Текст
Three-Dimensional Geometry
and Topology
Трехмерная геометрия
и топология
VOLUME 1
William P. Thurston
EDITED BY SILVIO LEVY
Уильям Тёрстон
ПОД РЕДАКЦИЕЙ СИЛЬВИО ЛЕВИ
ПЕРЕВОД С АНГЛИЙСКОГО
П.В.СЕРГЕЕВА, П.В.ТУМАРКИНА, А.А.ФЕЛИКСОН,
О.В.ШВАРЦМАНА
ПОД РЕДАКЦИЕЙ О.В.ШВАРЦМАНА
PRINCETON UNIVERSITY PRESS
PRINCETON, NEW JERSEY
1997
МЦНМО
МОСКВА, 2001
Предисловие редактора перевода
Предисловие
Советы читателю
5
6
7
1. Что такое многообразие? 9
1.1. Многоугольники и поверхности 9
1.2. Гиперболические поверхности 12
1.3. Мир поверхностей 22
1.4. Примеры трехмерных многообразий 36
2. Гиперболическая геометрия и ее друзья 47
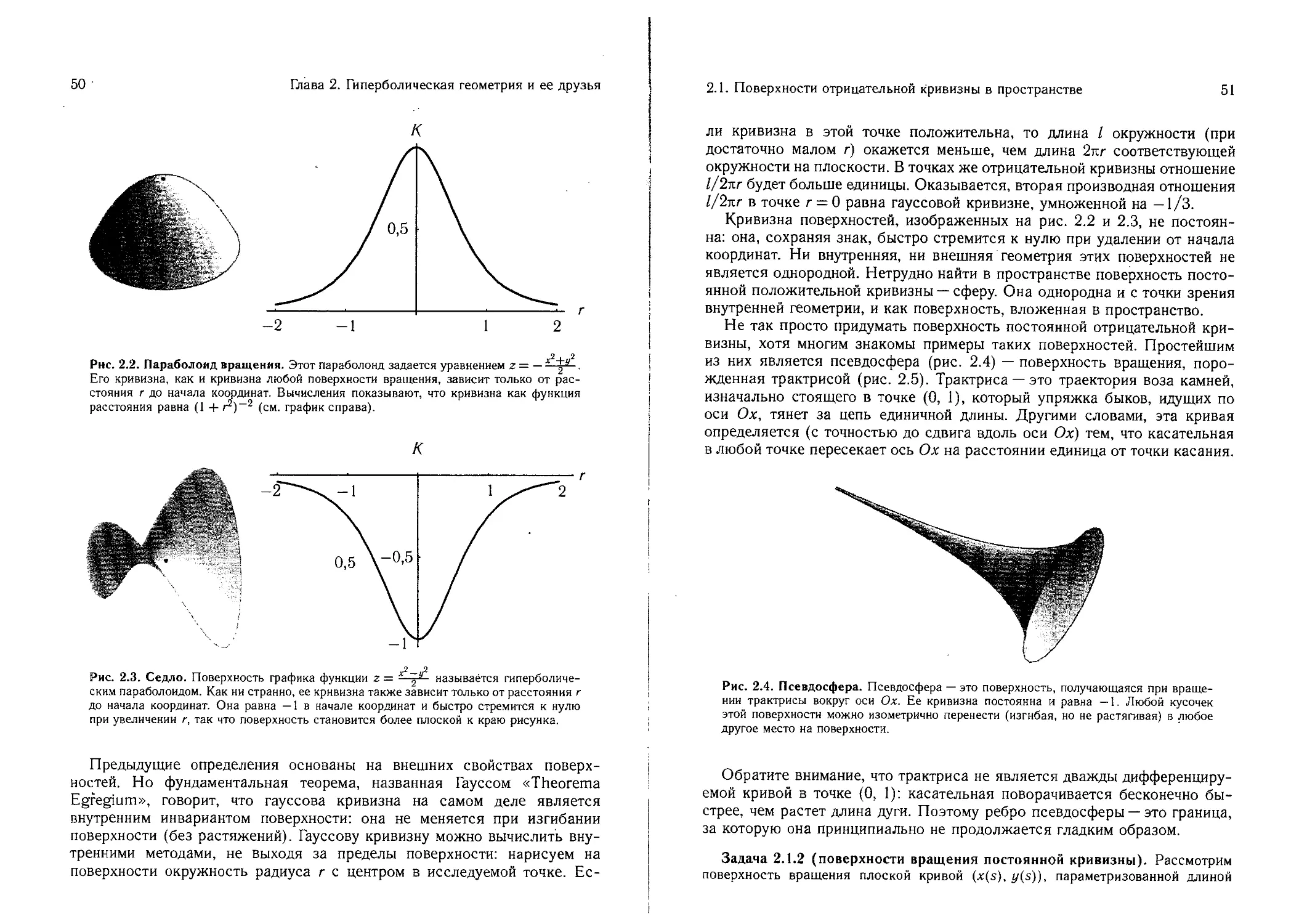
2.1. Поверхности отрицательной кривизны в пространстве .... 49
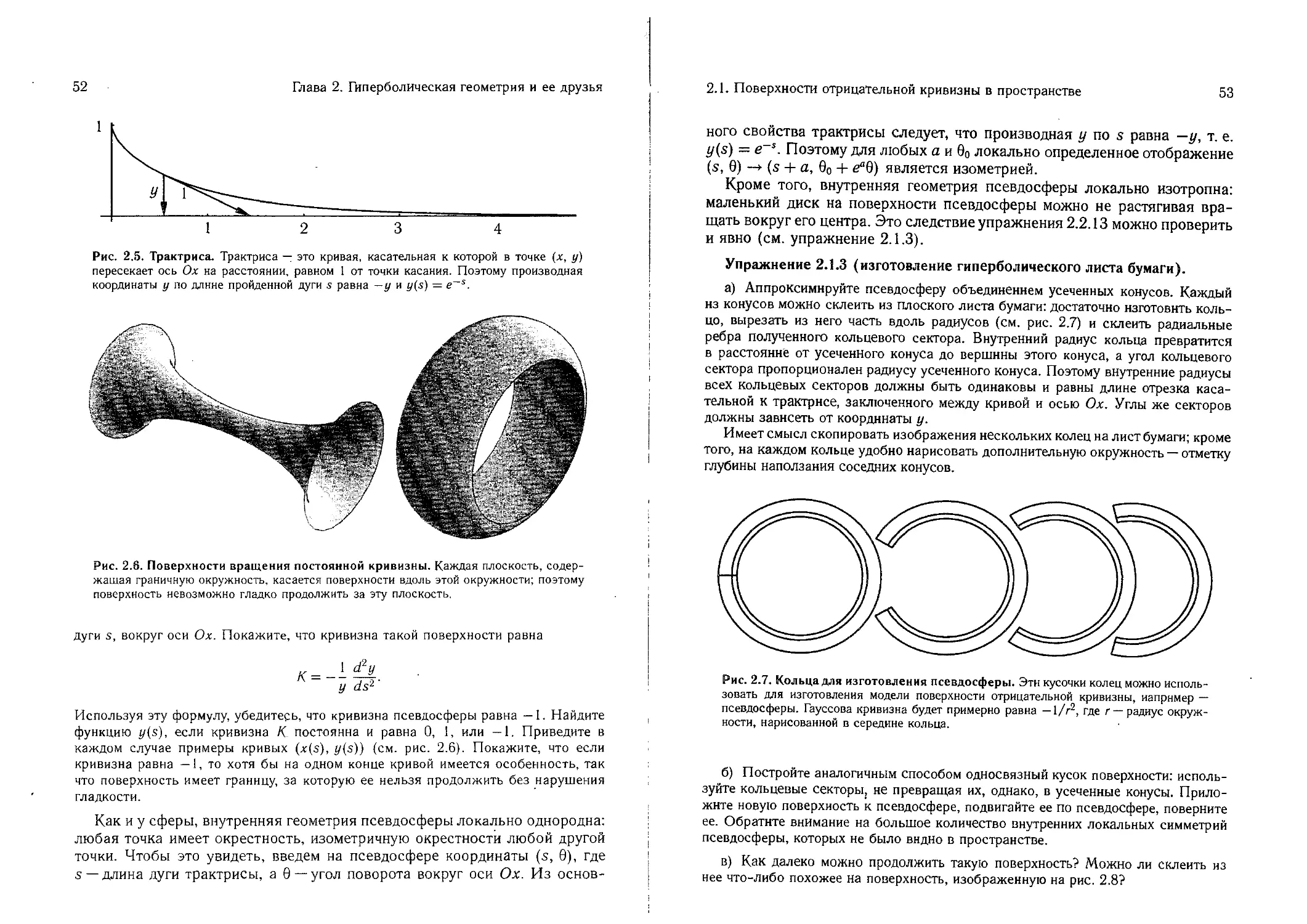
2.2. Инверсные модели 56
2.3. Модель на гиперболоиде и модель Клейна 67
2.4. Некоторые вычисления в гиперболической геометрии 76
2.5. Изометрии гиперболического пространства 89
2.6. Комплексные координаты на трехмерном гиперболическом
пространстве 101
2.7. Геометрия трехмерной сферы 105
3. Геометрические многообразия 112
3.1. Основные определения , 112
3.2. Триангуляции и склейки 121
3.3. Геометрические структуры на многообразиях 128
3.4. Отображение развертки и полнота 140
3.5.. Дискретные группы 156
3.6. Расслоения и связности 161
3.7. Контактные структуры 171
3.8. Восемь модельных геометрий 182
3.9. Кусочно-линейные многообразия 193
3.10. Сглаживания 197
312
Оглавление
4. Структура дискретных групп 212
4.1. Группы, порожденные малыми элементами 212
4.2. Евклидовы многообразия и кристаллографические группы . . 226
4.3. Трехмерные евклидовы многообразия 235
4.4. Эллиптические 3-многообразия 246
4.5. 7Ч-разложение 257
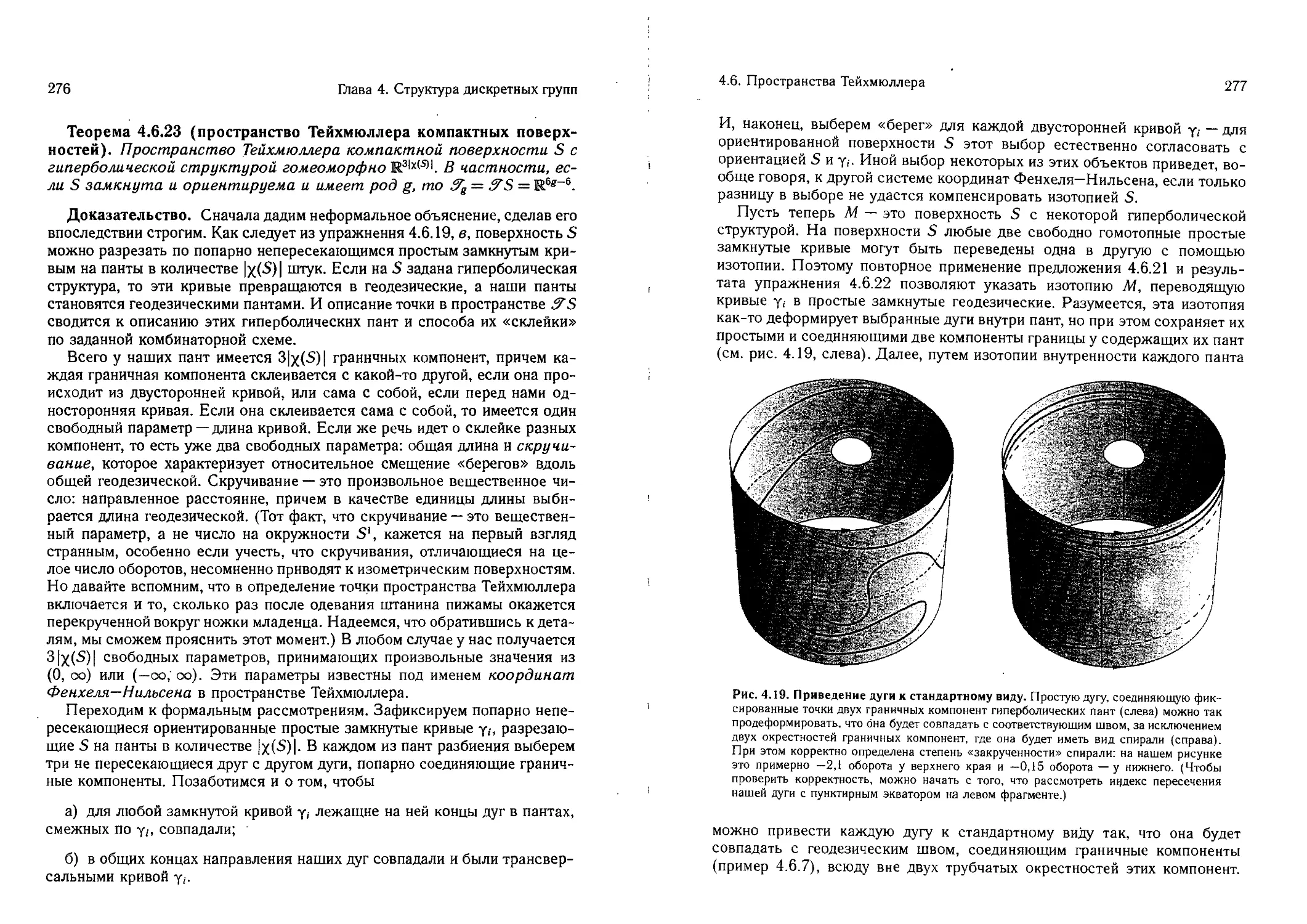
4.6. Пространства Тейхмюллера 263
4.7. 3-многообразия, моделируемые на расслоенных геометриях . 281
Словарь терминов 292
Литература 300
Предметный указатель 306
УДК 515.16+514.1+512.81
ББК 22.15
Т35
Издание осущствлено при поддержке РФФИ
(издательский проект № 99-01-14135).
И
Тёрстон У.
Т35 Трехмерная топология и геометрия / Перевод с англ. под ред.
О. В. Шварцмана.— М.: МЦНМО, 2001 — 312 с: ил.
ISBN 5-94057-013-5
Уникальная монография выдающегося американского тополога У. Тёрстона со-
содержит детальное изложение его глубоких идей о «геометризации» маломерной топо-
топологии. Первый том, посвященный геометрии и геометрическим структурам на много-
многообразиях, служит богатейшим источником информации, идей и ...энтузиазма.
Книга предназначена для студентов и аспирантов математических специальностей.
ББК 22.15
All rights reserved. No part of this book may be reproduced or transmitted in any form or by
any means, electronic or mechanical, including photocopying, recording or by any information
storage and retrieval system, whitout permission in writing form from the Publisher.
Уильям Тёрстон
ТРЕХМЕРНАЯ ГЕОМЕТРИЯ И ТОПОЛОГИЯ
Перевод с англ. П. В. Сергеева, П. В. Тумаркина, А. А. Феликсон, О. В. Шварцмана
под ред. О. В. Шварцмана.
Корректор С. Е. Твардовская.
Оригннал-макет подготовил В. Ю. Радионов.
Подписано в печать 9.12.2001 г. Формат 60 х 90 '/16- Бумага офсетная №1.
Печать офсетная. Печ. л. 19,5. Тираж 1000 экз. Заказ №516.
Издательство Московского Центра непрерывного математического образования.
121002, Москва, Бол. Власьевский пер., 11.
Лицензия ИД №01335 от 24.03.2000 г.
Отпечатано с готовых диапозитивов в типографии ОАО «Внешторгиздат».
127576, Москва, ул. Илимская, 7.
ISBN 0-691-08304-5 (англ.)
5SBN 5-94057-013-5 (рус.)
© Princeton University Press, 1997.
©МЦНМО, 2001.
Предисловие редактора перевода
Трехмерную топологию уже нельзя отделить от геометрии. Это стало ясно
после того, как в середине 70-х годов У. Тёрстон выдвинул смелую и очень
красивую гипотезу о геометризации трехмерных многообразий. Гипоте-
Гипотетически любое компактное 3-многообразие устроено так: его внутренность
можно представить в виде связной суммы и разрезать несжимаемыми то-
торами на «куски», причем каждый «кусок» несет полную локально одно-
однородную метрику конечного объема.
Тёрстон показал, что общая гипотеза о геометризации сводится к сле-
следующим двум.
Обобщенная гипотеза Пуанкаре. Если М — компактное 3-многооб-
3-многообразие с конечной фундаментальной группой щ(М), то М — многообразие
со сферической геометрией (сферическое многообразие).
Гиперболическая гипотеза. Пусть М — внутренность неприводимо-
неприводимого компактного 3-многообразия с бесконечной фундаментальной группой
tci(jW). Предположим, что а) фундаментальная группа края тс, (дМ) вклады-
вкладывается в тч(УИ); б) любая подгруппа Z © Z с щ(М) сопряжена подгруппе
в образе щ(дМ) при этом вложении. Тогда М — гиперболическое много-
многообразие.
Совсем недавно гиперболическая гипотеза была полностью доказана
для многообразий Хакена (так называются неприводимые 3-многообра-
3-многообразия, которые можно разрезать на шары вдоль несжимаемых поверхностей).
Обобщенная гипотеза Пуанкаре по сей день выглядит неприступной.
Поколение топологов н геометров, активно штурмующих гипотезу гео-
геометризации, выросло на принстонских записках лекций У. Тёрстона. Не
сомневаюсь, что и эта книга, поражающая богатством материала и идей,
столь же хорошо послужит новому поколению математиков.
Директор МЦНМО, выпускающего эту книгу, И. В. Ященко назвал кни-
книгу звездной. Мы согласны с ним и благодарим его за энергичную помощь
на всех этапах работы над проектом. Мы —это переводчики П. В.Тумар-
кин и А. А. Фелнксон A-2 глава), П. В. Сергеев C глава), О. В. Шварц-
Шварцман D глава), выпускающий редактор Ю. Н. Торхов, создатель оригинал-
макета В. Ю. Радионов. i
Отдельная благодарность РФФИ за финансовую поддержку русского
издания.
О. В. Шварцман
Предисловие
Эта книга возникла из курса лекций по геометрии и топологии 3-много-
образий, который я читал аспирантам Принстона в период 1978—1980 гг.
Записки курса, появившиеся при активной помощи Стива Керкхофа и Би-
Била Флойда, были размножены, и была организована рассылка по подписке.
Мы остановились, когда число заявок перевалило за тысячу.
Наш текст был рассчитан на математически зрелую аудиторию, да и
представленный материал был весьма нестандартен. Позднее через эти
записки пробивались участники нескольких семинаров. Их опыт, а также
мнения «одиночек», убедили меня в том, что первоначальное изложение
стоило бы дополнить деталями и уделить больше внимания основам. Ведь
в некоторых местах текста люди застревали на пару недель! И я решил
написать ясный, детальный и по-новому организованный текст, а уже по-
потом думать о книге. Это потребовало гораздо больше времени (и крови, и
пота, и слез), чем я мог себе представить. То, что вы прочтете, содержит
несколько глав из тех записок, но все они подверглись глубокой перера-
переработке.
Эта книга вряд ли бы вышла без поддержки Геометрического Центра и
доброй воли его директора Альберта Мардена. Ведь именно Геометриче-
Геометрический Центр в период с 1990 по 1992 г. организовал пять писательских кон-
конференций, где интенсивно обсуждался материал будущей книги. И многие
ее идеи, вместе с различными способами их показать,— результат коллек-
коллективных наблюдений и размышлений участников. Я особенно признателен
Дику Кэнэри, Джиму Кэннону, Дэвиду Эпштейну, Биллу Флойду, Стиву
Керкхофу, Яиру Мински. Благодаря их усилиям текст и рисунки в раз-
различных частях книги стали лучше. Особо хочу сказать о том, как приятно
мне было работать с Сильвно Леви. Он так увлекся этим проектом, что
прошел вместе со мной огонь и воду. Помимо всего прочего, он — автор
почти всех рисунков к этой книге.
Июнь, 1996 г.
Уильям П. Тёрстон
Советы читателю
Стиль изложения, принятый в этой книге, можно, вероятно, называть экс-
экспериментальным.
Наиболее эффективные логические подходы к предмету обычно сильно
отличаются от психологически комфортных способов его изучения. В ма-
математической литературе, как правило, преобладает дедуктивный подход,
когда дается большое количество определений (без примеров, их моти-
мотивирующих) либо большое количество ответов (без вопросов к ним). А в
результате у читателя, впервые знакомящегося с предметом, нет свобо-
свободы выбора, и он пассивно плетется за автором, свято веря, что усилия
затрачиваются ради чего-то стоящего.
Математика — это громадная структура с очень сильными взаимодей-
взаимодействиями. Эта структура нелинейна. Поэтому читатель математического
текста должен быть особенно активным, задавая вопросы, продумывая
связи текущего сюжета с другими известными ему идеями, и таким путем
формируя собственное представление о предмете в целом, а не просто
знакомясь с какой-то одной его стороной. Книга предполагает, что ее
читатель будет временами останавливаться, оглядываться и исследовать
местность. Я надеюсь, что вы не пожалеете времени на то, чтобы выра-
выработать свое собственное видение предмета, взаимосвязей его частей и его
связей с другими областями математики.
Представьте себе детский конструктор. Его главная идея —это просвер-
просверленные планки, соединяя которые винтиками, вы можете создавать более
сложные модели. Ни одна область математики не полна и не замкнута в
себе —скорее, она полна «дыр», а точнее, естественных вопросов, на кото-
которые ее методы ответить бессильны. Именно эти дыры и позволяют иногда
соединить две на первый взгляд никак не связанные области математики.
Но ради гладкости изложения этим «дырам» не остается места в матема-
математических текстах. Только что хорошего в конструкторе, планки которого
забыли рассверлить?
В нашем тексте все «соединительные отверстия» собраны в упражнени-
упражнениях, вопросах н задачах. Большинство из них мало похоже на упражнения
типа прогулки с собакой, которую ведут на поводке. Возможно, вы не смо-
сможете ответить на некоторые вопросы, даже если вы полностью понимаете
текст. Некоторые вопросы опережают события и связаны с идеями, кото-
которые детально обсуждаются позже. Другие же имеют дело с вещами, кото-
которые принято оставлять в качестве «упражнения для читателя». Наконец,
8
есть и такие вопросы, цель которых — перебросить мостик между тем, что
обсуждается в книге, и тем, что осталось вне ее.
Очень важно, читая книгу, думать над упражнениями и заданиями. По-
видимому, вы сможете ответить на большинство несложных вопросов. Но
если вам не удастся справиться с остальными, то огорчить вас это должно
не больше, чем неудачная попытка с ходу ответить на внезапно появив-
появившийся вопрос.
В нашей книге есть и другого сорта отступления от дедуктивной схемы.
Например, на интуитивном уровне многообразия и геометрические струк-
структуры обсуждаются в первых двух главах, хотя их точные определения и
основные свойства появляются лишь в третьей главе. Эти определения
тяжеловаты для понимания, если перед глазами нет хороших примеров.
Понятие орбифолда появится лишь в пятой главе второго тома, хотя оно
и важно для материала четвертой главы. Но иногда для удобства ссылок,
мы изменяем нашему принципу примата психологического над логическим.
Так, например, глава 2 содержит более полное изложение гиперболической
геометрии, чем требуется в книге на этот момент. Поэтому читатель может
здесь кое-что пропустить, в дальнейшем возвращаясь к этому материалу
по мере необходимости.
Очень часто начинающий бросает чтение, если попадает в дебри неиз-
неизвестных терминов и непонятных обозначений. С учетом нелинейного ха-
характера изложения, принятого в книге, вы наверняка столкнетесь с незна-
незнакомыми терминами, которые до этого в тексте не встречались. И в этом
случае не огорчайтесь: полезно бывает почитать дальше, а потом вернуть-
вернуться к фрагменту, который вас «держит». Некоторые понятия определены в
словаре терминов. Перед ними поставлен знак *.
Глава 1
Что такое многообразие?
Многообразия, нас окружающие, многолики. Нам, обитателям трехмерно-
трехмерного мира, наиболее знакомы двумерные многообразия: поверхность шара,
бублика; стена дома, поверхность дерева или волейбольная сетка... На
первый взгляд, трехмерные многообразия воспринимаются труднее. Но как
существа трехмерные, мы можем научиться воспринимать их как альтер-
альтернативные миры.
В математике многообразия чаще всего возникают не как какие-либо
объекты в пространстве, а косвенным образом: как пространства решений
при заданных условиях, как про-
пространства параметров для неко-
некоторой системы математических
объектов, и так далее. И там, где
это возможно, 'наше простран-
пространственное воображение помога-
помогает понять абстрактное описание
трехмерных многообразий.
Но даже с его помощью бы-
бывает нелегко распознать одина-
одинаковые многообразия: у одного и
того же топологического объек-
объекта может быть много абсолютно
разных описаний. Более того, у многообразия могут быть внутренние сим-
симметрии, неочевидные в выбранной модели.
Как же можно изучать многообразия?
Упражнение. Какое многообразие изображено на рисунке?
1.1. Многоугольники и поверхности
Простейшая и наиболее симметричная после сферы поверхность — это тор,
или поверхность бублика. Как у поверхности вращения, у тора есть явные
симметрии, но есть также «скрытые» симметрии. Топологически тор можно
8
есть и такие вопросы, цель которых — перебросить мостик между тем, что
обсуждается в книге, и тем, что осталось вне ее.
Очень важно, читая книгу, думать над упражнениями и заданиями. По-
видимому, вы сможете ответить на большинство несложных вопросов. Но
если вам не удастся справиться с остальными, то огорчить вас это должно
не больше, чем неудачная попытка с ходу ответить на внезапно появив-
появившийся вопрос.
В нашей книге есть и другого сорта отступления от дедуктивной схемы.
Например, на интуитивном уровне многообразия и геометрические струк-
структуры обсуждаются в первых двух главах, хотя их точные определения и
основные свойства появляются лишь в третьей главе. Эти определения
тяжеловаты для понимания, если перед глазами нет хороших примеров.
Понятие орбифолда появится лишь в пятой главе второго тома, хотя оно
н важно для материала четвертой главы. Но иногда для удобства ссылок,
мы изменяем нашему принципу примата психологического над логическим.
Так, например, глава 2 содержит более полное изложение гиперболической
геометрии, чем требуется в книге на этот момент. Поэтому читатель может
здесь кое-что пропустить, в дальнейшем возвращаясь к этому материалу
по мере необходимости.
Очень часто начинающий бросает чтение, если попадает в дебри неиз-
неизвестных терминов и непонятных обозначений. С учетом нелинейного ха-
характера изложения, принятого в книге, вы наверняка столкнетесь с незна-
незнакомыми терминами, которые до этого в тексте не встречались. И в этом
случае не огорчайтесь: полезно бывает почитать дальше, а потом вернуть-
вернуться к фрагменту, который вас «держит». Некоторые понятия определены в
словаре терминов. Перед ними поставлен знак *.
Глава 1
Что такое многообразие?
Многообразия, нас окружающие, многолики. Нам, обитателям трехмерно-
трехмерного мира, наиболее знакомы двумерные многообразия: поверхность шара,
бублика; стена дома, поверхность дерева или волейбольная сетка... На
первый взгляд, трехмерные многообразия воспринимаются труднее. Но как
существа трехмерные, мы можем научиться воспринимать их как альтер-
альтернативные миры.
В математике многообразия чаще всего возникают не как какие-либо
объекты в пространстве, а косвенным образом: как пространства решений
при заданных условиях, как про-
пространства параметров для неко-
некоторой системы математических
объектов, и так далее. И там, где
это возможно, 'наше простран-
пространственное воображение помога-
помогает понять абстрактное описание
трехмерных многообразий.
Но даже с его помощью бы-
бывает нелегко распознать одина-
одинаковые многообразия: у одного и
того же топологического объек-
объекта может быть много абсолютно
разных описаний. Более того, у многообразия могут быть внутренние сим-
симметрии, неочевидные в выбранной модели.
Как же можно изучать многообразия?
Упражнение. Какое многообразие изображено на рисунке?
1.1. Многоугольники и поверхности
Простейшая и наиболее симметричная после сферы поверхность — это тор,
или поверхность бублика. Как у поверхности вращения, у тора есть явные
симметрии, но есть также «скрытые» симметрии. Топологически тор можно
10
Глава 1. Что такое многообразие?
описать при помощи склеек противоположных сторон квадрата. Отраже-
Отражение относительно диагонали квадрата меняет местами оси а и Ь, сохраняя
схему склейки.
Задача 1.1.1 (квадратный тор в пространстве). Одноточечная компактифи-
кация R" пространства М" — это топологическое пространство, которое получит-
получится, если к М" добавить точку оо и объявить ее окрестностями множества вида
(Мл \ В) U оо для всех ограниченных замкнутых подмножеств В.
а) Докажите, что одноточечная компактификация R" гомеоморфна сфере 5".
б) Рассмотрим обычный тор в 53 =М3. Покажите, что кривые а и Ь на рис. 1.1
можно поменять местами, двигая тор в S3 (при этом его геометрическая форма
может меняться). (Эту задачу будет проще решать после чтения раздела 2.7.)
в) Докажите, что в М3 задачу б решить невозможно.
1.1. Многоугольники и поверхности
11
Рис. 1.1. Тор, получаемый склейкой квадрата. Топологически такой тор может быть
получен склеиванием параллельных сторон квадрата. Обратно, если разрезать тор
(рис. слева) вдоль нарисованных линий, то полученную фигуру можно развернуть на
квадрат (рис. справа).
Любопытно, что тор получается также склейкой параллельных сторон
правильного шестиугольника (рис. 1.2). У такой модели есть симметрия
шестого порядка, которая не видна в модели, приведенной выше.
Задача 1.1.2 (примирение симметрии тора). Итак, тор встретился нам в
трех видах: как физическая поверхность в пространстве, как квадрат'и как ше-
шестиугольник с соответствующими отождествлениями сторон. Попробуйте уяснить
связь этих трех моделей.
а) Проверьте, что указанная склейка шестиугольника дает тор. Нарисуйте на
торе разрезы, приводящие к шестиугольнику.
б) Придумайте преобразование, которое переводит склейку шестиугольника в
склейку квадрата.
в) Можно ли так *вложить тор в М3 или в S3, чтобы его симметрия шестого
порядка продолжалась на все *объемлющее пространство?
Рис. 1.2. Тор, получаемый склейкой шестиугольника. Здесь изображена другая
схема склейки, которая также приводит к тору. Очевидные в этой модели симметрии
тора не видны в предыдущей.
г) Тор можно так разбить иа семь стран, что каждая страна является связным
куском, и любые две страны граничат (ие по точке!) друг с другом. Иными словами,
для политической карты торического мира необходимо семь красок. Постройте
такую карту на торе. Можно ли построить симметричную карту?
Два встретившихся нам описания тора имеют прямое отношение к *за-
мощениям (укладкам) *евклидовой плоскости Е2. Запасемся бесконеч-
бесконечным числом квадратов, размеченных как на рис. 1.1, или шестиугольников
с разметкой как на рис. 1.2. Начнем с одного многоугольника на плос-
плоскости и будем последовательно добавлять его копии, соединяя их оди-
одинаково отмеченными сторонами. В процессе укладки будем внимательно
следить за тем, чтобы локальная картина вокруг любой вершины на плос-
плоскости в точности соответствовала локальной картине на склейке исходного
многоугольника. Если действовать таким образом, то процесс замощения
однозначен. В результате мы получаем замощение евклидовой плоскости
равными квадратами или шестиугольниками (см. рис. 1.3).
Построенные замощения показывают, что плоскость является *накры-
тием тора: *накрывающее отображение (скажем, для замощения квадрата-
квадратами) переводит соответствующие точки всех копий квадрата в одну и ту же
точку тора, полученного склейкой квадрата. Так как евклидова плоскость
*односвязна, наше накрытие будет *универсальным. Накрывающее ото-
отображение определяет группу гомеоморфизмов плоскости, элементы кото-
которой переводят любую точку плоскости в точку, имеющую тот же образ при
накрывающем отображении. Например, при замощении квадратами *груп-
па преобразований накрытия совпадает с группой параллельных переносов
плоскости, сохраняющих вершины. Тор является *факторпространством
плоскости по *действию этой *грутшы накрытия.
Так как накрывающие преобразования являются изометриями евкли-
евклидовой плоскости, на торе возникает *евклидова структура, т. е. такая ме-
метрика, которая локально изометрична евклидовой. А именно: для любой
12
Глава 1. Что такое многообразие?
1.2. Гиперболические поверхности
13
Рис. 1.3. Замощения плоскости, связанные с тором. Эти замощения плоскости
получаются из двух различных описаний склеек, приводящих к тору. Перед нами кон-
конструкция универсального накрытия тора, полученная путем его «развертки».
точки х на торе выберем ее столь малую окрестность U, что ее прообраз
на плоскости является объединением своих связных компонент, любую из
которых накрытие р гомеоморфно отображает на U. Уменьшив при необ-
необходимости U, можно считать, что диаметры компонент прообраза меньше,
чем расстояние между любыми двумя из них. Затем мы объявляем ото-
отображение р изометрией между любой из компонент и окрестностью U;
неважно, какую именно компоненту мы выбираем, так как все они изо-
метричны (рис. 1.4). Построенная локально евклидова геометрия на торе
не совпадает с геометрией тора как тела вращения в пространстве. Дело
в том, что мы построили плоскую геометрию, а на торе вращения есть
точки как с положительной, так н с отрицательной гауссовой кривизной
(см. раздел 2.1).
1.2. Гиперболические поверхности
Так же как и тор, крендель с двумя дырками, или поверхность рода два (см.
раздел 1.3), получается склейкой сторон многоугольника. Вот наиболее
известный способ, как это сделать: разрежем поверхность вдоль четырех
простых замкнутых кривых, пересекающихся ровно в одной точке, и по-
получим восьмиугольник (рис. 1.5). При этом кривые можно так снабдить
метками а, Ь, с, d, что символом склейки восьмиугольника будет слово
aba~!lb~lcdc~ld~l.
Можно ли по этой схеме склейки построить замощение плоскости пра-
правильными многоугольниками? Ясно, что на евклидовой плоскости это-
этого сделать нельзя: внутренний угол правильного восьмиугольника равен
ъР
<ЬР
Рис. 1.4. Перенос геометрии с плоскости на тор. Являясь факторпростраиством ев-
евклидовой плоскости по подгруппе группе изометрии, тор обладает локально евклидовой
геометрией: маленькое открытое множество U изометрично любой связной компоненте
его прообраза посредством накрывающего отображения р. В этой геометрии образы
прямых на плоскости являются "геодезическими на торе. Как правило, они не совпа-
совпадают с геодезическими на вложенном торе вращения.
Рис. 1.5. На кренделе с двумя дырами, или поверхности рода 2, существует система
разрезов, превращающая его в топологический многоугольник. На рисунке показана
каноническая система склейки такого многоугольника,
(8 — 2) ¦ к/8 = Зтс/4 = 135°. Следовательно, даже три таких многоугольни-
многоугольника не могут окружать одну вершину, тогда как требуется, чтобы их было
восемь.
Но это вовсе не значит, что из нашей затеи ничего не выйдет: если
на плоскости отказаться от *аксиомы Евклида о параллельности, то уже
ничто не мешает и сумме углов треугольника быть меньше к. А тогда есть
надежда построить правильный восьмиугольник с углами к/4, который
и решит нашу задачу. Вскоре мы все это проделаем явно.
14
Глава 1. Что такое многообразие?
До самого конца восемнадцатого века аксиома о параллельных счита-
считалась бесспорной. Было затрачено много усилий на безуспешные попытки
доказать избыточность этой аксиомы посредством вывода ее из остальных
аксиом Евклида и «общих» понятий, которые интуитивно казались более
ясными. Но к 1820 г. ситуация изменилась: три математика независимо
друг от друга пришли к выводу, что может существовать плоская геоме-
геометрия (с привычными точками, прямыми, углами), в которой не выполняется
аксиома о параллельных. Это были Янош Бойяи в Венгрии, Карл Фридрих
Гаусс в Германии и Николай Иванович Лобачевский в России. Гаусс был
первым, кто открыл эту геометрию, но он предпочел не публиковать своих
выводов; исследования Бойяи получили признание лишь после его смерти;
вот почему неевклидова геометрия впервые стала известна как геометрия
Лобачевского. Общепринятый термин «гиперболическая геометрия» был
введен Феликсом Клейном в начале XX в.
Отказ от одной из евклидовых аксиом был глубокой идеей, вызвав-
вызвавшей беспокойство математиков. И хотя интенсивные исследования Лоба-
Лобачевского и других не только не привели к противоречию, но и показали
богатые возможности новой геометрии, вопрос о ее непротиворечивости
был предметом многочисленных дискуссий на протяжении большей ча-
части XIX столетия. Наконец, в 1868 г. Эженио Бельтрами явно реализовал
часть гиперболической плоскости на поверхности постоянной отрицатель-
отрицательной кривизны в евклидовом пространстве. Идейно этому предшествовала
появившаяся намного раньше знаменитая работа Георга Фридриха Рима-
на «О гипотезах, лежащих в основании геометрии»1 A854 г.), в которой
он впервые рассматривал метрики постоянной кривизны. Из его описания
прямых и плоскостей в таких пространствах видно, как ясно он предста-
представлял себе их геометрию. Но лишь после открытия Бельтрами идеи Римана
стали постепенно завоевывать математическое сознание.
Позже появились и другие модели — каждая со своими достоинствами
и недостатками. Они подобны картам Земли: реальные размеры на них
искажены, но, изучая их, можно при некотором воображении восстановить
ландшафт.
Гиперболическая геометрия постоянно используется в этой книге. По-
Поэтому стоит с ней познакомиться прямо сейчас, а начать знакомство с ги-
гиперболической плоскости. Поначалу мы будем пользоваться конкретной
моделью, но стоит сразу уяснить, что у гиперболического пространства Н"
может быть много моделей. А пока наш план таков: мы введем гиперболи-
гиперболические прямые (геодезические) н рассмотрим некоторые преобразования,
их сохраняющие. С их помощью мы откроем много других свойств гипер-
гиперболической плоскости и гиперболической метрики. По мере продвижения
'Перевод см. в кн.: Об основаниях геометрии. Сборник классических работ по геометрии
Лобачевского н развитию ее идей. М.: ГИТТЛ, 1956.— Прим. ред.
1.2. Гиперболические поверхности
15
формируется и словарь, который позволит свободно переводить все поня-
понятия и термины с языка гиперболической геометрии на язык ее модели.
Гиперболическая плоскость Н2 гомеоморфна Е2, и модель диска Пу-
Пуанкаре, введенная Анри Пуанкаре в начале XX в., получается отображе-
отображением М2 на открытый единичный диск евклидовой плоскости. Гиперболи-
Гиперболические прямые, или геодезические, изображаются в этой модели дугами
окружностей, ортогональных границе 3D диска D, причем каждая дуга,
ортогональная 3D, является гиперболической прямой (рис. 1.6). Отме-
Отметим, что любой диаметр диска служит пределом последовательности дуг,
ортогональных 3D, а потому также является прямой. В дальнейшем, для
простоты, мы и о диаметрах будем говорить как о дугах, ортогональных 3D.
Рис. 1.6. Прямые в модели диска Пуанкаре. Прямые в этой модели выглядят как
дуги, ортогональные граничной окружности диска, или как диаметры.
Гиперболическое отражение относительно прямой, представленной диа-
диаметром, в нашей модели является обычным евклидовым отражением от-
относительно этого же диаметра. А что можно сказать об отражениях от-
относительно других прямых? Они переходят в некоторые преобразования
евклидовой плоскости, которые называются инверсиями и являются обоб-
обобщениями евклидовых отражений.
Определение 1.2.1 (инверсия относительно окружности). Пусть
С — окружность на евклидовой плоскости с центром в точке 0. Инвер-
Инверсией сс относительно С называется единственное отображение проколотой
(в точке 0) плоскости в себя, которое:
а) оставляет все точки С неподвижными;
б) меняет местами внутренность и внешность С;
в) любую окружность, ортогональную С, переводит в себя.
Упражнение 1.2.2 (инверсия корректно определена), а) Докажите сле-
следующий стандартный факт евклидовой геометрии на плоскости: если А — точка
вне окружности Си/ — прямая, проходящая через А и пересекающая С в точках
16
Глава 1. Что такое многообразие?
1.2. Гиперболические поверхности '
17
Рис. 1.7. Инверсия относительно окружности. Все окружности, ортогональные дан-
данной и проходящие через заданную точку Р, проходят также н через точку /". Точка Я7
называется образом точки Р при инверсии относительно окружности. Инверсия меняет
местами внутренность и внешность круга.
Я и Я', то произведение АР ¦ АР1 не зависит от / и равняется \АТ\2, где AT —
луч, касающийся С в точке Т. Это произведение называется степенью точки А
относительно окружности С.
б) При помощи упражнения а докажите, что определение 1.2.1 корректно.
(Указание: см. рис. 1.7, слева.)
в) Докажите, что если радиус С равен г, то образ Р' = ic(P) —это такая точка
луча ОР, что ОР ¦ ОР' = г.
Инверсии обладают многими приятными свойствами, но самое приятное
и в дальнейшем полезное свойство состоит в следующем.
Предложение 1.2.3 (свойства инверсии). Если С — окружность ев-
евклидовой плоскости, то ic ~ конформное преобразование, т. е. пре-
преобразование, сохраняющее углы. Кроме того, инверсия переводит
окружности, не проходящие через центр С, в окружности; окруж-
окружности, проходящие через центр, — в прямые; прямые, не проходящие
через центр, — в окружности, через него проходящие; а прямые, про-
проходящие через центр, — в такие же прямые.
Доказательство. Рассмотрим два вектора в точке, не лежащей на
окружности. Построим окружности, касательные соответственно к перво-
первому и второму векторам, и ортогональные окружности инверсии. Инверсия
сохраняет обе эти окружности, причем во второй их общей точке они пере-
пересекаются под тем же углом. Это доказывает конформность инверсии всюду
вне С. Конформность в точках С следует нз соображений непрерывностн.
Теперь покажем, что окружности и прямые, касательные к С, перехо-
переходят при инверсии соответственно в такие же прямые и окружности. При
доказательстве мы будем для удобства прямые также называть окружно-
окружностями. Для любой точки х на С рассмотрим семейство <FO окружностей,
ортогональных С в точке х, и аналогичное семейство &Т окружностей,
касающихся С в точке х (рис. 1.8). Любая окружность первого семейства
пересекает любую окружность второго семейства под прямым углом. Та-
Таким образом, &Т является семейством, ортогональным семейству &о. Мы
знаем, что семейство &о сохраняется при инверсии ic. Так как инверсия —
конформное преобразование, оно сохраняет и семейство окружностей &т,
ортогональных к &0. А это и значит, что множество окружностей, касаю-
касающихся С, переходит при инверсии в себя.
Рис. 1.8. Ортогональное семейство окружностей, проходящих через данную точ-
точку. Окружности, касающиеся С в данной точке х, суть ортогональные траектории
семейства окружностей, ортогональных к С в х.
Далее, с помощью подходящей гомотетии с центром в точке О любую
окружность, отличную от прямой, проходящей через центр О, можно пре-
преобразовать в окружность 5', касающуюся С. В силу упражнения 1.2.2, в
образы ic(S) и cc(S') связаны обратным преобразованием подобия. Образ
/сE') касающейся окружности есть окружность. Поэтому и образ ic(S)
есть окружность. Прямые, проходящие через центр, переходят в себя в
силу 1.2.2, в. Ц.2.31
Заметьте, что окружности, проходящие через центр, и прямые перехо-
переходят друг в друга по той простой* причине, что по мере приближения точки
к центру ее инверсный образ уходит на бесконечность.
Пример 1.2.4 (шарнирные механизмы). Расцвет теории шарнирных
механизмов относится к индустриальной эре (середина XIX в.). Актуаль-
Актуальной для того времени была такая задача: создать шарнирный механизм,
18
Глава 1. Что такое многообразие?
|
1.2. Гиперболические пойерхности
19
преобразующий вращательное движение в поступательное. В I860 г. эта
задача была независимо решена Липманом Липкиным и Понселе. Оба
механизма оказались одинаковыми, потому что в их основе лежала одна
и та же идея — идея инверсии. Устройство оказалось громоздким и силь-
сильно вибрирующим (семь стержней и шесть крепежных узлов). Поэтому на
практике использовались более простые механизмы, которые, выражаясь
математическим языком, лишь аппроксимировали прямолинейное движе-
движение.
Упражнение 1.2.5. а) Докажите, что изображенный на рис. 1.9 шарнирный
механизм работает согласно его описанию.
б) Постройте шарнирный механизм, обеспечивающий движение по прямой.
Рис. 1.9. Механический инверсор. Этот шарнирный механизм выполняет инверсию
относительно окружности радиуса г = -*/х2 — у2. Черный маленький треугольник —
точка крепления механизма. Если точка Р описывает плоскую фигуру, то точка Р1
движется по ее инверсному образу относительно окружности, отмеченной пунктиром.
Вернемся к модели Пуанкаре. Если гиперболическая прямая в модели
Пуанкаре — это дуга окружности, ортогональной 3D, то гиперболическое
отражение относительно этой прямой является в нашей модели ограниче-
ограничением на диск D инверсии относительно окружности. Это полностью согла-
согласуется с предложением 1.2.3 и показывает, среди прочего, что отражение
сохраняет гиперболические прямые. Теперь покажем, что оно сохраняет
и расстояние между точками, если его ввести разумным образом. Тем са-
самым смысл слова «отражение» будет полностью оправдан.
Как ввести расстояние на гиперболической плоскости? Фактически это
вопрос о *римановой метрике на гиперболической плоскости, т. е. вопрос
о выборе скалярного произведения в касательном пространстве каждой
точки плоскости. В разделе 2.2 мы укажем явную формулу, задающую
нашу метрику, а пока постараемся узнать о ней как можно больше, исходя
только из геометрических соображений, главное из которых заключается
в том, что гиперболические отражения должны быть изометриями. Это
требование определяет метрику с точностью до множителя.
Начнем с рассмотрения рис. 1.10. Рассмотрим две перпендикулярные
гиперболические прямые L и М, представленные в нашей модели дугами
евклидовых окружностей, ортогональных 3D, и еще одну евклидову окруж-
окружность С, пересекающую 3D в тех же точках, что и L. Простое рассуждение
позволяет убедиться, что окружность С перпендикулярна прямой М. По-
Поэтому, по определению инверсии, отражение относительно М переводит
окружности L и С в себя. Поскольку отражение сохраняет гиперболи-
гиперболические расстояния, точки окружности С, переходящие друг в друга при
отражении, должны быть равноудалены от прямой L. Изменяя М в классе
всех окружностей, ортогональных L, мы видим, что все точки окружно-
окружности С равноудалены от L, т. е. С должна быть эквидистантной кривой.
Область между L и С может быть заполнена ортогональными L сегментами
одинаковой гиперболической длины /.
Рис. 1.10. Эквидистанты к данной прямой. Все точки дуги С находятся на равных
гиперболических расстояниях от гиперболической прямой L.
Посмотрим, что делает с нашей областью произвольное гиперболиче-
гиперболическое отражение. Так как отражение является изометрией, оно переводит
нашу область в аналогичную, той же ширины /, и с тем же углом а при
«вершине» (в самом деле, инверсия сохраняет углы между окружностя-
окружностями). Но это означает, что / зависит только от угла а. Более того, / как
функция от а дифференцируема в нуле, поскольку евклидова длина 1Е лю-
любого трансверсального сегмента при малых а прямо пропорциональна а,
а гиперболическая длина / и евклидова длина 1Е сегмента должны быть бес-
бесконечно малыми одного порядка при а —> 0. Следовательно, можно считать,
что f I = 1.
da. la=0
20
Глава 1. Что такое многообразие?
1.2. Гиперболические поверхности
21
Теперь мы имеем все необходимое для того, чтобы ввести риманову
метрику с помощью следующей конструкции (рис. 1.11). Рассмотрим ка-
касательный вектор v в точке х. Проведем через х прямую L, перпендику-
перпендикулярную v, и эквидистантную окружность С через конец вектора v. Длина v
приблизительно равна гиперболическому расстоянию между С и L (для
небольших векторов w), которое, в свою очередь, приблизительно равно
евклидову углу между окружностями С и L в точке их пересечения.
Рис. 1.11. Гиперболическая длина вместо евклидовой. Отношение гиперолнческой
длины вектора к его евклидовой длине в модели Пуанкаре зависит только от рассто-
расстояния точки приложения вектора от центра круга.
Для того чтобы найти точное значение этой величины, рассмотрим
угол а, при вершине дугообразной области, построенной при помощи
вектора tv, и устремим / к нулю. Тогда длина вектора v равна ^|,_0-
На самом деле, все еще проще. Дело в том, что два вектора в точке х
с- одинаковой евклидовой длиной имеют и равные гиперболические длины.
Это следует из того, что, во-первых, существует отражение, оставляющее
точку х на месте и переводящее один вектор в другой, а, во-вторых, диф-
дифференциал инверсии в точке, лежащей на окружности инверсии, является
ортогональным преобразованием (см. текст после определения 1.2.1). Сле-
Следовательно, евклидово и гиперболическое скалярные произведения про-
пропорциональны, так как пропорциональны евклидова и гиперболическая
длины векторов. В частности, модель Пуанкаре является конформной, по-
поскольку евклидовы и гиперболические углы равны.
Теперь мы можем вернуться к задаче о замощении гиперболической
плоскости правильными восьмиугольниками. Напомним, что для этого нам
нужен правильный восьмиугольник с углом л/4, а так как модель Пуанкаре
конформна, то и евклидов угол между дугами окружностей, представля-
представляющих стороны восьмиугольника, будет таким же. Рассмотрим маленький
а)
б)
Рис. 1.12. Большие восьмиугольники в гиперболическом пространстве имеют
меньшие углы. Между крохотным евклидово-подобным восьмиугольником с больши-
большими углами (а) и очень большим восьмиугольником с произвольно малыми углами (в)
найдется восьмиугольник с углами ж/4.
восьмиугольник с центром в центре диска. Так как в нашей модели его сто-
стороны будут выгнуты очень слабо, его углы будут близки к Зл/4. С другой
стороны, уводя вершины восьмиугольника от центра, мы можем сделать
его углы сколь угодно малыми. В силу непрерывности (точнее, по "тео-
"теореме о промежуточном значении) найдется восьмиугольник с углом л/4
(рис. 1.12).
Коль скоро у нас есть нужный нам восьмиугольник, мы можем замо-
замостить гиперболическую плоскость его копиями, реализовав схему отожде-
отождествления, представленную на рис. 1.5. Результат изображен на рис. 1.13, а.
Восьмиугольники замощения выглядят в нашей модели по-разному: они
быстро становятся маленькими по мере удаления от центра, но все они
получаются один из другого с помощью гиперболического движения. На-
Например, два восьмиугольника на рис. 1.13, б переводятся один в другой
отражением относительно прямой L с последующим отражением относи-
относительно М.
Указанное разбиение гиперболической плоскости позволяет построить
гиперболическую структуру на поверхностях рода 2. (Геометрия таких
поверхностей локально сходна с геометрией гиперболической плоскости.)
Делается это с помощью конструкции, уже описанной нами в конце раз-
раздела 1.1. У нас снова есть накрывающее пространство — гиперболическая
плоскость, и риманова метрика на ней, инвариантная относительно группы
преобразований накрытия. Поэтому эта метрика определена и на фактор-
пространстве.
Тот факт, что тор накрывается евклидовой плоскостью, а поверхность
рода 2 — гиперболической плоскостью, не случаен. Как будет ясно из даль-
дальнейшего (см. раздел 1.3), все поверхности несут на себе простые геоме-
геометрические структуры.
22
Глава 1. Что такое многообразие?
1.3. Мир поверхностей
23
а)
б)
Рис. 1.13. Замощение гиперболической плоскости правильными восьмиугольни-
восьмиугольниками, (а) Так выглядит замощение гиперболической плоскости равными правильными
восьмиугольниками в модели Пуанкаре.
(б) Маленький восьмиугольник получается из большого с помощью двух отражений:
сначала относительно прямой L, а затем относительно М.
Задача 1.2.6 (симметрии поверхностей рода 2). Сколько симметрии может
иметь поверхность рода 2?
а) Укажите такое вложение поверхности рода 2 в R3, у которого есть симметрия
порядка 3.
б) Покажите, что поверхность рода 2 можно получить склейкой параллельных
сторон правильного восьмиугольника или правильного десятиугольника. Нарисуйте
разрезы на поверхности, дающие восьмиугольник или десятиугольник.
в) Через Гв обозначим поворот восьмиугольника на угол 2тс/8, а через Тю —
поворот десятиугольника на угол 2:т/10. Оба поворота индуцируют гомеоморфизмы
7в и Тю поверхности порядков 8 и 10 соответственно. Сколько неподвижных точек
у Гв и Гю? А сколько у Гв (соответственно Тю) периодических точек порядка,
меньшего чем 8 (соответственно 10)?
г) Можно ли вложить поверхность рода 2 в R3 так, чтобы вложенная поверх-
поверхность обладала симметрией порядка 8? Порядка 10? Тот же вопрос, если вложение
заменить *погружением, т. е. разрешить самопересечения.
1.3.'Мир поверхностей
.Склейки многоугольников всегда приводят к двумерным поверхностям.
Точнее, возьмем ориентированные многоугольники F], ..., Fk и предполо-
предположим, что общее число сторон (ребер) этих многоугольников четно. Снаб-
Снабдим ребра ориентацией, согласованной с ориентацией многоугольников.
Схема склейки — это указание пар сторон, при котором каждая пара снаб-
снабжена знаком «+» или «—», показывающим, сохраняется ли ориентация
при склейке. Например, схема склейки на рис. 1.1 отождествляет проти-
противоположные стороны, приписывая каждой паре знак «—», поскольку оба
склеивающих гомеоморфизма меняют ориентацию. (Заметьте, что стрел-
стрелки на рис. 1.1 означают не ориентацию, а направления, которые должны
совпасть при склейке. См. также рис. 1.14.)
а-Ь-
а-Ь+
а+Ь+
Рис. 1.14. Три склейки квадрата. Знак, соответствующий паре склеиваемых сторон,
показывает, изменяется ли при склейке ориентация. То же самое изображают стрелки.
Упражнение 1.3.1 (гомеоморфизмы интервала). Докажите, что два гомео-
гомеоморфизма интервала в себя *изотопны тогда и только тогда, когда они оба сохра-
сохраняют ориентацию (либо оба ее меняют). (Задайте изотопию явной формулой.)
Упражнение 1.3.2 (двумерные склейки), а) С помощью упражнения 1.3.1
покажите, что схема склейки определяет единственное топологическое простран-
пространство.
б) Покажите, что это пространство всегда является двумерным многообразием.
в) Покажите, что если склейка каждой пары сторон меняет ориентацию, то это
многообразие ориентируемо.
г) На рис. 1.14 показаны три схемы склейки, в которых отождествляются про-
противоположные стороны четырехугольника. Какие двумерные многообразия полу-
получатся в результате?
д) Найдите необходимое и достаточное условие ориентируемости двумерного
многообразия, которое компьютер мог бы проверить по схеме склейки.
Не так просто представить себе, какая поверхность получится после
склейки многоугольника с большим числом сторон или склейки нескольких
многоугольников. Однако у поверхностей есть просто вычисляемый чи-
численный инвариант, который позволяет бысто их опознать. Это эйлерова
характеристика поверхности. Если F — число склеиваемых многоуголь-
многоугольников (или граней), а ? и У —число ребер и вершин, получившихся после
склейки, то эйлерова характеристика склеенной поверхности S задается
формулой хE) = F - Е + V.
24
Глава 1. Что такое многообразие?
Например, при склейке тора из квадрата, изображенного на рис. 1.1,
получается одна грань, два ребра (противоположные стороны квадрата
склеиваются в одно ребро) и одна вершина (все четыре вершины склеива-
склеиваются в одну). Поэтому х(Т2) = 1 — 2 + 1 = 0. В случае тора, склеенного из
шестиугольника (см. рис. 1.2), получается три ребра и две вершины (по-
(поскольку вершины склеиваются по три), так что опять хПГ2) = 1—3 + 2 = 0.
Сферу можно разделить на четыре треугольника, образующих тетраэдр
с шестью ребрами и четырьмя вершинами, т. е. хE2) = 4 — 6 + 4 = 2. Ес-
Если сферу разделить на шесть квадратов, образующих куб, то получится
X(S2) =6-12 + 8 = 2.
Указанные разрезы поверхностей на многоугольники являются приме-
примерами клеточных разбиений. Клетка — это подмножество С с X произ-
произвольного хаусдорфова пространства X, гомеоморфное открытому диску
некоторой размерности, причем гомеоморфизм можно продолжить до не-
непрерывного отображения (называемого клеточным отображением) за-
замкнутого диска в X. Грани — это 2-клетки, ребра — 1 -клетки, а вершины —
0-клетки. Клеточным разбиением называется такое разбиение многооб-
многообразия X на клетки, у которого граница любой клетки содержится в объ-
объединении клеток меньшей размерности.
Если X — *дифференцируемое многообразие, то мы всегда будем пред-
предполагать, что наше клеточное разбиение дифференцируемо: это означа-
означает, что клеточное отображение каждой клетки С можно представить как
дифференцируемое отображение / выпуклого многогранника на замыка-
замыкание множества С, причем ранг / максимален в каждой точке. (Понятие
дифференцируемое™ в точке предполагает, что отображение определено
в окрестности этой точки. Поэтому, если X сШ" не является открытым
множеством, то говорят, что отображение X —> Шт дифференцируемо, если
оно является ограничением *дифференцируемого отображения открытой
окрестности X.)
Дифференцируемое клеточное разбиение близко к интуитивной идее
разрезания поверхности на многоугольники. Но иногда встречаются
клеточные разбиения других типов — например, в задаче 1.1.1, а сфера
представлена в виде объединения одной вершины и одной грани.
Эйлерова характеристика пространства X, имеющего конечное кле-
клеточное разбиение, определяется как число клеток четной размерности ми-
минус число клеток нечетной размерности. Возникает естественный вопрос:
зависит ли эйлерова характеристика от клеточного разбиения? Ответ от-
отрицательный. Мы докажем этодля дифференцируемых поверхностей.
По теореме об *инвариантн'ости области поверхность не может иметь
клетки размерности больше двух. Посмотрим, что происходит с эйлеровой
характеристикой при дальнейшем подразбиении двумерных и одномерных
клеток. Если в середину ребра поместить новую вершину, то добавится
одна вершина и одно ребро. В формулу для вычисления эйлеровой харак-
1.3. Мир поверхностей
25
теристики они входят с разными знаками. Если 2-клетка разделена на две
при помощи нового ребра, соединяющего уже существующие вершины, то
прибавится одна грань и одно ребро. Они также входят с разными знаками
и сокращаются.
Чтобы показать инвариантность эйлеровой характеристики, достаточно
доказать, что при помощи этих двух операций и операций, им обратных,
можно перейти от любого клеточного разбиения к любому другому. Но это
не самый лучший метод, поскольку при таком подходе легко увязнуть в
технических деталях, так и не поняв, что же происходит на самом деле.
Полезнее связать эйлерову характеристику с объектом, очевидно не зави-
зависящим от клеточного разбиения, — векторным полем на поверхности.
Рис. 1.15. Заряды на выпуклом многограннике. Стрелки представляют часть век-
векторного поля на поверхности многогранника; поле не определено только в самой верх-
верхней и в самой нижней вершинах. Если положительные заряды вершин и отрицательные
заряды ребер сдвинуть вдоль этого векторного поля, то этн заряды сократятся с по-
положительными зарядами граней.
Прежде чем решать общую задачу, разберем простой пример. Рассмо-
Рассмотрим сферу S2 с клеточным разбиением, реализованным в виде выпуклого
многогранника в Е3. Расположим многогранник в пространстве так, чтобы
ни одно ребро не было горизонтальным. Тогда найдется самая верхняя вер-
вершина U и самая нижняя вершина L. Поместим в каждую вершину и в центр
каждой грани единичный положительный заряд, а в середину каждого ре-
ребра — единичный отрицательный заряд. Покажем, что при суммировании
все заряды, кроме зарядов вершин U и L, сократятся. Для этого подвинем
заряды вершин и ребер так, чтобы каждый заряд двигался по многогран-
многограннику горизонтально и против часовой стрелки, если смотреть на все сверху
(рис. 1.15). В результате каждый заряд попадет внутрь какой-нибудь грани.
Теперь сложим заряды, попавшие в некоторую грань.
26
Глава 1. Что такое многообразие?
Каждая грань получает суммарный заряд некоторого открытого интер-
интервала своей границы. Этот интервал состоит из чередующихся ребер и вер-
вершин. Поскольку в начале и в конце идут ребра, минусов получается на один
больше; поэтому суммарный заряд грани равен нулю. Остается заряд +2
вершин U и L.
Обобщим эту идею на любую дифференцируемую поверхность с диф-
дифференцируемой триангуляцией. Дифференцируемая триангуляция — это
дифференцируемое клеточное разбиение, в котором клеточное отображе-
отображение каждой 2-клетки является * вложением, треугольника, причем клеточ-
клеточное отображение любого ребра согласовано с клеточным отображением
грани, которая содержит это ребро в своем замыкании (т. е. эти клеточные
отображения отличаются на аффинное отображение модельного интервала
на подходящую сторону модельного треугольника, см. рис. 1.16).
Рис. 1.16. Условие согласованности для триангуляции. Композиция клеточного
отображения /| модельного треугольника иа грань F\ с аффинным отображением
модельного интервала на подходящую сторону модельного треугольника совпадает
с клеточным отображением е модельного интервала на ребро Е. Аналогичная ком-
композиция для fi также дает е. Это означает, что мы можем измельчать триангуляцию
путем подразбиения модельного треугольника и модельного интервала.
Предположение о триангулируемости поверхности на самом деле несу-
несущественно: в любом дифференцируемом клеточном разбиении, не являю-
являющемся триангуляцией, можно подразделить все грани и ребра так, чтобы
замыкание каждой грани стало вложенным треугольником. Мы уже виде-
видели, что этот процесс не влияет на эйлерову характеристику. Кроме того,
надо подобрать клеточные отображения так, чтобы отображения ребер бы-
1.3. Мир поверхностей
27
ли согласованы с отображениями граней (это можно сделать с помощью
построения, аналогичного описанному в упр. 1.3.1).
Предложение 1.3.3 (невырожденные векторные поля). Если на
дифференцируемой триангулированной замкнутой поверхности су-
существует касательное векторное поле, нигде не обращающееся в
нуль, то эйлерова характеристика такой поверхности равна нулю.
Доказательство. Предположим, что векторное поле всюду трансвер-
сально триангуляции, т. е. не касается ни одного ребра. Этого всегда можно
добиться при помощи измельчения триангуляции и других преобразований,
не меняющих эйлерову характеристику (см. задачу 1.3.4). Измельчая раз-
разбиение, можно сделать так, чтобы векторное поле было почти постоянно
на каждой треугольной грани: точнее, для каждой грани существует ко-
координатная карта, в которой направление векторного поля изменяется не
более, чем на е, а направление ребра постоянно с точностью до е.
Расположив единичные заряды на построенной трансверсальной триан-
триангуляции, сдвинем их в направлении векторного поля. Если заряд вершины
попал в некоторую грань, то в ту же грань попадут и заряды двух прилегаю-
прилегающих ребер этой грани. Поэтому в каждую грань попадет либо заряд ровно
одного ребра, либо заряды двух ребер и одной вершины. Три или нуль
зарядов ребер попасть в одну грань не могут, поскольку это невозможно
в случае постоянного поля, а наше поле почти постоянно. В каждом из
возможных случаев суммарный заряд грани получается нулевым, а значит,
и эйлерова характеристика поверхности равна нулю. 11.3.31
Задача 1.3.4 (трансверсальная триангуляция). Для завершения доказатель-
доказательства предложения 1.3.3 нужно показать, что любую триангуляцию можно превра-
превратить в триангуляцию, трансверсальную векторному полю, причем направления поля
и ребер почти постоянны в каждой грани.
а) Покройте поверхность конечным числом координатных карт. Нарисовав до-
достаточно густую сетку параллельных линий, как на рис. 1.16, измельчите триан-
триангуляцию так, чтобы звезда каждой вершины v (т. е. объединение ребер и граней,
содержащих v) лежала в одной координатной карте, причем направление каждого
ребра и векторного поля изменялось в этих координатах не более чем на е.
б) Представьте множества направлений ребер и направлений поля в виде ин-
интервалов длины не более чем е на окружности. Покажите, что можно сделать так,
чтобы интервалы направлений ребер не пересекали интервалы направлений поля.
Для этого достаточно немного подвинуть вершину v в подходящем направлении
и продолжить движение на каждое ребро, содержащее а, с помощью евклидова
*подобия (в подходящих координатах), оставляющего на месте другой конец ребра.
' в) Распространите это на все вершины одновременно. Для этого сперва по-
покажите, что вершины можно покрасить в красный, синий и зеленый цвета так,
чтобы никакие две вершины одного цвета не были соединены ребром. (Указа-
(Указание: используйте *барицентрическое подразделение.) Сначала немного подвиньте
28
Глава 1. Что такое многообразие?
(одновременно) красные вершины, потом зеленые. В результате все ребра станут
траисверсальными полю.
На торе Т2 существует невырожденное векторное поле: рассмотрим по-
постоянное поле на Е2 и опустим его на факторпространство, как на рис. 1.4.
Ясно, что эйлерова характеристика тора равна нулю.
Что можно сказать о других поверхностях? Большинство из них не
имеет невырожденного векторного поля. В лучшем случае векторное по-
поле имеет изолированные нули (см. упражнение 1.3.8). Из доказательства
предложения 1.3.3 следует, что в областях, не содержащих нулей поля,
заряды сокращаются. Поэтому нам нужно изучить поведение зарядов в
окрестностях нулей.
Рассмотрим векторное поле X с изолированным нулем в точке z. Как
и при решении задачи 1.3.4, построим маленький многоугольник со сто-
сторонами трансверсальными полю X, содержащий z как внутреннюю точку.
Поместим по положительному заряду в каждую вершину, по отрицатель-
отрицательному заряду на каждое ребро, и положительный заряд во внутренность
многоугольника. Сдвинем заряды с границы многоугольника вдоль век-
векторного поля X. Индексом i(X, z) векторного поля X в точке z называется
сумма зарядов, оказавшихся внутри многоугольника после сдвига.
«Лемма 1.3.5 (корректность определения индекса). Пусть X — век-
векторное поле с изолированным нулем в точке z. Тогда индекс i(X, z)
зависит только от ограничения поля X на сколь угодно малую
окрестность точки z. В частности, индекс i(X, z) не зависит от
многоугольника, содержащего z.
Доказательство. Зафиксируем многоугольник, содержащий z, со сто-
сторонами, трансверсальными полю, и докажем, что индекс поля, подсчитан-
подсчитанный с помощью этого многоугольника, совпадает с индексом, подсчитан-
подсчитанным при помощи любого меньшего многоугольника с такими же свойства-
свойствами. Используя упражнение 1.3.6, разделим кольцо между двумя много-
многоугольниками на треугольники и сдвинем вершинытриангуляциитак, чтобы
все ребра были трансверсальны полю. Под действием поля одни заряды
попадут внутрь кольца через внешнюю границу, а другие покинут кольцо
через внутреннюю границу. В каждом треугольнике внутри кольца оста-
останется нулевой заряд, поэтому сумма входящих зарядов равна сумме выхо-
выходящих. |1.3.5|
Упражнение 1.3.6 (триангуляция кольца). Выше была опущена небольшая
техническая деталь: как триангулировать кольцо на плоскости? Покажем, что это
несложно сделать (впрочем, вместо этого было бы достаточно процитировать тео-
теорему о триангулируемости поверхностей).
а) Множество D называется звездным относительно внутренней точки v, если
для любой граничной точки и множества D интервал (v, и) состоит из внутренних
1.3. Мир поверхностей
29
точек множества D. Покажите, что звездный многоугольник можно триангулиро-
триангулировать так, чтобы точка v была вершиной триангуляции.
б) Триангулируйте кольцо между двумя многоугольниками, звездными относи-
относительно точки v, если один из них лежит внутри другого.
в) Покажите, что границу многоугольника, звездного относительно изолиро-
изолированного нуля z векторного поля X, можно сделать трансверсальной полю, сдви-
сдвинув вершины только в радиальном направлении, и значит, оставив многоугольник
звездным.
г)* Нельзя ли обойтись без предположения о звездности многоугольников?
Простейшим примером векторного поля с изолированными нулями
являются линейные векторные поля на плоскости, значения которых в
точке х можно получить применением линейного отображения к векто-
вектору Ох. Ясно, что начало координат 0 является нулем любого линейного
векторного поля; это изолированный нуль тогда и только тогда, когда
линейное отображение невырождено (т. е. имеет ненулевой определитель).
Если к векторному полю применить гомотопию, не двигающую нулей
поля, то индексы поля в нулях не изменятся, поскольку это целые числа.
Любые два линейных векторных поля с определителями одного знака мож-
можно связать гомотопией в пространстве невырожденных линейных полей.
Следовательно, их индексы одинаковы.
Упражнение 1.3.7 (индекс и знак определителя), а) Нарисовав достаточ-
достаточно много линейных векторных полей, попробуйте понять, как определитель связан
с качественным видом поля.
б) Докажите, что индекс линейного векторного поля равен знаку определителя.
Упражнение 1.3.8 (изолированные нули). По заданному конечному клеточ-
клеточному разбиению поверхности постройте дифференцируемое векторное поле с ис-
источником в центре каждой 2-клетки, стоком в каждой 0-клетке и седлом в центре
каждой 1-клетки (нужные определения даиы на рис. 1.17).
Задача 1.3.9. Какие значения может принимать i(X, z) в случае произвольного
векторного поля X? Можно ли написать формулу для i(X, z), верную для любого
векторного поля с изолированными нулями?
Предложение 1.3.10 (теорема Пуанкаре об индексе). Пусть S —
гладкая поверхность, а X — векторное поле на S с изолированными
нулями. Тогда
X(S) =
2: X(z)=O
, z).
В частности, эйлерова характеристика не зависит от клеточного
разбиения, использованного для ее вычисления, а является тополо-
топологическим инвариантом поверхности.
30
Глава 1. Что такое многообразие?
1.3. Мир поверхностей
31
i\->^-r'f iL-yyj-- ;\,
Рис. 1.17. Индекс векторного поля. Вблизи нуля векторного поля остается неболь-
небольшой участок, в котором заряды не сокращаются. Для векторного поля, изображенного
слева, общий заряд многоугольника, содержащего нуль, равен — 1 (этот заряд также
называется индексом поля в данной особой точке). Такая особая точка называется
седлом. Индекс особой точки, изображенной справа, равен 1; такие особые точки на-
называются источниками, или стоками, в зависимости от того, куда направлено поле:
к особой точке или от нее.
Доказательство. Как уже было сказано перед предложением 1.3.3,
любое конечное клеточное разбиение поверхности можно заменить на диф-
дифференцируемую триангуляцию. Измельчив и чуть-чуть пошевелив (если
необходимо) триангуляцию, можно добиться того, чтобы все нули лежа-
лежали внутри граней, причем не более одного на грани. Окружим каждый
нуль многоугольником, лежащим внутри соответствующей грани и транс-
версальным векторному полю. Триангулируем кольцо, получающееся, если
выкинуть многоугольник из соответствующей грани (см. упр. 1.3.6). Нако-
Наконец, сделаем триангуляцию колец трансверсальной полю', вновь используя
технику решения задачи 1.3.4.
Вклад каждого многоугольника в эйлерову характеристику равен индек-
индексу соответствующей особой точки. Вклад треугольников, лежащих снаружи
от многоугольников, равен нулю. Отсюда и следует нужная формула.
Инвариантность эйлеровой характеристики следует из того, что на лю-
любой поверхности есть векторное поле с изолированными нулями (упраж-
(упражнение 1.3.8). 11.3.101
Трудная задача 1.3.11. Покажите, что наши рассуждения об эйлеровой харак-
характеристике и индексах изолированных особых точек можно провести для любого
гладкого многообразия произвольной размерности.
Топология замкнутой поверхности определяет ее эйлерову характери-
характеристику. А возможно ли обратное? Невероятно, чтобы одно число несло
столько информации! Но, как ни странно, это почти что так: зная эйле-
эйлерову характеристику, а также ориентируема поверхность или нет, можно
определить, что это за поверхность. Этот важный факт известен уже более
века. Тем, кто с ним столкнулся впервые, необходимо проделать следую-
следующие шаги.
Задача 1.3.12 (классификация поверхностей), Рассмотрим (связную) по-
поверхность S, полученную склейкой многоугольников (среди которых могут быть
двуугольники, но не одноуголымки).
а) Покажите, что поверхность S можно получить при помощи склейки одного
многоугольника.
б) Если S имеет больше одной вершины, попробуйте уменьшить число вершин,
стянув одно из ребер. Это всегда можно сделать, если только многоугольник не
является двуугольником, вершины которого соответствуют двум различным точкам
поверхности S. В последнем случае S — сфера 52. Далее считаем, что S имеет
ровно одну вершину.
в) Обозначим через Е число ребер на поверхности S. Тогда многоугольник име-
имеет 2Е ребер и хE) = 2 — Е. Если Е = 1, то 5 является проективной плоскостью
2, а если Е = 2 —тором или бутылкой Клейна (рис. 1.14). Далее считаем, что
г) Назовем переклейкой следующее преобразование: разрежем многоугольник
по диагонали так, чтобы склеиваемые ребра е и е' оказались в разных частях,
и приклеим е к е'. Покажите, что переклейка не меняет топологии поверхности S.
д) Если поверхность ориентируема, то существует две пары склеиваемых ребер
х, х' и у, у', разделяющих друг друга.
е) Пусть х, х' и у, у' — пары склеиваемых ребер, разделяющие друг друга,
и склейка такова, что меняется ориентация. Пусть оставшиеся части многоуголь-
многоугольника содержат т, п, р и q ребер. При помощи одной переклейки преобразуйте
многоугольник так, чтобы т — п = 0, а затем при помощи еще одной переклейки
приведите его к виду т = п = р = 0.
ж) Если поверхность 5 ориентируема, то ее можно получить с помощью склей-
склейки с символом сида а^а^'бр'агбгаг'1^1 ¦¦¦asbgag[bgl. (В этих обозначениях
каждому ребру приписана ориентация, согласованная со склейкой, а символ есть
результат чтения полученного при обходе многоугольника слова.)
Из приведенных выше упражнений следует, что замкнутая ориентируемая по-
поверхность определяется с точностью до гомеоморфизма своей эйлеровой характе-
характеристикой, принимающей любое четное значение, не превосходящее двух. Число g
называется родом поверхности, а сама поверхность — сферой с g ручками.
з) Если 5 неориентируема, то с помощью одной переклейки можно добиться
того, чтобы какие-то два соседних ребра многоугольника склеивались отображе-
отображением, сохраняющим ориентацию.
32
Глава 1. Что такое многообразие?
и) Неориентируемая поверхность, склеенная из шестиугольника по схеме
aabbcc, гомеоморфна поверхности, склеенной по схеме aabcb с~*.
к) Любую неориентируемую поверхность можно склеить по схеме п\ а.\ а^а^ ¦ ¦ ¦
... asas. Число g называется родом неориентир у емой поверхности. Две за-
замкнутые неориентируемые поверхности с одинаковой эйлеровой характеристикой
гомеоморфны.
Упражнение 1.3.13. Сколько схем склейки можно задать на 2л-угольнике?
Сколько из них приводит к ориентируемым поверхностям? Сколько различных то-
топологических типов может получиться? Ответ показывает, как много различных
склеек приводят к одинаковым поверхностям.
Упражнение 1.3.14 (замкнутая поверхность без диска). Докажите, что если
из замкнутой связной поверхности удалить диск, то получится диск с лентами, как
на рис. 1.18. Всегда ли можно сделать так, чтобы все ленты были неперекручен-
ными? А все кроме одной?
Рис. 1.18. Диски с лентами. После удаления диска из замкнутой поверхности получа-
получается диск с приклеенными лентами. Слева мы начинали с ориентируемой поверхности
рода два; в середине — с неориентнруемой поверхности рода три, а справа — с проек-
проективной плоскости. Фигура, изображенная справа, называется лентой Мёбиуса.
В разделе 1.2 мы ввели гиперболическую структуру на ориентируемой
поверхности рода два. Используя задачу 1.3.12, можно провести аналогич-
аналогичное построение на любой поверхности отрицательной эйлеровой характе-
характеристики. В самом деле, такую поверхность можно склеить из 2л-угольника
(где л ^ 3) так, чтобы все вершины склеивались в одну. Сумма углов евкли-
евклидова многоугольника больше чем 2тс, так что на гиперболической плоскости
существует правильный 2л-угольник с нужными углами (см. рис. 1.12). Из
этого многоугольника можно склеить поверхность с гладкой гиперболиче-
гиперболической структурой.
Аналогично, поверхность нулевой эйлеровой характеристики можно
склеить из квадрата, у которого все вершины отождествляются. На такой
поверхности можно ввести евклидову структуру. В обозначениях рис. 1.14
эта поверхность может быть двух видов: а— Ь— или а— Ь+, т. е. это либо
тор, либо бутылка Клейна.
1.3. Мир поверхностей
33
Наконец, S2 и МР2 = 52/±1 —поверхности положительной эйлеровой
характеристики. На них можно ввести сферическую структуру (называе-
(называемую также эллиптической).
Нельзя ли каким-нибудь хитроумным способом ввести гиперболическую
структуру на торе или бутылке Клейна, или евклидову структуру на поверх-
поверхности рода два?
Задача 1.3.15 (знаки Гаусса—Бонне), а) Покажите, что эйлерова характе-
характеристика замкнутой поверхности с евклидовой структурой равна нулю.
б) Покажите, что сумма (внутренних) углов гиперболического треугольника
всегда меньше, чем л, а сумма углов сферического треугольника всегда больше,
чем л. (Указание: с помощью движений расположите треугольники так, чтобы
было удобней сравнивать углы.)
в) Покажите, что эйлерова характеристика замкнутой поверхности с гипербо-
гиперболической структурой отрицательна, а эйлерова характеристика замкнутой поверх-
поверхности с эллиптической структурой положительна.
Теперь уместно ввести некоторые операции, с помощью которых можно
получать новые поверхности из уже имеющихся (в дальнейшем нам по-
потребуются многомерные аналоги этих операций). Мы определим их для
произвольной размерности.
Связной суммой двух связных «-многообразий М\ и М2 называется
многообразие Mt#M2, получающееся, если удалить л-мерные диски D" из
М1 и М2 и склеить эти многообразия по границам удаленных дисков.
Упражнение 1.3.16. Докажите, что если поверхность S3 есть связная сумма
поверхностей St и S2, то хО$з) = xEi) + х(^2) — 2. Что происходит в случае мно-
многообразий других размерностей?
Это определение можно уточнить. Выберем диффеоморфные вложения
замкнутого л-мерного диска cpt: D" —> Мх и ср2: D" —>М2, удалим образы
D" из объединения М{ 1) М2 и отождествим границы cpi(dD") и ср2(д/?")
с помощью отображения ср2 q cpf'. Топология нового пространства зависит
от выбора вложений ср| и ср2 не слишком сильно, поскольку фактически
существует только один способ (с точностью до ориентации) вложить диск
в связное многообразие.
Точнее, при изменении вложения ср,, например, с помощью изотопии, то-
топология сохраняется, поскольку любую изотопию вложений диска в л-мер-
ное многообразие М можно продолжить до изотопии всего многообразия
(см. [Hir76, с. 185]). Сопоставим вложению ср: D" —*М *репер с началом
в точке ср(О), являющийся образом канонического базиса пространства Е"
при отображении dcp(O). Легко видеть (см. упражнение 1.3.17), что два вло-
вложения изотопны тогда и только тогда, когда соответствующие им реперы
можно непрерывно продеформировать один в другой, (т. е. в расслоении
реперов они лежат в одной компоненте связности). Поэтому диффеоморф-
диффеоморфные вложения D" —> М разбиваются на два класса изотопных вложений,
34
Глава 1. Что такое многообразие?.
если М ориентируемо. Если же М неориентируемо, то все вложения изо-
изотопны. Если на М выбрана ориентация, то можно определить, к какому
классу относится данное вложение: достаточно посмотреть, сохраняет оно
ориентацию или меняет.
Упражнение 1.3.17 (вложения диска и расслоение реперов).
а) Покажите, что два вложения диска D", переводящие начало координат в одну
и ту же точку и имеющие одинаковые производные в начале координат, изотопны.
б) Покажите, что они изотопны и тогда, когда отображают начало координат в
одну и ту же точку и задают в ней реперы, лежащие в одной связной компоненте
GL(n, Щ.
в) Покажите, что они изотопны, даже если отображают начало координат в
разные точки, но задают в них реперы, которые можно непрерывно деформировать
один в другой.
Связную сумму двух ориентированных многообразий имеет смысл опре-
определить так, чтобы снова получилось ориентированное многообразие, ори-
ориентация которого совпадает вне дисков с исходными ориентациями. Для
этого ровно одно из вложений cpi и ср2 должно сохранять ориентацию. При
этом условии ориентация на связной сумме двух ориентированных много-
многообразий оказывается корректно определенной.
Если одно из многообразий неориентируемо, то связная сумма не зави-
зависит от выбора ориентации склеивающего отображения.
Тем не менее, если оба многообразия ориентируемы, но не ориентиро-
ориентированы, могут возникнуть проблемы, поскольку при разном выборе знака
склеивающего отображения могут получиться разные результаты (однако
упражнение 1.3.18 показывает, что в случае поверхностей этого не проис-
происходит).
Упражнение 1.3.18 (полугруппа поверхностей), а) Докажите, что на ка-
каждой замкнутой ориентируемой поверхности существует гомеоморфизм, обращаю-
обращающий ориентацию.
б) Покажите, что связная сумма # — корректно определенная коммутатив-
коммутативная ассоциативная операция на классах гомеоморфных поверхностей (т. е. классы
гомеоморфных поверхностей образуют коммутативную полугруппу относительно
операции #).
в) Покажите, что S2 — единица этой полугруппы.
г) Покажите, что тор Т2 и проективная плоскость ЮР2 порождают эту полу-
полугруппу. Покажите, что Т2#КР2 =КР2#КР2#КР2.
д) Нарисуйте отмеченный ориентированный граф, вершины которого соответ-
соответствуют классам гомеоморфных поверхностей, ребра, отмеченные буквой А, изобра-
изображают сложение (в смысле связной суммы) с Т2, а ребра, отмеченные буквой В, —
сложение с НИР2.
1.3. Мир поверхностей
35
(*)/
Рис. 1.19. Раздутие точки. Раздутие многообразия М в точке х (рис. слева) состоит из
точек двух типов: точек множества М \ {х} и одномерных подпространств касательно-
касательного пространства ТХМ. Естественное отображение р этого многообразия в М переводит
каждую точку первого типа в себя, а каждую точку второго типа в х. Топология разду-
раздутия определяется следующими условиями: р — локальный гомеоморфизм вне р~1(х),
а окрестность точки / е р~1 (х), соответствующей прямой L, состоит нз точек второго
типа, которые соответствуют прямым, близким к L, и точек первого типа, лежащих на
этих прямых вблизи от точки X.
Упражнение 1.3.19 (раздутие точки), а) Пусть х — точка гладкого л-мер-
иого многообразия М. Замена точки х на множество прямых, касательных к мно-
многообразию в этой точке, называется раздутием точки х и приводит к топологии,
показанной на рис. 1.19. Докажите, что после раздутия получится гладкое много-
многообразие, гомеоморфное М#ШРп.
б) В двумерном случае раздутие равносильно вырезанию диска и вклейке на
его место ленты Мёбиуса.
в) Что произойдет, если в определении раздутия заменить касательные прямые
на касательные лучи?
Упражнение 1.3.20 (автосумма). Вместо связной суммы можно рассмотреть
следующую операцию: удалим два непересекающихся диска из одного и того же
многообразия и склеим две получившиеся граничные сферы. При отождествлении
этих сфер ориентацию можно выбрать двумя различными способами. Что произой-
произойдет с поверхностью при такой операции, называемой автосуммой?
Упражнение 1.3.21. Покажите, что полугруппу связных замкнутых поверхно-
поверхностей можно получить из единичного элемента S2 с помощью операций раздутия
и автосуммы.
36
Глава 1. Что такое многообразие?
1.4. Примеры трехмерных многообразий
Прочно обосновавшись на аэродроме под названием «поверхности», со-
совершим небольшой облет нескольких 3-многообразий.
Пример 1.4.1 (трехмерный тор). По-видимому, простейшим для по-
понимания трехмерным многообразием является трехмерный тор. Его можно
получить аналогично двумерному тору, отождествив каждую пару парал-
параллельных граней куба с помощью параллельного переноса.
Чтобы освоиться в трехмерном торе, представьте, что вы находитесь
внутри прямоугольной комнаты. Вообразите, что противоположные стены
отождествлены, а потолок приклеен к полу. При попытке посмотреть на
какую-либо стену ваш взгляд не упрется в нее, а скользнет в том же на-
направлении, стартовав из соответствующей точки противоположной стены.
Поэтому, глядя вперед, вы увидите свою спину, посмотрев влево — смо-
сможете рассмотреть себя справа, а посмотрев себе под ноги — обнаружите
собственную макушку. Рядом с вашей комнатой вы найдете шесть своих
двойников. Но их можно найти и глядя по диагонали, а также во мно-
многих других направлениях. Куда бы вы ни посмотрели, ваш взгляд будет
продолжаться бесконечно. Возникнет ощущение, что вы находитесь среди
бесконечного количества собственных двойников, раскиданных. по всему
трехмерному пространству (см. рис. 1.20). Сходный эффект возникает в
парикмахерской с зеркалами, висящими на противоположных стенах. Раз-
Разница состоит в том, что в парикмахерской ваши отражения повернуты к вам
то лицом, то спиной поочередно, в то время как в торе все ваши образы
стоят к вам спиной. Если вы повернетесь к своему образу в торе, то он от-
отвернется от вас, а если попытаетесь к нему приблизиться — он отодвинется,
и вы никогда его не встретите.
Пример 1.4.2 (внутренний вид трехмерной сферы). Следующим
по простоте восприятия трехмерным многообразием является трехмерная
сфера S3. Ее проще всего определить как единичную сферу х\ + х\ 4-
+ х\ + х\ = 1 в Е4. К сожалению, эта формула немного говорит людям,
не привыкшим разглядывать объекты в четырехмерном пространстве. Но
есть и другой способ представить трехмерную сферу — с точки зрения ее
обитателя.
Для начала хорошо бы представить, что видит житель двумерной сферы.
При этом мы будем предполагать, что с помощью некоторого приспосо-
приспособления лучи света искривлены так, что они следуют вдоль поверхности.
Например, можно представить, что «поверхность» — это тонкая прослойка
воздуха между двумя большими концентрическими стеклянными сферами,
от которых свет отражается, как в световоде. (К сожалению, не совсем
понятно, как жить в этой модели. В лучшем случае там хватит места для
ползания на животе.)
1.4. Примеры трехмерных многообразий
37
' ¦-* ii »i vi _ >4
и
it t Ji
/i
¦И Г А
*7*?±t
&щ
ii
Рис. 1.20. Внутри трехмерного тора. Жители трехмерного тора видят вместо любого
объекта бесконечное число его образов, расположенных в узлах трехмерной решетки.
Представьте, что на Северном полюсе сидит некто А, а некто В ползет
от него. Чтобы понять, каким житель В видится жителю А, посмотрим,
какие геодезические лучи, исходящие из глаз А, попадают в В (напомним,
что геодезические на сфере —это большие окружности). Итак, В ползет
от А. Сначала А покажется, что В уменьшается, но не так быстро, как
это происходило бы на плоскости. Но как только В достигнет экватора, А
увидит, что В увеличивается, причем все быстрее и быстрее, пока, наконец,
В не окажется на Южном полюсе и не займет все поле зрения Л, который
будет видеть В, глядя в любом направлении.
Примерно то же происходит и в трехмерной сфере. Чтобы нам было
попросторней, чем в торе Т3, переберемся внутрь трехмерного сфериче-
сферического мира, длина большой окружности которого равна двум милям. Си-
Силы тяготения нет. Нет необходимости думать о еде, ночлеге, освещении
и других мелочах. На спинах у нас небольшие пропеллеры, позволяю-
позволяющие перемещаться в любых направлениях. Если я удаляюсь от вас в
любом направлении, то вы видите, что мой образ уменьшается: сначала
быстро, потом — все медленнее. Когда я пролечу почти половину мили,
мой видимый размер будет меняться очень медленно — может показаться,
что я совсем не меняюсь. А после того, как я удалюсь на полмили, вам
покажется, что я снова стал расти. Приближаясь к вашему антиподу (на-
(находящемуся в миле от вас), я буду расти все быстрее и быстрее, и в двух
шагах от него вы увидите меня совершенно таким же, как если бы я был
в двух шагах от вас. Обернувшись назад и громко крикнув, я могу вас
случайно оглушить. Мы быстро поймем, что можем нормально перегова-
переговариваться, поскольку звуки, аналогично свету, сходятся в противоположной
точке.
38
Глава 1. Что такое многообразие?
И хотя я кажусь вам таким же, как если б я был в двух шагах от вас,
вы увидите все же нечто новое: вы сможете смотреть на меня с нескольких
сторон одновременно (есть, кроме того, различие в фокусном расстоянии,
но мы им пренебрежем: представим, что в этом пространстве настолько
светло, что наши зрачки сузились и мы этот эффект не замечаем). Я про-
продолжаю приближаться к точке, противоположной месту, где расположены
ваши глаза, и как только она окажется внутри меня, ситуация становится
драматической: вы обнаружите, что видите меня независимо от того, куда
смотрите, как будто я вывернулся наизнанку и стал внутренней поверхно-
поверхностью полой сферы, окружающей вас. И вы мне будете казаться внутренней
поверхностью полой сферы, окружающей меня.
В этом описании мы забыли одну существенную деталь: свет не оста-
останавливается, пройдя одну милю. Когда я нахожусь от вас на расстоянии
половины мили, я кажусь вам таким маленьким, что ваш взгляд продол-
продолжает беспрепятственно скользить вглубь сферы, в конце концов упираясь
в вас недалеко от места старта. Вы будете видеть все на фоне себя самого,
вывернутого наизнанку на внутренности полой сферы, и ваш затылок будет
красоваться перед вами.
Кроме того, мы упустили еще один момент: если я нахожусь от вас на
расстоянии меньше мили, то вы можете меня увидеть с двух противопо-
противоположных направлений. Например, если я нахожусь в двух шагах от вашего
антипода, то стоит вам повернуться ко мне спиной, как вы увидите меня
снова: я покажусь вам таким же, как если бы стоял лицом к вам и на-
находился бы в двух шагах от вас. Правда, несколько менее четким (из-за
голубой дымки от водяных паров в окружающем воздухе). Вы мне также
покажетесь стоящим рядом со мной. Но если мы захотим пожать друг
другу руки, то наши руки не встретятся.
Пример 1.4.3 (эллиптическое пространство). Утверждения сфе-
сферической геометрии часто требуют оговорок, вызванных существованием
противоположных точек. Например, любые две точки, если они не проти-
противоположны, определяют единственную прямую. Более разумно устроено
эллиптическое пространство, т. е. сфера, противоположные точки
которой- отождествлены.
Топологически л-мерное эллиптическое пространство совпадает с
л-мерным проективным пространством ЮР", но как фактор сферы по
группе, содержащей только тождественное и антиподальное отображения,
наследует у сферы геометрию, точно так же, как тор наследует геометрию
евклидова пространства. Факты сферической геометрии легко приспосо-
приспособить к эллиптическому пространству» и наоборот. Обычно они получаются
более простыми в случае эллиптического пространства: например, через
любые две точки эллиптического пространства можно провести единствен-
единственную прямую.
1.4. Примеры трехмерных многообразий
39
Мы уже знаем, что на сфере единичного радиуса видимый размер уда-
удаляющегося объекта уменьшается до тех пор, пока объект не окажется на
расстоянии тс/2. После этого он снова начнет увеличиваться, и, удалив-
удалившись на расстояние тс, покажется столь большим, как если бы он окружал
наблюдателя полностью. В эллиптическом же пространстве максималь-
максимальное расстояние равно тс/2, так что видимый размер объекта является мо-
монотонной функцией от расстояния. Наверное, обитатель эллиптического
пространства должен постоянно огорчаться, поскольку все, что он видит,
он видит на фоне своего собственного изображения. Глядя прямо вперед,
он видит свой перевернутый, сильно увеличенный затылок. Все остальные
предметы он видит дважды, причем в противоположных направлениях.
Пример 1.4.4 (сферическое пространство додекаэдра). Это знаме-
знаменитое пространство, открытое Пуанкаре, получается из додекаэдра склей-
склейкой противолежащих граней. Вершины пятиугольников, образующих про-
противоположные грани, расположены не в «фазе»: они перемежаются так,
что склеить эти пятиугольники с помощью параллельного переноса, как мы
делали это в случае тора, не удается. Посмотрим, что произойдет, если их
склеить с минимальной подкруткой: приклеивая переднюю грань к задней,
повернем ее на 1/10 полного оборота, скажем, по часовой стрелке, как в
случае правого винта (рис. 1.21, слева). Наш рецепт склейки симметричен,
поскольку, повернув додекаэдр на тс, мы не изменим принцип отождествле-
отождествления: правый винт, у которого шляпка приделана с другой стороны, остается
правым винтом.
Каждая грань додекаэдра имеет пять ребер, а каждое ребро принад-
принадлежит двум граням, так что в додекаэдре 12 • 5/2 = 30 ребер. Склейка
граней определяет многочисленные отождествления ребер, которые можно
проследить и убедиться, что в нашем случае ребра склеиваются по три,
образуя 10 троек.
Чтобы понять, что происходит с 12 • 5/3 = 20 вершинами додекаэдра,
рассмотрим сферические треугольники, высекаемые додекаэдром на ма-
маленьких сферах с центрами в вершинах додекаэдра. Эти треугольники
склеиваются так, что в каждой вершине сходится по четыре треугольника,
образуя нечто, похожее на тетраэдр. Поэтому вершины додекаэдра склеи-
склеиваются в пять групп по четыре, а получившееся пространство оказывается
многообразием (поскольку оно локально гомеоморфно Е3, даже в окрест-
окрестности вершины и в окрестности любой точки ребра).
Нельзя ли провести эту склейку так, чтобы не только топология, но
и Геометрия оказалась локально евклидовой? Тогда в получившемся про-
пространстве сумма углов вокруг любого ребра равнялась бы 2тс, и, если
исходный додекаэдр был правильным, его двугранные углы равнялись бы
2тс/3, т. е. 120°. Но двугранные углы евклидова додекаэдра немного меньше
этой величины: они равны arctg(—2), т. е. 116,565°.
40
Глава 1. Что такое многообразие?
Рис. 1.21. Сферическое пространство додекаэдра. Пятиугольные грани додекаэдра
разбиваются на пары противоположных, но противоположные пятиугольники повер-
повернуты друг относительно друга. Если склеить противоположные грани с поворотом по
часовой стрелке на одну десятую оборота, получится пространство додекаэдра. При
этом ребра склеятся по три штуки; поэтому, чтобы получить геометрическую структуру
на этом пространстве, нужно взять сферический додекаэдр, двугранные углы которо-
которого равны 120°. Это немного раздутое тело изображено (справа) в стереографической
проекции (см. упражнение 2.2.8); оно почти неотличимо от своего евклидова двойника,
двугранные углы которого равны 116,565°.
Вот тут на помощь приходит геометрия трехмерной сферы. Так же, как
углы геодезического треугольника на двумерной сфере несколько превос-
превосходят углы евклидова треугольника с теми же сторонами, двугранные углы
многогранника в трехмерной сфере превосходят углы евклидова много-
многогранника. Углы очень маленького сферического додекаэдра почти равны
евклидовым углам. С ростом додекаэдра его углы увеличиваются. И когда
вершины додекаэдра удалятся от центра на тс/2 (или на половину мили в
масштабе примера 1.4.2), додекаэдр станет двумерной сферой —его углы
будут равны тс.
Поэтому где-то по дороге встретится додекаэдр с углами ровно 2тс/3
(рис. 1.21, справа). После склейки такого додекаэдра получится геоме-
геометрическое (сферическое) многообразие.
Пространство додекаэдра можно развернуть так, что получится замо-
замощение сферы S3 (точно так же мы получали замощения пространств Е2
и Е3, разворачивая торы Т2 и Т3). Это означает, что пространство додека-
додекаэдра, как и эллиптическое пространство, является фактором сферы S3 по
группе изометрий. Сколько додекаэдров участвуют в замощении S3? Это
можно узнать двумя способами: либо с помощью координат в S3 С Е4,
либо изучив комбинаторную структуру замощения (опираясь на то, что
локальная структура нам известна). Но сейчас оба подхода потребуют от
1.4. Примеры трехмерных многообразий
41
нас больших усилий, так что мы вернемся к этому вопросу позже, в зада-
задаче 4.4.17. В результате получится, что для замощения трехмерной сферы
потребуется 120 додекаэдров. Это сферическое замощение определяет в Е4
многогранник со 120 гранями, каждая из которых является правильным
додекаэдром.
Пример 1.4.5 (пространство Зейферта-Вебера). Склеим противо-
противоположные грани додекаэдра, подкрутив их на этот раз на три десятых обо-
оборота (рис. 1.22). Присмотревшись к схеме склейки, мы увидим, что ребра
теперь склеиваются, образуя шесть групп по пять. Все двадцать вершин
склеиваются в одну, так что сферические треугольники (т. е. пересечения
маленьких сфер с додекаэдром) образуют правильный икосаэдр. Получив-
Получившееся пространство является многообразием и называется пространством
Зейферта—Вебера.
Рис. 1.22. Пространство Зейферта-Вебера. Противоположные грани додекаэдра
склеены с поворотом на три десятых оборота по часовой стрелке. Ребра склеиваются
по пять. Получившееся многообразие называется додекаэдрическим пространством
Зейферта—Вебера. Чтобы оно оказалось геометрическим, надо начать с гиперболиче-
гиперболического додекаэдра, двугранные углы которого равны 2тс/5. Этот многогранник изобра-
изображен (справа) в модели Пуанкаре.
Углы евклидова додекаэдра значительно превосходят 2тс/5, необходи-
необходимые для геометрической склейки. Теперь нам поможет трехмерное гипер-
гиперболическое пространство Ы3, которое, как и в двумерном случае, можно
отобразить на внутренность трехмерного шара. Такое описание гипербо-
гиперболического пространства называется моделью Пуанкаре в шаре. Плоско-
Плоскости представлены секторами сфер, перпендикулярных границе шара. Углы
между гиперболическими плоскостями совпадают с углами между соответ-
соответствующими сферами. Окружности, образованные пересечением этих сфер
42
Глава 1. Что такое многообразие?
с границей шара S2X, пересекаются под тем же самым углом, поскольку
наши сферы перпендикулярны границе шара.
Разумеется, углы правильного додекаэдра в Н3 меньше, чем в Е3, но
можно ли их сделать равными 2тс/5? Когда гиперболический додекаэдр
очень велик, его вершины почти лежат на границе шара. А в пределе по-
получается идеальный додекаэдр, у которого нет вершин — его идеальные
вершины лежат на S2^.
Три грани додекаэдра, сходящиеся в идеальной вершине, в пересечении
с S2^ дают три окружности. Учитывая их симметричное расположение,
легко понять, что двугранные углы идеального додекаэдра равны тс/3.
Поэтому подередине между очень маленьким гиперболическим доде-
додекаэдром с углами, близкими к arctg(—2), т. е. 116,565°, и очень боль-
большим додекаэдром с углами, стремящимися к тс/3, существует додекаэдр,
двугранные углы которого в точности равны 2тс/5. Из этого додекаэдра
можно склеить геометрическое пространство Зейферта—Вебера. Оно со-
соответствует замощению гиперболического пространства Н3 додекаэдрами,
при котором каждое ребро принадлежит пяти додекаэдрам, а каждая вер-
вершина — двадцати.
Пример 1.4.6 (линзовое пространство). Рассмотрим шар, поверх-
поверхность которого поделена экватором на две полусферы. Что будет, если
приклеить одну полусферу к другой?
Если склеить не перекручивая, т. е. с тождественным отображением
экватора иа себя, то получится многообразие S3. Точно так же, сферу S2
можно получить, разделив границу диска на два интервала и приклеив их
друг к другу, не меняя концы местами.
С другой стороны, если полусферы склеить, повернув одну относительно
другой на q/p оборота по часовой стрелке (где q и р — взаимно простые
целые числа), то каждая точка экватора склеится ср-1 другой точкой.
Окрестность каждой такой точки в пространстве склейки напоминает го-
головку сыра, сложенную из р клинышков. Многообразие, склеенное таким
образом, называется линзовым пространством ЬРЛ.
Для построения геометрической модели линзового пространства нам
понадобятся объекты, похожие на линзу, в которой угол между верхней
и нижней поверхностями равен 2тс//?. Их легко найти в трехмерной сфе-
сфере. Через любую окружность в S3 проходит целое семейство двумерных
сфер. Среди них нетрудно выбрать две сферы, пересекающиеся под нуж-
нужным углом. Приклеим теперь верхнюю грань линзы к нижней по нашему
правилу. При этом окрестности р склеиваемых точек ободка линзы склады-
складываются нужным образом. Это соответствует замощению трехмерной сферы
р линзами (рис. 1.23, слева).
Задача 1.4.7 (дальнейшее изучение линзового пространства), а) Линзу,
из которой склеено Lp,q, можно разрезать на р тетраэдров, имеющих общее
1.4. Примеры трехмерных многообразий
43
Рис. 1.23. Линзовое пространство. Слева показано поперечное сечение сферы S3,
замощенной двенадцатью копиями фундаментальной области пространства L\2,q (ис-
(использована стереографическая проекция: см. упражнение 2.2.8). Справа — простран-
пространство Lj2, разобранное и собранное по-другому, демонстрирует, что L7,2 = ^7,3-
ребро, проходящее по оси вращения линзы. После этого их можно склеить в
другом порядке, используя отождествление граней, лежащих на поверхности
линзы (рис. 1.23, справа). Что получится в результате склейки? Какие линзовые
пространства можно таким способом отождествить?
б) Возьмем линзу, использованную для склейки Lp,q, и высверлим из нее вдоль
центральной оси телесный цилиндр. При нашей склейке верхняя часть цилиндра
приклеится к нижней, образовав полноторие. Что при этом произойдет с оставшей-
оставшейся частью линзы, если склеить две компоненты ее границы, лежащие на поверхно-
поверхности линзы? Нарисуйте это для L3.2- Объясните, как склеить линзовое пространство
из двух полноторий.
в) Покажите, что Lp,q гомеоморфно Lpi qi тогда и только тогда, когда р = р'
и либо q' = ±q, либо qq' = ±1 mod p. (Это совсем не просто, см. доказательство
в [ВгобО].)
Пример 1.4.8 (заковыристый пример). На рис. 1.24 изображен про-
простейший пример трехмерной схемы склейки. Начнем с двух тетраэдров Г
и Г' с отмеченными гранями и ориентированными ребрами двух типов:
толстыми и тонкими. Склеим грани попарно, следя за тем, чтобы совпали
метки на гранях, а также направления и типы ребер: например, грань А
тетраэдра Г приклеивается к грани А тетраэдра V так, что толстые ребра
приклеиваются к толстым, а единственное тонкое — к тонкому. В полу-
получившемся комплексе К все толстые ребра в результате склеены в одно
ребро, а все тонкие — в другое. Более того, все вершины склеены в одну
вершину V.
44
Глава 1. Что такое многообразие?
Рис. 1.24. Простая трехмерная схема склейки. Простая схема склейкн двух тетра-
тетраэдров. В центре каждой грани находится метка. Одинаково отмеченные грани можно
единственным образом отождествить так, чтобы типы ребер (толстый нлн тонкий) и их
направления совпали. (На самом деле, этих условий достаточно, чтобы восстановить
даже спаривание граней.)
Является ли К многообразием? Нам надо проверить, что каждая точка
К имеет окрестность, гомеоморфную трехмерному шару. Для точек, лежав-
лежавших до склейки внутри тетраэдров, это очевидно, равно как и для точек,
лежавших внутри грани, где такая окрестность состоит из двух «встретив-
«встретившихся» на этой грани полупространств. Точка, лежавшая внутри ребра,
также имеет нужную шаровую окрестность, циклически склеенную из не-
нескольких долек. Каждая такая долька является окрестностью одного из
прообразов нашей точки в Т или Т.
Но с вершиной V возникают проблемы. Представьте себе маленькую
окрестность вершины V, пересекающую каждый тетраэдр по тетраэдраль-
тетраэдральным окрестностям вершин. При склейке внутренние грани этих тетраэдров
образуют поверхность, называемую линком вершины V. Можно прове-
проверить, что это — тор, увидев это явно или вычислив эйлерову характеристику
и вспомнив, что ориентируемая поверхность с нулевой эйлеровой характе-
характеристикой является тором. Поэтому окрестность вершины V в К является
*конусом над тором. Отсюда видно, что она не гомеоморфна шару. Так что
К — не многообразие. В каких же случаях комплекс, полученный склейкой
многогранников, будет многообразием? Детально и в более общей поста-
постановке этот вопрос обсуждается в разделе 3.2.
Хотя К и не многообразие, удалив непокорную вершину, можно полу-
получить некомпактное многообразие М = К — {V}. Поскольку каждая пара
граней склеивается отображением, обращающим ориентацию, многообра-
многообразие М ориентируемо. Удалив открытую окрестность вершины V, получим
компактное многообразие, граница которого является тором.
1.4. Примеры трехмерных многообразий
45
Упражнение 1.4.9. Постройте линк вершины V из восьми треугольников,
являющихся линками вершин двух исходных тетраэдров.
Оказывается, что многообразие М является дополнением (в сфере S3 =
= М.3 U {оо}) узла «восьмерка», изображенного на рис. 1.25. Чтобы убе-
убедиться в этом, расположим «восьмерку» вдоль ребер тетраэдра, как на
рис. 1.26, а. Видно, что на узел можно натянуть двумерный комплекс, со-
содержащий два ребра (стрелки) и четыре двумерных клетки (это четыре
грани тетраэдра, причем каждая грань украшена узкой полоской и уз-
узкой перекрученной ленточкой). Этот комплекс ограничивает в простран-
пространстве компактную область, внутренность R которой гомеоморфна открытому
шару.
Рис. 1.25. Два изображения узла «восьмерка». Два изображения узла «восьмер-
«восьмерка» — наиболее часто (после узла трилистника) встречающегося узла. Такой узел
можно увидеть на собачьих поводках, садовых шлангах, развернутых мотках веревки.
А теперь представим, что толстое ребро на рис. 1.26, а красного цвета,
тонкое — зеленого, а сам узел — черного цвета. Поместим внутрь области R
воздушный шарик и будем надувать его до тех пор, пока он не заполнит
все закоулки и трещинки внутреннего пространства. Затем вынем шарик
и рассмотрим его. На нем имеются четыре области, соответствующие че-
четырем двумерным клеткам, расположенные, как на рис. 1.26, б.
Граница каждой области состоит из пяти частей. Две черные, не отме-
отмеченные стрелками, получились из узла. Остальные три (две тонкие части
и одна толстая, или две толстые и одна тонкая) — из ребер комплекса.
Поскольку узел лежит не в М, а в дополнении, мы можем стягивать и рас-
растягивать черные кусочки, не меняя многообразия М. Если стянуть все
черные кусочки в точку, то области превратятся в треугольники, а_ вну-
внутренность воздушного шарика вместе с треугольными гранями окажется
ровно таким же тетраэдром Т, как на рис. 1.24.
Тетраэдр V получается точно так же, при раздувании шарика, содер-
содержащего бесконечно удаленную точку в S3 — R3 U {оо} (т. е. шарика, обле-
облепившего узел снаружи).
46
Глава 1. Что такое многообразие?
Рис. 1.26. Двумерный комплекс, натянутый на узел «восьмерка», (а) На «вось-
«восьмерку» можно натянуть двумерный комплекс с двумя одномерными клетками (изобра-
(изображенными стрелками) и четырьмя двумерными (это грани тетраэдра, каждая из которых
дополнена полоской, выходящей из вершины, и узкой перекрученной ленточкой, вы-
выходящей из противоположного ребра). Внутренность R этого комплекса гомеоморфна
открытому шару, (б) Продолжим гомеоморфизм до отображения замкнутого шара на
замыкание области R. Каждая одномерная клетка превратится в три ребра на грани-
границе, а каждая двумерная клетка будет ограничена тремя ребрами и двумя кусками узла.
Если стянуть куски узла в точку, то получится тетраэдр Т, изображенный на рис. 1.24.
Это разбиение непросто увидеть. В книге [Fra87, с. 151 — 155] вы найдете
два других описания этой конструкции, снабженных красивыми рисунками.
К этому пространству мы еще вернемся в примере 3.3.7. Тот поразитель-
поразительный факт, что дополнение к конкретному узлу можно получить специальной
склейкой двух тетраэдров, ясно указывает на необходимость поиска систе-
систематических методов сравнения и распознавания многообразий.
Упражнение 1.4.10. Вспомогательные
рнсункн могут оказаться обманчивыми. На
рис. 1.27 показано, что узел «трилистник»
также можно расположить вдоль ребер тетра-
тетраэдра и натянуть на него двумерный комплекс,
сильно напоминающий комплекс, натянутый
на «восьмерку». Раздуйте внутренний н внеш-
внешний воздушные шарики н нарисуйте следы уз-
узла и стрелок на их поверхности. Получатся ли
в результате тетраэдры?
Рис. 1.27. Двумерный комплекс, натянутый иа
трилистник. Несмотря на сходство с рис. 1.26, в
случае трилистника эта конструкция не приводит
к разбиению дополнения к узлу на два тетраэдра.
Глава 2
Гиперболическая геометрия и ее друзья
Смысл слова «геометрия» очень сильно зависит от контекста, в котором
оно употребляется. В этой главе мы изучим геометрию в ее классическом
понимании: наши геометрии будут аналогами обычной евклидовой геоме-
геометрии с ее прямыми (геодезическими), углами и плоскостями, измерением
расстояний, и большой степенью однородности.
Чтобы описать структуру геометрии, можно, например, ввести рима-
нову метрику. На любом римановом многообразии действует группа изо-
мепгрий — преобразований пространства, сохраняющих углы и расстоя-
расстояния (а следовательно, переводящих прямые в прямые). Правда, почти на
всех римановых многообразиях эта группа тривиальна. Мы же займемся
редкими исключениями — однородным и геометриями, т. е. геометриями, у
которых группа симметрии действует транзитивно: каждую точку можно с
помощью изометрии перевести в любую другую точку, так что все точки
«одинаковы».
Наши геометрии будут не только однородны, но и изотропны. Про-
Пространство называется изотропным, если все направления в нем равно-
равноправны; точнее, если для любых двух упорядоченных ортонормированных
базисов касательного пространства в точке х существует изометрия, со-
сохраняющая точку х и переводящая один из этих базисов в другой.
Однородность и изотропность вместе составляют очень сильное усло-
условие, из которого следует, например, что секционная кривизна не зависит от
точки и двумерной касательной плоскости. В каждой размерности суще-
существует только три существенно различных однородных изотропных геоме-
геометрий: геометрия нулевой секционной кривизны, постоянной положитель-
положительной кривизны К, и постоянной отрицательной кривизны -К (с помощью
перенормировки можно перейти к К= 1). Эти геометрии называются со-
соответственно евклидовой, сферической и гиперболической.
Евклидова геометрия знакома всем, поскольку она достаточно близка к
геометрии мира, в котором мы живем (если только не удаляться на слиш-
слишком большие расстояния). Сферическая геометрия — это обычная геоме-
геометрия я-мерной сферы, в которой геодезическими служат большие окруж-
окружности, а углы и расстояния наследуются из (п + 1)-мерного евклидова
46
Глава 1. Что такое многообразие?
Рис. 1.26. Двумерный комплекс, натянутый на узел «восьмерка», (а) На «вось-
«восьмерку» можно натянуть двумерный комплекс с двумя одномерными клетками (изобра-
(изображенными стрелками) и четырьмя двумерными (это грани тетраэдра, каждая из которых
дополнена полоской, выходящей из вершины, и узкой перекрученной ленточкой, вы-
выходящей из противоположного ребра). Внутренность R этого комплекса гомеоморфна
открытому шару, (б) Продолжим гомеоморфизм до отображения замкнутого шара на
замыкание области R. Каждая одномерная клетка превратится в три ребра на грани-
границе, а каждая двумерная клетка будет ограничена тремя ребрами и двумя кусками узла.
Если стянуть куски узла в точку, то получится тетраэдр Т, изображенный на рис. 1.24.
Это разбиение непросто увидеть. В книге [Fra87, с. 151—155] вы найдете
два других описания этой конструкции, снабженных красивыми рисунками.
К этому пространству мы еще вернемся в примере 3.3.7. Тот поразитель-
поразительный факт, что дополнение к конкретному узлу можно получить специальной
склейкой двух тетраэдров, ясно указывает на необходимость поиска систе-
систематических методов сравнения и распознавания многообразий.
Упражнение 1.4.10. Вспомогательные
рисунки могут оказаться обманчивыми. На
рнс. 1.27 показано, что узел «трилистник»
также можно расположить вдоль ребер тетра-
тетраэдра и натянуть на него двумерный комплекс,
сильно напоминающий комплекс, натянутый
на «восьмерку». Раздуйте внутренний и внеш-
внешний воздушные шарики и нарисуйте следы уз-
узла н стрелок на их поверхности. Получатся ли
в результате тетраэдры?
Рис. 1.27. Двумерный комплекс, натянутый на
трилистник. Несмотря на сходство с рис. 1.26, в
случае трилистника эта конструкция не приводит
к разбиению дополнения к узлу на два тетраэдра.
Глава 2
Гиперболическая геометрия и ее друзья
Смысл слова «геометрия» очень сильно зависит от контекста, в котором
оно употребляется. В этой главе мы изучим геометрию в ее классическом
понимании: наши геометрии будут аналогами обычной евклидовой геоме-
геометрии с ее прямыми (геодезическими), углами и плоскостями, измерением
расстояний, и большой степенью однородности.
Чтобы описать структуру геометрии, можно, например, ввести рима-
нову метрику. На любом римановом многообразии действует группа изо-
метрий — преобразований пространства, сохраняющих углы и расстоя-
расстояния (а следовательно, переводящих прямые в прямые). Правда, почти на
всех римановых многообразиях эта группа тривиальна. Мы же займемся
редкими исключениями — однородными геометриями, т. е. геометриями, у
которых группа симметрии действует транзитивно: каждую точку можно с
помощью изометрии перевести в любую другую точку, так что все точки
«одинаковы».
Наши геометрии будут не только однородны, но и изотропны. Про-
Пространство называется изотропным, если все направления в нем равно-
равноправны; точнее, если для любых двух упорядоченных ортонормированных
базисов касательного пространства в точке х существует изометрия, со-
сохраняющая точку х и переводящая один из этих базисов в другой.
Однородность и изотропность вместе составляют очень сильное усло-
условие, из которого следует, например, что секционная кривизна не зависит от
точки и двумерной касательной плоскости. В каждой размерности суще-
существует только три существенно различных однородных изотропных геоме-
геометрий: геометрия нулевой секционной кривизны, постоянной положитель-
положительной кривизны К, и постоянной отрицательной кривизны -К (с помощью
перенормировки можно перейти к К= 1). Эти геометрии называются со-
соответственно евклидовой, сферической и гиперболической.
Евклидова геометрия знакома всем, поскольку она достаточно близка к
геометрии мира, в котором мы живем (если только не удаляться на слиш-
слишком большие расстояния). Сферическая геометрия — это обычная геоме-
геометрия л-мерной сферы, в которой геодезическими служат большие окруж-
окружности, а углы и расстояния наследуются из (п 4- 1)-мерного евклидова
48
Глава 2. Гиперболическая геометрия и ее друзья
пространства. Мы уже обсуждали трехмерную сферу в примере 1.4.2, и
вернемся к сферической геометрии в конце этой главы. Гиперболическая
геометрия незнакома большинству людей. Она интересна сама по себе,
но, кроме того, именно она важна для двумерной и трехмерной тополо-
топологии. Поэтому мы не пожалеем времени на несколько различных описаний
гиперболической геометрии.
В главе 3 мы займемся еще пятью трехмерными геометриями, важными
для трехмерной топологии. Эти пять геометрий однородны, но не изотроп-
изотропны: в них не имеет значения, в какой точке находишься, но не все равно, в
какую сторону смотришь. Можно сказать, что в этих геометриях определе-
определено понятие «верх—низ», а в некоторых из них — еще и понятие «север—юг».
Рис. 2.1. Сфера обзора
Двумерную геометрию легко увидеть «снаружи», рисуя на листе бума-
бумаги. Начиная с размерности три, лучше всего представлять себя внутри
пространства. Чтобы формализовать это интуитивное понятие предста-
представим себе наблюдателя как точку я-мерного пространства., в которую свет
попадает по геодезическим (см. рис. 2.1). Каждая из геодезических опре-
определяет касательный вектор в этой точке. Назовем (п — 1)-мерную сферу
касательных векторов сферой обзора. По-другому ее можно предста-
представлять в виде маленькой сферы с центром в точке наблюдения, причем
каждая геодезическая, выходящая из точки наблюдения, пересекает эту
сферу в единственной точке. Если образ объекта на сфере обзора — ду-
дуга большой окружности, то объект воспринимается как отрезок прямой.
Величина объекта определяется длиной соответствующей дуги на сфере
обзора.
2.1. Поверхности отрицательной кривизны в пространстве
49
2.1. Поверхности отрицательной кривизны
в пространстве
Прежде чем описывать абстрактные модели гиперболической геометрии,
займемся объектами более естественного происхождения. Для этого нам
потребуются некоторые понятия дифференциальной геометрии поверхно-
поверхностей, которые мы будем вводить по мере необходимости. Мы не станем тра-
тратить время на подробности этой красивой науки, их можно найти во многих
уже имеющихся хороших книгах (см., например, [O'N66, Hic65, dC76]).
Внутренняя геометрия поверхности определяется ее гауссовой кри-
кривизной (или просто кривизной). Слова «внутренняя геометрия» здесь
означают свойства, которые не меняются при изгибаниях поверхности, со-
сохраняющих длины; иначе говоря, они зависят только от длин кривых на
самой поверхности. Внешние же свойства — это те, которые зависят от
вложения поверхности в пространство.
Внешний вид поверхности очень сильно зависит от знака кривизны. По-
Посмотрим на касательную плоскость к поверхности. В окрестности точки
касания поверхность положительной кривизны целиком находится с одной
стороны от касательной плоскости. Примером может служить резиновый
мяч. Касательная плоскость к поверхности нулевой кривизны всегда со-
содержит прямую, лежащую на поверхности. Для того чтобы убедиться в
этом, изогните (не сминая) лист бумаги в любом направлении и заметь-
заметьте, что через любую точку получившейся поверхности проходит прямая,
принадлежащая одновременно и поверхности, и касательной плоскости.
Касательная плоскость к поверхности отрицательной кривизны разрезает
поверхность — вспомните седло.
Значение кривизны определяется поведением поверхности с точностью
до членов второго порядка. Действительно, введем координаты так, чтобы
исследуемая точка находилась в начале координат, а касательная плос-
плоскость в ней была горизонтальна. Тогда поверхность локально является
графиком функции f(x, у), причем /@) = Д@) = fy@) = 0. Гауссова кри-
кривизна в начале координат равна определителю гессиана
B.1.1)
н =
fyyj'
Например, гауссова кривизна графика многочлена f{x, у) = Ах2 +
+ 2Вху + Су2 в начале координат равна К — ЦАС — В2). Для параболоида
вращения (рис. 2.2) это число положительно, а для гиперболического
параболоида (рис. 2.3) — отрицательно.
В этих примерах функция f(x, у) совпадает с квадратичной формой,
равной половине ее гессиана: f(x, у) = ±(х, у)Н{х, у)'. В общем случае,
эта квадратичная форма аппроксимирует f(x, у) с точностью до членов
второго порядка.
50
Глава 2. Гиперболическая геометрия и ее друзья
о 2
Рнс. 2.2. Параболоид вращения. Этот параболоид задается уравнением z = — "р* .
Его кривизна, как и кривизна любой поверхности вращения, зависит только от рас-
расстояния г до начала координат. Вычисления показывают, что кривизна как функция
расстояния равна A + г)~2 (см. график справа).
К
Рис. 2.3. Седло. Поверхность графика функции г = 2У называется гиперболиче-
гиперболическим параболоидом. Как ни странно, ее кривизна также зависит только от расстояния г
до начала координат. Она равна —1 в начале координат и быстро стремится к нулю
при увеличении г, так что поверхность становится более плоской к краю рисунка.
Предыдущие определения основаны на внешних свойствах поверх-
поверхностей. Но фундаментальная теорема, названная Гауссом «Theorema
Egfegium», говорит, что гауссова кривизна на самом деле является
внутренним инвариантом поверхности: она не меняется при изгибании
поверхности (без растяжений). Гауссову кривизну можно вычислить вну-
внутренними методами, не выходя за пределы поверхности: нарисуем на
поверхности окружность радиуса г с центром в исследуемой точке. Ес-
2.1. Поверхности отрицательной кривизны в пространстве
51
ли кривизна в этой точке положительна, то длина / окружности (при
достаточно малом г) окажется меньше, чем длина 2кг соответствующей
окружности на плоскости. В точках же отрицательной кривизны отношение
1/2тгг будет больше единицы. Оказывается, вторая производная отношения
1/Ъ.г в точке г = 0 равна гауссовой кривизне, умноженной на -1/3.
Кривизна поверхностей, изображенных на рис. 2.2 и 2.3, не постоян-
постоянна: она, сохраняя знак, быстро стремится к нулю при удалении от начала
координат. Ни внутренняя, ни внешняя геометрия этих поверхностей не
является однородной. Нетрудно найти в пространстве поверхность посто-
постоянной положительной кривизны — сферу. Она однородна и с точки зрения
внутренней геометрии, и как поверхность, вложенная в пространство.
Не так просто придумать поверхность постоянной отрицательной кри-
кривизны, хотя многим знакомы примеры таких поверхностей. Простейшим
из них является псевдосфера (рис. 2.4) — поверхность вращения, поро-
порожденная трактрисой (рис. 2.5). Трактриса — это траектория воза камней,
изначально стоящего в точке @, 1), который упряжка быков, идущих по
оси Ох, тянет за цепь единичной длины. Другими словами, эта кривая
определяется (с точностью до сдвига вдоль оси Ох) тем, что касательная
в любой точке пересекает ось Ох на расстоянии единица от точки касания.
Рис. 2.4. Псевдосфера. Псевдосфера — это поверхность, получающаяся при враще-
вращении трактрисы вокруг оси Ох. Ее кривизна постоянна и равна — 1. Любой кусочек
этой поверхности можно изометрично перенести (изгибая, но не растягивая) в любое
другое место на поверхности.
Обратите внимание, что трактриса не является дважды дифференциру-
дифференцируемой кривой в точке @, 1): касательная поворачивается бесконечно бы-
быстрее, чем растет длина дуги. Поэтому ребро псевдосферы — это граница,
за которую она принципиально не продолжается гладким образом.
Задача 2.1.2 (поверхности вращения постоянной кривизны). Рассмотрим
поверхность вращения плоской кривой (x(s), y(s)), параметризованной длиной
52
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.5. Трактриса. Трактриса — это кривая, касательная к которой в точке (х, у)
пересекает ось Ох на расстоянии, равном 1 от точки касания. Поэтому производная
координаты у по длине пройденной дуги s равна —у и y(s) = e~s.
Рис. 2.6. Поверхности вращения постоянной кривизны. Каждая плоскость, содер-
содержащая граничную окружность, касается поверхности вдоль этой окружности; поэтому
поверхность невозможно гладко продолжить за эту плоскость,
дуги s, вокруг оси Ох. Покажите, что кривизна такой поверхности равна
У ds2'
Используя эту формулу, убедитесь, что кривизна псевдосферы равна — 1. Найдите
функцию y(s), если кривизна К_ постоянна и равна 0, 1, или — 1. Приведите в
каждом случае примеры кривых (x(s), y(s)) (см. рис. 2.6). Покажите, что если
кривизна равна —1, то хотя бы на одном конце кривой имеется особенность, так
что поверхность имеет границу, за которую ее нельзя продолжить без нарушения
гладкости.
Как и у сферы, внутренняя геометрия псевдосферы локально однородна:
любая точка имеет окрестность, изометричную окрестности любой другой
точки. Чтобы это увидеть, введем на псевдосфере координаты (s, 9), где
s — длина дуги трактрисы, а 9 —угол поворота вокруг оси Ох. Из основ-
2.1. Поверхности отрицательной кривизны в пространстве
53
ного свойства трактрисы следует, что производная у по s равна —у, т. е.
y(s) — e~s. Поэтому для любых а и 90 локально определенное отображение
(s, 9) —> (s + а, 90 + еа9) является изометрией.
Кроме того, внутренняя геометрия псевдосферы локально изотропна:
маленький диск на поверхности псевдосферы можно не растягивая вра-
вращать вокруг его центра. Это следствие упражнения 2.2.13 можно проверить
и явно (см. упражнение 2.1.3).
Упражнение 2.1.3 (изготовление гиперболического листа бумаги).
а) Аппроксимируйте псевдосферу объединением усеченных конусов. Каждый
из конусов можно склеить из плоского листа бумаги: достаточно изготовить коль-
кольцо, вырезать из него часть вдоль радиусов (см. рис. 2.7) и склеить радиальные
ребра полученного кольцевого сектора. Внутренний радиус кольца превратится
в расстояние от усеченного конуса до вершины этого конуса, а угол кольцевого
сектора пропорционален радиусу усеченного конуса. Поэтому внутренние радиусы
всех кольцевых секторов должны быть одинаковы и равны длине отрезка каса-
касательной к трактрисе, заключенного между кривой и осью Ох. Углы же секторов
должны зависеть от координаты у.
Имеет смысл скопировать изображения нескольких колец на лист бумаги; кроме
того, на каждом кольце удобно нарисовать дополнительную окружность — отметку
глубины наползания соседних конусов.
Рис. 2.7. Кольца для изготовления псевдосферы. Эти кусочки колец можно исполь-
использовать для изготовления модели поверхности отрицательной кривизны, например —
псевдосферы. Гауссова кривизна будет примерно равна — 1/г2, где г —радиус окруж-
окружности, нарисованной в середине кольца.
б) Постройте аналогичным способом односвязный кусок поверхности: исполь-
используйте кольцевые секторы, не превращая их, однако, в усеченные конусы. Прило-
Приложите новую поверхность к псевдосфере, подвигайте ее по псевдосфере, поверните
ее. Обратите внимание на большое количество внутренних локальных симметрии
псевдосферы, которых не было видно в пространстве.
в) Как далеко можно продолжить такую поверхность? Можно ли склеить из
нее что-либо похожее на поверхность, изображенную на рис. 2.8?
54
Глава 2. Гиперболическая геометрия и ее друзья
В качестве материала для этих построений можно взять не бумагу, а ткань.
На самом деле, юбки-клеш (отрицательной кривизны!) шьют из больших секторов
колец (примерно из четвертей).
Рис. 2.8. Поверхность отрицательной кривизны в пространстве
Упражнение 2.1.4 (многогранные модели поверхностей отрицательной
кривизны). Модели, аппроксимирующие поверхности постоянной отрицательной
кривизны, можно изготовить и из треугольников.
а) Сделайте из бумаги (а лучше из плотного картона) достаточное количество
одинаковых равносторонних треугольников и соедините их так, чтобы в каждой
вершине было семь треугольников.
б) Сравните эту модель с бумажной моделью из упражнения 2.1.3. Сможете ли
вы вычислить или оценить, треугольники какого размера соответствуют кольцам
данной величины?
в) Попробуйте сделать такую же модель с восьмью треугольниками в каждой
вершине. Какого размера должны быть треугольники, чтобы получилась модель,
сравнимая с моделью из пункта а?
г) В этих многогранных моделях вся отрицательная кривизна сосредоточена в
вершинах. Но можно сделать более гладкие модели; распределив кривизну вдоль
сторон треугольников. Заменим каждую сторону равностороннего треугольника на
такую дугу окружности, чтобы все углы получившегося криволинейного треуголь-
треугольника были равны 2х/7. (Радиус окружности должен быть приблизительно в 6,69
раз больше длины стороны треугольника.)
д) Можно ли с помощью равных треугольников аппроксимировать геометрию
псевдосферы? А геометрию поверхностей вращения, изображенных на рис. 2.6?
После игр с бумажными моделями следующее утверждение может по-
показаться вам удивительным.
2.1. Поверхности отрицательной кривизны в пространстве
55
Теорема 2.1.5 (Гильберт). В трехмерном евклидовом простран-
пространстве не существует полной гладкой поверхности постоянной от-
отрицательной кривизны.
На самом деле, некоторые указания на то, что это так, уже встречались.
Мы видели, что псевдосферу и другие поверхности вращения невозможно
продолжить за их ребра. Другие физические поверхности отрицательной
кривизны, такие как листья многих растений, поля широкополых шляп
или бумажные модели из упражнения 2.1.3, имеют волнистые края, как на
рис. 2.8, если продолжать эти поверхности достаточно далеко. Это озна-
означает, что все они не являются гладкими, а в лучшем случае принадлежат
классу С
Чтобы это понять, нам потребуется чуть больше дифференциально-гео-
дифференциально-геометрической техники. Аппроксимируем поверхность квадратичной формой,
как мы уже это делали в начале главы, когда определяли гауссову кривиз-
кривизну. Поворотом в плоскости Оху эту квадратичную форму можно привести
к диагональному виду, т. е. к виду Ах2 + Су2, где, скажем, А ^ С. Тогда ось
Ох — это направление, в котором поверхность сильнее всего искривлена
вверх (или меньше всего искривлена вниз), а О у — направление, в котором
поверхность сильнее всего искривлена вниз (или меньше всего вверх). Эти
направления называются главными направлениями поверхности в дан-
данной точке. Если А — С, то главные направления не определены, а сама
точка называется омбилической.
На С2-поверхности отрицательной кривизны главные направления всю-
всюду определены, непрерывно зависят от точки и нигде не совпадают. Иными
словами, главные направления определяют два взаимно перпендикуляр-
перпендикулярных семейства кривых, в каждой точке касающихся главных направлений.
Это так называемые линии кривизны данной поверхности (см. рис. 2.9).
На поверхности с сильно волнистым краем линии кривизны обычно со-
совершают полоборота на каждую волну. Поэтому на таких поверхностях
линии кривизны не могут быть всюду определены: внутри у них должны
быть точки ветвления. Доказать это можно рассуждениями, аналогичны-
аналогичными использованным в теореме Пуанкаре об индексе (предложение 1.3.10).
Поэтому такие поверхности не могут быть С2-гладкими.
Гильберт доказал свою теорему [HilOl] для вещественно аналитических
вложений, но его доказательство годится и для вложений класса С4. Не-
Несколько труднее распространить теорему на класс С2 (см. [Mil72]). В клас-
классе С вложение полной поверхности отрицательной кривизны уже возмож-
возможно: в [Kui55] приведена явная конструкция.
Тем не менее, любое такое вложение будет чрезвычайно неуклюжим и
совершенно бесполезным в изучении внутренней геометрии поверхности, в
чем можно быстро убедиться, попробовав продолжить бумажную модель
дальше некоторых пределов. Например, длина окружности радиуса R на
56
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.9. Линии кривизны. Вид сверху линий кривизны гиперболического параболо-
параболоида с рис. 2.3 и поверхности с рис. 2.8. Видно, что вторая из этих поверхностей не
является гладкой, поскольку линии кривизны С2-гладкой поверхности отрицательной
кривизны не могут ветвиться.
поверхности постоянной кривизны —1 равна 2nshR. Длина окружности
радиуса 1 фут A фут равен 30,48 см) равна 7,38 футам, что еще не страшно:
получится модель средних размеров, вроде сферы радиуса 1 фут. Но длины
растут очень быстро. Окружность радиуса 2 фута имеет длину 22,78 футов,
радиуса 10 футов —уже длину 13,1 мили, а радиуса 20 футов —288 637
миль, что больше, чем расстояние до Луны.
Поэтому нам придется прибегнуть к искривленной картине гиперболи-
гиперболической плоскости и гиперболического пространства. Как для разных целей
удобны разные карты Земли (на некоторых из них лучше видна форма, на
других проще сравнивать площади, на третьих — прокладывать морские
пути), так и нам будут нужны различные карты гиперболического про-
пространства.
Мы рассмотрим несколько моделей гиперболического пространства. Их
польза состоит не только в помощи нашему воображению. Дело в том, что
являясь одной из простых и основных структур математики, гиперболи-
гиперболическая геометрия часто маскируется, встречаясь в самых разнообразных
вопросах. А маски, которые она выбирает, обычно связаны с одной из этих
моделей.
2.2. Инверсные модели
Одну из моделей гиперболической плоскости — модель Пуанкаре — мы уже
встречали в разделе 1.2. Здесь мы опишем ее многомерное обобщение
и познакомимся с ее ближайшими родственниками: моделью в верхней
2.2. Инверсные модели
57
полуплоскости и моделью в полусфере. Эти модели можно получить друг из
друга с помощью инверсии, поэтому первым делом нужно понять, что такое
инверсия в многомерном пространстве. Определение инверсии практически
совпадает с определением 1.2.1.
Определение 2.2.1 (инверсия в сфере). Пусть S — сфера в евклидо-
евклидовом пространстве Ея. Инверсией is в 5 называется единственное отобра-
отображение проколотого (в центре сферы) пространства в себя, которое
а) оставляет все точки 5 неподвижными,
б) меняет местами внутренность и внешность 5,
в) любую сферу, ортогональную 5, переводит в себя.
Образ is(P) произвольной точки Р можно найти, как и в двумерном
случае: если сфера 5 (с центром в 0) имеет радиус г, то is (P) — это такая
точка Р1 на луче ОР, что ОР ¦ ОР = г2.
Неудобно то, что инверсия никуда не переводит центр сферы. Но это
можно исправить, рассмотрев вместо пространства Е" его одноточечную
компактификацию Е" = Ея U {оо}, гомеоморфную сфере 5я (см. зада-
задачу 1.1.1). Тогда инверсию можно продолжить до гомеоморфизма Ёя на
себя, при этом центр О сферы 5 перейдет в оо, а оо — в точку О.
Упражнение 2.2.2 (прямые и окружности). Покажите, что гомеоморфизм
h: E" U {оо} —> S" можно выбрать так, чтобы он переводил окружности в окруж-
окружности, а прямые— в окружности без точки h(oo). (Указание: рассмотрите стерео-
стереографическую проекцию.)
Ввиду упражнения 2.2.2, прямые и плоскости можно рассматривать как
окружности и сферы, проходящие через оо. При таком соглашении, кото-
которое мы безоговорочно примем в этом разделе, многие свойства инверсии
и инверсных моделей выглядят проще. Если же понадобится рассмотреть
окружности, не являющиеся прямыми, мы будем говорить о собственных
окружностях (и, аналогично, собственных сферах). Вот, например, сжатая
версия предложения 1.2.3:
Предложение 2.2.3 (свойства инверсии). Пусть S — собственная
(п — \)-мерная сфера в Ея. Тогда инверсия is является конформным
отображением, переводящим сферы (любой размерности) в сферы.
Доказательство. Для доказательства конформности заметим, что лю-
любые два вектора с началом в одной точке являются нормалями к двум
(п — 1)-мерным сферам, ортогональным к 5. Поэтому угол между векто-
векторами, как и угол между их образами, равен двугранному углу между этими
сферами.
Второе утверждение следует из двумерного случая (предложение 1.2.3):
для сферы 5' коразмерности 1 достаточно рассмотреть группу поворо-
поворотов вокруг прямой, проходящей через центры сфер S и 5'. Но тогда
58
Глава 2. Гиперболическая геометрия и ее друзья
утверждение верно и для сфер меньшей размерности, поскольку их можно
получить пересечением сфер коразмерности 1. 12-2-31
Упражнение 2.2.4. а) Учитывая, что плоскость — частный случай сферы, как
бы вы определили инверсию относительно плоскости?
б) Что произойдет после двух последовательных инверсий относительно кон-
концентрических сфер? А если сферы являются плоскостями?
в) Покажите, что композиция инверсий относительно пересекающихся евкли-
евклидовых плоскостей является евклидовым поворотом. Как бы вы определили инверс-
инверсный поворот?
Модель Пуанкаре в шаре — это модель гиперболического простран-
пространства, определяемая при помощи единичного шара D" в Е". Назовем гипер-
гиперболическими прямыми дуги окружностей перпендикулярных границе шара.
Кроме того, объявим, что инверсии в (п — 1)-мерных сферах, перпенди-
перпендикулярных dDn, являются изометриями гиперболического пространства, и
назовем их гиперболическими отражениями. Ввиду задачи 2.2.17 было
бы достаточно указать только прямые или только изометрии, но мы не
стремимся к экономии.
Из предложения 2.2.3 можно вывести (и эти рассуждения уже были
приведены в разделе 1.2), что геодезические и изометрии определяют, с
точностью до постоянного множителя, гиперболическую метрику на D",
и что модель Пуанкаре оказывается конформной, т. е. гиперболические
углы в этой модели равны евклидовым углам. Более того, легко показать,
что сферы размерности k, перпендикулярные границе диска, представляют
все вполне геодезические fe-мерные гиперболические плоскости (римано-
во подмногообразие N многообразия М называется вполне геодезическим,
если любая геодезическая из объемлющего многообразия М, касающаяся
подмногообразия N, лежит в этом подмногообразии).
Чтобы явно задать метрику формулой, посмотрим снова, как гипер-
гиперболическая длина вектора, изображенного на рис. 1.11, связана с углом
дугообразной области, определяемой этим вектором. В силу конформно-
конформности, можно считать, что вектор v ортогонален диаметру. А тогда нетрудно
проверить, что в пределе при малых v угол рассматриваемой области в
2/A - г2) раз больше евклидовой длины v, где г — евклидово расстояние
от центра до точки приложения вектора v.
Упражнение 2.2.5. Нарисуйте картинку и убедитесь в справедливости этой
формулы.
Напомним, что при задании метрики мы можем выбрать постоянный
множитель. В разделе 1.2 мы выбрали этот множитель так, чтобы ги-
гиперболическая длина вектора v стремилась к величине угла дугообразной
области, когда обе величины стремятся к нулю. Это приводит к следую-
следующему выражению гиперболической метрики ds2 как функции евклидовой
2.2. Инверсные модели
метрики dx2;
B.2.6)
59
Упражнение 2.2.7 (кривизна модели Пуанкаре), а) Найдите в модели Пу-
Пуанкаре гиперболическое расстояние от центра шара до точки, находящейся от него
на евклидовом расстоянии г.
б) Найдите гиперболическую длину окружности заданного евклидового радиу-
радиуса г.
в) Найдите гауссову кривизну модели Пуанкаре в начале координат (восполь-
(воспользуйтесь рецептом на с. 52). Поскольку гиперболическое пространство однородно,
кривизна всюду одинакова. Тем самым оправдан выбор постоянного множителя в
формуле B.2.6).
Очевидно, что в модели Пуанкаре сильно искажены расстояния: евкли-
евклидова величина объекта вблизи границы, грубо говоря, пропорциональна
евклидовому расстоянию до нее (см. рис. 2.10 и 1.13). Человек, кото-
который движется к границе с постоянной скоростью, будет казаться нам все
меньше и меньше, а его движение — все более и более замедленным. Ра-
Разумеется, он никогда не достигнет границы, поскольку граница находится
на бесконечности, а не внутри пространства.
Тем не менее, границу дЬ" можно описать и в чисто гиперболических
терминах как сферу обзора. Каждый гиперболический луч, выходящий
из р, стремится к некоторой точке дЕУ. Если q — другая точка D", то
каждый луч, начинающийся в q, кажется из точки р дугой большой окруж-
окружности на сфере обзора с центром в р, поскольку р и луч определяют гипер-
гиперболическую два-плоскость. Эта дуга стремится к точке на сфере обзора с
центром в р; таким образом, получилось отображение сферы обзора с цен-
центром в q в сферу обзора с центром в р. Посмотрев из точки q на конечную
точку луча с началом в р, мы получим обратное отображение. Следова-
Следовательно, мы можем отождествить все сферы обзора. Эта конструкция не
зависит от модели, и значит, сопоставляет гиперболическому пространству
Ня сферу на бесконечности S"^1, или абсолют.
Займемся теперь очень полезным отображением, тесно связанным с
инверсией. Пусть S е Ея+| — собственная л-мерная сфера, касающаяся
плоскости П в точке х, а х' — точка сферы S, противоположная точке х.
Тогда стереографической проекцией сферы 5 на плоскость П называет-
называется отображение, переводящее каждую точку х е S в точку q, являющуюся
пересечением прямой рх' с плоскостью П.
Упражнение 2.2.8 (стереографическая проекция). Покажите, что стерео-
стереографическую проекцию можно продолжить до инверсии. (Указание: см. рис. 2.11.)
Из этого следует, что стереографическая проекция является конформным отобра-
отображением, переводящим сферы в сферы.
60
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.10. Замощение гиперболической плоскости в модели Пуанкаре одинако-
одинаковыми треугольниками с углами (п/2, п/3, тс/7)
Рис. 2.11. Стереографическая проекция и инверсия. Стереографическая проекция
совпадает с инверсией относительно сферы удвоенного радиуса.
2.2. Инверсные модели
61
С помощью стереографической проекции модель Пуанкаре можно пре-
превратить в другую модель гиперболического пространства. Расположим шар
Пуанкаре D" на плоскости {х0 — 0} пространства Ея+1 так, чтобы центр
шара лежал в начале координат. При этом граница шара окружена единич-
единичной сферой 5" сЕ"+|. Спроецируем D" из точки (—1, 0, ..., 0), южного
полюса сферы 5я, на верхнюю полусферу (см. рис. 2.12, а). Получается
отображение, обратное стереографической проекции, по крайней мере, с
точностью до растяжения (поскольку плоскость проекции экваториаль-
экваториальная, а не касательная). Таким образом, мы переносим геометрию эквато-
экваториального диска на северную полусферу и получаем модель гиперболи-
гиперболической геометрии в полусфере. Поскольку стереографическая проекция
конформна и переводит окружности в окружности, модель в полусфере
также конформна и ее геодезические являются полуокружностями, орто-
ортогональными экватору S"~l —dD".
Рис. 2.12. Модель в полусфере, (а) Стереографическая проекция из южного полюса
отображает экваториальный диск в северную полусферу. Это отображение преобра-
преобразует метрику диска Пуанкаре в метрику полусферы, геодезическими которой являются
полуокружности, перпендикулярные экватору.
(б) Окружность, проходящая через точки р и q и перпендикулярная диску, перпен-
перпендикулярна также и сфере. Следовательно, проекцию, определенную в п. а, можно
построить и с помощью гиперболических геодезических, перпендикулярных экватори-
экваториальному диску.
Как следует из рис. 2.12,6, окружность, перпендикулярная экватори-
экваториальному диску D" с Dn+i и сфере Sn = dDn+\ пересекает северную полу-
полусферу в точке р, являющейся образом точки q относительно нашей про-
проекции, и поэтому ее можно описать в чисто гиперболических терминах.
Зафиксируем в (п + 1)-мерном пространстве Ня+1 вполне геодезическое
я-мерное пространство Ня и выберем одно из получившихся полупро-
полупространств. Гиперболический луч, выходящий из произвольной точки q е Ня
62
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.13. Геодезические в модели в верхнем полупространстве. В модели в
верхнем полупространстве геодезические оказываются полуокружностями, перпенди-
перпендикулярными граничной плоскости, или перпендикулярными ей полупрямыми.
перпендикулярно к Ы" и лежащий в выбранном полупространстве, опре-
определяет точку на соответствующей сфере обзора. Тем самым получается
отображение Ы" -> S^,, Если считать Ыя экваториальным диском D" в
модели Пуанкаре D"+l пространства Ыя+\ то построенное отображение
совпадает с описанной выше проекцией.
Модель в верхней полусфере с помощью стереографической проек-
проекции можно преобразовать в другую важную модель. Теперь мы будем
проецировать сферу из точки экватора (например, @, ..., О, 1)) на вер-
вертикальное подпространство (например, {х„ = 0}), отождествленное с Е".
Тогда открытая северная полусфера отобразится на верхнее полупро-
полупространство {х0 > 0}, а экватор (т. е. абсолют полусферической модели)
без центра проекции перейдет в граничную плоскость Ея~' = {х0 = 0};
центр проекции отобразится в точку на бесконечности. Другими словами,
в данной модели абсолют представлен в виде одноточечной компактифи-
кации граничной плоскости S"j' = ЕЯ~' U {оо}. Геодезическими являются
полуокружности, перпендикулярные граничной плоскости (рис. 2.13), а
гиперболическими отражениями — инверсии относительно сфер, перпен-
перпендикулярных этой граничной плоскости. Ясно, что и эта модель кон-
конформна.
2.2. Инверсные модели
63
Гиперболическая метрика модели в верхнем полупространстве имеет
особенно простой вид, удобный для разнообразных вычислений. Чтобы
найти ее, можно написать явную формулу для композиции проекций, пе-
переводящей модель Пуанкаре в модель в верхнем полупространстве, после
чего воспользоваться формулой B.2.6); но проще заметить, что эта компо-
композиция конформна, так что можно снова использовать связь длины вектора
с углом соответствующей дугообразной области. Расположив эту область
так, чтобы одна из ее вершин была на бесконечности, превратим ее во
внутренность конуса. Теперь легко сравнить угол в вершине конуса с ев-
евклидовой длиной образующего этот конус вектора. В пределе, когда обе
величины очень малы, евклидова длина вектора в х0 раз больше величины
угла, где х0 — евклидово расстояние от начала вектора до граничной плос-
плоскости. Другими словами, гиперболическая метрика ds2 выражается через
евклидову метрику dx2 по формуле
B.2.9)
ds2 = \ dx2.
4
Поэтому евклидов размер фиксированного гиперболического объекта
пропорционален расстоянию от этого объекта до граничной плоско-
плоскости Е"~1. На рис. 2.14 показано, как выглядит замощение плоскости
треугольниками (ср. с рис. 2.10) в модели в верхней полуплоскости.
Упражнение 2.2.10 (евклидовы подобия как гиперболические изоме-
трии). Подобием пространства Ея называется преобразование, увеличивающее
все расстояния в одииаковое (ненулевое) количество раз. Любое подобие является
композицией элемента О(п) (начало координат в Е" мы выбираем произвольно),
растяжения или сжатия, и параллельного переноса.
Любое подобие пространства Ея~' можно единственным образом продолжить
до подобия Ея, сохраняющего верхнее полупространство. Покажите, что такое по-
подобие является гиперболической изометрией (представьте его в виде композиции
отражений).
Наглядность действия этой важной подгруппы изометрий гиперболического
пространства И" — одно из часто используемых достоинств модели в верхнем
полупространстве.
Упражнение 2.2.11. Мы уже знаем, что гиперболическое пространство одно-
однородно и изотропно. Явные формулы проще всего выглядят в модели в верхнем
полупространстве.
а) Найдите гиперболическое отражение, которое переводит одну заданную точ-
точку верхнего полупространства в другую.
б) Пусть О(п) — группа изометрий касательного пространства к И" в фиксиро-
фиксированной точке р. Покажите, что любой элемент О(п) можно представить в виде ком-
композиции гиперболических отражений..(Указание: докажите по индукции, что О(п)
порождается отражениями и что любое отражение из О(п) является отражением
относительно сферы, ортогональной абсолюту в модели в верхнем полупростран-
полупространстве.)
64
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.14. Гиперболическое замощение треугольниками с углами (§, §, f).
Другой вид разбиения гиперболического мира (в модели в верхней полуплоскости)
на одинаковые части.
в) Покажите, что отражения порождают всю группу изометрий простран-
пространства ВР. (Указание: изометрия определяется своей производной в неподвижной
точке.)
Горизонтальная евклидова плоскость {х0 = с}, где с > О, не является
гиперболической плоскостью: с настоящей гиперболической плоскостью —
евклидовой полусферой радиуса с — она пересекается всего в одной точ-
точке, и лежит с одной стороны от нее. (Кроме того, можно заметить, что
при сдвиге горизонтальной поверхности вверх вдоль перпендикулярных
ей геодезических гиперболическая метрика сжимается, а поверхность ис-
искривляется вверх.) Эти горизонтальные поверхности являются примерами
орисфер (или орициклов в двумерном случае). Любую орисферу можно
перевести в любую параллельную ей орисферу с помощью (евклидова)
растяжения с центром в точке абсолюта — это характеристическое свой-
свойство орисфер. Другое характеристическое свойство состоит в том, что ори-
орисфера перпендикулярна всем плоскостям, проходящим через некоторую
точку абсолюта; будем говорить, что орисфера касается 5^"' в этой точке.
Упражнение 2.2.12. Покажите, что эти два свойства эквивалентны. Выведите
из них, что орисферы в верхнем полупространстве—это или горизонтальные евкли-
2.2. Инверсные модели
65
довы плоскости, или евклидовы сферы, касающиеся абсолюта. Опишите орисферы
в модели диска Пуанкаре.
Внутренняя геометрия орисферы — евклидова. Проще всего это увидеть,
выбрав орисферу {х0 = с} и посмотрев на вид гиперболической метрики
(уравнение B.2.9)). Из этого же уравнения следует, что любую евклидову
изометрию орисферы можно продолжить до гиперболической изометрий
пространства Ы", сохраняющей нашу орисферу и все орисферы, парал-
параллельные ей.
Область {х0 ^ с} называется оришаром. Если орисфера представлена
евклидовой сферой, касающейся абсолюта, то соответствующий оришар —
это евклидов шар, ограниченный данной сферой.
С помощью орициклов можно установить связь между гиперболической
плоскостью и псевдосферой (рис. 2.4).
Упражнение 2.2.13 (псевдосфера — локально гиперболическая поверх-
поверхность). Рассмотрим отображение, накручивающее область у ~? 1 на псевдосферу,
переводя орициклы у — С в меридианы, а вертикальные геодезические х = С в
образующие (трактрисы). Покажите, что если отображение имеет период 2it по
оси х, то это локальная изометрия. (Указание: при удалении орицикла от прямой
у = 1 длина его дуги, ограниченной фиксированными вертикальными прямыми,
уменьшается экспоненциально. С той же скоростью уменьшается и длина дуги
меридиана псевдосферы, удаляющегося от ее края.)
Именно на орициклах основаны бумажные модели из упражнения 2.1.3.
При стремлении толщины колец к нулю метрика модели стремится к гипер-
гиперболической, а окружности становятся орициклами. Это показывает изо-
изотропность метрики псевдосферы — факт, который мы раньше не могли
объяснить.
Модель в верхнем полупространстве можно использовать для изучения
группы изометрий гиперболического пространства. Рассмотрим отражение
в Ы", заданное инверсией относительно (п — 1)-мерной сферы S, перпенди-
перпендикулярной к Ея~'. Ограничение этой инверсии на абсолют S"j' = Ея~' U оо
является инверсией относительно (п — 2)-мерной сферы 5п5^', при-
причем так можно получить любую инверсию сферы 5^"'. Преобразования
сферы S"^', являющиеся композициями инверсий, называются преобра-
преобразованиями Мёбиуса, а группа таких преобразований называется груп-
группой Мёбиуса и обозначается М6Ьд_ь Поскольку группа гиперболических
изометрий порождается отражениями (см. упражнение 2.2.11, в), группа
изометрий пространства Ня изоморфна группе Мебиуса МбЬ„_,.
Задача 2.2.14 (группа Мёбиуса). Для знакомства с группой Мёбиуса дока-
докажите следующие утверждения.
а) Подгруппа группы Мёбиуса, сохраняющая оо, изоморфна группе евклидовых
подобий.
66
Глава 2. Гиперболическая геометрия и ее друзья
б) Подгруппа группы МбЬ„, оставляющая на месте (я — 1)-мерную сферу и
точку, не лежащую на ней, изоморфна группе О(я).
в) При п > 1 группа Мёбиуса состоит из всех гомеоморфизмов сферы SJo,
переводящих (п — 1)-мерные сферы в (я — 1)-мерные.
г) Преобразование Мёбиуса, которое переводит сферу S в сферу R, сопрягает
инверсии is и //?.
д) Подгруппа группы Мёбиуса, переводящая /г-мерную сферу в себя, изоморф-
изоморфна группе Mob* х О(п — k).
е) Мёбиусова группа имеет подгруппу, изоморфную О(п + 1).
Чему равна размерность группы Мёбиуса?
Искусное использование преобразований Мёбиуса значительно упрощает
решение некоторых геометрических задач, в которых участвуют сферы.
Упражнение 2.2.15 (лоризм Штейнера). На плоскости даны две непересе-
непересекающиеся окружности Л и В и цепочка окружностей Хо, Х\, ..., Хп-\ таких, что Xi
касается окружностей А, В и Xi+i mod л- Окружности пересекаются только в точках
касания.
Покажите, что если окружности Хо, ..., Хп-\ стереть и нарисовать произволь-
произвольную окружность Yo, касающуюся Л и В, то аналогичная цепочка окружностей,
построенная по Л, В и Уо, замкнется ровно через п шагов.
Упражнение 2.2.16 (касающиеся сферы). Пусть Л, В и С — попарно касаю-
касающиеся двумерные сферы, а Хо — четвертая сфера, касающаяся А, В и С. Постройте
цепочку сфер, начинающуюся с Хо, и такую, что Xi касается сфер А, В, С, Xt-i
и Xi+i. Покажите, что цепочка замкнется на шестой сфере.
Задача 2.2.17 (экономные описания гиперболической геометрии). До сих
пор, обсуждая гиперболическую геометрию, мы не пытались описать ее С помощью
минимального числа структурных свойств. Вот несколько шагов в этом направле-
направлении.
а) Покажите, что гиперболические прямые можно описать в терминах метрики
как кривые, минимизирующие расстояние между двумя точками. (Указание: ис-
используйте модель в верхнем полупространстве; сведите задачу к случаю, когда обе
точки лежат на одной вертикальной прямой.)
б) Покажите, что гиперболические прямые можно описать непосредственно в
терминах группы изометрий как множества неподвижных точек.
в) Покажите, что диффеоморфизм верхнего полупространства в себя, пере-
переводящий гиперболические прямые в гиперболические прямые, является гипербо-
гиперболической изометрией. (В евклидовом случае это не так: аффинные отображения
переводят прямые в прямые.)
г) Покажите, что для того, чтобы задать гиперболическую геометрию, доста-
достаточно любого из следующих трех объектов: множества прямых, группы изометрий
или метрики, определенной с точностью до постоянного множителя.
д)* Покажите, что задания меры углов также достаточно для определения ги-
гиперболической геометрии.
2.3. Модель иа гиперболоиде и модель Клейна
67
2.3. Модель на гиперболоиде и модель Клейна
В евклидовом пространстве сфера радиуса г имеет постоянную кривиз-
кривизну 1/г2. Можно предположить, что поскольку гиперболическое простран-
пространство имеет постоянную кривизну — 1, оно должно быть сферой радиуса
Этому, казалось бы, невозможному условию можно придать разумный
смысл. Посмотрим, насколько далеко нас может увести рассуждение по
аналогии. Чтобы получить /г-мерную сферу, мы рассматривали *положи-
тельно определенную квадратичную форму Q+ в Ел+|, заданную формулой
Q+(x) = х\ + х\ + ... + х\, где х - (х0, ..., хп). В пространстве Ея+1 она
определяет евклидову метрику dx2 = dx% + dx\ + ... + dx2n, превращая это
пространство в евклидово пространство Ея+|. Сужая метрику на единич-
единичную сферу 5 = {Q+ = 1}, мы получаем риманову метрику постоянной по-
положительной кривизны, равной 1. Изометрий сферы 5 являются ограниче-
ограничениями линейных преобразований пространства Ел+1, сохраняющих Q+; эта
группа ортогональных преобразований обозначается через О(/г +1).
Теперь мы начнем с неопределенной метрики
B.3.1) ds2 = —dx% + dx\ +... + dx2n
в пространстве Ея+|, соответствующей квадратичной форме Q~(x) =
= -х\ + х2 + ... + х\. Пространство Ея+|, снабженное такой метрикой,
обычно называют пространством Лоренца и обозначают Е"-'. При /г = 3
это пространство специальной теории относительности; правда, физики
обычно меняют знак у формы Q~. В этой интерпретации вертикальное
направление х0 представляет время, а горизонтальные направления —
пространство. Вектор х называется пространственно-подобным, вре-
мени-подобным и свето-подобным, если значение Q~ {x) соответственно
положительно, отрицательно и равно нулю. По аналогии с евклидовым
случаем, длина вектора х равна VQ-(x), так что свето-подобные векторы
имеют нулевую длину, а времени-подобные — мнимую длину (выберем
ветвь корня так, чтобы получались числа из /Е+).
Сфера радиуса / с центром в начале координат пространства ЕяЛ —
это гиперболоид Н = {Q- = -1}. Ограничение на этот гиперболоид не-
неопределенной метрики ds2 (задаваемой формулой B.3.1)) является самой
настоящей положительно определенной римановой метрикой: легко про-
проверить, что любой касательный к гиперболоиду вектор имеет вещественную
длину. Топологически Н представляет собой объединение двух открытых
дисков.
Как и в случае сферы, превращенной в примере 1.4.3 в эллиптическое
пространство, после отождествления противоположных точек гиперболо-
гиперболоида получится подмножество проективного пространства ЕР. В отличие
68
Глава 2. Гиперболическая геометрия и ее друзья
от сферического случая, противоположные точки лежат в разных связных
компонентах гиперболоида, и подмножество в RP" может быть смодели-
смоделировано на любой из компонент. Возьмем, например, верхнюю половину
гиперболоида Н+, где х0 > 0. Мы получим модель гиперболического про-
пространства на гиперболоиде.
То же самое подмножество RP" можно смоделировать с помощью неод-
неоднородных координат, в которых точка {хи ..., х„) & R" изображает прямую
с параметрическим уравнением (t, x^t, ..., xnt). Тогда Н отображается на
единичный диск, и получается проективная модель, или модель Клейна.
Обратите внимание, что несмотря на то, что диск Клейна можно считать
вложенным в E"J (см. рис. 2.15), его метрика — это не индуцированная
метрика, а образ метрики гиперболоида при центральной проекции.
Рис. 2.15. Модель на гиперболоиде и модель Клейна. Точка р = {х0, х\, ..., хп)
гиперболоида отображается в точку (x\/xq, ..., x,,/xq) пространства К", изображен-.
ную на рисунке в виде горизонтальной плоскости {xq = 1}- При этом метрика гипер-
гиперболоида переносится на единичный диск D" в К", что дает проективную модель (или
модель Клейна) гиперболического пространства.
Как понять, что это и в самом деле модели /г-мерного гиперболического
пространства? Лучший способ состоит не в прямом вычислении, а, как и
в случае с инверсными моделями, в изучении прямых и изометрий.
С помощью скалярного произведения (х, у) = —хоуо + xty{ + ... + х„у„
в Е"'1 можно ввести понятие ортогональности. Ортогональным дополне-
дополнением ненулевого вектора х называется /г-мерное подпространство х1- =
= {у е Е"'1: (х, у) = 0}, которое содержит х тогда и только тогда, когда
2.3. Модель иа гиперболоиде и модель Клейиа
69
Q~(x) = 0. Ортогональное дополнение к подпространству — это пересече-
пересечение ортогональных дополнений к векторам этого подпространства.
Упражнение 2.3.2 (описание касательных векторов). Касательная плос-
плоскость в точке х гиперболоида Н совпадает с пространством -ех.
Рассмотрим теперь ортогональные преобразования, т. е. линейные пре-
преобразования пространства E"+I, сохраняющие форму Q~. Так же, как
группа изометрий сферы 5 совпадает с группой О(/г + 1) ортогональ-
ортогональных преобразований пространства Ея+|, группа изометрий гиперболои-
гиперболоида Н совпадает с группой О(/г, 1) ортогональных преобразований про-
пространства Е"-1.
Упражнение 2.3.3. Доказательство этого факта практически такое же, как и
в случае сферы. Ясно, что ограничение ортогонального преобразования Е4*1 на Н
является изометрией гиперболоида (нетривиальной, если преобразование нетриви-
нетривиально). Таким способом можно получить любую изометрию гиперболоида Н, т. е.
группа О(я, 1) действует на гиперболоиде траизитивно и изотропно.
а) Найдите элемент группы О(п, 1), меняющий местами точки р и q гипербо-
гиперболоида Н. (Указание: рассмотрите ортогональное дополнение вектора р — q.)
б) Покажите, что любая изометрия касательного пространства в точке р ? Н
индуцируется элементом группы О(п, 1). (Указание: вследствие пункта а можно
считать, что р — это «северный полюс», т. е. точка A,0,..., 0).)
Упражнение 2.3.4 (преобразования Лоренца). Элемент группы О (л, ^.пе-
^.переводящий каждую компоненту гиперболоида в себя, называется преобразовани-
преобразованием Лоренца. Покажите, что группа преобразований Лоренца (или группа Ло-
Лоренца) является подгруппой индекса два в группе О(п, 1) и совпадает с группой
изометрий пространства Н+.
Это открывает путь к описанию геодезических в модели на гиперболоиде
и в модели Клейна. Пусть р е Н+ — точка, a v — ненулевой касательный
вектор к #+ в точке р. Пусть Я—двумерная плоскость, содержащая начало
координат, точку р и вектор v. Тогда геодезическая, проходящая через р
в направлении и, совпадает с пересечением L = Н+ ПР (см. рис. 2.16). То
же самое получится, если гиперболоид Н+ заменить на диск Клейна К.
Для доказательства рассмотрим преобразование Лоренца, неподвижное
на Я и равное — 1 на ортогональном дополнении к Р. Соответствующая изо-
изометрия Н+ или К оставляет неподвижными ровно те точки, которые лежат
на L. В силу единственности геодезическая, проходящая через р в напра-
направлении v, неподвижна относительно этой изометрий, так что она должна
содержаться в L. Поскольку L — связная кривая, она и есть геодезическая.
В модели на гиперболоиде пересечение L является ветвью гипербо-
гиперболы, асимптоты которой — лучи, лежащие на световом конусе {Q~ = 0,
х0 > 0}. Это название пришло из теории относительности, где световой
конус — это объединение всех лучей света, выходящих в нулевой момент
70
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.16. Геодезические в модели на гиперболоиде и модели Клейиа. В модели
на гиперболоиде геодезическими являются пересечения гиперболоида с двумерными
плоскостями, проходящими через начало координат. В проективной модели — это от-
отрезки прямых.
времени из начала координат. Лучи светового конуса соответствуют бес-
бесконечно удаленным точкам этой модели.
Упражнение 2.3.5 (параметризация геодезических). Покажите, что если
длина вектора v равна 1, то точка р ch t + v sh t движется по L с единичной скоро-
скоростью. Как выглядит аналогичная формула для сферы в евклидовом пространстве?
В модели Клейна пересечение L является отрезком прямой, так что
модель корректна с точки зрения проективности: геодезические изобража-
изображаются прямыми. Поэтому модель Клейна очень полезна для понимания вза-
взаимного расположения прямых и плоскостей. Бесконечно удаленная сфера
совпадает с единичной сферой S?j' — образом светового конуса в ЮР".
В модели Клейна углы сильно искажены, однако (и это весьма удобно) их
можно точно вычислить в модели на гиперболоиде по тем же формулам,
что и в евклидовом пространстве. Нужно только не забывать пользоваться
метрикой Лоренца (см. формулу B.3.1)) вместо евклидовой.
Построим теперь отображение из модели в полусфере (см. раздел 2.2)
в модель Клейна, переводящее геодезические в геодезические. Поскольку.
для определения гиперболической геометрии достаточно задания множе-
множества геодезических (задача 2.2.17), мы получим, что К, а следовательно
и Н+, и в самом деле являются моделями Ы". Расположим К на экватори-
экваториальном диске единичной сферы в Ея+| и спроектируем ортогонально верх-
верхнюю полусферу на К. Это и есть искомое отображение. Действительно,
2.3. Модель на гиперболоиде и модель Клейна
71
Рис. 2.17. От полусферы к модели Клейна. С помощью (евклидовой) ортогональной
проекции на экваториальный диск можно перейти от модели в полусфере к модели
Клейиа. Сравните с рис. 2.12, а.
геодезические в полусфере, т. е. перпендикулярные экватору полуокруж-
полуокружности, спроектируются в отрезки прямых (см. рис. 2.17).
Те же конструкции (но с другой проекцией) мы использовали для пере-
перехода от диска Пуанкаре к модели в полусфере. Рассмотрим композицию
проекций из диска Пуанкаре в полусферу и «обратно», в диск Клейна.
В результате мы получили удивительное преобразование единичного диска
в себя, сохраняющее все радиусы диска, но переводящее все окружности,
перпендикулярные единичной сфере в отрезки.
Упражнение 2.3.6. Найдите формулу для перехода из модели Пуанкаре в про-
проективную модель (используйте полярные координаты (г, 6), где 0 < г < 1,8 е S").
Найдите формулу для обратного преобразования.
Упражнение 2.3.7. Стереографическая проекция отображает модель Пуанкаре
на модель в верхней полусфере (см. рис. 2.12). Покажите, что если эту проекцию
продолжить до проекции на Н+, то получится отображение этих моделей в модель
на гиперболоиде.
Как часть проективного пространства ЖР", модель Клейна имеет есте-
естественную интерпретацию в терминах гиперболической перспективы. На
самом деле, эта модель вложена в проективную сферу обзора — сферу
обзора, противоположные точки которой отождествлены. Представьте, что
вы парите в Ы"+| над плоскостью Ы". Поскольку все лучи света, идущие
к вам от геодезической на Ы", лежат в одной гиперболической плоскости,
касательные к ним векторы лежат на большой окружности вашей сферы
обзора; так что геодезические кажутся вам прямыми линиями. Итак, ги-
гиперболическая плоскость Ы" выглядит как модель Клейна! Сфера на бес-
бесконечности пространства Н" будет казаться вам настоящей сферой. В от-
отличие от евклидова случая, видимый радиус гиперболической плоскости в
72
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.18. Вид гиперболической плоскости с птичьего полета. Здесь изобра-
изображено то же разбиение гиперболической плоскости, что и на рис. 2.10 и 2.14, но в
проективной модели. Именно так выглядит это разбиение в перспективе трехмерного
гиперболического пространства. Посмотрите, как выглядит плоскость около ее гори-
горизонта; почувствуйте, как плоскость уходит от вас и как быстро (экспоненциально)
растет ее площадь с удалением от центра.
гиперболическом пространстве всегда строго меньше к, если только ваш
глаз не находится в этой плоскости. Образ плоскости уменьшается, когда
вы от нее удаляетесь, и увеличивается, когда вы приближаетесь к ней (см.
рис. 2.18).
Потренировавшись, можно научиться видеть объекты так, как будто и в
самом деле живешь в Н3. Чтобы все увидеть правильно, расположитесь ли-
либо в центре шара Пуанкаре, либо в центре модели Клейна. Если смотреть
из этой точки, то все предметы правильно расположатся на сфере обзора.
Наше евклидово пространственное зрение вводит нас в заблуждение: мы
2.3. Модель на гиперболоиде и модель Клейиа
73
оцениваем расстояние до предметов в модели Клейна так, как если бы эта
модель являлась внутренностью шара конечного радиуса. Но стоит нам
начать приближаться или удаляться от предмета, как мы тут же увидим
разницу — экспоненциальное увеличение или уменьшение его размеров с
расстоянием до него.
Рис. 2.19. Прямоугольный гиперболический додекаэдр в гиперболической пер-
перспективе. Заметьте, что ребра выглядят прямыми. Из фильма «Не узел» [GM91].
Это хорошо видно на рис. 2.19 и на обложке этой книги; оба рисунка
взяты из финальной сцены фильма «Не узел» [GM91], запрограммирован-
запрограммированного Чарли Гунном. «Не узел», созданный в рамках проекта «Геометриче-
«Геометрический суперкомпьютер» (позже из него возник геометрический центр), был
первой попыткой передать ощущение жизни и движения в гиперболическом
пространстве. На обложке показано замощение Н3 одинаковыми прямо-
прямоугольными додекаэдрами. Обратите внимание, что у многих, додекаэдров
одна грань находится впереди всех других. Это следствие быстрого умень-
уменьшения углового размера образа при увеличении расстояния. У остальных
додекаэдров бросается в глаза либо ближайшее к нам ребро, либо бли-
ближайшая к нам вершина. Каждый пятиугольник является частью замощения
плоскости прямоугольным'и пятиугольниками. Заметьте, как эти плоскости
уходят от вас вблизи горизонта. Правильное гиперболическое освещение
помогает передать этот эффект. Отражение света также помогает отли-
отличить вид гиперболического пространства от вида внутренности евклидового
шара.
74
Глава 2. Гиперболическая геометрия и ее друзья
2.3. Модель иа гиперболоиде и модель Клейна
75
Рис. 2.20. Двойственность гиперплоскостей и точек. Гиперплоскость, двойственная
точке х вне Н", пересекает W.
(а) Прямые, проходящие через х и пересекающие *х, перпендикулярны к *х, а пря-
прямые, перпендикулярные *х, проходят через х (доказательство см. в тексте).
(б) В пространстве RP" точка х является вершиной конуса, касающегося сферы S?T
по (п — 2)-мериой сфере (пересечению лгх с S1^1).
Упражнение 2.3.8. Как можно издалека определить, под каким углом пересе-
пересекаются две плоскости в Н3 ?
Теперь у нас есть геометрическая интерпретация точек пространства
RP", лежащих внутри единичного шара или на его границе. Но как быть
с точками, лежащими снаружи? Если х е КР" — такая точка, а X — соот-
соответствующая ей прямая в Е"-1, то Q~ положительно определена на X, т. е.
не определена на ортогональном дополнении Xх. Поэтому соответствую-
соответствующая гиперплоскость jcx с RP" пересекает гиперболическое пространство.
Гиперплоскость jcx называется двойственной к точке х. Благодаря про-
проективной двойственности любая прямая, проходящая через х и пересека-
пересекающая хх, перпендикулярна гиперплоскости Xх. Проще всего это увидеть
на гиперболоиде (см. рис. 2.20, а): если вектор р е Xх П Н+ представляет
точку из jcx и v e Xх — любой касательный вектор в точке р, представля-
представляющий направление в jcx, то мы хотим показать, что v перпендикулярен
касательному вектору w, который представляет направление от р к X. Но
w лежит в плоскости, проходящей через р и X, и ввиду упражнения 2.3.2,
вектор w ортогонален вектору р. Поскольку р ортогонален X, это означает,
что w на самом деле параллелен X, а следовательно, ортогонален вектору v.
Упражнение 2.3.9. а) Докажите утверждение, содержащееся в комментарии
к рис. 2.20, б.
б) Какой объект двойственен точке в Н"? А точке х € S^T1 ?
в) Что двойственно /г-мерной плоскости?
г) Покажите, что объект, двойственный к /г-мерной плоскости Р, является пе-
пересечением объектов, двойственных к точкам из Р. Напишите двойственное утвер-
утверждение.
Особенно просто все это выглядит в двумерном случае. В ЕР2 любые
две прямые где-то пересекаются. Если пересечение лежит внутри Н2, то
прямые пересекаются в обычном (с точки зрения гиперболического на-
наблюдателя) смысле. Если точка пересечения лежит на SJ^, то с точки
зрения наблюдателя прямые сходятся на сфере обзора и называются па-
параллельными. В остальных случаях прямые называются расходящимися;
они имеют общую перпендикулярную прямую в Н2, двойственную точке их
пересечения вне S1^.
Упражнение 2.3.10 (параллельность в гиперболическом пространстве).
Распространите понятия параллельных и расходящихся прямых на Л-мерные плос-
плоскости в Н". Покажите, что расходящиеся гиперплоскости имеют единственный
общий перпендикуляр. В предложении 2.5.3 содержится похожее утверждение о
прямых в Н3.
Задача 2.3.11 (проективные преобразования гиперболического простран-
пространства). Проективным преобразованием называется диффеоморфизм КР", инду-
индуцированный обратимым линейным преобразованием пространства R"+l. Ясно, что
любое ортогональное преобразование пространства Е"'1 индуцирует проективное
преобразование, переводящее S1^1 в себя. Покажите, что верно и обратное.
Отсюда следует, что любое проективное преобразование КРЯ, сохраняющее Ня,
является изометрией. Отметим контраст с евклидовым случаем, где есть много
проективных преобразований, не являющихся изометрнями (а именно, аффинные
преобразования). Вспомните также задачу 2.2.17.
Задача 2.3.12 (формы евклидовых многоугольников). Углы правильного
пятиугольника иа евклидовой плоскости равны Зл/б, но не любой пятиугольник с
такими углами является правильным. Рассмотрим пространство (возможно, са-
самопересекающихся) пятиугольников, все углы которых равны 3it/5, а стороны
параллельны соответствующим сторонам модельного правильного пятиугольника.
Параметризуем это пространство с помощью длин сторон s\, ..., 55 (длины бе-
берутся со знаком).
а) Покажите, что 5; удовлетворяют двум линейным уравнениям, задающим в R5
трехмерное линейное подпространство V.
б) Покажите, что площадь пятиугольника является квадратичной формой на V,
превращающей V в I?'1. Как определить площадь самопересекающегося пяти-
пятиугольника?
в) Опишите модель гиперболической плоскости в терминах подмножества про-
пространства V, состоящего из пятиугольников единичной площади. Сколько компо-
компонент связности имеет получениная модель?
г) Покажите, что пространство несамопересекающихся пятиугольников еди-
единичной площади является прямоугольным пятиугольником на гиперболической
плоскости.
76
Глава 2. Гиперболическая геометрия и ее друзья
д) На множестве пятиугольников можно ввести операцию «бабочка» (butterfly
operation), сохраняющую площадь пятиугольника. При этом преобразовании дли-
длина s одной из сторон пятиугольника заменяется на —s, а две соседние с ней стороны
удлиняются или укорачиваются так, чтобы сохранить площадь. Как выглядит это
преобразование в гиперболическом пространстве V?
е) Дан самопересекающийся пятиугольник из V. В каких случаях его можно
превратить в несамопересекающийся пятиугольник, пользуясь операциями «ба-
«бабочка»?
ж) Обобщите все это на многомерный случай. Рассмотрите пространство V
несамопересекающихся евклидовых (п + 3)-угольников единичной площади, сто-
стороны которых параллельны и сонаправлены сторонам фиксированного выпуклого
модельного многоугольника. Покажите, что V параметризуется точками выпуклого
многогранника в и-мерном гиперболическом пространстве. Какой трехмерный ги-
гиперболический миогогранник получится, если в качестве исходного многоугольника
выбрать правильный шестиугольник?
Задача 2.3.13 (модель на внутренности параболоида). Применив любое
проективное преобразование модели Клейна, можно получить другие проективные
модели гиперболического пространства.
а) Напишите явную форму проективного преобразования, отображающего еди-
единичную сферу в К" на параболоид хя = х\ + ¦ • ¦ + х2я_\. Применив это преобра-
преобразование к модели Клейна К, получим модель гиперболического пространства иа
внутренности параболоида.
б) Эта модель так же связана с моделью Клейна, как модель в верхнем полу-
полупространстве — с моделью Пуанкаре. Точнее, модель в верхнем полупространстве
выделяет точку сферы на бесконечности гиперболического пространства, и группа
гиперболических изометрий, сохраняющих эту точку, совпадает с группой евклидо-
евклидовых подобий, сохраняющих верхнее полупространство. Как эта группа проявляется
в модели на внутренности параболоида?
в) Покажите, что ортогональная проекция параболоида хп = х\ + ... + x^_, на
гиперплоскость хП = 0 пространства Е" индуцирует изоморфизм группы аффинных
отображений, сохраняющих параболоид, и группы подобий, сохраняющих верхнее
полупространство.
Задача 2.3.14. Мы видели, что преобразования Лоренца соответствуют изоме-
триям пространства Н3, но не обсуждали физическую интерпретацию этого про-
пространства. Каким образом люди могли бы увидеть или обнаружить с помощью
опыта пространство Н3 в релятивистской Вселенной?
2.4. Некоторые вычисления в гиперболической
геометрии
Изучая математику, мы, в конечном счете, хотим добиться качественного
понимания предмета. Но точные вычисления — эта черновая математи-
математическая работа — также важны. Это и способ достижения нашей цели, и
2.4. Некоторые вычисления в гш , юолической геометрии
77
проверка правильности нашего понимания. Изученные в двух последних
разделах модели гиперболического пространства дают хорошее предста-
представление обо всех гиперболических объектах; но все же в каждой из них не
видна вся симметричность гиперболического пространства. С другой сто-
стороны, образные представления могут оказать неоценимую помощь нашей
интуиции и со временем (и опытом) стать совершенно ясными и правиль-
правильными. Но все-таки по природе своей они неточны.
Сблизить два этих подхода можно с помощью формул гиперболической
геометрии, посмотрев на гиперболическое пространство глазами землемера
или строителя. Работая с формулами, мы продвигаемся медленно, но в
результате получаем точную, без малейших искажений, картину. В этом
разделе мы выведем тригонометрические формулы н вычислим площади
фигур на гиперболической плоскости.
В разделе 2.3 мы уже отмечали некоторые сходства и различия про-
пространства Лоренца Е2-1 и евклидова пространства Е3, а также сходства и
различия сферической и гиперболической геометрий. Сферическую триго-
тригонометрию нам зачастую предлагают в виде набора запутанных формул, на
самом деле эквивалентных нескольким утверждениям о скалярных произ-
произведениях единичных векторов в трехмерном пространстве и легко выводи-
выводимых из формулы для обратной матрицы 3x3.
Начнем с тройки (vu v2, v3) единичных векторов, лежащих в 52 е Е3.
Если эти векторы линейно независимы, т. е. не лежат на окружности
большого круга (сферической прямой), то они образуют сферический
треугольник — достаточно соединить и,- и V/ сферическим отрезком дли-
длины d(vj, vj) = Qi/ < тс. Двойственным базисом к (vlt v2, v3) называется
тройка (w,, w2, wz) (не обязательно единичных) векторов, определяемых
условиями Vj ¦ wt = 1, Vj ¦ Wj = 0 при / ф у; /, у = 1, 2, 3. Составив ма-
матрицы V и W из столбцов Vj и Wi соответственно, эти условия можно
переписать в виде W V = 1.
Геометрически Wi имеет направление вектора, нормального к плоскости,
содержащей v, и vk, если /, у, k различны. Поэтому угол <р,- при верши-
вершине Vj сферического треугольника V]V2v3 равен тс — Z(w/, wk), поскольку
угол между плоскостями дополняет угол между их внешними нормалями
до развернутого угла (см. рис. 2.21).
Чтобы учесть все соотношения между углами, рассмотрим матрицы
VV и WW скалярных произведений и заметим, что эти матрицы взаимно
обратны друг другу и что
V'V =
C12 С\з
С\1 1 С23
С13 С23 1
где с I/ = Vj-Vj = cos0,7.
78
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.21. К доказательству сферической теоремы косинусов
Поскольку W'W = {V'V)~\ то, записав обратную матрицу через алге-
алгебраические дополнения, получим
B.4.1)
W'W =
1
( 1 — C23 CI3C23 — C\2 C\2C2Z ~ Cl3^
deUV'V) I Cl3C23 ~ Cl2 ' ~ C'3 Cl2Cl31C23
V.C12C23 — C13 C12C13 — C23
Отсюда легко найти, например, что
• ДО2 _ COs6i2 — COS6i3 COS623
B.4.2) cos фз = — cos Z(wi, w2) = —-,—n—г — :—я—^rs
v ' YJ v ; |ayi||ay2| sin8i3Sine23
или, в более привычных обозначениях,
B.4.3) cos с = cos a cos b + sin a sin b cos C.
где Л, S, С—углы при вершинах vlt v2, v3 соответственно; a, b, с —про-
—противолежащие стороны.
Это соотношение называется сферической теоремой косинусов. По-
Поменяв местами (иь v2, v3) и (w\, w2, w3), получим двойственную сфе-
сферическую теорему косинусов (см. рис. 2.22). Теперь и; — не вершины,
а единичные векторы, ортогональные плоскостям, содержащим стороны.
При этом ср* = тс — Z(vh Vj), где /,у, k — различны, а 0,7 = Z(wh wj). Отсюда
следует, например, формула
2) =
COSCD2 + COSC03
— —
2.4. Некоторые вычисления в гиперболической геометрии
79
ИЛИ
Рис. 2.22. Двойственная сферическая теорема косинусов
cos С = — cos A cos В + sin A sin В cos с.
Упражнение 2.4.4. Предельный переход для очень маленьких треугольников
приводит к формулам евклидовой тригонометрии. Что можно получить из раз-
разложения в ряд сферической теоремы косинусов, если а, b-к с очень малы? Что
получится из двойственной теоремы косинусов?
Вернемся теперь к пространству Лоренца Е2-1. Здесь все почти так же,
но несколько сложнее из-за того, что ненулевой вектор может иметь ну-.
левую или мнимую длину. Чтобы уменьшить количество случаев, будем
рассматривать только векторы ненулевой длины. Будем считать, что они
нормированы так, что их длина равна 1 или /, причем в последнем случае
Хо > 0. Вспомним (см. раздел 2.3), что векторы хе Е2'1 длины i являются
точками гиперболоида Н+ — модели гиперболической плоскости, аналогич-
аналогично тому, как единичные векторы в Е3 являются точками сферы. Вектор х
длины 1 лежит снаружи от гиперболической плоскости и определяет на
гиперболической плоскости двойственную прямую хх.
Пусть теперь хну — различные нормированные векторы. Ограничение
квадратичной формы Q~ на плоскость, порожденную векторами х и у,
имеет сигнатуру A, 1), A, 0) или B, 0); в этих случаях плоскость соответ-
соответственно пересекает гиперболоид, касается конуса «на бесконечности» или
ни с чем из них не пересекается (см. рис. 2.23). В каждом из случаев нуж-
нужно понять, что означает величина х ¦ у, равная в евклидовом пространстве
косинусу угла между векторами (естественно, скалярное произведение бе-
берется относительно формы Q~). Это можно сделать в любой размерности.
80
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.23. Интерпретация скалярного произведения для различного расположе-
расположения точек. На рисунке (в проективной модели) представлены различные случаи из
предложения 2.4.5.
Предложение 2.4.5 (геометрический смысл скалярного произведе-
произведения). Пусть х и у — нормированные векторы ненулевой длины в ЕлЛ.
Тогда верно одно из следующих утверждений:
а) х, у б Н+ — векторы длины i и х ¦ у = — ch d(x, у);
б) х € Ш+ — вектор длины i, у — вектор длины 1, и произведение
, у-1);
в) х и у — векторы длины 1. Ограничение формы Q~ на плос-
плоскость, порожденную векторами х и у, имеет сигнатуру B, 0),
A,0) или A, 1). При этом гиперплоскости Xх и ух пересекаются,
параллельны или расходятся, а скалярное произведение х ¦ у равно
±cas/.(xx, ух), ±1 или =tohd{xx, ух), соответственно.
2.4. Некоторые вычисления в гиперболической геометрии
81
Доказательство. Пусть Я —плоскость, порожденная векторами хну.
В случаях а и б плоскость Я пересекает Н+ по гиперболической прямой
L э х. Выбрав единичный касательный вектор v к Н+ в точке х и восполь-
воспользовавшись результатом упражнения 2.3.5, запишем L в виде х ch t + v sh t.
Если у € H+, то у = xcht + vsht при t = ±d(x, у), в зависимости от
направления вектора v. Поскольку х и v ортогональны (упражнение 2.3.2),
получаем
х • у = х • (х ch t + v sh t) = — ch t = - ch d(x, y).
Если у ф. И+, то согласно упражнению 2.4.6 расстояние от точки х
до прямой ух равно расстоянию от х до точки у = L П ух, поскольку
L — единственный перпендикуляр к ух, проходящий через х. Поэтому у —
= xch/ + t/sh/ при t = d(x, yx). Заметим, что у — линейная комбина-
комбинация векторов х и v, причем у перпендикулярен у. Следовательно, у =
= ±(xsh/ + voht) (напомним, что векторы хну нормированы). Отсюда
следует, что
х-у =
, yx).
Анализ пункта в получается комбинацией рассуждений, использованных
при доказательстве пп. а к б. Пусть прямая L = Р Л Н+ не содержит ни х,
ни у, и мы ее параметризуем, начиная с точки х = L Г) Xх. Тогда х = ±и
и, вновь используя упражнение 2.4.6, получаем у = L п ух = х ch t + v sh t
при t = d(xx, yx) и y = ±(xsht + t>chf), так что х-у= ±chd(xx, yx).
Осталось разобраться с первыми двумя случаями пункта в. Если фор-
форма Q~ положительно определена на Я, то она не определена на ортого-
ортогональном дополнении Рх, так что множество Рх n H+ = Xх П ух не пусто.
Пусть р — точка лежащая в пересечении хх и ух. Для нахождения вели-
величины cosZ(xx, yx), определенной с точностью до знака, достаточно взять
касательные векторы к Н+ в точке р, перпендикулярные к хх и ух, н
вычислить косинус угла между ними. Но в качестве таких касательных
векторов можно взять сами векторы хну, так что cosZ(xx, yx) = ±jc • у.
Если Q~ *положительно полуопределена на Р, она также положительно
полуопределена и на Рх. Поэтому множество Рх Г) И+ = хх Г) ух пусто,
но Рх П S"^] содержит единственную прямую, проходящую через начало
координат. Следовательно, хх и ух пересекаются на бесконечности, т. е.
параллельны. Формулу х ¦ у = =Ы можно получить заметив, что этот случай
является предельным для двух предыдущих. 12.4.51
Упражнение 2.4.6 (минимум расстояния достигается на перпендикуляре).
а) Пусть L С ВТ — прямая, у — точка, не лежащая на ней, а х — такая точка
прямой L, что расстояние d(x, у) минимально. Тогда прямая ху перпендикулярна
прямой L.
82
Глава 2. Гиперболическая геометрия и ее друзья
б) Пусть L, М С Н" — непересекающиеся прямые, х е L, у &М — такие точки
этих прямых, что расстояние d(x, у) минимально. Тогда прямая ху перпендикуляр-
перпендикулярна прямым L и М.
Упражнение 2.4.7. а) Чтобы устранить неопределенность знака в предложе-
предложении 2.4.5, нужно задать ориентацию гиперплоскости, двойственной к вектору v
вещественной длины. Для этого надо выбрать одно из двух полупространств, опре-
определяемых гиперплоскостью v1 в Ея>1 — например, то, которое содержит вектор v.
Этим самым мы одновременно выберем и полупространство, определяемое гипер-
гиперплоскостью Vх в If. Проделав это, можно определить знак величины d(x, у1) в
пункте б. Как будет теперь выглядеть формула? А как она выглядит в различных
случаях пункта в?
б) Нельзя ли каким-нибудь разумным способом нормировать векторы нулевой
длины? Каков геометрический смысл скалярного произведения v ¦ w, если один или
оба вектора имеют нулевую длину?
Теперь мы можем вывести тригонометрические формулы для треуголь-
треугольников в Н2 или их обобщений — пересечений Н2 с треугольниками в RF2.
Как и прежде, (vlt v2, v3) означает базис нормированных векторов в Е2Л,
составляющий матрицу V, a (wly до2, w3) —двойственный базис, векторы
которого составляют матрицу W. Матрица W больше не является обратной
к V. Вместо этого выполнено соотношение WSV = /, где 5 — симметриче-
симметрическая матрица скалярного произведения, заданного формой Q~, записанная
в каноническом базисе. В данном случае, 5 — диагональная матрица с
числами (—1, 1, 1) на диагонали. Тем не менее, матрицы скалярных про-
произведений VSV и WSW обратны друг другу:
(V'SV)(W'SW) = (V'SV)(V-lW) = V'SW=(W'SVy = I.
Поскольку длины векторов v, могут оказаться мнимыми, диагональ ма-
матрицы VSV уже не обязана состоять из одних единиц; теперь эта матрица
выглядит так:
VtSV=[cX2 г2 с23),
\Cl3 C23 ЕЗ)
где Б/ = у,- • vt = ±1. Отсюда, как и прежде, следует, что
j / S2E3 —С23 CI3C23 —E3CI2 С|2С23 — Ег^зХ
B.4.8) WSW — det vtsv I C13C23 - езС12 ei?3 - 4з cl2cl3 - eic23 I •
V.C12C23 — E2C13 C[2C\3 — E\C23 Z\Z% —c\i )
Эту формулу можно использовать так же, как и 2.4.1, но нужно быть осто-
осторожным со знаками, поскольку при нормировании вектора мнимой длины
может потребоваться умножение на отрицательное число.
Рассмотрим случай, когда vu v2, v3 — векторы мнимой длины, так что
вершины образованного ими треугольника лежат в Н2 (см. рис. 2.24, а).
2.4. Некоторые вычисления в гиперболической геометрии
83
Рис. 2.24. Треугольник на гиперболической плоскости можно представить дву-
двумя способами, (а) Сопоставив единичным базисным векторам (v\, t>2, У3) верши-
вершины треугольника, получим формулу, связывающую длины сторон; (б) затем, выбрав
(v\, t>2, У3) двойственными к сторонам треугольника, выведем соотношения между его
углами.
Согласно предложению 2.4.5, а расстояния dy можно восстановить по ве-
величинам сц — Vi ¦ vh а именно, сц — — ch dn. Длина векторов до, веществен-
вещественна, и двойственные им прямые wj- представляют стороны треугольника. Из
предложения 2.4.5, в и упражнения 2.4.7, а следует, что до,- ¦ до//(|до,| (до;!) =
= — coscp*, где I, j, k различны и ср* — внутренний угол при вершине vk.
Полагая все е,- в формуле B.4.8) равными —1, мы видим, что перед нор-
нормированием нужно изменить знак матрицы, после чего все ее диагональные
элементы становятся положительными. Тогда получаем
C0ScP3 = -^i_J!L==
Обозначив через А, В, С углы при вершинах у,, v2, v3, а через а, Ь, с —
противолежащие стороны, получим гиперболическую теорему косину-
сов:
B.4.9)
ch с = ch a ch b — sh a sh b cos С.
Для доказательства двойственной теоремы возьмем векторы vh лежа-
лежащие вне гиперболического пространства, двойственные к сторонам рас-
рассматриваемого треугольника (см. рис. 2.24, б). Тогда ctj = — coscp* (/, /, k —
различные), и |(ш>/ • wj)/{\wt\ \Wj\)\ = chdlt. Поэтому
W\ ¦ W2
\W1\\W2\
_ С13С23 +С12 _ coscpi coscp2 +
84
Глава 2. Гиперболическая геометрия и ее друзья
или
cosC = — cos Л cos В + sin Л sinfichc.
Особо отметим формулы для прямоугольных треугольников, так как они
особенно просты. Поменяв в предыдущих формулах местами Л и С (а так-
также а и с) и положив С = тс/2, получим
cos A
cha =
sin В
(напомним, что в евклидовом прямоугольном треугольнике cos Л = sin?).
Из уравнения B.4.9) следует гиперболическая теорема Пифагора:
chc = cha ch b
Из формулы для chb, аналогичной формуле B.4.9), при помощи замен
сп с — ch a ch b и cos В = ch b sin А и тождества ch2 а = 1 + sh2 а получаем
sin Л =
sha
she'
Поэтому в каждом треугольнике высота h, опущенная на сторону с, удовле-
удовлетворяет равенствам sin В = sh /г/sh а и sin Л = shh/shb. Отсюда следует
гиперболическая теорема синусов:
sha _ sh6 _ she
sin Л sin В sin С
До сих пор мы применяли уравнение B.4.8) только к'треугольникам, це-
целиком находящимся внутри гиперболического пространства (или к двой-
двойственным к ним). Промежуточные случаи также представляют интерес.
Например, на рис. 2.25, а показано, что прямоугольный пятиугольник мож-.
но считать треугольником, две вершины которого лежат за абсолютом; эти
вершины представлены в пятиугольнике двойственными прямыми, образу-
образующими непересекающиеся стороны. Используя предложение 2.4.5 и следя
за знаками, можно убедиться, что в этом случае теорема Пифагора при-
принимает вид
shashfr = chd.
Отсюда следует теорема синусов для прямоугольных шестиугольни-
шестиугольников — достаточно провести общий перпендикуляр к паре противополож-
противоположных сторон и получить два прямоугольных пятиугольника. В обозначениях
рис. 2.25, б получится формула
B.4.10)
sha
shl
shb
shB
she
: sh~C'
Из того же рисунка следует, что прямоугольный шестиугольник можно
рассматривать как треугольник, все вершины которого лежат за абсолю-
абсолютом.
2.4. Некоторые вычисления в гиперболической геометрии
85
a) 6)
Рис. 2.25. Тригонометрия прямоугольного пятиугольника и прямоугольного ше-
шестиугольника.
Упражнение 2.4.11 (существование и единственность прямоугольных ше-
шестиугольников). Покажем, что для любых А, В, С > 0 в И? существует един-
единственный (с точностью до движения) прямоугольный шестиугольник Н, в котором
длины попарно непересекающихся сторон равны А, В и С (см. рнс. 2.25, б). Позже
мы воспользуемся этим фактом в разделе 4.6 при изучении пространства гипербо-
гиперболических структур на поверхностях.
а) Предположим, что шестиугольник Н существует. Обозначим через ах С Е2'
вектор, двойственный к стороне шестиугольника Н, лежащей против стороны дли-
длины А; аналогичный смысл имеют 6х и сх (см. рис. 2.25, б). Покажите, что можно
выбрать векторы ха е ах, хь G Ь1- и хс е сх так, что матрица их скалярных про-
произведений будет обладать следующими свойствами: внедиагольные элементы от-
отрицательны, а диагональные равны единице. Чему равен модуль внедиагональных
элементов?
б) Любой другой прямоугольный шестиугольник //', длины попарно непересе-
непересекающихся сторон которого равны А, В а С, можно перевести в шестиугольник Н с
помощью изометрии. (Указание: покажите, что линейное преобразование, перево-
переводящее тройку векторов (ха, Хь, хе) в аналогичную тройку для шестиугольника Н',
лежит в группе ОB, 1).)
в) Обратно, задавшись любыми А, В и С, можно выбрать векторы ха, Хь и хс
с нужными скалярными произведениями и, тем самым, восстановить шестиуголь-
шестиугольник Н. (Указание: приведите матрицу скалярных произведений к диагональному
виду.)
(По поводу других доказательств см. задачу 2.6.9 и рнс. 4.15.)
86
Глава 2. Гиперболическая геометрия и ее друзья
Евклидово пространство приучило нас к мысли, что масштаб можно вы-
выбирать как угодно: не так уж важно, в чем измерять расстояния — в метрах
или в футах. Любую фигуру можно произвольным образом уменьшить или
увеличить.
Но в гиперболической и сферической геометриях это не так. Удвоив
стороны гиперболического или сферического треугольника, мы неизбежно
изменим его углы (это можно проверить с помощью формул 2.4.9 и 2.4.3).
Евклидово подобие не имеет аналогов в гиперболической и сферической
геометриях (см. задачу 2.3.11).
При вычислении площадей еще лучше видна сильная зависимость раз-
размеров от углов. Хорошая область евклидова пространства — скажем, со
связной кусочно-гладкой границей — всегда обладает следующим свой-
свойством: общая кривизна вдоль границы равна 2тс, и, в частности, сумма
внешних (ориентированных) углов многоугольника равна 2тс. На гипер-
гиперболической плоскости с ростом площади области увеличивается и общая
кривизна ее границы. Это частный случай очень общего и глубокого утвер-
утверждения дифференциальной геометрии — теоремы Гаусса—Бонне. Мы не
станем формулировать эту теорему в большей общности; вместо этого
мы приведем принадлежащий Гауссу красивый элементарный метод вы-
вычисления площади гиперболического треугольника. Начнем с идеального
треугольника, т. е. треугольника, «вершины» которого лежат на беско-
бесконечности. Идеальный треугольник неограничен, но его площадь конечна.
Предложение 2.4.12 (идеальные треугольники). Все идеальные
треугольники равны и имеют площадь тс.
Доказательство. На модели в верхней полуплоскости легко видеть, что
с помощью изометрии любой идеальный треугольник можно перевести в
треугольник с вершинами сю, (—1,0) и A, 0) (см. рис. 2.26). Наш тре-
треугольник можно задать неравенствами — 1 < х < 1 и у ^ \/1 — х2. Гипербо-
Гиперболический элемент площади равен (\/y2)dxdy (формула B.2.9)). Поэтому
искомая площадь равна
¦1 г°°
/
dydx=
Предложение 2.4.13 (площадь гиперболического треугольника).
Площадь гиперболического треугольника равна тс минус сумма его
углов {угол при идеальной вершине равен нулю).
Доказательство. Если все углы треугольника равны нулю, то это иде-
идеальный треугольник. Рассмотрим теперь 2/3-идеальный треугольник, т. е.
треугольник, две вершины которого лежат на абсолюте. Обозначим че-
через Л (9) площадь такого треугольника, в котором угол при конечной вер-
вершине равен тс — 9. Это корректно определенная функция, поскольку все
2.4. Некоторые вычисления в гиперболической геометрии
87
** - t
:fe-'
-1
1
Рис. 2.26. Все идеальные треугольники конгруэнтны. Возьмем произвольный иде-
идеальный треугольник. Применив инверсию, переведем одну из его вершин в оо. После
этого применим евклидово подобие, переводящее две оставшихся вершины в (—1, 0)
и A,0).
2/3-идеальные треугольники с одинаковыми углами при конечной вершине
равны (доказательство аналогично случаю идеальных треугольников).
Ключевое наблюдение Гаусса состоит в том, что функция А аддитивна,
т. е. Л(9, + 92) = Л(90 + Л(92) при 9,, 92, 9, + 92 € @, тс). Доказательство
следует из рис. 2.27. Поэтому функция А: @, тс) —> Ш является Q-линей-
ной. Но А непрерывна, а значит, М-линейна. Вместе с тем Л (тс) — это
В'
Рис. 2.27. Площадь треугольника с двумя вершинами на абсолюте По определе-
определению, площади закрашенных треугольников, изображенных слева, равны А(в\) и А(в%).
Аналогично, площадь закрашенного треугольника на правом рисунке равна Л(б| + 9г).
Но площади изображенных на этих рисунках закрашенных фигур совпадают, по-
поскольку отражение относительно точки О переводит треугольник ОАВ в треугольник
ОА'В'. Поэтому функция /1(9) аддитивна. Это используется при вычислении площади
2/3-идеального треугольника.
88
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.28. Площадь произвольного гиперболического треугольника. После уда-
удаления ограниченного треугольника из подходящего идеального треугольника останутся
три 2/3-идеальных треугольника. Просуммировав углы и площади, получим предло-
предложение 2.4.13.
площадь идеального треугольника, равная тс по предложению 2.4.12. По-
Поэтому Л@) =0 и площадь 2/3-идеального треугольника равна внешнему
углу при конечной вершине.
Как показано на рис. 2.28, треугольник с двумя или тремя конечны-
конечными вершинами является разностью идеального треугольника и двух или
трех 2/3-идеальных треугольников. (Читателю следует проверить дета-
детали.) 12.4.131
Упражнение 2.4.14 (площадь сферического треугольника). С помощью
аналогичных рассуждений найдите площадь сферического треугольника, начав с
рассмотрения сферы, площадь которой равна 4тс.
Следствие 2.4.15 (площадь гиперболических многоугольников).
Сумма S внутренних углов плоского гиперболического п-угольника
меньше суммы внутренних углов евклидова п-угольника. Разность
(п — 2)тс — 5 называется дефектом и совпадает с площадью гипер-
гиперболического п-угольника.
Доказательство. Как и в евклидовом случае, разобьем многоугольник
на треугольники. |2.4.15|
Упражнение 2.4.16. а) Найдите площадь поверхности рода два, склеенной из
правильного восьмиугольника (см. рис. 1.12,6).
б)* Покажите, что все поверхности рода два постоянной кривизны —1 имеют
одинаковую площадь.
Упражнение 2.4.17. Как правильно определить площадь самопересекающего-
самопересекающегося многоугольника? Чему равна площадь самопересекающегося гиперболического
многоугольника? Сравните с задачей 2.3.12.
2.5. Изометрии гиперболического пространства 89
2.5. Изометрии гиперболического пространства
Как видно из задачи 2.2.14, движения гиперболического пространства
образуют большую группу. Для изучения этой группы можно применить
аппарат линейной алгебры, но для развития гиперболической интуиции
полезнее пользоваться прямыми геометрическими конструкциями. С ал-
алгебраическим подходом можно познакомиться в задаче 2.5.24.
Начнем с трехмерного случая. Пусть g: И3 —> Н3 — изометрия, сохраня-
сохраняющая ориентацию, отличная от тождественной. Осью g называется любая
прямая L, инвариантная относительно g, и на которой g действует сдвигом
(возможно, тривиальным).
Предложение 2.5.1 (единственность оси). Нетривиальная сохра-
сохраняющая ориентацию изометрия пространства Иъ, отличная от
тождественной, имеет не более одной оси.
Доказательство. Пусть L и М — различные оси сохраняющей ориен-
ориентацию изометрии g. Предположим, что g оставляет на месте каждую точку
прямых L и М и рассмотрим точку х прямой М, не лежащую на прямой L.
Тогда g сохраняет плоскость, содержащую L и х, поскольку сохраняет три
точки этой плоскости, не лежащие на одной прямой. Поскольку g сохра-
сохраняет ориентацию, это тождественное отображение.
С другой стороны, если g действует на L сдвигом, то для любой точки
хе L имеем d(x, M) — d(g(x), M), так что функция d(x, M) периодическая,
и следовательно, ограниченная. Но две различные прямые не могут нахо-
находиться на ограниченном расстоянии друг от друга в обоих направлениях.
Это означало бы, что их концы на абсолюте совпадают, а это противоречит
тому, что они различны. |2.5.1|
Упражнение 2.5.2. Найдите сохраняющую ориентацию изометрию простран-
пространства Н3, у которой больше чем одна инвариантная прямая.
Любая сохраняющая ориентацию изометрия евклидова пространства Е3
является сдвигом, вращением вокруг некоторой прямой или винтовым
движением, т. е. композицией вращения и сдвига вдоль оси вращения (в
упражнении 2.5.6 вам предстоит это доказать). В гиперболическом случае
выбор богаче, и здесь есть своя терминология.
Пусть g — нетривиальная сохраняющая ориентацию изометрия про-
пространства Н3. Если g имеет ось, на которой действует тождественно,
то g называется эллиптическим движением, или вращением, вокруг
своей оси. В этом случае орбита любой точки р, не лежащей на оси (т. е.
множество точек gk(p), где k € Z), лежит на окружности с центром на оси.
Если g имеет ось, на которой действует нетривиальным сдвигом, то g на-
называется гиперболическим движением. Здесь возможны два случая. Если
орбита точки, не лежащей на оси, лежит в одной плоскости всегда по од-
одну сторону от оси, то это гиперболический сдвиг. В этом случае орбита
90
Глава 2. Гиперболическая геометрия и ее друзья
2.5. Изометрии гиперболического пространства
91
лежит на одной из эквидистантных кривых (см. рис. 1.10). Если же ор-
орбита является множеством вершин многоугольной спирали вокруг оси, то
g является винтовым движением, что можно увидеть, применив компенси-
компенсирующий сдвиг. (Иногда термин «гиперболическое» движение используется
только для гиперболических сдвигов, а винтовые вращения называются
«локсодромическими» движениями. Такое деление не очень полезно, и мы
не будем им пользоваться).
Согласно предложению 2.5.1, движение не может быть одновременно
эллиптическим и гиперболическим. Но бывают движения, не являющиеся
ни эллиптическими, ни гиперболическими. Они называются параболиче-
параболическими. Таковой, например, является любая изометрия Н3, представленная
евклидовым сдвигом вдоль граничной плоскости в модели в верхнем по-
полупространстве.
В следующем предложении мы научимся находить ось (если она суще-
существует) нетривиальной сохраняющей ориентацию изометрии И3. Для этого
нам потребуется элементарный факт о взаиморасположении пары прямых;
вспомним (см. упражнение 2.3.10), что две прямые в И3 называются па-
параллельными, если у них есть общая точка на 5^,, или, что то же самое,
если расстояние между ними стремится к нулю в одном из направлений.
Лемма 2.5.3 (общий перпендикуляр к двум прямым в И3). Две
различные прямые в Н3 либо параллельны, либо имеют единственный
общий перпендикуляр.
Доказательство. Пусть X и Y — две различные прямые, a d(x, у) —
расстояние между точками х е X и у е У. Если эти прямые не параллель-
параллельны, то функция d(x, у) стремится к бесконечности, когда х или у, либо
и х, и у стремятся к бесконечности. Следовательно, эта функция достигает
минимума в некоторой точке (хо, Уо).
Если минимум равен нулю, т. е. прямые пересекаются, то любой общий
перпендикуляр должен проходить через точку пересечения, иначе получит-
получится треугольник с двумя прямыми углами, что невозможно согласно пред-
предложению 2.4.13. Поскольку существует единственная прямая, проходящая
через точку пересечения и перпендикулярная плоскости, содержащей X
и У, то в этом случае лемма доказана. (Заметьте, что эта часть леммы
неверна в пространстве размерности больше трех.)
Если минимальное расстояние не равно нулю, то прямая, проходящая
через Хо и у0, является, ввиду упражнения 2.4.6, искомым общим перпен-
перпендикуляром. Если бы существовал другой общий перпендикуляр, то мож-
можно было бы рассмотреть прямоугольный четырехугольник в пространстве
(быть может, самопересекающийся). Диагональ этого четырехугольника
делит его на два плоских треугольника, общая сумма углов которых не
меньше чем 2тс, что невозможно. |2.5.3[
Пусть L — прямая в И3. Обозначим через rL отражение относительно
прямой L, т. е. поворот на угол тс вокруг этой прямой.
Предложение 2.5.4 (в поисках оси). Всякая нетривиальная со-
сохраняющая ориентацию изометрия g пространства Н3 является
композицией отражений g = rL о гм. Прямые L и М параллельны, пе-
пересекаются или расходятся, если g—параболическое, эллиптическое
или гиперболическое движение соответственно. Ось движения g, ес-
если она существует, совпадает с общим перпендикуляром к прямым L
иМ.
Доказательство. Рассмотрим любую точку р такую, что g(p) ф р. Если
g(p) — р, то g сохраняет середину q отрезка pg(p) и плоскость, прохо-
проходящую через q и перпендикулярную прямой pg{p). Поскольку g должно
менять ориентацию этой плоскости, g действует на ней отражением от-
относительно некоторой прямой К- Поэтому g = rK является эллиптическим
движением порядка два. В этом случае в качестве L и М можно взять
любые две прямые, перпендикулярные К, проходящие через одну точку
х € К и перпендикулярные друг другу.
Если точки р, g(p) и ^(р)ф р лежат на одной прямой, то по счастливой
случайности р лежит на оси изометрии g и g —гиперболическое движение.
Заменив р на любую точку, не лежащую на оси, перейдем к следующему
случаю, когда три различные точки р, g(p) и g2(p) Ф р не лежат на одной
прямой.
В этом случае выберем биссектрису М угла pg{p)g2{p) так, чтобы гм
сохраняло g(p) и меняло местами р и ^(р). Рассмотрим далее двугранный
угол с ребром g(p)g2(p), грани которого содержат точки р и g^p). Пусть
П — плоскость, делящая этот двугранный угол пополам. Тогда в качестве L
возьмем серединный перпендикуляр к отрезку g(p)g2(p), лежащий в плос-
плоскости П (см. рис. 2.29). (Величина двугранного угла при этом может быть
равна 0 или тс, но это нам не помешает.) Вследствие симметрии отраже-
отражение rL меняет местами g(p) с ^(р), а также р с ^(р). Поэтому rL о гм
переводит р в g(p), g(p) в g2(p), a g2(p) в g*(p). Поскольку отображе-
отображения rL о гм и g совпадают в трех точках, не лежащих на одной прямой,
они совпадают и в плоскости, содержащей эти три точки. Но тогда они
совпадают всюду, так как каждое из них сохраняет ориентацию.
Общий перпендикуляр к прямым L и М, если он существует, являет-
является осью g, поскольку он инвариантен относительно композиции rL о гм,
действующей на нем сдвигом. Оставшееся утверждение о том, что чему
соответствует, следует теперь из леммы 2.5.3 и определений параболиче-
параболического, эллиптического и гиперболического движений. |2.5.4|
Упражнение 2.5.5. Используя предложение 2.5.4, покажите, что любая па-
параболическая изометрия, сохраняющая ориентацию пространства Н3, сопряжена
евклидову сдвигу в модели в верхнем полупространстве.
92
Глава 2. Гиперболическая геометрия и ее друзья
Рис. 2.29. Ось изометрии в трехмерном пространстве. В общем случае, ось изо-
метрии g пространства И3 можно построить, соединив ломаной точки орбиты р.
Упражнение 2.5.6 (изометрии пространства Е3). Докажите, что сохраня-
сохраняющая ориентацию изометрия пространства Е3 является сдвигом, вращением, или
винтовым движением. В последних двух случаях найдите ось движения с помощью,
геометрического построения.
Доказательство предложения 2.5.4 можно применить к любой изоме-
изометрии двумерного пространства, независимо от того, сохраняет она ори-
ориентацию или нет, поскольку такую изометрию всегда можно продолжить
до трехмерной изометрии, сохраняющей ориентацию. Но множества непо-
неподвижных точек трехмерных изометрии, обращающих ориентацию, а также
любых изометрии в больших размерностях не обязательно являются пря-
прямыми: рассмотрим, например, отражение относительно плоскости произ-
произвольной размерности или вращение относительно плоскости четной кораз-
коразмерности. Однако любое преобразование гиперболического пространства,
имеющее неподвижную точку, по-прежнему называется эллиптическим,
а сдвиг вдоль оси называется гиперболическим движением и имеет, как
и прежде, ровно одну ось. Любое другое нетривиальное преобразование
называется параболическим.
Задача 2.5.7 (изометрии пространства Н3, обращающие ориентацию).
Классифицируйте изометрии пространства Н3, обращающие ориентацию. Это
можно сделать по аналогии с предыдущим случаем, представив изометрни, обра-
обращающие ориентацию, в виде композиции отражения относительно плоскости и
отражения относительно прямой. Другой способ основан на том, что квадрат
2.5. Изометрии гиперболического пространства
93
изометрии, обращающей ориентацию, является изометрией, сохраняющей ориен-
ориентацию. Из каких изометрии пространства Н3 можно извлечь квадратный корень,
так чтобы полученное преобразование обращало ориентацию? Как выглядят ква-
квадратные корни из тождественного отображения? А квадратные корни из других
изометрии (разумеется, если они есть)?
Изучение изометрии в пространстве произвольной размерности будет
продолжено с геометрических позиций. Мы используем метод, основан-
основанный на выпуклости функции расстояния. Этот метод будет важен для нас
и в дальнейшем, поскольку его можно приспособить для изучения дру-
других метрик отрицательной кривизны в М". С алгебраическим подходом к
классификации изометрии можно познакомиться в задаче 2.5.24.
Вещественнозначная функция f на римановом многообразии называет-
называется выпуклой, если для любой геодезической у, проходимой с постоянной
скоростью, функция / о у выпукла. Другими словами,
для любого t € (О, 1). Если неравенство строгое для любого непостоянно-
непостоянного у, то / называется строго выпуклой.
Произведением двух римановых многообразий называется произведе-
произведение многообразий с римановой метрикой, являющейся суммой римановых
метрик сомножителей. Нетрудно показать, что кривая в произведении мно-
многообразий является геодезической (проходимой с постоянной скоростью)
тогда и только тогда, когда проекция на каждый множитель является гео-
геодезической (проходимой с постоянной скоростью). В частности, геодези-
геодезическая в Н" х И" — это кривая, проекция которой на каждый множитель
есть гиперболическая прямая или точка.
Теорема 2.5.8 (функция расстояния выпукла). Функция рассто-
расстояния d(x, у), рассматриваемая как отображение d: И" х И" —» М,
является выпуклой. Если геодезическая у в Н" х И" проецируется
на две различные прямые, то композиция day строго выпукла.
Доказательство. Без ограничения общности можно считать, что п ^ 3,
поскольку И" изометрически вложено в ВР+|. Кроме того, будем считать,
что проекции X и Y геодезической у являются прямыми, не лежащими в
одной плоскости; в частности, X не пересекает Y даже на бесконечности.
Параметризуем прямые X и Y длиной дуги и договоримся, что х и у
обозначают как точки на X и Y, так и значения их параметров. Для любых
точек х € X и у € Y обозначим через ?(jc, у) угол, образованный отрез-
отрезком Ту и положительным лучом прямой X с началом в точке х; аналогично,
г)(х, у) обознает угол между ~ух и положительным лучом прямой Y с нача-
началом в у (см. рис. 2.30).
Применив формулу площади (см. предложение 2.4.13), к треугольнику,
две вершины которого лежат на X, а одна на Y, мы увидим, что 5 являет-
94
Глава 2. Гиперболическая геометрия и ее друзья
х'
Рис. 2.30. Производная расстояния монотонна. Положение отрезка, соединяющего
прямые К и Y, однозначно определяется углами между этим отрезком и прямыми.
Используя этот факт, можно доказать, что расстояние между двумя прямыми является
выпуклой функцией.
ся монотонно возрастающей функцией от х при фиксированном у. Ясно,
что отображение (?, r\): R2 —> @, тс) х @, я) дифференцируемо; покажем,
что оно является биекцией. Для этого рассмотрим величину \Цх', у') —
- Цх, у)\ + \т)(х', у') - г](х, у)\, где (х, у) и (х', у') - произвольные пары
точек на X и Y. Можно считать, что х' ^ х. Если, кроме того, у' ^ у, как
изображено на рис. 2.30, то
\Цх!, у') - Цх, у)\ + |г](х', у') - г)(х, у)\ >
> Цх', у') - Цх, у) + ф, у') - г)(х, у) =
= {1{х>, у') - Цх', у)) + (Цх', у) - Цх, у)) +
+ (*](*', У1) - г)(х', У)) + (т)(*\ у) - ф, у)).
При этом
B.5.9) Цх', у') - Цх', у) > -Zyx'y',
если только у ф у'. Это — обычное неравенство треугольника для сфериче-
сферического треугольника, причем неравенство строгое, поскольку X и Y не лежат
в одной плоскости. Кроме того, из формулы площади (предложение 2.4.13)
следует, что т\{х', у') - г^х7, у) — /.ух1у' + S&yxiyl. Используя аналогичные
оценки для остальных разностей, получаем
B.5.10) \Цх', у') - Цх, у) | + !т)(х', у') -
при {х,у)ф{х',у').
, у) \ > SAxslx,
2.5. Изометрии гиперболического пространства
95
Таким же способом разбирается случай у' < у. Для этого надо начать с
неравенства
\Цх', у') - Цх, у)\
, у') - г](х, у)\ >
> Цх', у') - Цх, у) - (п(х', у1) - г](х, у)).
Тогда получается, что при (х, у) ф (х1, у') выражение \Цх', у') — Цх, у)\ +
+ h(x', у') - г](х, у)\ строго больше нуля, так что отображение (?, г)) явля-
является биекцией.
С другой стороны, из упражнения 2.5.13 следует, что градиент функции d
равен W = (dx, du) = (— cos?, — cosy)). Поэтому W также является би-
биективным дифференцируемым отображением изК2 в (—1, 1) х (—1, 1).
Производная отображения Vd равна гессиану функции расстояния,
jfx
Гладкая функция выпукла тогда и только тогда, когда ее вторая производ-
производная неотрицательна вдоль любой прямой в области определения, и строго
выпукла, если эта производная всюду положительна. Следовательно, мы
почти у цели, и нам осталось только показать, что матрица И положительно
определена.
Для этого нам понадобится инфинитезимальный аналог предыдущих
рассмотрений. Конечно же, хотелось бы снова использовать в наших рас-
рассуждениях площади. Но мы не будем этого делать, чтобы наше доказатель-
доказательство работало не только в гиперболическом пространстве, но и в любом
пространстве неположительной кривизны. Например, для евклидова про-
пространства площади в наших оценках вообще не фигурируют.
Обозначим через yv, y'v и Xv точки сферы обзора с центром в х', соответ-
соответствующие точкам у, у' и положительному концу прямой X. Пусть dv — рас-
расстояние на сфере обзора. Тогда dv(Xv, yv) = Цх', у), dv(Xv, y'v) = Цх', у')
и dv(yB, y'v) = /.ух1 у', и неравенство B.5.9) следует, как и раньше, из не-
неравенства треугольника. На самом деле, верно более сильное неравенство.
Использовав упражнение 2.5.13, в и предположение, что точки yv, y'v и Xv
не лежат на одной сферической прямой, получим
B.5.11)
Цх', у') - Цх', у) + Zyx'y' > е\у - у'\,
где е — некоторое положительное число, зависящее только от х и у.
Скомбинировав это с соответствующим неравенством для г\, получим
следующий аналог неравенства B.5.10):
B.5.12) \Цх', у') - Цх, у)\
при (х, у) ф (х', у').
, у') - г](х, у)\
\у -
96 Глава 2. Гиперболическая геометрия и ее друзья
Отсюда следует, что при дифференцируемом гомеоморфизме (?, rj) пло-
площадь увеличивается как минимум в е2 раз. Поэтому определитель гес-
гессиана функции расстояния всегда строго положителен или всегда строго
отрицателен. Функция расстояния является *собственным отображением
из R2 в [0, оо), и поэтому достигает своего минимума. В точке минимума
определитель гессиана не может быть отрицательным, поэтому он всюду
положителен. Но диагональные элементы матрицы Н положительны в силу
замечания о монотонности роста ? и г) при одном фиксированном аргумен-
аргументе. Поэтому матрица Н положительно определена. Таким образом, строгая
выпуклость расстояния установлена в предположении, что X и Y не лежат
в одной плоскости.
Условие выпуклости сохраняется при переходе к замыканию, так что
оно выполнено, даже если проекции X и Y геодезической у лежат в одной
плоскости или вырождаются в точку, поскольку эти случаи являются пре-
предельными для предыдущего. Но для доказательства строгой выпуклости
эти аргументы не годятся, тем более, что строгая выпуклость не имеет ме-
места, если X или Y являются точкой или если они совпадают. Поэтому нам
нужно найти другой метод доказательства строгой выпуклости для случая,
когда X и Y являются различными прямыми, лежащими в одной плоскости.
Теперь нам придется расстаться с надеждой получить доказательство,
работающее в любом пространстве неположительной кривизны: вспомним
о параллельных прямых в Е". Вместо этого мы можем использовать нера-
неравенство B.5.10) со знаком ^ вместо >. Из этого неравенства следует, что
при х 4- Y и у ? X выполнено неравенство B.5.12). Снова используя гра-
градиент Vd, получаем, что функция d: X х Y —> R строго выпукла всюду, за
исключением, быть может, двух прямых вида х — х0 и у = у0. В частности,
d о у: R —» R строго выпукла всюду, кроме, быть может, двух точек; но
выпуклая функция, строго выпуклая в дополнении к конечному множеству
точек, является строго выпуклой всюду. 12.5.81
Упражнение 2.5.13 (производная функции расстояния), а) Зафиксируем
в гиперболическом пространстве точку хо. Покажите, что градиент в точке х функ- •
ции расстояния х >-* d(x, x0) является единичным вектором с началом в точке х,
направленным вдоль геодезического луча Щх.
Пусть a(t) — дифференцируемая кривая в гиперболическом пространстве, t —
натуральный параметр. Предположим, что xq Ф a(to). Покажите, что производная
расстояния d(x0, а@) по t в точке t0 равна cos в, где в — угол между <х'(/о) и
геодезической, соединяющей хо с а(^о).
б) Покажите, что это верно и в евклидовом пространстве.
в) Покажите, что это верно и на сфере, если только х и х0 не являются проти-
противоположными точками.
г) Покажите, что этот же результат верен на любом римановом многообразии,
если только точки х и Xq не сопряжены.
2.5. Изометрии гиперболического пространства
97
Одно из стандартных введений в теорию пространств отрицательной
кривизны состоит в том, чтобы следующее их свойство принять за опре-
определение [Bus55, глава 5]:
Определение 2.5.14 (определение отрицательной кривизны по Бу-
земану). Метрическое пространство имеет отрицательную кривизну,
если в любом треугольнике ABC расстояние между серединами АВ и АС
меньше, чем половина расстояния между В а С.
Это определение полезно во многих ситуациях, в том числе при изучении
финслеровых многообразий, когда невозможно применить другие опре-
определения, взятые из римановой геометрии. Из теоремы 2.5.8 следует, что
гиперболическое пространство (как и любое односвязное полное риманово
многообразие строго отрицательной секционной кривизны) удовлетворяет
этому свойству.
Упражнение 2.5.15. Предположим, что выполнено свойство Буземана, но о
выпуклости функции расстояния ничего не известно. Пусть X и Y— середины гео-
геодезических отрезков АВ и CD. Докажите, что если все эти точки не лежат на одной
геодезической, то d(X, Y) < ^(d(A, С) + d(B, ?>)). (Указание: нарисуйте диагональ
четырехугольника.) Что произойдет, если все точки попадут на одну геодезическую?
Докажите, что теорема 2.5.8 выполнена в любом пространстве, имеющем отри-
отрицательную кривизну в смысле Буземана.
Функцией сдвига изометрии g: Ш" —> Н" называется функция dg =
= d(x, g{x)). Применив теорему 2.5.8 к графику функции g, который явля-
является сохраняющим геодезические вложением Й" в ЕР х Н", получаем
Следствие 2.5.16 (функция сдвига выпукла). Для любой изоме-
изометрии g пространства Й" функция сдвига ds является выпуклой в W
и строго выпуклой всюду, кроме прямых, инвариантных относи-
относительно g.
Предложение 2.5.17 (классификация изометрии пространства И").
Пусть g — изометрия пространства И". Тогда
а) изометрия g является гиперболическим движением тогда и
только тогда, когда точная нижняя грань de положительна. Эта
точная нижняя грань достигается в каждой точке прямой, явля-
являющейся единственной осью преобразования g. Концы оси являются
неподвижными точками действия g на 5^"';
б) изометрия g является параболическим .движением тогда и
только тогда, когда ds не достигает своей точной нижней грани.
. При этом точная нижняя грань равна нулю, g имеет единственную
неподвижную точку р на 5^"' и в модели в верхнем полупро-
полупространстве с точкой р на бесконечности действует евклидовой
изометрией;
Глава 2. Гиперболическая геометрия и ее друзья
в) изометрия g является эллиптическим движением тогда и
только тогда, когда существует такая точка х, что dg(x) = 0.
При этом множество djl(O) является гиперболическим подпро-
подпространством размерности k, 0 < k < п.
Доказательство. Пусть функция dg достигает положительной точной
нижней грани в точке х. Тогда точная нижняя грань достигается и в точ-
точке g(x). Ввиду выпуклости, функция dg постоянна на отрезке с конца-
концами х, g(x), и по следствию 2.5.16 прямая, проходящая через х и g(x),
инвариантна. Изометрия g действует на этой прямой сдвигом, т. е. является
гиперболическим преобразованием. Единственность оси преобразования g
следует из второй половины доказательства предложения 2.5.1. Докажем,
что g не имеет неподвижных точек на абсолюте, за исключением концов
оси. Действительно, пусть ось вертикальна в модели в верхнем полупро-
полупространстве. Тогда на граничной плоскости 5^"' \ {оо} преобразование g
действует как евклидово подобие с коэффициентом подобия, не равным
единице, а потому имеет не более одной неподвижной точки.
Пусть функция dg не достигает своей точной нижней грани. Тогда суще-
существует последовательность {*,} такая, что dg(xi) стремится к нижней гра-
грани. Вследствие компактности можно считать, что {*,} сходится к точке х
на 5^"', которая должна быть неподвижной относительно g. Пусть х = оо
в модели в верхнем полупространстве; тогда g действует на 5^"' \ {оо}
как евклидово подобие. Если это подобие не имеет неподвижных точек на
S^T1 \ {°°}i т0 эт0 евклидова изометрия, а следовательно, dg стремится к
нулю по любому вертикальному лучу, и inf dg — 0. А так как g не имеет
инвариантных прямых и неподвижных точек в Н", то g является парабо-
параболическим преобразованием.
Если же преобразование g имеет неподвижную точку у в 5^' \ {оо}, то
существует вертикальная прямая L, инвариантная относительно g. Пусть
П — (гиперболическая) гиперплоскость, перпендикулярная этой прямой.
Тогда замкнутая область F, лежащая между плоскостями П и g(TH), явля-
является фундаментальной областью преобразования g, т. е. для любой точ-
точки х 6 Н" существует k € Z такое, что g*(x) € /\ В частности, dg принимает
любое свое значение внутри области F.- Поскольку g не принимает своей
точной нижней грани, то из соображений компактности ясно, что g имеет
неподвижную точку в FnS1^1. Но если g сохраняет три точки на 5^', то
g тождественно действует на проходящей через них плоскости, что проти-
противоречит предположению о том, что значение inf dg не достигается.
Наконец, если в некоторой точке dg равно нулю, то по определению
g является эллиптическим преобразованием, а множество неподвижных
точек является /г-мерным подпространством, поскольку любая прямая,
проходящая через две неподвижные точки, полностью состоит из непо-
неподвижных точек. [2.5.171
2.5. Изометрии гиперболического пространства
99
Упражнение 2.5.18 (неподвижные точки и сопряженные изометрии).
а) Пусть аир- такие изометрии пространства ЕР, что множества неподвиж-
неподвижных точек на абсолюте у а и р~'ар совпадают. Тогда это множество неподвижных
точек инвариантно относительно р.
б) Пусть аир — две коммутирующие изометрии пространства ЕР, не явля-
являющиеся эллиптическими преобразованиями. Тогда это либо две гиперболические
изометрии с одной и той же осью, либо это две параболические изометрии, сохра-
сохраняющие одну и ту же точку абсолюта.
Выпуклости d(x, у) как функции одной переменной достаточно для
определения гиперболического среднего, т. е. центра масс конечного
числа точек пространства Н" с заданными весами. При гиперболических
изометриях центр масс должен переходить в центр масс; кроме того, центр
масс должен непрерывно зависеть от точек и их весов, а центр масс одной
точки должен совпадать с этой точкой.
Для определения гиперболического среднего можно воспользоваться
одним из определений среднего в евклидовом пространстве: для любого
набора {(pi, m,)} точек р{ с весами т{ центром масс называется точка х,
в которой функция S,m,d2(pb x) достигает своего минимума. В отличие
от d(pt, x), функция d2(pt, x) является строго выпуклой по х, поэтому и
сумма строго выпукла. А поскольку она неограниченно возрастает на лю-
любой прямой, минимум достигается, причем ровно в одной точке.
Следствие 2.5.19 (конечная группа имеет неподвижную точку).
Конечная группа изометрии W имеет хотя бы одну неподвижную
точку.
Доказательство. Пусть х — произвольная точка, a F — конечная группа
изометрии. Тогда центр масс орбиты любой точки х (точки орбиты берутся
с одинаковыми весами) является неподвижной точкой группы F. |2.5.19|
Упражнение 2.5.20 (компактная группа имеет неподвижную точку). На
любой компактной "топологической группе существует конечная инвариантная ме-
мера Хаара, т. е. конечная мера, инвариантная относительно действия группы на
себе левыми (или правыми) сдвигами [MZ55]. Используя этот факт, покажите,
что действие произвольной компактной группы G на ЕР имеет неподвижную точку.
(Указание: усредните образы точки х е ЕР с помощью меры Хаара на G.)
Упражнение 2.5.21 (гиперболическая медиана). Медианой взвешенной си-
системы точек (pit mi) в Е1 называется точка х, в которой функция J2tmid(Pi, x)
достигает своего минимума. Множество медиан либо состоит из одной точки, либо
является интервалом.
Это определение дословно переносится на случай Е" и ЕР. Продумайте вопрос о
существовании н единственности евклидовой и гиперболической медиан при п = 2
(типичный случай) и опишите их свойства. Дайте геометрическую характеристику
медианы трех точек.
100
Глава 2. Гиперболическая геометрия и ее друзья
Задача 2.5.22 (другие гиперболические средние). Используя модель на ги-
гиперболоиде, можно дать еще одно простое определение гиперболического среднего.
Для любого набора {(/?,-, mi)} рассмотрим pi как векторы в ВТ1" СЕ"'1, найдем их
среднее и умножим на число так, чтобы снова получилась точка на гиперболоиде.
Как связаны это среднее и среднее, определяемое при помощи функции «ква-
«квадрат расстояния»? Совпадают ли они? Можно ли это среднее выразить в виде
линейной комбинации выпуклых функций от расстояния?
Задача 2.5.23. Теорема Брауэра о неподвижной точке утверждает, что любое
непрерывное отображение D" —*• D" имеет неподвижную точку. Классифицируйте
изометрии ВТ (хотя бы при п = 2 или п = 3) при помощи теоремы Брауэра и
описания групп изометрии 5я и Е"~'.
Задача 2.5.24 (изометрии ВТ с алгебраической точки зрения). Соглас-
Согласно упражнению 2.3.4, изометрии пространства ВТ взаимно однозначно соответ-
соответствуют линейным преобразованиям пространства R"+1, сохраняющим множество
{Q~ = —1}, где Q~ — квадратичная форма сигнатуры (п, 1). С помощью этого
соответствия можно исследовать свойства гиперболических изометрии.
а) Пусть для начала V — двумерное вещественное векторное пространство, Q —
(быть может, вырожденная) квадратичная форма на V, а А: V —*¦ V — линейное
отображение, сохраняющее Q. Как связана форма Q с собственными векторами и
собственными значениями оператора Л?
б) Пусть V — (п + 1)-мерное вещественное векторное пространство, a Q — ква-
квадратичная форма сигнатуры (п, 1) на V. Покажите, что существует изоморфизм
пространств V и R"+1, переводящий Q в форму Q~ = — ir + x\ + ... + х\. Это
означает, что достаточно исследовать пространство Е"'1.
в) Начиная с этого момента считаем, что А — линейное преобразование про-
пространства Е?1', сохраняющее Q~. Если W — минимальное инвариантное подпро-
подпространство преобразования А, то оно одномерно или двумерно. (Это верно для
любого линейного преобразования любого нетривиального векторного простран-
пространства.) Если W двумерно, то форма Q~ положительно определена на W.
г) Разложим характеристический многочлен р оператора А на линейные и не-
неприводимые над R квадратичные множители. Пусть q —любой неприводимый ква-
квадратичный делитель многочлена р. Так как подпространство, аннулируемое опера-
оператором q(A), положительно определено, то корни многочлена q лежат на единичной
окружности.
д) Если среди корней многочлена р есть корни, не лежащие на единичной
окружности, то таких корней ровно два: X и X". В этом случае оператор А индуци-
индуцирует гиперболическое преобразование пространства И". (Иногда и сам оператор А
называется гиперболическим).
е) Если А сохраняет такой вектор и, что Q~(v) < О, то А индуцирует эл-
эллиптическое преобразование пространства ЕР. При этом А сохраняет некоторое
вполне геодезическое подпространство Р € ВТ, изометричное пространству И*, где
0 ^ k ^ п, и действует «вращением» на ортогональном дополнении к Р.
ж) Если все характеристические корни лежат на единичной окружности и Л не
сохраняет ни одного вектора v с условием Q~ (v) < 0, то А сохраняет такой нену-
2.6. Комплексные координаты на трехмерном гиперболическом пространстве 101
левой вектор v, что Q~(v) = 0. Все такие неподвижные векторы пропорциональны
друг другу, и оператор А индуцирует параболическое преобразование простран-
пространства Iff1. При этом А сохраняет гиперплоскость Р = {w: v ¦ w = 1}, где знаком
«¦» обозначено скалярное произведение, определяемое формой Q~, а гиперплос-
гиперплоскость Р пересекает область {Q~ < 0} в проективной модели (см. задачу 2.3.13).
Квадратичная форма Q~ вырождена на касательном пространстве к гиперплоско-
гиперплоскости Р и индуцирует евклидову метрику на факторпространстве Р/HLv. Оператор А
индуцирует на Р/Ш) евклидову изометрию, не имеющую неподвижных точек.
Упражнение 2.5.25 (возможности параболических элементов). Преобра-
Преобразование Мёбиуса, индуцируемое на абсолюте 5" эллиптическим, параболическим
или гиперболическим преобразованием пространства ВГ+|, также называется эл-
эллиптическим, параболическим или гиперболическим. Покажите, что для любых
различных точек а, Ь и с, лежащих на абсолюте, существует единственное па-
параболическое преобразование, сохраняющее а и переводящее b в с.
2.6. Комплексные координаты на трехмерном
гиперболическом пространстве
Трехмерная гиперболическая геометрия тесно связана с комплексными
числами. С их помощью можно дать красивое описание геометрии про-
пространства Н3.
Существует естественное вложение комплексной плоскости С в ком-
комплексную проективную прямую СР1, т. е. в множество комплексных прямых
(одномерных комплексных подпространств) пространства С2. При этом
вложении точка z € С переходит в комплексную прямую, порожденную
вектором (z, 1), и являющуюся точкой СР1. Величина z называется не-
неоднородной координатой этой точки, а пары (tz, t) б С2, где t S С* =
= С \ {0} — ее однородными координатами. Оставшаяся точка СР1, со-
соответствующая прямой, проходящей через A, 0), называется бесконечно
удаленной точкой; неоднородную координату этой точки можно обозна-
обозначить символом оо.
Топологически СР1 является одноточечной компактификацией С про-
пространства С (см. задачу 1.1.1), так что стандартное отождествление Е2 с С
можно продолжить на оо. Отсюда следует, что топологически СР1 является
сферой, называемой сферой Романа.
Как и в действительном случае (задача 2.3.11), проективным пре-
преобразованием пространства СР1 называется проективизация обратимого
линейного отображения пространства С2. Проективные преобразования
являются гомеоморфизмами пространства СР1. Линейное преобразование
с матрицей (~ Л приводит к проективному преобразованию А, имеющему
в неоднородных координатах вид
(МЛ)
102
Глава 2. Гиперболическая геометрия и ее друзья
(конечно же, Л (г) считают равным а/с при г = оо и равным оо при
г = —d/c). При условии, что ad — be ф 0, отображение А: СР1 —> СР1
вида B.6.1) называют дробно-линейным преобразованием. На самом
деле, мы уже встречались с дробно-линейными преобразованиями. .
Упражнение 2.6.2 (дробио-лииейные преобразования являются преобра-
преобразованиями Мёбиуса).
а) Покажите, что при стандартном отождествлении СР1 с S2 дробно-линейные
преобразования являются преобразованиями Мёбиуса, т. е. композицией инверсий.
(Указание: рассмотрите сначала преобразование z ¦-* l/z).
б) Покажите, что любое преобразование Мёбиуса, сохраняющее ориентацию
сферы S2, является дробно-линейиым.
Иногда преобразованиями Мёбиуса пространства <С называют именно
дробно-линейные преобразования. Чтобы избежать недоразумений, мы не
будем этого делать.
Задача 2.6.3. Из предложения 1.2.3 и упражнения 2.6.2 следует, что дроб-
дробно-линейные преобразования отображают окружности (в том числе, прямые) в
окружности. Для явного доказательства этого факта нужно применить дробно-ли-
дробно-линейное преобразование к общему уравнению окружности.
Нельзя ли объяснить без вычислений, почему окружности переходят в окруж-
окружности? Мы вернемся к этому вопросу в задаче 2.6.5.
Два невырожденных линейных преобразования пространства С2 поро-
порождают одно и то же проективное преобразование пространства СР1 тогда
и только тогда, когда они отличаются на постоянный множитель. Отожде-
Отождествив такие преобразования в GLB, С), получим группу проективных пре-
преобразований пространства СР1, обозначаемую PGLB, С) = GLB, С)/С*.
Иногда эту группу обозначают через PSLB, С), поскольку ее можно по-
получить и с помощью проективизации группы SLB, С), состоящей из ли-
линейных преобразований пространства С2 с определителем единица.
Как мы видели на странице 65, любое преобразование Мёбиуса абсо-
абсолюта S1^1 можно единственным образом продолжить до изометрии про-
пространства ВТ". Поскольку PGLB, С) действует на 5^ преобразованиями
Мёбиуса (упражнение 2.6.2), это действие можно продолжить на все про-
пространство Н3.
Теорема 2.6.4. Группа сохраняющих ориентацию изометрии про-
пространства Н3 совпадает с PGLB, С). (Изоморфизм устанавливает-
устанавливается с помощью действия на абсолюте 5^ = СР1.)
Впервые эту теорему доказал Пуанкаре с помощью практически тех же
соображений.
Можно дать и другое, внутреннее описание действия PGLB, С) на Н3.
Рассмотрим вещественное векторное пространство V эрмитовых форм
на С2, т. е. пространство отображений Н: С2 х С2 —> С, линейных по
2.6. Комплексные координаты на трехмерном гиперболическом пространстве 103
второй переменной и удовлетворяющих соотношению
) = H(v,w),
где v, w € С2. В каноническом базисе матрица эрмитовой формы имеет вид
П? §). где г, s € Е, a z € С. Поэтому размерность пространства V равна
четырем.
Определитель матрицы (? f) Равен rs ~ г^>так что функция det являет-
является квадратичной формой на V. Сигнатура этой формы равна A,3), так как,
например, матрицы @ i)> (о _i)> (i о) и (i ~о) образуютортонормиро-
ванный базис. Поэтому V с квадратичной формой -det изоморфно Езл. Из
сказанного в разделе 2.3 следует, что знакоопределенные эрмитовы формы,
взятые с точностью до умножения на ненулевые вещественные константы,
образуют модель пространства Н3!
В этом описании сфера на бесконечности S2^ состоит из эрмитовых
форм ранга один, определенных с точностью до умножения на число. Ка-
Каждой такой форме сопоставим ее ядро, являющееся точкой в СР1; посколь-
поскольку ядро определяет форму с точностью до умножения на число (проверьте
это), мы получаем каноническое отождествление сферы 5^ с СР1.
Теперь определим действие группы GLB, С) на V следующим образом:
преобразование А € GLB, С) переводит форму Н е V в форму А(Н), опре-
определенную равенством A(H)(v, w) =H(Av, Aw). Это действие с точностью
до множителя сохраняет форму —det (преобразование А умножает опре-
определитель каждой формы из V на |deti4|2). Поэтому индуцированное про-
проективное преобразование на V/Ш* является изометрией пространства Н3
(это обсуждалось на с. 69). Эта изометрия не меняется при умножении
преобразования А на скаляр, так что в результате мы получаем действие
группы PGLB, С) изометриями на пространстве Н3. Кроме того, возникает
и действие PGLB, С) на абсолюте 5^ = СР1.
Задача 2.6.5 (действие GLB, С) на абсолюте), а) Покажите, что дейст-
действие преобразования А € GLB, С) на СР1 в терминах описанного выше отожде-
отождествления совпадает (в однородных координатах) с умножением на А~х. Все ли
дробно-линейные преобразования можно получить таким способом?
б) Используя пункт а, покажите, что группа PGLB, С) совпадает с группой
сохраняющих ориентацию изометрии пространства Н3. (Указание: сохраняющие
ориентацию изометрии пространства И3 действуют просто транзитивио на тройках
различных точек абсолюта. Проверьте, написав явную формулу, что то же самое
верно и для действия проективных преобразований на СР1.)
в) Если форма Н € V представляет точку в V/W, лежащую за абсолютом, то
сигнатура Н равна A, 1), т. е. форма Н не определена. Опишите множество век-
векторов из С2, изотропных относительно формы Н. Покажите, что образ множества
изотропных векторов при канонической проекции С? на СР1 — это окружность.
104
Глава 2. Гиперболическая геометрия и ее друзья
2.7. Геометрия трехмерной сферы
105
Любую ли окружность на СР1 можно получить таким способом? Покажите, что
при отождествлении СР1 с множеством форм ранга 1 в V формы, отвечающие
Я-изотропиым векторам, будут ортогональны форме Н (относительно скалярного
произведения, ассоциированного с —det). Поэтому множество Я-изотропных век-
векторов совпадает с пересечением гиперплоскости, полярной вектору Н со сферой
на бесконечности.
г) Как преобразуется множество изотропных векторов под действием группы
PGLB, С) ? (Сравните с пунктом а.) Сможете ли вы теперь решить задачу 2.6.3?
Упражнение 2.6.6. Покажите двумя способами, что группа сохраняющих ори-
ориентацию изометрий пространства W совпадает с PGLB, R) = PSLB, Щ. (Ука-
(Указание: A) Используйте то, что PGLB, R) является подмножеством PGLB, С),
сохраняющим вещественные прямые. B) Замените в предыдущих рассуждениях
эрмитовы формы на С? квадратичными формами на R2.)
Упражнение 2.6.7 (классификация с помощью следа). С помощью инвари-
инварианта tr2 Л/det А определите, к какому типу (эллиптический, гиперболический или
параболический) принадлежит сохраняющее ориентацию движение Н3, предста-
представленное матрицей А € GLB, С). (Указание: можно считать, что det Л = 1 и что
после подходящего сопряжения А записана в жордановой нормальной форме, т. е.
является либо диагональной матрицей, либо матрицей ( g j J.) Пусть А € GLB, С)
представляет гиперболическую или эллиптическую изометрию. Как в терминах ма-
матрицы А найти ось этой изометрий? А угол поворота эллиптической изометрий?
Чему равен след вращения второго порядка?
Задача 2.6.8 (комплексная тригонометрия). Множество ориентируемых
прямых в Н3 несет на себе структуру двумерного комплексного многообразия: а
именно, оно диффеоморфно (СР х СР1) \ Д, где Д —диагональ {(z, z): z € СР1}.
Выведите формулы геометрии прямых в И3, решив следующие задачи.
а) Обозначим через W векторное пространство линейных преобразований С2 с
нулевым следом. Покажите, что неориентированные прямые в Н3 взаимно одно-
однозначно соответствуют таким одномерным подпространствам пространства W, нену-
ненулевые представители которых лежат в GLB, С). (Указание: см. упражнение 2.6.7.)
б) Рассмотрим на пространстве W скалярное произведение, ассоциированное
с формой —det; оно имеет вид А ¦ В = | irAB. Используя предложение 2.5.4 и
упражнение 2.6.7, объясните, как связаны скалярное произведение двух единич-
единичных векторов А к В и взаиморасположение прямых, заданных этими векторами
(сравните с предложением 2.4.5).
в) Выведите формулу, связывающую тройку прямых в И3 с двойственной трой-
тройкой их общих перпендикуляров. Эта формула дает удобное обобщение многих фор-
формул из раздела 2.4: например, можно получить сферические формулы, рассмотрев
три прямые в И3, пересекающиеся в одной точке.
г) Интерпретируйте W П SLB, С) как множество ориентированных прямых
в Ег. Уточните результаты пунктов баев случае, когда рассматриваемые прямые
ориентированы.
Задача 2.6.9 (утверждения для следов преобразований), а) Покажите,
что для любых матриц А, В & SLB, С) справедлива формула:
trAB + tr AB'1 =trAtrB.
(Указание: используйте то, что А — корень своего характеристического много-
многочлена.)
б) Покажите, что след любого элемента группы, порожденной матрицами Аи В,
является многочленом от trA, trB и trAB.
в) Пусть х, у и z — такие комплексные числа, что симметрическая матрица
1 х z\
х 1 у)
Z У I/
X
Z
невырождена. Покажите, что в SLB, Q существуют такие матрицы А и В, что
trA = 2x, trB — 2у и tr AB = 2z, и подгруппа группы SLB, С), порожденная ма-
матрицами А к В, определена однозначно с точностью до сопряженности.
(Указание: эту матрицу можно считать матрицей Грама тройки единичных век-
векторов из пространства W, введенного в задаче 2.6.8, причем эти векторы можно
выбрать так, чтобы они представляли некоторые повороты a, b и с на угол д.
Если матрица невырождена, то векторы составляют базис; используйте это, чтобы
объяснить однозначность (с точностью до сопряжения) группы G, порожденной а,
b и с. Далее, пусть А = be и В = са. Докажите, что группа, порожденная А к В
имеет индекс 2 в группе G и что она однозначно (с точностью до сопряженности)
определена.)
г) Что произойдет, если матрица из пункта в окажется вырожденной?
д) Покажите, что след любого элемента группы, порожденной матрицами А, В
и С, является многочленом от следов матриц А, В, С, АВ, ВС, СА и ABC. На самом
деле, и первых шести следов почти хватает: покажите (выразив tr(ABCJ через
эти величины), что tr ABC удовлетворяет квадратному уравнению, коэффициенты
которого выражаются через оставшиеся шесть следов, причем trACB является
вторым корнем этого уравнения.
е) С помощью п. в найдите новое доказательство существования и единствен-
единственности прямоугольного шестиугольника с заданными тремя попарно непересекаю-
непересекающимися сторонами (см. упражнение 2.4.11).
2.7. Геометрия трехмерной сферы
Так же, как окружность и двумерная сфера, трехмерная сфера — очень
круглый объект. Но некоторые ее красивые классические свойства нелегко
угадать, глядя на ее маломерных сестер.
Трехмерную сферу проще всего определить как единичную сферу {х\ +
+ х\ + х\ + х\ = 1} в четырехмерном пространстве, но большинству людей
увидеть это множество не так уж и просто. С помощью стереографической
проекции (с. 59) можно представить S3 в виде Й3 = R3 U {оо}. Трехмерная
106
Глава 2. Гиперболическая геометрия и ее друзья
сфера при этом станет более осязаемой и даже сохранит некоторые черты
своей геометрии: например, окружности и сферы останутся круглыми. Но
теряется часть симметрии: Й3 недостаточно круглое, и объекты одинако-
одинакового размера в 53 перестают быть такими в R3. Эти недостатки можно
преодолеть, представив, как выглядят движения 53 в модели Й3.
Отождествив R4 с С2, мы получим качественно новую картину. Взяв гх
и z2 за координаты в С2, перепишем уравнение единичной сферы в виде
|Z||2 + |z2|2 = 1. Каждая комплексная прямая (т. е. одномерное подпро-
подпространство в С2) пересекает S3 по большой окружности, называемой
окружностью Хопфа. Поскольку ровно одна окружность Хопфа прохо-
проходит через каждую точку 53, эти окружности заполняют всю трехмерную
сферу. При этом окружности Хопфа взаимно однозначно соответству-
соответствуют комплексным прямым в С2, т. е. точкам римановой сферы СР1 = <С.
Образно говоря, трехмерная сфера является двумерной сферой, точки
которой — окружности. Формально получается расслоенное простран-
пространство р: S3 —*• 52 со слоем S1. (Мы определим и подробно обсудим
расслоенные пространства в разделе 3.6, но основная идея состоит в
том, что часть S3, проецирующаяся на произвольную маленькую окрест-
окрестность 52, имеет структуру декартова произведения этой окрестности на S1.)
Эта структура традиционно называется расслоением Хопфа, хотя в те-
теории гомотопий слово «расслоение» означает более общее понятие, чем
расслоенное пространство.
На рис. 2.31 показано, как расслоение Хопфа выглядит в стерео-
стереографической проекции. Вертикальная ось изображает пересечение S3 с
комплексной прямой z{ — 0, горизонтальная окружность — пересечение с
2г = 0. Множество {|z2| < а}, где 0 < а < 1 является полноторием, со-
содержащим окружность 22 = 0. Его граница {|z2| = а} — это тор вращения,
заполненный окружностями Хопфа. Каждая из этих окружностей один
раз обмотана вокруг zx-окружности и один раз — вокруг z2-окружности.
С помощью подобия любой тор вращения в R3 можно превратить в
тор {|za| = а}. Но тот факт, что любой тор вращения имеет обмотку
окружностями такого вида, кажется настолько удивительным, что этим
окружностям дали специальное название: окружности Виларсо.
Упражнение 2.7.1 (расслоение Хопфа). а) Покажите, что для любого t€ R
отображение gt: 53 —>¦ S3, заданное умножением на е", является изометрией, со-
сохраняющей расслоение Хопфа. Отсюда следует, что у трехмерной сферы существу-
существуют изометрии, не имеющие выделенной оси: в каждой точке это движение выглядит
точно так же, как и в любой другой. Это показывает, что сфера 53 «более круглая»,
чем S2. Однопараметрическое семейство {gt} называется "потоком Хопфа.
б) Покажите, что любые две окружности Хопфа С и С' параллельны, т. е.
относительно метрики пространства S все точки окружности С находятся на оди-
одинаковом расстоянии от С.
2.7. Геометрия трехмерной сферы
107
Рис. 2.31. Расслоение Хопфа. Трехмерная сфера |z(|2 + |z2|2 = 1 расслаивает-
расслаивается над сферой Римана. Слоями служат большие окружности, заданные уравнением
Zi/z2 = const. Каждый тор вида {|z2| = а} (при 0 < а < 1) совпадает с тором вида
{|Z]| — b} и делит S3 на два полиотория (в стереографической проекции одно из иих
содержит бесконечно удаленную точку).
в) Покажите, что метрика пространства СР1 = 52, индуцированная отобра-
отображением Хопфа, является стандартной метрикой сферы. Куда переходят большие
окружности при этом отображении?
Как и окружность, трехмерная сфера является топологической группой.
Проще всего это увидеть с помощью кватернионов, являющихся рас-
расширением комплексных чисел. Мы потратим немного времени на изучение
кватернионов, так как и в дальнейшем нам представится случай ими вос-
воспользоваться.
Пространство Ж кватернионов — это просто R4 с некоторым некомму-
некоммутативным умножением Ж х Ж —> Ж'. Это умножение билинейно над М,
так что его достаточно определить на базисе пространства Ж. Базис обыч-
обычно обозначают через {1, /, /, k}, а умножение в этом базисе устроено так:
1 — это единица алгебры, а
// = k = —ji, jk = / = —kj, ki = / = —ik.
Подпространство, порожденное единицей 1, отождествляют с R, а его эле-
элементы называют вещественными; подпространство R/ и- R/ + R& назы-
называют пространством чисто мнимых кватернионов. Легко видеть, что
умножение в Ж ассоциативно, но ие коммутативно, и что R является цен-
центром Ж (так что структура Ж как кольца определяет его структуру как
вещественного векторного пространства). Кватернион является чисто мни-
мнимым, если его квадрат — вещественное неположительное число (поэтому
108
Глава 2. Гиперболическая геометрия и ее друзья
структура кольца определяет и разбиение на вещественное и чисто мнимое
подпространства).
Упражнение 2.7.2. Покажите, что любой автоморфизм кольца Ж является
линейным отображением (в отличие от поля С, где много и других автоморфизмов).
Кватернион q = а — Ы — с/ — dk называется сопряженным к кватер-
кватерниону q = а + Ы + с/ + dk. Число qq вещественно и положительно, ква-
квадратный корень из него называется модулем, или нормой, кватерниона q
и обозначается \q\. Эта величина совпадает с нормой q как вектора из Е4.
Кватернионы, норма которых равна единице, называются единичными
кватернионами. Любой ненулевой кватернион обратим: q~l = \q\~2q\ по-
поэтому Ж является телом. Для любых кватернионов р и q выполнены
равенства ~pq = qp и \pq\ = \p\ \q\. Поскольку множество единичных ква-
кватернионов образует трехмерную сферу S3 с Е4, мы получаем первое утвер-
утверждение следующей теоремы:
Теорема 2.7.3 (групповая структура трехмерной сферы). Трехмер-
Трехмерная сфера является некоммутативной группой с центром {±1}. Ле-
Левое и правое умножение задают действие S3 на себе изометриями,
сохраняющими ориентацию. Сопряжение с помощью элемента груп-
группы S3 также является изометрией, сохраняющей ориентацию и,
кроме того, переводящей в себя каждую двумерную сферу с центром
в точке 1. Факторпространство 53/{±1} изоморфно группе SOC)
изометрий сферы S2, сохраняющих ориентацию.
Доказательство. Расстояние между двумя точками на сфере S3 пол-
полностью определяется нормой разности между ними. Поскольку левое или
правое умножение на единичный кватернион сохраняет норму, оба отобра-
отображения являются изометриями. Так как сфера S3 связна, то по непрерыв-
непрерывности они сохраняют и ориентацию.
Сопряжение также является изометрией; оставляя на месте точку 1, оно
должно сохранять и множество точек, равноудаленных от 1, т. е. сопряже-
сопряжение сохраняет двумерные сферы.
Действие S3 на этих сферах сопряжениями определяет гомоморфизм
р: S3 —> SOC), причем его ядро лежит в центре S3; сюръективность про-
проверяется в упражнении 2.7.4. 12.7.31
Упражнение 2.7.4 (вращение сферы S с помощью кватернионов). Пусть
S2 — сфера чисто мнимых единичных кватернионов, а г + р — единичный кватерни-
кватернион с вещественной частью г и мнимой р. Покажите, что сопряжение кватернионом
г + р поворачивает S2 на угол 2arctg(|p|/|r[) вокруг оси, проходящей через р.
(Указание: для начала предположите, что г = cos 9, р — i sin 9. Распространите ре-
результат иа произвольное р, показав, что с помощью сопряжения точку i можно
перевести в любую точку сферы S2.)
2.7. Геометрия трехмерной сферы
109
Кватернионное и комплексное описания сферы 53 можно объединить.
Рассмотрев Л? как (левое) комплексное векторное пространство, заметим,
что умножение на кватернион / слева совпадает с умножением на ком-
комплексное число /; при этом векторное поле Х/(р) = ip для любого р € S3
определяет на S3 поток Хопфа. Это еще более симметричное описание,
поскольку / ничем не выделяется среди других кватернионов: вместо / мож-
можно взять любой чисто мнимый единичный кватернион и с его помощью
определить комплексную структуру в Jf (сравните с упражнением 2.7А).
Поэтому на трехмерной сфере есть много различных потоков Хопфа (соот-
(соответственно, и много слоений Хопфа). В частности, рассмотрев три взаимно
ортогональных векторных поля Х{, X/ и Xk, получим три взаимно перпен-
перпендикулярных семейства окружностей Хопфа.
Упражнение 2.7.5. Попробуйте понять, как выглядят три ортогональных слое-
слоения Хопфа. Используйте стереографическую проекцию, как на рис. 2.31, располо-
расположив точку 1 € Ж в начале координат, a i, / и k — на трех взаимно перпендикулярных
осях.
Групповую структуру на S3 можно описать и по-другому, используя уни-
унитарные преобразования пространства С2. Унитарными преобразовани-
преобразованиями называются комплексные линейные преобразования С2, сохраняющие
эрмитову форму (Zi, z2) • (w\, w2) = Z\W\ + z2w2. Здесь снова просматри-
просматривается аналогия с окружностью: группа SOB) ортогональных линейных
преобразований евклидовой плоскости, имеющих определитель 1, действу-
действует на S1 просто транзитивно. Зафиксировав любую точку х 6 51, отожде-
отождествим SOB) с 51 с помощью отображения, переводящего g.e SOB) в
g(x)eSl.
Точно так же группа SUB) унитарных преобразований пространства С2,
имеющих определитель 1, просто транзитивно действует на 53, и зафикси-
зафиксировав точку х € 53, получим отождествление SUB) = 53. Если х = A, 0) б
б 53 с С2, то точка (zi, z2) € S3 отождествляется с матрицей
fzx -z2\
\z2 zx)'
Упражнение 2.7.6. Умножение слева на заданный чисто мнимый единичный
кватернион определяет комплексную структуру на Ж. Покажите, что умножение
справа на произвольный кватернион определяет комплексно-лииейное отображе-
отображение (относительно этой структуры). Покажите, что умножение справа на единич-
единичный кватернион является унитарным отображением. Тем самым, снова получено
. отождествление SUB) es S3, которое превращает 53 в группу, сохраняющую одно-
одновременно все комплексные структуры, определенные умножением слева на чисто
мнимые единичные кватернионы.
С этой точки зрения можно установить и связь групповой структуры 53 с
геометрией 52. Каждый элемент SUB), действуя на 53 изометрией, перево-
переводит слой расслоения Хопфа снова в слой. Поэтому его действие опускается
no
Глава 2. Гиперболическая геометрия и ее друзья
на факторпространство, порождая проективное преобразование простран-
пространства СР1, которое одновременно является и изометрией сферы S2. Проек-
Проективное преобразование пространства СР1, рассматриваемое как отображе-
отображение сферы 52, сохраняет ее ориентацию, так что получается гомоморфизм
SUB) —* SOC). Элемент SUB) индуцирует на СР1 тождественное ото-
отображение тогда и только тогда, когда он действует в С2 умножением на
скаляр. Поскольку этому условию удовлетворяют только элементы ± Id,
получаем гомоморфизм PSUB) -> SOC), где PSUB) = SUB)/{±Id}.
Проверьте, что это отображение сюръективно, а следовательно, является
изоморфизмом.
Упражнение 2.7.7. Топологически PSUB) совпадает с S3/{±1} =RP3. По-
Постройте явное соответствие между КР3 и SOC); представьте для этого RP3 в виде
единичного шара в R3, противоположные точки границы которого отождествлены.
(Указание: пусть 0 € S2 и г€ [0, 1]. Рассмотрите поворот на угол %г вокруг оси,
содержащей в.)
Другой интересный вопрос об S3: как устроена группа ее движений.
Действия 53 на себе левыми и правыми сдвигами коммутируют, формула
т(?. h)(x)=gxh-{
определяет гомоморфизм х: 53 х 53 —> SOD). По теореме 2.7.3 для любого
ортонормированного репера с началом в точке 1 существует преобразо-
преобразование х(Л, Л), переводящее его в любой другой репер с началом в той же
точке. Последующее применение преобразования вида ~z(gh~\ 1) приводит
нас к произвольному ортонормированному реперу с началом в любой точ-
точке. Поэтому х является сюръективным гомоморфизмом с ядром {±A, 1)},
так что получается изоморфизм
B.7.8)
SOD) = (S3 х 53)/Z2,
где Z2 — циклическая группа порядка два.
Как получилось, что группа изометрий столь круглого пространства,
как 53, оказалась почти прямым произведением? Чтобы понять это, по-
посмотрим более внимательно на природу левого и правого умножения.
Для любого элемента g e S3, не равного ±1, преобразование x^gx
включается в единственный поток Хопфа, порожденный полем х н-> рх, где
р — единичный кватернион, пропорциональный мнимой компоненте ква-
кватерниона g. Аналогично, для любого элемента h € S3, не равного ±1,
преобразование х у-> xh включается в единственный поток Хопфа, поро-
порожденный векторным полем х н-> хр. Различие левого и правого потоков
Хопфа состоит в том, что окружности вблизи данной навиваются на нее
в разных направлениях (как резьба на шурупах или крышках консервных
банок). Алгебраическими средствами мы уже проверили, что любой левый
поток Хопфа коммутирует с любым правым потоком.
2.7. Геометрия трехмерной сферы
111
Задача 2.7.9. Пользуясь геометрическими соображениями, установите, что ле-
левые и правые потоки Хопфа коммутируют.
а) Представьте себе, что находясь в 53, вы подверглись левому действию од-
нопараметрической подгруппы трехмерной сферы. Опишите свои ощущения (т. е.
движение и скорость поворота).
б) Пусть X и Y — левое и правое поля Хопфа. Покажите, что начав с произ-
произвольной точки пространства 53 и передвигаясь в направлении, перпендикулярном
полям X и Y, можно достичь точки, в которой X = Y. Следовательно, в трехмер-
трехмерной сфере существует целая окружность С+, на которой X = Y. Аналогично, есть
окружность С~, на которой X = —Y, причем d{C+, С) =it.
в) Покажите, что множество точек, удаленных от С* на расстояние а, является
тором, инвариантным относительно X и Y. Кроме того, это геометрическое место
точек, удаленных от С~ на расстояние it — а. Покажите, что потоки X и Y являются
движениями этого тора, и, следовательно, коммутируют. Сравните с рис. 2.31.
г) Пусть умножение на х слева порождает поле X, а на у справа — поле Y.
Интерпретируйте С+ и С~ в терминах элементов SOD), соответствующих х и у.
д) Опишите ощущения обитателя сферы 53, на которого действуют произволь-
произвольной однопараметрической подгруппой группы SOD).
Задача 2.7.10. Опишите гомоморфизм SOD) —> SOC) x SOC) с геометриче-
геометрической точки зрения. (Указание: рассмотрите пространства левых и правых потоков
Хопфа.)
Глава 3
Геометрические многообразия
В первой главе мы познакомились с большим количеством многообразий.
При этом мы больше полагались на нашу интуицию и здравый смысл, чем
на определения. Теперь пришло время как следует заняться исследованием
многообразий.
Как в природе, так и в математике многообразия возникают самыми
разными путями. Очень часто они появляются уже с некоторыми дополни-
дополнительными структурами, и чтобы понять, как устроено данное многообразие,
необходимо «увидеть» эту структуру. В других случаях, мы встречаем мно-
многообразие само по себе, и, найдя подходящую ему структуру, можно под
другим углом зрения исследовать его, связать с другими многообразиями
и в итоге научиться правильно с ним обращаться.
Эти тонкости теории многообразий часто оставались незамеченными на
ранней стадии развития топологии. Несхожие конструкции воспринима-
воспринимались скорее как альтернативный материал для занятий топологией, чем
как строительные блоки для разных важных структур. Одним из замеча-
замечательных достижений топологов за последние сорок лет явилось то, что
они сконцентрировались на этих различиях, которые, как бы это ни про-
противоречило нашей интуиции, действительно имеют место. Так, например,
топологические, кусочно линейные и дифференцируемые многообразия не
являются эквивалентными в размерностях четыре и выше, хотя в размер-
размерностях два и три разница исчезает.
Среди огромного количества всевозможных структур — таких, как ком-
комплексная, гиперболическая, слоения и т. д., большую часть составляют
структуры значительно более требовательные к многообразию, чем диф-
дифференцируемая. «Требовательные» структуры играют очень важную роль
в размерностях два и три.
3.1. Основные определения
Многообразием называется топологическое пространство, локально
устроенное как R". Что именно понимать под словами «локально устроен-
устроенное как R"» зависит от того, какие свойства или структуры пространства
3.1. Основные определения
113
R" мы хотим наследовать. Идея состоит в том, что многообразие скле-
склеивается из нескольких маленьких лоскутков по данной выкройке. При
этом структура, которой наделяется многообразие, задается операционно,
в терминах сохраняющих ее преобразований; разрешая склеивать различ-
различные куски R" только с помощью заданных преобразований, мы получаем
многообразие с искомой структурой. Множество функций склейки должно
удовлетворять следующим естественным требованиям:
Определение 3.1.1 (псевдогруппа). Псевдогруппой на топологиче-
топологическом пространстве X называется множество #, состоящее из гомеомор-
гомеоморфизмов между открытыми подмножествами X, удовлетворяющее следую-
следующим условиям:
а) области определения элементов g е & покрывают X,
б) ограничение элемента g e & на любое открытое подмножество его
области определения также принадлежит <0,
в) композиция g, о g2 двух элементов из У принадлежит # (в тех слу-
случаях, когда она определена),
г) обратное отображение к элементу g e У принадлежит <&,
д) принадлежность к У является локальным понятием, т. е. если
g: U-+V — гомеоморфизм между открытыми подмножествами X, a Ua —
такое открытое покрытие U, что все ограничения g\Uai принадлежат <&, то
Из данных условий вытекает, что каждая псевдогруппа содержит то-
тождественное преобразование каждого открытого множества; псевдогруп-
псевдогруппа называется тривиальной, если она не содержит никаких других эле-
элементов. Другим крайним случаем является самая большая псевдогруппа
Тор на Е", состоящая из всех гомеоморфизмов между открытыми под-
подмножествами R". Многообразие называется топологическим, если его
гомеоморфизмы склейки принадлежат псевдогруппе Тор, т. е. на них не
накладывается никаких дополнительных ограничений. Такое многообразие
локально имеет топологию М" — и не более того.
Для каждой псевдогруппы У на R" можно определить &-многообразие
как многообразие, функции склейки которого принадлежат У. Приведем
более точную формулировку:
Определение 3.1.2 (^-многообразие). Пусть & — псевдогруппа
на R". У-многообразием, размерности п называется топологическое
пространство М, снабженное У-атласом, ^-атлас — это набор из У-со-
У-согласованных карт, области действия которых покрывают М. Картой,
или локальной системой координат, называется пара (U,, ср,-), где
Ut — открытое подмножество пространства М, а ф,: ?/, —> R" — гомео-
гомеоморфизм на образ. Согласованность означает, что если две области карт
(Uh ф,) и (U/, ф/) пересекаются, то функции перехода (функции замены
114
координат)
Глава 3. Геометрические многообразия
Гц = ф; о ф/ ': <fi(U, П U,) -»ср,({/, П
принадлежат псевдогруппе ??.
Пример 3.1.3 (дифференцируемые многообразия). Обозначим че-
через 4>г (г > 1) псевдофуппу, состоящую из всех С-диффеоморфизмов
между открытыми подмножествами Ш". ^'-многообразие называется диф-
дифференцируемым (класса С), или С-многообразием. ^-изоморфизмы на-
называются диффеоморфизмами. С°°-многообразия называются также глад-
гладкими многообразиями.
Соглашение 3.1.4 (все многообразия хаусдорфовы со счетной ба-
базой топологии). За исключением специально оговоренных случаев мы
будем придерживаться предположения, что рассматриваемые многообра-
многообразия являются хаусдорфовыми. В некоторых случаях естественно возникают
и нехаусдорфовы многообразия — см. пример 3.3.5. Будем также считать,
что все многообразия обладают счетной базой топологии. Тогда тополо-
топологические многообразия и многие другие классы многообразий с достаточ-
достаточно большой псевдогруппой if могут быть описаны с помощью конечного
^-атласа (где каждая карта состоит не более чем из счетного числа ком-
компонент). См., например, [Мипбб, с. 20—21].
Два ^-атласа определяют одну и ту же ^-структуру на топологиче-
топологическом пространстве М, если они согласованы, т. е. если их объединение
также является ^-атласом. Согласованность атласов является отноше-
отношением эквивалентности (ср. упражнение 3.1.8, б). Поскольку математики
неодобрительно относятся ко всякого рода неоднозначности, то структура
многообразия часто определяется с помощью одного из следующих двух
утонченных трюков: либо как класс эквивалентности ^-атласов, либо как
максимальный ^-атлас1. Каждый из этих объектов совершенно необъятен
и очень сложен, в противоположность конкретным ^-атласам, которые
обычно не так трудно построить и с которыми просто работать. Но при
этом нужно помнить, что выбор ^-атласа не является существенным для
структуры многообразия.
Столь же важным понятием, как и класс многообразий с ^-структурой,
является класс отображений, сохраняющих эту структуру. Простейшим
случаем является отображение одного ^-многообразия на другое с помо-
помощью гомеоморфизма, который в локальных координатах задается элемен-
элементом псевдогруппы У (в достаточно маленькой окрестности каждой точки).
Такое отображение называется У' -изоморфизмом (или У -автоморфиз-
-автоморфизмом, если это отображение многообразия на себя).
'Максимальный — относительно частичного порядка, заданного отношением вложения.
Для каждого (^-многообразия существует единственный максимальный атлас, который можно
задать, например, как объединение всех согласованных {^-атласов.— Прим. перев.
3.1. Основные определения
115
В целом, если отображение является локальным гомеоморфизмом (на-
(например, накрытие) и локально является элементом псевдогруппы <&, то оно
называется локальным У-изоморфизмом, или локальным гомеоморфиз-
гомеоморфизмом, сохраняющим ^-структуру.
Упражнение 3.1.5 (индуцированная структура). Пусть л: N -* М — локаль-
локальный гомеоморфизм топологического пространства N в ^-многообразие М. Надели-
Наделите N естественной #-структурой так, чтобы отображение -к сохраняло ^-структуру.
(Сравните с рис. 1.4).
Мы встретимся с множеством примеров, когда из двух рассматривае-
рассматриваемых псевдогрупп одна вложена в другую. Например, любая псевдогруп-
псевдогруппа содержится в Тор. Если Ж с &, то «/0°-атлас автоматически явля-
является и ^-атласом, так что каждое «/^-многообразие наделено некоторой
^-структурой. Такая Sf-структура называется 4'-ослаблением «^"-струк-
«^"-структуры, а Ж, в свою очередь, называется Ж-усилением <?-структуры; де-
дело в том, что имеется больше свободы при построении ё?-структур, чем
J^-структур.
Часто требуется исследовать все возможные усиления данной ^-струк-
^-структуры до «^"-структуры. При этом, как правило, полезно считать эквива-
эквивалентными те усиления, которые можно перевести друг в друга ^-автомор-
^-автоморфизмом. Точнее, пусть М — ^-многообразие и g: М —» М —^-автомор-
—^-автоморфизм многообразия М. Если N — ^-усиление ^-структуры на М, заданное
некоторым атласом {(?/,, /,•)}, то можно построить другое Ж -усиление gN,
заданное атласом {(g~l(Ul), frog)}. Таким образом, группа ^-автомор-
^-автоморфизмов многообразия М действует на множестве всех J^-усилений на М.
Отождествляя yv с gN для всех автоморфизмов g и всех yv, получаем
множество J^-усилений ^-структуры на М с точностью до if-авто-
if-автоморфизмов.
Пример 3.1.6 (сглаживание). Пусть & = &г (г< оо) и Ж = ^'со. То-
Тогда можно рассмотреть вопрос о ^""-усилениях, или сглаживаниях, дан-
данного С-многообразия М. Уитни [Whi36] доказал, что каждое многообразие
М имеет ровно одно (с точностью до С-диффеоморфизмов) сглаживание.
Менее формально это означает, что на каждом С-многообразии имеется •
ровно одна гладкая структура. Поэтому во многих случаях можно игнори^
ровать различие между дифференцируемой и гладкой структурами.
Вопрос о сглаживании топологических многообразий {& = Тор и
jrif = <У'°°) не так прост. Милнор [МП56] привел поразительный при-
пример нескольких неэквивалентных сглаживаний 57 (как топологического
многообразия). После появления этих экзотических сфер Милнора были
найдены как другие многообразия с неэквивалентными дифференцируе-
дифференцируемыми структурами, так и многообразия, вообще не допускающие никакой
дифференцируемой структуры.
116
Глава 3. Геометрические многообразия
Как уже было упомянуто, в малых размерностях это различие исчезает:
каждое двух- или трехмерное топологическое многообразие допускает ров-
ровно одну (с точностью до диффеоморфизма) дифференцируемую структуру.
См. раздел 3.10 и [МипбО].
Иногда полезно рассматривать другое отношение эквивалентности на
множестве всех Ж -усилений, которое возникает из действия некоторой
собственной подгруппы группы всех ^-автоморфизмов, и, следователь-
следовательно, тоньше только что описанного. Важный пример доставляет определе-
определение 4.6.4 (пространство модулей и пространство Тейхмюллера). Но пока
обратное не оговорено специально, при изучении усилений структуры бу-
будет рассматриваться именно отношение эквивалентности, полученное из
действия всей группы ^-автоморфизмов.
Мы не собираемся излагать полную теорию ^-структур и множество
красивых результатов и вопросов, связанных с ними, а сконцентрируем
наше внимание на изучении только малого класса жестких псевдогрупп.
Вместо обширной теории ниже приводится ряд примеров, большая часть
которых будет задействована в дальнейшем. За более подробным иссле-
исследованием псевдогрупп можно обратиться к книге [Нае58].
Пример 3.1.7 (вещественно-аналитические многообразия). Рас-
Рассмотрим псевдогруппу '&" вещественно-аналитических диффеоморфизмов
между открытыми подмножествами R". Такое ^""-многообразие называет-
называется вещественно-аналитическим многообразием. Вещественно-анали-
Вещественно-аналитические диффеоморфизмы однозначно определяются своим ограничением
на любое непустое открытое связное множество; это будет существенно
при изучении отображения развертки в разделе 3.4. Есть очень глубокая
теорема о том, что каждое гладкое многообразие имеет единственную ве-
вещественно-аналитическую структуру (см. [Whi36]).
Дифференцируемость и аналитичность являются локальными свойства-
свойствами, поэтому убедиться в том, что ^°° и "й*0 являются псевдогруппами
можно непосредственной проверкой. Однако другие интересные свойства,
которых можно ожидать от функций перехода, не являются локальными.
Поэтому, определяя псевдогруппу с подобными свойствами, нужно быть
чуть более внимательными при проверке условия 3.1.1, д.
Упражнение 3.1.8. а) Докажите, что для каждого множества #Ь-гомеомор-
физмов между открытыми подмножествами X существует единственная минималь-
минимальная псевдогруппа^ на X, содержания%• В этом случае говорят, что &о порожда-
порождает &'. (Как правило, мы начинаем с множества %, отвечающего всем условиям
определения 3.1.1, кроме локальности.)
б) Зачем вообще нужно условие 3.1.1, д? (Указание: рассмотрите множе-
множество #Ь. состоящее из ограничений параллельных переносов в К на открытые
подмножества Е. Докажите, что для %-атласов на S1 согласованность не будет
отношением эквивалентности.)
3.1. Основные определения
117
Пример 3.1.9 (слоения). Запишем R" как произведение R"~* х R* и
обозначим через & псевдогруппу, порожденную теми диффеоморфизмами
Ф (между открытыми подмножествами R"), которые сохраняют горизон-
горизонтальные слои, т. е. имеют вид
где х S R""*, у € R*. Псевдогруппа & состоит из тех диффеоморфизмов
между открытыми подмножествами R", для которых в каждой точке левый
нижний (п — k) х k блок матрицы Якоби состоит из нулей. Соответствую-
Соответствующая ^-структура называется слоением коразмерности k (или размерности
(я — /г)). Чтобы наглядно представить себе слоение, нужно рассматри-
рассматривать не сами локальные карты, а прообразы горизонтальных сомножителей
j?(n-ft) x ^уу^ КОТорые после склейки образуют на всем многообразии слои
или листы данного слоения.
Одномерные слоения существуют на очень многих многообразиях: с
любым векторным полем без нулей ассоциировано слоение его фазовых
кривых. Одним из примеров является расслоение Хопфа сферы S3, изо-
изображенное на рис. 2.31. В этом случае каждый лист является замкнутой
кривой, но, вообще говоря, листы могут завиваться в многообразии самым
причудливым образом. Вот один из примеров.
Упражнение 3.1.10 (иррациональная обмотка тора). На торе T2 = R2/Z2
рассмотрим постоянное векторное поле Х(х, у) = A, а). Фазовые кривые этого
поля являются образами прямых у = ах + уо на торе. Докажите, что листы данио-'
го слоения топологически являются окружностями, если а рационально, и всюду
плотны в торе, если а иррационально. Какому значению а соответствуют окруж-
окружности на рис. 2.31?
На торе есть и много других слоений. Например, факторпространство
К2 \ {0} по действию гомотетии с центром в начале координат топологиче-
топологически является тором. Так как слоение Ш2 \ {0} горизонтальными прямыми
переходит при гомотетии в себя, мы получаем слоение и на факторпро-
странстве (см. рис. 3.1).
Упражнение 3.1.11 (слоение Риба). Перенесите конструкцию рис. 3.1 в раз-
размерность три, т. е. начните со слоения R3 \ {0} горизонтальными плоскостями.
Каким будет факторпространство? Дайте качественное описание листов на фак-
торпространстве; докажите, что один из листов является тором. Разрезав многооб-
многообразие по этому тору, получим два полнотория, которые можно вновь склеить' так,
чтобы получить сферу S (в соответствии с рис. 2.31). Какова гладкость постро-
построенного слоения на S ?
Открытие этого слоения [Ree52] было своего рода неожиданностью —
до этого не было известно ни одного слоения S3 двумерными поверхно-
поверхностями. Позднее выяснилось, что слоения коразмерности один — типичное
явление; Ликориш [Lic65] и Новиков [Nov65] доказали, что такие слоения
118
Глава 3. Геометрические многообразия
Рис. 3.1. Слоение на торе, (а) Горизонтальное слоение сохраняется при гомотетии
х t—* 2х. (б) Слоение, полученное на факторпространстве (тор). Два листа этого слое-
слоения являются окружностями, и, следовательно, компактами; оии изображены жирными
линиями. Остальные листы (два из которых показаны на рисунке) завиваются вокруг,
накручиваясь на эти окружности.
существуют на любом ориентированном трехмерном многообразии, а Вуд
[Woo69] обобщил этот результат на неориентируемый случай. Вообще го-
говоря, на многообразии произвольной размерности слоение коразмерности
один существует тогда и только тогда, когда его эйлерова характеристика
равна нулю (см- [Thu76]). Родственные результаты о слоениях коразмер-
коразмерности большей единицы можно найти в [Нае58] и [Thu74].
С другой стороны, Хефлигер [Нае58] доказал, что никакое слоение на
S3 не может быть вещественно-аналитическим, а Новиков [Nov65] дока-
доказал, что каждое слоение коразмерности один на S3, так же как и на многих
других трехмерных многообразиях, имеет замкнутый слой, являющийся то-
тором1. Габай [Gab83, Gab87] построил слоения без замкнутых торических
листов на многих трехмерных многообразиях (не отвечающих условиям
теоремы Новикова). У этих результатов есть интересные для топологии
трехмерных многообразий следствия.
Пример 3.1.12 (многообразия с мерой). Диффеоморфизмы между
открытыми подмножествами Е", сохраняющие л-мерную меру Лебега, или
объем, образуют псевдогруппу Vol. Многообразие с Vol-структурой назы-
называется многообразием с мерой, так как на нем есть естественная мера.
'Точнее, любое слоение коразмерности один на трехмерном многообразии с нестягиваемым
универсальным накрытием имеет хотя бы один замкнутый лист, причем если данное слоение
ни в каком открытом подмножестве тотального пространства не является гладким рассло-
расслоением с компактным слоем, то один из замкнутых листов является тором, ограничивающим
компоненту Риба.— Прим. перев.
3.1. Основные определения
119
Упражнение 3.1.13 (векторные поля на плоскости, сохраняющие пло-
площадь). Векторное поле называется сохраняющим площадь, если его фазовый по-
поток сохраняет площадь. Докажите, что векторное поле, полученное поворотом на
к/2 градиентного поля гладкой функции Е2 -+ R, сохраняет площадь, и что любое
сохраняющее площадь векторное поле на плоскости может быть получено таким
образом.
Задача 3.1.14. Обобщите данный критерий сохранения площади для векторных
полей на произвольной римановой поверхности. (Подсказка: предыдущий крите-
критерий, вообще говоря, локален. Чтобы найти глобальный критерий, надо перейти от
гладких функций / к их дифференциалам df, которые задают замкнутую 1-форму
на всей поверхности. Если поверхность неориентируема, то получается замкнутая
1-форма, подкрученная ориентирующим расслоением1.)
Упражнение 3.1.15 (существование Vol-усиления). Докажите, что струк-
структура любого гладкого многообразия М может быть усилена до Vol-структуры.
(Подсказка: с помощью разбиения единицы склейте глобальную меру на М из ло-
локальных мер Лебега на картах атласа. Докажите, что для любой ограниченной по-
положительной функции /, определенной на открытом подмножестве К", существует
диффеоморфизм ее области определения на некоторое открытое подмножество R"
с якобианом, равным /. Используйте этот факт для нахождения атласа с мерой.)
Задача 3.1.16 (классификация Vol-усилений). Докажите, что два Vol-уси-
леиия дифференцируемой структуры на компактном связном многообразии диф-
дифференцируемо эквивалентны тогда и только тогда, когда многообразие имеет оди-
одинаковый объем (меру) относительно этих усилений. Для доказательства требуется
некоторое знакомство с дифференциальными формами и теоремой де Рама. Дадим
краткий обзор необходимых сведений: '
а) Объем многообразия с мерой является инвариантом относительно Vol-экви-
валеитности.
б) Пусть М — ориентируемое многообразие с мерой, заданной л-формой а. Ес-
Если w —дифференциальная форма, а X — векторное поле, то производная Ли Lxw
измеряет скорость изменения формы w под действием потока векторного поля X.
Точнее,
Tt (ф^*ш>
где <pjj — однопараметрическое семейство преобразований, ассоциированное с по-
полем X. Воспользуйтесь формулой
Lxw = ixdw + dixw,
где ix является внутренним умножением на поле X (т. е. ixw(X\, ..., Хп) =
= w(X, Х\, ..., Хп)), для доказательства того, что для любой (п — 1)-формы C
найдется такое векторное поле X, что L*a = ф.
'То есть 1-форма с коэффициентами в ориентирующем расслоении. Ориентирующее рас-
расслоение на гладком многообразии — это линейное расслоение, функции перехода которого
являются якобианами функций перехода атласа.— Прим. перев.
120
Глава 3. Геометрические многообразия
в) Для любых двух я-форм осо и ai таких, что
/ ою= / ai,
Jm Jm
реализуйте соединяющую их гомотопию а/ = A — /)ао + ta.\ с помощью построения
подходящего одиопараметрического семейства векторных полей Л/.
г) Докажите, что пространство Vol-усилений (с точностью до дифференциру-
дифференцируемой эквивалентности) компактного связного многообразия М параметризуется
положительными действительными числами.
Пример 3.1.17 (комплексные многообразия). В случае четного п
пространство R" можно отождествить с пространством С"/2. Обозначим
через Hoi псевдогруппу, состоящую из биголоморфных отображений от-
открытых подмножеств Сп/2. (Биголоморфным отображением называется
такое голоморфное отображение, для которого существует обратное голо-
голоморфное отображение. Оказывается, что каждый голоморфный гомеомор-
гомеоморфизм является биголоморфным.) Hol-многообразие называется комплекс-
комплексным многообразием (комплексной) размерности л/2. В случае п = 2 та-
такие многообразия называются также римановыми поверхностями.
При п — 2 гомеоморфизм является голоморфным тогда и только тогда,
когда он конформен и сохраняет ориентацию. Таким образом, сохраняю-
сохраняющие ориентацию изометрии модели Пуанкаре пространства ЕР являются
биголоморфными отображениями, и каждая ориентируемая гиперболиче-
гиперболическая поверхность наследует структуру комплексного многообразия.
Стереографическая проекция единичной сферы на С является конформ-
конформным отображением. Отображения, полученные композицией поворотов
сферы и стереографической проекции на С, задают (если только их обла-
области опеделения не лежат в дополении к некоторой точке) атлас для
комплексной структуры на S2. Мы получили комплексное многообразие
СР1 — сферу Римана.
Аналогично, сохраняющие ориентацию изометрии пространства Е2 го-
голоморфны. Отсюда следует, что гиперболическая, евклидова или элли-
эллиптическая структура на любой ориентируемой поверхности может быть
ослаблена до комплексной структуры.
Обратной к этому простому наблюдению является знаменитая теорема
униформизации: любую комплексную структуру на поверхности S мож-
можно усилить до гиперболической, евклидовой или эллиптической структуры,
причем так, что • получится полное метрическое пространство. Это очень
сильная теорема, так как она применима к любой римановой поверхности,
в том числе к незамкнутой или с бесконечным количеством дырок. Тео-
Теорема униформизации, тесно связанная с теоремой Римана, была объектом
особого внимания математиков второй половины XIX в., и здесь конкури-
конкурировали такие «звезды», как Пуанкаре и Клейн.
3.2. Триангуляции и склейки
121
Более того, любая риманова метрика на ориентируемой поверхности S
определяет комплексную структуру на S, так как в окрестности каждой
точки поверхности можно ввести изотермические координаты, т. е. ко-
координаты, в которых метрика имеет вид ds2 = f(u, v)(du2 + dv2); ясно что
функции перехода между двумя такими картами конформны. («Элемен-
(«Элементарное» доказательство существования изотермических координат мож-
можно найти в работе [sC55], а намного более подробное исследование —
в [НбгЭО].) Так как на каждом дифференцируемом многообразии можно
ввести риманову метрику (например, с помощью разбиения единицы), то
на любой ориентируемой поверхности имеется полная риманова метрика
постоянной кривизны. Как и в случае замкнутых поверхностей (см. зада-
задачу 1.3.15), эти три возможные структуры1 взаимно исключают друг друга
на всех поверхностях, кроме поверхностей, гомеоморфных R2, S1 x R или
листу Мёбиуса. На R2, S1 x R и листе Мёбиуса можно ввести как евкли-
евклидову, так и гиперболическую структуры.
Завершим этот раздел некоторыми замечаниями о терминологии, кото-
которая, являясь, впрочем, стандартной, может иногда ввести в заблуждение.
Многообразие с краем (границей), вообще говоря, многообразием не
является; это топологическое пространство локально устроенное так же,
как и полупространство R^. = {(х{, ..., хп) € R": хп > 0}. Это означает,
что каждая точка р многообразия с краем обладает окрестностью, которая
имеет тот же вид, что и окрестность некоторой точки R^, либо внутренней,
либо граничной. Точки, не имеющие таких же окрестностей, как у внутрен-
внутренних точек, образуют край (границу).
Многообразие (без края) называется замкнутым, если оно компакт-
компактно; в противном случае его часто называют открытым. Эти определения
могут и не соответствовать принятым в общей топологии терминам «от-
«открытый» и «замкнутый», но с этим уже ничего не поделаешь.
3.2. Триангуляции и склейки
Как и большинство «сырых» определений, определение 3.1.2 редко ис-
используется непосредственно. Атласы представляют собой достаточно не-
неудобный способ описания многообразия и, как правило, для построения
новых многообразий используются более конструктивные операции, та-
такие как склейка кусков пространства R" или взятие факторпространства
данного многообразия до действию некоторой группы. Так, в разделе 1.3
мы склеивали поверхности из многоугольников, а в разделе 1.4 задавали
трехмерное многообразие с помощью склейки многогранников.
Пока мы имели дело с поверхностями, можно было уверенно опираться
на интуицию. Тем не менее, приобретенного там опыта недостаточно для
1 Имеются в виду гиперболическая, евклидова и эллиптическая структуры.— Прим. перев.
122
Глава 3. Геометрические многообразия
работы со склейками в высших размерностях. Однако в размерности 3
новые трудности все еще можно обойти, сохранив наглядность и при работе
со склейками трехмерных многообразий. В этом и следующем разделах
мы подробно разберем необходимые технические приемы, с тем чтобы ие
возвращаться к ним в дальнейшем.
Рассмотрим сначала склейки симплексов, а затем и склейки выпук-
выпуклых многогранников, что чаще встречается на практике. Напомним, что
п-мерным симплексом а называется выпуклая оболочка п + 1 аффинно
независимых точек у0. vu ..., vn некоторого аффинного пространства (с
необходимостью не менее, чем я-мериого). Выпуклая оболочка какого-
либо подмножества всех вершин {и0, fi, •••. ^я} называется гранью или
подсимплексом симплекса а. Одномерную грань обычно называют ре-
ребром, а нульмерную грань (ее единственную точку) — вершиной. Грань
размерности п — 1 называется фасетой. Внутренность симплекса — это
то, что останется после удаления всех собственных граней; ее можно также
определить как топологическую внутренность симплекса, рассматриваемо-
рассматриваемого как подмножество своей аффинной оболочки.
Симплициальным комплексом называется локально конечная сово-
совокупность ? симплексов (принадлежащих некоторому аффинному про-
пространству), удовлетворяющих следующим двум условиям: любая грань
симплекса из ? содержится в ?, и пересечение двух симплексов из ? либо
пусто, либо является их общей гранью. Объединение всех симплексов
из ? называется полиэдром этого комплекса и обозначается через |?|.
k-остовом комплекса ? называется его подкомплекс, состоящий из
симплексов размерности не больше k.
Если симплициальный комплекс состоит из конечного числа симплек-
симплексов, объединение которых является выпуклым множеством, то мы прихо-
приходим к хорошо известному понятию выпуклого многогранника, опреде-
определенного, например, как выпуклая оболочка конечного числа точек. Говоря
о выпуклых многогранниках мы всегда будем иметь в виду именно это
определение, даже если условие конечности числа симплексов явно не
упоминается.
Для любого отображения вершин симплициального комплекса в аф-
аффинное пространство существует его единственное продолжение до ото-
отображения всего полиэдра, аффинного на каждом симплексе. Такое ото-
отображение называется симплициальным. Вполне естественно считать два
симплициальных комплекса изоморфными, если между ними существует
симплициальный гомеоморфизм.
Комплекс ?' называется подразделением комплекса ?, если их поли-
полиэдры совпадают и каждый симплекс комплекса ?' содержится в некотором
симплексе из ?. Основное достоинство симплициальных комплексов как
чисто технического инструмента состоит в том, что любое непрерывное
отображение полиэдра (скажем, в аффинное пространство) может быть
3.2. Триангуляции и склейки
123
аппроксимировано симплициальным отображением некоторого его подраз-
подразделения, причем это симплициальное отображение принадлежит тому же
гомотопическому классу, что и исходное (см., например, [Mun84, 89—95]).
Самым популярным подразделением является барицентрическое.
Оно индуктивно определяется на /г-остовах. Для того, чтобы подразде-
подразделить /г-мерный симплекс а, сначала подразделяется на симплексы его
(/г — 1)-мерная граница, а потом над каждым из этих симплексов строится
конус с вершиной в центре тяжести а.
Полиэдр симплициального комплекса (как и пространство, ему гомео-
морфное) триангулирован своим комплексом. Точнее, триангуляция
топологического пространства^—это симплициальный комплекс ? вместе
с гомеоморфизмом |?| -+Х; понятия из теории симплициальных комплек-
комплексов переносятся на пространство X с помощью этого гомеоморфизма. Мы
уже использовали триангулированные поверхности в разделе 1.3 (обратите
внимание на рнс. 1.16).
К числу триангулированных пространств принадлежат и пространства,
полученные склейкой симплексов.
Определение 3.2.1 (склейка), п-мерная (кусочно-линейная) склей-
склейка состоит из конечного множества л-мерных симплексов, разбиения всех
фасет этих симплексов на пары (причем каждая фасета входит ровно в
одну пару) и аффинных отображений отождествления между фасетами
каждой пары.
Интерес представляет факторпространство объединения этих симплек-
симплексов по отношению эквивалентности, которое устанавливается отображе-
отображениям отождествления. Иногда склейкой называют само это факторпро-
факторпространство. Наделим его структурой симплициального комплекса, вложив
в некоторое аффинное пространство так, чтобы все симплексы барицен-
барицентрического подразделения исходных симплексов оказались аффинно вло-
вложенными.
Упражнение 3.2.2. Докажите, что такое вложение существует.
Упражнение 3.2.3. При склейке трехмерных симплексов каждое ребро участ-
участвует в точности в двух склейках, соответствующих двум примыкающим к нему
граням. Компонуя их, можно получить цикл из склеек, возвращающийся к исход-
исходному ребру. Допустим, что композиция склеек из этого цикла обращает ориентацию
данного ребра. Дайте описание окрестности неподвижной точки построенного ото-
отображения в факторпространстве.
Возникает вопрос, когда пространство склейки (или, в общем случае,
триангулированное пространство) является многообразием. Упражне-
Упражнение 1.3.2 дает ответ в случае, когда размерность равна двум. Для более
высоких размерностей нам потребуются понятия линка и звезды симплек-
симплекса. Пусть о —симплекс комплекса ?, а Ть ..., xk — симплексы Е, содер-
содержащие а. Для каждого т,- обозначим через о( симплекс, противоположный
124
Глава 3. Геометрические многообразия
ксвт,, т.е. такой, что оПoi = 0 и т,- является выпуклой оболочкой aUа,-.
Липком а (обозначается через Ik а или 1кЕа) называется симшгациаль-
ный комплекс, состоящий из at. Звездой sta симплекса а называется
объединение внутренних точек симплексов т(.
Упражнение 3.2.4 (конус линка). Напомним, что конусом СХ над тополо-
топологическим пространством X называется цилиндр X х [0, 1] со стянутым в точку
верхним основанием X х {1}. Докажите, что если о —/7-мерный симплекс ком-
комплекса S, то sta является окрестностью в |S| произвольной внутренней точки о,
причем звезда sta гомеоморфиа произведению 1У х С\\ка\.
Предложение 3.2.5 (если линки сферичны, то пространство — мно-
многообразие). Пусть X — триангулированное п-мерное пространство.
Если линк каждого р-мерного симплекса гомеоморфен (п — р — 1)-
мерной сфере, то X является топологическим многообразием.
На самом деле, достаточно потребовать, чтобы линки вершин являлись
(п — 1)-мерными сферами.
Доказательство. Из упражнения 3.2.4 следует, что у каждой точки
пространства X есть окрестность вида Dp x CSn~p~l, которая гомеоморф-
на произведению Dp x Dn~p, так как конус над сферой есть шар. Такие
окрестности образуют покрытие X, и, следовательно, пространство X есть
многообразие. 13.2.51
Упражнение 3.2.6. Докажите, что многообразие, полученное при склейке,
является ориентируемым тогда и только тогда, когда при естественной ориентации
граней каждого симплекса все отображения отождествления меняют ориентацию1.
(См. упражнение 1.3.2.)
Естественно было бы предположить, что имеет место и обращение пред-
предложения 3.2.5, но это не так при п ^ 5. Первые контрпримеры были най-
найдены Р. Д. Эдвардсом. Приведенный ниже пример 3.2.11 имеет несколько
другой характер и был обнаружен Кэнноном [Сап79].
(Правильный критерий таков: полиэдр симплициального комплекса
является топологическим многообразием тогда и только тогда, когда линк
каждой клетки имеет гомологии сферы и линк каждой вершины одно-
связен. Доказательство этого факта лежит далеко за пределами нашего
исследования.)
В трехмерном случае ничего подобного не происходит.
Предложение 3.2.7 (в трехмерных многообразиях линки сферич-
сферичны). Трехмерная склейка тогда и только тогда является трехмер-
трехмерным многообразием, когда линк каждой вершины гомеоморфен сфе-
сфере S2.
'Ориентация симплекса индуцирует естественную ориентацию его гранен. Полученное
склейкой многообразие является ориентируемым тогда и только тогда, когда можно так задать
ориентации всех его симплексов максимальной размерности, чтобы все отображения склейки
меняли ориентацию фасет.— Прим. перев.
3.2. Триангуляции и склейки
125
Доказательство. Необходимое условие верно для любых триангулиро-
триангулированных пространств, как уже отмечалось после предложения 3.2.5. Впро-
Впрочем, легко убедиться, что для трехмерных склеек линк любого ребра явля-
является окружностью, так что можно непосредственно воспользоваться самим
предложением 3.2.5.
Для доказательства обратного утверждения нужен некоторый критерий,
отсекающий не-многообразия. В качестве такого критерия рассмотрим ло-
локальную односвязность. Топологическое пространство X называется (ло-
(локально) односвязным в точке х е X, если для любой окрестности U точки
х найдется такая ее меньшая окрестность V с U, что пространство V \ {х}
односвязно. Очевидно, что все многообразия размерности больше двух ло-
локально односвязны во всех точках.
Если X — трехмерная склейка, a v — вершина X, то линк v есть дву-
двумерная склейка, а значит (согласно упражнению 1.3.2, б) и многообразие.
Ясно, что пространство X локально односвязно в точке v тогда и только
тогда, когда линк Iky односвязен. Единственной замкнутой односвязной
поверхностью является сфера S2. Поэтому если линк вершины v отличен
от сферы, то пространство X — не является многообразием. 13.2.71
Даже если трехмерная склейка не является многообразием, из нее мож-
можно сделать многообразие, удалив все вершины, линки которых не сферы.
В точности это мы и проделали в примере 1.4.8. С другой стороны, можно
удалить открытые окрестности всех плохих вершин и получить многооб-
многообразие с краем.
Предложение 3.2.8 (склейка есть многообразие тогда и только
тогда, когда х = 0). Трехмерная склейка X тогда и только тогда
является трехмерным многообразием, когда ее эйлерова характе-
характеристика xW равна нулю. В общем случае, если склейка X имеет k
вершин vx, ..., vk, то
. 1 *
Доказательство. Обозначим через Р, Г и Т число ребер, граней и те-
тетраэдров склейки X. Тогда Г = 2Т, так как каждая грань принадлежит
ровно двум тетраэдрам, а у каждого тетраэдра четыре грани. Заметим так-
также, что
так как каждое ребро вносит в линки вершин два своих конца, каждая
грань— три ребра, каждый тетраэдр — четыре грани.
Из того, что эйлерова характеристика сферы равна двум, а эйлеровы ха-
характеристики остальных замкнутых двумерных поверхностей меньше двух,
126
Глава 3. Геометрические многообразия
следует, что хЩ ^ 0, причем равенство выполняется тогда и только тогда,
когда X — многообразие. j 3.2.8I
До сих пор мы интересовались только склейками симплексов и толь-
только с помощью аффинных отображений. Что получится, если мы станем
склеивать произвольные выпуклые полиэдры с помощью произвольных
непрерывных отображений? Задается ли топология склейки только ее ком-
комбинаторной схемой, или она зависит также и от выбора конкретных ото-
отображений склейки?
Множество вершин выпуклого полиэдра однозначно определяется как
минимальное множество точек, выпуклая оболочка которых совпадает с
самим полиэдром; грань есть такое пересечение выпуклого полиэдра с
полупространством, размерность которого меньше размерности полиэдра.
Грань коразмерности один называется фасетой.
Два выпуклых полиэдра называются комбинаторно эквивалентны-
эквивалентными, если существует сохраняющее инцидентность взаимно однозначное
соответствие между их гранями всех размерностей. Таким образом, их
вершины также находятся во взаимно однозначном соответствии; ребро
одного полиэдра отображается в то ребро другого полиэдра, концы кото-
которого соответствуют его концам, и т. д.
Если а — комбинаторная эквивалентность между полиэдрами Р и Q,
то гомеоморфизм h: P—> Q считается принадлежащим комбинаторному
классу а, если h переводит грань каждой размерности в грань, заданную
эквивалентностью а. Легко видеть, что каждую комбинаторную эквива-
эквивалентность можно реализовать некоторым гомеоморфизмом, но, конечно,
не все гомеоморфизмы определяют комбинаторную эквивалентность.
Зададим конечное число комбинаторных классов (типов) л-мерных вы-
выпуклых полиэдров. Схемой склейки называется разбиение множества фа-
фасет этих полиэдров на пары (так, что каждая фасета входит ровно в одну
пару) вместе с комбинаторными эквивалентностями между фасетами ка-
каждой пары. Склейкой, реализующей данную схему, называется набор вы-
выпуклых полиэдров данных комбинаторных типов вместе с гомеоморфизма-
гомеоморфизмами отождествления граней, реализующими заданные на них комбинаторные
эквивалентности.
Однако нам подходит не любой набор таких гомеоморфизмов — необ-
необходимо еще условие согласованности. Произвольная грань р размерности
п — 2 или меньше является гранью двух или более фасет, и поэтому она
встречается в двух или более парах. При композиции различных отображе-
отображений отождествления грань р склеивается с различными другими гранями.
Легко понять, что всегда будут встречаться такие цепочки отождествлений,
которые отображают грань р на себя. Условие же согласованности форму-
формулируется так: если композиция такой цепочки отображений принадлежит
комбинаторному классу тождественного отображения, то она сама должна
быть тождественным отображением.
3.2. Триангуляции и склейки
127
Упражнение 3.2.9 (стандартная склейка). Барицентрическое подразделе-
подразделение полиэдра определяется так же, как и барицентрическое подразделение сим-
симплекса, причем новые вершины выбираются произвольно среди внутренних точек
соответствующих граней.
а) Воспользуйтесь барицентрическим подразделением для построения гомео-
гомеоморфизма, реализующего данную комбинаторную эквивалентность между двумя
полиэдрами.
б) Докажите, что для заданной схемы склейки построенные таким способом
отображения отождествления отвечают условию согласованности.
в) Наделите факторпространство так определенной склейки структурой сим-
плициальиого комплекса, как в определении 3.2.1 и упражнении 3.2.2.
г) Обобщите предложения 3.2.7 и 3.2.8 на рассматриваемый случай.
Задача 3.2.10 (единственность склейки), а) Докажите, что гомеоморфизм
единичного шара пространства R", тождественный на границе, изотопен тожде-
тождественному отображению. (Подсказка: причешите все косы к одной макушке. Это
называется трюком Александера.1)
б) Докажите, что две склейки, построенные по одной и той же схеме, гомео-
морфны.
Пример 3.2.11 (двойная надстройка пространства Пуанкаре).
Надстройка Y.X топологического пространства X представляет собой
цилиндр X х [0, 1 ] над X, у которого верхнее и нижнее основания (X х {0}
и X х {1} соответственно) стянуты в точки, которые называются верши-
вершинами надстройки. Например, надстройкой л-мерной сферы является
(п + 1)-мерная сфера.
Пусть Я — пространство Пуанкаре додекаэдра из примера 1.4.4, на-
наделенное структурой симплициального комплекса способом упражне-
упражнения 3.2.9. Надстройка пространства Я не является многообразием, так
как линк вершины есть само пространство Р, а оно неодносвязно (см.
доказательство предложения 3.2.7). Но, как это ни странно, оказывается,
что двойная надстройка ?2Я = SSP гомеоморфна S5.
Это показывает, что обращение предложения 3.2.5 неверно, так как
на окружности надстройки (т. е. на надстройке над вершинами первой
надстройки) линки вершин и ребер не являются сферами. Линки вершин
на окружности надстройки гомеоморфны пространству SP, которое одно-
связно, так что это не мешает ?2Я быть многообразием. Линки ребер на
окружности надстройки гомеоморфны пространству Р, которое уже не од-
носвязно, и может показаться, что это препятствует пространству Р быть
многообразием, но оказывается, что дело обстоит не так.
Число различных склеек полиэдров растет очень быстро с ростом числа
фасет.
'Очень советуем заглянуть на с. 93 книги: В. В. Прасолов, А. Б. Сосинский. Узлы, зацеп-
зацепления, косы и тремерные многообразия. М.: МЦНМО, 1997.— Прим. ред.
128
Глава 3. Геометрические многообразия
Упражнение 3.2.12. а) Сколькими способами можно склеить каждую грань
куба с противоположной так, чтобы получить ориентированное трехмерное много-
многообразие?
б) Докажите, что число схем склейки для октаэдра равно 8! • 34/D! • 24) = 8505.
Попробуйте оценить число склеек, приводящих к многообразию (ориентированно-
(ориентированному многообразию).
в) Тот же вопрос для икосаэдра.
В силу симметрии многие различные схемы склеек приводят к гомео-
морфным пространствам; например, в случае икосаэдра это уменьшает чи-
число различных схем примерно в 120 раз. (Так как некоторые склейки сами
обладают симметриями, то реальное число склеек не так сильно уменьша-
уменьшается) . Все же остается огромное количество склеек, про которые нельзя с
уверенностью сказать, являются ли какие-нибудь из них гомеоморфными.
Непохоже, чтобы здесь дело обстояло так же, как и в размерности два,
где очень большое число схем приводит к гомеоморфным многообрази-
многообразиям. Но кто знает? Ясно одно — нам нужно расширить запас технических
средств, позволяющих распознавать и отличать трехмерные многообразия,
заданные разными способами.
3.3. Геометрические структуры на многообразиях
Удобно немного расширить определение ^-многообразия C.1.2), допуская,
что ^ может быть псевдогруппой на произвольном связном многообразии,
необязательно R". Пока псевдогруппа ^ действует транзитивно это не при-
приводит к появлению новых типов многообразий:
Упражнение 3.3.1 (локальность ^-структур). Пусть У — псевдогруппа на
произвольном многообразии Х,а U СХ— произвольное открытое множество обла-
обладающее тем свойством, что любую точку х из X можно некоторым преобразова-
преобразованием из ^ перевести в U. Обозначим через $у псевдоподгруппу, состоящую из
тех элементов 'ё', области определения и области значения которых вложены в U.
Докажите, что каждое ^-многообразие имеет единственное (с точностью до ^-изо-
^-изоморфизма) ^[/-усиление.
Многие важные псевдогруппы возникают из'действий групп на многооб-
многообразиях. Для данной группы G, действующей на многообразии X, обозначим
через ^ псевдогруппу, порожденную ограничениями элементов из G; см.
упражнение 3.1.8, а. Тогда каждый элемент g€& локально совпадает с
некоторым элементом из G: область определения элемента g можно так по-
покрыть открытыми множествами Ua, что g\Ua = ga\u. Лпя некоторых ga e G.
Такие ^ многообразия часто называются (G, Х)-многообразиями.
Пример 3.3.2 (евклидовы многообразия). В случае, когда G есть
группа изометрий евклидова пространства Е", (G, Ея)-многообразие на-
3.3. Геометрические структуры на многообразиях
129
зывается евклидовым, или плоским многообразием. Структуру этих мно-
многообразий мы уже обсуждали на неформальном уровне в разделе 1.1. Как
было замечено в разделе 1.3, из всех компактных двумерных поверхностей
только на торе и на бутылке Клейна можно ввести евклидову структуру, но
на них имеется много таких структур. Мы еще вернемся к исследованию
этого вопроса в примере 4.6.11.
Совсем нетривиальный результат Бибербаха [Biell, Bie 12] утверждает,
что в любой размерности существует только конечное число (с точностью
до гомеоморфизма) компактных евклидовых многообразий, причем каждое
из них допускает конечное накрытие тором той же размерности. Подроб-
Подробнее евклидовы многообразия рассмотрены в разделе 4.2, где упомянутые
результаты будут доказаны.
На рис. 3.2 приведена схема склейки для трехмерного случая, к которой
мы еще вернемся в разделе 4.3 при классификации трехмерных многооб-
многообразий (см. рис. 4.7).
Рис. 3.2. Евклидово трехмерное многообразие. Сначала поставим рядом два оди-
одинаковых куба, у которых на каждой грани проведена средняя линия так, что различные
линии не пересекаются. Теперь склеим одинаково расположенные грани этих кубов с
помощью отражения относительно средней линии этих граней. В итоге мы получим
трехмерное евклидово многообразие.
Упражнение 3.3.3. Докажите последнее утверждение из комментария к
рис. 3.2 по следующей схеме.
а) Докажите, что пространство склейки есть многообразие (обозначим его че-
через М).
б) Найдите группу, состоящую из изометрий пространства Е3, факторпростран-
ство по действию которой есть М. Тем самым будет доказано, что М обладает
евклидовой структурой.
130
Глава 3. Геометрические многообразия
в) Найдите в ией подгруппу конечного индекса, изоморфную Z3. Рассмотрев
факторпространство Е3 по действию этой подгруппы, получим, что М может быть
коиечиолистио накрыто тором (как и положено по теореме Бибербаха).
Пример 3.3.4 (аффинные многообразия). Если G — группа аффин-
аффинных преобразований R", то (G, R")-многообразие называется аффинным
многообразием.
В качестве примера снова рассмотрим гомотетию иа рис. 3.1. Как
факторпространство R2 \ {0} по группе аффинных преобразований (поро-
(порожденной гомотетией), построенный там тор обладает аффинной структурой
(почему?).
Есть и другой способ (принадлежащий Джону Смилли) построения аф-
аффинных структур на торе Т2 с помощью произвольного четырехугольни-
четырехугольника Q на евклидовой плоскости. Склеим противоположные стороны Q с
помощью (сохраняющих ориентацию) преобразований подобия. Так как
подобие сохраняет углы, то сумма всех углов при вершине получивше-
получившегося комплекса равна 2тс, а значит, в некоторой окрестности вершины
есть аффинная структура (почему?). Во втором томе мы увидим, что такие
структуры на торе Т2 тесно связаны с хирургиями Дена на трехмерных
многообразиях.
Дж. П. Бензекри (см. [МП58]) доказал, что из всех замкнутых двумерных
многообразий аффинными являются только торы и бутылки Клейна. Оста-
Остается открытым вопрос: верно ли, что эйлерова характеристика компактного
аффинного многообразия обязательно равна нулю?
Евклидова структура на многообразии автоматически задает и аффин-
аффинную структуру. Бибербах доказал, что замкнутые евклидовы многообразия
с изоморфными фундаментальными группами эквивалентны как аффинные
многообразия. Это будет доказано в теореме 4.2.2.
Пример 3.3.5 (эллиптические многообразия). Если G есть груп-
группа ортогональных преобразований О(я 4- 1), действующая на сфере S",
то (G, S")-многообразие называется сферическим, или эллиптическим.
Пространство Пуанкаре додекаэдра (см. пример 1.4.4) и пространства
линз (см. пример 1.4.6) являются сферическими многообразиями.
Пример 3.3.6 (гиперболические многообразия). Если G есть груп-
группа изометрий гиперболического пространства Ня, то (G, Ня)-многообразие
называется гиперболическим многообразием. Гиперболические поверх-
поверхности обсуждались в разделе 1.2, а трехмерный случай — пространство
Зейферта—Вебера был рассмотрен в примере 1.4.5.
В каждом из трех предыдущих случаев доказательство существования
данной геометрической структуры на многообразии сводилось к доказа-
доказательству того, что у каждой точки есть окрестность, изометричная подходя-
подходящему шару. (Дайте обоснование этому в свете определения 3.1.2.) Именно
3.3. Геометрические структуры иа многообразиях
131
так обстоит дело, когда многообразие является факторпространством Е3,
S3 или И3 по действию группы изометрий.
С другой стороны, если многообразие задано с помощью склейки вы-
выпуклых многогранников (т. е. пересечений замкнутых полупространств,
имеющих непустую внутренность) в Е3, S3 или И3, то проверить суще-
существование структуры можно, убедившись, что для каждого ребра сумма
двугранных углов, примыкающих к нему, равна 2к, а трехгранные углы
правильно смыкаются, образуя сферическую окрестность точки в модель-
модельном пространстве. (На самом деле второе условие следует из первого.)
Условие на ребра были проверены в примерах 1.4.4, 1.4.5 и 1.4.6. Точно
так же можно убедиться, что и многообразие на рис. 3.2 является евклидо-
евклидовым, просто заметив, что ребра куба склеиваются по четыре с двугранными
углами, равными к/2, а трехгранные углы смыкаются группами по восемь
октантов.
Воспользуемся предыдущими замечанием, чтобы наделить гиперболи-
гиперболической структурой некоторые открытые многообразия.
Пример 3.3.7 (дополнение к восьмерке). В примере 1.4.8 было по-
показано, как склейкой двух тетраэдров (без вершин) можно получить про-
пространство, гомеоморфное дополнению к узлу «восьмерка» в сфере S3. Вве-
Введем теперь на этом пространстве гиперболическую структуру.
Будем считать, что данные тетраэдры являются идеальными правиль-
правильными тетраэдрами гиперболического пространства, т. е. правильными те-
трпэлрами с вершинами на бесконечности. С комбинаторной точки зрения
идеальный правильный тетраэдр — это симплекс без вершин; геометри-
геометрически его можно представить как образ в модели Клейна правильного
евклидова тетраэдра, вписанного в единичную сферу. Из соображений сим-
симметрии все двугранные углы такого многогранника равны к/3 (см. рис. 3.3).
Упражнение 3.3.8. а) Обоснуйте комметарий к рис. 3.3, доказав, что угол
между двумя плоскостями в гиперболическом пространстве равен углу между огра-
ограничивающими нх на бесконечности окружностями в модели Пуанкаре.
б) Докажите, что сумма двугранных углов любого (не обязательно правильного)
идеального гиперболического тетраэдра равна 2тс. (Подсказка: стереографически
спроектируйте конфигурацию рис. 3.3 из вершины тетраэдра; тогда три нз четырех
окружностей перейдут в прямые.)
Склеим теперь грани двух данных тетраэдров с помощью гиперболиче-
гиперболических изометрий, сохраняя комбинаторную схему примера 1.4.8. Как уже
было отмечено, при этом ребра склеиваются по шесть, так что сумма дву-
двугранных углов при каждом ребре'равна 2тс. Условие на вершины проверять
не нужно просто потому, что вершин нет.
Выберем в гиперболическом пространстве два смежных идеальных пра-
правильных тетраэдра Г и Г' и пометим их грани и ребра в соответствии с
рис. 1.24, не забыв о согласовании меток на общей грани (назовем ее D).
132
Глава 3. Геометрические многообразия
Рис. 3.3. Правильный идеальный тетраэдр. Двугранный угол многогранника равен
углу между окружностями на абсолюте, органичивающими его грани в модели Пуан-
Пуанкаре (а); для правильного многогранника эти окружности те же, что и в проективной
модели, а значит, все углы равны тс/3 из соображений симметрии (б).
Тогда существует единственная сохраняющая ориентацию гиперболиче-
гиперболическая изометрия, переводящая (в соответствии со стрелками на ребрах)
грань А тетраэдра Т в грань А тетраэдра Г; то же верно и для В и С пар
ребер этих тетраэдров. Факторпространство пространства Н3 по действию
группы G, порожденной этими изометриями, и есть наше многообразие,
причем группа G является представлением его фундаментальной группы.
Этот пример тесно связан с семейством групп, исследованных Бьян-
ки [Bia92]: действительно, принимая за вершины тетраэдра Т точки О,
1, w и w, где w = -| + ^—i — кубический корень из единицы, получим,
что все образующие можно выбрать в группе PSLB, Z[w}) С PSLB, С).
(В действительности G есть подгруппа индекса 12 в PSLB, Z[ay]).) Другое
представление группы G (см. [Mag74, 153—155]) было известно Гизекингу
и содержится в его диссертации, опубликованной в 1912 г.
Впрочем, связь с узлом «восьмерка» является относительно новой. Рай-
ли [Ri!82] и Йоргенсен [Jor77] независимо друг от друга доказали, что на
дополнении к восьмерке имеется гиперболическая структура. Первый из
иих нашел представление фундаментальной группы этого дополнения, а
второй рассмотрел это пространство как расслоение над окружностью со
слоем «проколотый» тор.
Техника, использованная в примере 3,3.7, может показаться слишком
специфической, однако в действительности она применима к дополнениям
многих различных узлов и зацеплений. Сначала необходимо представить
данное дополнение в виде объединения многогранников без вершин, а за-
затем попытаться реализовать их как идеальные гиперболические многогран-
многогранники и склеить вместе так, чтобы получить гиперболическое многообра-
3.3. Геометрические структуры на многообразиях
133
зие. Некоторые исследователи, включая Дарела Купера, Колина Адамса и
Джефа Уикса, реализовали эту схему на компьютере (см. также [Hat83a]).
Конечно, не каждая склейка симплексов приводит к геометрическим мно-
многообразиям.
Пример 3.3.9 (зацепление Уайтхеда). На рис. 3.4 приведены две
плоские диаграммы зацепления Уайтхеда. На это зацепление можно на-
натянуть двумерный клеточный комплекс, который вырезает из дополнения к
зацеплению октаэдр без вершин; см. рис. 3.5 и 3.6. Как и в примере 1.4.8,
из двумерных клеток этого комплекса получаются грани октаэдра, если
разрезать комплекс вдоль стрелок и стянуть каждую получившуюся ком-
компоненту узла в удаляемую вершину.
Рис. 3.4. Зацепление Уайтхеда
Гиперболическую структуру на дополнении можно получить, если про-
произвести склейку на правильном идеальном гиперболическом октаэдре, ко-
который в модели Клейна можно представить как правильный евклидов ок-
октаэдр, вписанный в сферу. Все двугранные углы такого октаэдра равны к/2
(см. комментарий к рис. 3.3), так что ребра (и их окрестности) правильно
склеиваются по четыре. Склейка производится с помощью гиперболиче-
гиперболических изометрий граней октаэдра. Как и раньше, нет нужды заботиться о
вершинах.
Пример 3.3.10 (кольца Борромео). На рис. 3.7 изображены кольца
Борромео — зацепление со многими интересными свойствами; например,
если разрезать любое из колец, оставшиеся два расцепятся. Гиперболиче-
Гиперболическую структуру на дополнении к этому зацеплению можно ввести с помо-
помощью склейки двух идеальных октаэдров. Для этого соединим маленькими
отрезками пары ветвей у каждого перекрестка диаграммы (см. рис. 3.7,
справа) — это будут ребра октаэдров. Граням же соответствуют двумерные
клетки, натянутые на восемь областей (одна из которых неограниченна),
134
Глава 3. Геометрические многообразия
Рис. 3.5. Разрезание дополнения к зацеплению Уайтхеда. Двумерный клеточный
комплекс, натянутый на зацепление Уайтхеда, разрезает дополнение к зацеплению так,
что образуется октаэдр без вершин. В этом комплексе имеется четыре двумерные
клетки, две из которых изображены на данном рисунке; другие две клетки расположены
симметрично. Три одномерные клетки обозначены занумерованными стрелками. Схема
склейки, нарисованная на поверхности октаэдра, приведена на рис. 3.6.
Рис. 3,6. Зацепление Уайтхеда: склейка октаэдра. Здесь изображена поверхность
сферического октаэдра, стереографически спроектированная из одной из его вершин.
(Представьте, что его внутренность находится в полупространстве за плоскостью стра-
страницы.) Склеивая октаэдр по данной схеме, мы получим дополнение к зацеплению
Уайтхеда. Стрелки находятся в соответствии с рис. 3.5, а части поверхности, видимые
на рис. 3.5, изображены здесь тем же цветом.
3.3. Геометрические структуры на многообразиях
135
вырезанных на плоскости тремя окружностями диаграммы рис. 3.7 (слева).
Заметим, что расположение этих областей такое же, как и при стереогра-
стереографической проекции сферического октаэдра из центра его грани. Поэтому
мы можем считать, что каждый октаэдр раздут до полупространства с та-
таким же расположением граней на границе.
Рис. 3.7. Кольца Борромео. Вид на кольца Борромео сверху и сбоку; иа последнем
изображен 1 -остов натянутого иа кольца двумерного комплекса.
Один октаэдр подходит к зацеплению снизу, а второй — сверху, причем
перед соединением с зацеплением каждая грань превращается в шести-
шестиугольник: вершины срезаются, а ребра шестиугольника через одно укора-
укорачиваются и разворачиваются так, чтобы сойтись с вертикальными отрезка-
отрезками. Затем оставшиеся ребра шестиугольника стягиваются в точки, так что
грани снова становятся треугольниками. Каждая грань верхнего октаэдра
склеивается с находящейся прямо под ней гранью нижнего с помощью
поворота на 2к/3; причем направление поворота берется то по часовой
стрелке, то против — как у сцепленных шестеренок.
Чтобы ввести на дополнении гиперболическую структуру, можно вос-
воспользоваться двумя октаэдрами с прямыми двугранными углами (такими
же, как и в предыдущем примере с зацеплением Уайтхеда), так как в по-
полученном комплексе к каждому ребру примыкает по четыре грани.
Определение 3.3.11 (многообразия с геодезической границей).
Можно определять различные геометрические структуры и на многооб-
многообразиях с краем (смотри конец раздела 3.1), рассматривая подходящие
псевдогруппы на модельном многообразии с краем X. Пусть, например,
X — евклидово полупространство, X = E;j". Евклидовым многообразием с
геодезической границей называется произвольное ^-многообразие, где
<S — псевдогруппа, порожденная изометричными гомеоморфизмами между
136
Глава 3. Геометрические многообразия
3.3. Геометрические структуры на многообразиях
137
открытыми подмножествами X. Аналогично определяются эллиптические
и гиперболические многообразия с геодезической границей.
Евклидово (как и эллиптическое или гиперболическое) многообразие с
геодезической границей можно удвоить и получить обычное многообразие
(без края) с той же структурой; для этого достаточно взять два экземпля-
экземпляра этого многообразия и склеить их по тождественному отображению на
границе.
Пример 3.3.12 (гиперболическое многообразие с геодезической
границей). Опять склеим два тетраэдра, но по схеме, отличной от ис-
использованной в примере 3.3.7; см. рис. 3.8.
В
Рис. 3.8. Склейка двух тетраэдров. Два тетраэдра, склеенные по основаниям,
образуют шестигранник. Здесь изображена стереографическая проекция его границы
(сравните с рис. 3.6). Затем шесть граней разбиваются на пары, отмеченные одинако-
одинаковыми буквами и наборами точек. Затем пары склеиваются так, чтобы совпали точки.
(Так как все ребра склеиваются в одно, то для описания склейки нельзя обойтись
нумерованными стрелками, как на рис. 3.6.)
Упражнение 3.3.13. Опишите склейку из примера 3.3.7, воспользовавшись
обозначениями рис. 3.8. В чем отличие этой склейки от предыдущей?
Комплекс К, полученный при этой склейке, имеет только одну вершину,
одно ребро, четыре грани и две трехмерные грани (тетраэдры), так что
его эйлерова характеристика равна 2. Линк вершины есть поверхность
рода два, как легко убедиться непосредственно или применив предложе-
предложение 3.2.8. Как и в примере 3.2.7, можно удалить из К замкнутую «ко-
«коническую» окрестность вершины и получить многообразие М. Однако с
помощью техники примера 3.3.7 нельзя ввести (полную) гиперболическую
структуру на многообразии М, так как для этого потребовалось бы найти
два таких идеальных тетраэдра, у которых общая сумма их двугранных
углов равнялась бы 2тс, что невозможно в силу упражнения 3.3.8, б.
Вместо этого рассмотрим многообразие с краем М, полученное удале-
удалением из К открытой окрестности вершины. Мы введем на многообразии
М структуру гиперболического многообразия с геодезической границей.
Для этого снова рассмотрим правильный тетраэдр с вершинами на еди-
единичной сфере как правильный идеальный гиперболический тетраэдр (в
модели Клейна). Если мы теперь начнем двигать его вершины от центра,
то некоторые части тетраэдра вылезут за границу сферы на бесконечно-
бесконечности. Чтобы снова получить конечный объект, отрежем торчащие «уши»
плоскостями, двойственными к вершинам. Каждая из этих плоскостей пер-
перпендикулярна ребрам, сходящимся в двойственной вершине. В результате
будет получаться многогранник, комбинаторно эквивалентный изображен-
изображенному на рис. 3.9, до тех пор пока ребра тетраэдра не окажутся целиком
за абсолютом — в этом случае наши плоскости пересекутся внутри Н3 и
высекут конечный тетраэдр.
Рис. 3.9. Усеченный тетраэдр. Правильный гиперболический тетраэдр с вершинами
за абсолютом, усеченный плоскостями, двойственными его вершинам, приведен здесь
в проективной модели (слева) и модели Пуанкаре (справа). Все двугранные углы рав-
равны либо 7t/6 (между шестиугольными гранями), либо тг/3 (между шестиугольными и
треугольными).
В нашей, конструкции величина двугранного угла тетраэдра может быть
выбрана произвольно между тс/3 (для идеального тетраэдра) и 0 (для те-
тетраэдра, ребра которого касаются сферы на бесконечности). На рис. 3.9
изображен усеченный тетраэдр с углами тс/6; это то, что нужно для со-
состыковки 12 ребер двух тетраэдров. Склеивая два таких тетраэдра по
схеме рис. 3.8, получаем на многообразии М гиперболическую структуру с
138
Глава 3. Геометрические многообразия
геодезической границей: грани исходных тетраэдров подходят к краю под
прямыми углами.
Многообразие М примера 3.3.12 оказывается гомеоморфным подмно-
подмножеству R3, изображенному на рис. 3.10, чье дополнение в сфере S3 (т. е. три
лаза вместе с внешностью шара и бесконечно удаленной точкой) является
телом с ручками рода 2. Вообще говоря, есть способ попытаться реали-
реализовать подмногообразием в S3 любую склейку на одном многограннике
(без вершин). Он заведомо приводит к успеху, если каждая пара гра-
граней склеивается крест-накрест относительно вершины многогранника; в
обозначениях рис. 3.8 это означает, что одноименные грани примыкают к
вершине, которая помечена одинаково в каждой из них.
Рис. 3.10. Треножник, или скрученная рогатка. Многообразие из примера 3.3.12
похоже на изъеденное червем яблоко, где три лаза, переплетаясь, встречаются в цен-
центре, как показано на рисунке. Эти червоточины образуют тело с ручками в форме
скрученной рогатки, или «Y». См. также рис. 3.14.
Следуя Джорджу Франсису, проиллюстрируем этот метод склейки на
примере 3.3.12с помощью мультфильма из рисунков. Начав с рис. 3.8, уда-
удалим регулярные окрестности ребер и вершин (включая бесконечно удален-
удаленную вершину). Тем самым мы провели на поверхности борозды, соединя-
соединяющиеся друг с другом в ямах (рис. 3.11, слева). Далее ямы превращаются
в кратеры, а борозды становятся все шире и короче, пока не превратятся
в полосы, разделяющие кратеры (рис. 3.11, в центре). Грани становятся
3.3. Геометрические структуры на многообразиях
139
маленькими Т-образными пригорками, единственными возвышениями над
кратерами. Повернув внутреннее кольцо на 2л/3 по часовой стрелке, по-
поставим склеиваемые грани друг против друга (рис. 3.11, справа). Именно
здесь мы пользуемся тем, что каждая пара одноименных граней разделена
единственным кратером (вершиной). Теперь можно начинать клеить.
Рис. 3.11. Приготовления к склейке. Начав с рис. 3.8, удаляем окрестности граней
и вершин, а затем стягиваем грани и переставляем их так, чтобы одноименные грани
располагались друг против друга.
Каждая склейка происходит (как и показано на рис. 3.12) с помощью
наведения моста между противостоящими (одинаковыми) метками. Если
мост вдавить в землю, то в перпендикулярном направлении образуется
подземный переход. Общий вид местности после проведенных работ по-
показан на рис. 3.13 слева. Девять исходных полос превратились в одну
замкнутую полосу, которую мы максимально вытянем, чтобы было легче
вклеить удаленные окрестности ребер. Когда мы выпрямляем полосу, под-
подземным переходам приходится вытягиваться и перекрещиваться, так как
мы растаскиваем их входы, которые должны оставаться с одной и той же
стороны полосы (рис. 3.13, в центре).
Рис. 3.12. Склейка граней. Когда склеивается пара одноименных граней, образуется
мост (в центре), который затем можно вдавить в землю (справа).
140
Глава 3. Геометрические многообразия
Рис. 3.13. Склейка окрестностей ребер. После отождествления граней у нас оста-
осталась одна единственная полоса и три подземных перехода. Превратим полосу в кольцо
и приклеим к нему утолщенный диск, получениый из удаленных окрестностей ребер.
В итоге мы построили на земле иглу с тремя подземными лазами.
Для завершения построения необходимо вклеить обратно окрестности
ребер. Вначале они имеют вид (заполненных) полуцилиндров, но мы прида-
придадим им клинообразную форму так, чтобы они смыкались вокруг единствен-
единственного ребра склеиваемого пространства. В результате получим (заполнен-
(заполненный) цилиндр, или, что эквивалентно, утолщенный диск. Вклеим этот диск
обратно в виде купола так, чтобы его основание примкнуло к полосе (см.
рис. 3.13, справа). Наконец, вдавим этот купол в землю, загнав воздушный
пузырь под его сводом в три подземных перехода. Этот воздушный пузырь
и есть внутренний шар на рис. 3.10, где земля изображена не плоской, а
круглой.
Упражнение 3.3.14. Приведенный выше метод иногда работает не только в
тех случаях, когда каждая пара граней склеивается крест-накрест относительно
вершины. Например, возможно, что первоначально только одна пара граней на-
находится в нужном для склейки положении, но после того, как эта пара склеена,
происшедшее изменение топологии позволяет привести еще одну пару граней в
нужное положение, и так далее. Нарисуйте схемы склейки, иллюстрирующие этот
процесс, в случае упражнения 3.3.13 и рис. 3.6. (Первая из них приведена в работе
[Fra87, с. 153-155].)
3.4. Отображение развертки и полнота
Нам уже не раз приходилось обращаться к интуитивно понятной идее
развертывания геометрического многообразия. Например, развертывая в
разделе 1.1 евклидов тор, мы получили замощение плоскости. В данном
разделе дается определение развертки, которое потом рассматривается в
своей естественной общности.
3.4. Отображение развертки и полнота
141
Рис. 3.14. Скрученная рогатка Фергюсона. Мраморное изображение скрученного
«Y» (см. рис. 3.13) Хеламана Фергюсона украшает вход в Центр Геометрии Универси-
Университета штата Миннесота. Три переплетающиеся ветви «Y» встречаются в двух местах —
выпуклой части и пьедестале, которые нужно себе представлять отделенными друг
от друга (в скульптуре выпуклая часть опирается на пьедестал, а ветви — одна на
другую). Такое взаимное расположение навеяно формой трилистника; чтобы получить
из трилистника скрученный «Y», нужно разрезать три внешние петли, собрать шесть
свободных концов в две тройки и одеть в мрамор.
142
Глава 3. Геометрические многообразия
Пусть X — связное вещественно-аналитическое многообразие, а С-
группа вещественно-аналитических диффеоморфизмов, транзитивно дей-
действующая на X. В этом случае каждый элемент группы G однозначно
определяется своим ограничением на произвольное (непустое) открытое
подмножество в X. Рассмотрим некоторое (G, ^-многообразие М.
Пусть области Uly U2, .. ¦ и отображения ф(: Ut—*X задают локальные
системы координат на М с функциями перехода
Гц =
фу"
П
П U,).
По определению (G, ^-многообразия, каждое отображение у// локально
действует, как элемент из G, так что у,,- можно рассматривать как локально
постоянное отображение со значениями в G. После композиции с ср,- мы
получаем локально постоянное отображение Ut Л Uj —»• G, которое будем
также обозначать через у/у-
Предположим теперь, что две карты (U,, ф/) и (U,, ф;) покрывают одну
и ту же точку х. Тогда можно так изменить отображение фу (рассмотрев
его композицию с у,у), что оно будет совпадать с отображением ф( вблизи
точки х. На самом деле, если пересечение Us П Uj связно, то эти отображе-
отображения будут совпадать на всем пересечении, так что получится отображение
Uj U Uj —+ X, продолжающее ф,-. Но, вообще говоря, пытаясь таким образом
продолжить координатное отображение на все многообразие, мы придем
к несогласующимся значениям. Для того чтобы избежать несогласованно-
несогласованности, надо перейти к универсальной накрывающей.
Выберем отмеченную точку х0 s М и карту (?/0, фо), покрывающую эту
точку. Пусть к: М -* М —^универсальная накрывающая пространства М.
Будем представлять себе М как пространство гомотопических классов пу-
путей в М с началом_в отмеченной точке и рассмотрим путь а, представля-
представляющий класс [а] 6 М (так, что аA) =тс([а])). Разобьем путь а промежуточ-
промежуточными точками
= a(to),
х„ = а(/„)
(где /0 = 0 и /„ = 1) таким образом, чтобы каждый из получившихся ку-
кусочков пути целиком покрывался какой-то одной картой (?/,-, <р,). Затем,
двигаясь вдоль пути а, мы подправляем очередное отображение ф, таким
образом, чтобы оно совпало с (уже подправленными) отображением ф,_!
в некоторой окрестности jc, s i/,_i n ?/,-. Эти согласованные друг с дру-
другом карты образуют аналитическое продолжение отображения ф0 вдоль
данного пути (см. рис. 3.15). Последнее из новых координатных отобра-
отображений имеет вид
3.4. Отображение развертки и полнота
143
Рис. 3.15. Аналитическое продолжение. Пусть М — аффинный тор (слева). Путь
а (пунктиром) подразделен точками Xq, ..., Х4 (отмечены жирным шрифтом) так, что
каждая часть [х/, Xj+\ ] пути целиком содержится в области Ui действия координатной
карты. В окрестности первой части пути аналитическое продолжение отображения
<Ро есть оно само, в окрестности второй части это Yoi(*i)<Pb и так далее. Можно
представлять себе аналитическое продолжение как многозначное отображение из М в
X = Е2 или как отображение универсальной накрывающей М в X.
Упражнение 3.4.1 (аналитическое продолжение корректно определено).
Проверьте предыдущую формулу. Докажите, что росток отображения ф в точке ot( 1)
не зависит от произвола, допущенного при построении аналитического продолже-
продолжения, и даже от выбора пути а в том же гомотопическом классе. Таким образом,
можно положить ф'о = ф, и отображение ф корректно определено. А как зависит
Фо"' от выбора точки Хо или начального отображения фо?
Определение 3.4.2 (отображение развертки). Фиксировав базис-
базисную точку начальное отображение ф0, определим отображение раз-
развертки D: М -+ X как отображение, заданное локально с помощью ана-
аналитического продолжения ф0 вдоль каждого пути. То есть
D = ф^ о к
в некоторой окрестности a s M. При изменении начальных условий (базис-
(базисной точки и исходного отображения) образ отображения развертки меняет-
меняется под действием некоторого элемента из группы G (см. упражнение 3.4.1).
Если наделить пространство универсальной накрывающей (О,А)-струк-
турой, индуцированной накрытием к (см. упражнение 3.1.5), то отобра^
жение развертки является локальным (G, А")-гомеоморфизмом между М
пХ.
Хотя в наиболее интересных случаях группа G действует на X транзи-
транзитивно, это условие не является необходимым для определения отображе-
отображения D. Например, если группа G тривиальна, а многообразие X замкнуто,
то замкнутые (G, X)-многообразия — это в точности конечнолистные на-
накрытия над X с проекцией D.
144
Глава 3. Геометрические многообразия
Рис. 3.16. Голономия петли. Для тора на рис. 3.15 аналитическое продолжение
вдоль петли а требует двух замен координат: <ро на УоП^Офь а затем Yoi(-*j)<Pi
на Yoi(-ri)Yi2(-r2)(P2- Следовательно, голономией петлн а будет элемент g^ =
Рассмотрим теперь элемент а фундаментальной группы пространст-
пространства М. Аналитическое продолжение вдоль петли а приводит к ростку <#J,
который уже можно сравнить с сро, так как они оба определены в окрест-
окрестности базисной точки (см. рис. 3.16). Обозначим через ga такой элемент
группы G, для которого фо = gCTcpo; ga мы будем называть голономией а.
Из определения 3.4.2 легко вывести, что
где Та: х —»¦ ах есть преобразование накрытия, индуцированное элемен-
элементом а. Применяя это равенство к произведению петель, получаем, что
отображение Н: а-* ga из ^i(yW) в G является гомоморфизмом, который
мы будем называть голономией М. Его образ называется группой голо-
номии пространства М. Заметим, что отображение Н зависит от произвола
при построении D (см. определение 3.4.2): при изменении D образ отобра-
отображения Н сопрягается элементом из G.
Упражнение 3.4.3. Как выглядит развертка и голономия для
а) евклидова тора в примере 3.3.2,
б) аффинного тора в примере 3.3.4 (см. рис. 3.17).
Упражнение 3.4.4 (свободные гомотопические классы). Напомним, что две
петли линейно связного пространства называются свободно гомдпгопными, если
они гомотопны как отображения окружности S1 в пространство (без отмеченных
точек).
а) Свободные гомотопические классы петель находятся во взаимно однознач-
однозначном соответствии с классами сопряженности элементов фундаментальной группы.
3.4. Отображение развертки и полнота
145
Рис. 3.17. Развертка аффинного тора. Отображение развертки аффинного тора,
полученного из четырехугольника (см. пример 3.3.4) не покрывает ровно одну точку
плоскости.
б) Пусть D: М —> X — отображение развертки (G, X)-многообразия М. Тогда
каждому свободному гомотопическому классу петель в М соответствует некоторый
класс сопряженности в группе голономии пространства М. Для данного предста-
представителя a: S1 —> М этого класса выбор поднятия a: R -+ М уже однозначно задает
голономию петли а.
Вообще говоря, голономия пространства М не определяет (G, X)-струк-
X)-структуру на М, но в одном важном частном случае это все же имеет место. М
называется полным (G, Х)-многообразием, если отображение D: М -*Х
есть накрытие. Так как накрытие над односвязным пространством есть го-
гомеоморфизм, т<э в случае полного пространства М и односвязного X можно
отождествить М и X с помощью отображения развертки, что мы в дальней-
дальнейшем часто и будем делать без особого напоминания. Это отождествление
определено однозначно с точностью до действия группы G. Одновременно
мы получаем следующий результат.
Предложение 3.4.5 (группа голономии определяет многообразие).
Если G — группа аналитических диффеоморфизмов односвязно-
односвязного пространства X, то любое полное (G, Х)-многообразие можно
однозначно восстановить из его группы голономии Г как фактор-
пространство Х/Т.
146
Глава 3. Геометрические многообразия
Соглашение 3.4.6. Так как группа Г действует на X слева, то пра-
правильней было бы обозначать факторпространство через Г \ X. Однако для
наших рассуждений эта разница так несущественна, что из чисто эстети-
эстетических соображений мы все же будем писать Х/Г.
Упражнение 3.4.7. Ясно, что тор на рис. 3.17 не является полным многообра-
многообразием. Найдите условия, при которых аффинный тор, полученный в примере 3.3.4 с
помощью конструкции Смилли, будет полным многообразием.
Упражнение 3.4.8 (многообразия подобия). Структурой подобия назы-
называется (Sim(rt), Е")-структура, где Sim(n) есть группа преобразований подобия
пространства Е". Какие структуры подобия возможны на окружности S1? Какие
из них полны?
Учитывая важное соответствие, установленное в предложении 3.4.5,
часто оказывается полезным перейти от неодносвязного модельного про-
пространства X к его универсальной накрывающей X. На X действует накры-
накрывающая группа G, а именно группа, состоящая из тех гомеоморфизмов X,
которые являются всевозможными поднятиями элементов из G. Группу G
можно рассматривать как расширение:
1 -* щ(Х)-+б
1.
Существует взаимно однозначное соответствие между (G, X)- и (G, X)-
структурами, но голономия (G, ^-структуры несет больше информации.
Упражнение 3.4.9 (исследование стабилизаторов). Рассмотрим подробнее
структуру групп %i(X) и G в случае неодносвязного пространства X.
а) Докажите, что фундаментальная группа любой топологической группы ком-
коммутативна.
б) Пусть G — топологическая группа, а Н С G — ее замкнутая подгруппа. Будем
говорить, что группа G имеет локальное трансверсальное сечение (по отноше-
отношению к подгруппе Н), если найдется такое множество S представителей классов
смежности (по одному в классе) некоторой окрестности единицы в G/H, что ото-
отображение х —> Нх будет гомеоморфизмом на S.
Пусть X — многообразие, на котором группа G действует транзитивно гомео-
гомеоморфизмами. Рассмотрим точку х S X и ее стабилизатор Gx. Допустим, что группа
G имеет локальное трансверсальное сечеиие относительно Gx и что отображение
Р '¦ ё ~* 8х открыто.
Постройте гомоморфизм фундаментальной группы пространства X в группу ли-
линейно связных компонент стабилизатора Gx и докажите, что ядро этого гомомор-
гомоморфизма лежит в центре группы. В частности, если стабилизатор Gx линейно связей,
то фундаментальная группа пространства X коммутативна.
в)* Докажите, что условия существования локального трансверсального сече-
сечения и открытости отображения р заведомо выполнены, если, например, G — группа
Ли.
3.4. Отображение развертки и полнота 147
Вот полезное достаточное условие полноты.
Предложение 3.4.10 (компактность стабилизаторов влечет полно-
полноту). Пусть G — группа Ли, аналитически и транзитивно действу-
действующая на многообразии X, причем так, что *стабилизатор Gx не-
некоторой (а значит, и любой) точки х е X компактен. Тогда каждое
(G, Х)-многообразие М является полным.
Доказательство. Из транзитивности действия следует, что условие
компактности стабилизатора не зависит от точки. Теперь зафиксируем
точку х е X и рассмотрим касательное пространство ТХХ к многообра-
многообразию X в х. Существует аналитический гомоморфизм Gx в линейную группу
пространства ТХХ, образ которого компактен. Воспользуемся теперь сле-
следующим фактом, который интересен и сам по себе:
Лемма 3.4.11 (существование инвариантной метрики). Пусть
группа G транзитивно действует на аналитическом многообра-
многообразии X. Тогда X обладает G-инвариантной римановой метрикой в
том и только том случае, когда для некоторой точки xgX образ
стабилизатора Gx в GL(TXX) имеет компактное замыкание.
Доказательство. В одну сторону это утверждение очевидно: если груп-
группа G сохраняет метрику, то Gx отображается в подгруппу компактной груп-
группы О(ТХХ). Чтобы доказать обратное утверждение, рассмотрим точку х, у
которой образ стабилизатора Gx имеет компактное замыкание Нх. Пусть
Q — положительно определенная форма на ТХХ. Для того чтобы получить
//^-инвариантную квадратичную форму на ТХХ, усредним Q по мере Хаара
(см. упражнение 2.5.20) на Нх. Теперь перенесем эту метрику в касательное
пространство каждой точки у е X с помощью элемента g группы G, перево-
переводящего у в х (результат не зависит от выбора такого элемента). Полученная
риманова метрика инвариантна относительно действия G. 13.4.111
Упражнение 3.4.12. Воспользовавшись локальным трансверсальным сечени-
сечением (см. упражнение 3.4.9) группы G относительно Нх, докажите, что любая G-ин-
вариантная риманова метрика (в частности, построенная в предыдущей лемме)
является аналитической.
Если М — (G, X)-многообразие, то можно поднять риманову метрику с
X на М, воспользовавшись локальными картами; в результате получится
риманова метрика на М, инвариантная относительно всех (G, ^-отобра-
^-отображений. Но в римановом многообразии каждую точку у можно окружить
шаром Ве(у) радиуса г > 0, который является гомеоморфным образом
стандартного шара под действием экспоненциального отображения и ко-
который является выпуклым (т. е. любые две его точки можно соединить
единственной геодезической, лежащей в шаре). Если многообразие М за-
замкнуто, то из соображений компактности можно найти одно общее г > 0
148
Глава 3. Геометрические многообразия
для всех точек. Можно также считать, что все такие е-шары в X стя-
стягиваемы и выпуклы, так как G есть группа изометрий с транзитивным
действием. _
Тогда для любой точки у е М ограничение отображения D на шар
Вс(у) является гомеоморфизмом, так как из того, что D(y) = D{y') для
двух точек уф у1 шара, следует, что геодезическая, соединяющая учу",
переходит в самопересекаюшуюся геодезическую, что противоречит вы-
выпуклости е-шаров в X. Более того, по определению D является изометрией
между Вс(у) nBc(D(y)).
Рассмотрим теперь точки х <= X и у <= D~lBc/2(x). Шар Вс(у) отобра-
отображается изометрично, следовательно должен содержать как собственное
подмножество гомеоморфную копию шара Ве/2{х). Тогда полный прообраз
D~1Bc/u(x) распадается в дизъюнктное объединение таких гомеоморфных
копий. Следовательно, D: М —* X является накрытием, т. е. М — полное
многообразие. 13.4.101
Пример 3.4.13. Предложение 3.4.10 утверждает, что универсальная
накрывающая замкнутого эллиптического трехмерного многообразия М
есть сфера S3. Так как сфера компактна, то фундаментальная группа
щ(М) конечна. В частности, если многообразие М односвязно, то оно
обязательно гомеоморфно S3.
Пример 3.4.14. Топологическое пространство X со стягиваемой уни-
универсальной накрывающей называется пространством Эйленберга—
Маклейна и обозначается через K(G, 1), где G — фундаментальная группа
пространства X. (Число 1 в этой записи означает, что пространство X
удовлетворяет следующему условию: группа щ(Х) тривиальна при кф\\
есть аналогичные определения пространств K(G, п) для произвольного п.)
Пространства K(G, 1) определяются группой G однозначно, с точностью
до гомотопической эквивалентности. Как видно из предложения 3.4.10,
замкнутые гиперболические многообразия и замкнутые евклидовы много-
многообразия являются пространствами типа K(G, 1). Таким образом, главную
роль играет их фундаментальная группа.
Для незамкнутых многообразий проверка полноты — дело более тон-
тонкое. Часто оказывается полезным следующий критерий, который заодно
возвращает понятию «полнота» для (G, ^-многообразий его привычный
смысл.
Предложение 3.4.15 (смысл полноты). Пусть G — группа веще-
вещественно-аналитических диффеоморфизмов пространства X, тран-
транзитивно действующая на нем с компактными стабилизаторами
точек. Зафиксируем G-инвариантную метрику на X {которая су-
существует согласно предложению 3.4.11) и рассмотрим (G, Х)-мно-
гообразие М с метрикой, унаследованной от X. Следующие условия
3.4. Отображение развертки и полнота
149
эквивалентны:
а) М —полное (G, X)-многообразие,
б) для некоторого г > 0 все замкнутые е-шары в М компактны,
в) при всех а>0 все замкнутые а-шары в М компактны,
г) существует такое семейство компактных подмножеств S,
(/ € К+) многообразия М, что \J S, = М и множество S,+a содер-
жит а-окрестность множества St,
д) многообразие М полно как метри ческое пространство.
Доказательство, а =$¦ б. Если р: У-+ Z — накрытие одного риманова
многообразия другим и р сохраняет риманову метрику, то при всех у е Y
и г е R верно равенство Вс(р(у)) = р(Ве(у)), так как расстояния опреде-
определяются через длины путей, а пути в Z поднимаются в У. Таким образом,
если Е-шары компактны в У, то же верно и для Z, и обратно. Выберем
теперь е > 0 так, чтобы замкнутый шар, окружающий некоторую точку из
X был компактен. Так как группа G действует транзитивно, то найденное е
подойдет для Bjcex точек. Следовательно, замкнутые е-шары компактны в
X, а потому в М и М.
б =$¦ в. Докажем это по индукции. Предположим, что условие в выпол-
выполнено для какого-то значения а ^ е > 0. Тогда шар Bajx) можно покрыть
конечным числом е/2-шаров, и, следовательно, шар Ва+е/2(х) можно по-
покрыть конечным числом е-шаров, которые уже компактны. Тем самым
доказано, что шар Йа+€/2(х) — компакт.
в => г. Возьмем в качестве S, шар радиуса / вокруг некоторой фикси-
фиксированной точки.
г =$¦ д. Любая последовательность Коши в М должна содержаться в S,
для достаточного большого /, и, следовательно, должна сходиться.
д =$¦ а. Предположим, что М — полное метрическое пространство. Для
доказательства того, что отображение D: М —+ X является накрытием, до-
достаточно проверить, что любой путь а, в X можно поднять в М (так как
локальные гомеоморфизмы, допускающие поднятие путей, суть накрытия).
Сначала убедимся, что пространство М метрически полно. Действительно,
проекция на М любой последовательности Коши из М имеет предельную
точку х € М. Так как х обладает компактной окрестностью, компоненты
прообраза которой заведомо отделены в М, то последовательность Коши
сходится и в М.
Рассмотрим теперь произвольный путь а, в X. Если он допускает подня-
поднятие а, на отрезке [0, /0], то это поднятие можно продолжить на промежуток
[0, /0 + е) ДЛЯ некоторого е > 0. С другой стороны, если этот путь допускает
поднятие на полуоткрытом интервале [0, /0), то из полноты М следует, что
поднятие продолжается на отрезок [0, /<>]• Таким образом, М полно как
(G, ^-многообразие. |3.4.15|
150
Глава 3. Геометрические многообразия
Условия б—д эквивалентны для любого риманова многообразия, не
только для (G, Л)-многообразий. Это часть фундаментальной теоремы
Хопфа—Ринова [HR31], которая утверждает, что в римановой геометрии
метрическая полнота эквивалентна геодезической полноте (т. е. возможно-
возможности неограниченного продолжения геодезической). См., например, [dC92,
глава 7] и [GHL90].
Для гиперболических многообразий, полученных склейкой полиэдров,
условие г, по-видимому, наиболее полезно для проверки полноты структу-
структуры, а условие д — для проверки неполноты (см., например, пример 3.4.17).
Пример 3.4.16 (полнота пространства дополнения к узлу). Гипер-
Гиперболическая структура, построенная на дополнении к восьмерке в приме-
примере 3.3.7, полна. Напомним, что склеивались два правильных идеальных те-
тетраэдра Т и Т. Отображения склейки выглядели как евклидовы изометрии,
если тетраэдры Т и V были симметрично расположены в проективной мо-
модели, как на рис. 3.3, б. Правильный идеальный тетраэдр имеет конечную
группу симметрии, а у этой группы есть единственная неподвижная точка
(см. следствие 2.5.19), совпадающая с центром шара на рис. 3.3, б. Заме-
Заметим теперь, что при склейке Г и Г' те шары радиуса / вокруг их центров,
которые пересекаются со своими тетраэдрами, правильно склеиваются и
образуют семейство S,, отвечающее условию г предложения 3.4.15.
По тем же соображениям полны построенные нами гиперболические
структуры на дополнениях к зацеплению Уайтхеда (пример 3.3.9) и коль-
кольцам Борромео (пример 3.3.10).
Пример 3.4.17 (полнота двумерных склеек). При склейке двух иде-
идеальных гиперболических треугольников по схеме рис. 3.18 получается сфе-
сфера с тремя выколотыми точками. В отличие от предыдущего примера, здесь
больше свободы в выборе склеивающих отображений: любое отождествле-
отождествление склеиваемых сторон можно подправить произвольным гиперболиче-
гиперболическим сдвигом, так что на сфере с тремя выколотыми точками имеется не
Рис. 3.18. Диаграмма склейки для сферы с тремя выколотыми точками
3.4. Отображение развертки и полнота
151
одна гиперболическая структура, а целое семейство, параметризованное
пространством Е3. (Вообще говоря, они не обязаны все быть разными, и
они такими и не являются.) Какие же из этих структур полны?
Рассмотрим более общий вопрос. Пусть S — ориентированная гипербо-
гиперболическая поверхность, полученная такой склейкой идеальных тетраэдров,
при которой не остается свободных ребер. Идеальной вершиной поверх-
поверхности S называется класс эквивалентности вершин исходных треуголь-
треугольников, отождествленных при данной склейке. С каждой идеальной вер-
вершиной v ассоциирован некоторый инвариант d(p), который определяется
следующим образом. В одном из треугольников, чья вершина входит в
класс v, рассмотрим орициклический сегмент h «с центром» в v, заключен-
заключенный между сторонами данного треугольника, которые встречаются в v.
Будем последовательно продолжать h вокруг v (в направлении против ча-
часовой стрелки) с помощью орициклических сегментов, перпендикулярных
ребрам. В итоге кривая орициклов вернется в исходный треугольник в ви-
виде сегмента орицикла, концентричного первоначальному. Ориентированное
расстояние между этими орициклами и есть d(v) (считаем его положитель-
положительным в ситуации рис. 3.19). Легко видеть, что величина d(v) не зависит от
начального выбора Л.
Рис. 3.19. Продолжение орицикла. Расстояние d — d(v), ассоциированное с иде-
идеальной вершиной v, содержит информацию о голономни пути, однократно обходящего
вокруг и против часовой стрелки.
Предложение 3.4.18 (критерий полноты двумерных склеек). По-
Поверхность S полна тогда и только тогда, когда d(v) = 0 для всех
идеальных вершин v.
Доказательство. Предположим, что для некоторой вершины v вели-
величина d(v) > 0. Продолжая орицикл вокруг этой вершины, мы увидим, что
его длина ограничена, так как каждый следующий виток короче, чем пре-
предыдущий в некоторое фиксированное число раз, большее единицы. Таким
152
Глава 3. Геометрические многообразия
образом последовательность точек, высекаемых этой кривой на одном из
ребер, является последовательностью Коши, не имеющей предела, т. е. для
поверхности S нарушается последнее условие предложения 3.4.15. Случай
d(v) < 0 совершенно аналогичен, нужно лишь продолжать орицикл в про-
противоположном направлении — по часовой стрелке.
С другой стороны, если d(v) = 0 для всех вершин, то удалив малень-
маленькие окрестности вершин, ограниченные орициклами, получим компактное
множество So С S. Обозначим через S, множество, полученное удалени-
удалением из S меньших окрестностей, ограниченных орициклами, отстоящими на
расстояние / от исходных. Тогда семейство S, отвечает условию г предло-
предложения 3.4.15, что влечет полноту S. 13.4.181
Упражнение 3.4.19. Покажите, что для склейки на рис. 3.18 условия d(v) = О
приводят к трем линейно независимым линейным уравнениям от трех переменных,
так что получить полную поверхность можно единственным способом. Докажите
и обратное: любая полная сфера с тремя выколотыми точками может быть пред-
представлена в виде склейки двух идеальных треугольников. На языке раздела 4.6 это
означает, что пространство Тейхмюллера сферы с тремя выколотыми точками со-
состоит ровно из одной точки. См. также рис. 3.20.
Рис. 3.20. Развертка сферы с тремя выколотыми точками. Здесь изображены
развертки на гиперболическую плоскость полной (слева) и неполной (справа) ги-
гиперболических поверхностей, полученных из склейки на рис. 3.18. В первом случае
орициклическое продолжение приводит к замкнутой кривой, все время проходящей
через начальную точку треугольника; во втором (справа) случае получается кривая,
удаляющаяся от начальной точки. Обратите также внимание (справа) на области плос-
плоскости И2, которые не принадлежат образу отображения развертки.
Упражнение 3.4.20. Докажите, что голономия вокруг той идеальной вершины,
для которой d(v) = 0, является параболическим элементом, а соответствующий
«конец» поверхности («окрестность» идеальной вершины) изометричен тонкой ча-
3.4. Отображение развертки и полнота
153
стн псевдосферы. Такие идеальные вершины называются каспами — они будут
играть важную роль в разделе 4.5 («Г-/-разложение»). Следующее предложение
описывает ситуацию около вершины, где d{v) ф 0.
Предложение 3.4.21 (полнота гиперболических поверхностей).
Метрическое пополнение S поверхности S является гиперболиче-
гиперболической поверхностью с геодезическим краем. На каждую идеальную
вершину v с d(v) ф 0 приходится одна компонента края длины \d(v)\.
Доказательство. Для данной идеальной вершины v с d(v) ф 0 каждая
орициклическая спираль заканчивается в некоторой точке метрического
пополнения, причем так как различные спирали равномерно отделены, то
им соответствуют различные точки. Семейство таких спиралей параметри-
параметризуется точками их пересечения с некоторым выделенным ребром, заканчи-
заканчивающимся в вершине и, причем точки пересечения, идущие с шагом dip),
отвечают одной и той же спирали. Таким образом, для каждой идеальной
вершины v с d(v) Ф 0 предельные точки спиралей образуют окружность.
Эта окружность состоит из предельных точек геодезической (например,
ребра, оканчивающегося в и), а потому и сама является геодезической.
Легко проверить, что после присоединения всех таких предельных окруж-
окружностей получится полная поверхность S с геодезической границей. 13.4.211
Проще представить себе эту ситуацию, раскрутив рис. 3.19 в обрат-
обратном направлении — вместо геодезических, направленных к и, и закручи-
закручивающихся, спиралью орициклов появится более естественная картина: из
орициклов, направленных к граничной окружности, и ортогональных к ним
геодезических, наматывающихся на эту окружность, как на рис. 3.21.
Рис. 3.21. Геодезические накапливаются у границы. Идеальная вершина, для ко-
которой d(v) ф 0, порождает круг длины \A(ъ)\ в компактификации поверхности. Ребра
склеенных треугольников накручиваются на граничную окружность.
154
Глава 3. Геометрические многообразия
3.4. Отображение развертки и полнота
155
Ясно, что рассужения примера 3.4.17 применимы не только когда по-
поверхность S склеена из идеальных треугольников, но и когда поверхность 5
получена склейкой треугольников, у которых некоторые или все вершины
конечны. Требуется лишь, чтобы конечные вершины склеивались с ко-
конечными, а сумма углов в классе эквивалентных конечных вершин была
равна 2тс.
Переформулируем теперь предложение 3.4.18 так, чтобы его легко мож-
можно было обобщить на высшие размерности. Пусть v — идеальная верши-
вершина S, полученная при склейке гиперболических треугольников. Тогда на
линке lk(u), являющемся окружностью, есть каноническая структура по-
подобия (см. упражнение 3.4.8).
Чтобы убедиться в этом, отождествим часть линка, заключенную вну-
внутри треугольника с вершиной в и, с произвольно выбранным сегментом
орицикла с центром в v {см. рис. 3.19). Рассматривая модель верхней по-
полуплоскости с точкой v на бесконечности, заключаем, что на любом таком
сегменте орицикла имеется евклидова структура и что проекция одного сег-
сегмента на другой является евклидовым преобразованием подобия (упражне-
(упражнение 2.2.10). Следовательно линк lk(u) обладает структурой подобия внутри
каждого треугольника. Вместе эти локальные структуры образуют гло-
глобальную структуру подобия на всем lk(u), так как обход вокруг вершины
приводит к поперечному сегменту, параллельному начальному, так что они
отличаются на преобразование подобия. На самом деле несложно заме-
заметить, что это подобие есть сжатие с коэффициентом edl-v). Поэтому утвер-
утверждение о том, что d(v) = 0 эквивалентно тому, что голономия структуры
подобия на 1к(и) состоит только из изометрий. Это, в свою очередь, экви-
эквивалентно существованию евклидова усиления данной структуры подобия.
Упражнение 3.4.22 (критерий существования усиления). Если группа G
аналитически действует на многообразии X, а Н — подгруппа G, то G-структура
тогда и только тогда обладает //-усилением, когда ее группа голономии сопряжена
некоторой подгруппе группы Н.
Теперь можно приступить к обещанному обобщению предложения
3.4.18. Рассмотрим склейку л-мерных полиэдров (согласно определе-
определению на с. 126, это означает, что все фасеты разбиваются на пары).
Предположим, что эти полиэдры можно реализовать в И", пусть даже
поместив часть вершин на бесконечность. Предположим также, что все
отображения склейки — изометрий, а полученное пространство М (без
бесконечно удаленных вершин) является гиперболическим многообразием.
Идеальной вершиной многообразия М называется, разумеется, класс
эквивалентности бесконечно удаленных вершин исходных полиэдров. Ес-
Если v — идеальная вершина, то наделим ее линк lk(y) структурой подобия,
возникающей из поперечных орисферических сегментов в полиэдрах с
вершиной в v точно так же, как и в двумерном случае.
Теорема 3.4.23 (критерий полноты склеек). Следующие условия
эквивалентны:
а) М — полное многообразие,
б) для каждой идеальной вершины, v голономия линка Щу) состо-
состоит из изометрий,
в) для каждой идеальной вершины v структура подобия на линке
Щи) допускает усиление до евклидовой структуры,
г) для каждой идеальной вершины v линк Щи) является полным
как многообразие подобия.
Доказательство. То, что голономия линка lk(u) состоит из изометрий,
равносильно тому, что перемещаясь вдоль произвольной петли в линке,
мы возвращаемся к тому же орисферическому сегменту, с которого нача-
начали. Таким образом, частичные поперечные сегменты состыкуются и вме-
вместе образуют глобальное поперечное сечение, которое ограничивает «ори-
шарическую окрестность» вершины v. Удалив такие окрестности у всех
идеальных вершин, получим компактное подмножество Мо. Точно так же,
как и в доказательстве предложения 3.4.18, начнем стягивать удаляемые
окрестности и получим семейство компактных подмножеств Ми удовле-
удовлетворяющее условию г предложения 3.4.15.
С другой стороны, если голономия какой-то петли из lk(u) есть не изо-
метрия, а сжатие, то при каждом следующем обходе петли орисферический
сегмент приближается к и на фиксированное расстояние. Тем самым рас-
расстояние между соответствующими точками последовательных сегментов
убывает экспоненциально, так что эти точки образуют последовательность
Коши. Повторяя доказательство предложения 3.4.18, получаем, что эта по-
последовательность не имеет предельных точек на М, а значит, М не полно.
Тем самым доказана эквивалентность условий а и б.
Эквивалентность условий б я в следует из упражнения 3.4.22, так как
группа IsomE" — нормальная подгруппа Sim(«).
Для доказательства того, что из в следует г, заметим что линк lk(y)
есть замкнутое многообразие (так как в склейке нет свободных фасет) и
применим предложение 3.4.10.
Наконец, из г следует б: если линк \k{v) является полным как мно-
многообразие подобия, то его универсальная накрывающая это пространство
Е", а голономия не имеет неподвижных точек. Следовательно, голономия
состоит из изометрий. |3.4.23|
Упражнение 3.4.24. Проверьте, что в случае неполного многообразия М
структура подобия на \k{v) может зависеть от представления М в виде объединения
идеальных полиэдров.
Упражнение 3.4.25. Докажите, что единственной замкнутой ориентирован-
ориентированной поверхностью, имеющей структуру подобия, является тор. (Сравните с
задачей 1.3.15.) Следовательно, существование структуры подобия на линке накла-
156
Глава 3. Геометрические многообразия
дывает топологические ограничения иа гиперболическое многообразие, полученное
при склейке, даже если оно неполно.
Упражнение 3.4.26. Воспользуйтесь теоремой 3.4.23 для доказательства того,
что структуры на дополнениях к восьмерке (пример 3.3.7), зацеплению Уайтхеда
(пример 3.3.9) и кольцам Борромео (пример 3.3.10) полны. (Другим способом это
уже было доказано в примере 3.4.16.)
Упражнение 3.4.27. Каков трехмерный аналог предложения 3.4.21 и рис. 3.21 ?
К этому вопросу мы еще вернемся во втором томе, изучая преобразования Дена и
жесткость геометрических структур. Там мы убедимся, что, исследуя пополнения,
можно извлечь нетривиальную топологическую информацию о самих простран-
пространствах.
3.5. Дискретные группы
В соответствии с предложением 3.4.5, в случае, когда группа G состоит
из аналитических диффеоморфизмов односвязного многообразия X, клас-
классы изоморфных полных (G, ^-многообразий находятся во взаимно од-
однозначном соответствии с некоторыми подгруппами G (определенными с
точностью до сопряжения элементами из G). При описании групп, являю-
являющихся группами голономии полных (G, JQ-многообразий, часто возникают
определенные, уже ставшие традиционными, ошибки, так что необходимо
очень внимательно отнестись к следующим определениям.
Определение 3.5.1 (свойства группового действия). Пусть группа Г
действует на топологическом пространстве X гомеоморфизмами. Как пра-
правило, мы будем считать это действие эффективным в том смысле, что
только единичный элемент группы Г действует тривиально на X. В этом
случае можно считать, что группа Г состоит из гомеоморфизмов простран-
пространства X. Действие группы может обладать и другими свойствами:
(i) Действие называется свободным, если ни один неединичный элемент
группы Г не имеет неподвижных точек.
(ii) Действие называется дискретным, если Г является дискретной
подгруппой группы всех гомеоморфизмов пространства X в *компактно-
открытой топологии.
(ш) Действие имеет дискретные орбиты, если у каждой точки х € X
есть такая окрестность U, что множество элементов у € Г, переводящих х
в U, конечно.
(iv) Действие называется блуждающим, если у каждой точки х € X
есть такая окрестность U, что множество элементов у S Г, для которых
у?/ (~)U ф0, конечно.
3.5. Дискретные группы
157
(v) Предположим, что пространство X локально компактно. Действие
группы Г называется разрывным, если для каждого компактного под-
подмножества К пространства X множество элементов у € Г, для которых
¦хКпК^0, конечно.
Упражнение 3.5.2. Докажите, что группа Г действует разрывно тогда и толь-
только тогда, когда отображение Г х Х-> X х X, заданное формулой (у, х) >-+ (ух, х),
собственно. (Отображение называется собственным, если прообраз каждого ком-
компакта — компакт.)
Упражнение 3.5.3 (иерархия свойств). Докажите, что любое из трех послед-
последних свойств в 3.5.1 сильнее предыдущего. (Подсказка к неэквивалентности (III)
и (iv): задайте действие с дискретными орбитами Z на Sl x R х [-1, l]\{s0} x
xRx {0} с помощью семейства таких диффеоморфизмов цилиндров 51 х R х {(},
орбиты которых закручиваются по спирали под углом t.)
Предложение 3.5.4 (свободное блуждающее действие дает струк-
структуру многообразия на факторпространстве). Рассмотрим свободное
блуждающее действие группы Г на связном (хаусдорфовом) мно-
многообразии X. Тогда факторпространство Х/Т является (возможно
не хаусдорфовым) многообразием, а проекция на факторпростран-
факторпространство — накрытием.
Доказательство. Для произвольной точки хеX рассмотрим такую ее
окрестность U, которая пересекается только с конечным числом своих
сдвигов у?/. Так как пространство X хаусдорфово, а действие группы сво-
свободно, то можно найти меньшую окрестность точки х, сдвиги которой друг
с другом не пересекаются. Каждый сдвиг такой окрестности гомеоморфно
отображается на свой образ в факторпространстве. А это и означает, что
проекция на факторпространство есть накрытие. 13.5.41
Пример 3.5.5 (нехаусдорфово факторпространство). Рассмотрим
пространство А" = R2 \ 0 и группу диффеоморфизмов Г = Z, порожден-
порожденную отображением (х, у) ь-> Bх, у/2). Условия предложения 3.5.4 в этом
случае выполнены, но факторпространство М = Х/Т не хаусдорфово (см
рис. 3.22).
Немного изменив пространство X, а именно удалив отрицательную по-
полуось у, мы получим свободное блуждающее действие Z на М2. (На самом
деле, замечательная теорема Брауэра о сдвигах плоскости [Вго12], по-
помимо всего прочего, утверждает, что любое свободное действие Z на R2
является блуждающим.) И снова, факторпространство будет нехаусдор-
фовым многообразием. В частности, это означает, что встречаются него-
меоморфные нехаусдорфовы двумерные многообразия с фундаментальной
группой Z и универсальной накрывающей Ш.2.
Упражнение 3.5.6. Опишите факторпространство примера 3.5.5 как склейку
небольшого числа хаусдорфовых поверхностей.
158
Глава 3. Геометрические многообразия
Рис. 3.22. Действие с иехаусдорфовым факторпростраиством. Факторпростраи-
ство R2 \ 0 по группе, порожденной линейным преобразованием (х, у) ь-> Bх, у/2),
является многообразием (так как действие свободное и блуждающее), ио не является
хаусдорфовым пространством: любые две окрестности образов точек A, 0) и @, 1) пе-
пересекаются. Это происходит потому, что последовательные сдвиги любой окрестности
точки на оси х постепенно притягиваются к оси у, и наоборот.
Восстановим теперь наше соглашение о том, что все многообразия счи-
считаются хаусдорфовыми, если только специально не оговорено противное.
Предложение 3.5.7 (свободное разрывное действие дает хоро-
хорошее факторпространство). Пусть группа Г действует на многооб-
многообразии X. Факторпространство Х/Г является хаусдорфовым много-
многообразием, а проекция X -»Х/Г — накрытием тогда и только тогда,
когда группа Г действует свободно и разрывно.
Доказательство. Если действие свободно и разрывно, то в силу пред-
предложения 3.5.4 и упражнения 3.5.3 достаточно проверить хаусдорфовость.
Предположим, что х и // — точки из различных орбит на X. Обозначим через
К объединение двух непересекающихся компактных окрестностей точек х
и у, не содержащих сдвигов х или у. Тогда множество К \ U Y^ (гДе 1 ~
единичный элемент группы Г) все еще является объединением некоторой
окрестности точки х с некоторой окрестностью точки у, и эти окрестности
проецируются на непересекающиеся окрестности в Х/Г.
Обратно, предположим, что пространство Х/Г хаусдорфово и проекция
р: X —> Х/Г — накрытие. Для каждой пары точек {х\, j;2) € X х X мож-
можно найти такие окрестности U\(x\) и U2(x2), что yU\{x\) П U2(x2) ф 0 не
3.5. Дискретные группы
159
более чем для одного элемента у € Г. Действительно, если точка х2 не
принадлежит орбите точки хи то это следует из хаусдорфовости фак-
торпространства Х/Т, так как точки р(х{) и р(х2) обладают непересека-
непересекающимися окрестностями. Если же х2 имеет вид у*ь то это следует из
того, что р — накрытие; примем за Ui(xi) такую окрестность точки хь
которая гомеоморфно проецируется на факторпространство, и положим
U2(x2)=yUl{xl).
Рассмотрим теперь компактное подмножество К пространства X. Так
как произведение К х К тоже компактно, то из покрытия множества К х К
произведениями окрестностей вида U\ x U2, где не более одного сдвига ?Д
пересекается с 11%, можно выбрать конечное подпокрытие. Тогда множе-
множество элементов у ? Г таких, что уК П К Ф 0, конечно, и, следовательно,
группа Г действует свободно и блуждающе. 13.5.71
Следующий критерий часто оказывается удобным при проверке разрыв-
разрывности действия. Напомним, что отображение /: X —* Y называется эквива-
риантным относительно действия группы Г на пространствах X и У, если
/ коммутирует с действием группы Г.
Предложение 3.5.8 (собственные отображения сохраняют разрыв-
разрывность). Пусть группа Г действует на пространствах X и Y, а ото-
отображение /: X —» Y является собственным, сюръективным и экви-
вариантным относительно этого действия. Тогда действие Г на X
является разрывным в том и только том случае, когда разрывно
действие Т на У.,
Доказательство. Образы и прообразы компактов при отображении /
являются компактами. Каждое компактное подмножество X содержится в
множестве вида /~' (К), где К С Y — компакт, так что достаточно проверить
разрывность действия на таких множествах. Теперь все следует из того, что
/С п уК ф 0 тогда и только тогда, когда /""' (К) П yf~l{K) ф 0. 13.5.8I
Упражнение 3.5.9 (недискретная группа с хаусдорфовым факторпро-
странством). Приведите пример недискретной группы G, состоящей из гомео-
гомеоморфизмов М2, для которой факторпространство R /G хаусдорфово.
Упражнение 3.5.10 (дискретные подгруппы групп Ли разрывны). Рассмо-
Рассмотрим группу Ли G и ее дискретную подгруппу Г с G. Исследуем действие Г на G
левыми сдвигами.
а) Докажите, что это действие имеет дискретные орбиты.
б) Докажите, что Г действует блуждающе. (Подсказка: пусть t/ —такая окрест- .
ность единичного элемента 1 группы, что ГП 0= {[}. Найдите такую окрестность
V единицы, что V = V~l и \т с U. Докажите, что орбита группы Г пересекает
окрестность Vx произвольной точки х € G не более чем в одной точке.)
в) Докажите, что Г действует разрывно. (Подсказка: для данных точек х, у €
€ G найдите такие окрестности U = U(x) и V = У (у), что множество UV~lVU~l
160
Глава 3. Геометрические многообразия
пересекает Г только в единице. Тогда не более чем для одного элемента у е Г
окрестность yV может пересекаться с U.)
Альтернативный подход к этому вопросу состоит в использовании ле-
воинвариантной метрики.
Следствие 3.5.11. Пусть группа Ли G действует на многообразии
X транзитивно и с компактными стабилизаторами Gx. Тогда любая
дискретная подгруппа G действует на X разрывно.
Доказательство. Отображение G —* X = G/Gx собственно. Осталось
воспользоваться предложением 3.5.8 и упражнением 3.5.10. 13.5.11|
Таким образом, в наиболее интересных для нас случаях свойства (ii)—(v)
определения 3.5.1 оказываются эквивалентными. Вместе с предложением
3.4.5 (группа голономии определяет многообразие), предложением 3.4.10
(компактность стабилизаторов влечет полноту) и предложением 3.5.7 (сво-
(свободное разрывное действие дает хорошее факторпространство) это приво-
приводит нас к такому важному следствию:
Следствие 3.5.12 (классификация полных (G, X)-структур на мно-
многообразии). Пусть группа Ли G действует на односвязном много-
многообразии X транзитивно, аналитически и с компактными стабили-
стабилизаторами. Если М — замкнутое многообразие, то (G, Х)-структу-
ры на М (т. е. (G, Х)-усиления структуры М, рассматриваемые с
точностью до диффеоморфизма) находятся во взаимно однознач-
однозначном соответствии с классами сопряженности тех дискретных под-
подгрупп группы G, которые изоморфны щ(М) и свободно действуют
наХ с факторпространством М. Если многообразие М не замкнуто,
то взаимно однозначное соответствие получится, если рассматри-
рассматривать только полные (G, Х)-структуры на М.
Заметим, что условие «с факторпространством М» действительно необ-
необходимо, так как группа щ (М) не определяет М с точностью до диффеомор-
диффеоморфизма. Например, фундаментальная группа как тора с выколотой точкой,
так и сферы с тремя выколотыми точками одна и та же — свободная группа
Z * Z с двумя образующими.
Если группа Г действует на пространстве X разрывно, а факторпро-
факторпространство Х/Т компактно, то действие (или сама группа Г) называется
кокомпактным (-ной). Если X — риманово многообразие, группа Г со-
состоит из изометрий, а факторпространство Х/Т имеет конечный объем, то
действие (или сама группа) Г называется кофинитным (-ной). Ясно, что
кокомпактные группы кофинитны, однако обратное неверно: контрпример
дает дополнение к узлу «восьмерка» (см. пример 3.3.7).
Упражнение 3.5.13. Объясните, как определить объем факторпространства
Х/Г, если группа Г действует не свободно.
3.6. Расслоения и связности
161
Кокомпактные и кофинитные группы называют еще решетками (соот-
(соответственно, равномерными решетками), но мы не будем пользоваться
этой терминологией, так как она не согласуется с традиционным опреде-
определением решетки как дискретной подгруппы R", изоморфной Z".
Задача 3.5.14 (разрывность действия топологических групп). Продумайте
теорию, обобщающую определения и результаты этого раздела на случай действия
топологических групп на локально компактных пространствах и включающую в
себя результаты этого раздела в случае, когда группа G наделена дискретной то-
топологией.
3.6. Расслоения и связности
Геометрические структуры на многообразиях тесно связаны с другим важ-
важным понятием, которым мы неявно уже пользовались: локально тривиаль-
тривиальным расслоением, или просто расслоением.
Определение 3.6.1 (локально тривиальное расслоение). Пусть
топологическая группа G действует на топологическом пространстве X.
(G, Х)-расслоение, или, точнее, локально тривиальное расслоение со
структурной группой G и слоем X, определяется как совокупность
следующих данных: тотального пространства Е, базы расслое-
расслоения В, непрерывной проекции р: Е —»В и локальной тривиализации,
определенной ниже. Мы будем также говорить, что пространство Е рас-
слаивпется над В со слоем X.
Локальная тривиализация похожа на атлас: она дает возможность пред-
представить часть расслоения над маленькой окрестностью V в базе в виде
прямого произведения V х X с точностью до действия группы G на слоях.
Элементы группы G можно применять к различным слоям, лишь бы это
действие непрерывно зависело от точки базы.
Более формально, локальная тривиализация состоит из покрытия ба-
базы В открытыми множествами U; и набора гомеоморфизмов ср,: p~l(Ut) —»
¦ —» lli x X, которые при композиции с проекцией d х X —» U-, дают р.
Отображения ср,- должны отвечать следующему условию: для любых пе-
пересекающихся областей ?/,- и U/ композиция
= <р,
1: (U,
(U, n U,) х X
должна иметь вид
ф,Ды, х) = (и, уц(и)х),
где отображение ytj: ?/,• n U/ —»• G непрерывно.
(Отметим, что, вообще говоря, слово «расслоение» означает не то же
самое, что и «локально тривиальное расслоение». Расслоения, конечно,
включают в себя локально тривиальные расслоения, но, кроме них, еще
162
Глава 3. Геометрические многообразия
и отображения гораздо более общего вида, имеющие схожие с локаль-
локально тривиальными расслоениями гомотопические свойства, но не имеющие
такого хорошего геометрического описания, т. е. не устроенные локально
также, как проекция прямого произведения на один из сомножителей.)
Как и в ситуации с атласами, определяющими ^-структуру на мно-
многообразии, выбор конкретной локальной тривиализации не является су-
существенной частью структуры расслоения, а лишь способом ее задания.
Две локальные тривиализации эквивалентны, если их объединение также
является локальной тривиализацией.
Пример 3.6.2 (тривиальное расслоение). Тривиальное (G, ^-рас-
^-расслоение над пространством В есть прямое произведение В х X.
Пример 3.6.3 (накрытия). Любое накрытие связного пространства
В есть расслоение, слоем которого является некоторое множество Т с
дискретной топологией, а структурной группой — группа перестановок эле-
элементов из Т.
Пример 3.6.4 (лист Мёбиуса). Лист Мёбиуса есть (Z2, М)-рассло-
ение над S1 с нетривиальным действием Z2. На рис. 3.23 изображена
возможная локальная тривиализация.
Рис. 3.23. Нетривиальное одномерное расслоение на окружности. Лист Мёбиу-
Мёбиуса — это одно из двух возможных R-расслоений над S' (другое есть прямое произ-
произведение S1 х К). Представьте базу в виде объединения двух открытых дуг 11\ и Ич и
склейте локальные тривиализации U\ х R и С/2 х Ж так, чтобы на одной компоненте
пересечения они совпадали, а на другой склеивались с поворотом на п.
Пример 3.6.5 (тор отображения). Полезной конструкцией для по-
построения новых многообразий служит тор отображения. Если М —
гладкое многообразие, ср: М —» М — диффеоморфизм, то тор M,f отобра-
отображения ср получается из цилиндра М х [0, 1] склейкой его оснований с
помощью ср. Ясно, что M,f расслаивается над окружностью со слоем М.
Лист Мёбиуса является частным случаем этой конструкции.
3.6. Расслоения н связности
163
Упражнение 3.6.6. Опишите любым удобным вам способом (с помощью ло-
локальных тривиализации или как-ннбудь по-другому) следующие локально триви-
тривиальные расслоения:
а) бутылку Клейна как расслоение над окружностью со слоем окружность,
б) расслоение Хопфа (см. рис. 2.31),
в) RP3 как расслоение над сферой 52 со слоем окружность. (Подсказка: ото-
отображение Хопфа коммутирует с антиподальным отображением. Другой подход из-
изложен в примере 3.7.6.)
Пример 3.6.7 (векторные расслоения). Очень важен частный слу-
случай локально тривиального расслоения, когда X — векторное простран-
пространство, a G =¦ QL(X) — его группа линейных автоморфизмов. В этом случае
(G, >Y)-расслоение называется векторным расслоением.
Пример 3.6.8 ((G, Х)-слоения). Если база В есть л-мерное много-
многообразие, а слой X — m-мерное многообразие, то пространство расслоения
Е является (п + т)-мерным многообразием, на котором имеется слоение,
заданное во всех точках слоями расслоения. На нем есть геометрическая
структура, являющаяся усилением структуры слоения коразмерности п:
слоение с (G, А)-структурой на листах, или тангенциальное (G, Х)-сло-
ение. Не каждое тангенциальное (G, ^-слоение является локально три-
тривиальным расслоением, так как для этого каждый слой должен быть ко-
копией X, а не просто локально устроенным, как X.
Для задания расслоения над базой В реально требуется только покры-
покрытие базы U, и коцикл, т. е. набор функций перехода yih удовлетворяю-
удовлетворяющих условию коцикла у//Т/* = Y(* в0 всех точках множества ?// n U/ n Uk,
где данная композиция определена. Тотальное пространство получается
склейкой из произведений U; х X с помощью функций перехода. Для по-
построения расслоения подходит любой набор непрерывных функций у<у:
UtCiU/ —* G, удовлетворяющих условию коцикла. (В случае абелевой груп-
группы G с дискретной топологией у,7 есть 1-коцикл в смысле когомологий
Чеха.)
Так как коцикл никак не связан со слоем X, а только с группой G,
то мы можем для данного (G, JQ-расслоения над базой В и произволь-
произвольного пространства Y с действием группы G построить ассоциированное
(G, У)-расслоение над В. Более того, если р: G -»Я есть гомоморфизм
групп и Я действует на пространстве Z, то можно построить ассоциирован-
ассоциированное (Я, Z) -расслоение, функции перехода которого есть образы функций
перехода исходного расслоения при гомоморфизме р.
Упражнение 3.6.9. Докажите, что если группа G абелева, то существует ка-
каноническое действие группы G на каждом слое (G, X)-расслоения Е—>В, которое
продолжается до действия G на тотальном пространстве Е.
Морфизмом (G, X)-расслоений называется непрерывное послойное
отображение тотальных пространств двух расслоений, индуцирующее в
164
Глава 3. Геометрические многообразия
каждом слое G-изоморфизм, непрерывно зависящий от точки на базе.
Биективный морфизм расслоений, обратное отображение к которому
также является морфизмом расслоений, называется изоморфизмом рас-
расслоений. (G, X)-расслоения, изоморфные прямому произведению В х X,
называются тривиальными.
Часто встречается ситуация, когда элементы псевдогруппы if, действу-
действующей на многообразии У, порождают изоморфизмы определенного сорта
расслоений над (подмножествами) Y. В этом случае над любым ^-мно-
^-многообразием есть ассоциированное расслоение, полученное склейкой по-
посредством этого действия. Приведем наиболее важный пример.
Пример 3.6.10 (касательное расслоение). Пусть if = "%' — псев-
псевдогруппа С-диффеоморфизмов между открытыми подмножествами про-
пространства Y = Ж" (см. пример 3.1.3). Рассмотрим тривиальное рассло-
расслоение Ж" х R" над Ж" как векторное расслоение со структурной группой
GL(/i, R). Для любого диффеоморфизма /: U —>• V из if пара из ото-
отображения / и его производной задает изоморфизм расслоений U х Ш."
и V х R". Для данного дифференцируемого л-мерного многообразия М
с картами (U,, ср;) можно склеить тривиальные расслоения ?/,• х Ж" с
помощью производных функций перехода. Тем самым определено ка-
касательное расслоение ТМ многообразия М. Слой этого расслоения в
точке х называется касательным пространством к многообразию М в
х и обозначается через ТХМ.
Пример 3.6.11 (сферическое касательное расслоение). Сферичес-
Сферическое касательное расслоение (или, в размерности два, касательное рас-
расслоение окружностей) дифференцируемого л-мерного многообразия М
получается, если стянуть в точку каждый луч в ТХМ, так что слоем его
является сфера S"~l. Если на М есть риманова метрика, то это же рас-
расслоение определяется как расслоение сфер единичного радиуса. В этом
случае часто употребляют название единичное касательное расслоение
многообразия М и обозначение UTM.
Главным расслоением называется расслоение, слоем которого является
сама структурная группа, а действие задается левыми- сдвигами.
Пример 3.6.12 (расслоение реперов). Пусть, как и в примере 3.6.10,
^ = ^гиУ = 1". Рассмотрим главное расслоение R" x GL(/2, Ж) со слоем
и структурной группой GL(n, Ж). Слой этого расслоения можно предста-
представлять себе, как множество реперов, или упорядоченных базисов простран-
пространства R", так как группа GL(n, Ж) действует на этом пространстве просто
и транзитивно. Ассоциированное главное расслоение над произвольным
дифференцируемым я- мерным многообразием М называется расслоени-
расслоением реперов над М. Точки слоя над х € М называются реперами в точке х
3.6. Расслоения и связности
165
многообразия М и соответствуют выбору базиса в касательном простран-
пространстве ТХМ.
Сечением расслоения р. Е—* В называется отображение, обратное
слева к проекции, т. е. произвольное непрерывное отображение s: В —» Е
такое, что р о s = Id. Сечение выбирает непрерывным образом по одной
точке в каждом слое. Если слой X стягиваем, а база хорошая (например,
со счетной базой топологии), то любое (G, .X)-расслоение имеет сечение,
но в противном случае сечения, скорей всего, не существует.
Для каждой подгруппы Я с G любое (Я, X)-расслоение является так-
также и (G, ЛО-расслоением. Если (G, >Y)-расслоение представимо в виде
(Я, X)-расслоения, то говорят, что структурная группа G может быть ре-
редуцирована к группе Я. Редукция структурной группы аналогична усиле-
усилению ^-структуры.
Вообще говоря, если Я — замкнутая подгруппа G и G имеет локальное
трансверсальное сечение относительно Я (см. упражнение 3.4.9), то проек-
проекция G —» G/H задает главное Я-расслоение над G/H. Тогда любое главное
G-расслоение Е—> В можно представить в виде двухэтажного расслоения
Е —> Е/Н —»• В, где Е/Н есть (G, G/Я)-расслоение, ассоциированное с Е, а
Е—> Е/Н — главное Я-расслоение. Если структурная группа расслоения Е
редуцируется к Я, то все функции перехода у// принимают значения в Я,
и, следовательно, все отображения склейки ф(/ тотального пространства
сохраняют подгруппу Я. В этом случае у расслоения Е/Н —» В имеется
сечение: в каждом слое выбирается точка, соответствующая классу еди-
единицы при локальной тривиализации.
Верно также и обратное: если расслоение Е/Н имеет сечение, то струк-
структурная группа расслоения Е может быть редуцирована к Я. Для дока-
доказательства этого познакомимся еще с одним способом построения но-
новых расслоений из уже известных. Если Е —> В — (G, Я)-расслоение и
/: С —»• В — непрерывное отображение, то расслоением, индуцированным
из Е посредством f, называется расслоение f*E —* С с тотальным про-
пространством
ГЕ = {(с,е)еСхЕ:Нс)=р(е)},
проекцией расслоения (с, е) -»с и локальными тривиализациями (с, е) >->¦
н-> (с, tzx ° ф;(б)). где ср,- — локальные тривиализации расслоения Е, а пх —
проекция на Х-сомножитель.
Предложение 3.6.13 (редукция к подгруппе). Рассмотрим то-
топологическую группу G, ее замкнутую подгруппу Н и предпо-
предположим, что группа G имеет локальное трансверсальное сечение
относительно Я. (Это выполнено, например, если G — группа Ли.)
Структурная группа главного G-расслоения Е -» В тогда и толь-
только тогда может быть редуцирована к Н, когда ассоциированное
(G, G/Н)-расслоение над В имеет сечение.
166
Глава 3. Геометрические многообразия
Доказательство. Часть «только тогда» предложения доказана выше.
Если же расслоение Е/Н —*¦ В имеет сечение s, то расслоение, индуци-
индуцированное из Е —*¦ Е/Н посредством s, есть главное Я-расслоение над В.
Ассоциированное (Н, О)-расслоение и есть Е (проверьте это!). 136.131
Пример 3.6.14 (на каждом многообразии есть риманова метри-
метрика). Хороший пример такой ситуации дает касательное пространство
дифференцируемого многообразия (в действительности это тот самый
пример, с которым мы уже имели дело в лемме 3.4.11). Естественная
GL(/j, R)-структура на этом пространстве может быть редуцирована к ор-
ортогональной группе О(п) с GL(n, R). Факторпространство QL(n, Щ/О(п)
замечательным образом отождествляется с пространством Р положи-
положительно определенных квадратичных форм на R". Так как Р — выпуклое
подмножество векторного пространства, то Р стягиваемо. Следовательно,
(GL(/j, Ш), GL(n, Ш)/О(п))-расслоение, ассоциированное с касательным
расслоением многообразия, имеет сечение. Значит, структурная группа ка-
касательного расслоения всегда может быть редуцирована к ортогональной
группе О(п). Такая редукция эквивалентна выбору римановой метрики.
Интересный частный случай расслоений возникает, если структурная
группа G имеет дискретную топологию (сравните с примером 3.6.3), так
что все функции перехода локально постоянны. Такие расслоения называ-
называются плоскими. Если группа G не дискретна, то плоским G-расслоением
будем называть G-расслоение, структурная группа которого может быть
редуцирована к G, где G — это группа G с дискретной топологией.
Если база и слой плоского расслоения являются многообразиями, то
отображения склейки ф;/ тотального пространства сохраняют не только
слоение прообразами точек базы из примера 3.6.8, но и «горизонталь-
«горизонтальное» слоение, трансверсальное слоям. Трансверсальное слоение называ-
называется плоской связностью на данном расслоении. (Более общие связности
рассмотрены ниже; их чуть сложнее себе представить.)
Листы горизонтального слоения являются накрывающими простран-
пространствами для базы. Поднятие произвольного пути на базе, соединяющего
точки х и #, на листы горизонтального слоения задает гомеоморфизм сло-
слоев над точками хну, который называется отображением голономии и
зависит только от класса гомотопии в пространстве путей с закрепленными
концами. Этот изоморфизм, являясь композицией локальных склеек вдоль
пути, задается действием элемента группы G, который, конечно, зависит от
выбора локальных тривиализаций. Но в случае х = у имеется однозначно
определенный элемент группы G, который называется.голономией петли.
Если база В линейно связна, то, отметив на ней некоторую точку Ь, полу-
получаем гомоморфизм 7ti(B, b) =Ki(B) —>¦ G, заданный голономиями петель с
началом и концом в точке Ь, который называется голономией расслоения.
3.6. Расслоения и связности
167
Предложение 3.6.15 (классификация плоских расслоений). Рас-
Рассмотрим топологическую группу G, эффективно действующую на
пространстве X, и линейно связное пространство В с отмеченной
точкой Ь. Плоские (G, Х)-расслоения с базой В, для которых зафик-
зафиксировано отождествление слоя над Ь с пространством X, рассма-
рассматриваемые с точностью до тождественных на базе изоморфизмов,
сохраняющих данное отождествление, находятся во взаимно одно-
однозначном соответствии с гомоморфизмами щ(В) —*¦ G.
Доказательство. На самом деле^это утверждение относится к (б, X)-
расслоениям, поскольку группы G и 6 изоморфны как абстрактные группы,
так что можно далее считать группу G дискретной.
Нам уже известно, что (G, .X)-расслоение определяет гомоморфизм го-
голономии щ(В) —»• G, который, конечно, не изменяется при указанных выше
изоморфизмах.
Рассмотрим теперь произвольный гомоморфизм р: щ(В) —> G. Постро-
Построим сначала тривиальное (G, >Y)-расслоение над универсальной накрываю-
накрывающей В базы В, а затем профакторизуем его по действию щ (В) накрываю-
накрывающими преобразованиями на базе и действию р на слоях. Тогда мы получим
расслоение над В с голономией р.
Два таких расслоения с одной и той же голономией изоморфны: доста-
достаточно отобразить одно в другое, переводя друг в друга листы горизонталь-
горизонтальных слоений. [3.6.151
С помощью этого результата задачу о нахождении (G, >Y)-усиления
для гладкого многообразия можно разбить на две. Рассмотрим триви-
тривиальное расслоение X х X с очевидной плоской связностью и диагональ-
диагональным сечением {(х, х): х € X}, трансверсальным горизонтальному слое-
слоению. (G, >Y)-расслоение над данным (G, X)-многообразием М с атласом
{(?/;, <р;)} можно определить с помощью склейки тривиальных расслоений
Ui х X. Функции перехода у,/ определяются следующим образом: у//(")
есть элемент G, действующий как <р, о ср^1 в окрестности точки <р/(и).
Отображения склейки ф,7 сохраняют плоскую связность и диагональное
сечение X х X, так что полученное (G, ^-расслоение над М обладает
плоской связностью и сечением, трансверсальным горизонтальным листам.
Пространство листов слоения, ограниченного на маленькую окрестность,
имеет каноническую (G, ^-структуру, возникающую из проекции на слой
вдоль листов, так что и любое многообразие дополнительной размерно-
размерности, трансверсальное листам слоения, также наследует (G, JQ-структуру.
В частности, (G, ^-структуру на многообразии М можно восстановить из
плоского (G, X) -расслоения и сечения, трансверсального горизонтальному
слоению.
Таким образом, первая задача — найти гомоморфизм tci (M) —> G, ко-
который будет представлять голономию (G, .К)-структуры. Вторая задача —
168
Глава 3. Геометрические многообразия
построить сечение ассоциированного плоского расслоения, трансверсаль-
ное горизонтальному слоению. Такой метод особенно хорошо работает для
некомпактных пространств.
Приведем другую конструкцию, связывающую с каждым (G, ^-мно-
^-многообразием М каноническое плоское расслоение над М, на этот раз со
слоем G. Элемент нового тотального пространства состоит из точки х е М
и ростка в этой точке некоторого (G, ^-отображения со значениями в X.
Любые два таких ростка отличаются на элемент группы G. Локальная три-
виализация такого расслоения уже определена атласом многообразия М.
Листы горизонтального слоения накрывают М, и каждый из них снабжен
некоторым (G, ^-отображением в X: это и есть все возможные отобра-
отображения развертки для М.
Пример 3.6.16 (касательные расслоения евклидовых многообра-
многообразий—плоские). На евклидовом многообразии М имеется плоское глав-
главное (IsomE")-расслоение. Группа IsomE", очевидно, гомоморфно отобра-
отображается в О(п), а О(л) действует на R", так что можно образовать ассо-
ассоциированное плоское (О(/г), К")-расслоение. Эта операция эквивалентна
редукции структурной группы касательного расслоения многообразия М
к О{п) (см. пример 3.6.14). Таким образом, на касательном расслоении
любого евклидова многообразия (их также называют плоскими многооб-
многообразиями) имеется естественная плоская ортогональная связность.
Пример 3.6.17 (сферические расслоения гиперболических много-
многообразий — плоские). У предыдущего примера есть интересный аналог
для гиперболических многообразий. Каждый слой сферического касатель-
касательного расслоения пространства Н" можно, продолжая геодезические лучи на
бесконечность (см. с. 59), отождествить с бесконечно удаленной сферой
S"^1. Группа МбЬ„_1 изометрий гиперболического пространства действу-
действует на бесконечно удаленную сферу, поэтому над любым гиперболическим
многообразием существует ассоциированное плоское (МбЬл_ь S1^1) -рас-
-расслоение. Это расслоение канонически отождествляется со сферическим
касательным расслоением, на котором, таким образом, имеется плоская
связность. В частности, у гиперболической поверхности на касательном
расслоении окружностей (которое является трехмерным многообразием)
имеется слоение коразмерности один. Такие слоения имеют очень интерес-
интересные геометрические и динамические свойства. Заметим однако, что струк-
структурной группой указанных расслоений служит группа Мёбиуса, а не ор-
ортогональная или линейная группы. Структура касательного расслоения
гиперболического многообразия, вообще говоря, не может быть редуци-
редуцирована к дискретной ортогональной или даже линейной группе.
Как и было обещано, обратимся теперь к общему понятию связности.
Связность можно представлять себе, как инфинитезимальный случай ло-
локальной тривиализации. Пусть р: ? —>• В — гладкое (G, ^)-расслоение, т. е.
3.6. Расслоения и связности
169
Е, В и X — гладкие многообразия размерностей, скажем, т + п, п и т; р —
гладкое отображение, G — группа Ли, гладко действующая на X, и коцикл
Y,y, определяющий Е, состоит из гладких отображений. Связностью на Е
называется поле т, состоящее из /i-мерных плоскостей, трансверсальных
слоям и удовлетворяющих дополнительному условию (G, ^-согласован-
^-согласованности: для каждого слоя Ех должны найтись такие гладкие локальные
координаты, в которых поле т горизонтально.
Условие согласованности можно сформулировать еще и так: для про-
произвольного поля т, состоящего из л-мерных плоскостей, трансверсальных
слоям, и произвольного пути а на базе, соединяющего точки х и у, су-
существует, как и в случае плоской связности, отображение из некоторого
подмножества слоя Ех в некоторое подмножество слоя Еу. Это отобра-
отображение, называемое голономией поля т вдоль пути а, или параллельным
переносом вдоль а, получается поднятием пути а до пути а, касающегося
во всех точках поля т. Для фиксированного поднятия х начальной точки х,
поднятие пути, касательного к т, однозначно определено до тех пор, пока
оно не захочет убежать на бесконечность. В любом компактном подмноже-
подмножестве слоя Ех такое поднятие определено по крайней мере для достаточно
маленького начального участка пути а. Если пространство X связно, то
условие (G, .X)-согласованности для т означает, что параллельный перенос
сохраняет (G, >Y)-структуру на слоях.
Для двух данных связностей х и а можно рассмотреть их аффинную ком-
комбинацию tx + A — t)a: для произвольной точки ееЕ плоскость хе является
графиком линейного отображения, а множество линейных отббражений
образует аффинное пространство. Связности всегда существуют локаль-
локально (в окрестности локальной тривиализации) и, пользуясь предыдущим
замечанием, их можно склеить с помощью разбиения единицы, получив
глобальную связность.
Самым важным примером связности служит связность Леви-Чиви-
ты — ортогональная связность, определенная в касательном расслоении
любого риманова многообразия. Для данного пути а на /я-мерном мно-
многообразии М можно инфинитезимально наилучшим способом подогнать
окрестность а к окрестности некоторого пути а' в пространстве Ет. При
этом параллельный перенос для связности Леви-Чивиты перейдет в обык-
обыкновенный параллельный перенос в Е"' вдоль а'.
Связность Леви-Чивиты можно описать наглядней, если многообразие
М вложено в евклидово пространство Е" и метрика на М индуцирована
с Е". Проще сначала описать родственную евклидову связность. Для двух
почти параллельных m-мерных подпространств Р, Р' с Е" ортогональная
проекция одного на другое является почти изометрией: метрика портит-
портится на множитель, не больший косинуса угла между подпространствами.
Возьмем однопараметрическое семейство m-мерных подпространств, за-
заполняющих «угол» между Я и Я', и рассмотрим композицию ортогональных
170
Глава 3. Геометрические многообразия
проекций Р = Ро на Ри Pi на Р2 и так далее до проекции на Рп = Р, где
Pi, ..., Pn-i — идущие с некоторым шагом пространства этого семейства.
При уменьшении шага искажения метрики уменьшаются, ив пределе мы
получаем изометрию. Благодаря этой конструкции семейство касатель-
касательных пространств к М вдоль пути а задает поток евклидовых изометрий,
чьи траектории ортогональны этим пространствам. (Физически все сво-
сводится к тому, что касательное пространство к М катится вдоль пути а
без проскальзывания.) Этот поток определяет параллельный перенос для
некоторой евклидовой связности на ТМ. Параллельные переносы ортого-
ортогональной связности Леви-Чивиты — это линейные части (дифференциалы)
параллельных переносов построенной евклидовой связности.
Трансверсальное слоение плоского расслоения (как и любое слоение на
многообразии) определяет поле касательных подпространств. Можно
поставить обратный вопрос — когда некоторое поле пространств является
касательным к некоторому слоению? (Такие поля называются интегри-
интегрируемыми.)
Интегрируемость поля пространств связности равносильна тому, что эта
связность плоская, т. е. локальные горизонтальные части состыкуются в
трансверсальное слоение. Для плоской связности голономия вдоль пути
зависит только от гомотопического класса пути, и, в частности, тривиальна
для любой достаточно маленькой петли. В случае общей связности такая
голономия может оказаться нетривиальной, и мерой этой нетривиально-
нетривиальности является кривизна связности. Чтобы дать ее определение, напомним
некоторые факты об алгебрах Ли (см. [Нос65]).
Алгеброй Ли называется векторное пространство V с билинейной ан-
антикоммутативной операцией [ , ], удовлетворяющей тождеству Якоби:
C.6.18)
, у],
, z],
z, х], у] =
для всех х, у, ze V. Касательное пространство TeG к группе Ли G в едини-
единице имеет структуру алгебры Ли: TeG можно отождествить с пространством
левоинвариантных векторных полей на G (разнося касательные векторы в
единице по всей группе G левыми сдвигами), а скобка Ли (см. упражне-
упражнение 3.6.19) таких векторных полей принадлежит тому же пространству. Эта
алгебра называется алгеброй Ли группы G. Каждая конечномерная алгебра
Ли является касательной алгеброй некоторой группы Ли. Две группы Ли
имеют изоморфные касательные алгебры Ли тогда и только тогда, когда
их универсальные накрывающие изоморфны.
Упражнение 3.6.19 (скобка Ли). Скобка Ли [X, У] двух векторных полей X
и У на многообразии есть мера некоммутативности их потоков. Начав с точки р,
будем s мннут двигаться в потоке поля X, потом t минут в потоке поля У, потом s
минут в потоке поля — X и / минут в потоке поля —У. С большой вероятностью мы
окажемся не в точке старта, — четырехугольник не замкнется в точке р.
3.7. Контактные структуры
171
а) Докажите, что величина зазора сокращается не менее, чем линейно относи-
относительно произведения st. Следовательно, можно взять частную производную второго
порядка по s и t и получить корректно определенный вектор в точке р. Это и есть,
по определению, значение скобки [X, У] в точке р.
б) Докажите, что скобка Ли векторных полей удовлетворяет всем условиям из
определения алгебры Ли.
Кривизна есть отображение из пространства бивекторов на М в алгебру
Ли g группы Ли G, т. е. это g-значная 2-форма на М. Для двух данных
векторов v и w, приложенных в точке р е М, отобразим единичный квадрат
в многообразие М так, чтобы векторы A, 0) и @, 1) перешли воиш соот-
соответственно. Для каждых значений sat обозначим через H(s, t) голономию
связности Леви-Чивиты, порожденную обходом границы прямоугольника
[0, s] х [0, t]. Тогда частная производная второго порядка по s и t этой
голономии и есть значение кривизны на бивекторе v Aw (сравните с опре-
определением скобки Ли векторных полей из упражнения 3.6.19). Заметим,
что при v = w голономия равна нулю, так что вторая производная здесь
действительно кососимметрична.
В случае связности Леви-Чивиты на римановых поверхностях про-
пространство касательных бивекторов одномерно, как одномерно и простран-
пространство инфинитезимальных автоморфизмов слоя, или инфинитезимальных
вращений (т. е. касательная алгебра Ли группы 0B) одномерна). При
фиксированной ориентации, каждое из этих векторных пространств имеет
канонический базис — это соответственно форма объема и дифференциал
поворота с единичной скоростью против часовой стрелки («инфините-
зимальный поворот»). Гауссова кривизна поверхности и есть кривизна
связности Леви-Чивиты, вычисленная в этих базисах.
Желая обобщить, можно для каждой плоскости Р касательного про-
пространства к л-мерному риманову многообразию в точке р определить сек-
секционную кривизну, ограничив форму кривизны на бивекторы из Я и про-
проецируя значения формы на подалгебру Ли инфинитезимальных вращений
плоскости Р.
3.7. Контактные структуры
Точно так же, как слоения связаны с плоскими связностями и интегрируе-
интегрируемыми полями пространств, контактные структуры в размерности три
связаны с совсем другим типом полей — максимально неинтегрируемыми
полями плоскостей. Имеет смысл поближе познакомиться с контактной
структурой, потому что она является интересным примером такой часто
встречающейся структуры на многообразии, которую очень сложно заме-
заметить ненаметанным глазом.
170
Глава 3. Геометрические Многообразия
проекций Р = Ро на Ри Pi на Р2 и так далее до проекции на Рп = Р, где
Ри ..., Pn-i — идущие с некоторым шагом пространства этого семейства.
При уменьшении шага искажения метрики уменьшаются, ив пределе мы
получаем изометрию. Благодаря этой конструкции семейство касатель-
касательных пространств к М вдоль пути а задает поток евклидовых изометрий,
чьи траектории ортогональны этим пространствам. (Физически все сво-
сводится к тому, что касательное пространство к М катится вдоль пути а
без проскальзывания.) Этот поток определяет параллельный перенос для
некоторой евклидовой связности на ТМ. Параллельные переносы ортого-
ортогональной связности Леви-Чивиты — это линейные части (дифференциалы)
параллельных переносов построенной евклидовой связности.
Трансверсальное слоение плоского расслоения (как и любое слоение на
многообразии) определяет поле касательных подпространств. Можно
поставить обратный вопрос — когда некоторое поле пространств является
касательным к некоторому слоению? (Такие поля называются интегри-
интегрируемыми.)
Интегрируемость поля пространств связности равносильна тому, что эта
связность плоская, т. е. локальные горизонтальные части состыкуются в
трансверсальное слоение. Для плоской связности голономия вдоль пути
зависит только от гомотопического класса пути, и, в частности, тривиальна
для любой достаточно маленькой петли. В случае общей связности такая
голономия может оказаться нетривиальной, и мерой этой нетривиально-
нетривиальности является кривизна связности. Чтобы дать ее определение, напомним
некоторые факты об алгебрах Ли (см. [Нос65]).
Алгеброй Ли называется векторное пространство V с билинейной ан-
антикоммутативной операцией [ , ], удовлетворяющей тождеству Якоби:
C.6.18)
, у], г] + [[у, z], х] + [[z, х], у] = О
для всех х, у, z e V. Касательное пространство TeG к группе Ли G в едини-
единице имеет структуру алгебры Ли: TeG можно отождествить с пространством
левоинвариантных векторных полей на G (разнося касательные векторы в
единице по всей группе G левыми сдвигами), а скобка Ли (см. упражне-
упражнение 3.6.19) таких векторных полей принадлежит тому же пространству. Эта
алгебра называется алгеброй Ли группы G. Каждая конечномерная алгебра
Ли является касательной алгеброй некоторой группы Ли. Две группы Ли
имеют изоморфные касательные алгебры Ли тогда и только тогда, когда
их универсальные накрывающие изоморфны.
Упражнение 3.6.19 (скобка Ли). Скобка Ли [X, Y] двух векторных полей X
и У на многообразии есть мера некоммутатнвности их потоков. Начав с точки р,
будем s минут двигаться в потоке поля X, потом t минут в потоке поля Y, потом s
минут в потоке поля — X и / минут в потоке поля —У. С большой вероятностью мы
окажемся не в точке старта, — четырехугольник не замкнется в точке р.
3.7. Контактные структуры
171
а) Докажите, что величина зазора сокращается не менее, чем линейно относи-
относительно произведения st. Следовательно, можно взять частную производную второго
порядка по s и t и получить корректно определенный вектор в точке р. Это и есть,
по определению, значение скобки [X, Y] в точке р.
б) Докажите, что скобка Ли векторных полей удовлетворяет всем условиям из
определения алгебры Ли.
Кривизна есть отображение из пространства бивекторов на М в алгебру
Ли g группы Ли G, т. е. это g-значная 2-форма на М. Для двух данных
векторов vhw, приложенных в точке р е М, отобразим единичный квадрат
в многообразиеМ так, чтобы векторы A, 0) и @, 1) перешли ваиш соот-
соответственно. Для каждых значений sat обозначим через H(s, t) голономию
связности Леви-Чивиты, порожденную обходом границы прямоугольника
[0, s] х [0, t]. Тогда частная производная второго порядка по s и t этой
голономии и есть значение кривизны на бивекторе v Aw (сравните с опре-
определением скобки Ли векторных полей из упражнения 3.6.19). Заметим,
что при v = w голономия равна нулю, так что вторая производная здесь
действительно кососимметрична.
В случае связности Леви-Чивиты на римановых поверхностях про-
пространство касательных бивекторов одномерно, как одномерно и простран-
пространство инфинитезимальных автоморфизмов слоя, или инфинитезимальных
вращений (т. е. касательная алгебра Ли группы ОB) одномерна). При
фиксированной ориентации, каждое из этих векторных пространств имеет
канонический базис — это соответственно форма объема и дифференциал
поворота с единичной скоростью против часовой стрелки («инфините-
зимальный поворот»). Гауссова кривизна поверхности и есть кривизна
связности Леви-Чивиты, вычисленная в этих базисах.
Желая обобщить, можно для каждой плоскости Р касательного про-
пространства к л-мерному риманову многообразию в точке р определить сек-
секционную кривизну, ограничив форму кривизны на бивекторы из Р и про-
проецируя значения формы на подалгебру Ли инфинитезимальных вращений
плоскости Р.
3.7. Контактные структуры
Точно так же, как слоения связаны с плоскими связностями и интегрируе-
интегрируемыми полями пространств, контактные структуры в размерности три
связаны с совсем другим типом полей — максимально неинтегрируемыми
полями плоскостей. Имеет смысл поближе познакомиться с контактной
структурой, потому что она является интересным примером такой часто
встречающейся структуры на многообразии, которую очень сложно заме-
заметить ненаметанным глазом.
172
Глава 3. Геометрические многообразия
Пусть т — поле плоскостей в Ш.3, которое в точке (л:, у, z) € R3 порожде-
порождено векторами A, 0, 0) и @, 1, х) (рис. 3.24). Чтобы лучше понять строение
поля х, полезно обратиться к лежандровым кривым, т. е. кривым в R3,
касательные векторы которых принадлежат х. Теперь на минутку заду-
задумайтесь, и вы увидите, как можно добраться из любой точки R3 в любую
другую по лежандровой кривой. Это свойство сразу отличает т от поля
касательных плоскостей слоения.
Рис. 3.24. Поле плоскостей т. Это поле инвариантно относительно вертикальных
сдвигов, так что на рисунке показана только плоскость z = 0.
Упражнение 3.7.1 (лежандрово поднятие). Для данной кусочно-гладкой
кривой у: [0, 1]—»R2 на х(/-плоскости и произвольной точки из R3, проецирую-
проецирующейся в у@), существует единственное поднятие пути у до лежандровой кривой
у: [0, 1] —>R3 с началом в этой точке.
На языке раздела 3.6 поле х есть связность в (Ш, М)-расслоении
тг2: Ш3 —¦• R2, где п2 — проекция на ^-плоскость вдоль z-оси. Лежандро-
Лежандрово поднятие кривой определяет параллельный перенос вдоль этой кривой.
Поднятие петли у не обязательно будет снова петлей; на самом деле разни-
разница высот между началом и концом поднятия петли равна ориентированной
площади, ограниченной у- Понять это можно, представив т двойственным
образом как ядро 1 -формы со = — х dy + dz. Тогда cico = — dx l\dy — n'dS,
где dS — элемент площади на плоскости, а к* — перенос этой формы с
помощью тс2. Если соединить концы поднятой кривой у вертикальным
отрезком, то интеграл формы со по полученной замкнутой кривой сведется
к интегралу по добавленному вертикальному отрезку, который равен раз-
разнице высот между его концами (взятой с противоположным знаком). По
теореме Стокса эта величина равна интегралу формы — n*dS по поверхно-
поверхности, натянутой на эту замкнутую кривую. А сам интеграл, по определению,
3.7. Контактные структуры
173
равен ориентированной площади, ограниченной петлей у (также взятой с
противоположным знаком).
Таким образом, связность т имеет постоянную кривизну, равную 1. Па-
Параллельный перенос вдоль петли у тогда и только тогда является то-
тождественным преобразованием, когда суммарная кривизна в ограниченной
петлей у области равна нулю, а это, в свою очередь, имеет место тогда
и только тогда, когда ориентированная площадь, ограниченная у, равна
нулю.
Диффеоморфизм между открытыми подмножествами R3 называется
контактным, если он сохраняет поле т. Ясно, что контактный диф-
диффеоморфизм переводит лежандровы кривые в лежандровы кривые. Кон-
Контактная псевдогруппа Соп состоит из контактных диффеоморфизмов
между открытыми подмножествами Ш.3, а контактной структурой на
трехмерном многообразии называется Con-структура. Обратный образ т
при координатных отображениях называется контактным полем плос-
плоскостей на многообразии.
У R3 есть много контактных диффеоморфизмов. Для начала заметим,
что отображение
(х, у, z) !-»• (х + х0,
xoy)
сохраняет поле т. Это отображение сохраняет также и слоение Ш3 как
вертикальными прямыми, так и прямыми, параллельными х-оси (см. также
упражнение 3.8.6, в). Рассмотрим два обобщения этого преобразования.
Пример 3.7.2 (поднятие автоморфизмов, сохраняющих площадь).
Пусть ср — диффеоморфизм плоскости ху, который сохраняет площадь или
умножает ее на постоянный множитель. Тогда существует контактный ав-
автоморфизм ер пространства R3, сохраняющий слоение R3 вертикальными
прямыми и проецирующийся в ф отображением kz. Более того, любые два
таких автоморфизма отличаются на вертикальный сдвиг.
Произвольную точку р б R3 можно соединить гладкой лежандровой
кривой у с отмеченной точкой q € R3. Так как отображение <р должно
переводить лежандровы кривые в лежандровы, то для точки ф(р) есть
ровно одна возможность — она должна совпадать с конечной точкой
лежандрова поднятия кривой ф о тгг о у, которое начинается в точке ф(^)-
Конечная точка поднятия не зависит от выбора у. две кривых с общими
концами тогда и только тогда имеют общие концы при поднятии, когда
ориентированная площадь, ими ограниченная, равна нулю, а это свойство
сохраняется отображением ф.
Тем самым доказано как существование и единственность поднятия <р,
так и то, что любой контактный автоморфизм пространства R3, сохраняю-
сохраняющий его слоение вертикальными прямыми, имеет указанный вид.
174
Глава 3: Геометрические многообразия
Пример 3.7.3 (поднятие автоморфизмов уг-плоскости). Другой
хороший способ представить себе стандартную контактную структу-
структуру в R3 состоит в использовании проекции тсх на плоскость yz вдоль
прямых, параллельных оси х. Такие прямые являются лежандровыми
кривыми и образуют лежандрово слоение. Рассмотрим произвольную
лежандрову кривую у и ее проекцию тсх(у) на yz-плоскость. Если произ-
производная dnx(Y(t))/dt отлична от нуля, то по проекции можно восстановить
jc-координату. Она равна тангенсу угла наклона1 касательного вектора в
г/2-плоскости.
Пусть теперь ср — произвольный диффеоморфизм г/г-плоскости. Тогда
существует единственный контактный автоморфизм ср, определенный почти
на всем пространстве R3, сохраняющий слоение R3 прямыми, параллель-
параллельными jc-оси, и проецирующийся отображением тс* в ср.
Для данной точки р = (х, у, z) е К3 проекция поля т в точке р на
</2-плоскость есть прямая с наклоном х. Производная отображения ср
переводит вектор A, х) в точке (у, z) в какой-то другой вектор. На-
Наклон этого вектора и равен jc-координате точки ср(/?). По построению ср
сохраняет поле т. Если наклон равен бесконечности, то отображение ср
в точке р не определено. Но если ср переводит вертикальные прямые в
вертикальные, то наклон никогда не равен бесконечности, и мы имеем
контактный автоморфизм всего пространства R3.
Ясно, что контактные автоморфизмы, полученные таким способом, суть
в точности те, которые сохраняют слоение М3 прямыми, параллельными
JC-ОСИ.
В нашей конструкции можно избежать неудобств, связанных с неопре-
неопределенностью ср в некоторых точках, добавив бесконечно удаленную точку
к л-оси, т. е. пополнив множество направлений до окружности и про-
продолжив поле т на Ш2 х ЮР1, считая плоскости поля вертикальными при
х = оо. (Формально контактная структура на Ш2 х ЮР1 задается с помо-
помощью двух карт: одна, определенная для конечных значений х, есть просто
тождественное отображение, а другая, определенная при х Ф О, задает-
задается отображением (х, у, z) i-> (-l/x, z, —у)-) В таком случае поднятие ср
является контактным автоморфизмом пространства М2 х ЮР1.
В этой конструкции полезно рассматривать R2 х ЮР1 как проективиза-
цию касательного расслоения к М2, так что элемент пространства М2 х ЮР1
есть пара, состоящая из точки плоскости и прямой, проходящей через эту
точку. Лежандрова кривая соответствует такому движению этой пары, при
котором прямая является касательной к траектории движения точки2.
'Далее просто «наклон».— Прим. перев.
2Это и есть «условие конька», которое подробней описано ниже, после примера 3.7.6.
Очевидное обобщение этого условия определяет контактную структуру на проективизации
кокасательного расслоения любого гладкого многообразия.— Прим. перев.
3.7. Контактные структуры
175
Упражнение 3.7.4 (поднятие кривых из ^-плоскости). Предположим, что
имеется дифференцируемое отображение р открытого интервала на yz-шюскость.
Обозначим через кх проекцию вдоль х-оси иа yz-шюскость.
а) Докажите, что если производная отображения р нигде ие обращается в нуль
(т. е. р — погружение), то существует ровно одна лежаидрова кривая у, погруженная
в R2 х КР1, для которой izx о у = р. (Выпишите ее формулу.)
б) Общая лежандрова кривая как правило имеет касательную, параллельную
jc-оси, так что ее проекция на yz-плоскость уже не будет погружением. Напри-
Например, у проекции кривой C//2, Z2, t3) имеется касп в точке t = 0. Докажите, что
заключение пункта а все же имеет место, если только первая и вторая производ-
производная отображения р не обращаются в нуль одновременно. (Подсказка: разберитесь
сначала со случаем, когда касательная к р нигде не вертикальна.)
в) Докажите, что если для каждого значения параметра t найдется такое чи-
число г, что л-я производная отображения р не обращается в нуль, то исходное
утверждение все равно остается верным, за исключением того, что поднятие может
ие быть погружением.
г) Что можно сказать в общем случае?
Предложение 3.7.5 (касательное расслоение окружностей име-
имеет контактную структуру). Касательное расслоение окружностей к
гладкой поверхности имеет каноническую контактную структу-
структуру, которая сохраняется при любом диффеоморфизме.
Доказательство. Рассмотрим сначала М2 х S1 — касательное рассло-
расслоение окружностей на плоскости М2. Оно двулистно накрывает контакт-
контактное многообразие R2 х ЮР1, которое было введено после примера 3.7.3.
Действительно, его слоем служит окружность единичных векторов, а не
прямых, проходящих через точку О. Наделим пространство Е2 х S1 инду-
индуцированной контактной структурой. Диффеоморфизмы плоскости Ш2 точно
так же поднимаются до контактных автоморфизмов R2 x S1, как они под-
поднимались до контактных автоморфизмов пространства Ш2 х ИР1 в при-
примере 3.7.3. Таким образом, для фиксированного атласа поверхности кон-
контактные структуры на расслоениях окружностей в областях действия карт
правильно стыкуются и дают глобальную контактную структуру на каса-
касательном расслоении окружностей к данной поверхности. 13.7.51
Пример 3.7.6. Как следствие получаем, что пространства Т3, ЮР3 и 53
имеют контактную структуру. Тор Т3 диффеоморфен касательному рассло-
расслоению окружностей тора Т2, проективное пространство ЮР3 диффеоморфно
группе SOC) (см. упражнение 2.7.7), которую, в свою очередь, можно ото-
отождествить с касательным расслоением окружностей к сфере S2 (почему?).
Следовательно, на пространстве ЕР3 имеется контактная структура. Так
как сфера 53 двулистно накрывает S0C), то на ней тоже есть контактная
структура.
176
Глава 3. Геометрические многообразия
В действительности, как доказал Мартинэ [Маг71], каждое ориентиру-
ориентируемое трехмерное компактное многообразие имеет контактную структуру.
Чтобы понять физический смысл контактной структуры на касательном
расслоении окружностей к поверхности, обратимся к катанию на конь-
коньках или велосипеде. Идеальный конек описывает лежандрову кривую в
касательном расслоении окружностей к поверхности льда. Он может по-
повернуться в любую сторону, но в каждый момент времени его положение
меняется в том направлении, куда он смотрит. Точно так же, если вы едете
на велосипеде, то направление вашего движения определяет луч, каса-
касательный к земле в точке ее контакта с задним колесом. Если велосипед
не пробуксовывает, то заднее колесо движется в направлении этого лу-
луча, и его движение задает лежандрову кривую в касательном расслоении
окружностей к поверхности земли.
У маленьких детей бывают велосипеды с двумя дополнительными ко-
колесиками, расположенными на некотором расстоянии от заднего колеса.
Такое колесико также вычерчивает лежандрову кривую. На самом де-
деле, для любого действительного числа / диффеоморфизм ср( пространства
Ш2 х S1, который каждый касательный луч переносит влево параллельно
самому себе на расстояние / (расстояние со знаком), является контактным
автоморфизмом. Траектория колесика есть в точности образ траектории
заднего колеса при таком преобразовании. Заметим, что такое преобра-
преобразование, примененное к кривой, часто создает или устраняет каспы (см.
рис. 3.25). Вспомните об этом, когда будете стричь траву на лужайке и,
обойдя ее по краю, начнете двигаться внутрь.
Задние колеса автомобиля также едут по лежандровым кривым, связан-
связанным преобразованием ср(. (Благодаря специальному передаточному меха-
механизму колеса при повороте движутся со слегка разными скоростями, пото-
потому что в противном случае одно из колес обязательно пробуксовало бы при
движении по кривой.) Параллельные парковки возможны только потому,
что любые две точки можно соединить лежандровой кривой. С передними
колесами дело обстоит сложнее, так как передняя ось не перпендикулярна
их траектории, если, конечно, машина не движется по прямой. Зависи-
Зависимость между передними и задними колесами тоже не проста: движение
задних колес зависит не только от их положения в настоящий момент и
направления передних колес, но и от их предыдущего движения.
Контактный автоморфизм ср, можно определить не только для М2, но
и для любой ориентированной римановой поверхности. Он переносит ка-
каждый касательный луч влево (на расстояние /) по геодезической, перпен-
перпендикулярной направлению луча. (Поверхность должна быть ориентирована
именно для того, чтобы можно было говорить о движении влево или впра-
вправо.) При изменении / автоморфизмы ср/ определяют поток ср. Этот поток
тесно связан с геодезическим потоком на поверхности. Геодезический
поток ф на римановой поверхности перемещает каждый касательный век-
3.7. Контактные структуры
177
Рис. 3.25. Семейство параллельных кривых. Преобразование <р( касательного рас-
расслоения окружностей к плоскости, параллельно переносящее каждый касательный
луч влево от него иа расстояние /, является контактным автоморфизмом. На рисунке
изображены проекции иа плоскость образов одной единственной кривой при разных
значениях /. Обратите внимание на преобразования каспов.
тор вдоль своей геодезической с единичной скоростью. По сути, ср и ф —
это две реализации одного и того же потока, чтобы их отождествить доста-
достаточно повернуть каждый касательный вектор на угол к/2 против часовой
стрелки.
Упражнение 3.7.7. а) Предложение 3.7.5 дает пример канонического поля
плоскостей на касательном расслоении окружностей к гладкой поверхности. Если
на поверхности выбрана рнманова метрика, то есть и другой пример: ограниче-
ограничение связности Леви-Чивнты касательного расслоения иа касательное расслоение
окружностей. Сравните эти два поля и объясните, как связан геодезический поток
(или поток катящегося колеса) на поверхности со связностью Левн-Чивнты. См.
также следствие 3.7.16.
б) Дайте геометрическое описание контактной структуры примера 3.7.6.
в) Объясните, как связаны между собой контактная структура на S3, поток
Хопфа, связность Леви-Чивиты на S .
Задача 3.7.8 (лежандровы слоения). На контактном трехмерном многообра-
многообразии легко построить (по крайней мере, локально) одномерное лежандрово слоение,
т. е. слоение лежандровыми кривыми: в маленькой окрестности каждое ненулевое'
178
Глава 3. Геометрические многообразия
сечение контактного поля т является векторным полем, фазовые кривые которого
задают такое слоение.
а) Докажите, что каждое лежандрово слоение локально эквивалентно слоению
пространства R3 (с нашей модельной контактной структурой) прямыми, параллель-
параллельными х-оси.
б) Дайте интерпретацию контактных трехмерных многообразий с лежандровы-
ми слоениями как многообразий, локально устроенных так же, как касательное
расслоение окружностей на плоскости R2 с точностью до действия диффеомор-
диффеоморфизмов.
в) Приведите и проанализируйте какие-нибудь интересные примеры.
Вернемся к нашему модельному полю плоскостей т на R3. Пусть X —
произвольное гладкое векторное поле, касающееся т. Мы утверждаем, что
если только поле X не равно тождественно нулю, то его поток не может
состоять из контактных автоморфизмов. Действительно, рассмотрим ко-
короткую лежандрову дугу а, трансверсальную к X в точке р. Под действием
данного потока дуга а заметает четырехугольник, три стороны которого
являются лежандровыми кривыми. Если и четвертая сторона (сдвиг дуги а
потоком) тоже лежандрова, то получается замкнутая лежандрова кривая,
что невозможно, так как проекция этого четырехугольника на ху-плос-
кость имеет ненулевую площадь. На самом деле, легко понять, что поток
поля X поворачивает каждую плоскость поля т вокруг оси, проходящей
через вектор поля X, изменяя ее наклон в трансверсальном направлении
пропорционально длине вектора. Из этого следует
Предложение 3.7.9 (горизонтальные возмущения контактной
структуры). Для каждого инфинитезимального возмущения поля
х существует единственное касательное к х векторное поле X,
порождающее это возмущение.
Следствие 3.7.10 (локальная жесткость контактной структуры).
Пусть тг — контактное поле плоскостей на трехмерном многообра-
многообразии М. Существует такая окрестность (в С2-топологии) поля п,
что любое поле плоскостей к' из этой окрестности также задает
контактную структуру. Более того, поле л' эквивалентно полю
к при помощи С°°-диффеоморфизма, близкого к тождественному в
С2-топологии.
Доказательство. Близкое к к поле плоскостей к' можно соединить с
полем тг гладкой гомотопией. Согласно предложению 3.7.9, существует та-
такое векторное поле Хо, что его действие на л совпадает с точностью до
первого порядка с действием этой гомотетии при / = 0. Значение Хо в
каждой точке зависит от значения поля к и значения его первой про-
производной по времени в этой точке. Так как возмущение предполагается
С2-малым, то решения Xt существуют также при всех значениях параметра
3.7. Контактные структуры
179
0 < / < 1, и возникает зависящее от времени векторное поле, принадлежа-
принадлежащее классу С1, как функция на М х [0, 1 ]. Интегрируя это векторное поле,
получаем С2-близкий к тождественному диффеоморфизм, переводящий л
в л'. 13.7.101
Исходя из предложения 3.7.9, можно предположить, что находить кон-
контактные потоки — занятие непростое, но оказывается, что именно это пред-
предложение дает возможность построить многие (а на самом деле все) кон-
контактные потоки. Для данного контактного поля плоскостей к на трехмерном
многообразии М обозначим через N(n) факторрасслоение ТМ/п; это один
из способов определения нормального расслоения без использования ри-
мановой метрики.
Следствие 3.7.11 (классификация контактных потоков). Пусть п —
контактное поле плоскостей на трехмерном многообразии М. Про-
Проекция из ТМ на N(n) задает взаимно однозначное соответствие
между векторными полями, сохраняющими контактную структу-
структуру, и гладкими сечениями расслоения N(k).
Доказательство. Для данного гладкого сечения s расслоения N(n)
обозначим через X гладкое векторное поле, проецирующееся на s. Поле X
может и не сохранять к, но по предложению 3.7.9 это можно исправить,
добавив однозначно определенное содержащееся в к векторное поле,
получив тем самым контактное векторное поле.
Тем самым сюръективность отображения контактных векторных полей
в сечения N(iz) доказана. Инъективность же была установлена в замечании
перед предложением 3.7.9. 13.7.111
Упражнение 3.7.12 (площадь и контактная структура). Объясните, как
связаны между собой следствие 3.7.11, пример 3.7.2 и упражнение 3.1.13.
Степень закрученности, или неинтегрируемости, поля плоскостей можно
измерить примерно таким же образом, как н кривизну связности. Что-
Чтобы разобраться в этом, рассмотрим поле 6-мерных подпространств т на
я-мерном многообразии М. Пусть хну — векторы из т, приложенные в
некоторой точке р е М. Локально продолжим х и у до касательных к т
векторных полей X и Y и рассмотрим их скобку Ли [X, Y]. Кручением
поля т. называется 2-форма на т. со значениями в нормальном расслоении
N(x), которая паре векторов х и у сопоставляет образ скобки [X, Y] при
проекции на N(x).
Необходимо доказать, что значение формы не зависит от выбора про-
продолжений X и Y. Это делается с помощью стандартной техники: проверим,
что форма [X, Y]/x билинейна не только относительно комбинаций с. по-
постоянными коэффициентами, но и с коэффициентами в виде функций. Для
этого рассмотрим два векторных поля U н V, определенных в окрестности
точки р и касательных к т, и сравним значение [U, V]/x с [fU, gV]/x, где /
180
Глава 3. Геометрические многообразия
и g — функции. Новая скобка Ли имеет вид:
[fU, gV] = fg[U, V] + fU(g) V - gV(f) U,
так что
[fV,gV\/x=fg[U, V]/x.
Теперь рассмотрим набор {Хх, Х2. ¦ ¦, Хп) касательных к т векторных по-
полей, образующих базис т в окрестности точки р. Запишем поле U в виде ли-
линейной комбинации этих полей: 6/ = У}/А. Тогда [U, V]/x = J2fi[Xt, V]/x.
В частности, если Up = О, то ([?/, V]/x)p = 0. Точно так же, если Vp = 0, то
([?/, V]/x)p = 0.
Отсюда следует, что если X' и У - два векторных поля, совпадающих
с X и У в точке р, то
Р, Г]/х)р = Р' - X, Г]/х)Р + ([X, Y']/x)p =
= Р, У']Л)Р = Р, У]Л)„.
Например, стандартная контактная структура на М3 порождается век-
векторными полями X = A, 0, 0) и У = @, 1, х). Их скобка Ли равна @, 0, 1).
Форма кручения, записанная в базисе @, 0, 1) нормального расслоения, -
это перенос формы dx Ady с помощью проекции вдоль оси z.
Теорема 3.7.13 (Фробениус). Поле k-мерных подпространств ин-
интегрируемо тогда и только тогда, когда его форма кручения то-
тождественно равна нулю.
Доказательство. Если поле т интегрируемо, то поток векторного поля,
содержащегося в т., отображает каждый лист слоения на себя, и обрат-
обратно, каждое векторное поле, сохраняющее листы слоения, содержится в т.
Отсюда следует, что скобка Ли векторных полей, содержащихся в т, тоже
содержится в т. Таким образом, кручение тождественно равно нулю.
Чтобы доказать обратное, рассмотрим поле fc-мерных подпространств
с кручением, тождественно равным нулю. Выберем локальные координа-
координаты вК'в окрестности точки р так, чтобы поле т было трансверсально к
«вертикальному» координатному подпространству М"~*. Обозначим через
Хи ¦ ¦ ¦, Xk содержащиеся в т векторные поля, проецирующиеся в коорди-
координатные векторные поля горизонтального подпространства R*. Поток поля
Xt при проекции переходит в сдвиг в М* вдоль /-й оси координат, так что
скобка Ли [X,, X,] не имеет горизонтальной составляющей. Если круче-
кручение равно нулю, то необходимо [Х„ X,] = 0. Следовательно все поля Xt
коммутируют. Интегрируя их, получаем локальные координаты для слое-
слоения. ШШ
Если поле подпространств т является связностью в (G, Л)-Расслое'
нии р: Е -> В, то подпространство поля т в произвольной точке х е Е при
3.7. Контактные структуры
181
проекции р отождествляется с касательным пространством к базе в точке
р(х), и, следовательно, слой нормального расслоения Nxx = TxE/x отожде-
отождествляется с касательным пространством к слою Ех расслоения Е в точке х.
Кручение в точке х е Е — это 2-форма на ТР(Х)В со значениями в ТХЕХ. Если
фиксировать бивектор в ТУВ (у е 5), то на слое р~1(у) возникает векторное
поле (значений формы), соответствующее действию некоторого элемента
алгебры Ли g группы G. Рассматривая все слои вместе, получаем 2-форму
на базе В со значениями в g — это в точности кривизна связности т.
Упражнение 3.7.14. Пусть и> — невырожденная 1-форма на л-мерном мно-
многообразии (т. е. <о нигде не обращается в нуль). Докажите, что ядро этой формы
задает касательное поле к слоению коразмерности одни тогда и только тогда, когда
форма о Л da> тождественно равна нулю1.
Такой критерий очень удобен в случае двумерных полей на трехмерном
многообразии. Векторное пространство кососимметрических билинейных
форм на двумерном векторном пространстве, принимающих значения в од-
одномерном пространстве, имеет размерность один. Если и многообразие, и
поле плоскостей ориентированы (так что поле плоскостей оказывается и
трансверсально ориентированным), то кручению можно приписать опре-
определенный знак. Для этого выберем положительное направление в соответ-
соответствии с правилом буравчика при обходе маленькой петли, касательной к
х, в направлении против часовой стрелки.
В двойственных терминах поле т можно (по крайней мере, локально)
представить как ядро 1-формы о. Внешний дифференциал do при огра-
ограничении на х является формой, двойственной к кручению т, если о принять
за базис в jV(t).
Предложение 3.7.15. Поле плоскостей на трехмерном многооб-
многообразии тогда и только тогда определяет контактную структуру,
когда его кручение нигде не равно нулю.
Доказательство. Важно заметить, что если кручение поля т всюду
отлично от нуля, то можно воспользоваться доказательством предло-
предложения 3.7.9, чтобы затем из него получить следствие 3.7.10 и, наконец,
следствие 3.7.11.
Затем выберем локально сечение s расслоения jV(t), нигде не обра-
обращающееся в нуль. Пусть X — однозначно определенное векторное поле,
проецирующееся на s и сохраняющее т (следствие 3.7.11). Кручение поля т,
выраженное как кратное s(p) в каждой .точке р, является Х-инвариантной
скалярной 2-формой, определенной на векторах из т. Следовательно, она
1В этих же терминах можно сформулировать и общий критерий интегрируемости для полей
коразмерности q. Набор гладких линейно независимых в каждой точке форм шь ..., u>q
тогда и только тогда определяет касательное поле слоения коразмерности q, когда при всех /
(/ = 1, ..., q) формы Ш[ Л ... Л a>q Л du>i тождественно равны нулю.— Прим. перев.
182
Глава 3. Геометрические многообразия
определяет 2-форму, а значит, и меру, на локальном пространстве листов
слоения, ассоциированного с потоком векторного поля X. Построим сохра-
сохраняющее эту меру отображение пространства листов на плоскость так же,
как это было сделано в упражнении 3.1.15. Накроем, как в примере 3.7.2,
это отображение отображением из открытого подмножества трехмерного
многообразия в пространство М3, переводя каждую касательную к т кривую
в лежандрову кривую. Тем самым будет построена карта для контактной
структуры. 13.7.151
Следствие 3.7.16 (риманова контактная структура). Связность
Леви-Чивиты на единичном касательном расслоении римановой
поверхности S тогда и только тогда задает контактную струк-
структуру, когда гауссова кривизна S строго положительна или строго
отрицательна.
Упражнение 3.7.17. Докажите, что если <о — невырожденная 1 -форма на трех-
трехмерном многообразии, то ядро о задает контактное поле плоскостей тогда и только
тогда, когда форма и> A du> невырождена.
Невырожденные 1-формы со, для которых форма о> Ad<x> также невы-
невырождена, локально устроены как стандартная 1-форма а = dz — xdy, ко-
которая определяет модельную контактную структуру на R.3. Псевдогруппа,
сохраняющая форму а, называется строго контактной псевдогруппой.
Упражнение 3.7.18 (строго контактные структуры). Строго контактная
структура имеет канонический поток, определяющий слоение, трансверсальное
контактному полю плоскостей и локально эквивалентное слоению пространства
R3 (с модельной контактной структурой) прямыми, параллельными z-och.
Докажите, что на контактном трехмерном многообразии большинство слоеннй,
трансверсальных контактному полю плоскостей, не являются локально эквива-
эквивалентными такому слоению. (Сравните пример 3.7.2 н задачу 3.7.8.)
3.8. Восемь модельных геометрий
Что такое геометрия? До этого момента мы имели дело с тремя разными
трехмерными геометриями: гиперболической, евклидовой и сферической.
Все эти геометрии имеют одно общее свойство: они однородны и изо-
изотропны, причем настолько, насколько это вообще возможно. А именно,
в каждой из них можно с помощью изометрий перевести любую точку в
любую другую (однородность) и любой ортонормированный базис в каса-
касательном пространстве точки — в любрй другой ортонормированный базис
в этой же точке (изотропия). Новые возможности появятся, если мы по-
пожертвуем изотропностью, так что некоторые направления в каждой точке
будут геометрически выделенными.
Чтобы составить перечень дополнительных трехмерных геометрий, нуж-
нужно решить, какие пространства мы хотим рассматривать, какие структуры
3.8. Восемь модельных геометрий
183
на них выбирать для определения геометрии и как эти геометрии мы будем
различать. Например, будем ли мы считать ^еометрией пространство, на
котором определены такие понятия, как прямые и плоскости, или про-
пространство с конгруэнцией на нем, или же пространство с метрикой (рима-
(римановой метрикой)? Каждый из этих подходов имеет свои недостатки.
Проблема с использованием прямых и плоскостей состоит в недоста-
недостаточной общности такой геометрии. Ни в одной из пяти новых геометрий,
рассмотренных в этом разделе, мы не встретим хорошего определения
плоскости, так как в них нет вполне геодезических поверхностей. Кроме
того, даже в евклидовой геометрии информация о формах геометрических
объектов не может быть адекватно выражена в терминах отношений ин-
инцидентности прямых и плоскостей.
Использование понятия конгруэнтности в качестве ключевого приводит
к чрезмерному увеличению числа геометрий. Например, разные геометрии
получатся, если рассмотреть одно и то же евклидово пространство с груп-
группой конгруэнции, состоящей из параллельных переносов, и группой, состо-
состоящей из горизонтальных переносов и винтовых движений в вертикальном
направлении (когда угол поворота пропорционален вертикальному сдви-
сдвигу), и так далее. Иногда интересно различать такие структуры, но в целом
эти разнообразные вариации следовало бы рассматривать в рамках одной,
евклидовой, геометрии.
Использование расстояния для определения геометрии также малоудо-
малоудовлетворительно. Для начала просто изменим масштаб, например, в И3 или
S3 и получим разные метрические пространства. Даже если считать одина-
одинаковыми все метрические пространства с пропорциональными метриками,
останется много пространств, на которых имеются целые семейства одно-
однородных метрик (иногда разной степени однородности), которые не являют-
являются эквивалентными с точностью до масштаба. Например, на трехмерной
сфере есть интересное семейство однородных метрик, получающихся из
стандартной при ее сжатии или растяжении в слоях расслоения Хопфа
без изменения метрики в перпендикулярном направлении.
Лучше всего, конечно, представлять себе геометрию, помня о всех этих
трех точках зрения. Если считать изменения группы конгруэнции, не меня-
меняющие метрики, и изменения метрики, не меняющие группы конгруэнции, не
существенными для данной геометрии, а также считать геометрии одина-
одинаковыми, если множества компактных многообразий, смоделированных по
ним, совпадают, то мы придем к вполне приемлемому списку геометрий.
Из логических соображений нужно все-таки остановиться на каком-то
одном определении. Мы остановимся на понятии геометрии, соответству-
соответствующем пространству с группой конгруэнции, то есть (G, X)-пространству.
Определение 3.8.1 (модельная геометрия). Модельной геометри-
геометрией (G, X) называется пара, состоящая из многообразия X и подгруппы
184
Глава 3. Геометрические многообразия
3.8. Восемь модельных геометрий
185
G группы его диффеоморфизмов, для которой выполнены следующие
условия:
а) пространство X связно и односвязно,
б) группа G транзитивно действует на X, причем стабилизаторы всех
точек компактны,
в) группа G не содержится ни в какой большей подгруппе группы диф-
диффеоморфизмов, для которой стабилизаторы точек компактны, и
г) существует хотя бы одно компактное (G, ^-многообразие.
Условие а задает выбор ровно одного представителя из каждого класса
локально эквивалентных геометрий с разными фундаментальными груп-
группами, так как локально эквивалентные геометрии, взятые в качестве мо-
модельных, задают одинаковые классы многообразий (см. упражнение 3.3.1).
Условие б означает, что данное пространство обладает однородной G -ин-
-инвариантной римановой метрикой (см. лемму 3.4.11) и при этом является
полным относительно нее (см. предложение 3.4.15 и следующий за его
доказательством абзац). Условие в утверждает, что никакая G-инвариант-
ная риманова метрика не остается инвариантной под действием какой-
либо большей группы. В частности, это условие выделяет не более одного
представителя в каждом классе изометричных метрических пространств.
Другим соображением в пользу условия в служит то, что при увеличении
структурной группы G множество многообразий с данной структурой не
уменьшается. Условие г, хотя и не сформулировано во внутренних тер-
терминах,1 но тоже очень полезно, так как отбрасывает целое непрерывное,
семейство трехмерных геометрий, не способных служить моделями ни для
одного компактного многообразия.
Теорема 3.8.2 (двумерные модельные геометрии). Есть ровно
три двумерные модельные геометрии: сферическая, евклидова и
гиперболическая.
Доказательство. Так как группа G действует на пространстве X тран-
транзитивно, то любая G-инвариантная риманова метрика на X имеет постоян-
постоянную гауссову кривизну. Когда метрика домножается на коэффициент k, ее
гауссова кривизна умножается на k2, так что всегда можно найти метрику с
кривизной 0, 1, или — 1. Стандартная теорема римановой геометрии утвер-
утверждает, что единственными полными односвязными римановыми я-мерными
многообразиями постоянной секционной кривизны 0, 1, —1, являются про-
пространства Е", 5" и Н" соответственно (см., например, [dC92, с. 163] или
[GHL90, с. 135]). [3"М1
Другое доказательство этой теоремы содержится в упражнении 3.8.11.
1 Из сказанного в разделе 3.5 должно быть ясно, что условие г — это в точности условие
существования у G дискретной кокомпактной подгруппы.— Прим. ред.
Упражнение 3.8.3. Преобразования подобия на действительной прямой обра-
образуют двумерную группу Sim(l), которая действует на себе левыми сдвигами. По-
Почему (Sim(l), Sim(l)) не является двумерной модельной геометрией? (Подсказка:
см. упражнение 2.2.10).
При классификации трехмерных модельных геометрий (G, X) первым
делом нужно выделить связную компоненту единицы группы G — назовем
ее G'. Группа G' действует по-прежнему транзитивно, причем стабилизато-
стабилизаторы G'x точек х € X связны. Это объясняется тем, что факторпространства
G'x/(G'x)o, где (G'xH — связная компонента единицы стабилизатора G'x, слу-
служат слоями накрытия над X. Так как пространство X односвязно, то это
накрытие тривиально.
Таким образом, стабилизатор G'x есть связная замкнутая подгруппа
группы SOC). Так как связная замкнутая подгруппа группы Ли в свою
очередь является группой Ли и, следовательно, многообразием, то легко
видеть, что для G'x есть только три возможности: SOC), SOB), тривиаль-
тривиальная группа. Стабилизатор Gx является группой Ли той же размерности.
Теорема 3.8.4 (трехмерные модельные геометрии). Есть ровно
восемь трехмерных модельных геометрий, а именно:
а) Если стабилизаторы точек трехмерны, то X есть S3, Е3 или
Н3.
б) Если стабилизаторы точек одномерны, то пространство X
является G-инвариантным расслоением над одной из двумерных мо-
модельных геометрий. На X имеется такая G-инвариантная метрика,
что кривизна связности, ортогональной слоям, постоянна и равна
0 или 1.
б,) Если эта кривизна равна нулю, то X есть S2 х Е1 или В2 х Е1.
б2) Если кривизна равна единице, то X есть либо нильгеометрия
(расслаивающаяся над Е2), либо пространство SLB, M) (рас-
(расслаивающееся над Н2).
в) Единственной геометрией с дискретными стабилизаторами
является солвгеометрия, пространство которой расслаивается
над прямой.
Геометрии пункта а мы уже подробно рассматривали, а геометрии пунк-
пункта б; не требуют комментариев. Оставшиеся геометрии мы подробно ис-
исследуем в процессе доказательства. Начнем с того, что наделим простран-
пространство X римановой метрикой (см. комментарий к определению 3.8.1).
Доказательство 3.8.4, а. Если группа G' действует со стабилизатором
SOC), то любую плоскость в любом касательном пространстве действием
группы G можно перевести в любую другую плоскость в любом другом
касательном пространстве, так что метрика имеет постоянную секционную
186
Глава 3. Геометрические многообразия
кривизну. Так же, как и в двумерном случае, отсюда немедленно следует,
что данная геометрия есть сферическая, евклидова или гиперболическая.
Группа G' является подгруппой индекса 2 полной группы изометрий G,
которую можно получить, добавив произвольную меняющую ориентацию
изометрию. |3.8.4, а\
Доказательство 3.8.4, б. Если группа G' действует со стабилизатором
SOB), то существует единичное G-инвариантное векторное поле V на X,
которое задает в каждой точке х ось вращения элементов из G'x. Траектории
поля V образуют одномерное G'-инвариантное слоение &'. При этом поток
поля V (обозначим его через ср,) коммутирует с действием С, так что если
элемент группы С оставляет на месте какую-то точку листа F слоения &',
то он оставляет на месте все точки листа F: стабилизаторы всех точек листа
совпадают. Отсюда также следует, что если элемент группы С переводит
точку х € F в другую точку у € F, то он коммутирует со всеми элементами
стабилизатора G'x = G'y.
Зафиксируем теперь лист F слоения и точку х е F на нем. Обозначим
через g, элемент из С, переводящий (fi(x) обратно в х. Тогда преобра-
преобразование gt о ср, оставляет точку х на месте, а его производная в точке х
является линейным автоморфизмом касательного пространства ТХМ. На
оси вращения стабилизатора G'x эта производная совпадает с тождествен-
тождественным преобразованием. Она коммутирует с вращениями вокруг этой оси,
т. е. с элементами G'x. Но такое линейное преобразование само должно
быть вращением вокруг той же оси, возможно с дополнительным растя-
растяжением или сжатием. Но растяжения или сжатия исключены, так как по
условию существует компактное (G, ^-многообразие, откуда следует, что
поле V должно сохранять объем:
Упражнение 3.8.5 (дивергенция). Дивергенция векторного поля V на мно-
многообразии X с формой объема <о измеряет насколько это поле увеличивает илн
уменьшает объем. Точнее, div V есть, по определению, производная Ли (см. зада-
задачу 3.1.16) Lva> формы объема, отнесенная к самой форме.
Предположим теперь, что на многообразии X транзитивно действует группа Ли
G, а поле V и форма объема <о инвариантны относительно действия G. Докажите,
что дивергенция div V постоянна на X.
Вернемся к доказательству. Из того, что существует компактное (G, А)-мно-
А)-многообразие, следует, что это многообразие наследует у X векторное поле и форму
объема. Поле должно сохранять полный объем, а значит, и форму объема в ка-
каждой точке. Следовательно, дивергенция поля V равна нулю. Выведите отсюда,
что композиция gt о ф/ действует на ТХМ как вращение.
Таким образом, производная преобразования ср( изометрично отобража-
отображает ТХМ на Тъ{х)М. Так как это верно для любой точки х, то поток поля V
состоит из изометрий.
Рассмотрев окрестность какой-нибудь точки х на произвольном листе
слоения и учитывая, что рассматриваемый лист инвариантен относительно
3.8. Восемь модельных геометрий
187
подгруппы G'x, изоморфной SOB), заключаем, что лист не может накру-
накручиваться сам на себя, а является образом 51 или R1 при вложении. Более
того, легко видеть, что если слои различны, то у них существуют непере-
непересекающиеся окрестности. Следовательно, факторпространство Х/& есть
двумерное многообразие (обозначим его через У). Так как поле V действует
изометриями, то пространство У наследует у X риманову метрику (игно-
(игнорируя компоненту метрики в направлении слоя) и транзитивное действие
С изометриями. Из того, что пространство X связно и односвязно, следу-
следует, что этими свойствами обладает и У. Из доказательства теоремы 3.8.2
видно, что У является пространством одной из трех двумерных геометрий:
Е2, S2, Н2. К тому же X является главным расслоением над У со слоем и
структурной группой, равными 51 или R1.
Поле плоскостей т., ортогональное &, задает связность в этом рассло-
расслоении. Так как группа изометрий действует на X транзитивно, то кривизна
связности т постоянна.
б/) Если кривизна тождественно равна нулю, то т. определяет слоение.
Так как пространство У односвязно, то по предложению 3.6.15 наше рас-
расслоение тривиально. В зависимости от У может иметь место один из трех
следующих случаев (пустой кружок означает, что при этом новых геоме-
геометрий не появляется):
• Если У = S2, то получается модельная геометрия 52 х Е1. В качестве
компактного (G, ^-многообразия можно взять 52 х 51 (см. также
упражнение 4.7.1).
о Если У = Е2, то X = Е2 хЕ'= Е3. То есть группа С (а значит, и груп-
группа G) содержится в большей группе изометрий, и новой модельной
геометрии не возникает.
• Если У = Н2, то получается модельная геометрия И2 х Е1. Примером
компактного (G, Х)-мн°пюбразия служит любая компактная гипер-
гиперболическая поверхность, умноженная на окружность.
В каждой из этих двух новых геометрий полная группа изометрий G содер-
содержит G' в качестве подгруппы индекса 4, так как можно независимо менять
ориентацию на каждом из сомножителей.
бг) Если кривизна т отлична от нуля, то связность т определяет кон-
контактную структуру. После изменения масштаба в направлении слоев и
выбора подходящих ориентации на базе и слое можно считать, что кри-
кривизна тождественно равна 1 (в стандартных базисах пространств Д2 TY и
TF). Вместе с условием односвязности пространства X это, по существу,
уже определяет геометрию. Если у пространства У ненулевая кривизна,
то X можно считать пространством единичного касательного расслоения
многообразия У (точнее, универсальной накрывающей этого пространства)
со связностью Леви-Чивиты (см. следствие 3.7.16). Группа G состоит из
188
Глава 3. Геометрические многообразия
дифференциалов изометрий пространства Y и вращений единичных каса-
касательных векторов, причем на базе вращение действует тождественно.
о Если Y = S2, то единичное касательное расслоение есть SOC), а его
универсальная накрывающая — сфера S3 (см. пример 3.7.6). Группа G
в этом случае есть группа изометрий сферы S3, сохраняющих рассло-
расслоение Хопфа (см. упражнение 3.7.7, в). Это не максимальная группа
с компактными стабилизаторами, так что данная геометрия не может
быть модельной.
• Если Y = Е2, то мы имеем нильгеометрию. Ее можно определить в
терминах модельной контактной структуры т раздела 3.7 (стр. 172)
как группу контактных автоморфизмов, являющихся поднятиями изо-
изометрий .^-плоскости (см. пример 3.7.2). Из упражнения 3.8.6, д вы-
вытекает существование компактных нильмногообразий.
• Если Y = Н2, то единичное касательное расслоение есть группа
PSLB, R), сохраняющих ориентацию изометрий пространства Н2
(см. упражнение 2.6.6). Переходя к ее универсальной накрывающей,
получаем, что X = SLB, R). Примером компактного трехмерного
многообразия с такой геометрией служит единичное касательное
расслоение компактной гиперболической поверхности.
Для SLB, К) и нильгеометрии контактная структура определяет ори-
ориентацию, которую нельзя изменить изометриями. Тем не менее, можно
одновременно поменять ориентацию на базе (двумерной модельной гео-
метрии) и слое, а значит G' является подгруппой индекса 2 в G. [3.8.4, б\
Упражнение 3.8.6 (изометрий нильгеометрни). Пусть G — группа изоме-
изометрий нильгеометрни с контактной структурой т.
а) Вычислите разность между высотами концов лежандровой кривой, которая
проектируется на дгг/-плоскость Е2 в отрезок с концами (лго, уо) и (xi, у\). (Ответ:
\{xi +xo)(yi -Уо)-)
б) Воспользовавшись п. а и конструкцией примера 3.7.2, выпишите явно эле-
элемент группы G, проецирующийся в данную изометрию плоскости Е2. (Напомним,
что все такие элементы отличаются на вертикальный сдвиг.)
в) Как частный случай получаем, что изометрни, проецирующиеся в параллель-
параллельный перенос на Е2, имеют вид
(х, у, z)*-*(x + xo, y+yo,z + хоу + zo),
где л:о, уо, zo — произвольные действительные числа. Докажите, что группа И та-
таких изометрий изоморфна группе Гейзенберга, состоящей из верхнетреугольных
матриц 3 х 3 с единицами на главной диагонали. (Подсказка: группа И действует
на R3 свободно н транзитивно, что превращает К3 в группу с умножением
(дго, уо, го)(х, у, z) = (x + xo,
Сравните это с предыдущей формулой.)
3.8. Восемь модельных геометрий
189
г) Если элементы ha, к& € Н проецируются в сдвиги на векторы а и b соответ-
соответственно, то их коммутатор [Л„, А*] есть вертикальный сдвиг на расстояние, равное
ориентированной площади параллелограмма, натянутого на векторы а и Ь. Выве-
Выведите отсюда, что вертикальные сдвиги образуют центр группы Н, центр компоненты
единицы G' группы G, и, наконец, центр самой группы G.
д) Снова рассмотрим элементы Л„ и hb из п. г и допустим, что векторы а и Ь
линейно независимы. Докажите, что Л„ и hb порождают дискретную кокомпактную
подгруппу. В частности, если аи Ь — координатные орты, то получится группа це-
целочисленных верхиетреугольных 3x3 матриц с единицами на диагонали, которую
также называют целочисленной группой Гейзенберга (см. рнс. 3.26).
Рис. 3.26. Факторпространство R3 по действию группы Гейзенберга. Факторпро-
страиство Ш? по действию И совпадает с факторпространством R х Т2 по действию
циклической группы, порожденной отображением (х, у, z) i-> (х + 1, у, г + у). На ри-
рисунке изображено пространство IxT2 (противоположные стенки цилиндра нужно
мысленно отождествить); заштрихованные квадраты представляют собой торы, со-
соответствующие значениям х = 0 и х = 1. Чтобы получить пространство №?/Н, надо
рассмотреть область между этими торами, а потом склеить их так, чтобы совпала
штриховка.
Группа Гейзенберга *нильпотентна. На самом деле это единственная
трехмерная нильпотентная, но не абелева односвязная группа Ли. Этим
и объясняется термин «нильгеометрия» (см. также теорему 4.7.12).
Упражнение 3.8.7 (геодезические в нильгеометрии). Докажите, что лежан-
дровы кривые из упражнения 3.8.6, а являются геодезическими в нильгеометрии.
Какие там есть еще геодезические кроме них и вертикальных прямых?
Здесь проще работать с моделью, построенной на основе контактной структу-
структуры о, обладающей осевой симметрией (глава 4, с. 286).
190
Глава 3. Геометрические многообразия
Доказательство 3.8.4, в. Если при действии группы С стабилизаторы
тривиальны, то эту группу можно отождествить с ее единственной орбитой:
X = G'/G'x, так что само пространство X является группой Ли. Следова-
Следовательно, наша задача сводится к тому, чтобы исследовать связные и одно-
связные трехмерные группы Ли, еще не попавшие в список, и выяснить,
какие из них имеют дискретные кокомпактные подгруппы.
Алгебры Ли двух связных групп Ли изоморфны тогда и только тогда,
когда изоморфны универсальные накрывающие этих групп, так что начнем
с исследования трехмерных алгебр Ли. Иногда мы будем представлять себе
алгебру Ли группы Ли как касательное пространство в единице, а иногда
как множество левоинвариантных векторных полей.
Пусть G — группа Ли, а У — левоинвариантное векторное поле на ней.
С точностью до пропорциональности существует единственная левоинва-
риантная форма объема со на группе G. Поток поля Y задается правым
действием однопараметрической подгруппы группы G и, вообще говоря,
не обязан сохранять форму о>. Однако, как и при доказательстве теоре-
теоремы 3.8.4, б, из существования компактного (G, JQ-многообразия следует,
что Y сохраняет объем.
Упражнение 3.8.8 (присоединенное представление). Пусть G — группа Ли,
a jj — ее алгебра Ли. Действие элемента g € G на группе сопряжением являет-
является ее диффеоморфизмом, оставляющим единицу на месте. Следовательно, про-
производная этого преобразования в единице есть линейный автоморфизм алгебры д,
который мы обозначим через Ad(g). Гомоморфизм Ad: G —> GL(jj) называется при-
присоединенным представлением группы Ли G. Так как отображение Ad является
гладким, то можно рассмотреть его производную в единице и получить присоеди-
присоединенное представление алгебры Ли jj, которое обозначается через ad: jj t-+ jjl(jj).
а) Докажите, что (adv)(w) =[v, w] при всех v, wejj.
б) Докажите, что дивергенция (относительно инвариантной формы объема
на G) левоннварнантного векторного поля, соответствующего вектору v € jj, по-
постоянна на группе G и равна следу линейного отображения ad v: g —> q. (Подсказка:
производная в единице отображения det: GL(V) —>R есть оператор следа.)
Группа Ли, на которой каждое левоинвариантное векторное поле сохра-
сохраняет объем, называется унимодулярной. Далее можно считать группу G
унимодулярной, так что tr(ad V) = О для всех элементов V алгебры Ли д.
Антикоммутативное умножение (скобку Ли) на д можно рассматри-
рассматривать как отображение Д2 g —> g. Для трехмерной группы Ли G можно,
зафиксировав на g положительно определенную квадратичную форму (т. е.
скалярное произведение) и выбрав ориентацию, отождествить Д2 g и д,
отобразив V л W в векторное произведение V х W. Тогда скобку Ли мож-
можно рассматривать как линейное отображение L: g —> g, которое оказыва-
оказывается самосопряженным относительно данного скалярного произведения:
(L(V), W) = (V,L(W)) при всех V, W eg.
3.8. Восемь модельных геометрий
191
Чтобы убедиться в этом, выберем в g положительно ориентированный
ортонормальный базис, скажем, {е,, е2, е3}, и обозначим через //; коэф-
коэффициенты матрицы L в этом базисе. Применяя условие унимодулярности
з
tr(ad V) = О к вектору V = еи получаем, что 2((еь ei\ ед = 0. или
(Це3), е2) - (Це2), е3) = /гз - кг = 0.
Проделав то же с остальными базисными векторами, убеждаемся, что уни-
модулярность эквивалентна самосопряженности оператора L.
Для каждого самосопряженного линейного оператора можно найти ор-
тонормированный базис из его собственных векторов. Будем считать, что
{еь е2, е3} — это именно такой базис; в нем матрица оператора L является
диагональной с элементами с, = /й. Другими словами,
где нижние индексы рассматриваются по модулю 3. Если изменить квадра-
квадратичную форму так, чтобы ортонормальным был базис {ахех, а2е2, а3е3} (где
все а,- > 0), то коэффициент с, заменится на Ci(al+1ai+2/ai). Следовательно,
можно считать, что все с,- принадлежат множеству {±1, 0}. Дальнейшие
упрощения связаны с перестановкой базисных векторов. Здесь следует
иметь ввиду, что нечетная перестановка влечет изменение ориентации век-
векторного пространства, так что в итоге коэффициенты с, переставляются
и меняют знаки. Чтобы вернуть старые знаки, можно заменить векторы
базиса на противоположные. С помощью таких операций можно добиться
того, что С] ^с2^с3, причем число положительных коэффициентов с, не
меньше числа отрицательных. С точностью до изоморфизма мы получаем
шесть вариантов для алгебры д, и, следовательно, для группы Ли G. Только
один из них приводит к новой геометрии:
о Из С[ = с2 = с3 = 1 следует, что G = S3.
о Из С[ = с2 = 1 и с3 = — 1 следует, что G = SLB, R).
• При С[ = с2 = 1 и с3 = 0 получаем солвгеометрию.
Образующие в\ и е2 коммутируют, и поэтому группа Ли G содержит
подгруппу, изоморфную Ш2. Эта подгруппа нормальна, и факторгруппа
G/M2 есть Ш. Таким образом, группа Ли G есть полупрямое произведение
R к М2 и полностью определяется действием однопараметрической под-
подгруппы, порожденной е3, на R.2. Производная этого действия в единице
равна (j qJ. Повернув базис {еи е2} на угол л/4, перейдем к диагональ-
диагональному действию е3 с производной (I _°J при / = 0. Следовательно, действие
однопараметрической подгруппы в новом базисе записывается матрицами
192
Глава 3. Геометрические многообразия
(о е 0- ^ итоге получаем, что группа Ли G, являясь расширением типа
О —> К2 —»¦ G -»¦ R —>0, состоит из преобразований вида
(х, у, t) -» (е'°х + хОу
, t
Чтобы получить полную группу изометрий солвгеометрии, к ним еще нужно
добавить два коммутирующих отражения (х, у, t) —> (-х, у, t), (x, у, t) -*¦
—> (х, —у, t) и изометрию (х, у, t) —> (у, х, —i).
Таким образом, индекс связной компоненты единицы в полной группе
изометрий солвгеометрии равен 8.
Наконец, в 3.8.9 строится пример компактного солвмногообразия, так
что перед нами действительно модельная геометрия.
о При с, = 1, с2 = с3 = 0 получаем группу Гейзенберга.
о Из С[ = с2 = с3 = 0 следует, что G = М3.
о При С] = 1, с2 = 0 и с3 = — 1 получаем универсальную накрываю-
накрывающую группы изометрий плоскости Е2, где в\ и е3 действуют сдвигами
вдоль осей х и у, а е2 действует как поворот вокруг начала коорди-
координат. 13.8.4, в\
Пример 3.8.9 (солвмногообразие). Компактные солвмногообразия
возникают как торы отображений для диффеоморфизмов двумерного то-
тора на себя. Пусть ср: Т2 ->• Т2 — диффеоморфизм тора, происходящий из
линейного автоморфизма его универсальной накрывающей М2 с матрицей
А = Й П. Перейдем к новому декартовому базису, состоящему из соб-
собственных векторов матрицы А. В новых координатах действие линейного
автоморфизма записывается в виде (х, у) —> (е'°х, е~'°у) для некоторого
t0 e R. Тогда преобразование М3 вида <\>(х, у, t) = (e'°x, e~lot, t + t0) инду-
индуцирует заданный диффеоморфизм ср: Т2 х {0} —>• Т2 х {/0}. Следовательно,
тор отображения М9 является солвмногообразием: оно получается как
факторпространство М3 по действию дискретной группы изометрий сол-
солвгеометрии, порожденной элементом ф и целочисленными сдвигами вдоль
координатных осей.
Упражнение 3.8.10 (тор отображения для тора). Обобщите предыдущий
пример, рассмотрев отображение <р, возникающее из произвольного линейного ав-
автоморфизма плоскости R , сохраняющего целочисленную решетку Z2 с R2. Пусть
Хь Х2 — корни характеристического многочлена этого автоморфизма. Докажите
следующие утверждения.
а) Если корни Xt, X2 не являются действительными, то они суть корни из еди-
единицы, и отображение ср имеет конечный порядок. Тогда на Т2 есть евклидова струк-
структура, относительно которой ср является изометрией, и пространство М^ обладает
евклидовой структурой.
3.9. Кусочно-линейные многообразия
193
б) Если корни Xi, Хг действительны и различны, то у отображения ср есть два
собственных направления. На торе Т2 есть евклидова метрика, относительно кото-
которой эти направления ортогональны. Тогда пространство Mv есть солвмногообразие.
Найдите два линейных преобразования с одинаковыми характеристическими мно-
многочленами (с двумя различными вещественными корнями), для которых, тем ие
менее, торы соответствующих отображений не гомеоморфны.
в) В оставшемся случае Xi = Х2 = ±1, и либо ср2 = 1, и тогда пространство М9
обладает евклидовой структурой, либо ср сопряжено матрице вида ± ГА 7") (при
п ф 0), и пространство М9 — нильмногообразие.
В общем случае докажите, что М^ = G/Г, где Г — кокомпактная дискретная
подгруппа трехмерной группы Ли G. Как можно обобщить это утверждение для
линейных отображений л-мерных торов?
Интересно, что каждая из рассмотренных восьми модельных геометрий
изометрична некоторой трехмерной группе Ли с левоинвариантной метри-
метрикой. Все эти группы Ли, за исключением случая Н3, унимодулярны. Группой
Ли для Н3 служит группа гомотетий плоскости, которая действует просто
транзитивно, как группа изометрий верхнего полупространства. Во всех
случаях, кроме Н3, группа автоморфизмов геометрии является полупря-
полупрямым произведением односвязной группы Ли и ее группы автоморфизмов,
сохраняющих метрику.
Упражнение 3.8.11 (группы и двумерные геометрии). Получите классифи-
классификацию двумерных модельных геометрий из описания трехмерных унимодулярных
алгебр Ли без использования рнмановой геометрии.
3.9. Кусочно-линейные многообразия
Пример 3.2.11 показывает, что с триангулированными пространствами, да-
даже если они являются многообразиями, иногда довольно сложно иметь
дело. Если мы хотим получить пространства «высокого качества», то при-
придется потребовать от них существования некоторой дополнительной струк-
структуры, например дифференцируемой (см. пример З.Г.З). В теории скле-
склеек естественно рассматривать кусочно-линейные структуры, которые мы
сейчас определим.
Отображение из подмножества одного аффинного пространство в дру-
другое аффинное пространство называется кусочно-линейным, если оно
является ограничением некоторого симплициального отображения, за-
заданного на полиэдре симплициального комплекса. Кусочно-линейным
многообразием называется PL-многообразие, где PL — псевдогруппа,
порожденная кусочно-линейными гомеоморфизмами между открытыми
подмножествами М".
Задача 3.9.1. а) Кусочно-линейные отображения потому определяются в
терминах ограничений симплициальных отображений, что такому определению
194
Глава 3. Геометрические многообразия
заведомо удовлетворяют просто устроенные отображения, такие как тождествен-
тождественное. Докажите, что можно так триангулировать саму область определения для
кусочно-линейного отображения, что оно станет симплициальным.
б) Докажите, что кусочно-линейные гомеоморфизмы между открытыми под-
подмножествами W образуют псевдогруппу (так что слово «порожденная» в опреде-
определении PL на самом деле лишнее).
С помощью локальных координат понятие кусочно-линейного отобра-
отображения немедленно обобщается на отображения из подмножеств аффинных
пространств в кусочно-линейные многообразия.
Соглашение 3.9.2. Говоря о триангуляции кусочно-линейного много-
многообразия X, мы, как правило, будем иметь в виду кусочно-линейную три-
триангуляцию, т. е. такую триангуляцию S, что гомеоморфизм |S| —* X явля-
является кусочно-линейным отображением.
Задача 3.9.3 (триангуляции кусочно-линейных многообразий).
а) Докажите, что каждое кусочно-линейное многообразие может быть триангу-
триангулировано. (Подсказка: начните с выбора конечного атласа —см. соглашение 3.1.4.
Обратите внимание и на доказательство теоремы 3.10.2.)
б) Зафиксируем на данном многообразии какую-нибудь триангуляцию и ло-
локально конечный атлас. Докажите, что можно так измельчить атлас и сделать такое
подразбиение триангуляции, что локальные координаты измельченного атласа бу-
будут линейными на каждом симплексе своей карты.
Пример 3.9.4 (стандартная кусочно-линейная сфера). Рассмотрим
выпуклый (л + 1)-мерный многогранник К С Шп+1 вместе с его ортогональ-
ортогональной проекцией тс на некоторую гиперплоскость Р, которую мы отождествим
с К". Ограничение этой проекции на подходящее подмножество границы
дК (которая является сферой) дает гомеоморфное отображение на подмно-
подмножество гиперплоскости Р. Такие подмножества образуют покрытие грани-
границы, когда Р пробегает все гиперплоскости. С помощью так построенных
карт граница дК наделяется структурой кусочно-линейного многообразия,
которое называется стандартной кусочно-линейной сферой.
Упражнение 3.9.5. Докажите, что определение стандартной кусочно-линейной
сферы не зависит от выбора многогранника К в том смысле, что если провести та-
такое же построение для другого выпуклого многогранника К' (той же размерности),
то сферы дК и дК' будут кусочно-линейно гомеоморфны.
Пусть S — симплициальный комплекс. Можно ли превратить полиэдр
|Е| в кусочно-линейное многообразие X так, чтобы тождественное ото-
отображение |?| -* X являлось кусочно-линейным? Если это возможно, то
описание таких комплексов (их тоже называют кусочно-линейными мно-
многообразиями) значительно упрощается по сравнению с топологическим
случаем (см. предложение 3.2.5 и последующий комментарий).
3.9. Кусочно-линейные многообразия
195
Предложение 3.9.6 (линки кусочно-линейных многообразий сфе-
ричны). Симплициальный комплекс является кусочно-линейным
многообразием тогда и только тогда, когда линк каждой вер-
вершины является кусочно-линейным многообразием, эквивалентным
стандартной кусочно-линейной сфере.
Доказательство. Если линк каждого симплекса является стандартной
кусочно-линейной сферой, то звезда каждого симплекса кусочно-линейно
гомеоморфна кусочно-линейному шару (сравните с упражнением 3.2.4).
Набор из этих шаров и гомеоморфизмов и задает кусочно-линейный атлас.
Обратное утверждение следует из следующего факта.
Упражнение 3.9.7. Пусть Е' — подразделение симплициального комплекса ?.
Докажите, что если симплексы о € Б и ст' € Е' имеют одинаковую размерность и
|ст'| С |ст|, то линки ст н ст' кусочно-лииейно эквивалентны.
Теперь для данной вершины v симплициального комплекса и кусоч-
кусочно-линейной карты ср, покрывающей v, можно так подразбить триангуля-
триангуляцию маленькой окрестности v, что локальные координаты ср будут являться
аффинными отображениями на каждом симплексе, содержащем v. Легко
видеть, что в измельченной триангуляции линк каждого симплекса, содер-
содержащего v, кусочно-линейно гомеоморфен кусочно-линейной сфере подхо-
подходящей размерности. 13.9.61
Отсюда следует, что триангулированное пространство Е2Р из приме-
примера 3.2.11, гомеоморфное сфере S5, не является кусочно-линейным мно-
многообразием. Гомеоморфизм со сферой нельзя сделать кусочно-линейным;
на самом деле он переводит окружность надстройки в «дикий узел» на
сфере S5.
Так получается отрицательный ответ на знаменитую гипотезу Hauptver-
mutung, в которой утверждается, что любые две триангуляции простран-
пространства имеют изоморфные подразбиения. (Первый контрпример к Hauptver-
Hauptvermutung был найден Милнором [Mil61], но его пример не являлся много-
многообразием.) Тем не менее, условие Hauptvermutung выполнено для многих
классов пространств, в том числе для двумерных многообразий [Rad25],
двумерных комплексов [Рар43] и трехмерных многообразий [Bin54, Moi52].
Несколько более слабой разновидностью Hauptvermutung является во-
вопрос о том, любые ли две кусочно-линейные структуры на топологическом
многообразии эквивалентны. На этот и связанный с ним вопрос, любое
ли топологическое многообразие имеет кусочно-линейную структуру, от-
ответы отрицательные. Кирби и Зибенман [KS69] доказали, что существуют
шестимерные многообразия, не допускающие никакой кусочно-линейной
структуры, и пятимерные многообразия с неэквивалентными кусочно-ли-
кусочно-линейными структурами. Но в размерностях не выше трех все топологические
многообразия обладают кусочно-линейной структурой (см. [Bin59] и ссыл-
196
Глава 3. Геометрические многообразия
ки из предыдущего абзаца), и любые две такие структуры эквивалентны,
так как в этом случае выполнена Hauptvermutung-гипотеза.
Завершим этот раздел еще несколькими примерами ^-структур. Впро-
Впрочем, несмотря на то, что эти структуры связаны с кусочно-линейными, в
дальнейшем изложении они встречаться не будут.
Пример 3.9.8 (кусочно-проективные многообразия). Отображение
одного открытого подмножества R" на другое называется кусочно-проек-
кусочно-проективным, если его можно продолжить до такого отображения полиэдра
некоторого симплициального комплекса, ограничение которого на каждый
симплекс является проективным преобразованием. РР-многообразие, где
РР — псевдогруппа кусочно-проективных гомеоморфизмов между откры-
открытыми подмножествами R", называется кусочно-проективным многооб-
многообразием.
Пусть, как и в примере 3.9.4, К— выпуклый многогранник. На грани-
границе дК имеется кусочно-проективная структура, локальные координаты в
которой задаются проекцией из внутренней точки многогранника на ги-
гиперплоскость. Функции перехода при изменении точки и гиперплоскости,
являются проективными преобразованиями. Тем самым определена стан-
стандартная кусочно-проективная сфера.
Задача 3.9.9 (кусочно-линейные и кусочно-проективные структуры). Яс-
Ясно, что каждое кусочно-линейное отображение является также и кусочно-проек-
кусочно-проективным, так что каждое кусочно-линейное многообразие имеет кусочно-проектив-
кусочно-проективное ослабление структуры.
а) Докажите, что каждая кусочно-проективная структура имеет кусочно-ли-
кусочно-линейное усиление, и притом единственное, с точностью до кусочно-проективной
эквивалентности.
б) Докажите, что структура стандартной кусочно-линейной сферы являет-
является усилением структуры стандартной кусочно-проективной сферы. Имеет ли
линк вершины кусочно-лииейного многообразия каноническую кусочно-линейную
структуру или только каноническую кусочно-проективную структуру?
Не все интересные псевдогруппы действуют транзитивно. Приведем
один из наиболее любопытных примеров:
Пример 3.9.10 (целочисленно-проективные многообразия). Груп-
Группа PGL(n + 1, К) проективных преобразований пространства W содер-
содержит дискретную подгруппу PGL(/z + 1,Z). Псевдогруппа PIP целочи-
сленно-проективных преобразований состоит из таких гомеоморфизмов
между открытыми подмножествами R", для которых область определения
можно разбить на такие л-мерные симплексы, что сужение данного гомео-
гомеоморфизма на каждый из симплексов разбиения индуцируется действием
группы РОЦп + 1, Z) на Шп с.
3.10. Сглаживания
197
Так как элементы псевдогруппы PIP переводят точки с рациональны-
рациональными координатами в точки с рациональными координатами, ее действие не
транзитивно.
Задача 3.9.11 (кусочно-линейные и кусочно целочисленно-проективные
структуры). Докажите, что каждое кусочно-линейное многообразие допускает
целочисленно-проективное усиление структуры, причем единственным, с точно-
точностью до кусочно-линейной эквивалентности, способом.
Необычным в этой структуре является то, что группа кусочно цело-
численно-проективных гомеоморфизмов многообразия всего лишь счетна.
Ричард Томпсон доказал, что группа сохраняющих ориентацию кусочно
целочисленно-проективных преобразований окружности проста и конечно
представима. Неизвестно, является ли группа кусочно целочисленно-про-
целочисленно-проективных гомеоморфизмов поверхности конечно представимой.
Оказывается, что у пространства Тейхмюллера (см. раздел 4.6), так же
как и у гиперболического пространства, есть бесконечно удаленная сфе-
сфера, и ее преобразования, индуцированные гомеоморфизмами поверхности,
будут кусочно целочисленно-проективными.
3.10. Сглаживания
В предыдущем разделе мы разобрались в том, какие склейки полиэдров
приводят к кусочно-линейным многообразиям. Но остался еще один важ-
важный вопрос — когда пространство, полученное склейкой полиэдров, может
быть сглажено, т. е. наделено дифференцируемой структурой? (В этом раз-
разделе мы будем употреблять слова «гладкий» и «дифференцируемый» как
синонимы, так как большинство результатов применимо и к структурам
конечной гладкости: ср. пример 3.1.6.)
Оказывается, что в размерностях не выше трех ответ на поставленный
вопрос положителен: можно спокойно переходить от кусочно-линейной
структуры к гладкой и обратно. Это очень удобно для нас. Тем самым
стандартные идеи трехмерной топологии можно развивать, как в кусоч-
кусочно-линейной форме, так и в дифференцируемой; иногда намного проще
работать в одной теории, а иногда в другой.
Начнем с того, как вообще можно сравнить кусочно-линейную струк-
структуру на многообразии с гладкой структурой. Идеи усиления и ослабления
структуры нельзя применить непосредственно, так как диффеоморфизмы,
вообще говоря, не являются кусочно-линейными отображениями, и наобо-
наоборот. На самом деле, пересечением псевдогрупп PL и *€г при г ^ 1 является
псевдогруппа, возникающая из действия аффинных преобразований (см.
пример 3.3.4).
В этой ситуации ключевой является идея гладкой триангуляции глад-
гладкого многообразия. Триангуляция называется гладкой, если ее область
198
Глава 3. Геометрические многообразия
является триангулированным кусочно-линейным многообразием (см. со-
соглашение 3.9.2), а отображение — симплициально-гладким, т.е. его огра-
ограничение на каждый симплекс триангуляции есть гладкое вложение. Го-
Гомеоморфизм из кусочно-линейного многообразия на дифференцируемое
называется кусочно-гладким, если существует триангуляция области его
определения, индуцирующая гладкую триангуляцию на его образе. Сгла-
Сглаживанием кусочно-линейного многообразия М называется гладкое мно-
многообразие N, снабженное кусочно-гладким отображением N—> М.
Задача 3.10.1. Так как на пространстве R" присутствуют обе структуры: и
кусочно-линейная, и гладкая, то имеет смысл говорить о кусочно-гладких ото-
отображениях R" на себя.
а) Докажите, что такие отображения не образуют группу. Таким образом, ку-
кусочно-гладкие отображения служат лишь мостиком между кусочно-линейиыми и
гладкими структурами, не являясь полноценными сами по себе.
б) Обозначим через Sf группу, порожденную всеми кусочно-гладкими гомео-
гомеоморфизмами № на себя. Сможете ли вы дать какое-нибудь разумное описание
элементов из Sf ?
Теорема 3.10.2 (триангуляции гладких многообразий). Любое
гладкое многообразие можно гладко триангулировать. Любым двум
гладким триангуляциям одного многообразия соответствует одна
и та же кусочно-линейная структура, т. е. такие триангуляции
определяют изоморфные кусочно-линейные многообразия.
Доказательство. Мы приводим только основную идею доказательства.
Дж. Манкрес в своей книге [Мипбб, глава 2] дает полное и очень ясное
доказательство, в общих чертах основанное на первоначальном доказа-
доказательстве Дж. Уайтхеда [Whi40].
Сначала рассмотрим произвольную гладкую триангуляцию компактного
подмножества пространства W. Проведем очень тонкое подразбиение этой
триангуляции, точно следуя схеме, аналогичной той, которая приведена в
задаче 1.3.4. Заменим каждое гладкое вложение симплекса подразбиения
на аффинное отображение, совпадающее с ним в вершинах, и получим
кусочно-линейную триангуляцию. При этом отображение останется кусоч-
кусочно-гладким везде, где оно было таким.
Этим можно воспользоваться для доказательства единственности ку-
кусочно-линейной структуры, построенной по гладкой триангуляции. Рас-
Рассмотрим две гладкие триангуляции и будем их измельчать и аппроксими-
аппроксимировать до тех пор, пока отображение одной в другую не станет кусочно-ли-
кусочно-линейным. Этого можно добиться, перебирая карту за картой и отождествляя
каждую из них сМ°.
Аналогично можно доказать и существование триангуляции, следуя шаг
за шагом решению задачи 3.9.3. Начнем с выбора конечного атласа для
многообразия М. Для каждой карты (?/,-, ср,) выберем относительно ком-
3.10. Сглаживания
199
пактное открытое подмножество Щ так, чтобы все U\ по-прежнему по-
покрывали М, и зададим конечную триангуляцию компактного подмножества
в ?/,-, содержащего Щ. Теперь идея состоит в том, чтобы, карта за картой,
так подрегулировать эти частичные триангуляции, чтобы они стали PL-со-
PL-совместимыми на пересечениях. Чтобы продолжить гладкую триангуляцию в
область действия новой карты, рассмотрим область V = (fi{U',) с Rn. Глад-
Гладкая триангуляция уже определена на некотором подмножестве V; нужно
распространить ее на V. Измельчим, если потребуется, заданную на V три-
триангуляцию и аппроксимируем ее кусочно-линейным отображением. Этим
можно добиться согласования кусочно-линейной структуры в области V с
уже имеющейся структурой ее части, что и дает возможность продолжить
на V гладкую триангуляцию. 13.10.21
Итак, каждое гладкое многообразие является сглаживанием некоторо-
некоторого (по сути, однозначно определенного) кусочно-линейного многообразия.
Обратная задача о нахождении сглаживания данного кусочно-линейного
многообразия является более трудной. Самое сложное здесь — это четко
сформулировать, что именно требуется найти; сам процесс сглаживания
после этого становится более-менее очевидным.
В каждой точке х кусочно-линейного многообразия М можно опреде-
определить касательное пространство ТХМ как (например) множество классов
кусочно-линейных кривых [0, f) —* М с началом в точке х: класс состоит
из кривых с равными правыми производными в нуле. Это пространство
гомеоморфно Шп, где п — размерность многообразия М; гомеоморфизм за-
задается с помощью локальных координат. В отличие от дифференцируемого
случая, этот гомеоморфизм не определен однозначно с точностью до линей-
линейных отображений, так что на пространстве ТХМ нет естественной структуры
векторного пространства.
Еще хуже то, что на пространстве ТМ = \J TXM нет никакой естествен-
X
ной топологии, превращающей его в пространство расслоения1 над М. Для
дифференцируемого многообразия М топология на ТМ определяется так,
что для любого гладкого отображения f производная df: ТМ —* TN явля-
является непрерывным отображением. В случае кусочно-линейных многооб-
многообразий это уже не проходит: производная кусочно-линейного отображения
/: М —* N, определенная очевидным образом (см. рис. 3.27), может иметь
разрывы при переходе от одной точки к другой. Таким образом, если все
же требовать непрерывности от производной df: ТМ —* М" произвольно-
произвольного кусочно-линейного отображения, мы приходим к такой топологии на
ТМ, когда все слои независимы друг от друга (хоть их нули и образуют
подпространство, гомеоморфное М).
'Впрочем, для этого случая пригодно понятие кусочно-линейного микрорасслоения.
См.: Milnor J. W. Microbundles. I, Topology 3 A964), suppl. 1, 53-80.— Прим. перев.
200
Глава 3. Геометрические многообразия
Рис. 3.27. Производная кусочно-линейного отображения. Производная df: 7TR—>
-+ Ж кусочно-линейного отображения /: К -+ К при всех х переводит пространство
ТХШ в T/WK. В тех точках х, где график функции / имеет налом, производная dfx не
является линейной н, в частности, сильно отличается от значений djy даже для близких
к х точек у, находишихся по другую сторону излома.
Ситуация улучшается, если зафиксировать триангуляцию многообра-
многообразия М и ограничиться отображениями, аффинными на каждом симплексе
триангуляции. Производная такого отображения постоянна на любом от-
открытом симплексе произвольной размерности, так что пространство ТМ
над открытым симплексом а, содержащим точку х, есть просто а х ТХМ.
Более того, в этом случае пространство ТХМ составлено из полиэдральных
касательных конусов, по одному для каждого симплекса, содержащего х;
ограничение производной df на каждый из этих конусов является линейным
отображением.
Как стыкуются между собой такие куски касательного пространства
77W? Рассмотрим сначала триангуляцию М. Пространство касательного
расслоения к гладкой вещественной прямой есть R2: будем считать, что
горизонтальная координата — это точка базы, а координата по вертикаль-
вертикальной оси задает касательный вектор. Когда прямая триангулирована, мы
оказываемся в ситуации, изображенной на рис. 3.27: в каждой вершине
производные в положительном направлении совпадают с пределами спра-
справа, но, вообще говоря, не совпадают с пределами слева. Таким образом,
3.10. Сглаживания
201
вдоль касательного пространства в любой вершине делается разрез влево
от положительных векторов и вправо от отрицательных, как это показано
на рис. 3.28. (Подобную картинку можно увидеть, разделяя две дольки
грейпфрута, когда половинка пленки еще остается на одной дольке, а по-
половинка на другой.)
Рис. 3.28. Касательное пространство триангулированной прямой. Слой над вер-
вершиной не имеет линейной структуры: он является объединением двух касательных
конусов (лучей). Базис окрестностей для касательных векторов в этом случае зада-
задается замкнутыми полукругами, обращенными направо для положительных векторов и
налево — для отрицательных. ,
Для триангуляции пространства Е" картина аналогична. Начнем по-
построение с дизъюнктного объединения касательных пространств к К" над
открытыми симплексами. Для касательного вектора v, приложенного в
точке р, определим С„ как объединение всех симплексов а, содержащих
некоторый (пусть достаточно малый) начальный отрезок луча, исходяще-
исходящего из точки р в направлении v. Производная вдоль вектора и изменяет-
изменяется непрерывно, когда точка, в которой она вычисляется, перемещается
внутри конуса Со; в нем и нужно произвести склейку. (Формально базис
окрестностей для (р, v) состоит из произведений окрестностей вектора v в
касательном пространстве к!"в точке р на окрестности точки р в Со.)
Теперь у нас уже введена топология в тотальном касательном про-
пространстве триангулированного кусочно-линейного многообразия М. Если
некоторый симплициально-гладкий гомеоморфизм отображает многооб-
многообразие М на гладкое многообразие N, то его производная непрерывно и
взаимно однозначно отображает ТМ на 7W. Тем не менее, она не является
гомеоморфизмом, так как топология на образе более слабая. Итак, для
того чтобы превратить кусочно-линейное многообразие в триангулирован-
триангулированное гладкое многообразие, необходимо, во-первых, ослабить топологию
202
Глава 3. Геометрические многообразия
тотального касательного пространства ТМ, т. е. зафиксировать набор дан-
данных, задающий склейку разрезанных листов, изображенных на рис. 3.28,
которая наделяет ТМ структурой расслоения. Во-вторых, нужен набор
данных, определяющий линеаризацию каждого слоя ТХМ, т. е. задаю-
задающий на каждом слое линейную структуру, согласованную с частичными
линейными структурами на конусах, составляющих слой. (На самом деле,
оказывается, что эти два набора данных определяют друг друга: см. при-
пример 3.10.5.)
Займемся исследованием полиэдральной конической структуры на ТХМ.
Линеаризацию можно рассматривать как гомеоморфизм L: ТХМ —* Ш", ли-
линейный на каждом полиэдральном конусе, причем мы не будем различать
гомеоморфизмы, отличающиеся на линейное преобразование Ш". Можно
нормализовать линеаризацию, зафиксировав образы в Ия я линейно неза-
независимых векторов из выбранного конуса, после чего данная линеаризация
задается с помощью конечного числа своих значений.
Например, в размерности один касательное пространство в вершине
есть прямая Е, разбитая на положительную и отрицательную полуоси.
Нормализуем гомеоморфизм L: R —* М так, чтобы положительная ось то-
тождественно отображалась на себя. Тогда линеаризация задается значением
L{— 1), которое может быть любым отрицательным числом. (Вместо точ-
точки — 1 можно, разумеется, взять любую другую точку отрицательной полу-
полуоси.) Пространство линеаризации в этом случае есть открытая полуось.
, В размерности два рассмотрим сначала точку на ребре. Координаты
можно выбрать так, чтобы касательное пространство в этой точке предста-
представляло из себя плоскость Ш2, разбитую на верхнюю и нижнюю полуплос-
полуплоскость. Нормализуем L: R2 -*R2 так, чтобы верхняя полуплоскость то-
тождественно отображалась в себя. Зададим теперь линеаризацию образом
точки @, —1), который может быть любой точкой нижней полуплоскости.
Таким образом, пространство линеаризации является полуплоскостью.
Касательное пространство в вершине двумерной триангуляции Ш2 раз-
разбито на k > 3 сходящихся в этой точке углов. Нормализуем линеаризацию
L, отправив один из этих углов в первую четверть плоскости Ш2. Выбрав,
обходя вокруг вершины, по одной точке /?,• на каждом из оставшихся k — 2
лучей, мы однозначно зададим линеаризацию образами L{pt) этих точек.
Полярные координаты (г,, 6,) образов должны удовлетворять условиям
г,>0, 0<е,<...<е*_я<§*,
так что пространство линеаризации есть произведение открытого ортанта в
М?~2 (радиусы) на открытый (k — 2)-мерный симплекс (углы). В частности,
это пространство стягиваемо.
Упражнение 3.10.3 (линеаризации образуют многообразие). Обобщая
предыдущие рассуждения, докажите, что пространство линеаризации ТХМ есть
3.10. Сглаживания
203
открытое подмножество вида
(R+ xS"- хГ)'"-"",
где п — размерность триангуляции, m — размерность симплекса а, внутри которого
содержится точка х, j — число вершин линка Ik ст. В частности, это простран-
пространство всегда является многообразием. Опишите его явно в случаях m = п — 1 и
m = п - 2.
Определение 3.10.4 (спайка). Спайкой триангулированного кусоч-
кусочно-линейного многообразия М называется линеаризация его касательных
пространств, непрерывно зависящая от точки многообразия. Означает это
следующее.
Если х — точка М, а у € М — внутренняя точка симплекса а, содержаще-
содержащего х, то некоторое открытое подмножество ТХМ канонически отождествля-
отождествляется (с помощью параллельного переноса) с подмножеством ТУМ. (Если
обе точки х и у лежат внутри одного и того же открытого симплекса,
то касательные пространства в этих точках отождествляются полностью.)
Непрерывность означает, что когда у приближается к х внутри а, то ли-
линеаризация ТУМ сходится к линеаризации ТХМ на том множестве, где они
сравнимы (см. рис. 3.29).
Рис. 3.29. Условие непрерывности для спайки. Заштрихованные области изобража-
изображают те части пространств ТХМ и ТУМ, которые могут быть канонически отождествлены.
Линеаризация ТУМ задается, например, в точке у образами трех изображенных на
этом рисунке векторов. Когда у стремится ло ребру к х, образы этих векторов должны
стремиться к образам соответствующих векторов в х.
Ясно, что если М — триангулированное многообразие, а /: М —> N —
симплициально гладкий гомеоморфизм в гладкое многообразие, то лине-
линеаризация, заданная с помощью / на ТМ, определяет спайку. Однако не
204
Глава 3. Геометрические многообразия
каждая спайка многообразия М индуцирована кусочно дифференцируемым
отображением. Те, которые индуцированы, называются гладкими спай-
спайками.
Упражнение 3.10.5 (спайка и ослабление топологии). Докажите, что спай-
спайка, индуцированная отображением /, определяется на ТМ топологией, индуциро-
индуцированной /, и обратно.
Упражнение 3.10.6. Исследуйте вопрос, когда спайка является гладкой. В
частности, рассмотрите окрестность вершины триангуляции на плоскости. Попро-
Попробуйте найти содержательное необходимое условие, которому должны удовлетво-
удовлетворять в вершине вторые производные гладкой спайки вдоль ребер.
Предложение 3.10.7 (спайки могут быть сглажены). Любая спай-
спайка триангулированного кусочно-линейного многообразия М может
быть аппроксимирована гладкой спайкой.
Доказательство. Будем доказывать по индукции существование таких
гладких карт, покрывающих открытую окрестность /г-мерного остова мно-
многообразия М, что (соответствующим образом модифицированная) спайка
согласуется в этой окрестности со спайкой, заданной тождественным ото-
отображением.
Базой индукции служит это утверждение для вершины v. Некоторую
окрестность начала координат в TVM можно канонически отождествить с
окрестностью U вершины v в М. С помощью осуществляемой спайкой
линеаризации пространства TVM введем локальные координаты в II. Го-
Гомотопно продеформируем теперь спайку в U так, чтобы она совпала со
спайкой, заданной картой U, на меньшей окрестности точки и. Эту опера-
операцию нужно проделать для каждой вершины v.
Пусть теперь утверждение индукции выполнено для некоторого k. Рас-
Рассмотрим (k + 1)-мерный симплекс а. Спайка задает непрерывное отобра-
отображение ст в соответствующее пространство линеаризации, которое являет-
является многообразием (упражнение 3.10.3). Это отображение будет гладким
в окрестности границы симплекса. Аппроксимируем его другим отобра-
отображением, гладким везде в а и совпадающим с ним в некоторой меньшей
окрестности границы.
Тем самым, касательное расслоение к М над этим открытым симплексом
наделено структурой гладкого векторного расслоения. Касательное про-
пространство к симплексу задает гладкое подрасслоение размерности k + 1.
Выберем гладкое дополнительное подрасслоение и отождествим его с
а х К"-*-'. Экспоненциальное отображение в свою очередь отождествля-
отождествляет окрестность нулевого сечения этого подрасслоения с окрестностью U
открытого симплекса. Взяв композицию, мы получаем локальные коорди-
координаты на U, совместимые с построенными ранее картами в окрестностях
симплексов меньшей размерности.
3.10. Сглаживания
205
Проделав это для каждого (k + 1)-мерного симплекса, мы продолжим
гладкую структуру на окрестность {k + 1)-мерного остова. Как и в случае
с вершинами, можно так гомотопно продеформировать полученную спай-
спайку, чтобы она согласовывалась со спайкой, заданной в этой окрестности
гладкой структурой. Этим завершается доказательство индуктивного пе-
перехода. |3.10.71
Теорема 3.10.8 (существование сглаживания). Каждое кусочно-
линейное многообразие размерности не выше трех может быть
сглажено.
Доказательство. Выберем какую-нибудь триангуляцию данного мно-
многообразия (см. задачу 3.9.3). Согласно предложению 3.10.7, нам достаточ-
достаточно построить спайку на триангулированном многообразии.
В размерности один все тривиально. Выберем произвольные линеари-
линеаризации для касательных пространств в вершинах. Тогда касательное про-
пространство любой точки ребра уже имеет линейную структуру, а условие
непрерывности или определение 3.10.4 будет выполнено автоматически.
В размерности два все почти так же просто. Снова произвольно выбе-
выберем линеаризации для касательных пространств в вершинах. Как мы уже
убедились, пространство линеаризации касательного пространства к точке
на ребре параметризуется полуплоскостью. Следовательно, продолжение
спайки вдоль ребра сводится к нахождению пути, соединяющего две точки
в полуплоскости, что проще простого. Такое продолжение автоматически
распространяется на двумерные симплексы.
В размерности три применимы те же рассуждения. Согласно упражне-
упражнению 3.10.3, пространство линеаризации касательного пространства к точке
на ребре связно, так что спайка продолжается с вершин на ребра. Потом
нужно продолжить спайку с границы каждого треугольника на его внутрен-
внутренность. В этом случае пространство линеаризации есть полупространство в
М3, и поскольку оно стягиваемо, продолжение существует. 13.10.81
До сих пор мы не занимались вопросом о единственности сглаживания.
Может ли, к примеру, кусочно-линейное многообразие М иметь два сгла-
сглаживания М —> No и М —>Nt с недиффеоморфными No и Nt? Опять-таки,
в малых размерностях дела обстоят довольно просто.
Теорема 3.10.9 (единственность сглаживания). Если М -* No и
М —* Ni — два сглаживания кусочно-линейного многообразия раз-
размерности не выше трех, то сквозной гомеоморфизм No —> Nt может
быть аппроксимирован гладким отображением.
Доказательство. Два сглаживания определяют две спайки многообра-
многообразия М (с подходящей триангуляцией). Если многообразие М имеет размер-
размерность один или два, то пространство спаек многообразия М стягиваемо,
так что одну спайку можно гомотопно продеформировать в другую. Теперь
206
Глава 3. Геометрические многообразия
рассмотрим цилиндр М х [0, 1 ], разбитый на полиэдры вида ох[0, 1 ], где
а — некоторый симплекс. Эти клетки могут быть далее подразбиты на сим-
симплексы. Гомотопия между данными спайками задает спайку на М х [0, 1 ],
согласованную с исходными на краях. С помощью такой спайки можно
построить (см. предложение 3.10.7) сглаживание пространства М х [0, 1],
индуцирующее сглаживание No на нижнем основании цилиндра (М х {0}),
и сглаживание Nt на верхнем основании (М х {1}). Если чуть поаккурат-
поаккуратней проводить это построение, то можно добиться того, чтобы каждое се-
сечение М х {t} было гладким подмногообразием. Единичное векторное поле
в вертикальном [0, 1 ]-направлении может при этом оказаться не гладким,
но можно подкрутить его С°°-дифференцируемой сглаживающей функци-
функцией и получить аппроксимирующее гладкое поле V с постоянной единичной
скоростью в вертикальном направлении и малой горизонтальной составля-
составляющей. Интегрируя полученное поле от 0 до 1, получим диффеоморфизм
No —* Ni, аппроксимирующий сквозной гомеоморфизм.
Пространство спаек триангулированного трехмерного многообразия ис-
исследовать сложнее — мешают его вершины.
Трудная задача 3.10.10 (пространство триангуляции сферы S2). Является
ли пространство линеаризации касательного пространства в вершине триангуляции
R3 стягиваемым?
Вопрос можно переформулировать в терминах пересечений полиэдральных ко-
конусов с единичной сферой. Для данной триангуляции i сферы S2 обозначим через
Тх пространство триангуляции с геодезическими сторонами, снабженных комбина-
комбинаторным изоморфизмом сти рассматриваемых с точностью до изометрин. Является
ли пространство Гт стягиваемым?
Блох, Конли и Хендерсон дали положительный ответ в своей работе [ВСН84].
Игорь Ривнн [Riv] нашел элегантное решение, использующее трехмерные гипер-
гиперболические полиэдры.
Мы не будем пытаться глубже исследовать пространство спаек три-
триангулированного трехмерного многообразия. Воспользуемся вместо этого
другим методом сравнения сглаживаний, основанном на следующей инте-
интересной и самой по себе теореме Смейла:
Теорема 3.10.11 (продолжение диффеоморфизма). Каждый диф-
диффеоморфизм сферы S2 на себя можно продолжить до диффеомор-
диффеоморфизма на себя трехмерного шара.
Чуть позже мы докажем и обобщим эту теорему, а теперь применим
ее к доказательству теоремы 3.10.9. Имеется две спайки, индуцирован-
индуцированные на многообразии М сглаживаниями /0: М —> No и fx: М —* Nx. Так
как на ребрах пространства спаек стягиваются, то можно так гомотопно
продеформировать эти спайки, чтобы они совпадали везде, кроме малых
окрестностей вершин. Пусть Ро и Р\ получены из Nq и Nt удалением ма-
маленьких открытых шаров, построенных вокруг вершин. Как и ранее, гомо-
3.10. Сглаживания
' 207
топия, соединяющая спайки, позволяет нам построить диффеоморфизм из
Ро в Л, близкий к /, о /-'. По теореме 3.10.11 он может быть продолжен
до гомеоморфизма NO—>NU гладкого на Ро и на замыкании каждого из
удаленных шаров. Полученное кусочно-дифференцируемое отображение
No —> Ni легко может быть сглажено до диффеоморфизма. |з.10.9|
Доказательство. Мы докажем, что каждый диффеоморфизм единич-
единичной сферы S2 G Ш3 гладко изотопен ортогональному преобразованию
g е ОC). С помощью такой изотопии F, которую можно считать по-
постоянной около концов интервала, мы продолжим отображение / до
диффеоморфизма единичного шара, отображая каждую сферу Sr радиуса г
@ < г < 1) на себя диффеоморфизмом F,.
Теперь осталось доказать, что каждый диффеоморфизм сферы S2 € М3
можно изотопно продеформировать в ортогональное преобразование.
В действительности верно более общее утверждение: при п < 3 вложение
О(п + 1) С Diff5" есть *деформационный ретракт, если группу Diff S" диф-
диффеоморфизмов сферы снабдить С-топологией (т. е. два диффеоморфизма
считается близкими, если равномерно близки и их значения, и их производ-
производные). Для п = 1 этот факт прост, а для п = 2 доказан Смейлом. Наконец,
Смейл предположил, что утверждение верно в размерности п = 3, а Хатчер
[Hat83b] это доказал. Его длинное и трудное доказательство выходит за
рамки нашего исследования.
Итак, пусть / — диффеоморфизм сферы 52. Мы будем применять к /
различные операции, пока не превратим это отображение в ортогональное
преобразование. (В упражнении 3.10.13 и задаче 3.10.14 утверждается,
что если все этапы нашего построения применять одновременно ко всем
диффеоморфизмам, то результат будет непрерывен как функция от /. Та-
Таким образом, в действительности этот процесс задает деформационную
ретракцию группы DiffS2 на 0C).)
Сначала мы так продеформируем диффеоморфизм, чтобы он совпал с
ортогональным преобразованием внутри некоторого диска. Эта часть по-
построения применима и к диффеоморфизмам л-мерной сферы S", поэтому
доказательство проведем для любого п. Обозначим через е0, ..., е„ стан-
стандартный ортонормальный базис пространства Шп+1.
Лемма 3.10.12 (красивая заплатка). Пусть D — полусфера в S" с
центром в точке е0 € S". Любой диффеоморфизм f сферы S" глад-
гладко изотопен диффеоморфизму, который переводит е0 и —е0 в пару
антиподальных точек Хо и —xQ и чье ограничение на D совпадает с
ограничением некоторого элемента из О(п + 1).
Доказательство. Построение изотопии будет состоять из четырех ша-
шагов, причем на каждом шаге изотопия будет постоянной в окрестностях
начала и конца, что обеспечит гладкость конструкции.
208
Глава 3. Геометрические многообразия
Начнем с того, что сделаем производную диффеоморфизма в точке е0
ортогональным, а не просто линейным преобразованием. Пусть х0 = /(е0),
а хи ..., хп — образы векторов е{, ..., е„ под действием производной ото-
отображения / в точке во. Через Хо обозначим (п + 1) х (п + 1)-матрицу,
столбцами которой служат векторы х(, и пусть Xi — ортогональная матри-
матрица, полученная применением ортогонализации Грама—Шмидта к столбцам
матрицы Хо слева направо (заметим, что в первом столбце матрицы Xi
по=прежнему стоит вектор лс0). Гомотопно продеформируем Хо в Х1у пооче-
поочередно (слева направо) переводя столбец матрицы Хо в соответствующий
столбец матрицы Xt линейной гомотопией (тщательно следя каждый раз за
сохранением гладкости). В процессе гомотопии матрица Xt по-прежнему
содержится в GL(/z, Ж).
Изотопно изменим отображение /, взяв его композицию с XtX^1 и про-
проектируя обратно на сферу с помощью центральной проекции. Эта изотопия
сохраняет х0 как образ точки е0 и меняет производную в точке е0 от Хо к Xi.
Обозначим этот диффеоморфизм через Д. На этом первый шаг построения
закончен.
Теперь возьмем композицию Д с параболическим преобразованием, со-
сохраняющим точку х0, и начнем перемешать образ точки — е0 от /(—е0)
к — f(eQ) = —х0 по кратчайшей дуге. В каждый момент времени нужный
для этого параболический элемент существует и однозначен (см. упраж-
упражнение 2.5.25). Так как производная параболического преобразования в его
неподвижной точке является тождественным оператором, то производная в
точке е0 в процессе деформации не меняется. Полученное в конце второго
шага отображение обозначим через /2-
Пусть ср: Rn+l ->[0, 1 ] —сглаживающая функция, равная нулю вне еди-
единичного шара и единице внутри шара радиуса 1/2. Перенесем ср в точку е0
и так сожмем, чтобы ее носитель заключался в маленьком шаре с центром
в е0. Рассмотрим выпуклую комбинацию с коэффициентами 1 — ftp и ftp
отображения Д и аппроксимирующего его в точке е0 ортогонального пре-
преобразования. Если носитель ср заключен в достаточно маленьком шаре, то
все промежуточные отображения являются диффеоморфизмами (докажите
это!), так что третий шаг построения изотопии завершен. В итоге постро-
построено отображение, которое совпадает с ортогональным в окрестности е0 и
с отображением Д вне носителя ср.
Сопрягая это отображение подходящим гиперболическим преобразо-
преобразованием, сохраняющим точки х0 и —х0, растянем диск, на котором наш
диффеоморфизм ортогонален, в полусферу D из условия леммы. [3.10.121
Упражнение 3.10.13 (непрерывная зависимость 1). Докажите, что постро-
построенная в доказательстве леммы 3.10.12 изотопия непрерывно зависит от диффео-
диффеоморфизма /. Среди прочего, вам потребуется задать масштабирующий коэффици-
коэффициент для сглаживающей функции <р и доказать, что он непрерывно зависит от /.
(Напомним, что пространство DiffS" рассматривается в С'-топологии.)
3.10. Сглаживания
209
В силу леммы 3.10.12 можно считать, что на полусфере D диффео-
диффеоморфизм / является ортогональным преобразованием с центром в во. Нас
будет интересовать композиция / с преобразованием, обратным к это-
этому ортогональному. Воспользовавшись стереографической проекцией из
точки е0, можно рассматривать данную композицию как диффеоморфизм
h: Ш" ->R", тождественный вне единичного шара. Нам нужно изотопно
продеформировать h в тождественное отображение.
Вернемся теперь к предположению, что п = 2 (в случае п — 1 задача
легко решается с помощью усреднения). Пусть V — образ постоянного
векторного поля @, 1) под действием h. Нормируем V так, чтобы со-
сохранить информацию только о направлениях векторов, задав тем самым
отображение R2 —»S', постоянное вне единичного круга, а значит и вне
квадрата Q = [— 1, 1] х [—1, 1]. Не меняя построенного отображения вне Q,
его можно гладко гомотопно продеформироать в постоянное отображение.
Это легко сделать с помощью поднятия нашего отображения до отображе-
отображения R2 —> R1 в универсальную накрывающую окружности S1. Обозначим
через V, соответствующее векторное поле в момент /. По векторным полям
Vt и будет восстановлен диффеоморфизм Ш2.
Утверждается, что траектория любой точки квадрата под действием по-
поля Vt начинается на его нижнем основании и оканчивается на верхнем (см.
рис. 3.30). В противном случае у орбиты имелась бы некоторая предельная
1?
1
J
А
Рис. 3.30. Векторное поле на квадрате. Траектории гладкого векторного поля, ко-
которое постоянно и вертикально вне квадрата.
точка р в данном квадрате. Тогда можно было бы, слегка пошевелив век-
векторное поле в окрестности р, получить замкнутую орбиту, что невозможно
(см. упражнение 3.10.15).
Домножим теперь поле V, на скалярную функцию, постоянную на ка-
каждой траектории, так, чтобы время, затраченное на движение от нижнего
210
Глава 3. Геометрические многообразия
основания до верхнего, вдоль любой траектории было равно 2. Определим
/г, как гомеоморфизм квадрата Q, переводящий точку (х, у) в точку, отве-
отвечающую параметру у на траектории, выходящей из точки (х, — 1) (параметр
изменяется от —1 до 1). Начало и конец траектории поля Vt имеют, вообще
говоря, различные х-координаты (см. рис. 3.30), и задают некоторый диф-
диффеоморфизм ср, нижнего основания на верхнее. Рассмотрим композицию
ht с диффеоморфизмом, который переводит каждую горизонталь в себя и
изменяется от тождественного на нижнем основании до ср на верхнем.
После такой поправки новое отображение h, является тождественным на
границе квадрата и может быть продолжено до диффеоморфизма всего
пространства Ш2. При t, изменяющемся от 0 до 1, эти диффеоморфиз-
диффеоморфизмы задают искомую гомотопию между / и тождественным отображением.
13.10.111
Задача 3.10.14 (непрерывная зависимость 2). Проверьте, что нз прове-
проведенного выше построения вытекает, что пространство диффеоморфизмов плоско-
плоскости R2, тождественных вне квадрата Q, стягиваемо. (Вместе с упражнением 3.10.13
это означает, что пространство ОC) является деформационным ретрактом про-
пространства DiffS2.)
а) Докажите, что при подходящем выборе гомотопии, поле V, непрерывно за-
зависит от h (пространство гладких векторных полей на квадрате рассматривается в
С'-топологии).
б) Докажите, что скалярная функция, на которую домножалось поле Vt на по-
последнем шаге предыдущего доказательства, непрерывно зависит от поля V,. (Под-
(Подсказка: примените теорему об обратной функции к одному данному векторному
полю. Воспользуйтесь теоремой о непрерывной зависнмости обратной функции от
параметров и свойствами приближенных решений дифференциального уравнения
для доказательства непрерывности.)
в) Докажите, что поправка, необходимая для нейтрализации действия <р,, тоже
меняется непрерывно.
Задача 3.10.15 (замкнутые орбиты). Докажите, что нигде не обращающееся
в нуль векторное поле на плоскости не может иметь замкнутых орбит. (Подсказка:
воспользуйтесь задачей 1.3.12 и предложением 1.3.10. Измените векторное поле
так, чтобы на кривой оно стало направленным внутрь области, ограниченной этой
кривой.) Утверждение задачи является частью знаменитой теоремы Пуанкаре—
Бендиксона.
Упражнение 3.10.16. Почему вторая часть доказательства теоремы 3.10.11 не
проходит для больших размерностей?
Трудная задача 3.10.17 (сглаживание четырехмерных многообразий). До-
Докажите, что каждое кусочно-линейное четырехмерное многообразие имеет гладкую
структуру. Если следовать схеме доказательства теоремы 3.10.8, то сложности воз-
возникнут при продолжении спайкн вдоль ребер триангулированного четырехмерного
многообразия. Одна из идей состоит в том, чтобы вместо работы с фиксированной
триангуляцией обратиться к подразбиениям.
3.10. Сглаживания
211
а) Докажите, что для каждого кусочно-проективного отображения / сферы 52
на себя найдется такая триангуляция, что отображение / изотопно тождественно-
тождественному в классе гомеоморфизмов, проективных на каждом треугольнике. (Указание:
воспользуйтесь теоремой Смейла.)
б) Докажите, что на каждом кусочно-линейном четырехмерном многообразии
имеется триангуляция, допускающая спайку.
Еще раз подчеркнем, что гладкие и кусочно-линейные структуры разли-
различаются в старших размерностях. Есть примеры кусочно-линейных много-
многообразий, которые нельзя сделать гладкими, и примеры кусочно-линейных
многообразий, на которых есть несколько существенно различных глад-
гладких структур. Обратите также внимание на пример 3.1.6 и рассуждения,
следующие за доказательством предложения 3.9.6.
Задача 3.10.18. а) Рассмотрим гладкое многообразие М размерности т, ко-
которое гладко вложено в качестве замкнутого подмножества в многообразие N
размерности т + 1, причем оба многообразия М и N ориентируемы. Допустим,
что дано два таких вложения многообразия М в различные многообразия N\ н N%.
Докажите, что найдутся такие окрестности многообразия М в N\ и Л/г, которые
можно будет диффеоморфно отобразить одну в другую, оставляя при этом на месте
точки из М. Для наших нужд достаточно доказать это для т = 0, 1 и 2.
б) Докажите, что любое гладкое вложение единичного шара Вп в простран-
пространство К." изотопно в классе гладких вложений линейному отображению с той же
производной в нуле.
в) Докажите, что любой диффеоморфизм единичного диска D2 на себя, сохра-
сохраняющий три точки на границе, изотопен в классе таких диффеоморфизмов тожде-
тождественному отображению. (Подсказка: творчески воспользуйтесь теоремой Рнмана.)
Задача 3.10.19 (каноническое сглаживание двумерного многообразия).
Из теорем 3.10.8 и 3.10.9 уже известно, что гладкая структура на двумерном мно-
многообразии определяется канонически, с точностью до диффеоморфизма.
Определите каноническую гладкую структуру на триангулированном двумер-
двумерном многообразии М так, чтобы она зависела только от локальной комбинаторики
триангуляции и не оставляла никакого дополнительного произвола при своем по-
построении.
Точнее, постройте конечный гладкий атлас, который, во-первых, канонически
ассоциирован с триангулированным двумерным многообразием, во-вторых, мель-
мельче покрытия многообразия М открытыми звездами, в-третьих, любой изоморфизм
/: U —*• V между открытыми окрестностями звезд в триангулированных двумерных
многообразиях переводит карты атласа, содержащееся в U, в карты, содержащиеся
в V.
Трудная задача 3.10.20 (каноническое сглаживание трехмерного много-
многообразия). Обобщите задачу 3.10.19 на трехмерные многообразия. Для этого вам,
возможно, потребуется тяжелая артиллерия вроде теоремы униформизации для ри-
мановых метрик на S2, которую нужно применить с большой изобретательностью.
Глава 4
Структура дискретных групп
Довольно часто имеются сильные ограничения на топологию многообра-
многообразия М, представимого как факторпространство однородного пространства
(G, X) по действию дискретной группы Г с G. Они возникают как след-
следствие геометрических и алгебраических свойств дискретных групп и ока-
оказываются иногда настолько сильными, что позволяют получить полную
классификацию замкнутых (G, JQ-многообразий.
В этой главе мы исследуем структуру дискретных подгрупп автомор-
автоморфизмов однородных пространств. Особое внимание уделено модельным
трехмерным геометриям.
4.1. Группы, порожденные малыми элементами
Пусть G — группа Ли с левоинвариантной метрикой d (см. лемму 3.4.11).
Обозначим символом 1 единичный элемент группы G и назовем элемент
группы G малым, если он находится вблизи от единичного. Чтобы по-
получить полное представление о множестве всех дискретных подгрупп. Г в
группе G, нам следует разобраться не только с типичными примерами, но
и с крайними случаями, когда группа Г почти недискретна — в том смысле,
что в ней содержится много очень малых элементов.
В этом нам поможет хаусдорфова топология. Хаусдорфовым рас-
расстоянием dH(A, А') между двумя замкнутыми подмножествами А, А' с X
компактного метрического пространства X называется максимальное из
всевозможных расстояний, отделяющих точку одного из множеств от дру-
другого1. То есть:
dH(A, A') = (inf г. Леи Вг(х) и Л' с U В,(х)\,
где Вг(х) — шар радиуса г вокруг точки х.
'Расстоянием, отделяющим точку а множества А от множества А', автор называет число
min d(a, а').- Прим. перез.
а'еА'
4.1. Группы, порожденные малыми элементами
213
Упражнение 4.1.1. Докажите, что метрика Хаусдорфа превращает множество
замкнутых подмножеств пространства X в компактное метрическое пространство.
Топология, порожденная этой метрикой, определяется только топологией, но не
метрикой, пространства X.
Для подмножеств некомпактного метрического пространства правиль-
правильное определение хаусдорфовой топологии менее очевидно, и фактически
для ее определения есть два пути. Наиболее очевидный — сохранить опре-
определение, данное для компактных пространств. Но, к сожалению, простран-
пространство замкнутых подмножеств с такой топологией уже не будет ни ком-
компактным, ни даже паракомпактным. Лучший для наших целей способ —
определить хаусдорфову топологию с помощью пересечений с компактны-
компактными множествами. Точнее, если X — локально компактное полное метриче-
метрическое пространство и А с X — его замкнутое подмножество, то для любого
компакта К с X и любого числа е > О определим окрестность NKc(A) мно-
множества А в X как совокупность таких подмножеств В, что
dH(AnK, ВпК)<е.
Упражнение 4.1.2. Докажите, что в этой топологии пространство замкнутых
подмножеств компактно.
Предложение 4.1.3 (замкнутые подгруппы образуют замкнутое
хаусдорфово множество). Среди замкнутых подмножеств группы
Ли G ее замкнутые подгруппы образуют замкнутое, а потому
компактное подмножество.
Доказательство. Пусть А с X — замкнутое подмножество, которое
является предельной точкой для множества замкнутых подгрупп группы G.
Покажем, что для любых a, b € А, элементы а~1 и ab также лежат в А.
Для этого выберем такой компакт К с G, что множество его внутренних
точек содержит элементы a, b, ab и а. По определению в окрестности
NKtZ(A) найдется подгруппа, которая содержит элементы на расстоянии не
более, чем е, от а и b соответственно. А значит в этой группе содержатся
элементы, достаточно близкие к элементам a~l a ab. Переходя к пределу
при е —> 0, получаем наше утверждение1. 1-4-1.31
Про некоторое свойство замкнутых подгрупп в группе Ли будем го-
говорить, что оно уважает замыкание, если множество подгрупп, которые
обладают этим свойством, замкнуто в топологии Хаусдорфа.
Упражнение 4.1.4. Докажите, что нижеперечисленные свойства замкнутой
подгруппы Н уважают замыкание:
а) подгруппа Н связна,
'Полезно иметь в виду (и читатель это поймет, занимаясь упражнением 4.1.2), что если
lim Ап = А в топологии Хаусдорфа и последовательность ащ ? Ank сходится к а ? X, то
а е А.— Прим. ред.
214
Глава 4. Структура дискретных групп
б) подгруппа Н абелева,
в) подгруппа Н — нильпотентная группа ступени k. Это означает, что любой
&-й коммутатор [ho, [hi, ..., [hk-i. At]... ]] равен единице в группе Н. (Указание:
замыкание нильпотентной подгруппы ступени k есть нильпотентная подгруппа той
же ступени.)
Как показывает пример подгрупп п~хЪ в R, п = 1, 2, ..., дискретность
не является свойством, уважающим замыкание. Одна из важных задач
этого раздела — понять природу недискретных пределов дискретных групп:
см. теорему 4.1.7.
Любая замкнутая подгруппа Н группы Ли G является группой Ли. Тем
самым, связная компонента единицы в Н, обозначаемая через Н°, есть
группа Ли, и будучи связной, полностью определяется своим касатель-
касательным пространством в единице. Вся подгруппа Н представляет из себя
объединение дискретного множества смежных классов по подгруппе Н°;
в частности, группа Н дискретна, если Н° = {1}.
Как мы видели в разделе 3.6, алгебру Ли g группы Ли G можно пони-
понимать и как касательную алгебру в единице группы G, и как пространство
левоинвариантных векторных полей на группе G. Рассмотрим левоинварн-
антное векторное поле, принимающее значение v в единице группы. Поток
этого векторного поля получается при действии справа однопараметриче-
ской подгруппы ехр/и группы G, причем вещественный параметр / играет
роль времени в потоке. Отображение и н-> ехр и назвается экспоненциаль-
экспоненциальным отображением д —> G. Его производная в единице есть тождествен-
тождественный оператор, поэтому отображение ехр биективно отображает некоторую
окрестность нуля в g на окрестность единицы в С В этой окрестности
единицы можно определить обратное отображение, которое называется
логарифмическим отображением и обозначается через log. Оба ото-
отображения служат важными инструментами прн изучении групп Ли.
Пример 4.1.5. Функция е? — это и есть экспоненциальное отображение
для мультипликативной группы Щ_ положительных вещественных чисел.
Касательное пространство в точке Е е QL(n, Щ отождествляется с век-
векторным пространством Mat (я, R) линейных эндоморфизмов R", а экспо-
экспоненциальное отображение
ехр: Mat(«, R) ->• GL(«, E)
есть обычная матричная экспонента. Стандартным степенным рядом, схо-
сходящимся, в некоторой окрестности 0 в Mat(«, R), задается и матричная
логарифмическая функция \og(E + X).
Несложно проверить, что, как и в случае обычной экспоненты, ехр(яи) =
= (ехр v)n для любого целого п и любого v е д. Но равенство ехр(и + до) =
= ехр(и) ехр(до) для любых и и до верно только для групп Ли G с абелевой
группой G0.
4.1. Группы, порожденные малыми элементами
215
Теорема 4.1.6 (дискретная, порожденная малыми элементами
группа является нильпотентной). В группе Ли G существует такая
окрестность единицы U, что любая дискретная подгруппа Г с G,
порожденная множеством Г П U, нильпотентна.
Доказательство. Идея доказательства состоит в том, что умножение
маленьких элементов в группе G приближается сложением в алгебре Ли д,
а так как сложение в д коммутативно, то умножение маленьких элементов
коммутативно с точностью до величин второго порядка малости. Говоря
формально, существуют такие положительные константы е и С, что для
любых двух элементов а и b из группы G выполнено неравенство
если d{\, а) < е и d(\, b) < e.
В частности, коммутатор [а, Ь] находится значительно ближе к единице,
чем любой из исходных элементов. Наше неравенство получается, если
применить теорему Тейлора к отображению [ , ]: G x G -> G и принять во
внимание, что [ 1, Ь] = [а, 1 ] = 1.
Далее, выберем е настолько малым, чтобы для любых элементов a, b e
е U = ВеA) было выполнено неравенство rf(l, [a, b]) < id(l, а).
Пусть Г—дискретная подгруппа группы G, порожденная элементами из
ГП 0. Тогда для любых ^-элементов g,err\U,i=l,...,k, коммутатор
вида
[g\ ¦ ¦ ¦ gk] = [gl, [gi, [g3, ¦ ¦ ¦ , [gk-l ,gk].-- ]]]
удален от единицы не более чем на 2~*е. Но так как нетривиальные элемен-
элементы дискретной группы Г не могут находиться слишком близко от единицы,
то найдется такое k, что все коммутаторы рассматриваемого вида будут
тривиальны. Отсюда следует нильпотентность группы Г: достаточно рас-
рассмотреть центральный ряд
в котором подгруппа Г; порождена коммутаторами [g\... gt] ступени / с
элементами gs из пересечения Г П U. |4.1.6|
Ключевой результат о том, как устроено замыкание множества дискрет-
дискретных подгрупп, содержится в следующем обобщении теоремы 4.1.6:
Теорема 4.1.7 (нильпотентные пределы). Пусть G —группа Ли.
а) Существует такая окрестность U единицы в группе G, что
любая дискретная подгруппа Г с G, порожденная элементами из
Г П U, является кокомпактной подгруппой в некоторой связной,
замкнутой нильпотентной подгруппе N с G, пересекающейся с
окрестностью U по связному подмножеству.
216
Глава 4. Структура дискретных групп
б) Замыкание множества дискретных подгрупп группы G состо-
состоит из множества замкнутых подгрупп (не обязательно всех) с ниль-
потентной компонентой единицы.
Доказательство. Без потери общности можно считать, что группа G
связна.
В качестве окрестности U возьмем образ шара Ве@) в касательной ал-
алгебре g при экспоненциальном отображении, подбирая е настолько малым,
чтобы окрестность U удовлетворяла как требованиям теоремы 4.1.6, так и
некоторым другим, которые появятся по ходу доказательства. Предполо-
Предположив, что группа Г порождена пересечением Г П U, мы построим индукцией
по i башню замкнутых нильпотентных подгрупп возрастающей размерно-
размерности
Г = No С W, с . -. С Nk = N,
которая окончится связной подгруппой.
Первый шаг индукции — самый легкий. Можно считать, что группа Г не-
нетривиальна, и пусть а —ее нетривиальный элемент, ближайший к единице.
Ясно, что а € О (в противном случае Г П U = {1}, и группа Г тривиаль-
тривиальна). Далее, коммутатор а с любым элементом из Г П U тривиален, так
как он меньше самого а. Следовательно, элемент а коммутирует со всеми
элементами из окрестности U. Обозначим через v логарифм элемента а и
докажем, что однопараметрическая подгруппа М\ = expRu перестановочна
с элементами Г.
Для этого мы выберем окрестность U столь малой, чтобы
а) любой элемент из U обладал бы единственным квадратным корнем,
лежащим в U,
б) множество квадратных корней VU выдерживало бы сопряжения
элементами из U.
Если у S U ~ образующая группы Г, то элемент а[/2 = ехри/2 ком-
коммутирует с у, так как элемент уа1/2у~1 — это снова квадратный корень
из а, лежащий в U. Применяя индукцию, получаем, что все элементы вида
exp2~pv коммутируют с у. Но степени таких элементов всюду плотны в М i.
Поэтому элемент у лежит в централизаторе подгруппы Мх.
Заметим, что подгруппа Mi замкнута по той причине, что степени
а" = ехр/ги, neZ, образуют равномерную решетку в Мь а подгруппа
expZu замкнута в G. Точнее, факторпространство Afi/expZu гомеоморф-
но окружности R/Z, а потому компактно. Следовательно, оно замкнуто
в пространстве смежных классов G/expZu. А в силу замкнутости дис-
дискретной группы expZu отсюда уже следует, что подгруппа Mi замкнута1
1 Здесь полезно сослаться на следующий легко проверяемый общий факт: если Г — дис-
дискретная подгруппа группы G, а подгруппа Н такова, что Н П Г — кокомпактная подгруппа
d Я, то Н замкнута в G. Этот факт будет использован и в дальнейшем.— Прим. ред.
4.1. Группы, порожденные малыми элементами
217
в G. Итак, доказано, что N\ =M] Г — замкнутая нильпотентиая подгруппа
в группе G, а Г — кокомпактная подгруппа1 в N\.
Далее, воспользуемся индуктивным предположением и рассмотрим
башню Г = Nq с ... С Ni замкнутых нильпотентных подгрупп вида Nt =
= N?T, обладающих такими свойствами (см. рис. 4.1):
а) компонента единицы Mt группы N, имеет размерность /;
б) как Mj, так и N/ — нормальные подгруппы в N, при / < /, и, бо-
более того, действие подгруппы jV,- сопряжениями на факторгруппе j
тривиально, т. е. [W,, Mj] С Afy_(;
в) Г — кокомпактная подгруппа группы Л//.
Рис. 4.1. Дискретная подгруппа группы Ли, порожденная маленькими элемента-
элементами. Такая подгруппа Г напоминает решетку в R" с той лишь разницей, что умножение
в ней не совсем коммутативно: коммутаторы элементов, расположенных в указанных
на рисунке направлениях, могут оказаться нетривиальными в направлениях, где точки
расположены гуще.
Чтобы повысить размерность подгруппы М, на единицу, мы добавим
к ней однопараметрическую подгруппу вида exp(^loga), выбрав из пере-
пересечения Г П U элемент а, не принадлежащий подгруппе Mt. Если такого
элемента нет, индукция закончена.
В противном случае будет построена (/+ 1)-мерная связная замкнутая
нильпотентная группа Ли при условии, что добавленная однопараметриче-
однопараметрическая подгруппа нормализует Mh
'В самом деле,
~М{/ГnMi ~5{.-Прим. ред.
218
Глава 4. Структура дискретных групп
Обозначим через Lt связную компоненту единицы в пересечении Af, П U
и выберем самый маленький элемент а в Г \ L, (автоматически а е U).
Положим v = log а. Одновременно а будет и самым маленьким элемен-
элементом из Г П U, однопараметрическая группа которого ехр tv не лежит в Af,.
Мы покажем, что для всех / е К внутренний автоморфизм ср(/), индуциро-
индуцированный сопряжением с помощью элемента ехр tv, оставляет инвариантной
подгруппу Mj, j < i. Так как а е Г, то наше утверждение верно при t — 1
в силу предположения индукции. В силу связности подгруппы Af/ доста-
достаточно доказать, что производная автоморфизма ср(^) в единице оставляет
инвариантной касательную алгебру щ, которая однозначно определяет са-
саму группу (кстати, эта производная есть не что иное, как ad(expfo): см.
упражнение 3.8.8).
Теперь нам потребуется тот факт, что отображение, очень близкое к
тождественному, оставляет неподвижной некоторую точку тогда и только
тогда, когда эту же точку оставляет неподвижной его квадрат. Вот точная
формулировка:
Лемма 4.1.8 (надежный квадрат). Пусть V — сферическая окрест-
окрестность точки О € К" и пусть диффеоморфизм /: V —>• Ш" таков, что
производная отображения g- = / — Id ограничена по норме положи-
положительной константой г\. Тогда в тех точках, где определена компо-
композиция f2 — f(f(x)), имеет место неравенство
|/(/(и)) -u-2g(u)\<Г)\g(u)\.
В частности, если г\ < 2, то неподвижная точка отображения f
будет неподвижной и для отображения f.
Доказательство. Преобразуем левую часть неравенства
f{u) -и- 2g(u) = g(f(u)) + g(u) - 2g(u) = g(u + g(u)) - g(u).
Затем применим формулу Тейлора. Лемма доказана. |4.1.8|
Чтобы воспользоваться этой леммой, рассмотрим подпространство щ
как точку грассманиана /-мерных подпространств в касательной алгебре д.
Тогда, если автоморфизм ср(/) при некотором t, О < t < 1, сохраняет под-
подпространство Ш/, то этим же свойством обладает и <p(t/2) при условии, что
исходная окрестность U выбрана достаточно малой (причем этот выбор
можно сделать не зависящим от группы Г). В итоге получаем инвариант-
инвариантность подпространства т,- под действием всех автоморфизмов вида yB~pq)
для всех целых р и q, а стало быть, и под действием всей подгруппы <p(t),
Упражнение 4.1.9. Докажите, что подгруппа cp(R) нормализует М/, не приме-
применяя лемму 4.1.8. Используйте отображение cp(R) в GL(g) и exp-log функции.
4.1. Группы, Порожденные малыми элементами
219
Далее, согласно нашему плану, рассмотрим подгруппу AfI+I = Af, expRu.
Это —связная подгруппа группы С Кроме того, Mj —нормальная подгруп-
подгруппа в Mt+i при / < i.
Аргументы, с помощью которых была доказана замкнутость подгруп-
подгруппы Ми показывают, что подгруппа Af,+I также замкнута; снова рассмо-
рассмотрим пространство смежных классов G/M, ехр Zv и заметим, что подгруп-
подгруппа Mi ехр Zv замкнута, будучи объединением связных компонент подгруп-
подгруппы /V,-, которая замкнута по предположению индукции1.
Пришло время доказать,, что сопряжение элементом вида ехр tv, t € Ш,
тривиально действует на пространстве Af//Af/_,, если 1 </ < i + 1. Или,
что то же самое, доказать тривиальность такого действия на одномерном
линейном подпространстве щ/т^. Но при *= 1 это так. Следовательно,
это верно и для элементов вида <$B~pq). А значит, и вся однопараметри-
однопараметрическая подгруппа действует тривиально на mj/mj-i.
Заодно мы показали, что подгруппа Af/+I =Af,expRu тривиально дей-
действует иа Mj/MH1, поскольку этим свойством в силу индуктивного пред-
предположения уже обладает подгруппа М-,.
Докажем, наконец, что группа Г нормализует Mi+l и тривиально дей-
действует на M,+i/Mi. При доказательстве можно ограничиться элементами у,
лежащими в пересечении Г П U. В этом случае коммутатор [а, у] предста-
представляет элемент группы Г, меньший чем а. В силу выбора элемента а этот
коммутатор лежит в Af,-. Но это в точности означает, что автоморфизм срA)
оставляет на месте смежный класс элемента у в пространстве G/Mt. А нам
нужно показать, что это же верно для ср(^) при любом t: в самом деле, ведь
тогда ут ехр tvy~x e Mt ехр tv, если те Mi.
Возникает желание применить лемму 4.1.8 к многообразию G/Af,- и за-
заключить, что автоморфизм ср(^/2) сохраняет смежный класс элемента у,
если это делает автоморфизм y(t). Но здесь следует остеречься, так как от
нас потребуется выбрать константу, участвующую в формулировке леммы,
равномерно для всех замкнутых подгрупп, в то время как подгруппа Af,-
может достаточно плотно «заполнить» почти всю группу G. Поэтому мы
поступим иначе и рассмотрим слоение &и окрестности U, индуцированное
разбиением группы G на смежные классы, и будем работать в простран-
пространстве листов этого слоения, где все выглядит проще (см. рис. 4.2). При
О < t < 1 отображение ср(/) переводит листы слоения &и в листы слое-
слоения <&и> в чуть большей окрестности U'. С другой стороны, мы знаем, что
отображение срA) сохраняет слой, проходящий через у, и теперь мы мо-
можем применить лемму 4.1.8 к пространству листов 11/&и и сделать вывод
о ср(/)-инвариантности этого же слоя для всех t.
Наконец рассмотрим подгруппу /V/+1 = А1,+1Г. Из всего уже доказанного
следует, что:
'Напомним, что expZaer и что jM,+i/jM,expZa~ S1.— Прим. ред.
220
Глава 4. Структура дискретных групп
U
Рис. 4.2. Слоение G смежными классами по подгруппе А*/- Даже через маленькие
окрестности единицы подгруппа М-, может проходить много раз (рис. слева). По этой
причине, вместо пространства U/Mi, существенно зависящего от подгруппы Mi, удоб-
удобней работать с пространством слоев U/&u (рис. справа), к которому и применяется
лемма 4.1.8.
а) М+1 ~" подгруппа в G;
б) действуя сопряжениями в G, эта подгруппа сохраняет все Mh а на
пространстве MjMj-i ее действие тривиально;
в) пространство Ni+l/T расслаивается над Nt/T со слоем окружность.
Поэтому группа Г кокомпактна в Nl+U так как такова она в группе N,.
В частности, подгруппа /V/+1 замкнута1.
Осталось проверить, что построенная группа нильпотентна. В самом
деле, если {1} = Г0С...сГ* = Г- центральный ряд группы Г, то
{1} = Af0 С ... С Af,+i С
с ... С М,+{Гк
есть центральный ряд для группы /V/+1.
Так, по индукции, шаг за шагом, мы достроим нужную нам башню до
конца (ведь группа G конечномерна!) и докажем часть а теоремы. А часть б
есть лишь переформулировка части а. ШПп
Упражнение 4.1.10 (описание N). Докажите, что связная группа Ли N, по-
построенная в процессе доказательства теоремы 4.1.7, является замыканием группы,
порожденной всеми элементами вида а2 , р & Z+, а € Г П U.
Воспользовавшись такой характеристикой, покажите, что группа N растет вме-
вместе с группой Г в следующем смысле: зафиксируем окрестность U, которая возни-
возникла в доказательстве теоремы 4.1.7, выберем дискретную подгруппу Г в группе G и
обозначим через N(V) ту связную группу Ли, которая получится, если конструкцию
'См. сноску на с. 216.— Прим. ред.
4.1. Группы, порожденные малыми элементами
221
из доказательства применить к дискретной группе, порожденной элементами из пе-
пересечения группы Г с некоторой окрестностью единицы V с U. Тогда включение
U" с U' влечет включение N{U") с N(U') и, более того, если g~lU"g с V для
некоторого элемента g € Г, то и g~1N(U")g с N(U').
В частных случаях теорема 4.1.7 позволяет сделать более точные вы-
выводы.
Следствие 4.1.11 (дискретная ортогональная группа почти абеле-
ва). Для любой размерности п существует такое натуральное т,
что любая дискретная подгруппа ортогональной группы О(л) со-
содержит абелеву подгруппу индекса, не превосходящего т.
Доказательство. Пусть U — окрестность единицы, выбранная соглас-
согласно теореме 4.1.7. Для любой дискретной (т. е. конечной) подгруппы Г в
группе О (л) обозначим через Гу ее подгруппу, порожденную пересечением
Г П U. Покажем, что индекс [Г : Гу] ограничен. В самом деле, выберем
такую окрестность единицы W, что W = W'1 и W2 с V. Тогда окрест-
окрестности ctW и CjW не пересекаются для двух представителей различных
смежных классов по Ти. Следовательно, индекс [Г : Гу] не превосходит
отношения объема группы О(л) к объему окрестности W.
Так как группа О(л) компактна, то на ней имеется биинвариантная
метрика, т. е. риманова метрика, инвариантная при левых и правых сдви-
сдвигах элементами группы. Это доказывается методом усреднения точно так
же, как в лемме 3.4.11 доказывалось существование инвариантной мет-
метрики.
По теореме 4.1.7 группа Гу содержится в связной нильпотентной под-
подгруппе N с О(л), которая наследует биинвариантную метрику. Но связная
нильпотентная группа с биинвариантной метрикой оказывается абелевой.
Чтобы в этом убедиться, рассмотрим центр Z такой группы N. Биинвари-
Биинвариантная метрика на группе индуцирует в ее касательной алгебре п риманову
метрику, инвариантную относительно Ad-действия N на п (см. упражне-
упражнение 3.8.8). Кроме того, преобразования из Ad N оставляют неподвижными
все векторы касательного пространства з к подгруппе Z. Верно и обратное:
любой Ad /V-инвариантный вектор из п порождает центральную однопара-
метрическую подгруппу, а потому лежит в з-
В частности, в ортогональном дополнении з1 к j в п отсутствуют
Ad /V-инвариантные векторы. В силу Ad-инвариантности метрики подпро-
подпространство З" инвариантно относительно присоединенного представления
и изоморфно проектируется на алгебру Ли группы N/Z. Тем самым в
алгебре Ли группы N/Z отсутствуют инвариантные векторы присоеди-
присоединенного представления, т. е. центр этой группы тривиален. Но группа W
нильпотентна, и тривиальность центра означает, что она абелева. |4.1.11|
Похожее следствие мы получим и для евклидовых групп движений, но
вначале напомним стандартные факты о евклидовых изометриях.
222
Глава 4. Структура дискретных групп
Упражнение 4.1.12 (изометрии Е"). а) Любую изометрню <р аффинного ев-
евклидова пространства Е" можно представить, выбрав начало отсчета, в виде v ¦—>
i-+ A(v) + vq с линейной частью А из ортогональной группы О(я) и вектором сдви-
сдвига vq. Линейная часть А не зависит от выбора начала отсчета. Преобразование А
будем называть вращательной частью1 движения ср.
б) Если у А нет собственного значения, равного единице, то у движения <р есть
единственная неподвижная точка.
в) Дискретная группа сдвигов (параллельных переносов) Ж? изоморфна Z'™,
т ^ п, и кокомпактна тогда и только тогда, когда т = п.
г) Коммутатор любой изометрии ср пространства Е" со сдвигом v — это снова
сдвиг на вектор v — A~lv, где А — вращательная часть ср. В частности, если дви-
движение ср коммутирует с п линейно независимыми сдвигами, то оно само является
сдвигом.
д) Пусть G — группа движений Е". Тогда ее подгруппа Та, состоящая из всех
сдвигов, нормальна в G.
Следствие 4.1.13 (дискретная евклидова группа —почти абелева).
Для любой размерности п существует такое целое число т, что лю-
любая дискретная группа движений Е" содержит абелеву подгруппу,
индекс которой не превосходит т.
Доказательство. Пусть U — окрестность единицы в группе Isom E" из
формулировки теоремы 4.1.7. Можно считать, что U = RT, где R (соот-
(соответственно Т) — подходящие окрестности единицы в группе О(я) (соответ-
(соответственно в группе сдвигов R"). На самом деле, в качестве Т можно выбрать
всю группу сдвигов R"! Докажем это.
Рассмотрим подгруппу Г с IsomE", порожденную пересечением Гп
Г\ЯШ". Теперь заметим, что группа Гх, Х = 1, 2, ..., порожденная пересе-
пересечением Г П R(kT), сопряжена группе, порожденной множеством (ХГХ) П
П RT. Следовательно, применяя к группе Гх теорему 4.1.7, мы получаем
последовательность замкнутых связных нильпотентных подгрупп /Vx э Г\.
Кроме того, согласно упражнению 4.1.10, группа N\ растет с номером X,
т. е. Л/х Z> N^ при X > fi: Но такой рост связных групп может происходить
только за счет увеличения их размерности. По этой причине последо-
последовательность Nx стабилизируется, и мы получаем нужный нам результат:
группа Г содержится в связной замкнутой нильпотентнон подгруппе груп-
группы IsomE".
А теперь, как и при доказательстве следствия 4.1.11, мы получаем, что
для любой дискретной группы Г движений Е" индекс ее подгруппы, поро-
порожденной элементами из Г П RR", ограничен.
Осталось доказать коммутативность любой связной замкнутой ниль-
потентной подгруппы N с IsomE". Пусть TN — ее подгруппа сдвигов (в
'В оригинале rotational, что подчеркипает, что рассматриваемая матрица является орто-
ортогональной.— Прим. ред.
4.1. Группы, порожденные малыми элементами
223
обозначениях упражнения 4.1.12, д. Обозначим через V подпространство
в Ея, порожденное векторами сдвигов из Ты. Ясно, что N сохраняет как
подпространство V, так и его ортогональное дополнение V±. Рассмотрим
естественный гомоморфизм N -* O(VX) х Isom V. Покажем, что это мо-
мономорфизм. В самом деле, элемент ядра действует как сдвиг в простран-
пространстве Vх и тождественно в пространстве V, а по условию все сдвиги лежат
в V.
Итак, группа N вкладывается в прямое произведение О (л — k) x
х IsomE*, где k = dim V, причем ее проекции на оба множителя нильпо-
тентны, так как нильпотентна она сама. Поэтому, если k < n, то применяя
индукцию и следствие 4.1.11, приходим к выводу, что обе эти проекции
абелевы, а значит и сама группа N абелева. При k = п группа N содержит
«сдвиги во всех направлениях».
Покажем, что в этом случае N = Ш". Если это не так, то найдется эле-
элемент ф с нетривиальной вращательной частью А. Тогда, согласно упраж-
упражнению 4.1.12, г, линейная оболочка коммутаторов [ср, К"] совпадает с
подпространством 1т(Д — Id). Но линейное преобразование А — Id не-
невырожденно на подпространстве 1т(Д — Id). А это значит, что повтор-
повторные коммутаторы с ср~' будут порождать одно и то же подпространство
1т(Л — Id). При А ф Id это противоречит нильпотентности. [4.1.131
Задача 4.1.14 (абелевы подгруппы реализуются сдвигами). Докажите, что
для любой абелевой подгруппы А С IsomE" существует единственное максималь-
максимальное евклидово подпространство Е», на котором группа А действует сдвигами.
Чтобы применить теорему 4.1.7 к группе гиперболических движений,
мы должны ее усовершенствовать, распространив на случай, когда груп-
группа действует на многообразии X и порождается элементами, мало сдви-
сдвигающими фиксированную точку, но не обязательно близкими к едини-
единице. Начнем с простой леммы. Напомним определение слова в группе G.
Пусть А — подмножество элементов в группе G. Словом длины п над
множеством А называется я-вектор {аи ..., ап), координаты которого —
элементы из A U Л; будем говорить, что слово (аи ,.., ап) представля-
представляет элемент п\... ап группы, а там, где это не приведет к недоразумению,
мы будем часто и само слово записывать в виде а{ ...ап. Пустое слово,
или слово длины 0, представляет единицу группы. Введем норму элемента
группы как длину кратчайшего слова над А, представляющего этот эле-
элемент.
Лемма 4.1.15 (маленькая группа — короткие слова). Если число
элементов в группе G больше чем т, а А — множество образующих
группы, то в группе существует не менее чем (т + 1) различных
элементов с нормой, не превосходящей т.
В качестве обобщения рассмотрим некоторое множество S,
в котором больше чем т элементов, и транзитивную группу G
224
Глава 4. Структура дискретных групп
преобразований S. Пусть s eS. Тогда по крайней мере (т+1) эле-
элементов из группы G будут иметь норму, не большую чем т, и
переводить точку s в различные точки.
Доказательство. Докажем первое утверждение. Обозначим через г(п),
п > 0, число различных элементов группы G с нормой, не большей чем п.
Назовем г функцией роста группы G (по отношению к А). Следует пока-
показать, что г(т) > т. В противном случае, г{1 + 1) = r(i) < т для некоторого
/ < т. Но тогда и r(n) = r(i) для любого п > i, а это означает, что поря-
порядок группы \G\ = r(i) < m. Получили противоречие. Второе утверждение
доказывается аналогично. 14.1.151
Предложение 4.1.16 (короткие движения порождают почти ниль-
потентную группу). Пусть G — группа Ли, действующая на много-
многообразии X так, что стабилизаторы точек компактны. Выберем
произвольную точку х е X. Тогда существуют такое целое число т
и такое положительное е > О, что любая дискретная подгруппа Г
в группе G, порожденная элементами, сдвигающими точку х на
расстояние, меньшее чем г, содержит нормальную нильпотентную
подгруппу конечного индекса, не превосходящего т. Более того,
подгруппа Г содержится в замкнутой подгруппе группы G с чи-
числом компонент связности, не большим чем т, и с нильпотентной
компонентой единицы.
Доказательство. Пусть U — окрестность единицы, выбранная в тео-
теореме 4.1.7, а V — окрестность стабилизатора Gx, имеющая компактное
замыкание. Допустим, что окрестность V покрывается (т — 1) сдвигами
окрестности U. Выберем симметричную окрестность W = W~l стабилиза-
стабилизатора так, чтобы Wm с V. Рассмотрим дискретную группу Г, порожденную
элементами из Г П W, и пусть Ти — ее подгруппа, порожденная пересе-
пересечением Г Л U. Мы утверждаем, что индекс [Г : Гу] < т. В самом деле,
группа Г естественно действует на множестве смежных классов Г/Гу, и
если число элементов в этом множестве больше чем т, то по лемме 4.1.15
можно выбрать (т+1) элементов группы Г, лежащих в разных смежных
классах и имеющих норму, не большую чем т, относительно образующих
Г П W. Так как Wm с V, то все выбранные элементы лежат в V, и по
принципу Дирихле два из них, скажем, у и у', принадлежат одному и тому
же сдвигу окрестности U, т. е. y'y~' € Г П U. Приходим к противоречию,
так как в силу выбора элементы у' и у лежат в разных смежных классах
по подгруппе Гу.
А теперь выберем е > 0 таким, чтобы окрестность W содержала все
элементы из группы G, сдвигающие точку х на расстояние, меньшее чем е.
Итак, мы доказали почти все. Осталось позаботиться о нормальности вы-
выбранной нильпотентной подгруппы конечного индекса.
4.1. Группы, порожденные малыми элементами
225
Поступим так: определим по индукции убывающую цепочку множеств
U = иоэ Ui Э ..., полагая
gev
Каждое Ui является окрестностью единицы, так как замыкание V компакт-
компактно. Заменим окрестность U на окрестность Un, n = dim G, и переопределим
константы т и е, а также окрестность W.
Теперь наряду с дискретной группой Г, порожденной элементами из
Г П W, мы рассмотрим подгруппы Г,-, порожденные пересечениями Г П Ut.
По теореме 4.1.7 каждая подгруппа Г,- нильпотеитна и является коком-
пактной подгруппой в связной нильпотентной группе Nt cG. Кроме того,
N-, с /V,-_i для любого i (см. упражнение 4.1.10). Но уменьшение связ-
связных подгрупп происходит с уменьшением их размерности, и, следователь-
следовательно, наступлением такого момента /, что М = Ni-i, 1 < I < п. Если у ?
€ Г П W с V, то у-'?Лу С ?Л_1 по определению окрестности Ui, а значит
y~lN,y с М-1 =М согласно упражнению 4.1.10. Итак, мы доказали, что
группа Г нормализует подгруппу /V;. А тогда подгруппа Н = Г П Nt являет-
является нормальной нильпотентной подгруппой в Г, причем [Г: Н] < [Г : Г„] < т
(обратите внимание на то, что Н = Г П /V,- э Г П Nn = Г„).
И наконец, подгруппа IW,- замкнута, имеет максимум т компонент и
нильпотентную компоненту единицы. |4.1.16|
Следствие 4.1.17 (малая дискретная гиперболическая подгруппа —
почти абелева). Для любого п существует такое целое т и такое
положительное г, что любая дискретная подгруппа Г с Isom H", по-
порожденная элементами, сдвигающими некоторую точку х не даль-
дальше чем на г, содержит нормальную абелеву подгруппу, индекс ко-
которой не превосходит т.
Доказательство. После всего уже сказанного остается доказать, что
связная замкнутая нильпотентная подгруппа N группы IsomH" коммута-
коммутативна. Пусть ф — нетривиальный элемент из центра N.
Если ср — гиперболический элемент, то элементы из N сохраняют ось ср.
Следовательно, группа N является подгруппой группы О(я — 1) х R, а
потому абелева (см. следствие 4.1.11).
Если ф — параболический элемент, то группа N сохраняет его неподвиж-
неподвижную точку х е S^, т. е. является подгруппой группы евклидовых подобий.
Но фактически N является подгруппой группы евклидовых изометрий, так
как параболический элемент ф не коммутирует с подобиями, которые рас-
растягивают или сжимают. На этот раз группа абелева в силу следствия 4.1.13.
Наконец, если ф — эллиптическое движение, то N сохраняет d-мерное,
d < n, гиперболическое подпространство его неподвижных точек. Тем са-
самым, N с IsomHd х О(п — d), и наше утверждение получается с помощью
индукции с применением следствия 4.1.11. [4.1.171
226
Глава 4. Структура дискретных групп
4.2. Евклидовы многообразия и кристаллографические
группы
Согласно следствию 4.1.13, любая дискретная группа движений Е" содер-
содержит абелеву подгруппу конечного индекса. Этот результат обобщается в
красивой теории, созданной Бибербахом [Biel I, Biel2] (см. также [Zas48]).
Эта теория находит важные применения при изучении замкнутых евкли-
евклидовых многообразий и кристаллографических групп.
Определение 4.2.1 (кристаллографическая группа). Кокомпактные
дискретные группы движений пространства Е" называются п-мерными
кристаллографическими группами. Иногда их еще называют группами
Бибербаха.
Теорема 4.2.2 (Бибербах). а) Абстрактная группа Г изоморфна
дискретной группе движений евклидова пространства Ет для неко-
некоторого т, если и только если группа Г содержит свободную абелеву
группу конечного ранга в качестве подгруппы конечного индекса.
б) Любая т-мерная кристаллографическая группа Г содержит
свободную абелеву группу ранга т, совпадающую со своим центра-
централизатором, в качестве нормальной подгруппы конечного индекса.
Эта подгруппа характеризуется как единственная максимальная
абелева подгруппа конечного индекса или как подгруппа параллель-
параллельных переносов (сдвигов) в группе Г.
Наоборот, пусть группа Г обладает нормальной подгруппой А
конечного индекса, причем А совпадает со своим централизатором
и является свободной абелевой группой ранга т. Тогда Г изоморфна
т-мерной кристаллографической группе. Если же группа Г не имеет
кручения, то предположения о нормальности А и о ее централиза-
централизаторе излишни.
в) Пусть Г и Г" — две кристаллографические группы размерно-
размерности mum' соответственно. Если Г и Г" изоморфны как группы, то
т = т' и группы Г и Г" сопряжены с помощью некоторого аффинного
преобразования а: Е —> Ет.
г) Для любого числа т имеется лишь конечное число классов аф-
финно эквивалентных кристаллографических групп размерности т.
Следствие 4.2.3 (классификация евклидовых Многообразий).
Классы диффеоморфных замкнутых евклидовых т-мерных мно-
многообразий находятся в биективном соответствии с классами изо-
изоморфных групп без кручения, содержащих Z" в качестве подгруппы
конечного индекса.
4.2. Евклидовы многообразия и кристаллографические группы
227
Доказательство. Пункт в теоремы 4.2.2 и следствие 3.5.12 показыва-
показывают, что два замкнутых евклидовых m-многообразия диффеоморфны то-
тогда и только тогда, когда изоморфны их фундаментальные группы. Таким
образом, осталось доказать, что группа Г тогда и только тогда служит
фундаментальной группой замкнутого евклидова /п-многообразия, когда
она не имеет кручения и содержит свободную абелеву группу ранга т в
качестве подгруппы конечного индекса. Но дискретная подгруппа группы
движений евклидова пространства действует там свободно, если и только
если она не имеет кручения (вы уже можете доказать это самостоятель-
самостоятельно, или, в крайнем случае, обратиться к следствию 2.5.19). Поэтому наше
утверждение прямо следует из теоремы 4.2.2, б. | 4.2.31
Доказательство 4.2.2, а. Утверждение «только если» уже доказано в
следствии 4.1.13.
Доказательство оставшейся части будет получено прямой конструкцией
действия Г в евклидовом пространстве достаточно большой размерности.
Итак, пусть А — свободная абелева подгруппа ранга п и индекса р. Вы-
Выберем некоторое эффективное действие группы А в пространстве Е" с по-
помощью параллельных переносов, и пусть X — факторпространство прямо-
прямого произведения Г х Е" по отношению эквивалентности {ga, x) ~ (g, ax),
аеА. Пространство X состоит из копий пространства Е" —по одной для
каждого смежного класса Г/А; или, по-другому (см. раздел 3.6), X являет-
является Ея-расслоением, присоединенным к главному Л-расслоению Г над Т/А
(А действует на Г правыми сдвигами). Группа Г естественно действует в
расслоении X, а следовательно, и в пространстве его сечений, которое изо-
изоморфно W (оно есть произведение слоев, так как база дискретна). При
этом элемент у € Г как-то переставляет слои Е" и осуществляет сдвиг вну-
внутри каждого слоя, т. е. действует в Епр как изометрия. Несложно проверить
эффективность и дискретность построенного действия (наша конструкция,
которая по действию подгруппы Н с G на пространстве X строит действие
группы G в пространстве XG/H сечений присоединенного расслоения, носит
название индуцированного представления). 14.2.2, а\
Доказательства пункта б связано с двумя утверждениями об инвариант-
инвариантных подпространствах, представляющих самостоятельный интерес. Снача-
Сначала дадим определение: если G — группа движений Е", то подпростран-
подпространством сдвигов группы G называется (непустое) G-инвариантное евклидо-
евклидово подпространство, на котором G действует параллельными переносами.
Предложение 4.2.4 (максимальное подпространство сдвигов).
Любая абелева подгруппа А с IsomE" обладает единственным
максимальным подпространством сдвигов ЕА. Если А дискретна
и кокомпактна, то ЕА =Е".
Доказательство. Пусть Л —подгруппа группы IsomE". Проводя ин-
индукцию по я, предположим, что любая абелева подгруппа в группе IsomE*,
228
Глава 4. Структура дискретных групп
k < п, обладает единственным максимальным подпространством сдвигов.
Если группа А целиком состоит из параллельных переносов, то доказывать
нечего. В противном случае, пусть ср — элемент из А, который не является
сдвигом. Через U обозначим подпространство собственных векторов ли-
линейной части ф с собственным значением единица. (Возможно, U = {0}.)
Поскольку преобразование ср сохраняет слоение пространства Е" подпро-
подпространствами, параллельными U, то оно индуцирует движение евклидова
факторпространства En/U. Но у линейной части индуцированного дви-
движения уже нет собственного значения единица. Следовательно, согласно
упражнению 4.1.12, б, у него есть единственная неподвижная точка в E"/U.
В пространстве Е" этой неподвижной точке отвечает подпространство, ко-
которое мы обозначим через Е,, и на котором ср действует сдвигом. Любое
подпространство, на котором ср действует сдвигом, непременно содержит-
содержится в некотором подпространстве, параллельном U, и значит, лежит в ?9.
Следовательно, Еф единственно и максимально,
Таким образом, мы получаем внутреннее каноническое описание под-
подпространства Еф, а так как группа А абелева, то любой ее элемент должен
переводить Е9 в себя. В силу индуктивного предположения группа А, дей-
действующая в Еф, имеет единственное максимальное подпространство сдви-
сдвигов. Оно же будет и единственным максимальным подпространством сдви-
сдвигов для А в Е".
Пусть теперь А дискретна и кокомпактна. Тогда можно рассмотреть ее
ограниченную фундаментальную область F, пересекающую ЕА. С одной
стороны, любую точку Е" можно с помощью движений из А «загнать» в F,
с другой — элементы из А, будучи изометриями Е", сохраняют расстояние
любой точки до подпространства Ел, и, таким образом, очень далекие от Ел
точки не могут под их действием попасть в F. Выход один: Ел = Е". 14.2.41
Предложение 4.2.5 (инвариантное подпространство сдвигов).
Пусть Г —дискретная подгруппа движений Е". Предположим, что Г
содержит свободную абелеву подгруппу А ранга т, индекс которой
конечен. Тогда существует Г-инвариантное евклидово подпро-
подпространство размерности т, на котором группа А эффективно
действует параллельными переносами.
Доказательство. Пусть Ел — максимальное подпространство, иа кото-
котором группа А действует сдвигами (предложение 4.2.4). Действие А на ЕА
эффективно по той причине, что любой элемент из Г, имеющий непо-
неподвижную точку, имеет конечный порядок, а А — подгруппа без кручения.
Следовательно, размерность подпространства Г в Ел, порожденного век-
векторами сдвигов из группы А, равна гкЛ = т (т не может быть больше
чем dim 71, согласно упражнению 4.1.12, в). Расслоим ЕА подпростран-
подпространствами, параллельными Т, и предположим на минуточку, что подгруппа А
нормальна в Г. Тогда Г сохраняет листы этого слоения, и мы получаем
4.2. Евклидовы многообразия и кристаллографические группы
229
действие Г в пространстве листов, т. е. в евклидовом пространстве размер-
размерности dim ЕА — т. Но фактически речь идет о действии в этом пространстве
конечной факторгруппы Г/А. А у такого действия есть неподвижная точка,
т. е. инвариантный слой. Это доказывает наше предположение, при усло-
условии, что подгруппа А нормальна.
В общем случае воспользуемся тем, что индекс группы Л в Г коне-
конечен, и рассмотрим ее подгруппу В = f] yAy~l. Несложно показать1, что
тег
В — нормальная подгруппа конечного индекса в группе Г. Ясно также, что
В — свободная абелева группа ранга т. Следовательно, для нее найдет-
найдется Г-инвариантное m-мерное подпространство Е, на котором группа В
эффективно действует сдвигами. Докажем, что так же действует в Е и
группа А. В самом деле, любой элемент а € А коммутирует со сдвига-
сдвигами из В, порождающими Е. Поэтому его линейная часть действует в Е
тривиально. Таким образом, элемент а действует в Ет сдвигом, а эффек-
эффективность гарантируется отсутствием в группе А кручения. 14.2.51
Доказательство 4.2.2, б. Рассмотрим дискретную кокомпактную груп-
группу Г движений Ет. Согласно следствию 4.1.13, группа Г содержит абелеву
подгруппу В с Г конечного индекса (и по-прежнему кокомпактную).
Предложение 4.2.4 показывает, что группа В действует параллельными
переносами в Е и тем самым лежит в подгруппе параллельных перено-
переносов 7V группы Г. Подгруппа ТГ нормальна в Г (упражнение 4.1.12, д) и
изоморфна Zm (упражнение 4.1.12, в). Кроме того, любой элемент груп-
группы Г, коммутирующий с любым сдвигом из Тг, сам должен лежать в Тг
(упражнение 4.1.12, г). Поэтому централизатор подгруппы Тг совпадает
с ней самой. Тем самым, Тг не может содержаться ни в какой большей
абелевой подгруппе.
Докажем обратное утверждение. Пусть группа Г содержит свободную
абелеву подгруппу А ранга т, индекс которой конечен. По теореме 4.2.2, а
группа Г эффективно действует как дискретная группа движений неко-
некоторого евклидова пространства Е", п~^ т. Применив предложение 4.2.5,
найдем Г-инвариантное /п-мерное подпространство Е с Е", на котором
подгруппа А эффективно действует параллельными переносами. Обозна-
Обозначим через Гш подгруппу в Г, оставляющую неподвижной каждую точку Ега.
Сейчас мы покажем, что такая подгруппа тривиальиа, и значит, Г действует
как дискретная кокомпактная группа движений пространства Ет.
Подгруппа Тп конечна, так как она является подгруппой ортогональ-
ортогональной группы О(я — т). Поэтому если Г не содержит кручения, то все
доказано. Если мы не требуем от Г отсутствия кручения, то вступает в
силу предположение о нормальности подгруппы А. Но тогда коммутатор
[А, Гт] с А Л Г/п, а пересечение А П Г,„ тривиально. И снова получается,
'Алгебраисты иногда называют этот полезный факт леммой Пуанкаре.— Прим. ред.
230
Глава 4. Структура дискретных групп
что группа Гт тривиальна, так как подгруппа А совпадает со своим цен-
трализатором. 14.2.2, б\
Доказательство 4.2.2, в. Рассмотрим вложения р: Г-» IsomE™ и
р': Г -» IsomE'. Ясно, что т = т', так как, согласно б, размерность —
это ранг максимальной абелевой подгруппы конечного индекса в группе Г.
Группа Г посредством отображения (р, р') диагонально действует в прямом
произведении W х Е™. Воспользуемся предложением 4.2.5 и выберем еще
одну копию Е, вложенную в Em x E и инвариантную относительно этого
действия. В силу инвариантности выбранное подпространство эпиморфно
проектируется на каждый из множителей, т. е. является графиком аффин-
аффинного преобразования Е'™ —> Е, сопрягающего рассматриваемые действия р
ир'. 14.2.2, в\
Доказательство 4.2.2, г. После всего сказанного это утверждение вы-
выглядит очень правдоподобно. Действительно, в силу б для любой /и-мерной
кристаллографической группы Г имеется точная последовательность рас-
расширения
с абелевым ядром А = Z и конечной группой F, порядок которой ограни-
ограничен (ограниченность порядка получается из следствия 4.1.13).
Тонкость, однако, заключается в том, что, вообще говоря, группа Г вос-
восстанавливается по А и F многими способами. В связи с этим мы проведем
доказательство в два шага. Заметив, что группа F действует на А сопря-
сопряжениями, мы сначала покажем (теорема 4.4.6), что конечная группа может
действовать на А лишь конечным числом способов. А затем, зафиксировав
действие F на А, мы докажем, что для группы Г есть лишь конечное число
возможностей (другое доказательство этого факта вы найдете в упражне-
упражнении 4.2.12).
Теорема 4.2.6 (конечные подгруппы в GL(n, Z)). С точностью
до сопряженности, в группе GL(«, Z) имеется лишь конечное число
конечных подгрупп. Есть лишь конечное число действий, конечной
группы F на свободной абелевой группе А ранга п.
Доказательство. Второе утверждение следует из первого, потому что
действие F задается гомоморфизмом группы F в конечную подгруппу Aut A,
а группа Aut Л изоморфна QL(n, Z). Докажем первое утверждение.
Пусть G — конечная подгруппа группы GL(/2, Z). Мы укажем такой ба-
базис решетки Z", что группа G записывается в этом базисе матрицами,
элементы которых ограничены по абсолютной величине константой, зави-
зависящей только от п.
Для этого вложим решетку Z" в R" и будем рассматривать G как под-
подгруппу группы QL(n, Ш). Усредняя по группе G любую положительно опре-
определенную квадратичную форму, получим G-инвариантную форму. Меняя,
4.2. Евклидовы многообразия и кристаллографические группы
231
если нужно, масштаб, можно считать, что кратчайшие нетривиальные век-
векторы решетки имеют длину 1. Обозначим через V их линейную оболочку
в Ш". Затем, меняя масштаб в Vх, сделаем равной единице длину кратчай-
кратчайших векторов решетки, лежащих в R" \ V. Заметим, что после изменения
масштаба квадратичная форма остается G-инвариантной, так как G-инва-
риантны подпространства V и Vх. Будем продолжать этот процесс, пока на
каком-то шаге линейная оболочка кратчайших векторов (длины 1) решетки
не совпадет с Шп.
Может случиться, что решетка Z" не имеет базиса из кратчайших век-
векторов длины 1 (см. упражнение 4.2.9), но всегда можно выбрать базис
решетки, состоящий из векторов, длина которых ие больше чем (п + 1)/2.
Для этого рассмотрим линейно независимые векторы единичной длины
а,, ..., а„ в решетке Z". Применяя индукцию и обозначая через Wk ли-
линейную оболочку векторов аь ..., ak, можно считать, что для некоторо-
некоторого k < п в решетке Z" П Wk уже найден нужный нам базис Ьи ..., Ьк.
Пусть Ьш —кратчайший из векторов решетки Z" П Wk+l, не лежащий
в подпространстве Wk и обладающий кратчайшей проекцией на подпро-
подпространство, ортогональное Wk. Нетрудно сообразить, что в силу выбора
вектора bk+l длина этой проекции не больше единицы. Прибавив к векто-
вектору bk+l вектор из решетки Z" П Wk, получим новый вектор b'k+l, проекция
которого на подпространство Wk лежит в параллелепипеде Р, натянутом на
векторы аь ..., а* и сдвинутом так, что его центр находится в нуле. Диа-
Диаметр параллелепипеда Р не превосходит k, т. е. он целиком лежит в шаре
радиуса k/2 с центром в нуле. Но тогда \Ьк+1\ < \b'fc+l\ < y/(k/2J + 1 <
< (k + 2)/2, что и завершает доказательство по индукции.
Докажем, наконец, ограниченность матричных элементов в базисе
Ь\, ..., Ь„. Так как элементы группы G сохраняют длину, то достаточ-
достаточно доказать ограниченность в этом базисе координат любого вектора v
с длиной |и| < (п+ 1)/2. Но, как известно, /-я координата вектора v
равна отношению объема параллелепипеда Р, натянутого на векторы
Ь\, ..., &/_i, v, bi+i, ..., bn, к объему параллелепипеда Q, натянутого на
Ьи ..., Ьп. Объем Р не превосходит ((л + 1)/2)", тогда как объем Q боль-
больше объема шара радиуса 1/2 в пространстве Е„, поскольку Q содержит
шар такого радиуса.1 14.2 61
В предыдущем доказательстве решетка Z" с М" была фиксирована, а
скалярное произведение в W мы меняли так, чтобы решетка приобретала
нужные свойства. Иногда более наглядным оказывается дуальный под-
подход, когда меняется решетка в пространстве с фиксированным скалярным
1 Здесь неточность. Объем Q действительно ограничен снизу константой, зависящей толь-
только от размерности, но утверждение о шаре радиуса 1/2, содержащемся в Q, непонятно:
рассмотрим, например, правильную треугольную решетку, порожденную своими кратчайшими
единичными векторами. «Лечение» этого доказательства — еще одна задачка для читателя.—
Прим. ред.
232
Глава 4. Структура дискретных групп
произведением. С этой точки зрения в теореме 4.2.6 доказано, что для
конечной подгруппы F с GL(n, Z) существует такое вложение р: Z" -> W,
что кратчайшие (относительно стандартной метрики в Ж") векторы решетки
p(Z") порождают Е", а все преобразования р/р~\ /€ F, являются изоме-
триями.
В связи с этим интересно рассмотреть все такие вложения р: Z" —> R",
что группа F действует изометриями на образе. Рассматривая группу F с
точностью до сопряженности в GL(/j, Z), мы при этом забываем о самом
гомоморфизме р, а помним только о его образе — решетке в К". На этом
пути для каждого класса сопряженных конечных подгрупп в GL(n, Z) мы
получаем семейство решеток с группой симметрии F. Разумеется, некото-
некоторые из этих решеток могут обладать дополнительными симметриями. Мы
говорим, что F — полная группа решетки, если дополнительные симме-
симметрии отсутствуют. Пример неполной группы — тривиальная группа, так как
любая решетка наряду с тривиальной симметрией Id обладает симметри-
симметрией — Id. Если каждая решетка, допускающая группу симметрии F, дру-
другими симметриями не обладает, то F — максимальная конечная подгруппа
группы GL(/z, Z), а соответствующие решетки называются максимально
симметричными.
Упражнение 4.2.7 (конечные подгруппы SLB, Z)). Докажите, что любая
конечная подгруппа группы SLB, Z) сопряжена группе вращений одной из двух
решеток, изображенных на рис. 4.3. Сформулируйте аналогичное утверждение для
подгрупп в GLB, Z). Как выглядят полные подгруппы решеток в GLB, Z)?
Рис. 4.3. Правильные треугольная и квадратная решетки. Это максимальные
симметричные решетки в размерности 2; их группы симметрии в 0B) — это группы
диэдра D12 и Dg из 12 и 8 элементов соответственно.
Задача 4.2.8 (изометричные решетки), а) Покажите, что группа симме-
симметрии октаэдра порядка 48 допускает ровно три GLC, Z)-несопряженных вложения
в группу GLC, Z). Решетки с симметрией каждого из этих трех типов предста-
представлены на рис. 4.4. (Указание: воспользуйтесь следующим соображением. Пусть
F с 0(и) — конечная группа симметрии решетки L и / е F. Если v — вектор L
минимальной длины, причем f(v) ф v, то угол между векторами v и f{v) не меньше,
чем тс/3.)
4.2. Евклидовы многообразия и кристаллографические группы
233
б) Пространственно-центрированная кубическая решетка переходит в плоско-
центрированную при подходящем растяжении вдоль вертикальной оси. Аналогично,
все три изометрические решетки могут быть преобразованы друг в друга с помощью
изменения масштаба в направлении диагонали куба на рис. 4.4. Это означает, что
три вложения из п. а, различные в GLC, Z), сопряжены в GLC, R).
Рис. 4.4. Решетки с октаэдральной симметрией. Эти три решетки обладают мак-
максимальной возможной группой симметрии — группой октаэдра. (Здесь же изображены
фундаментальные области в каждом из трех случаев.) В кристаллографии у каждой из
трех решеток есть специальное название: кубическая решетка, объемноцентри-
рованная кубическая решетка и гранецентрированная кубическая решетка, а
все вместе их обычно называют изометрическими решетками. По этому поводу см
задачи 4.3.12 и 4.3.13.
Упражнение 4.2.9 (тонкая кубическая решетка). Постройте «-мерную ре-
решетку в К", минимальные векторы которой порождают R", но не образуют базис
решетки. (Указание: добавьте точки к стандартной кубической решетке размерно-
размерности п ^ 5.)
Задача 4.2.10 (оценка числа автоморфизмов решетки). Через Zm обозна-
обозначим циклическую группу порядка т и рассмотрим канонический гомоморфизм
moAm: SL(«,
• SL(n, Zm).
а) При т > 3 любая конечная подгруппа F С SL(«, Z) вкладывается в
SL(n, Zm). (Указание: единичный шар решетки Z" относительно метрики, по-
построенной в доказательстве теоремы 4.2.6, вкладывается в Bт)л.)
б) Порядок ядра F —> SL(n, Z2) есть степень двойки.
в) Порядок группы SL(«, Zp), где р — простое число, равен (рп - 1)(р" - р)...
... (рл-//-')/(/>-О-
г) Какие ограничения для конечных подгрупп в SL(«, Z) при небольших п не-
несет эта информация? Можно ли получить более сильные следствия, рассматривая
группы SL(«, Zm) для произвольного т?
Вернемся к доказательству теоремы 4.2.2, г. Напомню, что мы рас-
рассматриваем m-мерную кристаллографическую группу Г, которая является
расширением конечной группы F с помощью свободной абелевой группы А
234
Глава 4. Структура дискретных групп
ранга т, т. е. точную последовательность 0 -»Л —> Г —>F —> 1. При этом
действие Z7 на Л задано, и нас интересуют все такие Г с точностью до
изоморфизма.
Отождествим (не канонически) Г с прямым произведением А х F.
Для этого выберем представителей c(g) e Г из каждого смежного класса
g & F = Г/Л и поставим в соответствие паре (a, g), а € A, g € F, эле-
элемент c(g)a из группы Г. Разумеется, при таком отождествлении умножение
в А х F не похоже на стандартное, и их отличие происходит частично из-
за действия F на А, а частично — за счет «подкручивающей» функции
a: F х F —¦ А, которая определяется равенством
c(g)c(h)=c(gh)a(g,h).
(Если a(g, h) =0, то Г = А к F — полупрямое произведение.)
Имеются необходимые и достаточные условия, которым должна удовле-
удовлетворять функция a: F x F —>А, для того чтобы быть «подкручивающей»
функцией в расширении с заданным действием, но их точный вид нам
не важен (см. упражнение 4.2.11). Важно лишь то, что групповой закон
в А х F однозначно восстанавливается по а, и то, что (это мы увидим
позже) таких а, приводящих к неэквивалентным групповым законам, име-
имеется лишь конечное число. Эквивалентность означает здесь следующее:
выбирая по-другому представителей смежных классов c(g), мы меняем
«подкручивающую» функцию а и групповой закон в А х F, но при этом
получаем изоморфную группу.
Покажем, что за счет выбора представителей c(g) можно всегда до-
добиться того, чтобы все элементы a(g, h) лежали в ограниченном под-
подмножестве А. Сначала, как и при доказательстве теоремы 4.2.6, постро-
построим такую Г-инвариантную евклидову метрику в Шп, что все минимальные
векторы решетки А имеют длину 1 и порождают пространство R". Выбе-
Выберем т линейно независимых векторов аь ..., ат единичной длины из Л, и
пусть Р—натянутый на них параллелепипед. Этот параллелепипед являет-
является фундаментальной областью для подгруппы Л, порожденной элементами
п\, ..., ат. Диаметр Р не превосходит т. В качестве представителя клас-
класса ge F = T/A выберем такой элемент c(g), который сдвигает центр Р на
минимальное расстояние. Ясно, что оно меньше, чем т/2. Следовательно,
элемент a(g, h) = c(g, h)~lc{g)c{h) сдвигает центр Р не больше чем на
З/и/2. Очевидно, что число таких элементов ограничено, причем эта гра-
граница зависит только от действия группы F на Л, но не от группы Г. Итак,
для функции а имеется лишь конечное число возможностей, и теорема 4.2.2
полностью доказана. 14.2.2, г\
Задача 4.2.11 (когомологии групп). Выпишите в явном виде условие
на «подкручивающую» функцию a: F x F —>• А, происходящую из расширения
0—>А—>Г —> F —> 1, прн заданном действии р: F —> Aut A.
4.3. Трехмерные евклидовы многообразия
235
Подкручивающая функция называется коциклом, а наше условие, напоминаю-
напоминающее условие для функций перехода расслоения из раздела 3.6, условием коцикла.
В нашем контексте когомологическая точка зрения едва намечена, а полностью
представлена в [Cha86].
Упражнение 4.2.12 (полупрямое произведение как универсальная кри-
кристаллографическая надгруппа). Пусть Г — кристаллографическая группа, кото-
которая содержит группу А в качестве максимальной абелевой подгруппы конечного
индекса. Докажите, что Г является подгруппой конечного ограниченного индекса
в полупрямом произведении А к Г/А.
а) Г действует как группа аффинных преобразований А", где п — порядок груп-
группы Г/А. (Указание: рассмотрите, как и при доказательстве 4.2.2, а, индуцированное
представление.)
б) Обозначим через В орбиту точки @, ..., 0) е А" под действием группы А.
Тогда имеется индуцированное аффинное действие Г на А"/В, которое «пропуска-
«пропускается» через действие Т/А.
в) Обозначим через С свободную абелеву надгруппу группы А", порожденную
корнями степени п из всех элементов А". Пусть группа Г действует на С. Пусть D —
максимальная подгруппа в С, содержащая В и имеющая такой же ранг. Тогда Г
действует на C/D с неподвижной точкой, т. е. имеется Г-инвариантный смежный
класс Е.
г) Действие Г на ? эффективно. Каждый элемент группы ТЕ представляет из
себя композицию преобразования из Г и сдвига из Е. Группа ТЕ изоморфна полу-
полупрямому произведению А х Г/А.
д) Итак, если к группе Г добавить корни л-й степени из всех параллельных
переносов, в ней содержащихся, то полученная группа будет полупрямым произ-
произведением. Индекс Г в построенной подгруппе равен пт, где т — ранг группы А.
Покажите, что минимальный индекс, с которым Г может быть вложено в полупря-
полупрямое произведение, не превосходит пт. (Замечание: действие Г/А на решетке при
минимальном вложении может быть не изоморфно действию Г/А на А).
4.3. Трехмерные евклидовы многообразия
Геометрические исследования в трехмерной кристаллографии в основном
были выполнены в XIX в.
Имеются 32 подгруппы в 0C), которые служат группами линейных ча-
частей кристаллографических групп. В кристаллографии они известны как
точечные группы, и были впервые перечислены Гесселем [Hes30].
С точностью до аффинной эквивалентности, имеются 14 кристалло-
кристаллографических групп, являющихся полными группами симметрии решетки
(рассматриваемой как конфигурация точек) в Ш3. Они были перечисле-
перечислены Браве [Вга49], и классы соответствующих им решеток известны как
решетки Браве (см. задачу 4.3.13).
236
Глава 4. Структура дискретных групп
Существует 65 типов кристаллографических групп, сохраняющих ори-
ориентацию. Их классификация принадлежит Зонке [Soh79]. Наконец, три
исследователя независимо получили полный список 230 кристаллографи-
кристаллографических групп в М3 [Fed49, Sch91, Bar94].
Из этого списка групп, безусловно, можно извлечь список всех за-
замкнутых евклидовых 3-многообразий, отбросив все группы, действующие
с неподвижными точками [Now34]. Оказывается, что таких многообразий
всего 10, и поэтому такой способ требует затрат труда больших, чем хо-
хотелось бы. Прямая классификация была получена в [HW35].
Соглашение 4.3.1. В этой (и следующей) части мы будем иметь дело
только с замкнутыми многообразиями.
Приступим к классификации евклидовых трехмерных многообразий. И
на первом шаге постараемся лучше понять, как подгруппа F с 0C) ли-
линейных (вращательных) частей элементов из группы Г взаимодействует
с ее решеткой сдвигов. Если группа F тривиальна, то Г ~ Z3, а фактор-
пространство есть тор Т3. Следующий по сложности случай, когда F —
нетривиальная циклическая группа.
Лемма 4.3.2 (евклидово разложение). Пусть Г — трехмерная кри-
кристаллографическая группа без кручения, проекция которой в груп-
группу 0C) является циклической группой Ък, k > 1.
а) Имеется Y-инвариантное разложение Е3 = Е1 ф Е2, в том смы-
смысле, что Г сохраняет как слоение пространства прямыми, парал-
параллельными Е1, так и слоение плоскостями, параллельными Е2.
б) Пусть Т; обозначает подгруппу переносов в Е'. Если группа Г
сохраняет ориентацию, то она является подгруппой группы Tt x
х IsomE2, а ее подгруппа параллельных переносов ТГ есть прямая
сумма (rnr,) + (rnr2).
в) Если Г содержит элементы, меняющие ориентацию, то k = 2,
Г есть подгруппа IsomE1 х Т2, а индекс подгруппы (Г П Г,) + (ГП Т2)
в группе ТГ не превосходит двух.
Доказательство. Чтобы доказать п. а, выберем такой элемент а € Г,
что его линейная часть а порождает циклическую группу Ък. Согласно
упражнению 4.1.12, б, у а должно быть собственное значение единица. Ли-
Либо подпространство а-неподвижных векторов одномерно и а есть вращение
вокруг оси, либо оно двумерно и а есть отражение в плоскости. В любом из
двух случаев линейное пространство Ш3 раскладывается в прямую сумму
одномерного и двумерного а-инвариантных подпространств. Соответству-
Соответствующее разложение евклидова пространства Е3 инвариантно относительно
всей группы Г, так как линейная часть любого элемента из группы есть
4.3. Трехмерные евклидовы многообразия
237
степень а. В частности, Г является подгруппой группы IsomE1 x IsomE2.
Обозначим через рх и р2 проекции на множители этого произведения.
Если группа Г сохраняет ориентацию, то а — вращение, а само а —
винтовое движение с осью Е1. Так как а действует тождественно на одно-
одномерном слагаемом, то pi(g) — это параллельный перенос для любого g e Г.
На рис. 4.5 показано, что перенос pi(g) может не лежать в Г, но его k-я
степень — элемент группы Г. То есть подгруппа ?/?, (Г) содержится в Г П Г,,
и таким образом рх (Г) содержит Г П Т{ в качестве подгруппы, индекс кото-
которой не превосходит k. С другой стороны, ядро рх —это подгруппа IsomE2,
состоящая из одних параллельных переносов, по той причине, что любое
движение плоскости, отличное от сдвига, имеет неподвижную точку, что за-
запрещено условием. Следовательно, индекс подгруппы (Г П Т{) + (Г П Г2)
в Г не превосходит k. Но (Г П Т{) + (Г П Т2) с 7"г, а индекс [Г : Тг] = k.
Поэтому Тт = (Г п Г^ +• (Г П Т2), что доказывает п. б.
Рис. 4.5. k-я степень проекции pi(g) лежит в Г. Либо g— винтовое движение с
осью Е1, и в этом случае gk = p\(g)k, или g — параллельный перенос, но тогда, как
хорошо видно из рисунка, ? rgr~i — P\(g)k (короткие вертикальные стрелки всюду
гег
изображают p(g), а длинные пунктирные — их k-e степени).
Пусть теперь Г содержит элементы, меняющие ориентацию. Тогда k = 2
и а — отражение в плоскости.
Для доказательства пункта в можно в предыдущих рассуждениях про-
просто поменять местами индексы 1 и 2, но учесть, что на этот раз 2/?2(Г) —
подгруппа р2(Г) индекса 2 или 4, а потому индекс Г П Т2 в р2(Т) не пре-
превосходит четырех. Значит, и индекс подгруппы (Г П 7"i) + (Г П Т2) в Г не
превосходит четырёх. 14.3.21
Задача 4.3.3 (расщепление кристаллографических групп). Верен ли ре-
результат леммы 4.3.2, если группа Г содержит кручение? Если нет, то какое более
238
Глава 4. Структура дискретных групп
слабое утверждение все же верно? Что можно сказать в связи с этим по поводу
п -мерных кристаллографических групп?
Теорема 4.3.4 (евклидово многообразие, накрываемое произве-
произведением тора на Е1). Если Г — свободная от кручения трехмерная
кристаллографическая группа, то ее подгруппа параллельных пере-
переносов ТГ содержит подгруппу Z ранга 2, нормальную в группе Г. На
геометрическом языке это означает, что любое замкнутое евкли-
евклидово Ъ-многообразие является факторпространством простран-
пространства Т2 х Е1 (произведения^ 2-тора на евклидову прямую) по дей-
действию дискретной группы Г.
Доказательство. Пусть М = Е3/Г и Г = T/Z. Чтобы из алгебраиче-
алгебраической версии теоремы получить геометрическую, рассмотрим любую Z-ин-
вариантную плоскость Е2 и обозначим через Е1 ее ортогональное допол-
дополнение. Тогда тор Т2, о котором идет речь, есть факторпространство E2/Z.
Далее, любая изометрия Е3, нормализующая подгруппу Z, сохраняет раз-
разложение Е3 = Е2 ф Е1. Поэтому группа ? с Isom T2 x Isom E1.
Доказательство алгебраической части проведем путем перебора всех
возможностей для группы F с 0C) линейных частей элементов из Г. В ка-
каждом случае будет получено описание соответствующего евклидова мно-
многообразия.
Начнем с двух общих замечаний, которые будут постоянно использо-
использоваться.
(i) Если в теореме 4.3.4 выбрать Z максимальной, то ядро проекции Г —>
—> IsomE1 представляет из себя свободную от кручения группу симметрии
тора, которая не содержит параллельных переносов. Но такая группа либо
тривиальна, либо есть Z2, действующая как скользящее отражение, и тогда
в группе Г есть отражение в плоскости, содержащей слагаемое Е1, что
бывает лишь в случае д (см. ниже).
(ii) Образ группы Г в группе IsomE1, будучи ее дискретной кокомпакт-
ной подгруппой, есть Z или Z2 * Z2.
Переходим к разбору случаев.
Случай а: Если F тривиальна, то ТГ = Г, и в качестве Z можно вы-
выбрать любую максимальную подгруппу ранга 2 в группе Г. В этом случае
образующая группы Г = Z действует как сдвиг на торе Т2 и на Е1. Гео-
Геометрически факторпространство Е3/Г является тором диффеоморфизма
ср; т2 -> ТГ2, вызванного этим параллельным переносом (пример 3.6.5). По-
Поскольку действие образующей изотопно тождественному, то топологически
наше многообразие есть трехмерный тор Т2 х S1 = Т3. Оно известно как
многообразие G, в обозначениях Вольфа [Wol67] или как (®|) в обозначе-
обозначениях гл. 5.1
'Ссылка относится к тому 2, который пока не опубликован.- Прим. ред.
4.3. Трехмерные евклидовы многообразия
239
Случай б: Пусть F — сохраняющая ориентацию нетривиальная конеч-
конечная циклическая группа с образующей а € SO3. Через Та обозначим его
ось (а точнее, пространство параллельных переносов вдоль оси), и пусть
Т* — ортогональное дополнение к Та. По лемме 4.3.2, б
Тг = (Гг П Та) + (Тг П Т&.
Выберем Z = Тг П Т?.
Мы знаем, что в направлении Та группа Г действует параллельны-
параллельными переносами. Рассмотрим любой элемент р из Г с минимальным (но
ненулевым) сдвигом вдоль Та. Такой элемент представлен в Т? враще-
вращением, сохраняющим Z, т. е. он индуцирует изометрию тора Т2 = T^/Z.
Иными словами, любое из многообразий М = Е3/Г является тором для
диффеоморфизма ср: Т2 —¦ Т2, представленного вращением в Е2. В упраж-
упражнении 4.2.7 перечислены все такие возможности:
F
Угол вращения
Тип 2-тора
Имя по [Wol67]
Имя в гл. 5
Z2
71
произвольный
G2
B,2,2,2,), (|ее)
Z3
2к/3
шестиугольный
Сз
C,3,3,')
Z4
тг/2
квадратный
G4
D,4,2,')
z6
7t/3
шестиугольный
G5
F,3,2,')
Последние три из этих многообразий встречаются в двух различно ори-
ориентированных формах в зависимости от того, является ли р правым или
левым винтом.
Случай в: Группа F — нециклическая, но сохраняет ориентацию. Для
любого нетривиального элемента asF применим лемму 4.3.2, б к под-
подгруппе из Г, у которой линейные части содержатся в циклической группе
порожденной а. Получим разложение Тг = (Га П Гг) + (С П Гг)- Теперь
заметим, что различные оси Та и Гр для двух вращений а и р из группы F
должны быть ортогональны. В самом деле, если ортогонально спроекти-
спроектировать первую ненулевую точку решетки Та П Гг на ось Гр, а затем полу-
полученную точку решетки спроектировать обратно на Та, то мы обязательно
попадем в точку решетки Та П ГГ) а значит, в нуль. Таким образом, все
различные оси вращения в F попарно ортогональны. Результат упражне-
упражнения 4.3.5 показывает, что их ровно три, a F = Z2 Ф Z2 порождается двумя
поворотами на тс вокруг взаимно перпендикулярных осей.
Упражнение 4.3.5 (композиция вращений). Пусть f и g — вращения Е2, Н2
или эллиптической плоскости КР2 с заданными неподвижными точкам^. Опиши-
Опишите их композицию /оg и объясните, как найти неподвижные точки fog. (См.
рис. 4.6; неподвижные точки могут оказаться на абсолюте, или за его пределами
при проективном вложении Е2 илн Н2.)
Воспользуйтесь полученным описанием, чтобы доказать, что сохраняющая ори-
ориентацию группа движений сферы S2, имеющая лишь попарно ортогональные оси
240
Глава 4. Структура дискретных групп
f°g
Рис. 4.6. Нахождение неподвижных точек композиции вращении
вращений, есть либо циклическая группа, либо группа Z2 Ф Z2, действующая вра-
вращениями на 180° вокруг трех попарно ортогональных осей.
Выберем в качестве Z группу, порожденную переносами в направлени-
направлениях двух из этих осей, скажем, Га и 7"р. Группа Г должна быть изоморфна
Z2 * Z2, так как элементы из Г с линейной частью а или C действуют в Е1
как отражения. Кроме того, два элемента такого типа, порождающие груп-
группу Г, обязаны иметь различные оси: один — ось Та, второй — ось Гр (см.
рис. 4.7). Оба они представляют из себя винтовые движения, причем век-
вектор сдвига каждого не лежит в Z, но квадрат каждого движения — уже
параллельный перенос из Z. Получившееся многообразие единственно.
Оно обозначено через G6 в [Wol67] и символом B,2i'e) в гл. 5.
Рис. 4.7. Две фундаментальные области для евклидова многообразия B|2('®).
Цилиндры изображают оси винтовых движений с углом поворота к и параллельным
сдвигом на величину, равную высоте коробки (и равную половине ее ширины или
глубины). Многообразие является факторпространством Г2 х Е1 /Р. При этом тор Г
получается склейкой противоположных сторон верхней крышки коробки, Е1 напра-
направлено вертикально, а группа Г = Z2 * Z2 порождена двумя винтовыми движениями
вокруг горизонтальных осей верхнего и среднего слоя.
4.3. Трехмерные евклидовы многообразия
241
Упражнение 4.3.6. Покажите, что полученное многообразие совпадает с изо-
изображенным на рис. 3.2.
Разобравшись с ориентируемыми евклидовыми 3-многообразиями, зай-
займемся классификацией неориентируемых.
Случай г: Группа F = Z2 действует как отражение в плоскости V. Че-
Через Tv обозначим подгруппу переносов в Г, параллельных V. Положим
Z = Гг П Ту. Из результата и доказательства леммы 4.3.2, в следует, что
Г сохраняет разложение Е3 = V $ Vх, Г действует на V параллельными
переносами, а подгруппа Z', ими порожденная, содержит Z. Индекс [Z': Z]
равен 2 или 4. Меняющие ориентацию элементы группы Г — это скользя-
скользящие отражения в плоскостях, параллельных V. На Vх они действуют как
отражения. Поэтому f = Z2 * Z2.
О
О
О
о • о
о
о
• о • о • о
• о • о • о •
0 • О • G •
О • О • О •
о • о • о •
о • о • о • о
Рис. 4.8. Переносные части скользящих отражений. Белые точки — это векторы
решетки Z. Темно-серые точки изображают переносные части скользящих отражений
в плоскости страницы. У скользящих отражений в плоскости, ближайшей к плоскости
страницы, это множество может быть таким же (слева) или иным (светлые серые
точки справа). В последнем случае композиция двух скользящих отражений в соседних
плоскостях есть параллельный перенос, не лежащий в 2 (черные точки).
Пусть а и Ь — образующие группы Z. Тогда среди скользящих отражений
относительно данной плоскости существует ровно одно с вектором сдвига
а/2, b/2 или (а + Ь)/2. Действительно, если бы два скользящих отражения
сдвигали бы соответственно на любые два из указанных векторов, то третий
лежал бы в Z, что противоречит выбору а и Ь. Далее, если множества
сдвигов скользящих отражений одинаковы для всех плоскостей, то индекс
[Z' : Z] = 2 (рис. 4.8, слева), если же они совпадают лишь на плоскостях
«через одну», то индекс [Z': Z] = 4, и Г содержит сдвиги, У-компоненты
которых не лежат в Z (рис. 4.8, справа). В первом случае полученное
многообразие обозначено через В\ в [Wol67], а также (9|), или (+:+:), или
(|вв) в гл. 5. Во втором случае —через В2 или (+:э) = (е/).
Упражнение 4.3.7. Вдобавок к их описанию как факторпространств произ-
произведения Т х Е1 по действию Z2 * Z2, покажите, что каждое из этих двух мно-
многообразий является тором отображения ср: К2 —<¦ К2 евклидовой бутылки Клейна,
242
Глава 4. Структура дискретных групп
причем изометрия ср представлена параллельным переносом накрывающей плос-
плоскости. Установите, что эти многообразия различны, рассмотрев действие ср на двух
специальных простых замкнутых геодезических на К2 (эти геодезические— образы
осей скользящих отражений в группе движений накрывающей плоскости).
Случай д: F не сохраняет ориентацию и не является циклической груп-
группой. Тогда зеркало любого отражения должно содержать оси всех враще-
вращений, так как композиция отражения и вращения, ось которого не лежит
на зеркале отражения, не имеет неподвижных векторов согласно упраж-
упражнению 4.3.8; и у движения с такой линейной частью будет неподвижная
точка.
Упражнение 4.3.8 (композиция вращения и отражения). Рассмотрите ком-
композицию отражения в прямой и вращения вокруг точки на плоскости Е2. Покажите,
что если точка ие лежит на прямой, то их композиция не имеет неподвижных то-
точек. Перенесите это утверждение на сферу S2 и гиперболическую плоскость Н2;
используя сферический вариант опишите в Е3 композицию отражения в плоскости
и вращения вокруг оси, пересекающей эту плоскость в точке.
Вернемся к доказательству теоремы 4.3.4. Итак имеется лишь одна
такая ось Та, поскольку композиция вращений вокруг разных осей в од-
одной плоскости приводит к вращению, ось которого уже не лежит в этой
плоскости (упражнение 4.3.5). Далее, группа Г сохраняет разложение Е3 =
= Та ф Т^ и на Е1 = Та действует переносами. Пусть Z = Тг Л Ti~. Но на
этот раз отображение f —>¦ IsomE1 уже не взаимно однозначно. Действи-
Действительно, если бы группа f1 была изоморфна своему образу (состоящему
только из переносов), то она была бы циклической. Но тогда и ее фак-
факторгруппа F была бы циклической, что не так по условию. Таким обра-
образом, подгруппа в Г, тривиально действующая на 7"о и изоморфная фун-
фундаментальной группе бутылки Клейна является расширением группы Z с
помощью скользящего отражения в некоторой однозначно определенной
плоскости V, проходящей через Та. Элемент а нормализует эту подгруппу.
Поэтому он сохраняет плоскость V. Из всего сказанного следует, что а —
это поворот на 180°, а группа F = Z2 * Z2 и порождена отражениями в двух
ортогональных плоскостях, содержащих Та.
Вернемся снова к подгруппе, тривиально действующей на Та. Группа ее
линейных частей порождена отражением у в плоскости V. Линейные части
тех элементов из Г, которые минимально сдвигают вдоль Та, должны быть а
и ау. Имеются две возможности: оси таких элементов с линейной частью а
лежат на зеркалах скользящих отражений, параллельных V (рис. 4.9, сле-
слева), или их оси лежат между зеркалами, находясь на равном расстоянии
от ближайших к ним зеркал (рис. 4.9, справа). Получающиеся многооб-
многообразия в [Wol67] обозначены через В3 и ВА, или (~:~:) = (|ee) = BJi+:) и
(+:©) = С®е) = B,2,®) в гл. 5. \А2Л\
4.3. Трехмерные евклидовы многообразия
243
Рис. 4.9. Две фундаментальные области для евклидовых многообразий B[2[ + :)
и B|21®). Цилиндры представляют оси винтовых движений, с вращением на 180° и
параллельным переносом на нечетное кратное высоты коробки. Вертикальные прямо-
прямоугольники из жирных линий являются зеркалами скользящих отражений, чье действие
изображается жирными полунаконечниками стрелок. В любом случае, многообразие
имеет вид (Г2 х Е1 )/f с тором Г2, который получается из верхнего квадрата, вер-
вертикально направленным Е1 и группой f1 = Z2 * S2, порожденной одним винтовым
движением и одним скользящим отражением.
Упражнение 4.3.9. Попробуйте представить каждое из этих двух многообразий
как тор отображения бутылки Клейна (см. упражнение 4.3.7).
Задача 4.3.10. Требуется обобщить результат упражнения 4.3.5 на случай про-
произвольных сохраняющих ориентацию движений / и g пространств Е3, Н3 или RP3
(см. предложение 2.5.4).
Задача 4.3.11 (другие накрытия прямыми произведениями). Как по-дру-
по-другому можно представить десять евклидовых 3-многообразий в виде (М2 х Е1 )/f с
евклидовым 2-многообразием М2 и группой Г, изоморфной Z или Z2 * 2г?
Задача 4.3.12 (конечные подгруппы в SLC, Z)). С точностью до сопряжен-
сопряженности, в группе GLC, Z) существуют четыре максимальные конечные подгруппы F.
Они соответствуют четырем типам максимальных решеток (см. упражнение 4.2.7).
В GLC, Z) имеется еще десять подгрупп, которые являются точными группами
автоморфизмов решеток. В следующих задачах дан набросок нх классификации
(некоторые рассуждения встретятся нам и в дальнейшем прн классификации ко-
конечных подгрупп в SOC), которую мы проведем в задаче 4.4.6. Поэтому имеет
смысл взглянуть на эту задачу уже сейчас).
• а) Так как элемент —1 лежит в центре GLC,,Z) и сохраняет любую ре-
решетку, можно сосредоточить внимание на конечных подгруппах в SLC, Z).
б) Докажите, что если решетка А инвариантна относительно вращения
порядка m вокруг оси V, то гпА с (А П V) ® (А П V-1-) с А. (Указание: см.
рис. 4.5, справа.) Выведите отсюда, что m = 2, 3, 4 или 6.
244
Глава 4. Структура дискретных групп
в) Если т = 6, то решетка А — это произведение треугольной решетки в Е2
и решетки в Е1. (Указание: применить п. б к квадрату и кубу вращения шестого
порядка.) Группа сохраняющих ориентацию симметрии такой решетки — это группа
диэдра Di2 порядка 12, порожденная вращениями на 180° вокруг двух прямых
из V^. Такая группа максимальна.
г) Если т = 3, но решетка А не распадается, как в п. б, то ортогональная
проекция А на V1- содержит AnV±, как подрешетку индекса 3. Вдоль напра-
направления V три соответствующих смежных класса выглядят как на рис. 4.10. Группа
диэдра D6 автоматически входит в группу автоморфизмов решетки А. Это при-
приводит к другой точной решетчатой группе, которая ие максимальна — ее можно
расширить, применив растяжение в направлении V, которое превратит А в одну из
решеток, найденных в задаче 4.2.8.
х«ох«ох«о
• ох«ох«ох«
х*ох*ох*о
• ох*ох«ох«
х*ох*ох*о
• ох«ох«ох«
х*ох*ох*о
Рис. 4.10. Три слоя точек в кубической решетке при взгляде в направлении
диагонали
д) Если т = 4, то либо решетка А совпадает с (А П V) @ (А Г) V ), либо со-
содержит ее как подрешетку индекса 2. В любом случае, точная группа решетки есть
группа диэдра Da. Она не максимальна, так как растяжением вдоль направления V
решетку А можно превратить в кубическую (в первом случае), а во втором — в
объемноцентрированную или гранецентрированную кубическую решетку.
е) С точностью до сопряженности у группы Z2 есть два вложения в SLC, Z),
а у группы Z2 * Z2 — их четыре. Это дает еще шесть точных решетчатых групп. Ни
одна из них не максимальна; все они включаются в различные вложения группы D&.
ж) Если, кроме вращения вокруг оси V, у решетки А есть другие симметрии, не
сохраняющие V, то А обладает группой симметрии октаэдра и является кубической,
гранецентрированной или объемноцентрированной кубической решеткой.
з) Наконец, есть решетки, у которых подгруппа автоморфизмов, сохраняющих
ориентацию, тривиальна.
Кристаллографическая группа в размерности п, которая служит полной
группой автоморфизмов некоторой аффинной (без отмеченного нуля) ре-
решетки в пространстве Е", называется группой Браве, по имени математи-
математика, впервые перечислившего такие группы в Е3 [Вга49]. По теореме 4.2.2, в,
4.3. Трехмерные евклидовы многообразия
245
если группы Браве двух решеток изоморфны, то эти группы сопряжены
при помощи аффинного преобразования, которое автоматически перево-
переводит первую решетку во вторую. Соответствующие классы эквивалентных
решеток называются классами Браве, или, что менее удачно, решетками
Браве.
Задача 4.3.13 (точные группы решеток и группы Браве). Покажите, что две
л-мерные решетки тогда и только тогда принадлежат одному классу Браве, когда
группы линейных частей их групп Браве, вложенные в группу QL(n, Z), сопряжены
в GL(rt, Z). Другими словами, точные группы решеток в GL(/i, Z), рассматри-
рассматриваемые с точностью до сопряженности, находятся в биективном соответствии с
я-мериыми группами Браве, которые рассматриваются с точностью до аффинной
эквивалентности.
Используя это соображение и задачу 4.3.12, перечислите классы Браве в раз-
размерности 3. Правильность ответа проверьте по таблице 4.1.
Таблица 4.1. Классы Браве решеток. В трехмерной кристаллографии решетки Браве
(см. задачу 4.3.13) объединяются в системы по типу группы линейных частей в SOC).
(Тригоиальная система часто рассматривается как часть гексагональной.)
Система
Триклиническая
Моноклиническая
Орторомбическая
Тетрагональная
Тригональная
Гексагональная
Изометрическая
Симметрии в SOC)
{1}
Z2
Z2®Z2
z8
rjf
Ze
Zi2
группа октаэдра
Число
классов
I
2
4
2
1
1
3
Случай
в 4.3.12
3
е
е
д
г
в
ж
Задача 4.3.14. Проверьте, что существуют две такие трехмерные кристаллогра-
кристаллографические группы G\ и G2 (их выбор не однозначен), что любая другая трехмерная
кристаллографическая группа будет изоморфна подгруппе в одной нз них.
Задача 4.3.15 (двумерные группы, трехмерные многообразия). Докажите,
что каждое замкнутое ориентируемое евклидово 3-многообразие представляет из
себя пространство сферического расслоения некоторого евклидова 2-орбифолда
(нужные определения см. в главе 5 и особенно в разделе 5.11). Какие евклидовы
3-многообразия встречаются при таком их представлении дважды?
Трудная задача 4.3.16 (упрямые группы). В группе IsomE2 x IsomE2 есть
интересные дискретные подгруппы с недискретными проекциями на оба множителя.
Рассмотрим группу G с представлением
{«, р, Y: а2 = (З2 = у2 = (аCM = фг)" = (т«M = 1)
246
Глава 4. Структура дискретных групп
и два «золотых» равнобедренных треугольника 7"i и 7*2 с углами (л:/5, 2гс/5, 2л:/5)
и (Згс/5, к/5,7t/5) соответственно.
а) Группа, порожденная отражениями в сторонах треугольника 7"i, является го-
гомоморфным образом группы G. Это же верно и для треугольника 7г- Пусть pi
и р2 — соответствующие гомоморфизмы.
б) Докажите, что образ диагонального гомоморфизма pi х рг: G —* IsomlE? x
х IsomE2 является четырехмерной кристаллографической группой, но при этом
образы pi и р2 не дискретны. (Указание: перейдя к подгруппе индекса 2 в группе G,
рассмотрите действие pi х р2 на кольце Z[u>], где ш — примитивный корень 5-й
степени из 1; это кольцо вкладывается в С? как четырехмерная решетка.)
в) Покажите, что действие pi х р2 не является точным. Для этого сравните
его с действием р группы G на гиперболической плоскости. Чтобы понять, как
устроена кристаллографическая группа из п. б) поступим так: обозначим через Go
ядро естественного эпиморфизма G на группу диэдра Dm и рассмотрим поверх-
поверхность М = HVp(Go) рода 2. Тогда группа G, действуя на максимальном абелевом
накрытии М поверхности М, содержит Z4 (группу накрытия М —> М) в качестве
подгруппы индекса 10. Затем нужно эквивариантно отобразить G-триангуляцию М
в полиэдр в Е4, отправляя ее треугольники в копии двух золотых треугольников.
Является ли построенное отображение вложением?
г) Обобщите указанную конструкцию, построив для любого простого р кри-
кристаллографическую группу в Ер~', порожденную тремя элементами порядка 2 н
содержащую элемент порядка р. Заодно докажите, что (р — 1) —это минимальная
возможная размерность для кристаллографической группы, содержащей элементы
порядка р.
Задача 4.3.17. Задаче 4.3.16 можно придать комплексно-аналитическую фор-
форму, используя конформную эквивалентность треугольников вместо аффинной. По-
Поверхность М рода 2 представляет из себя регулярное разветвленное накрытие
степени 5 над сферой Римана QP1, т. е. ее можно представить в виде
{(х, у) е СР1 х СР1: х2 + у5 = 1}.
Два отображения универсального абелева накрытия М поверхности М в С имеют
дифференциалы, которые можно записать в виде dx/y3 и dx/y4 (это выводится из
явного локального поведения в точках ветвления). Что произойдет, если 5 заменить
любым простым числом?
4.4. Эллиптические 3-многообразия
Существует бесконечно много эллиптических 3-многообразий (в силу со-
соглашения 4.3.1 все они замкнуты). Следствие 4.1.11 показывает, что для
некоторого натурального т любое эллиптическое 3-многообразие допус-
допускает не более, чем m-листное накрытие с абелевой фундаментальной груп-
группой. Более того, эта абелева группа содержится в связной абелевой под-
подгруппе группы SOD).
4.4. Эллиптические 3-многообразия
247
Абелева подгруппа в SOD) диагонализируется над С, а над R это озна-
означает, что группа сохраняет разложение R4 = Е2 ф Е2; две инвариантные
плоскости пересекают сферу S3 по двум инвариантным окружностям, и,
если группа связна, то она действует вращениями на каждой из них, явля-
являясь тем самым подгруппой тора Sl x S1.
Итак, фундаментальная группа Г накрывающего многообразия М вкла-
вкладывается в S1 х S1. При этом проекции на оба множителя — инъективные
отображения. В противном случае нетривиальный элемент ядра поточеч-
поточечно сохраняет соответствующую окружность. Из инъективности проекций и
дискретности следует, что Г — циклическая группа (включая, как обычно, и
тривиальную группу). Таким образом, в комплексных координатах, связан-
связанных с инвариантными плоскостями, образующая группы Г записывается в
виде:
D 4 1) (z Zo) i—¦ ie^^z g^i^z ^
с некоторыми взаимно простыми целыми р и q. Рекомендуем убедиться в
том, что факторпространство М = S3/Y — это линзовое пространство (см.
пример 1.4.6).
И хотя в некотором смысле все эллиптические 3-многообразия являют-
являются «почти» линзовыми пространствами, т. е. линзовыми пространствами с
точностью до конечных накрытий ограниченной степени, наибольший ин-
интерес представляют примеры нелинзовых пространств.
Ниже будет получена классификация эллиптических 3-многообразий,
впервые намеченная в [Нор26] и детально выполненная в [ST30]. Наши
рассуждения не используют следствие 4.1.11. Они элементарны и опи-
опираются на два фундаментальных факта: каждое эллиптическое 3-много-
3-многообразие ориентируемо (упражнение 4.4.2) и каждая группа сохраняющих
ориентацию движений S3 есть «почти» прямое произведение (см. равест-
во 2.7.8).
Упражнение 4.4.2 (эллиптические 3-многообразия ориентируемы). Лю-
Любое движение сферы S3, не имеющее неподвижных точек, сохраняет ориентацию.
В частности, любое эллиптическое 3-многообразие ориентируемо. (Указание: для
любого элемента группы ОD) вычислите сумму размерностей подпространств его
собственных векторов с собственным значением —1, а также двумерных неприво-
неприводимых инвариантных подпространств, если таковые имеются. Другой способ: при
помощи теоремы Лефшеца о неподвижной точке докажите, что любой меняющий
ориентацию гомеоморфизм нечетномерной сферы имеет неподвижную точку.)
Эллиптическое многообразие тогда и только тогда бывает факторпро-
странством эллиптического пространства RP3, когда его группа голономии
содержит антиподальное отображение —Id.
Рассмотрим многообразие М, которое не является таким факторпро-
странством, т. е. в его группе голономии нет антиподального отображения.
248
Глава 4. Структура дискретных групп
Тем не менее, действие -Id иа сфере S3 опускается на М, так как эле-
элемент -Id лежит в центре. На М он действует без неподвижных точек;
в противном случае у(л:) = -х для некоторой точки х е S3 и некоторого
элемента у € Ki(Af). Но тогда у2(х) = х, т. е. у2 = Id и, наконец, у = -Id
(упражнение 4.4.3). Отсюда вывод: Af/{±Id} само является многообра-
многообразием, которое накрывается проективным пространством ШР3.
Упражнение 4.4.3 (элементы порядка два, действующие свободно). Эле-
Элемент —Id — это единственный элемент порядка два в группе О (л + 1), действующий
на сфере S" свободно.
Таким образом, классификацию эллиптических 3-многообразий можно
разбить на два этапа. Сначала найти все факторпространства КР3 по сво-
свободно действующим группам движений, сохраняющим ориентацию. А за-
затем добавить еще двойные иакрытия некоторых из них, а именно тех,
голономия которых не содержит —Id.
Второй этап совсем прост; с него и начнем.
Предложение 4.4.4 (существование двулистного накрытия). Трех-
Трехмерное многообразие М = КРУГ тогда и только тогда двулистно
накрывается многообразием М с группой голономии, не содержащей
—Id, когда Г — группа нечетного порядка.
Если такое накрытие М существует, то оно единственно, и
= Г, а щ(М) = Г х Z2.
Доказательство. Если порядок группы Г четен, то она содержит эле-
элемент у € IsornMP3 порядка 2. Пусть у —изометрия сферы 53, накрыва-
накрывающая у. Мы утверждаем, что у2 = —Id. В самом деле, если у2 = Id, то
у = ± Id, т. е. элемент у тривиально действует на ЖР3, что не так. Но если
любое поднятие у таково, что у2 = —Id, то у М не может быть двулистного
накрытия, как в условиях теоремы. _
Предположим теперь, что порядок Г нечетен. Обозначим через Г груп-
группу голономии М и рассмотрим двулистный гомоморфизм р: Г—> Г. Если
элемент группы Г мыслить как перестановку ее элементов, вызванную
умножением слева на этот элемент, то —Id дает нечетную перестановку —
произведение нечетного числа независимых транспозиций. Следовательно,
подгруппа Го С Г, состоящая из четных перестановок, изоморфна Г. А это
значит, что Г = Го х (-Id) = Г х Z2.
Искомое накрытие есть М = S3/To.
Докажем единственность двойного накрытия в случае, когда порядок Г
нечетен. С этой целью рассмотрим фундаментальную группу такого на-
накрытия; это некоторая подгруппа Г, индекса 2 в группе Г. Ясно, что про-
проекция р: Г\ —> Г —это изоморфизм. Но в таком случае подгруппа Г! пред-
4.4. Эллиптические 3-многообразия
249
ставляет из себя граф гомоморфизма Г —»Z2. Но такой гомоморфизм три-
тривиален, и поэтому Ti = Го. |4.4.4|
Преимущество работы с факторпространством проективного простран-
пространства ШР3 состоит в том, что группа сохраняющих ориентацию движе-
движений ШР3 есть произведение, а не «почти» произведение (как для сферы S3)
двух экземпляров группы SOC). В самом деле, если стандартным образом
отождествить ШР3 с SOC), то группа сохраняющих ориентацию изометрий
есть SOC) х SOC), действующая на себе двусторонними умножениями:
(g, h)(x) = gxh~l. Это действие эффективно, так как у группы SOC) три-
тривиальный центр (в отличии от S3). Проверив транзитивность действия этой
группы в расслоении ориентированных ортонормальных реперов на ШР3,
можно доказать, что SOC) x SOC) — это полная группа сохраняющих
ориентацию движений.
Классификация конечных подгрупп группы SOC) x SOC), свободно
действующих иа ШР3, включает в себя три задачи: классификацию ко-
конечных подгрупп в SOC), конструкцию подгрупп в прямом произведении,
если заданы подгруппы сомножителей, и поиск критерия того, что группа
свободно действует в ШР3. Начнем с последней задачи, как с наиболее
простой.
Упражнение 4.4.5 (свободное действие на КР3). а) Подгруппа Н группы
SOC) X SOC) тогда и только тогда действует свободно в КР , когда она не
содержит нетривиального элемента (hi, hi) e H с сопряженными в SOC) компо-
компонентами h\ и hi.
б) Любой элемент из SOC) есть вращение на некоторый угол вокруг некоторой
оси. Найдите необходимое и достаточное условие сопряженности двух элементов
в SOC).
Задача 4.4.6 (скучная классификация подгрупп в SOC)). В разделе 5.5
будет получена концептуальная классификация конечных подгрупп в SOC), но
предварительно ее все же стоит получить, применив прямой, но скучный подход.
а) Для любого сферического треугольника с углами а, р и у в группе SOC)
найдутся такие три вращения А, В и С на углы 2а, 2C и 2у соответственно, что
ABC = 1 (см. упражнение 4.3.5).
б) Наоборот, если элементы А, В, С е SOC), ABC= 1, н их оси не компла-
компланарны, то они связаны, как в а), с одним из восьми сферических треугольников.
в) Пусть а, C, у — три вещественных числа между Оии. Они тогда и только
тогда служат углами невырожденного сферического треугольника, когда а + р +
+ у>7с, а + C>у, C + Y>°<, Y + °<>p.
г) В сферическом треугольнике против самой короткой стороны лежит самый
маленький угол.
д) Пусть элементы А к В порождают конечную группу F с SOC), и предпо-
предположим, что расстояние между их осями строго меньше, чем между осями любой
другой пары элементов из F. Тогда один из них — элемент порядка 2, а другой имеет
порядок 2 или 3.
250
Глава 4. Структура дискретных групп
е) Если они оба — элементы второго порядка, то F = D2n — группа диэдра по-
порядка 2л.
ж) Если же один из них порядка 2, а другой 3, то порядок их произведения
равен 3, 4 или 5, и они порождают группу сохраняющих ориентацию симметрии
правильного многогранника: группу тетраэдра (порядка 12), октаэдра (порядка 24)
или икосаэдра (порядка 60) (см. также задачу 4.4.7).
з) Любая конечная подгруппа в SOC) порождена одним или двумя элементами.
и) Конечные подгруппы в SOC) — это циклические группы, группы диэдра,
группа тетраэдра, октаэдра и икосаэдра.
Задача 4.4.7 (многогранник и перестановки), а) Дайте геометрическое
описание следующих изоморфизмов групп: группы тетраэдра и знакопеременной
группы А\; группы октаэдра и симметрической группы S^; группы икосаэдра и
знакопеременной группы As- (Указание: рассмотрите действие группы симметрии
на различных геометрических фигурах внутри правильного многогранника.)
б) Найдите полную группу (включая и изометрии, меняющие ориентацию) сим-
симметрии каждого из правильных многогранников.
в) Покажите, что у группы икосаэдра есть автоморфизм, который не индуциру-
индуцируется изометрией. Опишите этот автоморфизм, представив ваш додекаэдр сделан-
сделанным из пентаграмм (пентаграмма — это пятиконечная звезда).
Один тип подгрупп в прямом произведении G\ x G2 — это граф любого
гомоморфизма Gi -* G2 (или G2 —¦ G{). В частности, таковы все подгруппы,
изоморфно проектирующиеся на один из множителей. Приведем общую
конструкцию, дающую все подгруппы прямого произведения и включаю-
включающую граф гомоморфизма как частный случай.
Пусть заданы группы Gb G2 и В и гомоморфизмы hi: G\ —> В, h2: G2 —>
-> В. Расслоенным произведением G(hu h2) называется подгруппа в
G, х G2, которая определяется условием
G(hu h2) = {(gb ft) e G, x G2: Л.Ы = h2(g2)}.
В специальном случае, когда Л, или h2 — изоморфизм, получаем граф
гомоморфизма.
Предложение 4.4.8 (диагональные группы являются расслоенны-
расслоенными произведениями). Каждая подгруппа Не Gi x G2, которая эпи-
морфно проектируется на каждый множитель, является расслоен-
расслоенным произведением для пары эпиморфизмов групп G{ и G2 в некото-
некоторую группу В.
Доказательство. Пусть HX=HC\GX х{1} H#2 = #n{l}xG2. Вос-
Воспользовавшись эпиморфностыо гомоморфизма Я —» G2, легко видеть,
что #i —нормальная подгруппа в G{ x {1}. Аналогично, подгруппа Н2
нормальна в {1} х G2. Профакторизовав подгруппы Я и G{ x G2 по
нормальной подгруппе Я, х Н2, получим подгруппу В = Я/Я, х Я2 в
4.4. Эллиптические 3-многообразия
251
прямом произведении G/Hx x G/H2, которая изоморфно проектиру-
проектируется на каждый из сомножителей, поскольку тривиально пересекает
любой из них. Путем композиции этих изоморфизмов с естественными
отображениями G, —» Gi/Я, и G2 —> О2/Я2 мы получаем эпиморфизмы
h\\ G\ —> В и /г2: G2 —¦ В, и не представляет большого труда проверить,
что Я =G(/i,, h2). \tlA\
Приступим к сведению воедино уже имеющихся фрагментов классифи-
классификации.
Предложение 4.4.9 (принцип элементов порядка два). Пусть Н с
С SOC) х SOC) — группа, свободно действующая в МР3, Г\ и Г2 — ее
проекции на множители, a Hi и Н2 — ее пересечения с множителями
SOC) х {1} и {1} х SOC) соответственно. Тогда, поменяв в случае
необходимости местами сомножители, можно утверждать, что
а) все элементы порядка два в Г, принадлежат Ни
б) Н2 — циклическая группа нечетного порядка. Более того, если
Т\ = Н\ или группа Г^ не является циклической, то и Г2 — циклическая
группа нечетного порядка.
Доказательство. Любые два элемента второго порядка сопряжены в
SOC), а потому в силу критерия свободного действия из упражнения 4.4.5
подгруппы Hi и Я2 не могут одновременно содержать элементы второго
порядка. Поэтому переставим, если нужно, множители местами и предпо-
предположим, что группа Я2 не содержит элементов второго порядка.
Выберем элемент второго порядка а € Г,, и пусть р е Г2 таков, что эле-
элемент (а, р) е Я. Ясно, что р2 е Я2. Порядок т элемента р2 нечетен, так
как в Я2 нет элементов второго порядка. Элемент (а'", р'") е Я имеет по-
порядок 2, а значит, C™ = 1. В противном случае, аш и р'" были бы двумя
сопряженными элементами второго порядка. Итак, поскольку а'п = а, эле-
элемент (а"', 1) е Я, т. е. а € Я,.
Далее, просмотрев список конечных подгрупп в SOC) (см. задачу
4.4.6, и), легко убедиться, что лишь циклические группы нечетного поряд-
порядка не содержат элементов порядка 2. Поэтому мы можем утверждать, что
Я2 — циклическая группа нечетного порядка.
Из доказательства предложения 4.4.8 следует, что Тх/Н\ = Т2/Н2. По-
Поэтому, если Г[ = Hi, то и Г2 = Я2, и все доказано. Осталось предположить,
что Fi — конечная нециклическая подгруппа в SOC), обладающая тем
свойством, что все ее элементы второго порядка лежат в ее собствен-
собственной нормальной подгруппе Яь Небольшая проверка с .использованием
задачи 4.4.6, и показывает, что Г! — группа тетраэдра, а Я, — подгруппа
индекса 3 в ней (см. также задачу 4.4.7). Следовательно, и индекс Я2 в Г2
равен трем. Но тогда Г2 — циклическая группа нечетного порядка, так как
она так же, как и группа Я2, не содержит элементов второго порядка.
[4А91
252
Глава 4. Структура дискретных групп
Упражнение 4.4.10. Сохраним обозначения предложения 4.4.9.
а) Докажите, что меняя, если необходимо, индексы, можно утверждать, что все
элементы порядка три в группе ГЛ принадлежат группе Hi, а группа Н2 таких
элементов вообще не содержит.
б) Постройте пример, когда порадок Н равен 5, а группы Н\ и Нч тривиальны.
в) Постройте пример, когда порядок Н есть степень двойки, н обе группы Т\
и Г2 нетривиальны. То же самое для порядка, равного степени тройки.
Следствие 4.4.11 (Зейферт). Если группа И с SOC) x SOC) сво-
свободно действует в МР3, то в одном из множителей найдется одно-
параметрическая подгруппа SOB), коммутирующая с действием Н.
Доказательство. Согласно предложению 4.4.9, группа Г2 является ци-
циклической, т. е. порождается поворотом вокруг некоторой оси. В каче-
качестве SOB) выберем группу всех поворотов вокруг этой оси. Если g €
G SOB), то элемент A, g) лежит в централизаторе группы SOC) x Г2, а
последняя содержит Н. 14.4.11|
Упражнение 4.4.12. Эллиптические 3-миогообразия находятся в биективном
соответствии с подгруппами в UB), которые свободно действуют в С? \ {0}.
Для нас важно то, что, согласно следствию 4.4.11, любое эллиптическое
3-многообразие М = ШВ^/Н (или его двулистное накрытие) расслаивается
на окружности. Эти окружности представляют из себя орбиты той самой
однопараметрической подгруппы, о которой говорится в следствии. (На
сфере S3 эти орбиты образуют расслоение Хопфа.) Это слоение не являет-
является расслоением, так как в нем могут присутствовать особые слои, т. е. такие
окружности, вокруг которых соседние обвиваются несколько раз прежде,
чем замкнуться. Такова рода слоения называются слоениями Зейферта;
общая теория слоений Зейферта будет обсуждаться в разделе 5.11.
А сейчас они потребуются для того, чтобы лучше понять топологию и
геометрию эллиптических 3-многообразий, интерпретируя их в терминах
геометрии S2. Удобней всего это сделать с помощью уже знакомого из
примера 3.7.6 отождествления группы SOC) с касательным расслоением
единичных векторов UTS2 на сфере S2 с R3. Производная любого дви-
движения сферы переводит это расслоение в себя. Возникающее действие
группы SOC) на UTS2 просто транзитивно. Поэтому после выбора про-
произвольного базисного вектора v0 € UTS2 мы можем отождествить элемент
группы SOC) с образом вектора v0 при его действии.
При таком отождествлении слои расслоения UTS2 будут слоями рассло-
расслоения Хопфа, спустившегося на SOC) при накрытий S3 —» SOC). Левый
сдвиг на группе с помощью элемента g переходит в действие производной
dg на расслоении UTS2. Правому же сдвигу на группе соответствует «ин-
«инструкция по навигации» из точки v0 в точку gvo (типа «поверните налево на
угол 12,7°, пройдите прямо 1219 километров, а потом поверните под углом
4.4. Эллиптические 3-многообразия
253
48,3° направо»). Эту инструкцию нужно применить ко всем единичным
касательным векторам.
Упражнение 4.4.13. По определению, производная сохраняющего ориентацию
движения сферы S2 принадлежит множителю SOC) x {1} с SOC) x SOC). Но и
производные меняющих ориентацию изометрий S2 сохраняют ориентацию UTS2 =
= КР3. Получите описание таких производных в терминах группы SOC) x SOC).
а) Какой элемент SOC) x SOC) отвечает антиподальному отображению на
сфере S2? Каким будет фактормногообразие?
б) Опишите полную группу симметрии икосаэдра как подгруппу в SOC) x
х SOC).
Пусть SOB) е {1} х SOC) состоит из тех изометрий, в инструкции у
которых нет указания о движении «прямо», т. е. изометрий, сохраняющих
каждый слой расслоения UTS2 (каждую окружность Хопфа). Согласно
следствию 4.4.11, для любой конечной группы Г, свободно действующей
в ЖР3, мы можем выбрать вектор v0 так, что группа Г содержится в
SOC) х SOB). А это позволяет уверенно рассуждать о факторпростран-
стве, используя лишь двумерные образы.
Так, например, факторпространство ЖР3 по группе Z5, которая действу-
действует справа, можно мыслить как множество всех единичных касательных
векторов к сфере S2, рассматриваемых с точностью до поворотов на углы,
кратные 2тс/5. Если рассмотреть фигуру Р с Zs-симметрией, такую как
правильный сферический пятиугольник, то наше факторпространство —
это множество фигур на S2, конгруэнтных Р. Его фундаментальная группа
есть Z10, порожденная петлей, возникающей при вращении Р до первого
самосовмещения. Если это повторить десять раз (т. е. сделать два полных
оборота), то полученная петля будет гомотопна тривиальной. На самом
деле, наше факторпространство — это линзовое пространство L1Oii (см.
упражнение 4.4.15 и задачу 4.4.16).
Факторпространство конечной подгруппы в SOC), действующей сле-
слева, можно представить как касательное расслоение единичных векторов
некоторого орбифолда (это понятие будет введено в главе 5).
Например, факторпространство группы икосаэдра топологически пред-
представляет из себя сферу с тремя особыми точками — образами вершин,
середин ребер и центров граней, т. е. образами неподвижных точек группы
при ее действии на сфере. Если закрыть глаза на особое поведение в трех
особых точках, то касательное расслоение единичных векторов факторпро-
странства есть факторпространство расслоения UTS2, и более тщательное
рассмотрение показывает, что оно является додекаэдрическим простран-
пространством Пуанкаре (см. задачу 4.4.17). Его же можно себе представлять и
как пространство всех конфигураций 60 касательных векторов к сфере,
обладающих икосаэдральной симметрией (группа порядка 60).
254
Глава 4. Структура дискретных групп
Эти два подхода можно объединить. Например, факторпространство
ЮР3 по группе тетраэдра, действующей слева, и циклической группе Zs,
действующей справа, отождествляется с факторпространством простран-
пространства пятиугольников, конгруэнтных Р, по действию на нем группы тетра-
тетраэдра. При этом действии ни один из пятиугольников не может перейти
точно в себя, так как в группе тетраэдра нет вращений пятого поряд-
порядка. Таким образом, это действие свободно, а факторпространство есть
эллиптическое 3-многообразие. Его можно представлять как множество
всех расположений 24 экземпляров пятиугольников, конгруэнтных Я, на
поверхности сферы 52, причем все рассматриваемые расположения до-
допускают тетраэдральную группу симметрии.
Теорема 4.4.14 (классификация эллиптических многообразий).
Пусть М — эллиптическое 3-многообразие.
а) Если фундаментальная группа щ(М) абелева, то она цикличе-
циклическая, а М — линзовое пространство.
Если это не так, то М = ЮРУЯ с группой Я одного из следующих
типов:
б) Я = Hi х Н2, где Hi — группа диэдра, тетраэдра Т, октаэдра О
или икосаэдра I, а Н2 — циклическая группа, порядок которой вза-
взаимно прост с порядком Ни
в) Н — подгруппа индекса 3 в группе Т х Z3,n, где m нечетно;
г) Н — подгруппа индекса 2 в Z2n x D2m с четным п и взаимно про-
простыми тип.
Доказательство. Пусть группа щ(М) абелева. Согласно плану, наме-
намеченному после упражнения 4.4.3, если М сразу не является факторпро-
факторпространством ЮР3, то мы можем свести все дело к случаю, когда это так,
рассмотрев многообразие N = М/{±Ы}. При этом, так как элемент -Id
лежит в центре, то из коммутативности ui(M) вытекает коммутативность
Ui(N), и, разумеется, если группа m(N) циклическая, то и щ(М) — цикли-
циклическая.
Таким образом, можно считать, что М = ЮРУЯ, где Н — абелева под-
подгруппа в SOC) х SOC). Далее, согласно предложению 4.4.9, проекция Н
на один из множителей, скажем Гь— циклическая группа нечетного поряд-
порядка. Тогда список конечных групп в SOC) оставляет для проекции Г2 две
возможности: циклическая группа или Z2 Ф %ъ = Dt. Покажем, что случай
Г2 = ?>4 невозможен. В самом деле, возьмем два различных нетривиаль-
нетривиальных элемента из Г2 и поднимем их в группу щ(Д) с E3 х S3)/Z2 = SOD).
Поднятия этих элементов имеют вид (рь р2) и (qu q2) с коммутирующи-
коммутирующими рх и qu но антикоммутирующими р2 и q2, поскольку оба элемента
не лежат в центре группы кватернионов {±1, =Ы, ±/, ±k}. Следователь-
Следовательно эти «поднятия» антикоммутируют, что противоречит коммутативности
группы щ(М).
4.4. Эллиптические 3-многообразия
255
Итак, теперь мы знаем, что Tt и Г2 — циклические группы, и должны
доказать, что Н — циклическая. Если это не так, то Н содержит подгруп-
подгруппу, изоморфную Zp х Zp для некоторого простого р. Но порядок любого
нетривиального элемента в такой подгруппе равен р, и поэтому она содер-
содержится в произведении Ър с Г, на Ър с Г2, а значит с ним и совпадает. В
итоге ZD с Hi
и Zp с Я2,
что противоречит условию свободного действия
Н (см. упражнение 4.4.5).
Осталось проверить, что группа щ(М) циклическая. Если элемент
(р,, pi) € SOC) x SOC) порождает Я, то HOK(ord(p,), ord(p2)) = ord(#).
Выберем такие поднятия рх и р2 в группе IsomS3, что ord(p,) = 2ord(p,),
i= 1, 2. Тогда HOK(ord(p"i), ord(p2)) =2ord(//), т.е. элемент (p,, p2) по-
порождает группу тс, (М). А в начале этого раздела мы уже показали, что М —
линзовое пространство, если группа щ(М) циклическая. Доказательство
п. а закончено.
Пусть теперь группа щ (М) неабелева. Сначала предположим, что М =
= ЮР^/Я. Тогда, как мы только что выяснили, группа Н не является ци-
циклической. Можно считать, опираясь на предложение 4.4.9, что Н2 = Z,,,,
т — нечетно, а нормальная подгруппа Hi содержит все элементы порядка 2
в группе Гь и тогда или Hi = Гь или Г! — группа тетраэдра Т и индекс
[Т: Hi ] = 3, или Fi — циклическая группа, a Hi—ее собственная подгруппа.
Если Hi = Гь то и Н2 = Г2, так как Тх/Нх = Т2/Н2 ввиду предложе-
предложения 4.4.8. То есть в этом случае Н = Нхх Н2, щ(М) = /7, х Я2 = Я, х Я2,
а порядки групп Ht и Я2 должны быть взаимно просты в силу упражне-
упражнения 4.4.5. Тем самым п. б доказан.
Если Г, = Г, и индекс [Т: Ht] = 3, то результат п. в получается с помо-
помощью тех же аргументов, что и п. б в предложении 4.4.9.
Если группа Г, циклическая и факторгруппа Г^Я, = Г2/Я2 нетриви-
нетривиальна, то Г2 может быть только группой диэдра D2m, так как ни одна из
групп Т, О или / не является циклическим расширением циклической груп-
группы. Но тогда Cm < D2m — единственная возможность для группы Я2 (нор-
(нормальная циклическая группа нечетного порядка). Следовательно, т нечет-
нечетно, Г1/Я1 = Г2/Я2 = Z2, и порядок Ti равен 2л, где п четно (в противном
случае в Tt найдется элемент порядка 2, не лежащий в Hi). Взаимная
простота тип снова следует из результата задачи 4.4.5. Пункт г доказан.
Наконец, пусть группа щ(М) неабелева и М не является факторпро-
факторпространством пространства ЮР3. Тогда, как мы уже знаем, М двулистно
накрывает многообразие ЮРУЯ, причем порядок группы Я нечетен. Но
такого не бывает, как показывает проведенное нами исследование. 14.4.141-
Упражнение 4.4.15 (характеристика линзовых пространств). Установите
взаимосвязь между следующими разными описаниями линзовых пространств.
а) Факторпространство КР3///, где Не Ът х Ъп с SOC) x SOC), или двой-
двойное накрытие многообразия такого вида.
256
Глава 4. Структура дискретных групп
4.5. Г-/-разложение
257
б) Факторпространство S3/T с циклической группой Г, действующей по фор-
формуле 4.4.1. Проведите классификацию линзовых'пространств с точностью до изо-
метрии в терминах пар (р, q). Сравните с задачей 1.4.7, в.
в) Результат склейки двух полноториев D2 x S1 с помощью такого аффинного
гомеоморфизма ср их границ, что <p(dD ) не параллельна дГР.
Задача 4.4.16 (другое описание эллиптических 3-многообразий). Попро-
Попробуйте описать различные эллиптические 3-многообразия, перечисленные в теоре-
теореме 4.4.14, используя касательное расслоение единичных векторов на S2, как это
уже объяснялось на примерах. Например, многообразие из п. в теоремы 4.4.14
с т = 5 можно описать как пространство правильных сферических пятиугольни-
пятиугольников, конгруэнтных Р, по модулю обычного действия группы Т на пятиугольники,
сопровождаемого поворотом пятиугольника на 0, 2тг/15 или 4тс/15, согласно гомо-
гомоморфизму х: Т —v Z3. Нельзя ли описать это многообразие как-нибудь получше?
Задача 4.4.17 (пересматривая додекаэдрическое пространство Пуанкаре).
Докажите, что факторпространство пространства КР3 = UTS2 по действию груп-
группы икосаэдра совпадает с додекаэдрическим пространством Пуанкаре из приме-
примера 1.4.4. (Указание: 12 граней додекаэдра дают инвариантное разбиение простран-
пространства UTS2 на 12 полиоториев. Стабилизатор грани — группа Z&. Фундаментальную
область для группы икосаэдра можно построить следующим образом: выберем
векторное поле на грани так, как это показано на рис. 4.11, и разрежем соответ-
Рис. 4.11. Почти постоянное единичное векторное поле на сферическом пяти-
пятиугольнике. Изображенный пятиугольник получен стереографической проекцией одно-
одного из пятиугольников додекаэдрального разбиения сферы. Центр проекции находится
в центре противоположного пятиугольника разбиения. Векторное поле постоянно на
плоскости. Его нормированный прообраз на сфере и есть нужное нам векторное поле.
ствующее полноторие вдоль пяти векторных полей на нем. Поля, о которых идет
речь, являются образами исходного векторного поля под действием стабилизатора
грани. Докажите, что получившиеся кусочки пространства UTS2 и есть додекаэдри-
ческие фундаментальные области для действия группы, а комбинаторная схема их
примыканий такая же, как и у додекаэдров в примере 1.4.4.)
Задача 4.4.18. Бинарной группой Г, ассоциированной с конечной подгруппой
Г с SOC), называется прообраз группы Г в S3 при двойном накрытии S3 —> SOC).
а) Группа Г тогда и только тогда изоморфна Г х Z2, когда порядок Г нечетен.
(Указание: фактически это уже было доказано в предложении 4.4.4.)
б) Как мы уже знаем из примера 1.4.4, факторпространство сферы S3 по би-
бинарной группе икосаэдра есть додекаэдральное пространство Пуанкаре. Получите
аналогичные геометрические описания факторпространств сферы 53 по бинарным
группа тетраэдра и октаэдра. Постройте фундаментальные многогранники для их
действий и укажите схемы склейки.
Задача 4.4.19 (отображение Фробениуса). Вот обобщение того факта, что
подгруппа изометрий в SOC) поднимается в S3 тогда и только тогда, когда ее
порядок нечетен. _
Рассмотри центральное расширение А -* G —> G с группой G порядка k. Дока-
Докажите, что отображение Фробениуса G —* A; gi—^g^, является гомоморфизмом.
(Указание: воспользуйтесь тем, что «подкручивающая» функция однозначно опре-
определяет расширение и аннулируется умножением на k.)
Воспользуйтесь отображением Фробеннуса, чтобы доказать, что _если группа А
конечна и порядок любого ее элемента взаимно прост с k, то группа G канонически
изоморфна группе G х А. Постройте контрпример в случае группы А бесконечного
порядка.
4.5. T-f-разложение
В разделах 4.3 и 4.4 был получен список евклидовых и эллиптических
3-многообразий. Другое дело — гиперболические 3-многообразия. Здесь
всё обстоит намного сложнее. В принципе можно указать алгоритм, пе-
перечисляющий гиперболические 3-многообразия, но ничего похожего на
систематическое описание мы этим не добьемся. В действительности, уже
полный анализ двумерных гиперболических поверхностей богат и чрезвы-
чрезвычайно интересен: это будет темой следующего раздела. Здесь же будут
получены общие структурные результаты о гиперболических многообрази-
многообразиях любых размерностей.
Пусть М — полное гиперболическое многообразие размерности п, воз-
возможно бесконечного объема. Для любой точки х е М множество ее про-
прообразов на универсальной накрывающей М = Н" представляет из себя ре-
регулярное множество точек, подобное атомам в кристалле. Поскольку груп-
группа накрывающих преобразований дискретна, то достигается минимум d
среди расстояний между двумя различными прообразами; этот минимум
равен длине кратчайшей гомотопически нетривиальной замкнутой петли в
точке х. Шар радиуса г = d/2 с центром в точке х вкладывается в М, так
как все его прообразы в Н" не пересекаются, но больший шар вложить
уже не удастся. Другими словами, г —это радиус максимального открыто-
открытого шара, в котором инъективно экспоненциальное отображение ТХМ ->¦ М.
Величина г = г(х) называется радиусом инъекпгивноспги многообразия
М в точке х.
258
Глава 4. Структура дискретных групп-
Можно рассмотреть разложение GW-разложение) М на толстую
часть
и ее дополнение
Если конкретное значение е роли не играет, то будем писать просто М^
и М<. Интерес представляет и тонкая часть М^ ~ М<, где черта, как
обычно, означает замыкание. Как правило, М^е совпадает с множеством
{хеМ: г(х) < е/2}, но наше определение исключает нежелательный по-
пограничный случай, когда имеется простая замкнутая геодезическая длины
ровно е. Вдоль такой геодезической радиус инъективности равен е/2, но
чуть в сторону — и он уже больше.
Мы увидим, что в силу следствия 4.1.17, M^t имеет стандартный вид,
если s не превосходит некоторой константы, зависящей только от размер-
размерности п.
Рассмотрим нетривиальный элемент у € щ(М), и пусть ГДу) (или Г(у),
если е уже выбрано) обозначает множество таких точек х е W, что
d(x, ух) < е. Поскольку функция dy(x) = d(x, у(х)) выпукла (теоре-
(теорема 2.5.8), то выпукло и каждое множество 7\у).
Например, в размерности 2 для гиперболического движения у область
Г(у) заключена между двумя эквидистантами, равноудаленными от его оси.
Объясняется это тем, что у коммутирует с отражением относительно оси,
а также с любыми сдвигами вдоль нее. В размерности три сохраняющее
ориентацию гиперболическое движение у есть композиция сдвига вдоль
прямой / и вращения вокруг /. В этом случае у коммутирует со всеми сдви-
сдвигами вдоль и вращениями вокруг /, и поэтому здесь Г(у) — это цилиндри-
цилиндрическая окрестность / (с круглыми сечениями), инвариантная относительно
сдвигов. Гиперболическое у, меняющее ориентацию,— это скользящее от-
отражение, т. е. композиция сдвига вдоль прямой / и отражения относительно
плоскости Р, которая содержит /. В этом случае Г(у) снова представляет из
себя цилиндрическую окрестность, но с овальными сечениями, у которых
большая ось симметрии лежит в Р.
Упражнение 4.5.1 (форма Т(у)). а) Найдите Г( у) для параболического или
эллиптического преобразования у на плоскости и в пространстве.
б) Приведите пример такого сохраняющего ориентацию гиперболического дви-
движения у в ЕР, что Г(у) — собственное подмножество Г(у100).
Выберем е и m так, как это было сделано в следствии 4.1.17. Тогда,
если пересечение нескольких множеств Г(у,) непусто, то группа, поро-
порожденная уь содержит нормальную абелеву подгруппу, индекс которой не
превосходит /га. С помощью этого соображения мы изучим связные ком-
компоненты множества М< = М<е, а также накрывающего его множества
4.5. Г-<-разложение
259
М< С М = W. Заметим, что /М< — это объединение 7(у) для всех нетри-
нетривиальных у € Tti(Af).
Компонента То с М< является объединением выпуклых множеств 7\у)
для элементов у из некоторого подмножества 5о Сщ(М). Допустим, что
Т(а) пересекается с 7\Р), а, р е 50. Обозначим через А нормальную абеле-
абелеву подгруппу конечного индекса в группе, порожденной элементами аир.
Пусть ф — нетривиальный элемент из А, который обязан быть параболи-
параболическим или гиперболическим, так как группа щ(М) свободна от кручения.
Если ф — параболический элемент, то у него есть единственная непо-
неподвижная точка р € Sj^'^-KQTQpyio оставляют на месте все элементы груп-
группы Л в силу упражнения 2.5.18. Результат этого же упражнения показы-
показывает, что и элемент т из нормализатора группы А оставляет точку р на
месте. Но элемент т не может быть гиперболическим. Действительно, если
бы он оказался гиперболическим, то, сопрягая элемент ф из А с помо-
помощью подходящих степеней его самого или к нему обратного элемента, мы
получили бы параболические элементы, сдвигающие любую данную точку
на сколь угодно малое расстояние, что противоречит дискретности груп-
группы щ(М). Следовательно, группа, порожденная аир, целиком состоит
из параболических движений с общей неподвижной точкой р. Поэтому
она изоморфна подгруппе группы IsomE". Каждый геодезический луч,
направленный в р, пересекает Т(а) (равно как и Г(Р)) по полубесконечно-
полубесконечному интервалу, поскольку функция сдвига da(x) стремится к иулю по мере
приближения х к р.
С помощью аналогичных рассуждений с неподвижными точками в слу-
случае гиперболического элемента ф с осью / получим, что группа, порожден-
порожденная элементами аир, состоит только из гиперболических движений с
осью / и тождественного преобразования. На оси / эта группа действу-
действует сдвигами. Поэтому она изоморфна подгруппе вЕ'х О(л — 1). Далее,
простое соображение показывает, что дискретная подгруппа без кручения
в группе Е1 х О(я — 1) является циклической. В частности, элементы а
и р коммутируют. Более того, / с Т(и), так как ось / — это геометрическое
место точек, минимально сдвигаемых движением а (предложение 2.5.17).
Ясно также, что образующая у циклической группы, порожденной аир,
лежит в 50: так как у сдвигает вдоль / не дальше, чем а, то / с 7(у).
Окончательный вывод таков: тип у (гиперболический или параболиче-
параболический) и неподвижные точки этого движения на бесконечности одииаковы
для всех у G So, так как в силу связности Го тип и неподвижные точ-
точки «распространяются» на все элементы 5о (по индукции). Итак, можно
говорить о параболической или гиперболической компоненте 7о. Полу-
Полученной классификацией мы немедленно воспользуемся для того, чтобы
разобраться с формой компоненты Мо (содержащейся в М<) — образом
компоненты То. Обозначим через Go подгруппу группы щ(М), порожден-
порожденную So. Тогда Мо = Tq/Gq.
260
Глава 4. Структура дискретных групп
4.5. 7Ч-разложение
261
Если компонента То гиперболическая, то GQ — циклическая группа, а
сама То является объединением конечного числа выпуклых окрестностей
оси / группы Go, а поэтому диффеоморфна открытому шару D" или, лучше
сказать, диффеоморфна Dn~l x R, причем диффеоморфизм эквивариантен
относительно действия группы Go =Z (задача 4.5.3, в). Если группа Go
сохраняет ориентацию, то компонента Мо диффеоморфна D"~l x 51, а ес-
если не сохраняет — то неор_иентируемому расслоению над окружностью со
слоем диск. Замыкание М0 оказывается компактным топологическим мно-
многообразием с краем.
Упражнение 4.5.2. а) Опишите компоненту То, если образующей группы
Go С Isom H3 служит скользящее отражение.
б) Приведите пример сохраняющей ориентацию циклической группы Со С
С Isom И* с невыпуклой областью То.
Задача 4.5.3 (звездная область есть шар), а) Открытое подмножество
С/сЕ", звездчатое относительно точки х е U, диффеоморфно Е". (Указание:
требуется модифицировать в U функцию расстояния до границы так, чтобы она
стала гладкой и вдоль любого луча из х до границы монотонно возрастала от 0
до оо. Обратитесь к [Вег87, 11.3.6.1], если возникнут проблемы; предложенную
там конструкцию можно сгладить.)
б) Обобщите на случай области U С Н".
в) Пусть U с Н" открытое множество, инвариантное относительно действия
циклической группы гиперболических движений. Если область U является звезд-
звездчатой относительно любой точки оси группы, то U эквивариантно диффеоморфно
ЕГ~' х Е1 (это означает, что действие группы в U отображается в действие Z на
Е"~' х Е1 изометриями, сохраняющими структуру прямого произведения).
г) Докажите аналогичное утверждение для области U с Н", звездчатой отно-
относительно точки х на бесконечности и инвариантной относительно группы парабо-
параболических движений с неподвижной точкой х. Кроме этого, мы предполагаем, что
любой луч, направленный в точку х, пересекает U.
Если компонента То параболическая с неподвижной точкой р е 5^"', то
она снова есть объединение выпуклых множеств, «касающихся» бесконеч-
бесконечности в точке р. Поэтому область То звездчата в том смысле, что любой луч
из точки х б Го в точку р целиком лежит в То. И, согласно задаче 4.5.3, г,
компонента То диффеоморфна полупространству Е" х @, оо). Профак-
торизовав по действию параболической группы Go, получим, что Мо диф-
диффеоморфна прямому произведению евклидова (я — 1)-многообразия и ин-
интервала @, оо); любое евклидово (я — 1)-многообразие может выступить
в этой роли. Замыкание Мо — это снова многообразие с границей, но на
этот раз некомпактное.
Удобно представить себе Мо как окрестность «точки на бесконечности»
или каспа многообразия М. Точнее, рассмотрим множество неподвижных
точек параболических элементов группы щ(М) и профакторизуем его по
действию самой группы. Соответствующие классы называются каспами М
(каспы не принадлежат М\), и каждая компонента М< с некомпактным
замыканием ассоциирована ровно с одним каспом.
Компонента То, будучи параболической или гиперболической, всегда од-
носвязна, и поэтому TCi(Af0) = Go (с точностью до сопряженности).
Упражнение 4.5.4. Опираясь на упражнение 4.5.1 н текст перед ним, попро-
попробуйте установить, как на самом деле выглядит Мо в размерностях два и три.
(Полезно рассмотреть рис. 4.12.)
Рис. 4.12. Г-<-разложение поверхности. Тонкая часть гиперболической поверхности
конечной площади состоит нз окрестностей коротких геодезических н окрестностей
каспов. Окрестность каспа изометрична псевдосфере.
Упражнение 4.5.5 (отсутствие каспов у компактных многообразий). Как
следует из наших рассмотрений, у компактных гиперболических многообразий ка-
каспы отсутствуют (т. е. фундаментальная группа состоит только из гиперболических
движений). Докажите это непосредственно. (Указание: на компактном многооб-
многообразии нижняя грань длин замкнутых кривых в каждом нетривиальном свободном
гомотопическом классе положительна.)
Подведем итоги:
Теорема 4.5.6 (структура тонкой части). Если величина е мень-
меньше некоторой константы, зависящей только от размерности, то
тонкая часть М^е полного гиперболического многообразия явля-
является объединением связных компонент одного из следующих ти-
типов: окрестности коротких геодезических, гомеоморфные расслое-
расслоению дисков над окружностью; окрестности каспов, гомеоморфные
262
Глава 4. Структура дискретных групп
произведению евклидовых многообразий на полубесконечные интер-
интервалы.
О толстой части М>6 в общем случае многого не скажешь, кроме, пожа-
пожалуй, того, что для маленьких е это многообразие с краем. Тем интересней
следующий результат.
Теорема 4.5.7 (толстая часть компактна тогда и только тогда, когда
объем конечен). Объем полного гиперболического многообразия ко-
конечен тогда и только тогда, когда толстая часть М-^е компактна
при всех е > 0.
Доказательство. Допустим, что объем многообразия М конечен, и рас-
рассмотрим множество точек S в М^с, обладающих тем свойством, что по-
попарные расстояния между любыми двумя из них не меньше чем е. Ясно,
что шары радиуса е/2 с центрами в этих точках попарно не пересекаются
и имеют одинаковый объем. Поэтому их число конечно. С другой стороны,
если выбрать множество 5 максимальным, то замкнутые е-шары вокруг
точек 5 покроют все М^в. Объединение таких шаров компактно. Поэтому
и Af;.s компактно, будучи замкнутым подмножеством в этом объединении.
Для доказательства обратного утверждения выберем s таким, чтобы
была применима структурная теорема 4.5.6. Если М^с компактно, нам
достаточно показать, что любая из конечного числа компонент многообра-
многообразия М<с имеет конечный объем. Для компонент с компактным замыканием
доказывать нечего. Если же компонента Мо не компактна, то обозначим
через То компоненту ее полного прообраза в Ня, выбранную так, что па-
параболическая неподвижная точка р соответствует точке на бесконечности
в модели верхнего полупространства. Группа Go сохраняет слоение на То,
индуцированное вертикальными лучами, и это слоение переносится на Мо,
поскольку gT0 П Го = 0, если элемент g из щ(М) не лежит в Go. Но каждый
лист этого слоения на Мо оканчивается в точке М^s, а так как М^ компакт-
компактно, то действие Go на горизонтальной (евклидовой) плоскости кокомпактно
с фундаментальной областью Р. Но это означает, что То отделено по вы-
высоте от нуля в верхнем полупространстве. Следовательно, объем Мо не
превосходит объема цилиндра Р х [п, оо), который, как легко сосчитать,
конечен. [4.5.71
Итак, для конечности объема М достаточно, чтобы М^е было компакт-
компактно при каком-нибудь е, для которого применима теорема 4.5.6. С другой
стороны, при больших е из компактности М^с не обязательно следует
конечность объема. Например, рассмотрим гиперболическое трехмерное
многообразие, расслаивающееся над окружностью со слоем замкнутая по-
поверхность, и его накрытие, которое получится, если все «развернуть» в
направлении окружности. Радиус инъективности накрытия все еще будет
ограничен, но его объем бесконечен.
4.6. Пространства Тейхмюллера
4.6. Пространства Тейхмюллера
263
Как нам уже известно из раздела 1.3, каждая замкнутая ориентируемая
поверхность рода g, g> 1, обладает гиперболической структурой. Од-
Однако в предложенной там конструкции имеется большой произвол. Это
согласуется с тем, что такая структура не одна. Чтобы понять, сколько их,
произведем грубый подсчет параметров.
Рассмотрим, например, поверхность рода 2, полученную склейкой про-
противоположных сторон восьмиугольника. Восьмиугольники на гиперболи-
гиперболической плоскости Н2 образуют 16-мерное пространство, так как каждая из
восьми вершин имеет две степени свободы. Конгруэнтные восьмиугольники
определяют одну и ту же структуру, поэтому мы вычтем три — размерность
группы IsomEP.
Далее, нас устраивают далеко не все восьмиугольники: длины проти-
противоположных сторон должны быть равны, чтобы их можно было склеить.
Это еще четыре условия. Наконец, сумма всех углов должна быть равна
2л, или, что то же самое, площадь равна 2к. Значит, нужно вычесть еще
единицу. В результате остается восемь степеней свободы.
Бывает и так, что два неконгруэнтных восьмиугольника дают при склей-
склейке изометричные поверхности. Заметим, что все вершины склеиваются в
одну базисную точку на поверхности и, перемещая эту точку по поверхно-
поверхности, мы получаем различные описания нашей поверхности как результата
склейки сторон восьмиугольника. Эта многозначность приводит к потере
еще двух степеней свободы. Итак, похоже, что пространство существен-
существенно различных гиперболических структур на поверхности рода два имеет
размерность шесть.
Наш грубый анализ оставляет без ответа многие вопросы. Какие вось-
восьмиугольники мы хотим использовать: требуется ли их выпуклость и требу-
требуется ли, чтобы они были вложены в Н2? Действует ли группа движений сво-
свободно, т. е. является ли факторпространство многообразием? Независимы
ли указанные нами условия, т. е. совпадает ли действительная размерность
пространства решений с ожидаемой? При перемещении базисной точки на
поверхности получаем ли мы метрически разные восьмиугольники склейки,
локально и глобально? Какова глобальная структура пространства гипер-
гиперболических многоугольников склейки? На все эти вопросы можно дать
точные и строгие ответы в рамках нашего подхода. Мы не станем этого
делать, а попробуем поменять точку зрения.
Но сначала нам придется четко ответить на вопрос: какие две гипер-
гиперболические поверхности следует считать одинаковыми? Дело в том, что
есть два разумных понятия эквивалентности, приводящие к двум различ-
различным пространствам: пространству модулей и пространству Тейхмюллера.
Если говорить неформально, то в пространстве Тейхмюллера мы следим не
264
Глава 4. Структура дискретных групп
только за тем, какую метрику «носит» поверхность, но и затем, как она ее
«носит». В пространстве модулей две поверхности с одинаковой метрикой
эквивалентны. Насколько важно различать эти случаи, ясно каждому, кто,
одев пижаму на младенца, обнаруживал перекрученную штанину.
Замечание 4.6.1. Модуль в комплексном анализе —это инвариант, ас-
ассоциированный с областью в С или, в общем случае, с римановой по-
поверхностью. В 1859 г. Риман высказал утверждение о том, что класс изо-
изоморфных замкнутых римановых поверхностей рода g, g > 2, зависит от
3g — 3 комплексных параметров, или модулей, т. е. пространство модулей
замкнутых поверхностей рода g имеет вещественную размерность 6g — 6.
Ввиду теоремы об униформизации (пример 3.1.17) изучать комплексные
структуры на поверхности — это в некотором смысле то же самое, что
изучать гиперболические структуры на ней. Эти две точки зрения легли в
основу двух главных направлений теории пространств Тейхмюллера.
Эвристические рассуждения Римана не были им превращены в строгие
доказательства. По-видимому, первые строгие рассмотрения этих вопро-
вопросов—заслуга Фрике и Клейна [FK12]. Само название пространств появи-
появилось после работ [Tei39, Tei43], в которых эта тема получила значительное
развитие (включая введение знаменитой метрики, которая появится у нас
на с. 272) и которые возродили интерес к ней.
Соглашение 4.6.2. Всюду в этом разделе поверхность — это любое
связное дифференцируемое 2-многообразие с границей, а гиперболическая
структура — это полная гиперболическая структура с геодезической грани-
границей: более точно, если Sf — псевдогруппа из определения 3.3.11, то гипер-
гиперболическая структура — это Sf-усиление поверхности 5, превращающее 5
в полное метрическое пространство. Так же нужно понимать евклидову и
сферическую структуры.
Упражнение 4.6.3. Как мы видели в примере 3.1.17, все поверхности без гра-
границы обладают одной из трех структур: гиперболической, евклидовой или сфери-
сферической. Распространите данные там объяснения на случай поверхности с границей.
Какие из них несут евклидову структуру? А какие сферическую?
Пусть 5 — поверхность, допускающая гиперболическую структуру, и
пусть S*S — пространство таких структур.
Определение 4.6.4 (пространство модулей и пространство Тейх-
Тейхмюллера). Пространством модулей MS поверхности S называется
факторпространство пространства S^S по действию на нем группы диф-
диффеоморфизмов DiffS поверхности S. Пространством Тейхмюллера SFS
поверхности 5 называется факторпространство S^S по действию группы
Diffo5 диффеоморфизмов S, гомотопных тождественному посредством
гомотопии, переводящей в каждый момент границу 5 в себя.
4.6. Пространства Тейхмюллера
265
Теорема Бэра [Вае28, Eps66] утверждает, что если поверхность 5 отлич-
отлична от открытого диска или открытого кольца, то два диффеоморфизма 5
тогда и только тогда изотопны, когда они гомотопны, причем эта гомо-
топия переводит границу в себя. Тем самым, если не обращать внимания
на два простых исключения, то определение пространства Тейхмюллера
можно сделать короче, используя изотопию, а группу Diffo5 естественно
интерпретировать как связную компоненту единицы в группе DiffS (тем
самым, Diff0 S — нормальная подгруппа в DiffS). И все же правильнее ра-
работать с отношением эквивалентности, определяемым гомотопией, нежели
изотопией, чему подтверждение — предложение 4.6.10 ниже.
Упражнение 4.6.5. В теореме Бэра требование к гомотопии переводить грани-
границу в себя нзлишие за исключением случаев, когда S — замкнутый диск, замкнутое
кольцо, илн когда среди компонент границы S есть интервалы. Предлагается найти
контрпримеры в каждом исключительном случае.
М
Рис. 4.13. Пространство Тейхмюллера тоньше пространства модулей. Изобра-
Изображенные здесь пары (/, М) и (/', М') совпадают в MS, так как М н М' переводятся
друг в друга изометрней, схематически изображенной параллельным переносом в R3.
Но как отмеченные эти поверхности представляют разные точки в &S, поскольку ото-
отображение /' о /-' не изотопно ни ft, ни какой-либо другой изометрии (случись такое,
и пунктирная кривая h(f(y)) оказалась бы изотопной кривой f'(f)).
Другая стандартная переформулировка определения 4.6.4 проиллю-
проиллюстрирована на рис. 4.13. Пара (/, М) состоящая из гиперболической
поверхности М и диффеоморфизма /: S —> М, называется отмеченной
поверхностью (см. также задачу 4.6.26). Рассмотрим все отмечен-
отмеченные S поверхности. Пространство Тейхмюллера S?S получается, если
отождествить такие (и только такие) пары (/, М) и (/', М'), для кото-
которых диффеоморфизм /' о /-' изотопен изометрии. Пространство модулей
266
Глава 4. Структура дискретных групп
MS получается путем «забывания» отметки, т. е. путем отождествления
изометрических поверхностей М и М', невзирая на отображения-метки /
и f. Как правило, отображения / и- f упоминаться не будут, и мы просто
будем писать М и М' для обозначения поверхности 5 с гиперболической
структурой.
Прежде чем обратиться к примерам, введем еще одно важное понятие.
По определению
где mcgS = DiffS/Diff0 5 — группа классов отображений или модуляр-
модулярная группа поверхности S.
Замечание 4.6.6. При комплексно-аналитическом подходе поверхно-
поверхности появляются с уже заданной на них ориентацией. В связи с этим тради-
традиционные определения основных понятий этой главы отличаются от наших
тем, что точкой отсчета служит ориентированная поверхность 5, а вместо
группы DiffS рассматривается группа Diff+ 5, сохраняющих ориентацию
диффеоморфизмов. Пространство гиперболических структур и простран-
пространство Тейхмюллера при этом не меняются (почему?), но модулярная группа
и пространство модулей могут измениться. Мы используем обозначения
mcg+ 5 и Ж+S для группы классов, сохраняющих ориентацию отображе-
отображений, и для соответствующего пространства модулей, так что по-прежнему
JK+S = ^5/mcg+ 5.
Пример 4.6.7 (панты). Поверхность Р на рис. 4.14 называется панты.
Топологически она является сферой без трех точек. Исследуем ее про-
пространство Тейхмюллера и пространство модулей.
Рис. 4.14. Панты
Каждой точке пространства SfP мы можем поставить в соответствие.
упорядоченную тройку положительных чисел: длины трех граничных ком-
компонент. (Заметьте, что упорядоченная тройка — это объект пространства
Тейхмюллера, но не пространства модулей, и причина здесь в том, что в
4.6. Пространства Тейхмюллера
267
модулярной группе есть элементы, меняющие местами граничные компо-
компоненты. По той же причине для точки из пространства Тейхмюллера, но не
из пространства модулей, мы можем говорить о свободном гомотопическом
классе петли и задаваться вопросом о длине его кратчайшего представи-
представителя.) Докажем, что построенное отображение SfP —> @, ооK биективно.
В самом деле, рассмотрим какую-нибудь гиперболическую структуру
на Р. Любую пару граничных компонент можно соединить швом — т. е. от-
отрезком геодезической, ортогональным границе, причем эти швы попарно не
пересекаются и определяются однозначно. Чтобы в этом убедиться, прове-
проведем три произвольные попарно непересекающиеся дуги, соединяющие три
пары граничных компонент. С точностью до изотопии это можно сделать
единственным образом. Затем рассмотрим дубль Я U Р1 поверхности Р (см.
определение 3.3.11): наши дуги превратятся в замкнутые кривые. Позже
мы докажем (предложение 4.6.20), что эти кривые на дубле можно изо-
топически продеформировать в три однозначно определенные, замкнутые,
попарно непересекающиеся геодезические. Такие геодезические автомати-
автоматически ортогональны границе: в противном случае, меняя местами Р и Р мы
вступаем в противоречие с их единственностью. Возвращаясь к пантам Р,
получаем три нужных нам шва.
Если разрезать панты Р вдоль швов, то получим два конгруэнтных ше-
шестиугольника, поскольку прямоугольный гиперболический шестиугольник
определяется с точностью до изометрии длинами трех несмежных сторон
(упражнение 2.4.11 или рис. 4.15 с наглядным доказательством).
Следовательно, швы делят каждую граничную компоненту на две равные
части, а длины граничных компонент определяют гиперболическую струк-
структуру на Р. Более того, согласно упражнению 2.4.11 или рис. 4.15, любая
тройка положительных чисел служит длинами граничных компонент.
Пространство модулей ЛР — это множество неупорядоченных поло-
положительных троек. Объясняется это тем, что группа mcg+ P совпадает с
симметрической группой 5з, действующей перестановками граничных ком-
компонент, а ЛР = Л+Р по той причине, что гиперболические панты все-
всегда допускают меняющую ориентацию изометрию. В этом смысле панты
являются исключением: для большинства поверхностей меняющие ориен-
ориентацию симметрии встречаются довольно редко, и, как правило, простран-
пространство Л+Р двулистно и (разветвленно) накрывает пространство JtP.
Упражнение 4.6.8. Найдите пространство Тейхмюллера и пространство мо-
модулей для сферы с тремя выколотыми точками (панты без границы). (Указание:
каждую граничную компоненту у Р можно заменить либо каспом, либо расширя-
расширяющейся гиперболической «трубой». Как будет показано в дальнейшем, речь идет
о двух принципиально разных структурах: см. задачу 4.6.16.)
Упражнение 4.6.9. Найдите пространство Тейхмюллера и пространство моду-
модулей открытого кольца, открытой ленты Мёбиуса, а также поверхности, полученной
удалением открытого диска из замкнутой верхней полуплоскости.
268
Глава 4. Структура дискретных групп
В
Рис. 4.15. Существует ровно один прямоугольный шестиугольник аСЬАсВ с
заданными а, Ь, с > 0. В предлагаемой конструкции на верхней полуплоскости сторо-
сторона а и длина стороны Ь фиксированы. Когда длина С меняется, то один конец стороны Ь
описывает изображенную пунктиром кривую d — дугу евклидовой окружности (см.
рис. 1.10). Прямая, на которой лежит сторона А, касается d в этой точке. Для длин С,
больших чем Со, продолжения сторон А и В расходятся, и с существует. По мере
увеличения С прямая, на которой лежит сторона А, оказывается «зажатой» между
кривой d и абсолютом Sj^; при этом евклидов радиус стороны с растет, а сторона В
становится короче. Отсюда по теореме синусов для шестиугольника (уравнение 2.4.10)
следует, что с является строго монотонной функцией от С, меняющейся от 0 до оо,
когда С пробегает промежуток (Со, оо). Таким образом, каждое значение с принимает
ровно один раз.
Предположим на минуту, что у поверхности 5 нет границы. Тогда из ре-
результатов раздела 3.5 следует, что пространство модулей как пространство
полных (IsomH2,!Р)-структур на 5 можно отождествить с пространством
классов сопряженных дискретных подгрупп группы IsomH2, действую-
действующих в Н2 с факторпространством 5. Пространство Тейхмюллера допускает
аналогичное алгебраическое описание как пространство классов точных
представлений (инъективных гомоморфизмов) Ui(S) —+ IsomH2 с дис-
дискретным образом.
Предложение 4.6.10 (голономия определяет структуру). Если S —
поверхность без границы, то две гиперболические структуры на S
тогда и только тогда эквивалентны в пространстве модулей, ко-
когда одинаковы их группы голономии, а в пространстве Тейхмюллера
они эквивалентны если, и только если, одинаковы их представления
голономии.
Разумеется, поскольку голономия определена лишь с точностью до со-
сопряженности, соответственно нужно понимать и слово «одинаковы».
4.6. Пространства Тейхмюллера
269
Доказательство. Утверждение о пространстве модулей — это в точно-
точности следствие 3.5.12. Что касается пространства Тейхмюллера, то пусть
М и М' — гиперболические структуры на 5, а р: Н2 —> М и р'\ Н2 —> М' —
локально изометричные накрытия. Поднимем тождественное отображение
М —> М' до отображения ср: ЕР —>• ЕР. Вообще говоря, ср не является ни
тождественным отображением, ни изометрией.
Обозначим представление голономии для М и М' через Я и Я' соот-
соответственно. Тогда если о? Ki(S), to сопряжение с помощью ср переводит
элемент Н(а) из группы накрытия М в элемент Н'(а) из группы накры-
накрытия М', т. е. ср сопрягает представления голономии Н и Н'. Поэтому ра-
равенство Н = Н' означает, что отображение ср коммутирует с голономией.
В таком случае, с голономией коммутирует и гомотопия вдоль отрезков
геодезических, соединяющая ср с тождественным отображением ЕР —> ЕР.
А такая гомотопия индуцирует гомотопию на 5, которая заканчивается
изометрией М —> М', так как в конце ее поднятие является изометрией Н2.
Следовательно, М н М' представляют одну и ту же точку пространства
Тейхмюллера.
И наоборот, если существует гомотопия, соединяющая тождественное
отображение М —> М' с изометрией, то ее можно поднять до гомотопии,
соединяющей ср и тождественное отображение Н2 —> ШР. А это и означает,
что у М и М' представления голономии одинаковы. |4.6.101
Аналогичное утверждение о пространстве Тейхмюллера SFS верно и в
случае, когда dS ф 0: два элемента из пространства структур УБ экви-
эквивалентны тогда и только тогда, когда одинаковы представления голономии
у их дублей. Чтобы в этом убедиться, нужно предыдущие рассуждения
применить к соответствующим дублям, а затем заметить, что поднятия гра-
граничных компонент, будучи геодезическими, должны совпасть при условии,
что Н = Н'.
Вообще говоря, совсем непросто выделить среди представлений группы
Тс! E) в группе Ли такие, у которых образ дискретен, а факторпространство
есть 5. Но в одном элементарном случае алгебраический подход торже-
торжествует:
Пример 4.6.11 (пространство Тейхмюллера для тора).. Если 5 до-
допускает евклидовы структуры, то точно так же можно определить про-
пространство Тейхмюллера и пространство модулей евклидовых структур с той
лишь разницей, что теперь S^S будет пространством евклидовых структур
на 5, рассматриваемых с точностью до умножения метрики на положитель-
положительное число (если поверхность 5 компактна, то можно нормировать метрику
так, чтобы площадь была равна единице).
Наиболее интересен случай Т2. Здесь нам нужно разобраться с дис-
дискретными представлениями тсДТ2) = Z2 —+ IsomE2. На самом деле, мы уже
знаем, что группа голономии тора состоит из параллельных переносов.
270
Глава 4. Структура дискретных групп
После подходящего сопряжения можно считать, что образующая A,0) в
7? представлена переносом на вектор A,0). Другая образующая @, 1) при
этом может перейти в любой вектор (х, у), где у ф 0, и снова после сопря-
сопряжения можно считать, что у > 0. Мы убедились в том, что пространством
Тейхмюллера для тора служит верхняя полуплоскость у > 0.
Упражнение 4.6.12 (классическая модулярная группа). Покажите, что
группа meg Т2 изоморфна PGLB, Z). Как группа meg Т2 действует на пространстве
Тейхмюллера &Т21 Что нз себя представляет факторпространство? (Указание:
обратитесь к рис. 4.16.) Название же модулярная группа относится к группе
-1
f
1
1
1
E
S
N
\
\
\
\
1
о
1/2
Рис. 4.16. Пространство Тейхмюллера для тора и действие модулярной груп-
группы. Группа meg Г2 = PGLB, Z) действует на пространстве Тейхмюллера тора как
группа гиперболических изометрий. Закрашенная область является фундаментальной
для действия группы mcg+f2 = PSLB, Ъ), порожденной элементами S= Го А и
?=(_! 0J, по формуле 2.6.1.
Упражнение 4.6.13. Опишите пространство Тейхмюллера и пространство мо-
модулей евклидовых структур на замкнутом кольце S1 х [0, 1], открытом кольце S1 х
@, 1), замкнутой и открытой лентах Мёбиуса и на бутылке Клейна.
Упражнение 4.6.14. Сферическое пространство Тейхмюллера поверхности,
допускающей сферические структуры, есть точка.
Снабдим теперь пространство 2?S естественной топологией, где близ-
близким точкам будут соответствовать «почти одинаковые» гиперболические
структуры. Это можно сделать многими способами, и один из них — ис-
использовать для этого метрику. Пусть К 5= 1 ¦ Назовем гомеоморфизм h двух
метрических пространств К-квазиизомешрией, если как /г, так и h~[ из-
4.6. Пространства Тейхмюллера
271
меняют расстояние между точками не более чем в К раз. Для диффеомор-
диффеоморфизма римановых многообразий это эквивалентно тому, что касательные
векторы растягиваются или сжимаются не более чем в К раз. Теперь, ес-
если М и М' — две структуры на 5, то положим
где нижний предел в правой части берется по всем таким /С, что в изото-
изотопическом классе тождественного отображения М —у М' есть /С-квазиизо-
метрия. Расстояние dqi определено на парах точек пространства &S, но в
силу его инвариантности относительно действия модулярной группы, оно
переносится и на пространство ^MS.
Несложно проверить, что выполнены все аксиомы метрического про-
пространства. Правда, расстояние dqi{M, M') может оказаться бесконечным.
Этого не происходит, если 5 компактно, поскольку в этом случае любой
диффеоморфизм будет квазиизометрией. Но вот пример, когда это так.
Упражнение 4.6.15 (неэквивалентные цилиндры). Пусть Ма — гиперболи-
гиперболический цилиндр толщины а, полученный, например, как факторпространство верх-
верхней полуплоскости по циклической группе, порожденной гиперболическим сдвигом
z>—>zea. Вычислите dqi(Ma, Мь), точно указав наилучшую квазиизометрию меж-
между Ма И Mb.
Обозначим через Mq факторпространство Н2 по параболическому сдвигу.
Докажите, что не существует квазиизометрий между Ма и Mq\ по этой причине
dqi(Ma, Mq) = оо, и пространство Тейхмюллера открытого цилиндра несвязно.
Задача 4.6.16 (неэквивалентные поверхности). Пусть М — связное мно-
многообразие. Рассмотрим такое его покрытие компактными множествами К\ С
С Кг С ... , что Ki С Ki+i. Такой согласованный выбор связной компоненты Aj
множества М \ Ki, что А; с Aj прн i > /, называется концом многообразия М.
а) Докажите, что данное определение не зависит от выбора компактного исчер-
исчерпывания {Ki} на М.
б) Пусть S — поверхность без границы, а М — гиперболическая структура на S
с группой голономии Г. Покажите, как каждому концу S поставить в соответствие
движение плоскости И2, определенное с точностью до Г-сопряженности, вместе с
Г-инвариаитным подмножеством абсолюта. Факторпространство этого подмноже-
подмножества по действию Г может быть точкой или окружностью. В первом случае конец S
называется параболическим (касп), во втором — гиперболическим (труба). Каспы
и трубы образуют идеальную границу М.
в) Две гиперболические структуры М и М' на S не могут быть квазиизометрнч-
ными, если соответствующие концы относительно этих структур имеют различный
тип.
г)* Если тип поверхности S конечен (т. е. группа tci(S) конечно порождена), то
различие типов концов — единственное препятствие к существованию квазнизоме-
трии между структурами М и М'.
272
Глава 4. Структура дискретных групп
Метрика, первоначально введенная Тейхмюллером [Tei39, Tei43], тес-
тесно связана с метрикой dqi. Метрика Тейхмюллера определяется точно так
же, но вместо квазиизометрий используются квазиконформные отображе-
отображения. Диффеоморфизм называется К-квазиконформным, если он изменяет
отношение длин двух любых касательных векторов в данной точке не бо-
более чем в К раз; другими словами, маленькая окружность в касательном
пространстве данной точки области отображается на эллипс, у которого
отношение осей не превосходит К. Расстояние Тейхмюллера показывает
меру конформного отклонения, тогда как расстояние dqi характеризует от-
отклонение метрик. При этом ясно, что dqc ^ dqi. Верно также, но далеко
не очевидно, что dql ^ Cdqc для некоторой константы С; всё вместе это
показывает, что обе метрики определяют одну и ту же топологию.
Одним из важных достижений Тейхмюллера было нахождение эконом-
экономной деформации поверхности: иными словами, он исследовал геодезиче-
геодезические в пространстве Тейхмюллера в метрике Тейхмюллера и доказал един-
единственность геодезической (хороший обзор на эту тему см. в [АЫ80]). Позд-
Позднее Ройден [Roy71 ] показал, что все изометрии метрики Тейхмюллера опре-
определяются действием модулярной группы. Альфорс [АЫ60] доказал, что в
пространстве Тейхмюллера есть единственная комплексная структура и что
через любые две точки проходит единственная комплексная геодезическая
(вложенная копия гиперболической плоскости). Ройден доказал совпа-
совпадение метрики Тейхмюллера и канонической метрики Кобаяси, ассоции-
ассоциированной с комплексной структурой. Все эти результаты, первоначально
полученные для компактных поверхностей, были затем обобщены на про-
произвольные поверхности (см. следующее замечание).
Замечание 4.6.17. По той причине, что расстояние между гипербо-
гиперболическими (или комплексными) структурами на открытой поверхности 5
может быть бесконечным, принято рассматривать пространство Тейхмюл-
Тейхмюллера, ассоциированное не с самой поверхностью 5, а с какой-либо кон-
конкретной гиперболической (или комплексной) структурой М на 5. В этом
случае пространство Тейхмюллера для М классифицирует только те струк-
структуры, которые квазиизометричны (или квазиконформно эквивалентны) М,
а именно, структуры из той же связной компоненты пространства SFS, что
нМ.
Более того, если М обладает концами в виде гиперболических труб, то
можно рассмотреть другую интересную группу диффеоморфизмов, которая
может заменить группу Diff0 5 в определении пространства Тейхмюллера:
это группа диффеоморфизмов, изотопных тождественному и тождествен-
тождественных на идеальной границе.. Факторпространство пространства структур,
квазиизометричных М, по действию этой меньшей группы, называют про-
пространством Тейхмюллера для М, тогда как факторпространство по дей-
действию Diff0 5 получило название редуцированного пространства Тейх-
4.6. Пространства Тейхмюллера
273
мюллера. Нередуцированное пространство во многих отношениях прият-
приятней редуцированного; в частности, именно для него имеются обобщения
всех упомянутых выше результатов, но оно бесконечномерно, за исключе-
исключением случаев, когда 5 компактна или имеет только каспы, т. е. когда между
этими пространствами нет разницы.
Задача 4.6.18. Согласно предложению 4.6.10, пространство &S можно рас-
рассматривать как подпространство пространства представлений (по модулю сопря-
сопряженности) фундаментальной группы S (или ее дубля). В свою очередь, простран-
пространство представлений— это алгебраическое подмножество в О'и', где G = IsomH2
и А — множество образующих фундаментальной группы. Как прн этом связана
топология, наследуемая &S от О|И|, с топологией, определяемой метрикой Тейх-
Тейхмюллера?
В оставшейся части раздела мы исследуем пространство Тейхмюллера
компактной поверхности 5 путем разрезания ее на панты и последующего
восстановления пространства S?S с помощью пространства Тейхмюллера
для пантов.
Упражнение 4.6.19 (разрезание поверхностей). Пусть S —компактная по-
поверхность. Докажите следующие утверждения.
а) S гомеоморфна замкнутой поверхности минус конечное число попарно не-
непересекающихся открытых дисков. Поверхность S полностью характеризуется чи-
числом Эйлера, числом граничных компонент и тем, ориентируема она или нет.
б) Простую замкнутую кривую на S назовем существенной, если она не гомо-
гомотопна нулю и не свободно гомотопна компоненте границы. На каких поверхностях
есть существенные кривые? Докажите, что разрезав S вдоль такой кривой, мы
получим поверхность или поверхности, любая из которых снова компактна и, в
некотором смысле, проще исходной.
в) Как это следует из б, если на S есть существенные кривые, то можно по-
последовательно сделать разрезы вдоль них, пока у нас не останутся только панты
и кольца (см. рис. 4.17). В каких случаях могут встретиться кольца? Когда их
появление неизбежно? Докажите, что число пант, получившихся при разрезании,
есть инвариант.
Таким образом, у нас есть топологическое разбиение поверхности. Для
геометрического разбиения мы должны суметь превратить простые за-
замкнутые кривые на 5 в геодезические. Часть этого процесса «выпрям-
«выпрямления» работает в любой размерности.
Предложение 4.6.20 (выпрямление замкнутых кривых). Пусть
М — полное компактное гиперболическое многообразие; возможно,
с геодезической границей, и пусть a: S1 —»• М замкнутая кривая,
не гомотопная нулю. Тогда в свободном гомотопическом классе а
имеется замкнутая геодезическая, единственная с точностью до
параметризации, которая либо не пересекает границу, либо в нее
входит.
274
Глава 4. Структура дискретных групп
Рис. 4.17. Разрезание поверхности на панты
Доказательство. Сначала рассмотрим случай, когда у М нет границы.
Зафиксируем проекцию р: W -> М и поднятие а: Е -> И" петли а (пусть
при этом р([0, 1]) =а). Обозначим через Га преобразование голономии,
отвечающее выбранному поднятию а (см. упражнение 3.4.4). Согласно
упражнению 4.5.5, преобразование голономии Та является гиперболиче-
гиперболическим движением. Рассмотрим его ось у: Ж -* W, параметризованную так,
что единичному сдвигу вдоль Ш. соответствует сдвиг Та вдоль геодезиче-
геодезической у (рис. 4.18, слева). В таком случае геодезическая гомотопия между
кривыми а и у инвариантна относительно группы, порожденной Та, а по-
потому проектируется в свободную гомотопию между а и у.
Наоборот, если петля а свободно гомотопна геодезической у, то гомо-
гомотопия между их поднятиями а и у сдвигает любую точку на ограниченное
гиперболическое расстояние. Следовательно, кривая а стремится с обе-
обеих сторон к соответствующим «концам» прямой у. По этой причине у
совпадает с осью голономии Та, и доказательство для случая замкнутого
многообразия закончено.
Если у многообразия М есть граница, то прежде всего рассмотрим
его дубль. Тогда универсальную накрывающую М можно рассматривать
как связную компоненту прообраза М на универсальной накрывающей И"
дубля (рнс^4.18, справа). Будучи пересечением полупространств, про-
пространство М выпукло, а потому проходят все предыдущие рассуждения:
поднятие петли а содержится в М, где его можно выпрямить в геодезиче-
геодезическую, снова лежащую в М, и эта геодезическая либо принадлежит границе,
либо с ней не пересекается. 14.6.20I
В размерности два можно сказать больше.
Предложение 4.6.21 (выпрямление сохраняет вложение). Пусть
М — компактная поверхность с гиперболической структурой и
4.6. Пространства Тейхмюллера
275
Рис. 4.18. Выпрямление замкнутой кривой. Слева: для нахождения геодезической,
свободно гомотопной замкнутой кривой а на замкнутом многообразии, мы сначала
поднимаем а на универсальную накрывающую, а затем берем ось голономии и про-
проектируем ее на многообразие. Справа: поверхность рода 2, полученная склейкой пра-
правильного гиперболического восьмиугольника (рис. 1.13),—это дубль поверхности М
с геодезической границей, гомеоморфной T2\D2. Каждая закрашенная область пред-
представляет собой универсальную накрывающую М, вложенную в Н2.
пусть а: 5' —* М простая замкнутая кривая, не гомотопная нулю.
Тогда геодезическая, представляющая класс а, кратна простой
замкнутой кривой.
Доказательство. Замкнутая кривая на М тогда н только тогда крат-
кратна простой кривой, когда любые два ее поднятия либо не пересекаются,
либо совпадают. Применим этот критерий к двум поднятиям <5i и а2 кри-
кривой а и рассмотрим взаимное расположение их концов на абсолюте 5^.
Мы видим, что оси соответствующих преобразований голономии либо не
пересекаются, либо совпадают. Но все эти оси — это в точности множе-
множество поднятий выпрямления а. Снова применяя критерий; получаем, что
выпрямление кратно простой геодезической у. 14.6.211
Упражнение 4.6.22 (кратность). Докажите, что кратность, о которой идет
речь в предложении 4.6.21, не превосходит двух и равна двум, если и только если
а ограничивает лист Мёбиуса. (Указание: рассмотрите возможные промежуточные
накрытия для ШР/С, где G — группа, порожденная голономией петлн у).
Можно ли по-другому убедиться в том, что граница листа Мёбиуса стягивается
в удвоенную геодезическую, ее выпрямляющую? Сравните с вопросом о кольце из
упражнения 4.6.19, в.
Заметьте, что все результаты пп. 4.6.20—4.6.22 верны и прн более сла-
слабых ограничениях, чем компактность: достаточно предполагать, что мно-
многообразие (или его дубль) не содержит каспов.
276
Глава 4. Структура дискретных групп
Теорема 4.6.23 (пространство Тейхмюллера компактных поверх-
поверхностей). Пространство Тейхмюллера компактной, поверхности S с
гиперболической структурой гомеоморф но М3|хE)|. В частности, ес-
если S замкнута и ориентируема и имеет род g, то SFg — SFS — М6в~6.
Доказательство. Сначала дадим неформальное объяснение, сделав его
впоследствии строгим. Как следует из упражнения 4.6.19, в, поверхность 5
можно разрезать по попарно непересекающимся простым замкнутым кри-
кривым на панты в количестве |хE) | штук. Если на 5 задана гиперболическая
структура, то эти кривые превращаются в геодезические, а наши панты
становятся геодезическими пантами. И описание точки в пространстве STS
сводится к описанию этих гиперболических пант и способа их «склейки»
по заданной комбинаторной схеме.
Всего у наших пант имеется 3|хE)| граничных компонент, причем ка-
каждая граничная компонента склеивается с какой-то другой, если она про-
происходит из двусторонней кривой, или сама с собой, если перед нами од-
односторонняя кривая. Если она склеивается сама с собой, то имеется один
свободный параметр — длина кривой. Если же речь идет о склейке разных
компонент, то есть уже два свободных параметра: общая длина и скручи-
скручивание, которое характеризует относительное смещение «берегов» вдоль
общей геодезической. Скручивание — это произвольное вещественное чи-
число: направленное расстояние, причем в качестве единицы длины выби-
выбирается длина геодезической. (Тот факт, что скручивание — это веществен-
вещественный параметр, а не число на окружности S1, кажется на первый взгляд
странным, особенно если учесть, что скручивания, отличающиеся на це-
целое число оборотов, несомненно приводят к изометрическим поверхностям.
Но давайте вспомним, что в определение точки пространства Тейхмюллера
включается и то, сколько раз после одевания штанина пижамы окажется
перекрученной вокруг ножки младенца. Надеемся, что обратившись к дета-
деталям, мы сможем прояснить этот момент.) В любом случае у нас получается
3|хE)| свободных параметров, принимающих произвольные значения из
(О, оо) или (—оо, оо). Эти параметры известны под именем координат
Фенхеля—Нильсена в пространстве Тейхмюллера.
Переходим к формальным рассмотрениям. Зафиксируем попарно непе-
непересекающиеся ориентированные простые замкнутые кривые уь разрезаю-
разрезающие 5 на панты в количестве |хE)|. В каждом из пант разбиения выберем
три не пересекающиеся друг с другом дуги, попарно соединяющие гранич-
граничные компоненты. Позаботимся и о том, чтобы
а) для любой замкнутой кривой у,- лежащие на ней концы дуг в пантах,
смежных по у/, совпадали;
б) в общих концах направления наших дуг совпадали и были трансвер-
сальными кривой у,.
4.6. Пространства Тейхмюллера
277
И, наконец, выберем «берег» для каждой двусторонней кривой у,- — для
ориентированной поверхности 5 этот выбор естественно согласовать с
ориентацией 5 и у,. Иной выбор некоторых из этих объектов приведет, во-
вообще говоря, к другой системе координат Фенхеля—Нильсена, если только
разницу в выборе не удастся компенсировать изотопией 5.
Пусть теперь М — это поверхность 5 с некоторой гиперболической
структурой. На поверхности 5 любые две свободно гомотопные простые
замкнутые кривые могут быть переведены одна в другую с помощью
изотопии. Поэтому повторное применение предложения 4.6.21 и резуль-
результата упражнения 4.6.22 позволяют указать изотопию М, переводящую
кривые у, в простые замкнутые геодезические. Разумеется, эта изотопия
как-то деформирует выбранные дуги внутри пант, но при этом сохраняет их
простыми и соединяющими две компоненты границы у содержащих их пант
(см. рис. 4.19, слева). Далее, путем изотопии внутренности каждого панта
Рис. 4.19. Приведение дуги к стандартному виду. Простую дугу, соединяющую фик-
фиксированные точки двух граничных компонент гиперболических пант (слева) можно так
продеформировать, что она будет совпадать с соответствующим швом, за исключением
двух окрестностей граничных компонент, где она будет иметь вид спирали (справа).
При этом корректно определена степень «закрученное™» спирали: на нашем рисунке
это примерно —2,1 оборота у верхнего края и —0,15 оборота — у нижнего. (Чтобы
проверить корректность, можно начать с того, что рассмотреть индекс пересечения
нашей дуги с пунктирным экватором на левом фрагменте.)
можно привести каждую дугу к стандартному виду так, что она будет
совпадать с геодезическим швом, соединяющим граничные компоненты
(пример 4.6.7), всюду вне двух трубчатых окрестностей этих компонент.
278
Глава 4. Структура дискретных групп
А в указанных окрестностях наша дуга будет выглядеть как дуга спирали,
так что картина в целом будет зависеть только от степени «закрученности»
этой спирали и длины соответствующей граничной кривой.
С учетом ориентации у,- получаем для каждой стандартной дуги два
вещественных числа, представляющих степень ее закрученности по мере
движения из середины к каждому из краев. Назовем параметром скру-
скручивания на кривой у/ разность соответствующих чисел у двух дуг, концы
которых соединяются на у;. При этом параметр скручивания не зависит от
того, какая из двух пар дуг выбрана для его вычисления (см. рис. 4.20), и
он равен 0, если кривая является односторонней (почему?).
1 1
А \ /
( ¦ ' Л (
гт-^ 1 г tr
1 1
Г, 1
i i
j i
1 Г^
1
1
1
1
1
^ . '
Рис. 4.20. Вычисление параметра скручивания. На рисунке показана развертка
трубчатой окрестности замкнутой геодезической y/- Толстая кривая получилась нз од-
одной пары стандартных дуг, соответствующих друг другу в смежных пантах, а тонкая —
из другой аналогичной пары. (Сравните с рис. 4.19: наш рисунок — это результат
склейки изображенных там пант самих с собой с сохранением ориентации). По той
причине, что концы швов (пунктирные линии) с обеих сторон от т/ расположены в
диаметрально противоположных точках кривой y/, толстая и тонкая кривые дают одно
и то же значение параметра скручивания.
Из конструкции ясно, что параметры скручивания одинаковы у двух
гиперболических структур М и М', связанных изометрией, изотопной то-
тождественному отображению. Прн этом, разумеется, одинаковы и длины
кривых у/, и длины граничных компонент. И, как следствие, мы полу-
получаем отображение &S -» @, ооM-6 х Е', где через s обозначено число
замкнутых кривых в разложении 5, через / — число двусторонних сре-
среди них, а через Ь — число граничных компонент. Как уже отмечалось,
s + b + t = 3|хE)|. Теперь мы должны показать, что полученное отобра-
отображение биективно.
Несложно доказать сюръективность. Пусть координаты Фенхеля-
Нильсена заданы. Выберем геометрические панты с нужными параме-
параметрами и проведем в них стандартные дуги с заданной закрученностью.
Затем построим диффеоморфизмы топологических пант из разбиения 5 на
выбранные геометрические (начать можно с диффеоморфизма кривых у/
и граничных компонент, затем продолжить его на дуги, а затем и на
шестиугольники). В результате, дополнительно позаботившись о согласо-
согласованности наших диффеоморфизмов, получим гиперболическую структуру
на 5.
4.6. Пространства Тейхмюллера
279
Чтобы доказать инъективность, предположим, что у гиперболических
структур М и М' на 5 координаты Фенхеля—Нильсена одинаковы. По-
После применения изотопии можно считать, что у,- являются геодезическими
на М и М'. Изометрии соответствующих пант соединяются в изометрию
/: М —» М'\ здесь используется только то, что параметры скручивания
сравнимы по модулю 1. Остается доказать, что отображение / изотоп-
изотопно тождественному. Для этого мы сначала подправим отображение / так,
чтобы оно стало тождественным на у,- — это делается так же, как и в
упражнении 1.3.1. Затем, приведя дуги в стандартное положение, мы еще
раз подправим /, сделав его тождественным и на дугах. Осталось рас-
рассмотреть / внутри шестиугольников, но здесь мы просто воспользуемся
тем фактом, что диффеоморфизм замкнутого диска, тождественный на его
границе, изотопен тождественному.
Если вы поняли, как работают координаты Фенхеля—Нильсена, то до-
доказательство того, что они являются глобальными непрерывными пара-
параметрами в пространстве STS, становится простым, и мы не будем его
объяснять. 14.6.231
В том случае, когда две гиперболические структуры отличаются пара-
параметром скручивания вдоль лишь одной кривой у,-, и это отличие составля-
составляет ±1, мы говорим, что одна структура получается из другой с помощью
скручивания Дена. Рассмотрим общую ситуацию, когда на ориентирован-
ориентированной поверхности 5 имеется существенная простая петля у. Скручиванием
Цена вдоль у называется класс изотопии такого диффеоморфизма: поверх-
поверхность S сначала разрезается вдоль у, а затем полученный разрез снова
склеивается после одного полного поворота его сторон относительно друг
друга. Скручивание считается положительным, если в трубчатой окрест-
окрестности у его можно привести к виду, показанному на рис. 4.21 > а вне этой
окрестности сделать тождественным. Положительное скручивание Дена
вдоль у обозначим через ty. Иногда скручиванием Дена называют и любую
степень т".
Упражнение 4.6.24. Пусть М замкнутая, ориентированная гиперболическая
поверхность, а у — простая замкнутая геодезическая.
а) Объясните,-что происходит на универсальной накрывающей поверхности М
при применении скручивания Дена хт. (Считайте, что хт тождественно вне трубча-
трубчатой окрестности у и рассмотрите такое его поднятие, которое будет тождественно
на некотором открытом множестве в Ш2. Воспользуйтесь правой частью рис. 4.18
как моделью.)
б) Докажите, что счетное множество на окружности Slo остается поточечно на
месте, тогда как остальные точки на S]^ при этом перемещаются, сохраняя цикли-
циклический порядок. Получите как следствие тот факт, что скручивание xY не гомотопно
изометрин, а потому скручивание Дена действует на пространстве Тейхмюллера без
неподвижных точек.
280
Глава 4. Структура дискретных групп
Рис. 4.21. Модель скручивания Дена. Положительное скручивание Деиа на по-
поверхности сопряжено диффеоморфизму кольца А, показанному на рисунке. При этом
кольцо А имеет в R2 стандартную ориентацию. Не имеет значения то, каким образом
сопрягающее отображение вкладывает А в поверхность, коль скоро оио сохраняет
ориентацию; по той же причине правый винт остается правым при любом его положе-
положении в пространстве.
в) Обобщите на случай композиции степеней скручиваний Дена вокруг не-
нескольких простых замкнутых геодезических. Этим обобщением подтверждается тот
факт, что координаты Фенхеля—Нильсена действительно определяют разные точки
пространства Тейхмюллера, если их параметры скручивания отличаются на целые
числа, не все равные нулю.
Группа классов, сохраняющих ориентацию отображений замкнутой ори-
ориентированной поверхности, порождается скручиваниями Дена вдоль ко-
конечного числа кривых. Этот результат, к которому мы еще вернемся в
одной из следующих глав, был впервые получен Деном в его длинной статье
[Deh38], которая до сих пор мало кому известна, и независимо переоткрыт
в [Lic62]. По-видимому, Ден был первооткрывателем и следующей теоре-
теоремы, впервые опубликованной Нильсеном (тем не менее, он приписывает ее
Дену).
Теорема 4.6.25 (Ден—Нильсен). Группа классов отображений за-
замкнутой поверхности S изоморфна группе внешних автоморфизмов
фундаментальной группы tii(S).
(Группа внешних автоморфизмов группы G — это факторгруппа группы
автоморфизмов Aut(G) по нормальной подгруппе внутренних автоморфиз-
автоморфизмов; заметьте, что действие диффеоморфизма 5 -* S на фундаментальную
группу определено лишь с точностью до сопряженности, поскольку у нас
нет базисной точки.) Прозрачное доказательство этой теоремы вместе с
историческими комментариями можно найти в [Sti87].
Задача 4.6.26 (метки). Термин «отмеченная поверхность» относится к следу-
следующей ситуации: пусть М — ориентируемая замкнутая гиперболическая поверхность
4.7. 3-многообразня, моделируемые на расслоенных геометриях
281
рода g. «Отметим» М с помощью набора из 2g попарно непересекающихся петель
{а,-, Ы), исходящих из одной точки, и разрежем М вдоль петель, превратив ее
в стандартный 4§-угольник (при стандартном разрезании требуется гомотопность
~'&~'&'&'&) Д
нулю петлн a~'&~'ai&
(А!' { \}
ру
). Две отмеченные поверхности (М, {а,-,
й /
jjgg) р (М, {а, }
и (А!', {а,-, Ь\}) назовем эквивалентными, если для некоторой нзометрии/: М —> М'
семейство кривых {/(а,), /(&<)} гомотопно семейству {a-, bfi. Рассмотрите отобра-
отображение Ф из пространства Тейхмюллера в множество отмеченных поверхностей по
модулю эквивалентности. Используя среди прочего теорему 4.6.25, докажите, что
Ф является биекцией.
Замечание 4.6.27. Литература на тему пространств Тейхмюллера весь-
весьма обширна, но большая часть книг предполагает знакомство с мощ-
мощной комплексно-аналитической техникой. Из книг, предъявляющих к чи-
читателю более скромные требования и не игнорирующих геометрический
подход, укажем на [IT92]. Вот некоторые другие известные учебники —
[Gar87, Leh87, Nag88]; рекомендуем также обзор [Вег81].
4.7. 3-многообразия, моделируемые на расслоенных
геометриях
В разделах 4.3 и 4.4 мы выяснили, что евклидовы и эллиптические 3-мно-
3-многообразия тесно связаны с дискретными группами, действующими в раз-
размерностях один и два. Поэтому нет ничего удивительного в том, что имеют-
имеются аналогичные описания многообразий, моделируемых на любой из пяти
анизотропных геометрий из теоремы 3.8.4, б—в, поскольку любая из этих
геометрий естественно расслаивается над геометрией меньшей размерно-
размерности.
Этот раздел целиком посвящен изучению свойств многообразий, моде-
моделируемых на этих пяти геометриях. Многие доказательства здесь будут еще
беднее деталями по сравнению с доказательствами из предыдущих разде-
разделов. Одним из результатов наших исследований окажется утверждение о
том, что дискретные кокомпактные (или коконечные) группы в любой из
восьми модельных геометрий отличаются от таких же групп в любой другой
геометрии чисто алгебраическими свойствами (теорема 4.7.8). В частно-
частности, компактное 3-многообразие может нести максимум одну структуру из
восьми типов геометрических структур.
Упражнение 4.7.1 (классификация S2 х Е1-многообразий). Если <р —
изометрия сферы S2, то тор отображения Mv (пример 3.6.5) является примером
S2 х Е1 -многообразия. В самом деле, Mv есть факторпространство S2 х Е1
по действию дискретной группы, порожденной элементом (v, t) н-» (<ра, / + 1),
v e S2. Наше многообразие диффеоморфно S2 x S', если <р сохраняет ориентацию;
в противном случае оно неориентируемо. Какие еще многообразия допускают
S2 х Е1 -структуру?
282
Глава 4. Структура дискретных групп
а) Любая дискретная подгруппа изометрий пространства 52 х Е1 действует
на ?' дискретно (но ие обязательно свободно нли эффективно).
б) Дискретная группа нзометрнй Е1 изоморфна либо группе Z, либо свободному
произведению Z2 * Z2 двух циклических групп второго порядка.
в) С точностью до диффеоморфизма существуют лишь три замкнутых 3-мно-
гообразия, допускающих S2 х Е1 -структуру. Два из них ориентируемы, а одно нет.
Переходим к анализу оставшихся четырех случаев: Н2 х Е1, PSLB, Е),
нильгеометрия и солвгеометрия. Как и в теореме 3.8.4, X будет обозна-
обозначать модельное пространство, G — группу его изометрий, и G0 — связную
компоненту единицы в группе С.1
Удобства ради условимся говорить о почти Р группе, если в этой группе
есть подгруппа конечного индекса, обладающая свойством Р. Например,
дискретная группа движений евклидова пространства является почти абе-
левой группой (следствие 4.1.13).
Прежде всего мы изучим геометрии И2 х Е1 и PSLB, Е), расслаива-
расслаивающиеся над И2. Обозначим через р: G -> IsomH2 проекцию на группу
движений базы. Любой элемент из G0, проектирующийся в тождествен-
тождественное преобразование, лежит в центре группы G, а потому коммутатор двух
элементов из G0 зависит только от их образов при проекции.
Предложение 4.7.2 (образ в IsomH2 дискретен или почти абелев).
Пусть Г дискретная группа изометрий пространств Н2 х Е1 или
PSLB, E). Тогда образ р(Т) с IsomH2 или дискретен или содержит
абелеву подгруппу конечного индекса.
Доказательство. Поскольку любое из свойств, указанных в заключе-
заключении теоремы, сохраняется при переходе к подгруппе конечного индекса,
можно с самого начала считать, что Г с G0.
Выберем такую окрестность U единичного элемента в G0, что [U, U]<zU
и U П Г = {1}. Утверждается, что два элемента из Г, которые проектиру-
проектируются в рф), коммутируют. В самом деле, их коммутатор лежит в Г и
в U одновременно (нужно сдвинуть элементы вдоль слоя так, чтобы они
попали в О, а затем воспользоваться наблюдением, сделанным перед фор-
формулировкой предложения). Поэтому группа Н, порожденная элементами
р(Т) np{U), коммутативна.
Аналогично, выбрав для данного у ? Г такую окрестность U^ единицы
в G0, что [у, Ur] с U, получим, что у коммутирует с любым элементом из Г,
который проектируется в p(Ur).
Если образ р(Г) не дискретен, то замыкание И группы И — это замкну-
замкнутая абелева подгруппа без изолированных точек, в группе IsomH2. Следо-
Следовательно, Н — однопараметрическая группа. Как мы уже знаем, проекция
1В главе 3 эта же связная компонента (в силу требований момента) обозначалась через О',
что непривычно.— Прим. перев.
4.7. 3-многообразня, моделируемые на расслоенных геометриях
283
р(у) любого элемента у 6 Г коммутирует с элементами из пересечения
р(Т) np(U^). Но такие элементы порождают в Я плотную подгруппу, и
поэтому р(у) входит в централизатор подгруппы Н. Остается заметить,
что централизатор однопараметрической подгруппы группы IsomH2 абе-
абеСледствие 4.7.3 (дискретные группы изометрий пространств Н2 х
х Е1 и PSLB, E)). Дискретная группа изометрий пространства
X = Н2 х Е1 или X = PSLB, R) тогда и только коконечна, когда ее
действие на Н2 дискретно, коконечно и имеет бесконечное ядро.
Доказательство. Если действие на Н2 дискретно, т. е. р(Т) —дискрет-
—дискретная подгруппа в Isom H2, то
уо!(Л:/Г) = шющадь(Н2/>(Г)) • длина(Е'/(Г П Кегр)).
Мы видим, что в этом случае коконечность Г эквивалентна коконечности
группы р(Т) и бесконечности ядра Г П Кегр.
С другой стороны, если р{Т) не дискретна, то, как ясно из доказатель-
доказательства предложения 4.7.2, она сохраняет прямую, точку или орицикл в Н2.
Следовательно, группа Г дискретно действует на прообразе в X точки,
прямой или орицикла. Но при этом, как легко видеть, объем Х/Г в любом
случае бесконечен. 14.7.31
Упражнение 4.7.4. Объясните формулу для объема из предыдущего доказа-
доказательства. Насколько общей она является?
Предложение 4.7.5 (дискретные группы изометрий нильгеоме-
трии). Проекция дискретной группы Г изометрий нильгеометрии
в группу IsomE2 либо дискретна, либо оставляет инвариантной
прямую или точку в Е2.
Доказательство. Пусть р: G —» IsomE2 проекция группы G в группу
IsomE2. Предположим, что Г содержится в связной компоненте едини-
единицы G0 группы движений G. Тогда коммутант группы Г действует на Е2 па-
параллельными переносами, поскольку коммутатор двух сохраняющих ори-
ориентацию движений плоскости есть перенос. Далее, если yi и у2 элементы
из коммутанта [Г, Г], то коммутатор [уь у2] —это вертикальный сдвиг в
нильгеометрии на расстояние, равное площади параллелограмма, постро-
построенного на векторах р(уО@) — 0 и р(у2)@) — 0 из Е2.
Предположим, что найдется такой параллелограмм с ненулевой площа-
площадью. Обозначим через Т подгруппу вертикальных сдвигов в Г. Подгруппа Т
лежит в центре группы Г, а группа G°/T действует на плоскости с компакт-
компактными стабилизаторами. Поэтому, в силу предложения 3.5.8 (собственное
отображение сохраняет разрывность действия), группа Т/Т = р(Т) дей-
действует на Е2 разрывно.
284
Глава 4. Структура дискретных групп
С другой стороны, если все параллельные переносы в р([Т, Г]) линейно
зависимы, то имеются две возможности.
(i) Проекция р([Т, Г]) действует на плоскости тривиально. Тогда р(Т)
сохраняет точку, если в р(Т) есть элемент с нетривиальной линейной ча-
частью. В противном случае р(Т) состоит из одних переносов, а потому
дискретна.
(ii) Проекция р([Т, Г]) состоит из переносов вдоль прямой. В этом слу-
случае линейная часть любого элемента из р(Т) либо тривиальна, либо —
поворот на тс. А тогда, как легко видеть, группа р(Т) сохраняет прямую
вЕ2.
Наконец, общий случай, когда Г <?. G0, автоматически следует из уже
сказанного. 14.7.51
Следствие 4.7.6 (коконечность влечет кокомпактность в ниль-
геометрии). Крконечная группа изомегприй нильгеомепгрии коком-
пакпгна, а ее образ в группе Isom E2 дискретен.
Теперь рассмотрим солвгеометрию. Обозначим ее пространство через X,
группу движений — через G, и пусть G0 — связная компонента единицы в
группе G. Напомним, что алгебраически группа G° является расширением
вида 0 -* Ш2 -> G0 -> Е -» 0.
Предложение 4.7.7 (дискретные группы изометрий солвгео-
метрии). Если Го — дискретная подгруппа в G0, то Г0/(Г0 П R2)
дискретно действует на R. Любая дискретная подгруппа Г с G
действует на прямой Е дискретно, причем ядро этого действия —
дискретная группа изометрий евклидовой плоскости.
Доказательство. Любой элемент у 6 Го, не лежащий в Е2, действует,
как аффинное преобразование Е3, сохраняющее единственную вертикаль-
вертикальную прямую и параллельно сдвигающее вдоль нее (так как у у. действую-
действующего в R2, нет собственного значения, равного 1).
Если группа Го абелева, то она либо целиком содержится в R2, либо
действует параллельными переносами на единственной вертикали. В лю-
любом из этих случаев наше утверждение верно.
Если группа Го не коммутативна, то ее коммутант содержится в R2. Если
t б Го П R2, а у ? Го — Е2, то t и y^Y ~ линейно независимые переносы.
Поэтому группа Го П Е2 компактна. Действие Го на Е «пропускается» че-
через ее действие на пространстве Х/(Т0 П Е2), и значит, согласно 3.5.8,
образ Го в Е дискретен.
Все утверждения, касающиеся группы Г, отсюда уже легко следуют.
14.7.71
4.7. 3-многообразия, моделируемые на расслоенных геометриях
285
Теперь мы обладаем достаточной информацией для того, чтобы указать
алгебраические свойства кокомпактных групп в любой из восьми геоме-
геометрий, позволяющие эту геометрию по группе однозначно восстановить.
Теорема 4.7.8 (различие геометрий кокомпактных групп). Дис-
Дискретная кокомпактная группа Г автоморфизмов одной из восьми
трехмерных геометрий не изоморфна кокомпактной группе любой
другой геометрии.
Схема на рис. 4.22 представляет процесс восстановления геоме-
геометрии.
Г — кокомпактная группа
изометрий чего-нибудь
Конечна ли Г?
Нет
Почти лн Г абелева?
Нет
Почти ли Г нильпотентна?
Нет
Почти ли Г разрешима?
Нет
Содержит ли Г
нормальную бесконечную
циклическую подгруппу?
Почти ли Г циклична?
нильгеометрия")
солвгеометрия)
Нет
Факторгруппа —
кокомпактная дискретная
группа гиперболических
движений. Есть ли в ней
расщепимая подгруппа
конечного индекса?
Нет
Рис. 4.22. Схема для кокомпактных групп. Если Г — дискретная кокомпактная
группа автоморфизмов одной из восьми геометрий, то она не может быть дискретной
кокомпактной группой ни в какой другой из них. Схема показывает, как узнать, в какой
из восьми геометрий действует группа.
286
Глава 4. Структура дискретных групп
Доказательство. Большая часть необходимой информации уже собра-
собрана, так что осталось прояснить всего несколько дополнительных пунктов.
Из упражнения 4.7.1 и следствий 4.1.13, 4.7.3 и 4.7.6 можно сделать вы-
вывод, что группа всегда однозначно выбирает стрелку «Да» там, где схема
предписывает ей это сделать. Фактически, в предложении 4.7.7 доказано
более сильное утверждение о том, что кокомпактная группа в солвгео-
метрии является почти полициклической. Так как Г кокомпактна, то ее
бесконечная циклическая нормальная подгруппа в случае PSLB, Е) или
Н2 х Е1 совпадает с пересечением Г П Zo, где Zo — центр G0. Осталось
объяснить, почему никакая группа не выбирает стрелку «Да», если схема
запрещает ей это сделать.
Нетривиальная разрешимая группа содержит нетривиальную абелеву
нормальную подгруппу. Так как кокомпактная группа движений Н3 не со-
содержит нетривиальных нормальных абелевых подгрупп, то она пропускает
все стрелки «Да». Если Г дискретная кокомпактная группа изометрий
Н2 хЕ1 или PSLB, R), то согласно следствию 4.7.3, ее образ в группе
Isom H2 дискретен и кокомпактен, а потому не может быть почти разрешим
из уже известных нам соображений. Поэтому и сама группа Г не может
быть почти разрешимой, кокомпактная подгруппа в PSLB, E) не подни-
поднимается в группу PSLB, R) (упражнение 4.7.9), а потому кокомпактная
подгруппа изометрий пространства PSLB, E) не может выбрать стрелку
«Да» на финише. Остальные случаи проверяются еще проще. 14.7.81
Упражнение 4.7.9. Кокомпактная подгруппа в PSLB, К.) не поднимается в
группу PSLB,R).
Немного по-другому обстоят дела с не кокомпактными, но коконечными
группами.
Теорема4.7.10 (различие геометрий коконечных групп), коконеч-
ные, но не кокомпактные группы автоморфизмов существую лишь в
геометриях Н3, ffxE'u PSLB, E) (из восьми основных геометрий).
Любая такая группа автоморфизмов геометрии Н2 х Е1 действу-
действует и как коконечная группа автоморфизмов PSLB, E) и наоборот.
Оставшиеся случаи различаются с помощью блок-схемы на рис. 4.23.
Геометрия Н3 выделяется из остальных так же, как для кокомпактных
групп. Остальные утверждения теоремы 4.7.10 мы не доказываем.
Дискретные кокомпактные группы в ниль- и солвгеометриях можно оха-
охарактеризовать способом, близким по идее к характеризации дискретных
кокомпактных евклидовых групп с помощью теорем Бибербаха. Начнем с
нильгеометрии.
Имеется более симметричное вложение нильгеометрии в Е3 нежели то,
которым мы до сих пор пользовались. В разделе 3.7 мы определили стан-
стандартную контактную структуру в Е3 как поле плоскостей т, порожденных в
4.7. 3-многообразия, моделируемые иа расслоенных геометриях
287
Г — коконечная, но не
кокомпактная группа
изометрий чего-нибудь
Есть ли в Г нормальная
бесконечная циклическая
подгруппа?
Нет
Н2 х Е1 или PSLBJR)^)
Рис. 4.23. Схема для кокоиечных групп. Коконечные, но ие кокомпактиые груп-
группы автоморфизмов существуют лишь в трех геометриях из восьми. Эта блок-схема
показывает, как их различить.
точке (х, у, z) б Е3 векторами A, 0, 0) и @, 1, х). А в разделе 3.8 нильгео-
метрия рассматривалась как пространство Е3 с группой автоморфизмов,
которая состоит из контактных автоморфизмов, сохраняющих расслое-
расслоение на вертикальные прямые, и проектирующихся в изометрни плоскости
(х, У).
Давайте вместо поля т рассмотрим поле плоскостей о, порожденное
векторами A, 0, —у/2) и @, 1, х/2). Такое поле по-прежнему задает связ-
связность с кривизной 1 и определяет изоморфную контактную структуру: в
самом деле, диффеоморфизм
(х, у, z) ^y (x, y,z- х/2)
переводит т в ст. Любая прямая, перпендикулярно пересекающая ось z,
является лежандровой для поля ст. Это свойство, вместе с требованием,
чтобы кривизна ст была равна 1, однозначно определяет поле о.
Одно из преимуществ поля ст —наличие вращательной симметрии от-
относительно оси z. Более того, если рассмотреть любое линейное преобра-
преобразование плоскости (х, у), сохраняющее площадь, и поднять его в R3 так,
чтобы оно поточечно фиксировало ось z и сохраняло поле ст, то такое
поднятие оказывается линейным преобразованием. И вообще, линейное
преобразование плоскости с определителем с продолжается до контактно-
контактного линейного преобразования Е3, изменяющего масштаб по оси z в с раз.
А параллельные переносы плоскости продолжаются до аффинных пре-
преобразований Е3, сохраняющих ст.
Предложение 4.7.11 (аффинная нильгеометрия). Нильгеометрия
обладает такой аффинной структурой, что все автоморфизмы
нильгеометрии являются автоморфизмами аффинной структуры.
288
Глава 4. Структура дискретных групп
Если через Я обозначить группу Гейзенберга (которая содержится
в группе автоморфизмов нильгеометрии), то все непрерывные ав-
автоморфизмы Я индуцируют автоморфизмы аффинной структуры.
Доказательство. Автоморфизмы группы Гейзенберга индуцируют ав-
автоморфизмы аффинной структуры — вот единственное, что остается еще
проверить.
Любой такой автоморфизм ф индуцирует автоморфизм факторгруппы
группы Я по ее центру Z, т. е. автоморфизм Е2. Как мы уже видели, это
линейное преобразование продолжается до аффинного преобразования ф',
сохраняющего ст. Поскольку группа Гейзенберга состоит из поднятий па-
параллельных переносов плоскости, сохраняющих ст, то аффинное преобра-
преобразование ср' автоматически является автоморфизмом Я.
Далее, рассмотрим функцию /: Я —> Z, заданную формулой f(h) =
= ф'~'(Л) • <р(Л). На самом деле функция / — это гомоморфизм группы Я
в Z (фактически речь идет о линейной функции Е2 —* Е). Таким обра-
образом, автоморфизм ф записывается в виде ф' • /, т. е. является аффинным
преобразованием. 14.7.11|
Теорема 4.7.12 (кокомпактные группы в нильгеометрии). Груп-
Группа Г тогда и только тогда изоморфна кокомпактной дискретной
группе автоморфизмов нильгеометрии, когда
(i) она содержит подгруппу конечного индекса, изоморфную це-
целочисленной группе Гейзенберга
H=(a,b:[a,[a,b]] = [b,[a,b]]=l),
(и) централизатор Я в Г — бесконечная циклическая группа.
Доказательство. Если Г дискретная кокомпактная группа изометрий
нильгеометрии, то и на плоскости R2 она действует как дискретная коком-
кокомпактная группа движений. Пусть а и й—два элемента из Г, действующие
на плоскости как два линейно независимых переноса. Подгруппа, которую
они порождают, изоморфна Я. Поскольку коммутатор [а, Ь] — это нену-
ненулевой вертикальный перенос, то факторпространство Е3/Я компактно, а
значит индекс Я конечен.
Наоборот, пусть группа Г содержит Я как подгруппу конечного ин-
индекса. Обозначим через Яо пересечение всех подгрупп в Г, сопряженных
подгруппе Я.
Тогда Яо — это нормальная подгруппа конечного индекса в Г, которая
служит дискретной кокомпактной группой изометрий нильгеометрии. Для
продолжения ее нильгеометрического действия на группу Г необходимо,
чтобы автоморфизм Но, вызванный сопряжением элементом у б Г, был
индуцирован изометрией нильгеометрии.
4.7. 3-многообразия, моделируемые на расслоенных геометриях
289
Объясним, как получить нужное геометрическое действие. Сопряжение
группы Яо элементом уеГ порождает автоморфизм решетки Z2 (фак-
(факторгруппа Яо по ее центру Zo), а любой такой автоморфизм индуцирован
линейным преобразованием плоскости. Таким образом, конечная группа
Т/Но действует на плоскости, как группа линейных преобразований, и
можно выбрать в Е2 метрику, инвариантную относительно этого действия
(см. доказательство теоремы 4.2.6).
Но действие группы изометрий нильгеометрии на плоскости еще не
определяет ее действия во всем пространстве. В самом деле, с любой ли-
линейной функцией /: М2 —* К связано линейное преобразование Lf: Ш? —* R3,
{X, z) -» (X, z + f(X)), X б Е2, индуцирующее автоморфизм группы Гензен-
берга. И два геометрических действия группы Но, совпадающие на плос-
плоскости, отличаются на некоторый автоморфизм Lf\ здесь стоит обратить
внимание на то, что действие коммутанта группы в нильгеометрин уже од-
однозначно, так как полностью определяется площадями соответствующих
параллелограммов на плоскости Е2.
Заметим также, что любой автоморфизм группы Но «пропускается» че-
через автоморфизм Z2, а потому однозначно продолжается до непрерывно-
непрерывного аффинного автоморфизма группы Н. Следовательно, конечная группа
Г/#о естественно действует на множестве всевозможных нильгеометриче-
ских продолжений группы На с плоскости, причем это действие аффинно.
Но конечная группа аффинных преобразований всегда имеет неподвижную
точку — центр масс любой своей орбиты. Соответствующее неподвижной
точке геометрическое действие Но и является искомым: при таком действии
элементы конечной группы реализуются изометриями нильгеометрии.
Наконец, нам нужно предъявить нильгеометрическое действие Г. С этой
целью мы сначала построим индуцированное аффинное действие Г на
декартовом произведении N(r/Ha). Конструкция такова: обозначим через
р: Но —* Isom N — найденное ранее геометрическое представление Но и
рассмотрим пространство
уу(г/яо) = (Г/Яо) х уу = (Г х N)/(gh, x) ~ (g, p(h)x).
Далее, если gt — автоморфизм ннльгеометрии, представляющий i-й смеж-
смежный класс в Г/Яо, то всевозможные вложения N в yV(r/Wo) вида х —*
-* (С?ь *)> •••> (ёгч х)), п = |Г/#0|, образуют Г-инвариантное слоение
пространства N(T/Ha) с Яо-инвариантнымн слоями. Так же, как и при до-
доказательстве предложения 4.2.5, можно убедиться в том, что существует
Г-инвариантный слой. Он то нам н нужен: действие Г на нем и есть
искомое нильгеометрическое действие Г.
Условие эффективности действия Г проверяется легко: тривиальное
действие у на N возможно лишь в том случае, когда у лежит в централи-
централизаторе Но (нли, что то же самое, в централизаторе Н). Но централизатор Яо
290
Глава 4. Структура дискретных групп
в группе Isom N совпадает с группой Е вертикальных переносов, а пото-
потому централизатор действует эффективно тогда и только тогда, когда он
является бесконечной циклической группой. 14.7.121
Теорема4.7.13 (кокомпактные группы в солвгеометрии). Группа Г
тогда и только тогда служит дискретной кокомпактной группой
автоморфизмов солвгеометрии, когда она содержит такую под-
подгруппу Н конечного индекса, что
(/) централизатор Н тривиален,
(ii) H есть расширение вида
Z2 _» Н -> Z,
причем действие Ъ на Z2 порождается гиперболическим элементом
группы SLB, Z).
Доказательство. Если Г—дискретная кокомпактная группа автомор-
автоморфизмов солвгеометрии, то группа И = Г П Go действительно является рас-
расширением указанного вида (нужно использовать 4.7.7).
Наоборот, если Г содержит подгруппу Н конечного индекса, указанного
в условии теоремы вида, то можно построить дискретное кокомпактное
действие И на X (см. упражнение 3.8.10). Без потери общности можно
считать, что Н — нормальная подгруппа в Г. Теперь нужно показать, что
любой автоморфизм Н индуцирован сопряжением с помощью некоторо-
некоторого элемента группы G, нормализующего действие И на X. В самом деле,
любой автоморфизм переводит в себя подгруппу Z2 и одновременно либо
сохраняет каждое из двух собственных подпространств гиперболического
элемента в К2 = Z2 ® Е, либо меняет их местами. Отсюда следует, что.
ограничение автоморфизма на Z2 можно реализовать с помощью элемента
конечного порядка из группы G, добавив к нему, в случае необходимости,
сдвиг в вертикальном направлении t, чтобы добиться нужного растяжения
собственных подпространств. Остается еще одна образующая группы И,
представляющая из себя сдвиг вдоль некоторой прямой. Автоморфизм пе-
переведет ее в сдвиг вдоль новой прямой, причем направление сдвига оста-
останется прежним или изменится на противоположное в зависимости от того,
сохраняет рассматриваемый автоморфизм собственные подпространства
в R2 или меняет их местами. Тогда с помощью горизонтального переноса
можно добиться нужного действия этой образующей, не изменив действия
остальных.
Заметим также, что разные элементы G не могут давать одинаковые
автоморфизмы Н. Поэтому наша конструкция приводит к гомоморфизму
Aut# -> G, который продолжает заданное вложение И в группу G. На-
Наконец, с помощью композиции отображений Г -»Aut И -» G мы получаем
все, что нужно. 14.7.131
4.7. 3-многообразия, моделируемые на расслоенных геометриях
291
Трудная задача 4.7.14 (нерасщепимые группы в расслоенных геометриях).
Докажите, что существуют интересные дискретные группы изометрнй в И2 х W
которые проектируются на оба множителя в недискретные группы. Но сначала
разберитесь с задачей 4.3.16.
а) Пусть G — группа с копредставленнем
(а, р, т | а2 = р2 = Y2 = (а|3O = фтO = (таO = 1).
Рассмотрим три треугольника: два с углами (тс/7, 2тс/7, 2тс/7) н (Зтс/7, тс/7, тс/7)
на гиперболической плоскости, а третий с углами Bтс/7, Зтс/7, Зтс/7) — на сфе-
сфере 5 . Тогда имеются три гомоморфизма группы G в группы движений соот-
соответствующих геометрий. Докажите, что у диагонального гомоморфизма в группу
Isom(H х Шг х 5 ) образ дискретен, и, как следствие, дискретна его проекция в
группу Isom(Er x Шг).
[Указание: выпишите в линейных моделях И2 и S2 матрицы Грама, связанные
с этими треугольниками (см. раздел 2.4). Обратите внимание на то, что все их
матричные элементы — целые алгебраические числа. Укажите решетку в R9, инва-
инвариантную относительно диагонального действия группы G. Выведите отсюда, что
группа G дискретна.]
б) Докажите, что образ группы G в группе Isom(H2) не дискретен. Для этого
проверьте, что обе проекции тц итс2 группы G в группу Isom(Н2) изоморфны, но прн
этом имеется такая подгруппа И с G, что проекция тс,(//) стоит из эллиптических,
а тсг(Я) — из гиперболических элементов.
в) Докажите, что все три гомоморфизма группы G не являются точными.
Словарь терминов
Абсолют. Принятое в отечественной литературе название сферы на
бесконечности S1^.
Аксиома Евклида о параллельности (пятый постулат). Пятый по-
постулат Евклида звучит так: «Через точку, не лежащую на прямой, проходит
ровно одна прямая, параллельная данной». У этой аксиомы евклидовой
геометрии имеется множество эквивалентных формулировок. Например,
такая: «Сумма углов треугольника равна 180°».
База. См. расслоение.
Барицентрическое подразделение. Барицентрическое подразделение
треугольника получается, если соединить его центр тяжести (т. е. точку
пересечения медиан) со всеми вершинами и серединами сторон. Барицен-
Барицентрическое подразделение триангуляции — это триангуляция, составленная
из треугольников барицентрических подразделений исходной триангуля-
триангуляции.
Вложение. См. погружение.
Геодезические [dC76]. Геодезические — это наикратчайшие кривые.
Точнее, кривая у: I —*Х (/ — интервал из К) на римановом многообразии
X называется геодезической, если для любых достаточно близких точек
х, у б /, у([х, у]) есть кратчайший путь, соединяющий у{х) и у{у) на X.
Обычно также требуется, чтобы путь у проходился с постоянной (возмож-
(возможно, нулевой) скоростью. Образ у(/) также часто называют геодезической.
Геометрия. Иногда мы используем слово «геометрия» как синоним
слова «метрика». Иногда термин «геометрия» относится к некоторому
набору свойств пространства, зависящих от его метрики. Иногда же это
понятие употребляется для обозначения свойств пространства, инвари-
инвариантных относительно действия некоторой (какой — зависит от контекста)
группы преобразований данного пространства. Именно так обстоит дело с
проективной, евклидовой и гиперболической геометрией.
Гладкость. См. дифференцируемое отображение.
• Словарь терминов
293
Гомотетия [Вег87, т. I, с. 39]. Гомотетией с центром в точке р € Е"
называется отображение, оставляющее р на месте, и «растягивающее» или
«сжимающее» все пространство по лучам, выходящим из точки р. Точнее,
гомотетия переводит точку q в точку k(q — р) + р, где вещественный ко-
коэффициент k фиксирован.
Гомотопия, гомотопные отображения, гомотопная деформация
[Мип75, с. 318—319]. Два непрерывных отображения f, g: X-*Y назы-
называются гомотопными, если их можно непрерывно продеформировать
одно в другое, т. е. если существует такое непрерывное отображение
F: X х [0, 1] -> Y, что F\Xx{oy = f и F\xX{iy = g- Это отображение на-
называется гомотопией между / и g; в этом случае мы будем говорить,
что отображение / можно гомотопно продеформировать в g с помо-
помощью F. Ограничения F\Xx{i} при / 6 [0, 1] называются промежуточными
отображениями гомотопии и обычно обозначаются через Ft: X —* У.
Группа изотропии, изотропность. Пусть группа G действует на про-
пространстве X Стабилизатором, или подгруппой изотропии, точки х е X
называется подгруппа Gx группы G, состоящая из элементов, оставляю-
оставляющих х на месте. Многообразие X называется изотропным (относительно
действия G), если стабилизатор каждой точки транзитивно действует на
касательном пространстве в этой точке.
Двугранный угол — это угол между двумя пересекающимися плоско-
плоскостями, который измеряется величиной плоского угла, высекаемого данны-
данными плоскостями на плоскости, перпендикулярной каждой из них.
Действие [Вег87, т. I, с. 5]. Действием группы G на топологическом
пространстве X называется гомоморфизм группы G в группу гомеомор-
гомеоморфизмов пространства X. Образ точки х € X под действием гомеоморфизма,
представляющего элемент g e G, будем обозначать через g(x). Такое дей-
действие (G-действие) определяет отношение эквивалентности на простран-
пространстве X: х ~ у тогда и только тогда, когда у = g(x) для некоторого g€.G. Со-
Соответствующие классы эквивалентности называются орбитами группы G.
Пространство орбит, снабженное фактортопологией, называется фактор-
пространством X по действию группы G.
Деформационный ретракт. Подпространство А пространства X на-
называется деформационным ретрактом X, если существует такая гомо-
гомотопия F: X х [0, 1] —* X, для которой Fo = Ых, Ft переводит X в А и все
отображения F, тождественны на А.
Диффеоморфизм, диффеоморфность. Взаимно однозначное отобра-
отображение /: X -> Y называется диффеоморфизмом, если и / и /-' дифферен-
дифференцируемы. Пространства X и Y в этом случае называются диффеоморф-
ными.
294
Словарь терминов
Дифференцируемое отображение [Hir76, с. 9, 15]. Отображение
/: U —» W, где U — открытое подмножество R", называется диффе-
дифференцируемым класса Сг (или Сг-отображением), если все частные
производные / до порядка г включительно определены и непрерывны в U.
Отображение /: X —>Rm произвольного подмножества XcR" называется
дифференцируемым класса С, если оно продожается до С-отображения
некоторой окрестности подмножества X.
Отображение /: X-+Y двух дифференцируемых многообразий с краем
называется С -дифференцируемым, если в любой точке многообразия X
оно имеет локальное представление класса С'.
Евклидова метрика, евклидово пространство [Вег87, с. 153, 202].
Евклидово п-мерное пространство Е" {евклидова плоскость при
п = 2) есть пространство Ш", наделенное евклидовой метрикой
d(x, у) =
где х = (Xi, ..., хп) и у = (ух, ..., уп) - точки из R". При п = 3 это окру-
окружающее нас пространство.
Замощение [Вег87, т. I, с. 11-31]. Грубо говоря, замощение про-
пространства X — это способ заполнить X экземплярами одного или несколь-
нескольких образцов, или черепиц. Есть много разных способов формализовать
и ограничить это определение так, чтобы с ним можно было работать.
Выберем следующее определение: замощение пространства X состоит из
связного компактного подмножества Р с X и подгруппы G группы изо-
метрий пространства X таких, что внутренность Р не пуста, объединение
образов Р под действием G есть X и никакие два различных G -образа Р
не имеют общих внутренних точек.
Изометрия, изометричность. Взаимно однозначное отображение ме-
метрических пространств называется изометрией, если оно сохраняет рас-
расстояние. При этом сами пространства называются изометричными. Ото-
Отображение /: X —> Y называется локальной изометрией, если у каждой
точки х е X имеется такая окрестность, что ограничение f на нее является
изометрией.
Изотопия. Изотопией между отображениями f и g называется та-
такая гомотопия F: X х [0, 1] -> Y, что все промежуточные отображения
F,: X —> Y при t е [0, 1] являются гомеоморфизмами на свой образ.
Инвариантность области. Если подмножество A c.R" гомеоморфно
открытому подмножеству Ж", то оно само открыто. Отсюда легко следует,
что m-мерное многообразие не может содержать подмножества, гомео-
морфного Ш", при п> т.
Словарь терминов
295
Компактно-открытая топология. На множестве S? непрерывных ото-
отображений X —> Y можно ввести компактно-открытую топологию,
задав базу, состоящую из открытых множеств вида {/ е J*: //С С ?/}, где
К — компакт в X, a U — открытое множество в U. Если пространства X
и Y хаусдорфовы, то это слабейшая топология, в которой отображение
{/, х) н-> f(x) непрерывно.
Конус (над пространством). Конусом над топологическим простран-
пространством X называется цилиндр X х [0, 1 ], у которого отождествлены между
собой все точки нижнего основания X х {0}.
Накрытие, накрывающее отображение, пространство накрытия,
преобразование накрытия, группа накрытия [Mun75, с. 331-341, 398].
Непрерывное отображение р: Х—*Х линейно связных пространств назы-
называется накрывающим, если у любой точки х е X найдется такая окрест-
окрестность V, что каждая связная компонента прообраза p~{(V) гомеоморф-
гомеоморфно отображается на V с помощью р. В этом случае X называется про-
пространством накрытия (или накрывающей пространства X), а тройка
(X, р, X) — накрытием. Преобразованием накрытия называется такое
непрерывное отображение ср: X —> X, что р о ср = р; преобразования на-
накрытия образуют группу, которая называется группой накрытия. Если
пространство X односвязно, то его называют универсальной накрыва-
накрывающей («его», потому что в этом случае оно определено однозначно, с
точностью до гомеоморфизма).
Нильпотентная группа. Обозначим через Z(G) центр группы G. Верх-
Верхний центральный ряд
Zo с Zi с ... с Z,- с ...
группы G определяется индуктивно. Положим Zo = {е} (где е — единич-
единичный элемент) и Zi/Zl_l = Z(G/Z,^i). Группа G называется нильпотентной
(ступени k), если Zk = G. Таким образом, группа абелева тогда и только
тогда, когда она является нильпотентной ступени 1.
Объемлющее пространство/гомеоморфизм. Если рассматриваются
два пространства (многообразия, ...), из которых одно содержится в дру-
другом, то большее пространство называется объемлющим. В этом случае
объемлющим гомеоморфизмом (диффеоморфизмом, ...) называется го-
гомеоморфизм (диффеоморфизм, ...) объемлющего пространства.
Односвязность. См. фундаментальная группа.
Орбита. См. действие.
296
Словарь терминов
Словарь терминов
297
Ориентация, ориентируемость, сохранение (обращение) ориен-
ориентации [МП65, с. 27]. Ориентацией конечномерного пространства назы-
называется класс эквивалентности (упорядоченных) базисов, для которых ма-
матрица перехода от одного к другому имеет положительный определитель.
Линейный оператор, действующий между двумя ориентированными век-
векторными пространствами, будем называть сохраняющим ориентацию
или меняющим ориентацию в зависимости от того, положителен или
отрицателен его определитель.
Многообразие М называется ориентируемым, если можно согласо-
согласованно ввести ориентацию на касательных пространствах к М во всех точ-
точках. Согласованность означает, что на М существует такой атлас, для
которого все производные координатных отображений являются сохра-
сохраняющими ориентацию операторами из Тх в R" со стандартной ориентаци-
ориентацией. Многообразие М называется ориентированным, если зафиксирована
такая ориентация касательных пространств. Локальный диффеоморфизм
ориентированных многообразий называется сохраняющим ориентацию
или меняющим ориентацию в данной точке х в зависимости от того,
каким оператором является его производная в данной точке.
Отмеченная точка. См. фундаментальная группа.
Погружение [Hir76, с. 21]. Дифференцируемое отображение /: М —>N
дифференцируемых многообразий называется погружением, если произ-
производная df имеет максимальный возможный ранг во всех точках р е М.
Если отображение f к тому же является гомеоморфизмом на свой образ,
то оно называется вложением. В частности, вложение есть взаимно од-
однозначное погружение.
Подобие [Вег87, т. I, с. 183]. Подобием называется преобразование
евклидова пространства, изменяющее все расстояния в фиксированное чи-
число k раз
Положительная (неотрицательная) определенность. См. сигна-
сигнатура.
Полугруппа. Полугруппой называется множество с ассоциативным
умножением.
Порядок. Порядком элемента g группы G называется такое наимень-
наименьшее натуральное число п {если оно существует), что g" = e.
Поток. Пусть X — топологическое пространство. Потоком1 на X на-
называется такое семейство непрерывных отображений f,: X —> X (t e R), что
/о = И* и fs+l = fsof, при всех s, t € R.
1 Или однопараметрической группой гомеоморфизмов.— Прим. перев.
Равномерно накрывающее отображение [Мип75, с. 331]. Пусть
р: X —> Y — непрерывное сюръективное отображение топологических про-
пространств, a U — открытое подмножество Y. Множество U равномерно
накрывается отображением р, если p~l(U) есть дизъюнктное объедине-
объединение открытых множеств, каждое их которых гомеоморфно проецируется
на U отображением р. Таким образом, р является проекцией накрытия,
если у каждой точки из Y есть окрестность, равномерно накрываемая р.
Расслоение, локально тривиальное расслоение [Spa66, с. 90].
Сюръективное отображение р: Е—> В топологических пространств назы-
называется проекцией расслоения, если локально оно выглядит как проекция
на сомножитель прямого произведения, т. е. если существует такое про-
пространство F, что для любой точки х € В найдется такая ее окрестность U
и отображение фу: U х F —»p~\U), что р о фу = ль где Л]: U х F —> U —
проекция на первый сомножитель. Четверка (Е, В, F, р) называется
локально тривиальным расслоением, где F — слой расслоения, Е —
тотальное пространство расслоения, а В — база расслоения. Ино-
Иногда расслоением также называют само пространство Е или говорят, что
пространство Е расслаивается над базой В.
Пусть G — подгруппа группы гомеоморфизмов слоя F. Локально триви-
тривиальное расслоение (Е, В, F, р) называется G-расслоением, если множе-
множества U и отображения фу, описанные выше, можно выбрать так, чтобы они
отвечали следующему дополнительному условию: для каждой точки х е В,
принадлежащей пересечению двух таких множеств Un V, гомеоморфизмы
F —> р~1(х), заданные ц>и и фу, отличаются на действие некоторого элемен-
элемента группы G.
Репер, расслоение реперов, r-репером векторного пространства V
называется упорядоченный набор г линейно независимых векторов из V.
Если размерность V равна п, то /г-репер есть не что иное, как упорядочен-
упорядоченный базис. Если М —дифференцируемое многообразие, то множество всех
r-реперов в касательных пространствах к М во всех точках образует ло-
локально тривиальное расслоение r-реперов над М, или просто расслоение
реперов, если г = dim M.
Риманово многообразие, риманова метрика [BG88, с. 126]. Рима-
ново многообразие — это многообразие X, в каждой точке р которого
задано положительно определенное скалярное произведение в касатель-
касательном пространстве ТРХ, причем это соответствие, называемое римановой
метрикой, гладко зависит от точки р. При заданном скалярном произве-
произведении можно говорить о длине касательного вектора и, следовательно, о
длине пути.
Сигнатура. Каждую квадратичную форму Q на Ж" можно линейной
заменой координат привести к одной из форм вида х\ + ... + х2г — (х2г+1 +
298
Словарь терминов
+ ... + x2r+s), где г + s < п. Сигнатурой формы называется пара (г, s),
которая однозначно определяет форму Q, с точностью до линейной замены
координат. Рангом формы Q называется число r + s. Форма Q называ-
называется положительно определенной, если г = п (т. е. если она принимает
положительное значение на любом ненулевом векторе) и неотрицатель-
неотрицательно определенной, если s = О {т. е. если она принимает неотрицательное
значение на любом векторе). Точно так же определяются отрицательно
определенные и неположительно определенные формы.
Собственное отображение. Отображение называется собственным,
если прообраз каждого компакта — компакт.
Стабилизатор. См. группа изотропии.
Стягиваемость. Топологическое пространство X называется стягива-
стягиваемым, если тождественное отображение X в себя гомотопно постоянному
отображению X *-* х0 € X.
Теорема о промежуточном значении. Непрерывная функция /:
[а, Ь] —> Ж, принимающая отрицательное значение в точке а и положитель-
положительное—в точке Ъ, обязательно где-нибудь на интервале (а, Ь) обращается в
нуль {тривиальное следствие связности интервала).
Топологическая группа. Топологической группой G называется та-
такое топологическое пространство, наделенное структурой группы, что ото-
отображения {gi, g2)^gig2 ng^g-1 непрерывны.
Тотальное пространство. См. расслоение.
Универсальная накрывающая. См. накрытие.
Факторпространство по действию группы. См. действие.
Фактортопология [Мип75, с. 134—136]. Для топологического про-
пространства X с некоторым отношение эквивалентности ~ определим фак-
тортопологию на множестве классов эквивалентности Х/~, объявив
открытыми1 те и только те множества классов эквивалентности, полный
прообраз которых открыт в X.
Фундаментальная группа [Mun75, с. 326]. Если X — связное топо-
топологическое пространство, то множество гомотопических классов петель,
начинающихся и кончающихся в данной отмеченной точке простран-
пространства X, образует группу относительно последовательного обхода петель.
Это и есть фундаментальная группа пространства X; если эта группа
тривиальна, то пространство X называется односвязным.
'То есть, фактортопология есть наименьшая из топологий, в которых непрерывна есте-
естественная проекция X —» Х/~ .— Прим. перев.
Словарь терминов
299
Эффективное действие. Действие группы G на пространстве X назы-
называется эффективным, если только единичный элемент группы Г действует
тождественно на X.
О(-). Для двух вещественнозначных функций / и g выражение / = O(g)
означает, что f(x) < Cg(x) для некоторой константы С и всех достаточно
больших х. В частности, / растет полиномиально, если для некоторого
п верно, что / = О(х"), т. е. функция / ограничена полиномом /г-й степени.
С, С°°. См. дифференцируемое отображение.
Литература
[АЫ80] Abikoff W. The real analytic theory of Teichmuller space. Berlin: Springer,
1980.
Имеется перевод: Абикоф У. Вещественно-аналитическая теория
пространств Тейхмюллера. М.: Мир, 1985. 119 с.
[АЫ60] A h I f о rs L. The complex analytic structure of the space of closed riemann
surfaces // Analytic Functions / Ed. Rolf Nevanlinna. Princeton: Princeton
University Press, 1960. P. 45-66.
Имеется перевод: Альфорс Л. Комплексно-аналитическая структу-
структура в пространстве римановых поверхностей// Альфорс Л., Берс Л.
Пространства римановых поверхностей и квазиконформные отображе-
отображения. М.: ИЛ, 1961. С. 51-80.
[Вае28] В а е г R. Isotopien von Kurven auf orientierbaren, geschlossenen Flachen //
Journal fur die Reine und Angewandte Mathematik 159 A928). P. 101-116.
[Bar94] Barlow W. Uber die geometrischen Eigenschaften homogener starrer
Strukturen und ihre Anwendung auf Krystalle // Zeitschrift fur Krystal-
lographie und Mineralogie 23 A894). P. 1-63.
[BCH84] Bloch E. D., Connelly R., Henderson D. W. The space of simplex-
wise linear homeomorphisms of a convex 2-disk // Topology 23 A984), №2.
P. 161-175.
[BerSl] Bers L. Finite-dimensional Teichmuller spaces and generalizations // Bull.
Amer. Math. Soc. (N.S.) 5 A981), №2. P. 131-172.
[Ber87] Berger M. Geometry. I, II. Berlin: Springer-Verlag, 1987.
Имеется перевод: Б е р ж е М. Геометрия: В 2-х т. М.: Мнр, 1984. Т. 1.
368 с; Т. 2. 560 с.
[BG88] Berger M., Gostiaux В. Differential Geometry: Manifolds, Curves and
Surfaces. New York: Springer-Verlag, 1988.
[Bia92] Bianchi L. Sui gruppi di sostituzioni Hneari con coefficienti appartenenti
a corpi quadratici immaginari // Math. Ann. 40 A892). P. 332-412.
[Biell] Bieberbach L..Uber die Bewegungsgruppen der euklidischen Raume I
// Math. Ann. 70 A911). P. 297-336.
[Biel2] Bieberbach L. Uber die Bewegungsgruppen der euklidischen Raume II
// Math. Ann. 72 A912). P. 400-412.
[Bin54] Bing R. H. Locally tame sets are tame // Ann. of Math. B) 59 A954).
P. 145-158.
Литература
301
[Bin59] Bing R. H. An alternative proof that 3-manifolds can be triangulated //
Ann. of Math. B) 69 A959). P. 37-65.
[Bra49] Bravais A. Memoire sur les polyedres de forme symetrique // J. Math.
Pures Appl. 14 A849). P. 141-180.
[Brol2] Brouwer L. E. J. Beweiss des ebenen Translationsatzes // Math. Ann.
72 A912). P. 37-54.
[ВгобО] В rod у Е. J. The topological classification of lens spaces // Ann. of Math.
B) 71 A960). P. 163-184.
[Bus55] Busemann H. The Geometry of Geodesies. New York: Academic Press,
1955.
Имеется перевод: Буземан Г. Геометрия геодезических. М.: Физ-
матгиз, 1962. 504 с.
[Can79] Cannon J. W. Shrinking cell-like decompositions of manifolds. Codimen-
sion three // Ann. of Math. B) 110 A979). P. 83-112.
[Cha86] Charlap L. S. Bieberbach groups and flat manifolds. New York: Springer-
Verlag, 1986.
[dC76] do С a rm о M. P. Differential Geometry of Curves and Surfaces. Englewood
Cliffs, NJ: Prentice-Hall, 1976.
[dC92] do Carmo M. P. Riemannian Geometry. Boston, MA: Birkhauser, 1992.
[DE86] Douady A., Earle C. J. Conformally natural extension of homeomor-
homeomorphisms of the circle // Acta Math. 157 A986), №1-2. P. 23-48.
[Deh38] Dehn M. Die gruppe der abbildungsklassen // Acta Math. 69 A938).
P. 135—206. English transl. in: Papers on Group Theory and Topology. New
York: Springer-Verlag, 1987. P. 256-362.
[Eps66] Epstein D. A. Curves on 2-manifoIds and isu'.pies // Acta Math. 115
A966). P. 83-107.
[Fed49] Фёдоров Е. С. Симметрия и структура кристаллов. М.: АН СССР,
1949. English transl.: Fedorov E. S. Symmetry of Crystals, New York:
American Crystallographic Association, 1971.
[FK12] Fricke R., Klein F. Vorlesungen uber die Theorie der automorphen
Funktionen. Stuttgart: Teubner Verlag. Band I, 1897; Band II, 1912.
[Fra87] Francis G. K- A Topological Picturebook. New York: Springer-Verlag,
1987.
Имеется перевод: Франсис Дж. Книжка с картинками по тополо-
топологии. М.: Мир, 1991.240 с.
[Gab83] Gabai D. Foliations and the topology of 3-manifolds // J. Differential
Geom. 18 A983), №3. P. 445-503.
[Gab87] Gabai D. Foliations and the topology of 3-manifolds. II, III//J. Differential
Geom. 26 A987), №3. p. 461-478, 479-536.
[Gar87] Gardiner F. P. Teichmuller theory and quadratic differentials. New York:
John Wiley & Sons, 1987.
302
Литература
[GHL90] Gallot S., Hulin D., Lafontaine J. Riemannian Geometry. 2nd ed.
Berlin: Springer-Verlag, 1990.
[GM91] Gunn Ch., Maxwell D. (directors). Not Knot. А К Peters, Wellesley,
1991. A6-minute video produced by The Geometry Center, University of
Minnesota; see http://www.geom.umtt.edu/video/NotKnot).
[Hae58] Haefliger A. Structures feuilletees et cohomologie a valeur dans un fais-
ceau de groupoldes // Comment. Math. Helv. 32 A958). P. 248-329.
[Hat83a] Hatcher A. E. Hyperbolic structures of arithmetic type on some link com-
complements // J. London Math. Soc. B) 27 A983), №2. P. 345-355.
[Hat83b] Hatcher A. E. A proof of a Smale conjecture, Diff(S3) ss OD) // Ann. of
Math. B) 117 A983). P. 553-607.
[Hes30] Hessel J. F. С Krystallometrie oder Kxystallometrie und Krystallographie
II Gehler's Phys. Worterbuch, Band 5, Abtheilung 2. Liepzig: Schwickert,
1830.
[Hic65] Hicks N. Notes on Differential Geometry. Princeton, NJ: Van Nostrand
Co., 1965.
[HilOl] Hilbert D. Uber Flachen von konstanter Gausscher Krummung Ц Trans.
Amer. Math. Soc. 2 A901), №1. P. 87-99.
[Hir76] Hirsch M. Differential Topology. New York-Heidelberg: Springer-Verlag,
1976.
Имеется перевод: Хирш М. Дифференциальная топология. М.: Мир,
1979. 279 с.
[Нос65] Hochschild G. The Structure of Lie Groups. San Francisco-London-
Amsterdam: Holden-Day Inc., 1965.
[Hop26] H о p f H. Zum Clifford-Kleinschen Raumproblem // Math. Ann. 95 A926).
P. 313-339.
[H6r90] Hormander L. An introduction to complex analysis in several variables.
3rd ed. Amsterdam: North-Holland Publ. Co., 1990.
Имеется перевод: Хермандер Л. Введение в теорию функций не-
нескольких комплексных переменных. М.: Мир, 1968. 279 с.
[HR31] Hopf H., Rinow W. Uber den Begriff der vollstandingen differentialge-
ometrischen Flachen // Comment. Math. Helv. 3 A931). P. 209-225.
[HW35] Hantschze W., Wendt H. Dreidimensionale euklidische Raumforme //
Math. Ann. 110 A935). P. 593-611.
[IT92] Imayoshi Y., Taniguchi M. An Introduction to Teichmiiller Spaces.
Tokyo: Springer-Verlag, 1992.
[Jor77] Jorgensen T. Compact 3-manifolds of constant negative curvature fiber-
ing over the circle // Ann. of Math. B) 106 A977). P. 61-72.
[KS69] Kirby R. C, Siebenmann L. С On the triangulation of manifolds and
the Hauptvermutung// Bull. Amer. Math. Soc. 75 A969). P. 742-749.
[Kui55] К u i p e r N. H. On C1 -isometric embeddings, III I Nederl. Akad. Wetensch.
Proc. Sen A 58 A955). P. 683-689.
Литература
303
[Leh87] Lehto O. Univalent Functions and Teichmuller spaces. New York: Sprin-
Springer-Verlag, 1987.
[Lic62] Lickorish W. B. R. A representation of orientable combinatorial 3-man-
3-manifolds // Ann. of Math. B) 76 A962). P. 531-540.
[Lic65] Lickorish W. B. R. A foliation for 3-manifolds // Ann. of Math. B) 82
A965). P. 414-420.
[Mag74] Magnus W. Non-Euclidean Tesselations and Their Groups. New York-
London: Academic Press, 1974.
[Mar71] Martinet J. Formes de contact sur les varietes de dimension 3 Ц Proc.
Liverpool Singularities Symposium. II / Ed. С. Т. С Wall. Berlin: Springer-
Verlag, 1971. P. 142-163. (Lecture Notes in Math. 209).
[MH56] Milnor J. On manifolds homeomorphic to the 7-sphere Ц Ann. of Math.
B) 64 A956). P. 399-405.
Имеется перевод: Ми л нор Дж. О многообразиях, гомеоморфных
семнмерной сфере Ц Сб. Математика 1 A957), вып. 3. С. 35—42.
[МИ58] Milnor J. On the existence of a connection with curvature zero // Com-
Comment. Math. Helv. 32 A958). P. 215-223.
[MiI61] Milnor J. Two complexes which are homeomorphic but combinatorially
distinct//Ann. of Math. B) 74 A961). P. 575-590.
[Mil65] Milnor J. Topology from a Differentiable Viewpoint. Charlottesville: The
University of Virginia, 1965.
Имеется перевод: М н л н о р Дж. Топология с дифференциальной точ-
точки зрения// Ми л нор Дж., Уоллес А. Дифференциальная топология:
начальный курс. М.: Мир, 1972. С. 177-270.
[Mil72] M i 1 п о г Т. К. Efimov's theorem about complete immersed surfaces of neg-
negative curvature I I Advances in Math. 8 A972). P. 474-543.
[Moi52] M о i s e E. E. Affine structures in 3-manifolds, V. The triangulation theorem
and the Hauptvermutung// Ann. of Math. B) 56 A952). P. 96-114.
[Mun60] Munkres J. Obstructions to the smoothing of piecewise differentiable
homeomorphisms // Ann. of Math. B) 72 A960). P. 521-554.
[Мипбб] Munkres J. Elementary Differential Topology. Princeton, N.J.: Princeton
University Press, 1966.
Имеется перевод: Манкрс Дж. Элементарная дифференциальная
топология// Мнлнор Дж., Сташеф Дж. Характеристические классы.
М.: Мир, 1979. С. 270-359.
[Mun75] Munkres J. Topology: A First Course. Englewood Cliffs, N.J.: Prentice-
Hall, 1975.
[Mun84] Munkres J. Elements of Algebraic Topology. Menlo Park, С A: Addison-
Wesley Publ. Co, 1984. "
[MZ55] Montgomery D., Zippin L. Topological Transformation Groups. New
York—London: Interscience Publ, 1955.
304
Литература
[Nag88] N a g S. The complex analytic theory of TeichmQller spaces. New York: John
Wiley & Sons, 1988.
[Nov65] Новиков СП. Топология слоений Ц Труды Моск. матем. о-ва 14
A965). С. 248-278. English transl.: Novikov S. P. Topology of foliations
// Trans. Moscow Math. Soc. 14 A965). P. 268-305.
[Now34] Nowacki W. Die euklidischen, dreidimensionalen, geschlossenen und of-
fenen Raumformen // Comment. Math. Helv. 7 A934). P. 81-93.
[O'N66] O'Neill B. Elementary Differential Geometry. New York-London: Aca-
Academic Press, 1966.
[Pap43] Papakyriakopoulos Ch. A new proof of the invariance of homology
groups of a complex // Bull. Soc. Math. Grece 22 A943). P. 1-154.
[Rad25] Rado T. Uber den Begriff der Riemannschen Flachen // Acta Litt. Sci.
Szeged 2 A925). P. 101-121.
[Ree52] Reeb G. Sur certaines proprietes topologiques des varietes feuilletees.
Paris: Hermann, 1952.
[Ril82] Riley R. Seven excellent knots // Low-Dimensional Topology / Eds.
R. Brown and T. L. Thickstun. Cambridge: Cambridge University Press,
1982. P. 81-151.
[Riv] Rivin I. Some applications of the hyperbolic volume formula of
Lobachevsky and Milnor. Preprint.
[Roy71] Royden H. L. Automorphisms and isometries of Teichmuller space // Ad-
Advances in the Theory of Riemann Surfaces / Eds. L. Ahlfors et al. Princeton,
N.J.: Princeton University Press, 1971. P. 369-384.
[sC55] С hern Shiing-shen. An elementary proof of the existence of isothermal
parameters on a surface // Proc. Amer. Math. Soc. 6 A955). P. 771-782.
[Sch91] Schoenfliess A. Krystalisysteme und Krystallstruktur. Depzig: Teubner
Verlag, 1891.
[Sma59] Smale S. Diffeomorphisms of the 2-sphere // Proc. Amer. Math. Soc. 10
A959). P. 621-626.
[Soh79] Sohncke L. Entwickelung einer Theorie der Krystallstruktur. Liepzig:
Teubner Verlag, 1879.
[Spa66] Spanier E. H. Algebraic Topology. New York: McGraw-Hill, 1966.
Имеется перевод: Спеньер Э. Алгебраическая топология. М.: Мир,
1971.680 с.
[ST30] Seifert H., Threlfall W. Topologische Untersuchung der Diskontinu-
itatsbereiche des dreidimensionalen spharischen Raumes // Math. Ann. 104
A930). P. 1-70; 107 A932). P. 543-586.
[Sti87] Still well J. The Dehn—Nielsen theorem // Dehn M. Papers on group
theory and topology. New York: Springer-Verlag, 1987. P. 363-396.
[Tei39] Те i с h m й 11 e r O. Extremale quasikonforme Abbildungen und quadratische
Differentiale // Abh. Preuss. Akad. Wiss. math-naturw. Ю-, 22 A939). P. 1-
197. Reprinted in: Collected Papers. Berlin: Springer, 1982. P. 335-531.
Литература
305
[Tei43] Teichmuller O. Bestimmungder extremalen quasikonformen Abbildun-
Abbildungen bei geschlossenen orientierten riemannschen Flachen // Abh. Preuss.
Akad. Wiss. math-naturw. Kl. 4 A943). P. 1-42. Reprinted in: Collected
Papers. Berlin: Springer, 1982. P. 635-676.
[Thu74] Thurston W. P. The theory of foliations of codimension greater then one
// Comment. Math. Helv. 49 A974). P. 214-231.
[Thu76] Th u rst о n W. P. Existence of codimension-one foliations // Ann. of Math.
B) 104 A976). P. 249-268.
[Whi36] Whitney H. Differentiable manifolds // Ann. of Math. B) 37 A936).
P. 645-680.
[Whi40] Whitehead J. H. C. On C1 -complexes // Ann. of Math. B) 41 A940).
P. 809-824.
[Wol67] Wolf J. A. Spaces of Constant Curvature. New York: McGraw-Hill, 1967.
Имеется перевод: Вольф Дж. Пространства постоянной кривизны.
М.: Наука, 1982.
[Woo69] Wood J. W. Foliations on 3-manifolds // Ann. of Math. B) 89 A969).
P. 336-358.
[Zas48] Zassenhaus H. Uber einen Algorithmus, zur Bestimmung der Raum-
gruppen // Comment. Math. Helv. 21 A948). P. 117-141.
Предметный указатель
С-многообразие 114
(G, ^-многообразие 128
— полное 145
(G, X)-слоение тангенциальное 163
#-автоморфизм 114
«f-атлас 113
^-атласы согласованные 114
^-изоморфизм 114
— локальный 115
^-многообразие 113
^-ослабление ^"-структуры 115
^-структура 113
^"-усиление ^-структуры 115
й-остов 122
Т-^-разложенне 257
А
абсолют 59
автосумма 35
алгебра Ли 170
аналитическое продолжение 142
Б
базнс двойственный 77
барицентрическое подразделение 127
вершина идеальная 42
многообразия 154
поверхности 151
— надстройки 127
— симплекса 122
вложение 10
внутренность симплекса 122
геометрия изотропная 47
геометрия модельная 183
— однородная 47
— сферическая 47
гиперплоскость, двойственная к точке
74
голономия (G, Л)-структуры 144
— расслоения 166
гомеоморфизм /С-квазиизометрия 270
—.меняющий ориентацию 23
грань 126
— симплекса 122
группа Бибербаха 226
— Браве 245
— Гейзенберга 188
целочисленная 189
— голономии 247
(G, Х)-структуры 144
— изометрий 47
— кокомпактная 160
— кофинитная 160
— кристаллографическая л-мерная
226
— Мёбиуса 65
— модулярная 266, 270
— нильпотентная 189
— топологическая 99
— унимодулярная 190
Д
движение гиперболическое 89, 92
— параболическое 90
— эллиптическое 92
действие блуждающее 156
—дискретное 156
— разрывное 157
— с дискретными орбитами 156
— свободное 156
Предметный указатель
307
действие эффективное 156
дивергенция 186
диффеоморфизм /(-квазиконформный
272
— контактный 173
додекаэдр идеальный 42
замощение евклидовой плоскости 11
зацепление Уайтхеда 133
звезда симплекса 124
И
изометрия аффинная евклидова, вра-
вращательная (линейная) часть 222
изоморфизм расслоений 164
инверсия 15
— в сфере 57
инверсор механический 18
индекс векторного поля 28
К
карта многообразия 113
касп 153
кватернион 107
— единичный 108
— чисто мнимый 107
классификация евклидовых многооб-
многообразий 226
— эллиптических многообразий 254
классификация поверхностей 31
классы Браве 245
— гомотопические, свободные 144
клетка 24
кольца Борромео 133
компактификация одноточечная 10
комплекс симплициальный 122
конус касательный 200
— линка 124
координаты изотермические 121
— неоднородные 101
— однородные 101
— Фенхеля—Нильсена 276
коцикл 235
край (граница) многообразия 121
кривая лежандрова 172
— существенная 273
кривая эквидистантная 19
кривизна 49
— гауссова 49
— связности 170
— секционная 171
кручение поля 179
Л
лента Мёбиуса 32
линеаризация 202
линия кривизны 55
линк вершины 44
— симплекса 124
М
мера Хаара 99
метрика бнннвариантная 221
— риманова 18
— Тейхмюллера 272
многогранник выпуклый 122
многообразие 112
— аффинное 130
— вещественно-аналитическое 116
— гиперболическое 130
с геодезической границей 136
— гладкое 114
— дифференцируемое 114
— евклидово 129
— замкнутое 121
— кусочно-линейное 193
— кусочно-проективное 196
— открытое 121
— плоское 129, 168
— с геодезической границей 135
— с краем (границей) 121
— с мерой 118
— топологическое 113
— эллиптическое 130
множество звездное 28
модель в верхнем полупространстве 63
— гиперболического пространства на
гиперболоиде 68
— гиперболической геометрии в полу-
полусфере 61
— диска Пуанкаре 15
— Клейна (проективная модель) 68
— на внутренности параболоида 76
308
Предметный указатель
модель Пуанкаре в шаре 58
морфизм (G, X) -расслоений 163
Н
надстройка 127
— двойная 127
накрытие 11
направление главное 55
нильгеометрия 188
норма элемента группы 223
норма кватерниона 108
О
окружности Виларсо 106
окружность Хопфа 106
орисфера 64
орицикл 64
оришар 65
ось движения 89
отображение G-эквивариаитное 159
— бнголоморфное 120
— голономии 166
— клеточное 24
— кусочно-линейное 193
— кусочно-проективное 196
— логарифмическое 214
— развертки 143
— симплициально-гладкое 198
— симплициальное 122
— собственное 96, 157
— Фробениуса 257
— экспоненциальное 214
отражение гиперболическое 15, 58
П
панты 266
параметр скручивания 278
перенос параллельный в расслоении
169
плоскость евклидова 11
поверхность отмеченная 265
— полная 55
— Римана 120
погружение 22
подмногообразие вполне геодезическое
58
подобие 63
подразделение барицентрическое 27,
123
подразделение комплекса 122
подсимплекс 122
поле векторное, трансверсальное три-
триангуляции 27
линейное 29
— интегрируемое 170
— касательных подпространств 170
полиэдр комплекса 122
полиэдры комбинаторно эквивалент-
эквивалентные 126
поризм Штейнера 66
поток геодезический 176
— Хопфа 106
представление индуцированное 227
— присоединенное алгебры Ли 190
группы Ли 190
преобразование параболическое 92
— проективное 75
— унитарное 109
преобразование Мёбиуса 65
проекция стереографическая 59
произведение римановых многообра-
многообразий 93
производная Ли 119
пространство гиперболическое 14
— Зейферта—Вебера 41
— линзовое 42
— метрическое отрицательной кривиз-
кривизны по Буземану 97
— модулей 263
— расслоенное 106
— сферическое додекаэдра 39, 256
— Тейхмюллера 263
редуцированное 272
— топологическое локально односвяз-
ное 125
— Эйленберга—Маклейна 148
— эллиптическое 38
прямые параллельные расходящиеся
75
псевдогруппа 113
— контактная 173
— строго контактная 182
псевдосфера 51
Предметный указатель
309
радиус инъективиости 257
разбиение клеточное 24
дифференцируемое 24
раздутие точки 35
расслоение ассоциированное 163
— векторное 163
— главное 164
—, индуцированное отображением 165
— касательное 164
единичное 164
сферическое 164
— локально тривиальное 161
— плоское 166
— реперов 33, 164
— Хопфа 106
расстояние хаусдорфово 212
ребро симплекса 122
редукция структурной группы 165
репер 33
ретракт деформационный 207
решетка 161
— равномерная 161
решетки Браве 245
род поверхности 31, 32
связность в расслоении 169
— Леви-Чивиты 169
—плоская 166
сглаживание 115
сдвиг гиперболический 89
седло 30
сечение 165
— локальное трансверсальное 146
символ склейки 12
симплекс л-мерный 122
склейка 126
— л-мерная 123
скобка Ли 170
скручивание 276
— Дена 279
слово длины п 223
слоение 117
— Зейферта 252
— лежандрово 174, 177
— Риба 117
слой (лист) слоения 117
солвгеометрия 191
солвмногообразие 192
спайка 203
— гладкая 204
структура гиперболическая 21
— контактная 173
риманова 182
— кусочно-линейная 193
— подобия 146
— строго контактная 182
— эллиптическая 33
сумма связная 33
сфера на бесконечности S1^1 59
— обзора 48, 71
— Римаиа 101
— стандартная кусочно-линейная 194
кусочно-проективная 196
сферы Милнора 115
схема склейки 10, 126
теорема Бибербаха 226
— Брауэра о сдвигах плоскости 157
— Гильберта 55
— косинусов гиперболическая 83
сферическая 78
двойственная 78
— Пифагора гиперболическая 84
— Пуанкаре об индексе 29
— синусов гиперболическая 84
— униформизации 120
топология компактно-открытая 156
— хаусдорфова 212
тор отображения 162
точка омбилическая 55
триангуляция 123
— гладкая 197
— дифференцируемая 26
— кусочно-линейная 194
трюк Александера 127
условие коцикла 235
Ф
фасета 122, 123, 126
310
Предметный указатель
форма квадратичная 55
— положительно полуопределеиная 81
Фробениуса теорема 180
функция, выпуклая на римановом мно-
многообразии 93
— строго выпуклая 93
— перехода 113
— расстояния 93
— роста 224
— сдвига 97
характеристика эйлерова 23, 24
Ц
центр масс гиперболический 99
часть (разложения) толстая 258
— тонкая 258