Автор: Чудовский А.Н. Сомова Л.А.
Теги: геометрия топология математика аналитическая геометрия издательство просвещение
Год: 1987
Текст
_(.А.Н.ЧУДОВСКИЙ Л.А.СОМОВА-
— ПРОВЕРЬТЕ —
СВОИ -ЗНАНИЯ -
III \т ill
ГЕОМЕТРИИ
К УЧАЩИМСЯ
Предлагаемая книга поможет вам самим проверить свои зна-
ния по геометрии.
Пособие состоит из двух частей: основной и дополнительной.
Основная часть содержит четыре параграфа: «Устные задачи»,
«Основные задачи» с подробными решениями всех задач, «Трени-
ровочные задачи» и «Задания для самоконтроля», являющиеся
главным материалом всей книги. «Тренировочные задачи» пред-
назначены для отработки навыка в решении основных задач лишь
в тех случаях, когда в этом возникает необходимость.
Вторая часть книги содержит дополнительный материал,
включающий задачи повышенной трудности, который поможет вам
расширить и углубить свои знания по геометрии и подготовиться
к вступительным экзаменам в вуз.
Степень усвоения вами геометрии можно установить, проверив
свои возможности в выполнении «Заданий для самоконтроля»
(с. 52). Варианты этих заданий составлены по аналогии с
экзаменационными билетами. Они охватывают основные темы
курса геометрии IX и X классов. Всего вариантов 20 и в каждом —
3 задания. По трудности самые простые — это первые задания.
Если вы справились с ними, то вы знаете по геометрии хотя и
немало, но достигли пока еще только первого, самого низкого
уровня знания геометрии. Чтобы достичь второго (среднего)
уровня знания геометрии, надо еще уметь в каждой задаче,
предлагаемой во вторых заданиях каждого варианта, выполнить
хотя бы одно из требований. И самым высоким уровнем знания
геометрии в этой книге считается тот уровень, при котором вы в
состоянии выполнить полностью все задания во всех вариан-
тах. Каждый ученик должен стремиться достичь по крайней мере
второго уровня знания геометрии.
Как работать с этой книгой?.. Сначала проверьте, что вы
могли бы решить из раздела «Устные задачи», подключая все
новые и новые задачи из этого параграфа по мере прохождения
материала в школе. Также решайте задачи из параграфа «Основ-
ные задачи». В начале выпускного класса начните выполнять
«Задания для самоконтроля», обращая особое внимание на пер-
вые два задания в каждом ^варианте. Имейте в виду, что наиболее
сложные задачи отмечены звездочкой' (*).
А.Н.ЧУДОВСКИЙ Л.А.СОМОВА
проверьте
свои ЗНАНИЯ
по
ГЕОМЕТРИИ
КНИГА ДЛЯ УЧАЩИХСЯ 9 И 10 КЛАССОВ
СРЕДНЕЙ ШКОЛЫ
МОСКВА «ПРОСВЕЩЕНИЕ» 1987
ББК 22.151
4-84
Рецензенты:
учитель-методист Е. Е. Егерман (Москва, школа № 467),
инспектор МП СССР Б. В. Сорокин
Чудозскнй Л. Н., Сомова JL А.
4-84 Проверьте сбоя знания по геометрии: Кн. для учащихся
9 и 10 кл. сред. шк.— 1Л.: Просвещение, 1S87.— 9G с.: ил.
Книга является Сборником задач и вопросов, с помощью которых учащийся
промерить степень усвоения нм геометрического материала за курс средней школы.
4306020009—842
4 103 (03)—87
218—87
ББК 22.151
© Издательство «Просвещение», 1987
ИСПОЛЬЗУЕМЫЕ ОБОЗНАЧЕНИЯ И ФОРМУЛЫ
ТРИГОНОМЕТРИЯ
1. Таблица значений тригонометрических функции
некоторых углов:
Функция Аргумент а
0 К |(0 л Т л т to| й
sin а 0 1 2 V2 2 о 1 1
cos а I л/з 2 V? 2 1 2 0
tga 0 У'З 3 1 <3
1 etg а — д/з 1 УЗ 3 0
Примечание. Связь между градусной и радианной мерами
измерения угла:
1 о Л
= 180
2. Формулы приведения:
ПЛАНИМЕТРИЯ
1. Треугольники (рис. 1)
а, Ь. с — стороны треугольника;
а, р, у — внутренние углы треугольника;
hby hc — высоты треугольника, опущенные из вершин тре-
Рис. 1
угольника на прямые, содержащие соответствующие противо-
положные стороны а, Ь, с\
та, ть, тс — медианы треугольника, соединяющие вершины
треугольника с серединами противолежащих сторон а, Ь, с\
1а, 1ь, 1с — биссектрисы треугольника, соединяющие вершины
треугольника с точками на противолежащих сторонах а, Ь, с;
MN — средняя линия треугольника;
р — полупериметр треугольника;
R — радиус окружности, описанной около треугольника;
г — радиус окружности, вписанной в треугольник;
S или Хддвс — площадь треугольника АВС.
Сумма углов треугольника
а + р + у = 180°
Неравенство треугольника
а<Ь-\-с,
с <Z а-\-Ь.
Теорема синусов
а ____ b _______ с
sin ос sin р sin у
Теорема косинусов
а2 = Ь2 + с2 — 2bc cos а
cos ос =
b2 — а2 + с2 — 2ас cos р
с2 == а2 + b2~%ab cos у
cos р —
cos y =
2ab
Полупериметр треугольника
а-\-Ь + с
4
Свойства средней линии треугольника
MN\\AB,
Л*
Площадь треугольника
S=4raha; S=-^bhb', S=~chc;
Mi Mi Mf
S =-5-ас sin Р; S=-^-ab sin у; S=-^-bc sin a;
S = ^jp(p — a) (p — Ь)(р — c) — формула Герона.
Равнобедренный треугольник
а —с; Z_a=/.у-, hb = mb = lb.
Равносторонний треугольник
a = b=^c\ а = р = 7==60°;
ha ~~ la ~~~hb lb П%ь\ he —— lc ~~~
ha — hb — hc.
Прямоугольный треугольник
a = 90°, b, c — катеты, a — гипотенуза;
a2~b2 + c'2 — теорема Пифагора,
R^=-^ = rna}
S = -^-bc;
Mi
sinY=^-; cosT=-y: *6 7 = ^
s,nP=T; COSP=V; tgf3 = T'
2. Четырехугольники
Параллелограмм ABCD
AB = a, BC = b — стороны параллелограмма;
ha, hb — высоты параллелограмма, опущенные из вершин
параллелограмма на прямые, содержащие стороны параллело-
грамма а и Ь\
d\, dz — диагонали параллелограмма;
а, у — углы параллелограмма;
а + у= 180°;
S — площадь параллелограмма;
S = aha, S = bhb, S = ab sin a;
5
d2i-]-d2 = 2 (a2 + fe2) — связь между сторонами и диагоналями
параллелограмма.
Если параллелограмм — прямоугольник:
а = 7 = 90°' d\ — d2\ S — ab.
Если параллелограмм — ромб:
d\JLd2\ d2 + d2==4a2; 5 = a2 sin a; S—^d\-d2.
Если параллелограмм — квадрат:
а = у —90°; d{ — d2; d\^d2\ S = a2.
Трапеция ABCD
BCM#; ВС — а\ AD — b; h — высота трапеции, опущенная из
вершины В на сторону AD. MN — m — средняя линия трапеции:
Равнобокая трапеция
AB — CD-, d\t d2— диагонали трапеции:
d\ = d2.
3. Окружность и круг
R— радиус окружности (круга);
/ = 2л7? — длина окружности;
S = n/?2 — площадь круга.
4. Правильные многоугольники
Треугольн и к.
аз — сторона правильного треугольника;
= —радиус описанной окружности;
С.\
г = —-^—радиус вписанной окружности.
Ч е т ы р е х у г о л ь н и к.
щ — сторона правильного четырехугольника;
/? = —-—радиус описанной окружности;
у2
г = ---радиус вписанной окружности.
Ш е с т и у г о л ь н и к.
Пб — сторона правильного шестиугольника;
р — — радиус описанной окружности;
г --------радиус вписанной окружности.
СТЕРЕОМЕТРИЯ
[АВС) — плоскость АВС — плоскость, проходящая через три
точки: Д, В и С.
6
I. Многогранники
Призма
Площадь боковой поверхности призмы равна произведению
периметра (р') перпендикулярного сечения на длину (/) бокового
ребрл: ' S- =Р'1
°оок Р
Для прямой призмы перпендикулярным сечением является
основание, боковым ребром — высота призмы Л, так что
*^бок ph.
Объем (I/) призмы равен произведению площади перпендику-
лярного сечения (S') на длину (/) бокового ребра:
V —S7,
или площади основания (S) на высоту, т. е.
V = Sh.
Пиралшда
Объем пирамиды
V~S‘h,
о
где S — площадь основания пирамиды, h — ее высота.
2. Цилиндр
Площадь боковой поверхности цилиндра
S=2nRH,
где R — радиус окружности, лежащей в основании цилиндра,
И — его высота.
Объем цилиндра
V = S*H.
3. Конус
Площадь боковой поверхности конуса
S = Tirl,
где г — радиус окружности, лежащей в основании конуса,
I — длина его образующей.
Объем конуса
v=4-S0C11/i ~^-nr2h,
О о
где h — высота конуса, S0CH — площадь круга, лежащего в осно-
вании конуса.
7
4. Векторы
Обозначения вектора: АВ , а\ на плоскости АВ (х, у), (х, у) в про-
странстве АВ (х, у, z), (х, у, z).
Если A (xi, уь 2(), В (х2, у2, z2), то АВ (х2 —х(, уг —Уь 22 —Zt).
Обозначения длины вектора: |ЛВ|, АВ, |а|, а. Если АВ =
= (х, у), то |ЛВ | ==д/х2 +у2; если АВ (х, у, z), то |ЛВ| =
=Vx2+y2+^2.
Обозначения угла между векторами:
^(AB,CD), ^(a,b\
Скалярное произведение векторов:
ab = |а] • \b\*cos Z.(a, b).
Если a(xi, у0, b(x2, y2), то a-F=xix2 + yiy2; если a(xh yh Z|),
b (x2t уг, z2), to a-fe = xix2+yiy2 + 2iz2.
Косинус угла между векторами а и Ь:
cos Z_(a, b)=
Если а(хь 4/i), b(x2, yi\ то cos Z.(а, 6) = : если
а (хь i/i, zi), Ъ(х2> у2( z2), то cos /.(а, Ь)= .
yi+zt-^Jxi + yi + 22
Равенство векторов: _ _ _
если а(хь z/t), b (х21 у2) и а = Ь, то xi=x2, yt = y2; если a(xi, уь zt),
b (л'2, у2, z2) и a — b, то Х|=х2, у\—у2, zi = z2.
Часть I
ОСНОВНОЙ МАТЕРИАЛ
§ 1. УСТНЫЕ ЗАДАЧИ
Эти задачи решаются устно, а если письменно, то на решение
одной задачи требуется примерно минуты три. Отметим, что под
одним номером чаще всего предлагается несколько задач. На-
пример, под номером 1 предлагается 4 задачи.
ПЛАНИМЕТРИЯ
1. Найдите площадь: а) треугольника, б) параллелограмма,
если стороны равны а —2, b = 3, а угол между этими сторонами
60°; 45°
2. Найдите площадь равнобедренной трапеции, если ее средняя
линия равна 5, а боковая сторона, равная 4, наклонена к осно-
ванию под углом: а) 30°; б) 45°.
3. Найдите: а) площадь круга; б) длину окружности, если
радиус равен 1; 0,5.
4. В квадрате диагональ равна: а) 4; б) 2-д/2. Найдите площадь
квадрата; радиусы описанной и вписанной окружностей.
5. В квадрате сторона равна: а) 4; б) 2 д/2. Найдите площадь
квадрата, радиусы вписанной и описанной окружностей.
6. Высота в ромбе равна: а) 2; б) 6. Найдите площадь круга,
вписанного в ромб; площадь ромба, если угол ромба равен 30°
7. Длина окружности равна: а) 4л; б) 2л. Найдите площадь
круга.
8. Площадь круга равна: а) 4л; б) л. Найдите длину окружности.
9. В прямоугольном треугольнике катеты равны: а) 3 и 4;
б) 5 и 12. Найдите площадь описанного около треугольника
круга; площадь треугольника; длину медианы, проведенной
к гипотенузе.
СТЕРЕОМЕТРИЯ
10. Из одной точки проведены две наклонные: одна имеет проек-
цию 2 м, а вторая — 0,5 м. Какая из наклонных образует с
плоскостью меньший угол?
11. Ребро куба равно 2. Найдите: а) полную поверхность и
объем куба; б) длину диагонали куба; в) радиусы вписанного
9
и описанного шаров; г) угол наклона диагонали куба к
плоскости основания куба.
12. В пирамиде плоскость сечения делит высоту в отношении:
а) 1:1; б) 2:1, считая от вершины. Найдите площадь сечения,
если площадь основания равна 60 м2; площадь основания, если
площадь сечения равна 2 м2.
13. В пирамиде площадь основания равна: а) 2; б) 4; в) 3.
Боковые грани наклонены к основанию под углом 30°; 60°-
45° Найдите площадь боковой поверхности пирамиды.
14. В правильной треугольной пирамиде: а) боковое ребро рав-
но 5, а высота равна 4; б) боковое ребро, равное 6, наклонено
к основанию под углом 30°; в) сторона основания равна д/З,
а высота пирамиды 4. Найдите объем пирамиды.
15. В правильной четырехугольной пирамиде: а) боковое ребро
равно 5, а высота равна 4; б) боковое ребро, равное 2 д/2, на-
клонено к основанию под углом 45°; в) сторона основания
равна 6, а высота пирамиды 4. Найдите объем пирамиды.
16. В конусе образующая равна 4 и наклонена к основанию под
углом 60°. Найдите площадь боковой поверхности конуса и
объем конуса.
17. Найдите площадь боковой поверхности конуса и объем
конуса, если образующая равна 5, а высота конуса 4.
18. Площадь поверхности шара равна: а) 36л; б) 16л. Найдите
объем шара.
32л
19. Объем шара равен: а) 36л; б) -у-. Найдите площадь поверх-
ности шара.
Векторы
20. Найдите длину вектора: а (3; —4; 0), b (5; 0; — 12), с (0; 0; —4),
/Ц0; —'3; 4).
21. Найдите угол между любой парой векторов, данных в зада-
че 20.
Плоскость и сфера
22. Составьте уравнение плоскости, проходящей через точку М
перпендикулярно вектору Л, если:
а) Л4(1; — 2; 3), /Ц2; 0; -1);
б) М(-2; 1; 1), £(1; 2; -3);
в) М (- 1; 0; 2), k (0; 2; 0);
г) М(0; 0; 0), 7г (— 1; -2; 7).
23. Укажите координаты какой-нибудь точки, принадлежащей
одной из плоскостей, заданных в задаче 22.
24. Составьте уравнение сфеоы с центром О и радиусом /?, если:
а) 0(2; -1; 3), Z? = 5; 6) 0(0; 0; —2), /? = 2; в) 0(0; 0; 0),
/? = 3.
25. Укажите координаты какой-нибудь точки, принадлежащей
какой-либо сфере, заданной в задаче 24.
10
ОТВЕТЫ К УСТНЫМ ЗАДАЧАМ
1. Указание. 5Д = 0,5а& sin С. S = ab sin а, где а — угол
между а и b. а) 1,5 у/3; 1,5 Л/2; б) 3 уЗ; 3 Л/2. 2. а) 10; б) 10 у/2.
3. а) л; у; б) 2л; л. 4. а) 8; 2; у2; б) 4; у/2; 1. 5. а) 16; 2; 2 у/2;
б) 8; д/2^ 2. 6. а) л; 8; б) 9л; 72. 7. а) 4л; б) л. 8. а) 4л;
б) 2л. 9. а) 25л; 6; 2,5 (медиана, проведенная к гипо-
тенузе, равна половине гипотенузы); б) 30; 13,5. 10. На-
клонная, у которой проекция равна 2, большая. 11. а) 24,8; б) 2 д/3;
в) R = д/З, г — I; г) sin а = -- -12. а) 15 м2; 8 м2; б) м2;
2 Л/3 -уЗ 3
4,5 м2. 13. Указание. 5Гп..==-^-, где а — угол наклона
СОЛ cos а
боковых граней к основанию, а) 4 д/3; 4; -—г; б) 8; 4т; в) -ут;
6;-^-. а) 9 л/3; б) в) -fi. 15. а) 24; б) у-; в) 48. 16. У ка-
зан и е. Н = 4 sin 60° = 2 у/З, R = 4 cos 60° — 2, SCoK = л/?/ = 8л,
V = nR2-^-=~^-. 17. Указание. /? = 3, SSoK = nRl = 15л,
О о
3
У=2^.= 12л. 18. а) 36л; б)
0
|fc| = 13, Id =4, (kI = 5. 21. Найдем угол ср между векторами:
ч “ Т а'Ь
а) а и о: cos ср =
а и
i л i • i b |
3-13 13
(3,-4,0) 70,0,-4)
b И
^(5.0, 12).(0, 3.4) = 22 а) 2 (д.__ 3)_0. б) (х + 2) +
4-2 (//— !)—3 (z —1) = 0; в) 2г/ = 0; г) — х — 2у + 7z = 0. 23. На-
пример, плоскости 2 (х—1) —(г —3) = 0 принадлежит точка
А (1^ 5, 3); плоскости (% + 2)-|-2 (у — 1) — 3 (z — 1) = 0 принадлежит
точка В ( — 2, I, 1); плоскости 2у =- 0 принадлежит точка С (5, 0, 17);
плоскости —х — 2r/ + 7z = 0 принадлежит тонка Z)(—1; 0,5; 0).
24. а) (х —2)2 + (п4-1)2 + (г — 3)2 = 25; б) х2 + //2 + (г + 2)2-4;
в) х2 -\-у2-f-z2 = 9. 25. Например, сфере (х — 2)3 + 0/ + 1)2 +
4-(г —3)2-~25 принадлежит точка Л(—1, 3, 3); сфере х2 + у2 +
+ (г4-2)3 = 4 принадлежит точка В (0, 0, 0); сфере x2 + j/2-|-z2 = 9
принадлежит точка С (-у'З, —2, -д/2).
И
§ 2. ОСНОВНЫЕ ЗАДАЧИ
ПЛАНИМЕТРИЯ*
Треугольник
Дан треугольник АВС.
1 (рис. 2). Найдите г, b, R, S и расстояние от точки С до пря-
мой АВ.
2 (рис. 3). Найдите b, at R, S и расстояние от точки С до пря-
мой АВУ если АВ = 2.
В
Рис. 2
Рис. 3
3 (рис. 4). Найдите АВ, ВС, R, S и расстояние от точки С
до прямой АВ.
4 (рис. 5). Найдите с, S, /? и расстояние от точки С до АВ.
5 (рис. 6). Найдите AC, BK=hby R, г и S.
6 (рис. 7) Найдите /?, АВ, S.
Рис. 5
Рис. 6
7 (рис. 8) /<Л1||ЛС. ^=|-.
/И С О
если S&АВС= 100.
Найдите КМ. Найдите
1 Здесь предлагаются такие планиметрические задачи, которые часто
используются при решении стереометрических задач.
12
Рис. 8
Рис. 9
8 (рис. 9).
Найдите /<1М|, к2М2.
1:2:3, ВС=6.
Прямоугольник
9 (рис. 10). Найдите R и S.
Ромб
10 (рис. 11). Найдите расстояние от точки В до прямой AD,
диагонали, 5, расстояние от точки А до прямой ВС.
Трапеция
Круг и окружность
12. В окружность вписан: а) треугольник АВС: Z./1 = 150°,
ВС = 4; б) правильный многоугольник, у которого «з = л/3’>
а4 = 6 д/2; «6 = 4.Найдите длину окружности и площадь круга.
Векторы
13 (рис. 13). Найдите: а) ВС; б) 18С|; в) /LABC; г) скалярное
произведение (2ЛС — АВ) ВС.
14 (рис. 14). а) Выразите в координатах векторы АВ и АС;
б) найдите скалярное произведение АВ-АС; в) найдите
|ЛВ| и |ЛС|; г) найдите угол между векторами АВ и АС.
13
Рис. 13
Рис. 14
СТЕРЕОМЕТРИЯ
Прямые и плоскости в пространстве
Аксиомы стереометрии и следствия из них
15. Сечение куба плоскостью1 На рисунках 15—18
изображены кубы. Постройте сечение куба плоскостью, про-
ходящей через точки М, Р, К-
16. а) Докажите, что все прямые, пересекающие прямую АС и
проходящие через точку В, не принадлежащую АС, лежат
в одной плоскости; б) докажите, что все прямые, пересекаю-
щие одновременно стороны АВ и ВС треугольника АВС,
лежат в одной плоскости.
Рис. 17
Рис. 18
Параллельные и скрещивающиеся прямые в пространстве
17. Дан куб ABCDA\B\C\D\. Основываясь на том, что все грани
куба — квадраты: а) докажите, что Д|В|||ОС и А।С\||ЛС;
б) укажите, какие ребра куба лежат на скрещивающихся
прямых (укажите 3—4 пары скрещивающихся прямых);
в) докажите, что точки А, С, М, К, где М — середина В\С\,
К — середина А|В|, лежат в одной плоскости.
18. Через конец А отрезка АВ проведена плоскость. Через конец В
и середину С этого отрезка проведены параллельные прямые,
пересекающие плоскость в точках В\ и Сь Найдите длину
отрезка ССЬ если длина отрезка BBi равна 12 см.
1 Напомним, что сечением тела плоскостью является плоская фигура,
состоящая из общих точек, принадлежащих телу и плоскости.
14
Точки А и В пс принадлежат плоскости а. Точка С при-
надлежит отрезку АВ. Через точки Л, В, С проведены
параллельные прямые, пересекающие плоскость а в точках
соответственно Bt, Сь Докажите, что точки /11, В|, С[
лежат на одной прямой, и найдите длину отрезка ССц если
АС
>1Д1=9 см, /323| —5 см, зная, что: а) ^=1; б)
xZz V-i
AC 1
ВС~ 3 *
20. Может ли прямая быть параллельной двум скрещивающимся
прямым?
Параллельность прямой и плоскости
21» Дан куб ABCDAiB\CiD\. Основываясь на том, что все грани
куба — квадраты: а) укажите, каким граням куба параллель-
на прямая ZiBj; ВС; АВ\; б) в ДАВ^С точки Л1 и К —
середины соответственно АВ\ и В\С. Докажите, что прямая
МК параллельна плоскости АВС.
22. На рисунках 19—22 изображены кубы. Постройте сечение куба
плоскостью, проходящей через прямую МК и точку Р. По-
строение проводить с помощью линейки и угольника так,
как строят параллельные прямые.
Рис. 19
Рис. 22
23. Дана прямая а, параллельная плоскости сс. Плоскость 0
проходит через прямую а и пересекает плоскость а по пря-
мой Ь, Будут ли а и Ь параллельны?
24. Даны две скрещивающиеся прямые. Можно ли через одну из
них провести плоскость, параллельную другой скрещиваю-
щейся прямой?
Параллельные плоскости
25. Дан куб ABCDA\B\C\D\ (грани — квадраты), а) Докажите,
что (ЛВС)||(ЛiBiCi); б) докажите, что любая прямая, при-
надлежащая плоскости АВВ\, параллельна плоскости DCC\\
в) докажите, что {АСВ\)\\{МРК\ где точки М, Р, К — середины
сторон соответственно AiDi, DtCj, BiD.
26. Постройте сечение параллелепипеда плоскостью, про?<одящей
через точки М, К, Р на рисунках 23—25.
27. а) Если прямая а параллельна двум прямым b и су то будет
ли fell с? Если прямая а параллельна двум плоскостям аир,
то будет ли а||0?
15
Рис. 23 Рис. 24 Рис. 25
б) Могут ли скрещивающиеся прямые быть и параллельными;
принадлежать параллельным плоскостям?
28. Дан куб ABCDA\BiCiD\. Проведите сечение в кубе через
данные точки и ответьте, какие фигуры получились в сечении:
а) Сь К, D\ б) Cj, К, С, где точка К — середина Л(Вь
Параллельное проектирование фигур на плоскость
29. При параллельном проектировании фигуры на плоскость мо-
жет ли быть изображен: а) прямоугольный треугольник —
равносторонним; б) равносторонний треугольник — прямо-
угольным; в) тупой угол — острым, а острый — тупым;
г) квадрат — параллелограммом (не квадратом), а парал-
лелограмм (не квадрат) — квадратом; д) параллелограмм —
трапецией, а трапеция — параллелограммом?
30. Отрезок МК, не имеющий общих точек с плоскостью а, раз-
делен точками Л, В в отношении МА :АВ:ВК= 1:2:3.
Пусть Mi, Ль В{ и Кл являются соответственно изображе-
ниями точек М, Л, В, К при параллельном проектировании
отрезка МК на плоскость а. Найдите отношения: a) MiBu
:ВЛь б) Mj/G^Br, в) ЛЛьММь г) Л,В, iBjKf :ЛЫь
31. дЛВС— равнобедренный: ЛС = СВ, CD — высота дЛСВ.
На рисунке 26 дано изображение треугольника ЛВС при
параллельном проектировании. Постройте изображение CD
в треугольнике Л1С1В1.
Перпендикуляр и наклонная к плоскости.
Угол между прямыми
Обратим внимание на то, что две прямые могут быть пер-
пендикулярны друг другу, даже если они и не пересекаются,
16
U
Рис. 27
например в кубе ABCDA\B{C\D\ ДД|ХОС, Д0ХСС1
(рис. 27) или если аХс, то aXfe и если аХ6, то aJLc
(рис. 28) — теорема о трех перпендикулярах. Это обстоятель-
ство, основанное на определении угла между скрещиваю-
щимися прямыми, учитывается нами при решении задач.
32. Дан куб ABCDA\B\C\D\. Основываясь на том, что у куба все
грани — квадраты, докажите, что: а) ВВ1Х(ДВС); б) AD X
X(OCCi); в) B^jXHiCiC); г) Д^ХВС,; д) Д^ХВО;
е) ДДВ1С( — прямоугольный.
33. Точка О — центр квадрата ABCD, ОЛ4Х(ДВС) и ОМ—12,
ДВ=8. а) Докажите, что МД = МВ; б) найдите расстояние
от точки М до прямой АВ\ в) найдите угол между AM и ДО
и между AM и ДВ; г) найдите площадь дДМВ.
34. Точка О — центр правильного треугольника, ОМХ(ДВС) и
0М=д/3, АВ =2~\13. а) Докажите, что МД = Л4В; б) найдите
расстояние от точки М до прямой ДВ; в) найдите угол между
AM и АО и между AM и ДВ; г) найдите площадь ДДМВ.
35. А В CD — прямоугольник, МДХ(ДВС), ОС=д/2, СВ=1,
Z-MCA =30°. а) Найдите расстояние от точки М до прямой
ОС; б) найдите угол между прямыми МВ и СВ; в) найдите
площадь ДМСВ.
36* В ДДВС Z_C = 90°, ДВ = 2, ДД = 30°, МСХ(ДВС),
МС —0,5. а) Найдите угол между МВ и СВ; б) найдите
расстояние от точки М до прямой ДВ; в) найдите площади
дМСВ и дДМВ.
37. В ДДВС ДС = 90°, ДС = 3, ДВ = 5, МДХ(ДВС), ДМВД =
= 60° а) Найдите угол между прямыми МС и ДС; б) найдите
расстояние от точки М до прямой ВС; в) найдите площади
ДМДС и ДМСВ.
38. В кубе ABCDA\B\C\Di найдите угол между прямыми:
а) АВ\ и ОС; б) АВ\ и Д1О; в) A\Ct и BD\ г) Д1С1 и BjC.
Угол между прямой и плоскостью и между плоскостями
Перпендикулярность плоскостей
39. Дан куб ABCDA\B\C\D{. Основываясь на том, что все
грани куба — квадраты: а) докажите, что (ДВС)Х(Д:ДО);
(ДВС)Х(ДСС|); (ДСС1)Х(ВОО1); б) найдите углы между:
2 Заказ 124 17
ABi и (ABC); BDi и (АВС); А1С1 и (£>1£>С); в) найдите углы
между плоскостями (ЛВС) и (AiAD); (Л|£)С) и (ЛВС); (ЛВ]С)
и (ЛВС).
40. Точка О — центр квадрата ABCD, OM-L(ABC), АВ = 8.
Прямая МА наклонена к (ЛВС) под углом 60°. Найдите:
а) расстояние от точки В до (АМС); б) угол между плоскостя-
ми ЛВС и АВМ; в) угол между плоскостями ЛВС и АМС;
г) угол между МВ и плоскостью АМС.
41. Точка О — центр правильного треугольника, OMJ-(ABC),
ЛВ = 2-\/3. Угол между прямой AM и (ЛВС) равен 45°.
Найдите: а) расстояние от точки М до (ЛВС); б) угол между
плоскостями ЛВС и АВМ; в) угол между прямой МА и (МОС);
г) угол между плоскостями АМО и ЛВС.
42. ABCD — прямоугольник, МА±(АВС), угол между плоскостя-
ми МВС и ЛВС равен 60°, МА = 4пД ЛС = 5. Найдите:
а) угол между прямой МС и (ЛВС); б) расстояние от точки
С до (DMA); в) угол между плоскостями СМА и АМВ;
г) угол между плоскостями АМС и АВС.
43*. В дЛВС Z.C = 90° MC_L(ABC), угол между плоскостями
АМВ и ЛВС равен 30°, АВ = 2, Z.BAC—600. Найдите: а) дли-
ну отрезка МС; б) площадь дАМВ; в) угол между плоскос-
тями МВС и АВС; г) угол между прямой МА и (АВС).
44. В ДАВС ZС=90°, МА±(АВС), угол между (АВС) и (МВС)
равен 45°, АС—2, Z_BAC=60°. Найдите: а) длину отрез-
ка МА; б) расстояние от точки В до (АМС); в) угол между
(АМС) и (АВС); г) угол между прямой МВ и (АВС).
Векторы в пространстве
45. Дано: Д(а, Ь)=90°, Д(а, с) = 60°, A(K,_F) = 60°, a==b = c= 1.
Найдите: а) скалярное произведение (а — 2Ь— 4с) Ь; б) угол
между (а— 2с) и Ь.
46. В параллелограмме ABCD А (0, 2, 0), В (— 1, 0, 2), С (2, — 1, 0).
Найдите: а) АВ; б) координаты точки D; в) ВО; г) скалярное
произведение AC*BD; д) АС и ВО; е) угол между векторами
АС и ВО.
Геометрические тела
Замечание. В задачах может встретиться требование на тему, еще не
пройденную, например найти объем или поверхность тела. В этом случае возмож-
ны два выхода: первый — отложить выполнение этого требования до прохожде-
ния соответствующей темы, второй — воспользоваться готовой формулой, взятой
из справочника данного пособия (с. 3).
Призма
47. В правильной треугольной призме ABCAiBiCi Z.A|CA = 30°,
A|C = 4. Найдите: а) двугранный угол между (ABBi) и
(BBiC), (А1ВС) и (АВС); б) площадь aBAiC; в) площадь
полной поверхности призмы; г) объем призмы.
18
48. В основании прямой призмы АВСА\В\С\ треугольник АВС.
у которого Z.C=90°, АВ — 2, Z.4 = 30°, /СВ1ЛВ = 45°. Найди-
те: а) двугранные углы между (АВВ\) и (СВВ\). (Л1СВ) и
(ЛВС); б) площадь ДЛ1СВ; в) объем призмы.
49. В правильной четырехугольной призме диагональ равна 4 -\/2
и наклонена к основанию призмы под углом 45°. Найдите:
а) площадь полной поверхности призмы; б) объем призмы.
50. Дан прямоугольный параллелепипед ABCDA\B\C\D\. в кото-
ром AD — 2 дм, ОС=3 дм, ЛЛ1 = 6 дм. Найдите: а) длину
диагоналей параллелепипеда; б) угол наклона диагонали па-
раллелепипеда к плоскости основания параллелепипеда;
к плоскостям боковых граней параллелепипеда; в) площадь
диагонального сечения; г) двугранный угол между плоскостя-
ми ADC\ и BAD*. д) площадь полной поверхности парал-
лелепипеда; е) объем параллелепипеда.
51. Основание прямого параллелепипеда — ромб со стороной 6 см
и углом 60°. Меньшая диагональ параллелепипеда наклонена
к основанию под углом 45°. Найдите: а) диагонали; б) пло-
щадь полной поверхности и в) объем параллелепипеда.
Пирамида
52. В правильной треугольной пирамиде сторона основания равна
6< а высота 3. Найдите: а) длину бокового ребра и угол
наклона этого ребра к плоскости основания; б) двугранный
угол между плоскостями боковой грани и основания; в) пло-
щадь боковой поверхности пирамиды; г) объем пирамиды.
53. В правильной четырехугольной пирамиде сторона основания
равна 10 см, а высота 12 см. Найдите: а) длину бокового
ребра и угол наклона этого ребра к плоскости основания
пирамиды; б) двугранный угол между плоскостями боковой
грани и основания пирамиды; в) площадь боковой поверх-
ности пирамиды; г) объем пирамиды.
54. В основании пирамиды MABCD — прямоугольник ABCD.
МАЛ_(АВС), АС=5. DC = 4. Двугранный угол между (MDC)
и (ADC) равен 60°. Найдите: а) длину МС и угол наклона МС
к (АВС); б) площади AMDC, ДСВЛ1 и ДЛА1В; в) объем
пирамиды.
55. В пирамиде проведены два сечения перпендикулярно высоте
пирамиды: а) одно сечение делит высоту пирамиды пополам;
б) другое — в отношении 1:3, считая от вершины пирамиды.
Найдите площади сечения, если в основании пирамиды лежит
треугольник со сторонами 5, 5, 6.
56. Высота МО правильной пирамиды MABCD равна 2д/3.
Двугранный угол при стороне АВ равен 60°. Найдите:
а) площадь поверхности пирамиды; б) объем пирамиды.
57. Высота МО правильной пирамиды МАВС равна 2д/3.
Двугранный угол при стороне ВС равен 45°. Найдите:
а) площадь поверхности пирамиды; б) объем пирамиды.
2* 19
Рис. 29
Цилиндр
Задачи, связанные с телами вращения: цилиндром, конусом, шаром, мы
иллюстрируем, как правило, рисунками, изображающими их осевые сечения;
еще на рисунках изображается сечение шара, проведенное через его полюсы
(рис. 29).
58. Диагональ осевого сечения цилиндра равна 8 см и наклонена
к основанию под углом 30° Найдите: а) площадь полной по-
верхности цилиндра; б) площадь полной поверхности
правильной треугольной призмы, вписанной в этот цилиндр;
в) площадь полной поверхности призмы, вписанной в этот
цилиндр, если в ее основании лежит прямоугольный треуголь-
ник с углом 30°; г) объем цилиндра.
59. В цилиндр вписана прямая призма, в основании которой —
прямоугольный треугольник с катетами 6 и 8 дм. Диагональ
большей по площади боковой грани призмы наклонена к
основанию призмы под углом 45°. Найдите: а) объем;
б) площадь боковой поверхности цилиндра.
60. В цилиндр вписана прямая призма, в основании которой —
треугольник со сторонами 6 и 6 дм и углом 120° между ними.
В осевом сечении цилиндра — квадрат. Найдите: а) объем;
б) площадь боковой поверхности цилиндра.
61. В цилиндр вписана прямая призма, в основании которой —
прямоугольник со сторонами 1 и д/З дм. Диагональ призмы
равна -у/5 дм. Найдите: а) объем; б) площадь боковой поверх-
ности цилиндра.
Конус
62. Образующая конуса равна 6, а угол между ней и плоскостью
основания равен 60°. Найдите: а) площадь полной поверх-
ности конуса; б) площадь сечения конуса плоскостью, парал-
лельной основанию и проходящей через середину высоты ко-
нуса; через точку К, принадлежащую высоте конуса и деля-
щую эту высоту в отношении 1:5, считая от вершины конуса;
в) объем конуса.
20
63. Высота конуса равна 5 -у/3 см, а угол при вершине осевого
сечения равен 60°. Найдите: а) площадь боковой поверх-
ности конуса; б) об^ьем конуса.
64. В конус вписана правильная треугольная пирамида. Сторона
основания пирамиды равна 6, боковое ребро 4 -д/3. Найдите:
а) площадь боковой поверхности конуса; б) объем конуса.
65, В конус вписана правильная четырехугольная пирамида.
Сторона основания пирамиды равна 2 д/2, высота пирамиды
равна 2 -\/3. Найдите: а) площадь боковой поверхности конуса;
б) объем конуса.
Шар
66. Перпендикулярно радиусу шара проведена секущая плоскость,
разделившая радиус пополам. Площадь сечения равна 75л.
Найдите: а) объем шара; б) длину касательной шара из
точки, отстоящей от центра шара на расстоянии 10д/5-
67. Шар касается плоскости. Расстояние от точки А, лежащей
в этой плоскости, до центра шара — точки О — равно 2 см,
а до точки касания -у/3 см. Найдите: а) площадь поверхности
шара; б) расстояние от точки касания до точки пересечения
прямой АО с поверхностью шара.
68. Перпендикулярно радиусу шара проведена секущая плоскость,
разделившая радиус шара в отношении 3:2, считая от центра
шара, и пересекающая поверхность шара по окружности,
равной 16л. Найдите: а) объем шара; б) расстояние от точки
до центра шара, если длина касательной к шару, проведенной
из этой точки, равна
69. Через конец радиуса шара проведена плоскость под углом
60° к радиусу. Площадь получившегося сечения равна
4л см2. Найдите: а) площадь поверхности шара; б) расстояние
от центра шара до плоскости сечения.
Расстояние между двумя точками, заданными координатами
70. Найдите расстояние от точки М (2, — 1, 1): а) .до начала О
координат; б) до координатной плоскости xz.
71. Найдите расстояние от точки Л4( — 3, 2, —1): а) до точки
К (1, —2, — 1); б) до оси х.
72. В параллелограмме A BCD А (1, —2, 3), В (0, 2, — 1), С (0, 0, 1).
Найдите: а) длину диагонали АС; б) длину диагонали BD.
Уравнение плоскости
73. а) Составьте уравнение плоскости, проходящей через точку
М (1, —2, 3) и перпендикулярной вектору п (2, 0, — 1). б) При-
надлежат ли точки Л 1(3, —5, 7) и Л2(1, 2, —3) плоскости?
в) Найдите точку пересечения этой плоскости с осью х.
74. а) Составьте уравнение плоскости, проходящей через точку
М и перпендикулярной вектору и, если М (0, 3, — 1),
п (5, — 3, 1). Укажите: б) координаты какой-нибудь точки,
21
принадлежащей плоскости; в) точку пересечения плоскости с
осью г.
Уравнение сферы
75. а) Составьте уравнение сферы с центром S (2, — 1, 3) и радиу-
сом Z? = 5; б) Принадлежит ли точка Л (5, —5, 3) сфере?
в) Пересекает ли сфера ось х и если пересекает, то укажите
точку пересечения?
76. а) Составьте уравнение сферы с центром 5( — 4, 0, 3),
если точка Л1 (— 1, 4, 3) принадлежит сфере; б) укажите
расстояние от центра сферы до плоскости yz.
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЯМ ОСНОВНЫХ ЗАДАЧ
Многие задачи допускают несколько способов решений. Мы
предлагаем один способ, наиболее общий при решении задач
подобного типа.
1 <*ис- 2>‘ b = 2ctg30’ = 2^3,
= 2t^3frO =2, S=0,5ad =2-\/3, CK=b sin 30°=л/3.
2 (рис. 3). b=2 cos 60°= 1, a —2 sin 60°=-\/3, /?== c _ =
'r 7 * 2 sin C
“«hr ->• ^ = 0.^=f • C« = 0sin60" = f.
3 u™. 4). АВ--^г=Ш BC = 2lg45°=2.
CK=ЛС sin 45° = 2 sin 45°=^2-
2 sm 45 v ¥
4 (рис. 5). c=-^a?4-6z = 5, S—0,5ab=6, = 2 sfo c = 2,5-
5 (рис. 6). ЛС=3, так как ДЛВС равносторонний, Иь —
=АВ sin 60°=-Ь^-. R = —?—= -! =V3, r=AO sin 30° =
2 2 sin Л 2 sin 60 v
=/? sin 30° = 0,5/?=^, S=^-.
6 (рис. 7). R =----= .-! =—. AB=-^—=—-=
' 2 sin 120° sin 60 sin 60 sin 60
=Д, ВК=Л/( ctg 60°—$=0,5ЛС-ВК—
т/з т/з
7 four JU KM KM_2“ KM — 4 SABKM. BAf S^bkm_
7 (рис. 8). AC BC , 10 5u , KM 4, S^ABC BC2 . 100
= 25^' ’ ^ABKM=^.
л z qs BC ____AB 6 ____6n KM ___4 __AB 6 ____
(рис. yj. KiAfi — AKi, KMl~5u’ л ’ k2m2~ak2’ KiMi ~
K2A42 = 3.
9 (рис. 10). 2R=AC, AC=-~—=4, R=2, AD = 2 ctg 30° =
SIH OvJ
= 2^/3, S=AD-CD=4^3.
22
В 4 С
Рис. 30
Рис. 31
Рис. 32
10 (рис. 11). В К — расстояние от точки В до прямой AD,
г.Л = 180° —В = 60°, ЛВ = 2, тогда ВК=АВ sin 60°=-Д Из
дЛВО, где Z-ABO=60° и АВ — 2, находим ВО=АВ cos 60°= 1,
значит, BD — 2, АО=АВ sin 60° = 2 sin 60° ==д/3, значит, АС=
=2-Д 5=Л£>-ВК = 2 V3, АЕ—АВ sin АВЕ=т/3.
11 (рис. 30). КМ = 4 + х, -^=g-, х = 4, /СМ = 8.
12 . а) Так как /?=-——-
2 sin А
= 2л/? = 8л, S = nR2 — 16л; б)
ТО 2 sin 150° 2 sin 30°
С—12л, 5 = 36л; R = а6 = 4, С = 8л, S = 16л.
13 (рис. 13). а) ВС=— АВ+АС; б) |ВС| =д/(ЛС—ЛВ)2 =
=-\/ЛС2-2ЛС-ЛВ+ЛВ2=^9-2+2с°5б0с+4 =л/7;
в) cos (ЛВС)=cos (ВЛ, ВС) = cos (—АВ, ВС)=-^^£ =
I-4BI4BCI
_ АВ-ВС АВ (АС—АВ) АВ-АС—АВ'- 2-3 cos 60°—4 _
~ 2^/7 — 2д/7 — 2-у/7 2т/7
=^, Z.ABC=arccos^; г) (2ЛС —АВ)-ВС=('2АС—АВ)Х
Х(ЛС—ЛВ)=2ЛС2 —2ЛС-2ЛВ-ЛВ-ЛС+ЛВ2=2ЛС2 —ЗЛСХ
ХЛВ+ЛВ2= 18-9 + 4= 13.
Замечание. -у/(а— b)2=/=a — Ь — обратите на это внимание.
14 (рис. 14). а) АВ (—1 — 1, 3 — 2), ЛВ(-2, 1), ЛС(-1, —4);
б) ЛВ-ЛС=-2-(-1)+1-(-4)=-2; в) ЛВ=^4+1=л/5,
ЛС=<Г+1б=л/Т7; г) cos (ЛВ, ЛС)=^|^=--^.
15 (рис. 31—34).
16 . а) Через точку В и прямую АС проведем плоскость а (через
три точки, не лежащие на одной прямой, можно провести плос-
кость и притом единственную). Проведем через точку В произ-
вольную прямую ВМ, пересекающую прямую АС (рис. 35).
23
Рис. 33
Рис. 34
Прямая ВМ имеет с плоскостью а две общие точки В и М, значит,
она лежит в плоскости а.
Обратите внимание! Согласно условию задачи мы должны
были доказать, что «все прямые... лежат в одной плоскости»,
мы доказали это утверждение только для одной прямой ВЛ4.
Но так как эта прямая произвольная (что может быть и не
оговорено специально), заключение этой теоремы будет справед-
ливо и для любых других прямых, удовлетворяющих условию
задачи.
б) Отрезки АВ и ВС лежат на пересекающихся прямых АВ и
ВС, значит, лежат в одной плоскости а. Проведем прямую DE,
пересекающую отрезки АВ и ВС (рис. 36). Прямая DE имеет
с плоскостью а две общие точки D и В, значит, она лежит в
плоскости а.
17 . а) Так как Л|В1||О|С| и DC||DiCi (как противоположные
стороны квадратов), то Л[В|ЦОС. Отрезок AAi равен и парал-
лелен отрезку CCi (они равны и параллельны DDi), следова-
тельно, ABiCiC — параллелограмм, т. е. Д|С1|]ЛС; б) например,
AAi и DC,AiCi и DC, B\D и AAi, и АС; в) Л1С1ЦЛС (доказа-
ли в а)) и МК||Л1С| (как средняя линия £±А\В\С\, т. е. МКЦДС),
поэтому МК и АС лежат в одной плоскости, а значит, и точки
А, С, М, К лежат в одной плоскости.
18 (рис. 37). СС1=-^-==6 см (как средняя линия ДДВВ1).
19 (рис. 38). По условию ВВ\ЦЛ/L, следовательно, эти прямые
принадлежат одной плоскости В AAi, которая пересекается с
плоскостью а по прямой В1Д|. В (ВЛД[) через точку С проведем
прямую CCi, параллельную AAi, которая пересечет плоскость а
в точке С, лежащей на прямой BtA]. Другой прямой, парал-
24
в
Рис. 37
Рис. 38
лельной AAi, через точку С провести ни на плоскости, ни в про-
странстве нельзя согласно аксиоме параллельности прямых.
Значит, точки Вь Сь Ai лежат на одной прямой, а) Так как
ЛС:ВС=1, то точка С — середина АВ, а СС\ —средняя линия
трапеции А\АВВ\. СС\ = 0,5 (ЛЛ14-ВВ1) = 0,5 (9+5) = 7 см;
б) то ЛС = и, ВС = Зи (рис. 39). ВО||В1Л| (по построе-
нию), тогда A\D=BB\ =5, Л£) = 9 —5 = 4. Пусть СЕ=х, ,
С* С Oil
х=3, тогда CCi = 5 + 3 = 8 см.
X о
20 . Не может. Докажем это. Пусть прямые а и Ь скрещивающиеся.
Если бы прямая с была параллельна а и Ь, т. е. с || а и с || &, тогда а|| Ь>
что противоречит условию.
21 . а) Л1В1 параллельна граням ABCD, DiCiCD; ВС парал-
лельна граням B\C[D\Ai, ADDiAc, ЛВ1||2)Сь значит, АВ\ парал-
лельна грани DCC\D\\ 6) в ДЛВ1С МК. — средняя линия, значит,
ЛТК|| Л С, следовательно, 7И/<||(ЛВС).
22 (рис. 40—43).
23 (рис. 44). Будут. Если бы прямая а пересекла прямую fr, а b
принадлежит плоскости а, то а пересекла бы плоскость а, что
противоречит условию. Значит, а||6.
24 (рис. 45). Можно. Пусть прямые а и Ь скрещивающиеся.
Возьмем на прямой а точку М. Через точку М и прямую b всегда
можно провести плоскость, а в ней прямую Л1/<|| Ь. Через прямые
Рис. 39
25
Рис. 40
Р
Рис. 41 Рис. 42
М
МК и а можно провести плоскость а,
которая будет параллельна прямой Ь.
25. а) (ЛВ<?)||(Л]В1С|), так как ЛВЦЛ1В1,
ВСЦВ1Сц и АВ с ВС пересекаются (или
А\В\ с BjCj пересекаются); б) если пря-
мая а. принадлежащая (ЛВВ|), пересе-
калась бы с (DCCi), например, в точке К,
то это означало бы, что точка К принад-
Р
Рис. 43
лежит и прямой а, а значит, и плоскостям ABBi и DCCi. Следо-
вательно, (ЛВВ1) и (DCCi) имеют общую точку К, т. е. пересекают-
ся, что противоречит условию; в) КР — средняя линия дВ£>|Сь
или KP\\DCi, а £>С|||ЛВ1, следовательно, КР\\АВ\. Так же дока-
жем, что Af/CHBjC (МЛЦAiD, A\D||BiC). Так как пересекающиеся
Рис. 45
прямые КР и МК соответственно параллельны ЛВ1 и BiC, значит,
(МР/ониад.
26 (рис. 46—48).
Рис. 46
Р
Рис. 48
26
Рис. 49
27. а) Если прямая а||Ь и а||с, то б||с. Если а||а, а|| 0, то плоскости
аир могут пересекаться. Так, например, в кубе ABCDA\B\C\D\
ДЛ|||(ОСС|) и AAi H(BiCiC), a (£>CCi) и (BiGC) пересекаются;
б) если бы скрещивающиеся прямые были параллельны, то они
обязательно принадлежали бы какой-то плоскости, что невозмож-
но, так как скрещивающиеся прямые согласно определению не
лежат в одной плоскости; скрещивающиеся прямые могут при-
надлежать параллельным плоскостям. Построим такие плоскости.
Пусть прямые а и b скрещивающиеся (рис. 49, а). Возьмем точки
М и К (рис. 49, б). В плоскости (Л1, Ь\ проходящей через точку М
и прямую 6, проведем прямую МС параллельно Ь. В плоскости
(/(, а) проведем прямую KD параллельно а. Через пересекающиеся
прямые а и МС, а также b и KD проведем плоскости, которые будут
параллельны (Ь||МС, a||KD) и в них будут лежать скрещивающие-
ся прямые (рис. 49, в).
28. а) (рис. 50). Равнобочная трапеция; б) (рис. 51). Прямо-
угольник.
29. а), б), в), г) — может, д) — не может. При выполнении этого
задания имеет смысл рассмотреть тени различных треугольников,
параллелограммов, трапеций, вырезанных из бумаги, в лучах лам-
пы или фильмоскопа. Полученный таким образом набор теневых
изображений, хотя и не является результатом точного парал-
лельного проектирования, все же с хорошей степенью точности
демонстрирует то, что можно получить при параллельном
проектировании.
30 (рис. 52). a) MiBl:BlKi=3t:3t==\: 1; б) ЛТ1К1:Л1В| =
Рис. 50
Рис. 51
27
Рис. 52
=6/:2/=3:1; в) A1K1:MiA.=5Z:/ = 5:l; г) AiBr.BiKr.MiAx =
=3/:3/:/=2:3:1.
31 (рис. 53).
32 (рис. 54). а) BiBJ-ЛВ, BiBJ_BC, АВ пересекает ВС, следо-
вательно, BiB_L(4BC); б) AD-LDDi, AD.LDC, DC пересекает
DD\, следовательно, AD J_(DiDC); в) BiD|_L4|Ci (как диагонали
квадрата), B\DiJlAA\ (так как AAi -L^iBjCi)), AAi пересекает
A iCi, следовательно, BiDi ±(ЛЛ|С); г) так как Л iBi JLBtCi, AtBi J_
±B|B, BtCi пересекает B\B, to AiBi _L(BB]Ci), откуда Л1В1±
J_BiC; д) так как Л1С1±В1£>1 (как диагонали квадрата),
BD||BiZ>i (так как BB\DiD — параллелограмм), то Л1С1ХВВ;
е) так как В|С1-ЬЛ|В1, B1C1.LBB1, A\Bi пересекает ВВг, то
В|С| _1_(Л1В|В), откуда В|С1_1_ЛВ1, т. е. АЛВ1С1=90° и треуголь-
ник ЛВ]С] прямоугольный.
33 (рис. 55). а) дМОА = /\МОВ (по двум катетам: МО — об-
щий катет, ЛО = ОВ, так как О — центр многоугольника),
следовательно, ЛЛ4=МВ; б) ОК Л-АВ (по построению), тогда
АВ±МК, OK=0,5AD=4, МК =^ОК2 + ОЛГ=^16 +144 =
= 4-\Я0; в) tg МАО=7^=-Ц==-тг; так как АО —ОК., то
v ' ’ s о А 4л/2 -y'S
smOAK=-r^=4^2, tgMAK=^=^=VlO; 0 5дЛМВ =
=АК-МК = 16 л/ТО-
Рис. 54
Рис. 55
28
Рис. 59
Рис. 57
Рис. 58
34 (рис. 56). а) См. решение задачи 33, а; б) ОК.Л-АВ (по по-
строению), АВ±МК, 0/(=4/<-tg 30°=3 tg 30° = Г, МК.~
=^/МО2 + ОК2 = 2; в) tg(MAO)=~=& так как АО =
XMK = 2V3.
35 (рис. 57). a) DC-LAD (по условию), MD-LDC (по теореме
о трех перпендикулярах), MD—^jAD2 + MA2 = ^Jl +1 =л/2» так
какЛС2=1 +2 = 3, то ЛС = -\/3, ЛЛ1 = ЯС-tg 30° = 1; б) Х_СМВ =
= 90°, так как СВ .LAB, то CB-LMB (по теореме о трех перпен-
дикулярах); в) МВ2=АМ2 + АВ2 — 3, МВ = ^3. £дЛШС = 0,5СВХ
ХМВ=£-.
36 (рис. 58). a) ВС=АВ-sin 30° = 2-0,5=1, tgМСВ=^ =
=215.-0,5; б) СК-LAB (по построению), MK-LKC (по теореме
о трех перпендикулярах), МК2 = КС2-\-МС2, 7(C=CB-sin В —
= I-sin 6О°=^-,Л1№=-|-+4-=1.Л1К=1; в) 5дЛ1СВ = 0,5МСХ
ХСВ=0,5-0,5-1 =0,25, 5дЛЛ1в=0,5ДВ-Л!К=0,5’2-1 = 1.
37 (рис. 59). а) МА =АВ tg 60° = 5 д/З, tg МАС=?~=5-^ ;
б) BC-LAC, где АС — проекция МС на (ЛВС), следоватряьно,
MC-LBC (по теореме о трех перпендикулярах), МС2 — АМ2 +
+ЯС2, МС2 = 9 + 75 = 84, A1C = 2-V^T; в) 5дЛЛ1С = 0,5МД-ДС =
5дА1СВ = 0,5ВС-Л1С=0,5-4-2 д/2Т=4д/2Т, так как ВСг=
=АВ2—АС2, ВС2=16, ВС = 4.
38 (рис. 60). а) Угол между прямыми АВ\ и DC равен углу между
прямыми ЛВ1 и АВ и равен 45°; б) угол между прямыми АВ\ и
A\D равен ZAB\C и равен 60°, так как ДЛВ1С равносторонний;
29
Рис. 60
Рис. 61
Рис. 62
в) угол между прямыми Л1С] и BD равен углу между прямыми
Д1С| и B|D| и равен 90°; г) угол между прямыми Л(С| и BiC
равен углу между прямыми Л1С1 и A\D и равен Z.C^iD=60°,
так как &А\С\В равносторонний.
39 (рис. 60). а) Так как АА\Л.(АВС), то (по признаку пер-
пендикулярности плоскостей) (AAiD)-L(ABCy, так как ЛЛ|й_
_1_(ЛВС), то (ЛЛ1С)_1_(ЛВС); так как DBA-АС (как диагонали
квадрата), ВВ_1_ЛЛ| (ЛЛ1_1_(ЛВС)), ЛЛ1 пересекает АС, то
DBJ-(AiAC), откуда (DBBi)A-(AiAC)‘, б) так как BiB_1_(ЛВС), то
ЛBiAB —45°; так как BD — проекция BDi на (ЛВС), то угол меж-
ду BDi и BD определим, найдя его тангенс: tg DiBD=l^ =
ТЯК КЯК В'С* — проекция Л.С1 на (DD\C\), то Z-AiCiDi
равен 45°; в) -90°, так как ЛЛ(±(ЛВС); 45°, так как Z-ADAi —
линейный угол двугранного AtDCB: DC Л. AD и DC.LA1D
(рис. 61); tg В\ОВ=-^——2 (рис. 62), так как Z-ByOB—
линейный угол двугранного В АС В г. АСА-ВО и ЛС_1_В1О.
40 (рис. 63). а) Так как диагонали квадрата перпендикулярны,
то ВОА-АС; так как МОА_(АВС), то МОА-ВО, или ВОА.АС и
В0±М0, следовательно, ВО±(АМС). ВО =^-=^=4 -у/2;
б) О/<±ЛВ (по построению), тогда AB.LMK (по теореме о трех
Рис. 64
30
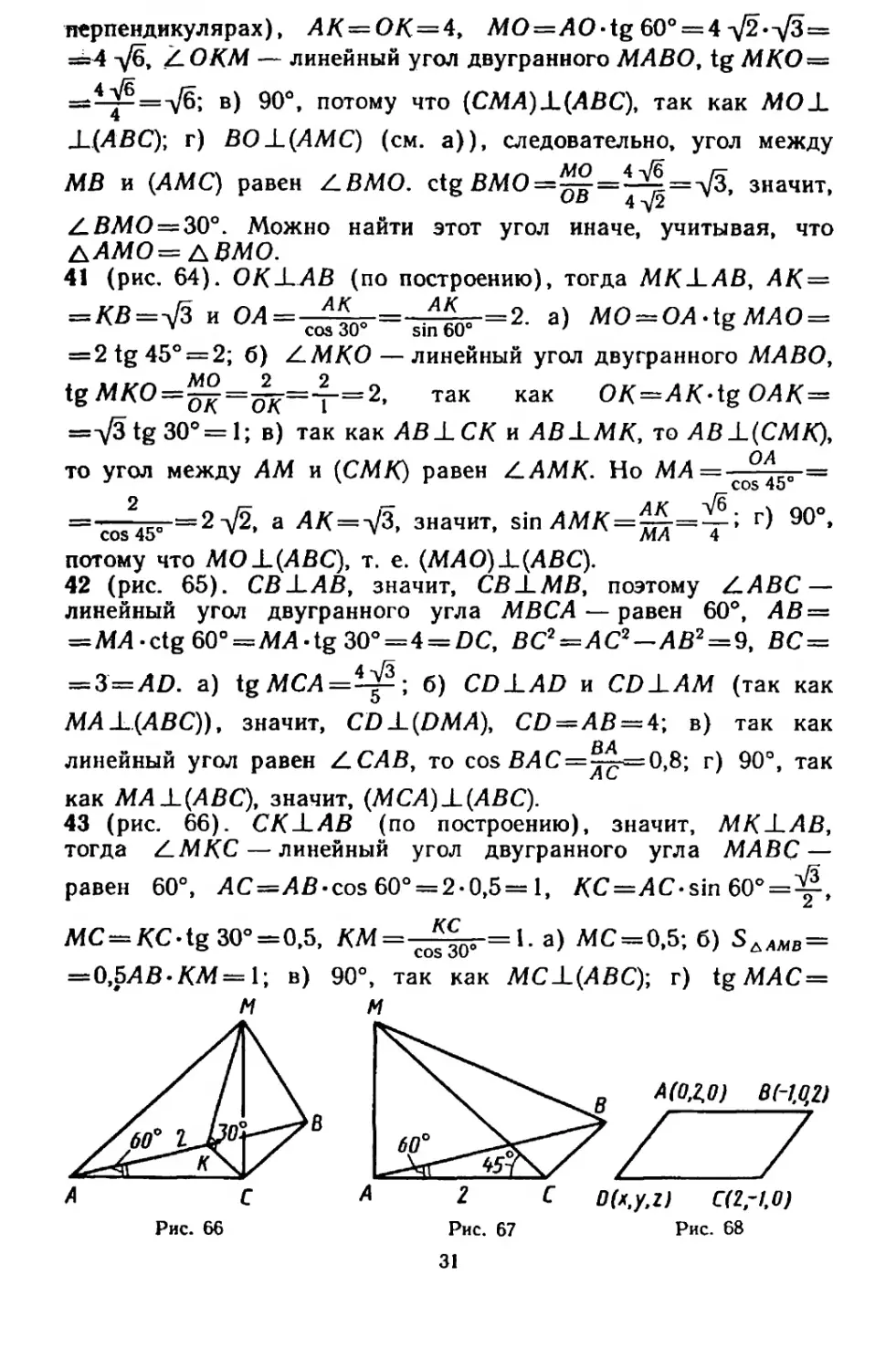
Рис. 65
Рис. 63
перпендикулярах), АК=ОК=4, MO=AO-tg 60° = 4 -\/2--^3=
=ь4 -у/б, Z.OK.M — линейный угол двугранного МАВО, tg МКО—
в) 90°, потому что (СМА)Л.(АВС), так как МО JL
Х.(АВС); г) ВОХ(АМС) (см. а)), следовательно, угол между
МВ и (АМС) равен Z.BMO. ctg ВМ0=^=^=^3, значит,
ив 4 -^2
Z_BMO = 30°. Можно найти этот угол иначе, учитывая, что
дЛМ0 = Д ВМО.
41 (рис, 64). 0/<_LAB (по построению), тогда МК-1_ЛВ, Л7< =
= КВ=д/3 и 0А = л* =-4g.-=2. a) MO = OA-tgMAO =
= 2tg45° = 2; 6) Л МКО— линейный угол двугранного МАВО,
tgMK0=^=^=-p=2, так как ОК^АК-tg ОАК=
=->/3 tg 30° = 1; в) так как АВ±СК и AB.LMK, то АВ±(СМК),
то угол между AM и {СМ К) равен ХАМЯ. Но МА=------7ёз-=
COS 4и
-----2д/2, а ЛЛ=д/3, значит, sin АМК = ^г=^-» г) 90°,
потому что МО-ЦЛВС), т. е. (MAO)_L(ABC).
42 (рис. 65). CBJ-ЛВ, значит, CBJ-MB, поэтому Z.ABC—
линейный угол двугранного угла МВСА— равен 60°, ЛВ =
=МЛ-ctg 60° = МЛ-tg 30°=4 = ВС, ВС2=ЛС2—ЛВ2 = 9, ВС =
= 3 = А£>. a) tg MCA =^; б) CD .LAD и CD±AM (так как
МА ±(ЛВС)), значит, CD J_(£>AfЛ), СО = ЛВ = 4; в) так как
ВА
линейный угол равен ДСЛВ, то cos В А С=^<=0,8; г) 90°, так
как МЛ ± (ЛВС), значит, (МСЛ)±(ЛВС).
43 (рис. 66). СК-LAB (по построению), значит, MK-LAB,
тогда Z-MKC — линейный угол двугранного угла МАВС —
равен 60°, AC=AB-cos60° = 2-0,5=l, КС=АС-sin 60°=^,
2^
МС —KC-tg 30°=0,5,
КМ=-^Г='-а> МС=0,5; б) 5дЛА,в=
90°, так как МС±(АВС); г) tg МАС=
Рис. 66
31
=МС-АС=0,5.
44 (рис. 67); ВС±АС, АМЦЛВС), значит, AMЛ.ВС и ВС±МС,
Z. MCA—линейный угол двугранного угла МАВС. а) МА =
-МС-tg 45° = 2-1 =2; б) ВС±АС и ВСА.АМ, значит, BC_L
±(ЛМС), ВС=AC-tg 60° = 2^/3; в) 90°, так как МА±(АВС),
то (ЛМС)±(ЛВС); г) ЛВ=-^—=4, tg MBA =j£=0,5.
45 . a) (a—2b— 4c)-b=ab—2b2 — 4cb = 0 — 2 — 2 =—4; 6) |a —
— 2c| =-\fa2 — 4ac+4c2 = 7a2 —4ac+4c2=71 —2 + 4 =73,
i~ d~ ~Z\ (o — 2c) b ab — 2bc 0 — 1
COS (a — 2c, b)= ' ’ =----=——= —
^з-\ -Vs V5 3
46 (рис. 68). а) ЛВ(— 1, — 2, 2); 6) DC (2-х, — I—у, —z),
так как AB=DC, то
или
£>(3, 1, -2); в) ВВ(3+1, 1-0, -2-2), BD (4, 1, -4);
г) АС (2, —3, 0), ЛС-ВВ = 8 —3 + 0 = 5; д) |ЛС| = 74 + 9 + 0 =
=713, |ВО| =716+1 + 16=733; е) cos (ЛС, В£))=^|^-=
5 5
~ д/ТЗ-д^З ~~ д/429 ‘
47 (рис. 69). а) 60°, так как Z.ABC— линейный между (ЛВВ1)
и (ВВ}С)\ АК J-ВС (по построению), значит, Л1К_1_ВС (потеореме
о трех перпендикулярах), поэтому АА\КА—линейный угол
двугранного угла AiBCA, но ЛК=ЛВ*51п АВК = 2^[% sin 60°==3,
А,А = Л,С-sin 30° = 4-0,5 = 2, tg Л.КЛ =^-=-?-; б) 5дВЛ1С=
- ЛА
= ВК-Л1К=73-713. так как Л^=7ЛЛ?+ЛК2=713; в) 2Х
ХВжи = ВС-АК=6^/3, 86ок = ЗАВ’АА1 = 12^, 5ПОЛ„ = 12ТЗ +
+ б73; г) У=ВК-ЛК-ЛЛ1=2 73-3=б73-
48 (рис. 70). а) 60°, так как Z14BC = 60o—линейный угол
двугранного угла ЛВ1ВС; (рис. 71) CB-L4C (по условию),
Рис. G9
Рис. 70
32
Рис. 71
Рис. 73
значит, СВХД1С (по теореме о трех перпендикулярах), поэтому
ЛА[СА — линейный угол двугранного угла AtCBA. tg Л]С71 —
=±£=А; б) 5дЛ,вс=0,5СВ-Л1С, но CB=4S-sin 30°= 1,
Л!С=д/ЛИ^Ь Л С1 2 3 = д/7, S^AiCB = 0,5^7; в) У=0,5ЛС-СВХ
хлл,=д/з.
49 (рис. 72). BD — B]D-cos 45° = 4; = 45° = 4.
£ОС11 = 0,5В£>2 = 8-2ЛВ2 = ВВ2, откуда ЛВ = ^=2 д/2; 5бок =
= 4ЛВ-В|В=32д/2; а) ВПОЛ11 = 16+32 д/2; б) V=SOC„-BiB = 32.
50 (рис. 73). a) V32 + 22 + 62 = 7; б)' sin В1£>В = |^-=-^-,
sin B\DA\ sin BiDA—^-; в) SBBlD1D — BBt-BD = 6 дЛЗ, где
BD=^13; г) ZLC.DC — линейный угол между (ADCi) и (BAD),
tg Ci£>C=-|-=3. S,I0.1H = 2-(2-3)4-(3 + 2 + 3 + 2)-6 = 72; д) V=
= 2-3-6 = 36.
5t (рис. 74) а) дАСВ равносторонний, поэтому ЛС = 6 —
меньшая диагональ ромба, тогда АС\=--—=бу2 —
меньшая диагональ параллелепипеда, СС)=/4С = 6. ВО =
= Л В • sin 60° = 3 д/3, BD = 6 д/3, BD, = 7ВР2-|-ВВт = д/Г08 + 36 =
=7144=12; б) 5ПОЛ11 = ВР-ЛС + 4ЛВ.ЛЛ|=б73-6 + 4-6Х
Хб = 36д'3+144; в) V=0,5BD • ЛС-ЛЛ । = 108 д/3.
52 (рис. 75) а) ХОДК=30°. ЛК=Зд/3, ОЛ=-^§==6,
COS »5U
МЛ=д/36 + 9=Зд/5, tgAMO=^=-|-==0’5; б) ОК=АКХ
Xtg 30° = 3 д/3 tg 30° = 3, Z_M/(O — линейный угол двугранного
угла МАСВ, tg МКО = ~^4-='1’ ^-МКО^45°; в) МК=
U л\ о
1 Для вычисления искомых углов найдем их синус: sinx = d. Этого вполне
достаточно, так как, используя формулу r=arcsinfc, угол всегда можно опре-
делить.
3 Заказ )24
33
=д/9+9 = Зд/2, S6oii=3 ЛЛ*Л1К=27 д/б; г) V^S^f/^^-X
X 0,5 -(6 д/3)2 • sin 60°•3 = 27 д/3.
53 (рис. 76). а) СА-—^-=10 д/% ОЛ = 5 д/2, МЛ =
' cos *5 о
=д/144 + 50=д/Т94, tgM4O=^?=^; б) ОК=5, Z.MK0 —
12
линейный угол двугранного угла МАВО, tg МК0=-^', в) А4/С=
=7144 + 25= 13, $6ок = 4Л/ОЛ1К=260; г) V=4-SOCI1//=400.
<J
54 (рис. 77). a) CD-LAD, Зхчачит, CD A-DM (по теореме о
трех перпендикулярах), поэтому /LMDC — линейный угол между
плоскостями MDC и ADC и равен 60° (по условию), AD =
= д/25-16 = 3 = ВС, ЛЛ1 = Л£»-1§60о = 3 73, tg МСЛ=^=
/1 С/
= 0,6 д/3; б) SaA1DC=0,5DC.DM, ОМ = ^Ж=_1__^6,
SA/>mc —0,5-4-6 — 12, СВ А. АВ,_значит, СВ А-МВ, ВлЛ13С =
= 0,5СВ-МВ, Л4В=-д/л1Л2 + ЛВ2 = 743, 5дЛ1ВС = 0,5-3.\/43 =
= 1,5д/43, 5дЛЛ(В=0,5Л4Л-ЛВ=6д/3; в) У=-рИЛ-ЛВ-Л£> =
+J 2-7v 5 + 5+6 а
55. Найдем площадь основания пирамиды: ---5---=8,
34
Swn=^p(p~a)(p~b)(p-c)=yl8-3>3^2 = 12
(площадь можно также найти по формуле
0,5а-йа). а) Используем рисунок 78,а:
«сеч _МК2_ и2_ I . с «осп__о
5осн — МОг~4и2— 4 ’ «ч— 4 — °-
б) Рассмотрим рисунок 78, б:
5«ч _МК2_ и2 _ 1 . 5 _12 3
SOCH МО2 16иг 16’ г>«ч—16~ 4 •
56 (рис. 79). ОК = 2 д/3-ctg 60° = 2=ДК,
д
МК=
МО
sin 60°
«поли = АВ2 + 4АК • МК = 16 + 32 = 48,
АВ2-МО _ 32 д/з
3 ~ 3
Рис. 82
57 (рис. 80). О К = 2 д/З-ctg 45°=2д/3; (рис. 81). ВК^ОКХ
Xctg 30° = 6 = CK^K=CK-tg 60° = 6д/3,5ос„ = ВК-ДК = 36 д/З;
(см. рис. 80). МК=-^А_=2д/б. Sn0JIH = Soc„ + 3BK-MK=
uUl ли
=36-^3+звк-мл=361/3+36 д/ё, =72.
58 (рис. 82). ДП = 8-соэ 30°=4д/з1 tf=8-sin 30<) = 4, AO = R =
=2д/3. a) SnojIH=2Soc„4-S6oK=2n* 12-}-2л«2 д/3-4 = 24л4-Ю д/Зл;
б) (рис. 83). А С—2R-sin 60° = 6 (по теореме синусов a=2R sin Д),
$пояи = 2$ос« 4- $бок = 2 • 0,5Д С2 • sin 60° 4- ЗД С • CD = 18 д/3 4- 72;
в) (рис. 84). AE=AD-sin 30° =2 д/3, ED=AD-cos 30° = 6,
5полн=25осн4-5бок=2.0,5Д£-ДП4-(ДС4-^Р4-ЛО).Я=12д/3 +
4-(2д/34-64-4 д£)-4=36д/34-24; г) У„,=л/?2Я=48л.
59 (рис. 85). АС=~\/аВ2^-СВ2= 10 = 2# (гипотенуза прямо-
угольного треугольника, вписанного в окружность, является
диаметром этой окружности), /? = 5, СС} =XC-tg 45° — 10 = Я,
У=лЯ2.Я = 250л, S6oK = 2nRH= 100л.
60. ze,u;„L’^l.L=3(J. (рис. 87). 7?=^=,^-^=
= 6==ЛО, значит, AD=l2 = DDit так как в осевом сечении
3*
Bi
Рис. 84
35
Рис. 83
Рис. 85
Рис. 86
Рис. 87
цилиндра — квадрат (рис. 86). V — л/?2// = 432л, S6oK — 2nRH—
= 144л.
61 (рис. 88). AC—^/AD2A-DC2 = 2 — 2R, следовательно, R=l,
СС, =лМс?-ЛС2 — \=Н, V = jiR2H = n, £бок = 2л/?//=2л.
62 (рис. 89). а) 5„0Л11 = Soc„ + S6oK = л/?2 + л/?/, но AO = R =
=6 • cos 60° = 6 • sin 30° == 3, •$„„„ = 9л-|- 18л = 27л; б) (рис. 89).
5осн = лЛ02 = л/?2 = 9л; (рис. 90). = £-=-%?-, 5сеч =
= — = ‘>9с\тт- (hue Qll МА'~ •Scc’i и _ ^сеч о __ __ л .
4 2,20л, (рис. У1). мо, , 36uj- дл , г>ссч 36 4 ,
в) /ИО = ЛМ • sin 60° = 3 д/3, Уй = -^-л/?2// = 9 73л.
63 (рис. 92). a) R=AO = MO-tg 30° = 5, l=AM=\0, 5б0к =
nr ел леч iz nR2H n-25-5-j3 125 \/Зл
= л./?/ = 50п; б) VK——z—=----- ~ =----=*
DO О
64 (рис. 93). ЛО = /? = -^ = 4=2 V3, так как а3 = 7?-^/з, SCoK =
V3 л/3 2
= л/?/ = л-2 V3-4 Т3 = 24л, Vk = ^., ЛЮ=д/дЛ12-ЛО2 =
О
=-748-12 = 6 = 7/, Ук = 21111±=24л.
О
Рис. 88
Рис. 89
36
Рис. 90
Рис. 91
МИМ
Рис. 92 Рис. 93 Рис. 94
65 (рис. 94). а) 7?=ЛО=^=2, l=MA=^OM^J±O2 = Ь,
V2
5б0К = л/?/=8л; б) Ук = ^=-М1.
66 (рис. 95). а) АВ = г, лг2 = 75л, г2 = 75, АВ2 = АО2 — ОВ2,
т. е. г2 = R2-(-^А 75=^. Я2 =100, R = 10, Уш=-^-=4000л;
б) МС2 = ОМ2 — ОС\ т. е. МС2 = 500— 100 = 400, МС=20.
67 (рис. 96). а) ОВ2 = /?2 = 4 —3=1, /?=1, 5 = 4л, V=^;
л/З
б) sin BOA =~2~' значит, Z.B0A = 60°, так как 0В = 0С и
ДВОС = 60°, то ДОВС равносторонний, ВС = ЛВ=1.
68 (рис. 97). а) значит, ОК=3«, АК = 2и> тогда ВО = 5«,
/\/1 Л
ВК = -\25а2 — 9u2 =4w, С = 2л• BK = 8nrz, 8зш=16л, н = 2, ВО =
= R = 5u=\0, V=^-=4-^; б) ОМ2 = ОА2 + АМ2= 100 +
+ 500 = 600, ОЛ4=Ю-у/6.
69 (рис. 98). а) л-ЛК2 = 4л, Л/<2 = 4, Л/( = 2 = гсс,„ АО=АВ=
= 2ЛК=4 = ВШ, 5ш = 4л/?2 = 64л; б) ОК=АКЛ% 60° = 2 ^3.
70. а) О (0, 0, 0), Л4О2 = (2 —0)2 + (— 1 -0)2+(1 -0)2 = 6, ЛЮ=6;
б) запишем координаты точки М\ (основание перпендикуляра,
опущенного из точки М на плоскость xz): Mi (2, 0, 1), /WiM2 =
= (2 —2)2 + (— 1 — 0)2Ч-(1 — 1)2= 1, т. е. ЛЛЛ4= 1.
Рис. 95
Рис. 96
37
10 W
Рис. 97
71. а) ЮИ2=(-3-1)2 + (2-}-2)2 + (-1 + 1)2 = 32, КЛ1 = 4л/2;
б) запишем координаты точки — основания перпендикуляра,
опущенного из точки М на осьх: Л4т ( — 3, О, 0), Л11Л12 = ( — 34~3)2 +
+ (2 —0)2 + (~ 1—О)2 —5, Л1М.=л/5.
72 (рис. 99). а) ЯС2=(0- 1 )2 + (0-’г2)2~Н 1 -3)2= 14, ЛС=д/Т4;
б) найдем координат;.! точки D (х, у, z'). Так как BA -—CD, то
( 1—0=х —О,
? —2 —2 = у —О,
I 34-1=2-1,
Тогда D (1, —4, 5),
В£>2 = (1 - 0)24-(-*-2)24-(5+ 1)2 = 73,
BD=-v/73.
73. а) 2(х—1)4-0(у4-2)—1 (г —3) = 0, 2 (х— 1) — (z — 3)=0;
б) подставим координаты точек 4i и А2 в уравнение плоскости:
2(3—1) — (7 — 3) —4 —4 —О, значит, точка Ai принадлежит
данной плоскости; 2 (1 — 1) — ( —3 — 3)=#0, т. е. точка А2 не
принадлежит данной плоскости; в) координаты точки /(— пере-
сечения плоскости с осью х: К (х, 0, 0). Подставим координаты
этой точки в уравнение плоскости: 2 (х—1) —(О —3) —О, 2х — 24-
4-3 = 0, х——0,5 или К ( — 0,5, О, 0).
74. а) 5 (х — 0)—-3 (у — 3)4- 1 (*+ 1) = 0; б) например, Р(1, 2, г)
(значения х и у взяли произвольными), вычислим теперь
z:5 (1 —0) —3 (2—-3)4-(^+1)~0, 54-34/+1 =0, z=-9. Итак,
Р(1, 2, —9); в) координаты точки д пересечения плоскости
с осью 2 вычислим аналогично: К (0, 0, г), 5(0 — 0) —3(0 —3)4-
4-(z4-l) = 0, г--10, К(0, 0, -10).
75. а) (х-2)24-(^+1)24-(г~3)-25; б) (5 — 2)2 4; (— 5 4~ 1 )2 + (3—
—-3)2 = 25 — верно, значит, точка А принадлежит сфере; в) коор-
динаты возможной точки К пересечения сферы с осью х: К (х, 0, 0).
Подставим в уравнение сферы координаты точки Л:(х — 2)24~
4-12 + (-3)2 = 25, (х —2)2 = 25—10= 15, х — 2=±Л^15, хи = 24-
38
+V15, %2 = 2—мы получили две точки пересечения сферы
с осью х: Ki (2+\Т5, 0, 0) и К2(2 —д/15. 0. 0).
76. а) /?2 = ОЛ42=(—1+4)2+(4—0)2 + (3-3)2=25. Уравнение
сферы: (х + 4)2 + (у- 1 )2 + (г- З)2 = 25. (х+4)2 + у2 + (2- З)2 = 25;
б) расстояние от центра сферы до плоскости уг равно модулю
координаты х центра сферы, т. е. | — 4| =4-
§ 3. ТРЕНИРОВОЧНЫЕ ЗАДАЧИ
ПЛАНИМЕТРИЯ
1. Дан ДАВС, причем Z.C = 90°. Найдите остальные стороны
треугольника, /?, 5 и расстояние от точки С до прямой АВ,
если: а) Z_A = 45°, а = 4; б) АА = 60°, 6=6; в) АД = 30°,
с = 8.
2. Дан А ЛВС, Z_C = 90°, а = 5, 6=12. Найдите третью сторону
треугольника, один из острых углов, R и расстояние от точки
С до прямой АВ.
3. В равностороннем треугольнике сторона равна 3 д/З. Найдите
высоту треугольника, /?, г и S.
4. Найдите /?, если угол при вершине В равнобедренного
треугольника АВС равен: а) 30°; б) 60°, сторона АС равна 2.
5. В треугольнике АВС КМЦАС, АС= 12. Найдите КМ, S^BKM,
зная, что ЗлАВС = 192, если отношение равно: а)
С* О
б> т-
6. В АЛВС сторона АВ разделена на три части точками Кь
Кг такг что отношение AKi:KiK?:K2B равно 4:3:5. Через
точки Ki и Кг проведены отрезки KrAli и КгМг параллель-
ные ВС (М। и Мг — точки на стороне АС). Найдите отрезки
К\М\ и КгЛ4г, если ВС = 24.
7. В прямоугольнике ABCD Z.CAD равен 60°. Найдите R и S,
если АВ = 4.
8* Дан ромб ABCD, DC = 2. Найдите расстояние от точки В
до прямой АВ, длины диагоналей, S, расстояние отточки А до
прямой ВСГ если угол В равен: а) 150°; б) 60°.
9. Найдите длину окружности и площадь круга, если в нее
вписаны: а) правильный треугольник со
стороной равной 3 д/З; б) правильный
четырехугольник со стороной, равной 2 д/2.
10. В окружность вписан n-угольник А|Аг...Ал й/2 и
(рис. 100), диагональ которого АгАп ран- Л/ у
на 2. Найдите длину окружности и J
площадь круга, если угол А2А1А/1 равен:
а) 150°; б) 90°. Рис. 100
39
11. В дАВС АВ = с, AC = b, с = 3,6 — 2, Z.(c, b) = 120° Найдите:
а) СВ; б) скалярное произведение (ЗЛС — АВ) СВ\ в) Z.ACB.
12. В параллелограмме ABCD А(—1, 2), В(—1, 3), С (2, 1).
а) Выразите в координатах векторы АВ и АС; б) найдите
координаты точки D; в) найдите скалярное произведение
АВ*АС\ г) найдите АВ и Л С; д) найдите Д(АВ, АС).
СТЕРЕОМЕТРИЯ
Прямые и плоскости в пространстве
Аксиомы стереометрии и следствия из них
13. Постройте сечение куба плоскостью, проходящей через точки
М, Р, К (рис. 101 — 104).
14. Три вершины параллелограмма лежат в некоторой плоскости.
/Можно ли утверждать, что и его четвертая вершина лежит в
этой плоскости?
15. Сколько можно провести перпендикуляров к данной прямой
через точку, лежащую на прямой?
16. Сколько можно провести перпендикуляров к данной прямой
через точку, лежащую вне прямой?
17. Сколько можно провести плоскостей через две параллель’
ные прямые?
Параллельные и скрещивающиеся прямые в пространстве
18. Дан куб ABCDA\B\C\D\. Основываясь на том, что все грани
куба — квадраты, укажите несколько пар ребер, лежащих на
параллельных, затем на скрещивающихся прямых.
19. Отрезок АВ разделен на 3 части точками Ki, Кг так:
A/<i:/<iK2’./<2B = 2:3:5. Только точка А отрезка АВ при-
надлежит плоскости а. Через точки Ki, Кг, В проведены парал-
лельные прямые, пересекающие плоскость а соответственно
в точках Mi, М2, Bi. Докажите, что точки Mi, М2, Bi лежат на
одной прямой. Найдите длины отрезков JCiAfi и BBi, если
K2M2 = 10.
20. Точки А и В не принадлежат плоскости а. Точки Ki и Кг при-
надлежат отрезку АВ, причем АК\:К1Кг-КгВ = 3:1:4. Через
Ри . 101
Рис. 102
Рис. 103
Рис. 104
40
A
точки A, Ki, K2, В проведены параллельные прямые, пере-
секающие плоскость а в точках соответственно А\, М\, М2. В\.
Докажите, что точки Ль Л15, ЛТр, В\ лежат на одной прямой.
Найдите К\М{. К2М2, если ВВ\ = 23, AAi = 7.
21. Дан куб ABCDA\B\C\D\. Докажите, что четырехугольник
К\К2КъКь— параллелограмм, если точки Ль ^2, Кз, Кь—
середины отрезков АВ\, В\С. CD и AD соответственно.
Параллельность прямой и плоскости
22. На рисунках 105—108 изображены пирамиды. Постройте
сечения этих пирамид плоскостью, проходящей через прямую
МК и точку Е, зная, что Л4КЦЛВ, точка Е принадлежит
плоскости АВС. При построении используйте линейку и уголь-
ник.
23. Дан дЛВС. Плоскость а, параллельная прямой АВ. пере-
секает сторону А С в точке К. а сторону ВС в точке М. Докажи-
те, что прямая МК параллельна прямой АВ. Найдите АВ. если
КС =12 см, АС = 18 см, /СМ = 36 см.
24. Будет ли отрезок, не имеющий общих точек ни с одной из
двух пересекающихся плоскостей, параллелен этим плоскос-
тям, если он параллелен линии их пересечения?
25. Даны две пересекающиеся плоскости. Существует ли плос-
кость, пересекающая данные плоскости по параллельным
прямым?
Параллельные плоскости
26. Дан куб ABCDAiB\CiDi. Докажите, что сечение куба плос-
костью Л1С1Л, где точка К — середина DC.— трапеция, а
сечения куба плоскостями AiB^K и АА\К — параллелограммы.
27. Две параллельные плоскости аир пересекают сторону ВА
угла АВС в точках D и Di, а сторону ВС соответственно в
точках Е и Е\. Найдите длину DE\ а) если BD = 12 см,
BZ)i = 18 см, DiEi = 54 см; б) если ВЕ = 3 см, ОВ = 4 см,
DDi=6 см. Найдите длину ЕЕ\\ в) DE~b см, DjEi = 10 см,
£Ю| = 12 см. Найдите длину DB.
28. Даны параллельные плоскости. Через точку А и В одной из
них проведены параллельные прямые, пересекающие вторую
41
плоскость соответственно в точках Ai и В1. Найдите длину
отрезка AjBi, если длина отрезка АВ равна 4. Объясните
решение.
Параллельное проектирование фигур на плоскость
29. На рисунке 109, а изображена трапеция ABCD с проведенными
в ней отрезками. На рисунке 109,6 вы видите частичное
изображение параллельной проекции этой трапеции. Закончи-
те рисунок 109, б и укажите в нем отрезки B|Mi, С1К1,
D\E\, являющиеся изображениями отрезков ВМ, СК. DE
соответственно.
30. ABCD — прямоугольник (рис. ПО), AM— биссектриса уг-
ла А. На рисунках Ill и 112 даны изображения двух
параллельных проекций этого прямоугольника, обозначенные
AiBiCiDi. На каждом из них постройте изображение AM.
31. & АВС равнобедренный: ЛС = СВ,
CD — высота ДЛСВ. На рисун-
ке ИЗ изображена параллельная
проекция этого треугольника. По-
стройте отрезок C\D\. являющий-
ся изображением CD.
Рис. М3
42
Перпендикуляр и наклонная к плоскости
32. Дан куб ABCDA\B\C\D\. Основываясь на том, что все грани
куба — квадраты, докажите: а) АВ±(ВСС|); б) ZLA|DC =
= 90°; в) ABYLBXC\ г) ACXBjD; д) AC±(BDBi);
е) A\B.LDC\\ ж) DCX_LAXDX.
33. Точка О — центр квадрата ABCD, МОЛ^{АВС). а) ОМ = 4,
АВ —6; б) АВ = 8, ЛМЛО — 60°; в) МО = Ь, Z-MAO — A&Y
Докажите, что AM — МС\ найдите расстояние от точки М до
прямой АВ; найдите угол между AM и АО и между AM и АВ;
найдите площадь Л AM В.
34. Точка О — центр правильного треугольника, OM_L(ABC) и
а) ОМ = 2 д/3, ЛВ = 3; б) АВ=2^3, ZAL4O = 60°; в) МО = 2,
Z. МАО — 45°. Докажите, что МВ —МС; найдите расстояние от
точки М до прямой АВ; найдите угол между ДМ и АО и между
AM и АВ; найдите площадь дАМВ.
35. ABCD — прямоугольник, MA.L(ABCY а) £)С = 3, СВ = 4,
ДМСА=60°; б) DC = 6, MD~6, ДМВА = 60°; в) МА==3,
ВС = 2 д/2, z!MCA=30o. Найдите расстояние от тонки М до
прямой ВС; найдите угол между прямыми МА и АВ; найдите
площадь д/rfBC.
36. В ДАВС Z.C = 90°, MC_L(ABC), МС = 2, АВ=4, ДА = 60°.
а) Найдите угол между прямыми МВ и СВ; б) найдите
расстояние от точки М до прямой АВ; в) найдите площади
ДМСВ и дАМВ.
37. В ДАВС ZC = 90°, МА±(АВС). а) АС = 5, ВС = 2, Z.MBA =
= 60°; б) ДС=л/3, А ВАС=60°, АМВС = 45°- в) АВ = 2,
ДВАС = 45°, Z.MBA = 30°. Найдите угол между прямыми
МС и АС; найдите расстояние от точки М до прямой ВС;
найдите площади ДМАС и дМСВ.
Угол между прямой и плоскостью и между плоскостями.
Перпендикулярность плоскостей
38. Дан куб ABCDAXBXCXDX. Основываясь на том, что все грани
куба — квадраты: а) докажите, что ADJLDXC, ADJ_CCi,
(ADCj)±(jDi£>C); б) докажите, что ACMDBX, AC-LDDXi
(ACCX)-L(BDDX); в) найдите углы между CXD и (ACCi), C\D
и (АВ£>1), C}D и (АВВ|); г) найдите углы между плоскостями
(АВ|С) и (ACCi), (АВ|С) и (ABD), (DCBX) и (АВС).
39. Точка О — центр квадрата ABCD, ОМ _i_(ABC), АВ = 6.
Угол между прямой МА и (АВС) равен 60°. Найдите: а) рас-
стояние от точки М до (АВС); 6) угол между (АВС) и (АВМ);
в) угол между (АВС) и (АМС); г) угол между МО и (АМВ).
40. Точка О — центр правильного треугольника, ОМЛ-(АВС\
АВ—ЗуЗ. Угол между прямой /ИА и (АВС) равен 30°.
Найдите: а) расстояние от точки М до (АВС); б) угол между
(АВС) и (АВМ); в) угол между МО и (МАВ); г) угол между
(АЛЮ) и (АВС).
43
41. ABCD — прямоугольник, Л1Л±(ДВС), ЛС=10, ЛВ = 8, угол
между (МВС) и (АВС) равен 60° Найдите: а) угол между
прямой МС и (АВС); б) угол между (MDC) и (ЛВС); в) угол
между (ОЛ4Л) и (AM В); г) угол между (ЛМС) и (ЛВС).
42*. В ДЛВС ZC = 90°, МС±(ЛВС), ЛВ = 4, ДВЛС = 30°
Угол между (Л7ИВ) и (ЛВС) равен 45° Найдите: а) длину
отрезка МС; б) площадь дЛМВ; в) угол между (МВС) и
(ЛВС); г) угол между прямой МА и (ЛВС).
43. В ДЛВС Z.C = 90°, МЛХ(ЛВС), ЛВ=4, ЛВАС = 30° Угол
между (ЛВС) и (МВС) равен 30° Найдите: а) длину МА;
б) площадь ДМСВ; в) угол между (ЛМС) и (ЛВС); г) угол
между прямой МВ и (ЛВС).
Векторы в пространстве
44. Дано Z.(a, 0=120°, Z_(a, с) = 60°, Z_(b, с) = 90°, |а| = |0 =
= [c|=J,. Найдите^ а) скалярное произведение-(2а — 0Х
Х(^ + 2с); б) \а — 2Ь|; в) угол между векторами (а— 20 и с,
45. В параллелограмме ABCD Л( —1, 1, —1), В ( — 2, — 1, 1),
С(1, —2, —1). Найдите: а) координаты векторов АВ и АС;
б) координаты точки D; в) длины векторов АВ и АС; г)_ скаляр-
ное произведение АВ •АС; д) угол между векторами АВ и Л С.
Геометрические тела
Призма
46. В правильной треугольной призме АВСА\В\С\ АВ = 2~у/3,
AAi=4. Найдите: а) двугранный угол между (ЛВВ1) и
(ВВ|С); (Л1ВС) и (ЛВС); б) площадь ДВЛ1С; в) площадь
полной поверхности призмы; г) объем призмы.
47. В основании прямой призмы ABCA\B\Ci — /±АВС, у которого
ДС = 9О°, ЛВ = 4, ДЛ=60°, ЛЛ1 = 1. Найдите двугранные
углы между: а) (ЛВВ|) и (CBBj); б) (/ICiC) и (ЛВС); в) (А\СВ)
и (ЛВС); площади: г) ДЛС1С; д) ДЛ]СВ; е) объем призмы.
48. В правильной шестиугольной призме большая диагональ рав-
на 4 -у/3 и наклонена к основанию под углом 60° Найдите
площадь полной поверхности и объем призмы.
49. Измерения прямоугольного параллелепипеда равны: AD =
= 4 дм, £>С = 2 дм, CCi=4 дм. Найдите: а) длину диагонали
параллелепипеда; б) угол наклона диагонали параллеле-
пипеда к плоскости основания параллелепипеда; к плоскостям
боковых граней параллелепипеда; в) площадь диагонального
сечения; г) двугранный угол между плоскостями ADC\ и BAD;
д) площадь полной поверхности параллелепипеда; е) объем
параллелепипеда.
50. Основание прямого параллелепипеда — ромб со стороной
2 д/3 см и углом 60° Меньшая диагональ параллелепипеда
наклонена к основанию под углом в 30° Найдите: а) диаго-
нали; б) площадь поверхности; в) объем параллелепипеда.
44
Пирамида
51. В правильной треугольной пирамиде сторона основания равна
Зд/3, а высота д/3. Найдите: а) длину бокового ребра и угол
наклона этого ребра к плоскости основания; б) двугранный
угол между боковой гранью и основанием; в) площадь
боковой поверхности пирамиды; г) объем пирамиды.
52. В правильной четырехугольной пирамиде сторона основания
равна 6, а высота 4. Найдите: а) длину бокового ребра и
угол наклона этого ребра к плоскости основания; б) двугран-
ный угол между боковой гранью и основанием; в) площадь
боковой поверхности пирамиды; г) объем пирамиды.
53. В основании пирамиды MABCD — прямоугольник, MA_L
_L(ABC), ДС=13, DC— 12. Двугранный угол между плоскос-
тями MDC и ADC равен 45°. Найдите: а) длину МС и угол
наклона МС к плоскости АВС; б) площади ДЛЮС, ДСВМ
и ДДМВ; в) объем пирамиды.
54. В правильной четырехугольной пирамиде ребро основания
равно 10. Высота пирамиды МО разделена на 3 части точками
К\ и К2 так: МК\'К]К2'К?О ==2:\:2, где М — вершина
пирамиды. Через каждую точку деления проведены плоскости,
параллельные плоскости основания пирамиды. Найдите пло-
щади получившихся сечений.
55. В правильной треугольной пирамиде сторона основания равна
2 д/3, а боковая грань наклонена к основанию под углом 30°
Найдите: а) высоту пирамиды; б) боковое ребро и угол на-
клона этого ребра к плоскости основания; в) площадь боковой
поверхности пирамиды; г) объем пирамиды.
56. МАВС — пирамида, МА — высота пирамиды, МА = 4 д/3,
ДЛСВ = 90°, ВС = 3. Двугранный угол при стороне ВС равен
60° Найдите: а) площадь грани МВС; б) объем пирамиды.
Цилиндр
57. Диагональ осевого сечения цилиндра равна 6 и наклонена к
основанию под углом 60° Найдите: а) площадь боковой
поверхности цилиндра; б) объем цилиндра; в) площадь
боковой поверхности правильной четырехугольной призмы,
вписанной в этот цилиндр, объем этой призмы; г) площадь
боковой поверхности вписанной в этот цилиндр призмы, если
в основании этой призмы — равнобедренный треугольник с
углом 120°; д) объем этой призмы.
58. В цилиндр вписана правильная треугольная призма, сторона
основания которой равна 2 д/3, а диагональ осевого сечения
цилиндра наклонена к основанию цилиндра под углом 60°
Найдите: а) объем; б) площадь боковой поверхности ци-
линдра.
59. Высота цилиндра 4 см, радиус его основания 10 см. а) Найдите
площадь полной поверхности цилиндра; б) найдите площадь
сечения, проведенного параллельно оси цилиндра на расстоя-
45
нии от оси 6 см; 8 см; в) найдите площадь боковой поверх-
ности правильной треугольной призмы, вписанной в этот ци-
линдр» и объем этой призмы; г) найдите объем цилиндра.
Конус
60. Образующая конуса равна 4, а угол между нею и плоскостью
основания равен 30°. Найдите: а) площадь полной поверх-
ности конуса; б) объем конуса; в) объем вписанной в конус
правильной четырехугольной пирамиды; г) объем вписанной
в конус пирамиды, в основании которой — прямоугольный
треугольник с углом 30°; д) площадь сечения конуса плос-
костью, параллельной основанию конуса и делящей высоту в
отношении 2:3, считая от вершины конуса.
61. Образующая конуса равна 6 см, а угол при вершине осевого
сечения равен 120°. Найдите: а) площадь боковой поверхности
конуса; б) объем конуса; в)* объем и полную поверхность
цилиндра, вписанного в конус, зная» что образующая цилинд-
ра в три раза больше радиуса цилиндра.
62. В конус вписана правильная четырехугольная пирамида.
Сторона основания пирамиды равна 2^/6. Боковое ребро
пирамиды наклонено к основанию пирамиды под углом 45°.
Найдите: а) площадь боковой поверхности конуса; б) объем
конуса.
Шар
63. В шаре радиуса 10 см проведена секущая плоскость на рас-
стоянии: а) 8 см; б) 6 см; в) 5 д/3 см от центра шара. Найдите
площадь сечения; площадь поверхности шара; объем шара.
64. Шар касается плоскости. Расстояние от точки Л, лежащей в
этой плоскости, до центра шара равно 15, а до точки касания
равно 5. Найдите: а) площадь поверхности шара; б) объем
шара.
65. Найдите объем и площадь поверхности шара, если сечение,
перпендикулярное радиусу шара: а) делит этот радиус в от-
ношении 4:1, считая от центра шара, площадь сечения равна
36л; б) делит этот радиус на части, одна из которых равна 2 м.
Радиус сечения равен 4 м.
66. Найдите объем и площадь поверхности шара, если фигура,
вписанная в большой круг шара, есть: а) правильный тре-
угольник со стороной 2 -у/3; б) квадрат со стороной 3 -у2;
в) равнобедренный треугольник с углом 150° и основанием,
равным 6; г) прямоугольный треугольник АВС с катетом
ЛС=3'\/3 и углом Л =60°.
Расстояние между двумя точками, заданными координатами
67. Найдите расстояние от точки М(—2, 2, — 1): а) до начала
координат; б) до координатной плоскости yz,
68. Найдите расстояние от точки М (—1, 2, 0): а) до точки
К (3, — 1, 1); б) до оси у. 46
69. В параллелограмме ABCD Л( —3, 2, —1), В(1, —1, 0),
С ( — 2, 1, 1). Найдите: а) длину диагонали АС\ б) длину
диагонали BD.
Уравнение плоскости
70. а) Составьте уравнение плоскости, проходящей через точку
Л4 (— 1, 2, — 2) и перпендикулярной вектору д( —3, —1, 4).
б) Укажите какую-нибудь точку С, принадлежащую этой
плоскости, в) Принадлежит ли этой плоскости точка
В (3, 0, —1)? г) Найдите точку пересечения этой плоскости
с осью у.
Уравнение сферы
71. а) Составьте уравнение сферы с центром 5(1, —2, — 1) и
радиусом /? = 1. б) Принадлежат ли этой сфере точки
А (1,6; — 2; —0,2), В ( — 2, 1, 0)? в) Пересекает ли сфера
ось у, и если пересекает, то в какой точке?
72. а) Составьте уравнение сферы с центром 5(3, 4, -2) и с
точкой М (— 3, 4, 6), принадлежащей сфере; б) укажите
расстояние центра сферы до плоскости ху и до оси у.
ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЯМ ТРЕНИРОВОЧНЫХ ЗАДАЧ
1. а) с = 4 Д, 4, 2Д, 8, 2Д; б) с=12, 6 Д, 6, 18 Д, З-Д;
в) а = 4, 4 Д, 4, 8 Д, 2 Д. 2. 13, tg4=-^-, 6,5, 3. 4,5, 3,
4. а) 2; б) 5. а) 4,5, 27; б) 3, 12. 6. 8, 14. 7.
8. а) 1, 4 sin 15° и 4 cos 15°, 2, 1; б) Д, 2 и 2 Д, 2 Д, Д. 9. а) 6л,
9л; б) 4л, 4л. 10. 4л, 4л, 2л, л. 11. а) —6Ч-с; б) —33;
в) cos(C4, СВ) = . 12. а) ЛВ(0, 1), Й'С(3, -1);
' 4 } 2-|с—Z>| 2 VI9
б) решение. Пусть D (х, у), точка DC (2 —х, 1 —у), но АВ = DC,
значит, (0, 1)=(2 — х, 1—у), откуда 0 = 2 — х и 1 = 1—у, следо-
вательно, х = 2, у = 0, D (2, 0); в) — 1; г) 1, дДО; д) cos (ЛВ, ЛС) =
=-----13 (рис. 114—117). 14. Да, так как 4 вершины парал-
Рис. 116
Рис. 114
Рис. 115
Рис. 117
47
лелограмма ABCD лежат на параллельных прямых АВ и CD,
которые принадлежат одной плоскости, значит, и все вершины
параллелограмма принадлежат этой плоскости. 15. Через точку,
лежащую на прямой, прямых, перпендикулярных к этой прямой,
можно провести на плоскости только одну, а в пространстве —
сколько угодно. 16. Через точку, лежащую вне прямой, прямых,
перпендикулярных к данной прямой, можно провести только одну
и на плоскости, и в пространстве. 17. Через две параллельные
прямые можно провести единственную плоскость. 18. На парал-
лельных прямых лежат, например, такие ребра AD и ВС, AD и
BiCj, AD и на скрещивающихся прямых, например,
AD и CCi, AD и D\Ct,AD и В\В. 19. Почему точки Мj, Л42, В лежат
на одной прямой? См. решение № 19 (§ 2), Z<|Afi = 4, ВВ2 —20.
20. См. решение задачи № 19 (§ 2), К\М\ =13, /С2М2=15.
21. КзКл — средняя линия в ДДС/), поэтому К3/С» = 0,5ДС и
КзКДИС, /С1Д2 — средняя линия в дДВ;С, поэтому ТС К? = 0,5/1 С
и K\Kz\\AC, значит, КзК^ = К\К2 и Яз/МЯлКг» поэтому /С#2/<з/<4 —
параллелограмм. 22 (рис. 118—121). 23. Так как а||ДВ и а пере-
секает плоскость АВС по прямой МК, то М7(|]ДВ: если бы МК
пересекала бы АВ, например, в точке В, то точка Р была бы точкой
пересечения прямой АВ и плоскости а (МК принадлежит плос-
кости а), что противоречит условию: ДВЦа; АВ = 54. 24. Да, будет,
на основании теоремы — признака параллельности прямой и
плоскости. 25. Да, существует. Эта плоскость должна быть
параллельна линии пересечения двух плоскостей. 26 (рис. 122).
МК||А1 Cj, потому что (41Р|С|)||(ДОС), а МК и 4iCi—линии
пересечения этих плоскостей. Так как МК~Л\С\ и Л1/СЦД1С1, то
МА\С\К — трапеция (рис. 123). Так как (ЛАiB])||(jD£hC), то
ABiHDC и A\Bi — DC, следовательно, A\13iCD — параллело-
грамм. Так как (ААiBi)H(DDiC), то A4i||A7G и AAt = KKi, следо-
71 М D
Рис. 122
Рис. 123
48
Рис. 124
Рис. 125
A, Df
Рис. 126
Ct
вательно, AA^KiK— параллелограмм. 27. DE — 36, EEi — 4,5,
DB = 3. 28 (рис. 124). a|| p по условию, тогда AZ31[AiB| и AAi||^Bi
по условию, следовательно, А\АВВ\ — параллелограмм, поэтому
АХВ\=АВ = 4. 29 (рис. 125). 30 (рис. 126, 127). 31 (рис. 128).
32. а) AB_L.BC, АВJLBBb следовательно, ABJL(BiBC); б) CDJ_
_LDDi, CDJLAD, следовательно, CD J_(AZ)Di), значит, CD J_Ai£>,
поэтому Z-A\DC — 90°; в) ABJ_BiB, АВ-ЕВС, следовательно,
АВ _L(B\BC), значит, АВА_ВХС\ г) ACJ_B£>, AC.LDD\ (так как
DD\.LADCy), следовательно, AC.L(BDD\), значит, AC.LBXD\
д) доказано в п. г); е) А\В_1_ЛВ|, а АВ\ ||DC\, значит, A\B-EDCX\
ж) /и£>1-LDiCi, A\D\A.D\D> следовательно, A\DX_L(B£>iCi),
откуда X|Di JLJDCi. 33. а) Так как О — центр квадрата, то
ОА — ОС, /\AMO—Z\CMO по двум катетам, откуда МС = АМ\
МК = 5, где точка К — середина АВ\ ОА=3 ~\2, tg МАО — ;
tg Л1АВ = -~; S= 15; б) АО==4^2, МО = 4^6, ОК = 4, где К —
середина АВ, МК — 4 д/7; tg А1АВ —л/7; 16^/7; в) АО = 6, О/( =
— 3 д/2, где К— середина АВ, MK = 3^f6; tgMAB = y/3,
гСМАВ — 60°; 3=18д/3. 34. а) Так как О — центр треугольника,
значит, АО — ОВ, /\МАО= &МОВ по двум катетам, поэтому
МА = МВ\ ОК~^-, где К — середина АВ, МК=^£-, АО = ^/3;
tSMAO=2, tgMAB = '^~, б) ^lt> = 2, О/И = 2^3,
О '1
tgM/W=^y-; S^y^; в) ЛО = 2, ОК=1 (К—
середина АВ), MK=-fi; AK=yf3, igMAB=^--, S=15.
О
Рис. 127 Рис. 128
49
35. а) ЛС = 5, АМ = 5^/3, MB = 2sj2\; 90°; 5 = 4^Т; б) АМ =
= 6^3, ЛВ = ОС = 6, Л4В= 12; 90°; AD = 3 = BC, 5=18;
в) DC = 2^2=AB, ВМ = ^/Т\; 90°; ЛС = 3, ВС=1, 5 = 0,5 ТГГ.
36. а) ВС=2-у/3, ctg МВС=у[3, значит, ZMBC=30°; б) Л4К±
-LAB (К — принадлежит АВ), ДС = 2, /(С = 3, 7ИК = п/7; в) 2<3,
2л/7. 37. а) ЛВ = 3, Л1Л = ЗУЗ, tgMO4=^^; МС = 4^2;
4^; б) ВС = 3=Л4С, cos МСА=&; МС=3; МА=^6,
£ о
$i=^, 52 = 4,5; в) ЛС=1, Л1Л=^, tg МСЛ=^; МС=^;
ВС=1, 51=^, 52=-ф-. 38. a) ADLDDi и ЛО±ОС, значит,
ЛО±(ОО1С), откуда ЛВ±В,С; ЛО±ССь (ЛОС|)±(ОО|С);
б) AC.LBD и AC-LDDi, значит, ЛС_1_(ВОО|), откуда AC-LBD\;
AC-LDDi; (ACC^A-^BDD^; в) sin OGD =0,5, где О — середина
AC; Z.O|OC=45°; 0°, так как DC\||(ЛВВ|); г) ZBiOOi, где О и
01 — центры соответственно ABCD и Л1В]С1Оь tgBiOOi =
==7)Zr’='^: * “"sF’ В\ОВ=-^/2; искомый угол равен
углу между прямыми ADi и DA\ и равен 90°. 39. а) ОА = 3 д/2, 3 -\/5;
б) ОК=3(ЛК = КВ), tgMKO=y6; в) 90°, так как МО±(ЛВС);
г) ОМК, ctg ОМ/С = д/б. 40. а) ОЛ = 3, МО=^/3; б) ОК=1,5
(ЛЯ = КВ), tgMKO=-^; в) ctg 0МК=-~; г) 90°. 41. a) DC=
уЗ *уЗ
=ЛВ=6, AM =6 л/3, tg MCA = 0,6 УЗ; б) Z-MDA, tg MDA =Ь^ ;
в) ZO/B = 90°; г) 90°, так как Л4Л±(ЛВС). 42. СК-LAB, тогда
КМ -LAB (К принадлежит ЛВ), значит, Z.MKC — линейный угол
двугранного угла МАВС, ЛС = 2д/3, СК=-\/3. а) МС=~^3;
б) Л4К=Уб, 5 = 2д/б; в) 90°; г) tg ЛЫС = 0,5. 43. ЛС = 2УЗ,
ВС=2. а) 2; б) Л4С=4, 5 = 4; в) 90°, так как МЛ±(ЛВС);
г) tg Л1ВЛ =0,5.44. а) 0; б) -у/7; в) arcccs-^,45. а) ЛВ(-1, —2,2),
АС (2, —3,0); б) 0(2,0, —3); в) ЛВ = 3, АС= 13; г) 4;
д) arccos - - . 46. а) 60°; К — середина ВС, ЛК = 3, tg АКА\
з -/13 3
б) Л|Д’ = 5, 5 = 5у/З; в) 5 = 30->/3, V= 12^/3. 47. а) 30°; б) 90°;
в) /LAiCA=arctgO,5; г) 1; д) 0,5-Л|С-СВ=0,5-л/5-2 ^3 =
=715; е) 2л/3-48. 5полн = 45Уз, У = 27 ^3. 49. а) 6; б) sin ai=-|-,
sin a2=-|~, sin a3 = -|-; в) BD = 2 \/5, S=8^r5; г) igC\DC = 2;
д) S = 64; e) V = 32. 5G\ a) 4, 2 <10; 6) 16<3; в) V-.-12-Д
50
Рис. 130
Рис. 129
51. а) 2^3, arctgf
52. а) д/34, arctgf^h ; б) arctgf-^-) > в) 6®* г) 48- 53. а) л/194;
б) 32,5, 30; в) 100. 54. 16,36.55. а) б) arctg(^) ;
в) 6; г) 1. 56 (рис. 129). МС=-^Ь=8; a) SйЛ)СВ=0,5МСХ
ХСВ=12, так как ZMCB =90°. АС —4 д/3-ctg 60° = 4; б) V=
= Р.-.5Лр-<?б.-2!?±. = 8 V3- 57. а) Я=4-, Я = 3д/3, 9л-у/3; б) ZL&-
в) 18^/6, 13,5-^3; г) 9д/3+13,5, 58. a3=R^3, 2^3 =
i=R-\f3, R—2, тогда ЛВ=4 (рис. 130), H=BC=AB<tg 60° =
=4 J3, V= 16л д/3, S=16n-V3. 59. а) 280л; б) 64, 48; в) 120т/3,
300 д/3; г) 400л. 60. а) 4л-(3+2д/3); б) 8я; в) 16; г) 4^3;
д) 1,92л. 61. а) 18л д/3; б) 27л; в) -j--„-=tg 60°, где Н=3,
х= — — радиус цилиндра, У=Злх3, НП0ЛИ=8лх2, где х=
= 27~^fi - 62- Я = 2л/3, /=2д/б, я=2^3. а) 12л ^2; б) 8л
63. а) 36л, 64л, 25л; б) 400л; в) 64. а) 800л; б) 8Q00"-^.
65. а) (рис. 131). Пусть ВК=и, тогда 0К=4и, 0A=*5u=^R.
АК=л/ОА'2—ОК2=Зи- лЛ№ = 36л; АК2=36, Л/^Зи=6; и=2.
Рис. 131
Рис. 132
51
Рис. 133
/? = 5п=10, У = 5Ш —4л/?2 = 400л; б) здесь
О О
возможны два случая:
1-й случай. Рис. 132. £^--2, тогда OK — R — 2. Л№ =
= 0Д2 —0/(2; 16 = /?2 —(/? —2)2; 16 = R2 -R2 + 4/?-4; 4Я = 20;
R — 5. Vlu = -|-nP3 =="5~л (м3). 5ш = 4л/?2= 100л (м2).
2-й с л у ч а й. Рис. 133. ОК = 2, ОА=-у/аК2 + ОК2 = 2 -fi=R.
рш = ±лР3 = 1£_^л (м3). Зш = 4лРг = 80л (м2). 66. a) R = 2,
о о
так как аз =/? д/3» V—5=16л; б) /? = 3, так как =
«3
V=3Gn, 5 = 36л; в) R = ъ ° 7 ----=6, У=288л, 5 =
’ 7 2 sin А 2 sin 150
= 144л; г) 2/?=ЛД=-^-=6 ^3. /? = 3 л/З. У=108^/Зл, S =
= 108л. 67. а) 3; б) 2. 68. а) 26; б) запишем координаты точки Мi,
являющейся основанием перпендикуляра, проведенного из точки
М к оси у: (0, 2, 0), тогда ММ2 = (0+ 1 )24-(2 — 2)2(0 — О)2 = I,
М\М— 1. 69. а) ЛС(1, —1,2), ЛС=д/б; б) найдем координаты
точки D (х, у, z}\ DC ( —2 —х, 1 — у, 1 — z), АВ (4, —3, 1), но АВ =
= DC, следовательно, — 2 —х = 4, 1— #=— 3, 1 — z = 1, откуда
х=—6, r/ = 4, z = 0, D(-6, 4, 0), BD ( — 7, 5, 0), B£> = V?4.
70. а) —3(х4-1)—1 (у — 2)4-4 (z 4-2) = 0; б) допустим, уточки С,
принадлежащей данной плоскости, х=1, «/ = 0 (произвольные
значения х и у), тогда С(1, 0, z). Подставим в уравнение коор-
динаты точки С: — 3 (1 4~ 1)"(0 — 2)4'4 (z4~2) = 0, откуда z = — 1,
значит, С(1,0, — 1); в) точка В не принадлежит данной плоскости;
г) пусть эта точка А (0, у, 0), тогда — 3 (0 4-1) — (у — 2) 4~ 4 (0 4- 2) =
= 0, откуда у = 7, А (0, 7, 0). 71. а) (х— 1 )2 + (у4-2)24-(z + 1)2= 1;
б) точка А принадлежит сфере, а точка В не принадлежит;
в) пусть точка К — предполагаемая точка пересечения сферы с
осью у: К(0, у, 0). Тогда (0 — 1 )2-f-(z/4-2)2 4-(0 4- 1 )2 = 1, откуда
(//-|-2д= — 1 —решения нет, значит, сфера не пересекается с
осью у. 72. а) R2 = СМ2 = (— 3 — З)2 444 — 4/4- (6 + 2/ = 100. Урав-
нение сферы (х — 3)244£/~*4)244z4-2f = 102; б) так как z= —2, то
расстояние от центра сферы до плоскости ху равно 2. Запишем
координаты точки Si — основания перпендикуляра, проведенного
из точки S на ось у\ Si (0, 4, 0). Теперь найдем SS2 = (3 —0)24-
4-(4 — 4)24-( — 2 — 0)2= 13, SSi=V13 — искомое расстояние.
§ 4. ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ
О МИНИМАЛЬНЫХ ТРЕБОВАНИЯХ К ЗНАНИЯМ ТЕОРИИ
Об определениях. Главное в определениях — понимание того,
что они означают. Например, можно не сформулировать опре-
52
деление призмы, но следует знать, что боковые грани призмы —
параллелограммы, а основаниями являются равные многоуголь-
ники, лежащие в параллельных плоскостях, так как без этих
знаний вы не сможете решать задачи этого раздела.
И все же некоторые особо важные определения без словесных
формулировок недостаточно хорошо усваиваются. К таким опре-
делениям отнесем определения равенства фигур; определения
параллельности и перпендикулярности прямых, прямых и,плоскос-
тей, плоскостей; определения угла между прямой и плоскостью,
между плоскостями, между скрещивающимися прямыми; опре-
деления расстояния между точкой и прямой, между точкой и
плоскостью.
О теоремах и формулах. Знание формул и формулировок
теорем и умение применять их при решении задач — необходи-
мое требование для всех учащихся. Если к тому же вы знаете
доказательства теорем и выводы формул, то это говорит о хоро-
шем знании вами геометрии, которое может быть оценено на 4
или 5 в зависимости от умения решать задачи.
ВАРИАНТЫ ЗАДАНИЙ
Всего вариантов 20, и в каждом — 3 задания. Наиболее
простым является первое задание. Вторым заданием является
решение задач, каждая из которых содержит два пункта. Задачи
берутся из § 2 «Основные задачи». Так, например, во втором зада-
нии l-ro варианта записано: № 45 а, б; 46 г, е, т. е. из § 2 «Основ-
ные задачи» надо взять либо № 45 и выполнить в нем пункты
а), б), либо № 46 и выполнить в нем пункты г), е). Необходимо
добиваться, чтобы по меньшей мере один из двух пунктов задачи
обязательно был выполнен. Третье задание — доказать теорему
или вывести формулу — отмечено восклицательным знаком, для
того чтобы предупредить, что без умения выполнить его уровень
знание геометрии не может считаться хорошим.
Предлагаемые в вариантах заданий задачи распределяются по
темам так:
Сечения параллелепипеда плоскостью: В.* 1 12 № 28 а), б); № 15
а) (рис. 15); 6) (рис. 17).
Нахождение расстояния от точки до прямой и угла между
пересекающимися прямыми: В. 5, 13 № 33 б), в); № 34 б), в).
Нахождение угла между скрещивающимися прямыми: В. 8
№ 38 а), б), в), г).
Нахождение расстояния от точки до плоскости и угла между
прямой и плоскостью: В. 10, 16 № 40 а), г); № 41 а), в).
Нахождение значения двугранного угла: В. 4, 20 № 40 б), в);
№41 б), г).
Нахождение площади граней призмы и объема призмы:
В. 6, 14 № 47 б), г); № 49 а), б).
.. I ”
1 Так здесь будем обозначать слово «Вариант».
53
Нахождение площади сечения пирамиды и конуса плоскостью,
параллельной плоскости основания пирамиды или конуса: В» 2
№ 55 а), б); № 62 б).
Нахождение площади боковых граней пирамиды и объема
пирамиды: В. 7, 15 № 52 в), г); № 53 в), г).
Нахождение площади поверхности и объема цилиндра: В. 18
№ 59 а), б); № 61 а), б).
Нахождение площади поверхности и объема конуса: В. 19
№ 62 а), в); № 63 а), б).
Нахождение площади поверхности и объема шаоа: В. 3
№ 66 а), б); № 67 а), б).
Нахождение скалярного произведения векторов и угла между
векторами: В. 1 № 45 а), б); № 46 г), е).
Нахождение расстояния между двумя точками, заданными
координатами: В. 1! № 70 а), б); № 71 а), б).
Составление уравнения плоскости: В. 17 № 73 а), в); № 74
а), б).
Составление уравнения сферы: В. 9 № 75 а), в); № 76 а), б).
Вариант 1
1. Сформулируйте определение параллельности прямой и плоскос-
ти и признак параллельности прямой и плоскости.
В основании пирамиды MABCD — квадрат. Докажите, что
AB\\MCD.
2. № 45 а), б); № 46 г), е).
3! Докажите признак параллельности прямой и плоскости.
Вариант 2
1. Сформулируйте определение перпендикулярности прямой и
плоскости и признак перпендикулярности прямой и плоскости.
Дан куб ABCDA\B\C\D\. Зная, что все грани куба квадраты,
докажите, что АА\ ХАВС.
2. № 55 а), б); № 62 б).
3! Докажите признак перпендикулярности прямой и плоскости.
Вариант 3
1. Сформулируйте определение параллельности плоскостей и
признак параллельности плоскостей.
Дан куб ABCDA\B\C\D\. Зная, что все грани куба — квадраты,
докажите, что ЛВСЦЛfB|Ci.
2. № 66 а), б); № 67 а), б).
3! Докажите признак параллельности плоскостей.
Вариант 4
1. Сформулируйте теорему о линиях пересечения двух парал-
лельных плоскостей третьей плоскостью.
Плоскости оснований куба пересечены плоскостью по прямым
МК и РЕ. Докажите, что МК\\РЕ>
2. № 40 б), в); № 41 б), г).
3! Докажите теорему о линиях пересечения двух параллельных
плоскостей третьей плоскостью.
54
Вариант 5
1. Сформулируйте определение перпендикулярности плоскостей
и признак перпендикулярности плоскостей.
Дан куб ABCDA\B\C\D\. Докажите, что любая плоскость,
проходящая через прямую AAi, перпендикулярна АВС,
2. № 33 б), в); № 34 б), в).
J! Докажите признак перпендикулярности плоскостей.
Вариант 6
1. Сформулируйте теорему о трех перпендикулярах.
Дан куб ABCDA1B1C1D1, Докажите, что DCX.A1D,
2. № 47 б), г); № 49 а), б).
3! Докажите теорему о трех перпендикулярах.
Вариант 7
I. Сформулируйте свойство диагоналей параллелепипеда.
Ребро куба равно 2. Найдите расстояние от точки пере-
сечения диагоналей куба до плоскости основания куба,
2. № 52 в), г); № 53 в), г).
3! Докажите свойство диагоналей параллелепипеда.
Вариант 8
1. Сформулируйте теорему о сечении шара плоскостью.
Диаметр шара равен 4 см. Чему равна площадь сечения
• шара плоскостью, проходящей через центр шара?
2. № 38 а), б), в), г).
3! Докажите теорему о сечении шара плоскостью.
Вариант 9
1. Возьмите модель правильной четырехугольной пирамиды и
укажите, какие измерения надо произвести, чтобы вычислить
объем и площадь боковой поверхности пирамиды.
2. № 75 а), в); № 76 а), б).
3! Выведите формулу для вычисления объема пирамиды.
Вариант 10
1. Возьмите модель правильной треугольной призмы и укажите,
какие измерения надо произвести, чтобы найти объем цилиндра,
описанного около этой призмы.
2. № 40 а), г); № 41 а), в).
3! Выведите формулу для вычисления объема цилиндра.
Вариант 11
1. Возьмите модель правильной треугольной пирамиды и укажите,
какие измерения надо произвести, чтобы найти площадь
боковой поверхности конуса, описанного около этой пирамиды.
2. № 70 а), б); № 71 а), б).
31 Выведите формулу для вычисления площади боковой поверх-
ности конуса.
55
Вариант 12
1. Возьмите модель шара (например, мяч) и укажите, какие
измерения надо произвести, чтобы найти объем шара.
2. № 28 а), б); № 15 а) (рис. 15), б) (рис. 17).
3! Выведите формулу объема шара.
Вариант 13
1. Запишите формулу площади поверхности сферы.
Чему равна площадь сферы, если диаметр сферы равен 2?
2. № 33 б), в); № 34 б), в).
3! Выведите формулу площади сферы.
Вариант 14
1. Запишите уравнение какой-нибудь плоскости и укажите
координату z точки А (1, 2, z), принадлежащей этой плоскости.
2. № 47 б), г); № 49 а), б).
3! Выведите уравнение плоскости. Запишите уравнение плоскос-
ти zy.
Вариант 15
1, Запишите уравнение какой-нибудь сферы и укажите координа-
ты точки S — центра этой сферы.
2. № 52 в), г); № 53 в), г).
3! Выведите уравнение сферы. Если сфера пересекается с какой-
нибудь осью координат, то в какой точке?
Вари а.нт 16
1. Дайте определение скалярного произведения векторов.
Дан куб ABCDA\B\C\D\. Чему равны скалярные произведе-
ния векторов: a) DC*AA\\ б) АВ*1)В\, если ЛВ (0, —1, 0),
DBi(-l, -1, 1)?
2. № 40 а), г); № 41 а), в).
3! Выведите формулу объема конуса.
Вариант 17
1. Выполните построение прямой, параллельной данной плоскости.
2. № 73 а), в); № 74 а), б).
3! Выведите формулу площади боковой поверхности цилиндра.
Вариант 18
1. Выполните построение плоскости, перпендикулярной данной
прямой.
2. № 59 а), б); № 61 а), б).
3! Докажите теорему о свойстве плоскости, перпендикулярной к
одной из двух параллельных прямых.
Вариант 19
1. Постройте плоскость, параллельную данной плоскости.
2. № 62 а), в); № 63 а), б).
3. Докажите теорему о свойстве диагонали прямоугольного
параллелепипеда.
Вариант 20
1. Запишите формулу вычисления расстояния между двумя точ-
ками, заданными своими координатами. Приведите пример.
56
2. № 40 б), в); № 41 б), г).
3! Выведите формулу вычисления расстояния между двумя
точками.
КОММЕНТАРИИ И УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПЕРВЫХ ЗАДАНИЙ
В. 1. Так как AB\\CD, то АВ||(MCD) по признаку параллель-
ности прямой и плоскости.
В. 2. Так как AA\A_AD и АВ пересекается с ADy
то ДЛ1±(ЛВС) по признаку перпендикулярности прямой и
плоскости.
В. 3. Так как АВЦД1В1, ВС||В{С\ и АВ пересекается с ВС, то
(ДВС)Ц(ЛiBjCi) по признаку параллельности плоскостей.
В. 4. Так как плоскости АВС и Л161С1 параллельны, то
AW||7<L как линии пересечения двух параллельных плоскостей
третьей.
В. 5. Так как ЛЛ1±(ЛВС), то любая плоскость, проходящая
через AAi, будет также перпендикулярна (ЛВС) по признаку
перпендикулярности прямой и плоскости.
В. 6. Так как ЛЛ| ±(Л£>С), то AD является проекцией A\D на
(ЛВС). 2?С±Л£>, следовательно, ВС±Л1£> по теореме о трех
перпендикулярах.
В. 7. Так как диагонали параллелепипеда делятся точкой
пересечения пополам, эта точка отстоит от плоскости основания на
расстоянии, равном 1, которое равно средней линии в треугольнике,
составленном диагональю параллелепипеда, боковым ребром и
диагональю основания параллелепипеда.
В. 8. Так как сечение шара плоскостью, проходящее через
центр шара,— большой круг, радиус которого равен радиусу шара,
то радиус этого круга равен 2 см. Поэтому Хсеч = л/?2 = 4л см2.
В. 9 . Поставив на стол пирамиду, прислонить к боковой грани
угольник так, чтобы один его катет находился на столе, а другой —
через апофему пирамиды. Затем измерить длину апофемы и ребра
основания. Чтобы найти высоту пирамиды, надо построить тре-
угольник, боковыми сторонами которого являются апофемы, а в
основании лежит отрезок, длина которого равна длине ребра
основания, и затем измерить его высоту, или с помощью тран-
спортира найти угол при основании треугольника и вычислить
высоту, или найти высоту, зная длины сторон равнобедренного
треугольника и угол между ними.
В. 10 (В. 11). Измерив боковое ребро, найти длину образую-
щей цилиндра (конуса). Измерив длину ребра основания, из
формулы аз = /?л/3 найти радиус основания цилиндра (конуса).
В. 12 (рис. 134). С помощью угольника найти АВ (радиус
шара), где В — точка касания угольника и шара, а А — вершина
прямого угла угольника.
1 Мы укажем лишь один из способов выполнения первых заданий в ва-
риантах 9—12.
57
4
Рис. 134
Рис. 135
В. 13. /? = 1, значит, 5 = 4л.
В. 14. Например: 2 (х—1) —3 (у + 2) + 4 (z —3) = 0. Поставим
в это уравнение координаты точки А, получим 2(1 — 1) —3(2 + 2)+
+ 4(z — 3)=0, откуда 0—12 + 4z—12 = 0, z = 6.
В. 15. Например: (х—l)2+(t/ + 2)2 + (z —3)2 = 52, тогда
5(1, -2,3). _____________
В. 16. Так как DCJ-Adi, следовательно, £>С-ЛЛ1 = |ОС| X
Х1ЛД||-соз 90° = 0.
4B-£>Bt=(0, —1, 0)-( —1, -1, 1 )=0+1 +0= 1.
В. 17. На плоскости а провести прямую а и вне плоскости а
взять произвольную точку М. В плоскости, заданной прямой а и
точкой М (ее строить не обязательно), провести прямую b
параллельно прямой а (рис. 135).
В. 18. R плоскости а провести две пересекающиеся прямые а
и Ь. Через точку М, взятую вне плоскости а, в плоскостях, задан-
ных прямой а и точкой М, прямой Ь и точкой М, провести прямые
а' и &' такие, что а'\\а и Ь'||6. Через эти две прямые а' и Ь' про-
вести плоскость р, которая будет параллельна плоскости а
(рис. 136).
В. 19. Через прямую а провести две пересекающиеся плос-
кости аир. Через точку М, взятую на прямой а, построить в
каждой из этих плоскостей перпендикуляры AM и ВМ к прямой а.
Через эти два перпендикуляра провести плоскость у, которая и
будет перпендикулярна прямой а (рис. 137).
В. 20. Пример: Л(— 1, 2, 0), В (2, —3, 1),
А В=V(2-(-l))24-(-3-2)24*(i—О)2 = л/9+25+1 = ^35.
Рис. 136
Рис. 137
Часть II
ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
§ 5. ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
ПЛАНИМЕТРИЯ
1. Докажите, что дЛВС — ДA\BiC\, если AB~AiBi, АС =
— А[С\ и hAC=hAtCl.
2. Докажите, что параллелограмм ABCD равен параллелограм-
му /IjBjCiDi, если ЛВ = Л1ВЬ AD=A[Di и hAD = hAiDl.
3. Докажите, что равнобочные трапеции ABCD и TliBiCiDi
равны, если ЛВ = Л|В1, AD = A\D\ и BD = B\D\.
4. Постройте треугольник ЛВС, зная длины сторон ЛВ, АС и
длину высоты hAC.
5. Постройте параллелограмм ABCD, зная длины сторон ЛВ, AD
и длину высоты hAD.
6. Постройте трапецию, у которой известны длины всех четырех
сторон.
7. В ДЛВС а=13, Ь = 14, с=15. Найдите S, R и г и углы
треугольника.
8. В ДЛВС а = 3, с = 8, А В = 60°. Найдите Ъ, углы треуголь-
ника, углы между медианами та и тс, 7? и г.
9. Верны ли утверждения: а) четырехугольник, у которого все
стороны равны, есть ромб; б) четырехугольник, у которого
диагональ делит противоположные углы пополам, есть ромб;
в) четырехугольник, у которого противоположные углы равны,
есть ромб; г) параллелограмм, у которого две стороны, имею-
щие общую вершину, равны, есть ромб; д) параллелограмм,
у которого диагональ делит противоположные углы пополам,
есть ромб?
10. Дан правильный шестиугольник ABCDEF со стороной, рав-
ной 6. а) Найдите АВЛГ; б) докажите, что четырехугольник
BCEF— прямоугольник; в) найдите площадь &BDF\ г) вы-
числите длины высот треугольника ACD\ д) вычислите
площадь шестиугольника; е) вычислите площадь круга,
описанного около этого шестиугольника.
11. Точки Л (1; 2); В (5; — 1) — вершины квадрата ABCD. Найдите
координаты остальных вершин квадрата.
12. Докажите, что если в четырехугольник можно вписать
окружность, то его площадь равна рг, где р — его полу-
периметр, г — радиус вписанной окружности.
59
13. Докажите, что ВлАвс=-^-
14. Докажите, что если ABCD — произвольный четырехугольник,
то £лясп=0,5ЛС• BD sin а, где а — угол между диагоналями
АС и BD этого четырехугольника,
15. Если в треугольнике АВС ВК— биссектриса, то Д/(:КС =
=АВ:ВС. Докажите.
16. В ДДВС а2А~Ь2 = с2. Этот треугольник прямоугольный.
Докажите.
17. В дДВС а + &>с. Допустим, ДС=90° Какой знак надо
поставить между а3 + &3 и с3?
18. В равнобедренном треугольнике длины двух сторон пропор-
циональны числам 3 и 5. Найдите длины сторон треугольника,
если его периметр равен 143.
СТЕРЕОМЕТРИЯ
Прямые и плоскости в пространстве
19. Постройте сечение многогранника плоскостью, проходящей
через точки М, Pt К: а) (рис. 138), точка К принадлежит
плоскости а; б) (рис. 139), точка К принадлежит плоскости а;
в) (рис. 140); г) (рис. 141).
20. Постройте сечение многогранника плоскостью, проходящей
через точку Е и параллельную плоскости МРК: а) (рис. 142);
б) (рис. 143); в) (рис. 144); г) (рис. 145). Сечения строить
с помощью линейки и угольника так же, как строят парал-
лельные прямые.
21. Дан куб ABCDA\BiCiDi. ДВ = 1, точка О — середина АС.
Найдите угол между: a) AtO и BDr, б) BD\ и АВ.
22. Точка О — центр правильного треугольника АВС. ОМ _L(ABC),
OM--\/3t ЛВ = 2д/3. Найдите: а) угол между СВ и АМ\
б) расстояние от точки О до (Л4СВ); в) величину двугранного
угла между плоскостями АМС и МСВ\ г) расстояние от
точки А до (МВС).
23. Точка О — центр квадрата ABCD. MO_L(ABC), МО = 12,
АВ =10. Найдите: а) угол между плоскостями АМВ и DMC\
б) расстояние от точки В до плоскости MDC.
24. Трапеция ABCD (ВС||Д/>) не имеет общих точек с плоскостью
Рис. 139
60
a, ВС:AD = 2:3. Расстояния точек А, В, С от плоскости а
соответственно равны 5; 8; 10. Найдите расстояние точки D
до плоскости а.
25. В дЛВС точка Е — середина АВ. Этот треугольник и плос-
кость так расположены, что расстояния точек В и Е до плоскос-
ти а соответственно равны 4 и 3. Найдите расстояние от
точки А до плоскости а, если: а) точка С находится по одну
сторону от плоскости а, а точки А и В — по другую; б) точка
А находится по одну сторону от плоскости а, а точки В и С —
по другую.
26. В кубе ABCDA\B[C\Di проведено сечение через вершины Л,
Bi, С. а) Будет ли BPt _1_(ЛВ|С)? б) В каком отношении BDi
делится плоскостью Л В] С?
27. В кубе ABCDA\BiC\Di АВ = 2. Найдите расстояние между
прямыми: a) B\D и ЛВ; б) B\D и АС.
28. Квадрат ABCD расположен в плоскости, образующей с плос-
костью а угол 60° Сторона ЛВ образует с плоскостью а
угол 30°. Какой угол образует с этой плоскостью сторона ЛВ?
Геометрические тела
29. Основание пирамиды МАВС— &АВС, /_ЛСВ = 90°, AL4_L
_1_(ЛВС), ЛМ = 3, АС —4, ВС = 3. Найдите площадь сечения,
проходящего через точку А перпендикулярно плоскости МСВ
и параллельно прямой ВС.
30. ABCA\B\Ci — прямая треугольная призма. Длина каждого из
ребер равна а. Найдите площадь сечения, проходящего
через АВ и образующего угол 60° с плоскостью ЛВС.
31. Докажите, что в параллелепипеде сумма квадратов его
диагоналей равна сумме квадратов всех его ребер.
32. Найдите длины диагоналей параллелепипеда, если все его
грани — ромбы с углом 60° и стороной, равной 1.
G1
33. В кубе ABCDAiBiCiDi с ребром, равным 1 м, найдите длину
кратчайшего пути между точками А и С.
34. В основании призмы ABCAjBiCi— правильный треугольник
со стороной, равной 6. Боковое ребро равно 5. Основание
перпендикуляра Л [О к плоскости АВС находится в центре
нижнего основания. Найдите площадь боковой поверхности
призмы.
35. Основанием прямой призмы служит ромб. Площади диаго-
нальных сечений этой призмы равны Р и Q. Найдите площадь
боковой поверхности призмы.
36. В пирамиде КАВС КА = КВ = КС= 13, ДС = 8, ВС=6,
21ЛСВ = 90о. Пирамида пересечена плоскостью, параллель-
ной ВС и АК так, что в сечении получился ромб. Найдите:
а) сторону этого ромба; б) угол ромба.
37. В правильной четырехугольной пирамиде MABCD величина
двугранного угла при боковом ребре равна 120°. Площадь
дМДС равна Q. Найдите площадь боковой поверхности
пирамиды.
38. В правильную треугольную пирамиду, боковые грани которой
наклонены к основанию под углом 60°, вписана правильная
треугольная призма так, что нижнее основание призмы лежит
в основании пирамиды, а вершины верхнего принадлежат
апофемам пирамиды. Длина каждого из ребер призмы равна 3.
Найдите площадь полной поверхности пирамиды.
39. В правильную четырехугольную пирамиду вписана правиль-
ная четырехугольная призма так, что нижнее основание приз-
мы принадлежит основанию пирамиды, а вершины верхнего
основания призмы лежат на боковых ребрах пирамиды. Найди-
те объем пирамиды, если ее боковое ребро наклонено к
основанию под углом 45°, сторона основания призмы равна
2 -у/2, а высота 2.
40. Основание пирамиды — равнобедренная трапеция, у которой
три стороны равны по 6 м и угол 60°. Боковые ребра пирамиды
наклонены к основанию под углом 45°. Найдите площадь
полной поверхности пирамиды.
41. Основание пирамиды МАВС — треугольник АВС, у которого
Z.C=90°, /_Л=а, АВ — с. Боковые грани пирамиды накло-
нены к основанию под углом 0. Найдите площадь боковой
поверхности пирамиды.
42. В правильной четырехугольной пирамиде MAOCD высота
равна Н, Л АМВ—2а. Найдите площадь боковой поверхности
и объем пирамиды.
43. В основании прямой призмы ABCDAiBiCiDi —* ромб,
Z.BCD==60°, С1Л4>з=5, где Л4| — середина BjDi, СС|=**д/8.
В этой призме проведено сечение плоскостью, проходящей
через отрезок BD и точку, принадлежащую CiMi. Найдите
значение наибольшей и наименьшей площади сечения.
44. Основание пирамиды МАВС — равнобедренный треугольник,
62
Z_ACB = QO°, МА l.(ABC\ MC-a. Найдите угол между
плоскостями МСВ и АВС, при котором объем пирамиды
будет наибольшим.
45. В осевом сечении конуса угол между образующими равен 120°.
Образующая конуса равна 2. Найдите наибольшую площадь
сечения, проходящего через две образующие конуса.
46. Боковая поверхность конуса рассечена плоскостью, парал-
лельной основанию, на две равные по площади части. В каком
отношении разделились образующие конуса плоскостью
сечения?
47. Конус рассечен плоскостью, параллельной основанию, на две
равные по объему части. В каком отношении разделилась
образующая конуса плоскостью сечения?
48. В правильную треугольную пирамиду вписан цилиндр так,
что его нижнее основание принадлежит основанию пирамиды,
а окружность верхнего основания касается боковых граней
пирамиды. Осевое сечение цилиндра — квадрат. Боковая
грань пирамиды наклонена к основанию под углом а, а
сторона основания равна 2а-д/3. Найдите объем цилиндра.
49. В пирамиду вписан шар, объем которого равен 36л, а полная
поверхность пирамиды равна 20. Найдите объем пирамиды.
50. В шар вписан конус так, что окружность основания конуса
и вершина конуса принадлежат поверхности шара. Расстоя-
ние от центра шара до основания конуса равно а. Образую-
щая конуса наклонена к основанию под углом а. Найдите
объем конуса.
51. Поверхность шара, диаметром которого является высота
конуса, делит образующие конуса в отношении 16:9, считая
от вершины конуса. Найдите объем шара, если радиус
основания конуса равен 3.
52. Каждое из ребер правильной пирамиды равно 1. Шар имеет с
каждым из ребер пирамиды только по одной общей точке.
Найдите объем шара.
53. Объемы шара и конуса равны. Осевое сечение конуса —
прямоугольный треугольник. Можно ли просверлить в шаре
такое отверстие, чтобы через него можно было вынуть
конус?
РЕШЕНИЯ И УКАЗАНИЯ К РЕШЕНИЯМ ЗАДАЧ
ПОВЫШЕННОЙ ТРУДНОСТИ
1. Прежде чем перейти к доказательству, обратим внимание на
следующее: две фигуры называются равными, если они движением
переводятся одна в другую, т. е. если две фигуры движением
можно совместить, то эти фигуры равны. И обратно: если две
фигуры равны, то их можно совместить.
Обратим внимание, что если многоугольники равны ЛВС...=
==Д1В]Сь.., то это будет означать, что Z_A = £А\, Z~B—
и т. д. и что = ВС --В\С\ и т. д.
G3
Рис. 147
Нам необходимо доказать, что &АВС= &А\В\С\ (рис. 146).
Рассмотрим &ВКА и &В\К\А\. Эти треугольники равны по катету
и гипотенузе: ВК — В^К^ АВ=А\В\. При совмещении треуголь-
ника ВКА с треугольником BiKiAi луч АС совместится с лучом
Л1С1, значит, и точка С совместится с точкой Ct, потому что по
условию AC — AiCit следовательно, стороны СВ и С\В\ сов-
местятся. Таким образом, ДЛВС совместится с дА^Сь значит,
дЛВС= ДАjBiCi, что и требовалось доказать.
2 (рис. 147). Докажем, что параллелограммы ABCD и
A\B\C\D\ можно совместить. Для этого совместим ДАВ7( с
&А\В\К\, что возможно, так как эти треугольники равны по
катету и гипотенузе. При совмещении этих треугольников сов-
местятся лучи AD и i4]Dt, а так как AD—A\Di, то точки D и Di
совместятся. Лучи ВС и В\С\ параллельны прямой AiDi, следо-
вательно, эти лучи по аксиоме параллельности совместятся.
Так как ВС = АЬ и B\Ci=A\D\, a AD—AiDj, то CB = BiCi, следо-
вательно, точка С совместится с точкой С|, значит, совместятся и
стороны CD и C[D\. Таким образом, параллелограмм ABCD
совместится с параллелограммом A\B\CiDi, т. е. они равйы, что и
требовалось доказать.
3 (рис. 148). Нам необходимо доказать, что трапеции ABCD
и Л1В1С|£>[ равны, т. е. что эти трапеции можно перевести дви-
жением одну в другую. Для этого совместим ДЛВ£) с дЛ^Рь
что возможно, так как они равны по трем сторонам. А так как
трапеции равнобочные, то ABAD = /CCDA и Z_BiAiD| =
= ZLC\D\A\, но zLBAD= Z-B}AiDit значит, ДCDA — ДCtDiAt,
поэтому при совмещении точки D с точкой D\ совместятся углы
CDA и C\D\A}t но AB = CD, A\B\ = C\D\ и АВ — А\В\, или CD —
— C\D\. Поэтому при совмещении лучей DC и D\C\ точки С и С\
совместятся и совместятся отрезки ВС и BiC|. Таким образом,
трапеции совместились, значит, они равны.
Рис. 148
G4
Рис. 149
Рис. 150
Рис. 151
Прежде чем строить требуемые фигуры, обратим внимание на следующее.
В ряде задач на построение в условии могут быть не даны конкретные длины
отрезков или величины углов для построения некоторой фигуры. Следователь-
но, длины отрезков и величины углов мы должны задать сами. Делать это мы
будем так. Допустим, надо построить треугольник по двум сторонам и углу
между ними. Для этого (примерно на четверти тетрадного листа) от руки
построим произвольный разносторонний треугольник AjBiCi (рис. 149). Будем
считать,"что этим построенным от руки треугольником мы задали необходимые
длины отрезков и величины углов.-Для построения треугольника АВС по двум
сторонам и углу необходимо знать длины, например, сторон АВ и ВС и угол ВАС.
Так, пусть будет длиной стороны АВ сторона Д|В1 нашего произвольного
треугольника, также сторона АС будет равна Д|С1 и угол ВАС будет равен
В1Д|Сь т. е. по отрезкам Д>В|, Д|С1 и углу В1Д1С1 построим треугольник АВС
с помощью циркуля и линейки.
4 (рис. 150). На произвольной прямой (назовем ее Ь) отметим
точку К и через нее проведем перпендикуляр к прямой Ь. На
этом перпендикуляре отложим отрезок КВ, равный К\В\, и про-
ведем дугу с центром в точке В радиусом ЛВ, равным Д]Вь до
пересечения с прямой Ь, найдя тем самым точку Л. На луче АК
отложим отрезок Л С, равный Л1Сь Соединив точки А и С с точ-
кой В отрезками, получим треугольник АВС. Задача решена
(рис. 151).
Замечание. Индексы при буквах К, В, С, А означают, что первой точкой
в нашем построении была точка К, второй — точка В, третьей — точка А и
четвертой — точка С. Тогда при наличии вспомогательных дуг и зная порядок
построения точек, легко восстановить его последовательность даже без
словесного описания.
5 (рис. 152). Построим сначала треугольник ABD по двум
сторонам ДВ=Л1В1, ЛО=Л1О| и высоте ВК=В\К\. Как строить
ДЛВК, рассказано в предыдущей задаче. Построив дДВО,
проведем дуги с центрами В и D радиусами, соответственно
равными В\С\ и D\C\. Точку пересечения С этих дуг соединим
с до.чками В и D. Задача решена (рис. 153).
Рис. 152
65
Рис. 154
Рис. 155
в. Допустим, дана трапеция .AiBi-CiDi (рис. 154). Проведем
в ней Bi/CJICiDt. Пусть АВ равен отрезку а, ВС—отрезку Ь,
CD — отрезку с и AD — отрезку d, тогда отрезок АК. равен
отрезку d — Ь, который обозначим /. Теперь построим треуголь-
ник АВК по трем сторонам: а, с, I. Далее на луче AD отложим
отрезок AD=d. Из точек D и В радиусами, равными соответ-
ственно с и Ь, проведем дуги, точка пересечения которых будет
точкой С. Задача решена (рис. 155).
7. По формуле Герона Vp О5-°) (Р—<=)в^д, р =
= 0,5 (13+14 +15)=21, ^21-8-7.6=3-4-7=84, R=^ =
13-14-15 65 о юк . 5 84 .
4-3-4-7 8 ’ 5’ р 21
Обратите внимание, что для решения мы использовали фор-
мулы, не являющиеся обязательными в школьном курсе геометрии.
8 (рис. 156). &2=g2+c2 —2accos60°=9+64 —2-3-8-0,5=
=49, Ь=7. Пусть ВА=с, ВС=а, тогда AMi = —с+0,5a, СМ?—
= — a + 0,5с=AM 1=-^с2+0,25a2 ^ас=-^64 + 2,25 — 24 • cos60°=
=0,5 V217, СМ2=~\[\3 cos <р= |
2ЛМ| СЛ42 I
л/217-т/13 '
= I .2(°^5а~4^5с~а) I =1------I3 - I ,г — ,HoS=4-acsin B =
' т/217-13 ’ 1 т/217-13 1 Р 2
= 0^3-8'^ =6 ^3, р = 0,5(а+6 + с)=9, г=^.
9. а) Да, так как такой четырехугольник — параллелограмм;
б) нет (рис. 157); в) нет (рис. 157): у любого параллелограмма,
даже не ромба, противоположные углы равны; г) да, так как при
этом все стороны будет равны: противоположные стороны парал-
лелограмма равны; д) да, так как у параллелограмма противо-
Рис. 156
66
положные углы равны, то по условию задачи будут равны и их
половины, поэтому д ЛВС равнобедренный: АВ—ВС, т. е. у парал-
лелограмма все сторонЫ’ будут равны.
10 (рис. 158). a) Z_BAF= 120°;
А
б) ZCBF=-^^-=-^-=90e, ZBC£=-^-=60°, CEF =
L At
—1^1=90°. ZEFB=90°; в) SBDF=0,5BD‘DF sin BDF =
=0,5 (12 sin 60°=27 -\/3, так как BD=2R sin BFD=DF, где
/?=6, ZB£D=60°; г) так как аЛС£) прямоугольный (Z С=90°)
и АЛ = 30°, то высоты Л С, DC, СМ вычислим следующим образом:
ЛС=ЛО*со8 Л = 12-C0S 30° = 6д/3, DC=ЛD sin 30° = 6, СМ =
=АС‘sin 30°=Зд/3; д) 5 = 65дЛ0Л. = 6-0,5ЛО-OF sin AOF=
=3*6-6-sin 60°=54-\/3; e) я/?2=36я.
11 (рис. 159). AD(x-l, y-2), AB (4,
Так как ABCD — квадрат, то
W ( AD • AB=AD‘AB cos 90°=0,
I AD=AB,
следовательно,
f (ж—1)«4 —3 (i/—2)=0,
t(x—1)2+(c/-2)2 = 164-9,
или
f 4x—3y= — 2,
I x2—2x-j-y2—4y=25—5,
J 4 ’
I (3w—-2J2 3«/ —2 । о a nn
I --4—----+yz—4y=20,
{ _3y—2 ,
9у»-^у4-4 _4y _20 = 0,
25j/2— 1W — 300 =0, y2 —4y—12=0,
у=2±4, t/i=6, i/2= — 2, X|=4, x2=—2.
A(1,Z) O(X,y)
Рис. 159
Di (4, 6) и Рг(—2, —2), так как AD= ВС, то ЛР1=(3, 4)=
==(Х1—5, t/i + l)=SCi, xi=8, t/.i=3, т. е. Ci (8, 3). AD2=
=(—3, —4)=(xl —5, 1/1 + 1)=ВС2, Xi=2, yi = — 5, т. e.
Сг(2, -5). Итак, D( (4, 6), С, (8, 3), D2(-2, -2), С2(2, -5), т. е.
получим два квадрата, удовлетворяющих условию задачи.
12 (рис. 160). Здвс1>=5ддор-|-£ддов4-£двос_1-,5дсор =
=0,5ЛР • OKi+0.5ЛВ • OKi +0.5ВС • ОК2+0,5ОС • ОК3=
=0,5r(AD+AB+BC+DC)=r‘p, где р=0,5 (ЛР+ЛВ-|-ВС+
+DC).
67
в
Рис. 160
О
РИС; 161
13. Используем две формулы: S = ^-sin С и c = 2/?sin С. Из
второй формулы найдем sinC = c/2/? и подставим в первую:
ab с abc
4Я“' •
14 (рис. 161). SABCD — S^BKA 4* S&BKC 4~ $&СК.О 4“
=0,5ВК ЛЯ-sin а + 0,5ВК-КС sin (180° —a)+0,5C/<-KD sin a +
4-0,5KD-AK- sin (180° — a). Так как sin (180° — a) = sin a, to
Sabcd = 0,5sma(BK-AK + BK-KC + CK-KD + KD-A K)=
=0,5 sin a (BK- (Л К + КС)+KD (СК + A K)) = 0,5 sin a (BK • A C +
+ К£>-ЛС) = 0,5 sin a-AC (BK+ KD) = 0,5AC-BD sin a.
15 (рис. 162). По теореме синусов из треугольников АВК
пг7п АК sin а КС sin a sin a
и BKC имеем -гд =-^r и = ст7Гяп» - Следова-
ло sm p dC sin (IoU — p) sin p
тельно, ^=^-, откуда АК'КС=АВ:ВС, так как в пропорции
можно менять местами средние (крайние) члены.
16. Докажем, что при условии а2 + 62==с2 /_ С будет равен 90°.
Для доказательства используем теорему косинусов. Для любого
треугольника верно с2 = а2-[-Ь2— 2ab cos С, где, учитывая условие
с* = а2 + Ь2> — 2ab cos С = 0, откуда cos С = 0, следовательно,
С = 90°.
17. Так как Z. С = 90°, сторона с больше стороны а и стороны 6.
а-\-Ь>с, следовательно, — Н—— >1, так как с>>0. Тогда
С с
Рис. 164
Рис. 165
теореме Пифагора а2-\-Ь2 = с2, что
равносильно
если
Но, учитывая, что — и —---правильные положительные дроби,
С с
убывающая,
3 3
0<а<1). Поэтому +('т)
, так как каждое из сла-
гаемых левой части неравенства меньше каждого из слагаемых
равенства +(-у) Но (’с’) < * и зна-
чит, а3 + &3 <с3, что и требовалось установить.
18 (рис. 163). Так как 6u>5u и 8u>5u, т. е. сумма двух
меньших сторон обоих треугольников больше третьей, значит, оба
треугольника существуют. Поэтому первое решение: 3а + 3и +
+ 5u = 143— и второе решение: 5и + 5и + 3и = 143, откуда
Ui —13, £Z2=11- Итак, длины сторон треугольников равны 39,
39, 65 и 55, 55, 33.
Замечание. Так бывает не всегда. Например, длины двух сторон
пропорциональны числам 2 и 5, а периметр равен 36. Здесь возможен только
один случай: 5:5:2 — таково отношение сторон. Случай 2:2:5 невозможен, так
как сумма двух меньших сторон меньше третьей: 4ж5п, а должна быть больше
третьей, как в первом случае: 7«>5м.
19 (рис. 164—167).
20 (рис. 168—171). _________ ____ _ ____
21 (рис. 172). Пусть AD = a, АВ~Ь и AAi =с, тогда Л|О =
=ЛИ+ 0,5X7? = — F+0,5AD + DC= —с + 0,5 (а + *)= — с +
+ 0,5а4-0,56. BDl = BA+AD-{-DDi=— b + a + c. AiO2=AA2t +
Рис. 166
Рис. .167
69
Е
Рис. 168
Рнс. 169
Рис. 170
Н Е
Рис. 171
Рис. 172
+ЛО2= 1+0,5, так как ЛО = 0,5ЛС = 0,5-\/2. Л1О=0,5-^6-
ВО|=д/3.
а) Пусть epi — угол
получим COS ф! — |
между Л|О и BDi, тогда соэф1 =
—, учитывая, что ab = 0, ас = 0 и £& = 0,
-с2 + 0,5а2 —0.5д2
2
2
= arccos
б) Пусть ф2 — угол между BD
__ | (а 4-с — tyb I | -- b2
л/3- ! ’ ' д/3
3 >
COS ф2 =
Обратим
внимание, что если надо было найти угол ABDi, то искали бы угол
между векторами ВА и BDi, тогда знак модуля не ставится,
где ВА = — Ь.
3 3
22. а) (рис. 173). AK-i-ВС по построению, ВС±МО, так
как Л4О±(ЛВС), тогда ВС-LAM, поэтому угол между СВ и AM
COS ф =
3
и ЛВ, тогда
q , ф2 = arccos
о о
Рис. 174
Рис. 175
70
равен 90°; б) OEJ-MK (по построению), О£±ВС, так как BCJ-
-LAK и BC.LMO, т. е. ВС JL (ОМА), следовательно, ОЕ Л_(ВМС).
2SOMK=MK*OE=MO.OKt OK = BK-tg 30°= 1, МК==УЗ+Т==2,
2-О£=-ТЗ-1, О£=^; в) (рис. 174). BP.LMC по построению,
тогда AP.LMC, так как дАРС=ДВРС по двум сторонам
(PC — общая, ВС = АС) и углу между ними. Тогда /LAPB —
линейный угол двугранного АМСВ. F— середина АВ. тогда
PFJbAB, так как &АРВ равнобедренный. Найдем угол FPB.
Сначала вычислим ВР. ВР*МС = МК*ВС (рис. 174, 173), МС=
=-\6и№+В№=у/7BP-V? = 2-2 д/3, ВР=^, sinFPB =
Z.FPB = arcsin^, ZLЛРВ = 2 arcsin ;
oP 4-д/З 4 8 4
г) рассмотрим сечение AMK (рис. 175). AD\\OE. но ОЕ Л_(ВСМ),
значит, AD±(BCM). AD-MK = AK-MO. AK=AB-s\n ABK =
= 2-V3sin60°=3 (рис. 173). AD-2 = 3-^3, Л£>=^ = 1,5-Д
23 (рис. 176). a) Z_EMK — линейный уге-л между плоскостями
DMC и АВМ, где ВВЦАВ, MK-LAB, ОК1.АВ, значит, EKJ.DC и
ME±PF. tg ZOjMK=arctg-^-, ЛЕМК=
=2 arctg-^-; б) расстояние от точки В до плоскости DMC равно
расстоянию от точки К до плоскости DMC. так как AB||(DAfC)
(потому что AB||DC). Расстояние от точки К до плоскости DMC
равно расстоянию от точки К до прямой ЕМ. т. е. KL.LEM
(КЕЛ, ЕМ по построению, /(LX DC, так как ВСЛ-ЕК и DC.LMO.
значит, ВС±(ЕМК)). ЕМ =-\[ЁО2 + ОМ2 = 13, 25дСМК = £КХ
XA1O=EM-KL, 1O-12=13-KL, KL=~-.
24 (рис. 177, а)/ Пусть CB = 2i^ AD~3ut тогда СО = 2/,
ОА = 3/ (рис. 177,6). 5:х = 5/:3/, х=3, 001=8. В трапеции
DiDBBtBBi = OOi=8, DDi=8, т. е. трапеция вырождается в
прямоугольник.
Рис. 176 Рис. 177
71
A
Рис. 178
25 . а) (рис. 178, a). ^±^=3, x=2; б) (рис. 178,6). AD =
= 2ME, x + 4 = 2-7, x=10, ЛР| = 10. Однако следует рас-
смотреть и еще один случай (рис. 178, в). AD = 2ME, 4-|-х = 2,
х=—2, но х>0, так как расстояния выражаются неотрица-
тельными ч'ислами. Следовательно, второй случай невозможен.
26 . а) (рис. 179, а). Докажем, что BD\_LAC и B£>iJ_Bp4.
Так как AC±BD и AC±BBi (BBi -ЦАВС)), то AC-L(BBiDx)t
значит, ЛС-LBDj. Аналогично доказывается, что BD\l.ABr.
AB\.L A\B и АВ\ ±Л(£>| (так как AiDi _1_(ЛЛ|В1), значит, AB|_L
_L(4iBZ>i), следовательно, AB\_LBDi. Таким образом, BD\Jl.AC
и BDi-LAB\, значит, BDi±(ABiC).
Другой способ решения проще, но он с векторами (рис. 179, а).
Пусть AD = a, ab = b, АА\=с и ЛВ=1. Выразив BD, ЛС, ЛВ<
через а, Ь, с, легко доказать, что BD\-AC = Q и BDi-ABt=O,
значит, BDi-LACi и ВВ1_1_ЛВ1, следовательно, ВО1_1_(ЛВ1С);
б) (рис. 179,6). aBiADjco АОКВ по двум углам, откуда
BlDi:BO = BiK:KO, (2ВО):ВО^В1А:/(О, В1А:АО = 2.
27 (рис. 180, а), а) 1-й ш а г. Построим плоскость, проходя-
щую через одну из данных прямых (например, B\D) и парал-
лельную другой прямой ЛВ. Такой плоскостью будет Л1В1Л.
2-й шаг. Проведем перпендикуляр из какой-нибудь точки прямой
Рис. 179
72
Рис. 180
АВ к плоскости (Д]В1О), например Л/С±Л1£>, тогда ЛК±Л(В по
построению, Л7<_1_Д1В1, так как Л1В1 ±(Л1Л£>), следовательно,
XK±(4iB!D), AK=AD sin 45°=^; б) (рис. 180,6). MO||B,D
по построению. Плоскость АМС проходит через одну из скрещи-
вающихся прямых АС и параллельна В]О. В плоскости MOD
проведем OPJLOM, тогда ОР_ЦЛМС). Действительно, OPJlOM
по построению, OP.LAC, так как ЛС-1_В£>, ЛС J_BBi. tg B\DB~
=tg d=^g-=-U, OP=OD sin а. Из условного треугольника
находим sina=-^-, тогда OP=^~=^.
д/3 уЗ 3
28 (рис. 181). A ABM со &ADH по гипотенузе и острому углу,
равному у, тогда МВ—АН, но МВ=^Д^-—^=АН, DH—
—^AD2-AH2=^, DDi = DA/sin60°=-J, sinx=^=^,
х=45°.
29 (рис. 182). AK-i-MC по построению, AK-LBC, так как
BCJLAC и BCJ-MA, следовательно, AKJ_(MCB), tga=4^-=
3 3
=—, следовательно, sin a=—. ЛК=ЛС-з1п a=2,4. Из дЛМЯ
Рис. 182
73
Рис. 183
Рис. 181
Af/C=M4.sina=l,8, MC=-^=5, tg₽=^=^-, KE=MKX
X tg ₽ = 1,08, Sce4 = 0.5Л К • KE = 1,296.
30 (рис. 183). CMA-AB по построению. Обозначим Z_C\MC=
= a. tg a=-£^==—^—==—==—L следовательно, tga<-\/3 =
д/з д/з
a ——
2
= tg 60°, значит, 60° > a, поэтому в сечении — трапеция АК\Е\В,
так как /(1£1||ЛВ (как линии пересечения двух параллельных
плоскостей — оснований призмы третьей) и KiEi^AB, Найдем
площадь проекции этого сечения на плоскость АВС,
5пр = S д Авс $ д ксе = 4 д KtCvEi;
KiCiEi — С\Р\ • P\Ki — С\Р\* CiPi • tg 30° —
_ CiP? ^(C|M|-P1M|)2^ (a sin 60°—c ctg 60°)2 ^д2 _!_\2 = a2
д/S д/3 дб д/3\2 д/3/ ~ 12д/з’
л ___д2 д/3 a2 __a2 (9—1)_2a2 __ 5np ___ 2д2«2 _ 4a2 д/3
np— 4 12 д/3~~ 12д/3 ~~Зд/З* сеч cos 60° Зл/з 9
31 . Пусть в параллелепипеде ABCDA\B[CiDi AD = a, AB = b,
AAi=c и |a|=a, |Ь|=&, |c|=c. Выразим диагонали через
a, b, с и найдем AC2, DB2t CA2, BD2, а потом их сумму. В итоге
должны получить DB2+ СЛ24-ЛС24-ВО2 = 4 (а2 + /г-|-£2).___
32 . Пусть в параллелепипеде ABCDAiBiCiDi AD —а, АВ = Ь,
АА\=с и |a| = |6| = |с| — 1. Найдем длину DBi, Остальные
диагонали находятся аналогично. DB\ = —а-\-Ь + с, DB\ =
=^Ja2 + 62 + с2 —2afr cos 60° — 2ас cos 60° + 2bc cos 60° =-\/2,
BDi=^/2, ЛС1=Л/б, CA 1=л/2. ________
33 . Нарисуем развертку куба (рис. 184), ЛС\ =уАС2 + СС? = 5.
34 (рис. 185). О£±ДС, АЕ=0,5АС=3, AiE=-^A^—AE^=
=4. Saa,c,c=AC‘A1E=24 — SAa,BiB, СВА_АК, CBA-AiO, значит,
СВХЛЛь следовательно, СВХССь так как СС|||ЛЛ|» значит,
CCiBiB — прямоугольник. Scc^b^CB-CCi — ^Q, S6ok = 78.
Рис. 184 Рис. 185
Рис. 186
74
Рис. 187
35 (рис. 186). Пусть АС=х, DB = y, AAt=z. Saa,c,c = xz=P,
sddiB,b = yz = Q-5бок = 4г-ЛО, но x=-^-, y=~ AD =
=У(0,5х)2+(0,5t/)2 = 0.5 У^+7=0,5 VP2 + Q2-
S6„=4z-A D = 2 Vp2 + Q2.
36 (рис. 187). а) т/n~=-7^-, значит, —=-^—, или — =-Д-,
'r ' ' MiMt AMi x AMt x AM,
KA AC 13 _ 8
MtM2~‘ (ЛС-ЛЛЛ) • T- e- x — (8-AM,) '
Пусть HAfi = y, j —=—, откуда х=4-^-.б) Легко доказать,
I 13 8
х ~(8-у) ’
что КОJ_(ЛВС), где О — середина гипотенузы АВ и ОК =12
из £\КОВ. Обозначим СВ=а, АС — b, ОК—с и найдем
cos M2MiAf4 = cos (СВ, АК)=-^, ZA42MiM4 = arccos
37 (рис. 188). Пусть МС=х, ОН—у, тогда, учитывая, что
ОН±МС, х^у—2-Samoc=S&amc = Q- Если ОН=у, то DH=
= ,JL-,..=2y. Так как DHA.MC, то SAMDC=0,5AfC.Dtf=
COS оо
= 0,5x-2y=xt/ = Q, 5^ = 40.
38 (рис. 189). KiK3 = 3, ОК=-уг=-\/3 (так как аз=/?УЗ),
К^К3 = 3, K3E = 3.ctg 6О°=УЗ, ОЕ = 2УЗ, Л£ = 3-ОЕ=6^,
СЯ=ЛЕ ctg 4CE=6y§.ctg 60° = 6, 50СЯ = СЕ-АЕ = 36 Уз. S6oK =
=^SiT=^=72^ S™“108
39 (рис. 190). 05 = 2-72-sin 45° = 2, 05 = 4, тогда ЯО=4.
1/ — KO'MP‘EF = 4-8-8 = 128
3-2 6 3 ’
40 . Так как боковые ребра наклонены к основанию под одним
углом, то ортогональная проекция вершины пирамиды есть центр
75
к
Рис. 189
к
окружности, описанной около основания (рис. 191). AD = 12,
ДАОВ= Д ВОС== ACOD, к тому же они равносторонние.
В ДЛ4ОС М0 = 0С = 6, OEi=AO-sin60°=6sin60° = 3V3 =
= ОВ2 = ОВ3. S0CH = 0,5 (AD + ВС). ОВ2 = 27-^3, Л!£1 =
=VMO2 + Otf=з V7. SeoK = 3 • + SAMD = 3 -0,5Д В • ME. +
+ 0,5A D • ЛЮ = 27 д/7 + 36. 5полH = 27 h/3+д/7) + 36.
41 (рис. 192). AC = c cos a, SOCH =0,5AC-AB sin a =0,25c2X
cin 9ry Q _ S°ch _ C S’n
/\ Sin ^Ot, ~~~ n “ л n *
0 cos ₽ 4 cos p
42 (рис. 193). AK=x, тогда QK=x иMK—x ctg a (O/C-LAB
по построению). MO=^MK2 — OK2==-ylxrctgYa—-x2 =
x -y/cos 2a
sin a
ctg2 a — 1 =
(cos2 a — sin2 a) _cos 2a
• 2
sm a
- 2
sin a
откуда
H sin a
V^s 2a
я tr ff cos a
тогда MK=------------
-tJcos 2a
S6ok = 4AK.MK = 4x.MK =
C
Рис. 192
Рис. 191
76
— — sin a‘cos a _Q 5//2 2a> Так как sin a*cos a = 0,5 sin 2a.
cos 2a
у__4х2*ЛК? _H3 sin a
. 3 . 3 cos 2a ’
43 (рис. 194). ClKi=x, тогда KiE=C,Ki tg30o=^r, AftK,=
________________________________ _________<3
=5 —x, тогда МК1=д/Л1Л1?4-Л11К? = л/33—10x4-x2. Sce.,=
=(KlE+MD)MKi, где MD=AfC-tg 30° =-p. 5сеч=^±Дх
Л - V3 д/З
XV33—1 Ox+x2=^V(* +5)433-1Ox 4-Х2). Пусть y=(x4-5)2X
X (33— 1 Ox 4-х2), где 0<x<5. / = 2 (x 4-5) (33—1 Ox 4-x2) 4-
4-(x4-5)2 (2x— 10) = 2 (x4-5)(33- 10x-bx24-x2-25)=4 (x-|-5)X
X(x2— 5x4-4), t/ = 0 при x2 —5x4-4=0, x=4, x=l. При x = 0
S=5 Vn=-^75, при x=l 5 = 12^/2 = 288, при x=4 5 = 9^3 =
т=-7243, при x = 5 S = 20~\/4j-=V266,6... . Наибольшая площадь
равна 12-\/2, наименьшая — 9д/3.
44 (рис. 195). Пусть /LMCA=x, тогда МА=а sin х, АС —
=ccosx, V==-------------------------, где 0<х<—. Рас-
О О Z
смотрим функцию t/ = cos2 x-sin х. Пусть sin x — ut тогда cos2 х =
= I~u2 и тогда у = и(1—и2) = и — u3t где 0<и<1, или рас-
Рис. 195
77
ширим несколько область определения функции у: O^w^l.
1 13
и' = 1—Зи, и=—. При и=0 у=0, при и—— у —2-^-, при
уЗ . -уЗ у
и=1 у=0. Следовательно» наибольшее значение у имеет при
1.1
ц=—, т. е. при sin х=—, следовательно, искомый угол равен
arcsin .
45 . Sce4 = 0,5/2 sin а, где I — образующая конуса, а — угол
между образующими в сечении (0<а< 180°). Наибольшее значе-
ние sin а при а = 90° (0 < а < 180°). Значит, $нанб = 0,5Z2 sin 90° = 2
(площадь этого сечения больше площади осевого сечения). /=2,
тогда R = I sin 60°=д/3. S6oK = nRl=2л д/3.
46 (рис. 196). Пусть НМ=х, АМ = у и Z.МАО = а, тогда
(лЛО-ЛЛ4> (у cos а)-// у2 _ ~ У_~-Л<) АН — (У~х) ~ У___i
(пМК-НМ) ’ (xcosa)«x ~х^ * х * ‘ НМ х х
=->/2—1.
л-7 / S-MO п S МО2 с лл/^2 е
47 (рис. 197). =2, 57= мор. откуда S = M02u, S( =
.<Л2 S-МО МО3и SMO\3 о МО Зсг
=MOlU, тогда J =2, откуда -^=^2.
значит, и ^-=Y' тогда MK=^2t, MKi = t, поэтому KiK=
=(Й- 1) t, откуда
48 (рис. 198, а). СК^а^/3, OK=a^/3-tg OCK=a-j3 tg30° =
=а; (рис. 198,6). OiK\=x, тогда К1Л1 = 2х и КМ = а—х9
78
Рис. 199
В
Рис. 200 Рис. 201
49 . В пирамиде, в которую вписан шар, соединим центр шара
со всеми вершинами пирамиды. Таким образом, мы данную
пирамиду можем рассматривать как сумму пирамид, каждая из
которых имеет основанием какую-нибудь грань пирамиды (в том
числе и основание пирамиды). Так, например, треугольная
пирамида будет составлена из четырех пирамид. Высотами каждой
из этих пирамид будет являться радиус вписанного в пирамиду
шара, так как радиус шара, проведенный в точку касания шара с
плоскостью, перпендикулярен этой плоскости. Значит, объем дан-
ной пирамиды можно рассматривать как произведение площади
полной поверхности многогранника на треть радиуса вписанного
4л/?3
в этот многогранник шара. Найдем радиус шара: —= 36л, /? = 3.
Упир = 20.1=20.
50 (рис. 199). ОК = а, (Ж = а- (90° - а)=2а-90°.
ЛК = а*ctg (2а —90°)=а-ctg (90° — 2 а) = — a*tg 2а, где 45° <
<а<90°, так как а>90° — а, зцачит, а>45°, следовательно,
2а>90°, /<B=i4/(-tga=—a-tg2a«tg а, что больше 0, так как
tg2a<0, то
51 (рис. 200). Пусть ЛЛ1=9«, тогда МВ = 1ба. Л№=ЛВХ
ХЛЛ4. В ДДВК Z.K=90°, КМ±ДВ (рис. 201). Обозначив
ЛК=Ь и Z_4 = a, докажите с помощью тригонометрии, что
Ь2=АВ-АМ, т. е. АК2=АВ-АМ. Следовательно, 9 = 25u*9u,
откуда В/(2=АВ*МВ, следовательно, В№ = 25и-16и =
=25-16t?=16, ВЛ=4. У=±^8.= Ю-|-л.
52 (рис. 202). Фигура DABC — тетраэдр, каждое из ребер
которого равно 1, тогда ВМ = 1 -sin 45°==^=СЛ4. Шар, вписан-
ный в куб, будет иметь с ребрами тетраэдра только по одной общей
точке. Тогда радиус шара будет равен 0,5ВЛ1=^,
79
Рис. 202
Рис. 203
53 (рис. 203). АО=х, тогда M0=x, Углн——. Пусть радиус
о
шара у, тогда
откуда
y = или
2х
1. Таким образом, диаметр конуса больше диаметра шара,
значит, нельзя конус «протащить» в отверстие, просверленное
в шаре.
§ 6. ЗАДАЧИ НА ИЗМЕРЕНИЯ
Как известно, слово «геометрия» означает «землемерие». Пред*
лагаем вам ряд практических задач, связанных с измерениями.
1. Объясните, какие измерения надо произвести на земле, чтобы
найти высоту строения, например высоту башни.
2. Объясните, какие измерения надо произвести на берегу рекщ
чтобы найти расстояние до пункта, находящегося на другом
берегу реки.
3. Какие измерения надо произвести на берегу реки, чтобы, не
переплывая реку, найти расстояние между двумя пунктами,
находящимися на другом берегу реки?
4. Какие измерения надо произвести с вертолета, находящегося
над землей на заданной высоте, чтобы определить ширину
озера?
Для решения следующих задач необходимо иметь набор моделей фигур:
конуса, куба (обозначим его ABCDAiBiCtDi), правильных треугольной и
четырехугольной пирамид (обозначим их МАВС и MABCD), где будем считать
точку О центром оснований каждой из этих фигур соответственно.
Эти модели можно склеить из плотной бумаги (развертки их даны на
рисунках 204—207) или изготовить, например, из дерева.
5. Возьмите модель куба (ABCDA\B\C\Di) и, произведя не-
обходимые измерения, найдите: а) угол наклона к плоскости
АВС медианы AM треугольника АВ\С\ б) угол наклона
плоскости АВ{С к плоскости АВС\ в) угол наклона плоскости
АВС\ к плоскости АВС\ г) радиус вписанного в куб шара;
д) радиус шара, описанного около этого куба.
80
Рис. 204
Рис. 205
И
Рис. 206
Рис. 207
6. Возьмите модель правильной треугольной пирамиды и, произ-
ведя необходимые измерения, найдите: а) площадь полной
поверхности и объем пирамиды; б) расстояние от центра
основания до плоскости боковой грани; в) углы наклона боко-
вого ребра и боковой грани к плоскости основания; г) радиус
вписанного в пирамиду шара; д) радиус описанного около
пирамиды шара; е) площадь полной поверхности и объем
вписанного в пирамиду конуса.
7. Возьмите модель правильной четырехугольной пирамиды и,
произведя необходимые измерения, найдите то, что указано
в пунктах а)—е) предыдущей задачи.
8. Возьмите модель конуса й, произведя необходимые измерения,
найдите: а) площадь полной поверхности и объем конуса;
б) угол наклона образующей к плоскости основания конуса;
в) радиусы вписанного и описанного шаров; г) полные
поверхности и объемы вписанных в конус правильных тре-
угольной и четырехугольной пирамид и пирамиды, в основании
которой лежит прямоугольный равнобедренный треугольник.
9. Возьмите модель шара, например мяч, и, произведя не-
обходимые измерения, найдите объем и площадь поверхности
шара.
81
ОТВЕТЫ И УКАЗАНИЯ К РЕШЕНИЯМ ЗАДАЧ
ИА ИЗМЕРЕНИЯ
1. Пусть АВ — высота башни (рис. 208), на земле отметим
так называемый базис СЕ, который измерим. Допустим, ваш
рост 1,5 м = ССь С помощью угломера найдем углы аир. Теперь
в A/4CtE], зная сторону CiEi = CE и прилежащие к ней два угла
а и 180° —р, находим высоту ABt, и тогда ЛВ = ЛВ( + 1>5 м.
2. Пусть АВ — расстояние, которое надо найти. На берегу
отметим базис AM и с помощью угломера найдем углы аир.
По стороне AM и прилежащим углам находим сторону АВ —
искомое расстояние (рис. 209).
Рис. 209
3. Пусть АВ — расстояние, которое надо найти. Измерим
расстояние МК (базис), а далее, как в задаче 2, найдем рас-
стояния АК и ВК. Кроме того (рис. 210), найдем угол АКВ и,
далее, по двум сторонам (А К и В К) и углу между ними АКВ найдем
в Л АВ К сторону АВ.
4 (рис. 211). Пусть вертолет находится в точке М на высоте
Н = МК. С помощью угломера определим углы а и р. Тогда в
&КВМ /LMBK=a, в ДЛ1Д/С ZLMAK = & и из этих треугольни-
ков находим КВ и КА и искомое расстояние АВ = КВ —КА.
82
§ 7. НЕКОТОРЫЕ ВОПРОСЫ ГЕОМЕТРИИ
ТЕОРЕМА, АКСИОМА ИЛИ ОПРЕДЕЛЕНИЕ?
Чем являются перечисленные ниже утверждения: теоремами,
аксиомами или определениями?
1. Если три стороны одного треугольника соответственно
равны трем сторонам другого треугольника, то такие треуголь-
ники равны.
2. Через точку вне прямой можно провести единственную
прямую, параллельную данной прямой.
Ответ на поставленные вопросы зависит от того, как построен
курс геометрии, какие из утверждений приняты в качестве аксиом,
системы аксиом. Так, в одном курсе геометрии первое утверждение
может быть теоремой, в другом курсе — аксиомой, а в третьем
(если его слегка изменить) — определением: «Треугольники
называются равными, если их стороны соответственно равны».
Второе утверждение в одном курсе геометрии может бь?ть
аксиомой, в другом —- теоремой. Можно было бы построить такой
курс геометрии, в котором за аксиому принять, например,
утверждение, называемое у нас теоремой Пифагора. Возможны
случаи, когда теорему, доказываемую на основе аксиомы, можно
поменять местами, т. е. теорему считать аксиомой, а аксиому
считать теоремой. Например, если считать предложение «Сумма
углов треугольника равна 180°» аксиомой, то утверждение «Через
точку вне прямой можно провести единственную прямую, парал-
лельную данной прямой» будет теоремой. Однако по какому бы
учебнику мы ни изучали геометрию, представление о точке, пря-
мой, плоскости и т. д. будет одно и то же, а треугольники по
трем сторонам будут равны независимо от того, как обосновывает-
ся их равенство: теоремой, аксиомой или определением. Доказьь
вать какую-либо теорему следует, используя только ту последо-
вательность понятий, аксиом, теорем, которые логически пред-
шествуют данной теореме в данном курсе геометрии, чтобы ни
одним из звеньев этой цепочки не оказалась доказываемая
теорема. Пожалуй, это самое трудное при поиске способа
доказательства теоремы.
Например, самым простым доказательством теоремы Пифаго-
ра будет такое.
Из теоремы косинусов с2 = а2-\-Ь2 — 2bc cos С при Z_C = 30°
следует: c2 = a2 + Z>2 (так как cos 90°==0), т. е. теорема Пифагора.
Но по учебникам, по которым большинство из вас учится, так
доказывать теорему Пифагора нельзя, хотя в них есть теорема
косинусов. Нельзя потому, что в этих учебниках теорема косинусов
следует за теоремой Пифагора.
83
О «ЗДРАВОМ» СМЫСЛЕ И ОЧЕВИДНОМ
Рассмотрим несколько задач, решение которых в связи с
очевидностью ответа не представляет никакой сложности.
L Можно ли заточить сверло так, чтобы оно высверливало
фигуру, очень напоминающую квадрат (рис. 212), если высверли-
вать отверстие обычной дрелью и обычным способом? Ответ
ясен: конечно, нельзя.
2. Из бумажной ленты, посередине которой проведен отрезок
АВ, разделивший ленту на две равные части, сделали кольцо
Рис. 213
Рис. 212
так, что при этом один конец ленты перед тем, как склеить,
повернули вокруг АВ на 180° (рис. 213). А теперь по линии АВ
разрежем кольцо. Сколько колец получится? И здесь в ответе
сомневаться не приходится: линия АВ разделила ленту пополам,
а разрезали мы кольцо по линии АВ, значит, получим два кольца.
3. Вообразим, что земной шар обтянут по экватору нитью и
что подобным же образом обтянут нитью обычный детский мячик
по окружности большого круга. Далее, вообразим, что длину каж-
дой из этих нитей увеличили на один метр и расположим их
соответственно вокруг экватора Земли и вокруг окружности боль-
шого круга мяча так, чтобы зазор между нитью и Землей (между
нитью и мячом) всюду был одинаков. В каком случае зазор боль-
ше: между нитью и Землей или между нитью и мячом? И здесь
ответ очевиден: какое значение имеет добавление к 40 млн. м —
длине экватора — одного метра, другое дело с мячом, у которого
длина окружности большего круга меньше метра. Поэтому зазор
в случае Земли практически равен нулю, а в случае с мячом
довольно значительный.
Хотя приведенные ответы, казалось бы, не вызывают сомне-
ний, но все они неверны: высверлить фигуру, мало отличающуюся
от квадрата, можно; при разрезании кольца по линии АВ получим
одно кольцо, а не два; а зазор в случае Земли и в случае с мячом
один и тот же, равный приблизительно 16 см. Объяснение этих
случаев смотри на с. 85.
Почему же «здравый» смысл нас хотя и очень редко, но под-
водит? Объяснить это можно тем, что где-то нам не хватает зна-
ний, где-то жизненного опыта, да и, кроме того, мы не отрабаты-
ваем у себя безошибочную интуицию, являющуюся чуть ли не
основой в любом виде творчества, и не только в науке, но и в
искусстве. Выдающийся ученый академик А. Н. Крылов говорил,
84
что, например, техник или инженер должен «развивать не только
свой ум, но и чувства, чтобы они его не обманывали... свои же
умозаключения он должен сводить к твердому, практическому:
<я это вижу, слышу, осязаю, чую, значит, это так и есть» (К ры-
ло в А. Н. Мои воспоминания: АН СССР, 1963).
К Казалось бы, что высверливать обычной дрелью можно
только круглые отверстия. Однако если особым образом заточить
сверло, то им можно высверлить квадратное отверстие (точнее,
отверстие, мало отличающееся от квадратного). Для этого сверло
должно иметь следующую форму. Возьмем равносторонний
треугольник АВС со стороной, равной а, и проведем дуги радиу-
сом а из вершин А, В и С до их пересечения (рис. 214). В любом
положении сверло будет касаться всех четырех сторон квадрата и
при вращении высверливать фигуру, указанную на рисунке 212.
2Г Объяснение со случаем ленты ограничим предложением
сделать такую ленту и, как указано в задании, разрезав ее по
средней линии, убедиться, что получится одно кольцо. Далее
полезно еще раз разрезать полученное кольцо вдоль опять по
средней линии и постараться угадать, что получится.
Рис. 214
Рис. 215
3.' Возьмем две окружности разного радиуса: /? и г Длина
одной окружности будет 2л/?, другой 2лг. Теперь к каждой
окружности добавим по 1 м, получим: 2л/? 4-1 и 2nrJ-l.
Теперь найдем радиусы следующих окружностей: —1 =/?( и
л* J Ь
2лг-^ 1
'—пт—= Л (рис. 215, а, 6). Далее, чтобы вычислить зазоры между
новой и старой окружностями в каждом случае, надо найти раз-
ности: Ri — R и rt— г. Найдем их: /?, —/?=2я*-+
2л
_^2n/?-f-l—2л/? 1 _______2лг+1 _ 2лг+1-2лг . 1
2л '~2? Г1 Г“~ 2л —г~~ 2л ~ 2л ’
R —
Таким
образом, зазор зависит только от прибавляемой к окружности
величины (в нашем случае от 1 м), а от радиуса не зависит.
Поэтому и в случае Земли, и мячика зазор будет одинаковым,
равным 1:2л 1:6,28~ 0,16 м = 16 см.
85
НЕ ТОРОПИТЕСЬ С ВЫВОДАМИ
Два тысячелетия известна аксиома о единственности прямой,
проходящей через данную точку параллельно другой прямой. Было
много попыток доказать справедливость утверждения аксиомы, т. е.
пытались доказать, что действительно прямую, параллельную дан-
ной, через данную точку можно провести только одну. Но попытки
доказать не увенчались успехом. Приведем одно из таких дока-
зательств.
Доказательство. Пусть даны прямая ВА и точка С
вне ее. Через точку С проведем прямую С А и отложим угол DC А,
равный углу САВ, так, как указано на рисунке 216, тогда прямая
CD (р ис. 217) будет параллельна прямой В А. Но через точку С
к прямой С А можно провести единственный луч CD (рис. 216),
чтобы он образовал угол ACD, накрест лежащий с углом САВ
и ему равный. Значит, прямая CD (рис. 217) является единствен-
ной прямой, параллельной АВ и проходящей через точку С.
Правилен ли наш вывод?
Приведем еще одно рассуждение, ошибочность которого
обнаружить не так просто.
Допустим, нам надо построить колонну из прямоугольных
параллелепипедов, отличающихся друг от друга только высотой,
устанавливая один параллелепипед на другой. Мы утверждаем,
что если число параллелепипедов не ограничено и не ограничено
время, то высота колонны может стать как угодно большой.
Действительно, добавляя по параллелепипеду, колонна становится
все время выше и выше и, наконец, когда-то, пусть через очень
продолжительное время (временем-то мы не ограничены), колонна
обязательно достигнет желаемой высоты.
Попробуйте найти ошибку в этих рассуждениях. И пусть эти
примеры служат вам предостережением в тот момент, когда в
результате рассуждений, связанных не только с математикой, вы
собираетесь сделать тот или иной вывод: не торопитесь с вывода-
ми, еще и еще раз подумайте...
1. Ошибка в доказательство единственности прямой
DC, параллельной прямой ЛВ, заключается в предположении, что
DC\\AB только в том случае, если выполняется равенство
или накрест лежащих углов, или соответственных углов п т. д. А
может быть, есть случай, когда накрест лежащие углы нс р а в-
Рис. 217
86
Рис. 218
ны, а при этом прямые будут параллельны? Доказать или
опровергнуть такое предположение не удалось, а поэтому приняли
-без доказательства теорему, называемую аксиомой параллель-
ности прямых: «Через точку вне данной прямой нельзя провести
более одной прямой, параллельной данной». Рассмотрим одно
рассуждение, приводящее к выводу, что через точку вне прямой
параллельно данной прямой можно провести сколько угодно
прямых. На рисунке 218 мы отметим штриховой линией прямую 6,
параллельную прямой а и отстоящей от прямой а, допустим,
на 1000 км. Будем вращать прямую СК, отмечая последова-
тельно точки пересечения прямой СК с прямой а: К\, Къ Кз, Kt,
Чтобы вращающейся прямой СК слиться с прямой b (что
безусловно возможно), вначале ей надо «оторваться» от прямой а
я затем, описав некоторый угол, слиться с прямой Ь. Описывая
этот угол, прямая СК не будет иметь общей точки с прямой а, т. е.,
занимая различные положения, все время будет парал-
лельна прямой а. Таким образом, через точку С парал-
лельно прямой а можно провести сколько угодно прямых. К
сожалению, справедливость этого утверждения практически
проверить невозможно, а теоретически доказать не удалось.
И поэтому есть геометрия, которую мы изучаем, где принимается
аксиома о единственности прямой, параллельной
прямой а, и есть геометрия, где принимается аксиома о возмож-
ности проведения более одной прямой, параллельной
прямой а.
2. Теперь рассмотрим другой вопрос: всегда ли высота колонны
может стать как угодно большой, если ставить один
параллелепипед на другой и если число параллелепипедов и
время не ограничены? Нет, не всегда. Например, пусть высоты
параллелепипедов являются квадратами натуральных чисел: I2,
Й2, З2, ..., и2. Ясно, что в этом случае, высота колонны, равная
Г4-4 + 9 + ... + П2, может стать как угодно большой, но может
быть и такой случай, когда, например, высоты параллелепипедов
Являются членами бесконечно убывающей геометрической про-
г | z । \ 2 / 1 \ 3 / 1 \ п
грессии: 1, —
В этом случае высота
2
2 ’
2
87
колонны будет всегда меньше 2, так как S = 1 4—g—|—-—1-„.=
=----р=2 как сумма бесконечно убывающей прогрессии
1 а
которая равна
1— я
ЧТО ОЗНАЧАЮТ НЕКОТОРЫЕ ФОРМУЛИРОВКИ?
1. В одном учебнике сформулирована аксиома: «Через точку,
не лежащую на данной прямой, можно провести на плоскости не
более одной прямой, параллельной данной».
Вопрос. Утверждается ли в этой аксиоме, что через точку,
.не лежащую на данной прямой, провести одну-то прямую, парал-
лельную данной, можно?
2. В другом учебнике сформулирована аксиома: «Через точку,
не лежащую на данной прямой, проходит только одна прямая,
параллельная данной».
Вопрос. Утверждается ли этой аксиомой, что через точку, не
лежащую на данной прямой, провести прямую, параллельную
данной прямой, можно?
3. В одном учебнике дано определение перпендикуляра к
прямой: «Перпендикуляром к данной прямой называется...».
К тому же дан рисунок этого перпендикуляра к прямой.
Вопрос. /Ложно ли на основании данного определения
и даже приведенного рисунка утверждать, что на самом деле
такой отрезок, перпендикулярный прямой, существует? И вообще,
означает ли, что то, чему мы дали определение, на самом деле
существует?
4. В одном учебнике сказано: «А к с и о м а. Через три точки,
не лежащие на одной прямой, проходит одна и только одна
плоскость». И далее: «Теорем а. Через прямую и не лежащую
на ней точку проходит одна и только одна плоскость».
Вопрос. Почему пишут «одна и только одна»? Не проще ли
написать «только одна» вместо «одна и только одна»?
5. В одном учебнике сказано: «Прямая, лежащая в плоскости,
перпендикулярна наклонной к этой плоскости тогда и только
тогда, когда она перпендикулярна ее проекции».
Вопрос. Почему и здесь повтор: «тогда и только тогда»?
Не проще ли сказать «только тогда» вместо «тогда и только
тогда»?
Кстати, теорема Пифагора иногда формулируется и так: «Сум-
ма квадратов двух сторон треугольника равна квадрату третьей
стороны тогда и только тогда, когда треугольник прямоуголь-
ный». И здесь опять: «тогда и только тогда». Зачем?
Ответы на вопросы
1. Не утверждается. Аксиома утверждает, что если бы
оказалось, что через данную точку провести прямую, параллель-
88
з&ю данной прямой, можно, то другой параллельной через эту
тдчку провести нельзя. А вот существует ли хотя бы одна прямая,
Параллельная другой, аксиома не утверждает. И если бы такой
прямой вообще не существовало, то аксиома продолжала бы быть
Нерно сформулированной.
2. Смысл этой аксиомы — в единственности прямой, парал-
лельной данной прямой и проходящей через данную точку. Однако
некоторые считают (и не без основания), что эта аксиома якобы
еще утверждает о возможности проведения прямой, парал-
лельной данной. Поэтому такую формулировку этой аксиомы
считать удачной нельзя: двух различных толкований не должно
быть.
3. Если считать, что все утверждения учебника верны, то
верить в существование данного понятия на основании его
определения и рисунка, приведенных в учебнике, можно. Однако
надо помнить, что, определяя какой-либо объект, мы должны
доказать, что он на самом деле существует, а не является плодом
нашего вымысла. Поэтому лучше было бы вначале обосновать
существование того или иного объекта, а потом дать ему опре-
деление, что, кстати, сделать бывает довольно трудно, поэтому
часто считают возможным принять определение какого-либо
объекта на веру либо доказательство существования его пере-
нести на более позднее время, когда знания у учащихся будут
и шире, и глубже.
4. Сформулируем эту аксиому несколько иначе: «Через три
точки, не лежащие на одной прямой, можно провести плоскость
й притом только одну» — или так: «Через три точки, не лежащие
-на одной прямой, проходит плоскость и притом только одна».
В любой из этих двух формулировок более четко видно, что в
этой аксиоме содержится два утверждения: во-первых, проходит
(или можно провести) плоскость, во-вторых, что эта плоскость
единственная. Сформулируем еще одно утверждение (не аксиому):
«Через две точки проходит (можно провести) плоскость и притом
бесконечное множество плоскостей». Аналогично сформулируем
теорему: «Через прямую и не лежащую на ней точку проходит
(можно провести) плоскость и при том единственная (един-
ственную)». Здесь также два утверждения: 1) проходит (можно
Провести) плоскость, 2) эта плоскость единственная.
5. Сформулируем две теоремы: «Если углы накрест лежащие,
то они равны» — теорема верна. А обратная теорема: «Если углы
равны, то они вертикальные» — утверждение неверное. Например,
в равностороннем треугольнике углы равны, но они не являются
Вертикальными. Еще теорема: «Если внутренние накрест лежащие
углы равны, то прямые параллельны» — теорема верна. Обратная
л»еорема: «Если прямые параллельны, то внутренние накрест
^фжащие углы равны» — и эта теорема верна. Эти две теоремы —
йфямую и обратную — можно сформулировать так: «Две прямые
параллельны тогда и только тогда, когда накрест лежащие углы
89
равны». Можно эти же две теоремы сформулировать и так:
«Накрест лежащие углы равны тогда и только тогда, когда
прямые параллельны». Наконец можно «тогда и только тогда»
заменить «в том и только в том случае», например: «Две прямые
параллельны в том и только в том случае, если накрест лежащие
углы равны», «Накрест лежащие углы равны в том и только
в том случае, если прямые параллельны». Таким образом,
только в том случае, когда прямая и обратная теоремы
в е р н ы, можно эти две теоремы записать в виде одной
формулировки, употребляя выражение «тогда и только тогда»
или «в том и только в том случае». Значит, если в формулировке
теоремы встречается выражение «тогда и только тогда» или
«в том и только в том случае», значит, формулируется не одна
теорема, а две (прямая и обратная) и доказывать в этом случае
надо не одну теорему, а две.
§ 8. О ДОКАЗАТЕЛЬСТВЕ ТЕОРЕМ
Переходя из класса в класс и получая новые знания, вы на
основе их можете доказывать теоремы иначе, чем доказывали
раньше, при этом часто новое доказательство либо проще,
либо более изящно.
Покажем ряд доказательств, которые могут отличаться от
известных вам. Конечно, если прежние доказательства вам
хорошо известны, то не имеет смысла учить новые. Может быть,
кто-нибудь из вас найдет свое доказательство. Только будьте
осторожны и вспомните о «цепочке», о которой мы говорили при
доказательстве теоремы Пифагора как следствия теоремы косину-
сов на с. 83.
О доказательстве равенства двух треугольников
по трем сторонам
Если три стороны одного треугольника Л, В, С соответ-
ственно равны трем сторонам другого А|, Bi, Ci, то согласно
теореме косинусов cos/l = cosyij, значит, АА — АА[. Поэтому
эти треугольники будут равны по двум сторонам (согласно
условию) и углу между ними: zLA~/LAi (согласно доказан-
ному) .
Рис. 219
Теорема Пифагора
Американский любитель математики
Э. Лумис собрал и опубликовал 367
различных доказательств теоремы Пифа-
гора. Приведем одно из доказательств.
Дано: дЛ,В,С, ZC = 90° (рис. 219).
Доказать: a2-\-b2 = c2 SA[3CD=^AB2 —
= (a-f-b)2 —4у-+с2, откуда a2+2ab-}-b2=
= 2аЬ + с\ а2 + Ь2 — с2
90
Признак перпендикулярности прямой и плоскости
ЦТ Теорема. Если прямая h перпендикулярна пересекающимся
прямым at Ь, то она перпендикулярна плоскости а, которой
Докажем, что Л±с, где с — произвольная прямая, при-
уфинадлежат эти пересекающиеся прямые,
Надлежащая плоскости а. Для доказательства на прямых а, Ь,
tr, ft отложим векторы а, Ь, с, h (рис. 220). Но /iJlq и ft_Lb,
значит, h_1_а и h±6, выразим с: c~xa-\~yb. Найдем скалярное
произведение h• с: h-c = h>(ха + yb)=xha + yhb =х-0 + */*0 = 0,
значит, й-с = О, следовательно, ft_Lc, поэтому и ft_Lc.
Так как с — произвольная прямая, принадлежащая плоскости
а, то прямая h перпендикулярна любой прямой, принадлежа-
щей плоскости а, значит, согласно определению ftJ_a.
Теорема о трех перпендикулярах
Теорема. Прямая, лежащая на плоскости, перпендикулярна
к наклонной тогда и только тогда, когда она перпендикулярна
к проекции этой наклонной на эту плоскость.
1. Докажем прямую теорему: если a .Lb, то aJ_c.
Доказательство. На рисунке 221 отрезок b — проекция
наклонной с на плоскость а, значит, ft_La, откуда h-La. Таким
образом, и по условию nJL6, следовательно, a_L(BC7Q,
откуда а±с.
г 2. Аналогично доказывается обратная теорема: если aJ_c,
та a -Lb.
Доказательство. ftJ_a, значит, h-La. Таким образом,
ЛЛа и по условию аЛ_с, следовательно, a_L(BCK), откуда a-Lb.
Замечание. Еще раз обращаем внимание па то, что предлагаемые
новые доказательства теорем и выводы формул не надо выучивать, если вам
Хорошо известны те доказательства теорем и выводы формул, которые вал
кфедлагали в школе.
3. Нахождение площадей плоских фигур и объемов тел с по-
мощью интеграла.
Докажем такие две очень похожие и по формулировке, и по
доказательству теоремы.
91
1) Если плоская фигура пересечена прямой, перпендикулярной
высоте фигуры, равной Я, и длина получившегося в сече-
нии отрезка I (х) — непрерывная функция, то площадь фигуры
н
S = (х) dx.
о
2) Если тело пересечено плоскостью, перпендикулярной вы-
соте тела, которая равна Н, и площадь получившейся в сечении
фигуры S (х) — непрерывная функция, то объем этого тела
н
V= (S (х) dx.
о
Доказательство. 1) Между прямыми х = 0 и х — Н расположена
фигура ABCD. где отрезок ОН будет высотой данной фигуры. При сечении этой
фигуры прямыми х и хЦ-Ах (т. е. прямыми, перпендикулярными высоте
тела) получим соответственно отрезки длиной / (х) и /(x-f-Ax) и фигуры AEFD
и AKMD имеют соответственно площади S (х) и S (х-^Ах). Можно записать
S (х-|- Ax) = S (х) + AS, где &S=S£xMf (рис. 222). Учитывая, что /(x)«Ax<AS,
запишем (/ (х) +е)* Ах--AS, где е (эпсилон) >0 и е->0 при Ах->0. Разделим обе час-
ти последнего равенства на Ах и получим / (х)е = Найдем пределы: lim (/ (х)-{-
Ах Дх->0
4-е)= lim —, но lim (/(х) + е)= lim /(x)-hlim г = 1 (х) + 0 = /(х), а
Дх->0 АХ Дх->0 Лх->0 Дх->0
lim — = S' (х), поэтому получаем /(x) = S'(x). Значит, S (х)—первообразная
Дх->-0 Ах
функции / (х), т. е. площадь фигуры есть первообразная от длины отрезка / (х).
//
А так как по определению ^l(x)dx = S(x) I = S (Н)—S (0) = S (Я)— 0 =
о ’
//
= S(/7), то S=t Цх) dx.
В качестве примера
(рис. 223): н
S = j / (х) dx — j adx = ах
о о
найдем площадь параллелограмма
н
о
Найдем площадь трапеции (рис. 224, 225): М# = /(х),
/1x2 Zj L
MN x b — a ,/4 b — а .
b а ~fj~* MN — x, МК I (x) jy x-f-a.
Конечно, этот вывод не проще, чем тот, что предлагается в школе
для нахождения площади трапеции. Мы его привели только как
пример использования интеграла для вычисления площадей фигур.
92
Рис. 223
Рис. 225
2) Между плоскостями а и р, которые перпендикулярны прямой Ох и находят-
ся друг от друга на расстоянии, равном Н, расположено тело ABCD, высота
которого равна И (расстояние между плоскостями а и Р). При сечении этого
тела плоскостями, перпендикулярными Ох и проходящими через точки х и
х-|-Лх (рис. 226), получаем фигуры соответственно площадью S (х) и 3(х4-/\х),
а тела AEFD и AKMD имеют соответственно объемы V (х) и 1/(х-4-Дх). Можно
записать (рис. 226): V (х + Дх) = V (х) + A V, где hV—VrKMj-. Учитывая, что
5(х)Дх<ЛУ, запишем (S (х)+ г)*Лх = ДV, где е->0 при Дх->0. Разделим обе
. о . Д V
части последнего равенства на Дх и получим 5(х)-|-е = —
Найдем предел: lim (S(x)+e)=lim —,
Дх-->-0 Дх->-0 Ах
+ lim e = S(x)+0 = S(x), lim ^-=V"(.r),
Дх->-0 Лх->0 Дх:
но lim (S (х)-|-е)= lim S (х)4~
Д.г-»-0 Лл->0
поэтому получаем S(x)=V"(x).
X
Рис. 226
Рис. 227
93
Значит, V (д) — первообразная функции S (х), т. е, объем тела есть первообразная
я !
от площади сечения S (х). А так как по определению J S (х) dx = V (х) I =
н 0
= V(//)-V(0)=:=V(№-0=V(W)( то V=Js(x)dx.
о
H=R
Теперь найдем объемы некоторых тел:
а) Найдем объем призмы (прямой или наклонной, но не прямо-
угольного параллелепипеда, рис. 227):
н н
S (x) = S, Vnp = j S (х) dx — \S dx = S-x \ " = S‘H-S-0=S-H.
О о
б) Найдем объем пирамиды (рис, 228):
Пусть 5ддвс = 3. ЗдЛ1В1С1—S (х). Найдем функцию 5 (х):
AiO, Д Л i ^i Ci __ уХ) Q f ' 5*Х
мо^—зГ^-’ 7Г-Т"’ ^W—^-
II II н .
1/ ( е / \ A f / 5 2ч J s ( 9 , S (х'\ \ Н SH
} S (х) dx=\ ) dx=Tf\ x dx = -Ц-) | o .
0 0 0
V--=4-SII.
о
в) Найдем объем конуса (рис. 229):
Пусть SOCH = S, SCC4 = S(x). Найдем функцию S (х):
ЛЮ? , ?ч х2 S (х) q ( \__ S-x2 , ч .. 1 е и
7лог~ (А)~~ //2 1 Т‘ Д' (см-б) ...V —
=4txR4l
о
г) Найдем объем полушара (рис. 230). Сначала найдем
к
функцию S (х): 3 (х) = л (V/?2 — х2)2 = л (R2 — х2). У = л$(/?2 —
о
— х2) dx -- л ^х/?2 — o=JI(^3~~4—о)=-|-л/?3, тогда объем
4 гз
шара равен —л/<
94
Обратим внимание, что с помощью интеграла выводить форму-
лу площади прямоугольника и объемов прямоугольного па-
раллелепипеда и цилиндра нельзя, так как при доказательстве
правильности утверждений, приведенных выше (о выводе формул
объемов и площадей с помощью интегралов), предполагается,
.что площадь прямоугольника и объемы прямоугольного парал-
лелепипеда и цилиндра мы уже знаем.
О выводе формулы площади поверхности тела
с использованием объема тела
а) Площадь боковой поверхности цилиндра.
Выразим объем цилиндра, у которого высота равна Н, как
функцию от х, где х — радиус основания цилиндра ABCD, тогда
лх2//= V (х). Если дадим значению х приращение Дх, то получим
цилиндр, имеющий объем V (х+Дх) — объем цилиндра AiBiC\Di,
V (х + Дх)— V (х)=Д V (х) — то, что на рисунке 231 заштриховано.
Чем меньше будет Дх, тем заштрихованная часть будет тоньше
и при Дх->0 будет стремиться к величине боковой поверхности
цилиндра, т. е. lim^ :=^бок‘ |*т0 Л'Ах^~ п0 0ПРеделе-
пию производной. Значит, = (х), т. е. Збок —(л/?2)7 — 2 л/?.
б) Площадь боковой поверхности конуса.
Выразим объем конуса, образующая которого наклонена под
постоянным углом, равныгл а, как функцию отх: х = КО (рис. 232),
КО-LAB. Тогда AO = R = OK: sin a=x:sin се. ВО=-Н—О1\:
:cos a = x:cos а. Значит, V=~3iR2H—-z~^~-----х3 Если да-
дим значению х приращение Дх, то получим конус, имеющий
объем У(х4~Дх) — объем конуса ThBiCi. V (х-ф Дх)— V (х)=-
==ДУ (х) (на рис. 232 заштрихованная часть). Чем меньше будет
Дх, тем заштрихованная часть будет тоньше и при Дх->-0 будет
стремиться к величине боковой поверхности конуса, т. е.
lim = 5Сок. Но lim V' (х) по определению производ-
Дх—>0 Да—> 0
Рис. 233
ной. Значит, S6OK
Зл
бок
О (на рис. 233 заштрихованная
, л___Г3 \ _
о—^“2-----Л I —
3 sin a cos а /
— о'~= •——--------— лАО>AB = jiRl, так как
3 sin a cos a sin a sin a cos а
х п х х , R f
——= R, ---—:cosa=---------=/.
sin a sin a cos a sin a cos а
Таким образом, 5бок = л7?/.
в) Площадь сферы.
Выразим объем шара как функцию от х, где х — радиус шара:
;/=Если дадим значению х приращение Ах, то получим
шар, имеющий объем V(x-}-A*) (объем шара радиуса x-f-Ax).
I/(x + AX)-V(x) = AV(x)
часть). Чем меньше будет Ах, тем заштрихованная часть будет
тоньше и при Дх->0 будет стремиться к площади сферы, т. е.
lim Но jjrn по определению производ-
ной. Значит, £ = (-^-лх3) = 4лх2, т. е. 5 = 4л/?2
г) Длина окружности.
Выразим площадь круга как функцию от х, где х — радиус
круга; 5 = лх2. Если дадим значению х приращение Ах, то получим
круг, имеющий площадь S(x + Ax)—площадь круга радиуса
х+Ах. S(x + Ax) — S(x) = AS(x). Чем меньше будет Ах, тем
заштрихованная часть будет тоньше и при Ах->0 будет стремиться
к длине окружности, т. е. lim —~——С (длина окружности).
Дх-»-0 &х
Но lim —-~^-=Sz (х) по определению производной. Значит,
Замечание. Еще раз обращаем внимание на то, что предлагаемые
новые доказательства теорем и выводы формул не надо выучивать, если вам
хорошо известны те доказательства теорем и выводы формул, которые вам
предлагали в школе.
СОДЕРЖАНИЕ
Используемые обозначения формулы 3
Часть 1 Основной материал 9
§ 1. Устные задачи
Планиметрия —
Стереометрия —
Ответы к устным задачам 11
§ 2. Основные задачи 12
Планиметрия
Стереометрия 14
Решения и указания к решениям основных задач 22
§ 3. Тренировочные задачи 39
Планиметрия —
Стереометрия 40
Ответы и указания к решениям тренировочных задач 47
§ 4. Задания для самоконтроля 52
О минимальных требованиях к знаниям теории —
Варианты заданий . 53
Комментарии и указания к выполнению первых заданий 57
Часть 11. Дополнительный материал 59
§ 5. Задачи повышенной трудности —
Планиметрия —
Стереометрия 60
Решения и указания к решениям задач повышенной трудности 63
§ 6. Задачи на измерения 80
Ответы и указания к решениям задач на измерения 82
§ 7 Некоторые вопросы геометрии . 83
Теорема, аксиома или определение? —
О «здравом» смысле и очевидном 84
Не торопитесь с выводами . 86
Что означают некоторые формулировки? 88
§ 8. О доказательстве теорем 90
Александр Николаевич Чудовский
Лидия Алексеевна Сомова
ПРОВЕРЬТЕ СВОИ ЗНАНИЯ ПО ГЕОМЕТРИИ
Зав. редакцией Р /X. Хабиб. Редактор Т В. Автономова. Младшие редакторы
О. В. Агапова, Л. Е. Козырева. Художник Г А. Алексеев. Художественный
редактор Е. Р. Дашук. Технический редактор М. С. Пузанова. Корректоры
Н. В. Красильникова, Е. В. Мамитова.
ИБ № 10303
Сдано в набор 12.05.87 Подписано к печати 10.11.87. Формат 60Х90'/|б-Бум.
кн. журн. импорт. Гарнит. литературная. Печать высокая Усл. иеч. л. 6,0.
Усл. кр. отт. 6,38. Уч.-изд. л. 5,39. Тираж 100000 экз. Заказ 124. Цена 15 коп.
Ордена Трудовою Крас Знамени издательство «Просвещение» Государственною комитета
РСФСР но ам ih.i<ih-. книжной ।. 1|нт»п.in Г»‘)н|G Москва. 3 й прог- Марьиной
р<)1НН. !1
Саратовский ордена Трудового Красного Знамени полиграфический комбинат Росг.1авиолиграфпрома
Государственного комитета РСФСР по делам издательства. полиграфии и книжкой торговли. 4Ю004.
('аратов, ул. Чернышевского, 59