Липман Берс
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
Lipman Bers
Calculus
HOLT, RINEHART AND WINSTON, INC.
New York Chicago San Francisco Atlanta Dallas Montreal Toronto London Sydney
Липман Берс Математический анализ
Том II
Перевод с английского Л. И. Головиной, под редакцией И. М. Яглома
МОСКВА «ВЫСШАЯ ШКОЛА» 1975
517.2+517.3
Б 48
УДК 517+516(075)
Рекомендовано учебно-методическим управлением по высшему образованию в качестве пособия для студентов высших технических учебных заведений
Берс Л.
Б 48 Математический анализ. Т. II. Перевод с англ. Л. И. Головиной. Под ред. И. М. Яглома. Учеб, пособие для втузов. М., «Высш, школа», 1975.
544 с. с ил.
Переведенная с английского языка книга Л. Берса представляет собой учебное пособие по курсу математического анализа (е элементами аналитической геометрии) и предназначается для первоначального ознакомления с предметом.
Книгу отличает большая тщательность в подборе и расположении материала, наглядность, соединяющаяся с высоким научным уровнем, а также органическая связь «чистой» математики и ее приложений.
Второй том посвящен аналитической геометрии на плоскости и в пространстве, рядам, дифференциальному и интегральному исчислению функций нескольких переменных.
Предназначается в качестве учебного пособия для студентов втузов; может быть также использована преподавателями высших учебных заведений.
Б"ООЦОГР75 Б3—16-7-75	5I7'2|S'7 '1
© Издательство «Высшая школа», 1975.
ОГЛАВЛЕНИЕ
8.	Ряды	9
§ 1.	Теоремы о конечном приращении 10
1.1.	Формулировка теоремы о конечном приращении (10). 1.2. Теорема Ролля (12). 1.3. Доказательство теоремы о конечном приращении (12). Упражнения (12). 1.4. Обобщенная теорема о конечном приращении (13). Упражнения (14). 1.5. Погрешность линейного приближения (15). Упражнения (17).
§ 2.	Теорема Тейлора	18
2.1.	Параболическое приближение (18). Упражнения (20). 2.2. Многочлены Тейлора (20).
Упражнения (24). 2.3. Теорема Тейлора (24). Упражнения (25). 2.4. Биномиальная теорема (26). Упражнения (27). 2.5. Биномиальные коэффициенты для произвольного показателя (27). Упражнения (28). 2.6. «Элементарные» варианты формулы Тейлора (29). 2.7. Вычисление логарифмов (29). 2.8. Вычисление Л (31). Упражнения (33). 2.9. Формула Тейлора для показательной функции (33). 2.10. Формулы Тейлора для синуса и косинуса (34). Упражнения (34). 2.11. Сигма-символика (34). Упражнения (36). 2.12. Сводка формул Тейлора (37).
§ 3.	Бесконечные последовательности 39
3.1.	Сложение бесконечного множества чисел (39). 3.2. Необходимость в точности (40).
3.3.	Бесконечные последовательности (41). Упражнения (42). 3.4. Сходящиеся последовательности. Пределы (43). Упражнения (45).
3.5.	Свойства пределов (46). 3.6. Вычисление пределов (47). 3.7. Расходящиеся последова-телыкхти (49). Упражнения (51). 3.8. Монотонные последовательности (52). Упражнения (53). 3.9. Постоянная Эйлера (54).
§ 4.	Бесконечные ряды	55
4.1.	Частные суммы (55). 4.2. Сходящиеся ряды (56). Упражнения (58). 4.3. Необходимое условие сходимости (58). 4.4. Расходящиеся ряды (59). Упражнения (60). 4.5. Геометрическая прогрессия (60). 4.6. Операции над рядами (62). Упражнения (62). 4.7. Ряды с положительными членами (63). 4.8. Признак сравнения (63). 4.9. Десятичные дроби как ряды (64). Упражнения (64). 4.10. Интегральный признак (65). Упражнения (67). 4.11. Критерий частных (68). Упражнения 69). 4.12. Знакопеременные ряды (70). 4.13. Абсолютная сходимость (70). 4.14. Перестановка членов (71). Упражнения (72). 4.15. Умножение рядов по Коши (72). Упражнения (73).
§ 5.	Степенные ряды	74
5.1.	Сходящиеся и расходящиеся степенные ряды (74).	5.2. Радиус сходимости (75).
5.3.	Дифференцирование и интегрирование степенных рядов (76). Упражнения (77). 5.4. Ряд Тейлора (78). 5.5. Аналитические функции (79). Упражнения (80). 5.6. Примеры рядов Тейлора (80). Упражнения (82). 5.7. Биномиальный ряд (83). Упражнения (85). 5.8.
Умножение степенны» рядов (85). 5.9. Деле-
ние степенных рядов (86). Упражнения (87).
5.10.	Четные и нечетные функции (88). Упражнения (88).	5.11. Подстановка ряда в
ряд (89). Упражнения (90). 5.12. Примечание (90).
Приложение к главе 8	90
§ 6.	Правило Лопиталя	90
6.1.	Неопределенности вида 0/0. (90). Упражнения (91). 6.2. Неопределенности вида оо/оо (92). 6.3. Обобщения (93). Упражнения (93).
6.4.	Другие неопределенные выражения (94). Упражнения (95).
§ 7.	Доказательства сходимости	96
7.1.	Монотонные последовательности (96).
Упражнение (96). 7.2. Перестановка членов ряда (96). Упражнения (99). 7.3. Произведение в смысле Коши (99).
§ 8.	Радиус сходимости	100
8.1.	Лемма Абеля (100). 8.2. Радиус сходимости (101). 8.3. Дифференцирование и интегрирование рядов (101). 8.4. Доказательство непрерывности (102). 8.5. Дифференцирование и интегрирование степенных рядов (103). Упражнения (104).
§ 9.	Погрешности методов численного интегрирования	104
9.1.	Оценка для правила трапеций (104). Упражнения (105). 9.2. Оценка для правила Симпсона (105). Упражнения (107). Задачи (107).
9.	Векторы	111
§ 1.	Векторная алгебра	112
1.1.	Направленные отрезки (112). 1.2. Векторы (114). Упражнения (115). 1.3. Сложение векторов (115). 1.4. Доказательства законов сложения (116). 1.5. Произведение вектора на число (118). 1.6. Доказательства законов умножения вектора на число (119). Упражнения (121). 1.7. Векторы на плоскости и в пространстве (121). 1.8. Базисы и реперы на плоскости (121). 1.9. Координаты (123). Упражнения (124). 1.10. Упорядоченные пары чисел как векторы (124). Упражнения (125).
1.11.	Произвольный базис. Независимость (125). Упражнения (126). 1.12. Базисы и реперы в пространстве (126). Упражнения (128).
§ 2.	Радиус-вектор	128
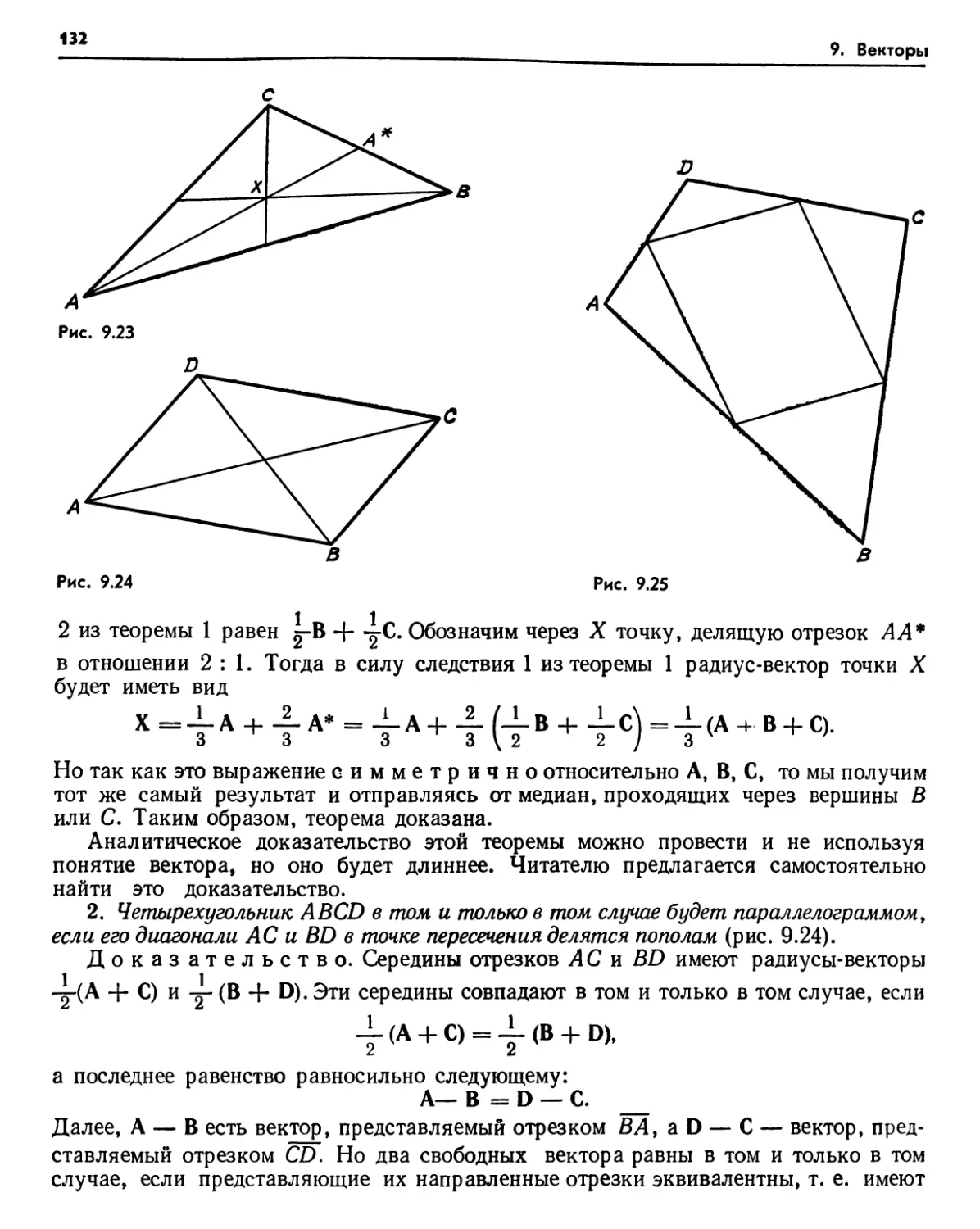
2.1.	Радиус-вектор точки (128). 2.2. Деление отрезка в данном отношении (130). Упражнения (131). 2.3. Векторные доказательства геометрических теорем (131). Упражнения (133). 2.4. Радиус-вектор в пространстве (134).
§ 3.	Полярные координаты	135
3.1.	Полярный угол вектора (135). 3.2. Полярные координаты (135). Упражнения (137).
3.3.	Уравнения линий в полярных координатах (138). 3.4. Изображение кривых (139). Упражнения (140).
6
Оглавление
§ 4.	Прямые и плоскости в пространстве 142
4.1. Формула деления (142). Упражнения (143).
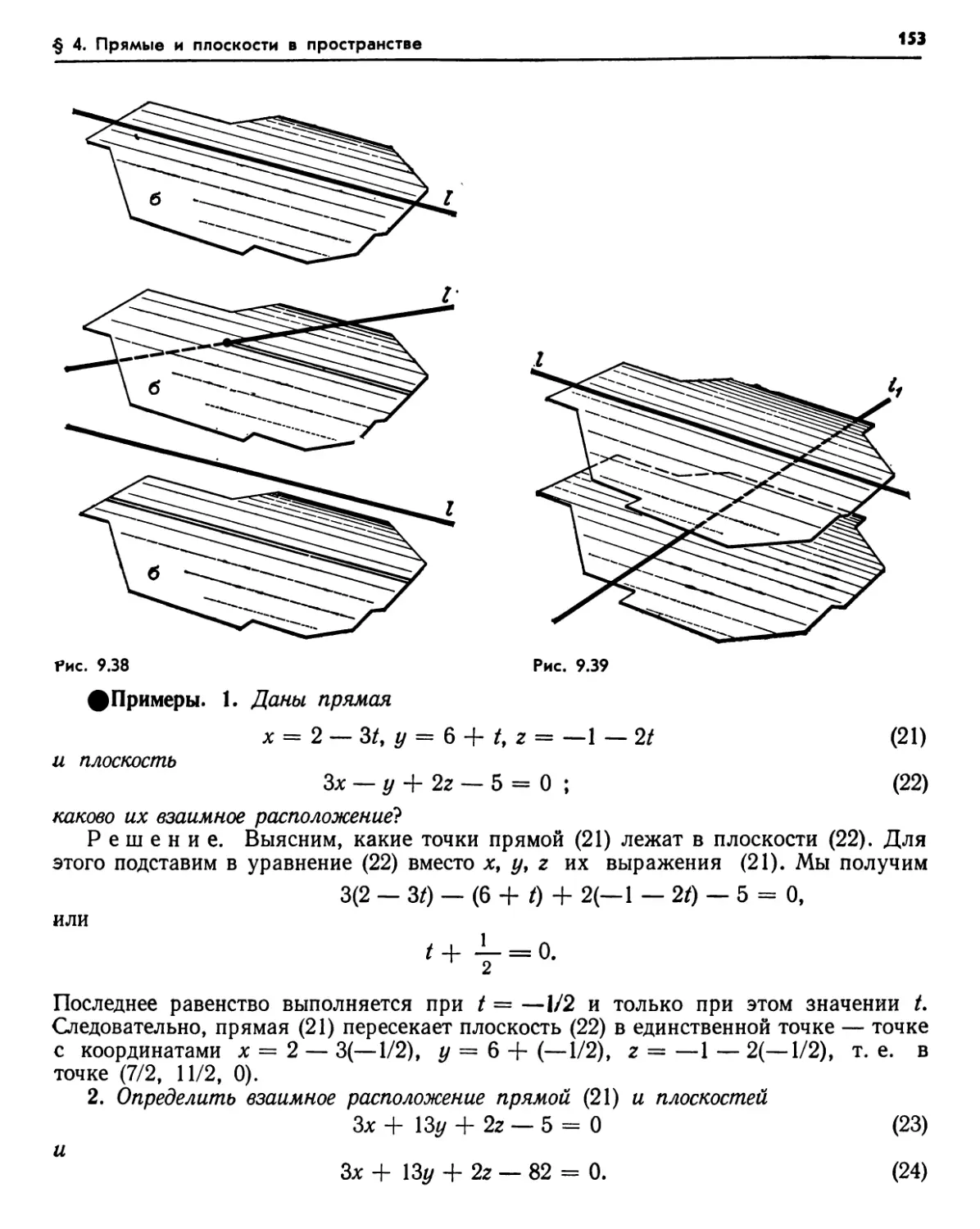
4.2.	Параметрическое представление прямой (143). Упражнения (145). 4.3. Уравнения плоскостей (145). Упражнения (148). 4.4. Параллельные плоскости (148). 4.5. Уравнения прямых (149). Упражнения (152). 4.6. Взаимное расположение прямых и плоскостей (152). Упражнения (154). 4.7. Сфера (155). Упражнения (156).
§ 5.	Цилиндрические и сферические координаты	157
5.1.	Цилиндрические координаты (157).
5.2.	Поверхности вращения (159). Упражнения (160). 5.3. Сферические координаты (160). Упражнения (163).
П наложение к главе 9	163
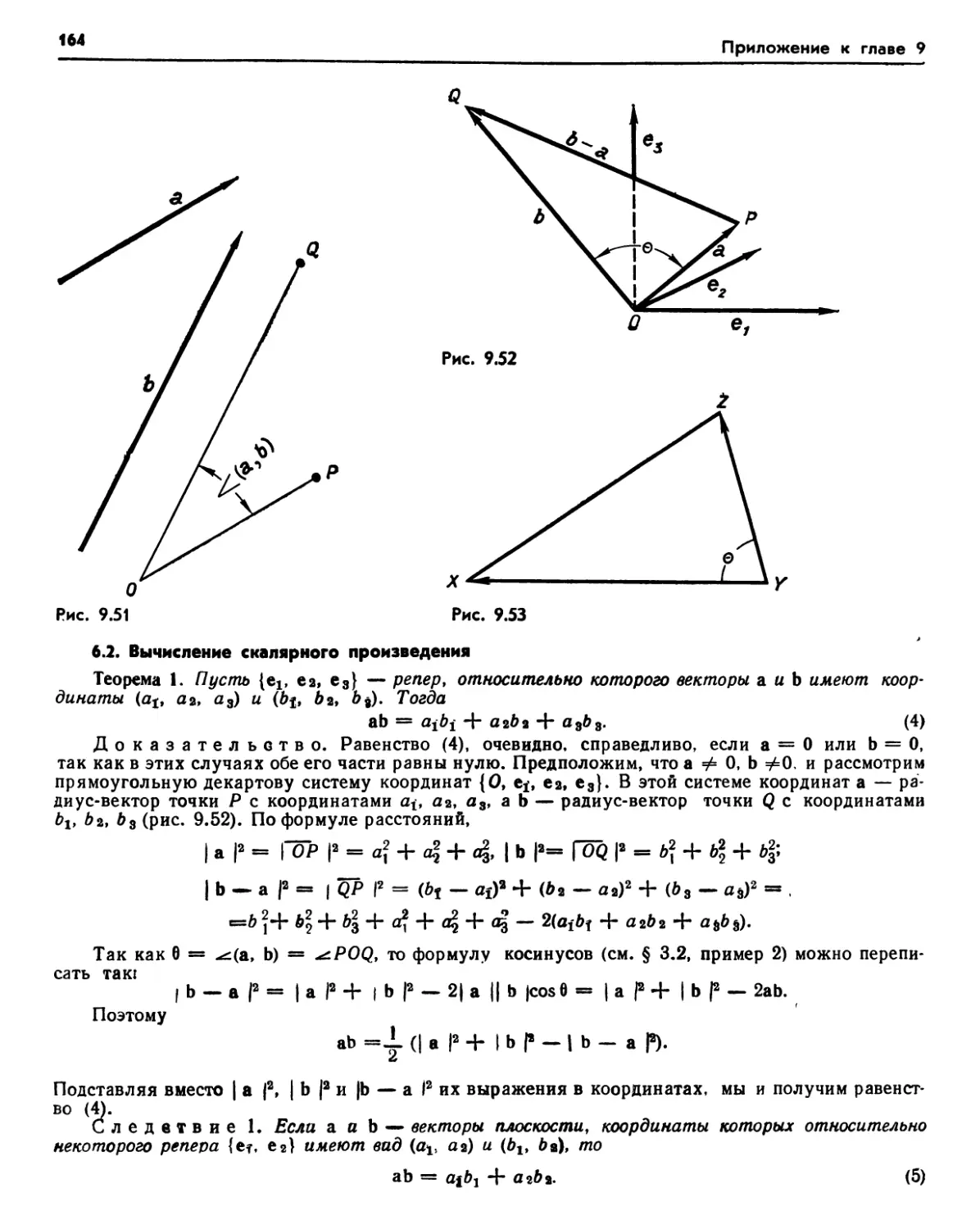
§ 6.	Скалярное произведение	163
6.1.	Определение	скалярного	произведе-
ния (163). 6.2. Вычисление скалярного произведения (164). Упражнения (165). 6.3. Свойства скалярного произведения (165).
6.4.	Применение свойств скалярного произведения (166). Упражнения (168). 6.5. Направляющие косинусы. Единичные векторы (168).
6.6.	Угол между двумя прямыми (170). Упражнения (170). 6.7. Нормаль к плоскости.
Угол между плоскостями (171). 6.8. Расстояние от точки до плоскости (172). 6.9. Расстояние от точки до прямой (173). Упражнения (173).
§ 7.	n-мерные пространства	174
7.1.	Пространство п-наборов (174). Упражнения (175). 7.2. Прямые и гиперплоскости (175). Упражнения (175). 7.3. a-мерное евклидово пространство (176). 7.4. Углы (176). Упражнения (177). Задачи (177).
10.	Квадрики	179
§ 1.	Коники	180
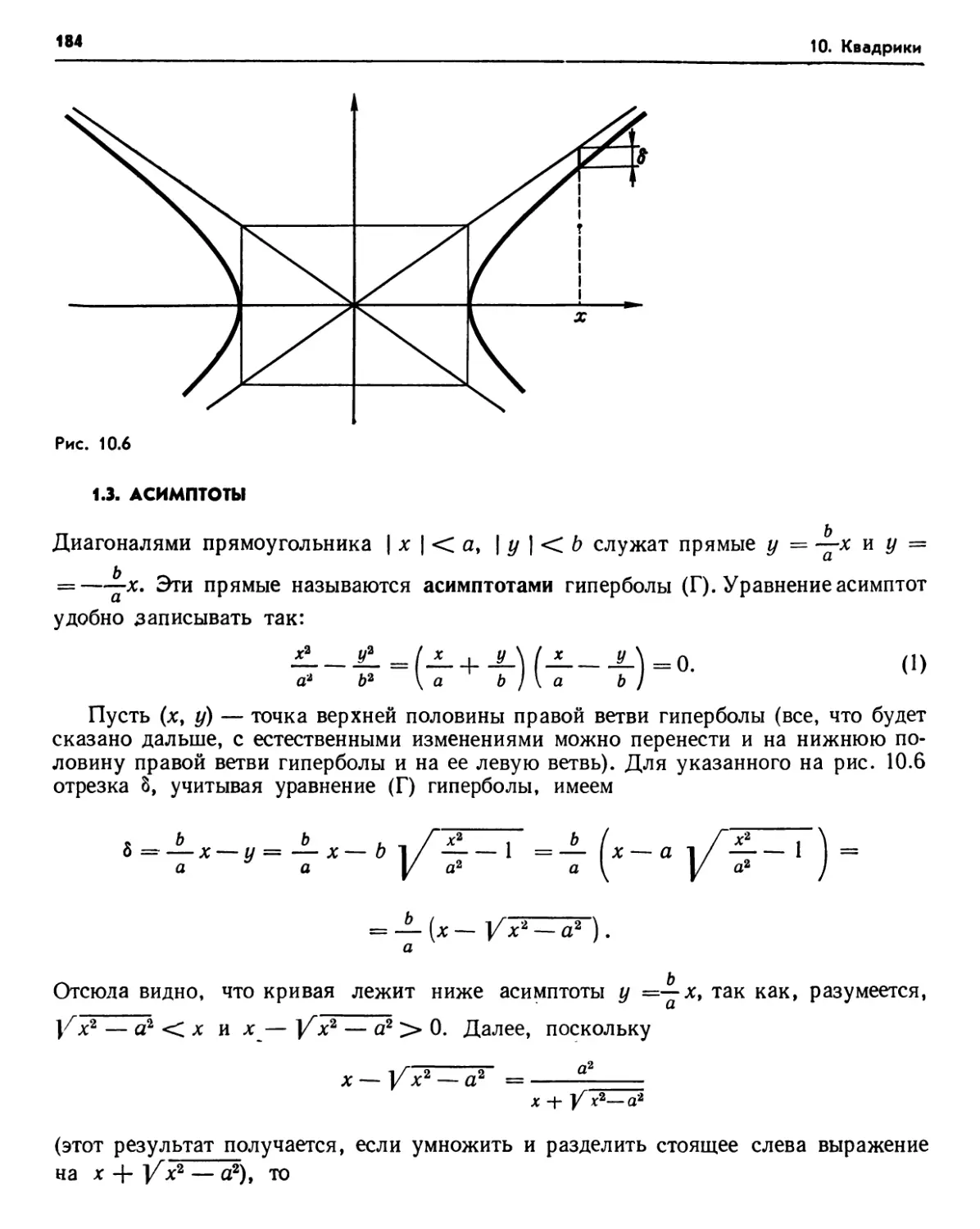
1.1.	Конические сечения (180). 1.2. Канонические уравнения (182). 1.3. Асимптоты (184).
1.4.	Фокусы и директрисы. Эксцентриситет (185). Упражнения (187). 1.5. Геометрические свойства коник (187). Упражнения (193). 1.6. Касательные (193). Упражнения (197). 1.7. Коники в полярных координатах (197). Упражнения (199). 1.8. Параметрические уравнения (200). Упражнения (202).
§ 2.	Повороты	202
2.1.	Отражения и повороты. Ориентация (202). Упражнения (205). 2.2. Замена системы координат (206). 2.3. Поворот осей координат (207). Упражнения (209). 2.4. Направленный угол между прямыми (209). Упражнения (211).
2.5.	Биссектрисы угла (212). Упражнения (213). 2.6. «Зеркальные* свойства коник (213). Упражнения (215). 2.7. Ориентация в пространстве (215).
§ 3.	Квадрики на плоскости	216
3.1.	Алгебраические кривые (216). Упражнения (217). 3.2. Кривые второго порядка (218).
3.3.	Дискриминант и след (218). 3.4. Основная теорема. Исключение смешанного члена (220). Упражнения (221). 3.5. Исключение линейных членов (222). Упражнения (223).
3.6	Положительный дискриминант (223).
3.7.	Отрицательный дискриминант (224).
3.8.	Нулевой дискриминант (225). Упражнения (228).
П наложение к главе 10	228
§ 4.	Квадрики в пространстве	228
4.1.	Поверхности второго порядка (228).
4.2.	Вырожденные случаи. Цилиндры (228).
4.3.	Конусы (229).	4.4. Эллипсоид (230).
4.5.	Гиперболоиды (232). 4.6. Параболоиды (232). Упражнения (233). 4.7. Линейчатые поверхности (235). Упражнения (236). 4.8. Замена системы координат в пространстве (236).
4.9.	Плоские сечения поверхностей второго порядка (237). 4.10. Вращения и отражения в пространстве (238). Упражнения (239).
4.11.	Приведение уравнения поверхности второго порядка к каноническому виду (239). Упражнения (241). Задачи (241).
11.	Векторные функции скалярного аргумента
§ 1.	Математический анализ векторных функций	244
1.1.	Векторные функции скалярного аргумента (244). 1.2. Кинематическая интерпретация (244). 1.3. Координаты векторной функции (245). Упражнения (246). 1.4. Применение математического анализа к исследованию векторных функций (247). 1.5. Основные правила математического анализа (248). Упражнения (249). 1.6. Независимость от базиса (251). Упражнения (253).
§ 2.	Ориентированные линии	253
2.1.	Параметрическое представление (253).
2.2.	Определение ориентированной линии (254). 2.3. Дуги кривой (255). Упражнения (257). 2.4. Непараметрическое представление (257). Упражнения (260). 2.5. Циклоида (261). Упражнения (262). 2.6. Формула площади в полярных координатах (262). Упражнения (265).
§ 3.	Касательная, длина, кривизна 266 3.1. Гладкие кривые (266). 3.2. Непараметрическое представление (267). 3.3. Единичный касательный вектор (267). 3.4. Полярный угол касательного вектора (269). Упражнения (270).
3.5.	Формулы в полярных координатах (270). Упражнения (272). 3.6. Единичный нормальный вектор (272). Упражнения (272). 3.7. Длина кривой (272). 3.8. Независимость от параметра (274). 3.9. Аддитивность (275). 3.10. Сравнение с прежней формулой длины (275). Упражнения (276). 3.11. Формула длины в полярных координатах (277). Упражнения (277). 3.12 Длина дуги как параметр (277). Упражнения (278). 3.13. Кривизна (279).
3.14.	Знак кривизны (280). 3.15. Кривизна графиков (281). 3.16. Радиус кривизны. Окружность кривизны (282). Упражнения (283).
3.17.	Кусочно-гладкие линии. Особые точки (283). 3.18. Пространственные кривые (284). Упражнения (284).
§ 4.	Движение	285
4.1.	Криволинейное движение (285). 4.2. Скорость и ускорение (285). 4.3. Вращательное движение (287). 4.4. Касательное и нормальное ускорения (288). Упражнения (291).
4.5.	Закон движения (291). 4.6. Движение брошенного тела (292). Упражнения (294).
4.7.	Движение по заданной траектории (295).
4.8.	Движение по наклонной плоскости (296).
4.9.	Математический маятник (297). 4.10. Движение планет. Второй закон Кеплера (299).
4.11.	Применение первого закона Кеплера (301). 4.12. Применение третьего закона Кеплера (302). 4.13. Небесная механика (304). Упражнения (305).
Приложение к главе 11	306
§ 5.	Движение по заданному пути 306
5.1.	Решение уравнения (306). 5.2. Периодическое движение (307). 5.3. Круговой маятник (309). 5.4. Циклоидальный маятник (310).
5.5.	Несимметричные траектории и пружи-
Оглавление
7
ны (311). Упражнения (311).
§ 6.	Движение систем	312
6.1.	Две взаимно притягивающиеся частицы (312). 6.2. Задача двух тел (313). Упражнения (314). 6.3. Третий закон Ньютона. Линейный импульс (314). 6.4. Центроид N частиц (315). Упражнения (316). 6.5. Твердое тело (316). 6.6. Свойство аддитивности (316).
6.7.	Положение центроида (317). 6.8. Свойство симметрии (317). Упражнения (318). Задачи (318).
12.	Частные производные	321
§ 1.	Функции нескольких переменных 322
1.1	. Функции двух переменных (322). Упражнения (323). 1.2. Интервалы (323). 1.3. Непрерывность (325). Упражнения (327).	1.4.
Функции трех и большего числа переменных (327). Упражнения (328). 1.5. Предельные точки. Пределы (328). 1.6. Открытые множества Границы (330). Упражнения (331).
1.7	< Геометрическая и физическая интерпретации (331).
§ 2.	Производные функций нескольких переменных	333
2.1.	Частные производные (333). 2.2. Обозначения частных производных (335). Упражнения (335). 2.3. Дифференцируемые функции (336). 2.4. Касательная плоскость (337).
2.5.	Частные производные дифференцируемой функции (337). 2.6. Непрерывно дифференцируемые функции (340). 2.7. Нормаль к поверхности (341). Упражнения (342).	2.8.
Цепное правило для функций двух переменных (343). 2.9. Производная в заданном направлении (345). 2.10. Градиент (347). 2.11. Линии уровня (347). Упражнения (349). 2.12. Дифференцирование неявной функции (350). Упражнения (351). 2.13. Дифференцирование функций трех и большего числа переменных (351). 2.14. Цепное правило для функций любого числа переменных (353). 2.15. Градиент, производная в заданном направлении и поверхности уровня (354). Упражнения (356). 2.16. Функции с нулевым градиентом (356).
2.17.	Дифференцирование под знаком интеграла (357). Упражнения (359).
5 3. Частные производные высших порядков	360
3.1.	Вторые частные производные. Равенство смешанных производных (360). Упражнения (361). 3.2. Функции с заданными частными производными (361). Упражнения (366).
3.3.	Высшие производные (367). Упражнения (368).	3.4. Критические точки (368).
3.5.	Максимум и минимум (370). Упражнения (372). 3.6. Производные высших порядков для функций более чем двух переменных (372). Упражнения (373). 3.7. Функции с наперед заданным градиентом (373). Упражнения (375).
§ 4.	Криволинейные интегралы	375
4.1.	Определение и обозначения (375). Упражнения (377). 4.2. Независимость от параметра (377). 4.3. Свойства криволинейных интегралов (378). Упражнения (380). 4.4. Язык дифференциалов (381). Упражнения (382).
4.3.	Независимость от пути (382). Упражнения (386). 4.6. Гомотопные пути. Односвязные области (386). Упражнения (389).
Приложение к главе 12	390
§ 5.	Энергия при криволинейном движении	390
5.1.	Векторные обозначения для криволиней
ных интегралов (390). 5.2. Работа (391). Упражнения (393). 5.3. Потенциальная энергия. (393). Упражнения (394). 5.4. Сохранение энергий (394). Упражнения (395).
§ 6.	Доказательства некоторых теорем о частных производных	395
6.1.	Дифференцируемые функции (395). 6.2. Цепное правило (397). 6.3. Смешанные производные (398).
§ 7.	Теорема Тейлора	399
7.1.	Теорема Тейлора для функции двух переменных. Частные случаи (399). 7.2. Теорема Тейлора для функции двух переменных. Общий случай (401). 7.3. Классификация критических точек (403). 7.4. Теорема Тейлора для функции п переменных (405). Упражнения (407). Задачи (407)
13.	Кратные интегралы	409
§ 1.	Двойные интегралы	410
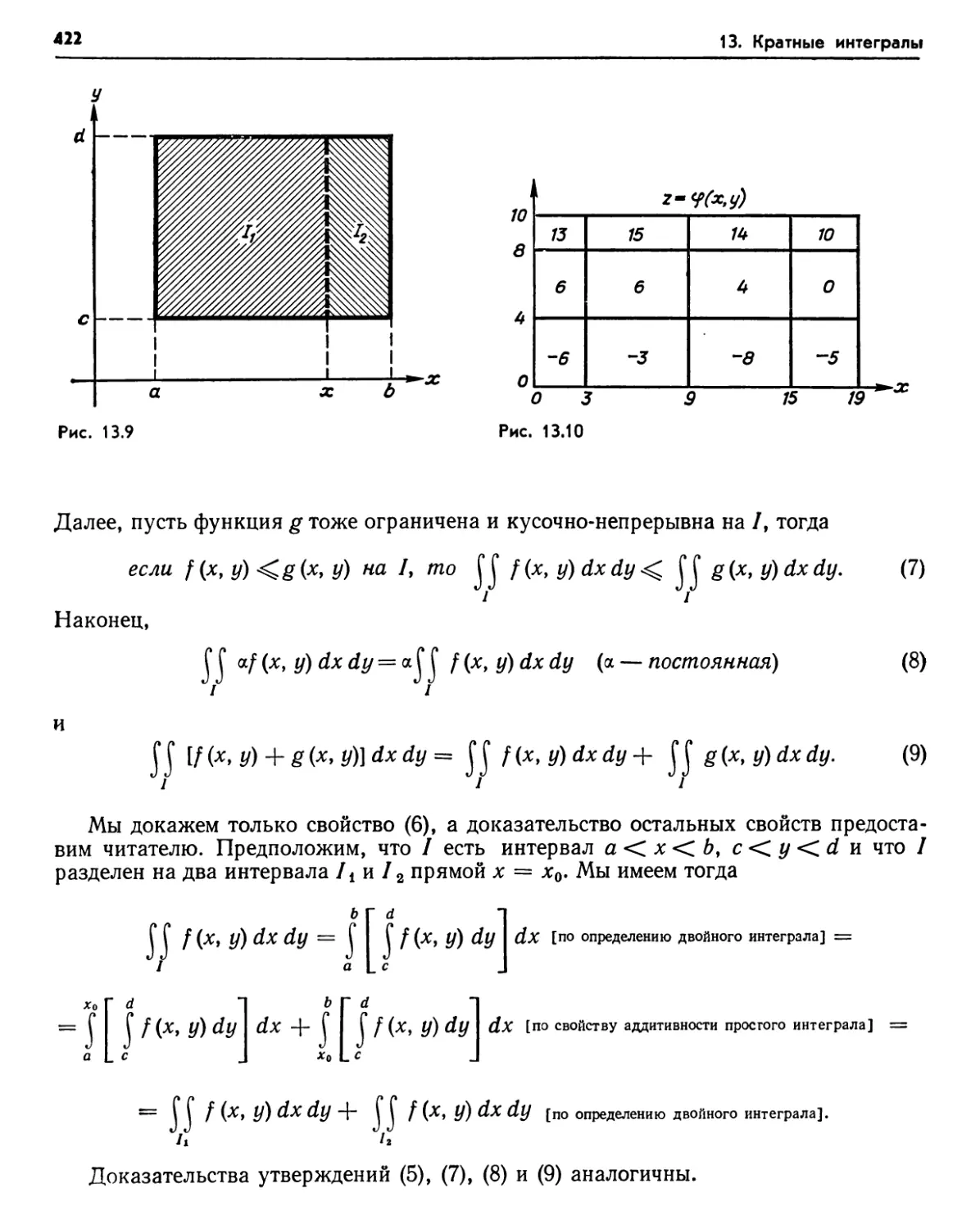
1.1.	Двойной интеграл от неотрицательной функции по интервалу (410). 1.2. Двойной интеграл как повторный интеграл (411). 1.3. Функции, принимающие значения разных знаков (417). Упражнения (418). 1.4. Кусочнонепрерывные функции (419). Упражнения (420). 1.5. Аналитическое определение интеграла (420). 1.6. Свойства интеграла (421). 1.7. Ступенчатые функции (423). Упражнения (425). 1.8. Суммы Римана (425). Упражнения (426). 1.9. Двойной интеграл по произвольному множеству (427).	1.10. Свойства
двойного интеграла в общем случае (429). Упражнения (434). 1.11. Двойные интегралы в полярных координатах (435). Упражнения (438).
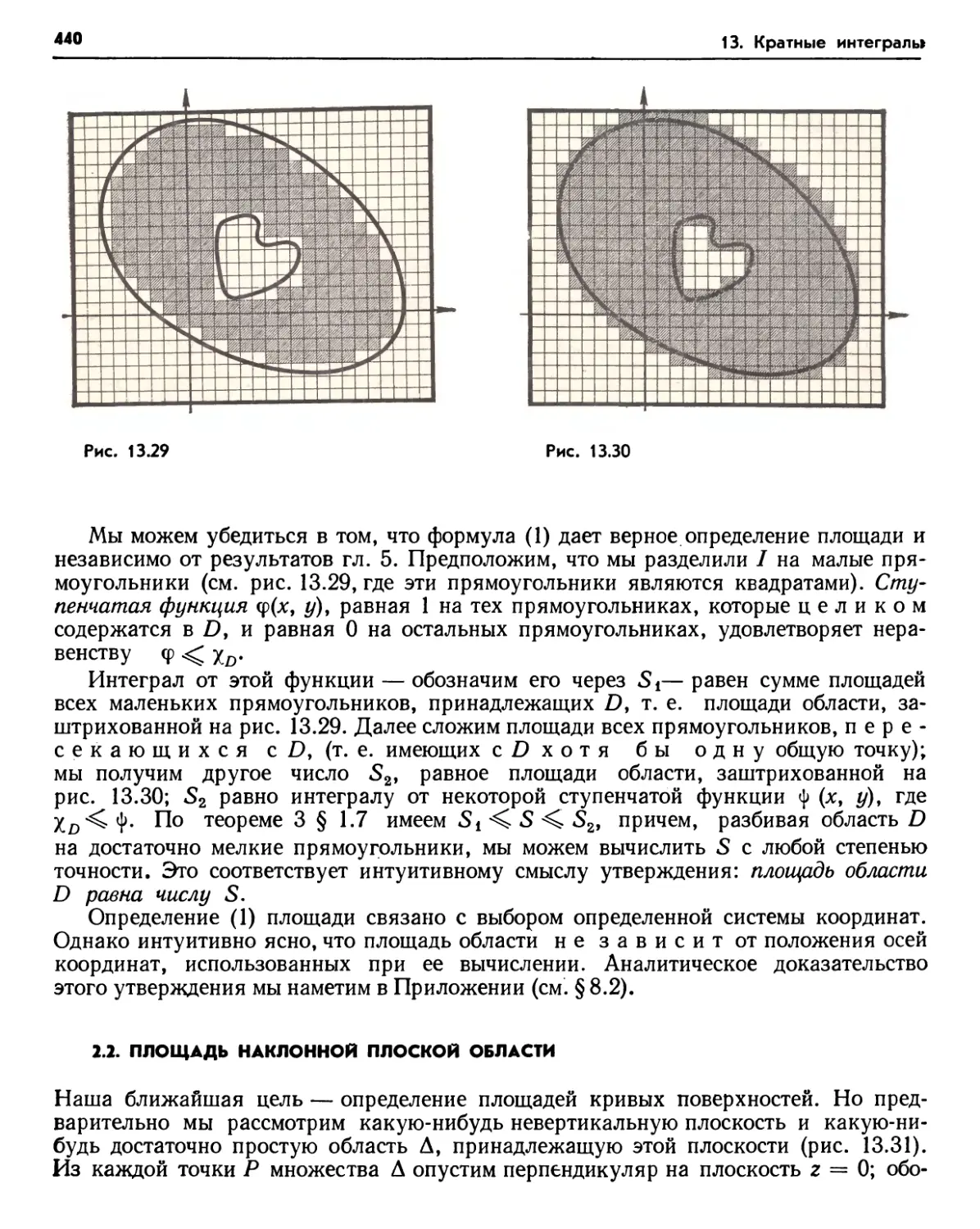
§ 2.	Площадь поверхности	439
2.1.	Площадь плоской области (439). 2.2. Площадь наклонной плоской области (440). 2.3. Формула площадей (442). Упражнения (444).
2.4.	Поверхности вращения (445). Упражнения (447).
§ 3.	Тройные интегралы	447
3.1.	Кусочно-непрерывные функции (447).
3.2.	Вычисление тройного интеграла (448). Упражнения (450). 3.3. Объем (450). Упражнения (451). 3.4. Интегрирование в цилиндрических координатах (451). Упражнения (453). 3.5. Тела вращения (454). Упражнения (455).
3.6.	Интегрирование в сферических координатах (455). Упражнения (458). 3.7. Плотность (458). Упражнения (459). 3.8. Гравитационная сила (460). Упражнения (461). 3.9. Сферическая симметрия (462). Упражнения (464).
§ 4.	Интегрирование функций п переменных	464
4.1.	Подынтегральные функции и области интегрирования (464). 4.2. Вычисление интеграла (464). Упражнения (465). 4.3. Объем в д-мерном пространстве (466). Упражнения (467).
Приложение к главе 13	467
§ 5.	Центроиды	467
5.1.	Центроиды материальных тел, пластинок и струн (467). Упражнения (468). 5.2. Центроиды областей (469). 5.3. Координаты центроидов (469). Упражнения (470). 5.4. Аддитивность и симметрия (470). Упражнения (472). 5.5. Теоремы Паппа (473). Упражнения (475).
8
Оглавление
§ 6.	Формула Грина	475
6.1.	Формулировка теоремы (475). Упражнения (476). 6.2. Частные случаи (477). Упражнения (478). 6.3. Набросок доказательства (478). Упражнение (480). 6.4. Обобщение (480). Упражнения (481).
§ 7.	Несобственные кратные интегралы 481 7.1. Неограниченные подынтегральные функции (481). Упражнения (483). 7.2. Интегрирование по неограниченным областям (484). Упражнения (485). 7.3. Важный пример (486). Упражнения (486).
§ 8.	Несколько доказательств	487
8.1.	Полярные координаты (487). 8.2. Об определении площади (4§8). Задачи (489).
Дополнение	491
§ 1.	Сходимость	492
1.1.	Верхний и нижний пределы (492).
1.2.	Ограниченные последовательности (492). Упражнения <493). 1.3. Теорема Больцано — Вейерштрасса (493). Упражнение (494). 1.4. Критерий сходимости Коши (404). Упражнение (494). 1.5. Последовательности точек (494).
§ 2.	Непрерывные функции	495
2.1.	Теорема об ограниченности (495). 2.2. Теорема о наибольшем значении (495). Упражнение (496). 2.3. Теорема Ролля и теорема о среднем значении (496). 2.4. Равномер-
ная непрерывность (496). Упражнения (497).
2.5.	Компактные множества (497). Упражнения (498). 2.6. Функции, непрерывные на компактных множествах (498)
§ 3.	Дифференцирование под знаком интеграла	498
3.1.	Формулировка результата (498). 3.2. Доказательство (499).
§ 4.	Интеграл Римана	499
4.1.	Ступенчатые функции (499). Упражнения (501). 4.2. Верхняя и нижняя суммы. Верхний и нижний интегралы (501). 4.3. Функции интегрируемые по Риману (501). Упражнения (502). 4.4. Непрерывные функции (502). 4.5. Покрытие кривой многоугольной областью малой площади (503). 4.6. Кусочно-непрерывные функции (504). Упражнение (505).
§ 5.	Повторные интегралы	505
5.1.	Повторные интегралы от непрерывных функций (505). 5.2. Повторные интегралы от ограниченных кусочно-непрерывных функций (506). 5.3. Повторные интегралы и двойные интегралы (508). Задачи (509).
Решения упражнений, помеченных знаком А	512
Алфавитный указатель	535
Указатель основных обозначений	543
8/РЯДЫ
В этой главе две основные темы: теорема о конечном приращении и бесконечные ряды.
Теорема о конечном приращении выражает геометрическое свойство дифференцируемых функций. Она имеет много применений, среди которых — формула Тейлора, позволяющая записать любую функцию, имеющую достаточное число производных, в виде суммы многочлена и остатка (или «остаточного члена»), обычно оказывающегося малым по величине.
Функции, для которых этот остаток может быть сделан сколь угодно малым (для чего только надо выбрать степень многочлена достаточно большой), называются аналитическими. Большинство важных функций, встречающихся в анализе, обладает этим свойством. Для изучения аналитических функций мы рассмотрим сначала (см. § 3 и 4) бесконечные последовательности и ряды.
Приложение к этой главе содержит четыре параграфа. В одном из них (см. § 6) излагается правило Лопиталя для вычисления пределов. Остальные три содержат доказательства некоторых теорем, формулируемых в тексте: в § 7 речь идет о последовательностях и рядах, в § 8 — о степенных рядах и в § 9 — об оценках погрешностей при численном интегрировании.
10
8. Ряды
§ 1.	ТЕОРЕМЫ О КОНЕЧНОМ ПРИРАЩЕНИИ
1.1.	ФОРМУЛИРОВКА ТЕОРЕМЫ О КОНЕЧНОМ ПРИРАЩЕНИИ
В самом начале нашего изложения анализа, как только было определено понятие производной, мы пришли к некоторому приближенному методу вычисления значений функции f(x) вблизи точки х0, в которой известны значения /(х0) и /'(*о) (см. гл. 4, § 1.8). Соответствующая формула имеет вид
f(x) « /<х0) + /'(х0)(х — %о),	(1)
где ««» означает «приближенно равно». Здесь мы снова займемся этим вопросом и придадим точный смысл словам «приближенно равно», оценив погрешность, допускаемую при использовании формулы (1). Вычисление этой погрешности имеет далеко идущие следствия. Мы покажем сначала, что некоторая формула, очень мало отличающаяся от формулы (1), в точности справедлива.
Рассмотрим график функции х /(х), определенной при а < х Ь. и допустим, что производная /'(х) существует и непрерывна. В таком случае график является гладкой кривой, соединяющей точки Р = (a. f(a))nQ = (b. Представляется геометрически очевидным, что на графике между Р и Q должна быть такая точка, в которой касательная к кривой параллельна хорде PQ (рис. 8.1).
Дадим теперь аналитическую формулировку предложения «существует касательная, параллельная хорде». Наклон хорды, разумеется, равен
b — а ’
а наклон касательной в точке (5, /(£)) равен /'(£). Касательная и хорда параллельны, если их наклоны равны. Мы рассчитываем поэтому, что справедлива следующая теорема.
Теорема 1 ( тео р е м а о конечном приращени и*). Если функция х /(х) непрерывна при а^х^Ь и имеет при а< х <Ь непрерывную производную. то существует такое число В, что
а < 5 < b
и
= ф	(2)
Ь — а
Положим а = х0, b = х, тогда можно записать (2) в виде /(х) — /(х0) = =/'(В)(х — х0), или
/(х)=/(х0) + Г(5)(х-х0).	(3)
* В нашей учебной литературе эта теорема чаше всего фигурирует как теорема Лаг-р а н ж а.
§ 1. Теоремы о конечном приращении
11
Это равенство весьма напоминает (1); но здесь вместо знака ««» стоит знак «=», а вместо стоит /'(0, где $ — некоторая точка между х0 и х.
Конечно, может случиться, что на дуге у = /(х), а х 6, найдется более чем одна точка, где касательная параллельна хорде. На рис. 8.1 есть лишь одна такая точка, а именно S; на рис. 8.2 таких точек три: $i, $2и53; на рис. 8.3 все точки между Р\ и Qi обладают требуемым свойством. Заметим еще, что если производная /'(х) не существует хотя бы в одной точке, то может не существовать никакой касательной, параллельной хорде, как это видно из рис. 8.4. Итак, условие существования производной функции f во всех точках между аиЬ существенно для справедливости теоремы 1.
12
8. Ряды
1.2.	ТЕОРЕМА РОЛЛЯ
Важный частный случай теоремы о конечном приращении (теоремы 1) представляет теорема Ролля: если f(a) = f(b), то между а и b существует такое число что f'(5) = = 0. Часто теорему Ролля формулируют следующим образом:
Между двумя нулями функции существует нуль ее производной.
Мы начнем с доказательства* теоремы Ролля. Если для всех х, а<х< производная /'(х) ¥= 0, то либо во всем интервале f'(x) > 0, либо во всем интервале f'(x) < 0; в самом деле, /'(х) непрерывна, и если она принимает и положительное, и отрицательное значения, то должна принимать и значение, равное нулю (см. теорему о промежуточном значении — теорему 5 § 3.6 гл. 3). Если f'(x) > 0 для всех х, то f возрастает [см. теорему 2 § 4.2 гл. 4) и f(b) > f(a).Если же f'(x) < 0 для всех х, то f убывает и f(b) < f(a). Оба эти неравенства невозможны; следовательно, f'($) = 0 для некоторого В между а и 6, что нам и требовалось доказать.
1.3.	ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О КОНЕЧНОМ ПРИРАЩЕНИИ
Общая теорема 1 легко следует из теоремы Ролля. В самом деле, определим функцию ср(х) так:
<Р (х) = f (х) - [/ (а) + -п^(а) (х - а)] .	(4)
Тогда ф непрерывна в тех же точках, где /, и имеет непрерывную производную
/ / \ г/ / \ f (Ь) — f (а) Ф (х) = f (X —	'
b — а
там же, где f. Сразу же видно, что ф(а) = ф(&) = 0; таким образом, к ф можно применить теорему Ролля, т. е. между а и b найдется такая точка £, что ф'(£) = 0- Но равенство ф'($) = 0 равносильно равенству (2).
Замечание. Теорему Ролля, а тем самым и теорему о конечном приращении, можно доказать и без предположения о непрерывности производной (см. Дополнение, § 2.3, где проводится такое доказательство). Однако и в только что доказанном виде она достаточна для большинства приложений.
УПРАЖНЕНИЯ
1. Пусть f (х) = 1 — Зх;
/(Я-
найдите все числа лежащие строго между 1 и 4, для которых
4— 1
2. Пусть f (х) = х2 + 1;
найдите все числа С, лежащие строго между 1 и 2, для которых
2—1
Мишель РОЛЛЬ (1652—1719)—французский математик. Теорему, носящую его имя, он сфор* мулировал как правило, позволяющее уточнить расположение корней многочлена.
§ 1. Теоремы о конечном приращении
13
3.	Пусть /(х) = 1пх; найдите все числа 6» лежащие строго между еа и для которых
Г & =
е^ — е2
4.	Пусть / (х) = х3 — х; найдите все числа лежащие строго между 0 и 1, для которых
К (6)=/(D-f(O).
5.	Пусть / (х) = 1^5 х3 4- ха; найдите все числа 6, лежащие строго между — 1 и 1, для ко-
торых /' (£) =
Н"- (-1) । - (- О
А6. Пусть f (х) = х9 10 В 4- х4 4- 1; найдите все числа 6, лежащие строго между — 1 и 1, для ко
торых (£) =
1 — (—1)
7. Пусть f (х) = х» -и х2 — 2х; найдите все числа 6, лежащие строго между 0 и 1, для ко-
торых /' ($) = /(!)—/(0).
8. Пусть f (х) = х5'3 4- х4/3: найдите все числа 6,
лежащие строго между —8 и
8, для ко-
торых Г (?) =
/(8)-/(-8)
*—(—8)
Г ® =
Z (4) — / (0) .
4
9. Пусть / (х) = J^x2 4- 9; найдите все числа лежащие строго между 0 и 4, для которых
10. Пусть f (х) = ел\ найдите все числа 5, лежащие строго между 1 и 2, для которых
Г (5) =
Z (2) — / (1) 2— 1
1.4. ОБОБЩЕННАЯ ТЕОРЕМА О КОНЕЧНОМ ПРИРАЩЕНИИ
Есть легко доказываемое, но весьма полезное обобщение теоремы о конечном приращении.
Теорема 2 (обобщенная теорема о конечном приращен и и*). Пусть F(x) и G(x) —непрерывные функции, заданные при а х Ь; предположим, что при a <Zx<Z b производные F' (х) и G' (х) существуют и непрерывны^ причем G'(x) =£ 0. Тогда существует такое число что
а<1<Ь
и
F (b) — F (а) = Г (5) ч G(d) — G (a) G' (с)
(5)
В нашей учебной литературе ее обычно называют теоремой Коши.
14
8. Ряды
Доказательство. Построим новую функцию*
Ф W = F (X) - Р (а) + F(b)~F(“\ (G (X) - G (а))1. L G(b)—G(a)	J
[Заметим, что здесь G(b) — G(a) =/= 0, так как в силу условия G'(x) =/= 0 функция G либо возрастает, либо убывает в интервале (а, Ь).]
Ясно, что ф непрерывна при а "С х Ь, а при а < х < b имеет непрерывную производную
/ / \	/?/ / \	F (Ь) — F (а)	/ \
Ф (х) = F (х)----—----— G	(х).
Y v V 7	G (b) — G (a)	v J
Далее, ф(а) = ф(&) = 0, и к функции ф можно применить теорему Ролля. Следовательно, существует такое число $ между а и &, что ф'(Е) = 0. Отсюда имеем
F’ (Е) - F(b}~F(a) G' G) = 0, G (b) — G (а)
что равносильно (5), так как, по условию, Gf(x) =И= 0.
Следствие. Если F(a) = G(a) = 0, то для любого Ь ф а существует такое
$ между а и Ь, что
= (6) О(»)	О'®
Здесь предполагается, что F'(0» G'(0 существуют и непрерывны при /, лежащих строго между а и 6, причем G'(t)	0. Следствие сразу же вытекает из теоремы (за-
метим, что в следствии может быть Ь < а).
УПРАЖНЕНИЯ
И . Пусть F (х) = 2х + 1 и G (х) = Зх — 4; найдите все числа Е, лежащие строго между 2 и
F (3) — F (2) F'(Е)
3, для которых О(3)_С(2) = —
12. Пусть F (х) = х3 и G (х) = 2— х; найдите все числа Е, лежащие строго между 0 и 9, для
которых
F(9)-F(0) _ F'(l) .
G(9)-G(0)	G'(E) ‘
13.
Пусть F (x) — 1/x и G (x) = x2;
F(2)-F(l)	F'(l)
КОТОрыХ G(2)-G(l)	G'(l)
найдите все числа E, лежащие строго между 1 и 2, для
14. Пусть F(x) = sinx и G(x) = cosx; найдите все числа Е, лежащие строго между к/4 и
Зк/4, для которых
F (Зк/4) - F (к/4) F' (Е)
G (Зк/4) — G (к/4)	G'(E)
* Чтобы получить эту функцию, надо заменить в (4) f(x) и х на F(x) и G(x), а значения функции х в точках а и b — на значения функции G(x) в тех же точках. Обобщение состоит, таким образом, в переходе от пары функций f, х к паре F, G,
§ 1. Теоремы о конечном приращении
15
15.
16.
17.
18.
19.
20.
Пусть F (х) = In х и G (х) = 1/х; найдите все числа лежащие строго между 1 и е, для
F(e)-F(l) F' (5)
К0Т0Р“Х G(e)-G (l) =^W
Пусть F (х) =	— х3 + х2 и G (х) = х2; найдите все числа $, лежащие строго между
F(2)-F(0)	F'($)
0 и 2. для которых G(2)-^=	’
Пусть F (х) = Ух4- 9 и G(x) = Ух ; найдите все числа 5, лежащие строго между 0 и
F(16)-F(0)	F'(£)
16, для которых -— --—— =	" •
и G(16) — G (0)	G'(5)
Пусть F(x) = x4 + 4x и G (х) = х2 Ч-2х; найдите все числа 5, лежащие строго между
F(2) —F(—1)	F'(S)
-1 и 2, для которых G(2}_G(_ ^ =	•
Пусть F (х) = У х2 + 9 и G(x) = х2+ 1; найдите все числа $, лежащие строго между 0
F(4)-F(0)	F'(£)
.4, .«тори. 0(4)_0(0) -'57^-'
Пусть F (х) = х3 и G (х) = Xs + Зх2 + Зх; найдите все числа 6, лежащие строго между 0
F(3)-F(0)	F'(£)
из, для которых	= — .
1.5. ПОГРЕШНОСТЬ ЛИНЕЙНОГО ПРИБЛИЖЕНИЯ
Мы располагаем теперь средствами, позволяющими оценить погрешность формулы линейного приближения (1). Смысл этой формулы состоит в замене графика f его касательной в точке (х0>/(*о))« Эта касательная есть график функции
X И-. Р (х) = f (х0) + f (х0) (х — х0),
имеющей в точке х0 то же значение и тот же наклон, что и f (рис. 8.5).
Пусть /?(х) — ошибка, допускаемая при вычислении значения /(х) с помощью функции Р вместо f, т. е. /?(х) = Дх) — Р(х). Тогда
/(х)==Чхв) + //(х0)(х —х0) + /?(х).	(7)
Отсюда
R(x) = /(X) — /<Хр) _^/)
= f (х0), X — Xq
lim -H-VL = о	(8)
X — Xq
Xo
и поскольку
lim x-*x0
имеем
16
8. Ряды
Это значит, что величина ] R(x) | мала, если х близко к х0, и даже становится сколь угодно малой по сравнению с | х — х0 | (ср. с теоремой 1 § 1.8 гл. 4). Однако из утверждения (8) не видно, насколько мало R(x) при заданном х =/= х0.
Чтобы ответить на этот вопрос, требуется добавочная информация о функции f(x). Мы предположим, что f имеет непрерывную вторую производную.
Рассмотрим теперь /?(х) при фиксированном х0 и переменном х; очевидно, /?(х«) = О
[это получается подстановкой х — х0 в (7)1. Далее, дифференцируя обе части (7) и замечая, что х0 фиксировано, получим
f'W = f (х0) 4- R'(x), откуда
R'(x0) = 0.
Вторично дифференцируя, получаем Г '(х) = R"{x).
Применим теперь следствие из теоремы 2, в котором положим F(t) = R(t), G(t) = (t — x0)2, a = x0,b = x. Тогда существует число т между х0 и х, для которого
R (х)	_ R' (г)
(х — х0)«	2 (г — х0)
Применим то же следствие снова, но на этот раз к F(f) = R’(t) и G(t) = 2(/ —х0); тогда оказывается, что существует 5 между х0 ит, для которого
R'M = R"(l) = Г® . 2(х —х0)	2	2
Отсюда /?(х)  /'(£)
(X — х0)»
2
§ 1. Теоремы о конечном приращении
17
ИЛИ
R{x}= ГЕН*
В частности, если
1Г(0 1<М
для всех t между х и х0, то
|Я(х)1<-^-(*~ *о)2-
Мы доказали, таким образом, что
(9)
(Ю)
f(x) = /(х0) + /'(х0)(х — х0) + /?(х),
где остаток /?(х) задается формулой (9), в которой $ заключено между х и х0; этот остаток удовлетворяет неравенству (10).
фПример. Какую погрешность мы допустим при вычислении ]/1 + h (edeh мало) по приближенной формуле У1 + й = 1 +
Решение. Приближенная формула является частным случаем (1) при Дх) = Ух. f'(x) = —L=, х0 = 1 и х = 1 + й. Имеем 2у х
Г М  -----=------------
4х/х 4(1-М)/1+Л
и, чтобы применить к погрешности R неравенство (10), надо найти такое число /И, чтобы при малых |й | было |/"(х)|<СЛ1.	_____
Отметим, что | /"(х)| = 1/4 при й = 0. Если й > 0, то (1 + й)У 1 + й > 1 и I f''(x)\< 1/4. Однако при й < 0 величина | /"(*) | — возрастающая функция от й. При й = —3/4 имеем 1 + й =1/4, У1 + й = 1/2, откуда | /"(х) | = 2. Таким образом, | /"(х) |	2 при | й | < 3/4. Применяя неравенство (10) при
М = 2, получаем | 7? | -С й2: для малых | й | (точнее, для | й | < 3/4) погрешность не больше h2.
Например, У1,02 = 1,01 и У0,98 =0,99 с точностью до 0,0004. (Последняя фраза означает, что ошибка здесь не превышает 0,0004.) Точно так же 1/1,03 = 1,015 и ]/0,97 = 0,985 с точностью до 0,0009.ф
Другим применением теоремы о конечном приращении является правило Ло-питаля для вычисления пределов, которое рассматривается в Приложении (см. § 6).
УПРАЖНЕНИЯ
В каждом из упражнений 21—30 найдите приближенное значение заданного выражения| воспользовавшись линейным приближением, и оцените погрешность.
21. /50. 22. /(Mi- 23. (0,025)1/3.	24.	9991/3.	27.	cos (0,01). 25	п	пз/5	28-	arctg zo-	•	29.	e-o.oi 26.	In	0,98.	30.	tg (0,24я).
18
8. Ряды
§ 2.	ТЕОРЕМА ТЕЙЛОРА
2.1.	ПАРАБОЛИЧЕСКОЕ ПРИБЛИЖЕНИЕ
Пусть f(x) — функция, определенная вблизи точки х0. Ранее мы вывели теорему о конечном приращении
/(х) =/(х0) +/'(В)(х — х0)	(1)
и формулу
f (X) = f (х0) + f' (х0) (х - ХО) + -2- /" (?) (х - хп)2.	(2)
Предполагается, что производные, входящие в эти соотношения, непрерывны. Число £, надлежащим образом выбранное между х и х0, не обязательно одно и то же в обеих формулах.
Следующий шаг исследования самоочевиден. Рассмотрим функцию /(х), для которой известны значения
/Uo), Л(Хо) и Их0).
Мы хотим вычислить приближенное значение Дх) в точке, близкой к х0, пользуясь уже не постоянной, как в (1), и не линейной функцией, как в (2), а квадратичным многочленом Р(х). Мы выберем этот многочлен так, чтобы было
РМ = Дх0), Р'(*о) =Г(х0), Р''М =	(3)
Иными словами: парабола у = Р(х) должна проходить через точку (х0, Дх0)) и должна иметь в этой точке тот же наклон, что график у = Дх), и ту же производную наклона1. Мы рассчитываем, что допускаемая при этом погрешность для х, близкого к х0, будет значительно меньше погрешности рассмотренного выше линейного приближения (рис. 8.6).
Найдем сначала Р(х). Легко догадаться, что
Р(х) = /(х0) + Г(х0)(х — х0) + у/"(хо)(х — х0)2.
В самом деле, Р(х) — квадратичный многочлен от х (х0 фиксировано) и легко проверить, что он удовлетворяет условиям (3). Чтобы найти остаток R{x), заметим, что
R(x0) = R'(x0) = Я"(х0) = О
1 Здесь можно также сказать: ту же кривизну (см. гл. 11, § 3.15).
§ 2. Теорема Тейлора
19
в силу условий (3), наложенных на Р, и что
Я"'(х) = /'"(х),	(4)
поскольку Р — квадратичный многочлен и, следовательно, Р'"(х) = 0. Теперь мы несколько раз применим следствие из теоремы о конечном приращении (см. § 1.4). Имеем:
—Уд для некоторого t, между хп и х, (х-*о)8	3(/!-х0)2	1	0
—R	— для некоторого t2 между х0 и /х,
3 (Zj х0)2	3 • 2 (/2 Xq)
з 2 v 7 ) = —- для некоторого $ между х0 и t2.
Принимая во внимание (4), мы выводим из этих результатов, что
-—- у  для некоторого 5 между х и х0.
То же можно переписать еще и так:
Я(х)=-£^-(х-х0)з.	(5)
Итак, мы пришли к формуле
f (X) = f (ХО) + /' (х0) (X - х0) + —Г (х0) (х - х0)2 + R (х),	(6)
1	’
где R задается выражением (5), при надлежащем $ между х0 и х. Если, кроме того, известно, что
I/'"(') КМ
20
8. Ряды
для всех t между х0 и то
|Я|
М|х-хор 6
(7)
фПример. Воспользуемся обозначениями примера из § 1.5 и заметим, что для /(х) = pGT имеем f"'(x) — 3/8 г~5/2. Легко убедиться, что при 1/4 -С х 7/4, т. е. при | h | = | 1 — х | -С 3/4, выполнено неравенство | f"(x) | < 12. Отсюда получаем соотношение
/1 +h =] -|_ JL h------Lh3 + R, |7?|<2Лз,
2	8
3	_______________________________
справедливое при I h | < [Полагаем в (6) и (7) f(x) = у х, х0 = 1, х = 1 + й,
М = 12.]
Например, /Ь2 = 1,1 —1-0,04 = 1,095, /6^8 = 0,99——0,04 = 0,985 с о	о
ошибкой, не превосходящей 2«(0,2)3 =0,016. Далее, ]/1,03 = 1 + ~0,03 —
---0,0009 = 1,0149 с ошибкой, не превосходящей 2* (0,ОЗ)3 < 0,00006.ф
УПРАЖНЕНИЯ
В каждом из упражнений 1—5 найдите все значения $, лежащие строго между х0 и Xf, для которых Дхг) = /(хо) +	— xq) +-1- f 'ft) (Xj —Xo)2. Затем найдите все значения ц,
лежащие строго между хо и хх, для которых
ftxr) = /(хо) + t'(xo)(xi — хо) + А Г'(хо)(Х1 — х0)2+ А /Г"('П)(^1 — *о)3. 2	о
1.	f(x) = х3, Хо = 1, Xf = 1/2.	4. f(x) = In х, Хо = 1, xt = е.
2.	f(x) = 1/х хо = 1, Xf = 1/8.	5. f(x) = х4 — х2, х0 = 1. xt = 2.
3.	t(x) = 6х, хо = 0, Xf = 1.
В каждом из упражнений 6—10 найдите приближенное значение данного выражения, применив квадратичное приближение и оценку погрешности. Сравните Ваши ответы с ответами упр. 21, 23, 25^27, 29 § 1.
6.	/50.	9. cos (0,01).
7.	(0,025)78.	А 10.
8.	(1,1)вЛ.
2.	2. МНОГОЧЛЕНЫ ТЕЙЛОРА
Три соотношения (1), (2) и (6) представляют собой ответы на следующий вопрос. Пусть х I-* /(х) — функция; пусть нам известны значения f и п первых ее производных /', /", ..., /(л)в точке х0. Как приближенно вычислить значение /(х) в точке х, близкой к х0?
На первый взгляд, вопрос этот кажется весьма специальным и даже несколько искусственным, однако на самом деле он служит введением в некоторые важнейшие обл асти математики.
§ 2. Теорема Тейлора
21
Ответ на поставленный вопрос можно разбить на два шага. На первом шаге мы построим многочлен Р(х) степени п, имеющий при х = х0 то же значение и такие же производные первого, второго, третьего, ...» n-го порядка, как и функция f. Мы увидим, что существует единственный многочлен такого рода, и назовем его п-м многочленом Тейлора функции f в точке х0. Мы рассчитываем, что при х, не слишком далеком от х0, значение Р(х) будет близко к /(х).
Второй шаг будет состоять в изучении остатка
R(X) = /(х) - Р(х).	(8)
Начнем с построения многочлена Р.
Теорема 1. Пусть даноп + 2 числа х0, а0, а4, ...» ап; тогда существует единственный многочлен Р(х) степени не выше и, удовлетворяющий условиям
Р = ао» ? (хо) = а1 ? W = а2» ••• » ?	(* *о) = а/1»	(Q)
а именно многочлен
р (X) = а0 + (х — х0) + (х — х0)2 +
+	(X - Х0)3 4- • • • +	°"	-- (X - х0)«.	(10)
1 • л • О	1 • Z • о . . . П
Доказательство. Ясно, что многочлен Р(х), заданный формулой (10), действительно имеет степень, не превосходящую п (степень может оказаться и меньше и, если ап = 0). Заметим, далее, что для целых положительных / и k имеем
d	= i(j — 1) (/ — 2) ...(/ — k + 1) (х — хоу-* при k < /,
dxR
^(х~х^ =1 . 2 • 3 ... /,	= 0 k > j
dxJ	dxk	Н J
(Читатель может сам убедиться в этом, произведя вычисления в каком-то частном случае, например при k = 4 или k = 5. Формальное доказательство потребовало бы использования метода математической индукции, но картина здесь настолько ясна, что такое формальное доказательство было бы ненужным педантизмом. В этой главе мы еще не раз встретимся с подобной ситуацией.)
Выпишем теперь производные многочлена (10), пользуясь предыдущими соотношениями:
Р' (X) = 04 + <Х2 (х — х0) + -рт- (X — х0)2 ч-1- ——-------— (X — х0)я-1,
Р№ (х) = «2 + аз (X — хо) + -р— (X — х0)2 + • • • +	---- (х — х0)«-2
1’4	— 4)
Брук ТЕЙЛОР (1685—1731) опубликовал ряд, который носит его имя, в книге, вышедшей в 1715 г. Тейлор одно время являлся секретарем Королевского общества *.
* Королевское общество играет в Англии роль нашей Академии наук.
22
8. Ряды
и т. д.; k-я производная (где /г<л) равна
(х) = «л + aA+i {х — х0) Ч---h - ап--------- (х — x0)«-ft,
1 • 2 ... (и — к) а n-я производная
Рп(х) = ап.
Подставив в эти выражения х = х0, получаем (9).
Допустим теперь, что есть другой многочлен степени не выше п, также удовлетворяющий условиям (9); обозначим его через Р(х). Требуется доказать, что Р=Р.
Положим Q(x) = Р(х) — Р(х). Тогда Q — многочлен степени не выше п, так что л-я производная Q(/l)(x) постоянна. Но Q(n)(x0) = Р(л)(х0) — Р(п,(хс) = ап— ап = 0; поэтому Q(n)(x) = 0, и степень Q(x) не вышел — 1. Следовательно, Q(n-1)(x) — постоянная. Но Q(n-1)(x0) = Pin~'4x0) — Р(п_1)(х0) = ал-1— ал-1 = 0; поэтому Q(n—о = о, и степень Q(x) не вышел — 2. Продолжая рассуждать таким же образом, мы придем, наконец, к заключению, что степень Q(x) равна нулю, т. е. что Q(x) — постоянная. Так как Q(x0) = Р(х0) — Р(х0) = а0— а0 = 0, то имеем Q(x) = 0.
Следствие. Если функция f(x) имеет п производных (т. е. производные порядков 1, 2, л) в точке х0, то п-й многочлен Тейлора функции f в точке х0 имеет вид
P(x)=f (Хо) + f-^~ (х - х0) 4- f" (*о) (х - х0)2 + 1	1 • Z
+ Т~ГТ (* - *о)3 + • • • +	f ’ (*о) (х - ХО)*.	(11)
1 • Z • О	1 • Z • о • • • И
Отметим некоторые свойства многочленов Тейлора. Прежде всего, (п + 1)-н многочлен Тейлора получается из п-го прибавлением единственного члена, а именно ;(n+i) ------------------------------~----—-----(* — *о)л+1-1 • 2 • 3 • • • (п + 1) v 07
Далее, пусть Р(х) — многочлен Тейлора степени п функции f(x) в точке х0’> тогда Р' (х) — многочлен Тейлора функции f' (х) в той же точке х0 степени п —1. В самом деле, Р‘—многочлен степени п—1. Поскольку Р(/)(*о) =/(/)х0) при / = 1, п, мы видим, что значения Р' и а также их соответствующих производных до (п — 1)-го порядка включительно совпадают в точке х0-х
Точно так же доказывается, что J P(f)dt есть многочлен Тейлора функции
X
j* f(f)dt опять в той же точке х0. Далее, сР(х), где с — постоянная, есть многочлен х0
Тейлора функции cf(x) в точке х0; Р(—х) — многочлен Тейлора степени п функции /(—х) в точке—х0; если хо=О, то P(xk) — многочлен Тейлора степени nk функции f(xk) в точке х0 = 0, и т. д.
§ 2. Теорема Тейлора ’
23
Коэффициенты многочлена Тейлора функции f в точке х0 называются коэффициентами Тейлора функции f в точке х0; коэффициент при (х — х0)7 называется j-м коэффициентом Тейлора.
•Примеры. 1. Найти четвертый многочлен Тейлора функции f(X) = /т в точке х0 = 0.
Решение. Имеем
ГМ = 4 (14 х)"1/2, /"(х) = -^-(1+х)"3/2> Г'(х) = А(1 +х)-5/2, А	4	о
/IV (х)=- 4г(1 +х)-7/2-10
Отсюда /(0) = 1, Г(0)=-|-, /"(0) = --р Г'(0)=-|-’ /,У(0) = ~4г-
Искомый многочлен имеет вид
1 ।	1	1	12.1	3 о	1	15 л
14--х----------- — х2 4------- — х3------------ -х4,
2	1-2	4	1.2*3	8	1-2.3-4	16
или . х х2 х3 5х4 1+Т“Т + Т~_^Г-
2.	Найти четвертый коэффициент Тейлора функции f (х) = 1 4- х в точке xft =-—.
0	2
Решение. Как мы видели,
f (х) =-----— (1 4-х)	. Отсюда f (х0) =
10
и четвертый коэффициент Тейлора равен
5
1 1 о о A I V*0/	Г— *
1 • 2 . 3 • 4	8/2
3.	Найти четвертый многочлен Тейлора функции Дх) = (1 4- х)3/2 в точке х = 0.
Решение. Заметим, что (1 4- *)3/2 = 1 + yj 1/1 + t dt. Пользуясь резуль-о
татом примера 1, заключаем, что искомый многочлен имеет вид
Конечно, то же можно было получить и прямым путем.
24
8. Ряды
4.	Функция /(х) = х11/3 имеет в точке х = 0 третий многочлен Тейлора Р(х) =
0, поскольку ДО) =/'(0) =/"(0) =/"'(0) =0. Четвертого многочлена Тейлора этой функции вообще не существует, так как рассматриваемая функция не имеет четвертой производной в точке х = О.ф
УПРАЖНЕНИЯ
11.	Найдите третий многочлен Тейлора функции х »-* \!(х + 1) в точке хо = 0.
12.	Найдите четвертый многочлен Тейлора функции г и-* (х + 1)4/я в точке х0 — 0.
13.	Найдите пятый многочлен Тейлора функции г >-► cos х в точке хо — 0.
14.	Найдите третий многочлен Тейлора функции х н* Iп(х2 + 1) в точке xq = 0.
X
15.	Найдите	четвертый многочлен Тейлора функции х J ln(u2 + l)dx в точке	х0	=	0.
16.	Найдите	четвертый многочлен Тейлора функции х н* х*’^* в точке х0 = 0.
17.	Найдите	третий многочлен Тейлора функции х »-> г4 — х3 + 2х2 — 1 в точке	хо	=	1.
18.	Найдите четвертый многочлен Тейлора функции х »-► 1п2х в точке х0 = 1.
19.	Найдите шестой многочлен Тейлора функции х »-► cos х в точке хо = л/2.
20.	Найдите десятый многочлен Тейлора функции х »-* е*6 в точке хо = 0.
X
21.	Найдите тридцать первый многочлен Тейлора функции х »-► Jarctg и10 du в точке хо = 0. о
22.	Найдите двенадцатый многочлен Тейлора функции х (х4 + 1)4/8 в точке хо = 0.
2.3	. ТЕОРЕМА ТЕЙЛОРА
Рассмотрим теперь «остаток»/?п+1 (х) = Дх)— Рп(х), гДе ?п есть п-Ъ многочлен Тейлора функции f в точке х0. Предположим, что Дх) определена и непрерывна в интервале /, содержащем х0 и х, что она имеет в / ( за исключением, быть может, его концов) непрерывную (п + 1)-ю производную. Для краткости мы будем часто писать /?(х) вместо /?п+1 (х). По построению, R(xQ) =R'(х0) = ... = /?(л)(х0) =0. Повторно применяя следствие из теоремы о конечном приращении (см. § 1.4), получаем
R(x)	R'lh)
-------—	 = ----------- [для некоторого tt между х0 и х] = (х-х0)«+’-------------------(л+1)(G—
Rff (t) = ------------------- (для некоторого t2 между х0 и G] =
(п+ 1)п(/г-«0)я-»
R'" (t.) = ------------------------ [для некоторого ta между х0 и G] —
(п + 1)п(п-1)(/3-х0)л-а
Rn+1 (« = • • • = ----------—---------- [для некоторого t между х0 и тем самым, между х0 и х].
(М+ 1)п(л—1) ...2-1	п
Поскольку, по построению, R(n+,)(x) = f(n+t)(x), имеем
Г"и /"+',(;)
1 - 2.3...(»+|>
Соберем полученные нами результаты в следующей теореме.
Теорема 2 (теорема Тейлора). Пусть f(x) определена и непрерывна в некотором интервале /, содержащем х и х0; пусть f имеет во всех внутренних точках I непрерывную производную (п + 1)-го порядка. Положим
§ 2. Теорема Тейлора
25
/(*) =/(х0) + -^-(х-х0) + ^^-(х-х0)2 +
+	(х - ХО)3 + ... + t /2(П)з(Ха) п (х - х0)" + Яя+1 (х).	(12)
Тогда существует такое число Л, заключенное между х0 и х, что
K^=-rh^T^-^’n-	"3>
Из формулы (13) очевидным образом вытекает следствие:
если | f<n+1>| в I, то |7?n+1(x)|< ^|х-х01л+1 .	(14)
Значение формулы Тейлора (12) состоит в том, что она позволяет представить по существу произвольную, достаточное число раз дифференцируемую функцию /(х), определенную вблизи точки х0, в виде суммы многочлена степени п и «остаточного члена» (или «остатка»), имеющего при х, близком кх0, порядок малости | х — х0 |л+1.
При х0= О формула Тейлора имеет вид
пх) = /(0) + -^х +	Х2+... +	хл+ 21^ хЯ+1. (15)
1	1-2	1 • 2 ... п 1 *2 ... п (п 4- 1)
Здесь £ — точка между х0 и х. Этот частный случай иногда называется формулой Маклорена.
Заметим, что в предыдущих рассуждениях интервал I может быть бесконечным. Далее, теорема и ее доказательство сохраняют силу, если х0—один из концов /; в этом случае /' (х0),..., /(п,(ло) следует рассматривать как односторонние производные.
УПРАЖНЕНИЯ
В упражнениях 23—32 найдите оценку (верхнюю границу) абсолютной величины остаточного члена R(x) = [(х) — Р(х).
23.	f (х) = х4, Р (х) — третий многочлен Тейлора, хо = О и х = — •
13/3	1
24.	f (х) = х , Р (х) — третий многочлен Тейлора, х0 = 0 и х = — •
3
25.	f (х) = arctg х, Р (х) — третий многочлен Тейлора, х0 = 1 и х = — •
26.	f(x) = ext Р (х)— четвертый многочлен Тейлора, хо = 0 и х=1.
27.	f (х) = Inx, Р (х) — четвертый многочлен Тейлора, х0 = 1 и х = е.
Копии МАКЛОРЕН (1698—1746) — профессор а Эдинбурге, а ранее — учении Ньютона.
26
8. Ряды
28.	f (х) = х + 1 , Р (х) — четвертый многочлен Тейлора, х0 = 0 и
I 1
29.	/(х) = 1/х, Р (х)— четвертый многочлен Тейлора, х0 = 1

АЗО. f(x) = cosx, Р (х) — шестой многочлен Тейлора, х0 = -у и -g-<x<-g-.
31.	f (х) = arctg х, Р (х)—третий многочлен Тейлора, хо = Ои-—
32.	f (х) = ех, Р (х) — многочлен Тейлора, х0 = 0 и х = 1. [Примечание. В этом случае ответ должен зависеть от п.]
2.4	. БИНОМИАЛЬНАЯ ТЕОРЕМА
В качестве первого применения формулы Тейлора мы рассмотрим функцию f(x) = (а х)п (где п — натуральное число); положим хо=О. Поскольку /(х) —многочлен степени и, имеем f(n+° (х) = 0 и R = 0. Далее, /(0) = ап. Так как/'(*) = = п(а + х)л“\ /"(х) = п(п — 1) (а + х)п~2 и вообще
/</) (х) = п(п — 1)...(и — / + 1)(а + х)л~' при i < и, то имеем
/(/) (0) = п(п— 1)... (п— / + 1)ал“Л
Подставляя эти значения в (12) и принимая во внимание, что R = 0, получаем тождество
(а + х)п=ап+ — ап~1 х + "(п~ °. ап~2х2 + п<п~п (п~2) ап-*х* +
V	1	1-2	1-2-3
I П (п — 1) (п — 2) (п — 3)	, л (л — 1) (п —2) ... 2  1
'	1 • 2 • 3 • 4	Ь2... л
Это—знаменитая формула бинома Ньютона*. Коэффициент при an~ixi называется биномиальным коэффициентом** и обозначается через (7). Таким образом,
©='• при'°'-2’3...................................- <|б>
Биномиальная теорема может быть записана еще так:
(а + х)п = (") ап + аГ'х + Q ап~2х2 Н----+ („)*“•	(17)
Конечно, это — алгебраическое тождество и, следовательно, формула бинома может быть доказана также и прямым путем.
* Впрочем, в таком виде эта формула была известна задолго до Ньютона; заслуга Ньютона заключается в том, что он распространил ее на не целые значения п (ср. с § 5.7, ниже).
** В нашей литературе более распространено обозначение С,/ для биномиальных коэффициентов.
§ 2. Теорема Тейлора
27
УПРАЖНЕНИЯ
33.
Покажите, (16).]
что
/ = 1, ... , п. [Воспользуйтесь равенствами
34.
Покажите,
что
О, 1, ... , п. [Воспользуйтесь равенствами (16) и
учтите, что достаточно рассмотреть случай / С п—/.]
35.
Покажите, что
/ > 1. [Воспользуйтесь равенствами (16).]
А36. Покажите, что
) = 2я. [Примените теорему о биноме при п /
х = 1 и при надлежащем а.]
37. Покажите,
что
= 0 при п > 1. [Примените
теорему о
биноме при
х = 1 и при надлежащем а.]
38. Покажите,
что
т • 2/и"1 при т > 2.
[Восполь-
зуйтесь результатом упр. 36 (где следует положить п = т— 1) и результатом
упр. 33.]
2.5	. БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ ДЛЯ ПРОИЗВОЛЬНОГО ПОКАЗАТЕЛЯ
Предыдущий вывод широко известной формулы бинома Ньютона из теоремы Тейлора, конечно, лишь любопытен. Но он имеет интересное продолжение. Рассмотрим функцию
f (х) =(14- х)а,
где а =# О — любое действительное число, не обязательно целое положительное.
Для х > —1 эта функция имеет производные всех порядков:
Г(х) =а(1 + х)а~‘, f (*) =а(а- 1)(1 + х)а-2, ...
и вообще,
/(,) (X) = а (а - 1) (а — 2)... (а — / ч- 1)(1+х)"-', так что
(0) = а(а- 1)(а - 2)... (а - / + 1).
Подстановка в формулу Маклорена (15) приводит к соотношению
(1+х)‘=1 + —х+ ^12).х2 + а(а-1)(»-2)хз+ ...
v '	1	1.2	1-2.3
• • • + Ма-1)..-(°-п+В хП +	(18)
1 • 2 ... п
28
8. Ряды
где
7? = ,«(«—0 ••• (« —»), п + п*-"-1 х«+1 1-2...(«+!)
а $ заключено между 0 их. Мы можем теперь обобщить определение биномиальных коэффициентов, полагая для любого a
И = 1, (?) = a(a-l)(tt-2) ... (а-,- + 1)	=| 2,3.... (19)
\0)	\11	1-2-3.../	'	' '
Тогда соотношение (18) можно записать так:
(1 +х)“ = 1 +	-----И (*)хП + Я ПРИ х>~ 1.	(2°)
где
/? = ( i iV1 + £)a-n_'Хл+*.	(21)
\п ~г 1 /
•Пример. Вычислить 1,03, пользуясь формулой (20) при п= 2, и оценить погрешность.
Решение. Полагая a = и х — 0,03, имеем о
-(--О
1,03 -(1 +0,03)'я - 1 + — -0,03-1-—-------!.-(0,03)1 +
.м»..............................
. . 0,03	(0,03)» . 5 (0,03)» . , п(1/3)-3
= 1+“-------“+—81	( +5)
Здесь 0<£<0,03, так что 0< (1 + 5)(1/3)_3 < 1, и последний член (т. е. R) не больше 5-0,000027/81 < 0,000002. Так как 1 + 0,03/3—(0,03)2/9 = = 1,0099, имеем 1,0099 < / 1,03 < 1,0099 + 0,000002.•
УПРАЖНЕНИЯ
В каждом из упражнений 39—46 найдите приближенное значение заданного числа и оцените погрешность. Примените формулы (20) и (21) для заданного значения л.
39. ^97	(п = 3).	43. (0,98)1/5 (л = 3),
40. ^П02	(п = 3).	44. ^2" (п = 4).
41. v'^75	(л =4).	45. (1,1)1Л (л = 3).
42. /Л	(л = 4).	Д46. (0,8)°’°‘ (л = 3).
§ 2. Теорема Тейлора
29
2.6. «ЭЛЕМЕНТАРНЫЕ» ВАРИАНТЫ ФОРМУЛЫ ТЕЙЛОРА
Некоторые из важнейших частных случаев формулы Тейлора могут быть получены без применения теоремы 1, с помощью элементарных методов.
Выражение для n-го многочлена Тейлора функции 1/(1 + х) в точке х0 = О имеет вид
1 _ х -f- х2— х3 + ... 4-(—1)лхл.	(22)
[Обратите внимание на то, что (—1)л равно 1 при четном п и —1 при нечетном п.\ Формулу (22) можно вывести либо прямо из определения, либо из (20), заметив, что
/— 1\ = (— 1) (— 1 — 1) (— 1 — 2)... (— 1 — /4- 1) = (-D (-2) ... (-/) =	1}/
\ j )	12.3.../	12.../	'	7
Заменив в равенстве (22) х на —х, получаем n-й многочлен Тейлора функции 1/(1 —х) в точке 0:
1 4-х 4-х2 4- ... +	(23)
Для вычисления остатка можно и не прибегать к теореме 1; в самом деле, имеет место тождество
1	«	гл+1
—— =1+х + х2+---+х'‘+ Y.	(24)
Заменив х на —х, получаем
—= 1 — х + х2------------ь (— 1)"хп ч- (~ 1)'тхП*1 .	(25)
14-х	14-х
Последними двумя формулами можно воспользоваться для того, чтобы ей е раз убедиться, что разложения (22) и (23) — это п-е многочлены Тейлора соответственно функций (1 — х)-1 и (1 4- х)"1. Так, например, из формулы (24) видно, что разность
—!-----(1 + х + х2 4------1- хл)
1 —X
обращается в нуль при х = 0 вместе со всеми своими производными порядков 1, 2. ..., п.
Заменив теперь в равенстве (25) х на х2, получим тождество
1	л	л (_____ ПЛ+1г2Л+з
— = 1	+Д4------+ (- 1ГХ2Л 4. L-1LA-.	(26)
2.7. ВЫЧИСЛЕНИЕ ЛОГАРИФМОВ
Интересные случаи формулы Тейлора мы получим, интегрируя только что найденные тождества от х = 0 до некоторого значения х. Перепишем сначала равенство (25), заменив х на t и п на п — 1:
= 1 _ t + ? _ t3 ------1_ i)n-i fK-i _|_,(- ВЩ.
14-/	14-<
30
8. Ряды
Отсюда
tndt
1-Н ‘
(27)
Чтобы оценить остаток, предположим сначала, что х > 0. При 0 < t < х имеем 1/(1 + 0 < 1, откуда
tndt
уЛ+1 tndt = -1—
о ' б
Если х < 0, то нам придется предположить, что х >—1. Тогда при имеем
tndl
Отсюда следует, что
где
1
1 —I Х|
tndt
| X |”+1
(1 — |х|) (И-к 1)
уП
— I)"’1 — + R, п
—*— при — 1 < х 0. л+ 1 Н
Отправляясь от соотношения (24), точно так же получаем
у2	уЗ	уП	п
-1П (1-х) =х + — + —+... + —+ [ Z	о	П	J
tndt
1 — t ’
(28)
(29)
Оценку остатка мы предоставляем читателю.
Записывая соотношения (27) и (29) для четного п, т. е. для п = 2т+2, и складывая их, получаем
ln2±i=2x + 4+...+4^- + R,	(30)
1 — х	3	2т + 1
где
и
1
1
— I *3 ~ + пг
хл+1
----- при х>-0, п+1 и ' '
J 1— /2 о
§ 2. Теорема Тейлора
31
Пусть х > 0. Тогда предыдущий интеграл возрастет при замене 1 — /2 на 1 — х2, а полученный таким путем интеграл легко вычисляется. Мы находим, следовательно, что
О у2/и+3
0 </? <------------при0<х<1.	(31)
1 — 2m + 3 Г
Заметим теперь, что любое число а > 0 можно представить в виде
1 + х 1-х ’
а
а — 1
где х =---------
При а > 1 число х удовлетворяет неравенству 0 < х < 1. Подставляя его в соотношения (30) и (31), имеем
+ 1	3 \ а + 1 У	2т + 1 \ а + 1)
(32)
причем
2а
1
2т + 3
а — 1 \ 2/и+з
о -|- 1 j
при а> 1.
Погрешность можно сделать сколь угодно малой, выбирая т достаточно большим; но если а — 1 мало, то даже при малых т формула оказывается довольно точной.
Примем, например, в (32) а = 2 и т = 1; тогда получим
1	1
5	З5 ’
откуда
1п2 = —+ ------------ + /?,
3	3 З3
0<7?< — 4
(33)
0,6914 <1п 2 < 0,6933
(в действительности In 2 = 0,6931...). С другой стороны, пользуясь формулой (28) при х = 1, получаем красивое соотношение:
1п2 = 1 - J- + -1— -L + ... + (- 1)»-1J_ + Rt |fl| <—L- .	(34)
2	3	4	n	п + 1
Однако для вычисления In 2 с точностью до 0,002 по этой формуле требуется взять около 500 членов.
2.8. ВЫЧИСЛЕНИЕ л
Перепишем теперь равенство (26), заменив х на t и п на п — 1:
—1— = 1 — /2 + /4---------р (— ПП-1/2Л-2 + (— ПЛ	.
Ц-Р	'	'	'	'	1-р Z3
Интегрируя, получаем
у8 уб у7	у2Л“*1
arctgx = x--£- + A--^-+ ...	+Я	(35)
3	5	7	2п — 1
где
32
8. Ряды
Я=(-1)л
t*ndt
и, поскольку 1/(1 4- /®)	1, имеем
(36) 1 1 2л + 1
Положим здесь х = 1; так как arctg 1 = мы приходим к следующему интересному соотношению:
Т = ‘—г + 4—Н-+^Т- + Л 1*1<5ГЛ-	(37)
Однако эта формула не представляет эффективного метода вычисления л/4: чтобы добиться точности в 1/л, понадобилось бы взять около п/2 членов.
Формула для арктангенса (35) дает хорошие результаты с относительно небольшим числом членов, если х близко к нулю. Но если мы можем с помощью этой формулы вычислить arctg и и arctg v, где и и v малы, то из теоремы сложения для тангенса (см. гл. 6, § 2.2) находим
arctg “~*~р = arctgи 4- arctg v.	(38)
1 —ио
•Пример. Для и =—, v = 4* имеем (и 4- о)/( 1 — ир)=1 и из равенства (38) 2	3
JL = arctg 4" + arctg -L -4	z	о
Для и = —, v = — и для и =—, v = — находим 3	7	6	8
arctg -i- = arctg -J- 4- arctg ~4» arctg 4“ = aretg 4” + arctg 4-.
Сопоставляя эти формулы, получаем
= 2 arctg -L 4- arctg -у + 2 arctg .
Вместе с (35) эта формула позволяет легко вычислить п о высокой степенью точности, ф
§ 2. Теорема Тейлора
33
УПРАЖНЕНИЯ
47.	Найдите n-й многочлен Тейлора для 1/(1 + х10) при хо = 0. Какова погрешность?
48.	Найдите n-й многочлен Тейлора для 1/(1 — Xs) при хо — 0. Какова погрешность?
49.	Пусть Р(х) — п-й многочлен Тейлора для f(x) при хо = 0 и f(x) имеет не менее п + 1 производных в точке 0. Покажите, что хР(х) есть (п + 1)-й многочлен Тейлора функции xf(x) в точке Хо = 0.
50.	Найдите n-й многочлен Тейлора для х2/( 1 + х) при хо = 0. Каков остаточный член? Воспользуйтесь результатом упр. 49.
51.	Найдите n-й многочлен Тейлора для х3/(1 +хб) при хо = 0. Каков остаточный член? Воспользуйтесь результатом упр. 49.
52.	Найдите n-й многочлен Тейлора для f"(x) в точке хо = 0, где f(x) = 1/(1 + х4). Каков остаточный член?
53.	Найдите n-й многочлен Тейлора для fIV(x) в точке хо = 0, если f(x) = 1/(1—х3). Каков остаточный член?
54.
Оцените остаточный член	—— равенства (29).
В каждом из упражнений 55—64 найдите приближенное значение заданного выражения и оцените погрешность. Воспользуйтесь в зависимости от условия соотношениями (32), (33), (35), (36).
55.	'4	(т = 1).	60. arctg -Ь 5	(n = 2).
56.	1п 4	(т = 1).	61. arctg А-	(« = 2).
57.	mA 4	(m = 1).	62. arctg 1 8	(n = 2).
58.	1п 3	(т = 2).	63. arctg 1	(n = 5)
59.	1п 9	(т - 1).	64. arctg -L	(n = 4).
2.9. ФОРМУЛА ТЕЙЛОРА ДЛЯ ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Вернемся теперь к общим формулам (12) и (13) и применим их к показательной функции f(x) = 3х при х0 = 0. Поскольку все производные 3х равны 3х, а потому обращаются в 1 при х = 0, имеем
Y	у2	уЗ	уЛ	уЛ+1
зх = 1 + — Ч-----------h —-------1-----1--------------1-------—-----------. (39)
11-2	1*2*3	1*2*3... п 1 *2*3 ... n (n + 1)	* 7
В частности, при х = 1 получаем1
з = 1 + 1 +---------1---------1-------------И * • • Н" —---------Ь --------------> (40)
1*2	1*2*3	1 . 2* 3* 4	1*2*3... п 1.2*3... (п + 1) V '
где 0 < Е < 1.
1 Последняя формула позволяет доказать, что число е не рационально. В самом деле, допустим, что е рационально. Тогда, поскольку 2	< 3, должно быть е = p/q, где р и q — це-
лые числа и q > 2. Выберем п так, чтобы было n > q. Умножим обе части равенства (40) на 1*2*3... п и заметим, что q — одно из чисел 2, 3, ..., п; поэтому все члены в (40), кроме, может быть, последнего, становятся при этом целыми. Отсюда следует, что & 1(п +1) — также целое число; но это невозможно, так как 0	< 3 и п +1 > 3.
34
8. Ряды
2.10. ФОРМУЛЫ ТЕЙЛОРА ДЛЯ СИНУСА И КОСИНУСА
Рассмотрим в качестве последнего примера формулы Тейлора для функций х cosx и х sin х при х0 = 0. Из таблицы
		Значение при x=0		Значение при x=0
Функция	cos X	1	in X	0
Первая производная	— sin х	0	COS X	1
Вторая производная	— cos X	— 1	— sin x	0
Третья производная	sin x	0	— cos X	—1
Четвертая производная	cosx	i	sin x	0
Пятая производная	— sin x	0	COS X	1
Шестая производная	— cos X	—1	— sin x	0
получаем
1
COS А' = 1--------------
1 • 2
—-----------+(—1)" —-----------+
1.2.3-4	1-2*3 ... (2п)
+ (— 1)л+1
х2П+2
1*2*3 ... (2л + 2)
COS В,
где $ заключено между 0 и х. Поскольку | cos £ |	1, имеем
г2	Г2П
cosx = 1_^ + ^_...+(_,)n__£_+^	(41)
----------ШГ!------. '	1	1*2*3... (2п 4- 2)
Точно так же находим
sin х = х-------1-----------------f- (— 1 )я------------F R, (42)
1-2-3	1-2-3-4-5	1-2-3 ... (2n+ 1)
I г 12П+3
1 1	1*2*3... (2л+ 3)
УПРАЖНЕНИЯ
65.	Найдите л-й многочлен Тейлора для х »-> е** в точке х0 = 0. Оцените остаток.
66.	Найдите п-й многочлен Тейлора для х sin(x2) в точке х0 = 0. Оцените остаток.
67.	Найдите п-й многочлен Тейлора для х cos(x3) в точке х0 = 0. Оцените остаток.
68.	Найдите п-й многочлен Тейлора для х х sinfx3) в точке хо = 0. Оцените остаток^
2.11. СИГМА-СИМВОЛИКА
Начиная с этого момента мы будем пользоваться сокращенным обозначением для сумм, содержащим буквуS (греческая прописная буква «сигма»). Пусть задано правило
/ »-> Ду,
§ 2. Теорема Тейлора
35
сопоставляющее каждому целому числу /, взятому из некоторого набора целых чисел, число а, (не обязательно целое), и пусть заданы два целых числа k и / k.
Условимся, что символ обозначает сумму ak+ ам + ...+ az. Переменная / здесь, конечно, «немая». Например,
^/ = 1 + 2 + 3 + • • • + и —— п (п + 1) /=1
или
2*=2р=2(<7+1) = 1+2 + 3 + “‘+л=тп(п + 1)-
fe=l р=1	q=0
2
•Примеры. 1. Чему равна сумма^]2—1)?
Л*=-2
Решение. Имеем
2
2 О’2 - о = ((- 2)2 - о + «- О2-I) + (О2 - 1) + (I2 - 1) + (22 - 1) = /=—2
= 3 -I- 0	(— 1) “I- 0 -J— 3 = 5.
2. Формула для суммы геометрической прогрессии записывается так:
п 2’' /=0
1 — qn+i
1 — q
Напомним еще обозначения
О! = 1, 11 = 1, 2! = Ь2, 3! = 1-2.3, ...	(43)
(/! читается «/ факториал»). Биномиальные коэффициенты выражаются следующим образом:
/а\  а (а — 1) (а — 2) ... (а — / + 1)
\П	i I
Если п — целое положительное число, то
л(л—1)(п—2)...(м—/+1)1(п—/)!) = п(л—1)(п—2)...(п—/+1)(и—/)(л—/—!)...2-1 ==и!,
откуда
п(п— 1)(п — 2).. .(п — 1+ 1) = п1 
(п —/) 1 и
.
U/ («-/)! Л
(44)
Этим объясняется свойство симметрии
(п\ _ ( п \
U7 U — П
36
В. Ряды-
Биномиальная формула может быть теперь записана в виде
(а 4- х)п = a”~J xJ'	(45>
/=о '
Полагая а = х = 1, а затем а = 1, х = —1, мы видим, что
Используем теперь сигма-символику для записи общей формулы Тейлора: П	/ ч	Дп-Ы)
f W = У	- V + Ял+1, 7?л+1 = 4—(X - xQr\ (46>
Здесь и дальше принимается соглашение, согласно которому /<0)(х) = f(x).
УПРАЖНЕНИЯ
Вычислите следующие суммы:
4
69. 2 /'• /=0
3
74.	(25)1-
е=о
5	5	14
»-2Л-	.
р=2 и	Х=1	Х	‘
71.	2	76.2^;-.
Zt=O	Z=1	v
72	У ——.	77 У Ь3'5 •••(2fe-l) #
’4i/2+1	’ Й 2-4.6... (2k)
73.	2 22Ж-
(3=0
Используйте сигма-символику для записи следующих сумм:
78.	+ /3" + К5 +/7 +/9 .
79. — + — + — + — + — +----------------------
2	6	10	14	18	22
£
1
1 • 3
1 • 4
80.
1-3-5
1 • 4 • 7
1 - 3  5 - 7
1 • 4 • 7 • 10 ’
§ 2. Теорема Тейлора
37
81. 1 — 8 + 27 — 64+ 125— 216.
82.
13	5	7	9
— + — + — 4- — +-
3^6^912	15
83 1>2_2-3,3-4_4>5,5>6 3-4	4 • 5 + 5 • 6	6 • 7 + 7 • 8 ’
1 - 4	9 - 16 25 • 36 49 • 64	81 - 100
4‘ 3 • 4 + 5-6 + 7-8 + 9 - 10 + 11-12
85.
ратите внимание на «сплошные сокращения». ]
при любом целом положительном п. [06-
86. Покажите, что (-од ) = (-Dn+i /=0	'	1	1
ного п.
для
любого целого неотрицатель-
[Указание: воспользуйтесь результатом упр. 35 и принципом «суммы со сплошными сокращениями». ]
— Х\ /п+Ц /0\
87. Покажите, что >	=	— для любого целого неотрицательного п и це-
' i / \i I
лого положительного /. [См. указание выше.]
88. Покажите, что
Для
любых целых неотрицательных п и k.
[См. указание выше.]
89. Покажите, что
для любого целого положительного л, где [0] означает, как обычно, целую часть числа 0, т. е. наибольшее целое число, не превосходящее 0. [Сначала докажите левое равенство, пользуясь результатом упр. 37 (может оказаться полезным рассмотреть отдельно случаи четного и нечетного л). Затем воспользуйтесь левым равенством и результатом упр. 36 для доказательства правого равенства.]
2.12. СВОДКА ФОРМУЛ ТЕЙЛОРА
Запишем теперь некоторые из формул Тейлора для часто встречающихся функций, используя при этом сигма-символику:
(1 4-х)а = 2(;)хУ+Я,	(47)
/=0	'
где R = ( а ) (1 + $)а~л”' хп*х и $ заключено между 0 и х;
\п + 1/
38
8. Ряды
где
и, в частности,
Далее,
и, в частности,
Наконец*,
1п(Ц-х) = У(-1Г‘4- + ^ Я I
|Я|<
x"*1 я 4-1
при к >• О,
| Х|п*‘
(1 - I X I) Л + 1)
1п2 = 2
(- 1)А1 /
при — 1 < х < О,
+ /?, |₽|<
1
Я +• 1
arctg*-£(-!)>« ^-+Я,
п
±^-+R, 2i-\
|Я|
1
2я+ Г
/=1
max (ех, 1) | г |”+| (я 4- I) I
“sx=i(-'’'-i5r+R'
/=0	4 ”
|Я|<
| X |ап+2 (2п 4- 2) I ’
sinx = 2<~ *V /=0
—---------R,
(2/+ 1)'
|Я|
| х |2П'1'3 (2я 4- 3) f ’
(48)
(49)
(50)
(51)
(52)
(53)
(54)
Читателю рекомендуется проверить, что это — те же разложения, которые были получены выше.
* Запись max Сех , 1) означает наибольшее из чисел 1 и ех . [Проверьте, что из неравенства (14) вытекает указанная в (52) оценка остаточного члена.]
§ 3. Бесконечные последовательности
39
§ 3. БЕСКОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
3.1. СЛОЖЕНИЕ БЕСКОНЕЧНОГО МНОЖЕСТВА ЧИСЕЛ
В силу теоремы Тейлора функция /(%) может быть при некоторых обстоятельствах представлена как многочлен плюс малый остаток. Но многочлен есть сумма конечного числа одночленов axJ. Естественно, возникает вопрос, нельзя ли избавиться от остатка и представить функцию как сумму бесконечного числа одночленов?
При этом, конечно, не ясно, что, собственно, означает сумма бесконечного числа слагаемых. Пожалуй, простейший способ наглядно изобразить такую сумму иллюстрирует следующий пример.
Рассмотрим отрезок длины 2 (рис. 8.7). Разделим его на два равных отрезка (каждый длины 1). Не трогая левого отрезка, разделим правый на два равных отрезка (каждый длины 1/2). Правый из них разделим на два равных отрезка (каждый длины 1/4). Продолжим этот процесс до бесконечности. Тогда мы приходим к разби-п	,1111	п
ению отрезка длины 2 на отрезки длины 1, у, -у, у, и т. д. «Поэтому»
Это рассуждение было известно еще грекам, и философ Зенон оспаривал его законность. Зенон известен нам лишь своими «парадоксами», сохранившимися в трудах других писателей.
Один из этих парадоксов утверждает, что бегущий человек никогда не сможет достичь своей цели, поскольку он должен сначала пробежать половину требуемой дистанции, затем половину оставшейся части дистанции, затем снова половину оставшейся части и т. д.; таким образом, он должен пробежать бесконечное множество расстояний, а это будет продолжаться вечно.
Конечно, Зенон видел бегунов, достигавших финиша; поэтому нам остается лишь догадываться, что он хотел сказать этим и другими своими парадоксами. Но если Зенон хотел сказать, что сложение бесконечного множества чисел нельзя толковать как процесс, аналогичный сложению конечного их числа, то он был, разумеется, прав.
Если бы мы попытались вычислить сумму (1), последовательно выполняя все указанные в ней сложения, то это, конечно, никогда бы не окончилось.
И все же мы. чувствуем, что равенство (1) в некотором смысле верно. В чем же заключается точный его смысл?
ЗЕНОН Элейский (ок. 490 г. до и. ».| оыл последователем философа алейской школы Парменида, учившего, что бытие в своей сущности неизменно. Парадоксы Зенона можно интерпретировать как попытку доказать иллюзорность движения.
40
8. Ряды
1	\	1/2	\ 7/4 |;/g| III’
Рис. 8.7
Если дано некоторое целое положительное число и, то мы можем вычислить сумму п первых членов левой части. По формуле для суммы геометрической прогрессии имеем
и вообще,
п членов	2
Таким образом, разность между суммой п первых членов левой части (1) и числом 2 есть число, которое становится сколь угодно малым при достаточно большом п. Мы рассматриваем формулу (1) просто как сокращенную запись только что сделанного утверждения.
3.2. НЕОБХОДИМОСТЬ В ТОЧНОСТИ
Читателю могут показаться слишком уж педантичными предыдущие рассуждения. «Но ведь это верно,— может он сказать,— что 1 +4-	+ 4- + ... = 2? Не все
ли равно тогда, какое истолкование дается этому равенству?» Приводимый ниже пример показывает, однако, что с бесконечными суммами не всегда можно обращаться, как с конечными. Как мы видели в § 2.12 [см. формулу (49)1 разность между конечной суммой 1 —+ 4-----------------— I)"-1 V и числом
1п 2 не превосходит по абсолютной величине, т. е. может быть сделана угодно малой, если п достаточно велико. Поэтому
2	3	4	5	6	7	8	9	10
Рассмотрим теперь бесконечную сумму
1 + -L —-L + _L + A^_L + _L + i__L 3	2	5	7	4	911	6
Она содержит те же члены, что и (2), и, по-видимому, должна иметь ту же сумму In 2. Но, с другой стороны, из (2) следует, что
J____L । J____L + 1
2	4^6 8 10
= In 2.
СКОЛЬ
(2)
(3)
= — In 2.
2
§ 3. Бесконечные последовательности
41
Запишем (2) и только что полученное соотношение рядом друг с другом:
1 j_______i_ j_______L_ _1_ _!_L_i_J______L _i__L
2 + 3	4	5	6	7	8	9	10	11
= 1п2,
2
8	+ 10
--= —1п2, 2
а затем сложим их. Тогда получаем
(4)
з
Каково же истинное значение суммы (3): In 2 или In 2? Чтобы ответить на это, необходимо дать точное определение суммы в случае бесконечного числа слагаемых Когда мы дадим такое определение, окажется, что правильно равенство (4).
3.3. БЕСКОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Чтобы построить строгую теорию бесконечных рядов, мы должны сначала рассмотреть бесконечные последовательности чисел. («Ряд» и «последовательность» — это тесно связанные между собой, но различные термины; их никак не следует смешивать.) Бесконечная последовательность есть правило, сопоставляющее каждому целому числу 1, 2, 3, ... некоторое число; число, сопоставляемое целому числу k, называется k-м членом последовательности. Для краткости далее мы будем говорить просто «последовательность» вместо «бесконечная последовательность».
Последовательности часто задают, выписав несколько первых их членов; при этом считается, что ясен закон построения «общего члена». Рассмотрим, например, последовательности
1, 3, 5, 7, ... ;	(5)
1, 0, 1, 0, 1, 0, ... ;	(6)
1, 1, 2, 3, 5, 8, 13, ... .	(7)
Многоточие указывает на бесконечность последовательности.
Последовательность (5) состоит из всех нечетных чисел; ее пятый член равен 9, n-й член ее 2п — 1.
В последовательности (6) n-й член равен 0 или 1 в зависимости от того, четно или нечетно п. Можно записать ее n-й член в виде
2
Наконец, (7) — это знаменитая последовательность Фибоначчи, каждый член которой получается сложением двух предыдущих, а первые два равны единице. Поэтому восьмой член последоват ельности (7) равен 8+ 13 =* 21f девятый равен 13 + 21 = 34, и т. д. Числа Фибоначчи обладают рядом любопытных свойств;
42
8. Ряды
в течение семи веков они были источником развлечения для профессиональных математиков и любителей*.
Всякий раз, когда идет речь о последовательностях, мы пользуемся переменными; термин «последовательность ait а2, а3, ...», или «последовательность ап, п = 1, 2. 3, ...», или «последовательность jazj», или просто «последовательность а » означает определенное, но не указанное конкретно правило k »-> akt сопоставляющее каждому целому положительному числу k число ah. Если мы хотим задать конкретную последовательность, то мы записываем это правило. Например,
ап= 2п — 1, п = 1, 2, ...
означает последовательность нечетных чисел (5), тогда как правило
^1 = ^2= К ап= ап-\ + ^п-2, п = 3, 4, ...
задает последовательность Фибоначчи. Конечно, в предыдущих формулах а и п — «немые переменные». Например, последовательность Фибоначчи может быть с таким же успехом задана правилом
br= b2 = 1, bj = bi-x + Z?/-2, j = 3, 4, ..., или
ak= 1 при £=1,2, ah= ak-2 + a*_i при k >> 3.
Заметим, наконец, что нумерация членов последовательности целыми положительными числами 1, 2, 3, ... — всего лишь дело удобства. Разумеется, мы могли бы начать с 0, с —1 или с 5.
УПРАЖНЕНИЯ
В упражнениях 1—9 выпишите шесть первых членов заданной последовательности.
1.ял = я2 — п, п = 1,2, ... .	4. kb= № — bt b = — 1,0,....
А2. ах = (—1)х (X — I)3, Х = 1,2...... 5-"/=^T’ / =	.....
3.	2)\ k = 0, 1.... 6. tx = xx~\ х=1,2..............
7.	хх = 1, х2=2, *п = 2*п-1 — ^л-2» и = 3,4.
8.	bs = 2s + (— l)5s, s = 3, 4.
9. ar
2r 4- 1 2r
r = 5, 6, ... .
10. Выпишите пять первых членов последовательности: st = 2,
s2 = 4,
п = 3, 4, ... .
ЛЕОНАРДО Пизанский, известный также под именем ФИБОНАЧЧИ (XIII в.), написал две мате* магические книги — одну по алгебре, другую по геометрии. Они содержат сведения, приобретенные Леонардо во время его путешествий по Востоку и, вероятно, также некоторые его ориги* нальные исследования.
* См. по этому поводу, например, Н. Н. Воробьев, Числа Фибоначчи, М., «Наука», 1969.
§ 3. Бесконечные последовательности
43
11.	Пусть a.j = 1, а0 = 4, ах = 9,а2 = 16,а3 = 25,а4 = 36,...; чему равно аЛ?
12.	Пусть bi = 1, b3 = 2, 64 = 4, Ьь = 8, Ь3 = 16, д7 = 32, чему равно bk?
13.	Каков «общий член» последовательности 0, 4, 8, 12, 16, 20, ... ? Укажите, с какого места Вы начинаете нумерацию членов.
14.	Каков «общий член» последовательности 1, —4, 7, —10, 13, —16, ... ? Укажите, с какого места Вы начинаете нумерацию членов.
15.	Пусть ak = (— 1)*-^ +	, k = 1,2, ... ; как следует определить bj9 / = — 1,0,... ,
чтобы было b^ = alt bQ = а2, Ьг = а3, ... ?
(2t 4- 2) (2t 4- 3)
16.	Пусть xt= -----2Г4--------- ’ r =	’ °’ • • • ’ ках слеДУет определить z^t X = 2, 3,... ,
чтобы было г2 = Х-t, г3 = х0, г4 = хг , ... ?
3.4	. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛЫ
Рассмотрим четыре последовательности:
1 1 1	.
3 ’ 4 ’ 5	’
1_______1_
3 ’	4 ’	5 ’
I 	1	1	1	1
/Г ’ /з" ’ /Г ’ /Г	/6"
Все они обладают общим свойством: если продвинуться в последовательности достаточно далеко, то члены ее становятся сколь угодно малыми по абсолютной величине. Например, в первой последовательности все члены после пятого лежат между 0 и 1/5, все члены после десятого —между 0 и 1/10 и т. д. Мы описываем это общее свойство наших четырех последовательностей, говоря, что они имеют предел 0, или что они стремятся, или сходятся к нулю.
Последовательность
5,1, 5,01, 5,001, 5,0001, ...
не сходится к нулю. Но если мы продвинемся достаточно далеко в этой последовательности, то члены ее станут сколь угодно близки к 5. Мы говорим, что эта последовательность имеет предел 5 (или стремится к 5, или сходится к 5).
Теперь мы дадим точное определение терминов сходимость и предел последовательности. При этом удобно пользоваться выражением «почти все» в смысле «все, кроме конечного числа». Например, в последовательности
—Ю, —9, —8, —7, ...
44
8. Ряды
почти все члены положительны (потому что одиннадцатый член равен 0, а все члены после одиннадцатого положительны).
Пусть alf а2, а3, ... — последовательность и а — число. Мы говорим, что последовательность сходится к а, или имеет предел а, и записываем это формулой
lim at = а, /->00
если выполнены следующие два условия'.
I. Если А — любое число, такое, что А > а, то почти все члены последовательности меньше А.
II. Если В — любое число, такое, что В < а, то почти все члены последовательности больше В.
Воспользуемся этими определениями для доказательства того, что последова-1	1	1	1	1	1	л
тельность 1, —, —, —, —, —,... сходится к 0, т. е. что
2	3	4	5	6
lim —=0.	(8)
/->00 I
Проверим сначала выполнимость условия I. Пусть А—любое положительное число (т. е. А >0). Спрашивается, для каких i выполнено неравенство \П < А? Конечно, для тех целых положительных I, для которых i > 1/Л. Пусть N — целое число, большее 1/Л. Тогда при всех i >> N имеем \/i < Л. Таким образом, все члены нашей последовательности, кроме, возможно, первых N — 1 членов, меньше Л, и условие I выполнено. Заметим, что найденное нами число N зависит от Л. Существенно здесь то, что для любого Л > 0 найдется N, обладающее требуемым свойством.
Проверим теперь условие II. В нашем частном случае это очень легко. В самом деле, если В — любое отрицательное число (т. е. В < 0), то в с е члены нашей последовательности больше В.
В качестве другого примера докажем, что последовательность
2—1,	2 + — ,	2— — ,	2+—,	2 — — ,...
2	3	4	5
сходится к 2, т. е. что
lim (2-Н— 1)" — ^=2.	(9)
п->оо \	П )
Проверим условие I. Возьмем число Л > 2. Тогда для нечетного п
ап=2--------<2<А.
п
Если же п четно, то неравенство
ап = 2+ — <А п
выполнено при условии 1/п < А — 2, т. е. при п > 1/(Л — 2). Если, таким образом, целое число N удовлетворяет условию N > 1/(Л — 2), то для всех п, кроме,
$ 3. Бесконечные последовательности
45
может быть, первых N, имеем an<Z А. Например, для А = 2,01 все члены последовательности, кроме первых 100, удовлетворяют неравенству ап<А, а для А = = 2,0001 — все, кроме первых 10000.
Проверка условия II аналогична и предоставляется читателю.
Имеется другая, равносильная форма определения предела последовательности. Утверждение
lim ап= а	(10)
означает, что для любого положительного числа е существует такое целое число N, что | ап—а | < е при п> N, т. е. при п = N + 1, V + 2, N + 3, ... и т. д.
Легко видеть, что это 4е-7V-определение» равносильно условиям I и II. В самом деле, каждое А > а можно записать в виде а + 8j при некотором е4 > 0, а каждое В < а — в виде а — е2 при некотором е2 > 0; неравенство же | ап— а |< в означает, что а — е < ап< а + е.
Отметим, что «e-jV-определение» вскрывает интуитивный смысл предела. Если равенство (9) справедливо, то члены последовательности aifa2,a3t..., достаточно далекие от ее начала, т. е. с достаточно большими номерами, сколь угодно близки к а.
Докажем теперь (9), пользуясь 8-Доопределением. Пусть е — заданное положительное число. Спрашивается, для каких целых положительных п справедливо неравенство
2-|-(— 1)" —2 I<е?
П / I
Конечно, для тех п, для которых Мп < в, откуда п > 1/е, т. е. при п> N, где N — наименьшее целое число, удовлетворяющее условию N >• 1/е. Это и доказывает равенство (9).
Везде, где это не вызывает сомнений, мы будем писать lim а£= а вместо lim af = a.
Многие авторы пишут также
a, а при / -> оо
(читается: «я, стремится к а, когда / стремится к бесконечности»).
УПРАЖНЕНИЯ
Прямое применение определения сходимости последовательности к конкретной задаче состоит из двух шагов. Во-первых, мы должны решить, будем ли мы пытаться доказывать, что последовательность сходится или что она не сходится, а в первом случае — к какому пределу. Лишь сделав эти предположения, мы можем перейти ко второму шагу, а именно к формальному доказательству. Конечно, если наша первоначальная догадка была неверна, то второй шаг осуществить не удастся. Помните, что если мы не дали формальное доказательство, то задача не может считаться решенной, но главное — правильно угадать ответ.
В каждом из упражнений 17—28 решите, сходится ли заданная последовательность, и если сходится, найдите ее предел.
1111
17. 0, 1, 0, — , 0, — , 0, — , 0, —....
2	3	4	5
19. -8. 27. -4, 9, -2, 3, -1, 1, --у, -у . - -j- ,	. ... ,
46
8. Ряды
А22 —	-L	_L __L
2 ’	2’2’	2’2’	2’2’	2........
23.	1. 1.1, 1,11, 1,111, 1,1111.
24.	11, 101, 1001, 10001, 100001, 1000001.
25.	1,1, 1,01, 1,001, 1,0001, 1,00001, 1,000001.
26.		 , - , - , -- , --- , - , — , ----------- , - , —.
2	3	5	7	1113	17	19	23	29
27.	0, 3, 1, 4, 2, 5, 3, 6, 4, 7, 5, 8, 6.
28	—	—
2 ’	2’4*	4’8*	8 ’ 16 ’	16.......
3.5.	СВОЙСТВА ПРЕДЕЛОВ
Как видно из определения, последовательность может иметь только один предел. (В самом деле, если lim = а и в то же время lim Р > а, то для почти всех j должно быть (а + Р)/2 и, с другой стороны, для почти всех j должно быть (а + Р)/2, что и приводит к противоречию.)
Из определения следует, что если lim aj= а и если последовательность bit b2, Ь3, ... получается из ait а2, а3, ... перестановкой конечного числа членов, то и lim bj= а. Далее, если clt с2, с3, ...— подпоследовательность последовательности а2, а3, ...,т. е. получается из alf a2t а3, ... удалением (возможно, бесконечного числа) членов, то lim с~ а. (В самом деле, все, что верно для почти всех ajt верно также для почти всех bj и для почти всех с;.)
Отметим, наконец, что утверждения
lim 0 и lim|	= 0
равносильны, равно как и утверждения
lim aj= а и lim ау+1 = а.
Читатель без труда убедится в этом самостоятельно.
•Примеры. 1. lim qn= 0 при 0<Zq<Z I.
П->ОО
Чтобы проверить это утверждение, мы должны показать, что, каково бы ни было положительное число е, всегда qn<Z е для почти всех п (условие II в рассматриваемом случае выполняется тривиально: если В < 0, то qn> В при всех и).
Первое доказательство. Пусть дано е >* 0. Спрашивается, для каких целых положительных п справёдливо неравенство qn< е? Поскольку логарифм — возрастающая функция, это неравенство можно записать в виде 1п(^п) < < In е, или п In q < In е. Так как 0 < q < 1, имеем In q< 0, и последнее неравенство
§ 3. Бесконечные последовательности
4?
можно записать также в виде п > In е/In q. Это верно при всех и, если In е О, и при всех достаточно больших и, т. е. почти при всех и, если In е < 0.
Второе доказательство. Положим 1/^=1+ а. Тогда а > 0 и (1 + а)л> 1 + ап, откуда (\/q)n = (1 + а)п> 1 + ап и qn < 1/(1 + ап) < \/ап. Но тогда, очевидно, имеем qn < в при \/(ап) < в, т. е. при п > 1/(ае) и, значит, почти при всех п.
2.	lim qn= 0 при I q | < 1.
Доказательство. Если q = Одо утверждение тривиально. Если q =/= 0, I q | < 1, то достаточно показать, что lim | qn | = 0. Но, согласно примеру 1, lim | qn | = lim | q\n = 0.
xn
3.	При любом x имеем lim — = 0. n->OO fll
Пусть т — фиксированное
Доказательство. Можно считать, что х > 0.
чи ело, большее х. При п > т имеем
п — т членов
Зададим теперь произвольное число е>0. Для каких п выполнено неравенство хп
< е? Конечно, для тех, для которых
Но в силу примера 1 это верно для почти всех п. (Чтобы убедиться в этом, достаточно положить q = —-— . т 1
4.	При любом х имеем
у2П+2	У2Л+3
lim —---------- 0, lim —-------= 0.
п-^оо (2л -f“ 2) I	п-*оо (2п 4~ 3) I
Доказательство. Заметим, что последовательности —, — , — , ... и
х? х®	х х% х^
—,	суть подпоследовательности последовательности — , — , — ..........
и воспользуемся результатом примера З.ф
3.6.	ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Понятие предела последовательности можно — и полезно — свести к понятию предела функции. Это нетрудно сделать. Напомним, что для любого числа х символ [х] означает наибольшее целое число, не превосходящее х (например, [2J = 2, [2,001] = 2, [л] = 3).
48
8. Ряды
Рис. 8.8
Пусть теперь имеется последовательностьа2, а3, ... . Мы поставим ей в соответствие функцию
определенную при всех х >- 1. Это — с тупенчатая функция, принимающая значение в интервале [1, 2), значение а2 в интервале [2, 3), значение а3 в интервале [3, 4) и т. д. На рис. 8.8 изображен график функции х н-> Я[Х] для последовательности ап= 5/Ynt п = 1, 2, ... .
Мы можем также поставить в соответствие нашей последовательности функцию
1/х |Г
определенную для всех значений х=/=0. Эта функция принимает значение аг при
х — 1 и х> 1, значение а2 при — 1	---— и — х < 1, значение а3
1	1	1	1	г2 гЬ 2	” rh
при-------<х<,— — и —<Сх< — и т. д. График такой функции для по-
2	3	3	2
следовательности ап — 5/]/~п показан на рис. 8.9.
Вспоминая определение пределов функции (гл. 3, § 4.1 и 4.3), мы видим, что три утверждения
lim at = a, lim а[х] = a, lim с 1/х п = а Z—>-ОО	х->--{-00	X—
равносильны.
Теперь мы можем перенести на последовательности доказанные выше теоремы о пределах функций (см. гл. 3, § 4.2).
§ 3. Бесконечные последовательности
4»
Теорема 1. Пусть
lima4 = a, lim bn = Р; тогда
lim (а„ + Ьп) = а + р, lim (сап) = са, \im(anbn) = <хр и lim — = — при р =/= 0. ьп ?
Теорема 2. Если функция х i-> /(х) непрерывна в точке х = а и если lim ап = а, то lim f(an) = /(а).
Пользуясь этими теоремами, можно вычислить многие пределы. Конечно, эти теоремы можно было бы доказать и непосредственно.
фПример. Вычислить
.. Зл2 + 2 lim ------—-----.
п-*оо 5/1^ — 2п + 1
Решение. Искомый предел равен 2	/	2 \	2
3 -1—	'	lirn 13 —1	lim 3 + lim ~~
..	п2	\ п2	п2
lim ------------=--------------------- ------------------------ =
2	1	/	2	1 \	2	1
5 — — + ~ lim(5— — + —I lim 5— lim —+ lim — n	n2	\	n	n2)	n	n2
__	3 + 0	= _3_
5—0 + 0 ~ 5 v
Мы воспользовались здесь тем фактом, что
lim —= 0. п2
Последнее соотношение можно вывести: (а) из определения; (б) из (8) и теоремы 1, поскольку lim -у = lim — lim —; (в) из (8) и теоремы 2, положив f(x) =х2, поскольку lim — = (lim —Y = О2 = 0. А п2 \ п )
3.7.	РАСХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
Не всякая последовательность имеет предел; последовательность, не имеющая предела, называется расходящейся. Говорят, что последовательность ait a2t а3, ... расходится к +оо*, если для любого числа А почти все ее члены	в
этом случае пишут lim = + оо.
* В русской учебной литературе иногда в таком случае говорят: «последовательность сходится к +оо».
$0
8. Ряды
То же можно выразить равносильным соотношением
lim = 4-оо.
Л-*Н~ОО
Аналогично,
lim а~ — оо
означает, что
lim а^) = — оо,
Х->Ч-со
т. е. что для любого числа А почти все члены А. (Вряд ли необходимо перечислять здесь правила, вытекающие из результатов о бесконечных пределах; см. гл. 3, § 5.2.)
Разумеется, последовательность может расходиться и не имея бесконечного предела; такова, например, последовательность
1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, ... .
^Примеры. 1. При а > 1 имеем
г аП lim — = 4-00.
«-►ОО П
Доказательство. Так как а > 1, можно положить а = 1 4- bt b > 0. По биномиальной теореме имеем
а" = (1 + ЬГ = V (п]& > («Ь* = fc2. W / W	2
Следовательно. — >* (п — 1) —» а это число может п	2
большим.
о т»	-л	3 4“
2. Имеет, ли последовательность а„ = —1-------,
п 1 — п
быть сделано сколь угодно
и = 1, 2,..., конечный пре-
дел? Бесконечный предел*?
Решение. Применив правило § 5. 2 гл. 3, заключаем, что
lim ап = lim--------------= lim (— п) lim---------------— = (— оо) • 2 = —- оо.
— п[ 1 — —1 —------------------------------
\ п I	п
Т. е. можно ли утверждать, что lim ап = 4~оо? Что lim ап = — оо?
§ 3. Бесконечные последовательности
Последовательность расходится к —оо; у нее нет конечного предела. Можно прийти к тому же выводу и прямым путем: величина
ап=(—п)-------—
1 — — п
в —п раз больше числа, которое при больших п очень близко к 2. Поэтому при больших п величина ап близка к —2п и lim ап= — оо.ф
УПРАЖНЕНИЯ
29.	Покажите,
30.	Покажите,
31.	Покажите,
32.	Покажите,
33.	Покажите,
34.	Покажите,
35.	Покажите,
что последовательность ап= -------- , л=0, 1, ... , сходится к L
п 4- 1
что
что
что
что
что
что
последовательность bj = —— , j = 1, 2, ... , сходится к 0. Vi
последовательность = (— 1)Л, k = 1, 2, ... , не сходится к 1.
2/	2
последовательность Wi = —------- , Z = 0, 1, ... , сходится к — •
1000
последовательность хи = -------- , и = 1,2, ... , сходится к 0.
и
последовательность bk = qk, k = 1,2, ... , при q > 1 не сходится к 0.
36.	Покажите, что последовательность иг = — sin г, г== 1,2, ... , сходится к 0. 1
37.	Покажите, что lim qп = 1 при 0<^q. [Указание: рассмотрите отдельно случаи п-*-оо
q < 1 и q > 1.]
38.	Покажите, что limg«/(«+l)= q. [Указание: рассмотрите отдельно случаи q <3 1 П-+00
и q > 1.]
В упражнениях 39—51 установите, какие из заданных последовательностей сходятся, какие расходятся к +оо или —оо и какие расходятся, не имея бесконечного предела. Ответы должны быть обоснованы либо прямым доказательством, опирающимся на определения, либо применением доказанных выше теорем.
39.	ап =
2п3 — п
Зп3 + п2 + !
40.	ап
1 — 2п2
1 + п, — п2
, п=0,1......
п = 1,2, ... .
41.	ип =
п3 — Зп + 4
П2 + п
п = 1,2,
fel/2+ 1
42-	=	\	, * = 2,3..........
к — 1
52
8. Ряды
*,/3+fe2/3
43. a-k— —	— ,
1 + fe1/2 + fe3/2
k= 1,2.......
A 44. o* =
2k + sin k
5/г + 1
fe = O, 1,
A ! + 1
45- “*= ГГП • x = 2’3....................
Л 1 — 1
an
47‘	= 7n-'l)'2' ’ rt = 2’3..... где a>h
48.	xn = nan, n = 0, 1, ... , где 0 < a < 1.
ПК
49.	an = cos — , n = 0, 1.......
7 nn
50.	an = — , n=l,2, ... • n I
8^ — 4/
51.	cj =-----j---, /==0,1........
3.8. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Существует чрезвычайно важная теорема, позволяющая установить сходимость некоторых последовательностей.
Последовательность aif а2, а3, ... называется возрастающей, если ai<a2< < а3 <...; неубывающей, если а2 аз • Таким образом, у возрастающей последовательности каждый член больше предыдущего, а у неубывающей — не меньше предыдущего. Последовательность {aj называется убывающей, если ai+1 для всех и невозрастающей, если at^> ai+l для всех I. Последовательность, которая является либо неубывающей, либо невозрастающей, называется монотонной.
Последовательность {aj называется ограниченной сверху, если существует такое число Л4, что а^М при всех L Последовательность называется ограниченной снизу, если существует такое число /и, что at т при всех I. Последовательность называется ограниченной, если она ограничена и сверху и снизу.
фПримеры. 1. Последовательность an=l+(—1)п/п2 не является ни невозрастающей, ни неубывающей, но ограничена.
2. Последовательность а = п2— (1/л) — возрастающая и неограниченная.
3. Последовательность ап= sin п — ограниченная, но не монотонная.ф
Теорема 3. Ограниченная неубывающая последовательность ait a2i а3, ... имеет предел*, предел этот — наименьшее число, не меньшее всех at.
Утверждение теоремы геометрически довольно очевидно (см. рис. 8.10).
Доказательство ее содержится в Приложении (см. § 7.1). В силу того что между пределами последовательностей и пределами функций существует тес-
<§ 3. Бесконечные последовательности
53
о, «4
Рис. 8.10
ная связь (см. § 3.6), теорема 3 следует также из теоремы об ограниченных монотонных функциях, доказанной в гл. 5 (теорема А § 9.1).
Отметим почти очевидное
Следствие. Ограниченная невозрастающая последовательность сходится.
В самом деле, если {aj не возрастает, то {—at} не убывает.
Заметим, что неубывающая последовательность {aj всегда ограничена снизу, так как а± <4 at для всех i. Поэтому в теореме 3 термин «ограниченная» можно заменить на «ограниченная сверху». Далее, если неубывающая последовательность {aj не ограничена сверху, то для любого числа А существует такое число /, что а/> А. Но тогда а^ А при всех i > j и тем самым lim af = + ©о. Поэтому теорему 3 можно формулировать еще и так:
Теорема 3'. Пусть <4 а2 а3 тогда либо lim at = +©о, либо существует такое число а, что lim = а. (В последнем случае а для всех j и а является наименьшим числом, обладающим этим свойством.)
УПРАЖНЕНИЯ
Установите, какие из следующих последовательностей являются неубывающими или невозрастающими, начиная с некоторого места; какие из этих последних ограничены (и тем самым сходятся), какие не ограничены (и тем самым расходятся к -|-оо или к —со). Может оказаться (не удивляйтесь этому!), что в некоторых случаях удастся, и даже легче, установить сходимость или расходимость последовательности прямым путем, не ссылаясь на теорему 3.
52.	2п—1	fe2+10fe °" - Зп + 4 ’ ”-1’2	 54-^~	410 ’
53.	k2 + 1	10" C*-fc2 + ft’		 55- “»= nl ’	Л=0>1	
56.	1 • 3 • 5 ... (2n — 1) an~ 2 • 4 • 6 ... (2n)	’ "~1,2	
57.	= (sin 1) (sin 2) ... (sin X), X = 1,2, ... .
58.	= (sin2 1) (sin2 2) ... (sin2 X), X = 1,2, ... .
59.	uk = 1 + ———-—г-----Л =1,2,... . [Указание: покажите, что при
л2 + k cos k + 1
производная функции х х2 + х cos х + 1 положительна.]
60.	ах =	. 1	, Х=1,2........
х X 4- sin (X2)
,, п
, n = 1,2, ... .
54
8. Ряды
7	2	3	4
Рис. 8.11
3.9. ПОСТОЯННАЯ ЭЙЛЕРА
В виде приложения теоремы 3 покажем, что существует число у, для которого
lim f1 + -Д + 4" Н-------------------Ь --------In л) = у
п-»»оо \	2	3	п	]
(11)
Число это называется постоянной Эйлера; первые цифры его десятичной записи таковы:
т « 0,5772... .
Рационально ли это число или нет, до сих пор не известно.
Равенство (11) равносильно утверждению:
In п — 1 Ч—-—|—-—|- • • • Ч-7 Ч- Игл — 0.
Чтобы доказать сходимость последовательности
a„ = l + -|- + -|*+-----------Н ------1пл, и = 1,2,.
«J	tl
начнем с неравенства
Справедливость этого неравенства ясна из рис. 8.11, где п = 4. Оно выражает тот факт, что площадь под графиком ступенчатой функции 1/[х Ч- 11 от х = 1 до х = п меньше площади под графиком функции 1/х, которая в свою очередь меньше площади под графиком ступенчатой функции 1/[х].
55
$ 4. Бесконечные ряды
Положим теперь
b„ = lnn- (v + T + "‘ +т)-
Вычитая из правого неравенства (*) сумму -у +	+ ... + имеем
0< Ьп< 1 — — < 1, п	п ’
так что последовательность (&п} ограничена. Так как Ьп есть сумма площадей, заштрихованных на рис. 8.11, то последовательность {Ьп} возрастающая. Поэтому существует конечный предел lim bn9 а тем самым и lim ап, где ап= 1— Ьп.
§ 4. БЕСКОНЕЧНЫЕ
РЯДЫ
4.1. ЧАСТНЫЕ СУММЫ
После подготовительного § 3 мы в состоянии рассмотреть бесконечные ряды. Бесконечным рядом называется последовательность чисел, соединенных знаками сложения. Числа эти, называемые членами ряда, можно занумеровать целыми числами О, 1, 2, ..., или числами 1, 2, 3, ..., или иным способом. Если некоторый член ряда — отрицательное число, например (—6), условимся писать — 6 вместо + (—6). В остальном мы будем придерживаться для рядов тех же соглашений, что и для последовательностей. Так, выражение «бесконечный ряд а0 +	+ а2 + ...» будет
означать, что — определенные, но не заданные конкретно числа. Для бесконечных рядов используется также сигма-символика, введенная в § 2.11: ряд
а0 + <21 + а2 +... записывается в виде
/=0
Для краткости мы будем отныне говорить «ряд» вместо «бесконечный ряд».
По определению, n-й частной суммой ряда (1) называется (конечная) сумма всех членов ряда до п-го члена включительно, т. е. сумма
ао + ai + • • • + ап = аг /=о
Тем самым возникает бесконечная последовательность, составленная из частных сумм; такая последовательность ставится в соответствие каждому бесконечному ряду. Обратно, любая последовательность может рассматриваться
56
8. Ряды
как последовательность частных сумм некоторого ряда', действительно, если задана последовательность
^1» ^2»	3» ^4» ••• »
то, как читатель легко проверит, частные суммы ряда
а* + («2 — «1) + (Яз — а2) + (а4— аз) + •••
совпадают с членами этой последовательности.
4.2. СХОДЯЩИЕСЯ РЯДЫ
00
Говорят, что бесконечный ряд aQ 4- а{ + а2 4- ... = 2 aj сходится, если сходится
/=0
последовательность его частных сумм, т. е. если существует конечный предел
S = lim = lim(an + aj + • • • + а„).	(2)
n->oo	П-+ОО
В этом случае S называют суммой бесконечного ряда и пишут
00
ао + а\ + а2 + * ’ * =5, или af = S. /=о
Точно так же утверждение со ап + а*+> + ам + • • • — S, или у а, = s /=Л есть сокращенная запись утверждения
lim (ak + ам + • • • + ап) = lim У а, = S. га-*оо	п-*оо
/=/?
Теорема 1. Если бесконечный ряд сходится, то сходятся и ряды, полученные из него добавлением, удалением или изменением конечного числа членов.
Доказательство. Достаточно рассмотреть, что происходит, когда меняется один член ряда. Пусть а0 4- at 4- а2 + ...= S. Это значит, что
lim (а0 4- аг 4- • • • 4- ап) = S. п-*со
Рассмотрим теперь ряд с измененным первым членом ап 4- а4 4- а2 4- ... . Его частные суммы имеют вид
а0 + ai + а2 4- * * * + ап = ао 4~ ai 4-	4- • • • 4- ап + (aQ — aQ).
По теореме 1 § 3.6 имеем
lim (а0 4- 4- • • • 4- ял) = S 4- (л0 — п-+со
тем самым ряд а0 + at + at + ... сходится.
$ 4. Бесконечные ряды
S7
Из теоремы Тейлора следуют интересные примеры сходящихся рядов. Например, из равенства (48) § 2.12 вытекает, что
j^(— iy+1	= In (1 + х) при — 1 <Zx
/=1 1
(3)
т. е.
+	+	---=ln(l+n
2	3	4	5
В самом деле, lim хп+1/(п 4- I) = 0 при 0 х 1 и lim ------------1—'------ = О
П-»СЮ	П—>ОО (1   | Я I) (п-}-1)
при —1<х<0. Частным случаем ряда (3) является ряд
1 — — + ----------н-----= 1п2,	(4)
2	3	4	' '
уже отмеченный в § 3.2.
Аналогично , из соотношения (50) § 2.12 получаем
“	у2/-1	у5
У(—1)Л‘-—-=х— —+--------------=arctgx при |х|<1,	(5)
1	О	О
откуда при х = 1 имеем
Оба замечательных ряда (4) и (6) были известны Лейбницу.
Как видно из равенств (52), (53) и (54) § 2.12, для всех х имеем:
= sinx.
(8)
(9)
В самом деле, /-я частная сумма 1 + — + ——!-••• + — отличается от ех не 1!	2!	/!
е\ х 11 х /+1	el * 11 х l/+1
более чем на*------!—!— , а в силу примера 3 § 3.5 lim---------—-----= 0. Разло-
(/+1)!	/-оо (/+1)1
жения (8) и (9) устанавливаются с помощью примера 4 § 3.5.
* См., впрочем, формулу (52) на стр. 38; уточнение предложенного доказательства результата (7) предоставляется читателю.
58
8. Ряды
УПРАЖНЕНИЯ
	°°
1.	Вычислите первые 6 частных сумм бесконечного ряда /=о ' +
2.	ОО Вычислите первые 6 частных сумм бесконечного ряда k=Q 00
3.	Вычислите первые 5 частных сумм бесконечного ряда	(—1) X!. х=о
4.	О	Л	*	V 1 • 3 - 5... (2п-1) Вычислите первые 4 частные суммы бесконечного ряда	2 4 6	2 п=1
5.	1 . 4 . 7 ... (Зп — 2) Вычислите первые 4 частные суммы бесконечного ряда п=1
A6.	п Найдите бесконечный ряд, п-я частная сумма которого равна	, где п— 1,2, .. п 4- 1
2Л
7.	Найдите бесконечный ряд, n-я частная сумма которого равна — , где п = 1,2, ... . п 1
В упражнениях 8—12 найдите n-й многочлен Тейлора Рп(х) заданной функции f(x) в точке хо. Затем найдите бесконечный ряд, последовательность частных сумм которого есть Р0(х), Р^х), P2(x)t...
8.	f(x) = е*2 при хо = 0. Сходится ли ряд для всех х? (См. упр. 65 из § 2.10.]
9.	t(x) == cos х3 при хо = 0. Сходится ли ряд для всех х? [См. упр. 67 из § 2.10.]
1
10.	f (х) = —— при х0= 1.
/х
— 1/3
11.	f (х) = х при Хо = 1 .
1
12.	f (х) = —= при х0= 1.
/2 — х
4.3. НЕОБХОДИМОЕ УСЛОВИЕ СХОДИМОСТИ
Существует очень простое необходимое условие сходимости бесконечных рядов, со
Теорема 2. Если ряд	aj сходится, то lim a, = 0.
/=о оо
Доказательство. Пусть 5 = 5? af. Тогда lim (а0 4-	4- ... 4- а,) =
/—*•00 /=0	'
= 5 и, следовательно, также lim (а0 4- Щ + ... + a/-i) = S (см. § 3.5). Отсюда /-►со
по теореме 1 имеем
lim cij = lim[(a0 4- ci\ 4- ... 4- aj) — (do 4-	4* ... 4~ &/_i)] = S — S = 0.
§ 4. Бесконечные ряды
59
Однако не следует думать, что каждый ряд, удовлетворяющий условию lim a,j = 0, сходится. Например, так называемый гармонический ряд
1 + — + — + — + —+ — + •••
2	3	4	5	6
не является сходящимся. В самом деле, согласно § 3.9, n-я частная сумма этого
при больших значениях п очень близка к 7 + In п, где у — постоянная Эйлера.
4.4. РАСХОДЯЩИЕСЯ РЯДЫ
Ряд, который не сходится, называется расходящимся. Следует иметь в виду, со
что если ряд не сходится, то символ ах + а2 4- ••• = не обозначает ника-
i=o
кого числа.
СО	00
Если lim = -f- 00, то говорят, что ряд Уа, расходится к 4- оо, и пишут П —► со 00 i=o	1=0
СО
2а/ = + о°-
i=0
оо
Смысл символа = — 00 ясен без дальнейших пояснений.
i—o
Например,
1 + 1 + 1 + ... = + оо, 14-2 + 3 + 4+... = + оо.
Далее,
1	+----1—-—|-----1-----!-•••= + оо.
2	3	4	5
Мы вывели это из результата, содержащего постоянную Эйлера; можно также заметить, что для любого целого числа k > 0 имеем
+	... + 2_>й-— = —
k 4- 1 k + 2	2k 2k 2
и что при достаточно большом k частная сумма 1 + ... + содержит сколь угодно большое число таких «отрезков» ряда, каждый из которых дает в эту сумму вклад, .	о	1
больший чем
60
8. Ряды
Ряд
2 (-1)7 = 1-1 + 1- 1 + 1-1 4-... /=0
расходится, поскольку частная сумма а0 + а{ + ... + ап равна 0 или 1 в зависимости от того, четно или нечетно п. Но этот ряд не расходится ни к +оо, ни к —оо.
УПРАЖНЕНИЯ
Установите, какие из приведенных ниже рядов сходятся, и какие расходятся.
/г
sin k
оо
22. > ---- —--------— . [Указание: избавьтесь от иррациональности в знаменателе
S /п+1 + /п
каждого члена.)
4.5. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Следующий очень простой результат в то же время весьма важен. Теорема 3. Бесконечная геометрическая прогрессия
1 + q + q2 + • • • = 2 qJ /=о
расходится при | q |>Л и сходится при | q | < 1, причем
1+<7 + <72Ч-=2^=TZ“
/=о
(Ю)
§ 4. Бесконечные ряды
61
Доказательство. Если | q |	1, то не выполняется условие lim | qi\ —
/->оо
= 0; следовательно, ряд не может сходиться (см. теорему 2). Если же | q | < 1, то
"	1 _ пп+1
= l+q-]--------h qn =	~
/=o	q
1 qn+l
1—q l—q
(1 । >
Qn+1
Поскольку Нш<7л+1=0 (см. пример 2 § 3.5), имеем lim —-------------------= 0, откуда и еле-
П-*-оо	П-+со 1 —q
дует (10).
При q =~Y получаем уже известное нам соотношение 1 +	+ • • • =2-
•Примеры. 1. Показать, что qk +	+ qk*2 + • • • = —— при | q | < 1.
1 — я
Решение. Умножим обе части (11) на qkt а затем найдем их пределы при п ->оо. Можно также вычесть 1 + q +	из обеих частей (10). Простейшим
способом кажется умножение обеих частей (10) на qk\ ниже мы увидим (см. § 4.6),. что такой прием законен.
2.	Найти сумму jq^1 = 1 + 2q + 3q2 + • • • при | q | < 1. /=1
Решение. Продифференцировав обе части (11) по q, имеем
1 . 2а +	+	= -("+!)?” (l-<7) + (l-*7w) = l-(n+l)^ + ^w.
(I-?)*	(1-^)2
переходя к пределу при п ->оо, мы получаем равенство* '+2’+3’г+--'-^-
3.	При | х | < 1
—Ц =2(— 1Ух2; = 1— х2 + х4 — х6Ч-.
Это получается подстановкой в (10) q = —х2.ф
* Тот же результат можно получить почленным дифференцированием по q обоих частей равенства (10) — ниже будет показано, что и этот метод законен.
«2
8. Ряды
4.	6. ОПЕРАЦИИ НАД РЯДАМИ
Следующее предложение сразу же следует из нашего определения и из теоремы 1 § 3.6.
Теорема 4. Если
V caf = сА. Если, далее,
(at + bj) = А + В.
/=Й
В словесном выражении: сходящийся бесконечный ряд можно почленно умножить на число; два сходящихся бесконечных ряда можно почленно сложить.
Применяя эту теорему, надо иметь в виду, что любой бесконечный ряд, почти все члены которого равны нулю, сходится и что любую конечную сумму можно рассматривать как бесконечный ряд, почти все члены которого равны нулю. Далее, между членами сходящегося ряда можно вставить сколько угодно нулей, что не меняет его суммы. Теперь можно убедиться в законности процедур, с помощью которых мы получили в § 3.2 соотношение (4).
УПРАЖНЕНИЯ
Установите, какие из приведенных ниже рядов сходятся. Если ряд сходится, найдите его
сумму, оо 23.	f10’” + 9'л>-
оо
24.	(IO'" + 2я).
п—1 со
25.	ПРИ I * I < 1 •
п=0 со
А 26. 2 (—1)А/Л/2 при 0 < 7 < 1.
Л=0 оо
27.	пгП ПРИ I г |< 1 •
п=0
со	со
29.	(2У -|- а/), где а,—любой сходящийся ряд.
/=0
00
30.	2 *ncos —— при |х|<1, п=0
£,	(2х)п + хп	1
31‘ 2 -------Tn-----' ПР"1И< —’
a=<j
со
32. 2 5,п2Л х при |*К“ п=0
00
33. 2 тгх271”1 при | х | < 1.
П=1
28.	(1-f-мл) при |«|<1.
п—о
34.	’’(/ ~ 0	ПРИ 191 < Ь
/=2
§ 4. Бесконечные ряды
63
4.7.	РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ
Рассмотрим теперь бесконечный ряд а0 + ai + а2 + ... , все члены которого положительны. Тогда последовательность его частных сумм — возрастающая,, поскольку (k + 1)-я частная сумма получается из &-й прибавлением положительного числа ak+}. Тем самым к последовательности частных сумм можно применить основную теорему 3 § 3.8. Это приводит к следующему результату.
со	оо
Теорема 5. Пусть все члены ряда ^ai положительны; тогда либо = +оо,
£==0	1=0
либо последовательность частных сумм ограничена, и ряд сходится. В этом случае оо	п
сумма ряда Yflt есть наименьшее число М, такое что ^pi << М при всех п.
1=0	1=0
Эта теорема имеет много важных применений. Ясно, что она справедлива и для рядов с неотрицательными членами.
4.8.	ПРИЗНАК СРАВНЕНИЯ
Теорема 6 (о мажорирующих рядах). Пусть
0 < Ьг при i = 0, 1, 2, ... .	(12>
Если ряд b0 + bi + b2 + ...	(13>
сходится, то сходится и ряд а0 + ai а2 4“ ••• 9	(14)»
причем
а0 + ai + а2 + ... b0 + bi + b2 + ... •
Если ряд (14) расходится, то расходится и ряд (13).
Примечание. Если выполнены неравенства (12), то говорят, что ряд (13> мажорирует ряд (14).
Доказательство. Пусть ряд	+ b2 -f-... сходится; положим-
оо	а	п
В = Тогда по теореме 5 имеем	откуда следует в силу (12), что J/z,
/=0	/==о	/=о
со
В для всех п. По теореме 5 ряд aQ + ai + а2 + ... сходится и В. Второе. /=о утверждение очевидным образом вытекает из первого.
«4
8. Ряды
4.9.	ДЕСЯТИЧНЫЕ ДРОБИ КАК РЯДЫ
Понятие сходящегося бесконечного ряда в неявном виде присутствует уже в употреблении десятичных дробей. В самом деле, рассмотрим десятичную дробь
CLq, CL 1CL 2^ 3* • •
{где а0 — целое положительное число, а остальные а; принимают значения 0, 1, 2,	9). Эту дробь можно записать как бесконечный ряд с неотрицательными чле-
нами:
~ । а1	I а2	। а3
ап —|----------------------
°	10	10а	103
(15)
Члены этого ряда не превосходят соответствующих членов сходящегося ряда
।	9	।	9	।	9	।	.	9 /i ।	1	।	1	.	\
0	10	10а	103	0	10 \	10	102	)
Следовательно, ряд (15) сходится; сумма его и есть, конечно, число а0, а1а2аз ••• Если а0, aia2a3... — периодическая дробь, то, как показывает формула для
суммы геометрической прогрессии, это число рационально. Например,
0,32 = 0,323232 ... =	-+	+
100	1002	1003
32	1	32
100 1	1	99
~~ 100
УПРАЖНЕНИЯ
Выразите следующие периодические десятичные дроби в виде частного двух целых чисел:
35.	0,Та	37. 0,1180.
36.	1,29.	38. 0.3 ПТ.
Выразите суммы следующих бесконечных рядов в виде частного двух целых чисел. (Эти ряды соответствуют периодическим дробям в системах счисления, отличных от общепринятой десятичной.)
QQ 1	1	2 ।	1 . .	2 ёГ + " +	1	2	-4-... .	
ээ. 3 +	9	27 +		32Л-1	'	32И		
2 40. —+ О	4	2	4 1	- I ,,	2 . 1 -	1	-	4 	 1 ,,,	
	25	125	625 '	~Г 52Л-1	”Г	52Л	
<1.-7 +	1		1 - । ।	1	1	0	।
	4	Н 16 +	32	‘'	23Л-2	’	2ЗЛ'	-1	2ЗЛ	-г ... •
3 42. — 4-0	3	3	3	3		0	3 	 1
	125	625	15625	• • • + 53л-	-2	'	5эл-1	5ЗЛ	— •
§ 4. Бесконечные ряды
65
Установите, какие из приведенных ниже рядов сходятся и какие расходятся; воспользуйтесь признаком сравнения, т. е. теоремой 6 о мажорирующих рядах.
«УI 2 * *?--
/1=0
оо
А48‘ 2 3* —sinfe *
Л=1
44.
2 4- cosfe k
49.
In г
2f-i ’
45.
1
2п 4- 1
50.
/i=:
46.
51.
п—2
1 л! —п
47.
1
2п — 1
52.
п=1 со со
Пусть0< qCa/Cbi при / = 0, 1,2, ... и ряды 2 сь 2 сходятся. Покажите, что ряд /=о	z=o
1
1
S ai сходится.
4.10.	ИНТЕГРАЛЬНЫЙ ПРИЗНАК
Следующий признак сходимости опирается на понятие несобственного интеграла (см. гл. 5, § 4.9 и 6.2).
Теорема 7 (интегральный признак сходимости ряда). Пусть t /(/) — непрерывная неотрицательная убывающая функция, определенная при / > 1. Если несобственный интеграл
существует, то ряд j/w /1=1 сходится. Если интеграл не существует, то ряд расходится. Прежде чем перейти к доказательству теоремы, отметим такое Следствие. Ряд
I + —+ -1- + —	V «-»
2s 3s 4J	n5
/i=l
сходится при s> 1, расходится при 1.
(16)
(17)
66
8. Ряды
В самом деле, если s > 0, то 1i-> t~s — убывающая функция от t и можно применить интегральный признак. При s Ф 1 имеем
4-00	А	А
С t~sdt = lim ^\t~sdt= lim —-—I = lim —J—(1 — Л1-*) =
J	| oo 1 ““ S j	А-и-|-<» S ~~ 1
fl	1
---------- при S> 1, _ s -— 1
+ оо При S< 1.
При s = 1 получается гармонический ряд, который, как мы знаем, расходится, со
Но интегральный признак также действует: несобственный интеграл не су-
ществует. При s 0 имеем lim n~s = +оо, так что ряд заведомо расходится. При п-*оо
s> 1 можно определить функцию
C(s) = 1 + —7- +	+ ... I
это так называемая дзета-функция Римана. Она играет очень важную роль в теории чисел.
Доказательство теоремы?. Заметим, что график функции t f(t) опускается. Поэтому
f (2) + f (3) -h ... + f (и) < p (0 dt < f (1) f (2) + ... + f (n - 1).
В самом деле (см. рис. 8.12, где п = 6), левая сумма равна площади от 1 до п под графиком ступенчатой функции, лежащим ниже кривой /»-►/(/); правая же сумма равна площади под графиком ступенчатой функции, лежащим выше той же кривой.
4-со
Пусть интеграл j* f(t)dt существует и равен числу /. Тогда
и сходимость ряда вытекает из теоремы 5 § 4.7.
Пусть теперь ряд сходится и имеет сумму 5. Тогда р(/)Л<5 1	г
откуда и вытекает сходимость несобственного интеграла.
§ 4. Бесконечные ряды
67
УПРАЖНЕНИЯ
С помощью интегрального признака сходимости установите, какие из приведенных ниже рядов сходятся, а какие расходятся:
53.
1
п In п
1 п In2 п
1 л1п1/2л
1
(п3+ 1)2/3 *
п2 + 2л л3 + Зл2 + 1 •
arctg л
1 +д2 *
59.
garctg п
14-п2 ‘
в1/« п2
2 Tib /г=1 со
63.	 л удХ п' Для любого действительного числа X. [Ответ зависит от X; см. упр. 53—55.]
/1=2
Докажите сходимость следующих ниже рядов, пользуясь теоремой 6 и разложением в ряд C(s) при надлежащем значении s.
68
8. Ряды
4.11.	КРИТЕРИЙ ЧАСТНЫХ
Существует другой полезный метод, позволяющий решать, сходится или расходится ряд с положительными членами.
Теорема 8 (критерий частны х*). Пусть все члены ряда ^ап положитель-/1=0
ны. Если
lim	1,
то ряд сходится. Если же
lim -2а±1_>1, ап то ряд расходится.
Прежде чем доказывать теорему, рассмотрим некоторые примеры ее приложения.
фПримеры. 1. Ряд
00
п«=»0
сходится, так как
lim ая+'  = lim —— = lim —1	= 0 < 1.
ап	/(п+1)1	/«+»
2.	Ряд
сходится (к числу 7), что читатель без труда проверит. Однако теорема 8 здесь неприменима, так как lim a'l+1  не существует: в самом деле, последовательность , а"	ill	°*
-^2-,	, ... в этом случае имеет вид —, 3, —, 3, —, 3, ....
ai аа	6	6	6
00
3.	Как мы знаем, ряд 2 n~s расходится при s<l и сходится при s>l. Но /1=1
lim a"+i.. = limf—-—V = 1 при всех s, так что теорема 8 здесь неприменима.® ап \л+1/
В нашей учебной литературе этот критерий обычно называют признаком Даламбера.
§ 4. Бесконечные ряды
69
Доказательство теоремы 8. Пусть сначала	Возь-
П-ХЮ dn
мем число 9, удовлетворяющее неравенству L<9<1. Тогда 0<-^2±а—<9 для
почти всех 9. Поскольку сходимость или расходимость ряда не нарушается в результате изменения или удаления конечного числа его членов, можно считать, что
-п+1 <9 при всех п. ап
Тогда < 9, откуда аА < 9 а0; затем < 9, откуда а2 < 9 ах < 92 а0; затем а0	01
-^2- < 9, откуда а3 <. 0 а2 <_ 93 а0. Вообще, 0<ап<а09я,
и поскольку ряд а0 + а09 + а092 4-ао03 4-... сходится (ибо 0<0<1), то, по теореме 6, сходится и ряд 2ап-
Пусть теперь lim в"*1 =L>1. Тогда °n+1 >• 1 для почти всех п. Начиная о ап	ап
некоторого п, члены ряда возрастают и, значит, не может быть выполнено условие liman = 0, т. е. ряд 2ап расходится.
н->оо
УПРАЖНЕНИЯ
Примените, где это возможно, следующие ряды:
критерий частных и установите, сходятся или расходятся
68.	со	1*3*5 ..	 (2л—1)		СО		2п
		2-4-6	... (2л)		/X.	£	(Д1)Х
69.	со 5	1-3-5 ..	. (2л —	1)	73.	co	п3
		1*4*7 ..	. (Зп—	2) •			
,	„ VI (п 4- 1)1 — л!
при Л > 0.	76.	.
П=1 77.	.
ЛА (»’)>
<1=1
±70.	со	1*6*11 ...	(Зп — 4)		ОО "•S <1=1	(2п)1 n! nl	со ,о	
		2*6*10 ...	(4п	-2) ’			I о.	п=1
71.	со 5	п\			со <1=1	еП* п!	79.	со V1 пя • п = 1
70
8. Ряды
4.12.	ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
Ряд называется знакопеременным, если его четные члены (т. е. члены с четными номерами) положительны, а нечетные — отрицательны (или наоборот). Примерами могут служить уже знакомые нам ряды
1 1	1,1	_ «
3 + 5	7 + 9	~ 4 
Теорема 9 (о знакопеременных ряда х*). Пусть Ро> Р1> Рг> > Рз >... > 0 и lim ра = 0; тогда ряд
Ро~ Pi + Pi— Рз + Pi — р5 4- ... сходится.
Доказательство. «Нечетные» частные суммы здесь образуют возрастающую последовательность, так как (2п 4- 1)-я сумма может быть записана в виде
5гп+1 = (Ро— Р1) + (Ра — Рз) + (р4 — р5) + ... + (p2n— р2п+1),
где все члены р0— pit рг— р3, ... положительны. Поскольку, далее,
2n+J Ро (РР а)	(Р 3 Р4) ~~	~~~ (Р 2n-l	Р 2n)	Р 2п+1
и члены Pi— р3, р3— р4, ... положительны, имеем S2n+i < Ро- По теореме 3 § 3.8 существует предел А = limS2n+1. Далее,
lim S2n = lim (S2n+, 4- p2n+1) = lim S2n+1 + lim p2n+1 = A 4- 0 == A.
Явно, что A — сумма нашего ряда.
4.13.	АБСОЛЮТНАЯ СХОДИМОСТЬ
Пусть задан ряд а3 4-	4- at 4- ... ; тогда представляет интерес также ряд, сос-
тавленный из абсолютных величин его членов: | а0 | 4- I at | 4- | а2 | 4- ... .
со	со
Теорема 10. Если ряд I а/1 сходится, то и ряд у а} сходится, причем
№	/е=0
СО
/=0
(18)
В случае, если сходится ряд ^1 I» говорят, что ряд сходится абсолютно. /=о	/=0
Теорему 9 часто называют также теоремой Лейбница.
§ 4. Бесконечные ряды
71
Доказательство. Пусть ряд S |	| сходится; положим
Тогда
отсюда
а,= \а>'
I 0.
если az^>0, если а,<0;
I I»
/=0
/=*0
/=о
р _ ( — Я/, если й) < 0, (	0, если af > 0.
IP/I5
/=о	/=о
п
п
п
Применяя к рядам
сходятся. Положим
Р/ теорему 6, приходим к выводу, что эти ряды /-о	/=о
/=о
<2 = 2?л
/=0 оо
тогда имеем \ а} | = ау + $jf =aj — Pj и, по теореме 4, ряд а] сходится, причем /=о
^aj=P — M, Р + N = А.
но
Поскольку Р >- О, N >* 0, отсюда следует, что |Р — Af | Р 4- W = Л, а это и доказывает (18).
4.14.	ПЕРЕСТАНОВКА ЧЛЕНОВ
Существуют сходящиеся ряды, которые не сходятся абсолютно; примером служит ряд Лейбница 1 —^‘ + 4’ — Т ’*’4" —'*• * Оказывается, что «парадоксальное» поведение, обнаруженное нами в § 3.2, не может иметь место в случае абсолютной сходимости, но обязательно имеет место для каждого сходящегося ряда, не являющегося абсолютно сходящимся.
со	со
Теорема И. Пусть ряд ^aj сходится. Если ряд 2 । а/ । сходится, то сходится i=om	i=0
и любой ряд, полученный из ^а} перестановкой членов, и притом к той же сумме. i=o
СО	00
Если же ряд |	| расходится, то ряд 2 aj можно превратить перестановкой
/=0	/=0
членов как в расходящийся ряд, так и в сходящийся ряд с произвольной наперед заданной суммой.
Доказательство этой теоремы* приведено в Приложении (см. § 7.2).
* Ее впервые доказал Б. Риман.
72
8. Ряды
УПРАЖНЕНИЯ
Сходящийся ряд, который не сходится абсолютно, называется условно сходящимся. Установите, сходятся ли следующие ряды абсолютно, условно или же расходятся:
00
80.	У р" при |р|<1. п=0
(— 1)*-1 п 2п — 1
и2 — и
А 88.
2п2+ 1 п34-3
(-1)” п in п
(-1)” и in2 п
п=0
4.15.	УМНОЖЕНИЕ РЯДОВ ПО КОШИ
Как видно из теоремы 11, коммутативный закон сложения в известном смысле сохраняет силу и для сумм бесконечного числа слагаемых, если только речь идет об абсолютно сходящихся рядах. Следующая теорема, доказываемая в § 7.3, утверждает, что в этих условиях справедлив и дистрибутивный закон.
Теорема 12. Если
^0 + а1 + а2 +	= 2 ' =	^0 + ^1 + ^2 +	~ 2 &J = Д
/=0	/=0
причем оба ряда абсолютно сходятся, то
АВ = 2 ( 2	= а°^° +	4”	4" (ао^2 + aiPi + аа^о) 4“
л=0 \	/
4* (я<Лз +	4*	4- аз^о) 4- ••• >
причем и этот ряд абсолютно сходится.
§ 4. Бесконечные ряды
Этот способ построения произведения двух бесконечных рядов называется умножением рядов по Коши, в честь Коши, одного из создателей строгой теории бесконечных рядов.
В качестве приложения только что введенного умножения рядов выведем, исходя из формулы
Т 1 I * I	I
ех = 1 Ч----Ч-------h ...,
11	2!	’
функциональное уравнение показательной функции. Требуется доказать, что еаед= Очевидно,
(здесь важно, что в качестве индексов суммирования в двух рядах выбраны разные немые индексы). Пользуясь умножением по Коши, определением биномиальных коэффициентов и биномиальной теоремой, можно проверить, что предыдущее произведение равно
V ( V = V V аУ»я~7 = V — V п' = 44 /I ki ] XJ 44 jt (П - /)1	44 ni
п=0 \	'	п=0 /=0	л=0	/=0
= 2-^2 (")
п=0	1—0	п=0
что и требовалось доказать.
УПРАЖНЕНИЯ
Докажите следующие соотношения, пользуясь умножением по Коши и отправляясь от формул
б) cos8 х = 1 +
(2/п)!
74
8. Ряды
[У к а з а н и е: воспользуйтесь частью (а) этого упражнения и результатами упр. 89 из § 2.11 при п = 2/п.]
со
93. a) sin2 х =
т—0
<-1)т
(2m 4-2)1
m=0
( i\m O2m+i
1___L -_____x2/n+2
(2m+ 2)!
[У к а з а н и e: воспользуйтесь частью (а) этого упражнения и результатами упр. 89 из § 2.11 при п = 2т + 2.]
94.	cos2 х + sin2 х=1 [Указание: воспользуйтесь результатами упр. 92 (б) и 93 (б).]
95.	cos 2х = 2cos2 х — 1 [У Казани е: воспользуйтесь результатом упр. 92 (б)].
§ 5. СТЕПЕННЫЕ
РЯДЫ
5.1.	СХОДЯЩИЕСЯ И РАСХОДЯЩИЕСЯ СТЕПЕННЫЕ РЯДЫ
Степенной ряд — это бесконечный ряд вида
a0 + ai(* —*о) + Мх —*о)2 + М* —*о)3 + ••• = ^ап(х — xQ)n, (1) д=0
где х0, Go, fli, о2,..« — фиксированные числа, ах пробегает некоторый интервал. Точнее, ряд (1) называется степенным рядом с центром х0, или рядом по степеням х — х0. Числа а0,	а2, ...называются коэффициентами степенного ряда.
Если почти все коэффициенты равны нулю, то степенной ряд обращается в многочлен. Поэтому можно считать, что степенной ряд — это в некотором смысле «многочлен бесконечной степени».
Если х0= 0, то степенной ряд имеет вид
а0 + atx 4- а^х* 4- а3х3 4- ... = ^ ап хП-	(Г)
п=0
Для упрощения записей мы будем часто рассматривать ряды только такого вида, что, конечно, не ограничивает общности рассуждений.
Если закрепить конкретное значение х, степенной ряд превращается в бесконечный числовой ряд, который может либо сходиться, либо расходиться. В точке х = х0 имеем а0 + 0 + 0 + ... ; таким образом, степенной ряд всегда сходится по крайней мере в одной точке.
§ 5. Степенные ряды
75
5.2.	РАДИУС СХОДИМОСТИ
Сформулируем теперь основную теорему о сходимости степенных рядов.
Теорема 1. Пусть дан степенной ряд у ап(х — тогда существует такое n—Q
число R >• 0 (которое может также принимать «значение» R = 4- оо), что ряд абсолютно сходится при | х — х0 | < R и расходится при | х — х0 R. (При х = х0+ R и х = х0— R ряд может либо сходиться, либо расходиться.)
Мы докажем эту теорему в Приложении (см. § 8). Приводимые ниже примеры иллюстрируют ее справедливость. Число R называется радиусом сходимости рассматриваемого ряда, а интервал | х — х0 | < R — его интервалом сходимости (в предположении, конечно, что R > 0).
•П	римеры. 1. Степенной ряд nl расходится при x=/=U. В самом деле, п=0
при х#=0 имеем Ит|п!хя| = 4- оо, поскольку lim|x|~n/nl =0 (пример 3 § 3.5) В этом случае R — 0. со
2.	Степенной ряд х" сходится при |х| < 1 и расходится при |х|> 1. Здесь л=0
/? = 1. со
3.	Степенной ряд	сходится при всех х (к сумме 6х). Здесь R = 4- оо.
л=0 оо ХП
4.	Степенной ряд Л’ (—I)”"1----сходится к сумме In(1 4- х) при — 1 <_х	1,
п—\
как мы уже видели выше. При х = — 1 ряд расходится, а именно обращается в
гармонический ряд 1 4-— 4-4- ... . Ряд расходится также при |х|> 1, так 2 о
I X как при | х | > 1 имеем lim =4- «>. В этом примере R = 1. /1-*оо Л оо ЖП	Х2л+1
5.	Степенной ряд Л (— 1)л —------- сходится (к сумме arctg х) при |х|<1;
jmJ	2п + 1
п=0
при |х|> 1 он расходится по той же причине, что выше. И в этом случае R — 1.ф
76
8. Ряды
5.3.	ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СТЕПЕННЫХ РЯДОВ
Рассмотрим теперь степенной ряд с положительным радиусом сходимости R и его
со
сумму f (х) = 2 ап (х — хо)п- Функция х »-+• / (х) определяется этим равенством при л=0
I х — х01 < 7?.
ОО
Теорема 2. Пусть f(x) = ап(х— х0)п при |х — х0 ] < R, где /?>0 — радиус п=0
сходимости этого степенного ряда. Тогда функция	непрерывна и диффе-
ренцируема в интервале сходимости и
со
f (X) = 2 пап (X — Яо)""1.
л=1
Л	00
= V-^_(x-X0)"+1.
J	л + 1
О	n=0
Более того, фигурирующие в двух предыдущих формулах ряды имеют тот же радиус сходимости R.
Эта теорема, которая будет доказана в § 8, утверждает, что степенной ряд можно почленно дифференцировать или интегрировать, как если бы он был обычным многочленом.
•Пример. Пусть нам ничего не известно о показательной функции и мы хотим найти функцию х определенную в окрестности точки х = 0, удовлетворяющую дифференциальному уравнению f'(x) = /(х) и условию /(0) = 1. Попытаемся
представить эту функцию в виде степенного ряда f(x) = апхп. Так как ДО) = а0»
п=0
то должно быть а0 = 1. Таким образом, мы хотим записать / в виде
/(х) = 1 + aix + а2х2 + ОзХ3 + а^+... .
Если ряд сходится, то по теореме 2 должно быть
/'(х) = at + 2a2x + ЗазХ2 + 4a4x® + ... .
Чтобы выполнялось равенство /'(х) = /(х), надо положить
а4 — 1, 2a 2 — а^, Заз а2, 4а^== а2, . . • , т. е.
„ , „ 1 1 1 1 1 1
— I > Оо —	—	, а? — — а» —-------, Ga — — а? —	, . . . •
2	2 1	2	3	3 2	2-3	4	4 3	2-3.4
§ 5. Степенные ряды
77
т. е. cij =	. Мы приходим к ряду
f (х) = 1 + — + — + — + ... • 'v ’	1	21	31
Сходится ли этот ряд? Применив к ряду абсолютных величин критерий частных (теорема 8 § 4.11), находим
I x"*i I lim J 7+2>!-L Л-СО	Xя
I nl I
= lim
Z1—*-ОО
\Х\ п+1
= 0.
Тем самым ряд сходится при всех х.
Если теперь вспомнить, что наложенные нами условия однозначно характеризуют показательную функцию е* (см. гл. 6, § 5.6), то мы получаем новое доказательство разложения ех = 1 Ч—р- +	+ ••• » независимое от теоремы Тейлора.ф
УПРАЖНЕНИЯ
Найдите радиусы сходимости следующих степенных рядов. Обычно это проще всего достигается применением к ряду из абсолютных величин критерия частных.
1-3-5 ... (2n —1)
2-5-8 ... (Зп —1)
1 S ПХп. п=0
2п — 1
Зп + 1
1-5-9 ... (4п —3)
(х + 2)«.
п=0
2-4-6 ... (2п)
(х-1)п.
Itz I
—= Ь. Покажите, что степенной ряд V ап (х— х0)п имеет радиус схо-ап ।	л=0
1
димости — при L =f= 0 и оо при L = 0.
00
8.	Пусть степенной ряд У, ап хп имеет радиус сходимости /?; каков радиус сходимости ряда п=0
со
2 ап рп хп, где р — постоянная?
п=0
78
8. Ряды
со
9.	Пусть степенной ряд 2 ЯпхП имеет радиус сходимости каков радиус сходимости ряда п—0
со
2 onxnkt где /г —целое положительное число? п—0
со
10.	Пусть степенной ряд 2 ап(х-~хо)п имеет радиус сходимости К; каков радиус сходимо-л=0
со
сти ряда 2 ап (х — xo)n+ft> где &— целое положительное число? л=о
В следующих упражнениях следует пользоваться лишь разложениями для cos х, sin х, arctg х, (1 + х)”1 и доказанными выше теоремами об операциях над рядами.
„	d sin х
11. Покажите, что-------= cos х при всех х.
dx
12.	„	d cos х Покажите, что	= — sin х при всех х. dx
13.	d arctg х	1 Покажите, что	,	— . Л при х <* 1. dx	1 + ха к
14.	X Представьте функцию f arctg t dt степенным рядом с центром 0 в интервале |х|<1.
5.4. РЯД ТЕЙЛОРА
Пусть х I-* f(x) — функция, представленная сходящимся рядом
/(х) = ^ап(х — х0)я.
/1=0
Применяя повторно теорему 2, заключаем, что функция f(x) имеет производные всех порядков. При этом
/' (х) = jp лап (х — Хо)*-1, Г (х) = 2 п (п — 0 ап <х — хо)""2. п= 1	п=2
/"'(х) = 2>1(п— 1)(л — 2)ап(х — х0)я-’ л=3
и т. д., вообще,
/(/) (х) = 2 л (л - 1) (л - 2)... (л - /+ 1) ап (х — х0)я'Л л=/
Подставляя х = х0 в ряды для Дх), f'(x), f"(x), f”(x) и т. д., находим /(х0) = л0, /'(х0) = Ль /"(хо) = 2аг, /'"(хо) = 3-2а3, вообще, /(/) (х0) = /!ау. Отсюда
а, =	, / = 0,1,2,...	(2)
§ 5. Степенные ряды
79
Как видно из этих формул, если данная функция может быть представлена степенным рядом с центром в точке х0, то лишь одним способом.
Пусть теперь f(x) — любая функция, определенная вблизи х0 и имеющая производные всех порядков; тогда мы можем вычислить по формуле (2) коэффициенты ар а затем построить степенной ряд
2 ai(х — V = 2 /(/)/|Х<>)~ — хо)У. /=0	/=о
называемый рядом Тейлора функции f в точке х0. Частные суммы ряда Тейлора суть многочлены Тейлора функции f в точке х0. (При х0 = 0 ряд Тейлора иногда называют рядом Маклорена.) Формулы (2) были доказаны в предположении, что f(x) = = 2а,(х— Xq)I-, это приводит к следующей теореме:
Теорема 3. Сходящийся степенной ряд (с центром в хь) есть ряд Тейлора его суммы (с центром в той же точке),
5.5. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Функция х ь-> /(х), определенная вблизи х0, называется аналитической в точке х0, если ее можно представить в виде суммы сходящегося степенного ряда с центром х0. Из теоремы 2 следует, что аналитическая функция имеет производные всех порядков.
Функция х »->/(х), определенная вблизи х0 и имеющая производные всех порядков, не обязана быть аналитической в этой точке; может случиться, что ее ряд Тейлора имеет нулевой радиус сходимости или ненулевой радиус сходимости, но сумма его не равна /(х).
Отметим следующий важный факт: сумма сходящегося степенного ряда есть аналитическая функция в любой точке интервала сходимости. Доказательство этого результата принадлежит общей теории аналитических функций и в этой книге не излагается.
Аналитические функции во многих отношениях ведут себя «наилучшим образом»; к счастью, функции, встречающиеся в приложениях анализа, как правило, аналитичны, за исключением некоторых отдельных точек.
•Примеры. 1. Функция х н* /(х) = — аналитична в каждой точке х0 =И= 0; в са-
мом деле, имеем
1 = 1____________= _1_________1 =
к (х — х9) + х0 xe ! x — Xq
хв
= — [i -	+ (х~Хв У-•••]= V (7+i)Z (х-
*о L хо \ хи J J JhJ xq
j=0
где ряд сходится при “— |<L т. е. при |х — х0|<х0. Функция х н* f (х) = 1/х не аналитична в точке хо = О, поскольку при любом определении /(0) функции не является непрерывной в этой точке.
80
8. Ряды
2. Показательная функция х*-+ е* может быть разложена в степенной ряд в любой точке х0; все полученные таким путем степенные ряды имеют радиус сходимости оо. Имеем
со
= е*»е*-*> =	+ х~х* _|_ (х~-х^2 + ...) = 2 -£-<* — хоИ-
/=о
3. Функция х *-> /(х), определенная условиями f(x) = е"1/х* при х =/= 0, /(0) = 0, имеет производные всех порядков (см. гл. 6, § 8.5), но не аналитична в точке х0= 0. Так как /(0) = f'(0) = /"(0) = ... = 0, то все коэффициенты Тейлора в точке х0 = 0 равны нулю и ряд Тейлора сходится к нулю; однако /(х) > 0 при х =/= 0.
Заметим, что та же функция является аналитической в любой точке х0 =/= О.ф
УПРАЖНЕНИЯ
Найдите ряд Тейлора с центром в данной точке Хо каждой из заданных функций. Затем найдите радиус сходимости ряда Тейлора [заметьте, что сходимость ряда Тейлора вовсе не означает. что он сходится обязательно к функции [(х), и даже не позволяет судить, где именно имеет место совпадение суммы ряда Тейлора и функции 1(х), разумеется, за исключением самой точки хо].
[Указание. В некоторых случаях легче найти ряд Тейлора функции Дх) посредством операций над рядами Тейлора других функций; в других же случаях проще всего найти ряд Тейлора прямо исходя из определения. Во всех случаях найдите общий член ряда и используйте для записи ответа X-символику (для этого может понадобиться выписать отдельно несколько первых членов ряда).]
15. £(х) = l/Vx, хо = 1.	20. /(х) = sin х, хо =	я/6.
16. f(x) = Х2/3, Хо = 1.	21. Дх) = 2», хо = 1.	
17. Их) = хЧ/4, Хо = 16.	22. [(х) = 1/(1 — х)а,	хо = 0.
18. Их) = 1/(2 — х)а, хо = 0.	23. Их) = х*/(1 — х),	хо = 0.
19- 1(х) = У 1 — х, хо = 0.	24. Цх) — ех*> хо = 0.	
25. Пусть f(x) «	, причем радиус сходимости ряда положителен. Дано, что ДО) = 1,
л—о
1М = К(х/Х) при постоянном X < 1; найдите коэффициенты ап. Затем найдите радиус сходимости. Отсюда видно, что существует одна и только одна функция аналитическая в точке 0 и удовлетворяющая поставленным условиям. При X = 1 имеем f(x) = ех . Что получается при X > 1?
5.6. ПРИМЕРЫ РЯДОВ ТЕЙЛОРА
Если дана функция /(х), имеющая ряд Тейлора в точке х0, то возникает вопрос, равна ли сумма этого ряда функции /(х) вблизи точки х0; решить его можно разными способами. Самый прямой путь доставляет нам теорема Тейлора: разложение
/(*) =
справедливо для тех х, для которых п-й остаток стремится к нулю при п -> оо. Этим путем мы выше получили разложения:
§ 5. Степенные ряды
81
е' = , + -п- + 1г + 1г + -’ * =	<3)
cosx = 1 £ = <»	(4)
sinx=x----£-+-£-----... . R = 00 •	(5)
□I 5!
1п(1+х)=х-----+ -----------?-+•••>	7? = 1>	<6>
2 о 4
ifS	jr5
arctgx=x------—+ —-----••• . R = 1-	(7)
О	□
Разложения (3) —(7) справедливы во всем интервале сходимости степенного ряда; радиус сходимости указан справа.
Другие разложения можно получить из этих простыми алгебраическими операциями (применяя в случае надобности теорему 4 § 4.6). Например, заменяя в (3) х на — х9 имеем
г	1	Я I &	1	D еГх = 1		h ••• > К = оо. 1!	2!	3!	(8)
Складывая и вычитая (3) и (8), а затем деля на 2, приходим к разложениям:	
и	.	х2 ,	X4	,	г, ch*	= ‘ +	2,	+	4,	+	- • «	“ »•	(9)
shх = х + ——h ——h ... , R = оо. 3!	51	(Ю)
Деля (5) на х, получаем	
sinx	.	ха , х4	Xе .	п 	 = 1	L 		F	,	А = ОО, х	3!	5!	7!	(И)
где стоящая слева функция при х = 0 условно считается равной единице. Далее, из (6) следует
1п(1 —х) = —х —-----------, Я = 1,	(12)
откуда, вычитая (12) из (6) и деля результат на 2, получаем
— |пТ^-=х+—+ —	, R = l.	(13)
2	1 — X	6	О	(
Можно также находить новые ряды Тейлора, почленно дифференцируя или интегрируя уже известные; законность этих операций гарантируется теоремой 2. Так, интегрирование геометрической прогрессии
—I— = 1 — х + ха — х3	...
1 + *
приводит к разложению (6); интегрирование ряда
—!_ = 1_х»_|_х* — х*+ ...
1 + *»
— к ряду для арктангенса (7).
82
8. Ряды
Дифференцируя (11), получаем ряд х cos х — sinx	2х , 4xs 6х6 ,
-------?----= —зГ + -й---------?Г + -	(14>
(который, можно, конечно, найти и другими способами). Интегрирование (11), как читатель легко проверит, дает разложение
представляющее интерес, поскольку функцию J,?1,” dt нельзя выразить через элементарные функции, не пользуясь знаком интеграла.
Подобное же положение возникает, если заменить в (8) х на х2, а затем почленно проинтегрировать полученный ряд. Имеем
	е~х = 1 —	— ч	X4	Xе 3! 1	(16)
		11 4	21		
И					
	X				
	J е~*‘ dt =х		X3 1! 3	4- xi 2! 5	X7 	-	1- ... . 31 7	(17)
	0				
Для малых значений х это разложение позволяет вычислить «интеграл ошибок» (см. гл. 6, § 8.3).
УПРАЖНЕНИЯ
Покажите, что ряд Тейлора функции f(x) в точке хо представляет f(x) для данных значений х. Сравните этот результат с радиусом сходимости ряда Тейлора.
А 26. Дх) = 1//7в точке xq = 1 для 1 < х < 2 (см. упр. 15). [В действительности ряд Тейлора представляет £(х) при 0 < х < 2, но это доказывается труднее; см. § 5.7.]
27.	1(х) = х~хК в точке xq = 16 для 16 < х < 32 (см. упр. 17). [В действительности ряд Тейлора представляет 1(х) при 0 < х < 32, но это доказывается труднее.]
28.	f(x)	=	sin х в точке xq —	л/6 для всех х (см. упр. 20).
29.	fix)	—	2х в точке xq = 1	для всех х (см. упр. 21).
30.	f(x)	=	1/(1 — х)2 в точке	xq = 0 для | х | < 1 (см. упр. 22).
31-	fix)	=	х*/(1 — х) в точке	xq = 0 для | х | < 1 (см. упр.	23).
32.	f(x)	=	ex2 в точке х0 = 0	для всех х (см. упр. 24).
X
33.	f(x) = f и ln(l + u)du в точке xq = 0 для |х | < 1. [Сначала найдите ряд Тейлора.] *0
X
34.	[(х) = J cos и2 du в точке xq = 0 для всех х. [Сначала найдите ряд Тейлора].
о
35.	Найдите представление функции l(x) = cosy х степенным рядом с центром хо = 0, справедливое при х > 0, т. е. во всей области определения f(x) = cos]/T. Найдите радиус сходимости этого степенного ряда. Таким путем получается функция, область определения которой содержит область определения первоначальной функции [(х) и которая совпадает с f(x) там, где f(x) определена.
§ 5. Степенные ряды
83
5.7. БИНОМИАЛЬНЫЙ РЯД
Есть другой способ убедиться в том, что функция представляется своим рядом Тейлора: доказывают, что этот ряд сходится и что сумма его обладает свойствами, характеризующими исходную функцию. Этим способом в § 5.3 мы показали, что X х*
ех = 1 + -jy 4- -gj- + ... . Применим тот же метод для доказательства биномиального разложения
(1 + х)л = 1 + «X4- “(‘"^х2 + °(“-П(а-2>хз + ... =
/1=1
а (а — 1) ... (а —п-Ь 1) хП _
|*1<1
(18)
(результат принадлежит самому Ньютону!). Сначала применим к ряду 2|(п)х" критерий частных:
lim Iа (а ~ Ч — (a — п + 1) (a — n) nl хп+' | = |jm I (а—п)х I /1->оо I Л (а— 1) ... (а — п4- 1) («4- 1)1 хп I я-оо| Л4-1 I
= lim /1->со
так что ряд сходится при | х | < 1 и расходится при | х | > 1. Для | х | < 1 положим
л=0
“ )х2 4-f “ ^х34-....
2 /	\ 3 /
Тогда
СО	00
//(х) = У (Z )лхя’1 = У (Л /1=1	л=0
(замена немого индекса) и
84
8. Ряды
Xf' W	( Л )
a=0 откуда следует, что оо
(1 +*)/'(*)= У? (( * , )(П + 1) + ( а ) nix".
I\Л + 1 /	\ п I I
о=0
Но
( ; ,)(n+D + (a)n= »(»-П(а-2)...(»-») (п+1) + \л+1/	\nj	(п 4-1)1
+ а(а-1)...(а-п-Ц) п = a(a l)...(g n+i) (а _ п +	= / а х
п\	п\	\ п /
Поэтому
(1 + х)/'(х) = а/(х), или
Г (х) = а f(x) 1 + X а это равносильно соотношению
d\nf(x) _ d In (1 4- х) __ d (а In (14-*)) _ d In (1 4- x)e dx	dx	dx	dx
Тем самым In f(x) — ln(l 4- x)a есть постоянная; назовем ее с. Тогда имеем 1п/(х) = 1п(1 + х)" + с, или Дх) =ес(1 + х)а; но ДО) =1 и (1 + 0)“ = 1, откуда ес = 1 и, наконец, Дх) = (1 + х)“, что и требовалось доказать.
ф Примеры. 1. При а = —получаем
7_
2
1-2-3-4
2. Заменяя х на —х2 в примере 1, имеем
1	] ха 1-Зх4	1-3-5х«	1-3-5-7Х8
у 1 _Х2 — + ~+ 2I22	312®	'	4\2*	!••••
Интегрирование дает
arcsinx- f dt -х+ х3 -к 13x6 4- Ь3-5х’ . Ь3.57х»
J У1 __/2	2-3	21225	3!237	4! 24 9
о
Это разложение справедливо при | х | < 1. ф
§ 5. Степенные ряды
85
УПРАЖНЕНИЯ
Применяя биномиальное разложение, найдите ряд Тейлора функции £(х) в точке хо и установите, в каких случаях этот ряд представляет [(х).
36.	f (х) = (х 4- 1)—1/3 в точке х0 = 0.
1
37.	f (х) = —	в точке х0 = 0.
У 1 4- ха
38.	f (х) = (х2 4- 1)2/5 в точке х0 = 0.
X
39.	f (х) = J /1 4- и2 du в точке х0 = 0.
X
40.	f (х) = J (1 4- и)5/2 du в точке х0 = 0.
41.	[ (х) в точке х0 = 0, где f (х) = arcsin х при х =£ 0, f (0) = 1.
5.8	. УМНОЖЕНИЕ СТЕПЕННЫХ РЯДОВ
Напомним, что степенной ряд абсолютно сходится внутри своего интервала сходимости. Теорема об умножении абсолютно сходящихся рядов в смысле Коши (теорема 12 § 4.15) в применении к степенным рядам приводит к следующему результату.
Теорема 4. Пусть
f (х) = а0 -4- аАх 4- а2х2 4- ... = а}х! при | х | < а,
/=о
g(x) = 60 + ьгх + Ь2х2 + ... = 2 ьих>) при |х|<р.
А=0
Тогда
f (х) g (х) = а0Ь0 + (аД + а, 50) х 4- (а0&2 4- а1й1 + а2Ь0) х2 4-
+ (аД 4- а1Ь2 4- а2Ь} 4- а3Ь0) х3 4- (а<Д + аД 4- а2Ь2 4- а3Ь3 4- а^0) xi 4-... =
= 2 ( 2 а) Ь*]х” =2 ( Х"
п=0	/	п=0 \ /=0	/
при | х | < 7, где f — меньшее* из двух чисел а, (3.
* Это записывается так: 7 = min (a,|J).
86
8. Ряды
Перемножив в качестве примера ряды
1	1	. ха । х3 । х* .
ш----= х Н--Н--------F ... ,
1—х	234
= 1 + х 4- х2 + X3 + ... , мы получим
1	1	/	у2	уЗ	у4	\
т4,пт4 = Г + Т + -Т + Т +-)(1 +* + х2 + *3+ ...) = 1 X 1 X \	£	О	/
=(х- 1)+(х.х+4 • iWx- *a+4-*+4- ’)+
+ (х-х3+^--х2+^-- х+^-.1)+ ...=
= 1+(1 + ±)д:. + (1 + 2. + Л^з+(| + Л + Л + 2_^. + ...=
Это разложение справедливо при | х | < 1.
5.9	. ДЕЛЕНИЕ СТЕПЕННЫХ РЯДОВ
В формулировке теоремы 4 лишь для краткости идет речь о рядах по степеням х вместо рядов по степеням х — х0. Из этой теоремы следует, что произведение двух функций, аналитических в некоторой точке, также является функцией, аналитической в этой точке. Есть и другая теорема, согласно которой частное двух аналитических функций также является аналитической функцией, если, конечно, делитель не обращается в нуль. Мы не станем доказывать эту теорему, а ограничимся сле-
дующим примером.
Функция х	sec х аналитична в точке xQ =0. Чтобы найти ее ряд
Тейлора, воспользуемся теоремой 4. Пусть sec х = а0 + QiX +	+ ••• ; на-
помним, что
Далее, мы имеем
1--------h
X* 4?
= а0. 1 +(0! • 1)х + (а0
^р- + а2- 1)х2+^а1 • -£р“ + аз- 1)*3 +
+ (“° 'Т + °2 ’ ~п~ + а‘ ’ О**+ С*1' «Г + °3 ’ ~гГ + а» ’ 9**+ •
§ 5. Степенные ряды
87
Итак, должно быть		
а0 • 1 = 1,	откуда	а0 — 1;
aj • 1 = 0,	»	О1 = 0;
а0-^— + «8’1 = 0,		1 1 а2 = —= — 1
° 2!	2		2	2!	2
о,	Н а3 * 1 == 0, 1 21	3	»	а3 =0;
° 4!	2!	4	»	1 .	1	5 Од — — — 4” *	= — > 4	41	(21)2	24
Qi	J- do	4" ^6 * 1 = 0, 1 4!	2!	»	а6 =0,
и т. д. Это — эффективный метод вычисления коэффициентов dj. Таким образом, sec х = 1 + — х2 4—— х4 4- ... .
2	24
Ясно, что метод, проиллюстрированный на этом примере, имеет общий характер.
УПРАЖНЕНИЯ
Примените технику умножения и деления рядов для вычисления первых пяти членов ряда Тейлора заданной функции f(x) в точке хо = 0.
42.	f(x) = ех sin х. Для каких х можно быть уверенным, что ряд Тейлора представляет Дх)?
43.	Дх) = ex arctg х. Для каких х можно быть уверенным, что ряд представляет Дх)?
ех
44.	f (х) = -j---. Для каких х можно быть уверенным, что ряд представляет f (х)?
45.	f (х) = tg х = sin х
46. Цх) =
COS X	е
-------— . Для каках х можно быть уверенным, что ряд представляет f (х)?
47.	f(x) =
1
1 + sin х
49. f (х) = ——
х
48. f(x) =
1 + 1п(1 + х) ’
51. a) f (х) = cos х • sin х.
б)
5°. f(x)=	.
1 + sin X
Покажите, что ряд Тейлора может быть записан в виде
(___	. 22/И
— ------——x2m+1. [Воспользуйтесь результатом упр. 89 из § 2.11 и умножением в
(2/п + 1)'
m=0
смысле Коши (см. § 4.15).]
88
8. Ряды
5.1	0. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
При вычислениях со степенными рядами может быть полезно следующее простое замечание. Если функция /(х) четна, то f'(x) нечетна; следовательно, /'(0) = = —f'(—0) = 0. Если /(х) нечетна, то /(0) = 0 и f(x) четна, так что f"(x) нечетна; отсюда/"(0) = 0 и т. д. Итак, ряд Маклорена (т. е. ряд Тейлора при х0 = 0) четной функции содержит лишь четные степени х, а ряд Маклорена нечетной функции — лишь нечетные степени х.
ф Пример. Функция
„ . е* — 1	1	. х х2 х* .
—- —+ —+ —+-
аналитична в точке х = 0 (где положено ДО) »1|. То же верно для g(x) = 1//(х)
(это следует из теоремы, приведенной без доказательства в § 5.9). Далее, функция
как читатель легко проверит, четна. Следовательно,
х _________*
е* — 1 + 2
=
/5о
Числа = /Ifty называются числами Бернулли; с ними приходится встречаться во многих вопросах анализа, ф
УПРАЖНЕНИЯ
Вычислите следующие числа Бернулли:
52. Во. 53.	54. В2.	55. В3.
56. Найдите коэффициенты а2, аз разложения
1 = аух2^ (справедливого
при малых | х |).
sin х — х cos х
57. Найдите первые три члена разложения Тейлора функции --------—---------в точке хо=О.
( оо	\ 2
2iajxJ | ПРИ малых 1*1 и а0= 1; найдите alta2t а3, М	'
59.	Пусть I 2	& 1	( 2 ai **) e 1	при	малых	I *1 • где af имеют 707 же смысл, что и в
\ л=о /	\ /=о	/
предыдущей задаче;	найдите Ьо, bit	b2t	b3.
§ 3. Степенные ряды
89
5.11. ПОДСТАНОВКА РЯДА В РЯД
Пусть f(x) = ап х" для малых |х| и g(x) = ^&>х4 так что g(0) = 0; /1=0	7=1
тогда функция f (g (х)) — аналитическая в точке х = 0. Мы не будем этого доказывать, но покажем на примере, как вычисляется ряд Тейлора композиции функций.
Пусть f (х) = ех, g (х) = sin х. Имеем
esin х = 1 ч- sin* I sin2* I sin3x 1!	2!	3!
Повторно применяя умножение по Коши, находим разложения sin2 х, sin3 х, sin4 х, ..., подставляем их в предыдущий ряд и «приводим подобные члены». Разумеется, мы имеем дело при этом с бесконечными суммами, но вычисление каждого из коэффициентов ряда Маклорена функции esln х требует лишь конечного числа шагов. Действительно,
и т. д. Точно так же разложение sin*x начинается с члена xk. Поэтому, чтобы получить в разложении е8,Пх член с х*. достаточно рассмотреть лишь члены до
—п *. Мы имеем, таким образом,
+	+	+ +	+	-7—Й-+--
Конечно, то же разложение прямо вытекает из теоремы Тейлора; читатель может самостоятельно убедиться в этом, если пожелает.
90
Приложение к главе 8
УПРАЖНЕНИЯ
Вычислите первые пять членов ряда Тейлора заданной функции [(х) в точке Хо = 0, поль-
зуясь изложенными выше приемами. А 60. f (х) = sin (	1	— l') . 61. [ (х) = cos ( е*2 — 1).	64. f(x) = garctgx 65. f (x) = arctg ( *	— 1) . \1 — xa /
62. f (х) = cos (sin х). 63. f (х) = arctg arctg x.	66. f (x) = cos (In (1 Ч-Х)). 67. (x) = In (14-sinx).
5.12. ПРИМЕЧАНИЕ
В заключение этой главы отметим любопытные аналогии между рядами Маклорена, казалось бы, совершенно различных функций:
х3 ।	%5	,	, х3 хБ ,
sinx = х--------------... , shx = х Ч-------------h ... ,
3!	5!	315!
i Ха , X4	i	1	, Ха , Х^ |
cosx = 1--------------... , chx = 1 Ч-------------И ... ,
21	4!	21	41
А	X3	, X6	1	.	1 4“ х	,	X3 . X6	,
arctg х = х-----------... ,	— In-1 - = х Ч------------h ... •
6	3	5	2	1 -х	'	3 ~ 5	'
Причина, лежащая в основе этих аналогий, выясняется лишь после введения комплексных чисел — при изучении степенных рядов с комплексными коэффициентами.
Приложение к главе 8
§ 6. Правило Лопиталя
Мы изложим теперь метод вычисления некоторых пределов, известный под названием правила Лопиталя\ он основан на следствии из обобщенной теоремы о конечном приращении (теорема 2 § 1.4).
6.1. Неопределенности вида 0/0
Основное правило Лопиталя относится к вычислению предела дроби F(x)/G(x) в точке а, если Г(а) = С(а) = 0. Оно применимо, когда F и G непрерывны в точке а и имеют непрерывные производные во всех точках вблизи а, кроме, возможно, точки х«=а, причем G'(x)=/=0 при х =/= а. Это правило гласит:
F'
если lim F(x) = lim G(x) «= 0 u предел lim - v существует, то x-*a	x-*a	x-*a G (x)
.. F(*) Iimf'(*)
lim " = nm —- .
x->a G (x) x-+a G (x)
(1)
§ 6. Правило Лопиталя
91
Доказательство не представляет труда: в силу следствия из теоремы 2 § 1.4 для любого х =/= а найдется такое 5 между а и х, что F(x)lG(x) = F'(£)/G'(£). Если х близко к а, то и 5 близко к а, и F'(S)/G'(>) близко к своему пределу.
Правило Лопиталя служит, как иногда говорят, для «раскрытия неопределенностей вида 0/0». Может случиться, конечно, что F'(а) = G'(a) = 0. В этом случае можно попытаться применить правило Лопиталя повторно. Если существует предел lim F"(x)/G''(x), то имеем
х-+а
.. F (х) f. F”(x) lim —т2— = lim	t .
G (x) x-+a Gn (x)
Иногда приходится повторять этот прием несколько раз. Конечно, успех при этом не гарантирован. Предел отношения в точке может не существовать, и даже если он существует, то не всегда поддается вычислению по правилу Лопиталя.
Правило Лопиталя в свое время произвело большое впечатление на специалистов; в современной математике оно оценивается гораздо скромнее.
rr , sin х — ех + 1
ф Примеры. 1. Найти lim------------------.
Решение. Дважды применив правило Лопиталя, получим
. sinx— 6х 4- 1 cos х — ех	— sinx —е* *	1
lim------------------ lim---------= lim--------------= — — .
х-*0 х2	х->о 2х х-*о 2	2
2.	В чем ошибка следующего рассуждения, основанного на правиле Лопиталя:
d (1 — 2х)
.. 1—2х .. dx	— 2	1
lim ------= lim--------------- lim------= — — ?
x-*0 2 + 4x x-*0 d (2 + 4x)	x-*0 4	2
dx
Ответ. Поскольку в точке х = 0 функции принимают значения 1 и 2 (а не 0 и 0), правило Лопиталя неприменимо, ф
УПРАЖНЕНИЯ
Вычислите следующие пределы, пользуясь правилом Лопиталя.
1.	lim х->1
4х3 — Зх2 4~ 4х — 1
Зх2 — 4х + 3
1п х
2.	lim------------.
х->о х —
„	х4-х2/3+4
3.	lim
8 2Х273 Ц-2х1/3 — 4
л .. х3 —2х2 — 4х + 8
4.	lim-------------1,
г-2	х3 —• 4х2 4- 4х
Гийом Франсуа маркиз де ЛОПИТАЛЬ (1661—1704), принадлежавший к высшей французской знати, был математиком-любителем и покровительствовал математикам. Он учил» у Иоганна Бернулли,  результате чего появился учебник анализа *, содержащий правило Лопиталя.
* Он переведен на русский язык: см. Г. Лопиталь, Анализ бесконечно малых, М.—Л., ОНТИ, 1935.
92
Приложение к главе 8
„ .. 1 — cos2 я 7. lim—г—— . х-*0 sin (х2)
8.	lim
(X— 1)а (х«—1)4/3 '
9.	lim х-*2
х — У~2х х3 —8
10.	lim х->0
In cos х
X2
arctg х2
11.	lim --------------.
x-*o x sin x
(arctg x)2 lim---------------
x-*o in (x2 + 1)
13.
r->0 1 — cos 2x
14. lim
X->k/4
cos x — sin x mtgx
sin (2x3)
15. lim——— x-*o sin3 (2x)
6.2.	Неопределенности вида оо / оо
Другой случай, к которому применимо правило Лопиталя, — это «неопределенности вида оо/оо». Соответствующая теорема гласит:
Fz (х)
если lim F (х) = + оо, lim G(x) = -f- оо и предел lim --- существует г то
х-+а	х-*а	х->а О (х)
lim х->а
G(x)
.. (*) lim —-------.
х-*а G (х)
(2)
В этом случае доказательство сложнее; мы лишь наметим его. Пусть
Возьмем число Xf а и рассмотрим число х. заключенное между а и х*. В силу обобщенной теоремы о конечном приращении (теорема 2 § 1.4) существует такое число хо, заключенное между х и Xf, что
F (х) — F (xt) = F' (х0)
G(x)-G(X1)	G'(x0) •	U
С другой стороны,
F(x)-F(x1) _ F(x) l-(Flx1)/F(x))
G(x)—G(xt) 6(x) 1 — (G(X1) / G (x)) ’
и (3) можно записать в виде
F(x) _ 1 — (хх) / G(х)) F' (х0) G (х) “ I - (F (хг) / F (х)) G' (х0) ’
Но точка Хо лежит между xj и а и, следовательно, она ближе к а, чем Xf. Поэтому, если xj достаточно близка к а, то дробь F'(xo)/G'(xo) будет сколь угодно близка к L. С другой стороны, если закрепить xj и взять затем х достаточно близким к а, то | F(x) | и | G(x) | будут сколь угодно велики, дроби G(xj)/G(x) и F(xt)/F(x) — сколь угодно близки к нулю и множитель
§ 6. Правило Лопиталя
93
заменить на —оо.
l-(G(xi)/6(x)) l-(F(x1)/F(x))
— сколь угодно близок к единице. Тем самым при х 4= а, но достаточно близком к а, дробь F(x)IG(x) будет сколь угодно близка к L, что и требовалось доказать Очевидно, правило (2) сохраняет силу, если +оо
, In sin2 х •Пример. Найти lim------- .
х-о ctg х
Решение. По правилу Лопиталя получаем
In sin2 x (1/sin2 x) 2 sin x cos x lim------------= im-----------------------------
x-o ctgx x->o — 1/sin2 x
= ‘lim (— 2 sin x cos x) = 0. *
6.3.	Обобщения
Правило Лопиталя справедливо также для односторонних пределов; здесь не нужно нового доказательства. Правило сохраняет силу и в случае, когда lim F'lG' равен +оо или —оо; это также не нуждается в новом доказательстве. То же верно и в случаях, когда а = +оо или а = = —оо; в самом деле, если lim F(x) = 0, lim G(x) =0, то, по определению пределов на бесконеч
ности,
.. F(x) n F(l/x) hm —- = lim ——; -*+« G(x) x_>oi-G(l/x)
и, по правилу Лопиталя, F(x)	dF(l/x)/dx .. F'(1/x) (—1/x2)	F'(l/x)	F' (x)
hm — -----= lim — ----------= lim —---------------— = um ——-------lim ——-----------
r^+oo G(x) x^o* dG(\/x)/dx x-o*G (1/x) (—1/x2)	x->o> G' (1/x)	t-4-00 G' (x)
в предположении, что последний предел существует.
УПРАЖНЕНИЯ
Вычислите с помощью
правила Лопиталя следующие пределы:
In X2 lim--------.
x->o 1/x
..	Intgx
hm ------------
х-Ик/2)- tgx
.. In (x — 1)
In (x2 — 1)
19. llm	.
x-»-l+ In (X — 1)
16.
17.
18.
21. lim
Х-И+ In (2x2 — X — 1) .. in (6х — 1) 22. hm ----------------- .
x«*0*	1/*
In (e* — 1) In 3x
. 9R llm arctg (2/x) A 26. lim -----------—-------
X—►-f-QO	1 / X
27. lim
23.	lim x-O*
24.	lim
28.
lim
20. lim г-(1/2)* In 2x
25.	lim
In (2x8 — x — 1) In (x2 — 1) X In X
• (x+i)2 ’
29.
30.
lim
J/x lim -4---- .
x^cn In x
х
94
Приложение к главе 8
6.4.	Другие неопределенные выражения
Правило Лопиталя позволяет «раскрывать» и другие «неопределенности», т. е. находить пределы других видов. В каждом случае надо сначала привести подлежащее исследованию выражение к виду F/G. Как это делается, лучше всего объяснить на примерах.
•Примеры. 1. (Случай оо/оо.) Hafynu предел lim ------------.
*-*+« 2х3 + х
Решение. Этот предел легко определить и прямым путем (ср. выше т. I, стр. 143, пример 2). Покажем, однако, что здесь применимо и правило Лопиталя:
x8-f-3 Jim Зх2	6х 1
2х3 + X	x-t—|-00 6x2 _|_ ] х->оо 12х	2 *
2.	(Случай 0 • оо.) Найти предел lim х 1пх.
Решение. Сводим задачу к случаю оо/оо:
1
1 п
lim х In х = lim ------ lim —-— = lim (— x) = 0
x-*o+	x-*o*	1	x->o+ i x->0+
x "~’72‘
(рекомендуем читателю сравнить это с рассуждением § 5.7 гл. 6).
3.	(Случай оо — оо.) Найти предел lim х-*о
Решение. Сведем задачу к случаю 0/0. Поскольку ctgx х — tgx --------, имеем
х tg х
1  ctgx X X
1
Ctgx
/ ,	1 \	X — tg X
lim I ctg x — — = lim--------------------= lim
x-*0 \	X J x-0 xtgX x-*-0
i_____L_
_____cos2x —= lim
.	x	x-*0 sinx C0SX4-X
tg x + —4-
COS2 X
cos2 х — 1
— sin2x w. — 2sinx cosx 0 = lim —---------------= lim-----------------= — = 0,
J_sin2x + x	cos2x-f-l 2
2
4.	(Случай l00.) Найти предел lim x-*--|-oo
Решение. Найдем этот предел с помощью логарифмирования. Положим <? (х) =
Тогда
§ 6. Правило Лопиталя
95
а так как логарифм и показательная функция непрерывны, имеем
,	. . „	lim ? (х)
lim 1 4- — = е	= е1 = е
х->4-оо \	х /
(сравните это рассуждение с доказательством теоремы 8 § 5.9 гл. 6).
5.	(Случай оо®.) Найти limx*”**
Решение. Поступаем, как и в случае 4:
г ..	In я	“7"
lim In Xе = elnx= hm —	 = lim —_— = 0.
X-»--]-00	X-*-f-09	X-*-|-00 C	x->4-00 0х
Отсюда
lim x?~x = e° = 1. ф
X->H-oo	W
УПРАЖНЕНИЯ
Найдите с помощью правила Лопиталя следующие пределы:
.. In sin х 31. lim ------------.
х-о* In (е* — 1)
32.	lim (— — —-—. х-*о \ х sin х /
33.	lim х1/3 In х3. х->(Н
34.	lim xln2x. х->0+
35.	lim (In x) (In (x + 1)').
X-*O*
36.	lim (secx—tgx).
x-*k/2
37.	lim (sin x) (Inx). x->0+
/	1
38.	limit-J-—-) . x-+o\	xa /
39.	lim (l+2x’)3/-'’. x->0
/ 1
40.	lim I 1 4- — | . x /
41.	lim (ln(x4- 1))* x->0
A42. lim (sin x)x. r->0
43.	limx1/(1 x) x-*l
44.	lim x2 . x->0+
45.	lim (arctg x)I/ln*.
96
Приложение к главе 8
§ 7. Доказательства сходимости
В этом параграфе мы докажем некоторые предложения о последовательностях и рядах, сформулированные в тексте без доказательства.
7.1. Монотонные последовательности
Докажем сначала основную теорему 3 § 3.8. Согласно этой теореме, неубывающая ограниченная последовательность
ai -С а а С < ...
имеет предел, и этот предел равен наименьшему числу, которое не меньше всех членов aj последовательности.
Доказательство несложно. Пусть наша последовательность ограничена. Тогда множество всех чисел aj ограничено и имеет в силу принципа верхней грани наименьшую верхнюю границу М. Надо показать, что
lim а/ = М. j-+QO
Чтобы проверить условие I в определении предела, допустим, что М <Л. Поскольку М — верхняя граница, aj < М для всех /. Следовательно, а/ < А для всех /.
Проверка условия II начинается с допущения, что В < М. Так как М — наименьшая верхняя граница, В не является верхней границей; поэтому последовательность содержит число ап ^>В. Поскольку последовательность не убывает, при j >п имеем ау > ал > В; следовательно, почти все члены последовательности больше В,
УПРАЖНЕНИЕ
1. Докажите прямым путем, что невозрастающая ограниченная последовательность имеет предел (видоизмените доказательство, данное выше для неубывающих последовательностей).
7.2. Перестановка членов ряда
Рассмотрим теперь сходящийся бесконечный ряд
00
/=0
и исследуем, к чему приводит перестановка его членов. Мы докажем тем самым теорему 11 § 4.14. Можно считать, что ни один из членов aj не равен нулю, поскольку такие члены ряда свободно могут быть опущены. В силу сходимости ряда имеем
lim at = О
/-*00
(теорема 2 § 4.3). Следовательно, для каждого числа Т>0 почти все aj удовлетворяют неравенству \aj | < Т. Поэтому мы можем собрать все положительные члены ау и расположить их в убывающем порядке. Обозначим эти члены через ао» а*, аа, ... . Тогда
ао > «1 > а« > ... » ау > 0, lim ау = 0.
§ 7. Доказательства сходимости
97
Аналогично, все отрицательные члены ду, расположенные в порядке убывания абсолютных величин, обозначим через —р0, —Pi, —Р 2....Тогда
Положим теперь
₽;>0,
lim Ру = 0. /-►оо
со	оо
/=0	/=0
Ро > ₽1 > ?2 >
(если не существует чисел а, считаем Р = 0, если не существует чисел р, считаем W = 0). Конечно, в качестве возможного значения Р или N следует допустить +оо. При этом, впрочем, либо Р = +оо и N = +оо, либо Р < +оо и N <+оо. (Иными словами, ряды, образованные положительными и отрицательными членами сходящегося ряда, либо оба сходятся, либо оба расходятся.) В самом деле, предположим, что Р = +оо и N < +оо. Тогда для любого т имеем т
^д/ = Sm— Тт, где Sm— сумма всех положительных членов из числа до, at, ...»	а —Тт
/=о
т
—сумма всех отрицательных членов из числа до, ар...» ат- Очевидно, Q<Tm<N, откуда ^aj > /=о
> Sm — N. Но если т достаточно велико, конечная последовательность aQ, д/,..., ат содержит
т
сколь угодно много членов ao, а$, а2,... и Sm, а значит, и ^д/ сколь угодно велика, что противо-/=о 00
речит предположению о сходимости ряда ^д;.
/=о
Мы показали, что случай Р = +00, N <+оо невозможен; точно так же устанавливается, что невозможен случай Р <+°o, N = +00.
00
Покажем теперь, что если Р <+00, N <+оо, то ^д; = Р — N. В самом деле, сохраняя /=о
предыдущие обозначения, достаточно заметить, что при большом т сумма Sm становится сколь угодно близкой к Р, а сумма Тт — kN.
00	00
Заметим, наконец, что ^1 aj I = ? + N (иначе говоря, ряд ^]д/ сходится абсолютно в том /=о	/=о
и только в том случае, если Р < +оо и N <+оо). Доказательство этого предоставляется читателю.
Предыдущие рассуждения содержат доказательство первой части теоремы И § 4.14: абсолютно сходящийся ряд остается сходящимся, если произвольным образом переставить его члены, причем перестановка не влияет на сумму ряда.
Пусть теперь
Р = -|-оо, N = 4~оо;
покажем, каким образом можно переставить члены	и —ру так, чтобы получился расходящий*
ся ряд.
98
Приложение к главе 8
со
Поскольку 2ай = +°°» можно разбить этот ряд на «отрезки* следующим образом: л=о
°о + а1 + а2 +•••+“/», + ал,4-1 + аЯ1+2 4~ ... 4~ % + ал,4-1 + ап,+2 + •• + ап, +
>₽1 + 1
>Рг4- 1
+	ал,+1+	 + %+ —
>Рз4-1
Ряд
ао + ai 4-... + °л, + (— Pi) + ап,-|-1 + •••+% + (— Рг) + an,+i 4- ••• 4-%, 4"
4- (— Рз) 4- an,+i 4- ••• 4- а„4 4- ...
получается перестановкой членов первоначального ряда и расходится (так как каждый из отмеченных скобкой «отрезков» ряда >1).
Пусть теперь з — какое угодно наперед заданное число. Покажем, что члены а«< Of,	—Ро, —pt, ... можно переставить так, чтобы получить ряд, сходящийся к з:
ao4-ai4- ... 4-а„, 4- — Ро — Pi — ••• — Рт, 4- ал,+1 4- ••• 4-%, 4- — Рт,-ц ~ ••• — Pm, 4-
°1	Т1	°2	т2
4- %+14~ ... 4-% 4- — Pm,4-1 ~	~ Pm, 4- “л,4-14- ... .
°3	Х3
Для этого примем за nt, т<, па, та, ... наименьшие целые числа, такие, что <*1 > s, 4~ Ti < з, Of + Ti ®2> $, 4* Ti 4- «г 4- т3< s, <Ti 4- 4- <та 4- та + a3>s 
00	00
Число ax существует, поскольку 2а/ = +°°; число существует, поскольку у = +оо; число /=о	/=о
00	00
02 существует, поскольку 2а/ — +оо; число Тя существует, поскольку УР / = +оо, и т. д» /=пх4-1
Частные суммы построенного таким образом ряда колеблются около s.
Далее, поскольку п± — наименьшее число, для которого <7$ > s, имеем | о^ —s | < аЛ1; точно так же, поскольку т± — наименьшее число, для которого ах +	< s, должно быть [(с^ +
+ Т1) — s I < PmU по той же причине |(аХ' + tx + ст2) — s| <си2; 1(^4- Tj + ст2 + Тг)| — s < < Рт2 и т. д. Так как lim ау- = lim (3у = 0, построенный нами ряд действительно сходится к s.
Тем самым мы доказали вторую часть теоремы 11: если ряд сходится, но не абсолютно, то его члены можно переставить таким образом, чтобы получился либо расходящийся ряд, либо ряд» сходящийся к любому наперед заданному числу.
§ 7. Доказательства сходимости
99
УПРАЖНЕНИЯ
оо
2.	Пусть ряд 2 I aj\ сходится; покажите, что Р<+ оои +оо. /=о
00
3.	Пусть P<Z + оо и Л'< H-оо; покажите; что ряд 2 I aj\ сходится.
1 /==°
4.	Переставьте члены ряда 1 ——— — —+ ... таким образом, чтобы полученный ряд расходился.
5.	Переставьте члены ряда 1 —— 2-|- t. таким образом, чтобы полученный ряд сходился к 1.
7.3. Произведение в смысле Коши
Наша следующая цель — доказательство теоремы об умножении абсолютно сходящихся рядов (теорема 12 § 4.15).
Пусть а/ = А» 2 ' aj । = < + 00» 2	=	2 I 1 ~ ^ < + °°; построим сначала
ряд
I До I I I + (I а91 I I + I ai I I I) + (| I I &21 4” I ai I I I 4“ I а21 I I) 4" ... =
= 2 । 2i«/i |ь»-/1) •	0)
п=0 \ /=0	/
N f п	\
Частная сумма этого ряда 2 I 2 । а)\ I ^л-/I 1 есть сумма положительных слагаемых. Все эти
п=о \ /=о	/
слагаемые входят в число тех, которые получаются при раскрытии скобок в произведении
N	\ ( N	\
2 I I) ( 2 I I Г» поэтому наша частная сумма не превосходит /?S. Но тогда из теоремы /=о	/ \ л=о	/
5 § 4.7 следует, что ряд (1) сходится; тем самым ряд
л=о \ /=0	/
(2)
(произведение по Коши) абсолютно сходится.
Обозначим сумму ряда (2) через С. Для завершения доказательства теоремы 12 остается показать, что С = АВ. Пусть Л у и By — N-e частные суммы рядов Zay, 2&у, Су — N-я частная сумма ряда (2). Тогда для любого целого положительного N
| ^2W	““	| —
2N	\	2N /
2	— 2 ( 2 aj
А=0 /	n=0 \ f+k=n
= | суммы всех членов ajbk\t где j < 2W, k < 2^, / +	> 2Af <
< суммы всех членов | ay || bk |, где j < 2Af, k < 22V, j + k > 2N <
< суммы всех членов |ау || bk (, где j < 2W, k < 2N и либо j > N, либо k > N =
2N	\ / 2N	\	/ N	\ / N
2i«/I 2i^i - 2lа)I 21 м
/—О	/ \Л=0	/	\/=о	/ \Л=0
100
Приложение к главе &
Но
поскольку
5 ifc*i
Л=0
Я$-Я5 = 0,
мы приходим к выводу, что /45 — С == 11Ш	=e
У-*»
Это и завершает доказательство.
§ 8. Радиус сходимости
Мы переходим теперь к доказательству предложений о степенных рядах, сформулированных без доказательства в § 5.2 (теоремы 1 и 2). Для упрощения записей можно, конечно, ограничиться рядами по степеням х (т. е. такими, что Хо = 0).
8.1. Лемма Абеля
Лемма 1 (лемма Абеля). Пусть степенной ряд
5 в»хЯ	а>
/1=0
сходится при некотором х = р ф Ъ тогда ряд абсолютно сходится и для | х |<р, причем су* ществует такая постоянная М что
Это основной результат теории степенных рядов. Доказательство его весьма просто. Пусть со
ряд 2апРл сходится; тогда по теореме 2 § 4.3 имеем lim а„р п = 0. Но в таком случае, по опреде-п=0
лению предела, ianpn 1< 1 для почти всех п;
пусть это верно для П. Обозначим через М наибольшее из чисел | во |, | Д(Р |, | а&Л |, ... ..., | ацрм |и 1; тогда при всех п имеем | апрл1 <М. или. что то же, ) ап ||р |Л<Л1. Поскольку р ф 0, отсюда следует утверждение (2).
Пусть теперь х — число, удовлетворяющее неравенству । х |< |р |. Тогда
и в силу (2)
I ап *п I <Л1|у"| •
Тем самым члены ряда (1) не превосходят по абсолютной величине членов геометрической прогрессии
ЛЦ-м|у-|+Л1| -у-| 4- ... .
Следовательно, по теореме 6 § 4.8, ряд 2| апхп | сходится и ряд (1) сходится абсолютно (см. теорему 10 § 4.13)
§ 8. Радиус сходимости
101
8 2. Радиус сходимости
Л е м м а 2. Пусть степенной ряд (1) сходится при некоторых х =£ 0, но не при всех х. Тогда существует такое число R^>0 (радиуссходимости), что ряд (1) абсолютно сходится при | х |< R и расходится при | х |> R.
Доказательство. Предположим, что ряд (1) сходится при х = р х 0 и расходится при х =р2- Тогда ряд (1) сходится при всех х, для которых | х |< |рх |, и расходится при всех | х |> |р2|, как это следует из леммы Абеля. Пусть S — множество всех таких положительных чисел р, что ряд (1) сходится при | х|<р. Это множество не пусто: оно содержит число |pt |. Оно ограничено: верхней границей служит |р2 |. Пусть R — наименьшая верхняя гра-
оо
ница (т. е. верхняя грань) S. Тогда при | Хо |< R ряд сходится, поскольку в противном /1=0
со
случае | х0 | была бы верхней границей S. Точно так же, p*Ji£aaXin сходится при всех хь удов-п=0
со летворяющих неравенствам | Хо |< | х± | < R; но тогда ряд	по лемме Абеля, сходится
п=0 со
абсолютно. Допустим, далее, что |х2 | > R. Тогда ряд 2 апх2 расходится, потому что если бы он л=0
сходился, то, по лемме Абеля, число | х2 | принадлежало бы S.
Итак, R — искомый радиус сходимости.
Если ряд сходится для всех значений х, полагают R = +©о; если он расходится при всех х =/= 0, полагают R = 0.
8.3. Дифференцирование и интегрирование рядов
Лемма 3. Три степенных ряда
2 апхЛ-
пап хп~х ,
X1
«4-1
хл+1
(3)
имеют один и тот же радиус сходимости.
Доказател ьство. Обозначим радиусы сходимости рядов (3) соответственно через R, R* и R* (эти символы могут быть неотрицательными числами или +оо).
Если RZ> 0, возьмем такое число р, что 0<р < R. Тогда по лемме Абеля имеем неравенство (2) и при |х |<р
хп'х
М | г | / | х|\л л-b i \ Р /
Q/i хп+' п + 1
\ р /
так что члены второго и третьего рядов (3) не превосходят по абсолютной величине соответствующих членов сходящихся рядов:
М М |х| М | х I2	М/ | х I \’2
+ 2	4- 3	- -f- ... = I 1 — j ,
р рр рр-	р \ р /
1x1	/ I х I \2	/	1x1 1
'А4| х|4-М|х| —-4-2И|хЦ *—L| 4- ... = М | xll 1 — —11 .
Р	\ Р /	\	Р /
102
Приложение к главе 8
Применив теорему 6 § 4.8, заключаем, что второй и третий ряды (3) сходятся при | х | <р < R и , следовательно, при всех | дг |< R. Отсюда R* > R и R# > R.
Но первый из рядов (3) получается из третьего точно тем же способом, как второй из первого, а именно почленным дифференцированием. Поэтому имеем также R > R* и R > R*, откуда
R= R* = R*.
8.4. Доказательство непрерывности
Лемма 4. Пусть
00
ряд ^алхп сходится при | х |< А (где А> 0); положим п=0
[(х) = 2апхп.
(4)
Тогда f,(x) непрерывна при | х |< А.
Доказательство. Докажем непрерывность [(х) в некоторой фиксированной, но произвольной точке 6 , где | Е |< А. Точнее, мы покажем, что при любом заданном е> 0 неравенство | f(x) —ДЕ) |<е выполняется для х, близких к 6.
Возьмем такие числа аир, что
|ё |<а<р< А.
(5)
В силу леммы Абеля справедливо неравенство (2). Положим
2 апхП-л=/л4-1
При | х | < а в силу теоремы 10 §4,13имеем
Р
Пусть задано число е> 0. Возьмем такое число т, что
I Rm (*)1 < при | х | < о;	(8)
/ о \m4-l
это возможно в силу (7), поскольку lim [—| =0. Закрепив значение т, положим т-*<х> \ Р /
Sm(x)= апхп.	(9)
n=Q
Тогда
ftx) = Sm(x) + Rm(x).	(10)
В частности, f(6) = Sm (6) + Rm(i) и вследствие (8) имеем
f(5)-y<SOT(5)</(6) + y .
§ 8. Радиус сходимости
103
Так как Sm(x) — многочлен и, значит, непрерывная функция, то для всех значений х, близких к £, мы имеем
ftf)-Y<Sm(x)</(e)+ Т‘
di)
Из (8), (10) и (11) следует, что при х, близких к 5, справедливо неравенство
I® -е<ах)<де)+8,
чем и завершается доказательство.
8.5. Дифференцирование и интегрирование степенных рядов
Лемма 5. В условиях леммы 4 имеем
(12)
при | х |< А.
Доказательство. Достаточно доказать (12), предполагая, что | х |< о<р < А. Пользуясь обозначениями предыдущего доказательства, имеем

В силу (7)
| X | При | X I < а.
Отсюда lim \R a) dt = O и m-*co J 0
b(t)di= lim f Sm(t)dt= lim f 2 a„tndt=z
/И-*ОО $
«-*°° o n=0
an Xn+1
an xn+1
m->oo
n—0
П 4- 1
П Ц- 1

что и требовалось доказать.
104
Приложение к главе 8
Лемма 6. В условиях леммы 4 имеем
f'(x)= 5 ««л*""1-
/1=1
\
00
Доказательство. Положим g (х) = 2 пап хП~х Для I х К А, по лемме 3, ряд схо-/1=1
дится, а по лемме 4, g (х) непрерывна. По лемме 5,
X	00
J g (0 dt = 2 вл *” = / (*) — а0.
О	л=1
Но тогда, по основной теореме анализа, g(x) = ['(х).
Очевидно, в леммах 1—6 содержится доказательство теорем 1 и 2 § 5.2 и 5.3 для случая хо =0;но ясно, что если упомянутые теоремы верны при xq=O, то они верны и при любом xq.
УПРАЖНЕНИЯ
1.	Пусть k—фиксированное целое положительное число. Покажите, что ряды
2 апхП и 2	—2) ... (Л —
п=0	п=Л4-1
имеют один и тот же радиус сходимости.
оо
2.	Сформулируйте и докажите аналог леммы Абеля для степенного ряда ^дл(х—хо)\ п=0
3.	Сформулируйте и докажите аналоги лемм 2—6 для степенного ряда с центром хо.
§ 9.	Погрешности методов численного
интегрирования
В этом параграфемы даем оценки для погрешностей методов численного интегрирования, приведенные в § 1 гл. 7. Подчеркнем, что в этих оценках не учитываются ошибки округления чисел, практически неизбежные при любых вычислениях.
9.1.	Оценка для правила трапеций
Пусть Дх) — непрерывная функция, заданная в конечном интервале [а, 6], аф (х)— линейная функция, совпадающая с f(x) в концах интервала, т. е. удовлетворяющая условиямф(а) = /(а), Ф(/?) — №)• Положим
ь ъ
Е* = [f(t)dt-^(t)dt.
а	а
§ 9. Погрешности методов численного интегрирования
105
Мы хотим оценить Е*, предполагая, что [(х) имеет в интервале [а, Ь] непрерывную вторую производную и что
|Г(0| < Л12.	(1)
Для этого положим
р	р	Г (х — а\з [х — а\2)
2(х) = р(')<«-Р(0<й+{2	_3
а	а
Тогда g(a) = 0, g(b) = 0 и, по теореме Ролля, найдется такая точка с, что a<Z c<Z b и g’(c) = 0. Легко подсчитать, что g'(a) = g’(b} = 0. Но тогда, опять по теореме Ролля, существуют такие точки и с2, что а< с, c<Z с2< b и g"(ci) = 0, g"(c2) = 0. Еще раз применив теорему Ролля, приходим к выводу, что между и с2 существует точка у, для которой g"'(y) =0. Поскольку ф"(х) = 0, имеем
0 = Г'(«/)=Г(</) + 7Г^7£*.
Принимая во внимание (1), получаем требуемую оценку
(Ь — а)3
IЕ* | < —----- М2.	(2)
Пусть теперь интервал [а, 6] разбит на п равных частей, длины h каждый; применим правило ь
трапеций для вычисления приближенного значения интеграла J Это значит, что для каж-а
дого подынтервала функция / заменяется линейной функцией, совпадающей с f на концах подынтервала, вычисляется интеграл от линейной функции, а затем полученные п чисел складываются. Согласно только что доказанному результату, погрешность при вычислении интеграла по каждому подынтервалу не превосходит по абсолютной величине Л3Тем самым общая абсолютная погрешность не больше
n/i3M2 t	М2
----Z- = (b — a} h? —-7- •
12	12
Это и есть оценка, приведенная в § 1.5 гл. 7.
УПРАЖНЕНИЯ
Найдите для заданной функции / и заданных	точек а,	b	число	у,	для	которого	0 = g'"(y) =
= 1"(у) + 12Е*/(& — а)3. [У к а з а	н и е:	вычислите <р(0,	а	затем	точное	значение	£*.]
1-	/W = *3 — * + L а = (О	= 1.
2.	t(x) = а = 1, b = 4.
3-	/(х) = 1п х, а = 1, b = е.
9.2.	Оценка для правила Симпсона
Пусть / — такая же функция, как и выше, с той разницей, что f имеет в [а, д] непрерывную четвертую производную /IV, причем
|/IV(x) ; < /И4.	(3)
Обозначим через ф(х) квадратичный многочлен, совпадающий с /(х) в концах и в середине рассматриваемого интервала, т. е. удовлетворяющий условиям
/ а 4- Ь \	/ а -+• Ь \
<р(а) = /(а), <р I—-—) = И—2—)’	=
106
Приложение к главе 8
Положим ь	ь
£* =	j9(Z) di
а	а
и приступим к оценке Е*.
Рассмотрим сначала функцию I а-\- Ь\ q (х) = (х-~а) I х — —-— I (х — Ь)
и убедимся в том, что
/ а . ь \	Ь	(а+Ь)/2
9(а) = ^| —l = ^W = 0,	Jg(/)d/ = O, J q(f)dt>0.
a	a
Следовательно, при любом выборе числа k функция <р о(-*Э = Ф (х) + kq(x) удовлетворяет условиям
(о -4- b \ (а 4~ b \
и ь	ь
£* = J НО Л - J ?0 (/) Л. а	а
Далее, k можно выбрать так, чтобы было
(<Ж>)/2	(а+Ь)/Ъ
J f(f)di= J <Ро(ОЛ. а	а
Построим теперь многочлен пятой степени /	а-\- Ь\2
4 (х — a)2 lx — —-—I (76 — а —6х) РW =-----------------77--------------------
(6 — а)5
и проверим, что он удовлетворяет условиям / л -|— b \ /о -р b \ Р (а) = р' (а) = р —-—\ = р'( —-—\ = р' (&) = 0, р (b) = 1.
Наконец, рассмотрим функцию
g(x) = j f (t)dt ~^<f0 (t) dt-E*p (X). a	a
Легко убедиться в том, что / CL b \ g(a) = g I——j = g(b) = 0, а также / ci -f” b \
(a) = g' (~ 2 -) = g' (6)=0.	(4)
Задачи
107
Повторно применяя теорему Ролля, приходим к заключению, что g' обращается в нуль и в точке между а и (а + &)/2, и в точке между (а + Ь)/2 и Ь, так что вследствие (4) функция g" равна нулю не менее чем в четырех точках интервала [а,&], функция g"'—не менее в чем в трех, функция g™— не менее чем в двух и, наконец, функция gV — по крайней мере в одной точке; обозначим эту точку через у. Поскольку <р о — многочлен третьей степени, имеем q>QV = 0. Далее, pV (х) = = —2880 (Ь — а)"6, откуда
V IV 0=g (f/)=/	(У) +
2880Е*
(Ь — а)5
Принимая во внимание (3), получаем оценку
|£*К
(Ь —a)sM4 2880
Если теперь разбить [а, Z?] на 2т равных интервалов (каждый длины h) и вычислить интеграл ь
J по правилу Симпсона, то для каждой из т последовательных пар интервалов можно вы-fl
полнить описанное выше построение. Для каждой пары подынтервалов абсолютная погрешность не превышает (2А)бМ4/2880, а общая абсолютная погрешность не больше
т (2Л)5 M4	/е4М4
= ( — a) lg0
Это и есть оценка, приведенная в § 1.7 гл. 7.
УПРАЖНЕНИЯ
Найдите для заданной функции I и заданных точек а, Ъ число р, для которого 0 = gv (у) = = №(у) + 2880 Е*/(д — а)5.
4.	f(x) = х3 — х + 1, а = 0, b = 1.
5.	f(x) = хЗ/2, а = 1, b = 4.
6.	[(х) = х\ а = 0, b = 1.
ЗАДАЧИ
1.	Дайте геометрическое истолкование функции ф(х), определенной равенством (4) в § 1.3 и использованной при выводе теоремы о конечном приращении из теоремы Ролля.
2.	Дайте геометрическое истолкование обобщенной теоремы о конечном приращении (теорема 2 § 1.4) [У к а з а н и е: рассмотрите в плоскости и, v кривую, заданную уравнениями и = G(x), v = F(x).] Решение этой задачи можно отложить до прочтения гл. 11.
3.	Докажите так называемую теорему о среднем значении для интегралов: если [(х) непрерывна и ограничена в (а, Ь), то существует такое число 6, что а <2 b и
I г
а
Проведите доказательство, не пользуясь теоремой о конечном приращении.
4.	Докажите, что теорема о среднем значении для интегралов (задача 3) вытекает из основной теоремы анализа и теоремы о конечном приращении. [Указание: рассмотрите
х
функцию F(x) = J t(t)di.]
108
Приложение к главе 8
\ f(x)dx + <f (b) J f (х) dx.
5.	Покажите, что теорема о среднем значении для интегралов может оказаться неверной даже для функции, имеющей единственную точку разрыва.
6.	Докажите обобщенную теорему о среднем значении для интегралов: пусть f(x) такова, как в задаче 3, а функция р(х) непрерывна, ограничена и положительна в (а, Ь); тогда существует такое число где	Ь, что
ь	ъ
J P(x)f (х) dx — f(i) J р (х) dx. а	а
7.	Сохраняет ли силу теорема задачи 6 для отрицательной функции р(х)7 Сохраняет ли силу та же теорема, если р(х) неотрицательна или неположительна, но может обращаться в нуль в некоторых точках интервала?
8.	Докажите вторую теорему о среднем значении для интегралов: для ограниченной непрерывной функции £(х) и монотонной непрерывно дифференцируемой функции <р(дг), определенных в [а, д], существует такая точка 6 между а и bt что
ь	е	ь
j f (х) <f (X) dx = <f (а)
a	at
9.	Остаточный член R равенства (11) § 1.5 зависит от точки xq. Запишем эту зависимость в явном виде:
[(*) =	f (*о)(Х — Xq) + R(X, Xq).
Это равенство при фиксированном х определяет R как функцию от xq. Вычислите производную R по xq. Вычислите значение R при х0 = х. Далее, применив к R как функции от хо теорему о конечном приращении, получите представление
R = f"G) (£ — *)(*о — х),
где 5 — число между х и xq. Совпадает ли число $ в этой формуле с числом 5 равенства (9) § 1.5? Приведите Ваши соображения по этому поводу.
10.	(Продолжение задачи 9.) Выведите интегральную форму остаточного члена:
X
(x-t) dt.
Xq
11.	Покажите, как получить для R формулу, приведенную в тексте [равенство (9) § 1.5], и формулу задачи 9 из интегральной формы остаточного члена (см. задачу 10).
[Указание: примените обобщенную теорему о среднем значении для интегралов сначала для p(t) = t — х, затем для p(t) = 1.J
12.	Применив теорему Ролля, покажите, что многочлен степени п может иметь не более п различных действительных корней. [Указание: пусть многочлен имеет k различных действительных корней; каково наименьшее число действительных корней его производной?]
13.	Остаток R формулы Тейлора
f(x) = 2 ---Т22- (x-xtf + R
1=о	1
Задачи
109
при фиксированном х является функцией от хо. Найдите производную от R по xq и значение R при хо = х. Далее, пользуясь теоремой о конечном приращении, получите остаточный член в так называемой форме Коши:
/п+,) (С)
R = —----г22- (х - 6)" (х - х0),
П I
где 5 заключено между х и хо.
14.	(Продолжение задачи 13.) Выведите интегральную форму остаточного члена:
К = ~Т f fin+" (0 (x-tydl.
п I J xe
15.	Покажите, что остаточный член в форме Коши (см. задачу 13) можно получить из интегральной формы. Покажите, как получить из интегральной формы остаточного члена остаточный член в форме Лагранжа, указанный в тексте:
R
/<п+1> (5) (п+ 1)1
(х-х0)я+1,
где 6 — число между х и хо (вообще говоря, отличное от числа 6 в формуле для остатка в форме Коши). [У казание: сравните с задачей 11.]
16.	Пусть функция х i-> Дх) определена для х, близких к хо (за исключением, возможно, самой точки хо). Пусть для произвольной последовательности чисел alf а2, а3, ... такой, что aj =/= хо при всех /, lim су = хо и для всех aj определены Да/), причем справедливо равенство lim Да/) = А. Докажите, что lim Дх) = А.
х-+х0 '
17.	Сформулируйте и докажите аналоги теоремы, приведенной в задаче 16, для односторонних пределов, пределов на бесконечности и бесконечных пределов.
18.	Считая доказанной теорему 3 § 3.8, выведите из нее теорему А § 9.1 гл. 5 об ограниченных монотонных функциях.
19.	В гл. 5 мы определили несобственный интеграл по бесконечному интервалу интегрирования лишь для неотрицательной подынтегральной функции. Пусть теперь Дх)— кусочно-непрерывная функция, определенная при х > 0; предположим, что она ограничена на любом конечном интервале [0, А]. Говорят, что несобственный интеграл 4-со
J t(x)dx сходится (или «существует»), если существует конечный предел
А
lim i/(x)dx.
оо	со
Говорят, что интеграл £ Дх) dx абсолютно сходится, если существует интеграл^ | Дх)| dx. со
Покажите, что если интеграл [(x)dx абсолютно сходится, то он сходится, но что обратное утверждение неверно.
20.	Постройте такую непрерывную функцию Дх), определенную при х > 0, что интеграл со
J t(x)dx существует и даже абсолютно сходится, но неверно, что lim Дх) = 0 (ср. с тео-о	+оо
ремой 2 § 4.3). 4-со .
21.	Сходится ли интеграл 1 -------- dx? Сходится ли он абсолютно?
oJ *
110
Приложение к главе 8
22.	Найдите такой расходящийся ряд а± + а% + а3 + что ряд
(«1 + а£ + («з + aj + (аз + а«) + ...
сходится, но не абсолютно.
23.	Пусть f(x) — функция, определенная вблизи х = 0 и аналитическая в точке х = 0. Пусть /(0) = 0 и =)= 0. Тогда %(х) имеет постоянный знак вблизи 0 (почему?) и, следовательно, существует обратная функция g(y), определенная вблизи у = 0; при этом f(g(y)) = У* glf.(x)) = х* Известно, что эта функция — аналитическая в точке у = 0. Приняв этот результат, покажите, как выразить коэффициенты ряда Тейлора функции g(y) в точке у = 0 через коэффициенты f{x) в точке х = 0.
24.	Сформулируйте результат, аналогичный приведенному в задаче 23, для более общего случая, когда f аналитична в точке х = а и f(a) = b.
25.	Получите с помощью метода задачи 23 три первых коэффициента Тейлора функции у н> tg у в точке у = 0 по известному разложению функции арктангенс. Проверьте результат по формуле Тейлора.
26.	Пусть g(y) — функция, обратная функции
с sin * л Xh*J ~т~
о
определенная вблизи точки у = 0. Пользуясь методом задачи 23, найдите несколько первых коэффициентов ряда Тейлора функции g(y) в точке у = 0.
9/ВЕКТОРЫ
В этой главе рассказывается про «язык векторов», широко используемый в аналитической геометрии, в особенности в аналитической геометрии в пространстве. Попутно здесь вводятся полярные, цилиндрические и сферические координаты. Материал настоящей главы можно изучать и непосредственно после (примыкающей к ней по содержанию) гл. 2.
Изложенные ниже сведения по стереометрии используются главным образом в гл. 12 и 13, посвященных изложению основных понятий «трехмерного» и «многомерного» математического анализа.
В Приложении вкратце изложены понятия скалярного произведения векторов и n-мерного векторного пространства.
112
9. Векторы
§ 1.	ВЕКТОРНАЯ	Прежде	чем продолжить изложение математического
АЛГЕБРА	анализа, мы посвятим несколько параграфов элементам
векторного исчисления, которое представляет интерес и само по себе, а также может быть использовано при дальнейшем построении аппарата математического анализа. Одновременно с этим здесь будет продолжено начатое в гл. 2 изучение аналитической геометрии.
Начало векторного исчисления восходит к XIX столетию. Его основы были заложены Гамильтоном*; настоящий свой вид оно приобрело главным образом благодаря работам американского физика и математика Гиббса. На первый взгляд, векторное исчисление может показаться только «языком», на котором удобно записывать формулы аналитической геометрии. В действительности, однако, дело обстоит совсем не так — векторный анализ представляет собой раздел математики, имеющий широкие приложения как в самой математике, так и в естественных науках.
1.1.	НАПРАВЛЕННЫЕ ОТРЕЗКИ
Направленным отрезком называется упорядоченная пара точек Р и Q. Такой направленный отрезок обозначают символом PQ и обычно изображают как стрелку (рис. 9.1). Первая из двух точек называется началом направленного отрезка, вторая — его концом. Расстояние между точками Р и Q называется длиной, или модулем, направленного отрезка PQ\ модуль отрезка PQ мы будем обозначать
Уильям Роуан ГАМИЛЬТОН (1805—1865). Его жизнь началась со стремительного подъема на интеллектуальные высоты и с больших научных успехов. Пятилетним мальчиком он читал по-древнееврейски, по-гречески и по-латыни; в 17 лет написал свою первую большую научную работу. В 22 года Гамильтон стал профессором Колледжа Троицы в Дублине, в 30 лет за научные заслуги был произведен в дворяне. Однако вторая половина жизни Гамильтона была омрачена домашними и личными несчастьями.
Гамильтон изобрел кватернионы — своеобразное обобщение алгебры комплексных чисел ♦; векторный анализ явился одним из результатов зтой обширной теории **. Однако наиболее важные его достижения — вто ранние исследования в области оптики и механики.
Джозайя Уиллард ГИББС (1839—1903) был заметной и в значительной степени уникальной фигурой в американской науке XIX столетия. Гиббс получил образование в Йельском университете, несколько лет учился в Европе, а затем вернулся обратно в Нью-Хейвен, где расположен Йельский университет; в этом городке он и жил до самой смерти.
Основные заслуги Гиббса относятся к области теоретической термодинамики, (в частности, статистической физики) и и применениям физически! методов к химии; однако и в области «чистой» математики его заслуги весьма значительны.
*	По этому поводу см., например, И. В. Арнольд, Теоретическая арифметика, М., Учпедгиз, 1939 или И. Л. Кантор и А. С. Солодовников, Гиперкомплексные числа, М., «Наука», 1973.
*	* Гамильтону принадлежит систематическая трактовка основных результатов векторного анализа на языке кватернионов; любопытно, что в соответствии с этим еще в знаменитом «Трактате об электричестве и магнетизме» Дж. К. Максвелла (1873) теория электромагнитного поля излагалась на языке квартернионов (на котором, в частности, были впервые записаны основные «уравнения Максвелла» электромагнитного поля, сегодня всегда записываемые на стандартном языке векторного анализа).
* Одновременно и независимо от Гамильтона к идеям векторного исчисления пришел немецкий математик Герман Г рассман (1809—1877). Любопытно, что как у Гамильтона, так и у Грассмана «трехмерное» векторное исчисление было связано с пространствами большего числа измерений («четырехмерные» кватернионы Гамильтона; «n-мерная» алгебра Грассмана).
§ 1. Векторная алгебра
113
Рис. 9.1
f I I I I I 1
через | PQ |. Длина PQ может быть и равной нулю — в этом случае начало отрезка совпадает с его концом. Направленные отрезки называют также связанными векторами.
Геометрический смысл утверждения «два направленных отрезка имеют одинаковые длины и направления, хотя, возможно, разные начала» ясен из рис. 9.2, где пять отрезков имеют одинаковые длины и направления (но один из двух пунктирных отрезков имеет иную длину, второй же — другое направление). Дадим теперь точное определение.
Направленный отрезок PQ имеет ту же длину и то же направление, что и направленный отрезок RS, если выполнено одно из следующих условий:
1°. Р = Q и R = S.	_	_
2°. Р ф Q', точки R и S принадлежат прямой PQ, причем I Z?S | = | PQ I, и точка S лежит с той же стороны от R, с какой точка Q — от Р (т. е. S лежит слева от R и Q слева от Р или 5 справа от R и Q справа от Р; рис. 9.3).
3°. Р, Q, R и S —четыре различные точки, никакие три из которых не принадлежат одной прямой*, прямые PQ и RS параллельны, и прямая PR параллельна прямой QS (рис. 9.4).
То, что направленный отрезок PQ имеет ту же длину и то же направление, что и RS, записывается так: PQ — RS. Отметим следующие свойства отношения
1.	PQ ~ PQ (отношение — рефлексивно).
2.	Если PQ~RS, то RS ~ PQ (отношение—симметрично).
3.	Если PQ~RS и RS — TU, то PQ ~ TU (отношение ~ транзитивно).
114
9. Векторы
Рис. 9.5
Выполнимость свойств 1—3 иногда формулируют в виде утверждения о том, что ~ есть отношение эквивалентности^
4.	Если PQ ~ &S, то | PQ | = | /?5 |.
5.	Если точки Р, Q и R даны, то существует единственная точка S такая, что PQ ~ /?5.
В доказательстве нуждается только свойство 3, причем это доказательство, хоть и очень простое по существу, требует довольно кропотливого разбора различных возможных случаев. Один из этих случаев изображен на рис. 9.5, где надо доказать, что прямые РТ и QU параллельны; но это сразу вытекает из равенства заштрихованных на рис. 9.5 треугольников. Другой случай изображен на рис. 9.6, и здесь снова доказательство следует из равенства заштрихованных треугольников.
Если PQ — RS, то для краткости мы будем говорить, что эти два направленных отрезка эквивалентны*.
1.	2. ВЕКТОРЫ
Рассмотрим направленный отрезок PQ и обозначим символом а множество всех направленных отрезков, эквивалентных PQ. Это множество а часто называют классом эквивалентности, отвечающим направленному отрезку PQ (или порожденным PQ). Если принадлежит а, т. е. если — PQ, то каждый направленный отрезок из а эквивалентен RS и все направленные отрезки, эквивалентные /?5, принадлежат а. Следовательно, а будет также и классом эквивалентности, порожденным отрезком 7?S.
Класс эквивалентности, т. е. определенное множество направленных отрезков, называется вектором (или свободным вектором, в отличие от связанного вектора, который является просто направленным отрезком). Конечно, свободные векторы тоже можно изображать в виде направленных отрезков или стрелок, помня, однако, что выбор начала вектора не имеет значения и что любые два направ
* В русской учебной литературе направленные отрезки PQ и PS, такие что PQ RS, иногда называют также эквиполентными. [Заметим также, что если PQ — RS, то PR ~ QS.J
§ 1. Векторная алгебра
115
ленные отрезка, имеющие равные длины и одинаковые направления, эквивалентны, т. е. порождают один и тот же вектор (или принадлежат одному вектору). Векторы мы в дальнейшем всегда будем обозначать латинскими буквами, набранными жирным шрифтом*.
Если а — вектор, a PQ — любой направленный отрезок, принадлежащий а, то говорят, что PQ представляет, или определяет, а. Если даны (свободный) вектор а и точка Р. то в силу свойства 5 из § 1.1 найдется в точности одна точка Q такая, что связанный вектор PQ представляет а. Мы будем иногда писать а = PQ. вместо того чтобы говорить, что PQ представляет** а.
Длина вектора а (она обозначается символом | а |) — это длина любого направленного отрезка, представляющего а. Это определение непротиворечиво в силу свойства 4 из § 1.1.
УПРАЖНЕНИЯ
В упражнениях 1—8 предполагается, что на плоскости задана некоторая фиксированная декартова система координат. Каждое из этих упражнений проиллюстрируйте примерным рисунком.
1.	Точка Р имеет координаты (0, 1), точка Q — координаты (2, 1); найдите такую точку R, что PQ — QR.
2.	Точка Р имеет координаты (—1, 2), точка Q — координаты (—1, —4); найдите такую точку R, что PQ — RP.
3.	Точка Р имеет координаты (2, 1), точка Q — координаты (2, —3), точка R — координаты (—1, 2); найдите координаты такой точки S, что PQ —
j^4. Точка Р имеет координаты (1 1), точка Q — координаты (4, 5); найдите координаты такой точки R, что PQ ~~ QR.
5.	Точка Р имеет координаты (2, —6), точка Q — координаты (1, —5) и PQ ~ RP; найдите координаты точки R.	__
6.	Точка Р имеет координаты (1^2, 1^3 ), точка Q — координаты ()^2 + 4, ]ЛЗ —2), а точка R — координаты (3, 1/2); найдите координаты такой точки S, что PQ — /?£.
7.	Точка Р лежит на прямой у = ах, а длина вектора, представленного направленным отрезком ОР, равна 20. Найдите все возможные координаты точки Р. (Здесь, как обычно, точка О является началом координат.)
8.	Точка Р имеет координаты (2 cos 21, 2 sin ^-) и OP ~ PQ; найдите координаты точки Q. (Точка О снова является началом координат.)
1.	3. СЛОЖЕНИЕ ВЕКТОРОВ
Сумма двух векторов а и Ь, обозначаемая а + Ь, тоже будет некоторым вектором.
Пусть даны векторы a ub. Выберем точки Р и Q так. чтобы направленный отрезок PQ представлял а; затем найдем такую точку R, что направленный отрезок QR представляет Ь. В таком случае вектор, представляемый направленным отрезком PR. называется суммой а + b (рис. 9.7).
* В тетрадях и на (классной) доске векторы принято обозначать латинскими буквами с черточками над ними: вектор а. вектор b и т. д.
** Более точной была бы (редко употребляемая) запись PQ € а (ибо а — это множество направленных отрезков).
116
9. Векторы
Докажем, что сложение векторов подчиняется тем же законам, что и сложение чисел, т. е. первым пяти аксиомам поля, сформулированным в § 2.2 гл. 1. (Запомните, что буквы жирного шрифта обозначают векторы, а обычные латинские буквы — числа.)
Теорема 1. Сложение векторов обладает следующими свойствами:
1.	Для любых двух векторов а и b существует единственный вектор а + Ь, называемый суммой векторов а и Ь.
2.	a + b= b + a для всех а и Ь.
3.	(а + Ь) + с = а + (Ь + с) для всех а, b и с.
4.	Существует единственный вектор 0, называемый нулевым вектором, такой что 0 + а = а для всех а.
5.	Для каждого вектора а существует единственный вектор —а, называемый противоположным а, такой что а + (—а) = 0.
Докажем сначала свойство 1. Определение сложения было дано выше; однако в этом определении фигурирует произвольная точка Р. Нам надо доказать, что выбор этой точки не влияет на окончательный результат. Иными словами, мы должны доказать, что если PQ — P\Qi и QR — то PR — PiRt-
В случае изображенном на рис. 9.8, когда точки Р, Q и R не принадлежат одной прямой, доказательство следует из того, что четырехугольники PQQiPi и QPPiQi являются параллелограммами, а значит, и PRRJ\ — параллелограмм. В остальных случаях доказательство аналогично, но проще.
14. ДОКАЗАТЕЛЬСТВА ЗАКОНОВ СЛОЖЕНИЯ
Для того чтобы доказать коммутативный закон 2, дадим другое, эквивалентное первому, определение сложения векторов. В этом определении векторы-слагаемые фигурируют совершенно симметричным образом, откуда и будет следовать, что а + b = b + а.	___ ____
Представим векторы а и b направленными отрезками ОР и OQ с общим началом О и определим а + b как вектор, представляемый таким отрезком OR, что:
§ 1. Векторная алгебра
1(7
(а) 7? = Q, если Р = О, и 7? = Р, если Q = О\
(Р) если О, Р и Q — три различные точки одной прямой, то точка 7? также принадлежит этой прямой; если точки Р и Q лежат по одну сторону от точки О, то 7? лежит по ту же сторону от О и | 07? | = | OP | + | 0Q | (рис. 9.9); если Р и Q лежат по разные стороны от О, то | 07? | = | | ОР | — | 0Q | |, причем R лежит по ту же сторону от О. что и точка Р, когда | OP | > | 0Q |; по ту же сторону от О, что и точка Q, когда | 0Q |>| 0Р|; совпадает с О, когда | OP | = | 0Q । (рис. 9.10);
(у) если точки О, Р и Q не принадлежат одной прямой, то точки О, Р, Q и 7? являются вершинами параллелограмма (рис. 9. 11).
Последний случай является здесь наиболее общим; поэтому сформулированное правило сложения векторов называется правилом параллелограмма*.
То, что новое определение сложения эквивалентно старому,легко проверяется.
Доказательство ассоциативного закона 3 непосредственно следует из рис. 9.12. Пусть а, b и с соответственно представлены направленными отрезками PQ, QR и RS. Тогда PR соответствует сумме а + b, a PS — сумме (а + Ь) + с. Но QS представляет сумму b + с,поэтому PS также изображает и сумму а + (Ь + с). (Заметим, что доказательство ассоциативного закона 3, основанное на правиле параллелограмма, было бы гораздо более громоздким.)
В силу ассоциативного закона такие выражения, как а + b + с (так же как и запись суммы большего числа векторов), имеют вполне определенный смысл.
Обозначим символом 0 вектор, представляемый направленным отрезком РР. Если вектору а соответствует отрезок PQ, то вектору 0 + а соответствует тот же отрезок PQ; значит, 0 + а = а. Если точка Pi не совпадает с Р и PiQi представляет
* В противоположность этому первоначальное определение сложения векторов, связанное с рассмотрением треугольника PQR, называется правилом треугольника.
118
9. Векторы
а, то вектор, изображаемый отрезком PQb отличен от а. Этим доказано свойство 4 сложения векторов. Вектор 0 называется нулевым вектором; его длина равна 0.
Пусть вектор а соответствует направленному отрезку PQ; обозначим через — а вектор, представленный отрезком QP. Тогда вектор а + (—а) изображается отрезком РР и, значит, равен 0. С другой стороны, если вектор х представлен отрезком QX, где X #= Р, то вектор а + х представляется отрезком РХ. отличным от 0. Это доказывает справедливость свойства 5 сложения. Как и в случае чисел, мы далее будем писать а — b вместо* а + (—Ь).
С помощью параллелограмма можно дать интересную интерпретацию разности а — Ь. Представим векторы а и b направленными отрезками ОР и OQ с одним и тем же началом и предположим, что три точки О, Р и Q не принадлежат одной прямой. Пусть R — четвертая вершина параллелограмма OPRQ. Тогда, как известно, направленный отрезок OR изображает сумму а + Ь. Докажем, что отрезок QP представляет разность а — Ь. Действительно, отрезок ОР. представляющий вектор а, изображает также сумму b + (вектор, представляемый отрезком QP) (рис. 9.13). Таким образом, одна из диагоналей параллелограмма, «натянутого на два данных вектора», представляет их сумму, а другая — разность.
1.5.	ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО
Определим теперь произведение вектора а на число а. Это произведение, обозначаемое символом аа, тоже является вектором.	___
Если а=£ 0 и а > 0, то выберем точку Р, направленный отрезок PQ, представляющий вектор а, и такую точку R. что:
(a)	R принадлежит прямой PQ;
(б)	R лежит по ту же сторону от точки Р, что и Q;
(в)	\PR | = а | PQ|.	___
Тогда аа есть вектор, представляемый отрезком PR (рис. 9.14). Если аУ=0 и а < 0, то будем считать, что, по определению, аа = —((—а)а). Наконец, положим
* Это соглашение легко обосновать: если а + х = Ь, то вектор х, который уместно обозначить символом b — а и назвать разностью векторов b и а, равен b + (—а) (проверьте это).
§ 1. Векторная алгебра
119
Оа = 0 для всех векторов а; аО = О для всех чисел а.
Иными словами, для того чтобы получить вектор аа, надо, сохраняя направление вектора а, если а > 0, и изменяя это направление на противоположное, если а < О, умножить длину вектора на | а |. Из этого определения вытекает, что
если аа = 0, то либо а = О, либо а = 0.	(2)
Теорема 2. Умножение вектора на число обладает следующими свойствами:
6.	Для каждого вектора а и произвольного числа а существует единственный вектор аа, называемый произведением а на а.
7.	1 • а = а для всех векторов а.
8.	а(ра) = (ар) а для всех а, р и всех а.
9.	(а + р)а = аа + ра для всех а, Р и всех а.
10.	а(а + Ь) = аа + ab для всех а и всех а, Ь.
Прежде чем доказывать эти свойства, сделаем два замечания. Говорить о справедливости равенства аа =аа не имеет смысла, поскольку произведение аа не было определено. Кроме того, заметим, что два дистрибутивных закона 9 и 10 выражают совершенно разные свойства операции умножения вектора на число.
Сформулированные выше законы 1—10 называют также аксиомами векторного пространства*. В вопросах, связанных с векторами, числа обычно называют скалярами. Вектор аа называется скалярным кратным вектора а.
1.6. ДОКАЗАТЕЛЬСТВА ЗАКОНОВ УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО
Произведение аа было нами определено выше. Для того чтобы показать непротиворечивость этого определения, а также доказать справедливость свойства 6 умножения вектора на число, нам остается только проверить, что используемый в этом определении выбор точки Р не влияет на результат. Достаточно показать следующее. Пусть Р, Р и R — три точки, принадлежащие одной прямой, причем точки
* Иными словами, векторным пространством называется множество некоторых объектов а, Ь, с ..., называемых «векторами», для которых определены операции сложения векторов (эта операция сопоставляет каждым двум векторам а и b новый вектор а + Ь) и умножения вектора на число (сопоставляющая вектору а и числу а новый вектор аа), обладающие свойствами 1—10 (или удовлетворяющие аксиомам 1—10).
120
9. Векторы
Q и /? лежат по одну сторону от точки Р; пусть, далее, Pif Qi =/= Pi и /?t — три точки, также принадлежащие одной прямой, причем Qi и Rt лежат по одну сторону от точки Если PQ - P&i и | РР | / | PQ | = |	| / |	|, то РР ~ P^t.
Доказательство сформулированного утверждения состоит в педантичном рассмотрении всех возможных здесь случаев; мы его опустим. Типичный случай изображен на рис. 9.15. Мы знаем, что отрезок PQ параллелен PjQi, а отрезок PPt параллелен QQp Надо показать, что отрезок PPt параллелен РРр Но это верно, так как, по предположению, расстояние РР равно расстоянию PiPi.
Справедливость утверждений 7, 8 и 9 очевидна, если а = 0. Пусть теперь а =# 0 и ОР — отрезок, представляющий вектор а. Примем прямую ОР за числовую ось, считая, что точка О есть «нулевая» точка этой числовой оси, а Р — ее «единичная» точка. Для каждого числа X обозначим через Qx точку этой прямой, представляемую числом X. Тогда отрезок OQx представит вектор Ха, как это следует из нашего определения. Сказанное делает совершенно очевидной справедливость законов 7, 8 и 9 умножения вектора на число.
Заметим, что в силу ассоциативного закона 8 такие выражения, как Хр-а, имеют вполне определенный смысл.
Доказательство дистрибутивного закона 10 мы проведем для случая, когда а > 0, а =И= 0 и b =И= 0, причем векторы а и b не пропорциональны (рассмотрение остальных, более простых, случаев предоставляется читателю).
Пусть отрезки ОР и PQ представляют векторы а и b соответственно; тогда отрезок OQ соответствует вектору а + b (см. рис. 9.16, где предполагается, что а> 1). Выберем точки R и S так, чтобы отрезок ОР изображал вектор аа, a OS — вектор а(а + Ь). Тогда
jOP |/ | ОР | = | OS | /| OQ | = а,
и значит, по известной теореме геометрии, RS параллельно PQ. Так как треугольники OPQ и ORS подобны, то I PS | = а | PQ |. Следовательно, отрезок PS со
§ 1. Векторная алгебра
121
ответствует вектору ab, а отрезок OS — вектору аа + ab. Но отрезок OS представляет и а(а + Ь), откуда и следует справедливость свойства 10.
УПРАЖНЕНИЯ
В упражнениях 9—15 предполагается, что на плоскости задана прямоугольная декартова система координат. Для каждого упражнения сделайте иллюстрирующий его рисунок.
9.	Пусть А (1, 2), В (2, 3). С (—1, 2) и D (0, —1). Найдите такую точку Р, чтобы вектор, представляемый отрезком АР, был равен сумме векторов, представляемых отрезками 'АВ и CD.
10.	Пусть А (0, 1), В (1, 3), С (1, 0) и D (0, —2). Найдите координаты такой точки Р. что вектор, представляемый отрезком DP, равен сумме векторов, представляемых отрезками ~АВ и CD.
11.	Пусть А (1, —1), В (2, —1), С (—1, 1) и D (0, 4). Найдите координаты такой точки Р, что вектор, представляемый отрезком ВР, равен сумме векторов, представляемых отрезками АВ и CD.
Пусть А (—2, 1), В (1, —3) и С (1, 0). Найдите координаты такой точки Р, что вектор, представляемый отрезком СР, равен JL вектора, представляемого отрезком АВ.
5
12.
13.
14.
15.
Пусть А = ()^2", 1^3 ), В (2 + У 2 , —1 + /3)иС (У7~. УТ! ). Найдите координаты такой точки Р, что вектор, представляемый отрезком СР, равен произведению вектора, представляемого отрезком АВ, на число —3.
Пусть А (2, —4), В (1, 1), С (—1, 2) и D (0, —2). Найдите координаты точки Р, если вектор, представляемый отрезком А Р, равен сумме удвоенного вектора, представляемого отрезком АВ, и утроенного вектора, представляемого отрезком CD.
Пусть А (0, 1), В (4, —1), С (3, 2) и D (2, 3). Найдите | а |, если вектор а равен разности удвоенного вектора, представляемого отрезком АВ, и удвоенного вектора, представляемого отрезком CD.
1.7. ВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
До сих пор мы все время подразумевали, что все рассматриваемые точки, а значит, и все фигурировавшие выше отрезки, принадлежат одной плоскости, т. е. что мы имеем дело исключительно с векторами на плоскости.
Но все сказанное выше сохраняет полную силу и в применении к векторам в пространстве, т. е. к классам эквивалентности направленных отрезков, которые не обязательно принадлежат одной плоскости. В частности, остаются в силе определения сложения и умножения на число, а также теоремы 1 и 2.
1.8. БАЗИСЫ И РЕПЕРЫ НА ПЛОСКОСТИ
Для того чтобы векторами было удобно пользоваться, надо связать их с числами. В этом нам поможет
Теорема 3. Векторы на плоскости обладают следующим свойством'.
112- Существуют такие два вектора et и е2, что каждый вектор а однозначно представляется в виде
а=а1е1 + а2е2,	(3)
где а 1 а а 2 — некоторые числа.
122
9. Векторьк
Только на первой стадии изучения планиметрии мы в явном виде используем предположение о том, что все рассматриваемые точки лежат в одной плоскости; в-дальнейшем же вместо этого мы просто будем считать справедливым свойство 112> которое вместе со свойствами 1—10 характеризует именно векторы на плоскости. Свойства 1—112 векторов называются аксиомами двумерного векторного пространства (или векторной плоскости).
Доказательство. Введем на плоскости прямоугольную декартову систему координат. Пусть О — начало координат, Ei—точка с координатами (1, 0) и Е2— точка с координатами (0, 1). Обозначим через ei и е2 векторы, представляемые соответственно отрезками OEt и ОЕ2.	___
Пусть а — произвольный вектор. Представим его направленным отрезком ОР и пусть точка Р имеет координаты (аь а^; обозначим, далее, через Pi точку с координатами (аь 0) а через Р2 — точку с координатами (0, а2); будем считать, что а!— это вектор, представляемый отрезком bPif а а2—вектор, представляемый отрезком PiP. Тогда
а = ai -f" а2,
по определению суммы векторов. Вспомнив затем определение умножения вектора на число, мы установим, что
at = ex |в1.
Вектор а 2 представляется отрезком Р{Р, а следовательно, и эквивалентным ему отрезком ОР2 (рис. 9.17). Теперь мы видим, что
а 2 = а 2^2*
Комбинируя три последние равенства, мы и получим равенство (3).
Обращая это рассуждение, мы можем установить, что если справедливо равенство (3), то вектор а может быть представлен отрезком ОР, где точка Р имеет координаты (ai,a2). Отсюда следует, что по вектору а числа си и а2 определяются о д-нозначно. Тем самым свойство 112 полностью доказано.
•§ 1. Векторная алгебра
123
Упорядоченная пара (е1} е2) векторов называется базисом, если каждый вектор может быть представлен в виде (3), и притом единственным образом. Из нашего доказательства вытекает, что если векторы ei и е2 представлены взаимно перпендикулярными отрезками длины 1, то {е4, е2} — базис. Такой базис называется ортонор-мированным базисом плоскости, или репером. В дальнейшем мы будем пользоваться почти исключительно ортонормированными базисами. Следует, однако, иметь в виду, что существуют также и другие базисы. (Примеры будут даны позднее.)
Замечание. Во многих книгах два вектора плоскости, образующие репер, обозначаются через i и j.
1.9. КООРДИНАТЫ
Выберем базис {еь е2}; тогда каждый вектор а может быть единственным способом представлен в виде а =	+ а2е2. Числа и а2 называются координатами век-
тора а в базисе {е4, е2}. Так устанавливается взаимнооднозначное соответствие между векторами плоскости и упорядоченными парами чисел. Иногда мы пользуемся сокращенным обозначением: 4
а = (аь а2) вместо а =	+ а2е2.
Это возможно только в том случае, если зафиксирован определенный базис, так как координаты вектора а зависят от базиса. Исключением является лишь нулевой вектор 0, координаты которого во всех базисах одинаковы [а именно (0, 0)1.
Теорема 4. В заданном базисе {еь е2} имеют место равенства
(^1е1 + а2ег) + (^1^1 + &2е2) = (Я1 + Mei + (а2 + &г)е2	(4)
X(fliei + а 2е 2) —	+ (Ха2)е2*
(5)
Доказательство теоремы 4 легко вытекает из свойств 1—10. Левая часть равенства (4) в силу коммутативного закона 2 и ассоциативного закона 3 равна + 616!)+ + (02е2 + 62е^, что в силу дистрибутивного закона 9 равно (ai + &i)ei + + (а2 + 6г)е2. Для установления справедливости равенства (5) важен дистрибутивный закон 10: в силу этого закона и ассоциативного закона 8 выражение М«1е1 + ^262) равно (Xai)et + (Хаг)^.
В сокращенных обозначениях, не использующих базиса, теорема 4 утверждает, что
(Qi, а2) + (&1, 62) =	+ &!, а2 + 62);	(4')
Х(Я1, aj = (Xfli, Ха2).	(5')
Это можно выразить так: сложение векторов сводится к сложению их координат*, умножение вектора на число равносильно умножению каждой из координат вектора на это число.
124
9. Векторы
УПРАЖНЕНИЯ
В упражнениях 16—27 предполагается, что для векторов на плоскости выбран некоторый фиксированный базис {в!, ез} и что координаты всех векторов заданы в этом базисе.
16.	Пусть вектор а имеет координаты (2, —4), а вектор b — координаты (4, —3); каковы координаты вектора а+ Ь? Вектора а — Ь? Вектора 2а? Вектора (—3)Ь?
17.	Пусть вектор а имеет координаты (3, У2), а вектор b — координаты (1, 3 1^2); каковы координаты вектора —2а + ЗЬ?
18.	Пусть вектор а имеет координаты (2, 3) и b = е, — ез + а; каковы координаты вектора За - 2Ь?
19.	Найдите координаты вектора (2, 3) + 4(6, 1) — 3(0, 2).
20.	Найдите	координаты	вектора 2(0, 1) — 4(3, 2) + 3(3.	1).
21.	Найдите	координаты	вектора 4(2, -L) — (0, 2) + 2(—1,	—А).
^22. Найдите аг и аз, если 3(аг, аз) + 2(3 0) = (9, 12).
23 Найдите и аз если 3(2. 0) — 2(ах аз) = (8. 4).
24.	Найдите	at и аа,	если 5(0. —1) + 2(аь а2) — 3(1, —1) =	(7,	3).
25.	Пусть a = Зех — 2е3,	b = —в! + 4е2, с = Aej и 2a +	b + 3v	=	2с.	Найдите коорди-
наты вектора у.
26.	Пусть а + b = ег и а — Ь = ез. Найдите координаты векторов а и Ь.
27.	Пусть et = 2а — ЗЬ и е2 = а + Ь. Если с =	— Зе2, то можно ли найти такие
числа а и fl, чтобы имело место равенство с = аа + pb?
1.10.	УПОРЯДОЧЕННЫЕ ПАРЫ ЧИСЕЛ КАК ВЕКТОРЫ
Забудем теперь на время о геометрических рассуждениях, приведших нас к равенствам (4') и (5'), и примем их за определения.
Теорема 5. Множество упорядоченных пар чисел, для которых равенства (4') и (5') определяют операции сложения пар чисел и умножения пары чисел на число, образует двумерное векторное пространство.
Это означает, что свойства 1—112 будут справедливы, если считать, что векторы (обозначаемые буквами жирного шрифта) — это упорядоченные пары чисел.
Первое доказательство. Вспомните, каким образом мы пришли к равенствам (4') и (5').
Второе доказательство. Докажем свойства 1—10, не обращаясь к геометрии, а исходя лишь из свойств чисел. Мы здесь сделаем это лишь для свойств 4 и 8; остальные же свойства читатель сможет доказать самостоятельно.
Утверждение 4 состоит в следующем: существуют такие два числа х{ и х2, что для любых двух чисел а4 и а2 имеет место равенство (xit х2) + (аи а2) = (аь а^. Но в силу нашего определения (%t, х2) + (аь а2) = (х< + alf х2 + аг)- Для того чтобы это было равно (alt а^, остается положить Xi = 0, х2 = 0. Никакая другая пара (хь х2), очевидно, нашему условию не удовлетворяет.
Утверждение 8 состоит в том, что
a(₽(at, а2)) = (а₽)(аь aj.
Согласно нашему определению, левую часть последнего равенства можно представить так: а(₽а4, pflg) = (aflat, afla2). Правая же его часть тоже равна (aflat, afla^, и наше утверждение доказано.
§ 1. Векторная алгебра
125
Рис. 9.18
Остается доказать для упорядоченных пар чисел справедливость утверждения 112. Но так как, очевидно,
(аи ад =(аь 0) + (0, ад.
(ai, ад 0)-Ь а2(0, 1).
Положим et = (1, 0),	= (0, 1). Векторы ej ие2и обладают свойством, требуемым
в равенстве (3).
УПРАЖНЕНИЯ
28.	Для множества упорядоченных пар чисел со сложением и умножением, определяемыми равенствами (4') и (5'), докажите утверждение 3. пользуясь только свойствами чисел.
29.	То же самое для утверждения 5.
30.	То же самое для утверждения 9.
31.	То же самое для утверждения 10.
32.	Рассмотрим снова множество упорядоченных пар чисел, сложение которых определим равенством (4'), а умножение на число — равенством Х(а12 ад = (Xaj, да). Образует ли эта система векторное пространство? [Указание : здесь нет необходимости проверять справедливость аксиом 1—5, поскольку они касаются только сложения векторов.]
1.11.	ПРОИЗВОЛЬНЫЙ БАЗИС. НЕЗАВИСИМОСТЬ
Приведем теперь пример неортогонального базиса. Пусть {е,, е2) — репер; положим f| =2еь f2 = в! + е2, или, короче,
=(2, 0), f2 =(1, 1)
(рис. 9.18). Каждая упорядоченная пара чисел может быть представлена, и притом единственным способом, в виде суммы a J, + a2f2, где гц и a2 — некоторые числа. В самом деле, предположим, что числа xt и х2 даны. Потребуем, чтобы имело место равенство
Но это означает, что
или
(Xi, х2) =04(2, 0) 4-a2(l, 1).
(хь Хг) = (2a t + a2, a-J,
Xi = 2at + a2, x2 = a2.
126
9. Векторы
Последние уравнения имеют единственное решение:
а2 =х2, он
Таким образом, пара векторов {ft, f2) образует базис. Из рис. 9.18 видно, что этот базис не является репером. Этот пример иллюстрирует общее свойство базисов.
Два вектора называются независимыми*, если они могут быть представлены такими направленными отрезками ОР и 0Q, что точки О, Р и Q не принадлежат одной прямой. Два вектора на плоскости образуют базис в том и только в том случае, если они независимы. Мы не будем пользоваться этой теоремой; поэтому ее доказательство мы опустим.
УПРАЖНЕНИЯ
В упражнениях 33—35 предполагается, что на плоскости выбран некоторый фиксированный репер {ех, еа}. Все координаты векторов относятся именно к этому реперу.
33.	Докажите, что векторы (3, 4) и (2, 6) независимы и образуют базис.
34.	Докажите, что векторы (3, 4) и (—6, —8) не являются независимыми и не образуют базиса.
35.	Найдите все такие числа и, что векторы (—1, 3) и (2, и) являются зависимыми (т. е. не являются независимыми).
36.	В плоскости дана точка Р. Можно ли найти такую точку Q, чтобы вектор, определяемый отрезком РР, и вектор, определяемый отрезком PQ, были независимы?
37.	Пусть а и b — независимые векторы и а — число, отличное от нуля. Будут ли векторы а и аЬ всегда независимыми, иногда независимыми или всегда зависимыми? Обоснуйте Ваш ответ.
38.	Пусть а и b — независимые векторы. Будут ли векторы а и а + b всегда независимы, иногда независимы или всегда зависимы? Обоснуйте Ваш ответ.
1.12.	БАЗИСЫ И РЕПЕРЫ В ПРОСТРАНСТВЕ
Все сказанное выше с некоторыми естественными видоизменениями сохраняет силу и для векторов в пространстве.
Теорема 6. Векторы в пространстве обладают следующим свойством'.
И3. Существуют такие три вектора еь е2 и е3, что каждый вектор а может быть единственным образом представлен в виде
а = a4ei + d2e2 + d3e3,	(6)
где at, a2ua3 — числа.
Упорядоченная тройка {еь е2, е3} векторов, для которой справедливо утверждение 113, называется базисом в (трехмерном) пространстве.
Доказательство утверждения 113. Введем в пространстве декартову систему координат. Пусть О — ее начало, а Е 2 и Е 3 — соответственно точки с координатами (1, 0, 0), (0, 1, 0) и (0,_0, 1); через еь е2 и е3 обозначим векторы, представленные отрезками ОЕ{, ОЕ2п ОЕ3 (рис. 9.19). Точно так же, как при доказательстве теоремы 3, убеждаемся в том, что {еь е2, е3}— базис. Точнее, если а есть вектор, представляемый отрезком ОР, и точка Р имеет координаты (di, d2, d3), то а = d^i + d2e2 + d3e3, причем нет никакого другого способа представить вектор а в виде суммы произведений векторов е1} % и е3 на числа.
* В русской учебной литературе такие векторы чаще называют линейно независимыми.
§ 1. Векторная алгебра
127
Базис, полученный таким способом из декартовой системы координат, называется репером в пространстве.
Три вектора в пространстве называются независимыми, если они могут быть представлены тремя направленными отрезками с общим началом, не лежащими в одной плоскости. Три вектора {еь е2, е3} в том и только в том случае образуют базис. если они независимы. Мы не будем пользоваться этой теоремой; поэтому доказательство ее мы опустим.
Если в пространстве выбран базис {еь е2, е3}, то каждый вектор а пространства однозначно представляется упорядоченной тройкой чисел (аь а2, aj — координат вектора а; при этом имеет место равенство
а = a 4ei + а 2е 2 + а Зе 3.
При сложении двух векторов их координаты складываются-.
(cti, а2, а3) + (Pi, Р2, Р3) = (сч + рь а2 + Р2, а3 + Р3), а при умножении вектора на число его координаты умножаются на это число-.
а2, а3) = (ХД1, Хд2, АДз).
Доказательства этих утверждений не отличаются от доказательств аналогичных утверждений для векторов плоскости.
Свойства 1—10 из § 1.3 и 1.5 вместе со свойством 113 образуют систему аксиом,, определяющую трехмерное векторное пространство.
Замечание. В литературе векторы, образующие репер, часто обозначаются через i, j, к (вместо еь е2, е3).
128
9. Векторы
УПРАЖНЕНИЯ
39.	Пусть а = b + с. Могут ли векторы а, b и с быть независимыми?
40.	Пусть а + b + с = 0. Могут ли векторы а, b и с быть независимыми?
41.	Пусть а = 2Ьис — произвольный вектор. Могут ли векторы а, Ьис быть независимыми?
В упражнениях 42—52 предполагается, что для векторов в пространстве выбран базис {ех, в2, е3}; координаты всех векторов заданы в этом базисе.
42.	Пусть вектор а имеет координаты (—I, 2, 3), а вектор b — координаты (3, —3, 0). Най* дите координаты вектора 2(а + Ь) — 3(2а — Ь).
43.	-Пусть вектор а имеет координаты (2, 0, I), а вектор b — координаты (—I, 4, —I). Найдите координаты вектора 2а — 3(Ь + ех) + 2(а — е3).
44.	Найдите координаты вектора 2(1, —1, 3) + 3(2, 1, 4) —3(1 0, —1) + 2(0, 0, —3).
45.	Найдите координаты вектора 2-.(уТГ, 0, —1) — 2(1, —1, 2) + У3(2., 0, 0).
46.	Найдите ах, аг и а3, если 2(ах, аг. а3) + 3(ах, 0, а3) = (10, —6, —3).
47.	Пусть a + b — 2с = ех, 2a — Ь + с = ег и 2a — b + Зс = е3. Найдите координаты векторов а, b и с.
48.	Пусть а + b + с = ех, а — Ь + с = ег и За — b — 2с=е3. Найдите координаты векторов а, b и с.
49.	Докажите, что векторы (1, 1, 1), (1, 1, 0) и (1, 0, 0) независимы и образуют базис.
50.	Докажите, что векторы (1, 1, 1), (1, 1, 0) и (2, 2, 1) не являются независимыми и не образуют базиса.
51.	Пусть v = ех + ег + ае3. Для каких значений а тройка {ех, ег, v) векторов образует базис?
Д52. Пусть v = aei + (1 — a)e3. Для каких значений а тройка {2ех, ег, v} векторов образует базис?
$ 2. РАДИУС-ВЕКТОР
2.1. РАДИУС-ВЕКТОР ТОЧКИ
Пусть О — некоторая фиксированная точка (обычно мы будем принимать ее за начало декартовой системы координат), а Р — произвольная другая точка. Тогда (свободный) вектор, представляемый направленным отрезком ОР, называется радиусом-вектором точки Р (относительно точки О).
Если точка О фиксирована, то радиус-вектор точки Р мы будем обозначать просто ’через Р. Ясно, что при заданной точке О каждый вектор будет являться радиусом-вектором некоторой точки, причем различным точкам отвечают различные радиусы-векторы. Нулевой вектор 0 служит радиусом-вектором точки О. В приложениях векторного исчисления к геометрии всегда предполагается, что «начало отсчета векторов» О заранее выбрано.
Предположим, что точка О и репер {ех, е2} нам известны. В таком случае на плоскости введена декартова система координат — такая система, в которой точка с радиусом-вектором ех имеет координаты (1, 0), а точка с радиусом-вектором е2 имеет координаты (0, 1). Если Р — произвольная точка, то ее радиус-вектор может быть представлен в виде
Р = ххех + х2е2.
Числа (xv %г) являются координатами точки Р в системе координат {О, еь е2}.
129
§ 2. Радиус-вектор
Рис. 9.22
Рис. 9.21
Если {ей е2} — репер, то мы придем к декартовой системе координат. Если базис {еь е2} не является репером, то мы получим более общую систему координат*; однако в этой книге мы не будем пользоваться такими системами.
ф Примеры. 1. Пусть Р и Q — две точки; вектор, определяемый направленным отрезком PQ, равен Q — Р (так что | PQ | = | Q — Р |). Доказательство видно из рис. 9.20.
2. Если точки Р и Q в некоторой координатной системе {О, еь е2} имеют координаты соответственно (pit р2) и (ql9 q2), то вектор а, представляемый отрезком PQ, имеет (в базисе {еь е2}) координаты q^—pi и q2— Рг-
Доказательство. По определению, координаты радиусов-векторов Р и Q равны (рь р^ и (qi9 q^\ наше утверждение следует из того, что а = Q — Р (см. пример 1).
3. Пусть точки Р, Q, R и S имеют соответственно координаты (р4, р2), (?ь <7г)> (П> гг) и ($1>$г)- Тогда PQ ~ PS в том и только в том случае, когда qi—pt =si—i\ и q2—Рг = s2 — г2.	___
Доказательст в о. Как показано в примере 1, отрезок PQ представляет вектор Q — Р, а отрезок RS — вектор S — R. Но два направленных отрезка эквивалентны тогда и только тогда, когда они представляют один и тот же вектор (это сразу следует из определения вектора; см. § 1.2). Поэтому условие PQ ~ RS озна-
* Отвечающие произвольному базису {е^, е2} системы координат впервые рассматривал П. Ферма; в настоящее время эти координаты обычно называют аффинными, или общими, декартовыми координатами (в противоположность декартовым прямоугольным координатам, к которым мы придем, приняв, что (elf ег} — репер).
130
9. Векторы
чает, что Q — Р = S — R. Как показано в примере 2, координаты вектора Q — Р равны	q2—Рг); координаты вектора S — R равны (si—rlt s2—г2). Сле-
довательно, Q — P = S — R тогда и только тогда, когда дч— Pi = Si— и ?2— р2 = «2— Г2.
Рассматриваемая ситуация изображена на рис. 9.21. (Мы могли бы доказать утверждение 3 и раньше, исходя из определения отношения эквивалентности для направленных отрезков, но это потребовало бы от нас больших усилий.) ф
2.2. ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
Во многих приложениях векторов в геометрии используется следующий результат: Теорема 1. Пусть Р и Q — две различные точки. Точка X в том и только в том случае принадлежит прямой PQ, если существуют такие числа а, 0, что радиусы-векторы Р, Q, X связаны соотношением
X = аР+ 0Q, а + Р = 1;	(1)
при этом точка X делит отрезок PQ в отношении 0/а.
[Поясним смысл последнего утверждения. Точками Ри Qпроходящая через них прямая делится на три части, отмеченные на рис. 9.22. Говорят, что точка Хэтой прямой делит отрезок PQ в отношении p/а, если: (а) точка X принадлежит части 1,11 или III прямой в зависимости от того, будет ли р < 0, 0 < р < 1 или р > Г, (б) отношение | РХ |/ | QX | = | 0/а |; здесь аир — такие числа, что а + р = = 1.]
Доказательство. Из определения умножения вектора на число (см. § 1.5) вытекает, что точка X в том и только в том случае принадлежит прямой PQ, если векторы, представляемые направленными отрезками РХ и PQ, пропорциональны. Но в силу результата примера 1 из § 2.1 последнее означает, что существует такое число 0, для которого
X — Р = P(Q — Р).
Отсюда (используя свойства 1—10 векторов) получаем
X = Р + p(Q — Р) = Р + pQ — рР = Р — рР + pQ = (1 — р) Р + pQ = aP+3Q, где положено a = 1 — 0, так что a + 0 =1. Следовательно, равенство (1) справедливо.
Предположим теперь, что равенство (1) имеет место. Примем точку Р за начало системы координат, а длину вектора PQ — за единицу длины. Вектор Q мы примем за первый вектор репера. Таким образом, имеем Р=0, 0=е!йХ = 0еР Иными словами, точки Р, Q, X принадлежат оси х и их координаты соответственно равны 0, 1 и 0. Следовательно, | РХ | = | 0 |, | QX | = | 1 — 0 | = | а |. Теперь ясно, что точка X делит отрезок PQ в отношении 0/а.
Отметим некоторые следствия теоремы 1.
Следствие 1. Пусть тип — два числа, не равные нулю одновременно. Радиус-вектор точки, делящей отрезок PQ в отношении п/т, равен
Р Ч---— Q.
п+ tn п + т
§ 2. Радиус-вектор
131
Это вытекает из теоремы 1, если положить а = т/(т + п), (3 = п/(т + п).
Заметим, что при а #= 0 и m =/= О имеем п/т = ₽/а.
Следствие 2. Радиус-вектор середины отрезка PQ равен
Доказательство. В предыдущей формуле положим т = п =1. Заметим, что если точка Р имеет координаты (р1э р^, а точка Q — координаты (<?,, q2), то точка, делящая отрезок PQ в отношении п/т, имеет координаты
mpi +	mfr + nq2
п + т ’ л + т В частности, координаты середины отрезка PQ равны
Р1 + и Р2 + ^2
2	2
УПРАЖНЕНИЯ
В упражнениях 1—8 предполагается, что в плоскости задана декартова система координат с началом в точке О. Для каждой точки Р через Р обозначен вектор, представляемый отрезком ОР.
1. Найдите координаты точки X— середины отрезка, соединяющего точки (2, 1) и (—3, 5).
1	3
2. Найдите середину отрезка, соединяющего точки (—, 3) и (—, —1).
В упражнениях 3—7 найдите координаты точки X и выразите вектор X через векторы Р и Q, как в § 2.2.
3. Точка Р имеет координаты (2, 3), а точка Q — координаты (—1, 9). Точка X принадлежит отрезку PQ и | РХ | = 2-| PQ |.
О
▲4- Точка Р имеет координаты (2, 0), а точка Q — координаты (3, 2); точка X принадлежит прямой PQ, причем Р лежит между Q и X и | РХ | =-L | PQ |.
4
5.	Точка Р имеет координаты (—1, 2), точка Q — координаты (2, 4); точка X принадлежит прямой PQ, причем Q и X лежат по одну сторону от Р и | РХ | = 3 | PQ |.
6.	Точка Р имеет координаты (—2, 1), точка Q — координаты (2, 5); точка X принадлежит прямой PQ, причем Р и X — по одну сторону от Q и | QX | = -L | QP |,
7.	Точка Р имеет координаты (1, 0), точка Q — координаты (0, 4); точка X принадлежит прямой PQ, причем Р и X — по разные стороны от точки Q и | PQ | = 2| QX |.
8.	Если точка X делит отрезок PQ в отношении —2/5, то в каком отношении точка Р делит отрезок QX?
2.	3. ВЕКТОРНЫЕ ДОКАЗАТЕЛЬСТВА ГЕОМЕТРИЧЕСКИХ ТЕОРЕМ
Приведем теперь несколько примеров, иллюстрирующих применение теоремы 1 для доказательства геометрических теорем.
•Примеры. 1. В треугольнике три медианы (отрезки, соединяющие вершины треугольника с серединами противоположных сторон) пересекаются в одной точке. Эта точка делит каждую из медиан в отношении 2:1, считая от вершины (рис. 9.23).
Доказательство. Обозначим вершины треугольника буквами Д, В, С. Радиус-вектор середины Д* стороны, противолежащей вершине Д, в силу следствия
132
9. Векторы
1 1
2 из теоремы 1 равен g-B + -g-C. Обозначим через X точку, делящую отрезок А А* в отношении 2:1. Тогда в силу следствия 1 из теоремы 1 радиус-вектор точки X будет иметь вид
X = — А + — А* = — А+ — В + — СА = — (А4 В + С).
3	3	3	' 3 \ 2	2 J 3 '	’
Но так как это выражение симметрично относительно А, В, С, то мы получим тот же самый результат и отправляясь от медиан, проходящих через вершины В или С. Таким образом, теорема доказана.
Аналитическое доказательство этой теоремы можно провести и не используя понятие вектора, но оно будет длиннее. Читателю предлагается самостоятельно найти это доказательство.
2. Четырехугольник ABCD в том и только в том случае будет параллелограммом, если его диагонали АС и BD в точке пересечения делятся пополам (рис. 9.24).
Доказательство. Середины отрезков АС и BD имеют радиусы-векторы
-i-(A + С) и (В + D). Эти середины совпадают в том и только в том случае, если
_L(a + c) = -L(B + d),
а последнее равенство равносильно следующему: А— В = D — С. _____________________________________
Далее, А — В есть вектор, представляемый отрезком BA, a D — С — вектор, представляемый отрезком CD. Но два свободных вектора равны в том и только в том случае, если представляющие их направленные отрезки эквивалентны, т. е. имеют
§ 2. Радиус-вектор
133
равные длины и одинаковые направления, а последнее выполняется в том и только в том случае, если четырехугольник ABCD является параллелограммом. Этим наша теорема доказана.
Заметим, что приведенная выше формулировка охватывает также и некоторые вырожденные случаи; так, мы не предполагаем, что наши четыре точки все различны или что они не принадлежат одной прямой. Подобные замечания можно сделать по поводу других рассматриваемых здесь и ниже геометрических теорем.
3. Пусть А, В, С, D — четыре точки. Середины отрезков АВ, ВС, CD и DA, взятые в этом именно порядке, являются вершинами параллелограмма (рис. 9.25).
Доказательство. Радиусы-векторы середин рассматриваемых отрезков соответственно равны
-L(A + B), -i-(B + C), -1-(C + D), -1-(A + D).
Середины диагоналей фигуры, образованной этими четырьмя точками, имеют один и тот же радиус-вектор, а именно
4- (4-(А 4- В) + 4- (С 4- D)) = -1- (4-(В + С) + 4 (А + D)] =
= JL(A + B4-C4-D).
4
Далее остается только воспользоваться результатом примера 2.ф
УПРАЖНЕНИЯ
При решении этих упражнений следует пользоваться векторной алгеброй.
9.	Даны точки Л(1. 4), В (—1, 2) и С (3, 3). Найдите точку пересечения медиан треугольника АВС.
10.	Точки А, В, С, D образуют параллелограмм. Пусть точка Р — середина отрезка CD и
прямая АР пересекает диагональ BD в точке X. Покажите, что точка X делит отрезок АР в отношении 2 : 1. В каком отношении точка X делит отрезок DB? [У к а-з а н и е: вспомните, что А + С = В + D.]
11.	Точки А В, С, D являются вершинами параллелограмма, Р — середина стороны CD, a Q — середина стороны ВС (см. рисунок). Отрезки АР и DQ пересекаются в точке X. Покажите, что точка X делит отрезок АР в отношении 4 • 1. В каком отношении точка X делит отрезок DQ? [Указание: вспомните, что А + С = В + D.]
12.	Точки А{ В, С, D являются вершинами параллелограмма; Р — середина стороны CD, а Q — середина стороны АD(cm. рисунок). Пусть отрезок PQ пересекает диагональ BD в точке X. Покажите, что точка X делит отрезок DB в отношении 1:3. В каком отношении точка X делит отрезок PQ? [Указание: вспомните, что А+.С =В + D.]
134
9. Векторы
13.	Точки А, В, С — вершины треугольника. Точка Р делит сторону ВС в отношении 2 :1, а точка Q делит в том же отношении сторону АС. Пусть прямые АР и BQ пересекаются в точке X. Покажите, что точка X делит отрезки АР и PQ в отношении 3 : 1.
14.	Точки А, В, С — вершины треугольника. Пусть точка Р делит сторону ВС в отношении (1 — а) : а, где 0 < а <; 1, а точка Q делит в том же отношении сторону АС. Точку пересечения прямых АР и BQ обозначим через X. Покажите, что точка X делит отрезки АР и BQ в отношении 1/а.
15.	Точки Д, В, С, D являются вершинами параллелограмма. Пусть точка Р делит сторону ДВ в отношении 2:1, точка Q делит в том же отношении сторону ВС и, аналогично, точка Р—сторону CD и точка В — сторону DA в том же отношении 2 : 1 (см. рисунок). Покажите, что точки Р, Q, Р, В являются вершинами параллелограмма.
16.	Пусть точки Д, В, С, D — вершины четырехугольника и точки Р, Q, Р, В определены, как и в упр. 15. Предположим,что точки Р, Q, Р, В являются вершинами некоторого параллелограмма. Покажите, что в таком случае исходный четырехугольник — тоже параллелограмм.
17.	Пусть точки Д, В, С, D —вершины трапеций с основанием ДВ. Так как прямая ДВ параллельна прямой CD, то найдется такое а > О, что DC = аАВ. Пусть X —точка пересечения диагоналей трапеции. Покажите, что точка X делит диагональ АС (и, аналогично, диагональ BD) в отношении 1/а.
2.4. РАДИУС-ВЕКТОР В ПРОСТРАНСТВЕ
Понятие радиуса-вектора сохраняет, конечно, смысл и в стереометрии. Если мы выберем точку О и репер {еь е2, е3}, то в пространстве будет задана декартова система координат. Координатами точки Р относительно этой системы координат будут такие числа (хь х2, х3), что радиус-вектор Р точки Р (относительно О)определяется равенством Р = x^i + х2е2 + х3е3.
Приложения векторов к аналитической геометрии в пространстве мы рассмотрим в § 4.
§ 3. Полярные координаты
135
§ 3. ПОЛЯРНЫЕ
КООРДИНАТЫ
3.1. ПОЛЯРНЫЙ УГОЛ ВЕКТОРА
Пусть {еь е2} — репер и а = atei + а2е2 — некоторый вектор. Если он представлен направленным отрезком PQ, где Р — (plt р2) и Q = (qlt q2), то at = qt— pit a 2 = q2— p2 (см. пример 2 из § 2.1 и рис. 9.26). Мы вычислим длину | а | вектор а по формуле расстояний между точками:
г = |а| = V & + а2.	(1)
Предположим, что а=/= О, так что г> 0. Так как
(—V + (—Y = h \ Г )	\ г /	’
то найдется такое 0, что
cos 9 = -у-, sin 9 = —	(2)
(ср. с теоремой 1 § 1.8 гл. 6). Это значение 0 определено не однозначно, но мы можем добиться его однозначности, если потребуем, чтобы было 0	0 < 2л; тогда 0 рав-
но длине дуги окружности, на рис. 9.26 помеченной буквой 9. Угол 0 мы будем называть аргументом (сокращенно arg), или полярным углом, вектора а относительно репера {е4, е2} и писать
0 = arg а.
Если г = 0, то 0 не определено.
Говорят, что вектор а имеет длину г и направление 9. Координаты ai и а2 вектора а выражаются через г и 0 так:
di = rcos0, a2=rsin0.	(3)
Если к 0 прибавить число, кратное 2л, то а не изменится. Заметим, что если г = =j а | и 0 = arg а, то
а = г cos 0 ei 4- г sin 0 е2.
3.2. ПОЛЯРНЫЕ КООРДИНАТЫ
Длина г и полярный угол 0 радиуса-вектора Р точки Р называются полярными координатами точки Р. Связь между полярными координатами (г, 0) и декартовыми координатами (х, у) точки задается равенствами
х = г cos 9, у = г sin 9,
г = У х2 -|- у2 , cos 9 = —, sin 9 = у- .	(4)
[В этом можно убедиться из рис. 9.27.)
136
9. Векторы
Рис» 9.28
Удобно каждую пару чисел (г, 0) рассматривать как полярные координаты точки, декартовы координаты (х, у) которой определяются равенствами (4). Условимся считать, что:
1)	если (г, 0) — полярные координаты точки Р, то и (г, 0 + 2л) — полярные координаты той же точки;
2)	если (г, 0) — полярные координаты точки Р, то и (—г, 0 + л) — полярные координаты той же точки;
3)	(0, 0), где 0 произвольно,— это полярные координаты начала О отсчета полярных координат.
Сетка, образованная линиями плоскости, для которых г = const (окружности с центром в начале О), соответственно 0 = const (лучи, выходящие из начала), изображена на рис. 9.28.
§ 3. Полярные координаты
137
•Примеры. 1. Формула расстояний в полярных координатах такова-, если две точки имеют полярные координаты (rlt 6^ и (г 2, 9^, то расстояние между ними равно
d = V rf — 2t\r2 cos (02 —	+ d •	(5)
Доказ ательство. Декартовы координаты рассматриваемых точек равны
(rjCosOj, п sin 0i) и (г2 cos 0 2, гг sin 0а).
Расстояние d между точками в силу формулы расстояний в декартовых координатах таково:
d2 = (/*! cos 0 i— г2 cos 0а)2 + (ri sin 0! — r2 sin 02)2 = = Г,2 COS2 0 1— 2Г1Га COS 0 1 COS 0 2 4" Г 2 COS2 0 2 4-4-ri2 sin2 01— 2Г1Г2 sin 01 sin 0 a+ r 22 sin2 0 2 =
= r, — гг^соз©! cos02 + sin 01 sin 0a) + /2 = r, — 2rir2cos (02— 0J + rl, что и требовалось доказать.
2. Теорема косинусов. Пусть АВС — произвольный треугольник-, тогда
& = а2 4- Ь2 — 2ab cos С.
(Здесь, как обычно, через С обозначена величина угла АСВ, через с — длина стороны АВ и т. д.; см. рис. 9.29.)
Доказательство. Выберем на плоскости декартову систему координат, приняв точку С за начало; пусть точка А принадлежит положительному лучу оси х, а точка В лежит в верхней полуплоскости. Тогда точка А будет иметь полярные координаты (Ь, 0), а точка В — координаты (а, С). Далее, нам остается лишь воспользоваться результатом примера 1, полагая г^—Ь, 0i=O, г2=а, 02 = С, d — с. Можно также непосредственно применить формулу расстояний в декартовых координатах, замечая, что точка А имеет декартовы координаты (&, 0), а точка В — координаты (a cos С, a sin С).ф
УПРАЖНЕНИЯ
В каждом из упражнений 1—6 координаты точек заданы в некоторой декартовой системе координат. Найдите полярные координаты этих точек.
1.	(0,1/2).	3. (—/ЗГ 1).	5. (1, —/3)
2.	(1, 1).	4. (—3, 3).	6. (— 2 sin тс/9.	2 cos «/9).
В каждом из упражнений 7—12 заданы полярные координаты точки. Найдите координаты этой точки в соответствующей декартовой системе координат.
7.	(2, тс/2).	9. (3, Зл/2).	11. (/3“, 5л/6).
8.	(2, Зл/4).	10. (1/2, л/4).	12. (/Т, 4л/3).
13.	Точка Р имеет полярные координаты (1, л/2), точка Q — координаты (2, л/6). Найдите расстояние между Р и Q.
14.	Точка Р имеет полярные координаты (3, л/3), а точка Q — координаты (1, л/12). Найдите расстояние между Р и Q.	__
15.	Точка Р имеет полярные координаты (р^З , 7л/6), а точка Q — координаты (2, л/3). Найдите расстояние между Р и Q.
16.	Для треугольника, изображенного на рис. 9.29, напишите формулу, выражающую а2 через Ь, с и cos А.
17.	В треугольнике а = 2, b = 3, с = 6. Найдите угол С (воспользуйтесь таблицей значений косинусов углов).
18.	В треугольнике а = 2,3, b = 4 и С = л/3. Найдите с.
19.	В треугольнике b = 1, с = 2, А = 45°. Найдите а.
138
9. Векторы
3.3.	УРАВНЕНИЯ ЛИНИЙ В ПОЛЯРНЫХ КООРДИНАТАХ
Полярные координаты, так же как и декартовы, можно использовать для составления уравнений линий; как это делается, мы покажем на примерах. Так как рассматриваемые уравнения могут приводить к отрицательным значениям г, то надо помнить условие 2 (стр. 136).
ф Примеры. 1. Найти уравнение (в полярных координатах) окружности с центром в точке Р (с полярными координатами г0, 6 о) и радиусом R.
Первое решение. Мы должны записать условие: расстояние от точки с полярными координатами (г, 0) до Р равно R. В силу формулы (5) это дает
г2 — 2гог cos (0 — 0 о) + ''о2 — R2 = 0.
Второе решение. Воспользуемся хорошо известным уравнением окружности в декартовых координатах (см. гл. 2, § 3.1). Декартовы координаты центра окружности равны rocos0o и r0 sin 0 0 [в силу равенств (4)1. Следовательно, уравнение нашей окружности в декартовых координатах имеет вид
(х — r0 cos 90)2 + (у — rQ sin 90)2 = 7?2.
Положим х = г cos 0, y=r sin 0 и преобразуем полученное выражение; мы получим то же уравнение, что и выше.
2.	Каково уравнение в полярных координатах прямой, проходящей через начало и имеющей наклон т?
Решение. Уравнение этой прямой в декартовых координатах имеет вид у = тх. Пользуясь равенствами (4), получим
г sin 0 = mr cos 0.
Если г =/= 0, то отсюда следует, что sin 0 = т cos 0, т. е. что tg 0 = т. Следовательно, ответ на наш вопрос таков:
tg 0 = т или г = 0.
(Последние равенства означают: рассматриваемой прямой принадлежат все точки, для которых tg 0 = т, а также начало координат, для которого г = 0.)
3.	Какие точки удовлетворяют уравнению cos 0 =0 или г = 0 (где г и Q — полярные координаты)?
Ответ. Точки вертикальной прямой, проходящей через начало координат. Читателю предлагается доказать это самостоятельно.
4.	Какие точки удовлетворяют уравнению г = 2 cosec 0 (где г и 0 — полярные координаты)?
Решение. Из уравнения получаем г = 2/sin 9, или г sin 0 = 2. Полагая х = г cos 0, у = г sin 0, перепишем это уравнение в виде у = 2. Эго уравнение горизонтальной прямой.
§ 3. Полярные координаты
139
5.	Уравнение линии в декартовых координатах имеет вид у2= 4х. Найти уравнение этой линии в полярных координатах.
Решение. Воспользовавшись равенствами (4), получим уравнение r2sin20 = 4r cos 0;
поделив обе части последнего равенства на г cos 0, найдем искомое уравнение: rsin0tg0 = 4 (и точка г = 0).
Эта кривая — парабола.ф
3.4.	ИЗОБРАЖЕНИЕ КРИВЫХ
При вычерчивании кривой, заданной уравнением г = /(0) в полярных координатах, удобно составить таблицу значений /(0) для различных значений 0. (Полезным здесь также окажется специально приготовленный лист бумаги с сеткой линий, изображенной на рис. 9.28.)
Необходимо заметить следующее:
Если /(0) — четная функция, то кривая симметрична относительно оси х. Если функция /(0) нечетна, то кривая симметрична относительно оси у. Если функция /(0) удовлетворяет условию /(0 + л) = /(0) для всех 0, то кривая симметрична относительно начала.
Мы докажем только первое из этих утверждений. Остальные два доказываются аналогично.
Предположим, что функция f четная. Пусть (х0, у0) — точка, принадлежащая кривой, где х0, у0 — декартовы координаты. Тогда найдется такое значение 0 0, что х0 =/(0П) cos0o и yo = f(Qo) sin0o. Поскольку /(—0О) cos (—0О) = х0 и /(—0o)sin (—0О) = —у0, точка (х0,— у0) также принадлежит нашей кривой. Но точки (х0, у0) и (х0, — у0) симметричны относительно оси х.
Если существует такое значение 0 0, что /(0 0) = 0, то кривая проходит через начало. В этом случае она имеет в начале координат касательную с наклоном tg 0 0 (вертикальную касательную, если 0О есть нечетное кратное л/2). Это мы докажем в гл. 11, § 3.5 [см. равенство (9) на стр. 271]. (Здесь предполагается, что функция /(0) имеет непрерывную производную.)
•Примеры. 1. г — cos 0.
Эта линия представляет собой окружность радиуса 1/2 с центром в точке х = = 1/2, у = 0. Чтобы убедиться в этом, достаточно, например, перейти к декартовым координатам: если г = cos 0, то г2 = г cos 0, или х2 + у2 — х. Последнее уравнение можно переписать так: (х — 1/2)2 + у2 = 1/4 (см. гл. 2, § 3.1).
Заметим также, что уравнение примера 1 § 3.3 приводится к виду г = cos 0, если положить 0 0= 0, /? = г0 = 1/2.
Рассматриваемая кривая изображена на рис. 9.30. При 0 = 90° мы получаем г — 0; касательная в этой точке вертикальна. Заметим также, что каждая точка кривой соответствует двум значениям 0 в пределах —180° <0 180’. Например, при 0 = —45° имеем г = 1/]/2^ а при 0 = 135° получаем г — —1/)/27Эти два значения 0 дают одну и ту же точку — точку, декартовы координаты которой X = 1//Г cos ( — 45°) = (— 1//2) cos 135° = 1/2, у = l/Z^sin ( — 45°) = =( — 1//2) sin 135° = — 1/2.
140
9. Векторы
2.	г = COS 2 6.
Эту линию, изображенную на рис. 9.31, называют четырехлепестковой розой. Поскольку cos 20 — четная функция, кривая симметрична относительно оси х. Так как cos 2(6 + л) = cos(20 + 2тс) = cos 26, кривая симметрична относительно начала. Следовательно, она симметрична также и относительно оси у. (Функция cos 26 не является нечетной, но здесь нет никакого противоречия. Выше мы утверждали лишь, что если функция /(0) нечетна, то линия г = /(0) симметрична относительно оси у\ но мы не утверждали, что если линия симметрична относительно оси у, то функция /(0) нечетна.)
3.	г = cos 30.
Эта линия называется трехлепестковой розой; она изображена на рис. 9.32.
4.	г = Ae“Q.
Эта линия изображена на рис.9.33. Она называется логарифмической спиралью; прилагательное «логарифмическая» объясняется тем, что уравнение линии можно переписать так:
слово «спираль» поясняет, что наша кривая делает бесконечно много оборотов вокруг начала О как при приближении к нему, так и при удалении от него.
5.	г = kQ.
Эта линия (изображенная на рис. 9.34, где& считается положительным) называется спиралью Архимеда. Она исходит из начала О и при удалении от него делает бесконечно много оборотов вокруг О.ф
УПРАЖНЕНИЯ
В каждом из упражнений 20—25 уравнение линии задано в декартовой системе координат (х, у). Найдите уравнение той же линии в соответствующей полярной системе координат (г, 0).
20.	Зу — 2х = 8.	23.	х2у2 = х2 + у2.
21.	(х — I)2 + (у — 2)2 = 4.	24.	arccos(x/y х2 + у2) = У х2	+	г/2.
Д22. (х2 + у2)№ = х + у.	25.	х2 + у2 — 2 /х2 + #2 — 3	=	0.
В каждом из упражнений	26—31 уравнение	линии задано в полярных координатах (г, 0).
Найдите ее уравнение в соответствующих декартовых координатах (х, у).
26.	г = l/(2cos0 + 3sin0).	29.	г2 cos 0 sin0 =	1.
27.	г = 4/(6cos 0 — 5 sin 0).	30.	г2 = sin 0.
28.	г2 — 2r cos 0 — 3 =0.	31.	r = cos 0 + sin	0.
В каждом из упражнений 32—46 требуется изобразить линию, заданную своим уравнением в полярных координатах (г, 0). Для облегчения построения линии составьте таблицу тех удовлетворяющих уравнению пар значений г и 0, которые Вам легко найти. Попытайтесь использовать соображения симметрии.
32.	г =	sin 20.	40.	r2 = sin 0.
33.	= г	cos 40.	41.	r2 = cos (0/2).
34.	г =	1 + cos 0.	42.	r = 2/cos 0.
35.	г =	cos (0/2).	43.	r = l/(sin 0— cosO).
36.	г =	1 — sin 0.	44.	r = cos 0 cos 20.
37.	г =	2 — sin0.	45.	r = cos(20/3).
38.	г =	1 — 2sin0.	46.	r = 3 + 2cos0.
39.	Г2 =	4 cos 20.		
§ 3. Полярные координаты
141
Рис. 9.32
Рис. 9.34
142
9. Векторы
§ 4.	ПРЯМЫЕ	В этом параграфе, используя векторную алгебру, мы из-
И ПЛОСКОСТИ ложим основные понятия аналитической геометрии в про-В ПРОСТРАНСТВЕ спгРанстве- Рассмотрение этих вопросов продолжится в в следующем параграфе. Вопросы, касающиеся углов, рассматриваются в Приложении (см. § 6).
Далее мы все время будем предполагать, что в пространстве введена некоторая декартова система координат, определяемая началом О и репером (е^ е2, е3}. Каждой точке Р соответствует радиус-вектор Р; координаты вектора Р равны координатам точки Р. Координаты точки будут записываться иногда как (х2, х2, х3), а иногда — как (х, у, г).
4.1.	ФОРМУЛА ДЕЛЕНИЯ
Пусть Р и Q — две различные точки в пространстве. Тогда радиус-вектор каждой точки X прямой PQ можно представить в виде
X = аР 4- 0Q, а 4- 0 = 1;	(1)
эта точка X делит отрезок PQ в отношении 0/а. Последнее утверждение есть не что иное как теорема 1 § 2.2. Правда, в § 2.2 речь шла о векторах на плоскости; однако доказательство теоремы 1 без каких-либо изменений переносится и на случай векторов пространства. Следствия из теоремы 1 § 2.2 тоже сохраняют силу и для пространства. Следовательно, если тй + па =/= 0, то вектор тЦт + п)Р + 4-n/(/n + zi)Q является радиусом-вектором точки, делящей отрезок PQ в отношении п/т\ в частности, -уР 4- -yQ есть радиус-вектор середины отрезка PQ.
Предположим, что точка Р имеет координаты (plt р2, р3); тогда Р = p^t + + Ргег + Р3е3 (см. § 2.4). Если точка Q имеет координаты (qi, q2, q3), а точка X — координаты (хь х2, х3), то Q = q^ + q2e2 4- q3e3 и X =	+ х2е2 + х3е3;
поэтому равенство (1) можно переписать так:
Xi = apt 4- ftyi, х2 = ар2 4- 0р2, х3 = ар3 4- Qq3, где а 4- 0 = 1.	(2)
• Пример. Принадлежат ли три точки (1, 2, 3), (4, —10, 8) и (— 7, 22, 9) одной прямой?
Решение. Пользуясь равенствами (2), где Р, Q и X — точки с координатами (1, 2, 3), (4, —10, 8) и (—7, 22, 9), мы видим, что, для того чтобы эти три точки принадлежали одной прямой, необходимо и достаточно, чтобы нашлись такие два числа а и 0, что
—7 = а4-40, 22 = 2а— 100, 9 = За 4-8р, а 4- 0 = 1.	(3)
Из первого и второго уравнений мы получаем значения а = 1, 0 = —2. Здесь а 4- 0 = —1 ¥= 1. Следовательно, наши точки не принадлежат одной ярямой.ф
§ 4. Прямые и плоскости в пространстве
143
УПРАЖНЕНИЯ
1. Пусть точки Р и Q имеют координаты (1, —3, 0) и (2, 5, —7). Найдите середину отрезка PQ.
А2. Пусть Р и Q — точки, заданные в упр. 1. Найдите точку, делящую отрезок PQ в отношении 4/5.
3.	Даны четыре точки Р (1, 2, 3), Q (3, 2, 1), R (2, 2, 2) и S (2, 2, 3). Какие три из них принадлежат одной прямой?
4.	Найдите такое число и, чтобы точка (1, 2, и) лежала на одной прямой с точками (2, 0, 5) и (0, 4, 7).
5.	Найдите такие числа х и «/, чтобы точка (х, у, 0) принадлежала прямой, проходящей через точки (4, 3, —1) и (2, 8, 2).
6.	Рассмотрим прямую, проходящую через точки (1, 5, 4) и (—2, 7, 9). Найдите точки пересечения этой прямой с координатными плоскостями (xj = 0, хъ = 0 и х3 = 0).
7.	Найдите точку Р в координатной плоскости ха = 0 и точку Q в координатной плоскости х3 = 0 так, чтобы точка (1, 2, 3) была серединой отрезка PQ.
4.2. ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРЯМОЙ
На плоскости прямая задается одним линейным уравнением, связывающим декартовы координаты ее точек. В пространстве задание прямой линии с помощью уравнений будет иным.
Теорема 1. Пусть Р и Q — две различные точки. Каждой точке X прямой PQ отвечает радиус-вектор вида
X = Р + t ( Q — Р),	(4)
где t — некоторое число. Обратно, для каждого t вектор X является радиусом-вектором некоторой точки прямой PQ, причем различные значения t соответствуют разным точкам.
Это утверждение непосредственно вытекает из равенства (1), в котором положено Р = /, а = 1 — t. Мы имеем в этом случае
аР + PQ = (1 — /)Р + /Q = Р + /(Q — Р).
Переменная t в равенстве (4) называется параметром, а само равенство (4) называется параметрическим представлением прямой.
Перепишем равенство (4) в координатной форме. Пусть (хь х2, х3) — координаты точки X, (pit р2, р3) — координаты точки Р и (qlt q2, ?з) — координаты точки Q. Мы получаем
Xi = Pi + (<71 — Pi)t, х3 = р3 +(q3 —p3)t, х3 = р3 + (<?3— pj)t. (5)
Часто бывает удобно координаты точки X обозначать не через (хь х2, х3), а через (х, у, z). В соответствии с этим координаты точки Р мы обозначим через (хь Уь ^1), а координаты точки Q — через (х2, р2, z2). Тогда равенство (5) можно переписать так:
х = Xi + (х2 — Xi)/, у = pi + (р2 — yjt, 2 = Zi + (z2 — Zi)t.	(5')
Теорема 2. Пусть а, ₽, 7, а, Ь, с — 6 чисел, такие что а2 + &2 + с2 =/= 0 (это означает, что а, Ь, с не равны нулю одновременно). Тогдавсе точки (х, у, г), для которых
х = а + at, у = Р + Ы9 г = 7 + ct,	(6)
144
9. Векторы
принадлежат одной прямой; причем все точки этой прямой могут быть представлены таким образом. Каждая прямая может быть задана равенствами (6).
Доказательство. Положим xt= a, У1 = fl, Zi— у, х3 = а + а, у2 = = fl + 6, z2 = y4-c. Тогда равенства (6) совпадут в равенствами (5'). В силу условия а2 4- Йа 4- & =/= 0 точки (хь уь Zi) и (х2, у3, г J — различные.
ф Примеры. 1. Найти параметрическое представление прямой, проходящей через точки (2, —1, 4) и (3, 2, 6).
Решение. Используя равенства (S') для точек (хь уи zj = (2, —1, 4) и (х2, у г, z2) = (3, 2, 6), мы и получим искомое представление:
х = 2 4- t, у = — 1 4- 3t, г = 4 4- 2t.	(7)
2. В каких точках прямая примера 1 пересекает координатные плоскости х = О, у = 0 и z = О?
Р е ш е н и е. Из равенств (7) видно, что х = О при t = —2. Но при t = —2 из тех же равенств (7) мы имеем у = —7, г = 0. Следовательно, плоскость х = 0 наша прямая пересекает в точке (0, —7, 0). Заметим, что эта же точка будет и точкой пересечения прямой (7) с плоскостью z = 0. Таким же образом находим, что у = 0 при t = 1/3. Для этого значения t равенства (7) дают значения х = 7/3, z = 14/3. Следовательно, наша прямая пересекает плоскость у = 0 в точке (у,0, у).
3. Совпадает ли прямая, определяемая уравнениями
х = 1 4- 2/, у = —4 4- 6/, z = 2 4- 4i,
(8)
с прямой, рассмотренной в примере 1?
Решение. Заметим прежде всего, что во избежание недоразумений параметры в двух представлениях лучше обозначить разными буквами. Поэтому мы перепишем уравнения (8) так:
х = 1 4- 2s, у = —4 4- 6s, z = 2 4- 4s.
(8')
Для того чтобы найти две точки прямой (8'), выберем два значения параметра s, например s = 0 и s = 1. Так мы получим две точки (1, —4, 2) и (3, 2, 6). Надо узнать, будут ли эти две точки принадлежать и первой прямой, т. е. можно ли их координаты представить в виде (7).
Итак, нам надо выяснить, существует ли такое t, что
1 = 2 4- t, —4 = — 1 4- 3/, 2 = 4 4- 2t ?
Из первого уравнения получаем t — —1, и для этого значения t два других уравнения тоже обращаются в тождества. Следовательно, точка (1,—4, 2) принадлежит прямой (7). Точно так же получаем, что и (3, 2, 6) есть точка прямой (7), соответствующая значению t — 1. Так как наши две прямые имеют две общие точки, то они совпадают, ф
Замечание. Точно таким же образом можно получить и параметрические представления прямых на плоскости.
§ 4. Прямые и плоскости в пространстве
145
УПРАЖНЕНИЯ
В упражнениях 8—13 требуется найти параметрическое представление прямой, проходящей через данные точки.
8.	(3, 4, 5) и (5, 4, 3).
9.	(—1, 2, 3) и (0, 4, 5).
10.	(0, 1, 0) и (1, 0, 0).
11.	(0, 12, 7) и (—5, 0, 3).
12.	(—3, 2, 0) и (12, —4, 0).
13.	(—1, 6, 8) и (—1, —2, —2).
± 14. В каких точках прямая упр. 8 пересекает координатные плоскости?
15.	В каких точках прямая упр. 11 пересекает координатные плоскости?
16.	Совпадают ли прямые упр. 10 и И?
17.	Совпадают ли прямые упр. 9 и 13?
18.	В какой точке прямая х =1 — t, у =1 + t, г — 2—'2t пересекает плоскость х = 2?
19.	Напишите параметрическое представление оси г.
20.	Пересекает ли ось г прямая, проходящая через точки (1, 3, 5) и (1, 3, 6)?
21.	Найдите такое число и, чтобы прямая х = 1 — ut, у = 1 + at. г = 2 — t совпадала с прямой, определенной в упр. 18.
4.3	. УРАВНЕНИЯ ПЛОСКОСТЕЙ
Следующая теорема аналогична теореме 1 § 2.1 гл. 2.
Теорема 3. Если А, В, С, D — такие числа, что А2 + В2+ С2 =4= 0, то множество точек, координаты которых удовлетворяют уравнению
Ах + By+ Cz +D = 0,	(9>
представляет собой плоскость; обратно, каждая плоскость может быть представлена уравнением вида (9).
Замечание. Уравнение вида (9) называется линейным уравнением, связывающим переменные х, у, z.
Доказательство. Пусть дано уравнение (9); обозначим через о множество всех тех точек, координаты которых удовлетворяют этому уравнению. Покажем прежде всего, что 1° если о содержит две различные точки прямой I, то и все точки этой прямой принадлежат о. В самом деле, пусть (х4, уи Zi) к (х2, у2, z 2)— две различные точки множества о; тогда
Ах^ “I* Byi -4- Cz± Ч- D = 0, Лх2 Ч~ ВУъ Ч” Cz2 -4- D = 0.
Пусть (х3, у3, z3) — точка прямой /. Тогда (см. § 6.1) найдутся такие числа аир, что
х3 = а%1 + Р*2, у3 = a#i + Р#2, 23 = aZi + Pza и а + Р = 1.
Но тогда
Ах3 Ч- Ву3 + Cz3+D = A(aXf + Px2)4-B(af/i + fiy 2)~l~C(aZi + pz2)+(a + P)D =
= а(Д%1 + By i + CZi + D) + Р(Лх2 4- By2 + Cz2 + D) = 0, так что и точка (х3, у3, z3) принадлежит а.
Покажем далее, что 2° найдутся три неколлинеарные точки, принадлежащие а, и существуют точки, не принадлежащие о. В самом деле, одно из чисел А, В, С, по предположению, не равно нулю. Пусть для определенности С =/= 0; разделив обе части уравнения (9) на С, получим
Л'х Ч- В'у Ч- z Ч- D' = 0,	(10)
146
9. Векторы
Рис. 9.35
Рис. 9.36
где А' = А/С, В' = В/С, D’ = D/С. Точки (0, 0, —D'), (I, О, —Л'—£>') и (О, I, —В'— D’), удовлетворяющие уравнению (Ю), не принадлежат одной прямой. С другой стороны, координаты точки (О, О, I —D') не удовлетворяют уравнению (Ю).
Свойства 1° и 2° показывают, что о действительно является плоскостью.
Докажем теперь, что каждая плоскость о может быть представлена уравнением вида (9). Предположим сперва, что плоскость о не совпадает с координатной плоскостью 2 = 0 и не параллельна ей. Тогда плоскость о пересекает плоскость ху по некоторой прямой I (рис. 9.35). Пусть уравнение прямой I имеет видах +Ьу + с= = 0, где а2 + Ь2 0.
Далее, пусть точка Р с координатами (xi9 yi9 2t) принадлежит о, но не лежит на прямой /. Тогда 21 =/= 0, так как в противном случае плоскость а содержала бы и прямую I и точку Р плоскости ху, не принадлежащую Z, а тогда о, вопреки предпо-ложеникц совпадала бы с плоскостью ху. Рассмотрим теперь уравнение
ах + by +с — 0X1 + *У1+с 2 = о.	(11)
Это уравнение вида (9), в котором А =а, В = Ь, С = — (ах1 4- Ьу1-[-с)/г1 и D = с. Значит, уравнение (11) определяет некоторую плоскость; обозначим ее через т. Каждая точка прямой I имеет координаты вида (х, у, 0), причем ах 4- by 4- с = 0; эти координаты удовлетворяют также и уравнению (11|. Кроме того, координаты (.Xi, Уzt) точки Р тоже удовлетворяют уравнению (11). Таким образом, т есть плоскость, проходящая через прямую I и через точку Р, не принадлежащую I. Этим плоскость т определена однозначно. Поэтому т совпадает с исходной плоскостью а.
Если данная плоскость о параллельна плоскости ху (рис. 9.36) или совпадает с ней, то все точки Р плоскости а имеют одну и ту же координату г, скажем, равную h. Но тогда плоскость а задается уравнением г = h,
которое является уравнением вида (9), где А = В — 0, С — 1 и D = —h. Теорема полностью доказана.
§ 4. Прямые и плоскости в пространстве
147
•Примеры. 1. Найти уравнение плоскости, проходящей через точки (5, 4, 1), (4, —2, —3) и (0, 6, 5).
Р е ш е н ие. Эти точки не принадлежат одной прямой, так что искомая плоскость однозначно определена. Ее уравнение должно иметь вид (9), и так как данные три точки лежат в рассматриваемой плоскости, то имеют место равенства:
5Л 4- 4В 4- С 4- D = О,
4А — 2В — ЗС 4- D = О,
6В 4- 5С 4- D = 0.
Мы получили три линейных уравнения, связывающие четыре неизвестных А, В, С и D. В этом находит отражение то обстоятельство, что, умножив все коэффициенты уравнения (9) на одно и то же число а 0, мы получим уравнение, равносильное исходному. Попытаемся выразить три из неизвестных А, В, С, D через четвертое. Из последнего уравнения имеем
D = —6В — 5С.
Подставляя это значение в первые два уравнения, получаем
5А 4- 4В 4- С — 6В — 5С = 0, 4А — 2В — ЗС — 6В — 5С = 0, или
5А — 2В — 4С = 0, 4А — 8В — 8С = 0.
Из второго уравнения теперь находим
А = 2В 4- 2С;
подставляя это значение в первое уравнение, получим
5(2В 4- 2С) — 2В — 4С = 0, или
В = — — С. 4
Следовательно,
А = 2 (— — С^4-2С= — С \	4	)	2
И
D------6 (— — С\ — 5С =------С.
\	4	/	2
Выбрав для С, скажем, значение 4, мы получим А =2, В=—3 иО=—2. Искомое уравнение имеет вид
2х — Зу + 4г — 2 = 0.
Легко видеть, что координаты заданных точек действительно удовлетворяют этому уравнению.
148
9. Векторы
2.	Если О, 0 и с=£ О, то плоскость, проходящая через точки (а, 0, 0), (0, Ь> 0), (0, 0, с), имеет уравнение
Доказательство. Это уравнение — вида (9) и координаты заданных точек ему удовлетворяют. Сравните этот результат с уравнением прямой на плоскости «в отрезках на осях» (см. гл. 2, § 2.4). ф
УПРАЖНЕНИЯ
В упражнениях 22—26 требуется найти уравнение плоскости, проходящей через заданные точки.	--
22.	(2, —1, 3), (4, 0, 5), (2, 1, 7).
23.	(1, —4, 5), (6, 7, 0), (3, —2, 5).
24.	(6, 1, 5), (—6, 2, 7), (1, 2, 3).
25.	(—1, 0, 0), (0, 3, 0), (0, 0, 2).
26.	(0, 0, 0), (2, 2, 2), (3, 3, 1).
В упражнениях 27—30 требуется найти уравнение плоскости, проходящей через заданные прямую I и точку Р.
27.	Р (0, 0, 0); I i х = 2 — /, у = 3 — t, г = 2/.
±28. Р (4, —1, 0); I : х = t, у = 2/, г = 3/.
29.	Р (1, 2, 3); I : х = 2 + /, у = 2 + 2/, г = —3/.
30.	Найдите такое число и, чтобы плоскость их у — г — 1 = 0 проходила через точку (100, и, и).
4.4. ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
Теорема 4. Пусть
Ах + By + Cz + D = 0,	(12)
-|- Bip	CiZ-|-Z)i = 0	(13)
— уравнения двух различных плоскостей. Для того чтобы эти плоскости были параллельны, необходимо и достаточно, чтобы нашлось такое число а =/= 0, для которого
Ai = аЛ, Bi = аВ, Cj = аС.	(14)
Доказательство. Предположим, что а =/= 0, удовлетворяющее условию (14), существует. Поделив обе части уравнения (13) на а, перепишем его так:
Ax + By + Cz+ -51 =0.	(13')
а
Если Dt /а. =/= D, то никакая точка (х, у, г) не может удовлетворять уравнениям (12) и (13') одновременно: эти две плоскости [а значит, и плоскости (12) и (13)] не имеют ни одной общей точки и, следовательно, они параллельны. В случае, когда Dt/a = D, уравнения (12) и (13') определяют од н у и ту же плоскость, а совпадающие плоскости можно считать параллельными*.
* Ср. с подстрочным примечанием на стр. 76, т. I.
§ 4. Прямые и плоскости в пространстве
149
Предположим теперь, что числа а ¥= О, удовлетворяющего условию (14), не существует. Мы покажем, что наши две плоскости имеют общие точки и, значит, не параллельны. Если не существует числа а =/= 0, удовлетворяющего условию (14), то по крайней мере одно из чисел
ABi — AiB, BCi—BiC, ACt—AiC	(15)
отлично от нуля. [В самом деле, если все числа (15) равны нулю и, например, А =/= 0, то, положив а =	, найдем, что = аВ и Cj = аС. При этом а дол-
жно быть отлично от нуля, так как хотя бы одно из чисел Д t, В ь С\ не равно нулю.] Предположим для определенности, что
A Bt— AtB^0.	(16)
Тогда для каждого данного значения г можно найти такие числа х и у, что точка (х, у, г) принадлежит обеим плоскостям (12) и (13). В самом деле, выбрав какое-нибудь значение z и рассматривая (12) и (13) как систему уравнений относительно х и у, мы сможем решить эти уравнения. Для этого умножим (12) на Blt а (13)—на В. Вычитая полученные уравнения, мы придем к уравнению
(ABi— A iB)x + (CBi— CiB)z +DBt—DiB = О, которое в силу условия (16) определит х; соответствующее значение у можно будет найти, подставляя это значение х в уравнение (12) и решая его относительно у.
фПример. Найти плоскость, проходящую через точку (2,—1,4) и параллельную плоскости
5х — 7у + 8z — 6 = 0.
Решение. Коэффициенты при х, у и z в уравнении искомой плоскости в силу теоремы 4 должны иметь вид 5а, —7а, 8а. Полагая а = 1, мы можем переписать искомое уравнение так:
5х — 7у -I- 8z -I- D = 0,
где D еще надо определить. Подставляя х = 2, у = —1 и г = 4, получаем 5-2 + +(—7) (— 1) -|-8-4 4- £> = 0. Следовательно, D = —49 и искомая плоскость имеет уравнение
5х — 7у + 8z — 49 = О.ф
4.5. УРАВНЕНИЯ ПРЯМЫХ
Две непараллельные плоскости, скажем,
2х — Зу + 4г — 5 = 0 и 6х — 9г/ + 5г — 1=0,	(17)
пересекаются по некоторой прямой I. Поэтому мы можем задать прямую I парой уравнений (17): прямая состоит из всех точек (х, у, г), удовлетворяющих обоим уравнениям.
Для того чтобы получить параметрическое представление этой прямой, будем рассматривать одну из трех переменных х, у, г как данную и решим полученную
150
9. Векторы
Рис. 9.37
систему относительно двух других. Какую из трех переменных выбрать, зависит от разностей (15), использованных в доказательстве теоремы 4 (схематический рис. 9.37 может помочь запомнить эти выражения). В нашем случае А = 2, В = —3, С = 4, Ai= 6, Bt = —9, С( = 5 и разности (15) таковы:
2(—9) — (—3)6 = 0; (—3)5 — 4(—9) =/= 0; 2-5 — 4-6 =/= 0.
Это означает, что можно решить уравнения (17) относительно у и г, выразив их через х, либо же относительно хи г, выражая их через у. Но мы н е можем выразить х и у через г (это читатель легко проверит сам). Дадим х произвольное значение, которое мы обозначим через t, и будем рассматривать (17) как систему двух уравнений с неизвестными у и г:
— Зу 4- 4z = 5 — 2t,	(18)
— 9у 4- 5z = 1 — 6t.
Умножив первое уравнение на 5, второе на 4 и вычитая из первого полученного таким путем уравнения второе, будем иметь
((_ 3)5 — 4( — 9)) у = 5(5 — 20— 4(1 — 60,
откуда 21# = 21 4- 14/, или
у = 1 +
Подставляя это значение у в первое из уравнений (18) и решая его относительно г, получим
Мы нашли параметрическое представление линии пересечения плоскостей (17):
§ 4. Прямые и плоскости в пространстве
151
X — t, у = 1 •+• t, z = 2. о
Если прямая / задана параметрическим представлением, то от него можно перейти и к заданию этой прямой двумя линейными уравнениями, т. е. в виде линии пересечения двух плоскостей. Последнее можно даже сделать бесконечным числом способов, так как существует бесконечно много плоскостей, проходящих через данную прямую.
Так, например, если прямая I задается равенствами
х = 2 — 2/, у = — 3 + 4/, z = 6 — t,	(19)
то мы можем следующим образом найти линейные уравнения, которым удовлетворяют все точки прямой /. Разрешим каждое из уравнений (19) относительно т. е. перепишем равенства (19) в виде
t=6 — z. 2	4
Теперь исключим t\ если (х, у, г) — точка прямой /, то для нее должны иметь место равенства
Я—- =1+± = б — г, 2	4
или после умножения на 4
4 — 2х = 3 + у = 24 — 4г.	(20)
Это — симметричная форма уравнений прямой (19). Мы можем теперь рассматривать нашу прямую как линию пересечения двух плоскостей
4 — 2х = 3 + # и 34"# = 24 — 4z, т. е.
2х 4- у — 1 = 0 и у 4- 4г — 21 = 0.
Можно рассматривать нашу прямую и как линию пересечения плоскостей
4 — 2х = 24 — 4г и 3 4- у = 24 — 4г, т. е.
х — 2г 4- 10 = 0 и у 4- 4г — 21 = 0,
И т. д.
ф Пример. Представить прямую х = 2 4- /, у = 2 — t, г = 2 как линию пересечения двух плоскостей.
Решение. Параметр t не входит в выражение для г. Исключая t из выражений для хи#, найдем, что рассматриваемая прямая является линией пересечения плоскостей х + # = 4 и г = 2.ф
152
9. Векторы
УПРАЖНЕНИЯ
В упражнениях 31—33 требуется найти плоскость, проходящую через заданную точку и параллельную заданной плоскости.
31.	(7, 4, 5), 2х — Зу — 6 = 0.
32.	(4, 0, 6), х + у + г = 0.
33.	(1, 1, 1), х —20у +7г —5 = 0.
34.	Найдите такое число а, что плоскость ах + 2ау + lOz — 2 = 0 параллельна плоскости х + 2у + 5z — 7 = 0.
35.	Плоскости х — у = 2 и 2х — ау + 7 = 0 параллельны. Найдите а.
36.	Закончите предложение: «для того чтобы плоскость Ах + By + Cz + D = 0 была параллельна плоскости yzt необходимо и достаточно...».
В упражнениях 37—43 определите, параллельны ли данные плоскости. Если они не параллельны, найдите параметрическое представление их линии пересечения.
37.	х = 0, у — 2=0.
38.	х — у = 1, у — 2=1.
39.	2х — Зу — 5 = 0, —4х + бу — 4 = 0.
40.	7х — 5г/ + 6г = 0, 21х — 15г/ + 18г — 62 = 0.
41.	х + у + 2г — 3 = 0, х + у — 2г + 3 = 0.
А 42. 2х — бу + 7г — 5 = 0, бх + у + 4г — 1 = 0.
43.	х — у — г = 5, х — у — г = 5,001.
В упражнениях 44—50 найдите два линейных уравнения, определяющих данную прямую.
44.	х = t, у = —t, г = 0.
45.	х = 2 — t, у = 2 — 2t, г = 6t,
46.	Прямую, проходящую через точки (0, 0, 0) и (7, 6, 3).
47.	х = — 1 + 2/, у = — 2 + 3t , г = 6 — 7t.
48.	Ось г.
49.	Прямую, проходящую через точки (2, —1, 4) и (6, 2, —3).
50.	х = 7 — 6/, у = 5*, z = 6 — I.
В упражнениях 51—57 уравнения прямой даны в симметричной форме. Найдите параметрическое представление этой прямой.
51.	х = у = 0.
52.	х = у = 1.
53.	х = у = г.
54.	х — у = х = у.
55.	2х — у = х + г = г — 4г/.
А 56. х — у + z = 2х — Зу + г = х 10# + 5г.
57.	2х + у — 4 = х — Зу + г + 5 = х + 2у — z — 10.
58.	Какая линия определяется уравнением
(х — у + I)2 4- (х •+ У — 2 + 4)2 = 0?
59.	Для каких значений q уравнение
(2х + Зу + 4г — 1)а + (qx + Зу + 4г — I)2 = 0 определяет прямую? Какое множество точек задает оно в иных случаях?
4.6. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
Пусть I — прямая и а — плоскость; тогда / либо целиком содержится в о, либо пересекает а в одной точке, либо параллельна* а (рис. 9.38).
Если I и It — две прямые, то либо совпадает** с /, либо пересекает /, либо параллельна /, либо li и / не лежат в одной плоскости; в этом последнем случае прямые 11 и / называются скрещивающимися (рис. 9.39). Мы покажем на примерах, как аналитически распознают взаимное расположение прямых и плоскостей.
* В ряде отношений удобно считать, что принадлежность прямой I плоскости а есть частный случай параллельности I и О’ (ср. G подстрочным примечанием на стр. 76, т. I).
** См., впрочем, ту же сноску.
§ 4. Прямые и плоскости в пространстве
153
Гис. 9.38
•Примеры. 1. Даны прямая
х = 2 — 3/, у = 6 + t, z — —1—2/	(21)
и плоскость
Зх — у + 2г — 5 = 0 ;	(22)
каково их взаимное расположение?
Решение. Выясним, какие точки прямой (21) лежат в плоскости (22). Для этого подставим в уравнение (22) вместо х, у, г их выражения (21). Мы получим
3(2 — 3/) — (6 + /) + 2(—1 — 2/) — 5 = О, или
t + — = 0.
2
Последнее равенство выполняется при t = —1/2 и только при этом значении t. Следовательно, прямая (21) пересекает плоскость (22) в единственной точке — точке с координатами х = 2 — 3(—1/2), у — 6 + (—1/2), г = —1 — 2(—1/2), т. е. в точке (7/2, 11/2, 0).
2. Определить взаимное расположение прямой (21) и плоскостей
Зх + 13г/ + 2г — 5 = 0	(23)
и
Зх + 13г/ + 2г — 82 = 0.	(24)
154
9. Векторы
Решение. Подставив выражения (21) в уравнение (23), получим равенство 77 = 0. Так как оно, конечно, неверно, то прямая (21) и плоскость (23) не пересекаются — они параллельны.
Подставляя (21) в уравнение (24), получим тождество 0 = 0 (оно не содержит /). Следовательно, прямая (21) принадлежит плоскости (24) — все ее точки являются также точками плоскости (24).
3. Определить взаимное расположение прямой (21) и прямой
х = —1 + 6s, у = —2s, z = 4 + 4s.	(25)
(Заметьте, что поскольку здесь мы имеем две прямые, то для обозначения параметра второй прямой мы вынуждены использовать другую букву!)
Решение. Выясним сначала, будут ли эти две прямые иметь общую точку. Если такая точка существует, то ей соответствует такое значение t и такое значение s, при которых получаются одни и те же значения х, у, z. Следовательно, мы должны иметь
2 — 3t = — 1 + 6s,
6 + t = —2s, — 1 — 2/ = 4 4- 4s.
Эти уравнения не удовлетворяются ни при каких значениях s и t. (Например, из первого уравнения следует 3/ + 6s = 3, т. е. t 4- 2s = I, в то время как в силу второго уравнения t 4- 2s = —6.) Следовательно, наши прямые не имеют общих точек, т. е. они либо параллельны (если лежат в одной плоскости), либо скрещиваются.
Чтобы определить, какой из этих случаев имеет место, выберем какие-либо две точки прямой (21), например (2, 6, —1) и (—1, 7, —3), и одну точку прямой (25), например (— 1, 0, 4). Плоскость, проходящая через эти три точки, содержит прямую (21). Уравнение этой плоскости
х — Зу — 3z 4- 13 = 0.
Возьмем теперь еще одну точку прямой (25), скажем точку (—7, 2, 0), и проверим, принадлежит ли она рассматриваемой плоскости. Оказывается, что дело обстоит именно так и, значит, наши прямые параллельны.ф
УПРАЖНЕНИЯ
В упражнениях 60—68 определите, будет ли прямая I содержаться в плоскости сг. параллельна ей или пересекать ее в одной точке. В последнем случае найдите точку пересечения.
60.	h х = 2у = Зг; at 8х — бу + 7г = 330.
61.	h х = t, у = 2 + 2/, z = 4^ <л 2х — Зу — 5г + 6 = 0.
62.	/» х = 2 — 2tt у = 3 4- 2t, г = 4 4- t\ о: х 4- 2у — 4г + 8 = 0.
63.	h х — 2у = 3 и х + г = 5; о? х + у 4* г = 1.
64.	Н х — 2у + г = 7 и х — у — 2г = 0; а: 2х — 4# = 0.
65.	li х — 2 = у — 3 = 2г — 5; <и 2х + Зу — 4г 4- 5 = 0.
66.	/! х — 2077у 4- ЮЗг — 4 = 0 и х 4~ 2у = 3; о: х — 2077// 4- ЮЗг — 4 = 0.
67.	Прямая I проходит через точки (0, 2, 1) и (4. —1, 0); плоскость о проходит через точки (0. 0. 0), (2, —1, 6) и (—2, 1, 7).
68.	Прямая / из упр. 67; плоскость (Л х 4" у — z = 2.
§ 4. Прямые и плоскости в пространстве
155
В упражнениях 69—78 определите, будут ли прямые Zj и /а скрещивающимися, параллельными, совпадающими или пересекающимися в единственной точке. В последнем случае определите точку пересечения.
69.	If.	х =	1	— Z,	у = 2 + Z,	z =	2Z; /2: х = 1 — s, у	= 1 + 2$, г =	4	— s.
70.	Ц:	х =	1	— Z,	у = 2 + t,	г —	2t\ 12: х = 3 — 2s,	у = 4 + 2s, г =	6	+ 4s.
71.	Zp	x —	1	= у	+ 2 = 2г — 3;	/2: x = s, у = s — 3, z =-b- s—	1.
72.	Zp	2x — 3y +	4z — 1 = x	— у	+ 2г = 0; 1%: Зх =	Зу = г — 2х.
73.	Zf х =	2 + 3/, у = — 2 + 3/, г = 4; Z2 : х + у — 2 = г — 4 = 0.
74.	Zx: х —	2у = г — 4 = Зх + г — 5; /2: х + у — г = х + у — 2г = 1.
75.	Прямая	Zx проходит через точки (2, 3, 4) и (1, 6, 7); Z2: х = 1 + Z, у =	г =	t.
А 76. Прямая	Zi проходит через точки (1,—1, 0) и (0, 1, 0); /2: х + у + г —2= х	— у	+	г — 2=
= х + г/ — г — 2.
77.	Прямая Zf совпадает с осью х; Z2: ЮООх = 1010г/ = 100100 г.
78.	Zx: х — у = х — 2г = у + г; Z2: 2х — Зу = г + 4у — 5 = х — у + 1.
4.7. СФЕРА
Множество всех точек пространства, отстоящих на одно и то же расстояние г >0 от некоторой фиксированной точки Q, называется сферой; точка Q называется центром сферы, а число г— ее радиусом. Таким образом, сфера есть множество всех точек (х, у, z), удовлетворяющих уравнению
(х — а)2 + (у — b)2 + (z — с)2 = г2,
где (а, 6, с) — координаты центра Q сферы. Множества точек, координаты которых удовлетворяют неравенствам
(х — а)2 + (у — b)2 + (z — с)2 < г2 и
(х — а)2 + (у — Ь)2 + (г — с)2 > г2,
— это соответственно все внутренние точки сферы и все точки, внешние по отношению к этой сфере.
Множество решений любого уравнения вида
х2 + у2 + z2 + ах + by + cz + d = 0
представляет собой либо сферу, либо точку, либо пустое множество. Это можно доказать, выделяя полные квадраты, точно так же как мы доказали соответствующее утверждение для случая плоскости (теорема 1 § 3.1 гл. 2).
•Примеры. 1. Каково множество решений уравнения
х2 + 2х + у2 — 2у + z2 — 4z + 6 = 0?
Решение. Выделяя полные квадраты, перепишем данное уравнение в виде
(х + I)2 — 1 + (у — I)2 — 1 + (г — 2)2 — 4 + 6 = 0, или
(X + I)2 + (у - I)2 + (г - 2)2 = 0.
Множество решений этого уравнения состоит из одной точки — точки (—1, 1, 2).
156
9. Векторы
Рис. 9.40
Рис. 9.41
2. Найти пересечение плоскости г = 13 и и сферы
(х — 2)? + (у — З)2 + (z — 4)2 = 100.
Решение. Подставив г = 13 в уравнение сферы, получим уравнение
(х — 2)2 + (у — З)2 = 19.
Величины х и у можно рассматривать как декартовы координаты на плоскости г = 13 (рис. 9.40); следовательно, линия пересечения является окружностью. Ее центр — точка (2, 3, 13), а радиус равен )/19.
Метод, использованный в этом примере, можно применить для аналитического доказательства теоремы: если плоскость имеет со сферой общие точки, то их пересечение представляет собой окружность или точку (рис. 9.41). ф
УПРАЖНЕНИЯ
79.	Плоскость г = 1 пересекает сферу г2 + и2 + г2 = 10 по некоторой окружности. Найдите ее центр и радиус.
80.	Плоскость у = 3 пересекает сферу х2 + уг + г2 — 2х + 2г = 16 по некоторой окружности. Найдите ее центр и радиус.
81.	Найдите уравнение сферы, имеющей центр в точке (1, —2, 2) и проходящей через точку (2, 0, 3).
82.	Найдите центр и радиус сферы, уравнение которой имеет вид
х2 + у2 + г2 — 4х + 6г/ — г + -12_= 1.
4
83.	Найдите центр и радиус сферы, уравнение которой имеет вид
4jt2 4- 4у2 4- 4г2 4- 40х — 32г/ — 4г = 31.
§ 5. Цилиндрические и сферические координаты
157
84.	Сферы х2 + у2 + г2 = 19 и х2 + у2 + г2 — Юг = —21 пересекаются по некоторой окружности. Найдите ее центр и радиус.
85.	Найдите уравнение сферы радиуса У114, проходящей через точки (2, 6,—3) и (1,—1, 5).
86.	Найдите точки пересечения прямой х = 2 + t, у = 3 — Л г = t со сферой радиуса 3 с центром в начале координат.
87.	Найдите точки пересечения прямой х = у = 2г со сферой (х — I)2 + у2 + г2 = 100.
88.	Найдите все плоскости о, параллельные плоскости ху и пересекающие сферу х2 + у2 + + г2 = 100 по окружности радиуса 4.
§ 5. ЦИЛИНДРИЧЕСКИЕ В этом параграфе мы введем две системы координат в про-И СФЕРИЧЕСКИЕ странстве, аналогичные полярным координатам на плос-КООРДИНАТЫ кости. Этими системами координат мы будем пользоваться ”	только в § 4 гл. 10 при исследовании поверхностей второго
порядка и в гл. 13 при вычислении кратных интегралов.
5.1.	ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ
Если точка Р имеет декартовы координаты (х, у, z), то ее цилиндрические координаты — это, по определению, три числа (г, 6, z), где (г, 6) — полярные координаты точки (х, у) в плоскости ху. Заметим, что г = ]/х2 + г/2 есть расстояние точки Р (х, у, z) от точки (0, 0, z), т. е. расстояние точки Р от оси z (рис. 9.42).
Поверхности, соответствующие фиксированным значениям г, являются круговыми цилиндрами (рис. 9.43); отсюда происходит и название «цилиндрические» координаты. Поверхности, соответствующие фиксированному значению 0, — плоскости, проходящие через ось z (рис. 9.44); поверхности, соответствующие фиксированному значению z, — это, конечно, плоскости, параллельные плоскости ху.
Связь между цилиндрическими координатами (г, 0, z) и декартовыми координатами (х, у, z) одной и той же точки определяется формулами:
г2 = х2 + у2,	(1)
cos 0 = —, sin 0 = —, z = г Г	Г
и
х = г cos 0, у = г sin 0, z = z.	(2)
Как и в случае полярных координат, здесь также удобно допускать и о т р и-цательные значения г.
•Пример. В цилиндрических координатах уравнение плоскости имеет вид
Rr cos(0 — а) + Cz + D =0,
где R, а, С, D — числа, такие что R2 + С2 =^= 0.
Для того чтобы убедиться в этом, рассмотрим линейное уравнение
Ах + By + Cz 4- D =0, где А2 + В2 + С2 =# 0. Пусть (/?, а) — полярные координаты точки (Л, В). Подставим вместо (х, у, z) их выражение (2) и заменим А и В на 7? cos а и /?sina. ф
2
Рис. 9.42"
Рис. 9.45
15*
§ 5. Цилиндрические и сферические координаты
5.2. ПОВЕРХНОСТИ ВРАЩЕНИЯ
Предположим, что в плоскости xz (в плоскости у = 0) задана кривая С, целиком расположенная в полуплоскости х >> 0. Будем вращать ее вокруг оси z, чтобы получить поверхность вращения S. Рассмотрим точку Р на поверхности S, удаленную на расстояние г от оси z. Пусть Ро — точка кривой С с той же координатой z, что и Р (рис. 9.45). Тогда г равно расстоянию х точки Ро от оси z. Отсюда вытекает следующий результат:
Уравнение поверхности S в цилиндрических координатах получается из уравнения кривой С заменой х на г.
Если уравнение поверхности S задано в цилиндрических координатах, то легко, конечно, получить и уравнение поверхности S в декартовых координатах — для этого достаточно заменить г2 на х2 + У2*
Ясно, что, вместо того чтобы считать кривую С лежащей в полуплоскости х >> 0, мы можем предположить, что она симметрична относительно оси z.
160
9. Векторы
Например, если линия С плоскости хг — это прямая х = р, где р — положительное число, то поверхность S, получающаяся при вращении С вокруг оси z, совпадает с поверхностью, которая получается при вращении пары прямых х = р и х = —р {рис. 9.46). Уравнение этой пары прямых х2 = р2. Следовательно, уравнение поверхности S будет иметь вид г2 — р2 = 0, или
х2 + у2 = р2.
Поверхность S является, конечно, круговым цилиндром.
фПример. Пусть т— положительное число. Будем вращать вокруг оси z прямую 2 = /их, или (что то же оамое) пару прямых z = тх и z = —тх (рис. 9.47). Уравнение этой пары прямых
(z + mx)(z — тх) = 0, или z2 — т2х2 = 0.	(3)
Следовательно, уравнение поверхности вращения таково: z2 — т2г2 = 0, откуда, l
полагая а = —, получим
а2 а2	V '
Эта поверхность называется круговым конусом', осью его служит ось z. ф
УПРАЖНЕНИЯ
В упражнениях 1—8 даны декартовы координаты точки в пространстве; требуется найти цилиндрические координаты этой точки.
1.	(2, —2^ —3).	5. (4cosl5°, — 4sinl5°, 1).
2.	(—/2, /2, 1).	6. (1, 2, 3).	__
3.	(2, — _2/з7 2).	7. (1/2 sin л/8, 1/2 cos л/8, УЗ /2).
4.	(—/3/2, 1/2, 1/4).	8. (3, 4, —1/2).
В упражнениях 9—12 требуется найти уравнение поверхности S в цилиндрических координатах.
9.	S совпадает с плоскостью уг.
10.	S описывается уравнением х2 + у2 + 2г2 + 2z — 5 = 0.'
11.	S есть сфера радиуса 1 с центром в начале координат.
12.	S есть плоскость х — 2у + Зг — 5 = 0.
В упражнениях 13—17 поверхность S получается вращением вокруг оси г линии С, лежащей в плоскости хг. Найдите уравнение поверхности S в декартовых координатах. Нарисуйте поверхность S.
13.	С: г = е~Х2.	16. С: г = х.
А14. С: г = I х3 I.	17. х2 + 4z2 = 100.
15.	С: (х — I)2 + г2 = 1.
5.3.	СФЕРИЧЕСКИЕ КООРДИНАТЫ
Сферические координаты точки Р, имеющей декартовы координаты (х, у, z), — это тройка чисел р, 0 и <р, определяемых следующим образом: р есть расстояние точки Р от начала координат О, 0 имеет то же значение, что и в случае цилиндрических координат, ср есть угол между положительным направлением оси z и лучом ОР (рис. 9.48). Если х2 + у2 -0, то 6 не определено; если р = 0, то не определено ф.
§ 5. Цилиндрические и сферические координаты
161
Рис. 9.48
Обозначим через Q точку с координатами (х, у, 0), а через Т — точку (0, 0, г). Из рис. 9.48 легко усмотреть, что г =pcos ф. С другой стороны,
х2 4- у2 = | OQ |2 = | TP |2 =р2 sin2 ф.
Следовательно, полярные координаты точки Q равны р sin ф и 6; поэтому ее декартовы координаты равны х =psin ф cos 6 и у =р5Шф$ш6. Окончательно мы приходим к следующим формулам, связывающим сферические координаты точки с ее декартовыми координатами:
°	р2 =х2 + у2 + г2,
cos 0 = — -*	, sin 0 = —-	,
+	Ух* + у‘
(5)
z . V х2 4- У2 COS ф =  »	Sin ф = ---
И	Р	Р
х =psin ф cos 6,
у =psin ф sin 0,	(6)
z =pcos ф.
Согласно нашему определению, р > 0 и 0	<л. Но удобно считать сфери-
ческими координатами точки (х, у, г) любую тройку чисел (р, 6, ф), для которых имеют места равенства (5).
162
9. Векторы
Рис. 9.49
Рис. 9.50
Вее точки, для которых ф = 0 или ф = 180°, принадлежат оси z. Поверхности, соответствующие фиксированному значению ф (где ф заключено между 0 и л/2 или между л/2 ил), — это круговые конусы, оси которых совпадают с осью z (рис. 9.49). Это геометрически очевидно и легко может быть доказано аналитически следующим образом.
Пусть а — данное положительное число; из равенств (6) имеем
а2 а2	\ а2 ]
Но если | tg ф | = а, то это уравнение равносильно уравнению (4), определяющему (круговой) конус (см. § 5.2). При ф = 90° получается плоскость ху.
Поверхности, соответствующие фиксированным значениям 6, — те же, что и в случае цилиндрических координат. Поверхности, соответствующие фиксированным значениям р, — это, конечно, сферы с центром в начале координат; отсюда и название этой координатной системы.
Рассмотрим теперь точку Р, принадлежащую некоторой фиксированной сфере с центром в начале координат. Положение точки на сфере можно определить заданием чисел ф и 6. Их значения мы ограничим неравенствами 0 ф 180°, —180° 'С
6	180°. Тогда 6 называется долготой точки Р, а (90° — ф) — ее широтой.
Это соответствует употреблению тех же терминов в географии, где значения ф = 0, Ф = 90° и ф = 180° отвечают Северному полюсу, экватору и Южному полюсу. Кривые на сфере, отвечающие фиксированному значению ф, называются параллелями, а кривые, соответствующие фиксированному значению 6, — меридианами (рис. 9.50).
§ 6. Скалярное произведение
163
УПРАЖНЕНИЯ
В упражнениях 18—24 требуется найти сферические координаты (р, 0, ф) точки, заданной своими	декартовыми	координатами (х, у, г).
18.	(1, 1, 1).	22.	(1,	2,	3).
19.	(7, —7, 5).	_	__	23.	(cos 77,	sin 77, 0).
20.	(5//2 , —5//2 .	5/3//2).	24.	(0,	1, 0).
21.	(0, 0, —л).
В упражнениях 25—29 требуется найти уравнение поверхности S в сферических координатах.
25.	S есть плоскость у = 0.
26.	S есть плоскость г = 1.
27.	3 есть сфера радиуса 1 с центром в точке с декартовыми координатами (0, 1, 0).
28.	S получается при вращении прямой х = 3 (лежащей в плоскости xz) вокруг оси г.
29.	3 получается вращением прямой х = г (лежащей в плоскости xz) вокруг оси г.
Приложение к главе 9
§ 6. Скалярное произведение
Существуют разные способы умножения векторов. Наиболее важным для изучения функций нескольких переменных и наиболее широко применимым в алгебре, геометрии и физике является так называемое скалярное умножение двух векторов. Впрочем, в настоящей книге мы лишь изредка будем пользоваться скалярным произведением векторов; именно поэтому § 6 отнесен в Приложение к основному тексту.
6.1.	Определение скалярного произведения
Пусть а и b — два вектора, причем а =/= 0, b =/= 0. Если выбрана точка О, то найдутся такие точки Р и Q, что направленный отрезок ОР представляет вектор а, а направленный отрезок OQ — вектор b (рис. 9.51). Угол ^POQ не зависит от выбора точки О, но только от векторов а и Ь. Этот угол, по определению, считается углом между векторами а и Ь; мы будем обозначать его символом ^(а, Ь).
Каждой паре векторов а и b сопоставляется некоторое число, называемое их скалярным произведением и обозначаемое через ab (или а«Ь). Это число определяется следующим образом:
ab = | а |« | b |« cos 0, где 0 — угол между а и b; ab = 0, если а = 0 или b = 0.	(1)
Скалярное произведение называется также «внутренним произведением» и иногда обозначается через (а, Ь)* *. Только что введенное определение применимо как к векторам на плоскости, так и к векторам в пространстве.
Из определения (1) следует, что
если ab = 0, то либо | а | = 0, либо | b | = 0, либо 0 = 90°.	(2)
Векторы а, Ь, для которых ab = 0, называются ортогональными, или перпендикулярными.
Если а = Ь, то 0 = 0 и cos 0=1. Следовательно,
или	а2 = а* а = | а |2.	(3)
	^1 = /^.	(3')
* Название «внутреннее произведение» (inner product) и запись (а, Ь) особенно распространены в (учебной и научной) литературе на английском языке.
164
Приложение к главе 9
6.2. Вычисление скалярного произведения
Теорема 1. Пусть {elf ез, е3} — репер, относительно которого векторы а и b имеют координаты (at, а а, а3) и (6j, 6з, b3). Тогда
ab = а±Ь± + 02^2 + а3Ь3.	(4)
Доказательство. Равенство (4), очевидно, справедливо, если а = 0 или b = О, так как в этих случаях обе его части равны нулю. Предположим, что а =/= О, b =/=0, и рассмотрим прямоугольную декартову систему координат {О, е^, ез, е3}. В этой системе координат а — радиус-вектор точки Р с координатами а^, а*, а3, а b — радиус-вектор точки Q с координатами
Ьъ, Ь3 (рис. 9.52). По формуле расстояний,
|	а |» = ГбР р = 4 + + 4 | b р= fOQ Р = 4 + % + 4
|	b — а Р = | QP Р = (&t - в1)» + (Ьз - аз)г + (b3 - а3)2 = .
=b ]+ 4 + 4	4 + 4 + 4 —	+ азЬз + a3b3).
Так как 6 = ^(а, b) = ^POQ, то формулу косинусов (см. § 3.2, пример 2) можно переписать так:
I b — а |2 == | а I2 + f b |2 — 2| а 11 b |cos O=|a|2+|b|2 — 2аЬ.
Поэтому
ab =^. (| а Р + I Ь р - | b - а Р).
Подставляя вместо | а |2, | b |2 и |Ь — а I2 их выражения в координатах, мы и получим равенство (4k
Следствие 1. Если а и b — векторы плоскости, координаты которых относительно некоторого репера {ег, ег) имеют вид (at, аз) и (blt bа), то
ab = ajdj + a 263.	(5)
§ 6. Скалярное произведение
16$
В самом деле, если е3 — такой вектор, что тройка {ех, е2, е3} является репером в пространстве, то векторы а и b можно рассматривать как векторы в пространстве, координаты которых относительно этого нового репера имеют вид (а^ аъ, 0) и (Ьъ bi, 0). Поэтому равенство (5) непосредственно вытекает из (4).
Теорема 1 позволяет найти угол 0 между двумя (ненулевыми) векторами а и b или между направленными отрезками, представляющими эти векторы. В самом деле, пользуясь равенствами (1) и (3), получаем
ab	ab
О =	(a, b) = arccos---= arccos —=—~ »	(6)
I а | |Ь|	/а2 j<b2
а пользуясь равенством (4), мы можем вычислить ab, а2 и Ь2.
•Примеры. 1. Если {еь ег, е3} — репер, то е^еу = 1 при i = j и еге/ = 0, если i Ф j. В самом деле, | ег | = 1 при i = 1, 2, 3 и ^(е/, е7) = 90д, если i =/= /.
2. Пусть точки X, Y и Z имеют декартовы координаты (1,2, 3), (4. —1, 7) и (6, —1. 4). Определить угол 0 = ^XYZ.
Решение. Очевидно, 0 = ^(Х—Y, Z—Y) (рис. 9. 53). Так как координаты вектора X—Y равны (1—4, 2+1,3 — 7) = (—3, 3, —4), а координаты вектора Z — Y равны (2, 0, —3), то мы имеем
| X — Y |2 = (—3)2+ З2 + (— 4)2 = 34, | Z — Y |2 = 22 + О2 + ( — З)2 = 13,
(X — Y). (Z — Y) = (—3). 2 + 3-0 + (—4)(—3) = 6 и, значит,
6
cos 0 = ———— % 0,28, т. е. О 74°. ф
/34/13
УПРАЖНЕНИЯ
В упражнениях 1—4 найдите скалярное произведение ab векторов а и Ь, имеющих указанные координаты относительно некоторого репера.
1.	(2, 0, 7), (—2, 0, —7).	3. (2, 4). (6, —1).
2.	(3, —5, 6), (0,01; 0,02; 0,3).	4. (51, 6, —3), (0. 7, 4).
В нижеследующих упражнениях {еь ез, е3}	— репер.
5.	Найдите такое число и, что cos (ег + 2еа + ие3, Звх + е2) =	.
6.	Найдите все такие числа и, что векторы ех + 5ез — 6е3 и 2ех —ез + ие3 ортогональны.
7.	Пусть Р, Q, R—точки, декартовы координаты которых соответственно равны (0, 1,3), (2,—1, 6) и (8, —2, 4). Найдите углы треугольника PQR (Поскольку здесь все вычисления приближенные, сумма полученных углов не должна точно равняться 180°).
В упражнениях 8—12 найдите угол между двумя данными векторами а и Ь.
8.	а = 2ех + (cos 10°)е2 — (sin 10°)е3, b = (l//2jei + (sinl0°)e2 + (cos 10°)е3.
9.	а = 2b, b = ej + е2 + e3.
10.	a = ex — e2, b = e2 — e3.
11.	a = 4ef — 0,5e2 + 6e3 b = 2(3ex — 4e2 + 0,5e3).
12.	a = (cos 3°)ех + (cos 20°)e2, b = —ex + 6e3.
6.3.	Свойства скалярного произведения
Отметим некоторые формальные свойства скалярного произведения.
Теорема 2. Скалярное произведение обладает следующими свойствами:
I.	Для любых двух векторов а и b существует однозначно определенное число, называемое их скалярным произведением и обозначаемое символом ab.
II.	ab = Ьа для всех а и Ь.
Ill.	(Xa)b = Х(аЬ) для всех векторов а, b и всех чисел X.
IV.	а(Ь + с) = ab + ас для всех а, Ь, с.
V.	Если а 4= 0, то а2 > 0.
166
Приложение к главе 9
Доказательство. Свойство 1 не нуждается в доказательстве. Остальные свойства можно доказать либо геометрически, пользуясь определением (1), либо аналитически, используя равенство (4) и свойства чисел. Мы пойдем по второму пути.
Пусть а, b и с — векторы, координаты которых в некотором репере мы обозначим через (alt az, а3), (bf, bz, Ь3) и (clt с2, с3). Коммутативный закон II вытекает из равенства (4), если заметить, что каждый член в правой части равенства (4) при перестановке сомножителей а и b не меняется. Ассоциативный закон III следует из того, что координаты вектора Ха равны (Хаг, Ха2, Ха3) и, значит, этот закон сводится к равенству
(XajJ^j + (Xa z)b 2 + (Ха3)63 = k(aib1 + а 262 + а3Ь^.
Так как координаты вектора b + с равны (Ьг + с19 bz + С2, b3 + с3), то дистрибутивный закон IV сводится к равенству
ai(^i + Ci) + az(bz + cz) + a3(b3 + с3) = (a^bi + azbz + a3b3) + (a^j + агсг + a3c3), которое, очевидно, справедливо. Наконец, а? + а| + а| > 0, где равенство имеет место лишь в том случае, если a$ = az = а3 = 0. Этим доказано и свойство V.
Заметим, что
а« 0 = 0 для всех а.	(7)
(Ь + с)а = ba -f- са.	(8)
Доказательства этих утверждений предоставляются читателю.
Векторное пространство, для которого справедливы свойства I—V, называется евклидовым векторным пространством. В следующем параграфе мы приведем примеры таких пространств.
6.4.	Применение свойств скалярного произведения
Докажем теперь некоторые следствия теоремы 2; при этом мы будем пользоваться только аксиомами 1—10 векторного пространства (см. § 1.5) и аксиомами I—V евклидова пространства (см. теорему 2). Следовательно, полученные результаты будут применимы ко всякому евклидову векторному пространству.
Теорема 3 (неравенство Шварц а*). Каковы бы ни были векторы а и Ь. всегда
। аЬ | < । а |. | b |.	(9)
Если воспользоваться определением 1, то справедливость этого утверждения очевидна, поскольку — 1 < cos 0 < 1. Мы же хотим доказать неравенство (9), пользуясь только свойствами 1—V скалярного произведения. Для этого заметим, что для каждого числа:
0 < (а + ХЬ)2 [по свойству VI =
= (а 4" ХЬ)(а 4“ ХЬ) [применим несколько раз свойства II, III. IV] ==
= а2 4- 2аЬХ 4- Ь2Х2 == । а |2 4- 2аЬХ 4- | b |2Х2.
Так как этот квадратный трехчлен относительно X не имеет (действительных) корней, то |а |2| b |2 — (аЬ)2> 0. а это равносильно неравенству (9).
Теорема 4. Длина вектора	__
|а| = /а2	(10)
обладает следующими свойствами'.
1)	для каждого вектора а его длина | а । неотрицательна',
2)	( а | = 0 « том и только в том случае, если а = 0;
3)	। Ха I — | X 11 а । для всех векторов а и всех чисел X;
4)	|а + Ь|<|а|4“|Ь| для всех а и b (неравенство треугольника).
Все эти утверждения геометрически очевидны. Но они также могут быть выведены из определения (10) и свойств скалярного произведения: так, свойство 2) вытекает из V, а свойство 3) — из III. Неравенство треугольника 4) эквивалентно тому, что
|а 4- Ь|2 < | а |2 4- 21 а 11 b । 4- | Ь |2, или
(а 4- Ь)2 < | а |2 + 21 а 11 b ( + |Ь (а.
* Это неравенство зачастую называют также неравенством Коши (или Коши—Шварца).
§ 6. Скалярное произведение
167
Рис. 9.54
Применяя к вектору (а + Ь)2 свойства II и IV. мы можем переписать последнее неравенство так: а2 + 2аЬ -Ь Ь2 < । а |2 + 2| а | | b | 4* | b2l.
что равносильно неравенству Шварца.
Выразим теперь координаты вектора через скалярные произведения. (Здесь мы предположим справедливость свойства 113.)
Теорема 5. Если {еъ ез, е3} — репер и а — вектор с координатами (а^, а 2, а3), то
Oj = аеъ аз = аез. а3 = ае3.	(11)
Доказательство. По определению координат (см. § 1.12), а = а1е1 4" аге г + а3е3.
Отсюда, используя свойства III—IV и соотношения еа1 = 1, еге1 = 0, e3ej = 0 (см. пример 1 § 6.2), получаем аег = (а^! + аге2 + a3e3)et = (а1е1)е1 4- (азег^ 4- (a3t3)e1 « =а1(е1е1) + а 2(^2,^) + а3(е3е!) = а^.
Остальные равенства (11) доказываются аналогично.
ф Примеры. 1. Найти угол между диагональю куба и его ребром.
Решение. Пусть {ev ез, е3} — репер Нам надо найти угол а между векторами ej + + ег + е3 и ег (это видно из рис. 9.54). Имеем
(ei 4~ е2 4” е3) ei	1*
cos a =  ---------;—;--— = —— »
I Ci 4- «2 4- е3 I • I ei I |<з так что приближенно .a » 54°41'.
2.	Найти угол между диагональю куба и диагональю его грани.
Решение. Здесь нам надо найти угол 0 между векторами ег + ез + е3 и ej 4- ез. Прое-/~ 2
тым подсчетом получаем cos 0 =j / — откуда 0 « 35°25'. W	&
3.	Диагонали параллелограмма равны (имеют одинаковые длины) в том и только в том слу-чае, если этот параллелограмм — прямоугольник.
Доказател ьство. Пусть две стороны параллелограмма с общей вершиной Р представляют векторы а и b (рис. 9.55). Тогда диагонали его будут представлять векторы а + Ьи а — Ь. Равенство диагоналей означает, что | а 4“ b | 2 = 1а — ЬР. или
168
Приложение к главе 9
О = (а + b)2 - (а - b)2= а2 + 2ab + b2 — (а2 — 2ab + b2) = 4аЬ.
Но равенство ab =0 означает, что векторы а и b ортогональны, т. е. что рассматриваемый параллелограмм — прямоугольник.
4.	Диагонали параллелограмма в том и только в том случае взаимно перпендикулярны, если этот параллелограмм является ромбом.
Доказательство. Воспользуемся обозначениями примера 3. Ортогональность диагоналей параллелограмма означает, что
0 = (а + b)(a — b) = а2 — b2 = ( а |2 — । b |2, откуда । а | = | b | и, значит, параллелограмм является ромбом.®
УПРАЖНЕНИЯ
В упражнениях 13—21 предполагается фиксированным некоторый репер {elt ег, е3}.
13.	Пусть (a. ej) = 1, (а, ег) = 2, (а, е3) = 3. (b, ej = 3, (b, ег) = 2, (b, е3) = 1. Найдите <(а, Ь).
14.	Пусть (a, ei) = (а, ег) = 2 и | а । = У17. Найдите (а, е3).
15.	Докажите тождество (а + b + с, а + b + с) = | а |2 + | b |2 + I с |2 + 2(а, Ь) + + 2(а, с) + 2 (Ь, с).
16.	Найдите угол между выходящими из одной вершины диагоналями двух граней куба. [Указание: сравните с примерами 1 и 2.]
17.	Найдите угол между ребром куба и диагональю его грани.
£ 18. Найдите вектор а, такой что (а, ех + ег) = 2, (а, ех — ег) = 3 и (а, е3) = 0.
19.	Найдите вектор а. такой что (а,	= (й, ег) = (а, е3) и । а | = 100.
20.	Если (а, ех) = (а, е2) = 5, то может ли быть | а | < 7?
21.	Покажите, что (а, ех)2 < (а, а) для всех а. В каком случае (a, ei)2 = (а, а)?
6.5.	Направляющие косинусы. Единичные векторы
В этом и в следующих разделах мы будем пользоваться фиксированным репером {ej, ег, е3} с заданным началом О.
Пусть а =/= 0 — вектор и alt a2, a3 — углы вектора а с ег, ег, е3 (рис. 9.56). Эти углы назы ваются направляющими углами вектора а, а числа cos alt cos a г, cos a3 — его направляющими косинусами.
Направляющие косинусы любого вектора обладают свойствами, напоминающими свойства косинуса и синуса полярного угла вектора на плоскости.
Если а =	+ аге г + а3е3, то направляющие косинусы вектора а равны
Д1	а2	аз	/1ОЧ
cos 04 = -—-,	cos a2 = ~—- ,	cosa3	= -—-	•	(12)
|а|	|а|	|а|
Действительно, имеем (см. теорему 3 § 6.3)
cos 04 = cos (а, еО = ——• = — >	(13)
I а 11 ех | I а |
так как ^ | = 1. Другие два равенства (12) доказываются аналогично. Зная длину | а | вектора а и его направляющие углы ах, а2, а3, мы можем представить этот вектор следующим образом:
а = | а | cos 04 ех + । а | cos a2 ег + | а । cos a3 е3.	(14)
Сравните формулы (12) и (14) с соответствующими формулами для векторов на плоскости (см. § 3.1);	’
cos0 = —, sin 6 = — , а = I а I cos 0 ei + I а I sin 0 е2.	(15)
§ 6. Скалярное произведение
IC9
Рис. 9.56
Для равенства cos2 6 + sin2 0 = 1 также можно найти аналог в стереометрии. Так как | а|2= = aj +	4“ а|, то из формулы (12) вытекает, что
cos2 ах + cos2 аз + cos2 а3 = 1.	(16)
Таким образом, эти три направляющих косинуса не независимы.
С другой стороны, если ах, аг, а3 — любые числа, заключенные между Ойл (включая и эти значения) и такие, что выполняется равенство (16), то они служат направляющими углами определенного единичного вектора (т. е. вектора длины единица). Этот вектор равен, конечно,
ао = (cos а^ех + (cos а2)е2 + (cos а3)е3.
Каждый вектор а с теми же направляющими углами аг, а2, а3 имеет вид a = Хао, где X— некоторое положительное число.
Замечание. Пусть а — вектор, ортогональный е3, так что а3 = 90° и cos а3 = 0. В этом случае мы можем представлять себе а как вектор в плоскости. Пусть 6— полярный угол вектора а в координатной системе {О, ех, е2}. Тогда cosa1=cosO и cos a2 = sin6, как можно видеть, сравнивая (14) с (15). Заметим, однако, что направляющие углы должны удовлетворять неравенству 0 < a < л, в то время как полярный угол может принимать любые значения. В случае, изображенном на рис. 9.57, мы имеем ах = 6, а2 = 90° — 6, в то время как в случае, представленном на рис. 9.58, имеем ах = 360° — 0, аз = 90° + ах.
ф Пример. Пусть 0 — угол между векторами а и b с направляющими углами ах, а 2, а3 и ₽i, ₽ 2, Р з- Тогда
cos 0 = cos ajCosPx + cos a2cosp 2 + cosa3cosP 3.	(17)
Доказательство. Воспользуемся разложением (14) и аналогичным разложением для вектора Ь:
b = I b | (cosPJej + | b |(cosp 2)е2 + | b |(cosP 3)е3.
Подставляя эти выражения для а и b в равенство (6), мы и получим (17).ф
170
Приложение к главе 9
6.6. Угол между двумя прямыми
Вектор а называется параллельным прямой Z, если он может быть представлен направленным отрезком прямой I] в этом случае вектор (—а) тоже параллелен I. Если а =£ 0. то направляющие косинусы вектора а называются направляющими косинусами прямой I.
Пусть I и k — две прямые, а и b — ненулевые векторы, им параллельные; положим 0 = — -^(а. Ь). Если 0< 6 < 90е, назовем ср = 6 острым углом между прямыми I и k. Если 90е <С < 6 < 180е, положим ср = 180 — би назовемф острым углом между нашими прямыми. Таким образом, во всех случаях coscp = |cos в | и, значит
cos ср =
I
|а| |Ь|
(18)
Как видно из рис. 9.59, если прямые I и k пересекаются, наше определение совпадает с общепринятым. Если I и k параллельны, то ф = 0.
УПРАЖНЕНИЯ
22.	Найдите направляющие косинусы вектора а = 2еТ' — Зег + 4е$.
23.	Найдите направляющие косинусы вектора а = —ej + 2ег — 10е3.
24.	Вектор а имеет равные направляющие углы: сц = аг = аа, при этом 0< а, < 90°. Найдите <ц.
25.	Вектор а имеет равные направляющие углы: aj = аг = ая, при этом 90° < а, < 180°. Найдите аг.
26.	Точка Р имеет координаты (7, —11, 6). Найдите направляющие косинусы вектора, представляемого отрезком ОР.
27.	Точка Р имеет координаты (3 cos 13°, —3 sin 13°, 0). Найдите направляющие косинусы и направляющие углы вектора, представляемого отрезком ОР.
28.	Найдите направляющие косинусы и направляющие углы вектора а с координатами (0. 20 cos 20°, 20 sin 20°).
29.	Точка Р имеет сферические координаты (р. 6, ср), где р >0. Найдите направляющие косинусы вектора, представляемого отрезком ОР.
30.	Точка Р имеет цилиндрические координаты (г, 6, г), где г > 0. Найдите направляющие косинусы вектора, представляемого отрезком ОР.
§ 6. Скалярное произведение
171
Рис. 9.60
31.	Точки Р и Q имеют соответственно сферические координаты (1, Of,Ф1) и (1, 6 2, <р 2). Найдите формулу для косинуса угла POQ. [Указание. Используйте упр. 29 и пример из § 6.4.]
32.	Найдите направляющие косинусы прямой, определяемой уравнениями х± = 2 — 2t, Х2 = 3 + /, х3 = 4 — 5/.
33.	Найдите острый угол между прямой упр. 32 и прямой, проходящей через точки (4, —1, 6) и (5, 2, —1).
6.7.	Нормаль к плоскости. Угол между плоскостями
Пусть о — плоскость, I — прямая, проходящая через начало О перпендикулярно к о, и Р — точка пересечения о и I (рис. 9.60). На прямой I найдутся две точки Q и Т, удаленные от точки Р на расстояние 1; направленные отрезки PQ и РТ определяют векторы, которые мы обозначим соответственно через п и —п. Эти векторы называются единичными нормалями к плоскости о. Если плоскость о не проходит через начало О, т. е. если Р Ф О, выберем точку Q так, чтобы О и Q лежали по разные стороны от плоскости ст. В этом случае мы назовем п единичной нормалью ко, направленной от начала. Если о проходит через О, то Р = О и выбор точки Q произволен.
Пусть cos alt cos 02, cos а3 — направляющие косинусы вектора п. Радиус-вектор точки Р равен рп, где р есть расстояние от точки О до плоскости о. Если X— точка с радиусом-вектором X и координатами jq, л*2, х3, то она тогда и только тогда принадлежит о, когда отрезок РХ ортогонален I. Так как отрезок РХ определяет вектор X — рп, то это условие можно записать следующим образом:
(X — рп)п = 0, или Хи — рп2 = 0, а так как па = 1, то это означает, что
Хп — р = 0,	(19)
или в координатах
jricos ах + х2cos аг + х3cos а3 — р = 0 (где р > 0).	(19')
Это линейное относительно xlt Х2, *з уравнение и есть уравнение плоскости (Т.
Обратно, каждое линейное уравнение
Л1Х1 + А 2X2 + А 3х3 + D = 0	(20 >
172
Приложение к главе 9
(где Alt Az, А з не равны нулю одновременно) можно привести к нормальной форме (19'). Для этого надо только умножить обе части уравнения нар, где
р = --- — , если D < О,
V А, + Л| + Л| и	(21)
р — —	• , если D > О
Уа2 + а2 + а2
(при D =0 можно взять любой знак). Мы получим тогда равносильное уравнению (20) уравнение вида (19'), где
cos С4 = р А!, cos аг = р А 2 cos а3 == р А 3, р = —рD > 0.	(22)
Так как cos2a1 + cos2a2 + cos2a3 = 1, то найдется вектор с направляющими углами alt аг, a3. Следовательно, направляющие углы ах, а2. а3 единичной нормали к плоскости (20) и расстояние р этой плоскости от начала координат определяются формулами (21) и (22). Если плоскость не проходит через начало координат, то этими формулами определяется нормаль, направленная от начала координат.
Приведенные выше рассуждения показывают, в частности, что вектор с координатами (A j, Аг, А з), т. е. вектор (1/р )п, параллелен единичной нормали к плоскости о. Пользуясь этим соображением, можно вычислить острый угол между двумя плоскостями. Он определяется как острый угол между ортогональными к ним прямыми. Острый угол <р между плоскостями
АЛЛА
А]Х} + А2Х2 + А3х3 -р D = 0 и AjXi 4" А2Х2 4“ А3х3 4" D = О
находится, следовательно, из равенства
I А А А I
COS <Р = *ЛМ1 + ЛгЛг+ ЛзЛ» I--------,	(23)
/(л2 + л2 + л23)(л2 + л2 + л2)
которое вытекает из формулы (18).
6.8.	Расстояние от точки до плоскости
В заключение этого параграфа мы выведем одну красивую формулу.
Теорема 6. Расстояние Ъот точки Р с координатами (alt az, а3) до плоскости а с уравнением A ijq 4- A zx 2 4- А 3х3 4- D = 0 равно
| А^ 4~ A2fl2 4- А3а3 4- D |
5 = ------ ------------------ (24)
)/ л? + л| + л|
Доказательство. Определим числа cos ax, cos аг, cos а3 и р по формулам (21) и (22) и обозначим через п вектор с координатами cos ax, cos a2, cos a3, т. e. единичный вектор нормали к плоскости а. Тогда уравнение плоскости о можно записать в виде (19х) и равенство (24), которое мы хотим установить, можно переписать так:
б = I пР - р |,	(24')
где Р есть радиус-вектор точки Р.
Пусть k — прямая, проходящая через точку Р и ортогональная а; обозначим через Q точку пересечения k и о (рис. 9.61). Тогда d = | PQ | = | Р — Q], где Q — радиус-вектор точки Q. Так как вектор Р—Q параллелен п, то Р — Q = tn, где t — некоторое число. Далее, поскольку точка Q принадлежат плоскости о, то в силу (19) имеем Qn = р, т. е.
(Р — /п)п = р, или Рп — /п2 = р,
§ 6. Скалярное произведение
173
и так как п2 = 1, то t = пР — р. Но
б=|Р—Q| = |fn|=p|.|n|=|f|, откуда и следует равенство (24х).
6.9.	Расстояние от точки до прямой
Равенство (24) имеет и планиметрический аналог. Если прямая I в плоскости ху задана уравнением Ах + By + С = 0, то расстояние д точки (а, Ь) этой плоскости от прямой I равно
|Ла+ВЬ + С| о = - "
V А*+ &
(25)
Можно доказать это аналогично теореме 6. Но проще заметить, что искомое расстояние д равно расстоянию от точки (а, Ь, 0) пространства до плоскости о, уравнение которой имеет вид Axi + Вх* + С = 0 (рис. 9.62). Следовательно, равенство (25) получается, если подставить в (24) at = а, а а = Ь, а8 = 0, 4$ = А, А% — В, Л3 = 0и£) = С.
УПРАЖНЕНИЯ
Следующие упражнения относятся к трехмерному пространству с координатами х±, ха, х8.
34.	Найдите координаты единичной нормали к плоскости 3xj — 2ха + 5х3 — 6 = 0.
35.	Найдите координаты единичной нормали к плоскости, проходящей через точки (1,0, 2), (4, 0, 0) и (1, 1, 1).
36.	Найдите острые углы между плоскостью Xf + ха + х3 = 0 и координатными плоскостями.
37.	Найдите острый угол между плоскостями упр. 34 и 35.
38.	Найдите расстояние от точки (1, 2, 3) до плоскости 2хг — Зха + 4х8 — 7 = 0.
39.	Найдите расстояние от начала координат до плоскости, проходящей через точки (6, 1, 0), (0, 0, 7) и (2, 0, 3).
40.	Найдите расстояние от точки (10, 10, —100) до плоскости упр. 39.
174
Приложение к главе 9
41.	Найдите положительное число л, такое что точка (2, и, 3) находится на расстоянии 100 от плоскости х1 + х2 + х3 = 8. А 42. Найдите такое число v > 0, что точка (и, 2v, и2) находится на расстоянии 1000 от плоскости 2*! — Х2 + 2дгз = 6. Следующие задачи относятся к плоскости ху» 43. Найдите расстояние от точки (2, 3) до прямой у — 7х = 5.
44.	На параболе у = х2 найдите точку (или точки), расстояние которой от прямой Зу = = —5 — 4х равно 4/5.
45.	Найдите такое число Л что точка (t, t2) находится на расстоянии 6 от прямой Зх— 4у = 0. Сколько существует таких чисел?
46.	Найдите все точки прямой у — 2х + 5 = 0, находящиеся на расстоянии 7 от прямой у + х _ 6 = 0.
§ 7. «-мерные пространства
7.1.	Пространство «-наборов
Мы уже упомянули в § 6.4 гл. 2, что «л-набор», т. е. упорядоченную последовательность п вещественных чисел, например (ар а2, ... ал), можно назвать точкой «-мерного пространства (или «-пространства). Здесь п может быть любым целым положительным числом. При этом точки удобно отождествлять с их радиусами-векторами. Следовательно, вектор — это просто упорядоченная последовательность из п чисел (л-набор): а = (ctj, аз» ...» ал).
Сложение и умножение векторов на числа определяются следующим образом: («1» а2, ...» art) + (Pi, ₽ 2» ...» Ря) = (С4 + Pi, а2 + Р 2» ...» аЛ + Рп); (1) Х(ах, а2» ...» ая) = (Хах, Хаг...................Хал).	(2)
Нулевым вектором 0 следует, конечно, назвать последовательность (0, 0, ..., 0), состоящую из л нулей. Свойства 1—10 векторов сохраняют силу и для л-наборов. (Доказывается это в точности так же, как и в случае л = 2; см. § 1.10.) Но теперь мы имеем такую дополнительную аксиому. 11л. Существуют такие п векторов elt ег, ...» еЛ, что каждый вектор а однозначно представляется в виде а =	+ агег + ... + апед.
Например, можно положить er = (1, 0, 0................................ 0),
е2 = (0, 1, 0..0),
е3 = (0, 0, 1.. 0),	(3)
 • • « . еЛ = (0, 0, 0.. 1).
Аксиомы 1 —10 вместе с аксиомой 11л называются аксиомами «-мерного векторного пространства. Совокупность векторов ех, е2, ...» ел, обладающая свойством 11п, называется базисом этого пространства. Невозможно, конечно, нарисовать картинку, изображающую ту или иную из л-мерных фигур (т. е. множеств точек л-мерного векторного пространства, где л > 3), но с л-мерными векторами можно производить вычисления. В настоящее время л-мерные векторные пространства играют очень большую и все возрастающую роль как в самой математике, так и в ее приложениях. (Это относится также и к бесконечномерным векторным пространствам, которых мы здесь не коснемся.)
§ 7. n-мерные пространства
175
УПРАЖНЕНИЯ
1.	Пусть а = (2, 7, 0, 6), b = (0, 0, 2, —3), с = (1, 1, —1, 5); вычислите а + Ь, а — с = = а + (—1)с, 2а — ЗЬ и 7с — 4Ь.
2.	Вычислите 33 (0, 6, —4, 5) — 32 (6, —7, 4, 6) + (2, 2, 100, 0).
3.	Составляют ли векторы (0, 1, 0, 0), (1, 0, 0, 0), (О, О, 1, 1) и (О, О, О, 1) базис четырех-. мерного векторного пространства (образованного всевозможными 4-наборами, т. е. упорядоченными четверками чисел)?
4.	Составляют ли векторы (1, 0, 1, 0), (1, 0, 0, 0), (0, 0, 1, 0) и (1, 0, 0, 1) базис четырехмерного векторного пространства?
5.	Составляют ли векторы (1, 1, 0, 0), (1, —1, 0, 0), (0, 0, 1, 1) и (0, 0, 1, —1) базис четырехмерного векторного пространства?
Д6. Составляют ли векторы (1, 1, 1, 0), (0, 1, 0, 0), (1, 0, 1, 0) и (0, 0, 0, 1) базис четырехмерного векторного пространства?
7.	Составляют ли векторы (1, 0, 0, 0, 1,), (1, 0, 0, 0, —1), (0, 1, 1, 0, 0), (0, 1, 0, 0, 0) и (О, 0, 0, 1, 0) базис пятимерного векторного пространства, образованного 5-наборами?
8.	Составляют ли векторы (1, 0, 2, 0, 1), (1, 0, 1,0, 0), (0, 0, 1, 0, 1), (0, 1, 0, 0, 1) и (О, 0, 0, 0, 1) базис пятимерного векторного пространства?
7.2.	Прямые и гиперплоскости
Прямая л-мерного пространства, — это, по определению, множество всех таких точек (векторов) х = (jq, хг, ..., хЛ), которые могут быть представлены в виде
х = а + /Ь,	(4)
где а и b =# 0 — данные векторы, a t —любое вещественное число. «Векторное уравнение» (4) равносильно п обычным (числовым) уравнениям:
Xi = aj + tbj, i = 1, 2.n.	(4')
Гиперплоскостью в л-мерном пространстве, по определению, называется множество всех точек (векторов), координаты которых удовлетворяют некоторому линейному уравнению, т. е. уравнению вида
+ Л 2X2 + ... + Апхп + D = 0,	(5)
где А±, А 2, ..., и D — числа, причем А% + А? + ... +	=£ 0. (При п = 1 гиперплос-
кость является точкой' при п — 2 — прямой, при п = 3 — обычной плоскостью.)
Многие привычные нам геометрические теоремы сохраняют силу и в л-мерном пространстве. Так, например, существует в точности одна прямая, проходящая через две несовпадающие точки; если две различные точки прямой принадлежат гиперплоскости, то и вся прямая ей принадлежит, и т. д.
УПРАЖНЕНИЯ
9.	Докажите, что если аир — такие числа, что а + р = 1, то точка х = аа + ₽Ь принадлежит прямой, проходящей через а и Ь.
10.	Найдите такие числа w, v, w, что точка (2, 4, л, v, w) принадлежит прямой, проходящей через точки (0, 2, 3, 4, 5) и (2, 2, —1, 6, 3).
11.	Найдите такие числа u, v, чтобы точки (3, 3, л, а), (4, 0, 5, 3) и (2, 6, 3, 5) принадлежали одной прямой.
12.	Найдите уравнение гиперплоскости четырехмерного пространства, содержащей точки (2, 0, 0, 0), (0, 4, 0, 0), (0,0, 1,0) и (0, 0, 0, 5).
13.	Найдите пересечение прямой х^ = хъ = х3 = t, х, =2 — 2t с гиперплоскостью 2xj— — Х2 — х3 — х4 — 6 = 0.
14.	Найдите точку, в которой прямая Xf = 2/, хг = х3 = 1 — t, х4 — 1 + t пересекает гиперплоскость упр. 12.
15.	Пересекаются ли гиперплоскости xj = 0 и хг + х3 = 0 пятимерного пространства? Попытайтесь описать множество точек их пересечения.
16.	Найдите гиперплоскость четырехмерного пространства, проходящую через начало координат (0, 0, 0, 0) и не пересекающую гиперплоскость 2х3 — х4 — 7 = 0.
176
Приложение к главе 9
7.3.	/г-мерное евклидово пространство
Пространство л-наборов а= (а*, аа, .... a^), b = (0i, р2> ---Рл) и т- Д- можно превратить в л-мерное евклидово (векторное) пространство (ср. с § 6.3). определяя скалярное произведение ab векторов а и b равенством
ab = 0x01 + 020 а + ... + аЛ0Л.	(6)
Заметим, что то утверждение, которое ранее являлось теоремой, здесь служит определением. Свойства I —V скалярного произведения (см. § 6.3) сохраняют силу и при таком определении числа ab. Это нетрудно доказать, и мы предоставляем читателю сделать это самостоятельно и заметим, что доказательство опирается на те же рассуждения, которые использовались в § 6.3 для случая л = 3.
Длина вектора а(ар аг, .... ад) определяется формулой
|а|= /?= У а?+а|4- ... +а2.	(6')
Неравенство Шварца (ср. с теоремой 3 § 6.4)
I ab | < |a || b |	(7)
тоже справедливо. Справедливы также и свойства 1)—4) длины вектора из § 6.4; в частности, имеет место неравенство треугольника
I а + Ь | < | а | + | b |.	(8)
Действительно, в доказательствах из § 6.4 использовались лишь общие аксиомы евклидова векторного пространства.
Расстояние d между двумя точками (векторами) а и b определяется теперь равенством
d = I а - b I = К (а, - ₽,)» + (аа-ОД» + ... + (а„ -	.	(9)
Пространство л-наборов с расстоянием, определяемым формулой (9), называется л-мерным евклидовым пространством. Неравенство треугольника (8) имеет простой «геометрический» смысл: расстояние между двумя точками а и —b не больше суммы их расстояний от третьей точки (начала 0).
Множество всех точек х л-мерного евклидова пространства, находящихся на данном расстоянии г > 0 от точки а, называют сферой радиуса г с центром в а (в случае л = 2 сфера — это окружность).
На самом деле неравенство Шварца (7) и неравенство треугольника (8)—это теоремы о вещественных числах. Мы сформулируем их следующим образом.
Для любых 2п чисел аь аг, ...» ал, 0Ь 0 г..0Л имеют место неравенства
(ах₽1 4- • •• 4- ап?л)2 < ( а1 4- • •• 4- ал) ( ?] + •• • 4- Зл)
и	_______________ __________________
V (“1 — fll)2 4---1- (“л — W2 < У а1 + •  • + ап + У	4— +1>« •
7.4.	Углы
Мы можем теперь определить угол в между двумя (ненулевыми) векторами а и Ь л-мерного евклидова пространства формулой _	ab
О = arccos : [— ,	(10)
|а|IЬ|
и развить «л-мерную аналитическую геометрию». Заметим, что в силу неравенства Шварца (7) ab
дробь г-.-|Г| в правой части равенства (10) всегда будет числом, заключенным между —1 и 4-1 1а| |°1
(включая сюда и оба крайних значения); поэтому формула (10) действительно определяет некоторый угол 0 (в обычном смысле этого слова). Заметим также, что базис (3), построенный в § 7.1, при наших соглашениях становится репером: векторы е/ являются единичными и взаимно ортогональными.
Пример. Чему равен угол 0 между векторами а = (1, 3, —7, 1) и b = (6, 0, —2, —20)?
Ответ. Так как ab = 1-64“ 3-04“ (—7)- (—2) 4- Ь (—20) = 0, то в = 90°.ф
Задачи
177
УПРАЖНЕНИЯ
17.	Найдите такое число и, что векторы (2, 7, —1, и) и (4, 6, 2, и2) ортогональны.
18.	В четырехмерном пространстве определите угол между вектором (1, 1, 1, 1) и вектором ех = (1, 0, 0, 0).
19.	Найдите направляющие косинусы вектора n-мерного пространства, следуя определению из § 6.5. Докажите, что сумма квадратов п направляющих косинусов равна 1.
20.	Докажите, что множество всех точек х n-мерного пространства, для которых ах = 0, где а —фиксированный (и отличный от нуля) вектор, является гиперплоскостью, проходящей через начало отсчета векторов.
21.	Уравнение гиперплоскости 2х± + Зхг—х3 —х4+ хб =100 перепишите в виде пх—р=0, где п — единичный вектор и р>0.
22.	Какое геометрическое место точек n-мерного пространства определяется уравнением (х — а)2 = а. где а — данное число, а — заданный вектор? (Рассмотрите случаи а>0, а = 0 и а< 0.)
ЗАДАЧИ
Задачи 1—4 относятся к векторам на плоскости.
1.	В тексте мы сначала определили произведение вектора на число, а затем доказали свойства 6—10 этой операции (см. § 1). Покажите, что если предположить справедливость предложений 1 —10, то можно доказать, что произведение вектора на рациональное числ ) обязано быть таким, как мы его определили. [Указание: рассмотрите сначала случай умножения на целое число.]
2.	Покажите, что два вектора независимы в том и только в том случае, когда они не пропорциональны.
3.	Пусть {ех, е2} — репер; а =	+ агег и b =	+ 0 гег — два вектора. Покажите, что эти два вектора независимы в том и только в том случае, если ахр2 —	=/= 0.
4.	Докажите теорему, сформулированную в тексте без доказательства: два вектора образуют базис на плоскости в том и только в том случае, если они независимы.
5.	Для данной последовательности векторов ах, аг, а3, ... (на плоскости или в пространстве) и вектора а утверждение а = lim а/, по определению, означает, что lim | а, — а | = = 0. Какие теоремы о пределах из § 3 гл. 8 сохраняют силу для пределов векторов?
6.	Определите сходимость и расходимость (бесконечного) ряда, составленного из векторов. Найдите, какие из теорем § 4 гл. 8 могут быть обобщены на векторы. В частности, до-
00	со
кажите, что если числовой ряд | а,- | сходится, то и ряд из векторов а/ тоже схо-/=1	/=1
дится. Что можно сказать относительно таких рядов?
Задачи 7 и 8 относятся к аффинной (или общей декартовой) системе координат на плоскости. Такая система определяется точкой О, называемой началом, и базисом {ех, ег}. Пусть Р — точка иР — ее радиус-вектор относительно О, т. е. вектор, определяемый направленным отрезком ОР. Тогда найдутся такие числа'*! и хг, что Р = х^ + хгег. Числа (хх, хг) называются координатами точки Р в системе координат (О, elf ег}.
Пусть £х и £г —точки с координатами (1, 0) и (0, 1) в этой системе координат. Координатными осями будут прямые, проходящие через О и Е± (ось хх) и через О и £2 (ось хг); они теперь не должны быть взаимно перпендикулярными. При этом нам даже не обязательно иметь одну «универсальную» единицу длины: длины вдоль оси хх мы измеряем длиной отрезка ех, а вдоль оси хг — длиной отрезка ег.
7.	Точки £х и £2 имеют декартовы (прямоугольные) координаты (2, 0) и (1, 1), точка О — начало декартовой системы координат. Начертите ось хх и ось хг. Постройте точки, координаты которых в этой системе {О, ех, ег} равны (1, 1), (2, —3), (—1, 0), (—2, —1). Найдите декартовы координаты этих точек.
8.	Решите задачу 7, предполагая на этот раз, что декартовы координаты точек £х и £2 соответственно равны (—1, 1) и (1, 1).
178
Приложение к главе 9
Задачи 9—11 относятся к векторам в обычном трехмерном пространстве.
9.	Пусть аь а2, а3 — три вектора. Покажите эквивалентность следующих условий: 1) эти три вектора не независимы, 2) один из этих трех векторов может быть представлен в виде линейной комбинации двух других, 3) найдутся три числа ах, аг, а3, не равные одновременно нулю, такие что ахах + а га г + а3а3 = 0. (Мы говорим, что вектор х является линейной комбинацией векторсв ух, у2, уЛ, если х = ^хух + £2у2 + ... + где 6/, /=1, 2, ... , k,— некоторые числа.)
10.	Докажите теорему, сформулированную в § 1 без доказательства: три вектора в пространстве в том и только в том случае образуют базис, если они независимы.
11.	Определите аффинную систему координат в пространстве, обобщая определение, данное перед задачей 7.
Задачи 12 и 13 относятся к векторному пространству, т. е. к любому множеству элементов, называемых векторами, для которых определены сложение и умножение на числа (скаляры) таким образом, что выполняются аксиомы 1 —10 из § 1. Векторное пространство называется «-мерным, если для него дополнительно выполняется аксиома 11л из § 7.1.
12.	Даны т векторов ах, .... а^; покажите эквивалентность следующих двух условий: 1) най дутся числа ах, а2, ... ат, не равные нулю одновременно и такие, что а1а1+агаг+... ... + ата^ = 0; 2) один из этих т векторов является линейной комбинацией остальных. [Указание: сравните с задачей 9; векторы ах, а2, ..., ат, обладающие этим свойством, называются зависимыми.]
13.	Покажите, что если т векторов независимы, то независимы и любые т — 1 из них.
14.	Покажите, что в пространстве «-наборов любые « + 1 векторов зависимы. (Если Вам никогда не приходилось встречаться с доказательством этого, то настоящая задача вряд ли покажется Вам особенно простой.)
15.	Покажите, что « векторов в пространстве «-наборов в том и только в том случае образуют базис, если они независимы.
16.	Рассмотрим множество всех многочленов р(х) от х. Многочлены можно складывать между собой и умножать на числа. Покажите,что многочлены образуют векторное пространство, т.е. что для них справедливы аксиомы 1—10 из § 1. Покажите, что это же верно для многочленов, степени которых не превосходят некоторого фиксированного целого положительного числа k.
17.	Покажите, что пространство многочленов, степени которых не превосходят k, имеет размерность k + 1; выведите отсюда, что пространство всех многочленов не является «-мерным пространством ни для какого «. (Такое пространство называется бесконечномерным.)
18.	Предположим, что в пространстве четверок вещественных чисел скалярное произведение двух векторов а = (ах, а2, а3, а4) и b = (Рх, р 2, р 3, р4) определено не так, как в § 7.3, а по формуле (а, Ь) = ахрх + 2а2р2 + За3р3 + 100а484. Будет ли это пространство евклидовым пространством, т. е. будут ли в нем справедливы равенства I—V из § 6.3? (Если нет, то какие именно аксиомы здесь не выполняются?)
19.	Ответьте на вопрос задачи 18 при следующих определениях:
ab = агрх + а2₽2 — а383 — а4р4*» ab = ахР] + 100а4Э4.
В задачах 20—23 используется математический анализ.
20.	Покажите, что все ограниченные непрерывные функции х »-► Дх), определенные на отрезке 0 < х < 1, образуют бесконечномерное векторное пространство. [Указание: вспомните, что многочлены являются непрерывными функциями.]
21.	В векторном пространстве задачи 20 определим скалярное произведение таким образом: 1
(/, g) = fax)g(x)dx. Покажите, что здесь выполняются все аксиомы евклидова пространства.
22.	Напишите неравенство Шварца и неравенство треугольника для только что определенного скалярного произведения (ср. с задачами 12 и 13 из гл. 5).
23.	Вычислите угол между «векторами» х х2 и х i~* 2х — 1 в векторном пространстве, определенном в задачах 20 и 21.
10/КВАДРИКИ
В этой главе продолжается изложение аналитической геометрии на плоскости. Математический анализ в ней практически не используется; ее можно читать непосредственно после первых трех параграфов гл. 9. Читатель, знакомый с аналитической геометрией, свободно может пропустить большую часть этой главы. Основное содержание главы составляет построение теории кривых второго порядка (конических сечений, или «коник»), для чего приходится рассматривать поворот системы координат. В последующих главах используется только материал § 1.
В Приложении продолжается изложение аналитической геометрии в пространстве; здесь содержится краткое введение в теорию поверхностей второго порядка («пространственных квадрик»).
180
10. Квадрики
§ 1. КОНИКИ
1.1. КОНИЧЕСКИЕ СЕЧЕНИЯ
Парабола, которую мы рассматривали в § 4.1 гл. 2, может быть определена как кривая, которая в соответственным образом выбранной декартовой системе координат описывается уравнением
у2 = 4ах (где а > 0 — некоторая постоянная).
(Для удобства мы поменяли ролями х и у и написали а вместо р.) Парабола — одна из замечательных кривых, знакомых еще древним грекам, назвавшим эти кривые коническими сечениями (или кониками).
Другие конические сечения — это эллипсы и гиперболы. Эллипсом называется линия, которая в соответственным образом выбранной декартовой системе координат задается уравнением
— + -^- = 1 (а > 0 — постоянные).
Гипербола — это кривая, которая в соответственно выбранной декартовой системе координат определяется уравнением
—----— = 1 (а>0, Ь>0 — постоянные).
а2 Ь2
Эллипс и гипербола, отвечающие значениям а = 4 и b = 3, изображены на рис. 10.1. Если а = Ьу то эллипс представляет собой окружность. Гипербола в случае а = b называется равнобочной гиперболой.
181
§ 1. Коники
а)
Рис. 10.2
Разумеется, греческие математики не использовали эти алгебраические определения. Вместо этого они рассматривали круговой конус (поверхность, которая получается при вращении прямой вокруг другой, пересекающей ее, прямой) и исследовали кривые, которые получаются при пересечении этого конуса плоскостью. Оказалось, что если исключить случай, когда плоскость проходит через вершину конуса, то линия пересечения будет либо а) эллипсом, либо б) параболой, либо в) гиперболой (рис. 10.2). В случаях а) и б) плоскость пересекает только одну «полость» конуса; в случаев) она пересекает обе полости. Если плоскость сечения проходит через вершину конуса, то пересечением будет либо а) точка, либо б) прямая, либо в) п ар а прямых (рис. 10.3). Сформулированное сейчас утверждение мы докажем в Приложении (см. § 4.9).
182
10. Квадрики
1.2. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Мы изложим теорию коник, отправляясь от трех канонических уравнений этих кривых:
у2 = 4ах, а > 0;
(П)
у2 /»2
—+ —= 1, а>д>0;	(Э)
а»	'
X2_______у2
~а? ~ "b2
а >0,
/?>0.
(Г)
Греки излагали теорию коник чисто геометрически. Их результаты собраны в известном трактате Аполлония, одном из наиболее замечательных достижений греческой математики. С изобретением аналитической геометрии эта теория, доступная лишь для лучших умов античности, превратилась в источник упражнений для начинающих студентов.
Вся информация о конических сечениях собрана в трех простых уравнениях (П), (Э) и (Г) и может быть выведена из этих уравнений по правилам алгебры. В математике каждое успешное продвижение вперед основывается на сделанном в этой области ранее; при этом все то, что было добыто предшественниками творцов новых идей, не отбрасывается а, напротив, сохраняется и только освещается по-новому. Так, и достижения Апполлония продолжают жить в аналитической геометрии; можно даже сказать, что мы сегодня понимаем их лучше, чем сам творец.
Уравнения (П), (Э) и (Г) называются каноническими уравнениями коник (точнее, параболы, эллипса и гиперболы).
Часть бывает удобно эллипс (Э) и гиперболу (Г) рассматривать совместно. Числа а и Ь называются длинами их полуосей. Ось х называется действительной осью гиперболы и большой осью эллипса. Ось у называется мнимой осью гиперболы и малой осью эллипса. Обе кривые, эллипс и гипербола, симметричны относительно обеих осей, так как при подстановке —х вместо х или —у вместо у равенства (Э) и (Г) сохраняют силу. Начало координат называется центром обеих кривых.
Напомним, что для параболы (П) ось х служит осью симметрии (то, что парабола симметрична относительно оси х, сразу следует из уравнения этой кривой); эту прямую называют просто осью параболы. Центра, парабола, очевидно, н е имеет.
Из уравнения (Э) вытекает, что | х | •< a, f у | < Ь. Таким образом, эллипс целиком лежит в прямоугольнике, образованном прямыми х = ±а, у = ±6. Четыре
АПОЛЛОНИЙ из Перги (ок. 260—170 г. до и. ».) преподавал в Александрии и в Пергаме. Из восьми книг (т. е. частей) его обширного трактата «Конические сечения» сохранилось лишь семь, причем некоторые из них — только в арабском переводе. Другие работы Аполлония тоже сохранились лишь частично.
§ 1. Коники
183
точки, в которых эллипс пересекается сего осями (и касается прямоугольника), называются вершинами эллипса (рис. 10.4).
Из уравнения (Г) вытекает, что ] х | >> а. Таким образом, гипербола состоит из двух частей, называемых ее ветвями. Гипербола пересекает свою действительную ось в двух точках, называемых вершинами (рис. 10.5).
Напомним, что парабола (П) имеет одну вершину — начало координат. Из уравнения этой кривой видно, что вся она лежит справа от прямой х = 0.
184
10. Квадрики
1.3. АСИМПТОТЫ
Диагоналями прямоугольника | х | < а, | у ] < b служат прямые у = -^-х и у = = —-х. Эти прямые называются асимптотами гиперболы (Г). Уравнение асимптот удобно записывать так:
“L-lL =(2L+JL\	И=0.	(1)
a2 b2 \ а b ) \ а b /
Пусть (х, у) — точка верхней половины правой ветви гиперболы (все, что будет сказано дальше, с естественными изменениями можно перенести и на нижнюю половину правой ветви гиперболы и на ее левую ветвь). Для указанного на рис. 10.6 отрезка 8, учитывая уравнение (Г) гиперболы, имеем
= — (х — ]/х2 — а2 ). а
Отсюда видно, что кривая лежит ниже асимптоты у так как, разумеется,
Ух2 — a2 <Z х и х — /х2 — а2 > 0. Далее, поскольку
х — j/x2 — а2 =---------
х -Ь У х2— а2
(этот результат получается, если умножить и разделить стоящее слева выражение на х + ]/х2 — а2), то
§ 1. Коники
185
и, значит,
lim (х—Ух2— а2 ) = lim -----------	 = О
х-*4-оо	х-*-4-оо х 4- f/” х2 — а2
lim 6 =0. Х-*+оо
Следовательно, измеренное по вертикали расстояние б между кривой и ее асимптотой при достаточно большом удалении от начала координат становится сколь угодно малым.
1.4. ФОКУСЫ И ДИРЕКТРИСЫ. ЭКСЦЕНТРИСИТЕТ
Все интересные геометрические свойства конических сечений связаны с точками, называемыми их фокусами. Эллипс (Э) и гипербола (Г) имеют по два фокуса: левый фокус F_ и правый фокус F+:
F.(—c, 0), F+(c, 0),
причем фокальное расстояние с (равное половине расстояния между фокусами) равно
с = ]/ а2 — Ь2 для эллипса
и
с = У а2 + Ь2 для гиперболы.
(2)
(3)
Геометрическое построение фокусов показано на рис. 10.7. Заметим, что если а = 6, т. е. если эллипс является окружностью, то оба его фокуса совпадают с центром этой окружности. Напомним еще (см. гл. 2, § 4.1), что парабола (П) имеет один фокус
F(a, 0),	(4)
который удобно называть ее левым фокусом.
Эксцентрисистет е эллипса и гиперболы определяется равенством
с =&а,	(5)
откуда с е = — . а Таким образом, О <^8 < 1 для эллипса
(причем для окружности 8 = 0) и
1 <8	для гиперболы
(причем для равнобочной гиперболы 8 = ]/2). Кроме того, по определению, имеем 8 = 1	для параболы.
186
10. Квадрики
Прямые
1	а
х ------------
е
называются левой и правой директрисами эллипса (Э) или гиперболы (Г) (так как для окружностие =0, то окружность директрис не имеет). Напомним, что прямая I: х = —а	(7)
называется директрисой параболы (П); нам будет удобно называть ее левой директрисой (и обозначать /_). Ни одна из точек конического сечения не принадлежит его директрисе (рис. 10.8).
Лемма. Если Р(х, у) — точка коники, заданной своим каноническим уравнением. то
\FJ I = |а+ех |,	(8)
\F,P\ = | а-ех |, расстояние от Р до /_ равно — + х
I е
расстояние от Р до 1+ равно —-----х
(9) (Ю)
(П)
§ 1. Коники
187
Справедливость равенств (10) и (11) можно усмотреть из рис. 10.8. Равенство (8) мы докажем только для эллипса — для гиперболы соответствующее доказательство аналогично, а для параболы даже проще, чем для эллипса. Опущенные нами доказательства, так же как и аналогичные доказательства равенства (9), предоставляются читателю.
Доказательство равенства (8) для эллипса проводится следующим образом. Если координаты точки Р(х, у) удовлетворяют уравнению (Э), то у2 =Ь2----х2, поэто-
му
|	|2= (х + с)2 + у2 = х2 4- 2сх4- с2 + Ь2 — —х2 =
а2
= X2 (1 — —) 4- 2сх + a2 f гак как с2 + &2 => а2] = а2
= х2 4- 2сх 4- а = а2 4- 2сх + — х2 1 а 4- — х Г = I а 4- ex I2 [так как с = aej. а2	а2 \ а \
Таким образом, наше утверждение доказано.
УПРАЖНЕНИЯ
В упражнениях 1—8 начертите кривую, уравнение которой задано. Найдите и четко отметьте на рисунке все то, что в данном случае имеет смысл: центр, фокусы, вершины, асимптоты, оси б директрисы.
х2	и2
1.	— — — = 1.	5. 16х2 —t/2=4.
4	16	*
X2	у2
2.	х2 — 44/2 = 36.	6. ----4-— =1.
25	4
3.	*2Ч- 44/2 = 36.	7. х2 — 44/2 = 100.
4.	4/2 = 36х.	8. 3*24-44/2=12.
1.	5. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА КОНИК
Теперь мы можем доказать основную теорему о кониках, которую часто кладут в основу самого их определения.
Теорема 1. Пусть дана кривая — коника с эксцентриситетом е.
1)	Если 0 е < 1 (эллипс), то для всех точек кривой сумма ее расстояний от фокусов есть величина постоянная.
2)	Если е > 1 (гипербола), то для всех точек кривой абсолютная величина разности ее расстояний от фокусов есть величина постоянная.
3)	Если г > 0 (не окружность), то для всех точек кривой отношение расстояния этой точки от фокуса к ее расстоянию от соответствующей директрисы (правой — для правого фокуса и левой — для левого) есть величина постоянная, а именно равная эксцентриситету 8.
Каждое из этих свойств полностью характеризует соответствующую кривую.
188
10. Квадрики
l^/’l + |FtP|=2a Рис. 10.9
Рис. 10.10
Утверждения теоремы 1 иллюстрируются на рис. 10.9, 10.10 и 10.11.
Доказательство. Достаточно доказать утверждения 1), 2) и 3) для коники, заданной своим каноническим уравнением.
1)	Если координаты точки Р(х, у) удовлетворяют уравнению (Э), то | х | а, и так как 0 в <1,тоа+ех>0иа — е х > 0. В силу равенств (8) и (9) |F_ Р | = = а +ех, | F*P | = а —гх и сумма
I Кр I + I I = 2а
имеет одно и то же значение для всех точек Р кривой.
2)	Если координаты точки Р (х, у) удовлетворяют уравнению (Г), причем это точка правой ветви гиперболы, то а < х. Поскольку е > 1, из равенств (8) и (9) находим, что | Р_Р| = а 4-ех, | F+P | = —а +ех и
I’fZP | — \~F\P\ = 2а.
Аналогично показывается, что для левой ветви \F_P\— |F+P| =—2а.
§ 1. Коники
189
3)	Это утверждение сразу вытекает из равенств (8)—(11). (Напомним, что парабола, по определению, имеет лишь левый фокус и левую директрису.)
Нам еще остается показать, что каждое из геометрических свойств 1), 2) и 3) рассматриваемых линий влечет за собой выполнимость соответствующего алгебраического уравнения. Мы ограничимся здесь лишь условием 1) и условием 3) при 8 > 1. Читателю предлагается рассмотреть остальные случаи.
1) Пусть даны две точки F_ и F+ и число а, такое что 2а > | F_F+ |. Мы должны показать, что множество всех таких точек Р, что
|PP:i+ |РР+ | = 2а,
есть эллипс с фокусами Р_ и Р+. Случай, когда Р_ = Р+, тривиален: здесь мы приходим к окружности радиуса а. Предположим, что Р_ #= Р+, и положим | Р_Р+ | = = 2с. Выберем декартову систему координат так, чтобы середина отрезка F_P+ была началом координат и чтобы точка F+ принадлежала положительному лучу оси х.
Тогда F_(—с, 0) и F+(c, 0). Если точка Р имеет координаты (х, у), то
| PF1 |2 = (х + с)2 + У2, I РР+ I2 = (* — с)2 + у2.
Так как | PF_ | + | РР+ | = 2а, мы получаем уравнение
У(х + с)2 + у2 + У(х — с)2 + у2 = 2а, из которого следует, что
(V(x + c)a + !/2 +V(x~c)2 + y2 )2 = 4а2, или
х2 + 2хс + с2 + у2 + х2 — 2хс + с2 + у2 +2 ]/ (х2 + с2 + У2)2 — 4с2х2 = 4а2, откуда после соответствующих преобразований получаем
У(х2 4- с2 + у2)2 — 4с2х2 — 2а2 — (х2 + у2 + с2}.
Возводя в квадрат обе части равенства, находим, что
(х2 + с2 + у2)2 — 4с2х2 = 4а4 + (х2 + у2 + с2)2 — 4а\х2 + у2 + с2)
и (после очевидных преобразований)
а4 — а2х2 — а2у2 — а2с2 + с2х2 = 0, откуда
а2(а2 — с2) = (а2 — с2)х2 + а2у2.
Положим Ь2 — а2 — с2. Тогда наше уравнение приведется к виду
Ь2х2 + а2у2 = а2Ь\ или
.*+£- = !.
а»
190
10. Квадрики
Это каноническое уравнение (Э) эллипса, фокусы которого имеют координаты (—с. 0) и (с. 0). (Мы уже знаем, что все точки (х, у), удовлетворяющие уравнению (Э), действительно обладают требуемым свойством.)
3)	Пусть даны прямая Z, точка F. не принадлежащая этой прямой, и числое > 1. Мы должны найти геометрическое место таких точек Р, для которых
| PF | равно г-кратному расстоянию от Р до I.	(12)
Выберем систему координат так, чтобы точка F была началом, а прямая I— вертикальной прямой, пересекающей ось х в точке х =—а, где а>0 (рис. 10.12). Если координаты точки Р равны (х, у), то расстояние Р от прямой I равно | х + a L а | FP | = Ух2 + у2. Считая, что условие (12) имеет место, находим
х2 + у2 =е2(х + а)2 =82х2 + 2ае2х + е2а2, или
(8 2 — 1)х2 + 2ае2х — у2 + е2а2 = 0, т. е.
/9	/ 9 . 2ае2 . а2е4 \ о а2е4 .99 л
е2—1) (х2+—-Х+ —---------— ]~У2—-—-+е2а2=0,
\ е2— 1	(е2—I)2 )	е2—1
Положим
5 = х +	у.	(13)
е2 — 1
Наше уравнение в новых координатах 5, rj (полученных переносом начала) приводится к виду
ея —. 1
ИЛИ
(14)
§ 1. Коники
191
Это каноническое уравнение (Г) гиперболы.
Однако нам надо еще убедиться, что все точки гиперболы (14) обладают требуемым свойством, т. е. мы должны проверить, что эксцентриситет гиперболы (14) равен е, a F и I являются соответственно ее фокусом и директрисой. Из уравнения (14) следует
аг .	аг
а =------, Ъ = —	.
е2 — 1	/е2 — 1
Поэтому
с2 = а2 + Ь2 = а2е2 (-----------5-----
\ (е2 — I)2
+ !\ .. £2— 1/	(£2— I)2
гр	осе2
1огдас =--------- = аг, так что е — действительно эксцентриситет
£2 — 1
Фокус кривой принадлежит оси 5, которая является в то же время
Следовательно, координата
Я£2
гиперболы.
и осью х.
х
Его координата 5 равна £ = ± с = ± ———.
£2 — 1
фокуса равна [сравните с (13)!] х = ±	"----t - Таким образом, точка
F (0, 0) является правым фокусом гиперболы, а ее правой директрисой будет прямая
J. _ а ___ а
г г2 — 1 ’
или
X =
а
£2 — 1
Я£2
£2 — 1
т. е. это и есть исходная прямая I. Последнее рассуждение и завершает доказательство.
•Пример. Найти уравнение эллипса, фокусами которого являются точки (0, 0) и (0, 8), а большая полуось а =5.
Первое решение. Воспользуемся свойством 1) теоремы 1. Расстояния от точки (х, у) до фокусов равны V х2 + t/2 и У х2 + (у— 8)2 . В силу условия (1) имеем
Ух2 + у2~ + Ух2 + (у-8)2 =10.
Упрощая это уравнение, получим
Ух2 + у2 _ 16у + 64 = 10 — Ух2 + у2 ,
или
х2_|_у2_ ]бу _рб4 = 100 — 20 Ух2 + у2 +х2 + у2,
или
16у + 36 = 20 у х2 +у2,
192
10. Квадрики
ИЛИ
4у + 9 = 5 У X2 + у2,
ИЛИ
16у2 + 72у + 81 = 25(х2 + г/2), или, наконец,
25х2 + 9у2 — 72у — 81 =0.
Второе решение. Мы можем воспользоваться каноническим уравнением эллипса. Для того чтобы сделать большую ось эллипса горизонтальной, введем новые координаты X, У, повернув координатную систему на 90°:
Х=у, Y =— х.	(15)
Новые координаты фокусов: X =0, У = 0 и X =8, У =0. Для того чтобы фокусы были симметричны относительно начала координат, изменим еще раз систему координат, осуществив перенос осей (рис. 10.13):
$ = Х-4,п = У.
В этой системе координаты фокусов 5= ±4, т] = 0. В системе координат 5, q уравнение эллипса будет каноническим. Так кака = 5, с=4, то b = У а2 — с2 = 3, и искомое уравнение имеет вид
т. е.
(X — 4)2 J2
25	+ 9
§ 1. Коники
193
Отсюда находим
Хз —8Х+16	J2
25	9
используя равенства (15), после упрощений получаем, как и выше, уравнение 25х2 + 9у2 — 72у — 81 = О.ф
УПРАЖНЕНИЯ
9.	Найдите уравнение эллипса с фокусами (0, 0) и (4, 0), длина большой полуоси которого а = /Г.
10.	Найдите уравнение эллипса с фокусами (—1, 0) и (5, 0), длина большой полуоси которого а = 2~У3 .
11.	Найдите уравнение эллипса, фокусы которого (—2, 1) и (6, 0), а эксцентриситете =-1.
5
12.	Найдите уравнение эллипса, фокусы которого (0, 0) и (0,10), а длина большой полуоси а = 5у/ 5 .
13.	Найдите уравнение эллипса с центром в точке (1, —1), длина большой полуоси которо-о
го а = 6, эксцентриситет е =—., причем большая ось эллипса горизонтальна.
14.	Найдите уравнение всех эллипсов с вершиной в точке (1, 1), другой вершиной в точке (3, 5) и вертикальной большой осью.
15.	Найдите фокусы, вершины, эксцентриситет, большую и малую оси эллипса 9х2 + 25г/2— — 225 = 0.
^16. Найдите уравнение гиперболы, фокусы которой (0, 0) и (6, 0), а эксцентриситете =
2
17. Найдите уравнение гиперболу, фокусы которой (—2,'—1) и (6, —1), а одна из вершин в
18.
точке (3, —1).
Найдите уравнение гиперболы с фокусами (0, —3) и (0, 5), одна из вершин которой совпадает с точкой (0, 1 + У10).
Найдите уравнение гиперболы с вершинами (1, 2) и (1, 12) и эксцентриситетом е = 2. Найдите уравнение гиперболы с вершинами (—2, 0) и (—2, 16), если один из ее фокусов имеет координаты (—2, 18). о
Найдите уравнение гиперболы, асимптоты которой имеют уравнения у = ±— (х—1) + + 2 и которая проходит через точку (4~Уз^ 6^2 ).
22. Найдите фокусы, вершины, эксцентриситет и асимптоты гиперболы 25х2 — 9г/2 = 225.
19.
20.
21.
1.6. КАСАТЕЛЬНЫЕ
Теория касательных к коническим сечениям может быть изложена либо «элементарными» методами (так строили ее древние греки), либо с помощью математического анализа. (Мы уже знаем, что именно так обстоит дело в случаях окружности и параболы.) Рассмотрим оба метода, причем начнем с использования математического анализа. (Читатель, еще не читавший гл. 4, может это рассуждение пропустить.)
Верхняя и нижняя половины параболы (П) — это графики функций
х*-+у = 2 Уах и х>->у =— 2угах.
При х #= 0 эти функции имеют производные:
194
10. Квадрики
dx 1/ х
dy =
Заметим, что оба выражения можно объединить следующим образом:
—	—	(для параболы),
dx	2 х у
(16)
Верхняя и нижняя половины эллипса (Э) и гиперболы (Г) — это графики функций	_________ __________________________
х*-+у = b 1 — — , х*-*у = — byf 1 — —
* у & '	* у а2
Если х2=И=а2, то, дифференцируя, получим dy  _______________________Ь_____х____ dy   b ___________х
dx	а2 у 1 — х2/а2 ’ dx	°2 У1 — х2/а2
И dy ____________________ b _____х_____ dy ______ b __________х____
dx а2 у х2/а2 — 1 ’ dx °2 У х2/а2—1 *
Эти формулы можно записать так:
— = — — — (для эллипса).	(17)
dx а2 у
— =— — (для гиперболы).	(18)
dx а2 у
Теорема 2. Пусть (х0> Уо) — точка коники, уравнение которой имеет канонический вид. Тогда уравнение касательной к кривой, проходящей через эту точку, имеет вид:
УУо = 2а (х + xQ)	(для параболы),	(19)
х*о  УУо = J а2	Ь2	(для эллипса),	(20)
хх^__УУо_ = j а2	Ь2	(для гиперболы).	(21)
Мы докажем теорему 2 только для гиперболы; остальные два случая читателю предлагается разобрать самостоятельно.
Если точка (х0, у0) является вершиной гиперболы, то yQ = 0, a xQ = а, либо х0 = = —а. Уравнение (21) будет в этом случае, как это и должно быть, уравнением вертикальной прямой х = а или х = —а.
§ 1. Коники
195
Предположим, теперь, что точка (х0, уо) принадлежит верхней половине правой ветви гиперболы (в остальных случаях рассуждение аналогично). В силу формулы (18) наклон касательной к гиперболе в точке х = х0 равен
и уравнение касательной имеет вид
У — Уо=т(х — х0), или
у — Уо =-т —(X — Хо), а* Уо
т. е.
а2уу0 — а2У2о = Ь2ХоХ — b2x2Q.
Разделив обе части на а2Ь2 и переставив члены, получим
хх9   уу0 = *о __ J/o_ аа	Ьа а2 62
Так как точка (х0, Уо) принадлежит гиперболе, то правая часть последнего равенства равна 1, и мы приходим к уравнению (21).
Следующая теорема дает элементарное описание свойств касательных. Временно «забыв» дифференциальное исчисление, мы теперь определим касательные уравнениями (19), (20) или (21) изатем покажем, что эти прямые обладают некоторыми замечательными свойствами, оправдывающими данное им название.
Теорема 3. Пусть Р — точка коники (К). Касательная к кривой (К) в точке Р— это единственная проходящая через Р прямая, которая не имеет с (К) второй общей точки [и в случае параболы не параллельна оси (К), а в случае гиперболы — не параллельна асимптоте (К)1.
Мы уже знаем, что сформулированное утверждение верно для окружности и для параболы (см. § 3.2 и 4.4 гл. 2). Проведем доказательство для равнобочной гиперболы х2 — у2 =1. Доказательства для гиперболы общего вида и для эллипса аналогичны, но вычисления в этих случаях более громоздки (см. также § 4.9).
Ясно, что вертикальная прямая либо пересекает гиперболу х2 — у2 =1 в двух точках, либо ни в одной точке, либо касается этой гиперболы в одной из ее вершин. Выясним теперь, в каком случае невертикальная прямая у = тх + р имеет с линией х2 — у2 = 1 в точности одну общую точку (х0, f/о)- Подставив в уравнение кривой значение у = тх + р, получим квадратное уравнение
х2 — (тх + р)2 = 1, или
(1 — т*)х2 — 2трх — (1 + р2) = 0.	(*)
Это уравнение имеет единственный корень (см. гл. 3, § 2.2) в том и только в том случае, когда 1 — т2=0, т. е. /и=±1 (асимптоты!), или когда
т2р2 + (1 — zn2)(l + р2) = 0,
т. е.
1 — т2 + р2 = 0.
196
10. Квадрики
Корни квадратного уравнения (*) — это абсциссы точек пересечения прямой с коническим сечением. В том случае, когда уравнение действительно является квадратным (т. е. т ± 1) и корень единствен, он равен х0 =—т/р, а соответствующее значение yQ = mxQ + р = —1/р, откуда, как читатель легко может проверить сам, т = ХоЛ/о» Р = —1/Уо- Уравнение нашей прямой приводится к виду
х0	1
у = — х-------,
Уо	Уо
или
Хох — УоУ = 1,
а это и есть уравнение (21) при а = Ь =1.
ф Пример. Найти касательную к эллипсу х2 + 4у2=32, наклон которой равен 1/2.
Первое решение. По теореме 2 уравнение каждой касательной к нашему эллипсу имеет вид
хх0 + 4уу0 = 32,
где (х0, у о) — точка касания. Наклон касательной должен быть равен 1/2; следовательно, должно выполняться равенство —х0/(4уа) = 1/2, или х0 = = —2у0. Но так как точка (х0, У о) принадлежит эллипсу, то Хо + 4«/о = 32, откуда 8х/о = 32. Таким образом, либо у0 = 2 и х0 = —4, либо у0 — —2 и х0 = 4. Мы получили две касательные с заданным наклоном: —4х + Зу = 32 и 4х — Зу = = 32, т. е.
х — 2у = —8 их — 2у =8;
они изображены на рис. 10.14.
Второе решение. Воспользуемся теоремой 3. Уравнение прямой с наклоном 1/2 имеет вид у = -ух + const, или х — 2у = р, где р — некоторое число. Определим р так, чтобы эта прямая имела с эллипсом в точности одну общую точку. Подставляя х = 2у + р в уравнение х2 + 4у* = 32, мы приходим к квадратному уравнению
§ 1. Коники
197
(2у + р)2 + 4у2 = 32, или 8у2 + 4ру + р2 — 32 =0.
Это уравнение будет иметь единственный корень, если (2р)2 — 8(р2 — 32) = 0, т. е. при р = 8 и при р = —8. Мы получили тот же результат, что и выше.ф
УПРАЖНЕНИЯ
В упражнениях 23—30 найдите уравнение касательной I к заданному коническому сечению в данной точке; используйте при этом как теорему 2. так и метод, примененный при втором решении примера. Покажите, что оба метода дают одинаковые ответы.
23.	9z/2 = х в точке (1, -7-
\	3
24. х2 + 25г/2 =
100 в точке
1	/3 \
4 ’	10 ) '
25.	25ха —уг= 100 в точке (—3. 5/5”)-
26.	t/a = 25x в точке (9, —15).
27.	4х2 4- 25z/a = 1 в точке
28.	4г/2 — ха = 1 в точке
точке
29. ху = 1 в
31.
32.
Найдите угол между касательной к эллипсу х2 + 4//2 = 5 в точке (—1. 1) и касательной к гиперболе х2 — 10г/2 = 90 в точке (10, 1).
о
Найдите все касательные к эллипсу 9х2 4- 25х/2 = 225, наклон которых равен —
25
33.	Найдите все касательные к гиперболе х2 — у2 = 1, наклон которых равен 2.
^34. Найдите касательную к параболе у2 = 10х, наклон которой равен 2.
35.	Найдите касательные к параболе у2 = 4х, преходящи. через точку (—2, 0).
36.	Имеются две касательные к эллипсу х2 + 4//2 = 32, проходящие через точку (10, 1).
Найдите их.	1
37.	Найдите касательные к гиперболе х2 — у2 = 16, проходящие через точку (3, —-g-).
1.7	. КОНИКИ В ПОЛЯРНЫХ КООРДИНАТАХ
Возможно, что построенная греками теория коник возникла из наблюдений над солнечными часами; однако она всегда рассматривалась как ветвь чистой математики. Многочисленные применения конических сечений в естественных науках и в технике были обнаружены лишь двумя тысячелетиями позже. Самое эффектное из этих приложений, связанное с изучением движений планет, мы рассмотрим в гл. 11. При этом нам понадобятся не уравнения (П), (Э) и (Г) коник, а уравнения конических сечений в полярных координатах.
198
10. Квадрики
Рассмотрим сначала кривую, эксцентриситет которой е =И= 0, т. е. не являющуюся окружностью. Пусть О — фокус кривой и I — отвечающая этому фокусу директриса. Введем декартову систему координат с началом в точке О, причем так, чтобы ось конического сечения (большая ось в случае эллипса, действительная ось в случае гиперболы) была осью х; положительное направление оси х выберем так, чтобы уравнение прямой I имело вид х = —р, где р есть расстояние от точки О до прямой /(рис. 10.15). Точка Р с декартовыми координатами (х, у) удалена от директрисы / на расстояние
S = I х — (—р) | = | х + р |.
Если (г, 6) — полярные координаты точки Р, то х = г cos 6 и
S = | г cos 0 + р |.
Расстояние между точками Р и О равно г. По теореме 1, точка Р в том и только в том случае принадлежит рассматриваемой кривой, если г =&$ . Считая, что г cos 0 + + р > 0, получим S = г cos 0 + р, и условие г =еб можно записать так:
г =e(r cos 0 + р).	(22)
Если же г cos 0 + р < 0, то S = —г cos 0 — р, и условие г =еб принимает вид г = —e(r cos 0 + р).
Разрешая уравнения (22) и (23) относительно г, получаем
г =-----------
1 — е COS 0 ИЛИ
г =	.
(23)
(24)
(25)
1 4- е COS 0
§ 1. Коники
199
Напомним теперь соглашение, сделанное в § 3.2 гл. 9. В соответствии с ним мы можем заменить в уравнении (25) г на —г и 0 на 0 + л. Но это равносильно тому, что мы заменим числитель —ер на ер, а знаменатель 1 + е cos 0 на 1 — ecos 0. При этом уравнение (25) превратится в (24).
Теорема 4. В соответственно выбранных полярных координатах уравнение конического сечения с эксцентриситетом & и фокусом О имеет вид
где А > 0 — некоторое фиксированное число. Обратно^ уравнение (26) всегда является уравнением некоторого конического сечения.
Мы уже доказали это для конического сечения, не являющегося окружностью (достаточно положить А =ер в уравнении (24)]. Если 8 = 0, то уравнение (26) принимает вид г = А, а это, конечно, — уравнение окружности.
Замечание 1. Для эллипса (О е < 1) знаменатель в уравнении (26) не обращается в нуль.
Для параболы (е = 1) знаменатель всегда неотрицателен. Он обращается в нуль, как этого и следует ожидать, при cos 0=1. Угол 0=0— это полярный угол точек, принадлежащих оси параболы (но расположенных в противоположном по сравнению с вершиной направлении от фокуса); однако парабола вовсе не содержит точек о таким полярным углом.
Для гиперболы (в > 1) знаменатель может быть и отрицательным, и положительным. Разные знаки соответствуют двум разным ветвям гиперболы. Знаменатель обращается в нуль при cos 0 =—, т. е. для двух значений 0, соответствующих асимптотам гиперболы.
Замечание 2. Изменяя единицу длины, мы можем числитель А в уравнении (26) сделать равным 1. Отсюда следует, что форма конического сечения зависит только от его эксцентриситета в.
УПРАЖНЕНИЯ
В упражнениях 38—44 найдите полярное уравнение данного конического сечения.
38.	Парабола с фокусом в начале координат и директрисой х = —5.
39.	Парабола с фокусом в начале координат и вершиной (—3, 0).
40.	Эллипс с эксцентриситетом -L и фокусами (0, 0) и (6, 0).
4
Эллипс с вершиной (—1, 0) и фокусами (0, 0) и (4, 0).
Гипербола, эксцентриситет которой равен 2, один из фокусов совпадает с началом координат, а соответствующая директриса имеет уравнение х = —1.
Равнобочная гипербола с фокусами (0, 0) и (—5, 0).
Гипербола, эксцентриситет которой равен 10, один из фокусов совпадает в началом координат, а соответствующая вершина — с точкой (—1, 0).
В упражнениях 45—50 определите, что собой представляет коника, заданная полярным уравнением, — эллипс, гиперболу или параболу. Найдите декартовы координаты этой коники. Начертите кривую, отметьте вершины, оси и асимптоты, 10
1 — cos О
46. г = ---—-
1 — cos О
41.
42.
43.
44.
45. г =
47. г =
1 — 20 cos 0
«—
1 — — cos 0
2
если они существуют. 1
49. г =-----------------
2 — 3 cos 0
1
50	20 — 25 cos 0
4
200
10. Квадрики
1.8	. ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ
В заключение этого параграфа мы выведем так называемые параметрические уравнения эллипса и гиперболы. Из результатов § 1.8 гл. 6 следует, что каждая точка Р(х, у) единичной окружности х2 + У2, = 1 может быть определена уравнениями
х = cos /, у = sin t.	(27)
(Если считать, что t изменяется в пределах 0 < t < 2л, то каждой точке Р этой окружности соответствует единственное значение /.) Итак, если только равенства (27) выполнены, то соответствующая точка Р(х, у) принадлежит единичной окружности. Мы знаем также (см. гл. 6, § 7.4), что координаты каждой точки Р правой ветви равнобочной гиперболы х2 — у2 = 1 однозначно представляются формулами
х = ch /, у = sh t	(28)
и что все точки с координатами (х, у}, удовлетворяющими равенствам (28), принадлежат этой ветви. Точки (х, у) левой ветви гиперболы х2 — у2 = 1 задаются уравнениями
х = —ch /, у = sh t.
Пусть а > 0 — некоторое число. Ясно, что уравнения
х = a cos /, у = a sin /, 0 t < 2л	(29)
определяют точки окружности
х 2 + у* = а2,	(30)
а уравнения
х = ± a ch /, у = a sh /, —оо < t < +оо	(31)
— точки равнобочной гиперболы
х2 — у2 = а2.	(32)
Далее, каноническое уравнение эллипса
можно переписать так: х2 + (а/Ь)2у2 = а2. Значит, точка (х, у} в том и только в том случае принадлежит линии (Э), если точка (х, а 1Ь у) принадлежит окружности (30), т. е. в том и только в том случае, если х = a cos /, (a/b) у = a sin t для некоторого t. Отсюда следует, что уравнения
х = a cos /, у = b sin /, 0 t < 2л
(33)
определяют точки эллипса (Э).
§ 1. Коники
101
Таким же образом получаем,
что точки гиперболы
X2 у2
определяются уравнениями
х = zb a ch t, у = b sh Z, —оо < t < оо.
(Г)
(34)
На рис. 10.16 и 10.17 мы отметили точки кривых (30) и (Э), а также кривых (32) и (Г), соответствующие одному и тому же значению /. Сравнивая уравнения (33) и (29), мы видим, что эллипс (Э) получается из окружности сжатием в направлении оси у с коэффициентом сжатия b/а. Сравнивая уравнения (34) и (31), мы видим, что гипербола (Г) получается из равнобочной гиперболы сжатием (или растяжением) в направлении оси у с коэффициентом сжатия Ыа.
(Эти замечания показывают, между прочим, что при доказательстве теоремы 3 § 1.6 достаточно было рассматривать окружность вместо произвольного эллипса и равнобочную гиперболу вместо произвольной гиперболы.)
фПример. Показать, что площадь э л л и п с а (т. е. площадь части плоскости, ограниченной эллипсом) с полуосями а и Ь равна лаЬ.
Первое решение (без применения математического анализа). Пусть мы уже знаем, что площадь круга радиуса а равна ла2. Наш эллипс получается из этого круга сжатием в вертикальном направлении с коэффициентом сжатия . Интуитив
202
10. Квадрики
но ясно, что при таком сжатии все площади умножаются* на Следовательно, площадь эллипса равна — ла2 = лад.
Второе решение (использующее математический анализ). Воспользуемся каноническим уравнением эллипса и формулой для вычисления площади, полученной в § 4.1 гл. 5. По этой формуле площадь эллипса равна
2J b 1 dx = 2 J ab р/ ] ~ =	1—^2 du = nab .
(Здесь мы воспользовались определением числа л, введенным в § 4.3, гл. 5.)ф
УПРАЖНЕНИЯ
В упражнениях 61—56 найдите декартовы координаты фокусов и вершин конического сечения. заданного своими, параметрическими уравнениями.
51.	x = 7cos?, г/= 8 sin г.
.	3	1
52.	х = — cos?, р=— sin?.
53.	x=±2ch/, y=3sh?.
2	1
54.	х = ± — ch г, у = “г- sh t. 3	о
55.	х=}^2 cosz, y = yr3 sin/.
56.	х = 0,01 cos?, у = 0,0001 sin/.
§ 2.	ПОВОРОТЫ В § 1 мы выбирали декартову систему координат так, чтобы получить возможно более простые уравнения изучаемых кривых. Но мы хотим иметь возможность изучать конические сечения и в произвольных системах координат. В качестве подготовки к этому мы рассмотрим важный вопрос о замене системы координат.
2.1.	ОТРАЖЕНИЯ И ПОВОРОТЫ. ОРИЕНТАЦИЯ
С помощью полярных координат легко описать все реперы на плоскости. Отправляясь от фиксированного репера {et, е2}, заметим, что {еь —е2} тоже является репером (рис. 10.18). Мы говорим, что репер {еь —е2} получается из репера {ei, е2} отражением от горизонтальной оси.
Пусть а 0 — произвольный вектор. Если его полярный угол относительно репера {еь е2} равен <р, то его полярный угол относительно репера {еь—е2) равен—<р.
* Это вытекает из того, что сеть равных малых квадратов плоскости (а площадь области приближенно равна числу «задеваемых» этой областью квадратов, умноженных на площадь'квадрата, причем при последовательном уменьшении размеров квадратов такое определение площади можно сделать сколь угодно точным!) переходит при таком сжатии в сеть равных прямоугольников, площадь каждого из которых равна площади квадрата, умноженной на Ыа.
§ 2. Повороты
2U3
Рис. 10.18
Это утверждение очевидно из рис. 10.19. Мы дадим ему и аналитическое доказательство. Пусты = | а |. Утверждение «полярный угол вектора а относительно репера {еь е^} равен ф» означает, что
Но в этом случае
или
а = (rcoscp)©! + (rsincp)ea.
а = (г cos(p)ei 4- (—г sin ф) (—е^,
а = г cos(—ф)в! + г sin(—ср) (—е^.
Это означает, что полярный угол вектора а относительно репера {еь—е2} равен —<р.
Пусть {fb f2} — какой-то другой репер. Тогда	Полярный
угол вектора f4 относительно репера {еь е2} обозначим через 0; тогда полярный угол вектора f 2, как это легко усмотреть из рис. 10.20, равен либо 0 + 909, либо 0 — 90Q. (Можно дать этому утверждению аналитическое доказательство, но мы его опускаем.)
204
10. Квадрики
Рис. 10.21
Рис. 10.22
Если полярный угол вектора f2 равен 0 + 90°, то
fi = cos 0 et + sin 0 е2,
f2 = cos (0 + 90°) в! + sin (0 + 90°) е2,
или, поскольку
cos (0 + 90°) = —sin 0, sin (0 + 90°) = cos 04 имеем
(fi = cos 9 e! + sin 0 e2, If 2 = —sin 0 et + cos 0 e2.
(I)
В этом случае мы говорим, что репер {fb f2} получается из репера {еь е2] поворотом на угол 0. Рис. 10.21 иллюстрирует смысл этого выражения.
Репер {еь —е2) не может быть получен поворотом репера [еь е2]. Действительно, если бы это было возможно, то нашлось бы такое число 0, что в! = cos 6 е± + sin 0 е2 и —е2= —sin 0 ef + cos 0 е2; но из первого равенства получаем, что cos 0 = = 1, а из второго — что cos 0 = —1.
Рассмотрим теперь такой репер {fd, f 2), что полярный угол вектора ft относительно репера {еь е2) равен 0, а полярный угол вектора f2 равен 0 — 90°. Такой репер изображен на рис. 10.22. Мы видим, что репер {fь f 2} получается из {еь —е2} поворотом на угол — 0 (это можно доказать и аналитически).
Следующие утверждения геометрически очевидны (и легко доказываются аналитически): поворот репера на угол 0° или на угол 360° не меняет репер; поворот репера на угол а и последующий поворот его на угол 0 равносилен повороту на угол а + 0-
§ 2. Повороты
205
Теорема 1. Зафиксируем раз и навсегда определенный репер {еь е2}. Каждый репер, который можно получить из репера {еь е2} поворотом, назовем правым, репер же, получающийся поворотом из {еь—е2}, назовем левым. Тогда: а) каждый поворот переводит правый репер снова в правый репер\ б) каждый поворот переводит левый репер снова в левый репер; в) каждый репер является либо правым, либо левым, но не может быть одновременно тем и другим.
Доказательство этой теоремы содержится в только что проведенном рассуждении.
В то время как различие между правым и левым реперами может быть определено математически, невозможно определить правый репер сам по себе; его можно только изобразить на рисунке. Иногда говорят, что правый репер образуют такие векторы в! и е2, что е2 получается из в! поворотом на угол 90° «против часовой стрелки». Однако не все часы на свете имеют одинаковый вид. (Известны средневековые часы на так называемой Еврейской ратуше в Праге, на которых числа заменены древнееврейскими буквами; их стрелки движутся в направлении, противоположном привычному нам, по тем часам, которые мы видим каждодневно. Учитель автора Ч. Лёвнер любил задавать вопрос: сможет ли человек, знающий только эти часы и читающий только математические книги, в которых нет рисунков, когда-либо обнаружить, что существуют часы, стрелки которых движутся в ином направлении?) Выбор репера, который, по определению, считается правым, равносилен ориентации плоскости. На ориентированной плоскости уже можно говорить о направлении вращения «против часовой стрелки»: это есть то направление, в котором надо повернуть на 90° первый вектор правого репера, для того чтобы он совпал со вторым вектором. Во всем дальнейшем изложении мы будем считать плоскость ориентированной.
УПРАЖНЕНИЯ
В упражнениях 1—5 предполагается, что {ej, е2] — фиксированный правый репер на плоскости. Определите, является ли данный репер {fx, f2) правым или левым.
Чарльз ЛЕВНЕР (1895—1968) переехал в Соединенные Штаты после того, как его родина Чехословакия была оккупирована нацистами. Он сделал важные открытия в некоторых областях математики * *.
* Известен, например «эллипс Лбвнера», однозначно сопоставляемый каждой (ограниченной) плоской фигуре.
206
10. Квадрики
2.2.	ЗАМЕНА СИСТЕМЫ КООРДИНАТ
Рассмотрим теперь вопрос о том, как изменяются координаты точки при замене декартовой системы координат. В § 1.2 гл. 2 мы выяснили, как сказывается на координатах точки перенос координатных осей, т. е. переход от системы {О, еь е2), где {elt е2} — некоторый репер, к системе {О', еь е2} с другим началом, но с теми же самыми направлениями осей. Напомним, что в этом случае старые координаты (х, у) точки Р и ее новые координаты (X, Y) связаны соотношениями
X = а + X, у = b + У.	(2)
где (а, Ь) — координаты точки О' в системе (О, elt еа). Теперь мы получим этот результат снова, используя векторы.
Пусть Т — вектор, определяемый направленным отрезком ОО'; тогда Т =	+
+ 6е2. Условимся обозначать через Р радиус-вектор точки Р по отношению к «началу отсчета» О и через Р' — ее радиус-вектор по отношению к О'; тогда Р = Т + 4- Р'. Но, очевидно,
Р = xei + f/e2 и Р' = Хе! + Уе2.
Следовательно,
хе4 + #е2 = ае4 + 6е2 + Xej + Уе2 = (а + X)et + (b + У)е2,
откуда и вытекают равенства (2).
Рассмотрим теперь два репера {еь е2} и {f4, f2} и две декартовы системы координат с одним и тем же началом: «старую» систему {О, в!, e2J и «новую» систему {О, fi, f2). Говорят, что новая система получается из старой заменой координатных осей. Замена координатных осей — это либо их поворот, либо отражение от оси х, либо, наконец, поворот и последующее отражение.
Начнем со случая отражения координатных осей: пусть fi = elf f 2 = —е2. Если обозначить старые координаты точки Р через (х, у), а ее новые координаты — через (X, У), то
Р = хе4 + уе2 = xfi — yt2 = Xfj + У12.
Следовательно,
x = X, у = —У.
(3)
Остается выяснить, что получается при повороте осей координат. Это будет сделано ниже; тем самым мы исчерпаем все возможные случаи. В самом деле, пусть даны любые две системы координат (О, et, е2} и {О', ft, f2}; тогда от одной из них можно перейти к другой с помощью переноса начала и последующего изменения осей или, наоборот, с помощью изменения осей и последующего переноса начала координат.
§ 2. Повороты
207
О	*,
Рис. 10.23
2.3.	ПОВОРОТ ОСЕЙ КООРДИНАТ
Теорема 2. Предположим, что репер {flt f2} получается из репера (ер е2} поворотом на угол 9. Пусть в системе {О, ер точка Р имеет декартовы координаты (х, у) и полярные координаты (г, <р), а декартовы и полярные координаты той же точки в системе {О, flt f2} будут (X, У) и (R, Ф). Тогда
г = 7?, <р = Ф + 9	(4)
х = X cos 9 — У sin 9,	.г.
у = Xsin9 4- Усов9.
Мы дадим два доказательства этой теоремы. Первое доказательство начинается с указания на то, что соотношения (4) геометрически очевидны: они следуют из рис. 10.23. Докажем теперь формулы (5). Так как X = R cos Ф, У = /?81пФ, то
х = г cos ср = R cos (Ф 4- 9) = /? cos Ф cos 9 — 7? sin Ф sin 9 = X cos 9 — У sin 9,
у = г sin ф = R sin (Ф 4- 9) = /? sin Ф cos 9 + R cos Ф sin 9 = X sin 9 4- У cos 9.
Второе доказательство — чисто аналитическое. Радиус-вектор Р точки Р равен х^ 4- уег=Х^ 4- Yt2. Воспользовавшись равенствами (1), получим
хе, 4- уег = X (cos 9 е, 4- sin 9	4- У (— sin 9 е1 4- cos 9 ej =
=(Х cos 9 — У sin 9) ej 4- (X sin 9 4- У cos 9) е2.
Отсюда и вытекают равенства (5). Далее, вспоминая § 3.2 гл. 9, имеем
г* = х® 4- уг = (X cos 9 — У sin 9)2 4- (X sin 9 4- У cos 9)® = Х®( cos® 9 4- sin® 9) 4-
4- 2ХУ (— cos 9 sin 9 4- sin 9 cos 9) 4- У2 (sin® 9 4- cos2 9) = X® 4- У2 = R2,
208
10. Квадрики
так что г = R. Кроме того,
_ ~ х X cos 0 — У sin 0 R cos Ф cos 0 — R sin Ф sin 0	,
COS ф ------ --------------------- = -----------------------------= COS (Ф +
Аналогично доказывается, что sin ф = sin(O + 0). Следовательно, ф = Ф + 0. Теперь и равенства (4) доказаны полностью.
ф Примеры. 1. Пусть репер {fp f2) получается из репера {ер е2} поворотом на угол 0, так что справедливы равенства (1). Выразить векторы ех и е2 через и f2.
Решение. Поскольку репер (ер е2} получается из {fp f2} поворотом на угол — 0, то
ех = cos 9 fx — sin 0 f2,
e2 = sin 9 fx + cos 0 f2.
Это можно получить также, разрешив уравнения (1) относительно ех и е2, для чего достаточно умножить первое из равенств (1) на cos 0, а второе — на —sin0 и сложить их; затем умножить первое равенство на sin 0, второе — на cos 0 и сложить их.
2.	Если {ер е2} — правый репер, то какими будут реперы {—ер е2} и {—ер —е2}: правыми или левыми?
Решение. Репер {—ер —е2} получается поворотом репера {ер е2} на 180°; значит, он правый. Репер {—ер е2} является левым, так как он получается поворотом на 180° репера {ер —е2).
3.	Пусть координаты точки Р в системе {О, ер е^ равны (х, у), а в системе {О, еь е2} , получающейся из {О, ер е2} поворотом на угол —45°, ее координаты (X, У); найти зависимость между (х, у) и (X, Y).
Решение. Используя формулы (5) при 9 = — 45°, получаем х = -±=- (Х+У),
у =	—X + И- Следовательно,
X = х + у Y = х^~у ут' ут ’
4.	Показать, что геометрическое место точек (х, у), удовлетворяющих уравнению х2 — у2 = 1, т. е. равнобочная гипербола, не отличается от графика обратной пропорциональной зависимости.
Решение. Повернем систему координат на угол — 45°; новые координаты обозначим через (X, У). Как следует из примера 3, х2 — у2 = = (х — у) (х + у) = 2ХУ. В новых координатах уравнение нашей кривой принимает вид 2ХУ = 1, или У = —, а это, по «школьному» определению, есть k 2Х
частный случай графика У = — обратной пропорциональной зависимости.^ X
§ 2. Повороты
209
УПРАЖНЕНИЯ
В упражнениях 6—13 предполагается, что репер {fj, f2} получается из репера {е^, ез} поворотом на угол 6.
6.	Пусть 0 = —• и декартовы координаты точки Р в системе {О, еА, е2} равны (2, —1); б
найдите ее декартовы координаты в системе {О, flt f2}.
Зтс	/	тс \
7.	Пусть 0 = — и полярные координаты точки Р в системе {О, еА, е2) равны! 2, — I; найдите 4	\	3 /
декартовы координаты этой точки в системе {О, fx, f2}.
8.	Пусть 0 = — и координаты точки Р в системе {О, в!, е2} равны (—2, 3); найдите декар-
товы координаты этой точки в системе {О, flt f2}. 4тс	/ 1	\
Пусть 0 =-— и декартовы координаты точки Р в системе {О, elt е2} равны ! —, 31;
3	у 2	j
дите декартовы координаты этой точки в системе {О, flf f2}.
7тс	/ /._
10. Пусть 0 = — и полярные координаты точки Р в системе {О, ех, с2} равны у 2 , • 6	\
декартовы координаты этой точки в системе {О, fx, f2}.
тс
= — — и декартовы координаты точки Р в системе {О, ех, е2} равны (3, декартовы координаты точки Р в системе {О, flt f2).
9.
най-
найдите
11. Пусть О найдите
тс
4
-8);
12. Пусть 0 = —
и пусть декартовы координаты точки Р в системе {О, е1э е2} равны
тс
2 cos —— 9
13. Пусть О
найдите
, 2sin найдите полярные координаты этой точки в системе {О, flt f2}.
тс	/ 1 тс
= — и полярные координаты точки Р в системе {О, еА, —е2} равны I— , — полярные координаты этой точки в системе {О,	f2}.
24. НАПРАВЛЕННЫЙ УГОЛ МЕЖДУ ПРЯМЫМИ
Теперь мы определим направленный угол между прямыми /1 и /2.
Пусть 1{ и 12 — две прямые; выберем правую систему координат, в которой является осью х; за угол а между 1^и 12 [обозначается (Zb Z2)] принимается любое число а, такое что наклон прямой 12 равен tg а. Если прямая 12 вертикальна, то ^(11912) = 90° или —90° (так как период тангенса равен те = 180°, то а определено с точностью до кратного л).
Рис. 10.24 показывает, что это определение соответствует нашим предыдущим рассуждениям. Заметим, что ^(Z2, ^i) = —^(Zp Iг)- Далее, если прямые Z± и Z2 параллельны, то (ZA, У = 0 или 180°. Всегда можно выбрать значение угла ^(Zb 12) так, что —90°	Z2) 90°. В этом случае неотрицательное число | -^(Zt, Z г)|
называется острым (точнее — не тупым) углом между прямыми Zt и Z2.
Теорема 3. Пусть It и 12 — две прямые, наклоны которых соответственно равны mt и т2. Тогда
(6) 1 -f- /711/7Z2
210
10. Квадрики
Доказательство. Обозначим через Zo ось х, и пусть си = (Zo, Л), ct2 = = ^(/0, /г). Из рис. 10.25 видно, что
^2) = а>2— СИ,
так что, по теореме сложения для тангенса (см. § 2.2 гл. 6),
/2)=	•
1 + *g а2 tg а1
Так как, по определению tg си = tg а2 = т2, то отсюда и следует равенство (6). Если /Him 2 = —1, то прямые li и 12 взаимно перпендикулярны', в этом случае тангенс -£(G, /2) не определен.
Замечание. Когда мы говорим о «(направленном) угле между прямыми /1 и /2», мы понимаем под этим углом 1^, но не (l2, li).
ф Примеры. 1. Найти угол между касательными к параболе у =-^-х2 в точках (1,1) и (2, 2).
Решение. Наклоны этих касательных равны
1, т	= 2.
2	\ dx
Пусть искомый угол равен ф. Тогда, по формуле (6), 2 — 1	1
10 ф —	“ —	,
1+2	3
tn.
так что <р = arctg -1, т. е. ф « 18°16'.
О
2. Найти угол между параболой у = х2 и кривой у чения. (Углом между двумя пересекающимися л называется угол между касательными к этим линиям
= 2х® — х в их точке Пересе-и н и я м и, по определению, в их общей точке.)
§ 2. Повороты
211
Решение. Чтобы найти точку пересечения кривых, решим уравнение х2 = = 2х3 — х, или 2л3 — х2 — х =0, т. е. х(х — 1)(2х + 1) =0.
Абсциссы точек пересечения равны х = —х = 0их =1. Обозначим углы между кривыми в этих точках через а, р и у. Так как и	= — 1	0, 2 при х ----—, 0, 1
dx	2
/(2хЗ-х)=_1_	5	х=—L, 0, 1,
dx	2	2
то мы имеем 1
.	2 +1 о . п —1—0	,	5 — 2	3
fg а =------= 3, tg р  ------------- — 1,	tg т =-------= — ,
ё	1	’	1	’	6 1	1+10	11
2
так что а « 72°, Р = —45° и у « 15°.ф
J - б = 0. 2у + Зх = —1.
УПРАЖНЕНИЯ
В упражнениях 14—25 предполагается, что на плоскости задана определенная декартова система координат. Используйте таблицы тригонометрических функций для получения числен* ных ответов.
14.	Найдите угол между осью у и прямой 2х — Зу — 5 = 0.
15.	Найдите угол между прямой If х — 2у = 0 и прямой hi 2х — Зу
16.	Найдите угол между прямой Зу — 6х = 2 и прямой 2у + Зх =
17.	Пусть прямая задается уравнением---i/ —-^-х = 1, 2	5
+ 6х= -5-. Найдите (/х> 1$. о
18.	Пусть If — касательная к кривой у и х3 в точке (1, кривой у = х3 в точке (2, 8). Найдите -4 (/^, /2).
1<2"
19.	Найдите угол между касательными к окружности ха + у2 = 1 в точках х = —-— и х
3
а прямая /2 —- уравнением ~У+
1), ah — прямая, касающаяся
21.
22.
23.
24.
25.
4
= — (касательные берутся в указанном в условии порядке). 5
20.	Найдите угол между касательными к кривой у — проведенными в точках с абсцисса-4
мих=1 и х = 2 и взятыми в указанном порядке.
Найдите угол между кривыми у = ха и у = У х ъ их точках пересечения.
Найдите угол между кривыми у = х3 — 4х2+ Зх и у = х в их точках пересечения.
Найдите угол между кривыми у = x*fi иу = х2/3 в их точках пересечения.
Прямая имеет уравнение —у +Ах= —1 и /а)=25°. Найдите наклон прямой h.
Прямая /х имеет уравнение Зу — 5х = 4 и (Zj, /2) = 100°; найдите наклон прямой Zj
212
10. Квадрики
2.5. БИССЕКТРИСЫ УГЛА
В качестве приложения теоремы 3 найдем наклон п прямой I, делящей пополам угол между двумя прямыми /4и /2 с наклонами т± и т2.
Так как ^(/ь /) = ^(1, 1^, то tg -4(1 lt /) = tg -=£(/, /2) и, по теореме 3,
т2 — п _ п — тг
1 + т2п 1 + т^п
После очевидных преобразований получаем
(/Hi + /и2)п2 + 2(1 — /П1/и2)п — (mi + т2) = 0.	(7)
Это — квадратное уравнение относительно п; оно имеет, вообще говоря, два различных корня. Но так и должно быть, потому что если заданы две прямые Ц и /2, то имеются не одна, а две прямые, делящие углы между ними пополам (рис. 10.26). Это хороший пример, иллюстрирующий выражение Эйлера, согласно которому зачастую «наше перо умнее нас самих»: мы могли забыть про вторую биссектрису, а формула нам напомнила про нее.
Если mi = —/и2, то прямые и /2 симметричны как относительно оси х, так и относительно оси у. В этом случае уравнение (7) приводится к виду (1 + /И12)/г = 0, откуда п = 0. Здесь она из биссектрис горизонтальна, а другая вертикальна (и не имеет наклона).
Если /П1 + /и2=7^ 0, то уравнение (7) можно переписать так:
n2 + 2 ?~w^2- п—1 =0.	(8)
mi + т2
В этом случае мы будем иметь два вещественных корня /Zj и п2, причем П1/г2 = —1. Следовательно, биссектрисы (смежных) углов между двумя прямыми взаимно перпендикулярны.
§ 2. Повороты
213
Рис. 10.28
УПРАЖНЕНИЯ
В упражнениях 26—31 найдите уравнения (в декартовых координатах) биссектрис углов между двумя данными прямыми и /г.
Д26. /х: у = х + 1, I2: у = 1х — 2.
27.	If 2у + 4х = 5, /2: у = -ух.
28.	If. у = х, 12: у = V7~__x.
29.	If у = 2х, I2: у = 19 х.
30.	If. у = V2~x + 1, /2: 2у —х = 1.	. .	__
31.	Прямая 1Г проходит через точки (2, 3) и (4, 5), прямая I2 — через точки (4, 1) и (3,—2).
2.6.	«ЗЕРКАЛЬНЫЕ» СВОЙСТВА КОНИК
Полученные выше результаты мы используем для вывода так называемых «зеркальных» свойств коник. Эти свойства используются, например, при устройстве параболических зеркал. Параболическое зеркало представляет собой параболоид, получающийся при вращении параболы вокруг ее оси. Такое зеркало преобразует падающий на него параллельный пучок лучей в пучок лучей, сходящихся в одной точке — в фокусе (таково применение параболического зеркала, скажем, в телескопе); напротив, пучок лучей, посылаемых источником, находящимся в фокусе зеркала, оно преобразует в пучок параллельных лучей, (так используется параболическое зеркало в прожекторе; см. рис. 10.27). В качестве несколько курьезного приложения зеркальных свойств коник можно указать так называемую «галерею шепотов» — комнату с эллипсоидальными стенами и потолком. Слова, произнесенные шепотом в одном из фокусов, ясно слышны человеку, находящемуся в другом фокусе, так как звуковые волны, выходящие из одного фокуса и отражающиеся от стен, собираются во втором фокусе (рис. 10.28).
214
10. Квадрики
Оба явления основаны на физическом законе, управляющем распространением волн («угол падения равен углу отражения») и на следующей математической теореме:
Теорема 4. Пусть Р — точка коники и I — касательная к этой кривой в точке Р. Если коника является эллипсом или гиперболой, то обозначим через 1^ и 12 прямые, соединяющие точку Р с фокусами (рис. 10.29). Если же коника является параболой, то обозначим через Ц прямую, соединяющую точку Р с фокусом, а через 12 — прямую, проходящую через точку Р и параллельную оси параболы (рис. 10.30). Тогда касательная I является биссектрисой угла между прямыми Ц и 12.
Доказательство. Предположим, что наше коническое сечение задано каноническим уравнением (см. § 1.1). Обозначим через т, mi9 т2 наклоны прямых I, It и 12. Мы должны доказать (см. § 2.5), что
(/ni + т^т2 + 2(1 — т^т^т — (гщ +	= 0.	(9)
Пусть (х0» У о) — координаты точки Р. Напомним (см. § 1.4), что для эллипса и для гиперболы фокусы имеют координаты (—с, 0) и (с, 0), а парабола имеет фокус в точке (а, 0). Следовательно,
тг =------—---, т2 = ———, если е#=1,
х0 + с	Xq — с
тЛ = ——— , тг = 0, если е = 1. х0—а
В § 1.6 мы нашли уравнения (19), (20) и (21) для касательной I, проходящей через точку (х0, уъ) коники. Из этих уравнений следует, что:
т = —— —, если 0 е < L Ро
2о	।
т = — , если е = 1,
«/о
А2 у
т ---------- , если е > 1.
О2 У»
Подставляя эти значения в равенство (9), мы и докажем наше утверждение.
§ 2. Повороты
215
Рассмотрим одно из приложений доказанного свойства конических сечений. Две коники называются конфокальными, если они имеют одни и те же фокусы.
Теорема 5. Конфокальные эллипс и гипербола пересекаются под прямым углом.
Доказательство. Пусть Р — точка пересечения, лежащая, например в первом квадранте (рис. 10.31). Обозначим через Ц и /2 прямые, соединяющие точку Р с фокусами. Касательная к эллипсу и касательная к гиперболе в точке Р будут (по теореме 4) двумя биссектрисами углов, образованных прямыми Ц и /2; значит, эти касательные (см. § 2.5) взаимно перпендикулярны. [Эти две касательные не могут совпасть, так как одна из них имеет положительный, а другая — отрицательный наклон; читатель может доказать это самостоятельно, пользуясь уравнениями (20) и (21) из § 1.6.]
Чисто аналитическое доказательство этой теоремы длиннее и не так изящно.
УПРАЖНЕНИЯ
32.	Проверьте утверждение теоремы 4 для параболы у2 = 4х и луча, выходящего из фокуса (4, 4).
33.	Проверьте утверждение теоремы 4 для эллипса х2 + 4у2 = 5 и принадлежащей ему точки (1, 1).
х2	у2	у2
34. Проверьте утверждение теоремы 5 для эллипса — + “ = 1 и гиперболы х2 — — = 1.
25	16	8
2.7.	ОРИЕНТАЦИЯ В ПРОСТРАНСТВЕ
Ориентация в пространстве задается выбором репера, который, по определению, считается правым. Тогда каждый другой репер будет либо правым, либо левым, но обязательно либо тем, либо другим. На рис. 10.32 репер а) [первый вектор которого изображен пунктирной линией, второй — тонкой, а третий — жирной] выбран в ка< честве правого; тогда реперы 6), в), г) и д) будут правыми, а реперы е) и ж) — левыми.
Интуитивно ясно, что если мы представим себе репер, сделанный из твердого материала, то любой правый репер можно движением перевести в любой другой правый репер, и аналогичное утверждение имеет место для левых реперов. Но совместить движением правый репер с левым невозможно, так же как невозможно надеть правую перчатку на левую руку.
216
10. Квадрики
Рис. 10.32
Только что сделанные утверждения необходимо подтвердить точными определениями и аналитическим доказательством. Мы не делаем этого здесь, поскольку нигде не будем пользоваться ориентацией в пространстве и поскольку эти доказательства привели бы нас к теории определителей, выходящей за. пределы содержания этой книги (см., однако, Приложение, § 4.10).
§ 3. КВАДРИКИ НА ПЛОСКОСТИ
3.1.	АЛГЕБРАИЧЕСКИЕ КРИВЫЕ
Парабола, гипербола и эллипс представляют собой примеры плоских алгебраических кривых. Определим точнее это понятие.
Одночленом от двух переменных х и у называется выражение вида axpyq. где а — какое-то число, а р и q — целые неотрицательные числа. Сумма р + q называется степенью одночлена, а число а — его коэффициентом. Многочлен от двух переменных — это сумма одночленов. Многочлен имеет степень и, если степень каждого из входящих в его состав одночленов (имеющих коэффициенты а =# 0) не превосходит а и по крайней мере один из этих одночленов имеет степень, равную п (так, например, Зх8 + 4х2(/2 — х — у — это многочлен от х и у степени 4).
Плоская алгебраическая линия (или алгебраическая кривая) порядка я — это множество всех точек Р плоскости, координаты (х, у) которых в некоторой декартовой системе координат удовлетворяют уравнению вида
(многочлен от х и у степени п) = 0.
Прямая, например, является алгебраической линией порядка 1, а окружность — алгебраической кривой порядка 2.
Теорема 1. Порядок алгебраической линии не зависит от выбора декартовой системы координат.
Доказательство. Рассмотрим две декартовы системы координат; каждая из них получается из другой посредством переноса начала и изменения осей. Следо-
§ 3. Квадрики на плоскости
217
взтельно, координаты точки Р в первой системе (назовем их х и у) и во второй системе (назовем их X и Y) связаны соотношениями вида
х = аХ + |ЗУ + а, у = '{Х + 6 Y 4” b, где числа а, Р, 7,6, а и b зависят от обеих систем координат, но не зависят от рассматриваемой точки (см. § 2.2 и 2.3). Предположим, что в первой системе координат нам дана кривая степени п\ пусть это будет, например, линия
21^0^5° _ 2х17^з _ *3 + з = о
(здесь п = 100). Для того чтобы получить уравнение этой линии во второй системе координат, мы должны просто подставить вместо х и у их выражения через X и Y. Но если мы возьмем выражение вида
(аХ + рУ + аУ(ТХ + 8У + Ь)^ выполним требуемые умножения и произведем приведение подобных членов, то получим многочлен от X и У степени не более чем р + q. Следовательно, в качестве уравнения нашей кривой в новых координатах мы получим алгебраическое уравнение, степень которого <л. На первый взгляд может показаться, что степень нового уравнения может быть и меньше, чем п (т. е. что, скажем, в нашем примере все члены, содержащие X и У в степени 100, могут и взаимно уничтожиться); однако на самом деле это невозможно. Действительно, ведь только от нас зависит, какие координаты считать «старыми», а какие — «новыми»; и если степень уравнения относительно X и У будет меньше п, то мы смогли бы преобразовать его в уравнение относительно х и у степени большей, чем первоначальная, что, как мы уже знаем, невозможно.
Это рассуждение и доказывает теорему.
Теория алгебраических кривых — одна из красивейших глав так называемой «алгебраической геометрии», которой математики занимаются уже более чем 300 лет. Но в этой книге мы коснемся только самого простого (и раньше всего изученного) ее частного случая—теории кривых второго порядка*.
УПРАЖНЕНИЯ
В упражнениях 1—6 найдите степень данного многочлена от х и у.
1.	бОх3//3.	4.	х3 — у3 + х2 — ху +	4Х3#.
2.	10х + 8у + 4х//.	5.	2х2у — ху2 + 10xi/ +	1.
3.	х2у + х4 — у2 — 100.	6.	х2у3 — 2х3у + 4х//6.
7.	Для каких действительных чисел	а многочлен х2 — у2	—	5ах6 — 7 имеет степень 6?
Степень 2?
8.	Для каких действительных чисел t многочлен х2//3 — tx + (t — I)//6 — 4t имеет степень 6? Степень 5?
9.	Для каких действительных чисел <о алгебраическая кривая, описываемая уравнением со2х5 + сох2// + (д2ху = сох5 + х2у + 1, имеет порядок 5? Порядок 3? Порядок 2?
10.	а) Для каждого действительного числа со 0 укажите отвечающий этому значению со порядок алгебраической кривой (относительно переменных х, //), уравнение которой имеет вид со2х3// — со4х21/ +1 = 0.
б)	Для каждого действительного числа х =/= 0 укажите порядок отвечающей этому зна чению х алгебраической кривой (относительно переменных со, //), уравнение которой имеет вид со2х3// — со4х2г/ +1 = 0.
в)	Для каждого действительного числа у =/= 0 укажите порядок отвечающей этому значению у алгебраической кривой (относительно переменных со, х), уравнение которой ___________имеет вид со2х3// — со4х21/ +1 = 0.
* Аналитическую геометрию зачастую описывают как учение о линиях первого порядка (прямых) и второго порядка; при этом теория алгебраических линий порядка п > 3 относится уже к области алгебраической геометрии.
218
10. Квадрики
3.2.	КРИВЫЕ ВТОРОГО ПОРЯДКА
Квадрикой, или кривой второго порядка, на плоскости называется плоская алгебраическая кривая порядка 2, т. е. множество точек плоскости, декартовы координаты (х, у) которых удовлетворяют уравнению второй степени
Дх2 + 2Вху + Су2 + Dx 4- Еу+ F = 0,	(1)
где Д, В, F — некоторые числа. В таком уравнении члены Дх2, 2Вху (часто называемый смешанным членом) и Су2 являются членами второй степени, Dx и Еу — линейными членами, a F — свободным членом. Коэффициент смешанного члена для удобства обозначается через 2В. Мы предполагаем, конечно, что Д, В и С не равны нулю одновременно.
Все коники являются кривыми второго порядка, поскольку их канонические уравнения (П), (Э), (Г) (см. § 1.2) представляют собой частные случаи уравнения (1).
Кривая второго порядка может и совсем не содержать точек (так, например, уравнение х2 + 1 =0 задает «пустое» множество точек); она может состоять из единственной точки (пример: х2 + у2 =0), из одной прямой (пример: х2 =0), из двух параллельных прямых (пример: х2 — 1 =0) или из двух пересекающихся прямых (пример: ху =0). Такие кривые называются вырожденными.
В этом параграфемы докажем замечательную теорему о том, что все невырожденные кривые второго порядка — это коники (см. ниже теорему 3).
3.3.	ДИСКРИМИНАНТ И СЛЕД
Числа
б = АС — В2 и t = А + С,
образованные из коэффициентов при членах второй степени в уравнении (1), называются соответственно дискриминантом и следом этого уравнения. Мы можем считать, что дискриминант и след не равны нулю одновременно. Действительно, из равенства t = 0 вытекало бы, что С = —А, и если б = 0, то —С2 — В2 =0, так что А = В = С = 0. В этом случае наше уравнение линейно. Мы покажем, что дискриминант и след определяют вид кривой, заданной уравнением (1).
Если уравнение (1) умножить на число а #= 0, то дискриминант умножится на а2, а след на а, так как
(аД)(аС) — (аВ)2 = а2(ДС — В2) = а2б,
аД + аС = а(Д + С) = а/.
Теорема 2. Дискриминант и след (кривой второго порядка) не меняются при поворотах и при переносах системы координат.
Мы докажем это сначала для переносов. Пусть система координат перенесена в новое положение. Если координаты точки (х, у) в новой системе равны (X, У), то (см. § 2.2)
§ 3. Квадрики на плоскости
219
х = X + а, у = Y + Ь, где точка (а, Ь) есть начало новой системы координат. Следовательно, х2 = X2 4- 2аХ + а2, ху = XY + ЬХ + aY + ab, у2 = У2 4- 2ЬУ 4- Я
Подставляя эти значения в уравнение (1), получим преобразованное уравнение
ЛХ2 + 2ВХУ + СУ2 + (2Аа 4- 2Bb + D) X 4- (2Ва + 2СЬ + Е)У + +Аа2 + 2Bab + Cb2 + Da 4- Eb 4- F = 0.
Так как члены второй степени этого уравнения не отличаются от членов второй степени исходного уравнения (1), то дискриминант нового уравнения по-прежнему равен АС — В2, а след равен А + С.
Пусть теперь координатные оси повернуты на угол 0. Тогда (см. теорему 2 § 2.3) новые координаты X, У связаны со старыми соотношениями:
х = Xcos 0 — ysin 9, у = Xsin 0 4- Уcos 0. Следовательно,
х2 = X2 cos2 9 — 2ХУсоз 9 sin 9 4- У2 sin2 9, ху = X2 cos 9 sin 9 4- ХУ (cos2 9 — sin2 9) — У2 sin 9 cos 9, у2 = X2 sin2 9 4- 2Xysin 9 cos 9 4- Y2 cos2 9.
Подставляя эти значения в уравнениё'(1), мы получим преобразованное уравнение, которое будет иметь вид
AX2+2BXY 4-СУ2 4-0X4- EY 4- F =0,	(2)
Л X
где буквы А, В и т. д. имеют следующий смысл:
А — A cos2 9 4- 2В cos 9 sin 9 4- С sin2 9,
В = (С — Л) sin 9 cos 9 4- В (cos2 9 — sin2 9),
(3) С — A sin2 9 — 2В sin 9 cos 9 4- С cos2 9,
D = Deos 9 4- В sin 9, E —— D sin 9 4- E cos 9, F — F.
220
10. Квадрики
Новый след
А + С = A (cos2 6 + sin2 6) + С (sin2 6 + cos2 0) = А 4- G
а новый дискриминант
АС — В2 = A2 sin2 9 cos2 9 — 2АВ sin 9 cos3 9 + AC cos4 9 + 2AB sin3 9 cos 9 —
—4B2sin29cos2 9 + 2BC sin 9 cos3 9 + AC sin4 9 — 2BCsin3 9 cos 9 + C2 sin2 9 cos2 9 —
— (C2 — 2AC+ A2) sin2 9cos2 9—2(BC — AB) (sin 9cos39 — sin39cos9) —
— B2(cos4 9 — 2 sin2 9 cos2 9 + sin4 9) = AC(cos49 + sin4 9 + 2 sin2 9 cos2 9) —
— B2(4 sin2 9 cos2 9 + cos4 9 — 2 sin2 9 cos2 9 + sin4 9) =
= (AC — B2)(cos2 9 + sin2 9)2 = AC — B2.
Это и завершает доказательство.
ф Примеры. 1. В примере 4 из § 2.3 мы показали, что уравнение х2 — у2 = 1 поворотом системы координат преобразуется в 2XY =1. Оба уравнения имеют дискриминант, равный —1.
2.	Если t2 =46 , то уравнение (1) определяет окружность, точку или пустое множество.
Доказательство. Если (А + С)2 = А2 + 2АС -I- С2 = 4АС — 4В2. то (А — С)2 =—4В2, т. е. (А—С)2 + 4В2 = 0; следовательно, А = С и В = 0. Да-। лее применяем результат § 3.1 гл. 2.ф
3.	4. ОСНОВНАЯ ТЕОРЕМА. ИСКЛЮЧЕНИЕ СМЕШАННОГО ЧЛЕНА
1 Приступим теперь к доказательству основного результата.
Теорема 3. Множество точек (х, у), удовлетворяющих уравнению второй степе-1 ни (1), либо пусто, либо состоит из одной точки, либо состоит из одной или двух 1 прямых, либо является параболой, эллипсом или гиперболой.
Мы докажем теорему 3, показав, чти можно преобразовать общее уравнение кривой второго порядка Ах2 + 2Вху + Су2 + Dx-\-Ey+F=Qu одному из канонических уравнений (П), (Э), (Г). При этом мы будем производить повороты координатной системы, ее переносы и в некоторых случаях умножать обе части уравнения на какое-то число а =й= 0. Доказательство состоит из нескольких шагов; вся описываемая процедура называется «приведением уравнения кривой второго порядка к каноническому виду». Первый шаг является наиболее важным.
Доказательство теоремы 3. Шаг I. Поворотом системы координат уравнение кривой второго порядка можно привести к виду, не содержащему смешанного члена.
Действительно, при повороте координатных осей на угол 9 уравнение (1) преобразуется в уравнение (2), причем новые коэффициенты определяются по формулам (3). Мы теперь перепишем формулу, определяющую В. так:
2В = (С — A)sin 29 + 2В cos 29.
Мы хотим подобрать 9 так, чтобы В было равно нулю. Если А =/= С, то положим
§ 3. Квадрики на плоскости
221
tg20 = ^rV-	(4)
Т ак мы получим, что В = 0 для четырех значений 0, а именно:
% = arctg -^-с , 0О + 90°, 0О + 180° и 60 + 270°.
Если А = С и В =/= 0, то В = 0 при cos 29= 0, т. е. если 0 имеет одно из следующих значений: 45°, 135°, 225° или 315°. Наконец, если Л = С и В = 0, то В = 0 для всех 9. (Ясно, что если В = 0, то нам вообще не требуется переходить к новой системе координат.)
ф Пример. При помощи поворота координатной системы преобразовать уравнение
Зх2 + 2ху + Зу2 — У<Гх = 0
в уравнение, не содержащее смешанного члена.
Решение. Так как А = 3, 2В = 2 и С = 3, то в качестве угла поворота 9 можно взять угол 45°. Так как cos 45° = sin 45° = то «новые» координаты X, Y определяются равенствами
х = -кг(Х-У),	y=^=(X + Y).
У 2	У 2
Подставляя эти значения х и у в наше уравнение [или просто воспользовавшись формулами (3)], получим
— (X2 — 2ХУ + У2) + (X2 — У«) 4- A (XJ + 2XY + Г3) — (X — У) = 0.
или после перегруппировки
4Х2 + 2У2 — X + Y = 0.®
УПРАЖНЕНИЯ
В каждом из упражнений 11—22 произведите такой поворот декартовой системы координат, чтобы в данном уравнении второй степени относительно х, у выпал смешанный член; напишите полученное уравнение в новой системе координат. (Это уравнение будет равнссильно старому; новые координаты уместно обозначить через X и У.) Изобразите на чертеже старые и новые оси координат. (В некоторых случаях будет легче определить cos 20 и sin 20 по tg 20, а затем, используя формулы половинного угла, найти sin 0 и cos 0. При этом отпадает необходимость явного определения угла 0.)
11.	2х2 + Зху + 2у2 — х + 1 = 0.
12.	ху + х + у == 0.
13.	х2 + /з"ху — 1 = 0.
14.	х2 + ху + у2 — 3 = 0.
15.	Зх» + 2/3- ху+у2 — 4 = 0.
16.	Зх2 — 4/Г Ху — у2 + 200 — 25 = 0.
222
10. Квадрики
17	Зх2 — 2/3 ху — у2 — 3/3 х 4- 7у = 0. Д 18. 4х24-4ху4-02— х = 0.
33	11
19.	5х2 — Зху + у2---— х 4----— у — 0.
/10	/10
20.	4x0 4-302 4- 2/5"х 4- 4/ЁГ 0 = 0.
21.	4х’ 4- 12x0 4- 902 4- 2/13 х 4- 2/13 0 = 0.
22.	14х2 4- 5x0 4- 2у2 — 2=0.
3.5. ИСКЛЮЧЕНИЕ ЛИНЕЙНЫХ ЧЛЕНОВ
Доказательство теоремы 3. Шаг II. Рассмотрим уравнение второй степени, не содержащее смешанного члена:
Ах2 + Cy2 + Dx + Ey + F = 0.
Если его дискриминант отличен от нуля, то линейные члены (члены с первыми степенями х и у) можно обратить в нуль переносом системы координат.
Действительно, так как дискриминант АС =# 0, тоЛ=/=0иС=/=0. Выделяя полный квадрат, мы получим
Х2.Г>	Л I 2	.	D	,	D’	\	D2	Л	f	.	О	V	D2
Ах2 4- Dx = Ах2	4-х 4------1------- А	(х 4---1---.
\	А	4А2	/	4А	\	2А)	4А
Аналогично,
п , . с	z>/21£	.	Е2	\	Е2	~	I	.	Е	\2	Е2
С у -J- Еу = С I у -4- —— у — I ~ = С I у -4- 	| —-,
J *	\ С У 4С2 ) 4С V 2С J 4С
и наше уравнение приводится к виду
(г) \2	/	р \2
х + " —) -4- С I у -J--]	= 0,
2А )	V	2С J	1
Перенесем теперь оси координат так, чтобы новое начало координат совпало с точкой (-----------Тогда новые координаты X, Y будут связаны со
старыми формулами
и уравнение приведется к виду
АХ* + CY* + F< =0.
Новое уравнение не содержит линейных членов.
§ 3. Квадрики на плоскости
223
фПример (продолжение). В уравнении
Зх2 + 2ху + 3i/2 — VTх = О исключить смешанный член и линейные члены.
Решение. Дискриминант уравнения равен 9 — 1 > 0. В предыдущем примере, повернув оси координат, мы уже исключили смешанный член и пришли к уравнению
4Х2 + 2Y2 — X + Y = 0.
Перепишем это уравнение так:
4 (X2---- X 4- — — — + 2(У2 + — У + ~Ц — — =0,
4	64]	16	\	2	16/	8
откуда
4(Х--Ч* + 2(Г+
\	8 )	\	4 )	16
Положим
$ = Х—L	= у _|_ _1_
8	4
(эта замена сводится к переносу осей координат). Тогда наше уравнение примет вид
4^+27i2=4-<
10
УПРАЖНЕНИЯ
В каждом из упражнений 23—34 определите дискриминант данного уравнения второй степени относительно X, У, не содержащего смешанного члена. Затем, если это возможно, перенесите оси декартовой системы координат так, чтобы исключить линейные члены; напишите эквивалентное первоначальному уравнение (новые координаты уместно обозначить через $ и *q). Изобразите на чертеже старые и новые оси координат, упр. 11. упр. 12. упр. 13. упр. 14. упр. 15. упр. 16.
23. Уравнение, полученное ^24. Уравнение, полученное
25.	Уравнение, полученное
26.	Уравнение, полученное
27.	Уравнение, полученное
28.	Уравнение, полученное
в в в в в в
29.
30.
31.
32.
33.
34.
Уравнение, полученное Уравнение, полученное Уравнение, полученное Уравнение, полученное Уравнение, полученное Уравнение, полученное
в в в в в в
упр. упр. Упр-упр. упр. упр.
17.
18.
19.
20.
21.
22.
3.6.	ПОЛОЖИТЕЛЬНЫЙ ДИСКРИМИНАНТ
Доказательство теоремы 3. Шаг III. Если дискриминант уравнения кривой второго порядка положителен, то это уравнение определяет либо пустое множество, либо точку, либо эллипс (который может быть и окружностью).
Действительно, используя преобразования шагов I и II, мы можем привести наше уравнение к виду
Дх2 + Су2 = F. где б = АС > 0.	(6)
Предположим, что А > 0 и С > 0: ведь если дело обстоит не так, то нам достаточно умножить обе части уравнения на —1.
224
10. Квадрики
Если F < 0, то уравнение (6) не удовлетворяется ни при каких х, у, оно определяет пустое множество. Если F =0, то уравнение (6) равносильно равенствам х = = у = 0; оно определяет одну точку.
Предположим, наконец, что F > 0. Будем считать также, что А С. [Если С < < Л, то мы повернем оси координат на 90°; новые координаты будут X = у, Y = = —х, так что уравнение (6) приведется к виду СХ2 + AY2 = F — здесь уже коэффициент при X2 меньше, чем при У2.] Обозначим а = У F/А, b = yF/С', тогда >> b > 0. Умножая обе части уравнения (6) на 1/F, получим каноническое уравнение эллипса:
фПример (продолжение). Привести уравнение
Зх2 + 2ху + Зу2 — /2 х = 0 к каноническому виду.
Решение. В предыдущих примерах после поворота и переноса системы координат мы получили уравнение
4^+ 2^ = А,
1О из которого умножением на 16/3 получаем
64_ $2 + 32 ^2 = ।
Так как коэффициент при £2 больше, чём коэффициент при т]2, мы повернем систему координат на 90°, т. е. произведем замену координат 5,т| на новые координаты:
U = , v = — $.
Наше уравнение приведется к виду
32	2 1	64	2	1
----и2 Ч-----v2 = I.
3	3	__
Это есть каноническое уравнение эллипса, у которого а = 1/ —, b =	3 .ф
3.7.	ОТРИЦАТЕЛЬНЫЙ ДИСКРИМИНАНТ
Доказательство теоремы 3. Шаг IV. Если дискриминант уравнения второй степени отрицателен, то это уравнение определяет либо пару пересекающихся прямых, либо гиперболу.
В самом деле, посредством преобразований шагов I и II мы можем привести уравнение кривой к виду
Ах2 + Су2 = F, где 6 = АС < 0.	(7)
Предположим сперва, что F = 0. Если Л > 0 и С < 0, то уравнение Лх2 + Су2 = = 0 приводится к виду (УАх + У—Су) (УАх — У —Су) = 0. Если Л < 0, а ОО, то мы получаем (У—Ах + У Су)(У—Ах — У Су) =0. В обоих случаях
§ 3. Квадрики на плоскости
225
уравнение определяет пару прямых, проходящих через начало координат;-наклоны этих прямых У—А/С и —У —А/С.
Если F =И= 0, то можно считать, что F = 1. (Если это не так, умножим обе части уравнения на 1/F.) В уравнении
Ах2 + Су2 =1, АС <0
знаки коэффициентов А и С противоположны. Можно считать, что А > 0. (Если это не так, повернем оси координат на 90°.) Положим а = У1/А, b = У—1/С. При этом наше уравнение приведется к виду
а это есть каноническое уравнение гиперболы.
3.8.	НУЛЕВОЙ ДИСКРИМИНАНТ
Доказательство теоремы 3. Шаг V. Если дискриминант уравнения второго порядка равен нулю, то это уравнение определяет либо пустое множество, либо прямую, либо пару параллельных прямых, либо параболу.
Действительно, осуществив преобразование шага I, мы можем привести уравнение к виду, не содержащему смешанного члена. Тогда б = АС и так как б = 0, то либо А = 0, либо С = 0. Ясно, что Л и С не равны нулю одновременно, ибо в противном случае наше уравнение было бы линейным. Далее, можно считать, что А = 0, а С =# 0. (Если было бы А =# 0, а С =0, то, повернув оси координат на 90°, мы поменяли бы местами коэффициенты при х2 и у2,) Можно даже положить, что Л = 0, а С = 1: ведь этого всегда можно достичь, умножая уравнение на 1/С.
Таким образом, нам осталось рассмотреть уравнение
у2 + Dx + Еу + F = о.	(8)
Предположим, сперва, что D = 0. Тогда наше уравнение будет квадратным уравнением относительно у. Если оно не имеет (действительных) корней, то ему отвечает пустое множество. Если оно имеет единственный действительный корень а, то это уравнение определяет прямую линию у = а. Если уравнение имеет два действительных корня fl и т, то оно определяет пару параллельных прямых у = fl и у = у.
Пусть теперь D #= 0. Выделив полный квадрат, мы перепишем уравнение (8) так:
(Р \2	Р2
у+ — I +Dx — — + F=0.
*	2 /	4
Другими словами, мы имеем
1у+ А? + о(л--5- + А)_о.
(ръ	F \
--------| , 4D------D /
Р
Y =«/ + — ; при этом наше уравнение примет следующий вид:
Y2 4- Dx = 0.
226
10. Квадрики
Можно предположить, что D < 0; в противном случае мы просто повернем оси координат на 180° — при этом X заменится на —X, а К на —Y. Положим а = — тогда а>0, и мы придем к уравнению
У2 = 4ах,	(П)
т. е. к каноническому уравнению параболы.
Этим доказательство теоремы 3 полностью завершено.
фПримеры. 1. Найти вершины эллипса
Зх2 + 2ху + 3z/2 — К2х = 0.
Решение. В предыдущих примерах мы преобразовали это уравнение к каноническому виду
—£— + —i— = 1.
(/!)’ (т^)
При этом мы перешли от координат х, у к кординатам X, Y по формулам
х = (X - Г). У-------(X + п
/2	уг
а затем к координатам В, т|, определяемым равенствами
е=х-А-, 4 = y+-L,
и, наконец, к координатам и и о, где
и =г), v ==—5.
В координатах и, v четыре вершины эллипса — это точки
/ЕЕ, oW-XL, o')/о, ХЕЕ /о,-ХЕЕ \ /32	/ \	/32	) \	8 /	\	8 /
/""з"	/ 3"
Далее, если и = 1/ —, v =0, то 5 =0, 'П = I/ — и, следовательно,
§ 3. Квадрики на плоскости
227
Таким образом, в первоначальной системе координат одна из вершин нашего эллипса имеет координаты
8/2	8/2
Читатель без труда найдет и координаты остальных трех вершин.
2. Найти асимптоты гиперболы
Уз'ху — у1 = 1.
Решение. Сначала приведем уравнение гиперболы к каноническому виду. Из формулы (4), где Л=0, В =/572 и С = — 1, находим угол поворота: О = -i- arctg /У = 30°. Так как sin 30° =	, cos 30° = -у-/3 , то при пово-
роте системы координат на угол 30° мы приходим к новым координатам X, Y, таким что	_	_
/зх — г х + /з Y х = —--------, у =----—-------
2	а	2
Подставляя эти значения в наше уравнение, получим
/3~ X2 — /3~ Y* + 2XY_____Х« + 2/3~ XY + 3Y*
У	4	4
ИЛИ — X2 — -2	1
а это каноническое уравнение гиперболы У равнение асимптот имеет вид
J-X2 —или /Уху —у2 =0.
Следовательно, асимптотами являются ось х и прямая у = /Ух.ф
2
в котором а = /2 и Ь =
228
Приложение к главе 10
УПРАЖНЕНИЯ
В упражнениях 35—46 предлагается следующим образом закончить работу, начатую в упражнениях 11—34: выясните, что именно определяется данным уравнением второй степени — эллипс, гипербола, парабола, точка, прямая, пара прямых или пустое множество. В невырожденных случаях найдите в исходной системе координат вершины, фокусы и асимптоты (если они существуют). Во всех случаях начертите кривую в первоначальной системе координат.
35.	Уравнение упр. 11 (см. 23).
36.	Уравнение упр. 12 (см. 24).
37.	Уравнение упр. 13 (см. 25).
Д38. Уравнение упр. 14 (см. 26).
39.	Уравнение упр. 15 (см. 27).
40.	Уравнение упр. 16 (см. 28).
41.	Уравнение упр. 17 (см. 29).
42.	Уравнение упр. 18 (см. 30).
43.	Уравнение упр. 19 (см. 31).
44.	Уравнение упр. 20 (см. 32).
45.	Уравнение упр. 21 (см. 33).
46.	Уравнение упр. 22 (см. 34).
В упражнениях 47—54 найдите уравнение второй степени относительно г, у, определяющее описанную кривую второго порядка, и в каждом случае найдите дискриминант уравнения. Определите геометрически угол, на который надо повернуть оси координат, чтобы исключить смешанный член, если этот член первоначально не равен нулю.
47. Пара прямых с наклоном 1, проходящих через точки (0, 0) и (0, 1).
48.	Пара прямых с наклонами 1 и —1, проходящих через точку (1, 1).
49.	Точка (2, —1).
50.	Прямая с наклоном 1/2, проходящая через точку (2, 3).
51. Пара прямых с наклонами }^3/3 и уЗ”, проходящих через точку (1, 0).
52. Эллипс с вершинами (±3, ±4) и (±—, ±1). О
53.	Гипербола с вершинами (±12, ±5) и фокусами (±24, ±10).
54.	Парабола с вершиной (1, 2) и фокусом (2, 3).
Приложение к главе 10
§ 4. Квадрики в пространстве
4.1.	Поверхности второго порядка
Определение многочлена степени п от трех переменных является естественным обобщением определения, введенного в § 3.1 для двух переменных. Алгебраическая поверхность порядка/г — это множество всех точек пространства, координаты х, у, z которых удовлетворяют некоторому уравнению вида F (х, у, z) = 0, где F (х, у, г) — многочлен от х, у и z степени п. Так, например, плоскость является алгебраической поверхностью первого порядка, а сфера — алгебраической поверхностью второго порядка.
Квадрика, или поверхность второго порядка, в пространстве — это алгебраическая поверхность порядка 2, т. е. множество всех точек, декартовы координаты (х, у, z) которых в некоторой системе координат удовлетворяют уравнению второй степени, т. е. уравнению вида
Ах2 + By 2 + Cz2 + 2Dxy + 2Eyz + 2Fxz + Gx + Hy + Iz + К = 0.	(1)
Сначала мы рассмотрим несколько примеров.
4.2.	Вырожденные случаи. Цилиндры
Мы начнем с рассмотрения нескольких вырожденных случаев поверхности второго порядка. Уравнением (1) может определяться пустое множество (пример: х2 = — 1), точка (пример: х2 + У2, + z2 = 0), прямая (пример: х2 + у2 = 0), плоскость (пример: z2 = 0), пара параллельных плоскостей (пример: z2 = 1) или пара пересекающихся плоскостей (пример: ху = 0).
Если уравнение (1) не содержит членов, в которые входит координата г, то соответствующая поверхность является цилиндром второго порядка. Для того чтобы построить такой цилиндр,
§ 4. Квадрики в пространстве
229
Рис. 10.33
рассмотрим в плоскости ху определяемую уравнением (1) кривую X второго порядка и «дополним» каждую ее точку (дг, у) всеми точками (х, у, г) пространства, где г произвольно, а (дг, у) — точка плоскости ху, принадлежащая линии X. Некоторые примеры (параболический цилиндр, эллиптический цилиндр и гиперболический цилиндр) изображены на рис. 10.33.
Цилиндром с направляющей линией X и образующими, параллельными оси г, называется поверхность S, которая состоит из всех точек всех прямых, перпендикулярных плоскости г — 0 и пересекающих эту плоскость в точках кривой X. (А вообще цилиндром называется любая поверхность, для которой существует система координат, в которой эта поверхность представляет собой цилиндр с образующей, параллельной оси г.)
(2)
4.3.	Конусы
В § 5.2 гл. 9 мы показали, что при вращении прямой z = тх плоскости хг вокруг оси z получается поверхность
4 + 4“га==о
а2 а2
(рис. 10.34). Эта поверхность второго порядка называется (прямым) круговым конусом.
Мы получим другую поверхность второго порядка, а именно эллиптический конус, если «сожмем» (или «растянем») круговой конус в направлении оси у. Если коэффициент сжатия равен b/а, то уравнение полученной поверхности будет иметь вид
х2 у2
— 4- — — г2 = 0;
а2 Ь2
эта поверхность изобоажена на рис. 10.35.
(3)
230
Приложение к главе 10
Рис. 1034
Для того чтобы исследовать полученную' поверхность, рассмотрим линии пересечения ее с плоскостями, параллельными координатным плоскостям. Плоскость, параллельная координатной плоскости г « 0 (т. е. плоскости ху), имеет уравнение г = у (где у — какое-то число). В этой плоскости х и у — декартовы координаты. Аналогично, yt г — это декартовы координаты в плоскости х  а и х, г — декартовы координаты в плоскости у = Р.
Уравнение линии пересечения конуса (3) с плоскостью г = у получается при подстановке г =у в уравнение (3):
а*	1
Оно определяет точку, если у *= 0, и эллипс с полуосями |у |а и |у |д, если у + 0. Линия пересечения конуса е плоскостью х = а имеет уравнение
аа и*
— 4- — — za = 0,
а»
или
у* а*
Ь» “ а»
Если а + 0 то это гипербола с полуосями |а|/а и b |а|/щ если же а = 0 — то пара прямых. Линия пересечения конуса с плоскостью у = Р также представляет собой либо гиперболу, либо пару прямых.
44. Эллипсоид
Вращая коническое сечение вокруг его оси, мы тоже получим некоторую поверхность второго порядка. Так, при вращении эллипса
$ 4. Квадрики в пространстве
231
вокруг оси г получается эллипсоид вращения. Уравнение этой поверхности в цилиндрических координатах (г, 6, г} имеет вид (см. гл. 9, § 5.2)
Следовательно, уравнение рассматриваемой поверхности в декартовых координатах таково (поскольку г2 = х2 + р2):
, У8 , га а» ва ** сг
(4)
Эта поверхность называется эллипсоидом вращения— вытянутым эллипсоидом при с > а (рис. 10.36) и сжатым эллипсоидом при с < а (рис. 10.37); ясно, что при с = а мы получаем сферу. Иными словами, вытянутый эллипсоид получается при вращении эллипса вокруг его большой оси, а сжатый эллипсоид — при вращении эллипса вокруг его малой оси. Поверхность Земли приближенно можно считать сжатым эллипсоидом.
Эллипсоид общего вида получается из (4) сжатием в направлении оси у\ его уравнение
имеет вид
X2	«2	z2
	 г I ---- а*--------------Ь*	с2
(5)
(см. рис. 10.38, где а > b > с). Читатель может легко проверить, что пересечение плоскости х = а, у = Р или г = у с поверхностью (5) либо пусто, либо состоит из одной точки, либо явля-
ется эллипсом.
232
Приложение к главе 10
4.5. Гиперболоиды
Вращая гиперболу вокруг ее действительной оси, получаем двуполостным гиперболоид вращения. Если уравнение гиперболы имеет вид
г2	х2
с2	а2
то уравнение соответствующего гиперболоида будет таково:
х2	у2	г2
а2	а2	с2
Сжатие в направлении оси у переводит наш гиперболоид вращения в двуполостный гиперболоид общего вида
(рис. 10.39). Легко видеть, что пересечение этой поверхности с плоскостью г = у либо пусто, либо состоит из одной точки, либо представляет собой эллипс, в то время как линия пересечения его с плоскостью х = а или с плоскостью у = Р всегда является гиперболой.
Однополостный гиперболоид вращения получается при вращении гиперболы вокруг ее мни-мой оси.. Если уравнение гиперболы имеет вид
то мы получим поверхность
Сжатие этой поверхности в направлении оси у переводит ее в однополостный гиперболоид общего вида
(рис. 10.40). В пересечении этой поверхности с плоскостями z = у получаются эллипсы, а с плоскостями х = а или у = р — гиперболы, которые при а = а илиР = b вырождаются в пары прямых.
4.6. Параболоиды
Существуют два типа поверхностей второго порядка, называемых параболоидами. Эллиптический параболоид определяется уравнением
Эта поверхность расположена в полупространстве z > 0 (рис. 10.41). При f > 0 плоскость г = = Т пересекает эту поверхность по эллипсу. Линии пересечения с плоскостями х = а или у = р являются параболами. Можно считать, что уравнение (8) получается при сжатии в направлении оси у параболоида вращения.
§ 4. Квадрики в пространстве
233
х2 + у2 = а2г,
получаемого вращением параболы
х2 — а2г = О вокруг ее оси.
Гиперболический параболоид (рис. 10.42) не может быть получек сжатием из какой-либо поверхности вращения. Его уравнение имеет вид
Линии пересечения этой поверхности с плоскостями х = а или у = 0 являются параболами, а с плоскостями г = % =/= 0 — гиперболами', при г = 0 мы получаем пару прямых.
Оказывается, что приведенными нами примерами поверхностей второго порядка исчерпываются все возможные случаи. Это основной результат теории поверхностей второго порядка, аналогичный теореме 3 § 3. Мы к нему вернемся в § 4.11. Уравнения (3), (5), (6), (7), (8) и (9) называются каноническими уравнениями соответствующих поверхностей.
УПРАЖНЕНИЯ
В упражнениях 1—14 определите линию пересечения данной поверхности второго порядка с данной плоскостью и, если эта линия является невырожденной, найдите ее фокусы и вершины. В случае параболы найдите уравнение директрисы, а для гиперболы — уравнения асимптот.
1. х2 + у2 — г = 0 и х = 2. г2 А2. 4х2 + у2 4- — = 1 и г = 2.
3.	4х2 + 25г/2 — 100z2 = 0 и х = 1.
4.	4х2 + 25г/2 — 100z2 = 0 и z = — 1.
X2	Z2
5.	-^- + 4^+	1 и 4у+ 1 = 0-
у2 х2
6-*-T-36=1 и х = 3-	...
И2 X2	'		- '	**
’•г2-v-^ = 1 и г^-Х5 •	-
4 Зо	*
г2	Л
8.	4х»+ у2— — = j и г=3. • 10	z	' .
г2	УТ *
9.	4х2 + у2--— = 1 и у = — --.
16	2
г»	/Г
10.	4ха + уа— — =..1 и	'
X2 . и2
н. г = — + 4- и х = — 2. 4	9
12.	4х2 — 16г/2 = г и г = 1.
13.	4х2 — 16у2 = г и г = —1.
14.	4х2 — 16у2 = г и 2х — 1 = 0.
234
Приложение к главе 10
Рис. 10.42
Рис 10.41
§ 4. Квадрики в пространстве
235
4J. Линейчатые поверхности
Поверхность S называется линейчатой, если через каждую ее точку Р проходит некоторая прямая /, целиком принадлежащая этой поверхности, т. е. такая, что каждая точка этой прямой является в то же время и точкой поверхности. Ясно, что все плоскости, цилиндры и конусы являются линейчатыми поверхностями.Существуют, однако, и другие линейчатые поверхности второ* го порядка.
Теорема 1. Однополостный гиперболоид и гиперболический параболоид являются линейчатыми поверхностями.
Доказательство. Пусть а — какое-то фиксированное число. Прямая, параметрическое представление которой имеет вид
х = a cosa + (a sin a)t, у = b sin a — (b cos a)/, z = ct,	(10)
целиком принадлежит поверхности (7). Это легко доказать, подставляя значения х, у, г, определяемые равенствами (10), в уравнение (7); при этом, как читатель легко может проверить сам, при всех значениях t получается тождество.
Предположим теперь, что точка P(xq, Уо, го) принадлежит гиперболоиду (7). Нам надо найти такое значение а, при котором прямая (10) проходит через точку Р. Значение t, соответствующее точке Р, должно быть равно zo/c. Следовательно, должны выполняться равенства
хо = a cos a + (a sin a)zo/c, yo = b sin a — (b cos a)zo/c.
Будем рассматривать эти равенства как систему уравнений с неизвестными cos а и sin а. Решая эти уравнения получим
х0/а — (у0/6) (г0/с)	(х0/а) (г0/с) + Уо/Ь
1 4-zg/с»	14-?g/ca
Для того чтобы нашлось а, удовлетворяющее этим условиям, необходимо, чтобы выполнялось равенство
ГXo/a — iyjb) (г,/с) 1«	Г(х0/а) (г0/с) + у0/&~|3 _
1 + 1 +
Но это равносильно тому, чтд координаты точки (хо, уо, го) удовлетворяют уравнению (7).
Имеется и другое семейство прямых, однократно покрывающих гиперболоид (7) [т. е. таких, что через каждую точку поверхности (7) проходит единственная прямая этого семейства],— это прямые x=a cos 0 — (a sin 0 )s, у = b sin р + (b cos р )s, z = cs,	(1
где р — некоторое фиксированное число, as — параметр.
Итак, наше утверждение для однополостного гиперболоида доказано. Из него следует, чт<Г модель этой поверхности можно сделать из прямолинейных стержней (такая модель изображена на рис. 10.43).
Далее, легко видеть, что для каждого фиксированного числа А прямая х = Аа + at, у = АЬ — bt, z = 4Л/	(12/
целиком принадлежит гиперболическому параболоиду (9). Если Р — (хо, Уо, 2о) — точка поверхности (9), то для прямой (12), проходящей через эту точку, л ^оМ+уо/Ь
2
Имеется и другое семейство прямых, однократно покрывающих поверхность (9), —это прямые
х = Ba + as, у = —Bb + bs, z = 4Bs,	(13)
где фиксированное число В задает прямую семейства, a s — параметр. Модель параболоида, построенного из прямолинейных стержней, изображена на рис. 10.44.
236
Приложение к главе 10
УПРАЖНЕНИЯ
15.	Найдите пару прямых, проходящих через точку ( у -L _L , 0j и принадлежащих гиперболоиду х2 + у2 — 100г2 = 1.
16.	Найдите пару прямых, проходящих через точку (2. 2, и принадлежащих гиперболоиду х2 + у2 — г2 = 1.
17.	Найдите пару прямых, проходящих через точку (0, 0, 0) и принадлежащих параболоиду 4х2 — 5уа = z.
18.	Найдите пару прямых, проходящих через точку (4, 5, —9) и принадлежащих параболоиду х2 — у2 = г.
19.	Покажите, что любые две прямые семейства (10), соответствующие двум разным значениям а, таким что 0 < а < 2л, скрещиваются.
20.	Покажите, что никакая прямая семейства (10) не совпадает ни с одной из прямых семейства (11).
21.	Покажите, что любые две прямые семейства (12), соответствующие разным значениям Д, скрещиваются.
22.	Покажите, что ни одна из прямых семейства (12) не совпадает ни с одной из прямых семейства (13).
4.8.	Замена системы координат в пространстве
До сих пор мы предполагали, что рассматриваемая квадрика задана своим каноническим уравнением, т. е. мы предполагали, что система координат в пространстве выбрана таким образом, чтобы уравнение нашей поверхности было возможно более простым. Для того чтобы рассмотреть всевозможные поверхности второго порядка, мы прежде всего сделаем некоторые замечания относительно замены системы координат в пространстве, складывающейся из переноса начала координат и изменения направлений координатных осей (сравните с рассуждением относительно замены системы координат на плоскости в § 2.2 и 2.3).
Предположим, сперва, что мы изменяем только положение начала координат, т. е. переходим от системы {О, е^, еа, е3) к системе {О', et> еа, е3}, где {elt еа, е3)-некоторый репер. Пусть Р — произвольная точка, а Р и Р' — ее радиусы-векторы относительно точек О и О'. Тогда Р = Т + Р', где вектор Т определяется направленным отрезком ОО' (рис. 10.45). Пусть в «ста-
§ 4. Квадрики в пространстве
237
рой> системе координат {О, ех, ез, е3} координаты точки Р будут (х, ул г), а в «новой» системе координат {О', ер ез, е3) ее координаты (Л, Y, Z), и пусть «старые» координаты точки О' будут (а, б, с). Тогда Т = аех + без + се3, Р =	“Г ze3 и Р' = Хех + Уе2 + Ze3, так что
х = а + X, у = b + Y. г = с + Z.	(14)
Рассмотрим теперь случай, когда новая система координат {О, fx, f3, f3) получается из старой изменением направлений координатных осей, т. е. посредством перехода к новому реперу {fx, fз, f3) Пусть (X, У, Z) — координаты точки Р в системе {О, fj, fa, f3} (рис. 10.46). Тогда
xej -f- z/ез + zea = Xtf + Из + Zf3.	(15)
Но мы имеем, кроме того,
fx = ах ех + а2 е2 + а3 е3, f2 = рх ех + ?2 е2 + З3 ©з»	= 71 е1 + 72 е2 + Тз ез» (16)
где а$, рi, у t (i =1,2 или 3) — числа, зависящие от обоих реперов {ех, е2, е3) и {ff, fs, f3}, но не зависящие от точки Р Подставляя (16) в правую часть равенства (15), группируя соответствующим образом полученные члены и учитывая, что коэффициенты при ех, ез, е3 в обеих частях равенства должны быть одинаковы, мы получим:
х= ахХ +рхУ +Yxz, у = а2х+р2У+y2Z, г= а3Х+рзУ + y3Z.	(17))
[сравните формулы (14) и (17) с соответствующими формулами из § 3.1]. Рассуждая в точности так же, как в § 3.1, мы можем получить следующий результат:
Теорема 2. Порядок алгебраической поверхности не зависит от выбора системы координат.
4.9.	Плоские сечения поверхностей второго порядка
Теперь мы в состоянии доказать следующее утверждение:
Теорема 3. Линия пересечения Поверхности второго порядка с плоскостью (не принадлежащей целиком этой поверхности) является кривой второго порядка (которая, в частности, может представлять собой пару прямых, прямую, точку или пустое множество).
238
Приложение к главе 10
Доказательство этого утверждения очень просто. По теореме 2 поверхность второго порядка остается поверхностью второго порядка и при изменении системы координат. Следовательно, можно выбрать систему координат так, чтобы рассматриваемая плоскость была бы плоскостью г = 0. Наша поверхность второго порядка определяется уравнением вида (1). Чтобы получить уравнение линии пересечения, подставим г = 0 в уравнение (1); мы получим тогда
Ах2 + By2 + 2Dxy + Gx + Ну + X = 0.	(18)
Числа Л, В, .... К не равны нулю одновременно, иначе плоскость г = 0 целиком принадлежала бы поверхности. Множество точек, удовлетворяющих уравнению (18), является кривой второго порядка, что и доказывает теорему 3.
Так как круговой конус, в частности, является поверхностью второго порядка, то линия пересечения кругового конуса с плоскостью является параболой, эллипсом, гиперболой, парой прямых, прямой или точкой. Так мы получили в качестве частного случая весьма общий результат — то свойство, которое греческие математики клали в основу определения конических сечений.
4.10.	Вращения и отражения в пространстве
Пусть {ei, еа, е3} — репер, который мы будем считать правым. Выберем некоторое число О и положим
fj = cos 0 ef + sin^ea, f a = —sin 0 ef + cos 0ea, f3 = e3.	(19)
Легко проверить, что {flt fa, f3} — тоже репер; мы будем называть его репером, полученным из {ei, еа, е3} поворотом вокруг оси г на угол 6 (см. § 2.1 и рис. 10.47). Если координаты точки Р равны (х, у, г) в системе {О, ех, еа, е3) и (X, Y, Z) — в системе {О, fi, fa, f3), то
х = XcosO — KsinO, у = XsinO + /cos 0, z = Z.	(19*)
Эти формулы выводятся в точности так же, как формулы (5) § 2.3, — ведь здесь мы имеем просто поворот в плоскости ху, в то время как в направлении оси г ничего не меняется.
Аналогично, можно сказать, что репер {^, fa, f3} получается из {ei, еа, е3} поворотом на угол 0 вокруг оси х или вокруг оси у, если
h = е1» Ь = cos бег + sin6e3, f3 = —- sinOea + cosOea	(20)
или соответственно
f3 = cos0e3 + sinOei, f2 = ea, fj = —sinO e3 + cosOef.	(21)
§ 4. Квадрики в пространстве
239
В этом случае старые и новые координаты точки связаны соотношениями:
х = X, у = Y cos 0 — ZsinO, г = Y sin 0 + Z cos 0,	(20')
или
г = ZcosO — XsinO, у = Y, х = ZsinO + X cosO.	(2Г)
Поворот системы координат в пространстве может быть определен как поворот сначала вокруг осиг, затем вокруг оси х, и наконец, вокруг оси у; при этом, разумеется, углы трех этих поворотов могут быть различными. Отражение от плоскости ху—это переход от репера {ej, ег, е8} к реперу {ei, ег, —е8} (рис. 10.48). Можно показать, что каждый репер в пространстве получается ив (elt еа, е8} либо поворотом, либо отражением с последующим поворотом. (В первом случае новый репер называется правым, аво втором —л е в ы м; ср. с §2.7.) Доказывать здесь это мы не будем.
УПРАЖНЕНИЯ
В упражнениях 23—28 определите вид линии пересечения конуса и плоскости. В том случае, когда полученная линия — невырожденная, найдите ее фокусы и вершины. В упражнениях 25—28 начните с переноса и поворота системы координат, переводящих данную плоскость в координатную плоскость.
23.	г2 = х2 + у2 и х = 2.
24.	9г2 = х2 + у2 и г » —2.
25.	г2 ® х2 + у2 и 2г = х + 1.
26.	г2 = 9х2 + 9г/2 и г = х + 1.
27.	г2 = 4х2 + 9у2 и г = 2х.
28.	4г2 - Збх2 + у2 и г = Зх + 1.
29.	Покажите, что при некотором повороте в пространстве репер (ex, ег, е8} переходит в {ег, —ег, —е8).
30.	Покажите, что при некоторых поворотах в пространстве репер (ех, ег, е8} переходит в {ег, е8,	} и в {е8, ex, ег}.
4.11. Приведение уравнения поверхности второго порядка к каноническому виду
Сформулируем теперь основную теорему о поверхностях второго порядка, аналогичную теореме о § 3.4.
Теорема 4. Уравнение (1) второй степени относительно х, у, г
Ах2 + By2 + Сг2 + 2Dxy + 2Eyz + 2Fxz + Gx + Ну + lz + К = 0
определяет в пространстве либо пустое множество, либо точку, либо прямую, либо некоторый цилиндр второго порядка, либо конус второго порядка, либо, наконец, эллипсоид, гиперболоид или параболоид.
Набросок доказательства. Мы хотели бы привести уравнение (1) к каноническому виду — поворотом координатных осей и переносом начала координат, а также умножением уравнения на числовой множитель.
Для каждого фиксированного значения z уравнение (1) можно рассматривать как уравнение второй степени относительно х и у. В §3.4 мы изучали, каким образом посредством поворота координатной системы в плоскости ху можно исключить смешанный член 2Dxy уравнения (1); при этом угол поворота зависит только от А, В и D. Следовательно, поворотом вокруг оси z [см. равенства (19х)] можно преобразовать уравнение (1) в некоторое равносильное (1) уравнение, не содержащее члена с произведением ху. Более сложное рассуждение, которое мы здесь не приводим показывает, как можно исключить все члены с произведениями координат.
240
Приложение к главе 10
произведя сначала поворот системы координат вокруг оси х, затем поворот вокруг оси у и, наконец, поворот вокруг оси z.
Предположим, теперь, что мы уже получили уравнение вида
Ах2 + By2 + Cz2 + Gx + Ну + lz + К = 0.	с22)
Рассмотрим сначала случай, когда С2 + I2 = 0 (т. е. когда С = 1 = 0). При этом уравнение (22) представляет собой уравнение второй степени относительно х, у. Если в плоскости ху оно определяет невырожденное коническое сечение, пару прямых или прямую, то во всем пространстве оно будет определять цилиндр (который может выродиться в пару плоскостей или в одну плоскость). Если же уравнение (22) при С2 + /2 = 0 в плоскости ху определяет точку или пустое множество, то во всем пространстве оно будет определять прямую или пустое множество. Аналогичные результаты получаются и в тех случаях, когда уравнение (22) не содержит членов с у или членов с х.
Предположим теперь, что ни одно из чисел A2+G2, В2+Н2, С2-|-/2 не равно нулю. Три числа A, В, С не могут равняться нулю одновременно, так как иначе степень уравнения (22) была бы равна 1, а не 2. Достаточно рассмотреть такие случаи: (I) А ф 0, В = С = 0; (II) А ф 0, В ф 0, С = 0; (III) А =/= 0, В =/= 0, С =# 0. [В самом деле, если, например, А = 0, В =/= 0, С = 0, то можно, сделав соответствующий поворот, заменить х, у, г на у, х, г и прийти к случаю (I).] В случае (I) мы можем избавиться от члена Gx, выделяя полный квадрат и перенося начало системы координат. Точнее говоря, мы пишем
/ G \2	G3
Ах2 + Gx = А х + —- —	>
\	2А )	4А
AZ	I G Z	V	G2
вводим новую переменную Х=х + — (это равносильно переносу начала) и присоединяем — — к свободному члену. Так мы получим уравнение вида
Ах2 + Ну + lz + К = 0, А =/= 0, Я 0, /	0.
Можно считать, что Н2 + I2 = 1, так как этого всегда можно достигнуть, разделив уравнение на + I2. Тогда найдется такое число а, что Н = cos а и / = sin а. Введем, далее, новые переменные X, Y, Z, такие, что X = х, a Y = у cos а + г sin а + К (это сводится к повороту вокруг оси х с последующим переносом начала). Наше уравнение примет теперь вид
АХ2 + Y = 0, А * 0.
Оно определяет параболический цилиндр.
В случае (II) посредством переноса начала, как и выше,мы ис ключим члены с х и г/;уравнение примет вид
АХ2 + BY2 + lz + К = 0 (А ± 0, В * 0, I * 0).
Можно предположить, что / = 1 (в противном случае мы разделим уравнение на /). Новый перенос начала (Z = z + К) приводит к уравнению
АХ2 + BY2 + Z = 0 (АВ * 0).
Оно определяет эллиптический параболоид, если АВ > 0, и гиперболический параболоид, если АВ < 0; ср. с § 4.6.
В случае (III) с помощью переноса начала удается исключить все линейные члены; при этом мы получаем уравнение вида
АХ2 + BY2 + CZ2 + К = 0 (где АВС * О).
Если К = 0 и все три числа А, В, С — одного знака, то уравнение определяет единственную точку. Если К = 0 и не все три числа А, В, С имеют один и тот же знак,то уравнение определяет конус (ср. с §4.3). Если X =/= 0, то мы можем предположить, что X = —1 (в противном случае поделим обе части уравнения на —X). Предположим еще, что в точности / (где / = 0, 2 или 3) из трех коэффициентов А, В и С положительны, так что 3—/ из этих коэффициентов отрицательны. Наше уравнение определяет пустое множество, если / =0,
Задачи
241
двуполостный гиперболоид, если / = 1, однополостный гиперболоид, если / = 2, и эллипсоид, если 1=3 (ср. с § 4.4 и 4.5). Тем самым наша теорема доказана.
Теорема 4 допускает соответствующее обобщение для n-мерного пространства. Это обобщение не имеет «наглядного^ геометрического смысла, но оно весьма важно для математики, физики и техники.
УПРАЖНЕНИЯ
Определите вид следующих поверхностей второго порядка. [Указание: воспользуйтесь методом § 4.11 для упрощения уравнения там, где это необходимо, но проявите также и изобретательность.]
31.	(х — у)2 — (х + у)2— г = 0.
32.	100(х + у)2 + 100(х — у)2 + (г — 100)2 = 1.
33.	ху + уг + гх = 1.
34.	ху + уг + гх = 0.
35.	х — уг = 5.
36.	10х2 — 2ху + у2 + г2 + 2г = 99.
37.	х2 + у2 + 5г2 — 10х — у — г = 0.
38.	х2 — у2 — 2г2 + Зх — г + 5 = 0.
39.	2ху — г2 + х — у = 100.
40.	х2 + уг — 5х = 1.
ЗАДАЧИ
Задачи 1 —11 относятся к произвольной аффинной системе координат на плоскости и в пространстве. О таких системах говорилось в замечании перед задачей 7 в конце гл. 9. Подчеркнем, что в нижеследующих задачах базисы {ех, е2} и {ех, ег, е3} не обязательно являются реперами.
1.	Пусть точка Р в системе координат (О, ег, еа) имеет координаты (х*, ха), а в системе координат (О', еь е2)— координаты (Хь Х2). (Говорят, что вторая система получается из первой переносом.) Пусть точка О' имеет в системе (О, ех, еа) координаты (ах, а2). Как связаны между собой старые и новые координаты точки Р? Сравните полученный результат с тем, который был установлен в § 2.2.
2.	Пусть точка Р имеет в системе (О, ех, еа) координаты (xf, ха), а в системе (О, fx, f 2) — координаты (Хх, Х2). (Говорят, что вторая система координат получается из первой посредством изменения координатных осей.) Координаты векторов ех и ег в базисе {fx, fa} обозначим через (а, Р)и (у ,&). Как связаны между собой старые и новые координаты точки Р? Сравните полученные результаты с теми, которые были установлены в § 2.3.
3.	В тексте мы доказали (см. § 2.1). что порядок алгебраической кривой не зависит от выбора декартовой системы координат. Покажите, что это верно и в случае произвольной аффинной системы координат. [У к а з а н и е: воспользуйтесь результатами задач 1 и 2.]
4.	Покажите, что прямая на плоскости есть геометрическое место точек, координаты которых в любой аффинной системе координат удовлетворяют линейному уравнению. Докажите это двумя способами: непосредственно и используя результат задачи 3.
5.	Пусть хх, х2 — аффинные координаты. Покажите, что линия хх2 + Х22 = 1 —эллипс. Можно ли уравнение произвольного эллипса привести к такому виду соответствующим выбором аффинной системы координат?
6.	Сформулируйте и докажите для гиперболы и для параболы предложения, аналогичные результату задачи 5.
7.	Найдите, как изменяются координаты точки пространства при переносе системы координат, т. е. при переходе от системы (О, ех, ег, е 3) к системе (О', ех, еа, е3). Сравните этот результат с тем, который был получен в § 4.8.
8.	Найдите, как изменяются координаты точки, если при фиксированном начале координат изменить направления осей, т. е. перейти от системы (О, elt ег, е3) к системе (О, fj, fa, f3). [У к а з а н и е: представьте базисные векторы fv f2, f3 в виде линейных комбинаций векторов ei, ег, е3. Сравните этот результат с тем, который был получен в § 4.8.]
242
Приложение к главе 10
9.	Пользуясь результатами двух предыдущих задач, покажите, что порядок алгебраической поверхности не меняется при переходе от одной аффинной системы координат к другой (для декартовой системы координат этот результат был получен в тексте).
10.	Покажите, что каждая плоскость — это множество точек, координаты которых в произвольно выбранной аффинной системе координат удовлетворяют некоторому линейному уравнению; сформулируйте и докажите обратный результат. [Указание: воспользуйтесь результатом предыдущей задачи; заметьте также,что для любой данной плоскости можно найти такую систему координат, в которой эта плоскость будет одной из координатных плоскостей. В тексте этот результат был получен для декартовой системы координат.]
11.	Рассмотрите все поверхности второго порядка, введенные в § 4. Для каждой из них укажите ту простейшую форму, к которой ее уравнение приводится в соответствующим образом выбранной аффинной системе координат. (Покажите, например, что уравнение любого эллипсоида можно привести к виду х^2 + хг2 + х82 = 1.)
12.	Покажите, что через каждую точку гиперболоида х2 + у2 — z2 = 1 проходят в точности две прямые, целиком принадлежащие этой поверхности. (В тексте в § 4.7 было доказано, что существуют по крайней мере две такие прямые.)
13.	Докажите то же утверждение, что в задаче 12, для гиперболического параболоида г = = А'2 — у2.
II/ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА
В этой главе понятия математического анализа и векторной алгебры применяются к изучению плоских кривых и к исследованию движений материальных точек. Кульминационным пунктом здесь является одно из важнейших приложений математического анализа — теория движения планет.
В Приложении излагаются и другие применения математического анализа к механике.
244
11. Векторные функции скалярного аргумента
§ 1.	МАТЕМАТИЧЕСКИЙ АНАЛИЗ ВЕКТОРНЫХ ФУНКЦИЙ
1.1.	ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА
Векторная функция скалярного аргумента (короче, векторнозначная функция, или даже просто векторная функция)
1f(0	(1)
— это правило, по которому каждому вещественному числу t из некоторого интервала или совокупности интервалов («области определения» функции f) ставится в соответствие определенный вектор f(/). В этом параграфе для простоты под «вектором» мы будем понимать «вектор плоскости». Однако все наши результаты с вполне понятными изменениями будут применимы и к векторам в пространстве (а также к векторам п-мерного векторного пространства).
Часто бывает удобно понимать векторы как радиусы-векторы точек относительно некоторой фиксированной точки О. Векторную функцию (1) можно представить геометрически, построив все точки с радиусами-векторами f(Z). Говорят, что функция l(t) задает параметрическое представление этого множества точек; само же это множество точек иногда называют годографом (или графиком) векторной функции f(0.
Примером векторной функции может служить линейная функция
f(/) = aZ + b,	—оо < t < +оо,	(2)
где а =# 0 и b — фиксированные векторы. Эта функция определяет прямую линию. В самом деле, уравнение (2) можно переписать так: f(0 = /(а 4- Ь) 4- (1 — ОЬ, а из этого уравнения видно, что все точки с радиусами-векторами f(0 принадлежат прямой, проходящей через точки с радиусами-векторами а 4- b и Ь, целиком заполняя эту прямую (см. § 2.2 гл. 9).
Приведем другой пример. Пусть (еА, е2} — некоторый репер (ср. с§ 1.8 гл. 9); рассмотрим векторную функцию
f(/) = cos t4- sin /е2,	0 t <Z 2д.	(3)
Множество точек, параметрически представленных этой функцией, является единичной окружностью.
1.2.	КИНЕМАТИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Часто бывает удобно считать, что векторная функция f(/) описывает движение некоторой точки плоскости, а именно точки с радиусом-вектором f(/). В этом случае независимая переменная t (называемая также параметром) интерпретируется как время. а годограф функции f(0 называют также траекторией.
§ 1. Математический анализ векторных функций
245
Так, уравнение (2) описывает движение точки вдоль некоторой прямой. При t = = 0 рассматриваемая точка находится в точке Р с радиусом-вектором Ь, а при t = = 1 — в точке Q с радиусом-вектором а + Ь. Вообще, в момент времени t эта точка делит отрезок PQ в отношении //(1 — 0-
Функция (3) определяет движение точки по единичной окружности в направлении против часовой стрелки, начиная от точки (1,0), отвечающей значению t = 0; при этом полная окружность проходится точкой за 2п единиц времени.
1.3.	КООРДИНАТЫ ВЕКТОРНОЙ ФУНКЦИИ
Выберем декартову систему координате началом О и базисными векторами {еь е2}. Каждую векторную функцию 1i-> f(0 можно представить в виде
f(0 =x(/)ei + f/(0e2.	(4)
Таким образом, векторная функция — это просто две обычные (скалярные) функцж :
11-> х(0, t y(t).	(5)
Эти функции называются координатами векторной функции f(/).
Так, например, рассмотрим линейную функцию (2) и предположим, что векторы а и b имеют координаты (аь а2) и (64, Ьг). Тогда
а =	#2е2/ b = &161 4“ &2ег
и
f(0 =	4- а2е2) 4“ (&iei 4" &2ег) =	4" &i)ei 4" (#2^ 4“ b^e2.
Следовательно, координаты функции (2) — это функции
х(0 =	4- 61, y(f) = a2t 4- b2.
Координаты функции (3), очевидно, имеют вид
x(t) = cos t, y(t) = sin t.
Векторная функция 1н-> f(0 может быть представлена и так:
Гн*г(0, t*-+ 9(0,
где г(0 и 0(0 — это соответственно модуль и полярный угол вектора f(0- Для функции (3) получаются очень простые формулы:
r(0 = 1, 0(0 = t.
(6)
246
11. Векторные функции скалярного аргумента
УПРАЖНЕНИЯ
В упражнениях 1—13 найдите векторную функцию, описывающую заданное движение. Предполагается, что (х, у) — это координаты точки в некоторой фиксированной декартовой системе координат, (г, 0) — соответствующие им полярные координаты и {е^, ej} — базисные векторы рассматриваемой декартовой системы координат.
1.	Точка движется вправо по параболе у = ха; значению t =0 отвечает ее положение (1, 1); при t = 3 она достигает точки (2, 4). При этом смещение точки от начального положения в горизонтальном направлении пропорционально квадрату времени, протекшего от начала движения.
2.	Точка движется вправо по кривой у = х3 +1; при t = 1 она занимает положение (—1, 0); при t = 2 она достигает положения (1, 2). При этом смещение точки от начального положения в горизонтальном направлении пропорционально корню квадратному из времени, протекшего от начала движения.
3.	Точка движется вправо по прямой у =8х; при t = 1 она находится в начале координат; при t = 2 она достигает положения (1, 8). При этом площадь прямоугольного треугольника, образованного началом координат, движущейся точкой и проекцией этой точки на ось х, пропорциональна кубу времени, протекшего от начала движения.
^4	. Точка движется вправо по кривой у = J'Gr2 + 1; при t = 1/4 она занимает положение (0, 1). При этом расстояние этой точки от начала координат пропорционально t.
5.	Точка движется вправо по кривой Зу —2х3/2= 0; при t =2 она находится в начале координат; при t = 16 ее абсцисса равна 3. При этом пройденное точкой расстояние (измеренное вдоль кривой!) пропорционально времени, протекшему от начала движения.
6.	Точка движется вправо по кривой у = х3; при t = 2 она находится в начале координат; при t = 4 она достигает положения (2, 8). При этом наклон проходящей через любое положение движущейся точки касательной к ее траектории пропорционален кубу времени, протекшего от начала движения.
7.	Точка движется по параболе у = х2 — х; при t = —1 она находится в начале координат и, двигаясь влево, достигает точки (—6, 42) при t = 1. При этом сумма горизонтального и вертикального смещений точки от начального положения пропорциональна квад^ рату времени, протекшего от начала движения.
8.	Точка движется по кривой у = 1пх; при / = —3 она занимает положение (1, 0); двига-. ясь, далее, вправо, она достигает положения (10, 1п 10) при t = 0. При этом скорость смещения точки в горизонтальном направлении (т. е. скорость движения проекции точки на ось х) пропорциональна времени, протекшему от начала движения.
9.	Точка движется по окружности г = 2; при t = 4 она находится в точке г = 2, 0 = 0} двигаясь, далее, против часовой стрелки, она достигает положения г = 2, 0 = к/2 прц t = 5. При этом полярный угол 0 точки пропорционален квадрату времени, протекшего от начала движения.
10.	Точка движется по окружности г = 1 + cos 0; при t =1 она занимает положение г = 2, 0 = 0; двигаясь, далее, против часовой стрелки, она достигает положения r= 1, 0 =л/2при t = 10. При этом полярный угол движущейся точки пропорционален корню квадратному из протекшего времени.
11.	Точка движется по спирали г = 0; при t = 1 она занимает положение г = 0 = 2л и приближается к началу координат; при t = 4 она достигает положения г = 0 = л. При этом скорость изменения расстояния движущейся точки от полюса обратно пропорциональна /2.
12.	Точка движется вправо по дуге трехлепестковой розы г = cos 30 (где 0< 0 < л/6); при t = 100 она занимает положение г = /з7 2, 0 = л/18; при t =144 достигает положения г = /F/2, 0= л/12. При этом скорость изменения полярного угла точки обратно пропорциональна /3/2,
13.	Точка движется против часовой стрелки по кривой г = 1—cosO; при t— —1 она находится в начале координат; при t = 3 достигает положения г =1, 0 = л/2. При этом скорость изменения полярного угла точки обратно пропорциональна корню квадратному из времени, протекшего от начала движения.
$ 1. Математический анализ векторных функций
247
М. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО АНАЛИЗА К ИССЛЕДОВАНИЮ ВЕКТОРНЫХ ФУНКЦИЯ
Векторная функция эквивалентна паре скалярных функций — ее координат x(t) и f/(0:
i н* f(0 = x(0et + t/(0e2.
Пользуясь этим, мы перенесем на векторные функции основные понятия математического анализа. Эмпирическое правило тут таково: математический анализ применяется обычным образом, причем базисные векторы ej и е2 рассматриваются как постоянные величины. Поясним это правило.
Функция f(0 называется ограниченной в некотором интервале, если ограничены обе ее координаты. Она называется непрерывной в некоторой точке, если обе ее координаты х(/) и y(t) непрерывны в этой точке. Запись
lim f (/) = аег +
по определению, означает, что
lim х (0 = a, lim у (/) = Ь. t-+t9	f-+r0
(Аналогично определяются односторонние пределы и пределы на бесконечности.)
Производная векторной функции определяется равенством
£=f'(/) =-£e> + ^Le»:	<7)
w	Ul	(U
она существует, если х'(0 и y'(f) в данной точке существуют. При фиксированном t эта производная f'(0 является вектором; рассматриваемая для всех допустимых значений /, она сама является векторной функцией. Поэтому можно определить вторую производную векторной функции:
и т. д.
Дифференцирование по параметру t часто обозначают точкой сверху:
~ = f (или, реже, f*), ~х (или
эта традиция восходит к Ньютону. При этом выписанные выше равенства можно переписать так:
f = хе, 4- f = хе, 4- уег.
248
П. Векторные функции скалярного аргумента
Часто бывает не обязательно указывать базисные векторы. Можно просто писать:
f = (X, у), f = (х,у), f - - (х,у) И т. д.
Векторная функция F(/) называется первообразной по отношению к f(/), если
F'(0 = ПО-
Интеграл от векторной функции определяется естественной формулой ь	( b	\	( ь	\
J f (/) dt = I f x (t) dt I ej + I J у (t) dt j e2.
a	\a	/	\a	J
Этот интеграл будет, конечно, вектором.
1.5.	ОСНОВНЫЕ ПРАВИЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Правила математического анализа, доказанные в предшествующих главах, сразу же распространяются и на векторные функции. Мы приведем только несколько примеров.
а)	Дифференцирование произведения вектора на число. Имеем
d («(0 f (0) = da(t) f	} dt (Q
dt	dt	у dt 9
или
(af) = af + af .
Доказательство. Мы предполагаем, конечно, что f и а существуют. В таком случае
(af)* = (a(xet 4- уе9))' = (axe, + aye^’ = (ax)*	+ (ay)* e2 =
= (ax 4- ax) ex + (ay + ay) e2 = axej + axex + aye2 + aye2 =
= a (xej + ye^ + a (xex + ye^ = af + ak
б)	Если f(/) = 0, mo t(t) — постоянный вектор.
Доказательство. Если f = 0, то х ^.0 и у = 0; следовательно, найдутся такие числа а^ и а2, что x(t) = а^ и y(t) = а2 для всех t. Тогда для всех t
f(0 = a^i 4“ ^2е2*
в)	Основная теорема математического анализа, первая часть. Если функция f(/) непрерывна при t =т, то
=f(T). dt J a
Доказательство этой теоремы предоставляется читателю.
§ 1. Математический анализ векторных функций
249
г)	Основная теорема математического анализа, вторая часть. Если функция 1(f) непрерывна и ограничена на интервале a <Z t <. b и функция F(0 является первообразной для f(/), то
j = F(&) —F(a). a
Доказательство снова предоставляется читателю.
д)	Предел длины (модуля) вектора равен модулю его предела: если lim f (t) = а, то lim |f (t) \ = | al.
t-t0
Доказательство. Положим a = a^ + а2ег- Наше предположение означает, что lim x(t) = ai9 lim y(t) = a2 при t t0. Следовательно, lim lx(/)2] = aA limlf/(/)2] = a22 и lim]/x(02 + f/(02 = jAij2 + o^2 = | a J, что и требовалось доказать.
2it
ф Пример. Вычислить Jf^a + sint Ь)Л, где а и b — фиксированные векторы.
Решение. Этот интеграл равен
j-i- /4а — cos t bp = 4тс4а. ф
УПРАЖНЕНИЯ
В упражнениях 14—33 предполагается , что {е^, ег) — фиксированный репер на плоскости; вычислите производные заданных векторных функций.
d
14.	— [(cos О2 ех + sin t • е2]. dt
15.	[tej — (In 0se2]. at
d r r—
16-	~ \fV t ex — sect • ег].
dt
d Г 1	1
17.	— — (/ех — ег) + cos t (t2ex + e2) • dt L *	J
5/2
18.	Вторая производная от t ex + (t — 1) ег.
19.	f" (t), если f (/) = cos t • ex + tg t • e2.
20.	(yT ei + e'ej. dt2
21	— f <ei + e2 \ . dt VUej + eal/
22.	Г(0), если f(0 = (a(0 +	— а(Пе2] и a(0) = 1. a'(0) =—2.
23.	f"(0), если f(/)	4- cos <e2) и a(0) = 1. a'(0) = —2, a"(0) = 4.
250
11. Векторные функции скалярного аргумента
Вычислите интегралы от векторных функций.
1/2
и- I '> о к/З
25. J (cos 2t ех + sin 3t е2) dt.
2
П"Ь + 7ТТ * ) “'•
1 3
27.	J ^2'ei — —г—- eaj dt. 1	У 4"
28.	J / (]/i2 + 1 ex + cos/2e2)dL
/3“
29.	f	/ei + 4e2 dt.
8	*2 +1
In 2
30.	J (ei 4- tt^ dt.
31.	Найдите такую векторную функцию f(Q, что f'(/) = (/1/Зех — г2еа и f(0) — 2ex+e2.
32.	Найдите такую векторную функцию f(/), что f"(/)=/2e1 и f(0)=e1+e2, f(l) = 2et —еа.
33.	Найдите такую векторную функцию f(/), что f"(/) = cos t ex + ea, причем f (0) =3e1— ea и f'(0)=l-e1-e2.
d }
34.	Докажите, что если функция f(0 непрерывна при t = т, то-^- j f(t)dt = f(T). а
b
35.	Докажите, что J t(t)dt = F(d) — F(a), если функция f(f) непрерывна и ограничена на а
интервале a<Z t<Z Ь, а функция F(0 является первообразной для f(/).
36.	Докажите, что если Игпф(/) = uq и lim f(w) = а, причем f непрерывна при и = uQ, то /-►/о	и-чл0
lim fo<p (/) = а.
/-►/о
37.	Докажите, что если <р (/о) = «о, причем функция <р дифференцируема в точке /о» а функция f — в точке w0, то (f о <р)'(М = 1'(мо)ф по)-
38.	Пусть f = aej + Рег. Докажите, что:
а)	если | f | < М, то | а | < Л4 и |Р|< Ajh
б)	если | а | < М и | Р | < Л4, то । f | < MV2.
Объясните, как можно проиллюстрировать эти результаты, рассматривая вписанную в квадрат окружность, причем этот квадрат в свою очередь вписан в некоторую окружность.
Ь	_
39.	Пусть । f(/) | < Л4 при а < t < b. Покажите, что |J t(t)dt | < (b — a) Л4]^2 (см. а
упр. 38).
40.	Пусть функции f (/) и f'(0 непрерывны при 0 < t < 1 и | Г(0 | > 0 для всех t. Возможно ли равенство f(0) = f(l)?
§ 1. Математический анализ векторных функций
251
1.6	. НЕЗАВИСИМОСТЬ ОТ БАЗИСА
Координаты вектора зависят от выбора базисных векторов. Нам надо доказать, что введенные выше понятия (ограниченность, непрерывность, предел, производная ит. д.)не зависят от выбора базиса.
Для этого мы дадим новые определения этих понятий, равносильные прежним, но уже не опирающиеся на понятия базисных векторов и координат. Мы используем то обстоятельство, что длина вектора не зависит от выбора репера.
1.	Для того чтобы векторная функция КО была ограниченной на данном интервале, необходимо и достаточно, чтобы скалярная функция |f (t) | была ограниченной.
Доказательство. Здесь и далее мы полагаем
f(0 -MOe. + iKOe».
Если функция f ограничена, то х(0 и y(t) ограничены, согласно данному выше определению. Следовательно, существуют такие числа М j и М 2, что на нашем интервале | x(t) | A4lt |	| -С М 2. А так как
|f(0 р =X(^ + y{t)\
(8)
то | КО р •’С М* + Мг2, откуда | f(0 I V М/ + М22, и, значит, | КО I ограничена. Обратно, если | f(0 I — ограниченная функция, то существует такое число М, что | КО | С М, а значит, | f(0 I2 М2. В силу равенства (8) мы имеем | х(01 "С М и I У(6 I Л4. Следовательно, функции х(1) и y(t) ограничены, а значит, по нашему прежнему определению, ограничена и векторная функция КО-
2.	Функция КО» определенная в окрестности точки t0, непрерывна при t0 в том и только в том случае, если
lim|f (O-fKo)l=0.
(9)
Доказательство. Предположим, что функция КО непрерывна в точке t0. По определению, данному выше, это означает, что скалярные функции х(0 и y(t) непрерывны при t = /0» т. е. что
lim х (0 = х Ко), lim у (0 = у Ко)«	(10)
t-*t,	t-^t.
Следовательно,
lim (х(0 —*Ко)) =°» Ит(у(0 — t/Ко)) = 0,	(11,
«-►<,	г-и,
откуда вытекает, что
lim {[х (0 - х К0)]2 + {у (0 - У Ко)]2} =0	<’ 21
252
11. Векторные функции скалярного аргумента
и, значит,
lim V [*(/)- <)]2 4- [у (/) - у(/0)]2 =0,	(13>
а это равносильно утверждению (9).
Обратно, если выполнено соотношение (9), то будут справедливы и утверждения (13), (12), (11) и (10), а значит, функции х(/) и y(t) будут непрерывны в точке /0- Следовательно, по нашему прежнему определению, функция f(0 непрерывна в точке /0.
3.	Предположим, что функция f(/) определена в окрестности точки tQ. Тогда
limf(/)=a	(14)
t->t0
в томи только в том случае, если
lim | f (0 — а | =0.	(15)
t^t0
Доказательство. Положим-а = a^i + а2е2. Утверждение (14) в соответствии с нашим прежним определением означает, что
limx(/)=ax и lim у(/) = а2, t-*t0	t-*t0
а это в свою очередь означает, что
' lim|x(/)— ах |2 = 0 и lim|t/(Z) — а2|2=0,
или
lim V |х(/) — ах|а + |у(0 — а2|2 = 0-
Но это лишь другой способ записи соотношения (15).
4.	Предположим, что функция f(/) определена в окрестности точки tQ. Тогда
Г(*о) = а	(16)
в том и только в том случае, если
НтГ4-(*(*о + Л)-»(*о))1=а.	(17)
л-о L h	J
Заметим, что поскольку мы уже знаем (из утверждения 3), что понятие предела не зависит от выбора базиса, то теперь утверждение 4 позволяет установить то же самое и для производной, а также в силу основной теоремы математического анализа [см. утверждения б) и в) в § 1.5] — и для понятия интеграла.
Для того чтобы доказать утверждение 4, положим а = aiex + я2е2. Равенство (16), по нашему определению, эквивалентно двум равенствам:
х'(/0) = ах и у'(/0) = аг-
Но эти два равенства можно переписать так:
,(«.+»-»«) _	,(<+»>-» и
*-.о	Л	1	h-0	Л
§ 2. Ориентированные линии
253
а это равносильно тому, что
lim j-x(<0 + ft)-x(U ei +	e2j = а,
т. е. равенству (17).
(Для односторонних производных и пределов, а также для пределов на бесконечности справедливы аналогичные утверждения.)
УПРАЖНЕНИЯ
В упражнениях 41—4Б воспользуйтесь утверждениями 1. 2, 3 и 4 хак определения-м и. Попытайтесь выполнить эти упражнения непосредственно, пользуясь только этими определениями и не обращаясь к координатам векторов.
41.	Пусть функции f(0 и g(/) ограничены на некотором интервале. Докажите, что их сумма f(/) + g(/) тоже ограничена на этом интервале.
42.	Пусть функции а(/) и f(/) ограничены на некотором интервале. Докажите, что произведение a(/)f(Z) ограничено на том же интервале.
43.	Докажите, что если lim f(/) = а и lim g(/) = b, то lim [f(0 + g(/)] = а + b.
t->t0	t^t0	t^t0
A44. Докажите, что если f'(fo) = а и g'(^o) — b, to (f + g)'(^o) = a + b.
45.	Докажите, что если cc'(fo) = a0 и Г (/о) = a, to (af)'(/o) = aof(fo) + a(/0)a.
46.	Докажите, что если функция f(/) непрерывна в точке /о, тэ и функция х н* | f(/) | непрерывна в этой точке.
§ 2. ОРИЕНТИРОВАН- В этом и в следующем параграфах векторные функции при-НЫЕ ЛИНИИ меняются к исследованию плоских линий. Для этого нам будет удобно выбрать и зафиксировать раз и навсегда начало координат О и репер {еь е2}.
2.1. ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
График скалярной функции у = /(/) дает нам полную информацию о функции: зная график, мы знаем функцию. Годограф векторной функции t >—► f(/) доставляет важную информацию относительно этой функции, однако н е в с ю информацию о ней: двум разным векторным функциям может отвечать один и тот ж е годограф. Последнее связано с тем, что точка может двигаться по одной и той же траектории, но разными способами.
Так, например, каждая из двух функций:
/	/а, где О t 1,
11-> /За, где О t < 1,
(1)
определяет прямолинейный отрезок, соединяющий точку О с точкой Л, радиус-вектор А которой равен а. Обе функции описывают движение точки от 0 к Л, но эти движения различны.
254
11. Векторные функции скалярного аргумента
Две функции: и
t H*cos^e1 + sin/e2,
ос
t С 2к,
t *+ cos 2t et -j- sin 2/ e2, 0 C t C 2n
описывают движение точки по единичной окружности, начинающееся и заканчивающееся в точке (1, 0); оба движения совершаются против часовой стрелки. Но в первом случае окружность пробегается один раз, а во втором — дважды. Функция
/-►cos/ei — sinfe2, 0 С t -С 2«
тоже описывает движение точки по единичной окружности, но на этот раз — в направлении вращения часовой стрелки.
2.2. ОПРЕДЕЛЕНИЕ ОРИЕНТИРОВАННОЙ ЛИНИИ
Эти примеры подсказывают такое определение: две непрерывные векторные функции t >-► f(Z), а С t С Ь и
* >-»б(т), а Ст С Р	(2)
определяют одну и ту же ориентированную линию (или ориентированную кривую) если существует такая возрастающая непрерывная функция
т >-► <р(т), а Ст < Р,	(3)
что
<р(а) = а, <р(Р) =Ь	(4)
и
Цф(т)) =g(x), а Ст < р.	(5)
Мы будем говорить при этом, что функция f(0 получается из g(r) изменением параметра: т »-► t = ф(т).
Под ориентированной линией С мы понимаем непрерывную векторную функцию t (/), определенную на некотором замкнутом конечном интервале [а, &] в м е с-т е со всеми векторными функциями, получающимися из нее изменениями параметра.
Заметим, что при изменении параметра можно использовать лишь возрастающие функции. Если
$ i-> ф(Е), а С Е С Р
— непрерывная убывающая функция, для которой
ф(а) =6, ф(Р) = а, и мы положим h(E) = f(<|>(E)), то ориентированная линия, определяемая функцией
Е н» h(0, а С Е С Р, называется противоположно ориентированной (или просто противоположной) по отношению к линии, определяемой функцией t f(f), а С t "Ч Ь. Начальная точка
§ 2. Ориентированные линии
255
Рис. 11.1
линии, определяемой функцией h, является концом линии, определяемой функцией f, и наоборот.
Множество точек, определяемых функцией t f(/), а 6, т. е. годограф векторной функции f(/), мы будем называть траекторией ориентированной линии, определяемой функцией f на интервале [а, Ь] (см. стр. 244; обратите внимание на различие понятий ориентированной линии и траектории: ориентированная линия и линия, ей противоположная, имеют одну и ту же траекторию).
Термины «линия» или «кривая» без прилагательного часто используются как для ориентированной линии, так и для траектории ориентированной линии. Мы тоже будем поступать так. Путаница здесь возникает редко, так как содержание этого термина обычно ясно из контекста.
Замечание. Иногда мы будем рассматривать еще и функции, определяющие ориентированные линии, и определенные на открытых интервалах (не включающих конечных точек), а также функции, определенные на бесконечных интервалах. В этом случае равенства (4) рассматриваются как предельные.
2.3. ДУГИ КРИВОЙ
Предположим, что А —ориентированная кривая, определяемая функцией
A:	f(0, t0 < t <
Пусть X — число, такое что t0 < X < Тогда ясно, что функция f(0, рассматриваемая только при /о < < X, тоже определяет некоторую кривую
В:	t f(/), tQ < t < X.
Говорят, что В является ограничением функции f на интервал Uo, XL
256
11. Векторные функции скалярного аргумента
Рис. 11.2
Аналогично,
С:
есть кривая, получаемая ограничением функции f на интервал [X, fj. При этих условиях мы можем сказать, что В и С являются дугами кривой А и что
А = В + С.
Шитается: «А состоит из дуги В и следующей за ней дуги С».]Заметим, что конечная точка В является начальной точкой для С (рис. 11.1).
Вообще, если мы разобьем интервал 1/0, М на k подынтервалов:
^0 = Хо < Х1 < Хг < ••• < Хд — ^1»
то ограничение функции f на каждый из этих интервалов [Х^х, X;] (где j =1, 2,...,&) определяет кривую
А/ 11-> f(f), ХМ</<Х7.
Говорят, что каждая из кривых А7 является дугой кривой А и что
А = Ах + А2 + ... + Aft.
(Читается: «А состоит из дуги Ai, следующей за ней дуги А2, следующей за ней дуги А3, ...» наконец, дуги АЛ».] Геометрический смысл такого разбиения кривой на ряд дуг иллюстрирует рис. 11.2.
§ 2. Ориентированные линии
257
УПРАЖНЕНИЯ
В каждом из упражнений 1—10 предлагается, решить, будут ли две данные векторные функции определять: а) одну и ту же ориентированную кривую; или б) противоположные кривые; или в) одна из них определяет дугу или противоположна дуге ориентированной кривой, определяемой второй функцией; или г) одна из них определяет ориентированную кривую, которая может быть представлена в виде суммы дуг кривой, задаваемой второй функцией,или в виде суммы дуг кривой, противоположной кривой, задаваемой второй функцией; или д) никакое из условий а) — г) не имеет места.
!./»-► t2er 4- Z<e2 при 0 < t < 1; и i-> (sin и) ех 4- (sin и)2 e2 при 0 < и < — •
t	/4-1	i	14-м	1	1
A2. t ь-> —• ex 4-  -Г e2 при 2 < / < 4; и	—— ex 4- “-------- e2 при — < и < — •
/4-1	/ — 1	u 4- 1	1 — и	4	2
3. t In (/ — 1) ex
b —---p e2 при 2 < t < 8;
и >-> 2 In и ex 4- н“2е2 при 1 < и < 2.
4.
/1-> eX 4- /е2 при 0</<l;
и н► u2ex 4--------- e2 при 0 < и < 1,
u-f- 1
5. /1-> (t2 4- 1) ex 4- /2е2 при 0 < / < 2;
6. t 4- /®2 ПРИ — 1 < / < 0;
и sec2 и ex 4- (sec2 и — 1) e2 при 0
1
и »-► — ex — In и e2 при 1 < и < e. и
< и < — 4
7.	/	(/4 — 2/2)ех 4- /2е2 при 0 < / <: 1; и (ы4 — 1) ех 4- (и2 — 1) е2 при 1 < и < У 2 .
8.	/	У / 4- 1 ех 4- (г 4- 1) е2 при — 1 < t < 3, и н* мех 4- ц2е2 при — 2 < и < 2.
9.	t !-► cos (к/2) ех 4- sin (тс/2) е2 при —1 < / < Г, и cos (тем3) ех 4“ sin (кц3) е2 при — 1 < и < 1.
и
10.	t »-► /2ех — УТ е2 при 0 < t < 1; и »-► е~2и ех — е 2 е2 при 0 < и < 1.
2.4	. НЕПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Каждая непрерывная скалярная функция, заданная на некотором интервале, определяет ориентированную линию; траектория этой линии является графиком функции.
Непараметрическое представление ориентированной линии — это представление ее в виде графика скалярной функции х у = ф(х). Такое представление в с е г-д а может быть преобразовано в параметрическое. Мы просто пишем
*(0 = t9 y(t) = Ф(0, или
11—► /ех 4- ф(0®2*
[Заметим, что мы не указываем интервал, на котором определена ф(0; обычно мы так и будем поступать, если этот интервал нам не понадобится.]
258
11. Векторные функции скалярного аргумента
Параметрическое представление иногда может быть преобразовано в непараметрическое. Рассмотрим, например, прямую, параметрически представляемую функцией t fa + b,
где а и b — два фиксированных вектора и а =/= О- Пусть а = (аь а2) и b = (blt b^. Наше параметрическое представление приводит к уравнениям
х = ait + 61, у = a2t + 62.
Если ai и а2 неравны нулю одновременно, то мы можем следующим образом исключить из последних уравнений t. Для каждого данного t значения x(t) и y(t) таковы, что z = и t=y-^h. а,\	а2
Следовательно, х—Ьх __ у— Ь2 ai	а2
ИЛИ 	 а2 „ ।_а1&2 — <*2^1 У___________________________________________л I	•
а1 а1
Это и есть искомое непараметрическое представление. Рассматриваемая линия является графиком скалярной функции х у.
Если а2 = 0, то эта линия допускает непараметрическое представление у = Ь2. Если а1 = 0, то уравнение нашей линии приводится к виду х =bi. Это не есть функция вида х у, но ее можно представлять себе как график функции, принимающей постоянное значение: у х = g(y) = 6А.
С другой стороны, единичная окружность х2 + у2 =1 допускает и параметрическое представление, например
х = cos /, у = sin /, но непараметрическое представление всей окружности, как известно, невозможно, независимо от того, как мы выберем систему координат.
Заметим также, что непараметрическое представление в полярных координатах (г, 0) г = можно рассматривать как параметрическое представление, полагая 0 = /, г = g(t), или х = g(t) cos/, у = g(t) sin/.
• Примеры. 1. Какое множество точек параметрически представляется векторной функцией
f(/) н* cos / а+ sin / b,	(5)
где а и b — два данных вектора?
§ 2. Ориентированные линии
259
Решение. Пусть а = aiei + а2е2, Ь = blel + b2e2. Тогда
f(Z) = (ах cos t 4- bi sin + (a2 cos t + b2 sin t)z2.
Переходя теперь к координатам, получим
x(t) = ai cos t + bi sin t, y(t) = a2 cos / -f- 62 sin t.	(6)
Далее нам остается рассмотреть два случая:
«1&2 — 02^1 = 0 и Я1&2 — 02^1 =/= 0.
В первом случае возможно, что ai = а2 — bi = b2 =0; однако это весьма малоинтересный случай, так как здесь f(/) =0 для всех /, и весь годограф функции состоит из одной точки. Если же а2, bit Ь2не равны одновременно нулю, умножим первое из уравнений (6) на b 2, второе — на bi и вычтем одно из другого (или умножим первое уравнение на а2, второе — на и вычтем одно из другого). Мы получим
Ь2х(0 — biy(t) = 0 и a2x(f) — aiy(t) = 0.
Так как а^2 — а2Ь{ = 0, то оба уравнения имеют один и тот же смысл — они означают, что точка (х(/), !/(0) принадлежит прямой а2х — aiy — 0 (или прямой Ь2х — — bty = 0, если ai = а2 = 0). Наша функция параметрически представляет отрезок этой прямой (но не всю прямую, так как sin t и cos t при всех t остаются в пределах между —1 и 1).
Во втором случае, когда ai&2 — а 2^1 =/= 0, мы можем решить уравнения (6) относительно cos t и sin t. При этом мы получим
< _ Ь2Х (0 — ьху (0 .	— а2х (0 + а1У (t)
I	9	will £ ——	*
01^2 — #2^1	#1^2 — O2^l
Но cos21 + sin21 = 1; это дает уравнение второй степени относительно’ x(t) и y(f): (b22 + а22)х(/)2 - 2(Ьф2 + а1а2)х(0у(0 + (6,2 + a2)y(f)2 = (аА - a2btf.
Его дискриминант равен
(а? + Ь2) а2 + Ь2) - (\Ь2 + аха^2 =
= а^а22 + Ьг2Ь22 + ах2622 -J- а22Ь,2 — 6Х2622 — ах2а22 — Ъа^Ь^ =
= (алЬ2 — аД)2>0;
значит, это — уравнение эллипса. Этот эллипс параметрически представляется заданной функцией.
2. Какое множество точек параметрически представляется функцией
....	а(1 — Р) , 2Ы	.
т (0 =-----—- ех Ч------е2,	— оо < / < + оо,
1 +12 1 1 +12 2
где а>0 и &>0 — некоторые числа ?
Решение. Координаты функции f равны x(/)=akzll> y(t) = ь 1+P	'	1+P
Легко видеть, что
x(t>2 , у (О2 = .
а2 Ь2
а это уравнение определяет эллипс.
260
11. Векторные функции скалярного аргумента
В этой задаче очень поучительно ввести новый параметр ср, такой что t = tg (т. е. ф = 2 arctg/). Так как t принимает все значения между—оо и +оо, то параметр ф принимает все значения между —тс и тс (исключая сами значения —тс и тс). При этом мы имеем
x(t) = a cos(p, y(t) = b sin ф, —л < ф < л,
а это — параметрическое представление эллипса (см. § 1.8 гл. 10).
Заметим, что точке эллипса с координатами х = —а, у = 0 не соответствует никакое значение /.•
УПРАЖНЕНИЯ
В упражнениях 11—18 требуется представить ориентированную кривую, определяемую данной векторной функцией, в виде графика некоторой скалярной функции или как кривую, противоположную графику скалярной функции, или, наконец, как сумму дуг, каждая из которых представляет собой такой график или кривую, противоположную такому графику.
11.	t /2е£ 4- /Зе2 при 0 < t <4- со.
12.	t У/2 4- 1 е£ 4- /Зе2 при 0</<4-~.
13.	t >-> -у- е£ 4- (/2 —2)е2 при 0<t<oo.
X
14.	1cos 4- sin 2t e2 при 0	•
it	n
15.	11-> cos 2t e£ 4~ cos t e2 при — — < t ’
2/3
16.	t / e£ 4- (t -h I)3 e2 при — oo < f < 4- °° •
17.	t»-> /2е£ 4~ У f2 4- 1 e2 при — oo < f <C 00 •
. Л	cos- t sin2/	Л t _
18.	e£ 4-e «2 при 0<^^2тс.
В упражнениях 19—24 требуется изобразить траекторию данной векторной функции. Определите, если это возможно, является ли полученная линия (бесконечной) прямой, окружностью, эллипсом, гиперболой, параболой или дугой одной из этих линий.
//2
19.	fb*eze£4~ * е2 при —оо < t <4- °° •
20.	t ^/2 — е£ 4-	ег при — оо < t < 4" °° •
/-- / ~
21.	t н* У In t е£ 4- 1/ In — е2 при 1 < / < е.
22.	t »-► V 1пе/ е£ 4’ У In t е2 при 1 < t < 4- со.
23.	t »-► sin 2/ е£ 4- (3 — sin 2t) е2 при —oo<f<4“°°-
24.	/»-}/Т^72е£ 4- У 1 4-/а е2 при — 1С/^1,
§ 2. Ориентированные линии
261
2.5. ЦИКЛОИДА
Мы определим сейчас интересную кривую, циклоиду, для которой легко можно указать ее параметрическое представление (тогда как найти ее непараметрическое представление было бы довольно трудно).
Рассмотрим окружность радиуса а, которая без скольжения катится по некоторой прямой; циклоида — это траектория, описываемая фиксированной точкой Р этой окружности.
Для того чтобы получить параметрическое представление циклоиды, предположим, что окружность катится вдоль оси х и что в начале движения точка Р совпадает с началом координат (рис. 11.3). Предположим, что окружность сместилась вправо на некоторое расстояние at, где 0 < t 2л, и пусть Q — та точка, в которой окружность касается теперь оси х. Тогда длина дуги окружности между точками Р и Q в точности равна at: именно это обстоятельство мы имели в виду, говоря, что окружность катится по прямой «без скольжения». (Если t > 2л, то длина этой дуги будет равна at — 2kna, где k — подходящим образом выбранное целое число.) Пусть А— центр окружности в рассматриваемый момент. Тогда координаты точки А равны, очевидно, (at, а), где t = ^QAP, а координаты (х, у) точки Р имеют вид х = at — — a sin t и у = а — a cost. Мы имеем, следовательно, такое представление:
х = a(t — sin f), у = а(1 — cos /).	(7)
Циклоида изображена на рис. 11.4. Точки циклоиды, принадлежащие оси х, называются точками возврата; они соответствуют значениям параметра: t = О, ±2л, ±4л, ... .
Циклоида была излюбленным объектом математических исследований в период создания математического анализа. В Приложении (см. § 5.4) мы упомянем некоторые из замечательных свойств этой кривой*.
* См. также весьма содержательную и доступно написанную книгу: Г. Н. Берман, Циклоида, М., Гостехиздат, 1954.
262
11. Векторные функции скалярного аргумента
УПРАЖНЕНИЯ
25.	Для каждой точки Q, принадлежащей верхней полуокружности единичной окружности (с центром в начале), проводится прямая, соединяющая эту точку с началом координат и пересекающая прямую I с уравнением у = 2 в точке Р. Обозначим через R середину отрезка PQ. Найдите параметрическое представление кривой, описываемой точкой R. j^26. Пусть Р — точка с декартовыми координатами (— 1, 0). Через каждую точку Q верхней полуокружности единичной окружности (с центром в начале)) проводится прямая PQ, на которой выбирается точка R так, что расстояние QR равно 1. Найдите параметрическое представление кривой, описываемой точкой R.
27.	Рассмотрим круг радиуса а, который катится вдоль прямой без скольжения. Предположим, что к нему приклеен концентрический с ним другой круг радиуса Ь. Отметим точку R на окружности второго круга. Найдите параметрическое представление кривой, описываемой точкой R. (Эта кривая называется трохоидой.)
28.	Предположим, что нитка длины 2ла разматывается с диска радиуса а (представлять себе можно, например, катушку), центр которого неподвижен. Найдите параметрическое уравнение кривой, описываемой свободным концом нити. (Эта кривая называется эвольвентой окружности.)
29.	Предположим, что круг радиуса b катится без скольжения по внешней стороне данной окружности радиуса а. Найдите параметрическое представление кривой, описываемой некоторой фиксированной точкой R окружности катящегося круга. (Эта кривая называется эпициклоидой; в частном случае, когда а = Ь, она называется кардиоидой.) 30. В упр. 29 предположим, что &<аи что меньший круг катится по внутренней стороне окружности большего круга. (Полученная таким путем кривая называется гипоциклоидой.)
2.6. ФОРМУЛА ПЛОЩАДИ В ПОЛЯРНЫХ КООРДИНАТАХ
В заключение этого параграфа мы получим один специальный, но важный результат — формулу для вычисления площади в полярных координатах.
Рассмотрим кривую, определяемую уравнением
г = 7(0), О<0 <2л, /(0) > 0	(8)
в полярных координатах, причем
/(2л) = /(0).	(9)
Мы предполагаем, конечно, что функция / непрерывна. Считая 0 параметром, получаем для этой кривой такое параметрическое представление:
6 h>/(0)cos0 ei + 7(0)sin 0 е2, или в координатах
х = /(0)cos 0, у = /(0 )sin 0.
В силу условия (9) начальная и конечная точка этой кривой совпадают; такая кривая называется замкнутой.
Внутренними по отношению к нашей кривой являются все точки Р области, ограниченной этой кривой, т. е. все точки, полярные координаты (г, 0) которых удовлетворяют неравенству
0 С г < /(0).
Мы хотим найти площадь S этой области. Сначала мы предположим, как обычно, что площадь существует, а затем воспользуемся нашим интуитивным представлением относительно площади для того, чтобы найти формулу для ее вычисления. После этого мы докажем, что эта формула дает то же самое численное значение, что и формула площади из § 4 гл. 5. Это, однако, будет сделано не здесь, а только в § 1.11 гл. 13.
§ 2. Ориентированные линии
263
Обозначим через 5(0) площадь области, ограниченной двумя лучами, выходящими из точки О и отвечающими полярным углам 0 и 0, и дугой рассматриваемой кривой, соответствующей интервалу [0, 0]; эта область заштрихована на рис. 11.5. Мы положим 5(0)= 0. Наше интуитивное представление о площади подсказывает нам, что 0	5(0) — непрерывная функция. Так как 5(2л) = 5, то
S= j S' (9) d6,
конечно, в предположении, что S'(0) существует и кусочно-непрерывна. Теперь мы найдем, или скорее угадаем значение производной S'(0).
Пусть h— малое положительное число. Разность S(0 + Л) — S(0) равна площади узкого сектора, заштрихованного на рис. 11.6. Эта площадь очень мало отличается от площади кругового сектора, изображенного на том же рисунке, а площадь кругового сектора равна половине квадрата радиуса, умноженного на величину центрального угла, т. е. равна f(G)2h. Следовательно,
S(6 + ft)-S(6) ~ 1 f ,0)2 h	~ 2 м ' ’
причем это приближенное равенство является тем более точным, чем меньше величина Л. Отсюда можно заключить, что
S'(0) = ^-/(0)2	(Ю)
и, значит, 2те
s=-bp(0m	(in
о
Это и есть та формула, которую мы хотели вывести.
Ясно, что
3
S=^-J/(0)2d0	(12)
а
есть площадь «сектора», ограниченного дугой нашей линии и двумя радиусами, полярные углы которых равны аир (рис. 11.7). Эта формула получается в точности так же, как и формула (11). Она применима и в том случае, когда начало координат О принадлежит кривой.
ф Примеры. 1. Найти площадь области, ограниченной кривой г = 2 + sin0, 0 <С0	2л.
Решение. Имеем 2те	2те
S = J (2 -|- s in 0)2 d0 = -у- J (4 + 4 sin 6 -I- sin2 0) d0 = о	о
2п	2п
= J (2 Ч- 2 sin 0 Ч- ?~^os29jd0 =	+ 2sin0 — -l-cos20)d0 =
о	о
--------2 cos 0---sin 20 ]	= —.
\ 4	8	До 2
264
11. Векторные функции скалярного аргумента
§ 2. Ориентированные линии
265
Здесь мы воспользовались тождеством 2 sin2x =1 — cos 2х. Соответствующая кривая изображена на рис. 11.8.
2. Найти площадь прямоугольного треугольника.
Решение. Предположим, что наш треугольник ограничен осью х, прямой х = 1 и прямой у = тх, где т > 0 (рис. 11.9). Уравнение прямой х = 1 в полярных координатах имеет вид rcos0 = 1, а наш треугольник получается при значениях 0, удовлетворяющих неравенству О<^0 arctg т. По формуле (11) площадь S треугольника равна
arctg tn
£ С = J_teelarctgm = -
2 J cos2 0	2 & [о	2
о
как и следовало ожидать.
3. Найти площадь области, ограниченной четырехлепестковой розой г = 2cos 20.
Решение. Мы начертим кривую (см. пример 2 § 3.4 гл. 9) и заметим, что в силу соображений симметрии искомая площадь в восемь раз больше площади половины лепестка, заштрихованной на рис. 11.10. Кривая, ограничивающая этот полулепесток, соответствует изменению полярного угла от 0 до Следовательно, искомая площадь равна к/4	тс/4	тс/4
•8.2- j (2cos20)2d0 = 16 j cos220d0 =8 у (1 +cos40)d0 = о	оо
= 8 (0 Ч—— sin 4б) р/4 = 2л.
\	4 J |о
Здесь мы воспользовались тождеством 2 cos2x = 1 + cos 2х.
Заметим, что площадь, ограниченная всей кривой, равна половине площади описанного около нее круга, ф
УПРАЖНЕНИЯ
Найдите площадь каждой из областей, ограниченной одной или несколькими кривыми которые заданы уравнениями в полярных координатах. В каждом случае, прежде чем вычислять площадь, полезно начертить кривую.
31.	г = 1 + cos 6, 0 < О 2л.
32.	г = 2 cos 0, 0 < 0 < л
33.	г = cos 30, 0 < О с л.
34.	г = l^cos 20 >	— — < 0< — •
4	4
36.
37.
38.
39.
40.
тс	тс
35.	г = 0, 0 < 0 < — , и линия, для которой 0 ~	•
г = tg0 и горизонтальные прямые, декартовы уравнения которых #=|^2 и у = — 1^2*. Меньшая (внутренняя) петля кривой г = 1 + 2 cos 0.
г = 0, 2л < 0 с 6л, и прямолинейный отрезок 0 = 0, 2л С г с 4л.
Одна из меньших (внутренних) петель кривой г = cos Д-0.
Одна из меньших (расположенных слева) петель кривой г = cos 0 cos 20.
266
11. Векторные функции скалярного аргумента
§ 3.	КАСАТЕЛЬНАЯ, ДЛИНА, КРИВИЗНА
3.1.	ГЛАДКИЕ КРИВЫЕ
Непрерывные векторные функции, введенные в § 1, образуют класс функций, слишком широкий для многих приложений. Кривые, ими определяемые, могут не иметь касательных, есть среди них и кривые, никакая дуга которых не имеет конечной длины, и даже такие странные кривые, которые проходят через каждую точку некоторой области (такие кривые называются кривыми Пеано). Чтобы получить более привычный класс кривых, мы условимся, что все рассматриваемые функции, в том числе и те, которые используются для замены параметра, имеют непрерывные производные.
Ориентированная кривая называется гладкой, если она задается векторной функцией
t н* * f(Z), а t b.
производная Г(0 которой существует, непрерывна и
f \t) =# О
для всех рассматриваемых значений /. Замена параметра т t = ср(т) называется допустимой, если производная <р'(/) существует, непрерывна и положительна. При такой замене параметра f(0 преобразуется в другое представление, g(r); при этом мы имеем
g(T) = f (<р(т)),
и так как g'(t) = Г(ф(т))ф'(т), то и
g'(T) ¥= о.
Векторная функция f(0 может быть представлена в виде
f(/) = х(/)е, + у(/)е2.	(1)
Если это удобно, мы будем обозначать ее через (x(/), y(f)). Производной этой функции будет (x'(i), y'(t)) и условие f'(/) #= 0 равносильно тому, что
x'(ty> + y’W Ф 0.	(2)
Джузеппе ПЕАНО (1858—1932) был блестящим математиком с разнообразными интересами (включая изобретение им некоторого искусственного всемирного языка, за основу которого была принята латынь *). Ему принадлежат знаменитые аксиомы Пеано, определяющие целые положительные числа.
* Наряду с этим Пеано принадлежит и своеобразный символический «математический язык», на котором он писал многие свои работы и который широко использовался в издаваемом Пеано в конце XIX в. журнале «Rivista di Matematica» (что делает, кстати говоря, напечатанные в этом журнале статьи сегодня весьма мало доступными).
§ 3. Касательная, длина, кривизна
267
3.2.	НЕПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Пусть х f(x) — скалярная функция, определенная при а х i и в этих пределах имеющая непрерывную производную/'(*)• График (или годограф) этой функции есть гладкая ориентированная кривая, которую можно задать векторной функцией
t	/е ± + /(/)е2, а t <1 Ь.	(3)
Заметим, что производная этой векторной функции есть с, + /'(/)е2 и, значит, она нигде не обращается в нуль.
3.3.	ЕДИНИЧНЫЙ КАСАТЕЛЬНЫЙ ВЕКТОР
Для гладкой кривой, определяемой функцией t >-> f(0, рассмотрим векторную функцию
Т«=ТгЖ'',,);	(4)
она вполне определена, так как, по предположению, | f'(Z) I =# 0. Мы назовем этот вектор Т(/) единичным касательным вектором к нашей кривой в точке Р с радиусом-вектором f(Z). Это название оправдывается следующими свойствами вектора Т.
1.	Т не изменяется при всех допустимых заменах параметра.
В самом деле, произведем замену параметра т »-> ф(т) = t\ при этом функция f(/) преобразуется в функцию
Т •-* gft) = f (ф(т)).
Эта функция тоже представляет нашу кривую. Пусть Р — точка этой кривой с радиусом-вектором f(/0) = g(t0), где /0 = ф(т0). По правилу дифференцирования сложной функции
g'fr) = ф'(т)Г(ф(т)).
По предположению ф'(т) >» 0, поскольку мы рассматриваем только допустимые замены параметра. Следовательно,
I g'W I = ф'(т) И'(<р(т)) |.
Таким образом, при т = т0 мы имеем
тгкд8' = ТЙТЙТГ ’’«=-й4г •'
Но левая часть этого равенства представляет вектор Т в точке Р, вычисленный с использованием функции g, а правая часть — это вектор Т в точке Р, вычисленный с использованием функции f. Наше утверждение доказано.
268
11. Векторные функции скалярного аргумента
2.	Вектор Т — единичный, т. е. | Т | = 1. Это очевидно, ибо
3.	Т является касательным вектором к рассматриваемой линии.
Другими словами, если выбрать систему координат [О, еь е2} так, чтобы та дуга кривой, которая содержит точку Р, являлась графиком скалярной функции х F(x), и если представить Т направленным отрезком PQ, то прямая PQ будет касательной к нашей кривой. Для того чтобы доказать это утверждение, заметим, что рассматриваемая дуга кривой имеет параметрическое представление
t ь-> f(/) = /ех + Г(/)е2.
Пусть Р — точка с координатами х0 = У о = Тогда наклон касательной к этой кривой в точке Р равен т = F'(t0). Мы имеем f'(/) =	+ F'(f)e2, так что
f'(/0) = ei + те2 и, значит, вектор f'(/0) направлен по касательной в точке Р. Точно так же направлен и вектор Т(/о), отличающийся от f'(/0) только длиной.
Геометрический смысл вектора Т можно усмотреть из следующего рассуждения. Пусть h — малое положительное число. Тогда вектор
п
$ 3. Касательная, длина, кривизна
269
близок к вектору Но вектор f(f0 + Л) — f(f0) представляется направленным от-резком РРН (рис. 11.11), где Ph — точка, радиус-вектор которой равен f(Z0 + Л). Следовательно, Ph есть точка нашей кривой, близкая к точке Р и расположенная на кривой по ту сторону от Р, которая соответствует возрастанию параметра t. Отсюда следует, что вектор Г(6>) направлен по касательной к кривой в направлении возрастания значений параметра, или, как говорят, в направлении рассматриваемой кривой. Единичный вектор T(f0) имеет то же направление, что и вектор f'(f0)-
Замечание. Для данной точки Р гладкой ориентированной кривой с у -шествует такая содержащая точку Р достаточно малая дуга кривой, которая в соответственно выбранной системе координат является графиком непрерывно дифференцируемой скалярной функции. Это геометрически очевидно (рис. 11.12). Если точка Р задана, то ее можно принять за начало координат, после чего репер |ео е2| можно выбрать так, чтобы вектор ej был направлен по касательному вектору в точке Р. (Аналитическое доказательство этого утверждения нетрудно, но мы его опускаем.)
3.4.	ПОЛЯРНЫЙ УГОЛ КАСАТЕЛЬНОГО ВЕКТОРА
Отметим полезные формулы: если гладкая кривая представлена уравнениями к — — x(Z), У — y(t)9 то вектор Т(0 имеел координаты
__И0___________ __£(0_____________	(5)
У х'(024-/(П2. ’ У *'(02 Н-/(О2 ’
В самом деле, если f = хс( + уе2, то Г = хе t 4- уе 2 и | Г |2 — х'1 4- у". Пусть ©(/) — полярный угол вектора Т(0- Тогда
cos 6 =	х —, sin в = у-----------	(6)
V/W	Гх'Ч/’
и, следовательно, fge = 44r-	(7)
X (t)
Если та же самая кривая представлена непараметрически как график функции х >-* у = F(x), то tg0 = F'(x) — потому что tg0 есть наклон касательной к кривой. Следовательно, из равенства (7) получаем
dy _ у’ (t) = dy/dt dx х' (0 dx/dt
Это соотношение еще раз показывает удобство обозначения Лейбница.
• Пример. Эллипс, заданный каноническим уравнением, можно представить параметрически:
х — a cos t, у = b sin t.
270
11. Векторные функции скалярного аргумента
Следовательно, dx	.	.	a du 1	. b
— = — a sin t ----------t/, —& cos / = — x
dt	b dt	a
и в силу равенства (8) dy _______________________________________b2 х
dx	a2 у
Выше мы получили этот результат другим способом (см. гл. 10, § 1.6).ф
УПРАЖНЕНИЯ
1.	Найдите единичный касательный вектор к кривой, представленной функцией f(/) = = (/3 + /)ех + /2е 2 в точке Р, декартовы координаты которой (—2, 1).
2.	Найдите единичный касательный вектор к кривой, представленной функцией f(/) = = e2t ех — (t + 8)4/3 егв точке Р, декартовы координаты которой (1, —16).
3.	Найдите единичный касательный вектор к кривой, представленной функцией f(/) = cos_2/ех + sin 3/ег (где —л/6< t<Z л/6) в точке Р, декартовы координаты которой /3/2, /2/2).
4.	Найдите единичный касательный вектор к графику кривой у = ln(x2 + 1) в точке Р с декартовыми координатами (—2, In 5).
5.	Найдите Т(/) для кривой, представленной функцией f(/) = cos /ех + /еа.
6.	Найдите Т(/) для кривой, представленной функцией f(/) = //2 + 1 ех + /ег.
7.	Найдите Т(х) для графика функции у = х3 + 2.
Д8. Найдите Т(г/) для графика функции у = х’/з — 2.
9. Рассмотрим кривую, представленную функцией f(/) = е1 ех — /Зег; пусть g(a) — параметрическое представление этой кривой, полученное из f(/) допустимой заменой параметра t = ф (и) = и2 + 1. Найдите Т(и).
10. Найдите Т(/) для кривой, представленной функцией f(/) = (/3 — 1)ех — /2ег.
3.5. ФОРМУЛЫ В ПОЛЯРНЫХ КООРДИНАТАХ
Вычислим вектор Т в полярных координатах (г, 0). Если кривая определяется уравнением
г =ле),
то она допускает параметрическое представление
х = f(Q) cos 0, у = /(0) sin 9,
где параметром служит полярный угол 0. Мы имеем
=f(9) cos 0-/(0) sin 9;	= f' (0) sin 0 + /(0)cos0.
Следовательно, как читатель легко может проверить сам,
+ (fY = f (S)2 + Г (0)2 = г* + (А)2.
\ du /	\ du /	\ du /
§ 3. Касательная, длина, кривизна
271
Рис. 11.13
Рис. 11.14
Координаты вектора Т таковы:
f' cos 6 — f sin О Г sin в + f cos О
V p+r2 ’ V P+r2
а наклон касательной равен
tg 0 =	<fl) sin 9 + / (9) COS e
dx f' (9) cos 9 — f (9) sin 9
Пусть P — какая-то точка кривой; найдем угол ф между прямой ОР и касательной к кривой, проходящей через точку Р (рис. 11.13). Так как ф = 0 — 0 и так как наклон касательной равен dyldx, а наклон прямой ОР равен tg 0, имеем (ср. с § 2.4 гл. 10)
f' sin 9 + f cos 9 sin 9
. . ___ tg 8 — tg 9 __ f' cos 9 — f sin 9 cos 9	_ f
1 + tg 8 tg 9	f' sin 9 + 7 cos 9 sin 9	[' *
[' cos 9 — f sin 9 cos 9
что можно также записать в следующем виде:
= ИЛИ =4* ‘S’*	(10)
dr [du	г du
272
11. Векторные функции скалярного аргумента
УПРАЖНЕНИЯ
Найдите вектор Т (6) и tg ф Для каждой из следующих кривых, заданных уравнением в полярных координатах.
11. Г = 2 + cos 0 для — л < 0 < тс.
А 12. г= 1 4" cos 0 для — л < 0< л.
13. г = cos2 0 для —л/2< 0 < тс/2.
15 г •*-“ е9 для — оо<^ 0	4“ оо.
16 г = 1/(cos 0 + sin 0)для —л/4<0< Зл/4.
17. г = In 0 для 0< 9 < 1.
14.	г = 0 для 0< 0< оо.
3.6.	ЕДИНИЧНЫЙ НОРМАЛЬНЫЙ ВЕКТОР
Пусть Т — единичный касательный вектор к ориентированной кривой в точке Р. Его полярный угол 0 определяется формулами (6). Вектор N, имеющий единичную длину и полярный угол 0 + 90°, называется единичным нормальным вектором в точке Р. Мы можем представить себе, что вектор N получается из Т поворотом против часовой стрелки на угол 90° (рис. 11.14). Так как cos (0 + 90°) =—sin©, sin (0 + 90°) = cos 0, то координаты вектора N(0 равны
"К х'2 + у'2
Ух'2+у'2
(11)
Заметим, что определение вектора N зависит от ориентации плоскости.
УПРАЖНЕНИЯ
18.	Найдите единичный нормальный вектор кривой, представленной функцией f (/) = = (/3 +/) ех 4-*2е2, в точке Р, декартовы координаты которой (—2, 1).
19.	Найдите единичный нормальный вектор кривой, представленной функцией f (/) = e2t ех— — (* 4" 8)4/3 е2, в точке Р, декартовы координаты которой (1, — 16).
20.	Найдите единичный нормальный вектор кривой, представленной функцией f (/) = = cos 2t ех4- sin 3t e2 (для — л/6< /<тс/6) в точке Р с декартовыми координатали (]ЛЗ/2, V 41^.
21.	Найдите единичный нормальный вектор графика функции у = In (х2 4- 1) в точке Р, декартовы координаты которой (—2, In 5).
22.	Найдите	N (/)	для кривой,	представленной функцией	f	(/)	= cos /	ех	4~	*е2.
23.	Найдите	N (t)	для кривой,	представленной функцией	f	(/)	— У Р	4-	1	ех 4- te2.
24.	Найдите	N (х)	для графика	функции у = х3 4- 2.
25.	Найдите	N (у)	для графика	функции у = х5^3 4“ 2.
3.7.	ДЛИНА КРИВОЙ
В § 4.8 гл. 5 мы вывели формулу для длины графика функции. Теперь мы рассмотрим более общий случай гладкой кривой, заданной параметрически. Сначала предположим существование длины кривой известным и с помощью интуитивного представления о длине попытаемся вычислить ее. Затем метод вычисления этой длины превратим в определение длины кривой. Наконец, проверим, что наше новое определение длины совпадает с определением, введенным в § 4.8 гл. 5.
Пусть А — гладкая кривая, определяемая векторной функцией t f(/), где а < t Ь\ обозначим через L длину кривой А. Пусть, далее, А$ — дуга кривой, определяемая ограничением функции f на отрезок la, El, a L($) — длина дуги /Ц.
§ 3. Касательная, длина, кривизна
273
Рис. 11.15
Иными словами, L($) есть длина дуги, определяемой функцией /н* f(f), где a -Cf-CE, и L = L(b). Мы положим еще Ца) = 0. Из нашего интуитивного представления о длине следует, что L(Sj) — непрерывная функция. Следовательно,
ь
L = J L' (/) dt, а
(12)
если производная L'(f) существует и непрерывна. Мы попытаемся «вычислить» L'(0> или, скорее, угадать, какое значение имеет эта величина.
Пусть t0 — какое-то значение параметра между а и 6, a h — малое положительное число (или отрицательное число, малое по абсолютной величине). Наше интуитивное представление о длине подсказывает нам, что разность L(tQ + Л) — L(/o) равна длине кривой, определяемой функцией t »-> f(/) на отрезке t0 -С t tQ + h. Но длина этой малой дуги будет, как мы можем ожидать, мало отличаться от расстояния между ее концами (рис. 11.15). Это расстояние равно | f(/0 + А) — f(/0) I, так как расстояние между двумя точками равно модулю разности их радиусов-векторов. Мы рассчитываем, следовательно, что
£«„ +ft)-£(/,) = 1 ] f + h} _ f (/о) (+ r> п	п
где г есть ошибка, которую мы делаем, заменяя дугу ее хордой, и которая становится сколь угодно малой при достаточно малом | h |. Другими словами, мы имеем основания полагать, что
Г W = lim .+
h-+0	h
= lim (4- |fa0 + fc)-f(Ql) =
fl->0 \ h	)
= lim l-L(f(/0 + ft)-f(/0)) h—>0 I h
274
11. Векторные функции скалярного аргумента
Пользуясь правилом д) из § 1.5, заключаем отсюда, что
L' (U = lim -L (f (t0 + h) - f (Q) I = | Г (/0) |. h—>0 n	|
Подставляя это значение L'(Z) в равенство (12), получаем
ь
L = ^\t'(t)\dt,	(13)
а
или в координатах,
ь
L =	+	(14)
а
Примем теперь эту формулу за определение длины дуги кривой.
3.8.	НЕЗАВИСИМОСТЬ ОТ ПАРАМЕТРА
Для того чтобы оправдать наше определение длины, покажем, что при допустимой замене параметра значение L не меняется. Это должно быть так, потому что длина должна зависеть только от кривой, а не от способа ее представления.
Пустьт »-► <р(т), где а <т *С Р — такая функция, что ф'(т) существует, положительна и непрерывна, причем ср(а) = а, ср(₽) = Ь. Так как g(x) = Т(ф(т)), то функция т g(x), а "Ст ’С Р тоже определяет кривую А. Применяя правило дифференцирования сложной функции и правило замены переменной под знаком интеграла, получим
ь
J1 g' (х) | dt = JIГ (ф (т)) ф' (т) I dt = а	а что и требовалось доказать.	J|f'(<p(x))||q)'(x)|dx=J|r(O|^. а	а
§ 3. Касательная, длина, кривизна
Пользуясь обозначениями di(t) = dx(t) — x'(t)dt, dy(t) = y'{t)dt, равенства (13) и (14) иногда записывают так:
L = J|df| и L=^Vdx* + dy* . А	А
Эти обозначения подчеркивают, что L не зависит от выбора параметра.
3.9.	АДДИТИВНОСТЬ
Если А = В + С (т. е. если линия А состоит из дуги В и следующей за ней дуги С; рис. 11.16), то мы можем рассчитывать на то, что длина А равна сумме длин кривых В и С. Докажем, что это действительно так. Пусть линия А определяется функцией 1>-> f(/), где /0 t tu В — ограничением f на отрезок [/0, /гЕ а С — ограничением f на отрезок [/2> ^il; тогда
ь длина линии А = С I f' (/) I dt [ПО определению] =
*0
G	Г1
= J | fZ (t) | dt -4- J | fZ (/) | dt [по свойству аддитивности интеграла] = to
= сумме длин линий В и С [ПО определению].
Аналогично можно показать, что линия А и линия, противоположная А (см. § 2.2), имеют одну и ту же длину.
3.10. СРАВНЕНИЕ С ПРЕЖНЕЙ ФОРМУЛОЙ ДЛИНЫ
Покажем, что наше новое определение длины согласуется с тем, которое мы ввели в § 4.8 гл. 5. Рассмотрим непрерывно дифференцируемую функцию х у = Дх), где а х 6. Ее график параметрически представляется векторной функцией
1► ц/) == /е4 + дое2, а t b.
Длина этого графика, по нашему новому определению, равна
ь
ь	ь
L = j|f' (0|d/ = J|ex + f (t) е2| d/ = j/ 1 +/'(*)2 dx,
а это в точности та же формула, которую мы получили в § 4.8 гл. 5.
Заметим, что определение длины формулой (13) дается в векторной форме. В ней не предполагается, что выбрана какая-то специальная система координат. Следовательно, длина кривой не зависит от положения декартовой системы координат, при помощи которой эта длина вычисляется. Конечно, так оно и должно быть. Теперь мы выяснили, наконец, вопрос, остававшийся открытым в § 4.8 гл. 5.
ф Примеры. 1. Длина дуги окружности. Эта дуга параметрически определяется так:
х = г cos 0, у = г sin 0, 0 'С 6 а,
276
11. Векторные функции скалярного аргумента
где а — ее центральный угол (рис. 11.17). Следовательно,

Для полной окружности (а — 2л) получаем L = 2л г.
2. Длина эллипса. Пусть а и b — полуоси эллипса. Из параметрического представления эллипса х = a cos 0, у = b sin 0 (где 0	0 -С 2л) получаем формулу
L - Г V Ш + Ш = J + М.
Так как Ь2 = а2 — с2 и с = ае, где е — эксцентриситет эллипса, мы имеем
L = a f У ' 1 — е2 cos8 9 d0 = 2а j У 1 — г2 cos2 9 d0; 6	о
последнее равенство объясняется тем, что функция 9 ь-* cos2 9 имеет период л. Мы получили так называемый эллиптический интеграл, который не может быть выражен через элементарные функции. •
УПРАЖНЕНИЯ
В каждом из упражнений 26—35 найдите длину кривой, определяемой данной векторной функцией, в указанных в условии границах.
26.	f (0= Р—l)ei + /3e2 для 1/3< t <2/3.
27.	f(0 = 4-/2ei + 4’ (2t + 1)3/2е2 для ОС t <1.
1	1	—
28.	f (/) = — /’е, + — t*e2 для 1 С t СУ 5 . о	4
29.	f (/) = 2е//2 в! + 4е3//4е2 для 0 < t < 2.
30.	f (0 = ~cos3f ei+(sinf —-sin3^e2 для к/6 </ <тс/3.
31.	f(/) = sin/ ei+sin3/2re2 для 0<	rc/4.
32.	f (/) = /2в! + (/s + t) e2 для 0 < t <1. (Ответ оставьте в форме интеграла.)
33.	f (0 = F*2 + 1 в! -f-	e2 для К t <4. [Ответ оставьте в форме интеграла.)
34.	f (t) = cosf8ei + sinfle2 для F"tc/4< t < F"k/2. [Ответ оставьте в форме интеграла.)
35.	f (0 = cos t ei + In t е% для те/4 < t < e/3. [Ответ оставьте в форме интеграла.)
§ 3. Касательная, длина, кривизна
277
3.11. ФОРМУЛА ДЛИНЫ В ПОЛЯРНЫХ КООРДИНАТАХ
Предположим, что кривая задана уравнением в полярных кординатах (г, 0): г = /(0), а <0 < fl.
Ту же самую кривую можно определить параметрически'. х(0) = /(0 )cos 0, у(0) = /(0 )sin 0.
Пользуясь формулой (13), легко можно получить формулу для вычисления длины дуги кривой, заданной уравнением в полярных координатах:
Р ____________
L = j yTwT/W do.	(15)
а
ф Пример. Логарифмическая спираль в полярных координатах определяется уравнением г = /(0) = ае? . Длина дуги этой спирали равна
L =	= ]/Ja(ep —еа) .ф
УПРАЖНЕНИЯ
В каждом из упражнений 36—41 найдите длину дуги кривой, заданной уравнением в полярных координатах (г, 1б),где 6 меняется в указанных пределах.
36.	г=е2, где /5<0<2/3.
37.	г = е^, где 0<6<1; а — фиксированное число.
38.	г = sec 6, где 0 < 6 < л/4.
39.	г — 1 + cos 0 , где 0 < 0 < л/2. [Ответ оставьте в форме интеграла.]
40.	r= pAosO, где л/6<-6< л/3. [Ответ оставьте в форме интеграла.]
41.	г = cos 6 + sin 0 , где 0 < 0 < л/2.
3.12. ДЛИНА ДУГИ КАК ПАРАМЕТР
Для каждой данной гладкой ориентированной кривой существует много параметрических представлений. Но имеется одно, в некотором смысле особенно простое представление — в нем за параметр принимается длина дуги кривой, измеренная от некоторой точки кривой. Покажем, как можно получить такое представление.
Рассмотрим гладкую линию, определяемую функцией t н-> f(/), где а -С t -С 6; пусть ее длина равна L. Обозначим через s($) длину дуги кривой, определяемой функцией t f(/), где а t В. Тогда
£
«(*) =	(16)
278
11. Векторные функции скалярного аргумента
Таким образом, ; »-> s (?) является непрерывной'возрастающей функцией, причем s(a) = 0, s(b) = L, а производная
s'G) = ! f'(0 I
непрерывна и положительна. Следовательно, существует обратная функция t = = <p(s), для которой <р(0) = a, cp(L) = b и <p'(s(Z))s'(/) = 1, откуда <p'(s(0) =	
Эта функция определяет допустимую замену параметра. Положим g(s) = f(cp(s)j. Тогда функция
s н* g(s), О s L
определяет нашу кривую и
lg'(s) I =1, так как
g' (s) = ф' ($) Г (ф ($)) = - 1 Г (/).
I I (I) I
Отсюда видно, что длина кривой между точками g(0) и g(s) равна s (или | $ |).
Если условиться брать в качестве параметра именно длину дуги s, то некоторые формулы можно упростить. Положим
g(s) = x(s)ei + z/(s)e2;
так как | g'(s) | = 1, то x'(s)2 4- y'(s)2 — 1, и формулы (5), (6) и (11) упрощаются следующим образом:
T(s) =xz(s)ef 4-y'(s)e2, N(s) =—t/'(s)et + x'(s)e2,	(17)
cos 0 = x'(s), sin 0 = y'(s).	(18)
УПРАЖНЕНИЯ
В каждом из упражнений 42—46 кривую, представленную векторной функцией или уравнением в декартовых координатах, задайте параметрически, используя в качестве параметра длину дуги $.
А 42. 2у = 3х—1, где х > 0.
.о „3/2 -3/2 3/2
43. у = 2 3 х , где х > 0.
44. /(/) = --— /в! 4-	(2/ 4- 1)3/2 е2, где t > 0.
2	и
46. у — У1 — я2 » где 0 < х < 1.
§ 3. Касательная, длина, кривизна
279
3.13.	КРИВИЗНА
Рассмотрим ориентированную линию, определяемую функцией t f(/), а < t < b.
и предположим, что функция f(/) имеет непрерывную производную второго порядка f"(0* Две такие кривые показаны на рис. 11.18. Ясно, что первая является «более искривленной», чем вторая, и что первая кривая является «более искривленной» в точке Р, чем в точке Q. Мы хотим найти способ численно измерить свойство линии «быть искривленной», ее «кривизну».
Вспомним определение полярного угла 0(/) единичного касательного вектора Т(/) линии. Если линия совсем не искривлена, т. е. является прямолинейным отрезком, то угол 0 не меняется. Поэтому естественно принять за меру искривленности кривой скорость изменения 0 при движении точки вдоль линии. Но скорость изменения по отношению к чему? На линии существует только один «натуральный параметр» — это длина ее дуги. Итак, по определению, кривизна k линии в точке Р — это вычисленное в этой точке значение производной по длине дуги полярного угла единичного касательного вектора.
Для того чтобы найти формулу для вычисления кривизны, предположим, что t »-> s(t)— функция, определяющая длину дуги через параметр t. Мы можем рассматривать полярный угол 0 и параметр t как функции s. По правилу дифференцирования сложной функции
. de dt k =------ ----,
dt ds
а так как s(t) определена формулой (16), то
dt 	1	 1
ds ds/dt I f'(Z) I
(19)
и, следовательно,
да =^и ds Ц'«>|
Но поскольку [см. формулу (7)] tg 0(0 = у , то *'(0
0(0 = arctg х '(0
(20)
(21)
©'(0 =
x'(t) y"(t) - x"(t) y'(f)	x'(t) y'(Q - x“(t) y'(t)
X'(O2	*'(02 + /(02
Для точек,
фор-
мулы ctg©
и, следовательно, ____________________1
1 + Г/'(О2/Х'(О2
в которых x'(0 = 0, мы получим тот же результат исходя из (t'}
= ——; напомним, что, по нашему предположению, х'(0 и у (i) не y'(t)
равны нулю одновременно.
280
11. Векторные функции скалярного аргумента
Подставляя значение 0'(О в формулу (20) и пользуясь тем, что |Г| =
V+ f/,3> получим окончательную формулу
*(0 =
xz(0 Г(0 - *zz(0 /(0 Lx'(О2 + /Ю213/2
(22)
3.14.	ЗНАК КРИВИЗНЫ
Может показаться, что величина кривизны зависит от выбора осей координат, поскольку полярный угол вектора зависит от системы координат; однако на самом деле это не так. Действительно, повернув оси координат, мы увеличим все углы 0(/) на постоянную величину, что не отразит ся на производной функции 0. С другой стороны; знак кривизны зависит от ориентации плоскости. Поэтому некоторые авторы называют кривизной абсолютную величину I k(f) | функции k(t).
Если k =	> 0, то угол 0 возрастает при движении вдоль кривой в направле-
нии возрастания значений параметра; это означает, что единичный касательный вектор поворачивается в направлении против часовой стрелки (рис. 11.19). Если k < 0, то 0 убывает и, значит, Т поворачивается по часовой стрелке. Точка, в которой кривизна изменяет знак, называется точкой перегиба (рис. 11.20).
§ 3. Касательная, длина, кривизна
281
В § 4.9 гл. 4 точкой перегиба мы называли такую точку (х0, f/o)> принадлежащую графику функции у == /(х), что f"(x) = 0 и f"(х) в точке х0 меняет знак. Понимаемые в таком смысле точки перегиба — частные случаи только что определенных (почему?).
3.15.	КРИВИЗНА ГРАФИКОВ
График скалярной функции х /(х), а х С b имеет параметрическое представление
х(0 =Z, y(t) так что
х'(0 =1, х"(0 =0, y'(f) =m y''(t)
Поэтому из формулы (22) следует такая формула для кривизны графика функции f в точке (х, /(х)):
<23’
фПримеры. 1. Окружность радиуса R. Ее параметрическое представление х — R cos t, у = R sin t, 0 "С 2л;	(24)
следовательно,
х’ = —R sin t, х" = —R cos t, у’ = R cos t, у" = —R sin t.
Поэтому по формуле (22) получаем k = —. R
Кривизна окружности во всех точках равна . Конечно, ее можно вычислить и непосредственно, замечая, что ©(/)=/+—, так что -^-=1,и$(0= 2	dt
dt	1
— Rt, так что— = — ; следовательно, ds	R
= 1 ds R
Верхняя половина нашей окружности является графиком функции
X » у = f (X) = ]/7?2 —х2.	(25)
Имеем

*—х
V Л2—*2
— R2
(^2_Х2)3/2 ’
(1 +т2]3/2
R3
(R2 —
f"(x) =
и, по формуле (23), k = . Это кажущееся расхождение легко объяснить. В параметрическом представлении (24) параметр t возрастает, как мы предполагали, вдоль кривой в направлении движения против часовой стрелки. В представлении (25) параметром является х, ах возрастает при движении по кривой в направлении движения по часовой стрелке.
282
11. Векторные функции скалярного аргумента
Рис. 11.21
2. Парабола у = х2. Здесь А(х) =--------------------------------------2—^г.
(14- 4х2)3/2
Точек перегиба парабола не имеет.
3.	Кубическая парабола. Это график функции = у. Мы имеем k(х) =-------------------------------------6*	.
(14- 9х«)3/2
Здесь имеется одна точка перегиба, а именно точка х = у = 0. ф
3.16.	РАДИУС КРИВИЗНЫ. ОКРУЖНОСТЬ КРИВИЗНЫ
Если кривизна k в точке Р линии А отлична от нуля, то величину
Р=^	(26>
называют радиусом кривизны линии А в точке Р. Это название естественно потому, что если А является окружностью, то р — это как раз радиус окружности (см. выше пример 1).
Окружность кривизны, или соприкасающаяся окружность, С линии А в точке Р определяется как окружность радиуса р, проходящая через точку Р, касающаяся линии А в точке Р и такая, что направления выпуклости кривых С и А совпадают. Центр окружности С называется центром кривизны (линии А в точке Р). Ясно, что если k > 0, то центр кривизны расположен от точки Р на расстояниир в направлении единичного нормального вектора N; если k < 0, то расстояние р нужно отложить в направлении, противоположном направлению N (рис. 11.21). Следовательно, радиус-вектор центра кривизны получится, если к радиусу-вектору точки Р прибавить -^-N, т. е. он равен
f(0 + TFN'	(27)
§ 3. Касательная, длина, кривизна
283
УПРАЖНЕНИЯ
В упражнениях 47—54 найдите кривизну и радиус кривизны данной линии. Найдите все точки перегиба кривой.
47.	у = 6х, где — оо < x<Z + оо.
48.	у = 1/х, где 0<	+ оо.
49.	у = 1пх, где 0<х<+ оо. Каков предел k(x), если х приближается к нулю справа? Если х стремится к + оо?
50.	у = —In cos х, где— те/2< x<Z л/2. Найдите все точки кривой, в которых ее кривизна имеет (локальный) максимум или минимум.
51.	f (t) = 2 cos t ej + 3sin/ ег, где 0 < t <2л. Найдите все точки кривой, в которых ее кривизна имеет (локальный) максимум или минимум.
52.	f(/) =	+ cos t е2, где — оо<^ t<Z + 00•
53.	f (/) = (/3 + /) ех +	t3 — t2 ^ег, где — оо < / < + оо.
54.	f(/) = (/3 — /) ef + /4ег, где — оо < t<Z + оо.
55.	Найдите окружность кривизны графика функции у = е~х в точке (0, 1). Начертите кривую и ее окружность кривизны.
56.	Найдите центры кривизны эллипса f(/) = a cos t ех + dsin/ег в точках (а, 0) и (0, Ь).
[Здесь а и b — произвольные положительные числа.]
57.	Найдите окружность кривизны кривой у = 1/х в точке (1,1). Изобразите на чертеже график кривой и ее окружность кривизны.
58.	Найдите центр кривизны кривой, определяемой функцией f (Z)= е* ex+sin 3t ег в точке (1, 0).
3.17.	КУСОЧНО-ГЛАДКИЕ ЛИНИИ. ОСОБЫЕ ТОЧКИ
Требование гладкости кривой иногда бывает слишком стеснительным. Тогда, например, такие обычные линии, как треугольник или квадрат, не являются гладкими линиями. Мы говорим, что непрерывная векторная функция t н-> f(/), а t b определяет кусочно-гладкую линию, если производная f'(0 существует, непрерывна и отлична от нуля на всем интервале [а, Ь], за исключением, быть может, конечного числа точек. Точки кривой 4, соответствующие таким «плохим» значениям параметра /, называются особыми точками кривой А.
Примером может служить циклоида, рассмотренная в § 2.5. Это кривая, определяемая функцией
f(0 = (t — sin Z)et + (1 — cos /)е2.
Для нее
f'(0 = (1 — cos/)e! + sin t e2.
Циклоида имеет особые точки при t =0, ±2л, ±4л, ... — это те точки, в которых кривая достигает оси х (см. рис. 11.4). Эти особые точки называются точками возврата (ср. с § 2.9 гл. 4).
Единичный касательный вектор Т и единичный нормальный вектор N можно, конечно, определить во всех неособых точках кусочно-гладкой кривой. На любой дуге кривой, свободной от особых точек, в качестве параметра можно использовать длину дуги, а формула длины дуги (13) может применяться и для всей кривой, если соответствующий интеграл имеет смысл (хотя бы как несобственный).
284
11. Векторные функции скалярного аргумента
3.18.	ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
Все, что рассказано в этом параграфе, за исключением тех рассуждений, в которых использовались непараметрические задания кривых, полярные углы, единичный нормальный вектор и кривизна, можно распространить и на кривые в пространстве.
Пусть {О, еь е2, е3} —декартова система координат в пространстве. Ориентированная пространственная кривая определяется непрерывной векторной функцией
/-> f(/) = x(/)ei + y(t)e2 + г(Оез, а < 6.
Если функция f(/) имеет непрерывную производную Г(0» отличную от нуля, то рассматриваемая кривая — гладкая. В этом случае можно определить единичный касательный вектор
1
Т ® = 77^77 f® ei + У' & ег + 2' ез) 1И01	Y x'(t)2 +y'(ty + z'(t)2
и натуральный параметр
s(0 = /|Г (O|dS.
а
Длина кривой А определяется формулой
ь
J | i'(01 dt = f ds = J Vx'(tf + г/'(02 + г'(02 dt. A	A	a
Распространение этих понятий на n-мерное векторное пространство не представляет затруднений.
УПРАЖНЕНИЯ
59.	Найдите единичный касательный вектор к пространственной кривой, определяемой функцией f(/) = (t2 + 1) ех + cos t ег + е3 в точке (1, 1, 1).
60.	Найдите единичный касательный вектор к пространственной кривой, определяемой функцией f(/) = (/ + l)2'ex + t3 ег + У t2 + 1 е3 в точке (1, —8, У 5).
61.	Найдите Т (/) для пространственной кривой, определяемой функцией f(/) = cos2/ех + 4- cos t sin t ег + sin t e3.
62.	Найдите T (/) для пространственной кривой, определяемой функцией f(/) = /cos/ex+ + t sin t ег + /е3.
63.	Найдите T(/) для пространственной кривой, определяемой функцией f(/) = = (t + cos t) ex + sin t e2 + /e3.
В упражнениях 64—68 найдите длину пространственной кривой, определяемой данной векторной функцией, где параметр t изменяется в указанных пределах.
64.	f(Z) = /3/3 ех + t2/y~2 ег + /е3, где 0 < t < 1.
65.	f(/) = sin t ei + cos t e2 + /3/2 e3, где 0 < t < 4.
66.	f(/) = e* ej +2 У2e^2 ег + /е3, где 0 < t <1.	__
67.	f(/) = t2/2 ex + 1/3 (t2 — 1)3/2 e2 + /2/2 e3, где 1 < t < У 3.
68.	f(/) = cos2 / ex + cos / sin t e2 + sin / e3, где 0 < t < л/2.
§ 4. Движение
285
§ 4.	ДВИЖЕНИЕ
4.1.	КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
В гл. 4 мы рассматривали прямолинейное движение частицы — «материальной точки», обладающей определенной массой; в этом параграфе мы рассмотрим более сложный случай криволинейного движения. Такое движение описывается векторной функцией
t н* г(/) = х(/)е! + г/(/)е2 + z(/)e3.
определяющей радиус-вектор г рассматриваемой частицы в момент времени /. (Мы предполагаем, что эта функция имеет непрерывную производную второго порядка. Радиус-вектор здесь обозначен через г, для того чтобы сохранить букву f для обозначения силы.) Частным случаем является плоское движение, когда в процессе движения частица все время остается в одной и той же плоскости. В этом случае можно выбрать систему координат так, чтобы эта плоскость была плоскостью ху (плоскостью z = 0); поэтому плоское движение описывается векторной функцией
t -* г(/) = x(/)et + z/(/)e2.
4.2.	СКОРОСТЬ И УСКОРЕНИЕ
Производная
v(0 =
' ’ dt
называется скоростью движения. Она тоже является векторной функцией. В этом и в следующем параграфах дифференцирование по времени мы будем обозначать точкой. Мы имеем, следовательно,
v = г
или в координатах
v = *ех 4- уе2 + ze3.
Для плоского движения г = 0, 2 = 0 и
Длина вектора скорости
v = хед + уе2.
| v | = | г | = V хг + у2 + z2 ,
286
11. Векторные функции скалярного аргумента
или для плоского движения
| VI = V X2 + у2, равна численному значению скорости*. Производная по времени вектора скорости а(/) = dv(Z) =
1	& Л2 ’
т. е.
а = v = г = xej + t/e2 -4- ze3, или для плоского движения
а = хе, 4- t/e2, называется ускорением.
Функция t >-> г(/), описывающая движение частицы, определяет некоторую ориентированную кривую, траекторию движения. В этом случае параметр t имеет вполне определенный смысл: он означает тот момент времени, в который частица проходит точку г(/).
Используемые в науке термины «скорость» и «ускорение» довольно близко соответствуют и повседневному значению этих слов. В самом деле, рассмотрим какое-то движение частицы и предположим, что в момент времени t0 она находится в точке Р с радиусом-вектором г(/0) , а еще через h единиц времени (где h мало) — в точке Q с радиусом-вектором г(/0 + Л) (рис. 11.22). Вектор
+ — ГО	0)
п
близок к вектору скорости v(^0). Его направление — от точки Р к точке Q — близко к направлению движения. Величина вектора (1) равна | PQ |/й, т. е. примерно равна пройденному расстоянию, разделенному на протекшее время. Можно сказать, таким образом, что вектор скорости v(Z0) характеризует изменение положения точки (или радиуса-вектора) в данный момент времени. Точно так же вектор ускорения характеризует изменение скорости в данный момент времени.
Рассмотрим теперь движение, определяемое векторной функцией t г(/), и предположим, что в некоторый момент времени tQ вектор скорости v(/0) отличен от нуля. Тогда вектор скорости v(/0) будет касаться траектории движения вточкег(/0). В самом деле, как было показано в § 3.3, единичный касательный вектор Т(/о) записывается в виде
т (Q = -4--------- г (t0) =	, V (Q
I r (t0) I	Iv (QI
и, значит, T и v имеют одно и то же направление.
* В английском языке существует специальный термин speed, обозначающий численную величину | v | скорости; можно только пожалеть, что в русской литературе такого термина нет.
§ 4. Движение
287
Пусть s(/) — длина траектории, измеренная от некоторого фиксированного момента времени /0 в направлении движения. Тогда, как было показано в § 3.7,
t .	t
s(t) = j* I г (/) I с?/ = J IV (t)1 dt,
^0	to
или
% =|v(OL at
и, значит, численная величина скорости равна скорости изменения пройденного расстояния
4.3.	ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Важным примером плоского движения является вращательное движение, задаваемое формулами
х = R cos у = R sin 2rcv/, где R и v — какие-то положительные числа. Траекторией этого движения является окружность радиуса R. Координаты скорости движения:
х = — 2kv/? sin 2irv/, у == 2twR cos 2 W, а численная величина скорости
| v(/)| х2 + у2 — 2™R
постоянна; за единицу времени частица проходит расстояние 2mR, т. е. она пробе-
288
11. Векторные функции скалярного аргумента
гает длину всей окружности,взятую v раз. Поэтому v называется частотой вращательного движения. Периодом этого движения называется то время, которое требуется для прохождения полной окружности; оно, очевидно, равно
7’=—.
Отметим интересную связь между вращательным движением и гармоническими колебаниями (см. § 1.14 гл. 6). Если точка движется по кругу так, что величина ее скорости постоянна, то каждая из проекций этой точки на оси декартовой системы координат совершает гармонические колебания.
Ускорение рассматриваемого вращательного движения имеет координаты
х = — 4tc2v2 R cos 2™/, У — — 4'Л2/? sin
или
X = — 4тс2У2Х, у = — 4к2 V2y.
Отсюда видно, что вектор ускорения а имеет направление, противоположное направлению радиуса-вектора г. Ускорение отлично от нуля, хотя численная величина скорости постоянна. Это не удивительно, так как направление вектора скорости меняется с течением времени. Однако численная величина ускорения постоянна: мы имеем
)а| =	+ у2 =	(2)
фПример. Движение искусственного спутника Земли в первом приближении может рассматриваться как вращательное движение по окружности, радиус которой равен радиусу Земли. Поэтому ускорение искусственного спутника направлено к центру Земли и по величине равно 4л2/?/Т2. Но на спутник при его движении по орбите действует только земное притяжение. Следовательно, 4л2/?/Г2 =g = 980 см/с2. Значит, период обращения спутника Т	можно вычислить, зная R.
Этим объясняется, почему величина периода обращения большинства искусственных спутников Земли имеет один и тот же порядок.ф
4.4.	КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ
Рассмотрим теперь плесков движение
t н-> г(0 = х^+ y(t)e2.
В каждый данный момент времени t единичный касательный вектор Т(/) и единичный нормальный вектор N(/) образуют репер. Выше мы видели, что вектор скорости по направлению совпадает с Т(/). Вектор ускорения a(Z) в общем случае можно разложить по касательному и нормальному направлениям, т. е.
а = аТ + |3N.
§ 4. Движение
289
Мы называем аТ и (JN соответственно касательным (или тангенциальным) и нормальным ускорениями:
аТ = а^, pN = а^ i
при этом
а=аг + ау.
Для того чтобы найти аг и ам, введем такой репер {еь е2}, что в рассматриваемый момент времени /0 имеем е4 = Т, е2 = N. В координатах наше движение пусть задается функциями
х =Х(О, У =y(t)-
Так как v(Z0) = |v(/0) |T(Z0) = |v(/0)|ei, то
i(*o)>O. i/Ko) = O.
Вектор ускорения в момент времени /0 имеет координаты х(/0), y(t0), так что
% (Q	у (/д) е2.
Поскольку = V X2	+ у2 , то	cPs	XX 4- у у	.	. 	 —		—. И ПОИ t = В СИЛУ УСЛОВИЙ
		
(3) имеем	ds	= Х	=х
	dt	dt2
Кривизна траектории в	силу равенства (22) из § 3.13 равна	
		ь— ху — х у ( •	• \3/2 (х»+ «/*)
и при t = ta получаем		
	k	= -т- , у — kx2. X*
Отсюда ясно, что при t = tQ cPs	и /	\2 кт
ат =----Т, av =k — IN.	лп
т	dt2 N \di )	* '
Если k > 0, то последнее равенство можно переписать так:
а« = Т (т) N'	<5>
290
11. Векторные функции скалярного аргумента
Рис. 11.23
где — радиус кривизны траектории. Так как все величины в равенстве (4) не зависят от выбора системы координат, то равенство (5) имеет совершенно общий характер.
Итак, ускорение плоского движения является суммой двух векторов — касательного ускорения ат .которое по величине равно производной по времени от численной величины скорости и направлено по касательной к траектории, и нормального ускорения адг, которое по величине равно произведению кривизны траектории на квадрат величины скорости и направлено по нормальному вектору. (Заметим, ds
что если k > 0 и 0» то вектор aw направлен к центру кривизны траектории; рис. 11.23.)
•Пример. Движение частицы описывается уравнениями
х = ф(0. У = —1<р(013.
где q(t) — возрастающая функция. Найти траекторию, величину скорости, нормальное и тангенциальное ускорения.
Решение. Траекторией является, очевидно, кубическая парабола у = —х3. Кривизна ее в точке (х, у) равна [ср. с равенством (23) из § 3.15]
= d2y!dx2 =6х .
[1 + (dj//dx)2]3/2	/(Н- 9*4)3
Величина скорости равна
= / ? +	= ]Л1 + Эх4 ф' (0. где X = ф (/).
Единичный касательный вектор и единичный нормальный вектор имеют координаты ( х	у и I ~у	х .
\У хг -|_ yi V х2+ у2 / VУ х2 + у2 У х2+ у2 /
Следовательно,
-г /	1	— Зх2 \	,,	/ Зх2	1	\
1 — ।	, 1	j , IM — ।	, —	“ I •
у 1 + 9х4 V 1 + Эх4 )	\ у 1 + 9х4 v 1 + 9х4 /
Далее,
4г = 4 (Vi + 9x4 ф' (0) = - 18x8	 Ф' (О2 + У1 + Эх4 <р" (0-
Л2	/14-Эх4
§ 4. Движение
291
Из формул (4) получаем
аг “	+ Ч’’ <0 )	~ W,
a»=-4r^-(3x>e‘+eJ-
В этих равенствах х = <р (0*ф
УПРАЖНЕНИЯ
Для каждого из следующих движений найдите скорость, ее численную величину, ускорение, нормальную и тангенциальную составляющие ускорения. Изобразите на чертеже траекторию движения.
1.	г(0 = ^+	/2е2.
2.	г (0 = cos31 ех + sin21 е2, где 0 < t < — • л»
3.	г (0 = cos t ег + cos 2t t%.
A 4. г (0 = a cos t ei + b sin t e2, где а и b — произвольные положительные числа.
1	1	3/2	1
5.	г (0 = — <2ех + — (2t + 1) е2, где t >----------—.
Z	О	£
6.	г (0 = е(е! + е-/е2.
7.	г(0 = cos31ег + cost е2, где 0<t<x.
8.	г (0 = t ef + In t е2, где t > 0.
9.	г (0 = tcos t ti + tsin te2 [У казание: начертите траекторию; воспользуйтесь полярными координатами.]
Ю. г (0 = cos(t + 1) ег + (t + 1) е2.
11. r(t) = tef +У 1 + t2 еа.
4.5. ЗАКОН ДВИЖЕНИЯ
Мы сформулируем теперь закон движения Ньютона: в каждый момент времени ускорение частицы, умноженное на ее массу т, равно действующей на частицу силе. Здесь т есть некоторое число, а так как ускорение а частицы является вектором, то и сила также должна рассматриваться как вектор. Если мы обозначим силу через f, то математическое выражение этого закона Ньютона примет вид
та = f.	(6)
Конечно, это утверждение становится законом природы, который можно подтвердить или опровергнуть экспериментально только в том случае, когда нам известно, как можно определять силу f.
Одно высказывание относительно силы неявно содержится в самой этой формулировке закона Ньютона, но здесь надо сделать пояснение: если на частицу дей
292
11. Векторные функции скалярного аргумента
ствуют две силы Ft и F2, то эта частица будет двигаться так, как если бы на нее действовала сила f, равная сумме векторов Ft и F2.
Читатель заметит, что «правило параллелограмма» для сложения векторов (см. гл. 9, § 1.4) является математическим определением; однако утверждение о том, что результат действия двух сил можно найти, образуя их векторную сумму по этому правилу, является физическим законом.
Если на частицу не действует никакая сила, то, по закону Ньютона, а = О, т. е. v(/) = 0, и v постоянна, а тогда г(/) = Zv -f- const. Частица, на которую не действуют никакие силы, движется прямолинейно с постоянной скоростью. Это утверждение называется законом инерции. Закон инерции часто называют также первым законом Ньютона, а соотношение (6) — вторым законом Ньютона. Имеется еще и третий закон Ньютона, который, однако, относится к движению не одной, а нескольких частиц; мы его здесь рассматривать не будем (см., впрочем, § 6.3).
4.6. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА
В качестве первого приложения закона Ньютона рассмотрим плоское движение частицы под действием силы тяжести. Плоскость, в которой происходит движение, будем считать плоскостью ху, ось у направим «вверх», так что вес частицы будет равен — mge2, где g есть ускорение силы тяжести (ср. с гл. 4, где мы рассматривали только вертикальное движение). Если вес— это единственная сила, действующая на частицу, то уравнение движения имеет вид
/пг = /па = — tnge2, или после сокращения на т и перехода к координатам
X = О, у = — g.
Эти уравнения решаются независимо. Мы имеем
x(t)=a, У (0 = — gt + ₽,	(7)
где а и Р — некоторые постоянные; следовательно,
х(0 = ^ + Т, y(9 = _-L^ + p/4 8,	(8)
где у» б — некоторые новые постоянные. Из равенств (8) видно, что (у, б) — это координаты нашей частицы в момент времени t = 0, а из равенств (7) следует, что (а, Р) — это координаты вектора скорости при t = 0. Та же формула показывает, что горизонтальная составляющая х вектора скорости постоянна во все время движения. (Так и должно быть, поскольку на тело не действует никакая горизонтально направленная сила.) Движение будет полностью определено, если мы знаем начальное положение (у, б) частицы и ее начальную скорость (а, Р).
Формулы (8) дают параметрическое представление траектории. Чтобы найти непараметрическое представление этой кривой, исключим t из уравнений (8). Из первого уравнения, полагая, что а #= 0, получаем t = (х — у)/а. Подставляя это значение t во второе уравнение, будем иметь
1	Iх — 7 \2 । о х — 7 I*
1/ = -——L +р—L + 8,
4	\ а /	л
§ 4. Движение
293
Рис. 11.24
ИЛИ
g х2 ц. gT +х _ g~t2 + 2а37 — 2я28 2а2	а2	2а2
Следовательно, траектория является параболой с вертикальной осью, обращенная выпуклостью вверх (рис. 11.24). Если а = 0, то х постоянно, и мы будем иметь прямолинейное движение по вертикали (такое движение рассматривалось в гл. 4).
Необходимо отметить, конечно, что при выводе уравнений (8) мы пренебрегли сопротивлением воздуха, ветром, влиянием вращения Земли и т. д.
фПримеры. 1. Частица движется по параболе под действием одной только силы тяжести. Показать, что кривизна k ее траектории в вершине параболы зависит только от горизонтальной составляющей скорости. (Здесь мы считаем, что k > 0.)
Первое решение. Обозначим горизонтальную составляющую скорости через а. В вершине параболы вектор скорости горизонтален. Следовательно, в этой точке абсолютная величина скорости равна | а |. Ускорение направлено по вертикали и по величине равно g. В вершине вектор ускорения направлен по нормали к кривой (а = ад/), и в силу равенств (4) g = &а2,или k = gla2. (Пожалуй, стоит проконтролировать полученный результат с помощью учета размерностей: g измеряется в см/с2, а — в см/с, следовательно, k измеряется в см"1, что, разумеется, верно, так как величина, обратная k. измеряется в единицах длины — ведь \/k есть радиус кривизны.)
Второе решение. Пользуясь формулами (8) и равенством (22) из § 3.13, находим
х у — х у
Так как в вершине парабоы у = 0, то в этой точке
=-«
V2	а2
294
11. Векторные функции скалярного аргумента
2. Начальная скорость брошенного тела равна <з cmzc. Его бросают с поверхности Земли под углом 0 к горизонту (где 0 < 0 < 90°); тело падает на Землю на расстоянии d см от первоначальной точки. Найти 0. [Мы предполагаем, конечно* что брошенное тело движется по закону (8).]
Решение. По условию, 6=0; можно предположить, что и у =0. Координаты начальной скорости а = a cos 9 и 3 = ° s*п ® (рис. 11 -25); Следовательно, y(t) =-----значит, у(/)=0 при t =0, т. е. в начальный момент, а также
.	29	2а sin 0 гт	.
при t = — = -----------. Для этого значения t имеем
g 8
.	2а2 sin6 cos в о2 .
х (/) = а/ =-----------= — sin 29;
g	g
эта величина должна равняться d. Следовательно, 9 можно найти из уравнения sin 29 =	, решая которое, получаем два значения 9 ; 9 = 9Х и 9 = 90° — 9Х
(рис. 11.26). е
УПРАЖНЕНИЯ
12.	Ядро вылетает из пушки (расположенной, конечно, на поверхности Земли) с начальной скоростью Оо и падает на Землю, имея скорость ах. Покажите, что о о =
13.	Ядро вылетает из пушки, расположенной на поверхности Земли,, в момент времени t = 0 и падает на Землю при / = tt. Покажите, что максимальной высоты оно достигает при t — t}/2 .
14.	Ядро вылетает из пушки, расположенной в точк§ О на поверхности Земли, с начальной скоростью aej + ре 2. Пусть Р — наивысшая точка траектории и Q — точка, в которой ядро падает на Землю. Обозначим через h высоту точки Р над поверхностью Земли и через г—расстояние между точками О и Q. Пусть 0 — полярный угол вектора началь* ной скорости (угол наклона траектории), а ф = 2 QOP.
а)	Вычислите h и г;
6)	Покажите, что 2 tg(p = tg 0.
[Указание: начертите траекторию; отметьте на ней точки О, Р и Q.]
§ 4. Движение
295
15.	Ядро вылетает из пушки, расположенной на поверхности Земли, с начальной скоростью 10ех + 12е2, где единицами измерения служат метры и секунды. На каком расстоянии от начальной точки ядро упадет на Землю?
16.	Ядро вылетает из пушки, расположенной на поверхности Земли, с начальной скоростью 8ej + 16еа, где единицами измерения являются метры и секунды. На какой высоте оно ударится о вертикальный утес, находящийся на расстоянии 17 м от начальной точки?
17.	Ядро вылетает из пушки, стоящей на поверхности Земли, с начальной скоростью 17е^ + + 13е2 (единицы измерения—метры и секунды). Оно ударяется о вертикальную скалу на высоте 4 м над поверхностью Земли. На каком расстоянии от начальной точки находится эта скала? Объясните, почему возможны два ответа.
18.	Ядро вылетает из пушки, стоящей на поверхности Земли, с углом наклона л/6 радиан (угол наклона — это полярный угол вектора начальной скорости.) Достигнув высоты 21 м, оно ударяется о вертикальную скалу,^находящуюся на расстоянии 27 м от начальной точки. Найдите величину начальной скорости ядра, а также величину скорости, с которой оно ударяется о скалу.
19.	Ядро вылетает из пушки, стоящей на поверхности Земли, достигает максимальной высоты 35 м и падает на Землю на расстоянии 70 м от начальной точки. Найдите начальную скорость ядра.
Д20. Ядро вылетает из пушки, установленной на платформе, высота которой равна 5 м, и через 2 с после выстрела падает на Землю. Тангенс угла наклона траектории равен 2. Найдите горизонтальное расстояние, пройденное ядром.
21.	Ядро вылетает из пушки, находящейся на поверхности Земли, и достигает цели, находящейся на высоте 80 м над поверхностью Земли. Скорость ядра в момент удара равна 16ех- — 10е2. Найдите его начальную скорость и расстояние по горизонтали от пушки до цели.
4.7	. ДВИЖЕНИЕ ПО ЗАДАННОЙ ТРАЕКТОРИИ
Рассмотрим теперь тяжелую частицу, которая вынуждена двигаться по совершенно гладкой траектории (рис. 11.27). Пусть уравнения траектории имеют вид
X = х($), у = t/(s),
где s — длина дуги. Действующие силы — это вес частицы — mge2 и неизвестная нам сила G, принуждающая частицу не сходить с траектории (сила реакции траектории). Мы предположим, что сила G всегда перпендикулярна траектории; это и имеют в виду, говоря, что траектория является совершенно гладкой (т. е. что силы трения, направленные по касательной к траектории, полностью отсутствуют).
Пусть T(s) и N(s) — соответственно единичный касательный и единичный нормальный векторы в точке траектории, отвечающие значению $ параметра (длины дуги). Тогда
Т = х'е, 4- /е2, N = —у'ei 4- х'е2, х'2 + у’1 =1,
где штрихом обозначено дифференцирование по s [см. равенства (17) из § 3.12]. Умножим первое из этих равенств на у', второе — на х' и сложим их; мы получим ®2 = у'Т 4- x'N. Следовательно, вес частицы равен
— mge2 = — mgy'(s)T(s) — mgx'(s)N(s).	(9)
296
11. Векторные функции скалярного аргумента
С другой стороны, направление силы G, по предположению, задается вектором N. Значит, существует такая функция y(s), что
G = t(s)N(s).	(10)
Выше мы видели [см. равенства (4)1, что вектор ускорения равен
где k = k(s) — кривизна траектории в рассматриваемой точке. Применяя к нашему движению закон Ньютона, получим равенство
—+ G = ma.
Используя равенства (9), (10) и (И), мы можем записать закон Ньютона так:
mgy'(s)+ tn -^-Yr(s) + [7(5) — rngx^s) —	N (s) =0.
dt2 )	[	\ dt / J
Так как [T, N| — репер, то это векторное уравнение равносильно двум скалярным уравнениям:
mgy'(s) + т = 0; т (s) = mgx'(s) + mk(s) .	(12)
Первое из них запишем в виде
=	(13)
dt2
это дифференциальное уравнение второго порядка относительно неизвестной функции /h->s(/), описывающей движение нашей частицы. Впоследствии мы покажем, как можно решить такое уравнение. Зная s(/), мы сможем воспользоваться вторым из уравнений (12), для того чтобы найти силу G = ?N, с которой траектория действует на частицу.
4.8	. ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ
Решение общего уравнения (13) мы изложим в Приложении (см. § 5); здесь же мы рассмотрим лишь два простых частных случая. Предположим сперва, что траектория частицы является прямолинейной; мы можем представлять себе, что частица скользит по абсолютно гладкой наклонной плоскости. Тогда (рис. 11.28)
х = х0 + s cos а, у = yQ + $ sin а, а = arctg р,
где р есть наклон траектории. При этом уравнение (13) примет вид
s"(t) = —g sin а.
Общее решение этого уравнения таково:
s(/) = — g t2 + at + b.
§ 4. Движение
297
Рис. 11.27
Поскольку при t = 0 мы имеем s = 6, то b — это значение s в «начальный момент времени». Аналогично, так как s'(/) = —gt sin а + а, то а есть «начальное значение» $'(/), т. е. s'(0). Считая, что начальная скорость частицы (скорость при t = 0) равна нулю и что b = 0, получаем
s(0=-
Так как sin а =------, то мы приходим к известному закону Галилея:
/1 +Ц2
3=--------------t\
2/1+ц2
который мы сформулировали без доказательства в § 1.14 гл. 4.
4.9	. МАТЕМАТИЧЕСКИЙ МАЯТНИК
Теперь мы рассмотрим «математический маятник», т. е. частицу массы /и, укрепленную на (невесомом!) стержне длины Z, вращающемся вокруг точки опоры (точки, в которой подвешен маятник; рис. 11.29) без трения. Мы предположим, что движущаяся частица находится ниже точки опоры, т. е. что частица движется по полуокружности
х = I sinO , у = —I cos0,	(14)
где угол 0 измеряет отклонение маятника от вертикали. Частица движется так, как если бы она скользила по гладкой дуге окружности, определяемой уравнениями (14).
Натуральный параметр $, выбранный так, что s = 0 при 0 = 0,— это s =/0. Следовательно,
, .	$	. s du . s
X = I sin —, у = — I cos —, — = sin ---.
/	I ds	I
298
11. Векторные функции скалярного аргумента
Уравнение (13) приводится теперь к виду
—+gsin —=0.	(15)
dt*	I	'
Это довольно сложное уравнение, решение которого содержит так называемые эллиптические функции. Мы, однако, ограничимся рассмотрением такого маятника, при котором он все время остается вблизи вертикали (как в случае маятника часов). Тогда 0 = у- мало, и мы мало ошибемся, заменив sin у на у. После такого упрощения наше уравнение примет вид
_^ +JLS = O) dt* I
а это уравнение нам хорошо известно (см. гл. 6, § 1.12). Его общее решение имеет вид	___ ______________
s = A cos р/"-у-1 + В sin рЛ-у-t.
Следовательно, если пренебречь ошибкой, которую мы допустили, заменив sin0 на 0, можно сказать, что маятник совершает простые гармонические колебания с периодом
этот период не зависит от амплитуды колебаний, а лишь от длины / стержня и величины ускорения силы тяжести g.
Последняя формула объясняет использование маятника в часовых механизмах, а также применение маятника для измерения ускорения силы тяжести g.
§ 4. Движение	299
4.1	0. ДВИЖЕНИЕ ПЛАНЕТ. ВТОРОЙ ЗАКОН КЕПЛЕРА
Мы переходим теперь к одному из наиболее драматических и в то же время наиболее важных приложений математического анализа: к выводу закона всемирного тяготения из астрономических наблюдений над движениями планет. Этот вывод принадлежит Ньютону; однако в опубликованной им по этому поводу работе Ньютон не пользовался математическим анализом (хотя, вероятно, само открытие было сделано им с помощью анализа).
Первый шаг, который ведет к этому важному открытию, является чисто умозрительным. Этим шагом является признание того факта (сегодня очевидного для нас, но во времена Ньютона требовавшего большой научной смелости, ибо он противоречил всем установкам древнегреческих ученых), что законы физики, полученные из наблюдений над обычными (земными) объектами, применимы также и к небесным телам. Так, например, одна и та же сила заставляет яблоко падать на Землю и Луну вращаться вокруг Земли.
Второй шаг имел чисто математический характер. Кеплер, анализируя астрономические наблюдения Тихо Браге, вывел из них свои знаменитые три закона, управляющие движением планет. Первые два из этих законов таковы:
(I)	Планеты движутся в плоскости, содержащей Солнце, причем их орбиты являются эллипсами, в одном из фокусов которых находится Солнце (рис. 11.30).
(II)	Отрезок, соединяющий планету с Солнцем, в равные промежутки времени «заметает» равные площади,
Ньютон показал (по-видимому, в возрасте 23 лет), что из законов Кеплера вытекает, что ускорение планеты направлено к Солнцу и что по величине оно обратно пропорционально квадрату расстояния планеты от Солнца.
То, что ускорение планеты направлено по прямой, соединяющей ее с Солнцем, вытекает уже из одного только второго закона Кеплера. Чтобы в этом убедиться, введем систему координат, в начале О которой находится Солнце. Пусть г и fl — полярные координаты планеты Р. Тогда движение планеты определяется двумя функциями:
0 =fl(0.
Площадь, заметаемая отрезком ОР от момента времени /0 до /, равна [см. рис. 11.31 и формулу (12) из § 2.61
t	*
-LJ гдаоо) =-L J r(^)dx.	(16)
to	^0
Иоганн КЕПЛЕР (1571—1630) посвятил годы трудным вычислениям, для того чтобы найти математическую гармонию, управляющую, по его убеждению, движениями планет. Не все из его предположений были верными, но в 1609 г. он опубликовал свои первые два закона, а 10 лет спустя сообщил о третьем. Кеплер сделал также первые исследования в оптике. Его трактат об измерении объемов винных бочек * предвосхитил математический анализ.
Однако древние суеверия оказали влияние на жизнь этого создателя современной астрономии. Его официальные обязанности как математика императора Рудольфа II включали составление гороскопов, а его мать была судима за колдовство (но, впрочем, оправдана). Тихо БРАГЕ (1546—1607), датский дворянин, усовершенствовал искусство астрономических наблюдений без телескопов и построил большую обсерваторию на острове Вен. Он обладал достаточной проницательностью для того, чтобы сообщить результаты своих наблюдений тому человеку, который лучше всех смог ими воспользоваться (т. е. Кеплеру).
* Он переведен и на русский язык: см. Й. Кеплер, Стереометрия винных бочек, М.—Л., ГТТИ, 1935.
300
11. Векторные функции скалярного аргумента
Рис. 11.31
В силу второго закона Кеплера производная по времени этой площади
= Yr(Z)2e(Z)
^0
постоянна. Обозначим эту постоянную величину через а; тогда
г20 = 2а.	(17)
Дифференцируя это равенство, получаем
2гг0 4- г20 = 0,
откуда
2/0+/0=0.	(18)
Декартовы координаты точки Р равны х = г cos 0, у = г sin 0, так что вектор скорости v имеет координаты
х = г cos 0 — r0 sin 0, у = г sin 0 + r0 cos 0. Координаты вектора ускорения а будут, следовательно, таковы:
х — г cos 0 — 2г*0 sin 0 — г02 cos 0 — г0 sin 0,
у = г sin 0 + 2 г0 cos 0 — г02 sin 0 4- r0 cos 0.
Пользуясь равенством (18), получим
х = (г — г02) cos 0, у = (г — г02) sin 0,
§ 4. Движение
301
т. е.
х = | —---б2 I X, У — \—------02 ) у.
\ Г	/	\ Г	]
Отсюда видно, что вектор ускорения {х, у} пропорционален радиусу-вектору (х, у\ планеты Р. Следовательно, ускорение планеты направлено к Солнцу.
Величина ускорения равна
|а|=|г’-гб2|.
Чтобы завершить рассуждение, мы должны показать, что величина |а) обратно пропорциональна квадрату расстояния планеты от Солнца. Это будет сделано, если мы покажем, что
= —	(19)
га
где р. — некоторое положительное число. Для доказательства этого мы воспользуемся первым законом Кеплера.
4.11.	ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА КЕПЛЕРА
Траектория планеты является эллипсом с одним из фокусов в точке О; обозначим через 8 эксцентриситет этого эллипса. Вспомним уравнение эллипса в полярных координатах (см. гл. 10, § 1.7): если полярная ось выбрана соответствующим образом, то это уравнение имеет вид
'	1 — е COS 6(0 ’
где А — некоторое положительное число. Из последнего равенства следует г(1 — е cos0) = А.	(20)
Дифференцируя это уравнение по времени, получим г (1 — е cos 9) 4- ег9 sin 9=0. Умножим теперь обе части полученного равенства на г: rr (1 — е cos 9) + er29 sin 9=0, что в силу равенств (17) и (20) можно переписать так: Аг 4- 2aesin9 = 0. Повторное дифференцирование дает
Аг 4- 2ае9 cos 9 = 0.	(21)
302
11. Векторные функции скалярного аргумента
Но из равенства (17) следует, что 9=^-.	(22)
Подставляя это значение 0 в уравнение (21), получим
••__ 4аа е cos в
7*
д
Так как в силу (20) — г cos 9 -----1, то
г
" = 4аа / J___1_\
г	* д г	к]'
Далее, в силу (22)
г92=^-, Г»
так что
7-г92 = -±1.-L.	(23)
А г2
Но это совпадает с равенством (19), которое нам и требовалось доказать; при этом
4.12.	ПРИМЕНЕНИЕ ТРЕТЬЕГО ЗАКОНА КЕПЛЕРА
Мы видели, что из первых двух законов Кеплера следует, что планета Р движется вокруг Солнца О, испытывая ускорение, по величине равное
4аа 1
А ’ г2 ’
Здесь г = ОР — расстояние планеты от Солнца и
1 — е cos о
— уравнение орбиты планеты в полярных координатах. Постоянная а определяется равенством (17), т. е. а — это площадь, заметаемая отрезком ОР в единицу времени. Пусть Т — период обращения планеты вокруг Солнца; тогда аТ равно площади эллипса. Если полуоси эллипса равны а и 6, то площадь его будет равна nab (см. пример в § 1.8 гл. 10). Следовательно,
а = ^-.	(25)
Из уравнения (20) видно, Что наибольшее и наименьшее расстояния планеты Р от Солнца О равны рр и Следовательно,
(рис. 11.32), или	' - - •
А = а(1 — s2).
§ 4. Движение
303
Далее,
b — a yi —в8,
так что в силу равенства (25)
ла» V1 — е3 а =-----------
Т
и, значит, 4аа 4каа3
<26>
Величина притяжения, испытываемого планетой со стороны Солнца, следовательно, равна
4тсад3ш 1	/07\
Г2 *	1 '
(так как она равна массе, умноженной на величину ускорения).
Теперь мы воспользуемся третьим законом Кеплера:
(III) Отношение а3/Т2 одинаково для всех планет.
Ньютон вывел отсюда, что сила притяжения со стороны Солнца единицы массы планеты «универсальна», т. е. одна и та же для всех планет и зависит только от расстояния планеты от Солнца. Далее, законы Кеплера справедливы также и для спутников планет, в частности для спутников Юпитера. Однако значение дроби аЧТ2 для спутников Юпитера отличается от ее значения для планет.
Эти соображения привели Ньютона к закону, состоящему в том, что между любыми двумя массами Мит действует сила взаимного притяжения, равная по величине
(28) где г есть расстояние между массами, а ? — некоторая универсальная постоянная.
304
11. Векторные функции скалярного аргумента
Сравнивая равенства (27) и (28), заключаем, что масса Солнца равна
7 Г»
Если — масса планеты (или другого Солнца), a Ci и Л — большая полуось и период обращения ее спутника (соответственно планеты), то мы имеем
и, следовательно,
М = а8Г? Mr ~ а^Т*
Так астрономические наблюдения позволяют сравнивать массы двух небесных тел. Однако для того чтобы вычислить действительные значения этих масс, надо непосредственно измерить гравитационную постоянную 7. Это сделал, и притом весьма тщательно, Кавендиш в 1798 г.
4.13. НЕБЕСНАЯ МЕХАНИКА
Читатель мог заметить, что при выводе ньютоновского закона всемирного тяготения из законов Кеплера мы нигде не использовали того обстоятельства, что эксцентриситет орбиты е< 1. Те же самые рассуждения годятся и для случаев, когда орбита является параболой (е = 1) или гиперболой (е > 1). Для круговой орбиты (8 == 0) эти рассуждения дали бы нам мало информации, так как в этом случае г было бы постоянным.
Можно обратить наше рассуждение и показать, что частица под действием притягивающей силы, направленной к постоянному центру О и по величине обратно пропорциональной квадрату расстояния от центра, всегда движется по коническому сечению с одним из фокусов в точке О и подчиняется второму закону Кеплера о постоянстве «секториальной скорости». Мы не будем проводить эти вычисления.
Однако в действительности планеты подчиняются законам Кеплера только приближенно. Каждая планета, а также и Солнце испытывают притяжение и со стороны всех других планет. Начиная с самого Ньютона, поколения математиков развивали основанные на математическом анализе методы, учитывающие эти побочные
Генри КАВЕНДИШ (1731 —1810) был очень богатым и очень эксцентричным английским аристократом, жившим почти как отшельник и выполнившим некоторые из самых блестящих экспериментов в истории науки.
Джон Кауч АДАМС (1819—1892) учился а Кембриджском университете и провел здесь также и всю последующую часть жизни. Еще будучи студентом, он заинтересовался неправильностями в движении планеты Уран л через несколько нот аьлшслмн движение более далекой планеты (впоследствии названной Нептуном), притяжением которой вызываются яти отклонения.
Урбен Жан Жозеф ЛЕВЕРЫ (1811—1877) быв директором Парижской обсерватории* когда он решил ту же проблему, что и Адамс. Оба ученых работали, ничего не зная друг о друге. Один немецкий астроном направил свой телескоп в точку небосвода* указанную Леяерье, и увидел новую планету. Сам Леверье, по-видимому, никогда не имел желания взглянуть на нее.
§ 4. Движение
305
эффекты, для решения проблем «небесной механики». Важным триумфом этой науки было открытие в 1846 г. планеты Нептун. Прежде чем кто-либо увидел эту планету в телескоп, Адамс и Леверье вычислили ее массу и определили ее орбиту, изучая отклонения в движении планеты Уран. Современное исследование Вселенной ставит перед небесной механикой новые задачи, и современные счетные машины позволяют нам эти задачи решать.
Существует, однако, планета, для описания движения которой недостаточно механики Ньютона. Некоторые особенности в движении Меркурия — самой близкой к Солнцу планеты солнечной системы — удается объяснить только с помощью общей теории относительности Эйнштейна.
УПРАЖНЕНИЯ
22.	Пусть $(/) — функция, определенная при 0 < t < + <х>; предположим, что для всех tz и а имеет место равенство S(t± + а) — 3(/г) = S(/a+ а) — S(tz). Если представлять себе t как время, это означает то, что S в одинаковые промежутки времени получает равные приращения. Положим а = S( 1) — S(0) и b = S(0).
а)	Покажите, что для каждого t > 0 и любого целого положительного числа т имеет место равенство S (mt) = mS (t) + (1 — m)b.
Указание. Запишите
S(mf) — S(0) = \S(mt) —S((m — 1) /)] + [S((m — 1) t) — S((m — 2)/)] + ... + [S(0 — S(O)J.
б)	Покажите, что для любого целого положительного числа п имее! место равенство
Указание. Запишите
S(l) —S|——| + S I 	) — S ( —==~ )+••• + s(— — S(0)
\ п /J L \ п /	\ « /j	L \ п /
в)	Покажите, что для любого положительного рационального числа г справедливо равенство S(r) = аг + Ь. Если предположить, что S непрерывна, то S(t) = at + b для всех t. По существу, этот результат был использован выше при применении второго закона Кеплера.
23.	Предположим, что вместо первого закона Кеплера справедлив закон, согласно которому орбиты планет являются спиралями, уравнения которых в полярной системе координат с началом в Солнце имеют вид г = ре® ; при этом предположим также, что второй закон Кеплера справедлив.
а)	Покажите, что г =	, где го = <(0).
б)	Покажите, что в этом случае ускорение обратно пропорционально кубу расстояния планеты от Солнца.
24.	В упр. 23 предположим, что спирали имеют уравнения г = 00.
а)	Покажите, что г = ( 6а0/ +	, где г0 = г(0).
б)	Покажите, что ускорение не пропорционально никакой степени (ни положительной, ни отрицательной) расстояния планеты от Солнца.
25.	Предположим, что вместо ньютонова закона всемирного тяготения имеет место закон: <сила притяжения планеты Солнцем пропорциональна расстоянию между ними». Какой вид примут в этом случае законы, управляющие движением планет?
306
Приложение к главе 11
Приложение к главе 11
§ 5. Движение по заданному пути
В § 4.7 мы вывели дифференциальное уравнение для движения тяжелой частицы, вынужденной скользить без трения по некоторой траектории, параметрические уравнения которой имеют вид г = x(s), у = y(s). Здесь s — длина дуги траектории, а отрицательное направление оси у совпадает с направлением силы тяжести. Это уравнение приводится к виду [см. уравнение (13) из § 4.7J
бРз dt2

(1)
-рде g —ускорение силы тяжести. В настоящем параграфе мы рассмотрим решение этого уравнения и те выводы, которые можно из него сделать.
5.1.	Решение уравнения
Уравнение (1) можно решить, пользуяоь таким искусственным приемом. Умножив обе части уравнения на ds/dt, получим
ds cPs	ds
dt dt2	dt
или
d f 1 / ds \*	\
зг(“г(й7 +	=°-
at \ z \ at /	/
Отсюда видно, что наше уравнение равносильно следующему утверждению: величина ~-s'(02 + gy{s) в процессе движения не меняется. Обозначив эту постоянную величину через
е, получим
1 / ds \2
тЫ =	(2)
\ di ]
(Это есть частный случай закона сохранения энергии, но нам здесь понятие энергии не понадобится.)
Пусть движение продолжается в течение некоторого временнбго интервала, причем производная s\t) сохраняет знак, скажем, все время положительна. Тогда из равенства (2) получаем
- = F2e-2®(S) dt
(3)
§ 5. Движение по заданному пути
307
Рис. 11.33
Рис. 11.34
Так как s'(t) > 0, то для функции t s(t) существует дифференцируемая обратная функция;, это значит, что мы можем рассматривать t (время) как функцию s (расстояния, измеренного вдоль траектории). В силу (3)
dt___________1
*	/2(е —gi/(s)j
и если I = 0 при s = «о, то
. г di
* =	------ (4>
Переходя опять к функции t s, мы и получим нужный результат.
Мы еще не знаем значения е, но его можно определить по величине а скорости ds/dt при /=0. Действительно, в силу уравнения (2) имеем
* = -7“°2 + g*/(so) •	(5>
&
Предположим, что при so s < Sf функция y(s) является убывающей (рис. 11.33) и что частица начинает движение на высоте у0 = y(so) с начальной скоростью 0. Пусть мы хотим-найти время т, которое потребуется на то, чтобы частица достигла высоты у^ = y(sf). Для этого мы должны взять в качестве е значение gy(so) (так как начальная скорость равна нулю) и применить равенство (4) при s = sj. Так мы получим, что
т=	——•	(6)
{ /2g [«/(«о) — </(s)l
5.2.	Периодическое движение
Предположим теперь, что рассматриваемая траектория является графиком четной функции уу которая сначала убывает, достигая своего минимума, а затем возрастает, как это показано на рис. 11.34. Пусть значения s = 0 и у = 0 соответствуют самой низкой точке этой кривой.Мы поместим частицу в точку Р, соответствующую значению параметра — so < О на высоте Ао и отпустим ее в момент времени t = 0 с начальной скоростью 0. Она будет скользить вниз к точке О, затратив на этот спуск время
308
Приложение к главе 11
-I l^2g 1у0 —у($)]
(7)
В момент времени т частица будет иметь некоторую скорость о, которую легко можно сосчитать. Действительно, в силу равенства (2) величина (ds/dt)2 + 2gy в процессе движения остается постоянной; при t = 0 она равна 2gy^. Следовательно, о = У2gyQ. Дальше частица будет подниматься до тех пор, пока ее скорость не станет равной нулю. Это случится именно в тот момент, когда будет достигнута высота уо. После этого частица снова будет скользить вниз, а затем подниматься до тех пор, пока не достигнет первоначального положения Р. Потом весь процесс повторится снова. (Это вечное движение оказалось возможным только потому, что мы пренебрегли трением.)
Первый подъем, второй спуск и второй подъем продолжаются столько же времени, как и первый спуск, т. е. т единиц времени. Это ясно из соображений симметрии и может быть проверено непосредственным вычислением. Период Т всего движения равен, следовательно, 4т, т. е.
S. K2g[i/0 — j/(s)j
или поскольку у — четная функция от s, то
•S, V2g[(y0— t/(s)|
(8)
Эта формула была выведена в предположении, что мы используем параметрическое представление траектории, причем за параметр принята длина дуги. Удобно переписать ее и для произвольного параметра 0 (мы не хотим здесь использовать букву t, сохраняя ее для обозначения времени). Если
sh>s(0), s(0) = 0, s(0o) = so, причем s(—0) = —s(0),
есть допустимая замена параметра, то
®о	1
г»	1	ds
Т=2	----------------- dO.	(♦)
_в, Г 2g [г/, - j/(s(«))J
3а мети м, что	_____________
ds	Г / dx \2 ( du V
d? = |/ \ de / + \ d? /
и что х и у можно рассматривать как функции 0; поэтому равенство (*) можно переписать так:
С , Л<dx/db)2+ (dy/dti)2
J v 2g(y0-y)	-
или в сокращенных обозначениях е. _________________________________________________
« С , / dx2 + dy2
J V 2g(y0-y) '
(9)
В общем случае Т зависит от траектории и от амплитуды уо.
§ 5. Движение по заданному пути
309
5.3.	Круговой маятник
Вычислим период Т для круговой траектории, т. е. период колебаний математического маятника (см. § 4.9). В этом случае кривая определяется уравнениями х = I sin 0, z/=—I cos 0. Следовательно,
где
О»
/а cos2 6 + /а sin2 6 2g (I cos 0 — I cos 0O)
* = sin “9°:
de
У cos e — cos eo
здесь мы воспользовались тождеством cos х = 1 — 2 sin1 2 — . 2
Если мы
теперь положим
1 . О
U~ k Sln 2 *
то получим, что
du
/(1 — u2) (1 — л2и2)
Это так называемый «эллиптический интеграл»; его значение зависит от начального смешения в,. Но если во мало, то
X» = sin2 — 2 очень мало (так, например, при Оо = 5° значение I2 = 0,0019). В этом случае можно пренебречь членом Х2и2; сделав это, получим приближенное значение
которое мы и имели в § 4.9.
Замечание. Интегралы (6), (7), (8) и (9) являются несобственными (см. гл. 5, §6.1), так как у = у0 при s = ± s0, т. е. при 0 = ± 0о. Но если y'(s) непрерывна и /(s0) #= 0, как мы предположили, то указанные интегралы сходятся, что можно доказать, пользуясь теоремой сравнения из § 6.4 гл. 5. Эти детали мы здесь опускаем.
310
Приложение к главе 11
5.4.	Циклоидальный маятник
Гюйгенс поставил вопрос о том, существуют ли кривые, для которых Т на самом деле ие зависит от амплитуды (начального смещения). Он нашел, что .этим свойством обладает циклоида (это доказать легко), и притом только циклоида. Последнее утверждение доказать не-просто,иэто доказательство мы здесь опустим. Циклоидалконечно, должна быть расположена так, чтобы ее точки возврата находились сверху (рис. 11.35).' Параметрическое представление такой кривой ср. с § 2.5) имеет вид
х = а (0 + sinG), у = а (1 — cos 0).	(10)
[Представление (10) можно получить из параметрического представления (7) в § 2.5, если заменить сперва х на х — ал, а у на 2а — у, а затем заменить параметр t на 0 + л.| В таком случае равенство (9) приводится к виду
Христиан ГЮЙГЕНС (1629—1695) — математик, астроном и физик, создатель волновой теории света *. (Эта теория была единственной, .принятой физиками, до появления квантовой теории, примирившей волновую теорию Гюйгенса с корпускулярной теорией света Ньютона.)
Голландец с независимыми средствами, Гюйгенс в течение многих лет жил в Париже. Здесь он встретил 26-летнего Лейбница, которого обучил современной ему математике.
Блез ПАСКАЛЬ (1623—1662) был, возможно, самой поразительной фигурой в истории матема-тики. Еще в детстве он самостоятельно понял необходимость доказательства того, что сумма углов треугольника равна 180°. В 16 лет он доказал основную теорему о конических сечениях и написал большой трактат об этих кривых, ныне утерянный. Наиболее замечательными достижениями Паскаля были создание (вместе с Ферма) теории вероятностей и' его работа о давлении газов и жидкостей. Он построил также первую вычислительную машину.
Однако позднее в жизни Паскаля стали преобладать мистические и религиозные интересы. Его «Письма провинциалу» (блестящая теологическая полемика) и особенно посмертно опубликованные «Мысли» ** являются шедеврами французской и мировой литературы.
* См.: X. Гюйгенс, Трактат о свете, М.—Л., ОНТИ, 1935.
** См.: Б. Паскаль, Мысли. В книге: «де Ларошфуко, Максимы; Мысли; Ж. де Л е б р ю й е р, Характеры», М., Худ. лит-ра, 1974.
Б. Паскаль,
§ 5. Движение по заданному пути
311
где мы положили
sin -ув
V~ . 1 ’ s,n-70o
Следовательно, Т, как и утверждалось, не зависит от 0о.
Гюйгенс указал также, как именно можно реализовать такой циклоидальный маятник: для этого гибкая нить с точечной массой, укрепленной в ее конце, должна качаться между двумя жесткими циклоидами (рис. 11.36). Тяжелая частица на конце маятника будет при этом описывать т.чк называемую эвольвенту циклоиды, которая также является циклоидой. (Мы не доказываем этого здесь; ср. с задачами 21 и 24 в конце главы.) В часах циклоидальные маятники не используются.
Циклоида (10) обладает и другим замечательным свойством, которое мы упомянем без доказательства. Если соединить точку Р циклоиды с ее самой низкой точкой Q л ю б о й кривой С, отличной от циклоиды (рис. 11.37), то на спуск от Р до Q вдоль этой другой кривой потребуется больше времени, чем на спуск по циклоиде, т. е. больше, чем л f^a/g. Несколько известных математиков получили этот результат независимо Друг от друга, среди них — два брата Бернулли (Якоб и Иоганн) и Паскаль*. Это открытие было важным шагом в создании той ветви математики, которая называется вариационным исчислением,
5.5.	Несимметричные траектории и пружины
Исследование движения тяжелой частицы по симметричной траектории с одним минимумом, такой как траектория, изображенная на рис. 11.34, можно повторить без существенных изменений и для случая кривой, которая сначала опускается, а затем поднимается, не будучи симметричной.
Результат Гюйгенса относительно циклоиды можно получить также, пользуясь новой интерпретацией уравнения (1). Выясним, для какой кривой х = х($), у = y(s) уравнение (1) является уравнением упругой пружины, которая совершает простые гармонические колебания с периодом, не зависящим от амплитуды (см. гл. 6, § 1.14). При этом мы должны иметь y'(s) =bs, где b >0— постоянная. Так как мы хотим, чтобы выполнялось равенство х'($)2 + y'(s)2 = 1, то x'(s) = = Y 1 — 62$2 • Если потребовать, чтобы при $ = 0 мы имели х = у = 0, то простым интегрированием получаем	________
arcsin (bs) -f- bs У" 1 — b2s2	bs2
*=-------’ *=—• <n>
Допустимая замена параметра 0=2 arcsin (bs) преобразует эти уравнения в уравнения (10)» где а = ---. Следовательно, искомая кривая является циклоидой.
4Ь
Уравнение (1) можно также рассматривать как уравнение движения пружины с массой т и восстанавливающей силой —(glm) y'(s). Это видно из определения пружины, данного в § 5.1 гл. 5. В этой интерпретации наше уравнение, записанное в виде (2), действительно совпадает с законом сохранения энергии, рассмотренным в § 5.4 гл. 5.
УПРАЖНЕНИЯ
1.	Предположим, что кинетическая энергия частицы, скользящей вниз по заданной гладкой 1	(ds\2 w
траектории, равна (df/ * ^ак Д°лжна быть определена потенциальная энергия, чтобы уравнение (2) было законом сохранения энергии?
2.	Проверьте, что циклоида является траекторией наибыстрейшего спуска, сравнивая спуск по циклоиде со спуском по прямой.
* А также — Лейбниц и Ньютон.
312
Приложение к главе 11
3.	Проверьте, что циклоида является траеторией наибыстрейшего спуска, сравнивая циклоиду с дугой окружности. [Замечание: учтите, что сделать это не очень легко.]
4.	Примените равенство (6) к случаю y(s) = —s. Что означает этот результат?
5.	Выполните замену переменной sh> 6, предложенную в конце § 5.5 для преобразования уравнений (11) в уравнения (10).
6.	Не используя знания тригонометрических функций, покажите, как можно прийти к первообразной для функции и н>(1 —	1/2 , решая дифференциальное уравнение
s"(t) + s(t) =0.
§ 6. Движение системы
В этом параграфе мы вкратце рассмотрим вопрос о движении системы, состоящей из н е-скольких частиц. При этом мы придем к важному понятию центроида.
6.1.	Две взаимно притягивающиеся частицы
Рассмотрим сначала две частицы с массами иц и т*, расположенные в точках Рх и Ра. Предположим, что единственная сила, действующая на частицы, — это сила взаимного их притяжения. Пусть гх и гз — радиусы-векторы точек Рх и Ра. Направленный отрезок РхРа представляет вектор Га—гх (рис. 11.38), расстояние между точками Рх и Рг равно | г2 — гх |. На первую частицу действует сила притяжения со стороны второй; эта сила, которую мы обозначим через f12, определяется равенством
где у — гравитационная постоянная, и и — единичный вектор (вектор длины единица), направленный от первой частицы ко второй. Ясно, что и = (га —rj/] —Гг |. Следовательно, и, аналогично, .	h — г2
-  Заметим, что
Ь1 + кз = 0.	(2)
Точка с ради у сом-вектором _ тхг1 4- т2г2
R = —L——	(3/
mx 4- т2 называется центроидом (пли центром масс) наших двух материальных точек. Напомним (см. гл. 9, § 2.1), что эта точка лежит на отрезке РхРа и делит его в отношении т^/т^ (см. рис. 11.39, где тх = 4/па). Мы утверждаем, что наши частицы движутся так, что ускорение их центроида равно нулю.
В самом деле, по второму закону Ньютона, л1хгх = tx2, т2т2 = la* Складывая эти два равенства и учитывая (2). получаем 01хгх 4- т^2 = 1х2 4- ^21 = 0, но это и означает, что R = 0.
Следовательно, центроид системы двух частиц движется прямолинейно и равномерно.
§ 6. Движение системы
313
Рис. 11.39
6.2. Задача двух тел
центроид

В § 4 мы рассматривали движение планеты вокруг Солнца. В этом рассуждении Солнце предполагалось неподвижным и сила притяжения, действующая на Солнце со стороны планеты, не принималась во внимание. Теперь мы рассмотрим так называемую задачу двух тел: движение двух частиц с массами тг и тг и радиусами-векторами гх и г2, притягивающими друг друга по закону всемирного тяготения.
Выше мы доказали, что ускорение центроида двух притягивающихся частиц равно нулю. Мы можем, следовательно, ввести такую систему координат, в которой этот центроид неподвижен. В этой системе координат все законы физики имеют обычный вид — последнее утверждение вытекает из так называемого принципа относительности классической механики (или принципа относительности Галилея). Далее, мы будем предполагать, что центроид совпадает с началом координат, т. е. что
R = 0.	(4)
Из равенства (3) следует, что
/п1г1 + т2Г2 = 0, или
mi г2 = — — Г!. т2 Поэтому
и сила f12, действующая на первую частицу, — это
[ср. с формулой (1)]. Положим
в таком случае получим
I П|
Этот результат означает, что первая частица движется так, как если бы она притягивалась неподвижным телом массы A4lf помещенным в пентроиде этих двух частиц. Она движется, следовательно, подчиняясь законам Кеплера, вокруг этого центроида; ее траектория является коническим сечением, один из фокусов которого совпадает с центроидом системы, причем отрезок, соединяющий центроид с частицей, в равные промежутки времени описывает равные площади.
314
Приложение к главе 11
Предположим, что масса мала по сравнению с т2, как в случае планеты, вращающейся вокруг Солнца, если, конечно, эта планета не является огромным Юпитером. Тогда центроид системы «планета—Солнце» находится вблизи от центра Солнца и «присоединенная масса» (5) близка к массе Солнца /иг. Поэтому мы не сделаем большой ошибки, считая Солнце неподвижным. Однако в случае системы «Солнце—Юпитер» и тем более в случае двойной звезды с двумя сравнимыми по массе компонентами приходится описывать это движение как движение (по законам Кеплера) каждой из компонент вокруг их центроида.
Мы только что показали, что задача двух тел легко сводится к «задаче одного тела», т. е. к задаче о движении частицы вокруг неподвижного центра притяжения. В случае трех и большего числа взаимно притягивающихся тел (задача трех тел и задача п тел) положение является гораздо более сложным. Успешное решение задачи л тел (где п > 3) может быть получено только с помощью громоздких численных расчетов.
УПРАЖНЕНИЯ
1. Предположим, что две частицы одинаковых масс, притягивающие друг друга по ньютоновскому закону всемирного тяготения, движутся по круговой орбите с одной и той же (постоянной по величине) скоростью. Предположим, что нет никаких других сил, действующих на эти две частицы. Что Вы можете сказать о взаимном положении этих двух частиц?
^2. Двойная звезда состоит из двух компонент. Каждая движется по некоторой эллиптической орбите, в одном из фокусов которой находится центроид двух компонент. Астрономическими наблюдениями установили периоды обоих движений и длины осей их орбит. Возможно ли вычислить отношение масс этих звезд? И если да, то как?
3.	Мы определили центроид двух частиц, используя понятие радиуса-вектора. Можно было бы думать, что центроид зависит от выбора начала отсчета радиусов-векторов. Покажите, что это не так.
6.3.	Третий закон Ньютона. Линейный импульс
Закона движения Ньютона (f = /па) недостаточно для описания движения системы, состоящей более чем из одной частицы. Для этого необходимо добавить третий закон Ньютона. Это некоторый закон симметрии, который утверждает следующее:
Силы, с которыми две частицы действуют друг на друга, противоположны.
Точнее, рассмотрим систему, состоящую из N частиц с массами т±, m%, ..., mN и радиусами-векторами rj, г2. .... Гд, . Предположим, что на каждую частицу mj действуют N—1 сил 1д, iy2,..., ijN со СТ0Р°НЬ1 Других частиц с массами mit m2t...t mN (где саму частицу с массой /Пу мы, естественно, пропускаем) и некоторая «внешняя» сила 1. Тогда «внутренние» силы 12у подчиняются условию симметрии [ср. с равенством (2)]:
V* + iki = 0-	(6)
(Критически мыслящий читатель может запротестовать против некоторого кажущегося антропоморфизма третьего закона, содержащего ссылку на «внутренние» силы частиц. Однако реальное содержание этого закона как раз и состоит в возможности разделения всех действующих на систему частиц сил на «внешние» и «внутренние», причем «внутренние» силы должны подчиняться закону симметрии.)
Применяя второй закон Ньютона к каждой из N частиц, получим W векторных уравнений:
= 112 4" Ьз 4" • • • + liy 4" h»
/П2Г2 = f21 4“ I23 4- • • • 4-	+ I2»
гл/ — 1дл 4- 1/V2 4- • • • 4- fv.v—i 4-fу.
§ 6. Движение системы	315
Сложим все эти уравнения. Так как в силу третьего закона Ньютона (6) все внутренние силы Друг друга уравновешивают, мы получим
/ПГ1 + /л2г2 + • •' 4“ mN = fi -р fa + • • • + fy.	(7)
Вектор v; = Гу — это скорость /й частицы. Произведение myVy называется линейным им-пульсом /-й частицы, а сумма
Q =	4- m2v2 4----b rnNyN
— (полным) линейным импульсом системы.'
Далее, обозначим через
F = fi 4- f-г 4~' • • •• 4- f#
сумму всех внешних сил. Равенство (7) можно переписать так:
Q = F;	(8)
оно утверждает, что производная по времени от линейного импульса системы равна сумме всех внешних сил. Если внешних сил нет, то Q = О и
Q = mxvi 4- m2v2 4----F *N = const
Это утверждение называется законом сохранения линейного импульса. Из него вытекает, что •если при отсутствии внешних сил скорости каких-либо частиц возрастают в одном, направлении, то скорости других частиц должны возрастать в противоположном направлении. Этим объясняются такие явления, как отдача орудия и реактивное движение.
6.4.	Центроид ЛГ частиц
Центроидом (центром масс) данных N частиц, по определению, является точка с радиусом-вектором
min 4- ш2г2 4----И rnN rN
R =------у— ----------" •	(9)
mi 4~ т2 4~ • •' 4-
Это определение оправдывается тем, что справедлива следующая
Теорема. Центроид системы частиц движется так, как двигалась бы помещенная в этой точке частица массы /их 4- /пг + .*. + niN = М. под действием силы F = fx 4" fa 4" • •• + f,v (полная внешняя сила).
Для того чтобы доказать это, нам надо только заметить, что производная по времени радиуса-вектора центроида N частиц равна
. /пхп 4- т2г2 -и > > > 4- гу Q mi 4- /п2 4- • • • 4- ты	М
Следовательно, MR = Q и в силу равенства (8)
MR= F.	(Ю)
Но это есть дифференциальное уравнение движения частицы массы М с радиусом-вектором R под действием силы F.
316
Приложение к главе 11
УПРАЖНЕНИЯ
4. Покажите, что положение центроида нескольких частиц не зависит от выбора начала отсчета радиусов-векторов (точки с радиусом-вектором 0).
5. Обычно мы не чувствуем своего веса. Можно ли объяснить это с помощью третьего закона Ньютона?
^6. Используя ответ на предыдущий вопрос, объясните, почему в условиях свободного падения (например, космонавт в своей кабине) человек становится «невесомым».
7.	Объясните, почему сохранение линейного импульса «виновно» в отдаче ружья. Объясните, как именно сохранение линейного импульса используется при реактивном движении.
6.5.	Твердое тело
Только что доказанная теорема применвма, в частности, к твердым телам.
Твердое тело — это система частиц, в которой внутренние силы между частицами таковы, что расстояния между частицами не меняются. [Такие понятия, как «частица» или «твердое тело» являются, конечно, идеализациями. Никакое тело в действительности не явлется вполне твердым, но многие тела в ряде случаев допустимо считать твердыми.) Предшествующие рассуждения показывают, что центроид (центр масс) твердого тела движется так, как если бы он был частицей, в которой сосредоточена вся масса тела, причем на эту фиктивную «частицу» действует сила, равная сумме всех действующих на тело внешних сил.
Для того чтобы полностью описать движение твердого тела или какой-нибудь другой системы, мы должны, следовательно, вычислить движение частиц по отношению к их центроиду. Это очень интересная задача, но обсуждение методов ее решения увело бы нас слишком далеко от нашей основной темы.
6.6.	Свойство аддитивности
Перечислим три свойства центроида W частиц.
1.	Предположим, что мы разделили все частицы системы на две группы. Пусть центроид частиц первой группы находится в точке Р^, а центроид частиц второй группы — в точке Ръ. Предположим также, что общая масса всех частиц первой группы равна Mv а частиц второй группы — равна М 2. Тогда центроид всей системы совпадает с центроидом двух частиц, одна из которых находится в точке Рх и имеет массу Л1х, а другая находится в точке Р% и имеет массу М 2.
Это свойство называется аддитивностью центроида. Оно легко обобщается на случай разбиения множества всех частиц на несколько групп.
Доказательство свойства 1. Мы можем предположить, что первая группа включает в себя частицы с массами т^, m2, ...» т^ и радиусами-векторами г^, г2,..., г*, а вторая— частицы с массами mk+l, mkJr2..mN и радиусами-векторами гЛ+1, г^+2, ...» тогда Mj =
= тА + m2 + ... + т^ и Л1 2 = mk+i + mk^2 + ... + Пусть Rj и R2 — радиусы-векторы точек Р^ и Р2. По определению центроида имеем
Л "ИЪ Н- • • • + mk^k ъ mk+irk+i + * ‘ ’ + mN r.v
Ri=	..	»	.	•
Mx	M2
Далее, центроид системы, состоящей из частицы с радиусом-вектором Rj и массой Mi и частицы с радиусом-вектором R2 и массой М 2, задается радиусом-вектором
M,R, + M2R2 от»г‘ 4-------+ тн rN
Мх-^-М2	т,+  +mN
а это и есть центроид всех рассматриваемых частиц.
§ 6. Движение системы
317
6.7.	Положение центроида
2.	Если все частицы системы принадлежат одной плоскости, то их центроид принадлежит той же плоскости. Если все частицы системы принадлежат одной прямой, то и их центроид принадлежит той же прямой.
Для того чтобы доказать это, выпишем координаты центроида системы частиц с массами тг, та...mN, расположенными в точках с координатами (xlt у19 zx), (х*, у2, z*),...,(xN, yN, zN).
Мы можем считать, что (xj, yj, zj) — это координаты радиуса-вектора Гу относительно некоторого репера. Пусть (X, Y, Z) — координаты радиуса-вектора R центроида, или, что то же самое, декартовы координаты центроида системы частиц. Из равенства (9) следует:
4-	т%хъ + • • • + т^ х^
^1 + ^2 4---н mN
т1У1 + ^2^2 4“ • • • 4" У
Y =------7-----7---7--------’	(п>
"h	4-	т2 4--4-	mN
miZi 4- m2z2 4- • • • 4~
Z=------------------------ .
mi 4- m2 4- • • • 4- mN
Доказательство свойства 2. Если все частицы принадлежат одной плоскости, то можно выбрать такую систему координат, длй которой эта плоскость совпадает с координатной плоскостью х = 0. Тогда Xj = 0 при всех j, а следовательно, в силу равенств (11) и X = 0. Поэтому центроид системы частиц принадлежит плоскости х = 0.
Если все частицы принадлежит одной прямой, то существуют две плоскости, пересекающиеся по этой прямой. По доказанному выше, центроид системы принадлежит каждой из этих плоскостей, а значит, и их линии пересечения.
6.	8. Свойство симметрии
3.	Если частицы расположены симметрично относительно некоторой плоскости, то их центроид принадлежит этой плоскости. Если все частицы принадлежат одной плоскости и расположены симметрично относительно некоторой прямой этой плоскости, то центроид системы частиц принадлежит этой прямой. Если все частицы принадлежат одной прямой и расположены симметрично относительно некоторой точки этой прямой, то их центроид совпадает с этой точкой.
Доказательство свойства 3. Говоря, что частицы расположены симметрично по отношению к некоторой плоскости о, мы имеем в виду, что если частица массы т, расположена в не принадлежащей о точке Pit то найдется другая частица той же массы mit расположенная в некоторой точке Pj, причем отрезок PjPi перпендикулярен плоскости о и делится этой плоскостью пополам.
Предположим, что плоскость симметрии о совпадает с координатной плоскостью х = 0; ясно, что этого всегда можно добиться соответствующим выбором системы координат. Если частица массы mf имеет координаты (xit yit z^), где xt =# 0, то существует и частица массы my = m-t с координатами ху = —jq, z/y = yit Zj = z^. Следовательно, в выражении для X в равенствах (11) все члены в числителе взаимно уничтожаются. Поэтому X = 0 и, значит, центроид системы частиц принадлежит плоскости х = 0, т. е. плоскости симметрии частиц.
Предположим теперь, что все частицы расположены в плоскости т симметрично относительно прямой I этой плоскости. Тогда все частицы расположены симметрично относительно плоскости о, проходящей через I и перпендикулярной т. Следовательно, по доказанвому выше, их центроид принадлежит плоскости о, а по свойству 2, он принадлежит также и плоскости т. Поэтому центроид системы принадлежит прямой I.
Предположим, наконец, что все частицы принадлежат прямой I и расположены симметрично относительно точки Р этой прямой. Это означает,что все частицы расположены симметрично отно
318
Приложение к главе 11
сительно плоскости о, проходящей через точку Р и перпендикулярной прямой Z. Центроид системы, по доказанному выше, принадлежит плоскости о; по свойству же 2, он принадлежит прямой I. Отсюда следует, что центроид системы совпадает с точкой Р.
УПРАЖНЕНИЯ
8.	Докажите следующее обобщение свойства 1. Если система из N частиц делится на К групп и если центроиды частиц этих К групп совпадают с точками Ръ Pz, ..., Р^, то центроид данной системы является также центроидом системы, состоящей из К частиц, расположенных в точках Pj, Рг, ..., Pk и имеющих массы М19 М2,..., М^, где Му есть полная масса у-й группы частиц.
9.	Покажите, что на концах данного отрезка можно поместить две (положительные) массы таким образом, что их центроид будет совпадать с любой наперед заданной внутренней точкой отрезка. Будут ли эти массы однозначно определенными? А их отношение?
10.	Пусть Pj, Р2, Р3 — три вершины треугольника, a Q —данная внутренняя точка этого треугольника. Покажите, что найдутся три положительных числа т19 m2, т8, такие что /Л1 + /Пг + щ8= 1, и что центроид трех частиц масс mv mz, т3, расположенных в точках Р^, Р2, Р3, совпадает с точкой Q. Будут ли эти три числа однозначно определенными?
11.	Покажите, что каждая внутренняя точка квадрата является центроидом четырех частиц, помещенных в четырех вершинах этого квадрата. Покажите, что массы этих частиц можно определить бесконечным числом способов, даже если потребовать, чтобы сумма всех масс была равна 1.
-ЗАДАЧИ
1. Пользуясь определением производной векторной функции, содержащимся в равенствах (16) и (17) из § 1.6, найдите производные следующих векторных функций, не обращаясь к их координатам: 11-> fa + b. i f2a + f3!) + Л |a| sin t а. [Здесь a, b и c —
постоянные векторы.]
2.	Докажите, что если t н* f(f) — непрерывная векторная функция, определенная на отрезке [а, Ь], то
ь	ъ
а	а
3.	Пусть t r(f)— определенная на [а, Ь] непрерывная дифференцируемая векторная функция. Она определяет некоторую кривую С. Покажите аналитически, что длина этой кривой не меньше расстояния между ее начальной и конечной точками, иными словами, — что прямолинейный отрезок является кратчайшей траекторией из всех, соединяющих его концы.
4.	Определите ориентированные кривые, изображениями которых на плоскости являются: цифра 8, буква Я, греческая буква 6, квадрат вместе с двумя его диагоналями. Какие из этих кривых могут быть гладкими?
5.	Пусть х f[x) — непрерывная скалярная функция, определенная на отрезке 0 <	1. Предположим, что существует такое число а, 0 < а < 1, что f(x) возрас-
тает на (0, а) и убывает на (а, 1), причем /(0) = f(l) = 0. С помощью формулы (12) из § 2.6 сосчитайте площадь области, ограниченной графиком функции Z и отрезком [0,1],
1
и покажите, что эта площадь равна J [(x)dx.
Б. Покажите, что результат предыдущей задачи остается справедливым, если f(0) и £(1) положительны.
7.	Покажите, что гладкая ориентированная кривая с постоянным единичным касательным вектором Т является прямолинейным отрезком.
3.	Найдите все кривые на плоскости, для которых угол между единичным касательным вектором в точке Р кривой и вектором, представляемым отрезком ОР, где О —фиксированная точка, является постоянным. [Указание: воспользуйтесь полярными координатами.]
Задачи
ЗИ*
9.	Докажите, что кривая, кривизна которой тождественно равна нулю, является прямолинейным отрезком.
10.	Докажите, что плоская кривая, кривизна которой постоянна, является дугой окружности.
11.	Пусть t f(0 и t g(0 —две дифференцируемые векторные функции, определенные на одном и том же интервале. Докажите, что (fg)* = f‘*g + f«g*. (Здесь точка означает дифференцирование по отношению к /, а произведение векторов — это их скалярное произведение, определенное в § 6 гл. 9.)
12.	Предположим, что частица движется в плоскости таким образом, что ее скорость постоянна по величине. Докажите, что в каждый момент времени ускорение частицы* перпендикулярно ее скорости.
13.	Сила взаимодействия между двумя электрически заряженными частицами пропорциональна их зарядам и обратно пропорциональна квадрату расстояния между ними; они притягиваются или отталкиваются в зависимости от того, будут ли их заряды разноименными или нет (закон Кулона). Рассмотрим две частицы: фиксированную Йоложительно заряженную частицу, находящуюся в начале координат, и другую, тоже положительно заряженную частицу, двигающуюся по гиперболе, один из фокусов которой совпадает с началом координат; будем считать еще, что движение частиц подчиняется второму закону Кеплера о постоянстве «секториальной скорости». (Такие движения встречались в опытах Резерфорда, относящихся к атомной физике.) Покажите, что такое движение согласуется с законом Кулона. [Указание: вспомните, что гипербола имеет два фокуса.]
14.	Понятие центроида системы материальных точек («частиц») можно распространить и на отрицательные массы. Условимся считать, что числа mj в формулах (9) и (11) из § 6 могут быть равными нулю или отрицательными. Покажите, что если Pf, Рг и Р3 — три фиксированные точки плоскости, не принадлежащие одной прямой, то каждая точка Q плоскости является центроидом расположенных в точках Pf, Рг, Р$ масс m2, m3 (не обязательно положительных). Покажите также, что если потребовать, чтобы выполнялось равенство mf + тг + т3 = 1,то эти массы т^ одиозна ч-н о определяются точкой Q. [В этом случае числа т^, m2, т3 называются барицентрическими координатами, точки Q по отношению к базисному треугольнику Р1Р2Р3.]
15.	Пусть mlt m2, m3 — барицентрические координаты точки Q по отношению к треугольнику РгР2Р3, Переведите следующие утверждения в утверждения относительно масс т^, m2, т3: Q = Р^; точка Q принадлежит прямой, проходящей через Р/ и Р2; точка Q лежит внутри или на границе треугольника Р1Р2Р3; Q есть внутренняя точка этого треугольника.
16.	Пусть Plt Р2, Р3 и Р4 — четыре точки пространства, не лежащие в одной плоскости. Определите барицентрические координаты точки пространства относительно тетраэдра (треугольной пирамиды) Р1Р2Р3Р4. Ответьте на вопросы, аналогичные тем, которые были поставлены в задаче 15 для случая плоскости.
17.	Пусть А — плоская кривая, определяемая уравнениями х = x(t), у = y(t), где x(t) и y(f) имеют непрерывные производные второго порядка. Обозначим через k(t) кривизну кривой в точке (x(f), y(t)) и через £(/)» 'n(Z) — координаты центра кривизны. Предполагая, что k =/= 0, докажите, что
= , (х'2+у'а)*'
Х х'у" — x"yf ’ У х'у" — х"у'
(для краткости мы опустили параметр /)• Кривая, определяемая векторной функцией t н► C(/)ei + т](/)е2, называется эволютой кривой А. Она может иметь особые точки и может вырождаться в точку (если А является окружностью).
18.	Как упрощаются формулы задачи 17, если:
a)	t является натуральным параметром для кривой А;
б)	кривая А является графиком функции х у = [(х)?
Шарль Огюстен КУЛОН (1736—1806), французский военный инженер, государственный служащий и физик, сделал несколько важныж открытий в области злектростатики.
Эрнест РЕЗЕРФОРД (1871—1937), новозеландец по происхождению, ббльшую часть жизни проведший в Англии; открыл атомное ядро. На основании своих экспериментов он предложил пер-вую модель внутренней структуры атома.
320
Приложение к главе 11
19 Найдите непараметрическое представление эволюты параболы л н> у = х2. (Эта парабола и ее эволюта изображены на рисунке.)
20.	Покажите, что эволюта циклоиды х = t — sin/, у = 1 —cos/ тоже является циклоидой, равной исходной, но смещенной по отношению к ней на 2 единицы вниз и на л единиц вправо. (Эти две циклоиде: изображены на рисунке.)
21.	Пусть А — гладкая кривая с ненулевой кривизной. В каждог очке Q кривой А проведем касательную к А и отметим на ней такую точку S, что Q лежит между Р и S и длина кривой, состоящей из дуги А, заключенной между точками Р и Q, и прямолинейного отрезка QS, равна а. Кривая В, состоящая из всех полученных таким путем точек S, называется эвольвентой (разверткой) А. Заметим, что если кривую А представлять себе сделанной из твердого материала, то эвольвента В может быть построена «механически», посредством разматывания нити, натянутой на «катушку» А (см. рисунок вверху.) Натянутая на А нить предполагается гибкой, но нерастяжимой.
Пусть параметрическое представление кривой А имеет вид и = u(t), v = v(t), где (и, и)— декартовы координаты, a t — длина дуги кривой А, измеренная от точки Р. Покажите, что параметрические уравнения эвольвенты В кривой А имеют вид
X = u(t) + (а — t)u'(t), У = v(t) + (а — /)и'(0-
22.	Покажите, что эволюта эвольвенты кривой А совпадает с А. (Здесь мы считаем, что параметрическое представление кривой А через натуральный параметр трижды непрерывно дифференцируемо.)
23.	Вычислите и начертите эвольвенту окружности и = cos /, v = sin t.
24.	Покажите, что эвольвента циклоиды f(/) = (t — sin /)ех + (1 — cos /)ег тоже является циклоидой (см. задачу 20). (Этот результат объясняет устройство циклоидального маятника Гюйгенса.)
12/ЧАСТНЫЕ ПРОИЗВОДНЫЕ
До сих пор в этой книге мы рассматривали лишь функции одной переменной, т. е. правила, согласно которым данному числу ставится в соответствие некоторое число или некоторый вектор. В этой и в следующей главах содержится введение в математический анализ функций нескольких переменных. Мы рассмотрим здесь только простейшие вопросы этой теории.
В настоящей главе на функции нескольких переменных распространяются понятия непрерывности и дифференцируемости, а в § 4 рассматривается некоторый способ интегрирования таких функций, приводящий к так называемым криволинейным интегралам.
В Приложении рассматриваются применения криволинейных интегралов к механике (см. § 5). Приложение содержит также доказательства некоторых теорем и формулы Тейлора для функций нескольких переменных.
322
12. Частные производные
§ 1. ФУНКЦИИ	Между функциями одной и функциями нескольких
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ	переменных имеются существенные различия. В то же время переход от двух переменных к большему их числу, как правило, не представляет затруднений; поэтому обычно мы будем подробно рассматривать только случай функций
	двух переменных.
1.1. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Функция двух переменных — это правило, ставящее в соответствие каждой упорядоченной паре чисел (из некоторого множества таких пар) определенное число. Множество пар чисел, которым ставятся в соответствие другие числа, называется областью определения этой функции. Область определения функции обычно будет видна из контекста. Для функций двух и большего числа переменных мы будем пользоваться точно такими же обозначениями переменных и стрелкой >->, как и для функций одной переменной.
Как и прежде, примем такое соглашение: в том случае, когда функция определена некоторой формулой, и если только не оговорено противное, мы принимаем за область определения этой функции наибольшее множество пар чисел, на котором наша формула имеет смысл.
Имея дело с функциями двух переменных (х, у) »-> z, обычно удобно рассматривать пару чисел х и у как координаты точки плоскости в некоторой декартовой системе координат. (Читатель помнит, что мы аналогично поступали и в случае функций одной переменной — только там мы отождествляли число х с соответствующей точкой числовой оси.) Функцию двух переменных мы можем представлять себе как правило, ставящее в соответствие каждой точке плоскости (или каждой точке из-некоторой области точек плоскости) определенное число.
Определения суммы, разности, произведения и частного двух функций, точно так же как и композиции функций, аналогичны соответствующим определениям для функций одной переменной; поэтому нет необходимости их здесь формулировать.
•Примеры. 1. Правило
(х, у) X + у
ставит в соответствие каждой паре чисел их сумму. Если мы обозначим это правило через /, то можем написать
Г ’	Кх, у) = х + у
и, например, /(2, 1) = 3, Д1, 2) = 3 и Дх, 0) = х для каждого значения х. Если обозначить через z то число, которое ставится в соответствие паре (х, у), то рассматриваемую функцию можно записать так:
z = х + у.
Эта функция определена для всех пар (х, у) или, как говорят, определена всюду.
§ 1. функции нескольких переменных
323
2.	Функция у) = ±
У определена для всех х и всех t/#=0. Так, мы имеем /(4, 2) =2, f(2, 4) = = 0,5, /(0, у) = 0 для всех у 0 и т. д.
3.	Функция
fix, у) = Ух—у
определена для всех (х, у), таких что х> у.
4.	Положим
fix,у) = х2 + у2, six,у) = х2— у2, ср(х) = cos х,
ф(х) = sin х.
Тогда, как легко проверить,
fix,у) + gix,y) = 2х2, fig(x,y), у2) = х4— 2х2у2 + 2/, /(ф(х), Ф(*)) = 1. gi<fix)> Ф(*)) = cos 2х.
<f>igix, у)) = cos(x2— у2), g(f(x, у), g(x, у)) = 4х2у2.
Каждая из этих функций определена всюду.
5.	Функция
х2 + у, если у 0,
определена всюду.ф
х3 + ху У
315,
если х>0, //>0,
если х < 0, у > 0,
(х, y)i->z =
УПРАЖНЕНИЯ
В упражнениях 1—4 предполагается, что <р(х) = In х, [(х, у) = хг + У2 + 1. ф(х) — 6х, Z(x) =	1/х. Вычислите	следующие	функции:
1.	М<Р«(3,1))).	3.	«ф(2),?(3)).
2.	Ф((«0,0))).	4.	Г[/(х,х)Р-2	.
5.	Положим h(s, 0 = | 1 — s | | 1 — t | — st — |s | — |/ | — 1. Для каких nap s, t имеем /i(s, t) = 0?
6.	Пусть k(a, b) = | a | + | b |. В (0, Q-плоскости начертите график функции 6(0 = = fc(sin /.cos Q.
7.	Пусть a(a, 0) = arctg a/0 , b(a, 0) = a2 + 0 2; покажите, что sina = an}/rd cos a = 0 . A 8. Покажите, что если r(/n, n) = eOTcos n, s(m, n) = e^sin n, to [r(/n, n)]2— [s(/n, n)]2 = = r(2/n, 2n) и 2r(/n, n) = s(2m, 2n).
9.	Пусть f(x) = x при x > 0, f(x) = 0 при г<0и пусть, далее, g(x, у) = х2е?. Упростите выражение h(x, у) = g(f(g(x, у)), g(xt у).
1.2	. ИНТЕРВАЛЫ
Множество внутренних точек некоторого прямоугольника со сторонами, параллельными координатным осям, называется конечным открытым двумерным интервалом. или, короче, открытым интервалом. Такое множество изображено на рис. 12.1. Его можно определить как множество всех таких точек (х, y)t координаты которых удовлетворяют неравенствам
а0<х<а,, Ро < У < Pi»	(1)
324
12. Частные производные
где а0, di, Ро, Pi— некоторые числа, такие что а0 < аь Ро < Pi. Точка с координатами х = (а4 + d0)/2, у = (₽! + ₽о)/2 называется центром этого интервала. (Это точка пересечения диагоналей прямоугольника.) Граница интервала состоит из четырех ограничивающих прямоугольник отрезков.
Множество, состоящее из всех точек открытого интервала и всех его граничных точек, называется замкнутым интервалом (рис. 12.2). Таким образом, замкнутый интервал, соответствующий открытому интервалу (1),— это множество всех точек (х, у), координаты которых удовлетворяют неравенствам
do<x<db p0<t/<Pi.	(2)
Условимся, что слова «в окрестности точки Р» (в плоскости) означают «в некотором интервале с центром в точке Р». Так как каждый интервал с центром в точке Р содержит некоторый круг с центром Р, и обратно (рис. 12.3), то слова «в окрестности точки Р» означают также «в некотором круге с центром Р», или «во всех точках Q, расстояние которых от Р меньше некоторого фиксированного положительного числа».
§ 1. Функции нескольких переменных
325
1.3	. НЕПРЕРЫВНОСТЬ
Понятие непрерывности для функций двух переменных является естественным обобщением понятия непрерывности для функций одной переменной (см. гл. 3, § 3.2). Грубо говоря, функция /(х, у) непрерывна, если небольшие изменения х и у вызывают небольшое же изменение Дх, у). Точное определение таково:
Функция f(x, у), определенная при х = х0, у = у0, называется непрерывной в точке (х0, у0), если она обладает следующими свойствами:
I. Если А — произвольное число, такое что f(x0, у0) < А, то f(x, у) < А для всех тех точек (х, у) в окрестности точки (х0, у0), для которых функция f определена.
II. Если В — произвольное число, такое, что В < f(x0,y0),mo В <Z f(x, у) для всех тех точек (х, у) в окрестности точки (х0 у0), для которых функция f определена.
Как и для функции однбй переменной (см. гл. 3, § 3.2), это определение эквивалентно такому е - 8-определению: функция f(x, у) называется непрерывной в точке (х0, (/0)> если для любого наперед заданного положительного числа & найдется такое положительное число 6, что
I f(x, у) — /(х0, у0) | <е для всех точек (х, у), для которых f(x, у) определена и
V (.х — х0)2 + (у — у^ <8.
Наконец, функция называется непрерывной на множестве S, если она определена и непрерывна в каждой точке множества S.
Сумма, разность и произведение непрерывных функций непрерывны; частное непрерывных функций непрерывно во всех тех точках, где его знаменатель не равен нулю. Композиция непрерывных функций тоже является непрерывной функцией. Все это доказывается точно так же, как для функций одной переменной (см. гл. 3, § 3 и 6). Далее, если f(x) — непрерывная функция одной переменной, то функции двух переменных F(x, у) = f(x) и G(x, у) = f(y) непрерывны; доказательство этого утверждения очевидно. Легко видеть, что каждый одночлен (х, у) ь-> схпут, где с — произвольно выбранное число, а п и т — некоторые неотрицательные целые числа, является непрерывной функцией. Следовательно, каждый многочлен от двух переменных, т. е. сумма конечного числа одночленов, всюду непрерывен. Рациональная функция от двух переменных, т. е. частное двух многочленов, непрерывна во всех точках, в которых знаменатель отличен от нуля. Иррациональная функция двух переменных (определение такой функции аналогично соответствующему определению, данному в § 2.7 гл. 3) непрерывна во всех тех точках, в которых она определена.
•Примеры. 1. В каких точках непрерывна функция (х, у) »-► esin (*2+2{/) + cos ху ?
Ответ. Эта функция непрерывна всюду, так как она представляет собой сумму двух функций, каждая из которых является композицией непрерывных функций.
326
12. Частные производные
2.	В какой области определена функция f(x, у} = tg -у ? Где она непрерывна?
Решение. Частное х/у определено при у =/= 0. Предполагая, что у =/= 0, мы видим, что функция f определена для всех тех значений х и у, для которых частное х/у не является нечетным кратным л/2, т. е. при
— =#= 2” + п = 0, ±1, ±2...............
У 2
Йными словами, функция f(x, у) определена для всех точек(х, у), не принадлежащих ни прямой у = 0 и ни одной из прямых
тс	тс	Зтс	Зтс	5тс
X =---у9 X =--------у, X =-----у, X ----------у9 X =---- у.....
.2	2 У 2	2	2
Будучи композицией непрерывных функций, функция f непрерывна всюду, где она определена.
3.	Функция
g(x, у) =
———, если (х, у) ф (0, 0), х2 + у2
----, если х = у = 0, 134-*
определена всюду; эта функция непрерывна всюду, за исключением точки х = у = 0.
4.	Рассмотрим определенную всюду функцию
Ф (X, у) =
———, если хг 4- у2 =#= 0,
(х2 + у2)2	J
0, если х = у = 0.
Если мы выберем фиксированное значение х и будем рассматривать ф(х, у) как функцию только у, то мы получим непрерывную функцию одной переменной. В самом деле, при фиксированном х = а ф 0 мы имеем ф(х, у) = -2- ПРИ всех ес* ли же х = 0, то ф(х, у) = 0 при всех у. Аналогично, для каждого фиксированного значения у функция х !-* ф(х, у) является непрерывной функцией х. Но функция ф, рассматриваемая как функция двух переменных (х, у), не является непрерывной в начале координат. В самом деле, ф(0, 0) = 0 < 1, но в каждом интервале с центром (0, 0) найдется точка (х, у), в которой ф(х, у) > 1, например точка х = у = Г, где 0 < t < у .
Этот пример показывает, что свойство функции быть непрерывной по каждой из переменных х, у в отдельности является более слабым, чем ее свойство быть непрерывной по совокупности переменных (х, г/).ф
§ 1. Функции нескольких переменных
327
УПРАЖНЕНИЯ
В упражнениях 10—23 для каждой функции найдите область ее определения и множество точек непрерывности.
10.	х"1 + у Ч
11.	(1 + r/2)/sin х.
12.	1/7 — /Я_
13.	/| X I - /I у |.
14.	sin (х/у).
15.	sin(xtgy).
16.	| х |У.
17.	| х |1/Ы.
18.	(х2 + t/a)/(Jr2 — уг).
19.	arctg ^(у/х).
20.	f(x, у) = ху при х> 0 и 0; f(x, у) = 0 при х < 0 или у < 0.
21.	f(x,	у)	=	ху, если х и у одного знака, и f(x, у) = 0 в противном	случае.
22.	f(x,	у)	=	ху, если х> 0; f(x, у) = 0, если х < 0.
23.	fix,	у)	=	ху, если х + yZ> 0; ft(x, у) = 0, если х + у < 0.
1.4	. ФУНКЦИИ ТРЕХ И БОЛЬШЕГО ЧИСЛА ПЕРЕМЕННЫХ
Едва ли необходимо даже говорить о том, что функция трех переменных — это правило (х, у. z) u=f(x, у, z), по которому каждой упорядоченной тройке чисел из некоторого множества таких троек ставится в соответствие определенное число. Аналогично, для каждого целого положительного числа п функция п переменных — это правило
(хь х2, .... Хп)^и = f(xlt х2, ...» хп),	(3)
ставящее в соответствие определенные числа и некоторым упорядоченным последовательностям из п чисел (n-наборам). Каждую такую упорядоченную последовательность из п чисел полезно представлять себе как совокупность координат точки или как совокупность координат радиуса-вектора х такой точки (в обычном, т. е. трехмерном, пространстве при п = 3 и в n-мерном пространстве при любом п > 0). При этом мы сможем писать вместо (3)
X U = /(х).
Открытый n-мерный интервал — это множество всех точек (хь х2, •••, координаты которых удовлетворяют неравенствам
ау< ху< ру, / = 1, 2, .., и,
где а; и Ру — числа, такие что ау < Ру. Соответствующий замкнутый интервал — это множество всех таких точек (хь х2, •••, *л), координаты которых удовлетворяют неравенствам
а7<Ху< Ру, j = 1, 2, ..., п.
Точка с координатами
называется центром рассматриваемого интервала.
Здесь можно повторить определение термина «окрестность», сохраняя его в том же виде, в каком оно было дано в § 1.2, и определение непрерывности, данное в §1.3. Мы сформулируем только e-8-определение непрерывности для функции п переменных.
328
12. Частные производные
Функция х ->f(x), определенная при х=х0, называется непрерывной в топке х0, если для каждого наперед заданного положительного числа г можно найти такое положительное число 6, что \f(x) —/fx0)|< в для всех х, для которых f(x) определена и | х — х0 | <6.
Теоремы о непрерывных функциях, установленные в § 1.3, справедливы и для функций трех и большего числа переменных.
Замечание. Непрерывная функция, определенная на множестве S, остается, конечно, непрерывной и на любом подмножестве множества S. В частности, непрерывная функция нескольких переменных остается непрерывной, если мы зафиксируем значения одной или нескольких переменных.
УПРАЖНЕНИЯ
Для каждой из указанных в упражнениях 24—29 функций найдите область определения и множество точек непрерывности этой функции.
24.	у/х + xlz + г/у.	21,	ху In г.
25.	у!(хг) + x/Q/z) +	z/(xy).	28.	(х2 + у2 + z2)/(x +	у + г).
26.	xs\n(y!z).	29.	(xz— yz)!(x — у).
1.5	. ПРЕДЕЛЬНЫЕ ТОЧКИ. ПРЕДЕЛЫ
Пусть S — множество точек (на числовой прямой, на плоскости, в обычном, трехмерном, пространстве или в n-мерном пространстве) и Р — некоторая точка. Эта точка может принадлежать или не принадлежать множеству S. Спрашивается, существует ли такой интервал с центром в точке Р, который не содержит точек множества S, отличных от Р? Если такого интервала не существует, то точка Р называется предельной точкой (или точкой накопления) множества S. Иными словами, точка Р является предельной точкой множества S, если каждый интервал с центром Р содержит точку множества S, отличную от Р (и, следовательно, содержит бесконечно много точек множества S, поскольку каждый интервал содержит бесконечно много меньших интервалов). Например, каждая точка границы открытого или замкнутого интервала является предельной точкой этого интервала. С другой стороны, точка (1, 1) не является предельной точкой для множества точек оси х.
Пусть S — некоторое множество, f — определенная на этом множестве функция и Р — предельная точка множества S с радиусом-вектором х0; в самой точке х0 функция f может и не быть определена. Поставим вопрос: существует ли число а, такое что если мы определим (или переопределим ) функцию f в точке Р, полагая ее значение /(х0) равным а, то эта функция станет непрерывной в точке Р? Если такое число а существует, то его называют пределом функции f в точке Р; это записывается так:
lim/(x) = а.
X—►Хо
Таким образом, утверждение
lim/(x) =/(х0) X—>х0
означает, что точка х0 является предельной точкой области определения функции f, причем эта функция в точке х0 определена и непрерывна в ней. [То, что функция
§ 1. Функции нескольких переменных
329
f может иметь в точке х0 не более одного предела, доказывается точно так же, как для функций одной переменной (ср. с. § 4.1 гл. 3).1
Понятие предела функции f в точках, не являющихся предельными для области S определения этой функции, не имеет смысла — в таких точках функцию f можно доопределять произвольным образом, это не скажется на ее непрерывности. Так, например, функция /(х, у), равная х\/~у при у > 0, равная — 7 в точке (—1, —1) и не определенная в остальных точках, непрерывна всюду, где она определена. Ее непрерывность не нарушится, если мы положим /(—1, —1) = 5 или /( — 1, —1) = Ю0 000.
Доказанные в § 4 гл. 3 теоремы о пределах при соответствующем изменении их формулировок сохраняют силу и для функций нескольких переменных; доказательства этих теорем по существу не меняются. Для функций нескольких переменных можно так же определить и бесконечные пределы. Так, например, утверждение
lim /(х) = + оо
(х. Ъ) означает, что
lim	—!— = 0,
(х, b) f(x, у)
причем /(х, у) >. 0 в окрестности точки (а, Ь). Мы не проводим здесь детального исследования понятия предела функции нескольких переменных, так как пользоваться им будем редко.
•Примеры. 1. Краков предел функции f(x, у) = х2 3— 2ху + у4 при (х, у) ->(—7, 2)?
Решение. Так как функция /(х, у) является многочленом, то она определена и непрерывна всюду; следовательно,
lim /(м)=/Н, 2) = 93.
(х. £/)—>(—7.2)
2. Найти предел функции /(х, у) = Vх2у при (х, у) -+(—1, —1).
Решение. Поставленный вопрос не имеет смысла. Функция /(х, у) определена при х2у 0, т. е. если у 0 или если х = 0. Таким образом, областью определения этой функции служит верхняя полуплоскость, дополненная лучом х = 0, у с 0. Точка (—1, —1) не является предельной точкой рассматриваемого множества; поэтому нельзя ставить вопрос о пределе/(х, у) в этой точке.
3. Найти предел
..	27
lim ---------------.
(X, t/)->(0,0) х4 4- 2х2 4- у*
Решение. Этот предел равен 4-оо, так как рассматриваемая функция больше нуля в окрестности точки (0, 0), а величина, ей обратная, является многочленом, принимающим значение 0 в точке х = у = 0.
4. Имеет ли функция f(x9 у) = sin 1п(х4 + у2) предел при (х, у) ->(0, 0)?
Ответ. Нет. Если х4 + У2 приближается к нулю, то функция ^(х4 4- у2) принимает отрицательные значения, сколь угодно большие по абсолютной величине, так что в каждом интервале с центром в начале координат /(х, у) принимает все значения между —1 и +1.ф
330
12. Частные производные
1
Рис. 12.6	Рис. 12.7
1.6	. ОТКРЫТЫЕ МНОЖЕСТВА. ГРАНИЦЫ
При изучении функций одной переменной мы всегда предполагали, что областью определения всех рассматриваемых функций является интервал или объединение нескольких интервалов. Для функций нескольких переменных такое ограничение является слишком жестким. Так, например, функция /(х, у) = К*2 + У2— 1 определена при х2 + у2 >• 1, ее область определения не является интервалом.
Множество S точек (прямой, плоскости, обычного трехмерного пространства или n-мерного пространства) называется открытым, если вместе с каждой точкой Р оно содержит также целиком некоторую окрестность точки Р (на прямой, на плоскости и т. д.), т. е. все точки некоторого интервала с центром в Р.
Так, например, открытый двумерный интервал (рис. 12.4) является открытым множеством плоскости. В то же время замкнутый интервал не является открытым множеством: сформулированное выше условие не выполнено, например, для угловых точек (рис. 12.5). Вся плоскость является открытым множеством. Пустое множество, совсем не содержащее точек, по определению, является открытым множеством.
Граничная точка множества S — это такая точка Q, что каждый интервал с центром Q содержит как точки, принадлежащие S, так и точки, не принадлежащие S. Совокупность всех граничных точек множества S называется его границей.
Так, например, если S есть множество всех таких точек (х, у). для которых х2 + у2 < 1 (это множество называется открытым единичным кругом), то граница множества S состоит из всех таких точек, для которых х2 + у2 = 1 (единичная окружность). Если S есть открытый или замкнутый двумерный интервал, ограниченный прямоугольником /?, то границей множества S служит прямоугольник /?.
Обычно нам придется иметь дело с функциями, определенными в некотором открытом множестве или в открытом множестве, дополненном его граничными точ
§ 1. Функции нескольких переменных
331
ками — всей его границей или ее частью. Это соответствует тому, что говорилось выше о функциях одной переменной, так как можно показать, что каждое открытое подмножество прямой является суммой непересекающихся открытых интервалов.
Замечание. Будет ли множество S открытым и каковы его граничные точки, зависит от того, рассматриваем ли мы это множество как подмножество прямой, или плоскости, и т. д. Так, например, множество всех таких точек х, что 1 < х < 2, можно рассматривать как множество точек прямой. В этом случае оно будет открытым множеством, и его граница состоит из двух точек х = 1 и х = 2 (рис. 12.6). Но множество всех точек вида (х, 0), где 1 <; х < 2, рассматриваемое как множество точек плоскости, не является открытым (рис. 12.7), причем каждая точка (х, 0), где 1 х 2, является для него граничной.
УПРАЖНЕНИЯ
В упражнениях 30—34 установите, будет ли данное множество точек плоскости открытым. (Система координат предполагается заданной.)
^30. Множество всех точек плоскости, сумма координат которых отрицательна.
31.	Множество всех точек плоскости, для каждой из которых по крайней мере одна из координат отрицательна.
32.	Множество всех точек плоскости, у каждой из которых обе координаты положительны.
33.	Множество всех точек плоскости, у которых ни одна из координат не является отрицательной
34.	Множество точек, абсциссы х которых удовлетворяют уравнению sin х = 0.
35.	Пусть А и В — открытые множества; множество С состоит из точек, принадлежащих хотя бы одному из множеств А и В, а множество D состоит из точек, принадлежащих обоим множествам* А и В. Будет ли множество С открытым? Будет ли множество D открытым?
^36. Пусть {Лх, А 2. ...} —бесконечная совокупность открытых множеств. Обозначим через Е множество всех точек, принадлежащих по крайней мере одному из множеств А}, а через F — множество точек, принадлежащих всем** Докажите, что множество Е открыто. Покажите, что можно найти такие множества {Л J, что F не будет открытым.
37.	Найдите границу множества, определенного в упр. 30.
38.	Найдите границу множества, определенного в упр. 31.
39.	Найдите границу множества, определенного в упр. 34.
40.	Пусть А — множество всех таких точек плоскости, обе кооординаты (х, у) которых являются рациональными числами; найдите границу множества А.
41.	Будет ли открытым множество таких точек (х, у), для которых ха + у2 1? Какова граница этого множества?
42.	Существуют в точности два таких множества точек плоскости ху, которые вовсе не имеют граничных точек. Какие это множества?
1.7.	ГЕОМЕТРИЧЕСКАЯ И ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИИ
Функция двух переменных (х, у) >-► /(х, у) = г, определенная на некотором множестве S, может быть представлена геометрически с помощью своего графика — множества всех таких точек (х, у, г) пространства, что точки (х, у) принадлежат S, а г = /(*> У)- График функции двух переменных, как и в случае функции одной переменной, содержит всю информацию относительно этой функции. К сожалению,
* С называется объединением (или суммой) множеств А и В, a D — их пересечением (или произведением); записывается это обыкновенно так: С = A U В; D = А П В (ср. ниже, стр. 430).
** Е называется объединением множеств А} (запись: Е= уДр, a F — пересечением
i
(это записывается так: Е = П Л f).
332
12. Частные производные
начертить такой график на бумаге не просто. Если /(х, у) — непрерывная функция, определенная на некотором открытом множестве или на открытом множестве, дополненном точками его границы — всей границей или ее частью, то график функции f называется поверхностью, или, точнее, поверхностью, заданной непараметрически. Вообще же множество точек называется поверхностью, если оно может быть разложено на несколько частей, каждую из которых при некотором выборе системы координат можно записать явным уравнением вида z = f(x, у).
фПримеры. 1. Функция нескольких переменных называется линейной, если она является многочленом первой степени. График линейной функции двух переменных представляет собой плоскость. В самом деле, такая функция может быть представлена в виде
(х, у) »-> z = ах + by + с,
где а, Ь, с — постоянные числа. Но мы знаем, что множество точек (х, у, z), координаты которых удовлетворяют уравнению ах + by + с — z = 0, является плоскостью (см. гл. 9, § 4.3).
2.	Графиком функции
(х, у) 1-> У\—х2 — у2
является верхняя полусфера единичной сферы. В самом деле, если г = У\ — х2—у2, то г >• О и х2 + у2 + г* = 1
3.	График функции
г = х2,
рассматриваемой как функция двух переменных, т. е. график функции
(х, у)л-+х2,
является параболическим цилиндром (ср. с § 4.2 гл. 10).
4.	График функции
/(х, у) = х2 — у2
является гиперболическим параболоидом. Эту поверхность мы рассматривали в § 4.6 гл. Ю.ф
Для функции трех (или большего числа) переменных также можно определить график, но это будет множество точек пространства четырех (или большего числа) измерений. Он не может быть изображен на чертеже или тем или иным способом построен; его также невозможно представить себе зрительно.
Иногда полезно интерпретировать функцию трех переменных (х, у, z) >-► и-> /(*, z) = Ф» скажем, как температуру ср в точке с координатами (х, у, z). Функцию четырех переменных (х, у, z, /) i-> ср можно представить себе как температуру в точке (х, у, z) в момент времени t. Существует много аналогичных представлений функций трех или большего числа переменных.
§ 2. Производные функций нескольких переменных
333
§ 2.	ПРОИЗВОДНЫЕ В этом параграфе мы применим к функциям нескольких ФУНКЦИЙ переменных первую из основных операций математического НЕСКОЛЬКИХ анализа — операцию дифференцирования.
ПЕРЕМЕННЫХ
2.1.	ЧАСТНЫЕ ПРОИЗВОДНЫЕ
Пусть дана функция двух переменных (х, у) f(x, у). Зафиксируем значение второй переменной у0 и рассмотрим функцию х i-»- f(x, у0) одной переменной. Возможно, что эта функция при х = х0 имеет производную; это означает, что существует (конечный) предел
jjm/(*» + &, Уо)~/(*о. Уо) ' h-*o	h
Этот предел называется частной производной по х функции (х, у) f(x, у) в точке (х0, Уо) и обозначается так:
/ dt \	df	д х/ .
——1	, ИЛИ —ИЛИ — f(x0,y0).
\ OX Jx=Xot У=Уо	их	ОХ
(Символ д читается как «дэ круглое».) Таким образом, заменив х0, у0 на х, у, мы получим
df  df(x, у) _ |-тf (x-f-ft, y)—f(x, у) .
dx dx л->о	h
Частная производная по у определяется аналогично:
df . |im ft*. y + h)—f(x, у) . dy h.-+o	h
Это есть производная функции f одной переменной у /(х, у}, где х считается фиксированным.
Так как частная производная — это в конечном счете производная от функции одной переменной, то ее нетрудно вычислить. Для этого мы пользуемся всеми рассмотренными до сих пор правилами дифференцирования, учитывая в каждом случае, какая из переменных фиксирована, т. е. принимается за постоянное число, а какая служит «переменной дифференцирования».
фПримеры. 1. Найти частные производные функции
f(x, у) = Зх3у + 4ху2 — 2х + 4у — 5 при х = 2, у = 3.
Решение. Имеем
/(х, 3) = 9х3 + 36х — 2х + 12 — 5 = 9х3 + 34х + 7.
Производная этой функции от х равна 27х2 + 34; при х = 2 мы получаем 142. Таким образом,
РЦ = 142.
\ дх Д=2, р=з
334
12. Частные производные
Далее, /(2, у) = 24у + 8у2 — 4 + 4у — 5 = 8у2 + 28г/ — 9. Эта функция одной переменной у имеет производную 16у + 28. При у = 3 мы получаем 76; следовательно,
РЦ =76.
\ ду /х=2, у=3
2.	Найти общие формулы для частных производных функции f(x, у) примера L Решение. Считая у постоянным числом и пользуясь обычными правилами дифференцирования, получаем
df = д (Зх3у + 4ху2 — 2х + 4у — 5) = 9%2	4у2 __ 2
дх	дх
Аналогично, при фиксированном х имеем
2L = _Э(Зх»у + 4^-2х + 4у-5) = Зд;3 g 4 ду	ду	*
Если подставить в эти формулы х = 2, у = 3, то будем иметь
=142,	=76,
\ дх )х=2, у=3	\ ду /х=2, у=3
что совпадает со значениями, найденными выше.
3.	Найти частные производные функции f(x, у) = sin (х2 + у) при х = 0, у = л. Первое решение. Пользуясь методом примера 1, получаем:
Psin<*2 + ^	=( dsin<*2 + n) \	= 2xcos(x2+k)| о = О,
\ дх /х=о, у=п \ дх /х=0
/gsin(z2 + y)\ =/asiny\ =[cosy]_ =-1.
\ ду /х=о, У=к \ ду )у=п	у к
Второе решение. Следуя методу примера 2, получим сначала общие формулы:
dsin(x2 + y) = 2х cos (х2 + у), dsin(*2 + y) = COS (X2 + у).! дх	ду
Если подставить в них х=0, у = л, то придем к тем же значениям 0 и —1 искомых частных производных, что и ранее.
4.	Каковы частные производные функции f(xt у) = | х | при х = у = О?
Ответ. Так как /(х, 0) = | х | и функция х >-► | х | при х = 0 не имеет производной, то частной производной по х наша функция не имеет. Так как /(0, у) = 0, то при х = у = 0 получим -^ = 0.
5.	Приведем пример функции двух переменных, которая имеет в некоторой точке частные производные, не будучи в этой точке непрерывной. Положим
f(x, У) = 0, если ху = 0, и /(х, у) = 1, если ху #= 0.
Ясно, что ~	= 0 в точке (0, 0), так как /(х, 0) = /(0, у) = 0. Далее заметим,
§ 2. Производные функций нескольких переменных
335
что /(0, 0) =0 и что в каждом интервале, содержащем точку (0, 0), имеются такие точки (х, у), что f(x, у) = 1. Следовательно, f не является непрерывной в точке (0, 0).ф
ОБОЗНАЧЕНИЯ ЧАСТНЫХ ПРОИЗВОДНЫХ
Для обозначения частных производных используются, кроме д, и многие другие символы. Так, например, вместо df/dx пишут
f'x, f\ или Dxf.
Аналогично, df/dy иногда обозначается через
f'y, f, или Dyf.
Так, например, если /(х, у) = 2х3 у — ху3, то
fx(x,y)=bx3y-y3, 4(1, 2) = 12-4 = 8,
Dy f(x, у) =2х3-2ху, 4 (1, 2) = 2 - 4 = - 2.
Мы будем пользоваться только символом д и обозначениями fx и f'y.
УПРАЖНЕНИЯ
В упражнениях 1—13 найдите частные производные df/dx и dfjdy функции [(х, у).
1.	f(x, у) = х + 21/.
2.	f(x, у) = х2у6.
3.	f(x, у) = х2у2 — 2ху2.
4.	f.(x, у) = У i + х2 + у2.
5.	Кх, у) = sin (№ + у).
6.	fix, у) = 5х10 — бху7.
13. f(x, у) — (ху) 1 — In у.
7.	f.(x, 41) = sin (х/у).
8.	Кх, У) = (Ux)ex‘+^
9.	f(x, у) = arctg (у/х).
А10. Кх, у) = ln(x tgy).
и
11. 1(х, у) = $ es,nidi.
12. Кх, у) = (х2 — у2)/(х2 + у2).
14.	Для функции f(x, у) определенной в упр. 7 , положим g(x) = f(xt 3). Вычислите значение g'(2) и сравните его со значением df/dx при х = 2, у = 3.
15.	Повторите упр. 14 для функции из упр. 11.
16.	Повторите упр. 14 для функции из упр. 12.
17.	Пусть f(x, у) — функция, определенная в упр. 8. Найдите fx (2,1) и [у(2, 1).
18.	Для функции из упр. 4 найдите f'x (0, 0) и fy (0, 0).
19.	Для функции Ди, о) = sin (u/v) положим g = dfjdu, h = dfjdv. Найдите dg/dv и dh/du.
20.	Повторите упр. 19 для функции fi = ln(u tg и).
21.	Найдите -7— g2x+s,n у. dx
22.	Найдите —— sin (cos 1 + ua + о2) . dv
23.	Пусть I (a, p) = a2 + e3^ cos a; найдите dl/da и dl/d$.
336
12. Частные производные
24.	Пусть z = ]/ 1 + и2 + /1 + и2 ; найдите ги (0,0) и z'o (0, 0).
25.	Пусть z = J sin tdt; чему равна разность z'x— г'у? х
Д26. Пусть v= J ех dx; найдите v'a приа=1, 6 = 2. а_____________________
27.	Пусть z = У х2 + г/2 ; покажите, что xzx + угу=г.
А 28. Пусть <р = 1п У а2 + 62; докажите, что аф^+ 6ф$ = 1.
2.3.	ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
Существование производной у функции одной переменной многое говорит о самой функции. Если /'(х0) существует, то функция х f(x) непрерывна при х = х0 и в окрестности точки х0 она может быть с большой степенью точности приближена линейной функцией (сравните с теоремой о линейном приближении — см. теорему 1 § 1.8 гл. 4). В случае функции двух переменных мы не можем рассчитывать на то, что из существования у функции (х, у) *-*f(x, у) частных производных в точке (х0, yQ) вытекают столь же глубокие следствия. В самом деле, при вычислении частных производных в точке (х0, г/0) мы пользуемся только значениями функции на проходящих через эту точку вертикальном и горизонтальном отрезках. Не удивительно поэтому, что только из существования частных производных не вытекает даже непрерывность функции (см. пример 5 в § 2.1).
Поэтому функцию /(х, у), имеющую в точке (х0, у0) обе частные производные, мы не станем называть дифференцируемой в этой точке. Дифференцируемой мы будем считать такую функцию, которую в окрестности рассматриваемой точки (х0, yQ) с большой степенью точности можно заменить линейной функцией. Точное определение дифференцируемости будет сейчас дано. Окажется, что все дифференцируемые функции обладают частными производными и что все функции с непрерывными частными производными дифференцируемы.
Функция f(x, у), определенная в точке (х0, yQ) и в окрестности этой точки, называется дифференцируемой в точке (х0, yQ), если существуют такие числа г0, а и Ь, что
ftx, у) = г0 + а(х — х0) + b(y — у9) + /(х — х0)2 +(у — y0)2r(x,y),	(1)
где
г(х, у) непрерывна в точке (х0, уй) и г(х0, у0) = 0,	(2)
или, что то же самое,
lim г(х, у)=0.	(2')
(X,	у9)
Чтобы пояснить смысл этого определения, заметим, что функция
(х, у) 1-> г0 4- а(х — х0) + Ь(у — уй)	(3)
§ 2. Производные функций нескольких переменных	337
является линейной. Выражение
К(х —Хо)2 + (у —l/о)2 г (X, у)
в равенстве (1) представляет собой погрешность, которую мы получим, заменяя данную функцию f(x. у) линейной функцией (3). Если расстояние У (х— х0)2 + (у — Уо)2 мало, то эта ошибка будет очень малой, значительно меньшей этого расстояния. В этом и заключается смысл утверждения (2).
Из определения дифференцируемости сразу же следует, что функция, дифференцируемая в некоторой точке. непрерывна в ней. Действительно, правая часть равенства (1) является суммой непрерывных функций и поэтому непрерывна.
Заметим, что слагаемое г0 в равенстве (1) равно
20 = f(x0, у0).	(4>
Это сразу получается, если в положить равенстве (1) х = х0. у = у0.
2.4.	КАСАТЕЛЬНАЯ ПЛОСКОСТЬ
График линейной функции (3) является плоскостью; эта плоскость называется касательной плоскостью к поверхности z = f(x. у) в точке Р = (х0, yQ. z0), где z0 = = /Uo» Уо)- Рис- 12.8 иллюстрирует геометрический смысл определения дифференцируемости. Плоскость (3) и поверхность z = f(x. у) проходят через одну и ту же точку Р. и в этой точке плоскость (3) «прижимается» к поверхности — в окрестности точки Р она почти совпадает с поверхностью, подобно тому как касательная к кривой в окрестности точки касания почти совпадает с этой кривой.
Обратимся теперь к вопросу о том, как найти уравнение касательной плоскости, т. е. как, зная функцию f. вычислить входящие в равенство (1) величины а и Ь.
2.5.	ЧАСТНЫЕ ПРОИЗВОДНЫЕ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Предположим, что функция (х, у) f(x. у) дифференцируема в точке (х0, у0). т. е. что справедливо равенство (1) из § 2.3 и, следовательно, поверхность z = f(x. у) имеет в точке Р = (х0, у0. г0) касательную плоскость (см. рис. 12.8). Пересечем плоскостью у = у0 и нашу поверхность и ее касательную плоскость. Линией пересечения плоскости у = у0 с поверхностью будет служить изображенная на рис. 12.9 кривая — график функции х f(x. у0). Пересечением плоскости у = yQ с касательной плоскостью является прямая линия. Естественно ожидать, что эта прямая будет касательной к кривой, т. е. что функция х н-> f(x. у0) в точке х0 будет иметь производную, а значит, функция f(x. у) в точке (х0, #0) будет иметь частную производную по х. Подтвердим это предположение выкладкой.
Пользуясь равенствами (1) и (4) и полагая у = yQ. получим
f(x, Уо) = f(x0, у0) + а(х — х0) + | х — х0 f/o)-	(5)
Здесь г(х. у0) — непрерывная функция переменной х и r(x0. yQ) = 0 в силу (2). По теореме 1 § 1.8 гл. 4 функция х ь-> f(x. у0) дифференцируема в точке х = х0 и ее производная равна а. Но это означает, что f(x. у) имеет в точке (х0, у^ частную про-
338
12. Частные производные
Рис. 12.8
Рис. 12.9
изводную по х, причем эта производная равна а. Последнее можно доказать и непосредственно: в силу (5)
и, значит,
f(x0 + h, у0) — /(х0, у0) = ah + | h ]г(х0 + h, y0)
l= lim +	Уо)-/(хо, у») = o + нт 1ALf (Xo + ft, у0) = a,
\ dx ]xOt y0 h-*0	h	h-+0 h
так как J-^-L равно 1 или —1.
Полагая в равенстве (1) х = х0, получим
f(xo, у) = f(x0, у0) + Ь(у — у0) + \ у — у0 |г(х0, у)-,
отсюда, как и выше, заключаем, что /(х, у) в точке (х0, у0) имеет частную производную по у и что эта производная равна Ь. Рис. 12.10 иллюстрирует геометрический смысл последнего утверждения. Плоскость х = х0 пересекает поверхность г = — f(x, у) по кривой, являющейся графиком функции у »-» /(х0, у), а касательную
§ 2. Производные функций нескольких переменных
339
Рис. 12.10
плоскость — по некоторой прямой. Эта прямая является касательной к кривой, ее наклон равен Ь.
Просуммируем полученные результаты:
Теорема 1. Пред положим, что функция f(x.y) дифференцируема в точке (х0> #о)> т. е. удовлетворяет условиям (1) и (2). В этом случае функция f(x, у) имеет в точке (х0, у^ обе частные производные, причем
df	df	.
—!—=а,	—!—	= b.
dx	dy
(6)
Отсюда, в частности, следует, что заданная функция f однозначно определяет числа а и Ь\ поверхность г = f(x, у) может иметь в данной точке (х0, у0. г0) н е б о-лее одной касательной плоскости.
340
12. Частные производные
2.6.	НЕПРЕРЫВНО ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ
Сформулируем теперь теорему, в определенном смысле «обратную» теореме 1.
Теорема 2. Пусть функция f(x, у) определена и имеет обе частные производные как в точке (х0, у0), так и во всех точках некоторой окрестности точки (х0, у0)\ предположим еще, что эти частные производные, рассматриваемые как функции от х и у, непрерывны в точке (xQ, у0). В таком случае функция f дифференцируема в точке (х0, у0).
Доказательство этой теоремы будет дано в Приложении (см. § 6.1). Эту теорему обычно применяют к функциям, определенным на некотором открытом множестве <S и имеющим частные производные по обеим переменным во всех точках множества S, причем эти производные непрерывны на S. Такие функции называются непрерывно дифференцируемыми (на S). На практике непрерывную дифференцируемость функции f(x, у) обычно легко усмотреть «на глаз».
ф Примеры. 1. Будет ли функция Дх, у) = sin(ex cos у + 2*3#) всюду непрерывно дифференцируемой?
Ответ. Да. Функция f, а также и функции df/dx и df/dy, которые вычисляются с помощью обычных правил дифференцирования, получаются из элементарных функций одной переменной, имеющих производные всех порядков, при помощи операций сложения, умножения и образования композиции функций.
2.	Функция f(x, у) = V |xz/[ всюду непрерывна; при этом	= 0 в
точке (0, 0). Однако эта функция в точке (0, 0) н е является дифференцируемой. В самом деле, если бы она была дифференцируемой, то мы должны были бы иметь	____ __________
1/Щ| = /х2 + у2 г (х, у), где г(х, у) непрерывна в точке (0, 0) и ДО, 0) = 0. Положив в последнем равенстве х = у, мы получим | х | = К2| х |Дх, х), откуда r(x, х) = l/j/*2 и, значит, ДО, 0)#= 0. Полученное противоречие и доказывает наше утверждение.
3.	Найти уравнение касательной плоскости к поверхности z = f(x, у) = = sin х + ех? + у в точке (0, 2, 3).
Решение. Имеем
= cosx + уех?, = хехУ + 1. дх	*	ду
Эти функции, очевидно, всюду непрерывны; поэтому здесь применимы теоремы 1 и 2. При х = 0, у = 2 находим:
ДО, 2) = z0 = sin 0 + + 2 = 3,
= cos О + 2е° = 3,	-^L=0e°+l=l.
дх	ду
Уравнение касательной плоскости [получаемое подстановкой в уравнение (3) значений х0 = 0, уо = 2, z0 = 3, а = 3, b = 1] имеет вид z = 3 + Зх + (у — 2), или
z = Зх 4- у + 1.
Заметим, что эта плоскость действительно проходит через точку (0, 2, 3).
§ 2. Производные функций нескольких переменных
341
4.	Найти касательную плоскость к сфере х2 + у2 + г2 = 29 в точке (2, 3, 4). Решение. Верхняя полусфера является графиком функции
z = ]/ 29 — х2 — у2;
эта функция непрерывно дифференцируема при х2 + у2 < 29. Искомое уравнение касательной плоскости мы получим, подставляя в равенство (3) значения
х0 = 2, у0 = 3, г0 = /29 —22 —З2 =4 и
/ д У 29 — х2 — у2	\	/х	\	__1_
\ дх	Л=2,	у=з	\	У 29 — х2 — у2 Л=г, и=з	2
ь = / 3/29 —х2 —у2 \	_ /_______У \	_____
\ дУ	Л=2,	у=3	\	/29 — х2 — у2 /х=2, у=з	4
Поэтому требуемое уравнение имеет вид
z=4--L(x-2)--------
ИЛИ
2х + Зу + 4z — 29 = О.ф
2.7.	НОРМАЛЬ К ПОВЕРХНОСТИ
Пусть P(xQi у о, Zq) — точка графика дифференцируемой функции z = Дх, у). Прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, называется нормалью к поверхности, являющейся графиком нашей функции {рис. 12.11).
Параметрическое представление нормали к поверхности таково:
х = х0 + at, у = yQ + bt, z = z0 — t,
(7)
где
— f (*o> Уо)>
\ &У JxQ,yo
(8)
Это вытекает из сравнения уравнения касательной плоскости (см. § 2.3—2.6) с результатами § 6.7 гл. 9. Таким образом, можно утверждать следующее: вектор с координатами
(fx, fy, 1)
перпендикулярен к поверхности z = f(x, у) в точке (х0, УоР
фПрммеры. 1. Найти нормаль к поверхности z = е* cos у в точке х = 1, у = л, z = \/е.
Решение. Используя формулы (7) и (8), где х0 = Ь Уа =7Г» 2о = и заме-
342
12. Частные производные-
чая, что ------ cosy exC0Sy,----= — xsiny exC0Sy, получим а =—Uet b = 0, так
дх	ду
что параметрическое представление нормали имеет вид
• t	1	.
X = 1----, У 2 =----------------t.
е	е
2.	В какой точке нормаль к поверхности г = хНу — 5xyQ в точке (2, 1, 6) пересекает координатную плоскость х = 0 ?
Решение. Находим = 4х3г/ — 5z/6, || = х4— 30xz/5. Поэтому в обозначениях (8) при xQ= 2, #о = L z0= 6 мы имеем а = 27, b = —44. Параметрическое представление нормали 1см. формулы (7)J в нашем случае принимает вид
х = 2 + 27/, у = 1 — 44/, z = 6—/.
Если х = 0, то /= —2/27, и, значит, у= 115/27, г= 164/27. Следовательно, искомой будет точка (0, 115/27, 164/27).ф
УПРАЖНЕНИЯ
В упражнениях 29—35 найдите уравнение касательной плоскости и уравнения нормали к данной поверхности в заданной точке.
29.	г = 5х2 + 2г/2 — 9; (3, 2, 44).
30.	г = ху; (3, —2, —6).
31.	г =	+ у3 + Зху; (1, -1, -3).
32.	г = 5х — у2; (4, 2, 16).
33.	г = ех2+у2 ; (0, 0, 1).
34.	г = х2 + у2; (1, 1, 2).
_________ /2	2	1 \
35.	г=/ 1-х2-у2;	— , — , — .
\ □ О □ ]
36.	Покажите, что поверхности z = х#/(4х — у) и z = "К(5х — г/)/3 в точке (1, 2, 1) пересекаются под прямым углом. (Последнее означает, что обе поверхности проходят через указанную точку и что их нормали в этой точке взаимно перпендикулярны.)
37.	Покажите, что касательная плоскость к сфере х2 + у2 + z2 = 1 в точке (хо, #о» го) этой сферы имеет уравнение ххо + УУо + zzq = 1. (Предполагается, что го> 0.)
Д 38. Покажите, что уравнение касательной плоскости к эллипсоиду (х/а) 2+ (у/b)2 + +(г/с)2 = 1 в его точке (хо. */о, го) таково: ххо/а2 + ууъ/b2 + zzq/c2 = 1.
39.	Найдите уравнение касательной плоскости к поверхности z = V1 — (х/10)2 — (у/\О)2 в точке х=1, 4/=7]Л2, z = 1/10 сначала непосредственно, а затем используя результат упр. 38.
А 40. По аналогии с упр. 38 угадайте вид уравнения касательной плоскости к гиперболоидам
(х/а)2 + (у/b)2 — (г/с)2 = 1 и (х/а)2 — (у/b)2 — (г/с)2 = 1.
Докажите ваше предположение.
§ 2. Производные функций нескольких переменных
343
2.8	. ЦЕПНОЕ ПРАВИЛО ДЛЯ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
Правило для вычисления частных производных композиции функций, или «сложной функции», нескольких переменных аналогично соответствующему правилу для функций одной переменной, хотя и несколько сложнее его.
Теорема 3 (цепное правило). Пусть функция F(xt у) дифференцируема в точке (х0, #о)> а функции ф(и, v) и ф(и, v) дифференцируемы в точке (и0, v0), и пусть ф(и0, ^о) = *о, ф(и0, ^о) = У о- Тогда сложная функция
z = f(u, v) = Г(ф(н, v), ф(и, и))	(9)
дифференцируема в точке (и0, ^о) и
JL —	J*L =	af ^10)
du dx du dy du dv dx dv dy dv
где частные производные no и и no v вычислены в точке (и0, vQ)t а частные производные по х и по у — в точке (xQi у0).
Можно выразить этот результат и иначе: если
z = F(x, у), х = ф(и, у), у = ф(и, v)
(причем все функции дифференцируемы), то
dz __ dF d<p । dF дф du dy du дф du
и аналогично для Если частные производные обозначать индексами (ср. с § 2.2), то цепное правило (10) можно записать так:
fu (Ц, v) = Fx (ф (и, у), ф (и, у)) ф^ (и, v) + Fy (ф (и, у), ф (а, сО) ф« (я, у),
Д (и, у) = Fx (ф(и, V), ф (и, V)) фо (и, v) + Fy (ф (и, у), ф (и, V)) фр (и, V).
Мы докажем теорему 3 в предположении, что функции F, ф и ф линейны. Этого достаточно, чтобы убедиться в справедливости теоремы, так как дифференцируемые функции в достаточной близости от данной точки всегда можно рассматривать как линейные. Итак, мы предполагаем, что
Г(х, У) = Ах + By + С, ф(ц, v) = аи + bv + с, ф(и, v) = аи + Ру + 7.
Тогда
Л=-^-, В = -^~, а = А_, b = -^-, a = -*L, p = (II) дх	dy	ди	dv	ди	dv
Далее,
г — F (<р (и, v), ф (a, о)) = Л<р (и, v) 4- Вф (и, v) 4- С =
=Л (аи + bv + с) 4- В (аи + jto + 7) + С =
== (Аа 4~ Вл) и 4~ (Ab 4~ BP) v 4“ (Ас 4~ В^ 4~ С),
Следовательно,
— = Аа 4- Ba, — = Ab 4- В?.	(12)
du	dv
344
12. Частные производные
Подставляя (11) в (12), мы получим (10). Более формальное доказательство теоремы 3 будет дано в Приложении (см. § 6.2).
фПримеры. 1. Предположим, что F(x, у) = Зх2у, <р(а, о) = и 4- о, ф(и, о) = ио. Пусть г = F($(u, о), ф (и, о)); найти частные производные -^-этой функции при и = 2, о = 3.
Первое решение. Имеем
г(и, о) = 3(и 4- о)2ио = Зи3о 4- 6и2о2 4- Зио3, так что
z'u = 9а2 о 4- 12мо2 4- Зо3, z'g = Зи3 4- 12и2о 4- 9ао2 и
z'u (2, 3)=405,	г0(2, 3) = 330.
Второе решение. Имеем:
Fx = Зху, Fy = Зх2, фи = 1, фо = 1, фй = V, фо = и.
При и = 2, о = 3 получаем:
фи = 1, Фо = 1, фи = 3, фр = 2
и, полагая х = ф(и, о) = и 4- о, у = ф(и, о) = ио, находим;
х = 5, у = 6, Fx = 180, Fy=73.
Пользуясь цепным правилом, имеем:
za — Fx хи 4- Fy у'и — Fx^'u 4- Fy ф^ = 180 • 1 4-75 • 3 = 405,
z„ = Fx x0 4- Fy y'o = Fx фо 4- Fy ф0 = 180 • 1 4- 75 • 2 = 330, что, разумеется, совпадает с полученными выше результатами.
2.	Найти частные производные пои и подфункции г =ех?, где х=иг и у=ио.
Решение. Подставляя значения х и у в выражение для г, получим г =еа’° и, значит, zu = Зи2ое“3° и г0 = и3е. Применяя цепное правило, надо иметь в виду, что функция одной переменной и может рассматриваться как функция от (и, о), частная производная которой по о равна нулю. Поэтому мы имеем:
гх — уеху, Zy = хе*?, хи — 2и, хд = 0, уи = о, у'о — и, так что по-прежнему
г'и — z’x х‘и + г’у у'и = уех? 2и 4- хе*?о = Зи2оеи’°, z'o = z'x х'о + г'у у'„ = уех? 0 4- хех? и — и3 еи\ %
§ 2. Производные функций нескольких переменных
345
2.9	. ПРОИЗВОДНАЯ В ЗАДАННОМ НАПРАВЛЕНИИ
Цепное правило применимо также и в том случае, когда мы из функции двух переменных F(x, у) образуем функцию одной переменной /	/(/), подставляя
в (F х, у) две функции х = ф(/), у = ф(/) одной переменной. Производная функции
’ г = Г(?(/), ф(0)	(13)
равна
JL. =	[ JL JL	(14)
dt dx dt dy dt ’
ИЛИ
Г (0 = Л (Ф (0, Ф (0) <p' (0+ Fy (<p (0, Ф (0) Ф' (0,	(И')
где для функции одной переменной мы используем обычные обозначения (d вместо д и штрих без индексов внизу).
Применим формулу (14) к очень простому случаю:
х = ф(/) = х0 + t cos а, у = ф(0 = у0 + t sin а.
Это параметрические уравнения прямой, проходящей через точку (х0, #0); t есть длина отрезка этой прямой [измеренная от точки х0 = ф(0), у0 = ф(0)], а а — полярный угол вектора, направленного в сторону возрастания t (рис. 12.12). Таким образом, (13) будет теперь значением функции F в точке, которую мы получим, пройдя от точки (х0> Уо) расстояние t «в направлении а». Производная (14) при /=0, т. е.
Рх (*о> У о)cos а + Ру (*о> f/o) s i п а»	(15)
или в сокращенной записи
Fxcosa + F^sina [в точке (х0, t/0)],	(15')
называется производной функции F в точке (х0, yQ) в направлении а (или «направленной производной»); она измеряет скорость изменения функции F в направлении а [по отношению к пройденному исходя из точки (х0, #0) расстоянию]. Полагая a = 0, мы получим производную в направлении оси х\ это есть не что иное как частная производная Fx. Аналогично, Fy есть производная в направлении оси у (здесь a = 90°), — Fx есть производная в направлении, противоположном оси х (здесь a = 180°) и т. д.
Точка, в которой обе частные производные обращаются в нуль, т. е. в которой
Fx = Fy = 0,
называется критической точкой функции F. В критической точке функции ее производная в любом направлении равна нулю. Такие точки мы рассмотрим ниже (см. § 3.4). Если же точка не является критической, положим а =	F'^j^p'2, ;
тогда найдется единственное число 0, 0 <^0 < 2л, такое что
Fx=acos9, F^ = asin9 (где а = I^f/ + Fy =/= 0) .	(16)
346
12. Частные производные
Производную в направлении а можно теперь записать так:
a cosQ cos а + asinQ sin а = а cos (0 — а).	(15")
Для какого значения а эта производная является наибольшей? Очевидно, что для такого а, при котором cos(0—а) имеет наибольшее возможное значение, т. е. 1. Это будет при а = 0; значение производной в направлении а = 9 будет равно а. Производная в направлении а принимает наименьшее значение, равное —а, если cos(0 — а) = —1, т. е. при а = 0 + 180°. [Если 0 + 180° не принадлежит интервалу (0, 360°), то прибавим к нему или вычтем из него подходящее кратное угла 360°.] А для какого угла а производная (15") равна нулю? Очевидно, для такого а, что 0 — а = 90° или 0 — а = —90°, т. е. при а = 0 ± 90°. Все это показано на рис. 12.13. Направление а = 0 есть направление наибыстрейшего возрастания функции /(х, у).
•Пример. Для функции F = х2у—2х—у найти\ а) критические точки; б) производную в направлении а = —4£° в точке (3, 1); в) направление 0 наибыстрейшего возрастания функции в точке (3, 1).
Решение, а) Имеем: Fx = 2ху — 2, Fy = х2 — 1. Следовательно, Fy = 0, когда х = 1 или х = —1. Если х = 1, то Fx = 0 при у = 1. Если х = —1, то Fx = О при у = —1. Следовательно, наша функция имеет две критические точки: (1, 1) и (-1,-1).
б)	В точке (3, 1) имеем Fx = 4, Fy = 8. Так как cos(—45°) = cos 45° = l/j/2 , sin(—45°)= —sin 45°= — 1/уЗГ, то в силу формулы (15') искомая производная в направлении а равна
4 /]/2 — 8//2 =	5,66.
$ 2. Производные функций нескольких переменных
347
в)	В точке (3, 1) имеем а = V Fx 4- Fu = р^80 = 4]Л5.
Следовательно, угол 9 наибыстрейшего возрастания определяется условиями Гер. с формулами (16)]:	_
4=4}Л5со59, 8 = 4]/5sin9, т. е. 0 « 63° 30'. ф
2.1	0. ГРАДИЕНТ
Пусть F(x, у) — непрерывно дифференцируемая функция (определенная на некотором открытом множестве). В каждой точке (х, у), в которой эта функция определена, построим вектор с координатами (FX1 Fy ); этот вектор называется градиентом функции F и обозначается символом grad F. Таким образом,
grad/' = -^eI +-^-е2.	(17)
дх	ду
где et и е2, как обычно, — единичные векторы, направленные по координатным осям (ср. с § 1.8 гл. 9). Заметим, что grad F — это правило, сопоставляющее каждой точке области определения функции F некоторой вектор; другими словами, grad F — это пример векторной (или «векторнозначной») функции двух переменных. Вспоминая равенства (16) из § 2.9, мы видим, что полярный угол градиента равен 0. Таким образом, градиент направлен в сторону наибыстрейшего возрастания, или, как еще говорят, наибыстрейшего подъема, функции двух переменных. Модуль градиента ^grad F | = |/ р'2	р'2 = а есть величина производной функции в направлении
наибыстрейшего подъема (в этом направлении производная функции является наибольшей). В критической точке функции ее градиент равен 0 (этот очевидный факт часто принимают за определение критической точки).
2.1	1. ЛИНИИ УРОВНЯ
Представим себе, что непрерывно дифференцируемая функция F двух переменных описывает горный ландшафт: z = F(x, у) есть высота точки земной поверхности, расположенной над точкой (х, у) плоскости z = 0; график функции z = F(x, у) — это поверхность горы. Линия уровня — это гладкая линия (ср. с § 3.1 гл. 11) х = <р(/), у = ф(0, такая что величина F(<p(/), ф(/)) имеет постоянное значение, например, равное С. Иными словами, линия уровня является проекцией на плоскость ху тропы, образованной всеми точками, находящимися на одной и той же высоте. Мы будем считать, что через каждую точку (х0, f/0), не являющуюся критической точкой функции F, проходит единственная линия уровня. (Если частные производные Fx и Fy сами являются непрерывно дифференцируемыми функциями, то это предположение можно доказать; однако в настоящей книге мы это доказательство опустим.)
Пусть (х0, yQ) — точка, не являющаяся критической точкой функции F. Тогда мы можем найти направление линии уровня, проходящей через эту точку. В самом деле, для линии уровня х = ф(/), у = ф(/), при t = tQ проходящей через точку х = ф(/0)» Уо = Ж), имеем
Лф(0, ф(0) = с.
(Это условие есть не что иное как определение линии уровня.) Продиффе-
348
12. Частные производные
У
Рис. 12.14
ренцировав по t (при t = /0) обе части последнего уравнения, получим [ср. с равенствами (13) и (14) из § 2.9]
Fx (х0, у о) ф' (t0) 4- Fy (х0, у0) ф' (/0) =0.	(18)
Напомним, что вектор ф'(^о)е1 + ф'(^о)е2 является касательным к нашей линии уровня в точке (х0, у0). Пусть b — длина этого вектора и Р — его полярный угол. Тогда ф '(/0) = b cos 3, ф'(/0) = b sin р. Принимая во внимание равенства (16) из § 2.9, мы можем переписать (18) так:
(a cos 0)(6 cos 3) 4- (а sin 0)(6 sin р) = ab cos (0 — Р) = 0.
Следовательно, cos(0 — Р) = 0 и, значит, либо р =0 + 90°» либо р =0 —90°. Иными словами, линия уровня, проходящая через (некритическую) точку, перпендикулярна градиенту в этой точке (рис. 12.14). Ясно, что этого и следовало ожидать:
§ 2. Производные функций нескольких переменных
349
направление градиента есть направление наибыстрейшего подъема функции, а направление, перпендикулярное к нему, есть направление линии уровня—производная по этому направлению равна нулю.
•Примеры. 1. Линии уровня функции F(x, у) = х2 + 4у2 —это, конечно, эллипсы х2 + 4г/2 = С. Мы имеем Fx = 2х, Fy = 8у, поэтому наша функция имеет одну критическую точку х = у = 0. Через эту точку не проходит ни одна линия уровня. Ряд линий уровня функции F изображен на рис. 12.15.
2.	Линии уровня функции Г(х, у) = х2 — 4у2 — это, конечно, гиперболы х2 — 4у2 = С; общие асимптоты всех этих гипербол также являются линиями уровня нашей функции. Мы имеем Fx = 2х, Fy' =—8у, точка (0,0) является единственной критической точкой. В этой точке пересекаются две линии уровня. Несколько линий уровня рассматриваемой функции изображены на рис. 12.16.ф
УПРАЖНЕНИЯ
Каждое из упражнений 41—45 выполните дважды: сначала находя производные непосредственно, а затем применяя цепное правило.
41.	Найдите du/ds и du/dt, где и = 2№ + ху + у2, х = 2s — t, у = s — 2t.
42.	Найдите dz/dx,	где z = ху2 + х2у, у = In х.
43.	Найдите dz/dt ,	где z = 1п(х2 + у2), х = е~1 , у = е*.
А 44. Найдите dz/dt,	где z = хУ, х = sin t, у = cos	t.
45.	Найдите dz/dt,	где z = х2 + у~\ х = ezcos	t,	у	= 1 + In t.
46.	Предположим, что функция [(х, у) дифференцируема в точке (0, 0) и fx(0, 0)=2, f (0, 0)= =3. Пусть, далее, функция ср (и, у) дифференцируема в точке (0, 0), ср (0, 0)=0,ф^(0, 0)= = Фу (0, 0) =9. Положим g(u, v) = Дф(и, v), и)). Вычислите gu (0, 0) и gv (0, 0).
47.	Пусть функция F(a, 0) дифференцируема при а = 0 =1 и пусть в этой точке Fa = 3, Гр = 5. Положим f(x, у) = F(x2, у3); найдите f*(l, 1) и fy(l, 1).
48.	Пусть f(f)—дифференцируемая функция и F(x, у) =1(х —2у)\ покажите, что 2FX (х, у) + + Fy (х, у) = 0.
49.	Пусть f(t) —дифференцируемая функция, f/(t)^>0 и ф(и, v)=[(u + v); что можете Вы сказать о величине ф^—ф^?
50.	Пусть функция f(x, у) всюду дифференцируема и пусть всюду 0, f:yZ> 0. Положим F(0 = № ^)- Является ли F возрастающей функцией? Обоснуйте свой ответ.
Для каждой из следующих пяти функций F найдите критические точки, градиент в данной точке Р и.производную по данному направлению а в точке Р.
51.	F =	Зх2 — 6z/2,	Р(8, 2), а = 120°.
52.	F =	уе2х, Р(0,	4), а = 135°.
53.	F = у + х cos ху, Р(0, 0), а = 2л/3.
54.	F =	х2 + у2 —	бдг + 4у + 25,	Р(1,	—4), а = 45°.
55.	F =	e^cos у, Р(0, 0), а = 60°.
56.	Для функции F и точки Р из упр. 51 напишите уравнение проходящей через эту точку линии уровня, найдите направление ее касательной и покажите, что эта касательная перпендикулярна градиенту.
57.	Выполните	упр.	56 для	функции,	заданной	в	упр.	52.
58.	Выполните	упр.	56 для	функции,	заданной	в	упр.	53.
59.	Выполните	упр.	56 для	функции,	заданной	в	упр.	54.
60.	Выполните	упр.	56 для	функции,	заданной	в	упр.	55.
350
12. Частные производные
2.1	2. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНОЙ ФУНКЦИИ
Пусть F(x, у) — функция двух переменных и (х0, Уо) — такая точка, что Ру' Uo, f/o) ¥= 0» т. е. в этой точке градиент не горизонтален. В таком случае касательная к линии уровня в этой точке (она перпендикулярна градиенту) не вертикальна. Поэтому линия уровня, проходящая через точку (х0, */о)> может быть представлена как график функции у = f(x) (рис. 12.17).
Таким образом, в рассматриваемом случае существует функция х у = /(х), определенная в окрестности точки х0 и такая, что = /(х0), причем
F(x, /(х)) = F(xOt у о) = const.	(19)
(Последнее утверждение следует из предположения, сделанного в § 2.11, которого мы в этой книге не доказываем.) Функция f(x) называется неявно заданной уравнением (19). Производную этой функции в точке х0 можно вычислить так: продифференцировав (в точке х = х0) по х обе части равенства (19) и используя в левой части цепное правило, получим
F х С^о» У о) “Ь РV	f/о) f W = 0*	(20)
[Здесь мы воспользовались тем, что /(х0) = уои что dx/dx = 1. Заметим, что (20) -есть просто частный случай равенства (18), где считается t = х, ср(/) = /, ф(/) = = /(/).] Из равенства (20) получаем
(21)
^(Хо, У о)
где знаменатель, по предположению, отличен от нуля.
При выполнении дифференцирования неявно заданной функции рекомендуется, не пытаясь вспомнить формулу (21), воспроизвести метод, которым она была получена.
Замечание. Если Fx' (х0, yQ) =# 0, то точно таким же способом можно найти производную функции х = g(y), неявно определяемой условиями g(yQ) = х0 и Р(ё(у), У) = У о) = const.
•Примеры. 1. Функция у = /(х) удовлетворяет уравнению
x2t/3 + 2х2у + Зх4 — у = 1.	(22)
Найти производную у'(х) при х = 1, у =—1.
Решение. Сперва мы проверим, что значения х = 1, у = —1 удовлетворяют уравнению (22). Затем продифференцируем по х обе части данного уравнения, помня, что у = /(х) есть некоторая функция от х. Так мы получим
2ху3 4- Ъх2у2у' + 4ху + 2х2у’ + 12Х3 — у' =0,
или
(Зх2у2 + 2х2 — 1)у' + (2xtf + 4ху + 12Х3) = 0.
При х = 1, у = —1 последнее равенство примет вид 4у' + 6 = 0. Следовательно, У(1) = —3/2. [Так как данная функция Г(х, у) является композицией элементар
§ 2. Производные функций нескольких переменных
35t
ных функций, то нам даже не пришлось применять цепное правило для функции двух переменных. Это типично для примеров, в которых фигурируют конкретные функции.]
2.	Найти производную функции у = f(x), неявно заданной равенствами
е~х cos у + sin у = е; у = л при х = 1.	(23)
Решение. Легко убедиться в том, что е-003* sin л = е. Дифференцируя обе части первого из равенств (23) по х, получаем
—cos у е~~х 005 у + х sin у е~х cos у у' 4- cos у-у' = 0.
Если х = 1, у = л, то отсюда следует,что е — у =0.Следовательно,у'(\) = е.ф
УПРАЖНЕНИЯ
В упражнениях 61—68 найдите производную dy/dx в данной точке, проверив сперва, что-график функции у = у(х) проходит через эту точку.
61.	у2 — 2х — 5 = 0, х = 10, у = 5.
62.	2tf — Зу2х — х6 — 40, х = —2, у = 1.
63.	г/10 + 2г/х10 — 3 = 0, х = 1, у = 1.
64.	\/у + 1/x = 1, х = 2, у = 2.
65.	х3 — ху + у3 = 1, х = 1, у = 1.
66.	х2 3 + У2^ = 2, х = 1, у = 1.
67.	ху — е* sin у = л, х = 1, у = л.
А 68. 1п (у2 + у2) = arctg г//х, х = 1, у = 0.
2.1	3. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ТРЕХ И БОЛЬШЕГО ЧИСЛА ПЕРЕМЕННЫХ
Обобщение понятий частных производных и дифференцируемости на функции трех и большего числа переменных совершенно очевидно.
Так, например, если (х, у, z) f(xt у, z) есть функция, определенная на некотором открытом множестве, то частная производная этой функции по z в точке (х0, Уо» 20) — это производная функции одной переменной z ь-> /(х0, у0, г) в точке г = z0. Эта частная производная обозначается символами
df	/ df \	д £	ч	ч
—ИЛИ -*-)	, ИЛИ — f(xo, у0, Zo), ИЛИ /2 (хо, у0, 20),
dz	\ ог )х0, уо, to	dz
а также символами Dzf(xQ, yOi z0) и f3' (х0, у0, 2о)» где индекс 3 внизу указывает, что дифференцирование производится по третьему аргументу.
Таким образом,
f	~ Ч iinnf(*o, У^ Zo + Л) — f (х0, t/о, г0)
/зНо> Уо> zo/ — 11111	7	•
Л
Для функции п переменных определение аналогично.
Функция /(х, у, z) трех переменных называется дифференцируемой в точке (х0, Уо, 20), если при всех (х, у, z) в окрестности точки (х0, у0, z0) имеет место равенство
f(x, у, г) =1 (х, у, г) + /(х — х0)2 + (у — у0)2 + (z — z0)2 г(х, у, z),
352
12. Частные производные
где I есть линейная функция, а г — функция, непрерывная в точке (х0, Уо» 2о) и равная в ней нулю. Линейная функция / может быть записана так:
l(x,y,z) = ах + by + cz 4- d —
= а(х — х0) + b(y — у о) + с(г — z0) + (d + ах0 + by0 + cz0).
Слагаемое d + ах0 + Ьу0 + сг0 равно, очевидно, значению f в точке (х0, у0, г0).
Для функций п > 3 переменных удобно использовать векторные обозначения. Обозначим через х вектор х = (xi, х2, ..., хл). Линейная функция от х имеет вид
/(х) = а +	+ а2х2 + ... 4- апхп.
Функция х !—► f(x) называется дифференцируемой в точке х0, если в окрестности точки х0
Дх) = /(х) 4- |х — х0|г(х),	(24)
где г(х) непрерывна в точке х0 и г(х0) = 0. Равносильное этому определение таково: функция х I-* f (х) дифференцируема в точке х0, если существует линейная функция /(х), такая что
lim J/W-/(x)| =0	5)
Х->Хо |х — Хо I
Эта функция I называется линейным приближением к / в точке х0. Дифференцируемая функция будет, очевидно, непрерывной.
Теорема 4. Пусть функция /(х) = /(xlt х2, .... хл) определена в точке х0 ы в окрестности этой точки. Если f дифференцируема в точке х0, то она имеет в ней частные производные, значения которых являются коэффициентами при xt, х2.х„
в записи линейного приближения /(х) функции Дх); если функция f в окрестности точки х0 и в самой этой точке имеет частные производные, непрерывные в точке х0, то функция f дифференцируема в точке х0.
Теорема 4 обобщает доказанные выше теоремы 1 и 2; доказывается она точно так же, как и эти две теоремы.
Мы будем рассматривать главным образом непрерывно дифференцируемые функции, т. е. функции, имеющие непрерывные частные производные.
•Примеры. 1. Найти fz (2, 6, 0), где f(x, у, z) = sin (xyz).
Решение. Принимая х и у за постоянные и дифференцируя f по г, получим fz (х, у, г) = ху cos(xz/z). Следовательно, fz (2, 6, 0) = 12.
2. Найти линейное приближение для функции F(x, у, z, t): (х, у, z, t) i-* ехУ-1- 2xz2i— xt2— е2 в точке (2, 1, —1, 3).
Решение. Частные производные функции F(x, у, z, t) равны:
Fx — уеху + 2z2t ~ t2, Fy=xexy, Fx = 4xzt, Ft=2xz2 — 2xt.
Они, очевидно, всюду непрерывны. При х =2, у = 1, г =—1, t =3 имеем
Fx=e2 — 3, Fy = 2e2, Л = —24, Л= —8.
§ 2. Производные функций нескольких переменных
353
Нам нужно найти линейную функцию, для которой эти числа служат коэффициентами при неизвестных. В точке (2, 1,—1, 3) значение функции F равно /'(2, 1, —1,3) =—6. Следовательно, искомая функция имеет вид
—6 + (е2 — 3)(х — 2) + 2е2(у — 1) — 24(z + 1) — 8(/ — 3).ф
2.14. ЦЕПНОЕ ПРАВИЛО ДЛЯ ФУНКЦИЙ ЛЮБОГО ЧИСЛА ПЕРЕМЕННЫХ
Цепное правило для функций более чем двух переменных аналогично правилу, сформулированному в теореме 3 § 2.8, и доказывается точно тем же способом.
Теорема 5. Пусть функция п переменных F (xv х2, ... , хп) дифференцируема в точке Р (хр х2,..., хп) и пусть даны п функций от т переменных ^(ц^и^ ... ,ит), Ф2(иг и2,..., ит),..., фп(ир и2,..., цт), дифференцируемых в точке Q [uv и2,..., wm) и таких, что ф7- =х7- в точке Q. Рассмотрим функцию f(uv ..., ит) от т переменных, полагая
f (^i> • ••» ит)	F (фг (ир..., Цт),..., Фп (их,... , Цт)).	(26)
Эта функция дифференцируема в точке Q и при j = 1, 2, ... , т имеем
df _ dF д^>! | dF dcp2 । dF dyn duj dx! du j	dx2 duj	dxn duj
где все производные no x берутся в точке Р, а все производные по и — в точке Q.
То же самое правило применимо, конечно, и в случае, если некоторые из ф являются функциями только части переменных и, так как функцию, зависящую от k < т переменных, можно рассматривать и как функцию всех т переменных, частные производные которой по «недостающим» переменным равны нулю.
•Пример. Предположим, что функция F(x,y,z) дифференцируема при х = = у = z = 0 и имеет в этой точке частные производные Fx =2, Fy = Fz = 3. Пусть
f(u,v)=F(u — v, и2—1, 3v — 3);
найти fu(\, 1) и fv(\, 1).
Решение. Пользуясь теоремой 5, получаем
df	dF d (и — v) , dF
---—		1	 du-dx----du--------dy
df   dF d (u — v) । dF dv	dx	dv	dy
При u = v = 1 находим отсюда
/	=2.1+3-2 + 3- 0=8,
\ du /1,1
Следовательно,
4(1,1) =8,
d(ua— 1) । dF d(3v — 3) du	dz	du
d(u2 — \) । dF d (3v — 3) dv	dz	dv
l-^L\ = 2 (—1) + 3 • 0 + 3 • 3 = 7.
\ dv /1,1
4(1, I) = 7. •
354
12. Частные производные
Z
Рис. 12.18
2.15. ГРАДИЕНТ, ПРОИЗВОДНАЯ В ЗАДАННОМ НАПРАВЛЕНИИ И ПОВЕРХНОСТИ УРОВНЯ
Если на нёкотором открытом множестве обыкновенного, трехмерного, пространства определена непрерывно дифференцируемая функция F(x, у, z), то вектор, координаты которого являются частными производными функции F, вычисленными в данной точке Р, называется градиентом функции F в точке Р и обозначается через grad F.
Таким образом,
gradF =-^-ех +-|^е2+-^-е3,	(27)
дх ду dz	' '
где еь е2, е3 — единичные векторы, направления которых совпадают с направлениями координатных осей (см. гл. 9, § 1.12). Точки, в которых grad F = 0, называются критическими точками функции F.
Предположим теперь, что радиус-вектор точки Р — это вектор Р с координатами х0» У о и z0 (совпадающими с координатами точки Р I). Пусть п — некоторый единичный вектор. Напомним (см. гл. 9, § 6.5), что координаты вектора п равны cos a, cos 0, cos у, где а, 0 и у — углы, образуемые вектором п с осями координат:
n = cos а е4 + cos 0 е2 + cos у е3.
Точка с радиусом-вектор ом Р + tn принадлежит прямой, проходящей через точку Р в направлении вектора п, и удалена на расстояние t от точки Р (рис. 12.18); ее координаты равны:
х = х0 + /cosa, у = у0 + /cos 0, z = zQ + /cosy.
Значение функции F в этой точке, т. е.
F(P + /п) = Р(х0 4- /cosа, г/о + /cos 0, zQ + /cosy),
§ 2. Производные функций нескольких переменных
355
является функцией одной переменной t. Производная этой функции при t — 0 называется производной функции F в точке Р в направлении п. Она показывает скорость изменения функции F при смещении (считая от точки Р) в направлении вектора п. По теореме 5, эта производная равна1
Fx (х0, у0, Zo) cos а + Fy (х0, у0, г0) cos 0 + Fz (х0, у0, z0) cos у.	(28)
Предположим теперь, что z = ф(х, у), где функция ф непрерывно дифференцируема, есть уравнение поверхности, на которой функция F принимает постоянное значение, т. е. такой, что
F(x, г/, ф(х, у)) = С.	(29)
Такая поверхность называется поверхностью уровня функции F. Дифференцируя обе части равенства (29) по х и по у, мы получим
Fx + Fz Фх = 0, Fy + Fz фг/ = 0.	(30)
В силу уравнений (7) и (8) из § 2.7 числа (ф*, ф^, — 1) являются координатами вектора, перпендикулярного к поверхности z = ф(х, у) в точке (х, у, z). Из равенств (30) получаем, что ф* = —Fx /F'z, ф^ = —P'JF'Z, так что рассматриваемый вектор имеет координаты
(Рх________р'у____Л
к Рг ’ Р’г ’	/
и, значит, он параллелен градиенту (F'x, F', FJ. Таким образом, градиент функции в каждой точке перпендикулярен к поверхности уровня этой функции, проходящей через рассматриваемую точку.
Тот же результат можно получить и в предположении, что поверхность уровня задается не уравнением z = ф(х, у), а уравнением вида х = ф(у, z) или у = /(z, х). Можно также доказать, хотя здесь мы и не будем делать этого, что если частные производные F'x, Fy, F'z непрерывно дифференцируемы, то существует единственная поверхность уровня, проходящая через любую точку, не являющуюся критической. (Если функция определяет распределение температуры, то ее поверхности уровня называются изометрическими поверхностями. Если функция определяет электрический потенциал, то поверхности уровня называются эквипотенциальными поверхностями.)
Шользуясь понятием скалярного произведения, введенным в Приложении к гл. 9 (см. § 6) мы можем переписать производную в заданном направлении (28) в виде скалярного произведения:
* '	grad F-п = | grad F | cos 0,	(*)
где 6 — угол между вектором п и градиентом.
Из равенства (*) следует, что в каждой точке, не являющейся критической, градиент направлен в сторону наибыстрейшего возрастания функции, а модуль градиента равен величине скорости этого возрастания. В самом деле, производная по направлению (*) принимает наибольшее значение, если cos 6 — 1, т. е. если 6 = 0, и вектор п имеет то же направление, что и grad F; в этом случае производная в заданном направлении равна | grad F |.
356
12. Частные производные
Все, что сказано в этом параграфе, с естественными изменениями формулировок можно перенести и на функции п > 3 переменных. Детали этих рассуждений предоставляются читателю.
УПРАЖНЕНИЯ
В упражнениях 69—76 найдите частные производные f'x, fy и f'2 данной функции 1(х, у, г).
69.	[(х,	у,	z) = xyz.	73.	£(х,	у,	г) =	arctg (1 + xyz).
70.	f(x,	у,	z)= 2xz2 + у? — хуг.	74.	fax,	у,	г) =	у cos [(1 + г2)х].
71.	l(x,	у,	z) = Ain (yz2).	75.	t(x,	у,	z) =	(x2 — y)/(y2 + z2).
72.	i(x,	y,	z) = (e*+sin ХУ)	£	76.	f(x,	y,	z) =?	xyz/(x2 + 2y2 + 4г2).
77.	Пусть ф (r, s, t) = rs/', найдите дф/дг, дф/ds, dq/dt.
78.	Пусть 0 (и, v, w)= euv+w /w, найдите d6/du, dfydv, dft/dw.
79.	Пусть f(a, p,y) = sin (a 0* ), найдите df/da, dfjdfi , дЦ/ду.
80.	Пусть F(x, у, г) = x2/a2-{-y2/b2+z2/c2. Выпишите уравнение поверхности уровня, проходящей через точку (—1, 3, 4). Найдите нормаль к этой поверхности в данной точке и покажите, что она параллельна градиенту F.
81.	Предположим, что температура в пространстве xyz задается функцией T—x2y-\-yz—е*?. Найдите скорость изменения температуры в точке (1, 1, 1) в направлении, ведущем от этой точки к началу координат.
А 82. Найдите все критические точки функции [(х, у, z) = Зх2у3г*.
83.	Найдите градиент функции <p(x, у, г) = tg(yz) + е210*.
84.	Пусть плотность распределения материи в пространстве rst задается формулой p=(r2+s2)/(l+^2). В каком направлении плотность меняется быстрее всего в начале координат?^В точке (—1, 3, 2)?
85.	Вычислите dF/dx, dF/dy, dFIdz, dF/dw для функции F = xyz/w + xylzw + xlyzw.
86.	Для функцииф(и, v, w, t) = sin (1 + uvVt) найдитефи , Фо , Фю и ф t.
2.1	6. ФУНКЦИИ С НУЛЕВЫМ ГРАДИЕНТОМ
Одна из основных теорем математического анализа для функций одной переменной состоит в том, что если ff = 0 на некотором интервале, то f на этом интервале постоянна (см. гл. 4, § 5.2). Аналогичное утверждение справедливо и для функций нескольких переменных.
Теорема 6. Если функция f нескольких переменных на некотором открытом интервале определена и имеет все частные производные, равные на этом интервале нулю, то эта функция на рассматриваемом интервале постоянна.
Иными словами, если градиент функции равен 0 на некотором интервале, то функция на этом интервале постоянна.
Доказательство. Достаточно рассмотреть случай функции двух переменных. Пусть s — отрезок, параллельный одной из координатных осей и принадлежащий, рассматриваемому интервалу. Вдоль этого отрезка s функция f может рассматриваться как функция одной переменной. Производная этой функции равна либо f'x, либо f'y и, значит, равна нулю, т. е. f постоянна вдоль s. Пусть теперь PQ и Pi — любые две точки рассматриваемого интервала. Их можно соединить ломаной, состоящей из двух отрезков PQP2 и Р2Рь параллельных координатным осям (рис. 12.19). Так как функция f постоянна вдоль каждого из этих отрезков, то она принимает одинаковые значения в точках Ро и Р2, а также одинаковые значения
§ 2. Производные функций нескольких переменных
357
Рис. 12.19
в точках Р2 и Р{. Следовательно, функция f принимает одинаковые значения в л ю-б ы х двух точках рассматриваемого интервала.
Только что проведенное рассуждение применимо к любому связному открытому множеству, т. е. к любому открытому множеству, каждые две точки которого можно соединить ломаной линией, состоящей из отрезков, параллельных координатным осям. (Грубо говоря, связное множество — это множество, состоящее из одного куска.)
Естественно, возникает вопрос: можно ли и при каких условиях найти функцию, определенную в некотором интервале и имеющую в этом интервале наперед заданные непрерывные частные производные? На этот вопрос мы ответим только в следующем параграфе (см. § 3.2 и 3.7). Но сначала мы выведем один очень полезный для дальнейшего результат.
2.1	7. ДИФФЕРЕНЦИРОВАНИЕ ПОД ЗНАКОМ ИНТЕГРАЛА
Мы теперь докажем типичную теорему о дифференцировании определенного интеграла, относящуюся к тому случаю, когда подынтегральная функция кроме обычной «переменной интегрирования» зависит и от другой переменной или от нескольких других переменных («параметров»). Переменную интегрирования мы условимся обозначать через у, а дополнительную переменную («параметр»), по которой мы будем дифференцировать наш интеграл, — через х; однако ясно, что полученные результаты не будут зависеть от используемых обозначений.
Установим, что при соответствующих условиях непрерывности дифференцирование по отношению к одной переменной и интегрирование по отношению к другой перестановочны.
Теорема 7. Пусть функция f(x, у) непрерывна и имеет непрерывную частную производную f'x (х, у) в некотором интервале а < х < 6, с у d. Тогда
d	d
-J-	f f(x, y)dy = f f'x(x, y)dy.
dx	j	j
c	c
Доказательство теоремы 7 не элементарно; мы его отнесем в Дополнение (см. § 3).
•Примеры. 1. Вычислить F'(x)t если
2
F (х) = J (х*у + ху3) dy.
О
358
12. Частные производные
Первое решение. Применим теорему 7 к функции /(х, у) = х2у + хг/3. Мы имеем f'x (х, у) =2ху + у3 и 2	2
F' (х) = J (х2у 4- ху3) dy = J f'x (х, у) dy = О	о
2
= f (2xt/ 4- у3) dy = [xt/2 4- J_ t/4?“2 = 4x 4- 4. J	L 4 J»=o
0
Второе решение. Так как, очевидно, 2
F (х) = С (х2у 4- ху3) dy = [4- х2у2 4-	= 2x2 + 4х«
J	L 2	4 Jo
О
то по-прежнему получаем F' (х) = 4х 4- 4.
2. Пусть ।
u(p,0 = J [ е*2 4- х sin (pt;2)] dx.
Найти и0 , и9.
Решение. В этом случае дифференцирование под знаком интеграла законно. Поэтому мы имеем 1 1
ир (Р> Я) = С ——	4- х sin(pq2)} dx = f xq2 cos (pq2) dx =
J dp \	/ J
о	о
i
= q2 cos (pq2) J xdx = -i- q2 cos (pq2). 0
Точно таким же образом находим, что иа(р, q) = pq cos (pq2).
3. Найти £'(1), если g(x) = j ex? dy.
0
Решение. «Переменная дифференцирования» x здесь встречается дважды: и под знаком интеграла и как верхний предел интегрирования. Поэтому удобно рассмотреть сначала функцию двух переменных
G(s, t) = J dy.
Мы имеем g(x) = G(x, x) и, значит, по цепному правилу, g' (х) = G's (х, х) 4- Gt (х, х).
Теперь в силу основной теоремы интегрального исчисления имеем G^s, t) =е“
§ 2. Производные функций нескольких переменных
359
Далее, по теореме 7, />' / a f de'* . f . С f d е‘У \ j Г е‘У	С j
G<(s, 0= \-zr-dy = \ уе‘? dy = у  ------— ]dy = у ——	— —— dy =
J dt J	J \ dy t J [ t J^° J *
0	0	0	0
= _L^_r±iy=s	—L^ + _L.
t L ** J»=o t <a t3
Таким образом,
g'(x) — ex +ex-----e-* + — = 2-------)e* + — ,
X2	X2 \ X2 j	X2
и окончательно получаем
g'(D = *+!••
УПРАЖНЕНИЯ
В упражнениях 87—92 найдите F’(x) двумя различными способами: сначала интегрируя, а затем дифференцируя полученный результат; потом — сначала дифференцируя под знаком интеграла, а затем интегрируя полученный результат.
2	8
87.	F (х) = J t2lx dt.	90. F (х) = J In (xt) di.
ь	1
88.	F (x) = J (y cos x + x cos y) dy.	91. F (x) = f (x 4- y)n dy.
89.	F (x) = f ехУ dy.	92. F (x) =
1
93.	Пусть g (s, t) = J cos (sye*y) dy, найдите gs и gt .
—1
1
94.	Пусть h (<p, <p) = J [(<pa + y)tty 4- У2] dy; найдите dh[dy и dh[dty.
95.	Пусть f (r) = j cos (rt) dt; найдите f' (2).
io
96.	Пусть h (6) = j* In (6 4- s) ds; найдите h' (5).
9
a2
97.	Пусть H (a) = J ear dr; найдите H' (2).
3(0
12. Частные производные
§ 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
3.1.	ВТОРЫЕ ЧАСТНЫЕ ПРОИЗВОДНЫЕ. РАВЕНСТВО СМЕШАННЫХ ПРОИЗВОДНЫХ
Если функция f(x, у) имеет частные производные
дх	ду
то эти частные производные сами являются функциями двух переменных и тоже могут иметь частные производные. Так, например, если /(х, у) = х2у + ху3, то
f'x = 2ху + у3, f'y =х2 + Зху3 и, следовательно,
^ = -S-JL=2y, ^L = J_JL = 2x + 3^ дх дх дх	ду ду дх
^L = -i-JL.2x + 3g>, i = ^_2L = 6x9. дх дх ду	ду ду ду
Частные производные от частных производных называются вторыми частными производными, или частными производными второго порядка.
Мы видим, что функция двух переменных, скажем, переменных х и у, может иметь четыре различные вторые производные: производная по х от производной по х, производная по у от производной по х, производная по х от производной по у и производная по у от производной по у. Но в только что рассмотренном примере (f = х2у + ху3) обе «смешанные» производные
и д df ду дх дх ду
оказались одинаковыми (а именно равными 2х + Зу2). Это не случайно, ибо имеет место следующая важная
Теорема 1 (о равенстве смешанных производных). Если функция /(х, у), определенная на некотором открытом множестве, имеет все вторые частные производные, являющиеся непрерывными функциями от х и у, то*
О df _ О df
ду дх дх ду
* Заключение теоремы 1 остается верным даже и при более слабых предположениях (напри-мер, достаточно потребовать лишь непрерывности функций fx , fyt fxy и fyx).
§ 3. Частные производные высших порядков
361
Иными словами, если функция f дважды непрерывно дифференцируема, т. е. функции, являющиеся ее частными производными, сами непрерывно дифференцируемы, то мы получаем один и тот же результат, продифференцировав f сначала по х, а затем по у, или сначала по у, а затем по х. Это можно выразить еще и так: дифференцирования по двум разным переменным перестановочны между собой.
Очень легко доказать теорему 1 для одночлена /(х, у) = схтуп, где с — некоторое число, а т и п — целые неотрицательные числа. В самом деле, в этом случае
f’x = тсхт~хуп, ( f'x)'y = птсхт~1 уп~\ fy = псхт уп~\	( f у )х = ппгсхт~* уп~\
так что (fx)y = (fyYx> как и утверждалось. Отсюда следует, что теорема 1 верна и для многочленов, а значит, для произвольных рациональных функций, являющихся отношениями многочленов. Доказательство этой теоремы для общего случая будет дано в Приложении (см. § 6.3).
Для вторых частных производных используются следующие обозначения:
д df _ d2f _ s дх дх дх2 ХХ
(читается «дэ два f по дэ х квадрат» или «вторая частная производная f по х» или «/ два штриха по х, х»). Аналогично,
д___df = d2f = / д df = d2f = г
ду дх дх ду ху ’ ду ду ду2 УУ
и т. д. По теореме 1, если fxy и f"yx непрерывны, то fxy = f”yx.
УПРАЖНЕНИЯ
1. Проверьте справедливость теоремы 1 для функции f (х, у) = sin (х cos у).
N
Д2. Докажите теорему 1 для функций вида f (х, у) =	(х) bj (у), т. е. для случая, когда f
1
является конечной суммой произведений дифференцируемых функций одной переменной.
3. Проверьте справедливость теоремы 1 для функции f (х, у) = ех2у / (у2 4- х).
А4. Пользуясь теоремой 1, докажите, что если функция f(x, у) имеет все третьи частные производные, причем все эти производные непрерывны, то ( [ххУу = ( fXy)'x = ( fyx}x •
5. Проверьте справедливость теоремы 1 для функции/(х, у) = J etx,v dt. X
3.2.	ФУНКЦИИ С ЗАДАННЫМИ ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Пусть и(х, у) и о(х, у) — непрерывно дифференцируемые функции, определенные на некотором открытом интервале /. Существует ли функция /(х, у), определенная на этом интервале и такая, что
f'x =и, f'v= v?
(1)
362
12. Частные производные
У
Рис. 12.20
В силу теоремы 1 ответ здесь не может быть всегда положительным. В самом деле, если выполняются равенства (1), то мы должны также иметь
uy = v'x.	(2)
Это равенство называется условием интегрируемости. В случае его справедливости ответ на наш вопрос действительно будет утвердительным:
Теорема 2. Если и(х, у) и v(x, у) — непрерывно дифференцируемые функции, определенные на некотором открытом интервале /, причем иу = v'x во всех точках этого интервала, то в этом интервале существует такая функция f(x, у), что
fx = fy — v.
Доказательство. Заметим сперва, что если функция f удовлетворяет условиям f'x = и, f = v и С — постоянная, то функция /4 = f + С тоже имеет частные производные и и о. Следовательно, если наша задача имеет решение, то мы можем предположить, что в некоторой точке (х0> У о) интервала 1 функция /принимает наперед заданное значение, скажем, А.
Пусть теперь функция / удовлетворяет требуемым условиям, причем
Кх0, У о) = А.	(3)
Если (х, у) — некоторая другая точка интервала /, то точка (х, у0) также принадлежит / (рис. 12.20). Вследствие условий (1), (3) и основной теоремы интегрального исчисления
/ (*. Уо) — А = f (х, у0) — /(х0, у0) = j f'x (t, ya)dt = J u (t, yQ) dt,
«0	Xo
У t	У
f(x,y) — f(x, y0) = j* f'y(x, s)ds = J v(x, s)ds
Vo	Vo
и, следовательно, x	V
«(t, y0) dt 4- jo (x, s) ds.	(4)
Xq	Vo
f(x,y)=A + ^
§ 3. Частные производные высших порядков
363
Отсюда видно, что если задано значение f(x0, yQ) = Д, то существует не более одной функции /, удовлетворяющей условиям (1). (Это вытекает также и из теоремы 6 § 2.16.)
Покажем теперь, что если условие интегрируемости (2) выполняется, то частные производные функции /, определенной равенством (4), имеют заданные значения. В самом деле, по основной теореме интегрального исчисления и по теореме об интегрировании под знаком интеграла (теорема 7 § 2.17) мы имеем (в предположении, что иу = vx)i
х	у	у
fx (X, у) =	С и (I, у0) dt 4- f V (х, s) ds = 0 + и (х, у0) + f vx (х, s) ds =
дх дх J	dx J	J
Хо	Уо	Уо
У
= И (X, Уо) + J Uy (х, s)ds=u (X, Уо) +	(X, у) — и (X, у0)] = и (х, у).
Уч
Точно так же *	У
fy(x, у) =-^- + -7- f u(t, yo)dt + -£- \v(x, s) ds =0 + 0 + v(x, у) = v(x, у), ду dy J	ду J
Хо	Уо
что и доказывает теорему.
Замечание 1. Наше доказательство указывает также и способ построения функции f с заданными частными пройзводными и и v [а именно формулу (4)]. Но, проще, пожалуй, не пользоваться этой формулой в ее окончательном виде, а поступать следующим образом. Считая у постоянным, можно найти «первообразную» ф функции и, рассматривая ее как функцию только от х. Так мы придем к функции f = ф + с, где «постоянная интегрирования» с = с(у) на самом деле зависит от у. Определим теперь с(у) из условий
(*» У) + с' (у) = v (х, у), ф (х0, у0) + с (у0) = Д.
Разумеется, здесь можно было бы поменять ролями х и у. Это рассуждение ниже иллюстрируется на примерах 2 и 3.
Замечание 2. Пусть D — связное открытое множество и пусть в области D даны две непрерывно дифференцируемые функции и и у, удовлетворяющие условию иу = v'x . Мы можем попытаться найти функцию /, удовлетворяющую условиям f'x = и, fy = vt определяя / сначала в одном из интервалов, содержащихся в Z), затем в некотором интервале, пересекающемся с первым, потом в третьем интервале, и т. д. (рис. 12.21). Так мы можем получить функцию, определенную на всем множестве Z), но можем и не получить такой функции: ведь возможен такой случай, что, попадая в некоторую точку Р по двум разным путям, исходящим из одной и той же точки (х0, у0), мы получим в ней разные значения функции f (см. рис. 12.22 и пример 4 ниже). Такая неприятность не может иметь места, если множество D является, как говорят, односвязным, грубо говоря — не имеющим дырок. (На рис. 12.21 область/) является односвязной; на рис. 12.22 — не является тако-
364
12. Частные производные
Рис. 12.21
Рис. 12.22
вой.) Мы коснулись здесь той области математического анализа, где он вынужден обращаться за помощью к одной не так давно возникшей ветви геометрии, а именно к топологии. (К этому вопросу мы еще вернемся в § 4.)
фПримеры. 1. Существует ли функция f(x,y), такая что[х=Ьу, fy=2x?
Ответ. Нет. Действительно, полагая и — Бу, v — 2х, мы имеем иу =5, v'x =2 и, значит, иу^=ох. Если мы попытаемся воспользоваться формулой (4), приняв, скажем, х0 = у0 = 1, А = 3, то получим
f (%> У) = 3 4- J 5 dt 4- J 2х ds = 3 4- 5 (х — 1) + 2х (у — 1) = 2ху 4- Зх — 2.
Тогда /(1,1) = 3, f 'y = 2х, но f'x = 2у 4- 3	5у.
2. Найти функцию f(x, у), для которой
f'x = 3х2у2у2, fy=x3 + 4xy—l, /(1,1)=4.
Первое решение. Проверим выполнимость условия интегрируемости:
?(3^ + 2У?), = Зх2 + 4у> а(хЗ + 4хУ-1) = Зх2 + 4у ду	дх
Применим теперь формулу (4), положив в ней х0 = у0 = 1, А = 4, и (х, у) = Зх2у 4-4- 2у2, v (х, у) = х3 4- 4ху — 1; мы получим
/ (х, у) = 4 4- (З/2 4- 2) dt 4- | (х34- 4xs — 1) ds =
= 44-(х3 — 1)4- 2(х — 1)4-JK3(«/— 1)4- 2x(f/a— 1) — (у— 1) = х^ 4-2xf/2 — у 4-2.
§ 3. Частные производные высших порядков
365
[Желательно всегда проверять ответ дифференцированием; в нашем случае
(х3у 4 2ху2 — у 4 2)'х = Зх2у 4 2у\
(х?у 4 2ху2 — у 4 2)'у= х3 + 4ху — 1, как нам и было нужно.]
Второе решение. После проверки условия интегрируемости из уравнения £ = Зх2у 4 2у2 находим, что
f(x, у) = х3у 4 2ху2 4 с(у).
Но f'u = xs 4 4ху 4 с'(у) = х3 4 4ху — 1 и, значит, с{у) = —у 4 С, где С — постоянная. Следовательно,
/ = Л/ 4 2ху2 — у + С
и из условия /(1, 1) = 4 получаем С — 2.
3. Найти все функции <р(х, у), для которых
<р* = еху 4 хуеху 4 cos х 4 1, <р^ = х2 еху.
Решение. Условие интегрируемости состоит в том, что
(еху + хуеху 4 cosx 4 1 ) 'у = (х2 еху}х.
В данном случае оно выполняется: обе части последнего равенства равны 2хеху 4 х2уеху. Из второго уравнения (q>j, = х2 еху) получаем
<Р (х, у) =хеху 4 с(х),
где функция с(х) подлежит еще определению. Для того чтобы удовлетворялось условие <рх = еху 4 х«/е*у 4 cosx4 1, мы должны иметь
еху 4 хуеху 4 с' (х) = еху 4 хуеху 4 cos х 4 1,
откуда с' (х) = cos х 4 1, или с (х) = sin х 4 х 4 С, где С — постоянная. Окончательный ответ здесь таков:
Ф (х> У) — хе*у 4 sin х 4 х 4 С;
его легко проверить дифференцированием.
4.	Приведем пример, иллюстрирующий феномен, упомянутый в замечании 2. Пусть D — множество всех таких точек (х, у), для которых 1 < № + / < 2. Обозначим через Do множество всех точек области D, за исключением точек отрезка, соединяющего точки (1, 0) и (2, 0) (рис. 12.23). Для каждой точки (х, у) области Do однозначно определен полярный угол 0, удовлетворяющий неравенству 0 <; 0 <; 2л. Таким образом, функция 0 = 0 (х, у) однозначно определена в области Do. Эта функция имеет частные производные
0=-------------, 0' =----------,
* х2 + у2 у х2 + у2
366
12. Частные производные
что нетрудно доказать, выражая 0(х, у) с помощью обратных тригонометрических функций. Так, например, при х > 0 и у > 0 имеем 0 = arctgу!х, при у > 0 имеем 0 = arccos(x/j/x2 + г/2) и т. д.
Положим теперь
и (•*, У)  ------------,	и (х, у)  ---------.
х2 + У2	х2 + г/2
Эти функции имеют в области D непрерывные частные производные всех порядков и удовлетворяют условию интегрируемости иу = v'x. Однако в области D не существует такой функции /(х, у), для которой f'x=u, a fy = v. Действительно, если бы такая функция нашлась, то в области Do она должна была бы иметь вид 0 + С, где С — постоянная. Но тогда в такой точке, как точка на рис. 12.24, она должна быть очень близкой к С, а в такой точке, как Р 2, она была бы близка к 2л + С. Однако такая функция f не может быть непрерывной в области D. [Заметим, что множество Do является односвязным, а множество D — нет.]ф
УПРАЖНЕНИЯ
6.	Найдите функцию f (х, у), для которой f'x= 12хб-{-24х2у6, f =40x3r/4+80r/® и f (0, 0)=1.
7.	Пусть а, 6, с — данные числа; найдите такую функцию f(x,y)t для которой fx=a, f'y^b> f(xotyQ) = c.
8.	Найдите такую функцию g (х, у), для которой gx = —е*2, gy = еу2, g (х, х) = 0.
9.	Предположим, что = ахпут nfu=bxrys. Докажите, что s=m—1, г—l=n, ma=rb. ?	*	А
10.	Найдите функцию f (г, 6), такую что f (1, 0) = 1, fr = г2 + sin 6,	= г cos 0 + е .
§ 3. Частные производные высших порядков
367
» s ,1
11.	Найдите функцию g (s, /), такую что gs = st + f ех* dx, g't = — s2+ln sin t, g (0, 1)=2. о	2
»	1	। x
A12. Найдите функцию f (x, у), такую что f == — ex/y , f' = —-ex^y и f (1, 1) = 0.
У	y У2
13. Пусть fxx = 24xr/2 + 6x, fxy=24x2y, fy = 8x3y + 2y, f (0, 0)=0, fx (0, 0) = 0, найдите t (x, y).
3.3. ВЫСШИЕ ПРОИЗВОДНЫЕ
Разумеется, запас частных производных функции не ограничен одними лишь первыми и вторыми частными производными. Мы можем пытаться находить частные производные от вторых частных производных, называемые третьими частными производными, или частными производными третьего порядка, затем, аналогично, четвертые частные производные (частные производные четвертого порядка) и т. д.
Если функция f(x. у) имеет все частные производные до порядка N включительно, причем все эти производные непрерывны, то функция f называется N раз непрерывно дифференцируемой функцией. В этом случае «смешанные» частные производные функции f зависят только от того, сколько раз мы дифференцируем f по каждой из переменных, но не от порядка, в котором производятся эти дифференцирования. Так, например,
д д df	= д д df	= d d	df
dx dy dy dy dx	dy dy	dy	dx
что можно записать еще и так:
fyyx = fуху = fxyyX
поэтому эта частная производная третьего порядка обозначается просто через
d3f
dx dy2
(читается: «третья производная функция f. один раз по х и два раза по у» или «дэ три f по дэ х. дэ у квадрат»). Никакого дополнительного доказательства этого факта, разумеется, не требуется; он вытекает из теоремы 1 § 3.1. Так, равенство
d d df __ d d df dx dy dy dy dx dy
получается применением теоремы 1 к функции fy. С другой стороны, по теореме 1, примененной к функции /, мы имеем, что
d df	d df	d d	df	d d	df
dx dy	dy dx	dy dx	dy	dy dy	dx
Аналогичное рассуждение применимо во всех случаях.
368
12. Частные производные
Функция f(x9 у) имеет четыре различные третьи частные производные: d3f d3f d3f д3?
дх3 ’ дх2ду ’ дхду2 ’ ду3
пять различных четвертых частных производных; ау	ау ау ау _ау_
дх4 ’ дх3ду ’ дх2ду2 ’ дхду3 ’ ду*
И Т. Д.
фПример. Найти значения всех третьих частных производных функции f (%, у) = ех2у в точке х = 0, у = 1.
Решение. Имеем fx = 2хуех\ f'y = х2ех2у. Следовательно,
/« = (/;); = 2^"+ fxy = (f'g)'x = 2xex*y + 2x3yex2y, fyy = (fy)y=^ex,y и, значит,
fxxx = ( fxx Ух = 4xy2ex2y + 8ху2ех2у + 8х3у3ех*у = 4ху2 (3 + 2х2у) ех2у;
fxxy = ( fxx = 2ех2у + 2х2уех2у + 8х2уех2у 4- 4xty2ex'y = 2(1+ Ьх2у + 2хУ/2) ех2у\
fxyy = ( fyy )* =	+ 2х5уех2у = 2х3 (2 + х2у)ех2у;
fyyy = ( fyy}У — х&е У*
Таким образом,
fxxx (0, 1) = 0, fXXy (0, 1) = 2, fXyy = О И fyyy = 0. ф
УПРАЖНЕНИЯ
14.	Найдите все третьи частные производные функции f (х, у) = sin (ху).
15.	Если f(x, у) = f(yt х) для всех х, у и если, по определению, g(x, у) есть сумма всех третьих частных производных функции f, то g(x, у) = g(y9 х) для всех х, у. Докажите это.
16.	Пусть f = xey‘-, вычислите f™xx, f™yy и f™xy.
17.	Пусть f= In (х2 + у), найдите все третьи частные производные функции f.
<18. Пусть f (х, у) — f (—х, у) =—f(x, —у) для всех х, у\ докажите, что fxy(x, у) = = “ fxy(—x> y)=f"xy(x> —У) Для всех х^ У и fmxxy(x^ У) = Г хху (—х —У) &ЛЯ всех х, у.
19. Проверьте, что fmxxy = Г"хух = f"'yXx Для Функции f (х, у) = х cos (ху2).
3.4. КРИТИЧЕСКИЕ ТОЧКИ
Напомним (см. § 2.9), что точка, в которой обе (первые) частные производные fx и fy функции f(x9 у) обращаются в нуль, называется ее критической точкой. Так, например, если функция f в точке (х0, yQ) имеет локальный максимум (или локальный минимум), т. е. если f(x, у) f(xOf у0) при всех (х, у) в окрестности точки
§ 3. Частные производные высших порядков
369
(х0, yQ) [или если /(х, у) /(х0, z/0) при всех (х, у) в окрестности (х0, r/0)L то (х0, z/0) является критической точкой. В самом деле, в этом случае обе функции одной переменной
х I—► fix, у0), у ->f(x0, у)
при х = х0 и у = Уо соответственно имеют локальный максимум (или локальный минимум) и, значит, их производные в этой точке равны нулю. Но это и означает, что Гх (х0, Уо) = О И f'y (Хо, Уо) = 0.
Обратное обстоятельство вовсе не обязательно должно иметь место: в критической точке функция не обязательно имеет максимум или минимум. Будет ли это так, иногда можно определить по вторым частным производным функции /, или, точнее, по знакам выражений f"xx fyy — fxy и, скажем, fxx + fyy (или любого из слагаемых последней суммы; ср. с соответствующим утверждением для функций одной переменной в § 4.4 гл. 4).
Прежде чем сформулировать правило, которое мы здесь имеем в виду, условимся относительно терминологии. Предположим, что функция /(х, у) определена в окрестности точки (х0, у0). Мы говорим, что точка (х0, у0) является точкой строгого минимума функции, если /(х0, у0) < /(х, у) при всех (х, у), близких к точке (х0, уо) и отличных от самой этой точки. Если /(х0, г/0) > /(х, у) при всех (х, у), близких к точке (х0, уо) и отличных от нее, мы говорим, что (х0, у0) есть точка строгого максимума функции. Наконец, если fx=zfy = O в точке (х0, #0) и в каждом интервале с центром (х0, уо) найдется такая точка (хь r/J, что /(хь r/J < /(х0, у0), а также такая точка (х2, у2), что /(х2, у2) >/(х0, Уо)> то точка (х0, у0) называется седлом.
Так, например, для функции /(х, у) = ху начало координат является седлом. В самом деле, в начале координат f = f'x = f =0, причем Дх, у) > 0 в первом и третьем квадрантах и /(х, у) < 0 во втором и четвертом квадрантах.
Теорема 3. Пусть функция f(x, у) трижды непрерывно дифференцируема в точке (х0, Уо) и пусть в этой точке f'x = fy = 0; тогда
если в этой точке	то эта точка является
1XX fyy	fxy<^ fxx fyy	fxy>^ fxx-^^ fxx fyy	fxy^*®' fxx^^	седлом точкой строгого минимума точкой строгого максимума 1
Доказательство теоремы 3 мы отнесем в Приложение (см. § 7.3). (Более тонкое исследование показывает, что утверждение теоремы 3 справедливо также и для дважды непрерывно дифференцируемых функций.)
370
12. Частные производные
3.5. МАКСИМУМ И МИНИМУМ
Предположим, что нам дана какая-то «хорошая» функция (х, у) ь-> /(х, у), определенная в замкнутом интервале или в некоторой другой «хорошей» области и на ее границе, и что мы хотим найти точки, в которых эта функция принимает наибольшее и наименьшее значения — абсолютный максимум и абсолютный минимум функции. (Пока мы предполагаем, что такие точки существуют; доказательство этого будет дано в Дополнении — см. § 2.6.) Максимум и минимум функции могут достигаться и на границе области. Если абсолютный максимум (или абсолютный минимум) функции f достигается в некоторой точке Р, не принадлежащей границе рассматриваемой области, то точка Р должна быть точкой локального максимума (или локального минимума), а следовательно, точка Р обязательно является критической.
Этим подсказывается следующий способ определения абсолютных максимума и минимума. Прежде всего находим все критические точки функции, расположенные внутри рассматриваемой области, для чего достаточно решить систему уравнений /*(х, У) = 0, fy(xt у) = 0. Затем находим те граничные точки области, которые могут быть точками максимума или минимума; это сводится к нахождению максимума и минимума функции одной переменной — параметра, к которому отнесены линии, ограничивающие рассматриваемую область. После этого нам остается только сравнить значения функции во всех найденных точках.
• Пример. Каковы наибольшее значение (абсолютный максимум) и наименьшее значение (абсолютный минимум) функции
f(x„ У) = 2х2 — ху + уг + 7х,
заданной в замкнутом интервале
—3	х 3, —3	у 3,
и в каких точках они достигаются^ Решение. Имеем
fx = 4х — у + 7, fy = — х + 2у.
Из системы уравнений f'x=f'y=O находим единственную критическую точку х = — 2, у = — 1; эта точка принадлежит рассматриваемому (замкнутому) интервалу. Так как fxx = 4, fxy = — 1, fyy = 2, то имеем	= 7 > 0,/хх+
_|_ fyy = 6 >> 0 (достаточно заметить, что f"(x) > 0). Следовательно (см. теорему 3 § 3.4), наша критическая точка является точкой локального минимума.
Рассмотрим теперь функцию f при у = —3, т. е. функцию
х Дх, —3) = 2х2 + 10х + 9,
где—3<^х<^3. Ее производная равна 4х + 10, что можно получить либо дифференцированием выписанной функции, либо подстановкой у = —3 в выражение
§ 3. Частные производные высших порядков
371
для fx. Эта производная равна нулю при х = —5/2. Следовательно, единственные значения х, при которых функция /(х, —3) может достичь максимума или минимума, — это концы интервала х = —3, х = 3 и корень х = —5/2 производной.
Аналогично рассматриваем и каждую из остальных трех сторон ограничивающего наш интервал прямоугольника; на стороне у = 3 функция х -> /(х, 3) имеет критическую точку при х = —1, а на двух вертикальных сторонах функции у »-► /(—3, у) и у ь-> /(3, у) имеют критические точки х = —3, у = —3/2 и х = 3, у = 3/2. Следовательно, функция f может достичь наибольшего и наименьшего значения только в критической точке внутри области ее определения, в одной из четырех вершин ограничивающего эту область прямоугольника, в двух точках горизонтальных сторон прямоугольника, где /' = 0, и в двух точках вертикальных сторон, где f = 0. Эти девять точек отмечены на рис. 12.25. Вычислив теперь значения функции f во всех этих девяти «подозрительных» точках, мы получим следующую таблицу:
X	—3	—1	3	—2	—3	5 ”” 2	3	—3	3
У	3	3	3	—1	—3	—3	—3	3 — 2	3 2
f	15	7	39	—7	—3	1 —3— 2	57	1 4	3 36т
Следовательно, наибольшее значение функции /(х, у) в замкнутом интервале | х |	3, | у |	3 равно 57 и достигается при х = 3, у = —3; наименьшее
значение, равное —7, достигается при х = —2, у = —1.ф
372
12. Частные производные
УПРАЖНЕНИЯ
^20. Покажите, что прямоугольный параллелепипед (коробка) максимального объема V с наперед заданной площадью поверхности S является кубом.
21.	Найдите наибольший объем прямоугольного параллелелипеда (коробки), грани которого параллельны координатным плоскостям и который вписан в эллипсоид
22.	Найдите три числа х, у, г, такие что х + у + г = 1, а сумма ху + xz + уг является наибольшей из возможных.
23.	Найдите кратчайшее расстояние от начала координат до плоскости ах + by + cz + d=0.
24.	Найдите ближайшую к началу координат точку поверхности г = ху — 1.
25.	а) Найдите наибольшее значение функции г = 2х + 4г/ — х2 — у2 — 3 из всех принимаемых ею в плоскости ху.
б)	Найдите наибольшее и наименьшее значения г в (замкнутом) интервале |х|< 1, I У I < 1-
J^26. а) Найдите все критические точки функции и = х3 + у3 — Зху и определите, какие из них являются точками максимума, точками минимума или седловыми точками.
б)	Найдите наибольшее и наименьшее значения функции а в треугольнике с вершинами (0, 0), (0, 1), (1, 0) (стороны треугольника причисляются к рассматриваемой области).
xz-{-yz~^-y
27.	Пусть/(х, у) = е ; найдите наибольшее и наименьшее значения, принимаемые функцией f в квадрате с вершинами (1,0), (0, 1), (— 1,0), (0, — 1) (учитывая и стороны этого квадрата).
28.	Пусть f(x, у) = ах2 + 2Ьху + су2\ найдите, при каких значениях a, Ь, с в области х2 + y2Z> 1 существует критическая точка функции /.
29.	Пусть f(x, у) = In (Зх2 + 4г/2 + 2х + 7).
а)	Найдите область D, в которой функция f определена.
б)	Найдите и определите все критические точки функции в области D.
в)	Найдите наибольшее и наименьшее значения функции t в единичном квадрате 0 < х < 1, 0 < у < 1.
3.6.	ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ДЛЯ ФУНКЦИИ БОЛЕЕ ЧЕМ ДВУХ ПЕРЕМЕННЫХ
Определение производных высших порядков и обозначения этих производных для функций более чем двух переменных вполне понятны. Если функция нескольких переменных дифференцируется несколько раз, то при условии непрерывности рассматриваемых производных результат зависит от того, сколько раз мы дифференцируем функцию по каждой переменной, но не от порядка, в котором производятся дифференцирования. Так, например, если и = f (х, у, г), то
дх ду dz дх dz ду ду дх dz
ду dz дх dz дх ду dz ду дх и общее значение этих шести производных обозначается через Г =-*L-.
хуг дхдудг
Доказывать это утверждение не надо: оно автоматически получается повторным применением теоремы 1 § 3.1. В самом деле, если мы выполняем дифференцирование по двум переменным, зафиксировав значения остальных переменных, то мы имеем дело, в сущности, с функцией двух переменных.
§ 3. Частные производные высших порядков
373
д ду	о
------------ геУг cos и2, ду дх
= — 2uze?z sin и2,
фПример. Пусть v = хеУ* cos и2; найти значение	пРи * = 0, у = 0,
z = 1, и = ]/пГ. Решение. Так как, очевидно, до	о д2у
-------------- еУг cos и2, 	 дх------------------дх ду
____д д2у ди дх ду
д v = — 2геУ* sin и2 — 4и2геУг cos и2,
д3у дх ду ди д*у ____ д
дх ду ди2	ди дх ду ди
то значение рассматриваемой производной при х = у = 0, z = 1, и=)Лгс равно 4л.
УПРАЖНЕНИЯ
Для данных функций найдите в заданных точках указанные производные.
д3/	к
А 30. f = a cos b sin t2, —------- , a = 1, b = — , / = jAu .
da db dt	2	r
31.	g = abc In (dsin/), g^abcdt' t = n/4, a = b = c = d=l.
32.	h = uvw -\-uv-\-uw-\-vw + u-\-v-\~w,	+ h"vw в точке (1 • 1» 1)•
33.	F = cos Xi sin Xi cos x2 sin x2 ... cosxN sinxN. Вычислите -gj--------
= x2 =	= xN = k/6.
34.	F = In [x In (y In z)]. Вычислите Fxyz (a, a, a).
при Xi =
35. G=(w + y + tt/ + x + f/ + z)10°. Пусть g — сотая частная производная функции G. Чему равно g?
^36. И = (Зи + 4у + боу/. Вычислите все третьи производные //.
37. Сколько имеет, вообще говоря, различных третьих частных производных функция г переменных, дифференцируемая достаточное чйсло раз?
3.7.	ФУНКЦИИ С НАПЕРЕД ЗАДАННЫМ ГРАДИЕНТОМ
Если f (xi, х2,... , хп)— дважды непрерывно дифференцируемая функция п переменных с частными производными
ut (%!..хп) = df(X1' Х2’ • • ,Хп),	1 = 1,2....п,	(5)
дх^
то эти производные удовлетворяютп (п— 1) условиям интегрируемости:
, I = 1, 2.....п; / = 1,2.....n, i=hj.	(6)
dxj dxi
d2f
В самом деле, обе части равенства (6) равны---------— •
dxi dxj
374
12. Частные производные
Обратно, если в некотором интервале I нам даны п непрерывно дифференцируемых функций удовлетворяющих условиям интегрируемости (6), то в / существует такая функция /, что df/dxt = ut при всех i. Решение системы уравнений (5) будет однозначно определено, если мы зададим значение / в какой-нибудь точке интервала /.
Все это доказывается в точности так же, как в случае функции двух переменных (см. § 3.2). Так, например, если п = 3 и и, v, w — это определенные в интервале / непрерывно дифференцируемые функции от (х, г/, z), то для нахождения определенной в интервале / функции /, для которой
fx = и, f'y — v, fz = w,
прежде всего должны быть выполнены условия интегрируемости9.
иу = vx, и2 = wx, v2 =wy.
Если эти условия имеют место и (х0, z/0, z0) — произвольная точка интервала /, то функция
xyz
f(x, у, z) = А + §u(t, у0, z0)dt + S. Za) ds + Jw(x,y, r)dr
Уо	?0
в точке (x0, y0, z0) принимает значение А и имеет заданные частные производные. Читатель может доказать это, копируя доказательство теоремы 2 § 3.2.
Мы упомянем еще без доказательства, что функцию с заданными частными производными в связном открытом множестве D можно найти только в том случае, если: 1) заданные частные производные удовлетворяют условиям интегрируемости', 2) множество D является односвязным. Последнее условие означает, что каждая замкнутая кривая в области D «может быть стянута в точку» так, что в процессе ее деформации она не выходит за пределы области D. (В случае плоскости условие односвязности означает, что область D не имеет «дырок»; мы вернемся к этому вопросу в § 4.)
фПример. Найти функцию f (х, у, z), для которой
fx = 2х, fy = 2у, fz = 2z и /(О, 0, 0) = 1.
Решение. Условия интегрируемости здесь выполнены. Так как f'x = 2х, то мы имеем / = х2 + с^у,г), где «постоянная интегрирования по х » является функцией у и z. Условие fy = 2у приводит к уравнению (с^у = 2у. Следовательно, Ci(y, г) = У2 + c2(z) и f = х2 + у2 + c2(z). Из условия fz = 2z получаем с2 (z) = 2z, т. е. c2(z) = z2 + С, где С — постоянная.. Таким образом, окончательно имеем
f = х2 + у2 + z2 + С.
Так как f = 1 при х = у = z = 0, то С = 1 и, значит,
f = х2 + у2 + z2 + 1.
Конечно, этот результат можно было предвидеть, ф
§ 4. Криволинейные интегралы
375
УПРАЖНЕНИЯ
В упражнениях 38—43 определите, существует ли функция [(х, у, г), удовлетворяющая заданным условиям; если такая функция существует, найдите ее.
38.	fx = ey+zZt f 'y = xezi 4- cos у, f '2 = 2xzey+zZ, f (0, 0, 0) = 1.
39.	fx = cos (z In (x + y)), fy = sin (z In (x + y)), f'z = cos (yz In (x + y)), f(0, 0, 0) = 1.
40.	fx = cos (x cos y) cos y,	f'y = — x (cos (x cos y)] sin у — sin z sin (y sin z), fг =
= — у cos z sin (y sin z), f (0, 0, 0) = 1.
41.	fx = yexy, fy= хехУ + ze~?z , f'2= ye^z, f (1, 1, 1) = e + 1/e.
A42. fx = cos у •_ exzosy— ylz, fy = — sin y-ex cos y — x/z, f2=xy/z2,	3, 4) = —4.
43.	f'x = ех/», fy = e-xW, 4 = 4, [ (1, 1, 1) = 0.
§ 4. КРИВОЛИНЕЙНЫЕ Существуют два пути обобщения понятия интеграла от ИНТЕГРАЛЫ функции одной переменной на функции нескольких переменных: на одном из них получаются так называемые кратные интегралы, которые мы рассмотрим в следующей главе, а на втором — интегралы, определенные на кривых линиях, искривленных поверхностях, и т. д. Мы рассмотрим здесь простейший и самый важный случай таких интегралов: интегралы по линиям, или криволинейные интегралы.
4.1.	ОПРЕДЕЛЕНИЕ И ОБОЗНАЧЕНИЯ
Пусть С — кусочно-гладкая кривая в трехмерном пространстве, в некоторой декартовой системе координат (х, у, z) заданная тремя функциями:
/»—► x(Z), t y(t), 11-> z(t), a t b.	(1)
Далее, пусть P (x, y, z), Q (x, y, z), P (x, y, z) — три непрерывные функции, определенные на некотором множестве, содержащем линию С. Тогда можно определить число, называемое криволинейным интегралом от Р dx + Q dy + Р dz по линии С и обозначаемое через
J Pdx + Q dy+R dz.	(2)
с
Это число равно
J [Р (X (t), у (/), г (0) X' (0 + Q (X (П, у (0, Z (0) / (0 + R (х (t), у (0, г (/)) г' (/)] dt. (2') а
Заметим, что мы могли догадаться о значении выражения (2), полагаясь на обозначения Лейбница: ведь ясно, что, например, dx не может означать ничего, кроме x'(t)dt.
376
12. Частные производные
Аналогично, если функции
1х (/), t\-+ у (/), где а	(3)
определяют кусочно-гладкую кривую С на плоскости и Р (х, у), Q (х, у) — непрерывные функции, то
^Pdx + Qdy	(4)
есть не что иное как сокращенная запись числа
J [Р (X (0, у (0) x\t) + Q (X (0, у (0) /(/)] dt.	(4')
а
Вообще, если даны п функций
t Х;(/), j = 1, 2, ... , п, а t b,	(5)
определяющих кусочно-гладкую кривую С в n-мерном пространстве, и если даны п непрерывных функций Р (хь х2, ... , хп), то, по определению,
Pi dx1 4- P2dx2 + • • • + Pndxn= J ^Pj dxj = c /=1
Вычислить
b Г n = j a L/=l
Примеры. 1. Пусть С — кривая
х = sin /, у = cos /, z = Z2, 0 t
xn(0)xj(0 dt.
(6)
Решение.
J ydx — xdy — z2dz.
Этот криволинейный интеграл равен
1	2
[cos t • cos t — sin t (— sin t} — (Z2)2 • 2/] dt = С (1 — 2/5) dt = — J	3
2.	Пусть С — кривая
х = t, у = г = 0, а < t Ь. Чему равен криволинейный интеграл
У /(х) dx+ g (у) dy + h (z) dz, С
где f, g, h — непрерывные функции?
Ответ. Так как dy/dt = dz/dt = 0, то этот криволинейный интеграл равен ь
J/ (t)dt.
а
Таким образом, обычный интеграл является частным случаем криволинейного интеграла, ф
§ 4. Криволинейные интегралы
377
УПРАЖНЕНИЯ
В упражнениях 1—4 вычислите интеграл J Р dx + Qdy+Rdzjuin данных Р, Q, R и С.
1.	С:	х= t, у = /2, z = Z3;	2 < t < 3; Р = еху, Q = sin х,	R = ху/г.
2.	С:	х	= у =	ё~*, г =	t2\	0 < t < 1; Р = ху, Q = x2z,	R = хуг.
3.	С:	х	= в3, у =	в, z = 02;	2	< 0 < 3; Р — yzix, Q = е?, R = sin z.
4.	C:	x	= s2 + s3,	у = y^s2	+	1, z = es*, —1 < s < 1; P =	x2, Q = y3, R = cos z.
5.	Вычислите J yndx + xndy, где кривая С задается равенствами x = asin0, i/=Z>cos0, О < 0 < 2тс.
Д6. Вычислите j Xi dxx + х2 dx2 + ... + хп dxn по кривой С, определяемой уравнениями хх =
— a^t, х2 —	, ••• , х— ant, tfg t
n
7.	Вычислите J dXi 110 КРИВО“ С, определяемой уравнениями x$ = tlt i = 1,2, ..., n, C Z=1
/() t /j.
n
8.	Вычислите J t* dtj по кривой Г, определяемой уравнениями tj=&, j = 1, 2, ... , n, г /=1
4.	2. НЕЗАВИСИМОСТЬ ОТ ПАРАМЕТРА
Значение криволинейного интеграла по кривой С не зависит от выбора параметра, использованного в представлении этой кривой.
Мы докажем это при п = 3 для криволинейного интеграла вида
f Pdx, с
(7)
т. е. для случая, когда Q = Ц = 0; однако наше рассуждение будет иметь совершенно общий характер. Предположим, что кривая С представляется уравнениями
х = х (/), у = у (0, z = z (t), a <Zt <Zb.
Пусть t = tp (т),	р — допустимая замена параметра (см. гл. 11, § 3.1).
Тогда ф (а) = а, ф (Р) = b и ф'(т) > 0; кривая С может быть также представлена тремя функциями
т I—► х (ф(т)), т у (ф(т)), т —>z (ф(т)), а < т < р.
378
12. Частные производные
Если мы вычислим наш криволинейный интеграл, используя ^-представление кривой, то мы получим
JP[(x(O, y{t), z(t)]x'(t)dt,	(8)
а
а вычисляя (7) с помощью параметра т, получим интеграл
0
Jp[x((p('t)), 1/(ф(т)), Z(<p(T))]V(<p(T))<p'(T)dT, а
который в силу правила замены переменной в обычном интеграле (см. гл. 5, § 3.5) равен интегралу (8).
4.3	. СВОЙСТВА КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
Имеем
(Л! + Bj) dxj + • • • + (Ап + Вл) dxn =
At dxt + • • • + Ап dxn + j Bj dxj + • • • + Bn dxn	(9)
и при постоянном k
kAt dxr +-----1- kAn'dxn = k I Aj dxA + • • • + An dxn.
(10)
Далее, если —С есть та же кривая С, но пробегаемая в противоположном направлении (см. гл. 11, § 2.2), то
^A1dx1 + ••• + Ап dxn= — § Aj dXj 4----Ь Andxn,	(11)
и если кривая + С2 состоит из кривой и следующей за ней кривой С2 (см. гл. 11, § 2.3), то
J Aj dxj • • • + Ап dxn = J Aj dxy 4- • • • 4- An dxn 4- j* At dXj + • • • 4- An dxn. (12) сДс,	ct
Все четыре равенства (9)—(12) доказываются непосредственным вычислением. Мы докажем здесь лишь равенство (И); при этом для краткости ограничимся интегралом (7). Если кривая С представляется уравнениями 1х (t). 11-> у (/), t »-► г (/), a t 6, to — С можно представить уравнениями s x(b — s), s »-> y(b — s), s -+z(b — s), 0 s b — а. Следовательно,
b—a
J Pdx = J P[x(b — s), y(b — s), z(b — s)] [—x'(b — s)]ds.
-с	о
§ 4. Криволинейные интегралы
379
Полагая т = Ь — s, будем иметь dx = —ds, причем т = b при s = 0 и т = а при s = b — а. Следовательно,
а	Ь
Pdx = J Р |х (т), у (т), г (х)) х/(х) dx = — j Р [х (х), у (х), г (х)] Xх (х) dt = — Jpdx, что и требовалось доказать.
фПример. Пусть С — кривая, изображенная на рис. 12.26, пробегаемая в указанном направлении от точки (0, 0) до точки (0, 1). Требуется вычислить
^(2 + у) dx + х dy.
Р е ш е н и е. Имеем С= Ct + С2, где Ci — отрезок прямой, задаваемый уравнениями x=t, у=0,	и С2— дуга окружности х = cos 0, у = sin 0, где
ТС
0	0 С “• Вдоль кривой Cj: dx = dt, dy—О. Вдоль кривой С2: dx = —sin 0d0.
dy = cos 0 d0. В силу равенств (9), (10) и (12)
f (2 -|- у) dx + x dy — 2 I dx -f- \ у dx+x dy =
c	Sb
= 2	j dx + 2	j dx	\ у	dx +	xdy	+	\y dx + xdy	=
Ci	C^	Ci	C*
1	ic/2	1	k/2
= 2 f	dt	+	2 C (— sin 9) dG + f 0	dt +	C	(— sin2 G	cos2 G) dG =a
oo	oo
я/2	ic/2
= 2 Ц- 2 cos GI 4- — sin 2G | = 0. ф
380
12. Частные производные
УПРАЖНЕНИЯ
В упражнениях 9—17 вычислите j* Pdx + Qdy + R dz или J P dx + Q dy для заданных линий С	С
С и подынтегральных функций Р, Q, R или Р, Q.
9.	С—треугольник с вершинами А (0, 0, 1), В (0, 1, 0) и С (1, 0, 0), пробегаемый в направлении АВС\ Р = xyz, Q = 1п(дг + у + г), R = 7.
10.	С — прямоугольник с вершинами А (0, 0, 1), В(1, 0, 1), С (1, 1,1),D (0, 1, 1), пробегаемый в направлении ABCD\ Р = х2 + у2, Q = xyz, R = х + у + г.
11.
12.
13.
14.
С — линия пересечения единичной сферы с плоскостью г = 0, пробегаемая один раз в направлении против часовой стрелки, если смотреть со стороны положительных значений г («сверху»); Р = уг, Q = хг, R = ху.
С — эллипс с центром в начале координат, с большой осью 2а, принадлежащей оси х, и малой осью 2d, пробегаемый один раз в направлении против часовой стрелки; Р = = х + у, Q = х — у.
С — полуокружность с центром (0, 4) и радиусом 2, лежащая справа от оси у и пробегаемая один раз в направлении против часовой стрелки; Р = х2 — у2, Q = гу.
С—единичная окружность, пробегаемая 1— раза в направлении против часовой стрелки 4
от точки (1, 0); Р = Ах + By, Q = Сх + Dy (Л, В, С, D — данные числа).
15.	С — правильный шестиугольник с центром в начале координат и одной из вершин в точке (1, 0), пробегаемый один раз в направлении против часовой стрелки; Р=3х2у —4у2х, Q = Зу2х + 4х2у.
±16. С — дуга окружности, начинающаяся в точке Л (—1, 1), проходящая через начало координат и заканчивающаяся в точке В (1, 1) (С пробегается в направлении от Л к В); Р = х + у, Q = х — у.
17.	С — кратчайший путь, по которому ползет жук в плоскости ху от точки (—2, 0) до точки (1, 0), не заходя в пределы единичного круга; Р = х3 + у2, Q = х2 + у3.
±18. Пусть С — кривая, определяемая уравнениями х = cos 0, у = sin 0,0 < 0 < 4л, и С2 — кривая, определяемая уравнениями х = cos Z2, у = sin t2, 0 < t < 2]/jT. Для
P = згу, Q = y2x покажите, что
JP dx+Q dy=§ P dx+Q dy. c 2
Объясните, почему это так.
19.	Пусть Сг — кривая, определяемая уравнениями х = е*, у = е~*, г — t2, 2 < t < 4, и Сз — кривая, определяемая уравнениями х — t, у = \/t, г — In2t, е2 < t < е4. Положим Р = е*Уг, Q = х sin уг, R— у sin хг. Докажите, не вычисляя ни одного из интегралов, что
У Р dx-j-Q dy + R dz = J P dx-h Q dy+ R dz.
20.	Пусть P(x, y) — наибольшее, Q(xt y) — наименьшее из двух чисел х и у\ обозначим через (*1(0, УМ) положение в момент времени t жука, который ползет по единичной окружности со скоростью один радиан в час. Положим: С^: x=Xf(t), у = y^t), 0 < t < 1 и Сз: х = =^(УТ), у = ух(УТ}, 0<Г<1. Вычислите JP dx+Qdy и J Pdx + Qdy.
21.	В упр. 1 и 2 из § 4.1 положите t = ^и вычислите предложенные интегралы, используя параметр s.
§ 4. Криволинейные интегралы
381
4.4. ЯЗЫК ДИФФЕРЕНЦИАЛОВ
Если 11-* ср (/) — функция одной переменной, то с?ф есть просто сокращенное обозначение для ф'(/)Л; в гл. 5 (см. § 3.4 и 3.5) мы видели, как полезно это обозначение. Теперь мы распространим «язык дифференциалов» на функции нескольких переменных. Если / (хь х2, ... , хп) — функция п переменных, то условимся писать
df=JLdX1 + ^dx2+ ... +-^-dxn.	(13)
дх!	dx2	дхп
Эту запись мы будем понимать формально: просто при вычислении криволинейных интегралов мы будем пользоваться левой частью равенства (13) для сокращенного обозначения правой части.
Цепное правило (ср. с § 2.14) можно хорошо объяснить на этом «языке дифференциалов». Если xt — функции от т новых переменных ui9 u2, ••• , т- е- если xi = = Ti (ui9 u2f ... , ит), i = 1 , 2, ... , n, to
dxt = du-i 4- du2 + • • • + ^-dumi 4 = 1.2,..., n. dur	du2	dum
Подставляя эти выражения в (13) и перегруппировывая члены, получим
d/	+ JL±i + ...+A. dU1 +
\ dx± dut dx2 du,!	dxn duv )
+ l_d[_ *h+JL dn + ... +JL *fl}du2 +
\ dx± du2 dx2 du2	dxn du2)
+....................................+
+ fJL + JL + . + JL dUm =
\^i dum dx2 dum	dxn dum)
— Аг dui + A2 du2 + • • • + Am dum,
где
= df	3?!	| df	3y2	df	d^n
f дхг	duj dx2	du j	dxn	du j
Так как Aj есть коэффициент при duf в выражении для dft то
как это и должно быть согласно цепному правилу.
Используя новые обозначения, мы вернемся к вопросу, рассматривавшемуся в § 3.2 и 3.7. Пусть даны п функций А 4, А 2, ... , Ап от п переменных xif х2, ... , хп; требуется найти, если это возможно, такую функцию f, для которой
« = 1,2,...,п.	(14)
dxt
382
12. Частные производные
Это условие можно переписать в следующем виде:
+ А 2е2 + ... + Апеп = grad F,	(15)
где {еь ej, , ед| — некоторый репер, или, иначе:
Aidxi + A 2dx2 + ... + Andxn = df.	(16)
В § 3 мы решили эту задачу для случая, когда все рассматриваемые функции определены в некотором интервале. Теперь мы рассмотрим более общие области.
УПРАЖНЕНИЯ
22.	Для каких х, у имеет место равенство d (ху) = О?
23.	Пусть и и v — функции п переменных (хх, №, ...» хя); верно ли, что d(u +и) = du-\-dv? Верно ли, что d(uv) = и dv + vdu?
В упражнениях 24—29 вычислите du для данной функции и = и(х, у, г).
24.	и = 8х cos (гу).
25.	и =	«г.
26.	и = — arccos (х + у).
27.	и = in (t/2 + sinz + ye*).
28.	и = arctg (хгеУ).
29.	и = sh (ху arcth г).
4.5. НЕЗАВИСИМОСТЬ ОТ ПУТИ
В этом и следующем параграфах через D обозначено некоторое открытое связное множество точек n-мерного пространства; конечно, особенно важны случаи, когда п = 2 и п = 3.
Теорема 1. Пусть Aif А2, ... , Ап—непрерывные функции переменных (х4, х2, ... , хп), определенные в области D. Если существует такая определенная в области D функция /, что
df = Aidxl + A 2dx2 + ... + Andxn,	(17)
то для каждой кусочно-гладкой кривой С в области D, идущей из точки Р в точку Q, имеем
^A.dx^.^+Andxn=f (Q) - f (Р),	(18)
так что, в частности, pxdxx+ ... +A„dx„=0	(19)
С
для каждой замкнутой кривой С в области D. Обратно, если условие (19) имеет место то существует функция f, определенная в области D и удовлетворяющая равенству (17).
Обозначения Лейбница подсказывают нам формулу (18), так как если выполняется равенство (17), то равенство (18) можно переписать в следующем виде:
§ 4. Криволинейные интегралы
383
Q df = f (Q) — f (Р),
напоминающем основную теорему интегрального исчисления. И в самом деле, наша теорема довольно просто вытекает из этой основной теоремы.
Доказательство теоремы I. Предположим, что равенство (17) справедливо и пусть кривая С задается уравнениями х = х (/), т. е. xt = хг(/), t = 1. 2...............л, причем Х}(а) = pt, xt(b) = qit где (plt р2, ... , рп) и
(qlt q2, ... , qn) — координаты точек Р и Q. В силу (17) Aj = df!dx} при / = I, 2, ... , п. Положим
Р (0 = f 1>1(0.	....хп(01.
Тогда
F(a) = /(P), Г (6) = / (Q) и в силу цепного правила
^'(0 = (4Ч	+	^(0 =
\d*l/x(f)	\^л/х(О
= А. (х (/)) х\ (/) + Л2 (х(0) х2 (/) + • • • + Ап (х (/)) < (0.
Далее, по определению криволинейного интеграла, ь
J Л dxt 4----F Ап dxn = j [Лх (х (/)) х\ (/) 4-А„ (х (/)) х'п (/)] dt =
С	а
b
= J F' (t) dt = F(b) — F (а) = f (Q) - f (P), a
что и требовалось доказать [см. формулу (18)1.
Предположим теперь, что справедливо утверждение (19). Если Ct и С 2 — две линии в области D с одним и тем же началом и одним и тем же концом, то С4 4-(—С 2) есть замкнутая кривая (рис. 12.27) и, значит,
0 = J Д dxr 4- • • • 4- Ап dxn = Ci+(—С2)
= J dx± + • • • + Лл dxn + J Л1 dxr + • • • 4- Ап dxn =
Ci	—ё2
= J A dx± + • • • + Ап dxn — J Аг dx± + • • • + Ап dxn. Ci	сг
Иными словами, условие (19) означает, что криволинейный интеграл
Лх dxx 4- • • • + Ап dxn
384
12. Частные производные
зависит только от начальной и конечной точек кривой С\ в этом случае говорят, что рассматриваемый интеграл не зависит от пути интегрирования.
Если это так, то можно однозначно определить функцию f(xlt x2f ..., хп), фик-
сируя какую-то точку х = (xl9 х2, ..., хп) и затем полагая
f (*) = f(xv ..., хп) = [Л, dxt н-Мпdxn,
где интегрирование производится вдоль некоторой кривой в области D от Л
точки х до х; так как этот интеграл не зависит от пути интегрирования, то выбор кривой не влияет на значение f(x^ ..., хп). Определенная таким образом функция f в свою очередь удовлетворяет условию (17).
Мы докажем последнее утверждение для случая п = 2, хотя используемые при этом рассуждения будут иметь общий характер. Условимся писать х и у вместо и х2У А и В вместо и А 2. Итак, предположим, что интеграл
J A dx+Bdy
не зависит от пути интегрирования. Определим функцию f(x, у) в области £>, полагая
(х, у) f(x,y)= J A dx л- В dy, (ХО, у0)
где (х0, У о) — какая-то произвольно выбранная точка области D, и покажем, что
f'x = A, fu=B	(20)
для всех точек области D.
Пусть (х1( уд — некоторая точка области D; покажем, что в этой точке выполняются равенства (20). Если Со— кривая, ведущая от точки (х0, у0) к точке (xlt уд, то, по определению функции f(x, у),
§ 4. Криволинейные интегралы
385
f (*1> У1)=\ Adx +В dy.
Обозначим через Cj горизонтальный отрезок, соединяющий точку (х1г уд с точкой (Xi + h, уд, где величина | h | мала. Тогда
/ (Xj 4- ft, уд = J A dx 4- Bdy = §Adx + Bdy+§ Adx + Bdy — Co~t~Ci	Co	Ci
= f <*!> У1) + j Adx + Bdy
(рис. 12.28). Далее, линия Ct имеет параметрическое представление х = xt 4- t, у = уи где t меняется от 0 до ft (причем ft может быть и отрицательным). Следовательно,
f (*i + h, уд = f(xy yj+
A(x, 4- t, yjdt.
(21)
Продифференцируем обе части (21) no ft, применим основную теорему интегрального исчисления и положим ft = 0. Мы получим
Уд =A(xv уг).
Второе из равенств (20) доказывается аналогично; Ct здесь будет вертикальным отрезком. Этим и завершается доказательство теоремы 1.
ф Примеры- 1. Пусть С—кривая, ведущая от точки (1, 2, 3) к точке (10, 20, 30). Чему равен интеграл
fjxdx + ydy — 2dzt
Решение. Поскольку, как легко видеть,
xdx + ydy — 2dz = d	У2 — 2zj,
этот интеграл равен
. юа 4-— . 202 —2 • 30^ —f—4-— • 22 — 2 • 3^ = 193,5.
\ 2	2	)	\ 2	2	/	’
2. Вычислим еще раз интеграл примера из § 4.3. Заметим, что
2dx = d(2x), ydx 4- xdy — d(xy), поэтому
(2 4- у) dx 4- x dy = d(2x -f- xy),
а кривая С ведет от точки (0, 0) к точке (0, 1). В этих граничных точках 2х+ху=0 Следовательно, рассматриваемый криволинейный интеграл равен 0 — 0 — О.ф.
386
12. Частные производные
УПРАЖНЕНИЯ
АЗО. Пусть С — кривая, ведущая от точки (—1, 2, 4) к точке (6, 0, —2). Вычислите интеграл J cos х dx + е~У dy 4- г2 dz.
с
31.	Пусть С — кривая, ведущая от точки (х0, г/0, z0) к точке (хх, zr). Вычислите J a dx + b dy + с dz, где а, Ь, с — заданные числа.
с
32.	Пусть С — кривая, ведущая из начала координат к точке (1, 1, 1). Вычислите интеграл J 2ху dx + (х2 + 2yz) dy + (у2 + 1) dz.
С
33.	Пусть С — кривая, ведущая от точки (1, 2, 3) к точке (10, 20, 30). Вычислите интеграл J 2xyz3 dx 4- (x2z3 + 2у) dy + 3x2f/z2 dz.
C
34.	Пусть C — некоторая кривая в плоскости ху и R (х, у, z)—данная функция. Вычислите f R (х, у, z) dx.
С
35.	Пусть С — кривая, ведущая от точки (х0, yQ) к точке (xlt уг). Вычислите интеграл j* еху2 dx 4- 2уех dy.
С
4.6	. ГОМОТОПНЫЕ ПУТИ. ОДНОСВЯЗНЫЕ ОБЛАСТИ
Продолжим исследование криволинейного интеграла
jX dx, Ч-----h А„ dxn,
С
предполагая теперь, что функции Ль А 2, ..., Ап непрерывно дифференцируемы. В § 3.2 и 3.7 мы видели, что если Aidxi + ... + Andxn = df, то At удовлетворяют п(п — 1)/2 условиям интегрируемости
дА‘ ' где »#=/.	(22)
dxj dxi
Если наша область является интервалом, обратное утверждение тоже справедливо — если выполняются условия интегрируемости, то все Л у являются частными производными некоторой функции. Но для произвольной области это уже неверно.
Рассмотрим, например, две функции
А =-------у—, В=---------х—,
х2 4- у2	х2 4- у2
непрерывно дифференцируемые в области D, представляющей собой всю плоскость, из которой удалено («выколото») начало координат. Пусть С — окружность с цен
§ 4. Криволинейные интегралы
387
тром в начале координат, пробегаемая один раз в положительном направлении. Это замкнутая кривая, причем
j A dx + В dy = 2гс.
(23)
В самом деле, кривая С допускает такое параметрическое представление: х = = R cos 0, у = R sin 0 , 0 < 0 < 2л. При этом dx = — 7? sin 0 dy = R cos 0 d9, A = — sin 0/7?, В = cos 0/7?. Следовательно, A dx + Bdy = d0, откуда и следует (23). Но для A dx + Bdy условия интегрируемости выполняются, так как
дА = дВ =	t/2 —х2
ду дх (х2 + у2)2
Читатель заметит, что проведенные выше рассуждения проливают новый свет на пример 4 из § 3.2 (функции А и В — это функции и и v этого примера).
Для того чтобы сформулировать результат, справедливый в произвольной области, нам понадобится одно геометрическое понятие, которое мы не станем строго определять, ограничившись чисто интуитивным его описанием. Две кривые и С2 в области D с одним и тем же началом и одним и тем же концом называются гомотопными в области D, если одну из них можно непрерывно деформировать в другую, не сдвигая концов линии и не выводя ее за пределы области D. Если мы будем представлять себе эти две кривые как гибкие и растяжимые нити, например как тонкие резинки, то смысл выражения «непрерывно деформируется» станет совершенно ясным. Так, например, кривую С2 на рис. 12.29 можно преобразовать в кривую С4 и нельзя — в кривую С3: преобразованию кривой С2вС3 мешает «дыра» в области D. Точное аналитическое определение гомотопии можно найти в любом изложении начал топологии*.
Теорема 2. Если все функции Aif А 2, ..., Ап переменных xi9 ..., хп непрерывно дифференцируемы в области D и удовлетворяют условиям интегрируемости (22), то
j Д dXj н----h Ап dxn = J Л, dxx н----+ Ап dxn	(24)
для любых двух кривых С и С, гомотопных в области D.
Мы не даем формального доказательства теоремы 2, ограничившись лишь некоторым наглядно очевидным рассуждением, мотивирующим ее справедливость. Если л
кривую С можно деформировать в С, то мы можем найти такие кривые Сь С 2,	С^,
л
что не только все кривые С, С2, ..., Си, С гомотопны между собой в области D, но, кроме того, кривая С очень близка к очень близка к С2 и т. д. (рис. 12.30). Достаточно показать, что интеграл от A i+... + Ллйхлпо кривой С равен интегралу по кривой Съ интеграл по кривой Ci равен интегралу по кривой С2 и т. д., а для этого достаточно рассмотреть кривые С и С4.
* См., например, Н. Стинрод, У. Чинн, Первые понятия топологии, М., «Мир», 1967, § 24.
12. Частные производные

Рис. 12.32
Рис. 12.31
§ 4. Криволинейные интегралы
389
Если кривые С и Сг достаточно близки одна к другой, то от С можно перейти к Ci с помощью последовательности нескольких гомотопных между собой кривых, любые две соседние из которых совпадают всюду, за исключением точек, попадающих внутрь некоторого маленького интервала, принадлежащего области D (рис. /2.31). Достаточно показать, что интегралы от A^dx^ 4- ... + Andxn по любым двум таким кривым равны между собой.
Типичная ситуация показана на рис. 12.32. Мы должны показать, что
J Аг dxx + • • • + Ап dxn = J Ai dx{ + • • • 4- Ai dxn. (25) К1+К2+/<3+К4	Л Л
К1+К2+Кз+К4
Вследствие правил, установленных в § 4.3, достаточно показать, что
J A.dx, + ••• +Andxn =0.	(26)
Л Л
К2+Кз~Н —Кз)+(—К2)
Но это справедливо, потому что /<2 4- /С3 4- (—К3) + (—Кесть замкнутая линия, принадлежащая некоторому интервалу, в котором функции ..., Ап определены и удовлетворяют условиям (22); поэтому в этом интервале существует, как мы видели выше, такая функция /, что df = A{dXi 4- ... + Andxn. Следовательно, равенство (26) справедливо по теореме 1.
Область D называется односвязной, если любые две кривые этой области, имеющие одно и то же начало и один и тот же конец, гомотопны. Ясно, что n-мерный интервал будет односвязен, каково бы ни было п. Если п = 2, то область D является односвязной в том и только в том случае, если в ней нет «дыр».
Теорема 3. Если область D односвязна и если в D определены п непрерывно дифф-ференцируемых функций Aif А 2, удовлетворяющих условиям интегрируемости, то в области D существует такая функция f, что df = A ^dx^ + ... 4- Andxn.
Этот результат получается комбинированием теорем 1 и 2.
УПРАЖНЕНИЯ
36.	Найдите функцию Цх, у, г), определенную при всех х, у, г и удовлетворяющую условию dt = г2 dx + 2xz dz.
37.	Найдите функцию t(x, у, г), определенную при всех х, у, г и удовлетворяющую условию dt = (У 4- в* у2) dx + (х + 2уех — г sin (yz))dy — у sin (уг) dz.
^38. Найдите функцию / (х, у. г), удовлетворяющую условию
df= (1 + —J—	+
\	*+У J
dy х+ У
~|- dz.
Укажите область, в которой эта функция определена.
39.	Найдите функцию f(x, у), определенную при всех х, у, за исключением точки (0, 0), и удовлетворяющую условию
х dx 4- у dy df= ---------
х2 4- У2
390
Приложение к главе 12
40.	Для каких постоянных А, В, С, D можно найти функцию f (х, у), удовлетворяющую условию df = хА ув dx + хс yD dy? Для каких А, В, С, D функция f(x,y) определена на всей плоскости ху?
41.	Пусть функции f^x, у) и /2 (*> У) удовлетворяют условию df± = df2, выполняющемуся при всех х, у. Что Вы можете сказать о разности — f2?
В упражнениях 42—47 через Ci обозначена линия, определяемая уравнениями х = cos f у = sin /, 0 < t < л, а через С2 — линия, определяемая уравнениями х = sin /, у = cos/, л/2 < t < Зл/2. Пользуясь интуитивным определением гомотопии, выясните, будут ли эти две кривые гомотопны в данной области D.
42.	Область D есть вся плоскость ху.
43.	Область D есть множество точек плоскости ху, координаты которых удовлетворяют неравенству х2 + у2^> 0.
44.	Пусть плоскость ху — это плоскость г = 0 в пространстве х у z, а область D — множество точек, координаты которых удовлетворяют неравенству х2 + у2 + г2>* 0.
45.	D есть единичная сфера х2 + у2 + г2 = 1.
46.	D есть единичная сфера, из которой удален северный полюс, т. е. это есть множество всех точек (х, у, г), для которых х2 + у2 + г2 = 1 и z< 1.
47.	D есть множество всех таких точек (х, у, г), что х2 + у2 + z2 = 1 и —1 < z< 1.
В упражнениях 48—50 используйте интуитивное понятие «односвязности».
^48. Предположим, что область D есть связное открытое множество точек плоскости, полученное удалением из интервала |х |<2, | у | < 2 всех точек, для которых х > 0, у = 0. Является ли область D односвязной? Будет ли это так, если мы удалим все точки, для которых х2 + y2<Z 1?
49.	Является ли односвязным множество точек (х, у, г), координаты которых удовлетворяют неравенствам 1 < х2 + у2 + г2< 7?
50.	Если множество D точек плоскости односвязно и если мы будем рассматривать D как множество точек трехмерного пространства, то останется ли оно при этом односвязным? Как обстоит дело, если D, рассматриваемое как множество точек плоскости, не является односвязным?
Приложение к главе 12
§ 5. Энергия при криволинейном движении
S.I.	Векторные обозначения для криволинейных интегралов
Применения криволинейных интегралов вида
J? dx + Q dy + R dz	(1)
c
к механике облегчаются, если использовать векторное исчисление. Пусть {е^, ег, е3) — некоторый репер, связанный с выбранной нами системой координат (см. гл. 9, § 1.12). Три функции, определяющие кривую С, мы запишем в виде одной векторной функции'.
/ !—► х(/) = х(/)е! +	+ г(/)е3, а </</>, ’	(2)
так что формально
dx = (x'Wei + /(0е2 + z'(/)e3)d/.
(3)
§ 5. Энергия при криволинейном движении
391
Рис. 12.34
Мы объединим также три функции Р, Q, R в одну векторную функцию точки х = xet + уе2 + + ге»:
F(x) = F(x. у, г) = Р(х, у. г)е( + (Цх, у, z)e, + R(x, у. z)e,.	(4)
Вспомнив определение скалярного пронзведення (см. гл. 9, $ 6), перепишем интеграл (I) так:
f F dx.	(1)
С
Это обозначение подсказывает один «математический миф», иллюстрируемый рис. 12.33. Кривую С можно представлять себе состоящей из бесконечно большого числа бесконечно малых направленных отрезков, каждый из которых определяет бесконечно малый векторах. Для каждого из отрезков возьмем соответствующее ему значение вектора F и образуем скалярное произведение
Fdx -= | F | | dx | cos 0,	(5)
где 0 — угол между векторами F и dx. Интеграл (Г) представляет собой сумму всех этих бесконечно малых величин.
S.2.	Работа
Напомним (см. гл. 5, § 5.2), что если частица проходит расстояние $ по прямой линии, подвергаясь действию постоянной силы F, действующей в направлении этой прямой, то работа UZ по преодолению этой силы равна, по определению, — | F |$, если частица движется в направлении силы F, и | F |$, если частица движется в противоположном направлении.
Если частица пробегает направленный отрезок PQ под действием постоянной силы F и если угол между F и PQ равен 0 (рис. 12.34), то работа W, совершаемая против этой силы, определяется как — | Р | | PQ |cos 0. Если обозначить через s вектор, определяемый направленным отрезком PQ, то
Г = —Fs.	(б)
[К этому определению мы приходим, полагая F = F> + Ft, где сила F> направлена по прямой PQt аГгперпендикулярна этой прямой. При естественном предположении о том, что при движении (без треиия) вдоль PQ с силой F2 не связана никакая работа, мы приходим к следующему заключению:
W = — | F j | | $ |, если 0 < 6 < л/2, V = | Fj | | S |, если л/2 < 0 < л.
Так как | Ft| = | F J cos 6 в первом случае и | Ft | = — | F | cos в — во втором, то отсюда н вытекает равенство (6).J
392
Приложение к главе 12
Предположим, теперь, что частица движется в силовом поле, определяемом функцией (4). Это означает, что если частица находится в точке с радиусом-вектором х, то действующая на нее сила равна F(x). Если наша частица движется по кривой С, определяемой векторной функцией (2), то мы определим работу, совершаемую против сил поля, как
IF = _ Jf du	<7)
С
[Это определение оправдывается тем «математическим мифом», о котором говорилось выше: W есть сумма чисел (5), каждое из которых представляет собой работу, совершаемую против сил поля на бесконечно малом отрезке линии С.]
Мы знаем (см. § 4.2), что интеграл (7) не зависит от параметрического представления, использованного для определения линии С. Это значит, что работа не зависит от скорости, с которой частица движется по линии С.
•Примеры. 1. Вблизи поверхности Земли сила тяжести, действующая в точке (х, у, z), равна
F = —tngt з,
если считать плоскость г = 0 совпадающей с поверхностью Земли, вектор е3 — направленным вверх и обозначить через g ускорение силы тяжести, а через т — массу частицы. Работа по преодолению силы тяжести, производимая при движении частицы от точки (л*о, */о, zo) до точки л*!, zt) кривой С, равна
— J — mg dz = mg f dz = mg (zx — z0). C	c
Она зависит только от координат zo и начальной и конечной точек, точнее, от разности их высот; ясно, что эта работа будет положительной, если го (т. е. если мы поднимаем тело массы т на высоту zx — Zo), и отрицательной, если zt < zo (в случае опускания тела).
2. Предположим, что
FU, у, z) = ej + *е2.
Рассмотрим две линии с одним и тем же началом (0, 0, 0) и одним и тем же концом (0, л, 0):
Сг: х(/) = /е2, т. е. х = 0, у = /, z = 0, 0 < t < л
и
С2: х(/) = sin/-ej + /е2, т. е. х = sin /, у = /, г = 0,	0 < t < л.
Работа, совершаемая вдоль кривой Сь равна
J F dx = J dx + х dy = J 0 dt = 0, Ci	Ci	о
а работа вдоль кривой C2 —
те
J F dx = dx + x dy = J (cos t + sin t) dt = 2.
C g	Cg	0
В этом случае работа зависит от пути интегрирования, а не только от концов этого пути.®
§ 5. Энергия при криволинейном движении
393
УПРАЖНЕНИЯ
В упражнениях 1—6 для каждого данного поля сил F и данной кривой С найдите работу W против силы F при движении по кривой С.
1.	F = Зе] + 4ег + 5е3; С — прямолинейный отрезок, ведущий от точки (хо, уо, го) к точке (X], ylt г,).
2.	F = дв] + уег + ze3; С — прямолинейный отрезок, ведущий от точки (хо, уо, го) к точке Уъ *1).
3.	F = Зв] + 4ег + 5е3; С — ломаная, состоящая из отрезков, первый из которых ведет из точки (до, Уо, го) в точку (дгх, ух, гх), а второй — из точки (хх, у±, гх) в точку (хг, у 2. гг).
4.	F — как в упр. 2, С — как в упр. 3.
5.	F = г/ех + гег + г/е3; С есть окружность большого круга, получающаяся при пересечении единичной сферы плоскостью г = у, пробегаемая один раз в направлении, которое из точки (—1/^2, —1/1^2, 0) видно как направление против часовой стрелки.
6.	F= x2yet + Лег + */z2e3; С— треугольник, который получается, если из начала координат идти к точке (1, 1, 0), затем к точке (0 0, 1) и, наконец, обратно к началу координат.
5.3. Потенциальная энергия
Силовое поле F(*, у, г) называется консервативным, если при движении частицы по замкнутой траектории* не совершается никакой работы:
j Fdx = 0, если С — замкнутая линия.
С
Так. например, поле в примере 1 из § 5.2 является консервативным, а поле из примера 2 не консервативно.
Мы знаем (теорема 1 §4.5), что поле консервативно в том и только в том случае, если работа, совершаемая при движении частицы по некоторому пути, зависит только от начала и конца пути. или — в том и только в гом случае, если существует функция с градиентом F. Но в этом последнем случае существует также и функция с градиентом — F; эта функция равна
(х, у, г)
W (х, у, z) = — J Fdx,	(8)
(х0. у0, г0)
т. е. работе, совершаемой при движении частицы по любому пути, ведущему из фиксированной точки Хо = (ло, уо, го) в точку х = (д, у. г). То. что F является на самом деле градиентом функции — U7, т. е. что координаты этой силы являются частными производными:
вытекает из рассуждения, использованного при доказательстве теоремы 1 § 4.5.
Функцию 1Г(х) называют потенциалом рассматриваемого силового поля, или потенциальной энергией частицы, находящейся в точке х. Функция №(х) определяется этим полем лишь с точностью до произвольной аддитивной постоянной, потому что выбор точки (хо, Уо, го), в которой W — 0, зависит от нас, а прибавление к W произвольной постоянной не нарушает справедливости равенств (9).
Если поле имеет потенциал, т. е. если оно консервативно, то выполняются условия интегрируемости:
Ру = Qt» = Rx ’	= *у
(мы всегда предполагаем, что координаты силового поля имеют непрерывные частные производные). Обратно, если эти условия выполнены и рассматриваемая область односвязна, то потенциал существует.
Поверхности уровня функции W называются эквипотенциальными поверхностями. Сила перпендикулярна к эквипотенциальным поверхностям (ср. с§ 2.15). В критических точках функции W имеем
F = — grad W = 0. т. е. здесь частица находится в равновесии.
* Интеграл по замкн утому контуру С часто обозначается символом ф.
394
Приложение к главе 12
•Примеры. 1. Согласно закону всемирного тяготения Ньютона (см. гл. 11, $ 4.12), масса М, сосредоточенная в начале координат, притягивает частицу с массой т, находящуюся в точке (аг, у, г), с силой F, величина которой равна ]тМ/г2; здесь т — масса частицы, 7 — гравитационная постоянная и г = К аг2 *4- у2 Ц- а2 — расстояние от начала координат до точки (лг, у, г). Далее, единичный вектор, направленный от точки (аг, у, z) к началу координат, равен (—1/| х|) х и имеет координаты —х/r, —ylr,—zlr. Следовательно, координаты вектора F равны:
—	~ ,	— улМ ,	_ fmM -L- ,
ИЛИ
упМх	-frnMy	ymMz
(X2 + j,2+ Z2)3/2 ’	(Х2+ yt + г^2 ’ “ (Х2_|_ у1 + г2) * 2
Легко видеть, что они противоположны частным производным функции
w,. v	1тМ
W (х, у, z) = —  ---= —	—— .
г	Ухг + у2 + Z2
Следовательно, эта функция UZ является потенциалом гравитационного поля, порождаемого массой М.
2.	Если мы ограничимся маленькой областью вблизи поверхности Земли и выберем систему координат так, как в примере 1 § 5.2, то потенциалом поля силы тяжести будет служить функция 9Р(аг, у, z) — mgz, где z — высота над поверхностью Земли. Это следует из результатов $ 5.3 гл. 5. В самом деле,
Wx =	= 0 и Wx = mg. •
УПРАЖНЕНИЯ
7.	Рассмотрите гравитационное поле, образованное двумя частицами с массами и тг, расположенными в точках Xj и хг. Найдя потенциал этого поля, убедитесь в его консервативности.
8.	Рассмотрите гравитационное поле, образованное п частицами с массами тъ mt.тп,
расположенными в точках х>, х«, ..., хя. Покажите, что это поле имеет потенциал и, следовательно, консервативно.
9.	Является ли консервативным поле вектора F = Агеж + уъ2 + Аа? Если Да, то каков его потенциал?
5.4	. Сохранение энергии
Кинетическая : жеиия (см. гл. 5, $ 5.4), по определению, равна
энергия движущейся частицы массы /я, как и в случае прямолинейного дв№
Если t обозначает
К = — то2, где v — численная величина скорости. время и если движение нашей частицы определяется функцией х(/) — хЩъ + y(t)ez + г(0е3, то вектор скорости равен x'(f), а численная величина скорости равна | х'(0 |, так что । т
* = у I *' (О I2 - — (*'(№ 4- /(О5 + *' №).
Мы можем теперь сформулировать и доказать основную теорему о сохранении энергии, из кото* рой как частный случай вытекает результат $ 5.4 гл. 5.
§ 6. Доказательства некоторых теорем о частных производных
395
Теорема \.Если частица движется в консервативном силовом поле, то ее полная энергия
Е = К + W
(т. е. сумма кинетической и потенциальной энергий) остается постоянной.
Доказательство. Мы предполагаем, конечно, что частица подчиняется закону движения Ньютона:
mx"(0 = F(x(0).
Так как сила F имеет потенциал W, то F = —grad W. Следовательно, /их" = —grad W. или
в координатах:
тх"(0 = —
д№ \
дх )х=х (/)
ту" (t) = —
dW \
ду Jx=x(t)
mz,f(t) = —
dW \
дг /х=х(О
(Ю)
Далее, энергия нашей частицы в момент времени t равна
£ (0 = у (*'W2 + У'(Ф + г'(02) + w (X (0, у (0, г (0).
Пользуясь цепным правилом, получаем
/ dW \	I dW\	( dW\
E'(t) —mx'(t) x"(t)+my'(t) y"(f)+mz'(t) z"(t) + —	x'(0 + —	/ (0 + — I z'(t) =
\ dx /x(O	\ dy	\ dz /x(n
Г	I dW\	1	Г	I dW \	1	Г	( dW\	1
=x'(t)\mx"(t) + —	+ y'(t) \my"(t) + —	+ z'(t) \mz"(t) + —	=0
L	\ dx Jx(t)	J	L	\ dy Jx(t)	J	L	\ dz Jx(t)	J
в силу равенств (10). Мы доказали, что величина Е постоянна.
Эта теорема является, конечно, только частным случаем некоторого весьма общего физического принципа.
УПРАЖНЕНИЯ
ХЮ. Покажите, что описанное в § 4.6 гл. 11 движение брошенного тела подчиняется закону сохранения энергии.
11.	Покажите, что планеты, вращающиеся вокруг Солнца по законам Кеплера (см. гл. 11, § 4.10, 4.11, 4.12), подчиняются закону сохранения энергии.
§ 6.	Доказательства некоторых теорем о частных производных
В этом параграфе мы докажем все утверждения, которые в основном тексте этой главы были сформулированы, но не были доказаны; исключение здесь составляет лишь теорема 7 § 2.17, которая будет доказана в § 3 Дополнения.
6.1.	Дифференцируемые функции
Предположим, что функция Дх, у) в окрестности точки (хо, Уо) имеет непрерывные частные производные. Мы покажем, что функция j дифференцируема в точке (хо, У о) в смысле § 2.3. Этим будет доказана теорема 2 § 2.6. Мы воспользуемся теоремой о среднем значении (см. гл. 8, § 1.1).
396
Приложение к главе 12
По предположению, существует такой интервал / с центром (х0, уо), в каждой точке которого t(x, у) имеет частные производные fx (х, у) и fy (х, у). Пусть (х, у) — произвольная точка интервала /, отличная от (хо, уо). Тогда
f(x,y)—f(x0, у0) = [/(*. y)—f(Xg, y)] + [f(x0, у) —f (х0. у0)].
(1)
Зафиксируем у и будем рассматривать f(x, у) как функцию только одного х; в таком случае, по
теореме о среднем значении, между х0 и х найдется такое число и (рис. 12.35), что f(x, y) — f(x0, у) = (x — x0)fx(u, у).	(2)
По той же причине между у0 и у найдется такое число v, что f<x0, y)—f(Xg, Уо) = (У — у0) f'u(x0, V).	(3)
Положим	теперь fx (х0, yQ) = а, ?у(хо,Уо) = Ь,	f (х0, yQ)	= z0	и заметим, что
f'x(u, у) = а 4- [ f'x(u, у) — а], f'y	(х0, v) =	Ь 4- [	fy (х0, и) — *].	(4)
В силу равенств (1), (2), (3) и (4) имеем
f(x,	у) = г0 + а (х — xft) + b (у — у0) + (х — х0) [	f'x (и ,у) —	а] +	(у — у0) [ f'u (х„, »)	— b ]=
= г0 + а (х — х0) + Ь (у — у0) 4-У (х — х0)2 4-	(у — У0)2 г(х, у),	(5)
где
х — ха
У — У„
' (х, у) =	------	- [ f'x (и, у) — а] 4- 	[ fy (Хд, v) — ь].
V (X— Хо)24- (у — Уо)2	V (х — Хд)* 4- (у — Уо)2
Обе дроби в правой части равенства по абсолютному значению не превосходят 1. Из неравенства треугольника следует, что
|г (*. у) I < I f'x («. У)~ «| + | f'y(Xg, о)— ь|.	(6)
§ 6. Доказательства некоторых теорем о частных производных
397
Числа и и v зависят от х и у, но и ближе к хо, чем х, а и ближе к г/о, чем у. Следовател ьно, если точка (х, у) достаточно близка к (хо, #о), то точки (и, у) и (хо, v) будут сколько угодно близки к (хо, уо) и величины
|f* («. У) — а | = | f'x (и, у) — f'x (х0, у0) |, I f'y (х0, о) — b | = | fy (х0, о) — f'u (х0, у0) | будут сколь угодно малы, ибо/* и^ непрерывны в точке (Хо, уо). Из неравенства (6) заключаем теперь, что
lim г (х, у) = О, (х, у)-+(х0, у0)
а это вместе с равенством (5) и означает дифференцируемость функции f в точке (хо, Уо)-
6.2.	Цепное правило
Докажем теперь цепное правило (теорема 3 § 2.8) для функции двух переменных. Мы предположим, что функции F(x, y)t <р(и, о), ф(ц, у) дифференцируемы в точках (хо, у о), (Цо, уо) и что ср (wo, Уо) = хо, ф(ао, Уо) = уо- Покажем, что сложная функция г = f(w, у) = = F(<p(w, у), ф(ц, у)) дифференцируема в точке (wo, уо), и вычислим ее частные производные.
Для упрощения записи предположим, что х0 = уо = ио = Уо = 0. В общем случае доказательство почти не меняется: нам придется только вместо и, у, х, у писать и — ио, и — Уо, х — хо, у — уо- Положим
F = Л, Fx= В, Fy = С при х = у = О,
=	?р=&- Фо = а» фр=₽ при и = о=0.
По предположению,
F (х, у) = А 4- Вх + Су + )<х2 +	t/2 R	(х,	у),
ср (и, у) = аи 4- bv 4- У и2 4- у2	г (и,	v),
ф (и, о) = aw 4“ ₽У 4“	4"	у2	Р (ц»	у) »
где R — непрерывная функция, равная нулю при х = у = 0,	г и	р	— непрерывные функции,
равные нулю при и = v = 0. Следовательно,
f(w, y) = F(cp(w, v), ф (w, у)) = А 4- В {аи 4- bv 4- У и2 4- у2 г(н,у)]4-
4-	С [aw 4- ?У 4" У “2 + У2 Р (Ц» у)] + К? (и > у)2 + Ф (ц» у)2 R (<р (w, у) , ф (w, у)) = = Л 4- (Ва 4- Са) и 4- (ВЬ 4- С₽) v 4- В }^w2 4- у2 г (и, у) 4- С J^w2 4- у2 р (w, у) 4-
4- К? (и» у)2 + Ф (м» v)2 R (? (и> у), Ф (м» у)) =
= л+ (Ва + Са)и+ (В& + СР) t>+	+ R (и, о),
где
А	Г <p(w, y)24-<Kw. и)2 11/2
R(u, o)=Br(u, i>)4-Cp(u, о) + ----------------------- о), ф(и, о)).
L w 4“ у J
А
Мы должны показать, что lim R (и, у) = 0; отсюда и будет следовать, что функция / дифферен-(и,0-(О,О)
цируема в точке и = у = 0 и что ее частные производные, как и утверждается в теореме, равны t'x = Ва 4- Са и f'y = Bb + Ср.
398
Приложение к главе 12
Функции r(u, v),p(u, v) и /?(ф(и, у), (а, и)) непрерывны при и = v = 0 и равны в этой точке нулю: первые две — по предположению, а третья — как композиция непрерывных функций. Так как В и С постоянны, то нам остается только показать, что выражение L..]^a в окрестности точки (0, 0) остается ограниченье. Но это действительно так. В самом деле, если и и и близки к нулю, то | r(u, v) | < 1 и | р(а, 0 |< 1, а значит,
|<P(U, р)|<(|а|4-|Ы + 1) Г«2 + у2,	|ф(«, 0)1 < (I«1 + 101 + 0 K+ + ^2.
Поэтому если М есть наибольшее из чисел (| а | + | b | 4" 1) и (| а | + | £ | + 1), то [... ]t/2 < М/Т.
6.3.	Смешанные производные
Докажем теперь теорему 1 § 3.1, утверждающую, если что f(xt у) определена и имеет непрерывные частные производные первого и второго порядков в некотором открытом множестве, т° fXy= fyx> r«e
г = JLJL г = _LJL. ху ду дх * ух дх ду
Для доказательства выберем определенную точку (хо, #о) рассматриваемого множества и составим выражение
Ь(Л) = /(х0+ Л, y^ + h)'— f(xQ + h, y0)—f(xQ, yQ+h) -f- f(xQ, y0)t	(7)
где ft =£ О, причем | ft | мало. (Это есть сумма значений функции f в двух противоположных вершинах квадрата, изображенного на рис. 12.36, минус сумма значений этой функции в двух других вершинах того же квадрата; на нашем рисунке ftj> 0.) Мы покажем, что
6(A)
Л?п~йГ“=	Уд.	(8)
а также что
lim ~мГ = fyx<xo> Уд>	(9)
h—>0 Л2 и
откуда и будет следовать равенство смешанных частных производных. Доказательство основывается на теореме о среднем значении (теорема 1 § 1.1 гл. 8) для функций одной переменной.
Рассмотрим функцию
F(x) — [(х, у9 + Л) — [(х, у0),	(10)
производная которой равна
F'(x)=f'x(xt уь + h)- f'x(xtyQ).	Ш)
Мы имеем
8 (ft) = F (Xq + ft) — F (x0) [В силу (7) и (10)] =
= hF' (?) [где £ заключено между 0 и Л. по теореме о среднем значении] =
= h [ fx (5> У» + Л) — fx (?> (/о)] [в силу (11)] =
= №’Ху$< ч) [по теореме о среднем значении; т] заключено между |/0 и yQ 4“ Л]« Таким образом,
^2 ^ху (S> ^l)’
Числа С и т] зависят от Л, но если | Л | достаточно мало, то точка (5, т]) сколь угодно близка к (х0, Уо)‘ Из непрерывности функции fxy вытекает равенство (8).
§ 7. Теорема Тейлора
399
Введем теперь в рассмотрение функцию
G(y) = f.(*o + h, у) — f(jr0, у).
Дважды пользуясь теоремой о среднем значений, получаем
S(h) = G(y0 + h)-G(y9) = hG'^)= h[fy(x0 + h, £)—/'(xe. h] = h*f"yx(l. $),
Л л
где 8 и т) — числа, зависящие от Л, которые лежат соответственно между х0 и х0 4- h и меж-
Л л
ду Уо и Уо + h. Следовательно, 6 (h)/h2 = f"yx ($, ц), откуда и следует равенство (9).
§ 7.	Теорема Тейлора
В этом параграфе мы обобщим теорему Тейлора, перенеся ее на функции нескольких переменных, и воспользуемся ею для доказательства теоремы 3 § 3.4 (теоремы о критических точках).
7.1.	Теорема Тейлора для функции двух переменных. Частные случаи
Теорема о среднем значении (см. гл. 8, § 1.1) и теорема Тейлора (см. гл. 8, § 2.3) переносятся на функции двух переменных с помощью очень простых соображений.
Пусть функция f(x, у) определена и достаточное число раз непрерывно дифференцируема а окрестности точки (х0, у0). Мы хотим, используя значения функции ft и ее производных до некоторого порядка в точке (х0, yQ), представить f(x, у) в виде суммы некоторого многочлена и остаточного члена, который становится очень малым, когда точка (х, у) приближается к (х0, у0). Для того чтобы сделать это, мы обозначим полярные кооодинаты точки (х — xQ, у — у0) через (г, 0), т. е. положим
х = х0+ г cos 0 , у = у0 + г sin 0
(рис. 12.37), и при некотором фиксированном 0 будем рассматривать значение функции £(х, у) в точке (х, у) как функцию от г. Иными словами, мы рассмотрим вспомогательную функцию
F(r) = t(x0+ г cose, у0 + rsinO).
Пользуясь цепным правилом, вычислим производную функции F:
F'(r) — fx (ха + г cos 6, у0 + г sin 0) cos 0 + fy (х0 + г cos 0, уа + г sin 0) sin 0,
F"(r) = f’xx ( ’') cos2 6 + %’xy (' • •) cos в sin 0 + f'yy (• • •) sin2 0,
F'"(r) = fxxx (...) cos3 0 + 3fxxy (...) cos2 0 sin 0 + 3/^ cos 0 sin2 0 +	(...) sin3 0,
fIVW = f™xxx (  ) cos4 0 +	(...) cos’ 0 sin 0 + 6fl^Xyy (...) cos2 0 sin2 0 +
+ 4?™ууу (•.) cos 0 sin3 0 + f™yy (...) si n4 0,
и т. д. (полностью все выкладки мы предлагаем читателю проделать самостоятельно). Здесь точки (...) означают: х0 + rcosO, yQ + г sin 0.
Выпишем теперь для функции F(r) теорему о среднем значении и различные частные случаи теоремы Тейлора:
P(r) = F(0) + F'(p)r,
400
Приложение к главе 12
F(r) = F(0) + F'(0) г + -^-F" (р) г2,
F (г) = F(0) + F' (0) r+ -J- F" (0) r2 4- 4- F'" (p) r»f Z!	01
1	1	1 JIV)
F (r) = F (0) 4- F' (0) r + — F" (0) r2 + — F'" (0) r3 +— F (p) r*
и т. д.; здесь p — такое число, что
0<p<r
(оно, вообще говоря, разное в разных формулах). Если мы подставим в эти равенства полученные выше выражения для F, F', F" и т. д., заметим, что г cos 0 = х — х0, г sin в = у — уа, и положим
5=х0+рсозв, т) = уа +psin 6,
то мы получим теорему о среднем значении и различные формы теоремы Тейлора для функции двух переменных:
fAx,y) = f(xn,y^+f'x(^,tf) (X — x0)-i-f'e(i,ti)(y — y0),	(10)
f (х,у) =f (х0,у0) 4- f'x (х0, у0) (х — х0) 4- f'y (х0,уа) (у — у0) 4-
+	[	fxx	(?’ ’l) Iх — *о)2 + tfxv (&• 1)	— хо) (У — Уо) + f‘vy (М) (У — !/о)а]>	(*i>
f (х,у) = f (х0,у0) 4- f'x (ха,у0) (х — хй) 4- f'y (х0,у0) (у — у0) 4-
+	[	fxx	(хо. Уо) (х — хо)2 + 2f’ty (хо • Уо) (х — хо) (У — Уо) + f'm (хо • Уо) (У — Уо)г	] +
+ 4т [fххх I) — *o)s + Zf'xxy ^•’1)	— *о)2 (У — Уо) +
+ Sf'xyy (S. <х - *о) (У - Уо)3 + iyyy «. Ч) (У - Уо)(12)
§ 7. Теорема Тейлора
40t
f(x, y)=f(x0, y0)+fx(xa, y0) (x —xa)fy(x0, Уо)(У — Уо) +
+	[ f’xx (хо>Уо) (X — XO)8 + W’xy (хо’Уо) (X — x0) (y — y0) 4- fyy (Xo,yo) (y — y0)2] +
+ ТГ [ f 'xx'x(xO' Уо) <X — xo)3 + 3f'x'xy (xo< Уо) (x — xo)2 (У — Уо) + o’
+ 3fxyy (хо.Уо) (*— xn) (y — Уо)2 + f'yyy (хо<Уо) (У — Уо)3] +
+	[ f”xx (’ - 1) (* — xo)4 + tf'xxxy К > ’))(*— *o)3 (У — Уо) +
+ У™уу (-1)) (* - *o)2 (У ~ Уо)2 + 4%yy (5. I) (x - x0) (у - у0У> 4- f%yy (5, -n) (y - f/0)4] (13> и т. д. [Заметим, что (5, т]) есть некоторая точка отрезка, соединяющего (х0, г/0) с (х, у), которая может быть разной в разных из выписанных формул; см. рис. 12.38.]
7.2. Теорема Тейлора для функции двух переменных. Общий случай
Теперь легко сформулировать и общую теорему Тейлора. Заметим, что в выписанных выше формулах f'x всегда умножается на (х — хо), [”хх — на (х — х0)2, f''xy — на (х — хо) (у — уо), ^хуу — на (* —	— J/o)2 и т. д. Далее, числовой множитель при производной, содержащей
р раз дифференцирование по х и q раз дифференцирование по у, равен 1/(р!^1). [Так, например, производная входит в эти формулы с коэффициентом 1/4! = 1/(410)!. а производная f™xxyy — с коэффициентом (1/4!)-6= 1/4= 1/(212)!.] Таким образом, мы можем надеяться, что верна следующая формула Тейлора:
У) = £(*о, Уо) + Рй(х, у) + /?л+1 (х, у),	(2)
где Рп есть /i-й многочлен Тейлора функции f в точке (хо, уо)> т. е. многочлен степени п, имеющий в точке (хо, уо) то же самое значение и те же самые частные производные что и функция /, а Rn+i У) указывает ошибку, получающуюся при замене функции f(x, у) многочленом f(x0, Уо) + Рп У) (т- е- это есть остаточный член формулы Тейлора). Точнее говоря, полагая
/ dp+qf \
apq~ ( дхРдуЯ )	(3)
\	/ х=х0, у=у0
имеем
Рп = “оо + °Ю (х — хо) + °01 (У — Уо) + (х — хо)2 + (х — Хо) (у — Уо) +
+ -т- (У — Уо)2 + чг — *<•) + 7ГГ7 (х ~ хо) ~ Уо) + "7777 (х — хо) (У — Уо) + Zl	OI	Zl II	1! Z!
+ (у - Уо)3 + • • • + -тг (х - *о)л + Т^ГТТТГ (х - Хо)"'1 (У - Уо) + OI	ГН	\П — 1J I II
+	(х -хо)Я“2 {у - у»)2+• • • + -тг <у - Уо)п'
\П> —~~	I ^1	П1
Но последнее выражение можно переписать так:
402
Приложение к главе 12
/=0 Р-Н7= /
аРЧ pl <?|
(х — xQ)P (у — у0)«
(4)
(не забудьте, что 01 = 1). Остаточный член имеет вид
Rn+1 = У -Т7" (X- Хо)р (У -Уо)4.	(5)
р+^п+1 где
_ ( dp+of \ a”4-[dxpw	(6)
и точка (£, т]) принадлежит отрезку соединяющему точку (х0, у о) с (х, у). Эта формула справедлива при условии, что f(x, у) определена и п + 1 раз непрерывно дифференцируема в некотором открытом множестве, содержащем этот отрезок. Мы опускаем формальное доказательство теоремы Тейлора, использующее математическую индукцию.
Заметим, что каждое слагаемое суммы (5) по абсолютному значению не превосходит [| apq \/р\q\]дЛ+1, где д есть расстояние между точками (хо, r/о) и (х, у). Следовательно, если абсолютные значения всех частных производных (п + 1)-го порядка функции f, не превосходят некоторого фиксированного числа, то остаточный член формулы Тейлора в окрестности точки (хо, Уо) удовлетворяет неравенству вида
|ЯЛ+1(*. У) I <	(7)
где М — некоторое постоянное число, не зависящее от х и у. Отсюда вытекает, что вблизи точки (хо, Уо)» т. е. при достаточно малых д, остаточный член формулы Тейлора будет по абсолютной величине много меньше, чем любой из (имеющих ненулевой коэффициент) членов многочлена Рп.
Нередким является тот случай, когда lim /?Л+1 (х, у) = 0. В этом случае функция f(x, у) мо-
П-*оо жет быть представлена в виде суммы (бесконечного) степенного ряда от двух переменных.
Заметим еще, что иногда формулу Тейлора для функции двух переменных проще получить не из общей формулы, а пользуясь разложением Тейлора для функции одной переменной, как мы покажем это на примерах.
•Примеры. 1. Найти третий многочлен Тейлора для функции [(х, у) — е*У в точке х = у=0.
Первое решение. Имеем:
f'x=y^y.
f'xx = у*е*>, fxy = е*У + хуехУ, fyy = xW, f'xxx =	• f'ixy =	+ xy*e*>.
С =	+	Q = x*e*y.
Следовательно, при x = у = 0 получаем: / = 1, f'x = f'y = fxx = f’yy= fxxx= fxxy = fxyy= fyyy= = 0, fxy = 1. Искомый многочлен Тейлора имеет вид 1 + хг/, так что
ехУ = 1 ху + члены порядка выше третьего.	(8)
Второе решение. Формула (8) вытекает также из того, что (см. гл. 8, § 5.6)
^-1 + 4 + -^ + ^-+....
2. Найти второй многочлен Тейлора функции f(x, у) = (1 + х + t/2)1^2 при х = 1, у = 0. Первое решение. Имеем:
§ 7. Теорема Тейлора
403
f'x= 1/2(1 +x+</2)-1/2, fy= у (I +x+y*)~l/2, f'xx = <- */4)(l + X + y2r3/2 , fxy = (- 1 /2)t/(l + X + t/2)-3/2 .
f"w = (1 + x + ya)-l/2 - j/2 (1+ x + у‘)~3/2 .
При x = 1, у = 0 получаем:
f=/2. /;=1/(2/2), /; = 0, 4=-1/(8/2), 4 = 0, /^=1//2.
Следовательно, искомый многочлен Тейлора имеет вид _ X — 1	(X—I)2 у2
Рг (х. У) = /2 +---— ----------— +------—
2/2	16/2	2/2
Второе решение. Положим х = 1+6. Из разложения в ряд бинома
§ 5.7) при малых |6 | и |.у | имеем
(1 + х + «/a)l/2 = (2 + е + у2)1/2 = /7 (i -ь LL^y/2 в
1 ( 1 _iW£+Ha 1 =
2 \ 2 Д 2 ) + "]
х—1	(х—I)2	у2
4	~	32
4
,см. гл. 8,
= /2-[1+-L 1±£+_L r L 2	2^2
= /2 p + -J- (6 + y2) _-^-($ + !/2)2+ ...J =
./-Г	1	1	1 „	1	/—Г x—l y2 (X—I)2	1
1'+тe+T it '+•]-[,+—+T—+ ••] 
где точками ... обозначены члены порядка выше 2 относительно х — 1 и у. Следовательно, искомый многочлен Тейлора имеет вид
/Г+J^L(x-i)--!jl(x-i)a-i-2j-{/2. • 4	32	4
7.3. Классификация критических точек
Применим теорему Тейлора для классификации таких критических точек функции Дх, у), в которых н е в с е вторые частные производные обращаются в нуль, причем fxx f'yy — fxy 0.
Для упрощения записей условимся считать, что критическая точка функции Дх, у) совпадает с началом координат (0, 0). Предположим также, что ДО, 0) = 0. Если функция f трижды непрерывно дифференцируема и если мы обозначим значения f"x, Цху, /уув точке (0, 0) через А, В и С, то в окрестности начала координат будем иметь
f (*.(/)= -у (4х2 + 2Вху + Су2) + R (х, у),	(9)
где остаточный член /?(х, у) удовлетворяет неравенству
|Я(х, </)| < M(x2 + /)3/2,	(10)
в котором Л4 — некоторое постоянное число. Это вытекает из теоремы Тейлора: в рассматриваемом нами случае многочлен Тейлора не содержит ни свободного члена, ни линейных членов, так как / =fx = fy = 0 при х = у = 0. Заметим, что, по предположению, Л2 + В2 + С2 =# 0. Введем теперь новую систему координат (X, Y), получаемую поворотом исходной системы (х, у) на некоторый угол 0 (рис. 12.39). Тогда (см. гл. 10, § 2.3)
х = X cos 6 — Y sin 0, у = X sin б + Y cos 0.	(11)
404
Приложение к главе 12
Будем рассматривать f как функцию новых переменных X и Y, т. е. рассмотрим функцию
f (X, Y) = f (X cos в —. Y sin 0, X sin 0 + Y cos 0).
Подставляя (11) в (9) и пользуясь тем, что X2 + Y2 = х2 + у2, получим
Л	1 /Л	Л Л \ Л
f (Х,Г) = — |ЛХ2 4- 2BXY 4- CY2J 4-R(X,F),	(12)
АЛЛ	Л
где A, В, С—числа, зависящие от А, В, С и 0, a R удовлетворяет неравенству
| R (X, Y) | < М (X2 + П)3/2 .	(13)
ЛАЛ
Нам нет необходимости вычислять А, В, С, так как мы уже это делали в § 3.3 гл. 10, где было показано, что
АЛЛ	АЛ
АС — В2 = АС — В2, А 4- С = А 4- С.
л
В § 3.4 гл. 10 мы показали, что можно выбрать такое 0, чтобы В обратилось в нуль. Предположим, что мы уже сделали это; тогда
А	1 /А Л \ Л
f (X, Y) = — (ЛХ2 4- CY2) 4- R (X, Y).	(14)
АЛ	АЛ
Если АС — В2 = 0, то АС = 0. В этом случае либо А = 0, либо С = 0, и из равенства (14) нельзя узнать, будет ли f вблизи начала координат сохранять один и тот же знак или нет.
АЛ	АЛ
Предположим теперь, что АС —	Тогда ДС<0. Если Д>0, С<0, то
Л	1 Л л
f(X,0) = —AX2 + R(Xt 0)
и пользуясь неравенством (13), заключаем, что при малых значениях | X |
§ 7. Теорема Тейлора
405
Л	1 Л	1 Л [	/ Л\ 1
/ (X, 0) > — ЛХ2-М|ХР= — АХ2 [ 1 — (2Л4/Л) | X |J > 0.
Аналогично получаем, что f(0, Y)<Z 0 при малых значениях | Y |. Следовательно, функция f не имеет в точке (0, 0) ни максимума, ни минимума; говорят, что точка (0, 0) является седлообразной точкой, или седлом, функции /. В окрестности точки (0. 0) линии уровня функции f похо-
1 л д
жи на линии уровня функции -^-(АХ2 — | С |У2), т. е. они выглядят как гиперболы (см. рис.
12.16). Если А < 0, а С>> 0, то мы приходим к аналогичному заключению.
АЛ	АЛ
Предположим теперь, что АС — В2^> 0, так что АС> 0. Если А + С> 0, то обозна-
Л л
чим через а меньшее из двух положительных чисел А и С. Для малых положительных значений суммы X2 + Y2 имеем
ЦХ, Г) > -у (ах2 + СГ2)— М (X2 + Г2)3/2 > -у (X2 + Г2) — М (X2 + Га)3/2 =
= — (Х24-Г2)Г1— -^-(Х2 +Г2)1/21>0. 2	I а	I
Следовательно, функция / имеет в начале координат строгий локальный минимум^ (х, г/)> f(0, 0) для всех точек (х, у), близких к точке (0, 0) и не совпадающих с ней. Аналогично доказывается, ЛА	Л Л
что если ACZ> 0 и А + С<0, то функция f имеет в начале координат строгий локальный максимум. В окрестности точки (0, 0) линии уровня функции f близки к линиям уровня функции 1 Л Л
(АХ2 + СУ2), т. е. они выглядят как эллипсы (см. рис. 12.15).
Проведенное рассуждение содержит доказательство теоремы 3 § 3.4.
7.4. Теорема Тейлора для функции п переменных
Формулу Тейлора для функции п переменных получают из соответствующего результата для функции одной переменной, повторяя ход рассуждений, использованный в § 7.1 и 7.2 для случая п = 2. Пусть функция f(xv х2, хп) = f(x) определена и N + 1 раз непрерывно диф-
Л Л Л л
ференцируема вблизи точки х = (xlt х2......хп) и пусть х есть некоторая точка, близкая к
л
точке х. Рассмотрим единичный вектор
n = (cos (ц, cos da, ...» cos an)
A	A
такой, что ay — это направляющие углы вектора х — х. Тогда х = х + гп, где г — некоторое положительное число. Применим теперь теорему Тейлора к функции одной переменной
f(x) = f(x + rn).
Не повторяя вычислений, сформулируем окончательный результат:
f (х) = PN (х) 4- ₽v+1 (х),
Л
где PN есть многочлен степени N — многочлен Тейлора функции в точке х. Этот многочлен
Л
имеет в точке х то же самое значение и те же самые производные до N-ro порядка включительно, что и функция /. Многочлен PN представляет собой сумму всех одночленов вида
406
Приложение к главе 12
1	(	^Р1Ч-Р2+...+Рл^
PJ Рг! ••• Рп\ у dxf1 дх£2 ... дхуп
где
Р1 + Р2+	+ Рп < N
(и, конечно, d°f / дх® ... дх„—это просто /). Остаточный член ^+1 представляет собой сумму всех членов вида
1	/	^+1 f
Pi’* P2I ... Р/Д дх^ дх%2 ... дх?п
х	х V1 (х	х Vе (х	х Vя
Х1	Х1) \*2	х2 J ••• \хп	хп) 9
где
Pi + р2 + ... + рп = Af + 1,
а g — некоторая точка отрезка, соединяющего х с х. В окрестности точки х остаточный член удовлетворяет неравенству
IЛ 1ЛЧ-1 | /?лг+1 (х) | < М | х — х I , где М — некоторая постоянная.
•Пример. Найти второй многочлен Тейлора функции [(xt yt z) = In (г2 + ху) при х = у = 0, 2 = 1.
Первое решение. Искомый многочлен Тейлора имеет вид
Р2 = /(0, о, 1) + f'x (0, 0, 1) х+ fy (0, 0, 1)р + /;<0, 0, l)(z—1)4*
+ f’xx (0. 0. D + 4” f"yy (°> °>	+ 4" (°’ °- <г - 1>2 +
+ f"xy (0, 0, 1) ху 4- 4 (0, 0, 1) х (г - 1) + fy2 (0, 0, 1) у (г - 1).
Но	f' = У f- = х f' = 2г
х г2 4- ху у г2 4- ху 2 г2 4- ху
* _ у2	J _ __ х2	г________2	_	4г2
хх (z2 4- ху)2 * уу (z2 4- ху)* ’	22 г2 4- ху (z2 4- ху)2
f _	2zy	f" =	1	_ ху	f = _ 2гх
хг (г2 4- ху) 2 ’ ху г2 4- ху	(г2 4- ху)2 ’ у2 (г2 4- ху)2
так что при х = у = 0, г = 1 мы имеем:
/ = о,	—	fz^^, fxx==fyy==^t fzz= 2» fxz = fyz = ^f fxy=l'
Следовательно,
P2 = 2(z - 1) - (2 - I)2 4- xy.
Второе решение. Воспользуемся разложением в ряд Тейлора логарифмической функции (см. гл. 8, § 5.6). Полагая г = 1 4" С и пренебрегая всеми членами степени выше второй, получим
Задачи
407
1п(г» 4- xy)=ln[(14-<;)’4-xyl= In [1 + (2С + С» + ху)] = (2С + С* + ху) - у (2С + С’ + ху)»4- ... =
= 2С 4-С’4-ху —4-...) = 2С — (? 4-ху 4-... = 2 (z—1) — (z —1)’4-ху 4-... .
Выписанные члены и образуют искомый многочлен Тейлора.ф
УПРАЖНЕНИЯ
1.	Найдите третий многочлен Тейлора (многочлен Тейлора степени 3) функции Дх, у) = = xsin(xy4) при х = у = 0.
2.	Найдите второй многочлен Тейлора функции /(я, р) = 1п(1 4- « + Р) при а = р = 0.
3.	Найдите третий многочлен Тейлора функции f(ut v) = (и2 + и)1/3в точке и = v = I.
А4. Найдите третий многочлен Тейлора функции Ди, о) = (и — о)3 в точке и = 2, v = — 1.
5.	Найдите второй многочлен Тейлора функции f(w, г) = ew/z в точке w = о, г = !.
х
6.	Найдите	второй многочлен Тейлора функции Дх, у)= J sin (/у) dt в точке х = О,	у =	0.
7.	Найдите	третий многочлен Тейлора функции Д$, /) = tgn(s + Г1) в точке s = 1,	t =	1.
▲8.	Найдите	многочлен Тейлора степени 2п функции Дх, у) = (1 + ху)'1 при х = 0,	у =	0.
[Попытайтесь доказать, что остаточный член /?л+1 стремится к нулю при стремлении п
к бесконечности и при условии, что | х |< 2, | у |< — .1
В упражнениях 9—14 найдите второй многочлен Тейлора (т. е. многочлен Тейлора степени 2) для данной функции в данной точке.
9. f (х, у, 0 = tg(x 4- VV+ г) в точке (0, к2/16, 0).
Ю. g (х, у, г) = 1/(2х 4- Зу 4- 4г) в точке (1,1, 1).
11.	F(e, 9, ф) =ев*/'<’ при 0 = 0, <р = 0, ф=|,
12.	f (х, у, г) = cos (х2 4- yz) в точке (0, 0, 0).
13.	g(r, s, t) =	в точке (1,1, 1).
14.	G (а, Р, 7) = In [оф — 7/а) при а = 1, Р=1, 7 = 0-
ЗАДАЧИ
1.	Предположим, что функция Дх, у) определена и непрерывно дифференцируема при всех (х, у). Покажите, что следующие два условия эквивалентны:
а)	|	(х, у) | < 1, | f'v (х, у) |	1 для всех (х, у);
6)	I/(х«. У») — /(*1. У1)| У(х0 — Xi)»4- (у0 — у,)« для всех х0, у0, х1( у,.
2.	Предположим, что Дх, у) — дважды непрерывно дифференцируемая функция при всех (х,у) и что fxy (х, у) = 0. Покажите, что Дх, у) = g(x) 4" h(y).
3.	Предположим, что функция Дх, у) дважды непрерывно дифференцируема при всех (х, у) и удовлетворяет дифференциальному уравнению (называемому волновым уравнением)
с* fxx fyy =0’
408
Приложение к главе 12
4.
5.
6.
где с — некоторое положительное число). Покажите, что
У) = g(x + о у) 4- h(x — су).
—— и вычислите 2с J
/(л,
|^У Казани е: рассмотрите Найдите все функции [(х,
функцию <р(£,т])=^—— у, г), для которых
р/ — Р/ — Р/ ______ Р/ ___ ffr __ fff _ л
I XX — I yv — ' zz — I ху f xz — I vz — u-
Найдите все функции /;(х, у, г), для которых все производные порядка k равны нулю. Функция £(хх, х2, ...» хл), определенная при xf + х% + ... +х? ф 0, называется однородной функцией порядка л, если для каждого 0
/(**1, ^2......ixn) = tnf (хг, х2, ... , хп).
что если такая функция является непрерывно дифференцируемой, то она у до так называемому уравнению Эйлера:
д/	с*/	dt	£ л
“7	4-	4- ... 4- ”— — п/ = 0.
дху	ох2	дхп
что для каждой непрерывной функции $ -► ф(6), определенной на отрезке
Покажите, влетворяет
7. Покажите, [а, Ь], функция
b
f (X, у) = У~{/2 J	(х—С)2/4Рф (£)
а
удовлетворяет дифференциальному уравнению (называемому уравнением теплопроводности} fxx = fy •
[У к а з а н и е: примените теорему 7 § 2.17.]
8. Покажите, что если | F | <! М и кривая С имеет длину L, то криволинейный интеграл f F du удовлетворяет неравенству

13/КРАТНЫЕ ИНТЕГРАЛЫ
В этой, последней, главе книги дается определение и рассматриваются свойства и приложения интегралов от функций нескольких переменных, определенных на интервалах и на областях более общего строения. Типичный случай — двойные интегралы — рассматривается подробно; затем двойные интегралы используются для вычисления площадей поверхностей. Дается краткий набросок обобщения понятия интеграла на случаи трех и большего числа переменных. Приложение к главе содержит четыре параграфа: о центроидах, о теореме Грина, связывающей двойные интегралы с криволинейными, о несобственных кратных интегралах; последний параграф Приложения посвящен доказательству некоторых теорем.
Строгая теория кратных интегралов сложнее теории обыкновенных интегралов; поэтому она отнесена в Дополнение (см. § 4 и 5),
410
13. Кратные интегралы
Рис. 13.1
$ 1. ДВОЙНЫЕ ИНТЕГРАЛЫ
В этом параграфе мы обобщим на функции двух переменных вторую основную операцию математического анализа — интегрирование. Мы поступим здесь так же, как это мы делали в гл. 5, в которой было введено понятие интеграла для функций одной переменной: сначала понятие двойного интеграла мы введем с помощью геометрической интуиции, а затем дадим этому понятию строгое аналитическое определение.
1.1. ДВОЙНОЙ ИНТЕГРАЛ ОТ НЕОТРИЦАТЕЛЬНОЙ ФУНКЦИИ ПО ИНТЕРВАЛУ
Рассмотрим непрерывную неотрицательную функцию двух переменных (х, у) •-►z = f(x, у), определенную в некотором интервале 1 :а< х < Ь,с < у <d и на его границе. Геометрическая интуиция подсказывает нам, что график этой функции, т. е. поверхность г — f(x, у), вместе с пятью плоскостями х = а, х = Ь, у = с, у — d и г = 0 ограничивают некоторое тело, которое имеет определенный объем V* (рис. 13.1).
Число V называется двойным интегралом от функции f(x, у) по /; обозначение Лейбница для него таково:
или
V = ^f(x, y)dxdy,
v= П f(x’0dxdy-a<x<b c<y<d
0)
(П
$ 1. Двойные интегралы
411
Рис. 13.2
Оправданием для этого обозначения служит следующий «математический миф». Считают, что рассматриваемый объем состоит из бесконечно большого числа бесконечно тонких трехмерных столбиков, имеющих форму прямоугольных параллелепипедов (трехмерных интервалов). Каждый из этих столбиков построен над «малой площадкой», окружающей точку (х, у) интервала /; он имеет бесконечно малые длину и ширину, dx и dy. и высоту z = /(х, у}. Объем этого столбика, следовательно, равен /(х, y)dxdy (рис. 13.2). Весь объем V равен сумме бесконечного числа таких бесконечно малых объемов.
1.2. ДВОЙНОЙ ИНТЕРВАЛ КАК ПОВТОРНЫЙ ИНТЕГРАЛ
Мы уже занимались вычислением объемов в § 4.4 гл. 5; использованный там метод можно применить теперь к вычислению двойных интегралов. При этом особенно поучительно будет еще раз провести все рассуждение, не используя прямо результатов гл. 5.
Мы ищем метод вычисления V, полагаясь на наше интуитивное представление об объемах. Для каждого /, где с< / <d, обозначим через У(/) объем тела, ограниченного поверхностью z = /(х, у) и пятью плоскостями: х = а. х = Ь.у = с, у ~ t и z = 0. Иными словами, V(/) есть «объем над интервалом a<Zx<Zb. с <Z у <Z t» или, иными словами,
V(0 = И f(x’y)dxdy.
а<х<Ь c<y<t
Наша интуиция подсказывает нам, что V(t) — непрерывная функция от t при t < / < d и что если положить У(с) = 0, то функция V(t) будет непрерывной и
412
13. Кратные интегралы
Рис. 13.3
при t = с, [Это просто означает, что V(7) будет сколь угодно мало, если t достаточно близко к c.J Следовательно, по основной теореме интегрального исчисления,
d
V = V(d) = §V'(t)dt С
(конечно, при условии, что производная V'(t) существует и является ограниченной кусочно-непрерывной функцией переменной /).
Нам остается еще угадать, чему равно значение Пусть h — малое положительное число. Интуитивное представление об объеме подсказывает, что
V(t 4-Л) — V(t) = jj f(x,y)dxdy
a<x<b t<y<t+h
— ведь стоящие слева и справа величины выражают объем узкого слоя, изображенного на рис. 13.3. Этот слой близок к цилиндру с высотой й, и его объем приближенно равен S(f)ht где S(t) есть «площадь основания» цилиндра, т. е. площадь пересечения рассматриваемого тела плоскостью у = t. Таким образам,
V(/ + /Q-V(O h
и мы можем рассчитывать, что
л-*о h
41J
§ 1. Двойные интегралы
Рис. 13.4
Если это так, то мы получаем формулу
d
V = j S (0 dt.
С
Но что такое S(/)? В плоскости у = t можно рассматривать х и z как декартовы координаты. Если с < t < rf, то пересечение плоскости у = t и рассматриваемого тела — это область, лежащая под дугой кривой z — f(x, f), взятой в пределах от х = а до х = Ь, как это видно из рис. 13.4. Площадь S(t) этого пересечения равна,
следовательно,
ь
и искомый объем равен
S(t) = § f(x, t)dx, а
f (х, t) dx
dt.
Обозначение переменной интегрирования здесь не играет роли; нам будет удобнее заменить t на у.
Учитывая обозначение (1), можно написать d Г b
Ц y)dxdy = J f(x, y) dx dy. /	c L a
(2>
Можно опустить скобки и писать просто:
b
JJ f(x, y)dxdy = j j f(x,y)dxdy. I	y=*c x=>a
(2'>
414
13. Кратные интегралы
Еще проще, условившись раз и навсегда, что внутренний знак интеграла соответствует внутреннему дифференциалу, а внешний знак интеграла — внешнему дифференциалу, писать
d ь
JJ f(x, y)dxdy = J Jf(x, y)dxdy. 1	c a
(2")
Можно, конечно, поменять роли х и у. В этом случае совершенно аналогичное рассуждение приводит к равенству
f (х, у) dx dy
f (х, У) dy
dx,
или b d
J j f <x, y)dxdy = J J f(x, y) dy dx.	(3')
I	a c
Формулы (2) и (3) сводят вычисление двойного интеграла к двум обыкновенным интегрированиям (можно сказать, к повторному интегрированию). Эти обыкновенные интегралы можно вычислить либо «формально» (с помощью разработанной техники отыскания первообразных функций), либо приближенными методами.
Замечание 1. Покажем, что формулы (2) и (3) являются частными случаями общей формулы объемов (см. гл. 5, § 4.4). Для того чтобы вычислить объем по «общей» фюрмуле, мы должны выбрать направленную прямую / и точку О на ней. После того как I и О выбраны, обозначим через S(t) площадь пересечения рассматриваемого тела с плоскостью Р, перпендикулярной I пересекающей I в некоторой точке, удаленной от О на расстояние t. Тогда искомый объем будет равен
+ со
V = J S(t)dt. — 00
Рассмотрим теперь тело, объем которого выражается формулой (1). Примем за прямую I ось у, за точку О — начало координат. При /< с и при t>d пересечение плоскости Р с рассматриваемым телом «пусто». Следовательно, £(/) = 0 при t < с и при t >* d, и интегрирование в формуле для объема производится только в пределах от t = с до t = d. Вычислив, как прежде, S(t), мы и получим равенство (2).
Приняв за прямую / ось х, мы точно так же придем к равенству (3).
Замечание 2. Поскольку мы пользовались обозначением Лейбница для двойного интеграла, то формулы (2) и (3) довольно очевидны — еще один случай, когда эти удивительно удобные обозначения прямо-таки думают за нас.
Замечание 3. Важным частным случаем формул (2) и (3) является следующее утверждение: двойной интеграл (по интервалу) от произведения двух функций, каждая из которых есть функция от одной переменной, является произведением двух обыкновенных интегралов:
§ 1. Двойные интегралы
415
с
b	d
JJ 4>(x)ty(y)dxdy = J<p (x)dx • dy. a<x<b c<y<d
В самом деле, в силу равенства (2) ь
d
d
JJ q(x)ty(y)dxdy = J J ф (x) <[> (y) dx dy = J <|> (y) a<x<b	c
c<y<d
с
а	-I
b	d
= J Ф (х) dx • J <|> (у) dy, а	с
что и требовалось доказать, фПример. Вычислить интеграл (6х2у + 8ху3) dx dy, J
распространенный no интервалу 1: 1 < x < 2, 3 <Z у < 4. Решение. Этот интеграл равен
4 2
С j (6х2у + 8ху3) dx dy =
- ь
J Ф (х) dx dy =
4 Г 2
Г j (6х2г/ 4- 8хг/3) dx dy.
Но для функции 6x2y + 8x#3, рассматриваемой как функция от х при постоянном уу первообразной будет функция 2х3у + 4х2#3. Следовательно,
2
J (6x2z/+8xi/3) dx = 2х3у + 4x2z/3
х=2
= 16у + 16г/3 — (2г/ + 4г/3) = 14г/ 4- 12г/3,
х=]
и наш двойной интеграл равен
(14г/+ 12г/3) dy = 7г/2 + Зу4
</=4
= 574.
у=3
Мы интегрировали сначала по х, а затем — по уу т. е. воспользовались формулой (2). Но можно было бы также интегрировать сначала по у у а затем — по х, т. е. воспользоваться формулой (3). В этом случае получаем
2
’ 4
2 4
J J (6х2г/ + вхг/3) dydx = J (6х2г/ 4- 8хг/3) dy
2	2
= J [(48х2 4- 512х) — (27х2 4- 162х)] dx = j (21х2 4- 350х) dx = (7xs 4- 175х2)
2	У=*
dx = \ [Зх2у2 + 2xz/4] dx =
2
= 574,
т. е. тот же результат, что и в первом случае.
§ 1. Двойные интегралы
417
1.3. ФУНКЦИИ, ПРИНИМАЮЩИЕ ЗНАЧЕНИЯ РАЗНЫХ ЗНАКОВ
Если функция /(х, у) принимает также и отрицательные значения, то двойной интеграл
а<х<Ь c<y<d
/(х, yjdxdy
рассматривается как сумма всех объемов, заключенных между поверхностью z = = /(х, у) и плоскостью z = 0 и ограниченных плоскостями х = а, х = Ь, у = с, у = d, причем объемы, расположенные выше плоскости г = 0, берутся со знаком плюс, а объемы, расположенные ниже этой плоскости,— со знаком минус. Так, например, в случае, изображенном на рис. 13.5, двойной интеграл равен разности двух положительных чисел.
Покажем, что и в этом случае вычисление двойного интеграла сводится к повторному интегрированию. Определим две функции:
г / ч f f (х, у), f+(X,y) = j 0
, .	.	( f(x, у),
f-(x, у) =	'
если f(x, у)>0, если f(x, t/)<0; если /(%,*/)< О, если f (х, у) О
(для случая, изображенного на рис. 13.5, графики этих функций приведены на рис. 13.6 и 13.7). Заметим, что
fix, у) = f+(x, у) + /_(х, у).
Так как /+(х, у) 0 всюду, то ясно, что
v+ = JJ f+(x, y)dxdy
есть объем над I — это объем тела, заключенного между плоскостью z = 0 и той частью поверхности z = f(x, у), которая расположена выше плоскости z = 0. Точно так же /_(х, у) < 0 всюду. Следовательно, всюду же [—f_(x,y)\ >• 0 и
V- = И [—/-(*. y)]dxdy
есть объем под интервалом I — это объем тела, заключенного между плоскостью z = 0 и той частью поверхности z = /(х, у), которая лежит ниже плоскости z — 0. Следовательно,
JJ /(X, y)dxdy = V+ — V. = JJ /+(х, y)dxdy — JJ [—f (x, y)] dx dy.
418
13. Кратные интегралы
В силу результатов § 1.2 и известных свойств обыкновенных интегралов имеем
d Г b	Ъ
= J J/+(X, y)dx + J/_(x, t/)dx c L a	a
d
с
b	d Г b
J [/+ (x> у) + /_ (X, I/)] dx dy = J J f (x, y) dx a	c L a
dy.
Отсюда видно, что формула (2) остается справедливой и для функций, принимающих как положительные, так и отрицательные значения. Формула (3) доказывается аналогично.
УПРАЖНЕНИЯ
В каждом из упражнений 1—22 заданы интервал и функция определенная на этом интервале. Проинтегрируйте f по этому интервалу. Каждую задачу попытайтесь решить дважды: применяя формулу (2) и применяя формулу (3).
1.	0<х<1, 2 < у < 3; f(xty) = xyex.
2.	—1<х<0, 0,1 < г/<0,2; f (х, у) = х2у3 -f- sin х.
3.	—1<6<1,	—1<<Р<1; /(6, <р) = 0<ре®2.
4.	— 1<х<1, — 1<г/<1; f(x, у) = ех+У.
5.	/2</<л, 0,37<m<0,4; f (I, т) = 1те1+т.
6.	10<Z< 11, —2тс < s < 0,5л; f (s, t) = 2/2 sin s.
7.	8<«<8,1, 0<d<100; f (u, v) = v/(u + v).
A8. 0,l<x<0,2, 0,25<p<0,3; f(xty) = yex^
9.	л/2 < x <л, л/2<р <л; f(x, у) = х cos ху.
10.	10<х<11, 4<р<5; f (х, у) = ех+У + In (ху).
11.	0<х<1, 0<р<1; f (х, у) = 4х3 У у + Зу2 Ух .
12.	—5<z< — 4, —3<иу<—2; f (z, ш) = 3z — 2ш3.
у—
13.	— 2 < х < 1, — 1 < у < 2; f (х, у) = 4t/2 V х + cos у.
14.	9<р<10, — 0,1<р<0; f (р, q) = cos (4р + 3q).
15.	0<х<л, 0<р<л; f (х, у) = cos (Ах + By) sin (Сх + Dy).
16.	3<4<6,7, 4,9<В<5,8; f (Л, В) = (Л3 + В3)2.
17.	0<х<1, 2 < у < 3; f (х, у) = (ех + cos у)3.
18.	0<z<l, 2 < w < 3; f(z, w) = w arcsin z.
19.	l<x<2, 2<//<3; f (x, у) = (х + у)3ех+У.
2O.	A<Zx<ZB, C<Zy<ZD\ f(x, y) = (x + y)n.
21.	хо<х<хь уо<у<Уъ У) = (* + У + 1А
22.	хо< х< хх; р0< y<Z Уъ t(x, у) = еах sin by.
§ 1. Двойные интегралы
419
1.4.	КУСОЧНО-НЕПРЕРЫВНЫЕ ФУНКЦИИ
Прежде чем дать аналитическое определение двойного интеграла, мы определим класс функций, которые только и будем интегрировать. Этот класс—более обширный, чем класс непрерывных функций, но достаточно ограниченный для того, чтобы мы не встретились в дальнейшем с какими-либо осложнениями.
Функция двух переменных (х, у) /(х, у) называется кусочно-непрерывной в некотором интервале, если она определена и непрерывна во всех точках этого интервала, за исключением, быть может, точек, принадлежащих конечному числу линий, каждая из которых представляет собой либо вертикальный отрезок, либо горизонтальный отрезок, либо может быть представлена как график непрерывной функции вида х >-► у = <р(х), а<-х<. 0 и в то же время как график непрерывной функции вида у »-> х = ф(^), 7 <. у <^6.
Это определение можно сравнить с определением, данным в § 1.5 гл. 5. Там мы назвали функцию одной переменной кусочно-непрерывной, если она непрерывна во всех точках некоторого (конечного) интервала, за исключением, быть может, конечного числа его точек.
Функция /(х, у) двух переменных называется ограниченной, если существует такое число Л4, что | /(х, у) \ < М всюду, где /(х, у) определена. Это определение в точности копирует аналогичное определение для функций одной переменной.
фПримеры. 1. Пусть х /(х), 0 < х < 1 — кусочно-непрерывная функция (ска-1	13
жем, функция /(х)= 0 при 0 <. х < —, f(x) — —1 при — < х < —, /(х) = 5 при з
— < х < 1). Тогда (х, £/)»->/(х) будет кусочно-непрерывной функцией на интервале 0 < х < 1, О <Z у <Z 1, потому что все точки разрыва этой функции принадлежат конечному числу вертикальных отрезков (в нашем случае отрезкам х = и х = -|-; 0< у< 1).
2.	Пусть /(х, у) — функция, непрерывная на интервале 0 < х< 1, 0 < у < 1, за исключением точек линии, имеющей форму восьмерки (рис. 13.8). Эта функция кусочно-непрерывна, так как наша восьмерка может быть разложена на дуги, каждая из которых удовлетворяет условиям определения. (На рисунке концы дуг разложения отмечены точками.)
3.	Если /(х, у) = 1 при х2 + у2 < 1, /(х, у) = 0 при х2 4- у2 > 1, то функция /(х, у) кусочно-непрерывна. Читателю предлагается доказать это.
1
4.	Функция /(х, у) =	• кусочно-непрерывна. Единственная точка
разрыва этой функции — начало координат — может быть покрыта горизонтальным отрезком.
5.	Если f и g — кусочно-непрерывные функции, то кусочно-непрерывны также fgyf 4- g,f — g. Читателю предлагается доказать это утверждение.
6.	Функция /(х, у), равная 0, если х и у рациональны, и равная 1 в противном случае, не является кусочно-непрерывной.ф '
420
13. Кратные интегралы
УПРАЖНЕНИЯ
23.	Если функции f(x, у) и g(x, у) кусочно-непрерывны в некотором интервале /, то будут ли функции f2+gHsin^ тоже кусочно-непрерывными? Попытайтесь обосновать Ваш ответ.
24.	Пусть выполнены условия упр. 23; при каком дополнительном условии частное [/g тоже будет кусочно-непрерывной функцией?
х2 + г/4 + 6
25.	Докажите, что функция Л(лг, у)=---------при ху 0, у) = 77 при ху = 0 ку-
ХУ
сочно-непрерывна в каждом интервале.
26.	Является ли функция Цх, у) из упр. 25 ограниченной?
1.5	. АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
Дадим теперь определение двойного интеграла от ограниченной кусочно-непрерывной функции. В § 1.1—1.3, исходя из интуитивного представления об объемах, мы показали, что двойной интеграл от непрерывной функции можно вычислить с помощью повторного (простого) интегрирования. Для кусочно-непрерывной функции мы хотим воспользоваться этим методом вычисленйя как определением; однако для этого необходимо убедиться в выполнимости описанного метода вычисления интеграла. Следующая теорема утверждает, что это на самом деле так.
Теорема 1. Пусть f(x, у) — ограниченная кусочно-непрерывная функция на интервале /: а<х<Ь, с < у <Zd. Тогда для каждого фиксированного у из интервала (с, d), за исключением, быть может, конечного числа точек, x*-+f(x, у) является кусочно-непрерывной функцией у, определенной на интервале (а, Ь). Аналогично, для каждого фиксированного х из интервала (а, Ь), за исключением, быть может, конечного числа точек, у i-> f(x, у) есть кусочно-непрерывная функция на интервале (с, d). Далее, ь
У*+ J/(X, y)dx а
§ 1. Двойные интегралы
421
есть ограниченная кусочно-непрерывная функция на интервале (с, d) и d
§f(x, y)dy С
— ограниченная кусочно-непрерывна я функция на интервале (а, Ь). Из теоремы 1 вытекает, что оба повторных интеграла
f(x, y)dx
f(x, y)dy
dx
(4)
имеют смысл.
Теорема 2. В предположениях теоремы 1 повторные интегралы (4) равны между собой.
Доказательства теорем 1 и 2 не вполне элементарны; мы их отнесем в Дополнение (см. § 4 и 5).
Двойной интеграл
JJ f(x, y)dxdy
I
мы теперь определим как общее значение двух интегралов (4):
d
JJ f(x, y)dxdy = J a<x<b	c
c<y<d
b
j f (x, y) dx
~ d
j f (x, y) dy dx.
(Это определение имеет то преимущество, что оно сразу показывает, как вычислить двойной интеграл. Другое определение будет рассмотрено в § 1.7 и в § 4 Дополнения.)
1.6	. СВОЙСТВА ИНТЕГРАЛА
Выразив двойной интеграл через интегралы от функций одной переменно й, мы можем сразу же перенести на двойные интегралы основные результаты, относящиеся к простым интегралам. (Эти свойства, впрочем, геометрически очевидны.) Так, для каждого интервала /
J J a dx dy = а • площадь / (а — постоян ная).	(5)
Если интервал I разделен вертикальной или горизонтальной прямой на два интервала и 12 (рис. 13.9) и функция / ограничена и кусочно-непрерывна на /, то
Jj f(x, y)dxdy = J J f(x, у) dx dy 4- f(x,y)dxdy.
422
13. Кратные интегралы
Рис. 13.9
Далее, пусть функция g тоже ограничена и кусочно-непрерывна на I, тогда
если f(x, у) ^g(x, у) на 1, то
Jj f (х, у) dx dy < jj g (x, у) dx dy.
Наконец,
j J af (*, У) dx dy = a J J f (x, y) dx dy (a — постоянная)
и
И [f(x,y) + g{x,y)]dxdy= JJ f(x,y)dxdy+ JJ g (x, y) dx dy.
(7)
(8)
(9)
Мы докажем только свойство (6), а доказательство остальных свойств предоставим читателю. Предположим, что I есть интервал a < х < 6, с <С у <Cd и что I разделен на два интервала Л и / 2 прямой х = xQ. Мы имеем тогда
ь Г d
f{x, y)dy
Г d
[по определению двойного интеграла] =
b
dx + J J f (x, y) dy dx
X0 L c
[по свойству аддитивности простого интеграла]
= JJ f(x,y)dxdy+ JJ f(x,y)dxdy [по определению двойного интеграла]. Ц	12
Доказательства утверждений (5), (7), (8) и (9) аналогичны.
§ 1. Двойные интегралы
423
Рис. 13.11
1.7	. СТУПЕНЧАТЫЕ ФУНКЦИИ
При рассмотрении интегралов от функций одной переменной мы часто пользовались понятием ступенчатой функции (см. гл. 5, § 1.5, 1.6 и 1.8). Теперь мы определим ступенчатую функцию двух переменных.
Если мы разобьем интервал а < х < b на некоторое число, скажем, р, подынтервалов и через каждую точку деления проведем вертикальную прямую, а интервал с <. У <Zd разделим на некоторое число, скажем, q, подынтервалов, и через каждую точку деления проведем горизонтальную прямую, то двумерный интервал / : а < х < Ь, с < у <Zd разобьется на pq двумерных подынтервалов. Так, например, на рис. 13.10 интервал 0 < х < 19 разбит на четыре подынтервала; интервал 0 < у < 10 — на три подынтервала, в силу чего весь двумерный интервал 0 < х < < 19, 0 < у < 10 разбился на 4-3 = 12 двумерных подынтервалов.
Ступенчатой функцией (х, £/)|->ф(х, у) в интервале / называется такая функция, которая для некоторого разбиения интервала / на подынтервалы постоянна на каждом из них. Для заданного разбиения интервала ступенчатую функцию г = ф(х, у) можно определить, задавая ее значения гь z2, г3, ... в различных подынтервалах. Мы сделали это на рис. 13.10; график полученной таким путем функции изображен на рис. 13.11. Ступенчатая функция всегда кусочно-непрерывна (и ограничена). (Ее значения на линиях разбиения интервала совершенно не важны — их можно задавать произвольно.)
424
13. Кратные интегралы
Интеграл от ступенчатой функции z = ф(х, у), принимающей постоянные значения zb z2, z3, ... на подынтервалах /ь/2,/3, •••, — это просто конечная сумма
ф(*. y)dxdy = z1S1 + z2S2 + ... ,	(10)
1
где Sk— площадь подынтервала Ik. В самом деле, применяя несколько раз свойство аддитивности (6), мы получим равенство
Jj <р(х, y)dxdy = ф(х, y)dxdy + fj ф(х, y)dxdy+ .... v
Но так как ср на интервале Ik постоянна и равна zk, то по свойству (5) мы имеем Jj Ф(Х, y)dxdy = JJ Zhdxdy = zkSh,
I k	1 k
откуда и вытекает равенство (10).
Так, например, для функции, изображенной на рис. 13.10, мы имеем
JJ ф(х, y)dxdy = 13-6+ 15-12 + 14-12+ 10-8+ 6-12+ 6-24+ 4-24 + 0<х<19 0<г/<10
+ 0-16 + (— 6)-12 + (— 3)-24 + (~ 8).24 + (— 5) • 16 = 818 — 416 = 402.
/(*, y)dxdy^ J J ф (х, у) dxdy.
Это есть, конечно, сумма объемов изображенных на рис. 13.11 «коробочек», лежащих выше плоскости z = 0, минус сумма объемов «коробочек», лежащих ниже этой плоскости.
Пусть /(х, у) — ограниченная кусочно-непрерывная функция, определенная в интервале /, и пусть ф(х, у) и ф(х, у) — ступенчатые функции, такие что ф f < ф в интервале /. По свойству монотонности (7) имеем
Ф(X, y)dxdy <
Так как интегралы от ступенчатых функций в левой и правой частях равенства легко вычисляются, то это есть способ приближенного вычисления двойного интеграла от функции /. Таким путем можно получить значение двойного интеграла с любой нужной нам степенью точности, если заключить / между двумя ступенчатыми функциями, интегралы от которых достаточно близки друг к другу. Это составляет содержание следующей теоремы.
Теорема 3. Пусть f(x, у) — ограниченная кусочно-непрерывная функция, определенная в некотором интервале /. Тогда существует одно и только одно число V, такое, что для любых двух ступенчатых функций ф(х, у) и ф(х, у), таких что функция f(x, у) «заключена между ними» [т. е. что ф(х, у) f(x, у) ф(х, г/)], выполняется неравенство
Jj ф(х, y)dxdy < V < 1
Этим числом является двойной интеграл от f по интервалу 1. Для каждого е > 0 можно найти такие ступенчатые функции ср и ф, что ф f <. ф и
JJ tydxdy— JJ ф dx dy <е.
/	j j
f f y)dxdy.	(11)
§ 1. Двойные интегралы
425
Это соответствует теореме 1 § 1.8 гл. 5, касающейся обыкновенных интегралов; однако доказательство для случая двух переменных сложнее; мы дадим его в Дополнении (см. § 4 и 5).
Замечание. Как и в случае функций одной переменной, равенство (10) можно принять за определение двойного интеграла от ступенчатой функции, после чего двойным интегралом от кусочно-непрерывной ограниченной функции можно назвать число, определяемое теоремой 3. В этом случае равенство двойного интеграла и соответствующего повторного интеграла будет уже не определением, а теоремой, требующей доказательства. Это доказательство дается в Дополнении.
УПРАЖНЕНИЯ
27. Еслиф и ф— ступенчатые функции, то такими же будут и ф + ф и фф. Докажите это. Д28. Еслиф(х, у) и ф(х, у) — ступенчатые функции, то такой же будет и функция со(х, у) = =тах[ф(х, у), ф(х, г/)] [наибольшее из чисел <р (х, у) и ф (х, #)]. Объясните, почему это так.
1.8. СУММЫ РИМАНА
Пусть f(x, у) — ограниченная кусочно-непрерывная функция, определенная в интервале I. Предположим, что мы разбили интервал /, как в § 1.7, на подынтервалы; выберем в каждом из подынтервалов Ij или на его границе точку (х;-, r/j) и образуем сумму
о = /(Xi, yt)Si + /(х2, y2)S2 + ....
где Sj есть площадь интервала IЧисло о называется суммой Римана (или интегральной суммой) для интеграла
V = JJ f(x, у) dxdy.
(12)
Мы можем определить ступенчатую функцию со(х, у), равную f(Xj, yj) в /7-. Тогда сумма о будет равна двойному интегралу от этой функции по интервалу /. Если Ф и ф — две ступенчатые функции, относящиеся к одному и тому же разбиению / и такие, что ф f ф, то имеет место и неравенство ф со ’С ф, так что по свойству монотонности (7) двойного интеграла имеем
Ф (х, у) dx dy < о < j |
/
ф (x, у) dx dy.
(13)
В силу теоремы 3 можно найти ступенчатые функции ф и ф, для которых ф f < ф, причем такие, что разность между двумя интегралами в равенствах (11) и (13) будет сколь угодно малой. При этом соответствующая сумма Римана отличается от двойного интеграла тоже сколь угодно мало.
426
13. Кратные интегралы
Пример. Рассмотрим интеграл
4 6
V = JJ (х2у + ху2) dxdy = J J (х2у + ху2) dx dy = 0<x<6	О О
О<#<4
4
= С (72у + 18z/2) dy = 576 + 384 = 960.
Разобьем интервал 0 < х < 6, 0 < # < 4 на 6 подынтервалов и в каждом из подынтервалов выберем точку так, как указано на рис. 13.12. Площадь каждого из подынтервалов равна 4. Значения суммы х2у + ху2 в каждой из точек (1, 1), (3, 1), (5, 1), (1, 3), (3, 3) и (5, 3) равны 2, 12, 30, 12, 54 и 120. Соответствующая сумма Римана, следовательно, равна
(2 + 12 + 30 + 12 + 54 + 120)4 = 920,
что примерно на 4% меньше точного значения интеграла.ф
УПРАЖНЕНИЯ
В упражнениях 29—32 задаются подынтегральная функция f(x, у) и интервал / = = {*о< x<Z хо+п, уо< у < у0 + т}. В каждом случае определите тп подынтервалов, используя разбиение осей х и у целыми значениями координат, и подсчитайте сумму Римана, используя ступенчатую функцию, равную f,(xo + i, Уо + /) в интервале %о + i — 1< *<С < *о + G уо + j — 1< y<Z уо + /. Сравните эту интегральную сумму с точным значе-
У
нием интеграла
f(x, у) dxdy.
29. t = х"2 + у, 100<jr< 102, 3<у<5.
Д30. (= x3y — 4z/2; 0 < x < 4, 0 < < 4.
31. f = ax+ by, 7<x<9, 13<^<15.
32. f, = x2 + ху +	10<x<13, —4<y<—I.
§ 1. Двойные интегралы
427
2
Рис. 13.13
Рис. 13.14
1.9. ДВОЙНОЙ ИНТЕГРАЛ ПО ПРОИЗВОЛЬНОМУ МНОЖЕСТВУ
Выше мы определили двойной интеграл по интервалу не только от непрерывной, но также и от кусочно-непрерывной функции. Это было очень полезно: теперь определение и вычисление интегралов по множествам более общего вида почти не потребует от нас дополнительной работы. Мы объясним это сначала на простом примере.
Пусть D — единичный круг, т. е. множество всех точек (х, z/), для которых хI 2 + + у2 <Z 1. Рассмотрим функцию г = f(x, у) = 3 + х\ пусть нам надо найти объем V, ограниченный кругом D, плоскостью z = 3 + х и цилиндром х2 + у2 = 1 (рис. 13.13). Этот объем естественно обозначить через
V = JJ (3 +x)dxdy.
Определим теперь новую функцию:
I 0, если х2 + t/2i>l.
(14)
(15)
Если / — произвольный интервал, содержащий круг D, то
И* 7 (х, у) dx dy = JJ (3 + x)dxdy.	(16)
1	D
Это просто означает, что объем V можно представлять себе как объем, заключенный между интервалом / плоскости z = 0 и графиком функции z = /(х, у) — ведь этот график в области, внешней по отношению к кругу D, совпадает с плоскостью z = О и ничего не добавляет к нашему объему V (ср. рис. 13.13 и рис. 13.14). Можно, конечно, доказать равенство (16) и используя формулу объемов из § 4.4 гл. 5.
428
13. Кратные интегралы
В силу равенств (15) и (16) объем V можно вычислить посредством повторного интегрирования. При этом размеры интервала /, содержащего круг О, не имеют значения; можно предположить, что / — это интервал — 1 < х <; 1, —1 < у <Z 1 (рис. 13.15). Мы имеем
V = JJ (3 + х) dxdy = J f (X, у) dxdy.
Но для каждого фиксированного у функция Дх, у) =0, если х2 + #2 > 1, т. е. если х2>1—г/2, а, значит, для всех х, лежащих вне интервала |хIC]/1—у2- Следовательно,
и
/1— у2	/1— Уг
J f (х, у) dx = J [ (х, у) dx = J (3 + х) dx
—1	-Vi^y2
1 /1-У2	1
V = J J (3 + x) dx dy = J 6 У 1 — у2 dy = Зтс -1 —VTqp	-1
(здесь мы использовали результат § 4.3 гл. 5).
Метод, которым мы только что воспользовались, применим, разумеется, не только в случае круга D и функции z = 3 + х. Для того чтобы дать точное описание этого метода, удобно воспользоваться понятием характеристической функции.
Пусть D — произвольное ограниченное множество точек плоскости, т. е. множество точек, содержащихся в некотором интервале. Характеристическая функция множества D, обозначаемая через (х, у), определяется следующим образом:
& у} __ ( Ь если точка (*> У) принадлежит множеству D,
1 0, если точка (х, у) не принадлежит D.
§ 1. Двойные интегралы
429
Пусть теперь f(x, у) — некоторая функция, определенная на множестве D и, возможно, на некотором объемлющем D множестве. Ясно, что функция xD (х, y)f(x, у) равна /(х, у), если точка (х, у) принадлежит D, и равна 0, если (х, у) не содержится в D. Так, например, если D есть множество точек единичного круга х- + у- <Z 1, то определение (15) равносильно следующему:
'f(x,y)=xD(x,y)f(x,y).
Далее, если xD кусочно-непрерывна и если f — такая функция, что произведение Xd/ — ограниченная кусочно-непрерывная функция, то мы полагаем, по определению,
£ j f (*> у) dx dy = J j /о (x, у) f (x, у) dx dy,	(18)
где / есть некоторый, содержащий D интервал. Ясно, что выбор интервала / не играет роли.
Иными словами, для того чтобы найти двойной интеграл от функции f по ограниченному множеству D, положим / = 0 вне множества D и проинтегрируем полученную функцию по некоторому интервалу, содержащему D. Область D обычно называется областью интегрирования.
В следующих параграфах мы будем предполагать, что все области интегрирования ограничены и имеют кусочно-непрерывные характеристические функции и что все подынтегральные функции ограничены и кусочно-непрерывны.
1.10.	СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА В ОБЩЕМ СЛУЧАЕ
Перечисленные в § 1.6 свойства двойных интегралов, распространенных по интервалам, можно обобщить на двойные интегралы, распространенные по произвольным ограниченным областям. В частности, постоянный множитель можно выносить за знак интеграла, интеграл от суммы функций равен сумме интегралов от слагаемых, большая функция имеет больший интеграл*.
JJа/dxdy = а JJf dxdy (а — постоянная), D	D JJ(/ + g)dxdy = J J fdxdy+ ^gdxdy, D	D	D если f^g на D, mo J J f dx dy	J J g dx dy. D	D	(19) (20) (21)
Это вытекает из определения (18) и свойств (8), (9) и (7) из § 1.6. Для того чтобы доказать, например, равенство (20), пишем
430
13. Кратные интегралы
JJ (f + g)dxdy = ff (f + g)xDdxdy = ff fxDdxdy + JJ g^Ddxdy = *D	I	/	Z
= jj fdxdy + ff gdxdy D	D
(где / — некоторый функция, то число
содержащий D интервал). Если — кусочно-непрерывная
Jf dxdy =	1 • dxdy = [J xD dxdy
D	D	i
есть площадь области D (подробнее мы обсудим это в § 2.1). Применяя свойство (19) к функции /= 1, заключаем, что
J J a dx dy = а • площадь D (а — постоянная).	(22)
Пусть теперь Dt и D2 — две области на плоскости; область, состоящая из всех точек, каждая из которых принадлежит хотя бы одной из областей Di nD2, называет-ется объединением, или суммой, Di и D 2 и обычно обозначается через Di (J D 2. Если D=Di (J£>2 и множества Di и D2 не пересекаются (не имеют общих точек), то, как легко видеть, (х, у) = %D (х, у) + XD (х, у). Пользуясь формулами (18) и (20), получаем
fdxdy = fdxdy-\- jj* fdxdy,	(23)
D	Dt	D2
где D есть сумма непересекающихся множеств Di и D 2. Эта формула обобщает свойство (6) из § 1.6. Свойство (23) нетрудно обобщить и на случай, когда множество D разложено не на два, а на большее число попарно непересекающихся множеств.
Двойной интеграл по области D часто вычисляют, как в примере из§ 1.8, посредством двух простых интегрирований. Говорят, что область D выпукла в направлении оси х, если существуют такие числа у иб, что при у0 < у и при у0 >6 горизонтальная прямая у = yQ не пересекает £>, а при у < yQ <6 пересекает ее по единственному отрезку а(#0) < х < Р(^о) (рис. 13.16). В этом случае мы имеем
5 Г Р (У)	1
Jj у) dxdy = у у f(x,y)dx dy, о	7 L а (У)
если условиться, что «внешний интеграл соответствует внешнему же дифференциалу», последнее равенство можно переписать еще и так:
8 Р(!/)
JJ/ (х, y)dxdy = j j f(x,y)dxdy. D	7	a(i/)
(24)
§ 1. Двойные интегралы
431
Если область D выпукла в направлении оси у (в смысле, показанном на рис. 13.17), то мы можем интегрировать сначала по у, а затем по х:
М W
J J f (*, У) dx dy = J J /(x, у) dy dx\ D	a t (x)
(25)
значения a, fl, 7 и б ясны из рисунка. На практике встречаются только такие области интегрирования, которые либо выпуклы в каком-то направлении, либо могут быть разложены на несколько непересекающихся областей такого вида.
•Примеры. 1. Пусть D — треугольная область, ограниченная прямыми 2у = х, у = 2х и х = л. Вычислить
sin у dx dy.
Решение. Изобразив область интегрирования на чертеже (рис. 13.18), мы видим, что область D выпукла в обоих направлениях — в направлении х и в направлении у. Сначала мы будем интегрировать по у. Для каждой точки (х, у) области D имеем О х л. Если вертикальная прямая удалена на расстояние х от оси у, то она пересечет область D в точках у = х/2 и у = 2х. Следовательно,
я 2х	«	=2л;
f sin у dx dy = f J sin у dy dx = f [— cos У\~x/2 dx =
D	0 X/2	0
ft = (7cos ——cos	dx = 2 sin —--------— sin 2x Г =2 sin — = 2.
J \	2	)	2	2 |o	2
432
13. Кратные интегралы
Если же мы хотим начать с интегрирования по х, то заметим, что 0 < у < 2л для каждой точки (х, у) области D и что горизонтальная прямая (прямая, отвечающая фиксированному у) пересекает область D по отрезку, концы которого отвечают значениям (рис. 13.19):
х = и х = 2у при 0 < у < гс/2
У
2
х =
и х = х при W2 < у <Z 2тс.
Следовательно, область D надо разбить на д в е области, после чего имеем
л/2 2у	2к я	/
f j sin у dxdy = J J sin у dxdy+ J J sin у dx dy = ( \2у
0 у/2	я/2 у/2	'
ч
2
2л	я/2	2к	2я
+ J («-----=0sinydy = -|- J ysmydy--------i- у ysinydy + те у siny dy.
я/2 4	0	я/2	я/2
Так как для функции у !-► у sin у первообразной служит функция у i-> sin у — — ycvsy [что можно найти, например, интегрированием по частям (ср. с § 3.3 гл. 5), а можно непосредственно проверить дифференцированием], то выписанный выше интеграл равен
4- Isi п у — yc©s]S/2-[sin у — у cos yf“ — те [cosy]^ = 4 + V + ~ л = 2*
§ 1. Двойные интегралы
433
У
Рис. 13.21
т. е. мы получили тот же результат, что и раньше.
2. Пусть D — множество точек (х, у), для которых х>0, y>x2uy<Z 2—х2. Вычислить
jj Vxy dxdy.
Решение. Множество точек (%, у), для которых х > 0, — это правая полуплоскость (рис. 13.20). Множество точек (х, г/), для которых у>х2,—это область, лежащая над параболой у = х2 (рис. 13.21). Множество точек (х, у), для которых у < 2 — х2, — это область, лежащая под параболой у = 2 — х2 (рис. 13.22). Множество D изображено на рис. 13.23; оно представляет собой пересечение этих трех множеств, т. е. состоит из точек, принадлежащих каждому из них. Две параболы пересекаются в точках, где 2—х2 = х2, т. е. при 2х2 = 2; точка пересечения, принадлежащая правой полуплоскости, имеет координаты (1, 1). Для точек области D абсцисса х изменяется от 0 до 1. Вертикальная прямая при постоянном х пересекает D по отрезку, концами которого являются точки у = х2 и у = 2—х2.
434
13. Кратные интегралы
Следовательно,
JJ Yxydxdy =
= j /7 А [(2 - х2)2- х<] dx = J (2х1/2 - 2х5/2 ) dx = [А х3/2 - А //2 О	о
Наша область интегрирования является выпуклой также и в направлении оси х. Читателю предлагается провести вычисления, интегрируя сначала по х, а затем ПО Г/.ф
УПРАЖНЕНИЯ
В упражнениях 33—52 заданы множество D и функция Дх, у). Начертите область D и вычислите П f(x, y)dx dy.
D
33.
34.
35
36.
37.
38
D	— внутренность треугольника с вершинами	(0, 0), (0, 1),	(1, 0); ft = х2у.
D	— внутренность треугольника с вершинами	(0, 0), (0, 1),	(1, 1); / = х2у;
D	—внутренность квадрата с вершинами (1, 0), (0, 1), (—1,	0), (0, —1); I =	уе*.
D	— область, ограниченная кривой у = sin х	и отрезком 0	< х < л; /j = ху.
D — внутренность треугольника с вершинами (хо, уо). (xj, У1), (хг, #з); Дх, у) = 1. (Дайте геометрическую интерпретацию полученного Вами результата.)
D — внутренность единичного круга; = Зх + 4у + 5. (После выполнения интегриро-
вания проведите рассуждение, которое позволяет найти этот интеграл без всяких
39.
вычислений.)
D — ограниченная область, заключенная между двумя параболами у = х2 и у = — х2 +
40.
+ 1; f (х, у) = х У~у.
X2	у2
D — пересечение внутренностей двух эллипсов—-------1- у2 = 1 и х2 Ч------ 1; / =х +
4	4
41.
42.
+ У + 1.
D — пересечение внутренностей двух треугольников: треугольника 7\ с вершинами (0, 0), (0 1), (1, 1) и треугольника Та с вершинами (0, 1), (1, 0), (2, 0); / = у sin х+х cos у. (Ответ можно оставить в виде повторного интеграла.)
D — сумма внутренностей двух треугольников из упр. 41; у sin х +х cos у. (Ответ можно оставить в виде повторного интеграла.)
43.	D — внутренность круга х2 + у2 = /?2;	= УR2 —х2—у2 . '(Укажите геометричес-
кую интерпретацию полученного результата.)
х2 у2	””Г””--~
44.	D — внутренность эллипса —— -|-	= 1; f = с у 1 ——. (Укажите
геометрическую интерпретацию полученного результата.)
45.	D — внутренность круга х2 + у2 = /?2; /; = /?[1— 7?"1 (х2 + у2)',г J. (Укажите геометрическую интерпретацию полученного результата.)
А46. D — внутренность треугольника с вершинами (—7, —6), (5, 3), (0, 0); f = е**?.
47.	D—внутренность треугольника с вершинами (—1, —1), (—4, —8); (—8, —4), t = (х2 - Зг/)2.
А48. D — кольцо, ограниченное двумя концентрическими окружностями с центрами в начале координат и радиусами и f = Ах3 + Вх2у + Су3.
49.	D — область, отсекаемая осями координат от полосы, заключенной между двумя параллельными прямыми с наклоном 2, проходящими через точку (1, 0) и через точку (2, 0); / = cos (х + у).
50.	D — сектор, отсекаемый от единичного круга лучами 0 =30° и 0 = 45°; ft(x, у) = 7х—9у.
51.	D — сектор, отсекаемый от единичного круга лучами 0 = Оо и 0 = 6^; f(x, у) = Ах + By. А 52. D — область, ограниченная параболами у = х2 и х = у2\ t = хпут, где пит — целые
положительные числа.
§ 1. Двойные интегралы
435
Рис. 13.24
1.11. ДВОЙНЫЕ ИНТЕГРАЛЫ В ПОЛЯРНЫХ КООРДИНАТАХ
Для некоторых областей интегрирования двойные интегралы удобнее вычислять, пользуясь полярными координатами (ср. с § 3.2 гл. 9).
Для того чтобы догадаться, какой вид должна иметь нужная нам формула, рассмотрим непрерывную неотрицательную функцию (х, у) к* z = /(х, у), определенную при х2 + г/2	7?2, и попытаемся вычислить объем V тела, заключенного между
графиком этой функции и кругом плоскости ху с центром (0, 0) и радиусом R. Это есть объем тела, ограниченного плоскостью z = 0, цилиндрической поверхностью х2 + у2 = Л?2 и графиком нашей функции (рис. 13.24).
Пусть (г, 6) — полярные координаты точки (х, у). Мы вернемся к упомянутому в § 1.1 «математическому мифу»: рассматриваемый объем состоит из бесконечно большого числа бесконечно тонких цилиндров. Основание каждого из цилиндров охватывает некоторую точку круга с координатами х = г cos 0, у = г sin 0; по форме оно представляет собой бесконечно малую фигуру, ограниченную двумя отрезками бесконечно малой длины dr, принадлежащими двум «соседним» радиусам, проходящим через начало координат, и дугами двух близких окружностей с центром в начале координат, соединяющими этим радиусы. Оба радиуса образуют бесконечно малый угол dQ (рис. 13.25). Высота соответствующего цилиндра, очевидно, равна
г = /(х, у) = f(r cos в, г sin 0).
Основание цилиндра близко к прямоугольнику, длины сторон которого dr и гdQ (последнее значение получается по формуле для длины дуги окружности). Следовательно, площадь основания малого цилиндра равна dr-г dQ= r-dr-dQ, а бесконечно малый объем этого цилиндра равен площади основания, умноженной на высоту, т. е.
f (г cos 0, г sin 0) г dr dQ.
436
13. Кратные интегралы
Полный объем будет равен сумме всех таких бесконечно малых объемов, и, значит, мы имеем
V = J J / (г cos 9, г sin 0) г dr d9,
по кругу
а руководствуясь обозначениями Лейбница, можем написать
2к Я
V = J J/(г cos 0, г sin 0) г dr d$, о о
(26)
или
R 2п
V = Г /(rcosO, г sin 9) г dQ dr.
о о
(Напомним соглашение: внешний знак интеграла соответствует внешнему дифференциалу.)
Мы пришли к двум равенствам, имеющим вполне определенный смысл; нам осталось только выяснить, будут ли они верны. Оказывается, что это так, и даже, более того, можно допустить, что функция f принимает и отрицательные значения, а непрерывность можно заменить кусочной непрерывностью. Для того чтобы не возиться с техническими деталями, мы только сформулируем следующий результат:
Теорема 4. Пусть f(x, у) — ограниченная кусочно-непрерывная функция, равная нулю вне круга х2 + у2 2, и пусть f(r cos 0, г sin 0) — кусочно-непрерывная функция от (г, 0). Тогда
2п R
f J f(x,y)dxdy = J J/(rcos9, l+y2<R*	о о
R 2к
г sin 0) г dr d$ =у у f(r cos 0, г sin 0) г dti dr. (27)
Доказательство этой теоремы будет дано в Приложении (см. § 8.1).
Применяя эту теорему, мы обычно имеем дело с функцией, равной нулю вне некоторого множества D, так что интеграл в левой части равенства может быть заменен интегралом по области D. Может случиться, что область интегрирования D «выпукла в радиальном направлении», т. е. что существуют такие числа и 02, что луч х = rcos0, у = rsin0, г > 0 пересекает область D только в том случае, если 0Х<0 < 02, причем пересечение является отрезком с концами г= а(0) и г = Р(0)>а(9). В этом случае (его иллюстрирует рис. 13.26) равенство (27) можно переписать так:
02 (3(0)
У У /(*> У) dx dy = у у / (г cos 0, г sin 0) г dr d0.	(28)
6i а(0)
§ 1. Двойные интегралы
437
Область D может оказаться выпуклой и по отношению к 0, и в таком случае мы имеем
Г2 0(г)
y)dxdy = J J f (r cos 9, r sin 9) r M dr.	(29)
D	a(r)
Геометрический смысл термина «выпуклая по отношению к 9», а также смысл чисел ri9 г2, a(r), Р(г) ясны из рис. 13.27.
•Примеры. 1. Предположим, что область D состоит из всех точек, полярные координаты (г, 0) которых удовлетворяют условиям
0! < 0 < 02, 0 < Г < ф (6),
где ф(0) — положительная непрерывная функция. Применим равенство (28) к функции fix, у) == 1. Так как а(0) = 0, (3(0) = ф(0) и
<р (6)
| rdr =ф (9)2,
ТО	о
02
площадь области D = — J ф (О)2 J9.
в.
Это (в других обозначениях) — та же формула, которую мы получили в§ 2.6 гл. 11.
2.	Пусть D — область, изображенная на рис. 13.28. Вычислить
ex*+y* dx dy.
438
13. Кратные интегралы
Рис. 13.28
Решение. Ясно, что в рассматриваемой области 0 изменяется от 0 до л/2, а г изменяется от 1 до 3. Далее, х2 + у2 = г2. Следовательно,
к/2 3	тс/2	тс/2
И - f j /7^» = j [±r p. _ j £^9
D	0 1	0	J	0
Без использования полярных координат этот интеграл можно вычислить, только применяя методы численного интегрирования.ф
УПРАЖНЕНИЯ
53.	Из упражнений 33—52 выберите пять таких, в которых целесообразно применить полярные координаты.
54.	В упр. 45 перейдите к полярным координатам и, вычислив интеграл, убедитесь, что
результат останется тем же, что и ранее.
Пусть D — область, ограниченная спиралью 6 = г и отрезком 0 < ;; < 2л. Вычислите двойной интеграл
55.
Обозначим через D интервал 0<х<1, | у\ <2. В интеграле dx dy перейдите к по<*
лярным координатам. Чему равно его значение?
57.	Вычислите (х2 4- у2)2 dx dy, где D — внутренность одного из лепестков четырехлепест-
ковой розы г = cos 20.
58.	Вычислите (1 + х2 + t/2)”1 dx dy, где D — внутренность лемнискаты г2 — cos 20.
59.	Пусть D — часть единичного круга, лежащая в первой четверти. Вычислите двойной интеграл у *2 + yi- dxdy''
60.	Пусть D — кольцо 1 < х2 -J- у2 < 2. Вычислите С С ——— dx dy.
J J (x2 + */2)2
61.	Пусть D — область, определяемая неравенствами тс <; 0<5тс/4, Ча < х2 + у2 < х/2к
Яху dx dy х2 + у2
D
§ 2. Площадь поверхности
439
§ 2. ПЛОЩАДЬ В этом параграфе мы рассмотрим применение двойных инте-ПОВЕРХНОСТИ градов для вычисления площадей поверхностей.
2.1. ПЛОЩАДЬ ПЛОСКОЙ ОБЛАСТИ
Мы уже видели, что если характеристическая функция iD(x, у) ограниченного множества D на плоскости кусочно-непрерывна, то интеграл
S
= JJ dx dy = J J	(x, у) dx dy
D	d 1
(1)
(где J есть некоторый интервал, содержащий область D), равен площади области D. Это соответствует определению, данному в § 4.2 гл. 5. В самом деле, так как двойной интеграл (1) можно вычислить посредством повторного интегрирования, то
здесь в качестве пределов интегрирования можно писать —оо и +<*>, поскольку функция вне / равна нулю. Далее, если для некоторого фиксированного х0 пересечение прямой х = х0 с областью D состоит из одного или нескольких отрезков, то интеграл
4-00
J Хэ(*0. y)dy =s(x0), — 00
где s(x0) — это сумма длин всех таких отрезков. Действительно,
О, если точка (х0, у) не принадлежит D,
Хд(*о- у) =
1, если точка (х0, у) принадлежит одному
из рассматриваемых отрезков.
Поэтому равенство (1) можно переписать так:
4-00
А = J s(x) dx, —00
а это в точности та формула площадей, которую мы имели в § 4.1 гл. 5 (если за прямую L принята ось х).
440
13. Кратные интегралы
Рис. 13.29
Рис. 13.30
Мы можем убедиться в том, что формула (1) дает верное определение площади и независимо от результатов гл. 5. Предположим, что мы разделили I на малые прямоугольники (см. рис. 13.29, где эти прямоугольники являются квадратами). Ступенчатая функция ф(х, у), равная 1 на тех прямоугольниках, которые целиком содержатся в D, и равная 0 на остальных прямоугольниках, удовлетворяет неравенству ф Хо*
Интеграл от этой функции — обозначим его через St— равен сумме площадей всех маленьких прямоугольников, принадлежащих D, т. е. площади области, заштрихованной на рис. 13.29. Далее сложим площади всех прямоугольников, пересекающихся с £>, (т. е. имеющих с О х от я бы одну общую точку); мы получим другое число S2, равное площади области, заштрихованной на рис. 13.30; S2 равно интегралу от некоторой ступенчатой функции ф (х, у), где ф. По теореме 3 § 1.7 имеем <. S <. S2, причем, разбивая область D на достаточно мелкие прямоугольники, мы можем вычислить S с любой степенью точности. Это соответствует интуитивному смыслу утверждения: площадь области D равна числу S.
Определение (1) площади связано с выбором определенной системы координат. Однако интуитивно ясно, что площадь области не зависит от положения осей координат, использованных при ее вычислении. Аналитическое доказательство этого утверждения мы наметим в Приложении (см. § 8.2).
2.2. ПЛОЩАДЬ НАКЛОННОЙ ПЛОСКОЙ ОБЛАСТИ
Наша ближайшая цель — определение площадей кривых поверхностей. Но предварительно мы рассмотрим какую-нибудь невертикальную плоскость и какую-нибудь достаточно простую область Д, принадлежащую этой плоскости (рис. 13.31). Из каждой точки Р множества Д опустим перпендикуляр на плоскость z = 0; обо-
§ 2. Площадь поверхности
441
Рис. 13.31
значим через Q точку пересечения этого перпендикуляра с плоскостью z = 0. Точка Q называется проекцией точки Р на плоскость z = 0. [Иными словами, если Р имеет координаты (х, у, z), то ее проекция Q имеет координаты (х, у, 0).] Множество Z), состоящее из проекций всех точек области Д, называется проекцией области Д на плоскость z = 0.
Площадь области Д, принадлежащей наклонной плоскости, равна площади ее проекции D, поделенной на cos0, где 0 есть угол между плоскостью области & и плоскостью области D.
Для того чтобы доказать это утверждение, предположим, что наклонная плоскость проходит через начало координат (мы можем добиться этого переносом системы координат в направлении оси z) и что эта плоскость проходит через ось у (этого можно добиться поворотом системы координат вокруг оси z). При этом мы приходим к такому расположению содержащих Д и D плоскостей, которое изображено на рис. 13.32. В плоскости, содержащей Д, введем декартову систему координат (X, у\. Точка этой плоскости с координатами (X, у) проектируется в точку (х, у), где х = X cos0. Это следует из рассмотрения прямоугольного треугольника ОАВ. (Заметим, что точка А есть проекция точки В, | ОА | = х и | OB | = X.) Следовательно, область Д получается из D сжатием к оси у, т. е. она получается, если сохраняя все расстояния в направлении оси у неизменными, мы умножим все расстояния в направлении оси х на l/cos0. Отсюда и вытекает наше утверждение. Для прямоугольного треугольника, расположенного так, как изображено на рис. 13.32, оно очевидно; для всех остальных фигур это вытекает, например, из формулы площадей (см. гл. 5, § 4.1), где за прямую I принимается ось у.
442
13. Кратные интегралы
2.3. ФОРМУЛА ПЛОЩАДЕЙ .
Рассмотрим теперь непрерывно дифференцируемую функцию (х, у) = f(x, у), определенную в некоторой ограниченной области D; предположим, что функция XD кусочно-непрерывна и что частные производные /*, f функции / ограничены. Мы хотим вычислить площадь S графика функции z = /(х, #), доверяя на этой первой стадии анализа задачи имеющемуся у нас интуитивному представлению о площади кривых поверхностей.
Предположим для простоты, что область D представляет собой интервал (как это изображено на рис. 13.33). Разобьем D на мелкие подынтервалы. Наша интуиция подсказывает, что «полная» площадь поверхности S есть сумма площадей всех малых «долек», которые проектируются на малые подынтервалы. Площадь же каждого из таких малых «кусочков» поверхности приближенно равна площади плоской фигуры, ибо малый участок кривой поверхности можно заменить соответствующим участком ее касательной плоскости. Но мы только что нашли, как вычислить площадь плоской области, образующей с горизонтальной плоскостью угол 0; поэтому можно рассчитывать, что мы сделаем лишь небольшую ошибку, если заменим площадь куска нашей поверхности, проектирующегося в подынтервал /у, числом, равным площади этого подынтервала, деленной на косинус угла Оу между плоскостью г = 0 и касательной плоскостью к поверхности, взятой в некоторой точке (xz, f/у) интервала /у.
Вычислим теперь угол Оу. Он равен острому углу между вектором нормали к поверхности в точке с координатами х;-, у^ Zj = /(х.-, z/y), где точка (Ху, yj) принадлежит /у, и вектором, направленным по оси z. Но, как мы уже знаем (см. гл. 12,
§ 2. Площадь поверхности
443
§ 2.7), вектор нормали к поверхности в точке (х,-, yjt Zj) имеет координаты (—f'x(Xj, у}, —fy(Xj< У})> О- А так как единичный вектор, направленный по оси г, имеет координаты (0, 0, 1), то (см. гл. 9, § 6.2)
cos 9у. = —	1	----,
V i + fx+fy
где f’x и f' вычисляются в точке (xj9 у у
Таким образом, мы приходим к следующему приближенному значению площади S:
площадь /х . площадь /2 . площадь /3 .
—	-j- -------- "Т"------------г • • • —
COS	COS в2	COS 63
= V 1 + fx{xlt у J2 4- fy (Xp yx)2 • площадь +
+ 1^1 + fx (x2, У2)2 + fy{x2, y2)2 • площадь /2 +
+	+ f'x(x3, y3)2 + f’y(x3, y3}2 • площадь /3 + • • • •
Но полученная таким образом сумма есть не что иное как сумма Римана для некоторого двойного интеграла (см. § 1.8), а именно интеграла от функции ]/* 1 + fx (х, у)2+ f (х, у)2 . Мы можем, следовательно, предположить, что
s = JJ V\ + f'x (X, у)2 + fy(x, у)2 dx dy.	(2)
D
Формула площадей (2) дает верный результат, когда/(х, у)=0 (т. е. когда подынтегральная функция равна 1), а также когда /(х, у) есть линейная функция f=ax+by+c (в этом случае подынтегральная функция равна У1 + а2 + 62 = l/cos0, где 0 — это угол между плоскостью z = ах + by + с и плоскостью z = 0).
Теперь мы изменим нашу точку зрения и примем формулу (2) за о п р е д е л е -н и е площади поверхности z = /(х, у), где (х, у) £ D.
•Примеры. 1. Найти площадь поверхности
z = — хУх	при 0 < х < 1, 1 < г/ < 2
3
Решение. Имеем z'x =У~х, гу=0. По формуле площадей (2)
S
__________ 2 1	____
+ г;а+ dxdy = J yi +xdxdy =
1 о
2	x=1
= Г [т<‘+*>’"]	(2/2-1)-
J L 3	Jx=0	д
444
13. Кратные интегралы
2. Найти площадь поверхности
г = 10 + ]ЛзГ V х2 + у2 , где у>х2, у<. 1.
Решение. Мы имеем z = j/T —- х , гу = ]ЛЗ — у . Следова-__________________ V X2 + у2	V х2 4- у2
тельно, V l + zx + zy = 2. Неравенства х2 < у < 1 определяют область, ограниченную параболой и горизонтальной прямой (рис. 13.34). Искомая площадь равна 1 1 1
2dy dx = J 2 (1 — х2) dx =	•
—1 X2	—i
Конечно, мы не можем рассчитывать, что при вычислении площадей поверхностей выкладки всегда будут столь же простыми.®
УПРАЖНЕНИЯ
1.	Найдите площадь поверхности z = 9хУх, где 1 < x<Z 2, —1 < y<Z 0.
2.	Найдите площадь поверхности г = 4х/х + Зх; 2< х< 3, 1 < у < 2.
3.	Найдите площадь поверхности г = 9х — у; х> 0, у >0, х2 + y2<Z 1.
4.	Плоскость Зх + 4г/ — 5 = —6 пересекает эллиптический цилиндр с образующими, параллельными оси z, и с основанием 2х2 + у2 = 1. Какова площадь сечения?
5.	Найдите	площадь	поверхности	г=У 1 — х2 — у2 , | х | < 1/2, |t/KVl—*2 •
6.	Найдите	площадь	поверхности	г=У x2+i/2 , 1/16 < х2 + у2 <1 /4 .
7.	Найдите	площадь	поверхности	z=9x2; 7<t/<8, 5<х<6.
А8.	Найдите	площадь	поверхности	i/ = xtgz; 1 < х2 + У2 < 18, —tc/2<z< тс/2 •
9.	Найдите	площадь	поверхности,	вырезаемой цилиндром х2 + у2 = 4 из сферыx2+y2+z2 =
= 36 и лежащей выше плоскости ху.
10.	Формула (2) определяет площадь поверхности, являющейся графиком некоторой функции г = /(х, у). Выпишите аналогичные формулы для площади поверхности, заданной уравнением х = g(r/, z) и вырезаемой и цилиндрической поверхностью с образующими, параллельными оси х, и с основанием D, принадлежащим плоскости уг.
fl. Пусть поверхность 2 определяется уравнением у = Л(х, г), где точка (х, г) принадлежит некоторой области D. Напишите формулу для вычисления площади поверхности 2.
12.	Найдите площадь той части поверхности у2 + г2 = 2х, которая отсекается от нее плоскостью х = 1.
13.	Найдите площадь части конуса х2 + у2 = г2, отсекаемой от него цилиндром х2 + у2 = = 2ах и расположенной выше плоскости ху.
14.	Найдите площадь куска параболоида х = у2 + г2, заключенного между плоскостями х = 0 и х = 12.
х2	у2
15.	Найдите площадь поверхности эллипсоида — + — + — = 1.
а2	Ь2	с*
§ 2. Площадь поверхности
445
2.4. ПОВЕРХНОСТИ ВРАЩЕНИЯ
Напомним, что поверхность вращения S получается вращением плоской линии С вокруг некоторой прямой /, принадлежащей плоскости этой линии (ср. с § 5.2 гл. 9). Предположим, что прямая / совпадает с осью z, что линия С принадлежит плоскости xz и что она является графиком функции
х н-> z = ф(х), О а < х < b
(рис. 13.35). Когда кривая С повернется вокруг оси z на 360°, она опишет некоторую поверхность S — график функции
(х, у) н-> г = ф (Ух2 + у2 ) = ср (г), а < г < Ь,
где г, 0 — полярные координаты точки (х, у). Согласно цепному правилу,
'	/ / v дт г , к х, ’	, . ч dr f / \ У
г* = Ф (И — = Ф (г) —, ги = <р (/) — = ф (г) —, dx	г	ду	г
так что
1 +zx + z'‘ = 1 + <р' (г)2.
По формуле (2) площадь поверхности S равна
S= JJ 1 + <р'(Ух2 + у2)2 dx dy = a2<x2+y2<b2
2к b
(3>
Переменную интегрирования можно обозначить любой буквой, так что формулу (3) можно переписать и так:
S = 2k
ь
J ]Л1 + ф' (х)а х dx. а
(4>
446
13. Кратные интегралы
Рис. 13.36
Эта же самая формула определяет и площадь поверхности, получающейся при вращении графика функции у = <р(х) вокруг оси у.
Замечание. Если линия С повернется не на «полный» угол 2л, а только на некоторый угол со, где 0 < со < 2л, то в формуле (4) нужно заменить множитель 2л на со. Действительно, в этом случае область интегрирования (в плоскости ху) в формуле (3) определяется неравенствами а < г < 6, 0 < 0 С со.
• Примеры. 1. Найти площадь боковой поверхности кругового конуса с высотой Н и радиусом основания R.
Решение. Эта поверхность получается при вращении вокруг оси г отрезка z = Н — (H/R)x, 0 < х < R (этот отрезок называется образующей конуса; рис. 13.36). Подставляя в формулу (4) значения а = О, b = R, <р(х) = Н — (H/R)x, находим
R	Г_________
S = 2к J У 1 + H‘l/R2 xdx — 2л	у.
О
Так как длина образующей L = ]//?2 4- /У2, то мы приходим к хорошо известной формуле элементарной геометрии:
S = nRL,
2.	Найти площадь поверхности сферы радиуса R.
Решение. Искомая площадь S равна удвоенной площади, полученной при вращении дуги окружности г ~ ]/ /?2 — х2, где 0 < х < /?, вокруг оси z, т. е.
___________ ч -.1/2	R
i V х dx = 4, f
-
как мы знаем из элементарной геометрии.
§ 3. Тройные интегралы
447
3.	Найти площадь S той части сферы х2 + у2 + z2 = /?2, которая лежит над сектором 0 < 0 < со < 2л в плоскости ху,
О т в е т. S = 2<о/?2 в силу результата примера 2 и сделанного выше замечания.ф
упражнения
16.	Пусть С — прямолинейный отрезок с концами (дг0. Уо) и (xf, yt), Вычислите площади поверхностей, получающихся при вращении С вокруг оси х и вокруг оси у.
17.	Пусть С — сектор, ограниченный лучами в = 0о, в = 01 и окружностью х2 + у2 = R2. Найдите площадь поверхности, получающейся при вращении С вокруг оси х.
18.	Выполните упр. 17, считая, что С вращается вокруг оси у.
19.	Найдите формулу для площади поверхности, получающейся при вращении кривой z = = ф(х) вокруг прямой г = 1.
20.	Найдите площадь поверхности, получающейся при вращении параболического сегмента у = х2, у < 1 вокруг оси у.
21.	Выполните упр. 20, принимая за ось вращения ось х.
22.	Выполните упр. 20, принимая за ось вращения прямую х = 10.
23.	Выполните упр. 20, принимая за ось вращения прямую у = —1.
^24. Найдите площадь части единичной сферы х2 + у2 + z2 = 1, заключенной между плоскостями г = А и г = В, где 0 < А < В < 1.
25. Среди всех кривых вида у = ф(х), проходящих через точки (0, 1) и (1, 1), прямая у = 1 является линией, которая при вращении вокруг оси х образует поверхность вращения наименьшей площади. Попытайтесь доказать это.
§ 3.	ТРОЙНЫЕ	Поскольку двойные интегралы мы рассмотрели довольно-
ИНТЕГРАЛЫ подробно, обобщение этой теории на функции трех и большего числа переменных уже не представит трудности. Здесь мы не столкнемся ни с какими существенно новыми явлениями, поэтому необходимость в строгих формулировках теорем отпадает.
3.1.	КУСОЧНО-НЕПРЕРЫВНЫЕ ФУНКЦИИ
Функцию/(х, у, z), определенную в трехмерном интервале х0 < х < хь у0 < у < z0 < z < zb мы будем называть кусочно-непрерывной, если она либо непрерывна на всем интервале, либо ее точки разрыва принадлежат конечному числу поверхностей^ каждая из которых представляет собой пересечение (трехмерного) интервала с плоскостью, параллельной координатной плоскости, либо является графиком функции х = ф1(у, z) и одновременно графиком функции у = ср 2(z, х) и графиком функции z = Фз(х, у), причем каждая из этих функций должна быть определена и непрерывна на некотором замкнутом двумерном интервале.
Из этого определения вытекает, что для всех значений х, за исключением, быть может, конечного их числа, функция f(x,y,z) является кусочно-непрерывной функцией от (yt z); аналогичное утверждение справедливо также и по отношению к переменным у и z.
448
13. Кратные интегралы
3.2.	ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА
Если /(х, у, z) — ограниченная кусочно-непрерывная функция, определенная в интервале /: х0 < х < хь у0 < у < У1, 20 < z < zt, то тройной интеграл от /(х, у, z) по /, обозначаемый
у, z)dxdydz,	(1)
I
— это число, которое можно вычислить, интегрируя /(х, у, z) сперва по х от х0 до хь затем по у от у0 до yi и, наконец, по z от z0 до zif причем эти три интегрирования можно производить влюбом порядке. Так, например, если мы решили интегрировать в порядке х, у, z, то получим
Zi ГУ1 (xx
Zi I/i *1	Z1 pi /Х1	\	"1
JJJ	dz=J J J/(x, у, z)dxdf/dz = j j I J/(x, yt z) dx I dy dz. (2)
1	zo Уо xo	z0 _y0 \x0	J
Л о
Заметим, что здесь мы снова вводим соглашение о том, что внешний знак интеграла соответствует внешнему дифференциалу.
Можно также вычислить (1) посредством одного простого и одного двойного ин-рирования. В самом деле, так как
J J/(x, у, z) dxdy=
Уо х0
JJ f{x,y,z)dxdy,
Уо<У<Ух x0<x<xt
то вместо (2) мы можем написать
2i
JJJ f(x, у, z)dxdydz= j	J J f(x,y,z)dxdy dz.
I	Zo L Уо<У<У1
(3)
X0<X<Xi
Все простые и двойные интегралы, встречающиеся в равенствах (2) и (3), являются интегралами от ограниченных кусочно-непрерывных функций. То же самое верно и по отношению к интегралам, получающимся изменением порядка интегрирования:
JJ (*, У> z)dxdz dy
XO<X<X1
Xi zt yi	yt
f (х, yt z) dy dzdx= J Xo Zo Уо	Уо
Z0<Z<Zi
и т. д. Это утверждение аналогично теореме 1 § 1.5. Изменение порядка интегрирования не меняет значения интеграла (1); в этом заключается «трехмерный» аналог теоремы 2 § 1.5. Приведенные в Дополнении (см. § 4 и 5) доказательства теорем 1 и 2 можно видоизменить так, чтобы получить и доказательства только что сформулированных утверждений.
Определение ступенчатых функций, сумм Римана (см. § 1.7 и 1.8) и теорема 3 § 1.7 сразу же распространяются на функции трех переменных, причем тройные интегралы обладают всеми свойствами, установленными в § 1.6 для двойных интегралов.
§ 3. Тройные интегралы
449
Наконец, тройной интеграл по ограниченной (трехмерной) области D определяется равенством
(х, у, z)dxdydz= j J J xD (x, у, z) f (x, y, z) dx dy dz,
где / есть некоторый интервал, содержащий D, а характеристическая функция %D предполагается кусочно-непрерывной. Иными словами, для того чтобы проинтегрировать функцию f(x, у, г) по области D, полагают f = 0 вне множества D, а затем интегрируют полученную функцию по некоторому содержащему D трехмерному интервалу.
•Примеры. 1. Пусть 1 — куб'. О < х < 1, 0 < < 1, 0 < z <; 1. Вычислить
ЦУ xy'z3 dx dy dz.
Решение. Имеем (см. замечание 3 из § 1.2)
ууу xy3z3 dx dy dz = J j j* xyaz3 dx dy dz —
z3 dz
1	'	1	t 1	= 1
2	*	3	* 4	24	*
2. Вычислить
J J Jyz3 cos (xyz) dx dy dz,
где I — тот же куб, что и в примере 1. Решение. Этот интеграл равен
ill	ii	11
j j ^yz3 cos(xyz) dxdydz=^ [za sin (xyz)]'“’ dy dz =J J za sin (yz) dy dz =
1	1	Ip
= f [— z cos (уг)]?~'о dz = \ (2 — z cosz) dz = —-I z cos z dz=
------[z sin z]z 1
2	*=o
sin z dz= —---sin 1 — [coszf 1 = —-----sin 1 — cos 1.
2	z=o 2
(На последнем шаге мы воспользовались методом интегрирования по частям.)
3. Пусть D — область, определяемая неравенствами х > О, у> 0, г < 4 и г >	+ у3. Вычислить
2х dx dy dz.
450
13. Кратные интегралы
Решение. Здесь D — это область, заключенная между плоскостями х = 0, у = 0, z = 4 и параболоидом z = х2 + у2. В области D аппликата z изменяется от 0 до 4. Для каждого фиксированного z переменные х и у положительны и изменяются так, что х2 + У2 < 2. Это означает, что у изменяется от 0 до j/z, а хизменяется от 0 до — у2. Следовательно, наш интеграл равен
4	4 Vz Vz—y*	4/г	____
f ff 2xdxdydz—{{ f 2xdx dy dz - f С [х2]х^г~уг dy dz =
0 x!+</2<z	__	000	00
= f f (2 — У2) dy dz = f \zy —
4	5/2
15 2
х=0
J 3
УПРАЖНЕНИЯ
В упражнениях 1—15 проинтегрируйте данную функцию f по данному интервалу.
1.	f = x2y*z\ —1 < х < 1, 0<«/<2, 0 < г <Z 1.
2.	f = \/(xyz);	1<х<2, —2<r/<—1, 2<z<3.
3.	f=(x + y)!z\ — 1<х<1, — 2<«/<2» 1<г<2.
4.	f = xyzexyZ , 0<х<1, 0 < у < 1, 0 < z < 1.
5.	f= (х+ r/ + z)2; 1<х<2, 2<«/<3, 3<г<4.
6.	f = uvYw\ —1 <2 и < 1, 0<и<2, 3<о><4.
7.	/ = г 4-2 (s/r)e'+ (1 + I/'); 2<r<3, 2<s<3, 2</<3.
8.	f= 1п(ха / г?); 1<х<2, 2<«/<3, 3<г<4.
9.	f = Уху 4- xyz2; 1<х<2, 2<«/<3, 3<г<4.
Ю. f=(x/y) + (y/z) + (z/x); 1<х<2, 1<г/<2, 1<г<2.
Н. f=[(x/y) + (y/z)]\ — 2<х<—1, —2<z/<—1; -2<z<-l.
12.	f— г cos 2/ 4-t sin 3s; 0<r<rc, 0<s <тс/2, 0</<к/4.
13.	/ = cos (2м— Зу4~4&у); тс/6 < и <тс/3, к/4	<Зтс/4, тс/2 < w < Зк/4.
14.	f = х In (yz) 4- 21 In (ху); 1<х<2, 1 <Z у < 2, l<z<2.
15.	f = (x 4-	+ cos г)2; 0<х<1, 0 < у < 1, —к/2 <г <л/2.
3.	3. ОБЪЕМ
Если D — некоторая достаточно «хорошая» область в пространстве (х, у, z) (т. е. если D содержится в некотором интервале и функция /D кусочно-непрерывна), то интеграл
j^dxdydz == j*JjxD(x,y, z)dxdydz D	I
выражает объем области D. Это определение соответствует формуле объемов, полученной в $ 4.4 гл. 5, и общему смыслу понятия объема. Его можно доказать с помощью
§ 3. Тройные интегралы
451
рассуждения, аналогичного тому, которое в § 2.1 использовалось для вывода формулы площадей. Объем, вычисленный таким образом, не зависит от выбора системы координат. Последнее геометрически очевидно; формально же это может быть доказано с помощью рассуждения, аналогичного тому, которое дается для площадей в Приложении (ср. с § 8.2).
Далее, объем, как и полагается, обладает свойством аддитивности: если область D разбита на две непересекающиеся части Di и D2 с объемами Vi и V2, то объем V области D равен Vi + V2. Это вытекает из свойства аддитивности тройного интеграла, которое аналогично соответствующему свойству двойных интегралов (см.
§ 1.Ю).
УПРАЖНЕНИЯ
J^16. Найдите объем тела, ограниченного цилиндром г2 + #2= 9, плоскостью г = 0 и плоскостью х + г = 4.
17.	Найдите объем тетраэдра, ограниченного плоскостями х = 0, у = 0, г = 0, 6х + 4# + + Зг = 12.
18.	Найдите объем тела, ограниченного параболоидом z = jr2 + 2у2 и цилиндром г = 4 — — х2.
19.	Найдите объем эллипсоида с полуосями а, Ь, о.
20.	Найдите объем тела, ограниченного двумя цилиндрами г2 + у2 = R2 и х2 + г2 = R2.
91.	Найдите объем тела, ограниченного двумя параболоидами г = х2 + Юг/2 и г = 20 — — х2 — 10у2.
22.	Найдите объем тетраэдра, ограниченного плоскостями г = 0, у = Q, z = 0 и х/а +у/Ь + 4- г!с = 1.
23.	Найдите объем области, определяемой неравенствами 0, г> 0, 0< у< г,	4—у2.
3.4.	ИНТЕГРИРОВАНИЕ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
В § 1.11 мы видели, что если нужно вычислить двойной интеграл, используя полярные координаты, то для этого недостаточно переписать подынтегральную функцию /(%, у), отнеся ее к полярным координатам (г, 0), но необходимо еще умножить ее на некоторый множитель, а именно на г (ср. с теоремой 4 § 1.11). Точно так же и в общем случае при переходе к новым координатам подынтегральная функция умножается на некоторый множитель, зависящий от выбранных координат. Этот множитель в честь математика Якоби называется якобианом.
Не обращаясь к общей теории, мы покажем, как вычислить тройной интеграл в цилиндрических координатах. Цилиндрические координаты, обычно обозначаемые через г, 0, z, были определены в § 5.1 гл. 9; этр определение иллюстрирует рис. 13.37. Напомним связь между декартовыми и цилиндрическими координатами:
х = г cos 0, у = г sin 0, z = z.
(4)
Карл Густав ЯКОБИ (1804—1857). Из числа его важнейших достижений можно назвать теорию так называемых «эллиптических* функций и новый математический подход к проблемам механики, продолжающий работу Гамильтона. Относвщався к классической механике теория Гамильтона — Якоби неожиданно сыграла очень большую роль в создании квантовой теории. Якоби был вдохновляющим учителем; он установил традицию сочетания университетского образования студентов с их самостоятельной научной работой.
452
13. Кратные интегралы
Предположим теперь, что /(х, у9 z) — ограниченная кусочно-непрерывная функция, равная нулю вне цилиндра х2 + у2 < /?2, | z | < Н (это не ограничивает общности нашего рассуждения), и что функция (г, 0, г) »->/(rcos0, rsin0, z) также кусочно-непрерывна. (Последнее можно было бы доказать, пользуясь несколько измененным определением кусочной непрерывности, но мы предпочитаем опустить эти технические детали.) При наших предположениях имеем
Н2к R
JJJ /(х, у, z) dx dy dz== J j J/(reosO, rsin0, z)rdrdf)dz. (5) жЧ-г<я*.	—но о
12 \<H
Якобиан здесь снова равен г, что не удивительно, так как цилиндрические координаты отличаются от полярных только наличием третьей координаты г.
Для того чтобы доказать равенство (5), вспомним равенство (3) из § 3.2. Так как функция f равна нулю вне цилиндра, то мы имеем
нг
fff / (%, у, 2} dxdy dz= С ff f(x,y,z)dxdy dz.
\г\<Н
(6)
Но по теореме 4 § 1.11 для каждого фиксированного z
J J f (x9 y9 z) dx dy= f J / (r cos 0, r sin 0, z) r dr dQ. x2+y2<R2	О о
Подставляя это в равенство (6), мы и получим (5). Конечно, равенство (5), можно переписать разными способами, изменяя порядок интегрирований в его правой части.
§ 3. Тройные интегралы
453
Можно также предсказать соотношение (5) исходя из некоторого «математического мифа», который иллюстрирует рис. 13.38. Мы рассматриваем точку с цилиндрическими координатами (г0, 0о> *о)> Два цилиндра г = rQ и г = r0 + dr. две плоскости 0 = 0О и 0 = 0 о + dQ и две плоскости z = z0 и г = г0 + dz\ здесь dr. dft, dz — бесконечно малые числа. Эти шесть поверхностей ограничивают бесконечно малую «коробочку», объем которой равен произведению длин ее сторон, т. е. (dr) (rodQ)(dz) = rQdrd§ dz. Тройной интеграл от функции f равен сумме бесконечно большого числа слагаемых, каждое из которых равно произведению значения функции f в некоторой точке одной из «коробочек» на объем этой «коробочки».
фПример. Пусть D — область, определяемая неравенствами
х2 + у2 < 1, 0 < z < х2 4- у2.	(7)
Вычислить
х2У2 dxdy dz.
Решение. Воспользуемся цилиндрическими координатами; неравенства (7) в цилиндрических координатах можно переписать так: 0<г<1, 0<z-<r2. Следовательно, рассматриваемый тройной интеграл равен
2л 1г’	2к 1 г‘
f J J (г cos 9)2 (г sin 9)2 г dz dr d8=J J f rs • — sin2 29 dz dr dO =
*o о о	о Jo о
2x1	2x	1
=	— f C r7	sin229 dr de=	— Csin229 d9 f	r’dr = —	к .	—	=	— .	>
4 J J	4 J J	4	8	32
_	o o	oo
УПРАЖНЕНИЯ
24.
x2 + у2 + za = 16
Найдите объем тела, ограниченного цилиндром г = 4 cos 0, сферой и плоскостью ху.
Найдите объем тела, вырезаемого из шара х2 + у2 + г2 < 36 цилиндром х2 + у2 < 9. Найдите объем тела, ограниченного параболоидом г = х2 + у2 и плоскостью z = 2у. Пусть D—область, определяемая неравенствамих>> 0, у^> 0, 0< г< 1, х2 + y2<Z 4. Вычислите J (х2 + У2)п cos г dx dy dz.
Пусть D — область, ограниченная плоскостями х=1, х = 2и круговыми цилиндрами у2 + г2 = 4 и у2 4- г2 = 9. Вычислите JJ* J ех у2 + z2 dx dy dz.
Два круговых цилиндра имеют одинаковые радиусы 7?, а их оси пересекаются под прямым углом. Покажите, что их пересечение имеет объем 16/?3/3.
Найдите объем тела, ограниченного плоскостью ху, круговым цилиндром х2+#2 = 1 и параболическим цилиндром х2 — 1 = г.
31.	Пусть D — тело, ограниченное цилиндром х2 + у2= 1 и двумя плоскостями 2х — 3# + + z — 0 и z = 100. Вычислите J J J (5х — 3z) dx dy dz.
32.	Вычислите J J J x dx dydz, где D есть область, определенная в упр. 30.
33.	Вычислите J^г/(У2 + г2) dx dy dz, где D есть область» определяемая неравенствами
25.
27.
28.
29.
30.
454
13. Кратные интегралы
3.5.	ТЕЛА ВРАЩЕНИЯ
Пусть D — плоская область и I — прямая, принадлежащая той же плоскости, что и D, причем область D лежит по одну сторону от прямой /. Если мы повернем область D вокруг прямой I на 360°, то она опишет некоторое тело вращения В. Для того чтобы вычислить объем этого тела, примем прямую I за ось г; пусть D принадлежит правой половине плоскости xz (рис. 13.39). Обзначим через /я (х, z) характеристическую функцию области D; тогда характеристическая функция множества В будет иметь вид (У*2 + z/2, z). В цилиндрических координатах объем V тела вращения В равен (здесь Т — некоторое достаточно большое число)
V=	Ш *D х2+у2>2) dx dy dz = J И xD(/-,z)rdrdzd0 = хг+иг+гг<Тг	0 г‘+г!<Г2
или, поскольку безразлично, как обозначить переменную интегрирования,
V
= 2к jjxdxdz.
Аналогично, если вращать вокруг оси у область D, принадлежащую правой полуплоскости плоскости ху, то объем полученного тела вращения будет равен
(8')
Наконец, если D есть область, принадлежащая верхней полуплоскости плоскости ху, то при вращении ее вокруг оси х получается тело объема
V = 2it dxdy.
(8")
В последнем случае предполагается, что D есть область, лежащая под графиком положительной функции у = /(х), где а < х < Ь. При этом
О	Ъ	1>
V — 2ir С С ydydx = 2nH—у2 = к f [/(х)]2 dx. а 0	a L 2	V=0 J
Мы уже получили эту формулу выше (см. гл. 5, § 4.6).
Замечание. Если область D поворачивается не на угол 2л, а на угол со, где 0 < со < 2л, то в формуле (8) надо лишь заменить множитель 2л на со. Доказательство этого предоставляется читателю.
§ 3. Тройные интегралы
455
2
Рис. 13.39
УПРАЖНЕНИЯ
34.	Найдите объем тела, полученного от вращения области 2<х<4, —x*<Zy<Zx* вокруг оси у.
35.	Найдите объем тела, полученного от вращения области | х | < л, 0< у < sin х вокруг оси х.
36.	Пусть D — область, ограниченная осью х, линией у = 6х и прямыми х = а и х = Ь. Найдите объем тела, полученного при вращении области D вокруг оси х.
37.	Найдите объем тела, полученного при вращении области D из упр. 36 вокруг оси у.
3.6.	ИНТЕГРИРОВАНИЕ В СФЕРИЧЕСКИХ КООРДИНАТАХ
Напомним (см. гл. 9, § 5.3 и рис. 13.40), что сферические координаты (р, 0, ф) связаны с декартовыми координатами формулами
х = р sin ф cos 0, у = р sin ф sin 0, z = р cos ф,	(9)
а с цилиндрическими координатами — формулами
г = р sin ф, 0=0, z = р cos ф.	(9')
Формула интегрирования в сферических координатах (справедливая при соответствующих предположениях о подынтегральной функции) имеет вид
JJJ dxdydz =
Х2+у2-|-22<₽2
л2л Я
= J J J/ (р sin ф cos 0, р sin ф sin 9, р cos ф) р2 sin <? dp df) d<p.
Якобиан здесь равен р2 sin ф.
456
13. Кратные интегралы
Рис. 13.40
Рис. 13.41
Прежде чем доказывать равенство (10), заметим, что его можно предсказать исходя из «математического мифа», аналогичного тому, который выше послужил нам для обоснования формулы интегрирования в цилиндрических координатах. Две бесконечно близкие сферы р = р0 и р = р0 + dp, две бесконечно близкие плоскости 0=0ои0=6о+^6 и два бесконечно близких конуса ф = ф0 и ф = ф0 + йф ограничивают некоторую «коробочку», объем которой равен
(dp)(posin фо^0)(ро^ф) = Po2sin фо dp Л) ^Ф (рис. 13.41).
Теперь докажем равенство (10); мы начнем с некоторого тождества, которое вытекает из равенства (5), если предположить, что функция f вне сферы радиуса R с центром в начале координат обращается в нуль. Так как неравенство *2 + f/2 + z2 <Я2 в цилиндрических координатах имеет вид z2 + г2 < 7?2, то
Я2я VR2—?2
fff f(x,y,z)dxdydz = fj С jr5+l/!+*!<«2	-Л 0	0
f (г cos 0, г sin 0, z) г dr dti dz =
2к R VR‘—z*
f (r cos 0, r sin 0, z) r dr dz d().
(П)
§ 3. Тройные интегралы
457
Рис. 13.42
Последний шаг является законным, поскольку законно изменение порядка интегрирования в кратном интеграле по интервалу. Для некоторого фиксированного 0 рассмотрим интеграл
г»
/ (г cos 9, г sin 9, г) г dr dz.
(12)
Примем г и г за декартовы координаты в плоскости zr. Тогда (12) будет двойным интегралом, распространенным на верхний полукруг (рис. 13.42). Имея в виду равенства (9'), примем р и <р за полярные координаты в плоскости zr, тогда получим
rVr^~
С f f (г cos 9, г sin 9, z) г dr dz =
* R
j J f (p sin <p cos 0, p sin ф sin 9, p cos <p) (p sin <p) p dp dtp.
Подставив это в равенство (11), мы придем к соотношению, отличающемуся от (10) только порядком интегрирования.
•Пример. Вычислим объем шара радиуса R-, эта задача как будто специально придумана для того, чтобы проиллюстрировать удобство использования сферических координат. Мы имеем

тс2тс R
dxdydz= С С С р2 sin ф dp d0
ООО
?рЗ = 2 • 2к • 2. = ±*R>,
как и следовало ожидать,
458
13. Кратные интегралы
УПРАЖНЕНИЯ

Л 38. Вычислите
xyz2 dx dy dz, где D — единичный шар .
39.	Найдите объем тела, получающегося удалением из полушара х2 + у2 + г2 < а2, г> 0
40.	конуса 3(х2 + у2) < г2. В шаре радиуса 2 просверлено цилиндрическое отверстие радиуса 1, ось которого проходит через центр шара.Найдите объем оставшейся части шара.
41.	Вычислите J (х2 + у2 + г2)3 dx dy dz, где D — область, определяемая неравенствами х>0, г/>0, х2 + У2 + г2 < Ю.
42.	Вычислите И 1 ху2 dx dy dz, где D — пересечение единичного шара, полупространства г > 0 и конуса х2 4- у2 < г2.
43.	Вычислите	х У х2 4- у2 -f- г2 dxdydz, где £> — пересечение единичного шара и цилин- дра х2 + {/2 <	•
44.	С С С	%2 “F у2 Вычислите 1 1 ] arctg 	dxdydz, где D — область, вырезаемая из верхней поло- d	z вины единичного шара двумя круговыми конусами с вершинами в начале координат, осью каждого из которых служит ось г, а углы при вершинах равны и 62.
45.	А Л A	Cl/2 Вычислите 1 1 1 (х2 4- у2 4- г2) dxdydz, где D — слой, заключенный между «внутрен- ней» сферой радиуса е и концентрической с ней «внешней» сферой радиуса R с центром в начале координат. Для каких значений а этот интеграл имеет конечный предел при
46.	/?->оо, и чему равен этот предел? Для интеграла из упр. 45 найдите, при каких значениях а он имеет (конечный) предел при стремлении е к нулю (R мы здесь считаем постоянным). Чему равен этот предел?
47.	Вычислите J^xyz dx dy dz, где D — пересечение единичного шара и «первого октанта», х>0, у>Ъ< г>0/
3.7. ПЛОТНОСТЬ
В некоторых приложениях тройного интеграла подынтегральную функцию /(х, у, г) удобно рассматривать как плотность материи в точке (х, у, г). Это означает, что мы представляем себе область интегрирования D как материальное тело, предполагая, что существует такая положительная непрерывная функция /(х, у, z), что масса каждой части Do области D равна
/(х, у, z) dx dy dz.
Масса всего тела равна в этом случае тому же интегралу, распространенному по всей области D. Так как масса не может быть отрицательной, то функция f (плотность) должна быть неотрицательной. (Отрицательная плотность может встретиться, например, при описании распределения электрических зарядов.) Размерность плотности равна размерности массы, деленной на куб единицы длины.
§ 3. Тройные интегралы
459
(Представление о непрерывно распределенной материи, определяемой некоторой функцией — плотностью, очень полезно во многих областях физики. Тем не менее не стоит забывать, что оно представляет собой лишь определенную «идеализацию», возникающую при «приближенном» описании естественно-научных фактов, поскольку оно игнорирует, например, то обстоятельство, что материя состоит из молекул, молекулы — из атомов и что сами атомы имеют сложную внутреннюю структуру.)
Иногда рассматривают также («двумерную»!) плотность, зависящую лишь от координат хи// (такая «плотность» измеряется в единицах массы, деленных на квадрат единицы длины), определенную в некоторой области D плоскости z = 0. В этом случае область D мы представляем себе как материальную пластинку настолько тонкую, что ее толщиной можно пренебречь. Можно также рассматривать непрерывное распределение материи по некоторой поверхности (такой пример нам встретится в следующем параграфе) или вдоль определенной линии. В последнем случае говорят о материальной струне, плотность которой измеряется в единицах массы, деленных на единицу длины.
•Примеры. 1. Если плотность равна /(х, у, z) = х2//4?8, то масса куба 0 < х <; 1, 0 < у < 1, 0 < z < 1, очевидно, равна
2.	Предположим, что плотность распределения материи в плоскости z = 0 равна /(х, у) = 1. Тогда масса, содержащаяся в любой (достаточно «хорошей») области D этой плоскости, равна площади области £).ф
УПРАЖНЕНИЯ
48.	В цилиндре, радиус основания и высота которого равны 1, плотность в данной точке пропорциональна высоте этой точки над основанием и обратно пропорциональна расстоянию точки от оси цилиндра. На окружности верхнего круга плотность равна Вычислите массу цилиндра.
49.	Полушар радиуса R в каждой своей точке имеет плотность, равную кубу расстояния’ точки от центра шара. Найдите массу полушара.
50.	Плоская пластинка имеет форму эллипса с полуосями а и Ь, где Ь. В каждой точке ее плотность равна расстоянию этой точки от большой оси. Найдите массу пластинки.
51.	Линейная плотность струны, имеющей форму окружности, равна 1 + sin2<р, гдеср есть угловая мера, измеряемая от некоторой фиксированной точки струны. Вычислите массу струны.
52.	Плотность электрического заряда куба с ребром 1 в каждой его точке равна расстоянию этой точки от нижней грани куба минус расстояние от левой грани. Найдите полный* заряд куба.
53.	Плоская пластинка имеет форму равнобедренного прямоугольного треугольника. Плотность в каждой ее точке равна расстоянию этой точки от вершины прямого угла. Площадь пластинки равна 1. Найдите ее массу.
54.	Площадь основания прямого кругового конуса равна 1, высота его h. Плотность в каждой точке равна расстоянию этой точки от центра основания. Какова масса конуса?
55.	Куб с ребром 1 устроен таким образом, что его грани и его внутренность имеют малую массу по сравнению с массой ребер, сделанных из тяжелой проволоки. Линейная плотность в каждой точке любого из ребер равна расстоянию этой точки от нижней правой передней вершины куба. Найдите массу этого куба.
460
13. Кратные интегралы
3.8.	ГРАВИТАЦИОННАЯ СИЛА
Согласно закону всемирного тяготения Ньютона, частица массы т притягивает другую частицу, скажем, единичной массы, с силой, величина которой равна ^ти/г2, где 7 — некоторая универсальная постоянная, аг — расстояние между частицами. Для простоты мы будем считать, что единицы выбраны таким образом, что 7=1. Тогда сила, с которой масса /и, помещенная в точку х = (х, у, г), притягивает массу 1, расположенную в точке X = (X, У, Z), равна
т
1 х — X Р
(х-Х),
(13)
лбо | х — X | есть расстояние между точками (х, у, z) и (X, У, Z), а | х — X |"х(х — X) — единичный вектор, направленный от точки (X, У, Z) к точке (х, у, г).
Предположим теперь, что нам даны N масс mit zn2, ..., mN, расположенных в ^точках с радиусами-векторами х4, х2, ...» xN. Полная сила, с которой эти N частиц действуют на единичную массу, расположенную в точке X, равна сумме
w
S^r-(x'-X) /=1
сил притяжения, порожденных всеми W частицами. Это наводит на мысль о том, что если дано твердое тело D с плотностью распределения массы /(х, yt z), то сила F, с которой тело D действует на единичную массу, помещенную в точку X, может быть найдена по формуле
(,4)
D
Это тройной интеграл от векторной функции; смысл его определяется правилами, установленными в § 1.4 гл. 11. Координаты подынтегральной функции в формуле (14) таковы:
________f(x, У, г)(х — Х)_____ [(х - ХУ+(у - У)2 + (г - Z)2]3'2 ’
________f(x, у, г) (у—У)______ [(х - ХУ + (У - УУ + (г - Z)213/2 ’
________f(x, у, г) (z — Z)____ [(х - ХУ + (у - УУ 4- (г - гу\л'2 ’
Пусть {е1( е2, е3}— репер, соответствующий выбранной системе координат (см. гл. 9, § 1.12). Тогда мы можем написать F = Ptt + Qe2 + Те3, где
§ 3. Тройные интегралы
461
Р = fff-------'<* « »>«-*>----_ dxdudx.
D
Q = f ff -----Z(x. У, г)(у-У)--- dx d d	(14')
JJJ [U-X)a+(y-F)2 + (z-Z)2]3/2
D
T = fff-------»*•	— dxdl/dz.
JJJ l(« - X)> + (»-!-)> + (г D
Формула (14) оправдывается следующим «математическим мифом»: F есть сумма сил, сшкоторыми бесконечно малые «коробочки» объемов dxdydz, каждую из которых можно считать «сосредоточенной» в своей точке х и имеющей массу f(x)dxdy dz. притягивают единичную массу, помещенную в точке X; каждая такая элементарная сила вследствие (13) равна
/(х) dxdydz | х — X |"3(х — X).
Аналогичные «математические мифы» подсказывают, что сила, с которой двумерная материальная пластинка притягивает единичную массу, помещенную в точке X, может быть вычислена по формуле
	f“j.l 1(>_w+^5,+2.jW	<15> D
ЧТО	F = f T-zT-(S)v .» <х <s) - Х» dS	0 6) J | x(s) — XI3
есть сила притяжения единичной массы струной, задаваемой уравнением х = x(s), где О s L, плотность которой в точке s равна /(s); здесь s — натуральный параметр (т. е. длина дуги; см. гл. 11, § 3.12).
Если в формулах (14), (15) и (16) положить f = const, то мы получим величину притягивающей силы в случае «однородного» твердого тела, «однородной» пластинки или «однородной» струны. /
УПРАЖНЕНИЯ
56.	Вычислите интегралы, определяющие силу притяжения, с которой однородная круглая пластинка плотности 1 действует на единичную массу, принадлежащую оси симметрии пластинки.
57.	Напишите интеграл, определяющий силу притяжения, с которой однородный куб плотности 1 действует на единичную массу, расположенную в произвольной наперед заданной внешней для куба точке.
58.	Вычислите силу, с которой круглая струна постоянной плотности притягивает частицу, расположенную в центре круга.
59.	Выполните упр. 58 для стр>ны, имеющей форму квадрата.
462
13. Кратные интегралы
3.9. СФЕРИЧЕСКАЯ СИММЕТРИЯ
Применим введенные выше определения для случая шара, плотность которого является сферически симметричной функцией, т. е. для случая, когда плотность в данной точке зависит только от расстояния этой точки от центра шара. Пусть М — масса шара. Мы покажем, что сила притяжения таким шаром точечной массы т, расположенной вне шара, равна силе притяжения массы т точечной массой М, сосредоточенной в центре шара.
Примем центр шара за начало координат. Тогда плотность в точке (х, у, z) шара равна
f(x,y,z) = g (Ух2 + у2 + z2) = g(p).	(17)
Полную массу шара проще всего вычислить, пользуясь сферическими координатами. Имеем [см. равенство (10) из § 3.6J
тс 2тс Я	Я
М ~ J J J g (р) р2 sin ф dp d6 = 4к J g (p) p2 dp, 0 0 0	0
(18)
где R — радиус шара.
Для того чтобы вычислить силу притяжения F, удобно изменить систему координат так, чтобы частица единичной массы, которая притягивается этим шаром, принадлежала положительной полуоси z, т. е. чтобы она имела радиус-вектор
X = Ze3.
В обозначениях § 3.8 X = Y = 0. Если мы перейдем к сферическим координатам, то знаменатель в формулах (14') примет вид
p2sin2cpcos20+ p2sin2<psin20+p2cos2(p — 2Zpcosq) + Z2)3/2=(p2—2Zp cos ф + Z2)3/2,
а первая координата P силы F ввиду равенств (14') запишется так:
тс 2тс Я
р _ Г С Г g (р) (р sin у cos 6) (р2 sin у dp d9 dy) __ J J J (p2 — 2Zp cos у + Z2)3/2 0 0 0
тс Я	2тс
= Г r _g(p)p2sin2ydpdy . f cos6 de = 0, J J (p2 — 2Zp cosy + Z2)3/2 J 0 0	0
поскольку второй сомножитель равен нулю. То же самое рассуждение применимо и ко второй координате Q силы F. Конечно, мы могли бы и опустить эти вычисления, так как вследствие симметрии шара сила F должна быть направлена по оси z.
Для того чтобы доказать сделанное выше утверждение, остается показать, что последняя координата Т силы F равна —M.IZ\ где М определяется равенством (18).
В силу равенств (14') имеем
тс 2тс Я	Я
т = f f f	_ Г
J J J (p2 — 2Zp cos у + Z2)°M	J
ooo	о
(p2 — 2Zp cos <p + Z2)3^2
§ 3. Тройные интегралы
463
где	2
ь-/Л\ _ f С (pcosy — Z)sinyd9dy _ 9 f (р cos у — Z) sin у dy	,]Q.
(P2 —2Zpcosy + Z2)3/2 J (pa — 2Zp cos у + Z2)3/2 '	( J
0 0	0
[Мы можем рассматривать К (р) как третью координату (аппликату) силы, с которой бесконечно тонкий сферический слой равномерной плотности и радиуса р притягивает частицу единичной массы, расположенную в точке (0, 0, Z).] Для того чтобы вычислить /<(р), введем вместо ф новую переменную
и = У р2 — 2Zp cos Ф + Z2
(что законно, так как выражение под знаком радикала неотрицательно). Мы имеем du _________________________ Zp sin	_ Zp sin ср
d<?	]/p2 —2Zp cos<?4-Za	u
а это можно переписать так:
, и du sin ф Цф ------.
Zp
Но и = Z — р при ф = 0 (так как Z > р) и и = Z + Р при ф = л; далее,
р2 — 2Zp cos ф + Z2 = и2, р cos ф = - и .
Подставляя это выражение в последний интеграл в равенстве (19), получим
Z-hp /р2 + Z2 — и2 \ и du	Z+p
о- I I 2Z	-о_ С (p»-Z«-tt*) du
К(р) - I	-	2« 1 2Z2pu2 —
Ъ	У-p
__ те	Гр2 — Z2 . l«=Z4-p   4те
Z2p [ и Ja=z— р Z2
Следовательно,
R
о что и требовалось доказать.
Этот важный результат впервые был получен самим Ньютоном, показавшим, что в астрономии при вычислении сил взаимного притяжения таких тел, как Земля, Солнце и Луна, можно заменять эти огромные тела точечными массами, сосредоточенными в их центрах. Но, по-видимому, Ньютон еще не знал этого в то время, когда он открыл связь между законом всемирного тяготения и законами Кеплера для планетных движений, что, возможно, и послужило причиной длительной задерж* ки публикации его работы.
464
13. Кратные интегралы
УПРАЖНЕНИЯ
60. Покажите, что однородный сферический слой не действует на массу, помещенную в любой точке его внутренней области.
61. Предположим, что вдоль оси Земли —от Северного полюса через ее центр к Южному полюсу — просверливается узкое отверстие Количество удаленной массы очень мало. Покажите, что сила притяжения Землей частицы, помещенной в этом туннеле, прямо пропорциональна расстоянию частицы от центра Земли. (Воспользуйтесь упр. 60 и результатом, полученным в тексте. Предположите, что поверхность Земли — сферическая и что плотность в данной точке зависит только от расстояния этой точки от центра.) Начертите график функции Я (г); покажите, что в точке г = R этот график имеет «клюв» (точку возврата).
§ 4. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ п ПЕРЕМЕННЫХ
4.1. ПОДЫНТЕГРАЛЬНЫЕ ФУНКЦИИ И ОБЛАСТИ ИНТЕГРИРОВАНИЯ
Едва лц надо говорить, что все сказанное выше с естественными видоизменениями можно перенести и на функции более чем трех переменных. Функция (хь х2,..., хп) i-> х2, ...» хп), определенная в некотором n-мерном интервале /, называется кусочно-непрерывной в /, если она непрерывна во всех точках этого интервала, за исключением, быть может, точек, принадлежащих конечному числу точечных множеств S2, ...» таких что каждое	— это либо множество, для которого одна из
координат xk фиксирована, либо это множество, которое может быть представлено в виде графика функции Xf = Ф1(х2, x3f ..., хп) и одновременно в виде графика функции х2 = <р2(хь *з> ...» хл) и т. д., причем каждая из функций фь ф2, ... определена и непрерывна в некотором замкнутом (п — 1)-мерном интервале. В этом параграфе все функции, которые мы будем интегрировать, предполагаются ограниченными и кусочно-непрерывными.
Мы условимся также, что все области, по которым производится интегрирование (области интегрирования), имеют кусочно-непрерывные характеристические функции.
4.2. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА
Интеграл от функции /(хь х2, ..., хл) по n-мерному интервалу /; aL<. Xj< bit i = = 1,2,..., n обозначается так:
J ...J [xi,...,xn)dx1...dxn\
(1)
его можно определить как число, получаемое путем последовательного интегрирования функции f по каждой из переменных xz от at до bi в любом порядке, например как
ьг ьп
J J • • • J f х2....Xn)dxn Jxn^ ...dxv	(2)
ax aa an
§ 4. Интегрирование функций п переменных
465
Мы всегда будем твердо придерживаться соглашения: внешний знак интеграла соответствует внешнему дифференциалу. Однако для того чтобы порядок интегрирований был более нагляден, вместо (2) иногда пишут
	bt	b, bn J	J ^2'“ J ^Хп[(х1> ••• »	Xnh (2	) »i	a, an
ИЛИ	b,	ь,	ьп J dxx j dx2... dxn_x J f (xx,..., xn) dxn.	(2") at	at	an
Все свойства двойных и тройных интегралов остаются справедливыми и для n-кратных интегралов. Это верно также и для интегралов, распространенных по произвольным областям.
ф Пример. Проинтегрировать функцию (х, у, г, t)*-*x по области, определяемой неравенствами
О < х < 1, х<_ у <2, 3 < г <	3 < / < 6.
Решение. Искомый интеграл равен 1	2 в z2	12	6	г=/2	1	2	6
[ dx j	dy j’	dt {xdz =	j’ dx j* dy	J [xz]*23 dt	= J	dx J dy	f (xt2	— 3x) dt =
6*33	6*3	0*3
12	f=6	1	2	1	_
= f dx f [— xt3 — 3xt 1 dy = C dx f 54xdy = C [54xyf~2 dx =
J J I 3	k=3 J J	J у=х
= J (108x — 54x2) dx = 54x2 — 18x31 = 36. о	0
Заметим, как это просто — и как скучно!, ф
УПРАЖНЕНИЯ
В упражнениях 1—10 проинтегрируйте данную функцию F по данной области D.
1.	F =	+ с2х2-j- ••• + спхп; D: a1<x1<blt a2<x2cb2.........ап < хп < Ьп.
2.	F = хгх^ х|... х£; D: а <	< Ь при 1=1,2.......п,
3.	F = х®‘ х£2 .. .хп п\ D: ai<.Xi<bit i = l.п. (Укажите, при каких а, а9
b интеграл не имеет смысла.)
Д4.	F =	In (	Х2Х3Х4); D: 1 < Xj < 2 < х2< 3<	х3 <; 4< х4	<;5.
5.	F =	х^2 (sin х3) (cos х4); D: 0<х^<1; Z=	1,2, 3,4.
6.	F =	tuvw\ D: t2 + и2 < v2 4- w2, v2 4- пу2 < 1.
466
13. Кратные интегралы
7.	F = (*i — х2 + х3 — х4)2; D: xf + х£ + xf + xf < 1.
8.	F = (Xi — cos x2) (x3 + sin x4); D: l<Xi<2,	2<x2<3, xf + xfcl.
9.	F = x® + 2xg + 3xg 4-4x4; D: Л<хг<В, /=1,2,3,4.
10.	F= txj(yz)\ D: — К/d, 1<г/<2, — 1<х<1, 1 < z < 2.
4.3.	ОБЪЕМ В n-MEPHOM ПРОСТРАНСТВЕ
Число
- j* dxi dx2... dxn
называется n-мерным объемом области D. Если D есть интервал < х < а2 < х < ^2» •••» х < Ьп и мы положим lt = bi— ait где i = 1, 2, ..., п, то объем области D будет равен произведению длин п его «сторон»: V = /4/2 ... /Л.
Множество всех таких точек (хь х2, •••» хл), для которых
X? + Х2 + • • • + Хп < R2,
называется /z-мерным шаром радиуса /?. Обозначим объем этого шара через ап (/?). Мы знаем, конечно, что
а1(7?)=2/?, а2(/?)=^2, а3(Я) О
Далее, имеем
поэтому, если условиться писать х вместо хп9 R	_____ R	______
«п (R) = J «п-1 (У^-х2) dx = 2 J (/я2 - X2) dx. —я	о
Пользуясь этой рекуррентной формулой, можно вычислять объемы п-мерных шаров. Так, например,
R
«4 (Я)	C(fl2-x2)3/2dZ
о J 0
Здесь мы сначала сделаем подстановку х = Rt, затем положим t = cos ф и, наконец, воспользуемся методами § 3.5 гл. 7. Так мы получим
§ 5. Центроиды
467
at (Я) =	J (R* _ 7?2/2)3/2 R dt =
0
__ 8тс/?4 Зте
~ ~ ’ "Тб
Этот метод применим при любом п.
J(l — t*)w dt = -^р- Jsin4q>d<p =
О	о
=~я4.
УПРАЖНЕНИЯ
11.	Вычислите Дб(/?).
12.	Вычислите ae(/?)«
13.	Четырехмерный конус высоты h, основанием которого служит шар радиуса 1, определяется как множество всех таких точек (л, у, г, 0» координаты которых удовлетворяют неравенствам 0< t<Z h, х2 + у2 + z2< (t/h)2. Вычислите объем этого четырехмерного конуса.
14.	«Единичный симплекс» в n-мерном пространстве определяется как множество точек (*1» *2, ...» хп), координаты которых удовлетворяют неравенствам 0, х2> 0,
0. х1 + х2+ ... + xn<Z 1. Вычислите длину единичного 1-симплекса, площадь единичного 2-симплекса, объем единичного 3-симплекса и четырехмерный объем 4-симплекса.
15.	Попытайтесь найти формулу для n-мерного объема единичного п-симплекса.
Приложение к главе 13
§ 5. Центроиды
В § 6.4 гл. 11, рассматривая движение системы (материальных) частиц, мы пришли к понятию центра масс, или центроида системы частиц. Однако в науке это понятие появилось раньше, чем динамика. Уже древнегреческие геометры, в частности Архимед и Папп, изучали центроиды кривых, поверхностей и тел. Эти рассмотрения становятся совсем простыми, если воспользоваться кратными интегралами.
5.1.	Центроиды материальных тел, пластинок и струн
Центроид (или центр масс) N частиц с радиусами-векторами хх, ха, ...» и массами m2, .... mN имеет радиус-вектор
jV	jV	Д'
х = ^Л-где M =
/=1	/=1	/=1
/=1
ПАПП Александрийский (ок. 340 г. н. э.) известен своими комментариями, к трудам греческих математиков, широко освещающими и существо, и историю разбираемых вопросов; его сочинение известно под названием Синанога (т. е. Собрание).
468
Приложение к главе 13
(см. гл. 11, § 6.4). Это подсказывает, что разумное определение положения центроида твердого тела D переменной плотности t(x, у, z) = f(x) должно быть таково:
X =	JJJ / (х) х dx dy dzt где М = JJJ f (х) dx dy dz.
(1)
Ясно, что это определение можно оправдать (имеющим характер «мифа») представлением о точке X как о центроиде бесконечно большого числа бесконечно малых «коробочек», имеющих объемы dx dy dz и массы f(x) dx dy dz.
Если D есть область плоскости г=0с определенной на ней функцией (плотностью) f(x, у), то центроид соответствующей материальной пластинки, по определению, имеет радиус-вектор
х =	(х. у) (хе, + r/e,) dx dy, где М = JJf (х, у) dx dy.	(2)
D	D
Если нам дана гладкая дуга (струна) длины L: х = x(s), 0< s< L, где s есть натуральный параметр (см. гл. 11, § 3.12), и если f(s), 0<s<L — функция, определяющая плотность этой
струны, то центроид струны имеет радиус-вектор
L
х = — I / (s)x (s) ds, где
Л4 J о
ds.
(3)
Определения (2) и (3) можно оправдать точно таким же образом, как и определение (1). Во всех трех случаях М есть полная масса (тела, пластинки или струны).
Замечание. Для того чтобы слово «струна» имело физический смысл, мы теперь будем требовать, чтобы кривая х = x(s) была простой', это значит, что различным значениям s должны соответствовать разные точки x(s) (за исключением случая замкнутой струны, для которой x(L) = = х(0)].
УПРАЖНЕНИЯ
1.	Найдите центроид прямого кругового цилиндра радиуса R и высоты Л, если плотность в данной точке цилиндра равна удвоенному расстоянию этой точки от основания цилиндра.
2.	Найдите центроид прямого кругового конуса радиуса R и высоты А, если плотность в каждой точке конуса равна квадрату расстояния этой точки от основания конуса.
3.	Найдите центроид куба с ребром а, если плотность в каждой точке куба равна квадрату расстояния этой точки от центра одной фиксированной грани куба.
4.	Найдите центроид плоской пластинки, имеющей форму правильного треугольника со стороной а, плотность в каждой точке которого равна расстоянию этой точки от одной (фиксированной) вершины пластинки.
5.	Найдите центроид струны длины 3, имеющей форму ломаной, которая на отрезке длины 1 направлена на восток, затем — на отрезке длины 1— направлена на север, и, наконец,— также на отрезке длины 1 — снова на восток. Плотность в каждой точке струны равна расстоянию этой точки от начальной точки струны (самого западного ее конца), измененному вдоль струны.
&	Струна имеет форму спирали: х = cos t, у = sin t, z = f, 0<	6л. Плотность в каждой
ее точке равна 4/. Найти центроид струны.
§ 5. Центроиды
469
5.2.	Центроиды областей
Центроидом некоторой разумным образом определенной области/^пространства (например, области с кусочно-непрерывной характеристической функцией xD ) называется центроид этой области, вычисленный в предположении, что ее плотность постоянна. Центроиды плоских областей, а также дуг кривых линий определяются аналогично. Формулы, определяющие положения центроидов, получаются из формул (1), (2) и (3) при условии, что 1. Так мы находим:
D
dx dy dz = объему области
D
х = -у (хе! 4- j/ej dx dy D
dx dy = площади области D
L
X = —- J x (s) ds (s есть длина дуги, m. e. | x'(s) | = Г). о
(4)
(5)
(6)
Вспомнив формулу длины дуги (см. гл. 11, § 3.12), мы можем переписать равенство (6), отнеся нашу «однородную струну» к произвольному параметру й
ь
X = -J-jx(/)|x' (t)\dt а
J | x' (/) | dt = длине кривой
(6')
Так как эти определения имеют векторную форму, то ясно, что они не зависят от выбора системы координат.
5.3.	Координаты центроидов
Для того чтобы найти положение центроида, мы должны переписать наши формулы в координатах. Это, конечно, совсем просто, и мы это сделаем только для центроидов областей. Ясно, что
X = JJJ х dx dy dz; Y =	JJJ у dx dy dz;	Z = -y J J ^zdx dy dz
(7)
— координаты центроида трехмерной области D объема V;
D
=	Z=0
координаты центроида (плоской) области D в плоскости z = О площади S;
L	L	L
If	If	1 г
X = — 1 х (s) ds, У = — | у (s) ds, Z = — \z(s) ds	(9)
J	‘-'J	L, J
0	0	0
—» координаты центроида линии x = x(s), у = y(s), z = z(s), 0< s< L, где x'($)2 + /(s)2 + + z'(sr — 1. Переходя в формулах (9) к произвольному параметру, получим, что
470
Приложение к главе 13
ь
х = т J х(0	+	<*•
а
b
r = Т Jy{t) Hx'WP + i/wp+i^a)]2 dt,	(У)
а
b
Z=T$^^'(w + ty'wp + izw dt а
— координаты центроида линии х = x(t), у = y(t), г — z(t), a<Z t<Z b, длины L.
УПРАЖНЕНИЯ
В упражнениях 7—24 найдите центроид заданной области. В каждом случае начертите эту область и отметьте ее центроид.
7.	Область, ограниченная прямыми у = 2х + 3, х — 1, х = 2, у = 0.
АЗ. Область, ограниченная параболой у = х2 и прямыми х = 4, у = 0.
9.	Область, ограниченная линией у = 2х^ — хи прямыми х = 1, х = 3, у = 0.
10.	Область, ограниченная кривой у = sin х и прямыми х = —, у = 0.
11.	Область, ограниченная кривой у = х2 и прямыми х + у = 0, х = 1.
12.	Область, заключенная между двумя параболами у = 4 — х2 и у = х2 — 4.
13.	Область, граница которой — прямоугольный треугольник.
14.	Область, ограниченная трапецией.
15.	Область, состоящая из всех таких точек (х, у), для которых	1 и у2<^х.
16.	Множество всех таких точек (х, у), для которых | у | < ех и 1 < | у | < е2.
17.	Прямой круговой конус с радиусом основания г и высотой Я.
18.	Тело, которое отсекается от одной полости конуса с углом 60° при вершине сферой радиуса 2 с центром в вершине конуса
19.	Полушар радиуса R.
20.	Тетраэдр с вершинами в точках (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1).
21.	Пересечение области Q<Zz2<Zxy с призмой, образующие которой параллельны оси г, а в основании лежит треугольник (0, 0), (4, 0), (4, 4).
22.	Часть шара х2 + у2 + z2 < R2, заключенная между полуплоскостями 0 = — я/4 и 0 = тс/4.
23.	Область, в которой х2 + у2 + г2 < 2R2 и х2 + у2.
24.	Часть единичного шара, отсекаемая от него двумя данными параллельными плоскостями.
В упражнениях 25—30 найдите центроид данной кривой. (Кривые упр. 25—29 принадлежат
плоскости ху.)
25. Окружность.
А26. Полуокружность.
27. Правильный треугольник.
28.	у = 2х\ | х | < 2.
29.	у = ch х, 0 < х < 2.
30.	t н* 3/ех “И З/еа 4“ 2/вз, 0 t 1.
5.4.	Аддитивность и симметрия
Определенные в § 5.1 центроиды материальных тел (пластинок, струн) обладают свойствами, аналогичными свойствам, доказанным в § 6 гл. 11 для центроидов конечных систем (материальных) частиц.
Отметим прежде всего свойство аддитивности. Пусть, например, область D формулы (1) разбита на две части Dx и Da. Обозначим через Мх и М а массы областей Dx и Da, а через Хх и Ха — радиусы-векторы их центроидов. Тогда
Х = + (10)
§ 5. Центроиды
471
Иными словами, X есть центроид двух частиц масс и ЛЬ, расположенных в точках Хт и Х2.
Для того чтобы доказать равенство (10), заметим, что в силу равенства (1) и по свойству аддитивности интегралов (установленному в § 1.6 для двойных интегралов) мы имеем
AliXj 4- M2X2 = JJJ f (x) x dx dy dz 4-
Аналогичное рассуждение доказывает свойство аддитивности центроидов для пластинок и для
х dx dy dz =
х dx dy dz — MX.
струн.
Свойство аддитивности сразу же обобщается и на случай, когда тело (или пластинка, или струна) делится на несколько частей.
Установим теперь различные свойства симметрии. Если плотность f.(x, у,г) и область D симметричны относительно некоторой плоскости, то центроид (1) принадлежит этой плоскости. Если плотность f(x, у) и область D, принадлежащая плоскости z = 0, симметричны относительно некоторой прямой этой плоскости, то центроид (2) принадлежит рассматриваемой прямой. Читатель легко сам сформулирует свойство симметрии центроида струны.
Мы докажем только одно из свойств симметрии. Предположим, что плоская область D и плотность fj(x, у) симметричны относительно некоторой прямой /. Выберем систему координат так, чтобы прямая I была осью х, a D —- интервалом вида —x<Z а, —b<Z y<Z b (если область D была не интервалом, мы можем положить = 0 вне первоначальной области D); при этом f(x, у) для каждого фиксированного х будет четной функцией у. Тогда функция у yf(x, у) нечетна и (ср. с § 3.6 гл. 5)
ъ
| УКХ> у) dy = о,
гак что ордината центроида равна
а Ъ
Y — j § yf(x, у) dy dx = 0,
—а —Ъ
что и требовалось доказать.
Свойства аддитивности и симметрии часто упрощают нахождение центроидов.
•Примеры. 1. Центроид прямоугольника совпадает с точкой пересечения его диагоналей.
Доказательство. Проведем через точку пересечения Р диагоналей прямоугольника прямые /f и /г, параллельные его сторонам. Так как прямоугольник симметричен относительно каждой из этих прямых, то его центроид принадлежит обеим прямым.
Читателю предлагается проверить этот результат выкладкой.
472
Приложение к главе 13
2. Центроид трехмерного интервала (прямоугольного параллелепипеда, коробки) совпадает с точкой пересечения его диагоналей. Иными словами, центроид совпадает с центром параллелепипеда.
Это доказывается в точности так же, как и предыдущее утверждение.
3. Найти центроид фигуры, изображенной на рис. 13.43.
Решение. Разобьем нашу область на четыре прямоугольника так, как это показано на рис. 13.44. Эти прямоугольники имеют площади 24, 8, 6 и 4, а их центроиды имеют координаты /	1 \	/	23 \
(1, 6), 16, — 1, I 5, —— ] и (9, 11). Следовательно, координаты центроида всей области таковы:
24»! 4- 8-6 + 6-5 + 4-9	23
24 + 8 4- 6 -Ь 4	7 ’
24.6+8.-^- + 6.-у-+4. 11 __261
24 + 8 + 6 + 4	31 * * * * * * * * * * 42
Так как наша фигура — плоская, то нет необходимости проверять, что Z = О.ф
УПРАЖНЕНИЯ
В упражнениях 31—42 найдите центроиды заданных плоских фигур, пространственных тел или кривых.
31 Кольцо, ограниченное окружностями ха 4" у2 я 1 и х2 4" У2 = 4.
32. Область, состоящая из кольца, определенного в упр. 31, и круга (х— 10)24-(#—10)а=4.
33. Область, состоящая из кольца и круга, определенных в упр. 32, и, кроме того, прямоугольника, ограниченного прямыми х = —11, х = —9, у = 1 и у = —3.
34. Объединение двух прямоугольников, один из которых ограничен прямыми у = 2, у = = —1. х = —10 и х = 11, а второй — прямыми у = —12, у = 4, х = 1 и х = 3.
35. Объединение двух кубов: ребра одного из кубов параллельны координатным осям и имеют длину, равную 2, причем нижняя левая передняя вершина куба находится в начале координат; второй куб определяется неравенствами 4 < г < 5, /2 < х 4е 4- у <2/2, б/Т<х — г/ <7/2.
36. Шар х2 + у2 4- г2< Ю, из которого удален куб 0< х< 1, 0< г/< 1, 0< г< 1.
37. Правильный тетраэдр. (Используйте соображения симметрии.)
38. Куб 0<х< 1, 0<^< 1, 0 < г<1, в котором просверлено вертикальное цилиндрическое отверстие радиуса 1/8 с осью х = 1/4, у = 1/4.
39. В кубе из упр. 38 параллельно оси х просверлено дополнительное отверстие радиуса 1/8, с осью у = 3/4, г = 1/2.
40. Просверленый куб из упр. 39, к которому приварен куб0<х<1/2, 0<^<1/2, - 1/2< г<0.
41. Искривленная струна из упр. 5.
42. Струна, имеющая форму буквы А, если угол при вершине равен 30°, а перекладина соединяет середины боковых сторон.
43. Полуокружность радиуса 1 в плоскости ху и прямолинейный отрезок, перпендикулярный плоскости ху, один из концов которого совпадает с серединой полуокружности.
44. Пересечение кругового цилиндра с плоскостью.
§ 5. Центроиды
473
I
Рис. 13.45
5.5. Теоремы Паппа
Две следующие теоремы принадлежат Паппу — последнему из великих греческих математиков*.
Теорема 1. Объем V тела, образованного вращением плоской фигуры площади S вокруг оси I, принадлежащей плоскости этой фигуры (причем линия лежит по одну сторону от I), равен
У=2лд$,	(11)
где д есть расстояние центроида фигуры от оси вращения.
Теорема 2. Площадь S поверхности, образованной вращением плоской линии длины L вокруг оси I, принадлежащей плоскости этой линии, но не пересекающей ее, равна
S = 2rtdL,	(12)
где д есть расстояние центроида линии от оси вращения.
В теореме 1 (рис. 13.45) предполагается, что S есть площадь фигуры D, лежащей по одну сторону от прямой I. Предположим, что фигура D принадлежит плоскости ху и что прямая I — это ось у. Тогда абсцисса центроида фигуры D, т. е. расстояние 6, по формуле (8) равна
& = X = xdx dU-dD
В силу формулы (8') из § 3.5 объем V тела В, образованного вращением фигуры D вокруг оси у равен
V = 2к jjx dx dy.
Из этих двух формул и вытекает равенство (11).
* В нашей учебной литературе эти теоремы зачастую необоснованно приписываются шгей-царскому математику XVII в. Паулю Гульдину. Однако Гульдин нашел эти теоремы значительно позже Паппа, возможно, даже заимствовал их у Паппа; что же касается пространных доказательств этих теорем Гульдином, то их никак нельзя признать математически корректными (в противоположность доказательствам современников Гульдина И. Кеплера и Ь. Кавальери, на которые Гульдин весьма яростно нападал).
474
Приложение к главе 13
В теореме 2 предполагается, что кривая, которую мы обозначим через С, лежит по одну сторону от прямой I (рис. 13.46). Предположим, что кривая С принадлежит плоскости ху, а прямая I является осью у. Пусть С служит графиком функции у = <р(х), 0 < а < x<Z b. Абсцисса центроида линии С, т. е. расстояние д, равна
b
8 = X = -j- j х V1 + [?'(х)]2 dx. а
В этом легко убедиться, если положить в (9') х = t, у =<р(0» z = 0. В силу формулы (4) из § 2.4 площадь S поверхности S, полученной вращением линии С вокруг оси у, равна
b
S = 2kJ х/1 +[<?' (х)]2 dx. а
Из двух последних формул и вытекает равенство (12). Еще проще доказать равенство (12) для случая, когда С есть прямолинейный отрезок х — a, a<Z y<Z £. Отсюда следует справедливость равенства (12) для общего случая, когда линия С состоит из вертикальных отрезков и графиков непрерывно дифференцируемых функций х к* <р(х).
Ниже мы даем несколько типичных примеров применения теорем Паппа. В некоторых из них, когда объемы и площади поверхностей известны из каких-то других соображений, эти теоремы применяются для нахождения центроидов. В других, наоборот, положение центроидов мы можем определить (например, используя соображения симметрии), и теоремы Паппа применяются для нахождения объемов тел и площадей их поверхностей.
ф Примеры. 1. Найти центроид полукруга.
Решение. Полукруг можно рассматривать как множество D точек (х, у), для которых х2 + */2< 1, х> 0. Его площадь S = л/2. В силу симметрии полукруга относительно оси х его центроид принадлежит оси х. Пусть X — абсцисса центроида. Вращая D вокруг оси у, мы получаем единичный шар, объем которого V = 4л/3. Следовательно, по первой теореме Паппа, 4л/3 = 2лХ*л/2 и, значит,
X = 4/(Зл).
2. Найти центроид полуокружности.
Решение. Полуокружность можно представлять себе как линию С, определяемую уравнением х2 + у2 = 1 при х> 0 . Длина ее равна л. Центроид полуокружности в силу соображений симметрии имеет координаты (X, 0). Вращая С вокруг оси у, мы получаем сферу, площадь поверхности которой равна 4л. По второй теореме Паппа 4л = 2лХл; значит,
X = 2/л.
§ 6. Формула Грина
475
3. При вращении окружности радиуса г вокруг прямой, удаленной на расстояние /?> г от ее центра, получается поверхность, называемая тором радиусов г и /?. (Тор выглядит как свернутая трубка.) Теоремы Паппа дают возможность определить площадь поверхности тора и объем, им ограниченный (соответствующее тело получается вращением круга радиуса г вокруг прямой, удаленной на расстояние /?>г от его центра), практически без всяких вычислений. В обоих случаях d = /?. Объем тора, следовательно, равен
2л/?- яг2 = 2л2/? г2, а площадь его поверхности равна
2л/? • 2лг = 4л2/?г. О
УПРАЖНЕНИЯ
В упражнениях 45—47, пользуясь первой теоремой Паппа, найдите объемы заданных тел вращения.
45. Круговой цилиндр радиуса г и высоты Н.
J^46. Тело, полученное от вращения вокруг оси х квадрата со стороной 1, одна из вершин которого совпадает с началом координат, а другая — с точкой (0,	).
47.	Тело, полученное от вращения вокруг оси х прямоугольника, ограниченного прямыми у = а> 0, у = Ь^> а, х = 0 и х = с.
В упражнениях 48—50, пользуясь первой теоремой Паппа, найдите центроиды заданных плоских фигур.
48.	Область, ограниченная двумя концентрическими окружностями и прямой, проходящей через их центр («полукольцо»),
49.	Правильный треугольник.
50.	Прямоугольный треугольник.
51.	Пользуясь второй теоремой Паппа, найдите центроид полуокружности.
52.	Пользуясь второй теоремой Паппа, найдите боковую поверхность прямого кругового конуса.
53.	Пусть С — окружность, проходящая через вершины данного прямоугольника /?. Докажите, что для всех прямых /, касающихся окружности С, площадь поверхности, полученной от вращения прямоугольника /? вокруг прямой /, будет одной и той же.
54.	Предположим, что в условии второй теоремы Паппа плоская кривая является прямолинейным отрезком, перпендикулярным прямой /. К какой теореме придем мы в этом случае?
55.	Используя соображения симметрии и вторую теорему Паппа, найдите центроид четверти окружности. (Какая поверхность известной площади может быть получена вращением четверти окружности вокруг некоторой оси?)
§ 6. Формула Грина
В этом параграфе мы рассмотрим формулу, связывающую криволинейные интегралы с двойными интегралами. Эта формула, полного доказательства которой мы здесь не даем, известна как теорема Грина\ она является простейшим и наиболее важным частным случаем некоторого весьма общего результата, которого мы здесь касаться не будем.
6.1.	Формулировка теоремы
Пусть D — некоторая открытая область на плоскости и С — ориентированная кусочно-гладкая простая замкнутая кривая
х = х (?), у — у (0 ,	0 < i < Т.
Напомним, что «простая» означает, что никакие два различных значения параметра /, отличные от 0 и Т, не отвечают одной и той же точке (x(t), y(t)). Говорят, что линия С является границей области D, если каждая точка (x(t), y(t)) является граничной для D и каждая граничная точка области D есть точка с координатами (x(t), y(t)) при подходящим образом выбранном t. (Понятие граничной точки было введено в § 1.6 гл. 12.) Типичный случай изображен на рис. 13.47.
476
Приложение к главе 13
Мы говорим, что граница С области D правильно ориентирована, если «при движении по линии С в направлении возрастания значений параметра область D остается слева». Это понятие мы принимаем как интуитивно ясное, хотя ему можно было бы дать и точное определение. На рис. 13.47 граница С области D правильно ориентирована.
Теорема 1 (теорема Грина). Пусть С — правильно ориентированная (кусочногладкая) граница открытого множества D плоскости и пусть функции Р(х,у) и Q(x, у) (определенные в некотором открытом множестве, содержащем С и D) непрерывно дифференцируемы, I огда
D
дР \
—— ]dx dy = ду 1
J Р dx + Q dy. С
О)
Формулу Грина (1) можно, конечно, заменить двумя равенствами:
(2)
(3)
В самом деле, полагая в формуле (1) Р=0 или Q= 0, мы и получим равенство (3) или (2); напротив. складывая (2) и (3), мы получим (1).
ф Пример. Пусть D — круг х2 4" f/a< 1; в таком случае С определяется уравнениями х = cos /, у = sin t, 0 < t < 2л (С является правильно ориентированной границей области D). Положим Р = у, Q = 0. Тогда
2х
С sin2 tdt = —’ Тс = — f J dx dy = о	JD
ИдР
D
УПРАЖНЕНИЯ
В упражнениях 1—10 проверьте формулу Грина, сравнивая между собой значения интегралов
О / dQ	дР \	С
| ---——— ] dx dy и I Р dx+Q dy, где С есть правильно ориентированная граница области D.
J\dx	ду ]	J
D	G
1.	D — единичный круг х2 + y2<Z 1; Р — Q = 1.
2.	D — единичный квадрат 0 < х < 1, 0< у < 1; Р = х3у, Q = х — у2.
3.	D — треугольник 0, у> 0, х + у<С 1; Р = х2 — у2, Q = Уху,
4.	D—область, определяемая неравенствами 0<х<1, 0< y<Z х2\ Р — ху^у , Q= = Ух + У у •
5.	D — единичный круг; Р = х2, Q = х2у2.
Джордж ГРИН (1793—1841) опубликовал теорему, теперь носящую его имя, в книге, посвященной математической теории влектричества и магнетизма. Грин был по существу самоучкой. Он поступил в Кембриджский университет, когда ему было уже 40 лет — через несколько лет после того, как его книга появилась в печати.
§ 6. Формула Грина
477
Аб. D — часть первого квадранта, задаваемая неравенством х* + y2<Z 2; Р = Q = ху.
7.	D — квадрат с вершинами в точках (1, 0), (0, 1), (1, 2), (2, 1); Р = хе? + 4, Q = 7 cos 4х.
8.	D—часть третьего квадранта, задаваемая неравенством —+	—3; Р =
= 1п (7 — х), Q = х cos у.
9.	D — треугольник с вершинами (хо, уо), (Xf, r/j), (лга» ^2); Р = хл у$ , Q = 0 (здесь а и 0 — данные целые положительные числа).
10.	D — прямоугольник Xq<Z.x<Zxi, yo^y^yil Р = 0» Q = cos пх» cos ту, где т и п — данные целые числа.
11.	D —область, определяемая неравенствами //> х2, xZ> У2', Р = х5^4 у1Q — =а х 10/9 ^1/8
6.2.	Частные случаи
Из формулы Грина (1) вытекает, что
если d-L=W- .то $Pdx + Qdy = 0.	(4)
ду дх	£
дР дО
Это согласуется с результатами § 4.6 гл. 12. Так как область D односвязна и — = -—, то существует такая функция для которой Р dx + Q dy = df, и, значит,
J Pdx+Qdy=^df = O.
Если применить формулу (1) к Р — —у и Q = х, мы получим интересные формулы для площади
S а именно:
S = — ^ydx	(5)
и
S = f xdy,	(6)
С
а значит, также
S = -у- J xdy — у dx	(7)
Q
[формула (7) получается сложением равенств (5) и (6)]. Предположим теперь, что линия С задана уравнением в полярных координатах:
г = ф (0), 0 < 0 < 2л.
Тогда она будет правильно ориентированной в параметрическом представлении:
х ® ф (0) cos 0, у = ф (0) sin 0, 0 < 0 < 2л, так что
dx = (<р'(0) cos 0 — <р(0) sin 0] dO, dy — [/(0) sin 0 + ?(0) cos 0] dO,
478
Приложение к главе 13
и, по формуле (7), площадь ограниченной линией С области равна 2я
— J {<р (0)ср'(6) sin 0 cos 0 + [<р(0)]2 cos2 0 — <р(0) <р'(в) sin 0 cos 0 + [<р(0) 12 sin2 0} d0 = о
2л
= yj[<p (e)]2d9-
о
Этим доказана формула (12) из § 2.6 гл. 11.
УПРАЖНЕНИЯ
12.	Пользуясь формулой Грина, вычислите площадь эллипса, границей которого является кривая х = a cost, y=bsint, 0<t<2it.
13.	Начертите график астроиды х2^ + у2/3 = /?2/3 и вычислите ограниченную ею площадь.
14.	Начертите график кардиоиды х = 2cos0 (1 — cos0) +1, у = 2 sin 0 (1 — cos 0) и вычислите ограниченную ею площадь.
15.	Вычислите площадь, ограниченную полукубической параболой у = х3/2 и прямыми у = 0, х = а, х = Ь.
16.	Вычислите площадь, ограниченную кривой г = 0, О<0 < 2л и отрезком оси х от х = 0 до х = 2л.
17.	Вычислите площадь, ограниченную одной аркой циклоиды х = t — sin t, у « 1 — — cos t и осью х.
6.3	. Набросок доказательства
Мы изложим здесь основные идеи доказательства теоремы Грина. Предположим, что область D разбита на две части D± и D2 (как это изображено на рис. 13.48) простой кусочно-гладкой кривой Со, концы которой разбивают линию С на две части Ct и Са. Покажем, что если формула Грина справедлива для областей Dt и D2, то она справедлива и для области D.
Правильно ориентированные границы областей и Dz— это Сг + Со (т. е. С и следующая за ней дуга Со) и (—Со) + Са (т. е. дуга Со,’пробегаемая в противоположном первоначальному направлении, и следующая за ней дуга Са). Мы предположим, что формула Грина для областей Dx и Da справедлива. Тогда
Складывая два последних равенства, получаем
' С дР	С С ЭР С С ЭР С. С С
J dx dy = — J J ~— dxdy — j j —— dx dy = J P dx -|- j P dx = j P dx,
D	D,	d2	ct c2 c
так как С = Cf + Са. Этим доказана формула (2). Аналогично доказывается и формула (3).
Последнее рассуждение можно сделать точным (пока оно не является совершенно точным, поскольку мы апеллировали в нем к чертежу). Далее, это рассуждение можно продолжить, разбивая области Df и Da на меньшие части, и т. д. Мы видим, что, для того чтобы доказать формулу Грина, достаточно: 1) разбить область D на простые куски, 2) доказать формулу Грина для каждого простого куска.
§ 6. Формула Грина
479
Рис. 13.48
Рис. 13.50
Некоторое разбиение области D изображено на рис. 13.49. Здесь каждый кусок либо является прямоугольником, либо ограничен двумя отрезками, параллельными координатным осям, и графиком монотонной гладкой функции.
Мы покажем теперь, как доказать часть (2) теоремы Грина для типичного куска, такого как, скажем, область D, изображенная на рис. 13.50. Ее правильно ориентированная граница — это кривая С = Сх + С2 + С3, где
: х = t, у = f(t)t	а < t	b	[f(t) >	0 при a<Z t<Z Ь],
Cz : х = b — t, у — с,	0 < t	< b	— а,
С3 : х = а, у = с — t,	0 С /	< с	— f(a).
Далее, по определению двойного интеграла и по основной теореме интегрального исчисления,
Ь с	b
J dx dy = — J у - - — dydx= — J [Р(х, с) — Р(х, f (х))] dx =
D	a f(x)	а
Ъ	Ь
= у Р(х, f (х)) dx — J Р(х, с) dx.	(8)
а	а
480
Приложение к главе 13
Но так как dx = 0 на линии Ся, то
b	Ь—а
Р dx = (Р ах + (Pdx= j Р (t, ЯП) dt — $P(b — t, c) di.
Ci	a	0
Воспользовавшись подстановками t = x и b — t = x, получаем о	b
P dx = jP (x, f (x)) dx — J P (x, c) dx, a	a
т. e. правую часть равенства (8); тем самым мы доказали равенство (2). Формула (3) доказывает* ся аналогично, только линию Cf здесь нужно задать уравнениями вида
Ct i х « g(t), у = t, t(a) <t < с,
где g есть функция, обратная функции /.
Доказательство теоремы Грина для интервала (прямоугольника со сторонами, параллель* ными координатным осям) совсем просто, мы предоставляем его читателю.
УПРАЖНЕНИЕ
А18. Докажите равенство (3) для рассмотренной выше области D.
6.4	. Обобщение
Теорема Грина может быть обобщена на области D, ограниченные несколькими прос* тыми замкнутыми кривыми. Типичный случай изображен на рис. 13.51. В этом случае формула Грина утверждает, что
J У (17—v) d“	J p +’
D	z=l Cj
Для доказательства этой формулы в случае «многосвязной» области D разобьем эту область D на две «односвязные» области Dj и Da, как показано на рис. 13.52, и воспользуемся тем, что если формула Грина справедлива для Di и для Da, то она справедлива и для области D.
§ 7. Несобственные кратные интегралы
481
УПРАЖНЕНИЯ
19.	Проверьте формулу Грина для случая, когда Р = —yj(x2 + г/2), Q= r/(x2 + у2), а область D представляет собой круговое кольцо 0<е < х2 + у2< 1.
20.	Проверьте формулу Грина, если область D определяется неравенствами х2 + y2<Z 10, х2 + у2> 1, (х — З)2 + (у — 3)2> 1 и Р = 1, Q = 0.
21.	Проверьте формулу Грина, если область D определяется неравенствами 3< | х | <С 5.
3 < | у | < 5 и Р = х2еу, Q = у2 cos х.
22.	Проверьте формулу Грина, если область D определяется неравенствами х2 + у2> 1.
I х | + | у | < 5 и Р = х + 7, Q = */ — 2.
§ 7. Несобственные кратные интегралы
Кратный интеграл называется несобственным, если либо область интегрирования, либо подынтегральная функция, либо и то и другое не ограничены. Мы будем рассматривать такие интегралы только для случая неотрицательных подынтегральных функций, как это мы делали и для простых интегралов (см. гл. 5, § 6).
7.1.	Неограниченные подынтегральные функции
Предположим, что f(x, у) — неотрицательная, кусочно-непрерывная, но не ограниченная функция, определенная в некотором интервале /. Какой смысл можно приписать выражению
y)dxdyt	(1)
Геометрический смысл двойного интеграла, состоящий в равенстве его объему тела, ограниченного сверху графиком функции z = f(x, у), подсказывает такое определение. Пусть А — какое-то положительное число. Обозначим через fA функцию, равную если [ < Я, и равную нулю в противном случае, т. е.
, . . f f(x> У) при f(x, у)<А, А ,У ( 0	при t (х, у) > А.
Функция fA ограничена, так как 0 < [Aj(x, у) < А во всем интервале /. Если кусочно-непрерывна, то существует интеграл
У JЛл <*• У) dxdy.	(3)
Это есть объем тела, ограниченного сверху той частью графика функции z = f(xt у), где f < А. Так как fA < fB при А < В, то числа (3) возрастают при возрастании А. Если А неограниченно возрастает, то либо интеграл (3) тоже неограниченно возрастает, либо он остается ограниченным и, значит, имеет некоторый конечный предел (см. теорему А § 9.1 гл. 5). В последнем случае мы говорим, что функция t интегрируема по интервалу / [или что интеграл (1) сходится], и полагаем
У У /О. У)	dy = Jim у J fA(x, у) dx dy.	(4)
Если интеграл (3) не ограничен при А -* + оо, то говорят, что интеграл (1) расходится, и пишут
УУ/(х. у) dxdy= + ОО .
482
Приложение к главе 13
Теорема сравнения (см. гл. 5, § 6.4) остается справедливой: если f < g в интервале / и функция g интегрируема в I, то функция Ц тоже интегрируема; данное ранее доказательство этого утверждения полностью переносится и на рассматриваемый здесь случай. Далее, можно показать, что если функция j интегрируема в интервале /, то
ь г d
d
b
jf t(x, y)dxdy = У $[(x,y)dy d*=j* $f(x,y)dx dy 1	a L c	J c L л
(где at b, c, d имеют обычное значение) при условии, что простые интегралы в последнем равенстве (в том числе и те, которые являются несобственными) существуют. (На самом деле последнее утверждение можно было бы доказать, даже если не ограничиваться лишь кусочнонепрерывными функциями.)
Все сказанное выше о несобственных интегралах распространяется и на функции п переменных при любом п. (Прил=1 только что данное определение несобственного интеграла эквивалентно определению, данному в § 6 гл. 5.) Ясно, что несобственные интегралы можно вычислять также и используя полярные, цилиндрические или сферические координаты.
•Примеры. 1. Вычислить несобственный интеграл
dx dy
V х2 + у2 л2+у2<1
Первое решение. Подынтегральная функция (х2 + i/2)”1/2 не ограничена вблизи начала координат. Для больших А > 0 подынтегральная функция меньше А при Ух2 + у2 > > 1/А. Следовательно, наш интеграл равен
Ит Л->+оо
dx dy
У х2 +у2
где Da есть множество таких точек (х, у), для которых НА < у/’х2 + y2<Z 1- Здесь полезно положить 1/А = е и перейти к полярным координатам:
dx dy
У х2 +у2
— г dr d0= г
2п 1
У J* dr d6 = 2л (1 — е).
О е
Таким образом,
И dxdy
У^+72
Х2+Уг<\
Второе решение. Сразу перейдем к полярным координатам:
2. Вычислить (ху)~1'2dx dy,
где I есть интервал 0<С*< Г, 0<*/< 1-
§ 7. Несобственные кратные интегралы
483
Решение. В этом случае удобно представить наш интеграл в виде повторного интеграла:
J j (xi/)“1/2	dx dy = j у	(х#)“1/2 dxdy = §	х”1/2 dx у	t/“1/2 dy = Г у	х“1/2 dx ;
1	0 0	0	0	L о
обозначение переменной интегрирования не имеет значения. Так как
У х”1/2 dx = 2х1/2 = 2 о	о
(это несобственный интеграл), то исходный интеграл равен 4.
3. Вычислить
У£У (х2 4- У2 4- z2)-а/2 dx dy dz,
где D — единичный шар (х2 + у2 + z2< 1) и а — положительное число.
Решение. Воспользуемся сферическими координатами. Рассматриваемый интеграл равен тс 2т-	1	я	2тс 1
У р“"а р2 sin <р dp d9 dtp = I sin ср dtp J dO J p2""® dp = о	ooo
4. Сходится ли интеграл
Ш 2 — sin x + е?г x24-!/2 + 2z2
dx dy dz?
Здесь 7 — некоторый открытый интервал, содержащий начало координат.
Ответ. Да. Действительно, пусть М — такое число, что 2 — sin х +	< М в
интервале / (легко видеть, что такое число существует). Тогда
2 — sin х 4- еУг	М
х2 Ч- у2 Ч~ 2г2 х2 -f- У2 + 22
Теперь используем пример 3 и теорему сравнения. •
УПРАЖНЕНИЯ
1.	Вычислите
, где D — единичный круг,
2.	Рассмотрите^ (х2 4- y2Y~a'/2 dx dy, где D —единичный круг, этот интеграл сходится, и вычислите его значение при этих примером 3 в тексте.
3.	Вычислите у^у | In Ух2 Ч- У2 + z2\dxdydz, где D —единичный шар.
Определите, при каких а
а; сравните этот пример с
484
Приложение к главе 13
В упражнениях 4—10 определите, сходится или расходится предложенный интеграл. В каждом случае область D является кругом или шаром с центром в начале координат и ра-
диусом 100. Д4. ф [(х - 1)» + ^ + (2 - 2)»]-г dx dy dz.	8.	| x — 11 1/2 (x 4- y)* dx dy. D
5. I cos xyz | [(x—2^+(y— l^+z^dx dy dz.	9- JJ Sin[(** + y^'2 | dxdy-D
6. JJJ | x Г1/2 | у Г2/3 | г I-374 dx dy dz.	10. JJJ | x”1 y2 z3 I dx dy dz.
(Х2 + у2+1) х2 4“ | ху |
dxdy.
7.
7.2. Интегрирование по неограниченным областям
Предположим, что мы хотим проинтегрировать неотрицательную функцию f}(x, у) по неограниченной области D. Мы можем положить, что [(х, у) = 0 для всех точек (х, у), не принадлежащих области D, и интегрировать функцию f(x, у) по всей плоскости. Такой интеграл мы обозначим через
$$f(x,y)dxdy	(5)
— 00
и будем рассматривать его как объем, заключенный между всей плоскостью ху и поверхностью 2 =	у)-
Для того чтобы приписать определенное числовое значение выражению (5), выберем последовательность ограниченных областей интегрирования Df, D2, D3, ... таких, чтобы: а) каждое Dj содержалось в следующей области D/+1; б) каждый круг х2 + y2<Z R2 еодержался бы в некотором Dj (а значит, также и во всех следующих Dj). Так, например, мы можем выбрать в качестве Dj интервал —j < х< /, —/ < у < j. Мы предполагаем, конечно, что все характеристические функции Xd кусочно-непрерывны.
Предположим также, что функция / кусочно-непрерывна и что интегралы
(х, у) dxdy,
которые могут быть и несобственными, сходятся. Так как f > 0 и условие а) выполняется, то числа (6) образуют возрастающую последовательность. Мы полагаем, по определению,
(6)
lim	y)dxdy = $$f(x, у) dxdy.	(7)
Если этот предел конечен, мы говорим, что интеграл (5) сходится или что функция f интегрируема на всей плоскости. В противном случае интеграл (5) расходится.
Может показаться, что определенное так значение интеграла (5) зависит от выбора областей
Dlt Dz, D3, ... . Но это не так. В самом деле, пусть Dt, Dz, D$, ... — другая последовательность областей, удовлетворяющая условиям а) и б). Зафиксируем какое-то k; область принадлежит некоторому кругу с центром в начале координат; следовательно, она принадлежит и всем Dj при достаточно больших /. Так как f > 0, то интеграл
6 7. Несобственные кратные интегралы
485
не больше, чем интеграл (6) при достаточно больших у и, значит, он не больше предела (7). Таким образом, значение интеграла (5), которое получается при использовании последовательнос-
ти Dt, D2, D3,	, не больше, чем то, которое получается при выборе последовательности
Di, Dz, ... . А так как аналогичное рассуждение показывает, что значение интеграла, получающееся при использовании последовательности Dy, не больше, чем то значение, которое получается
при выборе последовательности D*, то оба значения должны быть равны между собой.
Теорема сравнения справедлива и здесь (если Ос < g и функция g интегрируема по всей плоскости, то и функция f тоже интегрируема). Далее, интегралы по всей плоскости можно вычислять с помощью повторного интегрирования:
4-00
J р(х, y)dxdy =
fix, y)dx
dy =
J J f(x,y)dy
dx,
(8)
причем в некоторых случаях вычисления можно упростить, применяя полярные координаты.
Наконец, все сказанное выше распространяется и на функции более чем двух переменных.
• Пример. Вычислить
dx dy
(1 4- х2 4- у2)2
Решение. Выберем в качестве области Dy круг дг2+ y2<Z j2» Перейдя к полярным координатам, получим
2к /
dx dy___Km PC dxdy____________Г Г r dr d§
(\ + x2 + y2)2 “/J+oJj (1 + *2 + У2)2 “ /IT00J J (l+<2)2
2k /
f f r dr	Г 1	1	Y=/	/1	1	\
lim J I —-------------— = lim 2л — — ——-	= lim 2л I — —-------------------- = л,
J J (1 4~ f2)2	/->4-oo	2 1 + r2 _|r=o	/->--roo	\ 2	2(14“ /2) /
о 0
Но проще сразу же воспользоваться полярными координатами:
4“оо	2к -|-со	4“°°
JJ <l + «4-S">’ J J (l+r1)" J <!+'>	1	2 l+<"Jo
—со	0 0	О
Читателю следует попытаться вычислить этот интеграл с помощью повторного интегрирования в декартовых координатах (что, однако, потребует от него большего труда), ф
УПРАЖНЕНИЯ
11.	Фигура, ограниченная линией ху = 1 при х > 1 и осью х, вращается вокруг оси х. Покажите, что полученное тело вращения имеет конечный объем, но что площадь его поверхности бесконечна. (Если бы мы заполнили краской «бидон», имеющий форму только что построенной поверхности, то в нем поместилось бы лишь конечное количество краски, но для того чтобы покрасить этот бидон, не хватило бы никакого количества краски!)
12.	Область D определяется неравенством х2 4- у2 > 1; для каких значений а интеграл
J J (х2 4- у2)Л/2 dx dy сходится? Чему равно его значение? D
486
Приложение к главе 13
13.	Область D определена неравенством х? 4- у* 4- z54 > 1; для каких значений а интеграл j J У (х ‘ + V2 4- г2)а/2 dxdy dz сходится?
В упражнениях 14—20 определите, какие интегралы сходятся и какие расходятся. Здесь D — область, внешняя по отношению к единичному кругу.
14.	^J| х3| e~~y2dxdy	18.	j J e	dxdy.
15.	J j* х20 г/10 ё~ ^*1+ М dx dy.	19.	J J e~ ^x*+v‘ (1 + j^)-i dx dy.
А16.	С С 1 cos ху | dx dy J J (7 + x2 + у*)» • D	20.	f j e~	(1	yi)-\ dx dy.
17.	^e^+^dxdy.		
D
7.3. Важный пример
Мы докажем замечательное равенство
(9)
играющее большую роль в теории вероятностей и математической статистике (см. гл. 6, § 8.2.) Доказательство эюг® равенства основано на вычислении двойного интеграла
Т = J J е х* у2 dx dy.
—00 г Переходя к полярным координатам, получаем
С другой стороны, используя равенство (8) и свойства функции е*, имеем
4-00	4-00	-ТОО	4-00	4-0°	Г	+°°
Т = Ц е~*г e-^dxdy^ J j e~x'е~у2 dx dy = j е~х2 dx • j e^dy = J e~x2 dx
___QQ	—CO	—00	—CO	—00	|_	—co
так как обозначение переменной интегрирования не имеет значения. Отсюда и следует равенство (9).
УПРАЖНЕНИЯ
21.	Докажите, что С ( е""* / Уи^ du = УТт .
4-оо
22. Докажите, что
du = уТ/2.
487
§ 8. Несколько доказательств
§ 8. Несколько доказательств
8.1. Полярные координаты
Здесь мы докажем теорему 4 § 1.11 —формулу интегрирования в полярных координатах.
Пусть R — положительное число. В этом параграфе мы рассматриваем только такие ограниченные кусочно-непрерывные функции f(xt у), которые равны 0 при r> R и для которых функция (г, 0)i-> [(г cos 0, г sin 6) является кусочно-непрерывной функцией (г, 6) в круге 0 < г < R, О < 6 < 2л. Для такой функции £ положим
ПЛ =	(( t(x,y)dxdy
x2+y><R2 И
Т* [f] = J f f (r cos 0, r sin 0) r dr dO. о 0
Нам надо доказать, что
Т[[] = Г, [fl.	(I)
Так как ТДД вычисляется посредством двух простых интегрирований, то из неравенства ti < fa вытекает, что TJ/J < TJfaj. Далее, если функция дана, то можно найти такие ступенчатые функцииф иф, чтоф < fj < ф и» значит, Т [ф] < Т [fl < Т ]ф] и что, кроме того, разность Т [ф] — Т[ф] сколь угодно мала (теорема 3 § 1.7). В силу только что сделанного замечания имеет место неравенство 7\ [ф ] < Г* [fl < 7\ [ф]. Отсюда следует, что если равенство (I) выполняется для ступенчатых функций, то оно справедливо и в общем случае.
Так как Т*[[] есть повторный интеграл, то
T*[cf] — cT#[fl, где с — постоянная, и
т, [Л + Ы = т, [/1] + Г. (М.
Каждая ступенчатая функция является суммой функций вида , где / — некоторый интервал. Следовательно, равенство (1) достаточно доказать для случая, когда функция f является характеристической функцией некоторого интервала, т. е. если jj = 1 на некотором интервале и ft = О вне этого интервала. Но это можно сделать прямым вычислением.
Следует заметить, что любой интервал можно разложить на интервалы, каждый из которых лежит в одном из квадрантов. Далее, если интервал принадлежит некоторому квадранту, то его можно представить как интервал, одна из сторон которого принадлежит оси координат, из которого удален другой такой же интервал; интервал же, одна из сторон которого принадлежит координатной оси, может быть представлен как интервал, две стороны которого принадлежат осям координат, из которого удален другой такой же интервал. Наконец, интервал, две стороны которого принадлежат осям координат, может быть разложен на два прямоугольных треугольника с одной из вершин в начале координат и катетами, параллельными осям координат (рис. 13.53). Следовательно, равенство (1) надо доказать только для характеристических функций таких треугольников, что сделать легко (см. пример 2 в § 2.6 гл. 11).
488
Приложение к главе 13
У
Рис. 13.54
Для того чтобы завершить доказательство теоремы 4 § 1.11, заметим, что равенство
2п Я	R 2л
J J f (г cos е, г sin в) г dr d6 = J J f (r cos в, r sin в) r dz-является частным случаем теоремы 2 § 1.5.
8.2. Об определении площади
Мы упоминали в § 2.1, что площадь S ограниченной плоской области D может быть определена следующим образом:
S = И <*’ У) dxdy
I
при условии, что характеристическая функция кусочно-непрерывна; здесь / есть некоторый интервал, содержащий D; выбор этого интервала не сказывается на значении S.
Предположим, что мы перешли к новой декартовой системе координат (X, У) и что характеристическая функция множества D в новой системе координат Xd (X, У) остается кусочно-непрерывной. Будет ли площадь S, определяемая формулой
S = jflD (*• ПЫЖ
(где / — некоторый интервал, содержащий D), равняться S? Наша геометрическая интуиция говорит: конечно, да (рис. 13.54). Приведем доказательство этого интуитивно ясного ут-верждения.
Как мы видели в § 2.1, можно найти многоугольники Рг и Ра со сторонами, параллельными осям координат, и такие, что Рх содержится в D, a D содержится в Ра и
И dx dy <s < У J dx dy>
I	I
Задачи
499
причем
ffv,dxdy ~ И*₽. dxdy<e> / /
где е — любое наперед заданное положительное число (ср. с рис. 13.29 и 13.30, где и Ра — ЛАЛ
заштрихованные площади). Ясно, что < XD < Хр и, значит,
ПЛ	Л л л Л
dx dy < S < J J Xp2 dx dy*
Отсюда следует, что равенство S = S достаточно доказать для случая, когда D есть многоугольник, каждая из сторон которого параллельна одной из двух взаимно перпендикулярных прямых. Так как каждый такой многоугольник можно разбить на прямоугольники, то достаточно доказать, что если D — как угодно расположенный прямоугольник со сторонами а и Ь, лежащий внутри некоторого интервала /, то
$$lDdxdy = ab> I
а это получается элементарной выкладкой.
Читатель, которого удивит простота этого рассуждения, должен заметить, что существование введенных выше многоугольников Р$ и Ра вытекает из сравнительно трудной теоремы 3 § 1.7.
ЗАДАЧИ
В задачах 1—12 все функции предполагаются ограниченными и кусочно-непрерывными в каждой области D, по которой они интегрируются. Все области интегрирования D предполагаются ограниченными и имеющими кусочно-непрерывные характеристические функции.
1.	Предположим, что функция f(x, у) непрерывна в интервале 0<л,<1, 0< у <Z 1 и принимает в нем неотрицательные значения. Докажите, что если
1 1
f f / (х. у) dxdy = 0, 0 о
то f(x, у) тождественно равна нулю.
2.	Предположим, что [(х, у) ограничена и всюду непрерывна. Положим
F (*» У) = J* J /(и, v)dudv.
Уч х0
Чем у равна F” (х, у)?
3.	Предположим, что функция F(x, у) имеет ограниченную непрерывную частную производную Fxy (х, у) = [(х, у). Вычислите
у х
J J f (и, у) du dv.
Уч х0
4.	Перенесите результаты задач 2 и 3 на тройные интегралы.
5.	Пусть S — поверхность, определяемая уравнением z = f(x, у), где точка (х, у) принадлежит области D, в которой f(x, у) непрерывно дифференцируема, причем D есть «хорошая» ограниченная область. Покажите, что площадь поверхности S не меньше, чем площадь области D.
490
Приложение к главе 13
6.	Докажите, что для функций двух переменных справедливы неравенство Шварца
| J j f (х, у) g (х, у) dx dy | < |/ j j / (*, у)2 dxdy^gfx, у)2 dx dy и его следствие
]/y [/(X. F) + g (x, У)]2 dx dy < ^/Jj/(x, У)2 dxdy 4- j/ j j’g(x, y)2dxdy.
[Указание: сравните с задачами 12 и 13 из гл. 5.]
7.	Сформулируйте и докажите неравенство Шварца для функций трех-переменных, а также для функций п> 3 переменных.
8.	В трехмерном пространстве рассмотрим тело D плотности Дх, у, z). Ньютонов потенциал Ф этого тела, по определению, равен
. Y . Z) dX dY dZ _	---- —	... г ,
V(X - X)2 + (у-П2+ (г -Z)2 D
или, полагая х = xej + г/ег + ze8, X = Xtj 4- Уе2 + Ze3,
<Р (х) = j j J f (X) I X — X |-1 dX dY dZ. D
Вычислите F = grad9 в точке (x, у, г), не лежащей внутри или на границе области D, и докажите, что F есть сила, с которой D притягивает частицу массы 1, помещенную в точке (х, у, г). [Единицы выбраны так, что гравитационная постоянная равна 1. Мы можем предположить, что расстояние точки (х, у, г) от любой точки области D больше некоторого положительного числа].	_________
9.	Вычислите потенциал шара х2 + у2 4" z2< R2 с плотностью Дх, у, z)=g(yrx2 4“ у2 4*z2). Сравните этот результат g результатом § 3.8.
10.	Докажите, что потенциал ф(х, у, г), определенный в задаче 8, в точках, не лежащих внутри или на границе области D, удовлетворяет дифференциальному уравнению в частных производных
d2<f	д2?	д2? = 0
дх2	ду2	г2
(Это так называемое уравнение Лапласа; оно играет важную роль в математической физике.)
И. Пусть D — сферический слой 0</?,<х2 + у2 + г2 <	8 плотностью Их, у, г) =
= g (К*2 +	+ г2)- Какова вила притяжения, действующая на частицу, помещенную
внутри шара х2 4“ У2 + г2 < #1 ?
12. Функция
?(х,!/)= JJln[(x-X)2 + (j/-y)2|f (X. Y) dX dY D
называется логарифмическим потенциалом области D с плотностью В точках, не лежащих) внутри или на границе области D, логарифмический потенциал удовлетворяет уравнению Лапласа
д2? .	„
дх2 ду2
Докажите это. [Вы можете предположить, что рассматриваемая точка (х, у) обладает тем свойством, что ее расстояние от любой точки области D больше некоторого положительного числа.]
ДОПОЛНЕНИЕ
В этой книге мы попытались свести до минимума роль «чистой теории» и излагали математический анализ, обходя некоторые традиционные вопросы, которые представляют, однако, большой интерес и могут понадобиться читателю, собирающемуся продолжать изучение математики. Этот материал помещен в настоящем Дополнении.
В § 1 и 2 приводятся основные теоремы о сходимости и непрерывных функциях, не доказанные ранее. В § 3,4 и 5 мы докажем некоторые теоремы об интегралах, которые в основном тексте книги излагались без доказательства.
492
Дополнение
§ 1. Сходимость
Все рассуждения в этом Дополнении будут основаны на принципе верхней гра-н и: если непустое множество вещественных чисел ограничено сверху, то оно имеет (точную) верхнюю грань (наименьшую из верхних границ); если такое множество ограничено снизу, то оно имеет (точную) нижнюю грань (наибольшую из нижних границ) (см. гл. 1, § 6). В этом параграфе мы докажем две теоремы о сходимости. Первая из них, теорема Больцано — Вейерштрас-са, существенно используется в следующем параграфе. Вторая, критерий Коши, весьма важна, но в этом Дополнении она не используется.
1.1. Верхний и нижний пределы
В этом параграфе буквами i, j и k обозначаются целые положительные числа. Напомним что выражение «для почти всех / » означает «для всех /, за исключением конечного их числа», т. е. «для всех натуральных чисел /, за исключением каких-то N значений /», где W — некоторое целое число.
Пусть {Xj} = хх, Х2, х3, ... — последовательность действительных чисел. Число а* называется верхним пределом этой последовательности, если для каждого положительного числа е выполняются следующие условия: неравенство а* —е <С Xj имеет место для бесконечно большого числа значений j, а неравенство а* + е > Xj— для почти всех j. Число а* называется нижним пределом последовательности {ху}, если для каждого положительного числа е неравенство а* + Xj имеет место для бесконечно большого числа значений j, а неравенство а* —е < < Xj — для почти всех j.
Последовательность {ху} может иметь не более одного верхнего предела. Для доказательства предположим, что имеются два верхних предела, скажем, аг и а2> ях, и положим е = = (а2— а1)/3> 0; тогда ах + е> Xj для почти всех / и а2— Xj для бесконечно большого числа значений /. Но это невозможно — ведь мы выбрали е так, что ах + е < а2— е- Аналогично доказывается, что последовательность не может иметь более одного нижнего предела.
Нижний предел последовательности {xj} обычно обозначается символом lim xj (или символом lim inf Xj), верхний предел — символом lim Xj (или символом lim sup Xj).
Если последовательность имеет верхний предел а* и нижний предел а#, то а* > а*. В самом деле, для каждого е >0и для почти всех значений / имеем а* — е < ху< а* + е. Следовательно, а*—	—2е для любого е > 0, откуда и следует, что а* > а*.
Если а является одновременно и верхним и нижним пределом последовательности {ху}, то эта последовательность сходится к а. В самом деле, для каждого е> 0 неравенства а — e<Z Xj, а + е> Xj справедливы для почти всех /, т. е. | а — ху| < е Для почти всех у. Обратно, если последовательность имеет предел а, то а является одновременно и верхним, и нижним ее пределами.
1.2. Ограниченные последовательности
Мы докажем теперь основную теорему существования.
Теорема А. Ограниченная последовательность действительных чисел имеет верхний предел и нижний предел.
Доказательство. Рассмотрим последовательность xlt х2, х3, ... . По предположению, существует такое число М, что | Ху | < М для всех у. Для каждого k обозначим через ak верхнюю грань множества чисел {хд,, х^+х, х^+2, ... }; такое существует, так как наше множество ограничено. Поскольку ak является также верхней границей и для множества {хд+1, xk+2, ... к мы имеем ak > ak+1. Таким образом, ах > аз > а3...; значит, последовательность {а^} монотонно убывает. Кроме того, она ограничена снизу: так как х > —М для всех j, то > —М. Следовательно (по теореме 3 §3.8 гл. 8), последовательность {а^} имеет предел а.
(Напомним вкратце, как можно доказать сходимость последовательности {а^}. Обозначим через а нижнюю грань множества чисел {ах, а2, а3, ... }. Предположим, что существует такое число е> 0, что а + е для бесконечно большого числа значений k. Так как
§ 1. Сходимость
493
ат > ak ПРИ m<Zk, то неравенство а*> а + е будет справедливо для всех k, и а не будет тогда нижней гранью нашего множества. Следовательно, ak < а + е для каждого е > О и для почти всех k. Кроме того, а < а* для всех А; поэтому lim аЛ = а.)
k—►<»
Покажем теперь, что а является верхним пределом последовательности {*/}.
Пусть е — данное положительное число. Если бы было неверно, что а +е > xj для почти всех /, то неравенство а + е < xj выполнялось бы для бесконечно большого числа значений /. Следовательно, в каждом из множеств {*ь *л+1, *л+2> ••• } нашлись бы такие числа, которые не меньше, чем а + е, а тогда а* должно было бы удовлетворять неравенству > а + е. Но это невозможно, поскольку а есть предел а*. Далее, если бы было неверно, что а —е < xj для бесконечно большого числа значений /, то неравенство а —е > xj выполнялось бы для почти всех /. А тогда все числа множества {**, л>+1, *л+2, ••• }» где £ достаточно велико, были бы < а — ей, значит, выполнялось бы неравенство ak < а — е, что невозможно, так как а является пределом последовательности а*. Следовательно, а удовлетворяет обоим условиям определения верхнего предела.
Аналогично доказывается, что последовательность {xj} имеет также и нижний предел Р = lim р$, где р* — нижняя грань множества чисел {л>, *д+1» xk+2* ••• }•
fc—>оо
УПРАЖНЕНИЯ
1.	Докажите непосредственно существование нижнего предела р = lim р^. k—►<»
А2. Докажите, что определенный выше предел р действительно является нижним пределом последовательности {ху}.
1.3.	Теорема Больцано — Вейерштрасса
Пусть а*— верхний предел последовательности {ху} и пусть дано е> 0. По определению верхнего предела, а* — е<^у Для бесконечно большого числа значений / и ху< а* + е для почти всех /. Следовательно, | а* — лу |< е для бесконечно большого числа значений /.
Отсюда следует, что можно найти такое целое положительное число /f, что | х—а*|<Г,
другое целое положительное число /2, такое что /2> j± и | х^ — а*
1 КТ;
третье целое
и т. д. Последователь-
положительное число /3,
такое что /3> /а и | xf — а* |< — , /з	з
ность {xji ,	, х]з , ... } является сходящейся к а* подпоследовательностью последова-
тельности {*!, х2, х3, ... }. Аналогично доказывается, что если последовательность {лгу} имеет своим нижним пределом то некоторая ее подпоследовательность сходится к а*.
Из этих рассуждений и из теоремы А вытекает следующий важный результат:
Теорема Б (теорема Больцано — Вейерштрасса). Из каждой ограниченной последовательности вещественных чисел можно выделить сходящуюся подпоследовательность.
Бернард БОЛЬЦАНО (1781—1848), философ, логик и математик, во многом предвосхитивший свойственную Вейерштрассу тщательность в трактовке основных понятий математического анализа и созданную Кантором теорию множеств. Его основная математическая работа «Парадоксы бесконечности»* была опубликована посмертно.
Больцано был священником и профессором теологии в Пражском университете. В 1820 г. австрийское правительство уволило его, так как его лекции студентам были сочтены недостаточно лояльными (рассуждая о войне, он говорил о возникающем в этой связи конфликте между совестью человека и необходимостью повиноваться правительству).
♦ Имеется русский перевод: Одесса, «Матеэис», 1911.
494
Дополнение
УПРАЖНЕНИЕ
3. Приведите пример ограниченной последовательности рациональных чисел, которая не содержала бы подпоследовательности, имеющей рациональный предел.
1.4.	Критерий сходимости Коши
Последовательность чисел xlf х2, х3, ... называется удовлетворяющей условию Коши, если для любого е > 0 найдется такое целое число N, что | xj — хь | < е для всех j > N и k > N. Теорема В(критерий Коши). Для того чтобы последовательность действительных чисел имела предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство. Первая часть. Предположим, что последовательность {дгу} имеет предел а. Для данного е > 0 выберем такое число /V, что при всех / > 2V имеет место
£
неравенство | xj — a\<Z —(такое N существует
k > N, то
по определению предела).
Если j > N и
е
|ху —х*|<|ху —аЦ-lx*—а|<2 • — = е,
и условие Коши выполняется.
Мы доказали тривиальную часть теоремы (то, что из сходимости последовательности вытекает условие Коши). Это верно также и для рациональных чисел. Нетривиальная часть (то, что из условия Коши вытекает сходимость последовательности) эквивалентна свойству полноты множества действительных чисел.
Вторая часть. Предположим, что последовательность {ху} удовлетворяет условию Коши. Прие = 1 из этого условия получаем: существует такое число Nlt что при всех /> выполняется неравенство | xN —xj I < 1. Отсюда следует, что наша последовательность ограничена. (Ее ограничивает наибольшее из чисел I хх |, I х21, ... , I xN 1, | xN | + 1.)
В силу теоремы А эта последовательность имеет верхний предел а* и нижний предел а*. Если а* =/= то а*> Положим е = (а* — аж)/3 и заметим, что неравенство а* — e<Z.Xj справедливо для бесконечно большого числа значений/, а неравенство а* + е>х^ —для бесконечно большого числа значений k. Следовательно, —х£> —(а*+е) для бесконечно большого числа значений k. Тогда существуют такие сколь угодно большие числа / и k, что
ху — Xk > (а* — е) — (а* + е) = а* —	— 2е = е.
Но это противоречит условию Коши. Следовательно, а* = и, значит, последовательность {ху} имеет предел.
УПРАЖНЕНИЕ
А 4. Приведите пример последовательности рациональных чисел, удовлетворяющей условию Коши, но не имеющей рационального предела.
1.5.	Последовательности точек
Теорема Больцано — Вейерштрасса и критерий Коши могут быть обобщены на последовательности точек. В этом Дополнении слово «точка» обычно означает точку плоскости. Мы используем фиксированную декартову систему координат и отождествим точку с ее радиусом-вектором х, а также с парой координат (х, у) этой точки. (Мы ограничиваемся случаем плоскости тол ь к о для простоты рассуждений, но все сказанное ниже будет справедливо и для п-мер-ного пространства при любом п.)
Последовательность точек хх = (xj, у±), х2 = (х2, у2), х3 = (х3, у3), ... называется ограниченной, если ограничена последовательность чисел | хх I, | х2 |, | х3 |. Так	как |ху| =
-	то |ху|<|ху|, \yj\< | ху|, | ху| < | ху 1+| r/у |. Отсюда следует, что после-
довательность точек {Ху} ограничена в том и только в том случае, если ограничены обе числовые последовательности {ху} и [yj].
§ 2. Непрерывные функции
495
Последовательность точек {ху} называется сходящейся к точке а = (а, Ь) (или имеющей предел а), если числовая последовательность {| ху— а|} сходится к 0. Отсюда, как и выше, получаем, что последовательность {ху} сходится к а в том и только в том случае, если числовые последовательности {xj} и [yj] сходятся к а, соответственно к Ь.
Говорят, что последовательность точек {ху} удовлетворяет условию Коши, если для каждого числа е > 0 найдется такое целое число N, что | ху — х^ | < е при всех j > N и k Af. Отсюда, как и выше, получаем, что это будет иметь место в том и только в том случае, если условие Коши удовлетворяется для обеих числовых последовательностей {лгу} и {yj}.
Теорема Г. Критерий Коши (теорема В ) и теорема Больцано — Вейрштрасса (теорема Б) справедливы и для последовательностей точек.
Доказательство теоремы Г содержится в сделанных выше замечаниях.
§ 2.	Непрерывные функции
2.1.	Теорема об ограниченности
Теорема Д. Пусть функция £(х) определена и непрерывна на некотором конечном замкнутом интервале [а, д], т. е. для всех таких х, что а < х < Ь. Тогда f ограничена.
Прежде чем доказывать теорему, заметим, что все условия ее существенны. Функция f(x) = = х непрерывна на всей прямой —оо<х< + оо (бесконечном интервале), но не является на ней ограниченной. Функция f (x) = —непрерывна, но не ограничена на (открытом) конечном интервале 0 < х <Z 1.
Доказательство. Предположим, что f непрерывна, но не ограничена на интервале [а. 6]. Тогда для каждого / = 1, 2, 3.найдется такое ху, а < ху< Ь, что | f (xj) |> /. По тео-
реме Б из последовательности хх, х2, ... можно выбрать сходящуюся подпоследовательность Xyi , xj2 , ... . Пусть $ = lim Xj. . Тогда а < $ < b. Так как функция I непрерывна, то lim f (х )= i ►оо	i—►оо
— /($). Но поскольку | / (xj) |> /, то |f(£)| > / Для любого целого положительного /. А так как это невозможно, то наше предположение о неограниченности f было неверным.
2.2.	Теорема о наибольшем значении
Теорема Е. Пусть f, (х) определена и непрерывна на (замкнутом, конечном) интервале 1а, д]. Тогда на этом интервале существует такая точка 5, в которой f достигает своего наибольшего значения [т. е. такая точка £, что f(z) > f (х) для всех х, где а < х < 6].
Доказательство. По теореме Д множество значений, принимаемых функцией [ на интервале [а, Ь], ограничено. Обозначим через М верхнюю грань этого множества, т. е. такое число М, что М > 1(х) для всех х, а < х < Ь, причем для каждого N <ZM найдется такая точка х. х < Ь, что /(*)> N. Нам надо доказать, что найдется такая точка а < £<6, в которой /(£) = М. Предположим, что это не так. Тогда М — Дх)> 0 при а < х < b и, значит, функция g(x) = \/[М — [(х)] непрерывна на интервале [а, д]. По теореме Д найдется такое число А, что
g = А при ВСеХ х 1°’ Ь^ 1V1 ' I ^xj
Отсюда следует, что М — f(x) > 1/А, или f(x) < Л4 — 1/А для всех х, а < х < Ь. Но это противоречит определению числа Л4.
Следствие. В условиях теоремы Е на интервале [а, д] существует такая точка т), в которой функция f достигает своего наименьшего значения (т. е. такая точка т), что f (т|) < Дх) для всех х из интервала [а, Ь]).
Доказательство. Применим теорему Е к функции х i-> — f (х).
496
Дополнение
УПРАЖНЕНИЕ
1.	Докажите следствие из теоремы Е непосредственно (т. е. не используя теорему Е).
2.3.	Теорема Ролля и теорема о среднем значении
Теорема Ж ( те о р е м а Ролля в сильной ее форме). Пусть х f(x) — непрерывная функция, определенная на интервале а < х < Ь, и пусть ее производная f' (х) существует при всех х, а<^х<^Ь. Предположим, кроме того, что f(a) = f(b) = Q. Тогда найдется такая точка a<Z b. что [,'(£) = 0.
Доказательство. По теореме Е и ее следствию на интервале [a, Z?] существуют такие точки £ и т], в которых функция f достигает соответственно наибольшего и наименьшего значений. Если а<£< Ь, то точка 6 является точкой локального максимума и Если а<2 т] < Ь, то точка т] есть точка локального минимума и ^(Л) = 0. Если обе точки 6 и т) являются конечными точками интервала [а, 6], то и максимум и минимум функции f равны нулю. В этом случае [(х) = 0 и. следовательно, 1'(х) = 0.
Из теоремы Ролля вытекает теорема о среднем значении (см. гл. 8, § 1.3), а значит, и обобщенная теорема о среднем значении. Следовательно, эти теоремы справедливы, даже если фигурирующие в формулировках этих теорем производные не являются непрерывными.'Аналогично, и в теореме Тейлора нет необходимости требовать непрерывности производной, фигурирующей в остаточном члене формулы.
В § 8.1 гл. 4 мы получили такой основной результат: если f (x)Z> 0 на [а, /?), то функция /; строго возрастает. Сильная форма теоремы о среднем значении (без предположения о непрерывности производной) дает нам новое доказательство этого утверждения. Действительно, если а< Xi<2xzCb. то между хг и хъ обязательно найдется такое число что f(Xi) — fix,) = f (€) (х, — xt). Так как 0, то f(x2) —	0.
2.4.	Равномерная непрерывность
Функция х >-► /(^), определенная на некотором интервале, называется равномерно непрерывной на нем, если для любого наперед заданного положительного числа 8 найдется такое положительное число д, что если и хъ — любые две точки этого интервала, такие что I Xi — Xi |< д, то | t(xi) — l(xi) I <е.
Равномерно непрерывная функция всегда непрерывна; однако обратное может и не иметь места. Так, например, функция [(х) = 1/дг непрерывна, но не является равномерно непрерывной на интервале 0,<	1. В самом деле, пусть 3 — целое число; положим = 1/п, Х2=
= 2/п. Тогда 0< xi<Z 1, 0< *2< 1, | х* —	| = 1/п и । /(Xj) — Цхъ) | = п]2. Выбрав п
достаточно большим, мы можем сделать разность । Xj— ха I как угодно малой, а разность | 1(х±) — f(xz) | — как угодно большой.
Теорема 3. Пусть функция f(x) определена и непрерывна на (замкнутом) интервале 1а, Ь]. Тогда она равномерно непрерывна на этом интервале.
Доказательство. Предположим, что функция j не является равномерно непрерывной. Тогда найдется такое числов > 0, что ни для какого д> 0 из неравенства | хг—ха| не вытекает, что | f(Xf) — [(хъ) | <Z s* Иными словами, для этого 8>0 и для любого <5 Z> 0
А	Д	А
найдутся такие точки х и х на нашем интервале, что । х — х । < о, a I f(x) — f(x) |>е. Возьмем последовательность положительных чисел dj, да, б3, ..., стремящихся к нулю; мы получим
Л
тогда две последовательности чисел Xj и Xj интервала (а, Ь\, такие что
UO
a<xz<6, acx/Cb, lim | xf — xf\ = 0, /->ОО
I Z(X;) — f.(Xj) I >8 при всех /.
§ 2. Непрерывные функции
497'
Переходя, если это необходимо, к подпоследовательности, мы можем предположить, чго последовательность xj сходится (см. теорему Б). Положим 6 = lim Xj. Тогда а с 8 < b и, /->оо следовательне, так как функция f непрерывна на замкнутом интервале [а, 6],
Дт / (ху) = f (5).
Далее, АЛ	/Л	\
lim | ху —= Мт | ху —х7 + ху —£ | < lim I | ху — Ху | + | Ху — £ М = О, /-►оо	/-►оо	/-►оо 41	1	'
Л так что lim ху = 5 и lim / (ху) =/(6). /-►ОО
Отсюда вытекает, что если j — достаточно большое число, то |/(ху)—f (5)1 << е/2 и
I / (ху) — f (6) К е/2, а следовательно,
|/(ху) - f (х} | < | f (Xj) - f (£) 1 + | f (5) - f (xj) \ < -y- + -y = s.
что противоречит сделанному предположению. Таким образом, функция f(x) обязательно является равномерно непрерывной.
УПРАЖНЕНИЯ
2.	Является ли функция у = sin-— равномерно непрерывной в интервале 0< х< л? ^3. Дайте формальное доказательство теоремы: функция f(x), равномерно непрерывная в некотором интервале, непрерывна в каждой точке этого интервала.
2.5.	Компактные множества
Мы хотим обобщить некоторые из доказанных выше теорем на функции нескольких пере менных. Для этого нам придется рассматривать функции, определенные не только на интервалах, но также и на множествах более общего вида.
Напомним, что множество S точек (плоскости) называется ограниченным, если оно содержится в некотором интервале, т. е. если множество всех чисел | х |, где х £ S, ограничено.
Множество S точек (плоскости) называется замкнутым, если для любой последовательности точек {ху} из S, сходящейся к х, предел х тоже принадлежит S.
Множество S точек (плоскости) называется компактным, если для любой последовательности {ху} точек из S, можно найти подпоследовательность {ху^}, сходящуюся к некоторой точке х, тоже принадлежащей S.
Теорема И. Множество S точек (плоскости) компактно в том и только в том случае, ес-ла оно одновременно ограничено и замкнуто.
Доказател ьство. Если множество S не ограничено, то не существует такого числа М, что । х | < М для всех х £ S. Найдутся, следовательно, такие точки xt, Х2, х3, ... , принадлежащие S, для которых । ху |> /. Но тогда из последовательности {ху } нельзя выделить сходящейся подпоследовательности; следовательно, S не компактно.
Если множество S не замкнуто, то в S найдется последовательность точек {Ху}, сходящаяся к некоторой точке х, не принадлежащей S. Но тогда никакая подпоследовательность последовательности {ху} не может сходиться к точке, принадлежащей S; поэтому и здесь S не компактно.
498
Дополнение
Если множество S ограничено, то и каждая последовательность точек из S ограничена, а значит, содержит сходящуюся подпоследовательность (в силу теоремы Больцано—Вейерштрас-са). Если множество S, кроме того, замкнуто, то предел этой подпоследовательности принадлежит S и, значит, S компактно.
Эти определения и теорема переносятся также на множества точек прямой, обычного пространства или n-мерного пространства, где п—любое.
• Примеры. 1. Замкнутый двумерный интервал, т. е. множество всех таких точек х = (х, у), для которых а с х С б, с < у с d, является компактным множеством.
Доказател ьство. Это множество, очевидно, ограничено. Если Ху при всех / принадлежит нашему интервалу и последовательность {ху} сходится к х, то а < х< Ь, с < у < d, и, значит, пределы х = lim ху и у = lim yj удовлетворяют неравенствам а < х < b, с < t/ < d.
/-►оо	/->оо
Поэтому точка х= (х, у) принадлежит рассматриваемому интервалу.
2. Если Sx, Sa, ...» Sn — конечное число компактных множеств и S — их объединение, или сумма (множество, состоящее из всех точек, каждая из которых принадлежит хотя бы одному из множеств Sf, Sa, ...» Sn), то S компактно.
Доказательство. Пусть {ху} —бесконечная последовательность точек из S. Тогда некоторая бесконечная ее подпоследовательность должна принадлежать одному из множеств Sf, Sa, ...» Sn, скажем, Sx. Так как Sj компактно, то некоторая подпоследовательность этой подпоследовательности сходится к некоторой точке из 5$, т. е. к точке из S.Q
УПРАЖНЕНИЯ
4. Докажите, что объединение любого конечного числа замкнутых множеств замкнуто.
А5- Докажите, что пересечение любого числа замкнутых множеств замкнуто. (Пересечение множеств Slt Sa, ... состоит из всех точек, принадлежащих каждому из множеств Sj, Sa, ... .)
6. Докажите, что пересечение любого числа компактных множеств компактно.
2.6. Функции, непрерывные на компактных множествах
Определения наибольшего значения, наименьшего значения и равномерной непрерывности сразу же обобщаются и на функции нескольких переменных, определенные на некотором множестве.
Теорема К. Если f(x, у) = f(x) — непрерывная функция, определенная на компактном множестве S плоскости, то эта функция ограничена на S, принимает на множестве S наибольшее и наименьшее значения и равномерно непрерывна на S.
Это доказывается в точности так же, как теоремы Д, Е и 3. Теорема, аналогичная теореме К, справедлива и для функций п переменных при любом п.
§ 3. Дифференцирование под знаком интеграла
3.1. Формулировка результата
Рассмотрим непрерывную функцию f(x, у), определенную на замкнутом интервале /: а х < Ь, с < у < d и имеющую на нем непрерывную частную производную (х, у). Это означает, что обе функции (х, у) Дх, у) и (х, у) fx (х, у) непрерывны на /. Рассмотрим функцию одной переменной
а
F(x) = J f{x, у) dy,
(1)
§ 4. Интеграл Римана
499
тогда
d
F' (х) = J f'x (х, у) dy.
(2>
С точностью до обозначений — это теорема 7 § 2.17 гл. 12.
3.2. Доказательство
Заметим, что функция fx (х, у) равномерно непрерывна в интервале / (см. пример 1 из § 2.5 и теорему К). В частности, для каждого е > 0 найдется такое число д> 0, что
I f'x(x +$, У) — f'x(x, i/)| < е, если I е I < 8.	(3>
Пусть дана точка (х, у) интервала / и такое число /г =# О, что точка (х + /г, у) тоже принадлежит /; тогда по теореме о среднем значении найдется такое 6, зависящее от х, у и Л, что
Следовательно,
f(x + h,y)=f(x,y)+hf'x(x + ^,y), |£|<|Л|.
(4)

d
J [ f'x(.x + i,y) с
— f'x(x, !/)] dy
d
< J | fx (* + У) — f'x (x, у) I dy < (d — c) e, c
если | h [ <Z d, где d определяется из условия (3). Это означает, что
F(x + h)-F(x) р.
hm ------------------= fx (x, у) dx,
h—*0	n	J
c
чем и завершается доказательство равенства (2).
§ 4. Интеграл Римана
При изложении теории интеграла Римана в Приложении к гл. 5 (см. § 8) мы существенно использовали дифференциальное исчисление. Такое изложение не годится для двойных интегралов. Здесь мы дадим независимое изложение теории интеграла Римана для функций двух переменных. Все содержание настоящего параграфа без труда переносится и на функции любого числа п переменных (включая сюда и случай п = 1).
4.1. Ступенчатые функции
Все функции, рассматриваемые в этом параграфе, определены на некотором фиксированном интервале /: а < х С 6, с < у < d и ограничены на нем. Область интегрирования во всех случаях совпадает с этим интервалом /. В § 1.7 гл. 13 мы уже говорили об операции разбиения интервала / на меньшие подынтервалы 12, /3, ... ; такое разбиение осуществляется с помощью проведения нескольких прямых, параллельных оси х, и нескольких прямых, параллельных оси у. Проводя затем дополнительные прямые, как это показано на рис. Д. 1, мы получим новое раз-
$00
Дополнение
Рис. Д.1
биение /, являющееся более мелким, чем предыдущее. То, насколько мелким является данное разбиение, можно численно оценить его степенью измельчения, определяемой размером (mesh) разбиения, за который можно принять, например, длину наибольшей из диагоналей подынтервалов разбиения.
Напомним (ср. с § 1 7 гл. 13), что ступенчатая функция ф(х, у) — это функция, постоянная на каждом из подынтервалов некоторого разбиения. Значения, принимаемые функцией ф(х, у) на линиях раздела, никакой роли не играют. Если ступенчатая функция ф определена на некотором разбиении интервала / на N подынтервалов и принимает значения zlt Zz.zN на подын-
тервалах /j, /2, ...» /д , то, п о определению, интеграл от функции ф (по интервалу /) равен
J J ? (х> dy = ZjSi + Z2S2 + • • • + S	(1)
где S/г — площадь подынтервала /*. (Здесь нет необходимости писать под знаком интеграла букву /, поскольку интервал / в нашем рассуждении является фиксированным.) При желании можно заменить данное подразбиение более мелким и рассматривать функциюф как определенную на полученном таким путем подразбиении интервала/; это не изменяет значения интеграла (1) (ср. с соответствующим утверждением для функций одной переменной в § 8.1 гл. 5).
Очень легко проверить, что интегралы от ступенчатых функций ф, |ит. д. обладают следующими свойствами:
с<р dx dy = с J J<p dxdy (здесь с — постоянная),	(2)
(<Р + 40 dxdy=^<fdx dy+JJ Ф dxdy,	(3)
J J<p dx dy < JJ’pdxdy, если <p < ф	(4)
(ср. с соответствующими свойствами интегралов от функций одной переменной — см. гл. 5, § 8.1). В этом Дополнении запись «ф < ф» всегда будет пониматься как сокращенная запись сле~ дующего отношения между функциями: ф(х, г/)<ф(х, у) для всех точек (х, у) из интервала А (Это относится также и к функциям, не являющимися ступенчатыми.)
§ 4. Интеграл Римана
501
УПРАЖНЕНИЯ
1. Докажите равенство (2). ^2. Докажите равенство (3).
3. Докажите утверждение (4).
4J. Верхняя и нижняя суммы. Верхний и нижний интегралы
Пусть ф — некоторая ступенчатая функция и f(x, у) — произвольная ограниченная функция. Если Ф > то число
J J? dx dy
(5)
называется верхней суммой функции f (на интервале /); напротив, еслиф < f, то S называется ее нижней суммой. Множество всех верхних сумм функции f ограничено снизу (числом — MS, где S есть площадь интервала /, а М — верхняя граница функции | f |), а множество всех нижних сумм ограничено сверху (числом MS) —это непосредственно вытекает из свойства монотонности (4) (ср. с § 8.2 гл. 5).
Нижняя грань всех верхних сумм называется верхним интегралом функции f (на интервале /), а верхняя грань всех нижних сумм — нижним интегралом этой функции. Верхний и нижний интегралы обозначаются символами
JJ f (*, у) dxdy и у) dxdy .
(6)
Легко видеть, что для ступенчатой функции ее верхний и нижний интегралы совпадают между собой и совпадают с интегралом от этой функции (ср. с § 8.2 гл. 5).
Лемма А. Пусть функция f имеет (на интервале I) верхний интеграл J* и нижний интеграл и пусть е >0 — какое-то заданное число. Тогда найдутся такие верхняя сумма 2* и нижняя сумма 5* функции f, что
J* S* с J* -J- е и — е с S* с J*.
Доказательство. Для каждой верхней суммы 5 мы имеем S > J*. Если бы для каждой верхней суммы выполнялось неравенство 2 L> J* + £ , то J* не было бы нижней гранью верхних сумм; поэтому найдется такая верхняя сумма S*, что S* J* + е. Существование суммы 2# доказывается аналогично.
4.3. Функции, интегрируемые по Риману
Ограниченная функция f(x, у) называется интегрируемой по Риману (в интервале /), если ее верхний и нижний интегралы совпадают. Их общее значение называется интегралом Римана функции / (по интервалу /) и обозначается символом
JJ f(.x,y) dxdy.
(7)
В дальнейшем мы увидим, что для кусочно-непрерывной функции это определение интеграла совпадает с тем, которое мы ввели в § 1.5 гл. 13.
Теорема Л. Для того чтобы ограниченная функция f(x, у), определенная в интервале /, была интегрируема по Риману, необходимо и достаточно, чтобы для каждого £ > 0 существовали такие верхняя сумма и нижняя сумма (функции f по интервалу /), которые отличаются друг от друга меньше, чем на £.
Доказательство. Предположим, что J* = и что нам задано е > 0. Положим £х =е/2. По лемме А существуют верхняя сумма 5* и нижняя сумма такие что 5* < j* + + ех и	— ех. Следовательно, 5*—5*<2£1=£.
502
Дополнение
Обратно, пусть J* =/= J*. Тогда для каждой верхней суммы S* и каждой нижней суммы 2* имеем
£*-£* >•'*-•'*>0.
Из теоремы Л следует, что интеграл (7) — это единственное число, заключенное между каждой верхней суммой и каждой нижней суммой функции.
Пользуясь определением (7), свойствами (2), (3) и (4) ступенчатых функций, а также леммой А, нетрудно показать, что:
JJcf dx dy = с j*J fdx dy {с — постоянная),	(8)
J J If + g] dxdy=^ fdxdy + J J gdxdy,
J J f dx dy<. J J g dx dy, если f < g.
(9)
(10)
Здесь fug — функции, интегрируемые по Риману, и наше утверждение состоит, в частности, в том, что тогда и функции cf и f + g также являются интегрируемыми. Мы не приводим деталей доказательства, так как для кусочно-непрерывных функций свойства (8), (9) и (10) можно вывести из соответствующих утверждений о функциях одной переменной (см. гл. 13, § 1.6).
УПРАЖНЕНИЯ
В упражнениях 4—9 f и g — ограниченные функции, определенные на интервале /.
А4. Пусть с—положительное число и 2# и 5* — нижняя и верхняя суммы для Д покажите, что сЕ* и с2* — это нижняя и верхняя суммы функции cf.
5. Используя упр. 4, покажите, что если функция f интегрируема на интервале /, то функция cf, тоже интегрируема.
А 6. Докажите утверждение (8).
7. Покажите, что, для того чтобы число было нижней суммой (верхней суммой) функции f + g, необходимо и достаточно, чтобы оно могло быть представлено в виде суммы двух нижних сумм (верхних сумм) функций f и g.
AS. Докажите, что если функции [ и g интегрируемы, то и их сумма f+g тоже интегрируема.
9. Докажите утверждение (9).
А Ю. Докажите утверждение (10).
4.4.	Непрерывные функции
До сих пор мы близко следовали изложению, намеченному в § 8 гл. 5. Теперь мы отступим от принятой там линии изложения.
Теорема М. Функция f(x, у), определенная и непрерывная в замкнутом интервале, интегрируема по Риману.
Доказательство. Пусть е> 0 — какое-то наперед заданное число. Обозначим через S площадь интервала / и nycTbSj =e/S. В силу результата примера 1 из § 2.5 и теоремы К из § 2.6 функция I ограничена и равномерно непрерывна. Следовательно, найдется такое д > 0, что
если |х' — х"|< д, то | Дх') — Дх") |< ef.
Разобьем интервал / на такие подынтервалы, чтобы размер этого разбиения (см. § 4.1) был бы меньше д, и для этого разбиения определим две ступенчатые функции<р и ф, такие чтоф с f <<[». А именно, в каждом из подынтервалов будем считать функцию ср равной наименьшему, а функ-
§ 4. Интеграл Римана
503
цию ф — наибольшему значению функции f (они существуют по теореме К). Тогда ясно, что ф —	61. Далее, из свойств (2), (3) и (4) следует
0<
dxdy— J J <fdxdy=
J J (Ф — <f)dxdy < dx dy etS = s.
Мы нашли такие верхнюю и нижнюю суммы, которые отличаются друг от друга менее чем на е, и, значит, по теореме Л, функция I интегрируема.
4.5.	Покрытие кривой многоугольной областью малой площади
Мы хотим распространить наши рассуждения на кусочно-непрерывные функции. Для этого нам понадобится такой вспомогательный результат.
Лемма Б. Пусть С — график непрерывной функции х у = g(x), а < х <(3 и пусть & — произвольно заданное положительное число; тогда можно найти конечное число таких открытых двумерных интервалов, что каждая точка кривой С принадлежит хотя бы одному из этих интервалов, а сумма площадей всех интервалов меньше е.
Доказател ьство. Положим ех = e/f 4({3—а)]. По теореме 3 из § 2.4, функция g равномерно непрерывна. Следовательно, найдется такое число 0, что если | х' — х" | < б, то | g(x') — g(x") К ег. Пусть /V — такое целое число, что /Vd>P — а. Разделим интервал [а, р] на W равных подынтервалов и обозначим их концы через
а = х0< Xi <Z X2<Z ... < xN = p.
Длина каждого из этих подынтервалов равна бх = ф — a)/W<d.
Пусть /у — замкнутый интервал ху_ С х с х^ + dx = xj, । g(Xj_r) —у | < £р Тогда длина интервала /у равна бх, высота его равна 2ег а середина его левой стороны принадлежит кривой С и расположена над точкой х^. Следовательно, та часть кривой С, которая расположена над [ху-х, Ху], целиком содержится в интервале /у, потому что если х меняется не более чем на df, то у = g(x) меняется не более чем на ех (рис. Д. 2).
Сумма площадей интервалов /х, /2...... IN равна 2/Vdjef = 2бхф — а) = е/2. Заключим
А
теперь каждый из замкнутых интервалов /у в открытый интервал площадь которого превос-'	А А А
ходит площадь /у менее чем нае/22У (рис. Д. 3). Интервалы /г. /2, ..., lN обладают требуемым свойством.
504
Дополнение-
Рис. Д.5	Рис. Д.6
4.6.	Кусочно-непрерывные функции
Лемма В. Пусть f(x, у) — кусочно-непрерывная функция, определенная на интервале /, ое> 0 — какое-то выбранное нами число. Тогда можно разбить интервал I на подынтервалы и эти подынтервалы можно разделить на такие два класса, что функция f(x,y) непрерывна во всех внутренних и граничных точках каждого из интервалов первого класса, а сумма площадей интервалов второго класса меньше е.
Доказательство. По определению (ср. с § 1.4 гл. 13), функция f(x, у) может не быть непрерывной только на конечном числе множеств Сх, Сг, ...» Сг, каждое из которых представляет собой либо линию, подобную той, что рассматривалась в лемме Б, либо прямолинейный отрезок. (Стороны прямоугольника /, если функция / не является на них непрерывной, тоже будут входить в число этих линий Су.) Положим ег =е/г и покроем каждое из Су конечным числом открытых интервалов, сумма площадей которых менее чем ег (рис. Д. 4). Если Су — кривая, то это возможно по лемме Б; если Су — прямолинейный отрезок, то для этого достаточно даже одного интервала.
Продолжим теперь все стороны каждого из построенных интервалов и используем эти вертикальные и горизонтальные отрезки для построения разбиения интервала / (рис. Д. 5). Так мы получим разбиение, обладающее требуемым свойством — нам надо только отнести к первому классу все замкнутые подынтервалы, не пересекающие ни одно из Су.
•§ 5. Повторные интегралы
505
Лемма Г. В предположениях леммы В можно потребовать еще, чтэбы в каждом из замкнутых интервалов первого класса наибольшее и наименьшее значения функции /; отличались менее чем на е. (Наибольшее и наименьшее значения существуют по теореме К из § 2.6).
Доказател ьство. Сперва разобьем интервал / так, как это делалось в доказательстве леммы В. Обозначим через S множество всех точек, лежащих внутри и на границах всех интервалов первого класса. Это множество компактно (см. примеры в §2.5); следовательно, функция I равномерно непрерывна на S. Существует поэтому такое 6> 0, что если | х' — х" |< < б. то I f(x') — ftx") |< е.
Теперь мы заменим наше разбиение более мелким так, чтобы размер полученного разбиения был меньше д. Новое разбиение будет обладать требуемым свойством, если отнести к первому
классу все те из новых интервалов, которые содержатся в старых интервалах первого класса (рис. Д.6).
Теорема Н. Функция f(x, у), ограниченная и кусочно-непрерывная в некотором интервале, интегрируема в нем по Риману.
Доказательство. Выберем число е> 0. Мы построим две ступенчатые функции ф и
•ф, такие что
<ф,
ф dx dy —j* J<p dx dy <e.
(И)
После этого наше утверждение будет вытекать из теоремы Л.
Обозначим через S площадь интервала /, на котором определена функция f; пусть М — такое число, что । ft । < М. Положим Ej =e/(S + 2М) и рассмотрим разбиение, удовлетворяющее условиям лемм В и Г, где е заменено наЕг
В каждом из интервалов первого класса обозначим через ф и ф функции, равные соответственно наименьшему и наибольшему значениям функции / в этих интервалах. В каждом из интервалов второго класса положим ф = —/И, ф = М. Тогда первое из неравенств (11) будет справедливо.
Заметим теперь, что ф —ф <8^ в каждом из интервалов первого класса и ф —ф = 2М в каждом из интервалов второго класса. Так как общая площадь всех интервалов первого класса не превосходит S, а общая площадь всех интервалов второго класса меньше, чем elt то мы имеем
dxdy —
что нам и требовалось установить [см. (11)].
J J ср dx dy = j f (ф — ср) dx dy<2 4.S + 2Mex = e,
УПРАЖНЕНИЕ
11. Приведите пример ограниченной, ноне интегрируемой функции £(х, у), определенной в интервале 0 < х < 1, 0<r/< 1.
$ 5. Повторные интегралы
Теперь мы установим связь между определенным выше двойным интегралом и тем интегралом. который был определен в § 1 гл. 13, а также сформулируем некоторые новые теоремы, доказательства которых опустим.
5.1.	Повторные интегралы от непрерывных функций
Лемма Д. Пусть функция £(х, у) непрерывна в замкнутом интервале /: а < х < Ь, с < у < d. Тогда функция
d
xi-.F(x) = J/(x, у) dy
С непрерывна на интервале а < х < Ъ.
506
Дополнение
d
f(xQt у)] dy | <
Д о к а з а те л ьство. Пусть х0 — какая-то точка интервала [а, б] и пусть дано число е>0. Мы хотим установить существование такого числа 5, что если | х— х0 | < б, то | F(x) -FUo) |<е .
Положим ei = e/(d — с). В силу теоремы К функция равномерно непрерывна в интервале /; поэтому найдется такое б > 0, что если | х' — хЛ |< б, то | / (х') —	|<et- В частности,
если | х — х0 |< 6, то | 1(х, у) — £(х0, У) К при всех у, удовлетворяющих неравенству с < у < d и, следовательно, d	d
I F W — F Ue) I = I j f (*> </) dy — J c	c
d
< J I f (X. y) — f(x0, у) I dy < £1 (d — c) = e, c что и требовалось доказать.
Из этой леммы вытекает существование повторного интеграла b d J Jf (*. у) dy dx.
(1)
Аналогичное рассуждение показывает, что существует и повторный интеграл
d ь
J J f(x, у) dx dy. с а
(2)
Ниже мы покажем, что то же самое верно и для ограниченной кусочно-непрерывной функции.
5.2.	Повторные интегралы от ограниченных кусочно-непрерывных функций
Нам понадобится такой вспомогательный результат:
Лемма Е. Пусть х >-► F(x) —функция, определенная в окрестности точки дг0, и пусть для каждого е> 0 можно найти такие две функции Fr(x) uFt(x), определенные в окрестности точки *0, что F(x) = Fr(x) + Fz(x), причем Fr(x) непрерывна в точке х0, а | Fz(x) |<е для всех х, для которых она определена. Тогда функция F непрерывна в точке xq.
Доказательство. Выберем е > 0. Покажем, что можно найти такое б> 0. что если | х — Xq ।< б, то | F(x) — F(xq) i <е.
Положим ех= е/3. Найдем такие функции и F2, которые удовлетворяют условиям леммы, где теперь е заменено на ej (так что | Fz | < е J. Поскольку функция F± непрерывна в точке х0, найдется такое б> 0, что функции Fr и Fz определены при | х — xq |<б, и если | х— *о|< < б, то | Fi(x) — Fi(xq) I <ev Но при этом
| F(x) - F(xq) i = । F^x) + Fz(x)-F1(xQ) - F2(x0) | <
< | Fi(x) — F^xq) i + | Fz(x) | + | F2(a-o) |< Зб! = e
и, значит, функция F непрерывна в точке xQ.
Теорема О. Пусть Цх, у) —ограниченная кусочно-непрерывная функция, определенная в интервале /: а < х < Ь, с < у < d. Тогда повторные интегралы (1) и (2) существуют.
Доказательство. Заметим сперва, что если мы зафиксируем значение переменной х, например положим х = xq, то функция у ((xq, у) будет непрерывной при c<Z y<Z d, за исключением тех точек, в которых прямая х — xq пересекает кривые Clt С2.Сл, на которых
претерпевает разрыв функция f(x, у). Каждая из этих кривых либо является графиком функции х g(x), а < х < Р (прямая х = х0 пересекает график такой функции самое большее в одной точке), либо вертикальным отрезком. Следовательно, если точка xq не принадлежит конечному
§ 5. Повторные интегралы
507
Рис. Д.7
множеству значений, соответствующих вертикальным отрезкам Су, то функция у н* Дх0, у) кусочно-непрерывна при с < у < d.
Так как функция £ ограничена, то и функция
d
F (х) = § f(x, y)dy С
определена при всех х, a<Z x<Z b, за исключением конечного их числа. Функция F ограничена, так как если М. есть верхняя граница для । | |, то
d
I F (х) | < J|/(x, «/) I dy < M (d — с), с
Оказывается, что функция F(x) тоже кусочно-непрерывна. Пусть хо— одна из точек, в которых F(x) определена. Покажем, что F(x) непрерывна в точке xQ, поскольку для нее выполняются условия леммы Е.
Предположим для простоты, что прямая х = xq пересекает только три из кривых Су: прямую у = с, график функции у = g(x), а < х <0 (где а<х0<Р), и прямую у = d (см. рис. Д. 7; если прямая х = х© пересекает большее число линий Су, рассуждение аналогично). Положим yQ = g(xe) и выберем какое-то число е>0. Положим =8/(5 М). Так как функция g(x) непрерывна в точке Хо, то найдется такое б>0, что если | х — хо |< б, то | g(x)—g(xo) |< <8!’. Мы можем выбрать б настолько малым, чтобы при | х — хо |< б функция g(x) была определена и чтобы при | Xf — хо |< б прямая х = х: не пересекала никаких кривых Су, которые не пересекаются прямой х = хо.
При । х — хо | < б положим, по определению
Vo—е»	d—tt
Ft (х) = J f (x, у) dy + J f (x, y) dy,	(3)
<Ч-»1	Po+ei
H-ej	0o+6i	a
F2 (X) = J f(xty)dy+ J f(x9 y)dy+ j f(x9 y) dy.	(4)
c	^0—8t	rf—•!
508
Дополнение*
Так как функция [(х, у) непрерывна в (замкнутых) заштрихованных интервалах, изображенных на рис. Д. 7, то, по лемме Д, функция F^x) непрерывна в точке xq. Так как | / | <Л1 и суммарная длина всех путей, по которым в равенстве (4) производится интегрирование, равна 4elt то мы имеем | р2(х)| < 46^ = 4е/5< е. Далее, F(x) = F^x) + Fz(x). Следовательно, функция F непрерывна в точке %о в силу леммы Е.
Отсюда следует, что интеграл (1) существует; аналогичное рассуждение показывает, что существует и интеграл (2).
Рассуждения этого параграфа доказывают теорему 1 § 1.5 гл. 13.
5.3. Повторные интегралы и двойные интегралы
Теорема П. Предположим, что f(x, у) —ограниченная кусочно-непрерывная функция, определенная в интервале /: а < х С Ь, с < у d; тогда
Их, у) dy
d
Г ь
(Здесь двойной интеграл — это интеграл Римана, определенный в § 4.3).
Таким образом, оба повторных интеграла (1) и (2) равны между собой; это есть теорема 2 § 1.5 гл. 13. Из теоремы П следует также, что определение интеграла, данное в § 1.5 гл. 13, эквивалентно (для кусочно-непрерывных функций) определению из § 4. В силу теоремы J1 из § 4.3 справедлива теорема 3 § 1.7 гл. 13.
Доказательство теоремы П. Заметим прежде всего, что утверждение теоремы справедливо для ступенчатых функций. Это доказывается совершенно элементарным рассуждением, которое читатель легко может провести сам.
Пусть теперь f — ограниченная кусочно-непрерывная функция, а ф и — ступенчатые функции, такие что
Ф(*. У) < f.(x, у) < ф(х, у).
Следовательно, по свойству монотонности обыкновенного интеграла
add
(х, у) dy < J f (х, у) dy <	(х, y)dy, а<х<Ь
с	с	с
(за исключением конечного числа значений х, для которых один из этих интегралов не существует). Поэтому
В силу сделанного выше замечания это означает, что
ь
I	а
’ d J/(*. У) dy
-С
dx <
У У tydx dy.
Но единственное число, заключенное между каждой нижней и каждой верхней суммой, — это двойной интеграл (в смысле Римана), определенный в § 4.3. Этим доказано первое из равенств (5). Второе доказывается в точности таким же образом.
Рассуждения § 3,4 и 5 легко перенести и на функции более чем двух переменных.
Задачи
509"
ЗАДАЧИ
1.	Найдите нижний и верхний пределы следующих последовательностей:
а)	0, 1, 2, 0, 1, 2, 0, 1,
б)	1, 2, 1, 1, 2, 1, 1, 1, 2, 1,
в)	1; 1,1; 1; 1,11; 1; 1,111; 1; 1,1111; 1... .
2.	Найдите такую ограниченную последовательность, что каждая ее сходящаяся подпоследовательность сходится либо к 1, либо к 2, либо к 3, причем нашлась бы подпоследовательность, сходящаяся к каждому из этих чисел.
3.	Предположим, что дана такая последовательность, что для каждого целого числа k существует подпоследовательность нашей последовательности, сходящаяся к \lk. Покажите, что тогда найдется подпоследовательность, сходящаяся к 0.
4.	Найдите такую бесконечную ограниченную последовательность, что для каждого числа t, где 0 < t < 1, найдется подпоследовательность, сходящаяся к t. (Это может оказаться трудной задачей.)
5.	Предположим, что функция х i-> f(x) определена и ограничена при х> А. Для каждого-числа у^> А обозначим через а(у) верхнюю грань всех значений ft (х) при х > у. Далее, обозначим через 0 (у) нижнюю грань всех значений [(х) при х > у. Покажите, что существуют конечные пределы
Р = lim р (у) и а = lim а (у).
р—>4-«	«/—►+»
Числа Р и а называются соответственно нижним пределом и верхним пределом функции I при х -> + оо и обозначаются
р = Hm f(x), а = lim f (х) х—>4-оо	х—>4-°®
[или р = lim inf f (х), а = lim sup/ (х)].
х—►4-00	х—>4-0°
[Указание: Заметьте, что функции а(у) и fl (у) монотонны, и воспользуйтесь теоремой А из § 9.1 гл. 6.]
6.	Пусть /(х) — ограниченная функция, определенная для всех х в окрестности хо,за исключением, быть может, х = хо. По аналогии о условием предыдущей задачи, определите
lim / (х), lim /(х),	(♦>
X—>Хо
fim_ /(х),	Hm* /(х)	(♦*>
Х->Хо	х->х0
[или соответственно lim inf / (х), lim inf /(х), lim sup/(x), lim sup /(x)]. x->x^	x-^Xq	x->x0	x->x0
Меньшее из двух чисел (*) называется нижним пределом функции / в точке х0 и обозначается lim /(х), а большее из двух чисел (♦♦) — верхним пределом функции / г—►Хо	____
в точке х0 и обозначается lim / (х) [или соответственно lim inf / (х) и lim sup / (x)J. х—>Хв	X—*хо	х—*х0
7.	Докажите, что если в предположениях задачи 6 lim / (х) я» lim f (х) = А, то lim / (х)=Д. х—►Хо	Г—►г#	г—>х0
510
Дополнение
8.	Докажите принцип верхней грани (см. стр. 492) исходя из теоремы В, утверждающей, что каждая последовательность действительных чисел, удовлетворяющая условию Коши, сходится.
9.	Докажите следующий аналог теоремы В для функций. Пусть функция f (х) определена при всех х в окрестности точки х0, за исключением, быть может, самой точки х0. Предположим, что для каждого е > 0 найдется такое б > О, что если 0< | х' — х0 |< б и 0< | х" — х0 | <С б, то | f(x') — f(x") |<Се. Тогда существует предел /(х) в точке Хо. (Сформулированное условие существования предела функции тоже называется условием Коши.)
10.	Покажите, что условие Коши является не только достаточным, но и необходимым условием существования предела функции /(х). (Это легко.)
11.	Пусть /j(x), /г(х), f3(x), ... —последовательность функций, определенных в некотором интервале [а, д]. Эта последовательность называется равномерно сходящейся на интервале [а, 6] к функции /(х), если для каждого положительного8 найдется такое число N, что \fi (х) — f (х) । <8 при всех / > W и всех х, а < х < Ь, Покажите, что последовательность функций fj (х) = хЛ /= 1, 2, 3,..., рассматриваемая на интервале [0, 1], сходится к функции /(х)=0 (х=/=1),/(1)= 1, но что эта сходимость не является равномерной. Покажите, что та же самая последовательность, рассматриваемая на интервале [0, ?], где 1, сходится равномерно.
12.	Покажите, что если последовательность непрерывных функций, определенных на некотором интервале, сходится равномерно, то предельная функция непрерывна. (Это не очень просто.)
13.	Пусть f/y (х)} — последовательность непрерывных функций, определенных на интервале [а, Ь]. Предположим, что эта последовательность равномерно сходится к функции f(x); покажите, что тогда
ь	Ь
Hm J f.j (х) = J / (х) dx.
I"*00 а а
14.	Пусть {fj (х)} — последовательность функций, определенных на [а, б]. Предположим, что для каждого 8 > 0 можно найти такое целое число Af, что если j > N и k > N, то \ti(x)—fk(x) | <8 при всех х, а < х < Ь. Докажите, что последовательность
{fj W} сходится равномерно.
15.	Сформулируйте и докажите предложения, аналогичные результатам задач 12, 13 и 14 для функций двух переменных.
00
16.	Ряд 2 Ь (х), составленный из функций, определенных на интервале [а, Ь], называется /=0
равномерно сходящимся, если равномерно сходится последовательность его частных сумм. Покажите, что если степенной ряд с центром хо имеет положительный радиус сходимости R и если г — любое положительное ч исло, такое что r<Z R, то этот ряд на интервале [хо — г, хо + г] сходится равномерно. (В случае, когда /? = + оо, за г можно принять любое положительное число.)
17.	Пусть f (х) — функция, определенная следующим образом: f(x) = х, если 0 < х < 1, f (х) = 2 — х, если 1 < х < 2, и £ (х + 2) = f(x) для всех х. Докажите, что ряд
00
F (х) =	2"л /(2лх)
П=1
сходится равномерно на каждом интервале. Сумма F (х) является непрерывной функцией, не дифференцируемой ни в одной точке. Попытайтесь доказать это. [У Казани е: рассмотрите отношение приращения функции F (х) к приращению аргумента в некоторой точке хо; ограничьтесь сначала случаем Хо = 0.]
Задачи
511
18.	Если функция I (х, у) ограничена и интегрируема по Риману в интервале a<Z x<Z c<Zy<Zd, то справедливо следующее утверждение: функции
ь	ь
yt—^f(X, y)dx, y>->-^f(x, y)dx a	a
интегрируемы по Риману на интервале c<y<d; функции
xt-*
f(x, у) dy.
f(x. y) dy
интегрируемы по Риману на интервале a <; x < b и
d
^f(x,y)dy dx.
Попытайтесь доказать эти утверждения. [У к а з а н и е: рассмотрите ступенчатые функции ф(х, у) и ф (х, у), такие чгоф < f Докажите, что функции
ь	ъ
Ф (») = j ? (X, у) dx, Т (у) = j (х, у) dx
а	а
являются ступенчатыми, и заметьте, что ь	~ь
Ф (У) < J f (.х, у) dx < f (х, у) dx < Т (у), —	а
за исключением конечного числа точек, что несущественно.]
Решения упражнений, помеченных знаком ▲
Глава 8
§ 1
6. Так как /(1) = f(—1) = 3, то мы должны найти все такие значения 5, где —1 <	1,
для которых f (6) = 0. Но f (х) = 10х9 + 4х3 = х3(10х® + 4); поэтому единственным значением £, для которого /'(£) = 0» является £ = 0.
§ 2
10. Имеем: f (х) =	, х=0,01, хо=О. Далее, /' (х) = f'" (х) = — е~х и f" = е~х. Поль-
зуясь формулой (6), получаем
е—0.01 = во _ ео . 0>01 _1_ ео (0,01)2 + /? (х) = 0,99005 +R(x).
Третья производная | f" (/) | = I е~‘ | = е~‘ по модулю монотонно убывает, следовательно, если
(0.01)3
«</<0,01, то \fm (OKI/'" (0)1=1. Таким образом, |Я|<-	' <0,00000017.
6
30. Имеем | /vn (х) | = | sin х |. Так как | /vn (х) | < sin — = 1. то следовательно,
, „	. |х —л/2|’
1.2.3-4.S-6-7--
I	л I	л	1
Но поскольку в рассматриваемом интервале х — —- с < — I	2 |	8	z
, получаем
1
1.2-3-4.5-6-7 -27	645120.
36. Имеем 2” = (1 + 1)" = ( g ) + (")+•••+(«) •
46. В силу формул (20) и (21) имеем
(0,8)°’01 = (1 + (— О,2))0*01 = 1+ 0,01 (—0,2) + 0,01	(—0,2)^ +
0,01 (0,01 — 1) (0,01—2)
+ —~, о '	------~ (— 0,2)3 + Я = 0,997775732 + Я,
1 ‘Z’O
Решения упражнений, помеченных знаком А (глава 8)
513
где
R = 0,01 (0,01 — 1) (5,0J ~2) (0,01 ~3)' (1 + б)0’01-4 (—0,2)* = 0,0000013134 (1 + С)-3-99
1 . 2 • 3.4
для некоторого 6, такого что —0,2<6<0. Следовательно, 0,8< 1 +6< 1, откуда 0,8‘ > (1 + е)-3'99 > 1. Таким образом, (1 + 6)-3,99 < 1/0,83>" < 1/0,8* = 1/0,4096-наконец, | R | < 0,0000039402 < 0,000004.
Следовательно, О,О80,01 яг 0,99778.
и
. Вероят-
деле все они
число, такое
Но послед-
1
§ 3
2. Имеем: a, = (—1)41—I)8 =0, at = (—1)2(2—I)3 = 1, a, = (—I)8 (3—l)8 = —8, a4 = (—1)4(4—I)8 = 27. a6 = (—1)8(5—I)8 = —64. a« = (—1)«(6— I)3 = 125.
n — 1
18. Общий элемент последовательности имеет вид ап =---------, где п= 1,2,
п
ным пределом является Г, докажем это. (I) Пусть А — произвольное число, такое Ясно, что почти все элементы последовательности будут меньше, чем А; на самом
п — 1
меньше, чем А, так как --------< 1 < А для всех п. (II) Пусть В — произвольное
п
п — I что 1 > В. Мы должны показать, что если п достаточно велико, то------------> В.
п
нее неравенство будет справедливо при п—1>пВ, т. е. при п (1—В)>1, откуда п>
1 — В
(Так как В< 1, то разность 1 —В положительна.) Возьмем N > ---------— . Тогда для всех тех ап,
1 — В
для которых п >> N, выполняется неравенство ап > В.
22. Данная последовательность расходится. Это очевидно, потому что ее элементы, вместо того чтобы становиться сколь угодно близкими к одному фиксированному числу, колеблются между двумя различными числами. Доказательство: предположим, что существует предел после-
довательности, равный a. 1) Если а >, то не выполняется условие II, так как есть такое
число В, например В = 0, что а>В, но не верно, что почти все члены нашей последователь-
ности >> В = 0. 2) Если а с —	- , то не выполняется условие I при А = 0. 3) Если — —• <;
2	2
< а <	> то положим А = fa . Тогда а Д, но бесконечно много членов последо-
вательности превосходят А.
44. Имеем lim^= lim
Для того чтобы вычислить sin k 5k + 1 limo* =-7-4-0= -f-
sin/г _	„ 2k
—— . Далеее, lim —— = lim
OR + 1	OR + 1
положим b* =	1	. Тогда lim b* = 0. Так как
Ок + 1
2
2
5 ’
2/г
STf + 1,m
t. sin k h m ------ ,
5/г + 1
.	. sin k
< bk, то и lim —----= 0, что,
5k + 1
2 . л 2
5 1	б'*
впрочем, и следовало ожидать. Следовательно,
514
Решения упражнений, помеченных знаком А (глава 8)
§ 4
00	1	1
6. Пусть 2 aj — искомый ряд и Sn-* его n-я частная сумма. Тогда = --- = —, так
/=1	14-12
1 Л 2
ЧТО Ol=T, s2=—-
2	11
—-- =	4- а2 = — 4- а2> т. е. а2 = "Г" • Так как, вообще, Sn =
3	2	6
„	п п— 1	п п — 1	1
= 5л-1 4- ant Т. е. —— =--------4-ал, то ап =----— —--------= ——. Следовательно,
п 4- 1 п	п 4- 1 п п (п 4- 1)
искомый ряд имеет вид
00
1_________1_ 1 1
/(/ + 1) “ 2 + 6 + 12
/=1
26. Нам будет полезно выписать несколько первых членов ряда:
У (— 1)* tk/2 = 1 —/1/2 4-1 — /3/2 4- /2 — /5/2 4- ... . 6=0
Это геометрическая прогрессия со знаменателем g = — У t . Следовательно,
k=S	k=Q
48. Так как sin k <Z 1, то Зл — sin k > Зл	— 1	и -г----:—- < -г-------	< —— . (По-
3* — sin 6	3*	— 1	2*
следнее неравенство очевидно, поскольку Зл— 1	> 2Л	при k = 1, 2, ... ;	оно	легко доказы-
вается по индукции.)
Ряд
6=1	6=1
сходится. По теореме 6 сходится и дан-
ный ряд.
54. Пусть f (t) =-------. Тогда функция f (/) непрерывна, неотрицательна и убывает при
/ In21
t >2. Далее,
4-оо	А
с е .. с dt ..Г	1 Т4 V Г 1
1	[ (/) dt = lim I —— = lim I — ----- = lim —— J	Д->оо J t In21 Д-*оо [	In/ J2 Д-*оо L In 2
2	2
co
Так как этот несобственный интеграл сходится, то и ряд
п^2
1 1 1
1пД “ 1п2 <
00
/(л)= У 7^7 п = 2
является
сходящимся.
70. Имеем
an+l _ 1 -6-И ... (5п —4) (5п+ 1) 2-6-10 ... (4п —2) _ 5n + 1 5 ая ~ 2-610... (4п — 2) (4п + 2)-1-6-11 ... (5п — 4) ~ 4п + 2 4
Следовательно, данный ряд расходится.
Решения упражнений, помеченных знаком А (глава 8)
515
2л2 4- 1	1
88. В силу неравенства —j---— >— (вытекающего из того, что 2п3 + и>л3 + 3 при
2п2 4* 1
п > 1) наш ряд не может быть абсолютно сходящимся. Положим рп = —	—. Тогда рп >
п3 4~ 3
> pn+i при достаточно больших л. [Доказательство: (2л24~1)[(Л + 1)3 + 3]>»(л34-4-3) [2 (л 4- 1)24- 1] при достаточно больших л, что можно видеть, раскрывая скобки в обеих
частях неравенства и учитывая, что знак многочлена при л —► оо определяют члены наибольшей степени.] Далее, имеем
9 —L —-_
lim р„ = lim 2”	1 = lim-----— = 0.
п-к»	п 4" о />-*»	з
»+т?-
По теореме 9 данный ряд сходится (условно).
§5
2. Очевидно, имеем
I 2 (л 4-0 — 1	-	2л-1	I „	2л 4-1	Зл 4-1
Кт тт—гтг—:	*л+1»	;-;	*	= Кт	-—— .	—L—
п-+со | 3 (л 4-1) 4“ 1	Зл 4“ 1	I л-*»	Зл 4” 4	2л — 1
= ] х| Нт л->оо
6л2 4- 5л 4- 1
6л2 4- 5л — 4
1 = 1x1.
По теореме 8 из § 4 наш ряд сходится, если | х |< 1, и расходится, если | х |> 1, и значит, R = 1.
26. Используя результат упр. 15 и предложение (14) из § 2.3, получаем

_ 2л+3
1*1	2 .
Но поскольку 1 <*<2, правая часть меньше, чем 1-3-5... (2л + 1)/2л+1. Следовательно,
|^л+11
1-3-5 ... (2п+ 1)
2n+1 (п + 1)1
— 1 |л+1.
Так как 1 < x<Z 2, то | х — IIn*i<^ 1 и | х — 1 1Л+1	0 при п -> оо. С другой стороны,
1-3-5 ... (2л + 1)	1-3-5-7... (2л—1)(2л+ 1)
2л+‘ (л + 1)!	“	2-4-6-8... 2л (2л 4-2)
Следовательно, ( /?л+1| -* 0 ПРИ п -* °°- Так как радиус сходимости нашего ряда равен 1, то этот ряд сходится при | х — 1 |< I, т. е. в интервале 0< x<Z 2.
516
Решения упражнений, помеченных знаком А (глава 8)
60. Так как
у-1—= 1+	+	_	9
то
—= 1 + X2 + X4 4- X* + X® + ...
1 — X2 и
—-1=Х2+д4 + дв_|-Х8+ ...
1 — X2
Следовательно, (1	\	(х2 4- х4 4- х* 4- Р
--- -1) = (х2 + х4 + хв + хв + х10+	 т-> 4 1 — х2 /	3!
(х2 + а4 + ^+ ...)б	о. л. * о Зх* п 6*10	*10
+ -------------— ...= х24-х4+*«— — + х8 — —— + х1» — —— + —
о!	boo 120
5	1	1
= ха 4- х4 + — Xе 4- — х8 4--х10 4- ... .
6	2	120
[Заметим, что нам понадобился только первый член суммы (х2 + х4 + Xе + ...)6.]
§ 6
12. Дважды применяя правило Лопиталя, будем иметь
,. (arctg х)2	2 arctg х (х24-1) f. arctg х	1
lim -4------------= lim-----------------= lim-------= lim----------
x->o In (x2 4-1) x-*o (14-x2)2x x-+o x x->ox24-l
26. Это— неопределенность вида —. Мы имеем
__	2
arctg А	*2(1 + 4-) r 2х>
lim --------— = lim ----------2---------—L_ = hm —--------.
X->4~OO	1	X-*H-00	1	x->4-°0 X2 4“ 4
X	X2
4~00	„
Мы получили неопределенность вида----------- ; снова применяем правило Лопиталя:
4-00
2х2
11 гл ——
1-lim -----= 2.
42. Такой случай — неопределенность вида 0° — не рассматривался в наших примерах. Однако мы поступим, как и в случаях 4 и 5:
lim In (sin х)х = lim [х In sin x] = lim ?n sin .
x->0	x->0	x->o 1
X
Решения упражнений, помеченных знаком А (главы 8, 9)
$17
Мы получили неопределенность вида--------, допускающую применение правила Лопиталя:
оо
In sin х	ctgx „	—х2
lim----------= lim -------= lim--------,
x->o 1 x->o 1 x-*o tg x
x	x2
0 а это неопределенность вида —с ней мы поступаем так же:
£ 1
lim -------
х->о tgx
х-+о sec2 х
0.
Следовательно,
lim (sin х)х = е° = 1. х->0
Глава 9
§ 1
4. В соответствии с определением, данным в § 1.1, точка R должна принадлежать прямой
Z, проходящей через точки Р и Q, и | PQ | должно быть равно | QR |. Уравнение прямой I: у = 4	1	____
= —х — —, а | PQ | = 5. Пусть точка R имеет координаты (хо, уо). Тогда так как □	о
| QR | = 5, то У(х0 — 4)2 + (#0 — 5)2 = 5(*). Но поскольку точка R принадлежит прямой I, то
4	1
Уо = —х0 — •—(**). Возводя уравнение(*) в квадрат и подставляя в него значение у из (**) ,пос-о	о
ле упрощений получаем х$— 8х0 + 7 = 0; следовательно, х0 = 7 или х9 = 1. Значение х0 =
= 1 не подходит (так как иначе R = Р, но PQ не эквивалентно QP). Следовательно, точка R имеет координаты (7. 9).
22. Имеем 3(0!, а3) + 2(3, 0) = (Зах + 6, За3) = (3aj + 6)ех + За3еа = 9ех + 12ег.
В силу единственности координат вектора Зах + 6 = 9 и Заг = 12, откуда = 1 и о2 = 4.
52. Для того чтобы доказать, что векторы {ff, fa, f3} образуют базис, нам надо проверить, что: 1) к а ж д ы й вектор w может быть представлен в виде w = afj + Ma + cf 3; 2) для данного вектора w это разложение единственно.
Если а = 1, то тройка векторов {2ег, еа, v} не образует базиса, так как в этом случае О = 0(2ех) + Ov = 2ех — 2v.
Если а=/= 1, то тройка {2ef, еа, v} образует базис. В самом деле, имеем е3= --(v—аех).
1 — а
Пусть дан вектор w = Лех + Вег + Се3. Мы можем записать
1	1	а
w = А • 2 • — ej + Ве2 + С --v — С-------ех =
2	1 — а	1 — а
/1	С а
= — А —-------------
\ 2	2 1—а
—-— v = а (2ех) + Ье2 + су. 1 — а
Таким образом, условие 1) выполняется.
518
Решения упражнений, помеченных знаком А (глава 9)
Предположим теперь, что а (2ех) + Ье2 + cv = а (2ег) + 6е2 + се3, так что
О = (а — a) 2ej + (b — 6 ) е2 + (с— с ) v = 2 (а — a)ei+ (b — б) е2 -f-(c—c)ae1 + + (с — с ] (1 — а) е3= (2а — 2а + ас — ас ) ех + ( b — 6) е2 + (с — с ) (1 — а) е3.
Но так как векторы ех, е2, е3 образуют базис, то должно быть (с— с) (1 — а) = 0, b — b = О, 2а — 2а ас — ас= 0; и так как, по предположению, а =£ 1, то с = с, b = bt а = а. Таким образом, условие 2) тоже выполнено.
§ 2
4. Воспользуемся теоремой 1. Сделав рисунок, можно видеть, что | РХ | 4-1	| = I QX |.
Так как | РХ | = — 1 PQ | , то | QX1 = 51 РX | . Следовательно, | РХ | /1 QX | = -^-=|р/а|, или 4	5
|3| = —1«|. Поскольку точка X принадлежит интервалу I (см. рис. 9.22), тор<0 и, значит, 5
131 = — Р и а > 0 (ведь a -f- р = 1); следовательно, — р = а/5. Из равенства а -|- р = 1 получаем
5	1	5	1	/71
теперь а = — , р = — — , откуда X = — Р — — Q и, значит, X = — , — —
4	4	4	4	\ 4	2
§ 3
22. Так как х = г cos 0, у = г sin 0 и х2 + у2 = г2, то или г2 = cos 0 + sin 0.
имеем (r2)3/2 = r(cos0 + sin 0),
§ 4
2. Пусть (Xi, ха, х3) — координаты точки X. По условию п = 4, т = 5. Тогда вектор 5	4
X = т/(т + п) Р + п/(т + n) Q = — Р + —Q
есть радиус-вектор точки X. Следовательно, 5	4	13
'-т'+т-2-—•
5	„	4 г 5
х2 = —-(-3)+ 9 -5 = V
5	4
х’ = Т-°+Т(-7) = -
Таким образом, искомая точка —это (13/9, 5/9, —28/9).
14.	Прямая I упр. 8 (уравнения которой: х = 3 + 2/, у = 4, г = 5—2t) пересекает плоскость уг (плоскость х = 0) в точке х= 0, т. е. когда 3 + 2t = 0, или i = —3/2. При этом значении t имеем у = 4 и г = 5—2(—3/2) = 8. Следовательно, точка пересечения прямой I с плос
Решения упражнений, помеченных знаком А (глава 9)
519
костью уг имеет координаты (0, 4, 8). Прямая I не пересекается с плоскостью хг (плоскостью у = 0), так как ординаты всех точек этой прямой равны 4. Если г = 0, то 5—2/ = 0, откуда 8
t = -у. При этом значении t имеем х = 8 и у = 4. Следовательно, прямая I пересекает плоскость ху (плоскость г = 0) в точке (8, 4, 0).
28.	Заметим, что точка Р не принадлежит прямой /, так как в этом случае t было бы равно 4 и мы имели бы —1 = 2*4. Найдем две точки прямой /: полагая /=0, получим точку (0, 0, 0), при t = 1 — точку (1,2, 3). Теперь наша задача становится такой же, как в примере 1. Пусть Ах + By + Cz + D = 0 — уравнение искомой плоскости. Тогда так как точка (0, 0, 0) принадлежит этой плоскости, то 0* Л + 0* В + О» С + D = 0, откуда D = 0. Так как точки (1, 2, 3) и (4, —1, 0) тоже принадлежат плоскости, то Л+2В + ЗС + D = 0 и 4Л—В + D=
= 0, или А + 2В + ЗС = 0 и 4Л — В = 0. Отсюда ясно, что В = 4А и А = —так что 4
В = —-у С. Положим С = 3; тогда А = —1; В = —4, С = ЗиР = 0и, значит, уравнение искомой плоскости имеет вид —х — 4у + Зг = 0.
42.	Полагая Л = 2, В = —6, С = 7 и = 6,	= 1, Cj = 4, мы видим, что ни одно
из чисел (15) не равно нулю, т. е. мы можем выразить любые две из трех переменных х, у, г через третью. Следовательно, в качестве t мы можем выбрать л ю б у ю из этих переменных. Положим у = /; тогда наши уравнения примут вид 2х + 7z = 5 + 6t и 6х + 4г = 1 — t. Решая полученную систему уравнений, находим
х
31	13
34	34 '
х = 2/, у = t,
56.	Из первого равенства получаем х — у = 2х — Зу, откуда х = 2у. Второе равенство 9
можно записать так: у — г = 10# — 5z, откуда г = Положим у = t. Тогда х = 2t и г = 9
= -у /. Параметрическое представление прямой мы получим в таком виде:
76.	Параметрическое представление прямой If имеет вид: х = t, у = 1—2t, вив эти значения х, у, г в уравнения прямой /2> получим 1 — t = —1 + 3t = 1
1
нения удовлетворяются в том и только в том случае, когда t = -5“. Следовательно, прямые Л 1
и /2 пересекаются в единственной точке (-^-0, 0)«
г = 0. Подста-— /. Эти урав-
§ 5
14. Кривая симметрична относительно оси г. Следовательно, достаточно рассмотреть только ее часть С : z = х3, х > 0; это правая половина кривой, изображенной на рис. 3.3 (см. т. 1, стр. 105. Уравнение поверхности S имеет вид г = г3, или г = (х2 + #2)3/2.
§ 6
18. Пусть а = a1ef + ааеа 4“ 0363. Тогда а± 4“ 02 = aej 4“ аеа = а(в£ 4" еа) = 2, а± — аъ = а еу — а еа = afe, — еа) = 3 и а9 = а е$ = 0. Решая уравнения 4- as = 2 и
5	1	5	1
— а а = 3, находим ах = -у и а а = — Следовательно, а =?	— “у еа.
520
Решения упражнений, помеченных знаком А (главы 9, 10)
42. В силу теоремы 6 имеем
12v — 2v + 2v2 — 61	| 2v2 — 6 I
ft =------ --------------=-----------= 1000.
1/4-l 1 +4	3
Следовательно, 2и2 — 6 = ±3000. Отсюда вытекает, что 2и2 = 3006 или 2и2 = —2994. Но второе равенство невозможно. Поскольку 0, из первого получаем v = У1503.
§ 7
6. Обозначим эти векторы через f$, f2, f 3, f4. Тогда ff = е^ + е2 + е3, f 2 = еа, f 3 “ ei+e3, f4= e4. Заметим, что fx — f 3 = ег. Но в таком случае вектор ег может быть представлен в виде aih + «ata + азЬ + a4f4 двумя способами: можно положить aj = a3 = a4— 0, аг = 1 или aj; = 1, а3 = —1, аг = а4 =0, а это противоречит свойству базиса.
Глава 10
§ 1
16. С помощью переноса начала введем новую систему координат так, чтобы фокусы гиперболы были симметричны относительно начала: положим £ = х—3 и ц = у. В этой новой системе координат фокусы будут совпадать с точками (—3, 0) и (3, 0)* следовательно, с — 3. Так как е = 3/2 и е = da, то a = 2. А так как для гиперболы с = У a2-\-b2, то b = У5. В новой системе координат уравнение нашей гиперболы имеет вид £2/4 — т]2/5 = 1. Возвращаясь к первоначальной системе, получим уравнение-у (х — З)2 — у у2 = 1, или 5х2 — 4г/2 — ЗОх + 25 = 0.
5
34. Поскольку каноническое уравнение параболы имеет вид у2 =4ах, имеем а = у . В силу формулы (19) уравнение касательной в точке (хо, уо) примет вид уу^ = 5(дг + *о), или 5	5
у = у- х + y-xo (У о ¥= 0» так как в противном случае касательной была бы ось у). Наклон касательной равен 5/г/о, а так как он должен быть равен 2, то у0 = 5/2. Но тогда хо = 5/8 и уравнение касательной в точке (5/8, 5/2) имеет вид у — 5/2 = 2(х — 5/8), т. е. 4у — 8х = 5.
50. Для того чтобы привести уравнение кривой к виду (24), разделим числитель и знаменатель на 20; мы получим
1
,=________22__.
1—-L.COS0 4
5	1
Следовательно, е=— и р = —. Так как е>1, то это гипербола (сделайте рисунок). Один
4
1 из фокусов ее в начале координат, а соответствующая директриса имеет уравнение х = — “ =
25
a	5	1
= — — . Поэтому е = 25a и, поскольку е = — , находим а е	4
1	,----- 3
= — и b = У с2—а2 = —- .
16	80
. Таким образом, с = ае = 20
§ 2
Уз
4. Заметим, что при 0 = 150° мы имеем cos 0 = — —у и ные равенства можно переписать в следующем виде: 1$ = cos 0 ex + sin 0 ег и f г = —sin 0 ех + + cos Оег. В силу определения, следующего за формулой (1), и теоремы 1 репер {fj, fa} является правым.
sin 0 = -у Следовательно, дан-
Решения упражнений, помеченных знаком А (глава 10)
521
26. Наклон тг прямой равен 1; наклон т2 прямой /2 равен 7. Так как 1 4-7=/=0, то мож-
но воспользоваться уравнением (8), которое приведется к виду носительно и, получим и=2 или п =—	. Абсцисса точки
деляется из уравнения х4- 1 = 7х— 2; это A;==“^~- Значит,
и2 — — п — 1 = 0. Решая его от-2
пересечения прямых и /2 опре-
точка пересечения прямых имеет
/ 1	3 \
координаты I — , — I. Уравнения биссектрис:
3
у-~
или 2у = 4х + 1, и
3
у-~
или 4г/ 4“ 2х = 7.
§ 3
18. Так как А =£ С, то tg 20 = ------— = — . Поскольку угол 20 можно выбрать
А — С/ о
между 0 и 90° [см. замечание, следующее за формулой (4)], то 20 можно считать острым углом некоторого прямоугольного треугольника. Пусть катет, лежащий против угла 20, равен 4;
4	3
тогда другой катет равен 3, а гипотенуза оавна 5. Значит, sin 20 =—-, cos 20 = •—. Следова-5	5
тельно, sin 0 = у -1- (1 — cos 20) = 1 / УТГ и cos 0 = j/ -L- (1 4- cos 20) = 2 / уТГ. Поэтому
формулы преобразования координат будут_иметь вид х = У5~(2Х — Y)/5, у = У^Г(X 4- 2Y)/5, и наше уравнение приводится к 25Х2 — 2)^5”X 4- У 5 Y = 0.
24. После исключения смешанного члена получаем уравнение X2 — Y2 4“ 2}^2 X = 0. Дискриминант уравнения равен—1у=0. Далее воспользуемся формулами, полученными непосредственно перед разобранным в тексте примером; только теперь координаты X и Y играют роль хну, а £ и т] — роль Хи/. Мы имеем X = £ — У~2и У=т]. Уравнение X2 — Y2 4“ %У~2 Х= = 0 преобразуется в с2 — т)2 — 2 = 0.
X2 Y2
38. Сначала уравнение приводится к виду  4~	= 1. Чтобы получить большую кон-
станту под «первой переменной», повернем систему координат на 90°, полагая u=Y и v = — X Тогда мы получим уравнение «2/6 4-р2/2 = 1. В (u^ у)-координатах а=Уб, b=/2?с=2, фокусами служат точки (± 2, 0), вершинами — точки (± У"б, 0) и (0, ± У~2) (сделайте рисунок). Чтобы
вернуться к (х, у)-координатам, заметим, что х = .. KL (X —- Г) = -у- (-и-—у) и у = У 2“	У 2
а—5— (^ + ^) = —(и — v)- Следовательно, в (х, у)-координатах фокусы будут расположены в точках (—^2. V%) и (/Г, — /Г) , вершины —в точках (—/3, /з), (/3, — /3) ,
522
Решения упражнений, помеченных знаком А (главы 10, 11)
§ 4
5
2. При z = 2 уравнение линии пересечения имеет вид 4х2 4- у2 = — . Это эллипс; его кано-
ле2 у2
-------1. Ось у является его большой осью. Вершинами эллипса
ническое уравнение е/п_ 5/36	5/9
служат точки
, 0 и (0,
; фокусами — точки 10, ±
Глава 11
§ 1
в виде f(/) = x (t) ex + у (t) e2, где функции x и у удовлет-
воряют уравнению данной кривой, т. е. у (t) = Y х (t)2 4- 1 для каждого . Так как рас-4
4. Мы должны представить f(0
стояние точки от начала координат пропорционально Z, то мы имеем В частности,
также Yх (/)2 + у (/)2 = kt.
4
______» k
или YQ 4- 1 = “7“ » откуда k = 4. Следовательно, 4
(/)2 +j/(/)2 =-- 4t
Заменяя в последнем уравнении у (t) на Yx (О2 4- 1 и возводя обе
части равенства в квадрат,
получим 2х (О2 4- 1 =
. Знак минус можно отбросить, так как
наша точка находится в первом квадранте. Следовательно, х (t) =	8t2 — -А- и у (/) =
= / X (t)* + 1 =
2 *
26. Пользуясь данной в § 1.4 формулой для интеграла от векторной функции, получаем
2	/ 2	\	/ 2	\
Г / 1	1	\ С dt \ С dt \
j I — ej + —eJ di = I j — I*! + I J  -у le2 = (In 2 — In 1) ex + (In 3 — In 2)e2 =
i 4	\i / \i /
3 =ln 2 ei + In — e2.
44. Заметим сначала, что предел суммы векторных функций равен сумме пределов слагаемых. Это легко вытекает из соответствующих утверждений для скалярных функций. В силу п. 4 мы должны показать, что
lim {(f + g) (/о + h) - (f + g) (/о)} = a + b.
h-+o h
Но этот предел равен
Решения упражнений, помеченных знаком ▲ (глава 11)
523
lim -J- {f (t0 + ft) - f (/,)) + lim -J- {g («о + ft) - g (<o)h ft—>o h	h->o h
По предположениям, f'(/0) = а и g'(/o) = b. В силу п. 4 мы можем заменить последние два предела соответственно на а и Ь, откуда и получается требуемый результат.
§ 2
2. Если обе функции определяют одну и ту же траекторию, то для каждого t между 2 и 4 должно найтись такое и между 1/4 и 1/2, что t/(t + 1) = l/(u + 1) и (f+l)/(f— 1) = = (1 + «)/(! — и). Решая эти уравнения, мы в обоих случаях получим и= 1//. Следовательно
(ср. с § 2.2), функция ф (6) = — ;
она убывает на
отрезке а = — < 6 < — = £, ф I—
4= Ь.
Если мы обозначим первую функцию в этом упражнении через f, а
вторую — через h, то получим
1 № ’ —ГТГГГ'1 + тНгГ'1- dr '* +тй -=h ®-Следовательно, мы имеем случай б): противоположные кривые.
26. Пусть точка Q имеет координаты (cos 0, sin 0) для некоторого 0, где 0 < 0 < л. Прямая, проходящая через точку Р = (—1, 0) и точку Q, параметрически представляется в виде
х = —1 + (1 + cos 0)/, у = sin О* t.	(♦)
Точка R соответствует такому значению /, что /> 1 (Q лежит между Р и 7?) и
1 = (х — cos 6)а + (у — sin 0)2 = (/ — 1)2 [(1 + COS 0)2 + sin2 0] = (t — 1)2 2(1+ cos 0) =
= (/ — 1)2 4 cos2-у . 1	0
Следовательно, t = 1 + — sec — . Подставляя это значение в равенство ( *) и замечая, что . Л Л . О 0
sin 0 =2 sin — cos — , получим для координат точки R значения: 0	0
х = cos 0 + cos — , у = sin 0 + sin—• (гдеО<0<л). z	z
§ 3
8. Нам нужно найти Т(у), поэтому пусть у играет роль t, так что х = (у + 2)3/5 . Тогда f (У) = (у + 2)3/5 ех + уе2;
3	—2/5
е (У + 2) ех + е2	о	2/5
Т („> = -»	- ,	«, + 5to + 2)M
у -+ (У + 2)“ 4/5 + 1 V 9 + 25 (</ + 2)4/5	]Л9 + 25 (у + 2)4/5
F ZO
524
Решения упражнений, помеченных знаком А (глава 11)
12. Координаты Т(6) равны
(— sin 0) cos 0 — (1 + cos 0) sin 0 -----		— и
/(1 + cos 0)2 + (— sin 0)2
(— sin 0) sin 0 4- (1 + cos 0) cos 0 /(1 + cos 6)2 + (— sin 6)2
Упрощая эти выражения, получим
— (sin 0 4- sin 20) cos 0 4- cos 20 —— и —	- ------,
Y 2 (1 + cos в) v 2 (1 + cos fl)
кроме того, имеем
tg Ф =-------= —----------- .
6 Y dr/d0 sin 0
42. Имеем у = — x — — . Пусть x (t) = t и (/(/) = — t —	. Тогда f (/) = /ex 4-
/3	1 \
4- I — t — — le2, где 1 O’ представляет нашу кривую. Пользуясь равенством (16), получаем
s(6) = J ]/1+Ал = 1ф$.
О
Следовательно, представление кривой с помощью натурального параметра имеет вид 2	2	/ 3	1 \
£ = WS = <P(S) и g(s) = f(T(s)) = TTTsei + lkWs_Tje2-
§ 4
х2	у2
4. Имеем —— 4- —— = 1; эта траектория является эллипсом; v (/) = — a sin t в! + b cos t е2. а2	Ь2
Величина скорости равна длине вектора скорости, т. е. У a2 sin2t + b2 cos2 Л Ускорение а (/) = = — a cos t ех — b sin t е2. Для того чтобы вычислить нормальную и тангенциальную составляющие ускорения, нам нужно найти Т(/), k и N (/). Имеем
— a sin/ b cos t	ab sin2 t 4- ab cos21 ab
T (0 =	;  ex 4- —- — e2, k =	 -	= —
I v|	|v|	|vl3	|vl3
и
Далее, (ds \2 ab , Л	—ab2 cost	a2bs\nt
dt j | v |3	a2 sin21 4- b2 cos21 a2 sin2 t 4- b2 cos21
и d2s a2 sin t cos t — b2 sin t cos t =-----------------------------------T =-------------------------------- T =
T dt2	I v I
__ — g (a2 — b2) sin2 t cos t b (a2 — b2) sin / cos21 a2 sin21 4- b2 cos21	1 a2 sin21 4- b2 cos2/ в2’
Решения упражнений, помеченных знаком А (главы 11, 12)
525
8
20. Так как tg 0 = — = 2, то 0 = 2а и а
Г (0 = afe! + (~ 4"	+ ₽* + 16)	+ V + 2а/ + 16) в2’
Брошенное тело упадет на Землю через 2 с, т. е. когда t = 2, у (t) = 0, или — 2g 4- 4а -f- 16 = О
и *= —g —4.
Пройденное
им горизонтальное расстояние равно х (t) = 2а = g— 8,
или при-
ближенно 1,81 м.
§ 6
2. Да, возможно.
Предположим, что две компоненты двойной звезды имеют массы mj, /и2, периоды Tf, Тъ (относительно их общего центроида) и что они движутся по эллипсам с большими полуосями а^, аз. Согласно сделанному в тексте замечанию, первая компонента движется так, как если бы она была планетой некоторого неподвижного солнца с массой
Mf = /и 2/(1 + mJ m2)2 = /П23/(/П1 + m 2)2.
Аналогично, вторая компонента движется как планета некоторого неподвижного солнца с массой Mi= mjHmt + m2)2. В силу результатов § 4.12 имеем
/п|	4л2 af	mf	4л2
(«! + т2)2	7	’ (mi + т^2	7
Следовательно,
/И1 О2 I Т1 \2/3
^2	\ ^*2 /
6.	Ответ на вопрос упр. 5 положительный. Рассмотрим человека, сидящего на стуле в своей комнате. На его тело действует сила тяжести (его вес) W и реакция стула — W (в силу третьего закона Ньютона). Полная сила W + (—W) = 0, и ускорение равно 0. Взаимное давление между человеком и стулом воспринимается человеком как его вес.
Предположим теперь, что человек и стул свободно падают (как в лифте с отрезанным канатом или в ракете на орбите). Тело человека движется с ускорением — W, где т — его масса. Следовательно, кроме W, нет никакой другой силы, действующей на тело этого человека. Стул не оказывает ему никакого сопротивления, и человек ощущает «невесомость».
Глава 12
§ 1
8. Имеем
(em cos л)2 — (ет sin л)2 = е2т (cos2 п — sin2 п) = е2т cos 2п
2 (ет cos п) • (ет sin п) = е2т (2 cos п sin п) = е2т sin 2п.
30. Это множество открыто. Если точка (xj, yj принадлежит нашему множеству, то xj + У1 = —а, где а> 0. Если точка (х0, уо) удалена от точки (xj, yj на расстояние, меньшее, чем а/2, то хо <2*1 + <х/2, */о< У1 + а/2, так что хо + yo<Z Xf + у± + а = 0. Следовательно, все точки некоторой окрестности (х^, у±) принадлежат рассматриваемому множеству.
526
Решения упражнений, помеченных знаком А (глава 12)
36. Если точка (х$, уг) принадлежит Е, то (Xf, r/i) содержится в при некотором k. Так как множество открытое, то найдется интервал, содержащий точку (хр уг) и целиком содержащийся в A& а значит, и во всем Е. Следовательно, Е — открытое множество. С другой стороны, если Ak есть интервал |х|<-^-, \У I <	» то множеству F, т. е. всем Л* одновременно,
принадлежит только точка (0, 0). Значит, не существует интервала с центром (0, 0), который принадлежал бы всем Л^.
§2
10. Имеем
дх xtgy дх	xtgy х
df 1 d	х sec2 у 2
	=	—— (x tc и) =з	 = ~ 1
dy xtgy dy	xtgy sin2t/
(Можно также начать решение с того, что f = In х + In tg у.)
a*+b*
26. Так как v = j (dexfdx) dx, too = ea2+b2 —efl , v'a = 2aea2+b2 —ea и при a = 1, b = 2 a получаем
v'a — 2e6 — e,
28. Имеем	In (a2 + b2) и
,	1	°	' b
<Pa = ~ a2 + Z>2 = a2 + ft2 ’ <fb= a2 + 62 ’
так что a<fa + Ъуь =	= L
38. Рассмотрим точку (xo, у о, Zo) эллипсоида, для которой ?о> 0. Верхняя половина эллипсоида служит графиком функции
(х, у)*+с У 1 — (x/a)2 —(t//6)2.
Легко видеть, что zx = —c2x/(a2z), zy— — <?yl(b2z). Уравнение касательной плоскости в точке (хо, Уо> zo) имеет вид
. '.....................'	,	. , v с2*о (х — х0) с2у0 (у — Уо)
z = z0 + zx (х0, Уо) (х — х0) + zy (х0, yQ) (у — yQ) = *о —-—------—-------—-------=
a z9	о Zq
_ g2 / ZQ +— 4-—^  g%x  c2y0y  с2 / — xx0 ууо \
z0 \ c2 a2 b2 / a2z0 b2z9 z0 \ a2 b2 / или
xx0 ууо zzq a2 + b2 + c2	*
В случае, когда Zo<CO или го = 0, рассуждение аналогично. [В последнем случае, поменяв ролями у и г, рассмотрим функцию (х, г) »-* у.]
40. Как для эллипсоида, надо заменить х2, у2, г2 соответственно на Хох, уоу, ZoZ. Уравнения касательных плоскостей будут иметь вид
хх0	ууо  zzq	хх0  ууо  гг0
а2	Ь2	с2	а2	Ь2	с2
Доказывается это точно так же, как для случая эллипсоида (см. упр. 38).
Решения упражнений, помеченных знаком А (глава 12)
527
44. Имеем
dz	dz	dx	dz	du
	=	4- ---= t/x?’1 • cos t 4- x? In x (— sin i) = (y cos t — x In x • sin t) x?*1 = dt------------------------dx	dt-dy	dt
= (cos21 — sin21 • In sin t) (sin 0COS /’1.
Другой способ: z(f) = (sin 0cos/, откуда In z = cos bin sin t и, следовательно,
---= z (О [— sin t In sin t 4- cos2 £/sin /] <= (sin 0COS (cos2 t — sin21- In sin f), dt
68. Продифференцируем обе части равенства по х, рассматривая у как функцию от х: мы
получим
2х 4- 2уу' ху' — у х2 4- у2 х2 4- у2
, У+ %х откуда у' =-----— .
х —2t/
В точке (1, 0) получаем у' = 2.
82. Так как fJX = 6xy3z*, fy = §х2у2&, = 12x2y8z8, то fх	= 0 в том и только в
том случае, если по крайней мере одна из координат х, у, г равна 0. Все точки координатных плоскостей (и только они) являются критическими точками.
§ 3
2. Имеем
f=-£ 2а) (х) bj {у)=S [а/ (х) bf (y)1 = а''{х) ь> (у)'
Аналогично,
а', (х) b\ (у). Точно так же-^-ду	ду
b'l (У) и
а'/ (*) 6,’ (У).
4. Функция g — fY удовлетворяет условиям теоремы 1. Следовательно,	т. е.
rfl	*	ff	Л	HI	III	U*
fxxy = fxyx •	А так как	ху	= fyx	» ТО f хух*	= tyxx •
12. Сначала	вычислим	производные fyx и	f , для	того	чтобы	проверить их равенство
. л /	, х /	\	х
Н	1	““	I	X I	~~ И	1	““ I	X I	““
fvtt = — — е у 4-1 — — Iе у и ftJr = — — е у 4-1 — Т I еу • Следовательно, такая функ-ху	у2	\	у3 / у	у2 \	У3 /
х
ция f существует. Интегрируя f’x по х, мы получим f (х, у) у + g (у). Далее, должно вы по л-
9
няться равенство fy (х, у) = — — е у У
4- g' (У)
X
е у , откуда g' (у) == 0. Следователь
X
но, f (х, у) = е у 4-С, и так как f (1, 1) = 0, то С » —е.
18. Тождество f(x, y)=f(—x, y)=s^f(xt —у) продифференцируем дважды: сначала по х, затем по у, применяя ко второму и третьему членам цепное правило. Так мы получим fx (х, у) = = f'x(—x, у) (— 1) = — fx (х, —г/), а затем fx^(x, I/) = —/^(—х, у) = -~?ху (х, — у) (— 1). Из этих равенств вытекает, что fxy(x, у) = —fxy(—х, — у), откуда
Fхух (% *	fхух	X * " у} 1)’
528
Решения упражнений, помеченных знаком А (глава 12)
20. Пусть х, у и г — ребра параллелепипеда. Тогда V = xyz и S = 2(ху + yz + xz). Следовательно,
_.г у ( S \ ху ( S \ ху2 f у \2 { S	\
Х ~ У + X \. 2 Ху) ~~ (у + х)2 \ 2 Ху) у + х ~ ( у + х ) \ 2 2ху Х ) ’
Единственная критическая точка (при х>0, г/>0) —это х
А. ; ей соответствует
значение г =
что это максимум.
26. а) Имеем: и' = Зх2 — Зу, и' = За2 — Зх, а* = 6х, и” = —3, и== Зу. Положим и' = Лг	у	ЛЛ	лу	уу	*
= 0 = а* , получим две критические точки (0,0) и (1, 1). В точке (0,0) и"иш. — а„ =—9. У	ал уу лу
Следовательно, эта точка имеет вид седла. В точке (1,1) иххиуу— иху — 27 и ихх + иуу = 12; здесь мы имеем строгий минимум.
б) Внутри треугольника нет ни одной критической точки. Рассмотрим поведение функции и на границе треугольника. Функции а(0, у)=у3 и а(х, 0)=х3 не имеют критических точек внутри соответствующих областей. Функция и (х, 1 — х) = х3 + (1 — х)3 — Зх (1 — х) = 6х2 — 6х 4- 1
имеет критическую точку при х =. Далее, а(0,0)=0, а (0, 1) = 1, и (1,0)=1,
I 1	1 \	1	1	3	1 о	1
и \"Т~ *	=	""в” — ~4~ = —~2~ * Значит> минимальное значение функции равно —	,
максимальное значение равно 1.
30. Имеем:
^=cos6 sin t2, f^, = —sinft sin/2, /^ = —-2/sind cos/2.
В точке I 1, — , У л I эта производная равна 2 у п.
36. Заметим сперва, что если а, Ь, с — целые неотрицательные числа и a + &-f-c = 3, то лэ//
--------------= За • 4» • 5е t (t — 1) (t — 2) (3u + 4г. + 5w)‘~3.
dua dv° ди?
Далее,
H't = (3a + 4v + w)* In (3a -|- 4v 4- 5t<y),
= (3a 4- 4v 4- 5ay)* [In (3a 4- 4o 4- 5ку)]2,
= (3a 4- 4v 4- 5иу/ [In (3a 4- 4v -f- 5w)]3,
Hut = 3 (3a 4- 4v 4- бду/"1 4- 3/ (3a 4- 4v 4- In (3a 4- 4v 4- 5a;),
= [6 4-3/ In (3a 4- 4v 4- 5ку)] (3a 4- 4v 4- In (3a 4- 4v 4- 5w),
и т. д.
Решения упражнений, помеченных знаком А (глава 12)
529
а
42. Имеем
fyx = (— sin у) ех cos у cos у —-------,
fxy = (— sin у) ех cos У — х sin у cos у ех cos у —— .
Так как fxy =£ fyx , то не существует функции с данными частными производными.
§ 4
6. Так как dxt = a^dt, ... , dxn = andtt то наш интеграл равен
тг

16. Легко видеть, что С есть нижняя половина окружности радиуса 1 с центром в точке (О, 1), пробегаемая в направлении против часовой стрелки. Введем параметр на кривой С, используя полярные координаты с полюсом в точке (0, 1). При этом
С : х = cos 0, у = 1 + sin 6,	— л < 0 < 0.
Следовательно, на кривой С : Р = х + */ = 1 + cos 0 4“ sin 0, Q = х — у = —1 + cos 0 — — sin 0, dx = —sin 0 d0, dy = cos 0 d0 и
0
C P dx 4- Q dy= f (— sin 0 — sin 0 cos 0 — sin2 0 — cos 0 + cos2 0 — sin 0 cos 0) d0 =
о
= 2.
C	—тс
0
= j (— sin 0 — cos 0 -j- cos 20 — sin 20) d6 = cos 0 — sin 0 + — sin 20 4- — cos 20 —тс
18. Первый интеграл равен 4«	4тс
(cos 0 sin О)2 (1 — cos 0) d6 = — J (1 — cos 40) (1 — cos 0) dO = b	о
1 Г 1	1	1	Л
= — 0 — — sin 40 — sin 0 4- — sin 30 4-----------sin 50	= — .
8 [	4	6 T 10 Jo 2
Таково же значение и второго интеграла, что можно видеть, непосредственно вычислив его. Равенство этих двух интегралов проще всего получить, если, выполнив подстановку 0 = /2, заметить, что Сх и Са — это различные параметризации одной и той же кривой.
30. Поскольку cos х dx 4- е~у dy 4- г2 dz = df,	где f(x, у, z) = sin х — е~у 4- — г3, и
8	64	3
/(6,0, —2) = sin 6 — 1 —, f (— 1,2, 4) = — sin 1 —4- ——, наш интеграл равен sin 6 4-4- sin 1 4- е~2 — 25.
38. Требуется найти такую функцию /, для которой /„ = 1 4------------, f,, =-------,	=1-
х х + у у х 4- у
Условия интегрируемости выполняются. Зная fx , мы заключаем, что f (х, у, г) = х + 4-ln | х+у |4-g (у, г). Условие на f'y приводит к уравнению gy = 0. Следовательно, g(yt г) = = h(z). Условие на fz дает уравнение h' (z) = 1, откуда h (г) = z 4- С, где С — постоянная. Таким образом, f(x, yt z) = х 4- In |х 4- У\ 4-*4-С. Это решение годится для любой области, не содержащей никакого отрезка прямой х 4- у = 0.
530
Решения упражнений, помеченных знаком А (главы 12, 13)
48. Да. Любые две кривые, соединяющие одни и те же точки, можно непрерывно деформировать друг в друга, не выходя из области D.
3	3	3
Нет. Кривая Сх : х = — cos t, у = sin t, 0 < t < л и кривая С2 : х = — cos G у =
3 .	/	3	\	/	3	\
= —— sin t, 0 < t < л, соединяющие точки I — , 01 и I—— , 01 области D, не могут быть преобразованы друг в друга без выхода из области D.
1
— т [a2 -f- (gt)2 4- З2 — Его потенциальная
т
Полная энергия, равная — (а3 4- р2 4- 2bg),
§ 5
10. Имеем х'(0=а» у' (0 = —g/Ч-?- Кинётическая энергия брошенного тела равна величине энергия mgy = — — mg2t2 4- figtm 4- mgb.
постоянна.
§ 7
4. Имеем: f'=3(u—о)2, f'v = — 3 (и — а)2. f’a = 6 (а — о), f’m =6(u — v), f‘UB = =	6 (и v), fиии = 6, f =	6, fuuo =	6, fum — 6.
Следовательно, третий многочлен Тейлора в точке и = 2, v = —1 имеет вид
27 [1 + (и - 2) — (v + 1)] + 9 [(и - 2)а - 2 (и — 2) (с/ + 1) + (» + I)2] +
4- [(u — 2)3 — 3 (и — 2)2 (v 4- 1) + 3(и — 2) (о + I)2 — (v + I)3].
Так как наша функция сама является многочленом третьей степени, то эти вычисления на самом деле не обязательны. Мы могли просто написать
(и - v)3 = ((и - 2) - (v 4- 1) + З]3 и раскрыть скобки.
8. Если | и | < 1. то (1 + u)"1 = 1 — и + и2, — и3 + ... . При | х | < 2 , I у | <1/2 имеем । ху |< 1 и (1 + ху)'1 = 1 — ху + х2у3 — х3у3 + ... .
Если этот ряд оборвать на члене 2п-й степени, то остаточный член /?2л+1 не превзойдет (ху)2П+1 (1 — ху)'1; при | ху | < 1 он, очевидно, стремится к нулю.
Глава 13
§ 1
8. Имеем 0,3 0,2	о,з	0,3
J У уех? dxdy = У	dy = У ( е0’2» — е0,1г/) dy =
о;25 0,1	0,25	0,25
е0,1г/10,з
0,1 Jo,25
22. Имеем
J J еах sin by dy dx =
Хо Уо
= 5 ( е0,06 - е0,05 ) — 10 ( е0’03 - г0’025 ) .
еах dx
sin by dy
= —7- ( eax* — J [cos by^ — cos byt ] ab
28. Для интервала I возьмем все прямые, делящие / на такие подынтервалы, в которых функция <р или ф постоянна. Объединение этих разбиений дает такое разбиение /, что на каждом из подынтервалов обе функции — и <р и ф — постоянны и, следовательно, со постоянна.
Решения упражнений, помеченных знаком А (глава 13)
531
30. Находим 4 s= 5 (*3/— 4/2) = (—3 + 4 + 23 + 60) + 2 (—7 + 0 + 19 + 56)+ I. /=1
+ 3(—11 —4 + 15 + 52) 4-4 (—15 — 8+ 11 + 48) = 520; 4 4
J У (*3У — W) dx dy = 170,66.
В этом случае сумма Римана очень далека от интеграла.
46. Сторонами нашего треугольника служат прямые 6дг = 7у, Зх = 5 г/, Зх — 4у — 3. Как легко видеть из чертежа, искомый интеграл равен
0 (4f/+3)/3	3 (4JH-3) /з
J	J	е*+у dxdy + J J	ех+У dx dy~
—6 7у/6	0	5у/3
0 3
= С Г e(7i,+3)/3 _e13j//61 dy + Г Г е(7У+3)/3 _ А/31 dy = 3_ е8 + _2_ е-1з _ _2_ . J 1	1 J L	J 56	91	104
—6	о
48. Имеем f (—х, —у) = —f(x, у). Так как и функция /, и область D симметричны относительно начала, то j Jf dx dy = 0.
52. Имеем
С	1 С ( «4-	А	3
I 1 хпут dy dx =-------- lx 2 — ^4-2m4-2 I _	-----------------------
J J	m 4- 1 J '	'	(2n 4- m 4- 3) (2m 4- n 4- 3)
(Напомним, что m > 1, n > 1.)
56. Значение этого интеграла равно площади области D, т. е. равно 4. Эта площадь в четыре раза больше площади треугольника с вершинами (0, 0), (1, 0) и (1, 2) и, значит, равна arctg 2 sec 0	arctg 2
4 j J r drd 0 =2 f sec2 0 d6 = 2 tg (arctg 2) = 4. 0	0	0
§ 2
8. Воспользуемся полярными координатами и перепишем уравнение поверхности в следующем виде: г — arctg (у!х)= 0,—л/2<0<л/2, 1<г<4.Так как zх — — (sinO)/r, zy— =(cos6)/r, то эта площадь равна
к/2	4	______ к/2 4
1	(* Г	л /	__
1+—rdrd0= I I У 1 + г2 dr dO = — I 4 /17 — /7+ In
-я/2 1	—r./i 1
24. ВоспЬльзуемся полярными координатами:
1 /г2 4- X2 4- i/2__L
V г2 г '
,2 ,2__
1 “Ь 2х	2у
Следовательно,
s= г
J J____ /1 — Г2	/1-В*
0 V1—вг
532
Решения упражнений, помеченных знаком А (глава 13)
§ 3
16. Имеем 3	/9=^ 4_х	з	---
V = Г Г Г dz dx dy = J [4x — -5-] dy =
3 ________ Г __________________ у -|3
=8 f У 9 — у2 dy = 4 \y У 9 — i/2 4- 9 arcsin -т-	= 36л.
—3	L	3 J—з
26. Для всех точек (x, у, г) = (г cos 0, г sin 0, г) рассматриваемого тела х2 + y2<Z 2у и, значит, £/> 0, т. е. sin 0> 0. Мы видим, что рассматриваемое тело определяется неравенствами г2< z< 2г sin 0, 0< г<С 2 sin 0. Следовательно,
к 2 sin б 2г sin б	тс 2 sin б
sin4 0 — 4 sin4 6 ) d6 =
(2г2 sin 0 — г3) dr dO
л-f-— I (1 + cos 40) d6 = — л 4- — n = — л. O J	O	о	z
0
38. Находим xyz2 = p4 (cos cp sin <p)2 cos 0 sinO, и искомый интеграл, следовательно, равен тс 2тс 1
Ш81П 20	7
р° cos2 ср sin3 ср —-— dp d0 dcp = 0, так как J sin 20 d0 = 0.
ООО	0
§4
4. Имеем F = 2 In + 3 In х* 4“ 2 In х3 4“ 3 In х4. Следовательно, 2345	2	3	4	5
[ [ [ [ F dx± dx3 dx2 dx± = 2 [ In xt dxx 4- 3 [ In x2 dx2 4* 2 J In x3 dx3 + 3 j In x4 dx4 ==
| In Xi dXi 4- 3
8. Имеем:
515 33
= -10 + ,n — § 5
64 x2 dx = —“ о
4
3 С	24
х4 dx = —-
о
4 3 c xdj,dx=__j ^dx==3.	y=— ydydx- 128 J
0 0	0	0 0	0
26. Пусть полуокружность определяется уравнением х2 + у2 = R2, где ^>0. Тогда в силу симметрии X = 0 (см. ниже § 5.4) и
r=i
4 x2
4
2j?
sin 0 R d0=------
л
о
о
Решения упражнений, помеченных знаком Д (глава 13, Дополнение)
533
46. Центроид квадрата имеет координаты (0, 1^2/2) и расстояние его от оси X равно У2/2. Следовательно, V = 2л У 2/2 = л У2.
§ 6
6. В рассматриваемом случае двойной интеграл в формуле Грина равен
п/2 УТ
j J (у — х) dx dy = J Jr2 (sin 0 — cos 0) dr db = 0. d	о о
Далее, P dx + Q dy~xy(dx + dy) = 0 на ограничивающих область D кривых, за исключением дуги х = У2 cos 0, у = ^2 sin 0, где 0 < 0 <л/2. Следовательно, криволинейный интеграл в теореме Грина равен
тс/2	_
| 2 cos 0 sin 0 (— VTsin 0 4- У2 cos 0) d6 = 0.
18. Повторяя рассуждение, проведенное в тексте, при С3 : х = g(t), у = /, Да) < t < с, получаем
с g(y)	с
JJ ’^’dXd!/= f f ^dxdXdy= У У) —Ч(а, y)]dy-
L>	На) a	f(a)
С	f(a)
Так как dy = 0 на кривой С2, то J Q dy = J Q (g (у), у) dy + J Q (а, у) dy.
С	ца)	с
§ 7
4. Разобьем D на малый шар с центром (1, 0, 2) и остальное пространство. Сходимость интеграла сомнительна только в малом шаре радиуса г. В пределах этого шара полезно воспользоваться сферическими координатами с началом в центре шара, т. е. положить г = 2 4“ р coscp, у = р sin 0 sincp, х = 1 +pcosO sincp. Наш интеграл будет тогда равен
2т. и г
lim I I I р"2 sin ф dp d® d6 = lim 4л I—— — ) = 4- 00 .
e->O+J J J	6->0+ \ e r ]
0 0 6
Этот интеграл расходится.
16. Воспользуемся теоремой сравнения. Если х2 + #2>1, то подынтегральная функция не превосходит (х2 + г/2)-3, а
2т 4~оо
(х2 4- t/2)”3 dx dy = J J г“б dr d6 = — .
х24-г/2>1	0	1
Следовательно, заданный интеграл сходится.
Дополнение
§ 1
2. Пусть е —данное положительное число. Если 0 —е не меньше, чем xj, Для почти всех /, то в каждом множестве (х^, xk+it ...} должно найтись число, не превосходящее 0 —е. Но тогда < 0 —е для каждого k, что противоречит определению 0 как предела последовательности {₽&}. Следовательно, 0 —е < ху для почти всех /. Если 0 +е не больше xj для бесконечно большого числа значений /, то ху > 0 + е для почти всех /. А тогда ₽& > 0 +е для всех достаточно больших k, что противоречит определению 0. Следовательно, 0 4-е > ху для бесконечно большого числа значений /.
534
Решения упражнений, помеченных знаком Д (Дополнение)
4. Возьмем десятичное разложение иррационального числа х = 0,0402..., скажем л = = 3,1415926536..., и положим, по определению, ап = а,а1аг ... ал. Тогда {ал} есть последовательность рациональных чисел, сходящаяся к иррациональному числу х. По теореме В эта последовательность удовлетворяет условию Коши.
§ 2
3. Предположим, что нам дано число 8 > 0. Так как функция f равномерно непрерывна, то найдется такое б> 0, что если х и х — точки этого интервала и | х — х | <6, то \f(x)—f(x) | <8. Следовательно, если х — произвольная данная точка интервала, то функция f непрерывна в х.
5. Пусть S — пересечение замкнутых множеств (Sa }, где а пробегает некоторое множество индексов А. Пусть {хл} —последовательность из S, сходящаяся к точке х. Тогда {хл} будет последовательностью и каждого из Sa , сходящейся к х. Так как каждое из множеств Sa замкнуто, то точка х должна принадлежать каждому Sa , а значит, она принадлежит и S.
§4
2. Рассмотрим такое разбиение интервала /, что на каждом из подынтервалов /у функции ф и ф принимают постоянные значения Zj и (Оу. Тогда
J J (? + Ф) dx dy = (zi + ш1) 5i + (z2 4- <»2) S2 + ... + (гл + о>л) Sn =
= (г151 + z2S2 4-... 4- znSn) 4- (toiS14-to252 4- ... 4-шл5л) = J J? dx dy 4- J j* Ф dx dy.
4. Так как 2* есть верхняя сумма для /, то 2*=j>f? dxdy, где <р есть некоторая ступенчатая функция такая, что <р > f. Но если О 0, то с<р > cf и J J с<р dx dy — с J J (р dx dy = с 2 яв“ ляется верхней суммой для функции cf. Нижняя сумма 2 рассматривается точно таким же образом.
6. Так как функция f интегрируема, то в силу примера 5 интегрируема и функция cf. Далее, c^fdxdy = с 2 , где 2 есть нижняя грань всех верхних сумм 2 и одновременно верхняя грань всех нижних сумм 2 • Если О 0, то с2 есть нижняя грань для с2 —всех верхних сумм функции cf и одновременно верхняя грань с2 — нижних сумм функции cf. Следовательно, с2 = Jj* cf dx dy (Если с отрицательно, то рассуждение аналогично.)
8. Пусть 2g »	2 — соответственно верхние и нижние суммы для g и f.
Тогда в силу результата упр. 7,	4- 2f будет верхней, а	4- 2*f — нижней
суммой для f + g. Но так как функции fug интегрируемы, то найдутся такие суммы 2g > s. 2-,. 2-(.
l2’-S.I«=IX-2-8l + IS-2-f|<T+T-‘-
а тогда интегрируема и функция f 4- g.
10. Предположим, что f < g и пусть дано число е>0. Тогда найдутся такие ступенчатые функции <риф, что ср < f < g < ф и
f dx dy — J J <p dx dy < e,	JJ ф dx dy — J J* g dx dy < e.
В силу (4) J J у dxdy < J J ф dx dy. Следовательно, JJ f dxdy — J J g dx dy < 2e. Так как e произвольно мало, то наше утверждение доказано.
Алфавитный указатель
Абеля лемма 100
Абсолютно сходящийся ряд 70
—	— —, перестановка членов 71, 96, 97
—	— —, сходимость 71
--------, умножение рядов по Коши 72, 73, 99, 100
Абсолютный максимум 370
—	минимум 370
Адамс (Adams) 304, 305
Аддитивность длин 275
—	интегралов 421, 422, 429, 430, 451
—	центроидов 316, 470, 471
Аксиомы векторного пространства 116, 119,
121, 122, 126, 127, 174
Алгебраическая геометрия 217
—	кривая 216, 217
—	поверхность 228
Аналитическая геометрия 217
—	функция 79
Аполлоний (Appollonius) 182
Аргумент 135
Архимед (Archimedes) 467
Архимеда спираль 140, 141
Асимптоты гиперболы 184
Ассоциативность скалярного произведения 165, 166
—	сложения векторов 116, 117
— умножения вектора на число 119, 120
Аффинная система координат 129, 177, 241
Базис 123, 125, 126, 174
Бернулли Иоганн (Bernoulli Johann) 91, 311
Бернулли Якоб (Bernoulli Jacob) 311
Бернулли числа 88
Бесконечная геометрическая прогрессия 60, 61
— последовательность, см. Последовательность
Бесконечный ряд, см. Ряд
Биномиальная теорема 26
— формула 26, 36
Биномиальное разложение 83, 84
Биномиальные коэффициенты 26, 28
Биссектрисы угла 212
Больцано (Bolzano) 493
Больцано-Вейерштрасса теорема 493, 495
Большая ось эллипса 182
Браге (Brahe) 299
Вектор 114
—	, длина 115, 135, 166, 176
—	единичный 169
—	— касательный 267—271
—	— нормальный 272
—	, координаты 123, 127
—	, направление 135
—	нулевой 116, 118, 174
—	, параллельный данной прямой 170
—	, полярный угол 135
—	противоположный 116
Векторная функция 244
-----, годограф 244
—	— двух переменных 347
—	—, интеграл 248
—	—, кинематическая интерпретация 244, 245
-----, координаты 245
—	—, непрерывность 247, 251, 252
—	—, ограниченность 247, 251
—	—, основные правила математического анализа 248, 249
—	—, первообразная 248
-----, предел 247, 252
—	—, производная 247, 252, 253
Векторное пространство 119
—	— бесконечномерное 178
----- двумерное 122, 124
—	— п-мерное 174
----- трехмерное 127
Векторы в пространстве 121, 126, 127
—	— n-мерном пространстве 174
—	, вычитание 118
—	, доказательства геометрических теорем 131—133
—	зависимые 178
—	независимые 126, 127
—	на плоскости 121—126
—	ортогональные 163
—	свободные 114
—	связанные 113
—	, сложение 115—118, 123, 127, 174
—	, умножение на число 118—121, 123, 127, 174
—	, — скалярное, см. Скалярное произведение
—	, упорядоченные пары чисел как векторы 124, 125
536
Алфавитный указатель
Верхний интеграл 501
—	предел последовательности 492
—	— функции 509
Верхняя сумма 501
Вершина параболы 183
Вершины гиперболы 183
—	эллипса 183
Ветви гиперболы 183
Внутреннее произведение, см. Скалярное произведение
Возрастающая последовательность 52
Волновое уравнение 407
Вырожденная кривая 218
—	поверхность 228
Галилея закон 297
—	принцип относительности 313
Гамильтон (Hamilton) 112, 451
Гамильтона — Якоби теория 451
Гармонический ряд 59
Гиббс (Gibbs) 112
Гипербола 180
—	, асимптоты 184
—	. вершины 183
—	, ветви 183
—	, директрисы 186
—, каноническое уравнение 182, 224, 225
—. оси 182
—	, параметрические уравнения 201
—	равнобочная 180, 200
—	, уравнение в полярных координатах 199
—	, фокальное расстояние 185
—	, фокусы 185
—	, центр 182
—	, эксцентриситет 185, 199
(См. также Коники)
Гиперболический параболоид 233—235, 240
—	цилиндр 229
Гиперболоид, см. соотв. названия
Гиперплоскость 175
Гипоциклоида 262
Годограф 244
Гомотопные кривые 387
Гравитационная сила 460, 461
Градиент 347, 354
Граница интервала 324
—	множества 330
—	области 475
—	— правильно ориентированная 476
Граничная точка множества 330
—	— области 475
Грассман (Grassmann) 112
График векторной функции 244
— функции нескольких переменных 331, 332
Грин (Green) 476
Грина теорема 475—480
— формула 476
Гульдин (Guldin) 473
Гюйгенс (Huygens) 310, 311
Даламбера признак 68
Движение вращательное 287, 288
— криволинейное 285
— периодическое 307, 308
— планет 299—305
— плоское 285, 288—290
— под действием силы тяжести 292, 293
— по заданной траектории 295, 296, 306—311
— — наклонной плоскости 296, 297
— системы 312—316
(См. также Законы Кеплера, Законы Ньютона)
Двойной интеграл 410
— —, аналитическое определение 420, 421
— — в полярных координатах 435—437
— — как повторный 410—415
— — от ступенчатой функции 424, 425, 499, 500
— —, свойства 421, 422, 429, 430
— —, существование 424, 499—508
Двуполостный гиперболоид 232, 234, 240, 241
— — вращения 232
Действительная ось гиперболы 182
Деление отрезка в данном отношении 130, 142
Директриса параболы 186
Директрисы гиперболы 186
— эллипса 186
Дискриминант 218
— нулевой 225, 226
— отрицательный 224, 225
— положительный 223, 224
Дистрибутивность скалярного произведения 165, 166
— сложения и умножения вектора на число 119—121
Дифференцирование неявной функции 350 — под знаком интеграла 357—359, 498, 499 — степенного ряда 76, 104
(См. также Частные производные, Цепное правило)
Дифференцируемая функция 336, 337, 351, 352
Длина вектора 115, 135, 166, 176
— дуги 272—275, 277, 278
— направленного отрезка 112
Долгота 162
Допустимая замена параметра 266
Дуги кривой 256
Евклидово векторное пространство 166, 176
Единичная окружность 200, 244
Единичные нормали 171
Алфавитный указатель
537
Единичный вектор 169 -----касательный 267—271 ----- нормальный 272
Зависимые векторы 178
Задача двух тел 313, 314
Закон всемирного тяготения 299, 303
—	Галилея 297
—	Кеплера второй 299—301
-----первый 299, 301, 302
—	— третий 303
—	Кулона 319
— Ньютона второй (закон движения) 291, 292
—	— первый (закон инерции) 292
—	— третий 314
—	сохранения линейного импульса 315
Замена системы координат в пространстве 236, 237 —-------на плоскости 206
Замкнутая кривая 262 Замкнутое множество 497 Замкнутый интервал 324 — — п-мерный 327 Зенон (Zeno) 39
Зенона парадокс 39
«Зеркальные» свойства коник 213, 214
Знакопеременный ряд 70, см. также Абсолютно сходящийся ряд
Изменение параметра 254
Интеграл верхний 501
—	двойной, см. Двойной интеграл
—	криволинейный, см. Криволинейный интеграл
—	несобственный, см. Несобственные кратные интегралы
—	нижний 501
—	от векторной функции 248
—	повторный, см. Повторные интегралы
—	Римана 501
—	тройной, см. Тройной интеграл — эллиптический 276, 309 Интегральная сумма 425 Интегральный признак сходимости 65, 66
Интегрирование в полярных координатах 263, 277, 435—437, 487, 488 — — сферических координатах 455—457 -----цилиндрических координатах 451—453 — степенного ряда 76, 103 z Интервал замкнутый 324, 327 — открытый 324, 327 — сходимости степенного ряда 75
Кавальера (Cavalieri) 473
Кавендиш (Cavendish) 304
Канонические уравнения квадрик в пространстве 229, 231—233 --------на плоскости 182
Кардиоида 262
Касательная плоскость 337
Касательные к коникам 193—196
Касательный вектор 268, 269
Квадрики в пространстве 228
—	— —, канонические уравнения 229, 231 —233
—	— —, основная теорема 239—241
---------, плоские сечения 237, 238
—	на плоскости 218
— — —,	дискриминант	218
---------,	канонические	уравнения	182
—-------,	основная теорема 220—226
---------,	след 218
(См. также соотв. названия)
Кватернионы 112
Кеплер (Kepler) 299, 473
Кеплера законы 299—303
Класс эквивалентности 114
Коммутативность скалярного произведения 165, 166
—	сложения векторов 116
Компактное множество 497, 498
Конец направленного отрезка 112
Коники 180
—	в полярных координатах 197—199
—	, геометрические свойства 187
—	, «зеркальные» свойства 213, 214
—	, канонические уравнения 182
—	, касательные 193—196
—	конфокальные 215
—	, форма 199
(См. также Гипербола, Парабола, Эллипс)
Консервативное поле 393
Конус 240
— круговой 159, 160, 162, 181, 229, 230
— эллиптический 229, 230
Координаты аффинные 129, 177, 241
—	барицентрические 319
—	вектора 123. 127
—	векторной функции 245
— полярные, см. Полярные координаты
—, преобразования 206, 207, 236—239
— сферические, см. Сферические координаты
— цилиндрические, см. Цилиндрические координаты
Коши критерий 494, 495
—	неравенство 166
—	теорема 13
—	, умножение рядов 72, 73, 99, 100
—	условие 494, 495, 510
Коэффициенты биномиальные 26, 28
—	степенного ряда 74
—	Тейлора 23
Кривая алгебраическая 216, 217
—	второго порядка, см. Квадрики на плоскости
538
Алфавитный указатель
Кривая вырожденная 218
—	замкнутая 262
—	ориентированная, см. Ориентированная линия
—	простая 468
(См. также по названиям кривых)
Кривизна 279, 280
—	графика 281
—	, знак 280
—	, окружность 282
—	, радиус 282
—	, центр 282
Криволинейный интеграл 375, 376
— —, векторные обозначения 390, 391
— —, независимость от параметра 377, 378
— —,-------пути интегрирования 382—385
— —, свойства 378, 379
Критерий частных 68, 69
Критические точки 345, 354, 368, 369, 403—405
Круговой конус 159, 160, 162, 181, 229, 230
— маятник 309
— цилиндр 157, 159, 160
Кусочно-непрерывная функция 419, 447, 464, 504—508
Кулон (Coulomb) 319
Кулона закон 319
Лагранжа теорема 10—12
Лапласа уравнение 490
Лгверье (Leverrier) 304, 305
Левый репер 205, 239
Лейбниц (Leibniz) 310, 311
Лейбница ряд 71
— теорема 70
Леонардо (Leonardo) 42
Лёвнер (Loewner) 205
Лёвнера эллипс 205
Линейная векторная функция 244
— функция нескольких переменных 332, 336, 337, 351, 352
Линейное приближение 10, 17, 337, 352
— уравнение 145
Линейный импульс 315
Линейчатая поверхность 235
Линия алгебраическая 216, 217
—, длина 272—275, 277, 278
—, кривизна 279
— ориентированная, см. Ориентированная линия
— уровня 347—349
(См. также Кривая)
Логарифмическая спираль 140, 141
Логарифмический потенциал 490
Лопиталь (L' Hospital) 91
Лопиталя правило 90—95
Мажорирующий ряд 63
Маклорен (Macl aurin) 25
Маклорена ряд 79
—	формула 25
(См. также Тейлора ряд, Тейлора формула)
Максвелл (Maxwell) 112
Максимум абсолютный 370
—	локальный 368, 369
—	строгий 369
—	, существование 495, 498
Малая ось эллипса 182
Математический маятник 297 , 298
Материальная пластинка 459
—	струна 459
Меридианы 162
Минимум абсолютный 370
—	локальный 368, 369
— строгий 369
— существование 495, 498
Мнимая ось гиперболы 182
Многочлен от двух переменных 216
Множество замкнутое 497
— компактное 497, 498
—, объединение (сумма) множеств 331, 430, 498
— ограниченное 497
— односвязное 363, 374
— открытое 330, 331
—, пересечение (произведение) множеств 331
— связное 357
Модуль направленного отрезка 112
Монотонная последовательность 52, 96
Направление вектора 135
—	наибыстрейшего возрастания функции 346
Направленный отрезок 112
—	угол между прямыми 209
Направляющие косинусы 168—170
—	углы 168, 169
Начало направленного отрезка 112
Начальная скорость 292
Начальное положение 292
Невозрастающая последовательность 52
Независимые векторы 126, 127
Непараметрическое представление ориентированной линии 257, 258
—	— поверхности 332
Непересекающиеся множества 430
Непрерывно дифференцируемая функция 340, 352, 367
Непрерывность векторной функции 247, 251, 252
— суммы степенного ряда 76, 102, 103
—	функции двух переменных 325
—	— п переменных 328
(Cjh. также Теоремы о непрерывных функциях)
Неравенство треугольника 166, 176
—	Шварца 166, 176
Несобственные кратные интегралы 481
Алфавитный указатель
539
—-------от неограниченных подынтеграль-
ных функций 481, 482
--------по неограниченным областям интегрирования 484, 485
Неубывающая последовательность 52
Неявная функция 350
Нижний интеграл 501
— предел последовательности 492
----функции 509
Нижняя сумма 501
Нормаль к поверхности 341
n-мерное векторное пространство 174
-------- евклидово 176
Нулевой вектор 116, 118, 174
Ньютон (Newton) 25, 26, 83, 299, 303, 311, 463
Ньютона биномиальная формула 26
— законы 291, 292, 314
Ньютонов потенциал 490 х
Область выпуклая 430
—	интегрирования 429
—	односвязная 389
—	определения функции 322
Объединение множеств 331, 430, 498
Объем, вычисление 410—414, 450, 451
—	п-мерный 466
—	тела вращения 454
----, образованного вращением плоской фигуры 473
Ограничение функции 255
Ограниченная векторная функция 247, 251 — последовательность 52, 492—494 — функция двух переменных 419
Ограниченное множество 497
Однополостный гиперболоид 232, 234, 235, 240, 241
----вращения 232
Односвязное множество 363, 374
Одночлен от двух переменных 216
Окрестность 324
Окружность 180, 200
—	единичная 200, 244
—	кривизны 282
Ориентация в пространстве 215
—	на плоскости 205
Ориентированная линия 254, 284
---- гладкая 266
----, изменение параметра 254
----кусочно-гладкая 283
----, непараметрическое представление 257, 258
----—, параметрическое представление 253, 254, 257, 258, 277, 278
—	— противоположная 254
—	—, траектория 255
Ортогональные векторы 163
Ортонормированный базис, см. Репер
Оси гиперболы 182
—	эллипса 182
Особая точка кривой 283
Остаточный член формулы Тейлора 25, 401, 406
----------в форме Коши 109
----------------Лагранжа 109
Ось параболы 182
Открытое множество 330, 331
Открытый интервал 323
—	— п-мерный 327
Отношение эквивалентности 113, 114
Отражение в пространстве 239
—	на плоскости 202, 206
Папп (Pappus) 467, 473
Паппа теоремы 473, 474
Парабола 180
—	, вершина 183
—, директриса 186
—, каноническое уравнение 182, 225, 226
—, ось 182
—, уравнение в полярных координатах 199 i —, фокус 185
(См. также Коники)
Параболический цилиндр 229, 240
Параболоид вращения 232, 233
— гиперболический 233—235, 240
— эллиптический 232, 234, 240
Параллели 162
Параметр 143, 244
Параметрические уравнения гиперболы ’201
----окружности 200
— — циклоиды 261
---- эллипса 200
Параметрическое представление векторной функции 244
— — ориентированной линии 253, 254, 257, 258
----прямой 143, 144
Паскаль (Pascal) 310, 311
Пеано (Peano) 266
Пеано аксиомы 266
— кривые 266
Первообразная векторной функции 248
Пересечение множеств 331
Период 308
— вращательного движения 288
— колебаний кругового маятника 298, 309
---- циклоидального маятника 310
Плоскость 145
—, параллельность двух плоскостей 148, 149
—, пересечение с поверхностью второго порядка 237, 238
—, — — круговым конусом 181
—, положение относительно прямой 152
540
Алфавитный указатель
Плоскость, представление линейным уравнением 145, 146
—, — уравнением в нормальной форме 171, 172
Плотность 458, 459
Площадь 430, 439, 440, 488, 489
— в полярных координатах 262, 263, 437
—, вычисление с помощью криволинейного интеграла 477, 478
— наклонной плоской области 440, 441
— поверхности 442, 443
— — вращения 445, 446
— —, образованной вращением плоской линии 473
Поверхности второго порядка, см. Квадрики в пространстве
—	изотермические 355
—	эквипотенциальные 355, 393
Поверхность 332
—	алгебраическая 228
—	вращения 159, 445, 446
—	вырожденная 228
—	линейчатая 235
—	уровня 355
Повторные интегралы 414, 448, 505—508
Поворот в пространстве 238, 239
— на плоскости 204, 205
Погрешность линейного приближения 17, 337
—	, оценка для правила Симпсона 105—107
—	,------трапеций 104, 105
—	параболического приближения 19, 20 '
Подпоследовательность 46
Полярные координаты 135, 136
—	—, вычисление двойного интеграла 435—437, 487, 488
—	—, изображение кривых 139—141
—	—, связь с декартовыми 135
—	—, теорема косинусов 137
—	—, уравнения коник 197—199
—	—, формула длины дуги 277
---, площади 262, 263, 437, 477, 478
—	—, — расстояний 137
—	—, формулы для координат касательного вектора 270, 271
Полярный угол вектора 135
—	— единичного касательного вектора 269
Порядок алгебраической линии 216
--- поверхности 228, 237
Последовательность 41
— действительных чисел 492—494
— монотонная 52, 96	i
— ограниченная 52, 53, 492—494
—, предел 43—49, 492, 494, 495
— равномерно сходящаяся 510
— расходящаяся 49, 50
— сходящаяся 43, 44, 492, 495
— точек 494, 495
— частных сумм ряда 55, 56
Потенциал 393
Правило параллелограмма 117
— треугольника 115, 117
— цепное, см. Цепное правило
Правый репер 205, 239
Предел векторной функции 247, 252
— последовательности 43—49, 492, 494, 495
— функции нескольких переменных 328, 329
Предельная точка 328
Признак сравнения рядов 63
Проекция области 441
— точки 441
Произведение вектора на число 118, 119
— векторов скалярное, см. Скалярное произведение
— множеств 331
— рядов по Коши 72, 73, 99, 100
Производная в заданном направлении 345, 346, 355
— векторной функции 247, 252, 253
— частная, см. Частные производные
Противоположный вектор 116
Прямая в пространстве 143
— — —, параметрическое представление
143, 144
—-------, положение относительно плоскости
152
—	— —, представление в виде линии пересечения двух плоскостей 149—151
—	— n-мерном пространстве 175
Работа 392
Равномерно непрерывная функция 496
—	сходящаяся последовательность 510
—	сходящийся ряд 510
Радиус кривизны 282
—	сферы 155
—	сходимости степенного ряда 75, 101
Радиус-вектор 128, 134
Размер разбиения 500
Разность векторов 118
Раскрытие неопределенностей вида 0/0 91
—	— — оо/оо 92, 93
— — — других видов 94, 95
Расстояние между двумя точками п-мерного пространства 176
— от точки до плоскости 172, 173
----------- прямой 173
Расходящаяся последовательность 49, 50
Расходящийся несобственный интеграл 481, 484
— ряд 59, 60
Резерфорд (Rutherford) 319
Репер 123, 127
— левый 205, 239
— правый 205, 239
—, преобразования 202—205, 238, 239
Риман (Riemann) 71
Алфавитный указатель
541
Римана дзета-функция 66
— интеграл 499, 501
— сумма 425
Ролль (Rolle) 12
Ролля теорема 12
----в сильной форме 496
Ряд 55
— абсолютно сходящийся 70—73» 96, 97, 99, 100
—	биномиальный 83, 84
—	гармонический 59
—	знакопеременный 70
—	мажорирующий 63
—	, необходимое условие сходимости 58
—	, операции над рядами 62
—	, признаки сходимости 63, 65, 68, 70
—	равномерно сходящийся 510
—	расходящийся 59, 60
—	с положительными членами 63
—	степенной, см. Степенные ряды
—	, сумма 56
—	сходящийся 56, 57
—	Тейлора, см. Тейлора ряд
—	, частная сумма 55
Свободный вектор 114
Связанный вектор 113
Связное множество 357
Седло 369, 405
Сигма-символика 34, 35
Симметрия кривых 139
— сферическая 462
— центроидов 317, 471
Скаляр 119
Скалярное кратное 119
— произведение 163, 176
----, вычисление 164
----, свойства 165, 166
Скорость 285
—, численная величина 286, 287
Скрещивающиеся прямые 152
След 218
Соприкасающаяся окружность 282
Степенные ряды 74
----, деление 86, 87
----, дифференцирование и интегрирование 76, 103, 104
----, непрерывность суммы 76, 102, 103
----, основные определения 74, 75
----, подстановка ряда в ряд 89
----, сходимость 75, 100, 101
----, умножение 85
Степень одночлена от двух переменных 216
—	измельчения 500
Ступенчатая функция 423—425, 499, 500
Сумма векторов 115, 116
—	верхняя 501
—	интегральная 425
—	множеств 331, 430
—	нижняя 501
—	Римана 425
—	ряда 56
—	— частная 55
Сфера 155, 162, 231
—	в n-мерном евклидовом пространстве 176
Сферически симметричная функция 462
Сферические координаты 160
—	—, вычисление тройного интеграла 455—457
—	—, связь с декартовыми 161
----,------цилиндрическими 455
Сходящаяся последовательность 43, 44, 492, 495
Сходящийся несобственный интеграл 481, 484
—	ряд 56, 57
Твердое тело 316
Тейлор (Taylor) 21
Тейлора коэффициенты 23 ч.
— многочлен 21, 22, 401, 405
—	ряд 79
— — для основных элементарных функций 81
— теорема 24, 25
— — для функции двух переменных 399—402
—-------— п переменных 405, 406
— формула 25, 29, 36
— — для показательной функции 33, 38
-------- синуса и косинуса 34, 38
--------функции (1 + х)а 27, 28, 37
-----------In (1 + х) 30, 38
----— — двух переменных 401
----— — п переменных 405
Тело вращения 454
Теорема анализа основная (для векторных функций) 248, 249
— биномиальная 26
— Больцано—Вейерштрасса 493, 495
— Грина 475—480
— о движении центроида системы частиц 315
----дифференцировании под знаком интеграла 357, 498, 499
----знакопеременных рядах (теорема Лейбница) 70
----конечном приращении (теорема Лагранжа) 10—12
-----------обобщенная (теорема Коши) 13, 14
---- критических точках 369, 403—405
----мажорирующих рядах (признак-сравнения) 63
----независимости криволинейного интеграла от пути интегрирования 382—385
---- перестановке членов знакопеременного ряда 71, 96—98
----представлении плоскости линейным уравнением 145, 146
$42
Алфавитный указатель
Теорема о равенстве повторных интегралов 420, 421, 508
— — — смешанных производных 360, 398, 399
— — сохранении энергии 395
— — существовании двойного интеграла 424, 499—508
— — — функции с заданными частными производными 362, 363
— — сходимости монотонной последовательности 52, 53, 96
— — — степенного ряда 75, 100, 101
— об интегрировании в полярных координатах 436, 487, 488
— — умножении абсолютно сходящихся рядов 72, 99, 100
— — — степенных рядов 85
— Ролля 12, 496
— сравнения для несобственных кратных интегралов 482, 485
— Тейлора 24, 25, 399—402, 405, 406
Теоремы о квадриках в пространстве 235, 237—241
--------на плоскости 216—226
----кониках 187—191, 194—196, 199,
214, 215
— — непрерывных функциях 495—498, 502, 503
— — пределе последовательности 49
----свойствах векторов 116, 119, 121, 123, 124, 126
— — среднем значении для интегралов 107, 108
----степенных рядах 75, 76, 79, 100—104
----частных производных 339, 340, 352, 395—397
— об интегрируемости по Риману 501, 502, 505
— Паппа 473, 474
Тор 475
Точка возврата 261, 283
—	граничная 330
—	критическая, см. Критические точки
—	локального максимума 368, 369
----минимума 368, 369
—	n-мерного пространства 174
—	особая 283
—	перегиба 280
—	предельная 328
—	седлообразная 369, 405
—	строгого максимума 369
—	— минимума 369
Траектория 244, 255, 286
Трехлепестковая роза 140, 141
Тройной интеграл 448
----, вычисление в декартовых координатах 448, 449
— —,-------сферических координатах
455—457
-----,-----цилиндрических координатах 451—453
Трохоида 262
Убывающая последовательность 52
Угол между векторами 163, 165, 177 — — линиями 210 -----плоскостями 172 -----прямыми 170, 209
Уравнение теплопроводности 408
Ускорение 286
— вращательного движения 288
— касательное (тангенциальное) 289, 290
— нормальное 289, -290
Условие интегрируемости 362
Условия интегрируемости 373
Факториал 35
Ферма (Fermat) 129, 310
Фибоначчи (Fibonacci) 42
Фибоначчи последовательность 41
Фокус параболы 185
Фокусы гиперболы 185
— эллипса 185
Фокальное расстояние 185
Формула площадей 443
Функция двух переменных 322
-----—, графическая интерпретация 331, 332
— — —, дифференцирование, см. Цепное правило, Частные производные
--------дифференцируемая 336—339
--------интегрируемая 481, 484
— — —, — по Риману 501, 502, 505
--------кусочно-непрерывная 419
-----— непрерывно дифференцируемая 340
-----—, — — N раз 367
— — — неявная 350
----- — ограниченная 419
— — — с заданными частными производными 361 —364
— — — ступенчатая 423—425, 499, 500
Функция нескольких переменных 327
— — —, дифференцирование, см. Цепное правило, Частные производные
-----— дифференцируемая 351, 352
—-------, интегрирование 464, 465
—-------кусочно-непрерывная 447, 464
— ------ непрерывная 328
— ------ непрерывно дифференцируемая	352
-------- однородная 408
--------, предел 328, 329
--------с заданными частными производными 373, 374
Характеристическая функция 428, 449
Указатель основных обозначений
543
Центр интервала 324, 327
—	гиперболы 182
—	кривизны 282
—	масс, см. Центроид
—	степенного ряда 74
—	сферы 155
—	эллипса 182
Центроиды материальных тел, пластинок и струн 468, 470, 471
----частиц 312—318
—	областей 469
Цепное правило для функций двух переменных 343, 344, 397, 398
----------нескольких переменных 353
Циклоида 261, 310, 311, 320
Циклоидальный маятник 310, 311
Цилиндр 228, 229, 240
—	гиперболический 229
—	круговой 157, 159, 160
—	параболический 229, 240
— эллиптический 229
Цилиндрические координаты 157
----, вычисление тройного интеграла 451—453
----, связь с декартовыми 157
— —, — со сферическими 455
----, уравнение поверхности 159
Частная сумма ряда 55
Частные производные 333, 335, 351, 352
----второго порядка 360, 361
----высших порядков 367, 368
----, геометрическая интерпретация 337—339 ----смешанные 360, 367, 368, 372, 398, 399
Частота вращательного движения 288 Четырехлепестковая роза 140, 141 Число е 33 — л 62
Член последовательности 41
— ряда 55
Указатель основных обозначений
Некоторые постоянные
(/*), Сп биномиальные коэффициенты 26
7 постоянная Эйлера 54
By числа Бернулли 88
Функции (общие обозначения)
f (/) векторная функция 244
f(x, У) функция двух переменных 322
f (хх, х2, ... , хл), /(х) функция п переменных 327 F (*, У, г) = Р (х, yt г) ех -F Q (х, У. г) е2 + 4- R(x, у, г) е3 векторная функция трех переменных 391
Шар (п-мерный) 466
Шварца неравенство 166, 176
Широта 162
Эвольвента 320
—	окружности 262
—	циклоиды 311
Эволюта 319
Эйлера постоянная 54
—	уравнение 408
Эквивалентность направленных отрезков 114
Эксцентриситет 185, 199
Эллипс 180, 223, 224
—	, вершины 183
—	, директрисы 186
—	, длина 276
—, каноническое уравнение 182, 223, 224
—, оси 182
—, параметрические уравнения 200
—, площадь, ограниченная эллипсом 201, 202
—	, уравнение в полярных координатах 199
—	, фокальное расстояние 185
—	, фокусы 185
—	, центр 182
—	, эксцентриситет 185, 199
(См. также Коники)
Эллипсоид 231, 240, 241
—	вращения 230, 231
Эллиптическая функция 298
Эллиптический интеграл 276, 309
—	конус 229, 230
—	параболоид 232, 234, 240
—	цилиндр 229
Энергия кинетическая 394
—	полная 395
—	потенциальная 393
—	, теорема о сохранении энергии 395
Эпициклоида 262
Якоби (Jacohi) 451
Якобиан 451, 452, 455
Функции специального вида
[х] целая часть числа х 37
t(s) дзета-функция Римана 66
Id характеристическая функция 428
Знаки векторного исчисления
PQ направленный отрезок 112
PQ — RS эквивалентные направленные отрезки 113
а вектор 114
| а | длина вектора 115
0 нулевой вектор 116
544
Указатель основных обозначений
{elt е2) базис 123
a=(ai, а2) выражение вектора через координаты (в данном базисе) 123
arg а аргумент (полярный угол) вектора 135
а Ь, ab, (а, Ь) скалярное произведение 163
Знаки теории пределов lim ху, lim inf ху нижний предел последова-тельности 492 lim ху, lim sup Xj верхний предел последовательности 492 lim f(x), lim inf f(x) нижний предел функции 509 lim f(x), lim sup f(x) верхний предел функции 509
Знаки дифференциального исчисления
df	. .
— , f'(O> f » производная векторной dt	функции 247
(df\	д c
Г ’ Г	’ Т"Н*о,
дх \дх/х=х0, у=у0 дх частные производные 333 fx, f, Dxf «	«	335
fyy’77^’ f*y вторые част--ные производные 361 grad F градиент 347 Знаки интегрального исчисления ь (* f (t) dt интеграл от векторной функции 248 а
J Р dx + Q dy 4- Rdz криволинейный интег-С
рал 375
J F dx криволинейный интеграл в векторном с обозначении 391
ф криволинейный интеграл по замкнутому кон-
С туру 393
у) dxdy двойной интеграл 410
d г ь
j* J f (х, у) dx dy двукратный интеграл 413
с La J
z0
]*£[/(*» У» z)dxdydz тройной интеграл 448
zi Г У1 / xt	\
J J I J f (х> у, z) dx ] dy dz трехкратный
“ L УО \ Xq	/
интеграл 448
J ...jf(xu ... , xn)dx! ... dxn
п-мерный интеграл 464
г*	c‘
J	dxi	J dx2	...	dxn-1	J f(xt, ... , xn)dxn
Qi	a*	an
n-кратный	интеграл	465
4-00
J J f (*» У) dx dy несобственный двойной интег-— 00
рал 484
£[/(*, У) dxdy верхний интеграл 501
JJ*/(•*•» у) dxdy нижний интеграл 501
Некоторые другие знаки
I
2 суммирование 35
i=k
max (а, р) большее из двух чисел 38
min (а, р) меньшее из двух чисел 85
<4 направленный угол между двумя прямыми 209
U объединение множеств 331
П пересечение множеств 331
mesh размер разбиения 500
Липман Берс
МАТЕМ АТИЧЁСКИЙ	АНАЛИЗ
т. II
Редактор А. М. Суходский Художник-график Д. С. Котлов Художественный редактор В. И. Пономаренко Технический редактор Э. М. Чижевский Корректор Г. И. Кострикова
Сдано в набор 6/VI11-74 г. Подп. к печати 16/Х-75 г. Формат 70x90/16. Бум. тип. № 2. Объем 34 печ. л. Усл. п. л. 39,78. Уч.-изд. л. 35,33. Изд. № ФМ-5546. Тираж 33 000 экз. Зак. 20. Цена 1 р. 12 к. БЗ-16-7-75.
Москва, К-51, Неглинная ул. д.> 29/14, Издательство «Высшая школа*
Ярославский полиграфкомбинат «Союзполиграфпро-ма» при Государственном комитете Совета Министров СССР по делам издательств, полиграфии и книжной торговли. 150014, Ярославль, ул. Свободы, 97*