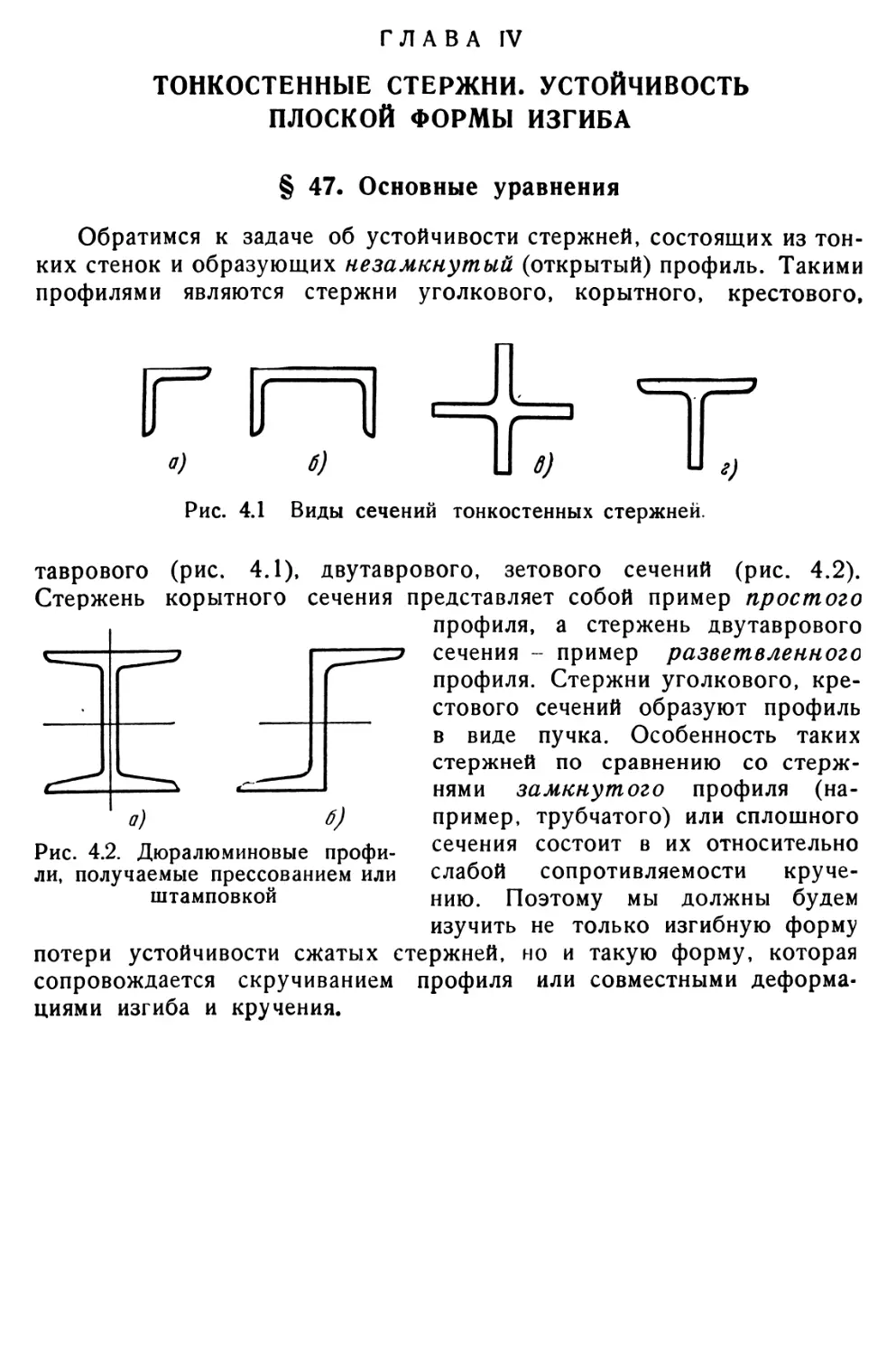
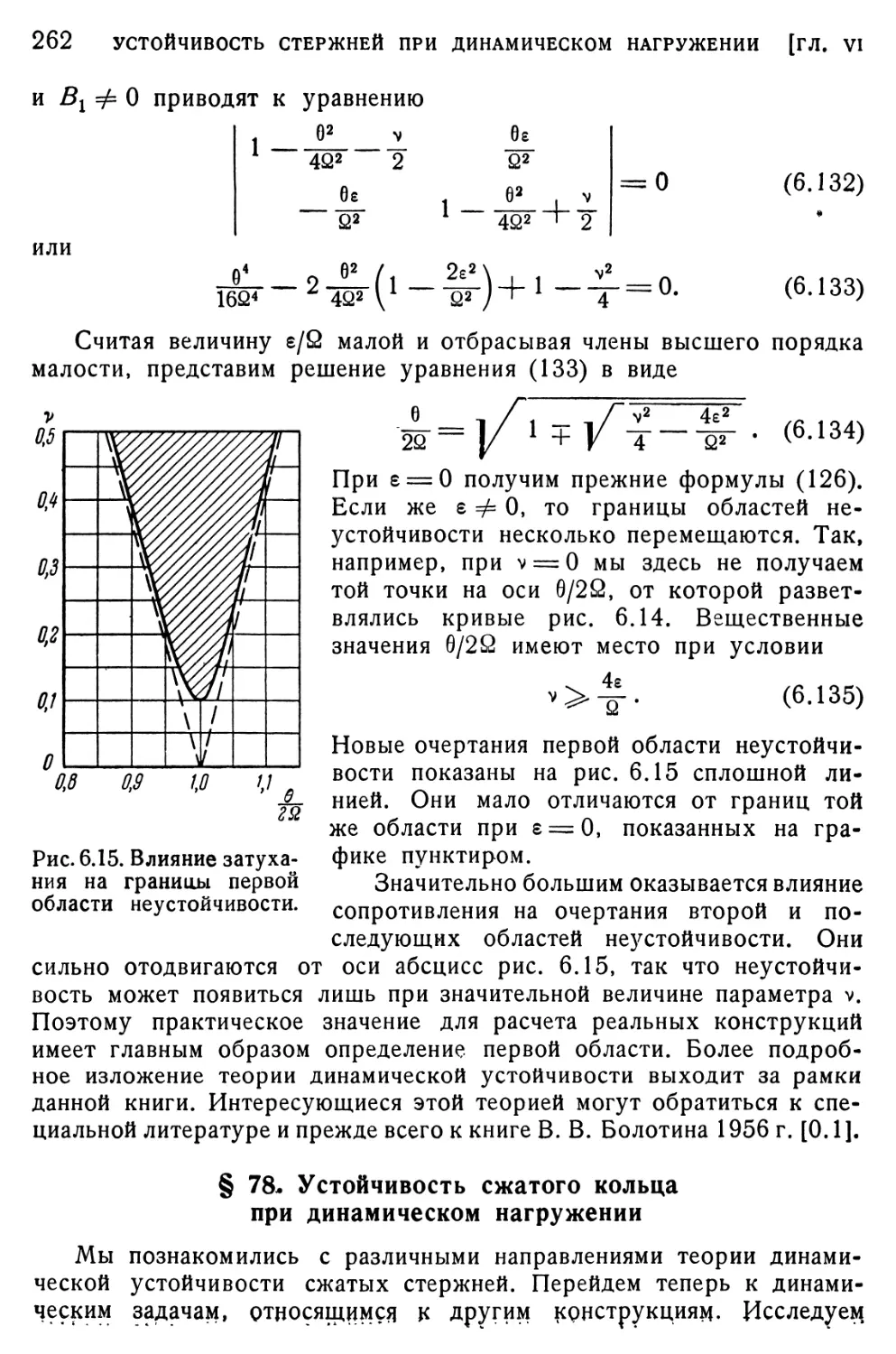
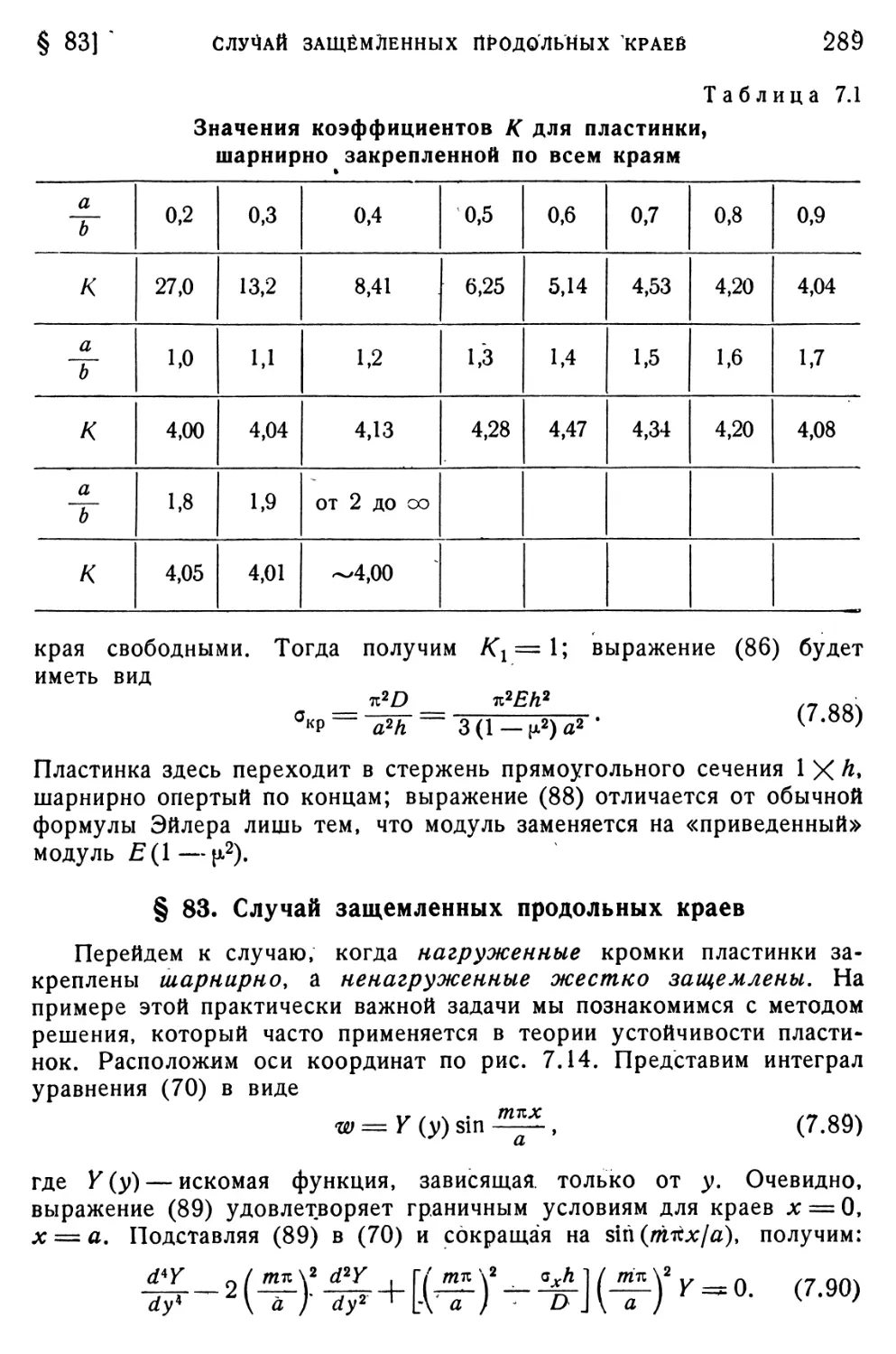
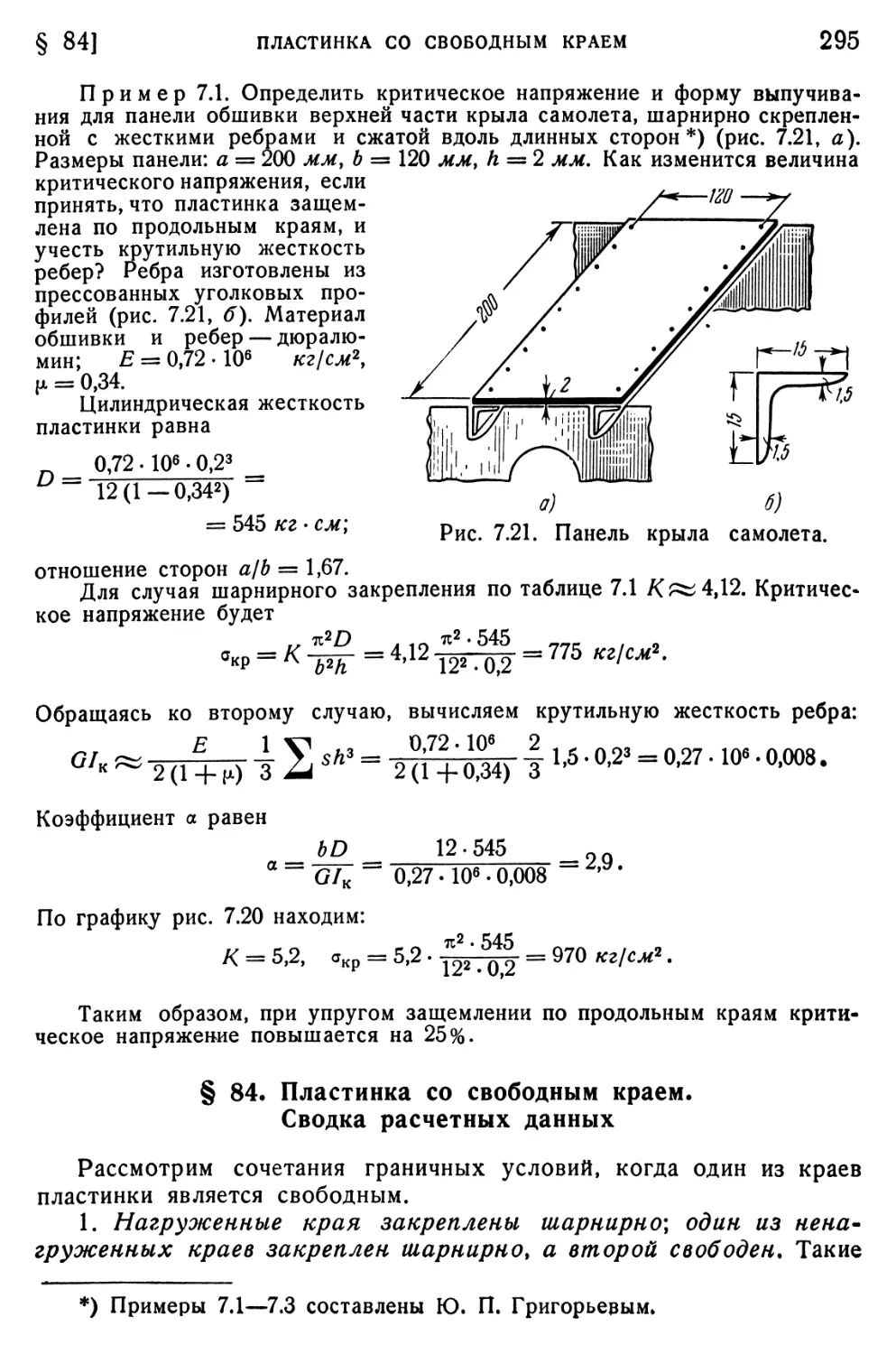
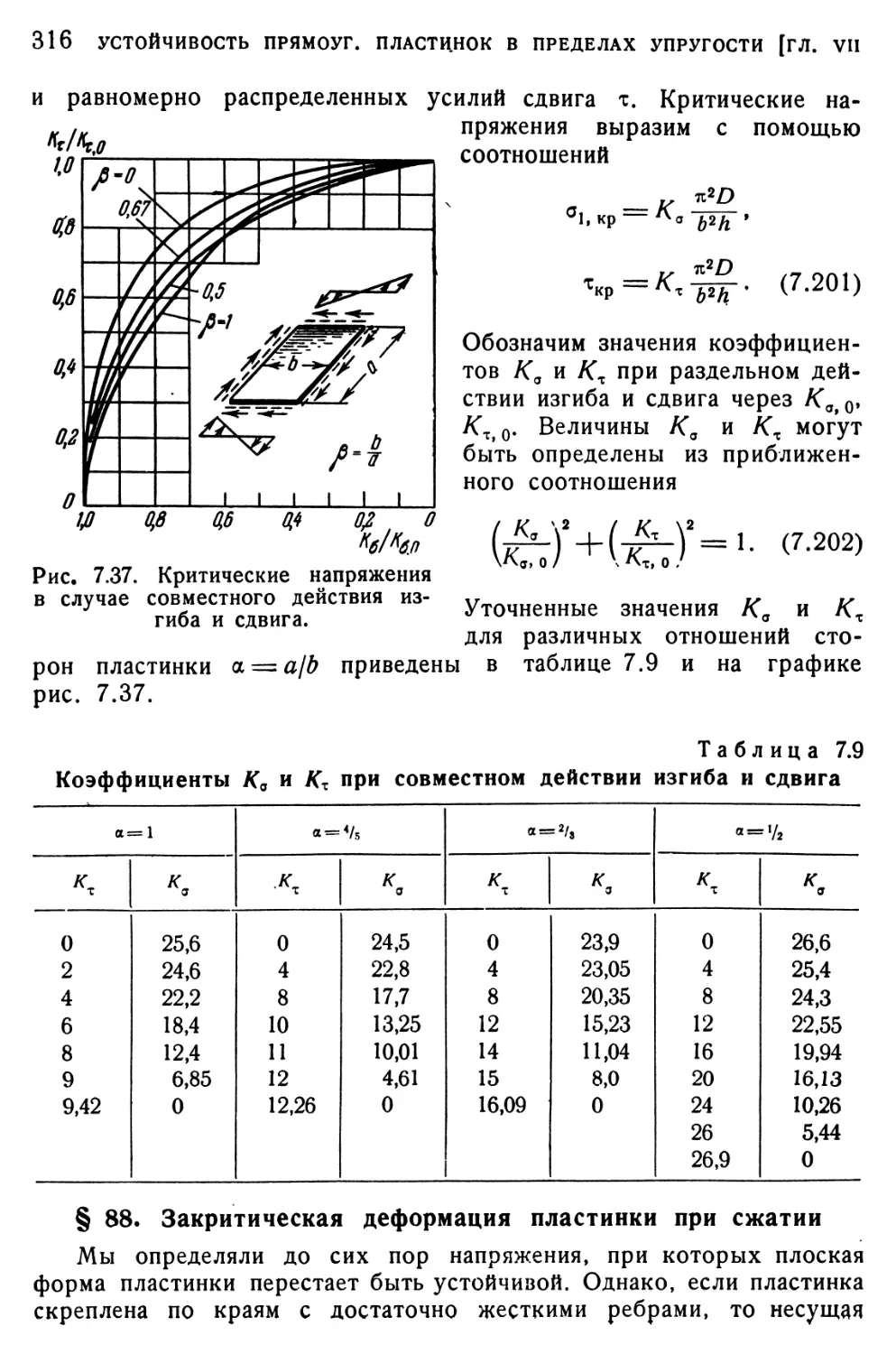
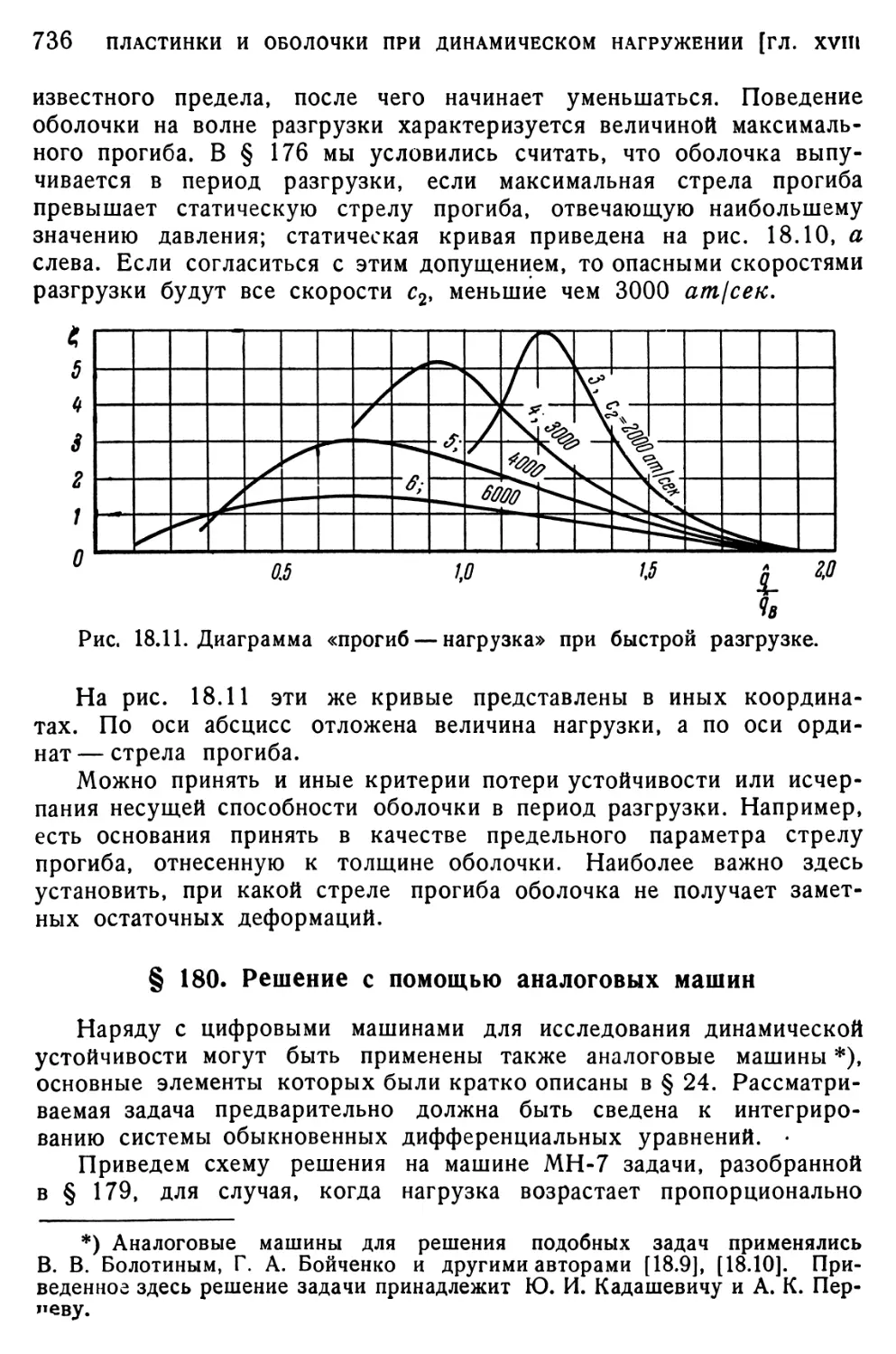
Текст
А. С. ВОЛьМИР
УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ
11
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА 1963
ОГЛАВЛЕНИЕ
Предисловие 10
Глава I. Устойчивость сжатых стержней в пределах упругости 13
§ 1. Основные понятия 13
§ 2. Устойчивость стержня, шарнирно опертого по концам. Формула Эйлера 15
§ 3. Другие случаи закрепления концов 21
§ 4. Пределы применимости формулы Эйлера 25
§ 5. Равновесные формы в закритической области 26
§ 6. Различные критерии устойчивости и методы решения
задач 32
§ 7. Приложение принципа возможных перемещений 36
§ 8. Энергетический критерий устойчивости 38
§ 9. Методы Ритца и Тимошенко 41
§ 10. Метод Бубнова—Галеркина,. 45
§ 11. Метод конечных разностей. Упругая шарнирная цепь... 47
§ 12. Метод ко л локации 50
§ 13. Метод последовательных приближений 51
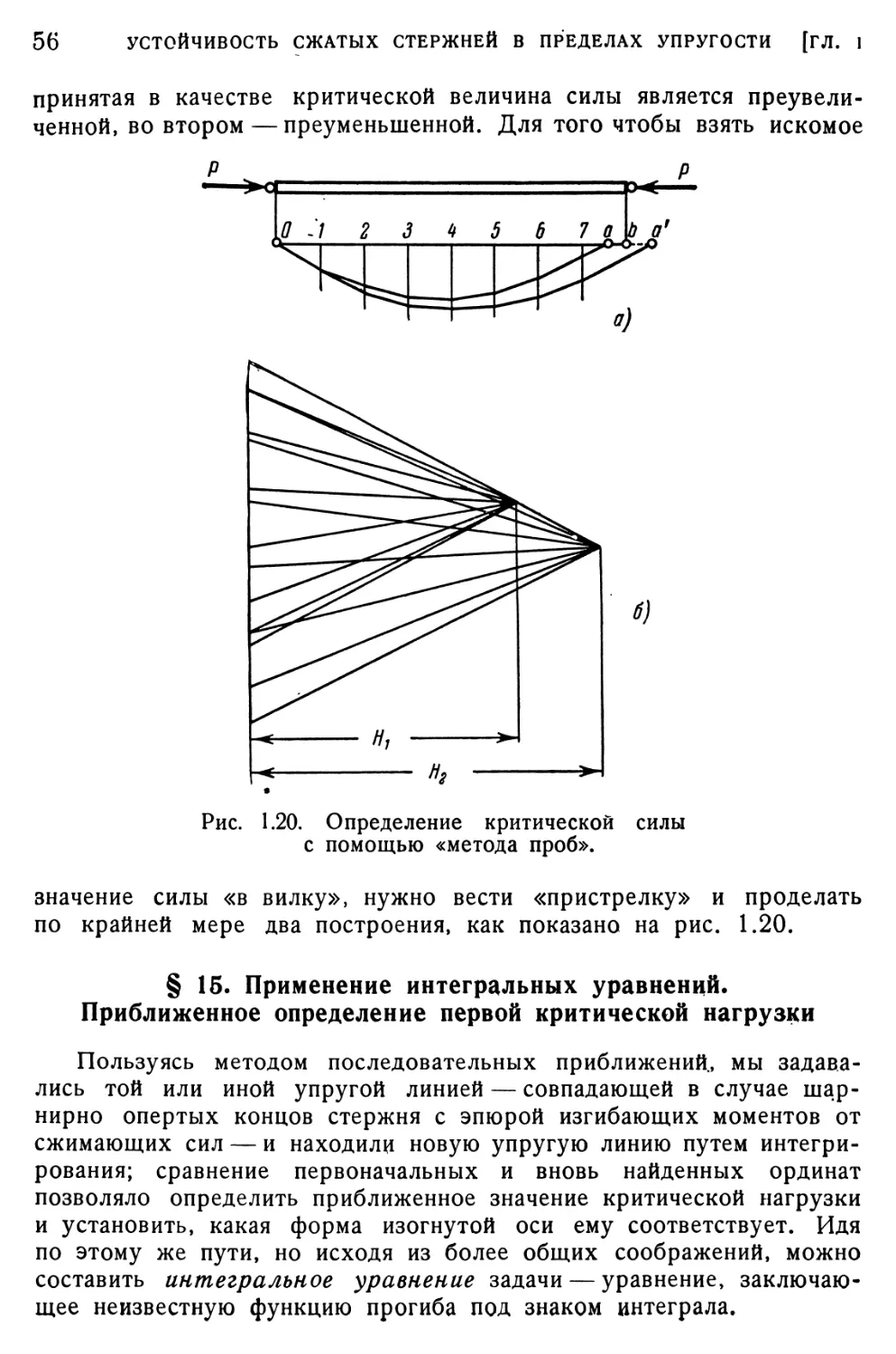
§ 14. Метод проб 55
§ 15. Применение интегральных уравнений. Приближенное определение первой критической нагрузки 56
§ 16. Динамический критерий устойчивости 60
§ 17. Критерий начальных несовершенств 63
§ 18. Эксцентричное сжатие. Приближенное решение 65
§ 19. Эксцентричное сжатие. Точное решение 67
§ 20. Влияние поперечной нагрузки 69
§ 21. Устойчивость неконсервативной системы. Случай следящей
силы 72
§ 22. Явление потери устойчивости «в большом» 75
§ 23. О выборе метода исследования. Применение цифровых электронных вычислительных машин 78
§ 24. Использование аналоговых машин 80
Глава II. Устойчивость сжатых стержней за пределами упругости 85
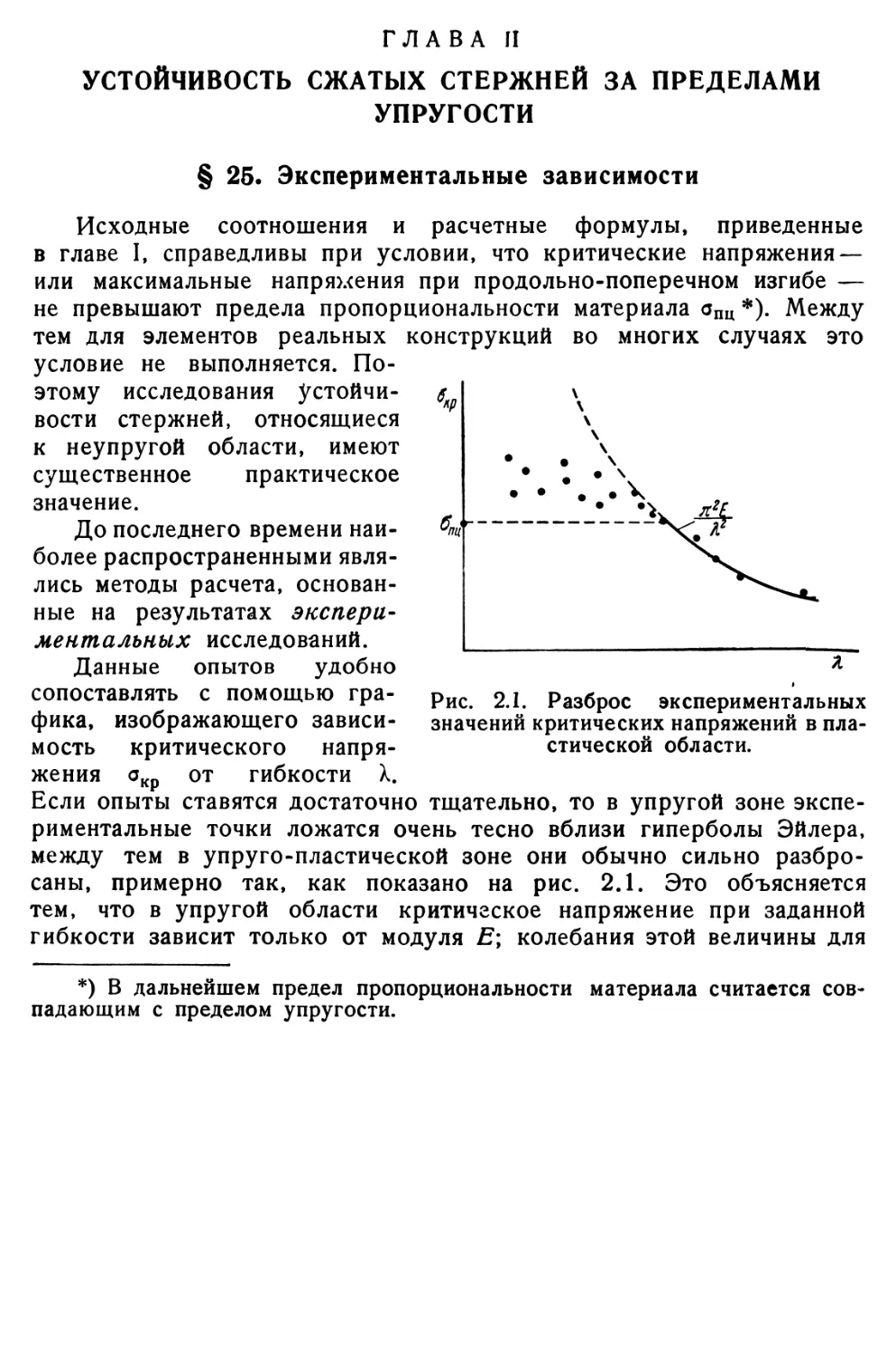
§ 25. Экспериментальные зависимости 85
§ 26. Выпучивание стержня при неизменной нагрузке 87
§ 27. Влияние формы сечения. Случаи двутаврового и прямоугольного сечений...».. • *. 90
4 ОГЛАВЛЕНИЕ
§ 28. Построение диаграммы «критическое напряжение — гибкость» 91
§ 29. Выпучивание стержня при изменяющейся нагрузке.... 95
§ 30. Стержни двутаврового и прямоугольного сечений при изменяющейся нагрузке 100
§ 31. Выбор критерия устойчивости и расчетной нагрузки... 105 § 32. Внецентренное сжатие в неупругой области. Приближенное
решение 107
§ 33. Внецентренное сжатие стержней прямоугольного и таврового сечений 110
Глава III. Более сложные задачи устойчивости стержней и стержневых систем *.. 114
§ 34. Стержни переменного сечения. Ступенчатое изменение
жесткости 114
§ 35. Случай непрерывного изменения жесткости по длине. Стержень наименьшего веса 116
§ 36. Случай сосредоточенной силы в пролете 121
37. Действие распределенной продольной нагрузки 123
§ 38. Одновременное действие распределенной и сосредоточенной
нагрузок 128
§ 39. Стержень, подвергающийся действию осевой силы и концевых пар 131
§ 40. Стержень, лежащий на нескольких жестких опорах.... 134 § 41. Случай упругой опоры. Задача о стержневом наборе. •. 137 § 42. Устойчивость стержня, связанного с упругим основанием 141 § 43. Влияние поперечной силы на критическую нагрузку.... 144
§ 44. Устойчивость составных стержней 145
§ 45. Устойчивость стержней, воспринимающих крутящий момент.
Совместное действие осевого сжатия и кручения 151
§ 46. Устойчивость кругового кольца и арки 154
Глава IV. Тонкостенные стержни. Устойчивость плоской формы
изгиба 158
§ 47. Основные уравнения 158
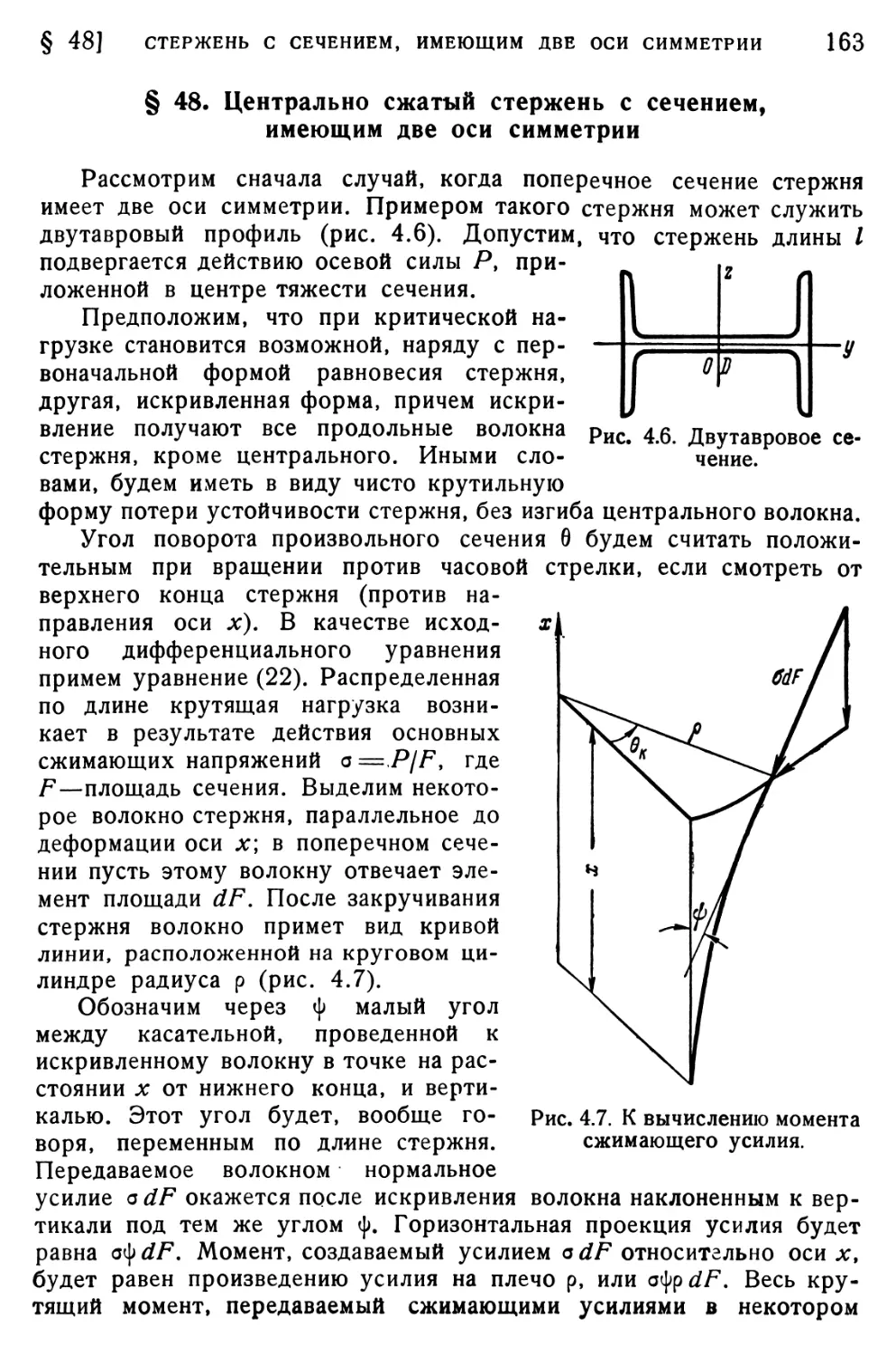
§ 48. Центрально сжатый стержень с сечением, имеющим две оси
симметрии 163
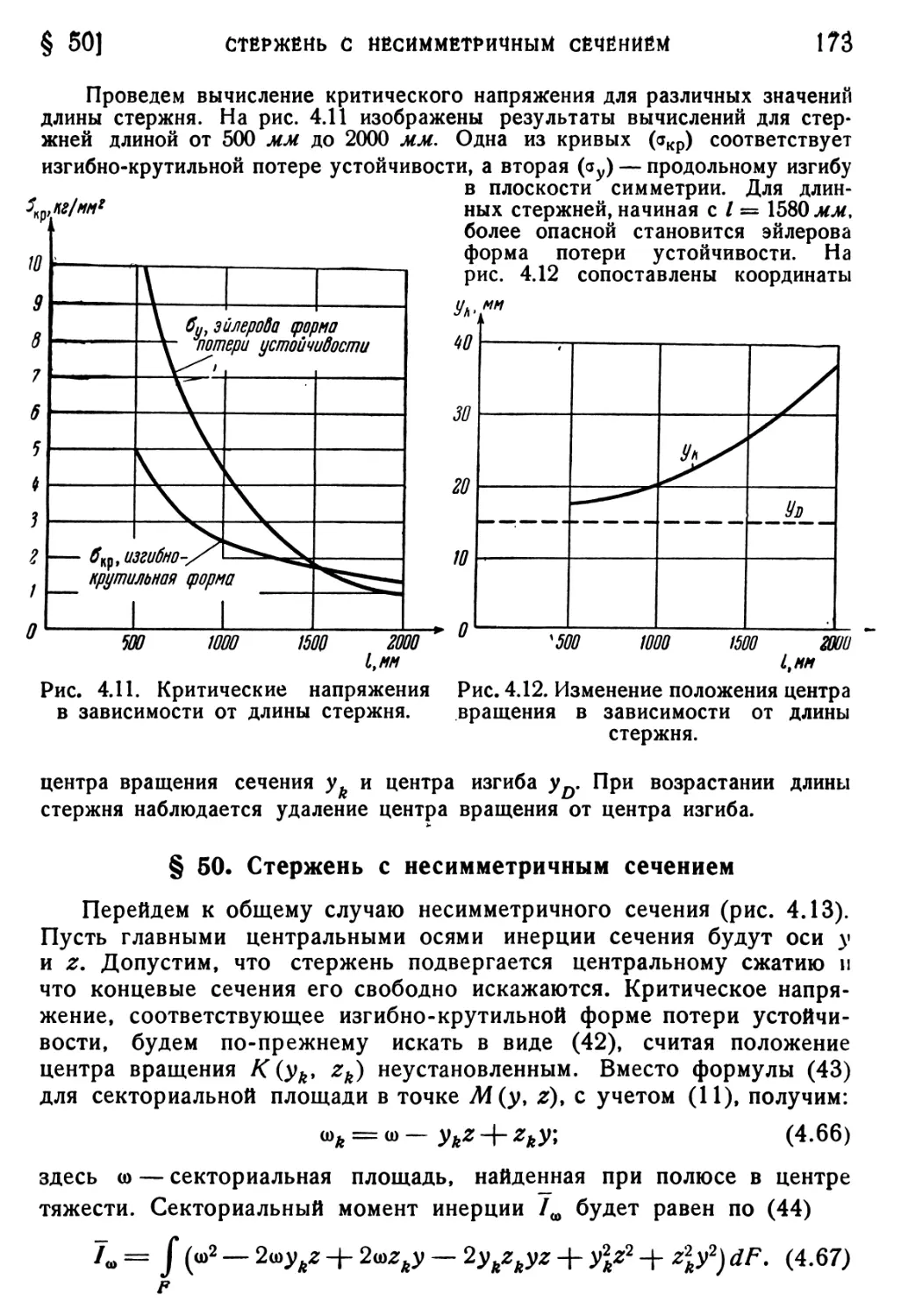
§ 49. Случай сечения с одной осью симметрии 166
§ 50. Стержень с несимметричным сечением 173
§ 51. Устойчивость плоской формы при чистом изгибе 175
§ 52. Случай внецентренного сжатия 179
§ 53. Более общие уравнения изгибно-крутильной деформации.. 183
§ 54. Устойчивость плоской формы полосы при изгибе 186
§ 55. Поперечный изгиб балок с сечением, имеющим две оси
симметрии 195
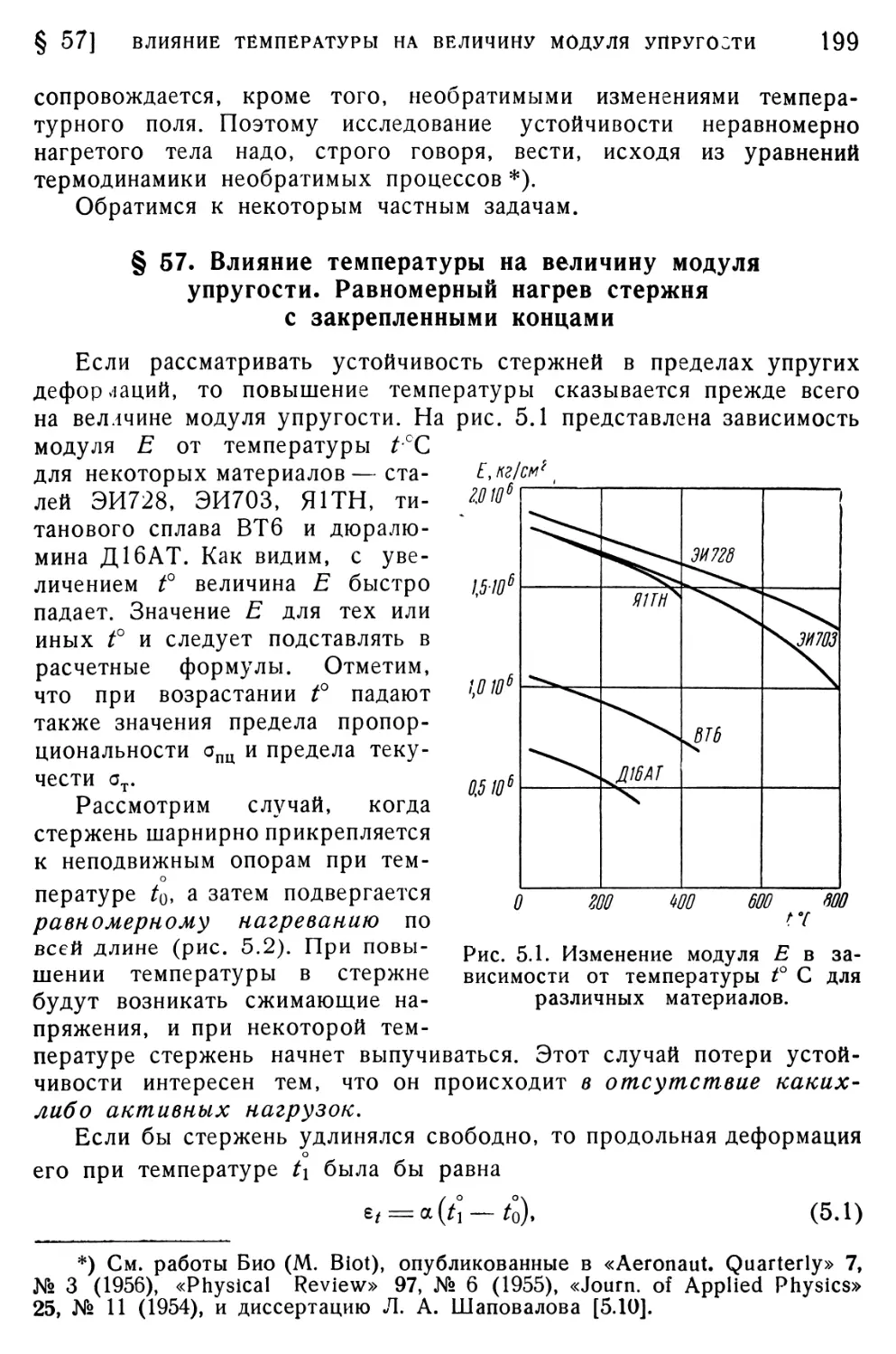
Глава V. Влияние температуры. Продольный изгиб при ползучести 198
§ 56. Задачи об устойчивости стержней, связанные с учетом
температуры 198
§ 57. Влияние температуры на величину модуля упругости. Равномерный нагрев стержня с закрепленными концами., *. 199
ОГЛАВЛЕНИЕ 5
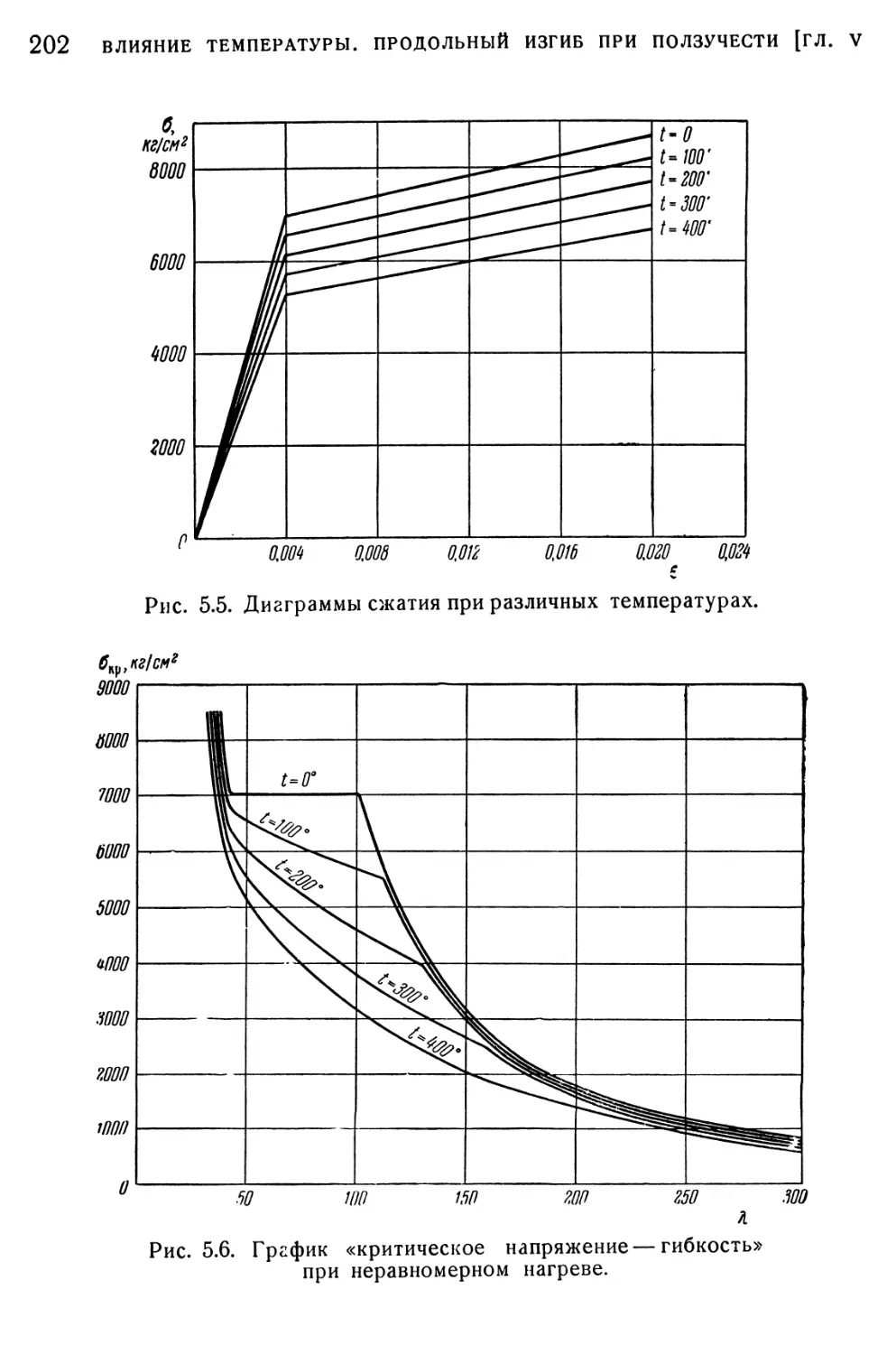
§ 58. Случай неравномерного нагрева 201
§ 59. Учет влияния теплопроводности 203
§ 60. Продольный изгиб при ползучести. Основные сведения.. 204
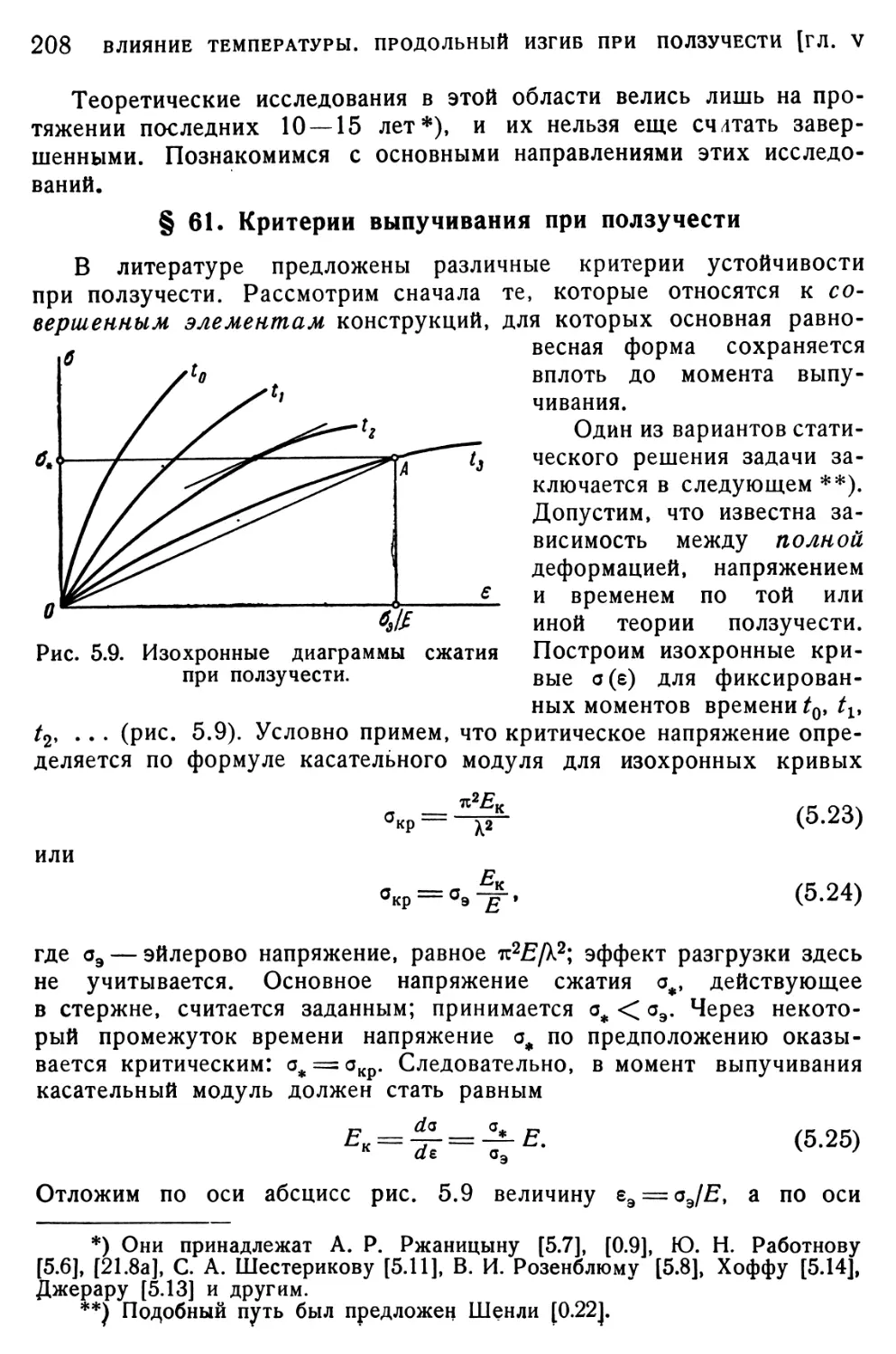
§ 61. Критерии выпучивания при ползучести 208
§ 62. Методы расчета по касательному и секущему модулям •. 210
§ 63. Динамический критерий 212
§ 64. Критерий начальных несовершенств 214
§ 65. Формулы для критического времени в случае двутаврового
сечения 225
§ 66. Сопоставление различных критериев выпучивания 232
Глава VI. Устойчивость стержней при динамическом нагружении 234
§ 67. Классификация динамических задач 234
§ 68. Динамическое нагружение стержня. Исходное уравнение.. 236
§ 69. Случай внезапного приложения нагрузки 238
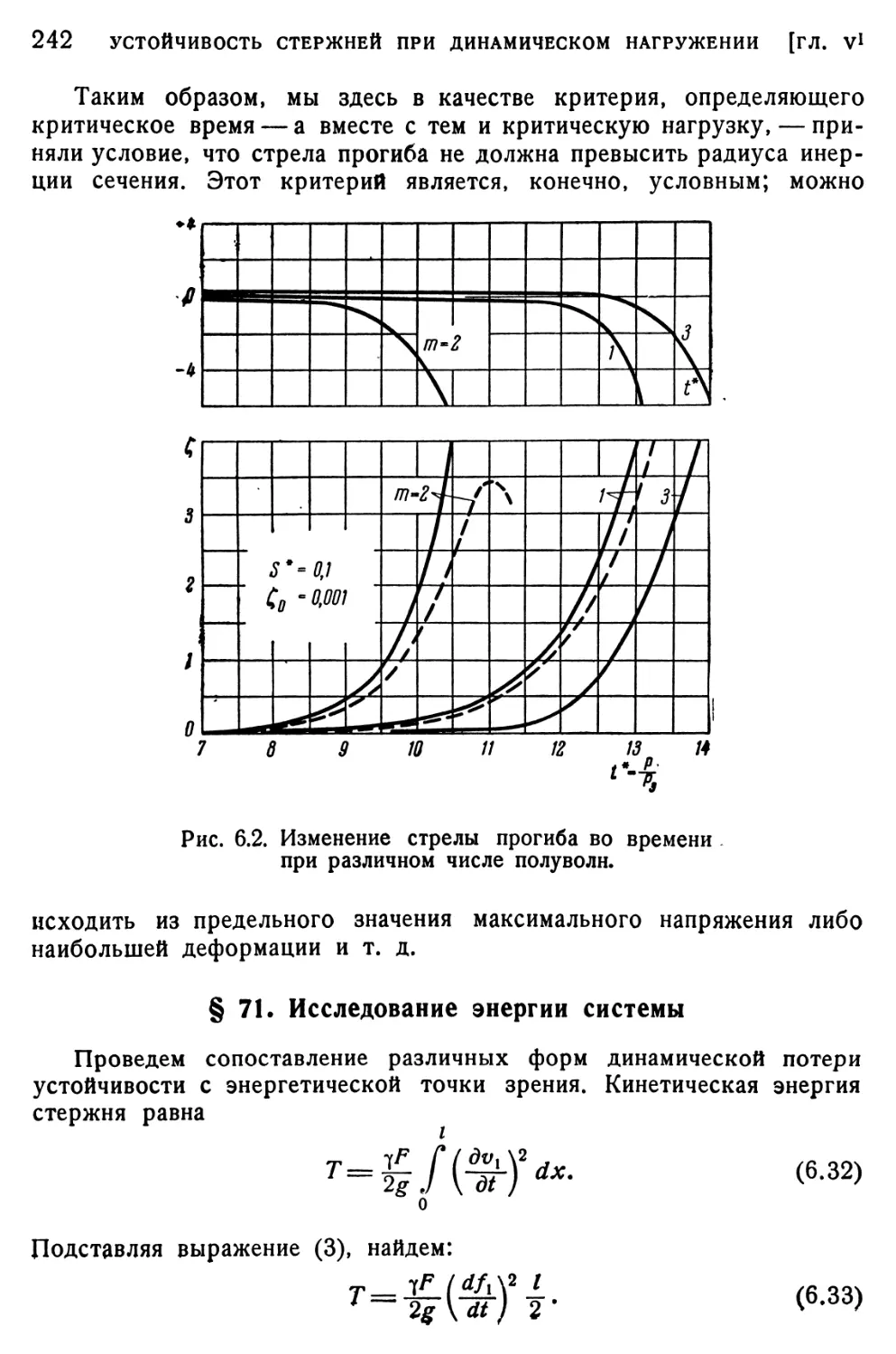
§ 70. Нагрузка, быстро возрастающая во времени 240
§ 71. Исследование энергии системы 242
§ 72. Решение в бесселевых функциях 245
§ 73. Эксперименты по продольному удару 248
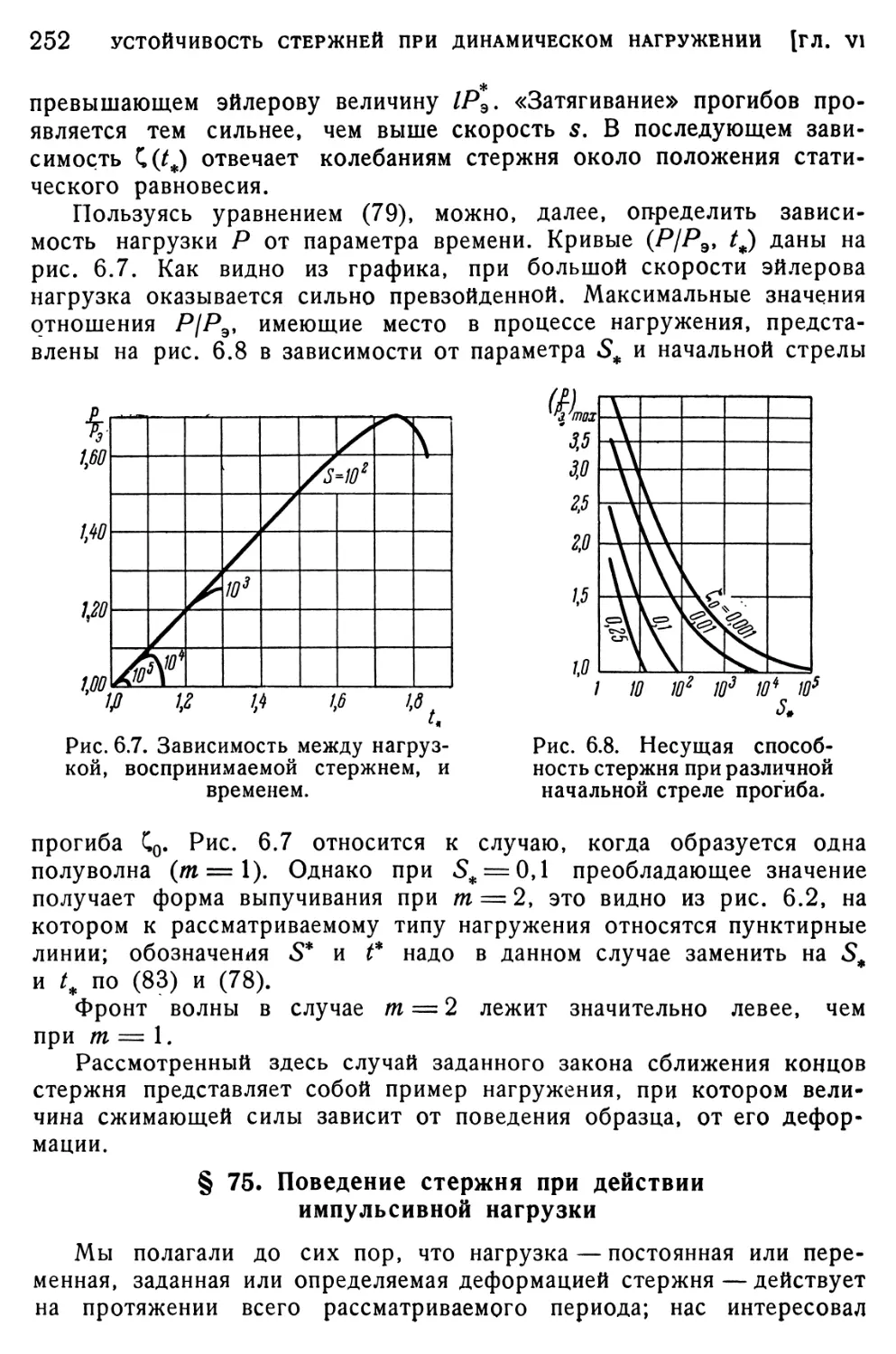
§ 74. Случай заданного закона сближения концов стержня... 249 § 75. Поведение стержня при действии импульсивной нагрузки 252 § 76. Случай пульсирующей нагрузки. Приближенное решение 253 § 77. Нагрузка, меняющаяся по гармоническому закону. Параметрические колебания 259
§ 78. Устойчивость сжатого кольца при динамическом нагружении 262
§ 79. Боковое искривление полосы при динамическом приложении
момента 265
Глава VII. Устойчивость прямоугольных пластинок в пределах
упругости 270
§ 80. Основные зависимости теории жестких пластинок 270
§ 81. Гибкие пластинки 282
§ 82. Устойчивость шарнирно опертой пластинки, сжатой в одном
направлении 285
§ 83. Случай защемленных продольных краев 289
§ 84. Пластинка со свободным краем. Сводка расчетных данных 295
§ 85. Устойчивость пластинок при сдвиге 300
§ 86. Неравномерное сжатие. Чистый изгиб 308
§ 87. Комбинированное нагружение 311
§ 88. Закритическая деформация пластинки при сжатии 316
§ 89. Приложение теории гибких пластинок 320
§ 90. Решение задачи с помощью цифровой электронной машины 325
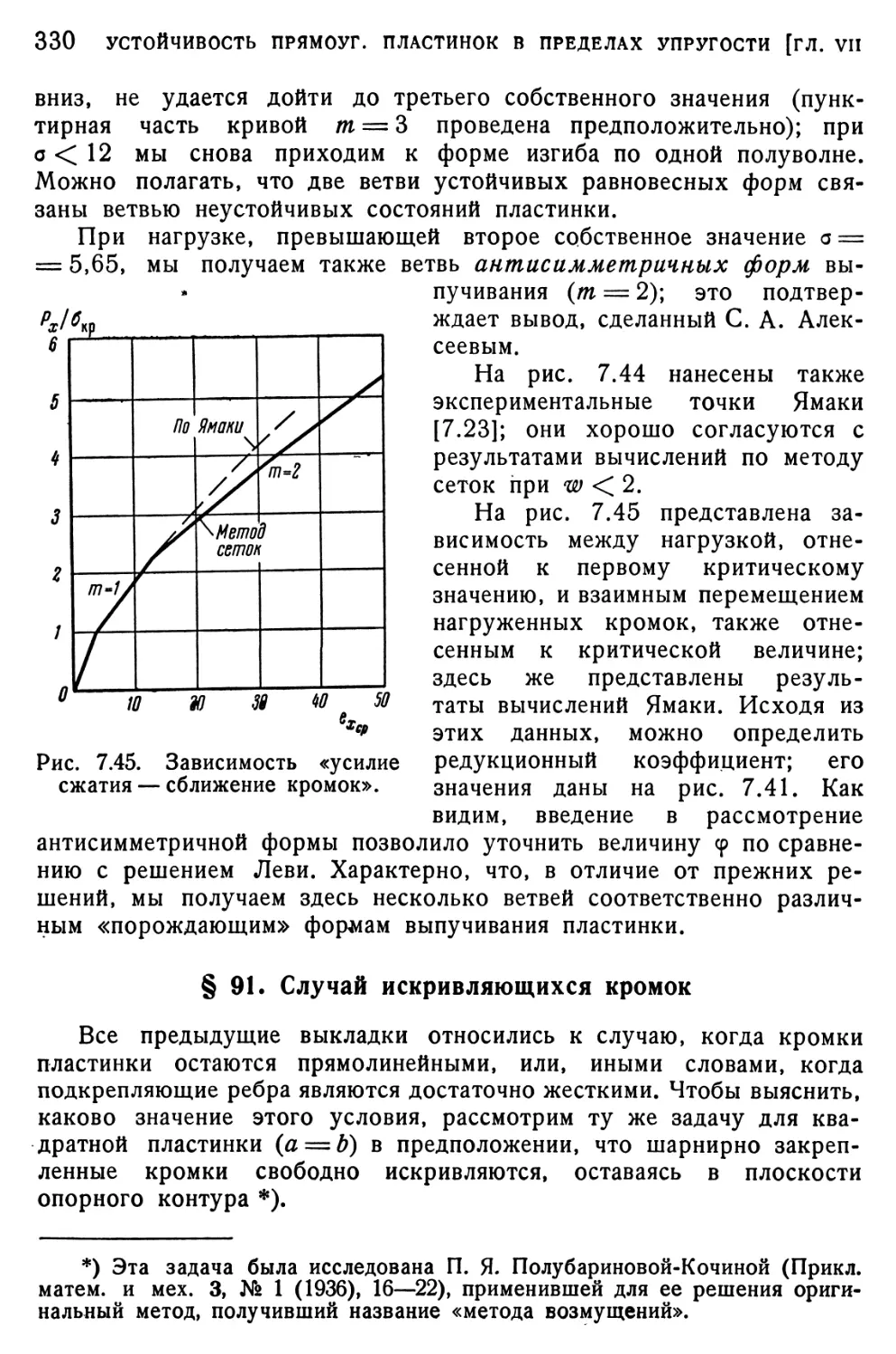
§ 91. Случай искривляющихся кромок 330
§ 92. Данные для практических расчетов 332
§ 93. Анизотропные пластинки 333
§ 94. Подкрепленные пластинки 335
§ 95. Несущая способность подкрепленных панелей при сжатии 340 § 96. Несущая способность сжатых тонкостенных стержней... 345 § 97. Закритическое поведение пластинки при сдвиге. Диагонально
растянутое поле 348
§ 98. Исследование закритического сдвига с помощью теории
гибких пластинок 351
б ОГЛАВЛЕНИЕ
Глава VIII. Устойчивость прямоугольных пластинок за пределами упругости § 99. Применение теорий пластичности к задачам об устойчивости пластинок § 100. Теория деформаций. Исходные зависимости § 101. Основное дифференциальное уравнение в случае несжимаемого материала § 102. Приложение вариационных методов § 103. Решение частных задач § 104. Вывод основного уравнения без учета эффекта разгрузки
§ 105. Выпучивание сжатой пластинки § 106. Выпучивание пластинки при сдвиге § 107. Обобщение теории деформаций на случай сжимаемого
материала * § 108. Применение теории течения § 109. Влияние сжимаемости материала по теории течения... § 110. Сопоставление расчетных формул для дюралюмина и стали § 111. Данные для практических расчетов Глава IX. Круглые пластинки § 112. Основные зависимости для жестких и гибких пластинок § 113. Защемленная по контуру пластинка под действием радиального сжатия § 114. Случай шарнирного закрепления по контуру § 115. Асимметричное выпучивание пластинки § 116. Кольцевые пластинки § 117. Закритическое поведение круглой пластинки Глава X. Общие сведения об оболочках § 118. Отличительные черты задач об устойчивости оболочек..
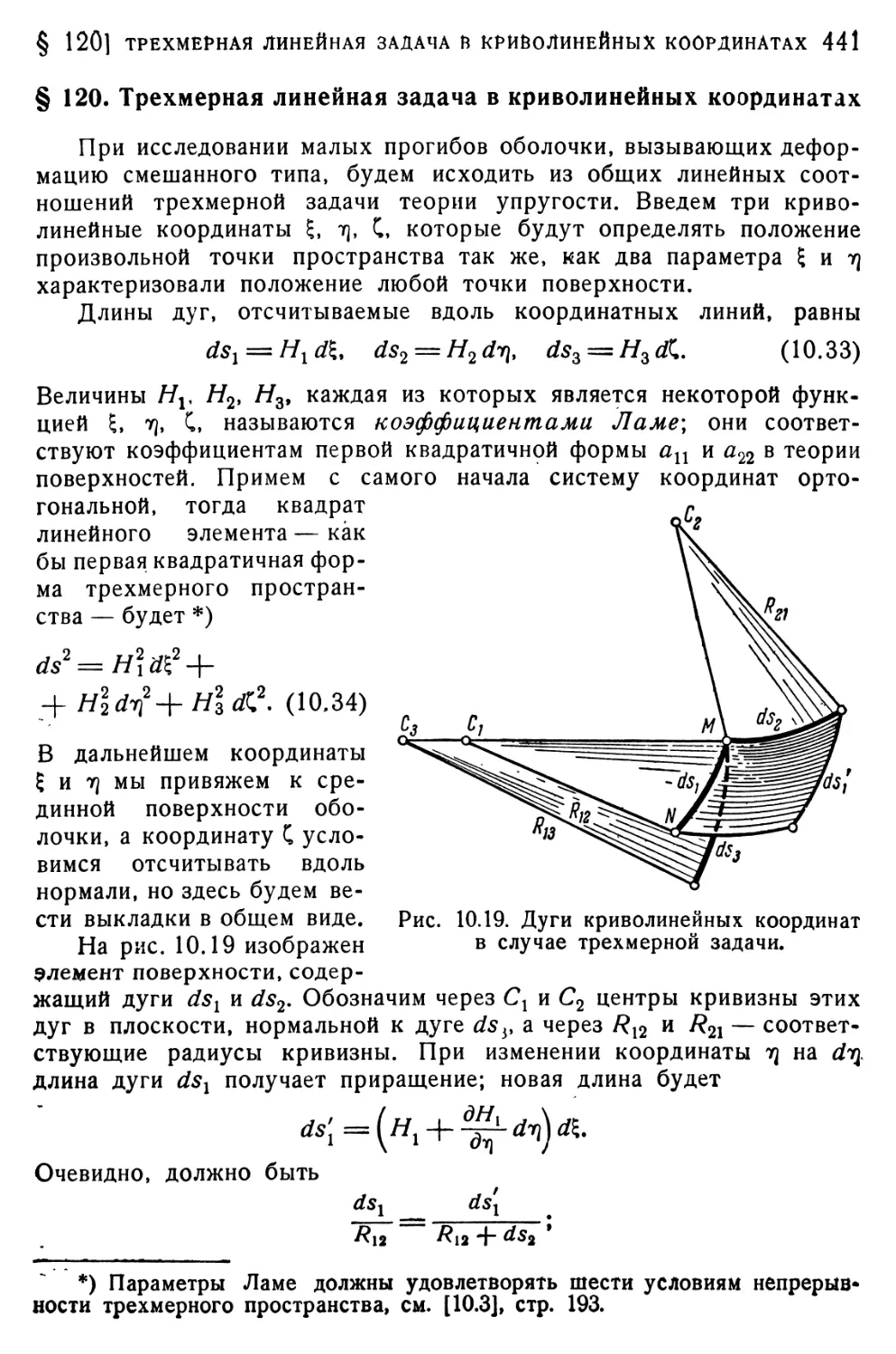
§ 119. Некоторые сведения из теории поверхностей § 120. Трехмерная линейная задача в криволинейных координатах § 121. Оболочка малого прогиба. Зависимость между деформациями и перемещениями § 122. Усилия и моменты. Уравнения равновесия элемента оболочки § 123. Упрощенный вариант основных уравнений линейной теории
оболочек § 124. Оболочки большого прогиба Глава XI. Устойчивость цилиндрических оболочек в пределах упругости § 125. Основные уравнения для оболочки кругового очертания § 126. Сжатие замкнутой оболочки вдоль образующей. Линейная
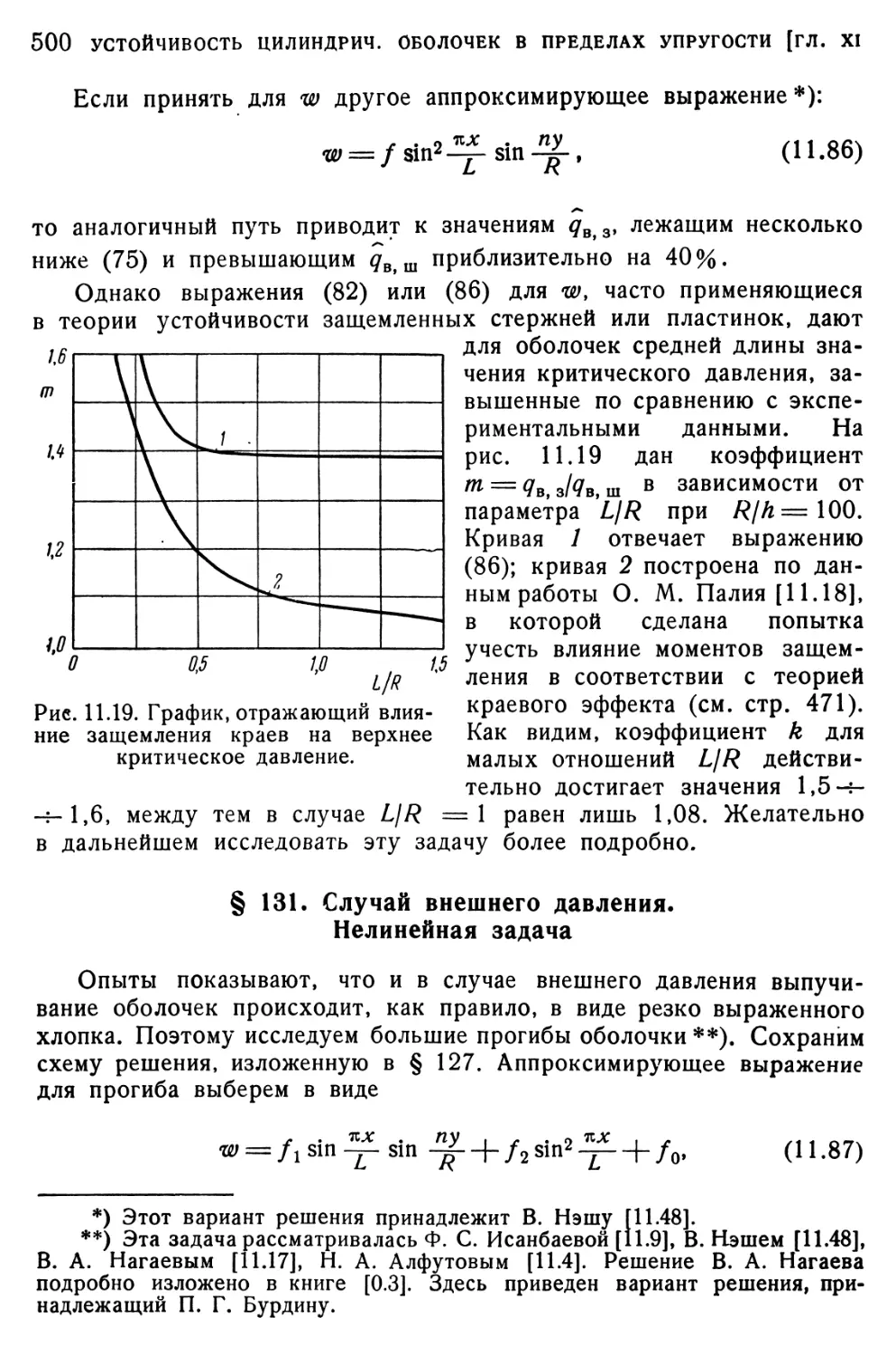
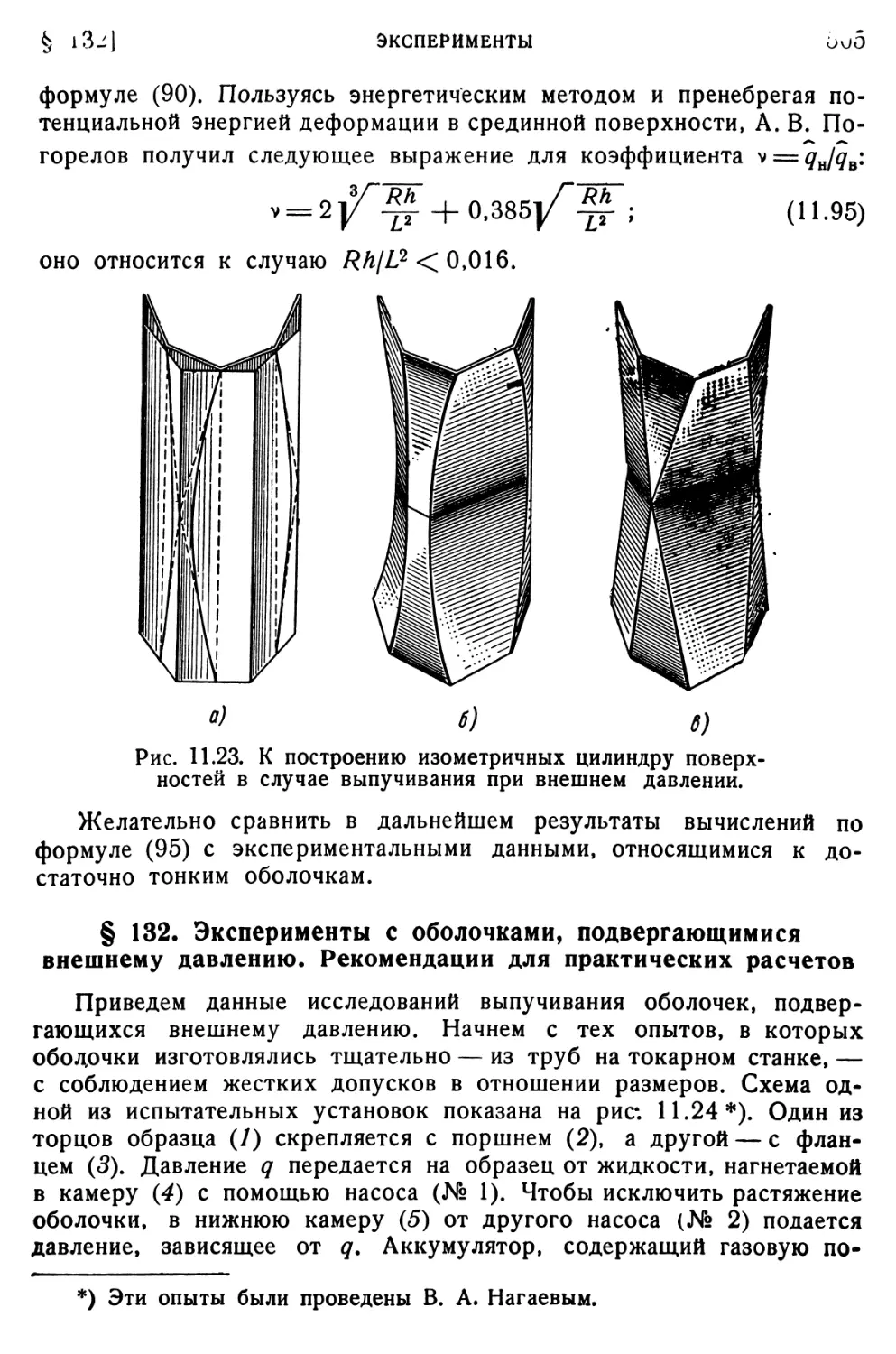
задача § 127. Нелинейная задача § 128. Геометрический подход к задаче § 129. Результаты экспериментов. Данные для практических расчетов § 130. Случай внешнего давления. Линейная задача § 131. Случай внешнего давления. Нелинейная задача § 132. Эксперименты с оболочками, подвергающимися внешнему давлению. Рекомендации для практических расчетов • •.
353
353
356
360
370
372
374
377
381
383
389
393
394 398
402
402
408
410
412
415
418
423
423
428
441*
444
448
454
458
462
462
471
478
487
491
495
500
505
ОГЛАВЛЕНИЕ 7
§ 133. Влияние начальных неправильностей при внешнем давлении 509
§ 134. Устойчивость оболочки при кручении 515
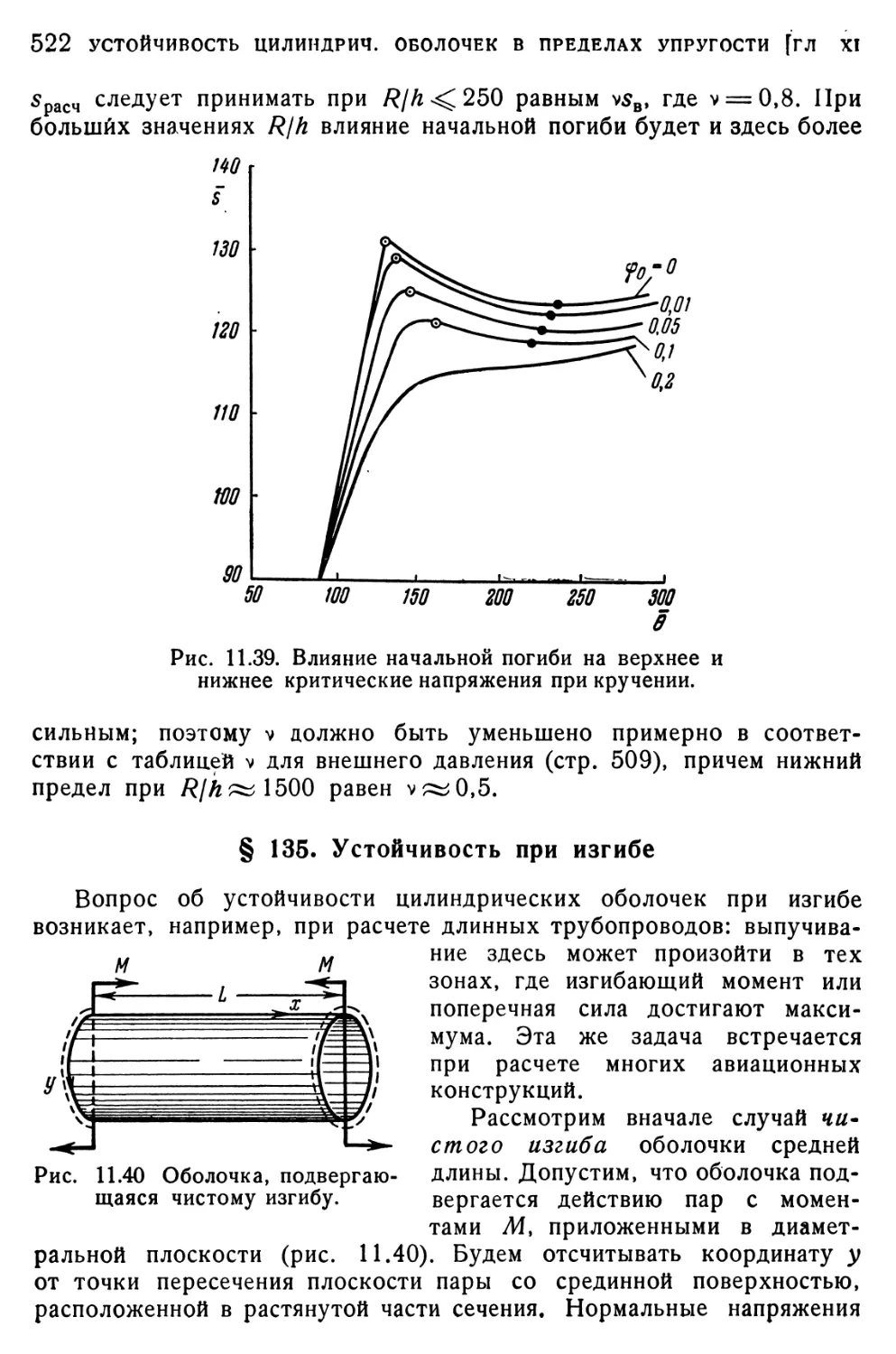
§ 135. Устойчивость при изгибе 522
§ 136. Замкнутые оболочки при комбинированном нагружении.. 530
§ 137. Подкрепленные оболочки. Общие уравнения 541
§ 138. Подкрепленные оболочки при осевом сжатии. Одновременное действие осевого сжатия и внутреннего давления 544 § 139. Устойчивость цилиндрической панели при осевом сжатии 550
§ 140. Устойчивость панели при сдвиге 554
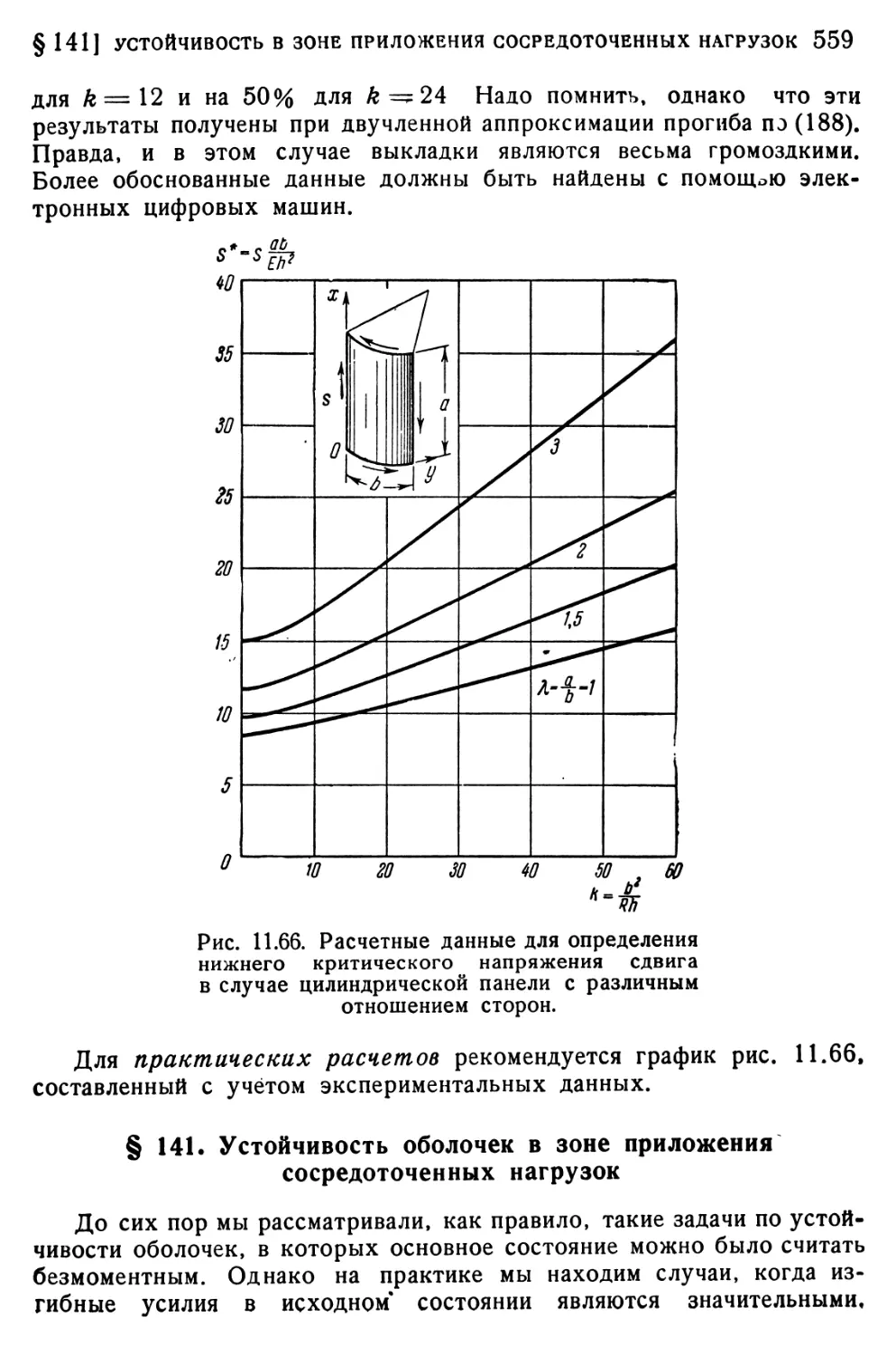
§ 141. Устойчивость оболочек в зоне приложения сосредоточенных нагрузок 559
Глава XII. Устойчивость цилиндрических оболочек за пределами
упругости 566
§ 142. Задача об устойчивости в малом 566
§ 143. Выпучивание замкнутой оболочки при осевом сжатии.. 569
§ 144. Замкнутая оболочка при внешнем давлении 575
§ 145. Кручение замкнутой оболочки 576
§ 146. Цилиндрическая панель при осевом сжатии. Устойчивость
в малом. 579
§ 147. Цилиндрическая панель при осевом сжатии. Устойчивость
в большом 580
Глава XIII. Конические оболочки 587
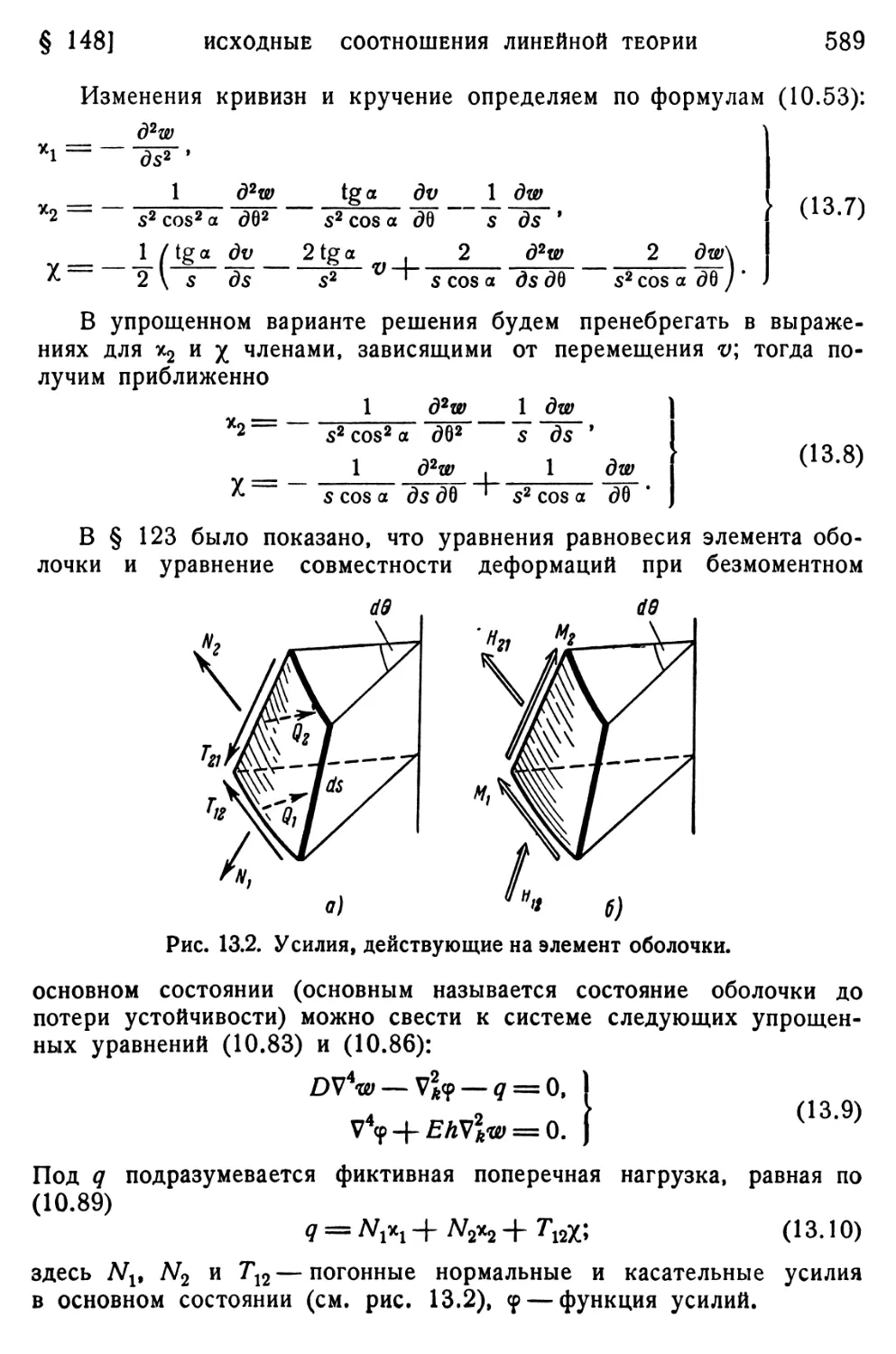
§ 148. Исходные соотношения линейной теории 587
§ 149. Осевое сжатие конической оболочки 591
§ 150. Случай внешнего давления 595
§ 151. Случай кручения 602
§ 152. Подкрепленные конические оболочки под действием внешнего давления 603
Глава XIV. Сферические оболочки 613
§ 153. Устойчивость в малом сферической оболочки при внешнем давлении 613
§ 154. Случай осесимметричного выпучивания. Линейная задача 616
§ 155. Устойчивость в большом 618
§ 156. Данные опытов и рекомендации для практических расчетов 627
§ 157. Эллипсоидальные оболочки 631
Глава XV. Устойчивость пологих оболочек при действии поперечной нагрузки 633
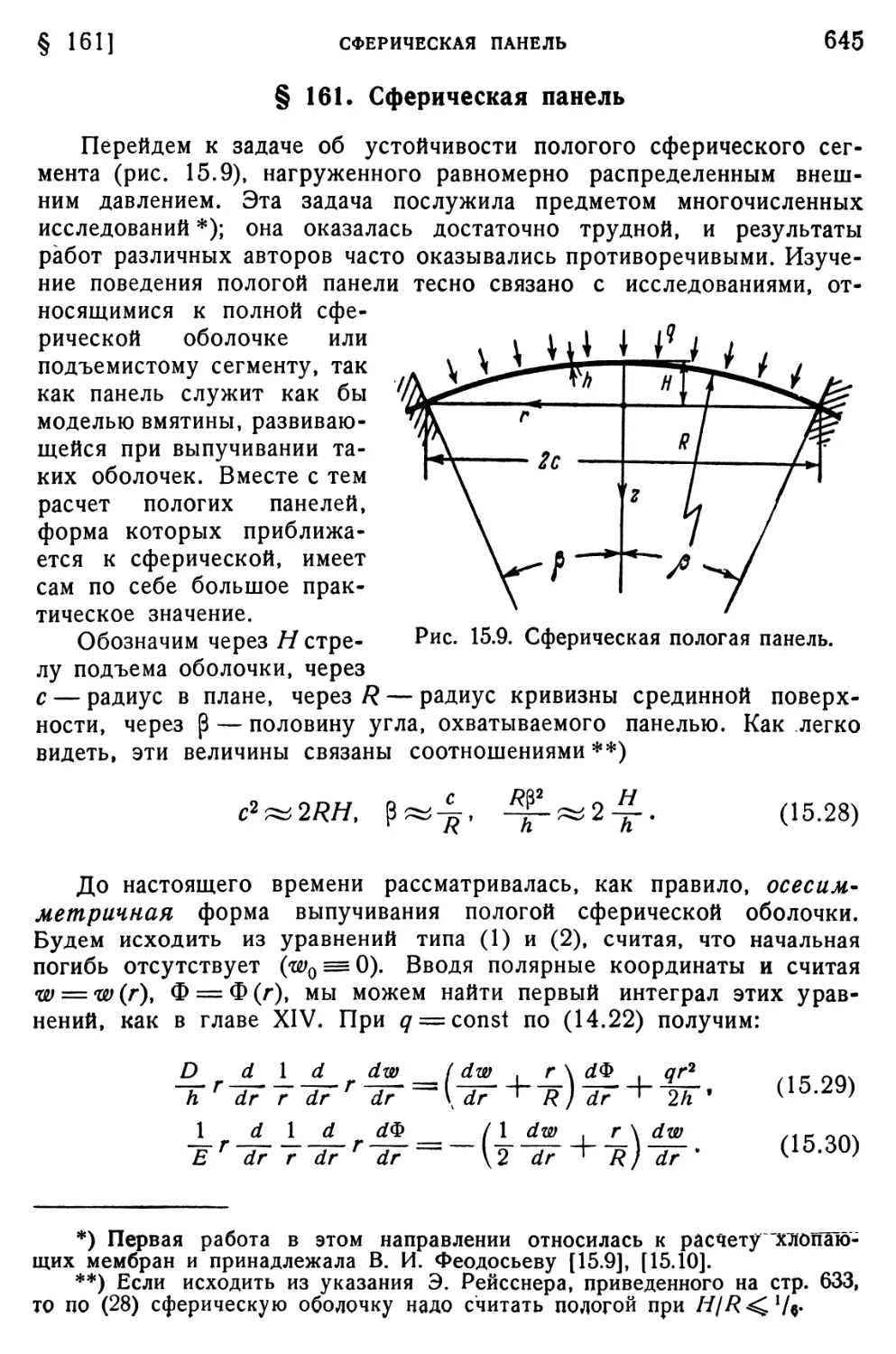
§ 158. Исходные зависимости 633
§ 159. Панель, прямоугольная в плане 636
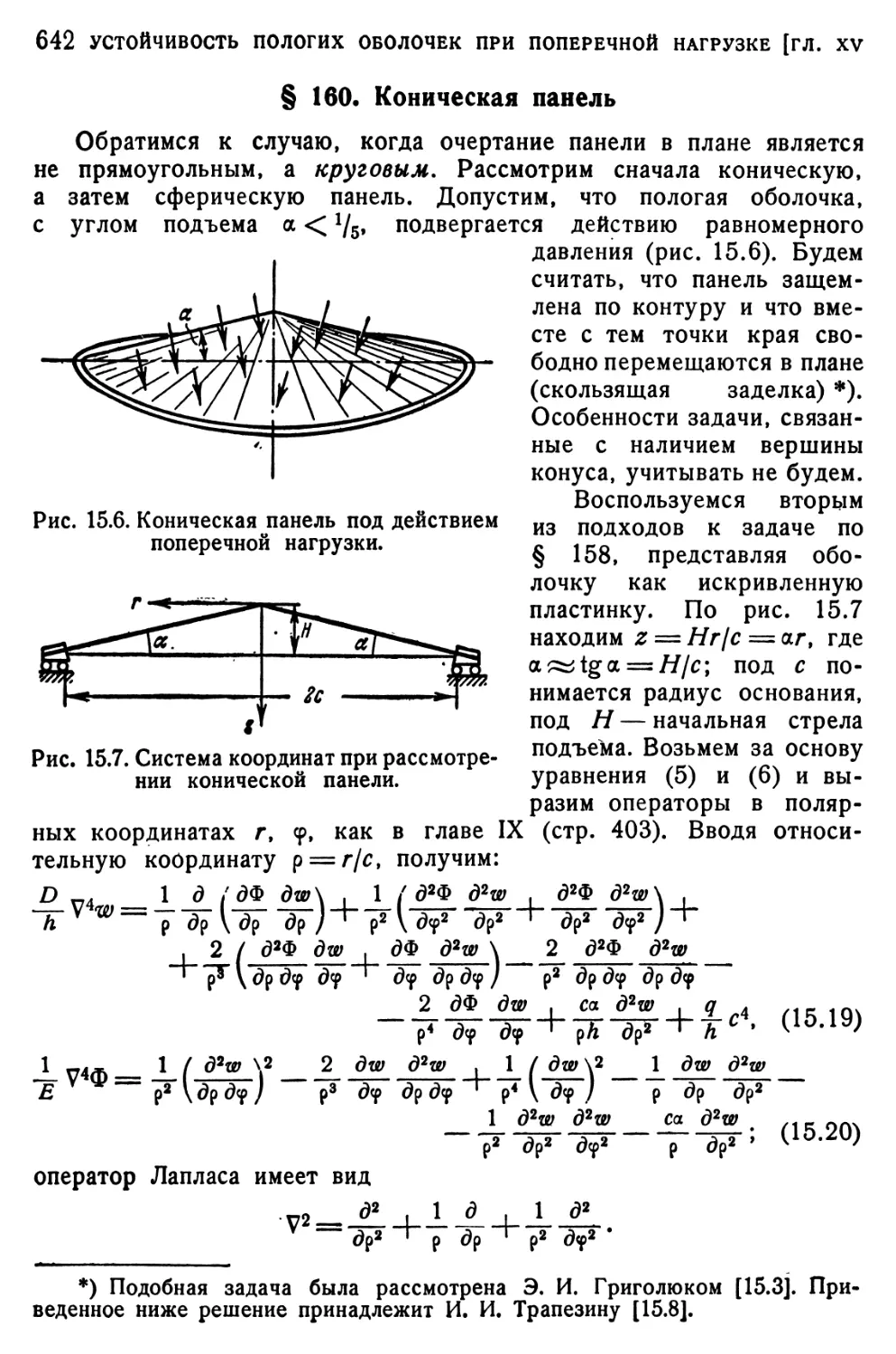
§ 160. Коническая панель •.. 642
§ 161. Сферическая панель 645
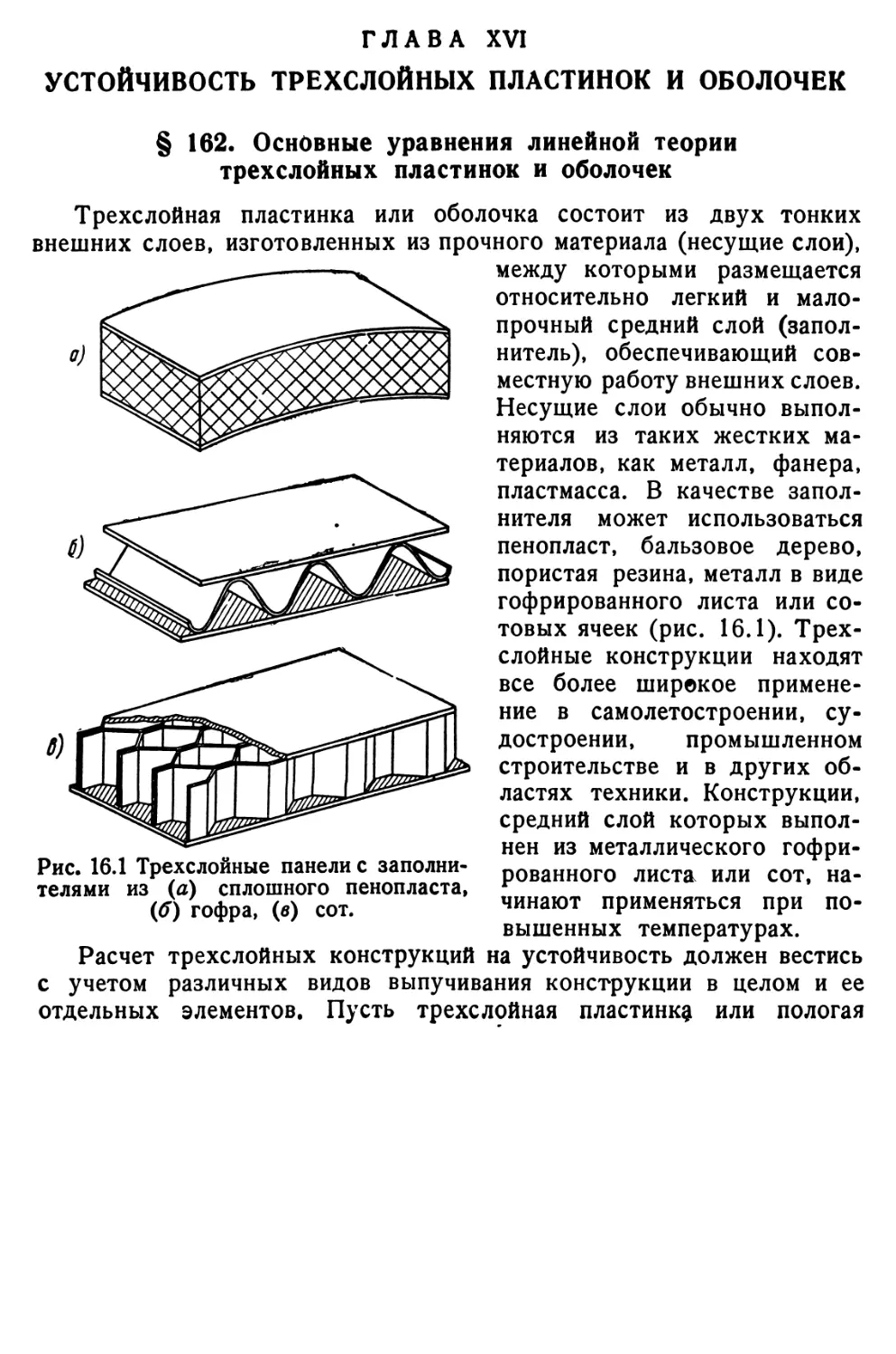
Глава XVI. Устойчивость трехслойных пластинок и оболочек.. 654
§ 162. Основные уравнения линейной теории трехслойных пластинок и оболочек 654
§ 163. Вариационное уравнение устойчивости. Граничные условия 669
8 ОГЛАВЛЕНИВ
§ 164. Устойчивость бесконечно широкой пластинки с легким
заполнителем при сжатии 674
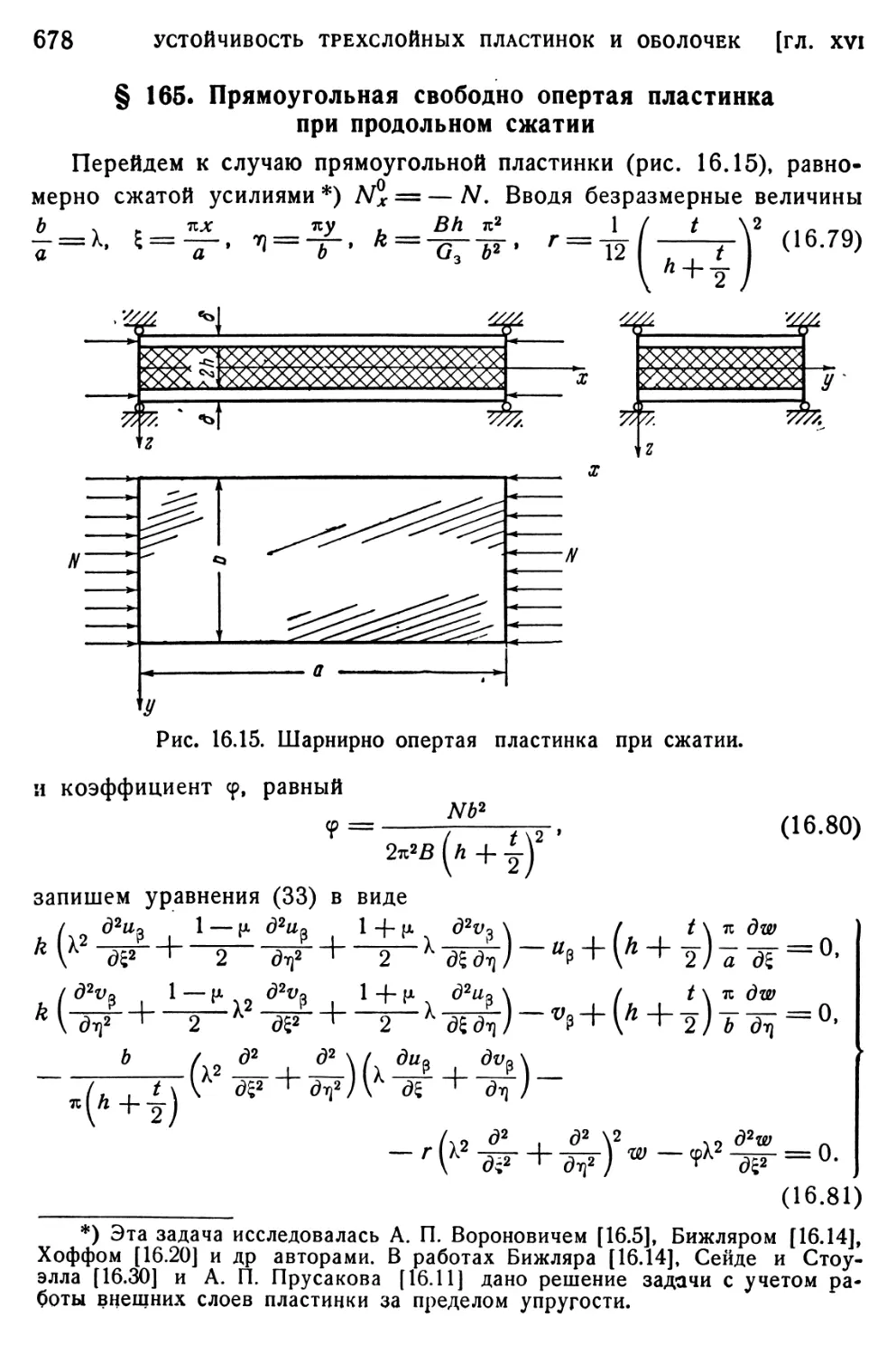
§ 165. Прямоугольная свободно опертая пластинка при продольном сжатии 678
§ 166. Другие условия закрепления краев. Метод разделения
жесткостей 681
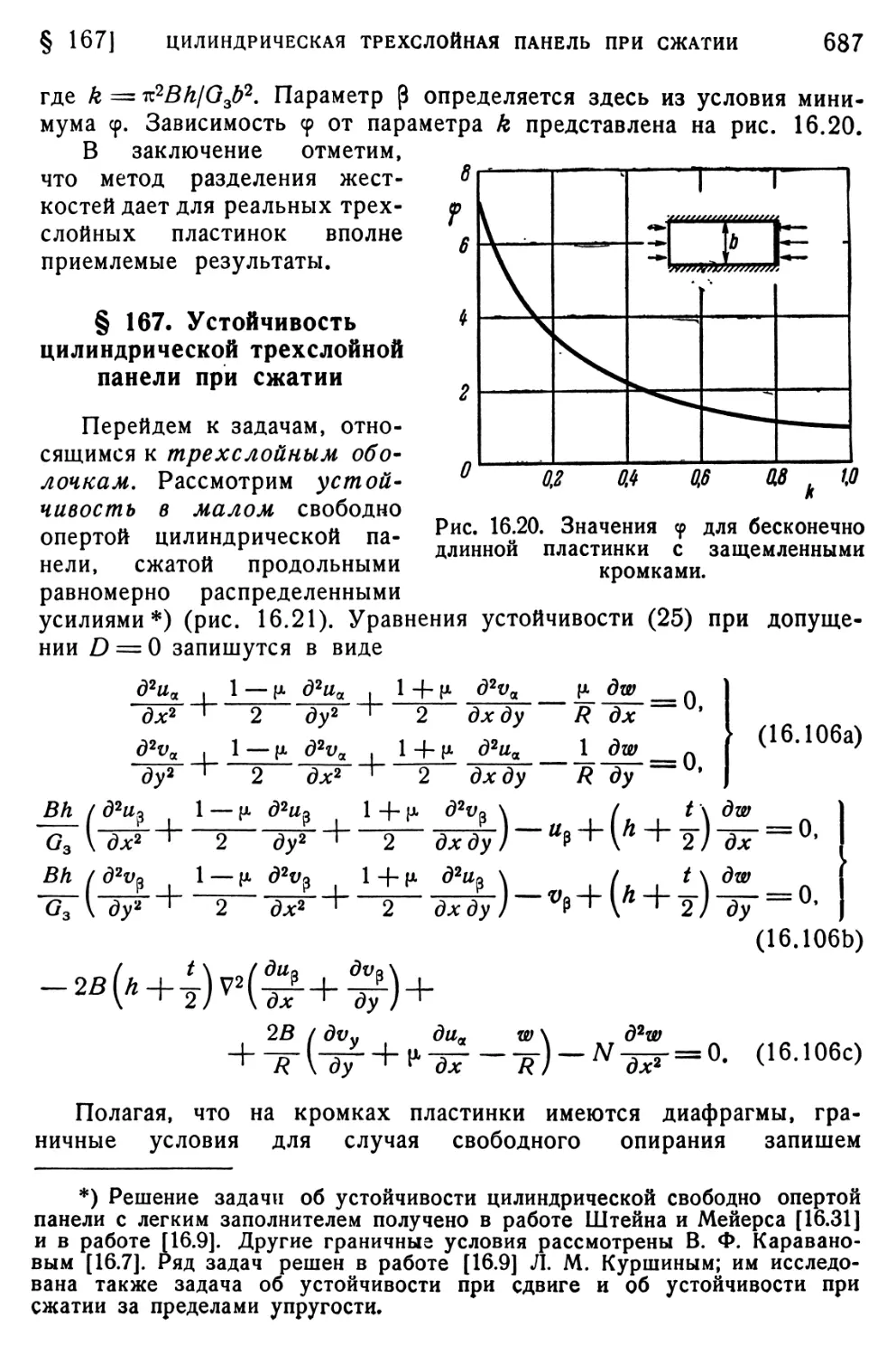
§ 167. Устойчивость цилиндрической трехслойной панели при
сжатии 687
§ 168. Устойчивость трехслойного цилиндра при продольном сжатии и внешнем давлении 690
Глава XVII. Пластинки и оболочки при высоких температурах 692
§ 169. Общие уравнения 692
§ 170. Плоская подкрепленная панель 695
§ 171. Подкрепленная цилиндрическая оболочка 698
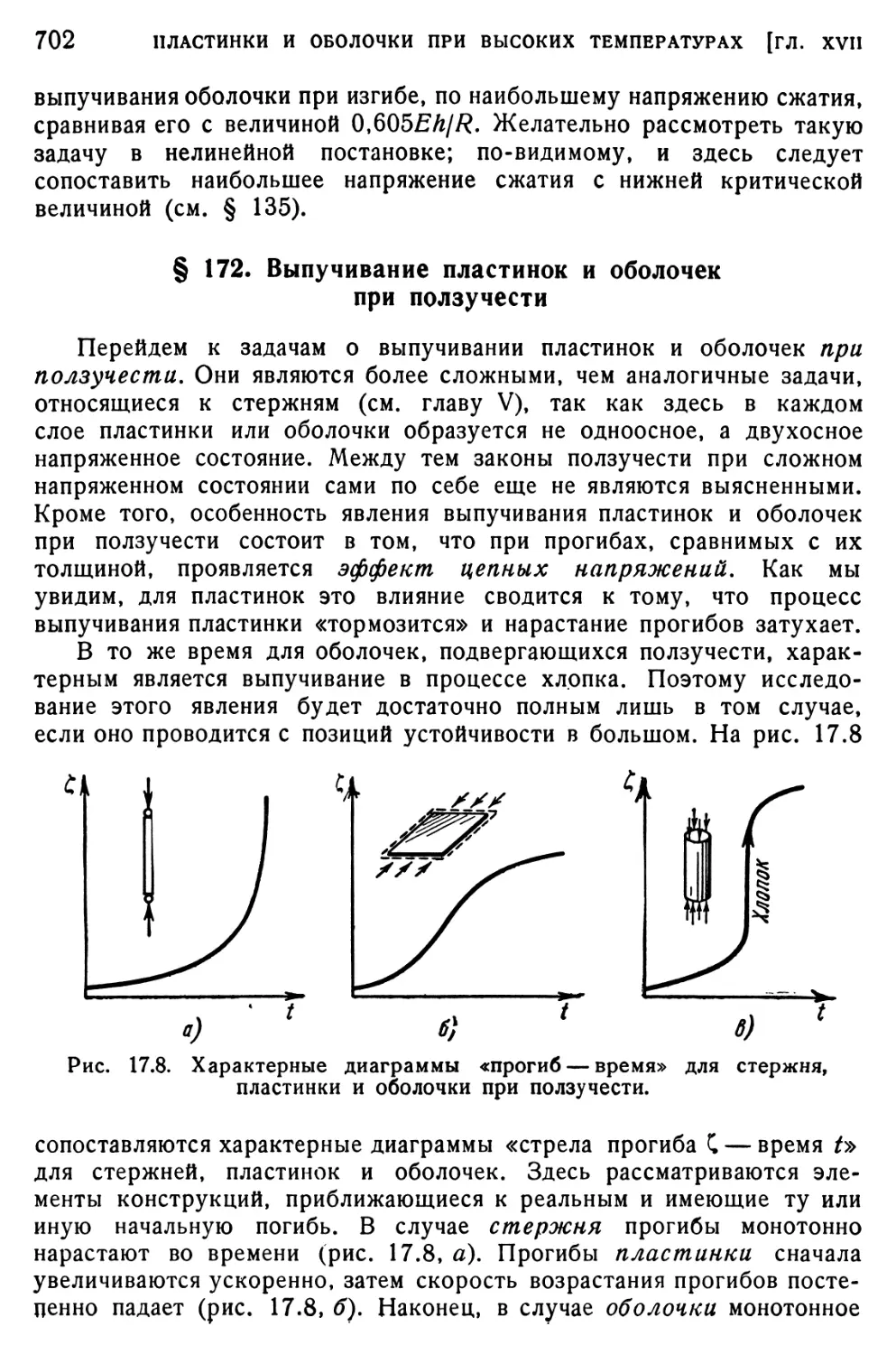
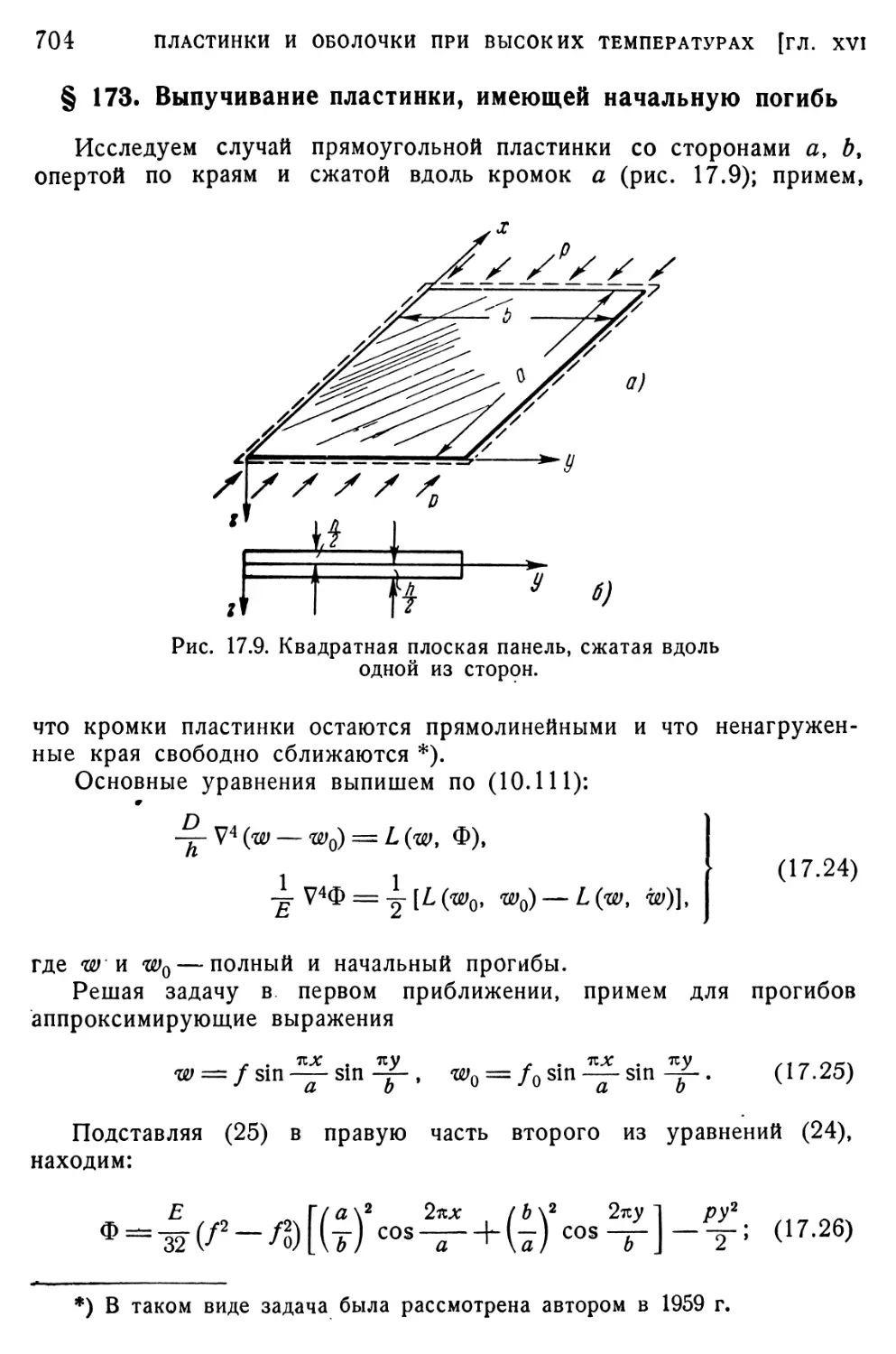
§ 172. Выпучивание пластинок и оболочек при ползучести... 702 § 173. Выпучивание пластинки, имеющей начальную погибь... 704
§ 174. Выпучивание в большом цилиндрической панели 710
§ 175. Данные экспериментов и рекомендации для практических
расчетов 714
Глава XVIII. Устойчивость пластинок и оболочек при динамическом нагружении 718
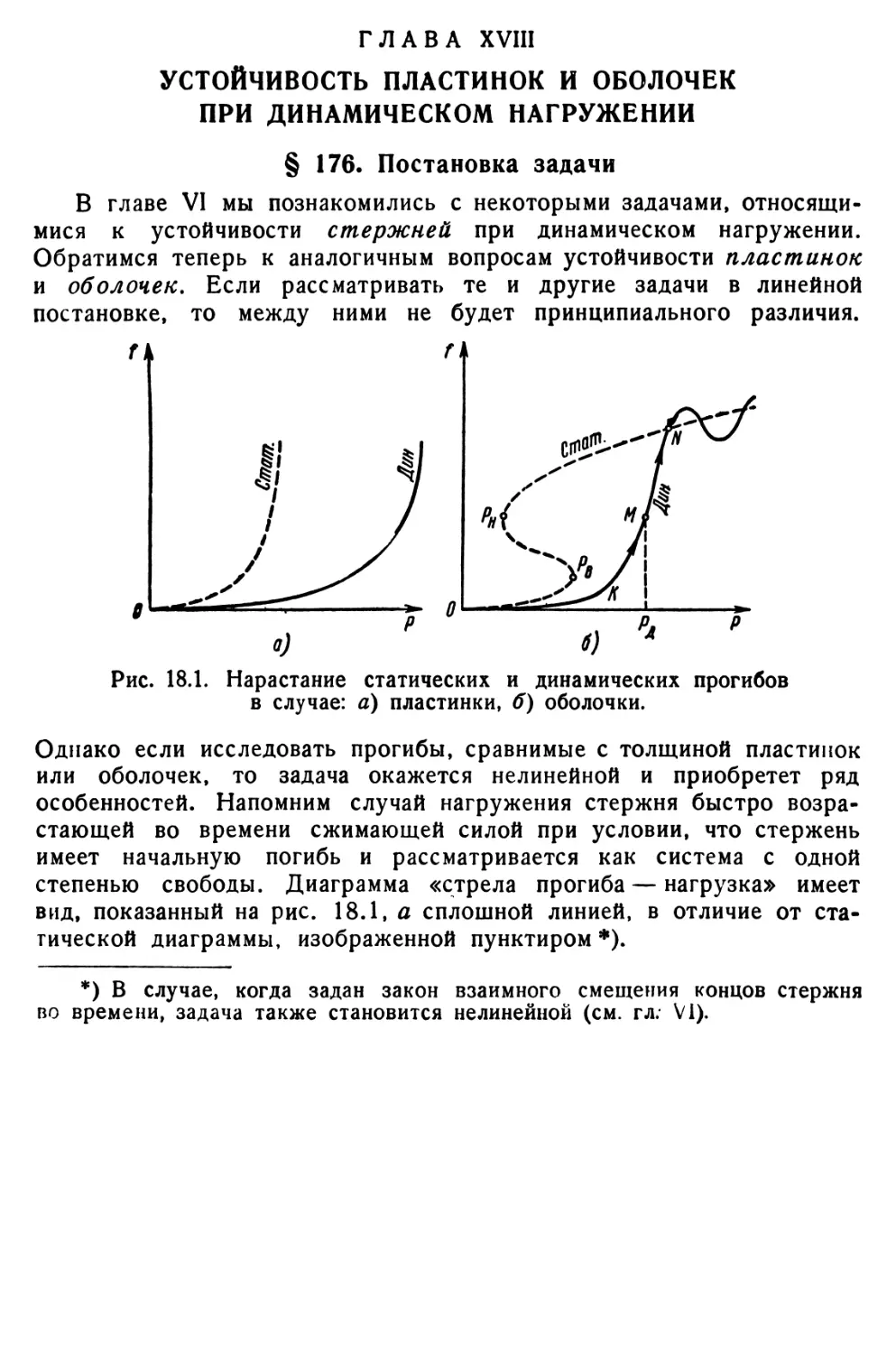
§ 176. Постановка задачи 718
§ 177. Устойчивость пластинок и цилиндрических панелей при
действии сжимающей нагрузки.... 720
§ 178. Применение цифровых машин 724
§ 179. Выпучивание замкнутых цилиндрических оболочек при
всестороннем давлении 729
§ 180. Решение с помощью аналоговых машин 736
§ 181. Экспериментальное исследование выпучивания оболочек
при всестороннем давлении 739
§ 182. Замкнутые цилиндрические оболочки при осевом сжатии 742
§ 183. Сферическая оболочка при внешнем давлении 747
§ 184. Практические выводы. Другие динамические задачи... 749
Глава XIX. Некоторые задачи аэроупругости 752
§ 185. Дивергенция и флаттер панели в потоке газа 752
§ 186. Определение нормального давления по поршневой теории 753 § 187. Исходные уравнения для пологой оболочки, обтекаемой
сверхзвуковым потоком 761
§ 188. Равновесные формы пластинки со смещающимися краями 763 § 189. Динамическая задача для пластинки со смещающимися
краями 768
§ 190. Пластинка с закрепленными краями 775
Глава XX. Применение статистических методов 781
§ 191. Основные понятия 781
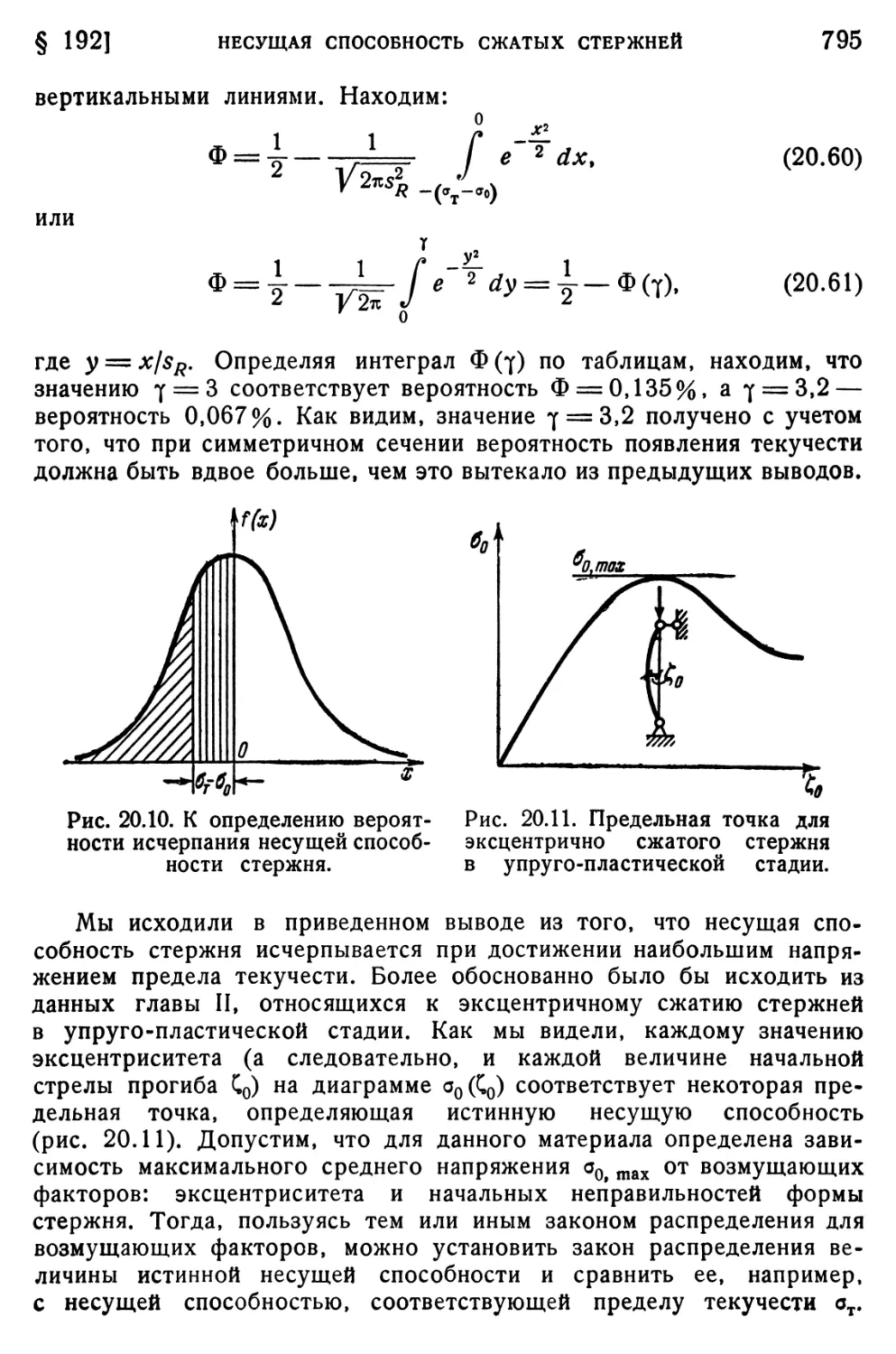
§ 192. Несущая способность сжатых стержней 791
§ 193. Влияние начальных неправильностей на поведение оболочек.
Цилиндрическая панель 796
ОГЛАВЛЕНИЕ
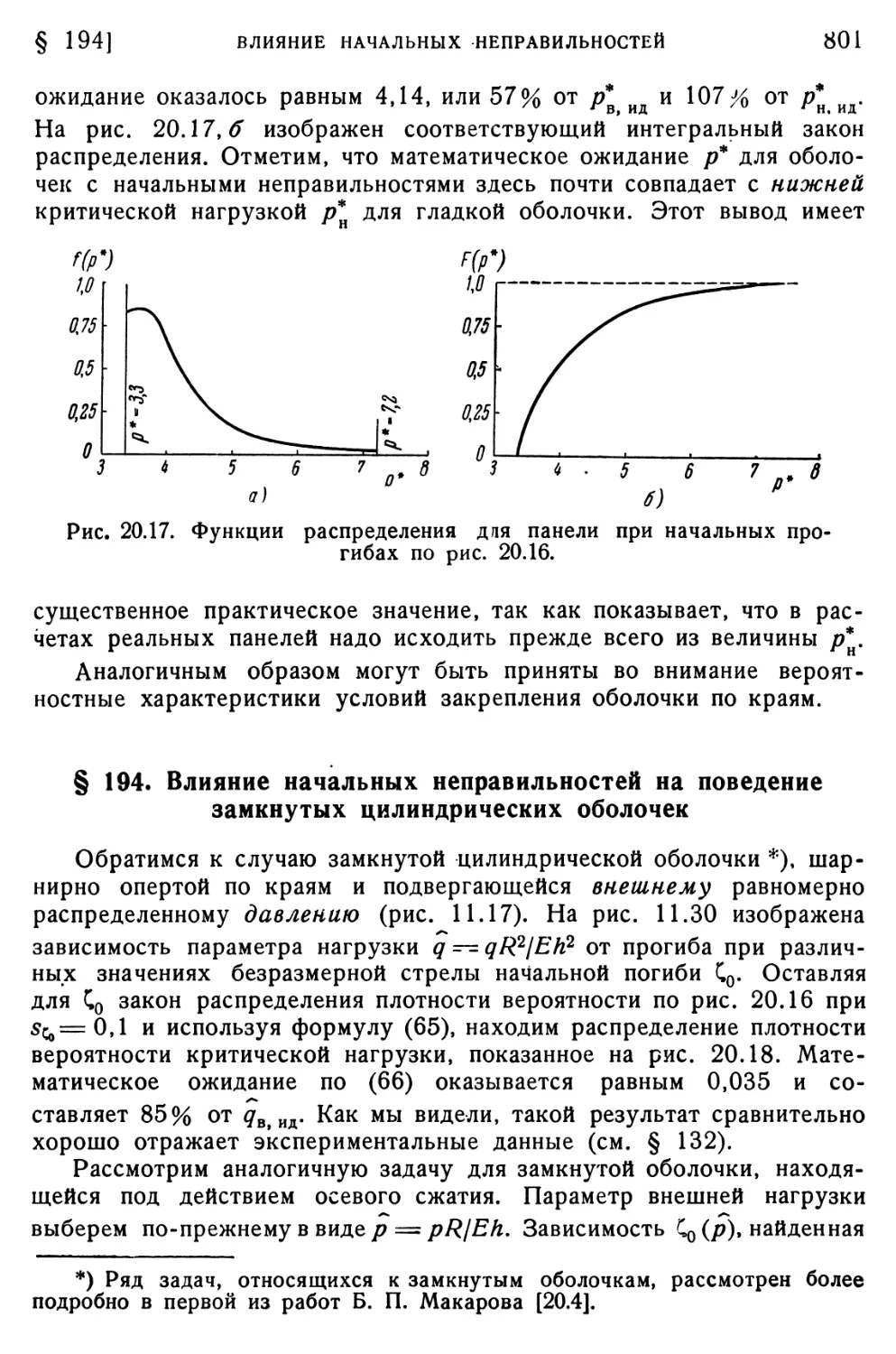
§ 194. Влияние начальных неправильностей на поведение замкнутых цилиндрических оболочек § 195. Влияние случайных нагрузок на поведение оболочек... § 196. Другие задачи статистической теории Глава XXI. Общие критерии устойчивости упругих систем...
§ 197. Динамический критерий устойчивости в малом § 198. Статический критерий устойчивости в малом. Исследование смежных равновесных форм для трехмерной задачи... § 199. Энергетический критерий устойчивости в малом. Теорема
Лагранжа—Дирихле § 200. Динамический критерий устойчивости в большом § 201. Статический критерий устойчивости в большом § 202. Энергетический критерий устойчивости в большом.... § 203. Критерий устойчивости при комбинированной нагрузке.. § 204. Некоторые задачи для дальнейших исследований Литература Именной указатель Предметный указатель 9
801
807
812
814
814
816
822
825
826
831
834
837
841
868
874
ПРЕДИСЛОВИЕ
Теории устойчивости упругих систем посвящен ряд монографий, опубликованных в СССР и за рубежом. В 1935—1950 гг. были изданы книги А. Н. Динника «Устойчивость упругих систем», «Продольный изгиб» и «Устойчивость арок». В 1936 г. была опубликована книга С. П. Тимошенко «Устойчивость упругих систем», перевод которой дважды издавался в Советском Союзе. В 1939 г. вышла книга И. Я. Штаермана и А. А. Пиковского «Теория устойчивости упругих систем».
В известных курсах строительной механики корабля, принадлежащих И. Г. Бубнову (1912—1914 гг.) и П. Ф. Папковичу (1941 г.), много внимания уделено расчетам на устойчивость стержней и пластинок. В книгах В. 3. Власова «Тонкостенные упругие стержни» (1-е изд.—1940 г.) и «Общая теория оболочек» (1949 г.) изложены его исследования по устойчивости тонкостенных стержней и оболочек. А. А. Ильюшин отвел значительное место в монографии «Пластичность» (1948 г.) задачам об устойчивости стержней и пластинок за пределами упругости. Вопросы устойчивости различных конструкций рассмотрены в книге К. Бицено и Р. Граммеля «Техническая динамика» (1940 г.) и в труде «Расчеты на прочность в машиностроении» под ред. С. Д. Пономарева (1952—1959 гг.). В последние годы были опубликованы монографии В. В. Болотина, X. М. Муштари и К. 3. Галимова, А. Р. Ржаницына, Н. С. Стрелецкого, Ф. Блейха, К. Колбруннера и М. Мейстера, В. Пфлюгера и других авторов, посвященные актуальным областям теории устойчивости и практическим методам расчета элементов конструкций.
От многих из перечисленных монографий эту книгу отличает прежде всего ее общая направленность. Автор поставил перед собой цель подытожить исследования по тем разделам теории устойчивости стержней, пластинок и оболочек, которые имеют в настоящее время наибольшее практическое значение. В книге рассмотрен ряд новых задач, возникших в последние годы в связи с требованиями промышленности (в особенности авиастроения) и строительства. Изложены, в частности, теоретические и экспериментальные данные, полученные автором и его сотрудниками по динамической устойчивости упругих систем, выпучиванию оболочек «в большом» при ползучести ц т. д,
ПРЕДИСЛОВИЕ
И
В книге приведены таблицы и графики, которые могут быть непосредственно использованы в практических расчетах. Даны некоторые числовые примеры.
Главы I—IV посвящены теории статической устойчивости стержней. Изложение начинается с задач, известных читателю по курсу сопротивления материалов; разбираются различные методы их решения. Наряду с широко распространенными энергетическими методами освещены: метод последовательных приближений, метод конечных разностей и некоторые графические приемы. В последующих главах эти методы применяются к решению более сложных задач.
Рассмотрены различные критерии устойчивости стержней за пределами упругости.
В главах VII—IX излагается теория устойчивости прямоугольных и круглых пластинок. Здесь представлены методы расчета прямоугольных пластинок на устойчивость при сжатии в одном и в двух направлениях, при сдвиге и комбинированной нагрузке. Уделено значительное внимание способам расчета пластинок на устойчивость за пределами упругости, вытекающим из различных теорий пластичности; указаны приближенные методы, основанные на некоторых упрощающих задачу допущениях; дано сравнение теоретических и экспериментальных результатов.
Главы X—XV относятся к устойчивости оболочек различного очертания. Здесь приведен ряд классических решений задач об устойчивости оболочек в линейной постановке. Кроме того, дается понятие об устойчивости оболочек «в большом» и приводятся основные результаты, полученные по отношению к различным частным задачам с помощью нелинейной теории. При этом частично используются данные, изложенные в последних разделах книги автора «Гибкие пластинки и оболочки» (Гостехиздат, 1956); некоторые же результаты являются новыми.
Глава XVI посвящена трехслойным пластинкам и оболочкам. Рассмотрены особенности выпучивания этих конструкций; используются наиболее приемлемые гипотезы, позволяющие решить ряд практически важных задач.
В главах V и XVII освещены температурные задачи. Исследуется выпучивание стержней, пластинок и оболочек при ползучести. Главы VI и XVIII посвящены динамической устойчивости упругих систем. В главе XIX изложены некоторые задачи аэроупругости, относящиеся к устойчивости плоской и искривленной панели в сверхзвуковом и гиперзвуковом потоке.
В главе XX изложены статистические методы в их приложении к задачам устойчивости стержней, пластинок и оболочек.
Глава XXI посвящена общей теории устойчивости упругих систем и объединяет сведения, полученные читателем из предшествующих разделов книги. Наибольшее внимание здесь уделяется уточнению
12
ПРЕДИСЛОВИЕ
понятия о нижней критической нагрузке, относящегося к устойчивости «в большом». В заключение перечислены некоторые актуальные задачи для последующих исследований.
В конце книги приведена библиография ко всей книге и по отдельным разделам. В списке литературы представлены далеко не все опубликованные работы. Автор стремился привести прежде всего те источники, в которых дана более подробная библиография по тем или иным частным задачам.
Формулы и рисунки нумеруются по главам. Ссылки на формулы в пределах данной главы даются без указания номера главы.
Глава XIII и § 160 главы XV написаны по просьбе автора И. И. Трапезиным, глава XVI — Л. М. Куршиным. Рукопись книги была внимательно прочитана В. И. Феодосьевым. Он сделал ряд ценных замечаний, учтенных при окончательном редактировании книги. Отдельные разделы книги были просмотрены В. В. Болотиным, И. И. Воровичем, В. М. Даревским, Б. Г. Кореневым, Г. Ф. Лаптевым, Б. П. Макаровым, Р. Г. Суркиным, А. А. Уманским. Помощь автору по техническому оформлению рукописи была оказана И. Н. Землянских, И. Г. Кильдибековым и Э. Д. Скурлатовым. Всем этим лицам автор выражает глубокую благодарность.
А. Волъмир
Теория, мой друг, суха, Но зеленеет жизни древо.
Гете, * Фауст».
ГЛАВА I
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ
§ 1. Основные понятия
С понятием устойчивости, которое будет неоднократно встречаться в этой книге, каждый читатель сталкивается повседневно. Рассмотрим, например, равновесные положения тяжелого шарика, помещенного на гладкую поверхность. На рис. 1.1 показаны равновесные состояния шарика в тех случаях, когда криволинейная поверхность обращена выпуклостью вниз (а) или вверх (<?). Легко
Рис. 1.1. Формы равновесия: а) устойчивая, б) неустойчивая, в) безразличная.
видеть, что эти положения шарика различаются между собой по характеру равновесия. Если слегка отклонить шарик от состояния равновесия, как показано пунктиром, и предоставить его самому себе, то в первом случае шарик начнет колебаться вокруг среднего положения, а во втором начнет сразу же удаляться от него. В первом из этих случаев равновесие является устойчивым, а во втором — неустойчивым. Отметим, что частота колебаний шарика по отношению к устойчивому положению зависит от кривизны поверхности: чем поверхность будет более пологой, тем частота окажется меньше41). На рис. 1,6 показан предельный случай, когда криволинейная
*) Это обстоятельство имеет значение для динамического критерия устойчивости, см. далее §§ 16 и 197.
14 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
поверхность переходит в плоскость. Здесь любое положение шарика является равновесным; такой вид равновесия называют безразличным.
Обратимся теперь к задаче, известной из курса сопротивления материалов. Представим себе гибкую упругую полосу, установленную вертикально и закрепленную нижним концом (рис. 1.2). Допустим,что на верхний конец полосы передается сжимающая сила Я, направленная вертикально вниз *). При малых значениях силы полоса будет сжиматься, оставаясь прямолинейной. Если верхний конец полосы слегка отогнуть (пунктир на рис. 1.2), а затем отпустить, то полоса будет совершать колебания относительно вертикального положения. Такое равновесное положение стержня является устойчивым. Частота колебаний оказывается и здесь различной в зависимости от величины сжимающей силы. При возрастании нагрузки частота будет уменьшаться. Когда сила достигнет некоторого критического значения, частота малых колебаний обращается в нуль: стержень будет как бы в безразличном равновесии**), какой бы прогиб мы ему ни придали. Стержень, изготовленный из реального материала, уже при сравнительно небольших прогибах может получить пластические деформации и останется в отклоненном положении, дойдя до упора а или Ь.
Допустим, что к полосе приложена сжимающая сила, превышающая критическую; вертикальное положение стержня будет по-прежнему равновесным, но равновесие это является уже неустойчивым: при любом возмущении полоса изогнется, после чего уже не будет возвращаться к вертикальному состоянию. Как видим, можно провести аналогию между равновесными состояниями сжатого стержня и тяжелого шарика по рис. 1.1.
Условимся называть в дальнейшем равновесное положение упругого стержня устойчивым, если, получив малое отклонение от этого положения, стержень будет возвращаться к нему ***). Происходящие вслед за этим малые колебания в реальных условиях быстро затухают из-за действия различного рода сил сопротивления.
*) Собственный вес полосы здесь во внимание не принимается.
**) Такую характеристику критического состояния стержня можно дать лишь в первом приближении, см. § 5.
***) Более строго понятия устойчивости и неустойчивости упругой системы разобраны в §§ 197 и 201.
Рис. 1.2. Колебания сжатого стержня.
§ 2] УСТОЙЧИВОСТЬ СТЕРЖНЯ, ШАРНИРНО ОПЕРТОГО ПО КОНЦАМ 15
Нагрузка, при которой начальная форма равновесия перестает быть устойчивой, называется критической. Приложение к стержню силы, равной критической или превышающей ее, ведет к продольному изгибу (изгибу, совершающемуся под действием продольных сил).
Устойчивыми в закритической области будут уже искривленные формы равновесия; в критической точке происходит разветвление (бифуркация) равновесных форм, характеризующееся обменом устойчивостью между этими формами (см. § 198).
§ 2. Устойчивость стержня, шарнирно опертого по концам. Формула Эйлера
Определим критическую сжимающую нагрузку для стержня с прямой осью и постоянным по длине поперечным сечением (рис. 1.3,а). Пусть один конец стержня О имеет шарнирно неподвижную опору, а второй конец а — шарнирно подвижную.
Будем считать, что сжимающая сила Р приложена в центре тяжести сечения и во все время нагружения направлена строго по вертикали. Расположим оси координат, как показано на рис. 1.3.
При малых значениях силы Р ось стержня остается прямой и в стержне возникают напряжения сжатия о = P/F, где F — площадь поперечного сечения.
Когда, постепенно возрастая, сила Р достигнет критического значения, то наряду с прямолинейной формой равновесия должна иметь место другая, искривленная форма, как изображено на рис. 1.3,tf. Мы предполагаем, что переход от прямолинейной формы к изогнутой происходит без изменения величины силы Р, т. е. при постоянной длине осевой линии. Но тогда точка а должна получить некоторое смещение А; можно показать, что при Рис. 1.3. Сжатый стержень,
малых прогибах Д пропорционально шарнирно опертый по концам,
квадрату стрелы прогиба упругой
линии и, таким образом, является величиной второго порядка
малости. В дальнейшем на рисунках условно будет приниматься, ЧТО трчкз а вообще не смещается по рертикади*
16
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
Выпишем выражение для кривизны изогнутой оси стержня:
*=±17 • <1Л>
где / — момент инерции поперечного сечения, М — изгибающий момент в некотором сечении.
Общее выражение для кривизны имеет вид
d2 у
(,'2)
где v — прогиб в сечении х; v — v (л:).
Будем считать здесь прогибы малыми по сравнению с длиной стержня. Изогнутая ось будет тогда пологой кривой; считая (dv/dx)2 1, можно при этом принять
*= + g. (1.8)
Изгибающий момент в сечении х равен
М = ± Pv. (1.4)
Получаем дифференциальное уравнение изогнутой оси в виде
“S—*• <15>
Как видно из рис. 1.3, при изгибе стержня, соответствующем сплошной линии, прогиб v положителен, а вторая производная отрицательна; таким образом, в уравнение типа (5) прогиб и вторая производная входят с разными знаками. Исходя из этого, мы, независимо от правила знаков для х и Ж, приходим к одному и тому же уравнению.
В курсах сопротивления материалов последующее решение задачи ведут, исходя из уравнения второго порядка типа (5). Здесь мы перейдем от (5) к уравнению четвертого порядка, так как это придаст решению более общий характер и позволит распространить его на другие граничные условия.
Принимая £У== const, продифференцируем (5) дважды по х\ тогда получим:
Это соотношение можно также непосредственно получить, исходя из известного уравнения упругой линии EI = q% вводя фиктивную поперечную нагрузку интенсивностью q. Рассмотрим деформированный
§ 2] УСТОЙЧИВОСТЬ СТЕРЖНЯ, ШАРНИРНО ОПЕРТОГО ПО КОНЦАМ 17
элемент стержня, находящийся под действием сжимающих усилий Р (рис. 1.4,а); равнодействующая этих усилий, направленная
(d я) \
— dx*)dX* а вели’ чина <7 равна q — — отсюда приходим к (6).
Введем обозначение
*2= т> (1.7)
тогда уравнение (6) примет вид
Й+*2Й=°- о-8)
Однородному линейному дифференциальному уравнению (6) соответствует характеристическое уравнение s2(s2 + 2) = 0; корни его Рис. 1.4. Интенсивность поперечной «нагрузки», вызываемой сжимающими силами.
равны st = s2 = 0, s3>4 = ± Ik. Следовательно, интеграл уравнения
(6) будет
v= A sin kx -f- В cos kx -f- Сх -f- D. (1.9)
Для решения задачи существенно то обстоятельство, что корни s3 и s4 получаются мнимыми; это в свою очередь объясняется тем, что в уравнение типа (5) величины v и cPvjd:с2 входят с разными знаками.
Решение (9) должно удовлетворять граничным условиям, которые в данном случае имеют вид
® = 0. 0=0 при * = 0, /. (1.10)
Пользуясь этими условиями, находим:
B + D = 0, В = 0,
A sin kl -f- В cos kl + Cl + D = 0, A sin kl -{- В cos kl =
Отсюда В = С = D = 0. Полагая А Ф 0, будем иметь
sin kl = 0,
! = 0. } (1П)
18 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
Для аргумента kl получаются значения
kl = nv, (1.13)
где п — произвольное целое число. Отбрасывая решение kl не отвечающее исходным данным задачи, находим:
£2 =, п= 1, 2, 3,...
или, по (6),
п п2к2ЕI
И— /2 *
Изменяя число я, получаем последовательный ряд значений силы А которым соответствуют различные искривленные равновесные формы.
Под критической силой мы условились понимать силу, при которой прямолинейная форма равновесия стержня перестает быть устойчивой. Следовательно, из всех возможных значений силы надо выбрать наименьшее и принять п= 1. Считая, что продольный изгиб произойдет в плоскости наименьшей жесткости стержня, будем под / понимать минимальный момент инерции сечения /т1п.
Вводя для критической силы обозначение Ркр, получаем:
рКр=- (ив)
Формула такого вида была получена Л. Эйлером [1.9], [1.10] и носит его имя.
Вернемся к уравнению изогнутой оси стержня
V— A sin kx — A sin х. (1-17)
Мы получили синусоиду, имеющую, вообще говоря, п полуволн. Критической силе (при п= 1) соответствует синусоида с одной полуволной:
Я • ТЬХ 4 Л Ч
v= A sin — = / sin —; (1-18)
здесь А = / — стрела прогиба.
Принимая последовательно п — 2, 3 и т. д., получим искривленные формы равновесия в виде синусоиды с двумя, тремя и более полуволнами в пределах длины стержня. При этом сила Р будет в четыре, девять и т. д. раз превышать критическую величину.
Эти формы равновесия, вообще говоря, неустойчивы, но их можно осуществить, если перейти к новой системе, поставив в точках перегиба синусоиды дополнительные шарнирные подкрепления.
Нами подразумевалось, что сжимающее напряжение в стержне лежит в пределах действия закона Гука, т. е. не превышает пре*
= 0, как
(1.14)
(1.15)
§ 2] УСТОЙЧИВОСТЬ СТЕРЖНЯ, ШАРНИРНО ОПЕРТОГО ПО КОНЦАМ 19
дела пропорциональности материала; следовательно, формулой Эйлера можно пользоваться лишь при этом условии. Напомним также, что мы применяем приближенное выражение (3) для кривизны изогнутой оси, что является уместным лишь при прогибах, достаточно малых по сравнению с длиной стержня. Именно поэтому величина стрелы прогиба / осталась в конечном счете неопределенной. В § 5 будет показано, что если исходить из «точного» уравнения упругой линии, то результат получится иной: каждому значению силы Р > Ркр будут отвечать равновесные формы со вполне определенными прогибами. Однако в окрестности точки разветвления равновесных состояний изогнутые формы стержня сколько угодно близки к прямолинейной форме, и поэтому при определении критической силы мы вправе исходить из приближенного выражения для кривизны.
С математической точки зрения рассмотренная нами задача представляет собой задачу о собственных значениях линейного однородного уравнения типа (5). Тривиальное решение v = 0 относится к начальному, неискривленному равновесному состоянию стержня. Нетривиальное решение соответствует так называемым собственным функциям задачи, которые в данном случае имеют вид (17). Первая и высшие критические силы (15) являются собственными значениями параметра Р, входящего в основное уравнение *).
Приведем два примера определения критической силы по формуле Эйлера.
Пример 1.1. Звено тяги управления к рулю высоты в самолете (рис. 1.5) передает сжимающее усилие. Звено представляет собой дюралюминовую трубу длиной L = 120 см; внешний диаметр сечения d = 3,5 см, толщина
стенки t = 1 мм. Определить критическую силу, принимая £ = 0,7 • 10е кг/см2 и предел пропорциональности материала апц = 2000 кг!см2.
Находим момент инерции сечения. Для тонкостенной трубы принимаем
*) Более подробно об этом см. в книге С. М. Михлина «Вариационные методы в математической физике», Гостехиздат, М., 1957. О месте таких линейных решений в общей теории устойчивости сказано ниже, в главе XXL
20 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [гл. I Критическая сила равна
п2.0,7 • 10е • 1,55 р 1202 кг'
Площадь сечения FnDt = п *3,5 *0,1 = 1,07 см2. Критической силе соответствует напряжение
о = = 690 кг/см2,
лежащее ниже предела пропорциональности.
Пример 1.2. Крыша цельнометаллического вагона, состоящая из обшивки и продольных подкрепляющих ребер (стрингеров), передает сжимающие усилия. Определить критическую нагрузку для панели крыши, состоящей из стрингера и присоединенной к нему плоской панели обшивки (рис. 1.6).
Рис. 1.6. К расчету на устойчивость крыши цельнометаллического
вагона.
Стрингер-уголок 25 X 25 X 1,5; толщина обшивки — 1,5 мм, ширина полосы— 70 мм. Материал — сталь Ст. 3, Е = 2 • 10б кг/см2, опц =* 2000 кг/см2. Считается, что потеря устойчивости возможна лишь в направлении, перпендикулярном плоскости обшивки. Концы панели принимаем присоединенными шарнирно к поперечным подкреплениям (шпангоутам), расстояние между которыми составляет 800 мм.
Определяем координату центра тяжести сечения г0:
105 * 0,75 + 37,5 • 22,5 + 35,3 • 14,75 0 ос
Zq —■ 177 8 — u,oo мм.
Момент инерции сечения относительно центральной оси равен. 70 • 1,53
-+105.3,1’ + Находим критическую силу:
’В'1*,-37.5.1,6.+Mi££ +
12
*2.2.10е* 0,695
12
+ 35,3 -10,92» 6950 мм\
: 2140 кг.
кр 802
Соответствующее напряжение а = 1190 кг/см2 лежит ниже спц.
§ 3]
ДРУГИЕ СЛУЧАИ ЗАКРЕПЛЕНИЯ КОНЦОВ
21
§ 3. Другие случаи закрепления концов
Рассмотрим, далее, случай, когда один коней, стержня защемлен, другой — свободен; сила Я, сохраняющая вертикальное направление, приложена к свободному концу (рис. 1.7). При потере устойчивости стержень получит прогиб по форме, изображенной на рис. 1.7.
Дифференциальное уравнение изогнутой линии сохраняет вид (8); общий интеграл уравнения по-прежнему имеет вид (9). Выпишем граничные условия. Для защемленного конца имеем:
v = 0t
— = 0 * ПРИ * = °dx J
(1.19)
На свободном конце изгибающий момент должен обратиться в нуль:
d2v
М = — Е1
dx2
:0 при X — L (1.20)
Поперечная сила нг верхнем конце может быть выражена через силу Р и угол поворота:
при х — 1.
(1.21)
Выражая поперечную силу через прогиб, получим:
=/>(§)„., с-*»
или
-*(SU <U3)
Используя выписанные условия, находим:
B-\-D = 0, ЛА + С = 0. \
,4£2sinA/4-BA2cosA/ = 0, А = 0. J (1'24) Отсюда А — С = 0, В = — D. При Вф 0 будет cos kl = 0 (1.25)
и
M = (2/t-f 1)-J. п = 0. 1. 2, 3,... (1.26)
П
ж!
II
II
I
I
I
I
/
Рис. 1.7. Стержень, защемленный одним концом и со свободным другим концом.
Рассуждая так же, как и в предыдущем параграфе, находим критическую величину силы Р равной (при я = 0)
n2EI min
~W~' (1.27)
P. р = -
22 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в ПРЕДЕЛАХ упругости [гл. I
Уравнение изогнутой оси получает вид
v = В (cos kx — 1). (1.28)
Если ввести обозначение / для перемещения свободного конца, то найдем при В = — /
= /(1 — cos*). (1.29)
Примем теперь, что один конец стержня защемлен и неподвижен, в то время как второй конец защемлен в подвижной опоре (рис. 1.8). Граничные условия здесь будут:
г; = 0 при jc = 0, /,
dv
= 0 при д: = 0, /.
(1.30)
(1.31)
Пользуясь (9), получаем:
B-\-D = 0, Ak+C = 0,
A sin kl В cos kl ~-J— Cl —j— D = 0, (1 »32)
Ak cos kl — Bk sin kl + С = 0.
Для постоянных А, В получаем уравнения
A (sin kl — kl) В (cos kl — 1) = 0,
A (cos kl—1) — В sin kl = 0. J
Условие нетривиального решения (А Ф 0, В Ф 0) имеет вид
Рис. 1.8. Стержень с защемленными концами.
sin kl — kl cos kl — 1 cos kl — 1 — sin kl
Отсюда для kl находим уравнение
= 0.
(1.34)
. kl I. kl kl kl\ л OC4
sin “2“ (sin ~2 2 cos~2~) ~ 0* (1.35)
Приравнивая нулю первый множитель, получим: kl = 2т, п = 1, 2, 3,...
(1.36)
Наименьшее возможное значение kl будет равно 2тг. Если же приравнять нулю выражение, стоящее в скобках, то наименьший корень будет kl =8,99. Таким образом, для определения критической силы мы должны положить kl = 2тс; тогда
кр*
4n2EI min 12
(1.37)
§ 3] ДРУГИЕ СЛУЧАИ ЗАКРЕПЛЕНИЯ КОНЦОВ 23
Уравнение упругой линии здесь получает вид (при 2В = — /)
V =y(i ~ cos = / sin2; (1.38)
через / по-прежнему обозначена стрела прогиба (рис. 1.8).
Наконец, обратимся к случаю, когда нижний коней, стержня неподвижно защемлен, в то время как верхний имеет шарнирную опору (рис. 1.9). Граничные условия будут:
dv
х/ = 0, — = 0 при лг = 0,
~ d2v л t
v — 0, -2=0 при х — I.
(1.39)
(1.40)
Между постоянными выражения (9) получим соотношения:
B + D = 0, Ak + C = 0, A sin kl —В cos kl —J~* Cl —j— D = 0, A sin kl + В cos kl = 0.
(1.41)
При АФ 0, —D = B = — Akl, C = ~ Ak будем иметь
Hi
W
w
I I / /
или
sin kl — kl cos kl = 0 tgkl = kl.
(1.42)
Рис. 1.9. Один конец стержня защемлен, а другой— оперт шарнирно.
Наименьшее значение kl, удовлетворяющее этому уравнению, будет
(1.43)
kl 4,4934.
Для критической силы находим выражение
EI.
кр
mln
/2
или, с известным приближением,
2я2£/
mln
Л кр ~ 12
Уравнение упругой линии будет
V = A\sin kx — kx kl(l — cos*)].
(1.44)
(1.45)
(1.46)
24 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [гл. I
На рис. 1.10 сопоставлены упругие линии для рассмотренных случаев закрепления. Формулу Эйлера можно записать теперь в обобщенном виде:
= (1-47)
ИЛИ
*2 EI
mln
кр'
(V/)*
(1.48)
Под 10 понимается приведенная длина стержня. При произвольных граничных условиях ее можно трактовать как длину эквивалентного
0,5
v-OJ
Рис. 1.10. Приведенная длина при различных условиях закрепления.
стержня, имеющего по концам шарнирные опоры. Величину v = /0// называют коэффициентом приведения длины *); он равен отношению длины полуволны синусоиды к действительной длине стержня; на рис. 1.10 полуволна синусоиды выделена; здесь же приведены значения v.
*) Это понятие было введено Ф. С. Ясинским [1.7]. В дальнейшем под «длиной полуволны» понимается длина проекции кривой на первоначальную
оь стержня.
§ 4] ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА
Величине Рк
25
кр по (47) соответствует критическое напряжение в поперечном сечении, равное
кр
*2£/
ntln
*кр '
(1.49)
Обозначим через /т1п минимальный радиус инерции поперечного сечения:
mln
тогда получим:
®кр ==
X2
(1.50)
(1.51)
Через X здесь обозначена так называемая гибкость стержня: у I
*mln
(1.52)
о)
б)
Рис. 1.11. Колонна испытательного пресса как сжатый стержень.
Пример 1.3. Определить приведенную длину колонны пресса, подвергающейся сжатию при испытании образца на растяжение (рис. 1.11, а). Верхний конец колонны защемлен, но может пе* ремещаться вместе с траверсой в горизонтальном направлении, как показано на рисунке.
Изогнутая ось имеет одну точку перегиба. Каждую половину
колонны можно уподобить стержню, один конец которого защемлен, а второй свободен (рис. 1.10 а). Следовательно, коэффициент приведения длины для половины колонны будет vl/a = 2. Для всей колонны получаем v = 1.
§ 4. Пределы применимости формулы Эйлера
Как уже говорилось, формула Эйлера справедлива при условии, что деформация сжатия стержня вплоть до момента потери устойчивости подчиняется закону Гука. Иными словами, критическое напряжение не должно превышать предела пропорциональности для данного материала:
26 УСТОЙЧИВОСТЬ С*КА?Ы СТЕРЖНЕЙ В ПРЕДЁЛаХ УПРУГОСТИ [гл. I
Предельная «упругая» гибкость стержня, т. е. наименьшая гибкость, при которой еще можно пользоваться формулой Эйлера, будет
(1.55)
f ®ПЦ
Условие (53) получает вид
(1.56)
Пример 1.4. Определить предельные гибкости К,, для стержней из стали и дюралюмина. Примем для стали марки Ст. 3 Е = 2 • 10е кг/см2 и опц = 2000 кг/см2. Тогда X* = п Y1000 100. Для дюралюмина будем считать Е = 7,5 • 105 кг/см2 и опц = 2000 кг/см2. При этом 1,; = % Y375 60.
§ 5. Равновесные формы в закритической области
До сих пор мы ставили перед собой цель определить первую критическую силу, предполагая, что для сжатого стержня она является предельной. Действительно, для элементов металлических конструкций достижение нагрузкой критической величины сопровождается значительными деформациями и, как правило, приводит к исчерпанию их несущей способности. Однако в некоторых случаях, например для гибких тонких полос, приходится вести расчет, исходя из того, что элемент конструкции подвергается действию нагрузок, превосходящих критическую. Перемещения концевых сечений такого стержня обычно ограничивают, исходя из конструктивных соображений.
Таким образом, для практических целей важно исследовать закритическую деформацию сжатых стержней. Кроме того, этот вопрос имеет большое теоретическое значение, так как позволяет установить случаи неприменимости линейных уравнений и уточнить критерий устойчивости *).
Рассмотрим закритические равновесные формы на примере стержня, защемленного нижним концом и при свободном втором конце. Будем считать, что к верхнему концу приложена сила Р, сохраняющая свое направление (рис. 1.12). Так как здесь прогибы уже нельзя считать малыми по сравнению с длиной стержня, то мы должны воспользоваться точным выражением (2) для кривизны упругой линии. Предполагая, что напряжения лежат в пределах пропор-
*) Равновесные закритические формы сжатых стержней были впервые подробно исследованы Лагранжем [1.12].
Рис. 1.12. К точному решению задачи о закритической деформации стержня.
§ б] РАВНОВЕСНЫЕ ФОРМЫ В ЗАКРИТИЧЕСКОЙ ОБЛАСТИ 27
циональности, получим нелинейное уравнение
d2v
е,¥+ШТ=~м' (,'57)
Обозначим горизонтальное смещение верхнего конца через /, тогда изгибающий момент в некотором сечении на расстоянии х от нижнего конца равен
М = ~ P(f — v). (1.58)
Введем вместо v новую переменную
y = v— / (1.59)
и воспользуемся обозначением (7); тогда уравнению (57) можно придать вид
d2y
Н
(1.60)
М£П
Граничные условия будут
У = —/. = 0 при д: = 0. (1.61)
Выпишем первый интеграл уравнения (60):
J **£_±_С; (1.62)
2
в справедливости этого соотношения легко убедиться непосредственным дифференцированием. Исходя из (61), находим:
с=1—(1.63)
уравнение (62) принимает вид
1 =1 — 4?-(/2 —у2). П.64)
/ 1+Ш
Отсюда вытекает
kVP — y2 ]/* 1— -f(/2—
£■=——о-ве) * 1-4- (Р-у*)
28 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах упругости [гл. I Разделяя переменные, получим:
к*
dx — ■
1—g- (/* — у2)
dy.
kVP-y2 ]/ 1 — (Я — у2)
Длина элемента изогнутой линии ds по рис. 1.13 равна
ds = dxjA+(-g-)’ +.
Пользуясь выражениями (64) и (66), приходим к зависимости
1
kds-
//’-у2 У 1—f (/2-у2)
dy.
(1.66)
(1.67)
(1.68)
Введем новые переменные <р и 8-, связанные с у, / и k такими соотношениями:
у2 — р cos2cp, = sin2 ft.
Тогда по (59) и (69)
У— + /cosср, v — /(1 q: cosср), dy = dv~ ± / sin ср fifcp.
Соотношение (68) приобретает вид
1
kds =
11 — sin2 Ь sin2 <р
£?ср.
(1.69)
(1.70)
(1.71)
Мы считаем, что длина осевой линии / является неизменной.
Относя значение ср = ср0 к нижнему концу стержня, примем
ср0 = — /гтс, д = 0, 1, 2,...
(1.71а)
С другой стороны, для верхнего конца должно быть у = 0. СоотРис. 1.13. Элемент изогнутой оси ветствующее значение <р полостержня. жим для 0Пределенн0сти равным
<р1=~. Интегрируя левую и правую части (71) по всей длине стержня, получим:
те/2
РАВНОВЕСНЫЕ ФОРМЫ В ЗАКРИТИЧЕСКОЙ ОБЛАСТИ
29
Выражение типа
ic/2
F(i> b)=f (1J3)
носит название полного эллиптического интеграла первого рода. Так как нижний предел интеграла (72) равен (—пк), то этот интеграл будет в (2я--1) раз больше выражения (73):
kl = (2n+l)F(. О). (1.74)
Интегралы вида (73) табулированы и приводятся во многих справочных книгах.
Вернемся теперь к соотношениям (69); второе из них дает
kf—± 2 sin». (1.75)
Сравнивая (70) и (75) и оставляя один из знаков, находим:
Aw = 2sinfr(l —coscp). (1*76)
Взятые вместе, соотношения (74) и (75) позволяют установить зависимость между отклонением верхнего конца стержня / и нагрузкой Р. Пусть известны жесткость стержня EI и длина /. Допустим, что задана величина нагрузки Р\ тогда по (7) можно найти k и из (74), при том или ином п, определить параметр. Наконец, по (75) может быть найдено отклонение /. Таким образом определяется соотношение P = P{f) для каждого значения п.
Если положить = 0, то при k Ф 0 получим / = 0. В этом предельном случае выражение (73) становится = Равнство
(74) тогда дает
Л, = -(2«+1>2 (1-77)
или, по (26),
/>„ = (2л-И)2Якр, (1.78)
где — первая критическая сила. Значения Рп при п— 1, 2, 3 и т. д. будут соответствовать другим точкам разветвления равновесных состояний по (26), т. е. высшим критическим силам. Соотношениям
(74) и (75) можно придать вид
30 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
иметь
Положим, например, Р = ЪРкр. Тогда при л = 0 из (79) будем
>ТЬ
F(j, ) = £уТ=2.72.
По таблице эллиптических интегралов*) находим ft = 74,5° и, далее,
f о s*n 74>5° 2 • 0,96 —/ q yQ0
Т 2,72 — 2,72 ~и’/ио-
На рис. 1.14 изображена зависимость между величинами Р/Ркр и /// для п = 0. С увеличением нагрузки прогиб верхнего конца
вначале возрастает до значения 0,806/, а затем начинает уменьшаться. В пре¬
деле, при Р-> оо, должно быть /->0.
Аналогичным образом может быть получена зависимость между нагрузкой и / /7j 2 3 ь прогибом верхнего конца
р/рц для л=1, 2, 3 и т. д.
Рис. 1.14. Зависимость между стрелой про- Отметим, что точки соот-
гиба и нагрузкой в закритической области, ветствующих кривых могут
быть получены по точкам первой кривой (для п = 0), если абсциссы их умножать на (2/t-f-1)2, а ординаты делить на (2лг —(— 1); это следует из (79) и (80). Несколько таких кривых приведено на рис. 1.15.
Форму упругой линии стержня, отвечающую тому или иному значению нагрузки, можно найти, исходя из зависимости (76). Как легко видеть по (60), вторая производная от у по
х обращается в нуль при у = 0, т. е. при значениях прогиба v, равных /; здесь будут лежать точки перегиба упругой линии. С другой стороны, из (69) для этих значений прогиба находим cos ср = 0 и ср = — тс (2п + 1)/2, так как верхний предел для ср мы приняли равным тс/2.
Рис. 1.15. Диаграммы «прогиб — нагрузка» при нагрузках, превышающих первую и высшие критические силы.
*) См., например, И. Н. Бронштейн и К. А. Семендяев, Справочник по математике, Гостехиздат, изд. 3-е, 1953, стр. 80.
§ 5] РАВНОВЕСНЫЕ ФОРМЫ В ЗАКРИТИЧЕСКОЙ ОЛАСТЙ
81
В случае п = 0 упругая линия не будет иметь точек перегиба; при п = 1 получим одну точку перегиба, при п — 2 — две и т. д. Упругие линии для случаев п= 1 и п = 2 представлены на рис. 1.16.
Для значений нагрузки, мало отличающихся от первой критической величины, можно установить простую приближенную зависимость между Р и /. Положим п = 0; тогда по (79) и (80)
V-г- = »)• т“-HrV
КР * -.2 ) I Л
(1.81)
Выражение для полного эллиптического интеграла может быть представлено в виде ряда по степеням sin
F(i’ ») = y(l+4s!n*a + *j.sln«d+...). (1-82)
При достаточно малом ряда, находим:
Р
ограничиваясь первыми
кр
1+- sin2ft. (1.83)
С другой стороны, во втором из равенств (81) можно положить
%
2
’(т- »)’
sin = ~ -у. 4 /
Тогда из (83) получим:
кр
= 1 +
32
ш1-
(1.84)
(1.85)
двумя членами f
Таким образом, первый уча- Рис. 1.16. Формы упругой линии стержня, сток кривой рис. 1.14 можно
с известным приближением заменить отрезком квадратной параболы. Судя по формуле (85) и графикам рис. 1.16, в закритической стадии стрела прогиба стержня возрастает весьма быстро. Если нагрузка превышает критическую лишь на 1 %, то стрела прогиба должна составить уже около 0,18/. Для стержней в% металлических конструкциях напряжения при подобных значениях прогиба обычно превышают предел пропорциональности. Следовательно, исследование закритической деформации имеет смысл только по отношению к стержням большой гибкости.
32 УСТОЙЧИВОСТЬ СЖАТЫХ СФЕРЖНЕЙ в пределах yrtpyrOcfH (гл. 1
§ 6. Различные критерии устойчивости и методы решения задач
Рассматривая сжатый стержень, различным образом закрепленный по концам, мы использовали один из наиболее употребительных критериев потери устойчивости: мы исследовали, при каких условиях наряду с начальным состоянием равновесия возникают соседние, новые равновесные формы. Такой подход к решению задач устойчивости будем называть статическим.
Другой критерий относится к потенциальной энергии, накапливаемой системой, и может быть назван энергетическим. Исследуем переход от начального равновесного состояния к изогнутому и определим приращение потенциальной энергии деформации, а также работу внешних сил. Если энергия деформации окажется больше работы внешних нагрузок, то, очевидно, система будет возвращаться к начальному положению равновесия; следовательно, это положение можно считать устойчивым. Напротив, условие неустойчивости состоит в том, что работа внешних сил превышает потенциальную энергию деформации. При безразличном равновесии (в линейной постановке задачи) приращение энергии деформации должно быть равно работе внешних сил. Если внешние силы являются консервативными, т. е. если работа их зависит только от начального и конечного положений точек приложения и не зависит от траекторий перемещения этих точек, то можно ввести понятия потенциала внешних сил и полной потенциальной энергии системы. Тогда данный критерий можно формулировать в применении к полной энергии системы, вернее, к ее приращению при переходе от начального равновесного состояния к соседнему.
Третий, наиболее общий путь состоит в исследовании движения системы, вызываемого некоторыми малыми возмущениями начального равновесного состояния. Такой критерий может быть назван динамическим. Если малые возмущения вызывают динамические перемещения системы, лежащие в определенных пределах, то начальное состояние является устойчивым. Точнее, при наличии устойчивости всегда можно подобрать такие начальные возмущения, чтобы при последующем движении системы перемещения ее точек не вышли за некоторые, наперед заданные границы (см. § 197). Есл речь идет о консервативной системе, на которую действуют консервативные заданные силы, а работа реакций связей и сил сопротивления равна нулю, то такая система будет совершать собственные колебания около положения равновесия. Критерием потери устойчивости будет при этом — как уже было сказано в § 1 — обращение в нуль частоты собственных колебаний.
Энергетический критерий, как он был формулирован выше, является, по существу, статическим, так как относится только к потенциаль¬
§ 6J РАЗЛИЧНЫЕ КРИТЕРИЙ УСТОЙЧИВОСТИ И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ 33
ной энергии системы и позволяет анализировать лишь различные равновесные формы. Однако энергетический критерий можно применить и при динамической постановке задачи, если ввести в рассмотрение кинетическую энергию системы и исследовать изменение функции, включающей как потенциальную, так и кинетическую энергии.
Определяя критическую нагрузку, отвечающую точке разветвления равновесных состояний, мы имеем в виду некоторую идеальную систему. Мы считаем, например, что ось сжатого стержня является строго прямолинейной, что нагрузка приложена в центре тяжести сечения, что материал является однородным и т. д. В реальных конструкциях такие условия, как правило, не выполняются. Можно определить характер устойчивости идеальной системы, изучая поведение близкой к ней несовершенной системы и устремляя параметры, характеризующие эти несовершенства, к нулю. Как мы увидим ниже, влияние начальных несовершенств резко возрастает, когда нагрузка приближается к критической величине, вычисленной для соответствующей идеальной конструкции, это и служит критерием устойчивости идеальной системы, который можно назвать критерием начальных несовершенств.
Приводят ли перечисленные выше критерии устойчивости той или иной системы к одному и тому же результату? Как мы убедимся ниже, в задачах, относящихся к консервативным системам, такое совпадение имеет место, поэтому применение различных критериев может служить для проверки правильности решения задачи. В случае же неконсервативной системы следует пользоваться наиболее общим динамическим критерием, так как статический (или энергостатический) подход может привести к ошибочным результатам; это будет показано на одном из примеров в § 21.
Определение критической нагрузки как точки бифуркации равновесных форм сводится, как мы видим, к решению линейной задачи; к такой задаче и относились перечисленные нами критерии устойчивости. Если же исследуется послекритическое поведение системы, как в § 5, то задача является нелинейной. Своеобразие нелинейной задачи состоит в том, что здесь одной и той же системе нагрузок может соответствовать несколько различных деформированных состо,ий, одни из которых являются устойчивыми, а другие — неустойчивыми, Так, например, в случае сжатого стержня при нагрузках, незначительно превышающих первую критическую величину, мы получали в § 5 две устойчивые изогнутые формы стержня (при изгибе стержня в одну и другую сторону) и неустойчивую форму — прямолинейную. Правда, при определении точки бифуркации мы также сталкиваемся с серией различных равновесных состояний, но от каждого из них можно непосредственно перейти к другому, соседнему; в нелинейной же системе равнЪвесные формы могут резко
34 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
различаться между собой. Это можно пояснить на примере, излагавшемся в § 1. Допустим, что тяжелый шарик перемещается по поверхности более сложной конфигурации, чем это было в § 1, и имеющей не одно, а два углубления (рис. 1.17). Если шарик первоначально находится в левой «ямке», то его поведение при отклонении от устойчивого равновесного состояния А зависит от характера возмущений.
Рис. 1.17. Устойчивость «в большом».
Если шарик получит малое отклонение или малую начальную скорость, то он будет испытывать ограниченные колебания около Л, не выходя за пределы ямки. Если же шарик получит достаточно большой толчок, то он может перескочить через неустойчивое равновесное положение В, попасть в правую «ямку» и начать колебаться около нового равновесного состояния С. Вероятность перескока шарика из одной ямки в другую зависит от того, насколько высок разделяющий их барьер. Например, в случае, показанном на рис. 1.17, б, эта вероятность больше, чем в случае рис. 1.17, а. Так как высота Н пропорциональна разности потенциалов силы веса шарика, то она характеризует потенциальный барьер, преодоление которого необходимо при перескоке *).
Мы будем говорить, что в положении А шарик устойчив «в малом», т. е. при сравнительно малых возмущениях. Вместе с тем он может оказаться неустойчивым «в большом», если возмущения превысят известный предел.
Многие нелинейные упругие системы, устойчивые в малом, могут быть неустойчивы в большом. В § 22 будет приведен анализ устойчивости в большом простейшей упругой конструкции. Наибольшее практическое значение эти понятия имеют в теории устойчивости оболочек (см. § 118). При исследовании характера равновесных
состояний нелинейных систем применяются те же критерии, что и для линейных систем: статический, энергетический и динамический (см. §§ 200—202).
*) Здесь имеется некоторая аналогия с понятием потенциального барьера в теории атомного ядра.
§ 6] РАЗЛИЧНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ 35
Выбрав тот или иной критерий, мы должны, далее, принять определенный метод решения задачи. Если применяется статический или динамический критерий, то можно исходить из дифференциальных уравнений* равновесия или движения для отклоненных положений и непосредственно интегрировать эти уравнения. Этот путь возможен, однако, лишь в простейших задачах. В более сложных случаях приходится пользоваться различными приближенными методами определения критической нагрузки. Так, например, дифференциальное уравнение равновесия или движения может быть заменено уравнением в конечных разностях; в зависимости от числа интервалов задача будет решена с той или иной степенью точности. Другой путь заключается в том, что дифференциальное уравнение — линейное или нелинейное — заменяется интегральным, т. е. таким, которое включает под знаком интеграла функции, характеризующие отклоненные состояния системы. Тогда для решения задачи можно применить метод последовательных приближений, позволяющий шаг за шагом уточнять характер равновесных форм системы и, в линейных задачах, величину критической нагрузки..Теория интегральных уравнений содержит также ряд других путей определения наименьшего параметра, характеризующего разветвление (бифуркацию) решений; это значение параметра соответствует интересующей нас критической нагрузке (см. §§ 15 и 141).
Пользуясь энергетическим критерием, мы должны представить себе, какой характер имеют отклоненные положения системы, и составить выражения для потенциальной энергии деформации и работы внешних сил. В линейных задачах критическая нагрузка приближенно определяется путем непосредственного сопоставления этих величин. Чаще всего энергетический подход осуществляется с помощью метода Ритца, в котором отклоненное положение равновесия или движения характеризуется с помощью нескольких независимых параметров. Подобная аппроксимация отклоненного состояния применяется и в методе Бубнова — Галеркина, который может быть обоснован из энергетических соображений — исходя из принципа возможных перемещений, — но, с другой стороны, может трактоваться как «формальный» прием приближенного интегрирования дифференциальных уравнений, когда форма интегральной кривой может быть заранее оценена из физических представлений.
Все перечисленные выше методы позволяли приближенно решать те или иные краевые задачи теории упругости, поскольку вместе с дифференциальными уравнениями задачи должны быть заданы граничные условия для перемещений или усилий. Существует, однако, путь—он назван ниже методом проб, — когда задача ставится как задача с начальными условиями: например, для стержня задается прогиб и угол поворота для одного из концевых сечений. Граничные условия, относящиеся ко второму концевому сечению,
36 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
выполняются после пробных попыток путем варьирования параметра нагрузки, входящего в дифференциальное уравнение.
Мы познакомились уже с одним из «статических» методов исследования устойчивости сжатого стержня — непосредственным интегрированием дифференциального уравнения упругой линии для отклоненного положения. В последующих разделах мы на том же простом примере познакомимся с другими критериями устойчивости и методами решения задач.
§ 7. Приложение принципа возможных перемещений
Как известно, наиболее общим принципом, позволяющим исследовать равновесные состояния упругих систем, является принцип возможных перемещений: он относится не только к линейным, но и к нелинейным статическим задачам; в соединении с принципом Даламбера его можно использовать и в динамических задачах. Поэтому изложение энергетических соотношений мы начнем с применения принципа возможных перемещений. Согласно этому принципу равновесное состояние упругой системы характеризуется тем, что сумма работ всех внешних и внутренних сил на любых кине¬
матически возможных перемещениях точек упругой системы равна нулю.
Допустим, что стержень длиной /, известным образом закрепленный по концам, подвергается действию сжимающей силы Р. Обозначим через ЬА работу внутренних сил при переходе от данной искривленной формы к другой, близкой к ней, а через
оW — соответствующую работу сжимающей нагрузки. Если исходная форма стержня является равновесной, то должно удовлетворяться равенство
Л + ВГ = 0. (1.86)
Работа внутренних сил может быть представлена выражением
/
lA = — jMUdx, (1.87)
О
где через Ьх обозначена вариация кривизны упругой линии. Примем для кривизны значение (3), так как речь идет о малом отклонении упругой линии стержня от оси х; тогда
SA = f m(S)dx=f мттНж)]‘!х- <'•“>
о о
§ 7] ПРИЛОЖЕНИЕ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
37
Интегрируя это выражение по частям, получим:
dM d dx dx
Повторное интегрирование дает
/
Пользуясь соотношениями
dM
(1.89)
находим:
Работа внешней нагрузки на возможном перемещении будет
где через е обозначена проекция взаимного смещения концов стержня, имеющего место при искривлении, на направление силы Р; величина е считается положительной при сближении концов. Напомним, что величина и направление сжимающих сил считаются неизменными. Воспользуемся соотношением (67) между длиной элемента изогнутой линии ds и проекцией его dx на направление Р:
Развертывая множитель при dx в ряд по формуле бинома Ньютона и ограничиваясь первыми двумя членами ряда, находим:
Полная длина изогнутой линии, равная длине стержня до искривления, будет
bW = Рое,
(1 91)
(1.93)
О
38 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах упругости [гл. I
здесь через 1г обозначена длина проекции изогнутой линии на направление оси х. Проекция смещения краев оказывается равной
, = l-l, = \f(£)'dx. (1.94)
О
Работа bW будет тогда
bW = ±pfb(-£.)’dx. «95)
О
или
w=pf <'-95а>
о
Интегрирование по частям дает
Ш = р[£ь*1-р/5-8 vdx. (1.96)
Уравнение (86) получает вид
И£)Н(« -р®Н-./ (£/w+p-S-)8'’ rf-'=o-
О (1.97)
Мы пришли к вариационному уравнению (97), вытекающему из принципа возможных перемещений.
Считая, что вариации bv произвольны и что первые два члена в левой части обращаются в нуль, получим отсюда дифференциальное уравнение (6). С другой стороны, рассмотрение внеинтегральных членов приводит к статическим граничным условиям задачи. Так,
в случае свободного конца, при условии §v=£ 0 и Ф О, по¬
лучим:
м = О, Q — Р- — 0,
что соответствует равенствам (20) и (21).
§ 8. Энергетический критерий устойчивости
При исследовании равновесных состояний консервативных систем можно вместо вариаций работы внутренних и внешних сил ввести вариацию полной потенциальной энергии системы. Как известно, работа внутренних сил на возможном перемещении равна взятой со знаком минуд вариации потенциальной энергии деформации:
ЬА=;-ги. (1.98)
§ 8] Энергетический критерий устойчивости 39
Сопоставляя (88) и (89), находим:
о
или
Ш=48/EI()'dx- 0-99)
0
Отсюда вытекает известное выражение для потенциальной энергии деформации изогнутого стержня:
1
u=if EI{dx- (1л°о)
О
Это выражение можно также записать в виде
i
,, 1 Г М2 dx „ <Л4ч
U=2 J —ВТ' <1Л01)
О
С другой стороны, по (95) находим работу внешней нагрузки, производимую силой Р при искривлении стержня:
v = ?p !(%;)'“*■ <U02>
о
Величина W равна взятому со знаком минус изменению потенциала нагрузки:
/
v=~w=~ipf (тР) ах- (ыоз)
О
Сумма потенциальной энергии деформации и изменения потенциала нагрузки представляет собой полную энергию упругой системы Э:
Э = и -\-V = U — W. (1.104)
Таким образом, в рассматриваемом случае полная энергия равна
э ” Т /(■)’<'*-7 р/<U05)
40 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в ПРЕДЕЛАХ УПРУГОСТИ [гл. I
При возможном отклонении стержня от равновесного положения
первая вариация от полной энергии должна быть равна нулю:
ЪЭ = 0, (1.106)
что соответствует равенству (86).
Об устойчивости равновесного положения можно судить по знаку второй вариации от полной энергии. Если исходное положение устойчиво, то вторая вариация положительна:
Ь2Э> 0. (1.107)
При этом энергия прямолинейной формы стержня будет минимальной по отношению к значениям энергии для близких к ней искрив¬
ленных форм.
Если вторая вариация от энергии отрицательна,
Ь2Э < 0, (1.108)
то рассматриваемая равновесная форма будет неустойчивой.
Безразличному равновесию стержня соответствует равенство нулю второй вариации:
о2Э = 0. (1.109)
Рассмотрим случай шарнирно закрепленного по концам стержня,
сжатого силами Р по концам. Принимая для искривленной упругой
линии уравнение (18), получим из (105):
3==Х£/7?'--ТЯТ- <1Л1°)
Введем безразмерные параметры
' = <1Ш>
где h — высота сечения стержня. Тогда по (110) и (16) будет
<М12>
Первая вариация от Э* равна
8Э* = (1 — JL)C8C. (1.113)
а вторая вариация
ь2э* = (1 —г) 2* (1Л14)
Любая прямолинейная форма является равновесной; при С = 0 будет всегда S3* = 0. Устойчивость равновесия зависит от соотношения между Р и Ркр; при Р < Якр, Р > Ркр и Р = Ркр будут соответственно выполняться равенства (107), (108) и (109).
МЕТОДЫ РИТЦА И ТИМОШЕНКО
41
§ 9. Методы Ритца и Тимошенко
Энергетический критерий служит основой для эффективных приближенных методов решения задач устойчивости, кратко охарактеризованных выше. Рассмотрим эти методы более подробно.
Примем, что изогнутая линия стержня при потере устойчивости приближенно может быть представлена с помощью ряда
п
V = fiV)l + f2rl2+ ••• +/яЧ« = 2М- (1.115)
Здесь под понимаются функции х, удовлетворяющие геометрическим граничным условиям задачи, т. е. таким условиям, которые относятся к прогибам или углам поворота. Подставим (115) в выражение для полной энергии системы (104). Тогда энергия окажется зависящей от параметров прогиба fВариацию ЬЭ можно при этом представить как сумму вариаций, соответствующих возможным изменениям параметров ft\
п
b9=YiW,bfL- (1Л1б>
/ = 1
Так как рассматриваемые нами изогнутые состояния являются равновесными, то вариация ЬЭ по (106) должна быть равна нулю:
п
2H8/i=a (1Л17)
/=1 1
Но вариации можно считать независимыми друг от друга; поэтому равенство (117) будет иметь место, если каждый из множителей при Ь/; будет равен нулю:
ffUo. 1= 1.2 га. (1.118)
Судя по (105), энергия должна являться квадратичной функцией параметров ft. Вычисляя производные по //э мы получим линейные
функции fi. Следовательно, равенства (118) представляют собой систему п линейных алгебраических однородных уравнений относительно ft\ в коэффициенты при ft входит нагрузка Р. Если считать 0, то условием наличия решения системы (118) будет являться равенство нулю определителя, составленного из коэффициентов при /,:
Д = 0. (1.119)
Уравнение (119) будет содержать нагрузку в степени п. Решая это уравнение, мы получим п значений Р. Наименьшее из этих значений
42 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах упругости [гл. I
и будет приближенно отвечать первой критической силе. Подобный метод решения вариационных задач носит название метода Ритца *).
Пример* 1.5. Определить критическую силу для сжатого стержня, защемленного одним концом и с другим свободным концом. Представим упругую линию в первом приближении в виде отрезка квадратной параболы
координата х отмеряется от защемленного конца. Нетрудно убедиться в том что это выражение удовлетворяет геометрическим граничным условиям
dv
прогиб v и угол поворота обращаются в нуль для точки х = 0. Вычислим энергию системы по формуле (105):
Точное решение (28) приводит для этого случая к коэффициенту гс2/4 = 2,47; таким образом, ошибка составляет около 20%.
Во втором приближении введем новый независимый параметр /4 и примем
Если приравнять нулю первые производные от Э по fx и /2, то придем к уравнениям:
(а)
о
о
или
9 = 2EIf\l-2Pfl-.
(b)
(с)
v — f2x2 + /4х4.
(Ф
Энергия будет равна
Э = 2EII
(А + W/ + -у /У) ~ 2Р1г ( Л + 4 V/ + J Л'6) • (е)
(El - ~ /*) U + (2EIP - Щ- /<) /4 = 0,
(ё1 - /*) Л + (j Ell* - Ц- /«) /4 = 0.
(0
*) W. R i t z, Ober eine neue Methode zur Ldsung gewisser Variationsprobleme der math. Physik, Journ. f. d. reine und angew. Math. 135, № 1 (1908); Gesammelte Werke, Paris, 1911.
МЕТОДЫ РИТЦА И ТИМОШЕНКО
43
Если принять /2=0 и /4 Ф 0, то определитель, составленный из коэффициентов при /2 и /4, должен быть равен нулю:
Р*
о
2 р*
3
Z —
5
Р*
18
2 Р*
5
5
7
= 0,
где
Р* =
Pi2 EI *
(g)
(h)
Развертывая этот определитель, придем к квадратному уравнению относительно Р:
Р*2_45Р*+105 = 0. (!)
Наименьший корень этого уравнения определяет критическую силу:
Ркр = 2,50 —j2~ > (к)
здесь ошибка по отношению к точному значению составляет лишь 1,2%. Вводя в третьем приближении параметр /б, примем
v = f2x2 + f4x4 + fex*. (1)
Идя тем же путем, получим окончательное уравнение в виде
'-4Р-
1—4-я*
5
6—у Р*
2
2—4-р* о
3-у Р*
J!
5
2Р* 7
45 7 “
180_ 1Р* 7 3
3
9
50 —£-Р* о
= 0.
(ш)
Определяя наименьший корень этого кубического уравнения, найдем:
Е/
Лер =2,48
/2
(п)
Ошибка снижается до 0,4%.
Как видим, увеличивая число параметров //f мы можем сколь угодно близко подойти к точному решению. Отметим, что в приведенном примере все приближенные решения были выше точного. Это не является случайным. Реальный стержень представляет собой систему с бесконечно большим числом степеней свободы. Между тем, пользуясь методом Ритца, мы вводим лишь один или несколько варьируемых параметров, как бы ограничивая число степеней свободы системы, т. е. накладывая на нее лишние связи. Это приводит к искусственному завышению жесткости стержня, так что критическая нагрузка получается более высокой.
Результаты, получаемые с помощью первых приближений по методу Ритца, можно несколько улучшить, представив выражение
44 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ в пределах упругости [гл. 1
для энергии (105) в ином виде. Пользуясь вторым из соотношений (89), напишем:
Изгибающий момент М в некотором сечении можно выразить через сжимающую силу Р и прогиба. Затем следует идти тем же путем, что и при использовании выражения (105). В этом случае нам не приходится вычислять вторых производных от v, как это приходилось делать раньше. Но при аппроксимации изогнутой линии обычно более или менее хорошо улавливается лишь общее очертание кривой, в то время как приближенные значения вторых производных сильно отличаются от истинных. Этим объясняется преимущество применения выражения (120) по сравнению со (105).
Пример 1.6. Решим пример 1.5, пользуясь выражением для энергии (120). Изгибающий момент в сечении, лежащем на расстоянии х от защемленного конца, булет равен [—P(vt — и)], где через vt обозначено отклонение свободного конца. В первом приближении, принимая v = f2x2, находим: vj = /2/2; отсюда
Если теперь приравнять нулю производную от Э по /2, то, считая /2 Ф 0, Р Ф 0, найдем:
Мы получили такой результат, который в примере 1.5 был получен лишь во втором приближении.
Метод Ритца в приложении к линейным задачам устойчивости может быть использован и в другой форме, указанной С. П. Тимошенко [0.23]. Как мы видели, при безразличном равновесии должно быть 83 = 0, 23 = 0. Если рассматривать весьма малые отклонения стержня, то можно принять полную энергию постоянной: Э = const. Условимся, что нулевой уровень будет соответствовать критической силе, и примем для Р = Ркр
о о
М = — Я/2(/2 — х2).
Энергия будет равна
(а)
(Ь)
(с)
кр — 2,5 -2- •
(d)
э==и — W = 0.
(1.121)
Это можно пояснить таким образом, что при продольном изгибе потенциальная энергия деформации изгиба U оказывается в точности
МЕТОД БУБНОВА — ГАЛЕРКИНА
45
равной работе внешней сжимающей нагрузки W. Пользуясь теперь выражением (105), находим:
i
\ 2
dx
.MS)’
PKp = —l • (1.122)
dx
0
Можно также воспользоваться вторым выражением для энергии (120). Обозначим через т изгибающий момент в некотором сечении, отвечающий силе Р= 1. Тогда вместо (120) можно написать
<u23>
о о
Исходя из (121), находим теперь
i
/ \ 2
dx
ЛсР = -—, • (1-124)
т2 dx
/
EI
Допустим, что изогнутая линия стержня приближенно представлена в виде ряда (115). Тогда в числителе и знаменателе дроби (122) или (124) мы получим функции параметров ft. Желая найти наименьшее значение нагрузки, приравняем нулю производные от Р no fi'
= 1= 1,2 п. (1.125)
Для линейных задач мы получим тогда точно те же результаты, что и по уравнениям (118).
§ 10. Метод Бубнова — Галеркина
Другой приближенный метод, предложенный И. Г. Бубновым *) и развитый Б. Г. Галеркиным **), можно связать с вариационным уравнением задачи (97). Допустим, что изогнутая линия стержня аппроксимируется рядом того же вида (115), причем каждая
*) Отзыв о работе проф. С. П. Тимошенко «Об устойчивости упругих систем», Сб. Ин*та инж. путей сообщ., 31 (1913); см. И. Г. Бубнов, Избранные труды, Судпромгиз, 1956, 136—139
**) Б. Г. Г а л е р к и н, Стержни и пластинки, Вестн. инженеров, № 19 (1915), 897—908; Собр. соч., т. 1, изд. АН СССР, М., 1952, 168—195.
46 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ в ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
из функций т)t удовлетворяет не только геометрическим, но и статическим граничным условиям задачи. Подставим выражение (115) в уравнение (97). Внеинтегральные члены, отвечающие статическим граничным условиям, должны тогда выпасть. Вместо bv можно подставить выражение
п
8* = 2ч,8/<; (1.126)
i = l
тогда уравнение (97) приобретет вид
S/(£/S-+p-3)4s/- = °-
/ = 10
Но если вариации bft независимы и произвольны, то отсюда вытекает система п уравнений типа
i
/(£'£- + рда)’И*“°. '='-2 »- (1-128)
о
Под v в выражении, стоящем в скобках, здесь понимается ряд (115). После интегрирования мы снова получим систему однородных линейных алгебраических уравнений относительно /*, из условия совместности которых (при нетривиальном решении) находим критическую нагрузку. Так как уравнения (128) метода Бубнова — Галеркина и уравнения (И8) метода Ритца отвечают одним и тем же энергетическим зависимостям, то получаемые по этим методам результаты должны совпадать.
Как легко заметить, в скобках под знаком интеграла в (128) содержится левая часть дифференциального уравнения, соответствующего уравнению (8). Метод Бубнова—Галеркина можно обобщить, подставляя вместо этих скобок другие операторы. Такой оператор может, например, отвечать уравнению (5); тогда будет
i
f {EI-j£r + Pv)'rlidx = 0 (1.129)
о
или, в более общей форме,
i
J(ei-m) 4dx=0. (1.130)
о
Но при этом результаты вычислений уже не будут, вообще говоря, совпадать с данными, полученными по методу Ритца. Если в основу
§ 11] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ. УПРУГАЯ ШАРНИРНАЯ ЦЕПЬ
47
вычислений берется уравнение (130), то уравнение избранной упругой линии должно быть подчинено лишь геометрическим граничным условиям для прогиба.
Пример 1.7. Найти критическую нагрузку для шарнирно опертого по концам стержня, взяв в качестве исходной кривой параболу
v = fx (/ — л:). (а)
Составляем уравнение типа (129):
/ [-2/+ж/х{1~ х)] х{1~х) dx=°-
о
После интегрирования, при / Ф 0, находим:
Р ЮEI
/2 *
(Ь)
(с)
§ 11. Метод конечных разностей.
* Упругая шарнирная цепь
Вернемся теперь к приближенным методам, относящимся по нашей классификации к статическому критерию устойчивости. Остановимся прежде всего на методе конечных разностей.
Пусть имеется в виду уравнение (5). Разделим общую длину стержня на п равных частей, длину каждого интервала обозначим через s. Вторую производную для некоторой точки, разделяющей два соседних интервала, можно заменить приближенно с помощью так называемой центральной разности:
под vt, vi+1 понимаются прогибы в соответствующих точках.
Этому значению второй производной отвечает изгибающий момент от силы Р в /-й точке: М = (—Pvt). Тогда уравнение (5) получит вид
EI(vl_x-2vi-{-vll)=—Pvl. (1.131)
Таких уравнений можно составить (п—1); в них будут входить значения прогибов в концевых точках. Таким образом, получаем систему (п — 1) алгебраических линейных уравнений относительно vt; условие совместности этих уравнений (при ненулевом решении) снова приводит к определению критической нагрузки.
48
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ в ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
Пример 1.8. Определить приближенное значение критической силы для шарнирно опертого сжатого стержня. Делим длину стержня на четыре
Рис. 1.18. К решению задачи в конечных разностях.
части (рис. 1.18). Составляем уравнения (131) для точек / = 1 и / = 2, считая 5 = //4:
El (v0 — 2v, -f t>2) = — Pvu
Введем обозначение
EI (t>, — 2t>2 f t/3) = - Pv2.
Для левой концевой точки
VQ = 0.
Кроме того, в силу симметрии упругой линии
Vx = vs.
PI2 “ “ Ш1 •
Тогда уравнения (а), (Ь) примут вид
(° 2) v -j-1»2 = 0,
2v, + (а — 2) i»2 = 0. j
Приравнивая нулю определитель этой системы, получаем квадратное уравнение относительно а:
ос2 — 4ос 2 = 0. (g)
Наименьший корень равен
а =2 — /2 як 0,586.
Приближенное значение критической силы оказывается равным
(a)
(b)
(c)
(d) (е)
(0
EI
EI
Ркр = 0,586. 16 = 9,38.
/2
0)
Это значение отклоняется от точного на 4,3%; в отличие от предыдущих примеров здесь критическая нагрузка получилась с преуменьшением.
Другой вариант метода конечных разностей, который получил в литературе название метода упругой шарнирной цепи *), состоит в следующем. Разделим длину стержня на п равных частей. Обо¬
*) Этот метод был предложен Г. Генки.
§ 11] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ. УПРУГАЯ ШАРНИРНАЯ ЦЕПЬ
49
значим прогибы в узлах через v0, vlt..., vn_v vn. Выпишем дифференциальное уравнение для шарнирно опертого стержня в виде
Аг/ Р
s
где s — ljrt, или, представляя производную vf через разность, «взятую вперед»,
Д(vi+l—vi) _ Р м
~0 тТТ V:,
BIVi'
PI2
Вводя прежнее обозначение — находим:
Д(«/+1— vt)=—pP‘vl.
Примем для одного из концов стержня v0 = 0, a vx— заданной величиной, не равной нулю. Будем определять последовательно приращения vt, пользуясь формулами:
Av2 = Av1--P*vl,
Дг/3 = Дг>2 — Jj- P*v2 = д®, — -L Р* {vx + v2),
hvi + l = kvx *(1+2+ ••• ~hvi)-
Считая Lvx=vv получим:
v2 = vx + A2 = 2vI~~2 P*Vl>
= V2 + A3 =3vi—~2 P* (2<Vl + V2)>
Vi + 1 = (* + 0 v\ P* — 1)2+ •••
(1.132)
Подставляя сюда значения v2,..., vi9 мы можем выразить прогиб любого узла через vx. Используя, далее, граничное условие для второго конца стержня, получаем из (132) при vx Ф О уравнение относительно критической нагрузки Р*,
Соотношения типа (132) можно пояснить следующим образом. Допустим, что стержень разделен на п абсолютно жестких звеньев, связанных между собой упругими шарнирами. Единичному углу поворота в /-м узле соответствует момент
EI
Е1п
50 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах УПРУГОСТИ [ГЛ. I
Если бы все звенья имели тот же угол наклона, что и первое звено, мы лолучили бы = l)vx. При наличии взаимного поворота звеньев в первом узле нужно ввести «поправку» к этой величине, равную для (/+1)-го узла P*lvjn2. Остальные члены в выражении для vi+l определяют «поправки» от углов поворота в других узлах, вплоть до /-го.
Пример 1.9. Определить критическую силу для шарнирно опертого стержня методом «упругой шарнирной цепи», разделяя стержень на четыре звена. Воспользуемся симметрией упругой линии относительно среднего сечения; очевидно, должно быть t>3 = v,. По формулам (132)
V» = 2», — P*vx,
1 f (а)
1»з = 3v, —Jg Р* (2t>, + t»j).
Отсюда
щ Р* (4v, - -jk ЯЧ»,) • (b)
Считая i/, Ф 0, приходим к уравнению
Р*1 — ЫР* + 512 = 0. (с)
Параметр критической силы оказывается равным Я* = 9,44; ошибка по отношению к точному решению составляет около 4,4%. Другой пример приме¬
нения этого метода будет приведен в § 22.
§ 12. Метод коллокации
Обратимся к методу коллокации *), который занимает как бы промежуточное положение между методом Бубнова — Галеркина и методом конечных разностей. Выражение для прогиба аппроксимируем снова с помощью ряда (115),
п
®=2 /л.
/* 1
причем каждая из функций должна соответствовать всем граничным условиям задачи. Параметры ft определяются таким образом, чтобы после подстановки выражения (115) основное дифференциальное уравнение задачи удовлетворялось для п значений независимой переменной. Точки, в которых выполняется уравнение, называются «точками коллокации». Они могут быть выбраны, вообще говоря, произвольным образом, но обычно их располагают на равных расстояниях друг от друга. Если имеется характерный участок резкого изменения функции, то желательно здесь располагать точки
*) Коллокация (collocation) — буквально расположение, размещение. Речь идет о размещении тоек» в которых выполняется определенное условие.
МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
61
коллокации более часто; при использовании метода конечных разностей интервалы в такой области также «размельчают».
Пример 1.10. Вновь определим критическую силу для стержня, один конец которого защемлен, а второй свободен. Дифференциальное уравнение задачи выпишем в виде (см. пример 1.6)
£/-0 = -/>(*,-«)• (а)
Аппроксимирующему выражению для v придадим форму
1/=/2лг2+/4дс4, (Ь)
как в одном из вариантов примера 1.5. Расположим точки коллокации в пунктах х = I/2 и х = /. Подставляя выражение (Ь) для этих точек в (а), получим следующие уравнения:
/2+6/’Л=0, (С)
(2 - 4 Р')л + (з-] Р*) I*f< = 0. (d)
Отсюда
PI2 48
тгтН2-53- <е>
Этот результат отклоняется от точного на 2,4% и очень близок к тому, который при том же аппроксимирующем выражении был получен нами по методу Ритца.
Энергетические методы, метод конечных разностей и метод коллокации можно объединить в том отношении, что при их применении задача сводится к рассмотрению системы алгебраических уравнений. Подобные методы в математической физике называют прямыми.
§ 13. Метод последовательных приближений
При использовании энергетических методов нам приходилось аппроксимировать упругую линию, причем погрешность результата зависела от того, насколько удачно выбрано выражение для прогиба. Правда, в примере 1.3 мы могли сколь угодно близко подойти к точной величине критической силы, но для этого нужно было всякий раз вводить новый параметр прогиба. Характер дополнительной составляющей мог быть выбран нами по тем или иным соображениям. Перейдем теперь к рассмотрению метода последовательных приближений, при котором каждое новое приближение целиком основывается на предыдущем и вытекает из него, не будучи связано с интуицией автора расчета.
Сущность этого метода состоит в том, что в качестве исходной упругой линии берется любая кривая, удовлетворяющая условиям на концах. Абсолютные значения ординат этой кривой могут быть выбраны произвольно, так как при критической нагрузке (если исходить
52 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах УПРУГОСТИ [гл. I
из приближенного дифференциального уравнения упругой линии) они определяются с точностью до постоянного множителя. Далее решается задача об изгибе стержня под действием данной системы внешних продольных сил. Если бы кривая была нами сразу подобрана правильно, то, определив изгибающие моменты и проинтегрировав дифференциальное уравнение упругой линии, мы должны были бы получить ту же кривую. Если же первоначальная кривая была подобрана лишь приближенно, то вторая кривая будет отличаться от первой. Иными словами, новая равновесная изогнутая форма окажется не той, что мы выбрали раньше. Чтобы прийти к новой упругой линии, надо изменить ординаты прежней. Но так как при наличии только осевой сжимающей силы изгибающие моменты пропорциональны ординатам, то это тождественно изменению в X раз величины внешней нагрузки. То обстоятельство, что ординаты новой кривой отличаются в X раз от ординат первоначальной кривой, указывает на то, что внешние силы надо увеличить или уменьшить в X раз, чтобы получить критическую нагрузку. Но, как правило, в различных сечениях стержня мы будем получать разные отношения ординат. Можно условиться определять критическую нагрузку через отношение максимальных ординат или отношение площадей, охватываемых упругой линией. Ниже будет указан также метод, когда истинное значение критической нагрузки окажется взятым «в вилку», т. е. представится возможным одновременно подходить к нему сверху и снизу. От первого приближения мы можем далее перейти ко второму и т. д. При этом мы будем получать ряд значений X, определяющих в пределе истинную величину критической нагрузки.
Методу последовательных приближений может быть придана аналитическая и графическая форма*).
Пример 1.11. Определить критическую нагрузку для шарнирно опертого по концам стержня, взяв в качестве исходной линии ломаную, состоящую из двух прямых отрезков (рис. 1.19) с ординатой / посредине.
Уравнение левой половины:
Принимая силу Р равной единице, определяем изгибающий момент в сечении х при х //2:
(а)
М = Pv = — х.
(b)
Дифференциальное уравнение упругой линии (5) принимает вид
(с)
*) Графический вариант метода был предложен Вианелло [1.16], а аналитический вариант Ф. Энгессером и в другой форме Б. Н. Горбуновым (Сб. исследований по теории сооружений, 2, 1936, Стройиздат).
§ 13]
МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
53
Интегрируя его дважды и находя постоянные из условий на концах, получаем уравнение упругой линии первого приближения:
£/и = -7Т+Ти
(d)
Отношение максимальных ординат первоначальной и полученной линии дает первое приближенное значение критической силы:
КI
кр UI / <2 *
(е)
Рис. 1.19. Форма упругой линии в нулевом и последующих приближениях.
выражение (d) в правую часть уравнения (с), тогда во втором приближении критическая сила получается равной
р(И)_Ы
KP-U,.L <2 ’
(О
ошибка равна здесь 1,4%.
Изменение формы упругой линии дано в следующей таблице (максимальная ордината взята за единицу):
\
/
6
/
1Г
/
2
Исходная форма 0
0,33
0,67
1
I приближение 0
0,48
0,85
1
II приближение 0
0,49
0,86
1
Точные значения (по синусоиде)..
0
0,50
0,87
1
Исходная форма (и0) сопоставлена с формами двух первых приближений (I/, и t/ц) на рис. 1.19.
Критерием для необходимого числа приближений может служить сравнение величины критической силы или ординат изогнутой линии в двух последовательных приближениях. Если эти значения
54 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах упругости [гл. I
совпадают с точностью до некоторой заданной величины,.то решение можно считать выполненным.
Как правило, последовательные приближения в той форме, как указано выше, приводят к значению наименьшей критической силы и при этом представляют собой сходящийся процесс.
Пусть дифференциальное уравнение изогнутой линии представлено в виде (5):
Разложим функцию v0, отвечающую упругой линии исходного приближения, по собственным формам потери устойчивости:
Напомним, что каждая из собственных форм соответствует своей критической силе — первой, второй и т. д. Для /-й собственной формы уравнение (133) принимает вид
Принимая /-ю форму в качестве эпюры моментов и находя отношение ординат предыдущей и последующей кривых, мы будем получать /-ю критическую силу. Так как исходная кривая (135) являлась произвольной, то в первом приближении мы получим следующее разложение:
®1—••• (1.137)
Повторяя такой цикл п раз, придем к уравнению
Но так как вторая, третья и последующие критические силы лежат всегда выше первой, то при увеличении числа циклов второй, третий и т. д. члены в правой части равенства (139) будут неизменно уменьшаться, так что в пределе получим:
d2v
~dx*
Xvt
(1.133)
и граничные условия будут
v = 0 при х = 0, I.
(1.134)
= f \Ч\ + fib + Мз +
(1.135)
(1.136)
ИЛИ
= + ••• 0-138)
Л1 л2 Л3
vnli = f\\ + А (17) \ + /з (17) 3 + ••• 0-139)
(1.140)
МЕТОД ПРОБ
55
Как видим, по мере возрастания номера п приближения vn с точностью до некоторого множителя приближается к первой собственной форме.
Критическую силу обычно вычисляют, сравнивая максимальные ординаты упругой линии в двух последовательных приближениях. Однако важная особенность метода состоит в следующем. Если найти отношение ординат в двух приближениях для одной точки, затем для второй и т. д., то истинное значение критической силы будет лежать между значениями, определяемыми максимальными и минимальными отношениями. Таким образом, точную величину критической силы удается взять «в вилку», которая сужается для каждого нового приближения *).
Так, делая вычисления в примере 1.11 для точек //6, 1/3 и //2, получаем в первом приближении 7,9 < PKJ2jEI < 12, во втором приближении 9,8 < < /VW < Ю и т. д.
§ 14. Метод проб
Если придать методу последовательных приближений графическую форму, то каждая новая упругая линия строится как веревочная кривая по отношению к предыдущей при произвольном полюсном расстоянии. Другой вариант графического метода можно предложить **), если задаваться некоторыми ориентировочными значениями критической нагрузки и строить соответствующую упругую линию, варьируя полюсное расстояние //. Величина Н берется равной
под п понимается число равных интервалов, на которце разделена длина стержня /, под 1 jm — масштаб чертежа (рис. 1.20). Первый участок веревочной линии проводим под произвольным углом. Далее выясняем, как расположена конечная точка а веревочной кривой, т. е. точка пересечения последнего участка с горизонтальной линией, проведенной через начальный пункт. Если эта конечная точка будет соответствовать правому концу стержня, то принятая для определения полюсного расстояния сила Р и является критической. Как правило, последний участок веревочной линии будет либо пересекать ось стержня, либо лежать ниже осевой линии. В первом случае
*) На это свойство метода последовательных приближений было указано С. Н. Каном; см. также книгу С. П. Тимошенко [0.23], изд. 1961 г»
**) Этот метод был предложен Саусвеллом.
56 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
принятая в качестве критической величина силы является преувеличенной, во втором — преуменьшенной. Для того чтобы взять искомое
Рис. 1.20. Определение критической силы с помощью «метода проб».
значение силы «в вилку», нужно вести «пристрелку» и проделать по крайней мере два построения, как показано на рис. 1.20.
§ 15. Применение интегральных уравнений.
Приближенное определение первой критической нагрузки
Пользуясь методом последовательных приближений, мы задавались той или иной упругой линией — совпадающей в случае шарнирно опертых концов стержня с эпюрой изгибающих моментов от сжимающих сил — и находили новую упругую линию путем интегрирования; сравнение первоначальных и вновь найденных ординат позволяло определить приближенное значение критической нагрузки и установить, какая форма изогнутой оси ему соответствует. Идя по этому же пути, но исходя из более общих соображений, можно составить интегральное уравнение задачи — уравнение, заключающее неизвестную функцию прогиба под знаком интеграла.
ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
57
Рассмотрим стержень, шарнирно опертый по концам. Определим прогиб в некотором сечении х, пользуясь формулой Максвелла — Мора:
* = /.
ММ
EI
(1.142)
где М — изгибающий момент в текущем сечении £ от заданных сил, М — момент в том же сечении от единичной силы, приложенной
Рис. 1.21. К выводу интегрального уравнения задачи.
в точке с координатой л:. Как видно из рис. 1.21, эти моменты будут (при сжимающей силе Р)
Ж = /М), М =
(l — -j) при
(l j'j х при
Воспользуемся безразмерными параметрами
— jc 1 —г
-J — XV £ —
(1.143)
(1.144)
и представим (142) в виде
«(*!>=*/ (l-*i)«i*«1)«1+/45r<l-Si)*i««i)*i. (1-145)
58 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в ПРЕДЕЛАХ УПРУГОСТИ [гл. t
Будем в дальнейшем опускать индексы при х и £. Введем обозначения (в безразмерных величинах)
( (1 — л:) £ при £<лг,
0(*, 5)= (1.146)
1(1- при '
Учтем также, что в общем случае момент инерции сечения / и модуль Е переменны по длине: / = /(£), Е = £(£), и выразим их через
некоторые приведенные величины Е0 и /0:
£(5)/(5) = (1.147)
тогда выражение (145) примет вид
1
<*• ® ® <*> • 148>
О
Функция О (л:, ), как легко видеть из (146), является симметричной относительно переменных х и Ь
Q(x, 5) га О (6, х). (1.149)
Обозначим
\ = К(х, 5) = 0(*. ЪУШУТй). y{x) = v{x)Vg{*)‘,
(1.150)
тогда вместо (148) получим:
1
у(*) = Х J/С(лг, 6)y(0«R. (1.151)
0
Судя по (150), функция К(х, £) также оказывается симметричной:
К(х, t) = K(l х). (1.152)
Уравнение (151) содержит функцию у(Е) под знаком интеграла, причем пределы интегрирования конечны и постоянны. Если функция К (х, £) в рассматриваемом интервале непрерывна, то уравнение (151) является однородным интегральным уравнением Фредгольма второго рода *). Теория Фредгольма распространяется также на функции /С, для которых интеграл
1 1
S2 = ff КНх, \)dxd% (1.153)
о о
*) См. С. Г. Михлин, Интегральные уравнения, Гостехиздат, М., 1949.
§ 15]
ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
59
имеет конечное значение. В нашей задаче это требование всегда выполняется. Функция К(х, £) носит название ядра, а величина X— параметра уравнения. Уравнение (151) имеет, вообще говоря, тривиальное решение: у(л;) = 0, отвечающее прямолинейной форме равновесия стержня. Нетривиальное решение у (л:) появляется в точках разветвления (бифуркации) равновесных состояний (см. стр. 15); соответствующие этим точкам значения параметра X называются характеристическими или фундаментальными числами, а также особыми или собственными значениями параметра (см. стр. 19), а нетривиальные решения—собственными, характеристическими или фундаментальными функциями. Характеристические числа уравнения (151) определяют в нашем случае первую и высшие критические нагрузки.
Таким образом, для определения первой критической нагрузки необходимо определить наименьшее характеристическое число интегрального уравнения; последнее заменяет дифференциальное уравнение задачи вместе с граничными условиями.
Интегральные уравнения решаются с помощью различных приближенных методов. Одним из наиболее распространенных методов является метод последовательных приближений, который уже рассматривался в § 13. Другой метод заключается в замене интегрального уравнения конечной системой линейных алгебраических уравнений, для чего правая часть (151) преобразуется по одной из формул приближенного интегрирования *).
Но для определения характеристических чисел можно воспользоваться также теорией симметричных интегральных уравнений Гильберта— Шмидта **). Этот путь приводит к примечательным формулам, выражающим первое характеристическое число через так называемые следы ядра. В первом приближении можно принять
где S2 — второй след ядра, определяемый по формуле (153). Такой метод интересен тем, что определение критической нагрузки (характеристического числа) как бы отделяется от установления формы потери устойчивости (собственной функции), в то время как в предшествующих случаях эти задачи выполнялись одновременно. Можно показать, что приближенное значение критической нагрузки по (154) всегда лежит ниже истинного.
Формулу (153) для двойного интеграла можно преобразовать следующим образом. Разделим площадь интегрирования на два равных
*) См. J1. В. Канторович, В. И. Крылов, Приближенные методы высшего анализа, 1962, стр. 110.
**) См. указанную выше книгу С. Г.. Михлина, стр. 108.
(1.154)
60
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ ГЛ. !
треугольника (рис. 1.22) линией х = %\ тогда, производя интегрирование по площади одного из этих треугольников, получим:
52 = 2 J dx J* К*{х, S.)d\.
(1.155)
Пример 1.12. Определить критическую нагрузку для шарнирно опертого стержня постоянного сечения, если сжимающие силы приложены по
концам. По (146) и (150) находим:
£(5) = 1, £(*) = 1, К(хЛ) = 0{х, S) =
(1 — x)z при
£) * при х < 5.
Пользуясь формулой (155), получим:
I х 1
2/(1 - *). /е * _ 1/(1 -,)’ д, _ А-.
• Л Л п
Рис. 1.22. К определению 0 (154)
величины 5 при симме- v ;
тричном ядре.
К = /90.
Приближенное значение критической нагрузки по (150) равно Лф =/90 = 9,487 ;
оно оказывается, как и следовало ожидать, меньшим, чем точная величина Ркр, и отличается от нее на 4,1%.
Мы составляли до сих пор интегральное уравнение, рассматривая задачу в линейной постановке. Если принять точное выражение (2) для кривизны изогнутой оси, то интегральное уравнение задачи окажется нелинейным. В литературе по нелинейным интегральным уравнениям рассматривается вопрос о правомерности их линеаризации при определении бифуркационных точек задачи (см. § 198).
§ 16. Динамический критерий устойчивости
Мы разобрали методы, основанные на статическом и энергетическом подходах к задаче об устойчивости стержня. Обратимся теперь к третьему, динамическому критерию и рассмотрим собственные колебания сжатого стержня, шарнирно опертого по концам.
ДИНАМИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
61
Выпишем дифференциальное уравнение изогнутой оси типа (6):
(1Л56)
где q— интенсивность поперечной нагрузки. В случае колебательного движения прогиб v будет функцией не только координаты х, но и времени t\ v = v(x, t). Поэтому полные производные по х должны быть заменены на частные. Пользуясь принципом Даламбера, примем в качестве интенсивности распределенной нагрузки силу инерции массы стержня, приходящуюся на единицу длины. Обозначая через р вес единицы длины стержня, получим:
Fl _ £.L Г1 157ч
дх4 + дх2 ~ g dt2 ’ (1.10/)
где g — ускорение силы тяжести. Вводя обозначение k2 = Р/El, придем к уравнению
4.ь2_ — о п П8ч
дх* ■ к дх2 Elg dt2 • (1.158)
Будем искать решение уравнения (158) в виде произведения двух функций:
v(xt t) = X(x)T(t); (1.159)
тогда вместо (158) получим:
d4X, а2т, d2X р vd2T
1 dx4 dx2 ~ Elg Л dt2
или
1 d4X.,9 1 d2X pi d2T
X Hr* FJa T НП • (1.160)
X dx4 X dx2 ~ Elg T dt2
Левая часть этого уравнения зависит только от х, а правая — только
от t\ уравнение может удовлетворяться лишь в том случае, если левая и правая части являются постоянными величинами:
1 d'X, а2 1 d2X, 1С1Ч
k у-й2=1» (1.161)
X dx4 г X dx2 р 1 d2T
Elg Т dt2 (1.162)
Второе из этих уравнений преобразуется к виду
62 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
Интеграл этого уравнения представим в форме
Т = A sin (о/ —J— ix)j 0*1
частота колебаний о определяется формулой
Ш2 = Х. (1.165)
Уравнение (161) перепишем в виде
<1Л66>
соответствующее характеристическое уравнение будет
s4 + k2s2 — X = 0. (1.167)
Это уравнение имеет два действительных корня и два мнимых. Вводя обозначения
s,= yw+b-k Л=УР+Ъ+»' (1168)
выпишем решение уравнения (166) в форме
X (л:) = A ch sxx + В sh sxx -f- С cos s2x -f- D sin s2x. (1.169)
Выражение (169), определяющее форму колебаний, должно удовлетворять граничным условиям (10). Первые два условия, относящиеся к сечению х = 0, дают: А = С = 0; два других приводят к равенствам: В = 0, Dsin2/ = 0. Считая Оф0, находим:
s2=™, л= 1, 2, 3.... (1.170)
Отсюда по (168)
<1.Ш)
Частота /t-го тона колебаний по (165) оказывается равной
_ я*** Г~Щ(Л Р1* \'1‘ „ 17ЛЧ
°>я— I2 У Р ' пгп*Ег} ’ (1.172)
Обозначим через а)0л частоту п-то тона колебаний стержня при отсутствии силы Р:
“О §Т' (1Л73>
Тогда окончательно
-„=“.,(1 -ни»)*-' С-.1М)
Эта формула является «ключевой» для динамического анализа
устойчивости стержня. В ней мы находим объяснение эксперимен¬
КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ
63
тальным данным, описанным в § 1. Частота колебаний стержня с образованием одной полуволны (п= 1) делается равной нулю, когда сила Р достигает кри- р тического значения Р9 = тс2£///2. 7*
Таким образом, наступление монотонной (статической) неустойчивости стержня характеризуется здесь обращением в нуль частоты собственных колебаний *). На графике (Р/Рэ, со2) получаем прямую, пересекающую ось ординат в точке бифуркации равновесных форм (рис. 1.23). Динамический критерий приводит в данном случае к тому же значению критической нагрузки, что и другие критерии — статический или энергетический. Однако, как уже было сказано, такое совпадение имеет место не для любой упругой системы.
§ 17. Критерий начальных несовершенств
До сих пор нами рассматривались идеальные стержни с прямолинейной осью, нагруженные сжимающей силой строго по центру тяжести поперечного сечения. Между тем реальные элементы конструкций всегда обладают известной начальной погибъю\ приложенные к ним сжимающие силы обычно действуют с некоторым эксцентриситетом) наряду с осевыми силами могут быть приложены те или иные поперечные нагрузки. Все эти факторы играют роль «возмущений», влияющих на поведение системы. Исследование «несовершенных» систем важно, прежде всего, с практической стороны, так как позволяет приблизить расчетную схему к реальным конструкциям. Правда, все перечисленные факторы являются, как правило, случайными, поэтому обоснованно оценить их эффект можно лишь с привлечением статистических методов. Подобные методы будут изложены ниже, в главе XX. Однако построение статистических зависимостей требует предварительного определения того, как ведет себя система при некотором заданном возмущении **). Кроме того, рассмотрение несовершенной системы в ряде случаев позволяет определить критическую нагрузку для ее идеальной модели: мы знаем уже, что эффект различных возмущений особенно сильно сказывается вблизи критической нагрузки.
*) Возможен также случай колебательной неустойчивости; он должен быть рассмотрен отдельно (см. § 21).
• **) Более подробно об этом см. в § 193.
Рис. 1.23. Зависимость между частотой колебаний и сжимающей силой.
64
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. 1
Рассмотрим последовательно влияние всех важнейших возмущающих факторов. Начнем со случая, когда стержень, шарнирно опертый по краям, имеет начальную погибь
v0 = v0(x) (1.175)
и сжимается силой Р, направление которой проходит через концевые шарниры. Дифференциальное уравнение (5) получает вид
T7I d2v п
El4*=-Pv
(1.176)
где под v понимается дополнительный прогиб, возникающий в процессе деформации, под v1 — полный прогиб:
«!=« + %
(1.177)
Вводя прежнее обозначение £2 = Р/£/, получим:
d2v
dx2
- k2v = — k2v0.
(1.178)
Пусть, например, в начальном состоянии стержень изогнут по полуволне синусоиды (рис. 1.24):
Л. пх vo — /о sin —.
(1.179)
Решением уравнения (176), удовлетворяющим граничным условиям v — 0 при л; = 0, /, будет
V-
Ж— sin-
-r — k2
(1.180)
Стрела дополнительного прогиба / оказывается равной
Рис. 1.24. Стержень с начальной погибью.
г /о
J р
* кр
(1.181)
— 1
где под Ркр понимается критическая сила (15). Полная стрела прогиба fx = f-\-f0 определится формулой
/о
/к
(1.182)
1.
кр
Зависимость между / и Р/Ркр при различных начальных неправильностях изображена на рис. 1.25; величины / и /0 отнесены
§ 18) Эксцентричное сжатие, приближенное решение
65
к радиусу инерции сечения стержня i:
(1.183)
Поведение системы оказывается качественно отличным от того, которое было характерно для «классической» задачи устойчивости. Прогиб возникает уже при малых значениях силы Р, в то время как в случае центрального сжатия при нагрузке РРкр стержень должен оставаться прямолинейным.
Скорость нарастания прогиба зависит от «возмущающего фактора» — стрелы начального прогиба.
При достаточно малых С0 кривая Я (С) лежит весьма близко от оси ординат. В то же время при нагрузке, приближающейся к критической, прогиб быстро нарастает; функция Р(С) является нелинейной. Когда Р приближается к Ркр, получаем /-> оо; стрела прогиба возрастает беспредельно.
Напомним, что материал стержня мы считаем здесь идеально упругим и что задачу решаем, исходя из линейного дифференциального уравнения.
Формула (181) может быть использована для определения критической силы при экспериментах со стержнями, имеющими начальную погибь *). Представим (181) в виде
Рис. 1.25. Диаграмма «дополнительный прогиб — нагрузка» для стержня с начальной погибью.
Ркр / — /о*
(1.181а)
Строим график, откладывая по оси абсцисс измеренные значения /, а по оси ординат — значения //Р. Тогда мы на графике должны получить прямую, причем величина, обратная угловому коэффициенту прямой, даст критическую силу.
§ 18. Эксцентричное сжатие. Приближенное решение
Рассмотрим, далее, другой возмущающий фактор — эксцентриситет в приложении нагрузки. Пусть стержень, шарнирно опертый по концам, подвергается действию сил Р9 точка приложения которых
*) Этот метод был предложен Саусвеллом.
66
УСТОЙЧИВОСТЬ СЖАТЫХ СТЁРЖНЕЙ в ПРЁДЕЛАХ УПРУГОСТИ [гл. I
отстоит от центра тяжести сечения на расстоянии е. Предполагается, что плечо е лежит в плоскости наименьшей жесткости стержня (рис. 1.26).
Дифференциальное уравнение (5) получит здесь вид
Е1
d2v
или
dx2 d2v.
= — P{v + e) k2v = — k2e.
(1.184)
(1.185)
Общее решение соответствующего однородного уравнения будет
v = A cos kx Bsmkx. (1.186)
Сюда надо присоединить частное решение v= — е; полное решение получает вид
v = A cos kxВ sin kx — е. (1.187)
Удовлетворяя граничным условиям задачи z; = 0 при л: = 0, /, найдем:
А = е, B = etgЦ-. (1.188)
Решение (187) теперь можно записать в форме
v= е cos kx -f- tg Ц- sin kx— l) (1.189)
Рис 1.26. Шарпи>но опертый стержень под действием эксцентрично приложенных сил.
или
v = е
cos
(?-*)
kl
Стрела прогиба равна при х =-j
1
f = e
(j« ■) ')
(1.190)
(1.191)
Отметим, что и здесь зависимость между / и Р будет нелинейной и что при Р->Ркр получим /->оо.
Решим ту же задачу с помощью метода Бубнова—Галеркина (см. § 10). Примем уравнение упругой линии в виде
-. пх V = / Sin -у-.
(1.192)
§ 19]
ЭКСЦЕНТРИЧНОЕ СЖАТИЕ. ТОЧНОЕ РЕШЕНИЕ
67
Составим уравнение типа i
/[£/ + P(v + O]sta5rfx = 0 (1.193)
О
и подставим вместо v выражение (192); после интегрирования получим:
f = (1.194)
— 1
Это уравнение имеет ту же структуру, что и зависимость (181), относившаяся к синусоидальной начальной погиби.
Если такого же типа нагружению подвергается стержень с одним защемленным концом и другим свободным концом (рис. 1.27), то уравнение (184) получит вид
d2v
EI
dx2
ИЛИ
(1.195)
(1.196)
dv
Подчиняя решение условиям v = 0, -- = 0 при х = 0, найдем:
v = (e-j-/)( 1 —cos kx). Полагая х = 1, получим:
f~e {coski ~1)~е( я / р
VC0S2K PZ
(1.197)
Рис. 1.27. Стержень с защемленным (1.198) концом под действием эксцентрично приложенной нагрузки.
Зависимость между / и Р оказалась точно той же, что и в случае шарнирно опертых концов.
§ 19. Эксцентричное сжатие. Точное решение
Подойдем к той же задаче об эксцентричном сжатии, исходя из точного дифференциального уравнения упругой линии, как в § 5. На рис. 1.28 изображен стержень длины I в изогнутом положении;
68 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ в ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. I
сила Р действует на плече е и сохраняет вертикальное направление. Кроме того, здесь же показан фиктивный стержень длиной lv конец которого лежит на линии действия силы Р. Очевидно, по отношению к этому фиктивному стержню можно использовать соотноше-
Пусть для верхнего конца стержня параметр ср приобретает значение ср = срх; тогда Рис. 1.28. К точному ре- стрела прогиба / будет равна шению задачи об эксцент-
ричном сжатии стержня. «/ = 2 sin ft (1 — cos срх). (1.200)
Определим, далее, угол поворота касательной к изогнутой линии 6. Воспользуемся соотношением
и подставим сюда значения dx и ds по (66) и (68); тогда получим:
Угол наклона верхнего торца при х = 1 найдется тогда по фор муле
Рассматривая рис. 1.28, выпишем зависимость между / и fx:
ние (75), связывающее стрелу прогиба /х с параметрами k и ft (оставляем знак плюс):
Прогиб v в некотором сечении х определяется по (76):
Будем рассматривать равновесные положения стержня вблизи первой критической силы, так что для ср0 в (71а) примем значение л = 0.
kv = 2 sin ft (1 — cos ср).
kfx = 2si nft. (1.199)
(1.201)
cos 6 = 1 п(/2 — У2)
или, no (69),
cos 6=1 — 2 sin2 ft sin2 cp.
(1.202)
cos 0Z = 1 — 2 sin2 ft sin2 cp1
(1.203)
fi = f cos 0Подставляя сюда выражения (199), (200) и (203), находим:
(1.204)
ВЛИЯНИЕ ПОПЕРЕЧНОЙ НАГРУЗКИ
69
Интегрируя выражение (71) для ds, получим полную длину стержня/: <pi
kl= f d2.. = = f((Pl, »). (1.206)
J у l — sin2 ft sin2 9 v ’
Подобный интеграл, в отличие от (73), носит название неполного эллиптического интеграла первого рода. Эти интегралы также табулированы.
Уравнения (204), (205) и (206) содержат три неизвестные величины: стрелу прогиба /, параметры ft и срх. Пользуясь ими, можно для каждого заданного эксцентриситета е установить зависимость между нагрузкой Р и стрелой прогиба /. Такие кривые для
* = 0,1/ и * = 0,01/ изображены на рис. 1.29 в сопоставлении с кривой, относящейся к случаю центрального сжатия (е = 0).
Наибольшее расхождение между кривыми получается в области, лежащей вблизи критической нагрузки; при Р > Якр влияние эксцентриситета падает.
Эти данные можно сопоставить с приближенным решением.
Если считать, что параметр ft мал для незначительных прогибов, то в (205) и (206) можно пренебречь sin2 ft sin2 ср по сравнению с 1; тогда получим:
kl = F (cpi, ft)«cPl, (1.207)
ke « 2 sin ft cos cpx 2 sin ft cos kl. (1.208)
Сравнивая с (200), найдем:
f = e(—-r-j l\,
J \ cos kl )
что совпадает с (198).
§ 20. Влияние поперечной нагрузки
Перейдем к случаю, когда наряду с осевой силой действует некоторая поперечная нагрузка. Пусть шарнирно опертый стержень,
сжатый силой Р, подвергается действию равномерно распределенной нагрузки интенсивности q (рис. 1.30). Уравнение (5) получает вид
т
0,8
0,6
0,4
0,2
02 0,4 0,6 0,8 w 1,2 1.4 16 18 2,8
РК р
Рис. 1.29. Зависимость между стрелой прогиба и нагрузкой по точному решению задачи.
d2v _ - ql _. qx»
70
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. Г
или, при k2 = PjEI,
d2 v dx?
*-)■
(1.210)
Соединяя общее решение однородного уравнения и частное решение, находим:
k2v = A cos kx + В sin kx— x ~~ Jr* 0-211)
Из граничных условий получаем:
л = -ь в.
Р £ 2
(1.212)
Окончательно:
kv = -jL(tg-sinkx-{- cos kx — у)' (1.213)
Стрела прогиба равна
_Л (1.214)
f ~ Pk* I
kl
Мы получили зависимость между / и Я того же типа, что и для эксцентрично сжатого стержня.
',4
:J..i J. L :.
I L.J 1. i ■
Р
Рис. 1.30. Стержень при продольно-поперечном изгибе.
В случае, если вместо распределенной нагрузки имеется сосредоточенная сила Q посередине пролета, таким же путем находим уравнение упругой линии для одной из половин стержня
О / 1
V =
и стрелу прогиба
2Р \ и kl
k COS
sin kx
1
(1.215)
(1.216)
Решим ту же задачу об одновременном действии осевой и поперечной нагрузок с помощью метода Бубнова—Галеркина. В случае
ВЛИЯНИЕ ПОПЕРЕЧНОЙ НАГРУЗКИ
71
равномерно распределенной нагрузки выпишем уравнение
+ (1-217)
Вводя в качестве аппроксимирующей кривой полуволну синусоиды
v = f sin, (1.218)
придем к уравнению
I)
Подставляя вместо v (218) и интегрируя, находим:
4 ql4
/ = i р/2 (1.220)
Числитель представляет собой здесь приближенное значение стрелы прогиба стержня при действии одной поперечной нагрузки:
/o = ssit-: (L221>
коэффициент равен 1/76,7 вместо известного значения 5/384 = = 1/76,8. Поэтому формулу (220) можно переписать в виде
/= /ор > (1.222)
* кр
что совпадает по структуре с (182). Эта простая формула может быть распространена и на другие случаи продольно-поперечного изгиба. Для определения максимальных нормальных напряжений надо воспользоваться формулой
_ Мтах
°шах — ур *
где W — момент сопротивления сечения.
Учитывая моменты, отвечающие продольной сжимающей и поперечной нагрузкам, найдем:
(1.223)
сжимающие напряжения считаются здесь положительными.
Как видим, при продольно-поперечном изгибе принцип независимости действия сил неприменим; величина (223) не равна сумме напря¬
жений, вызываемых продольной и поперечной нагрузками в отдельности.
72 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. 1
Поэтому при проверке стержня на «устойчивую прочность» (термин Н. В. Корноухова) умножают все нагрузки на коэффициент запаса п и сравнивают максимальное напряжение не с допускаемым, а с напряжением, принимаемым за предельное.
§ 21. Устойчивость неконсервативной системы.
Случай следящей силы
Все рассмотренные до сих пор упругие системы относились к числу консервативных: работа сил, приложенных к ним, не зависела от траекторий перемещения точек приложения и определялась только начальным и конечным положением этих точек. Обратимся теперь к одному из примеров неконсервативной системы, исследование устойчивости которой требует особого подхода *).
Допустим, что один из концов стержня постоянного сечения защемлен, а второй свободен и что
к свободному концу приложена сила Я, направленная при изгибе стержня вдоль касательной к упругой линии (рис. 1.31); такую силу называют следящей. Разложим силу Я на две составляющие: вертикальную V и горизонтальную Н. При малых углах поворота касательной силу V можно считать постоянной; она играет такую же роль, как «обыкновенные» силы в консервативных задачах. Напротив, сила Н является специфической: ее величина существенным образом зависит от угла поворота концевого сечения, а элементарная работа равна произведению силы на приращение прогиба.
Применим в этой задаче динамический критерий, подобно тому, как это было сделано в § 15. Уравнение движения элемента балки имеет по-прежнему вид (158). Принимая v = X(x)T(t) и идя тем же путем, приходим к выражению (169) для формы колебаний:
Х(х) = А ch sxx -f- В sh stx -+• С cos s2x + D sin s2x, (1.224)
где и 2 определяются по (168).
В сечении х = 0 обращаются в нуль прогиб и угол поворота,
а в сечении х = I — момент и поперечная сила; следовательно, гра¬
ничные условия для функции X (х) будут:
v л dX л л d2X л d*X л,
X — 0, = 0 при х = 0, -j-r = о, г = 0 при х = 1.
(1.225)
*) Подобная задача была рассмотрена М. Беком [1.8], К. С. Дейнеко и М. Я. Леоновым [1.2]; неконсервативным системам посвящена книга В. В. Болотина, 1961 [0.1].
х
I
Рис. 1.31. Стержень под действием следящей силы.
§ 21] УСТОЙЧИВОСТЬ НЕКОНСЕРВАТИ1НОЙ СИСТЕМЫ 73
Первые два условия дают:
А —}— С = 0, sB —— s2D = 0. (1.226)
Остальные условия приводят к уравнениям:
(s2 ch sxl -f- s2 cos s2/) A -f- (sx sh \l + s2 sin X2/) В = 0, 1
sh sin s2/) A -f- sx (s2 ch -f- s\ sin X2/) В = 0. j Приравнивая нулю определитель этой системы, приходим к сле¬
дующему уравнению:
Sl + 32 + 2s\s2 ch V C0S S2l — S1S2 (S1 — Sl) sh Sin S2l = 0*
Пользуясь выражениями (168), находим:
S* + s* = k* + 2X, s2s2 = X, s2 — s2 = — k\
Уравнение (228) принимает теперь вид
k4 + 2Х + 2Х ch sxl cos s2l -f- }X k2 sh sxl sin s2l = 0.
Перейдем к безразмерным параметрам
K=={klf = ER., 2 = Х/4 = -,
Sj ■1 1 <Sj/, S2 — 1 ■ S2l,
тогда получим зависимость
F (/С, 2) == /С2 22 -- 2Q ch sx cos s2 -f- Y® К sh S\ sin s2 = 0.
Параметр К представляет сжимающую силу, а 2 — частоту колебаний.
На рис. 1.32 приведен график, изображающий зависимость между К и 2 по уравнению (232).
Интересно сравнить его с аналогичным графиком рис. 1.23, относившимся к консервативной задаче. Тогда точка бифуркации равновесных состояний соответствовала «нулевой» частоте; теперь же на оси 2 = 0 мы не получаем точек бифуркации. Поэтому, если пользоваться только статическим критерием, то можно прийти к тому заключению, что потеря устойчивости стержня в данном случае вообще невозможна.
Другой результат мы получаем, пользуясь динамическим критерием, приобретающим при этом новую интерпретацию. Кривая (К* 2) имеет вид петли. Точки, лежащие на оси абсцисс, соответствуют двум первым собственным частотам изгибных колебаний стержня, не несущего сжимающей нагрузки. Если положить Р = 0, то
(1.228)
(1.229)
(1.230)
(1.231)
(1.232)
74 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в ПРЕДЕЛАХ УПРУГОСТИ
уравнение (228) переходит в следующее:
ch s1coss2= — 1;
(1.233)
корни его, как известно, определяют частоты собственных колебаний стержня с одним защемленным и другим свободным концом; формы этих колебаний показаны на ри
линия стержня сочетает первую и вторую собственные формы; для левой петли преобладающей является первая форма колебаний, для правой — вторая. В предельной точке петли частоты сливаются; этой точке соответствует значение К
При К > 20 система окажется неустойчивой и будет раскачиваться, снабжаясь дополнительной энергией за счет работы неконсервативной составляющей силы Р. Заметим, что изменгние направления силы Р, вытекающее из условия задачи, должно происходить благодаря некоторому внешнему для системы источнику энергии.
Если искать дополнительные корни уравнения (228), то мы, повидимому, получим новые петли, соединяющие третью и четвертую собственные частоты, пятую и шестую и т. д. Однако предельная точка для первой петли получается наименьшей; она и определяет критическую нагрузку, равную приблизительно
Рис. 1.32. «Петля» частот колебаний при различных сжимающих силах.
Рис. 1.33. Формы колебаний при действии следящей силы.
(1.234)
2 ъ2Е1
Лф = /2
(1.235)
Сравнение с формулой (27) показывает, что при следящей нагрузке критическая сила получается примерно в восемь раз больщей, чем при нагрузке постоянного направления,
ЯВЛЕНИЕ ПОТЕРИ УСТОЙЧИВОСТИ «В БОЛЬШОМ»
75
Мы рассматривали колебания стержня, не принимая во внимание влияние сил сопротивления. Учет этих сил может сказаться на величине критической силы и привести к ее уменьшению.
Другие примеры неконсервативных задач, связанные с задачами флаттера упругой системы, будут приведены в главе XIX.
§ 22. Явление потери устойчивости «в большом»
Познакомимся более подробно с явлением выпучивания упругой системы «в большом». В качестве примера такой системы может служить сжатый стержень, скре-
пружины с линейной характеристикой обозначим через к. Пусть первоначальная длина каждой пружины равна г, а расстояние от шарнира А до линии ВС
где гг — длина пружины после деформации. Суммарная реакция обеих пружин равна (см. рис. 1.34):
под / = AD понимается перемещение точки Л, характеризующее прогиб стержня. Рассматривая треугольник ABD, находим:
пленный с пружиной, имеющей нелинейную характеристику. Для упрощения задачи заменим упругий стержень двумя абсолютно жесткими звеньями длиной //2, соединенными упругим шарниром; два других конца звеньев будем считать свободно поворачивающимися (рис. 1.34). Примем, что шарнир А присоединен к двум пружинам АВ и АС, расположенным под некоторым углом друг к другу. Жесткость каждой
и
о
равно а.
Реакция каждой пружины при перемещении шарнира равна
S = k(r — rt), (1.236)
Рис. 1.34. Модель, иллюстрирующая явление потери устойчивости «в большом».
Q = 2S?-F-L = 2k(j-— l)(a — /); (1.237)
rV 0-238)
Q=2k
_ _ 11 (в _ /) * (2a2/—3a/2-)-/3). (1.239)
?6 устойчибстъ СЖАТЫК СТЕРЖНЕЙ В ПЕДЕЛАК УПРУГОСТИ [ГЛ. 1
Таким образом, при линейной характеристике каждой пружины в отдельности общая их реакция изменяется в зависимости от / по нелинейному закону.
Допустим, что стержни передают сжимающую нагрузку Р и что произошла потеря устойчивости системы. Условие равновесия каждого звена имеет вид
M = Pf — 4- (2а2/ — За/2 -f- /3) /. (1.240)
Считая отношение /// малым, примем взаимный угол поворота в шарнире ср равным 2//- = 4///. Жесткость шарнира С = М/ср подберем из условия, чтобы при отсутствии пружин критическая сила равнялась эйлеровой:
р f р /
С = = -р. (1.241)
При наличии пружин будет
P/--(2a2/-3a/2 + /3)=-if; (1.242)
отсюда при / Ф 0
Р — Рэ+ 4г (2я2 — За/ + /2) /. (1.243)
При потере устойчивости в малом нужно считать /<а, тогда получим критическую силу равной
Р* = Р* + -- (1-244)
Как видно из уравнения (243), при возрастании / сжимающая сила вначале падает (влияние среднего члена в скобках), а затем начинает снова возрастать (влияние третьего члена). Определим наименьшее значение Р = РН\ приравнивая нулю производную от Р по /, найдем: /=1,5 а. Отсюда
Ра = Р9—т*=Р>—ш *г1- (1.245)
При всех значениях силы Я, лежащих между Рн и Рв, система имеет три равновесных положения: одно, соответствующее начальному, и два смещенных. Начальное состояние становится неустойчивым при Р > Рв, поэтому по терминологии, принятой нами в § б, нагрузка Рв соответствует потере устойчивости в малом и может быть названа верхней критической силой. С другой стороны, сильно изогнутые равновесные формы возможны при всех значениях Р > Рн; при наличии известных возмущений возможен скачок
§ 22) ЯВЛЁНЙЁ ПОТЕРИ УСТОЙЧИВОСТИ «Ё БОЛЬШОМ* 77
системы от начального положения к изогнутому, характеризующий потерю устойчивости в большом. Нагрузку Рн называют нижней критической силой *).
Введем обозначения
о-246)
и перепишем уравнение (243) в виде
Р = 1 + ft (2 — ЗС + С2). (1.247)
На рис. 1.35 показана зависимость Р{С) между безразмерными параметрами нагрузки и прогиба, или, иными словами, диаграмма равновесных состояний системы при ft = 0,5; 1. На графике отмечены точки, отвечающие верхней и нижней критическим силам. На уровне нагрузки Я0 мы получаем, как уже было сказано, три равновесных состояния, соответствующих точкам а, b, с. Можно показать, что первое из них является устойчивым, второе — неустойчивым и третье — вновь устойчивым.
Это соответствует равновесным положениям шарика на рис. 1.17. При наличии известного возмущения система может перейти скачком из положения а в положение с.
Параметр k определяет «степень нелинейности» системы. Чем выше ft, тем большим получается перепад между верхней и нижней критическими нагрузками. Отметим, что при а — 0, когда пружины расположены по одной прямой, будет ft = 0.
Мы приходим к выводу, что для упругих систем, имеющих «падающую» характеристику Р(С), расчет по верхней критической силе, соответствующей потере устойчивости в малом и определяемой из линеаризованных уравнений, недостаточен. Обоснованный расчет подобных систем—это расчет на устойчивость в большом; он может быть проведен лишь с помощью нелинейной теории.
В качестве возмущения, вызывающего выпучивание системы при Р < РВ9 может служить начальное отклонение осевых линий
Рис. 1.35. Диаграмма «нагрузка — прогиб».
*) Это понятие более подробно рассмотрено ниже, в § 201,
?8 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ (гЛ. 1
звеньев от прямой FO (рис. 1.34). Тогда зависимость Р(С) будет иметь вид, показанный на рис. 1.35 пунктиром; как видим, верхняя критическая нагрузка Рв здесь не будет достигнута.
К таким же выводам приводит решение исходной, более сложной задачи об устойчивости в большом упругого стержня, скрепленного с пружиной, имеющей нелинейную характеристику *).
§ 23. О выборе метода исследования. Применение цифровых электронных вычислительных машин
Мы познакомились с различными критериями устойчивости и методами решения задач. Возникает вопрос: какой же из этих путей решения целесообразно выбрать в том или другом случае? Это зависит от цели решения задачи и от характера вычислительных средств, имеющихся в распоряжении расчетчика.
Если необходимо хотя бы грубо оценить величину критической нагрузки для консервативной системы, то уместно воспользоваться одним из энергетических методов, вводя минимальное число варьируемых параметров; обычно начинают с одного параметра. Результат решения здесь будет зависеть от инженерной интуиции автора расчета, позволяющей более или менее удачно аппроксимировать форму потери устойчивости. При увеличении числа независимых параметров вычисления сильно затрудняются.
В случае, когда желательна большая точность расчета (в пределах нескольких процентов), целесообразно применить метод последовательных приближений; он позволяет оценить сходимость вычислений и установить порядок погрешности. Для стержня переменной жесткости аналитическое определение упругой линии в каждом новом приближении является весьма трудоемким, поэтому целесообразно использовать графический или графоаналитический варианты метода последовательных приближений.
Для исследования неконсервативных систем следует применять наиболее общий критерий — динамический.
Все рекомендации, относящиеся к выбору метода решения, должны быть пересмотрены в том случае, если для выполнения расчетов используются электронные цифровые вычислительные машины (ЭЦВМ) или аналоговые машины.
Остановимся сначала на применении цифровых машин. Как известно, ЭЦВМ выполняют только простейшие арифметические действия, а также логические действия и операции управления вычислительным процессом. Поэтому выбранный метод расчета должен сводить решение задачи к выполнению последовательности простейших операций.
*) Такая задача была исследована Цянь Сюэ-сэнем [1.15].
§ 231
О ВЫБОРЕ МЕТОДА ИССЛЕДОВАНИЯ
79
Далее, необходимо обеспечить циклический ход решения задачи, т. е. многократное повторение расчетов по одним и тем же формулам с подстановкой в них при каждом повторении цикла новых числовых данных. Наконец, должна быть предусмотрена возможность контроля правильности решения задачи на машине.
При выборе численного метода надо учитывать «вычислительные возможности» применяемой машины *). Современные быстродействующие универсальные цифровые машины выполняют в секунду от нескольких десятков или сотен операций (малые машины, например «Урал-1») до нескольких десятков тысяч операций (большие машины). Числа, над которыми производятся арифметические действия, представляются в машинах с высокой степенью точности — от семи до десяти цифр в десятичной системе счисления. Оперативное запоминающее устройство большинства машин позволяет хранить одновременно от 1000 до 4000 чисел или команд программы, в то время как работающие с меньшей скоростью дополнительные (внешние) запоминающие устройства обладают практически безграничной емкостью. Следует также учитывать, что скорость ввода в машину исходной информации и вывода результатов является малой по сравнению со скоростью вычислений.
Электронные цифровые машины могут быть использованы, в принципе, для решения задач устойчивости любым из перечисленных выше методов. Однако некоторые из них являются предпочтительными. Укажем, прежде всего, на метод конечных разностей: характерным для него является многократное циклическое повторение расчетов по формулам, имеющим один и тот же вид для каждого интервала. Этот метод позволяет легко повысить точность расчета, так как дробление шага не вызывает принципиальных затруднений.
Мы видели выше, что при определении критической нагрузки с помощью метода конечных разностей мы получаем систему однородных линейных алгебраических уравнений относительно параметров прогиба. Условие нетривиальности решения этой системы состоит в том, что главный определитель системы равен нулю. Раскрывая определитель, мы приходим к нелинейному алгебраическому уравнению. Требуется найти наименьший вещественный корень уравнения. Такой процесс раскрытия определителя для нахождения коэффициентов нелинейного уравнения поддается программированию. Отыскание наименьшего корня алгебраического уравнения также выполняется на ЭЦВМ, например, одним из итерационных методов.
Аналогичный ход вычислений мы получим при использовании других прямых методов — Ритца или Бубнова—Галеркина. Отметим, однако, что применение машин для решения задач в тригонометри¬
*) См., например, А. И. Китов, Н. А. К р и н и ц к и й, Электронные цифровые машины и программирование, Физадатгиз, эд,? 1959,
80 УСТОЙЧИВОСТЬ СЖАТЫХ стержней в пределах упругости [гл. I
ческих рядах не вполне рационально, так как получение тригонометрических функций в машине требует вспомогательных вычислений по специальным подпрограммам или приводит к необходимости хранения в запоминающих устройствах громоздких таблиц.
Весьма удобными для программирования являются косвенные пути определения критической нагрузки. Целесообразно пользоваться критерием «начальных несовершенств», позволяющим ввести в уравнение «возмущающие» члены; само же уравнение может быть представлено в конечных разностях. Решение на ЭЦВМ позволяет определить равновесные формы стержня для различных начальных прогибов. Последовательно уменьшая параметр возмущения, определяем критическую нагрузку для «идеальной» конструкции.
Другой вариант заключается в применении метода последовательных приближений с заданием начальной аппроксимирующей функции. Этот же метод целесообразно применять при решении нелинейных задач, например при анализе закритических равновесных форм.
Динамические задачи с начальными условиями хорошо поддаются программированию, и поэтому применение динамического критерия для определения критической нагрузки на ЭЦВМ также вполне возможно.
Применение ЭЦВМ открывает перед различными областями механики и, в частности, перед теорией устойчивости упругих систем новые перспективы. Те задачи, которые раньше представлялись «недоступными» ввиду вычислительных трудностей, теперь оказываются вполне выполнимыми. Если в прошлом во многих случаях приходилось оставаться в пределах первого или второго приближения, то ЭЦВМ позволяют осуществить практически неограниченное число приближений. В настоящее время основное внимание, следовательно, надо уделить уточнению исходных уравнений, с тем чтобы они возможно полнее отображали свойства и условия нагружения реальных конструкций.
§ 24. Использование аналоговых машин
Обратимся к аналоговым (электромоделирующим) машинам. Основным элементом таких машин является операционный усилитель, схематически показанный на рис. 1.36. С помощью усилителя можно умножить некоторое напряжение на постоянное число, суммировать несколько напряжений и, наконец, произвести интегрирование. В качестве операционного усилителя может быть использован усилитель постоянного тока (ламповый, полупроводниковый, магнитный) с достаточно высоким коэффициентом усиления, в сочетании со входным сопротивлением Zt и сопротивлением обратной связи Z. Основное соотношение, описывающее режим операционного усили¬
ИСПОЛЬЗОВАНИЕ АНАЛОГОВЫХ МАШИН
81
теля, имеет вид
= (1.248)
где ех — подающееся на усилитель напряжение, е2 — выходное напряжение (рис. 1.36, а).
Если мы хотим умножить некоторое напряжение на величину k, то необходимо принять соотношение между входным сопротивлением и сопротивлением обратной связи, равным Ry/Ri = k. Подавая на усилитель несколько напряжений, можно выполнить операцию суммирования (рис. 1.36, tf).
Если в обратную связь включить конденсатор емкости С, а на входе ввести омическое сопротивление /?, то выходное напряжение будет пропорционально интегралу по времени от входного (рис. 1.36, в):
е~Ж f e'dt• (1249)
Вычислительная машина включает также блоки произведений (БП) и блоки нелинейности (БН), которые позволяют решать нелинейные задачи. Блок произведений перемножает две входящие в него переменные величины, при его помощи можно образовать, например, такие члены, как х2, х4, ху и т. д. Блок нелинейности позволяет аппроксимировать данную функцию одного аргумента кусочно-линейной.
Например, на машине МН-7 заданную функцию можно аппроксимировать десятью линейными участками. Блок переменных коэффициентов используется для набора заданных функций времени.
Усилители, интеграторы, блоки произведений и нелинейности работают по 100-вольтовой шкале; характерной особенностью блока произведений является то обстоятельство, что он алгебраически перемножает входящие величины и делит полученный результат на 100.
Для решения на вычислительной машине заданную систему уравнений обычно приводят к системе уравнений первого порядка
6)
Рис. 1.36. Элементы аналоговых машин.
82 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ JB ПРЕДЕЛАХ УПРУГОСТИ [гл. I
в безразмерных величинах и далее к машинному виду. Для этого необходимо знать порядок ожидаемых величин и диапазон изменения времени (или другого параметра, являющегося независимой переменной) и провести следующее линейное преобразование:
t = а Г, (1.250)
v = vn
где Vn—машинная переменная, vmSLX — ожидаемое максимальное значение функции, Т—машинное время в секундах, максимальное значение которого обычно ограничивается величиной порядка 50—100 сек.
Аналоговые машины общего типа приспособлены главным образом для интегрирования дифференциальных уравнений с начальными условиями. Поэтому для решения задач о собственных значениях, например об определении критических нагрузок, приходится прибегать к специальным приемам. Одним из таких приемов является метод проб, описанный в § 13 как графический.
В качестве примера рассмотрим стержень, шарнирно опертый по концам *). Исходное уравнение (5) заменяем двумя уравнениями первого порядка
п=0,ЗЮ
rVVV-
/77=/
Рис. 1.37. Структурная схема для определения критической нагрузки по методу проб.
и приводим их к безразмерному виду, вводя переменные х = хЦ, v = v/i, где / — радиус инерции сечения. Уравнения получают вид
dv г—= = — kvit dx
dv i т -
—~ = kv, dx
(a)
где k2 = PI2!El. Задаемся параметрами сжимающей нагрузки k2 и принимаем начальные условия v = 0, dv/dx = а при х = 0, причем величина а
*) Приведенное ниже решение задачи на анаогоой машине выполнено Д. Скурлатовдо,
ИСПОЛЬЗОВАНИЕ АНАЛОГОВЫХ МАШИН
83
выбирается произвольно. Интегрируя уравнения (а), проверяем, удовлетворяется ли условие v = 0 при х = / или дг = 1, и повторяем вычисления, варьируя параметр k. Вводим машинные переменные vN = v/vmax, kN = k/kmaj;
в качестве максимальных значений принимаем i/max = 0,2, kmix = 10, vu гаах = = 0,628. Вместо (а) выпишем следующие зависимости:
Принимаем интервал интегрирования (длину стержня) соответствующим 10 секундам машинного времени. Структурная схема, отвечающая уравнениям (Ь), изображена на рис. 1.37. Через П обозначены спиральные потенциометры, с помощью первых двух (Л, и П2) варьируется параметр kNt а третий (Л3) вводится для задания начальных условий. Значения проводимостей п в усилителях / и 2 имеют размерность [l/Мом], они соответствуют величинам
усилитель 3 служит для изменения знака. На рис. 1.38 представлены совмещенные осциллограммы, полученные с помощью приведенной схемы при различных параметрах k; эйлерова нагрузка отвечает k = 3,14. При меньших значениях k получаем решение «с недолетом», при больших — «с перелетом».
Этот путь может служить также для определения критических нагрузок в случае стержня переменного сечения.
Другой метод состоит в использовании специального блока регистрации и воспроизведения (БРВ), служащего для решения линейных однородных интегральных уравнений типа Фредгольма; в данной задаче это уравнение имеет вид (151). При этом применяется метод последовательных приближений, описанный в § 15. На машине приводятся следующие операции: образование ядра К(х, Е), перемножение функций К(х, Е) и у0(Е) по (151), интегрирование в пределах от 0 до 1 и умножение интеграла на варьируемый параметр X. В результате находим функцию зС*), которую вновь подставляем в правую часть уравнения. Блок БРВ служит для запоминания промежуточных решений интегрального уравнения, поступающих от модели, и для выдачи их в модель с целью получения новых приближений. Блок имеет электронно-лучевую трубку с послесвечением;
0,6281/j N = j* (10kN) (0,2г/уу) dx.
(b)
10 • 0,628 • 0,1 0,2
Рис. 1.38. Осциллограммы, полученные при трех пробах.
84 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ В ПРЕДЕЛАХ УПРУГОСТИ [гЛ. t
она позволяет фиксировать формы упругой линии для каждого приближения. При этом последовательно уточняются значения критического параметра X.
Наконец, могут быть составлены электрические моделирующие цепи, не содержащие операционных усилителей и осуществляющие так называемое прямое моделирование *). Критические нагрузки для различных конструкций определяются и здесь путем последовательных приближений, как описано в § 12.
*) Подобные схемы описаны в работе Сканлана [1.14]. Этому направлению посвящен ряд работ К. К. Керопяна, Г. Е. Пухова и других авторов.
ГЛАВА II
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ
УПРУГОСТИ
§ 25. Экспериментальные зависимости
Исходные соотношения и расчетные формулы, приведенные в главе I, справедливы при условии, что критические напряжения — или максимальные напряжения при продольно-поперечном изгибе — не превышают предела пропорциональности материала опц *). Между тем для элементов реальных конструкций во многих случаях это условие не выполняется. Поэтому исследования устойчивости стержней, относящиеся к неупругой области, имеют существенное практическое значение.
До последнего времени наиболее распространенными являлись методы расчета, основанные на результатах экспериментальных исследований.
Данные опытов удобно сопоставлять с помощью графика, изображающего зависимость критического напряжения окр от гибкости X.
Если опыты ставятся достаточно тщательно, то в упругой зоне экспериментальные точки ложатся очень тесно вблизи гиперболы Эйлера, между тем в упруго-пластической зоне они обычно сильно разбросаны, примерно так, как показано на рис. 2.1. Это объясняется тем, что в упругой области критическое напряжение при заданной гибкости зависит только от модуля Е; колебания этой величины для
Рис. 2.1. Разброс экспериментальных значений критических напряжений в пластической области.
*) В дальнейшем предел пропорциональности материала считается совпадающим с пределом упругости.
86 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. И
различных образцов, изготовленных из одного и того же материала, незначительны. В упруго-пластической области критические напряжения меняются в зависимости от диаграмм о(е) при сжатии, часто отличающихся друг от друга даже для образцов, принадлежащих к одной и той же партии. Влияние возмущающих факторов — эксцентриситета нагрузки, начальной погиби, остаточных напряжений от прокатки, сварки, правки и т. д. — в неупругой области также оказывается более значительным, чем в упругой. Поэтому анализ данных экспериментов и составление расчетных формул желательно проводить с помощью статистических методов *).
Различными авторами были предложены формулы для расчета на продольный изгиб за пределами упругости, из которых наиболее приемлемыми оказались следующие:
a) Линейная формула **)
°кр = л — М. (2.1)
где а, Ь—параметры, зависящие от материала.
При определении величин а, b желательно выполнить условие, чтобы при предельной гибкости \ уравнение (1) давало тот же результат, что и формула Эйлера. С другой стороны, можно было бы потребовать, чтобы при X —>0 величина окр приближалась к предельному напряжению на сжатие obt так что а = оь. Для хрупких материалов (например, дюралюмин) это предельное напряжение соответствует временному сопротивлению, найденному при сжатии образцов малой длины. В случае же материала, имеющего диаграмму с ясно выраженной площадкой текучести (мягкая сталь), критическое напряжение, как правило, не может превысить предела текучести от. Поэтому для пластичных материалов было бы более естественно принять а = ст. Однако основным требованием при составлении эмпирических формул является соответствие их конкретным данным серии опытов на продольный изгиб для стержней различной гибкости.
b) Гиперболическая формула***)
°кр= 1 _(.0ах2 ’ (2-2)
здесь с0—некоторое напряжение, а — эмпирический коэффициент.
c) Параболическая формула****)
окр = а-рХ2. (2.3)
*) Это было впервые отмечено Ф. С. Ясинским, применившим для обработки экспериментальных данных Тетмайера метод наименьших квадра-
**) Формулы этого типа были предложены Тетмайером [2.21] и Ф. С. Ясинским [1.7].
***) Подобная формула была предложена Ренкином (Rankine>
****) Эта формула предложена Джонсоном (J. В. Johnson).
§ 26] ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ НЕИЗМЕННОЙ НАГРУЗКЕ
87
Постоянные а, (3 можно подобрать таким образом, чтобы парабола на графике <зкр(Х) плавно переходила в гиперболу Эйлера, имея с ней при Х = ХФ общую касательную. Однако решающим и здесь является соответствие формулы экспериментальным данным.
Пример 2.1. При расчете корпуса корабля должна быть проверена устойчивость палубы: в определенных положениях корабля по отношению к гребням волн палуба оказывается сжатой (рис. 2.2, а). Определить критическое напряжение для панели, составленной из расположенных по длине корабля подкрепляющих ребер (бимсов) и присоединенных к ним полос обшивки, считая концы панели опертыми шарнирно. Потеря устойчивости
Рис. 2.2. Панель палубы корабля/
возможна лишь в направлении, перпендикулярном плоскости обшивки. Материал— сталь Ст. 4. Е = 2,1 • 106 кг/см2, ах = 2600 кг/см2, апц = 2200 кг/см2. При акр > апц применить формулу
акр =±= 3200 — 10Х (кг/см2) (а)
при условии акр<ат- Размеры сечения панели показаны на рис. 2.2, б (в мм), длина панели (шпация) равна 1 м.
Определяем координату центра тяжести сечения ус = см; площадь сечения равна F = 17,2 см2. Момент инерции сечения относительно центральной оси хс равен / = 190 см4. Вычисляем радиус инерции сечения и гибкость: '-1/~т§-зж ‘-таг-30'
Напряжение, вычисленное по формуле (а), равно 2900 кг/см2 > ат. Поэтому принимаем критическое напряжение равным акр = ат = 2600 кг/см2.
§ 26* Выпучивание стержня при неизменной нагрузке
Обратимся к теоретическому исследованию продольного изгиба за пределами упругости. Допустим, что стержень подвергается центральному осевому сжатию и что зависимость напряжения от деформации для коротких образцов из данного материала отвечает диаграмме рис. 2.3. Участок упругой деформации соответствует отрезку Оа. Предположим, что при нагружении образца мы дошли по диаграмме до некоторой точки т. Если после этого произвести разгрузку, то на графике мы получим прямую линию тт'% примернд
88 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. и
параллельную участку Оа; угол наклона этой линии характеризует модуль разгрузки.
Будем в дальнейшем считать, что модуль разгрузки равен начальному модулю Е. С другой стороны, при возрастающей от точки т деформации сжатия получим участок диаграммы тт. Если дополнительная деформация мала, то можно принять, что отношение приращений А о и Де определяется так называемым касательным модулем: р
Рис. 2.3. Диаграмма «напряжение-— Рис. 2.4. (а) Изогнутая линия, деформация». (б) сечение стержня, эпюры напря¬
жений и деформаций при неупругом продольном изгибе.
Пусть напряжение сжатия достигло величины о > опц. Допустим, что при этом напряжении происходит выпучивание, в процессе которого нагрузка остается постоянной. Тогда волокна, лежащие на вогнутой стороне, будут испытывать дополнительную деформацию укорочения, а на выпуклой — удлинения (рис. 2.4). Если рассматривать изогнутые формы, весьма близкие к прямолинейной, то можно принять для зоны нарастающего сжатия модуль Ек, а для зоны разгрузки — модуль Е. Нейтральная линия z, для точек которой дополнительные напряжения равны нулю, не будет проходить через центр тяжести сечения. Такая концепция «двух модулей» была впервые предложена*) Ф. С. Ясинским [2.14] и Ф. Энгессером, а в дальнейшем развита Т. Карманом [2.15].
*) Возникшая в связи с этим дискуссия между Ф. С. Ясинским и Ф. Энгессером освещена в статье А. Н. Митинского (см. книгу [1.7], изд.
§ 26] ВЫПУЧИВАНИЕ СТЕРЖНЯ ПРИ НЕИЗМЕННОЙ НАГРУЗКЕ
89
Пусть главные центральные оси инерции сечения будут у0 и zQ (рис. 2.4); примем, что выпучивание происходит в направлении у0. Считая, что поперечные сечения остаются при изгибе стержня плоскими, и отсчитывая у от нейтральной линии z> получим:
Де = —,
9
где р — радиус кривизны упругой линии. Напряжения в зонах догружения и разгрузки будут соответственно
Л«1 = £ку» До2 = Е~. (2.5)
Результирующая дополнительных усилий должна быть равна нулю, поэтому
fyiF + j-fydP-0
Fx
ИЛИ
EKS,+ES2 = 0. (2.6)
Здесь через Fx и Sx обозначены площадь и статический момент относительно нейтральной оси той части сечения, в которой имеет место догружение, а через F2 и S2 — части сечения, в которой происходит разгрузка. Приравнивая сумму моментов внутренних сил относительно нейтральной линии внешнему моменту, находим:
f y*dF-{- — Jy*dF = M,
или
1 {EJX + EI2) = M. (2.7)
Обозначим через Т результирующий или приведенный модуль, равный
Т= £к/'+£/», (2.8)
где / — момент инерции всего сечения относительно оси, проходящей через центр тяжести. Величину Т называют также модулем Кармана. Уравнение изогнутой оси приобретает вид, аналогичный (1.5):
Т'-Ш м■ <2'9>
Полагая для случая шарнирного опирания концов стержня М = = Pv, придем к уравнению
TI. + Pv = 0. (2.10)
90
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ (ГЛ. И
Величину Т можно при / = const считать не зависящей от х% так что все данные, полученные в главе I для упругого продольного изгиба, можно распространить на упруго-пластическую область при условии замены Е на Т. Сюда же относятся результаты, полученные с помощью энергетических методов, так как для любого волокна стержня по-прежнему принята линейная зависимость между приращениями напряжений и деформаций.
В обобщенном виде выражения для критической силы и критического напряжения будут
ркр= (v/» (2.11)
-кр ■
(2.12)
Коэффициент v здесь следует принимать таким же, как и в упругой области.
§ 27. Влияние формы сечения. Случаи двутаврового и прямоугольного сечений
Судя по формулам (6) и (8), результирующий модуль Т должен зависеть от формы сечения стержня. Вычислим величину Т для двутаврового сечения с тонкой стенкой (рис. 2.5) в предположении, что изгибающий момент воспринимается только полками двутавра и, благодаря определенным условиям закрепления стержня, выпучивание происходит в направлении оси у. Обозначим через h расстояние между центрами тяжести полок, площадь каждой из полок равна половине площади сечения, т. е. F/2. Пусть расстояние h делится
нейтральной при изгибе линией на отрезки hx (со стороны догружения) и h2
Г/2
I
1J
Г/2
Рис. 2.5. Зоны догружения и разгрузки в случае двутаврового сечения.
со стороны разгрузки). Из (6) получаем: - F1h1EK + F2h2E = 0;
отсюда
h\ — h Ек + Е ’ K — h Ек + Е Моменты инерции 1Х и /2 равны
л
2
л=
Ль
/ F L2
h~~ 2*
(2.13)
(2.14)
Момент инерции всего сечения относительно центральной оси будет
(2.15)
(2.16)
Формула (8) приобретает вид
Т =
•2ЕКЕ Ек + Е '
§ 28] ДИАГРАММА «КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ — ГИБКОСТЬ» 91
Для упругой области Т = Ек = Е. В общем случае результирующий модуль имеет некоторое среднее значение между Е и Ек. Для материала с ясно выраженной площадкой текучести, в пределах которой угол ак = 0, величины Ек и Т приближаются к нулю, как только сжимающее напряжение будет приближаться к пределу текучести. Это означает, что для сжатого стержня критическое напряжение практически не может превысить предела текучести.
В случае прямоугольного сечения (рис. 2.6) уравнение (6) получает вид
EKh\ — Eh\ — О
и, следовательно, h — А —
1 Vek+Ve ’
Моменты инерции будут
и _h Уек
2 Vek+Ve
(2.17)
bh
bh%
иПл. инп
/ L / — _
Л\— Q • 2 Q
bh6
Окончательно
T =
3
4 EEK
12
(Vek+Ye)2
Рис. 2.6. Зоны догружения и разгрузки в случае прямоугольного сечения.
Отклонения в величине Т для разных форм сечения незначительны, так что в практических расчетах и для других видов сечения можно пользоваться формулой (16) либо (19).
§ 28. Построение диаграммы «критическое напряжение — гибкость»
Представим формулу (12) в виде
—<2-2°> Задаемся последовательными значениями акр; зная соответствующие величины 7, находим по (20) связь между окр и X. Но для установления зависимости Т(о) должна быть известна диаграмма о (е), полученная при испытании на сжатие коротких образцов из данного материала*). На рис. 2.7 изображена подобная диаграмма для дюралюмина Д16Т. Модуль упругости принят равным £=7,5 • 105 кг/см2, предел пропорциональности опц = 2-103 кг!см2. Для определения Ек в различных точках диаграммы (а, Ъ% с и т. д.) проводим
*) Эти данные для дюралюмина и стали Ст. 3 получены автором в 1948 г.
92 УСТОЙЧИВОСТЬ СЖАТЫХ стержней за пределами упругости [гл. и
касательные и находим тангенсы углов их наклона к оси абсцисс. Величины Ек, соответствующие некоторым значениям айв, приведены в таблице 2.1. Здесь же даны вычисленные по формулам (16)
Рис. 2.7. Эпюра сжатия для дюралюмина Д16Т.
и (20) величины результирующего модуля Т и гибкости Хрез (индекс «рез» указывает на то, что значение X соответствует результирующему (приведенному) модулю). Полученная таким образом зависимость акр(Х)
Таблица 2.1 Расчетные параметры для дюралюмина Д16Т
Точки на диаграмме
8-10»
кг! cm2
к г/cm2
7M0-5,
кг/см2
рез
Хк
а
2,67
2000
7,50
7,50
60,5
60,5
b
3,0
2200
5,96
6,65
54,7
51,6
с
3,5
2460
4,34
5,50
47,0
42
d
4,0
2640
3,72
4,97
43,0
37,5
е
4,5
2780
2,55
3,81
36,8
30,2
f
5
2900
2,05
3,22
33,0
26,5
g
6
3080
1,50
2,50
28,3
22
h
7
3200
1,17
2,03
25,0
18,9
i
8
3320
0,97
1,72
22,6
17
k
9
3400
0,82
1,48
20,8
15,4
I
10
3450
0,82
1,48
20,6
15,3
m
11
3560
0,82
1,48
20,2
15,1
n
12
3640
0,82
1,48
20,0
14,9
§ 28] ДИАГРАММА «КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ - ГИБКОСТЬ» 93
представлена на рис. 2.8. Для упругой области, при Х60,5, кривая отвечает формуле Эйлера.
Рис. 2.8. Диаграмма «критическое напряжение — гибкость» для дюралюмина; кружки с крестиками — данные опытов.
В таблице 2.2 содержатся такие же данные для стали Ст. 3; соответствующая диаграмма акр(Х) дана на рис. 2.9.
Таблица 2.2
Расчетные параметры для стали Ст. 3
е*103
а,
KZlCM2
£-к.10-в, к г!см2
г.ю-в,
кг/см2
*рез
0,95
2000
2,10
2,10
102
102
1,0
2100
1,42
1,72
90
81,8
1Д
2200
0,99
1,39
79
66,6
1,2
2280
0,67
1,05
67,6
54
1,3
2340
0,46
0,85
59
44
1,4
2380
0,26
0,54
47,5
32,7
1,5
2390
0,13
0,33
37
23,1
1,6
2400
0,06
0,19
28
15,7
1,8—4,0
2400
0
0
0
0
4,5
2410
0,02
0,07
17
9,1
5
2420
0,04
0,13
23
12,7
6
2470
0,05
0,15
24,5
14,2
8
2575
0,05
0,15
24
13,8
10
2685
0,05
0,15
23,6
13,6
12
2800
0,05
0,15
23
13,5
94 УСТОЙЧИВОСТЬ СЖАТЫХ стержней за пределами упругости [гл. U
Полученные таким образом расчетные данные можно сопоставить с результатами опытов на продольный изгиб для стержней различной гибкости. В отдельных случаях при весьма тщательной постановке опытов удается получить точки на графике акр (X), лежащие достаточно близко к кривой Хрез. Однако, как правило, экспериментальные точки расположены ниже этой кривой (данные на рис. 2.8).
бнг/см2 2600
2600 гт то 2000 woo 1600 то 1200 1ШЩ
10 10 20 30 40 50 60 70 80 90 100 110 130 130 М
А
Рис. 2.9. Диаграмма «критическое напряжение — гибкость» для стали Ст. 3.
Было замечено, что лучший результат получается, если в формуле (12) заменить результирующий модуль на касательный и принять
Значения гибкостей, полученные по формуле
= пл/~ (2.22)
Т Glen
X
- °кр
будем отмечать индексом «к»; они помещены в последних графах таблиц 2.1 и 2.2. Соответствующие кривые нанесены на рис. 2.7.
Формула (21) отвечает первоначальным представлениям о выпучивании стержней за пределами упругости, изложенным в одной из статей Ф. Энгессера [2.11]. По этой концепции эффект разгрузки не учитывается; принимается, что во всем сечении соотношение между приращениями напряжений и деформаций содержит касательный
§ 29] выпучивание сТёржнй ПРи Изменяющейся НАгрузкЁ
модуль Ек. Но если это допущение относится к реальному материалу, то надо считать, что напряжения сжатия получают приращение во всех точках сечения, например, как показано на рис. 2.4 вверху. Иными словами, надо допустить, что одновременно с изгибом стержня имеет место возрастание сжимающей нагрузки *). Рассмотрим эту задачу в квазистатической постановке и исследуем изогнутые равновесные формы стержня.
§ 29. Выпучивание стержня при изменяющейся нагрузке
Будем считать, что сечение шарнирно закрепленного по концам стержня имеет по крайней мере одну ось симметрии у (рис. 2.10 а) и что упругая линия стержня лежит в плоскости ху.
Допустим, что выпучивание стержня началось при силе Pt и что при изгибе стержня нагрузка получает приращение. Тогда в некоторых сечениях может иметь место только догружение, а другие сечения разделятся на зоны догружения и разгрузки.
Примем здесь в качестве первого приближения, что появление разгрузки совпадает с началом выпучивания **).
Обозначим через с расстояние от центра тяжести сечения С до крайних волокон, лежащих на выпуклой стороне. Зоны догружения и разгрузки делятся нейтральной при изгибе линией тпУ отстоящей от крайних волокон на расстоянии s; эта величина меняется, вообще говоря, по длине: s = s(a:). Площадь
сечения F делится линией тп на площади Fx и F2. Примем, что при выпучивании стержня деформация в каждой части сечения характеризуется неизменными модулями: Ек при догружении и Е при разгрузке; эти модули определяются по диаграмме о (е) и соответствуют
исходному напряжению а = = PjF (рис. 2.10, б). В тех же сече¬
ниях, где зона разгрузки отсутствует, деформация полностью Определяется модулем Ек.
Рис. 2.10 а). Сечение стержня, подвергающегося выпучиванию; б) эпюра напряжений.
*) Такая гипотеза была выдвинута Ф. Шенли [2.19] и затем Ю. Н. Работновым [2.8] и развита рядом других авторов.
**) Такая постановка задачи. принадлежит А. Пфлюгеру [2.17]; ему принадлежат графики 2.16 — 2.20. Решение задачи в иной постановке дано Ю. Р. Лепиком [8.5J и И. С. Малютиным (канд. дисс., Москва, 1958),
96 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. I!
Обратимся к сечениям со смешанным законом деформации и введем обозначение Е/Ек = п. Представим себе некоторое преобразованное сечение, в котором ширина всех элементарных полосок, расположенных в зоне разгрузки, увеличена в п раз (рис. 2.11).
Площадь такого приведенного сечения Fe равна
F9 = Fx + nF2. (2.23)
Определим расстояние е между центрами тяжести исходного и приведенного сечений:
e=Sl+nS2. (2 24)
ге
через Sx и 52 обозначены статические
Рис. 2.11. Приведенное сечение стержня.
площадей Fx
ОТНОСИ-
моменты
тельно центральной оси исходного сечения. Обозначим, далее, через /е момент инерции приведенного сечения относительно оси, проходящей через центр тяжести Сх этого «нового» сечения:
Ie = Iu-\-nI2e= § У*еЛР + П f fedF\
(2.25)
координата уе отсчитывается от новой центральной оси.
Примем, что нагрузка Р получила приращение АР и достигла величины Р:
Р = Р* + ДЯ. (2.26)
Для преобразованного сечения деформацию можно определять, исходя из единого модуля Ек. Дополнительная деформация произвольного волокна равна
Ае == Дв_ ——,
(2,27)
где Де — деформация волокна, проходящего через центр тяжести приведенного сечения, р — радиус кривизны изогнутой оси. Приращение напряжения равно
(2.28)
Дополнительное усилие в сечении будет приложено в центре тяжести приведенного сечения и равно
§ 29] выпучивание стерший прй Изменяющейся нагрузке
97
здесь деформация укорочения считается положительной. Рассмотрим, далее, условие равновесия части стержня, показанной на рис. 2.12. В концевом сечении точка приложения полной силы Р совпадает с центром тяжести исходного сечения; в произвольном же сечении равнодействующая основных усилий приложена в том же центре тяжести, в то время как равнодействующая дополнительных усилий оказывается приложенной в новом центре тяжести приведенного сечения.
Сумма моментов сил РиЯ относительно новой центральной оси
M, = P(v + e) — Pme9 (2.30)
или
Me = Pv + ДА?. (2.31)
Рис. 2.12. Внешняя сила и внутренние усилия при выпучивании стержня.
Приравнивая этот момент сумме моментов дополнительных внутренних усилий, получим по (28):
Ме = - f b,yedFe = ffe.
(2.32)
Принимая для пологой изогнутой линии
1 d2v
Их*'
приходим к уравнению
EKIe+Pv + bPe = 0. (2.33)
В этом уравнении величины е, 1е являются функциями х. Для той части длины стержня, где область разгрузки отсутствует, нейтральная линия будет проходить через центр тяжести реального сечения и, следовательно, £ = 0, Ie = f, где /—момент инерции исходного сечения относительно центральной оси. Уравнение (33) принимает на этих участках вид
EJf + Pvо = 0. (2.34)
Граничные условия для концов стержня имеют вид:
(2.35)
98 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гЛ. \\
Кроме того, должны быть выполнены условия сопряжения на границе области, включающей разгрузку. Обозначая длину этой области через а (рис. 2.13), получим:
dv dv0 I — a I + а
V = V0, — dx dx ПРИ ** 2 * 2 е
Из (34) и (35) для концевых участков стержня получаем:
v0= A sin х.
Для точек нейтральной линии имеем:
с — е — 5
О = Дел
отсюда
Де,=
/ \ d2v
(c-e-s).
Сопоставляя это уравнение с (29), находим:
№ = — EKFe (с — е — s)
d2v Их2
d2v
Исключая из (33) и (40)’ буДем иметь:
P. Ie 1 ДР V~ Fe c — e — s
(2.36)
(2.37)
(2.38)
(2.39)
(2.40)
(2.41)
Так как по концам стержня изгибающий момент обращается в нуль, то из (31) вытекает:
LPe = 0 при jc = 0, х — I. (2.42)
Рассмотрим два предельных случая. Предположим, что область разгрузки занимает всю длину стержня, как это было принято
в § 26. Тогда в концевых сечениях должно быть еФ 0. Отсюда вытекает условие АР = 0. Идя по этому пути, мы получаем формулу для критической силы (11), включающую результирующий модуль Т.
Примем теперь, что область разгрузки занимает лишь некоторую часть длины стержня и что концевые участки деформируются чисто пластически. Тогда для лс = 0, х = 1 должно быть е = 0 и, следовательно, ДЯ=0. Этот путь приводит к решению С возрастающей нагрузкой. Предположим, что в момент начала
р
р
о
п»
Рис. 2.13. Граница зоны разгрузки.
§ 29] ВЫПУЧИВАНИЕ стержня при изменяющейся нагрузке
99
выпучивания весь стержень находится в чисто пластическом состоянии, так что для всех сечений модуль равен Ек. Зона разгрузки стягивается при этом в крайнюю точку среднего сечения, так что а->0. Понимая ниже под г; прогиб среднего сечения, получим по (41):
1 (2.43)
Fc
Таким образом, точка разветвления равновесных состояний, найденная при условии АРфО, соответствует критической силе
(2.44)
лежащей всегда ниже силы, определенной из (11). Отсюда вытекает формула (21), составленная ранее «интуитивно».
Будем называть критическую силу Ркр, находимую с помощью модуля Ек, касательно-модульной в отличие от приведенно-модульной Ррез, определяемой с помощью модуля Т. Принципиальное различие между этими понятиями можно видеть из рис. 2.14. По оси абсцисс здесь отложен безразмерный параметр прогиба v = v/c, по оси ординат — параметр нагрузки Р=Р/Ркр. Приведенно-модульной критической силе отвечает безразличное равновесие, так что прогиб остается неопределенным; на графике получаем горизонтальную прямую. Ветвь равновесных состояний, отходящая от касательно-модульной критической точки, имеет в этой точке наклонную касательную. Наклон этой касательной можно определить, пользуясь уравнением (41). Считая 5 = = 0, Ie = I, Fe = F, получим:
Рис. 2.14. Касательно-модульная и приведенно-модульная нагрузки.
или
/_ДР\ _р Fc_
Ut'L+o кр ' •
. dP Fc2
tga
dv I
(2.45)
(2.46)
кр
И P,
рез»
то наклон
Если точка разветвления лежит между касательной окажется меньшим; по мере приближения исходной силы к приведенно-модульной нагрузке угол наклона приближается к нулю.
100 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. II
§ 30. Стержни двутаврового и прямоугольного сечений при изменяющейся нагрузке
Рассмотрим случай двутаврового сечения с весьма тонкой стенкой. Приведенное сечение показано на рис. 2.15. Эксцентриситет центра тяжести этого сечения равен по (24)
И JL\ Jl\
2 \ 2 ~*~П 2 ) _ h п — 1
- £<, + „, -*« + !•
(2.47)
Площадь и момент инерции приведенного сечения будут по (23)
и (25) равны
/% = £(1+л), (2.48)
П+\) -Г
+ »(1-Т+т)’]=Тл,ТТ- <2«)
Уравнение (33) принимает вид
2 п d2v
EJ
п + 1 dx2
Вместо (40) получим:
(2.50)
BKF
Рис. 2.15. Приведенное двутавровое сечение.
d?v
При ДР = 0 и -2*0 из (51) находим:
s 1 h ~ п + 1 ’
что соответствует (13). Уравнение (50) принимает вид „, 2п d2v, ~ л
п+1 dx2
откуда находим приведенно-модульную критическую силу:
Р =
л рез
%2ЕК1 2 п
(2.52)
(2.53)
I2 п+1 *
это согласуется с формулой (16) для Г. Касательно-модульная критическая сила равна
Следовательно,
кр‘
рез.
*2£к/
12 *
2 п п 1
(2.54)
(2.55)
§ 30] СТЕРЖНИ ДВУТАВРОВОГО И ПРЯМОУГОЛЬНОГО СЕЧЕНИЙ Введем обозначения
h2 Р Л + 1 и2 Р
Ек/ 2п * *2—
Уравнение (50) принимает вид
d*V I А2 ДР РЬ- П—\ dx PJhT'
Интеграл его будет
а • *, о А Р h п — 1
v = Ax sin kxx-\-Bx coskx -p- *
Выпишем условие симметрии упругой линии:
dv ~ I
— = 0 при x = Y.
Пользуясь этим условием, из (58) получим:
= В} tg kx 2;
выражение для принимает вид
ДЯ А я—-1 I 1,-1. I Р 2 л +1 *
cos у
Уравнение (37), относящееся к концевым участкам, будет
г;0 = Л0 sin 2лг.
Условия сопряжения (36) приводят к соотношениям:
kxa
Aq sin
k2 (/ — a)
B>C0S~Y- ДЯАя-1
А,/ Я 2 Л + 1
cos-A-
A.a
/-« mT
4q/?2 COS /?2 2 11 отсюда
C08“
k{l
о ДР h n — 1 COS 2
=
/> 2 л + l cos M tgMtg*2I=iL
101
(2.56)
(2.57)
(2.58)
(2.59)
(2.60)
(2.61)
(2.62)
(2.63)
(2.64)
102 УСТОЙЧИВОСТЬ СЖАТЫХ стержней за пределами УПРУГОСТИ [гл. II
Обратимся к уравнению (51). Подставляя вместо v выражение (61), находим:
cos ~2
(2.65)
На границе зоны разгрузки должно быть
2
s = 0 при х = -~п а ; (2.66)
пользуясь (65) и (56), получим:
р _ АР h 2п coshT
1— Р 2 л-f 1 kxa • (2,67)
cos-±-
Приравнивая выражения (64) и (67), будем иметь: kx irf kxa ire h I — a n + 1
По (56) будет k2, Г 2n
TX~V n+1 *
и вместо (68) получим:
,гМ,б421 = 1А«ТГ. (2.6»)
Выражение (56) можно переписать в виде
к\ = Чг' *5 = 7££* (2‘70)
Уравнение (69) позволяет определить длину пластического
участка а, если задано, с одной стороны, значение п и, с другой стороны, отношение Р/Ркр.
Рассмотрим предельные случаи. Если область ра грузки отсутствует, должно быть а = 0, отсюда
tgM=00> = (2.71)
по (70) это дает Р = Ркр. Предполагая, с другой стороны, что область разгрузки занимает всю длину стержня (а = /), получим:
tgco, kx=Y> (2.72)
отсюда по (70)
Р = Р*9-Г[ = Р**3- (2.73)
§ 30] СТЕРЖНИ ДВУТАВРОВОГО И ПРЯМОУГОЛЬНОГО СЕЧЕНИЙ
103
На графике рис. 2.16 представлена зависимость между р — Р[Ркр и а// при п = 2; 4; 6 для промежуточных значений а/1. Пунктиром показан уровень, соответствующий силе Ррез по (73).
Рис. 2.16. Длина зоны разгрузки в случае двутаврового сечения.
двутаврового сечения.
Пользуясь выражениями (61) и (67), находим стрелу прогиба стержня:
(,7„
/h
Y в зависимости от Р — Р[РКр. для различных,. д.. Наклон касательной
104 УСТОЙЧИВОСТЬ СЖАТЫХ стержней ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. II
«р
р%01рк1г*£_
3-
стержня прямоугольного сечен я.
зоны разгрузки при выпучивании стержня.
Рис. 2.20. Диаграмма «нагрузка — прогиб» для стержня прямоугольного сечения.
§ 31] ВЫБОР КРИТЕРИЯ УСТОЙЧИВОСТИ И РАСЧЕТНОЙ НАГРУЗКИ 105
определяется выражением
dP _ 2 (/г 1) Я2 df h Р кр 2п
1
(2.75)
В точке разветвления будет Р = Ркр, Р=1, а = 0; отсюда
/ \ 2Р Кр
\*г)р-Ржр=~г~9
(2.76)
что соответствует выражению (45).
В случае прямоугольного сечения выкладки значительно усложняются. На рис. 2.18 представлен окончательный график зависимости Р = Р/Ркр от а/1. Из рис. 2.19 видно, насколько глубоко по сечению распространяется зона разгрузки в различных сечениях для того или иного уровня закритической деформации; принято п = 4. На рис. 2.20 дано изменение относительной стрелы прогиба v при возрастании нагрузки, начиная от Ркр.
§ 31. Выбор критерия устойчивости и расчетной нагрузки
Задача о выпучивании сжатого стержня за пределами упругости на первый взгляд представляется несложной. В самом деле, мы изучаем деформацию стержня, принимая прогибы малыми по сравнению с длиной, т. е. в геометрически линейной постановке. Закон распределения деформаций по сечению определяется гипотезой плоских сечений. Мы можем рассматривать стержень как систему продольно расположенных волокон, поскольку напряженное состояние считается одноосным. Закон напряжение — деформация принимается известным. И тем не менее, как мы видим теперь, задача эта таит в себе многие «подводные камни».
Первое затруднение состоит в распространении на упруго-пластическую область самого понятия устойчивости. Допустим, что сжимающее напряжение в стержне превзошло предел пропорциональности, но критическая нагрузка еще не достигнута, очевидно, прямолинейное состояние стержня должно быть устойчивым. Однако, если какое-либо возмущение вызовет искривление стержня, то в нем возникнут некоторые остаточные деформации. Можно понимать под устойчивым в малом такое равновесное положение системы, которое не имеет соседних искривленных равновесных форм. Под критической нагрузкой надо подразумевать тогда такую минимальную силу, при которой появляются соседние равновесные формы; но при этом надо исключить из рассмотрения те формы, которые соответствуют остаточным деформациям (см. (21.5а, 21.11]).
106 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. II
Такое определение может также вызвать возражения, если учесть, что пластическая деформация при нагружении конструкции представляет собой, в той или иной мере, процесс течения, развивающийся во времени. С этой точки зрения, говоря об устойчивости, надо сопоставлять величину малого возмущения, выводящего систему из рассматриваемого положения, с тем эффектом, который оно вызовет. Если этот эффект, заключающийся в искривлении стержня, является ограниченным и малым, то исходное состояние следует считать «устойчивым».
Как правило, мы будем все же считать, что процесс пластической деформации протекает весьма медленно и что использование понятия равновесного состояния системы является правомерным. Вернемся поэтому к определению критической нагрузки как точки разветвления равновесных форм. Здесь мы сталкиваемся с новой особенностью неупругого выпучивания: вместо определенной точки бифуркации, соответствовавшей первой критической нагрузке в упругой области, здесь возможные точки бифуркации заполняют весь промежуток, лежащий между касательно-модульной и приведенно-модульной нагрузками. В какой же точке должно произойти выпучивание образца, подвергающегося испытанию в лаборатории, либо элемента конструкции в реальных условиях? Это зависит от характеристики машины или связанных со стержнем частей конструкции. В предыдущих выкладках отношение APjbv не определялось, но его можно найти, если известны реакция сопряженных с образцом элементов конструкции при заданной стреле прогиба и характеристика нагрузки, приложенной к конструкции в целом *).
Возникает вопрос: какую же нагрузку — касательно-модульную. или приведенно-модульную — надо принимать в качестве расчетной при проектировании? Как мы видели, касательно-модульная нагрузка может при известных условиях соответствовать точке бифуркации равновесных форм, она всегда лежит ниже приведенно-модульной и лучше соответствует экспериментальным данным. Поэтому надо рекомендовать вести практические расчеты по касательно-модульной нагрузке. Правда, различие между касательно-модульной и приведенно-модульной нагрузками невелико; поэтому, как уже отмечалось Хоффом [6.13], существенного влияния на результаты расчета этот выбор не оказывает.
Проводя расчет по касательно-модульной нагрузке, мы как бы отказываемся учитывать эффект разгрузки при выпучивании. Это предположение сильно упрощает расчеты, особенно в более сложных задачах устойчивости пластинок и оболочек, и мы будем к нему в дальнейшем неоднократно прибегать.
*) См. статьи А. А. Ильюшина, В. Г. Зубчанинова (Инж. сб,. т, 27 я 28, 1960) и Я, Г. Пановко [2.6, 1962].
ВНЕЦЕНТРЕННОЕ СЖАТИЕ В НЕУПРУГОЙ ОБЛАСТИ
107
Независимо от того, какой модуль принять расчетным — Т или ЕКУ—для решения задач мы вправе применять приближенные методы, описанные в главе I. В случае стержня переменного сечения надо учитывать при этом изменение модуля Т или Ек по длине, зависящее от изменения напряжения о в сечении. Но так как само критическое напряжение обычно подлежит определению, то расчет приходится проводить путем нескольких проб.
§ 32. Внецентренное сжатие в неупругой области. Приближенное решение
Исследование форм равновесия стержней, подвергающихся внецентренному сжатию за пределами упругости, встречает новые затруднения. Здесь приходится рассматривать различные варианты расположения по сечению упругой и пластической зон при различных нагрузках. Поэтому был предложен ряд приближенных решений, вносящих значительные упрощения уже в самую постановку задачи*).
Одним из существенных допущений является введение модели идеально пластичного материала.
Под этим понимается воображаемый материал, диаграммы сжатия и растяжения которого имеют вид, показанный на рис. 2.21. Считается, что пределы текучести при сжатии и растяжении одинаковы.
Второе допущение состоит в том, что изогнутая линия для шарнирно опертого стержня представляет собой полуволну синусоиды.
На рис. 2.22, а изображено поперечное сечение стержня, имеющее ось симметрии. Будем считать, что точка Л приложения силы Р лежит на этой оси и отстоит от центра тяжести С на расстоянии е. Пусть высота сечения h делится точкой С на отрезки hx и h2. Обозначим через / стрелу прогиба стержня, отсчитываемую от линии действия силы Р. Представим себе, что деформации в некоторой части сжатой зоны превышают величину ет, отвечающую пределу текучести: ет = от/Е; граница этой зоны отстоит на £ от края сжатой области. Положение нейтральной линии пусть определяется отрезками С и т). Полные эпюры распределения деформаций и напряжений по высоте сечения даны на рис. 2.22, бив.
*) Эта задача рассматривалась Рошем [2.18], Хвалла [2.10], Фриче [2.12], Ежеком [2.13], А. В. Геммерлингом [2.3], В. В. Пинаджяном [2.7]. Здесь изложение построено по книге Ежека [2.13].
бпциб7
£
Рис. 2.21. Идеализированная диаграмма.
108 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. И
Составим уравнения равновесия для части стержня, отделенной средним сечением. Уравнение проекций сил на направление оси стержня имеет вид
VoT — f od/?j=0.
(2.77)
Здесь через F обозначена площадь сечения, через а — разность между
напряжением в точке с координатой и и пределом текучести от:
0 = 0.
(2.78)
Координата и отсчитывается от границы зоны текучести.
Уравнение моментов относительно линии, проходящей через крайнюю точку растянутой зоны, будет
P(f + h2)-
h-l
FaTh2 — J* о (/г — — и) dF = 0.
° (2.79)
Введем обозначения для статических моментов и моментов инерции частей
su — / «1 dF, /и = fu\ dF, (2.80)
о
h-i
Рис. 2.22. (а) Сечение стержня,
(б) эпюра деформаций и r „
(в) эпюра напряжений при экс- S2c — I u2dF, /2с = I u\dF. (2.81)
центричном сжатии. J о
Сопоставляя (80) и (81), можно записать
5* = 5i5+/7№ —?). (2.82)
Момент инерции всей площади относительно границы зоны текучести и момент инерции / относительно параллельной ей центральной оси связаны соотношением
A=/u+=/-h(Al-Q2-
(2.83)
ВНЕЦЕНТРЕННОЕ СЖАТИЕ В НЁУПРУГОЙ ОБЛАСТИ
109
Обозначим через c0 = P/F среднее сжимающее напряжение в сечении; тогда из (77) вытекает:
4=-nfT-, 07S)g*- <2-84)
Пользуясь (82) и (83), из уравнения (79) находим:
/ = 7-1/-/* — (А, — )Sie]. (2.85)
Для определенной формы сечения уравнение (85) вместе с (84) дают зависимость между стрелой прогиба / и средним напряжением о0.
Рассмотрим теперь геометрическую сторону задачи. Обозначим через р радиус кривизны упругой линии для среднего сечения, тогда
} = (2-86)
Пользуясь (1.3), для этого сечения получим:
(2.87)
Уравнение изогнутой линии стержня запишем в виде
v = e-\-(f — e) sin —, (2.88)
причем начало координат совпадает с точкой приложения одной из сил Р\ при * = //2 будет:
d2v п2
(2.89)
Сравнивая (87) и (89), находим:
it2 F
P = Tl(f — е) —. (2.90)
SJT
Окончательно по (84) и (85) имеем:
(*=!£[/-/„- <*, - S) S„ - -5!1+.,'’-.,,~5) Ч • (2 91)
Мы получили соотношение между средним напряжением о0 и шириной пластической области £. Анализ его показывает, что величина о0 вначале возрастает, а затем, после достижения некоторой предельной точки, падает. Поставим себе целью найти такое значение, при котором о0 является наибольшим; для этого приравняем нулю производную от Р по k при заданном а0; тогда получим
(*.-5+г)тГ—+ = <2-92>
Определяя отсюда Е, по (84) найдем «критическое» значение среднего напряжения, а по (85) соответствующую стрелу прогиба.
110 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. II
§ 33. Внецентренное сжатие стержней прямоугольного и таврового сечений
Рассмотрим случай прямоугольного сечения b X h. По формулам (80) при hx = /г/2 находим:
.15— “2» НГ’ (2.93)
Подставляем эти значения в (92), тогда получим значение ширины пластической зоны при критическом значении среднего напряжения
°о — акр:
Обозначим через k радиус ядра сечения:
W
k = -jr. (2.95)
где W — момент сопротивления сечения, и введем понятие меры эксцентриситета т:
В данном случае
k
Вместо (94) будем иметь:
е
еР
k ~
W •
h
6е
*6'
т =
= h
_1 т °кр h 3 скр
(2.96)
(2.97)
(2.98)
Подставим это выражение в уравнение (91); тогда получим:
»«>
чкр
Гибкость стержня равна
}_ 1 _ (V12 / h
Равенству (99) придадим вид
о.
(2.100)
(2101>
Отметим, что при 5 = 0, когда пластическая зона отсутствует, мы получаем обычную формулу Эйлера. Пользуясь выражением (98), получим: 9 к2Е (А т 1 \з
§ 33] ВНЕЦЕНТРЕННОЕ СЖАТИЕ ПРИ ПРЯМОУГ. И ТАВРОВОМ СЕЧЕНИЯХ 111
Мы пришли к уравнению относительно окр, позволяющему определить критическое напряжение при заданном относительном эксцентриситете. Соответствующие значения ч\ и / по (84) и (85) будут:
-w=ilr('-4)4
f кр
mh
~W
кр
■ + 4-4 ('-4)4 '
(2.103)
(2.104)
Сюда надо подставить выражение для ЦП по (98). На графике рис. 2.23 представлены кривые окр(Х), построенные по уравнению (102) для различных параметров т\ принято £ = 2,1 • 106 кг/см2,
бм,кг/см
Рис. 2.23. Диаграмма акр (К) в случае эксцентричного сжатия стального стержня прямоугольного сечения.
от = 2400 кг/см2. При т = 0 мы получаем горизонтальную прямую в пределах X < Х и гиперболу Эйлера для ХХ; здесь Х = 94. Небольшой левый участок диаграммы отвечает случаю двусторонней текучести, когда пластические деформации возникают не только в сжатой, но и в растянутой зоне.
В книге [2.13] рассмотрены аналогичным образом случаи поперечных сечений иной формы. Сопоставление результатов показало, что при значительных т критическое напряжение получается наименьшим для стержней таврового сечения, когда точка приложения силы лежит на оси стенки, по другую сторону от полки (рис. 2.24). Разберем тот случай, когда пластическая зона имеется ЛИШЬ на стороне сжатия и охватывает только часть полки. Выражения
112 УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. II
для и будут снова иметь вид (93), причем под b надо понимать ширину полки. Уравнение (92) оказывается квадратным относительно кр и приводится к форме
2 Fea.
кр
Ь (ат аКр)
(2.105)
Воспользуемся снова обозначением для меры эксцентриситета (96), причем здесь W = Wx — I\hx (см. рис. 2.22). Тогда наименьший корень уравнения (105) можно представить в виде
(2.106)
(2.107)
(2.108)
?кР = p — Vp2—Q’
где
кр
p = h 1 Я
mWx<3 Кр
F (®т акр) 2mW x<zK
Рис. 2.24. Тавровое сечение стержня.
Мат“ акр)
Сопоставляя (106) — (108), находим:
Ax-Skp =V7rzq-J%r- (2-109)
Подставим выражения (106) и (109) в уравнение (91); тогда после упрощений получим:
TEI [ + Ь Г / - о \3/а
икр
Отсюда при X = Iji п*Е
я)
(2.110)
Кр
тТ]}‘ (2-1П)
Развернем выражение (р2 — q)*/2 в ряд:
(р2—q)Vl = p3—тМ+4?—
2 гч I 8 р
После некоторых преобразований уравнение (111) примет вид
к2Е Г m<3vп Wj / тс,
2bh\ I а.
(2.112)
Х2 =
1
кр
ткр\2 _ 1
г скр / J
(2.113)
кр L Т кр
Если принять размеры сечения по рис. 2.25, при b = h, то коэффициент, содержащий Wx и hi% будет равен 0,38. Заметим, что разрешающее уравнение (102) для случая прямоугольного сечения можно также привести к форме
X2:
%*Е
°кр
§ 33] ВНЕЦЕНТРЕННОЕ СЖАТИЕ ПРИ ПРЯМОУГ. И ТАВРОВОМ СЕЧЕНИЯХ 113
оно отличается от (113) только коэффициентом при третьем члене ряда. Зависимость акр(Х) по (113) для сечения по рис. 2.25 представлена на графике рис. 2.26; здесь даны также участки кривых, соответствующих другим сочетаниям упругой и пластических зон сечения.
В. В. Пинаджяном [2.7] была решена более сложная задача в предположении, чго в диаграмме а(е) участок пластичности является не горизонтальным, а слегка наклонным (рис. 2.27). Такая зависимость о(е) лучше отвечает обычной диаграмме для стали Ст. 3. Вычисления показали, что критическое напряжение для такого материала лежит на 5 — 7% выше, чем в случае «идеальной пластичности».
Исследования устойчивости упруго-пластических стержней с учетом различных возмущений (внецентренность нагружения, начальная
Рис. 2.25. Размеры таврового сечения в численном примере.
кг/см*
погибь) лежат в основе современных норм расчета сжатых и сжато-изогнутых элементов строительных конструкций. Это направление освещено в книгах
Рис. 2.26. Зависимость акр (X) в слу- Рис. 2.27. Приближенная диаграмма чае стержня таврового сечения при сжатия для стали,
эксцентричном сжатии.
А. В. Геммерлинга [2.3], А. А. Пиковского [3.7], Г. Бюргермейстера и Г. Штойпа [0.16], К. Колбруннера и М. Мейстера [0.19].
ГЛАВА III
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ И СТЕРЖНЕВЫХ СИСТЕМ
§ 34. Стержни переменного сечения. Ступенчатое изменение жесткости
Мы рассматривали до сих пор только такие стержни, жесткость которых по длине является постоянной. Однако с точки зрения облегчения конструкции целесообразно применять сжатые стержни переменной жесткости, с увеличением ее в той зоне, где изгибающие моменты и нормальные усилия оказываются наибольшими. Правда, изготовление стержней переменной жесткости требует более сложной технологии. Но для крупных сооружений это заведомо окупается экономией материала, затрачиваемого на конструкцию. Особенно удобным является применение составных стержней переменной жесткости, имеющих две или несколько ветвей; такие стержни часто встречаются в конструкциях башен, мачтах, стрелах подъемных кранов и т. д.
Приведем решение нескольких задач, относящихся к устойчивости стержней переменной жесткости, шарнирно опертых по концам. Очевидно, в этом случае жесткость должна быть повышенной в средней части.
На рис. 3.1 представлен стержень, состоящий из трех частей. Крайние части, каждая длиной 1г, имеют жесткость EIV а средняя, длиной а = 2/2, — жесткость Е12, причем /2 > /х; / — общая длина стержня. Составим дифференциальные уравнения изогнутой оси для каждой части. Будем отсчитывать координату хг от конца стержня О, а х2 — от точки сопряжения участков. Уравнения будут иметь вид
El.- + Pv ! = 0, (3.1)
dx\
(3.2)
El
2 ал
■ Pv9 = 0.
§ 34]
СТЕРЖНИ ПЕРЕМЕННОГО СЕЧЕНИЯ
115
Вводя обозначения
р ь2
Р __ иЧ Е1г ~ 2'
запишем интегралы уравнений (1) и (2):
vx = A sin kxxx + В cos kxxv v2 = C sin k2x2 + D cos k2x2.
(3.3)
(3.4)
(3.5)
Граничные условия по концам и в точке сопряжения участков будут:
vx == О
vx = v2
dv
dvo
dx j dv2
dx«
dx2 = 0
при AT j = 0, (3.6)
при xx — lx и x2 = 0, (3.7)
при xx = lx и x2 = 0, (3.8)
при x2 = l2. (3.9)
Из этих условий находим:
В = 0, A sin kxlx = D,
Akx cos kxlx = Ck2, С cos k2l2 — D sin k2l2 -
sin kxlx = D, 1 sin2/2 = 0. J
10)
Сопоставляя уравнения (10), приходим к трансцендентному уравнению Ьх
t gWi
k2 tg k2l2.
Представим критическую нагрузку в виде
Eh
кр
:/С-
/2
(3.11)
(3.12)
“Л
“У/
Рис. 3.1. Случай ступенчатого изменения сечения.
В таблице 3.1 приведены значения коэффициента К для некоторых отношений
Т = Т = Х’ 7Г=“- <3J3)
Приведем пример решения той же задачи с помощью метода последовательных приближений.
Пример 3.1. Определить критическую нагрузку для стержня со ступенчатым изменением жесткости при А = 0,8. Примем начальное уравнение упругой линии в виде
4 №
v = -p-(lx — x2). (а)
116 ЁОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [гл. Ill
Таблица 3.1 Значения коэффициента К для стержня со ступенчатым изменением жесткости
0,2
0,4
0,6
0,8
0,1
1,47
2,40
4,50
8,59
0,2
2,796
4,222
6,694
9,330
0,4
5,089
6,680
8,512
9,675
0,6
6,978
8,187
9,240
9,790
0,8
8,550
9,177
9,632
9,840
Уравнения (1) и (2) перепишутся тогда следующим образом:
d2V\ ли (Х л\ d2v2 ли Iх л\
1W ~~ 1\т )’ ~ЗЖ ~~ г\Т~ )'
Интегрируя эти уравнения и используя условия (6) — (9) с учетом того, что х теперь отсчитывается от точки О, находим:
--2'*'[Нт),-з(т)‘ + ТТ + 7П5г(-1)]- <=>
Стрела прогиба будет
/(1) = /да (193 I _il \. (d)
1 Е/ т V 1875 3 • 104а / W
Критическая сила оказывается равной
_ei2 3.W
кр — /2 07 • \Ъ)
3088+ —
а
Для случаев, приведенных в таблице 3.1, получим следующие значения /<:
а 0,1 0,2 0,4 0,6 0,8
К 8,77 9,17 9,41 9,52 9,58
Ошибка по отношению к табличным значениям не превышает 5%.
§ 35. Случай непрерывного изменения жесткости по длине. Стержень наименьшего веса
Перейдем к случаю, когда жесткость стержня непрерывно изменяется вдоль длины *). Рассмотрим шарнирно опертый по концам стержень, для каждой половины которого момент инерции изменяется
*) Подобные задачи были впервые решены Лагранжем, ряд случаев стержней переменной жесткости был рассмотрен А. Н. Динником [3.1].
§ 35] СЛУЧАЙ НЕПРЕРЫВНОГО ИЗМЕНЕНИЯ ЖЕСТКОСТИ ПО ДЛИНЕ по степенному закону:
11?
(3.14)
х отсчитывается от точки, находящейся от середины стержня на расстоянии Ь. Если, например, стержень состоит из двух ветвей (рис. 3.2), имеющих прямолинейное очертание, и расстояние между ветвями h равно.
h=h2±,
то момент инерции сечения, если не учитывать собственного момента инерции сечения ветви, будет изменяться по соотношению (14) при т = 2.
Дифференциальное уравнение упругой линии будет
граничные условия имеют вид
dv п,
- = 0 при х = о\
dx
I
v = 0 при х — Ъ — = bv
Обозначим
(3.16)
рЬт
£/,
= k\
тогда вместо (15) получим: d2v
dx2
+ k2x'mv = 0.
(3.17)
Рис. 3.2. Момент инерции сечения изменяется по степенному закону.
Рассмотрим сначала случай, когда т = 2; при этом решение уравнения (17) будет
v = A Ylc sin (s In л;) + В Y~x cos (s In лг), (3.18)
где
(3.19)
в этом легко убедиться непосредственным дифференцированием. Производная равна
‘S' “ А [ W7sln (s п х)+у?s 008 (s In х)]+
+ В cos (s In х) - ~ s sin (sIn jr)J. (3.20)
118 ЬОЛЕЁ СЛОЖНЫЁ ЗАДАЧИ УСТОЙЧИВОСТИ CfEt>>KHEft (гЛ. Ill
Используем граничные условия (16). По второму из этих условий
В = — tgln).
Первое условие дает
[у (s 1° )Ч““f~В I*1 )J =
Отсюда получаем уравнение относительно s:
tg (s In -у-) = 2«. (3.21)
Наименьший корень этого уравнения определяет
критическую нагрузку:
кр = 1--. где (3.22)
Если тф 2, то решение уравнения (17) выпи¬
сывается следующим образом:
v = A yicJ (2Ьлг2')-1-£ V~xJ-, (ычх 211), (3.23) где
v = 2 — 'т—Драное число.
Под Уу понимается бесселева функция первого
рода с индексом v. Отметим, что при v
где п — целое число, функции 7V и могут быть выражены через элементарные функции.
Пусть, далее, шарнирно опертый стержень состоит из трех частей (рис. 3.3), причем на среднем участке /2 момент инерции постоянен и равен /2, а в крайних частях, длиной lv момент инерции меняется по закону (14). Тогда для среднего участка уравнение упругой линии запишется в виде (5) при / = /2, а для крайнего участка — в форме (15). Учитывая условия для концевого сечения, среднего сечения и точки сопряжения участков, определяем критическую нагрузку.
Данные для расчетов, относящиеся к случаю т = 2, приведены на графике рис. 3.4 [0.21]. Здесь по оси абсцисс отложено отношение /х//, по оси ординат — коэффициент Кх из формулы (22) при / = /9; серия кривых дана для различных отношений моментов инерции
Рис. 3.3. Стержень, состоящий из трех частей; средняя часть имеет постоянное сечение.
§ 35] СЛУЧАЙ НЕПРЕРЫВНОГО ИЗМЕНЕНИЯ ЖЕСТКОСТИ ПО ДЛИНЕ 119
Формулу (22) можно также представить в виде
р _ п2£1г.
КР~ (v/)2 *
коэффициент приведения длины равен у=1 /У~К[.
(3.24)
£ис. 3.4. График для расчета стержня переменного сечения.
Пример 3.2. Стрела АВ портального крана (рис. 3.5) состоит из четырех равнобоких уголков 75 X 75 X 6, связанных решеткой. Полная длина стрелы / = 17,5 м. Габаритные размеры сечения средней части DG постоянны, а на протяжении каждой из крайних частей меняются по линейному закону в зависимости от расстояния до опоры А или В. Размеры сечений в средней части и у опор показаны на рисунке. Требуется определить критическую нагрузку при Е = 2,1 • 106 кг/см2, апц = 2000 кг!см2.
Площадь сечения профиля равна 8,78 см2, расстояния от оси до центра тяжести сечения уголка в средней части — 17,94 см, у опор — 6,94 см. Момент инерции сечения в средней части
у опор
/2 = 4 (46,7 + 8,78.17,942) = 11 500 см\ /, = 4 (46,7 + 8,78.6,942) = 1900 см4;
здесь учтен собственный момент инерции профиля, равный 46,7 см*. Отношение Л// = 0,165, V 1x4 = 0,405. Из рисунка находим:
h 7
120
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ
[ГЛ. III
По графику рис. 3.4 при этих значениях Vl\4 и IJI будет Ki «0,73. Кри1ическую нагрузку без учета влияния поперечной силы (см. ниже, § 43) получаем равной
Соответствующее напряжение акр = 59 000/4 • 8,78 = 1570 кг/см2 лежит ниже 9ПЦ.
Рис. 3.5. К расчету стрелы портального крана.
Естественно поставить вопрос: какое очертание должен иметь сжатый стержень переменного сечения для того, чтобы при определенной нагрузке он имел наименьший вес *)? Приведем результаты решения такой задачи для случая, когда стержень имеет сплошное круглое сечение и шарнирно опирается по концам. Наивыгоднейшее очертание стержня отвечает закону
arcsin у] — т] У! — т]2 =,
(3.25)
*) Эта задача была впервые поставлена Лагранжем и в дальнейшем исследовалась Е. Л. Николаи (Труды по механике, Гостехиздат, М., 1955), Н- Г* Ченцовым [3.10J, А. Ф. Смирновым [0.11] и другими авторами.
СЛУЧАЙ СОСРЕДОТОЧЕННОЙ СИЛЫ В ПРОЛЕТЕ
121
где 7] — отношение текущего диаметра к диаметру среднего сечения, х отсчитывается от конца стержня. Форма стержня показана на рис. З.б, здесь отмечены значения rj в некоторых сечениях [1.13]. Вес такого «идеального» стержня оказывается на 13% меньше, чем вес стержня постоянного сечения. В случае трубчатого сечения экономия в весе может оказаться значительно большей.
§ 36. Случай сосредоточенной силы в пролете
Допустим, что стержень, шарнирно опертый по концам, подвергается действию сил Pv Р2 и Рг-±-Р2 и что сила Р2 приложена в некотором промежуточном
Л
\
\
п
кхг
Рис. 3.6. Очертание стержня наименьшего веса.
«г
Рис. 3.7. Случай силы, приложенной в пролете.
сечении, расположенном на расстояниях 1г и /2 от концов (рис. 3.7). Примем, что момент инерции сечения в верхней части равен Iv а в нижней /2.
Обозначим через / отклонение точки приложения силы Р2 при выпучивании стержня. Дифференциальное уравнение упругой линии для верхнего участка будет
Eli
d2Vi
dx f
2) vi'
Pit
(хг + l2) — P2(f — vx) =
p*.f
(*i—h);
(3.26)
здесь учитывается составляющая реакции опоры, равная P-Jlh координата X, отсчитывается от 0. Для нижнего участка получаем:
EI,
d2v2
dxi
= -(/>, +p2)<v
p,f
Воспользуемся обозначениями
Рх_
Eh
— k\,
х2.
Е1Х *4’
(3.27)
(3.28)
122 60ЛЁЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
тогда уравнения (26) и (27) перепишутся следующим образом:
(3.29)
й2Щ ич f
dx
Отсюда
dJx °х — **
-г k\v2 = Щ-Г Х2. (3.30)
CLX 2 L
k\ /
V\ = Ах cos kxxx —— Вх sin kxxx —)—2— (*i — i)» (3.31)
kx I
k\ f
*o2 = A2 cos k2x2 + B2 sin k2x2 -)—g x2- (3.32)
kn I
Граничные условия для концов стержня и точки сопряжения будут:
<vx == 0 при хх = lx% v2 = 0 при х2 = 0, - dv{ dv2 л. г (3.33)
Vl = v, = f И = при дс, = 0 И х2 = /2. J
Пользуясь этими условиями, находим:
А = о, '4‘=/(+ЗТ
B, = _f1+4Y B.-JLrU *
tg kxlx \ k\l J sin k2l2 \ k2l
и, наконец, приходим к окончательному уравнению k\ k\l+k\lx k\ k2l — k\l2
(3.34)
При заданном отношении сил и моментов инерции находим путем
проб значения kx>..., kA, отвечающие наименьшим значениям сил
Рх и Р2. Представим критическую величину Рх Р2 в виде
Р1 + Р2 = К. (3.35)
и обозначим
=т, -£- = «. (3.36)
Г\ 11
Коэффициенты К для случая /1 = /2» найденные по уравнению (34), дакы в таблице 3.2.
§ 37] ДЕЙСТВИЕ РАСПРЕДЕЛЕННОЙ ПРОДОЛЬНОЙ НАГРУЗКИ 123
Таблица 3.2
Коэффициенты К для случая сил, приложенных по концам и посередине пролета
т
П N.
1,00
1,25
1,50
1,75
2,00
3,00
1,00
9,87
10,9
11,9
12,5
13,0
14,7
1,25
8,81
9,77
10,5
11,2
11,6
—
1,50
7,90
8,86
9,53
10,1
10,7
—
1,75
7,11
8,04
8,52
9,10
9,77
—
2,00
6,40
7,30
7,90
8,43
8,97
—
Случай т = 1 относится к стержню переменного сечения, на который действуют только силы Рх по концам. Уравнение (34) переходит в следующее:
U U
(3.37)
k j /?2
tgk2i2 '
§ 37. Действие распределенной продольной нагрузки
Перейдем к случаю, когда продольная нагрузка распределена по длине стержня. Одним из примеров такого типа нагрузки является собственный вес стержня: при расчете колонн в крупных сооружениях, дымовых труб и т. д. его необходимо учитывать. Обычно в этих случаях один из концов колонны (верхний) является свободным, а второй (нижний) — защемленным. Рассмотрим Задачу об устойчивости такого стержня с постоянным по длине сечением сначала под действием только собственного веса, а затем — при1 совместном действии силы веса и других нагрузок *).
Примем систему координат по рис. 3.8. Обозначим силу веса, приходящуюся на единицу длины, через р. В сечении х сжимающая сила равна Рх = рх, а поперечная сила
<3-38>
Уравнение (2) преобразуем к виду
£/-g- = -Q; (3.39)
*) Задача о продольном изгибе колонн под действием собственного веса была поставлена Эйлером, а в дальнейшем рассматривалась Гринхиллом [3.11], изучившим в связи с этим также очертания стволов деревьев.
124 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ
подставляя (38), получим:
Введем обозначения
и г d3v ■ dxj л
EId*+Px47 = 0-
х t dv pi3 9
T — — W. El ~a;
тогда придем к уравнению
d2w
■ аЧи> = 0.
[ГЛ. Ill
(3.40)
(3.41)
(3.42)
Это уравнение интегрируется в бесселевых функциях *); решение имеет вид
w
р Здесь J1 —бесселева функция первого рода. Произ-
з*
водная от функции J(olz) по z равна
dJ'(а2) ---уЛ («) + ®Л-1 («)•
Основываясь на этой формуле, находим:
L з __ з
(3.44)
Рис. 3.8. К задаче об устой- Дифференцируя (43), получаем: чивости стержня под влиянием dw
собственного dt
веса.
Граничные условия задачи будут:
= AaV_2 (-а5*) - ВаУъ )
ИЛИ
М = — EI = 0 при х = 0,
. = 0 при лг = /
= 0 при 5 = 0, гг> = 0 при ?=1.
(а)
*) См., например, Э. Камке, Справочник по обыкновенным дифференциальным уравнениям, изд. 2-е, Физматгиз, 1961, стр. 453.
§ 37] ДЕЙСТВИЕ РАСПРЕДЕЛЕННОЙ ПРОДОЛЬНОЙ НАГРУЗКИ 125
Как известно, функции УДЕ) обращаются в нуль при Е = 0, если индекс v > 0; если же v < 0, то функция 7V(0) = оо. В нашем случае v = l/Zi следовательно, величина У1/3(0) = 0, в то время как J 2 (0) = °°- Но тогда первое из условий (а) может быть вы“
полнено лишь при А = 0. Считая В Ф 0, из второго условия находим:
у_1(та) = 0- (3-45)
3 '
Наименьшее значение аргумента, при котором функция J i обращу
щается в нуль, будет
• а = 1,866. (3.45а)
По (41) находим:
Ркр = «2j- = 7.84-. (3.46)
Введем понятие приведенной нагрузки, понимая под этим силу Р, сосредоточенную в известной точке и эквивалентную распределенной нагрузке в задаче устойчивости. Выберем центр приведения у свободного конца, тогда
I2 п2 7,84
и окончательно
Р=ЪйР1. (3.47)
Следовательно, приведенная сила составляет 1/3,18 часть от полного веса.
Познакомимся с решением этой же задачи без непосредственного применения бесселевых функций, с помощью метода степенных рядов; этот метод широко применяется в аналогичных задачах. Выпишем решение уравнения (42) в виде
w = C0-f- Сх%-\- С2Е2--С3Е3... (3.48)
Подставляя это выражение в (42), получим:
2С2 + 2.3С3Е+3.4С452+... +а2(С0Е + С1Е2 + С2Е3+...) = 0.
(3.49)
Сравнивая коэффициенты при одинаковых степенях Е, приходим к следующим соотношениям:
С2 = 0, 2 • ЗС3 = — а2С0, 3 • 4С4 = — a2Cv
С0 f (3.50)
4 • дСв = — а2С2 = 0, 5 - 6Сб = -а2С3 = а4,... j
} (З.Е
126 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
Таким образом, коэффициенты с индексами 2, 5, 8, 11 и т. д. обращаются в нуль:
С2+Зл = 0Ч при п = О, 1, 2,...
Остальные коэффициенты связаны зависимостями
*+2— (k + \)(k + 2) °*-1‘
Можно видеть, что все эти коэффициенты могут быть выражены через С0 и Сг:
с — 0,2 С С 0,4 С
3““ 2-3 °’ 6~~ 2-3-5-6 °’ ‘ * *
п д2 с С — Г
4— 3-4 l* 7~ 3-4-6-7 1' * • *
Выражение для w принимает вид Производная по £ будет равна
Ж = С<{-Ьг+---) +
+ з-,;3~Ь 3-4-6 •••)• (3.52)
Пользуясь первым из граничных условий (а), находим Сх = 0. Второе из этих условий при С0 Ф О приводит к уравнению
1 ~~ 1ГЗ 2-3-5-6 2• 3-5• 6• 8• 9 * =0, (3-53)
которое можно переписать в виде
, 3 /2 \2, З2 /2 \4 З3 (2 \б, л
1 2-4 \ 3 а) ~*~2-4-4-10\3 а) 2 • 4-4 • 6-10 • 16 \3 / ' °*
(3.54)
В левой части этого уравнения содержится ряд, соответствующий бесселевой функции J i Таким образом, мы получили урав-
“ 3 '
нение, эквивалентное (45); наименьший корень его определяется по (45а).
Реальные колонны больших размеров имеют, как правило, переменное сечение. В этом случае непосредственное интегрирование уравнения упругой линии усложняется, и потому расчет на устойчивость необходимо проводить с помощью приближенных методов. В качестве примера рассмотрим один из вариантов проектируемой
§ 37)
ДЕЙСТВИЕ РАСПРЕДЕЛЕННОЙ ПРОДОЛЬНОЙ НАГРУЗКИ
127
для Москвы телевизионной башни высотой в 520 м *) (рис. 3.9, ау б). На рис. 3.9, в приведена эпюра продольного сжимающего усилия (в тоннах). Определение коэффициента запаса устойчивости башни было выполнено с помощью метода последовательных приближений; одновременно устанавливалась форма упругой линии. Ордината г>тах
Рис. 3.9. К расчету телевизионной башни на устойчивость.
кривой первого приближения в точке у вершины антенны принимав лась равной единице. Далее определялись изгибающие моменты от вертикальных сил для ряда сечений. Считалось, что в этих сечениях имеются упругие шарниры, жесткость которых (в тонна-метрах) соответствует эпюре рис. 3.9, г; отсек, расположенный между расчетными сечениями, принимался абсолютно жестким (§ 11). Далее опре¬
*) Этот расчет принадлежит В. Ханджи. Ординаты эпюр в) и г) отве* чают сечениям, показанным точками на рис. 3.9, а.
128 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [гЛ. III
делялась новая упругая линия; сравнение полученной стрелы прогиба с исходной давало возможность найти запас устойчивости. На рис. 3.9, д пунктиром показана кривая третьего приближения, причем прогибы v вновь были отнесены к VmSLX.
§ 38. Одновременное действие распределенной и сосредоточенной нагрузок
Перейдем к тому случаю, когда стержень подвергается действию не только распределенной нагрузки р, но и сосредоточенной силы Р, приложенной к свободному концу (рис. 3.10). Для общности будем считать, что величина р является переменной: р = р(х). Воспользуемся методом Бубнова—Галеркина; предварительно выведем исходное уравнение с учетом распределенной I нагрузки. Обратимся к вариационному уравнению, полученному в § 6. Выражение для вариации работы внутренних сил представим в виде (1.88а):
U)]0+/zr(
в отличие от § 37 координата х отсчитывается от нижнего конца стержня.
Вычислим работу распределенной нагрузки, считая ее интенсивность переменной по длине. На элемент dx приходится нагрузка р dx; смещение центра тяжести элемента по отношению к нижнему концу равно
Рис. ЗЛО. Одновременное действие сосредоточенной силы и собственного веса для стержня с защемленным концом.
dv \2
zr) dx-
Полная работа распределенной нагрузки равна
о Lo
dx.
(3.56)
(3.57)
Введем обозначения Rt_x> Rt для результирующих нагрузки в пределах от 0 до л:, от х до I и по всей длине:
л / i
Rx = fpdu, R,_x = fpduR,-. R, = fpdx. (3.58)
§ 38] ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ РАСПРЕД. И СОСРЕДОТОЧ. НАГРУЗОК 129 Интегрируя выражение (57) по частям, получим:
л: -/ /
*■*4
О Jo о
или
w=iR‘.f Ш’х- 7/*•>Ш“х- (3 591
о о
Окончательно
i
w = ifRi-*(£fdx- (3-60)
О
Вариация равна
О
Эту величину надо прибавить к выражению (1.95а); полная вариация работы внешних сил будет
i
W = f (P+Ri-x)-()dx. (3.62)
О
Вариационное уравнение можно, следовательно, представить в виде
И* +/ [ h (el S-)+<р+ *i-j is] is
0 (3.63)
жесткость EI здесь для общности принята переменной. Подставляя вместо bv выражение (1.126) и принимая вне>интегральный член равным ну л ю, получим основное уравнение метода Бубнова—Галеркина:
f[{E,%?)+(p+«Z\Tt-dx = °- 2 0 (3.64)
Рассмотрим случай, когда наряду с сосредоточенной силой Р должен быть учтен собственный вес стержня р01, причем EI = const. Вместо (64) получим:
f{a 5- + 1р + Л1'-£--ЗГ = °- (3-65)
130 BOJtEfc СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [гл. Til
Уравнение упругой линии примем в виде, соответствующем случаю одной сосредоточенной силы:
i» = /(l —cos--). (3.66)
Принимая
' — cos— (3.67)
и подставляя два последних выражения в (65), находим:
f{-E/Wsin2W +
о
Ч-lP + Po (I — *)] sin2 Ц-}йх = 0. (3.68)
Выполняя интегрирование, получаем:
шт=р+{ъ—ъ)М' (3-69)
ИЛИ
(3.70)
Следовательно, расчет на продольный изгиб можно вести в рассматриваемом случае, присоединяя к сосредоточенной силе 3/10 от собственного веса стержня и Комбиниро- считая эту приведенную нагрузку приложенной к свованное дей- бодному концу стержня. Если нагрузка р0 значительна, ствие нагруз- то при суммарной критической силе, равной (70),
ки на стер- сила р может получиться отрицательной, т. е. растягижень, шар- м
нирно опер- вающей. Полученный нами результат хорошо соглатый по кон- суется с решением задачи в бесселевых функциях, так цам. как по (47) при Р = 0 мы получили приведенную нагрузку равной —0,31 р01.
Рассмотрим ту же задачу в предположении, что оба конца стержня оперты шарнирно (рис. 3.11). Выбирая выражение для v в виде
v = f sin-- (3.71)
и подставляя его в уравнение (65), придем к соотношению
£/ = Р + р0/. (3.72)
Здесь приведенная нагрузка оказывается равной половине собственного веса стержня.
Рис. 3.11.
§ 39] ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ОСЕВОЙ СИЛЫ И КОНЦЕВЫХ ПАР 131
§ 39. Стержень, подвергающийся действию осевой силы и концевых пар
Допустим, что стержень, шарнирно опертый по концам, подвергается совместному действию осевой силы Р и пары, приложенной к концевому сечению В, момент которой равен М0. Определим упругую
V7
Рис. 3.12 Изгиб стержня под действием осевой силы и пары.
линию стержня; это окажется важным в дальнейшем при исследовании устойчивости стержней, лежащих на нескольких опорах. Считая силу сжимающей (рис. 3.12), находим изгибающий момент в сечениях:
M=-x-{-Pv. (3.73)
Дифференциальное уравнение упругой линии имеет вид
E1L+Pv = -x (3.74)
или
~т ЁГ 1
Здесь ло-прежнему k2 = PjEL Решение уравнения (75) имеет вид
v = A cos kx-\- В sin kx £7” ~Т * (3.76)
Учитывая граничные условия v — О при л: = 0, лг = /, находим:
— ztf( жв—т)- <3-77>
Угол поворота у левой опоры будет
<8-78>
у правой опоры
( dv \ М01 /1 I \
133 вр/щр длрршыр задачи устойчивости стрржне [гл. ш
Таблиц 3.3
Вспомогательные функции
п
Дм сжатых алементо!
Для растянутых элементов
?(“)
Х(«>
Ь («>
XI (»)
0
0,1667
0,3333
0,1667
0,3333
0,1
0,1669
0,3336
0,1665
0,3331
0,2
0,1674
0,3342
0,1659
0,3324
0,3
0,1684
0,3354
0,1649
0,3314
0,4
0,1698
0,3369
0,1636
0,3298
0,5
0,1717
0,3390
0,1619
0,3279
0,6
0,1739
0,3416
0,1599
0,3256
0,7
0,1767
0,3448
0,1576
0,3229
0,8
0,1800
0,3485
0,1550
0,3199
0,9
0,1839
0,3528
0,1522
0,3166
1,0
0,1884
0,3579
0,1491
0,3130
1,1
0,1936
0,3637
0,1458
0,3092
12
0,1997
0,3705
0,1424
0,3052
1,3
0,2066
0,3782
0,1388
0,3009
1,4
0,2146
0,3870
0,1351
0,2966
1,5
0,2239
0,3972
0,1313
0,2921
1,6
0,2346
0,4089
0,1275
0,2875
1,7
0,2472
0,4224
0,1237
0,2828
1,8
0,2618
0,4383
0,1198
0,2781
1,9
0,2792
0,4568
0,1160
02734
2,0
0,2999
0,4788
0, 121
0,2687
2,1
0,3249
0,5053
0,1084
0,2639
2,2
0,3556
0,5375
0,1046
0,2592
2,3
0,3940
0,5775
0,1010
02546
2,4
0,4433
0,6285
0.0974
0,2500
2,5
0,5084
0,6955
0,0939
0,2454
2,6
0,5982
0,7873
0,0905
0,2410
2,7
0,7294
0,9207
0,0872
02366
2,8
0,9386
1,1321
0,0840
02322
2,9
1,3224
1,5183
0,0808
0,2280
3,0
2,2509
2,4495
0,0778
0,2239
3,1
7,6539
7,8553
0,0749
0,2198
3,2
—5,4511
—5,2466
0,0721
0,2159
3,3
—2,0128
—1,8051
0,0694
0,2120
3,4
—1,2375
—1,0262
0,0669
0,2083
3,5
—0,8961
—0,6811
0,0644
0,2046
3,6
—0,7049
—0,4858
0,0620
02010
§ 3PJ однрвррмрнчор дрЦдтэнв одвэой дцлы и концевых пар 133
Продолжение
и
Для сжатых элементов
Для растянутых »л*м«нто(
<р(и)
X (»)
?»(»>
Xi (и)
3,7
—0,5831
—0,3696
0,0597
0,1976
3,8
—0,4994
—0,2709
0,0575
0,1942
3,9
—0,4386
—0,2049
0,0554
0,1909
4,0
-0,3928
-0,1534
0,0533
0,1877
4,1
-0,3576
-0,1118
4,2
—0,3299
—0,0772
4,3
-0,3079
—0,0477
4,4
—0,2905
—0,0217
4,5
-0,2775
0,0015
4,6
—0,2660
0,0227
4,7
-0,2581
0,0426
4,8
—0,2525
0,0617
4,9
—0,2494
0,0804
5,0
—0,2486
0,0992
5,1
—0,2502
0,1185
5,2
—0,2547
0,1390
5,3
—0,2623
0,1613
5,4
—0,2739
0,1864
5,5
—0,2908
0,2157
5,6
—0,3148
0,2513
5,7
—0,3494
0,2967
5,8
—0,4008
0,3583
5,9
—0,4821
0,4492
6,0
—0,6243
0,6005
Воспользуемся обозначениями:
u — kl = l /~, (3.80)
<Р(И) = —J L, (3.81)
T v ' u sin и и2
y(w)==-L ?—, (3.82)
**v > и2 и ig и
гогда получим:
0Л = 9 ()■ = -г X ()• (3.83)
[опустим, что сила Р является растягивающей. Сопоставляя уравне-
ия (74) и (75), заключаем, что в этом случае мы можем восполь-
134 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. III
зоваться всеми расчетными формулами, заменив Л2 на (— ft2), к на Ik и и на tu> где / = У— 1. Тогда вместо (81) и (82) найдем:
На стр. 132 приведена таблица для функций ср, х» ?i и Xi при различных значениях и.
§ 40. Стержень, лежащий на нескольких жестких опорах
На рис. 3.13 изображен стержень, лежащий на трех шарнирных опорах. Будем полагать, что в левом пролете длиной 1Х жесткость стержня равна EXIV а в правом длиной /2 равна Е212 и что сжимающие силы Рх и Р2 различны.
Чтобы рассмотреть устойчивость такого стержня, воспользуемся формулами, полученными в § 39.
Для каждого пролета можно написать уравнение упругой линии типа (77), так как влияние соседнего пролета выражается в действии опорного момента М0. Угол поворота слева от опоры В будет
Углы 0В j и 0д 2 должны быть равны по величине и обратны по
Из уравнения (87) можно определить критическое сочетание нагрузок Рх и Р2. Предположим, что жесткости пролетов одинаковы
(3.84)
(3.85)
А
6
С
I, - — I2
Рис. 3.13. Двухпролетный стержень
а справа от опоры
здесь обозначено:
(3.86)
знаку; следовательно, при М0 Ф 0 это условие запишется в виде
I, 40J СТЕРЖЕНЬ, ЛЕЖАЩИЙ НА НЕСКОЛЬКИХ ЖЕСТКИХ ОПОРАХ 135
тогда по (87) находим:
X(“i)
(3.88)
Если же и длины пролетов равны, то условие (87) не может быть выполнено; при этом надо положить М0 = 0. Отсюда i(ux) =
— х(я2) = оо*» но тогда будет и = к и критическая нагрузка определится по обычной формуле Эйлера (1.15). Уравнение (88) можно истолковать так, что в более коротком пролете опорный момент «помогает» сжимающим силам Р изогнуть стержень, а в более длинном — «препятствует» им.
Если допустить, что в одном из пролетов (например, левом) сила Р является сжимающей, а в другом (правом) — растягивающей, то вместо (87) получим:
£7ГХ(и1>
(3.89)
h, ч « ’/ nTt п о -V-
z,('U Jx
Уравнения (88) или (89) ре- Рис. 3.14. Два участка многолролетного шаются путем пробных попы- стержня,
ток с помощью таблицы 3.3.
Предположим теперь, что число пролетов превышает два. Тогда можно рассмотреть два соседних пролета п — 1 и п (рис. 3.14) и снова выписать условие 0л } + 0л 2 = 0; но при этом надо учесть влияние второго опорного момента. Для трех соседних опор будем применять индексы п—1, п и п-1-1. Слева от средней опоры угол 0Л,1 будет равен
0„,, = Mn=jn.-yMUn_x) + MJn-г ( )t (3 90
С'П — \1 п— I
справа же от опоры угол дп2 будет
2 =%<Р(«П) + *(«„)• (3.91)
СЛ7Я Е'П1 п
Приравнивая нулю сумму этих выражений, получаем уравнение трех моментов
-/n-~ L 9(«л-i) + К [ Ё1-/ X (»«-i) + £Т X(«„)] +
СП-\ЛП-\ L С'П-\1 п- 1 сл;я J
+ -%Г<р(ия) = 0. (3.92)
Выписывая подобные уравнения для каждой пары пролетов, получаем :истему однородных трехчленных линейных уравнений относительно моментов Mv М2 и т. д. Система критических нагрузок будет
136 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
найдена, если приравнять нулю определитель, составленный из коэффициентов при Mv М2 и т. д. в этих уравнениях.
Допустим, что крайние опоры являются шарнирными. Введя
обозначение
I
s —
Е/ 9
найдем окончательное уравнение в виде
SqX (Wo) + sa (их)
О
О
Stf (Ml) s»X (“l)+2X («2) S (tt2)
О
О
Stf (U2)
S2l Ы+Szl (Из) s (Из)
о
о
*»<Р («з)
<5з7. (Ub)+S*l (И4) ■
(3.93)
= 0. (3.94)
Для двухпролетного стержня определитель будет состоять только из одного члена, для трехпролетного надо взять по два первых
члена в первой и второй строках и т. д.
Расчет стержня можно проводить по (87) или (89) и в том случае, если во всех пролетах или в некоторых из них критическое напряжение превышает предел упругости. В формулы (86) и последующие следует тогда ввести вместо модулей Е результирующие
модули Т или касательные Ек. Надо иметь в виду, что величины
этих модулей зависят от искомых критических напряжений; поэтому расчет может быть осуществлен лишь после нескольких попыток.
Пример 3.3. Ходовой винт АВ токарно-винторезного станка воспринимает усилие подачи, передающееся ему от режущего инструмента через перемещающуюся вдоль винта гайку С (рис. 3.15). Винт должен быть рассчитан на устойчивость в предположении, что гайка находится в крайнем
правом положении, на расстоянии /2 от опоры С, и передает участку винта АС, имеющему длину /,, сжимающую силу Р. Определить внутренний диаметр d винта в двух случаях: 1) гайка имеет малую длину и должна рассматриваться как промежуточная шарнирная опора (рис. 3.15, а); 2) длина гайки велика, и винт следует считать защемленным в опоре С (рис. 3.15, б).
Концы винта А, В в обоих случаях принимаются закрепленными шарнирно. Принять Р — 900 кг, коэффициент запаса устойчивости п = 3,5, 1Х = 150 см, /2 = 50 см. Материал — сталь Ст. 5, Е — 2,1 • 106 кг/см2, апц = 2800 кг/см2. При вычислении момента инерции сечения влиянием нарезки пренебречь.
В первом случае получаем стержень с тремя опорами, усилие в первом участке равно Якр, во втором — равно нулю. Так как жесткость по длине постоянна, воспользуемся уравнением (88):
X(«i) _ h
у Р
ItmmSw
ю П
\< Lf
Ц-4
38
6)
1ц
Р с\
Ft л
1Е---
--р—— 1,
V.
5-.J
Рис. 3.15. К расчету ходового винта токарно-винторезного станка.
§41] СЛУЧАЙ УПРУГОЙ ОПОРЫ. ЗАДАЧА О СТЕРЖНЕВОМ НАБОРЕ 137
По таблице 3.3 находим: х (0) = 0,333. Следовательно,
ко
х (и,)=~ w0,333=-0,11 L
Этому значению х отвечает и, 4,1. По формуле (80)
(£,/,)2 = и\ = 16,81.
Критическая сила должна быть равна Ркр = пР = 3150 кг. Момент инерции сечения будет
PKDl\ 3150 1502
/ — кр -- ~ 2 смА-
' 16,81£ 16,81 • 2,1 • 106 ~ М ’
отсюда диаметр винта d = 26 мм, площадь сечения 5,3 см2. Критическое напряжение
3150
<зкр = -g-g- = 600 кг/см2
лежит в пределах пропорциональности.
Если не учитывать влияние участка СВ и считать обе опоры А, С шарнирными, то получим параметр v?x равным п2; критическая нагрузка оказалась бы на 41% меньше.
Во втором случае винт на участке АС надо рассматривать как стержень, один конец которого закреплен шарнирно, а другой защемлен. Параметр aj равен 2тс2. Находим: / = 1,7 см4, d = 24 мм.
£,1 В
§ 41. Случай упругой опоры. Задача о стержневом наборе
Мы считали до сих пор промежуточные опоры жесткими. Однако в практических расчетах такое допущение не всегда можно сделать. Представим себе, например, стержень АВ (рис. 3.16, а), сжатый силами Р и связанный посередине длины с перпендикулярно к нему расположенным поперечным стержнем CD. При выпучивании первого из этих стержней второй является для него упругой опорой. В более общем случае вместо поперечного стержня можно представить себе некоторую линейную упругую опору жесткости с (рис. 3.16, tf). Определим критическую силу для
стержня АВ, считая сначала упругую линию симметричной относительно среднего сечения. Обозначим прогиб посередине длины через /; тогда составляющие реакций опор будут Р и с//2.
1 г *
О)
б)
Рис. 3.16. Стержень с упругой опорой.
138 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
Дифференциальное уравнение упругой линии для левой половины получает вид
£/-з5- = -/Ч» + 4*; (3.95.
решение его будет
cf
v — A cos kx + В sin kx -+* -ф х, (3.96)
где k2 = PlEI. Подчиним это решение условиям:
v=0 при x = 0, -- = 0 и v = f при х = -. (3.97)
Из первых двух условий находим:
Л —О, В= cf
kl *
2Pk cos -у
а третье при f Ф 0 приводит к соотношению
‘sl-T-l1 47г) = 0- (3-98)
Если же упругая линия антисимметрична, то среднее сечение
не получает прогиба. Но тогда каждая половина стержня выпучи¬
вается как самостоятельный стержень, шарнирно опертый по концам; критическая сила будет
Я9 = Ц- (3.99)
Приведем соотношение (98) к безразмерному виду
tg(* уТ)_ я /7(1 — у) = 0. (3.100)
где
‘=4г- <з>1)
Кривая v(c), найденная по (100), изображена на рис. 3.17*). При с = 0, когда средняя опора отсутствует, будет Я = 0,25РЭ. Если соо, то вместо (98) получим уравнение (1.42), соответствующее случаю стержня с одним из концов шарнирно опертым и другим защемленным, при этом Р2Р9. Но «симметричное» решение (100) имеет практическое значение только при Р<Р9, vl, что отве¬
*) Этот график взят из книги [0.21], стр. 96,
§41] СЛУЧАЙ УПРУГОЙ ОПОРЫ. ЗАДАЧА О СТЕРЖНЕВОМ НАБОРЕ 1Й9
чает с — 2. На наклонном участке зависимость может быть приближенно представлена как линейная:
1.3-
VSSST + T с-
(3.102)
Жесткость опоры с, при которой в задаче об устойчивости стержня эту опору можно рассматривать как нес мещающуюся, называют критической. В рассматриваемом случае критическая жесткость опоры равна
4 п2Е1
/3
(3.103)
Вернемся теперь к исходной схеме рис. 3.16, а, где роль упругой опоры выполнял стержень длиной 1Х и жесткостью ElJl. Предполагая, что этот стержень закреплен шарнирно по концам и что точка пересечения лежит посередине длины, найдем его критическую жесткость из соотношения 48£,/, _ 4п2Е/
/V
Г
отсюда
Эту же задачу легко решить с помощью энергетического метода. Примем для случая симметричного прогиба
v = / sin -
I
и выпишем уравнение энергии по (1.121), учитывая потенциальную энергию упругой опоры:
i I
р Г ( dv \2. EI Г ( d2v \2,, с/2.
2 J\dx) 2 J \ dx2) dx + 2 ’
тогда окончательно получим:
о
1,4:Т +
что мало отличается от (102).
Аналогичное исследование может быть проведено для более сложной системы - стержневого набора (рис. 3.18), составленного из сжатых балок главного направления и поддерживающих их
146 волкв сЛбжныё заАачй УсоЙчивостй стёрнёЙ [th. Ш
балок — поперечных связей. Задача об устойчивости такой системы имеет практическое значение для многих конструкций, как, например, перекрытий в корпусе корабля, и была впервые поставлена И. Г. Бубновым [0.2]. Основная цель и здесь состояла в определении критической жесткости поперечных связей. П. Ф. Папкович применил для решения этой задачи энергетический метод [0.7],
Рис. 3.18. Перекрестный стержневой набор.
а А. М. Пеньков — метод конечных разностей [3.6]. А. А. Курдюмов предложил рассматривать часто расположенные поперечные связи как сплошное упругое основание (см. § 42) для балок главного направления *).
Мы считали выше, что взаимодействие между пересекающимися стержнями выражается только в силе, нормальной к образуемой ими плоскости. В некоторых случаях, однако, необходимо учесть, что поперечные связи препятствуют не только нормальным смещениям, но и поворотам соответствующих сечений балок главного направления; в этом случае следует принять во внимание жесткость поперечных связей на кручение; кроме того, приходится учитывать условия закрепления балок одного и другого направления, отличные от шарнирного **).
В случае, если балки перекрестного набора расположены достаточно часто, набор может быть заменен анизотропной пластинкой ***); тогда для расчета набора могут быть использованы уравнения теории устойчивости пластинок, см. ниже главу VII.
*) См. работы А. А. Курдюмова в «Трудах Ленингр. кораблестр. ин-та», № 11 (1953) и в журнале «Судостроение», № 11—12 (1941).
**) Подобные задачи рассматривались с помощью метода конечных разностей Е. С. Войт в работе «Исследование устойчивости перекрестного стержневого набора» (канд. дисс., М., 1951) и Н. А. Венцель (Сб. трудов Ин-та строит, мех. АН УССР, № 15, 1950).
***) Такой метод был предложен Л. Я. Резницким.
§ 4й) устойчивое cffcf>ctoi, сШАййбГб t Vftpytm 6снойамиём 141 § 42. Устойчивость стержня, связанного с упругим основанием
Представим себе, что стержень, шарнирно опертый по концам, связан со сплошным упругим основанием (рис. 3.19). Пусть реакция основания, приходящаяся на единицу длины стержня, будет пропорциональна перемещению:
I R = cv\ (3.105)
д.,ттттттт
размерность коэффициента с Рис. ЗЛ9. Стержень на упругом осно-
будет кг/см2. вании.
Дифференциальное уравнение упругой линии примем в виде (1.7). Подставляя q = — /?, получим:
<3-106>
Если воспользоваться обозначениями
Ж = -ir = r. (3.107)
то вместо (106) будем иметь следующее однородное линейное
уравнение:
+ ™ = (3-1Q8)
Соответствующее характеристическое уравнение имеет вид
p* + k2p2+r = 0; (3.109)
его корни будут
4
Р2 = --± ]/Г• (3.110)
Примем p = im, где /=]/—1; тогда
/П2 = - + %-Г. (3.111)
Решение уравнения (108) получает форму
v = A sin тх -f- В cos тх -- Сх -f- D. (3.112)
Исходя из граничных условий (1.9), получим B = C = D = 0. При А Ф 0 будет
sin т/ = 0; (3.113)
отсюда
т2 = --. я=1, 2, 3,... (3.114)
142
БОЛЁЕ СЛОНЫЁ АДАЧЙ УСТОЙЧИВОСТЙ СТЕРЖНЕЙ
[гл. itt
Определяя к2 па (111) и пользуясь (114), находим:
к2 — — = к — EJ —
+
г/2
/2 _Г П2Т12
Изогнутая линия состоитиз п полуволн синусоиды
.. пп
v — A sin — х*
(3.1 id)
(3.116)
В отличие от свободно прогибающегося стержня здесь число полуволн п Ф 1, оно должно быть определено из условия минимума нагрузки. На рис. 3.20 по оси абсцисс отложены значения г = г (//тс)4,
Рис. 3.20. График для расчета стержня на упругом основании.
а по оси ординат — отношение Я/Р9, где Р9 — эйлерова сила для стержня, не имеющего упругого основания. Принимая п= 1, 2, 3, получим серию прямых; участки этих прямых, показанные жирной линией, являются расчетными. Переход от п-й ветви к(л+1)-й соответствует величине г, определяемой из равенства
п2п2. г/2 (я + I)2 rl2
~12~ + пЧ2'- Т2 Сп + I)2 тс2 ;
отсюда
г = й2и+ i )2-. (3.117)
Соответствующие значения k будут
Л2 = -1д2 + (я-Ь I)2].
(3.118)
§ 42] УСТОЙЧИВОСТЬ СТЕРЖНЯ, связанного с УПРУГИМ ОСНОВАНИЕМ 143
Если число полуволн п достаточно велико, то можно записать условие минимума ft2, приравнивая нулю производную от ft2 по mzjl:
dm
при этом
9 пп
z~r
rl6
= 0;
Критическая нагрузка по (115) оказывается равной
Ркр = 2EI ]/ 7 = 2 УШс.
В безразмерных величинах
кр
= 2 Vr.
(3.119;
(3.120)
Формуле (120) отвечает предельная линия, показанная на рис. 3.20 пунктиром.
Пример 3.4. Дюралюминовый стержень, расположенный в сжатой зоне фюзеляжа самолета (стрингер), должен быть рассчитан на устойчивость (рис. 3.21). Длина стрингера 1 = 2 м\ концы опираются на жесткие опоры; в пролете он поддерживается часто расположенными поперечными связями (нервюрами), лежащими на равных расстояниях одна от другой: s = 20 см. Нервюры можно рассматривать как балки на двух опорах, шарнирно опертые по концам, длиной л = 50 слг. Момент инерции сечения стрингера / = 1 см\ а нервюры — /1=г0,1 см\ площадь сечения стрингера У7 =1,5 см1.
Е = 0,7 • 10е кг!см2, апц = 2200 кг!см2 Определить критическую силу Ркр для стрингера и длину полуволны /кр при потере устойчивости.
Будем рассматривать стрингер как сжатую балку, лежащую на упругом основании. Реактивные силы, передающиеся на стрингер от нервюр, будем считать равномерно распределенными по длине стрингера. Реактивная сила для каждой нервюры равна
Рис. 3.21. К расчету стрингера в сжатой зоне фюзеляжа самолета.
где v — прогиб стрингера. Коэффициент жесткости упругого основания будет
с =
48Е/, 48 - 0,7. 10е. 0,1
503 • 20
1,34
кг/см прогиба СМ длины
144 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. III
Отсюда
//у с //у 1,34• 2004 1П-
Г ~Г[%) “£/(«) “ 0,7 • 10« • 1 • я4 ~ 9’5-
Значение г = 19,5 лежит между величинами г = 1 • 22 и 22 • З2; следовательно, при потере устойчивости стрингера должно образоваться две полуволны длиной /кр = 1 м. Находим по (115) (см. также график рис. 3.20)
Рк р я 7 _ 19,5
Р
где Р9 — эйлерова сила:
= „* + = 4 + = 8,9.
712Е1 712.7. 105 - 1
/2 2002 “ Кг'
Окончательно Якр = 1540 кг\ соответствующее напряжение акр = PKIF = = 1150 кг!см2 не превышает предела пропорциональности апц.
§ 43. Влияние поперечной силы на критическую нагрузку
Мы пользовались до сих пор уравнением изогнутой оси стержня, составленным без учета влияния поперечной силы. Как известно
из теории изгиба балок, влияние это в случае сплошного сечения
пренебрежимо мало. Однако для составных стержней со сравнительно слабой решеткой влияние поперечной силы надо принимать во внимание.
Выясним, насколько изменится величина критической нагрузки, если учесть влияние касательных напряжений на прогибы стержня. Для этого воспользуемся уточненным дифференциальным уравнением упругой линии
d2v М. 1 d2M. /о 1014
dx2 ~ EI т OF dx2 ’ (d.121)
здесь х — численный коэффициент, зависящий от формы поперечного сечения. Для случая стержня с шарнирно опертыми концами будет M = Pv\ уравнение (121) принимает вид
d2v х ~ d2v, Р ~ 1ГЬЛЧ
jV — 0. (3.122)
Решением этого уравнения, отвечающим условию v = 0 при л; = 0, будет
§ 44]
УСТОЙЧИВОСТЬ СОСТАВНЫХ СТЕРЖНЕЙ
145
Условие = 0 при х — 1 дает 1=:/nc//. Принимая п— 1 и определяя Р по (124), находим критическую нагрузку равной
ркр = Т7—£Г <ЗЛ25)
GF /2
или
K2FI 1
= 1 3-. (3.126)
1+2(1 +rtx-.
где [л — коэффициент Пуассона, X — гибкость стержня. Таким образом, желая определить критическую нагрузку с учетом влияния
касательных напряжений, мы должны вместо длины стержня I под¬
ставить в формулу Эйлера приведенную длину /0 = v/; коэффициент приведения равен
V = ]/ 1+2(1+11)*£. (3.127)
Как видим, значение критической силы получается несколько меньшим, чем вычисленное по формуле Эйлера. Формулу (125) можно распространить на упруго-пластическую область, заменив модуль Е на результирующий или касательный модули. Подставляя вместо ja наибольшее возможное значение 0,5 и считая х для прямоугольного сечения равным 1,2, получим:
v = 1Г1+. (3.128)
При X == 100 приведенная длина будет лишь на 0,18% превышать истинную длину стержня. Для коротких стержней значение будет ббльшим; но для них критическое напряжение сравнительно слабо меняется в зависимости от гибкости.
§ 44. Устойчивость составных стержней
В качестве сжатых элементов различных конструкций часто применяются стержни, составленные из двух ветвей, соединенных решеткой или планками *). Рассмотрим подобный стержень с решеткой, состоящей из диагоналей, как показано на рис. 3.22. Расстояние между центрами тяжести сечений ветвей обозначим через h\ длину отсека — через а, длину диагонали — через d. Будем считать, что
*) Принятый здесь путь решения задачи принадлежит (в различных вариантах) Ф. Энгессеру [2.11], С. П. Тимошенко (Изв. Киевск. полит, ин-та, 1908), Л. Прандтлю (Z. VDI, 1907), Ф. Блейху [0.15]. Другое направление, основанное на расчетной модели с непрерывными связями сдвига, развито А. Р. Ржаницыным [3.8]; см. также его книгу [0.10].
146 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. III
величина h значительно превышает высоту сечения отдельной ветви и. что момент инерции всего сечения можно приближенно определять по формуле
I == 1 Fxhl = Fh2, (3.129)
где F{ — площадь сечения ветви, F — полная площадь сечения.
Влияние поперечной силы, вызывающей деформацию стержней
решетки, можно учесть, пользуясь данными предыдущего параграфа.
1р Исходное уравнение (121) выведено в
предположении, что средняя по сечению
стержня деформация сдвига связана
с поперечной силой соотношением
Q
(3.130)
Для составных стержней в формулы § 43 можно подставить вместо х/О/7 отношение т/Q* отвечающее тому или иному типу соединительной решетки. На рис. 3.23 изображено, как меняется конфигурация
Рис. 3.22. Составной стержень с решеткой, состоящей из диагоналей.
Рис. 3.23. Искажение решетки составного стержня.
отсека стержня при деформации диагонали; число отсеков по длине считаем достаточно большим. Усилие в диагонали NA может быть выражено через поперечную силу:
Абсолютное удлинение диагонали будет равно
_ Qd*
* — EF.h '
(3.131)
(3.132)
УСТОЙЧИВОСТЬ COCtAfeHbljC СТЕРЖНЕЙ
14?
через Fa обозначена площадь сечения диагонали; модуль Е для стержней решетки считаем совпадающим с модулем материала ветвей. Смещение 5 узла С и угол сдвига у будут
5 d
Ь:
-Ь т = тг = хд
ah
(3.133)
отсюда
1
d3
Подставляя эту дим:
Р =
1 кр
величину
k2EJ
)
взамен
1
, ah2
*/GF
1 +
1 dz n2EI
в формулу (3.135)
EFa ah2 12
Коэффициент приведения длины определяется здесь
формулой • = <336> где через X обозначена гибкость стержня
Если ввести обозначение к* для приведенной гибкости составного стержня, то получим:
X* = v\ == V X2 Xf;
под понимается величина
d3 ah2
(3.137)
(3.138)
Рис. 3.24. Случай решетки, состоящей из диагоналей и стоек.
В случае, если критическое напряжение в ветвях превышает предел упругости, модуль Е для материала ветви надо заменить на результирующий модуль Т или на касательный ЕК. Величина Т определяется при этом по (2.16). Однако элементы решетки входят в работу лишь при изгибе стержня, поэтому для них деформации надо считать упругими. Формула (138) для Х1 приобретает вид
. ЛГ TF d3 к1 — “У EFa ah2
или
К
ъ\Г Е«
Et
F d3 EF„ ah2
(3.139)
Для упрощения расчета можно в запас прочности принять вместо (139) прежнюю формулу (138).
Если решетка состоит из диагоналей и стоек, как показано на рис. 3.24, то надо принять во внимание также деформацию стоек.
143
ЬОЛЁЁ СЛОЖНЫЙ ЗАДАЛИ УСТОЙЧИВОСТИ СФЕРЖНЕЙ
(ГЛ. ttl
Считая усилие в стойке равным 7VCT = Q, находим угол сдвига:
„ СТ Qh
EFcra
(3.140)
где Хст и FCT — удлинение и площадь сечения стойки. Формула (135) приобретает вид
-тг* HI 1
(3.141)
к2Е1
I2
1
1
1
Eah2
d3
,Fn
h3 \ 7i2El *
-_f —\l Д *CT / /2
Для применяемых на практике конструкций дополнительный член в скобках мал по сравнению с членом, содержащим d3, поэтому р. в расчетах можно пользоваться и здесь
прежней формулой (138).
Для составного стержня рамного типа (рис. 3.25) надо прежде всего принять во внимание деформацию ветвей, вызываемую поперечной силой, планки же в первом приближении будем считать жесткими. Точки, делящие длину каждой панели пополам.
Jj j
T
J!
Д
•и -
1 Сэ
i
jr
•г !
•L-H
4
V
■I*
Рис. 3.25. Стержень рамного типа.
Рис. 3.26. Искажение панели стержня рамного типа.
будут, очевидно, точками перегиба упругой линии при местном изгибе ветви (рис. 3.26). Поэтому мы можем приложить в этих точках поперечные силы QJ2 и определить прогиб ветви в пределах полуотсека: (3.142)
3EI,
где /{— момент инерции сечения ветви. Соответствующий «средний» угол поворота будет
> = *=»;• <3-Н3>
44)
Устойчивость COCtAfstibljC СТЁРЖНЕЙ
149
Подставляя отношение f/Q вместо х/О/7 в формулу (125), получим:
%2Е1 1
(3.144)
Р =
1 кр
I2
1
а2 п2Е/
24 £/, I2
Формулу (144) можно уточнить, приняв во внимание деформацию планок. Средняя точка планки также является точкой перегиба; в ней следует приложить поперечную силу для планки <?ПЛ, равную Qnjl == Qa/h. Прогиб одной из частей планки как балки длиной Л/2 будет равен
8 = т(т )'ткг- (3145)
где /ПЛ — момент инерции планки. Если планки лежат в двух плоскостях, как на рис. 3.27, то под /ПЛ надо понимать суммарный момент инерции двух планок. Угол поворота планки и скрепленного с ней участка ветви будет
25 Qah
Ti = ~h~
12 £/„
Рис. 3.27. Сечение составного стержня с (3 146) решеткой в двух плоv * ' скостях.
Кроме того, следует учесть деформацию сдвига планки. Если планка выполнена в виде пластинки, то угол сдвига равен
Т2:
Qa
1
h GFn
(3.147)
где Fnjl — площадь сечения планки (или двух планок, лежащих в разных плоскостях). Вводя отношение (71 + T2VQ в формулу (144), найдем:
%гш 1 W <ЗЛ48>
р —.
1 кр
ah
ШГп
GhF,
I2
Для обычных конструкций дополнительными членами, отвечающими деформации планок, можно пренебречь. Пользуясь формулой (144), снова найдем приведенную гибкость:
х2
, Fa2 24/,
(3.149)
Но полная площадь сечения составляет F = 2F1; отношение I<JFl дает квадрат радиуса инерции сечения ветви; поэтому во второй член в (149) можно ввести гибкость ветви /п в пределах отсека'.
Ь -1Г™ —У 2/, '
(3.150)
156
ВОЛЁЁ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ
(гл. lit
Считая приближенно тс2» 12, придем к прежней формуле (137):
X* = VV-f-X? (3.151)
с тем отличием, что под \ понимается теперь реальная гибкость ветви. В упруго-пластической области можно и здесь в запас устойчивости пользоваться формулой (151).
Пример 3.5. Катастрофа крупного сооружения (газохранилища) произошла в результате потери устойчивости сжатого раскоса, сконструированного из двух ветвей швеллерного сечения,
Jp соединенных планками (рис. 3.28). Общая длина
стержня 3600 мм. Расстояние между осями планок ' h-Ш-Н а — 00 мм. Сечение стержня составлено из швел■ • ■ леров № 16 Ь, расстояние в свету между которыми «
равно d = 28 мм. Планки изготовлены из полосы толщиной t = 7 мм; ширина их b = 140 мм. Для материала швеллеров и планок Е = 2,03 • 106 кг/см,
1 оо —j апц = 2700 кг/см2. Найти критическую силу: а) не
т учитывая влияния поперечной силы, б) с учетом
поперечной силы.
Моменты инерции швеллера:
/„ = 934,5 смА>
Х\
/Ух = 83,4 см4,
Рис. 3.28. Сжатый раскос в конструкции газохранилища.
расстояние от кромки до центра тяжести г0 = 1,75 см, площадь сечения Fx = 25,15 см2, h = d + 2г0 = 6,3 см. Определяем моменты инерции всего сечения:
Iх = 1869 см4,
/У = 2/у,+(М + 0 )21 =
= 2 [83,4 + 25,15 • 3.152] = 670 см*.
Сравнение /х и 1у показывает, что продольный изгиб произойдет в плоскости решетки. Радиус инерции
= 3,64 см.
Гибкость стержня в целом А. = -j- = = 99. Для отдельной ветви радиус
инерции Гибкость в пределах отсека равна
25,15 120
1,82
= 66.
Опасной является, таким образом, общая потеря устойчивости стержня. Эйлерово напряжение
тi*E 9,87. 2,03 • 106
оэг- X*
992
= 2020 кг (см2 у
и, следовательно, < эпц.
§ 45] УСТОЙЧИВОСТЬ СТЕРЖНЕЙ, ВОСПРИНИМАЮЩИХ КРУТЯЩИЙ МОМЕНТ 151
Критическая сила, вычисленная для стержня сплошного сечения, равна Р°кр = o9F = 2020 • 50,3 = 101 600 кг. (а)
С учетом влияния поперечной силы по формуле (148) будет
Якр = якр ч ( { аг j ; а • (Ь)
\24£/, + 12£/пл + QhFax ) ~Р~
Учитывая, что планки стоят в двух плоскостях, находим:
/пл = 2 0,712143 = 320 см*, Fh = 2 • 0,7 • 14 = 19,6 см2.
По формуле (Ь), принимая Q]E = 0,4, получим:
р 101 «ПО ! /■кр - iviwu 9,87 670 /120\2 9,87 670 120 - 6,3 9,87 670-120 “
+ 24 83,4 \360/ + 12 320 360* + 0,4 19,6 - 6,3 • 360»
= 101600 j 0 368 + 0 010 0,122 “ Jjg—=67600кг. (с)
Ослабление стержня из-за деформации решетки составляет 34%. Величина эта не является вполне точной, так как формула (148) для критической
силы составлена в предположении, что число панелей сравнительно велико. Ясно, однако, что стержень сконструирован неудачно.
Рассмотрение выражения (с) позволяет оценить удельный вес отдельных членов в знаменателе. Как видим, основную роль играет член, учитывающий деформацию ветвей, но все же влияние деформации сдвига планки относительно велико.
Найдем приведенную гибкость ослабленного стержня:
,/ 2,03 • 106 • 50,3 101
1вяжУ —67 600 =m-
Воспользуемся приближенной формулой (151), тогда получим: к* = + = /992 + 662 = 119,
что почти совпадает с прежним результатом. Если вместо двух промежуточных планок поставить пять, т. е. уменьшить вдвое длину отсека, то получим Ркр«92000 кг; ослабление стержня составит всего 9%.
§ 45. Устойчивость стержней, воспринимающих крутящий момент. Совместное действие осевого сжатия и кручения
Длинный стержень, подверженный действию скручивающих пар, может потерять устойчивость; ось стержня образует при этом пространственную кривую. Допустим, что концы стержня закреплены шарнирно и что пары, моменты которых равны Мк, приложены по концам стержня (рис. 3.29), причем векторы-моменты пар сохраняют свое направление вдоль начальной оси стержня»
162
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. III
Моменты инерции сечения стержня относительно всех центральных осей пусть будут одинаковы и равны /.
Рассматриваемая система является неконсервативной, так как в разных вариантах перехода стержня из начального положения в изогнутое, включающих поворот концевых сечений вокруг оси х, пары могут произвести различную работу. Следовательно, данная задача требует динамического подхода, см. [21.23]. Однако статический метод приводит здесь, в виде исключения, к правильным результатам, и мы им воспользуемся.
Выберем основную и «местную» системы координат, как показано на рис. 3.29. Обознаим через v и w перемещения вдоль у и z некоторой точки, принадлежащей осевой линии, стержня. Определяя проекции вектора-момента на оси ух и zv приходим к следующим дифференциальным уравнениям:
d2v dw
El
dx2
к dx dv
(3.152)
dx2 —лгл* dx Пользуясь обозначением
Ml
K~ El ’
перепишем систему уравнений (152) в виде d2 v
(3.153)
Рис. 3.29. Выпучивание стержня при кручении.
dx2 d2w ~dxJ
1 dx
-k = 0. dx
(3.154)
Этим уравнениям удовлетворяют следующие выражения для v и w: v = A sin kx Б cos kx -f- С, w = — A cos kx + Б sin kx + D. j Воспользуемся граничными условиями:
t/ = 0 при л; = 0, х = I, w = 0 при х = 0, х = 1. )
Условия, относящиеся к точке х = 0, дают:
С = — Б, D = A.
Другие условия приводят к уравнениям:
A sin kl — Б (1 — cos kl) — 0, \
Л( 1—cos kl) -f- Б sin kl = 0. j
(3.155)
(3.156)
(3.157)
(3.158)
§ 45] УСТОЙЧИВОСТЬ СТЕРЖНЕЙ, ВОСПРИНИМАЮЩИХ КРУТЯЩИЙ МОМЕНТ 153
Считая А Ф 0 и В Ф 0, приравниваем нулю определитель этой системы; получим:
sin2 kl + (1 — cos kl)2 — О,
откуда
cos/г/ = 1. (3.159)
Наименьшее значение kl> удовлетворяющее этому уравнению и не равное нулю, будет
k = ~. (3.160)
Следовательно, критическое значение крутящего момента равно
(3.161)
к, кр = -J- ■
Допустим теперь, что стержень подвергается совместному действию осевого сжатия силой Р и кручения (рис. 3.30). Уравнения (152) получат тогда вид
г> г d2v dw п
El = —Мк Pv%
dx2 к dx
Е!- — м --Pw
dx* ~~ K dx
Полагая
MK
El
= k,
El
(3.162)
(3.163)
r
лриходим к системе уравнений
dx2
d2w
Их2
dx
(3.164)
Решение этих уравнений будем искать в виде
(3.165)
v = A sin rxx -f- В cos гхх -f-
-- С sin r2x -f- D cos г2х, w = — A cos rxx -f-- В sin гхх — С cos r2x -f- D sin г2х.
Подставляя эти выражения в (164), находим, что величины гг и г2 должны удовлетворять одному и тому же квадратному уравнению
г2 -f- kr — s2 — 0. (3.166)
Рис. 3.30. Одновременное действие осевой силы и скручивающих пар.
154 БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
Считая гхФг2, находим:
г\= ~ ~2 » 2==z~ уТ}/4 + s2 • (3.167)
Принимая во внимание граничные условия (156) для л; = 0, будем иметь:
B-\-D = 0, А —— С = 0. (3.168)
Другие два условия приводят к уравнениям:
A (sin rxl — sin r2l) -- В (cos rxl — cos r2l) = 0, \
— A (cos rxl — cos r2l) + (s*n r\l — s*n = 0. J Приравнивая нулю определитель этой системы, получим:
(sin rxi — sin г2/)2 -J- (cos rxl — cos r2/)2 = 0,
или
cos(r1 — r2)/= 1. (3.170)
Наименьшая величина аргумента, не равная нулю, будет
('l — г2)1 = 2к. (3.171)
Но по (167) находим: fi-/а = 2 ]/-£• + «* ; (3.172)
следовательно,
<тр2 h2
~jr — Н“ (3.173)
Критические значения крутящего момента и сжимающей силы удовлетворяют уравнению:
<374>
В частных случаях простого кручения и сжатия получаем прежние формулы (161) и (1.16). Соотношение (174) может быть применено также при одновременном действии кручения и осевого растяжения; в этом случае перед Р следует поставить знак минус.
§ 46. Устойчивость кругового кольца и арки
Большое практическое значение имеет задача об устойчивости замкнутого кругового кольца, находящегося под действием радиальной нагрузки, равномерно распределенной вдоль окружности (рис. 3.31). Такие кольца (шпангоуты) служат обычно для восприятия радиальных сил, передающихся на скрепленную с ними цилиндрическую оболочку, или в качестве ребер, подкрепляющих оболочку.
46]
УСТОЙЧИВОСТЬ КРУГОВОГО КОЛЬЦА и АРКИ
155
Обозначим через q силу, приходящуюся на единицу длины ок* ружности, через М> Q и N — изгибающий момент, поперечную и осевую силы в сечении кольца, сила N считается положительной при сжатии. Составим уравнения равновесия элемента длиной dy
Q
Рис. 3.31. Кольцо под действием радиальной нагрузки.
Рис. 3.32. К выводу уравнений равновесия элемента кольца.
(рис. 3.32), определяя проекции сил на направления касательной и нормали, а также моменты относительно центра:
dN 1 Q. л —57 + р+?у — 0>
R
dQ N
+ —Ч*
:0,
ам
dy
(3.175)
(3.176)
(3.177)
координата у отсчитывается вдоль дуги, z - к центру; через R обозначен радиус окружности, проходящей через центр тяжести сечения, через qy и qz — проекции внешней нагрузки на соответствующие направления. Принимается, что нагрузка q всегда направлена вдоль нормали. Сопоставляя уравнения (175)—(177), получим:
Q = 7T’ (3.178)
dy
d3M
dy3
■f
1 dM, qy dqz R2 dy ' R dy ~u-
(3.179)
До момента выпучивания кольца осевая сила равна
NQ = qR. (3.180)
Изменение кривизны выражается через прогиб w следующим образом:
d2w w
+ (ЗЛ8!)
56
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ СТЕРЖНЕЙ [ГЛ. Ill
Первый член в этом выражении тот же. что и в случае прямой балки, второй находится по рис. 3.33 с учетом изменения радиуса кривизны:
' ' ' ' “ (3.182)
1
1
1
Я — v
1
7Г
W
Л»'
Момент М равен
М
(3.183)
Подставляя это выражение в (179), получим следующее дифференциальное уравнение для w:
' dbw * 2 d3w. 1 dw \ Qy dqz
~dy* ~dy* ' ~R* ~dy ) ~R dy~ *
Eli
(3.184)
В задачах устойчивости надо учесть радиальную составляющую усилий N, возникающую при выпучивании кольца:
Л/ / d2w w \
q, = N{
0 \ dy2
= »«(£+£)• <3'> Считая <7у = 0, находим окончательное дифференциальное уравнение:
dbw
2 d3w, 1 dw,
~dfr~W~df~'W4y'
• qR / dzw EI \ dy3
Рис. 3.33. К определению кривизны изогнутой линии.
Примем для w выражение = / sin
(3.187)
где п — число полных волн, образующихся по окружности. При п— 1 получим перемещение кольца как твердого тела. Исключая этот случай, примем 2. Подставляя выражение (187) в (186) и считая /=£0, приходим к следующей зависимости:
<7 = (я2 — 1)
(3.188)
Минимальная критическая нагрузка qK, соответствует двум волнам по окружности (п = 2) и равна
?кр=- (3.189)
Мы получили известную формулу для критическо1 о давления, часто применяемую в практических расчетах.
46]
УСТОЙЧИВОСТЬ КРУГОВОГО КОЛЬЦА И АРКИ
157
Перейдем к случаю круговой арки (рис. 3.34), охватывающей центральный угол 2<х и шарнирно закрепленной по концам. Примем выражение для прогиба в виде
w = / sln-2-, (3.190)
где / = 2Ra — длина средней линии. Подставим (190) в уравнение (186), тогда получим:
gR _ иУ 1
El ~ I2 R2 * (0.1У1)
Число полуволн т определим из того условия, что полная длина осевой линии остается неизменной. Деформация средней линии равна = <ЗЛ92>
где v — перемещение вдоль дуги. Второй член в этом выражении учитывает укорочение дуги по рис. 3.33. Полагая еу = 0, найдем:
£==■£• (ЗЛЭЗ>
Оба конца арки останутся неподвиж¬
ными при условии
Рис. 3.34. Круговая арка под. л /о 1л>1ч действием поперечной на-
wdy = 0. (3.194) грузки
о
Наименьшее число т, при котором выполняется равенство (194), будет т = 2. Критическая нагрузка оказывается равной
= ■%-(£-- !)• (3.195)
Отсюда можно получить формулу (189) для кольца, если положить t = ir/2, этот угол соответствует дуге, расположенной между точками 1ерегиба упругой линии кольца.
Как мы видели, шарнирно закрепленная арка с нерастяжимой эсью выпучивается по двум полуволнам. Однако для пологой арки ложет оказаться, что выпучивание произойдет при меньшей нагрузке, !сли считать среднюю линию деформируемой. Этот случай будет )азобран в дальнейшем.
Здесь были освещены лишь простейшие задачи устойчивости солец (шпангоутов) и арок. Более подробно эта область представлена в книгах А. Н. Динника [3.1, 1946], С. П. Тимошенко [0.23], 1. Ф. Папковича [0.7], А. Ф. Смирнова [0.11], А. Пфлюгера [0.21].
j
ГЛАВА IV
ТОНКОСТЕННЫЕ СТЕРЖНИ. УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА
§ 47. Основные уравнения
Обратимся к задаче об устойчивости стержней, состоящих из тонких стенок и образующих незамкнутый (открытый) профиль. Такими профилями являются стержни уголкового, корытного, крестового,
г п
о)
е)
нь
Рис. 4.1 Виды сечений тонкостенных стержней.
таврового (рис. 4.1), двутаврового, зетового сечений (рис. 4.2).
Стержень корытного сечения представляет собой пример простого
профиля, а стержень двутаврового сечения - пример разветвленного профиля. Стержни уголкового, крестового сечений образуют профиль в виде пучка. Особенность таких стержней по сравнению со стержнями замкнутого профиля (например, трубчатого) или сплошного сечения состоит в их относительно слабой сопротивляемости кручению. Поэтому мы должны будем изучить не только изгибную форму потери устойчивости сжатых стержней, но и такую форму, которая сопровождается скручиванием профиля или совместными деформациями изгиба и кручения.
а) б)
Рис. 4.2. Дюралюминовые профили, получаемые прессованием или штамповкой
Основные уравнений
159
Напомним некоторые определения и зависимости, относящиеся к общей теории тонкостенных стержней открытого профиля *). При скручивании таких стержней — если только они не образуют профиля в виде пучка — поперечные сечения искривляются: различные точки сечения получают разные перемещения вдоль оси стержня. Это продольное смещение называют искажением или депланацией. Если депланация сечений стержня не осуществляется свободно, то при кручении образуются нормальные напряжения, направленные вдоль оси. Нормальным напряжениям стесненного кручения сопутствуют касательные напряжения, распределяющиеся равномерно по толщине стенки (рис. 4.3) и накладывающиеся на касательные напряжения
Рис. 4.3. Касательные напряжения, и) стесненного кручения, б) свободного кручения.
свободного кручения. Как известно, эпюра касательных напряжений свободного кручения вдоль толщины стенки состоит из двух треугольников; средняя линия профиля оказывается свободной от напряжений в точках, достаточно удаленных от края профиля (рис. 4.3). Касательные усилия стесненного кручения образуют пару; момент
этой пары обозначим через М. Касательные усилия свободного кру¬
чения дают и свою очередь пару с моментом М. Суммируя их, получим полный крутящий момент Мк:
М-+М = МК. (4.1)
Депланация любой точки поперечного сечения и может быть выражена через единичный угол закручивания стержня а и так называемую секториальную площадь о>:
и = — ol(x)u>(s). (4.2)
Величина а является функцией координаты х% откладываемой вдоль оси стержня; сечение стержня считается в своей плоскости вполне жестким, неизменяемым. Под секториальной площадью со понимается удвоенная площадь, образуемая при перемещении радиуса-вектора»
*) Эта теория изложена в книгах В. 3. Власова [4.4] (см. там же библиографию) и А. А. У майского [4.12], см. также книгу Г. Ю. Джанелидзе и Я. Г. Пановко «Статика упругих тонкостенных стержней», Гостехиздат, 1948.
160
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. I
причем начало радиуса совпадает с некоторым полюсом /С, а конец скользит вдоль средней линии профиля (рис. 4.4); очевидно, величина а) будет функцией координаты s, отсчитываемой по средней линии. Знак минус в формуле (2) отвечает вращению радиуса-вектора против часовой стрелки. Мы считаем, что депланация и меняется, вообще говоря, вдоль оси стержня; частная производная от и по л:
даст деформацию удлинения соответствующего волокна. Нормальные напряжения стесненного кручения равны
г? ди „da
а — £ -з— = — п -т— аз.
дх
dx
Рис. 4.4. Секториальная площадь.
Единичный угол закручивания очередь равен производной от угла закручивания 0 по а = dbfdx. Следовательно, d2b
(4.3)
В свою полного длине, т. е.
dx2
(4.4)
Соответствующие касательные напряжения находятся по уравнению равновесия
=0
дх ds
откуда
_ Г да J дх
о
ds-
d3Q dx3
/
О) ds.
(4.5)
Введем обозначение для потока касательных усилий q = т/, где t — толщина стенки (рис. 4.4). Величина t в общем случае является переменной вдоль средней линии: t = t(s). По (5) находим:
S S
d4
q=E
dx3
f шtds = E-- f udF,
(4.6)
0
где под dF — t ds подразумевается площадь элемента стенки длиной ds. Введем обозначение
S
(о dF (4.7)
s. = /,
и назовем эту величину, измеряемую в см4, секториальным статическим моментом части площади профиля; тогда получим:
d3 0
ОСНОВНЫЁ УРАВНЁНЙЙ
161
Момент М% образуемый касательными усилиями стесненного кручения, будем определять относительно оси, проходящей через полюс К. Из рис. 4.5 видно, что момент элементарного усилия q ds относительно полюса равен qp ds или q Jo), где dm = р ds — приращение секториальной площади. Полный момент будет равен
М
а
= f q dm = Е f dm f со dF; (4.9)
интеграл распространяется на всю площадь сечения F. Интегрируя по частям, имеем:
М=Е-ш f <adF — J <JdF. (4.10)
Начальное положение радиуса-вектора при определении секториальной площади будем ниже выбирать из условия, что полный секториальный статический момент площади сечения равен нулю:
Sm.P= f *dF = 0. (4.11)
F
Секториальным моментом инерции профиля называют величину
/-=в J* (4.12)
она измеряется в см6. Вместо (10) теперь получим:
- EI -. (4.13) Рис. 4.5. К определению момен-
40 dx3 * та касательного усилия.
Что касается момента, образуемого касательными усилиями свободного кручения, то он равен
Ж = 0/ка = 0/к--, (4.14)
здесь 01к — крутильная жесткость профиля, /к — момент инерции сечения при кручении. Для профиля, состоящего из п прямоугольников, величина /к равна
п
'«<4Л5> lm 1
162
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
где st — длина и tt — толщина /-й стенки; — коэффициент, зависящий от формы сечения; /к измеряется в смА.
Общий крутящий момент должен по (1) складываться из (13) и (14):
d4. db.... 1СЧ
dx3 к —Мк. (4.16)
Мы получили дифференциальное уравнение стесненного кручения для стержня открытого профиля.
Момент касательных усилий стесненного кручения М изменяется по длине стержня. Введем новую функцию В(х), первая производная от которой равна М:
<4-17)
Величина В, измеряемая в кг • см2, носит название изгибно-крутиль-
ного бимомента или просто бимомента. Сравнивая (4) и (13),
находим:
Л—(4.18)
Сопоставляя теперь (17) и (18), будем иметь:
<s = -\ (4.19)
1 О)
предполагается, что при о==0 должно быть В = 0. Таким образом, нормальные напряжения стесненного кручения пропорциональны бимоменту; формула (19) построена аналогично известной формуле для нормальных напряжений при изгибе о = My/Iz, где у — расстояние точки сечения от нейтральной оси z.
Пользуясь (13) и считая В = 0 при d4/dx2 = 0, находим:
в=-е,-5- <42°)
Дифференцируя левую и правую части уравнения (16) по х> будем иметь:
+ = = (4.21)
под тк здесь подразумевается интенсивность внешней крутящей нагрузки; считаем эту величину положительной, если крутящий мо¬
мент Мк уменьшается при возрастании х. Исходя из (20), введем в уравнение (21) бимомент В\ тогда получим:
d2B GIK о ОГ)ч
~dxT ~ЁГ к* (422)
Мы пришли к дифференциальному уравнению второго порядка для бимомента.
§ 48] СТЕРЖЕНЬ С СЕЧЕНИЕМ, ИМЕЮЩИМ ДВЕ ОСИ СИММЕТРИИ 163
§ 48. Центрально сжатый стержень с сечением, имеющим две оси симметрии
LJU
m
Рис. 4.6. Двутавровое сечение.
Рассмотрим сначала случай, когда поперечное сечение стержня имеет две оси симметрии. Примером такого стержня может служить двутавровый профиль (рис. 4.6). Допустим, что стержень длины / подвергается действию осевой силы Я, приложенной в центре тяжести сечения.
Предположим, что при критической нагрузке становится возможной, наряду с первоначальной формой равновесия стержня, другая, искривленная форма, причем искривление получают все продольные волокна стержня, кроме центрального. Иными словами, будем иметь в виду чисто крутильную
форму потери устойчивости стержня, без изгиба центрального волокна.
Угол поворота произвольного сечения 0 будем считать положительным при вращении против часовой стрелки, если смотреть от верхнего конца стержня (против направления оси х). В качестве исходного дифференциального уравнения примем уравнение (22). Распределенная по длине крутящая нагрузка возникает в результате действия основных сжимающих напряжений a=,P/F, где F—площадь сечения. Выделим некоторое волокно стержня, параллельное до деформации оси х\ в поперечном сечении пусть этому волокну отвечает элемент площади dF. После закручивания стержня волокно примет вид кривой линии, расположенной на круговом цилиндре радиуса р (рис. 4.7).
Обозначим через ф малый угол между касательной, проведенной к искривленному волокну в точке на расстоянии х от нижнего конца, и вертикалью. Этот угол будет, вообще говоря, переменным по длине стержня.
Передаваемое волокном нормальное
усилие odF окажется после искривления волокна наклоненным к вертикали под тем же углом ф. Горизонтальная проекция усилия будет равна оф dF. Момент, создаваемый усилием о dF относительно оси лг, будет равен произведению усилия на плечо р, или atypdF. Весь крутящий момент, передаваемый сжимающими усилиями в некотором
Рис. 4.7. К вычислению момента сжимающего усилия.
164
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
сечении стержня, будет равен интегралу
J офр dF,
F
распространенному на всю площадь сечения. Если теперь взять соседнее сечение, удаленное от первого на расстояние dx, то угол ф получит приращение dty% а крутящий момент возрастет на величину
Интенсивность крутящей нагрузки тк определим, разделив эту величину на dx:
Знак минус здесь взят потому, что момент вращает относительно оси х по часовой стрелке, в то время как углы б и ф мы считаем положительными при вращении против часовой стрелки.
Заметим, что между приращениями углов ф и б имеется зависимость
Подставляя эти величины под знак интеграла в (23), получим:
под 1р здесь понимается полярный момент инерции относительно центра:
Но вторая производная от б по х связана зависимостью (20) с бимоментом В. Так как положительными мы теперь считаем сжимающие напряжения, то по (19) надо в (20) изменить перед В знак на обратный и положить
F
(4.23)
F
рб = <)dx;
отсюда
(4.24)
(4.24а)
F
ИЛИ
(4.25)
(4.26)
F
§ 48] СТЕРЖЕНЬ С СЕЧЕНИЕМ, ИМЕЮЩИМ ДВЕ ОСИ СИММЕТРИИ 165
Окончательно для интенсивности тк получаем выражение
шк = --5. (4.28)
Подставляя это значение тк в уравнение (22), получаем: d2B / a/., G/K \
-Ш+(т£-ш:)В = 0- (4-29)
Примем, что концевые сечения стержня свободны от нормальных напряжений стесненного кручения, т. е. что депланация этих сечений осуществляется свободно. Исходя из (19), мы можем формулировать граничные условия задачи следующим образом:
В = 0 при лг = 0, х — I, (4.30)
Полагая
а/0 GIK
Ж»~Ж>=к' (4-31)
получим решение уравнения (29) в виде
В = Сг sin kx + С2 cos kx. (4.32)
Из граничных условий находим С2 = 0. При СХФ 0 будет
kl = nn, /i=l, 2, 3,... (4.33)
Принимая п== 1, определяем по (31) наименьшее критическое значение напряжения о0:
0 — “72/ ' 7—• (4*4)
1 1р 7р
Эта формула справедлива, очевидно, лишь в пределах упругости. Если сечение состоит из относительно тонких стенок, то вторым членом в (34), учитывающим напряжения свободного кручения, можно пренебречь по сравнению с первым, отвечающим напряжениям стесненного кручения. Тогда получим формулу
п2Е/
<4-35>
по структуре аналогичную формуле Эйлера.
Для тех случаев, когда граничные условия (30) не выполняются, удобнее пользоваться дифференциальным уравнением в форме (21). Подставляя (25) в (21) и меняя знак перед о на обратный, получим:
к> 5=о- <4-36>
166
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
Пусть, например, задано, что торцевые сечения не поворачивакися и остаются плоскими. Исходя из (2), получаем граничные условия:
0 = 0 при х = 0, х = I, М Л Л I \ (4-37)
-£- = 0 при х = 0, х — I. I
По аналогии с задачей об устойчивости стержня сплошного сечения
с защемленными концами (§ 3) находим:
а MU I 0/к «04
e*-W'7+'r’ (4,38)
где коэффициент приведения длины v равен 0,5. При одном полностью защемленном конце, а другом свободном получим в (38) v = 2; при одном полностью защемленном конце, а другом, закрепленном только в отношении поворота, v = 0,7.
Величину <з9 следует сопоставить с критическими напряжениями, определяемыми по формуле Эйлера для изгибной потери устойчивости в плоскостях, содержащих главные оси инерции сечения z и у:
к2Е1у п2 EIZ
l2F ’ i2F * (4.39)
Расчет стержня надо вести по тому из значений критического напряжения ов, ау или az, которое окажется наименьшим.
Для прокатных двутавровых балок величина о9, как правило, оказывается более высокой, чем ау или ог, так что проверка крутильной устойчивости оказывается излишней. В то же время для стержней крестового сечения, когда / = 0, значение о0 может быть меньшим, чем ах и су
§ 49. Случай сечения с одной осью симметрии
Допустим, что поперечное сечение тонкостенного стержня имеет
только одну ось симметрии, например ось у (рис. 4.8). Здесь поло¬
жение оси, относительно которой поворачиваются сечения при потере устойчивости, заранее определить нельзя, можно лишь сказать, что центр вращения (К) должен лежать на оси симметрии.
Дифференциальное уравнение стесненного кручения запишем в виде
d2B G/K D —
— =?L В — — тк. (4.40)
dx2 Е/„ к v '
В отличие от (22) здесь над обозначениями и тк поставлены черточки; этим указано, что секториальный момент инерции и крутящий момент тк (а в последующем и полярный момент инерции 1р) вычисляются относительно оси вращения. Обозначения /* и 1р без
СЛУЧАЙ СЕЧЕНИЯ С ОДНОЙ ОСЬЮ СИММЕТРИЙ
167
черточек будут ниже применяться только для моментов инерции, отнесенных к центру тяжести сечения.
Составляя выражение для тк подобно тому, как было сделано в § 48, мы получим уравнение
d2B
1 / т
dx2
ЕГ
(°1р — G/K)2J = 0.
(4.41)
Примем, что торцевые сечения стержня свободно депланируют. Тогда интегрирование уравнения (41) приведет к выражению типа (34):
- — (4.42)
■'кр '
ЛР ЛР
Поставим себе целью найти координату центра вращения yk, исходя из выражения (42); начало координат выберем в центре тяжести. Примем, что из всех возможных положений центра вращения на оси симметрии у должно осуществиться такое его положение, при котором критическое напряжение будет наименьшим. Секториальная площадь о>л, вычисленная при полюсе в некоторой точке /С, выражается через секториальную площадь со, взятую при полюсе в центре тяжести, следующим образом [с учетом (11)]:
= “> — Уп2- (4.43)
д-
J
Рис. 4.8. Сечение с одной осью симметрии.
Подставим (43) в формулу сечения:
для секториального момента инерции
L= f <°l dF;
(4.44)
тогда получим:
/ш = j utdF — 2yft f tozdF + ylf z2dF. (4.45)
F F F
Первый интеграл равен секториальному моменту инерции /<„, вычисленному относительно центра тяжести. Для второго интеграла введем обозначение
Ry= j (oz dF; (4*46)
F
его можно назвать секториальным центробежным моментом инерции. Наконец, последний интеграл представляет собой момент инерции
сечения 1у. Вместо (45) находим:
'. = '.-2 + (4-47)
168 ТОНКОСТЕННЫЕ СТЕРЖНИ [гЛ. IV
Полярный момент инерции относительно точки К равен сумме осевых моментов инерции:
/, = /7+77: (4-48)
ось у совпадает с у, а ось z проходит через точку К. Имеем:
'у='у (4-49)
следовательно,
V=/у ■+ lz + y\F = !Р + y\F. (4.50)
Напоминаем, что оси у и z являются главными центральными осями.
Таким образом, критическое напряжение (42) оказывается равным
JT- (А. — Ьк Ry + y\iy) Л GIK
оКО= п. (4.51)
Р
Введем следующие обозначения:
* п2Е1ш G/K n2EIv
*“-7ЧГ + -?Г °v = -7W- <4-52>
Они уже встречались в предыдущем параграфе. Величину он можно истолковать как критическое напряжение при крутильной потере устойчивости вокруг центра тяжести сечения по (34); величину <зу— как критическое напряжение при изгибной потере устойчивости в плоскости zx. Кроме того, обозначим:
n2ERv ГТ
ру — /2ущ’ 71 — Ук \/ Тр' 4'53
Первая из этих величин, пропорциональная /?у, имеет размерность напряжения. Вторая является безразмерным параметром для координаты центра вращения yk.
Выражение (51) можно теперь переписать следующим образом:
(4 54
Желая найти минимум окр, приравняем нулю производную от (54) по т):
4(-2Ру + 23у,)(1-) — 2т}(ов —2py7)-l-<jy7j2) = 0. (4.55) Принимая во внимание (54), находим:
рУ /И KR4
§ 49]
СЛУЧАЙ СЕЧЕНИЯ С ОДНОЙ ОСЬЮ СИММЕТРИИ
169
Возвращаясь к (54), получаем квадратное уравнение относи¬
тельно о.
или
кр-
(«кр-кр--Р0
°кр - °кр («О + °у) + ( V» - Ру) = О-
Из двух корней этого уравнения выберем наименьший: ае + ау
(4.57)
(4.57а)
кр ■
2
у <4-58>
Корни уравнения (57) можно найти с помощью графического построения, аналогичного кругу напряжений в п лоской задаче (рис. 4.9) Откладываем по оси абсцисс отрезки АВ = <зу и АС = <з6, по вертикали СС' = ру (вверх) и ВВ' = ру (вниз). Отрезок AF отвечает в том же масштабе величине (58). Из рассмотрения рис. 4.9 заключаем, что критическое напряжение о
кр
для профиля с одной осью симметрии будет меньше величин сь и су.
Наряду с изгибно-крутильной формой потери устойчивости для профиля с одной
осью симметрии возможна и чисто изгибная потеря устойчивости в плоскости ху. Соответствующее критическое напряжение ог определяется по (39):
(4.59)
Рис. 4.9. Построение для определения параметров критических напряжений.
*2Е1Х
l2F
Расчетное критическое напряжение определяется как наименьшее из величин (58) и (59).
С помощью формул (53) и (56) мы можем теперь определить координату центра вращения:
У*
Ру
' акр
(4.60)
Как видим, центр вращения не лежит в центре тяжести сечения Вместе с тем он не совпадает с другой характерной точкой—центром изгиба сечения D (рис. 4.8). Это можно показать следующим
170
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
образом. Координата центра изгиба в случае тонкостенного стержня равна
Ry
Уо = п~-
У
По (53) находим:
Ру = «уУо Vг= VJo>
где г1о = УоУ т~'
’ ‘р
Формула (60) принимает вид
Ур°у
Ук
(4.61)
(4.62)
(4.63)
(4.64)
uKp
Отсюда заключаем, что в общем случае yk Ф yD. Вместо (64) можно также записать
Vy
укр
(4.65)
Пример 4.1. Определить критическую нагрузку для дюралевого стержня длиной / = 1 м, подвергающегося сжатию центральной силой Я. Сечение стержня имеет вид швеллера с отогнутыми полками. Толщина стенки и полок профиля равна 1 мм; остальные размеры (в мм) указаны на рис. 4.10,а.
22,b
Рис. 4.10. К определению геометрических характеристик сечения.
Допустим, что торцевые сечения стержня свободно депланируют. Примем Е = 7 • 103 кг/мм2, G = 2,8 • 103 кг/мм2, апц = 20 кг)мм2.
Определим положение центра тяжести О. Расстояние от точки О до средней линии отогнутых частей полок равно
19 • 19 + 2 • 19 • 9,5
е —
3-19 + 2-13
: 8,7 ММ,
§ 49] СЛУЧАЙ СЕЧЕНИЙ С ОДНОЙ ОСЬЮ СИММЕТРИЙ 1?1
Проведем через центр тяжести главные оси у, z, из которых первая совпадает с осью симметрии сечения. Вычислим главные центральные моменты инерции, считая площадь сечения сосредоточенной на средней линии профиля (пунктирная линия на рис. 4.10):
/у = 1 +219-9,52 + 2-- + 13• 162) = и. 10з ммку
/г = 2 (-Ц- + 19 • 0,82) + 213- 8,72 + 19 • 10,32 = 5,2 • 103 мм*.
Полярный момент инерции относительно центра тяжести равен Ip = Iy + !z= 16,2 • 103 мм\
Площадь сечения
F = 3- 19 + 2- 13 = 83 мм\
Величину /к вычисляем по формуле (15):
4 =-§-(2-13 + 3-19) = 28 мм*.
Определим секториальный статический момент Ry при полюсе в центре тяжести сечения. Вычисления сокращаются, если сначала найти значение R А при полюсе А, лежащем посередине стенки: у'
Ry.A=fdF- «
F
Для вычисления этого интеграла воспользуемся известным правилом Верещагина, построив предварительно эпюру секториальных площадей (рис. 4.10, tf) и эпюру величины z (рис. 4.10, в). Перемножая площади эпюр «>А (здесь толщина / = 1) и ординаты эпюр z> лежащие под центрами тяжести первых эпюр, получим:
0 Г 180,5• 19 п - 180,5-9,5 107 66.3,5 01Q1 0 1ЛЗ 4 /кч
А = 2 Н § 2— ’ J == ’ * м
Для перехода к полюсу, совпадающему с центром тяжести, запишем зависимость между секториальными площадями при переносе полюса по оси симметрии:
% = v;
здесь через у0 обозначено расстояние между центром тяжести О и прежним полюсом А: у0 = 10,3 мм. Величина Ry равна
Яу = / «•* dF = f (»А + у0г) г dF=Ry <A + yQ/y (d)
ИЛИ
Ry = 49,3 • 103 + 10,3. 1Ы08 = 163 • 103 мм5.
Для определения секториального момента инерции поступим таким же образом. При полюсе в точке А находим:
L.a= f ша dF- (е)
е
172 fOttkOctftHHbife ctEPWHli [гл. IV
Перемножаем эпюру <од на ее же ординаты, получаем:
0 / 181 • 19 2 101, 181-9,5 2 101, 66-3,5 2 сс\ *00 я
— з 181+—— -3 181 + 2“3-66j = 633*.
Для перехода к величине отнесенной к центру тяжести О, воспользуемся формулой (47), полученной при переносе полюса. Заменяя в ней 7 на и уъ на уо> имеем:
/ш = /т,А + 2УоЯу — Уо,у (О
Находим:
= 633 • 103 + 2 • 10,3 • 163 • 103 — (10,3)2 • 1ЫО3 = 282 • 10* мм\ Определим величины ау и <jq по (52):
9,87-7 -103.11 • 103
: 9,15 кг/мм2,
9,87 * 7 * 103 • 282 • 104, 2,8 • 103. 28 10,, ог 1Лвв «9 — IQ6. 2. ю3 16,2 • 103 — 16,85 кг/мм •
Далее, по формуле (53):
9.87-7-I0-..63-10.
10»/83 • 16,2 • 103
Критическое напряжение, соответствующее изгибно-крутильной форме потери устойчивости, будет по (58):
акр =
■<W+M-/(■»?.-9.15)» + 9,75,„г5г,г,м
При продольном изгибе в плоскости симметрии критическое напряжение аг будет по (59):
9,87 • 7 • 103 • 5,2 • 103. 0, 9
** = 1Q6. 83 = 4,3 кг/мм2.
Обе найденные величины лежат ниже предела пропорциональности спц = 20 кг/мм2.
Расчетным критическим напряжением оказывается напряжение окр, лежащее значительно ниже <зг. Критическая нагрузка при длине стержня / = 1 м равна
Якр = <sKpF = 2,52 • 83 = 209 кг.
Определим координату центра вращения О сечения по (60):
9,75, Г 16,2 • 103 ол с
У к — 9.11 — 2.52 V “ ' ММ'
9,11 — 2,52 V 83 Вычислим также координату центра изгиба по (61):
163.103
Как видим, центр вращения лежит значительно дальше от точки С, чем центр изгиба сечения.
СТЕРЖЕНЬ С НЕСИММЕТРИЧНЫМ СЁЧЁНИЁМ
173
Проведем вычисление критического напряжения для различных значений длины стержня. На рис. 4.11 изображены результаты вычислений для стер* жней длиной от 500 мм до 2000 мм. Одна из кривых (акр) соответствует изгибно-крутильной потере устойчивости, а вторая (ау) — продольному изгибу
в плоскости симметрии. Для длинных стержней, начиная с I = 1580 мм, более опасной становится эйлерова форма потери устойчивости. На рис. 4.12 сопоставлены координаты
40
Уп
1,мм
Рис. 4.11. Критические напряжения в зависимости от длины стержня.
'500
1000
1500
1,мм
Рис. 4.12. Изменение положения центра вращения в зависимости от длины стержня.
центра вращения сечения yk и центра изгиба yD. При возрастании длины стержня наблюдается удаление центра вращения от центра изгиба.
§ 50. Стержень с несимметричным сечением
Перейдем к общему случаю несимметричного сечения (рис. 4.13). Пусть главными центральными осями инерции сечения будут оси у и z. Допустим, что стержень подвергается центральному сжатию и что концевые сечения его свободно искажаются. Критическое напряжение, соответствующее изгибно-крутильной форме потери устойчивости, будем по-прежнему искать в виде (42), считая положение центра вращения К (yk, zk) неустановленным. Вместо формулы (43) для секториальной площади в точке М(у, z)> с учетом (11), получим:
ш — Укг + 2ку, (4.66)
здесь со — секториальная площадь, найденная при полюсе в центре тяжести. Секториальный момент инерции /в будет равен по (44)
7а = f (<»2 — 2u)укг + 2шгку — 2ykzkyz + ур2 -(- z*y2) dF. (4.67)
174
ТОНКОСТЕННЫЙ СТЁРЖНЙ
[гЛ. IV
Введем обозначение для второго секториального центробежного момента инерции:
ftz = J v>ydF. (4.68)
F
Учитывая, что для главных осей центробежный момент инерции
7 равен нулю:
fyz = f yzdF = 0, (4.69)
находим:
/„ = /.-2 ykRy+2zkRz + ?kIy+zlIz.
(4.70)
Для полярного момента инерции относи-
Рис. 4.13. Несимметрич- / = /у +1г + y\F + z\F
ное сечение тонкостенного стержня.
IP + F{ylrzD- (4.71)
Формула (42) для критического напряжения приобретает вид ¥ (/. - bkR> + 2гкЯж + у\1у + г\1г) + GIК
кр
Воспользуемся новыми обозначениями:
%*ERZ -.ГУ,
Рг 1*УТГР ’ Zkr 1р ’ тогда с учетом (52), (53) и (59) найдем:
а0 — 2рут) 4- 2ргС + <Jy7]2 -- а2с2
КР 1 + 1J2 + С2
Приравниваем нулю частные производные от окр по т) и С:
да.
кр
= 0,
да.
J2. = 0-
<ЭС
пользуясь (70), получим:
Ру
С =
Рг
икр
(4.72)
(4.73)
(4.74)
(4.75)
(4.76)
Формула (74) приводит теперь к следующему кубическому уравнению относительно <зкр:
(°кр - «■) (°К,. - «,) (°кр - «,) - РI (°кр - аг) - р! (°кр - °у) = °- (4.77)
*§ 51] УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ПРИ ЧИСТОМ ИЗГИБЕ
175
Это уравнение обобщает полученные ранее результаты. Для сечения с двумя осями симметрии ру = = 0; три корня уравнения (77)
будут:
(°KP)l = (°кр)2 = 0у Кр)з = °г> (4.78)
что согласуется с формулами (34) и (39). В случае сечения с одной осью симметрии ру Ф 0, p* = 0; тогда получим (окр)1>2 по уравнению (57) и (окр)3 = ог по (59).
Исследование уравнения (77) показывает, что, каково бы ни было соотношение между величинами а}, ау, oz, наименьший его корень будет всегда лежать ниже любой из этих величин. Следовательно, потеря устойчивости стержня с несимметричным сечением возможна только в изгибно-крутильной форме.
§ 51. Устойчивость плоской формы при чистом изгибе
Рассмотрим случай, когда тонкостенный стержень с сечением, имеющим одну ось симметрии, подвергается чистому изгибу в плоскости симметрии ху. Пусть каждая из пар, приложенных по тор-
м м
Рис. 4.14. Тонкостенный стержень подвергается чистому изгибу в плоскости симметрии (опоры изображены условно).
Рис. 4.15. К определению напряжений в краевых волокнах.
цам, имеет момент М (рис. 4.14). Нормальные напряжения в любом сечении стержня будут распределяться по закону
о = ~у; (4.79)
1 Z
напряжения в краевых волокнах ом будут
вж = ТР7- (4-8°)
где Wz — момент сопротивления сечения, относящийся к тому или
иному краевому волокну (точкам с или d на рис. 4.15).
В первой стадии нагружения упругая линия стержня является
плоской кривой; однако при известном значении момента М может произойти выпучивание стержня по направлению oc*i zt перпендику*
176 ТОНКОСТЕННЫЕ СТЕРЖНИ [гл. IV
лярной плоскости изгиба. Это явление носит название потери устойчивости плоской формы изгиба. Очевидно, при этом любое сечение стержня совершает поворот вокруг некоторого центра К, лежащего на оси симметрии сечения. Поэтому мы можем снова воспользоваться дифференциальным уравнением стесненного кручения (40). Составим выражения для интенсивности крутящего момента тк. По (23) и (24) имеем:
f 9 ?dF' <4-81)
F
причем под р понимается радиус-вектор площадки dF относительно центра вращения. Пользуясь (79), находим:
Введем обозначение
— d4 М Г -о олч
т«==~ШТ J ур dF' (4,82)
* F
f y?dF = Sy, (4.83)
Sy d*b M Sy
тогда по (27) получим:
mK — — М — — = — — В; (4.84)
1г dx* Е/ш /г ’
величину 1Ш надо также определять относительно центра вращения К. Уравнение (40) принимает вид
d2B / М Sv GIK\
+(жпг-ж;)в=0- (4-85)
Считая, что концевые сечения свободно депланируют, получим решение уравнения (85) снова в виде (32), причем
М Sy GIK
/г2 — — *- (4.86)
Е/ш 1г Е1Ш
Принимая по (33) kl = mt и п= 1, найдем критическое значение момента:
М«Р _ I GIK (Л о7ч
h i% + Sy • ( }
Мы пришли к формуле той же структуры, что и для критического напряжения при центральном сжатии по (42), но вместо 1р входит величина Sy. Координату центра вращения будем по-прежнему обозначать через у, тогда для сохранится выражение (47). Восполь¬
§ 51] УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ПРИ ЧИСТОМ ИЗГИБЕ 177
зуемся далее соотношением между радиусами-векторами, отнесенными к центру вращения и центру тяжести:
р2 = y2--z2 = (y— ykf -j~z =р2 — 2yky + у2; (4.88)
отсюда по (83)
Sy= f (p2 — ЬкУ + fk) ydF = Sy — 2ук1г, (4.89)
/-
Вместо (87) находим:
_2 p
MKp —p- (7ш — ЬцРу 4 уУу) + G/K
(4.90)
/* Sy 2 Уь! z
где
Sy= f Р2У dF. (4.91)
F
Введем наряду с (53), (63) и (80) обозначения
Р»=(!£-*>)/ *—<4-92>
тогда от (90) можно перейти к критическому значению напряжения в краевом волокне:
°е-2<у)0ъ4-<у)* НОоч
2(P, + 40-V- <4'93>
Определяем положение центра вращения, приравнивая нулю производную от (soM) по т]Л; тогда получим при + — y]k Ф 0
— Уо + 2<3У % + 2s°m = 0.
откуда
rlk = 'flD — (4‘94)
Qy
Подставляем теперь (94) в (93); для критического напряжения будем иметь квадратное уравнение
(s<3mT + 2Ру°у (5ам) + <*№ — °е°у = °; (4-95)
корни его будут
««“«у (— Ру ± + Г - Ч?> ) • (4.96;
178 ТОНКОСТЕННЫЕ СТЕРЖНИ [гл. IV
Критические величины момента оказываются равными
М = Ру(-Ь±уГ Т2+АГ2_У2) (4 97)
где !J-. v =й лГ=L
' V F Ту Ру Г Р ОТ _
Уо* Ру °у’ °G•
(4.98)
Отрицательный знак Ж относится к парам, придающим упругой линии стержня выпуклость не вниз, как на рис. 4.14, а вверх.
Обратимся к частному случаю, когда сечение стержня имеет две оси симметрии. Тогда будет Ry = Sy = y = yD = 0; для критических значений ам и М получим простые формулы:
°м, кр = 7 У а*°у ’ кр = r VP*Py • (4.99)
Для профиля, состоящего из пучка полос, будет
/ =0 *L=°Ll р.
следовательно,
°ж,кР = тг7Щ мкр = уоЩ,. (4.100)
При изгибе полосы прямоугольного сечения byh парами, ле¬
жащими в ее плоскости, получим IK — bhzj3, Iy=zbhzj 12 и
:тг VgW -?■ = -■- * (4.101)
r I /2(1+1*) I '
В случае двутавровой балки (рис. 4.16) секториальный момент инерции сечения может быть определен по (12). Для точек стенки
секториальная площадь <d обращается в нуль. Для точек полки имеем: о> = у/г/2, где
'Jj h — высота профиля; у отсчитывается от
средней линии стенки, и начальный ра-
2 диус-вектор совпадает с этой же линией. Следовательно,
У
Рис. 4.16. К вычислению секториальной площади. р\
/„ = 2--/ уЧу = --; (4.102)
интеграл распространяется на площадь полки, 1г — момент инерции полки относительно оси стенки. По (52) и (92) будет
( _ \ F п2Е/у
§ 52] СЛУЧАЙ ВНЁЦЁНТРЁННОГО сжатия 179
отсюда
кт >+w- <4'104)
Эта формула относится к случаю, когда изгибающие пары лежат в плоскости стенки.
§ 52. Случай внецентренного сжатия
Допустим, что стержень подвергается внецентренному сжатию силами Р, причем точка приложения силы лежит на оси у\ эту ось будем считать осью симметрии сечения (рис. 4.17). При малых
Рис. 4.17. Тонкостенный стержень, подвергающийся внецентренному сжатию.
нагрузках и здесь упругая линия окажется плоской. Однако, если сила Р превысит известную критическую величину, может произойти потеря устойчивости плоской формы, так что стержень начнет выпучиваться по направлению оси 2. Для разыскания критического значения Р воспользуемся тем же методом, что и в предыдущих параграфах. Предположим, что в момент потери устойчивости сечение стержня вращается вокруг точки /С, удаленной от центра тяжести на yk, и определим это расстояние. Нормальные напряжения в любом сечении до выпучивания будут равны
° = + У = °о(1 +тг); <4-105>
здесь a0 = P/F, = сжимающие напряжения по-прежнему счи¬
таем положительными. Интенсивность крутящего момента по (81) равна
d2 О
f р2 dF + /* ур2 dF\,
Р ** F )
\Р
ИЛИ _ _
Tp+4sy
d2b
■о,
dx2
° (•ГР + jr 5У ) = °0 —в- (4.106)
180 ТОНКОСТЁННЫЁ СТЁРЖНЙ [гл. IV
Вместо (85) и (86) получаем:
d*B
dx2
j-k2B= 0, (4.107)
*—-з:—ж:- <4108>
При k = v// будем иметь:
*2ЕТ„
+ 0/к
Оо=- J— —. (4.109)
+ ТГ 5У lz
Воспользуемся прежними формулами перехода (47), (89) и введем дополнительно обозначение
.-/4-
(4.110)
(4.111)
тогда получим:
в —У1й(2,1р-\)
° 1 +’)! + 2i)(.(py + Ti£) — ft)
Приравнивая нулю производную от о0 по v\kt найдем:
(4.П2)
<Л ау — а0 ш ау— о0 4 7
В частном случае центрального сжатия при = 0 придем к формуле (65). Подставим (112) в выражение (111); это приведет к квадратному уравнению относительно о0:
(°о — «о) (°0 — °у) + 2о0 (о0 — оу) 7)г Фу + 70) — (о01), — OyTjo)2 = О
(4.113)
или
[1 + 2 (Ру + T}D) — fill cl — (о, + ау-Ь 2oyPyT)e) О0 + о,о, — о* ig, = 0.
(4.114)
Отсюда при г}е = 0 вытекают уравнения (57) и (57а).
Рассмотрим случай, когда сжимающая сила приложена в центре изгиба сечения D, так что v\e — v\D. При этом из (112) получим rik — т}D, если оу Ф о0. Это означает, что центр вращения будет лежать в той же точке D. По (113) теперь найдем:
q<1*= °*~У>р, (4115)
1 ’Id +
СЛУЧАЙ ВНЕЦЁНТРЁИНОГб СЖАТИЙ
181
Второй корень уравнения (ИЗ) будет
= V (4.115а)
Мы видели, что при центральном сжатии стержня с несимметричным сечением критическое напряжение всегда лежит ниже оу. Если же сила приложена эксцентрично и именно в центре изгиба, то критическое напряжение в точности равно эйлеровому значению.
Исследование уравнения (114) показывает, что при известных условиях потеря плоской формы изгиба имеет место и в случае, когда сила Р является растягивающей. Это может произойти при достаточно большом эксцентриситете приложения нагрузки; один из корней уравнения (114) становится отрицательным. Граничные значения эксцентриситетов, при которых критическая сила Р будет растягивающей, определяются из того условия, что корень уравнения (114) равен ± оо. Но тогда должен быть равен нулю коэффициент при о:
Ц—Ъ'ПеЬ—1 =°;
здесь безразмерная k принята равной
А = Чс + Рг (4.1156)
Два значения т, отвечающие уравнению (113), будут _ r\e = k± Vk2-\- 1.
Мы найдем соответствующие точки на
оси 7] (или у на рис. 4.18), если отложим от центра отрезок kv а от него в одну и
другую сторону отрезки Yk2x-f-1 ; принято
k1 = k(Ip/F)il\ Если сила приложена в промежутке между точками с и d, то критическое значение ее может быть только сжимающим.
В более общем случае эксцентриситета в двух плоскостях найдем, что область сжимающих критических значений лежит внутри «круга устойчивости» *), безразмерный радиус которого будет
Y\k2~\-12, а координаты центра равны /; здесь под / понимается величина
т=27-V~r;fw-
*) Такое распространение решения на случай двухосного эксцентриситета является совершенно условным, так как в этом случае оно относится лишь к специфической линейной задаче, см. [4.3].
б
h
п
ус
г
У
Рис. 4.18. Область приложения сжимающей нагрузки при потере устойчивости плоской формы изгиба.
182
ТОНКОСТЁННЫЁ СТЕРЖНИ
(ГЛ. IV
Мы рассматривали здесь задачу об устойчивости тонкостенных стержней при внецентренном сжатии. При определении несущей способности стержня надо также исходить из условия, чтобы наибольшие напряжения или перемещения не достигали опасной величины (см. [4.3], [3.7]).
Пример 4.2. Для стержня, описанного в примере 4.1, определить критические значения среднего напряжения а0 = Р/F при нагрузке Ру приложенной по оси симметрии сечения на различных расстояниях ус от центра тяжести С.
Определяем величину Sy по (91):
Рис. 4.19. «Круг устойчивости» для сечения с одной осью симметрии.
Sy = J* р2у dF = j* у3 dF-j- J z2y dF.
F F F
Для стенки
+ 9,5
Sv, = 10,33 • 19 + 10,3 f z*dz =
У*./
= 20800+ 10,3 6859
12
26 700 мм5.
Для частей полок, параллельных оси у,
10,3 10,3
Sy, 2 ~ 2 f y*dF + 2 f у (9,5)2 dF =
-8,7
-8,7
: у (11 230 — 5780) + -19,52 (106 •
. 76) = 5420 ммК
Для отогнутых частей полок
Sy> 3 = 2 (- 8,7)313 + (_ 8)7) fiJ-iJ) = -78 000 мм\
Полное значение Sy будет
Sy = *Sy, -f- Syf 2 *4 Sy, з = — 45 900 мм*. Размерные величины и no (92) и (1156) равны
45 900 2-5156
= — 4,4 MMy py = — У0 — — 4,4 — 14,8 = — 19,2 мм.
Вычисляем значение г:
16 179
= 14,2 мм.
F — r 83 Радиус круга устойчивости будет
R = У г2 + k\ = у 14,22 + 4,4Г = 14,8 мм.
§ 53] БОЛЕЕ ОБЩИЕ УРАВНЕНИЯ ИЗГИБНО-КРУТИЛЬНОЙ ДЕФОРМАЦИИ 183
На рис. 4.19 нанесен круг устойчивости, центр его находится на расстоянии 4,4 мм от центра тяжести сечения.
Задаваясь различными значениями уе (или це), находим критические величины а0 по уравнению (114). В частном случае, когда сила приложена в центре изгиба сечения D (см. рис. 4.10 а), по (115) и (115а) получаем:
(1) _ 16,85 • (14,2)г — 9,15 (14.8)2 _
о “ 14,22 + 14,82 + 2 • 14,8 (—19,2) - ’ ' ’
«{?> = а = 9,15 кг/мм2.
Расчетным критическим напряжением здесь будет сг = 4,3 кг/мм2, эта величина была найдена выше, в примере 4.1.
Из примера 4.2 видно, что при значительных эксцентриситетах одно из критических напряжений является растягивающим.
§ 53. Более общие уравнения изгибно-крутильной деформации
6dF
До сих пор мы принимали в качестве полюса центр вращения сечения. В некоторых случаях более удобным оказывается выбрать в качестве полюса центр изгиба сечения. Выведем соответствующие уравнения, принимая, что, в дополнение к центральным сжимающим силам Р, по торцам стержня приложены пары в плоскостях xz и ху с моментами Му и Мг. Рассмотрим стержень в состоянии, отклоненном от основного, и определим интенсивности «нагрузок», соответствующих повернутым усилиям основного состояния. При этом сначала рассмотрим повороты, вызванные искривлением оси центров изгиба, а затем повороты, связанные с закручиванием вокруг этой оси. Перемещения центров изгиба различных сечений вдоль осей у, z будем обозначать через v, w. На рис. 4.20 показано элементарное усилие adF, повернутое в плоскости xz. Соответствующие углы в плоскостях ху и xz равны dvfdx и dwjdx. Дополнительные проекции на оси у и z усилий о dF будут o(dv/dx)dF и o(dw/dx)dF; эти* проекции дают моменты относительно центра изгиба, равные
Рис. 4.20. К определению момента элементарного усилия.
[«£<*-Sri'’] « [- «ЗгО’-Л.)’];
184 ТОНКОСТЕННЫЕ СТЕРЖНИ [гл. IV
через yD и zD обозначены координаты центра изгиба. На единицу длины осевой линии будут приходиться нагрузки
«•=- S°i-dF <4иб>
F F
и момент интенсивностью
m=s I (4-117)
F
интегралы относятся ко всему сечению.
При действии сжимающей центральной силы Р и моментов Му, Мг напряжение о в точке у, z равно
* Р м. м„
°=T--rry+-rfz' (4Л18)
Додставляя это выражение в (116), найдем:
d d2v п d2w /А
Я у dx2' Чг ~dx2~t (4.119)
остальные интегралы обращаются в нуль. Момент (117) будет равен т = - (PzD - Му) -g- + (PyD +Мг). (4.120)
Обратимся к поворотам усилий, вызванных закручиванием стержня. Приращение составляющей элементарного усилия в плоскости yz оказалось равным (стр. 164)
adtydF, или ad(dF\ проекции его на оси у и z будут
» [-°*(£Ь4
под р! понимается радиус-вектор, проведенный из центра изгиба к элементу dF. Погонные интенсивности нагрузок равны
Яу= f ai{z~ZD)dF'
h F
Подставляя (118), получим:
/У2В /У2А
Я,= - <Ргр-Му)-, 4, — iPyp + M. (4.121)
§ 53] БОЛЁЁ ОВЩИЁ УРА6НЁНИЙ ЙЗГИЁНО-КРУТИЛЬНОЙ ДЕФОРМАЦИИ 185
Составим дифференциальные уравнения для перемещений vt w и угла поворота 0:
dAv
Е1*Ч*=Ъ'
1г/ dAw
У 1Гх*~ ~ Я*’
d'6 л, d4
“ к dx* ~ т'
(4.122)
Здесь под /о понимается секториальный момент инерции относительно центра изгиба. Исходя из формулы перехода (47), находим:
C=A»-2V?y+2v?,+ jfc/y+4/-
Но по (61) имеем:
Яу = Уо/у. Л, = - V*. (4.123)
следовательно,
С = Vb-'A <4-124)
Крутящий момент (25) равен
20 /* / Р Mz Mv \
\T-nr> + -T7g)*dP- (4Л25)
или
т
По формуле (71)
rP = lP + (yl + zl)F'> (4-126)
отсюда
/•*2=4 = г2+у20+4.
(4.127)
Величины S’ и 5 по (89) равны
S; = Sy-2yD/z, S* =Sz~2zD/r (4.128)
Выражение (125) приобретает вид
““ - ш.{шг-и>) + 2/И>(377-■*«)]
Вводя обозначения типа (92):
d4 dx2
Ру — 2/г Уо* Р* — 2/у 2°'
получим:
я* = - (Рг*2— 2Жгру + 2MyfjJ U. (4.129)
186
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
Собирая выражения для погонных нагрузок (119) и (121), а также для моментов (120) и (129) и подставляя их в уравнения (122), приходим к следующей системе дифференциальных уравнений:
EI
d4v
El,
z dx* d4w
EI\
у dx4 d46
P+(Pzo~M = <lr P-(.PyD+Mz)™=qz,
dx2
dx4
(/V*2-2MR +2Myp2-G/K)
d2e
+ (PZD ~ ™y)
У d2v
dx2
У dx2
(РУй 4“ Mz) — m.
(4.130)
Аналогичные уравнения для случая переменных по длине моментов имеют несколько иную структуру ([4.4], стр. 369). В бифуркационных задачах пользоваться уравнениями такого типа следует с осторожностью (см. сноску на стр. 181).
§ 54. Устойчивость плоской формы полосы при изгибе
Рассмотрим частный случай полосы прямоугольного сечения, подвергающейся изгибу в плоскости ху.
Мы должны при этом положить /*=py = 3z = 0. Примем в (130) Р = Му = qz = т = 0 и проинтегрируем дважды второе из этих уравнений, считая постоянные интегрирования равными нулю. Окончательно второе и третье уравнения примут вид
£/y-g_Mz0 = O, (4.131)
Of + = (4-132)
Исключая отсюда w, получаем одно уравнение второго порядка относительно 6:
d4. Ml
dx2 1 GIKEIy
1 = 0. (4.133)
При чистом изгибе Mz = const; решение уравнения имеет вид
0 = A sin kx + В cos kx, (4.134)
где
к~~ УЩЩ’ (4.135)
§ 54) устойчивость плоской формы полосы 187
Граничные условия выберем в виде
6 = 0 при х — 0, х = 1; (4.136)
тогда первое критическое значение k будет тс//; отсюда по (100)
МК9 = УШЖу (4.137)
Уравнениями (131) — (132) можно пользоваться в нашем случае и при переменном по длине моменте.
Пусть, например, правый торец полосы защемлен, а левый свободен. Предположим, что в центре тяжести левого торцевого сечения приложена сила Р, направленная по вертикали (рис.4.21). В этом случае Мг= — Рх, вместо (133) будем иметь
d4, dx2 +
Введя обозначение а =
01кЕ1у
ч
я
\
h
\ *
У GIKEIу ’ мы приведем уравнение (138) к виду
(4.139)
+в2*«+10 = О,
Рис. 4.21. Изгиб полосы сосредоточенной силой.
с которым мы уже встречались в § 35 и 37. Если положить
1
л + 3
(4.140)
и учесть, что v является дробным числом, то решение уравнения (139) принимает вид (3.23):
6 = A Yx jXx)-\-B Ух J.Xtavx'b), (4.141)
где 7V — бесселева функция первого рода с индексом v. Производная от выражения типа (141) была нами уже вычислена; по (3.44) имеем:
dx
— Аах 2v «/_(!_>) (яду*2*)—Вах 2v {flavx 2v). (4.142)
В разбираемом нами примере п= 1, v = 1/4; следовательно, о = А Ух j\ (y л:2) -- В Ух J (у х2,
3 3
~ = Аах*]_г - Bax2JL( х2).
(4.143)
(4.144)
188 ТОНКОСТЕННЫЕ СТЕРЖНИ [гл. IV
Будем считать, что на левом конце обращается в нуль крутящий момент Мк. По зависимостям (13) и (14) эта величина, при 1Ш = 0 равна
Жк = ж = 0/к-. (4.145)
Следовательно, на этом конце должно быть
- = 0 при х = 0. (4.146)
С другой стороны, на защемленном торце должен быть равен нулю угол закручивания:
6 = 0 при х — 1. (4.147)
Как известно (см. § 37), функция J_з(0) = оо, в то время как ве-
~Т
личина Jз (0) обращается в нуль. Поэтому условие (146) дает Л = 0. Т
При В Ф 0 из условия (147) находим:
•/_i(y/2) = °- (4Л48>
Определив наименьший корень этого уравнения, мы найдем критическую нагрузку. В следующей таблице приведены корни уравнений, аналогичных (148), для функций с различными индексами.
Таблица 4.1
J.
j 4
J 0
Корни
1
3
1
3
4
4
Т
4
1-Й
2,781
3,492
2,006
1,058
2-й
5,910
6,650
5,120
4,290
Таким образом, в данной задаче имеем:
~Р = —ГР Р = 2,006; (4.149)
2 2 VEIyG/K
следовательно, первая критическая нагрузка равна
Р=-УЩЩ~Г (4.150)
По структуре зависимость (150) сходна с формулой Эйлера.
§ 54]
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ полосы
189
Эту же задачу можно решать также приближенными методами. Примем, например, для функции б зависимость
б = б0(/2-*2),
(4.151)
удовлетворяющую граничным условиям. Уравнение метода Бубнова — Галеркина, отвечающее (138), будет
/
f a2jc2®) V2 ~ *2)dx = 0. (4.152)
о
Подставляя (151) и интегрируя, найдем: а2/4=17,5. Коэффициент в формуле типа (150) получает приближенное значение 117,5 = = 4,18.
Допустим теперь, что сила Р приложена не в центре тяжести торцевого сечения, а на расстоянии d от центра (рис. 4.22); будем считать d положительным, если точка приложения силы лежит над центром тяжести. Тогда крутящий момент на левом конце будет равен Mx = PdQ; следовательно, вместо (146) получаем граничное условие
о/. *-=-/*6
при х = 0,
(4.153)
условие же (147) остается.
Функция Бесселя с индексом в виде ряда
Рис. 4.22. Случай, когда сила приложена не в центре тяжести сечения.
v может быть представлена
Л(*) =
———Г
2Т (v) L
л:4
2 (2м -J- 2) 2 • 4 (2v + 2) (2м + 4)
здесь I» — гамма-функция, таблицы величин T(v) содержатся в справочных книгах. По (143) находим:
190 ТОНКОСТЕННЫЕ СТЕРЖНИ
При х —> 0 будем иметь:
6(0 ) = В [гл. IV (4.15б/
Далее, по (144)
41=а«-ШЛ_
2'7г(-)
_я
dx
йг(-1)
,_(И
2 0,5
27г() (—\ =
V /ж =0
.-М+ 1.
2-3,5 •••]*
з 2 2а4
(4.156)
г(-т)'
Подставляя эти значения в (153), получим:
2Г (- т) 01 «А +Г(- т) аР* (01«Е/у в = °- (4-157>
Второе условие, т. е. (147), дает:
J1 (тР) A+J-l(jl2)B = °- (4.158)
Приравниваем нулю определитель системы уравнений (157) и (158); Т01;да будем иметь:
2Г (-1) 0/KJ_, ( р) - Г (_ ) dP* (GIKEIyf<» Л ( Р) = 0.
(4.159)
В таблице 4.2 приведены значения коэффициента К в формуле для критической силы
Ркр = К
V GIKEfy
Р
(4.160)
отвечающей уравнению (159); они оказываются зависящими от параметра d УЩ/i VgT*-
§ 54] УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ полосы 191
Таблица 4.2
Коэффициенты К для случая, когда сила Р приложена к консоли не в центре тяжести
Над центром тяжести
d,/Ely I V GIK
0
0,0031
0,0887
0,164
0,238
0,322
0,425
0,568
0,791
1,224
2,485
К
4.013
4,0
3,6
3,2
2.8
2,4
2,0
1,6
1,2
0,8
0,4
Под центром тяжести
d,/E/y
1 V а/к
0
0,114
0,320
0,923
со
к
4,013
4,4
4,8
5,2
5,562
Здесь даны также коэффициенты К для предельных случаев,
когда сила передается через весьма длинный рычаг (у->оо. Для
малых отношений djl может быть использована простая приближенная формула
p,p=4.oii£t(i-4»/* -стг); <416>
это можно легко проверить по таблице 4.2.
Перейдем к случаю, когда консоль подвергается действию равномерно распределенной по всей длине нагрузки q = const (рис. 4.23). При этом Mz = qx2/2; уравнение (133) получает вид
ЛЧ, q2
dx2 ~ GIKEIy 4
Если принять
> = 0. (4.162)
2 V 01КЕ1
==, (4.163)
получим уравнение типа (139) при п = 3 и v = 7б. Повторяя выкладки, приведенные для случая сосредоточенной силы, приходим вместо (148) к уравнению
J_i(P) = 0. (4.164)
192
ТОНКОСТЕННЫЕ СТЕРЖНИ
[ГЛ. IV
Наименьший корень этого уравнения будет 2,142; критическое значение интенсивности распределенной нагрузки равно
г V GIKE/V
q = 2aY GIKEIy == 12,85 (4.165)
Если нагрузка распределена вдоль длины балки по закону треугольника q = q0x/l, то получим уравнение типа (139) при
Я
Яо
При п = 5 и будем иметь
(4.166) = 1/8 вместо (164)
Ы\Гв1кЕГу
.V
Рис. 4.23. Полоса подвергается действию равномерно распределенной нагрузки.
J i(f*4) = 0. (4.167)
8 1
Наименьший корень уравнения (167) равен —2,2; поэтому критическое значение q0 будет
<70 = 52,8
V 01кЕ1у /3
(4.168)
Приведем значения коэффициента в формуле для критиче¬
ского максимального изгибающего момента:
УШЖу
I
'1'
\
У
i
max 1
(4.169)
При чистом изгибе /С1 = тс, в случае сосредоточенной силы К\ = 4,01, при равномерно распределенной нагрузке Кх = 6,43, в случае нагрузки, распределенной по закону треугольника, Кг = 8,8.
Обратимся к случаю, когда полоса шарнирно оперта по торцам, а сила Р сосредоточена посередине пролета (рис. 4.24). Расположим начало координат у левого конца, тогда момент М для левой половины балки будет равен
М = -7Г X.
Рис. 4.24. Случай сосредоточенной силы, приложенной посередине пролета.
Уравнение (133) приобретает вид
d4, Р2
/Л 1
УСТОЙЧИВОСТЬ плоской ФОРМЫ полосы
193
Решение его можно по-прежнему выписать в форме (143), но вместо (138) надо положить
а = —tJL=. (4.171)
2V GIKE/y
Будем считать, что опорное сечение не поворачивается:
6 = 0 при л; = 0. (4.172)
С другой стороны, при искривлении по одной полуволне угол поворота среднего сечения должен быть максимальным, так что здесь
должно быть
d О Л /
_ = 0 при x = -z-
(4.173)
Пользуясь выражением (143), из первого условия находим В = 0. Второе условие дает
= (4.174)
4 4 1
Судя по таблице 4.1 (стр. 188), первый корень этого уравнения равен 1,058; следовательно, критическая сила равна
V 01кЕ1у
Р= 16,94
/2
(4.175)
Допустим, что сила Р приложена в точке, удаленной от центра тяжести сечения на расстояние d. Тогда граничное условие (172) остается, а условие (173) надо заменить на следующее:
01 * in=тQd при х=4 • (4-176)
Принимая В = 0, получим отсюда
М.Л/~БГ7,, 1°р\
— т
Р
}
1
1 —
W-
Рис. 4.25. Сосредоточенная сила приложена на разных расстояниях от опор.
(4.177)
Коэффициенты К в формуле типа (160), полученные по уравнению (177), приведены в таблице 4.3.
Рассмотрим, наконец, случай, когда сила Р приложена к шарнирно опертой полосе на разных расстояниях от торцевых сечений (рис. 4.25). Обозначая эти расстояния через т, п, имеем для левой половины Mz = Pnxjl и для правой половины Мг = Ртхх11.
194
'ГОНКОСТЕННЫЁ СТЕРЖНИ
[ГЛ. IV
Таблица 4.3
Коэффициенты К для случая, когда сила Р приложена к балке на двух опорах не в центре тяжести
Над центром тяжести
I V G/K
0
0,030
0,143
0,293
0,544
1,210
К
16,94
16,0
12,8
9,6
6,4
3,2
Под центром тяжести
I I GIK
0
0,069
0,166
0,271
0,396
0,562
0,815
1,30
2,78
К
16,94
19,2
22,4
25,6
28,8
32,0
35,2
38,4
41,6
Мы можем использовать уравнение (143), полагая
Рп Рт
1 lVGIKEIy’ 2 iVQUEIy '
(4.178)
Граничные условия составляем для концевых сечений в виде
61 = 0 при хх = О, 02 = О при лг2 = 0 (4.179)
и для точки сопряжения
и ~dx dx ’
Уравнение для определения критической нагрузки будет
В таблице 4.4 приведены значения коэффициента К для разных отношений т/1, вычисленные по (181).
В случае, если концы полосы защемлены, а сила Р приложена посередине пролета, коэффициент К в формуле типа (175) оказывается равным 26,6, а в формуле типа (169) — равным 3,54.
dQj _ db2
(4.180)
ПОПЕРЕЧНЫЙ ИЗГИБ
195
Таблица 4.4
Коэффициенты К для случая сосредоточенной силы, приложенной на разных расстояниях от опор
т
~Т
0,5
0,45
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,05
К
16,94
17,15
17,82
19,04
21,01
24,10
29,11
37,88
56,01
111,6
При действии равномерно распределенной нагрузки на шарнирно опертую по концам балку коэффициент К в формуле (169) равен 28,3/8 = 3,54.
§ 55. Поперечный изгиб балок с сечением, имеющим две оси симметрии
Обратимся к более общему случаю, когда стержень представляет собой произвольный профиль, имеющий две оси симметрии; примером может служить двутавровая балка. Для такого профиля центр изгиба совпадает с центром тяжести и = 0. Если балка подвергается поперечному изгибу в плоскости ху, то дополненные уравнения (131) и (132) примут по (130) вид
l,Sr-MJ=qz.
d* 9
EIy
El,.
d2w
Мг=т.
(4.182)
Считая gz = 0 и исключая w, придем к уравнению четвертого порядка
EL
.(Г
dx*
О/,
Mi
к dx2
(4.183)
Если на балку действует распределенная нагрузка q, приложенная на расстоянии d от центра тяжести (рис. 4.23), то интенсивность момента т равна (— qd • 6); учитывая зависимость между q и Mz, получим вместо (183)
rf40 d4 (
Е1<л ~dx* ~ GIk ~dx* ~ \
Ml
EIV
dx2
d} 0 = 0.
(4.184)
Интегрирование этого уравнения в общем случае может быть выполнено лишь с помощью приближенных методов.
Рассмотрим случай балки на двух опорах, к которой приложена сосредоточенная сила Р посередине пролета (рис. 4.24). Тогда
196 ТОНКОСТЕННЫЕ СТЕРЖНИ [гл. IV
уравнение (184) примет вид при 0 х ч
d4 4 М* л
£/<“Их* ~01«!П? Ш7хВ~0; (4.185)
здесь Мтах — момент в среднем сечении. Будем считать, что угол поворота торцевых сечений равен нулю:
0 = 0 при л; = 0, х = 1. (4.186)
Кроме того, допустим, что' бимомент в торцевых сечениях обращается в нуль. Тогда должно быть
= 0 при л; = 0, х = 1. (4.187)
Примем для 0 приближенное выражение
*тг
0 = Л sin -j-, (4.188)
удовлетворяющее граничным условиям. Уравнение Бубнова — Галеркина будет
i_
Л* я2 4Af \ %х
/2~Лс /2£/ х J sin —dx = 0
или
I ( П4 J \ 4<ах / /3 /3 \
т (тгш-Ь-тгк) /2£/у ~0- (4.189)
Отсюда критическое значение Мтах:
/• -gr-
Жшах = —==_]/ 1+тпя?- (4.190)
Для частного случая, когда 7 = 0, получим:
Мтах = У1ЩЕГу. (4.191)
В § 54 мы получили точное значение коэффициента в этой формуле, равное 4,23. Воспользуемся формулой (190), чтобы оценить влияние дополнительного множителя, содержащего Отметим, что в случае чистого изгиба наш прием привел бы к точному резуль¬
тату (104):
§ 55]
ПОПЕРЕЧНЫЙ ИЗГИБ
197
где под х понимается выражение
X = j/l + 7ЩГ- (4.193)
дает основание представить расчетную формулу для рассматриваемого случая сосредоточенной силы в форме
/ GIKEIV
Мтах = 4,23 J—(4.194)
По-видимому, этот же множитель % может быть использован и в других случаях загружения шарнирно опертой балки. Например, при действии равномерно распределенной нагрузки, приложенной по центральной линии, мы получим:
мтах = УШЖу X- (4.195)
Если нагрузка приложена не в центре тяжести, а по верхней или нижней полкам, то вместо (195) получим:
Мтп = Ц-УЩ,Хк. (4.196)
Дополнительный множитель k оказывается равным *=/
Знак минус относится к случаю, когда нагрузка передается на верхнюю полку, а знак плюс — при нагружении нижней полки.
В предыдущих главах рассматривалась устойчивость стержней и простейших стержневых систем. Вне рамок данной книги остается теория устойчивости сложных стержневых систем, и прежде всего статически неопределимых рам. Эта область освещена в книгах Н. В. Корноухова [0.5], А. Р. Ржаницына [0.10], В. Г. Чудновского [0.12], А. Ф. Смирнова [0.11], Н. К. Снитко [3.9], Я. Л. Нудельмана [3.5], И. К. Снитко (Практические методы расчета статически неопределимых систем, Москва, 1960), А. А. Пиковского [3.7], С. А. Рогицкого (Новый метод расчета на прочность и устойчивость, Свердловск, 1961), Р. Р. Матевосяна (Труды ЦНИИСК, № 3, 1961), Ф. Блейха [0.151, Г. Бюргеймейстера и Г. Штойпа [0.16].
ГЛАВА V
ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ § 56. Задачи об устойчивости стержней, связанные с учетом температуры
Благодаря развитию новых областей техники и прежде всего сверхзвуковой авиации в последнее время возникли новые задачи — об устойчивости упругих систем при высоких температурах. Как известно, аэродинамический нагрев приводит к образованию неравномерного поля температур в конструкции летательного аппарата. С этим связано появление некоторых напряжений. Подобные температурные напряжения не всегда являются опасными для прочности конструкции, так как «рассасываются» по мере развития деформации. Но те элементы конструкции, в которых развиваются сжимающие напряжения, могут потерять устойчивость, что в ряде случаев равносильно исчерпанию несущей способности и является недопустимым.
Далее, при высоких температурах проявляется ползучесть конструкционных материалов (стали, дюралюмина, титановых сплавов и т. д.), которая в свою очередь приводит к потере устойчивости сжатых элементов при напряжениях, лежащих значительно ниже эйлеровой величины. Отметим, что у некоторых материалов (пластмассы) ползучесть имеет место и при относительно низких температурах. Явление ползучести протекает во времени; малозаметная деформация сжатого стержня по истечении определенного периода завершается резким выпучиванием. Таким образом, здесь, наряду с установившимся понятием критического напряжения, появилось новое понятие критического времени. Возникла новая область те<эрии устойчивости упругих систем — теория выпучивания при ползучести.
При решении задач, относящихся к неравномерно нагретым конструкциям, надо вновь пересмотреть критерии устойчивости. Существование неравномерного температурного поля связано с явлением теплопроводности внутри тела и с рассеянием энергии в окружающую среду. Процесс деформации при нагружении и выпучивании тела
§ 57] ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА ВЕЛИЧИНУ МОДУЛЯ УПРУГОСТИ 199
сопровождается, кроме того, необратимыми изменениями температурного поля. Поэтому исследование устойчивости неравномерно нагретого тела надо, строго говоря, вести, исходя из уравнений термодинамики необратимых процессов *).
Обратимся к некоторым частным задачам.
§ 67. Влияние температуры на величину модуля упругости. Равномерный нагрев стержня с закрепленными концами
Если рассматривать устойчивость стержней в пределах упругих дефор лаций, то повышение температуры сказывается прежде всего на веллчине модуля упругости. На рис. 5.1 представлена зависимость модуля Е от температуры t°С для некоторых материалов—ста- Е,кг!см} лей ЭИ728, ЭИ703, Я1ТН, титанового сплава ВТб и дюралюмина Д16АТ. Как видим, с увеличением t° величина Е быстро падает. Значение Е для тех или иных t° и следует подставлять в расчетные формулы. Отметим, что при возрастании t° падают также значения предела пропорциональности опц и предела текучести от.
Рассмотрим случай, когда стержень шарнирно прикрепляется к неподвижным опорам при температуре о, а затем подвергается равномерному нагреванию по всей длине (рис. 5.2). При повышении температуры в стержне будут возникать сжимающие напряжения, и при некоторой температуре стержень начнет выпучиваться. Этот случай потери устойчивости интересен тем, что он происходит в отсутствие какихлибо активных нагрузок.
Если бы стержень удлинялся свободно, то продольная деформация его при температуре t\ была бы равна
е< = а(*1 —/о). (5.1)
*) См. работы Био (М. Biot), опубликованные в «Aeronaut. Quarterly» 7, № 3 (1956), «Physical Review» 97, N® 6 (1955), «Journ. of Applied Physics» 25, № 11 (1954), и диссертацию Л. А. Шаповалова [5.10].
Рис. 5.1. Изменение модуля Е в зависимости от температуры t° С для различных материалов.
200 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гЛ. V
где а — коэффициент линейного расширения. В случае закрепленных концов имеют место сжимающие напряжения, равные
о* = Eet = Еа (t\ — to). (5.2)
тг2Е
После того как величина о/ достигнет эйлерова значения -j2~>
прямолинейная форма равновесия стержня станет неустойчивой. При шарнирном закреплении концов стержня разность температур, соответствующая критическому напряжению, будет равна
о о 7г2
*‘-*0 = W (5-3)
где X — гибкость стержня. Так, например, для дюралюмина Д16АТ коэффи¬
циент а составляет 25 • 10_6. В случае стержня, гибкость которого равна X = 100, выпучивание начнется, когда разность температур достигнет величины t\ — to = 40°. Соответствующее сжимающее напряжение составляет около 700 кг)см2.
Если напряжения в стержне превосходят предел пропорциональности, то деформации (1) будет отвечать напряжение, равное
= Ecet, (5.2')
где Ес — секущий модуль, отвечающий температуре t\. Пользуясь формулой для критического напряжения с касательным модулем Ек> найдем разность температур, при которой возникает выпучивание:
<5-4>
Модуль Ек также вычисляется для температуры t\.
Своеобразие этой задачи состоит в том, что, как только начнется выпучивание стержня, реакции опор, равные сжимающему усилию в стержне, будут уменьшаться; поэтому интенсивное выпучивание может иметь место лишь при продолжающемся возрастании температуры.
1.06
»л
105
№
ч
103
t;
102
101
100
V/
С
Рис. 5.2. Стержень с неподвижными концами при изменяющейся температуре.
Рис. 5.3. Зависимость между нагрузкой и прогибом после потери устойчивости.
СЛУЧАЙ НЕРАВНОМЕРНОГО НАГРЕВА
201
Это обстоятельство иллюстрируется графиком рис. 5.3 *). По оси абсцисс здесь отложен угол 8 наклона касательной к упругой линии стержня в концевом сечении (см. рис. 5.2), по оси ординат — температурное усилие
Рт = EFcl (t\ — tl\
которое должно иметь место в прямом стержне для того, чтобы после искривления угол поворота достиг значения 0; величина РТ отнесена к эйлеровой силе Р9. Как видно из графика, соотношение между Рт/Р9 и 0 зависит от гибкости стержня X. Например, при X = 100 и 0 = 0,015 усилие Рт на 6% превышает критическую величину. Для сравнения здесь приведена диаграмма закритической деформации стержня с верхним подвижным шарниром для постоянной температуры. При прежнем значении 0 = 0,015 сжимающее усилие Р° превысило бы эйлерову величину лишь на 0,003%.
§ 68. Случай неравномерного нагрева
Перейдем теперь к случаю, когда температурное поле не являзтся равномерным. Рассмотрим центрально сжатый стержень прямоугольного сечения, защемленный по концам. Допустим для примера, что подобный образец установлен между плитами испытательной
о
машины при температуре t0, после чего подвергается нагреванию до температуры, изменяющейся вдоль одного из размеров сечения (рис. 5.4) по линейному закону; приращение температуры равно
Г = -Ц—У, (5.5)
вдоль каждого продольного
Щ
6)
Рис. 5.4. Стержень, подвергающийся неравномерному нагреву.
волокна
величина t° является постоянной **).
Так как концы стержня защемлены, то ось его останется прямой до момента выпучивания. Допустим, далее, что на стержень передается возрастающая нагрузка; требуется определить ее критическую величину. Подобная задача представляет особый интерес в случае, если напряжение в стержне превосходит предел пропорциональности.
*) Этот график составлен В. И. Усюкиным.
**) Эта задача была поставлена Л. И. Балабухом и решена Л. А. Шаповаловым [5.10].
202 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
Рис. 5.5. Диаграммы сжатия при различных температурах.
бы,кг/смг
Рис. 5.6. Гргфик «критическое напряжение—гибкость» при неравномерном нагреве.
УЧЕТ ВЛИЯНИЯ ТЕПЛОПРОВОДНОСТИ
203
Каждому волокну стержня будет тогда соответствовать своя диаграмма о (в), характер которой изменяется в зависимости от температуры. Будем считать, что выпучивание стержня происходит при постоянной силе и что поэтому сечение делится на зоны догрузки и разгрузки (рис. 5.4, б). Примем для примера, что диаграмма сжатия материала (стали) состоит из двух прямых линий (случай «линейного упрочнения») и что при повышении температуры одновременно изменяются: основной модуль Е, касательный модуль
на втором участке Ек и предел пропорциональности, как показано на рис. 5.5.
Деформация каждого волокна до потери устойчивости складывается из двух составляющих, одна из которых вызвана активной нагрузкой, а вторая связана с повышением температуры:
е = ео + а°* (5.6)
Коэффициент а будем считать не зависящим от температуры. Деформации в момент выпучивания распределяются по закону плоских сечений. Исходя из этого и рассматривая условия равновесия части стержня, как это было сделано в § 26, можно найти результирующий модуль Т и построить диаграмму зависимости критического напряжения акр от гибкости стержня X. На рис. 5.6 показана такая окончательная диаграмма для случая, когда /° = 0, t°2 = i°. Как видим, при возрастании перепада температур критическое напряжение резко уменьшается.
§ 59. Учет влияния теплопроводности
Обращаясь к термодинамической постановке задачи об устойчивости сжатого стержня, мы должны уточнить исходные предпосылки. До сих пор, по существу, предполагалось, что первоначальное сжатие и последующее выпучивание стержня происходят при постоянной температуре, т. е. изотермически. Но, как известно, любая упругая или неупругая деформация изолированного тела сопровождается некоторым, хотя и незначительным для конструкционных материалов, изменением температуры. Упругое удлинение стержня связано с падением температуры, а укорочение — с повышением ее. Следовательно, при выпучивании стержня должен возникнуть весьма слабый тепловой поток от сжатых волокон к растянутым. Поведение стержня в процессе продольного изгиба должно зависеть, таким образом, от коэффициента теплопроводности материала *). Если этот коэффициент бесконечно велик, то температура во всем объеме в любой момент времени одинакова. Если поддерживается
*) Такая зависимость была установлена Л. А. Шаповаловым [5.10]. См. также книгу А. Пфлюгера [0.21].
204 ВЛИЯНИЕ ТЁМПЁРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
постоянство этой единой температуры — в частности, благодаря внешним источникам и стокам тепла, — то процесс выпучивания является изотермическим. Напротив, если коэффициент теплопроводности бесконечно мал, то теплообмена между участками сжатия и растяжения, а также между телом и внешней средой не происходит, и процесс будет адиабатическим. Подобный случай мог бы иметь место при весьма быстром выпучивании.
Можно показать, что критическое напряжение в обоих предельных случаях определяется по формуле Эйлера, но с введением в нее различных модулей упругости — изотермического Et или адиабатического Еа. Модули эти отличаются друг от друга незначительно, так, для стали найдено
Еа1,00Щ. (5.7)
Если коэффициент теплопроводности имеет малое, но конечное значение, то критическое напряжение определяется по изотермическому модулю. Таким образом, с практической точки зрения нет необходимости отличать изотермический и адиабатический процессы потери устойчивости, но различие между ними имеет принципиальное значение.
Из сказанного вытекает, что энергетический критерий устойчивости, относящийся к консервативным системам, может быть применен к реальным стержням лишь с известной оговоркой. Предпочтительным и здесь оказывается динамический критерий, позволяющий определить области устойчивости возмущенного движения термодинамической системы.
§ 60. Продольный изгиб при ползучести.
Основные сведения
Обратимся к исследованию выпучивания сжатых стержней при ползучести. Под ползучестью понимают изменение деформаций тела во времени при заданных нагрузках *). Как было уже сказано, для таких материалов, как сталь и дюралюмин, с ползучестью надо считаться лишь при повышенных температурах. Процесс одноосного растяжения в условиях повышенной температуры можно представить в виде графика, изображенного на рис. 5.7. По оси абсцисс откладывается время, по оси ординат — деформация. Непосредственно при приложении нагрузки, которая в дальнейшем поддерживается постоянной, происходит упругая или упруго-пластическая «мгновенная» деформация, отвечающая участку О А. Вслед за этим начинается процесс ползучести, сначала более быстрый, а затем замедляющийся. На диаграмме получим криволинейный участок АВ, нося¬
*) Мы оставляем в стороне явление релаксации (изменения напряжений при заданных смещениях).
ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ
205
щий название первичной или неустановившейся фазы ползучести. В последующем скорость ползучести делается почти постоянной, так что диаграмма принимает вид прямой линии (участок ВС). Эта вторичная фаза процесса называется установившейся ползучестью. Затем на образце появляется шейка, и деформация ускоряется (участок CD), после чего происходит разрушение. В случае, если короткий образец подвергается центральному сжатию, диаграмма е(£) имеет такие же участки, отвечающие «мгновенной» деформации, первичной и вторичной фазам ползучести.
Будем полагать, что постоянное сжимающее напряжение равно о.
Упругая деформация равна ее =
= о/Е(°, причем модуль Et° отвечает заданной температуре /°. Деформация ползучести ес, соответствующая установившейся фазе *), зависит от времени, свойств материала и величины приложенного напряжения. Предложен ряд приближенных формул, описывающих этот участок диаграммы, например:
zc = kontt (5.8)
где k и п — коэффициенты, зависящие от свойств материала**).
Другая приближенная формула имеет вид
sc = AeBat, (5.9)
где Л, В — постоянные материала, е — основание натуральных логарифмов. Если принять уравнения (8) или (9) и считать здесь о не зависящим от t, то скорость изменения деформации во времени будет
величиной постоянной:
Рис. 5.7. Деформация при растяжении в состоянии ползучести.
или
с — —ь0п
dt —ка*
s. = Аев°.
(5.10)
(5.11)
Фазу неустановившейся ползучести можно объединить с мгновенной пластической деформацией, появляющейся при приложении нагрузки. Эту деформацию представляют с помощью зависимости типа
(5.12)
*) Мы применяем здесь обозначения для составляющих деформации, принятые в книге Л. М. Качанова [5.3], 1960.
**) Значения их приведены, например, в «Справочнике машиностроителя», изд. 2-е, т. 3, 1956, стр. 290.
206 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [ГЛ. V
включающей параметры материала kx и т\ при этом напряжение а считается зависящим от t. Так как эта деформация является необратимой, то в случае разгрузки коэффициент kx надо считать равным нулю. Скорость деформации для этой фазы равна
ер = m£1om1=mklGnt~le. (5.13)
Во многих случаях принимают т = 2.
Если учитывать все составляющие деформации, то скорость е можно представить в виде
s = —g- g —— rasa -f- kon\ (5.14)
здесь принято r = mk1 и s = m—1. Принимая во внимание только упругие деформации и установившуюся ползучесть, получим:
ъ=-о-\-коп. (5.15)
Считая п— 1, мы придем к известному уравнению Максвелла для скорости течения упруго-вязкой среды:
* = 4- + ?- №16)
где [х — коэффициент вязкости. Поведение такой среды может быть описано с помощью механической модели, представленной на рис. 5.8. Она состоит из пружины, жесткость которой отвечает модулю материала Е, и поршня; последний движется в цилиндре с жидкостью. Оба эти элемента, упругий и вязкий, соединены последовательно и нагружены постоянным усилием, пропорциональным о. Скорость деформации этой системы отвечает формуле (16).
Формулам типа (8) и (9) придают также вид
ес = А>Л1/г (5.17)
или
ес = лЛ1/т (5.18)
при 7> 1; это дает возможность учесть одновременно первичную и вторичную фазы ползучести.
Мы привели некоторые соотношения, описывающие процесс ползучести. Уравнения (8), (9) или (17), (18) связывают деформацию ползучести с напряжением и временем. В более общем виде
г
Рис. 5.8. Механическая модель упруго» вязкой среды.
ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ
207
эту зависимость можно представить следующим образом:
Ф (ес> о. 0 = 0.
(5.19)
где Ф — некоторая функция величин ег, а и t. Уравнение (19) соответствует так называемой теории старения в ее деформационном варианте. Название теории объясняется тем, что с течением времени механические свойства материала меняются, он «стареет». Можно также предложить другой вариант теории, связывающий скорость изменения деформации ползучести, ес, напряжение и время:
его можно назвать вариантом течения. В обоих уравнениях (19) и (20) явно содержится время t. Недостаток этих теорий заключается в том, что при описании отдельных участков процесса ползучести надо учитывать, от какого момента отсчитывается параметр времени; иными словами, уравнения не являются инвариантными относительно начала отсчета времени
Другая теория ползучести — так называемая теория упрочнения— описывает деформацию с помощью уравнения
где а, р, 7 — параметры материала *). В это уравнение параметр t явно не входит, но оно позволяет установить закон изменения гс во времени.
Эксперименты со сжатыми стержнями, подвергающимися ползучести, проводят обычно с помощью специальных установок, в которых автоматически обеспечивается постоянство усилия и температуры либо изменение этих величин по заданному закону. Как показывают опыты, процесс ползучести сжатого стержня завершается явлением быстрого выпучивания с резким нарастанием стрелы прогиба **). Напряжение в стержне, которое считается постоянным, может быть значительно меньше критического напряжения, соответствующего данной температуре при «мгновенной» деформации.
*) Во многих работах вместо гс здесь фигурирует пластическая деформация, объединяющая деформацию ползучести с мгновенной пластической деформацией (см. [5.3]). Параметры, соответствующие уравнению (21) для дюралюмина Д16Т, приведены в статье Н. Г. Торшенова [Журн. прикл. мех. и техн. физ., № 6 (1961), 158—159].
**) Описание таких экспериментов дано чиже, в главе XVII, См. такж работу [5.4].
Ф (ес, а, 0 = 0;
(5.20)
Ф (ес. ес. о) = 0.
Подобное уравнение может, например, иметь вид
(5.21)
(5.22)
208 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
Теоретические исследования в этой области велись лишь на протяжении последних 10—15 лет*), и их нельзя еще считать завершенными. Познакомимся с основными направлениями этих исследований.
§ 61. Критерии выпучивания при ползучести
В литературе предложены различные критерии устойчивости при ползучести. Рассмотрим сначала те, которые относятся к совершенным элементам конструкций, для которых основная равновесная форма сохраняется вплоть до момента выпучивания.
Один из вариантов статического решения задачи заключается в следующем **). Допустим, что известна зависимость между полной деформацией, напряжением и временем по той или иной теории ползучести. Построим изохронные кривые о (е) для фиксированных моментов времени /0, tv
• (рис. 5.9). Условно примем, что критическое напряжение определяется по формуле касательного модуля для изохронных кривых
Рис. 5.9. Изохронные диаграммы сжатия при ползучести.
п2Ек
-кр-
\2
или
(5.23)
(5.24)
где аэ — эйлерово напряжение, равное ъ2Е[к2\ эффект разгрузки здесь не учитывается. Основное напряжение сжатия а, действующее в стержне, считается заданным; принимается о* < оэ. Через некоторый промежуток времени напряжение а* по предположению оказывается критическим: о* = акр. Следовательно, в момент выпучивания касательный модуль должен стать равным
ЕК = - = — Е.
к dz о*
(5.25)
Отложим по оси абсцисс рис. 5.9 величину еэ = оэ/Е, а по оси
*) Они принадлежат А. Р. Ржаницыну [5.7], [0.9], Ю. Н. Работнову [5.6], [21.8а], С. А. Шестерикову [5.11], В. И. Розенблюму [5.8], Хоффу [5.14], Джерару [5.13] и другим.
**) Подобный путь был предложен Шенли [0.22].
КРИТЕРИИ ВЫПУЧИВАНИЯ ПРИ ПОЛЗУЧЕСТИ
209
ординат о. Величина модуля Ек по (25) характеризуется углом а наклона линии ОА. Изохронные кривые пересекают линию о* под разными углами. Выпучивание, очевидно, произойдет в тот момент (на рисунке t2), когда касательная к кривой о(е), проведенная на уровне о*, станет параллельной линии ОА. Период времени t2 по этой теории и будет критическим. Итак, первый подход к задаче соответствует касательно-модульной теории.
Во втором случае в качестве основного критерия выбрана критическая деформация *). Принимается, что элемент конструкции теряет устойчивость при определенной полной деформации независимо от того, является ли она упругой или упруго-пластической, и от того, какими факторами она вызвана. Если вернуться к рис. 5.9, то по этой теории выпучивание стержня должно иметь место в тот момент (на рисунке /3), когда изохронная кривая о (е) пройдет через точку А\ последняя как раз соответствует эйлеровой критической деформации еэ. Очевидно, критическое время по этой теории окажется всегда большим, чем по касательно-модульному варианту. Угол а характеризует наклон секущей для диаграммы а(е), поэтому мы, по существу, пользуемся секущим модулем Ес, считая критическое напряжение равным
Отметим, что формула типа (26) может быть выведена с помощью деформационной теории пластичности в применении «к некоторым случаям упруго-пластической теории устойчивости пластинок и оболочек (см. главы VII и XI).
Третий критерий устойчивости является динамическим **); он сводится к исследованию движения стержня, происходящего в результате некоторого малого возмущения. Составляется уравнение, связывающее стрелу прогиба со временем; после линеаризации этого уравнения ищется условие, при котором стрела прогиба остается ограниченной.
Наконец, четвертый подход к задаче относится к несовершенной системе и распространяет на случай ползучести критерий начальных неправильностей ***). Допустим, что ось стержня до деформации слегка искривлена либо что усилие приложено с некоторым эксцентриситетом. Тогда в различных сечениях стержня будет с самого начала действовать не только осевая сила, но и изгибающий момент. В процессе ползучести деформации будут возрастать — как на вогнутой, так и на выпуклой стороне искривленного стержня. Но
*) Этот подход был предложен Джераром [5.13).
**) Он был предложен Ю. Н. Работновым и С. А. Шестериковым [5.6].
***) Такой подход был развит в работах Хоффа [5.14] и других авторов
210 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [ГЛ. V
деформации эти не будут одинаковыми, так как скорость ползучести зависит от уровня напряжения в данном волокне. Поэтому произойдет увеличение кривизны изогнутой оси, что в свою очередь связано с возрастанием изгибающего момента и напряжений в различных волокнах. Это приведет к быстрому нарастанию прогибов, равносильному явлению выпучивания стержня. Критическое время можно здесь условно определить, выбрав некоторое предельное значение для стрелы прогиба стержня либо для скорости возрастания прогиба. В не которых же случаях удается найти «истинное» критическое время по истечении которого скорость возрастания прогиба становится бесконечно большой.
Познакомимся более подробно с каждым из критериев устойчивости.
§ 62. Методы расчета по касательному и секущему модулям
Рассмотрим первые два подхода к задаче об устойчивости стержня, используя теорию старения и принимая закон ползучести в виде
e = -g4~kont. (5.27)
Найдем соотношение между изохронными приращениями е и а: йг = -f- ktiGn~lt do
или, по (27),
de = [ + T(s-!)K (5-28)
Введем касательный модуль Ек = do/dz, тогда соотношение (28) примет форму
fW+тК1—;)• <5-29>
Далее, по (25), принимая о = и е = е, получим:
£* J I q* / j L\
аэ п ' аэ \ п) *
Введем обозначения:
вЕ — а -
тогда уравнение (30) примет вид
S = o,+l(l-of). (5.32,
(5.30)
(5.31)
§ 62] МЕТОДЫ РАСЧЕТА ПО КАСАТЕЛЬНОМУ И СЕКУЩЕМУ МОДУЛЯМ 211
Мы пришли к простой зависимости между параметрами деформации и напряжения, характеризующими момент выпучивания. Построим график о(е) и отложим по осям отрезки, равные 1 (рис. 5.10), и, роме того, по оси абсцисс отрезок 1/я, тогда получим линии ОМ КМ. Проводя горизонтальную прямую на уровне с*, находим е*. дин из участков этого отрезка —
0 линии ОМ — характеризует гновенную деформацию, равную а*,
второй — деформацию ползучести
1 — oj/л. Чем ниже уровень нафяжения, тем больший удельный *ес будет иметь деформация получести *).
Исходя из (32), можно и непосредственно определить «критическое время» t*. Представим (27) в виде
-1
е = о-\- Ekoni<3э По (32) получим:
_1 1-51
п Eka%v\
пп—\
(5.33)
(5.34)
Рис. 5.10. К расчету по «касательномодульной» нагрузке.
Примем, далее, закон ползучести в более общем виде (19) и введем обозначения:
дФ
= v,
дФ
да
= Х.
Тогда находим:
X da —j- v d отсюда, идя тем же путем, находим:
1
Е ~ *
В нашем примере было
X/v = — kmn Ч\
(5.35)
(5.36)
(5.37)
(5.38)
исходя из (37), снова приходим к (34).
Формула (37) относится, в частности, к зависимости (17) с коэффициентом у Ф 1. При определении критического времени по формуле типа (34) следует вместо /* подставить 4/т.
*) График такого типа был предложен в работе [5.6].
212 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИВ ПРИ ПОЛЗУЧЕСТИ [гл, V
Обратимся ко второму варианту решения задачи и примем в качестве критерия устойчивости полную деформацию; тогда во всех случаях должно быть
е* = -> е.= 1. (5.39
На графике рис. 5.10 критической деформации будет отвечать вер тикальный отрезок MN. Из частного закона (27) вытекает формул для критического времени
t,= 1~а* (5.40
EkoSо»1 V
Таким образом, период времени до выпучивания по теории критической деформации получается при ]=1 в п раз больше, чем по касательно-модульной теории. При f Ф I по (17) надо в (40) снова заменить t* на £J/t.
§ 63. Динамический критерий
Рассмотрим, далее, возмущенное движение стержня, исходя из теории упрочнения и считая по (21) Ф(е, ес, о) = 0. Введем обозначения типа (35) и примем здесь условно ес неваръируемой величиной. Тогда получим по-прежнему
(Ек — v) do + Zfv de = 0. (5.41)
Согласно закону плоских сечений 8е = ъу, где х—кривизна изогнутой оси стержня, у — расстояние от нейтральной оси до некоторой точки сечения. Интегрируя по площади сечения, придем к соотношению
(Ек — v) М + Ehх = 0 (5.42)
или
(ia-v)-*™+E/v*®=0. (5.43)
где v — прогиб. Считая, что «погонная нагрузка» q = д2М/дх2 соот¬
ветствует сжимающим усилиям oF и силе инерции, найдем:
-(Ек-,)(»f 0 + iF) + £/»g_°. (5.44)
Примем для шарнирно опертого стержня
тогда будет
v = x(t) sin, (5.45)
(v — Ек) x -)- [fXo -f- v (o — o)] x = 0. (5.46)
ДИНАМИЧЕСКИЙ КРИТЕРИЙ
213
(5.47)
Частота колебаний обращается в нуль при
ЕХа -f- у (о9 — g)
v — EX *
отсюда
1
°* X 9
1 — Еv
что по форме совпадает с (37).
Воспользуемся для примера зависимостью
ф = е*ес — ке°/А = 0. (5.48)
Находим:
Х = те°/А* v = — е°/А. (5.49)
А £с
Отсюда по (47)
■+%
(5.50)
Критическое значение безразмерной деформации ползучести будет
(551)
<*э
Отсюда можно сделать заключение, что динамический подход в применении к теории упрочнения приводит снова к касательномодульному критерию. Отметим, что приведенный здесь вывод содержал, по существу, те же выкладки, что и в § 16, но для упругопластической задачи, без учета эффекта разгрузки.
В статье Ю. Н. Работнова и С. А. Шестерикова [5.6] содержалась иная, более обоснованная трактовка динамического критерия, хотя конечные зависимости имели тот же вид. Эти авторы считали вначале ес варьируемой величиной и получали вместо (46) уравнение третьего порядка для т. В более поздней работе [21.8а] Ю. Н. Работнов предложил другой вариант вывода аналогичных зависимостей — квазистатический.
Допустим, что в некоторый момент процесса ползучести стержень переведен в смежное изогнутое положение и предоставлен самому себе. Если характерный прогиб v после этого начнет уменьшаться, то критическое состояние не достигнуто. При возрастании прогиба критическое состояние будем считать превзойденным. Следовательно, об устойчивости можно судить по знаку скорости v. В том же случае, если стержню придана начальная поперечная скорость vt то об устойчивости следует судить по знаку ускорения v. Обсуждение критериев устойчивости при ползучести содержится также в работах Г. В. Иванова [21.5а] и Л. М. Куршина [5.5].
214 влияние температуры, продольный изгиб прй ползучести [гл. V
§ 64. Критерий начальных несовершенств
Примем, что до нагружения стержень имеет некоторую начальную погибь (рис. 5.11)
v0 = v0(x). (5.52)
Приложим к стержню центральную сжимающую нагрузку, лежащую ниже эйлеровой силы Рэ; тогда прогибы различных сечений сразу
возрастут. Обозначая через v(x) дополнительный прогиб, найдем
изгибающий момент в произвольном сечении:
My=P(v + v о). (5.53)
Дифференциальное уравнение (1.178) перепишем в виде
d2v, Р Р /с _,ч
17 v ~ ~ W v°' (5.54)
Разложим функцию гС*) в ряд по синусам:
s
Vo(x) = 2 а< sin ’ (5-55)
/ = 1
ограничиваясь первыми 5 членами ряда. Решение уравнения (13) будем искать в виде
v(*) = 2dnip-. (5.56)
i = 1
Подставляя последние выражения в (54), найдем:
Рис. 5.11. Сжа- ’ (5-57)
тый стержень —- 1
с начальной Р
погибью, под- где p(J) есть ЭйЛерова сила: вергающиися *
ползучести. D(/j i2%2EI
э — I2 •
(5.58)
Напряжения в некоторой точке поперечного сечения будут
Р Р (у + v0) у
(5.59)
где через у обозначено расстояние до центральной оси; сжимающие напряжения считаются положительными. Далее совершится первый «пластический» шаг деформации стержня *). Допустим, что зависи¬
*) Приведенный здесь метод расчета «шаг за шагом» был предложен Лином [5.20J.
§ 64] КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ 215
мость между деформацией ползучести и временем задана в виде
= О* (5.60)
Примем интервал времени равным At и вычислим Аес для различных точек поперечных сечений; практически приходится ограничился некоторым числом точек (например, пятью или семью) в нескольких сечениях по длине стержня (трех или пяти), напряжения в этих
точках предварительно определяются по (59). Совместно с пластическими деформациями происходят упругие, связанные с приращениями напряжений соотношением
Ao = £Aetf. (5.61)
Полные изменения деформаций в некотором волокне равны
Asj = Аес-—As; (5.62)
они должны удовлетворять закону плоских сечений. Если обозначить приращение деформации волокна, проходящего через центры т*ж> сти сечений, через As0, а изменения кривизны через Ах, то приращение деформации произвольного волокна, удаленного от центра
тяжести на расстояние у, будет
Aej = Ае° — Аху. (5.63)
Вместо (61) имеем:
Ао = £(Ае° — А ку — ДеД (5.64)
Составим выражения для изменений осевой силы и изгибающего момента в произвольном сечении:
ДР= f До dF=E Де0/7 — Е J scdF, (5.65)
F F
АМ=— J Асу dF = EI Ах Е j scydF. (5.66)
F F
Так как статический момент относительно центральной оси равен
нулю, то при составлении (65) и (66) соответствующие выражения
выпадают; под I понимается момент инерции сечения относительно центральной оси.
По предположению осевая сила считается неизменной, так что АР =9 0; отсюда получаем:
Дг° = -±fecdF. (5.67)
F
Составим дифференциальное уравнение для функции приращецця
216 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [ГЛ. V
прогиба Дг/(лг). Изменение кривизны равно
d2 Дг/ dx2
с другой стороны, имеем:
ДМ = Р Av. (5.69)
Таким образом, по (66) получаем:
(РДи, Р
dx* ' EI
д W dFj • (5-70>
Уравнение (70) имеет ту же структуру, что и (54); для интегрирования его применяем прежний прием. Разложим выражение, стоящее в скобках и имеющее размерность [см], в тригонометрический ряд:
S
- A f *cydF = % Аа( sin(5.71)
F 1 = 1
Представляя решение уравнения (70) в виде
S
Av = Дbt sin, (5.72)
1
найдем по-прежнему
<5-73>
-т--'
Таким образом определяются приращения коэффициентов Ъь в разложении (56) для функции прогиба v; зная их, находим новую упругую линию. Стрела прогиба после первого шага получит приращение
s
A/ = 2Adis,nT- = Ai — Д*з+Д*5— ••• (5.74)
1 = 1
Пользуясь (72), определим изменение кривизны в каждом из рассматриваемых сечений:
А d2 Av V4 /2те2. inx /е
Дх — dx2 — I J2 in j • (5.75)
/-1
*
Изменение деформации волокна, удаленного на расстояние у от центра тяжести, вычисляем по (63), а приращение напряжения — ПО (64). Новые полные напряжения будут равны
0 = о —J— До, (5.76)
КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ
217
Переходя ко второму шагу, рассматриваем следующий отрезок времени по (60) определяем изменения пластических деформаций Дес, отвечающие напряжениям av и т. д. Продолжая этот процесс, находим зависимость между стрелой прогиба стержня и временем. Непосредственно после приложения нагрузки напряжения распределяются в сечении по линейному закону (59). Однако по мере развития пластических деформаций эпюра напряжений в любом сечении будет все более отходить от прямой линии.
Пример 5.1. Дюралюминовый стержень длиной / = 21,4 см прямоугольного поперечного сечения (Ь = 2 см, h = 0,8 см) с шарнирно опертыми концами подвергается действию центральной сжимающей силы Р — 500 кг при температуре 300° С. Осевая линия изогнута до приложения нагрузки по полуволне синусоиды:
v = 0,01 sin см. (а)
При t° = 300° С считаем модуль Е = 4 • 105 кг/см2. Определить зависимость стрелы прогиба от времени с учетом упругих деформаций и установившейся ползучести; для заданной температуры закон ползучести представляем в виде
е, = 5.1(Г12Л, (Ь)
причем с измеряется в кг/см2, a t — в часах.
Радиус инерции сечения равен
i = W = 0,232 см.
/12
Гибкость стержня составляет
К = — = - — 92
/ 0,232
Эйлерово напряжение равно
тс2 • 4 • 105 °э = -=470 кг/см2;
ему соответствует нагрузка
pW = <зэР = 470 • 1,6 = 750 кг.
Разобьем длину стержня / на шесть равных частей, а высоту сечения h — на четыре равные части. Определим напряжения в каждой из пяти точек с координатами
По формуле (57) находим стрелу дополнительно прогиба:
а, 0,01
218 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГЙВ ПРЙ ПОЛЗУЧЕСТИ [ГЛ. V
Полная стрела прогиба равна/ = 0,03 см. Напряжения определяются по (59):
._4[,+ ><«! + *!>*],
ИЛИ
о = 310 (l +0,56у sin (С)
Пол}чзнные по (с) значения а выписаны в первой строке таблицы 5.1.
Первый интервал времени выберем равным 30 минутам. Находим пластические деформации кгс по (Ь), подставляя t = 0,5 и значения напряженлй (с). Величины Дес • 105 даны во второй строке таблицы. Далее находим удлинение осевой линии по (67), используя в каждом случае формулу Симпсона:
-i- /*e‘Wr=-jj('*A_+ 4«А_+2е0+4в_+£_ (d)
F \ 2 4 4 2/
индексы у, j и т. д. соответствуют координатам точек сечения. Значения Де занесены в третью строку таблицы.
Определим интеграл (71) для рассматриваемых сечений, пользуясь той же формулой:
Е Г 4 • 105 • 2 • 0,8 / h h h h\
p J tcydF — 500-12 E‘ 2+ 14.14 e_±2)’
p \ 2 4 4 2 /
(e)
ИЛИ
£ h <2 г л \ 2 T “T _ Т/
По выражению (f) получена следующая строка таблицы. Пользуясь этими данными, мы должны определить коэффициенты тригонометрического ряда (71) Да/ при /, меняющемся от 1 до 6. Так как функция симметрична относительно точки х = //2, то величины Да/ с четными индексами равны нулю.
Таким образом, будет
Е Г А тъх а Зпх, А 5пх. ч
~~~Р I gcydF= sm + Дд3 sin —j l»Aa5sin —j—. (g)
F
Заметим, что для всех точек концевых сечений а = const = Р/F. Но тогда в этих сечениях и =г const, так что интеграл (71) обратится в нуль. Окончательно для точек 0, 1,..., 6, отстоящих на //6 одна от другой, получаем следующие значения функции (умноженные на 105):
у = уб = 0, У\ ==г у5 = 360, Уг = У4 = 760, у3 = 900.
Дополняя интервал 0 <;.*:<;/ участком /<;.*<; 2/, будем иметь следующие шесть точек с ординатами у7 = уи= — уи у8 = у10 = —у2, у9 = — Уз- На-
IгсУ dF==~
F
Таблица 5.1
§ 64] КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ 219
II
<м
1
00
о со 8 -*
7,90
900
37,5.
22,9
9,1
36,4
416
1
348
10,5
15.4 4,9
19.5 368
О
о ГС
СО
7,9
0,45
1,7
312
•si
276
5,25
0,4
—4,85
—19,5
256
Jg <N
240
3,45
—7,1
—10,6
—42
198
— оо
II
Ч
< <N 1
372
12,9
7,75
760
32,3
20,7
9,8
39
411
•Si 1
340
9,85
14,3
4,45
17,8
358
о
010
7,75
0,3
1.2
311
•si
280
5,50
1,25
—4,25
—9
217
•st <м
250
3,90
—5,25
—9,15
—36,6
213
ч®
II
н
•si <м 1
348
10,5
7,60
360
17,4
СО г-н_ Tt
СО
•ss r 1
щ. 00 00 со
г—1 со СМ ci of
8
о
310
7,45
7,60
0,15
0,6
311
293
6,30
4,10 —2,2 —8,8 284
•s; <n
275
5,20
0,60
—4,6
—18,5
256
Сечение
Координаты
Cl
3 о
го
* * Ui
О <1
ю
О
<1
>ч
ю
S «ч а. о I S
<3 v <1
CVJ
Ю Ю г! 2 2 ■§■ * g ш а) Ь
<1 <3 <1 о
220 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
ходим коэффициенты А а/ по формулам Бесселя (при числе участков, равном 12, на длине 21)
и
>Даг = V
6
о
В нашем случае получим:
1ПП /1-4
У‘ Sln “R-' (h)
Ла‘= ■§■ (4у‘sin if+4уг sin •
Да3 = 1(4У1—2у3),
Aa® = т(4у 1 sin 7Г~ 4уг sin Т“2уз) •
Подставляя значения ординат, имеем:
Ьах = 855/ 10~5 см, Аа3 = — 60 • 10-5 см, Аа6 = — 16,5 • 10“5 см. Теперь по (73) можно определить приращения Д:
д», - —-А-1- ■= 855 • 10~5. = 1710.10-ж,
(0
750
Я 500
— 1
д«з 60 -КГ5. 1Л_5
Дз = ——— = = — 5-10 см,
/><3) 9-750
э
Р 500
о-5
см.
и,—**! Pi51 25 - 750
э
Р 500
Изменение кривизны в каждом сечении определяем, пользуясь формулой (75). Так, например, для сечения х = //6 имеем:
а /и *2 ■ 11 I it тс 25те2. 5тс\
Д% = Д6 -р sin g—f- Д*з sin -j + Д*6 —р- sin -g-j =
= 2fr (0,5 Д,+9Д63 + 12,5 Д*5) = 17,5 • Ю5.
Таким же путем вычисляем значения Ах для сечений х = 1/3, х — //2; они выписаны в таблице 5.2. Зная Ах, мы можем по (23) найти полные деформации е j в каждой из рассматриваемых точек. Так, например, для точки с координатами х = //6, у = Л/2 получаем:
Ае, • 105 = 7,6 — 17,4 • 0,4 = 0,6.
В таблице 5.2 помещены приращения полных и упругих деформаций Де* = = Де, — Агс для каждой точки. Здесь же даны приращения напряжений Да = Е Де* и полные напряжения, имеющие место к концу 30-й минуты: о! = о + Да. Стрела прогиба получает приращение Д6, = 1710 • 105 см и, следовательно, составляет
/, = /+ Д, = 0,0471 см.
§ 64] КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ 221
Таблица 5.2
h
h
h
h
Координаты у
Т
Т
0
4~
2
Интервал 0—30 мин
кг/см2
240
276
310
348
380
£с' Ю5
3,45
5,25
7,45
10,5
13,8
«о • 105
7,90
i—L СyuedF\w
900
\ F /
1% • 105
39
Atc-105
—7,6
0,15
7,90
15,7
23,4
i-105
—10,1
—4,4
0,45
5,2
9,6
Аа, кг/см2
—40
—16
1,8
21
38
flt СМ
0,048
Интервал 30—60 мин
Dj, кг/см2
200
260
312
369
418
• 105
2,0
4,4
7,56
12,6
18,3
1>
СО
о
1 о
СЛ
8,80
f-Л- fyfrcdpyw
1570
К Р J
in • 105
68
К-10*
—18,2
—4,7
8,8
22,3
35,8
\ге ■ 10»
—20,2
—9,1
1,24
9,7
17,5
Уз, кг/см2
—81
—36
5,0
39
70
f,, см
0,079
222 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
Продолжение
h
h
h
h
Координаты у
Т
т
0
А
~т
Интервал 60—90 мин
о, кг/см2
119
224
317
408
488
• 105
0,42
2,8
8
17
29
Де° • 10s
10,6
(-■i f yedA-w
2740
\ P J
>
s
о
СЛ
118
Агс • 105
—36,4
—12,9
10,6
34,1
57,6
Аге • 105
—36,8
—15,7
2,6
17,1
28,6
Да, кг/см2
—147
—63
10
68
114
/з, см
0,134
Интервал 90—120 мин
а, кг/см2
—28
161
327
476
602
Ьгс • 105
—0,005
1,04
8,75
27
54,5
>
со
о
о
СЛ
16,0
Л-4 ГуА.Л.10*
5120
\ р ;
Ах • 105
220
Агс. 105
—72
—28
16
60
104
Аее • 105
—72
—29
7
33
50
Да, кг/см2
—284
—126
28
132
200
/4, см
0,236
§ 64] КРИТЕРИЙ НАЧАЛЬНЫХ НЕСОВЕРШЕНСТВ 223
Продолжение
h
h
0
h
h
Координаты у
2
4
4
~Y
Интервал 120—150 мин
4, кг/см2
*c-io5
—312
—7,6
35
0,01
355
11,2
608
56
802
129
u° ■ ios
32
/—-f- f У cdt\-105
11600
\ F /
Ay. ■ 105
500
Дс • 105
—168
—68
32
132
232
Дее • 105
—160
—68
21
76
103
Да, кг/см2
—640
—272
84
304
412
U см
0,468
а5, кг/см2
—952
—237
439
912
1214
Судя по таблице 5.1, в данном случае, когда исходная изогнутая ось стержня была полуволной синусоиды, можно принять, что и вновь полученная упругая линия является полуволной синусоиды. Иными словами, мы могли бы вести вычисления только для среднего сечения, считая Аахф0 и да3 = Ааь = 0; тогда величина Аах находится по формуле
Дя,= — -jr f уДtcdF, (k)
F
причем интеграл относится именно к среднему сечению. Это дает в нашем примере Adi = 900 • 10“5. Отсюда
900•КГ5
А Ьх
750 1
500
Изменение кривизны в сечении х = //2 теперь будет
Ду. = ~ Д6, = 39 • 10-5
224 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
вместо ранее полученной величины 37,5 • 10”. Новые значения деформаций и напряжений для среднего сечения представлены в таблице 5.2. Как видим, принятое нами допущение вполне приемлемо. Поэтому продолжим вычисления для следующих интервалов времени: от 30-й минуты до 60-й, 6т 60-й до 90-й и т. д., считая, что упру гая линия остается полуволной сину соиды. Результаты вычислений прь ведены в той же таблице 5.2.
На рис. 5.12 изображено изма нение стрелы прогиба во времени Величина / быстро растет; можн считать, что в течение 150 мину несущая способность стержня буде исчерпанной. Эпюры распределений напряжений по высоте среднего се чения представлены на рис. 5.13 Как видим, неравномерность распределения напряжений усиливается на каждой ступени. Таким образом, данный критерий приводит к значению критического времени, приблизительно равному
= 2,5 часа.
Определим критическое время для того же примера, считая стержень 380 418 488 602 802 1214
Рис. 5.12. Изменение стрелы прогиба / при ползучести (/— в см, t—в часах).
f
240
Рис. 5.13. Эпюры распределения напряжений в различные моменты времени.
не имеющим начальной погиби и пользуясь первыми двумя критериями выпучивания. Основные параметры равны
оэ = 470 кг/см2, в = = 0,67, k = 5 • 1012, п = 3, Е = 4 • 105 кг/см2,
причем t измеряется в часах.
Воспользуемся касательно-модульной теорией. По формуле (34) находим:
1 1—0,67
3 4 • 10® • 5 • 10“12 • 0,673 • 4702
- = 0,83 часа.
Если, далее, воспользоваться теорией критической деформации, то по (40) получим:
= 2,5 часа.
Совпадение со значением, найденным для стержня с начальной погибью, является, конечно, случайным.
§ 65] критическое время в СЛУЧАЕ ДВУТАВРОВОГО СЕЧЕНИЯ 225
§ 65. Формулы для критического времени в случае двутаврового сечения
Рассматриваемая нами задача может быть решена и иным путем для «идеализированного» двутаврового сечения *), состоящего из двух одинаковых полок, соединенных тонкой стенкой высотой h (рис. 5.14). Момент инерции сечения будем считать равным
радиус инерции равен /=/г/2.
Рассмотрим сечение стержня на расстоянии х от левого конца. На рис. 5.15 изображена одна из его частей в изогнутом положении. Обозначим через ах напряжение в полке, находящейся на вогнутой стороне, а через о2 — напряжение в полке, лежащей на выпуклой стороне. Условие равновесия в проекциях на ось х дает
(oj -)- а2) = Р* (5.78)
где Р — сжимающая сила, принимаемая нами постоянной. Определяя
Рис. 5.15. Силы, действующие на отсеченную часть сжатого стержня.
моменты относительно центральной линии сечения (рис. 5.15), найдем:
(°i -<з2)~- = М = Pv, (5.79)
где М — изгибающий момент, равный произведению силы на прогиб v. В настоящем параграфе под v понимается полный прогиб
*) Решение, приведенное здесь и в следующем параграфе, принадлежит Н. Хоффу [5.14].
II
Рис. 5.14. Сечение двутавра с тонкой стенкой.
(5.80)
226 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [ГЛ. V
в сечении х. Сопоставляя (77) и (79), найдем:
Примем зависимость (14) между скоростью деформации и напряжением, исключив вначале мгновенные пластические деформации и
первичную фазу ползучести. Тогда будет
e = i- o+fto*; (5.81)
показатель степени п будем считать нечетным. Для полки на вогнутой стороне получим (при Р = const):
2Р dv. и(Р\п(л, 2v\n, /е ооч
Sl EFh dt \FJ \ h) ' (5.82)
для второй полки
2 Р dv
EFh dt
Выразим кривизну изогнутой линии стержня через деформации волокон, принадлежащих полкам:
Учитывая зависимость
находим:
е1 — е2 х— h *
(5.84)
d2v
7 дх2'
(5.85)
d2v
дх2 h *
(5.86)
Дифференцируя левую и правую части по t и подставляя (82), (83), получим:
d3v 4 Р
дх2 dt ~ EFh2
В дальнейшем примем п = 3. После простых преобразований с учетом (87) придем к основному дифференциальному уравнению задачи:
d3v. Р dv -,, / Р \3 1 /Q v.. v3 \ п /к ооч
дх2 dt + El dt kyF) Л \3 A + Л3 ) ’ 5-88
Это уравнение является нелинейным. Допустим, что концы стержня оперты шарнирно и что изогнутая линия является полуволной синусоиды:
v = f(t) sin. (5.89)
§ 65] КРИТИЧЕСКОЕ ВРЕМЯ В СЛУЧАЕ ДВУТАВРОВОГО СЕЧЕНИЯ 227
Подставим (89) в уравнение (88) и проинтегрируем его по методу Бубнова — Галеркина; получим:
i
. пх, Р df. пх, л и (р\9 1 (о f. и,
dt 12 sm / ~b~ EI dt Sin I + * (F) h\h sin ~l I
0
I + 4 p- sin3 sin dx = 0. (5.90)
Вычислим интеграл
i
J (5.91)
0
тогда вместо (90) будем иметь:
f(-_p)-m(4)-(z+5)=0. (5.92)
Подставляя вместо I выражение (77) и деля на F, получим следующее дифференциальное уравнение относительно /:
(с3-О) § = (5.93)
где оэ — по-прежнему эйлерово напряжение. Здесь введен знак полной производной, так как стрела прогиба / зависит только от времени.
Вводя безразмерный параметр прогиба С = //Л, получим:
dt ~ Т+Р ' 5‘94)
Будем считать, что в момент времени / = 0 относительная стрела
прогиба равна С = Cq = fo/h. Интегрируя уравнение (94) для проме¬
жутка времени от 0 до t, найдем:
с
<Ja <3
t =
fwrm- (595)
3Eke*.1 С (1 + С4) '
Со
Как легко убедиться непосредственным дифференцированием, входящий сюда интеграл равен
/сгЬг='”тт- (5-96)
Выражение для t принимает вид
а9 — а С2 1 + Cq
1 и ! /К 07\
228 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
Таков промежуток времени, необходимый, чтобы стрела прогиба стержня возросла от значения С0 до С. Определим время t, при котором прогиб сделается бесконечно большим, и будем считать его критическим. Полагая в (97) С->оо, найдем:
'•=-£г?-сГ- <5-М)
Это выражение можно упростить, если считать, что начальная стрела прогиба мала по сравнению с высотой сечения тогда будет
In Со. (5.99)
6Eka3
Иной результат мы получим, если характеристика ползучести материала является линейной, т. е. если показатель степени в (81) равен единице. Считая в зависимости (87) п= 1, придем к линейному дифференциальному уравнению
dsv, Р dv,, Р п. /с 1ЛЛЧ
“Ь ~~рт Т v — 0. (5* юо)
дх2 dt El dt Принимая v в форме (89), получим:
(P,-P)% = kEPf. (5.101)
так что скорость возрастания / пропорциональна самой величине /. Интегрирование (101) дает
'=тй<5-02>
Из формулы (102) следует, что бесконечно большой прогиб может быть достигнут лишь в течение бесконечно большого времени. Поэтому в данном случае должен быть введен иной критерий для определения критического времени.
Пример 5.2. Определить критический промежуток времени для стержня двутаврового сечения с площадью сечения F = 1,6 см2, сжатого силой Р = 500 кг, так что а = 310 кг/см2. Высоту сечения h подберем таким образом, чтобы радиус инерции двутаврового сечения / был равен радиусу инерции прямоугольного сечения стержня, рассмотренного в примере 5.1: h = 2 • 0,23 = 0,46 см. Тогда гибкость стержня останется той же: \ = 92; эйлерово напряжение будет равно аэ = 470 кг/см2. По-прежнему примем /0 = 0,01 см, п = 3, Е = 4 • 105 кг/см2, k = 5 • 10 ~12. Имеем /о<СЛ; по формуле (99) находим:
ЗЮ — 470. / 1 \ 0„
= = 5- In( ) =з 3,4 часа.
6 • 4 • 10 • 5 • 10~12 • З103 \ 462 /
Мы пришли к результату, близкому к тому, который был найден численным методом в примере 5.1; здесь величина должна была получиться большей, так как мы применили несколько иной критерий выпучивания.
§ 65] КРИТИЧЕСКОЕ ВРЕМЯ В СЛУЧАЕ ДВУТАВРОВОГО СЕЧЕНИЯ 229
Формулы (98) и (99) можно для «прикидочных» расчетов применить к стержням любой формы сечения, считая гибкость фиктивного стержня двутаврового сечения равной гибкости рассматриваемого стержня.
Напомним, что для соответствующего «идеального» стержня мы нашли по касательно-модульной теории = 0,83 часа и по теории критической деформации = 2,5 часа.
Обратимся к более общему случаю, когда мгновенные деформации, появляющиеся вслед за приложением нагрузки или при последующем возрастании напряжений, не будут чисто упругими. Исходную зависимость (81)
нении (14). Как было уже сказано, введение этого члена дает также возможность учесть фазу неустановившейся ползучести. Будем принимать и здесь, что показатель степени 5 является нечетным. Новый член должен вводиться со знаком плюс в том случае, если происходит возрастание напряжений сжатия, т. е. при о > 0 и о > 0, и со знаком минус при возрастании растягивающих напряжений. При разгрузке мгновенные пластические деформации будут отсутствовать, так что для процесса разгрузки надо принимать г — 0.
Если стержень двутаврового сечения имеет легкое искривление до приложения нагрузки, то можно считать, что на первой стадии нагружения в обеих полках будут иметь место напряжения сжатия, причем на вогнутой стороне они будут возрастать (дополнительное нагружение), а на выпукло»—уменьшаться (разгрузка). Примем для et дополнительный член
это выражение надо ввести в (82); значение же е2 по (83) останется без изменений. Уравнение (87) примет теперь вид
Примем в последующих выкладках п — 3 и s = 1; значения отвечают данным опытов над некоторыми сталями, а также алюминиевыми сплавами. Кривая г (а) будет представлена в этом случае квадратной параболой
Примем v (ty х) по (89); тогда левая часть уравнения (90) должна быть дополнена выражением
мы должны, следовательно, дополнить членом r<ssat фигурирующим в урав
(5.103)
дх2 dt
dzv
4 Р dv EFh2 dt
(5.104)
(5.105)
/
<5Л06>
о
Вычисляя интеграл
или
230 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
получим вместо (92) уравнение
(•• ■— т '»’*) ж- ж 5 - 3*’’£ «+с'>- (5ЛМ)
Введем обозначения
~ гя'Е = X, 3Aa*£ = v (5.110)
и приведем (109) к виду
оэ — о — X 16 X rfC /е111.
7” С + С3 3tcv1+C2‘ ( *
Найдем интеграл
с
о. С — Со
/,
= arctg С — arctg ZB = arctg. (5.112)
Со
Вместо (96) получим теперь новое выражение для t:
оэ — в — X С2 1 +Й 16 X г г
(5Ш>
Судя по уравнению (113), эффект упругой деформации и первичной фазы ползучести сводится здесь к уменьшению времени, необходимого для достижения заданного значения С.
Скорость поперечного перемещения djdt становится бесконечно большой в том случае, если коэффициент при ней в левой части уравнения (1Q9) обращается в нуль:
,э_0_х—iixc = 0. (5.114)
Отсюда находим «критическое» значение относительной стрелы прогиба:
О-
С'=ТЖ(3э-а- (5.115)
Подставляя выражение (115) в (113), находим критический промежуток
времени t... Если принять Х = 0, т. е. предположить, что мгновенные пласти¬
ческие деформации отсутствуют, то (115) дает С*->оо, и формула для критического промежутка времени (113) перейдет в формулу (99) предыдущего параграфа.
Мы принимали здесь, что напряжения на выпуклой стороне изогнутого стержня являются сжимающими, В действительности, как
§ 65] КРИТИЧЕСКОЕ ВРЕМЯ В СЛУЧАЕ ДВУТАВРОВОГО СЕЧЕНИЯ 231
это мы видели в примере 5.1, они могут перейти в растягивающие. Тогда вместо разгрузки на выпуклой стороне мы получим уже догружение; в выражение (83) для е2 придется ввести дополнительный член, учитывающий мгновенные пластические деформации. Как видно из формул (80), величина с2 меняет знак при 2v = h. В среднем сечении напряжение изменит знак при / = /г/2 или при С = 0,5. Таким образом, все предыдущие соотношения справедливы, строго говоря, лишь для С <0,5. Если пользоваться расчетными формулами (113) и (115) при С> 0,5, то мы получим несколько преувеличенное значение t+. В одной из работ [5.14] предложена аналогичная формула, дающая преуменьшенное* значение tt; она выведена в предположении, что во всех точках полки, лежащей на выпуклой стороне, мгновенные пластические деформации растяжения возникают одновременно.
Пример 5.3. Определить критический промежуток времени для стержня, описанного в примере 5.2, принимая п = 3, s = 1, Е = 4 • 105 кг/см2, 6 = 5-10~12, г = 3*Ю”10. При таком значении г зависимость о(е) имеет вид (напряжение выражено в кг/см2)
10бе = 2,5а—1,5-10“4о2. (а)
Величины К и v составляют по (110):
X = i 3 • Ю-10 • 3102 • 4 • 105 = 5,8, v = 3 • 5 • 10-12 • З103 • 4 • 105 = 179. (Ь)
По формуле (115) критическое значение безразмерной стрелы прогиба будет
9-
С* = I6T53 (47° “ 310 ~5’8) = 15Д <с>
Мы получили С* > 0,5. Воспользуемся все же формулой (113), чтобы найти приближенное значение критического промежутка времени; найдем:
470 — 310 — 5,8 15.62 1 + (4б)
*“ 2-179 /1\* 1 +15,62
\46/ 16 5 8 15,6 ■” 46
3 arctg 15б“ = 3,34-0,1 = 3,4 часа. (d)
1 + ~ш~
Результат получился в данном случае тот же, что и в примере 5.2, когда мгновенные пластические деформации во внимание не принимались. Это объясняется тем, что мгновенные пластические деформации при заданном
значении а малы по сравнению с упругими деформациями: второй член
в выражении (а) для с составляет лишь около 2% по сравнению с первым.
232 ВЛИЯНИЕ ТЕМПЕРАТУРЫ. ПРОДОЛЬНЫЙ ИЗГИБ ПРИ ПОЛЗУЧЕСТИ [гл. V
§ 66. Сопоставление различных критериев выпучивания
Мы познакомились с различными подходами к задаче об устойчивости стержней при ползучести. Каждый из них обладает своими преимуществами и недостатками.
Критерий касательного модуля согласуется в известной мере с общей теорией устойчивости сжатых стержней при пластических деформациях. Расчетные формулы получаются простыми по структуре и позволяют использовать разные теории и законы ползучести Вместе с тем. вывод основных зависимостей этого критерия содержит некоторые допущения, требующие дополнительного анализа. Возможно, что закон ползучести, хорошо описывающий общий процесс! изменения деформации во времени, нельзя распространять на изохронные деформации, являющиеся следствием малых возмущений; особенно это относится к деформации на стороне разгрузки.
Критерий критической деформации является предельно простым с точки зрения практического применения. Однако, как уже было сказано, он не соответствует теории упруго-пластического выпучивания стержней и не имеет, по существу, определенного обоснования, являясь своего рода «догадкой». Значения критического времени получаются по этой теории в несколько раз большими, чем по предыдущей. Надо вместе с тем отметить, что имеющиеся немногочисленные экспериментальные данные довольно хорошо согласуются с критерием критической деформации *).
Динамический критерий, который мог бы служить для оценки всех других методов, разработан в настоящее время лишь в применении к теории упрочнения. Здесь он приводит практически к тем же результатам, что и «касательно-модульный» подход. Желательно найти непротиворечивые пути приложения этого критерия к зависимостям теории старения.
Наконец, критерий начальных несовершенств полностью основывается на известных соотношениях теории изгиба стержней и с точки зрения логики расчета является вполне оправданным. Однако исходные данные — характер и стрела начальной погиби — зависят от многих обстоятельств, которые трудно учесть при конструировании. Можно рекомендовать пользоваться приближенными формулами для стрелы начальной погиби в зависимости от гибкости стержня (см. главу XX) и применить статистический подход к задаче. Надо отметить также, что вычисления, необходимые для решения задачи численным методом, «шаг за шагом», являются сравнительно трудоемкими. Правда, они легко поддаются программированию для выполнения на цифровых электронных машинах, в этом случае нет
*) Об этом свидетельствуют результаты экспериментального исследования, принадлежащие А. П. Кузнецову [5.4].
§ 66] СОПОСТАВЛЕНИЕ РАЗЛИЧНЫХ КРИТЕРИЕВ ВЫПУЧИВАНИЯ 233
необходимости искать аналитические зависимости, аппроксимирующие процесс ползучести; можно непосредственно использовать табличные данные или диаграммы, полученные экспериментально.
В итоге надо рекомендовать для «прикидочных» расчетов пользоваться теорией касательного модуля или критической деформации, помня, что первая из них дает, как правило, преуменьшенные значения критического времени и определяет возможный исходный момент выпучивания. Для более обоснованного определения ресурса реального стержня следует применить критерий начальных несовершенств. Крайне важно накопить экспериментальные данные в сопоставлении с результатами расчетов.
Другое направление в теории устойчивости при ползучести, важное прежде всего для расчета бетонных и железобетонных конструкций, связано с использованием так называемой теории на* следственности, представляющей связь между полной деформацией* напряжением и временем с помощью уравнения Больцмана — Вольтерра; оно выражает влияние на процесс ползучести единичных «импульсов», действовавших в моменты времени, предшествовавшие данному (см. книги А. Р. Ржаницына [0.9], Н. X. Арутюняна «Некоторые вопросы теории ползучести», Москва, 1952 и Jl. М. Качанова [5.3]). Это направление развивается Г. С. Григоряном (Труды Ереванской конференции по теории оболочек, 1962).
ГЛАВА VI
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
§ 67. Классификация динамических задач
Все задачи, которые мы рассматривали до сих пор, являлись статическими и относились к устойчивости равновесных форм. Правда, при исследовании устойчивости стержней в пластической области, или в состоянии ползучести, фигурировали процессы, происходящие во времени; но они считались настолько медленными, что силами инерции элементов тела можно было пренебречь. Обратимся теперь к динамическим задачам, в которых необходимо учитывать ускорения элементов тела.
Одна из таких задач состоит в исследовании поведения сжатого стержня при быстром нагружении. Если скорость возрастания сжимающей силы достаточно велика, то элементы стержня не успевают переместиться в направлении, нормальном к оси стержня. Благодаря этому сжимающее усилие может достигнуть первой критической величины и даже значительно превысить ее, раньше чем прогибы достигнут заметных значений. Поскольку в таком динамическом процессе сжимающая сила может пробежать не только первое, но и более высокие критические значения, то при этом следует ожидать появления высших форм потери устойчивости. Эта особенность процесса быстрого нагружения является важной, так как связана с существенным повышением несущей способности стержня. Подобно тому как это было в задаче о ползучести, нас здесь будет интересовать критическое время, по истечении которого напряжения или перемещения достигают предельных значений, определяемых из условий эксплуатации конструкции.
При решении задач, относящихся к поведению стержня при быстром нагружении, мы будем пользоваться принципом Даламбера, в уравнение «равновесия» элемента стержня будут вводиться силы инерции. В дальнейшем учитываются, как правило, лишь силы инерции, соответствующие поперечным перемещениям (прогибам) элемен¬
КЛАССИФИКАЦИЯ ДИНАМИЧЕСКИХ ЗАДАЧ
235
тов стержня. Легко убедиться в том, что такое решение справедливо только для сравнительно быстрого, но не ударного нагружения.
Допустим, что импульсивно приложенная сжимающая нагрузка воспринимается одним из концов стержня. Примыкающие к этому концу элементы стержня будут испытывать упругую деформацию, которая начнет распространяться по длине стержня со скоростью, совпадающей со скоростью звука в материале стержня, равной
v = V т1’ <6Л)
где j — удельный вес материала. Для стали и дюралюмина эта величина составляет V = 5 • 105 с м/сек.
Примем, что отрезок времени, необходимый для распространения упругой волны по длине стержня, мал по сравнению с интересующим нас «критическим временем». Тогда можно рассматривать поперечные смещения как относительно медленные и условно принять, что сжимающая сила в каждый момент времени имеет во всех сечениях стержня одно и то же значение, передаваясь по длине как бы мгновенно.
Иначе должна ставиться задача об устойчивости стержня в случае собственно ударной нагрузки, передающейся на стержень в течение весьма короткого промежутка времени. Здесь существо задачи состоит в том, чтобы проследить процесс передачи усилий вдоль длины стержня. Иными словами, в этом случае необходимо дополнительно учитывать силы инерции элементов стержня, отвечающие продольным перемещениям.
Наряду с задачами о быстром или ударном нагружении, состоящем в однократном приложении силы, большое значение имеют также задачи, в которых сжимающая сила является периодической функцией времени. Возникающие в этом случае поперечные колебания стержня носят название параметрических. Они имеют своеобразные черты, отличающие их от обычных вынужденных колебаний. В зависимости от характера параметрических колебаний стержень может быть динамически устойчив либо неустойчив. Термин динамическая устойчивость в литературе часто связывают именно с поведением конструкций под действием периодической силы. В дальнейшем мы будем иногда применять этот термин и в более общей трактовке, распространяя его на случай импульсивного приложения нагрузки.
Промежуточное место занимают случаи, когда нагрузка изменяется не периодически, а по определенной заданной программе либо когда ее изменение отчасти задано, а отчасти зависит от поведения самой упругой системы.
236 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом НАГРУЖЕНИИ [гл. VI
Исследования, относящиеся к устойчивости упругих систем при динамическом нагружении, привлекли к себе внимание главным образом в связи с требованиями современной авиационной техники и машиностроения. Опасные для конструкций параметрические колебания наблюдались также в висячих мостах.
В данной главе мы рассмотрим задачи динамической устойчивости стержней, круговых колец и высоких балок. Говоря об устойчивости при быстром нагружении, мы будем, как правило, исследовать системы, имеющие начальные отклонения от идеальной формы, и определять развитие этих отклонений во времени. В предыдущей главе уже говорилось о том, что такой путь дает возможность определить несущую способность реальных конструкций, всегда получающих те или иные начальные дефекты при изготовлении, транспортировке, сборке. Правда, для единичной конструкции начальные несовершенства имеют, как правило, случайный характер; поэтому при разработке практических методов расчета надо пользоваться статистическими методами и данными о возможном разбросе начальных возмущений.
§ 68. Динамическое нагружение стержня. Исходное уравнение
Начнем с задачи о стержне, шарнирно закрепленном по концам и подвергающемся сжатию, силой Р, изменяющейся во времени t\ P = P(t). Примем, что стержень имеет начальную погибь; другие возмущающие факторы, например эксцентриситет в приложении нагрузки, будут как бы заменяться эквивалентным искривлением стержня.
Обозначим начальный прогиб через = v0 (л;), полный и дополнительный прогибы (рис. 6.1) будут являться функциями координаты и времени — соответственно vx(x, t) и v(х, t).
Дифференциальное уравнение изогнутой оси стержня имеет вид
Ff d*{vt—v0) _ рЛ, ьЛ.
С дх* — дх2 g dt2 ’ (-D-
где / и F — момент инерции и площадь сечения стержня. В левой части фигурирует производная от дополнительного (упругого) прогиба v = vx— v0. В правой части сила множится на производную от полного прогиба; из рис. 6.1 видно, что при вычислении изгибающего момента силу Р следует множить именно на vx. Последний член представляет собой силу инерции, приходящуюся на единицу длины стержня; здесь может фигурировать либо функция vx, либо V.
Поставим перед собой цель — определить характер движения элементов стержня при том или ином законе изменения сжимающей
§6 8] ДИНАМИЧЕСКОЕ НАГРУЖЕНИЕ СТЕРЖНЯ. ИСХОДНОЕ УРАВНЕНИЕ 237
силы во времени. Как было уже сказано, сжимающее усилие во всех сечениях стержня считается равным Р *).
Уравнение (2) выписано в предположении, что прогибы vx и v0 весьма малы по отношению к длине стержня. При рассмотрении прогибов, сравнимых с длиной, следует составить нелинейное уравнение, пользуясь точным выражением для кривизны упругой линии.
Функцию v0(xt t) можно в общем случае разложить в ряд Фурье по формам статической потери устойчивости или по формам колебаний; в случае стержня эти формы совпадают между собой. В зависимости от обстоятельств изгиба наибольшее значение может иметь форма начальной погиби с определенным числом полуволн т. Поэтому в дальнейшем мы будем принимать для v0 и vx выражения:
т %х
v0 = f0 sin ;
т= 1, 2, 3,
vx = fx sin -
(6.3)
Стрелу начального прогиба /0 считаем заданной; стрела полного прогиба fx является функцией времени: fx = fx (t). Подставим выражение (3) в уравнение (2); тогда получим:
т4 (/, — /о) — р~ m2ft = * э
ГДеР9
п2Е1
Eg %Ч dt2
I2
Рис. 6.1. Стержень с начальной погибью, воспринимаю44 щий динамиче' скую нагрузку
Если считать Р = 0, получим отсюда уравнение собственных поперечных колебаний стержня, имеющего начальную погибь:
d2fx. Eg n4Jm4 (f _ f dt2 7 HP yj \ Jo)-
Частота /я-го главного колебания равна
(6.5)
(6.6)
Частоту основного тона колебаний обозначим через k (без индекса); она равна
Г Eg_J__p*V_
Р V ч F * /
(6.7)
*) Подобная задача была поставлена И. М. Рабиновичем в 1947 г.
238 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом нагружении [гл. VI
Здесь под Р* понимается безразмерный параметр эйлеровой нагрузки (равный соответствующей деформации), под I — радиус инерции сечения, а именно:
pi=w=£-- х==т- /==/Т: (е-8>
величина V выражается формулой (1).
Полагая в (4) инерционный член равным нулю, найдем полную стрелу прогиба стержня, имеющего до загружения силой Р начальное искривление по т полуволнам и получившего дополнительный прогиб по той же форме:
/1 = /ор - (6.9)
1 —
т2Р9
Введем безразмерный параметр времени
9ir
tk = kt = Art, (6.Ю)
где Т — период основного тона колебаний; тогда исходное уравнение (4) примет вид
-L + m2m2_ = (6.11)
Используем это уравнение для решения ряда частных задач.
§ 69. Случай внезапного приложения нагрузки
Предположим, что стержень подвергается действию внезапно приложенной силы Р, которая затем остается постоянной *).
Такая постановка задачи не вполне согласуется со сделанными выше допущениями. Мы считали, что скорость нарастания сжимающего усилия находится в известных пределах, в связи с чем можно пренебречь инерцией продольных перемещений; между тем в данной задаче принимается, что в начальный момент времени сжимающее усилие по всей длине стержня возрастает мгновенно до величины Р. Однако изучение этого простейшего случая важно с методической стороны.
Воспользуемся уравнением (И), принимая следующие начальные условия:
/1 = /о- -- = ° npk tk — 0. (6.12)
*) В излагаемой здесь постановке эта задача была впервые исследована М. А. Лаврентьевым и А. Ю. Ишлинским [6.4J в 1949 г.
§ 69] СЛУЧАЙ ВНЕЗАПНОГО ПРИЛОЖЕНИЯ НАГРУЗКИ 239
Рассмотрим случай, когда Р/Рэ<т2; тогда вместо (11) получим:
+0)2/l=OT4/o( (6<13)
atk
где
ш2 = т2 [т2— J5~)' (6.14)
Интеграл этого уравнения будет
ni4
/1 = A sin <s>tk -f- В cos 10tk + /0. (6.15)
Пользуясь условиями (12), находим:
— cos (О tk\f0. (6.16)
■ 1
Мы пришли к уравнению собственных колебаний стержня около положения равновесия, характеризуемого стрелой прогиба (9).
Колебания делаются невозможными при Р/Р9 т2. При Р/Р9 = т2 получим:
=m4U (6Л7)
atk
откуда
/i = /o(l +-г **)• (6.18)
При Р/Р9> т2 уравнение (11) принимает вид
22/i==»4/0. (6.19)
atk
где
22 = т2 (-р- /я2. (6.20)
Решение уравнения (19) будет
Р1 У о- (6-21)
7W -1/
Таким образом, при PjP9m2 стрела прогиба неограниченно возрастает во времени. Как только нагрузка достигнет эйлерова критического значения Рэ, начнет развиваться форма с одной полуволной (ш= 1). При Р — 4Р9 возможно нарастание стрелы прогиба для форм с одной, двумя полуволнами (т— 1, 2) и т. д. Темп возрастания прогиба определяется величиной 22, Если при достаточно
/1=1
ch Шь
/i = l
т*Ра
т2Ра
240 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом НАГРУЖЕНИИ [гл. VI
большом числе т считать его непрерывно изменяющимся, то условие максимума 22 получит вид
Следовательно, максимум 22 имеет место при значении т*> равном
Между тем статическая высшая равновесная форма стержня имеет номер, равный
или ближайший к этой величине.
Как видим, наибольшим темпом нарастания будут обладать не те формы, которые соответствуют числу у, а формы с меньшим номером, равным приблизительно 0Jr\. Допустим, например, что к стержню внезапно приложена сила Р=9РЭ. Тогда имеем 3, с наибольшей интенсивностью будет нарастать форма прогиба по двум полуволнам {т* = 2); при Р= 16РЭ будет т* = 3 и т. д. Этот вывод имеет существенное значение для последующих разделов.
Мы считали,, что начальная упругая линия может быть представлена с помощью ряда Фурье и что все составляющие гармоники являются равновозможными. Если же характер начальной погиби является вполне определенным, то сравнение различных вариантов искривления стержня теряет смысл. Отметим, однако, что форма прогиба, развивающаяся в соответствии с начальной погибью, может в результате малых возмущений, возникших уже в процессе движения, перейти в другую форму, с преобладанием гармоники, характерной для данной скорости нагружения.
§ 70. Нагрузка, быстро возрастающая во времени
Рассмотрим далее случай, когда сила Р возрастает пропорционально времени: Р = ctF; величина с, измеряемая в кг/см2 • сек, характеризует скорость изменения сжимающего напряжения *).
Введем новый параметр времени
(6.22)
(6.23)
либо при т*, равном ближайшему
числу.
(6.24)
Р _ cFt. ~ Рэ~ Р9г
(6.25)
*) Эта задача разобрана автором [6.2а].
НАГРУЗКА, БЫСТРО ВОЗРАСТАЮЩАЯ ВО ВРЕМЕНИ
241
он связан с величиной tk (10) соотношением
--*• = -4-/,. (6.26)
cF P*9V * v '
Воспользуемся безразмерным параметром скорости изменения напряжения
(6 27)
тогда получим:
tk = yS*t*. (6.28)
Уравнение (11) приобретает вид
т2) h=т*и (6-29)
Разделим каждый член на радиус инерции сечения / и обозначим:
с=4* <б-зо>
тогда получим:
= (6-31)
Уравнение (31) может быть проинтегрировано в бесселевых функциях (см. § 72). Кроме того, интегрирование уравнения (31) и более сложных уравнений такого типа может осуществляться численными методами, а также с помощью аналоговых и цифровых машин.
На рис. 6.2 представлены результаты вычислений, проведенных численным методом Адамса, для случая S* = 0,1, С0 = 0,001. По оси абсцисс отложен параметр t*, равный отношению переменной величины сжимающей силы к эйлеровой нагрузке, а по оси ординат — безразмерная стрела прогиба С. Различные кривые отвечают значениям т = 1, 2, 3. Как видим, резкое увеличение прогибов имеет место раньше всего при изгибе стержня по двум полуволнам (т = 2); правее лежат кривые для т= 1 и т == 3. Судя по кривой т = 2, прогибы начинают резко возрастать лишь при силе, в семь раз превышающей эйлерову нагрузку. Прогиб, равный радиусу инерции сечения, достигается при нагрузке Я=9,6ЯЭ.
Если воспользоваться формулой (9), то можно определить зависимость С от Р/Р9 для статического нагружения при разных т. Левее всего здесь лежит кривая т= 1, изображенная на рис. 6.2 пунктиром. Прогиб С=1 достигается при Р/Р9 1.
Интересно отметить, что нагрузке Р9Р9 отвечает статическая форма потери устойчивости с тремя полуволнами, в то время как динамический процесс происходит при двух полуволнах; объяснение этому было дано выше, в § 69.
242 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при ДИНАМИЧЕСКОМ нагружении [гл. V1
Таким образом, мы здесь в качестве критерия, определяющего критическое время — а вместе с тем и критическую нагрузку, — приняли условие, что стрела прогиба не должна превысить радиуса инерции сечения. Этот критерий является, конечно, условным; можно
Рис. 6.2. Изменение стрелы прогиба во времени при различном числе полуволн.
исходить из предельного значения максимального напряжения либо наибольшей деформации и т. д.
§ 71. Исследование энергии системы
Проведем сопоставление различных форм динамической потери устойчивости с энергетической точки зрения. Кинетическая энергия стержня равна
т=щ.[Ш“х- <6-з2)
о
Подставляя выражение (3), найдем:
<6-33>
§ 71] ИССЛЕДОВАНИЕ ЭНЕРГИИ СИСТЕМЫ 243
Воспользуемся безразмерным параметром
= %АЕИ2 Т (6.34)
и введем параметр времени по (25)г тогда будет
т* — ~§* (м*) • (6.35)
Потенциальная энергия деформации складывается из энергии
изгиба и сжатия:
(6.36,
О
Чтобы вычислить потенциал нагрузки, определим сближение концов стержня Д. Начальное расстояние между шарнирами равно
/
=l~i f {-ж)2**’ <6-37)
о
а конечное расстояние
i
,, Р1 1 f(dvx \2, 0.
/1 —1 EF 2,)\дх)ах' 6-38
о
где I — длина стержня в прямолинейном состоянии. Сближение краев равно
А = V~ I, = +1 / - ()'J dx. (6.39)
о
Пользуясь (3), находим:
д = -£7?-+47 ю2*2 (/? — /о)* (6.40)
Потенциал нагрузки будет иметь вид
У = = тЧ2(К “ )- (6-41)
Общая потенциальная энергия равна
Э = и + У = Ц-И%-Цх-и?mW(/?-/2). (6.42)
Отсюда в безразмерных величинах 4/з
Э = «4 (С — С0)2 — тЧ* (С2 — С2) - 2Г. (6.43)
244 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
Определим безразмерную функцию Лагранжа
L* = Г — Э* = ± С2 — т* (С — С0)2 + тЧ* (С2 — С2) + 2t*\ (6.44) где t =, и составим уравнение Лагранжа
(6.45)
dt* ас ас
тогда придем к основному уравнению (31).
Найдем, далее, полную энергию системы
II* = Т + Э* = С2+ /и4 (С — с0)2 — тЧ*(С2 — С2) — 2Г2. (6.46)
Рассматриваемая нами система не является консервативной — заданная сила явно зависит от времени, — и потому полная энергия не остается здесь постоянной.
Введем обозначение
Hi = П +21. (6.47)
На рис. 6.2 вверху изображена зависимость П*(£*) для различных значений т. Судя по графику, в любой момент времени уровень полной энергии, отвечающий т = 2, ниже, чем уровень энергии для т— 1 или т — Ъ. По-видимому, форма потери устойчивости по двум полуволнам является при данном значении S* наиболее вероятной.
Рис. 6.3. Диаграмма «прогиб—нагрузка» при различных скоростях нагружения.
Графики, аналогичные рис. 6.2, были построены для различных значений 5*; были найдены кривые, отвечающие такому значению т% при котором возрастание прогибов является наиболее интенсивным. На рис. 6.3 дан сводный график функций С(£*) при С0 = 0,001 для
§ 72] РЕШЕНИЕ В БЕССЕЛЕВЫХ ФУНКЦИЯХ 247
Воспользуемся известными соотношениями для гамма-функции *)
тогда найдем:
и, далее,
Г (г + 1) = zT (*), Г (г) Г (1 —z) =, (6.66)
г(т)г(-ж)—ГШГ(1) (6'67>
тс
О Sin -5-
* = 7TrV-rT = А (6.68)
Окончательно имеем:
■Ш-i)
71
3
W = ~%T- (6-69)
Выполняя интегрирование **) по (59), подставляем найденное выражение для С3 в решение (56); постоянные Сх и С2 должны быть определены из начальных условий:
dt С = С0, =° при t* = 0 и г = (S*ms)3. (6.70)
Функции (56) изменяются периодически, так что движение системы на протяжении первого этапа имеет колебательный характер. Изменение С происходит с амплитудой порядка С0; поэтому на графике рис. 6.3, составленном для С0 = 0,001, колебания незаметны.
При возрастании параметра времени t* величина z падает. Определив С dC
и для z = 0, мы получим начальные данные для следующего, второго этапа движения. Уравнение (52) для второго этапа принимает вид
dK -
*С = Ж0, (6.71)
dz2
где
z = —z = (t* — m2) (S*m2) 6. (6.72)
Решение уравнения (71) выпишем в виде
С = СхCi -f- С22 “Ь Сз* (6.73)
Решения однородного уравнения
-7Т~?С = 0 (6-74)
dz2
*) См., например, Н. Н. Лебедев, Специальные функции и их приложения, Гостехиздат, М., 1958, стр. 13.
**) Подробные выкладки для частного примера приведены Н. Хоффом [6.12]. Другой закон изменения нагрузки рассмотрен с помощью подобного метода Б. Д. Олисовым.
248 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом нагружении [гл. VI
будут *)
= <6-75> где/j,7 y—модифицированные (видоизмененные) бесселевы функции
3 ““3
первого рода. Эти функции меняются монотонно; амплитуда прогиба будет при t* > т2 неограниченно возрастать. К этому результату мы уже пришли в § 70, пользуясь численным методом. Частное решение С3 определяется по формуле типа (59); определитель Вронского по-прежнему выражается формулой (68).
§ 73. Эксперименты по продольному удару
Образцы 6*20*Шмм
Особенности явления динамической потери устойчивости, отмеченные выше, обнаруживаются и в экспериментах. В работе [6.5] описаны интересные опыты над деревянными стержнями, подвергавшимися ударному нагружению падающим грузом. Была применена
скоростная киносъемка последовательных конфигураций стержня (от 2200 до 2700 кадров в секунду); кроме того, проводилось осциллографирование деформаций в отдельных точках.
Судя по этим данным, весь процесс деформации образца делился на несколько фаз. В течение первого периода, который в одном из опытов составлял около Vsoo сек> весь образец испытывал сжатие. На протяжении второго периода, примерно той же продолжительности, через образец проходила
отраженная волна и возникали поперечные колебания. При этом в различных образцах в зависимости от гибкости возникало различное число полуволн по длине,
в то время как нагрузка, приходящаяся на единицу площади сечения, оставалась одной и той же. В течение третьего периода, составлявшего V250 сек» происходило изменение формы потери устойчивости с переходом к одной полуволне. Наконец, четвертый период (х/ю сек) состоял в затухающих колебаниях образца по одной полуволне. На рис. 6.4 изображены различные конфигурации стержней двух типов, а на рис. 6.5 — три кадра киносъемки, отражающих динамическую потерю устойчивости по трем полуволнам.
Таким образом, теоретически выше нами была описана только одна из фаз изгиба стержня при ударе; не была исследована пред-
Рис. 6.4. Искривление стержней при динамическом нагружении.
*) См. указанную выше книгу Э. Камке, стр. 453.
§ 72] РЕШЕНИЕ В БЕССЕЛЕВЫХ ФУНКЦИЯХ 245
последовательно возрастающих скоростей нагружения с\ напомним, что параметр 5* обратно пропорционален с2. Значение т для каждой кривой указано.
Из графика видно, что при относительно малой начальной стреле прогиба и большой скорости нагружения сила, воспринимаемая стержнем, может во много раз превзойти эйлерову нагрузку. Прогибы развиваются преимущественно при некоторой определенной форме упругой линии, зависящей от скорости нарастания сжимающей силы; чем выше эта скорость, тем большее число полуволн образуется по длине стержня.
§ 72. Решение в бесселевых функциях
Мы уже говорили о том, что рассматриваемая задача может быть решена точно без применения численных методов. Обратимся к такому пути решения.
Представим уравнение (31) в виде
S*m2 (t* — т2) С = S*m%. (6.48)
Воспользуемся подстановкой
t* = т2 — z (S*m2) 3 (6.49)
и введем новую переменную z. Имея в виду соотношения
£
S*т2 (т2 — t*) = (S*m2) 2 z, (6.50)
получим:
где
(dt*)2 = (dz)2(S*m2) *9 (6.51)
d2 С
dz2
+ гС = Ж0, (6.52)
A = irS*mi. (6.53)
Рассмотрим сначала случай, когда
Г <т2у z> 0. (6.54)
Эти соотношения справедливы для первого этапа движения, когда сжимающая нагрузка не превосходит тя-й статической эйлеровой силы:
Р < гп2Рэ. (6.55)
Общее решение уравнения (52) может быть представлено в виде
C = CjCi + C2C 2 + С3. (6.56)
Под Ci и С2 понимаются линейно независимые решения однородного уравнения
U + = °. (6.57)
246 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
Сз==тг(С2 / dz~t'\
f C,i«).
определитель Вронского:
С, с2
W ==
dtjx dt2 dz dz
•
образующие так называемую фундаментальную систему решения; под Сз подразумевается частное решение исходного уравнения.
С уравнением типа (57) мы уже встречались в § 37; как мы видели, оно имеет решения *):
С1 = *7л(-*7). с* = j**)> (6.58)
где J\, J i —бесселевы функции первого рода с индексами -i- и —
— —— о о
з з
Частное решение С3 можно выписать в виде
(6.59)
(6.60)
dz
Вычислим производные от функций Ci, С2*-
3 3
Подставляя эти выражения в (60), получим:
«бга>
Выражение (63) может быть представлено через гамма-функции с помощью формулы типа
= Л (*> J'-, (г) - J-y (*> К (2) =
= 7[r(v + l)r(—v) — Г(м)Г(— V + 1)]- (6,64)
В нашем случае
О Г 1 11
(6.65)
W— — 2
.г(4)гЮ гШг(1).
*) См. указанную на стр. 124 книгу Э. Камке, стр. 453.
§ 74] СЛУЧАЙ ЗАДАННОГО ЗАКОНА СБЛИЖЕНИЯ концов СТЕРЖНЯ 249
верительная фаза распространения деформации по длине стержня, и не нашел отражения переход от большего числа полуволн к меньшему в заключительной фазе.
*)
Рис. 6.5. Выпучивание стержня по трем полуволнам.
Судя по данным опытов, работа падающего груза, затраченная в процессе выпучивания стержня, может оказаться для более гибких стержней выше, чем для жестких, так как в случае гибкого стержня образуется большее число полуволн.
§ 74. Случай заданного закона сближения концов стержня
Перейдем к другому случаю, когда заданной переменной величиной является не сжимающая сила Р, а взаимное смещение концов стержня А. Такой случай характерен для нагружения стержня с помощью «жесткой» испытательной машины *). Если одна из траверс машины приводится в движение от электродвигателя через редуктор, то можно считать, что взаимное сближение концов стержня возрастает пропорционально времени. Пользуясь силоизмерителем машины, определяем зависимость между нагрузкой и взаимным перемещением концов образца.
*) Этот случай был рассмотрен в ряде работ Хоффа и других авторов [6.12], [6.13] при условии, что по длине стержня образуется одна полуволна.
250 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
Обозначим скорость взаимного смещения концов стержня через
5 см/сек, примем
A = st. (6.76)
По (40) получим:
-§j? = st-±mW (fi-fl). (6.77)
Введем новый параметр времени
t — —
* 1Р\ '
Разделив обе части уравнения (77) на 1РЭ, будем иметь:
(6.78)
£ = (6.79)
Сравнивая выражения (25), (26) и (78), находим:
1Р1 1
— = (6.80)
отсюда
P**Vl
tk = —7s— * <6-81)
Подставим выражения (79) и (81) в уравнение (31); тогда придем к следующему основному уравнению:
-J- Jr + т2 [№ + ~ (С* - Ф с] = т\-, (6.82)
здесь через S* обозначен параметр
<«>
Отметим, что величина, S* зависит от отношения скорости взаимного смещения концов стержня 5 к скорости распространения звука в материале. По принятому выше основному допущению это отношение должно быть малым.
Положим инерционный член в уравнении (82) равным нулю; тогда получим зависимость С(£ф), отвечающую статическому нагружению:
[»2 + Ф] С = (6.84)
Значение /*=1 соответствует по (78) эйлеровой деформации. Заметим, что, в отличие от случая заданной нагрузки (§ 70), здесь
§ 74] СЛУЧАЙ ЗАДАННОГО ЗАКОНА СБЛИЖЕНИЯ КОНЦОВ СТЕРЖНЯ 251
величина С при t*= 1 и т= 1 не становится бесконечно большой. Стрела прогиба остается конечной при любом конечном параметре t+, поскольку в данном случае фиксировано сближение концов стержня. Если положить С0 = 0, то получим:
С = 0 либо —= — т2. (6.85)
При < т2 будет С = 0, а при t > т2 возможны три значения С: одно из них будет С = 0, а два других определяются вторым уравнением (85).
Поведение стержня при динамическом нагружении описывается уравнением (82). Оно было проинтегрировано численным методом*) [6.13]; результаты для случая т = 1 и С0 = 0,001 представлены на рис. 6.6.
С
1,60
0,80
0,40
2,0
1,0
0
ь
* с,
0-0,001
/
/
/
S'
У
/
/
А
/
/
/
i Js.-io3
А
/
Oi 2,0 3,0 4,0 5JJ
\
/
/
А
k
А
и
100
1Д 1,40
1,60
1,80
t.
т
Рис. 6.6. Случай, когда задан закон сближения концов стержня во времени.
Сплошными линиями здесь дана зависимость С() при различных значениях параметра «S*. Напомним, что под tm понимается отношение переменного сближения концов стержня к укорочению прямого стержня при эйлеровой нагрузке, равному (1РЭ). Пунктиром показана статическая кривая (84). Общий характер кривых C(Q на первом участке — до момента резкого возрастания С — тот же, что и на рис. 6.3. Рост прогибов имеет место при значении А, значительно
*) В статьях [6.13] изложены другие методы интегрирования уравнения (82), при т = 1.
252 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом НАГРУЖЕНИИ [гл. VI
превышающем эйлерову величину 1Р9. «Затягивание» прогибов проявляется тем сильнее, чем выше скорость s. В последующем зависимость С() отвечает колебаниям стержня около положения статического равновесия.
Пользуясь уравнением (79), можно, далее, определить зависимость нагрузки Р от параметра времени. Кривые (Р/Р9, /*) даны на рис. 6.7. Как видно из графика, при большой скорости эйлерова нагрузка оказывается сильно превзойденной. Максимальные значения отношения Я/Яэ, имеющие место в процессе нагружения, представлены на рис. 6.8 в зависимости от параметра S* и начальной стрелы
Рис. 6.7. Зависимость между нагрузкой, воспринимаемой стержнем, и временем.
Рис. 6.8. Несущая способность стержня при различной начальной стреле прогиба.
прогиба С0. Рис. 6.7 относится к случаю, когда образуется одна полуволна (т = 1). Однако при 5 = 0,1 преобладающее значение получает форма выпучивания при т = 2, это видно из рис. 6.2, на котором к рассматриваемому типу нагружения относятся пунктирные линии; обозначения S* и t* надо в данном случае заменить на S* и по (83) и (78).
Фронт волны в случае т = 2 лежит значительно левее, чем при т= 1.
Рассмотренный здесь случай заданного закона сближения концов стержня представляет собой пример нагружения, при котором вели* чина сжимающей силы зависит от поведения образца, от его деформации.
§ 75. Поведение стержня при действии импульсивной нагрузки
Мы полагали до сих пор, что нагрузка — постоянная или переменная, заданная или определяемая деформацией стержня — действует на протяжении всего рассматриваемого периода; нас интересовал
§ 76] СЛУЧАЙ ПУЛЬСИРУЮЩЕЙ НАГРУЗКИ. ПРИБЛИЖЕННОЕ РЕШЕНИЕ 253
«критический» промежуток времени, за который несущая способность стержня считается исчерпанной.
Для практических расчетов интересен также случай нагрузки типа взрывной, которая вначале возрастает, а затем падает по некоторому закону. В качестве простейшего примера рассмотрим поведение стержня при условии, что к нему внезапно приложена сжимающая сила Р, остающаяся постоянной на протяжении короткого промежутка времени т и затем исчезающая. Форму начальной погиби считаем по-прежнему совпадающей с формой дополнительного прогиба.
Поведение стержня в период т описывается уравнением (13) при Я<ЯЭ и уравнением (19) при Р > Рэ\ переменная tk по (10) меняется от 0 до kx = 2izx/Г, где Т—период колебаний в отсутствие сжимающей силы.
Для участка 0 < tk < уравнение движения будет
f\ = С\ cos kxtk-\-C2 sin —2~/0 при Р<РЭ (6.86)
*1
ИЛИ
ж4
fi = Ci ch kxtk -f- C2 sh k2tk -\—75-/о при Р>РЭ; (6.87)
2
постоянные Cv С2 определяются из начальных условий. Для последующего периода дифференциальное уравнение имеет вид
= (6.88)
atk
решение его запишем в виде
f \ == С3 cos nfitfo —(— sin nfitfc —(— fq, (6.89)
Постоянные C3, C4 находим, приравнивая значения прогибов и скоростей при tk = k'Z.
Как видим, во втором случае стрела прогиба, вообще говоря, получает максимальное значение в момент времени, не совпадающий с моментом прекращения действия силы Р. В дальнейшем имеют место колебания относительно начальной изогнутой линии.
§ 76. Случай пульсирующей нагрузки. Приближенное решение
Перейдем к случаю, когда импульсы повторяются один за другим и стержень подвергается действию периодической нагрузки, равной Р в одни промежутки времени и падающей до нуля в другие промежутки (рис. 6.9). Обозначим через б частоту приложения силы Р и
через т = у—полупериод изменения силы. Первые два интервала
254 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
мы уже изучали в § 56. Новое условие состоит в том, что отрезок времени tk > kx является ограниченным и завершается в момент tk = 2ki новым приложением силы Р.
Важно выяснить, какой характер будут носить колебания стержня, вызываемые такой пульсирующей нагрузкой. Если колебания будут
затухать, то начальную форму стержня можно назвать динамически устойчивой. При колебаниях, нарастающих от одного импульса к другому, начальная форма является динамически неустойчивой. В промежуточном случае, когда колебания стержня будут периодическими или близкими к периодическим, исходную форму можно считать динамически безразличной. Отметим, что в дифференциальное уравнение движения стержня (13) нагрузка входит не в качестве возмущающей силы, а в качестве параметра, определяющего жесткость системы. Поэтому колебания, возникающие при периодическом изменении силы Р, называют параметрическими колебаниями.
Для того чтобы исследовать характер движения стержня, достаточно проследить изменение прогибов и скоростей в течение одного полного периода 2т. Очевидно, при Р > Р9 прогибы, вызванные повторной нагрузкой, всегда будут нарастать. Поэтому рассмотрим случай Р<Р9. При этом надо принять т— 1.
Для первого полупериода уравнение (13) примет вид
'
< г »
t
Рис. 6.9. Закон изменения нагрузки во времени.
d2fx
2/г-=0,
где
Отсюда
О2 = 1 7Т—.
Д = Аг cos wtk + Вх sin <s>tk.
Для второго полупериода будет ш2 = 1 и, следовательно, fx — А2 cos tk В2 sin tk.
(6.90)
(6.91)
(6.92)
(6.93)
Допустим, что при tk — 0 начальная стрела прогиба составляет /0, а производная по tk будет равна /0, причем начальная скорость будет v0 = f0k. То1гда по (92)
1
А\ — /о* — — /о-
(6.94)
§ 76] СЛУЧАЙ ПУЛЬСИРУЮЩЕЙ НАГРУЗКИ. ПРИБЛИЖЁННОЕ РЕШЕНИЕ 255
В конце полного периода параметр tk по (10) равен tk = 2kfzl = —g—.
Примем *), что прогиб и скорость изменяются к концу периода в одно и то же число раз s:
/г — sfo* — sfo-
Тогда по (93) будет
Отсюда
. 2nk, о. 2%k -
Аг cos -j—\-В2 sin -j- = sf0,
•. 2nk I q 2tcAj i
— A2 sin — -f- £2 cos — = s/0.
. - 2nk ;. 2rc
Л2 = sf о cos -g s/0 sin —,
D.. 2тс%, \ 2%k
B2 = s/0 sin -jj—I- sf0 cos —.
(6.95)
(6.96)
(6.97)
В конце первого полупериода, при tk = itkjb, стрела прогиба и скорость, вычисленные по (92) или (93), должны быть одними и теми же; это условие приводит к равенствам;
(6.98)
« a Ttk I л. Ttk
jCOS—g 1-Bx Sin —0- = Acos-y-f J32Sin -y,
. пшк. о. Tttok \ a * Tk 1 nk
— Ax sin —g f- Bx sin —0-) = — A2 sin -g- B2cos -g-.
Подставляя в (98) выражения (94) и (97), приходим к следующим уравнениям:
(а-ш)/0+(С + 4)/о=0,
где
(С + а>й)/0-(а-£)/0=0,
2nk nonk Tzk,, 71 (£>k. %k
а = S COS —g COS—0—cos-g-, 0 — Sin —J—Sin -g-
. 2 nk 7Z(nk. nk
c = s sin —g cos —g- sin -y-,
,, noik Tzk
а = sin g— cos—g-
(6.99)
(6.100)
Если принять /0 Ф 0, /0 Ф 0, то определитель системы (99) должен быть равен нулю:
а — mb с “ ' О)
— (c + wd) а —
= 0.
(6.101)
*) Такой путь решения задачи принят в книге Ден-Гартога [6.10].
256 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ гл. V*
Развертывая этот определитель, приходим к уравнению а2 + £2+с2 + йР + (о> + Л-) (cd — ab) = 0.
По (100) находим:
а2 -f- Ь2 + с2 + d2 = s2 — 25 cos cos + 1,
■ f. C07u/j.
cd — ab = s sin —к— sin.
о 0
Уравнение (102) принимает вид
s2 — 2ns1 =0,
где
ГССО Tlk 1 /, 1 \. 7Ш. nk
n = cos — cos-0 2 Г + sin ПГ sin “0
Коэффициент 5 оказывается равным
s = n ± Yn2— 1.
Если величина n2 меньше 1, то для s получаем комплексное выражение. Очевидно, исходное допущение об одновременном возрастании прогиба /о и скорости /0 в s раз в этом случае невыполнимо. Однако вещественная часть 5 оказывается правильной дробью; колебания стержня не будут нарастать, так что начальную форму движения стержня надо считать устойчивой.
Напротив, при п2 > 1 коэффициент 5 будет больше 1, так что колебания к концу каждого периода будут усиливаться; следовательно, начальная форма окажется неустойчивой.
Промежуточный случай п2= 1 отвечает как бы безразличной форме движения. Таким образом, равенство
%(£>k nk 1 /, 1 \. TCG0 %k,. 1
п ==cos —Q— cos—q -g- (о) + —) sin -Q—sin -jp= ± 1 (6.107)
определяет границу, отделяющую зону устойчивого движения от зоны неустойчивости. Отметим, что при /г < 1 прогиб и скорость меняют знак в конце периода по отношению к началу того же периода, а при п > 1 сохраняют знак.
Допустим, что величина пульсирующей нагрузки весьма мала по сравнению с эйлеровой: Я<СРЭ; тогда можно считать о>->1. Условие (107) принимает вид
(6.102)
(6.103)
(6.104)
(6.105)
(6.106)
§ 76] случай пульсирующей нагрузки, приближенное решение 257
Отсюда получаем следующие две серии значений /г/0:
k__ J_ 3_ 5
0 — 2 ’ 2 ’ 2 ’ *
т=1. 2» 3,
при
при
Л= — 1. k=l.
(6.109)
Первая зона неустойчивости имеет место при частоте пульсирующей нагрузки 0, вдвое превышающей частоту свободных колебаний стержня k. Это можно пояснить следующим образом. Допустим, что сила Р прикладывается к стержню в те ин-
2;8
тервалы времени, когда, искривляясь, он перемещается от среднего положения к W крайнему; так как точка приложения силы будет перемещаться вниз, то сила 2,0 совершит положительную работу. В те же интервалы времени, когда стержень вы- 1,6 прямляется, перемещаясь к среднему положению, сила Р снимается, так что 1,2. работа совершаться не будет. За полный период колебаний стержня сила окажется до приложенной дважды, что отвечает значению в/k = 2. Работа силы Р будет, таким ofi образом, непрерывно возрастать, и это должно сопровождаться нарастающими колебаниями стержня. *>ис* Области неустой-
~ г м „ чивости при параметриче-
Рассмотрим второй предельный слу- ских колебаниях.
чай, когда сила Р близка к эйлеровой; Р
0,6 до р/р3
Р9 и (0->О. Соотношение (107) перепишется в виде
п = lim
со -» 0
ИЛИ
1tO) ftk I со. 7ТО) cos —g— cos—g 2 sin —g—
Ttk
sin ■
20
ncak
~T~
sin
nk
nk nk,
П = COS — gjf sin
UK t nk I «
-Sjt Sin -s- = ± l.
= ±l
(6.110)
Найдем первые два корня уравнения (110). Первый из них соответствует отношению /0 = 0,548, тогда будет
П = — 0,157 — ± 0,548*. 0,988;
1.
Второй корень отвечает k/Q—l; при этом вновь /г = —1.
Результаты вычислений для других значений ш приведены на рис. 6.10 *). Для всех значений £/б, заключенных внутри заштрихо¬
*) Подобный график приведен в работе В. М. Макушина [6.6], стр. 65*
258 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
ванных областей, величина п будет либо меньше (— 1), что имеет место в первой, третьей и т. д. зонах, либо больше (-(- 1)—во второй, четвертой и т. д. зонах. В точках граничных линий будет п= ± 1.
Таким образом, при ш Ф 0 мы получаем области значений k/B, для которых имеет место динамическая неустойчивость. Надо оговориться, что нами не принимались во внимание силы сопротивления, оказывающие влияние на колебательный процесс. При учете этих сил зоны неустойчивости оказываются несколько иными (см. § 77).
Представим полученные результаты в другой форме. Отнесем частоту пульсирующей нагрузки б к частоте собственных колебаний Q стержня при среднем значении силы Р, равном Р/2. Как легко видеть, будет
й = к\Г\ —2р- • (6.111)
С другой стороны, введем параметр нагрузки
Р
2 Рл
1-
(6.112)
2 Я,
характеризующий отношение между переменной частью нагрузки и ее средним значением. В координатах v, первая область не¬
устойчивости имеет вид, показанный на рис. 6.11. Границы области
представляют собой
линии,
близкие к прямым.
Рис. 6.11. Первая зона неустойчивости.
Рис. 6.12. Характер изменения нагрузки.
Аналогичное исследование можно провести для случая, когда пульсирующая нагрузка меняется по тому же закону относительно некоторого среднего значения Р0, а переменная часть ее равна Pt (рис. 6.12), причем Р0 + Р,<;Р9. Частоты колебаний стержня для двух интервалов периода изменения силы будут
px = ky[ 1 --°+р<, 1 --р°-р‘. (6.113)
§ 77] НАГРУЗКА, МЕНЯЮЩАЯСЯ ПО ГАРМОНИЧЕСКОМУ ЗАКОНУ 259
Условие (107) получает вид
n = coscos--i( + -)sin-sin-=+ 1; (6.114)
отсюда определяются граничные линии зон неустойчивости. Как легко видеть, для разобранного выше примера надо принять
px = k to, р2 — k.
Параметры Q и v в общем случае равны
Я
=*/v=
Рэ
1-*Рэ
(6.115)
§ 77. Нагрузка, меняющаяся по гармоническому закону. Параметрические колебания
Мы исследовали поведение стержня при ступенчатом периодическом изменении сжимающей силы. Естественно перейти отсюда к случаю, когда величина нагрузки следует гармоническому закону (рис. 6.13)
Р = Р0 + Pt COS (6.116)
или
/> = P0 + P,cos-i, (6.117)
где tk определяется по-прежнему по (10).
Уравнение (11) при /0 = 0 и т— 1 приобретает вид
-f + fl — — — -§-cos-J-*V = 0. dt\ \ Р9 Рэ k 4J
(6.118)
Воспользуемся обозначениями (115) и введем новый параметр времени
t, = уГ 1-
L
Рис. 6.13. Нагрузка изменяется по гармоническому закону.
(6.119)
тогда вместо (118) получим: d2f
dti
(6.120)
Уравнение такого типа носит название уравнения Матье\ оно встречается в астрономии и в некоторых задачах математической физики. Подробные исследования показали, что при отношениях 0/2,
260 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. VI
лежащих внутри некоторых определенных областей, решение уравнения делается неустойчивым. Иными словами, при изменении сжимающей силы по (116) мы получаем некоторые области динамической неустойчивости, как это было в примере § 76: прогибы и скорости нарастают на протяжении каждого периода изменения нагрузки. Естественно ожидать, что и здесь явление параметрического резонанса при малых Р будет возникать вблизи значений 2/0, равных
Границы областей неустойчивости снова определяются из того условия, что динамическая форма стержня является как бы безразличной: колебания должны поддерживаться, не усиливаясь и не ослабляясь. Поставим перед собой цель приближенно определить границы первой области неустойчивости, лежащей вблизи значения
0 = 22. Считая, что движение стержня должно быть периодическим, примем в качестве первого приближения выражение для / в виде ♦)
Считая Ах Ф 0 и Вх Ф 0, приравниваем нулю выражения, стоящие в скобках; тогда найдем:
На рис. 6.14 изображены нижняя и верхняя границы первой области неустойчивости, построенные по (126). Этот график очень близок к графику рис. 6.11.
(6.121)
✓ А 61 I D • 0*1
f = Ax Cos-H-Bjsin--.
(6.122)
Подставляя (122) в уравнение (120), будем иметь:
-)sin-§- = 0. (6.123)
Учитывая соотношения
(6.124)
и отбрасывая члены с утроенной частотой, получим:
§- = 0. (6.125)
■4=/
2 ’ 2Q
V
Ш = \/~ '+J' <6Л26>
*) Этот метод решения уравнения Матье бы дан Рэлеем [6.17].
§ 77] НАГРУЗКА, МЕНЯЮЩАЯСЯ ПО ГАРМОНИЧЕСКОМУ ЗАКОНУ 261
Уточненное решение задачи можно получить, принимая выражение для / в виде ряда
/ = 2(Л»С03 + В*81п) (6Л27)
П
и удерживая новые члены ряда дополнительно к Аг и Вг. Подробное исследование показывает [6.2], что при значениях v<0,6 поправка к формулам (126) лежит в пределах 1%.
Выражениям (126) можно придать иной вид, раскладывая правую часть по формуле бинома Ньютона. В первом приближении получим *):
i = 1-T* ш = 1+т- <6Л28>
Формулам (126) соответствуют на рис. 6.14 пунктирные линии.
При выводе формул не учитывались силы сопротивления колебаниям. Чтобы оценить влияние этих сил, будем считать их пропорциональными. скорости движения и выпишем исходное уравнение в более полном виде:
2. + *>(■ g-cos„<)/=0.
(6.129)
Переходя к переменной tt по (119), получим вместо (120)
<6-130>
Воспользуемся снова решением (122); тогда уравнение (130) примет вид
г. Л 02 v\, n Osl 0/,.
[А 1 4Q2 2 ) 1 Q2 J C0S 2Q
+[M1-w+i)~]sin-=°- (6Л31)
Приравнивая нулю выражения, стоящие в квадратных скобках, получим два уравнения относительно Ах и В{; условия Аг Ф 0
*) Эти формулы были предложены Н. М, Беляевым [6.1].
у
Рис. 6.14. Сравнение точного и приближенного решений.
262 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом нагружении [гл. VI
и Вх Ф 0 приводят к уравнению
О2 v
1
4Q2
или
1624
Ъг_ Й2
62
4Q2
0е
22
1 —
0J. v
W+2
2£2N 22,
)+'-т
= 0
(6.132)
(6.133)
Считая величину е/2 малой и отбрасывая члены высшего порядка малости, представим решение уравнения (133) в виде
JL— Л\ - i/
2Q ~ \/ + V 4 Q2
(6.134)
При е = 0 получим прежние формулы (126). Если же г Ф 0, то границы областей неустойчивости несколько перемещаются. Так, например, при v = 0 мы здесь не получаем той точки на оси 6/22, от которой разветвлялись кривые рис. 6.14. Вещественные значения 0/22 имеют место при условии
(6.135)
0,8 0,9 1,0 1,1
Рис. 6.15. Влияние затухания на границы первой области неустойчивости.
Новые очертания первой области неустойчивости показаны на рис. 6.15 сплошной линией. Они мало отличаются от границ той же области при е = 0, показанных на графике пунктиром.
Значительно большим оказывается влияние сопротивления на очертания второй и последующих областей неустойчивости. Они сильно отодвигаются от оси абсцисс рис. 6.15, так что неустойчивость может появиться лишь при значительной величине параметра v. Поэтому практическое значение для расчета реальных конструкций имеет главным образом определение первой области. Более подробное изложение теории динамической устойчивости выходит за рамки данной книги. Интересующиеся этой теорией могут обратиться к специальной литературе и прежде всего к книге В. В. Болотина 1956 г. [0.1].
§ 78- Устойчивость сжатого кольца при динамическом нагружении
Мы познакомились с различными направлениями теории динамической устойчивости сжатых стержней. Перейдем теперь к динамическим задачам, относящимся к другим крнструкциям. Исследуем
§ 78] УСТОЙЧИВОСТЬ СЖАТОГО кольца при дйнамйч. нагружении 263
прежде всего поведение кругового замкнутого кольца при быстром нагружении радиальными усилиями (рис. 3.31). Эта задача представляет интерес для расчета шпангоутов в подкрепленных оболочках, подвергающихся динамическому приложению внешнего давления.
Сохраним прежний подход к решению задачи и допустим, что кольцо имеет некоторые начальные отклонения от круговой формы. Воспользуемся основными зависимостями, выведенными для «идеального» кольца в § 46, и дополним их, учитывая начальный прогиб. Под w в дальнейшем будем понимать полный прогиб.
Уравнения равновесия (3.175)—(3.177) остаются в силе, однако полные производные по у надо заменить на частные. Изменение кривизны х по (3.181) теперь будет определяться выражением
(6Л36)
изгибающий момент М в произвольном сечении равен
+-=а-]. (6.137)
Пользуясь (3.179), получим вместо (3.184) дифференциальное уравнение для w в таком виде:
rd5 (да — w0) 2 д3 (w — w0) 1 d(w — w0) - qy dqz
E/[ djs I~~R* ду~3 Я7 dy J= ~R dy~'
(6.138)
В динамических задачах должны быть учтены составляющие силы инерции
qz g dt2 9 qy g dt2 * здесь v — перемещение вдоль дуги, F — площадь сечения, f — удельный вес материала.
Выпишем выражение для деформации вдоль дуги:
= (6.Н0)
и примем по-прежнему ось кольца нерастяжимой: еу = 0, тогда будет
264 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при ДЙНАМИЧЁСКОМ нагружёнйи [гл. VI
Пользуясь (138)—(141), приходим к следующему окончательному дифференциальному уравнению:
р,Г d6(w — w0). 2 d4(w — w0). 1 д2 (w — w0) ],
L ду6 “T R2 ду4 R4 ду2 J
, n I d4w. 1 d2w\, 7F ( d4w 1 d2w\ Л
\ dy4 R2 dy* ) ~g~ \ дуг dt* ’№~dir)~°- (6-142>
Примем для w и w0 выражения
<w = f sin--, w0 = /0sln —jjT' (6.143)
Считая n >-2, получим:
(/-/о) «2 (»2 - l)2 -/ »2 (»2 - 1) + --(»2+1) = о.
(6.144)
Вводя выражение (3.188) для статического критического давления <7Э, представим (144) в виде
d2f. л2(пг—1) /,, ъ <1 \ * ns(ns — 1)J,,с
Ж+а~ п*+1ЛЛп l-si)f = a >Ь+i к (6Л45)
здесь введено обозначение
в=-- (6-146)
Предположим сначала, что кольцо подвергается внезапному нагружению *). При q < получим колебания около положения
статического равновесия. При q > q3 стрела прогиба начнет неограниченно возрастать. Рассуждая таким же образом, как в § 70,
найдем формы с наибольшим темпом возрастания. Будем считать п> 1, тогда в уравнении (145) можно пренебречь 1 по сравнению с п2, и оно примет вид
W--k\f = m'fо, (6.147)
где
k\ = are2 (З--re2). (6.148)
Приравнивая нулю производную dk\jdn, найдем значение п:
(би9)
Мы получили тот же результат, что и в § 70: наиболее бурно возрастает та форма потери устойчивости, номер которой состав¬
*) Эта задача была исследована М. А. Лаврентьевым и А. Ю. Ишлинским (см. сноску на стр. 238).
§ 79] БОКОВОЕ ИСКРИВЛЕНИЕ полосы 265
ляет около 0,7 от номера статической формы, отвечающей данному уровню нагрузки.
Примем, далее, что давление возрастает во времени по за¬
кону q — ct. Тогда уравнение (145) перепишется в виде:
1 d2f, п2(п2-1) / о « *ct\f— Чп2-1)2 f
7F+T- \п ~ 1 - 3 )f ~ ■ /**+Т /о- (6.150)
Воспользуемся параметрами
к=Г.=Т,- <6151)
под V по-прежнему подразумевается скорость звука, под s3=q3R/EF — дуговая деформация, соответствующая давлению q9. Уравнение (150) получает вид
J_ d2f. п2 (п2 1). 2 j t ) f п2 f Гб 152
Sdt\ n2 +1 /z2 -{— 1 *
При пГ> 1 уравнение (152) переходит в следующее:
\ ~ «2 «2 ~ П2) / = Vo- (6-153)
S dt
Это уравнение по структуре совпадает с уравнением (31), относящимся к случаю стержня. Поэтому при п >- 4 можно в случае
кольца пользоваться всеми результатами, полученными для стержней,
при условии определения t2 и 5 по формулам (151).
§ 79. Боковое искривление полосы при динамическом приложении момента
Обратимся к задаче о боковом выпучивании узкой полосы, нагруженной парой сил в ее плоскости. На рис. 6.16 изображен
элемент полосы в деформированном состоянии. Допустим, что оси координат х, у, z> проведенные в некотором сечении полосы (рис. 6.16,а), принимают после деформации направления £, С (рис. 6.16, б). Обозначим через w полный прогиб центра тяжести полосы вдоль оси z и через б — полный угол поворота сечения в плоскости yz.
Уравнения равновесия элемента в проекциях на ось Сив моментах относительно осей у и z имеют вид
266 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [ГЛ. VI
где М—изгибающие моменты, Q — поперечная сила, qс—интенсивность нагрузки вдоль оси С, т, — составляющие момент-
ной нагрузки. Величины ?с, т, т выражаются через момент приложенной пары М и инерционные нагрузки:
d2w
g dt2
АЛ W.
m = Ж-/v dx ’
, (6.157)
Ж
d*2 *
(6.158)
(6.159)
здесь F — площадь сечения Рис. 6.16. Боковое искривление полосы при полосы, У—момент инерции динамическом нагружении. массы балки, приходящейся
на единицу длины. Изгибающие моменты могут быть выражены через полные перемещения w, р и их начальные значения w0, р0:
(6.160)
(6.161)
под 1у понимается момент инерции сечения относительно оси у, под G/K — крутильная жесткость.
Сопоставляя выписанные выше соотношения, приходим к следующим уравнениям:
гд20
д., d*(w — w0),
У дх4
, д2 (0 — 0О) и к дх2
АГ
дл:2
g dt2
(6.162)
(6.163)
Если принять Wq = 0О = 0 и исключить инерционные члены, получим статические уравнения (4.131), (4.132), выведенные другим путем
в главе IV.
Предполагая, что торцы полосы оперты шарнирно, и рассматривая основную форму выпучивания, положим:
§ 79] БОКОВОЕ ИСКРИВЛЕНИЕ полосы 267
тогда уравнения (162) и (163) получат вид
*£+ £/,.*(/_/о) = 0. (6.165)
J4W + О/к-£(<р-<р0)-М-£/ = 0. (6.166)
Полагая инерционные члены равными нулю и считая ср0 = /0 = 0, находим отсюда статическую критическую нагрузку:
мэ = УШ~оЦ = УРЖ> (6.167)
где через Р9 по-прежнему обозначена эйлерова сила; эта формула
совпадает с (4.100).
С другой стороны, принимая Ж = 0, определяем основные частоты юи и о)к изгибных и крутильных колебаний:
«>„ = -£]/шк — j (6.168)
Пользуясь этими обозначениями, придадим уравнениям (162) и (163)
окончательную форму:
1 d2f М Мэ,, -
1 d*v М Рэ,.
4 dt2 Мэ Мэ
(6.169)
Допустим, что момент приложенной пары изменяется во времени по закону М = M(t). Интегрируя уравнения (169), можно тогда определить величины / и (3 как функции времени.
Рассмотрим случай, подобный тому, который исследовался в § 69, когда полоса подвергается внезапному нагружению моментом М > Мэ, сохраняющим постоянную величину в течение периода т и затем падающим до нуля *). Начальные условия примем следующими:
/ = /<>• ? = ?о. If =0- -§- = 0 при * = 0. (6.170)
Исключая./ из (169), получим уравнение для ср:
*£ __ (Ш2 + Ю2 + ша j 9 = w2yK _J_ /о j
(6.171)
*) Эта задача была исследована Дэвидсоном [6.9].
268 УСТОЙЧИВОСТЬ СТЕРЖНЕЙ при динамическом НАГРУЖЕНИИ [гл. VI Интеграл этого уравнения выпишем в форме
—я- (Л ch оijt + В sh -- С cos v>at + D sin a>at) —
9o M — M9
Ml
-(
Ж+Ж1' (6Л72)
причем
2а>2 = 0)2 -f 0)2 4- р/'(<о* - о,2)+4шук-
т1— 0)? = шк+ши-
Принимая во внимание начальные условия, находим:
P-Jo МЪ ’
f—1 т° f
\ M~w \
у
ч
/✓]
\у
nn
>
V1
✓
/
X
1 п
/
/
/
/ А
1 V
\ 6 1 1
Л+С = 1 +
(6.173)
В = D = 0,
(6.174)
Аш] — Са>* = „
1 а Ml
Pb M2-Ml /о
М
<fo
f.a>J
Рис. 6.17. Изменение параметров прогиба полосы во времени.
О)2 0) к
(6.175)
соотношение
= -“>*• <6Л76>
вытекающее из рассмотрения уравнений (173), приходим к следующему выражению для ср:
М2
<оа ch (Лft -f- (I)2 COS соat
Ml
M2 — Ml
Мг
+
+
P3fo м3<р о
“а 1 1 + ch <°(( + “? 1 — J j cos “a *
(6.177)
Подобное же выражение может быть выписано для /. Зависимость типа (177) имеет ту особенность по сравнению с аналогичным соотношением (87) для сжатого стержня, что наряду с экспоненциальными составляющими содержит гармонический компонент. На рис. 6.17 показано, как изменяются во времени величины <р/ср0 (сплошные линии) и ///0 (пунктирные линии) при условии, что при-
БОКОВОЕ ИСКРИВЛЕНИЕ ПОЛОСЫ
269
ложенный момент составляет М = 2МЭ и М=\0М9 и что отношение (ои/(ок равно 0,2; кроме того, принято -Рэ/0/Жэср0= 1. По оси абсцисс отложена величина t* = о)и£; периоду изгибных колебаний Ги соответствует значение t* = 2тс. Время действия нагрузки в одном случае выбрано равным t* = 0,25, в другом оно соответствует периоду крутильных колебаний и равно £*=1,25. Кружками показаны моменты, когда нагрузка снимается. Как видим, при данном соотношении частот колебаний угол закручивания растет, а затем падает значительно более интенсивно, чем стрела прогиба.
Литература по устойчивости стержней при динамическом нагружении приведена ниже (стр. 846); отметим также работы Л. Н. Воробьева (Труды Новочеркасского полит, ин-та 21/35, 1949), И. А. Бурнашева (Изв. АН Узб. ССР № 11, 1951), Ш. С. Мазитова (Изв. АН Тадж. ССР, № 16, 1956), Е. Прокоповича, С. Рэуту и Ф. Динке (Журн. прикл. мех. АН Рум. Респ., 1957), О. И. Кацитадзе (канд. дисс., Тбилиси, 1958), Севина (S. Sevin, J. Appl. Mech., № 1, 1960), А. И. Оселедько (Труды Воронеж, инж.-стр. ин-та, № 4, 1958), У. Р. Упманиса (Вопросы динамики и прочности, № 7 и 9, Рига, 1961).
ГЛАВА VII
УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
В ПРЕДЕЛАХ УПРУГОСТИ
§ 80. Основные зависимости теории жестких пластинок
Пластинки прямоугольного очертания входят в состав различных конструкций — крыла самолета, днища, палубы и бортовых стенок корабля, стенок цельнометаллического вагона и т. д. — обычно в виде панелей обшивки, скрепленных с системой подкрепляющих ребер. Обшивка подвергается в этих конструкциях действию той или иной «местной» поперечной нагрузки, например аэродинамического давления, и кроме того воспринимает «основные» усилия вместе с другими элементами конструкции — от общего изгиба крыла самолета, корпуса судна или вагона. Во многих случаях эти основные усилия являются превалирующими: они вызывают' сжатие, изгиб либо сдвиг пластинки в ее плоскости и приводят, при известных условиях, к выпучиванию пластинок (рис. 7.1); поэтому расчет пластинок на
LiLLll
/7/7/7 p~7~FJ7
а) 9) В)
Рис. 7.1. Выпучивание пластинки при сжатии, изгибе и сдвиге.
устойчивость представляет собой неотъемлемую часть общего расчета конструкции. Пластинки, подкрепленные по продольным краям, способны и после потери устойчивости нести возрастающую нагрузку. Для некоторых конструкций считается вполне допустимым, чтобы обшивка получала относительно мелкие вмятины, с тем, однако,
§ 80] ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ЖЕСТКИХ ПЛАСТИНОК 271
условием, чтобы подкрепляющие ее элементы оставались достаточно жесткими. Следовательно, конструктора должно интересовать не только само явление потери устойчивости пластинок, но и их закритическое поведение. Стенки высоких балок, а также элементы различных тонкостенных стержней и балок также представляют собой прямоугольные пластинки, подвергающиеся выпучиванию, следовательно, и здесь расчет на устойчивость имеет первостепенное значение.
При определении критических нагрузок, когда исследуются равновесные состояния, соседние с исходным, можно полагать, что появляющиеся в процессе выпучивания напряжения в срединной поверхности пластинки малы по сравнению с напряжениями собственно изгиба; прогибы пластинки считаются также малыми по сравнению с толщиной. В этом случае можно пользоваться теорией жестких пластинок, пренебрегающей напряжениями в срединной поверхности пластинки. Если же исследуется закритическое поведение пластинки, то надо исходить из более общей теории гибких пластинок, учитывающей одновременно напряжения в срединной поверхности и напряжения изгиба *).
Напомним сначала важнейшие положения теории жестких пластинок. Рассмотрим прямоугольную пластинку со сторонами а, b и толщиной h (рис. 7.2). Пусть координатная плоскость ху совпадает
х
Рис. 7.3. Сечение изогнутой поверхности пластинки.
со срединной плоскостью пластинки; ось х будем, как правило, проводить вдоль длинной стороны а, ось у — вдоль короткой стороны b. Обозначим перемещения точек срединной поверхности вдоль осей х, у, z через и, v, w.
Рассечем срединную поверхность изогнутой пластинки плоскостью, параллельной плоскости xz (рис. 7.3). Так как прогибы малы, то
Рис. 7.2. Система координат при рассмотрении прямоугольной пластинки.
*) Более подробно об этом см. в книге [0. 3], стр. 13.
272 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах упругости [гл. VU
в сечении мы получим пологую кривую. Угол наклона 0. касательной к кривой равен
е* = ж* (7Л>
(7.2)
аналогично для сечения, параллельного плоскости yzt
д dw
°y = W
Кривизну сечения будем считать положительной, если выпуклость обращена в сторону положительного направления оси z. Тогда кривизны в сечениях, параллельных плоскостям xz и yz, будут равны
дЬх дву
%х= /ГГ' У'у = ду~ * (7-3)
или
дх d2w
V
d2w
ду2
(7.4)
При изменении у угол 0. в общем случае также меняется; относя приращение угла 0 к приращению координаты у (или приращение ву к приращению х), находим кручение срединной поверхности: ддх dOv
Х = —3T = --3F’ <7-5>
Рис. 7.4. Нормальные и касательные напряжения при изгибе.
или
d2w
(7.6)
л дх ду *
Если речь идет о жестких пластинках, то срединная поверхность считается свободной от деформаций, сопровождающих изгиб. Для
произвольного слоя пластинки, лежащего на расстоянии z от сре¬
динной поверхности, деформации удлинения еи и еу>и равны
£ЛГ, и === еу, HZKy, (7.7)
деформация сдвига будет
Ти = 2zX- (7.8)
Этим деформациям соответствуют нормальные напряжения <зх, оу и касательные напряжения т (рис. 7.4). Пользуясь законом Гука и пренебрегая напряжениями ог, получим:
§ 80] ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ЖЕСТКИХ ПЛАСТИНОК 273
В сечениях пластинки, параллельных осям х п у> выделим полоски длиной, равной единице. Усилия ох и оу образуют изгибающие моменты, приходящиеся на единицу длины сечения:
М
h_ h
2 Т
= f ax,»zdz> Му= f °у,« zdz.
ях
—h. i.
T ~J
или
Mx — D(xx-\- (j,yy), My = D (xy + (7.11)
где D — цилиндрическая жесткость пластинки:
°-= 12 (.-W <7I2>
Касательные усилия т образуют крутящий момент, приходящийся на единицу длины сечения:
и_
2
Я
= f xzdz, (7.13)
—А ~~~2
или
H=D(\-p.)x. (7.14)
Введем, далее, обозначения Qx, Qy для поперечных сил в сечениях xz и yzt также приходящихся на единицу длины.
Допустим, что пластинка подвергается действию поперечной нагрузки интенсивностью q. На рис. 7.5 показан элемент пластинки dxdy с действующими на него силами. Двойными стрелками обозначены вектор-моменты. Если в сечении с координатой х действует момент Mxdy, то в соседнем сечении, имеющем координату x-\-dxt
будет действовать момент dxJ dy. Аналогичные прираще¬
ния получают остальные компоненты моментов и поперечных сил. Составим уравнения равновесия элемента в проекциях на ось z и в моментах относительно осей хну. После простых преобразований эти уравнения приобретают вид
dQx, dQy
дх 1 ду, дН
-q, (7.15)
«, = 0. (7.16)
О,--«, = <>■ Р-1?)
дх 1 ду дН дМу
274 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Отсюда
д*Мх дгН d*Mv
2Jxdy~~dy*~ = ~q- (7.18)
Пользуясь выражениями для моментов и кривизн, приходим к известному дифференциальному уравнению изгиба жестких пластинок
~ / dAw, 0 dAw, dAw \ /7 1ЛХ
\ дх' + дх* ду* + ду< ) ~q (7Л9
ИЛИ
DV4w = q, (7.20)
где
V% = V2V2W> * = £ +
— двухмерный оператор Лапласа.
В «классических» задачах устойчивости внешняя поперечная нагрузка не учитывается: начальное напряженное состояние считается
Рис. 7.5. Усилия, приложенные к деформированному элементу пластинки.
безмоментным. Но вместе с тем при рассмотрении «соседних» изогнутых состояний пластинки надо принять во внимание проекции повернутых внутренних усилий на оси неподвижной системы координат. На рис. 7.6 показан элемент пластинки dxdy после изгиба с действующими на него нормальными усилиями о, ау и касатель-
§ 80]
ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ЖЁСТКИХ ПЛАСТИНОК
275
ными т. Напряжения ах, оу считаются положительными при сжатии; касательные напряжения будем принимать положительными, если они направлены, как показано на рис. 7.6; соответствующая им деформация сдвига увеличивает угол между гранями элемента, расположенными ближе к началу координат. Определим результирующую усилий axhdy. Левая грань элемента поворачивается вокруг
оси у на угол
dw
вая — на угол
а правда
- dx
Рис. 7.6. Усилия в срединной поверхности.
дх ' дх2 (рис. 7.7). Суммарная проекция сил oxhdy на ось z, равная, с точностью до малых высшего порядка, их равнодействующей, будет (оси координат на рис. 7.7, 7.8 отличаются от принятых на рис 7.6):
dy — °xh (Й + S dx) аУ = — cxh -г dx dy. (7.21) Аналогичное выражение для усилий су имеет вид
(7.21а)
а*Н~дх
, d2w,,
— °У h~df-dydx-
Найдем, далее, равнодействующую касательных усилий т/г, также получивших новые направления. Если одна из граней, параллельных у,
Рис. 7.7. К определению результирующей повернутых усилий сжатия.
г fid у
Рйс. 7.8. К определению результирующей повернутых усилий сдвига.
повернулась вокруг оси х на угол а вторая, ближайшая к чи-
dw
d2w
тателю (рис. 7.8),—на угол ~f~ ~§х'ду Х' то силы дадут
276 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах УПРУГОСТИ (гл. VII суммарную проекцию, равную
~xhSwdxdy- (7.22)
гг dw
Левая грань поворачивается вокруг оси у на угол а правая —
dw
на угол -jx dy. Полная проекция усилий xhdx будет
также равна
— тА dx dy. (7.22а)
Найдем сумму проекций «повернутых» усилий и разделим ее на dx dy;
эту величину надо ввести в левую часть уравнения (15); при = 0 оно получает вид
dQx dQy, d2w t d2w л t d2w
—,— Grh-5-0 — 2x/z -5—-r— = 0. (7.23)
dx 1 ду x дх2 у dy2 dxdy 4 y
Отсюда
dQx dQv 1 d2w d2w d2w \
-п-+-ь-=\°’-ш + ъ <724)
Сравним это уравнение с (15); как легко видеть, выражение, стоящее в скобках, можно трактовать как интенсивность фиктивной поперечной нагрузки
Ч° = - («* + «у + 2т г) А=(«л+Vy + 2хХ)А- <7-25>
Окончательно уравнение (20) получает вид (при q = 0)
<7-26>
При интегрировании уравнения (26) мы должны удовлетворить граничным условиям. Рассмотрим некоторые из вариантов таких условий.
1. Один из краев, например край л; = 0, шарнирно оперт. Такое предположение можно сделать, если пластинка соединена с подкрепляющим ребром, имеющим малую жесткость на кручение
(тонкостенный стержень открытого профиля), либо если прикрепление пластинки к ребру осуществляется по узкой полосе (один ряд заклепок, точечная сварка) (рис. 7.9, а). Тогда граничные условия имеют вид
w — 0, (7.27)
м=-°+)=0- <7-28>
Если выполнено условие (27), то вдоль края лг = 0 заведомо
§ SO]
d*w
~dy*
ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ЖЕСТКИХ ПЛАСТИНОК 277
= 0; следовательно, условие (28) перепишется в виде
d2w дх2
= 0.
(7.29)
2. Край л; = 0 защемлен. Такое допущение соответствует случаю пластинки, прочно сочлененной (например, с помощью двухрядного заклепочного шва) с ребром, достаточно жестким на кручение (рис. 7.9,6). Граничные условия будут
<2/ = 0, (7.30)
dw
дх
= 0.
(7.31)
3. Пластинка скреплена по краю лг = 0 с упругим ребром, имеющим изгибную жесткость EI. Одно из условий сопряжения состоит в равенстве прогибов:
Щ = («0,=о; (7-32)
через wx обозначен прогиб ребра. Второе условие выражает равенство погонного усилия, передающегося от пластинки на ребро,
Рис. 7.9. Граничные условия: а) шарнирное закрепление; б) защемление.
реакции со стороны ребра. Можно показать (см. [0.3], стр. 40), что погонная реактивная сила, нормальная к поверхности пластинкет, будет для рассматриваемого края
или
Второе граничное условие приобретает вид
(7.33)
(7.34)
(7.35)
278 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
4. Край лг = 0 свободен. Тогда должно быть
или
d3w
дх3
II II р р
(7.36)
d2w. d2w ~дх2 г ду2
— 0,
(7.37)
/о \ d3w
дх ду2
= 0.
(7.38)
Определим работу внутренних усилий на возможном перемещении пластинки. Если кривизна ъх получает приращение Ъхх, то работа момента Mxdy, приходящаяся на длину элемента dx, будет равна (—Mxbxxdx dy). Вычисляя таким же образом работу остальных усилий и интегрируя по площади пластинки F — аЪ, получим:
ЬА = — f f (МхЪхЛ + Му8чу + 2Я 8х) dx dy.
F
Приращение потенциальной энергии равно SU = — ЬА; пользуясь выражениями для моментов и кривизн, находим:
=D//Ks+)8(S)+(+)8()+
+ *<‘-»-£И£5-)]л«W = I D5 / / {(S + £)’ (Д)■}
или
F
Полная энергия изгиба равна
U = D j J {(V%>)2 — (1 — j») L(w, w)) dxdy; (7.39)
F
под L(w,<w) понимается выражение
t / \ о Г d2<w d2w ( d2w \21.Лч
L(WtW) = 2[-w— (-) J. (7.40)
Вычислим, далее, работу внешних сил, совершающуюся при выпучивании пластинки. Допустим, что пластинка подвергается действию усилий ох> оу, т, приложенных в срединной плоскости. Обозначим через и, v перемещения некоторой точки срединной плоскости вдоль осей х, у. Найдем взаимное смещение кромок пластинки,
Выделим элемент АВ волокна,
§ 80]
ОСНОВНЫЕ ЗАВИСИМОСТИ ТЕОРИИ ЖЕСТКИХ ПЛАСТИНОК
279
параллельного оси х (рис. 7.10). Пусть перемещения точки А вдоль осей х и z будут и и w% а точки В — и -f- dx и w -f- г/лг: новые положения точек обозначим через Ах и В{. Длина ds{ элемента после деформации будет
dSl=[(**+.g. )2+(4*)2]2.
или
Раскладывая это выражение в ряд и ограничиваясь первыми членами разложения, получим:
*, = [>+£+Мж)'+!(£)>-
Мы рассматриваем случай, когда пластинка выпучивается из своей плоскости; поэтому величиной можно пренебречь по сравнению с Окончательно W
находим:
да. 1 / dw \2 /7 л 1 \ *
6* = ¥+2Ы' <7-41> г'
По аналогии выпишем выражения для деформации удлинения элемента, параллельного оси у:
в, ~ dx
dv I J_ / w \2 2\ Рис. 7.10. К определению работы сжима-
dy ' 2 \ dy / * ' ющих сил при выпучивании пластинки.
Но для жестких пластинок деформации в срединной поверхности еу надо считать равными нулю. Следовательно, должно быть
ди 1 / dw \2
~ — —2VdJT) ’
dx
dv J[ / dw \2
~dy 2\5y/ *
(7.43)
Взаимное смещение точек, принадлежащих кромкам х = 0 и х = а, отнесенное к размеру а, равно
—if Т**—}:/(<*■■ (*•««>
280 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
величину ех считаем положительной при сближении кромок. Будем принимать, что в процессе выпучивания усилия ох остаются постоянными. Тогда их работа будет равна
Wl = aJCexha = ±f axh f (-£)* dx
o Lo
dy;
(7.45)
величина ox оставлена под знаком интеграла, так как в общем случае усилия ах меняются вдоль размера Ь. Аналогично взаимное смещение
кромок у = 0, у — b будет
о
<7-46>
Рис. 7.11. Деформация сдвига в срединной поверхности.
а работа усилий оу
V,=±f',h f(%py
Рис. 7.12. К определению работы сдвигающих сил.
dx. (7.47)
Перейдем к определению работы касательных усилий т/г. Найдем деформацию сдвига элемента dx dy, соответствующую перемещениям и, V. Как видно из рис. 7.11, она равна
vr _ ди. dv, -
Т —ду+дх’ (Э)
На следующем рис. 7.12 показано, как искажается треугольник ОМЫ со сторонами dx, dy при деформации сдвига *j, вызванной перемещениями w. Рассматривая рисунок, находим:
WW = [(dx? + (-g- dx)2 + (dy? 4- (4 dy)2 -
_ 2 уГ<«*?+(-£«*)’ - -rf <ь>
§ 80] Основные зависимости теории жестких пластинок 281 или, приближенно,
WW= {(dx? [ 1 + (-g-)*] + (dy? [l+(-)S]-2T dyf. (Ь0 С другой стороны, из рассмотрения треугольника N'N'fM вытекает
MN= [(dx? -f- (dy? + dy-- dxjj2. (с)
Сравнение выражений (b') и (с) дает
„ dw dw /J4
Ч ~ дх ду ‘
Полная деформация сдвига будет
ду. дх дх ду ' ' '
Считая для жестких пластинок у = 0, находим у' = — или
т--4!г-?г (7-49>
Примем, что касательные усилия т постоянны вдоль кромок пластинки а, b. Им соответствует «интегральное» искажение пластинки
а b
Г Г dw dw,, __ч
* = } J -d7-Wdxd»- (7-5°)
о о
Работа сил тh будет
а Ь
Wz = xhg = xhff4* rfx rfy. (7.51)
0 6
Окончательное выражение для работы внешних сил получает вид ь
Ръ I
W :
=4{/0
lo Lo
+ / °У / )2 } + // ж-wdx dy■ (7-52)
0 L0 J J 0 0
Полная энергия системы равна
Э—U — W. (7.5 3)
Приведенными выше выражениями для £/ и f мы воспользуемся, при решении задач устойчивости пластинок с помощью энергетического метода.
282 УСТОЙЧИВОСТЬ ПРЙМОУГ. пластинок В ПРЕДЕЛАХ УПРУГОСТИ (гл. VII
§ 81. Гибкие пластинки
Приведем зависимости, относящиеся к гибкам пластинкам; как уже было сказано, они понадобятся нам при изучении поведения пластинок в закритической области. Выпишем выражения для деформаций в срединной поверхности, которые только что были выведены:
ди. 1 / dw \2
dv, 1 / dw \2
е = -д7+2\—'
— ду ~ 2 \ду ) *
ди. dv_.dw dw
7 ду дх дх ду
(7.54)
Положительными здесь считаются деформации удлинения. Отметим, что правые части всех этих выражений содержат одни и те же функции и, v% w; следовательно, величины е, е, у не являются незави* симыми. Связывающее их уравнение совместности, или непрерывности деформаций, имеет вид
д2гх д2£у д2у I j)2w d2w d2w
ду2 ' дх2 дх ду \ дх ду / дх2 ду2 или, если воспользоваться оператором L,
дЧх дЧу д2ч 1
~д?- + -д?— w)- (7-56)
В справедливости соотношения (56) легко убедиться непосредственным дифференцированием. С физической точки зрения оно означает, что соседние элементы пластинки не могут деформироваться самостоятельно, как изолированные, так как в этом случае между ними возникнут пустоты и будет нарушена непрерывность материала. Деформации е, еу, у связаны с напряжениями в срединной поверхности ох, су, х выражениями
QX °у Оу °Х 2 (1 + fl)
tX £ V4 £ » еу “ Е ? — Е Х
ИЛИ
Е Е Е
7372-(®r+f*ey)< °у = ТГ («у+ !***)• * = gfl+jt) т- (7-58)
Эти напряжения должны удовлетворять уравнениям равновесия.
На рис. 7Л6 изображены усилия, действующие по граням dx, dy. Направления усилий, показанные на рисунке, принимаются положи-
§ 81] ГИБКИЕ ПЛАСТИНКИ 283
тельными. Проектируя все силы на оси х, у, находим:
(7.59)
дах. дх _п дх ' ду
дч dav
Уравнения (59) будут автоматически выполняться, если выразить ах, оу, х через функцию напряжений Ф следующим образом:
д2Ф д*ф __ д2Ф
°У дх* » Т drriv * (7.60)
— ду2 у дх2’ дх ду *
Обратимся теперь к уравнению равновесия в проекциях на ось z. Здесь элемент пластинки должен быть рассмотрен в деформированном состоянии. Но это было сделано нами уже раньше. Поэтому мы можем воспользоваться
уравнениями (23) и (26); надо
только изменить перед ох, а, Tdx
х знак на обратный, так как tdys/ЩШ 7(tJj-dx)dy
при выводе этих уравнений ' ~ х
положительными считались об- // - * ~:~S/гб + \d
ратные направления усилий. ж/ ' х+1х х} У
Окончательно уравнение (26) принимает вид
(tdy)dx7,
j® у4 i! + 0 i АъЩ-ъ)**
h дх2 у ду2
d2w Рис. 7.13. Усилия в срединной поверх-
~~Z~dx~dy' ности гибкой пластинки.
Выразим напряжения ох, оу, х через функцию Ф по (60) и введем оператор L(w, Ф):
,, d2w д2Ф. д2т д2Ф 0 d2w д2Ф _ _ч
L(w, Ф)— дх2 ду2 + ду2 дх2 2 дхду дхду ; (7.62)
тогда уравнение равновесия (61) примет вид
--44w = L(w, Ф). (7.63)
Если, далее, подставить в уравнение совместности деформаций (56)
выражения (54) для е, sy, у, то оно примет вид
-I- V4<3> = _.1 L (w, w). (7.64)
Отметим, что операторы L(w, ф) по (62) и w) по (40) имеют
рдну и ту же структуру,
284 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Уравнения (63) и (64), связывающие функцию Ф напряжений в срединной поверхности и функцию прогиба wt являются основными в теории гибких пластинок. При интегрировании этих уравнений надо удовлетворить тем или иным граничным условиям. Условия, зависящие от прогиба пластинки, имеют такой же вид, что и для жестких пластинок. Что касается условий, относящихся к деформации в срединной поверхности, то они формулируются следующим образом.
1. Точки края лг = 0 свободно смещаются вдоль осей хну. Тогда здесь должны равняться нулю напряжения ах и х:
<*2ф л <*2ф Л /7
5 = 0. *-—5 = 0. (7.65)
2. Точки края лг == 0 остаются неподвижными; тогда должно быть при л: = 0
и = 0, v = 0.
3. Кромки пластинки остаются прямолинейными. Если полагать, что одна из кромок, например л; = 0, неподвижна, при этом получится, что взаимное смещение кромок х = 0 и х — а должно иметь фиксированное значение. Обозначая через ех относительное сближение краев:
ех—\ («ж=а — Ог-о).
по (54) получим:
т / [е- - т (4г)1dx=const <7-66>
или
U
Пдо д*ф Е I dw \21.. с_ч
- р -зр- - т Ur) г * =const- <7-67>
О
Как показал П. Ф. Папкович *), условие может быть упрощено, если считать, что изогнутая поверхность симметрична относительно осей симметрии пластинки, или, иными словами, если функции w и Ф имеют одни и те же значения в симметричных точках. Тогда условие (67) переходит в следующее:
-- = 0 при х — а. (7.67а)
Потенциальная энергия деформации гибкой пластинки складывается из двух составляющих: энергии изгиба Ux и энергии дефор-
*) См. книгу [0.7], стр. 899.
§ 82] устойчивость шарнирно опертой пластинки 285
мации в срединной поверхности U2. Первая из этих величин опре*
деляется по-прежнему формулой (26). Энергия U2 равна
U2 = hj J (<3xsx-{-<3yby-{-*4)dx dyt
F
или, по формулам (57),
и2 = Ц f f К + °у “ 21ХЗЛ + 2 (1 + I1) х2] d»-
F
Вводя функцию напряжений Ф, получим:
-2<‘ + rt[-Sp— <7М>
ИЛИ
и2=ш/11(у2ф)2 ~(1+1 (ф* ф)] dx аУ' <7-69)
F
Перейдем к различным частным задачам устойчивости и закритической деформации пластинок*).
§ 82. Устойчивость шарнирно опертой пластинки, сжатой в одном направлении
Выпучивание пластинок в авиационных и судовых конструкциях чаще всего вызывается действием сжимающих усилий, расположенных в плоскости пластинки. Так как ширина пластинки, являющейся панелью крыла самолета, палубы судна и т. д., обычно мала по сравнению с габаритами конструкции, то во многих случаях сжимающие усилия можно считать равномерно распределенными по ширине пластинки. Поэтому задача об устойчивости пластинок при равномерном сжатии является той «классической» задачей, которая привлекает к себе наибольшее внимание; решение ее **) является отправным пунктом для формулировки и исследования других, более сложных задач.
*) Обзор исследований в этой области дан в книге Колбруннера и Мейстера [0.19], 1958; из этой книги взяты некоторые из приведенных далее графиков.
**) Эта задача была впервые решена Брайеном [7.14] в 1888 г. с помощью энергетического метода. Уравнение типа (70) было составлено Навье еще
286 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Рассмотрим сначала пластинку, удлиненную вдоль оси х (а>Ь) и сжатую вдоль длинной стороны усилиями ох (рис. 7.14). Допустим, что пластинка шарнирно закреплена по длинным краям; граничные условия по коротким краям в данном случае являются несущественными.
Уравнение (26) получает
вид
D _4. d2w
-hVw+c*-d*
:0.(7.70)
Граничные условия имеют вид
d2w
ду2
: 0 ПрИ
у = 0,Ь. (7.71)
х777
Рис. 7.14. Пластинка, сжатая в одном направлении.
Выпишем решение, удовлетворяющее этим условиям, в виде
/.. пх. п%у _лч
w = f sin — sin. (7.72)
Мы считаем, что вдоль короткой стороны образуется п полуволн. Так как для удлиненной пластинки можно принять, что волнообразование осуществляется по направлению х свободно, то через I обозначена длина полуволны по этому направлению. Подставляя (72) в (70), получим:
+ (7-73>
Отсюда
(Ь, n2/\2 Dn2 _,ч
(т+т )~ш- (7’74>
Для того чтобы найти критическое напряжение, надо положить
п= 1. Считая, далее, напряжение вх функцией переменной Ijb и
желая найти минимум ах, приравниваем нулю производную:
да
Отсюда находим:
’Ш
1 = Ь.
0.
(7.75)
(7.76)
Таким образом, изогнутая поверхность удлиненной пластинки состоит в данном случае из квадратных участков размером Ъ X Ъ, в пределах каждого участка по направлениям х и у образуется одна
§ 82)
УСТОЙЧИВОСТЬ ШАРНИРНО ОПЕРТОЙ ПЛАСТИНКИ
287
полуволна синусоиды. Для смежных участков выпуклость синусоиды направлена в разные стороны, как показано на рис. 7.15.
Подставляя (76) в (74), находим критическое напряжение равным
(7.77)
или
Принимая [л;
КР“~ 3(1 —(X2) ;0,3, получим:
кр '
(7.7 8)
(7.79)
Эта формула справедлива лишь в том случае, если критическое напряжение лежит в пределах упругости.
Рис. 7.15. Волнообразование удлиненной шарнирно опертой пластинки.
Предположим, далее, что стороны пластинки сравнимы между собой по величине. Принимая прежние граничные условия (71), выберем решение уравнения (70) в виде
j.. тих. w = / sin —J— sin
my
~
(7.80)
где m, n — числа полуволн по направлениям xt у. После подстановки этого выражения в (70) имеем:
Drt2 / mb. пга \* С1ч
(7l8I)
Здесь надо положить л=1. Считая, что достаточно велико, найдем, что минимум выражения (81) имеет место при
(7.82)
Подставляя (82) в (81), находим, что критическое напряжение По-прежнему определяется выражениями (77) (79). Этот результат
легко было предвидеть: мы как бы отсекаем от удлиненной пластинки
288 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах УПРУГОСТИ [гл. VII
(по рис. 7.15) столько квадратов, сколько раз ширина пластинки укладывается вдоль длины.
Выражения (77)—(79) являются точными в том случае, если отношение afb является целым числом. Если же число не целое, то следует по-прежнему принять п= 1, а из двух ближайших значений т взять такое, которое придает выражению (81) наименьшую величину. Переход от т к т-\- 1 полуволнам будет иметь место при
* “ - '(m + 1)2, 1 I2
22 “Г Ь* J
»2
т*
(т + I)2
отсюда
(7.83)
Например, при afb < V2 будем иметь т = 1, а при а/£> У~2 т. = 2.
При а/b =У2 одинаково возможно образование одной и двух полуволн.
Введем обозначение
K=(4+-sf <7-84>
Тогда выражение для критического напряжения можно представить в виде
7l2D
°кр = к-
b*h
(7.85)
числе полуволн.
В таблице 7.1 и на графике рис. 7.16 приведены значения К, вычисленные по формуле (84).
В случае, если ширина пластинки b велика по сравнению с продольным размером а, надо принять т = п= 1; формуле (85) удобнее придать вид
л* D
•ф
=*,•
a2h
где
К,
(7.86)
(7.87)
При достаточно большом значении Ь/а можно пренебречь вторым членом в выражении (87), или, иными словами, считать продольные
СЛУЧАЙ ЗАЩЁМЙЕННЫХ ПРОДОЛЬНЫХ КРАЕВ
289
Таблица 7.1
Значения коэффициентов К для пластинки, шарнирно закрепленной по всем краям
а
Т
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
К
27,0
13,2
8,41,
6,25
5,14
4,53
4,20
4,04
а
~Т
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
К
4,00
4,04
4,13
4,28
4,47
4,34
4,20
4,08
а
Т
1,8
1,9
от 2 до оо
К
4,05
4,01
—4,00
края свободными. Тогда получим /С1=1; выражение (86) будет иметь вид
пЮ п*ЕН* (7.88)
кр '
a2h
3(1 — (х2) а2 •
Пластинка здесь переходит в стержень прямоугольного сечения 1 X шарнирно опертый по концам; выражение (88) отличается от обычной формулы Эйлера лишь тем, что модуль заменяется на «приведенный» модуль £(1—2).
§ 83. Случай защемленных продольных краев
Перейдем к случаю, когда нагруженные кромки пластинки закреплены шарнирно, а ненагруженные жестко защемлены. На примере этой практически важной задачи мы познакомимся с методом решения, который часто применяется в теории устойчивости пластинок. Расположим оси координат по рис. 7.14. Представим интеграл уравнения (70) в виде
W = Y (у) sin, (7.89)
где У (у) — искомая функция, зависящая, только от у. Очевидно, выражение (89) удовлетворяет граничным условиям для краев х = 0, х = а. Подставляя (89) в (70) и сокращая на sin (ткх/а)* получим:
d*Y
dy
г-г(т)’?+[Ш'-тг]Нг)’к=°- <7-90>
290 УСТОЙЧИВОСТЬ ПРЯМОУГ, ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
От уравнения (70) в частных производных мы перешли, таким образом, к обыкновенному дифференциальному уравнению относительно функции К; в этом и заключается основной шаг. Интегрирование уравнения (90) в данном случае не представляет трудностей; в более же сложных задачах оно может быть выполнено с помощью различных приближенных методов, например метода Бубнова — Галеркина.
Обращаясь к уравнению (90), введем обозначение
(7.91)
и составим характеристическое уравнение
k4 _ 2Ш + (х2 — X2 = 0; (7.92)
корни его будут
*i,2 = lA(x+j/’--)> А3,4 = ‘/'х(х — (7.93)
Как мы видели, в предельном случае пластинки со свободными продольными сторонами критическое напряжение определяется формулой (88); при закреплении продольных сторон должно быть
ах > \2D/h. (7.94)
Следовательно, корни 3>4 являются мнимыми. Полагая
a = Л(х+/*-.). р = (7.95)
получим интеграл уравнения (90) в виде
К (у) = Сх ch а у + С2 sh а у -f- С3 cos (Зу С4 sin ру. (7.96) Г раничные условия имеют вид
К = 0, =0 при у = 0, у = Ь. (7.97)
Пользуясь этими условиями, находим:
Cj + С3 = 0, <хС2 + рС4 = 0 (7.98)
и, далее,
С) (ch ab — cos P)+ С2 sh аb — у sin р£ = 0, (7.99)
Сх (sh ab -f- -Ц* sin р С2 (ch аb — cos р£) = 0 (7.100)
§ 83]
СЛУЧАЙ ЗАЩЕМЛЕННЫХ ПРОДОЛЬНЫХ КРАЕВ
291
Система уравнений (99), (100) имеет решения, отличные от нуля, при условии
ch cab — cos fib sh ab — ~ sin fib
= 0;
(7.101)
sh ab + sin fib ch ab — cos fib отсюда получаем:
(ch ab — cos fib)2 — sh ab -f- sin sh ab — sin (3 = 0. (7.102)
Из (95) имеем:
а*+Р* = 2Ху/Г, a2 — (32 = 2X2. (7.103)
Пользуясь уравнениями (102) и (103), определяем критическое напряжение.
Задача упрощается, если учесть симметрию упругой поверхности пластинки относительно оси х' (рис. 7.17). Выражение (96) перепишется в виде
У (у) = A ch ay -f- С cos fiy. (7.104)
Граничные условия будут
к=0, 4у=° при у=т*
(7.105)
Вместо уравнений (100) получаем следующие:
A ch + С cos -у- = 0,
Acl sh 4 — Ср sin-- = 0.
(7.106) рис уду Пластинка с защемленными продольными краями.
Приравнивая нулю определитель системы (106), находим: ath- + ptg-- = 0.
Следуя Гартману [0.18J, введем обозначения:
ab Р
%— 2 • 'J— 2
Тогда вместо (107) будем иметь:
—% th 5 = У) tg -q.
(7.107)
(7.108)
(7.109)
292 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Уравнения (103) получают вид
Определяем величины £ и т) из уравнений (109) и (111) и по (110) находим критическое значение <зх. На рис. 7.18 по оси абсцисс отложены значения £, а по оси ординат rj. Кривые т](£) по уравнению(109) пересекают ось ординат в точках т] = it, 2тс, Зтс,... и располагаются одна над другой. Величина ех по (110) пропорциональна (£2+ т]2)2; следовательно, мы должны выбрать кривую, имеющую наименьшие ординаты; она изображена на рис. 7.18 и обозначена через S. Здесь же даны кривые—гиперболы,— соответствующие уравнению (111), при различных значениях mb/a. Точки пересечения этих кривых с линией S определяют искомые величины £ и *г\\ они даны в скобках. Представим критическое напряжение формулой (85); коэффициент К будет равен
K=lA£f + ■*?■ (7.42)
При a/mb= 1 получаем К = 8,67; при a/mb = 0,67 К = 7,00; при a/mb = 0,5 К = 7,80. Более подробное исследование показывет, что напряжение получается наименьшим при a/mb=0,662, причем /С=6,97.,
Таблица 7.2
Значения коэффициента К в случае шарнирного опирания нагруженных краев и защемления ненагруженных
а/Ь
0,4
0,5
0,6
0,7
0,8
0,9
1,0
К
9,44
7,69.
7,05
7,00
7,29
7,83
7,69
В таблице 7.2 приведены значения К для различных отношений а\Ь. В случае а >Ь изогнутая поверхность пластинки состоит из вмятин,
?
4,495
4
Д
■—_
у/ JL JL 2 /
2
1
54
N
-Sv
mw)mm i f / ill
; f 1
я\ - m 1' 2л 7,0
Щ m
f
Рис. 7.18. К определению критического напряжения в случае защемленных краев.
§ 83]
СЛУЧАЙ ЗАЩЕМЛЕННЫХ ПРОДОЛЬНЫХ КРАЕВ
293
длина которых I = ajm. составляет приблизительно 2/3 ширины Ь (рис. 7.19).
бх
б£
■пг
—м I
I I
!f —V 11 I I
I Г I! п и
j LJ <~> > 1 I J 1 V J
1 1 и IVu ) 11 J1
4*0,7 b
Рис. 7.19. Волнообразование удлиненной пластинки, защемленной по длинным краям.
Применим для решения этой же задачи метод Ритца. Граничные условия задачи удовлетворяются, если выбрать выражение для прогиба в виде
,. тпх. о 7CV /_ 1 1 оч
w = / sin sin2--. (7.113)
Составим выражение для потенциальной энергии изгиба по формуле (39):
3 m4b, 8т2, 16а \
ab
Работа внешних сил равна по (45)
о о
или
W=-±-*xhfW
Приравнивая выражения (114) и (116), находим: ■кЮ ( 1, 8. 16,2\
(7.114)
(7.115)
(7.116)
(7.117)
где Х-а/тЬ. Если считать а>Ь, то минимальное значение <зх найдем из условия
:0. (7.118)
д\
откуда
Х2 =
V з
<?кр —7,3 Ь2(1.
(7.119)
(7.120)
294 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах УПРУГОСТИ [гл. vn
Отметим, что значение X получилось близким к найденному выше (0,662); значение критического напряжения оказалось выше точного на 4%.
Мы рассмотрели случай, когда продольные края пластинки не поворачиваются. Критическое напряжение по сравнению со случаем шарнирного опирания здесь значительно повышается: минимальная величина окр возрастает в 7/4 раза. Это обстоятельство надо учитывать при проектировании. Условиям полного защемления можно, как уже было сказано, удовлетворить, прикрепляя пластинку с помощью двухрядного заклепочного шва.
Вместе с тем подкрепляющие ребра должны обладать достаточной крутильной жесткостью: сечение их, совместно с сечением прилегающего участка обшивки, должно иметь замкнутый контур, как показано на рис. 7.9, б.
Если необходимо провести уточненный расчет с учетом фактической крутильной жесткости ребер, то надо обратиться к задаче
об устойчивости пластинки с упруго защемленными продольными
защемленными краями.
краями *). Результаты решения этой задачи приведены на рис. 7.20. Каждая серия кривых относится к определенному значению коэффициента а, равного
где b — ширина пластинки, GIK—крутильная жесткость продольных ребер. При а = оо и а = 0 получаем предельные случаи, соответственно, шарнирного опирания и жесткого защемления.
*) Эта задача исследована Ландквистом и Стоуэллом (Е. Lundquist, £. Stpwell, NACA Rep. № 733, 1942).
§ 84] ПЛАСТИНКА СО СВОБОДНЫМ КРАЕМ 295
Пример 7.1. Определить критическое напряжение и форму выпучивания для панели обшивки верхней части крыла самолета, шарнирно скрепленной с жесткими ребрами и сжатой вдоль длинных сторон*) (рис. 7.21, а). Размеры панели: а = 200 мм, b = 120 мм, h = 2 мм. Как изменится величина критического напряжения, если принять, что пластинка защемлена по продольным краям, и учесть крутильную жесткость ребер? Ребра изготовлены из прессованных уголковых профилей (рис. 7.21, б). Материал обшивки и ребер — дюралюмин; Е =г 0,72 • 106 кг!см2, р. = 0,34.
Цилиндрическая жесткость пластинки равна
0,72.106 • 0,23 D~ 12(1—0,342)
= 545 кг • см;
отношение сторон alb = 1,67.
Для случая шарнирного закрепления по таблице 7.1 /<4,12. Критическое напряжение будет
°“Р = к W = 4)12 =775 кг/см2-
Обращаясь ко второму случаю, вычисляем крутильную жесткость ребра:
Коэффициент а равен
ЬР 12-545 д.
GIK~ 0,27 • 10е • 0,008 ~ ’ '
По графику рис. 7.20 находим:
п2. КАК
К = 5,2, акр = Ъ,2--шщШкг/см2.
Таким образом, при упругом защемлении по продольным краям критическое напряжение повышается на 25%.
§ 84. Пластинка со свободным краем.
Сводка расчетных данных
Рассмотрим сочетания граничных условий, когда один из краев пластинки является свободным.
1. Нагруженные края закреплены шарнирно; один из ненагруженных краев закреплен шарнирно, а второй свободен. Такие
*) Примеры 7.1—7.3 составлены Ю. П. Григорьевым.
Рис. 7.21. Панель крыла самолета.
296 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Граничные условия имеют место, например, для каждой из полок равнобокого уголка, сжатого вдоль оси (рис. 7.22, а). Для продольных
Рис. 7.22. Выпучивание пластинки, одна из сторон которой свободна
краев соотношения пп. 1 и 4 § 80 принимают вид
d2w, d2w
w=°’ -w+v-w
d2w, d2w d3w
= 0 при у — 0,
0 при у = Ь.
(7.121)
(7.122)
~ду* “Г ~дх* ~ ’ ~ду*~ ( ~ дх2 ду
Представляя w по-прежнему в форме (89), находим для К выражение (96). Условия (121) дают:
+ С3 = о,
т2 л2
Сх* - C - (Pi + Q = 0,
(7.123)
(7.124)
откуда С1 = С3 = 0. Из условий (122), далее, получим: с2 (а2 — jj. Sh ab — С4 (а2 •+- sin
С2а [<х2 — (2 — ц) --J ch аb — С [р2 + (2 — у.) -Lj cos §b
= 0,
= 0.
(7.125)
§ 84]
ПЛАСТИНКА СО СВОБОДНЫМ КРАЕМ
297
Приравнивая нулю определитель этой системы, приходим к уравнению
т2п2
■Р-
(7.126)
* + f*-
В th ab
Исследование этого уравнения показывает, что при любых значениях а/b наименьшее значение ох соответствует т = 1, так что в продольном направлении всегда образуется только одна полуволна (рис. 7.22, б). Значения коэффициента К в окончательном выражении (85) даны в таблице 7.3 (при [х = 0,25).
Таблица 7.3 Значения коэффициента К в случае, когда один из ненагруженных краев закреплен шарнирно, а другой свободен
а/Ь
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
3,0
оо
К
3,65
2,15
1,44
1,14
0,95
0,84
0,76
0,70
0,56
0,456
Обратимся к энергетическому методу. Представим w в виде
тпх
w = f у sin ■
(7.127)
считая каждое сечение х = const срединной поверхности прямой линией. Энергия изгиба U равна (см, формулы (39)—(45))
D х9 т2к2 г т2п2, Л *]'
тг/2—[-
работа внешних сил
(7.128)
(7.129)
(7.130)
2 J а2 6
Приравнивая эти выражения, находим:
Сх=-£н[тЧ2 + 6(1-\
Очевидно, здесь надо принять т= 1. При (х = 0,3 коэффициент К оказывается равным
К= 1,03 (4)2+ 0,427. (7.131)
Эта формула дает значения /С, весьма близкие к тем, которые помещены в таблице 7.3.
298 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
2. Один из ненагруженних краев защемлен, другой свободен. В этом случае условия (121) приобретают вид
л dw f, л
w = 0t = 0 при у = 0,
(7.132)
(7.133)
условия (122) остаются прежними. Из (132) следует
С3= С1 С4 = р- С 2-
По (122) находим:
Схо? ch aft -- C2a2 sh aft -f- C2 cos 0ft -f- C2a[3 sin (3ft —
_ (i JHL (c1 ch ab + C2 sh a£ — C, cos — j C2 sin = 0, (7.134)
CjOt3 sh aft -f- C2a3 ch aft — CjP3 sin (3ft -- C2a(32 cos (3ft -f-
+ (2 — [a) (Cxa sh aft — C2a ch aft -f-
sin (3ft— C2a cos (3ft) = 0. (7.135)
Приравнивая нулю определитель этой системы, получим уравнение
2уЬ -f- (у2 -f- 82) ch a ft cos (3ft:
sh a* sin p*. (7.136)
где
T = «2-(2-t*) 8 = p2 + (2-rt
ml n*
(7.137)
Анализ уравнения (136) показывает, что при а>Ь изогнутая поверхность делится на полуволны длиной 1,64ft. Значения коэффициента К при различных отношениях a/ft даны в таблице 7.4 ( = 0,25).
Т а б л иц.а 7.4 Значения коэффициента К в случае, когда один из ненагруженных краев защемлен, а другой свободен
а\Ь
0,8
1,0
1,2
1,4
1,6
1,8
2,0
3,0
со
К
2,70
1,70
1,47
1,36
1,33
1,34
1,38
1,36
1,33
Решение этой же задачи энергетическим методом можно получить, полагая
-. тпх. о пу 1 о о ч
w = / sin —— sin2. (7.138)
§ 84] ПЛАСТИНКА СО СВОБОДНЫМ КРАЕМ 299
Выражение для К получает вид
К = 1,04 (У' + ОЛзЦ-у2 + 0,684. (7.139)
При а>Ь минимальное значение К соответствует a/mb= 1,64 и равно К =1,43. Ошибка по отношению к точному решению составляет около 8%.
Рис. 7.23. Коэффициент К при различных условиях закрепления пластинки, сжатой в одном направлении.
На рис. 7.23 приведены значения К в зависимости от отноше» ния а/Ь для случаев, разобранных выше, а также для тех случаев,
300 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
когда нагруженные края защемлены, а ненагруженные закреплены шарнирно или защемлены *).
Приводим также сводку значений минимальных критических напряжений; наряду с величиной К в таблице 7.5 помещены значения коэффициента k в формуле, удобной для практических расчетов:
°Kp = k(J, (7.140)
в применении к стали (принято Е= 2V1 • 106 кг/см2, jjl = 0,3) и дюралюмину (£ = 0,7 • 106 кг/см2, р, = 0,3).
Таблица 7.5
Минимальные критические напряжения при сжатии в одном направлении
Граничные условия для ненагруженных кромок
К а=0,3
k в кг!см2
сталь
дюралюмин
Шарнирное опирание 4,00
760
253
Защемление 6,97
1320
440
Один из краев шарнирно оперт,
другой свободен 0,425
80,5
26,8
Один из краев защемлен, другой
свободен..
1,28
243
80,8
§ 85. Устойчивость пластинок при сдвиге
Вторая классическая задача теории устойчивости пластинок относится к случаю чистого сдвига (рис. 7.24). В таком напряженном состоянии находится панель коробчатой (кессонной) конструкции, передающей крутящий момент. Другой пример — тонкие стенки балок, воспринимающие поперечную силу, при условии, что нормальными напряжениями в стенке можно пренебречь.
Определение критических усилий для пластинки при сдвиге — задача более трудная, чем в случае равномерного сжатия, так как вмятины, образующиеся при потере устойчивости, имеют своеобразную форму, сильно меняющуюся в зависимости от отношения сторон пластинки.
Рассмотрим и здесь прежде всего случай удлиненной пластинки шарнирно опертой по длинным краям, и приведем приближенное решение задачи. Эксперименты показывают [7.22], что
*) Некоторые расхождения в значениях /С, указанных в таблице 7.5 и предыдущих таблицах и графиках, объясняются различием в величинах у. и тем,что задачи решались в разных приближениях.
§ 85]
устойчивость пластинок При сдвиге
301
при выпучивании такой пластинки образуются. наклонные складки, близкие к прямолинейным. Поэтому изогнутую поверхность можно представить с помощью выражения
W -
= / sin sin у (х — ky).
(7.141)
Прогиб обращается здесь в нуль по продольным краям пластинки и, кроме того, по «узловым» линиям y = kx, наклон которых характеризуется параметром k\ величина / представляет здесь расстояние между узловыми линиями..
Потенциальная энергия по (39) оказывается равной
с/ = °ти-[(!)г+да+2+( 4/(1+]/';
работа внешних сил по (51) будет
(7.142)
(7.143)
Приравнивая эти величины, находим:
7i2D
[б + 2 + ()2 +(А)2(1+)2]. (7.144)
2 kb2h
4 Определяем параметры k, / из условий, что т принимает наименьшее значение при
отсюда
1
£ = —, /=1,22£. (7.146)
Таким образом, угол наклона узловых линий к оси равен приблизительно 35°. Подставляя (146) /Ж
в выражение (144), определяем коэф- фициент К в формуле г
т is. 7 Рис. 7.24. Пластинка, подвергаю-
а ми » щаяся сдвигу.
кр
b2h
он оказывается равным /С= 4 ]/2 = 5,64. Решение задачи в замкнутом виде*) приводит к точному значению К =5,34; таким образом, погрешность приближенного решения составляет около 6%. Форма горизонталей изогнутой поверхности и изогнутых линий в сечениях, нормальных к оси х, соответствующая точному решению,
, Г,), °«° было получено Саусвеллом и Скзн (R. V. S о u t h w е 11, Sylvia W. Skan, Proc. Roy. Soc. London, Ser. A 105 (1924), 582).
302 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
показана на рис. 7.25; расстояние между «узловыми» линиями составляет /=1,25.
В случае жестко защемленной по длинным краям пластинки коэффициент К достигает величины 8,98; таким образом, эффект «заделки» краев оказывается приблизительно таким же, как и при
Рис. 7.25. Волнообразование удлиненной пластинки с шарнирно опертыми краями при сдвиге.
сжатии. Изогнутая поверхность для этого случая изображена на рис. 7.26; узловые линии здесь также сближаются, и расстояние между ними снижается до / = 0,8ft.
Сечения
Рис. 7.26. Волнообразование удлиненной пластинки с защемленными краями при сдвиге.
Перейдем к задаче о выпучивании пластинки с конечным отношением сторон; решение ее оказалось особенно сложным. Воспользуемся методом Ритца, аппроксимируя выражение для прогиба с помощью ряда
22 А°
т*= \ л« 1
. тпх. пъу sin Sin —г—
(7.148)
§ 851 устойчивость пластинок при сдвиге 303
Вычислим энергию изгиба по (39), принимая во внимание соотношения
? ( а
тих. Ых, ] о ПРИ — ’
С1П П У0 — < sin sin — dx
о а а I 0 при т Ф 1\
(7.149)
тогда получим:
слщ
т п
Далее определим работу внешних сил по (51); учитывая соотношения
2а
Г. Ых тъх,, j
j sin —— cos —— dx dy = \
% /2 _ m2 ПРИ нечетной сумме
0 при четной сумме / + т,
(7.151)
получим:
w• <7-152>
т n I j
здесь должны быть приняты во внимание лишь те сочетания индексов т-\-1 и л + у, которые одновременно являются нечетными. Условия экстремума энергии
<?Э _d(U-W)_
Ш— —дЛ 0 (7.153)
итп и-птп
получают вид 4 п sIl а __п2 \2 U 4 тп \а2 ПГ- Ь2 )
(7.154)
i j
суммы т + /t + У должны быть нечетными.
В первом приближении выберем следующие сочетания индексов:
т, n
I, J
l; 1
2; 2
2; 2
l; 1
Система (154) сведется к двум уравнениям:
D-An(± + ±.J--xhA22 = 0. (7Л55)
f-Ai-4DaM22(-l-+-i-)2 = 0. (7.156)
304 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII Введем обозначения:
а = -г-, А :
ь
тс 4D
' 32ахЬ2/1 ’
тогда уравнения (155), (156) примут следующую форму:
+**)■> Ап+Ап=0,
■§■ -11 “Ь (1 + ®2)2 22 = 0.
Приравниваем нулю определитель системы:
гО + *2)2
4
9
9
(1 + а2)2
= 0,
отсюда
Х== ±
9(1+ а2)2 *
Критическое напряжение ткр будет равно
_ 9тс4£(1+а2)2 ТкР — 32a 4%h
Для квадратной пластинки получим:
t * 1 тс2D
ТКР — 11,1 -рд-.
Далее из (158) можно найти соотношение между Ап и Л22; при а = Ь будет Л22 = 0,25ЛП.
Во втором приближении возьмем такие сочетания индексов:
(7.157)
(7.158)
(7.159)
(7.160)
(7.161)
(7.162)
(7.163)
т, п
i. j
1,1; 1,3; 3,1; 3,3 2,2
.2,2
1.1;
СО
СО
со
со
Определитель системы (149) имеет вид 4
9
4 _
2
0
9
0
0
0
(! + «>>■ -±
-ТГ
5
_4
5
36
25
О
О
4-(9+а2)2
36
25
О
О
81Х.
О -d + a2)2
= 0. (7.164)
§ 85]
УСТОЙЧИВОСТЬ ПЛАСТИНОК ПРИ СДВИГЕ
305
Во всех строках, кроме одной, здесь содержится только по два члена. Благодаря этому уравнение, полученное после развертывания определителя, можно сократить на X3. В итоге находим:
X = ±
9(1+«2)2
s,
где
81
81 (1+а2)2, 81 (1 + а2)2
625 25 (1 + 9«2)2 25 (9 +а2)2
этому соответствует критическое напряжение
9n4D (1 -)- о2)2
ткр
32 a3b2hs
(7.165)
(7.166)
(7.167)
Поправочный коэффициент по отношению к значению первого приближения (161) равен. Для квадратной пластинки он составляет s=l,18; поэтому во втором приближении вместо (163) получим:
*кР = 9,4 -5-. (7.163а)
Мы исследовали только тот случай, когда сумма индексов т-\-п является четной. В общем случае определитель типа (164) представляет собой произведение двух определителей, из которых один содержит четные т-\-п, а другой — нечетные. В случае 1 < а < 2,5 наименьшее значение дает определитель с четными т-\-п; при
больших а надо попеременно учитывать первый и второй опре¬
делители *).
В итоге критическое напряжение ткр можно по-прежнему представить в виде
*кр = (7Л68)
Уточненные значения коэффициента К даны в таблице 7.6.
Таблица 7.6
Коэффициенты К в случае шарнирно опертой пластинки при сдвиге
a/b
1,0
1,1
1,2
1,3
1,4
1,6
1,8
2,0
3,0
5,0
oo
К
9,34
8,47
7,97
7,57
7,30
6,90
6,64
6,47
6,04
5,71
5,34
*) Это исследование было проведено Зейделем [7.19], Гартманом [0.18] и Штейном и Неффом (Н. Stein, J. Neff, NACA TN 1222, 1947).
306 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Для определения К можно также пользоваться приближенной формулой (а>1)
К = 5,34+. (7.169)
Для предельных значений а=1 и а = оо эта формула дает величины /С, совпадающие с приведенными в таблице 7.6. На рис. 7.27
Рис. 7.27. Волнообразование пластинки с отношением сторон 0,5 и 1 при сдвиге.
Рис. 7.28. Выпученная поверхность подкрепленной пластинки при сдвиге: а) в момент потери устойчивости, б) при ЗсГкритической деформации.
показана форма изогнутой поверхности пластинки при а = 0,5 и а= 1,0.
Если пластинка защемлена по всем кромкам, то формула (169) принимает вид (а>1)
к= 8,98 + --. (7.170)
В заключение приведем фотографии удлиненной пластинки, подкрепленной по краям, в момент потери устойчивости (рис. 7.28, а) и при значительном превышении сдвигающими усилиями критической величины (рис. 7.28, б).
Сводный график для определения К в зависимости от aft дан на рис. 7.29. Здесь приведены расчетные кривые не только для рассмотренных выше граничных условий, но и для случаев, когда два края пластинки (длинные или короткие) защемлены, а два других закреплены шарнирно.
Пример 7.2. Подкрепленная цилиндрическая оболочка (рис. 7.30) испытывает действие крутящего момента Мк = 5000 кгм. Нервюры располагаются на расстоянии а = 250 мм друг от друга. Определить максимальный шаг Ь стрингеров из условия, что критическое напряжение сдвига в обшивке достигает предела пропорциональности тпц = 2000 кг/см2; толщина обшивки h = 2 мм. Проверить на устойчивость вертикальные стенки лонжеронов,
УСТОЙЧИВОСТЬ ПЛАСТИНОК ПРИ СДВИГЕ
307
Рис. 7.29. Коэффициент К при различных условиях закрепления пластинки, подвергающейся сдвигу.
Нердюро
Рис. 7.30. К расчету на устойчивость при сдвиге оболочки типа крыла самолета.
308 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах упругости [ГЛ. VII
толщина которых равна h = 4 мм. Принять, что панели обшивки жестко защемлены по краям, прикрепленным к поясам лонжеронов, и шарнирно закреплены по двум другим краям. Материал — дюралюмин,£ = 7,2 • 105 кг/см2, [х = 0,32.
Принимаем, что крутящий момент передается центральным отсеком оболочки, имеющим размеры 600 X 200 мм. Погонное касательное усилие по формуле Бредта равно
т=-2Ш9т-==Шкг/см'
Напряжение в обшивке будет
Т 208,..л,,
=1 = Т = 1040*г/сл2-
Шаг стрингеров находим из условия
*2.0,72.10°. 0,23 Л 12 (1 — 0,322) b2 -AUW»
отсюда Ь2/К = 25. Так как К зависит от отношения а/b, то при а = 260 мм решение приходится искать путем проб, задаваясь значением Ь и оценивая по графику рис. 7.29 соответствующую величину К Окончательно получаем:
К ~ 6,7, а = 130 мм.
Напряжения в стенке лонжерона
Т 908
TcT = t7 = Ж = 520лг/слг-
Стенку лонжерона рассматриваем как пластинку, защемленную на поясах и шарнирно опертую по смежным стойкам. При а/b = 26/20 = 1,3 по графику рис. 7.29 /С» 11,6. Критическое напряжение равно
я2. ft 72. Ifte. ft 43
ТкР = 11>6 ~ 12 (1- 0,32») 20* •= 3060 Кг/См2-
Так как величина ткр превышает тпц, то ее следует уточнить, пользуясь формулами, выведенными с учетом пластических деформаций. Во всяком случае очевидно, что устойчивость стенки лонжерона обеспечена.
§ 86. Неравномерное сжатие. Чистый изгиб
Обратимся к случаю, когда по двум кромкам пластинки распределены нормальные усилия, изменяющиеся по линейному закону*) (рис. 7.31):
= -«-£)• (7.171)
При а = 0 получим случай равномерного сжатия, при а = 1 — случай сжимающих усилий, распределенных по закону треугольника.
*) Эта задача исследована И. Г. Бубновым [0.21 и С. П. Тимошенко [0.23].
НЕРАВНОМЕРНОЕ СЖАТИЕ. ЧИСТЫЙ ИЗГИБ
309
Если а>1, то известная часть пластинки будет испытывать растяжение. При а = 2 придем к случаю чистого изгиба. Таким образом, здесь объединяются различные виды нагружения панелей обшивки и тонких стенок, включающие внецентренное сжатие и изгиб.
Рис. 7.31. Пластинка под действием нормальных усилий, распределенных по линейному закону.
Будем считать, что все кромки пластинки закреплены шарнирно, и используем тот же путь решения, что и в § 85. Аппроксимируем прогиб по-прежнему с помощью ряда
у
а
оо оо
(7.172)
т = \ л=1
Энергия деформации изгиба будет равна
т п
Работа внешних сил будет
а Ь
г=т//»»й(1-“ )(£!***>■ <7-174>
О О
Принимая во внимание соотношения
о
ъ
16b2 ij если / ± J — нечетное
я О*2 —У2)2* число,
О, если t±j — четное, >
Ь2
-у, если / = у,
(7.175)
310 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
найдем:
W
2 т2%2
4
аа
т L п п i JJ
при п ± / нечетном. Уравнения
получают вид DAmn (2 + -Ja) —
d(U— W)
дА„
= 0
— °крА •
m2Tz2
а*
ат2%2
~2аГ
26 у тс2 iL' 1=1
Amini (n2 — /*)*
(7.177)
В первом приближении положим, что Ап Ф 0, а все остальные коэффициенты равны нулю; тогда придем к единственному уравнению
(т+тГт- (7178>
откуда
и2£)
b2h
Это решение имеет смысл лишь для малых а. Рассматривая последовательно системы двух, трех и т. д. уравнений типа (177), находим уточненные значения критических напряжений. Представим критическое значение о0 в виде
Рис. 7.32. Коэффициент К в различных случаях нагружения.
а —К%2° ао, кр А f)2h
(7.179)
Уточненные значения К для разных случаев нагружения представлены в таблице 7.7; в отличие от предыдущих случаев а не всегда является большей стороной пластинки.
В случае чистого изгиба минимальное значение К получается при а/Ь = 2/г. На рис. 7.32 сравниваются наименьшие величины К для некоторых видов нагружения при шарнирно опертых кромках
§ 87] КОМБИНИРОВАННОЕ НАГРУЖЕНИЕ 311
Таблица 7.7
Коэффициенты К для случая неравномерно распределенных нормальных усилий
>ччча/Ь
0,4
0,5
0,6
0,667
0,75
0,8
0,9
!,°
1,5
2
29,1
25,6
24,1
23,9
24,1
24,4
25,6
25,6
24,3
4/з
18,7
12,9
11,5
11,2
11,0
11,5
1
15,1
9,7
8,4
8,1
7,8
8,4
АЫ
13,3
8,3
7,1
6,9
6,6
7,1
2/з
10,8
7,1
6,1
6,0
5,8
6,1
Во многих конструкциях, однако, *gmt
♦ МММ
пластинки. Как видим, коэффициент /С, относящийся к наибольшим напряжениям изгиба, оказывается приблизительно в 6 раз большим, чем при равномерном сжатии.
§ 87. Комбинированное нагружение
Мы определили критические напряжения при сжатии (растяжении) в одном направлении и сдвиге, пластинки испытывают одновременно усилия различного типа.
Один из примеров — обшивка крыла летательного аппарата; изгиб крыла вызывает появление сжимающих (растягивающих) напряжений в обшивке, кручение — напряжений сдвига. Рассмотрим различные виды комбинированных нагрузок.
1. Сжатие в двух направлениях. Допустим,что шарнирно закрепленная по всем краям пластинка сжата одновременно усилиями ах и ау, равномерно распределенными вдоль соответствующих сторон*) (рис. 7.33).
Уравнение (26) получает вид
D -_4, d2w
Выпишем решение в виде
/ / -С
П - -
Г а
£
ГГ4
I t f f t t I
Рис. 7.33. Пластинка сжимается одновременно в двух направлениях.
d2w
ду2
: 0.
.. тпх. /гтсу
w = Атп sin sin —тг~
mn а b
(7.180)
(7.181)
!) Эта задача была впервые рассмотрена Брайеном [7.14].
312 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Подставляя в (180), получим:
\2 /п\212
°[(т)’+(т)Т=£Ыт)+»,(т)']-
Введем обозначения
а =
(7.182)
(7.183)
и выразим критические напряжения следующим образом:
°Х, кр Кх b2h
n2D
°у, кр ку yifo кр> (7.184)
тогда из (182) найдем:
К,
£)• + *
(7.185)
На рис. 7.34 даны минимальные значения Кх в зависимости от а при разных ср; для отдельных ветвей указаны индексы тип. Для квадратной пластинки получаем всегда т — п— 1; при этом
4
К — \+9 ’
(7.186)
(7.187)
отсюда
КХ + КУ = А.
2. Равномерное сжатие (растяжение) в одном направлении и сдвиг. Перейдем к случаю совместного действия сжимающих или растягивающих усилий о в одном направлении и касательных усилий х (рис. 7.35). Края пластинки примем закрепленными шарнирно.
Для весьма длинной пластинки прогиб может быть аппроксимирован выражением, аналогичным (141):
Рис. 7.34. Критические напряжения для пластинки, сжатой в двух направлениях.
w = f sin -у- sin j(x — ky).
(7.188)
§ 87] КОМБИНИРОВАННОЕ НАГРУЖЕНИЕ 313
Потенциальная энергия изгиба по-прежнему определяется равенством (142). Дополняв (143), получаем для работы внешних сил новое выражение:
W = ) р. (7.189)
Сравнивая (142) и (189), находим:
о + 2т* = [()2 + 6*2 + 2 4- (А)2 (1 + *2)2]. (7.! 90)
Выражение, заключенное в скобки, приобретает минимальное значе-
л?
Рис. 7.35. Одновременное действие сжатия в одном направлении и сдвига.
ние при длине полувсл [ы
i = bV\+k?.
Таким образом, система критических напряжений уравнению
Лте 2
акр + = -frfyT (4 + 82).
При раздельном действии сжатия и сдвига будет
л %2D л л/- те2D
°о, кр 4 b2h * Т°» КР ' ~Wh *
Уравнение (192) получает вид
Jl+2l/T-5*-*=l + 2A Пусть отношение ткр/т0>кр задано; тогда минимальное значение окр соответствует углу наклона узловых линий, определяемому следующим образом:
- (7.195)
(7.191) удовлетворяет
(7.192)
(7.193)
(7.194)
314 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
При простом сжатии = 0, при сдвиге =l//2, при комбинированной нагрузке k имеет промежуточное значение. Подставляя (195) в (194), находим соотношение
= 1- (7Л96)
Зо.кр 1 \Ч,кр/
Как и следовало ожидать, изменение направления касательных усилий (перемена знака т) не влияет на величину критического напряжения.
Уравнение (196) может быть использовано и в том случае, если
усилия а являются растягивающими; знак перед а следует при этом изменить на обратный. Критическое касательное напряжение будет при этом больше, чем при простом сдвиге.
В случае пластинки с конечным отношением сторон можно пользоваться тем же уравнением (196). Уточненное решение задачи было получено путем аппроксимации прогиба выражением (141). Если удержать при решении пять параметров Атп, то приходим к следующим результатам. Введем обозначения:
% =к.т£. v=K.w- <7-197>
Значения Ка и Кх для различных отношений а = а/b даны в таблице 7.8. Знак минус перед К0 соответствует растягивающим усилиям *).
(Г а б л и ц а 7.8 Коэффициенты Ка и в случае комбинированного действия сжатия и сдвига
К'
-1,0
0
1,0
2,0
3,0
3,6
4,0
а = 1
КX
10,57
9,42
8,15
6,67
4,72
3,02
0
к9
—2,0
0
2,0
2,83
3,6
3,9
4,2
а = 1,6
Кх
8,46
7,0
5,31
4,46
2,95
2,09
0,06
а
и
СО
ю
К9
—1,0
0
1,7
2,5
3,0
3,7
4,017
Кв
7,45
1
6,75
5,4
4,66
4,14
3,29
2,19
На графике рис. 7.36 дана уточненная, по сравнению с (196), зависимость акр/ао, кр и ткр/т0> кр для различных отношений bja.
3. Сжатие в двух направлениях и сдвиг. Пусть удлиненная пластинка, шарнирно опертая по краям, подвергается действию сжи¬
*) Незначительное расхождение между величинами Кх при Ка =5 0, помещенными в таблицах 7.8 и 7.6, объясняется тем, что задача решена в ином приближении.
§ 87]
КОМБИНИРОВАННОЕ НАГРУЖЕНИЕ
315
мающих (растягивающих) усилий вдоль длинной стороны ах, вдоль короткой стороны оу, а также касательных усилий х. Пользуясь
Рис. 7.36. Критические напряжения в случае совместного действия сжатия и сдвига.
тем же методом, что и в предыдущем случае, приходим к следующей зависимости между критическими напряжениями:
х[!(з + 1Л-4)-]; (7.198)
П°Д хо, кр и °о, кр понимаются критические напряжения при раздельном действии сдвига и сжатия в направлении х; под о — величина
те 2D
— ТЯГ- (7-199)
4. Чистый изгиб и сдвиг. Рассмотрим, далее, шарнирно опертую пластинку, находящуюся под действием нормальных усилий по двум кромкам,
0 = вх(1—т)* (7-200>
316 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
и равномерно распределенных усилий сдвига т. Критические напряжения выразим с помощью соотношений
в —к *£.
ь кр —ЬгН * те* П
ткР = Кх ■щ' • (7.201)
Обозначим значения коэффициентов К0 и Кх при раздельном действии изгиба и сдвига через /Св>0, KXt0. Величины Ка и Кх могут быть определены из приближенного соотношения
<7-202)
V
Рис. 7.37. Критические напряжения в случае совместного действия изгиба и сдвига.
Уточненные значения Ка и Кх для различных отношений сторон пластинки а = a/ft приведены в таблице 7.9 и на графике рис. 7.37.
Таблица 7.9
Коэффициенты Ка и Кт при совместном действии изгиба и сдвига
а =
= 1
а —
%
а =
= 2/з
а =
■-'!г
К
к
К
К
К
К„
К
К
X
<3
т
9
X
а
X
а
0
25,6
0
24,5
0
23,9
0
26,6
2
24,6
4
22,8
4
23,05
4
25,4
4
22,2
8
17,7
8
20,35
8
24,3
6
18,4
10
13,25
12
15,23
12
22,55
8
12,4
11
10,01
14
11,04
16
19,94
9
6,85
12
4,61
15
8,0
20
16,13
9,42
0
12,26
0
16,09
0
24
26
26,9
10,26
5,44
0
§ 88. Закритическая деформация пластинки при сжатии
Мы определяли до сих пор напряжения, при которых плоская форма пластинки перестает быть устойчивой. Однако, если пластинка скреплена по краям с достаточно жесткими ребрами, то несущая
§ 88] ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПЛАСТИНКИ ПРИ СЖАТИИ 317
способность ее в момент потери устойчивости не исчерпывается; пластинка в состоянии и после этого нести возрастающую нагрузку. Поэтому для того, чтобы судить о несущей способности пластинки, необходимо исследовать ее закритическое поведение.
Как мы видели, в момент выпучивания пластинки в ней возникают только напряжения изгиба; при вычислении потенциальной энергии деформации можно было ограничиться определением энергии, соответствующей изгибным напряжениям. В послекритической стадии, когда прогибы становятся сравнимыми с толщиной пластинки, важную роль начинают играть напряжения в срединной поверхности. В каждой точке пластинки напряжения будут складываться из напряжений собственно изгиба и напряжений в срединной поверхности; по мере развития выпучин роль последних возрастает.
Напряжения в срединной поверхности появляются благодаря двум обстоятельствам. С одной стороны, при больших прогибах неподкрепленной пластинки заметно искривляются ее края, как показано
///////
Рис. 7.38. Усилия в срединной поверхности при выпучивании пластинки.
на рис. 7.38, а\ здесь принято, что краевые волокна остаются в первоначальной плоскости пластинки. Но в том случае, когда пластинка снабжена жесткими ребрами, они сопротивляются искривлению краевых полос. При выпрямлении краев образуются дополнительные усилия — сжимающие вблизи углов и растягивающие в средней части (рис. 7.38, б)\ при этом накапливается дополнительная потенциальная энергия. С другой стороны, выпучивание пластинки происходит таким образом, что срединная плоскость переходит в неразвертывающуюся поверхность;.это вызывает новые напряжения, зависящие от характера искривления пластинки в той или иной точке. Как мы увидим ниже, влияние на поведение пластинки первого фактора — жесткости подкрепляющих ребер — значи¬
318 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
г
[М
т ель но больше, чем эффект, связанный с волнообразованием срединной поверхности.
Характерная особенность закритической деформации пластинки состоит в изменении формы вмятин: если в момент потери устойчивости удлиненной пластинки вмятины являются квадратными, то затем длина их уменьшается, причем переход от одного числа волн к другому сопровождается обычно хлопками. На рис. 7.39 показана форма волнообразования пластинки для момента, когда напряжение в подкрепляющих ребрах в 40 раз превышает критическое напряжение для пластинки *).
Рассмотрим сначала закритическую деформацию пластинки, шарнирно скрепленной по краям с жесткими ребрами и сжатой в одном
о)
Рис. 7.39. Закритическое волнообразование пластинки при сжатии.
Рис. 7.40. Распределение напряжений при закритической деформации пластинки.
направлении. Будем принимать, что подкрепляющие ребра остаются прямолинейными, но что точки пластинки могут свободно скользить вдоль ребер. Рассмотрим сечение пластинки, перпендикулярное к направлению сжатия. Если до потери устойчивости пластинки напряжения сжатия распределяются по ширине равномерно, то после выпучивания они более интенсивно возрастают у краев; в центральной же части напряжения мало отличаются от критического значения (рис. 7.40, d).
Обозначим через о0 напряжение в краевом волокне пластинки, расположенном в срединной поверхности, а через о — среднее на•
*) По Ладе и Вагнеру (R. L a h d е, Н. W a g п е г, Lufttahrtiorschung 13, № 7 (1936)).
§ 88] ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПЛАСТИНКИ ПРИ СЖАТИЙ 319
пряжение по ширине:
ъ
0 = jf Cxdy. (7.203)
о
Полное сжимающее усилие, передающееся пластинкой, равно Р = Ыго. Выразим его через краевое напряжение:
Pz=<fbhOy (7.204)
введя так называемый редукционный коэффициент ср. Этот коэффициент равен
?=■£• (7.205)
Можно условно принимать, что работающими частями пластинки являются только полосы, прилегающие к краям, как показано на рис. 7.40, б\ суммарную ширину этих двух полос назовем приведенной шириной и обозначим через b0 — bn9; тогда будет
пр
* = -/• (7.206)
Если известно, как меняется редукционный коэффициент при возрастании ар, то можно определить сопротивление пластинки сжимающей силе на каждом этапе нагружения. В свою очередь величина ар связана с деформацией подкрепляющих ребер. В зависимости от условий деформации ребер надо принять
Е е
°Р=Г=- или °р = £,рер> (7.207)
где Ер — модуль упругости материала, ер — деформация укорочения ребер. Определение редукционных коэффициентов позволяет установить роль, которую играет пластинка в качестве элемента той или иной конструкции, например корпуса летательного аппарата или корабля.
Приведем вывод простой приближенной формулы для редукционного коэффициента, не претендующий на учет всех обстоятельств закритической деформации пластинки *). Выделим работающие краевые полосы пластинки и мысленно сочленим их между собой; тогда получим пластинку шириной £пр. Будем считать, что напряжения ср в приведенной таким образом пластинке таковы, что пластинка находится на грани выпучивания; иными словами, примем, что вели-
*) Этот вывод принадлежит Карману, Зехлеру и Доннеллу [7.16].
320 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII чина ор равна критическому напряжению для пластинки шириной йпр:
cp = K-St- <7-208>
*орЛ
С другой стороны, в момент выпучивания исходной пластинки критическое напряжение равно
°кр = *1ЯГ- (7-209)
Сопоставляя (208) и (209), находим:
(7.210)
Здесь через п* обозначено отношение напряжения в краевом волокне к критическому напряжению:
(7.211)
акр
эта величина характеризует уровень развития закритической деформации. Отметим, что при я*—>оо редукционный коэффициент приближается к нулю. Во всех рассуждениях здесь принимается, что
напряжения в пластинке и ребрах лежат в пределах упругости.
Приближенная формула (210) часто применяется в практических расчетах. Ниже дано более строгое решение задачи о закритическом поведении пластинки.
§ 89. Приложение теории гибких пластинок
После выпучивания пластинки прогибы ее нельзя считать малыми по сравнению с толщиной. Поэтому при исследовании закритической деформации надо исходить из общих уравнений теории гибких пластинок (63), (64). Примем, что все края пластинки остаются прямолинейными и что продольные края при изгибе пластинки свободно смещаются друг по отношению к другу; кроме того, будем считать, что точки, принадлежащие кромкам пластинки, свободно скользят вдоль подкрепляющих ребер. Это последнее предположение не соответствует, как правило, реальным условиям прикрепления пластинок к ребрам, но значительно облегчает вычисления. Более строгое решение [7.11], принадлежащее Г. Г. Ростовцеву, показало, что погрешность, вносимая этим допущением для таких «интегральных» характеристик, как редукционный коэффициент, невелика.
Решение системы нелинейных уравнений (63), (64) при принятых граничных условиях выполняется с помощью различных приближенных методов. Чаще всего принимают следующий путь.
§ 89] ПРИЛОЖЕНИЕ ТЕОРИИ ГИБКИХ ПЛАСТИНОК 321
Выберем аппроксимирующее выражение для прогиба w в виде ряда
оо оо
- = 2 (7.212)
т-1 л = 1
Подставим это выражение в правую часть уравнения (64); тогда получим линейное дифференциальное уравнение относительно функции Ф. Интеграл его имеет вид
® = ;SpIcoscoSiE-ii. (7.213,
р—0 <7=0
Отсюда по (60) находим напряжения ох, оу, т. Коэффициенты Bpq выражаются через Атп\ под а понимается среднее сжимающее напряжение по ширине пластинки.
Полная сжимающая сила в любом сечении пластинки, параллельном у, будет
ь
Р= j haxdy = cbh; (7.214)
0
отметим, что эта величина не зависит от координат и, таким образом, остается постоянной по всей длине пластинки.
Определим, далее, взаимное смещение точек пластинки, имеющих координаты (лс, 0) и (л;, b), по (54)
u=f[**-i(jP}]dx- <7-215>
о
Деформация по (57) и (60) равна
1 (д*Ф б*Ф\ /7 01*4
*х~ Е\дуг djc* ) * (7.216)
Подставляя (212) и (213), получим:
ОО оо
гг2
22 р-2'7)
т-1 /1=1
Аналогичным образом найдем взаимное смещение точек с координатами (0, у) и (д, у):
»=/IW(f)>’ (7-218>
322 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
или
00 оо
(7.219)
т = 1 /1 = 1
Как видим, величины и и v не зависят от координат; следовательно, условие прямолинейности кромок выполняется.
Пользуясь выражениями для f и Ф, приближенно интегрируем уравнение (63). Для этого можно применить метод Ритца или Бубнова—Галеркина *). При этом находятся коэффициенты Атп и Bpqy определяющие прогиб и напряжения в срединной поверхности. Далее по формуле (205) вычисляется редукционный коэффициент.
Рассмотрим для простоты квадратную пластинку со стороной b и примем в первом приближении АпФ0 и все остальные коэффициенты равными нулю. Иными словами, будем полагать, что пластинка искривляется по одной полуволне вдоль осей х и у. Тогда для выражения (213) получим:
другие коэффициенты обращаются в нуль. Как легко видеть, пара метр Ап представляет собой здесь стрелу прогиба пластинки, по этому обозначим далее An = f. По (217) находим:
Взаимное сближение нагруженных кромок, отнесенное к стороне пластинки, будет
Примем, что эта величина отвечает деформации продольного ребра и что модули упругости пластинки и ребер одинаковы (Ер = Е); по (207) напряжение ор оказывается равным
20 — 02 — 32 9
(7.220)
(7.222)
(7.223)
множитель 1/(1— (J-2) здесь опущен.
*) Такой путь решения задачи разработан в исследованиях П. Ф. Пап* Ковича, первое из которых относится к 1920 г., П. А. Соколова и других авторов; обзор этих работ см. в книге [0.3}, стр. 390.
ПРИЛОЖЕНИЕ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
323
Применяя для интегрирования уравнения (63) метод Бубнова— Галеркина, выпишем соотношение
Подставляя значения w и Ф и проводя вычисления, приходим к следующей зависимости:
Примем /=£0 и учтем, что во втором члене фигурирует критическое напряжение окр; тогда найдем:
Редукционный коэффициент по (205) оказывается равным *)
где под п* по-прежнему понимается отношение (211). Эта зависимость отличается от формулы Кармана (210) уже тем, что при /г*—> оо редукционный коэффициент приближается к значению 0,5, а не к нулю; вообще же величина ср получается значительно выше, чем по (210).
Уточненные решения можно строить, увеличивая число варьируемых параметров Атп. В книге [0.3] проведены выкладки, сделанные с учетом двух параметров: Ап и А31 (первый индекс — число полуволн в направлении лг, второй — вдоль у); оказалось, что значения редукционных коэффициентов лежат несколько ниже, чем по данным первого приближения.
В статье Маргерра [7.18] были проведены также вычисления с удержанием коэффициентов Ли, Л13, Л31. В результате была получена следующая приближенная формула для редукционного коэффициента:
а ъ
(7.224)
о о
где
X = -rV*w — L(w, Ф).
(7.225)
(7.226)
(7.227)
Сравнивая формулы (223) и (227), получим:
(7.228)
(7.229)
(7.230)
*) Эта формула была указана Маргерром [7.18J.
324 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
очевидно, она также дает более высокие значения ср, чем формула Кармана (210).
Далее, в работе Леви [7.17] содержатся данные, полученные с сохранением коэффициентов Лп, Л13, Л33, Л15, Л51. Найденная при этом зависимость ср(п*) изображена на рис. 7.41 в сопоставлении
Рис. 7.41. Значения редукционных коэффициентов по результатам различных решений.
с формулами (210) и (230). Кривую Леви, на первый взгляд, можно считать наиболее обоснованной. Однако решение С. А. Алексеева [7.1 ],• выполненное с помощью метода последовательных приближений, привело к иным результатам. Оказывается, в тех вычислениях, которые были до сих пор выполнены по методу Ритца, выпадали коэффициенты, относящиеся к четным числам полуволн (например, Л21). Между тем, как было показано С. А. Алексеевым, кривая т = 2 (т — число полуволн по длине) дает в определенной области изменения п* меньшие значения ср, чем соседние кривые т= 1 и т = 3. Поэтому решение Леви давало при п* > 3,5 преувеличенные значения редукционного коэффициента.
Простые опыты, в которых осуществляется сжатие подкрепленной пластинки в пределах упругости, подтверждают этот вывод. При незначительном превышении критического напряжения квадратная
§ 90] РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЦИФРОВОЙ ЭЛЕКТРОННОЙ МАШИНЫ 325
пластинка выпучивается таким образом, что по длине образуется одна полуволна. Дальнейшее нагружение пластинки приводит, как мы уже видели, к хлопку, в процессе которого появляются две полуволны; в последующем образуются три полуволны и т. д.
§ 90. Решение задачи с помощью цифровой электронной машины
Применение метода Ритца или Бубнова—Галеркина к задаче о закритическом поведении пластинки приводит к решению системы кубических уравнений типа (226) относительно параметров прогиба. При значительном числе удерживаемых параметров вычисления оказываются весьма трудоемкими. Сложные выкладки приходится осуществлять также при использовании метода последовательных приближений. Поэтому решение этой задачи желательно выполнять с помощью электронных цифровых машин. Процесс вычислений, связанный с применением метода Ритца или метода последовательных приближений, поддается, вообще говоря, программированию. Однако наиболее удобным здесь оказывается применение метода конечных разностей или метода коллокации. Ниже излагается решение задачи о закритическом поведении пластинки, проведенное с помощью метода конечных разностей *).
Введем в основные уравнения (63) и (64) безразмерные величины:
\ — а Х-Т'
— Ф
Ф =
Eh2
w =
w
т
£ UJ ’ У~ Е [а) ’
ab
W
(7.231)
тогда эти уравнения примут вид
vd+2- + ) = I(®, Ф), (7.232)
\ дх* дх*ду2 - дуЧ
—f-X2-= — \l(w, да); (7.233)
*2 дх* дх*ду2 ду< 2 >' >
операторы L включают производные по л: и у. Напряжения в срединной поверхности равны
д2ф - д2Ф - д2Ф /7 00,ч
ду2 у дх2 дх ду
*) Это решение принадлежит А. Ю. Биркгану,
326 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Наибольшие по толщине напряжения изгиба будут
d2w ~дх2
х, и
2(1
2(1
1 /1 d2w
1 /1 d2w
—I1-2) \ № ду*
+
d2w \
d2w \
'*1*V
1
d2w
(7.235)
(7.236)
(7.237)
и 2(1+р.) дхду
Заметим, что в безразмерных переменных х> у прямоугольная область с любым отношением сторон X отображается в квадратную
со стороной, равной единице. Систему уравнений (232), (233) представим в конечных разностях. Воспользуемся квадратной сеткой и разделим каждую сторону на т равных частей. Шаг сетки будет с = 1/т. Введем также внеконтурные узлы на расстоянии с и 2с от кромок (рис. 7.42).
Исследуем по-прежнему случай пластинки, шарнирно закрепленной по всем сторонам и загруженной усилиями а, равномерно распределенными вдоль кромок д: = 0 и х=\. Очевидно, изогнутая поверхность будет симметричной относительно линии )> = ~ и симметричной или 1
относительно линии х = -, поэтому достаточно
-1/6
1
- c-
*
с
1/2
0
X
I
i
1
i
Рис. 7.42. К применению метода сеток.
антисимметричной
рассмотреть 1/4 часть пластинки.
Для перехода к конечным разностям применим центральные операторы, имеющие погрешность квадрата шага (черточки над w и Ф далее опускаем):
d2w
1
dx2
c2 (
d2w
1
dy2
c2
d2w
1
d4w
1
dx4
cA
d4w
1
dy4
c4
d4w
1
Ox2 dy2 ~
C4
дх ду
4 с2
(w2 — 2w0+w4),
(w5 — w6+w7 — w8),
(7.238)
(w9 — 4wj 6w0 — 4w3 wu),
(«10 — 4w2 + 6®0 — 4w4 +
(7.239)
§ 90] РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЦИФРОВОЙ ЭЛЕКТРОННОЙ МАШИНЫ 327
Нумерация узлов в расчетной ячейке дана на рис. 7.43. Аналогичные формулы составляем для функции напряжений Ф. Подставляя разностные операторы в уравнения (232) и (233), находим значения прогиба и функции напряжений в текущем узле, являющемся «центром» расчетной ячейки (при Х=1)
wQ = {(wl -f- wz) (Ф2 — 2Ф0 -- Ф4 + 8v) -f-
+ (w2 4“ wd (®i — 2Ф0 + Ф3 + 8v) —
— J (W5 + Wl) (Ф5 — Ф6 + Ф7 — Ф8 + 16v) ~
— (да6 + да8)(Ф5 —Ф6 + Ф7 —Ф8— 16v) —
— v + W10 + Wn + Wtt)} ’• 2(®l + ®2 + ®3 + ®4 — 4Ф0-}- lOv),
(7.240)
Фо = -[8(Ф1 + Ф2+Фз + Ф4)-2(Ф5Ч-Фб + Ф7 + Ф8)-
(Ф9 + ф10 + Ф11 + Ф12) + fg (% — Щ 4“ W1 — Ws)2 —
— (Wi — 2w0 + w3) (w2 — 2w0 + w4)]. (7.241)
Составляем столько нелинейных алгебраических уравнений типа (240), сколько значений прогиба необходимо найти во внутренних узлах сеточной области. Функция напряжений определяется во внутренних и граничных узлах; в угловой точке х = 0, у = 0 принимается Ф = 0.
Величины w и Ф во внеконтурных узлах выражаются через значения во внутренних узлах с помощью граничных условий. Примем, что края пластинки шарнирно оперты и что перемещения точек каждой кромки в плоскости пластинки не стеснены; тогда граничные условия для краев jc = 0 и х = 1 имеют вид
л d2w л д2Ф
w = 0* -zr — 0, = — а,
дх2 д2Ф дх ду
ду2
= 0.
(7.242) рис 7 4з Расчетная ячейка.
Этим условиям соответствует нечетное продолжение функции w и четное продолжение функции Ф за контур пластинки; в точках контура w == 0. Если учесть эти соотношения, то значения w и Ф в узлах, лежащих на прямых х=\-\-с, х=\-\-2с, у=\-±-с, у = 1 + 2с, не будут являться дополнительными неизвестными.
328 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Решение системы разностных уравнений (240), (241) можно искать путем последовательных приближений по следующей схеме. Задаемся в узлах сеточной области начальным (нулевым) приближением функций w и Ф. Выбрав направление обхода сетки (например, от узла х = с> у = 0 вдоль строки у = const с переходом между строками в сторону возрастания у), подставляем принятые значения wи Ф(0) в уравнение (241). Первое приближение и нулевое приближение функций в остальных двенадцати соседних точках используем для определения функции напряжений в узле х = 2с, у = 0 и т. д. Найдя Ф(1) в первой строке, переходим к строке у = с. Во внутренних узлах сетки вычисления начинаются с применения формулы (240), причем найденное значение прогиба используется для вычисления функции напряжений в той же точке. Одно приближение заканчивается, если вычислены значения функций во всех узлах области, включая внеконтурные. При выбранном порядке обхода рабочие формулы имеют вид
W{0+1) = Cp(wi2, 5, 6, 9, 10» 8, И, 12» Фол, 2, 5, 6, Ф£ 4/7, с),
Ф+1) = ф (12, 5, 6» зД, 7, 8» Ф%, 5, 6, 9, 10» Фз? 4,*7, 8, И, 12» с),
где v — номер приближения. Значения, относящиеся K(v-J-1)-My приближению, используем для ускорения итерационного процесса.
Итерации повторяются до тех пор, пока не будет получено решение системы разностных уравнений с необходимой степенью точности. Погрешность решения приблизительно пропорциональна квадрату шага. Проведя вычисление для различных значений шага, например, V6, 7в» V12» можно косвенно оценить погрешность решения с любым шагом. Пробные расчеты показали, что погрешность в определении прогиба и напряжений в различных точках квадратной пластинки составляет около 1,5—2,5% при шаге с = 1/12 и 3—5% при шаге с — 78.
Описанный метод был использован для исследования закритической деформации пластинки в предположении, что края ее закреплены шарнирно и остаются прямолинейными и что точки каждой кромки свободно смещаются вдоль нее. Этому случаю отвечают, как мы видели, граничные условия
л d2w п д2Ф л д3Ф n /7 0iQ4
•W — о, дхг — 0. дхду—0, дх — 0 (7.243)
для кромок д: = 0, х = I.
Надо помнить, что решение системы основных уравнений гибкой пластинки в закритической области является многозначным. Важно составить такой план вычислительного процесса, чтобы не были по*» теряны решения, относящиеся к устойчивым формам равновесия пла¬
§ 90] РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЦИФРОВОЙ ЭЛЕКТРОННОЙ МАШИНЫ 329
стинки при заданной нагрузке. Целесообразно, например, строить процесс вычислений, исходя из форм выпучивания пластинки с одной двумя, тремя и т. д. полуволнами в направлении сжатия (т = 1, 2,
3,...) и с одной полуволной (я= 1) в перпендикулярном направлении. Эти формы соответствуют первым собственным значениям линейной задачи об устойчивости пластинки:
_ %*(т2 + П*)2 в*~ 12(1—ц2)т2 ’
Приведем результаты вычислений, выполненных на электронной цифровой машине «Стрела» с шагом с = 1/8. На рис. 7.44 изображена зависимость между нагрузкой о и прогибом в центре пластинки
б
2Ь
W
15
W
5
0,5 \0 1.5 2,0 2,5 ЗД
ш
Рис. 7.44. Зависимость «усилие сжатия—прогиб» по данным вычислений на цифровой машине.
(при т — 1 и 3) либо в центре половины пластинки (при т— 2). Для случая т = Ъ прогиб отложен с обратным знаком. Как видно из графика, на первом этапе закритической деформации, при 3,62 < <о<5,65, имеется единственная равновесная форма пластинки с одной полуволной в направлении сжатия. С ростом сжимающей нагрузки в центральной части пластинки постепенно развивается вмятина, направленная в обратную сторону по отношению к «основному» прогибу. Поэтому рост стрелы прогиба замедляется; при а >16 стрела прогиба начинает уменьшаться. Наконец, при а =18,5 первая форма становится неустойчивой, по крайней мере в «вычислительном смысле»: итерационный процесс сходится здесь уже к форме выпучивания с тремя полуволнами. Идя по ветви решения для т = Ъ
330 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК В ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
вниз, не удается дойти до третьего собственного значения (пунктирная часть кривой т = 3 проведена предположительно); при
о < 12 мы снова приходим к форме изгиба по одной полуволне.
Можно полагать, что две ветви устойчивых равновесных форм свя¬
заны ветвью неустойчивых состояний пластинки.
При нагрузке, превышающей второе собственное значение а = = 5,65, мы получаем также ветвь антисимметричных форм выпучивания (т = 2); это подтверждает вывод, сделанный С. А. Алексеевым.
На рис. 7.44 нанесены также экспериментальные точки Ямаки [7.23]; они хорошо согласуются с результатами вычислений по методу сеток при w < 2.
На рис. 7.45 представлена зависимость между нагрузкой, отнесенной к первому критическому значению, и взаимным перемещением нагруженных кромок, также отнесенным к критической величине; здесь же представлены результаты вычислений Ямаки. Исходя из этих данных, можно определить редукционный коэффициент; его значения даны на рис. 7.41. Как видим, введение в рассмотрение антисимметричной формы позволило уточнить величину ср по сравнению с решением Леви. Характерно, что, в отличие от прежних решений, мы получаем здесь несколько ветвей соответственно различным «порождающим» формам выпучивания пластинки.
По
Ямаки
\
/ /
7.
/У
/ х
/т=2
А
'Memo,
сетол
г
т-1/
Рис. 7.45. Зависимость «усилие сжатия — сближение кромок».
§ 91. Случай искривляющихся кромок
Все предыдущие выкладки относились к случаю, когда кромки пластинки остаются прямолинейными, или, иными словами, когда подкрепляющие ребра являются достаточно жесткими. Чтобы выяснить, каково значение этого условия, рассмотрим ту же задачу для квадратной пластинки (а = Ь) в предположении, что шарнирно закрепленные кромки свободно искривляются, оставаясь в плоскости опорного контура *).
*) Эта задача была исследована П. Я. Полубариновой-Кочиной (Прикл. матем. и мех. 3, № 1 (1936), 16—22), применившей для ее решения оригинальный метод, получивший название «метода возмущений».
§ 91] СЛУЧАЙ ИСКРИВЛЯЮЩИХСЯ КРОМОК 331
При этом напряжения ах> ау в срединной поверхности должны для точек кромок быть такими:
о„= —о при х = 0, Ь: )
., = 0 при „ = <,.».} <7244>
Будем считать, кроме того, что касательные напряжения равны нулю «в среднем» вдоль каждой кромки пластинки:
ъ
J т dy = 0 при л; = 0, b, у = 0, Ь. (7.245)
о
Выберем путь решения задачи, отличающийся от принятого в § 89: будем применять метод Бубнова — Галеркина не только по отношению к уравнению равновесия (63), как это было раньше, но и к уравнению совместности деформаций (64)*).
В первом приближении выберем для функций w и Ф выражения
J.. %х. %У о. пх. пу су2 0
w = f sin —sin —, <D = £sin — sin (7.246)
Как легко видеть, все принятые граничные условия будут при этом выполнены.
Составим уравнения
ь ь ъ ъ
j j* X sin sin dx dy = 0, j* J Ysin siny- dx йГу = 0, (7.247)
0 0 0 0
где через X обозначено по-прежнему выражение (225), а под К понимается по (64) выражение
Y = -±- У4Ф + -j L (w, w). (7.248)
Подставляя (246) в (247) и считая /=£0, приходим к следующим
соотношениям:
— 4п2Р 32 — —Ef2 (7 249)
b2h 3 b2* 3it2 * ((.МУ)
Отсюда
e = «KP + -g-(4)2. (7.250)
*) Этот путь был предложен В. 3. Власовым [10.3] и применен в работах М. А. Колтунов а [7.6] и других авторов.
332 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Сравним эту формулу с (227); коэффициент во втором члене, равный здесь приблизительно 1,44, при прямолинейных кромках был равен 1,23*). Сопоставление этих величин надо проводить с осторожностью, так как они получены различными методами. Желательно продолжить приведенное здесь решение и найти уточненные результаты, как это сделано для другой задачи М. А. Колтуновым (см. стр. 638).
Мы познакомились с некоторыми методами решения задачи о закритическом поведении пластинки, приводящими к различным расчетным графикам и формулам. Какие же из них надо рекомендовать для практических расчетов?
Сравнение результатов, полученных для случаев прямолинейных и искривляющихся кромок, показывает, что работоспособность обшивки после потери устойчивости в большой мере определяется жесткостью подкрепляющих ребер. В том случае, если ребра являются заведомо жесткими и обшивка делится на ряд смежных панелей, редукционные коэффициенты следует определять по кривой на рис. 7.41, полученной с помощью метода сеток; это решение надо, по-видимому, считать наиболее обоснованным.
Решения Леви и Маргерра дают для этой области изменения п* (которая охвачена графиком рис. 7.41) значения ср, близкие к кривой метода сеток.
Однако в случае относительно слабых подкрепляющих ребер и если панель является изолированной, так что нет уверенности, что условие прямолинейности кромок будет выполнено, надо пользоваться формулой Кармана (210):
дающей обычно значения ср в запас устойчивости. Подставляя минимальное значение окр по (79), получим:
§ 92. Данные для практических расчетов
(7.210а)
(7.210Ь)
Приведенная ширина равна тогда
(7.210с)
*) В работе П. Я. Полубариновой-Кочиной (см. ссылку на стр. 330) при той же структуре формулы был получен несколько иной коэффициент, равный 1,804.
§ 93]
АНИЗОТРОПНЫЕ ПЛАСТИНКИ
333
Для случая, когда одна из ненагруженных сторон пластинки закреплена шарнирно, а другая свободна, рекомендуется формула, близкая к (229):
Исследование устойчивости пластинок, обладающих различными механическими свойствами по разным направлениям, привлекло к себе первоначально внимание в связи с применением в конструкциях такого материала, как фанера, обладающая резкой анизотропией *). В настоящее время эта область приобрела особенную актуальность благодаря быстрому внедрению стеклопластиков, также являющихся анизотропными. Это подчеркнуто в названии одного из видов пластмассы — «СВАМ», что означает: «стекловолокнистый анизотропный материал». Кроме того, некоторые пластинки могут рассматриваться как «конструктивно-анизотропные» (см. § 94).
Рассмотрим ортотропные пластинки, упругие свойства которых характеризуются четырьмя независимыми величинами: модулями
упругости Ег и Е2 по двум взаимно перпендикулярным главным направлениям хну, модулем сдвига О и коэффициентом Пуассона {Хр отвечающим поперечной деформации вдоль оси у. Второй коэффициент а2, соответствующий поперечной деформации по направлению х, связан с {хх соотношением
(7.21 Od)
Все эти методы расчета относятся к упругой области.
§ 93. Анизотропные пластинки
е2
(7.251)
Уравнения закона Гука принимают вид
(7.252)
*) Основные работы в этой области принадлежат Г уберу (М. Т. Huber, Teoria sprezystdsci, Варшава, 1950) и С. Г. Лехницкому, Анизотропные пластинки, Гостехиздат, М., 1947.
ПОДКРЕПЛЕННЫЕ ПЛАСТИНКИ
335
Исследуем устойчивость ортотропной пластинки, шарнирно закрепленной по краям и сжатой в одном направлении; координатные оси расположим по рис. 7.14. Граничные условия имеют вид:
л d2w, d2w ~ А
w = 0. -г + 2-г = 0 при х = 0, х = а,
л d2w, d2w ~ л *
w==0, ■■+(Ai=0 при у=0, у=ь-
Принимая для w прежнее выражение (80) и полагая в уравнении (259) су = т = 0, получим:
Очевидно, в этом выражении надо положить п= 1. Критическое напряжение акр определим, варьируя число полуволн т. Для пластинки, удлиненной вдоль оси х(а§>Ь), будет
= (7.264)
Считая Dv D2, D3 равными D, придем к прежней формуле (77) для изотропной пластинки. Для пластинки с конечным отношением сторон следует принимать:
т= 1 при 0 <
т = 2 при уЛ4-<< уЗб!-,
m = 3 при j/~36 <j< /~ 144 и т. д.
Отметим, что число полуволн, образующихся по направлению сжатия, существенным образом зависит от отношения жесткостей Dx/D2. Пластинка с малой жесткостью выпучится, при прочих равных условиях, по большему числу полуволн, чем изотропная
пластинка.
§ 94. Подкрепленные пластинки
Пластинки, входящие в конструкцию корпуса самолета, корабля, цельнометаллического вагона и т. д., как правило, подкреплены ребрами жесткости. В практических расчетах приходится определять критическую нагрузку не только для полосы пластинки, лежащей между ребрами, но и для подкрепленной пластинки в целом. Здесь возможны два подхода к задаче. Первый из них состоит в рассмотрении приведенной анизотропной пластинки с «разнесенной» вдоль
336 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
сечения жесткостью ребер. Если пластинка снабжена только продольными ребрами, как показано на рис. 7.46, то жесткости эквивалентной анизотропной пластинки можно считать равными
°«“-Т + Т5(ПГрГ D* = D3=n>(' (7-265>
где / — момент инерции сечения ребра относительно оси, проходящей через центр тяжести сечения, I — расстояние между ребрами.
Рис. 7.46. К определению приведенной жесткости подкрепленной пластинки.
Очевидно, этот путь расчета применим в том случае, если ребра расположены достаточно часто: величина 1 //г, где п — число ребер, приходящихся на всю ширину пластинки, должна быть малой
по сравнению с единицей [7.5]. Жесткость ребер на кручение в формулах (265) не учитывается.
Другой подход состоит в исследовании пластинки с дискретно расположенными ребрами. Рассмотрим в качестве примера задачу об устойчивости пластинки, Шарнирно закрепленной по краям и подкрепленной одним продольным ребром, расположенным посередине пролета *) (рис. 7.47). Будем учитывать лишь жесткость ребра на изгиб в плоскости, перпендикулярной плоскости пластинки. Выпишем дифференциальное уравнение (70) в применении к одной из половин
Рис. 7.47. Пластинка, подкрепленная одним продольным ребром.
*) Эта задача рассматривалась С. П. Тимошенко (Изв. Ин-та инж. путей сообщ., Петербург, 1915). Барбре (R. В а г b г ё, Ingenieur-Archiv, 1937, стр. 117). Графики рис. 7.48, 7.50 взяты из книги [0.19].
§ 94] ПОДКРЕПЛЕННЫЕ ПЛАСТИНКИ 337
пластинки. Интеграл его представим в виде (89):
«, = К(у) sin —• (7.266)
тогда придем к уравнению (90) для функции У (у). Решение его имеет форму (96):
У (у) = Сг ch а у + С2 sh а у С3 cos (Зу + С4 sin Ру; (7.267)
аир определяются выражениями (95). Граничные условия для края у —Ь/2 будут
w = 0' ■■==0 Ри У = -Т- (7.268)
Если считать, что пластинка выпучивается вместе с ребром, то,
очевидно, изогнутая поверхность должна быть симметрична относительно линии у = 0; это приводит к условию
г) 70)
_=0 при у = 0. (7.269)
Далее, на ребро будет передаваться разность реактивных усилий от двух полос пластинки, определяемая по формуле типа (34):
Как легко видеть, при составлении разности усилий следует учитывать только первые члены в квадратных скобках. Если считать, что ребро вместе с пластинкой подвергается действию сжимающих напряжений ах, то для изогнутой линии ребра получим следующее уравнение:
(*'0 + S+)y==O; <7.271,
здесь / и F — момент инерции и площадь сечения ребра. Воспользуемся параметрами
а = Т' Т=-ш-. 8 = Ж- (7.272)
Величины 8 и у характеризуют соотношение между жесткостями и площадями сечений ребра и пластинки. Вводя в условия (268)—(272) выражение (266), получим систему уравнений относительно Сг,..., С4. Приравнивая нулю определитель этой системы, приходим к следующему уравнению:
a,h т- ■- w* f) № - ■m) т -4 т у* =• °- (7-ш)
334 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII ИЛИ
= Т-1,Л2 <eJT Н- 1*2еу>.
(£у+1х1елг)’
т
= от.
(7.253)
Введем обозначения для изгибных жесткостей по главным направлениям
F h3
Dx = 1 D2= ion г (7.254)
1 12(1 —(x,(x2) * 12 (1 — y
и для крутильной жесткости
Dft=-i-0A3; (7.255)
тогда вместо (И) получим следующие выражения для изгибающих и крутящего моментов:
= Di + W,)' -Му==02(ху +H — 2Dkx. (7.256)
Из уравнений равновесия элемента пластинки (16), (17) находим:
Qx = -<L(Dx*x+D3b), Qy = (ZVy + D3*,); (7.257)
под Z)3 понимается приведенная жесткость:
D3 = Dx)x2 -f- 2D = + 21 + 4D). (7.258)
Для ортотропной пластинки уравнение (23) принимает вид
D.l£ + 2D»W + D’ +
<7-259>
что соответствует уравнению (26).
Уравнения (63) и (64), относящиеся к гибким пластинкам, надо заменить на следующие [0.3J:
А 45 + 2D3 + D2- = hL (w, Ф), (7.260)
* д4ф, д4Ф, s> дАФ 1 / / ч /7 ОС1Ч
82 1- + 28зтар- + 81-5р- = -Т(.«'). (7.261)
где
338 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Под К здесь подразумевается отношение критического напряжения к эйлеровому напряжению, определяемому для пластинки со свободными краями:
п ___ nh%h
(7.274)
ако cb2h is КР Уравнение (273) решается путем проб. Результаты решения для случаев 8 = 0, 8 = 0,2 представлены на рис. 7.48. Каждой паре
Рис. 7.48. Данные для расчета подкрепленных пластинок.
значений 8 соответствует серия кривых, построенных для различных чисел полуволн т. Кривые j = 0, 8 = 0 отвечают неподкрепленной пластинке и повторяют график рис. 7.15. Интересно отметить, что при 7 = 0, 8 = 0,2 мы получаем значения /С, лежащие ниже, чем для гладкой пластинки. В этом случае, очевидно, ребро уже не является подкрепляющим элементом, а само поддерживается пластинкой.
Постепенно повышая жесткость ребра, можно добиться того, чтобы критическое напряжение местного выпучивания каждой половины пластинки (рис. 7.49, а) было меньше, чем критическое напряжение общей потери устойчивости пластинки вместе с ребром (рис. 7.49, б).
Кривые местной потери устойчивости ограничивают на рис. 7.48 серию кривых, характеризующих общую потерю устойчивости; в случае а> Ъ минимальное значение К близко к 16. По аналогии с задачей об устойчивости стержня на упругих опорах назовем критической или эквивалентной такую жесткость ребра, при которой оно может рассматриваться как абсолютно жесткое. Эквивалентная
§ 94] ПОДКРЕПЛЕННЫЕ ПЛАСТИНКИ 339
жесткость ребра уэкв определяется, очевидно, по точке пересечения кривых, относящихся к общей и местной потере устойчивости, на
Рис. 7.49. Различные формы потери устойчивости подкрепленной пластинки.
графиках типа рис. 7.48. Например, при 8 = 0,2 и afb = 1 находим ТэквЮ. На рис. 7.50 даны значения уэкв в зависимости от
Рис. 7.50. Эквивалентная жесткость ребер.
параметров а и 8 по (272). Так как критические напряжения общей и местной потери устойчивости зависят от числа полуволн изогнутой поверхности, то кривые рис. 7.50 имеют «впадины». Практически
340 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах УПРУГОСТИ [гл. VII
эти кривые сглаживаются за первым максимумом, как показано пунктирными линиями.
Мы разобрали простейший пример пластинки, соединенной с одним упругим продольным ребром. Допустим теперь, что пластинка подкреплена системой продольных и поперечных ребер. Тогда путь решения задачи, которым мы воспользовались, оказался бы весьма сложным: необходимо было бы составить условия сопряжения пластинки и ребер по многим линиям. Если система является «регулярной», например, если расстояния между ребрами одинаковы, а жесткости их равны между ссбэй, то для решения задачи можно использовать метод конечных разностей. В общем же случае для исследования устойчивости комбинированной системы часто пользуются энергетическим методом, присоединяя к энергии деформации пластинки энергию изгиба ребер и учитывая также работу внешних усилий, приложенных к ребрам *). В результате были получены в применении к различным конструкциям таблицы и графики для определения критических усилий и эквивалентной жесткости ребер**).
§ 95. Несущая способность подкрепленных панелей при сжатии
Мы рассмотрели различные подходы к расчету подкрепленных пластинок на общую и местную устойчивость. Каким же образом определить оптимальное соотношение между жесткостями пластинки и подкрепляющих элементов? Как определить несущую способность комбинированной конструкции? Эти вопросы неизбежно возникают при проектировании.
Для некоторых конструкций по условиям эксплуатации местное выпучивание обшивки между ребрами считается недопустимым. Тогда критерием наименьшего веса конструкции будет равенство критических напряжений, относящихся к местной устойчивости отдельной панели пластинки и к общей устойчивости конструкции.
Однако во многих случаях местная потеря устойчивости обшивки является допустимой. Например, пассажиры самолетов, наблюдающие за деформацией крыла, могут убедиться в том, что обшивка сжатой зоны крыла получает вмятины, расположенные между стрингерами и нервюрами (рис. 7.51)***). Влияние повторяющихся хлопков обшивки на усталость конструкции должно быть рассмотрено особо.
*) Этот метод был применен к подкрепленным пластинкам С. П. Тимошенко {7.13], решившим ряд конкретных задач; впоследствии он использовался П. Ф. Папковичем [0.7], А. В. Кармишиным [7.5] и другими авторами.
**) См., например, «Справочник проектировщика (расчетно-теоретический)», под ред. А. А. У майского, Стройиздат, М., 1960.
***) Фотографии рис. 7.51, 7.53 и 7.57—7.59 взяты из книги Гертеля (Н. Н е г t е 1, Lelchtbau, Springer-Verlag, 1960).
§ 95] НЕСУЩАЯ СПОСОБНОСТЬ ПОДКРЕПЛЕННЫХ ПАНЕЛЕЙ ПРИ СЖАТИИ 341
Процесс деформации подкрепленной пластинки при постепенном нагружении сжимающими силами состоит в следующем. Если пластинка является достаточно тонкой,* то местное выпучивание ее наступает при сравнительно небольших сжимающих напряжениях (рис. 7.52)
Рис. 7.51. Выпучивание обшивки в сжатой зоне крыла самолета.
В дальнейшем вмятины углубляются; при этом время от времени происходит изменение числа вмятин, нередко сопровождающееся хлопками. В том случае, если обшивка делится на панели различной
Рис. 7.52. Последовательные стадии выпучивания пластинки, подкрепленной тонкостенными ребрами.
ширины, например при подкреплении П-образными ребрами, то на более поздней стадии происходит потеря устойчивости «узких» панелей (рис. 7.53). Если подкрепляющее ребро является тонкостенным, то следующий этап состоит в местной потере устойчивости элементов ребра — стенки или полок. На отдельных этапах нагружения в обшивке и стенках подкрепляющих профилей возникают пластические деформации. Наконец, наступает общая потеря устойчивости конструкции; она выпучивается в целом, как сжатый
342 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Рис. 7.53. Выпучивание различных полос сжатой подкрепленной панели.
стержень либо как закрепленная по краям пластинка; вместе с этим дополнительно изгибаются обшивка и стенки профилей. В этот момент несущая способность конструкции оказывается исчерпанной.
Таким образом, определение несущей способности конструкции сводится к расчету ее на общую устойчивость, причем обшивка,
а в отдельных случаях и стенки подкрепляющих профилей должны приниматься во внимание с учетом редукционных коэффициентов. Так как редукционные коэффициенты зависят от величины сжимающих напряжений в ребрах, то расчет проводят путем последовательных приближений: задаются ориентировочным значением максимальной нагрузки, находят редукционные коэффициенты, вновь определяют нагрузку и т. д. При рассмотрении общей устойчивости редукционные коэффициенты для обшивки и стенок профилей принимают обычно теми же самыми, что и в случае «статического» сжатия *), т. е. по данным § 92.
Пример 7.3. Определить несущую способность для панели шириной В = 450 мм, толщиной h = 1 мм (рис. 7.54, а), подкрепленной четырьмя
стрингерами и сжатой в продольном направлении. Сечение стрингера показано на рис. 7.54, б, под С понимается центр тяжести. Материал обшивки и стрингеров— дюралюмин, Е — 0,72 • 10б кг/см2, (л = 0,32, апц = 2800 кг/см2. Вычислить толщину обшивки в предположении, что два промежуточных стрингера удалены, а несущая способность осталась прежней. Сравнить вес новой панели с весом исходной.
Примем сначала, что несущая способность определяется местной потерей устойчивости свободной полки стрингера. Рассматривая эту полку как пластинку, у которой один из ненагруженных краев защемлен, а другой свободен, находим критическое напряжение по рис. 7.23 равным
Рис. 7.54. К вычислению несущей способности панели, подкрепленной четырьмя стрингерами.
0,46тс2£> 0,46 • тс2 • 0,72 • 10б • 0,152
wCTp
b2h
12 (1 —0,322) 202
= 1680 кг/см2.
*) Более строгий подход к задаче требует определения редукционных коэффициентов с учетом того, что сжатые края пластинки перемещаются друг относительно друга (см. [0.3], стр. 155).
§ 95] НЕСУЩАЯ СПОСОБНОСТЬ ПОДКРЕПЛЕННЫХ ПАНЕЛЕЙ ПРИ СЖАТИИ 343
Вычисляем редукционный коэффициент для обшивки (при этом напряжении в ребре) по (210 Ь):
m ОД 0,72.10° лоло
= ~ПГ V - 1680~ = 0’262-
Несущая способность панели равна
Р = 1680 (4 • 0,584 + 0,262 • 0,1 • 45) = 1680 • 3,52 = 5900 кг.
Определим критическую нагрузку общей потери устойчивости, рассматривая панель как сжатый стержень. Будем условно учитывать площадь обшивки
,\f> г' Г !■*
Рис. 7.55. К определению редукционных коэффициентов.
с прежним редукционным коэффициентом 0,261, а сечение стрингера—с коэффициентом 1. Вычислим координату центра тяжести редуцированного сечения уц.х, отсчитывая ее от оси ус, проходящей через центры тяжести угольников (рис. 7.55):
- 0,1 • 45 • 0,262 • 0,6 ло
Уц. т = 32 = °'2 см-
Момент инерции редуцированного сечения равен
45. 0 262. 0 I3
/ = 4 • (0,222 + 0,584.0,22) + 0,1.45 • 0,262.0,42 + -, = 1,17 см*.
Ориентировочное значение критической эйлеровой силы оказывается равным
82»«г.
а соответствующее напряжение будет
9250 оллл, 9
аэ —1 52 ~” къ[СМ ®пц*
Таким, образом, разрушающая нагрузка соответствует общей потере устойчивости конструкции. Чтобы уточнить величину Рэ, следует найти новые редукционные коэффициенты для обшивки, исходя из напряжения ар = 2600 кг/см2, а затем провести новое приближение (см. след, пример).
Рассмотрим далее случай, когда два промежуточных стрингера удалены, и допустим, что несущая способность определяется местной устойчивостью стрингера, так что напряжение ар равно 1680 кг/см2. Найдем толщину обшивки hx из условия, что нагрузка составляет Р = 5900 кг:
5900 = 1680 (2 • 0,584 + сbhx 45); (а)
редукционный коэффициент <pj для обшивки равен
1ЛА,,/“0,72-10° ло
<е‘ 45 г 1680 ~ ~ * 5 I*
344 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Подставляя это значение <р, в (а), приходим к уравнению
3,5 = 1,168 + 39,34
Отсюда Н\ = 0,224 см. Выбираем стандартную толщину h{ = 0,25 см. Определяя, аналогично предыдущему случаю, эйлерову силу для панели в целом, находим Рэ = 6450 кг.
Веса исходной и новой панелей относятся, как площади их сечений:
О, 4-0,584 + 0,1.45
G2 2-0,584+ 0,25‘45
Таким образом, при одинаковой несущей способности панель с тонкой обшивкой и четырьмя стрингерами оказывается приблизительно вдвое более легкой, чем панель с толстой обшивкой и двумя стрингерами.
Пример 7.4. Вычислить несущую способность на сжатие для дюралюминовой панели, изображенной на рис. 7.56, а. Сечение продольных ребер
показано на рис. 7.56, б; площадь сечения /? = 0,684 см2, момент инерции относительно центральной оси / = 0,204 см4. Принять Е = 0,72 • 10б кг/см2, р. = 0,32, апц = 2800 кг/см2. Насколько увеличится предельная нагрузка, если длину панели уменьшить до I = 150 мм?
Определим нагрузку, соответствующую местной потере устойчивости свободной стенки стрингера:
-. ft*.и.0,72.10..„г1смК
wCTp '
12 (1 —0,322) 182
Эта величина превышает предел пропорциональности материала, поэтому ее необходимо уточнить, исходя из теории устойчивости пластинок в пластической области (см. главу. VIII). Примем в качестве предельного напряжения апц = 2800 кг/см2. Редукционный коэффициент для обшивки равен
<¥> = 1,9
0,2
Г 28С
10е
= 0,3,
20 V 2800 при этом нагрузка будет
Р = 2800(2-0,684 + 0,2-20-0,3) = 7200 кг.
§ 96] НЕСУЩАЯ СПОСОБНОСТЬ СЖАТЫХ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 345
Рассмотрим, далее, общую устойчивость панели, принимая для обшивки в качестве исходного тот же редукционный коэффициент <р = 0,3, а для полки стрингера <р = 1. Центр тяжести редуцированного сечения будет находиться на расстоянии от центра тяжести сечения стрингера, равном
0,2 • 20 • 0,3 • 0,62 Л 0 У п. т = 257 ~ ’ СМ'
Момент инерции редуцированного сечения оказывается равным (см. вычисления в предыдущем примере) / = 0,66 см4. Критическая сила для панелей разной длины:
;1) = *2• 0,72_А°в'0,66 = 1300 кг, Р(2) = 16P<!) = 20800 кг.
602 9
Для первой панели местная потеря устойчивости полки стрингера, очевидно, исключена. В следующем приближении примем напряжение ар равным
1300 *пп, 2
Ср = 2 сд = 500 кг/см2;
тогда редукционный коэффициент по (210Ь) будет <р = 0,72 и Р = 2130 кг. Снова вычислим координату центра тяжести редуцированного сечения, уц т = 0,42 см, и найдем момент инерции сечения, / = 0,77 см4. Эйлерова сила равна Р = 1520 кг. Это значение все же сильно отличается от предыдущего (2130 кг), поэтому необходимо сделать еще одно приближение, принимая
®стр = 25 = кг!см2,
тогда = 0,85, Р = 1720 кг. Новая координата центра тяжести уц< т = 0,44 см, при этом / = 0,792 см4. Значение критической силы Р = 1570 кг, что отличается от исходного на 9%. Ограничиваясь этим приближением, находим окончательно несущую способность панели равной Р « 1600 кг.
Несущую способность второй панели необходимо уточнить, учитывая местную потерю устойчивости полки стрингера. Принимая условно для этой панели в качестве предельной нагрузки Р = 7200 кг, приходим к заключению, что укорочение панели привело к увеличению несущей способности в 7200/1600 = 4,5 раза.
§ 96. Несущая способность сжатых тонкостенных стержней
В главе IV мы выяснили, что общая потеря устойчивости для сжатых тонкостенных стержней происходит в изгибно-крутилъной либо изгибной форме; при этом предполагалось, что сечение стержня сохраняет свое очертание. Теперь мы можем учесть новое обстоятельство— местную потерю устойчивости стенок профиля, причем каждая стенка здесь не может выпучиться изолированно, а лишь совместно с другими. Это явление приводит к искажению формы сечения; оно либо предшествует общей потере устойчивости, либо происходит после нее, в зависимости от соотношения между размерами сечения и алиной профиля.
Рассмотрим случай стержня швеллерного сечения. При достаточно большой длине стержня наиболее опасной оказывается изгибная
346 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
либо изгибно-крутильная форма потери устойчивости. Если ширина полки b сравнима с шириной стенки а, то профиль теряет устойчивость в изгибно-крутильной форме, при Ь<а — в изгибной. На рис. 7.57, а, б показан случай изгибной потери устойчивости; в процессе продольного изгиба может дополнительно произойти местное выпучивание, если полки оказываются на вогнутой стороне (рис. 7.57, а).
а) б) а) б) а) б)
Рис. 7.57. Изгибная Рис.7.58. Выпучивание Рис. 7.59. Местное выпучиформа потери устойчи- тонкостенного стерж- вание стенок стержня,
вости тонкостенного ня, сопровождающестержня. еся закручиванием.
Для более коротких стержней сначала происходит местное выпучивание полок и стенки (рис. 7.58, а), а затем закручивание профиля (рис. 7.58, б). Наконец, в случае короткого стержня опасным будет местное выпучивание (рис. 7.59, а и б).
Исследование местного выпучивания швеллерного профиля проводится с учетом одновременного изгиба полок и стенки *) в предположении, что углы профиля остаются прямыми. Для каждого из этих элементов выписываются дифференциальные уравнения изгиба типа (70), а также условия сопряжения. Результаты вычислений для швеллера с постоянной толщиной стенки показаны **) на рис. 7.60.
•) Оно было выполнено Киммом (К i m m, Luftfahrtforschung, № 5 (1941)).
**) Они принадлежат Винклеру (по книге Гертеля, см. ссылку на стр. 340).
§ 96] НЕСУЩАЯ СПОСОБНОСТЬ СЖАТЫХ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 347
Критическое напряжение сжатия представлено формулой
По оси абсцисс на рис. 7.60 отложено отношение Ь/а, по оси ординат — значения k. Вверху расположена зона местной неустойчивости. Здесь же приведены кривые, определяющие наступление
Рис. 7.60. Различные варианты выпучивания швеллерного профиля.
изгибной либо изгибно-крутильной неустойчивости, параметром служит величина
Как и следовало ожидать, при малых значениях т опасной оказывается общая потеря устойчивости. Зона изгибно-крутильной неустойчивости выделена.
График рис. 7.60 позволяет лишь определить начальное критическое состояние. Важным является определение несущей способности для того случая, когда изгибная или изгибно-крутильная неустойчивость наступает после местного выпучивания (рис. 7.58). Решение этой задачи является трудным: «подкрепляющие ребра», которыми здесь являются углы профиля, не остаются прямыми, как это считалось в § 89, а закручиваются вместе со всем сечением.
348 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
Один из предложенных подходов к задаче *) состоит в том, что критическая сила, соответствующая местной потере устойчивости, сохраняется по величине и направлению, оставаясь приложенной в центре тяжести сечения. Дальнейшее увеличение нагрузки отвечает надкритической силе, которая уравновешивается дополнительными напряжениями сжатия, причем сопротивляемость стержня действию этих надкритических напряжений определяется меньшим (касательным) модулем, различным для каждого волокна. Эта важная задача ждет своего более полного решения.
§ 97. Закритическое поведение пластинки при сдвиге.
Диагонально растянутое поле
Мы рассматривали до сих пор закритическую деформацию пластинки лишь при сжатии в одном направлении. Однако при расчете
некоторых конструкций надо принять во внимание поведение пластинки после потери устойчивости от сдвига. Это относится, например, к некоторым панелям крыла или фюзеляжа самолета, а также к стенкам высоких балок.
Так же как и в случае сжатия, здесь имеются два подхода к задаче. Один из них состоит в использовании модели, позволяющей описать характер выпучивания пластинки при значительном превышении касательными напряжениями критической величины. Другой подход заключается в решении задачи на основе нелинейной теории гибких пластинок. Познакомимся сначала с первым направлением.
Напомним, что при чистом сдвиге оси главных напряжений составляют с кромками угол, равный 45°, и одно из главных напряжений является растягивающим, а другое — сжимающим. При потере устойчивости происходит как бы гофрирование пластинки по направлению главного сжимающего напряжения (рис. 7.61). Если края пластинки остаются в первоначальной плоскости, то и здесь выпучивание ведет к образованию напряжений в срединной поверхности. Случай сдвига интересен тем, что волокна пластинки, параллельные складкам, могут нести весьма значительные растягивающие усилия, передающиеся на
Рис. 7.61. Гофрирование пластинки при сдвиге.
*) Задача поставлена А. А. Уманским и решена Б. И. Иванием.
§ 97] ЗАКРИТИЧЕСКОЕ ПОВЕДЕНИЕ ПЛАСТИНКИ ПРИ СДВИГЕ 349
продольные ребра. Реакции от продольных ребер воспринимаются в свою очередь поперечными элементами; последние оказываются сжатыми. Таким образом, создается система наклонных растягивающих усилий, уравновешенных реакциями поперечных ребер (стоек). Такая модель, упрощающая истинное распределение напряжений в срединной поверхности и напряжений изгиба, носит название диагонально-растянутого поля *).
Будем в первом приближении полагать, что направление складок совпадает с направлением главного растягивающего напряжения и что главное сжимающее напряжение равно нулю. Иными словами, мы считаем, что пластинка не способна передавать какие-либо усилия нормально к гофрам.
Обозначим: т — напряжение сдвига в сечениях, параллельных
координатным осям, а — главное растягивающее напряжение, а — угол наклона вектора а к продольным кромкам, е и —деформации по направлению а и перпендикулярно ему.
Принимаем е = с/Е. Величина ед складывается из упругой деформации (— ро/Е) и сближения точек пластинки, вызываемого образованием складок.
Рассмотрим деформацию квадрата со стороной, равной единице (рис. 7.62). Деформации по направлениям х и у равны
*) Теория диагонально растянутого поля была разработана Вагнером [7.22].
У
Рис. 7.62. Деформации в случае диагонально растянутого поля.
(7.275)
350 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок в пределах УПРУГОСТИ [гл. VII
Прямые, параллельные осям х, у, при деформации повернутся на
углы ух% уу, равные
ух=уу = (е — вд) sin a cos а, (7.276)
Деформация сдвига будет
Т = ?*+ Ту = (•- **) sin 2а. (7.277)
Пользуясь выписанными соотношениями, находим:
tg 2а = -—I—, (7.278)
елг у
£х + £у, 1
е =
6
+ (7.279)
- 4- У(~02 + Т2- (7.280)
я 2 2 Y ух У
Эти уравнения позволяют определить угол наклона складок и угол сдвига, если заданы деформации подкрепляющих ребер и деформация по направлению главного растягивающего напряжения:
tg2 а = —» (7.281)
у
Т = 2 У(е — ех)(е — еу). (7.282)
Последнее выражение можно также представить в виде
у = 2 (е — ьх) ctg а. (7.283)
Отметим соотношение
е + е</ — елг + еу (7.284)
Напряжение сдвига х выражается через главное растягивающее напряжение следующим образом:
x = --sin2a. (7.285)
Рассмотрим случай, когда подкрепляющие ребра можно считать недеформируемыми, так что eJC = ey = 0. Тогда по (281) получим:
tg2 a = 1. (7.286)
Таким образом, угол наклона складок будет равен 45°. Далее найдем:
х =, 7 = 2--. (7.287)
Отсюда
т = 0,2 ЪЕу. (7.288)
§ 98] ИССЛЕДОВАНИЕ С ПОМОЩЬЮ ТЕОРИИ ГИБКИХ ПЛАСТИНОК 351
Вводя понятие приведенного модуля Gv характеризующего жесткость пластинки после потери устойчивости, будем иметь:
Ох = -у = 0,25£. (7.289)
По отношению к начальному модулю сдвига О величина Gx составит
Gt = - (12+ (7.290)
или, при х = 0,3,
0! = 0,650. (7.291)
Таким образом, при недеформируемых подкрепляющих ребрах
жесткость пластинки на сдвиг падает после потери устойчи¬
вости на 35%; в случае деформируемых ребер это снижение будет больше.
§ 98. Исследование закритического сдвига с помощью теории
гибких пластинок
Модель диагонально растянутого поля уместна лишь при достаточно развитой закритической деформации пластинки. В случае, если критическое напряжение сдвига превышено незначительно, исследование должно основываться на теории гибких пластинок.
Рассмотрим квадратную пластинку со стороной Ъ, шарнирно опертую по краям, подвергающуюся действию сдвигающих усилий s по всем кромкам. Предполагается, что края могут искривляться в плоскости опорного контура. Воспользуемся уравнениями (232), (233); граничные условия для краев х = 0, х = 1 примем в виде
• = °. 5 = °. - = 0. -3 = *. (7.292)
Представим основные уравнения и условия (292) в конечных разностях, как это было описано в § 90. Ниже представлены результаты решения задачи *), выполненного на цифровой машине. «Урал-2», с шагом сетки с = 1/ъ. Контур сеточной области составляет кромки л; = 0, у = 0 и диагональ у=1—х. Внеконтурные точки лежали на прямых х =» — с, у — — с. Считалось, что пластинка изгибается симметрично относительно диагонали у= 1—х.
На рис. 7.63 сплошными линиями изображена зависимость между параметром нагрузки s, равным
“т(4У-
*) Оно было проведено А. Ю. Биркганом.
352 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК в ПРЕДЕЛАХ УПРУГОСТИ [гл. VII
и прогибом w в точках А(1/2, 1/2) и £(3/4, 11А), причем величина Wq отложена с обратным знаком. Критическое напряжение составляет по (161) sKO = 9,4. Пунктирные линии представляют данные решения той же задачи с помощью метода Бубнова— Галеркина (см. [0.3], стр. 157) с введением двух варьируемых параметров. Как видим, погрешность подобного решения оказывается значительной *).
На рис. 7.64 нанесены горизонтали изогнутой поверхности, относящиеся к различным значениям w, при 5=12 и
5 = 50. Критическое напряжение было
га» после потери устойчивости.
S-M
Рис. 7.64. Выпучивание квадратной пластинки при сдвиге.
превзойдено в первом случае в 1,25 раза, а во втором — в 5,3 раза. Судя по рис. 7.51, при относительно большом превышении критического напряжения в средней части пластинки образуются густо расположенные складки, подобные тем, которые соответствуют модели диагонально растянутого поля.
*) Отметим, что в решении по методу Бубнова — Галеркина граничные условия (292), относящиеся к функции Ф, выполнялись лишь «в среднем».
ГЛАВА VIII
УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
ЗА ПРЕДЕЛАМИ УПРУГОСТИ
§ 99. Применение теорий пластичности к задачам
об устойчивости пластинок
Формулы для расчета пластинок на устойчивость, выведенные для упругой области, применимы только при относительно малой толщине пластинки. Рассмотрим, например, сжатую в одном направлении удлиненную шарнирно опертую пластинку. Критическое напряжение скр для такой пластинки определяется формулой (7.79), справедливой при условии, что величина акр не превышает предела пропорциональности материала: акр <зпц. Отношение ширины пластинки к толщине должно составлять
Предельное значение bjh оказывается равным для мягкой стали около 60, а для дюралюмина — 36.
Между тем в реальных конструкциях часто встречаются пластинки, для которых отношение bjh лежит ниже указанного предела. Это относится, в частности, к авиационным конструкциям: в тяжелых летательных аппаратах в связи с новыми аэродинамическими требованиями толщина обшивки в последнее время значительно возросла. Поэтому исследование устойчивости пластинок при пластических деформациях является весьма важным, оно необходимо и для конструкций из стеклопластиков: предел пропорциональности этих материалов сравнительно низок.
В главе II было показано, как осложняется задача об устойчивости стержней в упруго-пластической области, если определять соотношение между зонами догружения и разгрузки в сечении стержня в зависимости от условий приложения внешних сил. Тем более трудным является исследование выпучивания пластинок\ в каждом слое пластинки образуется не одноосное, как, в случае стержня, а плоское напряженное состояние..
23 Д. С. Вольмир
354 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами упругости (гл. VIII
В настоящее время имеются два подхода к решению задачи об устойчивости пластинок при пластических деформациях. Один из них заключается в рассмотрении пластинки как анизотропной, т. е, имеющей не ту цилиндрическую жесткость, которая определяется для упругой области, а различные жесткости на изгиб в двух направлениях и на кручение. Соотношение между жесткостями зависит от того, в какой мере превзойден предел пропорциональности теми или иными «основными» (докритическими) усилиями.
Например, в случае одноосного сжатия вместо дифференциального уравнения (7.70)*)
Коэффициент уменьшения жесткости X в направлении х одни авторы считают равным \=Т/Е, где Т—результирующий модуль для стержня прямоугольного сечения, а другие — X = EJE, где Ек — касательный модуль. Коэффициент крутильной жесткости принимают лежащим в пределах Х<Х*<1; чаще всего считается Х*=угХ. При этом предполагается, что пластические свойства материала должны проявляться главным образом в направлении основного напряжения ох, величина которого превосходит предел пропорциональности. Что касается направления у, то здесь материал является как бы «свежим» и имеющим упругий модуль. Для крутильной жесткости принимается некоторая промежуточная характеристика. Этот подход позволяет получить без особых трудностей расчетные формулы для критических напряжений, но его надо считать лишь приближенным. Хорошо известно, что при сложном напряженном состоянии пластические свойства материала в каждой данной точке тела зависят от некоторых суммарных характеристик, в которые напряжение и деформация по направлению данной оси входят лишь как некоторые составляющие. Эти характеристики определяются теориями пластичности. Поэтому обоснованное исследование выпучивания пластинок в упруго-пластической области может быть проведено лишь с помощью той или иной теории пластичности; в этом и состоит второй подход к решению задачи. Применение теорий пластичности приводит в конечном счете к дифференциальным уравнениям, близким по форме к уравнениям типа (Ь) для анизотропных пластинок; но коэффициенты анизотропии здесь уже не выбираются по интуиции.
предлагается взять за основу следующее:
(Ь)
*) Такой подход содержится в книгах С. П. Тимошенко [0.23], Ф. Блейха и И. Геккелера, а также в ряде работ Колбруннера (см. [0.19]).
ПРИМЕНЕНИЕ ТЕОРИЙ ПЛАСТИЧНОСТИ
355
Наиболее ценные результаты в этой области были получены, начиная с 1944 г., с помощью теории малых упруго-пластических деформаций*). Эта теория**) связывает величины главных деформаций сдвига с соответствующими касательными напряжениями. Использование теории деформаций равносильно рассмотрению пластинки в пластической стадии как нелинейно-упругого тела. Преимуществом этой теории является сравнительная простота исходных зависимостей. Все же в задачах о выпучивании пластинок теорией деформаций надо пользоваться с осторожностью, так как, строго говоря, она относится лишь к случаю простого нагружения, когда все составляющие тензора деформаций изменяются пропорционально одному параметру и, следовательно, направления главных осей деформации остаются неизменными. Но это допущение выполняется лишь в процессе нагружения пластинки до момента выпучивания. При потере устойчивости пластинки в различных точках возникают дополнительные деформации изгиба, и главные оси деформации меняют свое направление. Правда, можно считать, что при слабом искривлении пластинки дополнительные деформации малы по сравнению с основными и что поэтому нагружение является близким к простому.
Естественное желание освободиться от ограничений деформационной теории привело к появлению исследований по устойчивости пластинок, основанных на теории течения; эта теория устанавливает соотношения между напряжениями и приращениями пластических деформаций, т. е. скоростями изменения деформаций, в то время как предыдущая теория оперировала с полными деформациями.
Мы познакомимся с приложением к различным задачам устойчивости пластинок как теории деформаций, так и теории течения и сравним результаты вычислений с экспериментальными данными.
Не надо забывать, что термин «устойчивость» применяется к конструкции, испытывающей упруго-пластические деформации, в условном смысле. В самом деле, здесь любое малое возмущение вызывает необратимые деформации конструкции. Выведенная из положения устойчивого равновесия, конструкция. будет совершать затухающие колебания уже около некоторого нового изогнутого положения, характеризуемого остаточными прогибами. Поэтому здесь остаются в силе те оговорки, которые были сделаны в § 31 (стр. 105) по отношению к определению устойчивости. Мы будем считать состояние пластинки устойчивым в малом, если отсутствуют соседние «нетривиальные» равновесные формы.
*) Первые исследования этой задачи принадлежат А. А. Ильюшину [8.1], [8.2].
**) Ниже она коротко названа теорией деформаций.
356 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ [гл. VIII
Эффект цепных напряжений, благодаря которому пластилка способна воспринимать возрастающую нагрузку после выпучивания, распространяется и на упруго-пластическую область. Задача о закритическом поведении пластинок при пластических деформациях является весьма сложной. Мы познакомимся с возможными подходами к ее решению в главе XII; кроме того, в § 111 будет изложен приближенный прием для определения редукционных коэффициентов.
§ 100. Теория деформаций. Исходные зависимости
Обратимся прежде всего к теории деформаций и приведем некоторые основные зависимости.
Будем исходить из диаграммы а (в), полученной при одноосном растяжении образцов из данного материала (рис. 8.1). Тангенс угла наклона а0 начального участка диаграммы отвечает модулю упругости Е. Проведем в некоторой точке N касательную к кривой а (в); тангенс угла ак между этой касательной и осью абсцисс
определяет касательный модуль *)
Е°к:
da
dt
(8.1)
Соединим точку N с началом О; тангенс угла наклона полученной прямой к оси абсцисс соответствует так называемому секущему модулю £?, который, подобно основному модулю Е, равен отношению оке:
Е°~с f •
(8.2)
Рис. 8.1. К определению секущего и касательного модулей.
Величины и Е являются функциями е* Что касается коэффициента Пуассона [х, то в упругой области, как известно, он лежит для стали и дюралюмина между значениями 0,25 и 0,33. При появлении пластических деформаций величина р. быстро возрастает, приближаясь к предельному значению [х = 0,5. Принимая (х = 0,5, мы считаем материал несжимаемым: кубик из такого материала, подвергающийся всестороннему сжатию, не будет испытывать изменения объема.
Чтобы определить зависимость а(е) в случае одноосного сжатия* проводят испытания коротких образцов, причем тонкие пластинки соединяют в пакеты. В дальнейшем будем принимать, что в преде-
*) Индекс «0» обозначает, что величина £к отвечает одноосному напряженному состоянию.
§ 100] ТЕОРИЯ ДЕФОРМАЦИЙ. ИСХОДНЫЕ ЗАВИСИМОСТИ 357
лах сравнительно малых деформаций диаграммы о(е), отвечающие одноосному сжатию и растяжению, совпадают между собой.
В случае сложного напряженного состояния вводятся понятия интенсивности напряжений ot и интенсивности деформаций
— — °у)2-Нву—вж)2+6 (У+ • + '). (8.3)
= Ц-V(£'~ev)2+(ev -T(ir2y+Ty,+TL); (8-4)
здесь <зх, oy, oz — нормальные напряжения в координатных площадках, проходящих через данную точку, хху% хуг, хгх— касательные напряжения, гх% еу,ег—деформации удлинения, fxy9 yv —Деформации сдвига.
Допустим, что интенсивность деформаций в данной точке возрастает и выполняется условие «простого нагружения». Тогда величины ot и ef связаны между собой, независимо от вида напряженного состояния, зависимостью
°i = £сее (8.5)
Под Ес здесь понимается секущий модуль в диаграмме ot (Bt); связь его с модулем отвечающим одноосному растяжению, будет установлена ниже.
Компоненты деформаций связаны в свою очередь с компонентами напряжений следующими соотношениями:
е* 3 0 — 2Ес S'
гу J 0 ~ 2£с °у ~
__3_
Тху £ Хху-
(8.6)
Аналогичные выражения могут быть выписаны для остальных компонентов. Под 0 в (6) понимается объемная деформация:
® я=*ж~Ь ®у“Ье*> (8.7)
под 5 — «среднее» нормальное напряжение:
3 —■!* + «>+.««.. (8.8)
Величины 9 и <5 связаны зависимостью
а 3(1 — 2ц)
(8.9)
358 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Для несжимаемого материала надо принимать 0 = 0. При деформации относительно тонкой пластинки в каждом ее слое, параллель* ном срединной плоскости, имеет место плоское напряженное состояние; по известным допущениям теории пластинок можно принимать
б* = °- tyz = Тм = 0- (8-10)
Выражение для интенсивности напряжений (3) получает вид
oi=V<5x — oxoy-j-oy-f-Зт2. (8.11)
Величина 5 будет равна
О Y “f G\I
5=, (8.12)
Здесь и в последующем введены обозначения: тху = х, уху = у. Пользуясь (9), перепишем соотношения (6) в виде
_3_0 _
Г з
1—2х
2ЕС 1
\2ЕС
Е
3 _
( 3
1—2(1.
2£с У '
V 2£с
Е
3
ЕсХ‘
)s,
(8.13)
В выражениях (13) можно выделить составляющие упругой и пластической деформации, если положить *)
Gc O' Опл '
(8.14)
Здесь под G понимается модуль сдвига в пределах упругости, под Ос — секущий модуль сдвига, под Опл — модуль сдвига для собственно пластических деформаций. Величина G связана с модулем Е известной зависимостью:
° = 5ПТД- <8-,6>
Для Gc и Опл можно выписать аналогичные соотношения, принимая [х = 0,5:
°с = -у-» Опя =
(8.16).
*) См. книгу Jl. М. Качанова [8.3], стр. 41,
§ 100] ТЕОРИЯ ДЕФОРМАЦИЙ. ИСХОДНЫЕ ЗАВИСИМОСТИ 359
Вместо (14) можно записать соотношение
1 2(1 1
Ес 3Е Г Епл •
Вводя (17) и (12) в выражения (13), получим:
— (?х 1АОу) + (ах ~ ) •
-т.
(8.17)
(8.18)
Первый член в каждом из этих выражений отвечает упругой деформации, а второй — чисто пластической.
Допустим, что известна диаграмма о(е), относящаяся к одноосному растяжению или сжатию. Тогда по (18) и (2), полагая ох = а, оу = 0, будем иметь:
с с, 3/ а \
з];
отсюда
(8J9)
ПЛ С С
Зависимость (19) позволяет найти значения Еая по диаграмме, полученной для одноосного растяжения или сжатия. Пользуясь соотношением (17), имеем, далее,
J- = _L_I=3i Г8 20
Ес Е° ЗЕ * ' *
В случае несжимаемого материала всегда будет £? = £с. Иными словами, считая л = 0,5, мы получаем диаграмму оДе) совпадающей с диаграммой о(е).
Если выписать выражение для интенсивности деформаций (4) в применении к плоскому напряженному состоянию и положить [х = 0,5, то оно примет вид
** + V, + e* + T Т2- (8-21)
Допустим, далее, что в данной точке тела имеет место разгрузка,
выражающаяся в уменьшении тогда в известных пределах изме¬
нения интенсивности напряжений и деформаций будут связаны между собой- законом Гука:
Aoj = Е Ае(, (8.22)
где Е — основной модуль растяжения — сжатия для данного материала.
360 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. VIII
§ 101. Основное дифференциальное уравнение в случае несжимаемого материала
Применим выведенные зависимости к задачам об устойчивости пластинок в предположении, что материал является несжимаемым. Будем считать, что в. некоторой точке пластинки к моменту потери устойчивости напряжения имеют значения ах, су, т, соответствующие им деформации равны ех, еу, 7, и что докритическое нагружение было простым.
Принимая в соотношениях (6) 0 = 0 и пользуясь (12), получим:
Введем обозначения:
тогда будет
sx — ох - 2 V Sy Су 2 9 (8.24)
Sr sv Зх
e = -g-, *У = -[Г’ (8.25)
Пользуясь соотношением (5), получим:
±L = — £у _ sy Gi ’ Qi
В момент потери устойчивости пластинка принимает изогнутое равновесное положение, бесконечно близкое к первоначальному. Определим вариации Ъвх, Ьау, Ьх напряжений, имеющие место при выпучивании пластинки. Исходя из (23), находим:
е/
Зх
(8.26)
— 3 (е* + 2 ®у) ’
°у=~3 (еУ ~2 е*) ’
Х = ЕсЬ
(8.27)
§ 101]
ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
361
Вычислим вариации этих величин, помня, что модуль Ес является переменным и зависит от
Ьах =4 (8ех + 4'8®у) + т(е* + геу) 4 8ei’
8оу = Т Ес (8еУ + i8е*) + Т (®у + Т **) Si’ 8х = 1£с8Т+1Т-8£<.
(8.28)
По аналогии с (1) введем понятие касательного модуля для диаграммы оДе):
(8.29)
(8.30)
По (5) имеем: дифференцируя, находим:
Ес=-
dEc
dz.
. Ц-=-(Ек-Ес).
ei dh zi h
Зависимости (28) принимают с учетом (31) вид
Ъх = ЕС (bex + \ 8еу) - (Ес - Ек)
8а,
= ±ЕС (оеу +1 Ых) - (Ес - Ек) Ц,
Ъх = ±ЕсЪ1-(.Ес-Ек)Ы1. Вариации составляющих sx, sv по (24) равны
ЬХ = Ь°Х—
Пользуясь (32), получим:
Ч = 8зу— 21
bsx = EcUx-(Ec-EK)Ui<
bsy = Ес оеу — (Ес — Ек) — Ц, M = jEcbj-(Ec-EK)±be
(8.31)
(8.32)
(8.33)
(8.34)
362 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Определим вариацию интенсивности деформаций е/в Пользуясь (21), получим:
1
2 (е* + *у у) + *у Ьгх -f е* £у + у Ьу
л?,
После умножения на а, найдем:
= у [(едг + у еу) 8ел: + (еу + У е*) 8еу + \ Т 8т] • Подстановка соотношений (27) дает
<*1 Ц = алг 8едг'
, +т8т.
(8.35)
Выражению (35) может быть придан энергетический смысл: оно равно работе усилий, приложенных к элементу тела, на возможном перемещении.
Допустим, что при нагружении пластинки до потери устойчивости интенсивность напряжений во всех точках превысила предел пропорциональности. В момент выпучивания к основным напряжениям добавятся напряжения изгиба. Пластинка разделится по толщине на две зоны: в одной будет происходить догружение, а в другой—разгрузка (рис. 8.2). Пользуясь гипотезой прямых нормалей, выразим вариации деформаций в произвольной точке пластинки через вариации деформаций в срединной поверхности Ьех, 8еу, 87 и вариации кривизн хх, ху, у:
— Чг + Z%x' 8бу — Ч + Z\,
8тг = 8т + 2гх. (8.36)
Рис. 8.2. Зоны догружения и разгрузки при выпучивании пластинки.
Как и ранее, под z понимается координата, отсчитываемая от срединной поверхности вдоль нормали к ней. Определим положение той нейтральной точки нормали, которая лежит на границе зон догрузки и разгрузки. Очевидно, вариация 8е/ в этой точке должна быть равна нулю. Исходя из (35), находим:
о, 8е* + оу 8е* + х 8Т* = 0. (8.37)
Подставляя значения (36) и обозначая через z0 координату нейтральной точки, будем иметь:
°jc*xzo) + ау (ь*у %yzo)4“Х(5Т + 2Хо)= (8.38)
§ 101] ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 363
Отсюда
(8.39)
0 ~ »л + °у*у + 2хХ
Введем обозначения:
П(о, е) = сл.8е-(-су8еу + т8, (8.40)
П(°> Х) = °Л +Vy + 2xX! (8-41)
тогда будет
Вариация 8е* для произвольной точки с координатой z оказывается по (35) равной
*, (5елг + 2%х) + °у (еу + 2*у) + z (7 +
8е/ = • (8-43)
Используя (42), находим:
= - (8.44)
Обратимся к зоне догружения; примем, что она охватывает слой пластинки между точками z = — и z = zo• Здесь вариации величин szx и 8е* связаны первым из соотношений (34):
К=Е<К-(Е,-£.)К (8.45)
Используя (36) и (44), получим:
Ьзгх = Ес (8еж+гжх) + (£с - Ек)Ыг*~г) ° (з'. (8.46)
ai
По аналогии будет
bsl = Ес (8еу +2ху) -f- (Ес — Ек) —=— -, (8.47)
Qi
8т* = 1 Ес (8Т + 2zX) + (Ес - Ек) х Ц — ■?) П (з, к.). (8>48)
* °<
h
Для зоны разгрузки, лежащей между точками г = г0 и г =,
надо положить ЕС = ЕК = Е, тогда найдем:
Ьб = Е*я + гхх). bsy = Е (8еу -(- zxy), 8t* = j£(8y-1-2zx).
(8.49)
864 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Обозначим через bNx, bNy и ЬТ вариации результирующих усилий, приходящихся на единицу длины сечения пластинки:
h
2 2 2 bNx — fbazxdz, bNy= f bo*dz, ЬТ= j dz. (8.50)
h h h_
“2 ~~~2 *2
Введем вспомогательные величины:
A h
2 T
8Rx = bNx — ±Wy = f bsx dz, bRy = Wy — ±bNx = f bszydz.
A A
* 2 2
(8.51)
По (46) и (49) будет h_
2 *o
bRx = J E (8e л -f - zvx) dz-\- j Ec (aex -j- z*x) dz-j-
+ f (£g —£к) Дд:П(а, *) (Zo_2)d2. (8<52)
1 h 9t
отсюда
8 Rx = [(£ +Ec)-—(E— Ec) z0] 8er +
+ I- (E - Ec) (-£ - 4) *, + (Ec - EK) -(PX (y + z0J. (8.53)
Аналогичным путем находим:
bRy = [(£ + Ec) A _ (£ _ £c) *0] 8ey +
+ ‘(£-£J(-_4),y + (Ec-£K)iiL(+,0J.
(8.54)
8 T = i [(£ + Ec) A - (E - Ec) z0] 8T + j (E - Ec) (-£ - z) X +
+ (£с_Як)Л1(А+го)2. (8.55)
§ 101] ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 365
Примем здесь, что процесс потери устойчивости происходит при
неизменных внешних усилиях. Распространим это допущение на вариации внутренних результирующих усилий и положим *)
bRx = bRy = bT=0. (8.56)
Умножим выражения (53) — (55) соответственно на ах> ау и Зх и сложим эти произведения между собой. Учитывая соотношение
sxax + say + Зх2 = о2 (8.57)
и пользуясь обозначениями (40) и (41), получим:
[(£ + £с)4-_(£_££)*0]п(о> е) + у(£-£с)(х-*о)П(°- *) +
+ (Ее - Ек) ( * + z0f = 0.
Деление на П (о, х) с учетом (42) дает
- [(£ + ЕС)\-(Е- Ес) г0] z0 + ±(E- Ес) (-* - z2) +
+ -£с7£к (4+о)2 = 0. (8.58)
или
Е(т-го)2-£к(т + г0)2 = 0. (8.59)
Если обозначить через hx толщину зоны дополнительного нагружения, а через h2 — толщину зоны разгрузки, то будем иметь:
£й!-ЕкЛ? = 0. A2 = A_Zo> a1 = ---_20. (8.60)
Мы получили точно такое же соотношение между hx и /г2, как и в случае сжатого стержня прямоугольного сечения при использовании теории двух модулей (см. § 27). Из (60) находим:
h, = h, h2=h.Ек,. (8.61)
1 УЩ+Ув 2 Yek + Ve к 1
Координата z0 равна
<8.62)
2 УЁ + УХ
*) Более точное решение задачи, при котором вариации внутренних усилий не считаются равными нулю, было дано А. А. Ильюшиным [8.2] и Ю. Р. Лепиком [8.5].
366 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. VIII
Определим, далее, изгибающие и крутящий моменты, приходящиеся на единицу длины сечения:
мх
A A L
2 2 2
= У* 0zxzdz, му= I* ozzdz> Н= f i*zdz. (8.63)
A il a
2 “2 * 2
Введем дополнительные обозначения:
JL h
2 2
Шх= Mx — My = j szxzdz> My = My — jMx= j* szyzdz.
h *h
” T (8.64)
Подставляя выражения (46) и, (49), находим: h_
2 z0
= j E(lsx-\-z-*.x)zdz-\- jE<.(Ux-\-ZY.x)zdz-\-
z0 h
2
4- / (£c ~ £к) ** П (g> X) (g0 — *) ■dz. (8.65)
J± 1 2
Интегрируя, будем иметь:
mx=±(E-Ec)(£ - -
- (E - Ec) zl] хя-± (Ec - EK) (A3 - 4zl + 3*0A*). (8.66)
При p. = 0,5 цилиндрическая жесткость пластинки в пределах упругости окажется равной
-ЫКйЦ.--
Вводя обозначения
<Рс = §. = (8.68)
перепишем (66) в виде
а»,=o' {з (1 + *) - (1 - ъ> (т)’] ь +
' (8.69)
§ 101]
ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
367
Выразим величину через кривизны. Для этого определим 8е, пользуясь (53) и (56):
8е
J (1 —?c)(-jp—*о)*» ! (?с — <Рк) П (з, %) + ZoJ
(1+»е)-5—2 [О+*>т~~(1 “ *>*•]•< *
(8.70)
Подставляя это значение в (69), находим:
<й, = О' ( 3 [i (1 + - (1 — *) 4] -
4 1
(l — 4zo-}-3z0) -J-
n (3. *) sx
(8.71)
(8.72)
(8.73)
2 0 + Tc) — (1 — ¥с) гч
t 60-Te)(-g + g.)2(j—
4(l+?c)-(l-?c),
здесь введено обозначение
2
Z°— h '
Представим (71) в виде
2K,=D'0-r)*.,-(l -g) где
,-!(■-» [о+*a+7 0,7, ] • <8>
. = 1 -1 (fc -*> [ I - iii+зг0+i (‘ (i+)to,ls!'’)] •
(8.75)
D> Ц(1-г)ху-(1-5)П (°'J? Sy j, (8.76)
[f (1 - ОX ~ (1 ~ ~} '-j •' (8.77)
Аналогичным путем получаем: 2K =-
По (64) имеем:
368 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Отсюда
мх=
D' [(1 - г) (гх+1 ху) -1 (1 - j,
Г / 1 \ 3 П (а, %) sv 1
= D(i_r)+___(i_S)_LrbLj.
(8.79)
гиб:
Выразим кривизны и кручение изогнутой поверхности через про-
d2w
d2w
d2w
х дх2 ’ У ду2 * л дх ду
Тогда выражения (79) и (77) с учетом (41) примут вид
М
= _D'0-r)
Му = -
d2w дх2 / dw
2 ду 1 d2w
Н = где
= — D'[-(l — г)
[2 дхду
ду2 2 дх2
d2w
(1 — S)-J II (о, w)j
II (о, w) = о
4
d2w
3 (l—s)~n (о, да) j,
х дх*
ai
d2w. 9 °У ду2 ‘ Z дх ду'
(8.80)
(8.81), (8.82) (8.83)
(8.83а)
Рассматривая малые прогибы пластинки и пользуясь соотношениями (7.16), (7.17), (7.156), выпишем уравнение равновесия элемента
д2Мл
дх2
+ 2
д2Н
д2М„
дх ду
ду2
-[- MI (a, w) = 0.
(8.84)
Здесь напряжения ох и оу считаются положительными при сжатии. Подставляя сюда выражения (81) — (83), приходим к следующему дифференциальному уравнению для прогиба*):
О
3 1-s С
4 1 —г
)-5-+Ф
з 1—s + 2т
2 1
+ 1
3 1 — S atl
4 1 — г J ду
дw
4 1 —г 1 — S х
дw
1-
Г О;
d*w
дх2 ду2 d4w
дх3 ду
дх дус
+
h
(1 —г) D
— П (a, w) = 0. (8.85)
*) Это уравнение было впервые выведено А. А. Ильюшиным [8.1], [8.2]. В его работах содержатся также решения ряда частных задач для пластинок, сжатых в одном и в двух направлениях.
§ 101] ОСНОВНОЕ ДИФФЕРЕНЦИАЛЬНОЕ. УРАВНЕНИЕ 369
Уравнение (85) вместе с граничными условиями является исходным при решении различных частных задач. Если положить срс = срк = 1, то будет г = 0, 5=1; тогда вместо (85) - получим известное уравнение, относящееся к устойчивости пластинок в пределах упругости, если считать в нем jx = 0,5:
D'V4w-j- hU(o, w) = 0. (8.86)
Отметим некоторые соотношения, облегчающие вычисление параметров г и s. Как мы видели, координата (62) слоя, разделяющего зоны догрузки и разгрузки, получается той же, что и в задаче об устойчивости -стержня прямоугольного сечения. Введем безразмерную величину, отвечающую результирующему модулю Т в этой задаче:
/ Л 4ук. ~ _
е - (ГЁ+ГЮ2 ~ (1 +Уп)2 ’ { ’
следовательно,
По (62) будет
отсюда
l-V*= \,t~- (8-88)
1 + У Ук
г°=7ттйг <8'89)
(\—2z0? = t, (8.90)
1 —4i? = 2 V7(l — (8.91)
l + 8 = 2(l -)[(l+ (8-92)
Используя эти зависимости, приведем выражение (74) к виду
(8.93)
Обратимся к выражению (75). Представим его в виде
«=(1—2+4?„(1 - - ?,»in+21„я п - г„, +
+ 3(i-w(.+s»>,(i-c;>i
„ /лл 4 0+?с) — (1— <Рс)2го. J
По (89) имеем:
*-(тт§)\ <8'95)
370 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ [гл. VIII Пользуясь, кроме того, соотношением (90), получим: s = t + j (1 - 9с) (1 ~ *о)0 + 2z0? -
3 [(1 + 2F0)*-ус(1 -2г0)2](1 -jfc)(1 - 411)
® (1 + ?с) + (1 — ?с) 2*0
(8.96)
или
(8.97)
И- 4- (r—'Рс) {(1Н- — 48)—
3 [(1 + 2?р)г - Ус (1 - 2го)* ] (1 - у с) (1 - 45»)
8 (1+Те) + (1-Т«)2г0 j
Объединяя последние два члена, содержащиеся в скобках, и сопоставляя полученное выражение с (74), приходим к следующему простому соотношению:
s = t + г. (8.98)
Располагая для определенного материала пластинки значениями секущего и результирующего модулей, можно определить параметры г по (93) и 5 по (98); такие вычисления сделаны в § 110 для дюралюмина и стали.
§ 102. Приложение вариационных методов
Составим выражение для работы усилий Мх, Му> Н на возможных перемещениях, при которых кривизны получают приращения 8х., 8ху, 8Х. Участку пластинки с размерами вдоль осей х, у, равными
единице, будет соответствовать удельная работа
ЪА* = — (Мх 8хх + Му 8ху + 2Я 8Х). (8.99)
Учитывая соотношения (77) и (79), находим:
84* = — D' j (I — г) [(*, + у *у) 8*г + (*у + •? *х) Ч + X Ч] —
• 3 (1 с)П (*’ q) (вхЬ%х + + 2т8х) \. (8.100)
4 е] \
Выражение (100) можно представить в виде полной вариации*): ЪА* = -£>'8 у(1-г) (** + Vy + *2 + Х2) _
— A(l-s)IE-(y))a. (8.101)
*) Напряжения о*, х считаются неварьируемыми,
§ 102)
ПРИЛОЖЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ
371
Введем понятие потенциальной энергии деформации, вариация которой равна
bU*=bA\ (8.102)
Такой шаг является оправданным: как уже было сказано, теорию малых упруго-пластических деформаций можно рассматривать как теорию нелинейно-упругого тела. Далее находим:
и'=%{(1 -г)(хх+ v>4-+ Х2)-то -}•
(8.103)
Моменты будут равны частным производным от потенциальной энергии:
му=1' 2Я=1г> (8Л04>
это отвечает известной теореме Лагранжа.
Полная потенциальная энергия будет
U = J J U* dx dy. (8.105)
F
Определим работу внешних сил при малом искривлении пластинки, считая усилия axh, ayh равномерно распределенными вдоль соответствующих кромок пластинки. По (7.52) находим:
*-т//[•<(£-)'+*(£)'+*£]*'<* (8'106>
F
Если рассматривать переход от начальной равновесной формы к изогнутой как возможное перемещение пластинки, то должно быть
bA + bW = 0 (8.107)
или
b(U — W) = b3 = 0, (8.108)
где Э — U — W — приращение полной энергии системы при выпучи¬
вании пластинки.
Пользуясь вариационным уравнением (108), можно истолковать с энергетической точки зрения применение метода Бубнова — Галеркина для приближенного интегрирования исходного уравнения (85). С другой стороны, при рассмотрении потери устойчивости «в малом» каждую возможную равновесную форму пластинки надо считать безразличной; в процессе перехода от начальной формы к изогнутой полная энергия должна оставаться неизменной. Иными словами, работа внешних сил при выпучивании пластинки должна равняться
372 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
потенциальной энергии, отвечающей возникающим при изгибе внутренним усилиям. Исходя из этого условия, можно применять для
приближенного решения задач устойчивости пластинки метод Ритца — Тимошенко (см. § 9).
§ 103. Решение частных задач
Рассмотрим для примера случай шарнирно опертой по краям пластинки, сжатой в направлении х (см. рис. 7.14). В уравнении (85) следует положить
о1 = ох — о, оу = т = 0. (8.109)
В результате, пользуясь (98), получим:
Л 3_ 1 —t — r\ d4w. су d*w. d*w, ha d2w Л
\ Т 1 — г ) дх4 ' дх2 ду2 ду4 (1 — г) D' дх2
(8.110)
Примем решение в виде
-. тпх. ту w — f sin —— sin ~y~ ; (8.111)
после подстановки в (ПО) будем иметь:
/1.3 t \ т<. 0 т2п2. п' ho т2 _ „ - по
\J-T- 4 1 — г) а* Z аЧ2 ь4 (1 — г) D' о2*2” *
отсюда
-т+ттМ’+’+-пг)’]- <8-ш>
Критическое напряжение определится как минимум выражения (113). При этом надо прежде всего положить п= 1; следовательно, пластинка должна выпучиваться, образуя одну полуволну вдоль стороны Ь. Полагая а/Ьт = К запишем, далее, условие *минимума о в виде
= 0; (8.114)
д\
это дает
Т
t
4*4 1 —г * Критическое напряжение оказывается равным
(8.115)
кр v b2h
где
°ко = *. (8.116)
/С = 2 (1 — г) (/~ -Ь-1- -ПГ7+ O’ (ЗЛ1?>1
§ 103]
РЕШЕНИЕ ЧАСТНЫХ ЗАДАЧ
373
Формула (117) относится к удлиненной пластинке, для которой волнообразование вдоль стороны а является свободным. При значении а% сравнимом с b, следует отыскать число полуволн т% придающее коэффициенту К наименьшее значение.
Допустим, что для квадратной пластинки минимуму К соответствует т= 1, тогда величина К в формуле (116) по (113) равна
К = 3,25 -f~ ~Г~7~) (1 — г)= 13(1-r)+g-. (8.118)
В предельном случае упругой задачи надо положить г = О н t— 1, тогда формулы (117) и (118) приведут к известному значению К —А. Если диаграмма оДе,), соответствующая данному материалу, имеет площадку текучести, то для точек этой площадки имеем по (93) r = 1—<рс, * = 0; вместо (117) получим /С = 3срс, а вместо (118)
к- 13 «
Л = <Рс-
В случае удлиненной пластинки выражение для критического напряжения можно тогда представить в виде
oKp = 3-pf; (8.119)
здесь через D' обозначена, по аналогии с (67), цилиндрическая жесткость, отвечающая секущему модулю, при [i, = 0,5:
Напомним, что при £->0 несущая способность сжатых стержней всегда оказывалась исчерпанной. В теории устойчивости пластинок мы приходим к иному результату: для точек площадки текучести величина зкр=£0. Иными словами, переход «порога» площадки текучести не обязательно сопровождается выпучиванием пластинки *). Это объясняется тем, что при выпучивании пластинки, в отличие от случая стержня, образуется двухосное напряженное состояние. Судя по формулам (32), здесь могут иметь место приращения ох, ау и х и в том случае, когда материал находится в состоянии текучести (при Ес =£ 0, Ек = 0). Допустим, что величины сх, оу их получили приращения, в то время как величина интенсив-
*) Этот вывод относится к «бесконечно медленному» процессу нагружения. Если принять во внимание динамический эффект, имеющий место в упругой испытательной машине при достижений площадки текучести, то состояние пластики може! все же оказаться неустойчивым.
374 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ [гл. VIII
ности напряжений (11) остается неизменной. Тогда должно быть (о, + Ьсх? - (сх+Ьох) (cy-f- So,) + (оу + So/ + 3 (т + 5х)2 =
= <-V,+ пренебрегая малыми высшего порядка, будем иметь
ох(2Ьох— 8ву)+
°у — 28оу) + Зт8т == 0.
(8.121)
бу-й6х полагая здесь оу = т = 0, по5) лучим:
9б* 2Ьох = Ьау. (8.122)
Именно такое соотношение — должно быть в рассматриваете оо w мой задаче между Ьаг и Ьои
Рис. 8.3. К случаю выпучивания пластин- J х У
ки при напряжении, равном пределу те- для точек диаграммы о(е), кучести. лежащих на площадке теку¬
чести (рис. 8.3).
Мы рассмотрели здесь лишь одну частную задачу об устойчивости сжатой пластинки с шарнирно закрепленными краями. Ряд задач, относящихся к другим видам нагрузки и иным граничным условиям,
исследован с помощью тех же исходных соотношений Б. М. Броуде
[7.3], С. М. Поповым [8.6] и Ю. Р. Лепиком [8.5].
§ 104. Вывод основного уравнения
без учета эффекта разгрузки
Теория устойчивости пластинок, изложенная выше, в частном случае сжатого стержня сводится к теории «двух модулей». Судя по (61), толщина пластинки делится на зоны догрузки и разгрузки таким же образом, как делится высота прямоугольного сечения стержня при продольном изгибе. Естественно попытаться распространить на пластинки другой подход, при. котором эффект разгрузки не учитывается. В применении к стержням эта концепция соответствует, как мы видели в главе И, случаю, когда сжимающая сила возрастает в процессе выпучивания.
Итак, будем считать, что соотношения между приращениями напряжений и деформаций являются в зонах догружения и разгрузки одними и теми же. Тогда, очевидно, «нейтральная» поверхность, разделяющая эти зоны, будет совпадать со срединной поверхностью пластинки. Следовательно, вариации деформаций для точек срединной поверхности будут при выпучивании пластинки равны нулю.
§ 104] ВЫВОД ОСНОВНОГО УРАВНЕНИЯ без учета эффекта разгрузки 375
Воспользуемся соотношениями типа (46) между вариациями напряжений и деформаций, найденными выше для зоны догрузки:
Ч = Е<Ч~(Ес ~ЕК)~ Ч (8.123)
**; = ЕС 8еу - (ЕС - Ек) % Ч- (8.124)
8тг = 1яс8т*-(£с_£к)-±-8е*. (8.125)
Считая Ьех = 8еу = Ьу = 0, по (36) получим:
Ы*х = г%х, = 8 = 2. (8.126)
Вариация интенсивности деформаций (42) равна
(аЛ + ауху + 2%/) г П(а, %)
=. у ’г. (8.127)
Выражения (46) — (48) заменятся на следующие:
8®£ = [fc*, - (Ее - Ек) М.4* *) j z, (8.128)
8s* = j £exy - (£c - EK) 5ytI’ X) j г, (8.129)
8т* = ~ EeX - (Ec - EK) -TtI <*’ *> j г. (8.130)
Как можно видеть, условие (56) выполнено: вариации результирующих усилий bRx, §Ryi ЬТ оказываются равными нулю. Величина Шх будет равна
2
шх
= f Ъф dz = Ес*я - (Ес -. (8.131)
Вводя значение цилиндрической жесткости (67), получим:
= т D' [Ъ*х- (?« -<Рк) --I’--] • (8.132)
Таким же путем находим:
аи, = т о' —(«ре — <рк) j, (8.133)
V = JD' [} Тех - (CPC - <Рк) — (з2 Х)'] - (8.134)
376 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Изгибающие моменты по (78) равны:
MX = D' [<рс (чж+1*у) -2(<рс_срк) Цр-j. (8.135)
[/ 1 \ 3 avTl (<j, х)
Тс (уу + у)-Т(Ус-Тк) У g2 I • (8-136)
Пользуясь выражениями (80) для кривизн, будем иметь:
= -0'[f,(g + i)-(<P.-<P,)n<a. „)j. (8.137)
[/d2w 1 d2w\ 3 av _ ”1
(8138> ->]• <fu39)
Уравнение равновесия (84) приобретает вид *)
+с’1)+-5Г11(’-) = 0- (8140)
Здесь введена цилиндрическая жесткость (129), соответствующая секущему модулю.
Все соотношения — от (132) до (140) •*— мы могли бы непосред-
ственно получить из зависимостей § 101, считая = zQ = -g-.
В самом деле, при таком значении z0 вся толщина пластинки оказывается охваченной зоной догрузки. Параметры г и 5 по (74) и (75) будут равны --
Г= 1 —Тс- * = 1 — (?С — ?«)• (8.141)
При рассмотрении упругой задачи надо считать Ф == ср =-1, D' = D'.
Тк Тс с
*) Это уравнение было получено СтоуэлЛом [8.16]. Им же был решен ряд частных задач для пластинок, сжатых в одном направлении.
§ 105] ВЫПУЧИВАНИЕ СЖАТОЙ пластинки 377
Вариационное уравнение (113) и энергетический критерий остаются в силе и при решении задачи без учета разгрузки; изменится лишь выражение для удельной энергии U*t :вместо (103) получаем:
и*= it {+**+у2)—т (?с—?«) -(у)]2 J • (8-142>
§ 105. Выпучивание сжатой пластинки
Будем исходить из нового дифференциального уравнения (140). В случае сжатия пластинки в одном направлении оно принимает вид
/ 1 I 3 <рк \ d*w. 0 d*w. d4w. hi d2w _ ~
(i + 7)+2W+7+d=0- (8Л43)
Рассмотрим различные условия закрепления.
1. Все края пластинки шарнирно оперты. Принимая w попрежнему в виде (111), получим:
tD' Г / 1 3 <р„\ 1 „ 1
0=w l(t+т и+2п + 4X2J ’ <8-144)
где \ = а/Ьт. Принимаем п— 1 и выписываем условие (114) для удлиненной пластинки; тогда находим:
>■=¥ <8-145>
Судя по (145), в упруго-пластической области волны укорачиваются в направлении сжатия, и тем интенсивнее, чем меньше отношение срк/срс. Это и естественно: относительная жесткость пластинки вдоль х
при развитии пластических деформаций падает.
Коэффициент К в формуле (116) получает значение
К = 2срс (/~ + (8Л46>
В случае квадратной пластинки, если принять /ю=1, получим:.
К = 3,25срс—— 0,75срк. (8.146а)
При сильно развитой пластической деформации можно положить <рк = срс, тогда вместо (146) и (146а) получим:
378 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
таким образом, критическое напряжение будет определяться «секущим модулем». Для точек площадок текучести при срк = 0 в случае удлиненной пластинки будем иметь:
а -3
°кр—6 b2h ’
что совпадает с (124). Длина полуволн при этом составляет по (145) около 0,7 от ширины пластинки. Как и следовало ожидать, значение /С, найденное без учета эффекта разгрузки, лежит, как правило,
ниже, чем с учетом разгрузки.
Введем обозначение для «приведенного» коэффициента:
<Рпр == у <Рс ]/ ' + (8-148)
и перепишем формулу (116) для удлиненной пластинки в виде
«кр = 2 -щ- (?пр + <Рс)- (8.116а)
Для упругой области српр = срс=1. При вычислении D' принимается р. = 6,5. Поэтому (116а) не переходит в известную формулу (7.77). Этот переход будет осуществлен ниже, в § 107; здесь же условно примем D' = D и обозначим критическое напряжение для упругой области через акрэ; тогда вместо (116а) получим:
°кр == кр. э» (8.149)
где под ч\ понимается поправочный коэффициент для упруго-пластической области:
т) = 0,5(<рс +<рпр). (8.150)
Для квадратной пластинки по (147)
т) = 0,81срс + 0,19срк. (8.150а)
Рассмотрим, далее, пластинку, сжатую вдоль короткой сто¬
роны, при а<Ь, Х2<1, тогда
K*D' г Q \
акр = -4й-(?с + 39к)-
Относя эту величину к значению <зкр.э и принимая Dr — D, придем к поправочному коэффициенту для случая «цилиндрического выпучивания» пластинки в виде
т) = 0,25срс + 0,75срк. (8.150Ь)
Напомним, что так как мы не учитываем эффекта разгрузки, то в пре¬
дельном случае сжатого стержня должно быть
т} = срк. (8.150с)
§ 105] ВЫПУЧИВАНИЕ СЖАТОЙ ПЛАСТИНКИ 379
2. Нагруженные края пластинки закреплены шарнирно, а ненагруженные — защемлены (рис. 7.17). Воспользуемся энергетическим методом решения задачи. При одноосном сжатии выражение (142) для U* примет вид
U*= Т [*с (х*+'W+*у + х2) — Т (<Ре ■— <Р«)'] ’ (8 •151)
отсюда
и D'c f С171 -1-3 ?к Wd2w V I d2w,
U—~2~JJ 4 ъ )\д* ) ~*~ д* ду*
+(4)2+(йг)2]dx dy- (8Л51а)
Работа внешних сил по (106) будет
г=4/А (£)’■** ■'у-
F
Пользуясь (108) и полагая ох = а, находим:
*//(■)’ d*d>
F
(8.153)
Выражение для прогиба выпишем в виде
w = / sin - sin2 > (8.154)
После подстановки этого выражения в (153) и интегрирования находим:
п2Р'с 11 f 3 <рк m2b2 t 8л2 ( 16 а2п4 *]
0 = ~Wh~ L vT Т / л* ' 3~ + ~5ЬЬп*\•
Величина о будет по-прежнему минимальной при п= 1. Примем, что пластинка является удлиненной и нагруженные края свободны. Полагая -~ = \, получим:
*2d; 0 b*h
К1 3 <рк\ 1 8 16 1
4+T)iF+3+x4- (8Л55)
380 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ [гл. VIII
Условие (114) приводит к соотношению
отсюда
<jkp==8~6W~('3 + T + 'if)*' (8.156)
При срк = Тс = 1 и D' = D придем к формулам § 83 для упругой области:
У _ V 3 _ 8(/3 + 1)
АЭ— 2 ’ °кр.9— 3 b2h •
Поправочный коэффициент 17 при D' = D получает значение
<Рс + V3 <Рпр
/3 + 1 '
или
т1«0,3бсрс+0,64?прв (8.157)
3. Нагруженные края оперты шарнирно, а из ненагружен/шл; краев один закреплен шарнирно, а второй свободен. В этом случае примем такое выражение для до:
—/тг sin —r-J (8.158)
6 а
оси координат расположены, как показано на рис. 7.22. По формуле (153) получаем:
>171 ■ 3 ук \ кЧт*, п*тг 1
А-б5-
Выражение (159) будет наименьшим при т— 1; так же, как в упругой задаче, здесь вдоль оси х образуется одна полуволна; следовательно,
«■.■=[(т + т£)()!+4-]- <<U60)
В случае удлиненной пластинки при b <d а
3D' 1 / h \2
b2h 3
Поправочный коэффициент оказывается при D' = D равным
•»1 = <Рс- (8.161)
§ 106]
ВЫПУЧИВАНИЕ ПЛАСТИНКИ ПРИ СДВИГЕ
381
Критическое напряжение оказалось здесь пропорциональным секущему модулю. Это позволяет значительно облегчить практические расчеты. При заданном отношении bfh находим критическую деформацию:
е-=-Нт)!- <8-62>
и по диаграмме о (в) для данного материала соответствующее значение секущего модуля Ес, тогда
°кр =:: секр*
Джерар предложил [8.10] пользоваться этим приемом для определения критических напряжений при других граничных условиях; в формуле типа (162) рн рекомендует подставлять вместо коэффициента 73 такой коэффициент kt который вытекает из решения упругой задачи; например, в случае удлиненной пластинки с шарнирно закрепленными краями k = 3,6.
Как мы видели, такой расчет по секущему модулю, часто встречающийся в литературе, вытекает из теории деформаций в случае одноосного сжатия лишь в одном частном случае. Во всех других задачах этот прием надо рассматривать как приближенный, причем погрешность при пользовании им может быть значительной.
4. Нагруженные кромки шарнирно оперты; один из ненагруженных краев защемлен, а второй свободен. Пользуясь тем же методом, что и в п. 3, находим следующее окончательное выражение для поправочного коэффициента у при D' — D:
71 = 0,43срс + 0,57српр. (8 Л 63)
Значения rj для дюралюминовых и стальных пластинок приведены ниже, в § 110.
§ 106. Выпучивание пластинки при сдвиге
Обратимся к случаю квадратной пластинки со стороной а, подвергающейся действию касательных напряжений т по всем кромкам (см. рис. 7.24). По (11) находим:
С; = j/3 т. (8.164)
Уравнение (140) приобретает вид
dAw, (Л, <рк \ d4w, dAw, 2h d2w
382 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ [гл. VIII
Здесь принято
ф=1—.St.
т 9с
Выражение для прогиба примем в виде (7.148):
т п
Выпишем уравнение метода Бубнова — Галеркина:
J* J X sin sin dx dy = 0.
F
Принимая во внимание соотношения (7.151), получим:
f Г (т2 + п2)2 } 1 У1 У f Яд2 mrUJ ft
fmn а4 [ 4 ViJ (т2 — i2) (п2 — у2) — °*
(8.170)
Введем обозначения:
х ~ Ezh2 ' Р ~ 3 (1 — (л2) * (8.171)
Идя тем же путем, что и в § 85, рассмотрим сначала сочетания
индексов: (1, 1), (2, 2) и (2, 2), (1, 1), тогда получим систему урав¬
нений относительно /п и /22. Приравниваем нулю определитель системы:
(4-ф)/
1 128 „
9 *2 х
Параметр т*р, отвечающий критическому напряжению сдвига, оказывается в первом приближении равным
.“тётО-т)’ <8-173>
отсюда
TKpil=12,l(l-±)fc(A)2. (8.173а)
Выберем в качестве второго приближения индексы /я, п следующими: (1, 1), (1, 3), (3, 1), (3, 3), а /, j — (2, 2), а затем поменяем
4 128, 9 ** Х
(16_4ф)/>*
= 0.
(8.172)
(8.167)
(8.168)
(8.169)
§ 107] ОБОБЩЕНИЕ НА СЛУЧАЙ СЖИМАЕМОГО МАТЕРИАЛА
383
их местами. Это приведет к уравнению, обобщающему прежнее уравнение (7.164) на упруго-пластическую область:
(4 — <0 р*
4
9
128 *
2~ *
п2
0
0
0
1 128 *
(16 —
1
128,
1
128,
9 128,
9 п2 т
Ц)Р*
5
5
2 Х
п2
25 я* х
0
4
5
128
7Z2
(33-
-Зф)р*
0
0
0
4
15
_128. п2
0
(33-
-3 ф)/>*
0
0
4
15
128,
2 Х
0
0
(36—9<Юр'
= 0.
(8.174)
Определяя отсюда т*р 2 второго приближения и сравнивая эту величину с v получим:
'-“ТПргferiT- (8Л75)
V 25 L 100 — 9ф 25 J
В § 85 было видно, что величина, стоящая в знаменателе, при ф = 0 равна 1,18. Распространяя это значение на случай ф=£0, получим:
или
<р= 10,2£(0.75(рс + 0,25срк)(А)2. (8.177)
Поправочный коэффициент оказывается равным
= 0,75срс —j— 0»25срк. (8.178)
Это значение примем условно и для пластинок с произвольным отношением сторон. Отметим, что Джерар рекомендует в случае сдвига вести расчет по секущему модулю [8.10] и принимать т] = <рс.
§ 107. Обобщение теории деформаций на случай сжимаемого материала
Предыдущие решения задачи об упруго-пластической устойчивости пластинок имеют тот недостаток, что для всех точек диаграммы (е*) коэффициент Пуассона считался равным 0,5. Поэтому основные дифференциальные уравнения (85) или (140) не сводятся в частном слу¬
384 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
чае чисто упругой деформации к известному уравнению классической теории пластинок; это же относится к отдельным расчетным формулам.
Чтобы получить уточненное решение для материала, сжимаемого в упругой области, воспользуемся более полными зависимостями § 100 между деформациями и напряжениями *). Ограничимся при этом случаем одноосного напряженного состояния до потери устойчивости (ау = % = 0) и не будем учитывать эффект разгрузки.
Воспользуемся соотношениями
ox-S = ox-j- = lsx, 0y-S=-§sy) (8.179)
тогда выражения (18) для деформаций можно переписать следующим образом:
ех=г-£- К — t*«y) -Ь ££■ sx, (8.180)
S = (8.181)
T = [2(1ifT'i'' + r]T- (8Л82)
Выразим вариации величин е, еу, у через вариации напряжений в таком общем виде:
Цг = 11а.*:+12°у + = Л21 8а-(- А22 8ау Л23 8т, (8.183)
= А31 Ьах + AZ2 + лзз *
Коэффициенты Лп, Л12,... равны соответствующим производным:
дгг я дгх я дг*
ь
Рассматривая выражения (182), сразу же. находим:
Л13 = Л23 = Л31 = Л32 = 0. (8.185)
Определим остальные коэффициенты. Пользуясь равенством (180),
= A2=-g. и т.д. (8.184)
получим:
dtx 1. 1 ds»-, д
А — ~ дах — Е
Производная от sx равна
dsx
(<U86)
1. (8.187)
*) Такое решение было впервые дано. Л. А. Толоконниковым [8*8]. Другой путь решения, изложенный ниже, был предложен для случая = х == 0 Бижляром [8.9], а в более общем виде — А. П. Прусаковым [16.12]. Последние два автора рассматривали задачу без учета эффекта разгрузки.
§ 107] ОБОБЩЕНИЕ НА СЛУЧАЙ СЖИМАЕМОГО МАТЕРИАЛА 385
Найдем производную от 1 /:пл. Исходя из соотношения (17), будем иметь:
д
д<зх
Ox Um)“ ** (ie)* (8Л88)
Запишем это выражение в виде
Находим:
<8,90)
и, далее,
dai
= —— i/o* — а о ч- а* ч- дх* — ~—— =
в/
Окончательно
дах
(8.191)
(i)=(i-i)t- <8i92> Выражение (186) получает вид
1 1 /1 Л \ 4
Лп“ £г+;+(Г_3)
Аналогичным образом вычисляем остальные коэффициенты:
(X 1 /1 1 \ sxsv
(8.194,
1 1 /1 1 \ 4
•22 = Т ~z—I- ( ~z ТГ ) ~Т' 22 Е Епл \ЕК Ес) °У Считая основное напряженное состояние одноосным, примем:
= sy = -t’ б< = °*; (8.196)
тогда получим:
1,1,1
386 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. Vlft
Воспользуемся соотношением (17), тогда выражения (197) можно привести к виду:
и _ 1 I !—2
11 — £к ZE
А А 1
л12 21 2 Ек
A -1-L л22 — 4 Ес
1 —2fx
4 £к
3£
(8.198)
(8.199)
(8.200)
Коэффициент Л33 находим непосредственно по (182); используя (17), будем иметь:
(8-201>
Выразим вариации напряжений через вариации деформаций; в общем виде будет
Ьох = п Ьвх + 12 8еу + 13 Ьу,
5оу = 21 5елг + 22 Sey + 23 (8.202)
St = 31+ 32 8еу + 33 й?. «
Мы должны найти матрицу коэффициентов и, 12,..., обратную матрице величин Ап, Л12,... Как легко видеть, в данном случае
13 = 23 =: 31 32 0. (8.203)
Остальные коэффициенты равны
11 ~ д2 * 12 = 21 — » 22 — » 33 = 4зз • (8.204)
Под А здесь подразумевается определитель, составленный из коэффициентов Ап Л22:
А =
Ац А12 21 22
(8.205)
Подставляя выражения (198)—(200), после упрощений находим:
А = -
1 —2(х / 1
(ik+i)- (8-206)
Перейдем к безразмерным величинам:
§ 107] ОБОБЩЕНИЕ НА СЛУЧАЙ СЖИМАЕМОГО МАТЕРИАЛА 387
тогда получим:
an = i(— + — + e = i(r_L+.L=>\1
Д \ 4<(с 4<рк 3 / А \ ук 3 /
(8.208)
ги=г,,=(--
г+о- ад(г+тг)- (8-210)
‘2<рк
где
_ Q
Если не учитывать эффекта разгрузки при выпучивании пластинки, то для всех точек по толщине будут справедливы соотношения (202). Изгибающие и крутящий моменты будут равны
А А А
2 2 2
М
.= J bcjzdz. Му — J bayzdz, Н= J 8тzdz. (8.211)
Приращения деформаций изгиба выразим через кривизны:
bex = z%x, 8ey = zxy, by = 2zx; (8.212)
тогда получим:
12 Мх _ _ 12Му
12ху» £дз = 21** + 22*у»
12// 0gF- — 2аззХ-
(8.213)
Если воспользоваться выражениями (80) для кривизн, то уравнение равновесия (84) приобретает вид
“ d4w, п /-, г>~ \ » “ d4w, 12 d2w л /о г»1>1ч
длг*- 12 33 длг2ду2 +а22“г + £Д2 0 2 0* (8.214)
Перед последним членом взят знак плюс, так как напряжение считается положительным при сжатии.
Дифференциальное уравнение (214) справедливо как для чисто упругой, так и для упруго-пластической области; коэффициент Пуассона р. может быть выбран в соответствии с данными опытов для рассматриваемого материала. В предельном случае упругой деформации надо воспользоваться зависимостью (20). Считая для одноосного растяжения или сжатия £? = £, получим:
1 1/, 1 — 2(i \ 2 (1 + {*),001*4
388 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VII]
Аналогичную формулу будем иметь для величины, обратной касательному модулю в диаграмме оДе):
ж = <8-2,6>
отсюда
1 = 1 = 2(1+ Ю
Тс Тк 3
(8.217)
Формула (210) получает вид
К= 1 — [х2. (8.218)
Вместо (208) и (209) находим:
а11 — а<22 = 1—2 ’ а12 = а21 = » а33 = 2 (1 + (1) * (8.219)
Пользуясь этими значениями, вместо (214) получим известное уравнение (7.70), относящееся к упругой области.
Если считать материал несжимаемым и положить = 0,5, то будет
=4Г’ «11 = CPk+J?c ei2 = -J*c. 22 = 4 Те. «33=-.
(8.220)
и тогда уравнение (214) приобретает вид
/1, 3 ук \ d*w. о d'w d*w. a /•0 9014
W “Г 4 ?с)дх* дх*ду* ду4 дх2 — и’
что совпадает с полученным выше уравнением (143).
Рассмотрим случай удлиненной шарнирно опертой пластинки, сжатой в одном направлении. Принимаем для прогиба выражение (111) и подставим его в уравнение (214); полагая п— 1, будем иметь:
0 = W Р» Ж+2 + 2зз) +. X =. (8.222)
Условие (114) дает
4
.=l/ 1. К <*22
Критическое напряжение оказывается равным
акр = 52 ' ( апа22 + а12 + 233). (8.223)
Если воспользоваться значениями коэффициентов (219), то для упругой области получим известную формулу
_ *2Eh2 _4 пЮ
°КР з (1 — (X2)Ь2~~ b2h 9
§ 108]
ПРИМЕНЕНИЕ ТЕОРИИ ТЕЧЕНИЯ
389
Подставляя в (223) выражение (220), придем, к прежней формуле (146), относящейся к несжимаемому материалу.
Обратимся к случаю квадратной шарнирно опертой пластинки. Принимая в (222) т — п— 1, найдем критическое напряжение равным
В упругой области получим формулу, совпадающую с (224). При р, = 0,5 вновь придем к выражению (146а).
Приложим к решению задач об устойчивости пластинок другую теорию пластичности — теорию течения, непосредственно связывающую приращения деформаций и напряжений с компонентами напряжений *). Напомним, что в основные зависимости (5) и (6) теории упруго-пластических деформаций входили полные значения деформаций.
Будем считать, что приращения деформаций имеют упругую и пластическую составляющие. Примем, что обе эти составляющие определяются для несжимаемого материала при х = 0,5. Упругие составляющие в случае плоского напряженного состояния равны
Пластические составляющие по теории течения определяются еле дующим образом [8.3]:
В случае одноосного растяжения полное приращение деформации будет
%2Eh2 °КР 12Ь2
\.аи 4“ 22 “Ь 2 (12 Ч~ 2а33)]. (8.225)
§ 108. Применение теории течения
(8.226)
(8.227)
(8.228)
*) Теория течения была приложена к задачам об устойчивости пластинок Хандельманом п Прагером [8.12], Пирсоном [8.14] и Л. М. Качановым [8.3].
390 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
отсюда
*-£ (к-т8«*) = тг(-т)- <8-229)
Пользуясь прежним обозначением для касательного модуля
получим:
== 1 Sa/J j\
£ °х \?к )
Будем в дальнейшем обозначать
(8.230)
(8.231)
(8.232)
Соотношение (231) обобщается на случай сложного напряженного состояния таким образом, что вместо ах сюда вводится интенсивность напряжений at; тогда будет
(8.233)
(8.234)
(8.235)
(8.236)
Е <3i 7
Окончательно приращения, деформаций оказываются равными K = + Sx)’
ыу = т{ьу+*у)'
8т = -§.(* + <!>
Находя вариацию от интенсивности напряжений (11), имеем:
8о, =
s% Stfjf -f- Syboy -f- Зт Вт
a/
Пользуясь (236), перепишем выражения (234) и (235) в виде (183); коэффициентами здесь служат величины
Л, = i-(> + К), Ли = ±(14- «14). Л* = -§. (1 + 3<rf).
А и — A2l g 2 ’
Аз = 31 = ~£ 23 == 32 = ~£ 45ут»
под sx, s, т понимаются безразмерные параметры
(8.237)
§ 108]
ПРИМЕНЕНИЕ ТЕОРИИ ТЕЧЕНИЙ
391
Определим приращения напряжений по формулам (202). Коэффициенты ап, а12,... и здесь образуют матрицу, обратную по отно-
шению к матрице коэффициентов Alv
12»
... Обозначим через А
главный определитель системы (183):
11 12
Аз
=
21 22
23
(8.239)
31 32
33
Вычисляя этот определитель, находим:
£3Д = (1 + ф) [3 (1 + <) (1 + 3-Й - Ц%х*\ +
+(--?+ [92 (w2> -3 + 32> (- i +■ Л)] +■
+ ЭДV [(— т + *Кл) 3Ф5ух — (! + tsy) 3fv ] • (8.240)
Принимая во внимание соотношение
4+*у + Vy + 7 — -ц (а1+°у — Vy + Зт2) = 7 * (8.241)
после упрощений будем иметь:
£3Д = -(1 + ф) = 1. (8.242)
Коэффициент аи оказывается равным А2% А2ь
dw —
*32 33
А/Е
:4-[1+Ф(52-(-Зх2)]. (8.243)
Аналогичным образом находим остальные коэффициенты. Окончательно получим:
“.. = 3(iwI1 + *« + 3',)l’
4 Е
«22 = 3(ТТФ)-Г1 + 'Н4+Зт2)]-
21 3(1+4-) [2 ( 2 х2 ~ ’
4 Е
flj2 * а
33 — з (1 __ ф)‘ [-Т + i (sl + sl + 5л)] •
й13 = а31 — — 3(1 Т (д Sy + S.r) •
4£ф — / 1 — — \
fi23 fl32 3(1 _ ф) Х (2 + SyJ •
(8.244)
392 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
Будем решать задачу без учета эффекта разгрузки. Тогда для всех точек по толщине пластинки следует принять соотношения (202).
Выразим приращения деформаций через кривизны по (212) и придадим выражениям для моментов следующий вид:
~ /*з Х — аП%х + а12ху + 21зХ’
12 Му
—дз = а2\хх + а22ху + 22зХ»..о
—— — аг1*х + а32ху -f- 2 а33х.
(8.245)
Выразим кривизны через прогиб по формулам (80). Подставляя выражения (245) в уравнение равновесия (84), получим следующее дифференциальное уравнение относительно прогиба:
[?К + (1 - <Рк) (Ц + )] 15 + 2 {<рк + (1 - срк) [4 й + ?,) -
- 4 +i *2] +['Рк+(1 - Тк) (4+Щ -0- -
4(1 срк) X [(4Sy + Sx)-*Zy +{iSx+ sy) S°xdy3 ] +
+ -гП(9, w)=0. (8.246)
Уравнение (246) является исходным при решении частных задач.
Обратимся для примера к задаче о сжатии шарнирно опертой пластинки в направлении х усилиями а; тогда
sx = o, sy = — т = '0. (8.247)
Вместо (246) получим:
/1,3 \ d4w, 0 d4w. d4w, h d2w л /о ола\
(4 + 4 'f’v дх* + дх*ду2 ду* + £>' а дх2 (8-248)
Уравнение (248) имеет такую же структуру, что и уравнение (143), относящееся к теории деформаций; они совпадают, если в уравнении (143) положить срс = 1, Dc = D » т. е. если вместо секущего модуля подставить модуль Е. Поэтому мы можем воспользоваться при этой замене всеми формулами § 105. Ясно, что теория течения приводит к более высоким значениям критического напряжения, чем теория деформаций; различие будет тем резче, чем ниже модуль Ес по сравнению с Е. При слабо развитых пластических деформациях обе теории дают близкие результаты.
§ 109] ВЛИЯНИЕ СЖИМАЕМОСТИ МАТЕРИАЛА ПО ТЕОРИИ ТЕЧЕНИЯ 393
§ 109. Влияние сжимаемости материала по теории течения
В § 108 было принято, что материал является несжимаемым как в упругой, так и в пластической области. Допустим теперь, что компоненты упругой деформации связаны с напряжениями законом Гука в его обычной форме, т. е. будем считать материал сжимаемым. Вместо соотношения (226) получим:
Ком: ''ченты пластической деформации по-прежнему определяются формулами (227).
Рассмотрим случай, когда исходное напряженное состояние является одноосным: = а = а, оу = т = 0. Вариация 8о/ по (236) равна
Ц = 8о —§ог (8.250)
Полные приращения деформаций оказываются с учетом (233) равными
(8.249)
 [(1 + Ф) — (t1 Н—2'ф) 8оу] ’
Sey = [— (tA+T'l>)8 + (1 +Т'1')8оу] ’
87 = J- (1 4- (А) 8т.
(8.251)
Определяя отсюда приращения напряжений, получим:
Ьах — 5”) “1“((*■ '2') 8еу] ’
8оу = [1(•* + т) (1 8еу] ’
(8.252)
где
Д1 = 1 — t*2.+ — -4- Ф-
(8.253)
394 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
В общих формулах (202) мы должны, следовательно,, положить:
11 — (l 4“ Ip) » 22 = О + ф)» 12 — 21 = (1х 4“ ~2 ) ’
_ П _ Е
23 — 32 — 13 — 31 — 33 '
(8.254)
2(1+10
Дифференциальное уравнение типа (214) получает вид
(> + t)4f+4+!+t)w+<‘+rt£+
+ РА,(1-) = <8-255>
где D определяется по (7.12). Пользуясь формулами (253) и (232), после несложных преобразований приводим уравнение (255) к виду
(1 + Зсрк) (1 — t*2) d*w I
(5 _ 4fx) — (1 — 2)2 срк дх*
О 2(l + g)(l +9к) + (5 —4fx)(l—ук) д*т ■
“Т- (5 — 4{Х) — (1 — 2,а)2 <рк up; 2 -Г
I 4(1—fX2) d4w, h<z d2w __ л
-Г (5 — 4(л) —(1 — 2)2 срк ду4 ~т~ D <jc2 — и*
В частном случае ц, = 0,5 уравнение (256) получит прежний вид (246), если принять ау = х = 0.
Воспользуемся уравнением (256) для случая квадратной пластинки. Примем выражение (111) для прогиба, считая т = п= 1. Тогда получим для критического напряжения формулу (116) с заменой D' на £>, причем коэффициент К будет равен
к _ (9 ■+ 7ук) О - У-2) + 2 (1 - у) (5 - 4р.) (1 - Ук)
(5 — 4р.) — (1 — 2р.)2 <рк ‘ V • ;
Если принять срк = 1, то придем к величине К = 4, отвечающей решению задачи для упругой области.
§ 110. Сопоставление расчетных формул для дюралюмина и стали
Приведенные выше формулы для критических напряжений можно применить, если известна зависимость а(е) при одноосном сжатии и растяжении. От этой зависимости можно перейти к соотношению между at и е; как было показано в § 100, диаграммы c(s) и оДег) совпадут, если принять jx = 0,5.
Воспользуемся приведенной выше (§ 28) примерной диаграммой о(е) для дюралюмина Д16Т (стр. 92) и дополним таблицу 2.1 значениями t, г и [л (см. табл. 8.1). Ниже приведена, также дополненная, таблица 8.2 для стали (Ст. 3).
§ 110] СОПОСТАВЛЕНИЕ РАСЧЕТНЫХ ФОРМУЛ ДЛЯ ДЮРАЛЮМИНА И СТАЛИ 395
Таблица 8.1
Расчетные параметры для дюралюмина Д16Т
s-103
с,
кг/см2
£с.10-5,
кг!смг
V10~6'
кг/см*
Г 10”®,
кг/см2
*с
1
Г
1»
2,67
2000
7,50
7,50
7,50
1
1
1
0
0,320
3,0
2200
7,33
5,96
6,65
0,98
0,79
0,88
0,01
0,320
3,5
2460
7,03
4,34
5,50
0,94
0,58
0,73
0,03
0,322
4,0
2640
6,55
3,72
4,97
0,87
0,50
0,66
0,067
0,323
4,5
2780
6,18
2,55
3,81
0,82
0,34
0,51
0,10
0,326
5,0
2900
5,80
2,05
3,22
0,77
0,27
0,43
0,13
0,330
6,0
3080
5,13
1,50
2,50
0,68
0,20
0,33
0,19
0,338
7,0
3200
4,57
1,17
2,03
0,61
0,16
0,27
0,24
0,344
8,0
3320
4,15
0,97
1,72
0,55
0,13
0,23
0,29
0,350
9,0
3400
3,78
0,82
1,48
0,49
0,11
0,20
0,33
0,352
10,0
3450
3,48
0,82
1,48
0,46
0,11
0,20
0,35
0,356
11,0
3560
3,24
0,82
1,48
0,43
0,11
0,20
0,38
0,358
12,0
3640
3,03
0,82
1,48
0,40
0,11
0,20
0,40
0,360
Исходя из этих данных, сопоставим значения критических напряжений, получаемые по различным вариантам теории деформаций и теории течения.
На рис. 8.4 и 8.5 изображена зависимость между критическим напряжением акр и отношением bjh для удлиненной пластинки, подвергающейся сжатию в одном направлении и шарнирно закрепленной по всем краям. Рис. 8.4 относится к дюралюмину Д16Т. Сплошные кривые соответствуют теории деформаций; одна из кривых получена по формуле (117) для несжимаемого материала с учетом эффекта разгрузки; вторая — по формуле (146) для несжимаемого материала без учета разгрузки; третья — по формуле (223) для сжимаемого материала без учета эффекта, разгрузки. Пунктирная кривая соответствует теории течения, она построена по формуле (257) при [а = 0,5 без учета эффекта разгрузки.
Аналогичные кривые, приведенные на рис. 8.5, относятся к стали (Ст. 3). Горизонтальные участки кривых соответствуют площадке текучести. Если вести вычисления по формуле (146), то на участке упрочнения, строго говоря, мы получаем для каждого значения bjh две различные величины окр; кривая окр (£//*) имеет здесь петлю. ДЛтрих-пунктирный участок сглаживает переход от одной ветви кривой к другой *).
*) Об использовании для практических расчетов тех участков кривых, которые лежат выше предела текучести, см. в § 111.
396 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами упругости [гл. VIII
бкг/см*
т
3000
т
2000
15 20 25 30 35 W
,, o/h
Рис. 8.4. Критические напряжения для дюралюминовых пластинок по теории деформаций и по теории течения в сравнении с экспериментальными данными.
бфуМ/СМ*
2800
2700
2600
2500
2400
2300
2200
2100
2000
1900
Ю 15 20 25 30 35 40 45 50 55 60 65 70
0/Ь
Рис. 8.5. Критические напряжения для стальных пластинок по теории деформаций и по теории течения.
Cm
Эфф(
ьРазгр<
шм 1 екта \ 'tfKUjtyk
Дюраммин Д16Т По теории деформаций
По теории течения
о Экспериментальные данные
.о
\о
\
\
без учета разгрузки,
- и-Ц5 Вез учета / сжимаемый
S6
Ss
\
\
тгрузки, f материал
\
\л
1 Г
Ж б {Ш1/1
\
чЛл
Вез учета ~ разгрузки, /1-0,5
i\
4s
// /г**,.\1.1 i б -бпц
Ш///.
¥//////
ш/Ь
ШЯ
§ 110] СОПОСТАВЛЕНИЕ РАСЧЕТНЫХ ФОРМУЛ ДЛЯ ДЮРАЛЮМИНА И СТАЛИ 397
Таблица 8.2
Расчетные параметры для стали Ст. 3
e-103
<*>
кг/см2
К 2/CM2
Як.Ю-«. кг/см1
7М(Га,
кг! cm2 -
*c
“Pk
t
r
0,95
2000
2,10
2,10
2,10
1
1
1
0
0,270
1,0
2100
2,08
1,42
1,72
0,99
0,68
0,82
0,005
0,272
1,1
2200
2,00
0,99
1,39
0,95
0,47
0,66
0,025
0,274
1,2
2280
1,90
0,67
1,05
0,90
0,32
0,50
0,052
0,280
1,3
2340
1,80
0,46
0,85
0,86
0,22
0,41
0,075
0,285
1,4
2380
1,70
0,26
0,54
0,81.
0,12
0,26
0,11
0,290
1,5
2390
1,60
0,13
0,33
0,76
0,062
0,16
0,15
0,293
1,6
2400
1,50
0,06
0,19
0,71
0,029
0,094
0,19
0,304
1,8
2400
1,33
0
0
0,63
0
0
0,33
0,318
2,0
2400
1,20
0
0
0,57
0
0
0,43
0,330
2,5
2400
0,96
0
0
0,46
0
0
0,54
0,358
3,0
2400
0,80
0
0
0,38
0
0
0,62
0,375
3,5
2400
0,69
0
0
0,33
0
0
0,68
0,390
4,0
2400
0,60
0
0
0,25
0
0
0,71
0,400
4,5
2410
0,54
0,02
0,07
0,26
0,010
0,033
0,61
0,405
5,0
2420
0,48
0,04
0,13
0,23
0,019
0,062
0,60
0,408
6,0
2470
0,41
0,05
015
0,20
0,024
0,071
0,63
0,414
7,0
2520
0,36
0,05
0,15
0,17
0,024
0,071
0,65
0,417
8,0
2575
0,32
0,05
0,15
0,15
0,024
0,071
0,68
0,420
9,0
2630
0,29
0,05
0,15
0,14
0,024
0,071
0,70
0,424
10,0
2685
0,27
0,05
0,15
0,13
0,024
0,071
0,71
0,426
11,0
2740
0,25
0,05
0,15
0,12
0,024
0,071
0,73
0,428
12,0
2800
0,23
0,05
0,15
0,11
0,024
0,071
0,74
0,430
Имеющиеся в литературе экспериментальные данные относятся к дюралюминовым пластинкам с упруго защемленными краями [8.16]. Если воспользоваться коэффициентами закрепления краев, взятыми из решения упругой задачи, то их можно условно привести к случаю шарнирно закрепленных краев. Найденные таким образом экспериментальные точки приведены на рис. 8.4; материал испытанных образцов близок по механическим свойствам к дюралюмину Д16Т. Как видим, эти точки лежат вблизи кривых, полученных по теории деформаций, но без учета разгрузки.
На рис. 8.6 также сделано сопоставление расчетных данных с экспериментальными для дюралюминовых сжатых пластинок, но в иной интерпретации *). По оси абсцисс откладываются деформа¬
*) См. работу Прайд и Хаймерля (R. A, Pride, О. I. Heimerl, NACA Techn. Note № 1817, 1949).
398 УСТОЙЧИВОСТЬ ПРЯМОУГ. пластинок за пределами УПРУГОСТИ (гл. VIII
ции ер, по оси ординат — напряжения <зкр. На рисунке нанесена кривая 0кр(екр), относящаяся к одноосному сжатию, и здесь же кривые, построенные по теории деформаций — с учетом и без учета эффекта разгрузки — и по теории течения. Экспериментальные точки располагаются по-прежнему вблизи кривой, относящейся к теории деформаций.
Судя по рис. 8.4 и 8.6, теория течения приводит к значениям критических напряжений, лежащих значительно выше экспериментальных данных. Следовательно, при разработке практических методов расчета пластинок на устойчивость в настоящее время надо отдать предпочтение теории деформаций. Возможно, теорию течения удастся эффективно использовать при исследовании поведения пластинок с начальными неправильностями. Отметим, что условия простого нагружения в этом случае не будут выполняться на протяжении всего процесса деформации пластинки.
§ 111. Данные для практических расчетов
Мы пришли к выводу, что впредь до накопления более обширного экспериментального материала для практических расчетов целесообразно пользоваться теорией деформаций в том ее упрощенном варианте, который не учитывает эффекта разгрузки. При этом расчетные критические напряжения будут, как правило, лежать по отношению к реальным значениям в запас устойчивости, как при расчете сжатых стержней по касательно-модульной нагрузке. Необходимые расчетные формулы приведены в §§ 105 и 106. Для определения критического напряжения следует вычислить его значения по известным формулам и графикам, относящимся к упругой области, а затем умножить на поправочный коэффициент % приближенно принимается Df = D.
На рис. 8.7 дана сводка формул для поправочного коэффициента, относящихся в случае сжатия к удлиненным пластинкам, однако в практических расчетах их можно использовать и для пластинок с иным отношением сторон.
6K9,tхг/см*
Рис. 8.6. Сопоставление расчетных и экспериментальных данных.
§ 111]
ДАННЫЕ ДЛЯ ПРАКТИЧЕСКИХ РАСЧЕТОВ
399
На рис. 8.8 и 8.9 изображена зависимость окр(6/А) для сжатых в. одном направлении дюралюминовых и стальных пластинок, найденная по этим формулам при различных условиях закрепления.
Участки кривых, лежащие на рис. 8.9 выше предела текучести, показаны пунктиром; для материала с ярко выраженной площадкой текучести следует, по-видимому, считать предел текучести верхней границей для критических напряжений. Хотя теории пластичности приводят к иному результату, но при этом не учитывается, как было
SXXX
Х_/_Х.'-/_х
X X X X X а«Ь
_////
ХХХХ
XXXX
хххх
/XXX
Рис. 8.7. Поправочные коэффициенты для расчета сжатых пластинок при различных условиях.
400 УСТОЙЧИВОСТЬ ПРЯМОУГ. ПЛАСТИНОК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. VIII
уже сказано в § 103, своеобразная «неустойчивость» процесса пластического течения и чувствительность конструкции, испытывающей
Рис. 8.8. Критические напряжения для дюралюминовых пластинок по приближенным формулам.
4ф, кг/см2
Рис. 8.9. Критические напряжения для стальных пластинок по приближенным формулам.
этот процесс, ко всякого рода возмущениям. Возможно, пластинка окажется в состоянии практически перейти порог площадки текучести, если она будет скреплена по краям с достаточно жесткими ребрами, изготовленными из иного материала.
ДАННЫЕ ДЛЯ ПРАКТИЧЕСКИХ РАСЧЕТОВ
401
Приведем приближенный прием, позволяющий определять редукционные коэффициенты для сжатой пластинки после потери устойчивости в том случае, если напряжения в полосах пластинки, прилегающих к продольным краям, лежат за пределами упругости *) и если подкрепляющие ребра остаются прямолинейными **). Допустим, что деформация ех изменяется вдоль ширины пластинки таким же образом, как и в упругой области. Тогда по мере развития пластических деформаций неравномерность распределения напряжений должна сглаживаться — так же, как и в известной задаче о концентрации напряжений вокруг отверстий. Это обстоятельство можно учесть, применяя уже известные нам формулы для редукционных коэффициентов и подставляя вместо критического напряжения акр и напряжения в крайних волокнах ор их истинные значения — независимо от того, лежат ли они в пределах или за пределами упругости.
*) Сл. статью Джерара (G. Gerard, Journ. of Aeron. Sciences 10 (1946), 518—523) и книгу [0.3], стр. 144.
**) Более подробно об этом см. в главе XII.
ГЛАВА IX
КРУГЛЫЕ ПЛАСТИНКИ
§ 112. Основные зависимости для жестких и гибких пластинок
Круглые пластинки в измерительных приборах обычно служат чувствительными элементами (мембранами), реагирующими на изменение поперечного давления* В некоторых случаях — при изменениях температуры, в процессе сборки и т. д. — «мембрана» подвергается действию радиальных сжимающих усилий со стороны опорного устройства; это может привести к выпучиванию мембраны. В конструкциях ускорителей элементарных частиц имеются пластинки, которые облучаются потоком нейтронов; при этом происходит деформация пластинок, связанная с тепловым эффектом, ядерными превращениями и изменением кристаллической решетки [9.6], и здесь может произойти потеря устойчивости пластинки.
Выпучивание наблюдается и в тех случаях, когда пластинки не связаны по контуру с жестким кольцом и воспринимают только поперечное давление. При больших прогибах пластинки вблизи контура образуется сжатая зона, которая и является очагом потери устойчивости.
В общем случае при потере устойчивости пластинки может образоваться ряд мелких вмятин различного направления как вдоль радиуса, так и по окружности. Такое несимметричное выпучивание имеет место, например, в случае пластинки, испытывающей большие прогибы, либо пластинки, подкрепленной ребрами. Однако наибольшее практическое значение имеют случаи осесимметричного выпучивания, когда срединная плоскость пластинки переходит в поверхность вращения (рис* 9.1); подобные частные задачи мы прежде всего и рассмотрим.
Напомним предварительно некоторые зависимости теории круглых пластинок, относящиеся к малым прогибам, для несимметричной изогнутой поверхности. Будем пользоваться цилиндрической системой координат, основная плоскость которой совпадает со срединной плоскостью пластинки (рис. 9.2). Длину радиуса-вектора обозначим
§ 112] ОСНОВНЫЕ ЗАВИСИМОСТИ ДЛЯ ЖЕСТКИХ* и ГИБКИХ ПЛАСТИНОК 403
через г, полярный угол — через ср. Мы можем применить все известные нам соотношения теории прямоугольных пластинок, перейдя к новой системе координат. Формулы перехода можно получить, совместив ось х прямоугольной системы с радиусом-вектором г.
Рис. 9.1. Осесимметричное выпучивание круглой пластинки.
Рис. 9.2. Система координат при рассмотрении круглых пластинок
как показано на рис. 9.2. Производные от некоторой функции Z по х, у выражаются через производные от Z по г, ср следующим образом:
dZ _ dZ dZ _ 1 dZ
дх dr * ду г ду *
d2Z д ( 1 dZ \ d2Z 1 dZ, 1 d2Z
d2Z
d2Z
д /1 dZ\
dx2 dr2 * dx dy dr \ r dy /* dy2
r dr
dy2
(9.1)
(9.2)
Оператор V2Z оказывается равным d2Z, d2Z d2Z
V2Z =
1 dZ
dx2
dy2
dr2
r dr
1 d ( dZ\. zTW{rF) +
1 d2Z r2 dy2
1 d2Z
r2 dy2 *
(9.3)
Находим no (2) кривйзны изогнутой поверхности в сечении вдоль диаметра и в перпендикулярном направлении:
d2w 1 dw 1 d2w J4
Х.= —г— — —. (9.4)
г dr2 9
Кручение поверхности будет равно
_д_ /1 dw \
dr \Т dy )
г дг г2 ду2 •
(9.5)
Изгибающие и крутящий моменты определяются прежними соотношениями:
M, = D(*r + P9). Mf = D(v-у-f-[XX,.), H = D(l — \x)x. (9.6)
404
КРУГЛЫЕ ПЛАСТИНКИ
[гл. IX
Определим поперечную силу в дуговом сечении Qr Если исходить из условия равновесия элемента пластинки, вырезанного двумя радиальными и двумя дуговыми сечениями (рис. 9.3), то получим:
0*? dr)(r*dr)dy> (Mr'jjFdr)(r./lr)(ip
Qr-
дМг Mr — М9
дН
дг
rdf
• (9-7)
(м?
По сравнению со случаем прямоугольной пластинки новым является здесь второй член: он должен быть введен, так как моменты Мт и
Мг ~rr- dr действуют по дугам
различной длины, а вектор-моменты дМ9
и Му-1—составляют между собой угол tfcp.
Поперечное реактивное усилие /?г, приходящееся на единицу длины контура и передающееся на опорное устройство, складывается из поперечной силы и производной от крутящего момента (см. [0.3], стр. 41):
Рис. 9.3 Моменты и поперечные силы.
Rr = Qr-
дН
г dy
(9.8)
Допустим, что пластинка подвергается действию усилий ог, т в срединной поверхности (рис. 9.4); растягивающие §йлия будем считать положительными. Дифференциальное уравнение изгиба пла~
стинки (7.26) перепишется в виде
— V%== ПДа, w),
(9.9)
где
Рис. 9.4. Напряжения в срединной поверхности.
1 dw
1 d2w
dr
(9.10)
Основные напряжения в срединной поверхности можно выразить через функцию напряжений *Ф по формулам типа (7.60), если воспользоваться соотношениями
§ 112] ОСНОВНЫЕ ЗАВИСИМОСТИ ДЛЯ ЖЕСТКИХ И ГИБКИХ ПЛАСТИНОК 405
Граничные условия на контуре пластинки в случае жесткого защемления имеют вид
w = 0, 0 = 0 или 4 = 0. (9.12)
При шарнирном опирании будет
« = 0, Мг = 0 или + _*•. = <). (9.13)
Для осесимметричных задач все соотношения значительно упрощаются: любая функция Z будет зависеть только от г, так что вместо частных производных по г мы получим полные производные. Формулы перехода (1) — (3) получают вид
dZ dZ dZ
-te=W -di = 0’ <914>
d2Z d2Z d2Z n d2Z 1 dZ /ft t K4
= 0’ -2- = T77’ (9Л5>
dx2 dr2 dx dy ’ dy2 r dr
y2z——- 4- — — = — — (гЩ (9 16)
dr2 ' r dr r dr X dr )'
Кривизны и кручение изогнутой поверхности будут равны
d2w 1 dw л /л 1 _ч
JjT' \ — dr ’ (9-17)
Пользуясь (16) и считая Z=V2w, перепишем уравнение (9) в виде
D 1 d Г d /гг9 '1 d2w, 1 dw /л 1£h
Выражения (11) принимают форму
1 аФ а*ф л /п юч
°r = T4F' \ = т = 0- (9Л9>
Отсюда вытекает зависимость между радиальным и дуговым напряжениями:
°9 = 1?ГагУ (9-2°)
Правую часть уравнения (18) можно, следовательно, представить в виде
dw\.
чту
1 d I
TdF\rar
отсюда вместо (18) получаем:
D <921>
406 КРУГЛЫЕ ПЛАСТИНКИ
Находим первый интеграл этого уравнения:
[гл. IX
(9.22)
Очевидно, постоянная С0 должна обратиться в нуль, если область интегрирования содержит точку г = 0, т. е. если пластинка не имеет центрального, отверстия.
Введем обозначение 6 для угла поворота нормали к срединной поверхности (рис. 9.5):
0 = --- (9.23)
Знак минус объясняется тем, что, как видно из рис. 9.5, отсчет угла 0 происходит в направлении, обратном повороту от оси г
к оси z или w. Вместо (17) получим:
db 0 Q 0 х' = -27’ \ = Т> <9-24)
изгибающие моменты равны
=o(f + r±), м,=°{у + ?£)■
Выражение для V2w по (16) приобретает форму
= -{w+t)’ <9-26>
поэтому для сплошной пластинки вместо (22) имеем
(9.27)
“Д
г]
\ ш / r
r
fu>
(9.25)
Рис. 9.5. Прогиб при осесимметричном выпучивании.
Это уравнение будет являться исходным при решении частных задач.
Уравнения нелинейной теории гибких пластинок по-прежнему имеют вид (7.63), (7.64); оператор L(w, Ф) здесь равен
/ / ( 1 <?Ф. 1 д2Ф \ 1
L(w, Ф) — д/.3 дг + rt д<(2 ) +
. /1 dw. 1 d2w\ д*Ф п д (1 дФ\ д (I dw\ q
Mr dr “t г2 dy2 ) dr2 * dr \r d<f ) dr\r d<( )’
заменой Ф на w находим L(w, w). При наличии осевой симметрии будет
/ л™, tfw 1 / dw dФ\ ч Id (dw\%,n от
L(W. Ф) = 7 —i(Wi (9.29)
§ 112] ОСНОВНЫЕ ЗАВИСИМОСТИ ДЛЯ ЖЕСТКИХ И ГИБКИХ ПЛАСТИНОК 407
Находим; первый интеграл уравнений (7.63) й (7Л4) аналогично тому, как это было сделано по отношению к уравнению (21):
А(РФ)= _£(£)•; (9.3,)
здесь принято = 0.
При использовании метода Бубнова — Галеркина в задачах,
относящихся к круглым пластинкам, надо соблюдать осторожность.
Если речь идет об осесимметричных задачах, то естественно исходить из тех соотношений, которые являются первым интегралом исходных уравнений. Однако здесь могут получиться различные результаты в зависимости of структуры подынтегрального выражения в разрешающем уравнении.
Рассмотрим для примера линейную задачу. Допустим, что прогиб аппроксимируется с помощью ряда
®» = 2-‘Vb(r)- (9.32)
Введем обозначение
+!!?-£)-‘«а <9-зз>
тогда уравнение метода Бубнова — Галеркина, отвечающее (22), лучше всего записать в виде
f X-rdr = 0; (9.34)
F
интеграл распространяется на площадь пластинки F. Можно показать (см. [0.3], стр. 183), что (34) соответствует вариационному
уравнению, составленному по принципу возможных перемещений. В литературе часто используется уравнение типа
jXrildr = Q, (9.35)
F
которое приводит к несколько иным окончательным зависимостям.
Аналогичное замечание относится к нелинейным уравнениям (30) и (31).
Перейдем к решению отдельных задач: начнем с определения
критических усилий при осесимметричном выпучивании пластинки, затем обратимся к несимметричным задачам и в заключение, рассмо* трим.закрияическую деформацшо пластинок.
408 КРУГЛЫЕ ПЛАСТИНКИ [гл. IX
§ 113. Защемленная по контуру пластинка под действием радиального сжатия
Исследуем устойчивость круглой пластинки радиуса с, защемленной по контуру и находящейся под действием радиальных сжимающих усилий р, равномерно распределенных вдоль контура
D y/у/Л
р
и— -
Рис. 9.6. Пластинка, защемленная по контуру, под действием радиального сжатия.
(рис. 9.6). Будем считать, что точки контура могут свободно смещаться в плоскости пластинки и что изогнутая поверхность является
осесимметричной *).
Принимая ог = — р, вместо (22) получим:
D(u+}5-)+*'’e=°’ <9-зб>
или
г2+г47+(тгл2-1)9=0- (9-37)
Обозначим:
=а2; и = га. (9.38)
Вводя в уравнение (37) вместо г переменную и, придем к уравнению
и25+йж+<“2-1)6=0’ <9-39>
представляющему собой уравнение Бесселя. Интеграл его имеет вид
0 = CXJX (и) + C2YX (и), (9.40)
где Jx (и) — бесселева функция первого рода с индексом 1, Yx (и) — бесселева функция второго рода с индексом 1.
Функция Yx (и) при и = 0 становится бесконечно большой; так
как угол поворота 0 в центре, вообще говоря, ограничен (здесь
равен нулю), то следует положить С2 — 0, поэтому
d = CxJx(u). (9.41)
Второе из граничных условий (12) принимает вид
0 = 0 при г — с. (9.42)
*) Эта задача была впервые рассмотрена Брайеном [7.14J в 1891 г.
§ 113] ЗАЩЁМЛЕННАЯ ПО КОНТУРУ ПЛАСТИНКА 409
Считая СХФ 0, из (16) находим:
У1(ас) = 0. (9.43)
Функция Jx(u) выражается рядом
40-7ТТЛ(тЬ -]• (9'44)
Уравнение (18) удовлетворяется при следующих значениях и = а.с (если исключить и = 0):
а!£ = 3,83, a2£ = 7,02, a3c=10,2,... (9.45)
Пользуясь первым из этих корней, находим по (38) критическое
напряжение:
„
РкР с2 А ’
или
Ркр — К-£2 (9.46)
при
К = 14,68. (9.47)
Критические усилия высшего порядка при осесимметричном выпучивании соответствуют корням а2, а3 и т. д.
Определим изогнутую поверхность пластинки после выпучивания. Интегрируя (41), находим:
■w = — ~Cl У* J1(u)da = -ClJ0(u)-\-C0, (9.48)
где J0(u) — бесселева функция с индексом нуль:
Л> («) = 1 — (у)2 + (f) — (Г2з)2- (j) + • • • (9-49)
Постоянную С0 выражаем через Cv исходя из первого граничного условия (10):
w = 0 при и — сас. (9.50)
Воспользуемся для решения той же задачи методом Бубнова — Галеркина. Представим изогнутую поверхность с помощью выражения
= (9-51)
удовлетворяющего условиям (37) и (45); оно соответствует решению задачи о малых прогибах пластинки под действием равномерно распределенной поперечной нагрузки. Находим:
л dw 4/ / г г3 \ /г.
410 КРУГЛЫЕ ПЛАСТИНКИ [гл. IX
Выпишем уравнение Бубнова — Галеркина в виде (34):
с ___
/ х{т~1)гаг=:0- (9-53)
О
. V
Найдем выражение для X по (33):
* = -32D/£ + 4A/4(£—£). (9.34)
и воспользуемся обозначением
с
тогда вместо (53) получим:
Т = Р5.@-55)
О
Вычисления дают Отсюда при / Ф 0
J [32 D/p — 4Ар/с2 (р — рЗ)] (р _ р3) р dp = 0. (9.56)
±Df-±fphc2 = 0. (9.57)
Ркр=--. К = 16; (9.58)
отклонение от точного значения (47) составляет около 9%.
§ 114. Случай шарнирного закрепления по контуру
Решим такую же задачу, что и в § 113, но в предположении, что пластинка шарнирно закреплена по контуру (рис. 9.7) *). Второе из граничных условий (13) имеет вид
-7 + !* 7 = 0 при г — с. (9.59)
Приведем формулу дифференцирования:
-i=70(a)-A. (9.60)
Подставляя (41) в (59), получим:
Л(«с)--./1(ас) = °. (9.61)
*) Первое исследование этой задачи принадлежит А. Н. Диннику [9.4]; в его работах содержится также решение ряда более сложных задач, как, йапример, об устойчивости пластинки, лежащей на упругом основании.
§ 114J
СЛУЧАЙ ШАРНИРНОГО ЗАКРЕПЛЕНИЯ ПО КОНТУРУ
411
Пользуясь таблицами функций J0(u) и Jx(u)t можно определить корни уравнения (61); первые из них оказываются равными (при [х = 0,3)
а1>с = 2,05, а2с = 5,39, <х3с = 8,57. (9.62)
В выражении для критического напряжения коэффициент К оказывается равным
К = 4,2.
(9.63)
Это значение близко к критическому напряжению для шарнирно.опертой квадратной пластинки со стороной 2с, сжатой в двух направлениях усилиями р; в этом случае мы получали
Обратимся к приближенному решению задачи по методу Бубнова — Галеркина. Аппроксимирующее выражение для w выберем
по-прежнему таким же, как и в случае малых прогибов пластинки при поперечной нагрузке:
Рис. 9.7. Пластинка, шарнирно опертая по контуру, под действием радиального сжатия.'
W
где
5 + ц
Вместо уравнения (56) получим:
Ь= i+A 3 + ц *
(9.64)
(9.65)
J* [32 Dabfp — 4hpfc*a (р — V)1 (р — *Р3) р dp = 0. (9.66)
о
После вычислений находим: 8
-£>а£(3 — 2Ь) / — Р16-8Й + Э62) Ас2а/ = 0> Величина К равна
К-
16Ь(3 — 2Ь)
При (л = 0,3 будет
6 —8* + 362 ' а — 0,623, £ — 0,394.
(9.67)
(9.68),
(9.69)1
412
КРУГЛЫЕ ПЛАСТИНКИ
[гл. IX
Отсюда
К = 4,21,
(9.70)
что почти совпадает с точным решением.
Отметим, что выкладки для случая защемленной пластинки вытекают из приведенных здесь, если положить a = b= 1. Критическое напряжение для защемленной пластинки получается примерно в 3,5 раза большим, чем для шарнирно опертой.
До сих пор мы предполагали, что изогнутая поверхность пластинки при выпучивании является осесимметричной. Рассмотрим теперь случай, когда прогиб изменяется не только вдоль радиуса, но и по дуге *).
Сначала рассмотрим прежнюю задачу, когда пластинка подвергается действию радиального сжатия. Принимая
и пользуясь прежними обозначениями (38) и (16), приводим уравнение (9) к виду
Аналогичное уравнение мы получали в главе VII в случае прямоугольной пластинки, сжатой в двух направлениях (стр.,311). Выпишем интеграл уравнения (72) в виде
где Jw(cLr) = Jm(u) — бесселева функция с индексами т= 1, 2,
3,... Отметим, что выражение rm sin аяф является интегралом уравнения V2w = 0.
Примем, что пластинка защемлена по контуру. Граничные условия (12) приводят к следующим уравнениям:
Приравниваем нулю определитель системы (74); тогда получим:
*) Эта задача рассматривалась Брайеном [7.14] и Надаи [9.13]. Обзор исследований по устойчивости круглых пластинок и решение некоторых новых задач содержатся в работах В. М. Макушина [9.5]. Случай, когда пластинка на одной части контура защемлена, а на другой шарнирно оперта, разбирался В. Новацким и 3. Олесяком [9.7].
§ 115. Асимметричное выпучивание пластинки
<*г = е9 = — Р
(9.71)
V% -j- a2V% = 0.
(9.72)
w — [CxJm (ar) + C3rm] sin mcp,
(9.73)
(9.74)
(9.75)
§ 115]
АСИММЕТРИЧНОЕ ВЫПУЧИВАНИЕ ПЛАСТИНКИ
413
Воспользуемся формулой дифференцирования
dJm (») _ т
du
HL I /
и Jm Jm+1>
(9.76)
тогда уравнение (75) перейдет в следующее:
Jm+l («0 = 0.
(9.77)
Находя корни этого уравнения определяем критические напряжения.
На рис. 9.8 показан характер выпучивания пластинки при различных значениях т. Число узловых диаметров равно т, число узловых окружностей зависит также от а. Например, при т= 1 первый корень уравнения (77) соответствует коэффициенту К = 26,4; выпученная поверхность показана на рис. 9.9, а. Второму корню отвечает К = 70,6, здесь появляется одна узловая окружность (рис. 9.9, б).
Как видим, асимметричному сокие
при различных m= 1, 2, 3,
Рис. 9.8. Несимметричное выпучивание круглой пластинки.
выпучиванию отвечают более высобственные значения задачи, чем осесимметричному; поэтому
Рис. 9.9. Волнообразование пластинки: а) при одном узловом диаметре; б) при одном узловом диаметре и одной узловой окружности.
асимметрия может иметь место лишь в случае подкрепленной пластинки.
Как было уже сказано, несимметричное выпучивание круглой пластинки может возникнуть и в другом случае, когда нагрузка
414
КРУГЛЫЕ ПЛАСТИНКИ
[ГЛ. IX
является поперечной*) {рис. 9.10). Примем, что точки контура пластинки свободно смещаются в радиальном направлении. При достаточно больших прогибах; у контура появляются значительные сжимающие напряжения, это и ведет к потере устойчивости. Особенность
этой задачи состоит в том, что основное напряженное состояние, предшествующее выпучиванию, характеризуется наличием переменных усилий в срединной поверхности и моментов и что пластинка получила предварительно искривление. Поэтому здесь надо пользоваться ббновными уравнениями теории гибких пластинок, учитывающими влияние начального прогиба w0 и функции начальных напряжений срединной поверхности Ф0. Зависимость между параметрами ин-
* 0С4
тенсивности давления q = jym-5 и стрелы прогиба пластинки
/ / J9 С =, найденная в статьях
/ л h
[9.8], изображена на рис. 9.11. При изучении симметричных форм мы получаем соотношение типа (см. [0.3], стр. 186)
Рис. 9.10. Гибкая пластинка под действием поперечной нагрузки.
<7* = Ж3 + Ж;
(а)
ему отвечает кривая 1. Исследование несимметричных Рис. 9.1Ь Образование несимметричных форм при тф 0 приводит к форм выпучивания. таким же уравнениям, но с
другими коэффициентами Л, В. Кривая 2 соответствует числу узловых диаметров, равному т = 8; кривые для ближайших значений т — 7\ 9 и т. д. лежат выше линии 2.
В точке пересечения кривых 1 и 2, соответствующей q*=880 и С 9,6, должна произойти потеря устойчивости осесимметричной формы-прогиба; при этом возникает восемь вмятин вдоль окружности. Т1осле этого одновременно будут возрастать прогиб в центре пластинки и стрелы прогиба «местных вмятин». В дальнейшем, очевидно, наступит новое изменение формы волнообразования, с последовательным возрастанием числа «местных вмятин».
*) Эта задача была впервые исследована Д. Ю. Пановым и В. И. Феодосьевым [9.8]; см. также работу -Боднера [9.9].
§ 116)
КОЛЬЦЕВЫЕ ПЛАСТИНКИ
ч\ъ
§ 116. Кольцевые пластинки
Во многие конструкции входят кольцевые пластинки, различным образом закрепленные по краям. Такой кольцевой пластинкой является, например, стенка кругового шпангоута фюзеляжа самолета или подводной лодки. Кольцевые пластинки встречаются также в приборостроении. Рассмотрим устойчивость кольцевой пластинки,
(рис. 9.12), если по ее внутреннему и внешнему контурам, радиусы которых равны а и Ь, действуют усилия одинаковой интенсивности *)
Р\=Рг = Р-
Если ограничиться случаем осевой симметрии изогнутой поверхности, то можно исходить из уравнения (22) с учетом члена CQ/r; тогда вместо (40) получим:
6 = С1У1(аг)+С2К1(аг) + -. (9.78)
Отсюда
« = т [<Vo(«') + Wo(«О! + С31пг + с4. (9.79)
Но можно допустить, что для кольцевой пластинки, подкрепленной по внутреннему краю, решающим будет асимметричный случай, й потому надо исследовать более общее уравнение (72). Дополняя (73), находим:
w (осг)СгКщ (осг) ———\Cf sin/rtcp. (9.80)
Выражения (79) или (80) должны удовлетворять граничным условиям на внутреннем и внешнем контурах. Условия, соответствующие защемлению и шарнирному опиранию, имеют вид (12) и (13). Разберем практически важный случай, когда один из краев
*) Устойчивость кольцевых пластинок исследовалась первоначально Ди* ном (W. R. Dean, Ргос. Royal Soc. London, ser. A 106 (1924)) и А. С. Локшиным (Comptes rendus (1924)). Решение данной задачи было дано для осесимметричного случая В. М. Макушиным [9.5], а в более общем виде Ямаки [9.14]. График рис. 9.13 дан по (9.14].
Рис.9Л2, Кольцевая пластинка под действием радиального сжатия.
416
КРУГЛЫЕ ПЛАСТИНКИ
[ГЛ. IX
пластинки (например, внутренний) может смещаться в направлении оси пластинки, но при этом не поворачивается. Тогда здесь должно быть
-»■ «--«•
(9.81)
Если подставить в выражения (8) и (7) значения кривизн, то после некоторых преобразований можно привести второе из условий (81) к виду
/ d2w
1 dw
1 d2w
dr \ dr2
r dr
r2 dy2
)+Шг£)Н- <9-82>
уравнений относительно Cv
w
Подчиняя (79) или (80) граничным условиям, приходим к системе
С4; приравнивая нулю определитель системы, находим критическое значение р.
На рис. 9.13 представлены результаты вычислений *) для различных случаев закрепления: а — за¬
щемление по обоим краям; Ъ — шарнирное опирание по обоим краям; с — защемление по внешнему контуру и свободное смещение, без поворота, по внутреннему; d— шарнирное закрепление по внешнему контуру и такое же свободное смещение по внутреннему. По оси абсцисс отложено отношение а/b, по оси ординат — значение где К — коэффициент в формуле
Ц8 0,9 W а/Ь
Рис. 9.13. Расчетный график для случая кольцевой пластинки при различных условиях закрепления.
Ркр = К -щ;- (9.83)
На графике указано число т узловых диаметров, которому соответствует наименьшее напряжение при данном а/b. В предельном случае -у—>0 и при граничных условиях а и b мы, очевидно, приходим к случаю сплошной пластинки с подкрепленным центром; изогнутая поверхность образует здесь один узловой диаметр, как на
*) Для {х = 0*3; принято, что h мало по сравнению с (Ь — а).
§ 1161
КОЛЬЦЕВЫЕ ПЛАСТИНКИ
417
рис. 9.9, а. Однако при у >0,1 пластинки выпучиваются различным образом: защемленная пластинка имеет тем больше вмятин по окружности, чем она уже, а шарнирно опертая изгибается осесимметрично (т = 0).
При граничных условиях с и d> и — -> 0 приходим к обычному
случаю сплошной пластинки со свободно смещающимся центром, поэтому здесь будет т = 0, и критические напряжения определяются формулами (47) и (63).
При возрастании а/Ь формы изогнутой поверхности получаются различными; шарнирно опертая пластинка во всех случаях изгибается осесимметрично. В другом предельном случае ~ —■► 1
мы получаем такое же критическое напряжение, как если бы удлиненная прямоугольная пластинка ширины Ъ — а была сжата в двух направлениях усилиями р и имела бы аналогичные граничные условия по длинным краям.
Рис. 9.14. Кольцевая пластинка, нагруженная по внутреннему контуру.
В литературе рассмотрены также случаи, когда кольцевая пластинка подвергается действию радиальных усилий только по внутреннему [9.11] или внешнему краю [9.12]. В этих задачах «основные» усилия аг и о • будут изменяться вдоль радиуса. Если по внутреннему контуру приложены сжимающие усилия, то напряжения аг будут во всех точках пластинки сжимающими, а — растягивающими; если же приложены растягивающие усилия, то наоборот. Интересным является случай нагружения по внутреннему краю при Ь>а. В случае сжатия (рис. 9.14, а) критическое значение р равно (при условии, что внутренний край не поворачивается)
Р9~ а2А ’
(9.84)
418
кРУГЛЫЁ ПЛАСТИНКИ
[гл. IX
а при растягивающих усилиях независимо от условий закрепления (рис. 9.14, б)
т. е. в три раза больше, чем при сжатии. В случае сжатия пластинка изгибается осесимметрично, а при растяжении — с двумя узловыми диаметрами.
§ 117. Закритическое поведение круглой пластинки
Круглая пластинка способна нести возрастающую нагрузку после потери устойчивости, так же как и прямоугольная пластинка. Как мы видели, сплошная пластинка, так или иначе закрепленная по контуру*) и подвергающаяся действию радиального сжатия, выпучивается по осесимметричной форме. Естественно, что и в начальной стадии закритической деформации осесимметричность изогнутой поверхности сохраняется. Однако при дальнейшем возрастании нагрузки происходит образование более мелких волн и симметрия нарушается. Чем выше нагрузка, тем ббльшим должно становиться число волн по окружности. Решение этой задачи относилось до сих пор, как правило, к осесимметричным формам изгиба **) пластинки.
Рассмотрим шарнирно опертую пластинку радиуса с со свободно смещающимися кромками, сжатую усилиями р. Для исследования закритической области при осесимметричном выпучивании мы должны обратиться к общим уравнениям (30) и (31), относящимся к гибким пластинкам. Примем для w прежнее аппроксимирующее выражение (64). Подставляя его в правую часть уравнения (31), находим:
Постоянные Сг и С2 находим из условия ограниченности в центре пластинки (С2 = 0) и условия
*) Предполагается, что точки контура свободно перемещаются в радиальном направлении.
**) Оно было дано Фридрихсом и Стокером в 1939 г. [9.10], Э. И. Григолюком [9.3], применившим метод Бубнова — Галеркина, И. И. Воровичем [9.1J и Боднером [9.91.
(9.85)
и, далее,
(9.88)
§ 117] ЗАКРИТИЧЕСКОЕ ПОВЕДЕНИЕ КРУГЛОЙ ПЛАСТИНКИ 419
Тогда окончательно
= + + <9-89> Воспользуемся методом Бубнова—Галеркина и выпишем уравнение (34); величины X и по (30) и (32) будут равны
Х-°4г™-7£%- -г-7-Т-
После интегрирования приходим к уравнению i Db (3 — 2ft) f — -g- p (6 — 8ft+ 3 ft2) hc2f +
4- 2- Eha2f3 (84— 1680+140ft2— 56ft3+ 9ft4) = 0. (9.91)
Опуская нелинейный член, найдем критическое напряжение ркр по (70). Определим зависимость между нагрузкой и стрелой прогиба, вводя безразмерные параметры
'•=£(!)■• '-{■ (9-92>
найдем
Р*кр = 0,385. (9.93)
Величина п* показывает, во сколько раз краевые напряжения р превышают критическое значение; здесь р играет ту же роль, что и напряжение в краевых волокнах ор для прямоугольных пластинок. Принимая а, b по (69) для jx = 0,3, находим из (91) при /=£0
л*1+0,16С2. (9.94)
Отсюда = я>- <••»»>
Если предположить, что критическое усилие сильно превзойдено, так что \/п* можно пренебречь по сравнению с 1, и в то же время деформации остаются упругими, то получим:
С 5» 1.96 Уя\ (9.96)
Зависимость (95) изображена на рис. 9.15 пунктирной линией. Как мы видели, в случае защемленной пластинки решение остается в силе, но надо принять a = b— 1. Тогда (91) получает вид
jDf — phcy + -gg- Ehp = 0. (9.97)
420
КРУГЛЫЕ ПЛАСТИНКИ
[ГЛ. IX
Подставляя значение /?кр по (58), получим при /=£0
п*= 1 +0,16С2; (9.98)
отсюда (9>
При получим С/уГ*->2,5.
Эффект защемления пластинки по контуру проявляется сильнее всего в момент выпучивания, по мере роста прогибов он ослабевает.
Поэтому при одинаковой степени превышения критического напряжения стрела прогиба защемленной пластинки получается несколько большей, чем для шарнирно опертой.
В работах [9.9] и [9.10] эта же задача была решена методом возмущений *). В качестве параметра выбирается величина s = п*— 1, равная нулю в момент вы-
о 1 <*Ф
пучивания. Величины —
и — раскладываются в ряды по степеням этого параметра,
а затем подставляются в основные уравнения (30) и (31). Приравнивая коэффициенты при одинаковых степенях е, приходим к системе линейных дифференциальных уравнений относительно функций, входящих в ряды. Задача сводится к последовательному решению этих уравнений. Очевидно, этот метод применим при относительно малой величине е.
Другой подход к задаче [9.10] состоит в применении метода
л. 1 ЛФ 1 dw
степенных рядов**). Функции и у раскладываются
в ряды по степеням г; первый член ряда определяет значения этих функций в центре пластинки, при г = 0.
Пользуясь граничными условиями, сводим задачу к решению системы трансцендентных уравнений.
На рис. 9.15 представлены результаты вычислений по методу рядов для случая шарнирного опирания (сплошная линия); она ле-
*) Этот метод был ранее предложен для аналогичной задачи П. Я. Полубариновой-Кочиной, см. ссылку на стр. 330.
**) Метод рядов был применен Уэем при решении задачи о больших прогибах круглой пластинки при действии поперечной нагрузки,
С/ур*
Рис. 9.15. Диаграмма закритической деформации круглой пластинки.
1 dw
§ 117] ЗАКРИТИЧЕСКОЕ ПОВЕДЕНИЕ КРУГЛОЙ ПЛАСТИНКИ 421
жит сравнительно близко к кривой, полученной по методу Бубнова — Галеркина. На рис. 9.16 изображен закон распределения вдоль радиуса при различных п*. Как
Рис. 9.16. Дуговые напряжения при закритической деформации пластинки.
видим, при п* =14,7 во всей центральной зоне пластинки, занимающей около 0,7с, имеют место растягивающие напряжения. Сжимающие напряжения концентрируются в «пограничной зоне», у контура пластинки. При этом центральная часть пластинки становится поч¬
ти плоской, как изображено на рис. 9.17 для я*=14,7. В пределе
л*-14.7
Рис. 9.17. Изогнутая поверхность круглой пластинки на различных ступенях закритической деформации.
эта центральная часть охватывает всю пластинку, как показано на рис. 9.17 пунктиэом. Сопоставление данных, относящихся к напря-
Рис. 9.18. Напряжения в центре шарнирно опертой и защемленной пластинок при закритической деформации.
жению Оц в центре пластинки для шарнирно опертых и защемленных пластинок, дано на рис. 9.18. Штрих-пунктирная линия относится к решению по методу Бубнова — Галеркина.
422
КРУГЛЫЕ ПЛАСТИНКИ
[ГЛ. IX
Таким образом, при значительном п* функции Ф и f резко меняются лишь у самого края пластинки. Это позволяет упростить исходные уравнения и воспользоваться асимптотическим решением задачи о краевом эффекте, подобно тому как это делается в теории оболочек [10.6] и при рассмотрении пограничного слоя в аэродинамике. Такое асимптотическое решение задачи привело к следующим результатам. Для шарнирно опертой пластинки при л*-> оо получаем:
С = 2 Уп*. (9.100)
что очень близко к (96). Напряжения в центре при я*—>оо приближаются к значениям, показанным на рис. 9.18.
Все эти данные относятся к осесимметричному выпучиванию. При некотором значении л*, приблизительно равном п* = 15 для шарнирно опертой пластинки, в пограничной зоне должно произойти «вторичное» выпучивание; осесимметричное изогнутое состояние пластинки становится неустойчивым. Исследование этого явления представляет собой интересную задачу.
ГЛАВА X
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
§ 118. Отличительные черты задач об устойчивости оболочек
Перейдем к задачам, относящимся к устойчивости оболочек. Эти задачи представляют особый интерес для многих областей новой техники, а также для всех тех «устоявшихся» областей, в которых происходит внедрение облегченных конструкций и новых материалов. С расчетами на устойчивость оболочек различной формы, гладких и подкрепленных, изотропных и анизотропных, деформируемых в пределах и за пределами упругости, мы неизменно сталкиваемся прежде всего при конструировании летательных аппаратов и их двигателей. Около полувека тому назад И. Г. Бубнов отмечал, что корпус корабля почти целиком состоит из пластинок. Теперь мы можем сказать, что конструкция летательного аппарата состоит главным образом из оболочек. Криволинейные панели обшивки в этих конструкциях представляют собой пологие оболочки; вместе с тем, корпус летательного аппарата в целом можно рассматривать как подкрепленную оболочку. Запросами авиационной техники прежде всего и объясняется интенсивное развитие теории устойчивости оболочек в последнее время. Расчеты оболочек на устойчивость имеют существенное значение при проектировании надводных и подводных кораблей, тепловозов и вагонов, трубопроводов, резервуаров, куполов и покрытий в инженерных сооружениях и т. д.
Поведение оболочек при потере устойчивости существенно отличается от поведения стержней и пластинок. Выпучивание оболочек, как правило, сопровождается появлением не только напряжений изгиба, но и дополнительных напряжений в срединной поверхности (цепных напряжений), в то время как для стержней и пластинок мы могли учитывать только напряжения изгиба*). Некоторая часть потенциала внешней нагрузки «расходуется» в случае оболочки на увеличение
*) Как мы видели, при исследовании закритической деформации пластинок также учитываются напряжения того и другого типа.
424
ОБЩИЁ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
(гл. X
энергии изгиба, а другая часть — на изменение энергии срединной поверхности. Соотношение между этими величинами зависит от того, какую конфигурацию принимает оболочка при выпучивании.
Представим стержень, пластинку и оболочку как системы с одной степенью свободы и рассмотрим характерные для них диаграммы зависимости между нагрузкой Р и параметром прогиба / в задачах устойчивости (рис. 10.1). Будем считать, что прогибы остаются
о) б)
Рис. 10.1. Диаграммы «нагрузка — прогиб» для стержня и пластинки.
малыми по сравнению с габаритными размерами конструкции, но могут быть сравнимы с высотой сечения стержня или толщиной пластинки и оболочки. Участок О А относится во всех случаях к исходным равновесным состояниям, которые здесь считаются безмоментными, а участки AD и АС — к изогнутым, моментным равновесным состояниям.
В случае стержня диаграмма P(f) имеет вид горизонтальной линии (рис. 10.1, а), что соответствует «безразличному» равновесию. Для пластинки мы получаем кривую закритических устойчивых состояний, симметричную относительно оси ординат (рис. 10.1, б): очевидно, что для идеально плоской пластинки, как и для идеально прямого стержня, оба направления прогиба (-(- /) и (— /) являются равноправными. Между тем в случае оболочки ветвь изогнутых равновесных форм CABD оказывается несимметричной, как показано на рис. 10.2.
Такое своеобразие в поведении оболочки можно пояснить на примере арки-полоски АСВ, показанной на рис. 10.3 и закрепленной по краям А, В. Если придать арке дополнительный прогиб (— /) от центра кривизны, как показано пунктирам, волокна срединного слоя должны удлиниться. Напротив, при прогибе (-(-/) к центру кривизны (сплошная тонкая линия) срединные волокна укорачиваются. Когда арка получает очертание АС'В, зеркальное па отношению к исходному, напряжения в срединном слое станут равными нулю. Лишь при дальнейшем изгибе (по штрих-пунктирной линии)
§ 118] ОТЛИЧИТЕЛЬНЫЕ ЧЕРТЫ ЗАДАЧ ОБ устойчивости ОБОЛОЧЕК 425
срединные волокна будут удлиняться. Для оболочки связь между усилиями растяжения — сжатия в срединной поверхности более сложная, чем в случае, арки, так как задача является двухмерной. Но
Рис. 10.2. Характерные диаграммы «нагрузка — прогиб» для оболочки идеальной формы и с начальной погибью.
общая тенденция остается той же: оболочка «предпочитает» выпучиваться внутрь, к центру кривизны *). Это показано на рис. 10.4 на примере цилиндрической панели, сжатой вдоль образующей.
Вернемся к рис. 10.2; здесь прогиб к центру кривизны от-
Ъ*
Рис. 10.3. Прощелкивание арки- Рис. 10.4. Цилиндрическая панель «пред-
полоски. почитает» выпучиваться к центру кри¬
визны.
кладывается по оси абсцисс вправо, а от центра — влево. Несимметричность диаграммы равновесных состояний связана с тем, что ветвь диаграммы ABF лежит ниже точка разветвления (бифуркации) А.
*) Здесь имеются в виду оболочки, у которых центры кривизны всех нормальных сечений лежат по одну сторону от срединной поверхности (см»
426
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
На участке АВ равновесные формы являются неустойчивыми, а на участке BF — устойчивыми. Участки АС и FD соответствуют устойчивым состояниям. Но подобную диаграмму мы уже получали в главе I (стр. 77) для сжатого стержня, снабженного нелинейной упругой опорой. По аналогии с этой задачей в теории устойчивости оболочек применяются понятия верхней и нижней критических нагрузок*). Под верхней критической нагрузкой Рв будем по-прежнему понимать наибольшую нагрузку, до которой начальное равновесное состояние является устойчивым в малом, т. е. по отношению к соседним равновесным состояниям. Применительно к модели, которая описывается диаграммой OABD, верхняя критическая сила соответствует точке бифуркации равновесных состояний. Под нижней критической нагрузкой Рн будем подразумевать нагрузку, до которой начальное состояние является единственным устойчивым состоянием **); при нагрузках, лежащих ниже Рн, обеспечивается устойчивость оболочки не только в малом, но и в большом.
Допустим, что исходная форма оболочки — идеальная (отсутствуют какие-либо начальные прогибы), а нагружение является статическим и происходит таким образом, что напряженное состояние является строго безмоментным; тогда прикладываемая к оболочке нагрузка должна возрасти до верхнего критического значения Рв, после чего оболочка совершит скачок (хлопок) от равновесного положения А к положению F, после чего нагрузка вновь начнет увеличиваться ***), но уже по ветви FD. Обратный процесс состоит в падении нагрузки по линии DB, «выхлопу» оболочки по линии BG, а затем в новом снижении нагрузки от О до О. Следовательно, скачок при разгрузке происходит на уровне нижней критической силы Рн. Что касается равновесных состояний, соответствующих линии АС, то они обычно не реализуются, так как им отвечает более высокий уровень энергии.
Реальные оболочки всегда имеют, однако, те или иные начальные неправильности формы. Для таких оболочек исходное состояние, как правило, уже нельзя считать безмоментным, так что ветвь равновесных состояний при нарастающей нагрузке уже не будет совпадать с осью ординат. Во многих случаях диаграмма Я(/) по рис. 10.2 и здесь состоит из устойчивых ветвей О А' и B'D' и
*) Эти понятия были впервые введены Карманом и Цянь Сюэ-сэнем [11.351 в 1939 г; более подробно они разобраны в § 201.
**) Напоминаем, что здесь рассматриваются прогибы, сопоставимые с толщиной оболочки; они могут превышать толщину в несколько раз, даже в 10—20 раз, но все же должны оставаться малыми по сравнению с радиусами кривизны. Поэтому, например, случай полного продавливания резинового мяча в рамки этой теории не входит.
***) Здесь предполагается, что нагрузка в процессе хлопка поддерживается постоянной. Другие варианты изменения нагрузки разбираются ниже, в §§ 127 и 129,
§ 118] ОТЛИЧИТЕЛЬНЫЕ ЧЕРТЫ ЗАДАЧ ОБ УСТОЙЧИВОСТИ ОБОЛОЧЕК 427
неустойчивой А'В'. Переход от одного устойчивого состояния к другому также должен происходить скачком — на уровне А'. Нагрузки, соответствующие точкам А' и В', будем, по аналогии с предыдущим случаем, называть верхней и нижней критическими нагрузками Рв и Рн. Мы предполагали, что начальный прогиб направлен в ту же сторону, что и дополнительный, — преимущественно к центру кривизны. Если исходный прогиб направлен от центра кривизны, то начальная ветвь ОМ будет идти влево от оси ординат. Другие возможные равновесные формы характеризуются участками NB и £D. Здесь также имеет место (хотя и не во всех случаях) перескок от ветви ОМ к ветви BD\ уровень энергии для точек второй из этих ветвей может оказаться значительно ниже, чем для соответствующих точек первой ветви.
Как видим, начальные неправильности формы и другие возмущения проявляются в случае оболочки совсем иначе, чем для пластинки; они приводят к сильному снижению верхней критической нагрузки. Поэтому экспериментальные данные, относящиеся к критическим нагрузкам для оболочек, обычно характеризуются значительным разбросом *). Само выпучивание оболочек на практике во многих случаях сопровождается резким хлопком. Отсюда вытекает вывод, что в практических расчетах следует учитывать как верхнюю, так и, в особенности, нижнюю критические нагрузки. Эксплуатационная нагрузка должна составлять некоторую долю от верхней критической величины и вместе с тем, как правило, не должна превышать нижнее критическое значение. Правда, для некоторых конструкций второе требование не удается выполнить, если, например, нижняя критическая нагрузка близка к нулю или даже является отрицательной, т. е. имеет обратное направление по сравнению с основным состоянием. Во всех случаях наиболее обоснованным будет расчет, непосредственно учитывающий влияние начальных неправильностей формы и иных возмущающих факторов. Если речь идет о большом числе одинаковых элементов конструкции, то самый естественный подход при этом — статистический (см. главу XX).
Так или иначе, практические расчеты оболочек на устойчивость должны вестись с учетом поведения оболочек при больших прогибах. Если для стержней и пластинок можно было разделить определение точек бифуркации и исследование закритической области, то здесь этого сделать в большинстве случаев нельзя**). Поэтому в дальнейшем мы будем, как правило, параллельно рассматривать
*) За исключением таких лабораторных испытаний, в которых обращается особое внимание на технологию изготовления оболочек и условия нагружения.
**) Как мы увидим дальше, в некоторых задачах нижняя критическая нагрузка оказывается весьма близкой к верхней; тогда необходимость отдельного расчета на устойчивость в большом может отпасть.
428
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
одну и ту же задачу, подходя к ней с точки зрения устойчивости в малом и в большом. В первом случае надо исходить из линейной теории жестких оболочек, во втором — из нелинейной теории гибких оболочек.
Обратимся к основным положениям линейной и нелинейной теории.
§ 119* Некоторые сведения из теории поверхностей
Если подходить к оболочкам с геометрической точки зрения, то они характеризуются, прежде всего, формой срединной поверхности. Поэтому при выводе основных зависимостей, относящихся к оболочкам, приходится пользоваться многими понятиями общей теории поверхностей *).
Рассмотрим участок поверхности, показанный на рис. 10.5, и выберем на нем систему (семейство) линий U таким образом, чтобы
Рис. 10.5. Сеть координатных линий Рис. 10.6. Координатные линии на ци-
£ = £2 и т. д. Далее, выберем новую систему линий V, каждая из которых отвечала бы некоторому значению второго параметра 7]:tj = 7]0, 7j = rjlt yj = rj2 и т. д., и при этом так, чтобы линии V пересекали все линии U. Выполним требование, чтобы через любую точку поверхности проходила одна и только одна линия каждого семейства; выбранная таким образом сеть линий называется правильной. Если линии систем U и V пересекаются под прямым углом (т. е. угол между касательными к этим линиям равен прямому), то сеть называют ортогональной.
Конкретный смысл параметров £, г\ может быть различным. Для примера на рис. 10.6 изображены координатные линии на участке цилиндрической поверхности, причем линии U совпадают с образующими, а линии V лежат в поперечных сечениях цилиндра.
каждая из них соответствовала определенному значению некоторого параметра £: £ = £0, 5 = Si.
Ы0
на поверхности.
линдрическои поверхности.
*) См., например, курсы дифференциальной геометрии М. Я. Выгодского (М., 1949), А. В. Погорелова (Харьков, 1961), П. К. Рашевского (М., 1956), С. П. Финикова (М., 1961).
§ 119] НЁКОТОРЫЁ СБЁДЁНИЯ ИЗ ТЕОРИЙ ПОВЕРХНОСТЕЙ
429
В качестве параметров т] здесь можно избрать непосредственно длины отрезков, отложенных вдоль линий. На рис. 10.7 показан
участок сферической поверхности. Здесь удобно пользоваться географическими координатами и в каче-
Рис. 10.7. Географические координаты на сфере.
Рис. 10.8. Координатные линии, характеризующие пологую поверхность.
стве параметров у\ выбирать угол широты а и угол долготы р.
Заметим, что в этом примере полюс А является особой точкой,
так как для него не выполняется требование правильности координатной сети.
В случае пологой поверхности МУ близкой к плоскости N, параметрами могут служить декартовы координаты соответствующих точек плоскости (рис. 10.8) либо по-. лярные координаты этих точек.
Как бы ни были выбраны параметры 7j, положение каждой точки поверхности определяется их значениями; они являются криволинейными координатами точек поверхности; координата £ отсчитывается вдоль линий т = 7]0, у] = а координата
7}—вдоль линий £ = £о» £ = £i> Сами линии* семейств U п V носят название координатных линий.
Если обозначить через г радиус-вектор точки поверхности относительно произвольного начала О (рис. 10.9), то г будет однозначной векторной функцией криволинейт ных координат Е и т):
Г = г, У\).
(10.1)
Рис. 10.9. Радиус-вектор точки поверхности как функция криволинейных координат.
Проведем векторы г и r-f-Ar, соответствующие двум соседним точкам Ж и Ж' линии 7j = const. Относя приращение функции Аг к приращению параметра Д£ и считая Д£->0, получаем в пределе
430
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[гл. X
частную производную от г по Ь
\ Д6 М -► о д£
Направление вектора совпадает с направлением касательной к линии £ в данной точке; поэтому он носит название координатного
дг
вектора. Второй координатный вектор направлен вдоль касательной к линии rj (рис. 10.10).
Плоскость L, проведенная через векторы и является
плоскостью, касательной к поверхности в точке М. Линия, перпендикулярная к плоскости Z,, представляет собой нормаль
к поверхности; направление нормали определяется векторным про-
dr дг
изведением векторов -щ и
ЛГ—— X — х ац •
Единичный вектор нормали равен
(10.2)
дг дг
<% х
Рис. 10.10. Координатные векторы в точке М поверхности.
I £_ чх £_ I дЬ А дц
в знаменателе здесь — абсолютная величина N. Вектор п не должен, конечно, зависеть от выбора параметров I*, Если координатные линии составляют угол а, то, пользуясь определением скалярного произведения, получим:
дг_дг_
dl drj
fll2
здесь введены обозначения:
_(дг\2 _ дг дг
°п~\дь) ’ fll2 ~ di dt) ’
Пользуясь (3), находим:
ш
sin а = —г *
У аиа22
<“= V ЛцОи —ах2
где
(10.3)
(10.4)
(10.5)
(10.6)
§ 119] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОВЕРХНОСТЕЙ
431
Исходя из определения векторного произведения, приводим (2) к виду
— у—
п _ <% А dv (Ю.7)
<0
Поставим перед собой цель исследовать поверхность вблизи некоторой точки М (рис. 10.11). В первом приближении бесконечно малый участок поверхности можно заменить бесконечно малым участком касательной плоскости. Воспользуемся этим, чтобы определить дифференциал ds дуги, проходящей через точку М. Направление дуги будет фиксировано, если задано отношение соответствующих дифференциалов криволинейных координат dy\\d% (при d-Ф0). Будем под dr понимать дифференциал радиуса-вектора г при перемещении из точки М по касательной к данной дуге. Квадрат ds можно вычислить, составив скалярное произведение
ds2 — dr • dr — dr2.
Полный дифференциал dr равен
dr = -dl + dr> (10.8)
отсюда
ds2 = and№-\- 2and% dr\ + a22flfy2. (10.9)
Выражение (9) носит название первой квадратичной формы поверхности, а величины ап, а12, а< по (4)—коэффициентов первой квадратичной формы. Эти коэффициенты зависят от криволинейных координат для точки Ж, но не зависят от их дифференциалов; следовательно, для данной точки поверхности величины ап, 12» 22 определяются однозначно. Зная первую квадратичную форму поверхности, можно найти угол между любыми линиями, проходящими через эту точку (т. е. угол между касательными к этим линиям); примером может служить формула (3), позволяющая найти угол между координатными линиями. Интегрируя выражение для ds вдоль некоторой кривой, можно вычислить полную длину дуги кривой.
Так как при исследовании выпучивания оболочек важно определить удлинения и сдвиги срединной поверхности, т. е. изменения длин дуг и углов между дугами, то, очевидно, первая квадратичная форма срединной поверхности оболочки должна играть в таком исследовании существенную роль. Отметим, кроме того, что с помощью первой квадратичной формы можно вычислить площади тех или иных участков поверхности.
Рис. 10.11. К исследованию поверхности вблизи точки М в первом приближении.
432
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
Будем в дальнейшем обозначать первую квадратичную форму через /:
/ = aud¥-\-2al2dtdri-\-a22drf. (10.9а)
Для ортогональной координатной сети будет по (3) а12 = 0, при этом
/ = аи а22 drf. (10.10)
Если радиус-вектор г выразить через декартовы координаты х, у, z, то по (4) получим:
*..Ч)!+Шг+(§)г- I
г dz [ is ~аГ“ »
дх дх, ду ду, dz
12 ду ' д£ dq ' dz dri
=№+№+№■
а,
(10.11)
Далее исследуем поверхность во втором приближении и выясним, как отклоняется поверхность от касательной плоскости в окрестности точки касания. Проведем через М произвольную линию /, лежащую на поверхности, и касательную т к этой линии (рис. 10.12). Представим себе плоскость, проходящую через касательную к линии I и некоторую точку N, лежащую на линии вблизи точки касания М. Проследим за изменением положения этой плоскости, устремив длину дуги MN к нулю; в пределе получим так называемую соприкасающуюся плоскость S. Если бы кривая I лежала в одной плоскости, то эта плоскость являлась бы соприкасающейся для всех точек кривой. Нормаль к кривой, лежащая в соприкасающейся плоскости, называется главной нормалью. Единичный вектор (орт) главной нормали обозначим через v; он показан на рис. 10.12. Если г — радиус-вектор точки Ж, а 5 — длина дуги, отмеряемой вдоль
линии, то орт касательной будет Производная от этого вектора d2r
П9 s, равная определяет кривизну кривой k и называется век¬
Рис. 10.12. К исследованию поверхности вблизи точки М во втором приближении.
§ 119] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОВЕРХНОСТЕЙ 433
тором кривизны; он направлен вдоль орта главной нормали v, подобно нормальному ускорению при движении точки по кривой. Таким образом, приходим к известной формуле Френе:
S- = *v. (10.12)
Спроектируем вектор кривизны линии I на нормаль к поверхности, как показано на рис. 10,12; тогда найдем так называемую нормальную кривизну линии kn. Для определения kn сос.авим скалярное произведение вектора на орт нормали к поверхностй п\ тогда найдем:
d*r
kn = kvn, или kn = -j-2n- (10.13)
Если обозначить через 0 угол между направлениями v и я, будет v/* = cos0 и, следовательно,
kn = k cos 0. (10.14)
Эта зависимость позволяет определить кривизну k любого наклонного сечения поверхности по нормальной кривизне kn (Упеорема Менье).
Вьбрем в качестве параметра, определяющего положение точки на кривой /, длину дуги s\ тогда криволинейные координаты точки
будут функциями 5, т. е. £ = £(s), 7] = tj(s). По (8) получим:
dr __ЙГ _Л_, dr_ *1 по _
ds ~ dt ds ' dr, ds ‘ (ШЛО)
Дифференцируя это выражение вновь по 5, найдем:
d2r дг_ d4 дг_ d2. д2г / d\ \2. ~ d2r t d\ (drf\, д2г (dr\\2
ds2 ds2 dri ds2 ' di2 Ws / dr\ \ds )\ds) ' drf \ds)
(10.16)
Выпишем скалярное произведение (13), учитывая, что каждый
дг дг
из координатных векторов и -щ ортогонален орту нормали п\ тогда будет
где
ьи = п-г> ьп = п дг, ' b<n~n • (10.18)
Выражение (17) можно переписать в виде
11 bu di2 4- 2й12 d£ d-ц + b22 drf.
я I au dr\-2andSdri. + ai2drf ’ uu.iy;
434
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
под II здесь понимается выражение, построенное аналогично (9а) и носящее название второй квадратичной формы поверхности:
II = bu d\2 + 2bx2 d\ dr\ + 22 dtf.
(10.20)
Величины bn, bx2. b22 носят название коэффициентов второй квадратичной формы. Судя по формулам (18) — (20), для всех линий на поверхности, имеющих общую касательную, т. е. характеризуемых одним и тем же соотношением dr\: нормальная кривизна kn
булег одна и та же. Следовательно, величина kn дает суммарное представление о кривизне поверхности по выбранному направлению; ее можно назвать нормальной кривизной поверхности.
Если в (19) положить dr\ = 0, а затем dl = 0, то получим соответственно kxx~ bxx/axxy k22 = b<nla22. Таким образом, коэффициенты второй квадратичной формы Ьхх и £22 характеризуют нормальную кривизну линий rj = const и £ = const. Что касается коэффициента Ь12, то он отвечает параметру кручения поверхности. Внося (7) в (18), представим скалярно-векторные произведения в виде:
h —JL(LLJL\ h — 1 (д*г дг дг\
11 <о \ дф д ду )9 12 а) \ д£ дц д£ д-ц )*
, _1_ / д2г дг дг\
22 <о \ дг? д£ dri) *
где (о определяется по (6).
Если выразить г через декартовы координаты х% у, zt то для ЬХ1 можно составить определитель
Ьхх = —
11 О)
д2х
д2у
д2г
д?
д
д?
дх
ду
дг
~W
дЦ
я
дх
ду
дг
07)
Ibj
(10.21)
Аналогичные определители можно составить для Ьх2 и Ь22.
Подойдем к определению второй квадратичной формы с иной точки зрения. Принимая по-прежнему длину дуги кривой 5 в качестве параметра, выпишем соотношение
£»=«•
Дифференцируя это произведение по, получим:
§ 119] НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОВЕРХНОСТЕЙ
435
Сопоставляя эту зависимость с (13) и (19), находим:
II = — dr • dn.
Таким образом, вторая квадратичная форма зависит от того, насколько интенсивно изменяется в окрестности данной точки ориентация орта нормали п.
Сопоставляя сведения, относящиеся к первой и второй квадратичным формам поверхности, можно сказать, что форма I характеризует длины дуг, углы между кривыми и площади областей на поверхности, в то время как форма II позволяет определить нормальные кривизны поверхности. Можно показать, что формы I и II, взятые вместе, полностью определяют очертание поверхности с точностью до ее положения в пространстве.
Перейдем к исследованию различных нормальных сечений поверхности, проведенных в какой-либо точке М поверхности (рис. 10.13), т. е. сечений, содержащих нормаль к поверхности п. Если зафиксировать направление касательной, через которую про- Рис. 1013 Нормальное сечение ходит некоторое сечение Р, то кривизна поверхности,
этого сечения будет равна по абсолютной величине нормальной кривизне поверхности kn в соответствующем направлении: векторы v и п составляют для нормального сечения угол 0 или тс. Проследим за изменением kn при повороте сечения вокруг нормали к поверхности при переходе, например, от плоскости Я к плоскости R. Такой поворот равносилен изменению отношения d*f\: d% при фиксированных т и £. Для гладкой поверхности это отношение меняется непрерывно и вместе с тем периодически; следовательно, кривизна kn должна принимать при определенных положениях сечения максимальное и минимальное значения. Найдем эти значения; для этого перепишем (19) в виде
*п + 2*12 Л йщ + *22dr? — kn (п + 2al2 d% dr\ + a22 dtp) = 0.
(10.22)
Примем вначале, что дифференциал dr\ постоянен; дифференцируя (22) по d\ и приравнивая производную нулю, получим:
*и Л + *12 drl — kn (и + 12 d7l) = 0.
Аналогично, считая постоянным дифференциал d\, находим:
*12 Л + *22 dri — kn (12 + 22 dri) — 0.
436
0Ё1ДИЁ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
(ГЛ. X
Исключим отсюда отношение dr\: d\\ тогда придем к квадратному уравнению относительно kn\
Отсюда находим два экстремальных значения kn, которые называются главными кривйзнами поверхности в данной точке; соответствующие направления, определяемые отношением dr\: d\ по (22), носят название главных направлений. Будем считать, что кривизна kny отвечает линии rj = const, a kn— линии = const; тогда из (22) получим, считая последовательно dri = 0 и d% = 0:
Принимая kn>i=kn> находим для главных направлений Ь12 = 0, а[2 — 0. Отсюда следует, что главные направления взаимно перпендикулярны. В дальнейшем будем обозначать главные кривйзны
Проведем линии на поверхности таким образом, чтобы в каждой точке касательные к ним шли вдоль главных направлений. Такие кривые называются линиями кривизны; их удобно выбирать в качестве координатных кривых.
Определим произведение и полусумму главных кривизн, исходя из уравнения (23):
Первая из этих величин называется гауссовой кривизной поверхности в данной точке, а вторая—средней кривизной.
В качестве примера вычислим коэффициенты первой и второй квадратичных форм и гауссову кривизну для поверхности,'заданной уравнением z = f(x,y). Примем х, у в качестве криволинейных координат: х = 1> У = г\\ тогда по (11) и (6)
(вн'«22 —<*?2) kl - (ai Аг + Vn - 2anbn) kn + (Va2 - bn) = 0-
(10.23)
12 а\Фп, 5 — 0* 12 а12л. ц — 0-
через kx и k2.
Г = kxk2 =
(10.24)
k\ 4 2
21212 1122 2211
(10.25)
2
2 (ii22 12)
(10.26)
и, далее, по формулам типа (21) 1 д2г
1 д2г
1 d2z
§ 119]
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОВЕРХНОСТЕЙ
43?
/ dz \2 / dz \2
Отметим, что для пологой оболочки при у-) <С11> 1
можно принять о)«1, тогда коэффициенты Ьц будут иыражаться так же, как кривйзны и кручение изогнутой поверхности пластинки. Гауссова кривизна по (24) будет
Г — 1 \д*2 d*z ( д*г \2
со4 [ dx2 dy2 \dxdy) J '
(10.28)
Интересно отметить, что для пологой оболочки при 1 мы получаем выражение, которое фигурировало в одном из основных уравнений теории гибких пластинок. Сравнивая (7.40) и (28), находим:
•i L (w, w) = Г.
(10.29)
Таким образом, цепные напряжения, образующиеся при больших прогибах пластинки, непосредственно связаны с гауссовой кривизной изогнутой поверхности.
Рассмотрим, далее, поверхность вращения (рис. 10.14), заданную уравнениями
х = г (z) cos ср,
, v. } (10.30)
у = Г (z) Sin ср, Z — * 1 J
Рис. 10.14. Центры кривизны Сх и С2 в случае поверхности вращения.
Под г понимается радиус параллельного круга в сечении z, под ср — угол
поворота меридиональной плоскости. В качестве параметров примем £ = <р, т] = £. По формулам (11), (6) и (21) находим:
«22= 1 +Г' >
ь* г
/1 +.
а12 — 0, 12 = 0,
г2
Ьи=-
> = rV 1-+-
г'
(10.31)
Vl+r'2
через г' и г обозначены производные от г по z, характеризующие очертание меридиана. Гауссова кривизна равна по (24)
Г =
г(1 + г'2)2’
(10.32)
Если выпуклость меридиана обращена к оси z, как изображено на рис, 10.14, то будет г > 0; такая оболочка имеет отрицательную гауссову кривизну. На рис. 10.14 показаны центры кривизны С2 и Сх нормальных сечений, одно из которых совпадает с плоскостью меридиана, а второе перпендикулярно к этой плоскости.
438
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
Заметим, что кривизна параллельного круга 1 /г должна быть по теореме Менье (14) равна (1/рх sin 0г), где — главный радиус МСХ кривизны сечения. Отсюда следует, что центр кривизны Сх является точкой пересечения нормали к поверхности с осью симметрии; как легко видеть, соответствующая кривизна равна
ь - 1 - 1
1 Р, rVl + r
Вторая главная кривизна равна
к - 1 -
р. “а+/•'*)%'
Понятие гауссовой кривизны является в теории поверхностей фундаментальным. Преобразуя выражение (24) для Г, можно показать, что гауссова кривизна зависит только от коэффициентов первой квадратичной формы и их производных. Вместе с другими величинами, зависящими от коэффициентов формы I, гауссова кривизна относится к так называемой внутренней геометрии поверхности.
По знаку гауссовой кривизны можно судить о форме поверхности в окрестности данной точки. Если Г > 0, то, как видно из (24), кривизны kx и k2 имеют одинаковый знак. Это означает, что центры кривизны Сх и С2 по главным направлениям находятся по одну сторону от поверхности, как показано на рис. 10.15, а;
о)
6)
в)
Рис. 10.15. Расположение центров кривизны Сх и С2 для (а) эллиптической, (б) гиперболической и (в) параболической точек поверхности.
центры кривизны всех других нормальных сечений будут лежать на отрезке СХС2. Точка М поверхности, для которой центры кривизны располагаются таким образом, называется эллиптической. Напротив, при Г < 0 центры Сх и С2 лежат, как мы видели, по разные стороны от поверхности (рис. 10.15, б); центры кривизны остальных нормальных сечений находятся на внешних областях
§ 1191 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ПОВЕРХНОСТЕЙ 439
отрезка СХС2\ соответствующая точка поверхности носит название гиперболической. Наконец, в случае Г = 0 точка называется параболической. Здесь одна из главных кривизн обращается в нуль; центры кривизны лежат по одну сторону от Cv и центр С2 находится на бесконечности. Это относится, например, к точке М на рис. 10.15, в, принадлежащей цилиндрической поверхности.
На рис. 10.16 изображена поверхность вращения; в точках верхней части будет Г < 0, как на рис. 10.14, в точках нижней части Г > 0; эти части разделяются параболической линией, для точек которой Г = 0.
Примерами поверхностей, во всех точках которых гауссова кривизна положительна, могут служить сфера или эллипсоид.
Отрицательную гауссову кривизну, и притом постоянную для всех точек, имеет так называемая псевдосфера; здесь kx = — k2 =
= const. Цилиндрическая и коническая поверхности имеют нул вую гауссову кривизну.
Гауссова кривизна играет особую роль в теории изгибания поверхностей. Под изгибанием понимается преобразование поверхности, при котором длины любых кривых, проведенных на поверхности, остаются неизменными; вместе с тем сохраняются и углы между пересекающимися кривыми. Такое преобразование называют также изометрическим. Поверхность при изгибании надо представить себе как абсолютно гибкую нерастяжимую оболочку, которая может изменять (во о форму без складок и разрывов *).
При изометрическом преобразовании первая квадратичная форма, равная квадрату длины линейного элемента, должна оставаться неизменной; но тогда и гауссова кривизна будет сохраняться. Следовательно, изометричные поверхности имеют в соответствующих точках одинаковую гауссову кривизну •*). Интересно отметить, что при изгибании поверхности меняются все три коэффициента формы И, но таким образом, что дискриминант этой формы, равный b\\b<n — b]? и содержащийся в выражении (24), остается постоянным. Примером изометричных поверхностей являются поверхности, развертывающиеся на плоскость; все они имеют нулевую гауссову кривизну.
*) Простое перемещение поверхности в пространстве при этом исключается.
**) Эта замечательная теорема была доказана Гауссом в 1816 г. Говоря об изометрическом преобразовании, Гаусс представлял поверхность именно как «гибкое, но нерастяжимое тело, одно из измерений которого принимается исчезающим» («Общие исследования о кривых поверхностях», перевод 1887 г., стр. 34).
вращения с участками, имеющими различную гауссову кривизну.
440
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
Мы до сих пор не ставили условия, чтобы изгибание поверх¬
ности было непрерывным процессом. Поэтому можно сказать, что переход выпуклого сегмента с закрепленным контуром (рис. 10.17) из положения 1 в положение 2, являющееся зеркальным отражением первого, является изгибанием *), но оно происходит в большом. Если же речь идет о бесконечно малом изгибании, то оно может осуществляться лишь для ограниченного класса поверхностей. Такое изгибание оказывается. невозможным для любой выпуклой непре-
ванне выпуклого сег- Рывн0„й “мку™й повеРхнос™ (например,
мента. полной сферы). Иными словами, такая выпуклая
поверхность является жесткой в малом **). С другой стороны, для поверхностей нулевой и отрицательной гауссовой кривизны бесконечно малое изгибание, вообще говоря, возможно. Это можно иллюстрировать на простом примере стержневой системы, показанной на рис. 10.18. Если стержни нерастяжимы, то
бесконечно малые перемеа) щения среднего шарнира в первом случае (рис. а) исключены, а во втором (рис. б), когда стержни вытянуты в одну линию, могут осущеРис. 10.18. а) «Неизменяемая» и б) «изме- ствиться.
няемая» в малом стержневые системы. gce эти ВЫВОдЫ> содер¬
жащиеся в теории поверхностей, как мы увидим ниже, имеют прямое отношение к задачам устойчивости оболочек в малом и в большом. Если бы оболочка была бесконечно тонкой, то ее деформацию можно было бы охарактеризовать полностью с помощью теории поверхностей. Однако в реальных оболочках любое изменение формы, даже если оно сопровождается изометрическим преобразованием срединной поверхности, вызывает поярлние деформаций изгиба, неравномерно распределенных по толщине. Поэтому мы будем пользоваться приведенными выше зависимостями, изучая деформации срединной поверхности, но должны вместе с тем учесть деформации собственно изгиба оболочки. Иными словами, нам необходимо как бы объединить теорию абсолютно гибких оболочек с теорией жестких пластинок.
*) Сравни деформацию арки-полоски по рис. 10.3.
**) Обзор исследований по качественным вопросам теории деформации поверхностей был опубликован Н. В. Ефимовым (Успехи матем. наук 3, № 2 (1948), 47—158); ряд относящихся сюда общих теорем получен А. В. Погореловым (см., напр., его работу «Некоторые результаты по геометрии В целом», Харьков, 1961).
§ 120] ТРЕХМЕРНАЯ ЛИНЕЙНАЯ ЗАДАЧА ft КРИВОЛИНЕЙНЫХ КООРДИНАТАХ 441
§ 120. Трехмерная линейная задача в криволинейных координатах
При исследовании малых прогибов оболочки, вызывающих деформацию смешанного типа, будем исходить из общих линейных соотношений трехмерной задачи теории упругости. Введем три криволинейные координаты £, т], С, которые будут определять положение произвольной точки пространства так же, как два параметра £ и yj характеризовали положение любой точки поверхности.
Длины дуг, отсчитываемые вдоль координатных линий, равны
dsl = Hldti% ds2 = H2dr\% dte3 = //3dC (10.33)
Величины Hv 2, каждая из которых является некоторой функцией £, у], С, называются коэффициентами Ламе\ они соответствуют коэффициентам первой квадратичной формы аи и а22 в теории поверхностей. Примем с самого начала систему координат ортогональной, тогда квадрат линейного элемента — как бы первая квадратичная форма трехмерного пространства — будет *)
<й8=Я?а*-+ H\dif Н\ Л2. (10.34)
В дальнейшем координаты {• и т] мы привяжем к срединной поверхности оболочки, а координату С условимся отсчитывать вдоль нормали, но здесь будем вести выкладки в общем виде.
На рис. 10.19 изображен Элемент поверхности, содержащий дуги dsx и ds2. Обозначим через Сх и С2 центры кривизны этих дуг в плоскости, нормальной к дуге dsb> а через /?12 и R2l — соответствующие радиусы кривизны. При изменении координаты на dц длина дуги dsx получает приращение; новая длина будет
Рис. 10.19. Дуги криволинейных координат в случае трехмерной задачи.
ds
Очевидно, должно быть
;=(
Нл
дНх
dsл
дц
ds\
dl
*) Параметры Ламе должны удовлетворять шести условиям непрерыв* ности трехмерного пространства, см. [10.3], стр. 193.
442
06ЩИЁ СВЕДЕНИЯ ОВ ОБОЛОЧКАХ
[гл. X
отсюда находим кривизну дуги dsх:
1 ds[ — dsx
или
1
R\2
dsx ds2 9
1 дНу HXH2 дт\
Аналогично кривизна дуги ds2 будет
1 _ 1 дН2
Н2НХ дЬ
(10.35)
(10.36)
Если теперь рассмотреть элемент поверхности, образованной дугами dsx и ds2, то таким же образом найдем кривизну дуги dsx в плоскости, нормальной к ds2:
1 _ 1 дНх
Я, з НХНЪ <?С
(10.37)
Идя подобным путем, можно определить кривизну дуги ds2 в плоскости, нормальной к dsv и кривизны дуги ds3 в плоскостях, нормальных к dsx и ds2.
Допустим, что при деформации упругого тела принадлежащая ему точка М получает перемещения вдоль координатных линий £, rj, С, равные соответственно и, v, w. Определим деформации удлинения, которые получают дуги dsx, ds2 и ds3, а также сдвиги в плоскостях, образованных различными дугами.
Деформация удлинения дуги dsx равна
Рис. 10.20. К определению деформа- 1 12 13
ции, вызванной перемещениями v. Первая составляющая соответствует
приращению и при переходе от точки М к смежной точке N (рис. 10.20); если бы и зависело только
от sx, то было бы б£ = --. Если бы все точки дуги dsx — Rn dBl2
получили перемещения v (рис. 10.20), то радиус кривизны Rx2 увеличился бы на v. При этом дуга dsx получит длину (/?12 + v)dbx2t и относительная деформация будет
(R\2 ~f* 0 db2 RX2 dbх2 v
RX2 dbl2 Rx2
Это дает вторую составляющую в выражении (38). Аналогичное рассуждение относится к перемещению w, что дает третью составляю-
§ 120] ТРЕХМЕРНАЯ ЛИНЕЙНАЯ ЗАДАЧА В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ 443
щую. Подставим в (38) выражения (35) и (37) для 1 //?12 и 1 //?13, тогда найдем:
Деформация сдвига в плоскости, касательной к дугам dsl и ds2, равная изменению прямого угла между этими дугами, будет
положительный знак здесь, как обычно, отвечает уменьшению угла между дугами. Первые две составляющие соответствуют поворотам дуг dsx и d2, вызванным перемещениями точек L и N относительно точки М (рис. 10.21), и имеют такой же вид, как для элемента пластинки (см. стр. 280). Представим себе, далее, что все точки
дуги ds2 получают смещение v (рис. 10.22); тогда угол между ds{ и ds2 должен увеличиться на v/R2l; если же точки дуги dsx сместятся на и, то угол увеличится на u/Rl2. Это дает третью и четвертую составляющие в (40). Подставим сюда выражения (35) и (36), тогда будет
Рис. 10.21. К определению деформаций, вызванных поворотами элементов.
Рис. 10.22. К определению дополнительных деформаций от поворотов.
нли
(10.41а)
444
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[гл. X
Аналогичные выкладки позволяют получить выражение для других составляющих деформации. Окончательно деформации удлинения получаются такими:
1 ди
1
дН{
1
дЬ
dv
НХН2
1
ег —
н2
1
Иг
dri
dw
1
drj
дН2
dt
dH3
v -
1 dHx
w-
H\HZ
1
<?c
dH2
HXH2
1
d4 dH*
w,
U,
HZHX dt
HZH2 drt
v,
(10.42)
а деформации сдвига-
v _Я1 д ( u \ \ H* d ( v \
H2 dri\Hl)~t' H{ dt \H2)’
„ _J±2 — (—\
нъ dx. \H2n H2 dyi\Hs)*
_ H3 d ( w \. Hx d ( u\
Hi dg \ //3 / Hz dt \HX )'
(10.43)
Используем эти выражения для построения теории тонких оболочек. Напомним, что все выведенные зависимости относятся только к малым перемещениям; поэтому они могут быть применены лишь в случае, если прогибы оболочки малы по сравнению с ее толщиной.
§ 121. Оболочка малого прогиба. Зависимость между деформациями и перемещениями
В основе теории изгиба тонких оболочек лежит гипотеза прямых нормалей, по которой точки, принадлежавшие нормали к срединной поверхности до деформации, остаются и после деформации лежать на прямой, нормальной к срединной поверхности. Строго говоря, в процессе деформации оболочки прямолинейность нормалей несколько нарушается: это связано со сдвигами в сечениях, нормальных к срединной поверхности. Поэтому гипотеза прямых нормалей, по существу, сводится к предположению о том, что сдвиги в нормальных сечениях малы по сравнению с углами поворота нормалей и что поэтому сдвиги можно, как правило, принимать равными нулю *).
Отнесем срединную поверхность к линиям кривизны и будем откладывать вдоль этих линий координаты £ и г) (рис. 10.23). Такая сеть линий является ортогональной; коэффициенты первой квадратичной формы срединной поверхности обозначим следующим образом:
и
alt = Ai, а22 = А2, причем а12 = 0. Величины Ах
коэффициентам Ламе: А1 = Н1,
А2 = Н2.
А2 эквивалентны
Линию С совместим с нор¬
малью к срединной поверхности и примем Hs= 1. Введем, далее,
*) См. Б. Б. Нозожидов, Теория тонких оболочек 110.11].
§ 121]
ОБОЛОЧКА МАЛОГО ПРОГИБА
445
обозначения Rx и /?2 Для. радиусов кривизны нормальных сечений
срединной поверхности соответственно вдоль линий £ и tj.
Рассмотрим слой оболочки, отстоящий на расстоянии С = 2 от
срединной поверхности; здесь где — толщина
оболочки. Положительное направление z и w условимся откладывать к центру кривизны *). Так как длины дуг пропорциональны расстояниям до центра кривизны, то коэффициенты А\ и данного слоя будут
Л\ для
6 —
(10.44)
Производные от них по z равны Ал
дА\
дг дА* дг
(10.45)
Рис. 10.23. Элемент оболочки, образованный линиями кривизны срединной поверхности.
После того, как вычислены производные, мы будем в (44) принимать z<_Rv z<R2 и, следовательно, A\AV A*zA2; производные (45) будут одними и теми же для любой точки нормали.
По гипотезе прямых нормалей мы должны принять = 0.
Развертывая выражения (43) для и по типу (41) и полагая А3= 1, получим:
duz uz дАх, 1 dwz
dz
dvz
Ai dz vz дЛ2
dz
+
At di 1 dwz
= 0, = 0,
(10.46)
A2 dz ' A2 drj
wz — перемещения произвольной точки нормали. Для точек прямого элемента, нормального к срединной поверхности, duz dvz
производные и должны сохранять постоянные значения,
равные
nZ 11 *Z п •
(10.47>
диг
dz
ди
dz
dvz
dz
dv
dz
*).Это относится к эллиптическим и параболическим точкам срединной поверхности.
446
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
Но, с другой стороны, принимая 2 = 0 в (46) и пользуясь (45), получим:
ди и 1 dw dv v 1 dw /1Л Ао\
дг ~ Я, Ax dt * dz ~ ~ R2 А2~д' <1и-48>
Сравнивая (47) и (48), находим:
*■—*(т+хтг)- *■—*(*+т)- “°-49>
Обозначим деформации удлинения вдоль линий кривизны через
и е2, а деформацию сдвига через у; если принять в общих выражениях (42) и (43) Нх = Ау Н2 = А2, з=1, wz = wt то при любом z будет
61 ~ А. д£ ' А,Ап дъ * A. dz W%
W,
Ах дЬ АхА2 ду
, 1 dv* 1 дЛ2.
2 — А2 дг1~г~ АХА2 дЬ и ”
Ах dz 1 дА2 Л2 дг
„г_А± — (—\
Т — А2 U, V Ах dt \А2)'
(10.50)
Пользуясь (49), можно теперь представить деформации в виде*) *J = ej 4-**г < = e24-*V 1г=1+2гХ' (Ю.51)
Под е1 е2, 7 здесь понимаются деформации в срединной поверхности:
1 ди. 1 дАх w
ei X л. л* v д, •
А, дЬ ' АхА2 дц 1 dv. 1 дА2 w
б2__ 12 я U R3’
v — A JL (JL\ _i_ А (JL\
» ~ А, дц\AJ~ Ах di \At)’
(10.52)
*) Выражения типа (52) и (53) были получены различным путем многими авторами; подробный их анализ дан в книгах В. 3. Власова [10.3], А. Л. Гольденвейзера [10.6], В. В. Новожилова [10.11]. Приведенный здесь вывод принадлежит Э. Рейсснеру [10.21]. Первые пять выражений (52) и (53) совпадают у всех этих авторов; шестое же выражение — для кручения — имеет несколько вариантов, незначительно отличающихся друг от друга.
§ 121]
ОБОЛОЧКА МАЛОГО ПРОГЙБА
447
под х1э х2—изменения кривизн и под х—«кручение» срединной поверхности:
I д ( и. \ dw \ 1 / и. 1 dw\ dAt
*1_ — Л, di \/?, A, di ) уМДя2'+ А2~д)~д'
1 д / v * 1 1 / и * 1 dw \ дЛ2
%2~~Ad4\R2~A3 df,) ’“‘ЯГ di)~dT'
L Г Л / у. 1 dw \ Ах д (и. 1 dw \1
~ 2 [ Аг дЦ A2R2 А\ dr, ) А2 d-n \ А _t~ А\ di J J
(10.53)
Принимая в (53) Л, = А2 = 1 и /?, = R2 = оо, придем к прежним выражениям для кривизны и кручения пластинки:
d2w d2w d2w
Х1 = W ’ Х2 = ~ ~д * X = — -щ •
Отметим, что шесть величин — деформации в срединной поверх¬
ности и изменения кривизн — выражаются через три функции перемещений и, v, w. Очевидно, эти шесть величин не являются независимыми, для них можно выписать три уравнения совместности. Приведем одно из этих уравнений *):
1 } d 1 Г л dg2 I dА2, V А± ду_ дА\ 1.
AXdi А,[ 2 di *• 2 V 2 d-ч di) +
d 1 Г л d*i ■ dA,, A2 df dA2 11 x, x,
+ a2 L 1 дт, + дц {1 2’ 2 di di ш Ri Ж~
(10.54)
Это уравнение можно проверить непосредственной подстановкой выражений для деформаций ev е2, f и параметров изменения кривизны Xj, х2; ПРИ этом надо воспользоваться следующими соотношениями, известными из теории поверхностей**) (формулы Петерсона — Кодацци и Гаусса):
д (А2\ 1 dA2 d (АЛ 1 дАх
1 1 Г d ( 1 <М2\, d I 1 <М,У...
RtR2 — Л,лД(?«1л. di )~ dr, \At dij )J * (10-56>
Зависимости (55) и (56), выписанные здесь для главных направлений, выражают, по существу, связь между коэффициентами первой и второй квадратичных форм срединной поверхности. Формула (56) свидетельствует о том, что гауссова кривизна, равная 1//?х/?2, зависит
*) См. книгу А. Л. Гольденвейзера [10.6], стр. 58. Два других уравнения приведены ниже, на стр. 455.
**) См. П. К. Рашевский, Курс дифференциальной геометрии, 1956, стр. 350.
448 ОВЩИЁ СВЕДЕНИЯ Ofc ОБОЛОЧКАХ *
только от коэффициентов первой квадратичной формы и их производных; об этом уже было сказано в § 119.
В частном случае, если Ах и А2 постоянны и могут быть приняты равными Л1 = Л2= 1, уравнение совместности (54) переходит в следующее:
д2£2. д2г{ д2ч 1 d2w 1 d2w
дк2 ~ dr? dtdrt ~ R2 д¥ Rx дч\2
(10.54а)
Как мы увидим ниже, во многих задачах, относящихся к устойчивости оболочек, можно упростить выражения (53) для параметров изменения кривизны и кручения, считая перемещения «в массиве» материала и, v малыми по сравнению с прогибом w\ тогда получим:
1 d / 1 dw \ 1 dw дАх
Ч~ ~ А,Л2
1 д I 1 dw \ 1
А2 дг/ \а2 д-г) J A\j
А2 dy drj dw dA2
(10.57)
\A2 di dt
1 Г Аъ_ d I 1 dw_ \, d I 1 dw \ 1
1 ~ ~ 2 [ 7 ~di \ 4 j+ \ ~di j J'
Перейдем к исследованию напряженного состояния оболочки.
§ 122. Усилия и моменты. Уравнения равновесия элемента оболочки
Проведем нормальные сечения оболочки вдоль линий кривизны. Обозначим через ov о2, т напряжения в срединной поверхности по этим сечениям, а через о*, о*, хг—напряжения в некотором слое на расстоянии z от срединной поверхности.
Нормальные и касательные усилия, приходящиеся на единицу длины дуги линии Y, обозначим через Nx и (рис. 10.24); они будут равны
/г/2 Л/2
W'“X37 / «MS*!*». =
-Л/2 -Л/2
Эти выражения составлены с учетом того, что длина дуги A2ch\ в срединном слое не равна длине дуги (A%dri) произвольного слоя. Подставив сюда значение А% по (44), получим:
Л/2 Л/2
§ 122]
УСИЛИЯ И МОМЕНТЫ
449
По аналогии находим усилия в сечении по линии
ЛГ2= f 4[\—±.yz, Г21 = f T*(l--*S)dz. (10.59)
-Л/2
-Л/2
В общем случае, при Rx Ф /?2, касательные усилия Т12 и Г21 оказываются различными. Если учесть, однако, что для тонких оболочек z R\ и z /?2, можно в выражениях (58) и (59) принять
Рис. 10.24. Положительные напра- Рис. 10.25. Положительные направле-
вления усилий в срединной поверх- ния моментов, поперечных сил и по-
1—z/R2 1, 1—z/Rittl, тогда получим TX2 = T2V как это было в случае пластинки. Выпишем, далее, выражения для изгибающих и крутящих моментов (рис. 10.25):
И здесь можно приближенно принять Н12 = Н21. Поперечные силы в сечениях вдоль т и Е пусть будут Qx и Q2; приходящуюся на единицу площади внешнюю нагрузку вдоль линий £, z обозначим через qv q2, qz.
Составим уравнения равновесия элемента оболочки, вырезанного сечениями вдоль линий кривизны *). Длины дуг в срединной поверх-
*) Приведенное здесь изложение построено по Ван Цзи-де (см. [21.21], стр. 366).
ности.
перечной нагрузки.
(10.60)
(10.61)
450
Общиё свёдения ofc Оболочках
[гл. х
ности, отложенных вдоль Е, т), равны Axd%> A2dri> а длины соседАх dr\ d\% {а2-{-r-ddy\. Уравнение равновесия
них дуг
в проекциях на касательную к линии £ имеет вид
- nxa2 (л/j+ ds) (л2 4 -L dlj) dij -
ТпАг d\ 4 (г214- dt,) (л, 4 <*ч)* -
2-d<dr,+ ri2-d!;d7i-
- Qi Р«Й11 + МЛЛ = 0. (10.62)
Здесь члены, зависящие от N2 и Г12, появляются вследствие изменения длин дуг при переменных Ах'и А2. Из рис. 10.26, а видно,
drj
пг*Щ‘лЬ)й71 о)
Рис. 10.26. К выводу уравнений равновесия элемента оболочки. Система координат здесь отличается от принятой на рис. 10.24.
что малый «угол поворота» р дуги {Ах-\-dyjd\ равен разности отрезков [А2-\- d£jdr\ и A2dy], разделенной на длину дуги:
дЛ2
dt
dt\
(
А{ -+*
дАг
dt\ \ d\
V
Угол а получается равным (рис. 10.26, б)
дА, дг1
dy\ db
о
Умножая усилие (д/2 4- —drj 4- на угол р и
соответственно усилие Т12 4- d\ А2 4- dj dr\ на угол а и
отбрасывая малые высшего порядка, приходим к выражениям, фигу-
§ 122]
УСИЛИЯ И МОМЕНТЫ
451
рирующим в (62). Далее, заметим, что сечение, в котором действует поперечная сила («+- наклонено к сече¬
нию с силой QxA2dr\ под углом df, равным df = Axdt/Rx (рис. 10.27); отсюда находим проекцию первой из этих сил, выписанную в (62). Приходящаяся на элемент проекция внешней нагрузки равна qxAxA2d%dr\\ этой величине отвечает последний член уравнения.
Пренебрегая в (62) малыми высшего порядка и представляя члены, зависящие от Nx и Т12, в виде
(*£-Аг+ N)4idn = _ d(A2Nt)
dt
{4%A'+T*ik)dld
_ д(А,Т21)
dvi
d\ dr\,
dtdrq,
приходим к следующему уравнению: d(A2Nl) д (AxT2\) xr dA2
dt
No
Qi
Л'А* -иии2 = о.
dr\ 2 dt '
Рис. 10.27. К определению результирующей поперечных сил.
(10.63)
Таким же образом получаем уравнения равновесия в проекциях на касательную к линии г\
дАх
д-ц
д (AxN2), д(А2Т12)
dyi
dt
дАй
1 21 ‘
dt
Q2
2 (10.64)
Проектируя, далее, все усилия на направление нормали, находим:
d(2@i) 1 d (41 2) дт 12 j\j *12
■Nt
-<7ZV12 = 0. (10.65)
2 R,
появляются благодаря тому,
dt dyi 1 Rx
Здесь члены, зависящие от Nx и N2, что соответствующие усилия действуют под углами Axdt/Rx и A2dr\IR2 друг по отношению к другу.
Проектируя вектор-моменты, показанные на рис. 10.25, и находя момент поперечной силы, получаем уравнение моментов относи¬
тельно касательной к линии т/:
Md-ц - (ж, + dt) (л2 + dk) drt +
dH2\ j \ (A I dA{
+ HnAx d% - (tf21 + dij) (Л, + dTj) d% +
tf,
dri
dAx
drid%-\-
452 ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ [ГЛ. X
Члены, зависящие от М2 и 12, вычислены с учетом углов поворота аир, аналогично тому, как это было сделано выше для Nx и Г12; малые высшего порядка отброшены. После простых преобразований приходим к уравнению
-d(У2)--Ж2+Я12~= 0. (10.66)
Уравнение моментов относительно касательной к £ принимает
вид
а (ЛЯ,г) + W) _ Mt д£_ _ = Q (10 67)
Нам осталось составить уравнение моментов относительно оси z, направленной вдоль нормали в точке (£, tj); оно имеет вид
(*•«+Цг л) (■Л* + л) d7! -
- (г,, + dri) (лг + d\ AJn -
— Нп-йЫг[ + Н2Х-с1\(1г; = 0
или
7’12-7'21-4г+‘ = 0- (10-68)
Введем в шестое уравнение равновесия (68) исходные выражения (58) — (61) для входящих в него величин, тогда окажется, что оно удовлетворяется тождественно. Если же принять приближенно Т\2 — Т2Х и Н12 — Н21, то при ИгФ R2 шестое уравнение не будет удовлетворяться; можно показать, однако, что вносимая при этом погрешность, как правило, того же порядка, что и погрешность других соотношений теории оболочек.
Перейдем к соотношениям между усилиями и деформациями, а также моментами и изменениями кривизн, ofBe4aioiuHM закону Гука. Примем для некоторого слоя оболочки, отстоящего на z от срединной поверхности, зависимости того же типа, что и для пластинки:
= °1 = Т=(е2г + К)* = 2(пЬ)1Г*- (10-69)
Выражения (69) соответствуют обобщенному плоскому напряженному состоянию слоя оболочки; иными словами, считается, что напряжение а2 не влияет на напряжения ах и <з2.
§ 122]
УСИЛИЯ и МОМЕНТЫ
453
Введем (69) в выражения для усилий (58) и (59) и воспользуемся соотношениями (51); тогда, считая z<Rx и z<R2, получим:
— 1 —[х* (ei + !хег)’ М2 — _2 (е2 + Pei)>
Г,2 = Г21 = Г=-
Eh
2(1+) Т-
Аналогично находим выражения для моментов:
Мх = D(x, +ХХ2), ж2 = 0(х2+ {!.*,),
Hi2 = H2i=H = D(l
(10.70)
(10.71)
Мы получили точно такие же соотношения, что и в теории пластинок; они подкупают своей простотой. Но мы отмечали уже некоторые противоречия, к которым приводит это упрощение; появляются и другие затруднения, например, при рассмотрении потенциальной энергии деформации оболочки. Эти противоречия можно устранить, принимая условно выражения для Г12 и Г21 следующими *):
1 12 *
Eh 2(1+
(т—Щ*)' Т21
Eh
2(1+1*)
Подставляя (72) в (68), убеждаемся, что шестое уравнение равновесия теперь удовлетворяется тождественно. Таким образом, в этом варианте теории оболочек по-прежнему будет 12 = 21 = Я, но касательные усилия Т12 и Т21 оказываются различными.
В нашем распоряжении теперь имеются 6 зависимостей (52) и (53), связывающих деформации с перемещениями, 5 уравнений равновесия и 8 соотношений закона Гука. Неизвестными являются 3 перемещения и, v, w, 4 усилия в срединной поверхности, 4 момента, 2 поперечные силы, 3 деформации в срединной поверхности и 3 параметра кривизны. Общее число уравнений (19) соответствует числу неизвестных. Решая уравнения, мы должны удовлетворить граничным условиям, составленным для конкретной задачи.
Пути решения уравнений могут быть выбраны различными в зависимости от того, какие величины выбраны в качестве основных неизвестных— перемещения либо усилия и моменты. В дальнейшем мы будем также часто пользоваться смешанным методом, как в теории гибких пластинок; основными неизвестными будут прогиб и функция усилий в срединной поверхности.
*) Эти выражения были предложены Л. И. Балабухом и В. В. Новожиловым; см. книгу [10.11], стр. 47.
454
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
§ 123. Упрощенный вариант основных уравнений линейной теории оболочек
Как мы видели, структура исходных уравнений общей теории оболочек даже для области малых прогибов сравнительно сложна; поэтому решение конкретных задач представляет значительные трудности. К счастью, для многих задач по устойчивости оболочек, имеющих наибольшее практическое значение, основные уравнения удается сильно упростить. Это относится к тем случаям, когда выпучивание оболочек сопровождается появлением сравнительно мелких волн, т. е. таких волн, размеры которых, хотя бы в одном направлении, малы по сравнению с радиусами кривизны срединной поверхности или габаритными размерами оболочки. При этом в пределах каждой вмятины оболочку можно рассматривать как пологую. Это позволяет применить в подобных задачах устойчивости оболочек произвольного очертания аппарат теории пологих оболочек *).
При построении теории пологих оболочек можно считать, что внутренняя геометрия срединной поверхности независимо от ее гауссовой кривизны является на некотором участке такой же, как и геометрия на плоскости **). Иными словами, первая квадратичная форма поверхности считается той же, что и для плоскости:
/ = Л1 dt + drf.
Но тогда зависимость (56) гауссовой кривизны от коэффициентов первой квадратичной формы нарушается, и надо положить
д ( 1 дАо \, д ( 1 дАх \ л /1Л _оч
-зНзг-ю+Ьгтт)®0- <10-73>
Другой критерий заключается в том, что функции, через которые выражаются перемещения, деформации и напряжения, изменяются сравнительно быстро хотя бы вдоль одной координаты, так что при дифференцировании по данной координате функция значительно возрастает.
Вместе с тем надо принять, что перемещения и, v вдоль линий кривизны срединной поверхности малы по сравнению с прогибами w. Это позволяет воспользоваться упрощенными выражениями (57) для изменений кривизны.
Далее, шестое уравнение равновесия во внимание не принимается; соотношения упругости получают вид (70) и (71), причем Т12 — Г21 — т
*) Эта теория была разработана для круговых цилиндрических оболочек Доннелом [10.16], а для оболочек произвольного очертания — В. 3. Власовым [10.3], А. Л. Гольденвейзером [10.6], X. М. Муштари [10.9], В. В. Новожиловым [10.11], [10.12], Ю. Н. Работновым [10.13] и С. Фейнбергом [10.14].
**) Это допущение было впервые сформулировано В. 3. Власовым ([10.3], стр. 303); см. также статью С. А. Амбарцумяна, Прикл. мат. и мех., 11
§ 123] УПРОЩЕННЫЙ ВАРИАНТ ОСНОВНЫХ УР-НИЙ ЛИНЕЙНОЙ ТЕОРИИ 455
и Н12 — Н21 = Н. Что касается первых двух уравнений равновесия (63) и (64), то в них оказывается возможным пренебречь членами, зависящими от поперечных сил; уравнения эти переходят в следующие:
д (A2Nt) i д (АХТ) до дА2. j дАх _
д£ ' дг\ 2 dZ ' дт
= 0,
д(А,М2), д (А2Т)
dZ
■N,
dAt
дг,
дАг
дг
= 0.
(10.74а)
(10.74Ь)
Уравнения (74) будут тождественно удовлетворяться, если ввести функцию усилий в срединной поверхности <р по формулам:
А2 ду \ А2 дг, j
_1 д_ I 1 дер \
~ dZ )
1 дА2 д<*>
а\а2
n2 =
dZ
дА{
dZ
дер
А А1 12
г= —IГАА/
2 [А1 dZ \
д / 1 дер \
+
1
А\А2 \ д<* df]
дАх
drj
дт) дт)
А! д / 1 др\ А2 ду дер
Ж
U*)]-
1 дА2 дер \
А2 д; дт) /'
(10.75)
Величина <р аналогична функции напряжений в срединной поверхности Ф, которая фигурирует в теории гибких пластинок. Если положить Аг = А2= 1 и ввести координаты х и у, то будет, например,
лг <?2ф
N1 = hcx = h-r,
так что ср = Ф/г.
Отметим, что усилия Л, N2, Т выражаются по (75) через функцию <р таким же образом (с точностью до знака), как кривизны х2, Xj и у через функцию прогиба w по (57). Очевидно, кривизны должны удовлетворять соотношениям, аналогичным уравнениям равновесия (74):
д (А2Ъ) MiX) дЛ2 дА{
Л
dZ
дг]
дт)
д(А2Х)
dZ
dZ
дА{
дт)
— X
дг\
дА2
dZ
= 0,
= 0.
(10.76)
Эти зависимости представляют собой упрощенный вариант двух дополнительных уравнений совместности, упоминавшихся в § 121 (стр. 447).
Найдем, далее, поперечные силы Qi и 09 из уравнений равновесия (66) и (67):
д (А\Н) дА2 I j_j дАх
9 ' drj.
дА. гт дА2 ~
дт] ' дб Jв
Qi
1
■[
д (А2М1)
А\А2 _ д?
д(Л{М2)
(10.77)
456 ОБЩИЕ СВЕДЕНИЯ ОВ ОБОЛОЧКАХ [ГЛ. X
Воспользуемся соотношениями упругости (71). Если принять во внимание соотношения (76), то получим при этом
«о-78»
С другой стороны, по (57) находим:
1 дА2 dw
_1 д_ I 1 dw \
~A~dZ \ л7дГ/
+
А\А2 di dZ
_i_ _L_£. / J_ _j no 79>
+ A2 dr, \ A2 dr, ) + A,Al dr, dr, J ’ (IU 79)
или
*1 + x2 = ~ (10.80)
здесь под V2 понимается оператор Лапласа в криволинейных координатах:
(10-81)
Оператор V2 в декартовых координатах получим при ЛХ = Л2=\.
Окончательно находим следующие выражения для поперечных сил:
1 —<ь—<'°-82>
подобные же выражения мы получали в теории пластинок.
Введем (82) в оставшееся уравнение равновесия (65) и выразим усилия Nx и N2 через функцию ср по (75); тогда придем к уравнению
D44w = V2k<f + q; (10.83)
здесь введен новый оператор [10.3]:
+ (,0-84>
который отличается от V2 коэффициентами 1 /R2 и 1 /Rv учитывающими кривизны оболочки.
Воспользуемся, далее, уравнением совместности деформаций (54). Если ввести в него выражения для деформаций по (70):
= е2 = -Г(-1), Т = (10.85)
и, далее, выразить Nv N2, Т через функцию усилий по (75), а изменения кривизн — через w по (57), то придем к следующему уравнению:
(10.86)
§ 123] УПРОЩЕННЫЙ ВАРИАНТ ОСНОВНЫХ УР-НИЙ ЛИНЕЙНОЙ ТЕОРИИ 457
Таким образом, мы получили систему симметрично построенных линейных уравнений четвертого порядка относительно функции прогиба w и функции усилий <р; при q = О эта система принимает вид
DV4w — v£cp, -1- V4<p = — V\w.
(10.87)
В частном случае Ах = А2 = 1, если ввести х и у вместо £ и получим:
Г72 Г72_ 1 д2 1 д2 п
V — дх2 + ду2 ’ к~ R2 дх2 + Я, ду2 * (W.88)
Однако в задачах устойчивости первое из уравнений (87) надо допол¬
нить членами, учитывающими основные усилия в оболочке. Если основное состояние является безмоментным, то необходимо учесть докритические усилия в срединной поверхности, в общем случае надо принять во внимание и усилия изгиба. Рассмотрим случай безмоментного основного состояния; при этом можно ввести в уравнение (83) фиктивную поперечную нагрузку qz — q, равную сумме дополнительных проекций основных усилий рх% pyt s на направление нормали к изогнутой поверхности:
q = h(px%l + pyx2 + 2sx) = hU(p, %). (10.89)
Положительными здесь считаются усилия, способствующие увеличению параметров кривизны; в применении к рх и ру положительными принимаются усилия сжатия. При Аг — А2 = 1 получим:
-Щу) = -шw>- <10-89a> Применим к первому из уравнений (87) оператор V4, а ко второму— оператор v; тогда систему (87) можно привести к одному разрешающему уравнению восьмого порядка:
Vsw + = 0 (10.90)
или
12(1-) = 0. (10.90а)
В задачах устойчивости уравнение (90) надо дополнить членом V4<7;
оно получит по (89а) вид
у»да + V2* V4n (р, X) = 0; (10.91)
458
ОБЩИЕ СВЕДЕНИЯ ОБ ОБОЛОЧКАХ
[ГЛ. X
здесь параметры изменения кривизны должны быть выражены через w по (57). При Аг =* Л2 =* 1 будет
--V>sW-j-Vlvlw + -±-V4U(р, «0 = 0. (10.91а)
В дальнейшем мы будем пользоваться уравнениями типа (91) при решении многих частных задач. В случае, когда будет применяться энергетический метод, нам придется находить потенциальную энергию деформации оболочки, складывающуюся из энергии деформации в срединной поверхности и энергии изгиба. Первая из этих составляющих вычисляется по формуле, аналогичной той, которая была приведена в главе VII для гибких пластинок (см. стр. 285):
U‘ = wf /[(в, + а*)2 -2 (10.92)
интеграл распространяется на срединную поверхность оболочки. Используя соотношения типа (70), выразим Uc через деформации:
ЕН
/ /[(eiW-2(l-tf(*i«2-7)]ii4atfrf4. (10.93)
«— 2(l-i*) р
Энергия изгиба определяется по-прежнему формулой типа (7.39): t/„ = 4//к*1 + )2-2(1-Ж*Л-Х2)МИ2<ЗД. (10.94)
F
Для пологой оболочки можно ввести сюда функции напряжений и прогиба; тогда получим:
= f 1(2Ф)2-(1 + )(Ф. Ф)]dxdy,
F *
— f t(V2w)2 —(1 —\x)L(w, w)\dxdy.
(10.95)
Обратимся к основным соотношениям теории гибких оболочек. § 124. Ободочки большого прогиба
Линейная теория оболочек дает возможность исследовать устойчивость в малом. Но полное решение задачи, включающее подход К ней в большом, может быть дано, как мы знаем, лишь с позиций
§ 1241
ОБОЛОЧКИ БОЛЬШОГО ПРОГИБА
459
нелинейной Тебрйй. Приведем основные соотношения, б>гн<яш‘ие€» к оболочкам большого прогиба *).
Будем исходить иэ упрощенного варианта, в котором оболочка' считается пологой, по крайней мере в пределах отдельной вмятины. Примем поэтому Аг = Л2 = I и будем откладывать вдоль линий кривизны координаты х и у. Начальные кривизны срединной поверхности будем обозначать через kx—\/Rx и 2=1 /R2 и примем их для данного участка оболочки постоянными.
Выражения для деформаций в срединной поверхности для линейной задачи имеют вид (52):
ди и dv и ди, dv /ЛГк л/*ч
вх = ж-к, Sy=--k2w, т = _+-5_. (10.96)
Дополняя их теми же нелинейными членами, что и в теории гибких пластинок, получим:
00.97)
s = <10-98)
Уравнение совместности деформаций (54а) принимает вид
Т+Ту- Дг = -7 о)-*1-: П0.100)
под L(w, w) здесь понимается прежний оператор (7.40), а под V* — упрощенный оператор (84):
*-*2 и d2w. - д2т / л г\,Л1\
— 2 дх2 1 ду2 * (10.101)
Формулы (57) для изменений кривизн переходят в следующие:
d2w d2w d2w /1Л 1ЛОЧ
*1_ дх2 • *2— ду2 ’ х~ дхду ; (Ю.102)
новых нелинейных членов здесь вводить не будем. Таким образом, параметры х и )( будут теми же, что и в случае пластинки.
Соотношения закона Гука (70) и (71) также остаются прежними. Первые два уравнения равновесия (74а) и (74Ь) принимают вид
д<з г dz dz dcv
+ W = 17+TF = 0; <10103>
здесь принято cx = N1jhi ay = N2/h.
*) Эти соотношения были выведены в более общем виде Цянь Вэй-чаном [10.15], Н. А. Алумяэ [10.1], X. М. Муштари и К. 3. Галимовым [10.10].
460
ОВЩИЁ СВЕДЕНИЙ 0Ё ОЁОЛОЧкАХ
[гл. X
Третье уравнение равновесия (65) перепишем в виде
ъг + + {a*k*+e h+Я-= 0; (10.104)
оно должно быть дополнено членами, зависящими от изменений кривизн, как в случае гибкой пластинки, и приобретает форму
Внося эти выражения в (105), приходим к следующему уравнению:
Вводя в уравнение совместности деформаций (100) напряжения по соотношениям упругости типа (85), получим:
Воспользуемся теперь функцией напряжений Ф = ср/Л и выразим ох% оу, т в (107) и (108) через Ф по известным формулам (7.60); тогда придем к окончательным уравнениям (при q = 0):
Эти уравнения обобщают систему (87) на случай оболочки большого прогиба. С другой стороны, полагая здесь равными нулю
относящиеся к гибким пластинкам. Как мы видели, первое из уравнений (109) выражает условие равновесия элемента оболочки,, а второе — условие совместности деформаций.
Допустим теперь, что оболочка имеет до нагружения некоторые отклонения от идеальной формы, или, иными словами, начальные
+ 2тАж5г + <7==0’ (10-,05>
причем x=T/h.
Поперечные силы по (82) будут
(10.107)
дН д\ (дЧх, 0 t д2ву ~
дх ду ' ду2 \ ду2 ' дх ду дх2 / J
= — у L (w, w) — (10.108)
= /. (да, Ф)+Ф,
-i- У4Ф = — у L (w, w) — V2kw.
(10.109)
члены, содержащие оператор V*. получим уравнения (7.63) и (7.64),
§ 124]
ОБОЛОЧКИ Ё0ЛЫ110Г0 ПРОГИБА
461
прогибы w0(x, у). Тогда выражения для деформаций (97) — (99) получают вид
\2
ди и, ч. 1 / dw \2 1 / д*0о \2
: = ж-кх-Щ)+2\Ж) -ТЫ-)
ду
ди, dv да; ддо
ду ' д* ' д* ду
ду; dwQ dw0 дх ду
1 ( dwQ v2
2 \ ду / *
(10.110)
под <а> здесь понимается полный прогиб. Повторяя вывод основных уравнений, получим вместо (109)
V4 (w — w0) = L (w, Ф)Н-УФ,
-L у4ф = _ -![£(«,, w) — L(w0, та»о)] — V\(w-
■w0).
(10.111)
Перейдем к конкретным задачам об устойчивости в малом и в большом оболочек различного очертания. Начнем с круговых цилиндрических оболочек.
ГЛАВА XI
УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
В ПРЕДЕЛАХ УПРУГОСТИ
§ 125. Основные уравнения для оболочки кругового очертания
В исследованиях по устойчивости оболочек наибольшее внимание уделяется круговым цилиндрическим оболочкам. Оболочки такого очертания отвечают, как правило, требованиям наименьшего веса конструкции и простоты изготовления; поэтому они широко применяются в различных областях техники. Цилиндрические оболочки входят в конструкции летательных аппаратов и двигателей, подводных лодок, резервуаров, трубопроводов и т. д.
Выпучивание цилиндрических оболочек может произойти в тех случаях, когда они подвергаются действию осевого сжатия, поперечного давления, кручения, изгиба, причем эти нагрузки встречаются отдельно либо в различных сочетаниях. В дальнейшем мы рассмотрим последовательно задачи об устойчивости оболочек при этих видах нагружения.
Прежде всего приведем основные соотношения линейной теории круговых цилиндрических оболочек постоянной толщины h. Обозначим радиус кривизны средин¬
ной поверхности через R. В качестве параметров, определяющих положение любой точки срединной поверхности, выберем координаты х и у, откладываемые соответственно вдоль образующей и по дуге (рис. 11.1). Перемещения вдоль этих линий и по нормали по-прежнему обозначаем через и, v и w;
прогибы w считаем положительными, если они направлены к центру
кривизны.
Первая квадратичная форма срединной поверхности будет здесь
Рис. 11.1. Координатные линии при рассмотрении цилиндрической оболочки.
I = dx2-\-dy2.
(ил)
§ 125] ОСНОВНЫЕ УРАВНЕНИЯ ДЛЯ ОБОЛОЧКИ КРУГОВОГО ОЧЕРТАНИЯ 463
Следовательно, мы должны принять в обозначениях предыдущей главы ап = Ах=1, а22 = А2 — 1, а12 = 0 и, далее, Ь = х, rj = y. Кроме того, надо положить Rx — оо, R2 = R. Так как коэффициенты Аг и А2 здесь постоянны, все соотношения теории оболочек сильно упрощаются.
Выражения (10.52) для деформаций в срединной поверхности получают вид
ди dv w ди. dv /л л лч
е* = Ж* еу = Sy—R' 1 = + <п-2)
параметры изменения кривизны по (10.53) будут
d2w 1 dv d2w 1 dv d2w „
*у~ ~ R Tf ~~~W' % — ~ 2R~dx~~dxdy'
Отметим, что для параметра ху в литературе применяется и другое выражение:
w d*w. /1 1 л\
%у R2 ду2 ’ О***)
его можно получить из (3), если принять условие «нерастяжимости» срединной поверхности в направлении дуги: еу = 0; тогда будет *)
dv w.. _
dJ = ~R- <1L5>
В дальнейшем при рассмотрении изотропных оболочек будем вводить в основные соотношения не усилия Мх, Ny, 7\ а непосредственно напряжения в срединной поверхности ох = NJhy ay=Ny/h и т = T/h. Уравнения равновесия (10.63) — (10.65) в проекциях на ось Ху касательную к линии у, и ось z перепишутся в виде
dax дх 1 dx дау Q у 1
дх ду h дх~~ ду Rh
dQx. dQy hay
' ' Ь<7*=0.
(11.6)
дх ' ду ' R
Уравнения моментов (10.66) — (10.68) получают форму дМх дН dH dMv
-d + sr~Q, = °- ■w + sr-Q> = 0- (“'7>
*) В варианте основных соотношений, принятом В. 3. Власовым [10.3],
выражение (4) не связано с условием нерастяжиморти.
464 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. оболочек в пределах упругости [гл. XI
Найдем Qx и Qy из (7) и подставим в (6); тогда получим: dax дт 1 дт dav 1 / дН дМ» \ 1
+ Т =0* + Rh (dF ~дГ' )~Tqy = 0'
дх
д*М,
дх2
д*Н д2Мч 2+ у
ha.,
' дхду
ду2
-h?2 = 0. (П.8)
Шестое уравнение равновесия (10.68) учитывать не будем.
Определим, палее, напряжение в срединной поверхности по (10.70) и (2):
Е Г ди. (dv w\
°х — + —
Е Г dv w, ди ]
°у~ 1 — (Д.2 [~dy~~R 1х\‘
(ди. dv\
~ду~гШ)’
(11.9)
2(1+1*) и моменты по (10.71) и (3):
м nf I М dv I d*w\l
х ~ [ дх2 ду ду2 )J ’
М,
, 1 dv, d2w 1
Н= -D( 1
d2w dy2 R ду
\ ( 1 dv {*)( 9i
\ 2 R dx
d2w• \
(11.10)
дхду / *
Введем выражения (9) и (10) в условия равновесия (8); тогда придем к следующим уравнениям:
1 — {а д2и, 1 + fi. d2v fx dw, 1 — fx2
~R~W
d2u
dx2
d2v 1 — dy2
т 2
fx d2v
dy2
h2
2 d2v
' 2 dx2
1 + f* d2u
12У?2 \ dy2
1 dw, h2 I ~R~dy~ Y1R \i
dx dy
1 fA d2i/
2
d3w
Eh
d3w \, 1 — fi2
qx = 0,
' 2 dx dy /? йу T 12/? V d*2 dy
, JL_ JLfL L *!. _i_
l2 v w-t- R dx R d -r
dy
\, 1 — [l* л
3 ) + £Д— — 0,
+
h2
12 R
/ dbv, d3v\ \ dx2 dy ' dy3 /
Eh
** Яг — 0 (11.11)
где V4=V2V2 — двойной оператор Лапласа по (7.20а).
Мы получили один из вариантов уравнений теории цилиндрических оболочек в перемещениях *). Перепишем эти уравнения в виде
См. книгу Ван Цзи-де (21.21J, стр. 39§,
§ 125] ОСНОВНЫЕ УРАВНЕНИЯ ДЛЯ ОБОЛОЧКИ КРУГОВОГО ОЧЕРТАНИЯ 465
таблицы операторов по отношению к и, v, w (грузовые члены опущены).
Таблица 11.1
Дифференциальные операторы основных уравнений
и
V
W
д2, 1—и д*
1+t* д2
IX д
R дх
R ду +
. А2 / д3 д* \
дх2 1 2 ду2 1+И
2 дхду
( д 1 —(а d2 W
2 дх ду R дх
\(Эу2 1 2 дх*)*
xh1 А2 А
Х\ + 12 R2)
-1± +
R ду
h2 / д* д* \
1 12 R \дх2 ду 1 ду» ]
+ 12 R \дх2 ду 1 ду3)
hi. v« j L
12 Л*
Отметим, что недиагональные члены этой таблицы построены симметрично. В. 3. Власов считает [10.3], что это свойство находится в соответствии с энергетическими принципами теории упругости и, в частности, с теоремой о взаимности работ.
Обратимся теперь к упрощенному варианту линейной теории оболочек, изложенному в § 123. Новые выражения для изменений кривизны по (10.57) имеют вид
d2w d2w d2w /лл
~ Тх2' ду* ' дхду • О1-12)
Как легко видеть, окончательные выражения для деформаций (2) и параметров кривизны (12) совпадают с такими же выражениями в теории пластинок; исключение составляет формула для еу, заключающая здесь дополнительный член (—w/R). Первые два уравнения равновесия (8) приобретают вид
466 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
они аналогичны соответствующим уравнениям для элемента пластинки. Это позволяет ввести функцию напряжений Ф по (10.75)
_ д*Ф _ д2Ф _ д2Ф /11104
°х— ду2 ’ °У дх2' х ' дхду • (11.13)
Уравнение совместности деформаций (10.54а) получает вид
д2гх д2Ву д2у 1 d2w
~ду* дхду ==~~R~dxr‘ (11-14)
Идя далее по пути, описанному в § 123, приходим к окончательным уравнениям (10.83) и (10.86). Полагая по (10.84)
«2 1 d2w
Wk~~R~dx2''
находим:
4=45+’ <1115>
= (П.16)
Мы получили известную систему уравнений смешанного типа относительно прогиба w и функции напряжений Ф, лежащую в основе многих исследований. При решении задач устойчивости оболочек в уравнение (15) надо подставить вместо qjh величину П(а, х) по (10.89); в полном виде уравнение будет
D -4 1 д2Ф d2w d2w n d2w /л л _ ч
Т ~ ~R~dx* ~ Рх !h? ~ РУ ~ду* дхду ' (11Л5а)
Далее, уравнения (15а) и (16) можно привести к одному разрешающему уравнению вида (10.91а). Если напряжения рх> pyt s не зависят от координат, получим:
D -л, Е d4w, m / d2w \. -А( d2w \.
+2sV,(r)-°- <>7>
Упрощенный вариант теории цилиндрических оболочек можно представить и в виде уравнений в перемещениях. В таблице 11.1 можно при этом отбросить члены со вторыми и третьими производными, коэффициенты в которых содержат /г2; тогда придем к следующей таблице*) 11.2.
*) Эти уравнения были приведены В. 3. Власовым (см. [10.3], стр. 316) у Доннелом [11.30].
§ 125] ОСНОВНЫЕ УРАВНЕЙЙЙ ДЛЯ ОБОЛОЧКИ кгоьбгб ОЕТАНИЙ 4б7
Таблица 11.2 Дифференциальные операторы упрощенных уравнений
и
V
W
д2 l-(i д2
1+Р д2
д
дх2 1 2 ду2
2 дх ду
R дх
1+(х д2
д2 1 — fx 2
1 д
2 дх ду
ду2 1 2 дх2
R ду
(л _д_
1 д
h2 „а, 1
R дх
R ду
12 + Л*
Эти операторы также обладают полной симметрией. Приведенные в таблице 11.2 уравнения можно преобразовать. Дифференцируя второе уравнение по х и у, находим:
1 + н* д4и * d4v. 1 — fx d4v 1 dzw л
2 дх2 ду2 дх ду3 ' 2 дх3 ду R дх ду2 *
Пользуясь первым уравнением, определяем входящие сюда производные v; тогда придем к уравнению
Т74 dsw л _.
V и~Р дх3 дх дуг ' (П.17а)
Аналогичное уравнение для v имеет вид
(,1Л7Ь)
Эти два соотношения дополняют уравнение (17) для w.
Мы привели вариант упрощенных уравнений, относящийся к случаю, когда размер выпучин мал по сравнению с размерами оболочки хотя бы в одном направлении. Например, если оболочка получает осесимметричные (кольцевые) выпучины, то длина их должна быть мала по отношению к полной длине оболочки. Если же, напротив, вмятина занимает всю длину оболочки, то число п волн вдоль окружности должно удовлетворять условию п2> 1. Практически упрощенные уравнения можно применять при п 4; это условие выполняется в различных случаях нагружения оболочки, если отношение L/R не слишком велико. Вместе с тем, это отношение не должно быть и чрезмерно малым: в зонах оболочки, прилегающих к торцам, будут сильно сказываться местные напряжения. Таким образом, в применении к задачам устойчивости, упрощенные уравнения
468 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах УПРУГОСТИ [гл. XI
по таблице 11.2 справедливы для оболочек средней длины; этот термин часто встречается в литературе. Более подробный анализ показывает, что параметры оболочек средней длины должны удовлетворять условию (по В. М. Даревскому)
-7- 1 — <с(—У (11.18)
Y 12(1 —(л2) R \kR) ' ’
/12(1-4 »Й)2- (11-18Ю
Сделаем попытку установить более определенные границы для L/R, записав вместо (18) и (18а) следующие неравенства:
]/, ” »-*']/ (U.lSb)
V /12(1 — (X2) R R V * h ’
или
В дальнейшем мы уточним эти соотношения на примере задачи об осевом сжатии оболочки.
Рассмотрим другой вариант упрощения основных уравнений, относящийся к случаю слабо выраженного волнообразования по длине оболочки. Этот вариант состоит в том, чтобы принять срединную поверхность нерастяжимой в дуговом направлении (sy = 0) и считать, кроме того, что сдвиги в срединной поверхности отсутствуют (7 = 0). Далее, можно положить равными нулю поперечные силы и изгибающие моменты в осевом направлении, а также крутящие моменты: Qx = Мх = Н — 0, и принимать во внимание только усилия Qy и Му. Такая теория оболочек получила название полубезмоментной *). При этом выполняется условие (5), поэтому для ху получаем выражение (4):
ди / d2w. w \ dv w ди dv
г*~~дх' %y~~\dyrW)' Ty~~R' ~dj~ ~ ~дх‘
Отсюда вытекает соотношение
д2гх 1 д2т
ду2 R дх2
*) Эта теория, применение которой особенно уместно для подкрепленных (ортотропных) оболочек, была разработана В. 3. Власовым [10.3]. Ему принадлежат уравнения (23).
§ 125] ОСНОВНЫЕ УРАВНЕНИЙ ДЛЯ ОБОЛОЧкЙ КРУГОВОГО ОЧЕРТАНИЯ 469
Сопоставляя его с выражением для ху, приходим к следующему уравнению совместности деформаций:
д4гх 1 д2ех d2xv
~ду*~ ду2 = дх2 ‘ (11.19)
Уравнения (8) приобретают вид
дзх дх 1 дх д<3у 1 дМу 1
~дх ~ду~ ~h q* ~ ~дх~ Ну ~Rh ~ду~ + Т 4у ~
У ' -cy+qt = 0.
ду2 ' R У
Объединяя их, получаем уравнение равновесия d*Mv 1 d2Mv дЧх
R~ду5 ~R~df k ~дх*~ = ’ (11.20)
где
_дЧхl, п, 20яч
Р— д* + dy ду2 • (11.20а)
Соотношения закона Гука выпишем в виде
с р/,3
М = 19 1. x=Dx (11.21)
Введем переменные а = лс//?, (3 = у/ и воспользуемся оператором
2 =-ргН-2 5 (11.22)
тогда уравнения (19) и (20) примут вид
12R dWv д2ах
Qc* jT-SI = 0’ Rh- + QMy = R*P*. (11.23)
где
D* Г Т- dp dp2
я, = _fyx, дЯу__Яг_ (1124)
Исключая ox и подставляя Му по (21), приходим после исключения (для задач устойчивости) оператора (д2/д2 + 1) к уравнению
DQQw + EhR>- = -R4?f. (11.25)
Этим уравнением следует пользоваться, исследуя устойчивость оболочек средней и особенно большой длины при том характере волнообразования, о котором говорилось выше.
Отметим, что уравнение (19) непосредственно связывает изменение кривизны ху, характеризующее искажение контура поперечного сечения, с деформацией ех, определяющей искажение сечения
470 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в прёдёлах упругости (гл.
в направлении образующей, т. е. депланацию сечения. Напряжения ох> возникающие при такой депланации, образуют в поперечном сечении систему усилий, которую мы в главе IV называли бимоментом. Таким образом, данный вариант теории оболочек тесно
связан с теорией тонкостенных стержней.
К приведенным выше уравнениям мы будем обращаться в последующем при решении линейных задач. В нелинейных задачах будем пользоваться уравнениями теории гибких оболочек, приведенными в § 124, полагая 1 = 0, k2—l /R- Окончательные уравнения (10.109) получают вид *)
£v4r = Z,(w, + (11.26)
= (11.27)
Дополненное разрешающее уравнение типа (17) будет П F г)4™ F /)2
Ф) + -«» = 0. (11.28)
При исследовании оболочек с начальной погибью надо воспользоваться уравнениями (10.111); они переходят в следующие (при Я = 0):
Л 1 г)2Ф
-~(w — w0) = L(w, +
-L У4Ф = —[I (w, w) — L(w0, та>0)1 — d*(wd~Wo).
(11.29)
Если с помощью уравнений (26) — (29) исследуется закритическая деформация оболочки, то производные от Ф по формулам (13) определяют полные напряжения и включают, таким образом, критические усилия.
Интегрируя приведенные выше линейные (либо нелинейные) уравнения, мы должны удовлетворить граничным условиям. Выясним, каковы будут эти условия для торцевых сечений замкнутой оболочки**). При шарнирном опирании или защемлении оболочки по
краям х = 0, х = L должно быть соответственно
л d2vv л л dw л
<а/=0, -g-£- = 0 или w = 0, -- = 0.
Далее, необходимо формулировать условия, касающиеся перемещений и> v, а также усилий в срединной поверхности. Если точки
*) Эти уравнения были впервые составлены Карманом и Цянь Сюэ-сэнем [11.35]. Уравнение (28) было получено Цянь Вэй-чаном [10.15].
**) О граничных условиях для открытой оболочки (цилиндрической панели) см. в § 139.
§ 126] СЖАТИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ВДОЛЬ ОБРАЗУЮЩЕЙ 471
краев свободно смещаются вдоль образующей и по дуге, в этих точках будет о* = 0, т = 0. В другом предельном случае несмещающихся кромок надо положить и — О, *0 = 0. Одно из важных свойств оболочки как упругой конструкции состоит в том, что эффект воздействий, сосредоточенных в некоторой зоне, выражающийся в образовании моментов и поперечных сил в сечениях оболочки, при удалении сечения от этой зоны существенно затухает*). Это обстоятельство надо учитывать при исследовании влияния граничных условий в конкретных задачах.
§ 126. Сжатие замкнутой оболочки вдоль образующей. Линейная задача
Обратимся прежде всего к задаче об устойчивости замкнутой круговой цилиндрической оболочки, подвергающейся сжатию вдоль образующей усилиями /?, равномерно распределенными вдоль дуговых кромок (рис. 11.2). Этот случай нагружения представляет большой практический интерес. Например, корпус летательного аппарата подвергается на участке разгона действию сжимающих усилий, передающихся от двигателя. Некоторые другие задачи, в том числе задача об устойчивости оболочек при изгибе, сводятся, как мы увидим, к применению результатов, относящихся к случаю центрального сжатия. Вместе с тем, круговая оболочка, сжатая вдоль образующей, является своего рода эталоном, служащим для сопоставления теоретических и экспериментальных данных и для проверки различных подходов в теории устойчивости оболочек.
Эксперименты и наблюдения над реальными конструкциями показывают, что характер выпучивания сжатых оболочек на практике совсем не такой, каким он рисуется, если исходить из линейной теории. Критические напряжения в опытах получаются здесь в тричетыре раза меньшими, чем это вытекает из исследования устойчивости оболочки в малом. Более полное решение этой задачи может быть осуществлено с помощью нелинейной теории оболочек. Таким образом, эта классическая задача, являющаяся на первый взгляд
*) Исключение составляет случай, когда воздействия происходят вдоль асимптотических линий, т. е. линий нулевой нормальной кривизны, См* книп? [10.6], [10.8], [10.2]. * г г
Рис. 11.2. Оболочка, сжатая вдоль образующей.
472 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
элементарной, таит в себе неожиданные затруднения; их до сих пор не удалось полностью преодолеть.
Начнем с рассмотрения устойчивости оболочки в малом*). Будем считать, что оболочка длиной L шарнирно оперта по торцам. Воспользуемся дифференциальным уравнением (17); оно принимает в данном случае вид
х’-+£ + ',(£)-* ‘-а»
Граничные условия для w будут
п п л г
w = О, = О при л; = О, L.
Определенных условий, относящихся к перемещениям и, v, ставить
не будем.
В качестве первого варианта решения примем, что изогнутая поверхность оболочки после выпучивания является осесимметричной, т. е. что поперечные сечения остаются круговыми. Тогда w будет зависеть только от а; и уравнение (30) переходит в следующее:
D dbw. d6w. Е dAw л 1t
A dx* Р dx6 + R2 dx* ~ (11.30а)
Примем для w выражение
w = f sin-, (11.31)
удовлетворяющее граничным условиям; здесь т — число полуволн изогнутой поверхности вдоль длины. Очевидно, при таком характере выпучивания каждая продольная полоска находится в тех же условиях, что и сжатый стержень на упругом основании (см. главу III); таким «основанием» здесь служат дуговые волокна.
Подставляя (31) в уравнение (30а), находим:
' = 4 + 4’ (П.32)
где \ = mtKR/L = v:Rllx. Определим минимальное значение р, приравнивая нулю производную от р по X; при этом мы считаем т> 1.
Тогда получим:
Х = 12(1 — р2)]/~ (11.32а)
*) Решение этой задачи, принадлежащее Р. Лоренцу [U*45J и С* П. Тимощенко [11.23], было дано в 190В—J9J4 гг.
§ 126] СЖАТИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ВДОЛЬ ОБРАЗУЮЩЕЙ
473
Обозначим через рв верхнее критическое значение напряжения, соответствующее точке бифуркации для линейной задачи; предыдущие соотношения дают
рв =. 1 Е —. (11.33)
/3(1—) R к ’
При = 0,3 будет
pB = 0,605£-jp (11.34)
Формула (33) является фундаментальной в теории устойчивости оболочек. Она показывает, что отношение верхнего критического напряжения сжатия к модулю упругости материала — того же порядка,
что и отношение толщины оболочки к радиусу кривизны срединной
поверхности.
Судя по (32а), длина полуволны 1Х равна
/, = -4 - уш. (11.35)
к 12 (1-1**) так что величина ее — порядка УRh.
В случае весьма короткой оболочки, если (L/R)2< 1, надо
положить т= 1, и дифференцирование выражения (32) по X ста¬
новится неправомерным. Но тогда X будет велико, так что вторым членом в (32) окажется возможным пренебречь по сравнению с первым; отсюда
Р«р = ППТ- (П-32Ь)
Мы получили формулу Эйлера для полоски, вырезанной из оболочки в направлении образующей.
Обратимся теперь к более общему варианту решения задачи и допустим, что изогнутая поверхность не является осесимметричной; тогда надо исходить из дифференциального уравнения (30). Примем для w выражение, также удовлетворяющее граничным условиям:
w = f sin--sin--, (11.36)
где т — число полуволн по образующей, п — число полных волн вдоль окружности.
Подставляя (36) в уравнение (30), находим:
D (т2п2. /г2 \4. Е т4п4 (т2п2 п2 \2 т2ъ2 л /ЛЛ 0<7Ч
1Г(-Р- + Ж) +1? — + - = 0- (1137)
Введем безразмерные параметры
pR а mnR n2h
474 УСТОЙЧИВОСТЬ ЦИЛЙНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ (гл. XI
Отметим, что величины и г\ можно выразить через длины полуволн изогнутой1 поверхности вдоль дуги (ly = izRjn) и по образующей (lx — L/m):
lv %2Rh
* = 4 = (H.38a)
x у
Таким образом, параметр Ь характеризует очертания вмятины,
а т] — длину полуволны /у. Из (37) находим:
~ 1 (1+02)2
Р— 12(1 — 1*2) о* 4-1- (1 + 02)2 • UA.ayj
Считая числа w и п достаточно большими, найдем минимум р из
условия
др
где
это дает
= 0,
<?Р
(1 + О2)2 Р = о2 Ч
р= у 12(1 — tx2).
Верхнее критическое значение параметра р равно
'■=7Щ=РГ~0-605- (“'40)
Соответствующее напряжение рв определяется формулой, в точности совпадающей с (33).
В рамках приведенного решения нельзя установить однозначно форму волнообразования оболочки; величины 7] и должны лишь удовлетворять условию
ч(Ь +г)2== -f*2)3,3. (11.41)
Если предположить, что волны являются квадратными (fr=l), получим т] = 0,825; отсюда
ив« 0,91 (11.42)
Следовательно, потеря устойчивости оболочки в малом с образованием вмятин, расположенных в шахматном порядке, происходит при том же критическом напряжении, что и в случае осесимметричного выпучивания, причем число волн вдоль дуги — порядка YRjh. Мы увидим
в дальнейшем, что этот вывод относится только к изотропным обо¬
лочкам.
§ 126]
СЖАТИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ВДОЛЬ ОБРАЗУЮЩЕЙ
475
Аналогичные результаты можно получить, исходя из уравнений относительно перемещений, по таблице 11.2. При этом надо положить
и = A cos
rrmx
L
sin
пу R ’
v = В sin
тпх
L
cos
пу R ’
(11.43)
w = С sin
тъх
L
sin
пу
R J
и ввести в третье уравнение грузовой член
1 — м.2 id2w d2w
= где
тогда придем к системе алгебраических линейных уравнений относительно А, В, С. Приравниваем нулю определитель, составленный из коэффициентов при этих величинах:
X2-
1 - Iх и2
2 П
= 0, (11.44)
д,Х п е (я2+Х2)2 --1—Х2ср
где по-прежнему Х = tmzRIL = n и е = h2/\2R2. Находим отсюда ср:
+, (l-f*2)X*.
? X2 “1 (п2 + X2)2 ’
это соответствует выражению (39) для р.
Все приведенные выше формулы относятся к случаю п2> 1, при более общем решении задачи мы должны исходить из системы уравнений по таблице 11.1. Если воспользоваться выражениями (43) для и, v, w, то придем к следующему уравнению ♦):
1+И-
И2
\п
хХ
= 0.
2 2
Хл (1 +е)п2-1- * — Х2ср п [ 1 -\-eti (я2+Х2)]
\хк п [ 1 + еп (п2 + X2)] е (/*2-f-X2)2+1 —Х2ср
(11.44а)
Определяя отсюда <р и р в зависимости от относительной длины оболочки и числа волн, приходим к результатам, изображенным на
*) См. книгу Ван Цзи-де [21.21], стр. 396.
476 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах упругости [гл. XI
рис. 11.3*). Здесь по оси абсцисс отложены (на участках а и б рис. 11.3) различные величины:
_ 12(1-) l /Т 1 L „ГТГ
0)1 « ~RV Т' Ш2 — -4 У -R •
пу 12(1 —р.*) *
а по оси ординат — величина kp, где = Л — ц2. Очевидно, рис. а относится к коротким оболочкам, рис. б — к длинным. Нисходящая линия в левом углу рис. а соответствует уравнению (32Ь);
;
0,8
0,6
0,5
Ofi
0,3
0.2
0.1
S—
\
X
0,50,6 0 1.0 {5 2.0 0.02
а) (°>
02 0,3 Ofi 0,50.6 03 W 1.5
б)
Рис. 11.3. Значения верхнего критического напряжения в случае сжатия вдоль образующей.
каждая полоска оболочки выпучивается, как пластинка. Далее мы получаем горизонтальную линию на уровне l/]/3 = 0,577, что отвечает выражению (33). Числа п здесь настолько велики, что изменение при переходе от п к (п— 1) является незаметным. Однако в правой части диаграммы, для относительно длинных оболочек, переход от одного целого числа п к другому становится ощутительным. На (рисунке изображены лишь нижние части кривых для разных я, лежащие между точками их пересечения. Как видим, при 4 значения рв лежат близко к значению (33). Однако при п = 3 к, особенно, при п = 2 минимум рв резко отклоняется вниз. Наконец, справа кривая п = 2 ограничена линией п= 1; эта линия отвечает
*) График рис. 11.3 построен для fx =* 7в и R/h = 100, см. книгу Флюгге [10.18], стр. 248. Участки, лежащие между кривыми п = 2, п = 1 и т. д., получены параллельным переносом ветвей, лежащих слева; они отвечают другим формам волнообразования.
§ 126] СЖАТИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ВДОЛЬ ОБРАЗУЮЩЕЙ 477
эйлеровой форме потери устойчивости оболочки как стержня; в самом деле, при п = 1 любое сечение трубы перемещается, как жесткое целое.
Радиус инерции кругового сечения тонкой трубы равен / = RlY\ эйлерово напряжение равно os = tz2ER2/2L2, при этом
H2R* р~ 2L2h *
Таким образом, здесь мы переходим от местной потери устойчивости к общей. Рассмотрение рис. 11.3 позволяет определить область значений L/R, для которых можно считать справедливой формулу (33). Слева она ограничена значением о>10,8, справа — значением о)2~0,1. При этом отношение L/R лежит в пределах
‘•з8/?<4<°'57/¥-
что приблизительно соответствует (18Ь). Например, при R/h= 100 находим 0,14 < L/R < 5,7. Как видим., границы применимости теории оболочек средней длины сравнительно велики и охватывают значительную часть диапазона значений L/R, встречающихся на практике.
Рассмотрим теперь более подробно случаи п = 2 и п = 3, когда оболочка выпучивается с образованием длинных волн. В § 125 подготовлен для этого аппарат полубезмоментной теории оболочек. Воспользуемся уравнением (25). Здесь надо принять перемещения v и w
d2v
сравнимыми между собой и положить в,(24) qx=cOtqy = — ph, d2w
Яг = — рЬ-ш> TOra
п» д ( u \ дг I u d*w \
д \р №до?) \р R*da*)‘
Но из исходных соотношений (стр. 468) следует: = w, поэтому
г>* h д2 ( d2w \
Р R* W Г ) *
Полагая w = W (a) sin nfi, приводим (25) к виду *)
EhR2 4n*-\yw = -phR44n?+\).
(11.25a)
Принимая W = f sin mitRa/L, получим:
g_ В ГА2 гп*(п2-1)2-. p ~ n2 + 1L n* X2 (1 — jx2) J *
*) Уравнение типа (25a) выведено для подкрепленной оболочки другим путем К. Д. Туркиным [11.24].
478 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
где по-прежнему e = h2/\2R2. Минимизируя р по X, находим: X2 = е11*п2 (п2 — 1)/(1 — [л2)1/-; отсюда
Г— 1 ”2-1
/3(1-)п* + 1
или, при jjl = 0,3,
P.«0,605-j£=i. (11.45)
Эту примечательную формулу можно получить также из общего уравнения (44а), пренебрегая некоторыми членами. Весьма интересен предельный случай п = 2, когда минимум рв уходит далеко вниз; из (45) находим: рв — 0,363. Таким образом, здесь рв составляет 0,6 от «классического» значения. При п = Ъ это отношение равно 0,8. При п2§> 1 отсюда снова получаем рв0,605.
Итак, для весьма длинных оболочек мы должны получить снижение критического напряжения по сравнению с (33).
§ 127. Нелинейная задача
Как мы видели, верхнему критическому напряжению (33) соответствует форма изогнутой поверхности по (31)—при осесимметричном выпучивании и по (36) — при отсутствии симметрии. Эти два варианта изображены на рис. 11.4, а и б. Однако характер выпучивания реальных оболочек средней длины не согласуется ни с одним из этих вариантов. Вместо вмятин прямоугольного очертания, расположенных в шахматном порядке и обращенных поочередно к центру и от центра кривизны (рис. 11.4, б)> в действительности образуются ромбовидные вмятины, похожие на грани кристалла, как показано на рис. 11.4, в. Эти вмятины, глубина которых уже в первоначальный момент сравнима с толщиной оболочки, появляются обычно в процессе резко выраженного хлопка. В большинстве случаев вмятины составляют два или три смежных пояса. Однако в отдельных опытах со тщательно изготовленными образцами удается получить сетку ромбовидных углублений на всей поверхности оболочки или на большей ее части. Таким образом, здесь совершенно четко реализуется потеря устойчивости оболочки в большом. Отсюда вытекает необходимость решения задачи с позиций нелинейной теории; впервые оно было дано Карманом и Цянь Сюэ-сэнем [11.27]. Эти авторы использовали такой же метод, какой обычно применяется в теории гибких пластинок (см. главу VII). Он состоит в выборе аппроксимирующего выражения для прогиба wt содержащего несколько варьируемых параметров, и подстановке этого выражения в правую часть уравнения (27). Интегрирование этого уравнения определяет функцию напряжений Ф. Далее вычисляем энергию системы; варьируя энергию по параметрам прогиба, находим диаграмму равновесных состояний оболочки. Задача
§ 1271
НЕЛИНЕЙНАЯ ЗАДАЧА
479
осложняется тем, что в процессе выпучивания число и размеры вмятин являются переменными; поэтому диаграмма равновесных форм представляет собой огибающую некоторой серии кривых, отвечающих тем или иным числам волн. В работах других авторов, опубликованных за последние два десятилетия, были предложены уточненные
а) б) б)
Рис. 11.4. Различные формы выпучивания оболочки: а) осесимметричная, б) «шахматная», в) ромбовидная.
варианты решения задачи. В некоторых работах вместо метода Ритца был использован метод Бубнова—Галеркина в применении к уравнению (26).
Приведем один из наиболее простых вариантов решения задачи с помощью метода Ритца *). Выберем выражение для w в виде
= /lSin-Sin- + /2Sin2- + /0. (11.46)
Первый из этих членов взят исходя из решения задачи об устойчивости в малом и совпадает с (36). Второй член отражает несимметричность прогиба относительно срединной поверхности, с преимущественным направлением к центру кривизны. Если, суммируя
*) Это решение принадлежит П. Г. Бурдину.
480 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕк В ПРЕДЕЛАХ УПРУГОСТИ (гл. XI
первые два члена, построить линии равного прогиба, то они дадут очертания вмятин, напоминающие рис. 11.4, в. Наконец, третий член в (46) соответствует радиальным перемещениям точек, принадлежащих торцевым сечениям, при л: = 0, L. Этот член не зависит от у: считается, что при выпучивании оболочки торцевые сечения остаются круговыми.
Введем обозначение
г = - = я (11.47)
для отношения длины полуокружности к длине полуволны вдоль
образующей; вместо (46) получим:
•a» = /,sin-- sin-- + /2sin2- + /0. (11.48)
Подставляя (48) в правую часть уравнения (27), находим:
Т~-Лф(“тг+С“т?) +
+ /Л-91 (stH sin % - sin +
+ 2/cos. (11.49)
Интеграл этого уравнения будет
+ А/»*-2»2 [<*h)sin ITsin- W7T)sin nrsln nr] +
+ Asinsin--/2cos--; (11.49a)
здесь под p понимается среднее значение сжимающих усилий в торцевом сечении; введено обозначение
(аг, Ьп) = [(аг)2 + (Ьп)2]2. (11.50)
Зная функции Ф и w, можно определить напряжения и деформации в срединной поверхности, а также перемещения и и v. Особое внимание надо уделить тому, чтобы эти функции удовлетворяли
условию периодичности или замкнутости. Это относится, прежде
всего, к перемещению v: приращение v при изменении у на 2tzR должно быть равно нулю:
2те/?
/
= 0. (11.51)
§127] НЕЛИНЕЙНАЯ ЗАДАЧА 481
Пользуясь соотношениями (10.98) и.(13), находим:
dv. 1 / dw\2 w п. R04
b = -iy + -2Uy) ~R’ (U-52)
1 (дЩ д2Ф\,n
sy~ E [dx2 ay2)’ (11.53)
отсюда вместо (51) получим:
2icR
Л1 / д2Ф д2Ф\ 1 (dw\2, w 1, л /11 с >1ч ~Ё\Ш *~ду2)~ 2 Uy ) (11.54)
о
Подставляя (48) и (49а), находим:
-7I = — Р f\ (11.55)
Определим, далее, полную энергию системы:
Э=ис-\-ии — W, (11.56)
где Uc — потенциальная энергия деформации срединной поверхности, ия — потенциальная энергия изгиба, W — работа внешних сил. Первые две величины находим по формулам (10.95). Для вычисления работы усилий р найдем среднее значение сближения точек, принадлежащих торцам оболочки:
—/К-(1,57)
о о
тогда
L 2* R
IV/ Ь С Г /д2Ф\ Гд2Ф д2Ф E(dw\21, /t < еоч
о о Окончательно
W'-)+{w /;(г<+«*)+
+ПП w [)+<]+«,/?(7fir+f П-
- т Л/»* [:1 + wht] }'-*тг г’-'ым? (Лш+ Я - дг) •
(11.59)
Решая задачу в первом приближении, будем варьировать энергию по двум параметрам:
_0. Ц = 0. (11.60)
482 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах УПРУГОСТИ [гл. X
Введем обозначения в дополнение к (38):
тогда уравнения (60) примут вид ?)(1+»4)
7lsi 1 / 8{И \ ~
12(1 — (х2) s2 t*2 = P- (11.62)
г i ч»2
U»V23(i—t*2) р\
Ч=-г
16Э2
(1+тК(тЧК
(11.63)
где
s, = 1 + »« s2 = 1 -f 9»2.
Подставляя С2 по (63) в (62), приходим к уравнению, связывающему
р и С2, а считая С2 = 0, — к прежней формуле (39) для р, полученной с помощью линейной теории. Выбирая, далее, определенные
А
Р 0.4
0,3
0,2
0,1
V 1
0,25
0,20
X
V
1
50
1 0,45 OJk
од
> V.
Г
17 - 0,15 /
”71
0J68
1
_
Г
1
0,1 Я
II
5
1
12 3 4 5 6
Ьг
Рис. 11.5. Равновесные формы оболочки при 0 = 1у!1х = 0,5; к исследованию в первом и втором приближениях.
значения и tj, строим кривые р(С2). На рис. 11.5 и 11.6 показаны две серии таких кривых для ft = 0,5 и = 0,6; вычисления были также приведены для 12 других значений ft, лежащих в пределах 0,3 < ft <2,4. Пунктирные линии являются огибающими кривых,
§ 127]
НЕЛИНЕЙНАЯ ЗАДАЧА
483
соответствующих различным значениям tj. При сопоставлении всех вариантов оказалось, что наименьшая величина р — нижнее критическое напряжение — соответствует параметрам 0 = 0,6, tj = 0,19, Cj = 7,2, Сг = 3,04 и равна рн = 0,124.
Рис. 11.6. Равновесные формы оболочки при Ь = 1у/1х = 0,6.
Во втором приближении будем варьировать энергию системы дополнительно по й и составим уравнение
Ж- = °: <-б4)
оно получает вид
_ Т (2.
202
162
-тгЬг]=°-<“-65)
Комбинируя уравнение (65) с (62) и (63), находим новую зависимость р(С2). Соответствующие кривые для различных т] и 0 показаны на рис. 11.5 и 11.6 пунктирными линиями. Соединяя вновь полученные точки пересечения, находим новую огибающую (сплошная линия). На рис. 11.7 сопоставлены огибающие для различных Наименьшее значение р имеет место при 0 = 0,48, т) = 0,4, ( = 3,45, С2=1,9 и равно /?н = 0,186. Таким образом, во втором приближении нижнее критическое напряжение оказалось равным
рн = 0,186, (11.68) что составляет приблизительно 30% от верхнего значения (34).
484 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах УПРУГОСТИ [гл. XI
Полученные данные позволяют построить диаграмму зависимости параметра нагрузки от величины е, характеризующей взаимное
Рис. 11.7. Равновесные формы оболочки приО=* = iy/ix = 0,48. Нижнее критическое напряжение соответствует /Г =0,186.
Рис. 11.8. Диаграмма «сжимающее усилие — сближение краев».
сближение торцов оболочки: = ДR/Lh. По формуле (57) находим: e = ? + -(tf +jd). (11.67)
При Cj = С2 = 0 получаем прямую е = р, изображенную на рис. 11.8; она соответствует исходному равновесному состоянию. Точка бифур*
§ 127]
НЕЛИНЕЙНАЯ ЗАДАЧА
485
нации А отвечает рв = 0,605. Здесь ответвляется кривая ABC изогнутых форм, разные точки которой отвечают различным 0 и rj; значения указаны на рисунке. Как видим, переход от неустойчивых форм к устойчивым и дальнейшее развитие закритической деформации связаны с возрастанием параметра ; судя по (38а), это означает, что вмятины вытягиваются вдоль дуги. Надо полагать, что на участке АВ параметр 0 резко падает, а вблизи точки В начинает постепенно возрастать.
Итак, закритическая диаграмма р (е) состоит из «падающей» ветви, соответствующей неустойчивым равновесным состояниям, и «восходящей» ветви устойчивых состояний. Мы считали, что процесс перехода от одних равновесных форм к другим является статическим. Но так как неустойчивые равновесные состояния не осуществляются, то оболочка должна перейти от начальной формы к изогнутой устойчивой форме динамически, путем хлопка.
В § 118 мы говорили только о таком случае, когда хлопок происходит при неизменней внешней нагрузке. Но этот случай сравнительно редко осуществляется на практике. Если бы оболочка была расположена вертикально и подвергалась сжатию грузом определенного веса, то требование р = const могло быть реализовано, однако такие опыты провести трудно. При сжатии оболочки в испытательной машине можно также создать фиксированную нагрузку, но для этого машина должна быть снабжена специальным приспособлением, включающим газовую «подушку»: во время хлопка оболочки содержащийся в такой «подушке» газ (например, воздух или азот*)) расширяется, поддерживая давление неизменным. Другой предельный случай состоит в том, что в процессе хлопка фиксируется общая деформация оболочки е. Такое требование е = const может быть осуществлено лишь в условиях весьма жесткой испытательной машины, расстояние между плитами которой остается при хлопке неизменным. Обычно, однако, конструкция испытательной машины является упругой, так что при резко возрастающей деформации оболочки одновременно снижается приложенная к ней нагрузка. Это можно иллюстрировать рис. 11.9: сжатая пружина А, моделирующая упругую часть нагружающего
*) Во избежание взрыва лучше пользоваться азотом.
Рис. 11.9. Оболочка в испытательной машине.
486 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
устройства машины, разгружается при хлопке оболочки. В реальных конструкциях элементы, связанные с оболочками, обычно также являются упругими. Характер хлопка в двух предельных случаях и при наличии упругой связи изображен на рис. 11.10. Обратный хлопок должен произойти по пунктирным линиям. Так или иначе, диаграмма равновесных состояний ограничивается снизу нагрузкой рн,
поэтому, как было уже сказано в § 118, для практических расчетов она представляет большой интерес.
Обратимся к другим решениям задачи об устойчивости сжатой цилиндрической оболочки в большом. В книге [0.3] подробно изложен вариант решения задачи, принадлежащий В. J1. Агамирову, с выбором аппроксимирующего выражения для w в виде
х. тъх. пу. х. 9 ткх. 9 пу..,л л с<<\
w = Д sin —j- sin -\-f2 sin2 —J— sin2 -t- /о, (11.68)
отличающегося от (48) вторым членом. Величина рн оказалась в первом приближении равной (при варьировании энергии по двум параметрам) 0,284, а во втором (при четырех варьируемых параметрах)— 0,334; соответствующее значение = 0,59. Сравнение с предыдущим вариантом показывает, как влияет малозначительное, казалось бы, изменение структуры второго члена в (48) на результаты решения: значение рн возросло примерно в два раза. Это
относится и к другим нелинейным задачам по устойчивости оболочек. Подобно тому как реальные оболочки резко реагируют на малые возмущения, что приводит к большому разбросу критических напряжений (см. § 129), результаты решения соответствующих задач по методу Ритца сильно меняются даже при незначительном изменении аппроксимирующего выражения для прогиба,
§ 128]
ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ЗАДАЧЕ
487
В первоначальном решении Кармана и Цянь Сюэ-сэня [11.27]
второй член выражения (48) был выбран в виде /2 (cos -[-cos
и было получено для квадратных волн (0 = 1) /?н = 0,194. Позднее Михилсен [11.46] нашел в уточненном решении рн= 0,195. Кемп-
нер [11.38] ввел вместо второго члена выражение /2cos —тх --
+ /3C0S~r~) и провел варьирование по пяти параметрам (fv /2,
/з» и ЧУ в результате было получено /?н = 0,182 при 0 = 0,36.
Таким образом, имеющиеся решения по методу Ритца *) приводят к значениям /?н, лежащим в пределах от 0,182 до 0,334.
Во всех перечисленных выше решениях параметр рн оказывался не зависящим от отношения R/h; это вытекало уже из структуры исходных соотношений. Однако С. А. Алексеев [11.2], пользуясь методом последовательных приближений, пришел к иному выводу, состоящему в том, что величина рн падает с возрастанием R/h.
Такая неопределенность найденных до сих пор значений рн вновь свидетельствует о большой чувствительности результатов приближенного решения к методике расчета. В дальнейших исследованиях большую роль должно сыграть применение цифровых электронных машин (см. § 139).
§ 128* Геометрический подход к задаче
Выбирая аппроксимирующее выражение для прогиба, мы стремились отразить склонность оболочки выпучиваться по ромбической форме. Подойдем теперь к явлению хлопка оболочки с геометрической точки зрения и постараемся более подробно изучить характер волнообразования, проявляющегося в результате хлопка. Если бы оболочка продолжала после потери устойчивости выпучиваться по той симметричной форме**) (31) или (36), какую отражает линейная теория, то это было бы связано с затратой значительной работы на деформацию срединной поверхности. Как было уже сказано в § 118, оболочка во многих случаях «предпочитает» выпучиваться внутрь, л именно потому, что при этом срединная поверхность не получает значительных деформаций растяжения — сжатия. Поэтому целесообразно рассмотреть такой предельный случай волнообразования оболочки, при котором дополнительная энергия деформации в сре¬
*) См. также работы Е. Д. Голицинской [11.6] и Н. Н. Леонтьева [11.13].
**) Под симметрией здесь условно понимается равенство стрел прогиба к центру и от центра кривизны.
468 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
динной поверхности вообще отсутствует *). Но как мы знаем из § 118, при этом изогнутая поверхность должна быть изометрична первоначальной поверхности кругового цилиндра. Иными словами, гауссова кривизна в каждой точке новой поверхности должна остаться равной нулю.
Такое геометрическое изгибание не является непрерывным и осуществляется в процессе хлопка оболочки.
Чтобы получить искомую поверхность, изометричную круговому цилиндру, поступим следующим образом. Пусть дана правильная
призма с четным числом граней, как изображено на рис. 11.11. Проведем на одной из боковых граней otj некоторую гладкую кривую однозначно проектирующуюся на ось призмы; на рисунке эта кривая изображена для примера в виде синусоиды, нулевые точки которой проходят через среднюю линию грани. Далее нанесем на соседней грани а2 кривую 72» являющуюся зеркальным отображением относительно плоскости р12, проходящей через ось призмы и ребро Ь12. Повторяем такое же построение для следующих граней, тогда получим кривые 73, 74 и т. д.
Построим теперь цилиндрическую поверхность Z12 таким образом, чтобы она проходила через кривые 7lt у2 и чтобы ее образующие были перпендикулярны к плоскости (312 (рис. 11.11,). Этим же путем проведем поверхности Z23, ZM и т. д. Трубчатая поверхность, состоящая из Z12, Z23,..., и является искомой. Это легко показать.
В самом деле, очевидно, что в точках, не принадлежащих кривым Ti> Т2» • • •» вновь образованная поверхность имеет нулевую гауссову кривизну, так что она изометрична исходной. Но и в точках кривых 7!, 72,... изометрия сохраняется, так как, если отразить цилиндрическую поверхность Z23 зеркально в плоскости грани а2, то полученная при этом поверхность Z23 будет являться продолжением поверхности Z12.
о)
6)
Рис. 11.11. К построению поверхности, изометричной цилиндру.
*) Подробные исследования в этой области принадлежат А. В. Погорелову [11.19], [11.20]. Ниже излагается предложенный им метод построения изометричных поверхностей. См. также статью Кирсте [11.38].
§ 128]
ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ЗАДАЧЕ
489
В поперечном сечении вновь образованной трубчатой поверхности чы получим замкнутую линию. Можно показать, что длина этой шнии окажется во всех сечениях одной и той же независимо от вида линий Yi» Т2» •••» она равна периметру правильного многоугольника (см. рис. 11.11, я), вершины которого совпадают с серединами сторон в сечении первоначальной призмы. Будем считать длину этой линии равной 2тг/?, где R— радиус кривизны изометричной цилиндрической поверхности. Отметим также, что длина линии пересечения трубчатой поверхности с плоскостью, проходящей через ось призмы и любое ребро, равна высоте цилиндра.
Следовательно, полученная трубчатая поверхность изометрична круговому цилиндру радиуса R.
Так как этот вывод не зависит от вида кривой у, то подобное построение является, по существу, универсальным.
По мере развития закритической деформации оболочки форма изогнутой поверхности должна изменяться; это можно отобразить, увеличивая амплитуду синусоиды по рис. 11.12, а. Если теперь заменить синусоиду прямолинейными отрезками со сглаженными участками в местах сопряжений, то в пределе получим поверхность, изображенную на рис. 11.12, б’. Мы пришли к тем характерным «граням кристалла», о которых говорилось в § 127. Таким образом, геометрический подход к задаче позволяет исследовать характер поверхности оболочки после хлопка с качественной стороны. Можно попытаться использовать полученную изометрическую модель и для количественной оценки нижнего критического напряжения.
Коль скоро мы пренебрегаем деформациями в срединной поверхности, связанные с ними нелинейные члены в основных уравнениях выпадают. Потенциальная энергия деформации оболочки при выпучивании будет состоять только из энергии изгиба.
Познакомимся сначала с приближенным методом Кирсте [11.39], заключающимся в выделении из оболочки в продольном направлении криволинейных полосок. Рассматривается устойчивость подобной полоски радиуса R, длины 1Х и ширины 1у, сжатой вдоль длины, с учетом «упругого основания», образующегося благодаря поддерживающему влиянию дуговых полосок (см. пример 3.4, стр. 143).
о)
6)
Рис. 11.12. Изометричная цилиндру поверхность с «гранями кристалла».
490 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Сечение двух соседних полосок показано на рис. 11.13. Момент инерции полоски приближенно принимается равным / = /у/г/720/?2. Считая, что в поперечном направлении полоска изогнута по синусоиде «aj = /sm(>ry//y), определяем реакцию упругого основания, приходящуюся на единицу прогиба:
Определяя критическое напряжение ркр по формуле типа (3.115), найдем:
s _ я2/Я I r l*R — n2R ( ly I
Ркр ~ l%h2 ъЧуК 6 (1 - ц*) h \ 120/?2/2 Ъ1\)'
Минимизируя ркр, получим:
Ь- = л/~ — Rh, ркр = —=. яь 0,187. (11.69)
/2 V « кр 3 (1 — н-2) /120л v '
Первое из этих равенств дает в обозначениях § 126 = 0,75 *1.
Интересно отметить, что такой элементарный подход приводит к ве.
личине ркр, весьма близкой к нижнему критическому напряжению § 127; даже соотношение между Ь и rj отвечает данным приведенного выше варианта решения по методу Ритца.
В работе А. В. Погорелова ([11.19], части 1 и 2) дано определение рКр с помощью энергетического метода, исходя из описанного выше представления изогнутой поверхности. Потенциальная энергия изгиба вычисляется отдельно для гладких участков поверхности и для зон, прилегающих к гребням на границах вмятин. В одном из вариантов решения было принято, что вмятины являются квадратными, а линии j были представлены прямолинейными участками, сопряженными между собой дугами парабол. Нижняя критическая нагрузка для упругой оболочки определялась из условия «смыкания» гребней соседних вмятин, и было получено рн = 0,138. Если же линии j выбрать в виде дуг синусоид, то при различных предположениях относительно начального напряженного состояния оболочки будет />„ = 0,15 и /*„ = 0,18,
Рис. 11.13. К приближенному определению нижнего критического напряжения.
§ 129]
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
491
§ 129. Результаты экспериментов.
Данные для практических расчетов
Обратимся к экспериментальным данным, относящимся к величине критического напряжения и характеру волнообразования. Данные эти являются разноречивыми, так как сильно зависят от начальных неправильностей в форме оболочки и условий нагружения.
Рассмотрим прежде всего результаты испытаний металлических оболочек, изготовленных с большой тщательностью, — как правило, обточкой на токарном станке по специальному копиру, с минимальными отклонениями толщины стенки и радиуса кривизны от заданных величин *).
В подобных испытаниях еще до хлопка удается наблюдать — лучше всего по искажению световых полос на поверхности образца — образование едва заметных прямоугольных вмятин того
типа, какой отвечает выпучиванию в малом по
рис. 11.4, tf. Такие предварительные вмятины оказываются примерно «квадратными»: размеры их вдоль образующей и по дуге близки между собой. Затем происходит резкий хлопок, после которого на образце появляются вмятины
ромбического типа по рис. 11.4, в, причем и здесь диагонали вмя¬
тины получаются приблизительно равными. Нагрузка, регистрируемая манометром машины, при хлопке резко падает. Если же продолжать нагружение образца, то усилие сжатия слегка повышается, а вмятины вытягиваются вдоль дуги. К сожалению, при испытаниях стальных или дюралюминовых образцов обычно не удается провести опыт в чистом виде, так как в зонах, прилегающих к гребням вмятин, образуются пластические деформации. Если бы равновесные формы оболочки сменялись статически, по диаграмме р(е) рис. 11.10, то первоначальные вмятины, отвечающие точке А на рис. 11.14, должны были бы сильно вытянуться вдоль образующей, как показано для точки £, и лишь затем постепенно изменить форму, удлиняясь по дуге. Но в реальном динамическом процессе оболочка, по-видимому, «проскакивает» промежуточные равновесные формы, так что
*) Такие испытания были проведены Л. Р. Исправниковым, В. Л. Агамировым и др. авторами, см. [0.3], стр. 320—325.
Рис. 11.14. Формы вмятин при различных вариантах хлопка.
492 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
на диаграмме рис. 11.14 мы попадаем непосредственно в точку С с «квадратными» вмятинами. Параметр напряжения, при котором гроисходит хлопок, для таких образцов составляет ркр 0,230,35. Как видим, даже при весьма тщательном проведении опыта критическое напряжение составляет лишь около половины от верхнего значения рв.
Рис. 11.15. Последовательные стадии образования ромбовидных
вмятин.
При испытаниях оболочек, изготовленных более грубо — например, из свернутого плоского листа,—обычно можно заметить уже при малых нагрузках образование одиночных вмятин в местах, где имеются те или иные возмущения — начальная погибь или концентрация напряжений. В дальнейшем происходит серия хлопков, ведущих к появлению новых вмятин.
Такой прэцгсс отражен на фотографиях рис. 11.15, относящихся к стальным оболочкам (L/R = 1,4, R\h = 1870) *). В конечном счете
*) Эти фотографии получены Канемитцу и Найима (S. К a n е ш i t s u, N. М. N о j i m a).
§ 129]
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
493
образуется та же система ромбических вмятин, что и в случае тщательно изготовленных образцов.
На рис. 11.16 указана область экспериментальных значений /?кр, взятых из работ различных авторов. Как видим, величина рв = 0,605 действительно является верхней границей для реальных критических напряжений. Из теоретического исследования вытекает, что выпучивание оболочек должно происходить при безразмерных напряжениях, лежащих между рн и рв. Так как окончательное значение рн еще
Рис. 11.16. Область экспериментальных данных для критического напряжения сжатия.
не найдено, трудно судить о том, насколько это предположение осуществляется. Значительная часть опытов приводит к значениям /?кр, лежащим выше 0,18. Однако некоторые экспериментальные точки лежат ниже этой величины и в отдельных случаях оказываются равными 0,06-f-0,15. Рис. 11.16 указывает на явную тенденцию к падению ркр при возрастании*) отношения R/h. Такой результат,
как мы видели, не был получен ни в одной из работ, основанных на методе Ритца, и вытекал лишь из исследования С. А. Алексеева. Надо иметь в виду, что по мере увеличения R/h вероятность появления начальных прогибов должна повышаться; это, несомненно, должно приводить к снижению средней величины реальных критических напряжений (см. главу XX). Подтверждение этому мы находим в статье [11.33, 1957 г.], содержащей статистическую обработку ряда экспериментальных данных. Будем, например, определять нижнюю границу критических напряжений, исходя из того требования, чтобы вероятность попадания экспериментальной точки в вышележащую
*) Снижение /?кр при весьма малых R/h объясняется тем, что в этой области выпучивание оболочек происходит за пределами упругости (см. следующую главу).
494 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
область составляла 90% или 99% *); тогда получим следующие значения р в зависимости от Rjh:
R/h
250
500
750
1000
1500
2000
2500
По критерию 90% вероятности 0,18
0,16
0,14
0,13
0,11
0,09
0,08
По критерию 99% вероятности 0,14
0,12
0,10
0,08
0,07
0,065
0,06
Как видим, при увеличении Rjh значения р действительно резко падают.
Какие же данные надо положить в основу практических расчетов? Общее требование, изложенное в § 118, состоит в том, что эксплуатационная нагрузка должна определяться со значительным коэффициентом запаса по отношению к верхней критической величине рв и, как правило, лежать ниже рн. В рассматриваемом нами случае верхняя критическая нагрузка настолько высока по сравнению с экспериментальными значениями, что допускаемые напряжения следует определять, исходя из нижней критической нагрузки, найденной теоретически и вместе с тем с учетом данных опытов. Такое сопоставление приводит к следующей таблице значений /?расч, которой рекомендуется пользоваться на практике для тщательно изготовленных оболочек, в пределах упругости.
R/h
<250
500
750
1000
1500
Р расч
0,18
0,14
0,12
0,10
0,09
Если же оболочки изготовляются недостаточно тщательно и начальные прогибы достигают величины порядка толщины h, расчетные значения р следует снижать примерно вдвое. Начальные прогибы, заметно превышающие толщину оболочки, вообще недопустимы, так как жесткость конструкции при этом резко снижается.
*) Приведенные ниже таблицы составлены Б. М. Броуде на основании данных, имеющихся в статье [11.33] и других работах.
§ 130]
СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ. ЛИНЕЙНАЯ ЗАДАЧА
495
§ 130. Случай внешнего давления. Линейная задача
Перейдем к случаю, когда оболочка подвергается действию равномерно распределенного по боковой поверхности внешнего давления q (рис. 11.17). Такой вид нагружения характерен для корпусов подводных лодок и оболочек авиационных двигателей. Резервуары в химической промышленности также часто испытывают избыточное внешнее давление.
Допустим, что по торцам оболочка шарнирно скреплена со шпангоутами, точки которых могут получать некоторые радиальные перемещения, причем шпангоуты остаются круговыми.
Рассмотрим задачу об устойчивости такой оболочки сначала в линейной постановке *). Если круговая оболочка подвергается действию внешнего давления q и изгиб оболочки отсутствует, то из
уравнений (6) получим при Qx = Qy = 0 напряжение вдоль дуги равным зу = — qR\h. Таким образом, действие поперечной нагрузки q эквивалентно действию сжимающих напряжений py=zqRjh. Поэтому мы можем воспользоваться однородным уравнением (17), учитывая лишь усилия р \ тогда получим:
т’-+££+г *•(£)-<•• С»-*»
Примем для w то же выражение (36), удовлетворяющее граничным условиям, что и в случае сжатия; тогда вместо (37) получим:
Рис. 11.17. Цилиндрическая оболочка подвергающаяся внешнему давлению
D / т2те2. п2 \4
~Т\ТГ '
R2 L4
т(т?+Я-£‘“*
отсюда
гп /т2%2, п \2 « Eh 1
q_DR\jr+ R2J + —— -
\ №
n2L2 \2 R2m2Tz2 )
(П.72)
Очевидно, при определении критического давления надо принять т= 1. Следовательно, в отличие от случая осевого сжатия, при
*) Линейная задача была решена Р. Мизесом [11.47], а в дальнейшем X. М. Муштари и А. И. Саченковым [11.16] и другими авторами. Иные граничные условия были рассмотрены Н. А. Алфутовым (Труды Ереванской конференции по теории оболочек, 1962),
496 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
внешнем давлении оболочка должна выпучиваться вдоль образующей всегда по одной полуволне; это заключение подтверждается экспериментами. Введем обозначение
Подставляя (76) в выражение (74), определяем верхнее критическое значение qB:
Формулами (77) можно пользоваться, если выполняется условие (75). В противном случае надо вернуться к полному выражению (74) и найти значение я, отвечающее минимуму q. На рис. 11.18 представлены значения qQi вычисленные *) по (74) для большего диапазона отношений R/h и L/R.
*) Расчетные графики рис. 11.18 и 11.20 принадлежат В. Д. Нагаеву [11.17].
(11.73)
вместо (72) находим: h п2 q~ R 12 (1 — fx2)
Я2/?2\2
n2£2 )
r+
те4/?5 L'hn*
гс2Я2\2 ’ n2£2 )
1
)
(11.74)
Эта формула упрощается, если можно принять
(11.75)
тогда будет
1 n*h. п<Я5
Я ~ 12 (1 — (л2) Я г- L'hn* '
Минимизируя q по и, получим:
(11.76)
или, при х = 0,3,
(11.76а)
0,5
(11.77)
или, при (а = 0,3,
(11.77а)
Соответствующее окружное напряжение равно
(11,77Ь)
§ 130J СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ. ЛИНЕЙНАЯ ЗАДАЧА
497
Рис. 11.18. Расчетные данные для определения верхнего критического давления.
498 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах УПРУГОСТИ [гл. XI
Выражение (74) справедливо и здесь при условии 1 /я2<1, относящемся к исходному уравнению (71). Будем по-прежнему считать, что это условие выполняется при п >4. Случаи п = 2; 3 надо рассматривать, исходя из уточненного выражения для кривизны изогнутой поверхности вдоль дуги. Воспользуемся выражением (4), содержащим по сравнению с (12) дополнительный член (—w/R2); тогда вместо (10) получим:
лл гч I d2w, w, d2w \
My — — D(-df+-W+V--dW)'
Если ввести это выражение в третье из уравнений (8), а нагрузку д2 для задач устойчивости определить по (10.89), то придем к следующему уравнению *):
£[+7И2>*0 + 2+ж)]+
R2 дх4
Подставляя сюда выражение (36), получим:
D / т2п2. п2\2 i (т2ъ2. п2 \2. 1 Г1 0/ m2n2R2. о\П,
тЬт+т?) tb*4/?) +ж[1-2([Х-т+п2Ж+
Е гпАп4 q [ т2п2 п2 \2, 2 t л
1-23-+-) 1> = °-
R L* Rh
Отсюда при т= 1
*-{(£+*)*+т{г['-*ИР+*)]}+
+ -f73 <п-79)
(т*+)
Рассмотрим случай весьма длинной оболочки, когда L> R; выражение (79) переходит в следующее:
<7в=—з1—• (П.80;
Минимальное значение q находим при п = 2:
3D /it о 1 \
Яв дз • (11.81)
Отметим, что формула (72) дает при R q = n2D/R3\ при п = 2 будет qB = 4D/R3, что превышает (81) на 33%. Этот пример иллюстрирует то, что область применения приближенных уравнений теории оболочек средней длины является ограниченной и что погрешность результатов вычислений в отдельных случаях может бьт
*) Это уравнение было получено С. В. Александровским [11.1], а впоследствии Тилеманом [11.51], [11.52] для общего случая анизотропной ободочки.
§ 130] СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ. ЛИНЕЙНАЯ ЗАДАЧА 499
значительной *). Впрочем, с практической точки зрения такие случаи являются скорее исключениями.
Так как в случае внешнего давления оболочка получает вдоль образующей только одну вмятину, то, в отличие от задачи об осевом сжатии, здесь влияние граничных условий оказывается более заметным. Поэтому рассмотрим отдельно случай оболочки средней длины, защемленной по торцам.
Примем в качестве первого приближения выражение для прогиба в виде **)
да = 16/ (0 (i _ £-)2 sin 2L, (11.82)
удовлетворяющее условиям = 0, -=0 при л; = 0, L. Подставим (82) в правую часть уравнения (16); после интегрирования на¬
ходим:
ф = -32т(т)'тЧ[1 + 24Ш’]-6г+
+ 6(т)■}*■-£—*гтг- <и-83>
Уравнение (15а) при px = q = 0 и py = qR/h принимает вид
—— — 4-- —= 0 h R дх2 h ду2
Пользуясь методом Бубнова — Галеркина, составим уравнение
L
II Х{т)‘{'-т = (П-84)
о о
После интегрирования получим:
? = 12R (1 - [1 + 24 () +504 (--j
(11.85)
Верхнее критическое давление qB3 определяем, минимизируя q по п (при достаточно больших значениях п)\ оно примерно на 55% превышает величину qBt ш относящуюся к шарнирно закрепленным кромкам.
*) Пользуясь уравнением типа (79), можно составить график для qB, охватывающий весь диапазон отношений L/R, как на рис. 11.3; подобный график приведен в книге Флюгге [10.18].
**) Это решение принадлежит В. А. Нагаеву [11.17].
500 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI Если принять для w другое аппроксимирующее выражение*):
(11.86)
то аналогичный путь приводит к значениям qB3, лежащим несколько ниже (75) и превышающим qBtUJ приблизительно на 40%.
Однако выражения (82) или (86) для w, часто применяющиеся в теории устойчивости защемленных стержней или пластинок, дают
для оболочек средней длины значения критического давления, завышенные по сравнению с экспериментальными данными. На рис. 11.19 дан коэффициент т = qBt JqBt ш в зависимости от параметра L/R при R/h =100. Кривая 1 отвечает выражению (86); кривая 2 построена по данным работы О. М. Палия [11.18], в которой сделана попытка учесть влияние моментов защемления в соответствии с теорией краевого эффекта (см. стр. 471). Как видим, коэффициент k для малых отношений L/R действительно достигает значения 1,5 -г-1,6, между тем в случае L/R =1 равен лишь 1,08. Желательно в дальнейшем исследовать эту задачу более подробно.
16
1Л
12
1,0
\
\
\
г
0,5
10
L/R
Рис. 11.19. График, отражающий влияние защемления краев на верхнее критическое давление.
§ 131. Случай внешнего давления.
Нелинейная задача
Опыты показывают, что и в случае внешнего давления выпучивание оболочек происходит, как правило, в виде резко выраженного хлопка. Поэтому исследуем большие прогибы оболочки**). Сохраним схему решения, изложенную в § 127. Аппроксимирующее выражение для прогиба выберем в виде
w = fx sin ~ sin + /2 sin2 + /0, (11.87)
*) Этот вариант решения принадлежит В. Нэшу [11.48].
**) Эта задача рассматривалась Ф. С. Исанбаевой [11.9], В. Нэшем [11.48], В. А. Нагаевым [11.17], Н. А. Алфутовым [11.4]. Решение В. А. Нагаева подробно изложено в книге [0.3]. Здесь приведен вариант решения, принадлежащий П. Г. Бурдину.
§ 131] СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ. НЕЛИНЕЙНАЯ ЗАДАЧА 501
оно совпадает с (46), если принять т= 1. Вместо (47) примем обозначение
Уравнение типа (49) сохраняется. В выражение (49а) для Ф/Е должна быть введена величина
(-тт) вместо (-)*
Уравнение периодичности (51) принимает в отличие от (55) вид
А — _l /2 tl- /11 qq\
R — Eh ryi W 2R * Uboyj
Работу нормального давления будем вычислять по приближенной формуле
L 2
W = q ff wdxdy; (11.90)
о о
находим:
W = qTz RL (2/0 -- /2). (11.91)
Эту величину следует ввести в выражение для энергии (59) вместо
двух последних членов.
Сохраним обозначения (61); тогда уравнение (62) останется в силе, но с заменой р на q/Ь2; в уравнении (63) следует положить р = 0. Подставляя С? из (63) в уравнение (62), получим (при у\ = n2h/R):
884 о <И Г 1 I 1 1 Г
(1 4- 92)2 [(!_)_ 92)2 + (1 + 992)2 J [ (1 + »2)2 (1 + 9»2)2 ] **2+ (1 + 92)2 v -Г
I ч (I + в2)2 L Г1 _1_ 1 г — q (ц до’»
12(1—ц2) 4 [ (1 + »2)2 J — Я'
Это уравнение определяет q как функцию параметра. Полагая С2 = 0, находим:
~ + П193ч
Я— 12(1 _2) -т (1 -_92)21) •
что согласуется с решением линейной задачи по (74).
Далее, пользуясь зависимостью (92), можно определить нижнее критическое давление в первом приближении.
602 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Рис. 11.20. Расчетные данные для определения нижнего критического давления.
§ 131] СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ. НЕЛИНЕЙНАЯ ЗАДАЧА 503
ё
Варьируя энергию Э дополнительно по п, как в§ 127, приходим к уравнению
’i(1 + 82), 2*4, о„ Г 1
6 (1 —(*2) Т 16 (1 + д2)* 1) “Г 71 L(1 + »2)3
, 9 1Г2 1 h (1 — О2) -] г - /11Л/1Ч
Н“ (l-f-g»2)3] 4 [ (1 + 92)3 J2— Ч- (11.94)
Комбинируя это уравнение с (92), получаем решение задачи во в.пог ром приближении.
На рис. 11.20 представлены окончательные значения нижнего
критического давления дн для различных отношений L/R и R/h. Этот график, полученный В. А. Нагаевым, можно сравнить с данными рис. 11.18 для qB. Если зафиксировать величину R/h, то соотношение между нижним и верхним критическими давлениями будет
зависеть от L/R. Для весьма длинных оболочек {LfR > 4), а также
для коротких (L/R < 0,8) величины qB и qH близки между собой. Наиболее резко отношение v = H/B снижается при значении L/R,
L/R
Рис. 11.21. Отношение v нижнего критического давления к верхнему в зависимости от L/R.
лежащем в пределах от 0,8 до 2, как показано на рис. 11.21. С увеличением R/h минимум сдвигается в сторону меньших L/R.
На рис. 11.22 изображена зависимость коэффициента v от параметра ft, характеризующего форму волнообразования при нижней критической нагрузке. Кривую v(ft) можно считать не зависящей от отношения R/h. Минимальное значение v, полученное во втором приближении (кривая /), равно vmin = 0,73 и относится к Ь=я 0,3. Здесь уце приведена кривая (4) первого приближения и дань*
504 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
зависимости, полученные в работах Ф. С. Исанбаевой [11.9] (кривая 2) и Н. А. Алфутова [11.4] (кривая 3).
Как видим, влияние нелинейности задачи здесь значительно слабее, чем в случае осевого сжатия: уровень qH составляет около 70—75% от qB, в. то время как при сжатии он снижался до 30—35%. Волнообразование также оказывается иным: вместо серии местных вмятин, характерных для случая сжатия, здесь возникает «кристалл» со своеобразными удлиненными гранями, охватывающими всю длину образца.
Ччч2
—
4
пц 0,1 0,2 0,3 0Л 0,5 0,6
Д
Рис. 11.22. Зависимость v = н/в от параметра, характеризующего форму волнообразования по различным решениям задачи.
Такая изогнутая поверхность также должна быть близка к поверхности, изометричной по отношению к круговому цилиндру. Поэтому мы можем и в данном случае использовать геометрическое построение *), описанное в § 128. В качестве линии у можно принять полуволну синусоиды, проведенную через средние точки сторон торцевых сечений призмы (сплошные линии на рис. 11.23, а), либо прямоугольные отрезки, сглаженные у середины грани (пунктирные линии). ♦Снова проведем плоскость, перпендикулярную к оси призмы, и отметим многоугольник, соединяющий точки пересечения плоскости с линиями. При перемещении плоскости вдоль оси призмы получим трубчатые поверхности, показанные на рис. 11.23, для случая, когда в качестве линий у взяты синусоиды, и на рис. 11.23,6 — для случая прямых отрезков. Эти трубчатые поверхности оболочки хорошо отображают характер выпучивания реальной оболочки. Рассмотрение геометрической модели по рис. 11.23 позволяет сравнительно легко найти разность между объемом трубки и исходного цилиндра; но тогда можно определить работу внешнего давления по
*) См. работы А. В. Погорелова [11.19], ч. 2 и [11.20], относящиеся к случаю внешнего давления,
§ 13;]
ЭКСПЕРИМЕНТЫ
формуле (90). Пользуясь энергетическим методом и пренебрегая потенциальной энергией деформации в срединной поверхности, А. В. Погорелое получил следующее выражение для коэффициента v = qJqB:
у = 2уГ J-+ 0,385j/ ; (11.95)
оно относится к случаю Rh/L2 < 0,016.
а
в)
Рис. 11.23. К построению изометричных цилиндру поверхностей в случае выпучивания при внешнем давлении.
Желательно сравнить в дальнейшем результаты вычислений по формуле (95) с экспериментальными данными, относящимися к достаточно тонким оболочкам.
§ 132. Эксперименты с оболочками, подвергающимися внешнему давлению. Рекомендации для практических расчетов
Приведем данные исследований выпучивания оболочек, подвергающихся внешнему давлению. Начнем с тех опытов, в которых ободочки изготовлялись тщательно — из труб на токарном станке, — с соблюдением жестких допусков в отношении размеров. Схема одной из испытательных установок показана на рис*. 11.24*). Один из торцов образца (/) скрепляется с поршнем (2), а другой — с фланцем (3). Давление q передается на образец от жидкости, нагнетаемой в камеру (4) с помощью насоса (№ 1). Чтобы исключить растяжение оболочки, в нижнюю камеру (5) от другого насоса (№ 2) подается давление, зависящее от q. Аккумулятор, содержащий газовую по¬
*) Эти опыты были проведены В. А. Нагаевым.
606 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [ГЛ. XI
душку, создает, если это необходимо, условие постоянства давления во время хлопка.
Потеря устойчивости оболочек, как правило, происходит внезапно, с образованием глубоких, регулярно расположенных вмятин, обращенных к центру кривизны, именно той формы, какая была положена в основу решения нелинейной задачи. Если газовая подушка отключена, то во время первого хлопка возникают лишь одна — три волны, и лишь в процессе последующих хлопков появляются остальные волны. На рис. 11.25 показаны фотографии двух образцов, имевших одинаковое отношение Rjh. Исследуемая цилиндрическая часть образца была частично защемлена. Отметим, что более короткая оболочка (б) выпучивается по большему числу волн, чем оболочка (а); этот результат вытекает из формулы (76). Случай шарнирного опирания торцов показан на рис. 11.26; очертание волн здесь приближается к прямоугольному. Наконец, на фотографиях рис. 11.27 показаны образцы, имевшие диафрагму — жесткое внутреннее кольцо, разделявшее оболочку на две равные части. Для каждой из этих частей внутренний край можно было считать шарнирно опертым.
На рис. 11.28 даны результаты опытов, относящиеся к форме волнообразования. По оси абсцисс отложена величина L/R, по оси ординат — отношение ширины 1у вмятины вдоль окружности к длине Z,. Сплошная линия соответствует теоретическим выкладкам § 130.
Рис. 11.24. Установка для испытаний оболочек на устойчивость при внешнем давлении.
§ 1321
ЭКСПЕРИМЕНТЫ
507
Приведем, далее, сводку экспериментальных значений v = qKp/qB* полученных различными авторами при разнообразных условиях изготовления и испытания образцов (рис. 11.29); под qKp понимается реальная величина давления при выпучивании. В некоторых сериях
б)
Рис. 11.25. Форма выпучивания оболочек Рис. 11.26. При шарнирном за-
в случае частичного защемления по креплении по краям оболочки
краям. образуют «прямоугольные»
волны.
опытов модели были получены из плоских листов и имели значи-
а) б)
Рис. 11.27. Оболочки, снабженные жесткой на изгиб диафрагмой, после потери устойчивости.
тельные начальные неправильности; при этом разброс экспериментальных точек оказался более значительным и уровень критического
508 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
давления—гораздо ниже, чем в случае тщательно изготовленных оболочек. Для тонких оболочек (R/h от 1000 до 1500) критическое давление падает особенно сильно из-за большего влияния начальных
Рис. 11.28. Экспериментальные данные, относящиеся к форме вмятин.
неправильностей. Анализ данных экспериментов показывает также, что для дюралюминовых образцов значения v лежат в среднем
v
V
1,0
0,9
0,8
0,7
0,6
о
э
ВТ*--с
1
о
о
1денбурь о
' и Трил
Г ft
инз
1
f !
ев
бурдш
у ®,
г
••
о
о
л
О
Q-®
> <
•
... @
Г • •
'V
§ е
о <
)
36
1
тр
1
•
комщ
ооб
1
0,1 0,15 0,2 0,25 0,3 0,35 «4 (5 0.5 0,55
В
Рис. 11.29. Экспериментальные значения критического давления по данным различных авторов.
несколько ниже, чем для стальных. Возможно, это объясняется большей чувствительностью дюралюминовых оболочек к термическим эффектам во время обработки, хранения и т. д.
Пунктирная линия на рис. 11.29 отвечает, очевидно, qB; сплошная же получена по данным второго приближения для qH. Подавляющее
§ 133] ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ ПРИ ВНЕШНЕМ ДАВЛЕНИИ 509
число экспериментальных точек лежит и здесь между этими линиями. Наименьшее значение v составляет в этих сериях опытов 0,68.
Таким образом, практические расчеты на устойчивость при внешнем давлении нужно вести по верхнему критическому значению (см. график рис. 11.18 и формулы (77)), умноженному на коэффициент v; значение v будем считать зависящим только от отношения Rjh. Ориентировочно рекомендуем следующие значениия v:
R/h
250
500
1000
1500
V
0,7
0,6
0,5
0,4
Эти данные можно использовать и для всестороннего сжатия.
§ 133. Влияние начальных неправильностей при внешнем давлении
Есть все основания считать, что наибольшее влияние на разброс экспериментальных значений критических нагрузок оказывают начальные неправильности формы оболочки. Обратимся поэтому к более подробному исследованию поведения оболочек, имеющих начальную погибь. Удобнее всего это сделать по отношению к оболочкам, подвергающимся внешнему давлению, так как конфигурация вмятин здесь более определенная, чем в случае осевого сжатия. Рассмотрим задачу в нелинейной постановке и будем исходить из системы уравнений (29). Напомним, что под w понимается полный прогиб, под w0 — начальный прогиб. По-прежнему для w примем выражение
w = /(sin-sin --H-sln2 -77- + ?)- (11.96)
Будем предполагать, что начальные прогибы распределяются по аналогичному закону:
wo = /o(sin ■■ + 1' sin2T+ ?)• (11.97)
и что величины ф и ср в (96) и (97) совпадают. Иными словами, мы считаем, что форма начального волнообразования, характеризуемая параметрами ф и ср, находится «в резонансе» с волнообразованием оболочки в процессе деформации и что единственным наперед заданным параметром является величина /0. Такое допущение несколько усиливает влияние начальных неправильностей *).
*) Это предположение, значительно облегчающее выкладки, принято также в работе Лу [11.44], Доннела [11.30] и др. Приведенное здесь решение дано Б. Е. Минеевым и автором (см. [11.5], статья 1957 г.).
510 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Подставим (96) и (97) в правую часть второго из уравнений (29); интегрируя уравнение, получим следующее выражение для функции напряжений:
i ф = ( w - да) 005 2ал:+ ж02 cos2 +
+ К (1 _Дэ2)2 /Ц Sin 3 S‘n —
[(1 __ §2)2 /it (fqrpjr ]sin ax sin Ж ~2 ' 1 -98)
Здесь введены обозначения:
a = T’ P = 7?-’ fi = f — U =1 + 2- = 7; (П.99)
под fx понимается стрела дополнительного (упругого) прогиба.
Вычислим полную энергию системы (56), пользуясь выражениями (10.95) и (90), но с заменой w на w — w0. Если ввести, кроме того, безразмерные параметры
5=Э-®?' <* = ■ % 01.100)
то получим:
3=у с, С? (С, + 2С о)2С2 (С! + 2С0)2 Р -
- С3 (С, + 2С0) V +1 сД + i С£2 - QA (С, + 2С0) 4- 3?.
(11.101)
где
/■> _ 1 + 84 2 _ ЬА Г 1 I 1 1 2
Ч — 64 Ч - Ч — 2 _ (1 + а2)2 (1 + 992)2 J ’
г _ 1 Г, и С_П 1, (1 + 2)У
°з— 16 (1 -j-2)2J 4— 2 L(l + »2)2 12(1 — ц2) J’
с* = т+тчггг c«=f 4 = PiR4-
Уравнения метода Ритца в применении к параметрам С и 5 выпишем в виде
4=о, 4=0; <ило2>
пренебрегая некоторыми несущественными членами, представим эти уравнения в виде
2СА (Cj + 2С0) (Сг + Со) + с2 (С, + 2Q S2 - 2С3 (С, + С0) I+ 2С4С,
-2Св?(С, + Со) = 0. (11.103)
С* (Ci + 2С0)2 ? - С3С, (Сх + 2С0) + С6 = 0. (11.10.4)
§ 133] ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ ПРИ ВНЕШНЕМ ДАВЛЕНИИ 511
Отметим, что такие же соотношения можно получить, пользуясь методом Бубнова — Галеркина в применении к первому из уравнений (29). На рис. 11.30 представлены результаты вычислений по уравнениям (103) — (104) для случая R/h = 112,5, L/R = 2,2. По оси абсцисс отложен параметр полного прогиба С, по оси ординат — безразмерная нагрузка q\ принято jx = 0,3. Каждая сплошная линия
Рис. 11.30. Диаграммы «давление — прогиб» для оболочек с начальной
погибью.
отвечает определенной величине С0 и представляет собой огибающую серии кривых, построенных для различных значений параметра ri = n2hlR; на рисунке показаны пунктиром подобные кривые, соответствующие оболочке круговой формы (С0 = 0). Кружок на оси ординат отмечает величину qB для идеальной оболочки. Как видим, при наличии начальных неправильностей верхняя критическая нагрузка (наивысшая точка петли) снижается: так, например, для
С0 = 0,1 снижение составляет около 12%. Между тем нижнее давление qH остается почти постоянным.
Если стрела начального прогиба превышает толщину оболочки, то нагрузка изменяется монотонно. Отметим, что на известной стадии нагружения характеристика деформации оболочки (С) оказывается тем более крутой, чем выше величина С0; возрастание жесткости -объясняется тем, что при значительных начальных прогибах оболочка становится как бы гофрированной. На рис. 11.31 показана зависимость qB от амплитуды начального прогиба С0 для разных отношений R/h в случае всестороннего* сжатия; было принято L/Rtt 2,5*
512 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. X!
Приведем, далее, данные экспериментов, поставленных для исследования влияния начальной погиби *). До испытания дюралюминовым образцам придавались вмятины с помощью специального штампа. Поведение оболочек было различным в зависимости от числа и расположения начальных вмятин. Например, если образцу придается
Рис. 11.31. Снижение верхнего критического давления для оболочек с начальной погибью.
лишь одна вмятина, имеет место плавное нарастание прогибов и напряжений в прилегающей к ней зоне, а остальная часть поверхности оболочки остается почти гладкой. Затем происходит выпучивание путем хлопка (или нескольких хлопков) в других точках по окружности. Это иллюстрирует график рис. 11.32 изменения напряжений изгиба оХ'И вдоль окружности среднего сечения оболочки; под aXtH понимается величина ах> Hb2IEh2t где oXt и — напряжение, наибольшее по толщине. В точке 1 располагалась начальная вмятина. Напряжения распределялись на первой стадии нагружения по рис. а), а затем по рис. б), как показано сплошными линиями.
Интересно сравнить нагрузку, которую выдерживает оболочка при различных числах начальных вмятин. Гладкая оболочка принятых размеров выпучивается по шести волнам. На рис. 11.33 отмечены нагрузки, отвечающие первому хлопку (нижняя линия) и окончательному волнообразованию (верхняя линия), в зависимости от числа п
*) Эти эксперименты были проведены В. Е. Минеевым.
§133] ВЛИЯНИЕ НАЧАЛЬНЫХ-НЕПРАВИЛЬНОСТЕЙ ПРИ ВНЕШНЕМ ДАВЛЕНИИ 513
одинаковых начальных вмятин, равномерно распределенных по окружности оболочки, от п = 1 до п = 7; значение п = О относится к гладкой оболочке. Рис. 11.33, а соответствует стреле начального прогиба С0 = 1, рис. 11.33, — стреле С0 = 2.
Как видим, наиболее опасными являются случаи, когда число вмятин отвечает форме потери устойчивости гладкой оболочки (три
Рис. 11.32. Изменение наибольших напряжений изгиба в случае одной начальной вмятины.
или шесть начальных вмятин). В случае же, если расположение начальных неправильностей не соответствует форме выпучивания идеальной оболочки (п = 4), в процессе деформации происходит перестройка волнообразования; несущая способность оболочки может оказаться даже выше, чем при отсутствии начальных неправильностей. Во многих опытах удалось наблюдать как бы упрочнение образцов при значительном развитии выпучин, связанное с образованием жестких гребней волн. Окончательное разрушение образцов наступало при надломе этих своеобразных ребер.
В заключение сравним экспериментальные зависимости q (С), показанные на рис. 11.34 сплошными линиями, с теоретическими (пунктир).
514 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Рис. 11.33. Несущая способность оболочек при различном числе начальных вмятин по данным опытов.
2,5 5,0 7,5 10,0 12,5
Рис. 11.34. Кривые «давление — прогиб» для «идеальной» оболочки (С0 = 0) и оболочек с начальной погибью (С0 от 0,1 до 5).
§ 134]
УСТОЙЧИВОСТЬ ОБОЛОЧКИ ПРИ КРУЧЕНИИ
515
Заметим, что в опытах торцы оболочки были частично защемлены. Начальные ветви кривых, относящихся к одним и тем же значениям С0, оказываются близкими друг к другу, однако в последующем кривые расходятся. Это объясняется, по-видимому, тем, что в теоретическом решении были сделаны некоторые ограничения, касавшиеся характера выпучивания; в действительности картина волнообразования оболочки оказывается более сложной. Желательно в последующем вернуться к этой важной задаче, принимая, в частности, более строгую процедуру варьирования энергии системы.
§ 134. Устойчивость оболочки при кручении
Обратимся теперь к случаю кручения оболочки парами AfK, приложенными по торцам (рис. 11.35). Здесь основное состояние определяется касательными напряжениями; для тонкой оболочки их можно считать равными
Мк 2%R2h *
S = ■
(11.105)
Выпучивание при действии такой нагрузки может иметь место при известных условиях для оболочек летательных аппаратов и двигателей.
Рассмотрим сначала линейную задачу *), считая, что оболочка средней длины шарнирно оперта по торцам. Уравнение (17) приобретает вид
h
V8-
Е dAw
R2 дх*
™'(£k)=°- <п-,06>
Рис. 11.35. Оболочка, подвергающаяся кручению.
По аналогии с задачей об устойчивости пластинки при сдвиге можно предполагать, что выпучивание оболочки в случае кручения будет сопровождаться образованием регулярно расположенных по окружности волн, наклоненных под известным углом к образующей. Поэтому примем для w выражение
г пх п.,
w — f COS-J- COS -д- (у + T*)>
(11.107)
считая, что начало отсчета х расположено посередине длины оболочки; под п понимается число полных волн по окружности, под у — тангенс угла наклона гребней волн к образующей. Выражение (107)
*) Эта задача рассматривалась Доннелом (11.30], X. М. Муштари [10.9], В. М. Даревским [11.7]. Излагаемое ниже решение дано В. А. Марьиным
516 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
удовлетворяет условию w = 0 при х=± 1/2. Находим, далее, dw г я п (, L \
i===_/Tcos_(y±T_j,
дх
d2w
дх2
- 2кпч. ti (, L \
L=f-LRSm
Как видим, избранное нами выражение для прогиба, строго говоря, не удовлетворяет ни условию шарнирного опирания, ни условию защемления. Вместе с тем, получаем:
2itR 2 itR
/()„, А*-/=
О 2 0 **2
Таким образом, оба эти условия удовлетворяются одновременно в интегральном смысле. Выражение (107) можно переписать в виде w = w1-j-w2, где
wx = / (cos ~ cos тх — sin sin тх j, (11.108)
w2 = -g- / (cos cos — sin sin » (11.109)
причем
= / = (11Л1°) Подставляя в уравнение (106), получим:
[(mI+ж)' Т+ж -2s -г (!+ж)’] +
+[(',+ -S),T+,,-2s'l('!+)>*=0- (•')
Приравнивая нулю коэффициенты при wx и w2, получаем два уравнения:
2s _ (m2R2 + n2)2 ( h\2 m*R>
E — 12 (1 — a2) mRn \R ) _r (m2R2 + n2)2 n ’
2s (l2R2 + n2)2 (h\2 PR*
E — 12 (1 — fx2) IRn \ R ) (l2R2 + n2)2 n 9 1,10)
Уравнения (112) и (113) должны давать одно и то же значение 5. Задавшись числом волн и отношением R/L, мы можем построить по этим уравнениям кривые s = s(rif), как показано на рис. 11.36. Эти кривые одинаковы по форме (так как величины т и / в (112) и (113) взаимозаменяемы), но смещены одна относительно другой вдоль оси абсцисс на величину
(»-0Л =. (11.114)
§ 134]
УСТОЙЧИВОСТЬ ОБОЛОЧКИ ПРИ КРУЧЕНИИ
517
Ордината точки К пересечения кривых дает критическое значение s при принятых условиях. Задавшись различными значениями п, ищем минимальную величину s, определяющую верхнее критическое напряжение sB. Заметим, что достаточно построить одну из кривых по (112) или (113) и вписать в нее параллельно оси абсцисс хорду длиной c = 2>kRIL. Если кривая построена по (112), то точка К будет находиться на правом конце хорды. Введем обозначения:
v = raT+—
Р2=:
1
(*)*’
(11.114а)
12(1-»*) тогда уравнение (112) примет вид
4-
Е v/i (v2 -{- л2)2
Пренебрегая v2 по сравнению с п2, получим:
я.8 р2 + v4 vn5
Учитывая, что значениям v и v величины 5, находим:
пу + v4
(11.116)
27zR
пу
Рис. 11.36. К вычислению верхнего критического напряжения при кручении.
соответствуют одинаковые
»v+(*+T*)4
vn5
(’
2тс/?\ 5
—г
(11.117)
Отсюда при заданном отношении L/R необходимо, определить п, Решая уравнение (117), находим *):
а = 4,2 Уxl/'-F' (11.118)
Пользуясь (116), определяем далее верхнее критическое напряжение: Sg = 0.74.. £ JLfW
или, при [х = 0,3,
(1— [*2)s/’ R
L2
(11.119)
: 0,78 Е
Rh L2 ’
(11.120)
*) См. работы В. М. Даревского [11.7],
518 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Введем безразмерные параметры
'i 5 /? <\ « Rh. /111014
S==_£T ’ ~nL ' Ь = !Т’ <11121>
тогда получим:
s„ = 0,78 Vb. (11.122)
При этом значении s будет
= «0.75 {'■§'. т «1,73 V'T. (11.123)
4,2 У \ — ц2
Судя по (118) и (123), число волн, образующихся вдоль дуги, падает по мере увеличения относительной длины оболочки L/R и менее резко при увеличении относительной толщины h/R.
Для оболочек большой длины число волн становится равным п = 2, так что сечение приобретает вид овала. Если исходить при этом из более общих уравнений типа (И), то придем к следующей формуле для критического напряжения *):
1 Е / h \Ь5
Sb — ЗУ! (1-ц2)0’75 (л) ’ (11.124)
при этом, считая jx = 0,3, получим:
sB = 0,254 А. (11.125)
Для весьма длинных оболочек sB не зависит от отношения L/R:
граничные условия по торсам здесь становятся несущественными.
На графике рис. 11.37 объединены расчетные данные для оболочек различной длины **) при разных отношениях R/h. Здесь по оси абсцисс отложено отношение L/R, по оси ординат — параметр ?в = =sR2/Eh2; применена логарифмическая шкала. Судя по формулам (120) и (125), в случае оболочки средней длины мы должны получить на таком графике наклонные прямые, а для весьма длинной оболочки — горизонтальную линию. Строго говоря, наклонные прямые в левой части диаграммы являются огибающими кривых, соответствующих различному числу волн п\ эти числа указаны на графике. Кривые п=2 при значительном L/R переходят в горизонтальные линии. Из графика можно убедиться в том, что наибольшее значение отношения L/R, при котором число волн составляет п 4, соответствует приблизительно величине это согласуется с неравенством (18Ь), уста¬
*) Формула такого типа принадлежит Шверину [11.50].
**) Этот график принадлежит Штурму [11.49].
§ 134]
УСТОЙЧИВОСТЬ ОБОЛОЧКИ ПРИ КРУЧЕНИИ
519
навливающим пределы применимости теории оболочек средней длины. На рис. 11.37 дана также величина у, равная тангенсу угла наклона гребня волн к образующей.
Исследование влияния защемления краев на критическое напряжение *) показало, как и следовало ожидать, что оно является существенным лишь для сравнительно коротких оболочек.
Рис. 11.37. Расчетные данные для определения верхнего критического напряжения при кручении.
Как показывают опыты, реальные оболочки выпучиваются при кручении приблизительно таким же образом, как в случае внешнего давления, но вмятины расположены под некоторым углом к образующей **) (рис. 11.38). Появление вмятин у оболочек средней длины, как правило, сопровождается хлопком. Поэтому и здесь надо обратиться к решению нелинейной задачи об устойчивости в большом ***). Аппроксимируем прогиб с помощью выражения
w = fx sin-—-sin --(У — T**') /2sJn2 “Т-* (11.126)
*) Оно было выполнено Доннелом [11.30].
**) Фотография рис. 11.38 получена О. И. Теребушко.
***) Это решение дано Лу [11.44]; см. также работу Иошимура и Ниизава [11.55].
520 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. X!
Первый член аналогичен выражению (107), относящемуся к линейной задаче. Второй член выбран в том же виде, как и в случаях осевого сжатия и внешнего давления. После подстановки (126) во второе из уравнений (29) и интегрирования находим:
Ф 2 Г 1 2п (у — ух), 1 2пх 1 л
~Ё 32 [ (1 + f)2 cos R ~
_ *L Г 1 cn- ”(y~aJf) 1 cn~ n(y — bxx)
2 R (1+*?/ R
4- 1 со: п<У-ь*х'> I f f.
{1+4? Я +(1 + blfC0S R J/l/2 +
Г a?
[(!+.
. R Г ax п(у — а,х) bx n (y — byx) 1
A 5- 5-5- COS 7 5-5- COS /, —
2n [ (1 + a\f R (1 4- b\f R J1
D o_ Y
“ W /2cos НГ + sx* (11 •127)
где
a1==T-f, bx = y — », a3 = 7 + 3», *3 = T~ 3». (11.128)
Если положить 7 = 0, придем к прежнему выражению (49а) для Ф с заменой (— ру2/2) на sxy.
Определим полную энергию системы Э по (56). Величины Эс и Эи вычисляются по формулам (10.95) *). Работа внешних сил равна
W = Мкв = 2 nR2hsd, (11.129)
где б — взаимный угол поворота торцов. По формуле (10.99) будет
ди, dv, dw dw _1_ 1_ д2Ф п < « оПч
ду ' дх ' дх ду G Х G дх ду * '
Угол б равен.yL/R, где у— среднее значение той составляющей деформации сдвига, которая не зависит от w:
т = — 2RL If + дх)dX йУ
F
1 Г Г ( 1 д2Ф, dw dw\ г, /11 Ю1Ч
2nRL J J \ 0 dxdv dx ~dy)dxdy- (11131) F
Пользуясь выражениями (126) и (127), находим:
fi — (J- ±_ J’l.JL Л v2\_L0 — \0 4 L2 02 Ix) R *
отсюда
/i)*1 (i i.i32)
*) Выражения для Эс и «Эи приведены в книге [0.3], стр. 348.
§ 134]
УСТОЙЧИВОСТЬ ОБОЛОЧКИ ПРИ КРУЧЕНИИ
521
Далее составляем уравнения метода Ритца:
дЭ
Vi
= 0,
дЭ
д/2
= 0.
(11.133)
Примем в первом приближении, что в процессе закритической деформации вид волнообразования будет тот, который соответствует решению линейной задачи об устойчивости в малом, по (123). Тогда можно определить соотношение между параметром s и углом поворота б и найти нижнее критическое напряжение v Отношение v=sH/ sB оказывается зависящим от параметра 8 = RhjL2.
При 8=1/20; 1/200; 1/2000 получаем соответственно v = 0,94; 0,80; 0,87.
Таким образом, наименьшее значение составляет около 80%. Как видим, эффект нелинейности задачи оказывается здесь несколько более слабым, чем в случае внешнего давления.
Геометрический подход к задаче (см. § 128) позволяет и в случае кручения построить поверхность, изометричную исходному круговому цилиндру и воспроизводящую форму выпучивания оболочки в большом *).
Исследование влияния начальных неправильностей формы для оболочки **) средней длины может быть проведено тем же путем, что и в § 133. На рис. 11.39 изображена
чиной = (s/G) (Ljh)2 и параметром угла закручивания 0 = 0 (Lfh)2 для оболочки идеальной формы и для оболочек с начальной погибью при 8= 1/200. Отношение стрелы начального прогиба к толщине обозначено через ср0. На графике отмечены точки, отвечающие верхнему и нижнему критическим напряжениям sQ и sH. Общий характер этих кривых тот же, что и в случае внешнего давления.
Судя по данным опытов, экспериментальные значения критического напряжения лежат, как правило, в вилке, составляемой верхним и нижним критическими напряжениями. Поэтому в практических расчетах для определения sB надо пользоваться графиком рис. 11.37 либо (для оболочек средней длины) формулой (120). Расчетное значение
Рис. 11.38. Оболочка после выпучивания при кручении.
зависимость между вели-
*) См. работы А. В. Погорелова [11.19], ч. 3 и [11.20].
**) Оно было выполнено Нэшем [11.48].
522 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл XI
следует принимать при R/h 250 равным vsB, где v = 0,8. При больших значениях R/h влияние начальной погиби будет и здесь более
расч
Рис. 11.39. Влияние начальной погиби на верхнее и нижнее критические напряжения при кручении.
сильным; поэтому v должно быть уменьшено примерно в соответствии с таблицей v для внешнего давления (стр. 509), причем нижний предел при R/htt 1500 равен v0,5.
§ 136. Устойчивость при изгибе
Вопрос об устойчивости цилиндрических оболочек при изгибе возникает, например, при расчете длинных трубопроводов: выпучива-
М
М
ние здесь может произойти в тех зонах, где изгибающий момент или поперечная сила достигают максимума. Эта же задача встречается при расчете многих авиационных конструкций.
Рассмотрим вначале случай чистого изгиба оболочки средней длины. Допустим, что оболочка подвергается действию пар с моментами МУ приложенными в диаметральной плоскости (рис. 11.40). Будем отсчитывать координату у от точки пересечения плоскости пары со срединной поверхностью, расположенной в растянутой части сечения. Нормальные напряжения
Рис. 11.40 Оболочка, подвергающаяся чистому изгибу.
§ 135]
УСТОЙЧИВОСТЬ ПРИ ИЗГИБЕ
523
в поперечных сечениях распределяются до выпучивания оболочки по закону
= PiC0s-- = -C0s--. (11.134)
Соответствующие деформации в срединной поверхности равны
р..— ди - Рх р Л — — _ IEjl v — п
х> 0 — дх ~ Е 9 у>°~ ду R Е 9 — °‘
Считая v = 0 и w = 0 по торцам при х = 0 и х = L, получим следующие выражения для начальных перемещений:
“о=тг (т ~*)cosтг'
0 2 * ~ Sin ТГ ’
w° = I* — л:) — 2(а/?2] cos.
Как видим, сечения оболочки не остаются круговыми; максимальные прогибы равны
w°> max = 2Ё~ ( JR2 *
Однако мы не будем принимать во внимание этих перемещений, понимая в дальнейшем под w дополнительный прогиб; легко показать, что погрешность решения будет незначительна.
При исследовании устойчивости оболочки в малом будем исходить из уравнения (17); оно принимает вид
Т+£4 + Л7,(!£со*-£)=0- (11.135)
Принимая, что торцевые сечения оболочки оперты шарнирно, выберем решение уравнения (135> в виде ряда
w=:Sin 2/яяп-ЛУ. (11.136)
/2=1
Подставим это выражение в (135) и приравняем нулю коэффициенты при однородных членах; тогда придем к трехчленным уравнениям относительно параметров fп такого вида:
Г D I т2п2, п2\2, Е ( тп
[Т \7? “Г'ЖХ L ) }fn~
1)=°; (11.137)
524 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
здесь принимается во внимание, что
лгу у 1 sin-cosi'= 2
Если ограничиться некоторым числом параметров fп и положить равным нулю определитель системы (137), то можно приближенно определить верхнее критическое значение р0. Судя по расчетам, принадлежащим А. В. Кармишину, Ю. Г. Одинокову *) и Флюгге [10.18], величина ри в отличается на несколько процентов от верхнего критического напряжения (33) для центрально сжатой оболочки. Можно показать, что по мере увеличения числа параметров это расхождение падает **). Такой результат легко объяснить, если принять во внимание, что характер потери устойчивости в обоих случаях один и тот же. Таким образом, верхнее критическое значение pifB определяется по (33):
Эксперименты показывают, что выпучивание оболочек средней длины при чистом изгибе происходит путем хлопка с образованием сравнительно мелких вмятин в сжатой зоне. Поэтому, переходя к решению задачи об устойчивости оболочки в большом, примем условно, что дополнительные прогибы имеют место только в сжатой половине сечения и что сопряжение частей оболочки по нейтральному диаметру соответствует условиям жесткого защемления. Аппроксимирующее выражение для прогиба в сжатой зоне выберем в виде
где /ж, 1у — длины полуволн в осевом и дуговом направлениях. Это выражение взято по аналогии с решением Кемпнера, относящимся к случаю осевого сжатия (см. § 127); введен дополнительно множитель cos2(y/R)- Если ограничиться первым членом в скобках и принять для сжатой зоны
то, решая линейную задачу с помощью методов Ритца или Бубнова— Галеркина, получим верхнее критическое напряжение, близкое к (138).
.*) См. Труды Казанского авиац. ин-та, 1940.
**) Этот вывод был сделан Ю. А. Шевляковым и Л. И. Маневичем. Им же принадлежит изложенное ниже решение задачи об устойчивости в большом; см. Доклады АН УССР, Кг 5 (I960), 605—608.
(11.138)
- их пу 9 у W — J COS -j— COS COS2 ~, lx ly К
(11.139a)
§ 135]
УСТОЙЧИВОСТЬ ПРИ ИЗГИБЕ
525
Подставляя (139) в правую часть уравнения (16), находим функцию Ф. Далее определяем полную энергию системы Э. Воспользуемся параметрами /?, Ь, по (38) и (38а) и введем новые обозначения:
(п. 140)
тогда получим:
Э*
=N8,[
62
(,г + ьу+4а*ь2 (1 + »2)2, 1, 17
+-
(1 + 9»2)2
+
Ь*
(9 + 82)2 ' 128 ' 12-256 1 ' J ' 4 (1+92)2
■ (а + Ь) -f- (Cj — 8а)2 j — -j /?2 -f
(1 -f »2)2
+ 48 (Г-ZF) С? [ (1 + »2)2 + 32 (а2»4 -+- Ь2) ] - 0,225 (1 + 8а2).
(11.141)
Будем минимизировать полную энергию по пяти параметрам, принимая
л л л л л 1}*
(11.142)
дЭ*
дЭ*
дЭ*
да
дЭ*
дЪ
дЭ*
дЬ
= 0.
дС,
Первые три уравнения будут такими же, как если бы задача решалась для случая равномерного сжатия (рх =ь= const = р). Чтобы удовлетворялись остальные два уравнения (142) для простого сжатия, параметры р и рх должны быть связаны зависимостью
Г- 17 Й02 1
рг= 1,1 ~—(1 +8а2) J • (11.143)
Поэтому, зная закритические формы дболочки при чистом сжатии, найденные в решении Кемпнера, можно перейти к случаю изгиба. Такой переход сделан в следующей таблице:
р
0,24
0,22
0,21
0,2
0,19
0,18
с,
1,1
1,2
1,24
1,27
1,35
1,4
Р\
0,29
0,28
0,27
0,2о
0,265
0,27
Наименьший параметр нагрузки равен ри н== 0,26; остальные параметры будут: т) = 0,19, Ь = 0,3, а = 0,5.
Эта задача была решена также в предположении, что по линии сопряжения сжатой и растянутой зон имеет место упругое защемление;
526 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в пределах УПРУГОСТИ [гл. X!
было принято несколько иное выражение для w. В сжатой зоне прогибы мало отличались от (139), а на нейтральном диаметре и в растянутой зоне являлись пренебрежимо малыми. Повторяя выкладки, придем к следующему значению нижнего критического напряжения:
при этом будет (=1,4, т) = 0,22, fr = 0,36, а = 0,18.
Таким образом, амплитуда нижнего критического напряжения равна pl a = 0t24EhlRt в то время как при равномерном сжатии коэффициент в этой формуле был равен 0,18. Судя по этому варианту решения, наличие растянутой зоны и неравномерность распределения сжимающих напряжений здесь сказываются существенным образом: амплитуда нижнего критического напряжения превышает на 33% величину /?н, относящуюся к равномерному сжатию. Это, на первый взгляд, противоречит результату, полученному при решении линейной задачи. Окончательные выводы окажется возможным сделать лишь впоследствии, когда эта сложная задача будет решена с помощью цифровых электронных машин.
В практических расчетах следует исходить, как и в случае центрального сжатия, из величины нижнего критического напряжения с учетом экспериментальных данных. Влияние начальных неправильностей в форме оболочки в случае изгиба должно быть не так велико, как при осевом сжатии; начальные вмятины в растянутой зоне не должны сказываться сколько-нибудь существенно на поведении оболочки. Следовательно, со статистической точки зрения вероятность прощелкивания оболочки в случае изгиба будет меньшей. С другой стороны, при изгибе оболочки происходит некоторое сплющивание поперечного сечения, которое ведет к повышению максимального напряжения по сравнению с расчетным значением. Все же здесь расчетные напряжения надо принимать несколько более высокими, чем при центральном сжатии. Так, при R/h = 250 следует принимать /?Ьрасч=0,22 вместо значения 0,18, указанного для случая центрального сжатия.
В общем случае внецентренного сжатия следует вычислить коэффициент а, равный а = 1 — p2lPv где Р\ — максимальное напряжение сжатия, р2 — напряжение у противоположного конца диаметра (с учетом знака). Тогда для расчета можно воспользоваться данными таблицы для /?расч в случае центрального сжатия (стр. 494) (в зависимости от отношения R/h) и найти значение наибольшего сжимающего напряжения по формуле *)
/>1,11 = 0.24;
(11.144)
*) Эта формула предложена Б. М. Броуде.
§ 135]
УСТОЙЧИВОСТЬ ПРИ ИЗГИБЕ
527
В случае чистого изгиба будет ос = 2; отсюда при R/h 250 приходим к величине расч = 1,25 • 0,18 = 0,225, что соответствует указанному выше значению 0,22.
Все приведенные выше данные относились к оболочкам средней длины. Для тонких оболочек со значительным отношением длины к радиусу можно ожидать иного явления — выпучивания по длинным полуволнам, подобно случаю равномерного сжатия (стр. 477) *). Пользуясь тем же аппаратом «полубезмоментной» теории оболочек, можно решить в линейной постановке задачу о потере устойчивости с образованием таких длинных полуволн. Результаты приближенного
Pi,В 0,6
0,5
0,4
0,3
0,2
0,1
В Ю 02 0,3 0* 0.0 8£ 0.7 0.8 0 10 1;i
Рис. 11.41. Верхнее критическое напряжение при чистом изгибе.
решения представлены на рис. 11.41. По оси ординат отложен параметр ph в, по оси абсцисс — величина £ = (L/mR) Vh!R\ здесь т — число продольных полуволн. Наименьшее значение рх в = 0,38 имеет место при 5 = 0,58. Например, при R/h = 330 этот минимум получается для оболочки с отношением L/R= 10, L/R = 20 и т. д. Как видно из графика, снижение ри в по сравнению со случаем изгиба по коротким полуволнам, когда рЬъ 0.605, происходит, начиная с £ = 0,35. При расчетах по рис. 11.41 следует вычислить £, подставляя т= 1, 2 и т. д., и выбрать затем меньшее значение р1в. На рис. 11.42 показана оболочка после выпучивания по длинным полуволнам. Судя по предварительным вычислениям, учет геометрической нелинейности задачи здесь не приводит к такому «катастрофическому» падению расчетного напряжения, как при выпучивании по коротким полуволнам. Об этом свидетельствуют и показанные
*) На это обстоятельство было впервые указано Е. Д. Плетниковой в 1949 г. В дальнейшем данная задача исследовалась в применении к различным случаям изгиба гладких и подкрепленных оболочек К. Д. Туркиным [11.24]. Ему принадлежат график рис. 11.41 и приведенные на нем экспериментальные данные, а также фотография, воспроизведенная на рис. 11.42,
528 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
на рис. 11.41 кружочками экспериментальные значения рх\ разброс их сравнительно невелик.
Если вести расчет по значению phpacч = 0,22, то, по-видимому, это даст для длинных оболочек некоторый дополнительный запас
устойчивости. Отметим, что все представленные на рис. 11.41 экспериментальные точки лежат выше уровня рх = 0,22.
Мы разобрали случай чистого изгиба оболочки. Обратимся теперь к другому, практически важному случаю, когда оболочка подвергается поперечному изгибу под действием сосредоточенных сил или распределенной нагрузки. Здесь возможны два подхода к задаче. Один из них состоит в исследовании волнообразования в зоне наибольших нормальных напряжений сжатия, как при чистом изгибе; он относится к сравнительно длинным оболочкам (L > 4R). Другой подход заключается в рассмотрении зоны наибольших касательных напряжений ттах, расположенной у нейтрального слоя. Отметим, что в случае оболочки, защемленной одним концом и нагруженной сосредоточенной силой на другом, свободном конце, величина ттах составляет pxR/L.
Влияние касательных напряжений будет, естественно, возрастать с уменьшением длины оболочки. Поэтому расчет на устойчивость по ттах имеет значение для коротких оболочек при L < 4R; его можно вести, исходя из данных о верхнем и нижнем критических напряжениях*) при кручении (см. § 134). В окончательный расчет вводится наименьшая из критических нагрузок, найденных по pi и ттах.
Исходя из формулы (119), приходим к следующим окончательным выражениям для верхней критической поперечной силы. Для оболочки, защемленной по одному торцу и подвергающейся действию сосредоточенной нагрузки на свободном конце, будет (при х=0,3)
QB = 0,781, (а)
*) Такой подход был развит В. М. Даревским [11.7]; ему же принадлежат формулы (а), (Ь); см. также книгу [0.3], стр. 351. Судя по вычислениям В. В. Сердюкова, верхнее критическое значение тв, из для поперечного изгиба несколько отклоняется от тВ) кр в случае кручения, причем расхождение это зависит от отношения LfR. Этот вопрос желательно исследовать более подробно.
Рис. 11.42. Выпучивание при изгибе по «длинным волнам».
§ 135] устойчивость при изгибе 529
в случае же нагрузки Q, распределенной по всей длине оболочки, QB = 1.12ic£A* Щ- • (b)
Пример 11.1. Внутризаводской газопровод представляет собой цилиндрическую оболочку, имеющую ряд опор (рис. 11.43) *). Толщина стенки газопровода h — 6 мм, радиус поперечного сечения R = 1010 мм\ материал — низколегированная сталь марки 14ХГС с пределом текучести ат=3500 kzJcm2.
Погонный вес трубы dT? = 246 кг/м, погонный вес изоляции dm = 600 кг]м\ давление в газопроводе во время испытания воздухом составляет q=3,75 кг!см2. Расстояние между опорами, найденное по нормам прочности **), равно L = 68 м. Провести проверку оболочки на устойчивость, учитывая, что газопровод имеет так называемые линзовые компенсаторы температурных деформаций, показанные на рис. 11.43, и что вблизи одной из опор газопровод может быть снабжен задвижкой.
Оболочка подвергается здесь совместному действию изгиба и осевого сжатия. Максимальное сжимающее напряжение в сечении над опорой равно
(тр 4~ из), л 0 qR
Р' = VM г- ’ *2Л =
= (2’l2 Лб 100°2 + 1,2 ~ 25 0?б1 = 2°°0 + 380 = 2380 кг/см*,
где W — момент сопротивления сечения.
Первое слагаемое учитывает изгибные напряжения, вызываемые весовой нагрузкой в средних пролетах трубопровода, рассматриваемого как неразрезная балка. Второй член соответствует продольным усилиям от внутреннего
*) Этот пример предложен М. Н. Ручимским.
**) Указания по определению нагрузок, действующих на опоры трубопроводов, и допускаемых пролетов между их опорами, 1959.
530 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
давления; коэффициент 1,2 введен для учета дополнительного давления на линзу компенсатора.
Растягивающее напряжение у противоположного конца диаметра равно р2 = — 2000 + 380 =з — 1620 кг!см2. Вычисляем коэффициент а:
_ л, 1620 _ а - 1 + 2380 ~ ’
При R/h =* 1010/6 находим по приведенным выше данным (стр. 526):
Ри расч = 0,18 (\+Щ = 0,216.
Отсюда
Pi, расч = 0,216 • 2,1 • 10° яа 2700 кг/см2.
Принимая коэффициент запаса устойчивости равным 1,5, находим допускаемое напряжение /?ьдоп = 1800 кг/см2. Сравнение этой величины с вычисленным напряжением 2380 кг/см2 показывает, что конструкция не является надежной. Следует уменьшить длину пролета примерно до 50 м.
В дополнение к этому исследуем устойчивость оболочки по длинным полуволнам (стр. 527). По данным примера L/R = 6,7; R/h = 168; считая т = 1, получим £ = 0,51.
По графику рис. 11.41 параметр /?ьв составляет 0,38; эта величина лежит выше принятого нами значения рх = 0,216.
§ 136. Замкнутые оболочки при комбинированном нагружении
Во многих конструкциях замкнутые цилиндрические оболочки подвергаются одновременному действию нагрузок разного типа.' Приведем данные для определения критических напряжений при таком комбинированном нагружении.
1. Осевое сжатие или изгиб и внешнее давление. Сочетание этих нагрузок характерно, например, для высоких башен резервуаров, используемых в химической промышленности. В нижнем поясе башни создаются сжимающие напряжения от собственного веса, вместе с тем, внутри башни может иметь место некоторый вакуум.
Рассмотрим сначала задачу об устойчивости оболочки в малом. Комбинируя (30) и (70), получаем исходное уравнение для оболочек средней длины в виде
Подставляя решение (36) и пользуясь безразмерными параметрами (38) и (73), приходим к следующей зависимости:
~ \ Я 1 (1+2)2, О2 /1t 1/Сч
Р-\- Э2 — 12(1— ц2) 2 ЧЧ- (11.146)
Как видим, критические сочетания величин pug связаны между собой, при определенных fr и т), линейной зависимостью. Гра¬
§ 1 Зб] ЗАМКНУТЫЕ ОБОЛОЧКИ ПРИ КОМБИНИРОВАННОМ НАГРУЖЕНИИ 531
фик р (<q) должен представлять собой некоторую ломаную линию АСОВ такого типа, как показано на рис. 11.44. Ниже (см. глару XXI) мы убедимся в том, что подобные диаграммы устойчивости при комбинированных нагрузках всегда обращены выпуклостью наружу — от начала координат: это вытекает из общих соображений. Отметим, что точки А и В на рис. 11.44 соответствуют верхним критическим нагрузкам осевого сжатия р0гВ и внешнего давления
Яо, в» приложенным отдельно друг от друга. Если мы соединим эти точки прямой линией, то получим промежуточные значения р и q, отвечающие уравнению
j-+J- = 1
Ро> в Я о» в
или
—1—— = 1.(11.147)
РоI в Я о, в
Как легко видеть, значения р и q по (147) будут всегда определять верхние критические нагрузки с некоторым запасом устойчивости по сравнению с ломаной линией. Поэтому в практических расчетах в качестве первого приближения можно пользоваться уравнением (147).
Судя по экспериментальным данным, потеря устойчивости оболочек в большом при комбинированном нагружении сопровождается волнообразованием смешанного характера: вмятины оказываются
более вытянутыми вдоль образующей, чем при чистом сжатии *). Решение нелинейной задачи **) позволяет определить зависимость между нижними критическими нагрузками. Отметим, что и здесь диаграмма р (q) должна быть очерчена по отношению к началу координат таким же образом, как и в предыдущем случае (см. главу XXI). Следовательно, при вычислении нижних критических нагрузок можно пользоваться уравнениями типа (147):
-§■ — 1. (11.148)
Ро» н Яо, ш
действии осевого сжатия и внешнего давления.
*) Эти опыты описаны более подробно в книге [0.3], стр. 344.
**) Оно было выполнено В. Л. Агамировым и О. И. Теребушко.
532 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Экспериментальные значения критических нагрузок, полученные для комбинированного нагружения В. Л. Агамировым (см. [0.3], стр. 344), заполняют область, лежащую между прямыми (147) и (148).
Разберем, далее, случай всестороннего давления, часто встречающийся на практике. При этом будет p = q/2, формула (146) приобретает вид *)
п =.J— Г (1+У)2Ц 1
1. «L 112о—(j-2) (i + 2)2J + 2
Приближенное уравнение (147) дает
Воспользуемся формулами (40) и (77а) для p0tB и qQt в; тогда получим:
(0,83+1,1 1.
Если отношение R/h велико, первый член в скобках* будет мал по сравнению со вторым; поэтому, как уже было сказано выше, критическое давление в случае всестороннего сжатия слабо отличается от значения, отвечающего чистому поперечному давлению.
2. Внешнее давление и кручение. Такому сочетанию нагрузок подвергается, например, оболочка корпуса трансмиссии газотурбинного двигателя. Избыточное давление возникает в расположенной с внешней стороны камере сгорания, а крутящий момент передается от диска, несущего направляющие лопатки.
Решения задачи об устойчивости оболочки в малом и в большом**) приводят здесь к приближенным формулам такого же типа, как и в случае пластинки, подвергающейся одновременному действию сжатия и сдвига:
_£н_4-.(-4м_\2= 1. (11.150)
Яо, в \ so, в / Яо, н \ so> н /
Под s здесь понимается параметр (121); случаю самостоятельного кручения соответствует параметр верхнего или нижнего критического напряжения s0tB или 0>н (см. § 134).
*) Формула такого типа была получена Мизесом [11.47].
**) Решение линейной задачи принадлежит В. М. Даревскому [11.7], [11.8], а нелинейной — О. И. Теребушко [11.22]. Некоторые авторы рекомендуют показатель степени при s/s0 в формуле (150) принимать равным 3.
§ 136] ЗАМКНУТЫЕ ОБОЛОЧКИ ПРИ КОМБИНИРОВАННОМ НАГРУЖЕНИИ 533
Наконец, при совместном действии осевого сжатия, внешнего давления и кручения можно пользоваться формулой, комбинирую-
аналогичную формулу надо рекомендовать для нижних критических напряжений.
Эксперименты показывают, что вмятины, образующиеся при совместном действии внешнего давления и кручения (рис. 11.45), имеют более четкие границы, чем в случае простого кручения (см. рис. 11.38). Если в дополнение к внешнему давлению и кручению имеется осевое сжатие, грани вмятин наклонены под меньшим углом к образующей (рис. 11.46)*).
Рис. 11.45. Форма вол- Рис. 11.46. Случай совместного
кручения и внешнего давления.
3. Внешнее давление, кручение и изгиб. В предыдущем пункте было указано, что корпус трансмиссии газотурбинного двигателя подвергается действию внешнего давления и кручения. К этим усилиям надо присоединить напряжения от изгиба, если учесть силы инерции корпуса двигателя при вращательных перемещениях самолета.
Из § 135 мы знаем, что в случае поперечного изгиба надо разделять оболочки в зависимости от относительной длины. При
щей (147) и (150):
(11.151)
нообразования при совместном действии
действия осевого сжатия, внешнего давления и кручения.
*) Фотографии рис. 11.45 и 11.46 получены О. И. Теребушко.
534 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
сравнительно большой длине (L > 4/?) основное значение имеет потеря устойчивости типа сжатия с образованием мелких вмятин в сжатой зоне. Поэтому здесь уместно вести расчет на комбинированную нагрузку, исходя из формулы типа (151), подставляя вместо р0 величину максимального напряжения при изгибе рх. В случае же оболочки малой длины должно произойти выпучивание типа кручения, с концентрацией вмятин в нейтральной зоне. Тогда необходимо воспользоваться формулой типа (150), понимая под 5 сумму касательных усилий, вызванных кручением, и максимальных касательных усилий от изгиба.
4. Влияние внутреннего давления. Вопрос об устойчивости при осевом сжатии или изгибе и внутреннем давлении возникает, например, в задаче о расчете несущей оболочки топливного бака летательного аппарата. Как известно, на стартовом участке в корпусе летательного аппарата возникают сжимающие усилия, связанные с силами инерции; на других участках траектории корпус подвергается изгибу; в то же время внутри бака поддерживается значительное давление. Так как с целью экономии веса оболочка топливного бака проектируется возможно более тонкостенной, то эта задача имеет актуальное значение.
Рассмотрим случай совместного действия осевого сжатия и внутреннего давления, не принимая во внимание местного напряженного состояния в зоне сопряжения оболочки с жестким шпангоутом, т. е. считая начальное напряженное состояние безмоментным *). Если исследовать устойчивость оболочки, подвергающейся осевому сжатию, с помощью линейной теории **), то окажется, что дополнительное внутреннее давление не влияет на величину критического напряжения, так что значение рв по-прежнему должно определяться формулой (34). К иному выводу мы приходим с позиций нелинейной теории. В самом деле, выпучивание оболочки в большом сопровождается образованием глубоких вмятин, обращенных к центру кривизны; но при наличии внутреннего давления такое прощелкивание оболочки будет затруднено. Отсюда ясно, что характер волнообразования должен здесь измениться. Это подтверждается экспериментами. При малом внутреннем давлении мы получаем вмятины типа сжатия, но вытянутые вдоль дуги (напомним, что при внешнем давлении они вытягивались вдоль образующей). Это можно видеть по фотографиям ***) на рис. 11.47; здесь сопоставлен образец (а), испытанный на простое сжатие, и образцы {б) — (г), подвергавшиеся сжатию в сочетании с внутренним давлением. По мере увеличения интенсивности давления эффект удлинения вмятин вдоль дуги
*) Об учете этого эффекта см. ниже, в § 141.
**) См. W. Fltigge, Die Stabilitat der Kreiszylinderschale, Ing. Archiv
3, № 5 (1932).
***) Фотографии рис. 11.47 взяты из статьи [11.33], 1957.
§ 136] ЗАМКНУТЫЕ ОБОЛОЧКИ ПРИ КОМБИНИРОВАННОМ НАГРУЖЕНИИ 535
усиливается. При значительном внутреннем давлении цепочку мелких выпучин заменяют сплошные кольцевые складки, так что потеря устойчивости становится осесимметричной (рис. 11.47, tf).
Рис. 11.47. Форма волнообразования при действии: а) осевого сжатия, б)— г) внутреннего давления в сочетании с осевым сжатием.
Но в этом случае эффект нелинейности уже не будет существенным, и, как это видно из § 126, мы снова придем к формуле (34) для критического напряжения.
536 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Эти выводы вытекают также из теоретического исследования *). Если обобщить решение Кемпнера на случай, когда осевое сжатие сочетается с внутренним давлением, то окажется, что нижнее критическое напряжение /?н возрастает по мере увеличения внутреннего давления.
На графике рис. 11.48 вдоль оси ординат отложено отношение
PJPo, в» гДе Ро, в — параметр верхнего критического напряжения для простого осевого сжатия по (40), а по оси абсцисс — величина q = (q/E) (R/h)2 (1 — jx2). При q = 0 получаем ptt— 0,18, что
отвечает формуле (66). Судя по графику, в области изменения параметра 0 < q < 0,5 поддерживающее влияние внутреннего давления резко возрастает. Когда q приближается к q = 2, вели чина рн практически достигает верхнего предела p0t в. На рис. 11.48 отмечены также значения ft = 1у/1х, характеризующие относительные размеры вмятин при напряжении /?н; как видим, отношение lyjlx быстро
увеличивается по мере роста q. Здесь же указана область экспериментальных точек.
К несколько иным результатам приводит исследование совместного действия кручения и внутреннего давления. Решение, основанное на линейной теории**) и относящееся к оболочкам средней длины, указывает на некоторое возрастание верхнего критического напряжения кручения sB, определяемого по (121), при увеличении параметра внутреннего давления q по (73). Это видно из графика рис. 11.49. Здесь по оси ординат отложено отношение sjs0t в, гДе so, в находится по формуле (120), а по оси абсцисс — величина я!яо, в» гДе Яо, в отвечает критическому значению внешнего давления для такой же оболочки, вычисляемому по (77) или (77а). Расчетной
*) Это решение содержится в статье Тилеманна [11.51], [11.52], см. также работы Ло, Крзйт и Шварца [11.43] и Клейна [11.40].
**) Оно было дано В. М. Даревским [11.7] и В. А. Марьиным [11.14]. См. также работу Клейна [11.40].
Рис. 11.48. К определению нижних критических нагрузок при совместном действии осевого сжатия и внутреннего давления.
§ 136] ЗАМКНУТЫЕ ОБОЛОЧКИ ПРИ КОМБИНИРОВАННОМ НАГРУЖЕНИИ 537
является сплошная линия; пунктирная линия соответствует приближенной параболической зависимости
_££_\*= 0.907 тД-,
50, В / Яо, В
относящейся лишь к большим значениям q. Если рассмотреть встречающиеся обычно на практике значения внутреннего давления, то влияние его на устойчивость при кручении в малом может оказаться слабым. Вместе с тем, несомненно, внутреннее давление должно
Л А
Sb/S0.8
7
о
Рис. 11.49. Верхние критические нагрузки при
совместном действии кручения и „ внутреннего
давления.
существенно повысить нижнее критическое напряжение кручения.
Желательно дать решение подобной нелинейной задачи.
В экспериментах отмечаются два различных типа волнообразования оболочки. При малых значениях внутреннего давления
хлопком возникает выпучина, расположенная по винтовой линии (рис. 11.50). При относительно большом давлении образуются короткие сплошные волны, развивающиеся в дальнейшем у торцов. На рис. 11.51 показана фотография такого образца, уже получившего пластические деформации *).
На графике рис. 11.49 показаны экспериментальные точки для критических напряжений, относящиеся к одному стальному (зачерненный кружок) и 18 дюралевым образцам **). Большая часть экспериментальных значений напряжения лежит несколько ниже верхней критической величины; для некоторых из них снижение составляет 12—15%. В итоге можно рекомендовать вести практические расчеты по графику рис. 11.49, вводя поправочный коэффициент v несколько более высокий, чем при простом кручении (см. § 134), например v = 0,85 при R/h 250.
*) Фотографии рис. 11.50 и 11.51 принадлежат В. А. Марьину.
**) По опытам, выполненным Р. И. Кшнякиным, М. В. Никулиным и В. В. Сердюковым, см. [11.11].
538 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
При комбинированном действии внутреннего давления и изгиба *) надо пользоваться различными данными в зависимости от того, являются ли при простом изгибе данной оболочки решающими нормальные или касательные напряжения. В первом случае можно определять нижние критические значения максимального напряжения изгиба по графику рис. 11.48, повышая рн (при <7 < 0,5) примерно на 25%. Во втором случае надо вести расчет, пользуясь
графиком рис. 11.49, по аналогии с задачей о кручении.
Все приведенные данные относятся к упругой области. В ходе
Рис. 11.50. Выпучива- Рис. 11.51. Случай одновре-
ние оболочки при одно- менного действия кручения и
временном действии значительного внутреннего
кручения и малого давления,
внутреннего давления.
расчета важно выяснить, не превышает ли максимальное значение интенсивности напряжений предел пропорциональности материала. Если напряжения, вызываемые внутренним давлением, настолько велики, что это требование нарушается, то поддерживающее влияние внутреннего давления будет ослабевать. Обратимся, например, к случаю совместного действия внутреннего давления и сжатия; дополненный график рис. 11.48 получит форму, показанную на рис. 11.52 (см. [11.30а]). Падение несущей способности оболочки имеет место, начиная с точки Л, соответствующей пределу пропорциональности.
*) Эта задача рассмотрена В. М. Даревским [11.7].
§ 136] ЗАМКНУТЫЕ ОБОЛОЧКИ ПРИ КОМБИНИРОВАННОМ НАГРУЖЕНИИ 539
Пример 11.2. Корпус (а) топливного бака ракеты (рис. 11.53).представляющий собой цилиндрическую оболочку, передает на стартовом участке сжимающую силу Р при внутреннем давлении q — 2 am. Длина бака составляет L = 6,5 м, диаметр D = 2,44 м> толщина стенки h = 2 мм. Материал — дюралюмин, Е = 7 • 105 кг/см2, р = 0,32, спц = 2400 кг/см2. Определить критическую сжи-
при этом q = 13 (1 — fx2) q = 1,91. По графику рис. 11.48 находим: v = 0,92, рн = 0,56. Нижняя критическая нагрузка сжатия составляет
Ри = 2nRhpH = 2 nEph2 =
= 2п. 7 • 105.0,56 • 0,22 = 98 000 кг.
Растягивающее напряжение в дуговом направлении равно ау = qRjh = 1220 кг/см2, сжимающее напряжение от силы Р составляет ах = = — 0,56 EhjR = — 640 кг!см2. Интенсивность
напряжений = V + <*у — зОу = 2380 кг/см2 лежит в пределах пропорциональности.
В том случае, если внутреннее давление отсутствует, надо было бы принять рн = 0,18; нижняя критическая нагрузка при этом ЯН = 98000Х X (0,18/0,56) = 31 500 кг. Таким образом, благодаря поддерживающему влиянию внутреннего давления несущая способность бака повышается примерно втрое.
*) Рис. 11.53 взят из журнала «Weltraumfahrt», N° 3 (1961), стр. 75 Размеры бака приняты на основе данных, приведенных в журнале «Flight», № 2 43 (1959), 507—532. * '
мающую нагрузку.
Находим параметр внутреннего давления:
г
Рис. 11.52. Несущая способность оболочки при совместном действии осевого сжатия и внутреннего давления падает при разви¬
тии пластических деформаций.
Рис. 11.53. Корпус ракеты с несущим топливным баком.
540 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Пример 11.3. Рассчитать на устойчивость корпус А трансмиссионного вала и наружный корпус В камеры сгорания газотурбинного двигателя, имеющего осевой компрессор *). Схема двигателя изображена на рис. 11.54. Оболочки А, В воспринимают крутящий момент Мк от сил а, Sb, передаваемых от лопаток соплового аппарата а, Ь. Оболочка А, кроме того, подвергается действию внешнего давления q — 8 am. Размеры этой оболочки: /,==560 мм, =160 мм, h = 1,6 мм. Учитывая, что оболочка подкреплена кольцами, примем приведенную толщину равной /гпр = 2,5 мм. Наружный
Рис. 11.54. К расчету на устойчивость оболочек газотурбинного двигателя.
корпус В испытывает такое же давление, которое для него является уже внутренним', размеры оболочки примем: L = 800 мм, R = 400 мм, h = 2 мм. Определить критическое значение Л1кр> А и Мкр> в для каждой из оболочек. Материал — сталь, Е = 2,1 • 106 кг!см2, Iх = 0,3, ап„ = 5000 кг/см2.
Для оболочки А находим по графикам рис. 11.18 и 11.20 при L/R = Z,5 и R/hnр = 64 (см. также формулу (77а))
£о, в = 0,0329, q0,n =0,0263.
Величину q0, н принимаем в качестве расчетной: q0, н = (fo, расч- Далее, по формуле (122) ?о. в = 0,78 У Bjy = 0,78 16 = 0,1475.
Принимая v = 0,8, получим:
0, расч = 0,8s0, в = 0,118.
Параметр q, отвечающий q = 8 am, равен
- _ 8*642 ПЛ1*7
*7расч — 2 \. юб “ 0,0157.
Для комбинированного нагружения по формуле типа (150)
т / £Расч -ш f 0,0157
«расч = so, расч / 1 - =0.118 j/ 1-_ =0,075.
Отсюда по (121) и (105)
5оасч /ч
«расч = — = 2460 кг/см2, Мкр> А = 2%R2hsp3C4 = 9,88 • 105 кг ■ см.
*) Этот пример предложен И. А. Биргером.
§ 137] ПОДКРЕПЛЕННЫЕ ОБОЛОЧКИ. ОБЩИЕ УРАВНЕНИЯ
541
Для оболочки В при L/R = 2, R/h == 200 аналогичным образом находим: q0 в* 0,033, q0t расч = 0,026, о, в = 0,147,
50, расч “ 0,118, расч == 0,152, *7расчА7о> расч = 5,86.
При совместном действии кручения и внутреннего давления по графику рис. 11.49, вводя условно расчетные критические напряжения, получим:
-iL- = 2,3, ?расч = 0,271
So, расч
и, следовательно,
5расч кг/см2, MKf в = 5,72 • 10б кг • см.
Таким образом, внешний корпус камеры сгорания может передать крутящий момент в 6 раз больший, чем внутренний корпус; в этом сказывается. отчасти влияние направления поперечной нагрузки.
§ 137. Подкрепленные оболочки. Общие уравнения
В летательных аппаратах и двигателях, в кораблестроении и инженерных сооружениях часто применяются круговые цилиндрические оболочки, имеющие продольные подкрепляющие ребра (стрингеры) и кольцевые ребра (шпангоуты). Такими подкрепленными оболочками являются, например, фюзеляж самолета и корпус подводной лодки. Подобно тому как это было при исследовании подкрепленных пластинок (см. главу VII), в случае оболочки возможны два подхода. Если ребра расположены достаточно часто, то конструкцию можно рассматривать как ортотропную; жесткость ребер распределяется, или, как иногда выражаются, «размазывается», по длине соответствующего отсека. Если же ребра находятся на большом расстоянии друг от друга, то их приходится рассматривать как дискретные элементы *). Основное внимание ниже будет уделено первому подходу к задаче. Полученные при этом результаты могут быть с известным приближением применены к оболочкам, изготовленным из стекловолокна **).
Примем, что цилиндрическая оболочка является ортотропной и что главные направления жесткости совпадают с образующей цилиндра и дугой поперечного сечения. Выведем основные дифференциальные уравнения изгиба такой оболочки сначала для случая, когда прогибы являются малыми. Будем следовать упрощенному варианту соотношений между изменениями кривизн и перемещениями по (12).
*) Устойчивость оболочек, подкрепленных дискретными ребрами и подвергающихся внешнему давлению, была рассмотрена В. М. Даревским и Р. И. Кшнякиным [11.8, 1960 г.].
**) См. ниже пример 11.4.
542 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Уравнения равновесия по (8а) и (8) выпишем в усилиях Nx, А/у, 7 и моментах Мх, Му, И, при qz — q:
= о I — о
а* ду и’ дх ду ~и’
ЛИ, (W <?2MV A/v
~д~ + 2 Way + + ~r~ + q = °-
(11.152)
Зависимости закона Гука, относящиеся к деформации в срединной поверхности, будут иметь такой же вид, как и для ортотропной пластинки; представим их следующим образом*):
-у. (ПЛ53)
Т
причем в обозначениях § 93 будет
* 1 * — L а 2 * 1 •
1 Exh 9 2~~ E2h * E2h Eyh * 0О ~ Gh '
Развернем для примера матрицу (153) для е.; тогда получим:
Nx v-oN v
■- = 8. + W + 0-r='ET~Er
¥У
Моменты выразим в соответствии с (7.256):
МЛ (D, 0 \,
Му =1 D2 0 чу); (11.154)
,Н / \0 0 2Da / Vх
здесь в обозначениях § 93 = 0 — D2\t.
Первые два уравнения равновесия (152) удовлетворяются при введении функции напряжений по формулам типа (13):
N —*3. N — £3. Т— — ду2 • — дх2' дхду'
Третье уравнение принимает вид
п» dAw, 0~ d4w. d4w 1 д2Ф,лл
1 дх' + 3 дх2 ду2 + 2ду< R дх2 ~Я' (П Л55)
где D3 = D-±- 2Dg\ оно переходит в соответствующее уравнение (7.259) для пластинки при R-> оо. Уравнение совместности (14) переходит в следующее:
Ме? + 28» t£w + *'?• + 7? й? = °- (1М56)
*)См. работы Гилеманна и др. авторов [11.51], [11.52].
§ 137] ПОДКРЕПЛЕННЫЕ ОБОЛОЧКИ. ОБЩИЕ УРАВНЕНИЯ
Введем операторы
д4
* дх2 ду2
д4
3 дл:2 ду2
543
тогда уравнения (155) и (156) можно представить в более компактной форме:
гг4 1 д2ср п4,
V0w —-5- = 9, Vecp--
R дх2
Для изотропной оболочки будет
1 d2w Я Л*2
= 0.
(11.157)
V4d = DV4, vl=--v4.
В задачах об устойчивости в малом вместо q следует подставлять, интенсивность фиктивной нагрузки по (10.89); тогда пе*рвое из уравнений (157) примет вид
_4 1 д2Ф - - / d2w, d2w. 0 d2w \ Л
VDw — + h урх дх2 -f ру 2-+ 2s — о.
Обратимся к случаю, когда прогибы являются большими. Поступая таким же образом, как в § 125, приходим к следующим уравнениям *) (при q = 0):
vl>w = Z,(w, +
п4 1,, ч 1 d2W
Vt<p = -TA(«.
(11.158)
где оператор L выражается по формулам (7.40) и (7.62). Если же исследуется поведение оболочки с начальными неправильностями, то по (29) будет
Vi?:
Vd(w — w0) = L(w, т)+1, 4iHw.
(11.159)
Под w и w0 по-прежнему понимаются функции полного и начального прогибов.
*) Уравнения такого типа были выведены С. В. Александровским [11.1].
544 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
В заключение приведем выражения для энергии деформации в срединной поверхности и энергии изгиба по (10.95):
Uc=jf f (Si/Vj? + 28р.А/*Л/у -- b2Ny-{-boT2)dx dy, (11.160)
- т If t°. <f+Ш'+
+ 4D0 (ш)2} dx dy- (11Л61>
Перейдем к решению некоторых частных задач.
§ 138. Подкрепленные оболочки при осевом сжатии. Одновременное действие осевого сжатия и внутреннего давления
Рассмотрим устойчивость ортотропной оболочки при осевом сжатии. Будем решать общую задачу об устойчивости в большом *); линейная задача явится предельным случаем. Примем аппроксимирующее выражение для прогиба, выбранное Кемпнером (см. стр. 524):
w — f (cos ~ cos + acos?-f-£cos-+. (11.162)
\ 1Х 1у 1>х /
Подставляя, как обычно, это выражение в правую часть второго из уравнений (158) и интегрируя его, находим функцию напряжений:
л С п л Г s2 — 8л 2ъх
ч ~ Т]2 2 У 8,1 32й2 C0S 17
. 02С 2пу О2 юг / I ь\ 11 пх %У I
+ 32 C0S if+ l+2vc»2 + l2C <a+ *) ■- 11 cos Tt C0s Ту +
I О г Зтсх %y,
+ 2flC J _j_ 2)gVca» + 81»4 cos ~l~ cos 7 +
. ur ft2 2tzx 2ny
+ 1 + 2vca2 + a4 cos ТГcos ~T~ 'T'
+ 26 81 + 2,9vc»2 4- cos 7J cos ~T7~ 1— N* \ ’ (11.163)
Lx
здесь введены следующие параметры:
V+ 2 50 2у?я2 r / Г \
-■ -, Ч = уЬдВа. С = —==~. » = ~ I/ В,
У 5152 у 2 У 52D2 ж
*) Это исследование проведено О. И. Теребушко [11.22], а также В. Тилеманном и другими авторами [11.51], [11.52]. Ниже приводится решение, содержащееся в этих последних статьях.
§ 138] ПОДКРЕПЛЕННЫЕ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ
545
Для изотропной оболочки будет vc = 1, а величины т] и ft переходят в следующие:
7) = fRh -, » = (11.164)
4 Лз(1-2) /ж
Аналогичные обозначения вводились выше, в § 126; они характеризуют размеры и форму вмятины.
Определим относительное укорочение оболочки по формуле, аналогичной (57):
•'= т ■-- т /в ■**’ -- т / К8.. + V ) •-1 (ж)']
О о
(11.165)
Вычисляем, далее, полную безразмерную энергию системы Э*:
э*=(СМ, - сл2+л3+,)М4+т,л5)+э;: (11.166)
коэффициенты Av..., Аъ зависят от a, b% ft, vc и от величины vIi = D3/yrD1D2. Минимизируя энергию по параметрам С, vj, a, b, ft, приходим к системе пяти нелинейных уравнений.
Полагая С —> 0, находим решение линейной задачи, определяющее точку бифуркации равновесных состояний. При этом будет а — Ъ = О, так что для прогиба получаем выражение w = / sin (nx/lx) sin (ny/ly); выпученная поверхность делится на прямоугольные клетки. Отдельно надо исследовать случай ft->oo, когда образуются осесимметричные кольцевые выпучины; при этом w = / sin (ъх/1х). Верхнее критическое усилие получается в последнем случае равным
<М67)
к
Для изотропной оболочки отсюда вытекает классическая формула (33). Введем обозначения:
я-тт/' -ВТ- 1=-щг <-168>
Величине NB соответствует параметр NB = длина полуволны 1Х
оказывается при этом равной lx = тс У R2Dxb2.
Вернемся к уравнениям, описывающим большие прогибы оболочки. На следующих графиках представлены результаты их решения, полученного с помощью электронных цифровых машин. Наиболее существенной характеристикой ортотропности оболочки оказывается параметр 7; судя по (168), при относительно сильных стрингерах
546 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
велико, а при сильных шпангоутах — мало. На рис. 11.55 показано, как зависят величина верхнего критического усилия NB и вид диаграммы от т при vc = 4 и vH = 0,5. За единицу по оси ординат взято верхнее критическое усилие осесимметричной потери устойчивости N0t в, вычисляемое по (167); по оси абсцисс отложено отношение e/e0f в, где е0> в — критическая деформация кольцевого выпучивания. Как видим, для ортотропных оболочек точки бифуркации
Рис. 11.55. Диаграмма равновесных форм сжатой ортотропной оболочки при больших прогибах.
«клеточного» типа NB и «кольцевого» типа N0t в не совпадают. Выпучивание в малом должно, очевидно, сопровождаться образованием клеток, причем с возрастанием 7 отношение NJN0t в падает. Закритические диаграммы относятся к выпучиванию «по ромбам»; характер их резко меняется в зависимости от 7.
При значительных 7, т. е. в случае усиленных стрингеров, диаграмма имеет за точкой бифуркации обычный падающий участок. Однако при уменьшении 7 наклон этого участка изменяется, и, начиная с 7 < 1/9, мы получаем уже не падающую, а восходящую характеристику. Правда, в последующем напряжение вновь снижается и оказывается возможным определить нижнее критическое напряжение. По-видимому, при испытаниях реальных оболочек мы будем наблюдать переход от одной ветви к другой путем хлопков.
На рис. 11.56 показано, как меняется отношение нижнего критического усилия к верхнему в зависимости от 7 при тех же vc и vH. Судя по этим данным, эффект нелинейности оказывается наибольшим для изотропных оболочек. Он несколько ослабевает в случае оболочки, усиленной в продольном направлении, и резко падает для оболочек, имеющих поперечные подкрепления. Различной оказывается и форма волнообразования: как и естественно ожидать, в случае сильных стрингеров вмятины вытянуты вдоль образующей, а при сильных шпангоутах — вдоль дуги.
§ 138] ПОДКРЕПЛЕННЫЕ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ 547
Для случая, когда подкрепленная оболочка подвергается одновременному действию осевого сжатия и внутреннего давления, решение может быть проведено аналогичным образом. Если воспользоваться для w прежней аппроксимацией (162), то выражение (163) для ср надо дополнить членом (qRx2!2), где q — интенсивность внутреннего давления.
Введем параметры
в случае изотропной оболочки они равны
1 Е А2 ’
На рис. 11.57 изображена зависимость между сжимающим усилием N и величиной e-f-Stt//’8182 при определенных значениях vc, v„ (они
Рис. 11.57. Диаграммы «усилие — приведенная деформация» для оболочки, испытывающей осевое сжатие в сочетании с внутренним давлением.
указаны на рисунке) для оболочки, усиленной в осевом направлении (7 = 8,064). Нижняя кривая относится к случаю, когда внутреннее давление отсутствует (q= 0), а вышележащие кривые — к последова¬
Рис. 11.56. Изменение нижнего критического напряжения сжатия в зависимости от характера подкрепления оболочки.
548 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
тельно возрастающим значениям q. График ограничен сверху линией, отвечающей случаю осесимметричного выпучивания. Как видим, с увеличением q здесь возрастает не только нижнее, но и верхнее критическое усилие; этим ортотропная оболочка отличается от изотропной. Вместе с тем, как видно из рисунка, от интенсивности q зависит вид начального участка закритической диаграммы, при значительном q и здесь мы получаем восходящие участки, при q = 4 начальный участок получает форму петли.
Мы можем сделать вывод, что при наличии значительного внутреннего давления более эффективным оказывается усиление оболочки в продольном направлении: в этом случае величины NB и NH оказываются относительно выше, чем для оболочек, усиленных в дуговом направлении.
О. И. Теребушко рассмотрел нелинейную задачу об осевом сжатии конструктивно анизотропной оболочки, пользуясь методом Ритца и принимая аппроксимацию для w в виде (68). Решение проводилось
также с помощью электронных цифровых машин. Исследуя закритическое поведение оболочек для разных типов подкрепления, приходим к заключению, что требованию наименьшего веса отвечает оболочка вафельного типа с весьма часто расставленными продольными и кольцевыми ребрами (рис. 11.58).
Рис. 11.58. Оболочка «вафельного» При этом ставилось требова-
типа. r „ s
ние равноустойчивости в большом
для замкнутой оболочки и для отдельных цилиндрических панелей, расположенных между подкреплениями (см. § 139). Такой вывод станет понятным, если учесть, что редко расставленные стрингеры или шпангоуты не могут заметно повлиять на образование местных вмятин. Конструкция должна быть рассчитана таким образом, чтобы в пределах каждой вмятины было расположено несколько подкрепляющих ребер; лишь тогда критическое напряжение может значительно возрасти по сравнению со случаем неподкрепленной оболочки. Пример выпучивания гофрированной оболочки, удовлетворяющего этому требованию, показан на рис. 11.59*).
Изображенная на предыдущем рис. 11.58 вафельная конструкция является необычной, возникает вопрос о технологии ее изготовления. Здесь могут быть применены штамповка, фрезерование или другие методы. Однако преимущество такой конструкции является очевид-
*) Испытания таких оболочек были проведены Г. Л. Комиссаровой.
§ 138] ПОДКРЕПЛЕННЫЕ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ
549
ным. Как показал О. И. Теребушко, при обоснованном выборе раз¬
ними можно спроектировать под-
меров ребер и расстояний между крепленную оболочку, которая будет в 1,5 раза легче равноустойчивой с ней изотропной оболочки.
Важно отметить также, что влияние ребер на верхнее и нижнее критические напряжения будет различным в зависимости от того, как расположены ребра относительно срединной поверхности. Можно показать, что в случае ребер, находящихся со стороны выпуклости, верхнее и нижнее критические напряжения будут (при прочих равных условиях) выше, чем в случае ребер, расположенных с вогнутой стороны.
По-видимому, исследования устойчивости в большом для подкрепленных оболочек могут привести здесь к модели облегченной конструкции. Мы получаем здесь пример того, как совершенствование методов расчета,
связанное с применением современной вычислительной техники, может дать толчок к появлению новых типов конструкций.
Пример 11.4. Определить критическую нагрузку для сжатой вдоль оси замкнутой стеклопластиковой оболочки, изготовленной из стеклоткани типа корд и полиэфирной смолы. Направление основы совпадает с образующей цилиндра. Размеры: R = 108 мм, h = 1,5 мм. Такого типа оболочку можно приближенно рассматривать как ортотропную. Заданы следующие значения модулей упругости и коэффициентов Пуассона: Ех = 2 • 105 кг/см2 (вдоль оси), Е2== 1 • Ю5 кг!см2 (в кольцевом направлении), = 0,1, ja2 = 0,05.
Находим верхнее критическое усилие по (167) для осесимметричной потери устойчивости:
Рис. 11.59. Выпучивание гофрированной оболочки, подвергающейся осевому сжатию.
Nn
отсюда
или
-tV %-ТУ°'в'Ъ j/El
V Е, R’
К3(1 — Ц,(Аг)
2 • 105 г_ 0,15
(а)
(Ь)
V 3(1—ОД 0,05)
V0,5
10,8
= 112Q кг/см2.
550 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. X!
Эта величина лежит в пределах упругости материала. Полная критическая нагрузка равна
Р0, в = в = 11>4 т-
Испытание такой оболочки в лаборатории*) показало, что в действительности выпучивание происходит по ромбической форме, как показано на
рис. 11.60. Критическая нагрузка составила 6 т, т. е. около 53% от верхней критической величины.
Отметим, что стеклопластиковые оболочки, армированные тканью или жгутами, находят все большее распространение в различных областях техники. Желательно, чтобы были даны уточнен* ные методы расчета таких оболочек, основанные на нелинейной теории и учитывающие особенности структуры того или иного материала.
§ 139. Устойчивость цилиндрической панели при осевом сжатии
При проектировании подкрепленных оболочек необходимо, как мы видели, рассчитывать на устойчивость отдельные панели, лежащие между ребрами. Обратимся поэтому к задачам об устойчивости таких панелей — открытых круговых цилиндрических оболочек—при сжатии и сдвиге. Условия закрепления панели по кромкам зависят от размеров подкрепляющих ребер. Обычно ребра имеют достаточную жесткость на изгиб в плоскости, перпендикулярной к срединной поверхности, и потому прогиб панели по кромкам можно принимать равным нулю. В зависимости от крутильной жёсткости ребер различают случаи полного или упругого защемления, либо шарнирного опирания. Кроме того, должны быть сформулированы условия, касающиеся перемещений точек, принадлежащих кромкам панели, в плоскости, касательной к срединной поверхности.. В одних случаях — при ребрах, слабых на изгиб в этой плоскости, — можно считать, что точки кромки перемещаются свободно в направлении, перпендикулярном к кромке. Если же ребра обладают большой жесткостью, ставится условие равенства нулю этих перемещений. Далее, должны быть рассмотрены условия, касающиеся перемещений точек панели вдоль кромок. При наличии сварного шва или заклепочного соединения следовало бы считать, что перемещения точек панели “по отношению к ребру в этом направлении отсутствуют; это условие в большой мере относится к «цельным» или «интеграль¬
*) Оно было проведено Б. В. Ивановым.
Рис. 11 60. Выпучивание сжатой оболочки, изготовленной из стекловолокна.
§ 139] УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ ПРИ ОСЕВОМ СЖАТИИ 551
ным» конструкциям, в которых ребра изготовляются заодно с обшивкой. Однако для упрощения задачи чаще всего принимают, что точки панели свободно скользят вдоль кромок.
Рассмотрим прежде всего случай, когда круговая цилиндрическая панель сжата усилиями /?, равномерно распределенными вдоль криволинейных кромок. Обозначим через а и b длину и ширину панели, через 0 — охватываемый ею центральный угол (рис. 11.61). Рассмо* трим случай шарнирного опирания панели по всем кромкам. При решении линейной задачи *) бу-
w = f sin тпХ sin ппу (11 170) Рис Цилиндрическая панель
J а Ь ' у ' ' при осевом сжатии.
где т и п — числа полуволн вдоль образующей и по дуге. Подставляя это выражение в (169), получим:
D / т2п2 п2п2 \2 Е т4п4 / т2%2. п2п2 у
Т \а?~ ~Ь*~) p\aT~'~bi~)
п2п2 2 т2к2 ~Ь2~) W
откуда
или
(11.171)
где
(11.172)
Минимизируя р по ср, находим:
(11.172а)
Верхнее критическое напряжение оказывается равным
(11.173)
*) Эта задача была впервые рассмотрена С. П. Тимошенко, см. его «Курс теории упругости», ч. 2, Петербург, 1916, стр. 395.
552 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. *1
Мы пришли вновь к хорошо известной нам формуле (33), полученной выше для замкнутой оболочки. Однако эта формула справедлива лишь для панели, охватывающей сравнительно большой центральный угол, когда операция дифференцирования по ср является допустимой.
Как и для замкнутой оболочки, форма волнообразования здесь однозначно не определяется, известна лишь величина ср, зависящая от чисел т и я. В случае весьма пологой панели следует в (172) принять п = 1, т = а/Ь; тогда будет ср = 2. Отсюда по (171)
Pb==4~¥F~{~r) Е' (11.173а)
Эта формула справедлива при условии
ИЛИ
9<lV г* /i-
К 12 (1 — 1*)
Введем безразмерные параметры, характеризующие сжимающее усилие и кривизну панели:
•“id)'- * = 4 = ж: <1М74>
тогда из (173) получаем для панели большой кривизны
р* = 1 k 0,605/е, (11.175)
а для пологой панели при k. 12
Ра— 3(1 — fxa) 4~3,6-*~39£ * (11.176)
Решим ту же задачу в нелинейной постановке *). Примем сначала для простоты, что речь идет о шарнирно опертой квадратной панели (Ь = а) и что ненагружепные кромки сближаются свободно, оставаясь прямолинейными. В первом приближении выберем выражение для w по-прежнему в виде (170), считая при этом, что в обоих направлениях образуется лишь по-едной полуволне (т = п— 1). Подставляя w в правую часть уравнения (27) и интегрируя, находим:
1 л 1 го ( 2т1лг 2пу \ I - а2. пх. лу ру2
£Ф = ЖЛС05—+C0S а ) + ТЯ 5Ш —
*) Приведенное ниже решение предложено автором [11.5], причем условие прямолинейности кромок выполняется лишь приближенно. Исследования устойчивости панелей в большом принадлежат также В. Койтеру [11.41], Легге (Legget D., Rep. and Меш., № 1899 (1942), № 1972 (1943)) и другим.
§ 139] УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ ПРИ ОСЕВОМ СЖАТИИ 553
Статические граничные условия на кромках: <зу = 0, х = 0 при у — О, b; ах = — р, т = 0 при jc = 0; они выполняются для каждой кромки лишь в среднем.
Воспользуемся методом Бубнова — Галеркина и составим уравнение
If Hr “ L {W' Ф) “ i S] sin -X sin dxdy = 0.
0 0
Подставляя выражения для w приходим к уравнению
w£/’-w£/+w£+
, TZ4 ~ 712 r\
Считая /-> 0, находим прежнюю формулу (173) для верхнего критического напряжения рв. Далее находим:
р = Рв + §я Ef-
Полагая С = ///г, получим: р’=р\+-
(11.177)
Минимизируя /?* по С, находим нижнее критическое напряжение равным
Я2 200 2 /1 1 1 TQ4
/’и—3 (1 — р.2) (11.178)
и Ф и выполняя интегрирование,
l\
\ \
1
\\ \ \
/
г,
if
\ \
1
//
\
\
\
/
II
и
J
/
1
1
1
\
\{.
//
/
/
/'
у
/
/
-/ 0 1 2 3 4 £ 5
Рис. 11.62. К определению нижнего критического напряжения сжатия для цилиндрической панели при различных условиях закрепления.
при С «0,14; оно лежит несколько ниже критического напряжения для плоской панели, равного тс2/3(1—а2)»3,6. В последнее время эта задача для квадратной панели была решена в конечных разностях с помощью электронной цифровой машины*). На рис. 11.62 представлена зависимость р*(С), относящаяся к случаю ==12; пред-» полагалось, что кромки панели остаются прямолинейными (кривая /) или свободно искривляются (кривая 3). Часть кривой У, соответ-.
*) Эти результаты принадлежат А. Ю. Биркгану. См. также статью М. А. Колтунова «Устойчивость гибкой панели цилиндрической оболочки* в «Вестнике Моск. гос. ун-та», М*2 5 (1962).
554 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
ствующую неустойчивым равновесным состояниям панели, данным методом получить не удалось. Штрих-пунктирная линия 2 соответствует уравнению (177), полученному при граничных условиях, приближающихся к случаю прямолинейных кромок. Как видим, общий характер изменения р* описывается приближенным решением удовле-
В более общем решении *) задачи, для панели произвольной кривизны и а Ф Ь, прогиб был задан с помощью выражения типа (68):
Нижнее критическое напряжение оказалось равным (при £>20) /?*v= 0,26. Надо полагать, что при более точном решении задачи теоретическое значение р* должно упасть и приблизиться к значению 0,18£, полученному для замкнутой цилиндрической оболочки. В то же время для пологой панели (при k 20) величина /?*, как мы видели, мало отличается от критического напряжения для плоской пластинки. Поэтому можно рекомендовать вести практические расчеты, определяя верхнее критическое напряжение по формулам (175) и (176), а для нижнего критического напряжения принимать (в случае тщательно изготовленных оболочек):
Если же панели получают при изготовлении и сборке конструкции значительную начальную погибь, сравнимую с толщиной оболочки, следует принимать /?* = 0,12 (при k > 20).
Цилиндрические панели, входящие в конструкцию крыла летательного аппарата, передают не только нормальные, но и сдвигающие усилия. Перейдем к исследованию устойчивости панели при сдвиге. Допустим, что панель со сторонами а, Ъ, шарнирно закрепленная по краям, подвергается действию касательных усилий, равномерно распределенных по всем кромкам (рис. 11.63)**). Исследуя устойчивость панели в малом, примем за основу уравнения (15а) и (16):
*) Оно дано О. Н. Ленько и автором, см. [0.3], стр. 296.
**) Впервые эта задача была рассмотрена Н. В. Зволинским (Труды ЦАГИ, № 246 (1936)). Приведенное здесь решение задачи принадлежит В. А. Марьину [11.14].
творительно, но величина /?нП0(178) лежит ниже уточненного значения.
sin + /2sin2-sin. (11.179)
р*и = 3,6 при k <20; =0,18А при k>20.
§ 140. Устойчивость панели при сдвиге
(11.180)
(11.181)
§ 140] УСТОЙЧИВОСТЬ ПАНЕЛИ ПРИ СДВИГЕ 555
Примем выражение для w в виде
W :
ъ
т п
Подставляя это выражение в правую часть уравнения (171) и интегрируя, получим:
- Е V4 V4 х яг2. тпх. ппу,
~ ZAjfmn / m2 П2 \ 2 ап —яп-+му.
т п yw + “р-;
Воспользуемся методом Бубнова — Галеркина и вместо (180) возьмем уравнение
Г Г ( D -уд 1 д2Ф, 0 d2w \. Ых, /тсу л
J ) (irv%-«+2s)sin —sinZr=°-
(П
Подставляя выражения для ге; и Ф, после интегрирования находим:
- ab
I тп 4
1т4Е
i4D / т2, п2\2 7Г V'o2' *+■ Ж J
— S 2 f V8s (m2 — г'2) (п* — /) — 0;
* Рис. 11.63. Цилиндрическая панель
здесь должны учитываться лишь те при сдвиге,
члены, для которых суммы т-\-1.и n-\-j нечетны. Это следует из соотношений (7.151). Вводя в дополнение к (174) обозначения
= х==т* (11Л82>
приходим к уравнениям типа
Amnf тп Р f if (т2 /2) (п2 jsy == 0» (11.183)
где
А - 112 (т2 + п*\2)2 k2 АтЯ2 1285* -
3(1— it2) тпгй2 ' п2 (т2 + п2к2)2 п ’ р тс2 •
В первом приближении примем числа т, л, /, j равными 1, 2. Выпишем соответствующую систему уравнений типа (183):
4 1
Ai/n 9 Р/22 = 22/22 9 Р/u =
2 2
Аг/12 + gT Р/21= 0* 21/21 + “9 Р/12 — 0*
556 устойчивость ЦиЛйнДРйЧ. СёоЛочёк Пределах упругости [гл. XI Условие нетривиального решения этой системы имеет вид
Лп -Q р О
]_
‘ 9 О
О
9
А 22
О
о
о
о о
а2 4р
Р Л2
(11.185)
Уравнение (185) распадается на два: А,
4
¥ Р
1
—-Q р А
22
А\2
2
¥ Р
= 0,
2
9 Р
Л2Х
первое из них соответствует четной сумме индексов т-\-п, второе — нечетной. Отсюда находим два корня для р:
9 г 9 г Pi = ~2 У Al Ай’ Р2 = Y У 1221’
и значения верхнего касательного напряжения:
О* лГл А, s* %2 l/~4 ~А~
1 — 256 ' 22 2 — 256 '
В случае квадратной панели (Х=1) получим:
5’
(11.186)
'+44 <187>
Во втором приближении учтем все возможные комбинации индексов, равных 1, 2 и 3, причем система уравнений по-прежнему распадается на системы, относящиеся к индексам с четной и нечетной суммами т-\-п. Для случая четных сумм получим уравнение вида
Ац
4
~ 9 Р
0
0.
0
1
“ TP
22
1
5 Р
1
5 Р
9
25 Р
0
4
15 Р
A\z
0
0
0
4
15 Р
0
31
0
0
4
25 Р
0
0
33
:0.
§ 140] устойчивость панели при сдвиге 557
Отсюда
с* ГС2 /“ 4и -Д22-413Л31Л33
~ 128 г
где
= АИ13 (- 31 + -ft; зз) Н5 зИзз 13) •
Для нечетных сумм т-\-п будет
л* п2 ъГ “412-21 -23-32
- *2 — 128 V L2
причем
36 4 4
2 025 1221 Н gj2332 Ч (1223 “1“ 2132)*
Наконец, в третьем приближении учтены все комбинации индексов от 1 до 4. Оказалось, что это приближение дает малые поправки к результатам второго приближения.
Верхнее критическое напряжение *, как правило, определяется величинами, относящимися к четным суммам индексов. Исключение составляют удлиненные панели (к 3) малой кривизны (k < 7).
Обратимся к решению нелинейной задачи. Примем выражение для w в виде
.. пх. пу,.. 2пх. 2пу...
w = fx sin — sin -f- /2 sin —— sin —jj-. (11.188)
Из уравнения (27) находим:
i ф=iw- (а*cos +b*cos Ч) К+
iщ- (а4 cos пг +м cos г) Я+
32аЧ* + 4 аЧ2
пх Зпу Зпх пу
cos COS —~ COS COS
CL О j CL I f f Г
(A2 + 9a2)2 1 (a2 + 962)2 I/1/2 ~r
a2b*. nx. nv,
sinrsin-/i +
■I»
~ Ji2 (a2 + 62)2 /? a b
, a2b4. 2ялг. 2-y
+ 4rc2 (a2 + b*Y~R Sln “Г Sln -Г fr+ e-
Выпишем уравнения метода Бубнова—Галеркина:
J J X sin sin dxdy = 0, j* J X sin sin - dx dy = 0,
F * F
где
x = -L(w, тогда получим уравнения относительно fx и /2. Вводя дополнительные
558 устойчивость цилиндрич. оболочек в пределах упругости [гл. xi
обозначения /i/A = C, fh = \, приведем эти уравнения к виду Ср + CJ — Cpk — Cfk + С5Ш
+ 12(1-„-) + <П-'89>
16 С3 + С£Ч — С6«Л + С5№ -1-
+ 3(1-,.) (Ч' (+л-о.-оим>
где Сг,..., Сб — некоторые функции X.
Введем параметр ф = £/С, определяющий форму волнообразования. Исключая s* из уравнений (189) и (190), получим биквадратное уравнение относительно ф:
Ц4_ /?.2_5 = 0,
где 7, /?, 5 — некоторые функции X, kt С. Определив отсюда ф, находим далее 5*.
Ц*
0,3
0,2
0J
к=24
У
\
\
V \ \\
к=0
\
Jr /
/ / у / / / /
//
\N
N j \
>с
V
\
*5 \
/
24
i
1
i
1
1
1
50
40
30
10
II
/
7
/
1
2
3 4
С
Рис 11.64. Изменение характера волнообразования панели при сдвиге.
7 2 3 4
Рис. 11.65. Диаграмма «усилие — прогиб» для цилиндрической панели при сдвиге.
На рис. 11.64 показана зависимость ф от С для случаев Х=1 (сплошные кривые) и Х = 2 (пунктир). На следующем рис. 11.65 даны кривые s* (С) для плоской пластинки (/5 = 0) и цилиндрической панели с кривизной =12 и 24 при Х=1. Нижнее критическое напряжение s* снижается по сравнению с s*B примерно на 30%
§141] устойчивость В ЗОНЕ ПРИЛОЖЕНИЯ СОСРЕДОТОЧЕННЫХ НАГРУЗОК 559
для =12 и на 50% для 6=?24 Надо помнить, однако что эти результаты получены при двучленной аппроксимации прогиба по (188). Правда, и в этом случае выкладки являются весьма громоздкими. Более обоснованные данные должны быть найдены с помощью электронных цифровых машин.
Рис. 11.66. Расчетные данные для определения нижнего критического напряжения сдвига в случае цилиндрической панели с различным отношением сторон.
Для практических расчетов рекомендуется график рис. 11.66, составленный с учётом экспериментальных данных.
§ 141* Устойчивость оболочек в зоне приложения сосредоточенных нагрузок
До сих пор мы рассматривали, как правило, такие задачи по устойчивости оболочек, в которых основное состояние можно было считать безмоментным. Однако на практике мы находим случаи, когда изгибные усилия в исходном* состоянии являются значительными.
560 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК В ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
Мы уже видели это в § 130, когда надо было учесть влияние
защемления торцов оболочки на устойчивость при действии внеш¬
него давления. Вообще с такого рода задачами мы встречаемся, если к оболочке приложены нагрузки, сосредоточенные в некоторой узкой области, например в районе сопряжения оболочки с днищем или жестким шпангоутом. Допустим, что оболочка подвергается осевому сжатию и внутреннему давлению или одному внутреннему давлению; так как днище или шпангоут препятствуют деформации оболочки, то от них на оболочку передаются сжимающие радиальные усилия. В зоне краевого эффекта, прилегающей к месту сопряжения, прогиб резко изменяется; при этом моменты и поперечные силы имеют большую амплитуду, и следовательно, моментное напряженное состояние оказывается ярко выраженным.
Здесь мы сталкиваемся, с одной стороны, с задачей о бифуркации равновесных состояний оболочки для зоны краевого эффекта
и, с другой стороны, с определением
несущей способности из условия, что
напряжения достигают опасной величины. Остановимся сначала на бифуркационных задачах.
Допустим, что замкнутая оболочка длины L подвергается действию внешнего давления, распределенного равномерно по поясу b, расположенному посередине длины (рис. 11.67). Такая задача может встретиться при расчете оболочек, снабженных шпангоутами, в различных конструкциях, в случае, если продольные подкрепляющие ребра отсутствуют. Примем, что деформации в срединной поверхности v изменения кривизн для исходного осесимметричного напря¬
женного состояния оболочки определяются по (2) и (4) выражениями
л *
'Ъ'®
II
9.4
II
*о*
w0
R ’
О
II
о
II
°*Н
d2w0 дх2 ’
1
II
w0 R2 »
II
О
где я0, w0—начальные перемещения; принято о£ = 0. Будем считать, что потеря устойчивости оболочки сопровождается волнообразованием как по образующ й, так и вдоль дуги. Решая задачу об устойчивости в малом с помощию метода Ритца *), представим начальные
*) См статью Элмрота и Браша (В. О. А1 ш г о t h, D. О. Brush, Journ. Aerospace Sciences 28, № 7 (1961), 573—578, 592); этими авторами получены данные, приведенные на рис. 11.68 и 11.69.
Рис. 11.67. Оболочка подвергается внешнему давлению по поясу шириной Ь.
§141] УСТОЙЧИВОСТЬ В ЗОНЕ ПРИЛОЖЕНИЯ СОСРЕДОТОЧЕННЫХ НАГРУЗОК 561
и дополнительные прогибы с помощью рядов wo = -§- 2 /о,т*п. « = cos 2 /Ps,n£r-
т=1, 3, 5,... /? = 1, 3, 5,...
Аналогичные выражения могут быть выписаны для перемещений и, V-
Oflt 0,10 1,00
0,01 0,10, 1,00 в)1'1
Ofit 0,10 в)
t/L
Рис. 11.68. Данные для вычисления верхнего критического давления при местном приложении нагрузки.
Определяя полную энергию системы и минимизируя ее по пара метрам /р, определяем верхнее критическое давление qB. На рис. 11.68 даны значения параметра qB — qB R/Eh для различных bjL при отношении /,//? = тс/4, ти/2 и тс. Эксперименты показали, что оболочки теряют устойчивость хлопком, причем вмятины располагаются в зоне пояса b (рис. 11.69). Желательно, чтобы в дальнейшем эта задача была исследована с помощью нелинейной теории.
Рассмотрим теперь, снова в линейной постановку предельный случай, когда отношение L/R весьма велико, а ширина пояса b стремится к нулю, так что давление оказы-, вается приложенным по линии (рис. 11.70);
под N понимается погонная интенсивность нагрузки. Здесь можно избрать другой подход к задаче, связанный с составлением интегрального уравнения *). Изучим начальное состояние. В задачах типа
Рис. 11.69. Характер волнообразования при местном приложении внешнего давления.
*) Это решение задачи было дано Л. И. Балабухом и В. М. Марченко, Приведенный здесь вариант вывода принадлежит А. И. Тюленеву.
562 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
краевого эффекта можно пренебречь величиной w0/R2, фигурирующей в выражении (191) для *у. Тогда мы придем к известному упрощенному варианту разрешающего уравнения типа (17). Повторяя вывод,
, \
\tu : /* ■ \«- \V
ГО —=Ш
\
* У
/ j-r -1
\~ ’ 1
Г~ \
V / ■ — “А
AJ x~Rx ЧЕЕ\
V' К
Рис. 11.70. К расчету на устойчивость оболочки в зоне приложения сосредоточенной нагрузки.
убеждаемся, что в осесимметричной задаче уравнение (17) может быть заменено уравнением четвертого порядка (при рх = ру = s = 0)
D d4w0. Е А /11 1ЛЛЧ
ir-d+ww о=°- (11Л92>
Введем переменную a = x/R и положим Х2 = zVl—R/h, тогда (17) получит вид
+ 4Х%0 = 0. (11.192а)
В среднем сечении при а = 0 должно быть
п D d3w0 N dw0 п
Чх— /?з daз — 2 ’ da —и*
Учитывая эти условия, используем решение уравнения (192) в виде
NR3
w0 = -g£xT е~Ха (cos + sin а)-
Усилия вдоль дуги будут равны
oyh = — w0 = — 2 Ne-la (cos Ха -f-- sin Ха). (11.193)
Перейдем теперь к рассмотрению выпученного равновесного состояния оболочки, уже не являющегося осесимметричным. Представим функцию прогиба, как и в предыдущем примере, в форме тригонометрического ряда по переменной р = y/R:
со
W = 2/i(a)c°S. п—1
§ 141] устойчивость в зОнё Приложений сосрёдСточённых нагрузок 563
Воспользуемся полным уравнением (17), считая ру =— оу, рх = = 0; тогда получим уравнение относительно амплитуд прогиба wn:
[{--п2)4 + 4X4!■] ®« = ПГРуп2(- ~ л2}2»«• О1-194)
Применим, далее, преобразование Фурье *). Имея в виду, что напряженное состояние является симметричным относительно параллели а = 0, выберем преобразование Фурье по косинусам. Иными словами, введем наряду с оригиналом функции /(а) ее изображение (трансформанту) F (s) по формуле
ОО
F (s) = ~ У* / (а) cos sol da. (11.195)
о
Обратная зависимость, связывающая оригинал /(ос) с изображением F(s), имеет вид
ОО
/(«>= /4/ F (s) cos sads. (11.196)
о
Следует учесть, что при симметричном относительно нулевой параллели а = 0 напряженном состоянии нечетные производные от функ¬
ции прогиба равны нулю при а = 0.
Применяя преобразование Фурье по косинусам к уравнению (194), получаем следующее изображающее уравнение:
00
l(s2 + я2)4 -(- 4XV] W (s) = 4 ]/~(s2 + /г2)2 п2 J pywn cos sa da.
о
(11.197)
Здесь через W обозначена трансформанта Фурье функции прогиба. Интеграл, входящий в правую часть (197), представляет собой трансформанту Фурье произведения функций ру(а) и wn(a). В соответствии с теоремой о свертках трансформант **) находим:
ОО ОО
J ру10п cos sa </а = j W (p)lP(s - p\)-\- P(s + p)]dp, (11.198)
0 0
где P — трансформанта Фурье функции py(ос). Производя преобразо-
*) См. Снеддон, Преобразование Фурье, И Л, М., 1955, стр. 27 и сл-
**) См. предыдущую ссылку, стр. 35.
564 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК в ПРЕДЕЛАХ УПРУГОСТИ [гл. XI
вание Фурье (195) над выражением (193), получаем: р)+ («+/>)=
= (1 — ***>/>)4 + 4Х< + (s-+-/>)“Н-4X4]* (П.199) Введем обозначение
„()=уе±щтн:Г(5,;
тогда соотношения (197) — (199) дадут
ОО
V(s) = N f К (s, р) V (р) dp, (11.200)
о
где
1С( с nV 2Х<п2 12 (1 — х2) /?2 s2 + n2 v
A {S. р)— п Eh3 а
Х У(р* + Jp'+'4Ay [ (~РУ + W + (s+ РУ + 4x0* (И-201)
Мы получили однородное интегральное уравнение (200) Фредгольма второго рода с симметричным ядром, причем внешнюю нагрузку N можно рассматривать как независимый параметр. Нашей целью является определить верхнюю критическую величину NB, т. е. наименьшее собственное значение уравнения (200). Но с такой задачей мы уже встречались в § 15 при рассмотрении устойчивости сжатого стержня. Как мы видели, NB приближенно находится из соотношения
оо оо
V-// К2(s, p)dsdp.
N2
о о
Для упрощения выкладок заменим входящую в выражение (201) величину
1, 1
(s — ру + 4Х4 ' (s + р)4 + 4Х4 на заведомо большую: 1/2Х4; тогда найдем:
ОО оо
1 144<1-ц2)2Д4«< Г Г (s2+n2)2 (/>2 + п2)2
Ч»— r*E?h* J J [(s2 + л2)4 + 4X4s4] [(р2 + л2)4 + 4XV] р'
о о
Как легко видеть, величина 1/N равна
оо
1 —12 (1 ц2) R2n2 Г (s2 + n2)2 d П1 202)
N * ■ nEh* J (s2 + п2)4 + 4XV *•11 * ’
о
§141] УСТОЙЧИВОСТЬ В ЗОНЕ ПРИЛОЖЕНИЯ СОСРЕДОТОЧЕННЫХ НАГРУЗОК 565
Введем обозначения: z = sjn, v = X//t; выражение (202) примет вид
ОО
1 _ 12 (1 — ц2) Я2ы г (1+г‘)2 N %Eh*\ J (1 -(- z2)4 + 4v*4
о
Вычисляя входящий сюда интеграл, находим: Eh3l У4+-»4
N,
В '
3(1,YVfW+2
Минимизируя N по X, найдем:
V4 — 4 — 21/4 + И = 0;
отсюда v4 = 12. Окончательно
ЕНЯ 4 У12 Eh / h \1,5 2
3(1-)и>/¥ 9 (1 _ 0,75.203)
Эту формулу можно сопоставить с формулой (77) для верхнего критического давления в случае оболочки, подвергающейся равномерно распределенной поперечной нагрузке.
Обратимся к задаче об определении несущей способности оболочки в зоне краевого эффекта. Допустим, что оболочка конечной длины, скрепленная по торцам со шпангоутами, подвергается совместному действию внутреннего давления и осевого сжатия. Исследуем напряженное состояние вблизи шпангоута *). Если ограничиться линейной постановкой этой осесимметричной задачи, то уравнение (192) надо дополнить членами, зависящими от осевого усилия Nx и давления q:
~ d4w, d2w, Eh
При интегрировании этого уравнения надо учесть условия сопряжения оболочки со шпангоутом. Определяем максимальные напряжения, складывающиеся из напряжений в срединной поверхности и напряжений изгиба. Пользуясь той или иной теорией пластичности, находим сочетание усилий и q, при котором напряжения достигают опасной величины. Полученные таким образом расчетные графики для Nx и q приведены в статье [11.12], относящейся к 1960 г.
*) Эта задача была рассмотрена О. Н. Ленько [11.12]. Им было показано, что учет нелинейных членов в выражениях типа (191) в данном случае мало влияет на результат решения.
ГЛАВА XII
УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
ЗА ПРЕДЕЛАМИ УПРУГОСТИ
§ 142. Задача об устойчивости в малом
Выведенные в главе XI зависимости справедливы лишь в пределах упругости. Так, например, формулой (11.33) для верхнего критического напряжения при осевом сжатии круговой цилиндрической оболочки можно пользоваться при условии /?в<пЦ; отсюда
Для дюралюмина при [х = 0,3, опц = 2 • 103 кг/см2, Е=7 • 105 кг/см2 должно быть R/h> 210. Формула (11.66) для нижнего критического напряжения применима, если R/h70. Однако во многих случаях выпучивание оболочек происходит в пластической области. Это относится, прежде всего, к инженерным сооружениям, например к трубопроводам. В главе VIII говорилось уже, что панели современных тяжелых самолетов также выпучиваются при напряжениях, превышающих предел пропорциональности. Поэтому исследование устойчивости оболочек за пределами упругости, слабо еще представленное в литературе, имеет существенное практическое значение.
Как показывают экспериментальные данные (см. § 143), при слабо развитых пластических деформациях необходимо так же, как и в пределах упругости, отличать устойчивость оболочек в малом и в большом.
Подойдем сначала к задаче с точки зрения устойчивости в малом. Естественно распространить на решение этой задачи те методы, которыми мы пользовались при исследовании устойчивости пластинок (глава VIII), и применить теорию деформаций, либо теорию течения.
Обратимся вначале к теории деформаций *). Так как по сравнению со случаем пластинки задача здесь усложняется, выберем наи¬
*) Надо помнить, что все ограничения, касающиеся применения деформационной теории в задачах такого типа (см. § 99), остаются здесь в'силе.
§ 142]
ЗАДАЧА ОБ УСТОЙЧИВОСТИ В МАЛОМ
567
более простой вариант решения и не будем учитывать эффект раз грузки. Иными словами, будем считать, что срединный слой является нейтральным в том смысле, что напряжения и деформации собственно изгиба в точках этого слоя равны нулю. Но для оболочки надо учесть приращения напряжений в срединной поверхности 80, 8оу, 8т и соответствующие деформации Ьвх, 8еу, Ьу; координаты дг, у будем отсчитывать по-прежнему вдоль образующей и по дуге. Пользуясь обозначениями (8.33), перепишем выражения (8.123—5) в виде
8 = £с8е,-(Ес-£к)-Ц,
У_
\ — (Ес — EK)~Ut,
bSy — (£с £к)
8х
(12.2)
где sx = ox— 0,5ау, sy = oy— 0,5а,*., а 8 и ot — интенсивность деформаций и интенсивность напряжений в срединной поверхности *). Умножим левые и правые части уравнений (2) соответственно на ох, оу, Зх и сложим; принимая во внимание соотношение
получим:
Отсюда
sx°x + sy°y + = °2i>
°xbsx + °ybsy + Зх8т = лЦaxbsx + + 3x5т П (a, s)
где
1 чЕк
П(а, 8) = П(, 8о) = sxbox -- syboy -f-Зх8х. Пользуясь (2), находим:
8’=i[38’+fn<‘-84
(12.3)
(12.4)
(12.51
(12.6)
*) В главе VIII мы пользовались обозначением s (без индекса!) для другой величины — интенсивности усилий сдвига; мы сохраним это обозначение и здесь.
568 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [ГЛ. XII
Выпишем уравнения равновесия элемента оболочки в проекциях на направления образующей и касательной к дуге:
д(Ъ,х), д(Ъг)
дх
д(Ъх)
ду д (5ау)
дх
ду
■ О,
:0.
(12.7)
Эти уравнения будут удовлетворены, если ввести функцию дополнительных напряжений по формулам:
Тогда
* д2Ф аду2
д2Ф
дх2 9
Ъх :
д2Ф
дх ду
Л2ф Л2ф
П («. bs) = П (S, Ф) = «д.+ sv
У дх2
Зт
д2Ф дх ду
(12.8)
(12.9)
Выражения (6) принимают вид дщ 1 д2Ф
дf д*Ф
Ес[ *>-*[
2 дх2 1
%-=--П(о, ф).
’]
Sy Ес Ек
дх2 2 ду2
д2Ф. дх ду
П (а, Ф),
Зт. ф)1
°1 К J
]
(12.10)
Проектируя силы, действующие на элемент оболочки, на направление нормали к срединной поверхности, мы получили ранее следующее уравнение равновесия (стр. 464):
д2Мх
дх2
д2М,
д2Н
d2w
х дх2
у ду2
■2т
d2w
дх ду
(12.11)
Основные напряжения, соответствующие моменту потери устойчивости, обозначим по-прежнему через рх, ру% s\ величины рх, ру считаются положительными при сжатии. Соответствующая интенсивность напряжений равна
Pi = Vр1 -Ь р\ — РхРу+3s2.
(12.12)
Моменты Мх% Му и Н будем и здесь определять с помощью выражений (8.137)—(8.139). Пользуясь, кроме того, соотношениями (8),
§ 143] выпучиваний замкнутой оболочки При бсЁвдм сжатии 569 представим уравнение (11) в виде
2 1 d4w [ сp \ s / d4w d4w
3-3О-тЬг +
1 1 P? J <Ъ>4 Л' 'РсУ Pi дх* дУ 'Уу дх дУгJ
, h / d2w. n d2w, d2w 1 д2Ф \ Л /in
~ted+Py~d?~T¥f 5 ( • 3)
уравнение (8.140), составленное ранее для пластинки, дополнено здесь членом, содержащим Ф.
Возьмем уравнение совместности деформаций, в случае малых прогибов оно имеет форму (11.14):
д2Ьгх д2Ьгу д2Ьу 1 d2w
ду2 ~~~дх* дх ду ~~~R Их* * (12.14)
Подставляя выражения (10), приходим к следующему уравнению*):
У4Ф+ Ус-уГ/ _1 \<?ги(л ф), / _ 1 \ дт(р, Ф)
+ iJi Ll 2 ) д? 2 j А**
агП (р, Ф) 1 __ ус£ d2a> 1
J Л <?■*» • U-lO)
В уравнениях (13) и (15) приняты прежние обозначения (8.68) и (8.120) для срс, срк и Dc.
Воспользуемся теорией течения. Как мы видели выше (§ 108), соотношения типа (6) сохраняются в этом случае, если положить Ес — Е. Поэтому мы придем к тем же дифференциальным уравнениям (13) и (15), считая срс=1, DC = D.
§ 143. Выпучивание замкнутой оболочки при осевом сжатии
Обратимся к случаю шарнирно опертой по торцам оболочки, сжатой вдоль образующей усилиями р. Уравнение (13) принимает вид (при px = pi=py Py = s = 0)
О'Чс [У1 I 3 М d*w I о d*w I d4w] I nd*w— 1 дЩ П* 1 fa —JT L\T“t“4 ус) дх L дх2ду2~ ду4 J ~р дх2 ~ R дх2 '
Выражение (9) оказывается равным
тт/ лчч /<?2ф 1 <*2ф\
П (о, Ф) — р ду2 2 дх2 у
*) Уравнения (13) и (15) содержатся в работах Э. И. Григолюка [12.4].
570 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII Уравнение (15) переходит в следующее:
/3. 1 Ус\ д4ф I /о 9с \ <?4Ф I Ус <?4ф _ ?с£ П9,7ч
\4 4 <?к) дх* М <fK) дх2ду2 'i“ <рк ду* ~ R дх* ' гл,>
Примем для w выражение
х. тпх пу,л л, оч
<aj = /sin —cos-(12.18)
и подставим его в правую часть уравнения (17); тогда получим:
/3, 1 <рс\ <?«ф, /о «Рс\ <?4Ф I Ус <?4Ф
\4 ' 4 % j дх* <?к j <bc2<ty2 Т <fK ду*■
= 02.ISO
Будем искать частный интеграл уравнения (19) в виде
ф = Л sin cos--; (12.20)
находим:
А==Е~Я( 3.1 Ус\/\г, /3?С 9c\/«V, 9с / /л* \2;
1т+тгД-г) +13_г>ы +
отсюда 2ф у
Я /3 1 ус\ / ус\/ Ln X2 • ?с / 17ГуХ
\ 4 4 9к / \ <pK/\'”5t/ 9к \mKR)
.,. тпх пу...
X sin—cos--. (12.21)
Подставляя выражения (18) и (21) в (16) и полагая D' = Eh3/9, приходим к следующему выражению для р:
+wmwwzw¥m\ <12'22)
Введем безразмерные параметры
п — П— ”2fe ft —1—l!L /1 о ооч
Р~ Eh’ R ' п£ ’ <рс (12.23)
Все эти величины, кроме X, встречались в главе XI. Выражение (22) получает вид
+ А2 I О. 1 \ I X
(
С12 I О 1 1 \ I А I / о пл\
§ 143] ВЫПУЧИВАНИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ 571
Если осуществляется осесимметричная форма потери устойчивости * то п = 0 и из (22) получим:
Минимизируя полученное выражение по mic/L, находим параметр, соответствующий критическому напряжению *):
Это выражение вытекает из (11.33), если принять (д, = 0,5.
Если воспользоваться теорией секущего модуля [12.10], о которой говорилось в главе VIII (стр. 381), мы получили бы
Сравнение (26) и (28) показывает, что решение задачи по теории деформаций без учета эффекта разгрузки приводит к более низкому значению для рв.
Основываясь на теории течения и идя тем же путем, придем к формулам:
Рассмотрим теперь более общий случай несимметричной формы потери устойчивости оболочки. Критическое напряжение по (24) представляет собой функцию параметров г\ и 2. Минимизируя функцию (24) по т), находим:
р = Е<.рс
(12.25)
при этом
а = /ЗД-£-
(12.26)
В упругой области, при <рк = <рс = 1, будет
(12.27)
(12.28)
Я = - /<Рк. рш = 4 VEJE 4. (12.29)
Если условно принять ’ то эти формулы совпадут с (28).
7) =
. (12.30)
/*( 1+3L»> + 2 + -£■)(1+» 9* + зх_! +.)
*) Формула (25) получена в работах [8.9], [12.3], [12.10] и обобщена на случай сжимаемого материала Э. И. Григолюком [12.4].
572 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII
Подставляя это значение в (24), получим:
Рв з d\ VkTc* (12.31)
где
d -l/“1 1 П2
и\ —у I (1+ЗХ)4 + 4(ЗХ —1)д2 + 4 •
Если теперь исследовать выражение (32), то окажется, что оно получает «локальный» минимум при
<12'33)
Так как Ь характеризует отношение длин полуволн в окружном и продольном направлениях, то из (33) следует, что при переходе из упругой области в пластическую волны должны вытягиваться вдоль дуги; как мы увидим ниже, это подтверждается экспериментами.
Окончательно формула для критического напряжения при несимметричном выпучивании оболочки будет
Pb = jE(?cV \f -2 + 1 + 3 А. (12.34)
3 V ЗА—1+1+3*. R v ’
Для точек площадки текучести (Х = 0) формула (31) получает / 2 \1,5
вид /7в = срс(-у. Отсюда можно определить критическую деформацию
V1’5 h
кр
=(!П- с»-»»
Сопоставление формул (25) и (31) показывает, что при X Ф 1 будет dx > 1 и, следовательно, выпучивание оболочек в малом при наличии пластических деформаций должно происходить по осесимметричной форме, поэтому для практических расчетов надо пользоваться формулой (26). Ее следует представить в виде
Т7==К' <12'26‘>
Зная зависимость срс и срк от о (см. § 110), находим отсюда критические значения рв для различных отношений R/h. Такой же путь применяется при расчетах по формуле (29).
Приведем данные серии экспериментов по устойчивости дюралюминовых оболочек в упруго-пластической области *). Отношение длины к радиусу составляло L/R = 2; величина R/h менялась в пределах от 130 до 20. Образцы изготовлялись из труб на токарном
*) Эти опыты были проведены А. Н. Божинским [12.1].
§ 143] ВЫПУЧИВАНИЕ ЗАМКНУТОЙ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ 573
станке, так что начальные неправильности формы были незначительными.
В тех случаях, когда потеря устойчивости происходила при слабо развитых пластических деформациях, она всегда сопровождалась хлопком. Появляющиеся при этом вмятины имели ромбовидное очертание, как в упругой области. По мере уменьшения отношения R/h число волн по окружности падало. На рлс. 12.1, а, б, в приведены фотографии испытанных образцов при отношении R/h, соответственно равном 50, 30 и 25.
В случае, если пластическая деформация до потери устойчивости была значительной, эффект хлопка исчезал и образовывалась сплошная кольцевая выпучина (рис. 12.1, в), как в упругой области при наличии внутреннего давления. Таким образом, судя по этим опытам, чисто пластическое выпучивание оболочки действительно является осесимметричным *).
На рис. 12.2 знаком Д отмечены значения парамет-
ра Ркр* полученные в опытах, в зависимости от отношения R/h. Сплошная и штрих-пунктирная линии построены по формулам (26) и (29), первая из которых отвечает теории деформаций, а вторая — теории течения. Интересно отметить, что графики pB(R/h), построенные по двум этим теориям, мало отличаются друг от друга, в то время как в случае плоской пластинки диаграммы pKp(b/h) резко отличались одна от другой. Пунктирная линия на рис. 12.2 относится к упругой области, причем принято а = 0,5. При выпучивании в пределах упругости реальное критическое напряжение оказалось равным ркр0,27, что составляет около 40% от рв = 0,667 (при jx = 0,5) и 45% от рв = 0,606 (при р, = 0,3). Таким образом, здесь налицо резкое расхождение между реальными критическими напряжениями и верхним значением ркр. Однако, как это видно из графика, при возрастающей пластической деформации это расхождение сглаживается. Так, например, лри деформации екр = 1,4епц, где епц = опц/В, критическое напряжение составляет уже 80% от рв, а при е>1,67епц величины ркр и рв оказываются весьма близкими между собой.
Рис. 12.1. Сжатие вдоль оси оболочки после выпучивания при пластических деформациях; для образца в) пластические деформации являются наибольшими.
*) Аналогичные результаты были получены В. Г. Зубчаниновым [12.2].
674 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. Xlf
р*р№/сн\£ 3500
Рис. 12.2. Зависимость верхнего критического напряжения сжатия от отношения Rjh по различным теориям пластичности в сопоставлении с экспериментальными данными.
По теории деформаций
/ / / / / / S / / J /'?У / / / / /7 / у / / / 73
50 W0
W0qlt 250
Рис. 12.3. Зависимость между безразмерным пара* метром сжимающего усилия и отношением Rjh,.
§ 144]
ЗАМКНУТАЯ ОБОЛОЧКА ПРИ ВНЕШНЕМ ДАВЛЕНИИ
575
На рис. 12.3 результаты экспериментов представлены в иной форме. По оси абсцисс по-прежнему отложено отношение R/h, а по оси ординат — коэффициент v = Ркр/Рв’ причем рв вычислено по теории деформаций. Здесь же отмечен характер волнообразования в различных случаях.
Из графиков рис. 12.2 и 12.3 можно сделать вывод, что при сравнительно малых значениях R/h (для дюралюминовых оболочек при R/h < 25), когда пластические деформации значительны, можно вести практические расчеты лишь на устойчивость в малом. Однако при слабо развитых пластических деформациях эффект геометрической нелинейности продолжает сказываться; здесь расчетные разрушающие напряжения должны составлять известную долю от рв. Поэтому задача об устойчивости в большом сохраняет значение и для упруго-пластической области. Попытка решения такой задачи будет сделана ниже (§ 147) в применении к цилиндрическим панелям.
§ 144. Замкнутая оболочка при внешнем давлении
Перейдем к случаю, когда оболочка средней длины подвергается действию равномерно распределенного внешнего давления *) q. Рассматривая устойчивость в малэм, будем исходить из уравнений (13) и (15) деформационной теории. Примем рх = s = 0, py = qR/ht тогда получим:
Из уравнения совместности (37) находим функцию напряжений в виде
Примем для w выражение
-. ткх. пу W = / Sin —J— sin.
(12.ЭБ>
.. тпх. пу
ф = Ах sin —j— sin,
sin —~-
(12.39)
где
*) Это решение принадлежит Джерару [12.10].
576 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. оболочек за пределами упругости [гл. хи Подставляя (38) и (39) в уравнение (36), получим:
J=-i[a<+294-(!+4£)] +
•’+(!+т*)]’
(12.40)
здесь по-прежнему обозначено
*=££ = Ш‘> <12'41>
величины и т] определяются по (23). Как мы видели из рассмотрения упругой задачи, для оболочек средней длины можно принять т = 1, fr2<l; тогда получим:
JL — 2L (1 _j_ -i Tc9U'+4 ?с/
,(i+i±V
44 + 4
или
«Рс + З<fK n2h 4<pK R I kRV1 /19 404
’ Збус R 3<fK + <fc n2h \nL ) *
9c
Находя минимум по я2, имеем:
,Ь5/9к\°’5 4<рс
«4 _ О ‘’7 Ук 4<рс ««/У
Кр \<рс/ <Рс + 3<Рк Л£2 *
Подставляя это выражение в формулу (42), находим верхнее критическое давление:
hL = _i_ / Ус + Зук \Vi / ук \v< / h \!/« /12 43)
Ус 39/“ \ 4срс / \ срс / L \r)
ll
?С 3' \ 4сРс / \ <Рс>
Если принять срк = срс = 1, то найдем отсюда
4 %R ( h ч V*
<7в:
4 tdR /Ау/ ‘ 39/< L \R)
мы приходим к прежней формуле (11.77) при [х = 0,5. И здесь при слабо развитых пластических деформациях может происходить выпучивание оболочки в большом. Поэтому в практических расчетах следует пользоваться формулой (43), вводя затем поправочный коэффициент vO,7.
§ 145. Кручение замкнутой оболочки
Рассмотрим теперь случай нагружения замкнутой оболочки по торцам скручивающими парами *) с моментом
MK=2nR2hs. (12.44)
) Эта задача впервые исследовалась Джераром [12.10].
§ 145] КРУЧЕНИЕ ЗАМКНУТОЙ ОБОЛОЧКИ 577
Уравнения (13) и (15) принимают вид D' Г d4w d4w d4w 1 d2w 1 д2Ф
D'c Г dAw d4w d*w 1
ir L'r+(1 +
+ 2s3W-K-sr-o- <,2-45>
д'Ф J_/3 l\ L <i1' Бе <>*«>
*4 X ) dx2 dy2 dy4 /? d*2 * ( • По аналогии с упругой задачей примем для w выражение
w = / sin sin (у Т*)» (12.47)
где у —тангенс угла наклона волны к образующей цилиндра. Частный интеграл уравнения (46) можно искать в виде
Ф = В, cos [у + (f -f- d) X] -Ь В2 cos [у + (Т — -«1; (12.48)
здесь b = vRjn.L. Подставим выражение (48) в (46), находим:
в EcR(i + Wf
2«2 [(т + ьу + (- -1) (Т + »)2 +1] ’
EcR(t-bYf
S, = -
2п* [(7 - Ь)' + (j - 1) (7 - »)’ -Ь1 ]'
Далее подставляем да и Ф по (47) и (48) в уравнение (45) и приравниваем нулю коэффициенты при cos (га/) [у + (7 + )jc] и cos (re//?) [у + (*f — ft) х]- тогда получим два соотношения между сдвигающим напряжением s и параметрами оболочки:
2s п» М\2 (т + »)4 + (1 + *)(т+»)г+1,
£с — 9 \R) т + _r
Н г ч. (12.49)
«г [(T + V + y-d+V + lJ
2L — (t- + P + Wt-W + i j_
ве ~ 9 1 — 9 1_
+ —Г (JZ=T r <12-50)
[(T _ »)«+±—L (t _ »)2 + 1J
Введем обозначения:
Т+ = т№ + т)=4'”>==1Г* vi = /?'P). Pi=3R' (12,51)
578 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. оболочек за ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII
и придадим уравнению (49) форму
2s о о
1Г=л2Р?
(*)'+«>+*>(*/+
1
(*)•
Для оболочек средней длины цожно пренебречь v2 по сравнению с я2, тогда получим:
2 пЧ + yi
1 1 (12.52)
v,nD
Сравнение этого результата с (11.116) показывает, что правая часть уравнения получается той же, что и при решении упругой задачи.
Рис. 12.4. Критическое напряжение кручения при пластических деформациях.
Но в § 134 мы пришли к выражениям (11.118) и (11.119), определяющим число волн вдоль дуги и верхнее критическое напряжение. Полагая в этих выражениях (л = 0,5 и вводя Ес вместо Е, получим •для нашего случая
» = 4,2 (0,75 >“(£)*(4)\
S. = 0.74 (0.75Е, (-£У* (4)1'' •
(12.53)
(12.54)
Таким образом, в задаче о кручении мы приходим непосредственно к расчету по секущему модулю, как это было в некоторых задачах по устойчивости пластинок. Диаграмма sB(R/h) для дюралюминовых оболочек при L/R = 0,5; 1; 2 представлена на рис. 12.4; здесь sB = sBR/Eh. Учитывая возможность выпучивания оболочки в большом, рекомендуется в практических расчетах вводить поправочный коэффициент к величине sB9 равный уя0,75.
§ 146] ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ОСЕВОМ СЖАТИИ 579
Аналогичное решение задачи может быть дано для оболочек большой длины [12.10], тогда придем к уравнению, аналогичному (11.124):
sB = 0,272 • 0,75~’/4Ес (12.55)
и здесь расчет может быть проведен по секущему модулю.
§ 146. Цилиндрическая панель при осевом сжатии. Устойчивость в малом
Исследуем случай круговой цилиндрической панели, шарнирно закрепленной по краям и сжатой вдоль образующей. Рассмотрим сначала устойчивость панели в малом с применением теории деформаций, тогда надо воспользоваться уравнениями (16) и (17). Примем следующее выражение для w:
w = /sini£sin--. (12.56)
Подставляя (56) в (17), находим:
ф = Л2ап-п-, (12.57)
где
/ Ус.
А0 = Е
отсюда
р f 9с /10 СО\
дх*~ R /3 i_ 1 ?с\/о ?с\/ ап\* <Рс (пау ’
V4 + 4 п) + \3-п)\Ш) +П\Ь)
Пользуясь уравнением (16) и вводя обозначения:
— = lx, - = L, - = \,
т х п У <рс
где 1Х, /у — длины полуволн вдоль сторон панели, находим:
Р = Щ с
*Y(i±+JL+-i)+
3 А 41\ + 1}
+
\
fi+зх 1 i\ 1
(12.59)
580• УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК ЗА ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII
Исследование этого выражения значительно упрощается, если принять во втором члене ЗХ— 12; как легко видеть, это ведет к несколько преуменьшенному значению р. Делая такую замену, находим:
Р = Е(?С (“*§ V1 + 7c22Vi)> (12.60)
где
_ 1+ЗХ 2 /*
Vl— 4,2 -Г л -Г А'
1у 1у
Считая, что для панели большой кривизны волнообразование осуществляется свободно, запишем условие минимума р по vt; тогда для получим выражение
_ 3 tf~.
Vl — те V Rh’
верхнее критическое напряжение будет равно
= (12.61)
Эта формула совпадает с выражением (26), относящимся к замкнутой оболочке.
В случае панели малой кривизны надо принять п= 1; тогда
получим выражение (59) с заменой 1у на Ь. Если панель является
удлиненной, то надо определить минимальное значение рв, варьируя число полуволн т = а/1х. Для квадратной панели, условно считая т = п = 1, будем иметь:
р /Л\*Г о 13 + 3A, 1 ( b2 \2 4Х I
Рв — [я 36 +те2\лл) 1 + 15ХJ' (12.62)
При /?->оо придем к прежней формуле (8.147), относящейся к пластинке.
§ 147. Цилиндрическая панель при осевом сжатии. Устойчивость в большом
Мы видели, что в случае слабо развитых пластических деформаций следует подойти ко всем задачам данной главы с точки зрения устойчивости в большом. Необходимость учесть в таких задачах одновременно физическую и геометрическую нелинейность делает решение исключительно трудным, и, прежде всего, с принципиальной стороны. Если говорить о теории деформаций, то здесь, когда должны исследоваться большие прогибы оболочки, возможность использования гипотезы о простом нагружении становится особенно сомнительной. Вместе с тем, применение других теорий
§ 147]
ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ОСЕВОМ СЖАТИИ
581
пластичности ведет к сильному усложнению задачи. Поэтому примем условно, что теория деформаций может быть использована, по крайней мере, на первых ступенях закритического выпучивания оболочки. Но и тогда мы сталкиваемся с трудностями, поскольку интенсивность напряжений меняется от точки к точке, как вдоль определенной нормали к срединной поверхности, так и для различных нормалей. Можно подойти к исследованию такого поля напряжений двояким образом. Один подход состоит в решении задачи «в лоб», т. е. в определении закона изменения интенсивности напряжений от точки к точке; при решении задачи по методу конечных разностей *) рассматривают определенное число точек по нормали и вдоль координат х, у. Другой путь, значительно упрощающий решение задачи, основан на предположении, что пластические свойства материала проявляются лишь в отношении основного напряжения в срединной поверхности **). Попытаемся использовать этот второй путь для решения задачи об устойчивости в большой пологой цилиндрической панели, сжатой вдоль образующей. Будем при этом считать, что физические характеристики материала — секущий и касательный модули — являются функцией лишь средней интенсивности напряжений в срединной поверхности. Очевидно, при исследовании закритического поведения оболочки мы должны исходить из соотношений, соответствующих теории оболочек большого прогиба. Поэтому введем в уравнения (16) и (17), описывающие малые прогибы оболочки (сжатой вдоль образующей), нелинейные члены из уравнений (11.26), (11.27). Тогда придем к следующим основным уравнениям:
Допустим для простоты, что панель является квадратной (а = Ь). Поставим перед собой цель определить равновесные состояния панели при р Ф рв. Считая, что пологая панель будет выпучиваться в обоих направлениях по одной полуволне, примем аппроксимирующее
*) Такой метод был предложен П. А. Лукашем и В. М. Проскуриной для пластинок; по-видимому, он может быть реализован при условии применения цифровых электронных машин.
**) Этот путь указан в первой работе Ли и Адеса [12.11]. См. также [12.12]. Приведенное здесь решение принадлежит А. Н. Божинскому.
/3,1 \ д4Ф - / 1\ д<Ф.1 д*Ф _
\4 ' 4Х) дх4 “Г\ X) дх2ду* + X ду4 ~
582 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. оболочек за пределами УПРУГОСТИ [гл. XII
выражение для прогиба в виде
w = / sin -
(12.65)
Подставляя это выражение в (64) и интегрируя, получим:
где
(12.67)
Применяя, далее, метод Бубнова — Галеркина для интегрирования уравнения (63), находим соотношения между нагрузкой и стрелой прогиба:
При С->0 находим верхнее критическое напряжение по (62). Поэтому (68) можно переписать в виде
Считая Cj=l (/=1, 2, 3) и срс = 1, придем к уравнению (11.177). относящемуся к упругой задаче.
Результаты вычислений по (69) в применении к дюралюмину Д16Т приведены на рис. 12.5; принято /5=12. Кривые 1—3 построены для различных отношений b/fi. При b/h> 55 выпучивание происходит в упругой области, этому случаю соответствует кривая /; напомним, что здесь принято р, = 0,5. Следующие кривые построены для более толстых оболочек при £//г = 40,1 и 27,4 и относятся к упругопластической области. Судя по кривым 1—3, во всех случаях может быть найдено нижнее критическое напряжение /?*. Отношение р*н/р* составляет в упругой области 59% и для кривых 2 и 3 соответственно 74 и 80%. Этот результат является очень интересным, так как свидетельствует о постепенном сглаживании явления хлопка оболочки по мере развития пластических деформаций. Такой вывод со-
здесь введены обычные параметры:
/>*=/>;+<рс[
(С. + С,)»»
16
С2-з(2С34-)к]. (12.69)
§ 147) ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ОСЕВОМ СЖАТИИ
583
гласуется с экспериментальными данными для замкнутых оболочек, описанными в § 143.
Заслуживает внимания предельный случай плоской пластинки (k = 0). На рис. 12.6 построены по (69) кривые р*(С), характеризующие закритическое поведение пластинок различной толщины. Кривая 1 соответствует случаю, когда критическое напряжение лежит
Рис. 12.5. Диаграммы «усилие сжатия — прогиб» для цилиндрической панели в зависимости от развития пластических деформаций.
в пределах пропорциональности и закритическая деформация относится целиком к упругой области. Кривые 3—5 отражают деформацию пластинки полностью в пластической стадии при bfh = 37,5; 29,5; 25,2. Кривая 2 (для £/Л = 50) ответвляется от линии 1 в точке Л, соответствующей пределу пропорциональности, так что начальная стадия деформации пластинки является упругой, а последующая — чисто пластической. Как видим, в случае упругой деформации по кривой 1 среднее напряжение уже при С = 3 более чем в два раза превышает критическое. В пластической же области возрастание напряжения сверх критического значения оказывается значительно меньшим, так что несущая способность пластинки приближается к критической нагрузке. Таким образом, при развитых пластических- деформациях цепные напряжения, появляющиеся при больших
584 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК за ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII
прогибах, не оказывают существенного влияния на поведение пластинки.
Если по этим данным определить редукционные коэффициенты, то в пластической области они окажутся более высокими, чем в упругой. Это и естественно, так как при развитых пластических
деформациях неравномерность напряжений сглаживается. Для примера на рис. 12.7 приведены значения редукционных коэффициентов, относящиеся к тем же случаям, что и на рис. 12.6; нумерация кривых сохранена. По оси абсцисс здесь отложены значения пг = е/екр, где е — деформация продольных волокон вблизи подкрепляющих ребер, екр — критическая деформация; по оси ординат — редукционный коэффициент ср. Интересно сопоставить эти данные с теми, которые могут быть получены по формуле, аналогичной формуле Кармана (см. [0.3], стр. 145). Общий характер кривых
n in л т т /f v/vjLu,riri Aauaiviu i\unDuiA
Рис* 12.6. Несущая способность подкреп* / /\ >
ленной пластинки за пределами пропорцио- 9\п) оказывается в обоих нальности. случаях одним и тем же;
конкретные значения ср получаются несколько иными. Отметим, что кривая 1 рис. 12.7 для упругой области скорее соответствует формуле Папковича, приведенной в главе VII.
Аналогичный путь может быть принят для исследования влияния начальных неправильностей на поведение оболочки или пластинки. Исходные уравнения (63)—(64) при этом получают вид £>'<рс / 1 + ЗХ д4, 0 д4, д4 \,
А ( 4 дх* + дх2 ду2 + dy4) ~
= L(w, (12.70)
, / 1\ д*Ф. 1 д*Ф _
X / дх2ду2 ' X ду4
= -£<pc[iz.(W, «0-1 Цщ, o)+lSj; (12.71)
(i+i)
д4Ф
дх4
§ 147] ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ ПРИ ОСЕВОМ СЖАТИИ
585
Рис. 12.7. Редукционные коэффициенты Для сжатой пластинки при наличии пластических деформаций.
Сцш0
7
'Г'0,05
--0,1
1 L
-V
0,25
’2345
Рис. 12.8. Влияние начальной погиби на несущую способность сжатой цилиндрической панели.
586 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧ. ОБОЛОЧЕК за ПРЕДЕЛАМИ УПРУГОСТИ [гл. XII
под w и Wq здесь подразумеваются, как обычно, полный и начальный прогибы. Идя по тому же пути, что и раньше, приходим к результатам, изображенным на рис. 12.8; здесь*принято k—12, b/h = 27,4; параметр начальной стрелы прогиба составляет С0 = /0//*=0; 0,05; 0,1; 0,25. Как видим, начальные неправильности оказывают в пластической области значительно меньшее влияние на поведение оболочки,,чем в упругой.
Мы применили здесь приближенный прием, отказавшись от детального исследования пластических свойств материала в различных точках и сосредоточив внимание на изменении пластических свойств в зависимости от основного сжимающего напряжения. По-видимому, этот путь позволяет прийти к практически ценным качественным выводам.
В уточненных исследованиях следует исходить из более общих уравнений, описывающих большие прогибы оболочки при пластических деформациях *). Интегрирование этих уравнений можно провести по методу конечных разностей, о чем говорилось выше (стр. 325), либо с помощью метода последовательных приближений, исходя из решения упругой задачи **).
*) Такие уравнения для пластинок были составлены Ю. Р. Лепиком [12.7].
**) Подобное исследование закритической деформации сжатой пластинки было выполнено Н. Ф. Ершовым (См. сборник «Теория пластин и оболочек», Киев, 1962, 344—346).
ГЛАВА XIII
КОНИЧЕСКИЕ ОБОЛОЧКИ
§ 148. Исходные соотношения линейной теории
Круговые конические оболочки входят в конструкции реактивных двигателей, летательных аппаратов, резервуаров и т. д. Решение задачи об устойчивости конических оболочек значительно труднее, чем в случае цилиндрических оболочек, так как структура исходных уравнений является более сложной.
Приведем основные уравнения линейной теории конических оболочек. Определим вначале коэффициенты первой и второй квадратичных форм недеформированной срединной поверхности оболочки. Расположим оси координат так, как показано на рис. 13.1, а. Начало координат пусть совпадает с вершиной конуса. Будем определять положение точки К срединной поверхности радиусом-вектором г, проведенным из вершины конуса О, и углом 0 между осевой плоскостью, проходящей через рассматриваемую точку, и некоторой неподвижной осевой плоскостью.
Длину вектора г обозначим через s, а угол наклона образующей к основанию — через а. Проекции г на оси координат равны
х = s sin а, у = cos ос cos 0, z = s cos а sin 0. (13.1)
Вектор г можно разложить по ортам i9 у, k:
r — s(i sin a-j- у cos a cos 0-f- £cosa sin 0). (13.2)
Величины 5 и 0 будем рассматривать как криволинейные координаты на срединной поверхности £ = s, т}==0.
Коэффициенты первой квадратичной формы ап = А* и а22 = А% определятся по формулам (10.4):
л1=Ш2' (13*3)
Отсюда
Л1=1, i42 = scosa. (13.4)
Далее вычислим деформации срединной поверхности и параметры изменения кривизн, учитывая, что радиусы кривизны срединной
588
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
поверхности Rx и R2 равны (см. рис. 13.1,6)
/?! = оо, R2 =
(13.5)
Удлинения и сдвиг в срединной поверхности по формулам (10.52) с учетом (4) и (5) оказываются равными
ди
ei ~ ds * 1
dv
s cos а дв 1 ди
, U_ W tga
' 1 5
. dv v
S COS a <70
ds
(13.6)
Здесь я, v и w — смещения точек срединной поверхности соответственно в направлении образующей, вдоль параллельного круга (по
б)
Рис. 13.1. Система координат при рассмотрении конических оболочек.
окружности, получающейся при пересечении срединной поверхности с плоскостью, перпендикулярной к оси оболочки) и по внутренней нормали к поверхности.
§ 148]
ИСХОДНЫЕ СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
589
Изменения кривизн и кручение определяем по формулам (10.53): d2w
ds2 ’ 1
d2w
2 s2 COS2 a dO2
dv ds
v _ 1 (l8a dv 2tg“
X— 2 I,
tgg dv 1 dw
s2 cos a dO s ds *
2 d2w
v-\-
s cos a ds db
s2 cos
dw\ a dft /
(13.7)
В упрощенном варианте решения будем пренебрегать в выражениях для х2 и х членами, зависящими от перемещения х/; тогда получим приближенно
1 d2w 1 dw
*2 =
х=-
52 cos2 a dб2
1 d2ze>
s cos a ds dO
s2 cos a dO
(13.8)
В § 123 было показано, что уравнения равновесия элемента оболочки и уравнение совместности деформаций при безмоментном
Рис. 13.2. Усилия, действующие на элемент оболочки.
основном состоянии (основным называется состояние оболочки до потери устойчивости) можно свести к системе следующих упрощенных уравнений (10.83) и (10.86):
DV4w — V*cp— q — 0, I
4 2 ( (13.9)
V4<p + £AV*w = 0. )
Под q подразумевается фиктивная поперечная нагрузка, равная по (10.89)
Ч = Nih -Ь М<*2 + Т'кХ? (13.10)
здесь Nv N2 и Г12—погонные нормальные и касательные усилия в основном состоянии (см. рис. 13.2), <р — функция усилий.
590 КОНИЧЕСКИЕ ОБОЛОЧКИ [гл. XIII
Подставляя в (13.10) выражения (13.7) и (13.8) для уп и х2, при Т12 = 0 получим:
А7 d2w кт ( 1 d2w, 1 dw\ /ю m \
ч~ i ds2 2 \ s cos a d№ + 5 do)' (13.10a)
2 2
Операторы V и V* находим по формулам (10.81) и (10.84):
?2 = S COS а [ж SC0Sa йг) + Ж (scosa ж)] ’
2 _ tga _д*_. s ds2 ’
отсюда
оз.»)
03.12)
Далее находим:
п4 п2 /, 1 1 d2w \
?%, = V2_- —=—— — » =
5 ds ‘ 52 COS2 a дО2 / '
1 f (d2w, I dw. 1 d2w\'] f
cos a ( ds l C°S a ds \ ds2 ' s ds ' s2 cos2 a d62 / J
, d Г 1 d I d2w dw, 1 d2w \11
' dd [ 5 cos a d0 \ ds2 s ds ‘ s2 cos2 a d0 / J j *
или
_4 d4w. 2 d3w 1 d2w. 1 dw,
'ds4' >“7 “5s5 s2 “ds2* 7~c7 '
2 d4ze> 2 d3tp,
' S2 COS2 a ds2 d02 S3 COS2 a ds d02 '
- 4 d*w I 1 d4» ПЗ ш
' s4 cos2 a d02 ' s4 cos4 a d04 ' ’ '
Подставляя выражения (12) и (13) в уравнения (9), приходим
к следующим окончательным уравнениям линейной теории:
о{
d4w. 2 d4w, 1 d4w
ds4 * s2 cos2 a ds2 dO2 * S4 COS4 a <?04
2 d3a>, 4 d2a>
S3 COS2 a ds d02 ~ S4 COS2 a d02
. 2 d3ze> 1 d2w 1 dw \. tga d2y,
' S ds3 S2 <?S2 S3 ds / 5 ds2 '
. \/ d2*e> i \t i 1 i 1 л /ln liv
+ JV1'F + 2 U2cos2a w +Т'5г) — °* (13-14)
§ 149] ОСЕВОЕ СЖАТИЕ КОНИЧЕСКОЙ ОБОЛОЧКИ 591
д4<р, 2 д4<р 1 d4? ds4 S2 COS2 a ds2 dQ2 S4 COS4 а дб4
2 d3y, 4 d2<p, 2 д3<р
S3 COS2 а ds dO2 S4 COS2 а dO2 • S ds3
«*«>
Воспользуемся этими уравнениями для решения частных задач.
§ 149. Осевое сжатие конической оболочки
Рассмотрим прежде всего задачу об устойчивости в малом круговой конической усеченной оболочки, сжатой вдоль оси. По аналогии с решением задачи для цилиндрической оболочки примем сначала, что выпучивание оболочки является осесимметричным. Тогда будет w = w(s)9 <р = <р(), и уравнения (14) и (15) приведутся к виду
л ( -L- 1 d2w i 1 \
\ ds4 ' ~s ~ds3 ~s* ds2 ' s3 ds )
+,t?(13.16)
+ —'Tt +.-+Eh'.Si-=o (13.1?)
ds4 1 s ds3 s2 ds2 1 s3 tfs 1 s ds2 v 7
или, в более компактной форме,
-•-,iK[*-,£(‘£)]} + ¥ +.S:-<>- <13,8>
ss{[s-e(sIf)]} + £4-¥-0- <1319>
Будем считать, что при потере устойчивости образуется большое число волн; длина каждой волны будет невелика, и потому величину s в пределах одной волны можно считать постоянной *). Рассмотрим волну, примыкающую к большому основанию конуса. Положив s = lv где 1Х — расстояние по образующей от вершины до большего основания, и N\ = — Nu где N\ — сжимающее усилие на окружности большего основания, согласно (18) и (19) получим:
D dw_ _ дгО dw, tga d_ _ 0
ds4 /V ds2 T /, ds2 — *
d*<? iFh tg* d2w _n
ds4 h lx ds2
(13.20)
*) Такое предположение было сделано И. Я. Штаерманом [13.11]; ему принадлежит формула (25).
592 КОНИЧЕСКИЕ ОБОЛОЧКИ
Будем искать решение уравнений (20) в форме
w = A sin — (s — 1Х){ ср = В sin у (S — 1Х\
где X — длина волны. Подставляя (21) в (20), получим:
*ИхУ-.(тЛ+в]Ш-«-
(ГЛ. XIII
(13.21)
(13.22)
Приравнивая нулю определитель системы (22) и вводя обозначение ic/X=ji, находим:
N°l = Df + --. (13.23)
Р 1\
Минимизируя N\ по р2, определяем величину 2:
g2==, f EhtgU
У D 1\ '
(13.24)
Подставляя это значение в (23), приходим к следующему значению верхнего критического усилия:
1.в*
Eh2 tg а
/./3(1-) '
При [а = 0,3, получим:
Eh2 Eh2
Nx з = 0,605 tg а = 0,605,
Ч *<0
(13.25)
(13.26)
где R0—радиус кривизны срединной поверхности у большего основания.
Исследуя, далее, случай, когда выпучивание оболочки не является осесимметричным, примем:
w = wx cos nfi, <p = (fxco snti, (13.27)
где wx = wx (s)t <fx — fx (s), n — число волн по параллельному кругу.
§ 149] ОСЕВОЕ СЖАТИЕ КОНИЧЕСКОЙ ОБОЛОЧКИ 593
Подставляя (27) в (14) и (15) и вводя обозначение n = n1cosa, получим:
Г rfVj 2 d3wl 1 -f- 2п\ d2wx 1 + 2Л[ dw{
L ds* s ds3 s2 ds2 ' s3 ds
n?(4— л?) d2w} tga 2<fil
d\i 2 1 -j~ 2/г2 rf2<pj
г/s4 s ds3 s2 dfs2 '
1 + 2л? dy* /2? (4 — /г?) tg a d2wx
+ TrJ--£- Х?-±Ъ + £1’ — -ш- = <>- (13.29)
Легко убедиться в том, что уравнения (28) и (29) можно переписать в виде [13.10]
— Ds'-* [V-2/,> S2--1 [,1 -2п' (*•«>!)] }• j +
<13-30>
**-1 *_ р-2„, Л_ S2„,-1 d_ [Sa«,-1 J*. (sY)] } ] +
+ Eh~-- = (13.31)
Заменяя в (30) и (31), как и в предыдущем выводе, 5 на 1г и Nx на — N\, придем к прежнему выражению (26) для верхнего критического усилия. Оно получается таким же, как в случае осевого сжатия цилиндрической оболочки радиуса R0.
Как показывают эксперименты, реальные конические оболочки, сжатые вдоль оси, выпучиваются хлопком по ромбической форме с образованием двух или нескольких поясов выпучин у большего основания. Поэтому здесь должен быть принят тот же подход к задаче, что и в случае цилиндрической оболочки, с рассмотрением устойчивости в большом. Полное решение нелинейной задачи для сжатой конической оболочки в литературе еще отсутствует. Примем поэтому с достаточно большой уверенностью, что нижнее критическое давление может быть определено по аналогии с принятым для цилиндрической оболочки *) по формуле
Nx а=0,18Е~. (13.32)
* /<о
Формулы (26) и (32) пригодны для практических расчетов; при этом надо принять во внимание указания, сделанные в § 129
*) В пользу законности такой аналогии говорят также и теоретические соображения (см. [13.9]).
594
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
по отношению к цилиндрическим оболочкам. Значения полной осевой сжимающей силы получаются при этом равными:
PB = 0,605£ic/,sin2a. I
I (13.33)
Рн — 0,1SE -5- ъ1х sin 2a = 0,18Eh2n tg a sin 2a; I
/vO )
здесь принято во внимание соотношение /?0 = /1/tga.
Формула (26) справедлива при условии, что число волн вдоль образующей достаточно велико. Следуя И. Я. Штаерману [13.11], будем считать, что это условие выполняется, если оболочка является достаточно подъемистой (угол а 30°).
Желательно, чтобы задача об устойчивости конической оболочки при осевом сжатии была разработана более подробно, с учетом влияния угла подъема а на характер волнообразования. Кроме того, интересно распространить на коническую оболочку геометрический подход к задаче, освещенный в § 131.
Пример 13.1. Коническая диафрагма средней опоры (днище) воздушнореактивного двигателя, выполненная из стали, нагружена осевой силой Р = 2500 кг (рис. 13.3). Провести проверку диафрагмы на устойчивость.
2 205
Находим tg а = —20 ' в 0»533 и а да 28°. Длина образующей равна /j = 5=5 мм' РадиУс кривизны у большего основания R0 =
КАО
= _ = 980 лл.
§ 150] СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ 595
По формуле (32) значение нижнего критического сжимающего усилия будет
А2 О 42 к?
Nu н = 0,18£-£- = 0,18 •2 • 106 = 586 —.
ь н Ro 98 см
Полная осевая критическая сила согласно (33) равна
Рн = 0,18£Л2гс tg a sin 2а = 0,18 • 2 • 10е * 0,42. тс 0,533.0,829 = 8 • 104 кг.
Критическое напряжение у верхнего основания
80 000 лллл, 2
•ь = *34-0,4-sin 28° = 4000 Кг/СМ-
Критическое напряжение не превосходит предела пропорциональности. Величина Рн оказалась во много раз большей величины заданной осевой силы Р.
§ 150. Случай внешнего давления
В конструкциях реактивных двигателей, резервуаров и т. д. конические оболочки подвергаются внешнему давлению. Обратимся к рассмотрению этого случая, причем сначала рассмотрим оболочку, замкнутую в вершине. Предварительно упростим исходные уравнения, следуя Н. А. Алумяэ [13.1]. Представим функции w и ср в виде
w = ty(s)tgoicosnb, )
cp = 1(5)s2£’/1 tg2acos/i0. } (13.34)
Здесь n — число волн, образующихся по параллельной окружности при потере устойчивости; под s понимается величина
е — I f —ctga А, (13.35)
У У 12(l-i)* /,
где 1г — длина образующей от вершины до большего основания.
Такая подстановка позволяет выделить в разрешающих уравнениях малые члены, которыми можно пренебречь. Усилия докритического напряженного состояния при равномерном внешнем давлении q выражаются следующим образом:
w>“-7fcs- W> = -T<13-36> Введем безразмерные параметры
р~£-' (13.37)
и безразмерную координату
_£ h
x — j-. (13.38)
*1
596 КОНИЧЕСКИЕ ОБОЛОЧКИ [гл. XIII
Тогда выражения (36) примут вид
N, = — 4-™3Ehtg*a, I
2 (13.39)
Л/2 = — xve3Eh tg2 a. j
Если принять во внимание равенства (34) и (37) — (39), то урав¬
нениям (14) и (15) можно придать такую форму:
♦ — * {Ч~ (— 4? ~ 7 тк—Р ♦)+'
о3-4»)
2л:
. Чр (d*xi 1 dtx. 2Х \.
dx2 ’ х3 *л х \ dx2 х dx ' х2 )'
I Ахгх I ° rf3xi 1 а*Ъ I 1 dll\ — n П*4П
+ e dx* x4Wx°4F} — °* <I3-41>
Величина e мала по сравнению с единицей, если только угол a
не близок к нулю, величина же р становится большей по сравне¬
нию с единицей, если угол а близок к тс/2. В случае, если угол a не близок ни к нулю, ни к тс/2, в уравнениях (40) и (41) можно пренебречь членами, содержащими е и е2. Сделав это, получим:
+ —(13.42)
5-+£х, = 0- (13.43)
Исключив из этих уравнений функцию придем к следующему разрешающему уравнению:
ет(5) + (5— /Л) + -0. (13.44)
Примем это упрощенное уравнение в качестве исходного. При решении задачи воспользуемся сначала методом Бубнова — Галеркина.
Для случая шарнирно опертой оболочки зададимся функцией ф в таком виде:
ф = Ахг (1 + ах) sin тслг, (13.45)
где
(13.46)
При {* = 0,3 будет а = — 0,759. Функция (45) удовлетворяет условиям шарнирного опирания ф(1) = 0 и =0 (момент Мх по¬
казан на рис. 13.2, б).
§ 150J
СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ
597
Уравнение метода Бубнова—Галеркина, соответствующее (44), запишем в виде
1 1 1
/ ш{х31П?)**ах + р'/dx~Ph f t2 = 0. (13.47)
о 'о о
Пользуясь формулой интегрирования по частям, находим:
1
1
о о
1 1
= _*3
dx2 dx
+_M5)! <13-48»
тогда из (47) получим:
1
о о J
. (13.49)
2 dx
Если бы оболочка была жестко защемлена по краю, то граничное условие имело бы вид = 0 и мы пришли бы к формуле *)
р dx+p Si?dx
(13.50)
Подставляя выражение (45) в (49) и определяя величину р из условия минимума v, найдем vmIn = 20,4. Используя формулы (35), (36) и (39), получим следующее значение верхнего критического давления:
q = 3,15£ (-T-Y tg « л/~4- у tg° =
49 \tl) У h /(1 —,12)3
= г,15Е(±)'\Ы>- (13.51)
*) Эта формула была получена Н. А. Алумяэ.
598
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
Решим эту же задачу методом конечных разностей*). Перепишем уравнение (44) в виде
Для оболочки, замкнутой в вершине, будет Разделим
этот интервал на п частей. Примем следующие граничные условия.
В вершине, при х = 0, положим ф = 0, -- = 0. Для точек основания, при х=1, примем условия шарнирного опирания
Выражая в (52) и в граничных условиях производные через конечные разности по известным формулам **), составим систему алгебраических уравнений относительно значений ф в узлах. Положив п = 4, придем к следующим уравнениям:
Приравнивая определитель этой системы нулю, получим уравнение, из которого может быть определена величина v. Минимизируя v по р, находим значение v=17,8. При более мелком шаге (п = 5) будет vmIn = 18,2; формула для критического давления примет тогда вид
Мы получили формулу той же структуры, что и раньше (см. выражение (51)), но численный коэффициент оказался здесь равным 2,8 вместо 3,15. Формулу (54) и следует рекомендовать для практических расчетов при определении верхнего критического давления. Судя по экспериментальным данным (см. ниже), значения реальных критических давлений для тщательно изготовленных оболочек лежат
*) Это решение проведено И. И. Трапезиным [13.10]. Ему же принадлежат формулы (51), (57), (103), (104).
**) См., например, Э. Камке, Справочник по обыкновенным дифференциальным уравнениям, ИЛ, 1950, стр. 326. Целесообразно для точек х = 1 /п и х = 1 воспользоваться выражениями для производных, дающими приближения первого порядка, а для всех остальных точек — приближениями второго порядка.
Xх
7фз-Щ2 + (13 + 16р4 - -) ф, = 0, -53>48фз-ь(з1,36 + 1р4---р3ф2 = 0> [ (13.53)
(27,83 + -Ц- р* - v) ф3 - 12,4ф2 - О.бф, = 0.
(13.54)
§ 150]
СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ
599
несколько выше величин, получающихся по формуле (54). Поэтому расчет по формуле (54) будет, как правило, идти в запас устойчивости. Для оболочек, имеющих начальную погибь, следует вести расчет с учетом нижнего критического давления. Соответствующая нелинейная задача еще не решена, поэтому здесь целесообразно пользоваться теми же поправочными коэффициентами, которые рекомендовались в § 132 для цилиндрических оболочек.
Обратимся к случаю усеченной оболочки (рис. 13.4), чаще встречающемуся в реальных конструкциях. Докритические усилия определяются здесь формулами:
')• —ТГ*- <355>
где /0 — расстояние по образующей от вершины до меньшего основания. Введя безразмерную координату x = sllv представим эти выражения в виде
Nj = -у ve3Eh tg2 a * N2 = —xEhiga.. (13.56)
Величины e и v определяются по-прежнему по (35) и (37). Поступая так же, как и в случае замкнутой оболочки, после упрощений придем к уравнению (44). Но если в случае оболочки, замкнутой в вершине, величина х изменялась в пределах 0x<l, то теперь она лежит в пределах 1.
600
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XII!
Решая задачу об устойчивости усеченной оболочки методом конечных разностей, получим для случая, когда оболочка по меньшему
основанию защемлена, а по большему шарнирно оперта, следующую формулу:
в -СЕ( h \% (tga)Vl 1 W, / (1—ц2)*'**
(13.57)
Коэффициент Cj определяется по кривой рис. 13.5.
Полученные формулы применимы, как уже говорилось, при угле <xv не близком ни к нулю, ни к тс/2. Эксперименты показывают, что этими формулами можно пользоваться при угле, лежащем в пределах 20° < а <80°; при а > 80° можно коническую оболочку при вычислении qB заменить цилиндрической с радиусом, равным среднему радиусу конической оболочки.
Приведем данные испытаний тщательно изготовленных замкнутых и усеченных конических оболочек *), подвергшихся внешнему гидростатическому давлению. Края оболочек были жестко защемлены. Давление измерялось с помощью манометров и датчика; показания датчика записывались на ленте осциллографа. Момент потери устойчивости отмечался скачкообразным уменьшением ординаты кривой давления. На рис. 13.6 показана оболочка, замкнутая в вершине, после выпучивания. На рис. 13.7 изображена усеченная коническая оболочка после испытания; фотография сделана со стороны большего основания.
Углы а замкнутых в вершине оболочек менялись в пределах от 30 до 75°, а усеченных — от 81 до 86°. Отношение /е/ изменялось от 0,235 • 10”2 до 0,57 • 10~2. Потеря устойчивости сопро¬
Рис. 13.5. График для расчета усеченной оболочки с меньшим защемленным и большим шарнирно опертым торцами.
*) Эти испытания были проведены И. И. Трапезиным [13.10].
§ 150]
СЛУЧАЙ ВНЕШНЕГО ДАВЛЕНИЯ
601
вождалась хлопком, хотя и не резким. Хлопок был более сильным, если давление на оболочку осуществлялось не жидкостью, а воздухом.
Для всех тщательно изготовленных оболочек экспериментальное значение критического давления оказалось несколько выше теоретического» определенного по формуле (54) (для замкнутых в вершине
риментальная величина критического давления была приблизительно на 5% выше значения по (54) и примерно настолько же ниже величины, определенной по (51).
В практических расчетах можно использовать формулы (54) и (57) для верхнего критического давления; при этом следует вводить коэффициент v, аналогично тому как это рекомендовалось для цилиндрических оболочек (см. § 132).
Пример 13.2. Проверить на устойчивость коническую часть внутренней стенки диффузора, толщиной h = 2,5 мм, расположенную между соседними ребрами жесткости (рис. 13.8) и находящуюся под действием внешнего давления q = 6,3 кг/см2. Размеры даны на рисунке; пользуясь ими, находим:
оболочек) и по (57) (для усеченных оболочек), и ниже давления по (51). В среднем экспе-
Рис. 13.6. Форма волнообразования при выпучивании конической оболочки.
Рис. 13.7. Вид на образец с торца.
= 1,5, а = 56° 20',
Расчет ведем по формуле (57). Значения Сх на рис. 13.5 даны для значений f0/llt изменяющихся от нуля до 0,8; в нашем случае /0// = 0,81.
602
КОНИЧЕСКИЕ ОБОЛОЧКИ
[гл. XIII
Экстраполяцией находим С, = 6,2. Далее по формуле (57) находим:
qB = 6,2.2,1.10». (3,22 -10-»)%
(1.5)*/! _ 15 1 кг
(1 — 0,32)а/< 'см2
Формула (57) получена в предположении, что оболочка защемлена по меньшему основанию и свободно оперта по большему. В нашем случае оба
Ф700-
-Ф860
Рис. 13.8. Внутренняя стенка диффузора газотурбинного двигателя.
основания упруго защемлены, но ребра, на которые опирается оболочка, являются настолько мощными, что закрепление можно считать приближающимся к жесткому. Расчетное критическое давление оказывается в 2,4 раза больше избыточного внешнего давления.
§ 161. Случай кручения
Рассмотрим задачу об устойчивости усеченной, свободно опертой конической оболочки, нагруженной равномерно распределенными по торцевым сечениям сдвигающими усилиями *).
Погонное усилие в плоскости меньшего основания (s = l0) обозначим через Г/о, а в плоскости большего основания (s = 1Х) через Г/,.
Эти усилия равны
ер МК
2тс (/0 cos а)2
7V
2п (/ j COS а)2
(13.58)
где Мк — крутящий момент.
Для добавочных смещений, возникающих при выпучивании оболочки, примем следующие выражения, соответствующие винтообразным волнам, образующимся при потере устойчивости:
и — Cxez {sin (kxz -f пд) — sin (kz + nb)), v = C2ez {sin (\xz nd) — sin (k2z -f- пЩ, w = — 2Czez sin (te -f- nB) sin mxzt
(13.59)
•) Приведенное здесь решение принадлежит X. М. Муштари [13.6]
§ 152] ПОДКРЕПЛЕННЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ 603
причем
* = In-f-, ml = = hh-, c=ln(l+-£). \ = h+h..
Под I понимается длина оболочки по образующей, через Сг, С2, С3 обозначены неопределенные постоянные.
Формулы (59) удовлетворяют кинематическим граничным условиям на торцах оболочки: при z = 0 и z — С, u = v = w = 0.
Используя для решения задач метод Ритца, приходим к следующей приближенной формуле для критического сдвигающего усилия:
п=eV’co fs2 *; (13-6°)
здесь введены обозначения:
<**•«>
с.=2-61 (:т-)['+о-ШгТ+«.)]. ».=тоте- 113-62)
Условия применимости приведенных формул состоят в следующем: е«С0,1, 0,25 О<0,33.
Приводим таблицу для величины С0 (при ц = 0,3):
е
0,12
0,10
0,07
0,05
0,03
Со
3,75
3,87
3,95
4,08
4,31
Необходимо отметить, что при решении этой задачи значительную роль должны играть нелинейные члены; было бы желательно исследовать устойчивость конической оболочки при кручении в большом.
§ 152. Подкрепленные конические оболочки под действием внешнего давления
В летательных аппаратах и двигателях, кораблестроении и инженерных сооружениях, наряду с подкрепленными ребрами цилиндрическими оболочками (см. § 137), применяются и подкрепленные конические оболочки. Кроме того, возможны случаи, когда материал, из которого выполнена коническая оболочка, является анизотропным.
Рассмотрим сначала задачу устойчивости конической оболочки, выполненной из анизотропного материала, ограничиваясь случаем
604
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
ортотропии. Примем, что главные направления жесткости совпадают с образующей конуса и дугой поперечного сечения.
Зависимости закона Гука, относящиеся к деформации срединной поверхности, представим аналогично тому, как это было сделано в § 137 (см. формулы (11.153)):
через Ev Е2, и \ь2 обозначены модули упругости и коэффициенты Пуассона в направлении образующей и в направлении параллельной окружности (см. рис. 13.2, а).
Развернув для примера матрицу (63) для elf получим:
Рассмотрим теперь уравнения равновесия по (10.63)—(10.68). Они могут быть написаны как для основной формы равновесия, так и для формы нейтрального равновесия, отличной От основной.
Назовем первые уравнения, относящиеся к основной форме равновесия, уравнениями (а), а вторые — уравнениями (б).
Положив в уравнениях (б) Z — s, у} = 6> i41=l, A2 = s cos а и приняв во внимание уравнения (а), мы приведем эти уравнения
(13.63)
Здесь
2 f*l
E2h Eih ’
Моменты выразим по аналогии с (11.154):
(13.64)
ВбЛИпмии v v м v лппопопаштга паооигтооим (7\•
= Di\h = D2Pi-
(13.65)
§ 152] ПОДКРЕПЛЕННЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ 605
к такому виду:
--scosa-l- Nj cos a -j— — N2cosa = 0, (13.66)
ПЯГ ”1 s cos a + Л2 cos a + r2ieos a — Q2 sin a, (13.67)
dOi,, dQ2, KT d2w,
--scosa + Qicosa4- -4-W10-rscosa +
+ WI*'»« + W»(ji; + cos«)=0. (13.68)
s cos a -- Mx cos a — M2 cos a — Qts cos a = 0, (13.69)
s cos a -f- + H12 cos a -f- H2l cos a — Q2s sin a =0. (13.70)
В этих уравнениях Nl0 и N20— нормальные усилия, возникающие в оболочке перед потерей устойчивости; все остальные усилия и моменты являются дополнительными, т. е. возникающими при переходе оболочки от основной осесимметричной формы к новой форме равновесия (усилия и моменты показаны на рис. 13.2, а и 13.2, б).
Члены, содержащие Nl0 и N2Qt связаны с изменениями кривизн (—хх) и (—х2) [см. (7) и (8)]. Последнее из шести уравнений равновесия мы не написали, так как оно, как это было показано в гл. X,
тождественно удовлетворяется.
Если в уравнении (67) пренебречь поперечной силой, то уравнениям (66) и (67) можно удовлетворить, положив
дг = 1, I _j_ jty ПЗ 7П
1 52 cos2 а дО2 ' s ds 9 Uo./iJ
2 =. (13.72)
71 'г 1 У I 1 ду /1 о 70ч
№ s cos a ds db s2 cos a dQ * v • /
где ср — функция усилий. Исключив из остальных трех уравнений Q и Q2, получим:
d2M{,01 1 д*и2\ д2Н12 dM2,
ds2 s cos a + 2 ds cos a ds db ds <?9 ds cos a
. 1 dHn, 1 dHtl. 1 d*M2..,
H Ай— — -чао “I-* sin a —j—
1 s d0 s d0 ' s cos a dO2 1 2 '
• kt d2w x \i I 1 d2w, dw \ ~ плч
+ 10 cos a + Л/20 _ + _ cos aj = G. (13.74)
606 КОНИЧЕСКИЕ ОБОЛОЧКИ [ГЛ. ХЩ
Обратимся к уравнению совместности деформаций (10.54); в данном случае при = s, г} = 6, Ах= 1, Л2 = со8а оно примет такой
вид:
1 1 д'(, д2г2.
R2 s cos a ds dd s2 cos а дв ds2 '
I 1 д2г2 2 дв2 1 де, п Ло 7,ч
s2cos2a дЬ2 s ds 7 ~ds~~v' Uo./Oj
Выражая Afle Ж2 и Hl2 = H2l = H с помощью соотношения (64) и учитывая равенства (7) и (8) и (72), придадим уравнению равновесия (74) форму
p. d4w р. / 2 2 д3да. 2 d2ze> \
1 ds4 i* \s2 cos2 a ds2дв2 s3 cos2 a ds дв2 s4 cos2 а дв2 )
on П ( 1 d4w 1 d2w. 1 dw, 2 d2w\
1 s ds3 2\s4cos4a d04 s2 ds2 * s ds s4cos2a d02 /
П ( 2 I 2 2 d3w \, tga d2y.
0 \s4 cos2 a dO2 г s2 cos2 a ds2 dO2 s3 cos2 a ds db2 ) ' s ds2 *
, «т d2w, KT ( 1 d2w. 1 dw \ л /10
+ -2- + 2o (S2 C0S2 a -jp- H- 7 5J- J — 0. (13.76)
Используя, далее, равенство (63), с учетом (7) и (8) приведем уравнение совместности (75) к такому виду:
ft ( 1 а4Т I 2 1 I 1 *f\ I
1 \S4 COS4 a d04 ' S4 COS2 a d02 S2 ds2 S3 ds /
_L.ft (д4<? I 2 d3<f> \ I ft / 2 A
2 \ ds4 ' s ds3 / _r Iх \52 COS2 a ds2 dQ2
2 d3y, 2 d2(p \,
s3 cos2 a ds dO2 ' s4 cos2 a dQ2 /
, / 1 d4(p 1 d3cp. 1 d2<p.
' \s2 cos2 a ds2 dO2 s3 cos2 a ds dO2 ' s4 cos2 a dO2
1 d2? 1 t\ 1 i *££. _ f m 771
* s3 cos2 a ds db s4 cos2 a dO / ' s ds2 • v • /
Уравнения (76) и (77) являются исходными при решении задачи
об устойчивости ортотропной оболочки в малом.
Рассмотрим случай, когда оболочка подкреплена круговыми и продольными ребрами, симметрично расположенными относительно срединной поверхности Хрис. 13.9, а и 13.9, б). Ребра считаются
§ 152]
ПОДКРЕПЛЕННЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ
607
расположенными достаточно часто, так что жесткость ребра можно равномерно распределить («размазать») по длине шага.
Будем считать, что ребра обладают жесткостью только в их плоскости. При этом условии ребра не будут оказывать влияния на сдвиг и кручение оболочки. Учитывая это, примем для Т12 — Т21 — Т, Нх2 = Н21—Н те же выражения, что и для гладкой оболочки. Остальные усилия и моменты должны быть рассмотрены отдельно.
Для волокна, параллельного образующей и расположенного на расстоянии z от срединной поверхности, получим такое выражение для деформации удлинения:
а)
б)
Рис. 13.9. Сечения подкрепляющих ребер.
е? =е,— ълг.
(13.78)
Для волокна, перпендикулярного к образующей, будет
е = е2 Х2*
(13.79)
Для напряжения аг получим:
и, далее,
при
(13.81)
и
Здесь под понимается напряжение в ребре.
608 КОНИЧЕСКИЕ ОБОЛОЧКИ [гл. XIII
Аналогично находим:
= ь§-£2[е2+ ~2(*2 -ЬО] ПРИ (13.82)
о *=ЕЦ=Е(-г*2)
при
[—(j + S?)<2< —и [ <г<(- + 8£)]Усилие Nx равно
(13.83)
2 2
W, = / oJdz + 2E- f oz = T?iI5(e1 + (xe2)-(-2£i-Sfe1 =
Jh_ 1 h_ 1
2 2
= Г{[1+28’(1-)Ь + Ь <13-84>
Таким же образом получим:
{[l +2 jjj-0 -1*2)]е2 + }. (13.85)
Момент Мг оказывается равным
£+sP
2 2 + 1
Мх = — У zo\dz — 2f zdf>dz = h_ 1 h_
2 2
= щГЙ (Х1 + +2£ТГ /?Х1>
или
Ж1=Г2(!- {[1+2—(-1-i /1 + R2}- (13.86)
Для момента М2 получаем такое же выражение:
U1 + 2 /{Ь +'*’■'}• <13-87)
В равенствах (86) и (87) под 1\ и / понимаются моменты инерции половины сечения ребра относительно осей, лежащих в срединной
§ 1521 ПОДКРЕПЛЕННЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ 609
поверхности:
/р — h 12 4
1f = + 7 (л + 8'Р)2'
1Р=ШТ { }_ Ь2Щ(к + 3Р)2_
Вводя обозначения:
1+ТГ'(1-1а2>==0)1’ (13.88)
1 +g*jbjg!)/f = /„ 1 +-Х2) /2р=/2. (13.89)
представим равенства (84) — (87) в форме Eh Eh
N\ = 'j—72 (“ii + г)' Ni = XZI75 (W2S2 4- t*e,). (13.90)
£A3 Eh3
Ж1 = 12 (1-1*2) (/l1Cl + t*X2)> ж2 — 12 (1 — (X2) (*2*2 + Fl)- (13.91)
Выражая et и e2, исходя из равенств (90), получим:
(13.92)
*l~ Eh(o), —ц2) (г! Рг),
e2 = ~ №
Сравнивая выражения для ег и е2 по (92) с формулами (63), получим следующие значения 81 82, 8:
* ш2 (1 — t*2) S = tOl(l—2) * fX (1 fx2)
1 Eh(a>ia)2 — p-2) * 2 Eh((i>l(i>2 — (л2) * Iх Elг (<02 — [x2)
(13.93)
Сопоставляя, далее, равенства (91) с выражениями для моментов, даваемыми равенством (64), найдем:
_ Eh%.EhH2 D y-Eh* —G —
Ul 12 (1 — p.2) * u* 12 (1 — fx2) * uv 12 (1 — (x2) * uO u 6 *
(13.94)
Подставляя (93) и (94) в уравнения (76) и (77), получим, что в случае конических оболочек, подкрепленных продольными и
610
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
поперечными ребрами, задача сводится к решению следующих уравнений:
Eh3 [ dAw, 2 dAw 2 d3w. i2 dAw.
12 (1 — (x2) _ 1 ds4 ' s2 cos2 a ds2 d02 s3 cos2 a ds d02 ' s4 cos4 a d04 ■
, 2 (1 + i2) d2w, 2/j d3w
' sA cos2 a d02
s ds3
t i2 d2w, i2 dw “I
s2 ds2 ' s3 ds J
tgad2(p KT d2w KT I 1 d2w. 1 dw\ n /10 nc.
T'Js2 nio-m—n*>(S2 cosa dT + T'di-)-0’ (13-95)
d4<f
(1 — fj.2) (0, g4y 2/ 1-t*» \ 1 W<o2 —x2 ds4 \ a>,<»2 — (x2 '•) s2 COS2 a ds2 dt)2 ~
, (1 — fx2) o>, 1 r 1-(X2 -I 1 d*<f
i — p.2 s4 cos4 a ds4 ' li«2 — f2 ir/J s3 cos2 a ds dd2 '
a)jO)2 ■
+ S< COS2 a [sfi, - n2 (U)2 — Iх) + ('1 “ +
. 2(1 —fx2) a>, d3v J_ df_
* a)jO)2—fx2 5 ds3 0)2 <o j co2 — f*2 S ds2
tga£/,=0 o),co2 — fx2 s3 ds 1 s ds2
(13.96)
T
t
vJl
t
4-
ГТ
—— / —■ £ —■» »j
Рис. 13.10. Одностороннее расположение ребер.
В случае оболочки, снабженной односторонними ребрами (рис. 13.10), изменяются выражения для iv coj и /2, о>2. В этом случае *)
12 (1 — (х2) р 12 (1 — {х2) -р
Ь— 1_1 7JT* '2—1Н р3 2»
°1= 1
vf
Л/г
(1 —Х2), а)2= 1 -f _(1 — JX2),
(13.97)
Здесь /? — момент инерции сечения продольного ребра относительно
*) Более подробное исследование случая односторонних ребер в применении к цилиндрическим оболочкам было дано В. В. Новожиловым, В. И. Королевым, а также О. И. Теребушко [11.22], см. работу 1962 г.
§ 152]
ПОДКРЕПЛЕННЫЕ КОНИЧЕСКИЕ ОБОЛОЧКИ
611
центральной оси профиля кругового сечения оболочки, /£ — момент инерции сечения кругового ребра относительно центральной оси профиля осевого сечения оболочки. При отсутствии продольных ребер будет ix = 1.
Рассмотрим задачу об устойчивости конической оболочки, подкрепленной ребрами, при действии равномерного поперечного внешнего давления. Уравнения (95) и (96) можно упростить так же, как это было сделано выше по отношению к соотношениям (14) и (15) (см. § 150); тогда получим уравнение
d2 dx2
(Jf83-) + PiP4-i—РаР8у = °г <13-98)
здесь
Pl=
f*2:
(1-р*)»1
“l“2 (*2
(1 — f*2) (Я2 (01(02 (X2
<13.99)
(13.100)
Функция ф связана с функцией w равенством (34), а величины v и р даются формулами (37). Решая уравнение (98) методом Бубнова— Галеркина, мы вместо равенства (49) получим:
1 1
1
— х3
d2ф д?ф dx2 dx
+
I *'(w)' ix+p'h.f £ix
(13.101)
2 dx
Задаваясь, как и в случае гладкой оболочки, выражением (45) для функции ф, из условия (Af1)JK.=1 = 0 найдем:
6/1 +Iх
8/1 +fx
(13.102)
Таким образом, при наличии не только круговых, но и продольных ребер величина а зависит от /х; изменение а оказывается незначительным: при ix= 1 будет а = — 0,759, а при /х=5
а = — 0,75. Это дает возможность принять при [х = 0,3 для а значение, соответствующее 1г — 1.
В результате, найдя р из условия минимума v, приходим к такой формуле для критического давления:
р, 1 W, / О -1*4'
Напомним здесь, что уравнение (98), а следовательно, и равенство (103) получены в предположении, что угол а не близок ни к нулю,
(13.103)
612
КОНИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIII
ни к ir/2. Как показывают вычисления, круговые ребра существенно повышают критическое давление; продольные же ребра оказываются значительно менее эффективными. Решая ту же задачу с помощью метода конечных разностей, получим формулу (103) с коэффициентом 2,8 вместо 3,15.
В случае усеченной оболочки будет
Величины коэффициентов Сх можно определить по кривой рис. 13.5, при тех же граничных условиях.
(13.104)
ГЛАВА XIV
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
§ 163. Устойчивость в малом сферической оболочки при внешнем давлении
Оболочки вращения, имеющие сферическое очертание или форму, близкую к сферической, применяются во многих областях техники. Примерами могут служить обтекатели радиолокационных антенн в летательных аппаратах, переборки подводных лодок, днища резервуаров и т. д. Наиболее важная задача устойчивости таких оболочек относится к случаю, когда оболочка нагружена равномерно распределенным внешним давлением. В реальных конструкциях чаще всего встречаются сферические сегменты, закрепленные по краю. Мы будем различать сегменты с большим углом охвата, стрела подъема Н которых сравнима с радиусом кривизны срединной поверхности R (рис. 14.1), и пологие панели, для Которых H<R. В данной главе рассматриваются только сегменты большого подъема *). Так как выпучивание такого сегмента сопровождается образованием сравнительно мелких вмятин, то критические напряжения для него будут теми же, что и для полной сферической оболочки (рис. 14.2).
Обратимся поэтому к определению критической нагрузки длу полной сферической оболочки, подвергающейся внешнему равномерному давлению. На первый взгляд, ввиду предельной простоты формы оболочки и симметрии нагрузки, эта задача не должна быть сложной. И действительно, она не представляет особых трудностей,
Рис. 14.1. Сферический купол, нагруженный внешним давлением.
*) Пологим сферическим панелям посвящен § 161 следующей главы.
614
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
если решать ее в линейной постановке. Однако реальные сферические оболочки оказываются такими же чувствительными к малейшим начальным несовершенствам, как и сжатые вдоль оси цилиндрические оболочки. Выпучивание сферических оболочек, как правило, сопровождается хлопком, и истинные значения критических усилий
лежат обычно гораздо ниже значений, найденных по линейной тео¬
рии. Поэтому задача об устойчивости сферической оболочки должна ставиться как нелинейная. Экспериментальные исследования устойчивости полной сферической обо¬
лочки или подъемистых сегментов являются более сложными, чем для цилиндрических оболочек. Особенность процесса выпучивания реальной сферической оболочки состоит в том, что в одних случаях он сопровождается появлением одной
быстро развивающейся вмятины, а в других — серии волн, распо¬
ложенных по окружности. Поэтому построение приближенных решений, связанных с аппроксимацией изогнутой поверхности, требует здесь особой тщательности. Таким образом, практически важ¬
ная классическая задача о выпучивании сферической оболочки является одной из наиболее тонких и сложных задач этого круга как в теоретическом, так и в экспериментальном отношении.
Начнем с решения линейной задачи *). Будем полагать, что в пределах зоны первичной вмятины оболочка является пологой, и воспользуемся уравнениями (10.83) и (10.86). В нашем случае по (10.88)
2 2
будет Vfc = (l//?) V, где R—радиус срединной поверхности; следовательно, приходим к следующей системе уравнений:
DV% = -i- V2cp -- qz,
Рис. 14.2. Полная сферическая оболочка под действием внешнего давления.
(14.1)
Исключая отсюда ср, получим окончательно уравнение шестого порядка относительно w\
Fh
DV*w + -2w = V2qz, (14.2)
*) Эта задача рассматривалась впервые Цолли [14.14] и Л. С. Лейбензоном [14.2] s 1915—1917 гг.
§ 153]
УСТОЙЧИВОСТЬ в МАЛОМ
615
где V6 = V2V2V2. При действии внешнего равномерного давления начальные усилия во всех нормальных сечениях оболочки будут по (10.65)
N1==N2=- sg-.
Если считать сжимающие усилия N и напряжения а положительными, найдем:
W ° = (14.3)
Определим радиальное перемещение w0 всех точек срединной поверхности, соответствующее начальным напряжениям а. Деформация укорочения вдоль дуги любого нормального сечения равна е = Wq/R; с другой стороны, е = а(1—р)/Е = qR( 1—p)/2Eht отсюда
<14-4>
В дальнейшем через w будем обозначать дополнительный прогиб, имеющий место при выпучивании оболочки; сама нагрузка q непосредственно в уравнение (2) входить не будет. Фиктивную же нагрузку qZy отвечающую напряжениям о, найдем по (10.89а); qz = — hoV2w. Таким образом, уравнение (2) получает вид
VQw-\-oV4w-\--j'V2w = 0. (14.5)
Следуя В. 3. Власову [10.3], примем, что решение уравнения (5) должно удовлетворять соотношению
V2w = — \2w, (14.6)
где X — неопределенный параметр. Тогда из (5) получим (при \Ф 0)
тх,_лг + ж=°
и, далее,
Минимизируя а по X2, находим:
l2 = V -Ш = ж/*20-«*•*>• (14-8)
Далее по (6) определяем верхнее критическое напряжение:
1 £ * «О.бОбеА. (14.9)
в“ У 3(1 —(а2) Я R
Соответствующее давление равно
2
616
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
Таким образом, величина верхнего критического напряжения для сферической оболочки по (9) получается в точности такой же, как для цилиндрической оболочки радиуса /?, сжатой вдоль оси.
§ 154. Случай осесимметричного выпучивания.
Линейная задача
До сих пор мы интересовались только значением критического давления и не определяли формы вмпучивания оболочки. Выясним теперь, какой является форма изогнутой поверхности в случае, если выпучивание является осесимметричным.
Будем сначала исходить из уравнения (6), соответствующего теории пологих оболочек. Введем полярные координаты г, ср и примем, что прогиб является функцией только расстояния г данной
точки от полюса: w = w (г). Определяя по формуле (9.16),
приходим к уравнению
- + - + Х% = °. (14.11)
Уравнение такого типа уже встречалось выше, при рассмотрении
устойчивости радиально сжатой пластинки. В самом деле, соотно¬
шению (9.3) можно при ог = о<р=— р придать вид
• Р- __ p2w — о
или, при k2 = ph/D,
V2 (V2w k2w) = 0;
отсюда вытекает уравнение (11). Как мы видели, подобное уравнение интегрируется в бесселевых функциях. Считая, что в полюсе w = ft примем
W = fj0(kr)t (14.12)
где J0Q>r) — бесселева функция первого рода с индексом 0. График этой функции показан на рис. 14.3. Как видим, осесимметричное выпучивание оболочки должно сопровождаться появлением сравни¬
§ 154] СЛУЧАЙ ОСЕСИММЕТРИЧНОГО ВЫПУЧИВАНИЯ. ЛИНЕЙНАЯ ЗАДАЧА 617
тельно глубокой вмятины у полюса и ряда кольцевых складок, размельчающихся по мере удаления от полюса.
Если теперь воспользоваться теорией непологих оболочек, то естественно перейти к географическим координатам (рис. 14.4). В общем случае несимметричной задачи первая квадратичная форма будет
I — R2 dot2 -- г2 d62 =
= R2 (doс2 + sin2a dp2), (14.13)
где а и р — углы широты и долготы. Коэффициенты формы / равны ап = Л2 = /?2, а22 = А\ =
= R2 sin2 а, а12 = 0. Оператор Лапласа по (10.81) получает вид
Т79 1 I д2, х д,
да д2 \
sin
д?2)'
(14.14)
Возвращаясь к симметричной задаче, найдем:
'”=ib+cls»i)-<14-15>
Введем безразмерный оператор V2 = /?2V2; тогда, исходя из общих соотношений главы X, можно прийти (см. [ 10.3]) к следующему уточненному соотношению, заменяющему (6):
(V2+2 )w-
sw,
(14.16)
где 5 — новый неопределенный параметр.
Подставляя значение V2, приходим к уравнению d2w. dw
da2
da
ctg a + (s -f- 2) w = 0.
Примем 5 + 2 = n(n-\- 1), где n= 1,2,3,..., тогда вместо (16) получим:
- + -ctga + n(n+l)w = 0. (14.17)
Уравнение такого типа относится к классу так называемых гипергеометрических уравнений. Ему удовлетворяют гармонические сферические функции Лежандра первого рода (полиномы Лежандра первого рода). Каждому индексу п отвечает функция определенного вида. Попытаемся связать величину 5 с геометрическими параметрами
618
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
оболочки. Сравнивая уравнения (6) и (16), приближенно примем sR2X2 или, по (8), = /?]/ 12(1—\ь2) /htt3,3R/h.
На рис. 14.5 приведен график функции w(a), которая, исходя из этих приближенных зависимостей, соответствует отношению R/h = 50. Как видим, изогнутая поверхность здесь имеет тот же характер, что и по рис. 14.3. Отметим, что число волн,
Рис. 14.5. Форма выпучивания, описываемая сферическими функциями.
помещающихся на данном отрезке меридиана, увеличивается по мере возрастания отношения R/h\ следовательно, чем тоньше оболочка, тем волны будут короче. Если амплитуду основной вмятины принять за 1, то амплитуда соседней складки окажется равной лишь 0,4; в дальнейшем амплитуды постепенно уменьшаются при возрастании а. При выпучивании реальных оболочек положение полюса центра основной вмятины является случайным. В экспериментах, как мы увидим ниже, могут одновременно возникнуть несколько очагов выпучивания, расположенных в различных местах оболочки. Нужно считать, что на достаточном удалении от полюса эффект данного очага не будет ощущаться. Если же расстояние между полюсами меньше, чем радиус действия этого эффекта, то волны, принадлежащие различным очагам, должны накладываться друг на друга.
§ 155. Устойчивость в большом
Обратимся к исследованию устойчивости сферической оболочки в большом. Как уже было сказано, в опытах наблюдается либо прощелкивание и развитие одной вмятины, завершающиеся «опрокидыванием» оболочки, либо образование группы волн, соединяющихся затем обычно в одну глубокую вмятину. В соответствии с этим возможны два подхода к задаче: а) рассмотрение процесса развития одиночной вмятины, заключающееся в решении осесимметричной задачи; б) исследование несимметричного выпучивания. До настоящего времени применялся преимущественно первый из этих подходов; он и будет освещен ниже *). Будем считать, что на первой стадии развития вмятины, вплоть до достижения нагрузкой нижнего критического значения, поведение упругой сферы может быть опи-
*) Задача о несимметричном выпучивании пологой сферической оболочки была рассмотрена Э. И. Григолюком (см. § 161, стр. 653.).
§ 155]
УСТОЙЧИВОСТЬ В БОЛЬШОМ
619
сано теорией пологих оболочек. Основные нелинейные уравнения (10.109) имеют вид (с учетом поперечной нагрузки q)
2-V*w = L(w. Ф)Н- ?аФН-£.
у4ф _ — А (w_ w) — v\w.
(14.18)
(14.19)
Считая по-прежнему V = (1//?)V2, получим:
Ц- V4w = L(w, ф)+-1 у2ф+-,
_i- \74Ф = — Z, («о/, w) V2w.
Воспользуемся полярными координатами г, ср. совмещая начало
радиуса-вектора с центром вмятины. Считая, что функции w и Ф
не зависят от ср, найдем по (9.16) и (9.29):
., -. 1 / d2w йФ, dw d2Ф \
L(w, ф)=7(__+_:
1 d / dw d \ г dr \ dr dr ) *
2 d2w dw L{WtW)=- — 4F
_ JL _i_ 1 J- — i JL I d \
~ dr2 r dr ~~ r dr X dr)'
(14.20)
Уравнения (19) можно представить следующим образом (после сокращения на г):
(14.21)
Проинтегрируем эти уравнения по г; тогда получим (после деления на г):
x£<*»>=i-£ +T-3r-f-+T,r-
под ЧГ подразумевается функция нагрузки:
(14.22)
Г
W = jf Яг dr.
(14.23)
Напряжения в срединной поверхности равны (в общем случае) д2Ф д2Ф д ( 1 дФ >
1 дФ. 1
/ 1 дФ\
620
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[гл XIV
В осесимметричных задачах будет
1 йФ t
°г г dr * 0<р
В дальнейшем нам понадобятся выражения для радиального перемещения и точек срединной поверхности. Найдем сначала деформацию удлинения в кольцевом направлении:
_ 1 / d2Ф jx 1Ф\
Е\ dr2 г dr ]’
С другой стороны, величина равна е<p==w/r, отсюда
Приложим эти соотношения к решению конкретной задачи.
Поставим перед собой цель проследить за изменением стрелы прогиба одиночной вмятины, образующейся в полной сферической оболочке, в зависимости от давления; это должно привести к определению нижней критической нагрузки. Все имеющиеся в литературе решения этой задачи можно разделить на две группы. Значительная часть работ основана на использовании вариационных методов Ритца и Бубнова — Галеркина *), и лишь в двух последних работах проводилось численное интегрирование дифференциальных уравнений с помощью цифровых электронных машин **). Остановимся сначала на применении вариационных методов. Трудность задачи состоит здесь в установлении граничных условий на контуре вмятины, поскольку остальная часть оболочки также подвергается деформации. Вообще говоря, участок вмятины надо считать упруго защемленным, однако аппроксимировать изогнутую поверхность вмятины с учетом деформации «гладкой» зоны нелегко. Кроме того, возник ряд методических вопросов. В одном из первых вариантов решения [14.10] по методу Ритца изогнутая поверхность аппроксимировалась с помощью нескольких параметров и далее производилась минимизация по одним параметрам полной энергии системы, а по другим — величины давления. X. М. Муштари и Р. Г. Суркин показали [14.4], что правильнее минимизировать по всем параметрам непосредственно полную энергию***). Далее, в работе [14.9] были
*) Первая работа в этой области принадлежит Карману и Цянь Сюэ-сэню [14.10]; дальнейшие исследования были проведены Фридрихсом [14.9], X. М. Муштари и Р. Г. Суркиным [14.4], [14.6], В. И. Феодосьевым [14.7], Мацуя и Иошимура [14.12] и другими авторами.
**) Эти работы выполнены в 1961 г. А. Г. Габрильянцем, В. И. Феодосьевым [14.1], а также Мэреем и Райтом [14.13].
***) Такой путь был избран выше, в гл. XI, при рассмотрении устойчивости цилиндрической оболочки при осевом сжатии и внешнем давлении.
(14.25)
§ 155]
УСТОЙЧИВОСТЬ В БОЛЬШОМ
621
допущены погрешности в формулировке граничных условий для усилий в срединной поверхности. Что касается применения метода Бубнова—Галеркина, то здесь оказалось существенным, учитывается ли изменение радиуса вмятины в процессе выпучивания и соответствует ли основное уравнение метода принципу возможных перемещений (см. [14.7], [14.3]).
Приведем один из простейших вариантов решения задачи с помощью метода Ритца *). Примем (в качестве первого приближения), что на
>-
— с f \ш
Рис. 14.6. Форма вмятины при осесимметричном выпучивании сферической оболочки.
контуре вмятины (рис. 14.6) выполняется условие полного защемления:
= 0, -- = 0 при г = с\ (14.26)
здесь под с подразумевается радиус вмятины. Положим, далее, что
по краю вмятины отсутствуют радиальные перемещения:
и —0 при г = с; (14.27)
по (25) получим:
d2 Ф р.
ч-г—тчг = 0 при г = с. (14.28)
В полюсе, при г->0, радиальные напряжения ог, очевидно, должны быть ограничены по величине. Отсюда по (24) вытекает четвертое граничное условие:
dQ
-— = 0 при г — 0. (14.29)
Аппроксимирующее выражение для прогиба, удовлетворяющее условиям (26), примем виде
= J)2; (14.30)
это соответствует форме изогнутой поверхности круглой пластинки, защемленной по контуру и подвергающейся действию равномерной поперечной нагрузки.
*) Этот вариант был предложен автором [0.3], стр. 364 в развитие работы [14.12].
622 СФЕРИЧЕСКИЕ ОБОЛОЧКИ [гл. XIV
Подставляя (30) в правую часть второго из уравнений (22)» получим:
_*_П72АЛ — Е 16Я (Г г* \2. Е 4/ / г г*\
rfr 2г с2 \с с3) + Я с U °3)'
Интегрируя это выражение, находим:
+■*-¥(£--£)+<>.• <>«■)
Новое интегрирование дает
2£/2 / г3 г5 - г7 \ - Efc /3г3 г5\ г, r 1
dr — с \2с3 3с5 “Т” 12с7j1 6/? \ с3 с5/*1 2 “tC2 г ’
Постоянная С2 равна нулю в силу условия (29). Определяя, далее, Сх из условия (28), находим:
*Ф = Е£_ ( 5-3 г _ 6 rj_ _ rjx _
dr 6с \ 1 — р. с с3 ' с5 с7/
£/с Г 2 (2 ц) г г*. г* -I у/?
6Я L 1—1* с с3 с5 J 2А (14.о)
Последний член соответствует основным напряжениям рг = /? = = f/?/2A.
Определим энергию системы. Потенциальная энергия деформации
срединной поверхности равна по (10.95)
</« = 5z/[<va®»‘-2(l+l‘)7<,4'33>
О
Величину V2<D находим, пользуясь (31), по выражению (32):
*•-4Р(т=£-“£+■»£-«£)-
-w[ifeiri-67-+3f]--Sr-- (И'34)
Выражение для Uc по (33) получает вид
п (23 —9ц)я р h f4 (3 — f*)“ Eh «,.
с 126(1—(х) с2 3 9(1 —(х) R 1
Потенциальная энергия изгиба равна по (10.95)
= \ I [(W- 2 О ■~ Ю 7 Tf] 2ur dr* (14>36)
§ 155] устойчивость в большом 623
Величина V2w равна по (20) и (30)
V2W :
*L
с2
Окончательно
(1-2 £). (14.37)
£/и = -у-»£>(4)*- (14.38)
Определим работу внешних сил, равную приближенно
с
W = j* q (w -f- w0) 2кг dr; (14.39)
о
под w0 здесь подразумевается радиальное смещение, соответствующее основным напряжениям. Подставляя в (39) выражения (30) и (4)
для w и wQt находим:
w = jqfc2+£jjh{ l-rty- (14.40)
Полная энергия равна
Э = ие-\~ин — W. (14.41)
Введем безразмерные параметры
у с2 Р2 д QR2 г f_ Ъ 3 R о. /14494
k~~Rh~ h ' Eh~ 2Eh*' ~h' Э~2 nEh*Э’
тогда получим:
£ 23 — 9fx -4 3 fx -3, 4 *2,
Л А (Л 4 I Я /1 „2\ b 4
84 (1—fx) Лг 6(1— fx) * r30—
+ <14«>
Будем считать варьируемыми параметры С и k\ первый из них
характеризует стрелу прогиба вмятины, а второй — ее радиус. Уравнения метода Ритца получают вид
f-=°. ж = 0. (14.44)
Выполняя дифференцирование, приходим при С Ф 0 к уравнениям: 23 9{х ~2 3 — fx * 8 7 —2fx 2о = 0
4 О /1 • ЯЛ (1.2 \Ь Ч 1С/1 (1\ *
21 (1 — fx) 2(1 — р.) ' 3 (1 — \2)k 15(1 —fx)
84(1 — (*) Л2 **4 + [ 3(1 — (х2) ~ 30(1 — р) j'*2 + 2'(1 —°2 = °-
(14.45)
624
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
Эта система уравнений связывает величины а, С, k. Исключим
отсюда k и найдем зависимость о(С); тогда получим график, изображенный на рис. 14.7. Наинизшая тсчса кривой о соответствует значению *)
= 0,155 или он = 0,155Е (14.46)
и стреле прогиба С = 9,16.
Формула (46) определяет нижнее критическое напряжение; ему соответствует давление
<7Н —0.31f(-2. (14.47)
Полученное нами значение он почти в четыре раза меньше верхнего
А критического напряжения ов.
Если сравнить формулы (46) и
(11.66) для сферической и
цилиндрической оболочек, то окажется, что коэффициенты в них близки между собой, подобно тому как это было в линейной задаче.
X. М. Муштари и Р. Г. Суркин [14.4], [14.6] дали уточненное решение задачи. Они составили несколько различных аппроксимирующих выражений для w и, кроме того, для меридионального перемещения а. В одном из вариантов было принято
Рис. 14.7. Диаграмма «напряжение — прогиб» при потере устойчивости в большом.
(а)
Далее использовался метод Ритца, и энергия системы минимизировалась по параметрам /, с и и0. Нижнее критическое напряжение оказалось равным он = 0,193/]/l—jj.2 0,203.
Как было уже сказано, принятые при выводе формулы (46) граничные условия не вполне соответствуют истинному характеру сопряжения зоны вмятины с остальной частью оболочки: защемление по контуру вмятины надо считать не жестким, а упругим. Такое предположение было сделано в работе В. И. Феодосьева [14.7]; им принималось следующее аппроксимирующее выражение для угла поворота нормали 0:
0 = Лр(1 _р2)*-*Р, (Ь)
*) Более подробно выкладки приведены в книге [0.3], стр. 367.
§ 155]
УСТОЙЧИВОСТЬ В БОЛЬШОМ
625
d%sj г
где 6 = р = —. Отметим, что в предыдущем решении,
исходя из формулы (30), мы получили бы 0 = 2/р(1—р2).
Таким образом, новым в (Ь) является множитель е~к?, учитывающий затухание прогибов по мере удаления от вмятины. Если воспользоваться методом Бубнова—Галеркина и в первом приближении варьировать только параметр /, то нижнее критическое давление оказывается отрицательным: <зн——0,13; это соответствует
давлению, направленному от центра кривизны. Если же в дополнение к этому варьировать и радиус вмятины г (как это сделано в статье X. М. Муштари [14.3]), то получим для он положительное значение он = 0,1 /)А—х20,П.
Если сопоставить между собой различные варианты решения задачи, то окажется, _что найденная в них величина ан колеблется в очзнь широких пределах. Здесь сказывается та резкая чувствительность результатов применения вариационных методов к выбору аппроксимирующих функций, которую мы отмечали выше. Очевидно,, дальнейшее уточнение решения возможно либо путем повышения числа варьируемых параметров при использовании методов Ритца или Бубнова—Галеркина, либо путем применения иных методов интегрирования основных дифференциальных уравнений. И в том и в другом случае, по-видимому, нельзя обойтись без применения цифровых электронных машин. В связи с этим обратимся к результатам вычислений, выполненных с помощью ЭЦВМ в работе [14.1] (см. также статью [14.13]).
А. Г. Габрильянц и В. И. Феодосьев [14.1] преобразовали уравнение (22), введя новые переменные; при этом было показано, что полученная в результате решения величина он не должна зависеть от отношения R/h. Этот важный кывод относится, конечно, лишь к исходным уравнениям теории пологих оболочек. Далее, было принято, что нелинейные зависимости распространяются на некоторую область со сравнительно большими прогибами, размеры которой можно было менять в достаточно широком диапазоне. Что касается остальной зоны оболочки, то для нее основные уравнения были линеаризованы. Как мы видели в § 154, решение таких линейных уравнений выражается в бесселевых функциях и может считаться известным.
Граничные условия были приняты следующими. Для центра вмятины, при г = 0, считалось 0 =—dw/dr — 0, а также йФг = 0 по (29). Кроме того, были выписаны четыре условия непрерывности функций б и аг = (\/г)№Ф№г) по линии сопряжения линейной и нелинейной областей; эти условия выражают равенство по этой линии углов поворота нормали, изгибающих моментов, а также меридиональных усилий и перемещений. Машинный счет применялся для
626
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
численного интегрирования шаг за шагом уравнений типа (22) в пределах нелинейного участка, от центра к границе. Интегрирование проводилось пробами, с тем, чтобы удовлетворить приведенным выше условиям сопряжения. Результаты вычислений приведены на рис. 14.8.
Рис. 14.8. Диаграммы равновесных состояний, полученные с помощью цифровых машин.
По оси абсцисс отложен безразмерный прогиб в центре С = wjh, по оси ординат — величина о. Сплошная линия соответствует основным формам равновесия, а пунктирные — высшим формам; эти формы показаны на рисунке. Наинизшая точка основной кривой, отвечающая стреле прогиба до да 22,5 /г, дает величину ан= 0,067. Таким образом, судя по этому решению осесимметричной задачи, величина ан лежит значительно ниже, чем это вытекает из решений по методу Ритца, и вместе с тем выше того значения (—0,13), которое было получено при неварьируемом радиусе вмятины с помощью метода Бубнова—Галеркина. Все же надо полагать, что коэффициент о = 0,067 не является еще окончательным. Прежде всего, описанное решение построено на основе теории пологих оболочек и результаты могут быть иными, если использовать уточненные уравнения. Кроме того, задача считалась осесимметричной. Между тем, во многих опытах скачкообразное выпучивание оболочки выражается в развитии ряда вмятин, заполняющих некоторую область оболочки, и сопровождается взаимным влиянием (интерференцией) вмятин, подобно тому, как это происходит в случае цилиндрической оболочки. Но тогда задача должна рассматриваться как несимметричная. Поэтому теоретическое исследование этой важной задачи необходимо продолжить.
Влияние начальных неправильностей формы на поведение сферических оболочек при осесимметричном выпучивании было изучено Р. Г. Суркиным [14.6] с помощью метода Ритца и аналогично тому, как это было описано выше для цилиндрических оболочек (§ 133),
§ 156]
ДАННЫЕ ОПЫТОВ
627
Оказалось, что, например, при стреле начальной погиби вмятины, равной толщине оболочки, верхнее критическое давление ов снижается на 39% по сравнению с ав для оболочки идеальной формы.
Геометрический подход к задаче, предложенный А. В. Погореловым [14.5], основан на том, что выпучивание сферической оболочки (или выпуклой оболочки иной формы) в большом должно соответствовать изометрическому преобразованию срединной поверхности. Но тогда, как мы видели в § 119, форма вмятины будет отвечать зеркальному отражению сегмента оболочки в отсекающей его плоскости (см. рис. 10.17). Рассмотрим энергию деформации, образующуюся при таком выпучивании, как это было сделано для цилиндрических оболочек: ее можно составить из энергии изгиба в зоне вмятины и энергии деформации пояска, лежащего между вмятиной и гладкой зоной. Определяя эту энергию через параметры вмятины, можно приближенно определить нижнее критическое давление.
§ 156. Данные опытов и рекомендации для практических расчетов
Как уже отмечалось выше, проведение экспериментов с полными сферическими оболочками затруднительно. В статье [14.10] приведены данные испытания сферического сегмента с углом раствора в 180° при Rjh = 900. Потеря устойчивости заключалась в скачкообразном продавливании вмятины, охватывавшей центральный угол в 16°, со стрелой прогиба /=12,5 /г. Критическое напряжение оказалось равным о=0,154. Многочисленные опыты со сферическими сегментами были также проведены Р. Г. Суркиным *). Образцы изготовлялись из листового материала (стали, латуни, меди, алюминия) вытяжкой под давлением масла**). Характер выпучивания оболочки зависел от вида нагружения. В тех случаях, когда во внутренней области создавался вакуум, потеря устойчивости происходила в процессе резкого хлопка. При нагружении жидкостью (маслом) эффект хлопка был значительно меньшим. Оболочки первоначально теряли устойчивость, как правило, по несимметричной форме. Для высокоподъемистых оболочек при Н/с = 0,6 -г- 0,75 (см. рис. 14.1, стр. 613) наблюдались различные картины выпучивания. У некоторых образцов появлялась серповидная вмятина, прилегающая к контуру; при последующем нагружении эта вмятина последовательно расширялась, охватывая всю периферийную часть сегмента (рис. 14.9).
*) Р. Г. Суркин, С. Г. Степанов, статья в сборнике «Теория пластин и оболочек», Киев, 1962, 311—313.
**) Отметим оригинальный метод изготовления аналогичных образцов, предложенный Л. С. Палатником и заключавшийся в конденсации на стеклянную форму металла, испаряемого в вакууме (см. книгу А. В. Погорелова [14.5], стр. 62).
628
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ XIV
Другой пример показан на рис. 14.10, выполненном по результатам скоростной киносъемки. Первоначально вблизи контура здесь образовывалась одна вмятина, быстро углублявшаяся; затем возникали соседние вмятины. Сопоставление отдельных кадров показывает, что границы вмятин меняли свои очертания в процессе выпучивания. Случай ярко выраженной несимметричной потери устойчивости, происходившей в виде очень сильного хлопка и сопровождавшейся образованием нескольких волн по окружности, отражен на рис. 14.11. Наконец, в отдельных случаях имело место продавливание центральной зоны оболочки (рис. 14.12).
Судя по этим экспериментальным данным, имеющиеся теоретические исследования далеко не охватывают всего диапазона различных форм потери устойчивости в боль«, л шом.
Рис. 14.9. Серповидная вмятина. ц?0 касается экспериментальных
значений критического давления, то они оказались очень разнообразными и при этом зависящими от величины угла, охватываемого сегментом. Будем характеризовать кривизну сегмента с помощью параметра (см. рис. 14.1)
Х2=У 12(1—(14.48)
принимаем 0180°.
В случае стальных оболочек с полным углом охвата 0 от 9 до 45°, параметром X2 от 70 до 350 и отношением Rjh от 800 до 3900, испытанных путем создания вакуума, было получено о в пределах от 0,606/4,11 до 0,606/2,23; при испытании давлением масла величина о составляла от 0,606/3,8 до 0,606/2,61. Отметим, что испытания при постоянном объеме дают меньшее рассеяние экспериментальных точек, чем при постоянном давлении. Для медных оболочек с углом охвата от 106 до 140°, X2 от 1700 до 2350 и Rjh от 813 до 860 были зафиксированы наименьшие значения а, в пределах от 0,606/6,14 до 0,606/4,19.
В итоге надо считать, что реальные критические напряжения окр подъемистых.сферических сегментов лежат между верхним критическим значением ав = 0,605 и нижним значением, которое мы условно будем считать равным он = 0,155. Вмес:те с тем, расчетные значения орасч должны зависеть от угла, охватываемого сегментом, параметра кривизны X2 и отношения Rjh. Картина здесь
§ 156] ДАННЫЕ опытов 629
получается примерно та же, что и для цилиндрических оболочек: хотя теоретически нижнее критическое давление не связано с отно-
Рис. 14.10. Процесс выпучивания сферической оболочки по данным
киносъемки.
шением R/ht при больших значениях R/h надо ожидать значительных начальных неправильностей в форме оболочки, а это ведет к снижению окр. Впредь до накопления новых теоретических и
630 СФЕРИЧЕСКИЕ ОБОЛОЧКИ [ГЛ. XIV
экспериментальных данных в практических расчетах следует исходить из различных значений орасч в зависимости от параметра кривизны
Рис. 14.11. Несимметричная форма потери устойчивости.
сегмента. Ориентировочно можно предложить следующую таблицу для орасч и критического давления <7расч> относящуюся к тщательно изготовленным оболочкам:
А2 по (48)
От 100 до 500
От 500 до 1500
Более 1500
арасч ПО (42)
0,15
0,12
0,09
расч
0,3 Eh2/R2
0,24 Eh2/R2
0,18 Eh2lR2
При начальных прогибах, достигающих величины порядка толщины
оболочки, эти значения следует снизить приблизительно вдвое.
Приведем также экспериментальную формулу, рекомендуемую в работе [14.11] для оболочек с отношением R/h, лежащим в пределах от 400 до 2000, и углом охвата 0 от 40 до 120°:
<7расч = 0,36£(-)2;
здесь коэффициент k определяется по формуле
*=(1-0.175X
хО-тш-)-
В заключение отметим, что в последнее время при возведении некоторых сооружений применяют купола в виде оболочек вращения с ромбовидными «вмятинами». Форма этих предварительных вмятин*
Рис. 14.12. Выпучивание оболочки с продавливанием центральной части.
§ 157]
ЭЛЛИПСОИДАЛЬНЫЕ ОБОЛОЧКИ
631
как легко заметить, характерна для потери устойчивости оболочки в большом. Зависимость между поперечной нагрузкой и перемещениями для такой оболочки должна соответствовать восходящей ветви BD рис. 10.2, так что оболочка как бы.заранее находится в прощелкнутом состоянии. Изучение диаграмм состояния для оболочек различного вида позволяет сделать ряд заключений, относящихся к прочности и устойчивости таких куполов; желательно этот вопрос разобрать более подробно.
§ 157. Эллипсоидальные оболочки
Приведем, далее, данные для расчета на устойчивость эллипсоидальных оболочек вращения, встречающихся в авиастроении, химической промышленности, приборостроении. Следует различать вытянутые эллипсоиды, образованные вращением вокруг оси АВ эллипса с полуосями а, b, причем а <£ (рис. 14.13), и сплющенные (сжатые) эллипсоиды, при а>Ь (рис. 14.14). Допустим, что эллипсоидальная оболочка подвергается действию внешнего равномерно
Рис. 14.13. Вытянутая эллипсоидаль- Рис. 14.14. Сплющенная (сжатая) ная оболочка. эллипсоидальная оболочка.
распределенного давления q. Задача об устойчивости такой оболочки *) родственна аналогичной задаче, относящейся к сферической оболочке, так как в обоих случаях речь идет об образовании местных вмятин. Для вытянутой эллипсоидальной оболочки следует ожидать появления таких вмятин в зоне экватора, так как главные радиусы кривизны срединной поверхности здесь являются наибольшими. Верхнее критическое давление равно
2 F />2 А 2
дв = -» 1,21 —г. (14.49)
}3(1 fx2) 2 b2— а2 2 Ь2 — а2 4 '
*) Эта задача была рассмотрена в линейной постановке X. М. Муштари [10.9], а в нелинейной — Р. Г. Суркиным [14.6], см. также книгу [0.6].
632
СФЕРИЧЕСКИЕ ОБОЛОЧКИ
[ГЛ. XIV
В случае сплющенной оболочки, напротив, первые вмятины должны образоваться в зоне полюсов Л, В. Главные кривизны в полюсах равны R{—R2 = a2lb\ здесь оказывается применимой известная формула (10) для сферической оболочки с заменой R на a2lb:
2Е k2b2 101*72 /ц
дп = —— —г-~ 1>21£—т—. (14.50)
Чв К 3 (1 — (х2) а a4 v OKJ>
Интересен случай, когда сплющенная оболочка подвергается действию внутреннего давления *). Более подробное исследование показывает, что приа>£]/2 кольцевые напряжения в оболочке будут сжимающими. Это можно пояснить на разобранном в главе VIII примере круглой пластинки со свободно смещающимся в плане контуром: при значительных прогибах в зоне пластинки, прилегающей к контуру, также появлялись сжимающие напряжения. Для эллипсоида, испыРис. 14.15. Выпучивание сплющенной эллипсо- тывающего внутреннее идальной оболочки в зоне экватора. 'давление, сжимающие напряжения будут наибольшими у экватора; здесь и образуются начальные вмятины. Пример такой потери устойчивости показан**) на рис. 14.15. Критическое давление определяется в этом случае формулой***)
2 Е h2 loir? h2 / i еп
<7в— /3(1 — Иг) я2 — 2*2 я2 — 2*2 ’ (14.51)
совпадающей по структуре с (49).
Что касается нижнего критического давления qH, то оно составляет для эллипсоидальных оболочек приблизительно такую же долю от qB, как и для сферических оболочек; практические расчеты надо вести по величине qH.
*) Этот случай был впервые исследован И. В. Геккелером (Статика упругого тела, 1934, стр. 281).
**) По данным Н. И. Спиридоновой (Расчет на прочность тонких эллипсоидальных оболочек, канд. дисс., 1961).
***) Эта формула получена X. М. Муштари [10.9].
ГЛАВА XV
УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ДЕЙСТВИИ ПОПЕРЕЧНОЙ НАГРУЗКИ § 158. Исходные зависимости
Мы рассматривали до сих пор оболочки различного очертания, считая, что начальные кривизны срединной поверхности могут быть значительными. Выделим теперь особо пологие оболочки, имеющие малые кривизны. На рис. 15.1 показаны примеры пологих оболочек,
Рис. 15.1. Пологие оболочки: а) прямоугольная в плане, б) круговая
в плане.
одна из которых является прямоугольной в плане, а другая — круговой в плане. Условимся считать оболочку пологой, если стрела подъема Н не превышает 1/5 от наименьшего размера в плане *). Примем, далее, что оболочка* подвергается действию нагрузки, направленной нормально к срединной поверхности (давление газа или жидкости), либо нагрузки, направленной перпендикулярно к основной плоскости (собственный вес оболочки, вес снега для покрытий и т. д.). Пологие оболочки применяются в настоящее время все
*) Такое ограничение было указано В. 3. Власовым (см. [10.3], стр. 303). Э. Рейсснер при рассмотрении оболочек вращения принял, что для пологой оболочки максимальный угол наклона касательной не должен превышать ]/з (Е. R е i s s п е г, Journ. Math, and Mech. 7, № 2 (1958), стр. 128).
634 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ [гл. XV
шире в строительных конструкциях; они входят также в конструкции летательных аппаратов, подводных лодок и т. д.
При исследовании пологих оболочек, находящихся под действием поперечных сил, приходится, как правило, считать напряженное состояние моментным уже на первых ступенях нагружения. Если ограничиться определением напряженного состояния оболочки при малых прогибах, то его можно вести в рамках линейной теории. Различие между пологой оболочкой и плоской пластинкой скажется тогда лишь в том, что для оболочки надо учитывать дополнительные напряжения в срединной поверхности. Однако для расчета на устойчивость пологой оболочки важным является исследование больших прогибов с позиций нелинейной теории.
Рассмотрим различные варианты диаграммы «нагрузка — стрела прогиба», которые являются характерными для пологих оболочек различной кривизны. В случае весьма пологой оболочки параметр нагрузки q монотонно возрастает с увеличением стрелы прогиба /
?* 4k и п
Рис. 15.2. Различные варианты диаграммы «нагрузка — стрела прогиба».
(рис. 15.2, а); диаграмма имеет при этом точку перегиба С, причем на первом участке ОС жесткость оболочки падает, а на втором возрастает. В случае, если начальная стрела подъема оболочки сравнима с толщиной, диаграмма получает предельную точку А (рис. 15.2, б); здесь при известных условиях — когда нагрузка является «мертвой» — становится возможной потеря устойчивости, выражающаяся в прощелкивании оболочки к новому устойчивому равновесному состоянию. Далее, на рис. 15.2, в изображена диаграмма q(f), соответствующая оболочкам большой кривизны; падающая ветвь АВ неустойчивых состояний лежит вблизи начальной ветви ОЛ. Такого типа кривые анализировались нами в главе XI; прощелкивание становится возможным здесь при любом поведении нагрузки. Наконец, встречаются примеры, когда прогиб в центре оболочки на некотором этапе нагружения уменьшается и диаграмма q(f) становится петлеобразной (рис. 15.2, г); это связано с изменением формы волнообразования*).
О
*) Такой тип диаграммы был получен А. Ю. Биркганом для цилиндрических панелей; см. также работу Будянского [15.12].
§ 158]
ИСХОДНЫЕ ЗАВИСИМОСТИ
635
В некоторых случаях прощелкивание пологих оболочек является необходимым их свойством (хлопающие мембраны в приборах). С другой стороны, для оболочек, служащих покрытиями в строительных конструкциях, и во многих других примерах явление прощелкивания недопустимо. Так или иначе для расчета пологих оболочек на устойчивость должны быть известны характерные точки диаграммы «нагрузка — прогиб».
При выводе основных зависимостей нелинейной теории пологих оболочек возможны два подхода. Первый из них состоит в непосредственном использовании уравнений главы X. Будем исходить из уравнений (10.111) для оболочки, имеющей начальные отклонения от идеальной формы, и введем в них вместо полного прогиба дополнительный прогиб wl = w — w0; в развернутом виде уравнения примут вид
D л д2 Ф / d2w{, d2w0 \, д2 Ф / d2wx. d2w0 \
~~dx\dyi ' ду2') I Ш~)~
о д2 Ф / d2wl, d2w0 \., дгФ.. д2Ф, q
дх ду \ дх ду ' дх ду) ' х ду2 ' У дх2 ' h ’
(15.1)
J_ у4ф _ ( d*w\ \2 d*wi d*wi I о d*w\ д2®>о E \dxdy ) dx2 dy2 ' dx dy dx dy
d2wx d2w0 d2wx d2w0. d2w{ u d2wx /1KO\
dx2 dy2 dy2 dx2 x dy2 У ~~dx2~ *
Уравнения (1) и (2) получены в предположении, что перемещения и, v, w точки срединной поверхности отсчитываются вдоль касательных к линиям кривизны х, у и по нормали к поверхности; все размеры оболочки также естественно измерять вдоль линий кривизны. Под кх% ky подразумеваются начальные кривизны линий х, у.
Другой подход заключается в рассмотрении оболочки как пластинки с начальной погибью. Допустим, что контур оболочки в плане является прямоугольным. Тогда удобно ввести декартовы координаты х, у, откладывая их в основной плоскости 1—4 вдоль сторон контура (рис. 15.3). Пусть, далее, координата z определяет
начальное положение точек срединной поверхности *). Прогиб wx
теперь надо отсчитывать от исходной срединной поверхности
Рис. 15.3. Пологая оболочка, рассматриваемая как пластинка с начальной погибью.
*) При расположении системы координат на рис. 15.3 значения % будут отрицательными.
636 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ [ГЛ. XV
параллельно оси z. В такой трактовке надо в уравнениях (1), (2) положить kx = ky = 0 и ввести z вместо w0; тогда будет*)
D -4 д2Ф (d2wy. d2z \. д2Ф (d2wx, d2z \
~hVw' — ~Ш’\~ду2~ + ду2 ду2 \ дх2 + дх2)
д*Ф / д\ ■ q
дхду \дхду Т дхду)-\- h >
1 u4ffi / d*w, \2 d2Wi d2a>,. 2 d2 d2z E \ дх ду ) дх2 dy2 дх ду дх dy
d2wx d2z d2wx d2z.
dx2 dy2 dlfx2 t15’4'
или, в компактной записи,
1 /l'l <15-5>
— 74Ф = — L(wx> -j-wH~z)‘
Если используется этот подход, то размеры оболочки целесообразно представлять как размеры в плоскости ху.
Системы уравнений (1) — (2) и (3) — (4) являются эквивалентными **) при условии, если центральный угол 2ср, охватываемый наибольшим размером рболочки, достаточно мал, так что можно принять coscpl, sincpcp. Перейдем к отдельным задачам, относящимся к оболочкам различной формы.
§ 159. Панель, прямоугольная в плане
\
Начнем со случая, когда панель с главными кривизнами kx, ky имеет очертание, прямоугольное в плане (рис. 15.1, а); величины kx и ky принимаются постоянными. Размеры сторон опорного контура обозначим через а, Ь. Предположим, что по краям оболочка шарнирно скреплена с ребрами, абсолютно жесткими на изгиб в направлении нормали и в то же время имеющими малую жесткость на изгиб в плоскостях, касательных к срединной поверхности. Кроме того, будем считать, что точки, принадлежащие концевым сечениям оболочки, свободно скользят вдоль ребер. Этим допущениям соответствуют следующие граничные условия для краев л; = 0, х = а:
« = 0, 5- = 0; сх = 0, т = 0, (15.6)
*) Эти уравнения были даны Маргерром (К. Marguerre, Ргос. of 5th Internat. Congress of Appl. Mech., 1938).
**) Этот вопрос рассматривается в книге X. М. Муштари и К. 3. Галимова [0.6], стр. 181.
§ 159]
ПАНЕЛЬ, ПРЯМОУГОЛЬНАЯ В ПЛАНЕ
637
и аналогичные условия для краев у = 0, у = Ь. Примем, что нагрузка интенсивности q равномерно распределена по всей поверхности и действует со стороны выпуклости *).
Используем уравнения (1) — (2); принимая 0 = 0, представим их в виде
При заданных выше граничных условиях можно воспользоваться для интегрирования системы (7) — (8) методом Бубнова — Галеркина, применяя его одновременно к двум уравнениям системы **). Аппроксимируем функции w и Ф в первом приближении с помощью выражений
Как легко видеть, первые три граничных условия типа (6) удовлетворяются на всех кромках; четвертое же условие выполняется лишь
*) Это относится к оболочкам положительной и нулевой гауссовой кривизны.
**) Такой путь был уже принят в § 91, см. стр. 331.
wx = fx sin -j- sin ~y, Ф = Ax sin
b
«в среднем»; так, для кромок
о
Выпишем уравнения Бубнова—Галеркина:
а ь
а b
0 0
0 0
(15.10)
Подставляя сюда (7) — (9) и интегрируя, получим: D, ( 1, 1 \2 А f 2,
ТТб —ли\
(15.11)
(15.12)
638 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ [гл. XV
тогда по (11) придем к следующей зависимости между нагрузкой и прогибом *):
32я2
1
Ы)2 (ч4У
-t2+
+
— k* 16 *
*в(т+х)*
192 (1 — р.2)
С. (15.13)
Если панель является квадратной (а = Ь)> то при х = 0,3 будет
q* = 8,77С3 — 2,46*C2-f- (0,154fc*2 + 22)С. (15.14)
В случае, когда оболочка имеет цилиндрическую форму и координата у отсчитывается вдоль дуги, надо принять kx = 0, ky=\/R; тогда будет k* = b2jRh. Для сферической оболочки получим: kx = = ky = \jR\ при a = b найдем: k* = 2b2/Rh. Интересно рассмотреть случай оболочки отрицательной гауссовой кривизны. В § 119 приводился пример псевдосферы, для которой kx =— ky\ если считать а = Ь, то при этом будет * = 0. Уравнение (14) получает вид
4* = 8,77С3 + 22С.
Если судить по этим данным, панель псевдосферы будет вести себя, как плоская пластинка; потери устойчивости по форме, отвечающей (9), здесь произойти не может.
На графике рис. 15.4 пунктирными линиями изображены диаграммы * (С) по (13) для различных значений k* при X = 1. Как видим, при малых k* величина q* непрерывно возрастает, подобно случаю плоской пластинки; при больших k* диаграмма имеет нисходящий участок. Для того чтобы найти значение k*, при котором становится возможным прощелкивание, надо исследовать производную dq*/dL Приравнивая ее нулю, находим значения С, соответствующие верхней и нижней критическим нагрузкам:
’ 32 R +32 Г 2(1— ц2)
(15.15)
Граница области прощелкивания соответствует тому случаю, когда диаграмма <7* (С) имеет точку перегиба с горизонтальной каса¬
*) Эта зависимость была получена М. А. Колтуновым [15.4]; ему же принадлежит приводимое ниже уточненное решение, выполненное с помощью цифровых электронных мащин.
§ 159]
ПАНЕЛЬ, ПРЯМОУГОЛЬНАЯ В ПЛАНЕ
639
тельной *); при этом подкоренное выражение в (15) должно обратиться в нуль. Таким образом, предельное значение k* будет
при С = — k*. v 32
V6(l-fO
На первый взгляд, в ходе проектирования желательно назначать такие значения кривизн, при которых прощелкивание оболочек будет
Рис. 15.4. График «нагрузка — прогиб» для квадратной в плане панели.
исключено. Легко видеть, однако, что при этом начальный участок диаграммы будет иметь малый угол с осью абсцисс, так что жесткость оболочки окажется незначительной. Поэтому с практической точки зрения важно возможно точнее определить q* и <7* для оболочек относительно большой кривизны. Представим для этого функции w и Ф в виде рядов:
w — sin sin, Ф = 2 sin ~ir sln ь~‘ (15-16)
i.J i.)
*) При этом мы переходим от диаграммы по рис. 15.2, а к диаграмме такого типа, какой изображен на рис. 15.2, б.
640 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ нагрузке [гл. XV
Решение будет тем ближе к точному, чем большее число членов ряда принимается во внимание при вычислениях. Приводим результаты такого решения, выполненного с помощью цифровой электронной машины. Если удержать в рядах (16) члены с индексами (1; 1) и (2; 2), а затем присоединять к ним члены (3; 3) и (4; 4), то получим сплошные кривые рис. 15.4, обозначенные соответственно через 2; 3\ 4\ на рисунке они сливаются между собой. Однако отличие от данных первого приближения оказывается очень ощутительным, начиная с *36. Уточненные диаграммы дают несколько меньшие верхние критические нагрузки, причем пик кривой перемещается в сторону меньших прогибов. Но особенно меняется, и при этом в сторону возрастания, нижняя критическая нагрузка; в некоторых случаях она меняет знак и становится положительной. Вблизи qB кривая становится более крутой, а вблизи qH— более пологой*). Отсюда видно, что при k* < 60 второе приближение дает практически точные результаты; правда, прежде чем делать окончательные выводы, следует провести дополнительно счет для сочетаний индексов (1; 3); (3; 1) и т. д., а также рассмотреть антисимметричные формы выпучивания. На графике рис. 15.5 даны значения верхней и нижней критических нагрузок в зависимости от к* для пластинок с различным отношением сторон по данным четвертого приближения (X = 1, X = 1 //2,Х = 0,5); принято [л = 0,3. Прощелкивание имеет место при k* > 18 для X = 1, при k* > 20,4 для X = 1 jY2 и при k* > 30 для Х = 0,5. Очевидно, с увеличением X жесткость оболочки понижается.
Отметим, что четвертое граничное условие (6) может быть удовлетворено во всех точках края, если выбрать аппроксимирующее выражение для Ф в виде Ф = U (л;) V (у), где U и V—«балочные» функции, удовлетворяющие условию защемления балки по краям**). Если рассмотреть квадратную панель, то при этом в уравнении (14) существенно изменяется только коэффициент при С3; он получает значение 7,48 вместо 8,77.
Обратимся к другим случаям закрепления краев панели. Предположим, например, что ребра, окаймляющие панель, остаются прямолинейными, но вместе с тем свободно сближаются между собой. Идя аналогичным путем, приходим для квадратной панели в первом приближении к уравнению (при л = 0,3)
q* = 7.5С3 — 2,06ft*;2+(о, 154ft*2 + 22>С. (15.17)
*) К аналогичным выводам пришел В. И. Феодосьев, исследовавший с помощью цифровой машины прощелкивание пологих сферических сегментов (см. § 161, стр. 650).
**) Это решение дано М. М. Козаровым, канд. дисс., МИСИ, 1955.
§ 159}
ПАНЕЛЬ, ПРЯМОУГОЛЬНАЯ В ПЛАНЕ
641
Существенное влияние на характер диаграммы оказывает коэффициент при С2; нижние критические нагрузки по сравнению с предыдущим случаем сильно повышаются. Прощелкивание оказывается возможным
Рис. 15.5. Значения нижней и верхней критических нагрузок для пологих панелей.
при k* > 25,3. Если же ребра являются несмещающимися, зависимость (17) получает вид
д* =х 28.9С3 — 6,\k%2 + (0,5k2 + 22)С. (15.18)
Желательно, чтобы для этих случаев, важных с точки зрения практических приложений, были даны уточненные решения.
Отметим, что для удлиненной цилиндрической панели (а>Ь) может быть получено точное решение задачи *); при этом исследуется поведение арки-полоски с соответствующими условиями закрепления.
*) Это решение было дано. И. Г. Бубновым [0.2] и М. С. Корнишиным и X. М. Муштари [15.5].
642 УСТОЙЧИВОСТЬ пологих ОБОЛОЧЕК при поперечной НАГРУЗКЕ [гл. XV
§ 160. Коническая панель
Обратимся к случаю, когда очертание панели в плане является не прямоугольным, а круговым. Рассмотрим сначала коническую, а затем сферическую панель. Допустим, что пологая оболочка, с углом подъема а < у5, подвергается действию равномерного
давления (рис. 15.6). Будем считать, что панель защемлена по контуру и что вместе с тем точки края свободно перемещаются в плане (скользящая заделка) ♦). Особенности задачи, связанные с наличием вершины конуса, учитывать не будем.
Воспользуемся вторым из подходов к задаче по § 158, представляя обо¬
лочку как искривленную пластинку. По рис. 15.7 находим z = Hr {с = аг, где
a«tga = tf/c; под с по¬
нимается радиус основания, под Н — начальная стрела подъема. Возьмем за основу уравнения (5) и (6) и выразим операторы в полярных координатах г, ср, как в главе IX (стр. 403). Вводя относительную координату р = г/с, получим:
D -4 1 д / дФ dw \ * 1 / д2Ф d2w. д2Ф d2w \.
. 2 / д2Ф dw, дФ d2w \ 2_ д2Ф d2w 7 \ д? ду др ду ) р2 др ду др ду
2 дФ dw, са d2w
Рис. 15.6. Коническая панель под действием поперечной нагрузки.
Г
Т
яш 9»
S
Рис. 15.7. Система координат при рассмотрении конической панели.
р4 ду ду
1
1 / d2w \2 2 dw d2w, / dw \2 1 dw d2z
\ dp dy) p3 dy dp dy ' p4 \ dy ) p dp dp
p h dp2 ~T” h
1 dw d2w
vy
1 d2w d2w ca d2w
оператор Лапласа имеет вид
J2 dp
p2 dp2 dy2 p dp2
(15.19)
(15.20)
1 d2
p2 dy2
*) Подобная задача была рассмотрена Э. И. Григолюком [15.3]. Приведенное ниже решение принадлежит И. И. Трапезину [15.8].
§ 160]
КОНИЧЕСКАЯ ПАНЕЛЬ
643
Граничные условия будут
w — О, -~р=0, ог = 0, х == 0 при р = 1. (15.21)
Выберем аппроксимирующее выражение для прогиба, удовлетворяющее первым двум условиям (21), в виде*)
w = fx( 1 — р2)2Ч-/2р4(1 — р2)2 cos /tcp. (15.22)
Первый член в (22) соответствует, как уже указывалось в главе IX, решению осесимметричной линейной задачи для защемленной пластинки, а второй отображает изгиб по п волнам вдоль дуги с равными амплитудами к центру и от центра кривизны. Во взаимном сочетании эти два члена характеризуют образование ряда вмятин, преимущественно направленных к центру кривизны.
Подставляя (22) в правую часть уравнения (20), находим:
у4ф = /?0+ /?л cos лер -- R2n cos 2/tcp, (15.23)
где /?0, Rn — некоторые функции р, содержащие параметры /х, /2. Интегрируя (23), с учетом того, что в центре панели, при р = 0, величина сг должна быть ограниченной, получим:
-1. Ф = Ф0 Фл cos щ + Ф2п cos 2/tcp, (15.24)
где Ф0, Ф„, Ф2п — новые функции р, fv /2. Проинтегрируем далее уравнение (19) по методу Бубнова — Галеркина; тогда придем к следующим двум зависимостям:
д* = ср + ср + С3С+Ср+од, (15.25)
Bf? + B£ + Вр + ВР + ВР + ВР? = 0; (15.26)
здесь введены параметры
*=№)'• с=4' *=4- <15-27>
Коэффициенты Сх,..., С5 и Bv..., В6 зависят от числа волн п. Отметим, что безразмерная величина С характеризует по (27) прогиб центра панели. Исключая £ из системы (25) — (26), находим зависимость д*(С), причем случай п — 0 соответствует осесимметричной
форме прогиба.
На рис. 15.8 приведена диаграмма д*(С) для cfh —100 при
а = 0,1 и п = 0 (сплошная линия). Если построить кривые для п Ф 0, то до значения С = 7,5 они будут идти выше кривой, соответствующей осесимметричной форме равновесия, а при С > 7,5 — ниже этой
*) Это выражение было ранее использовано В. И. Феодосьевым при рассмотрении гибких круглых пластинок [15.10].
644 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ [гл. XV
кривой. Для примера на рис. 15.8 приведена пунктирная линия, относящаяся к л =10. Следовательно, несимметричная форма выпучивания должна проявиться при прогибе в центре, равном 7,5 толщинам оболочки. Огибающая семейства кривых, соответствующих различным п, при С > 7,5 мало отличается от кривой, соответствующей осесимметричной форме *). Нижнее критическое давление оказывается близким к нулю.
т Г
125
100
75
50
25
2.5 5 7t5 Ю 12,5 15 17,5
Рис. 15.8. Диаграмма равновесных форм для конической панели.
Если рассмотреть аналогичным образом случай жесткой заделки панели, когда точки кромки не смещаются, то нижнее критическое давление при c/h= 100 окажется отрицательным.
Допустим, далее, что коническая панель со скользящей заделкой по контуру подвергается действию сосредоточенной силы Р в центре, направленной вдоль оси. Исследование осесимметричного выпучивания панели приводит к следующей зависимости между нагрузкой Р и стрелой прогиба /:
Р* = 0,294С3 — 0,332 --С2 + [о,16 + 1,47] С,
где Р* = Pc2/Eh2, С = //А.
*) Этот вывод относится лишь к данному примеру. При других параметрах оболочки результат может быть иным, так что исследование несимметричного выпучивания окажется необходимым.
§ 161]
СФЕРИЧЕСКАЯ ПАНЕЛЬ
645
§ 161. Сферическая панель
Перейдем к задаче об устойчивости пологого сферического сегмента (рис. 15.9), нагруженного равномерно распределенным внешним давлением. Эта задача послужила предметом многочисленных исследований *); она оказалась достаточно трудной, и результаты работ различных авторов часто оказывались противоречивыми. Изучение поведения пологой панели тесно связано с исследованиями, относящимися к полной сферической оболочке или подъемистому сегменту, так как панель служит как бы моделью вмятины, развивающейся при выпучивании таких оболочек. Вместе с тем расчет пологих панелей, форма которых приближается к сферической, имеет сам по себе большое практическое значение.
Обозначим через //стрелу подъема оболочки, через
с — радиус в плане, через R — радиус кривизны срединной поверхности, через р — половину угла, охватываемого панелью. Как легко видеть, эти величины связаны соотношениями**)
:2 RH,
А
(15.28)
До настоящего времени рассматривалась, как правило, осесимметричная форма выпучивания пологой сферической оболочки. Будем исходить из уравнений типа (1) и (2), считая, что начальная погибь отсутствует ( = 0). Вводя полярные координаты и считая w = w(r)t Ф = Ф (г), мы можем найти первый интеграл этих уравнений, как в главе XIV. При q = const по (14.22) получим:
D d 1 d dw i dw. r \ dФ. qr2
h Г dr r dr Г dr I dr ' R) dF ' 2 h *
/1 dw, r \
V2~~drR)'
J_ d 1 d йФ
Er dr r dr r dr
dw
dr
(15.29)
(15.30)
*) Пер вая работа в этом направлении относилась к расчету хлопающих мембран и принадлежала В. И. Феодосьеву [15.9], [15.10].
**) Если исходить из указания Э. Рейсснера, приведенного на стр. 633, то по (28) сферическую оболочку надо считать пологой при ////?< V*.
646 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ [ГЛ. XV
Введем безразмерные параметры *)
в — —, а———0, т= 1 (15.31)
с М 1 ЕЩУ т dr 4 ’
= Р = —~д (~)2, т = ; (15.32)
V Vm h 2EVm \h) 12(1—ц*) v '
тогда уравнения (29) и (30) перейдут в следующие:
L' (а) = р' (ау Рв2), (15.33)
(T) = jP'(62-a2). (15.34)
где под U понимается линейный оператор
(15.35)
Параметры р' и Р связаны с введенными нами в главе XIV величинами k и о соотношениями
f,=THk- р=-йг (15-38)
Будем считать, что панель защемлена по контуру и что радиальные смещения точек контура отсутствуют, как показано на рис. 15.9. Тогда граничные условия получают вид
а = 0, 7 = 0 при 0 = 0, (15.37)
а = 1, — Mf = 0 при 0 = 1. (15.38)
Один из вариантов решения задачи состоит в следующем [15.16]. Представим величины а и у в виде рядов по степеням 0:
а = 2ап02'-1, Т = 2ъ,02Я1. (15.39)
п п
Первое из выражений (39) представляет собой обобщение аппроксимирующей формулы, которой мы пользовались в § 113**) главы IX. В самом деле, по (9.51) находим:
Увеличивая число удерживаемых членов в (39) по сравнению с (9.52), мы повышаем точность решения.
*) Такие параметры введены Рейссом, Гринбергом и Келлером [15.16].
**) См. также первый член выражения (22), относящегося к конической панели.
§ 161]
СФЕРИЧЕСКАЯ ПАНЕЛЬ
647
Выражения (39) удовлетворяют граничным условиям (37). По (38) получаем:
2 «„-i-о,
2[2я-(1+х)]Тп = 0.
(15.40)
Подставляя (39) в уравнения (33) и (34), имеем: „ р р 72 =
для п>
и, далее,
4п (п — 1)
8(«,Т1 + Я)' ’* 8(1— af)
— ~ 4п (п — 1) а‘*п-1
л-1
/=1
л-1
для
/«1
Эти формулы позволяют выразить все коэффициенты через ах и Уравнения (40) принимают тогда вид
(«1. Tfi) = 0. О (*!, Ti) = о.
(15.11)
я > 2.
(15.42) ** н Тя
(15.43)
где F, О — нелинейные функции аг и fi- В работе [15.16] определение корней уравнений (43) было проведено с помощью цифровых электронных машин; находились р. точки /, 2, 3,... на диаграмме «нагрузка Р—стрела прогиба С», как показано на рис. 15.10. Наиболее благоприятным был случай, когда линия ОАВ, соединяющая эти точки, имела нисходящую ветвь АВ: это давало возможность с известной уверенностью найти верхнюю критическую нагрузку. Однако процесс вычислений не всегда приводил к нужным результатам. Так, например, в отдельных случаях зависимость Р (С) получала вид, изображенный на рис. 15.10 пунктирной линией; в некоторой точке С процесс вычислений начинал расходиться. Такие случаи вообще нередко встречаются при решении систем нелинейных уравнений в задачах устойчивости; они требуют дополнительного исследования, так как могут быть вызваны особенностями принятой программы вычислений. Во всяком случае, рискованно принимать точку С для определения верхней критической нагрузки. Приводим сравнительно надежные результаты, относящиеся к определению верхней
Рис. 15.10. Диаграммы «нагрузка — прогиб» по данным вычислений на цифровых машинах.
648 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК при поперечной НАГРУЗКЕ [гл. XV
критической нагрузки*). На рис. 15.11 приведена зависимость верхнего критического давления qQ от геометрических параметров оболочки при различных условиях закрепления: жесткого защемления по контуру (кривая /), шарнирного закрепления с несмещающимися в плане точками контура (кривая 2) и шарнирного опирания со
Рис. 15.11. Верхняя критическая нагрузка для пологой сферической панели при разных условиях закрепления.
свободно смещающимся в плане контуром (кривая 3). По оси абсцисс отложена величина
р= -j/2p' = 12(1 — jj.2) = (15.44)
Пользуясь соотношениями (28), выразим также параметр р через отношение Hjh:
р:=2Л2(1—или» ПРИ [* = 0,3, р6,6~. (15.45) По оси ординат откладываются значения параметра
vB = -= /3(1 — 1**),g./ Я\а (15.46)
в 2/2 2 Е\h)
Судя по выражению (14.10), в (46) фигурирует величина верх¬
него критического давления для полной сферы; обозначим ее через q0t в. Следовательно, величина vB характеризует верхнюю критическую нагрузку для пологой панели, отнесенную к q0tB; vB = B/0)B. При
*) Они получены Вейнитшке [15.19].
§ 161]
СФЕРИЧЕСКАЯ ПАНЕЛЬ
649
р > 40 (k > 12) процесс вычислений сходился настолько медленно, что результаты нельзя считать окончательными; соответствующие участки кривых показаны на рис. 15.11 пунктиром, Обратимся прежде всего к случаю защемленной по контуру панели. Значения vB лежат при р < 25 значительно ниже 1; в то же время при 35 < р < 75 они превышают 1 и, наконец, при р > 75 снова лежат ниже 1. Такой, на первый взгляд, неправдоподобный вид кривой vB(p) объясняется тем, что в зависимости от значения р характер волнообразования оболочки оказывается различным. Это обстоятельство подтверждается экспериментами *), проведенными над оболочками, изготовленными из магниевого сплава и жестко защемленными по контуру. При малых р прогиб являлся максимальным в центре и монотонно уменьшался по направлению к краю (рис. 15.12, а). При ббльших значениях р средняя часть вмятины становилась более пологой, при р > 20 максимальный прогиб всегда имел место не в центре (рис. 15.12, б).
Рис. 15.12. Формы волнообразования сферических панелей различной
кривизны. В случае развитой вмятины максимум прогиба будет уже на расстоянии половины радиуса от центра. При р > 55 появлялся новый пик в центре (рис. 15.12, в).
Вернемся к графику рис. 15.11. Сравнение кривой 2 с кривой 1 показывает, что в определенной области, при 15 < р < 30, величина qB для случая шарнирного закрепления лежит выше, чем при защемлении панели по контуру. Это объясняется, возможно, различным влиянием изгибных напряжений, образующихся у края. В остальной области изменения р для шарнирно закрепленной оболочки мы по« лучаем значения vB меньшие, чем для защемленной. Особенно резко падает vB при свободно смещающемся в плане контуре.
Отметим, что постановка задачи здесь отличается от принятой в § 155. Там мы условно предполагали, что основное состояние является безмоментным, и вводили первоначальный прогиб w0. Если все же, пользуясь уравнениями (14.45), попытаться найти верхнее критическое давление при С—>0, то получим:
\
8
3(1-**) Л
*) Ряд опытов с пологими сферическими сегментами был проведен
Г. Н. Гениевым и Н. С. Чаусовым [15.2], а также Р. Г. Суркиным (см. § 156). Здесь приводятся данные, полученные Капланом и Фыном [15.14].
650 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ нагрузке [гл. XV
Если, далее, построить по этому уравнению кривую св(), то она будет напоминать начальный участок кривой 1 рис. 15.11.
Все эти данные относятся к верхнему критическому давлению. Судя по результатам экспериментов (см. ниже рис. 15.15), выпучивание реальных оболочек происходит при нагрузке, лежащей, как правило, значительно ниже qB. Очевидно, здесь проявляются те же особенности задачи, что и в случае полной сферы. Поэтому надежные основания для расчета можно получить лишь после исследования характера других участков кривой q(С) и определения нижнего критического давления. Такие данные были получены в самое
Рис. 15.13. Верхние и нижние критические нагрузки для сферических
панелей.
последнее время также с помощью электронных цифровых машин *). Приведем окончательные результаты вычислений. На рис. 15.13 **) предложена зависимость между параметром нагрузки q* = qc4/Eh4 и безразмерной стрелой прогиба в центре С = тах/Л для панелей, имеющих различную начальную кривизну и жестко защемленных по
*) Эти исследования выполнены почти одновременно В. И. Феодосьевым и Тёрстоном [15.18]; отметим, что результаты этих работ, полученные разными методами, оказались очень близкими между собой.
**) Графики рис. 15.13 и 15.16 принадлежат В. И. Феодосьеву.
§ 161]
СФЕРИЧЕСКАЯ ПАНЕЛЬ
651
контуру. При H/h = 0 пол>ча м случай плоской пластинки. Далее, для весьма пологой панели (Hjh < 1,5 или р < 11) нагрузка возрастает с увеличением С монотонно, что соответствует рис. 15.2, а. Для панелей большей кривизны график *(С) получает вид, показанный на рис. 15.2, б. На графике отмечены значения верхнего и нижнего критических давлений, причем
д JS-36 О/>-49 о Jo-64 о jo-81
максимальное значение H(h здесь составляет 4; это отвечает р » 26.
В случае р > 26 процесс вычислений значительно осложняется: это объясняется изменением характера волнообразования в процессе выпучивания оболочки. Как мы видели из рис. 15.12, максимальный прогиб будет при р > 26 иметь место, как правило, не в центре панели; на некоторых участках нагружения прогиб в центре будет уменьшаться (см. рис. 15.2, г). Будем все же определять параметр С как прогиб в центре, отнесенный к толщине: С = ‘К>0//*. На рис. 15.14*) изображены результаты вычислений, относящиеся к панелям несколько большего подъема, при 36 < р < 81. Для значений р = 49 и р = 64 было получено несколько различных ветвей равновесных состояний оболочки, не связанных между собой. Одни из этих ветвей соответствуют, по-видимому, устойчивым, а другие — неустойчивым формам равновесия. Отложенный здесь по оси ординат параметр f равен
7 = 6(1 — ц2) У 3(1 — р.2) q* или, при р = 0,3, т « 9*. (15.47)
Исследование кривых рис. 15.13 и 15.14 позволило определить верхние и нижние значения критического давления qB и qH при
0 < р < 80. Эти окончательные данные приведены на рис. 15.15; по оси ординат отложены по-прежнему параметры vB и vH, характеризующие отношения qB и qH к величине q0tb для полной сферы. Кривая для vB почти совпадает с той, которая была получена другими методами (см. кривую 1 рис. 15.11); линия vH является для нас новой. На графике рис. 15.15 даны также результаты экспе-
Рис. 15.14. Ветви равновесных состояний пологих оболочек различной кри~ визны.
*) Графики рис. 15.14 и 15.15 получены Тёрстоном [15.18].
652 УСТОЙЧИВОСТЬ ПОЛОГИХ ОБОЛОЧЕК при поперечной НАГРУЗКЕ [гл. XV
риментов [15.14]; одна часть из них получена при нагружении оболочки маслом (ромбы), а другая часть — при нагружении воздухом (кружки). Можно считать, что в первом случае выпучивание происходило при постоянном объеме, а во втором — при постоянном давлении. Хлопок проявлялся наиболее резко во втором случае; отмеченное в опытах падение нагрузки показано на рис. 15.15 стрелками. Как видим, экспериментальные значения v лежат в вилке, образуемой vB и vH, и при этом для р > 40 ближе к vH. В практических расчетах следует пользоваться графиком рис. 15.15, определяя для
Рис. 15.15. Теоретические значения верхней и ннжней критических нагрузок в сопоставлении с данными экспериментов.
тщательно изготовленных оболочек vH непосредственно по кривой графика, а при относительно большой начальной погиби — с уменьшением vH приблизительно на 40%. В случае шарнирного закрепления оболочки можно получить ориентировочные расчетные данные, сравнивая графики рис. 15.11 и 15.15.
В заключение приведем интересные данные, позволяющие судить
о том, в каком соотношении потенциальная энергия деформации оболочки делится на две части — энергию деформации срединной поверхности Uc и энергию изгиба £/и. На рис. 15.16 повторена кривая q * (С), относящаяся к защемленной по контуру панели, при H[h — 4. Здесь же показано, как меняется в процессе выпучивания отношение UJUc-)-Unt выраженное в %. Как видим, при малых прогибах (ч < 1) основную долю — около-90% общей энергии — занимает энергия деформации срединной поверхности; эта пропорция сохраняется при q = qB. Затем удельный вес (Jc быстро падает, но все же при нижнем критическом давлении Uc составляет примерно 23% от общей энергии. При последующем выпучивании доля Uc снижается уже до 6%; вычисления для значений С>8 еще пока не
§ 161]
СФЕРИЧЕСКАЯ ПАНЕЛЬ
653
проводились. Эти данные проясняют вопрос о возможности пренебрежения величинами Uc или UB при исследовании различных этапов процесса выпучивания оболочки; надо, впрочем, иметь в виду, что они относятся только к отдельному примеру.
Рис. 15.16. Изменение удельного веса энергии деформации срединной поверхности при выпучивании оболочки в большом.
Мы рассматривали выше лишь осесимметричную задачу. Однако по аналогии со случаем конической панели естественно предположить, что при некотором значении прогиба должно произойти образование волн по окружности, причем число волн будет зависеть от интенсивности нагрузки. Как уже отмечалось выше, рассмотрение такой задачи было начато Э. И. Григолюком [15.3], принявшим аппроксимирующее выражение в форме, аналогичной (22). Желательно, чтобы в дальнейшем эти исследования были продолжены как для оболочки идеальной формы, так и для случая оболочки с начальной погибью с рассмотрением различных условий закрепления оболочки по контуру.
Отметим своеобразный путь решения нелинейных задач теории оболочек, предложенный Н. А. Кильчевским (Докл. АН УССР, № 7, 1962), заключающийся в использовании эквивалентной линейной модели с переменными упругими характеристиками.
ГЛАВА XVI
УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК
§ 162. Основные уравнения линейной теории трехслойных пластинок и оболочек
Трехслойная пластинка или оболочка состоит из двух тонких внешних слоев, изготовленных из прочного материала (несущие слои),
между которыми размещается относительно легкий и малопрочный средний слой (заполнитель), обеспечивающий совместную работу внешних слоев. Несущие слои обычно выполняются из таких жестких материалов, как металл, фанера, пластмасса. В качестве заполнителя может использоваться пенопласт, бальзовое дерево, пористая резина, металл в виде гофрированного листа или сотовых ячеек (рис. 16.1). Трехслойные конструкции находят все более широкое применение в самолетостроении, судостроении, промышленном строительстве и в других областях техники. Конструкции, средний слой которых выполнен из металлического гофрированного листа или сот, начинают применяться при повышенных температурах.
Рис. 16.1 Трехслойные панели с заполнителями из (а) сплошного пенопласта, (б) гофра, (в) сот.
Расчет трехслойных конструкций на устойчивость должен вестись с учетом различных видов выпучивания конструкции в целом и ее отдельных элементов. Пусть трехслойная пластинка или пологая
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
655
оболочка * со сплошным заполнителем нагружена симметрично относительно срединной поверхности. Прежде всего, надо различать две формы потери устойчивости: общую, обусловленную, в основном, искривлением срединной поверхности конструкции (рис. 16.2, а), и местную, выражающуюся, главным образом, в искривлении (сморщивании) внешних слоев (рис. 16.2, б) и происходящую без искривления пластинки или оболочки в целом. При местной потере устойчивости внешнего слоя он может быть представлен как пластинка или оболочка на упругом основании.
В случае, если средний слой выполнен в виде листа гофра или в виде ячеек сот, возможна, кроме того, местная потеря устойчивости стенок гофра или пластинок сот.
Исследования трехслойных конструкций на устойчивость общего и местного типа представляют собой две самостоятельные области, в каждой из которых применяются свои допущения. Такое разделение оказывается возможным в связи с тем, что для трехслойных пластинок отсутствует взаимное влияние этих форм [16.5], а для трехслойных оболочек взаимным влиянием можно пренебречь, если оболочка пологая [16.9].
В настоящей главе мы будем рассматривать лишь вопросы общей устойчивости трехслойных пластинок и оболочек *).
Тонкие несущие слои трехслойных пластинок и оболочек естественно представлять как обычные пластинки и оболочки, используя при составлении уравнений для них гипотезу прямых нормалей.
Заполнитель трехслойной конструкции необходимо, вообще говоря, рассматривать как тело трех измерений. В такой точной постановке был выполнен ряд исследований устойчивости трехслойных пластинок **). Эти исследования сыграли роль в обосновании эффективных приближенных методов расчета трехслойных пластинок и оболочек, использующих некоторые допущения о работе заполнителя.
*) Местная устойчивость внешних слоев в случае сплошного заполнителя рассмотрена в работах А. П. Вороновича [16.5], В. И. Королева [16.8], А. Л. Рабиновича [16.13], Кокса [16.15], Марча [16.24], Юсуффа [16.37]; местная устойчивость в случае заполнителя типа гофра рассмотрена в работе [16.3].
**) В этом направлении были выполнены работы А. П. Вороновичем [16.5], Коксом [16.15], Гудьиром и Нео [16.18], Хантер — Тодом [16.21], Нейбером [16.26], Легге и Хопкинсом [16.22J и другими авторами,
Рис. 16.2. Кососимметричная и симметричная формы потери устойчивости.
656 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
Приближенная теория устойчивости трехслойных пластинок и оболочек в пределах упругости и будет предметом настоящей главы *).
Сделаем некоторые допущения, касающиеся деформаций заполнителя при общей потере устойчивости пластинок и оболочек. Прежде всего, будем пренебрегать поперечной сжимаемостью заполнителя, и прогибы внешни слоев будем считать одинаковыми. Это допущение, как показано в ряде работ [16.11], [16.27], оказывается приемлемым для практических расчетов в весьма широком диапазоне.
Если заполнитель имеет жесткость того же порядка, что и несущие слои, или отношение размеров пластинки к ее толщине велико, то при расчете можно считать справедливой гипотезу прямых нормалей для всего трехслойного пакета. Расчет в этом случае не будет отличаться от расчета обычных однослойных пластинок и оболочек, с той лишь разницей, что в нем будут использоваться
жесткости составных сечений. Однако, в большинстве случаев, из
соображений экономии веса трехслойная конструкция выполняется
таким образом, что заполнитель оказывается недостаточно жестким, и расчет приходится вести с учетом деформаций поперечного сдвига заполнителя. Собственно в учете влияния сдвига среднего слоя на работу внешних слоев и состоит главное отличие расчета трехслойных конструкций от расчета обычных однослойных пластинок и оболочек.
Для учета деформаций поперечного сдвига заполнителя введем следующее допущение.
Будем считать, что в заполнителе прямая
линия, перпендикулярная к его срединной поРис. 16.3. Характер веРхн0СТИ Д° деформации, остается прямой и
распределения пере- в процессе деформации, но за счет сдвига мещений по толщине перпендикулярность нарушается; иными сло-
трехслойной оболочки, вами, по толщине заполнителя задается линей¬
ный закон смещений. К тонким внешним слоям будем применять гипотезу прямых нормалей. Таким образом, нормаль, проведенная через все три слоя, в процессе деформации
становится ломаной (рис. 16.3).
Такая расчетная схема для трехслойных пластинок и оболочек является весьма общей и позволяет учесть как деформации сдвига заполнителя, так и работу его на продольные силы и моменты. Но учет воспринимаемых заполнителем продольных сил и моментов далеко не всегда является необходимым. В случае, если отношение
*) Эта теория получила свое развитие в работах Нейта [16.25], A. Л. Рабиновича [16.13], Рейсснера [16.27], А. П. Прусакова [16.11], [16.12],
Хемпа [16.19], Лайбева и Батдорфа [16.23], Штейна и Мейерса [16.31], Хоффа [16.20], Э. И. Григолюка [16.6], В. Ф. Караванова [16.7], Л. М. Куршина [16.9], [16.10] и других авторов.
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
657
/Л
модуля упругости несущего слоя Е к модулю упругости заполнителя Е3 в плоскости, параллельной несущим слоям, велико, а отношение толщины несущего слоя t к толщине заполнителя 2А не очень мало (Е3 h/Et <i 0,1), то продольные силы воспринимаются почти целиком внешними слоями. Такие заполнители по установившейся терминологии принято называть легкими. Таким образом, при расчете трехслойных пластинок и оболочек с легким заполнителем можно пренебрегать в среднем слое нормальными и касательными напряжениями, лежащими в плоскости, параллельной несущим слоям. В случае, если заполнитель воспринимает заметную часть продольных усилий, его принято называть жестким заполнителем.
Гипотеза ломаной линии для смещений позволяет получить уравнения трехслойных оболочек как с легким, так и с жестким заполнителем. Мы дадим здесь вывод уравнений для случая легких заполнителей, представляющих наибольший интерес для практики. Попутно кратко остановимся и на уравнениях для жестких заполнителей.
Рассмотрим трехслойную пологую оболочку с одинаковыми внешними слоями и легким заполнителем. Обозначим через Rx и R2 главные радиусы кривизн ее срединной по- Рис- 16.4. Элемент трехслойной оболочки, верхности (рис. 16.4). Криволинейные координаты л:, у на срединной поверхности оболочки пусть совпадают с линиями главных кривизн.
Для перемещений точек верхнего слоя при потере устойчивости в соответствии с гипотезой прямых нормалей и с учетом пологости оболочки находим (при (— A — t) z (— А) ) *):
wb = wi> ub = u\ — + A + 4) ' vB = tV\ — [z + * + 4) ;
(16.1)
здесь uv vv wx — смещения точек срединной поверхности верхнего несущего слоя.
Аналогично для смещений точек нижнего слоя (при А А + /) / и t \ dw2 / и t\ dw2
= Ян = Я2 — (z — h — v* = v* — \z~h—2)~dT'
(16.2)
*) Индексы «в» и «н» здесь относятся к верхнему и нижнему слою, в то время как в других разделах они соответствуют верхней и нижней критической нагрузке.
658 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ пластинок и ОБОЛОЧЕК [гл. XVI
причем я2» v2* w2 — смещения точек срединной поверхности нижнего несущего слоя. При исследовании деформаций общей потери устойчивости трехслойной конструкции можно, как было указано выше, принять
w1 = w2 = w. (16.3)
Смещения среднего слоя, в соответствии с гипотезой прямых линий в заполнителе, равны (при — A<z<A)
wc = w.
Для деформаций слоев используем выражения
да w dv w
г*~~дх~~'Щ’ еУ~~ду~~Ъ'
ди. dv dv. dw ди. dw
~ ~дуг~дх’ Ъ*—дг~т~ ду ’ 'дх
Последние два соотношения необходимы только для среднего слоя, где имеют место деформации сдвига.
Будем рассматривать трехслойную оболочку с внутренними и внешними слоями из изотропных материалов. Обозначим модуль сдвига материала заполнителя через 03. Для напряжений во внешних слоях имеем выражения
°х— 1 — р.2 (здг+у)* °У~ 1 — fi,2 (еУ “I I*6*) * Хху = 2(1 + (X)
(16.6)
Касательные напряжения txz, ху2 во внешних слоях, как обычно при использовании гипотезы о прямых нормалях, определяются из уравнений равновесия элемента внешнего слоя. Для касательных напряжений в заполнителе имеем:
= Оз т,г, V = 03 1гу2. (16.7)
Определим усилия во внешнем слое. Для этого проинтегрируем напряжения (6) по толщине внешнего слоя и учтем выражения для деформаций (5) и смещений (1). Для усилий в верхнем несущем
(16.4)
(16.5)
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
659
слое получим:
\i d (ди\, dvx w w \
N‘.' = в Ьх-+ W-f W'•
АТ в(>1. и\ W W\
ь1 =в (-37+1* W - ЪГ *г)’
Т JLniift (dv' JL.du'\-
— Xte'dy)'
(16.8)
здесь В = £//(1 — р2) — жесткость внешнего слоя.
Аналогичным образом для усилий в нижнем несущем слое NXt2> Nyt 2» Т2 получим те же выражения (8) с заменой в них uv vx соответственно через и2, v2. Положительные направления усилий показаны на рис. 16.5, по аналогии с рис. 10.24.
Рис. 16.5. Положительные направления усилий в срединной поверхности.
Для изгибающих (Мх, Му) и крутящих (Н) моментов во внешних слоях относительно соответствующих срединных поверхностей получим, вычисляя интегралы вида
—Л
/ °х(г — А— )аг==М*’»
-<*+«
известные выражения:
М
d2w \
лл АЛ r\( d2W. d2W \
Му, 1 — Му12 — D +1*. дхъ J.
Н1—Н2 = — (1 — ja)D
d2w
дх~ду;
(16.9)
здесь D—цилиндрическая жесткость внешнего слоя: D=Ets/12(1—jx2). Положительные направления моментов показаны на рис. 16.6.
660 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. XVI
Определим касательные напряжения в заполнителе. Из (7), (5). (4) имеем:
yz*
(16.10)
Поперечные силы в заполнителе:
-го, [!■(«,-«,>-(*+!-) £.].
<?„,= - 20, [I <»,-,*)-(* + !■) -£■].
Выделим из верхнего внешнего слоя элемент dx, dy. Рассмотрим условия равновесия моментов (рис. 16.7) и продольных сил (рис. 16.8),
(16.11)
действующих на элемент. Обозначим через zXZt v xyz> t касательные напряжения, действующие в месте сопряжения внешнего слоя с заполнителем. Из условия равновесия моментов найдем:
дМ*
дН*
дх
Qy> 1 =
дМ
у>1
ду
дН{
2 т» 1*
1 — ду Условия равновесия сил дают
dNr.t, дТ.
дх
2 V-1-
дх
dN,
у, 1
ду
dTt
ду
дх
Г + xz, 1 = 0, ту * 1 = 0.
(16.12)
(16.13)
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
661
Исключая из (12) напряжения rXZtlt TyZfl, с помощью (13) получим выражения для поперечных сил во внешнем с'лое:
дМ.
*х, 1
дх
£ii _L — ( i d7*i \
Qy.i=-
dM
dy
dHx
2 \ dx
dy
dTt
dy
dx
IdNy,, dT{\ \ dy ' dx)
(16.14)
Рис. 16.7. Моменты и поперечные силы, действующие на элемент внешнего слоя.
к
Рис. 16.8. Усилия, действующие на элемент Рис. 16.9. Касательные навнешнего слоя. пряжения, обусловленные
взаимодействием внешних слоев с заполнителем.
Аналогичным образом для нижнего слоя, учитывая направление напряжений txz, %уг (рис. 16.9), из уравнений равновесия элемента
662 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
будем иметь:
Qx, 2 —'
дМ\
Ж, 2
дН2
t (dNx
дх
Фу, 2 —'
дм
у, 2
ду
дН2
ду
дх
+;( + т(-
дх
dN.
у, 2
ду
дТ2
ду
г).
)•
(16.15)
Суммируя поперечные силы в заполнителе и внешних слоях, получим для поперечных сил в трехслойной оболочке выражения
«,=<и.■+ ш,■+ >>+w <•+•> -
-7 [i <*'•.--.!)+ -5-<г. - г>>] •
О, = <?„(«„,■+ МГ:,)+ (Я, + Я,) -
(16.16)
Введем обозначения:
e« = -g-(«i+и2), ®« = y(®i + v2)«й = 4- («1 — «2). «В = Т (®1 — «2>-
(16.17)
Выразим суммарные усилия и моменты в трехслойной оболочке через смещения срединных поверхностей внешни* слоев. По (8) и (17) получим:
W,=+1* _-г-_,
N, = «,., + N,., = ™ --Щ - I* ж) ■
7-= Г, + 7-, = (1 - р) В + i).
(16.18)
Изгибающие и крутящие моменты в трехслойной оболочке относительно ее срединной поверхности будут
М* =М,.1-Ь Мх, 2 - (а + 4) (Nx,, - NXJ.
Му = Myil + My, 2 - (A + 4) (Ny,, - /Vy, 2).
Я = Hx + Ht- (A + 1) (7\ - TJ.
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
663
Используя (8), (9) и (17), получим: d*w d2w \
Mx = -2d(
ду
duo
дх2 \ г ду21
/ d2w d2w \ ( t\( dvo duo \
жу = -20('3 + ~3)-2(А + т)Яг37+1*'дг)’ I (16-19>
d2w ( t\ (dvo dua\
H = — 2D (1 -Jl) — (l-i) \h + )B (-gj- + -gp-).
Для поперечных сил в трехслойной оболочке (16) с учетом (8), (9), (11) и (17) получим выражения через перемещения:
■*{!>
дх2
1 — (1 д2и 1+fi d2v \
2 ~ду2~ 2~~дхду)'
q,=■- го. Ь - (*+4) £] - го г* -
-Bt{-
d2Vo
L _J L_ L_1 dy2 ‘ 2 dx2 ‘2 d*dy
i—ft d*v? i + x
)■
(16.20)
Обратимся к уравнениям равновесия элемента пологой трехслойной оболочки в целом. Из условий равновесия сил в направлениях хну получим (рис. 16.10):
dNx
дТ
= 0.
dNv
дТ
+-лТ = 0.
дх 1 ду dy ■ дх
Уравнения равновесия моментов (рис. 16.11) дают
дМх
дН
дх
дМч
дН
дх
= Qv-
(16.21)
(16.22)
ду '*■*’ ду
Уравнение проекций сил на направление нормали с учетом составляющих, обусловленных поворотом элемента (рис. 16.12), дает
Nr
Nv
Я.
+
dQx
dQy
dx
d
dy
dx
(w?
dw\
и)+
(')+w(7£)+T5F(r,,£H' <16-23>
•усилия в оболочке до потери устойчивости.
Здесь Nx, Ny, Т°-
Учитывая, что усилия N%, Ny, Т° удовлетворяют уравнениям равновесия, запишем уравнение- (23) в виде
Nr
ЛГ„
dQx
dQv
дх
ду
„о d*w_ -+- N* fa*
■N,
о d2w
d2w
dy2
-=0- <16-24>
V
Рис. 16.10. Усилия, действующие на элемент трехслойной оболочки.
Рис. 16.11. Моменты, действующие на элемент трехслойной оболочки.
Рис. 16.12. К выводу уравнения равновесия проекций сил на нормаль.
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
665
Выразим в уравнениях (21), (22), (24) усилия и моменты через
перемещения срединных поверхностей внешних слоев с помощью формул (18), (19), (20).
Кроме того, преобразуем уравнение (24), прибавив к нему уравнения (22); продифференцировав их по х и у и умножив на 203, получим систему уравнений устойчивости пологой трехслойной оболочки в перемещениях:
д2иа, 1 — р д2иа, 1 + (х d2va д / w w \ _ '
\ R\ /?2 /
дх2 d2va
2 ду2 1 — {х d2va
2 дх ду 1 “4“ Р д2ил
дх
ду2 1 Bh / d2w.
дх2 1 1—fx д2и
дх ду 1 + f*
d2i/fi
В/г /
7Г
, дх2
г 2 dy2 1
1 2
dA: dy
— «р-
дЧ,
1 — (х d2i/o
1 р -1
! 1 + Iх
d2wp
. ду2
1 2 d*2
1 2
d.*: dy
U
)-
(16.25а)
-2В(„ + 4) V’ (% + - 207% +
_L.. dv«
, 25 /di/a.
dy
dwa
w
Ж
w
W \.
1‘T?r) +
W w \
а* ~ дг- ЯГ/-1-
d2a>
d*2
Л7о d2w Ny~dfr
2T°4 = 0.
d.*: dy
(16.25b)
Систему уравнений (25) можно привести к одному разрешающему уравнению. Введем функцию усилий ср, полагая
дг e ** iV* dy2
дг =ii
iVy d;c2 ’
T =
d2<p
d*dy *
(16.26)
Очевидно, уравнения (21), соответствующие двум первым уравнениям системы (25), при этом выполняются.
Исключив из трех соотношений (18) с учетом (26) функции ич и получим уравнение
d2w * 1 d2w \
'd2+ Rx ду2 ) *
Обозначив
дил. dvо
(16.27)
р.— _L_l_ г ~~ дх ду '
(16.28)
666 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК и ОБОЛОЧЕК [гл. XVI
дифференцируя третье уравнение системы (25) по х, а четвертое — по у и складывая, получим:
BNPF=tOt\P — + (16.29)
Последнее уравнение системы (25) с учетом соотношений (26) и (28) запишется в виде
+ w;j-+w;-+2r»r = 0. (16.30)
Из уравнений (29), (30) можно исключить функцию F. Получим уравнение
2В(й+4)5 V% + (l - Q V»)[2DV%--i-0_
Таким образом, для функции усилий <р и прогиба w мы получили систему из двух уравнений (27), (31); их можно привести к одному уравнению относительно прогиба:
2В (h + -)2 V% + (l — VJ) [2DV*w +
+ 2(1 + *]_ _v<(N;0+w;+2)=o. (I6.32)
Заметим, что решение задач устойчивости с помощью одного уравнения оказывается возможным в тех случаях, когда граничные условия удается выразить через w. В противном случае приходится обращаться к системе уравнений (25), позволяющей удовлетворить граничным условиям, сформулированным относительно иа, va.
В случае трехслойной пластинки (Rx = 00, R2 = 00) система уравнений (25) распадается на две независимые системы: два уравнения относительно функций иа, va, имеющих тривиальное решение, и три уравнения для функций vр, w. Эти три последних уравнения и будут уравнениями устойчивости трехслойной пластинки
§ 162]
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
667
Bh (d*v9 1—ft d*v? 1 + 1* д*и? \
GTWy* 2~ 2 дхду)
Bh /d*v.
(16.33)
—*+(*+т)ж=0’
- 28 (* + 4) Т» (£ + %) - 2ОТ<« +
Систему (33) можно привести к одному разрешающему уравнению относительно прогиба:
Отметим, что в предельном случае, когда модуль сдвига 03 стремится к бесконечности, уравнения трехслойных пластинок и оболочек приводятся к уравнениям однородных пластинок и пологих оболочек
составного сечения из двух слоев, разнесенных на высоту заполнителя. В другом предельном случае, когда 03~> 0, получаются уравнения для изолированных внешних слоев.
Итак, исходя из допущения о линейном распределении перемещений по толщине заполнителя, мы получили уравнения устойчивости пологой трехслойной оболочки с легким заполнителем, т. е. без учета нормальных и касательных напряжений в заполнителе, параллельных внешним слоям.
В практике расчета трехслойных пластинок и оболочек, как уже было сказано, могут встретиться случаи и более жестких заполнителей, когда в трехслойной конструкции заполнителем воспринимается заметная часть продольных сил и моментов. В этом случае необходимо учитывать напряжения в заполнителе, направленные параллельно внешним слоям. Уравнения можно тогда получить, исходя из линейности смещений по толщине заполнителя и пренебрегая поперечной деформацией заполнителя. Принципиально этот вывод не будет отличаться от приведенного выше для легких заполнителей: необходимо лишь ввести в выражения для сил и моментов составляющие,
с изгибной жесткостью
т. е. с жесткостью
668 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
обусловленные напряжениями ах, су% хху в заполнителе. Не приводя этого вывода, выпишем окончательные уравнения устойчивости трехслойной пологой оболочки с жестким изотропным заполнителем:
дТ dNv. дТ
dNy
£(*+!«■)(
дх
4- л — о,
1 ду
ч-
ду г
, —0 дх
д*и9
1 — М- д2и
, 1 + Iх
d2v? \
, дх2
2 ду2
1 2
дхду )
Bcht 6 Gc
дхy2w
+ (*4-
t \ dw ~2)Их
■2Г4
1— ц d2v?
О „2
. 1 + к-
1 о
д2и \
(16.35а)
ВСЫ
6GC ду
+(*+4)=0.
(16.35b)
- [2В (й+ т) ■+ \ ВА 72 (■ж + w) + (тв'и -2D) +
+
Nx
Nv n d2w
dx2
n d2w d2w
+-A'»V+2to7
0. (16.35c)
Усилия и перемещения связаны соотношениями
+ + J-).
r=(l-,)(S+B,)(- + ).
(16.36)
Здесь B3 = E3h/( 1—jx2); коэффициенты Пуассона [x материалов заполнителя и внешних слоев приняты одинаковыми.
При решении задач устойчивости трехслойных пластинок и оболочек со средним слоем типа гофра, сот или армированного пенопласта можно введением приведенных жесткостных параметров заменить такие заполнители некоторым эквивалентным однородным заполнителем *).
Отметим, что использовавшееся в этом параграфе положение
о линейности смещений по толщине заполнителя в случае легких заполнителей является следствием следующих допущений: а) равенства нулю напряжений ах, ау, хху, б) нерастяжимости заполнителя
*) Для определения приведенных модулей упругости гофра и сот можно воспользоваться работой [16.2]. Уравнения устойчивости пологих оболочек с жестким ортотропным заполнителем можно найти в работе [16.6].
§ 163] ВАРИАЦИОННОЕ УРАВНЕНИЕ УСТОЙЧИВОСТИ. ГРАНИЧНЫЕ УСЛОВИЯ 669
в поперечном направлении: w = w(x, у). Это непосредственно следует из уравнений равновесия элемента
-asr = °- ~тг=° <16-37>
и соотношений
да dw zxz dv dw zyz
dz dx G3 ' dz dy G3
Тем не менее, методика вывода уравнений с заданием закона изменения смещений по толщине заполнителя представляется более удобной: она может быть почти целиком перенесена на более общий случай трехслойных конструкций с жестким заполнителем, при рассмотрении которого необходимо учитывать напряжения ах, ау, z в заполнителе; тогда гипотеза о линейном законе смещений окажется суще¬
ственной.
§ 163. Вариационное уравнение устойчивости. Граничные условия
Энергетическое уравнение устойчивости трехслойной пологой оболочки эапишем в виде
и+НflN°(£),+N°>(wf+2T°wwldx‘'!,=0- (16'38)
где U — потенциальная энергия, обусловленная усилиями, возникающими при потере устойчивости оболочки.
Для потенциальной энергии верхнего внешнего слоя имеем: h+t
U\ = 2 f f f (axex~\~ayBy~~xxyTxy)dX(tydz. (16.39)
h
Вводя в (39) выражения (5) для деформаций и (1) для смещений и выполнив интегрирование по z, получим:
\,/7К.(tS-- ж)+■ (w~%)■+
+(£+)-*-■ (1М0)
Аналогичным образом для нижнего несущего слоя найдем:
+ Т>№ + %УМ‘.’-М*>%Г-2н*т£ф}<1*<11’- 06.41)
670 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
Потенциальная энергия заполнителя будет
h
UQ = 2 J* J j* ixzTxz **yzTyz) dx dy dz. (16.42)
-h
Вводя выражения для деформаций (5) и смещений (4) и выполнив интегрирование по z9 будем иметь:
U3=ihff{Q*’a[—i(u 1—“2)+(a+t)ij]+
+ Qy, з [— *5“ (Vi — +;§*) -г] } 16.43)
Суммируя (40), (41) и (42) с учетом обозначений (17) и формул (18), (9), (20) для потенциальной энергии, получим:
U -5 //{ N>(Ж -ж) + “>('W-- ж) + Т№ + тг) +
+(W„, -
/ dvo дил \ d2w d2w
+<T,-JV) (.jf+ -Л).s.-■2M
'dy') 1 53F— У’1 “dy*
4Яг+т»[— ae+(A+ir)'sr]+
+ '£?у3[— vv + {h + T)w\\dxdy’ (I6-44>
или
u-iff {Н(ж-ж)'+(%-ж?+
I 0,Jdu* V)\(dva w \. 1— f» ( dua. dva\2,
“г *4 А* Я, ) Wy Rt ) + 2 \ dy “Г dx )
+(£)*+«?У+*££+(£+£Л+
+ 2D[W-2(1-,)(-()] +
+i0sh“ (a+4)w] +i03K—(A+)i?]
(16.45)
Варьируя в уравнении (38) перемещения, получим вариационное уравнение
w + * / / И (£)’ + (£)’+2 А (£ )] “у =
(16.46)
Будем считать, далее, оболочку ограниченной координатными линиями х = Oj, jc = аг и у = Ьх, у = bv Выполнив интегрирование по
§ 163] ВАРИАЦИОННОЕ УРАВНЕНИЕ УСТОЙЧИВОСТИ. ГРАНИЧНЫЕ УСЛОВИЯ 671 частям в уравнении (46), т. е. проделав преобразования по формулам
Да 5 '//()!=2/ /£»(£)<**-
fli bi а\ Ь\
1[i£u-T.ixd»-2 f f
J<*i
fli
приведем вариационное уравнение к виду
-//{(+408“.+(тГ + £Н + +иг+1?+!?й)-х(«г(‘+7)а]ч+
Г (d2Vo 1—{a d2Va 1+м* д2ил\ 2<73/ /
+ [2Л (др-“• 2~Ш + ~2 57) Г\v»-\h+т) ay)] Ч +
Г 2(?с / t \ / ди*, dv8 \ 2GC i t \2
+1-т-(*+т)№+-)+тг(*+т) 20v<®+
Nv 0 ft д2до л d2w 1 \
+~RT'~Rr~Nx~r + N>,W~2aWJ**>}dxdy+
+ / {,4+n-.+ae+i* £?)s+
a\
+»<«-*(£+£K-4£+>£)»(£)+
20(if +(2 “w TOj)]!jw f d*+ f (А+ГЧ +
+Ц£+К+«о->>Ъ+Ъь-
_ o, («,-(*+4) £)-*>£(£-<>-« fc)] 4*+
+'“i-i*)D{[3wtoI!C=0- <16-,7>
672 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
Усилия Nx, Ny, Т в этом уравнении связаны с перемещениями формулами (18).
Поскольку вариации Ьиа, произвольны, множители при
каждой из вариаций в первом интеграле должны быть равны нулю. Отсюда следуют пять дифференциальных уравнений устойчивости. Легко видеть, что эти уравнения совпадают с уравнениями (25); для того чтобы убедиться в этом, следует проделать очевидные преобразования последнего уравнения с помощью третьего и четвертого уравнений.
Второй и третий интегралы соответствуют однородным статическим граничным условиям на каждом крае оболочки; они получаются приравниванием нулю множителей при вариациях перемещений, произвольных на контуре. Как видим, в отличие от однородных оболочек, где на контуре можно задать четыре условия, для трехслойных оболочек должно быть задано шесть условий.
Обратимся к краю оболочки х — const и выпишем для него основные граничные условия.
1. Два граничных условия связаны с прогибами и поворотами на контуре или, при статических граничных условиях, с поперечной силой и моментами. В случае шарнирного опирания внешнего
слоя или свободной кромки величина произвольна и гранич-
При защемлении внешних слоев вместо (48) будем иметь
Если прогибы на контуре произвольны (край свободен от опор), имеем:
При наличии опор вместо этого условия имеем геометрическое условие
2. Два граничных условия, связанных с перемещениями иа и v9 или соответственно с усилиями Nx, Г, определяются характером закрепления края оболочки в целом относительно смещений в направлении, перпендикулярном к краю (иа), и в направлении, касательном к краю (vj.
ное условие согласно (47) будет
(16.48)
w — 0.
(16.51)
§ 163] ВАРИАЦИОННОЕ УРАВНЕНИЕ УСТОЙЧИВОСТИ. ГРАНИЧНЫЕ УСЛОВИЯ 673
В случае, если опоры препятствуют таким перемещениям, имеем:
иа = О, (16.52)
va = 0. (16.53)
Если смещения иа, va ничем не стеснены, вместо этих условий имеем:
диа, dva w w л е.ч
+ = <16-54> <16-55)
3. Последние два граничных условия связаны с перемещениями ир, или соответствующими усилиями и определяются характером закрепления края оболочки в целом относительно поворотов в направлении, перпендикулярном к опоре (яр), и относительно взаимных перемещений внешних слоев в направлении, касательном к кон-
туру (V-
Если край оболочки закреплен в целом от поворота (защемление), то
Uq = 0. (16.56)
При шарнирном опирании или свободной кромке
ди* dvo
Ж+Ы=°- <16'57)
Если внешние слои закреплены от взаимных перемещений в касательном к контуру направлении, будет
г>р = 0. (16.58)
В этом случае внешние слои в плоскости опоры соединены жесткой на сдвиг диафрагмой. Если такая диафрагма отсутствует, то должно быть
dvo дил
SF + W=°- <16-59>
Кроме того, как это следует из уравнения (47), в свободных углах должны быть выполнены особые условия, имеющие тот же вид, что и в теории однородных пластинок и оболочек:
г = °- (1б-60>
При приближенном решении задач устойчивости перемещения могут разыскиваться в виде, удовлетворяющем не только геометрическим, но и статическим граничным условиям. В этом случае можно использовать метод Бубнова — Галеркина.
674 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК и ОБОЛОЧЕК [гл. XVI
Для трехслойных пластинок (/?1 = /?2 = оо) при потере устойчивости имеем: ua = va = 0. В соответствии с этим число граничных условий сокращается до четырех, а из уравнения (47) выпадают первые два.
Решение задач устойчивости трехслойных пластинок и оболочек можно упростить, если пренебречь неравномерностью распределения напряжений по толщине внешних слоев, т. е. принять в уравнениях устойчивости жесткость изгиба внешних слоев D равной нулю. Это допущение при решении задач устойчивости вводится большинством авторов. При этом порядок системы уравнений устойчивости оболочек (25) и пластинок (33) понизится. В соответствии с этим сократится и число граничных условий. Вместо шести условий для оболочек будем иметь пять, а для пластинок вместо четырех — три: выпадает условие (49) относительно угла поворота внешнего слоя или (48) относительно момента.
Перейдем к рассмотрению конкретных задач, относящихся к трехслойным пластинкам и оболочкам.
§ 164. Устойчивость бесконечно широкой пластинки с легким заполнителем при сжатии
Начнем со случая, когда бесконечно широкая пластинка с легким заполнителем, имеющая пролет а, сжата равномерно распределенными
N
1
Рис. 16.13. Трехслойная пластинка при сжатии в условиях плоской деформации.
усилиями*) N (рис. 16.13). Будем рассматривать цилиндрическую форму потери устойчивости, так что
Яр = Яр (jc), = 0, w — w (л:), Nx — — N, №у = Т°
:0.
*) Эта задача рассматривалась при различных допущениях в работах А. Л. Рабиновича [16.13], А. П. Вороновича [16.5] и многих других авторов. Различные случаи опирания рассматривали А. П. Прусаков [16.11], Бижляр [16.14]. Мы приводим здесь результаты из работы [16.11].
§ 164] УСТОЙЧИВОСТЬ БЕСКОНЕЧНО ШИРОКОЙ ПЛАСТИНКИ
Уравнения (33) запишутся в виде
Bh d2uo / t \ dw
~3T~dF2 ®*~H h+2)~dF=0-
f t\ d3uQ d4w d2w
здесь
1— ц2 ’ 12(1—f*2) '
Введем безразмерные величины
.. nx, Bh к2 1 / t
\ = -z~* k
a, — 12 I 4 +
Уравнения (61) примут вид
. d2uo
( t\ те dw
2-j-J-dT=0>
d4w d2w
d? r Ж4 V~d£r~0'
v di2
a d3u d4w d2w
%{h+i)
параметр
:(Л+)
Здесь cp — безразмерный параметр критической нагрузки, с N соотношением
2 *в(- П2
= V *
Найдем решение системы (63), полагая г — О (D = 0), ристическое уравнение системы в этом случае будет
а2 [а2 (1 — ср) — ср] = 0.
Решение запишется в виде
w = Ах sin ос£ -- А2 cos а£ -- Л3£ -- Л4,
и% = — J (h + -0 [ х _Дад (А2 sin а — Л, cos а?) — Ай], где
k<t • Отсюда
<Р =•
1 + fta2
675
(16.61)
(16.62)
(16.63)
связанный
(16.64) Характе-
(16.65)
(16.66)
(16.67)
Значение а определяется условиями закрепления кромок пластинки.
Обратимся к граничным условиям. В связи с тем, что в рассматриваемом случае условия, связанные с Vg, выпадают, должны быть
676 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
поставлены (с учетом допущения D = 0) два граничных условия на каждой из кромок пластинки: относительно w и или соответствующих усилий. При шарнирном опирании граничные условия согласно (51) и (57) будут
ди8
w = 0, ~dx == ПРИ х = 0, х = а или, в безразмерном виде,
dUa,
w — - = 0 при 5 = 0, 5 = тс. (16.68)
Подчиняя решение (66) граничным условиям (68), получим:
А2 ~j~ А === 0, Ах sin сстс —j- А2 cos остс —J~ Ar —1~ A = 0,
A2 = 0, A2a cos атс -f- ia s*n aTC = 0.
Нетривиальное решение имеет место при равенстве нулю определителя однородной системы, что дает уравнение sin arc = 0. Наименьшему значению критической нагрузки соответствует a= 1. Таким образом, параметр критической нагрузки ср в формуле (64) оказывается по (67) равным
»=ттт- <16-69>
В случае, если кромки пластинки защемлены, граничные условия согласно (51) и (56) будут
w = Hq = 0 при 5 = 0, 5 = тс. (16.70)
Определитель системы, полученной в результате подчинения решения (66) условиям (70), сводится к уравнению
ап Гл ап ап ап 1 л
sin -g- [2 sin - ттш cos -2-J = 0, из которого наименьшее а будет a = 2. Тогда
»=ТТ«- <16П>
В случае, если кромка х = С защемлена, а кромка х = а свободна (консоль), граничные условия при л; = 0 согласно (51), (56) будут
w = u = 0; (16.72)
при х = а по (57), (50) имеем (с учетом D = 0):
.
duo dw '9 Г / dw 1
--2-Чие-(л + 2Ы=0-
§ 164] УСТОЙЧИВОСТЬ БЕСКОНЕЧНО ШИРОКОЙ ПЛАСТИНКИ 677
С учетом первого из уравнений (61) и обозначений (62), (64) последние условия примут вид:
dua d2ua i t\% dw
при = * -rfT0’ dp_ + '()(A+ * (16J3)
Тем же путем в этом случае получим для а уравнение cosaic = 0, из которого ос = 0,5. При этом
»=тЬг <16J4)
В случае, когда кромка х — 0 защемлена, а кромка х — а свободно оперта, граничные условия будут:
при 5 = 0 w = Uq = 0,
da. } (16.75)
при £==« w = —г = 0. J
Уравнение для определения а будет tg air
1 +6a2
(16.76)
Наименьшее значение ср согласно (67) и (76) в зависимости от k дано на графике рис. 16.14.
Оценим пределы применимости полученных решений на основе допущения D = 0 (г = 0). Вводя решение (66) во второе уравнение (63), запишем условие прием-
40 ?
1,5
лемости этого допущения в виде
1 лД; (16.77)
1,0
считая допустимой ошибку в 5% и учитывая обозначения (62), получаем:
<06 + Gc а2 аЧ2
1 HIHW
ПГ1
т—t t f
■ft t,
0,25
0,5
0,75
1.0
(16.78)
Рис. 16.14. График для параметра <р в случае, когда одна кромка пластинки защемлена, а другая свободно оперта.
где а определяется в зависимости от граничных условий (0,5 < a < 2). Заметим, что случай k = 0 соответствует однородной пластинку
(t ' 2
/?+2) *
678 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
§ 165. Прямоугольная свободно опертая пластинка при продольном сжатии
Перейдем к случаю прямоугольной пластинки (рис. 16.15), равномерно сжатой усилиями *) = — N. Вводя безразмерные величины
b * е пх пу, Bh л2 1 / t \2 /ia
— — X, £ —, т] b, k G b2, г — -ру I — (16.79)
Рис. 16.15. Шарнирно опертая пластинка при сжатии, и коэффициент ср, равный
Nb2
т / t \2 * WB (л+)
запишем уравнения (33) в виде
(16.80)
(х2
д*и.
1 fX <Э2Ид 1 + fJL 62V
1
\ dr?
X2
dr?
d2v*
1 + Iх
as
d2a
-(л+4)
d52 -r 2
—(v—+—\
t \ \ d? + dr?) \K дб + dr) J
\ / Г \ 7C <7*0
) — «Р + (л -b -g) — -gg- = 0. з \ / t \ n dw
9—s+(*+2)7=0.
a2
X2- +
\2 ajr)
d2w
d
:0.
(16.81)
*) Эта задача исследовалась А. П. Вороновичем [16.5], Бижляром [16.14], Хоффом [16.20] и др авторами. В работах Бижляра [16.14], Сейде и Стоуэлла [16.30] и А. П. Прусакова [16.11] дано решение задачи с учетом работы внешних слоев пластинки за пределом упругости.
§ 165]
ПРЯМОУГОЛЬНАЯ СВОБОДНО ОПЕРТАЯ ПЛАСТИНКА
679
Получим сначала решение, полагая г = О (D = 0). На каждом из краев пластинки должны быть поставлены три граничных условия.
При свободном опирании пластинки в соответствии с (51) и (57) имеем условия:
Третье условие можно сформулировать различно в зависимости от наличия или отсутствия жестких на сдвиг диафрагм, соединяющих внешние слои на опорах. Если внешние слои соединены диафрагмами, то согласно (58) должно быть:
при х =• О, х = а г/р = 0; при у = 0, у = Ь и — 0. (16.83)
Если диафрагмы отсутствуют, то согласно (59) при лг = О, х = а, у = 0, у = Ь будет
Найдем решение задачи, полагая, что на контуре имеются диафрагмы. С учетом обозначений (79) граничные условия запишутся в виде:
Граничным условиям (85) и уравнениям (81) можно удовлетворить, разыскивая решение в виде
w = A sin т% sin и = В cos т\ sin пу\, = С sin тЦ cos nv\, (16.86)
где т и п — целые числа. Уравнения (81) дают однородную систему, равенство нулю определителя которой приводит к уравнению для параметра критической нагрузки
Очевидно, наименьшему значению ср соответствует п = 1. Обозначив mk = mb/a = ф, получим:
(16.84)
(16.85)
/и2Х2 [1 + к (л2 + т2Х2)]
(n2 + т2Х2)2
680
УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [ГЛ. XVI
Целое число т в формуле (87) выбирается таким образом, чтобы значение ср было наименьшим. Критическая нагрузка определяется по формуле
2”2Д(*+т)2
А/' = ср -
Ъ2
На графике рис. 16.16 даны значения ср в зависимости от отношения ajb для ряда значений параметра k. В случае, если
0,5
1,0
15
2,0
2,5 3,0
а/Ь
Рис. 16.16. Графики для параметра ср в случае свободно опертой пластинки.
отношение ajb велико (ajb > 2,5), значение ф в формуле (87) можно найти из условия минимума
-г. = о
Уравнение (88) запишется в виде
(1 + ф2)[ф2(1-*)-(! + *)] _ ф3[1 + *(1 + ф2)]2 —
При k < 1 имеем:
,2_1 + * 4
0.
1 — к ’
(1 + kf'
(16.88)
(16.89)
(16.90)
При k > 1 единственный положительный корень уравнения (89) равен ф2 — со, следовательно,
¥ = -*. 06.91)
§ 166]
ДРУГИЕ УСЛОВИЯ ЗАКРЕПЛЕНИЯ КРАЕВ
681
Отметим, что когда k->\, в продольном направлении должны по нашим выводам возникнуть волны, длина которых а/т-> 0. Нетрудно видеть, что этот результат является следствием допущения г== 0 при D = 0. В связи с этим можно записать решение задачи с учетом жесткости изгиба внешних слоев и попытаться оценить пределы применимости допущения D — 0.
В результате оказывается целесообразным ограничить пределы применимости допущения D = 0 условием k < 1. При £> 1 допущение D = 0 приводит к существенному искажению истинного характера волнообразования.
Неравенство k < 1 можно принять в качестве критерия приемлемости допущения D = 0 и при иных условиях закрепления и иных видах нагрузки. Такой вывод подтверждается сравнением с более точными решениями, полученными без этого допущения.
§ 166. Другие условия закрепления краев.
Метод разделения жесткостей
При решении задач устойчивости прямоугольных пластинок, две противоположные кромки которых свободно оперты, на двух же других заданы различные условия, можно использовать метод Леви, известный в теории однородных пластинок. Рассмотрим случай прямоугольной пластинки, сжатой равномерно усилиями №х = — N, ненагруженные кромки которой защемлены, а нагруженные свободно оперты *) (рис. 16.17). Полагая, что на кромках пластинки имеются диафрагмы, запишем граничные условия с учетом обозначений (79) в виде
дио
£ = 0, ? = «, w = = 0,
(16.92)
7} = 0, У] = TZ, W = Vp—Up = 0.
Решение уравнений (81) при г = 0 будем разыскивать в виде w = /i Ofl) sin/ю S, Up = f2(rj) cos ml, = /3(т) sin m 5, (16.93)
*) Решение этой задачи было получено в работах Сейде [16.29], Иена, Салерно и Хоффа [16.36], А. П. Прусакова [16.11]. Другие граничные условия рассмотрены Тёрстоном [16.32] и А. П. Прусаковым [16.11]. Задача об устойчивости длинной свободно опертой пластинки при сдвиге рассматривалась Сейде [16.29], прямоугольной свободно опертой пластинки при сдвиге — А. П. Вороновичем [16.5], при сдвиге совместно со сжатием —
А. П. Прусаковым [16.11], при сжатии в двух направлениях — Рейссне[>ом [16.27]. Устойчивость трехслойных пластинок с заполнителем типа гофра рассматривалась Сейде [16.29].
682 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ пластинок и ОБОЛОЧЕК [ГЛ. XVI
где т — целое число. Граничные условия на кромках £ = 0, £ = ic, очевидно, выполняются. Вводя выражения (93) в уравнения (81),
Рис. 16.17. Сжатая пластинка с защемленными продольными кромками.
получим систему обыкновенных дифференциальных уравнений для функций /(?]):
— Ц2/2 4- 1 2 kfl + 1_2 14 Wb — /2 + (А + 4') т Ф/» = °*
2
1 + (X
— /з + (* + у) y/i = 0*
где
— Ч»3/г + '\h + fh — /з + ffi = 0..
(16.94)
Nb*
ф = — = ш, ' a
WB (a + -0 Характеристическое уравнение системы будет
[l --Ц(?2 —f)]{(T2 —f)2 —[1—MT2-f»)=0. (16.95) Обозначив
+, 15=,ЛЗ=Г.
(16.96)
§ 166] ДРУГИЕ УСЛОВИЯ ЗАКРЕПЛЕНИЯ КРАЕВ 683
запишем решение системы (94) в виде
з
/2 = 2 (4 ch f jTJ 4- Cj sh 7,7)),
/«=1
2
/з = S J (C‘ ch Ъ71 + Л' sh Ъ7)) + (С, ch Тз7! + A3 sh Тз7!).
/si
2
/ = — 7 1\—Ц — Ф2) — П(4 — chijij + CjshTfiii).
V /=1
(16.97)
Подчиняя решение (97) граничным условиям, которые согласно (92) и (93) имеют вид
/i = /2 = /з = 0 ПРИ *1 = 0, 7J = п,
получим систему однородных уравнений относительно произвольных постоянных Aly Ct. Приравнивая определитель этой системы нулю, получим уравнение, которое распадается на два уравнения. Первое из них имеет вид
Ti [Mi -12) - Чth - f 2 f* (if? -12) - 11th +
ф2 (т? — T2) 7зте
—Mthii- = 0. (16.98)
13 *
Второе уравнение получается из уравнения (98) заменой всюду функции th на cth. Расчеты показывают, что наименьшее значение ср дает уравнение (98). При расчетах по уравнению (98) число полуволн т должно выбираться из условия минимума ср. На графике
рис. 16.18 даны значения ср, полученные по уравнению (98), для ряда значений k в функции от отношения сторон а/д.
Особо рассмотрим случай сжатой длинной пластинки с защемленными продольными кромками (рис. 16.19). Обратимся для решения этой задачи к приближенному методу разделения жесткостей *), заключающемуся в следующем. В уравнении устойчивости трехслойной пластинки (34)
2В (а + j)2 + (1—7- ?2) [2DV*w —
дг0 d*w к/0 d*w 07м д2® 1 _ n
Nx dx* 21 — 0
*) Этот метод был предложен Бижляром [16.14], решившим с его помощью большое число различных задач.
684 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК И ОБОЛОЧЕК [гл. XVI
полагаем Л = — Nnx% Ny = — Ntiy, Т° =
NnXt у; здесь N — иско-
*Х* ‘•'•'у*
мый критический параметр при заданном характере нагружения
Рис. 16.18. Значения параметра ср для прямоугольной пластинки с защемленными продольными кромками.
Рис. 16.19. Сжатая бесконечно длинная пластинка, пластинки усилиями пх, пу, nXty. Уравнение примет вид
2s(A + -02V%+(l — -V2)[2DV%+NP(w)] = 0, (16.99)
где
„.. d2w. d2w
р№ = пх-дЖ + пу~д?-
-2 п
d2w *У~дхду •
Далее рассмотрим три задачи устойчивости.
Допустим, прежде всего, что жесткость сдвига среднего слоя бесконечно велика (03->оо), а изгибная жесткость внешних слоев
§ 1661
ДРУГИЕ УСЛОВИЯ ЗАКРЕПЛЕНИЯ КРАЕВ
685
равна нулю. Уравнение (99) примет вид
2B(h + 4*w-\-NP{w) = 0. (16.100)
Далее, примем, что пластинка в основном работает на сдвиг (Ос-> 0), и, кроме того, как и в первом случае, примем D = 0. Уравнение этой задачи будет
2B(h-\-V*w — !§LnWP(w) = Q. (16.101)
Наконец, будем считать равной нулю жесткость на растяжение внешнего слоя (В = 0), тогда уравнение (99) перейдет в следующее:
2DV%>-f NP(w) = 0. (16.102)
Предположим, что во всех случаях формы потери устойчивости w одинаковы. Если обозначить через Л, N2> N0 критические нагрузки соответственно для каждой из трех задач, то получим:
2В [h. + Щ V4® -= — NXP («),
V2/> — (w),
2 DV*w = — 4rP(w)JV0
Вводя эти выражения в основное уравнение (99), находим:
-Р(«)+(1 + *£.)(дг_лдя(®)=о,
отсюда
N = N0-i—,■ 1 ■ (16.103)
— -А- —
N, N2
Эта формула и является основной в методе разделения жесткостей. Длина полуволны выпучивания для N0, Nv N2 принимается одной и той же, она определяется из условия минимума N.
Проиллюстрируем метод разделения жесткостей на примере задачи по рис. 16.19. Находя Nv мы, по существу, рассматриваем случай однородной пластинки. Полагая
w— sin 1 —cos-y
и интегрируя по методу Бубнова — Галеркина уравнение типа (100):
2B(h+fv*w + Nl-r=0,
686 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ ПЛАСТИНОК и ОБОЛОЧЕК [гл. XVI
получим:
N _ Й+O+WI, (16.104)
здесь L — половина длины волны при выпучивании.
Для определения N2 представим уравнение (101) в виде
г.. V h V -W,4g.= 0.
Полагая
получим уравнение G(
w = F(y) sinL,
(*+2) /av _** Fy, N * P_Q
Интеграл этого уравнения будет
Z7 (3;) = С, sin %у -f- С2 cos ху,
где
-.2 Г ЛГ
1
х L2
20с(л + -)2
Используем граничные условия F (0) = F ф) = 0; тогда найдем £х = ?с, отсюда
(а+4)2
N2 = 2GC - - h ; (1 + Е2)- (16.105)
Обращаясь к формуле (103) и пренебрегая в ней изгибной жесткостью внешних слоев (N0 = 0), получим окончательно:
N-
2«>в(и + 1.)
t \2
f2-b(l + 4m 1
Ь2 Зр2.. n2Bh [2 Н- (1 Н- 42)2]
+ Gcb2 3(32 (1 -f р2)
Параметр <р в формуле
n=<p—v-12-
будет равен
[2 + (l+4PV](l+p!)
3p2(l + p2) + A[2 + (l+4p2)ij •
§ 167] ЦИЛИНДРИЧЕСКАЯ ТРЕХСЛОЙНАЯ ПАНЕЛЬ ПРИ СЖАТИИ
687
где k = к2ВН/03Ь2. Параметр [3 определяется здесь из условия минимума ср. Зависимость ср от параметра k представлена на рис. 16.20.
В заключение отметим, что метод разделения жесткостей дает для реальных трехслойных пластинок вполне приемлемые результаты.
§ 167* Устойчивость цилиндрической трехслойной панели при сжатии
Перейдем к задачам, относящимся к трехслойным оболочкам. Рассмотрим устойчивость в малом свободно опертой цилиндрической панели, сжатой продольными равномерно распределенными
Рис. 16.20. Значения <р для бесконечно длинной пластинки с защемленными кромками.
усилиями*) (рис. 16.21). Уравнения устойчивости (25) при допущении D = 0 запишутся в виде
д2иа. 1 — [а д2иа, 1
d2va
дх2
d2va
2 ду2 1 — Р d2va
2 дх ду 1 -h р д2иа
1 dw
Bh 1 д2и{
Bh / G3 V (
ду2
1 _!_
1 2 дх2
1 — p. д2и*
1 + p.
дх ду d2v.
J3
Bh
Ж
дх2
d2Vo
2
1 —fx
dy2
d2Vo
2
1+P
dy2
dx2
dx dy d2u dx dy
R dy
’я \ / t \ dw
17)— “p + (A + j) 'ar = °-
= 0,
(16.106a)
\ / t \ dw
) — *,+ (*+ 2-)-gTT = 0.
_2b(*+4)v»(+) +
(16.106b)
2В / dvv da„ w \ d2w
+ тг(тг + 'жг—r)-nw=-°- (,6106c)
Полагая, что на кромках пластинки имеются диафрагмы, граничные условия для случая свободного опирания запишем
*) Решение задачи об устойчивости цилиндрической свободно опертой панели с легким заполнителем получено в работе Штейна и Мейерса [16.31] и в работе [16.9]. Другие граничныз условия рассмотрены В. Ф. Каравановым [16.7]. Ряд задач решен в работе [16.9] Л. М. Куршиным; им исследована также задача об устойчивости при сдвиге и об устойчивости при сжатии за пределами упругости.
688 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ пластинок и ОБОЛОЧЕК [гл. XVI
в виде (см. § 163)
при л; = 0, х — а w = при у = О, y = b w =
да
дх
dva
-va
■Vn —
дил
дх
ди
= а = и о
ду «Р ду
Разыскиваем решение уравнений (106) в виде w = Ах sin т sin иа = Л2 cos т\ sin пг\, ир = Л3 cos т\ sin /itj, va = Л4 sin cos /гт], = Лъ sin т\ cos nr\
8десь m и n — целые числа, £ = iu;/a, т] = тсу/.
О,
0.
(16.107)
;!
(16.108)
Рис. 16.21. Цилиндрическая свободно опертая панель при сжатии.
Вводя перемещения (108) в уравнения (106), из условия равенства нулю определителя системы найдем для параметра критической нагрузки выражение
(п2 + т212)2, т2\2.
здесь
Nb 2
т2к2 [1 + k (тЧ2 + п2)]
тi2Bh
2тъ2В
ыг
асьг ’
~ (mW + л2)2 ’
(»+*)*
(16.109)
Значения целых чисел т и п в формуле (109) определяются таким образом, чтобы получить наименьшее значение ср. На рис. 16.22 и 16.23 даны минимальные величины ср для некоторых значений а и k. Полученные результаты применимы, как показано в работе [16.10],
167] ЦИЛИНДРИЧЕСКАЯ ТРЕХСЛОЙНАЯ ПАНЕЛЬ ПРИ СЖАТИИ
s/d
Рис. 16.22. Значения параметра ср для цилиндрической панели
при а2 = 5.
690 УСТОЙЧИВОСТЬ ТРЕХСЛОЙНЫХ пластинок и оболочек [гл. XV1
при а2<(1—Щк2. В случае а2>(1—k)jk2 надо учитывать жесткость внешних слоев (см. [16.10]). Результаты без учета D дают в этом случае несколько заниженное значение критической нагрузки.
Некоторые исследования устойчивости трехслойных панелей в большом [16.10] приводят к предварительному заключению, что эффект нелинейности задачи сказывается здесь не столь значительно, как в случае однородной оболочки. Рассмотрение этого вопроса желательно продолжить.
§ 168. Устойчивость трехслойного цилиндра при продольном сжатии и внешнем давлении
Рассмотрим длинный трехслойный цилиндр с легким заполнителем, нагруженный равномерной сжимающей продольной нагрузкой*) №х = —N (рис. 16.24). Будем и здесь исходить из линейных уравнений.
Рис. 16.24. Трехслойный цилиндр, сжатый вдоль образующей.
Уравнение устойчивости (32) относительно прогиба при условии D — 0 запишется в виде
2S(* + 4)V. + (1 - f-V)+ 7<(дг **)] = 0.
(16.110)
Если потеря устойчивости является осесимметричной, уравнение (110) примет вид
(16.111)
*) Линейные задачи об устойчивости трехслойных цилиндрических оболочек с легким заполнителем при сжатии рассматривались в работах Легге и Хопкинса [16.22], Штейна и Мейерса [16.31], Джерара [16.17]. Слу¬
чай заполнителя типа гофра рассмотрен в работах [16.311 и [16.9]. Устойчивость трехслойного цилиндра при сжатии за пределом упругости рассмотрел Э. И. Григолюк [16.6]. Задача об устойчивости длинного трехслойного цилиндра с легким заполнителем при кручении решалась в работах Джерара [16.17] и Л. М. Куршина [16.9].
§ 168]
ТРЕХСЛОЙНЫЙ ЦИЛИНДР
691
Полагая w = A sin (тиг/Z.), где L — длина полуволны в продольном направлении, из (111) найдем:
Исследование, проведенное для общего случая потери устойчивости [ 16.9], показывает, что для трехслойных цилиндров при
симметричная форма. Отметим, что формула (114), полученная без учета изгибной жесткости внешних слоев, дает заниженное значение нагрузки.
Желательно рассмотреть задачу об устойчивости цилиндрической трехслойной оболочки с позиций нелинейной теории и провести экспериментальные исследования, которые позволили бы оценить практическое значение приведенных выше формул.
В заключение приведем без вывода формулу для расчета на устойчивость в малом длинного трехслойного цилиндра с легким заполнителем, нагруженного равномерно распределенным наружным давлением. Критическое давление определяется по формуле
(16.112)
где
Из условия минимума (112) получим:
О
при k< 1 у = 1 _ 6 р '* ПРИ > 1 Т2 = °о.
(16.113)
и во втором
(16.114)
наименьшее значение критической нагрузки дает
(16.115)
Потеря устойчивости здесь, как и в случае длинного однослойного цилиндра, происходит с образованием двух волн в окружном направлении.
ГЛАВА XVII
ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
§ 169. Общие уравнения
В настоящей главе мы вернемся к вопросу о влиянии высоких температур на устойчивость упругих систем, который отчасти разбирался в главе V. Как уже говорилось в § 56, относящиеся сюда задачи являются актуальными для авиационных конструкций: расчет обшивки летательных аппаратов, имеющих сверхзвуковую скорость полета, ведется с учетом аэродинамического нагрева. Вопрос о влиянии высоких температур важен также для расчета оболочек в конструкциях двигателей. Но выпучивание оболочек под влиянием температурных воздействий может произойти и в конструкциях, относящихся к другим областям техники, например в оболочках башен или резервуаров, испытывающих неравномерный нагрев в разных направлениях.
Дополним основные уравнения теории гибких пологих оболочек (приведенные в главе X) в предположении, что температура изменяется как в срединной поверхности, так и по толщине оболочки. Запишем выражение для деформации е* вдоль линии кривизны х на расстоянии z от срединной поверхности:
= <а> под о* и о* здесь понимаются напряжения в этом же слое оболочки, под t°*z — температура в градусах С в данном слое, под Ег и \хг — модуль упругости и коэффициент Пуассона, зависящие, вообще говоря, от температуры, и под а — коэффициент линейного расширения материала. В дальнейшем будем считать величины Ег = Е и = постоянными по толщине и отвечающими температуре срединного слоя.
Величина е*, с другой стороны, равна
§ 169]
ОБЩИЕ УРАВНЕНИЯ
693
где под гх понимается деформация в срединной поверхности. Таким образом, находим:
е* — zn5'=\(<s*x-V-(3Zy)+'l1f>'Z (17.1)
и аналогично
** т(°уг-К) + °,г- (17-2)
еу г ду2
Умножим все члены выражений (1) и (2) на z и проинтегрируем по толщине пластинки, тогда получим:
Л3 d2w
12 дх2 № d2w
-£«е,
12
(М —рМх) — а.в;
(17.3)
здесь Мх% Му — изгибающие моменты, а 0 — приведенная величина
t°'zzdz.
12 ду2 изгиб*
«температурного момента»:
/
L
~2
Найдем моменты по (3):
ял (d2w. d2w\. и h2 1 ~
м*~ D + 12 i—(х ав>
л/f Г\( I d2w\, д. h2 1 0
му \ду2 + ** дх2)~ \2 1— (X ав’
(17.4)
(17.5)
Подставляя эти выражения в уравнение равновесия элемента оболочки (10.105), придем к следующему окончательному уравнению *), заменяющему (10.107):
= Ф) + *,« + *, g + (17.6)
Далее, выпишем по (1) и (2) выражения для деформаций в срединной поверхности:
e* = i(0* — у) + а7’>
e*=i(ay—)+ar;
(17.7)
*) Уравнения (6) и (9) содержатся в книге X. М. Муштари и К. 3. Галимова [0.6]. Общие линейные уравнения приведены в книге В. Новацкого
(W. Nowacki) «Вопросы термоупругости», см. русский перевод 1962 г.
694 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
здесь под Т понимается величина
j* t0,zdz,
(17.8)
h
2
ох, оу — напряжения в срединной поверхности. Подставляя (7) в уравнение совместности деформаций (10.93), получим взамен (10.109) такое уравнение:
Рассмотрение уравнений (6) и (9) показывает, что температурный эффект сказывается в них только через лапласианы У2Г и V29. Следовательно, если величины Т и 0 остаются вдоль линий лг, у постоянными или меняются по линейному закону, основные дифференциальные уравнения будут такими же, как и для «холодной» конструкции. Однако влияние температуры может все же сказаться через граничные условия. Такой случай характерен для подкрепленных конструкций. Если обшивка нагревается быстрее, чем подкрепляющие ребра, то температурная деформация обшивки будет стеснена и в обшивке могут возникнуть значительные сжимающие напряжения, вызывающие выпучивание.
Если исследуются малые прогибы оболочки с учетом заданных усилий в срединной поверхности, то уравнения (6) и (9) перейдут в следующие:
под рх% ру по-прежнему понимаются заданные нормальные усилия (положительные при сжатии), под — касательные усилия.
Исключая отсюда Ф, получим следующее разрешающее уравнение относительно w (при постоянных kx и ky):
d2w d2w 9 d2w -
P* dx2 Py dy2 S dx dy'
г**®-
§ 170]
ПЛОСКАЯ ПОДКРЕПЛЕННАЯ ПАНЕЛЬ
695
Для круговой цилиндрической оболочки будет
5'<(з?)+
+1 v‘(siSir)+i v‘(>d)-whv,‘i'
ha TlRCk a d2
-I20)v6e-sw-'',r=°- <17-,2>
Для тонких оболочек можно считать, что температура t°'z меняется вдоль толщины по линейному закону. При таком допущении найдем:
7 =/сред. е = —АЛ (17.13)
Здесь Af характеризует перепад температур /внеш и /ВНуТр между
внешней (z = — /г/2) и внутренней (z = Л/2) поверхностями, а ред— среднюю температуру:
д jo внеш внутр внеш внутр /17 t >(ч
til — 2 » Гсред — 2 * ' • '
Если считать = 0. то по (9) получим известное уравнение плоской задачи термоупругости *):
1у4Ф.= — <xV27\ (17.15)
Если же принять Ф = 0, то придем к исходному уравнению задачи об изгибе пластинок при неравномерном температурном поле:
D=-,щ- (,716) При исследовании устойчивости оболочек в малом следует выписать уравнения «в вариациях», которые можно получить из (10) — (12), если под w н Ф понимать прогиб и функцию напряжений, связанные с выпучиванием, и положить = 0; температурные члены при этом выпадают.
§ 170* Плоская подкрепленная панель
Рассмотрим случай, когда плоская прямоугольная панель обшивки шарнирно скреплена по краям с жесткими на изгиб ребрами, так что точки всех краев панели не смещаются ни в плоскости пластинки, ни в поперечном направлении. Примем, что температура изменяется
*) Здесь рассматривается случай плоского напряженного состояния.
696 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
вдоль осей х, у (рис. 17.1) по параболическому закону
r=r0+r,[i _(*£=£.)’] [i
а по толщине, является постоянной. Определим критические значения параметров Т0 и 7\, при которых произойдет выпучивание пластинки *).
Рис. 17.1. Подкрепленная пластинка при неравномерном нагреве.
Напряжения основного состояния определяются из уравнения (15). Интеграл этого уравнения выпишем в виде
®=2-tF+
тп п
m п
где рх, ру — средние сжимающие напряжения вдоль х и у. Входящие сюда постоянные определяются из граничных условий, отвечающих неподвижным кромкам. Далее применяем метод Ритца. Выбираем аппроксимирующее выражение для прогиба в виде
<ь>
m п
*) Эта задача была рассмотрена Клоснером и Форреем [17.15].
§ 170]
ПЛОСКАЯ ПОДКРЕПЛЕННАЯ ПАНЕЛЬ
697
Минимизируя полную энергию системы по /„„, приходим к системе линейных уравнений относительно fmn. Приравнивая, как обычно, нулю определитель этой системы, находим критическое напряжение. Результаты расчетов по [17.15], проведенных с удержанием четырех членов ряда (Ь), приведены сплошными линиями на рис. 17.2 (принято [л = 0,32). По оси абсцисс отложено отношение ajb, по оси ординат — значение коэффициента/, определяющего критический перепад температур Тикр по формуле К
kT 1 (h\>
1 _ jj.2 а \b )
Кривые построены для различных отношений TJTV характеризующих температурное поле.
Пунктирными линиями даны результаты приближенного решения, в котором температура принимается равномерной и соответствующей некоторому среднему значению между Т0 и Tv При TJT 2 результаты уточненного и приближенного решений можно считать совпадающими, между тем как в случае Т0/Тх < 2 эффект неравномерности температурного поля оказывается существенным.
Если рассмотреть случай, когда подкрепляющие ребра
являются упругими и деформация пластинки менее стесненной, то неравномерность распределения температуры скажется еще сильнее.
Вопрос о закрыт инее кой деформации пластинок при наличии равномерного или неравномерного распределения температур является важным, прежде всего, для расчета обшивки летательных аппаратов. Как уже говорилось в главе VII, от амплитуд местных выпучин зависят аэродинамические характеристики конструкции. С одной стороны, волнообразование обшивки ведет к увеличению лобового сопротивления, а с другой — к усилению турбулентности потока, что, в свою очередь, связано с появлением опасных колебаний и развитием усталостных трещин *). Наконец, необходимо определить влияние высоких температур на редукционные коэффициенты. Задачи о закритическом термическом выпучивании пластинок должны решаться
*) На это указывается, в частности, в статье Ван-дер-Нойта [17.18].
а/Ь
Рис. 17.2. К определению критических температур в случае подкрепленной пластинки.
698 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
с помощью уравнений (6) и (9). Некоторые результаты в этой области были получены Ван-дер-Нсйтом [17.18], а также В. В. Болотиным и Ю. Н. Новичковым [19.5].
Случай цилиндрической панели при неравномерном распределении температуры по толщине был рассмотрен с помощью уравнения (6) и (9) М. С. Ганеевой [17.3]. Задачи, относящиеся к устойчивости круговых пластинок при неравномерном распределении температур вдоль радиуса, исследовались С. Г. Винокуровым [17.1] и Э. И. Григолюком [17.4].
§ 171. Подкрепленная цилиндрическая оболочка
Обратимся к задачам об устойчивости оболочек при повышенных температурах. Эти задачи представляют особый интерес для расчета тонкостенных конструкций: термическое выпучивание оболочки, часто сопровождающееся хлопками, ведет к появлению остаточных деформаций и снижению жесткости конструкции; такое явление, как правило, является недопустимым. Кроме того, температурные напряжения, даже если они являются сами по себе незначительными, могут служить тем возмущающим фактором, который в соединении с основными усилиями вызывает потерю устойчивости оболочки в большом.
Рассмотрим сначала случай равномерно нагретой круговой цилиндрической
~ 1о оболочки, скрепленной по торцам с «хо-
Рис. 17.3. Оболочка в случае г, * л _ оч
неравномерного распределе- лодными» шпангоутами (рис. 17.3), при
ния температур вдоль обра- условии, что торцы свободно смещаются
зующей. в осевом направлении друг относительно
друга. Примем, что разность температур оболочки и шпангоутов составляет 7\ «Холодный» шпангоут препятствует температурному удлинению оболочки в окружном направлении; поэтому в оболочке возникают кольцевые сжимающие напряжения. Величина их падает по мере удаления рассматриваемой точки от шпангоута; мы получаем здесь напряженное состояние типа краевого эффекта. В тот момент, когда сжимающие напряжения достигают критического уровня, вблизи шпангоута возникают выпучины; осевая симметрия изгиба оболочки нарушается. Определим критическую температуру, при которой происходит такое выпучивание оболочки в малом *).
*) Подобная задача рассматривалась Цуком [17.22], Джонсом [17.11], Хоффом [17.14], Л. М. Куршиным.
§ 171] ПОДКРЕПЛЕННАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА 699
Эта задача очень близка к тем задачам об устойчивости оболочек в зоне краевого эффекта, которые рассматривались в § 141.
Будем считать, что в осевом направлении оболочка деформируется свободно и что по торцам имеет место защемление. Для того чтобы найти напряжения в докритическом состоянии, воспользуемся первым из уравнений (10). Для осесимметричной задачи при равномерном распределении температур будет
D d'w _°у_£е (17 17)
~h ~dx* R R y’ ( Л }
или
DVw_EtT—pi== 0.
h dx4 R \ R /
Отсюда вытекает следующее уравнение:
Rh2 d4w, w ~
12 (1 — p.2) dx* ■+■ R ~ 9
(17.18)
при Г=0 оно переходит в уравнение (11.192). Интегрируя (18) с учетом граничных условий
w — 0, g = 0 при jc = 0, х = L,
находим:
w = a,RT [1 — е-2**(Ахсо 2(3*+ i42sin 2рлг) —
_-20(i-7) [Лх cos 2р(1 — *)-f А2 sin 2р(1 —x)l (17.19) где P=birj/'j£.
Через Av A2 обозначены некоторые функции величины р, характеризующей относительную длину оболочки. Пользуясь (17), определяем по (19) кольцевые напряжения оу. На рис. 17.4 сплошными линиями показана зависимость величины оу/ЕаТ от х при различных значениях р. Пунктирной линией изображена функция
g*ji- = cos2 ъх. (17.20)
Как видно из графика, она приблизительно отвечает параметру р = 2,
Рис. 17.4. К расчету на устойчивость оболочки при неравномерном распределении температур.
700 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
Возьмем для примера зависимость (20) в качестве исходной *) и определим критический перепад температур. Будем исходить из уравнения (12); в нашем случае оно принимает вид
Ave»4-—— —-We !Е\ = оEh v w Я2 дх4 Е \°у ду2 / ’
здесь под w понимается дополнительный прогиб. ч Аппроксимируя w с помощью выражения
£. 9 ЪХ. пу
w = / Sin2 -J- Sin -Щ-,
как это было сделано в § 131 (стр. 500), и пользуясь методом Бубнова— Галеркина, приходим к следующему выражению для критической температуры **):
Т - 1 - h I *2 h I (1+42)41 I 108*6Н П7 9П
кр~ /3(i-fx~2j /г«1 W L1 + 2 J+1*5*2/’
где ф = 'гс/?/яА. Фигурирующее здесь число волн п должно быть определено из условия минимума Гкр.
Приведем полученные другим путем расчетные формулы, относящиеся к длинным оболочкам, при р > 5. При защемлении по торцу критическая температура равна
Ткр=->-6,41=-4. (17.22)
р /3(1—(д.2) aR
а при шарнирном опирании по торцу
(17-23)
Соответствующее кольцевое напряжение вблизи шпангоутов равно в первом случае окр = 3,88Eh/R, а во втором окр = 7AEh/R. То обстоятельство, что величина Ткр получается для шарнирно опертой оболочки выше, чем для защемленной, объясняется большей податливостью шарнирно опертой оболочки при нагреве. Судя по приведенным выражениям для окр, термическое выпучивание защемленных по торцам дюралюминовых оболочек при R/h < 1500 будет происходить уже за пределами упругости.
В случае, если торцы оболочки не могут смещаться друг относительно друга, при возрастании температуры в оболочке воз-
*) Такое предположение было сделано Цуком [17.22].
**) Это выражение получено Л. М. Куршиным; ему же принадлежат
формулы (22) и (23).
§ 171] ПОДКРЕПЛЕННАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
701
никнут осевые сжимающие напряжения. При этом следует ожидать выпучивания по рис. 17.5 а в пределах упругости и по рис. 17.5 б-в упруго-пластической области.
Значительный интерес представляют также задачи о выпучивании цилиндрических оболочек при температуре, изменяющейся вдоль окружности. Примером может служить оболочка, частично наполненная жидкостью *) (рис. 17.6, а).
Допустим, что -зона оболочки,
°)
б)
6)
Рис. 17.5. Термическое выпучивание оболочки: а) с образованием ромбовидных вмятин, б) осесимметричное.
Рис. 17.6. Оболочка в случае температуры, изменяющейся вдоль окружности.
соприкасающаяся с жидкостью, имеет температуру более низкую, чем остальная зона, и разность температур составляет Т (рис. 17.6, б). Тогда в области повышенных температур возникнут участки со сжимающими напряжениями (рис. 17.6, а) и здесь может произойти выпучивание. Такой вывод подтверждается экспериментами. Вмятины имеют форму ромба и располагаются в средней части оболочки по длине (рис. 17.7); появление вмятин обычно сопровождается хлопком.
Путь решения подобной задачи состоит в следующем. Определяется эпюра распределения началь- рис Выпучивание оболочки ных напряжений; решающее зна- при неравномерном распределении чение здесь имеют осевые напря- температур вдоль окружности, жения ох. Эпюра имеет различный
вид в зависимости от соотношения между размерами нагретой и холодной зон. Далее, для решения задачи об устойчивости в ма~ лом используется уравнение (12). Подробное исследование показывает, что практические расчеты можно производить, как в случае
*) Эта задача была рассмотрена В. И. Ускжиным; им же проведены описанные здесь эксперименты.
702 ИЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [гл. XVII
выпучивания оболочки при изгибе, по наибольшему напряжению сжатия, сравнивая его с величиной 0,605£/г//?. Желательно рассмотреть такую задачу в нелинейной постановке; по-видимому, и здесь следует сопоставить наибольшее напряжение сжатия с нижней критической величиной (см. § 135).
Перейдем к задачам о выпучивании пластинок и оболочек при ползучести. Они являются более сложными, чем аналогичные задачи, относящиеся к стержням (см. главу V), так как здесь в каждом слое пластинки или оболочки образуется не одноосное, а двухосное напряженное состояние. Между тем законы ползучести при сложном напряженном состоянии сами по себе еще не являются выясненными. Кроме того, особенность явления выпучивания пластинок и оболочек при ползучести состоит в том, что при прогибах, сравнимых с их толщиной, проявляется эффект цепных напряжений. Как мы увидим, для пластинок это влияние сводится к тому, что процесс выпучивания пластинки «тормозится» и нарастание прогибов затухает.
В то же время для оболочек, подвергающихся ползучести, характерным является выпучивание в процессе хлопка. Поэтому исследование этого явления будет достаточно полным лишь в том случае, если оно проводится с позиций устойчивости в большом. На рис. 17.8
Рис. 17.8. Характерные диаграммы «прогиб — время» для стержня, пластинки и оболочки при ползучести.
сопоставляются характерные диаграммы «стрела прогиба С — время t» для стержней, пластинок и оболочек. Здесь рассматриваются элементы конструкций, приближающиеся к реальным и имеющие ту или иную начальную погибь. В случае стержня прогибы монотонно нарастают во времени (рис. 17.8, а). Прогибы пластинки сначала увеличиваются ускоренно, затем скорость возрастания прогибов постепенно падает (рис. 17.8, б). Наконец, в случае оболочки монотонное
§ 172. Выпучивание пластинок и оболочек при ползучести
§ 172] ВЫПУЧИВАНИЕ ПЛАСТИНОК И ОБОЛОЧЕК ПРИ ПОЛЗУЧЕСТИ 703
увеличение прогибов завершается хлопком (рис. 17.8, в). Эти диаграммы намеренно упрощены; в отдельных опытах может проявиться влияние таких факторов, как несоответствие формы начального прогиба и формы выпучивания, соотношение между неустановившейся и установившейся ползучестью и т. д. Какой же вид будет иметь диаграмма «прогиб — время» для идеального элемента конструкции, не имеющего начальных несовершенств? Можно ли получить такую зависимость как предельную по диаграммам типа рис. 17.8, устремляя начальные прогибы к нулю? По-видимому, на этот вопрос в настоящее время еще нельзя дать окончательного ответа. Все же в ряде работ предложены критерии выпучивания идеальных конструкций, изложенные в § 61. Для пластинок и оболочек часто применяют критерий критической деформации *). Например, для сжатой в одном направлении удлиненной пластинки ширины b критическая деформация в упругой области равна
«кр«3.62(-А)в. (а)
Принимают, что выпучивание при ползучести наступит, когда сближение нагруженных кромок достигнет этой величины. Для сжатой круговой цилиндрической оболочки аналогичный подход приводит к формуле
екР> в = 0,605, (Ь)
если за основу брать верхнюю критическую нагрузку. Но, как мы увидим ниже, расчет по (Ь) дает резко завышенные значения критического времени; лучше согласуется с опытами расчет по нижней критической деформации:
екР,,, ~0,18--. (с)
Динамический критерий устойчивости пластинок при ползучести был развит Ю. Н. Работновым и С. А. Шестериковым [5.6].
В. М. Панферов предложил метод определения критического времени при неустановившейся ползучести на основе серии экспериментов по растяжению образцов при заданных скоростях изменения деформации.
В дальнейшем мы подробно остановимся на критерии начальных несовершенств\ будем при этом считать, что начальные и дополнительные прогибы сравнимы с толщиной пластинки или оболочки.
*) См. работу Джерара и Гильберта [17.10]. Несколько иной подход предложен в другой статье Джерара (J. Aerospace Sci., 29, № 9, 1962).
704 ПЛАСТИНКИ И ОБОЛОЧКИ при высоких ТЕМПЕРАТУРАХ [гл. XVI
§ 173. Выпучивание пластинки, имеющей начальную погибь
Исследуем случай прямоугольной пластинки со сторонами а, b, опертой по краям и сжатой вдоль кромок а (рис. 17.9); примем,
Рис. 17.9. Квадратная плоская панель, сжатая вдоль одной из сторон.
что кромки пластинки остаются прямолинейными и что ненагруженные края свободно сближаются *).
Основные уравнения выпишем по (10.111):
D
_ у4 (w — w0) = L (w, Ф),
-1 V4® = j \L (w0, w0) — L (w, w)],
(17.24)
где w и w0 — полный и начальный прогибы.
Решая задачу в первом приближении, примем для прогибов аппроксимирующие выражения
пу
w.
= /0sinsinf-. (17.25)
Подставляя (25) в правую часть второго из уравнений (24), находим:
Е « « \(а\2 2пх /Ь\2 2пу 1 ру2 /4_л/,ч
Ф= 32(/ -о)[(т) cos —+ Ы cos—J--; <17-26>
*) В таком виде задача была рассмотрена автором в 1959 г.
§ 173] ВЫПУЧИВАНИЕ ПЛАСТИНКИ, ИМЕЮЩЕЙ НАЧАЛЬНУЮ ПОГИБЬ 705
под р понимается интенсивность усилий сжатия. Напряжения в срединной поверхности будут
д2Ф д2Ф д2Ф
Т дх ду *
ду2 ’ У дх2
Напряжения изгиба, наибольшие по толщине пластинки, равны
Eh ~ д2 (w — w0)
ах, и 4 У(Т
(17.27)
•f*2)
дх2
д2 (т — w0) ■]
ду2 J ’
°у, И + 2(1
Eh г.
-и2) L
ду2
Eh д2 (w — Wq)
тн — + 2 (1 + fx) дхду
д2 (w — w0)
дх2
]•
(17.28)
Знак минус относится к точкам пластинки (рис. 17.9, б), лежащим у нижней поверхности (z — h/2)t знак плюс — к точкам у верхней поверхности (z = — /г/2). Определим полные напряжения для центра пластинки (л; = а/2, у = Ь/2):
°*> — 8а2 (- П) 2(1-(л2) У ( аг Г2 ) Р'
СУ> п = 8Р- (f2 ~' fo) — 2 (1 — ц2) — /о) (-р- 4 Jr) >
т„ = 0.
(17.29)
Интенсивность напряжений в каждой из точек с координатами z — ± Щ2 равна
о == lo2 -f-o2 —о о ;
/ Г ЛГ, п у, п дг, п у, п*
этой величине соответствует интенсивность деформаций е1 = а1/Е во всех случаях под Е понимается модуль упругости материала при соответствующей температуре; принимается, что в течение всего процесса деформации пластинки напряжения лежат в пределах пропорциональности.
Перейдем к безразмерным параметрам
е* — а* — ЧЬ2 — Qib2 а* —аХ,П ( Ь \2 а* — Су,П ( а V (\7 ЧП)
i~ t~~ h* ~ Eh* ' Е \ Л J * ау~ Б \h) ’ (17-30)
<о=т-. х = т- Р'=т(т)'- <7-31>
Условимся в дальнейшем сжимающие напряжения считать положительными. Тогда получим:
2(f-ff2 + (17.32)
п2\2 /„2 ф п2 (X2 + fx)
2 (1 — f*2)
(17.33)
(17.34)
706 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
Допустим, что в начальный момент времени пластинка испытывает сжатие усилиями р. В дополнение к начальным прогибам она сразу же получает упругие прогибы. Для определения дополнительной стрелы прогиба надо обратиться к первому из уравнений (24). Если подставить в это уравнение выражения для w> w0 и Ф и воспользоваться методом Бубнова — Галеркина, то придем к следующей зависимости (см. книгу [0.3], стр. 286):
Здесь под р*кр понимается параметр критического сжимающего напряжения:
При заданном параметре сжимающего усилия р* из (35) можно найти стрелу полного прогиба С. Зная С, можем определить интенсивность деформаций в любой точке пластинки. Будем для упрощения ограничиваться определением интенсивности деформаций в двух точках нормали z = ± /г/2 для центра пластинки при х = а/2, у = Ь/2.
Для характеристики процесса ползучести при сложном напряженном состоянии будем пользоваться зависимостями теории упругопластических деформаций. Введем понятие интенсивности деформаций ползучести:
Воспользуемся теорией старения и примем для примера, что при установившейся ползучести величина является функцией интенсивности напряжений о,- и времени t:
Предполагается, что этот закон имеет место, в частности, при одноосном растяжении и сжатии с неизменными для данного материала параметрами Лит. Для определения составляющих деформации ползучести будем пользоваться соотношениями
(17.35)
(17.36)
(17.37)
е = Aoft.
(17.38)
е
'X
(17.39)
Введем обозначения:
*ХЬ2 -* еуД2
А2 * еу~ А2 *
/А \2m-2
А* = АЕтуТ\ ; (17.40)
§ 173] ВЫПУЧИВАНИЕ ПЛАСТИНКИ, ИМЕЮЩЕЙ НАЧАЛЬНУЮ ПОГИБЬ 707 тогда соотношения (38) и (39) примут вид
Примем следующий порядок расчета. Допустим, что пластинка подвергается действию постоянных по величине усилий р. Рассмотрим некоторый промежуток времени At, считая от начала процесса ползучести. Вычислим интенсивность напряжений в точках z= ± h/2 для центра пластинки. Далее по выражению (41) установим интенсивность деформаций ползучести и по (42) — составляющие е* и 1*. Следующий шаг должен состоять в определении дополнительных прогибов Aw пластинки, вызванных ползучестью. Для этого воспользуемся соотношением, относящимся к точке z = hj2:
От деформаций изгиба можно перейти к полным деформациям, так как деформации в срединной поверхности будут при вычитании исключаться. Получим:
Прибавляя приращение стрелы прогиба АС к начальной стреле
(17.42)
(17.41)
,. h д2 Aw
(е*. «>/г/2 — 2 дх2 ‘
(17.43)
Принимая
A<K> = A/sin--siny-, ДС = --,
(17.44)
для центра пластинки получим:
(17.45)
При г — — А/2 будет
(17.46)
Запишем выражение для АС в виде
(17.47)
(17.48)
найдем новую стрелу прогиба Со:
Со = Со+ДС.
(17.49)
708
ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
Величину Со рассматриваем как начальную стрелу прогиба для следующего промежутка времени Д/. Повторяя эту процедуру, можно проследить за развитием пластических и упругих деформаций пластинки.
Пример 17.1. Рассмотрим случай квадратной дюралюминовой пластинки, для которой отношение ajh составляет 60. Усилия сжатия примем равными 80% от критической величины:
р = 0,8ркр = 0,8.3,6 = 2,8
(а)
Составим соотношение (35). Вводя обозначение k = С/Со» получим:
р* = 3,6 + 1,23 (k2 - 1) t*
В данном примере будет
5 — k
4
1,7* (k2 — 1) •
(b)
(с)
Рис. 17.10. Зависимость между полной и начальной стрелами прогиба для пластинки.
Пользуясь выражением (Ь), составляем таблицу или график для зависимости С0 (k). Подобный график изображен на рис. 17.10.
Пусть температура окружающей среды составляет 300° С. Модуль упругости дюралюмина при этой температуре примем равным Е = 4 • 105 кг!см2. Закон ползучести зададим в виде
(d)
*, = 9- 1(Г12<ф,
причем а; выражается в кг/см2, t — в часах. При т = 3 по выражению (40)
(е)
А* = 9-10“12 (4 • Ю5)3 -gL- = 0,0445,
и, далее,
s-* = 0,0445 (а*)3 г.
(0
Примем начальную стрелу прогиба равной /0 = 0,1Л или С0 = 0,1. Пользуясь графиком рис. 17.10, находим соответствующее значение k = 4; безразмерная стрела полного прогиба составляет С = 0,4.
По выражениям (32) — (33) при = 0,3 находим:
о* = —1,23*0,15 + 7,05-0,3 +2,88 = —0,19 — 2,12+2,88 = 4,81 при * = —Л/2,
с* = —0,19 — 2,12 + 2,88 = 0,57 с*у = —0,19+2,12= 1,93
а’ = —0,19 — 2,12 = —2,31
Интенсивность напряжений по (34) равна
а* = Y4,812 4- 1,932 — 4,81 • 1,93 = 4,17 при г = — Л/2, oj = /0,572 + 2,312 + 0,57 • 2,31 = 2,64 при г = Л/2.
при z = Л/2, при z = — Л/2, при z = Л/2.
§ 173] ВЫПУЧИВАНИЕ ПЛАСТИНКИ, ИМЕЮЩЕЙ НАЧАЛЬНУЮ погивь 709
Выберем интервал времени t = 0,5 часа. По выражению (41) определяем интенсивность деформаций ползучести:
1* = 0,0445 • 0,5 • 4,173 = 1,62 при г = — Л/2,
г* = 0,0445 • 0,5 • 2,643 = 0,42 при г = Л/2.
Составляющие деформации вдоль оси по выражению (42) будут
1,62 (4,81 — 0,5 -1,93)
1,5
вляет
* 4,17
при z = — Л/2,
0,42 (0,57 + 0,5* 2,31)
8* ” 2,64
при z = /г/2.
Приращение стрелы прогиба соста-
Мы получили бы несколько иной результат, если бы вели расчет по деБолее последовательно
формациям г*
У*
было бы исправить полученные значения е* и е* с тем, чтобы величина АС оказалась одной и той же. Будем, однако, продолжать выкладки, пользуясь значениями гх.
Рассматривая интервал времени от 30 до 60 мин, мы должны считать начальную стрелу прогиба равной
с; = Со + АС = 0,23.
tfmbi)
Рис. 17.11. Нарастание стрелы прогиба пластинки во времени (t — в часах).
Пользуясь рис. 17.10, находим k = 3 и С' = 3 • 0,23 = 0,69. Далее повторяем выкладки по той же схеме. Ниже приведены результаты вычислений, относящихся к первым девяти интервалам времени (по 30 мин); здесь даны безразмерная стрела полного прогиба С в начале интервала и приращение стрелы прогиба АС, имеющее место на протяжении данного интервала вследствие ползучести.
Номер
шага
1
2
3
4
5
6
7
8
9
С
0,4
0,69
0,92
1,14
1,38
1,51
1,67
1,79
1,92
АС
0,13
0,17
0,20
0,21
0,20
0,17
0,14
0,11
0,05
График зависимости С(0 приведен на рис. 17.11 (сплошная линия).
Как видим, скорость нарастания прогибов, связанных с ползучестью, сначала увеличивается, а затем начинает падать; штрих-пунктирная линия на рис. 17.11 отвечает приращениям АС. По-видимому, в случае подкреплен-
710 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ XVII
ной пластинки вообще нельзя определить критический период времени, по истечении которого скорость нарастания прогибов становится бесконечно большой. Как уже говорилось, в этом проявляется эффект цепных напряжений, возникающих при прогибах пластинки, сравнимых <? толщиной.
Решение задачи было дано здесь лишь в первом приближении. Однако полученные результаты интересны с качественной стороны: они свидетельствуют о своеобразии в поведении пластинки, выражающемся в повышении ее несущей способности по сравнению со случаем сжатого стержня.
§ 174. Выпучивание в большом цилиндрической панели
Выясним теперь особенности поведения оболочек при ползучести на примере пологой круговой цилиндрической панели, сжатой вдоль
образующей (рис. 17.12)*). Основные уравнения получают такой вид по (10.111):
Л 1 /}2Ф
V4(w-w0) = L(w, (17.50)
= 1 [£(«,„, w0) — L(w, tt>)]-2(d~Wo). (17.51)
Принимая прежние выражения для прогиба (25) и подставляя их в уравнение (51), найдем вместо (26)
Ф+(±)r~q+
+ £f. (17.52)
*) Эта задача рассмотрена П. Г. Зыкиным; им же проведены эксперименты, описанные в § 175.
§ 174J ВЫПУЧИВАНИЕ В БОЛЬШОМ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ 711
Напряжения в срединной поверхности определяются по-прежнему по (27), а напряжения изгиба — по (23). Пользуясь безразмерными параметрами (30) и (31), найдем полные напряжения для центра пластинки (считая их положительными при сжатии):
°*х = ~ 8Х* — k (1 -}- I2)2 — + 2(1—р.») X* (£ — Со) + Р*.
(17.53)
«;=-т р - ч)+4 гту <с - w т 5<п)(Х!+ (17.54)
где k = b2jRh. Интегрируя уравнение (50) по методу Бубнова — Галеркина, получим вместо (35)
(17.55)
где р* — параметр верхнего критического напряжения. Будем считать, что параметр кривизны панели k лежит в пределах k < 24 и что выпучивание панели происходит по одной полуволне вдоль сторон а, Ъ.
Попытаемся ввести здесь вместо (38) более общий закон ползучести с тем, чтобы описать не только установившуюся, но и неустановившуюся фазу. Примем
ll = KeB’t\ (17.56)
где К у В, у— постоянные для данного материала при определенной температуре. Воспользуемся прежними соотношениями (40) и введем обозначения:
к* = к(, В* = ВЕ(±)\ й = е/)2, (17.57)
тогда будет
1\= К*еВ*’Ч\ (17.58)
Сохраним тот же порядок вычислений, что и в § 173. Выражения (45) — (49) остаются без изменений.
Пример 17.2. Проведем вычисления для дюралюминовой панели при следующих данных: К = 1, а — Ъ — 200 мм, R = 615 мм, Л = 1,9 мм, Со = 0,3. Параметры, входящие в формулу (56), примем для материала Д16АТВ при температуре 250° С равными: К =* 4,51 • 10”5, В = 327 • 10 “5, у = 0,63; о выражается в кг[см2, t — в часах. Будем считать, кроме того, Е = 5,38 • 105 кг[см2> р. = 0,42.
712 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ (ГЛ. XVII
По формулам (57) имеем.
К* = 0,503, В* = 0,159.
Если построить по (55) зависимость р* (Q для различных значений С0> то получим график рис. 17.13. Параметры верхнего и нижнего критических
напряжений при С0 = 0 равны р*в = 33,6, р* = 6,6. Пользуясь кривыми рис. 17.13, можно перейти к зависимости С (С0) при заданных усилиях сжатия р*9 определяемых в зависимости от параметра /?* по отношению а = p*Jpa.
§ 174] ВЫПУЧИВАНИЕ В БОЛЬШОМ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ
713
График С(С0) изображен на рис. 17.14. При значениях а>2 имеет место скачок от одного устойчивого равновесного состояния к другому.
Рис. 17.14. Соотношение между полной и начальной стрелами прогиба для цилиндрической панели.
напряжению р по (53) — (54):
• кг!см2. В качестве первого шага вычислений находим
Примем для примера а = 0,35, что соответствует среднему сжимающему = 570; 1 “ о* = 15,36, о* = 3,61 при z = — Л/2;
» «у
а* = 11,53, а* = — 0,22 при z = /г/2
и, далее,
а* = 14,6 при z — — /г/2, а* = 11,63 при z = h/2.
Отсюда
Интервал времени примем равным 0,2 часа. По (58) интенсивность деформаций ползучести равна
z* = 1,86 при z — — Л/2, е* = 1,16 при z = Л/2.
ё* = 1,72 при z = — Л/2, е* = 1,16 при z = Л/2.
Приращение прогиба составляет
ДС = 1’72~1,16. = 0,057.
Для следующего интервала, от 0,2 до 0,4 часа, начальная стрела прогиба
714 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
равна Cq = С0 + АС = 0,357. Пользуясь графиком рис. 17.14, находим С = 0,634. Продолжая вычисления, составляем следующую таблицу:
Номер шага
1
2
3
4
5
6
7
Интервал времени в часах
С АС 0,2
0,525
0,057
0,2
0,634
0,039
0,2
0,710
0,031
0,2
0,785
0,034
0,2
0,880
0,039
0,2
1,050
0,058
од
1,430
0,054
На рис. 17.15 изображены графики С (t) и AC (t). Уменьшение приращения прогиба на первых ступенях объясняется падением скорости ползучести в первой фазе.х По мере увеличения прогибов деформации ползучести накапливаются все быстрее; это приводит, в свою очередь, к ускоренному
росту упругих прогибов. В конце 7-го интервала времени прогиб достигает такой величины, что должен произойти хлопок с резким возрастанием прогиба. Как мы увидим ниже, подобные хлопки наблюдаются и в экспериментах.
Хлопок оболочки сопровождается, как правило, появлением значительных пластических деформаций. Поэтому мы снова вернемся к понятию критического времени, понимая под ним период накопления прогибов, заканчивающийся хлопком. Если обратиться к графику р* (С) по рис. 17.13, то для заданного значения усилий сжатия р* = 0,35р* мы постепенно переходим от одной кривой к другой; после того как достигнут «горб» кривой Со = 0,5, имеет место скачок.
§ 175. Данные экспериментов и рекомендации для практических расчетов
Приведем данные серии опытов по устойчивости плоских и цилиндрических панелей в условиях ползучести. Образцы были изго¬
товлены из дюралюмина Д16АТВ. Панели нагружались с помощью специального приспособления, позволявшего осуществить различные условия закрепления кромок. Прогибы измерялись индикаторами часового типа. Напряженное состояние исследовалось с помощью электрических термостойких датчиков сопротивления.
Предварительные испытания на устойчивость при нормальной
температуре дали возможность установить порядок погрешности при определении критических напряжений; для плоских панелей она
Рис. 17.15. Нарастание прогибов панели во времени, заканчивающееся хлопком.
§ 175]
ДАННЫЕ ЭКСПЕРИМЕНТОВ
715
составляла не более 5% по отношению к теоретическим значениям. Далее были проведены кратковременные испытания на устойчивость пластинок при повышенных температурах (до 250° С); они показали, что в этом случае применимы обычные расчетные формулы с измененным модулем Е. Для цилиндрических панелей реальные критические напряжения (при хлопке) составляли (0,65-М),7) от верхних теоретических значений; экспериментальные значения /?кр можно было аппроксимировать формулой pKp0,4lEh/R.
Испытания на ползучесть были проведены при температуре 250° С; сжимающие усилия р составляли от критических такие доли:
а = -£- = 0,65; 0,8; 0,94.
Ркр
Сводный график зависимости стрелы прогиба от времени (пунктирные линии) для трех плоских панелей дан на рис. 17.16; под а понимается отношение сжимающего напряжения к статическому критическому значению. Как видим, здесь имеет место монотонное изменение прогибов с уменьшающейся скоростью. Ползучесть не приводит, таким образом, к бурному росту прогибов; это подтверждают результаты, полученные выше, в § 173; теоретические кривые показаны сплошными линиями. Для контроля был проведен опыт с пластинкой, продольные края которой перемещались свободно, иными словами, был исследован случай балки-полоски. Полученная при этом кривая С.(0 изображена на рис. 17.16 штрих-пунктирной линией; она соответствует обычным диаграммам, относящимся к стержням, и позволяет определить критическое время tKр.
Данные испытаний десяти цилиндрических панелей приведены на рис. 17.17 и 17.18. Сплошные кривые и здесь изображают зависимость С(/), полученную в опытах; пунктирные построены по данным приближенного решения, изложенного в § 174; через Со обозначен параметр начального прогиба, через а — отношение сжимающего напряжения к верхней критической величине. В случае, если среднее напряжение равнялось нижнему критическому значению (о = рп% а = 0,3), оболочка вела себя подобно плоской панели. Если же
Рис. 17.16. Диаграммы «прогиб — время» для плоских панелей (t — в часах).
716 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. XVII
напряжение лежало в пределах рн < о < рв, выпучивание оболочки во всех случаях заканчивалось хлопком.
С помощью графиков рис. 17.17 и 17.18 устанавливалось критическое время £крэ по истечении которого происходило выпучивание в большом. Эти данные изображены на рис. 17.19.
Если условно принять величину начального прогиба для всех испытанных образцов примерно одинаковой, то можно, пользуясь
SJJ С
V гя
!t5 КО
V
О
Рис. 17.17. Диаграммы «прогиб — время» для цилиндрических панелей первой серии в сравнении с данными экспериментов.
Рис. 17.18. Диаграммы «прогиб — время» для цилиндрических панелей второй серии.
экспериментальными данными (треугольники), построить график зависимости критического времени tKp от среднего напряжения сжатия, (пунктир на рис. 17.19). Как видим, критическое время резко падает при увеличении сжимающего напряжения. При нагрузках, составлявших 90-*-95% от ръ> критическое время в ряде случаев исчислялось секундами.
Таким образом, данные расчета по критерию начальных несовершенств достаточно хорошо согласуются с экспериментами.
§ 175]
ДАННЫЕ ЭКСПЕРИМЕНТОВ
717
кр»
если
иг/смг
№
iio
\
1
1 \
ч
А
\
4*
Aj
Р
-
На рис. 17.19 сплошными линиями нанесены также значения полученные по критерию критической деформации екр считать ее равной 0,605h/R или 0,41/г//?. Как видим, результаты расчета по этим формулам сильно отклоняются от экспериментальных данных. Как уже говорилось, правильнее в основу расчета брать нижнюю критическую деформацию 0,18 h/R.
В итоге можно рекомендовать для прикидочных расчетов на выпучивание пластинок и оболочек при ползучести пользоваться критерием критической деформации. Дая пластинок при этом будет определен, повидимому, тот отрезок времени, по истечении которого скорость нарастания прогибов является наибольшей.
Что касается оболочек, то здесь, таким образом, будет найден момент времени, соответствующий явлению хлопка. При этом в качестве исходной надо принимать деформацию, соответствующую нижнему критическому напряжению, найденному для упругой области (см. главы XI—XV). Это относится не только к случаю сжатия, но и к другим нагрузкам.
Более достоверные данные о поведении пластинок и оболочек
при ползучести можно получить, используя критерий начальных несовершенств, как это было описано в §§ 173 и 174. Но здесь надо располагать сведениями о примерных значениях начальных прогибов для конструкций того или иного типа. И в этом случае
наиболее обоснованным является статистический подход к задаче.
Мы не касались здесь важного вопроса об уменьшении крутильной жесткости и о возможной потере устойчивости тонкостенной конструкции типа крыла самолета, связанными с температурными напряжениями; этот вопрос освещен в статьях Будянского и Мейерса (В. Budiansky, J. Mayers, J. Aeron. Sci., 23, № 12, 1956), Ван-дерНойта [17.18] и других авторов, см. книгу А. А. Уманского [4.12] 1961 г.
Рис. 17.19. Критическое время для цилиндрических панелей при различных уровнях сжимающего напряжения.
ГЛАВА XVIII
УСТОЙЧИВОСТЬ ПЛАСТИНОК И ОБОЛОЧЕК
ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
§ 176. Постановка задачи
В главе VI мы познакомились с некоторыми задачами, относящимися к устойчивости стержней при динамическом нагружении. Обратимся теперь к аналогичным вопросам устойчивости пластинок и оболочек. Если рассматривать те и другие задачи в линейной постановке, то между ними не будет принципиального различия.
Рис. 18.1. Нарастание статических и динамических прогибов в случае: а) пластинки, б) оболочки.
Однако если исследовать прогибы, сравнимые с толщиной пластинок или оболочек, то задача окажется нелинейной и приобретет ряд особенностей. Напомним случай нагружения стержня быстро возрастающей во времени сжимающей силой при условии, что стержень имеет начальную погибь и рассматривается как система с одной степенью свободы. Диаграмма «стрела прогиба — нагрузка» имеет вид, показанный на рис. 18.1, а сплошной линией, в отличие от статической диаграммы, изображенной пунктиром *).
*) В случае, когда задан закон взаимного смещения концов стержня во времени, задача также становится нелинейной (см. г л; VI).
§ 176]
ПОСТАНОВКА ЗАДАЧИ
719
Обратимся к такой же задаче для оболочки с начальной погибью, подвергающейся выпучиванию под действием некоторой нагрузки. Будем и здесь условно считать оболочку системой с одной степенью свободы. Допустим, что, исследуя равновесные формы при статическом нагружении, мы получаем на диаграмме «нагрузка — стрела прогиба» линию с верхней и нижней критическими точками Рв и Рн (рис. 18.1, б). Если нагрузка бистро возрастает во времена, то параметр внешних сил может «пробежать» уровни как нижней, так и верхней критических нагрузок (участок сплошной линии ОК на рис. 18.1,6), причем на начальном участке (при Р < Рв) будут происходить колебания вокруг равновесных положений, характеризующихся «малыми» прогибами.
В некоторый момент, наступление которого определяется программой нагружения и различными возмущающим-и факторами, происходит скачкообразное перемещение оболочки к равновесным положениям с большими прогибами (линия KN на рис. 18.1, б); после этого начнутся колебания вокруг новых равновесных форм, имеющие ярко выраженный нелинейный характер. В дальнейшем этот процесс хлопка оболочки при быстро возрастающей нагрузке мы будем условно называть динамическим выпучиванием или динамической потерей устойчивости. Введем также понятие динамической критической нагрузки Рд, отвечающей моменту хлопка. Мы будем находить ее условно по диаграмме типа 18.1, б, определяя абсциссу точки М перегиба кривой Р(/), т. е. точки, отвечающей наибольшей «скорости выпучивания» оболочки. Можно также условиться определять Ра с помощью других величин, характеризующих участок хлопка KN.
До сих пор мы полагали, что приложенная к оболочке нагрузка возрастает во времени и что прощелкивание оболочки происходит на этой восходящей ветви нагружения. Допустим теперь, что йагрузка возрастает лишь до некоторой величины Рл < Яд (рис. 18.2) (причем прощелкивание оболочки не осуществляется) и что затем нагрузка начинает уменьшаться во времени по заданному закону. Если падение нагрузки будет совершаться достаточно интенсивно, то оболочка получит колебания вокруг начального положения равновесия и после затухания колебаний вернется к этому положению. В том же случае, если нагрузка будет падать сравнительно медленно, прощелкивание панели все же может иметь место на нисходящей ветви нагружения. Примерная кривая, характеризующая изменение / при падении Р, показана на рис. 18.2 жирной линией. Мы будем условно считать, что прощелкивание оболочки совершилось, если наибольший прогиб /д достигает значения /ст; под /ст понимается статический прогиб, соответствующий нагрузке Яд. Такое сопоставление необходимо для Тргр, чтрбы выяснить, возникнут ли при динамическом нагружении,
720 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл.* XVIII
совершающемся по сложной программе, заметные остаточные деформации.
Описанные здесь задачи являются важными для авиастроения и других областей техники. Например, корпус летательного аппарата подвергается динамическому нагружению на стартовом участке.
Быстрое изменение нагрузки во времени испытывают также некоторые оболочки двигателей.
Выпишем основные динамические уравнения нелинейной теории пологих оболочек с учетом начальных неправильностей формы оболочки. Будем исходить из уравнений (10.111) и дополним их инерционным членом, соответствующим нормальному перемещению (прогибу оболочки) w. Инерционные нагрузки, отвечающие перемещениям и и v в срединной поверхности, учитывать не будем. Таким образом, мы отказываемся здесь от исследования процесса распространения упругих волн в срединной поверхности; ограничения в отношении характера приложения нагрузки, приведенные в главе VI для стержней, остаются в силе *). Окончательно получим уравнения в виде
D „Ач t д2Ф,, д2Ф
Рис. 18.2. Динамические прогибы на нисходящей ветви нагружения.
= + + + (18.1) = w)]-kx=L
(18.2)
под у понимается удельный вес материала оболочки.
§ 177. Устойчивость пластинок и цилиндрических панелей при действии сжимающей нагрузки
Рассмотрим пологую цилиндрическую панель, шарнирно закрепленную по краям (см. рис. 11.61). Допустим, что панель подвергается динамическому сжатию вдоль образующей; исследуем ее поведение во времени при условии, что оболочка имеет начальные
*) Более общие задачи рассматривались Н. А. Алумяэ [18.2] и В. Л. Агамировым.
§ 177] устойчивость при действии сжимающей нагрузки 721
прогибы. Уравнения (1) и (2) принимают вид
X=°-4*(w—w0)-L{w, 1=0. (18.3)
V«S = - i [L (w, w) — L («0, «о)] - - J- -2(<g*°>-. (18.4)
Разберем сначала случай, когда усилие сжатия р возрастает во времени по закону р = ct. Примем для полного и начального прогибов выражения
х. ПХ. ПУ х. ПХ. Пу /ю гч
w = / sin sin -у-, Wq = /0 sin -у sin —. (18.5)
Подставляя эти выражения в уравнение (4), находим, как обычно, функцию Ф (см. стр. 710):
,± '_Ц, (18.6)
j
где р — интенсивность среднего сжимающего усилия, зависящая от времени, С = ///г, С0 = /0/й. Далее, воспользуемся методом Бубнова — Галеркина в применении к уравнению (1). Выполняя интегрирование, придадим для квадратной панели (а = Ь) к следующей зависимости:
[р*-х(с2-]с+ё (5;2 -- Ф -
здесь введены прежние безразмерные параметры р* = pa2\Eh2t k = a2/Rh.
Опуская в (7) инерционный член, получим решение статической задачи об устойчивости в большом. Считая С0 = 0 и С—>0, найдем параметр верхнего критического напряжения для панели, не имеющей начальной погиби:
. 1L
рв~ Eh2 3(1— ц2) ' 4к2 '
С другой стороны, отбрасывая нелинейные члены и полагая р* = 0, С0 = 0, придем к уравнению малых колебаний незагруженной панели без начальной погиби:
-.г.
Л£ + n*Egh2 dt2 —
722 ПЛАСТИНКИ и ОБОЛОЧКИ при ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
Квадрат основной частоты колебаний оказывается равным
„ 7z2Egh2
ш — 47*
Разделим каждый из членов уравнения (7) на рв и введем обозначение t\ для параметра времени:
—= 4-; (18.8) Рв Рв
тогда получим обыкновенное дифференциальное уравнение для стрелы прогиба:
2k
з *ув
Под Sj понимается величина
*»/ nVEh* \2
(5С2 — 4ССо — Со) — (С — Со) J = 0. (18.9)
,з /*УЕ»
>1 — Рв \ са4 ) *
где V — скорость звука в материале оболочки. Сравнивая выражения для оо2 и Sv находим: отличие от уравнения (6.31),
составленного выше для сжатого стержня, уравнение (9) является нелинейным; интегрируя его, находим зависимость С(Г).
Перейдем к другому случаю, когда задан закон взаимного смещения криволинейных кромок панели *). Деформация в срединной поверхности вдоль образующей равна
1 ( д2Ф д2Ф \ е*. = — I IX
tjc ~ Е ду* ** дх* /'
С другой стороны,
- ди. I Г( dw\2 I dw0\2~
* ~ дх 2 LV дх ) \ дх ) J ’
где и — перемещение точки срединной поверхности вдоль образующей. Укорочение некоторого волокна, параллельного образующей,
а
равно ех = — j* dx. Обозначим через е среднее значение ех по
*) Эта задача была рассмотрена автором [18.11].
§ 177) устойчивость при действии сжимающей нагрузки 723
ь
дуговой кромке: е = у У* rfy; тогда получим:
о
а b
1 Г f 1 (дЩ д*Ф\ 1 Г/ dw \2 /й®0\21..
* —~ Ь J J Е\ду* Р дх* ) 2 [\ дх ) [~дГ) \dx d?‘
О о
Примем e = st. В случае квадратной панели в прежних обозначениях получим:
или
4 =.tl - -f- (С2 - eg) - i (12~ (С - Со). (18.9а)
Рв 0РВ КРВ
Здесь введен новый параметр времени
« = <1810>
Подставим р* по (9а) в уравнение (7) и выразим t по (10); тогда придем к зависимости
JK
dtt
«“ (I *р. “V. J
+ (5C2-4CCo-CS)-(C-Co)1 = 0; (18.11)
з* рв • J
под 52 здесь понимается новая величина:
0 *з / nVh3 \2
5* = М1гН*
Уравнение (И) было проинтегрировано численным методом, а также с помощью моделирующей машины для различных значений Cq и «S2. Были приняты начальные условия
С = Со, -*=0 при 4 = 0. dt2
Результаты интегрирования для случая k — 0 (плоская панель) при С0 = 0,001 и 52=Ю00 представлены на рис. 18.3, а. По оси абсцисс откладывается параметр t*v по оси ординат — величина С, и отношение сжимающего усилия к критическому p*fp* Статическим
кр
зависимостям соответствуют: для стрелы прогиба — участки О В
и BLt\ а для нагрузки — участки О А и АС. При динамическом
724 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
нагружении происходит затягивание начального участка до точки М (или К)\ затем прогибы резко нарастают, и возникают установившиеся нелинейные колебания. Эти результаты очень близки к тем, которые были получены в главе VI для стержней; но закритическая диаграмма для нагрузки АС здесь является восходящей. На рис. 18.3, б
Рис. 18.3. Диаграммы «нагрузка — время» для: а) пластинки и б) оболочки при статическом и динамическом нагружении.
изображены аналогичные графики для квадратной в плане цилиндрической панели при k =12; значения С0 и S2 оставлены прежними. Статической задаче отвечают кривые OBLF и ОЛС, динамической— линии ОВМ и ОАК. При динамическом приложении нагрузка достигает, как и для пластинки, примерно 165% от верхней статической величины. Затем происходит резкое падение /?*, причем величина р* становится отрицательной, что соответствует растяжению панели.
В предыдущем мы приводили пластинку или оболочку к системе с одной степенью свободы и определяли зависимость стрелы прогиба от времени. При этом не удавалось проследить за изменением характера изогнутой поверхности пластинки или оболочки в процессе нагружения. Более точное решение задачи можно дать, если аппроксимировать изогнутую поверхность с помощью нескольких параметров либо представить исходные уравнения в конечных разностях. Как в одном, так и в другом случаях вычисления сильно осложняются и для их выполнения должны быть привлечены электронные цифровые машины.
Ниже изложено решение задачи с помощью метода конечных разностей *). Рассмотрим общий случай пологой панели со сторо¬
§ 178. Применение цифровых машин
*) Это решение дано А. Ю. Биркганом и автором [18.6].
§ 178]
ПРИМЕНЕНИЕ ЦИФРОВЫХ МАШИН
725
нами в плане а, Ъ, имеющей некоторые начальные прогибы. Воспользуемся безразмерными параметрами
х — у — th г, — w
У Г 1/ ГГ/19... Eh2 *
Х==Т' у=т- t = ikv' W=T' ф=т: (18л2)
тогда исходные уравнения (1) и (2) можно представить в виде
d2w d2w /д2Ф
(0*9 - \, d2w (д2Ф — \ Рх) ду* ~ Ру)
dt2 дх2 \ ду2
ду2
2 d2w д2Ф
1
дх ду дх ду 12 (1 — (х2)
V4 (w — w0) +
kv / д2Ф \ -- п / д2Ф _ \ —
(?—<18ЛЗ>
У4ф
/ d2w \2
~\д!ду)
d2w d2w
дх2 ду2
(дУо_\ I
\д*ду/
d2wo d2w0 ky d2 (w — w0) — 2 d2(w — w0)
kxK
’ dx2 dy2 I2
* •
Здесь введены соотношения
b2kx
дх2
ду2
X
Ь \2
h
ky=-
a2ky>
Рх I О Y - Ру I а \2 _ q (ab\2
р*~ Е\ h) ' ру~ Е \ h) ' 4 ~ E\h2) '
Оператор V4 имеет вид 1
V4= -—t—1-2 _d4 _
к2 дх< дх2 ду2
-X»-
_д*_
дуА
(18.14)
(18.15)
(18.16)
Заметим, что при выборе безразмерных параметров по (12) и (15) прямоугольная в плане панель преобразуется в квадратную со стороной, равной единице.
Граничные условия, заданные в виде линейных однородных зависимостей, будем считать неизменными по времени. Начальные
()<(£) —
условия могут, например, иметь вид w = w0, —— = 0 при / = 0.
dt
В дальнейшем черточки над обозначениями w, xt у, t и т. д. будем опускать.
В пространстве переменных х, у, t, ограниченном плоскостью t — 0 и плоскостями х = 0, х=\, у — 0, у=1, построим систему плоскостей t — О, t = At, t = 2Аt,..., t — mkt,..., покрытых сеткой прямых х = 0, х = s, х = 2s,..., х — 1, у = 0, у = s,......» у — 1. Здесь Ы — шаг по времени, — шаг по пространственным
726 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [ГЛ. XVIII
координатам х и у (рис. 18.4). В узлах построенной таким образом трехмерной сеточной области должны выполняться уравнения в конечных разностях, аппроксимирующие систему дифференциальных уравнений. Кроме того, для выражения граничных условий
с помощью симметричных конечных разностей введем необходимое количество внеконтурных узлов, расположенных на плоскостях
х = — 2s, х = — s, * = 1 s, х = 1 + 2s,
у = — 2s, у = — S, у = 1 S, у = 1 + 25.
Производные по пространственным координатам заменим разностными операторами по формулам типа (7.238) и (7.239),
d2w wx — 2wq -f- w3
~dx*~ s2
d2w w5 — w6-j-w7 — w8
dxdy 4s2 ’
d4w wg — 4wx + 6w0 — 4w3 + wu
dx4 ~ s4
d4w 4w0 — 2 (wx + w2 + wb + w4) + w5 + we + w7 + wb
dx2dy* s4
с погрешностью, имеющей порядок квадрата шага. Нумерация узлов счетной ячейки дана на рис. 18.4. Производную по времени заменим соотношением
Рис. 18.4. Трехмерная сеточная область.
§ 178] ПРИМЕНЕНИЕ ЦИФРОВЫХ МАШИН 727
Подставив эти выражения в уравнения (13) и (14) и опустив члены порядка квадрата шага, получим в текущей (нулевой) точке слоя tim) по два уравнения в конечных разностях. Переход от т-го к (ая--1)‘мУ слою по времени производится по формуле, в правой части которой находятся уже известные значения функций (такая разностная схема называется явной):
w(m+\) — 2wffl) — w~l) — 2w'™] -(- w(gl)s) —
— 2Фт) + ФМ — ps2} + (w{™] — 2w<0m) (Ф<да> —
— 2ф(,т> 4- Фзт> — PS*) — J (wM — W<6m> -j- w'f> — •ш£п>) (ф>) —
„ 1 (At)* гkv
- Ф<”> + Ф<”> - Ф<р> + rs*)\ + (Фр*> -
— 2Фт) + Ф<т> — pf s \ -f- kl2 (Ф§»> — 2ФМ + —
- P'f**)]-Cj[(+8 + 6X2) wm _
— 4 (1 + jr) (wf> H- «£•>) — 4(1 + X2) (> + «■>) -f
-4-2 (wm> w<6m> -- o<®) + •да{)т)) -(- j--
Н-(Д02(/.0+?Г> (18-17>
Для определения функции напряжений в момент времени t'm+1} нужно решить совместно систему разностных уравнений такого типа:
ф(т+1) — -g—— 1 А. (т+1) — w(m+l) _j_w(m+l) —
— — 2wt+l) —— w1 *■ —(—
-f-«><>*+»)-f 4(1 +(ф(я«+» -_ф+1)) +
+ 4 (1 + X2) (ф('»+1> + ф<*+1>) _ -1 (ф+1) -f Ф<«+1>) —
— X2 (Ф<*+1> + Ф+1>) — 2 (Ф£»+« + Ф+D + Ф+D + Ф§»+») —
— s1 -р- (w(1m+1> — 2«п+1> -(- + kl2 —
— 2w('»+1> + wf+»)] + H0s* j. (18.18)
Здесь L0 и H0 — функции, зависящие от начального прогиба, с = = 1/12(1-).
Процесс вычислений начинается с того, что последовательным обходом узлов сетки определяется прогиб w2)(x, у, 2Дt) по формуле (17). Далее находится функция напряжений Ф(2)(*» У» 2Д)
728 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
путем решения методом последовательных приближений системы разностных уравнений по формуле (18). По существу, на данном этапе решается линейная задача, так как входящие в правую часть уравнения (18) значения прогиба уже вычислены в предыду¬
щем пункте. В качестве начального приближения функции напряжений могут быть взяты ее значения на предыдущем шаге по времени, если они не равны нулю, или значения функции Hs4. Итерации заканчиваются после того, как достигнута требуемая степень точности.
Шаг по времени завершается пересчетом внеконтурных значений ' w и Ф в соответствии с принятыми граничными условиями.
ш 3
I ;
о /
г з
Рис. 18.5. Изменение стрелы прогиба пластинки при динамическом нагружении с различными скоростями (по данным вычислений на цифровой машине).
Далее вычисления повторяются: находятся значения w(ху у, ЗА/) и Ф(3)(лг, у у ЗА/), определяются функции во внеконтурных узлах и т. д. После каждого шага по времени либо через определенные промежутки можно определять значения напряжений.
Конкретные вычисления были проведены на вычислительной машине для квадратной плоской пластинки с шагом s=xj8. Шаг по времени выбирался таким образом, чтобы была обеспечена устойчивость разностных уравнений. Предварительно были определены статические равновесные формы пластинки при закритической деформации, соответствующие различным «порождающим» изогнутым формам. Последние отвечали собственным значениям линейной задачи при числе полуволн т = 1 и т == 3 в направлении х и одной полуволне вдоль у. На рис. 18.5 пунктирными, линиями представлена статическая зависимость прогиба в центре пластинки w* от параметра t* = p/pKр при начальной стреле- прогиба -до* = 0,001; под Ркр = = тс2/3(1—л2) понимается параметр статического критического напряжения. Прогибы, направленные в сторону начальной погиби, от¬
§ 179] ВЫПУЧИВАНИЕ ЗАМКНУТЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК 729
ложены вверх. Далее, сплошными линиями показаны результаты решения динамической задачи при нагрузке, возрастающей пропорционально времени. В случае, когда скорость нагружения относительно мала (p/t = 2,15), бурное нарастание прогибов имеет место
Рис. 18.6. Изогнутые формы пластинки в различные моменты времени.
при нагрузке р«1,8/?кр; затем происходят нелинейные колебания относительно положений статического равновесия. При большей скорости нагружения (р = 5/) прогиб резко возрастает, когда р« ~2,6/?кр; после этого на протяжении каждого периода колебаний пластинка перескакивает от одной равновесной формы к другой, так что прогиб меняет знак. При резком нарастании прогибов и последующих колебаниях форма изогнутой поверхности сильно меняется. Это можно видеть из рис. 18.6; здесь представлены изогнутые формы пластинки в среднем сечении, параллельном х. Каждая из этих форм соответствует точкам кривой рис. 18.5, обозначенным той же буквой (a, bt с и т. д.).
Отметим, что для решения динамической задачи описанным методом необходимо выполнить около 50 миллионов операций.
§ 179* Выпучивание замкнутых цилиндрических оболочек при всестороннем давлении
Перейдем к случаю замкнутой круговой цилиндрической оболочки, подвергающейся динамическому приложению всестороннего давления. Примем, что по торцам оболочка скреплена со шпангоутами (см. рис. 10.17), остающимися при деформации оболочки круговыми.
730 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [ГЛ. XVI11
Для полного и начального прогибов по аналогии с решением статической задачи (§ 133) выберем следующие аппроксимирующие выражения (см. работу [18.1]):
где а = тс/L, = n/R.
Подставим в правую часть уравнения (2) выражения (19). Тогда интеграл этого уравнения может быть представлен в виде
ф = Е (Кх cos 2ах -f- К2 cos 2фу + /С3 sin сих sin фу -f-
Последние два члена в выражении (20) отвечают напряжениям в срединной поверхности, определяемым по безмоментной теории.
Сравнивая выражения для еу через прогиб и функцию напряжений, подобно тому как это было сделано в § 127, находим:
Выпишем условие замкнутости, которым мы уже пользовались при решении статической задачи (стр. 480):
Подставляя (22), с учетом предыдущих соотношений находим:
Таким образом, величина ср оказывается выраженной через фи/. Остается составить уравнения для определения этих параметров.
w = / (sin ах sin фу + ф sin2 ах + ср), Wq = /0 (sin ах sin (ty + ф sin2 ах + <р)<
(18.19)
+ К4 sin Зад: sin фу) —
Здесь
§dy = 0.
(!-)-1 + Т + /о)Р2- <18-23>
§ 179) ВЫПУЧИВАНИЕ ЗАМКНУТЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
731
Воспользуемся методом Бубнова — Галеркина и запишем уравнения
L 2*/?
И X sin ах sin [Зу dx dy = О,
о о
L 2nR
и X sin2 ах dx dy = 0;
о о
(18.24)
здесь X определяется по (3). Подставим под знак интеграла выписанные выше выражения для w\ wQ и Ф. Выполняя интегрирование, придем к следующему уравнению, связывающему параметры прогиба с изменяющейся во времени нагрузкой:
<7 = Со(1 —+ — Со)Н-С2(С2 — Со)<>2 — С 2 1 ——
-C3(C-to)t-bC4I-g-, (18.25)
где
С,
- 1 Г ** 0+€2)2*1
0— 1 + _LS» L*2(i+e*)sb~~ isa-n2) р J’
—
16
я* 1+64 х г *Н* Г 1, 1 ъ
(l + p) 52 ’ 2 l+yP I-(l+£2)2 (l+J
c2=
c3 =
(l + £2)2(l+-5-«2)’ 3 4(1+45’)
-Г1Ч-—1 L (1+52)* J*
r tR1
В выписанных выше уравнениях были введены безразмерные параметры
а—±(3\2 г_/ г —А
q~ E\h) ’ A ’ А ’
р kR nL~ 8
Я ’
Rh L2 •
(18.26)
Второе уравнение системы (24) здесь развертывать не будем и, чтобы упростить выкладки, примем для параметра ф то выражение, которое вытекает из решения статической задачи:
И. _ W,
где
Nx-
2(ЛГаС* + ЛМ * 1
8. N.
С»ч
4
(18.25 а) (■+!)•
732 ПЛАСТИНКИ и ОБОЛОЧКИ при динамическом нагружении [гл. XVIII
Это означает, что при заданном значении С форма волнообразования считается в случае быстрого нагружения такой же, как и при медленном.
Ограничиваясь в (25) первым членом и считая С0 = 0, найдем параметр верхнего критического давления для данного значения равным qB = С0 или
Это выражение соответствует формулам (11.74) и (11.93) с учетом £=0. Чтобы получить расчетное верхнее критическое значение qB, следует найти такую величину т. (или такое число волн /г), при которой выражение для qB будет минимальным.
Примем, что интенсивность давления возрастает по закону q = ct, и введем параметр времени
(18.28)
Eh2qB qB qB
тогда уравнению (25) можно придать вид
■§—[(< —Ц)с-яг(с2-сЗК-
в (Е2-фс3. в (С-ЦР <С-С,)К,1_0. П8 29)
2 (NJ? + NiY + 3 Ntf + 4 Ntf + Ni J ~ ( )
здесь
в -С * ' В -С В - СгЩ R + Н
В2~С2Ж’ 4~ W*
Уравнение (29) для безразмерной стрелы прогиба С было проинтегрировано численным методом, а также с помощью моделирующих и цифровых, машин при следующих начальных данных:
С = £0, - = 0 при ?= 0. dt
При вычислениях было принято в применении к дюралюминовым оболочкам V — 5 • 105 см/сек, jjl = 0,3, £ = 7,75 • 105 кг/см2. Кроме того, принималось R/L = 0,45, R/h = 112, 3 = 1,8- 10”3.
На рис. 18.7 представлен график С (/)> отражающий зависимость между стрелой полного прогиба и временем нагружения (или нагрузкой) для случая С0 = 0,001. Первая кривая слева отвечает решению статической задачи при с -> 0; это решение можно получить по
§ 179] ВЫПУЧИВАНИЕ ЗАМКНУТЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК 733
методу, указанному в § 133. На графике изображена огибающая различных кривых, отвечающих тому или иному числу волн п.
Рис. 18.7. Диаграммы «прогиб—нагрузка» при начальной стреле прогиба в 0,001 толщины оболочки.
Верхнее критическое давление имеет место при п = 6, нижнее — при п = 5. На том же рис. 18.7 нанесены кривые, найденные для случая динамического нагружения при скоростях с = 0,2* 104, с = 1 • 104, с = 2 • 104 ат/сек. Все кривые перестроены таким образом, что в качестве базы взято наименьшее верхнее критическое давление qB. На рисунке приведены кривые для тех чисел волн п, при которых бурное возрастание прогибов соответствует наименьшему параметру t.
Как видим, динамический эффект и здесь проявляется в последовательном возрастании числа волн и значительном увеличении критического давления.
График рис. 18.8 содержит такие же кривые для случая большей начальной погиби (( = 0,1). Как и следовало ожидать, при сравнимых значениях скорости с здесь проявляются менее высокие формы потери устойчивости по отношению к случаю С0 = 0,001; меньшими
Рис. 18.8. Случай, когда начальная стрела прогиба составляет 0,1 толщины оболочки.
734 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
(примерно в 1,5 раза) оказываются и критические значения давления. Общий вид кривых также несколько иной: нарастание прогибов получается менее резким, чем при Cq = 0,001.
Приведенная схема решения задачи была использована В. Л. Агамировым *) для определения критического параметра t при самых различных значениях R/L, R/h' и с. В качестве примера продемонстрируем результаты своеобразного исследования, выполненного с помощью цифровой машины. На рис. 18.9.изображена зависимость
между коэффициентом динамической перегрузки д, равным отношению условной динамической критической нагрузки к верхнему статическому значению, и стрелой начального прогиба для L/R = 2 и R/h=\QQ. Здесь намеренно были выбраны исчезающе малые безразмерные стрелы начального прогиба от 10~4 до _20
10. Величина kA монотонно
возрастала от 4,21 до 8,56. Возникает естественный вопрос, можно ли найти конечное значение д для предельного случая идеальной оболочки (при С()->0). Этот вопрос важен с теоретической стороны, и его желательно рассмотреть подробнее. Однако можно считать, что случай исчезающе малых величин С0 (порядка Ю~20) может быть практически исследован.
Рассмотрим более сложную программу нагружения оболочки. Допустим, что оболочка подвергается давлению, нарастающему со скоростью с = 2000 ат/сек и достигающему значения, равного 80% от динамической критической нагрузки. Как мы видели, при этом в процессе нагружения оболочка не получает заметных прогибов. Предположим, что в дальнейшем нагрузка меняется по различным законам, как показано на рис. 18.10, б. Вариант 1 совпадает с тем, который был разобран ранее; здесь нагрузка продолжает нарастать
с прежней скоростью. В варианте 2 нагрузка на втором этапе ос¬
тается постоянной. В остальных вариантах (3—9) нагрузка падает по линейному закону; скорость падения нагрузки обозначена через с2 и меняется от 2 • 103 до 2 - 104 ат/сек. На рис. 18.10, а показаны графики изменения стрелы прогиба во времени. Несмотря на то, что в вариантах 3—9 нагрузка падает, стрела прогиба нарастает до
*) Другое решение задачи было дано Ю. И. Кадашевичем и А. К. Перцевым [18.15], учитывавшими инерционность осесимметричного.обжатия* оболочки.
Рис. 18.9. Динамические «критические* нагрузки в зависимости от начальной стрелы прогиба.
§ 179] ВЫПУЧИВАНИЕ ЗАМКНУТЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
735
Рис. 18.10. Нарастание прогибов оболочки при более сложной программе нагружения.
736 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [ГЛ. XVIII
известного предела, после чего начинает уменьшаться. Поведение оболочки на волне разгрузки характеризуется величиной максимального прогиба. В § 176 мы условились считать, что оболочка выпучивается в период разгрузки, если максимальная стрела прогиба превышает статическую стрелу прогиба, отвечающую наибольшему значению давления; статическая кривая приведена на рис. 18.10, а слева. Если согласиться с этим допущением, то опасными скоростями разгрузки будут все скорости с2, меньшие чем 3000 ат/сек.
Рис. 18.11. Диаграмма «прогиб — нагрузка» при быстрой разгрузке.
На рис. 18.11 эти же кривые представлены в иных координатах. По оси абсцисс отложена величина нагрузки, а по оси ординат — стрела прогиба.
Можно принять и иные критерии потери устойчивости или исчерпания несущей способности оболочки в период разгрузки. Например, есть основания принять в качестве предельного параметра стрелу прогиба, отнесенную к толщине оболочки. Наиболее важно здесь установить, при какой стреле прогиба оболочка не получает заметных остаточных деформаций.
§ 180. Решение с помощью аналоговых машин
Наряду с цифровыми машинами для исследования динамической устойчивости могут быть применены также аналоговые машины *), основные элементы которых были кратко описаны в § 24. Рассматриваемая задача предварительно должна быть сведена к интегрированию системы обыкновенных дифференциальных уравнений. •
Приведем схему решения на машине МН-7 задачи, разобранной в § 179, для случая, когда нагрузка возрастает пропорционально
*) Аналоговые машины для решения подобных задач применялись В. В. Болотиным, Г. А. Бойченко и другими авторами [18.9], [18.10]. Приведенное здесь решение задачи принадлежит Ю. И. Кадашевичу и А. К. Периеву.
§ 180) РЕШЕНИЕ С ПОМОЩЬЮ АНАЛОГОВЫХ МАШИН 737
времени. Перепишем уравнение типа (29) в форме
С= Ж-(- Ш + C + DC2-)- £С3 + К5
или в виде системы уравнений
Х\ = Х2 (л -f~ St —J— Dx2 —j— Ex2 —j— FX2) —\- С, X2:== X\, (18.30)
где л;2 = £, лг2=~_- Рассмотрим оболочку с прежними параметрами,
принимая h = 0,8 мм, /? = 90 л/л/, L = 200 мм, С0 = 0,001, /г = б, <7В = 0,0402, £ = 6000 ат/сек.
В этом случае система (30) примет вид
*a = x2(?— 1 —0,508 • 10_3*2 + 0,02*2 — 0,234 • 10_34) 6,9 -f-
-4- 6,9 - 10_3; х2 = хг. (18.31)
Выберем максимальное значение функций л;1=100, лг2=20.
Для того чтобы процесс в схеме не шел очень быстро, что неудобно для снятия показаний приборов и наблюдения за функциями на лучевом индикаторе, увеличим машинное время в 10 раз. Тогда будет
~ 100 - 20
Т 10/f, ХХ JQQ XV Х2 JQQ *2*
Теперь систему (31) можно записать в машинном виде:
= (0,138- 100+ 1,387-1-1,1 — 5,3) + 6,9- 104,
jc2 = 0,5jc1. (18.32)
Здесь учтено, что при перемножении двух функций блок произведений делит произведение на 100.
Для набора задачи на машине составляется блок-схема. В данном случае нагрузка линейно зависит от времени, и на блоке нелинейности была набрана функция F (Т) = Т. Так как блок нелинейности позволяет набрать функцию любого вида, то на машине легко можно исследовать и более сложные случаи нагружения. Блок-схема для системы (32) показана на рис. 18.12.
Заметим, что машина практически работает хорошо при увеличении начальных значений функции в 30—50 раз. Специфическим условием задач исследования вопросов потери устойчивости оболочек является требование получить увеличение функции в несколько тысяч раз. Поэтому такие задачи приходится решать, либо вычисляя начальный участок кривой численно (что облегчается тем, что при малых прогибах уравнения линеаризируются), либо решая задачу на машине поэтапно, перестраивая на каждом этапе блок-схему.
738 ПЛАСТИНКИ И ОБОЛОЧКИ при динамическом нагружении [гл. XVIII
Данный пример был решен на машине МН-7, начиная со времени /к 3,3. Значения функции С и ее производной в этот момент
Начальные условия
иниикатор
Рис. 18.12. Блок-схема набора задачи на моделирующей машине.
получено численным интегрированием. Система уравнений (32) преобразована к новому машинному времени: ТХ = Т—33. Решение
Рис. 18.13. Диаграммы «прогиб — нагрузка», полученные на моделирующей машине (сплошная линия) и с помощью ручного счета (пунктир).
задачи записано на искрописце и показано на рис. 18.13 (сплошная кривая). Здесь же пунктиром нанесен участок кривой, полученный численным интегрированием. Как видно из графика, точность решения на машине оказалась достаточно высокой.
§ 181]
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
739
§ 181. Экспериментальные исследования выпучивания оболочек при всестороннем давлении
Приведем результаты экспериментального исследования, проведенного над серией тщательно изготовленных (точеных) дюралюминовых образцов*), при R/h = 220 и L/R = 2,2. Специально спроектированная установка состояла из двух резервуаров, вставленных один в другой и заполненных маслом (рис. 18.14). Образец, представляющий собой круговую цилиндрическую оболочку, находился во внутреннем резервуаре; верхний торец образца оставался открытым. Отверстие в днище внутреннего резервуара закрывалось клапаном, связанным с системой пружин. В наружном резервуаре создавалось повышенное давление в пределах от 5 до 50 am; при этом сжималась находящаяся в верхней части резервуара газовая «подушка». При внезапном открытии клапана во внутреннем резервуаре происходил гидравлический удар, передававшийся на образец; с известным приближением можно было считать, что образец подвергался при этом динамическому нагружению всесторонним внешним давлением. Изменение во времени давления в нескольких точках резервуара измерялось специальными датчиками, сигналы от которых фиксировались на ленте шлейфового осциллографа. Датчики омического сопротивления, наклеенные на наружную и внутреннюю поверхности образца, позволяли определить деформации удлинения
в соответствующих точках; показания датчиков также передавались на осциллограф (линии 1—3 на рис. 18.15). При испытаниях варьи¬
Рис. 18.14. Установка для опытов; образец (3), внутренний (1) и внешний (2) резервуары, датчики (6, 7).
*) Опыты были проведены В. Е. Минеевым при участии В. С. Смирнова. Частично данные этих опытов были приведены в статье [18.12].
740 ПЛАСТИНКИ и ОБОЛОЧКИ при динамическом НАГРУЖЕНИИ [гл. ХУШ
ровалась разность давлений во внешнем и внутреннем резервуарах, а также время открытия клапана, что позволило получить различные скорости нарастания давления в пределах от 2 • 103 до 6,5 • 103 ат/сек.
2
I
— 1 1 1 1 1 »- « «
Рис. 18.15. Осциллограмма динамического нагружения оболочки.
На рис. 18.16 приведены фотографии образцов, подвергнувшихся статическому нагруя.ению (рис. 18.16, а) и динамическому нагружению со скоростью нарастания давления в 4700 и 5000 amjcetc (рис. 18.16, б, в). Общий характер глубоких вмятин, обращенных,
главным образом, к центру кривизны, во всех случаях один и тот же, однако конфигурация вмятин несколько меняется: при динамическом приложении давления они имеют очертание, близкое к прямоугольнику. Как видим, с увеличением скорости нагружения изменяется форма волнообразования, как это вытекает из теоретического решения. Вместе с тем резко повышается несущая способность оболочки в стадии нагружения.
На графике рис. 18.17 экспериментальные данные сопоставлены с результатами, полученными в § 179, для оболочек с теми же размерами. По оси абсцисс отложена скорость с в ат/сек, по оси ординат — коэффициент динамической перегрузки д. Сплошной линией соединены точки, полученные из графиков рис. 18.7 для Со = 0,001. Треугольниками помечены экспериментальные данные для первоначально «гладких» оболочек, кружками — для оболочек
Рис. 18.16. Оболочки после выпучивания: а) при статическом нагружении, б) при нагружении со скоростью 4700 ат/сек, в) для скорости 5000 ат/сек.
§ 181]
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
741
с начальной погибью, причем стрела начального прогиба составляла 2h. Суля по графику, эксперименты подтвердили теоретические выводы, по крайней мере, с качественной стороны.
Рис. 18.17. Сравнение теоретических данных для случая С = 0,001 (сплошная линия) с экспериментальными.
Некоторое отклонение опытных значений критического давления для оболочек «идеальной формы» вверх от теоретической кривой можно объяснить тем, что в экспериментах края оболочек были защемлены и что к силам инерции массы оболочки присоединялись силы инерции прилегающего слоя жидкости. Кроме того, теоретическое решение нельзя считать окончательным; желательно, в частности, выяснить подробнее характер изменения параметра ф.
Другая серия опытов была проведена над стальными оболочками *), параметры которых составляли: R/h = 200, L/R = 2,9.
Оболочки, снабженные вставными днищами, помещались в резервуар, заполненный жидкостью. По свободной поверхности жидкости производился удар падающим грузом. Изменение высоты падения груза позволяло варьировать скорость нарастания всестороннего давления, передававшегося на оболочку. На рис. 18.18 изображены образцы после выпучивания (днища были удалены). При статическом нагружении оболочка получала шесть
вмятин по окружности (рис. а), при динамическом нагружении с различными скоростями — восемь (рис. б) и девять вмятин (рис. в).
Рис. 18.18. Форма выпучивания оболочек при ударном нагружении.
*) Это исследование было выполнено В. В. Сорокины.
742 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
§ 182. Замкнутые цилиндрические оболочки при осевом сжатии
Перейдем к случаю, когда круговая цилиндрическая оболочка подвергается динамическому воздействию осевого сжатия (см. рис. 11.2)*).
Полный и начальный прогиб аппроксимируем по аналогии с (19) следующим образом:
w — / (s*n arn х sJn фу + Ф sin2 атх + ?)»
Щ = /о (sin am х sin ру -f- <* sin2 атх + ср).
В эти выражения входит новый коэффициент am, равный am = где т — число полуволн по длине оболочки, в то время как в § 179 соответствующий коэффициент принимался в виде a = тс/Z,. Напомним, что при осевом сжатии, в отличие от случая всестороннего давления, потеря устойчивости оболочки в большом выражается в появлении ромбовидных вмятин, расположенных в шахматном порядке и образующих несколько поясов по длине L. Подставляя w и w0 в уравнение (6) и интегрируя, находим:
Ф = Е (К\ cos 2атх + Кч cos 2у -f-
-f- Kz sin а,тх sin py + K\ sin 3amjc sin y) —
Коэффициенты K[t..., K\ определяются прежними выражениями (21) с заменой а на ат; под р понимается средняя интенсивность сжимающих усилий, приложенных к торцам оболочки.
Применяя метод Бубнова—Галеркина, воспользуемся уравнением (3). После интегрирования придем к следующему соотношению:
р = с; (1 - !f) + с; (с2 - Ф + с'2 (С2 - Ф <>2- Сз (С - Со) f+
\ £2 2
+ С*Т-Щ--С'5—<18-33>
где
1 (!+й)2 „
12(1 f»2) £ %
< 1 _f2i ет
/1 е° 2 I * 4 г е2 * 5 /1 i с2 \2 *
*) Здесь излагается решение задачи, полученное С. Н. Кирюшиной. Другие работы по этому вопросу принадлежат В. Л. Агамирову и автору [18.1], О. И. Теребушко [18 19]. Подробное исследование линейной осесимметричной задачи проведено А. И. Блохиной [18.7].
Со
Сх
(1+£Ь
1 1+4 16 £.
«--kb
§ 182] ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ 743
В дополнение к (26) здесь введены безразмерные параметры
с mnR _ ат Р ~ Е h ' *т~ nL ~ Р *
Если из уравнения (33) исключить инерционный член и положить Cq = 0, то придем к решению статической задачи для оболочки идеальной формы. Верхнее критическое напряжение для некоторой заданной формы выпучивания будет равно
п С' 1 + I Рш 0 12(1—(X*) ?т 7,+(1+4)21)'
что соответствует формуле (11.39). Минимизируя р, находим известное значение рв = 0,605. Что касается нижнего критического напряжения, то данный вариант решения приводит к параметру *)
рн= 0,15рв = 0,09; он отвечает значению 5т = 0,6.
Вернемся к динамической задаче. Примем, что внешние усилия возрастают по закону p = ct, и введем безразмерный параметр
t* _ ctR _ р_.
EhPs Рв ’
тогда уравнение (33) примет вид (индексы т опущены):
1 \ ( +* ° \ Г (г3 ?Т2
—К' с—)С —Т55Г4-Р--%)~
-t[«Ti¥+«r+W](e-+'+
+ jk[l + (T«v]w_w+aWS(i:!_'i)*)='
(18.34)
Уравнение (34) было проинтегрировано численным методом и с помощью цифровой машины. При этом была принята форма вмятин, которая отвечает наименьшему верхнему критическому напряжению. Параметр ф принимался тем же, что и в соответствующей статической задаче для оболочки идеальной формы (см. § 127). Кроме того, было принято R/h— 180, L/R = 2,2. Результаты вычислений представлены на рис. 18.19. По оси абсцисс отложены значения
= =
Рв Рв
здесь в знаменатель входит наименьшее верхнее критическое напряжение. По оси ординат на рис. 18.19 откладываются значения
*) Выше (см. § 127) в этом приближении была получена несколько иная величина (0,124). В §126 величина £т обозначена
744 ПЛАСТИНКИ И ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVII)
стрелы прогиба С. Различные серии кривых относятся к динамическому нагружению со скоростями с = 1 • 106; 2 • 106; 5 • 106 кг!см2сек. Каждая кривая отвечает известному числу волн я, указанному на графике. Как видим, бурный рост прогибов имеет место ь первом
с =2-10 6 кг/см2-сек
Рис. 18.19. Кривые «прогиб — нагрузка» при динамическом сжатии вдоль образующей.
случае при п— 11, во втором — при п= 12, в третьем — при п — 13.
В другом варианте решения задачи (см. [18.1] и [18.19]) прогиб аппроксимировался выражением
- /. ткх. пу,.. о т%х. 9 пу \
w = / (sin - L Sin -Г+ ф Sin2 —j— sin2.
В выкладках, проведенных тем же путем, было принято, что волны являются квадратными: £т = rmzRlnL=: 1. Интегрирование уравнения типа (34) было осуществлено с помощью цифровой машины «Урал-2» и численным методом; данные оказались очень близкими между собой. Результаты вычислений приведены в работе О. И. Теребушко [18.19].
Теоретические выводы можно сопоставить с данными серии опытов над дюралюминовыми оболочками *), проведенных с помощью той же установки, какая была описана в § 181. На рис. 18.20 указаны экспериментальные значения коэффициента динамической перегрузки; он был получен делением величины нагрузки, при которой происходило динамическое выпучивание, на статическое критическое значение нагрузки, также найденное из опытов. Сплошная
*) Эти опыты принадлежат С. Н. Кирюшиной*
§ 182] ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ПРИ ОСЕВОМ СЖАТИИ 745
линия проведена через точки, полученные интегрированием уравнения (34). Отметим, что экспериментальные точки имеют здесь больший разброс, чем в случае всестороннего сжатия (см. рис. 18.17). Эффект динамичности в случае осевого сжатия оказывается меньшим.
Рис. 18.20. Сопоставление теоретической кривой с данными опытов (треугольники).
В случае сжатия выпучивание выражается в образовании мелких вмятин, занимающих обычно лишь часть поверхности оболочки;
Рис. 18.21. Фотографии образцов (с торца) после выпучивания.
поэтому силы инерции здесь не оказывают такого влияния, как при поперечной нагрузке, когда в движение приходит, как правило, вся масса оболочки.
На рис. 18.21 изображены фотографии (с торца) оболочек толщиной40,5л1л*, одна из которых была испытана статически (рис. 18.21, а). а вторая — при динамическом нагружении со скоростью с = 0,65 X X Ю6 кг/см2 (рис. 18.21, б).
746 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
Ряд интересных опытов по динамическому выпучиванию оболочек при осевом сжатии был проведен также Шмиттом [ 18.23] и Коппа [ 18.22].
Правда, эксперименты этих авторов относились скорее к чисто ударному нагружению оболочки, чем к тому случаю умеренной скорости возрастания нагрузки, который рассматривался выше. Тем не менее качественные результаты опытов соответствуют полученным нами теоретическим выводам. Оказалось, что при динамическом нагружении размеры вмятин меньше и число вмятин в поперечном сечении больше, чем при статическом приложении силы. В работе Рис. 18.22. Выпучивание [18.22] особое внимание было уделено оболочки при резком форме выпучивания оболочки при ударе.
УдаРе* Оказалось, что здесь может быть применен
тот же геометрический подход к задаче, какой был предложен для статических задач (см. § 128). На рис. 18.22 показана форма волнообразования реальной оболочки, приближаю-
Рис. 18.23. Оболочка выпучивается при ударе (рис. б) по форме, весьма близкой к изометрической (рис. а).
щаяся к изометрической. На следующем рисунке полученная построением изометрическая форма (рис. 18.23, а) сравнивается с фактической конфигурацией вмятин (рис. 18.23, б).
§ 183] СФЕРИЧЕСКАЯ ОБОЛОЧКА ПРИ ВНЕШНЕМ ДАВЛЕНИИ
747
§ 183. Сферическая оболочка при внешнем давлении
Рассмотрим теперь сферическую оболочку, подвергающуюся динамическому действию равномерно распределенного внешнего давления. Речь идет как о замкнутой сферической оболочке, так и о сферическом сегменте, охватывающем достаточно большой центральный угол (см. рис. 14.1 и 14.2). До потери устойчивости оболочки сжимающие напряжения в стенке равны a = qR/2h.
Ограничимся решением задачи о динамической устойчивости оболочки в линейной постановке. Полагая в (1) и (2) kx = ky=\/R и отбрасывая нелинейные члены, придем к уравнениям
= (18.35)
Х-У4Ф = — V2 (w — w0). (18.36)
Объед шяя эти два уравнения, получаем следующее разрешающее уравнение для прогиба:
Я. ve (да _ щ) +V2 (да _ Wo) + f* v% + JL (уада) = 0. (18.37)
Идя тем же путем, что и в § 153, не будем выписывать для функций w и w0 конкретных выражений, а примем следующую зависимость, вытекающую из периодического характера этих функций:
V2w = — \2w, V2w0 = — X2w0; тогда уравнение (37) примет вид
— w0) + (w — w0) — + j 5 = 0. (18.38)
Введем обозначения:
w r. 9 0. о qR2 <*R
— mh = r?, 0=q. ж = °;
тогда после простых преобразований получим:
[12(1 — ц2) + *](£ о) \ + “2“ =0* (18.39)
Если в этом уравнении опустить инерционный член, то при Cq-->0 найдем статическое критическое давление, отвечающее данному параметру tj:
)~2[l2(l— (л.*) +1?]'
Минимизируя эту величину по % находим известное значение верхнего критического давления фв=1,21. Соответствующее безразмерное мембранное напряжение равно ов = 0,605.
748 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVI11 Динамическое уравнение (39) можно теперь переписать в виде
с-0
ИЛИ
gEi? dt* iR2 dK
+ T<C-Co)-
■C = 0.
(18.40)
gEfq* в at‘ ' 2 w 2<r„.
Примем, что давление меняется по закону q = ct, и введем безразмерный параметр времени
ctR2
Eh%
Тогда уравнение (40) перейдет в следующее:
где
е 1 -з /V£A*\*,
2 qr> \ cR3 ) '
(18.41)
(18.42)
Интегрируя уравнение (41), найдем зависимость С(/*) при заданном 5. Затем следует перейти к «единому» времени
t:=s-=(*L
Я в Яв
и сравнить кривые отвечающие различным значениям т). Находя
кривую, которой соответствует наиболее бурный рост прогибов, определяем динамическое критическое давление.
На рис. 18.24 изображены кри- ? вые С(. полученные с помощью
Т,1* эс, 7А 1П
\ ’ ✓
s-5, Сд-т
1
1
1
и
/
Рис. 18.24. Диаграмма «прогиб — на- Рис. 18.25. Графики динамического
грузка» для сферической оболочки, выпучивания сферической оболочки
при различной начальной погиби.
электронной цифровой машины «Урал-1». Они относятся к значениям 5 = 5, Cq=10~4 и различным т)2. Как видим, бурное возраста-
§ 184] ПРАКТИЧЕСКИЕ ВЫВОДЫ. ДРУГИЕ ДИНАМИЧЕСКИЕ ЗАДАЧИ 749
ние прогибов имеет место прежде всего в случае т]2 = 5. Наследующем рисунке 18.25 сопоставлены кривые относящиеся к пара¬
метру 5 = 5 и различным С0; здесь выбраны лишь кривые, лежащие ближе всего к оси ординат.
§ 184. Практические выводы. Другие динамические задачи
В настоящей главе мы подробно рассмотрели различные подходы к решению динамической задачи, которая с практической точки зрения является наиболее актуальной,— о поведении пластинок и оболочек различной формы при быстром монотонном возрастании нагрузки. Были намечены также пути исследования более сложных программ нагружения. Общий вывод состоит в том, что характер выпучивания пластинок и оболочки при динамическом нагружении является иным, чем при статическом, и что в первом случае проявляются высшие формы потери устойчивости. Это позволяет проектировать облегченные тонкостенные конструкции, заранее предусматривая их перегрузку в короткий период приложения сил.
Приведенные данные интересны и с теоретической стороны, так как открывают новую область в проблеме устойчивости пластинок и оболочек. Они указывают, в частности, на важность изучения не только первой формы потери устойчивости, но и высших форм. Кроме того, некоторые свойства оболочек, как, например, переход к почти изометричной поверхности при выпучивании, проявляются в динамическом процессе более отчетливо.
Мы рассматривали поведение оболочек, как правило, с позиций нелинейной теории. Отметим, однако, что интегрирование линейных уравнений (см. § 183) также позволяет, хотя и с некоторой погрешностью, судить о начальной стадии бурного возрастания прогибов.
Нами учитывались только силы инерции, соответствующие нормальному перемещению. Более полные уравнения включают инерционные члены для перемещений и и v. Предварительные вычисления *) показывают, что в ряде случаев изучение влияния инерции в направлении нормали можно отделить от рассмотрения влияния инерции в срединной поверхности. Этот вопрос желательно исследовать дополнительно.
Обратимся теперь к другим динамическим задачам, рассмотренным в главе VI в применении к стержням. Наибольшее внимание в литературе было уделено задаче о параметрических колебаниях пластинок и оболочек **). И здесь полная картина поведения
*) Они были выполнены В. Л. Агамировым, см. также указанные выше работы Н. А. Алумяэ [18.2] и Коппа [18.22].
**) Эти задачи были впервые рассмотрены В. В. Болотиным [18.8], а в дальнейшем — С. А. Амбарцумяном, Ж. Е. Багдасаряном и другими [18.3J — [18.5], [18.13]. Ниже приведены данные, полученные В. Ц. Гнуни.
750 ПЛАСТИНКИ и ОБОЛОЧКИ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ [гл. XVIII
пластинок и оболочек может быть получена лишь при использовании нелинейной теории. Это имеет особенно большое значение для оболочек, так как процесс колебаний может сопровождаться их прощелкиванием. Рассмотрим для примера случай замкнутой цилиндрической оболочки, находящейся под действием пульсирующего нормального давления. Воспользуемся схемой решения задачи, принятой в § 179, в применении к идеальной оболочке, т. е. считая С0 = 0. Уравнениям (25) и (25а) можно придать вид
С4г+[Со-Я (01 с - Ctf* + (Pi + C2f) с» = 0.
N1
'2(NJ? + Nty
(18.43)
Примем q (t) = q° cos 0 и положим приближенно ф = (NZ/2NX) С; тогда первое из уравнений примет вид
_g_+a)2(1_2[*cos0f)C — аС3-НС5 = 0, (18.44)
где
а2 t ?° a 1 Q 23
C4 ‘ 2 C0 2CaNx C49 r 4 CX*
Если исключить из (44) нелинейные члены, то придем к известному уравнению Матье (6.118). Результаты исследования такого линейного
уравнения совпадают с теми, которые были изложены в § 77. Между тем решение нелинейной задачи имеет существенные особенности. Если учитывать линейное демпфирование, то для тzR/nL < 2,66 мы получим зависимость между квадратом амплитуды установившихся колебаний С2 и квадратом частоты возмущающей силы 02 в области главРис. 18.26. Амплитуды колебаний оболоч- ного (первого) параметриче-
ки в зоне параметрического резонанса, ского резонанса, изображен¬
ную на рис. 18.26. Как видим, кривые С2 (б2) имеют характерную петлеобразную форму; это указывает на возможность осуществления хлопков оболочки от одних устойчивых установившихся положений к другим *).
*) На это обстоятельство было обращено внимание В. В. Болотиным в работе 1958 г. [18.8J.
§ 184] ПРАКТИЧЕСКИЕ ВЫВОДЫ. ДРУГИЕ ДИНАМИЧЕСКИЕ ЗАДАЧИ 751
Исследуя поведение оболочек при динамическом приложении нагрузки, мы знакомились уже с собственными нелинейными колебаниями оболочки вокруг устойчивых равновесных состояний. Интересные особенности таких колебаний были изучены Э. И. Григолюком [18.14] и О. Д. Ониашвили (18.18]. Специфические черты вынужденных колебаний оболочек были рассмотрены в работах С. А. Амбарцумяна и В. Ц. Гнуни [18.3], Г. В. Мишенкова [18.17] и других авторов.
В заключение отметим, что приведённые выше исследования являются лишь первым шагом в разработке теории устойчивости оболочек и пластинок при динамическом нагружении, включающей описание явления прощелкивания оболочки. „Уязвимым местом решений по методам Ритца и Бубнова — Галеркина, особенно в применении к замкнутым цилиндрическим оболочкам, являются допущения, касающиеся характера волнообразования оболочки в процессе выпучивания. Желательно продолжить уточнение решений различных задач с применением цифровых электронных машин (см. § 178), а также провести новые серии экспериментов. Другие направления возможных исследований в этой области намечены в § 204 (стр. 838).
ГЛАВА XIX
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
§ 185. Дивергенция и флаттер панели в потоке газа
Обратимся к задачам устойчивости пластинок и оболочек, относящимся к области аэроупругости, когда поведение пластинки или оболочки тесно связано с воздействием обтекающего их газового потока. Рассмотрение этих задач является важным, поскольку вопрос об упругой устойчивости неизбежно возникает при расчете конструкции любого летательного аппарата. Не менее интересны эти исследования и с теоретической точки зрения, так как они позволяют выявить различные виды потери устойчивости. Один из них состоит в монотонном выпучивании; например, при наступлении определенных условий становится устойчивой не плоская форма панели, а изогнутая. В авиационной литературе такой процесс статической потери устойчивости обычно называют дивергенцией. Другой, колебательный вид наступления неустойчивости выражается в возникновении незатухающих вибраций конструкции. С этим вторым типом неустойчивости мы уже сталкивались при изучении параметрических колебаний. Особенность того колебательного движения, с которым мы познакомимся в настоящей главе, состоит в том, что оно поддерживается за счет энергии, доставляемой газовым потоком, причем скорость и направление потока могут оставаться постоянными. Такого рода вибрации называются автоколебаниями или колебаниями типа флаттера. Мы будем здесь касаться только статического выпучивания и автоколебаний подкрепленных пластинок либо оболочек, являющихся панелями обшивки крыла, фюзеляжа или оперения летательного аппарата; такие колебания получили название панельного флаттера.
Допустим, что удлиненная панель, закрепленная по краям, обтекается потоком газа вдоль линии АВ (рис. 19.1); причем скорость потока равна U. Если панель отклоняется от плоскости АВ, то она будет подвергаться поперечному давлению, зависящему в каждой данной точке от угла между нормалью к срединной поверхности и направлением потока. В том случае, когда изогнутое очертание
§ 1 86] ОПРЕДЕЛЕНИЕ НОРМАЛЬН. ДАВЛЕНИЯ ПО ПОРШНЕВОЙ ТЕОРИИ 753
панели симметрично по отношению к среднему сечению, нормальное давление оказывается в первом приближении антисимметричным, как показано на рис. 19.1. Панель получает своеобразную деформированную конфигурацию, сочетающую симметричные и антисимметричные прогибы. Поведение панели при этом зависит от характера закрепления краев и от того, имеются ли начальные усилия в срединной поверхности. Если пластинка в исходном положении является плоской и подвергается действию сжимающих усилий, то при известной скорости потока эта начальная форма может стать неустойчивой, между тем как устойчивыми будут изогнутье формы; в этом случае наступает статическое выпучивание панели (дивергенция). С другой стороны, при известном сочетании сжимающих усилий и скорости потока могут возникнуть колебания типа панельного флаттера. Так как колебания вызывают ускоренное развитие усталостных трещин в обшивке *), то они являются нежелательными, хотя бы их амплитуда и была ограниченной.
Для летательных аппаратов, имеющих сверхзвуковую или гиперзвуковую скорость, начальные усилия в обшивке могут быть вызваны повышением температуры, связанным с воздействием того же газового потока. Поэтому основные уравнения, описывающие поведение пластинок и оболочек в потоке газа, должны учитывать влияние температурного поля, и их надо отнести к области аэротермоупругости.
Определение аэродинамического давления при больших сверхзвуковых скоростях облегчается благодаря возможности применения так называемой поршневой теории. Нам придется в дальнейшем пользоваться основными соотношениями этой теории, поэтому приведем их краткий вывод.
§ 186. Определение нормального давления по поршневой теории
Рассмотрим одномерную задачу о неустановившемся изэнтропическом движении идеального газа, заключенного в цилиндрическую трубу и находящегося справа от поршня А (рис. 19.2). Поршень перемещается вправо со скоростью и, малой по сравнению со
*) В литературе имеются сведения, что воздействие газового потока вызвало в свое время разрушение некоторых панелей обшивки немецкой ракеты V-2.
Рис. 19.1. Панель под воздействием потока газа: распределение нормального давления.
754
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
и
. и=0
скоростью звука в невозмущенной газовой среде; очевидно, этой же скоростью обладают прилегающие к поршню частицы газа. Скорость распространения малых возмущений (скорость звука) в газовой среде обозначим через с, давление — через р% плотность — через р. Все эти величины изменяются по мере удаления от поршня. На
достаточно большом расА стоянии от поршня точки
газа находятся в покое, так что скорость и = 0; остальные характерные величины cQ'№* соответственно равны с0, Ро> Ро*
j Выберем на некотором
удалении от поршня два бесконечно близких сечения т и т' таким образом, что малое возмущение передается от т к тг со скоростью звука с за время dt; расстояние между сечениями будет dx = с dt. Пусть в сечении т давление равно р, а в сечении т' равно р — dp.
Составим уравнение импульсов для элементарной массы газа pdx заключенной между сечениями с единичной площадью, считая, что под влиянием возмущения эта масса за время dt приобретает дополнительную скорость du:
Рис. 19.2. К выводу уравнения движения газа при перемещении поршня.
Отсюда
р dxdu — pdt — (р — dp) dt.
1
du = — dp.
P с
(19.1)
Полагая, что за время dt внутрь элемента через сечение втекает масса газа р dudt, определяем новое значение плотности в том же объеме:
,, р dx + р du dt
p+rfp=JL-—
следовательно,
du = — dp. P r
(19.2)
Другой вывод полученных зависимостей состоит в следующем. Запишем известные в аэродинамике уравнения движения элементарной массы газа и неразрывности:
г ди
ди
др
§ 186) ОПРЕДЕЛЕНИЕ НОРМАЛЬН. ДАВЛЕНИЯ ПО ПОРШНЕВОЙ ТЕОРИИ 755
Считая, что величины скорости и и приращений и и р малы, будем пренебрегать их произведениями; тогда уравнения (3) примут вид
ди др
рЖ~~~д7'
др ди
~dt Р дх ’ J
(19.4)
Для возмущения, передающегося через газ справа от поршня, все характерные величины будут зависеть от одной переменной*) xf = х — ct. Для некоторой функции / имеем:
df(x') _ df df(x') _ df
dx — dx' * dt ~ 0 dx'* (АУ*
Заменяя частные производные в (4) через полные производные по х\ приходим к соотношениям (1) и (2).
Сопоставляя (1) и (2), получаем известную формулу для скорости звука:
<“>•«>
С другой стороны, для изэнтропического процесса имеет место зависимость
Р = Ср1,
где С—постоянная величина, х — отношение теплоемкости газа при неизменном давлении к теплоемкости при постоянном объеме. Находим, считая х = const,
= = (19.7)
И
e=V *f • (19-8)
Равенства (1) и (8) дают
du = -dp. (19.9)
Пользуясь (7) и (8), выразим скорость звука с в произвольном сечении через скорость звука с0 на бесконечности:
-к=Уг¥=(т:Гг- <19-»
*) Это положение неявно фигурировало и в предыдущем выводе, когда принималось dx = с dt.
756 НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ [ГЛ. XIX
Соотношение (9) приобретает вид
= (19.11)
* V Ро ) Р
Интегрируя (11), будем иметь:
р/ро *-1,
«-«•=/Ш)«
1
Отсюда при и0 = О
“ = Т [(Г-1]-
Далее получаем:
здесь и надо брать со знаком плюс при выталкивании газа поршнем (рис. 19.2) и минус при всасывании в трубу.
Для воздуха при х=1,4 будет -==(14-0,2—).
Ро \ со /
Считая и.с0, разложим выражение (13) в ряд по формуле бинома Ньютона:
*-'+Ч+Ш,+2£аШ'+
+>(,+«13-,)Ш,+-
Отсюда
р-рр+ч1а)'+ч}-ш+
+ О»-!*)
Пользуясь (8), находим: pQ = CqPo/*» следовательно, множитель перед
скобками в (15) можно записать в виде (р0).
Для малых возмущений в первом приближении будем иметь:
Р — Ро = я = РсАИ- (19.16)
С0
Мы получили линейные соотношения, связывающие приращение давления со скоростью потока. Заметим, что (16) также непосредственно вытекает из (2). Удерживая в выражении (15) два или три члена ряда, получаем соответственно нелинейные зависимости второго или третьего приближения.
§ 186] ОПРЕДЕЛЕНИЕ НОРМАЛЬН. ДАВЛЕНИЯ ПО ПОРШНЕВОЙ ТЕОРИИ 757
Рассмотрим случай, когда удлиненная слабо искривленная панель подвергается действию сверхзвукового или гиперзвукового потока (см. рис. 19.1). Обозначим скорость невозмущенного потока через £/, скорость звука в невозмущенном потоке — через с0, а соответствующее число Маха — через М =U/c0. Будем считать, что число это лежит выше значения М = 2.
Если длина панели b значительно больше ширины а, то для исследования деформации панели достаточно рассмотреть полоску шириной, равной 1 (рис. 19.3), и считать все искомые величины
Рис. 19.3. Случай удлиненной панели; задача становится одномерной.
функциями координаты х и времени t. Обозначим через 0(лг, f) полный угол наклона нормали к срединной поверхности по отношению к плоскости, перпендикулярной к вектору U; величину б, выраженную в радианах, будем полагать малой: 02 1.
Рис. 19.4. Различныеслучаи искривления панели: а) выпуклостью вверх, б) выпуклостью вниз.
Допустим, что слева от панели (рис. 19.4) имеется жесткая преграда, так что панель обтекается потоком только Снизу. Примем сначала, что панель изогнута выпуклостью вверх (рис. 19.4, а). Тогда непосредственно за точкой А будет лежать зона
758
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
разрежения потока. В этой зоне течение является изэнтропическим; отметим, что если бы оно было одномерным, то оно описывалось бы точно теми же уравнениями (2) и (4), как и для дозвукового потока; надо считать, что поршень, изображенный на рис. 19.2, движется влево. Однако рассматриваемая задача гораздо более сложна, так как является двухмерной. Предположим теперь, что панель искривлена выпуклостью вниз (рис. 19.4,6). Тогда в ближайшей к точке А зоне будет иметь место сжатие газа; от А берет свое начало фронт скачка уплотнения. Возможное очертание этого скачка изображено на рисунке. Возмущенная зона потока (заштрихована на рис. 19.4,6) находится в пределах между поверхностью пластинки и фронтом скачка. Здесь уже и одномерная задача должна быть поставлена по-новому, так как между прилегающим к поршню слоем газа и остальной областью расположена ударная волна; в пределах возмущенной зоны энтропия газа меняется.
Таким образом, по сравнению с описанной выше одномерной задачей о дозвуковом движении поршня мы сталкиваемся здесь с двумя основными затруднениями: (а) задача оказывается двухмерной, и (б) имеются скачки уплотнения в сжатой зоне, причем энтропию газа нельзя считать постоянной.
Первое из этих затруднений может быть преодолено введением так называемой гипотезы плоских сечений. Как показывают более подробные исследования, при достаточно больших числах М фронт скачка уплотнения лежит сравнительно близко к поверхности пластинки. При прохождении через скачок скорость частицы газа меняется незначительно; после соприкосновения с пластинкой частица газа продолжает перемещаться с почти неизменной касательной скоростью. Эту касательную скорость Ux можно при малых углах 0 считать равной скорости невозмущенного потока Ц. Возмущение потока, вызванное контактом с пластинкой, состоит, главным образом, в поперечных перемещениях частиц газа. Картина течения получается такой, как если бы частицы газа продолжали перемещаться с неизменной скоростью U, отклоняясь по направлению нормали к поверхности пластинки. Обратим движение, т. е. примем, что пластинка движется со скоростью U в покоящейся газовой среде (рис. 19.5). Тогда получится, что пластинка «разрезает» среду, придавая частицам поперечные смещения. Выделим слой частиц газа двумя плоскостями тп и mxnv нормальными к вектору U. Можно считать, что при больших сверхзвуковых скоростях перемещения пластинки частицы слоя получают смещения лишь в пределах данного слоя; плоскости тп и тхп% оказываются
Рис. 19.5. К формулировке гипотезы плоских сечений.
§ 186] ОПРЕДЕЛЕНИЕ НОРМАЛЬН. ДАВЛЕНИЯ ПО ПОРШНЕВОЙ ТЕОРИИ 759
как бы «непроницаемыми стенками» *). В этом и состоит гипотеза плоских сечений.
Если вернуться к первоначальной картине обтекания панели и принять, что панель неподвижна, то поперечная составляющая скорости (рис. 19.6) будет равна Uв; для пластинки, совершающей
колебания, необходимо учесть также переносную скорость которой обладает точка срединной поверхности с координатой z. Иначе говоря, задача об определении давления на пластинку сводится к рассмотрению неустановившегося движения частиц газа при наличии жесткой стенки, перемещающейся со скоростью
и = 1/е + -г. (19.16а)
Рис. 19.6. Поперечная составляющая скорости потока и переносная скорость.
Если бы это возмущенное движение газа было изэнтропическим, то мы могли бы для решения задачи воспользоваться результатами, полученными при рассмотрении одномерного распространения возмущений в газе, вытесняемом поршнем; скорость поршня надо, очевидно, определять по формуле (16а). Для зоны разрежения мы можем сделать это без всяких новых допущений. Однако для зоны сжатия газа необходимы дополнительные гипотезы.
Можно показать, что при использовании нелинейного выражения (15), в котором удержана кубическая степень (и/с0), мы получаем значения давления, весьма близкие к «точным», даже если эти последние найдены с учетом наиболее сильного присоединенного скачка уплотнения. Таким образом, и здесь процесс распространения возмущений в газе можно приближенно принимать изэнтропическим.
Поршневая теория дает удовлетворительные результаты, если число М потока удовлетворяет требованию М2>1; практически она может быть применена уже при М > 2. Отметим, далее, что при выводе соотношений, относящихся к одномерной задаче о движении поршня, мы считали, что скорость поршня мала по сравнению со скоростью звука с0. Следовательно, должно быть и < с0 или
(t/6 +
dz
dt )n
<с0
(а)
*) Такая формулировка гипотезы плоских сечений дана в работе А. А. Ильюшина [19.6]. Исследования в этой области принадлежат, кроме того, Хэйсу [19.19], Лайтхиллу [19.25], Эшли и Зартярьяну [19.14] и другим авторам.
760 НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ [ГЛ XIX
Допустим, что исследуемый процесс является колебательным и что величина z меняется по закону z = A sin а)/, где Л и со — амплитуда
и частота колебаний; тогда (-4?- =Ла). При этом условие (а)
\ at /тах
перепишется в виде
о с0
где бтах — наибольшее значение б, или
м(етах4-4г)<1- (Ь)
Отнесем амплитуду А к ширине панели b, тогда вместо (Ь) найдем:
Mf0raax+4-)<L <с>
Дополнительные исследования показали, что формулы поршневой теории применимы и в случае, когда основной поток является нестационарным, т. е. при U — U (t); при этом должны быть выдержаны определенные условия в отношении характера изменения U.
Во многих случаях второй составляющей в выражении (16а) можно пренебречь по сравнению с первой и положить
и = иО = Мс0Ъ. (19.16b)
Такая постановка задачи носит название квазистатической: мы условно считаем, что в каждый данный момент времени давление по поверхности колеблющейся пластинки распределяется так же, как и для неподвижной пластинки той же конфигурации.
В курсах аэродинамики приводится известное выражение для избыточного давления:
р — Ро = —-• 6,
У0 /м2 — 1
где qA — динамическое давление, равное дл = рои2/2. Принимая Ц == Мс0, находим:
М2
Р — Ро = Росо 9-
При м2> 1 можно считать ум2— 1«м. Тогда придем к линейной зависимости *)
р — /\, = РосоМ9;
*) Вводя вместо М множитель М2/}М2 — 1, можно отодвинуть нижнюю границу применимости поршневой теории приблизительно до М=]2, см. книгу В. В. Болотина [0.1] 1961 г.
§ 187] ПОЛОГАЯ ОБОЛОЧКА, ОБТЕКАЕМАЯ СВЕРХЗВУКОВЫМ ПОТОКОМ 761
она совпадает с формулой (16), выведенной с помощью поршневой теории, если определять и по (16Ь).
Перейдем к случаю, когда стороны а, b панели сравнимы между собой. При этом прогибы пластинки зависят как от координаты х, так и от у. Гипотеза плоских сечений остается в силе; поперечное перемещение частицы газа надо и здесь считать происходящим вдоль нормали к деформированной поверхности пластинки. Если направление скорости потока совпадает с направлением х, то под углом 0 мы должны понимать поворот нормали в плоскости xz:
все остальные соотношения остаются в силе. Рассуждая таким образом, мы пренебрегаем эффектом отклонения вектора скорости потока от плоскости xz.
§ 187. Исходные уравнения для пологой оболочки, обтекаемой сверхзвуковым потоком
Будем в дальнейшем рассматривать пологую оболочку как слабо искривленную пластинку, считая начальные и дополнительные прогибы сравнимыми с толщиной. В качестве исходных зависимостей примем динамические нелинейные уравнения, данные в предыдущей главе (стр. 720):
-LУ4Ф = — [L(w,w) — L(w0, w0)];
(19.17)
здесь по-прежнему w и w0 — полный и начальный прогибы.
Интенсивность поперечной нагрузки q определим, пользуясь (13):
<7 = - (/> — />о) = />о [ 1 — (! + -У * ‘]* (19.18)
Знак минус перед (р — /?0) объясняется тем, что при положительном значении б нагрузка оказывается направленной вверх, т. е. в сторону, обратную оси z\ при отрицательном же 0 нагрузка будет действовать вниз (см. рис. 19.1).
Считая по (16Ь)
и шш dw
т;=м-д7'
введем (18) в уравнения (17) и дополним их температурными членами по (17.6) и (17.9). Кроме того, примем во внимание линейное демпфирование, как это обычно делается в теории колебаний. Тогда
762
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
получим следующие динамические уравнения аэротермоупругости для пологой оболочки большого прогиба *), обтекаемой сверхзвуковым потоком газа в направлении х:
h
V4 (w — wQ) = L (Ф, w) -
d2w
g dt2
dw,
•eir +
Eha
dx J J 12 (1 — fx) У4Ф = — ~ [L (w, w) — L (w0i w0)] — aV27\
V20,
(19.19)
Если представить q по формулам третьего приближения (15) в виде
dw х —f- 1 ■ «л ( dw \2 i “x. —f~ 1
Я — — Pox [m
dx
то первое из уравнений (19) примет форму
V4(w — w0) = L(Ф, w) ■
Y d2w
g dt2
dw
~dt
1 и dw Г1. x+1 u dw Л, 1 dw\l
- Ао*Мж[Ц--М-д]Г(1 + 3
Eha
V2A
12(1-ц) V *
(19.20)
Уравнения (19) и (20) являются нелинейными с двух точек зрения: с одной стороны, они учитывают геометрическую нелинейность в соответствии с основными допущениями теории гибких пластинок и, с другой, — аэродинамическую нелинейность зависимости нормального давления от скорости потока. Если принять аэродинамические соотношения линейными, получим уравнение (20) в виде
V4(w — wq) = L(Ф, w) -
у d2w dw
_J S dt
g it' T*«
Po..KA dw
Eha
dx 12 (1 — jx)
V20.
(19.20a)
Перейдем к частному случаю удлиненной пластинки, испытывающей цилиндрический изгиб. Прогиб w будет здесь зависеть только от х и t% т. е. w = w(x, t). Из напряжений в срединной поверхности надо учесть только ах=о0, причем эту величину следует считать постоянной по ширине пластинки. Второе из уравнений (19)
*) Уравнения такого типа были составлены В. В. Болотиным (сб. «Расчеты на прочность» 6, I960).
§ 1881 РАВНОВЕСНЫЕ ФОРМЫ ПЛАСТИНКИ СО СМЕЩАЮЩИМИСЯ КРАЯМИ 763
отпадает, а первое получает по (20) форму
D д4 (w — w0) d2w у d2w e dw
h дх4 °° дх2 g dt2 6 dt
1 ьл dw Гi. х + 1 шл dw f., 1 dw\“ Eha d28
+-1-М-5г11 + 3Mir)-l2(i-) !'
(19.21)
Вместо уравнения (20a) будем иметь (сжимающие напряжения считаем здесь положительными):
D d4 (w — w0) h dx4
d2w 7 d2w dw 1 dw Eha d20
~ ~ 0 ~dx* ~ ~g BTt H P(>*M ~dx 12 (1 — (x) !h? ■
(19.21a)
Если длинные края пластинки не смещаются, то величина о связана с начальным и полным прогибом по (7.44) и (7.207) соотношением
Перейдем к решению некоторых конкретных задач.
§ 188* Равновесные формы пластинки со смещающимися краями
Рассмотрим сначала удлиненную пластинку, обтекаемую с одной стороны газовым потоком при условии, что длинные края оперты
Рис. 19.7. Начальный и полный прогибы пластинки.
шарнирно и могут свободно сближаться в плоскости пластинки. Допустим, что пластинка в начальном состоянии является плоской и что она подвергается действию постоянных сжимающих усилий о0 вдоль оси х (рис. 19.7).
Сжимающие усилия могут быть вызваны общим изгибом конструкции и, кроме того, температурной деформацией обшивки.
764
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
Правда, температурные напряжения определяются теми или иными условиями сочленения обшивки с подкрепляющими элементами, между тем как мы считаем края панели свободно перемещающимися. Однако исследование случая постоянных сжимающих усилий позволяет выяснить основные особенности задачи.
Примем, далее, что прогибы малы по сравнёнию с толщиной пластинки, и будем решать задачу как линейную и геометрически, и аэродинамически. Перепишем уравнение (21а) в виде (о = о0):
D d4w h dx4
d2w
0 dx2
!(VM-gf=0; (19.23)
здесь принято e = 0 и 0 = const. Мы отмечали уже, что своеобразие задачи заключается в сочетании симметричных и антисимметричных форм изгиба пластинки. Поэтому выражение, аппроксимирующее прогиб, выберем следующим образом:
2%х
w — f\ sin —г + /2sin
(19.24)
Применяя метод Бубнова - Галеркина, выпишем уравнения
и и
У* X sin dx = 0, f X
. 2пх, *~
sin dx — 0.
а
(19.25)
Подставляя сюда (24) и интегрируя, получим:
D
~h~ J1 а0 о-/
h 2а3 D 8тс4 ha3-'2
2 а 2*2
3 h
/>о*М/2 = о,
/‘2 + зд PoMfi = 0.
Введем безразмерные параметры
А г
1 — h * 2
р0ъМа3 тz4D
(19.26)
(19.27)
под оэ понимается эйлерово критическое напряжение: оэ = K2D/a2h. Уравнения (26) принимают вид
01 = 0- I
<7*С1+(16-4ац*);2 = 0.
(19.28)
Считая параметры прогиба Сг и С2 отличными от нуля, приравниваем нулю определитель этой системы, тогда найдем:
w - о
(19.29)
§ 188] РАВНОВЕСНЫЕ ФОРМЫ ПЛАСТИНКИ СО СМЕЩАЮЩИМИСЯ КРАЯМИ 765
Это решение имеет, очевидно, смысл при 1 о* 4, так что величина о* лежит между критическими значениями, отвечающими выпучиванию пластинки по одной и двум полуволнам. Интересно отметить, что в некоторой зоне значений М критическое напряжение сжатия для пластинки, обтекаемой газовым потоком, оказывается ббльшим, чем в отсутствие потока. Таким образом, здесь газовый поток оказывает стабилизирующее действие, «выпрямляя» пластинку. Конечно, исследование закритической деформации пластинки, когда прогибы становятся сравнимыми с ее толщиной, должно проводиться с помощью общих нелинейных уравнений.
Рис. 19.8. Зависимость между давлением и сжимающими усилиями для удлиненной пластинки по точному решению (сплошная линия) и приближенному решению задачи (пунктир).
На графике рис. 19.8 пунктиром изображена зависимость по (29); кривая имеет вид петли. Каждому значению q* соответствуют две равновесные формы *) с различным соотношением и С2. При некоторой предельной величине q* эти формы сливаются; очевидно, для больших значений q* вообще не существует никаких равновесных форм, комбинирующих одну и две полуволны синусоиды. Минимизируя q* по о*, находим значения о* и q* для предельной точки: о* = 5/2, q* = 9/8. Если выбрать форму прогиба в виде комбинации трех и четырех полуволн, то получим на графике <7*(<Зо) сле” дующую петлю, заключенную между значениями о* = 9 и о* =16. Соответствующий максимум q* лежит гораздо выше первого, поэтому
*) По-видимому, устойчивой является лишь форма, относящаяся к левой части петли.
766
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
здесь с практической точки зрения достаточно рассмотреть первую петлю.
Перейдем к случаю шарнирно опертой по краям пластинки со сторонами а, Ъ, сравнимыми между собой, и предположим, что направление потока параллельно стороне а. Допустим, что пластинка сжата в том же направлении усилиями о0. Решая задачу в той же постановке, что и в предыдущем случае, запишем уравнение (20а) в виде
вводя, дополнительно к форме изгиба по одной полуволне вдоль обеих сторон, антисимметричную форму вдоль направления потока.
Выпишем обычные уравнения метода Бубнова—Галеркина; после интегрирования находим:
Если принять в первом уравнении р0 = 0, найдем величину критического напряжения:
Это выражение справедливо при условии, что размеры пластинки
к (27) безразмерные параметры о0 = о0/аэ, а = а/Ь; тогда уравнения (31) примут вид
значение Од соответствует высшей критической силе для второй из
Аппроксимируем прогиб с помощью выражения
,. %х. пу, £. 2пх пу _Лч
w = fx sin — sin -f- /2 sin —— sin, (19.30)
(1*9.3 la)
мало отличаются друг от друга: <12. Введем в дополнение
Приравнивая нулю определитель системы, находим:
§ 188] РАВНОВЕСНЫЕ ФОРМЫ ПЛАСТИНКИ СО СМЕЩАЮЩИМИСЯ КРАЯМИ 767
принятых нами форм выпучивания (две полуволны в направлении х и одна — вдоль у).
В случае квадратной пластинки получим:
= f / (зо-1)(т-~4®о)- (19.34)
Предельное значение q* будет иметь место при а0 —41/32 и равно q* = 27/32.
Мы познакомились с решением задач, относящихся к удлиненной пластинке, а также к пластинке конечных размеров, в первом приближении. Однако для этих задач можно получить и точное решение. Вернемся к исходному уравнению (23) для удлиненной пластинки и перепишем его в виде
d4w, o0h d2w, р0%М dw /inon
-3F + -5--33H D~4F = °- (19-35>
Введем обозначения:
- x — Q0ha2 9 * - р0ъМа?, * /1Л
х — —, <3q— р тс Oq, q— q —ic*q ; (19.36)
вместо (35) получим:
w]V 4- o0w + qw' — 0; (19.37)
штрихами обозначены производные по х. Соответствующее характеристическое уравнение будет
—— —— = 0. (19.38)
Один из корней его равен гх — 0, остальные находим из кубического уравнения
r*+o0r + q = 0. (19.39)
Дискриминант этого уравнения положителен, следовательно, один из корней является вещественным, два других — комплексные. Обозначим их г2 = а, /*з>4=7 ± ib. Корни уравнения связаны с его коэффициентами следующими зависимостями:
г2гзг4~ ~Я> г2 + г3 + г4 = 0, г2гз+-г1г2 + /-1г3 = а0.
Отсюда находим:
а = -2Т> 8 = /з-Г2+-о0. ? = 2Т(4Т*+>. (19.40)
Корням rv..., г4 соответствует решение уравнения (37):
w = А 4- Веах 4“ Схе+1ЬХ 4- Dxe-ib)xt
или
w = А 4- Be~2l(X 4-Сеухcos Ьх 4~ Deix sin Ьх. (19.41)
768
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
Граничные условия выпишем в виде
/72 яг л.
w = 0, —7~y = 0 при л; = 0; 1.
Подставляя сюда (41), получаем четыре уравнения, связывающие постоянные Л,..., D. Первое из них имеет вид Л-j-£-j-С = 0. Выражая отсюда А через В и С, приравниваем нулю определитель оставшихся трех уравнений:
1(Т2 + 2)2 “Ь Т2 (2 — Т2)] 7 sin 8 = у3Ъ (ch у cos S — ch 2y). (19.42)
Пользуясь (40) и (42), можно найти зависимость между о0 и qt или, иначе говоря, между а* и q*. В случае <7 = 0 получим по (42)
у = 0; при этом будет sin S = 0, 5 = тс, 2тс,... или а0 = тс2, 4тс2, что соответствует значениям а*= 1, 4,... При у Ф 0 и 1 < а* < 4 получаем сплошную кривую <7*(<з*) на рис. 19.8; она слегка отклоняется от пунктирной кривой первого приближения. Предельное значение q* по точному решению оказывается равным 1,17, что очень близко к приближенному значению 9/8= 1,12.
Аналогичное решение можно получить для пластинки с конечным отношением сторон [19.3], если исходить из уравнения (20а) и представить w в виде w = X (х) sin (ку/b). Перейдем к изучению второго типа потери устойчивости — колебательного.
Будем исходить из уравнений (21) и (21а), описывающих процесс движения удлиненной пластинки во времени. Снова рассмотрим случай, когда пластинка не имеет начальной погиби и края смещаются свободно; прогибы будем считать малыми по сравнению с толщиной. Принимая линейное выражение для давления и не учитывая демпфи-
*) Подобное уравнение для более общей динамической задачи было получено А. А. Мовчаном, а также Хеджпетом, см. ссылку на стр. 772.
4*(2 — Ь2 2fb
42£-2Г et (2 cos 5—25 sin 5—52 cos Ь) ё* (*(2 sin 5 -f- 25 cos 5—52 sin Ь)
1 — cos Ь
— er sin 5
= 0.
Развертывая этот определитель, приходим к уравнению *)
1(Т2 4“ 2)2 + Т2 (2 — 72)] s*n (е —е~т) —
— 8 fb cos 8 (ei -f e-i) -+• 8 fb (e* + *”2T) = 0
или
§ 189. Динамическая задача для пластинки со смещающимися краями 1
§ 189]
ПЛАСТИНКА СО СМЕЩАЮЩИМИСЯ КРАЯМИ
769
рования и влияния неравномерности температуры, получим следующее исходное уравнение по (21а), при о = о0:
Допустим, что в результате некоторых возмущений панель начала совершать малые гармонические колебания частоты а> около положения равновесия. Тогда прогиб w можно представить в виде
Примем для w по-прежнему аппроксимирующее выражение (24) и выпишем уравнения Бубнова — Галеркина типа (25). После интегрирования получим уравнения, аналогичные (26), но в первое из них войдет дополнительный член (—ay/2g) ш2/ а во второе (— ay/2g) (о2/2. Если принять в этих уравнениях о = 0 и р0 = 0, то придем к известным значениям первых двух частот собственных колебаний удлиненной пластинки:
Мы получили зависимость между приведенной скоростью потока q* и частотой установившихся колебаний пластинки <о*, если считать заданной величину начального сжимающего усилия о*. Примем сначала о* = 0; тогда будет
D d4w Т~дх*
w = w (х) sin (a)t -f- а).
Подставляя это выражение в (43), придем к уравнению
Введем дополнительно к (27) параметр (о* = Yтогда система уравнений типа (28) примет вид
4«*Ч + (1в —4»; —»-)Сг = 0.
(19.45)
Приравнивая нулю определитель системы, находим:
Эта зависимость изображена на графике рис. 19.9 пунктиром; по оси ординат отложены значения со*4. И здесь кривая q*\w**) имеет вид
77и
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[гл. XIX
петли. Для каждого значения q* мы получаем в пределах этой петли два различных типа колебаний, с частотами о* и о>*. При колебаниях с частотой ш*, очевидно, преобладает симметричная форма прогиба, а при частоте со* — антисимметричная. При некотором предельном значении q* = q* эти частоты сливаются, и в случае q* > q* установившиеся колебания пластинки становятся невозможными. Очевидно,
Рис. 19.9. Зависимость между скоростью потока и частотой колебаний пластинки при отсутствии сжимающих усилий.
в этом случае должно возникнуть неустановившееся движение типа флаттера, сопровождающееся (при отсутствии демпфирования) возрастанием амплитуд. Величина <7* является безразмерной критической скоростью потока. Для определения этой величины запишем условие dq*/dis)*A = 0, откуда о>*4=17/2. Соответствующее значение q* будет 45/162,81. Мы пользовались методом Бубнова — Галеркина, причем аппроксимирующее выражение для прогиба содержало два параметра. Если принять во внимание три параметра, отвечающие трем первым собственным формам колебаний, то найдем <7* = 3,68.
Обратимся теперь к общему случаю о*=£0. На рис. 19.10 дан пространственный график *), изображающий зависимость q* от о*
*) Графики рис. 19.10 и 19.12 построены Э. Д. Скурлатовым. График, аналогичный изображенному на рис. 19.11, был предложен В. В. Болотиным, см. книгу [0.1, 1961 г.], стр. 268.
§ 189]
ПЛАСТИНКА СО СМЕЩАЮЩИМИСЯ КРАЯМИ
771
Рис. 19.10. Петли статической и колебательной неустойчивост удлиненной панели.
772
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
и <!>* по (46). Здесь показана поверхность, заключающая петли <7*(<о*) при различных о*, а также петля д*(о0), отвечающая статическому выпучиванию.
На рис. 19.11 показан окончательный график (gq) по данным первого приближения. Наклонная прямая, определяющая границу флаттера, касается петли статического выпучивания в точке * = 0,9, о* =3,4. Анализ этого графика приводит к интересным выводам, касающимся поведения панели при возрастании скорости потока. Допустим, что сжимающие усилия малы и лежат ниже аэ. При возрастании д* и = const мы будем двигаться на графике на уровне некоторой линии тп. Пластинка будет оставаться плоской вплоть до момента, соответствующего точке п\ здесь должен возникнуть флаттер. Предположим теперь, что величина д* остается постоянной и
в обшивке возникают сжимающие усилия. Тогда, идя по линии 1р, мы подходим к точке р, соответствующей дивергенции панели.
Следовательно, перемещаясь на графике из области плоских равновесных форм, мы можем в одном случае пересечь границу монотонной, а в другом — границу колебательной неустойчивости.
Точное решение линейной задачи можно дать подобно тому, как это было сделано в § 188. Пользуясь обозначениями
- X
х = — > а
Рис. 19.11. График критических скоростей потока для удлиненной панели.
D Dg
перепишем уравнение (44) в виде
wiy -j- o0wf/ -f- gwr — kw = 0. Вместо характеристического уравнения (39) мы получаем здесь уравнение
г4 -\-о0г2-{-дг— /5 = 0. (19.47)
Исследование его корней *) приводит к графику, показанному на рис. 19.9 сплошной линиьй, причем величина д* оказывается ра,..ой 3,54, т. е. лежащей на 26% выше д* первого приближения и На 4% ниже д* второго приближения. Отметим, однако, что при
*) Оно было проведено А. А. Мовчаном [19.9] и Хеджпетом [19.22]; им Принадлежит также исследование случая пластинки с конечным отношением Сторон. Здесь изложение построено по [19.22].
§ 189]
ПЛАСТИНКА СО СМЕЩАЮЩИМИСЯ КРАЯМИ
773
исследовании равновесных форм панели в закритической области и, особенно, в зоне, лежащей на графике рис. 19.11 над точкой касания А, следует пользоваться нелинейными зависимостями (см. § 190).
Рис. 19.12. Петли статической и колебательной неустойчивости квадратной панели.
Обратимся к случаю пластинки с конечным отношением сторон. Решая задачу в той же постановке, что и выше, примем, что пластинка сжата вдоль оси х усилиями с0. Уравнение (20а) принимает вид
V%> —— а„ — h у w — а0 dxt
d2w
g дt*
Полагая w — w sin(atf + a), приходим к функции w = w(x, у):
(19.48)
уравнению относительно
d2w
<>№
p0%M dw 7 9— л
(19.49)
774
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
Пользуясь по-прежнему аппроксимирующим выражениемдля прогиба типа (30), выпишем уравнения Бубнова — Галеркина; тогда придем к уравнениям
2
3 ah
(19.50)
Полагая в первом уравнении о> = р0 = 0, снова находим статическое значение критического напряжения (31а). С другой стороны,
считая в обоих уравнениях с0 = р0 = 0, получим две частоты собственных колебаний:
= -Ь-рг)-5jb <I9-5I>
они соответствуют формам прогиба, фигурирующим в (30).
Последующие выкладки проведем для квадратной пластинки («а = Ь)\ тогда будет
4rc2D
2п2
л Г
Dg
5тс2
,г
Dg
§ 190]
ПЛАСТИНКА С ЗАКРЕПЛЕННЫМИ КРАЯМИ
775
Введем безразмерные параметры
<30b2h <J0 -, / аГ - р0ъМЬ*. /1П ег»\
= Ш==У Я = *!>*-• (19.52)
уравнения (50) примут вид
(1 _;01-о. I
2, /25 -л. „ <19-И)
3 Я\ Ч~“4 4оо <в jC2 = О I
Приравнивая нулю определитель этой системы, найдем:
? = (ш4+о0-1)(т-~4®0 — “4)* О9-54)
л 29 5 -
Из условия dq/da> = 0 находим: а)4=- у о0. Максимальное зна¬
чение q> которое мы считаем критическим, равно
?Ф = т(т-®о)- <19-55)
При отсутствии сжимающего усилия будет q — 63/i3. На рис. 19.12 изображен график изменения q в зависимости от о0 и а>4, аналогичный графику рис. 19.10. На рис. 19.13 показана петля статических равновесных форм и прямая (55); точка касания соответствует значениям q = 0,675 и о0=1,45.
§ 190. Пластинка с закрепленными краями
Во всех предыдущих примерах мы предполагали, что сжимающее усилие а0 является заданным и что края пластинки свободно смещаются. В реальных конструкциях, однако, панель обшивки связана с подкрепляющими ребрами. Поэтому для практических расчетов важно определить поведение панели во взаимодействии с другими элементами конструкции. Примем, например, что вдоль линий х = 0, х = а удлиненная пластинка шарнирно скреплена с настолько жесткими ребрами, что эти края надо считать неподвижными. Исследуем равновесные положения пластинки, принимая, что в начальном состоянии пластинка искривлена по полуволне синусоиды w0 = /0 sin (кх/а) и что начальная стрела прогиба /0 сравнима с толщиной пластинки*). Таким образом, здесь мы рассматриваем задачу с позиций геометрически нелинейной теории. В то же время
*) Подобная задача была решена Фыном [19.16] с учетом начальных усилий в срединиой поверхности.
776 НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ [ГЛ. XIX
аэродинамику будем считать в первом варианте линейной. Следовательно, мы должны исходить из уравнения (21а):
D d4 (w — wQ), d2w,1 шА dw ~
+ + M-ZF=°-
Величина о здесь не является заданной, а связана с прогибом соотношением (22).
Принимая для w аппроксимирующее выражение (24), находим:
•=-sr(/5-/?-Vt) т=р- <19-5в>
Выпишем уравнения Бубнова — Галеркина (25). После интегрирования придем к следующим уравнениям:
D, 2*2, 4 м, ( (19-57)
Введем дополнительно к (27) обозначение С0 — /о/ и подставим
выражение а по (56); тогда уравнения (57) примут вид
3 (С? + 4C,Cl -,) + (Cl - Со) - 4 <?*С2 = 0,1
о } (19.58)
3 (4Сг + С1С2 — С0С2) 4“ з* = 0. j
Пользуясь этой системой кубических уравнений относительно параметров прогиба С2> мы можем при заданных значениях q* и Cq определить равновесные формы панели.
Более точное решение (с учетом аэродинамической нелинейности) ведет к весьма сложным выкладкам, поэтому оно было осуществлено с помощью цифровых электронных машин *). Введем безразмерные параметры
— х — w г /о — 12л2
х——, W Y' t*o —Т' 0 — 0
12(1—ц2)хМ а’..Л
Я = Ро — -ЕЪ • Ч = М-
(19.59)
Если считать х=1,4, то основное уравнение (21), содержащее три члена ряда в выражении для q, примет вид (черточки над безразмерными величинами опущены)
dUw — w0). d2w, dw h, 3 dw Л. 1 dwY\ Л /ЛГх ~ЛЧ
■ dx* +a-5 + [1+57i-57l1 + 3)J==0- <1960>
*) Это решение для удлиненной пластинки и панели с конечным отношением сторон (см. ниже) лринадлежит А. Ю. Биркгану.
§ 190]
ПЛАСТИНКА С ЗАКРЕПЛЕННЫМИ КРАЯМИ
777
Выражение (22) приводится к следующей форме:
1
= е/Ш-(£)’Ь
(19.61)
коэффициент (1—j**) здесь опущен. Как видно из (60), параметр tj позволяет здесь учесть высшие члены разложения аэродинамической нагрузки в ряд по (15). Представим (60) и (61) в конечных разностях, пользуясь симметричными операторами второго порядка точности по (7.238) и (7.239). В /-м узле уравнение имеет вид
wt_2 — + Bwt — Awi+l -f- wi+2 = Clt
(19.62)
m
wo
50
где A = 4-f-os2, B = 6-1-2os2. Под понимается шаг интегрирования, Ct зависит от аэродинамической нагрузки и начального прогиба.
Величина о определяется численным интегрированием, например, по формуле Симпсона. Таким образом, мы приходим к системе нелинейных алгебраических уравнений, которая решается последовательными приближениями.
На рис. 19.14 показана зависимость между величиной q и прогибом в центре панели = fjh при С0 = 5 и т] = 0. Кривая 1 соответствует результатам машинного счета, кривая 2 получена методом Бубнова — Г алеркина по (58). Как мы видели, величина т\ учитывает здесь аэродинамическую нелинейность; случай = 0 отвечает линейной аэродинамике. Точки правого участка ветви определить с помощью машинного счета не удалось; видимо, для этого должны быть найдены специальные приемы (см. сноску на стр. 765).
На рис. 19.15 показана зависимость q(o) при различных значениях rj. Напомним, что сжимающее напряжение о здесь является результатом изгиба панели. Как видим, учет аэродинамической нелинейности ведет здесь к снижению предельной точки *). Формы
/
м~
V
\
Рис. 19.14. Равновесные формы панели с закрепленными краями.
*) На это обстоятельство было указано В. В. Болотиным (Научн. докл.
высщ. щк., Маш. и приб., № 3, 1958).
778
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТИ
[ГЛ. XIX
изогнутых поверхностей, соответствующие различным значениям q при т = 0,2 представлены на рис. 19.16.
Перейдем к случаю панели конечных размеров. Рассмотрим квадратную в плане шарнирно опертую панель со стороной а, имеющую начальный прогиб wQ = /0 sin (кх/а) sin (ку/а) и обтекаемую со стороны выпуклости потоком с параметрами М, р0. Примем, что края панели могут смещаться, оставаясь прямолинейными. Будем решать
Рис. 19.15. Определение равновесных форм панели с учетом аэродинамической нелинейности.
эту задачу, учитывая одновременно геометрическую и аэродинамическую нелинейность, без разложения величины (р — р0) в ряд; тогда будет (при х=1,4)
где по-прежнему*) ri=Mh/a. Принимая безразмерные параметры
- х — у — w г /л
- Ф рйа< 1 (19-63>
ф = П — ZO—. с — w Eh2 * Р Eh*' L 12(1—t*2)'
*) Здесь параметр -ц является единственной величиной, отвечающей скорости потока.
§ 190]
ПЛАСТИНКА С ЗАКРЕПЛЕННЫМИ КРАЯМИ
779
приводим систему уравнений (19) к виду (черточки над w, Ф и т. д. опущены)
здесь ф, ср — функции, зависящие от начального прогиба. Уравнения (64) и (65) могут быть представлены в конечных разностях и вычисления проведены с помощью цифровых машин, как в § 90.
Решение динамической задачи для удлиненной панели и панели с конечным отношением сторон также может быть выполнено с помощью цифровых машин. Для этого используется путь, описанный в предыдущей главе (§ 178). Если обратиться для примера к уравнению (60), то оно преобразуется к виду
лебаний *). Сеточная область строится
в общем случае в пространстве х, у, t. Шаг по времени выбирается из условия устойчивости решения разностных уравнений. В результате вычислений были получены следующие результаты. Допустим, что панель с начальной погибью помещена в поток с параметрами т), р. Поведение панели в значительной мере зависит от значений tj, р и коэффициента демпфирования. При относительно малых tj, р колебания быстро гасятся. Когда параметры rj, р достигают некоторой критической величины, амплитудные значения прогибов и напряжений имеют тенденцию к возрастанию или, по крайней мере, не убывают, несмотря на наличие демпфирования; это соответствует явлению флаттера. Особенно интересной получается картина
cV*w = L(w, Ф) + /ф — (l — -i + (19.64)
V4® = — у L(w, w) — ср; (19.65)
Здесь “ ЛПЛЯиЛШ1Л ~ DunoWeuiiau Л* (ft
q-40
введен]
Рис. 19.16. Формы изогнутой поверхности панели при различных q.
величина е учитывает демпфирование ко-
*) В уравнении (66) черточки над t и е опущены.
7S0
НЕКОТОРЫЕ ЗАДАЧИ АЭРОУПРУГОСТЙ
[ГЛ. XIX
при сжимающих усилиях, значительно превышающих критическую величину. На протяжении каждого периода колебаний прогиб меняет знак, так что панель должна совершать один хлопок за другим. Подобный процесс колебаний с большими амплитудами можно охарактеризовать как бурный флаттер*). Если проследить за какойлибо узловой точкой панели, то окажется, что она перемещается во времени вдоль пролета. Таким образом, здесь отчетливо наблюдается явление так называемых бегущих волн. Желательно в дальнейшем провести более полное решение динамической задачи для панелей различного очертания и при разных условиях закрепления, а также осуществить дополнительные экспериментальные исследования.
Здесь мы остановились лишь на некоторых задачах, относящихся к флаттеру плоских и слегка искривленных пластинок, с определением аэродинамических сил по поршневой теории. Обзор литературы по этому вопросу, а также о границах применения поршневой теории, содержится в работах Гудмана и Раттайи [19.18] 1960 г. и В. В. Болотина ([0.1] 1961 г. и [21.1] 1962 г.). Влияние пограничного слоя на критическую скорость флаттера обсуждается в статье Майлса [19.26] 1959 г., влияние магнитного поля — в статье
А. Д. Лисунова (Журн. прикл. мех. и техн. физ. № 4, 1960).
Понятие панельного флаттера распространяется также на автоколебания замкнутых цилиндрических оболочек, сопровождающиеся образованием местных вмятин. Эта задача исследовалась В. В. Болотиным [19.3], Майлсом [19.26], Р. Д. Степановым [19.11],
А. А. Мовчаном [19.9], Ю. Ю. Швейко [19.12] и другими.
Вычисления и эксперименты показывают, что практически явление панельного флаттера опасно для относительно тонких пластинок и оболочек (см. экспериментальные данные Г. Н. Микишева
[19.8] и Э. И. Григолюка, Р. Е. Лампера, Л. Г. Шандарова, Труды Ереванской конф. по теории оболочек 1962 г.); поэтому исследования, основанные на геометрически нелинейной теории, представляют особый интерес. Это относится, в особенности, к случаю замкнутых цилиндрических оболочек.
*) Он наблюдался в экспериментах, описанных Фыном [19.16J, а также в опытах В. Л. Агамирова.
ГЛАВА XX
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
§ 191. Основные понятия
В предыдущих разделах книги мы рассматривали, по существу, некоторые модели конкретных конструкций, отражающие с тем или иным приближением физические свойства материала, геометрические характеристики элементов, условия нагружения. В некоторых случаях мы пытались приблизить выбранную нами модель к реальным конструкциям, учитывая переход упругих деформаций материала к упруго-пластическим, начальные неправильности формы элемента или характер изменения нагрузки в процессе выпучивания, изучая устойчивость в большом и т. д. Тем не менее и здесь мы оставались в рамках определенных схем. С индивидуальными конструкциями мы сталкивались лишь тогда, когда приводили окончательные данные отдельных экспериментов, хотя некоторые характеристики опытов оставались для нас неизвестными либо не были отмечены.
Все это вполне естественно: характеристики материала данного элемента конструкции, начальные несовершенства, реакции других частей конструкции, прикладываемые нагрузки являются случайными величинами. Располагая известными теоретическими результатами или данными серии экспериментов, мы можем судить о поведении какой-либо новой для нас конструкции лишь с известной вероятностью. В некоторых случаях мы можем считать наши суждения практически достоверными, в других — нет. Поэтому очень важно воспользоваться статистическими методами и попытаться установить вероятность реализации того или иного полученного нами вывода для конкретных конструкций.
Приведем некоторые положения и формулы теории вероятностей, которые понадобятся нам в дальнейшем *). Событие, наступление
*) См. Е. С. В е н т ц е л ь, Теория вероятностей, изд. 2, Физматгиз, М., 1962; В. С. П у г а ч е в, Теория случайных функций, изд. 2, Физматгиз, М., 1960 и др. В настоящем параграфе изложение построено в основном по книге Б. Р. Левина, Теория случайных процессов и ее применение в радиотехнике, изд. 2, «Советское радио», М., 1960.
782
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
или ненаступление которого нельзя определенно предсказать, называется случайным. Таким случайным событием мы можем считать результат отдельного эксперимента. Допустим, что после п экспериментов, проведенных при определенных условиях, появилось т раз случайное событие А. Отношение
V = f- (20.1)
называется относительной частотой появления события А. Установлено, что эта частота при достаточно большом числе опытов стабилизируется около некоторой величины, которая называется вероятностью события при данных условиях. Будем обозначать вероятность через Ф. Очевидно, частота события и его вероятность должны удовлетворять неравенствам
0<v<l, 0<Ф<1. (20.2)
Вероятность достоверного события равна единице, невозможного — нулю. Случайные события называются несовместимыми, если не могут произойти одновременно, и независимыми, если вероятность одного из них не зависит от того, произошло второе или нет.
Если события Av Л2,..., Ап являются несовместимыми, то вероятность появления одного из них равна сумме вероятностей каждого события в отдельности:
Ф(ЛХ, или А2,..или Ап) = Ф(Аг)-\-Ф(А2)-{-... +Ф(ЛЯ). (20,3)
Если события Bv В2,..., Вп являются совместимыми, но независимыми, то вероятность одновременного их наступления равна произведению вероятностей каждого события:
Ф(Вг. и В2% и Вп) = Ф(Вг)ХФ(В2)Х --- ХФ(Л). (20.4)
Результат отдельного эксперимента представляют также с помощью некоторой случайной величины 5; таким образом, вместо качественной характеристики опыта вводится его количественная оценка. В некоторых случаях возможные значения случайной величины можно заранее перенумеровать с помощью натурального ряда чисел; такая величина является дискретной. В других случаях случайная величина может принимать любое значение на некотором интервале; тогда вероятность того, что величина примет заданное значение, равна нулю. Можно, однако, определить вероятность того, что такая случайная величина будет находиться в некотором интервале возможных значений.
Допустим, что случайная величина £ может принимать любые действительные значения от —оо до +°°- Тогда важно бывает установить вероятность того, что £ не превосходит некоторого заданного уровня х9 т. е. установить вероятность выполнения нера¬
§ 191]
ОСНОВНЫЕ ПОНЯТИЯ
783
венства £ < х. Эта вероятность носит название интегральной функции распределения случайной величины £ и зависит от значения х. Обозначим функцию распределения через F (х):
/>(*) = Ф (5 <*). (20.5)
Вероятность того, что величина £ будет находиться в интервале
между значениями хх и лг2, равна
ф (*1 < 5 < Х2) = F (*2) — F (лгг); (20.6)
всегда должно быть F (х2) F (дгг) при х2> xv
Предположим, что случайная величина изменяется непрерывно и что интегральная функция распределения также непрерывна и дифференцируема. Тогда можно ввести новую важную характеристику
Г(*)‘
1
У
6)
Рис. 20.1. Графики (а) плотности вероятности и (б) интегральной функции распределения.
случайной величины, называемую плотностью вероятности или дифференциальной функцией распределения, равной
dF(x). dx '
/(*) =
(20.7)
так как функция F (х) является неубывающей с возрастанием х, то всегда будет /(*)>. 0.
Из предыдущих соотношений вытекает:
X
Ф ( < X) = F (*) = f / (X) dx, (20.8)
— ОО
X2
Ф
(*! < 5 < *2) = f / (*) dx.
(20.9)
На рис. 20.1 изображен вид дифференциальной и интегральной функций распределения f(x) я F(x). Вероятность того, что £ ежчт
784
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
между значениями хх и х2 (по (9)), графически отвечает заштрихованной площади на рисунке 20.1, а, расположенной в этих пределах* Так как вероятность того, что величина ? примет любое значение от —оо до -(-оо, равна единице, то полная площадь под кривой плотности вероятности равна
J f(x)dx = 1.
— ОО
Соответственно интегральная
кривая на рис. 20.1, б
между осью абсцисс и прямой
Г = 1. Значение Е — х
плотность вероятности максимальна, называется модой.
/(*)
0,5
¥
о,з\
0,2 \
0,1 \
■ ■ 1 /Vr- £4
(20.10)
при котором
-3 -2
-1 О 1
I— 68,3%—\
95,67. 99,71 Рис. 20.2. Нормальный закон распределения.
На практике часто встречаются случайные величины, имеющие так называемый нормальный закон распределения:
f(x) = ce 2s2. (20.11)
Коэффициент с находится из условия (10); он оказывается равным
с = тЛ==- (20.12)
V2«2
Мода нормального закона распределения равна а\ на рис. 20.2 отложены значения f (х) в зависимости от (л; — a)/s. Как легко видеть, вторая производная d2f(x)jdx2 обращается в нуль при х = а±;
§ 191]
ОСНОВНЫЕ понятия
785
следовательно, при этих значениях х кривая f(x) имеет точки перегиба. Максимальное значение f(x) равно
/ (а) = /max — = С' 13)
На рис. 20.2 показано, какой процент общей площади под кривой распределения занимает площадь полосы между линиями а ± s, а ± 2s, а ± 3s. Судя по этим данным, можно практически считать* что любая случайная величина, распределенная по нормальному закону, лежит в пределах а ± 3s. Вероятность такого события равна 0,997, и его поэтому можно принимать практически достоверным. Чем больше параметр s, тем более пологими оказываются кривые f(x) и тем значительнее разброс случайной величины. На рис. 20.3 изображены кривые f(x) и F (х) для различных параметров s.
Рис. 20.3. Плотность вероятности (а) и интегральная функция (б) для нормального закона при различных параметрах s.
Одной из характеристик распределения случайной величины является так называемое математическое ожидание или среднее значение, равное
ОО
т{%)= j xf(x)dx. (20.14)
— ОО
Величина /я(£) численно равна статическому моменту площади, лежащей между линией f(x) и осью абсцисс, относительно оси ординат. Но так как сама площадь равна единице, то выражение (14) одновременно определяет абсциссу центра тяжести площади. Отклонение случайной величины от математического ожидания равно « — *«)]•
786
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
Выражение
£>(£)= f (x — m(%)ff(x)dx
(20.15)
представляет собой математическое ожидание или среднее значение квадрата отклонения и носит название дисперсии величины £. Вычисляя квадратный корень из дисперсии, т. е. /D(£), находим среднеквадратичное отклонение или так называемый стандарт закона распределения.
Для нормального закона распределения после простых вычислений находим:
т = а, D — s2. (20.16)
Следовательно, под а надо понимать математическое ожидание (и вместе с тем моду), а под 5 — среднеквадратичное отклонение или стандарт нормального закона распределения. Для распределения, симметричного относительно оси ординат, математическое ожидание равно нулю.
б)
/
f(y)
/Ж
Рис. 20.4. Плотности вероятности / и <р для величин 5 и 1) = 1) (£).
В дальнейшем нам придется определять плотность вероятности <р(>0 случайной величины 77, если известна зависимость 77 = £/(£) от другой случайной величины £ и задана плотность вероятности f(x) этой второй величины (рис. 20.4). Допустим, что имеется однозначное соответствие между £ и г\. Если £ лежит в пределах х < £ < <x-\-dxt то отсюда вытекает неравенство У<?]<У + У при y = U (х). Вероятности выполнения этих неравенств равны между собой. Но так как эти вероятности соответствуют заштрихованным площадям f{x)dx и <р (y)dy на рис. 20.4, а и б, то можно записать равенство
/ (л:) dx = <р (у) dy. (20.17)
§ 191]
ОСНОВНЫЕ понятия
787
Отсюда находим простейшую формулу преобразования вероятностей:
(20.18)
dx
Напоминаем, что здесь предполагается наличие однозначной обратной функции x = V(y). Так как всегда <р(у)0 и /(*)<> 0, то в (18) надо подставлять абсолютное значение dy/dx.
Допустим, что величина £ распределена по нормальному закону (11):
/(*) =
1
(■r-g)2
2s2
(20.19)
Если вторая случайная величина г\ линейно зависит от первой:
т] = £, y — kx, (20.20)
то по (18) получаем:
1
У2it (sA)2
(у -ka)* Рис. 20.5. К определению
е 2(ks)* в (20.21) двумерной функции распределения.
Таким образом, математическое ожидание, стандарт и дисперсия для новой величины т) равны
ax = kat sl = ks, Dl — k2D. (20.22)
Преобразование сводится к изменению масштабов вдоль координатных осей в k раз.
Перейдем к рассмотрению двумерной задачи, когда определяется вероятность одновременного выполнения неравенств £ < х,
т) < у для двух зависимых, в общем случае, случайных величин £
и т]. Обозначим интегральную функцию через F(xt у):
Ф (S < *, т] < у) = F (дг, у). (20.23)
На графике рис. 20.5 дана геометрическая интерпретация неравенств, входящих в (23): координаты (5, т]) точки на плоскости не должны превышать уровней х и у, т. е. должны находиться в пределах заштрихованной площади. Двумерная плотность вероятности f(x, у) определяется как смешанная вторая производная от F(x, у):
fix у)т= У)
ЦХ.у)— дхду.
(20.24)
788 ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ [гл. XX
Двумерную плотность вероятности можно геометрически изобразить в виде поверхности, расположенной над плоскостью х% у. Вероятность F (х; у) по (23) равна
X у
F(x,y)=f f/(x,y)dxdy. (20.25)
— ОО —оо
Считая верхние пределы лг—>оо и оо, приходим к'формуле
ОО оо
/ f f(x, y)dxdy=l. (20.26)
—оо —оо
Следовательно, объем под поверхностью распределения равен единице. Допустим, далее, что в (25) второй из пределов оо; тогда двухмерная плотность переходит в одномерную, относящуюся к величине £:
X оо
F(л:, +оо)= J J/(*, y)dxdy — Fx(x). (20.27)
—оо —оо
Производная от этой величины равна плотности вероятности fx(x):
оо
fx (*) =//(■*• У)аУ- (20.28)
— ОО
Если случайные величины и т] независимы, то по правилу умножения вероятностей получим:
F (х. у) = Ф (5 < т] < у) = Fг (х) F2 (у), (20.29)
где Fl(x)t F2(y)—интегральные функции распределения для каждой из величин и г\. Такое же соотношение имеет место для плотностей вероятности:
/(*. y) = fl(x)f2(y). (20.30)
Допустим, что известны математические ожидания а, Ъ двух случайных величин £,
оо оо
а~ f xfl(x)dx, b— j yf2(y)dy. (20.31)
—OO —OO
Найдем математическое ожидание для суммы этих величин С = + '*]:
оо оо
С = f f (X + у) f (х, у) dx dy. (20.32)
— ОО —ОО
§ 191] Основные понятий 789
Сопоставляя (28) и (31), имеем:
оо оо оо оо
xf(x, y)dxdy, b = J1 yf(x,y)dxdy. (20.33)
— CO — oo
Следовательно, величина с равна сумме математических ожиданий:
с = а-\-Ь. (20.34)
Пусть, далее, заданы дисперсии Dv D2 независимых случайных величин S, у\:
оо оо
D,= f(x — a)2f1(x)dx, D2= f (y — 6)2f2(y)dy. (20.35)
— OO —oo
Определим дисперсию суммы C = как математическое ожидание
величины (С — с)2 или ( + ?]— а — Ь)2. По (34) имеем:
D( = m [(5 — а) + (т] — Ь)\\ (20.36)
или
D (С) = т (5 — a)2 +m(ri — b)2 2т (£ — a)(rj — b). (20.37)
Для независимых величин последнее слагаемое обращается в нуль, так как для каждого из множителей (5 — а) и (tj — b) соответствующий интеграл равен нулю, например:
оо оо
J f (х — a)f(x, y)dxdy= J(х — a)fl(x)dx = 0. (20.38)
— OO —oo —oo
Окончательно находим, что величина D равна сумме дисперсий:
D (С) = D«)+ £>(*)). (20.39)
Предположим, что величины и г\ независимы и что каждая из них распределена по нормальному закону:
(х-а)* (у-6)*
/l(*)=-r4=Te : (20.40)
у 2ks\ У 2ns
тогда двумерная плотность вероятности по (30) равна
_1 Г (х-а)2 I (У“Ь>21
i”2L 4 4 1.
/(*• *>= 2г* L 1 2 J; <20-41>
соответствующая /(л:, у) поверхность с сечениями, параллельными координатным плоскостям, показана на рис. 20.6.
790
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
Плотность вероятности для суммы величин x-j-y = z по (39) и (34) будет равна *)
1 1
f=2e'2 i ’ (20‘42>
где
c = a + b, s2 = s\-\-sl (20.43)
Пусть'требуется по двумерной функции распределения f(xv х2) случайных величин и £2 определить двумерную функцию распределения <р(Ух» у2) случайных величин и т]2, являющихся функциями
ffcy)
Рис. 20.6. Сечение поверхности, соответствующей двумерному нормальному закону распределения.
первых: Ч1 = *Л(?1* У» Ъ = 2(1» У; если Функции ? и г\ взаимно однозначны, будем иметь:
‘PO'i* y2) = /Oi- *2)\v\; (20.44)
под V понимается определитель, составленный из производных:
дхх dxt ~<>У2 дх2 дх2 дуГ
*) Непосредственный вывод формулы (42) из (41) см. в книге С. Н. Бернштейна «Теория вероятностей», М., 1946, стр. 270.
d(*i. х2) д (У. Уг)
(20.45)
§ 192] НЕСУЩАЯ СПОСОБНОСТЬ СЖАТЫХ СТЕРЖНЕЙ 791
Если преобразуются п случайных величин, то будет
?(У1. У2 У„) = /(* 1. 2 я)11; (20.46)
определитель V составляется по аналогии с (45):
у _ д(х1г х2,хп) (20.47)
d(yi, у*,.... ул) v '
Обратимся к приложению статистических методов для определения несущей способности реальных стержней, пластинок и оболочек.
§ 192. Несущая способность сжатых стержней
Как мы видели, несущая способность сжатых стержней сильно зависит от начальных неправильностей в форме стержня, от эксцентриситета в приложении нагрузки, условий закрепления и т. д. Эти факторы являются случайными, и для них могут быть установлены некоторые законы распределения. Для функции этих величин — несущей способности — можно также найти известный закон распределения и, таким образом, установить вероятность исчерпания несущей способности в тех или иных условиях.
В работе А. Р. Ржаницына [20.5] был предложен следующий подход к этой задаче. Предположим, что ось шарнирно опертого стержня имеет начальную погибь, изменяющуюся по закону w0 = /о sin (тсл;//). Составляя дифференциальное уравнение изогнутой линии
El(-d*w
dx2
dx2
Pw,
где w и w0 — полный и начальный прогибы (рис. 20.7), и полагая w = / sin (bxjl), приходим к известной формуле (1.182):
/о
1-
Р12
(20.48)
п2Е1
Рис. 20.7. Стержень с начальной погибью, подвергающийся эксцентричному сжатию.
Определим напряжение ог в краевом волокне для среднего сечения:
°1 = £ + ТГ’ (20-49)
где F и W — площадь сечения и момент сопротивления сечения. Вводя обозначение для среднего напряжения а0 = PfF и для радиуса
792 ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ [гл. XX
ядра сечения р = W/F, находим:
<20'50)
где т — /0/р. В случае, если сила приложена с эксцентриситетом е0, усиливающим начальную кривизну, можно положить т =(f0-j-е0)/р.
Анализ экспериментальных данных показывает, что величина т тем выше, чем больше гибкость стержня. Воспользуемся формулой *)
т=а -fp(-i)2 (20.51)
и предположим, что значения / и р, а также нагрузка заданы, а величины аир являются случайными и что они распределяются по нормальному закону с центром (модой) в начале координат. Тогда величина ох будет также случайной. Будем считать, что материал подчиняется закону Гука вплоть до площадки текучести. Тогда несущую способность стержня можно определить по напряжению о0, при котором в крайних волокнах достигается предел текучести **).
Определим разность между «абсолютной» несущей способностью стержня, соответствующей пределу текучести от, и фактической несущей способностью:
(а + Р1)я2£
R — от — а0 — в0 ъ2Е — з0\г ’ (20.52)
Величина R характеризует как бы неиспользованную часть абсолютной несущей способности стержня.
Поставим перед собой цель определить закон распределения R. Он будет нормальным в том случае, если R выражается через аир линейно. Поэтому приближенно примем R в виде
R z==‘ оТ — 6q —j— А<х —— BQ (20.53)
и определим А и В как частные производные от R по а и р:
в={{)'*■ <20И>
Центр распределения R будет
aR = oT — о0, (20.55)
*) Такая зависимость была предложена А. Р. Ржаницыным [20.5]; близкая к этому формула рекомендуется также Доннелом и Ваном [11.30а].
**) В уточненном решении задачи следует также принять во внимание, что нагрузка Р и предел текучести материала ат являются случайными величинами, и, кроме того, учесть возможные изменении в способе закрепления концов стержня [20.5J.
§ 192]
НЕСУЩАЯ СПОСОБНОСТЬ СЖАТЫХ СТЕРЖНЕЙ
.793
а стандарт по (22) и (43) равен-
+(f)‘s5’ <20-56>
где sa и — стандарты распределений величин аир.
Введем обозначения:
Под ф понимается коэффициент снижения несущей способности стержня по сравнению с пределом текучести, или, иными словами, коэффициент снижения допускаемого напряжения. Величина 7 определяет разброс отклонений предельных напряжений от предела текучести по отношению к среднему отклонению; чем выше 7, тем этот разброс меньше. А. Р. Ржаницын рекомендует принять ориентировочное значение у для стержней несимметричного сечения равным 3, а для стержней симметричного сечения равным 3,2. Это означает, что точки перегиба кривой распределения будут лежать в случае несимметричного сечения на расстояниях от точки /? = О, равных 2/3(от — с0) и %(от — Oq). При симметричном сеченйи вероятность достижения предела текучести в крайних волокнах получается большей; этим объясняется повышение у. Под Хт понимается гибкость идеального стержня, соответствующая критическому напряжению, равному пределу текучести от. Наконец, параметр I* равен отношению радиуса инерции к радиусу ядра сечения; для прямоугольного сечения будет е = Уз. для двутаврового сечения при изгибе в плоскости стенки Пользуясь (57), приводим выражение (56) к виду
1 — ф Х2ф ~Г = Va. + WV (20.58)
2 2
где Da = sa, D — s — дисперсии распределений а, р.
Задаваясь значениями Da, Dp, Хт и у, определяем из (58) зависимость между коэффициентом ф и гибкостью стержня X при у — 3, £ = 13, Хт«90. На рис. 20.8 и 20.9 приведены кривые *) ф (X) для стали Ст. 3 при различных значениях Da; принято Dp = 0 и Dp = 25 • 10“12. При Da = Dp = 0 по уравнению (58) получаем ф= 1. Однако по графику 20.8 при Da = Dp = 0 находим ф = 0,7. Это объясняется тем, что при построении кривых рисунков 20.8 и 20.9 учтен также возможный разброс значений предела текучести стали по нормальному закону. Было принято, что отношение дисперсии
*) Эти графики взяты из работы [20.5].
794
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
распределения от к среднему значению равно 0,1. Если принять Da = Dp = 0, то найдем (1 — ф)/*у = 0,1; при = 3 будет ф = 0,7.
Приняв определенное значение 7, мы фиксируем тем самым закон распределения величины /?. Теперь мы можем определить вероятность Ф исчерпания несущей способности стержня из условия, что
Рис. 20.8. Коэффициент снижения несущей способности </ для стержней различной гибкости А при дисперсии Dp = 0.
величина R обращается в нуль. На рис. 20.10 показана примерная кривая распределения величины
тс 2Еап
х — т
п2Е — q0\2
R — (oT — о0).
(20.59)
Если эта величина делается равной [—(ат — а0)], то несущую способность стержня надо считать исчерпанной. Соответствующая вероят-
t
0,7 0,6 0,5 0А 0,3 0,2 0,1
сг»
II
<
r=J
Вв-25Ю',г
и
По Зил еру
- 0J 0,15 0.2 0.3 0,4 Da= 0,5
- • 1 1 1
' 50 100 150
200 Л 250
Рис. 20.9. Коэффициент ф при дисперсии D3 = 25 • 10 12.
ность равна площади, заштрихованной косыми линиями на рис. 20 10, или, иными словами, разности между полуплощадью под всей кривой распределения, равной г/2, и площадью, заштрихованной
§ 192]
НЕСУЩАЯ СПОСОБНОСТЬ СЖАТЫХ СТЕРЖНЕЙ
795
вертикальными линиями. Находим:
(20.60)
или
или
1 1 г 1
Ф==4-тЫ* 2=4-Ф(т).
о
(20.61)
где у = x/sR. Определяя интеграл Ф() по таблицам, находим, что значению 7 = 3 соответствует вероятность Ф = 0,135%, а у == 3,2 — вероятность 0,067%. Как видим, значение у = 3,2 получено с учетом того, что при симметричном сечении вероятность появления текучести должна быть вдвое больше, чем это вытекало из предыдущих выводов.
Рис. 20.10. К определению вероят- Рис. 20.11. Предельная точка для
ности исчерпания несущей способ- эксцентрично сжатого стержня
ности стержня. в упруго-пластической стадии.
Мы исходили в приведенном выводе из того, что несущая способность стержня исчерпывается при достижении наибольшим напряжением предела текучести. Более обоснованно было бы исходить из данных главы И, относящихся к эксцентричному сжатию стержней в упруго-пластической стадии. Как мы видели, каждому значению эксцентриситета (а следовательно, и каждой величине начальной стрелы прогиба С0) на диаграмме а0(С0) соответствует некоторая предельная точка, определяющая истинную несущую способность (рис. 20.11). Допустим, что для данного материала определена зависимость максимального среднего напряжения о0> тах от возмущающих факторов: эксцентриситета и начальных неправильностей формы
стержня. Тогда, пользуясь тем или иным законом распределения для возмущающих факторов, можно установить закон распределения величины истинной несущей способности и сравнить ее, например, с несущей способностью, соответствующей пределу текучести от.
т
%
796
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
Правда, закон распределения несущей способности уже не будет нормальным, так как зависимость <з0, тах от эксцентриситета и начальной погиби нельзя принять линейной. Задача становится при этом более сложной и может быть решена тем путем, какой указан ниже в применении к оболочкам. Желательно, чтобы именно такой подход к задаче был принят в дальнейших исследованиях.
§ 193. Влияние начальных неправильностей на поведение оболочек. Цилиндрическая панель
Применение статистических методов является особенно важным при рассмотрении устойчивости упругих систем в большом. Как мы видели на примерах оболочек, подвергающихся различного рода нагрузкам, влияние возмущающих факторов на их поведение и несущую способность очень велико. Оболочки, а также некоторые другие системы, склонные к прощелкиванию, чувствительны к самым незначительным неправильностям в форме срединной поверхности, эксцентриситетам в приложении нагрузки, погрешностям в технологии изготовления и т. д. Этим объясняется сильный разброс в критических нагрузках для реальных конструкций и при экспериментах. Обоснованный анализ таких экспериментальных данных и попытки предсказать поведение элементов реальных конструкций, по-видимому, невозможны без вероятностного подхода.
Будем в дальнейшем условно считать, что опасным событием для оболочки является выпучивание в большом*). Очевидно, вероятность этого события при нагрузке, меньшей нижней критической величины, равна нулю, а при нагрузке, достигшей верхней критической величины, равна единице. Допустим, что верхняя и нижняя нагрузки определены для оболочки идеальной формы и для оболочек, имеющих различные начальные несовершенства, и вместе с тем при разных граничных условиях. Тогда статистический подход может заключаться в том, чтобы по заданным вероятностным характеристикам начальных неправильностей и условий закрепления оболочек определить вероятностные характеристики критических нагрузок. Задача сводится, таким образом, к преобразованию вероятностей. Очень важно при этом условиться о том, как ведет себя оболочка при изменении нагрузки. Один из подходов к решению задачи состоит в следующем. Будем здесь считать, что нагрузка меняется сравнительно медленно и что деформация оболочки непрерывно следит за нагрузкой. Очевидно, такая система является безынерционной, и поведение оболочки полностью определяется нелинейной диаграммой равновесных состоя¬
*) Это соответствует приведенным выше теоретическим и экспериментальным данным. Более общая постановка задачи заключается в том, чтобы учесть возможность наступления других опасных состояний, например перехода из упругой области в пластическую и т. д.
§ 193]
ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
797
ний p(f) такого типа, какая изображена на рис. 20.12, а. Подобный подход к задаче можно охарактеризовать как статический *). Необходимо, далее, установить, какая из ветвей диаграммы рис. 20.12, а используется при решении задачи, с тем чтобы зависимость p(f) была однозначной. Будем принимать, что при возрастании нагрузки от р < рн равновесные состояния оболочки соответствуют ветви ОЛ; при достижении нагрузкой значения рв происходит хлопок. Если же нагрузка падает от значения р > рв, то надо пользоваться ветвью СВ;
Рис. 20.12. Диаграммы равновесных состояний оболочки.
при р = Рн осуществляется обратный хлопок. Неустойчивые состояния, отвечающие ветви АВ% вообще не реализуются. Таким образом, строго говоря, состояние оболочки зависит от истории нагружения. В дальнейшем будем для простоты считать, что нагрузка всегда является возрастающей и что, следовательно, состояния оболочки однозначно определяются диаграммой по рис. 20.12,6.
Применим такой подход к решению задачи прежде всего к случаю квадратной цилиндрической панели, шарнирно опертой по краям и сжатой вдоль образующей усилиями р (см. рис. 11.61). Примем, что все важнейшие возмущающие факторы сведены к эквивалентным начальным неправильностям в форме срединной поверхности. Будем считать панель системой с одной степенью свободы, при этом формулы преобразования вероятностей значительно упрощаются. Если аппроксимировать полный и начальный прогибы с помощью выражений (17.25) и ввести безразмерные параметры по (17.31), то зависимость между сжимающим усилием р* = pb2jEh2 и стрелой прогиба С
*) Или, лучше сказать, как квазистатический\ с его помощью могут быть решены и некоторые динамические задачи. Этот подход принадлежит
В. В. Болотину [20.1].
798
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
примет вид (17.55). Для квадратной пластинки (Х=1) получим:
Р' = [< ид + Т- С (5С + Ч • (2°. 62)
где k = b2/Rh; под р* ид понимается верхнее критическое усилие для оболочки идеальной формы, под С0— стрела начального прогиба. Примем k = 12. Кривые р* (С), построенные по (62) для различных значений С0 при такой величине k, приведены в книге [0.3], стр. 288;
они имеют такой же характер, что и кривые рис. 17.13. Определим с помощью этого графика значения верхних критических усилий /?* нач для оболочек с различными начальными прогибами С0. На рис. 20.13 изображен график С0 (/>*); величины р\ нач лежат в пределах между нагрузкой Р\, нач = 3>3> отвечающей Cq = = 0,25, и верхней критической нагрузкой р* ид = 7,2 для идеальной оболочки. При С0 > 0,25 прощелкивания обо¬
лочки не происходит. На д* рис. 20.13 даны также абсо-
Рис. 20.13. Данные для преобразования ™bl.e значения производной
функции распределения в случае сжатой •
цилиндрической панели. Таким образом, нами уста¬
новлена зависимость между верхними критическими усилиями и начальным прогибом для той области, где имеет место прощелкивание оболочки. Задача ставится теперь таким образом: по заданным вероятностным характеристикам для Со установить вероятностные характеристики для р\ Наиболее трудная часть решения задачи состоит в определении вероятностных параметров для начального прогиба. В настоящее время имеется еще мало данных для выбора этих параметров. Примем в качестве первого приближения, что величина С(, распределена по нормальному закону с центром в начале координат:
to 1 0,25 т
0,15
0,10
0,05
§ 193]
ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
799
Воспользуемся, далее, формулой (18) преобразования вероятностей. Но следует принять во внимание, что, по нашему предположению, С0 принимает любое значение от —со до +оо, в то время как явление хлопка имеет место лишь при ОС0<С0» где С0 = 0,25. Поэтому при преобразовании вероятностей следует ввести нормирующий множитель (см. [20.1]). Определим вероятность того, что С0 лежит в указанных пределах:
- с°
F=f /(С о)Ло. (20.64)
0
На эту величину, меньшую единицы, надо разделить плотность (63); тогда мы от кривой / рис. 20.14 перейдем к кривой 2, причем
Рис. 20.14. «Нормирование» кривой распределения начальных прогибов.
Рис. 20.15. Функция распределения критической нагрузки для сжатой панели.
площадь под этой кривой останется равной единице. Окончательно плотность вероятности / (р*) оказывается равной
<*Ср
dp*
(20.65)
На рис. 20.15 изображена кривая /(/?*), полученная в работе [20.1] для случая sCo = 0,l. В результате преобразования плотность особенно повышается ДЛ5Г тех значений /?*, где велики абсолютные значения производной djdp*, т. е. для зоны, ближайшей к нижней критической нагрузке. Математическое ожидание т (р*) и
800
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
дисперсия D(p*) нового закона распределения определяются по формулам (14) и (15) с учетом множителя 1 /F:
Со
«00 = 4- f Р*(So)/Go)«Ко. (20.66)
F о
Со
D (р*) = ±r f[p’ (Со) -т (р*)р / (Со) dCo. (20.67)
Р о
По данным работы В. В. Болотина [20.1, 1958 г.], в случае *(£0) = 0,1 математическое ожидание равно 4,84, или 67% от /?* ид и 146% от р* ид; при (С0) = 0,25 оно равно 4,5, или соответственно 62% и 136%. Как видим, величина т(р*) при принятом законе распределения мало зависит от разброса начальных прогибов.
Рис. 20.16. Плотность вероятности начальных прогибов, преимущественно направленных к центру кривизны.
Надо, однако, учесть, что начальные неправильности в форме оболочки возникают в результате технологической обработки, различного рода ударов при транспортировке и монтаже конструкций; следует полагать, что реакция оболочки на эти возмущения имеет такой же характер, как и при действии рабочей нагрузки: предпочтительнее будут возникать начальные вмятины, направленные к центру кривизны. Поэтому центр распределения начальных прогибов уместно выбирать в точке, расположенной на некотором удалении от начала координат—в сторону положительных прогибов, обращенных к цен14у кривизны. На рис. 20.16 изображен такой закон распределения плотности вероятности с центром, равным С0 = 0,1, и стандартом =0,1. На рис. 20.17, а показано соответствующее распределение вероятности /(р*), вычисленное по (65). Математическое
§ 194]
ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
801
ожидание оказалось равным 4,14, или 57% от /?* ид и 107 от /?* ид. На рис. 20.17, изображен соответствующий интегральный закон распределения. Отметим, что математическое ожидание р* для оболочек с начальными неправильностями здесь почти совпадает с нижней критической нагрузкой р* для гладкой оболочки. Этот вывод имеет
Г(р') Г(р')
Рис. 20.17. Функции распределения для панели при начальных прогибах по рис. 20.16.
существенное практическое значение, так как показывает, что в расчетах реальных панелей надо исходить прежде всего из величины /?*.
Аналогичным образом могут быть приняты во внимание вероятностные характеристики условий закрепления оболочки по краям.
§ 194. Влияние начальных неправильностей на поведение замкнутых цилиндрических оболочек
Обратимся к случаю замкнутой цилиндрической оболочки *), шарнирно опертой по краям и подвергающейся внешнему равномерно распределенному давлению (рис. 11.17). На рис. 11.30 изображена зависимость параметра нагрузки q — qR2/Eh2 от прогиба при различных значениях безразмерной стрелы начальной погиби С0. Оставляя для С0 закон распределения плотности вероятности по рис. 20.16 при s= 0,1 и используя формулу (65), находим распределение плотности вероятности критической нагрузки, показанное на рис. 20.18. Математическое ожидание по (66) оказывается равным 0,035 и составляет 85% от Ид. Как мы видели, такой результат сравнительно хорошо отражает экспериментальные данные (см. § 132).
Рассмотрим аналогичную задачу для замкнутой оболочки, находящейся под действием осевого сжатия. Параметр внешней нагрузки выберем по-прежнему в виде р = pR/Eh. Зависимость С0 (р), найденная
*) Ряд задач, относящихся к замкнутым оболочкам, рассмотрен более подробно в первой из работ Б. П. Макарова [20.4].
802 ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ [ГЛ. XX
по данным работы [11.30а] при R/h — 1000, изображена на рис. 20.19. Сохраняя прежний закон распределения рис. 20.16, при-
Г(91
¥
0,5
0
0,025 0,03 0,035 ОМ л
Ч
Рис. 20.18. Функция распределения для критической нагрузки в случае замкнутой оболочки, подвергающейся внешнему давлению.
ходим к распределению плотности вероятности нагрузки (рис. 20.20, а) и к интегральной функции распределения (рис. 20.20, б). Математическое ожидание р равно 0,369, или 61% от верхнего критического напряжения /?в> ид.
До сих пор мы считали заданным закон распределения безотносительно к размерам оболочки. В действительности, однако, амплитуда и форма начальной погиби зависят от геометрических параметров оболочки. Для стержней выше принималось, что безразмерная стрела начального прогиба пропорциональна квадрату отношения длины стержня или, лучше сказать, длины полуволны изогнутой линии к характерному поперечному размеру. Для оболочек можно ввести аналогичное до¬
Рис. 20.19. Зависимость «начальный прогиб — верхняя критическая нагрузка» для случая осевого сжатия.
§ 194]
ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
803
пущение, но здесь амплитуда вмятины должна зависеть от размеров вмятины не в одном, а по крайней мере в двух направлениях. В случае цилиндрической оболочки естественно связать
Рис. 20.20. Функции распределения для критической нагрузки в случае замкнутой оболочки при осевом сжатии.
стрелу возможного начального прогиба с длинами полуволн изогнутой поверхности в двух направлениях (рис. 20.21, а) — вдоль образующей (1Х) и по дуге (/ ). В работах [11.30], [11.30а] была предложена
о)
6)
в)
Рис. 20.21. Возможные очертания начальных неправильностей.
формула для безразмерной стрелы начального прогиба (отношения стрелы прогиба к толщине) такой структуры:
С ( lxlv 1 \«
<•=(77 той) • (20-68)
где С, 8 — эмпирические коэффициенты.
Судя по некоторым эмпирическим данным, параметр о колеблется от 1,5 до 3. По аналогии со случаем стержня можно выбрать среднее значение 8 = 2.
804
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
Доннел и Ван [11.30а] считают, что при 8 = 2 коэффициент С будет равен: для оболочек, изготовленных из труб, С=1,5-*-3, для цилиндров, тщательно изготовленных из специально обработанных плоских листов, С =’3-ч-5, и, наконец, для оболочек, полученных из листа без особых требований к технологии, С = 5-5-10. В одной из статей Нэша [11.48] величина С была принята значительно большей: С = 30. Таким образом, каких-либо определенных данных относительно коэффициента С в настоящее время нет; очевидно, он будет резко меняться в зависимости от технологии изготовления оболочек и условий их хранения, транспортировки, испытаний и т. д.
Было обращено также внимание [11.30а] на то, что при изготовлении оболочек вмятины, вытянутые вдоль образующей (рис. 20.21, б), имеются чаще, чем вдоль дуги (рис. 20.21, в). Поэтому была предложена формула типа
С
(100Л)2 ’ (20.69)
где Х< 1. Принимая Х = 0,5, получим:
Сг
0==! (100Л)2 * (20.70)
Значение Cv судя по структуре формулы, должно быть примерно в 4 раза меньше С.
Если принять lx = Ljm и 1у = tzR/п, где т — число полуволн вдоль образующей оболочки и п — число волн вдоль поперечного сечения, то получим:
=(товУ'!(твгГ- <20-71>
Вводя прежний параметр (11.38)
rmzR
nL
приведем (71) к виду
(20.72)
'»=cw(w)J- <20-73>
Величины С и Сг зависят, главным образом, от технологии изготовления образцов. Если условно принять, что С и Сх не зависят от R/hf то по (73) окажется, что стрела прогиба начальных вмятин пропорциональна (R/h)2. Можно наметить следующий путь определения зависимости математического ожидания р от Rjh. Принимая для Сг некоторый закон распределения и пользуясь формулами преобразования вероятностей, находим математическое ожидание р для различных отношений R/h. В результате мы должны будем прийти
§ 194]
ВЛИЯНИЕ НАЧАЛЬНЫХ НЕПРАВИЛЬНОСТЕЙ
805
к тому выводу, что среднее критическое напряжение для реальных оболочек должно снижаться с увеличением Rjh. Между тем по классической линейной теории верхнее безразмерное критическое напряжение pBt ид = 0,606 не зависит от Rfh. Аналогичный вывод вытекает из нелинейных решений по методу Ритца в отношении нижнего критического напряжения, равного рн, ид = 0»18* Следовательно, со статистической точки зрения мы должны получить последовательное снижение математического ожидания рв от уровня рв>ид к уровню Рн, ид» а возможно, и далее, к уровню нижнего критического напряжения для заданного начального прогиба pHt нач, как показано на рис. 20.22. Такой вывод, как мы видели в главе XI, согласуется
с экспериментальными данными; он положен в основу рекомендаций § 129 для практических расчетов*).
Мы принимали в примерах для простоты, что начальные прогибы распределяются по нормальному закону. Однако это предположение не является вполне обоснованным. В самом деле, при изготовлении элементов реальных конструкций обычно исходят из определенных технических условий. Если эти условия регламентируют наибольшие отклонения от заданной формы оболочки, то изделия, не отвечающие им, идут в брак и исключаются из серии. Поэтому закон распределения начальных прогибов необходимо подбирать особо для каждой исследуемой серии образцов. Можно ожидать, что для ограниченной серии образцов плотность вероятности начального прогиба будет более или менее равномерно распределена на ограниченном участке <С<С2.
Далее, при рассмотрении влияния тех или иных возмущающих факторов далеко не всегда окажется удобным сводить их к экви-
Рис. 20.22. Снижение уровня верхнего критического напряжения при возрастании R/h.
*) Это касается лишь того случая, когда напряжения в оболочке лежат в пределах упругости.
806
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
валентным начальным прогибам. Тогда следует перейти к решению более сложной задачи, преобразуя вероятности по формулам (44) или (46).
Так как законы распреде-
ь
¥
0,2
о
8
...
Р в,идт.
1
1
1
1
!_ S
ш
0
ЗсР° о
о
о 0
о
ЩРЯ
о
f
о \
о
8> о >
WUU ZUUU OUUU
Рис. 20.23. Критические напряжения сжатия по экспериментальным данным.
шений R/h. По этим данным можно гистограммы величины v = /?//?B IW,
ления начальных несовершенств еще мало изучены, интересно поставить обратную задачу: по окончательным данным результатов опытов над реальными оболочками определить вероятностные характеристики начальных прогибов. Рассмотрим тот же случай осевого сжатия *) и воспользуемся экспериментальными данными статьи [11.33]. На рис. 20.23 приведены значения безразмерного критического напряжения р для различных отнодля различных R/h построить т. е. диаграммы, состоящие из
Ф)
К/
1 1 Ь=0*500
1
гт
ш
//у/уу
Т/
8
ГМ
0,2
0J2
0,4 0,6
о)
1
1
(1=1000
I
000
d
ш.
L
0,4 0,6
в)
0,8
fM
к
II
1
W00
..... 0
Ж
1
ш,
2Z) 0,8 1,0
8
fM
W
Of 0,4
б)
0,6
0,8
0,2
0,4
0,6
1,0
1
Я/
1
II
1
то
и!
Р
1
ш,
0,8 1,0
Рис. 20.24. Гистограммы значений реальных критических напряжений.
прямоугольников и указывающие, какое число опытов соответствует данному промежутку изменения отношения v реального критического напряжения к величине /?в, ид = 0,605. Такие гистограммы изображены
*) Этот случай был исследован Б. П. Макаровым во второй работе [20.4]; ему принадлежат приведенные ниже данные.
§ 195] ВЛИЯНИЕ СЛУЧАЙНЫХ НАГРУЗОК НА ПОВЕДЕНИЕ ОБОЛОЧЕК 807
на рис. 20.24. Отметим, что по мере возрастания отношения R/h спектр реальных значений р сужается и перемещается в зону меньших v. Кроме того, интересно указать на то, что две первые гистограммы имеют два максимума плотности вероятностей, так что закон распределения оказывается «двугорбым» *). Если, далее, провести преобразование вероятностей по графику рис. 20.19 и использовать формулы типа (73), то можно найти гистограмму для параметра и, соответствующего Сх. Такая окончательная диаграмма показана на рис. 20.25. Сплошная линия соответствует нормальному закону распределения и с центром и = 0,1 и стандартом 5 = 0,06. Мы находим здесь подтверждение сделанному
выше предположению, что центр закона распределения начальных прогибов должен быть смещен в сторону положительных С0.
Рис. 20.25. Определение закона распределения начальных прогибов по данным о реальных критических напряжениях.
§ 196. Влияние случайных нагрузок на поведение оболочек
До сих пор мы уделяли основное внимание влиянию на поведение оболочки начальных несовершенств ее формы, а также граничных условий. Но весьма важную роль в явлении прощелкивания оболочки играет также характер изменения нагрузки. Далеко не всегда нагрузка меняется во времени настолько медленно, чтобы можно было ограничиться рассмотрением равновесных диаграмм «нагрузка — прогиб». Так, например, оболочки самолетов, расположенные вблизи реактивных двигателей, подвергаются акустическому давлению, спектральное представление которого почти постоянно в весьма широкой области частот. Другой пример — воздействие на оболочки летательных аппаратов турбулентности атмосферы.
Будем считать, что нагрузка, приложенная к оболочке, состоит из двух частей: основной, являющейся систематической неслучайной величиной, и дополнительной, имеющей характер случайных воздействий. Примем, что эти случайные колебания нагрузки независимы от факторов, характеризующих рассеяние начальных неправильностей и других параметров оболочки. Далее, предположим, что
*) Аналогичный двугорбый закон распределения получил В. М. Гончаренко в другой задаче, см. вторую из работ [20.3]. Является ли такой результат закономерным, остается пока неясным.
808
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
случайные воздействия имеют характер белого шума, т. е. равномерно распределены на широком диапазоне частот. Термин «белый шум» соответствует белому свету, характеризующемуся равномерным спектром.
При изучении влияния переменной нагрузки на явление хлопка оболочки естественно прежде всего использовать энергетический подход *). В главе X мы говорили о том, что «самопроизвольный» хлопок для идеальной оболочки имеет место лишь при верхней критической нагрузке pBt ид. Но так как реальные оболочки выпучиваются, как правило, при более низкой нагрузке, то при этом должен быть преодолен известный энергетический барьер. Этот барьер тем выше, чем ниже нагрузка. Конечно, речь здесь идет только о таких нагрузках, при которых имеется возможность потери устойчивости в большом. Произойдет ли хлопок оболочки при нагрузке /?, лежащей в пределах рн> ид Р Рв, ид» зависит от наличия случайных возмущающих факторов, позволяющих преодолеть энергетический барьер. Здесь имеется некоторая аналогия с задачами о прохождении через потенциальный барьер, встречающимися в других областях физики, например при рассмотрении броуновского движения, где также используются статистические методы.
Очевидно, вероятность преодоления системой потенциального барьера зависит от уровня полной энергии системы при данной нагрузке и от его возможных колебаний в процессе испытаний или эксплуатации конструкции. Можно попытаться установить вероятность скачка, используя выражение для полной энергии через обобщенные координаты, не переходя — как это было в предыдущих параграфах — к непосредственной зависимости между этими координатами и возмущающими факторами. Обозначим безразмерную полную потенциальную энергию системы через Э и введем параметр 8, определяющий рассеяние случайных динамических нагрузок, которым может подвергнуться конструкция, так что уровень случайной нагрузки может достигнуть величины 3/8. Условия испытаний или эксплуатации конструкции будут особенно «неспокойны» при малых значениях 8.
Вместе с тем будем учитывать различные геометрические и упругие несовершенства системы с помощью эквивалентных начальных неправильностей формы; для простоты примем по-прежнему, что эти неправильности определяются одним параметром С0. В результате приложения случайных нагрузок система может получить деформации того или иного масштаба. Будем эти деформации описывать условно также с помощью одного параметра С (безразмерного прогиба).
Допустим, что начальные несовершенства оболочки заданы, и определим установившуюся плотность вероятности fx (С) для времен, больших по сравнению с так называемым временем релаксации (/>р).
*) Такой подход к задаче принадлежит И. И. Воровичу [20.2].
§ 195] ВЛИЯНИЕ СЛУЧАЙНЫХ НАГРУЗОК НА ПОВЕДЕНИЕ ОБОЛОЧЕК 809
Воспользуемся для этого известным из статистической физики распределением Гиббса. При фиксированном С0 искомая плотность вероятности будет равна
/,(0 = 7Э(С). (20.74)
где а — некоторый коэффициент, зависящий от характера конструкции*); под 1/У понимается «нормирующий» множитель, причем
00 а
J= fe~T9XVd:. (20.75)
— ОО
Отметим, что плотность вероятности того или иного значения С зависит здесь от величины энергии системы: плотность тем больше, чем ниже уровень энергии. Это и естественно, так как чаще всего должны осуществляться более устойчивые состояния системы с минимальной энергией.
Примем во внимание, далее, рассеяние начальных прогибов, считая, что при этом учитываются и другие отклонения от расчетной модели оболочки. Обозначая плотность вероятности С0 через ср(С0), на основании теоремы об умножении вероятностей получим:
/<C) = /i(t) ср (Со); (20.76)
здесь принято, что параметры, определяющие разброс значений на¬
грузки и начальных несовершенств, независимы. Вероятность того, что прогиб С будет лежать в интервале < С С2» равна
С2 оо
F=f /АЮтОУЛсД. (20.77)
Ci -ОО
В качестве примера рассмотрим ту же пологую цилиндрическую панель, что и в § 193. Безразмерная энергия системы равна**)
э р++«j) - ( v+«о)+
+ (20-78)
где р*>ид— параметр верхней критической нагрузки, р* — параметр заданной статической нагрузки, k — параметр кривизны.
*) В работе [20.2] этот коэффициент выражен через параметры, характеризующие колебания конструкции с учетом затухания.
**) См. книгу [0.3], стр. 282—286 и работу [20.2].
810
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
Поведение системы при случайных воздействиях зависит от относительного уровня статической нагрузки v = /?*/Pb ид» распределения начальных несовершенств С0 и параметра а/8.
Рис. 20.26. Вероятность F, относящаяся к стреле полного прогиба панели при уровне средней нагрузки р = 0,5.
Рис. 20.27. Вероятность F для стрелы полного прогиба панели при различных уровнях средней нагрузки.
На рис. 20.26 и следующих приведены результаты вычислений, содержащиеся в работе И. И. Воровича [20.2]. На рис. 20.26 по оси ординат отложена вероятность F того, что безразмерный прогиб С
по модулю не достигнет единицы, а по В (С )-0015 оси абсцисс — дисперсия D начального
°00267 пР0ГИа в предположении, что для С0
7 выбран треугольный симметричный закон
распределения. Принято k = 12 и v = 0,5. График показывает, как этого и следовало ожидать, что, чем больше а/8, а следовательно, и разброс динамических нагрузок, тем вероятность получения предельного прогиба станет более высокой. Отметим, что при малых а/8 дисперсия начальных прогибов почти не влияет на вероятность F.
На рис. 20.27 показано, как вероятность F зависит от дисперсии С0 и уровня нагрузки v при а/8 = 1. Чем выше v, тем меньше вероятность того, что прогиб останется в пределах (—1)<С< 1. На рис. 20.28 та же зависимость приведена в координатах F, V. Отметим, что уровень нижней критической нагрузки характеризуется параметром v = 0,544. Как видим, при v > 0,544 вероятность возникновения опасных прогибов резко усиливается.
Рис. 20.28. Вероятность F для величины полного прогиба панели в зависимости от нагрузки.
§ 195] ВЛИЯНИЕ СЛУЧАЙНЫХ НАГРУЗОК НА ПОВЕДЕНИЕ ОБОЛОЧЕК 811
Определим теперь вероятность Fm того, что в любой наугад взятый момент времени t§>tp оболочка окажется в окрестности прощелкнутого состояния; в дальнейшем будем условно называть F+ вероятностью хлопка. По (77) эта вероятность будет равна
ОО ОО
/ //i(t)<P(C0)fiMt. (20.79)
С* -оо
Как мы видели, хлопок может произойти лишь при условии, что С0 не превосходит известной величины С0 (для k =12 значение С0 равнялось 0,25). Таким образом, получаем:
оо Со
F.= / //i(C)<p(C0)rfC0dC. (20.80)
С* -оо
В отличие от § 193, здесь учитываются не только положительные, но и отрицательные начальные прогибы, т. е. направленные как к центру, так и от центра кривизны: хлопки имеют место в реальных испытаниях и при отрицательных прогибах (см. рис. 20.29),
Рис. 20.29. Хлопок оболочки с переходом от «отрицательных» прогибов к «положительным».
Рис. 20.30. Вероятность хлопка цилиндрической панели в зависимости от уровня нагрузки.
хотя для бесконечно медленного процесса здесь нельзя получить диаграмму постепенного перехода от одной формы равновесия к другой.
На рис. 20.30 показано, как вероятность хлопка Fm зависит от уровня нагрузки v и дисперсии величины С0. При возрастании v вблизи нижнего критического значения вероятность хлопка быстро возрастает.
Отметим, что энергетический подход позволяет установить некоторые статистические зависимости и прийти к определенным
812
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
[ГЛ. XX
качественным выводам без непосредственного использования диаграмм состояния для оболочки; необходимо иметь лишь выражение для полной потенциальной энергии системы.
§ 196. Другие задачи статистической теории
Описанный выше подход приводит к характеристикам поведения оболочек, устанавливающимся на протяжении сравнительно большого промежутка времени. Можно поставить и другую задачу — определить вероятностные характеристики поведения оболочек на достаточно малом промежутке времени. В первом случае оболочку можно было рассматривать как упругую систему с незначительной инерцией или с сильным затуханием. Во втором случае систему надо рассматривать как инерционную, т. е. воспользоваться как бы динамическим подходом *).
Так, например, может быть решена следующая задача: установить вероятность того, что оболочка будет в окрестности прощелкнутого состояния в момент времени t при t <tp. Эта вероятность оказывается зависящей от высоты потенциального барьера, разделяющего устойчивые формы равновесия оболочки, и декремента затухания, который здесь играет существенную роль. Другая задача формулируется следующим образом: определить вероятность того, что в течение некоторого промежутка времени оболочка окажется хотя бы один раз в прощелкнутом состоянии. В работе [20.3] 1961 г. рассмотрен, например, случай, когда удлиненная пологая цилиндрическая панель находится под действием нормального давления, характеристики которого соответствуют акустическому давлению на фюзеляж самолета. Особенно важной является задача об определении вероятностных характеристик процесса последовательных прямых и обратных хлопков оболочки, приводящих к развитию усталостных трещин в материале.
Вообще говоря, исследование влияния случайных воздействий, имеющих характер белого шума, связано с применением теории так называемых марковских процессов. Решение задачи о вероятностных характеристиках поведения системы сводится при этом к интегрированию уравнения Фоккера — Планка — Колмогорова **); в общем случае такое интегрирование можно провести пока только численно. Поэтому необходимо искать пути эффективного решения различных частных задач.
Мы предполагали до сих пор, что «основная» часть нагрузки является неслучайной заданной функцией времени. Но иначе должна быть поставлена задача, если речь идет, например, о поведении оболо¬
*) На это было указано В. М. Гончаренко [20.3].
**) См. Р. Л. Стратонович, Избранные вопросы теории флюктуаций в радиотехнике, М., 1961, стр. 59.
§ 196]
ДРУГИЕ ЗАДАЧИ СТАТИСТИЧЕСКОЙ ТЕОРИИ
813
чек при динамическом нагружении (см. главу XVIII). На рис. 20.31 приведена для примера диаграмма «прогиб — время» для нагрузки, основная часть которой является также случайной функцией времени. Хотя характер процесса остается, как правило, одним и
Рис. 20.31. Случайные динамические процессы для оболочек.
тем же, конкретные очертания диаграммы меняются от случая к случаю. Поэтому в экспериментах для образцов одной и той же серии мы получаем различные динамические «критические» нагрузки <7Д, разные «выбросы» прогиба и т. д.
Исследован также важный случай высокочастотных изменений нагрузки, приводящих к повышению нижних и верхних критических усилий (см. работы В. Н. Челомея [18.21] и В. М. Гончаренко, ДАН УССР, № 7, 1962).
Таким образом, статистический подход к задачам об устойчивости оболочек должен учитывать, с одной стороны, рассеивание параметров оболочки и граничных условий и, с другой, влияние на поведение оболочек различных групп нагрузок: а) случайных нагрузок типа белого шума, б) нагрузок, изменение которых может быть описано конечным числом случайных параметров с известным законом распределения.
В заключение отметим, что применение вероятностных методов в теории устойчивости упругих систем окажется эффективным лишь после того, как будут собраны более подробные данные о начальных несовершенствах конструкций, получены характеристики случайных нагрузок и т. д. Желательно, чтобы в дальнейшем эксперименты, ч проводящиеся над достаточно большими сериями образцов, всегда сопровождались статистической обработкой результатов.
ГЛАВА XX!
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
§ 197. Динамический критерий устойчивости в малом
В предыдущих разделах книги был разобран ряд задач, относящихся к выпучиванию стержней, пластинок и оболочек. Мы познакомились с различными методами решения задач, в основе которых лежали статический, энергетический или динамический критерии устойчивости. В настоящей главе мы рассмотрим эти критерии с более общей точки зрения, связывая их с теми подходами к понятию устойчивости, которые приняты в аналитической механике и нелинейной теории упругости.
Еще в § 1, вводя понятие устойчивости сжатого стержня, мы как бы интуитивно воспользовались простой динамической моделью. И здесь мы начнем с динамического критерия, применяя его прежде всего к устойчивости в малом. При этом естественно обратиться к тем понятиям устойчивости и неустойчивости механических систем с конечным числом степеней свободы, которые были в свое время введены Лагранжем *). Он говорил об устойчивом равновесии «в том смысле, что если сначала система находилась в состоянии равновесия, а затем была немного из него выведена, то она сама собою стремится вернуться к этому состоянию, совершая около него бесконечно малые колебания». Далее, при неустойчивом равновесии «система, будучи однажды выведена из этого состояния, может совершать колебания, которые не будут уже очень малыми и которые могут все более и более отклонять систему от ее первоначального состояния».
Строгое определение устойчивости равновесия, как частного случая движения, было впервые дано А. М. Ляпуновым **). Допустим, что
*) Ж. Лагранж, Аналитическая механика, т. 1, Гостехиздат, 1950, стр. 97.
**) А. М. Ляпунов, Общая задача об устойчивости движения, Гостехиздат, 1950, стр. 17—21. См. также Н. Г. Четаев, Устойчивость движения, Гостехиздат, 1955.
§ 197] ДИНАМИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В МАЛОМ 815
положение системы определяется п обобщенными координатами qt (/=1, 2, /г), причем в равновесном состоянии будет <7* = 0
при тех же /.
Примем, что в начальный момент t — О абсолютные значения координат и скоростей лежат в пределах
К<5. £ <5
и что в любой последующий момент времени / > О мы сопоставляем координаты qt{t) и скорости qi(f) с некоторой величиной е. Устойчивое равновесное состояние характеризуется тем, что для любого е > О можно подобрать соответствующую величину 8 (е) > О такую, при которой в течение всего периода времени t > О величины \qt\ и \qt\ будут находиться в пределах
I ?/1 < •• кг I < *•
Иными словами, в случае устойчивого равновесия системы всегда можно подобрать такие начальные условия, что обобщенные координаты и скорости не будут выходить за некоторые наперед заданные границы, лежащие в окрестности основного состояния. Если подойти к этому определению с геометрической точки зрения, то нужно представить себе некоторую трубку в (2п-\- 1)-мерном пространстве. Пусть величины qt и qt откладываются в воображаемом сечении такой трубки, имеющем 2п измерений, а время t — вдоль ее оси. Устойчивое равновесие характеризуется тем, что если подобрать должным образом начальные значения q° и q°l% то величины qt и qt будут при любом t лежать внутри трубки с заданным сечением.
А. М. Ляпуновым было введено также понятие асимптотической устойчивости: этот вид устойчивости относится к случаю, когда система при неограниченном возрастании t возвращается к основному состоянию, т. е. qi(t)Ot если t-> оо.
Предположим, далее, что механическая система при заданных параметрах имеет не одно, а несколько устойчивых равновесных состояний: ряд подобных примеров мы встречали выше. Тогда приведенное здесь определение устойчивости в малом должно быть отнесено к окрестности каждого из этих равновесных состояний.
Приведенные выше критерии устойчивости и неустойчивости можно обобщить на деформируемую конструкцию, являющуюся системой с бесконечно большим числом степеней свободы. Круг величин, характеризующих поведение такой системы во времени, расширяется: здесь могут быть введены, наряду с перемещениями точек системы и скоростями, такие величины, как компоненты дополнительных деформаций и напряжений. Выходя из рамок собственно механики,
816 ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
мы можем рассматривать также изменение температуры в различных точках системы и т. д.
Величины, которые выбираются в той или иной задаче для описания поведения конструкции, будем в дальнейшем (для краткости) называть характеристиками.
§ 198. Статический критерий устойчивости в малом.
Исследование смежных равновесных форм для трехмерной задачи
Перейдем к статическому критерию, которым мы неоднократно пользовались при исследовании устойчивости в малом. Допустим, что нагрузка, воспринимаемая конструкцией, пропорциональна некоторому параметру и что малым значениям параметра соответствует единственное в рассматриваемом диапазоне характеристик устойчивое состояние системы. Будем увеличивать параметр пагрузки, исследуя при этом состояния конструкции, близкие к основному. То значение параметра, при котором хотя бы одно из смежных состояний конструкции впервые становится равновесным, мы называем критическим значением. При нагрузке, превышающей критическую величину, основное состояние, как правило, перестает быть устойчивым *).
Мы занимались исследованием окрестности основного равновесного состояния во многих частных задачах, когда оно являлось одноосным (стержень) или двухосным (пластинка, оболочка); в практических приложениях именно эти задачи являются существенными. Но для того, чтобы установить общие черты в постановке различных задач, рассмотрим случай трехосного напряженного состояния **).
Отнесем деформированное и напряженное состояние упругого тела к декартовой системе координат. Обозначим, как и прежде, через и> v, w перемещения точек тела вдоль осей х, у, z, через е., уху и т. д.—деформации удлинейия и сдвига, через ох, хху и т. д.— нормальные и касательные напряжения. В дальнейшем составляющие деформаций и напряжений, соответствующие основному состоянию, будем обозначать е°, с£, х°ху и. т. д. При возрастании параметра нагрузки величины е°,,... изменяются в каждой точке
тела монотонно. Постановка и решение задач значительно облегчаются в случае простого нагружения, когда главные деформации и напряжения в любой точке сохраняют свое направление, или, иными словами, когда все составляющие деформаций и напряжений изменяются
*) Для некоторых механических систем возможны и исключения, см. А. Ю. И ш л и н с к и й, С. И. М а л а ш е н к о, М. Е. Т е м ч е н к о, Изв. АН СССР, ОТЛ, № 8 (1958), 53—61.
**) В дальнейшем изложении мы следуем В. В. Новожилову [21.8J.
§ 198] СТАТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В МАЛОМ
817
пропорционально одному и тому же параметру нагрузки. Это требование выполняется, например, для оболочек, если основное состояние является безмоментным. Однако нам встречались и случаи сложного нагружения *), когда направление главных деформаций и напряжений для тех или иных точек в процессе нагружения меняется (моментное основное состояние для оболочек).
Так или иначе мы можем выразить деформации через перемещения по известным формулам линейной теории упругости **):
о ди° о dv° о дт°
гх дх * еу ду * 6* дг *
о = ди°.
ду '
у
dv°
дх
о dv°
~dz
dw°
dw°
ду
дх
, ди° + дг '
(21.1)
Мы считаем здесь, что величины е°, у,... малы по сравнению с 1. Составим, далее, уравнения равновесия элемента, имеющего размеры dx, dy, dz. Если не учитывать массовых сил (например, силы веса), то эти уравнения в проекциях на оси координат примут вид ***)
даж ■
дх ду
dzv
dz,
ух
да„
dz
di
= 0,
дх
дСг
ду
дх
ху
дх
ду
dz
дг
у± = 0,
= 0,
(21.2)
а уравнения моментов приводят к равенствам
ху
: Т, Т = Т, X
ух* XZ ZX’ yz
zy
Далее, выпишем зависимости закона Гука:
(о о о\
2 (1 + Iх)
(21.3)
• ху
т°у и т. д. (21.4а)
Пользуясь (4а), можно выразить напряжения через деформации; тогда получим формулы типа
°;=ttfK+t=V6°)* и т- д- (21-4Ь)
где 0° = е°х -f- е° -f- е° — объемная деформация.
*) Термины «простое нагружение» и «сложное нагружение» часто применяются в литературе по теории пластичности.
**) См., например, П. Ф. П а п к о в и ч, Теория упругости, Оборонгиз, 1939, стр. 44—48.
***) См. указанную выше книгу П. Ф. Папковича, стр. 19 и 31.
818
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
Если подставить эти выражения в уравнения равновесия (2) и использовать соотношения (1), то получим линейные уравнения относительно перемещений и°, v°, w°. Решение этих уравнений должно удовлетворять граничным условиям. Допустим, что на поверхности тела заданы компоненты внешней нагрузки р°х, р°у, р°г. Тогда из условия равновесия пограничного элемента получаем:
где /, т, п — косинусы углов, составляемых нормалью к данной площадке поверхности с осями х, у, z.
Из известной теоремы Кирхгофа следует, что при заданных граничных условиях решение линейных статических уравнений теории упругости является единственным *). Следовательно, возможность определения соседнего равновесного состояния с помощью обычных линейных уравнений исключена. Если обратиться к примеру пластинки, испытывающей усилия в своей плоскости, то в этом случае невозможно исследовать устойчивость пластинки, используя линейные уравнения плоской задачи и соответствующие граничные условия.
Особенность задач устойчивости в малом состоит в том, что при исследовании соседнего равновесного состояния не обходимо принять во внимание изменение ориентации граней элемента тела, в то время как при составлении обычных уравнений классической теории упругости типа (2) это изменение не учитывается. Иными словами, в задачах устойчивости должны быть введены в рассмотрение повороты элемента вокруг координатных осей.
Рассмотрим переход от основного состояния тела к соседнему. Обозначим дополнительные перемещения любой точки тела, возникающие при таком переходе, через и', г/', w' и соответственно дополнительные деформации и напряжения через е, о'х и т. д. Для деформаций выпишем выражения типа (1):
Поставим перед собой цель охарактеризовать повороты элемента вокруг координатных осей. На рис. 21.1 представлена грань элемента тела, перпендикулярная к оси z. Поворот орта оси х в плоско-
(21.5)
, да', дг/, dw'
дх * еу ду * е* dz 9
, ди', dv', dv', dw', dw', du'
Уху ду ' dx * Уг dz ' dy* zx dx dz
(21.6)
*) См., например, А. Л я в, Математическая теория упругости, ОНТИ, 1935, стр. 181.
§ 198] СТАТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В МАЛОМ
819
сти ху равен dv'jdx, а поворот орта оси у в той же плоскости равен ди'/ду, причем он будет положительным, если происходит в сторону положительных и', т. е. в направлении, обратном первому
повороту. Под поворотом а)' грани ху вокруг оси z будем понимать
полусумму величин dv'jdx и —ди'/ду, определяющую как бы «среднее» значение пово¬
ротов вокруг z различных прямых, проходящих через точку О и лежащих на грани ху.
Аналогичные рассуждения приводят к следующим формулам для поворотов элемента вокруг осей х, у, z:
, 1 (dw' dv'\
Ш* — Т\'ду~~дг)’, 1 iduf dw'\
— 2\~dz~~ dx)*
, 1 (dv1 da' \
~2 \ длГ dy ) *
(21.7)
Рис. 21.1. К определению поворота элемента вокруг оси z.
Будем считать, что деформации удлинения и сдвига по (6), происходящие в плоскости каждой грани, малы по сравнению со «средними» поворотами грани <о', со., ю'у и, в свою очередь, эти последние величины малы по отношению к 1. Но тогда при определении нового положения ортов координатных осей следует рассматривать, например, грань элемента ху как жесткий диск, поворачивающийся вокруг оси z на угол, равный о>'. Это дает возможность выписать таблицу приближенных значений косинусов углов, которые составят повернутые орты у', kf осей х, у, z с их первоначальными направлениями (рис. 21.2).
V
/
V
X
1
/
/
“у
У
/
1
/
Z
/
<•>*
1
Рис. 21.2. Повороты ортов координатных осей.
Выпишем теперь уравнения равновесия элемента тела в соседнем состоянии, учитывая основные напряжения после поворота, дополнительные напряжения и массовые силы. Считая дополнительные
820
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
напряжения малыми по сравнению с основными, поворота их учитывать не будем.
Уравнение типа (1) в проекциях на ось х будет иметь вид *)
3 / О О f. О / / \ I д / о Of,
al (ах — Хху “z + Ххж*у + 0*)+ (V _ °У “г +
+ + V)+ «ж — ХгуШ'г + °>у + Xzx) = °- (21 -8)
Здесь приращения усилий в площадках с нормалями у', последовательно проектируются на ось л: с учетом первой строчки таблицы косинусов. Вычитая (2) из (8), получим окончательно:
0 / f О /. О /\ I 3 / t о /.
— (О — х о) —4— х (о )Н- -т— (X — ао)Н~ дх\ * *У * ' хг у) ~ ду V ух у г *
+*>',)+и«. - <,<+°у,) - »• <г -9>
По аналогии выпишем два других уравнения:
д /. t I Of О ' \ I / / I О f О / \ д-х('*у+вх®. - х*л)+ж; (°у + V®. - V«+
+ 5г(+т>-0Х) = °- (2,л°)
(?// 0/1 О /\ I / / О / 0/\
5* (Т “I Х*у ®х) “1“ ду (ТУ-г + S +£«-<Л+<у<)=°- (21Л1)
Эти уравнения можно представить в несколько ином виде. Так как мы условились пренебрегать деформациями по сравнению с поворотами, то при вычислении о>, о>', со' положим
, ди', dv'
dy ‘ dx'
Далее, по (7) находим:
, dw' dv', da'
о) г—, о) ——
ду dz у дг
у'
j
\уг
дг
dw'
дх
, _L I
* zx г) г * дг
’ о, ;0.
(21.12)
dw,
• ~л—. ;
дх г
<2МЗ>
du
ду
Если обратиться для примера к уравнению (11), то, пользуясь (13), ему можно придать вид
dx\xz * х дх * ху ду ду \ у* ■ ух дх •
, о dw'\, d /,. чо dw'. о dw'\ л /01 -
+ оу!7) + 5?(°* + х~-§7 + у-57) = 0- <21Л4>
*) Уравнения такого типа были составлены в работе Бицено и Генки
[21.9].
§ 198]
СТАТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В МАЛОМ
821
В уравнениях типа (9) или (14) напряжения можно по-прежнему выразить через деформации по формулам
»;=т1тг(*;+гв')’ =5<пЬът-д-(2115)
где 0' = e-f-e' -f- е'г, а затем деформации и повороты — через перемещения по (6) и (7). Тогда получим три однородных уравнения относительно и', v\ wf.
Обратимся к граничным условиям для соседнего состояния тела. Допустим здесь, что при переходе от основного состояния к смежному внешняя нагрузка остается неизменной по величине и направлению. Тогда для нового положения будет
(«; - +«у <+—«>;+
<21Л6>
Вычитая первое равенство (5) из (16), получим:
(°ж - Х°ху< + Х*гшу) 1 + {?ух - °у К +
+*;,»;)т+- v»;+<*■>;)»=°- <21 •17>
Другие два условия можно записать по аналогии.
Таким образом, задача сводится к исследованию системы однородных уравнений, содержащих перемещения а', г>\ w' (либо уравнений, эквивалентных им), причем основные напряжения о°, т°у,... в (17) считаются заданными функциями координат. Если основные напряжения пропорциональны некоторому параметру X, то, находя величины X, при которых эти уравнения имеют нетривиальное решение, получим так называемые собственные значения задачи об устойчивости в малом; они соответствуют точкам разветвления (<бифуркации) равновесных форм (при рассмотрении задачи в линейной постановке). Как правило, в упругих системах каждому собственному значению задачи соответствует одна собственная форма, т. е. одна определенная форма потери устойчивости. Можно, однако, представить себе, что в некоторых слунаях (например, для пластинок или оболочек) тому или иному собственному значению будут отвечать две, три и т. д. формы потери устойчивости (различные выпученные состояния); тогда мы получим собственные значения второй, третьей и т. д. кратности. Если сопоставить последовательные собственные значения задачи об устойчивости системы, то окажется, что наименьшее из них имеет непосредственный практический смысл, так как соответствует потере устойчивости основного состояния; это значение и определяет первую эйлерову критическую нагрузку или, по принятой нами терминологии, верхнюю критическую нагрузку. Что касается следующих точек бифуркации, то к ним сходятся лишь
822
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
неустойчивые ветви, и отвечающие всем этим ветвям равновесные состояния не реализуются.
Сопоставим полученные нами уравнения с теми, которыми мы пользовались для пластинок. Возьмем, например, уравнение (14). Считая о°, о° и т°у не зависящими от координат и, кроме того, принимая х°гх = х°гу = 0 и <з' = 0, получим
dzxz d2w' d2w' d2w'
l)x~~dy~~>r9*lh? 2V dx dy + S dy2 =
После интегрирования по толщине пластинки легко получить те уравнения, которые лежали в основе решения линейных задач устойчивости. Для того чтобы получить аналогичные зависимости теории устойчивости оболочек, следует выразить основные зависимости в криволинейных координатах [см. § 120].
Сравним между собой уравнения равновесия типа (2), относящиеся к основному состоянию, и уравнения (14), соответствующие переходу от основного состояния к смежному. И те и другие уравнения являются линейными, но они имеют различный смысл. Уравнения второго типа надо рассматривать как уравнения, полученные линеаризацией некоторых нелинейных зависимостей, описывающих большие перемещения системы (см. § 201), так как эти уравнения второго типа выведены с учетом поворота элемента тела. Поэтому можно сказать, что в конечном счете каждая задача устойчивости является нелинейной. Возникает вопрос: являются ли точки бифуркации, найденные с помощью линеаризованных уравнений, теми же, как если бы они были получены исходя из нелинейных зависимостей? Этот вопрос был рассмотрен с помощью методов функционального анализа *). Оказалось, что для практически важных случаев, когда критическим значениям параметра \ отвечает лишь одна определенная форма выпучивания (или, вообще говоря, нечетное число таких форм, т. е. когда собственные значения имеют нечетную кратность), все собственные значения линеаризованных уравнений являются точками бифуркации нелинейной задачи. Между тем, если собственные значения имеют четную кратность, такое совпадение может не иметь места.
§ 199. Энергетический критерий устойчивости в малом.
Теорема Лагранжа — Дирихле
Обратимся к энергетическому критерию устойчивости в малом. Этот критерий в применении к консервативной системе с конечным числом степеней свободы основывается на известной теореме
*) См. М. А. Красносельский, Топологические методы в теории нелинейных интегральных уравнений, Гостехиздат, 1956; И. И. В орочи ч, ДАН СССР, 122, № 1 (1958).
§ 199] ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В МАЛОМ 823
Лагранжа-- Дирихле *), которая формулируется следующим образом: Если в некотором (основном) состоянии консервативной системы потенциальная энергия минимальна по отношению к значениям энергии для всех смежных (отклоненных) состояний системы, то основное положение является положением устойчивого равновесия. Для доказательства примем, что в основном положении обобщенные координаты qv q2 qn равны нулю; потенциальную
энергию Э для этого положения также примем равной нулю. Для смежных положений системы при <е и <е и условии Э(0, 0, 0) = min = 0 будет Э>0. Но тогда суммарная энер¬
гия Е, состоящая из кинетической Т и потенциальной Э, будет для этих положений Е= 7,+ Э> 0, так как всегда Г> 0. Отметим значения Е для различных состояний на границе области е и установим наименьшее из этих значений Е*. Примем, что величина Е меняется внутри области е непрерывно; при этом можно найти такую более узкую область 8 внутри е, для которой будет qt < 8, qt < 8, а энергия окажется Е < Е*. Выберем координаты qt и скорости qi% удовлетворяющие этому условию, в качестве начальных, тогда и начальная энергия Е° (при t = 0) будет Е° < Е*. Но так как для консервативной системы полная энергия остается постоянной, то и во все последующее время энергия системы будет Е = Е° < Е*. При этом система окажется устойчивой, так как при любом £> 0 координаты и скорости не будут выходить за пределы е.
Судя по приведенному доказательству, теорема Лагранжа — Дирихле может быть распространена на системы, на которые действуют, в дополнение к потенциальным силам, также диссипативные силы: для таких систем Е < Е° < £*, т. е. движение будет сопровождаться рассеянием энергии.
А. М. Ляпунов дал для двух важных случаев обращение теоремы Лагранжа — Дирихле. В одном случае рассматривается некоторое (основное) равновесное положение системы, в котором потенциальная энергия является максимальной по отношению к энергии смежных положений, причем этот максимум отвечает членам наинизшего порядка (не обязательно второго) в разложении потенциальной энергии по координатам qt\ в этом случае основное положение является неустойчивым. В другой теореме речь идет о случае, когда известно лишь, что энергия в основном равновесном положении не является минимальной; такое положение будет неустойчиво, если отсутствие минимума определяется членами второго порядка в разложении потенциальной энергии.
*) Эта теорема была формулирована впервые Ж. Лагранжем (см. его «Аналитическую механику», т. 1, 1950, стр. 97); доказательство принадлежит П. Г. Лежен-Дирихле (см. ту же книгу Лагранжа, стр. 537). Здесь мы следуем Ф. Р. Гантмахеру, см. его «Лекции по аналитической механике», I960,
824
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
Все приведенные теоремы относились к системам с конечным числом степеней свободы. Обобщение их на случай системы с бесконечно большим числом степеней свободы было предметом ряда исследований *) и не является еще завершенным. Но, как было уже сказано, при решении многих задач упругая конструкция рассматривается как система с конечным числом степеней свободы, и тогда основные теоремы могут быть непосредственно приложены.
Теоремы Лагранжа — Дирихле и Ляпунова указывают путь для отыскания критической нагрузки. Рассматривая малые отклонения системы от основного состояния, представим приращение полной потенциальной энергии в виде
ДЭ = 8Э + у2Э;
в линейных задачах следующие члены разложения будут отсутствовать, так как энергия является квадратичной формой обобщенных координат. Для любого равновесного состояния 83 = 0; поэтому о характере равновесия надо судить по знаку второй вариации. Равновесие будет устойчивым при Ь2Э > 0 и неустойчивым при й2Э < 0. Но первая верхняя критическая нагрузка соответствует переходу от устойчивых равновесных положений к неустойчивым, следовательно, для этого значения нагрузки должно быть 82Э = 0. Если система имеет п степеней свободы и отклонения от основного состояния определяется с помощью обобщенных координат qv q2,.. -, qn, то вторую вариацию можно представить в виде
52Э=И-
д*Э
0,\ Ч+
.. +2
д2Э dqx dq2
bqx bq2 -j-.
Условие й23 = 0 эквивалентно здесь следующему уравнению, содержащему коэффициенты приведенного ряда **):
д2Э
dq\
д2Э
д2Э Ч\ Я2 д2Э
dq2 dqx dqz2
= 0.
(21.18)
Корни этого уравнения определяют все критические нагрузки и, в том числе, наименьшую из них.
*) См., например, А. А. М о в ч а н, Прикл. мат. и мех. 24 (I960), 988—1001.
**) См. Н. Г. Четаев, Устойчивость движения, Гостехиздат, 1955, стр. 52.
§ 20Q] ДИНАМИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В БОЛЬШОМ 825
Мы не различали здесь «классических» задач устойчивости, в которых докритическое нагружение является простым, а верхняя критическая нагрузка — точкой бифуркации, и задач со сложным нагружением, когда критическая нагрузка представляет собой предельную точку. В обоих случаях ветвь устойчивых решений сопрягается в первой критической точке с ветвью неустойчивых решений. Вопрос о том, к какой ветви относится сама критическая точка, остается при этом неясным; он может быть рассмотрен лишь при решении нелинейной задачи с учетом высших членов разложения АЭ (см. § 202).
Ряд примеров применения энергетического критерия был приведен в разделах, относящихся к стержням и пластинкам.
§ 200. Динамический критерий устойчивости в большом
До сих пор рассматривались критерии устойчивости основного равновесного состояния упругой системы по сравнению со смежными состояниями. Как мы знаем, во многих задачах, относящихся, прежде всего, к оболочкам, более важным является изучение устойчивости в большом. Потеря устойчивости практически совершается для таких систем не путем непрерывной смены равновесных форм, а скачкообразно. Так как новые состояния равновесия оказываются удаленными от первоначальных, то задачи об устойчивости в большом являются существенно нелинейными. Приложение динамического критерия состоит при этом в исследовании характера нелинейных колебаний системы вокруг ее равновесных положений.
Особый интерес представляет здесь случай, когда конструкция может быть приведена к консервативной системе с одной степенью свободы. Тогда характер равновесия определяется с помощью графиков на так называемой фазовой плоскости *). Эти графики выражают зависимость между обобщенной координатой С и обобщенной скоростью С, вытекающую из закона сохранения энергии Е = Т -\-Э= const, при условии неизменности уровня нагрузки. Под Е здесь понимается полный запас энергии, полученный системой в начальный момент времени. На рис. 21.3, а показан график С (С) для случая, когда нагрузка не достигает нижнего критического значения. Система имеет здесь единственное устойчивое равновесное положение, отвечающее точке А. Эта особая точка носит название центра; она окружена замкнутыми непересекающимися линиями (фазовыми траекториями), каждая из которых соответствует определенному запасу энергии Е. Вверху на том же рисунке изображена
*) См., например, И. М. Бабаков, Теория колебаний, 1958, Гостехиздат, стр. 510 и сл.
826
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
зависимость Э(С). Как видим, центру А соответствует минимальное значение Э.
Следующий график, рис. 21.3, tf, содержит фазовые траектории для случая, когда нагрузка превышает нижнее критическое значение. Здесь имеются два центра Л и С, между которыми лежит другая особая точка В, называемая седлом; оно отвечает неустойчивому равновесному состоянию. В зависимости от того, какие начальные значения С0 и С0 приданы системе, мы получим колебания вокруг
одного из устойчивых положений либо колебания, охватывающие оба эти положения. Как видно из верхнего графика, седлу соответствует максимальное значение Э.
Наконец, график, рис. 21.3, в, отвечает случаю, когда нагрузка в точности равна нижней критической величине. В точке D один из центров совмещается с седлом. На графике энергии положению D соответствует точка перегиба с горизонтальной касательной.
Примеры фазовых траекторий для оболочек, рассматриваемых как системы с одной степенью свободы, были даны Э. И. Григолюком *) и автором [0.3, стр. 294]. Выше, в главе XVIII, был приведен также пример, относящийся к цилиндрической панели, когда колебания охватывали различные устойчивые равновесные состояния; при этом панель была представлена как система с несколькими степенями свободы.
§ 201. Статический критерий устойчивости в большом
Как мы видели, для системы с одной степенью свободы анализ характера нелинейных колебаний конструкции является относительно простым; но для системы с большим числом степеней свободы он значительно осложняется. Поэтому исследования по устойчивости в большом основываются, как правило, на статическом критерии. Уравнения, описывающие различные удаленные друг от друга равновесные состояния, остаются при этом нелинейными. Познакомимся со структурой таких статических уравнений, относящихся к трех¬
С
I
Рис. 21.3. Графики на фазовой плоскости.
*) См. Изв. АН СССР, ОТН, № з (1955), 35—68.
§ 201] СТАТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В БОЛЬШОМ
827
мерной задаче *). Мы не будем приводить здесь общих соотношений нелинейной теории упругости, а сразу же введем те допущения, которые уместны при исследовании устойчивости гибкой конструкции. Они заключаются в том, что составляющими деформаций можно пренебрегать, если они входят в уравнения наряду с поворотами, и что как деформации, так и повороты являются малыми по сравнению с 1.
В дальнейшем откажемся от раздельного рассмотрения деформации тела в основном состоянии и при переходе к новому состоянию, как это было принято в § 198, и будем считать недеформированное положение тела исходным.
Обозначим через и, v, w перемещения точек тела вдоль осей декартовой системы координат х, у, z. Деформации удлинения оказываются равными **)
ди, 1 г/ди \2, / dv\%, (dw\2l
+ + W J’
dv. 1 [7 du\2. ( dv \2. / dw \
*y = -W+ 2 IxW) + iw) + iw)
dw, 1 Г/ du \2, / dv\%, (dw\21
e-=iF+2 [Ы +Ы +Ы J’
(21.19)
а деформации сдвига равны
ди, dv,
fХУ ду г дх '
dv. dw
Чу* дг ' dv
fix ' г)? ' ft?
dy
du
~dz
du
du
i
dv
dv
i
dw
dw
dx
~dy
~dx
17
+
dx
~dy
du
du
-f
dv
dv
i
dw
dw
~dy
~dl
dy
~dl
+
~Sy
~dz
du
du
i
dv
dv
+
dw
dw
~dz
dx
~r
~dz
dx
~dz
dx
(21.20)
Если считать перемещения и, v малыми по сравнению с w и пренебречь в (19) и (20) нелинейными членами, содержащими и их;, то получим формулы для ех, еу, уху, которые были выведены в главе VII для гибких пластинок.
Воспользуемся, далее, приближенными зависимостями типа (13):
dw
dy
dv
dz
du
~dz
dw
dx
dv
~dx
*) Этот вопрос исследовался В. В. Новожиловым [21.8], В. В. Болотиным [21.1] и другими. Обзор литературы по общим соотношениям нелинейной теории упругости дан К. 3. Галимовым [21.4]. Дальнейшее изложение построено в основном по книге В. В. Новожилова [21.8].
**) См. указанную в § 198 книгу П. Ф. Папковича, стр. 69»
828
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
и обозначим линейные составляющие гх, и т. д. через е., л,
Тлгу, л» • • • 5 пренебрегая квадратами этих величин по сравнению с квад-
Уравнения равновесия элемента тела составим, пользуясь прежними допущениями об относительной величине деформаций и поворотов. Тогда косинусы углов, составляемых ортами повернутых осей координат с неподвижными осями х, у, zt определяются той же таблицей, что и на стр. 819, но с заменой и/ на и т. д. Рассуждая так же, как в § 198, получим уравнения равновесия в виде (массовые силы по-прежнему не учитываем)
Рассмотрим вновь в качестве примера гибкую пластинку. Примем повороты в плоскости пластинки пренебрежимо малыми (о)2 = 0) и не будем учитывать в первых двух уравнениях члены, зависящие от касательных напряжений xxz, xyz. Если, кроме того, принять соотношения (21), то система (23) получит вид
эти уравнения и лежат в основе нелинейной теории пластинок (см. главу VII).
ратами поворотов, получим:
(21.22)
+ ~дг Xjcz<0* ~ С*(0*) =
(ZX2 °ХШу + Ххушх) Н~ V®* ауШх) +
~дг (°г — Xzx<0y хгушл) = °-
(21.23)
' XZ
да г dzvx dzxv d<sv
£4--/1==0, -5+ -5 = 0,
дх 1 ду дх 1 ду
dzV2 d2w d2w d2w
У2 i j l ~ — rv
dy °x dx2 x dy + °y dy2 0»
dx
§201] СТАТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ в БОЛЬШОМ 829
Граничные условия в общем случае сохраняют ту же форму, что и в § 198; первое из условий составляется по (16):
(Рх xyz “Ь хг®у) I Н” ух yz yzy) 4
+ i'zx — *zy<»z + n = Px> (21 *24)
где px — составляющая внешней нагрузки; принимаем, что внешние силы не меняют своей величины и направления.
Выпишем, далее, соотношения между напряжениями и деформациями по типу (15):
°* = тЫв* + -йГЩГе)* 2(пЬ) и т- д- (21-25)
Если подставить в (23) значения ох, хху9... по (25) и воспользоваться зависимостями (19)—(20), то придем к уравнениям относительно перемещений и, v, w. В отличие от уравнений, составленных в § 198, они будут уже нелинейными, и это объясняется структурой формул (19)—(20) или (22) для составляющих деформаций. Таким образом, нелинейность здесь имеет геометрический смысл и вызвана тем, что перемещения считаются не малыми, а конечными. Если необходимо учесть еще и физическую нелинейность, то соотношения (25) надо заменить на соответствующие зависимости, относящиеся к рассматриваемой системе. Во всех предыдущих выкладках мы считали деформации и повороты малыми по сравнению с 1; в противном случае нам пришлось бы учесть не только изменение ориентации граней элемента, но и изменение площади граней; кроме того, таблица косинусов, приведенная на стр. 819, получила бы иной вид (см. [21.8]).
Система уравнений относительно и, v, w может быть заменена эквивалентной системой, содержащей, например, одно из перемещений и, кроме того, функцию напряжений, как это было сделано при рассмотрении гибкой пластинки; но тогда должны быть выписаны зависимости, вытекающие из (19) и (20) и выражающие условие совместности деформаций.
Решение окончательной системы уравнений определяет зависимость между параметром нагрузки X и величинами, характеризующими деформированное состояние тела. В ряде задач мы стремились установить значение нижней критической нагрузки. Попытаемся дать теперь более строгое определение этого понятия. Напомним сначала тот ход рассуждения, который привел нас к понятию верхней критической нагрузки. Мы рассматривали основное устойчивое напряженное состояние. Далее, мы увеличивали параметр X и опред ляли точку разветвления решений, считая, что в этой точке при* Х = ХВ основное состояние перестает быть устойчивым. /
Теперь подойдем к задаче с другой стороны. Примем, что при достаточно большом значении X в заданной области характеристик
830 ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
имеют место устойчивые вторичные равновесные состояния, отличающиеся от основного (например, моментные состояния для оболочки, в то время как основное состояние является безмоментным). Будем уменьшать параметр X и следить за характером решений, определяющих вторичные состояния. То значение параметра X, при котором вторичные состояния тела перестают быть устойчивыми, назовем нижним критическим значением Хн. Мы допускаем вместе с тем, что при значениях X, меньших, чем Хн, могут иметь место вторичные состояния (например, моментные состояния для оболочки), но уже неустойчивые *). Если конструкция является идеальной, т. е. полностью соответствует принятой модели, то при нагрузке, отвечающей Хн, и может произойти скачкообразный переход конструкции от вторичного состояния к основному.
Из приведенных определений вытекает, что «первая» нижняя критическая нагрузка не должна лежать выше «первой» верхней. В самом деле, при Х = ХВ в окрестности основного состояния появляются некоторые вторичные состояния, которые мы считаем устойчивыми. Следовательно, должно иметь место соотношение **) Хн Хв.
В предыдущих главах мы понимали под нижней критической нагрузкой такую нагрузку, при которой основная форма равновесия перестает быть единственной. Для системы с одной степенью свободы оба подхода приводят к одному и тому же результату. Но в случае системы с двумя и более степенями свободы вместе с возрастанием числа точек бифуркации (собственных значений линеаризованной задачи) увеличивается и число нижних точек ветвей диаграммы «нагрузка — характеристика деформации»***).
Но из этих нижних точек практическое значение имеет лишь та, которая соответствует потере устойчивости вторичных форм равновесия. Следующая точка отвечает переходу от одного вида неустойчивости к другому. Следовательно, при определении нижнего критического параметра нагрузки, являющегося основой для практических расчетов, надо исследовать именно те решения исходных уравнений, которые соответвуют устойчивым вторичным положениям. Это обстоятельство надо иметь в виду при использовании различных приближенных методов интегрирования исходных уравнений. Метод Ритца дает возможность непосредственно исследовать энергию системы и отобрать решения, отвечающие устойчивым состояниям.
*) Такие состояния найдены, например, для удлиненной цилиндрической панели, подвергающейся поперечной нагрузке (см. [0.3], стр. 244).
**) Можно, правда, представить себе, что интервал основных устойчивых состояний обрывается в некоторой точке X = Хв, а вторичные устойчивые состояния возникают лишь при более высоком значении X, но такой случай является гипотетическим.
***) В указанном выше примере с цилиндрической панелью, приведенной к системе с двумя степенями свободы, были найдены две верхние и две нижние точки диаграмму.
§ 202] ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ в БОЛЬШОМ 831
Метод Бубнова — Галеркина, примененный к уравнениям формально, может привести к неустойчивым решениям *). Если используется метод конечных разностей и вычисления проводятся с помощью цифровых электронных машин, то и здесь надо относиться к результатам с осторожностью. Впрочем, опыт показывает, что неустойчивые решения можно получить в процессе машинного счета лишь в виде исключения.
Таким образом, теория устойчивости упругих систем в большом тесно соприкасается с качественной теорией нелинейных дифференциальных уравнений. Ряд результатов, относящихся к пологим гибким оболочкам, был получен в этом направлении И. И. Воровичем [21.3]. С помощью методов функционального анализа он показал, что в тех случаях, когда начальное состояние оболочки является безмоментным, всегда существует число \ > — оо такое, что при X < \ в >зможна единственная форма равновесия и в то же время в интервале значений параметра \ X < \ е (где е — любое сколько угодно малое положительное число) существуют такие X, которым, кроме безмоментной, соответствует по крайней мере одна моментная форма равновесия оболочки. Эти значения \ удовлетворяют соотношению \ < Хв, где Хв — наинизшее собственное число линеаризованной задачи, отвечающее точке бифуркации исходных уравнений. Таким образом, для наиболее важного класса нелинейных задач строго доказана возможность получения не единственного решения исходных уравнений при нагрузках, лежащих ниже эйлеровой.
§ 202. Энергетический критерий устойчивости в большом
Как мы видели, при отыскании практически ценных ветвей решений нелинейной задачи важно определить характер соответствующих форм равновесия; существенную роль при этом играет энергетический критерий. Пользуясь им, мы можем, прежде всего, уточнить наши представления о равновесных формах консервативной системы вблизи точки бифуркации, т. е. при нагрузках, мало отличающихся от верхнего критического значения.
Рассмотрим случай системы с одной степенью свободы **). Обозначим параметр нагрузки через р и параметр характерного перемещения (например, стрелы прогиба оболочки) — через С. В отличие от линейной задачи (§ 199), мы можем теперь представить энергию с учетом высших степеней С Допустим, что в выражении для безразмерной полной энергии Э* удержаны степени С до четвертой включительно и это выражение имеет вид
•э* = с2 (Рв — р) С2 — ср + ср, (21.26)
*) Под этим здесь понимаются решения, соответствующие неустойчивым формам равновесия.
**) Исследование этого случая принадлежит В. Койтеру [21.14].
832
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
где рв — параметр верхней критической нагрузки, Ct — некоторые постоянные. Примеры выражений такого типа для энергии встречались нам в задачах, относящихся к гибким пластинкам и оболочкам.
Рассмотрим прежде всего критическое состояние и положим р = рв. Допустим сначала, что С3 Ф 0; тогда член, содержащий С4
можно или С3 < 0 ждаться
отбросить, так что будет 3* = — С3С3. Ори С3 > 0 и С> 0 и С < 0 переход к смежному состоянию будет сопровопадением полной энергии, поэтому здесь равновесное
состояние, отвечающее /?в, окажется неустойчивым; это заключение вытекает также из первой теоремы Ляпунова (стр. 823). Если же С3 = 0, то надо исследовать выражение 3* = С4С4. При С4 > 0 отклонение системы от основного состояния будет связано с повышением уровня энергии, и критическое состояние окажется устойчивым. Напротив, при
С4 < 0 оно будет неустойчивым.
Обратимся теперь к равновесным формам для уровней нагрузки, лежащих несколько выше или ниже критического. Если учитывать только члены второго порядка, получим: 3* = С2 (рв — р)С2. Считая основное состояние устой-
Рис. 21.4. Диаграмма «нагрузка—прогиб» при С3 > 0; точка разветвления принадлежит к неустойчивой ветви.
чивым при р < /?в, получим: С2 > 0. В случае С3 Ф 0 отбросим снова член с С4. Учитывая, что смежное состояние является равновесным, выпишем равенство дЭ*/дС = 0 при С ф 0; тогда получим:
Г 2 / Ч с2 д*Э* 0, ч -
3 (рв р) » £2 2 (Р рв) С2'
Если С3 > 0, то при нагрузке, превышающей /?в, т. е. при Р> Рв> будет С < 0, д2Э*/дС2 > 0, так что отклоненные состояния будут устойчивыми; при р < рв получим: С > 0, д2Э*/д2 < 0, что указывает на неустойчивость. На рис. 21.4 изображена диаграмма р(С) при С3>0 и С4 = 0, относящаяся к С0 = 0 (отсутствие начальных отклонений); ветви устойчивых состояний изображены сплошными линиями, неустойчивых — пунктиром. В верхней критической точке А происходит обмен устойчивостью между ветвями *), причем сама
*) Свойства подобных диаграмм, содержащих точки бифуркации, впервые исследовались Пуанкаре (Acta mathematica 7 (1885), 259—380) в связи с изучением фигур равновесия небесных тел; в задачах упругой устойчивости эти диаграммы исследовались Г. Ю. Джанелидзе [21.5],
В. В. Болотиным [21.1] и другими авторами.
§ 2021 ЭНЕРГЕТИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ В БОЛЬШОМ 833
критическая точка принадлежит, как мы видели, к неустойчивой
ветви (зачерненный кружок).
Разберем, далее, случаи С3 = 0 и С4 Ф 0. При С4 > 0 будет
Г9 12/ \ д2Э* ЛГУ, ч
~2 С 4 — С2 (/* Рв)*
Отсюда заключаем, что при р > /?в смежные равновесные состояния будут устойчивыми, как показано на рис. 21.5, причем точку А
для рв = ркр надо отнести к ус-
ветвления принадлежит к устойчивой ветви.
р (С) будет обращен выпуклостью вверх (рис. 21.6) и точка А будет относиться к ветви неустойчивости.
Рассмотрим, далее, влияние начальных возмущений (например, начальной погиби в случае оболочки) на поведение системы. Выпишем дополненное выражение для энергии в виде
= ОV ид -р)С2- ср + ср - СМ, (21.27)
где Cq — параметр начального возмущения, /?в> ид — верхняя критическая нагрузка для идеальной системы. Анализ выражений для дЭ*/д(, и д2Э*/дС2 приводит к следующим выводам. В случае С3 > 0, С > 0 или С3=0, С4 < 0 диаграммы р(С) имеют предельные точки, как показано на рис.' 21.4 и 21.6, причем эти точки относятся к неустойчивым ветвям. При С3 = 0, С4 > 0 все равновесные формы оказываются устойчивыми (рис. 21.5).
В качестве примера, отвечающего рис. 21.4, может служить цилиндрическая панель, сжатая вдоль образующей (§ 139), а для рис. 21.5 — сжатая подкрепленная пластинка (§ 88). Пример
834 ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
конструкции, соответствующей диаграмме рис. 21.6, приведен в статье Б. JI. Николаи [21.7].
Аналогичным образом могут быть исследованы равновесные состояния, смежные с нижней критической точкой /?н. Эта точка, как мы видели, разделяет области неустойчивости и устойчивости. Следовательно, при р=рн вторая вариация от полной энергии должна обращаться в нуль: Ъ2Э* = 0.
Наконец, энергетический критерий может в известной мере служить для определения нагрузки, при которой надо ожидать прощелкивания реальных конструкций. Некоторые авторы предлагали принимать за основу при расчете на устойчивость в большом не нижнюю критическую нагрузку, а такую нагрузку /?э, при которой энергия основного состояния равна энергии прощелкнутого состояния. Надо отметить, однако, что в тех конкретных задачах, которые были до сих пор решены, величина рэ превышает рн незначительно (в пределах 10%); поэтому существенного практического значения это предложение не имеет. В то же время при наличии достаточных возмущений прощелкивание к устойчивому состоянию с более высоким уровнем энергии может произойти. Очевидно, вопрос о реализации тех или иных равновесных форм может быть решен лишь вероятностными методами.
Мы обсуждали выше только критерии устойчивости равновесия деформируемых тел в применении к консервативным и отчасти к диссипативным системам; эти критерии лежат в основе всех знакомых нам методов решения частных задач для таких систем. Критерии устойчивости систем, имеющих приток энергии извне, должны быть рассмотрены особо (см., например, § 21).
Обратимся теперь к случаю, когда консервативная система подвергается комбинированному нагружению.
§ 203. Критерий устойчивости при комбинированной нагрузке
Допустим, что потеря устойчивости упругой системы может произойти при действии нагрузок различного вида. Например, для подкрепленной прямоугольной пластинки такими нагрузками могут являться сжимающие усилия в одном и другом направлениях либо усилия сдвига.
Предположим, что найдены критические значения нагрузок при их раздельном применении, и рассмотрим случай, когда они действуют совместно в том или ином сочетании *).
Примем, что система, имеющая одну степень свободы, подвергается действию двух нагрузок разного типа и что исследуется устойчивость системы в малом.
*) В общем виде задача об устойчивости при комбинированном нагружении была впервые решена П. Ф. Папковичем [0.7].
§ 203] КРИТЕРИЙ УСТОЙЧИВОСТИ ПРИ КОМБИНИРОВАННОЙ НАГРУЗКЕ 835
На рис. 21.7 по осям откладываются параметры нагрузок Р, Q; критические значения их при раздельном приложении обозначим через Р* и Q*. а при совместном действии — через Рв и QB. Отмеченная на рис. 21.7 точка А имеет координаты Р0, (?0, лежащие в пределах 0 < Р0 < Рв, 0 < Q0 < QB. Очевидно, точка А находится в области устойчивости, относящейся к основному состоянию.
Полную энергию, соответствующую точке Л, представим в виде
5o = y(a — РЛ> — TQo) <72 = 4
(21.28)
где q — обобщенная координата, изменяющаяся при переходе от основного состояния к смежному. Производная ddjdq обращается в нуль лишь при q = 0; исходя из критерия устойчивости основного состояния, находим:
д2Э dq2
= 90 > 0.
Далее, будем изменять нагрузки, приложенные к системе, полагая:
Р = P0-\-Xk, Q = Q0-\- XL
На рис. 21.7 величина X откладывается вдоль луча Ап; параметры k и / представляют собой направляющие косинусы луча:
Рис. 21.7. Переход из области устойчивости в область неустойчивости при комбинированной нагрузке.
k — cos(x, п), / = cos(<y, п). Так как работа внешних нагрузок вычитается из полной энергии системы, то для нового состояния будет
Э = \ (a — РР — TQ) q* = 1 [0О — X ®k + Т/)] q\ (21.29) Обозначая ф/г+7/) через ft, получим:
Э = \(Ь0-ЬХ)Ч\ - = В0-ЬХ. (21.30)
Если параметры, / положительны, то всегда ft > 0; при отрицательных kt I имеем ft < 0. В случае же, если один из параметров k, / положителен, а другой отрицателен (луч А'п' на рис. 21.7), может быть ft >- 0 либо ft < 0. В зависимости от знака ft система будет вести себя при увеличении X различно.
Предположим, что ft > 0. Тогда при некотором значении X мы получим:
Щ- = %-ЪХ = 0, (21.31)
836
ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [ГЛ. XXI
что соответствует критерию потери устойчивости; следовательно, мы найдем первую пару критических нагрузок Яв, QB. При дальнейшем возрастании X всегда будет
д2Э
dq2
= 0О — ьх < О,
(21.32)
так что равновесие будет неустойчивым.
Допустим, что на рис. 21.7 равенство (31) выполняется для точек В и Вг\ эти точки будут лежать на граничной линии, отделяющей устойчивую область от неустойчивой. Если мы движемся вдоль луча Ап от точки А, то после того, как пройдена точка В, мы уже не можем вернуться в область устойчивости; это же относится к переходу от А' к В' вдоль Л V. В случае, когда ft < О, величина d29/dq2 не может обратиться в нуль, и следовательно, мы всегда будем находиться в области устойчивости.
Таким образом, проводя луч из любой точки области устойчивости в произвольном направлении, мы можем либо пересечь граничную линию, и при этом только один раз, либо вовсе не пересечь
ее. Легко видеть, что граничная линия, удовлетворяющая таким
Рис. 21.8. Граничные линии, отделяющие устойчивую область от неустойчивой.
Рис. 21.9. Приближенное определение граничной линии для зоны устойчивости.
требованиям, не может быть обращена выпуклостью к области устойчивости. Это означает, что граничная линия должна состоять из участков прямых или из участков кривых, обращенных выпуклостью к области неустойчивости (рис. 21.8). При этом угол наклона прямых участков, касательных к криволинейным участкам, должен изменяться монотонно.
Этот вывод дает возможность установить приближенные значения критических усилий при комбинированной нагрузке. В самом деле, соединим точки Рт и Qm прямой (рис. 21.9); очевидно, ее точки дают критические сочетания усилий Р, Q либо точно, либо приближенно, но во втором случае всегда с известным запасом устойчивости.
§ 204] НЕКОТОРЫЕ ЗАДАЧИ ДЛЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ 837
Допустим, что нам известно положение касательных к граничным линиям в точках Р = Р„ и Q = Q (рис. 21.9); тогда искомые граничные кривые должны лежать между прямой PjQ* и этими касательными. Уравнение «безопасной» прямой имеет вид
- + --=1. (21.33)
Эти результаты нетрудно распространить на случай, когда система подвергается действию трех нагрузок различного типа: Я, Q, R; вместо плоской картины мы получим пространственную, вместо граничной линии — поверхность, вместо прямых участков — плоскости. При числе нагрузок большем трех необходимо перейти к многомерному пространству.
Аналогичные выводы можно получить также в более сложном случае, когда система имеет п степеней свободы [0.7]. Б. М. Броуде распространил эти выводы на нелинейные задачи, относящиеся к устойчивости в большом. Оказалось, что приведенные критерии устойчивости при комбинированном нагружении могут в известных случаях служить для определения не только верхних, но и нижних критических нагрузок. Этот вопрос желательно подвергнуть дополнительному исследованию.
§ 204. Некоторые задачи для дальнейших исследований
В заключение перечислим некоторые актуальные задачи теории устойчивости упругих систем, о которых отчасти говорилось уже выше. Наиболее важными с практической точки зрения — особенно для авиационной техники — являются в настоящее время задачи, относящиеся к устойчивости оболочек. Необходимо, пользуясь электронными цифровыми машинами, получить надежные данные для расчета оболочек на устойчивость в большом. Основная цель при этом — определение уточненных значений нижних критических нагрузок. Желательно рассмотреть вновь случаи круговой цилиндрической оболочки, подвергающейся осевому сжатию, внешнему давлению и кручению; сферической и эллипсоидальной оболочек при внешнем давлении; пологих оболочек различного очертания в плане при действии поперечной нагрузки. Желательно исследовать различные случаи комбинированного нагружения круговых цилиндрических оболочек; особое внимание должны привлечь задачи о совместном действии внутреннего давления и осевого сжатия или кручения.
Существенное практическое значение имеют задачи об устойчивости подкрепленных оболочек. Необходимо рассмотреть более подробно различные модели таких конструкций — анизотропную оболочку с разнесенной жесткостью ребер и гладкую оболочку с дискретными ребрами — и установить границы применения таких
838 ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
моделей. Важно найти методы для рационального конструирования подкрепленных оболочек наименьшего веса.
Все более широкое применение в различных областях техники получают оболочки, изготовленные из стеклопластиков, однако данных для расчета таких оболочек крайне мало. Здесь важно установить, какие модели должны быть положены в основу исследований для оболочек той или иной структуры, и в зависимости от этого составить исходные уравнения, исходя из теории ортотропных оболочек либо из общей теории анизотропных оболочек. Далее, необходимо выяснить, для какого круга таких оболочек должна быть рассмотрена устойчивость в большом. Необходимо экспериментально установить основные упругие характеристики для оболочек различной структуры.
Число работ, посвященных трехслойным оболочкам, достаточно велико; но в настоящее время еще нет надежных данных для расчета на устойчивость трехслойных оболочек средней длины, подвергающихся внешнему давлению и кручению, а также этим видам нагрузки в сочетании с осевым сжатием. Эти задачи должны быть решены не только в линейной, но и в нелинейной постановке. Экспериментальных данных для таких оболочек накоплено мало.
Вопрос об устойчивости оболочек в малом и1 в большом за пределами упругости требует значительного внимания. Желательно выяснить, насколько уместно пользоваться здесь той или иной теорией пластичности, особенно при конечных перемещениях, и получить практически доступные методы решения конкретных задач. Далее, необходимо определить верхние и нижние критические нагрузки для оболочек различного очертания.
Вопрос о температурном выпучивании оболочек и пластинок ждет дальнейшей разработки. Здесь важно рассмотреть подкрепленные оболочки с тем или иным законом распределения температур по сечению обшивки и подкрепляющих ребер, а также по поверхности обшивки, и определить значения критических температур. Мало разработан еще вопрос о выпучивании пластинок и оболочек при тепловом ударе.
Проблема устойчивости оболочек, пластинок и стержней при ползучести также нуждается в разработке. Необходимо вновь проанализировать имеющиеся критерии и методы определения критического времени, сопоставив их с экспериментальными данными для различных материалов. Существенным является вопрос об устойчивости оболочек в большом при ползучести. Критерии устойчивости в температ} рных задачах должны быть обобщены исходя из термодинамических соотношений для обратимых и необратимых процессов.
Актуальными являются задачи, относящиеся к устойчивости оболочек, пластинок и стержней при динамическом нагружении. Же¬
§ 204] НЕКОТОРЫЕ ЗАДАЧИ ДЛЯ ДАЛЬНЕЙШИХ ИССЛЕДОВАНИЙ 839
лательно исследовать устойчивость оболочек и пластинок при весьма быстром (ударном) нагружении, с учетом распространения волн в срединной поверхности. В имеющихся работах рассматривались, как правило, элементы конструкций с «равновозможными» начальными несовершенствами различного типа. Для реальных конструкций те или иные виды начальных несовершенств могут явиться преобладающими, в этом случае надо ожидать перескоков от одних форм выпучивания к другим в процессе динамического нагружения. Возникает вопрос: можно ли осуществить предельный переход от задачи для конструкции с начальными несовершенствами к задаче о поведении идеальной конструкции? Решение этого вопроса даст возможность более строго подойти к понятию динамической критической нагрузки. Для практических расчетов важно также определить величину работы, которая может быть поглощена конструкцией до момента выпучивания. Желательно исследовать вопрос о динамической устойчивости замкнутых оболочек, содержащих жидкость, с учетом приведенной массы жидкости.
Желательно продолжить решение задач об устойчивости оболочек для того случая, когда основное напряженное состояние является моментным. Это относится к коротким цилиндрическим оболочкам, подвергающимся внешнему давлению или совместному действию осевого сжатия и внутреннего давления, к пологим оболочкам, несущим нормальную нагрузку, и т. д. Здесь целесообразно рассмотреть бифуркационные задачи, когда исходная форма оболочки сменяется последовательно формами различного типа и появляется разное число мелких вмятин. В некоторых задачах (например, при наличии внутреннего давления в замкнутых оболочках) надо учесть развитие пластических деформаций в основном состоянии.
Особенно важными являются исследования по применению статистических методов для расчета конструкций на устойчивость. Это относится, прежде всего, к устойчивости оболочек в большом. Все имеющиеся статистические подходы к задаче должны интенсивно развиваться. Необходимо изучить законы распределения начальных несовершенств для реальных оболочек при различной технологии изготовления и вероятностные характеристики нагрузок, испытываемых элементами разных конструкций. Применение статистических методов должно объяснить экспериментальные данные по разбросу критических нагрузок и вместе с тем подвести более надежную базу под проектирование реальных конструкций. При рассмотрении динамической устойчивости конструкций надо применять статистические методы, относящиеся к случайным процессам.
Разнообразные методы решения частных задач на устойчивость должны быть пересмотрены, исходя из возможностей электронной цифровой вычислительной техники. Желательно приложить цифровые машины к предварительным этапам решения задач по методу
840 ОБЩИЕ КРИТЕРИИ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ [гл. XXI
Ритца, начиная с определения энергии. Надо научиться отделять устойчивые ветви решений от неустойчивых при применении метода конечных разностей или метода коллокации. Целесообразно разработать специальную программу для определения нижних критических нагрузок без исследования всей области выпучивания оболочек.
Для многих конструкций расчет на устойчивость является решающим. До сих пор при определении размеров проектируемых конструкций исходят обычно из сопоставления с аналогичными уже осуществленными сооружениями либо из «интуитивных» соображений, а затем проводят проверку на устойчивость. Между тем применение электронных вычислительных машин должно позволить сопоставить большое число вариантов конструкции и найти наивыгоднейший из них. Это относится, например, к конструкциям из стеклопластиков, для которых может быть установлено наиболее выгодное сочетание различных слоев с тем или иньщ направлением волокон. Таким об разом были бы найдены основания для определения не только размеров, но и желательной технологии изготовления конструкции.
Необходимо вернуться к исходным уравнениям нелинейной теории оболочек и составить систему уравнений, которая могла бы описать выпучивание оболочек по длинным волнам. Ждут своего дальнейшего развития методы функционального анализа для качественного исследования нелинейных уравнений теории оболочек и, в особенности, для выяснения свойств решений вблизи нижних критических точек.
Общая линейная теория устойчивости оболочек также еще не является завершенной. Здесь особенно важно уточнить пределы применимости ур£В1ений различного типа и выяснить — в какой мере влияет на решение задач устойчивости «точечное» удовлетворение граничным условиям на кромках оболочки.
ЛИТЕРАТУРА
Ко всей книге
0. 1. В. В. Болотин, Динамическая устойчивость упругих систем, Гостехиздат, М., 1956; Неконсервативные задачи теории упругой устойчивости, Физматгиз, М., 1961.
0. 2. И. Г. Бубнов, Строительная механика корабля, часть I, 1912; часть II,
1914.
0. 3. А. С. Вольмир, Гибкие пластинки и оболочки, Гостехиздат, М., 1956.
0. 4. А. Н. Д и н н и к, Устойчивость упругих систем, ОНТИ, 1935; Продольный изгиб, ОНТИ, М., 1936.
0. 5. Н. В. К о р н о у х о в, Прочность и устойчивость стержневых систем, Стройиздат, М., 1949.
0. 6. X. М. М у ш т а р и, К. 3. Г а л и м о в, Нелинейная теория упругих оболочек, Таткнигоиздат, Казань, 1957.
0. 7. П. Ф. Папкович, Строительная механика корабля, часть II, Судпромгиз, Л., 1939.
0. 8. С. Д. Пономарев, В. Л. Б и д е р м а н, К. К. Лихарев, В. М. Ма* кушин, Н. Н. Малинин, В. И. Феодосьев, Расчеты на прочность в машиностроении, изд. 1-е, т. II, Машгиз, М., 1952, изд. 2-е, т. III, 1959.
0. 9. А. Р. Р ж а н и ц ы н, Некоторые вопросы механики систем, деформирующихся во времени, Гостехиздат., М., 1949.
0.10. А. Р. Ржаницын, Устойчивость равновесия упругих систем, Гостехиздат, М., 1955.
0.11. А. Ф. Смирнов, Статическая и динамическая устойчивость сооружений, 1947; Устойчивость и колебания сооружений, 1958.
0.12. В. Г. Ч у д н о в с к и й, Методы расчета колебаний и устойчивости упругих систем, изд. АН УССР, Киев, 1952.
0.13. И. Я. Штаерман и А. А. Пиковский, Основы теории устойчивости строительных конструкций, Госстройиздат, М., 1939.
0.14. С В. Biezeno, R. Gramme 1, Technische Dynamik, Berlin, 1939 (в переводе; К. Б. Бицено, Р. Граммель, Техническая динамика, часть I, Гостехиздат, J1., 1950).
0.15. F. Bleich, Buckling strength о! metal structures, NY, 1952 (в переводе: Ф. Блейх, Устойчивость металлических конструкций, Физматгиз, М.*
1959).
0.16. G. Burgermeister, Н. Steup, Stabilitatstheorie, Ak. Verlag, Berlin, Teil I, 1957.
0.17. G. Gerard, Weight analysis of compression structures, NY, Un-ty Press, 1956; Introduction to structural stability, 1962.
0.18. F. Hartmann, Knickung, Kippung, Beulung (в переводе: Ф. Гартман» Устойчивость инженерных сооружений, Госстройиздат, М.г 1939),
842
ЛИТЕРАТУРА
0.19. С. F. Kollbrunner, М. Meister, Knieken, Springer-V., Berlin, 1955; Ausbeulen, 1958.
0.20. R. Mayer, Die Knickfestigkeit, Springer-V., Berlin, 1921.
0.21. A. Pfltiger, Stabilitatsprobleme der Elastostatik, Springer-V., Berlin, 1950.
0.22. F. R. S h a n 1 e y, Weight-strength analysis of aircraft structures, NY, 1952 (в переводе: Шенли, Анализ веса и прочности самолетных конструкций, Оборонгиз, М., 1957).
0.23. S. Timoshenko, Theory of elastic stability, NY, 1936 (в переводе:
С. П. Тимошенко, Устойчивость упругих систем, Гостехиздат, М., изд. 1-е,
1946, изд. 2-е, 1955); S. Т i ш о s h е n к о, J. Gere, Theory of elastic stability,. NY, 1961.
К главе I
1. 1. Б. Г. Г а л e p к и н, Теория продольного изгиба и опыт применения
теории продольного изгиба к многоэтажным стержням, стойкам с жесткими соединениями и системам стоек, Изв. C.-Пет. полит, ин-та 12, № 1 (1909), 167—241, № 2 (1909), 383—451, Собр. соч., т. 1, изд. АН СССР, М., 1952, 24—124.
1.2. К. С. Д е й н е к о, М. Я. Леонов, Динамический метод исследования устойчивости сжатого стержня, Прикл. мат. и мех. 19 (1955),. 738—744.
1. 3. Г. Ю. Джанелидзе, Об устойчивости стержня под действием следящей силы, Труды Ленингр. политехи, ин-та, № 192 (1958).
1. 4. Ю. Д. Копей кин, М. Я. Леонов, Об одном особом случае потери устойчивости равновесия сжатого стержня, Прикл. мат. и мех. 19
(1955), 736—737.
1. 5. А. Н. Крылов, О формах равновесия вертикально нагруженных элементов, Изв. АН СССР (1931), 963.
1. 6. Е. П. Попов, Нелинейные задачи статики тонких стержней, Гостехиздат, М., 1948.
1. 7. Ф. С. Ясинский, О сопротивлении продольному изгибу, 1894; Избранные работы по устойчивости сжатых стержней, Гостехиздат, 1952.
1. 8. М. Beck, Die Knicklast des einseitig eingespannten, tangential gedriickten Stabes, Zeitschr. angew. Math, und Phys. 3, № 3 (1952), 225—228.
1. 9. L. Euler, Methodus inveniendi lineas curvas..., Lausanne et Geneve, 1744; Additamentum 1: De curvis elasticis, p. 267 (Л. Эйлер, Метод нахождения кривых линий, обладающих свойствами максимума либо минимума, М., Гостехиздат, 1934; Приложение 1: Об упругих кривых).
1.10. L. Euler, Sur la force des colonnes, Mem. de l’Acad., Berlin, 13, (1757), 251—282.
1.11. F. Engesser, Ueber die Berechnung auf Knickfestigkeit beanspruchten Stabe aus Schweifi- und Gufieisen, Z. osterr. Ing. Arch. Ver., № 45 (1893), 506—508.
1.12. L. Lagrange, Sur la figure des collonnes, Oeuvres, 2, Paris
(1868), 125—170, Sur la force des ressorts plies, Oeuvres 3 (1869),
77—110.
1.13. J. Ratzersdorfer, Die Knickfestigkeit von Staben und Stabwerken, Wien, 1936.
1.14. R. H. Scan lan, Resistance network solution of some structurul problems in deflection and stability, Proc. Soc. Exp. Stress Anal. 16, No 1 (1958), 117—128.
1.15. H. S. Tsien, Lower buckling Joad in the nonlinear buckling theory for thin shells, Quart. Appl. Math. 5, № 2 (1947), 236—237.
1.16. L. V i a n e 11 o, Graphische Untersuchung der Knickfestigkeit gerader Stabe, Z. Ver. deutsch. Ing. 42 (1898), 1436—1443.
ЛИТЕРАТУРА
843
К главе II
2. 1. Б. М. Броуде, Предельные состояния стальных балок, Госстройиздат, М.—Л., 1953.
2. 2. А. С. Вольмир, К вопросу о продольном изгибе за пределом упругости, Научн. зап. Харьковск. мех.-маш. ин-та (1935), 137—145.
2. 3. А. В. Геммерлинг, О несущей способности сжатых стальных конструкций, Труды ЦНИПС, № 7, М. (1952).
2. 4. С. Д. Л ей тес, Устойчивость сжатых стальных стержней, Госстройиздат, М., 1954.
2. 5. С. Н. Никифоров, Устойчивость сжатых стержней сварных ферм, ГИЗ, М.—Л., 1938.
2. 6. Я. Г. П а н о в к о, О критической силе сжатого стержня в неупругой области. Инж. сб. 20 (1954); О продольном упруго-пластическом изгибе стержней в статически неопределимых системах, Изв. АН СССР, Механика и маш., № 2 (1962), 160—165.
2. 7. В. В. П и н а д ж я н, Некоторые вопросы предельного состояния сжатых элементов стальных конструкций, Изд. АН АрмССР, Ереван, 1956.
2. 8. Ю. Н. Р а б о т н о в, О равновесии сжатых стержней за пределом пропорциональности, Инж. сб. 11 (1952).
2. 9. Н. С. Стрелецкий, Материалы к курсу стальных конструкций, Работа сжатых стоек, Госстройиздат, Москва, 1959.
2.10. Е. Chwalla, Theorie der aufiermittig gedruckten Stabes aus Baustahl, Stahlbau, № 21—23 (1934).
2.11. F. Engesser, Ueber Knickfestigkeit gerader Stabe, Z. Arch. u. Ing.
Ver. zu Hannover 35 (1889), 455; Die Knickfestigkeit gerader Stabe, Zentralblatt der Bauverwaltung 11 (1891), 483; Ueber Knickfragen,
Schweiz. Bauzeitung 26 (1895), 24.
2.12. J. Fritsche, Naherungsverfahren zur Berechnung der Tragfahigkeit aufiermittig gedruckter Stabe aus Baustahl, Stahlbau, № 18 (1935).
2.13. K- Jezek, Die Festigkeit von Druckstaben aus Stahl, Wien, 1937.
2.14. F. J a sin ski, Zu den Knickfragen, Schweiz. Bauzeitung 26 (1895), 24 (см. Ясинский Ф. С., Избранные труды, Гостехиздат, М., 1952).
2.15. Th. К а г m a n, Untersuchungen fiber Knickfestigkeit, Physik. Z. (1908), 138; Mitteilungen fiber Forschungsarb. auf dem Gebiet d. Ing. Wesens, № 81, Berlin (1910); J. Aeron. Sciences 14 (1947), 267.
2.16. L. Navier, Resume de lemons, Paris, 1826.
2.17. A. Pfluger, Zur plastischen Knickung gerader Stabe, Ing. Archiv 20, № 5 (1952), 291—301.
2.18. M R о s, Le fcstabilite de barres comprimees par des forces excentrees, Paris, 1932.
2.19. F. R. Shanley, Inelastic column theory, J. Aeron, Sci, 13, № 12 (1946), 678; 14, No 5 (1947); Proc. Am. Soc. Civ. Eng. 75 (1949), 759.
2.20. F. Schleicher, Ueber die Grundlagen der Plastizitatstheorie und des plastischen Knickens, Stahlbau, № Ю (1951), 118.
2.21. L. Tetmajer, Die Gesetze der Knickungs- und zusammengesetzten Festigkeit der technisch wichtigsten Baustoffe, Leipzig, 1907.
К главе III
3. 1. A. H. Дин ник, О продольном изгибе стержней переменного сечения, Изв. Донск. полит, ин-та 1 (1913), 390—404; Приложение функций
Бесселя к задачам теории упругости, Избранные труды, т. 2, Изд. АН УССР, 1952, 73—78; О расчете сжатых стоек переменного сечения, Вестн. инж., No 1, 2 (1929); Устойчивость арок, М., 1946.
844
ЛИТЕРАТУРА
3. 2. Б. Г. Коренев, Некоторые задачи теории упругости и теплопроводности, 1960.
3. 3. Я. И. К о р о т к и н, А. 3. J1 о к ш и н, Н. Л. Сивере, Изгиб и устойчивость стержней и стержневых систем, Машгиз, 1953.
3. 4. Е. Л. Николаи, Об устойчивости прямолинейной формы равновесия сжатого и скрученного стержня, Труды по механике, Гостехиздат, 1955.
3. 5. Я. Л. Н у д е л ь м а н, Методы определения собственных частот и критических сил для стержневых систем, Гостехиздат, М., 1949.
3. 6. А. М. Пеньков, Устойчивость стержневых наборов, Труды Киевского технол. ин-та пищ. пром-сти, № 6 (1947).
3. 7. А. А. П и к о в с к и й, Статика стержневых систем со сжатыми элементами, Физматгиз, М., 1961.
3. 8. А. Р. Ржанидын, Теория составных стержней строительных конструкций, Стройиздат, 1948.
3. 9. Н. К. Снитко, Устойчивость стержневых систем, Госстройиздат, М.,
1952; Устойчивость сжатых и сжато-изогнутых стержневых систем, 1956.
3.10. Н. Г. Ч е н ц о в, Стойки наименьшего реса, Труды ЦАГИ, Mb 265 (1936).
3.11. A. Greenhill, On height consistent with stability, Proc. Camb. Phil. Soc. 4 (1881), 65—75.
К главе IV
4. l.C. А. Амбарцумян, К вопросу расчета устойчивости тонкостенных
стержней, ДАН АрмССР 17, № 1 (1953)*.
4. 2. В. В. Болотин, Интегральные уравнения стесненного кручения и устойчивости тонкостенных стержней, Прикл. мат. и мех. 17, № 2
(1953); О пространственных деформациях балок после потери устойчивости, Расчет пространств, констр. 4 (1959), 3—18; Конечные деформации гибких трубопроводов, Труды Моск. энергет. ин-та 19 (1956); Об устойчивости балок, соединенных упругими связями, Расчеты на прочность 1 (1954), 223—230.
4. 3. Б. М. Б р о у д е, Об устойчивости и колебаниях упруго защемленного стержня, «Сб. по теории сооружений» 5 (1954); Об устойчивости слегка искривленных и внецентренно нагруженных двутавровых балок, Расчет пространств, констр. 4 (1958), 5—36; Уточнение решения задачи
Прандтля — Тимошенко, там же, 5 (1959); Об устойчивости стержней, сжатых с двухосным эксцентриситетом, там же, 31—50; О линеаризации уравнений устойчивости, равновесия внецентренно сжатого стержня, Исследования по теории сооруж. 8 (1959), 205—221.
4. 4. В. 3. Власов, Тонкостенные упругие стержни, изд. 1-е, 1940, изд 2-е, Физматгиз, М., 1959.
4. 5. В. 3. Власов, Кручение и устойчивость тонкостенных открытых профилей, Строит, пром., № 6—7 (1938); Кручение, устойчивость и колебания тонкостенного стержня, Прикл. мат. и мех. 3, N° 1 (1939).
4. 6. А. В. Г е м м е р л и н г, К расчету внецентренно сжатых тонкостенных стержней, Труды лабор. строит, мех. ЦНИПС, Стройиздат (1949).
4. 7. И. И. Г о л ь д е н б л а т, Современные проблемы колебаний и устойчивости инженерных сооружений, Стройиздат, 1947.
4. 8. Л. М. Качанов, Устойчивость тонкостенных стержней при упругопластических деформациях, ДАН СССР 107, № 6 (1956), 803—806.
4 9. И. Ф. Образцов, К расчету тонкостенных стержней на устойчивость при изгибе, Труды МАИ, № 26, Оборонгиз (1953).
4.10. А. Р. Р ж а н и ц ы н, Устойчивость тонкостенных стержней за пределом упругости, Труды лабор. строит, мех. ЦНИПС, Стройиздат (1949).
4.11. А. И. Стрельбицкая, Несущая способность тонкостенных стержней при сложном сопротивлении, Прикладная механика, изд. АН УССР 2, Ко 3 (1956).
ЛИТЕРАТУРА
845
4.12. А. А. Уманский, Кручение и изгиб тонкостенных авиаконструкций, М., 1939; Строительная механика самолета, М., 1961.
4.13. Ху а Хай-чан, Цзе Бо-минь, Общая теория равновесия и устойчивости упругих тонкостенных стержней (на китайском языке), Acta Phys. Sinica, № 4 (1955).
4.14. J. Goodier, Torsional und flexural buckling of bars of thin-walled open section under compressive and bending loads, J. of the Aeron, Sci. (1942), 103—107.
4.15. R. Kappus, Drehknicken zentrisch gedruckten Stabe mit offenem Profil in elastisch Bereich, Luftfahrtforschung 14, № 9 (1937).
4.16. H. L. Langhaar, On torsional-flexural buckling of columns, The Journal of the Franklin Institute, № 2 (1953), 101—112.
4.17. H Nylander, Torsion, bending and lateral buckling of I-beams, Kgl. tekn. hogskolans handl., № 102 (1956), 140.
4.18. L P r a n d 11, Kipperscheinungen, Niirenberg, 1899.
4.19. S. Timoshenko, Theory of bending, torsion and buckling of thin walled members of open cross section, The Journ. of the Franklin Institute, № 3, 201—219; № 4, 249—268; № 5, 343—361 (1945).
4.20. H. Wagner, Verdrehung und Knickung von offenen Profilen, Festschrift 25-Jahre Т. H. Danzig, 1929.
К главе V
б. 1. JI. Б. Бунатян, Устойчивость тонкостенных стержней с учетом ползучести материала, Изв. АН АрмССР, серия физ.-мат., ест. и техн.
наук 6, № 2 (1953), 43—53.
5. 2. В. Ф. Воробьев, Устойчивость стержней в состоянии ползучести,
Журн. прикл. мех. и техн. физ., № 6 (1961), 135—144.
5. 3. Л. М. Качанов, Некоторые вопросы теории ползучести, Гостехиздат, 1948; Теория ползучести, Физматгиз, 1960.
5. 4. А. П. Кузнецов, Устойчивость сжатых стержней из дуралюмина
в условиях ползучести, Журн. прикл. мех. и техн. физ., № 6 (1961), 160—162.
5. 5. Л. М. К у р ш и н, Устойчивость стержней в условиях ползучести, Журн. прикл. мех. и техн. физ., № 6 (1961), 128—134; № 2 (1962).
5. 6. Ю. Н. P а б о т н о в, С. А. Шестериков, Устойчивость стержней
и пластинок в состоянии ползучести, Прикл. мат. и мех. 21, № 3 (1957).
406—412; Journ. Mech. and Phys. Solids 6 (1957), 27.
6. 7. A. P. Ржаницын, Процессы деформирования конструкций из упруго¬
вязких элементов, ДАН СССР 52, № 1 (1946), 25—28.
5. 8. В. И. P о з е н б л ю м, Устойчивость сжатого стержня в состоянии ползучести, Инж. сб. 18 (1954), 99—104.
5. 9. М. Р. Фельдман, Продольный изгиб стержня с учетом пластического последействия, Изв. АН АрмССР, серия физ.-мат., ест. и техн. наук 9, Ms 1 (1956), 75—86.
5.10. Л. А. Шаповалов, Влияние неравномерного нагрева на устойчивость сжатого стержня, Прикл. мат. и мех. 22, JNb 1 (1958), 119—123; Уравнения термоупругости и устойчивости при действии внешних сил и температурных напряжений, канд. дисс., М., 1960.
5.11. С. А. Шестериков, К вопросу устойчивости при ползучести, канд. дисс., Моск. госуд. ун-т, 1957; О критерии устойчивости стержня при ползучее, Прикл. мат. и мех., № 3 (1959).
5.12. R. L. Carlson, Time-dependent tangent modulus applied to column creep buckling, J. Appl. Mech. 23, № 3 (1956), 390.
846
ЛИТЕРАТУРА
5.13. G. Gerard, Note on creep buckling of columns, J. Aeron. Sci. 19, № 10
(1954), 714; A creep buckling hypothesis, J. Aeron. Sci. 23, № 9 (1956),
879—882, 887; J. Aerospace Sci., 29 № 6 (1962).
5.14. N. J. Hoff, Creep buckling, Aeron. Quarterly 7, № 1 (1956), 1—20
(см. сб. переводов «Механика», ИЛ, № 6, 1956); Buckling at high temperature, J. of the Royal Aer. Soc. 61, № 563 (1957), 756—774 (cm.
сб. переводов «Механика», ИЛ, № 5, 1958, 65—100); A survey of the
theories of creep buckling, Stanford Un-ty Division of Aeronaut. Eng. Research, № 80, 1958 (сб. «Механика», ИЛ, № 1, 1960, 63—96).
5.15. L. W. Hu, N. H. T r i n e r, Bending creep and its applications to beam columns, J. Appl. Mech. 23, № 1 (1956), 35—42.
5.16. J. A. H u 11, Critical time in creep buckling, J. Appl. Mech., 22, № 3
(1955), 432.
5.17. J. Kempner, Creep bending and buckling of non-linearly visco-elastic columns, NACA Techn. Note 3137, 1954.
5.18. J. Kempner, V. Pohl, On the non-existence of a finite critical time for linear visco-elastic columns, J. Aeron. Sci. 20 (1953).
5.19. C. Libove, Creep buckling of columns, J. Aeron, Sci. 19, № 7 (1952), 459—467; Creep buckling analysis of rectangular section columns, NACA Techn. Note № 2956, 1953.
5.20. Т. H. L i n, Creep stresses and deflections of columns, J. Appl. Mech. 23, № 2 (1966), 214—218; Creep deflections and stresses of beam-columns. J. Appl. Mech. 25, № 1 (1958), 75.
5.21. J. Marin, Creep buckling in columns, J. Appl. Physics 18, № 1 (1947), 103—109.
5.22. F. К. О d q u i s t, Influence of primary buckling on column buckling, J. Appl. Mech. 21, № 3 (1954), 295; Trans. Roy. Inst. Techn., № 66, Stockholm (1953).
5.23. S. A. Patel, J. Kempner, Effect of higher-harmonic deflection components on the creep buckling of columns, Aeronaut. Quarterly 8» № 3 (1957), 215—225.
5.24. D. Rosenthal, H. W. Baer, An elementary theory of creep buckling of columns, Proc. of the 1st U. S. Congr. of Appl. Mech., 1951.
5.25. F. В. V e u b e k e, Creep buckling, «High temperature effects in aircraft structures», 1958.
К главе VI
6. 1. H. М. Беляев, Устойчивость призматических стержней под действием переменных продольных сил, сб. «Инженерные сооружения и строительная механика», Изд. «Путь», 1924.
6. 2. В. В. Болотин, О поперечных колебаниях стержней, вызываемых периодическими силами, «Поперечные колебания и критические скорости», 1, изд. АН СССР (1961), 46—77; О параметрически возбуждаемых колебаниях упругих арок, ДАН СССР 83, № 4 (1952), 537—539; Определение амплитуд поперечных колебаний, «Поперечные колебания и критические скорости», изд. АН СССР 2 (1953), 45—64; О параметрическом возбуждении поперечных колебаний, там же, 5—44; Динамическая устойчивость плоской формы изгиба, Инж. сб. 14 (1953), 109—122; О взаимодействии вынужденных и параметрически возбужденных колебаний, Изв. АН СССР, ОТН, No 4 (1954).
6.2а. А. С. В о л ь м и р, Устойчивость сжатых стержней при динамическом нагружении, Строит, механика и расчет сооруж., № 1 (1960), 6—9.
6. 3. И. И. Г о л ь д е н б л а т, Современные проблемы колебаний и устойчивости инженерных сооружений, Стройиздат, М., 1947; Динамическая устойчивость сооружений, Стройиздат, М., 1948.
ЛИТЕРАТУРА
847
6. 4. М. А. Лаврентьев, А. Ю. И ш л и н с к и й, Динамические формы потери устойчивости упругих систем, ДАН СССР, 65, № 6 (1949).
6 5. М. Е. Каган, Н. Д. Г е н я, Экспериментальные исследования работы деревянных стержней на продольный удар, Изв. вузов, Строительство и архит., № 3 (1961), 33—38.
6. 6. В. М. М а к у ш и н, Труды МВТУ им. Баумана, кафедра сопротивления материалов, разд. 3 (1947).
6. 7. В. Н. Ч е л о м е й, Динамическая устойчивость элементов авиационных конструкций, Изд. Аэрофлота, 1938.
6. 8. J. Р. С h a w 1 a, Numerical analysis of the process of buckling of elastic and inelastic columns, Proc. of the 1st U. S. Congr. of Applied Mech., 1952, 435—440.
6. 9. J. F. Davidson, Impact buckling of deep beams in pure bending.
Quarterly Journ. of Mech. and Appl. Math. 8, № 1 (1955), 81—87 (cm. сб. «Механика», ИЛ, № 2 (36), 1956, 133—139).
6.10. D e n - H a r t о g, Theory of vibrations, 1940 (в переводе: Дж. ДенГартог, Теория колебаний, Гостехиздат, 1942).
6.11. N. J. Hoff, The process of the buckling of elastic columns, Rep. № 163, Polit. Inst, of Brookline, 1949; Dynamic criteria of buckling, Research Eng. Struct. Supplement, Butterworths Publ., 1949; The dynamics of the buckling of elastic columns, J. Appl. Mech., № 1 (1951), 68—74 (см. сб. «Механика», ИЛ, № 3, 1952).
6.12. N. J. Hoff, Buckling and stability, J. of the Royal Aeron. Soc. 58, № 1 (1954) (перевод: H. Хофф, Продольный изгиб и устойчивость, ИЛ, 1955).
6.13. N. J. Hoff, S. N а г d о, В. Erickson, The maximum load supported by an elastic column in a rapid compression test, Proc. of the 1st U. S. Nat. Congress of Appl. Mech., 1952, 419—423; An experimental investigation of the process of buckling of columns, Roc. of the Soc. for Exper. Stress analysis 9, № 1 (1951), 201—208.
6.14. S. Kaliski, Statecznosc udarowa preta, Biuletyn Wojckowei Akademj technicznej, Warszawa, 1955.
6.15. C. Koning, J. Taub, Stossartige Knickbeanspruchung schlanker Stabe in elastischen Bereich, Luftfahrtforschung 10, № 2 (1933), 55—64.
6.16. S. Lubkin, J. J. Stoker, Stability of columns and springs under periodically varying forces, Quart, of Appl. Math. 1, № 3 (1943).
6.17. Rayleigh, The theory of sound, v. 1, London, 1926 (в переводе: Рэлей, Теория звука, т. 1, Гостехиздат, 1940, стр. 311—313).
6.18. J. S. Rinehart, J. Pearson, Behaviour of metal under impulsive loads, 1953 (в переводе: Дж. Райнхарт, Дж. Пирсен, Поведение металлов при импульсивных нагрузках, ИЛ, 1958).
6.19. V. L. Salerno, F. Bauer, I. S h е n g, The behaviour of a simply supported column under constant or varying end load. Proc. of the 1st IJ. S. Nat. Congr. of Appl. Mech., 1952, 425—434.
6.20. J. Taub, Stossartige Knickbeanspruchung schlauker Stabe im elastischen Bereich, Luftfahrtforschung 10, № 2 (1933), 65—85.
К главе VII
7. 1. С. А. Алексеев, Послекритическая работа гибких упругих пластинок,
Прикл. мат. и мех. 20, № 6 (1956), 673—679.
7. 2. В. П. Белкин, Работа элементов палубных перекрытий после потери устойчивости, Судпромгиз, Л., 1956.
7. 3. Б. М. Б р о у д е, Устойчивость пластинок в элементах стальных конструкций, Машстройиздат, М. 1949.
7. 4. А. С. К а л м а н о к, Строительная механика пластинок, Машстройиздат, 1950.
848
ЛИТЕРАТУРА
7. 5. А. В. К а р м и ш и н, Устойчивость свободно опертых прямоугольных пластинок, подкрепленных ребрами жесткости, под действием равномерной нагрузки, Инж. сб. АН СССР 24 (1956).
7. 6. М. А. Колтунов, Поведение пластинки после потери устойчивости, Вест. Моск. гос. ун-та, Кя 10 (1953); № 6 (1962), 43—50.
7. 7. А. С. J1 о к ш и н, К расчету пластин, подкрепленных жесткими ребрами, Прикл. мат. и мех. 2, № 2 (1935).
7. 8. С. Н. Никифоров, Сжатая прямоугольная пластинка со свободно искривляющимися в ее плоскости продольными краями, Уч. зап. Моск. гос. ун-та 117, Механика, № 1 (1946).
7. 9. П. М. О г и б а л о в, Изгиб, устойчивость и колебания пластинок, изд.
МГУ, 1958.
7.10. П. Ф. П а п к о в и ч, К вопросу о выпучивании плоских пластин, сжимаемых усилиями, превосходящими их эйлерову нагрузку, Морск. сб., No 8—9 (1920).
7.11. Г. Г. Ростовцев, Продольно-поперечный изгиб гибкой прямоугольной пластины, Инж. сб. 8 (1950), 83—104.
7.12. П. А. Соколов, О напряжениях в сжатой пластинке после потери устойчивости, Труды НИСС, № 7 (1932).
7.13. С. П. Тимошенко, Об устойчивости пластинок, подкрепленных упругими ребрами, изд. Ин-та инж. путей сообщ., 1915.
7.14. G. Н. В г у a n, On the stability of a plane plate under thrusts in its own plane, Proc. of the London Math. Soc. 22 (1891).
7.15. H. L. Cox, Buckling of thin plates in compression, Rep. and Memor., №№ 1553, 1554 (1933).
7.16. Th. Karman, E. E. Sechler, L. H. Donnell, The strength of thin plates in compression, Trans. ASME 54 (1932), 53—57.
7.17. S. Levy, Bending of rectangular plates with large deflections, NACA Rep. No 737 (1942).
7.18. K. Marguerre, Die mittragende Breite des gedruckten Plattenstreifens, Luftfahrtforschung 14, JSfe 3 (1937) (перевод в сб. переводов под ред. А. А. У майского, Оборонгиз, Москва, 1938).
7.19. Е. Seydel, Ueber das Ausbeulen von rechteckigen isotropen oder
orthogonal anisotropen Platten bei Schubbeanspruchung, Ing. Archiv 4 (1933), 169.
7.20. R. V. Southwell, S. W. S k a n, On the stability under shearing forces of a flat elastic strip, Proc. of Royal Society, A105 (1924), 582.
7.21. E. Trefftz, Die Bestimmung der Knicklast gedriickter rechteckiger
Platten, Z. fur angew. Math. u. Phys. 15 (1935).
7.22. H. Wagner, Ebene Blechwandtragermifsehrdtinner Stegblech, Zeitschr. f. Flugtechnik and Motorluftschiffahrt 20, № 8—12 (1922), 200 (перевод в сборнике под ред. А. А. Уманского и П. М. Знаменского, изд. ЦАГИ, 1937, 58—117).
7.23. N. Y a m a k i, Postbuckling behaviour of rectangular plates with small
initial curvature loaded in edge compression, J. Appl. Mech. 26 (1959),
407—414; 28 (1960), 335—342; Experiments on the postbuckling behaviour of square plates loaded in edge compression, J. Appl. Mech. 29 (1961), 238—244.
К главе VIII
8. 1. А. А. Ильюшин, Устойчивость пластинок и оболочек за пределами
упругости, Прикл. мат. и мех. 8, № 5, 337—360.
8. 2. А. А. Ильюшин, Пластичность. Гостехиздат, 1948.
8. 3. JI. М. Качанов, Основы теории пластичности, Гостехиздат, 1956,
165—173.
ЛИТЕРАТУРА
849
8. 4. В. Д. К л ю ш н и к о в, Устойчивость пластин за пределами упругости, Изв. АН СССР, ОТН, Ко 7 (1957), 41—56.
8. 5. Ю. Р. Лепи к, Одна • возможность решения задачи об устойчивости упруго-пластических пластинок в точной постановке, Изв. АН СССР, СТН, Ко 8 (1957), 13—19; Об устойчивости упруго-пластической пластинки, сжатой в одном направлении, Прикл. матем. и мех. 21, № 5
(1957), 722—724; Устойчивость прямоугольной упруго-пластической
пластинки, неравномерно сжатой в одном направлении, Инж. сб. 18,
(1954), 161—164; Некоторые вопросы равновесия упруго-пластических пластинок и стержней, докт. дисс., МГУ, 1957.
8. 6. С. М. П о п о в, Устойчивость свободно опертых пластинок за пределами упругости, Инж. сб. 9 (1951); О распространении метода смягчения граничных условий на устойчивость за пределами упругости прямоугольных пластинок, Прикл. мат. и мех. 15, № 1 (1951); Устойчивость за пределом упругости пластинок при внецентренном растяжении или сжатии, Инж. сб. 18 (1954), 165—173.
8. 7. А. П. Прусаков, Устойчивость и свободные колебания трехслойных пластин с легким заполнителем, докт. дисс., Днепропетровск, 1955.
8. 8. Л. А, Т о л о к о н н и к о в, О влиянии сжимаемости материи на упругопластическую устойчивость пластин и оболочек, Вестник МГУ, № 6
(1949), 35—44; К вопросу об устойчивости круглых пластин, сжатых равномерно распределенным давлением по контуру, Уч. зап. Рост, ун-та 18, Ко 3 (1953).
8. 9. Р. В i j 1 а а г d, Theory of plastic stability, Proc. * Kon. Ned. Akad. d. Wet. 41, № 5 (1948) (перевод в сб. «Теория пластичности», ИЛ, 1948, 392—404); Theory and tests on the plastic stability of plates and shells,. J. Aeron. Sci. 16, № 9 (1949), 529—541.
8.10. G. Gerard, Secant modulus method for determining plate instability above the proportional limit, J. Aeron. Sci. 13, № 1 (1946), 38—41, 48; Critical shear stress of plates above the proportional limit; J. Appl. Mech., Ks 3 (1948), 7—11; Effective width of elastically supported flat plates, J. Aeron. Sci. 13, № 10 (1946), 518—524.
8.11. G. J. Heimerl, Determination of plate compression strength, NACA Techn. Note № 1480, 1947.
8.12. G. H. H a n d e 1 m a n, W. P r a g e r, Plastic buckling of a rectangular plate under edge thrusts, NACA Techn. Note № 1530, 1948.
8.13. H G. Hopkins, The plastic instability of plates, Quart, of Appl. Math. 11, № 2 (1953).
8.14. С. E. Pearson, Bifurcation criterion and plastic buckling of plates and shells, J. Aeron. Sci. 17, № 7 (1950), 417—424, 455 (см. сб. «Механика», ИЛ, № 5, 1951).
8.15. R. A. Preide, G. J. Heimerl, Plastic buckling of simply supported compression plates, NACA Techn. Note № 1817, 1949.
8.16. E. Z. S to well, A unified theory of plastic buckling of columns and plates, NACA Techn. Note № 1556, 1948
8.17. E. H. Shuette, Buckling of curved sheet in compression and its relation to the secant modulus, J. Aeron. Sci. 15, № 1 (1948), 18—22.
К главе IX
9. 1. И. И. В о р о в и ч, О поведении круглой плиты после потери устойчивости, Уч. зап. Рост. гос. ун-та 32, № 4 (1955), 55—60.
9. 2. Б. Г. Газизов, К вопросу об устойчивости кольцевой пластины, Изв. Казан, ф-ла АН СССР 12 (1958), 155—164.
850
ЛИТЕРАТУРА
9. 3. Э. И. Гр и го люк, К вопросу о поведении круглых пластинок после ■потери устойчивости, Вест. инж. и техн., № 3 (1949).
9. 4. А. Н. Д и н н и к, Об устойчивости сжатой круглой пластинки, Изв.
Киев, полит, ин-та (1911); Приложение функций Бесселя к задачам теории упругости, 1913; Избранные труды, т. 2, изд. АН УССР, Киев, 1955, 62—72.
9. 5. В. М. М а к у ш и н, Критические значения интенсивности радиальных сжимающих сил для круглых тонких пластин, «Расчеты на прочность» 4 (1959), 270—298; 5 (1960), 236—248; 6 (1960), 171—181.
9. 6. Ю. И. Р е м н е в, Об устойчивости круглой пластины при облучении,
Научн. докл. высшей школы, физ.-мат. науки, № 3 (1959), 145—147.
9. 7. В. Новацкий, 3. Олеся к, Колебания, устойчивость и изгиб круговой пластинки на части окружности, защемленной полностью и частично опертой, Бюллетень Польской АН, отд. 4, 4, № 4 (1956).
9. 8. Д. Ю. Панов, В. И. Ф е о д о с ь е в, О равновесии и потере устой¬
чивости пологих оболочек при больших прогибах, Прикл. мат. и мех.
12, № 4 (1948), 384—406; 13, N° 1 (1949), 116.
9. 9. S. R. В о d n е г, The postbuckling behaviour of a clamped circular plate,
Quart. Appl. Math. 12, N° 4 (1955), 397—401.
9.10. К Friedrichs, J. Stoker, The non-linear boundary value problem of the buckled plate, Proc. of the Nat. Acad, of Sci. 25 (1939), 535—540; Amer. J. Math 63 (1941), 839—888; Buckling of the circular plate beyond the critical thrust, J. Appl. Mech. 9, N° 1 (1942), 7—14.
9.11. E. H. M a n s f l e 1 d, On the buckling of an annular plate, Quart. Journ. of Mech. and Appl. Math. 13, N° 1 (1960), 16—23.
9.12. E. Meissner, Ueber das Knicken kreisformiger Scheiben, Schweiz. Bauzeitung 101 (1933), 87—89.
9.13. A. N a d a i, Ueber das Ausbeulen von kreisformigen Platten, Zeitschr. VDJ, N° 9 (1915), 10.
9.14. N. Y a m a k i, Buckling of a thin annular plate under uniform compression, J. Appl. Mech. 25 (1958), 267—273.
К главе X
10. 1. H. А. Ал у м я э, Равновесие тонкостенных упругих оболочек в после-
критической стадии, Тарту, 1948; Прикл. мат. и мех. 13, Jsfe 1 (1949); О представлении основных соотношений нелинейной теории оболочек, Прикл. мат. и мех. 20, № 1 (1956), 136—139.
10. 2. С. А. А м б а р ц у м я н, Теория анизотропных оболочек, Физматгиз, М., 1961.
10. 3. В. 3. Власов, Основные дифференциальные уравнения общей теории упругих оболочек, Прикл. мат. и мех. 8, № 2 (1944).
10. 4. В. 3. Власов, Общая теория оболочек и ее приложение в технике, Гостехиздат, М., 1949.
10. 5. А. Л. Гольденвейзер, Дополнения и поправки к теории тонких оболочек Лява, сб. «Пластинки и оболочки», Госстройиздат, 1939; Уравнения теории оболочек в перемещениях и функциях напряжений, Прикл. мат. и мех. 21, № 6 (1957); 801—814; Асимптотические свойства собственных значений в задачах теории упругих тонких оболочек, Прикл. мат. и мех. 25, N° 4 (1961), 729—741.
10. 6. А. Л. Гольденвейзер, Теория упругих тонких оболочек, Гостехиздат, М., 1953.
10. 7. Н. А. Кильчевский, Обобщение современной теории оболочек, Прикл. мат. и мех. 2, N° 4 (1939).
10. 8. А. И. Лурье, Статика тонкостенных упругих оболочек, Гостехиздат,
1947.
ЛИТЕРАТУРА
851
10. 9. X. М. М у ш т а р и, Некоторые обобщения теории тонких оболочек
с приложением к задаче устойчивости упругого равновесия, Изв. физ.мат. о-ва при Каз. гос. ун-те (1938), 71—97, Прикл. мат. и мех. 2, № 4 (1939); Об упругом равновесии тонкой оболочки с начальными неправильностями в форме срединной поверхности, там же, 15, Mb 6 (1951).
10.10. X. М. Муштари, К. 3. Галимов, Нелинейная теория упругих оболочек, Таткнигоиздат, Казань, 1957.
10.11. В. В. Новожилов, Теория тонких оболочек, Оборонгиз, 1941; Судпромгиз, 1951.
10.12. В. В. Новожилов, Общая теория устойчивости тонких оболочек, ДАН СССР 32, № 5 (1941).
10.13. Ю. Н. Ра бот нов, Основные уравнения теории оболочек, ДАН СССР 47, Mb 2 (1945); Уравнения пограничной зоны в теории оболочек, там же, 47, Mb 5 (1945); Локальная устойчивость оболочек, там же, 52, Mb 2 (1946).
10.14. С. Ф е й н б е р г, К вопросу о построении приближенной теории тонкостенных оболочек произвольного очертания, сб. «Исслед. по теории сооружений», Госстройиздат, 1939.
10.15. Wei-Zang Chien, The intrinsic theory of thin shells and plates, Quart, of Appl. Math. 1, Mb 4 (1944), 297—327; 2, Mb 1, 43—59, Mb 2, 120-135 (1945).
10.16. L. Donnell, A discussion of thin shell theory, Proc. 5th congr. for Appl. Mech., 1939.
10.17. Y. C. Fung, E. E. Sechler, Instability of thin elastic shells, «Structural Mechanics», Pergamon-Press (1960), 115—168.
10.18. W. Fliigge, Statik und Dynamik der Schalen, 2. Auflage, SpringerVerlag, 1957 (перевод: В. Флюгге, Статика и динамика оболочек, Госстройиздат, М., 1961).
10.19. A. Love, Mathematical theory of elasticity, 1927 (А. Ляв, Математическая теория упругости, ОНТИ, М., 1935).
10.20 К Marguerre, Zur theorie der gerkrummten Platte grosser Formanderung, Jahrbuch 1939 der deutschen Luftfahrtforschung, 413—418.
10.21. E. Reissner, A new derivation of the equations for the deformation of elastic shells, Am. Journ. of Math. 63, Mb 1 (1941), 177—184; On some problems in shell theory, «Structural Mechanics», PergamonPress (1960), 74—114.
10.22 J. L. Synge, W. Z. Chien, The intrinsic theory of elastic shells and plates, Th. Karman Ann. Volume (1941), 103—120.
К главе XI
11. 1. С. В. Александровский, Об устойчивости цилиндрической обо¬
лочки при больших прогибах, «Расчет пространств, конструкций» 3, Стройиздат (1955), 453—492.
11. 2. С. А. Алексеев, Послекритическая деформация пластинок и оболочек, докт. дисс., М., 1958.
11. 3. Н. А. Алумяэ, Критическая нагрузка длинной цилиндрической круговой оболочки при кручении, Прикл. мат. и мех. 18, Mb 1 (1954Y, 27—34.
11. 4. Н. А. Алфутов, Устойчивость цилиндрических и конических подкрепленных оболочек, нагруженных внешним давлением, канд. дисс., Моск. высш. техн. уч-ще, 1956? К расчету оболочек на устойчивость энергетическим методом, Инж. сб. 22 (1955).
11.4а. Н. А. Алфутов, В. Ф. Соколов, Определение нижнего критического давления упругой цилиндрической оболочки и поведение оболочки
852
ЛИТЕРАТУРА
после потери устойчивости, Расчеты на прочность в машиностроении, Труды МВТУ, № 89 (1959).
11. 5. А. С. Вольмир, Теория устойчивости и больших деформаций цилиндрической оболочки при сжатии и сдвиге, «Расчет пространств, конструкций» 1, Машгиз (1950), 285—316; О влиянии начальных неправильностей на устойчивость цилиндрических оболочек при внешнем давлении, ДАН СССР 113, № 2 (1957), 291—293.
11. 6. Е. Д. Голицинская, Устойчивость тонких замкнутых цилиндрических оболочек, Труды Белорусской сельскохоз. академии 31 (1959), 75—82.
11. 7. В. М. Д а р е в с к и й, Устойчивость цилиндрической оболочки при одновременном действии крутящего момента и нормального давления, Изв. АН СССР, ОТН, № 11 (1957), 137—147; Устойчивость консольной
цилиндрической оболочки при изгибе поперечной силой с кручением и внутренним давлением, «Прочность цилиндрических оболочек», Оборонгиз, 1959, 72—94; «Расчет пространств, конструкций» 5 (1959), 431—449.
11. 8. В. М. Д а р е в с к и й, Р. И. Кшнякин, Устойчивость консольной цилиндрической оболочки с подкрепленным краем при действии внешнего давления, ДАН СССР 131, № 6 (1960), 1294—1297; Устойчивость подкрепленной кольцами цилиндрической оболочки при действии внешнего давления, ДАН СССР 134, № 3 (1960), 548—551.
11. 9. Ф. С. Исанбаева, Определение нижней критической нагрузки цилиндрической оболочки при всестороннем сжатии, Изв. Казан, ф-ла АН СССР 7 (1955), 51—59; К теории устойчивости защемленной цилиндрической оболочки при гидростатическом давлении, там же, 12 (1958), 149—154.
11.10. Н. И. Кривошеев, Об устойчивости цилиндрической оболочки под действием сдвига, Изв. Казан, ф-ла АН СССР 12 (1958), 133—142; Об устойчивости цилиндрической оболочки при совместном действии кручения и равномерного поперечного давления, там же, 143—148.
11.11. Р. И. Кшнякин, Влияние осевой растягивающей силы на устойчивость цилиндрических оболочек при кручении и при внешнем нормальном давлении, «Прочность цилиндрических оболочек», Оборонгиз, 1959, 55—71.
11.12. О. Н. Ленько, Устойчивость круговой цилиндрической ортотропной оболочки, сб. «Расчет пространств, конструкций» 4 (1956), 499—524; Влияние краевого эффекта на прочность цилиндрической оболочки, нагруженной внутренним давлением и осевым сжатием, Строит, механика и расчет сооружений, № 1 (1960), 1—6.
11.13. Н. Н. Леонтьев, К вопросу устойчивости замкнутой цилиндрической оболочки, Научн. докл. высшей школы, Строительство, № 1 (1958), 26—34.
11.13а. П. А. Лукаш, Об устойчивости ортотропных цилиндрических оболочек, Научн. докл. высшей школы, Строительство, № 2 (1958), 5—13.
11.14. В. А. Марьин, Устойчивость цилиндрической оболочки при кручении и внутреннем давлении, «Расчет пространств, конструкций» 5 (1959), 475-484; Устойчивость цилиндрической панели при сдвиге, там же, 485—501.
11.15. X. М. Муштари, Об упругом равновесии цилиндрической оболочки под действием продольного сжатия в закритической области; Труды Каз. авиац. ин-та 17 (1946); Приближенное определение редукционного коэффициента обшивки при осевом сжатии, Изв. Казан, ф-ла АН СССР 7 (1955), 23—35.
11.16. X. М. Муштари, А. В. Саченков, Об устойчивости цилиндрических и конических оболочек кругового сечения при совместном действии
ЛИТЕРАТУРА
853
осевого сжатия и внешнего нормального давления, Прикл. мат. и мех. 18, № 6 (1954), 667—674.
11.17. В. А. Нагаев, Определение нижней критической нагрузки цилиндрической оболочки при внешнем поперечном давлении, Изв. Высш. уч. зав., серия машиностр., № 6 (1959), 46—52.
11.18. О. М. Палий, Устойчивость круговой цилиндрической оболочки, защемленной на криволинейных кромках, Изв. АН СССР, ОТН, JSfe 1 (1958), 126—128.
11.19. А. В. П ого ре лов, Цилиндрические оболочки при закритических деформациях, части 1—3, изд. Харьк. ун-та, 1962.
11.20. А. В. Погорело в, О закритических деформациях сжатых цилиндрических оболочек, ДАН СССР 134, № 1 (1960), 62—63; Закритические деформации цилиндрических оболочек под внешним давлением, ДАН СССР 138, № 6 (1961), 1325—1327; Закритическая деформация цилиндрических оболочек при кручении, ДАН СССР 16, № 2 (1962).
11.21. Ю. Н. Работнов, Локальная устойчивость оболочек, ДАН СССР 52, № 2 (1946).
11.22. О. И. Теребушко, Расчет несущей способности круговой цилиндрической панели, подкрепленной ребрами, «Расчет пространств, конструкций» 4 (1958), 531—554; Устойчивость цилиндрической оболочки при кручении, внешнем давлении и сжатии, там же, 5 (1959), 502—522; К расчету на устойчивость и проектирование цилиндрических подкрепленных оболочек, там же, 7 (1962), 119—133.
11.23. С. П. Тимошенко, Известия Электротехнического ин-та 11 (1914).
11.24. К. Д. Т у р к и н, Устойчивость подкрепленной цилиндрической оболочки при сжатии и чистом изгибе, «Расчет пространств, конструкций» 4
(1958), 477—498; Общая устойчивость подкрепленной цилиндрической оболочки при поперечном изгибе, там же, 5 (1959), 450—474.
11.24а. В. М. Ч е б а н о в, Некоторые вопросы исследования устойчивости оболочек, Вестн. Ленингр. гос. ун-та, Мех. и матем., № 1 (1959), 79—93.
11.25. Л. А. Шаповалов, Прикл. мат. и мех. 20, № 5 (1956), 669—671.
11.26. М. Коза ров, Исследования устойчивости тонких упругих ортотропных цилиндрических оболочек по нелинейной теории В. 3. Власова, Ежегодник Инжен.-строит. ин-та, София, 1957 (на болгарском языке), 93—136.
11.27. Цянь Сюэ-сэнь (Н. S. Tsien), A theory for the buckling of thin shells 9 (1942), 373—384.
11.28. H. Becker, G. Gerard, Torsional buckling of moderate length cylinders, J. Appl. Mech. 23, № 4 (1956), 647—648.
11.29. P. P. В i j 1 a a r d, Buckling stress of thin cylindrical clamped shells subject to hydrostatic pressure, J. Aeron. Sci. 21, № 12 (1954).
11.30. L. H. Donnell, Stability of thin walled tubes under torsion NACA Rep. № 479 (1933) (перевод в сб. переводов под ред. А. А. Уманского и П. М. Знаменского, изд. ЦАГИ, М., 1937, 29—57); Effect of imperfections on the buckling of thin cylinders under external pressure, J. Appl. Mech. 23, No 4 (1956), 569—575.
11.30a. L. H. Donnell, С. C. Wan, Effect of imperfections on the buckling of thin cylinders and columns under axial compression, J. Appl. Mech.
17, No 1 (1950), 73—83.
11.31. G. D. Galletly,.R. Bart, Effects of boundary conditions and initial out of roundness on the strength of thin-walled cylinders subject to external hydrostatic pressure, Paper Am. Soc. Mech. Eng., NAPM-9, 1956.
11.32. G. Gerard, An evaluation of structural sheet materials in missile application, Jet Propulsion 28, № 8 (1958), 511—520.
11.33. L. A. Harris, H. S. Suer, W. T. Skene, R. J. В e n d j a m i n e, The stability of thin-walled unstiffened circular cylinders under axial com¬
854 ЛИТЕРАТУРА
pression including the effects of internal pressure, J. Aeron. Sci. 24, № 8
(1957), 587—596; The bending stability of thin walled unstiffened circular cylinders uncluding the effects of internal pressure, J. Aeron. Sci. 25, № 5 (1958), 281—287.
11.34. H. G. H о p к i n s, E. H. Brown, The effect of internal pressure on the initial buckling of thin-walled cylinders under torsion, Aer. Res. Com. Rep. and Memo, № 2423 (1951).
11.35 Th. К a r m a n, H. S. T s i e n, The buckling of thin cylindrical shells under axial compression, J. Aeron. Sci. 8, N° 8 (1941), 303—312.
11.36. J. К e m p n e r, Postbuckling behaviour of axially compressed circular cylindrical shells, J. Aeron. Sci. 21, № 5 (1954), 329—335, 342 (перевод в сб. «Механика», ИЛ, т. 2, 1955, 105—116).
11.37 J. Kemp пег, К. Pandalai, S. Patel, J. Crouze-Pascal, Postbuckling behaviour of circular cylindrical shells under hydrostatic pressure, J. Aeron. Sci. 24, № 4 (1957), 253—264.
11.38. L. Kirste, Abwickelbare Verformung diinnwandiger Kreiszylinder, Oesterr. Ing. Archiv 8, № 2—3 (1954), 149—151.
11.39 A. К i r s t e i n, E. W e n k, Observations of shap-through action of thin cylindrical shells under external pressure, Proc. Soc. Exper. Stress Analysis 14, N9 1 (1956), 205—214.
11.40 B. Klein, Interaction equation for the buckling of unstiffened cylinders under combined bending, torsion and internal pressure, J. Aeron. Sci.
22. № 8 (1955), 583; Buckling of unstiffened thin-walled circular cylindrical shells subjected to various loading conditions with and without internal pressure, Am. Rocket Society, 1958.
11.41. W. T. Koiter, Buckling and postbuckling behaviour of * cvb'ndnral panel under axial compression, Nat. Luchtvaart laborat., Rep. № 476, Amsterdam, 1956.
11.42. D. Leg get, R. Jones, The buckling of a cylindrical shell under axial compression when the buckling load has been exceeded, Rep. and Memo., № 2190 (1942); Pubis. Inst. math. Acad. Serbe Sci. 7 (1954).
11.43. H. Lo, H. Crate, E. Schwartz, Buckling of thin walled cylinders under axial compression and internal pressure, NACA Rep. № 1027, 1951.
11*44 Tsu-Tao Loo, Effects of large deflections and imperfections on the elastic buckling of cylinders under torsion and axial compression, Proc. of the 2nd US Nat. Congr. of Appl. Mech., NY, 1954, 345—357.
11.45. R. Lorentz, Zeitschr. d. Ver. deutsche Ing. 52 (1908), 1706; Physik. Zeitschr. 12 (1911), 241.
Я1.46. H. F. M i с h i e 1 s e n, The behaviour of thin cylindrical shells after
buckling under axial compression, J. Aeron. Sci., № 12 (1948), 738—744.
11.47 R. Mises, Der kritische Aufiendruck fur allseits belastete cylindrischer Rohre, «Festschr. zum. 70 Geburtstag von prof. A. Stodola», Zurich, 1929, 418—432.
11.48. W. Nash, Effect of large deflections and initial imperfections on the
buckling of cylindrical shells, J. Aeron. Sci. 22, № 4 (1955), 264—269; An experimental analysis of the bucking of thin initially imperfect cylindrical shells subject to torsion, Paper of the Soc. Experim. Stress
Anal., № 476 (1957); Buckling of initially imperfect cylindrical shells subjected to torsion, J. Appl. Mech. 24, № 1 (1957), 125—130.
11.49. R. G. Sturm, Stability of thin cylindrical shells in torsion, Proc. Am. Soc. Civil. Eng. 73, № 4 (1947), 471—495.
1150 E. Schwerin, Die Torsionsstabilitat des dunnwandigen Rohres,
Zeitschr. angew. Math, und Mech. 5, № 3 (1925), 235—243.
11*51. W. F. Thielemann, New developments in the nonlinear theories of the buckling of thin cylindrical shells, «Aeronautics and Astronautics», Pergamon-Press, 1960, 76—121.
ЛИТЕРАТУРА
855
11.52. W. Thielemann, W. S с h n e 11, G. Fischer, Beul- und Nachbeulverhalten orthotroper Kreiszylinderschalen unter Axial und Innendruck, Zeitschr. fur Flugwissenschaften 8, № 10/11 (1960), 284—293.
11.53. E. Wenk, R. S. Sea nl and, W. A. Nash, Experimental analysis of the buckling of cylindrical shells subjected to external hydrostatic pressure, Proc. of the Soc. Exper. Stress. Anal. 12, № 1 (1954).
11.54 D. F. Windenburg, C. Trilling, Collapse by instability of thin cylindrical shells under external pressure, Trans. ASME 56 (1934), 819—825.
11.55. Y. Yoshimura, J. Niisawa, Lower buckling stress of circular cylindrical shells subjected to torsion, J. Aeron. Sci. 24, № 3 (1957), 211—216.
К главе XII
12. 1. A. H. Божи некий, А. С. Вольмир, Экспериментальное исследование устойчивости цилиндрических оболочек за пределами упругости, ДАН СССР 142, № 2 (1962).
12. 2. В. Г. 3 у б ч а н и н о в, Осесимметричная форма потери устойчивости круговой цилиндрической оболочки за пределами упругости, Изв. АН СССР, Мех. и маш. № 5 (1961), 131—132.
12. 3. Н. С. Ганиев, Определение критической нагрузки цилиндрической оболочки за пределом упругости при осевом сжатии и внешнем нормальном давлении, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук, 7 (1955).
12. 4. Э. И. Г р и г о л ю к, О выпучивании тонких оболочек за пределами упругости, Изв. АН СССР, ОТН, № 10 (1957), 3—11; Чистопластическая потеря устойчивости тонких оболочек, Прикл. мат. и мех. 21, № 7
(1957); Об учете сжимаемости материала при определении нижних критических нагрузок, Изв. АН СССР, ОТН, № 5 (1958); Касательномодульная нагрузка круговых цилиндрических оболочек при комбинированной нагрузке, Вестник Моск. гос. ун-та, № 1 (1958).
12. 5. Л. М. Качанов, К вопросу устойчивости упруго-пластического равновесия, Вестник ЛГУ 19, серия мат., мех. и астр., № 4 (1956).
12. 6. В. Д. Клюш ников, Устойчивость пластин за пределом упругости, Изв. АН СССР, ОТН, № 7 (1957).
12. 7. Ю. Р. Лепи к, Одна возможность решения задачи об устойчивости упруго-пластических пластинок в точной постановке, Изв. АН СССР, ОТН, № 8 (1957); Равновесие упруго-пластических пластинок при больших прогибах, Инж. сб. 24 (1956), 37—62.
12. 8. А. В. С а ч е н к о в, Об устойчивости оболочек за пределом упругости, Изв. Каз. ф-ла АН СССР 10 (1956), 81—100.
12. 9. Л. А. Т о л о к о н н и к о в, О влиянии сжимаемости материала на упруго-пластическую устойчивость пластин и оболочек, Вестник Моск. Гос. ун-та, № 6 (1949), 35—44.
12.10. G. Gerard, Plastic stability theory of thin shells, J. Aeron. Sci. 24, N° 4 (1957), 264—279; J. Aerospace Sci., 29, № 10 (1962).
12.11. L. Lee, C. A d e s, Plastic torsional buckling strength of cylinders including the effects of imperfections, J. Aeron. Sci. 24, N° 4
(1957).
12.12. L Lee, Inelastic buckling of initially imperfect cylindrical shells
subject to axial compression, J. Aerospace Sci. 29, № 1 (1962),
87—96.
12.13 S. Radhakrishnan, Plastic buckling of circular cylinders, J. Aeron. Sci. 23, N° 9 (1956), 822—894.
856
ЛИТЕРАТУРА
К главе XIII
13. 1. Н. А. Алумяэ, Об определении состояния равновесия круговой оболочки при осесимметричной нагрузке, Прикл. мат. и мех. 17, № 5
(1958); К определению критической нагрузки замкнутой в вершине конической оболочки вращения, находящейся под действием внешнего давления. Труды Таллинского политехи, ин-та 66 (1955); Асимптотическое интегрирование уравнений статической устойчивости конической оболочки вращения, Прикл. мат. и мех. 21, № 1 (1957).
13. 2. Н. А. Ал футов, К расчету оболочек на устойчивость энергетическим методом, Инж. сб. 21 (1955).
13. 3. JI. М. Бунич, О. М. Палий, И. А. П и с к о в и т и н а, Устойчивость усеченной конической оболочки, находящейся под действием равномерного внешнего давления, Инж. сб. 23 (1956).
13. 4. Г. Н. Гениев и Н. С. Ч а у с о в, Некоторые вопросы нелинейной теории устойчивости пологих оболочек, Гос. издат. по строит, и архит., 1954.
13. 5. Э. И. Гр иголюк, Об устойчивости замкнутой двухслойной конической оболочки под действием равномерного нормального давления, Инж. сб. 19 (1954); Нелинейные колебания и устойчивость пологих стержней и оболочек, Изв. АН СССР, ОТН, № 3 (1965); К потере устойчивости при больших прогибах замкнутой слоистой конической оболочки под действием равномерного нормального давления, Инж. сб. Ин-та механики АН СССР 22 (1965); Упругая устойчивость ортотропных и слоистых конических и цилиндрических оболочек, сб. статей «Расчет пространств. конструкций» 3 (1955).
13. 6. X. М. Муштари, Некоторые обобщения теории тонких оболочек с приложением к задаче устойчивости упругого равновесия, Изв. Физ.мат. научно-исслед. ин-та математ. и мех. при Казанском ун-те, сер. 3, 11 (1933); Приближенное решение некоторых задач устойчивости тонкостенной конической оболочки кругового сечения, Прикл. мат. и мех. 7, № 3 (1943).
13. 7. X. М. Муштари, А. В. С а ч е н к о в, Об устойчивости цилиндрических и конических оболочек кругового сечения при совместном дей¬
ствии сжатия и внешнего нормального давления, Прикл. мат. и мех,
23, No 6 (1954).
13. 8. Р. К. Ряямет, Критическая нагрузка конической оболочки, находящейся под действием равномерно распределенного внешнего давления, Труды Таллинского политехи, ин-та 66 (1951); Равновесие упругих конических оболочек в послекритической стадии, Труды Таллинского политехи, ин-та, серия А, № 82 (1956); Равновесие тонкостенных упругих конических оболочек в послекритической стадии, Труды Таллинского политехи, ин-та, серия А, № 82 (1956).
13. 9. А. В. С а ч е н к о в, Приближенное определение нижней границы критической нагрузки при продольном сжатии тонкой конической обо¬
лочки, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук,
7 (1955); Об устойчивости оболочек за пределом упругости, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук, 10 (1956); Об устойчивости конических оболочек кругового сечения под действием равномерного внешнего давления, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук № 12 (1953).
13.10. И. И. Трапезин, Об устойч’ивости тонкостенной конической оболочки кругового сечения при нагрузках, осесимметричных относительно ее оси, Труды Моск. авиационного ин-та, N2 17 (1952); Устойчивость конструктивно ортотропной тонкостенной конической оболочки, нагруженной равномерным внешним давлением, Труды МАИ, вып. 69, Обо-
ЛИТЕРАТУРА 857
ронгиз (1956); Об устойчивости конической оболочки, находящейся под гидростатическим давлением, «Расчеты на прочность, жесткость, устойчивость и колебания», Машгиз (1956); Устойчивость тонкостенной конической оболочки, замкнутой в вершине, нагруженной боковым гидростатическим давлением. «Расчеты на прочность», Машгиз 5 (1960); Экспериментальное определение величин критического давления для конических оболочек, там же.
13.11. И. Я. Штаерман, Устойчивость оболочек, Труды Киевского авиац. ин-та, № 1 (1936).
13.12. J. Fritiof, N. Niordson, Buckling о! conical schells subjected to uniform external lateral pressure, Acta Polytechnica Transactions of the Royal Institute of Technology, Stocholm, № 10 (1947).
13.13. N. Hoff and J. Singer, Buckling of circular conical shells under external pressure, Proc. of the JUTAM Symposium on the theory of thin elastic shells, Delft, 1959.
13.14. A. Pfluger, Stabilitat diinner Kegelschalen, Ing. Archiv 8,№3 (1957).
13.15. P. Seide, On the buckling of truncated conical shell's under uniform hydrostatic pressure, Proc. of the JUTAM Symposium on the theory of thin elastic shells, Delft, 1959.
13.16. С. E. Taylor, Elastic stability of conical shells loaded by uniform external pressure, Proc. of the 3d midwestern conference on solid mechanics, Michigan, 1957.
К главе XIV
!4. 1. А. Г. Габрильянц, В. И. Феодосьев, Об осесимметричных формах равновесия упругой сферической оболочки, находящейся под действием равномерно распределенного давления, Прикл. мат. и мех. 25, № 6 (1961), 1091—1101.
14. 2. JI. С. Л е й б е н з о н, О применении гармонических функций к вопросу об устойчивости сферической и цилиндрической оболочек, Уч. зап. Юрьевского ун-та, № 1 (1917); Собр. трудов, т. 1, изд. АН СССР, 50—85.
14. 3. X. М. М у ш т а р и, К теории устойчивости сферической оболочки под действием внешнего давления, Прикл. мат. и мех. 19, № 2 (1955).
14. 4. X. М. М у ш т а р и, Р. Г. С у р к и н, О нелинейной теории устойчивости упругого равновесия сферической оболочки при действии равномерно распределенного внешнего давления, Прикл. мат. и мех. 14, № 6
(1950), 573.
14. 5. А. В. По го ре л о в, К теории выпуклых упругих оболочек в закритической области, изд. Харьк. ун-та, 1960.
14. 6. Р. Г. С у р к и н, К теории устойчивости и прочности сферических и эллипсоидных оболочек, днищ и мембран, канд. дисс., Казан, филиал АН СССР, 1952; К вопросу о потере устойчивости сферической оболочки, Изв. Казан, ф-ла* АН СССР 10 (1956).
14. 7. В. И. Феодосьев, Об устойчивости сферической оболочки, находящейся под действием внешнего равномерно распределенного давления, Прикл. мат. и мех. 18, № 1 (1954), 35—42.
14. 8. Цянь Вэй-чан, Хуа Хай-чаи (W. Z. Chien, Н. С. Hu), On the snapping of a thin spherical cap, 9th Congress Int. Mech. Appl., Univ. Bruxelles 6 (1956), 309—320.
14. 9. K- O. Friedrichs, On the minimum load for spherical shells, Th. Karman ann. volume, 1941, 258—272.
14.10. Th. Karman, H. S. Tsien, The buckling of spherical shells on external pressure, J. Aeron. Sci. 7 (1949), 43.
.14.11. K. Kloppel, O. Jungbluth, Beitrag zum Durchschlagsproblem diinnwandiger Kugelschalen, Stahlbau 22, Ns 6 (1953), 121—130.
858
ЛИТЕРАТУРА
14.12. U. Masuja, Y. Yoshimura. The buckling of spherical shells by external pressure, Proc. 2nd Japan Nat. Congress Appl. Mech., 1953, 145—148.
14.13. F. J. Murray, F. W. Wright, The buckling of thin spherical shells, J. Aerospace Sciences 28, № 3 (1961).
14.14. R. Zoelly, Ueber ein Knickungsproblem an der Kugelschale, Zurich
1915.
К главе XV
15. 1. E. Ф. Бурмистров, Расчет пологих ортотропных оболочек с учетом конечных деформаций, Инж. сб. 22 (1955), 83—97.
15. 2. Г. А. Гениев, Н. С. Чаусов, Некоторые вопросы нелинейной теории устойчивости пологих металлических оболочек, Стройиздат, М., 1954.
15. 3. Э. И. Г р и г о л ю к, Нелинейные колебания и устойчивость пологих стержней и оболочек, Изв. АН СССР, ОТН, № 3 (1955), 35—68; Прикл. матем. и мех. 19, № 3 (1955); 376—382; О несимметричном выпучивании оболочек вращения, Изв. АН СССР, ОТН, Мех. и машиностр.
(1960); Proc. IUTAM Symposium on the theory of thin elastic shells, Amsterdam (1960), 112—121.
15. 4. М. А. Колтунов, Учет конечных перемещений в задаче об изгибе и устойчивости пластинок и пологих оболочек, Вестник Моск. ун-та, № 5 (1952); Уточненное решение задачи об устойчивости прямоугольных панелей гибких пологих оболочек, там же, № 3 (1961), 37—45.
15. 5. М. С. К о р н и ш и н, X. М. Муштари, Устойчивость бесконечно длинной пологой цилиндрической панели под действием нормального равномерного давления, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук 7 (1955).
15. 6. X. М. Муштари, И. В. С в и р с к и й, Определение больших прогибов цилиндрической панели, опертой на гибкие нерастяжимые ребра, под действием внешнего нормального давления, Прикл. мат. и мех. 17, №6
(1953), 755—760.
15. 7. А. А. Назаров, О больших прогибах пологих оболочек, Уч. зап. Сарат. гос. ун-та (1956); О больших прогибах и устойчивости пологой оболочки двоякой кривизны с жестко закрепленными краями, ДАН УССР, № 3 (1956).
15. 8. И. И. Т р а п е з и н, Конечные деформации конической оболочки с малым углом подъема, нагруженной равномерным гидростатическим давлением, «Расчеты на прочность» 3 (1958), Машгиз, 151—159.
15. 9. В. И. Ф е о д о с ь е в, К расчету хлопающей мембраны, Прикл. мат. и мех. 10, № 2 (1946), 295—300; Расчет хлопающей мембраны, Труды каф. строит, мех. МВТУ, Машгиз, М. (1947).
15.10. В. И. Феодосьев, Упругие элементы точного приборостроения, Оборонгиз, М., 1949, 206—337.
15.11. R. R. Archer, Stability limits for a clamped spherical shell segment under uniform pressure, Quart. Appl. Math. 15 (1958), 355.
15.12. B. Budiansky, Buckling of clamped shallow spherical shells, Proc. IUTAM Symposium (cm. [15.3]), 1960, 64—94.
15.13. B. Budiansky, H. J. Weinitschke, On axisymmetrical buckling of clamped shallow spherical shells, J. Aerospace Sci. 27 (1960), 545.
15.14. A. Kaplan, Y. C. Fung, A nonlinear theory of bending and buckling of thin elastic shallow spherical shells, NACA TN 3212, 1954.
15.15 H. B. Keller, E. L. Reiss, Spherical cap snapping, J. Aerospace Sci. 26 (1959), 643.
15.16. E. L. Reiss, H. J. Greenberg, H. B. Keller, Nonlinear deflections pf shallow spherical shells, J. Аегоц. Sci. 24 (1957), 533.
ЛИТЕРАТУРА
до
15.17. Е. Reiss пег, Symmetrical bending of shallow gftells of revolution1, J. Math, and Mech. 7 (1958), 121.
15.18. G. A. Thurston, A numerical solution of the nonlinear equations* for axisymmetrical bending of shallow spherical shells, J. Appl. Mech'. 28, No 4 (1961), 557—562.
15.19. H. W e i n i t s с h к e, On the stability problem for shallow spherical shells, J. Math, and Phys. 38 (1960), 209; On the nonlinear theory of shallow spherical shells, J. Soc. Ind. and Appl. Math. 6 (1958), 209.
15.20. G. R. W i 11 i с h, The elastic stability of thin spherical shells, Proc. Am. Soc. Civ. Eng. 185, № 1 (1959).
К главе XVI
16. 1. А. Я. Александров, JI. Э. Б р ю к к е р, Л. М. К у р ш и н, А. П. П р усаков, Расчет трехслойных панелей, Оборонгиз, 1960.
16. 2. А. Я. Александров, Упругие параметры ребристых заполнителей трехслойных панелей, «Вопросы расчета элементов авиационных конструкций», Оборонгиз, 1 (1959); Определение приведенных упругих параметров сотовых заполнителей трехслойных панелей (совместно с
Э. П. Трофимовой), там же, 2.
16. 3. А. Я. Александров, Г. С. Саввина, Г. М. Таланова, Местная устойчивость трехслойных панелей с ребристым заполнителем при сжатии, «Вопросы расчета элементов авиационных конструкций», сб. статей 2, Оборонгиз (1959). -
16. 4. Л. Э. Б р ю к к е р, Л. М. К у р ш и н, О выводе статическим путем уравнений изгиба трехслойной пластины с жестким заполнителем, Изв. АН СССР, ОТН, Мех. и машиностр., № 3 (1959).
16. 5, А. П. Воронович, Устойчивость обшивки с заполнителем при сжатии и сдвиге, канд. дисс., 1948.
16. 6. Э. И. Григолюк, Уравнения трехслойных оболочек с легким заполнителем, Изв. АН СССР, ОТН, № 1 (1957); Конечные прогибы трехслойных оболочек с жестким заполнителем, Изв. АН СССР, ОТН, № 1
(1958); Об устойчивости трехслойных оболочек и пластин за пределом упругости, там же, № 6 (1958).
16. 7. В. Ф. Караванов, Уравнения пологих трехслойных оболочек с легким заполнителем при конечных смещениях, Изв. вузов «Авиационная техника», № 1 (1958); Осесимметричные трехслойные оболочки с легким заполнителем, Изв. вузов, «Машиностроение», № 6 (1958); Устойчивость трехслойной пологой цилиндрической панели с легким заполнителем с защемленными продольными кромками при осевом сжатии, Изв. вузов «Авиационная техника», № 2 (1960); Уравнения осесимметрических трехслойных оболочек с легким заполнителем, «Прочность авиационных конструкций», Труды МАИ, № 130 (1960), 110—132.
16. 8. В. И. Короле в, Симметричная форма потери устойчивости трехслойных пластин и оболочек, Вестник МГУ, серия физ.-мат. наук, № 5 (1956).
16. 9. Л. М. К у р ш и н, Некоторые вопросы изгиба и устойчивости трехслойных цилиндрических оболочек, дисс., Ин-т механики АН СССР, 1958.
16.10. Л. М. К у р ш и н, Уравнения трехслойных цилиндрических оболочек, Изв. АН СССР, ОТН, № 3 (1958); Об устойчивости трехслойной пологой цилиндрической оболочки при сжатии, там же, № 8 (1958); Об учете изгибной жесткости трехслойной криволинейной панели, работающей на продольное сжатие, «Вопросы расчета элементов авиационных конструкций», сб. статей 1, Оборонгиз (1959); Устойчивость при сжатии трехслойной криволинейной цилиндрической панели, продольные кромки которой свободно оперты, а поперечные защемлены, там же;
860 ЛИТЕРАТУРА
Устойчивость при сжатии трехслойной цилиндрической свободно опертой панели и цилиндра с заполнителем из гофра, там же; Устойчивость трехслойной цилиндрической оболочки за пределом упругости, там же,
2, Оборонгиз (1959); Об устойчивости трехслойной пластины при изгибе, Изв. вузов, серия «Строит, и архит.», № 9 (1959).
16.1 К А. П. Прусаков, Устойчивость и свободные колебания трехслойных пластин с легким заполнителем, докт. дисс., Ин-т механики АН УССР, 1958.
16.12. А. П. Прусаков, Основные уравнения изгиба и устойчивости трехслойных пластин с легким заполнителем, Прикл. мат. и мех. 15, № 1
(1951); Устойчивость и свободные колебания трехслойных пластин с легким заполнителем, Сборник трудов Днепропетровского инж.-строит. ин-та, № 4 (1958).
16.13. A. JI. Рабинович, Устойчивость обшивки с заполнителем при сжатии, Оборонгиз, 1946.
16.14. P. P. Bijlaard, Stability о! sandwich plates, J. Aeron. Sci. 16, № 9 (1949); Stability of sandwich plates in combined shear and compression, там же, 17, N° 1 (1950); Analysis of the elastic and plastic stability of sandwich plates by the method of split rigities, J. Aeron. Sci. 18, № 5, № 12 (1951); 19, № 7 (1952); Buckling of sandwich cylinders under combined compression, torsion and bending loads, J. Appl. Mech. 23, N° 1
(1956).
16.15. H. L. Cox, J. R. Riddel, Sandwich construction and core materials, part 3, Instability of sandwich struts and beams, ARC Rep. and Memo., N° 2125, 1945.
16.16. A. C. Erin gen, Bending and buckling of rectangular sandwich plates, Proc. of the 1st US Nat. Congr. of Appl. Mech., 1952.
16.17. G. Gerard, Buckling of a sandwich cylinder under uniform axial compressive load, J. Appl. Mech. 18, N° 4 (1951); Compressive and torsional instability of sandwich cylinders, Symp. of Struct. Sandwich Constr., ASTM, Spec. Techn. Publ:, 118, 1951; Torsional instability of a long sandwich cylinder, Proc. of the 1st U. S. Nat. Congr. of Appl. Mech., NY, 1952.
16.18. J. N. Goodier, J. M. Neou, The evaluation of theoretical critical compression in sandwich plates, J. Aeron. Sci. 18, N° 10 (1951).
16.19. W. S. Hemp, On a theory of sandwich construction, ARC Rep. and Memo., N° 2672, 1952; Proc. 7th Intern. Congr. Appl. Mech. 1, 1948.
16.20. N. J. Hoff, Bending and buckling of rectangular sandwich plates,
* NACA TN N° 2225, 1950.
16.21. J. H. Hunter-Tod, The elastic stability of sandwich plates, ARC Rep. and Memo, № 2778, 1953.
16.22. D. Legget, H. Hopkins, Sandwich panels and cylinders under compressive end loads, ARC Rep. and Memo, N° 2262, 1942.
16.23. C. Libove, S. В a t d о r f, A general small deflection theory for flat sandwich plates, NACA Rep. N° 899, 1948; NACA TN N° 1526, 1948.
16.24. H. W. March, Sandwich construction in the elastic range, Symp. Struct. Sand. Constr., ASTM, Spec. Tech. Publ. N° 118, 1952; Elastic stability of the facings of sandwich columns, Proc. Symp. Appl. Math
3 (1950).
16.25. A. Neut, Die Stabilitat geschichteter Streifen, Netterlands Nat. Luchtvaartlabor., Amsterdam, Bericht № 284 (1943).
16.26. H Neuber, Theorie der Druckstabilitat der Sandwich Platte, Teil 1, Zeit. fur angv. Math, und Mech., № Ц/12 (1952); Teil 2, N° 1/2 (1953).
16.27. E. Reissner, Finite deflections of sandwich plates, J. Aeron. Sci. 15, N° 7 (1948); 17, № 2 (1950); Small bending and stretching of sandwichtype shells, NACA TN N° 1832, 1949; NACA Rep. N° 975, 1950.
ЛИТЕРАТУРА 861
16.28. J. R. Robinson, The buckling and bending of orthotropic sandwich panels with all edges simply-supported, the Aeron. Quart. 6, N2 2 (1955).
16.29. P. S e i d e, The stability under longitudinal compression of flat symmetric corrugated-core sandwich plates with simply-supported loaded edges and simply supported or clamped unloaded edges, NACA TN № 2679, 1952; Compressive buckling of flat rectangular metalite type sandwich plates with simply supported loaded edges and clamped unloaded edges, NACA TN N2 1886, 1949; N2 2637, 1952; Shear buckling of infinitely long simply supported metalite type sandwich plates, NACA TN № 1910, 1949; On the torsion of rectangular sandwich plates, J. Appl. Mech. 23, No 2 (1956), 191—194.
16.30. P. Seide, E. S towel 1, Elastic and plastic buckling of simply supported metalite tipe sandwich plates in compression, NACA TN N2 1822, 1949; NACA Rep. N2 967, 1950.
16.31. M. Stein, J. Mayers, A small deflection theory for curved sandwich plates, NACA TN № 2017, 1950; NACA Rep. N2 1008, 1951; Compressive buckling of simply supported curved plates and cylinders of sandwich construction, NACA TN N2 2601, 1952.
16.32. G. A. Thurston, Bending and buckling of clamped sandwich plates, J. Aeron. Sci. 24, N2 6 (1957), 407—412.
16.33. С. T. Wang, Principle and applications of complementary energy method for thin homogeneous and sandwich plates and shells with finite deflections, NACA TN N2 2620, 1952.
16.34. С. T. Wang, G. V. R a 0, A study of an analogues model giving the nonlinear characterictics in the buckling theory of sandwich cylinder, J. Aeron. Sci. 19, N2 2 (1952).
16.35. С. T. Wang, R. J. Vaccaro, D. F. de Santo, Buckling of sandwich cylinders under combined compression, torsion and bending loads, J. Appl. Mech. 22, № 3 (1955).
16.36. К- T. Yen, V. G. S a 1 e r n 0, N. J. H о f f, Buckling of rectangular sandwich plates subjected to edgewise compression with loaded edges simply supported and unloaded edges clamped, NACA TN N2 2556, 1952.
16.37. S. Y u s s u f f, Theory of wrinkling in sandwich construction, J. Roy. Aeron. Soc. 59, N2 529 (1955).
К главе XVII
17. 1. С. Г. Винокуров, Температурные напряжения в пластинках и оболочках, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук, N2 3 (1953).
17. 2. А. С. В о л ь м и р, П. Г. 3 ы к и н, Устойчивость в большом цилиндрических оболочек при ползучести, Труды 2-й конференции по температурным напряжениям, Киев, 1962.
17. 3. М. С. Ганеева, Устойчивость прямоугольной цилиндрической панели, жестко заделанной по краям и находящейся в неравномерном температурном поле, Уч. зап. Казан, ун-та 116, N2 1 (1956), 41—44.
17.4.3. И. Гр иго люк, Некоторые задачи устойчивости круглых пластич при неравномерном нагреве, Инж. сб. 6 (1950).
17. 5. Л. М. Кур шин, Устойчивость панелей крыла при нагреве, Доклады АН СССР 136, N2 2 (1960).
17. 6. Л. А. Шаповалов, Термическая устойчивость пластин и оболочек, «Прочность и деформации в неравномерных температурных полях», М. (1961), 241—255.
17. 7. С. А. Шестериков, Устойчивость прямоугольных пластинок при ползучести, Журнал прикл. мех. и техн. физ., № 3 (1961), 93—100;
862
ЛИТЕРАТУРА
Устойчивость пластинок при ползучести по теории течения, там же, № 5 (1961), 100—108.
17. 8. P. P. Bijlaard, Differential equations for cylindrical shells with arbitrary temperature distribution, J. Aeron. Sci. 25, №9 (1958),594—595.
17. 9. С. С Chang, J. К. E b с i о g 1 u, Thermoelastic behaviour of a simply
supported sandwich panel under large temperature gradient and edge compression, J. Aerospace Sci. 28, № 6 (1961), 480—492.
17.10. G. Gerard, A. Gilbert, A critical strain approach to creep buckling of plates and shells, J. Aerospace Sci. 25, № 7 (1958), 429—438; 458 (перевод в сб. «Механика», ИЛ, № 2, 1959).
17.11. D J. Johns, Comments on «Thermal buckling of clamped cylindrical shells», J. Aeron. Sci. 26, № 1 (1959), 59.
17.12. L. A. Harris, Axial compression buckling of a pressurized cylinder with a thermally induced ring compression, J. Aeron. Sci. 23, No 12
(1956), 1120—1121.
17.13. W S. Hemp, Fundamental principles and theorems of thermoelasticity, Aeron. Quarterly 7, № 3 (1956), 184—192.
17.14. N. J. Hoff, Thermal buckling of supersonic wing panels, J. Aeron. Sci.
23, No 11 (1956), 1019—1028; Buckling of thin cylindrical shell under hoop stresses varying in axial direction, J. Appl. Mech. 24, Mb 3 (1957). 405—412; Buckling at high temperature, J. Roy. Aeron Soc. 61, № 563
(1957), 756—774 (перевод в сб. «Механика», ИЛ, № 5, 1958).
17.15. J. Klosner, М. Forray, Buckling of simply supported plates under arbitrary symmetrical temperature distributions, J. Aeron. Sci. 25, JSIb 3
(1958), 181—184.
17.16. Т. H. Lin, Creep deflection of wiscoelastic plate under uniform edge compression, J. Aeron. Sci. 23, № 9 (1956), 883—887.
17.17. К. M i u r a, Thermal buckling of rectangular plates, J. Aerospace Sci. 28, No 4 (1961), 341—343.
17.18. A. van der Neut, Buckling caused by thermal stresses, «High temperature effects in aircraft structures» (1958), 215—247 (перевод в книге «Проблемы высоких температур в авиационных конструкциях», М., 1961).
17.19. J. S. Przemieniecki, Transient temperature distributions and thermal stresses in fuselage shells with bulkheads of frames, J. Roy. Aeron. Soc. 60, No 552 (1956), 799—804.
17.20. J. Singer, Thermal buckling of solid wings of arbitrary aspect ratio, J. Aeron. Sci. 25, № 9 (1958), 573—580.
17.21. T. Wan, R. K. Gregory, Creep collapse of long cylindrical shells under high temperature and external pressure, J. Aerospace Sci. 28, № 3 (1961), 177—188, 208.
17.22. W. Z u k, Thermal buckling of clamped cylindrical shells, J. Aeron. Sci.
24, No 5 (1957), 389.
К главе XVIII
18. 1. В. Л. Ага миров, А. С. Вольмир, Поведение цилиндрических обо¬
лочек при динамическом приложении всестороннего давления и осевого сжатия, Изв. АН СССР, ОТН, Мех. и машиностр., № 3 (1959), 78—83.
18. 2. Н. А. А л у м я э, О применении метода расчленения напряженного состояния при решении осесимметричной задачи динамики замкнутой цилиндрической оболочки, Изв. АН ЭстССР 10, № 3 (1961).
18. 3. С. А. Амбарцумян, В. Ц. Г н у н и, О динамической устойчивости нелинейно.упругих трехслойных пластинок, Прикл. мат. и мех. 25, №4
(1961); О вынужденных- колебаниях и динамической устойчивости трехслойных ортотропных пластинок, Изв. АН СССР, ОТН, Мех. и мат. No 3 (1961).
ЛИТЕРАТУРА
863
18. 4. С. А. Амбарцумян, А. А. Хачатрян, Об устойчивости и колебаниях анизотропных пластинок, Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1960); Об устойчивости и колебаниях пологой ортотропной цилиндрической панели, ДАН АрмССР 30» № 1 (1960).
18. 5. Ж. Е. Б а г д а с а р я н, В. Ц. Г н у н и, К теории динамической устойчивости слоистых анизотропных оболочек вращения, Изв. АН АрмССР, серия физ.-мат. наук, 13, № 5 (1960).
18. 6. А. Ю. Б и р к г а н, А. С. Воль мир, Применение электронных цифровых машин к задаче о динамической устойчивости оболочек, ДАН СССР 135, № 5 (1960).
18. 7. А. И. Блохин а, Динамическая устойчивость цилиндрической оболочки с начальным изгибом при заданной скорости сближения торцов, Инж. сб. 31 (1961).
18. 8. В. В. Б о л о т и н, Некоторые нелинейные задачи динамической устойчивости пластинок, Изв. АН СССР, ОТН, № 10 (1954), 48—59; Динамическая устойчивость пластинок, Труды МЭИ, Госэнергоиздат, № 7
(1955), 22—40; Устойчивость тонкостенной сферической оболочки под действием периодических сил, сб. «Расчеты на прочность», Машгиз, 2 (1958), 284—299.
18. 9. В. В. Болотин, Г. А. Бойченко, Исследование прощелкивания тонких упругих оболочек под действием динамических нагрузок, сб. «Расчеты на прочность», Машгиз, 5 (1960), 259—282.
18.10. В. В. Болотин, Г. А. Бойченко, Б. П.. Макаров, Н. И. Судаков а, Ю. Ю. Ш в е й к о, О потере устойчивости тонких упругих оболочек под действием импульсивной нагрузки, «Строительная механика и расчет сооружений», № 2 (1959).
18.11. А. С. Вольмир, Об устойчивости цилиндрических оболочек при динамическом нагружении, ДАН СССР 123, № 5 (1958), 806—808.
18.12. А. С. Вольмир, В. Е. Минеев, Экспериментальное исследование процесса выпучивания оболочки при динамическом нагружении, ДАН СССР 125, № 5 (1959).
18.13. В. Ц. Г н у н и, К теории динамической устойчивости оболочек, Изв. АН АрмССР, серия физ.-мат. наук, 13, № 1 (I960); Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1961), 181—182; О границах динамической неустойчивости оболочек, Труды по теории оболочек, Казань, 1960; О параметрически возбуждаемых колебаниях слоистых анизотропных оболочек, Изв. АН АрмССР, серия физ.-мат. наук, 15, № 3 (1962).
18.14. Э. И. Гр и го люк, О колебаниях пологой круговой цилиндрической панели, испытывающей конечные прогибы, Прикл. мат. и мех. 19, №3 (1955).
18.15. Ю. И. Кадашевич, А. К. Перцев, О потере устойчивости цилиндрической оболочки, Изв. АН СССР, ОТН, Мех. и машиностр. № 3
(1960).
18.16. Л. А. М о в с и с я н, Об одной динамической задаче дая цилиндрической оболочки, ДАН АрмССР 32, № 5 (1961).
18.17. Г. В. М и ш е н к о в, О вынужденных нелинейных колебаниях упругих панелей, Изв. АН СССР, ОТН, Мех. и машиностр., № 4 (1961), 97—103.
18.18. О. Д. О ни а ш вил и, Некоторые динамические задачи теории оболочек, изд. АН СССР, 1951.
18.19.0. И. Теребушко, Устойчивость цилиндрической оболочки при быстром нагружении осевой силы, «Строительная механика и расчет сооружений», № 1 (1960).
18.19а. У. Р. У п м а н и с, Обзор исследований по динамическому продольному изгибу, Уч. зап. Рижского политехи, ин-та, 1 (1959), 171—186.
18.20. А. А. X а ч а т р я н, Об устойчивости и колебаниях круглых трансверсально-изотропных цластинок, Изв. АН АрмССР, серия физ*-мат, наук,
864
ЛИТЕРАТУРА
13, Ко 1 (1960); Об устойчивости и колебаниях трансверсально-изотропной сферической оболочки, там же, 13, № 4 (1960).
18.21. В. Н. Челомей, О возможности повышения устойчивости упругих систем при помощи вибраций, ДАН СССР 110, № 3 (1956).
18.22. А. Р. С о р р a, On the mechanism of buckling of a circular cylindrical shell under longitudinal impact, Space Sciences Laboratory, General Electric, 1960.
18.23. A. F. S m i 11, Dynamic buckling tests of aluminum shells, Aeronaut Eng. Review, Sept. 1956, 54—58.
К главе XIX
19. 1. С. А. Амбарцумян, Ж. Е. Б а г д а с а р я н, Об устойчивости ортотропных* пластинок, обтекаемых сверхзвуковым потоком газа, Изв. АН СССР, ОТН, Мех. и машиностр., № 4 (1961), 91; Об устойчивости нелинейно-упругих трехслойных пластинок, обтекаемых сверхзвуковым потоком газа, там же, № 5 (1961), 96.
19. 2. Ж. Е. Багдасарян, Об устойчивости трехслойной ортотропной пластинки в сверхзвуковом потоке газа, Изв. АН АрмССР, серия физ.-мат, наук, 14, № 5 (1961).
19. 3. В. В. Волошин, Колебания и устойчивость упругой цилиндрической оболочки в потоке сжимаемой жидкости, Инж. сб. 24 (1956), 3—16; К вопросу об устойчивости пластинок в потоке сжимаемого газа, «Вопросы прочности материалов и конструкций», изд. АН СССР; Некоторые новые задачи теории оболочек, сб. «Расчеты на прочность»
4 (1959); О применении метода Галеркина к задачам флаттера упругих панелей, Изв. высш. уч. зав., серия «Машиностр.», № 12 (1959), 25—32; Нелинейный флаттер пластин и оболочек, Инж. сб. 28 (I960), 55—75; О применении «закона плоских сечений» для определения аэродинамического давления на колеблющиеся оболочки, Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1961).
19. 4. В. В. Болотин, Ю. В. Г а в р и л о в, * Б. П. Макаров, Ю. Ю. Ш в е й к о, Нелинейные задачи устойчивости плоских панелей при больших сверхзвуковых скоростях, Изв. АН СССР, ОТН, Мех. и машиностр., № 3 (1959), 59—64.
19. 5. В. В. Болотин, Ю. Н. Новичков, Выпучивание и установившийся флаттер термически сжатых панелей, находящихся в сверхзвуковом потоке, Инж. журнал.1, № 2 (1961), 82—96.
19. 6. А. А. Ильюшин, Закон плоских сечений в аэродинамике больших
сверхзвуковых скоростей, Прикл. мат. и мех. 20, № 6 (1956), 733—755.
19. 7. Б. П. М а к а р о в, Об устойчивости защемленных пластин в потоке
сжимаемого газа, Изв. высш. школы, серия «Машиностр.», № 1 (1961);
Об амплитудах установившегося флаттера защемленных панелей, там же, Ко 5 (1961).
19. 8. Г. Н. М и к и ш е в, Экспериментальное исследование автоколебаний квадратной пластинки в сверхзвуковом потоке, Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1959), 154—157.
19. 9. А. А. М о в ч а н, О колебаниях пластинки, движущейся в газе, Прикл.
мат. и мех. 20, № 2 (1956), 211—222; Об устойчивости панели, движущейся в газе, там же, 21, № 2 (1957), 211—243; Устойчивость лопатки, движущейся в газе, там же, 21, № 5 (1957), 700—706.
19.10. П. М. О г и балов, К постановке задачи о флаттере оболочек и панелей, Вестник Моск. ун-та, Матем., механ., № 5 (1961), 60—66.
19.11. Р. Д. Степанов, О флаттере цилиндрических оболочек и панелей, движущихся в потоке газа, Прикл. мат. и мех. 21, № 5 (1957),644—657; }4зв. высш. 1пколы? Мащиностр. и приборостр., № 8 (I960),
ЛИТЕРАТУРА 865
19.12. Ю. Ю. Швейко, Устойчивость круговой цилиндрической оболочки в потоке газа, Изв. АН СССР, ОТН, Мех. и машиностр., Mb 6 (1960), 71—79; О влиянии сверхзвукового потока газа на нижнее критическое усилие для цилиндрической панели, там же, № 4 (1961), 14—19.
19.13. Дун Мин-дэ, Об устойчивости упругой пластинки при сверхзвуковом обтекании, ДАН СССР 120, Mb 4 (1958), 726—729.
19.14. Н. Ashley, G. Zartarian, Piston theory —a new aerodynamic tool for the aeroelastician, J. Aeron. Sci. 23, Mb 12 (1956), 1109—1118.
19.15. J. P. Chawla, Aeroelastic instability at high Mach numbers, J. Aerospace Sci., 25, № 4 (1958), 246—258.
19.16. Y. Fung, An introduction to the theory of aeroelasticity, NY, 1955, 260—261 (перевод: Фын, Введение в аэроупругость, Физматгиз, М.,
1960); The static stability of a two-dimensional curved panel in a supersonic flow, with an application to p.anel flutter, J. Aeron. Sci. 21, Mb 8
(1954); Flutter of curved plates with edge compression in a supersonic flow, Proc. of the 3th midwestern conf. on solid mech., Ann-Arbor, 1957, 221—245; On two-dimensional panel flutter, J. Aeron. Sci. 25, №3 (1958); (перевод: «Механика», ИЛ, № 1, 1959, 75—*106).
19.17. M. Goland, Y. L. Luke, An exact solution for two-dimensional linear panel flutter at supersonic speeds, J. Aeron. Sci., Mb 4 (1954), 275—276.
19.18. L. E. Goodman, J. V. R a 11 a у a, Review of panel flutter, Applied Mech. Reviews 13, № 1 (1960), 2—1 (перевод: «Механика», И Л, Mb 5,1960).
19.19. W. Н. Hayes, Quart. Appl. Math. 5, N 1 (1947), 105—106.
19.20. D. J. Johns, Some panel-flutter studies using piston theory, J. Aeron. Sci. 25, Mb 11 (1958), 679—684.
19.21. P. F. Jordan, The physical nature of panel flutter, Aero-Digest, Mb 2 U956), 34—38.
19.22. J. M. Hedgepeth, On the flutter of panels at high Mach numbers, J. Aeron. Sci. 23, Mb 6 (1956), 609—610; Flutter of rectangular simply supported panels at high supersonic speeds, там же, 24, Mb 8, 1957, 563—573 (перевод: «Механика», ИЛ, № 2, 1958, 103—126).
19.23. J. М. Hedgepeth, В. Budiansky, R. W. Leonard, Analysis of flutter in compressiible flow of a panel on many supports, J. Aeron. Sci. 21, No 7 (1954), 475—486.
19.24. F. D. H a i n s, Flutter of a thin membrane in hypersonic flow, J. Aeron. Sci. 25, No 9 (1958).
19.25. M. J. L i g h t h i 11, Oscillating airfoils at high Mach number, J. Aeron. Sci. 20, No 6 (1953), 402—406.
19.26. J. W. Miles, On panel flutter in the presence of a boundary layer,
J. Aerospace Sci. 26, № 2 (1959), 81—93 (см. сб. «Механика», ИЛ, No 4, 1959, 97—122); On the aerodynamic stability of thin panels,
J. Aeron. Sci. 23, Mb 8 (1956); 24, Mb 2 (1957), 25, Mb 5 (1958).
19.27. J. W. Miles, W. P. R о d d e n, On the supersonic flutter of two-dimensional infinite panels, J. Aerospace Od. 26, Mb 3 (1959).
19.28. S. F. S h e n, Remarks on «An exact solution for two-dimensional linear flutter»,-J. Aeron. Sci., Mb 9 (1955), 656—657; An approximate analysis of nonlinear flutter problems, J. Aerospace Sci. 26, Mb 1 (1959), (перевод: «Механика», ИЛ, Mb 4, 1959, 79—96).
К главе XX
20. 1. В. В. Болотин, Статистические методы в нелинейной теории упругих.оболочек, Изв. АН СССР, ОТН, Mb 3 (1958); Статистические методы в строительной механике, Госстройиздат, М., 1961.
20. 2. И. И. В о р о в и ч, Статистический метод теории устойчивости тонких упругих оболочек, Прикл. мат, и мех. 23, Mb 5 (1959), 88§—§9?.
866
ЛИТЕРАТУРА
20. 3. В. М. Гончаренко, Исследование устойчивости оболочек методами теории вероятностей, канд. дисс., Киев, 1961; К определению вероятности потери устойчивости оболочкой, Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1962), 159—160.
20. 4. Б. П. М а к а р о в, Применение статистического метода для анализа нелинейных задач устойчивости оболочек, Труды Львовской конференции по теории оболочек, Киев, 1962; Применение статистического метода для анализа экспериментальных данных по устойчивости оболочек, Изв. АН СССР, ОТН, Мех. и машиностр., № 1 (1962), 157—158.
20. 5. А. Р. Р ж а н и ц ы н, Статистический метод определения допускаемых
напряжений при продольном изгибе, Госстройиздат, М., 1951.
К главе XXI
21. 1. В. В. Болотин, Вопросы общей теории упругой устойчивости, Прикл.
мат. и мех. 20, № 5 (1956), 561—577; Нелинейная теория упругой устойчивости в большом, «Расчеты на прочность» 3 (1958), 310—354; Современные направления в области динамики пластин и оболочек, «Теория пластин и оболочек», Киев, 1962, 16—32.
21. 2. А. С. В оль мир, Современные проблемы теории устойчивости оболочек, Доклад на Львовской конференции по теории пластин и оболочек, 1961.
21. 3. И. И. В о р о в и ч, О существовании решений в нелинейной теории оболочек, Изв. АН СССР, серия мат. 19 (1955); О некоторых приближенных методах в нелинейной теории пологих оболочек, ДАН СССР 105, № 1 (1955); Прикл. мат. и мех. 20, № 4 (1956); О существовании решений в нелинейной теории оболочек, ДАН СССР 117, № 2 (1957); Некоторые математические вопросы нелинейной теории оболочек, докт. дисс., 1958.
21. 4. К. 3. Галимов, Уравнения равновесия теории упругости при конечных перемещениях и их приложение к теории оболочек, Изв. Казан, ф-ла АН СССР, серия физ.-мат. и техн. наук, № 1 (1948), 25—45.
21. 5. Г. Ю. Джанелидзе, Устойчивость равновесия нелинейно деформируемых систем, Труды Ленингр. политехи, ин-та 178 (1955).
21.5а. Г. В. Иванов, Об устойчивости равновесия при неупругих деформациях, Журн. прикл. мех. и техн. физики, № 1 (1961), 47—55; № 3
(1961), 74—84.
21. 6. А. Ю. Ишлинский, Рассмотрение вопросов об устойчивости равновесия упругих тел с точки зрения математической теории упругости, Укр. матем. журнал 6, № 2 (1954), 140—146.
21. 7. Б. Л. Николаи, О критерии устойчивости упругих систем, Труды
Одесского ин-та инж. гражд. и комм, стр-ва, 1 (1939), 191—208.
21. 8. В. В. Новожилов, Основы нелинейной теории упругости, Гостех¬
издат, 1948.
21.8а. Ю. Н. Работнов, Теория ползучести и ее приложения; в сборнике «Plasticity», Pergamon-Press, 1960, 338—346.
21. 9. С. В. Biezeno, Н. Hen с к у, On the general theory of elastic stability, Proc. Roy. Neth. Acad. Sci., Amsterdam 31 (1928), 569—592; 32
(1929), 444.
21.10. G. H. Bryan, On the stability of elastic systems, Proc. of the Cambridge Phil. Soc. 6 (1888), 199.
21.11. D. C. Dr иске г, E. Т. О n a t, On the concept of stability of inelastic
systems, J. Aeron. Sci. 21, № 8 (1954).
21.12. R. Hill, On uniqueness and stability in the theory of finite elastic
strain, J. Mech. Phys. Solids 5, № 4 (1957), 229—241; Stability of rigidplastic solids, 6, № 1 (1957), i—8.
ЛИТЕРАТУРА 867
21.12а. R. Hill, М Sewell, A general theory of inelastic columm failure, J. Mech. Phys. 8, № 2 (I960), 105—118.
21.13. R. Kappus, Zur Elastizitatstheorie endlischer Verschiebungen, Zeitschr. angew. Math, und Mech. 19, № 5 (1939), 271—285; № 6, 344—361.
21.14. W. T. Koiter, Over de stabiliteit van het elastisch evenwicht, Amsterdam, 1945; Elastic stability and postbuckling behaviour, 1960 (В. Койтер, Устойчивость и закритическое поведение упругих систем, «Механика», ИЛ, М> 5, 1960).
21.15. F. Murnaghan, Finite deformation of an elastic solid, NY, 1951.
21.16. С. E. Pearson, General theory of elastic stability, Quart. Appl. Math.
14 (1956), 133.
21.17. W. Prager, The general variational principle of the theory of structural stability, Quart. Appl. Math. 4 (1957), 378.
21.18. R. V. Southwell, On the general theory of elastic stability, Phil.
Trans. Roy. Soc. London A213 (1913), 187.
21.19. M. Ska loud, Pokriticka pevnost stn ocelovych nosnikii, Praha, 1962.
21.20. E. Trefftz, Ueber die Ableitung des Stabilitatskriterien des elastischen
Gleichgewichts, Verhandl. Ill Intern. Kongr. techn. Mech. 3 (1930),
44—50.
21.21. Chi-The Wang, Applied elasticity, NY, 1953 (перевод: Ван Цзи-де, Прикладная теория упругости, М., 1959).
21.22.0. Zanaboni, Premesse alio studio della stabilita del d’equilibrio elastico, G. Genio civile 99, № 6 (1961), 457—473.
21.23. H. Ziegler, Die Stabilitatskriterien der Elastomechanik, Ing. Arch.
20, № 1 (1952); Advances in applied mechanics 4 (1956) (перевод в сб, «Проблемы механики» 2, ИЛ, 1959, 116—160).
ИМЕННОЙ УКАЗАТЕЛЬ
Агамиров В. Л. 491, 531, 532, 720, 734, 742, 749, 780, 862 Адес С. (Ades С.) 581, 856 Александров А. Я. 859 Александровский С. В. 498, 543, 851 Алексеев С. А. 324, 330, 487, 493,
847, 851
Алумяэ Н. А. 459, 597, 720, 749, 850, 851, 856, 862 Алфутов Н. А. 495, 500, 504, 851, 856 Амбарцумян С. А. 454, 749, 751, 844, 850, 862, 863, 864 Арутюнян Н. X. 233 Арчер П. П. (Archer Р. Р.) 858
Бабаков И. М. 825 Багдасарян Ж. Е. 749, 863, 864 Балабух Л. И. 201, 453, 561 Барбре P. (Barbre R.) 336 Батдорф С. (Batdorf S. В.) 656, 860 Бек М. (Beck М.) 72, 842 Беккер Г. (Becker Н.) 853 Белкин В. П. 847 Беляев Н. М. 261, 846 Бенджемайн Р. Дж. (Benjamine R.)
. 853
Бер Г. В. (Baer Н. W.) 846 Бернштейн С. Н. 790 Бидерман В. Л. 841 Бижляр П. П. (Bijlaard Р. Р.) 384, 674, 678, 683, 849, 853, 860, 862 Био М. (Biot М.) 199 Биргер И. А. 540
Биркган А. Ю. 325, 351, 553, 634, 724, 776, 863 Бицено К. Б. (Biezeno С. В.) 10, 820, 841, 866
Блейх Ф. (Bleich F.) 10, 145, 137, 354, 841 Блохина А. И. 742, 863 Боднер С. P. (Bodner S. R.) 414,418, 850
Божинский А. Н. 572, 581, 855
Бойченко Г. А. 736, 863 Болотин В. В. 10, 72, 262, 698, 736, 749, 750, 760, 762, 770, 780, 797, 800, 827, 832, 841, 844, 846, 863—866 Брайен Г. Г. (Bryan G. Н.) 285, 311, 408, 412, 848, 866 Браш Д. О. (Brush D. О.) 560 Бронштейн И. Н. 30 Броуде Б. М. 374, 494, 526, 837, 843,
844, 847.
Броун Э. Г. (Brown Е. Н.) 854 Брюккер Л. Э. 859 Бубнов И. Г. 10, 45, 140, 308, 423,
641, 841
Будянский Б. (Budiansky В.) 634,
858, 865 Бунатян Л. В. 845 Бунич Л. М. 856 Бурдин П. Г. 479, 500 Бурмистров Е. Ф. 858 Бурнашев И. А. 269 Бюргермейстер Г. (Btirgermeister G.) 113, 197, 841
Вагнер Г. (Wagner Н.) 318, 349,845,
848
Ваккаро Р. И. (Vaccaro R. J.) 861 Ван К. К. (Wan С. С.) 792, 804, 863 Ван Т. (Wan Т.) 861 Ван Цзи-де (Wang С. Т.) 449, 464, 475, 861, 867 Ван-дер-Нойт A. (Van der Neut А.)
697, 698, 717, 862 Вебек В. (Veubeke В. F.) 846 Вейничке Г. И. (Weinitschke Н. J.)
648, 858, 859 Венк Э. (Wenk Е.) 854, 855 Вентцель Е. С. 781.
Венцель Н. А. 140 Вианелло Л. (Vianello L.) 52, 842 Виллих Г. (Willich G. R.) 859 Винденбург Д. Ф. (Windenburg D. F.) 855
ИМЕННОЙ УКАЗАТЕЛЬ
869
Винклер (Winkler) 346 Винокуров С. Г. 698, 861 Власов В. 3. 10, 159, 331, 446, 454,
463, 466, 468, 615, 633, 844, 850 Войт Е. С. 140
Вольмир А. С. 841, 843, 846, 852, 855, 861—863, 866 Воробьев В. Ф. 845 Воробьев Jl. Н. 269 Ворович И. И. 418, 808, 810, 822,831,
849, 866
Воронович А. П. 655, 674, 678, 681, 859
Выгодский М. Я. 428
Габрильянц А. П. 620, 625, 857 Гаврилов Ю. В*. 864 Газизов Б. Г. 849 Галеркин Б. Г. 45, 842 Галимов К. 3. 10, 459, 636, 693, 827,
841, 851, 866 Ганеева М. С. 698, 861 Ганиев Н. С. 855 Гантмахер Ф. Р. 823 Гартман Ф. (Hartmann F.) 291, 305,
841
Гаусс К- (Gauss К ) 439 Геккелер И. (Geckeler J.) 354, 632 Геммерлинг А. В. 107, 113, 843, 844 Гениев Г. Н. 649, 856, 858 Генки Г. (Hencky Н.) 48, 820, 866 Геня Н. Д. 847
Гертель Г. (Hertel Н.) 340, 346 Гильберт A. (Gilbert А.) 703, 862 Гиэр Дж. (Gere J.) 842 Гнуни В. Ц. 749, 751, 862, 863 Голанд М. (Goland М.) 865 Голицинская Е. Д. 487, 85 Гольденблат И. И. 844, 846 Гольденвейзер A. JI. 446, 447, 454,
850
Гончаренко В. М. 807, 812, 813, 866 Горбунов Б. Н. 52 Граммель P. (Grammel R.) 10, 841 Грегори Р. К. (Gregory R. К.) 862 Григолюк Э. И. 418, 569, 571, 618,
642, 656, 690, 698, 751, 780, 826,
850, 855, 856, 858, 859, 861, 863 Григорьев Ю. П. 295 Григорян Г. С. 233 Гринберг Г. Дж. (Greenberg Н. J.) 646, 858
Гринхилл A. (Greenhill A. G.) 123, 844
Губер М. Т. (Huber М. Т.) 333
Гудмэн J1. Э. (Goodman L. Е.) 780,
865
Гудьир Дж. (Goodier J. N.) 655,
845, 860
Даревский В. М. 12, 515, 517, 528, 532.536, 538, 541, 852 Дейнеко К. С. 72, 842 Ден-Гартог П. (Den-Hartog Р.) 255, 847
Де-Санто Д. Ф. (de Santo D. F.) 861 Джанелидзе Г. Ю. 159, 832, 842,
866
Джерар Г. (Gerard G.) 208, 209,381, 383, 401, 575, 576, 690, 703, 841,
846, 849, 853, 865, 860, 862 Джонс Д. Дж. (Johns D. J.) 698,
862, 865 Джонс P. (Jones R.) 854 Джонсон Дж. (Johnson J. B.j' 86 Дин В. P. (Dean W. R.) 415 Динке Ф. 269
Динник А. Н. 10, 116, 157, 410, 841,
843, 850
Доннел Л. Г. (Donnel L. Н.) 319,
464, 466, 509, 515, 519, 792, 804,
848, 851, 853 Друккер Д. К. (Drucker D. С.) 866 Дун Мин-дэ 865
Дэвидсон Дж. Ф. (Davidson J. F.) 267, 847
Ежек К. (Jezek К.) 107, 843 Ершов Н. Ф. 586 Ефимов Н. Е. 440
Зартарьян Г. (Zartarian G.) 759,865 Зволинский Н. В. 554 Зейдель Э. (Seydel Е.) 305, 848 Зехлер Э. Э. (Sechler Е. Е.) 319, 848,
851
Зингер И. (Singer J.) 857, 862 Зубчанинов В. Г. 106, 573, 855 Зыкин П. Г. 710, 861
Иваний Б. И. 348
Иванов В. В. 550
Иванов Г. В. 866
Иен К. (Yen К. Т.) 681, 861
Ильюшин А. А. 10, 106, 355, 365, 368.
759, 848, 864 Иордан П. Ф. (Jordan P. F.) 865 Иошимура И. (Yoshimura Y.) 519, 620, 855, 858 Исанбаева Ф. С. 500, 504, 852 Исправников Л. Р. 491
870
ИМЕННОЙ УКАЗАТЕЛЬ
Ишлинский А. Ю. 238, 264, 816, 847,
866
Каган М. Е. 847 Калиский С. (Kaliski S.) 847 Калманок А. С. 847 Камке Э. (Кашке Е.) 124, 246, 248, 598
Кан С. Н. 55
Канемитцу С. (Kanemitsu S.) 492 Канторович Л. В. 59 Каплан A. (Kaplan А.) 649, 858 Каппус P. (Kappus R.) 845, 867 Караванов В. Ф. 656, 687, 859
Карлсон Р. Л. (Carlson R. L.) 845
Карман Т. (Karman Th.) 88, 319, 426, 470, 478, 487, 620, 843, 848, 854, 857 Кармишин А. В. 340, 524, 848
Кацитадзе О. И. 269
Качанов Л. М. 205, 233, 358, 389,
844, 845, 848, 855 Келлер Г. Б. (Keller Н. В.) 646,858 Кемпнер И. (Kempner J.)) 524, 536, 544, 846, 854 Кильчевский Н. А. 653, 850 Кимм (Kimm) 346 Кирсте Л. (Kirste L.) 489, 854 Кирштейн A. (Kirstein А.) 854 Кирюшина С. Н. 742, 744 Китов А. И. 79 Клейн Б. (Klein В.) 536, 854 Клёппель К. (Kloppel К.) 857 Клоснер И. (Klosner J.) 696, 862 Клюшников В. Д. 849, 855 Козаров М. 640, 853 Койтер В. Т. (Koiter W. Т.) 552, 831 854, 867
Кокс Г. Л. (Сох Н. L.) 655, 848, 860 Колбруннер К. Ф. (Kollbrunner С. F.)
10, 113, 286, 354, 842 Колтунов М. А. 331, 553, 638, 848, 858
Комиссарова Г. Л. 548 Конинг К- (Koning С.) 847 Копейкин Ю. Д. 842 Коппа А. П. (Сорра А. Р.) 746, 749,
864
Коренев Б. Г. 12, 844 Корнишин М. С. 641, 858
Корноухов Н. В. 72, 197, 841
Королев В. И. 610, 655, 859 Короткин Я. И. 844 Красносельский М. А. 822 Кривошеев Н. И. 852
Криницкий Н. А. 79
Ж. (Crouze-Pas*
Круз-Паскаль cal J.) 854 Крылов А. Н. 842 Крылов В. И. 59 Крэйт Г. (Crate Н.) 536, 854 Кузнецов А. П. 232, 845 Курдюмов А. А. 140 Куршин Л. М. 12, 213, 656, 687, 690 698, 700, 845, 859, 861 Кшнякин Р. И. 537, 541, 852
Лаврентьев М. А. 238, 264, 847 Лагранж Ж. (Lagrange J. L.) 26 116, 120, 814, 823, 842 Ладе P. (Lahde R.) 318
Л 860вВ 4 (Libove Ch) 656> 846,
Лайтхилл М. Дж. (Lighthill М. J.)
/оУ, ооо
Лангхаар Г. Л. (Langhaar Н. L.) 845 Ландквист Е. (Lundqiust Е. Е.) 294 Лебедев Н. Н. 247 Леви С. (Levy S.) 324, 332, 848 Левин Б. Р. 781
Д- (Legget D.) 552, 655, 690, о54, 860
Лежен Дирихле П. Г. (Dirichlet P. G. Lejenne) 823 Лейбензон Л. С. 614, 857 Лейтес С. Д. 843
Леонард Р. В. (Leonard R. W) 865
Леонов М. Я. 72, 842
Леонтьев Н. Н. 487, 852
Лепик Ю Р. 365, 374, 586, 849, 855
Лехницкии С. Г. 333
Ли Л. (Lee L.) 581, 855
Лин Т. X (Lin Т. Н.) 215, 846, 862
Лисунов А. Д. 780
Лихарев К. К. 841
Ло Г. (Lo Н.) 536, 854
Локшин А. С. 415, 848
Лоренц P. (Lorentz R.) 472, 854
Лу Т. Т. (Loo Tsu-tao) 509, 854
Лукаш П. А. 581, 852
Лурье А. И. 850
Льюк И. Л. (Luke Y L.) 865
Любкин С. (Lubkin S.) 847
Ляв A. (Love А. Е. Н.) 818, 851
Ляпунов А. М. 814, 815, 823, 824
Мазитов Ш. С. 269 Майер P. (Mayer R.) 842 Майлс Дж. В. (Miles J. W.) 780,
865
Макаров Б. П. 801, 806, 863, 864, 866
ИМЕННОЙ УКАЗАТЕЛЬ
871
Макушин В. М. 257, 412, 415, 841, 847, 850 Малашенко С. И 816 Малинин Н. Н. 841 Маневич Л. И. 524 Маргерр К. (Marguerre К.) 323, 332, 636, 848, 851 Марч Г. В. (March Н. W.) 655, 860 Марченко В. М. 561 Марьин В. А. 515, 536, 537, 554, 852 Матевосян Р. Р. 197 Мацу я У. (Masuja U.) 620, 858 Мейерс Дж. (Mayers J.) 656, 687, 690, 717, 861 Мейсснер Э. (Meissner Е.) 850 Мейстер М. (Meister М.) 10, 113,842 Мизес P. (Mises R.) 495, 532, 854 Микишев Г. Н. 780, 864 Минеев, В. Е. 509, 512, 739, 863 Митинский А. Н. 88 Миура К- (Miura К.) 862 Михилсен Г. Ф. (Michilsen Н. F.)
487, 854 Михлин С. М. 19, 58, 59 Мишенков Г. В. 751, 863 Мовсисян Л. А. 863 Мовчан А. А. 824, 864 Муштари X. М. 10, 454, 459, 495,515, 602, 620, 624, 625, 631, 632, 636, 641, 693, 841, 851, 852, 856—858 Мэнсфильд Э. Г. (Mansfield Е. Н.) 850 Мэрей Ф. (Murray F. J.) 620, 858 Мэрин Дж. (Marin J.) 846 Мэрнаган Ф. (Murnaghan F.) 867
Навье Л. (Navier L.) 285, 843 Нагаев В. А. 496, 499, 500, 503, 505, 853
Надаи A. (Nadai А.) 412, 850 Назаров А. А. 858 Найима Н. М. 492 Нардо С. (Nardo S.) 847 Нейбер Г. (Neuber Н.) 655, 860 Нейт A. (Neut А.) 656, 860 Нео Дж. (Neou J. М.) 655, 860 Нефф Дж. (Neff J.) 305 Ниизава И. (Niisawa J.) 519, 855 Никифоров С. Н. 843, 848 Николаи Б. Л. 834, 866 Николаи Е. Л. 120, 844 Никулин М. В. 537 Ниландер Г. (Nylander Н.) 845 Новацкий В. 412, 693, 850 Новичков Ю. Н. 698, 864 Новожилов В. В 444, 446, 453, 454, 610, 816, 827, 851, 896
Нудельман Я. Л. 197, 844 Ньордсен Н. (Niordson N.) 857 Нэш В. A. (Nash W. А.) 500, 521. 804, 854, 855
Образцов И. Ф. 844
Огибалов П. М. 848, 864
Одиноков Ю. Г. 524
Одквист Ф. К. (Odquist F. К.) 846
Олесяк 3. 412, 850
Олисов В. А. 247
Онат Э. Т. (Onat Е. Т.) 866
Ониашвили О. Д. 751, 863
Оселедько А. И. 269
Палий О. М. 500, 853, 856 Пандалаи К- (Pandalai К.) 854 Панов Д. Ю. 414, 850 Пановко Я. Г. 106, 159, 843 Папкович П. Ф. 10, 140, 157, 322, 340, 817, 827, 834, 841, 848 Патель Ш. A. (Patel Sh. А.) 846,854 Пеньков А. М. 140, 844 Перцев А. К. 734, 736, 863 Пиковский А. А. 10, 113, 197, 841,
844
Пинаджян В. В. 107, 113, 843 Пирсон Дж. (Pearson J.) 847 Пирсон К. Э. (Pearson С. Е.) 389,
849, 867 Писковитина И. А. 856 Плетникова Е. Д. 527 Погорелов А. В. 428, 440, 488, 490,
504, 505, 521, 627, 853, 857 Полубаринова-Кочина П. Я. 330,332, 420
Поль В. (Pohl V.) 846 Пономарев С. Д. 10, 841 Попов Е. П. 842 Попов С. М. 374, 849 Прагер В. (Prager W.) 389, 849, 867 Прайд P. A. (Preide R. А.) 397, 849 Прандтль Л. (Prandtl L.) 145, 845 Пржеминецкий И. С. (Przemieniecki J. S.) 862 Прокопович Е. 269 Проскурина В. М. 581 Прусаков А. П. 384, 656, 674, 678, 681, 849, 860 Пуанкаре A. (Poincare Н.) 832 Пугачев В. С. 781
Пфлюгер A. (Pfliiger А.) 10, 95, 157, 203, 842, 843, 857
Рабинович А. Л., 655, 656. 674* 8QQ Рабинович И. М. 237
872
ИМЕННОЙ УКАЗАТЕЛЬ
Работнов Ю. Н. 95, 208, 209, 213, 454, 703, 843, 845, 851, 853, 866 Радхакришнан С. (Radhakrishnan S.) 855
Райнхарт Дж. С. (Reinchart J. S.) 847
Райт Ф. (Wright F. W.) 620, 858 Рао Г. В. (Rao G. V.) 861 Раттайа И. В. (Rattaya J. V.) 780,
865
Ратцерсдорфер И. (Ratzersdorfer J.) 842 '
Резницкий Л. Я. 140 Рейсснер Э. (Reissner Е.) 446, 633, 645, 656, 681, 851, 859, 860 Рейсс Э Л. (Reiss Е. L.) 646, 858 Релей — см. Стретт Дж. В.
Ремнев Ю. И. 850 Ренкин (Rankine) 86 Ржаницын А. Р. 10, 145, 197, 208, 233, 791, 792, 793, 841, 844, 845,
866
Риддел Дж. P. (Riddell J. R.) 860 Ритд В. (Ritz W.) 42 Робинсон Дж. P. (Robinson J. R.) 861
Рогицкий С. А. 197
Родден В. P. (Rodden W. R.) 865
Розенблюм В. И. 208, 845
Розенталь Д. (Rozenthal D.) 846
Ростовцев Г. Г. 320, 848
Рош М. (Ros М.) 107, 843
Ручимский М. Н. 529
Рэуту С. 269
Ряямет Р. К. 856
Саввина Г. С. 859
Салерно В. Г. (Salerno V. G.) 681, 861
Сальвадори Д. (Salvadori D.) 777 Саусвелл Р. В. (Southwell R. V.) 65, 301, 848, 867 Саченков А. В. 495, 852, 855, 856 Свирский И. В. 858 Севин С. (Sevin S.) 269 Сейде П. (Seide Р.) 678, 681, 857,
861
Семендяев К. А. 30 Сердюков Л. В. 528, 537 Сивере Н. Л. 844 Синг Дж. Л. (Synge J. L.) 851 Сканлан Р. Г. (Scanlan R. Н.) 84,
842
Скен В. Г. (Skene W.) 853
Скурлатов Э. Д. 82, 770
Скэн Сильвия (Skan S. W.) 301, 848
Скэнлэнд Р. С. (Scanland R. S.) 855 Смирнов А. Ф. 120, 157, 197, 841 Снитко И. К. 197 Снитко Н. К. 197, 844 Соколов В. Ф. 851 Соколов П. А. 322, 848 Оорокин В. В. 741 Спиридонова Н. И. 632 Степанов Р. Д. 780, 864 Степанов С. Г. 627 Стокер Дж. Дж. (Stoker J. J.) 418,
847, 850
Стоуэлл Э. (Stowell Е. Z.) 294, 376, 678, 849, 861 Стратонович Р. Л. 812 Стрелецкий Н. С. 10, 843 Стрельбицкая А. И. 844 Стретт Дж. В. (Strutt J. W., Lord Rayleigh), 260, 847 Судакова Н. И. 863 Суркин Р. Г. 620, 626, 627, 631, 649,
857
Сюэл М. (Sewell М.) 867 Сюэр Г. С. (Suer Н. S.) 853
Таланова Г. М. 859 Тауб И. (Taub J.) 847 Темченко М. Е. 816 Теребушко О. И. 519, 531, 532, 533, 544, 548, 549, 610, 742, 853, 863 Тёрстон Г. A. (Thurston G. А.) 650, 651, 859, 861 Тетмайер Л. (Tetmayer L.) 86, 843 Гилеман В. Ф. (Thielemann W. F.)
498, 536, 542,. 544, 854, 865 Тимошенко С. П. 10, 44, 45, 145, 157, 308, 336, 340, 354, 472, 551, 842,
845, 848, 853 Толоконников Л. А. 384, 849, 855 Торшенов Н. Г. 207 Трайнер Н. Г. (Triner N. Н.) 846. Трапезин И. И. 12, 598, 600, 642,856,
858
Треффц Е. (Trefftz Е.) 848, 867 Триллинг К. (Trilling С.) 855 Туркин К. Д. 477, 527, 853 Тэйлор К. Э. (Taylor С. Е.) 857 Тюленев А. И. 561
Уманский А. А. 159, 340, 348, 717.
845
Упманис У. Р. 269, 863 Усюкин В. И. 201, 701 Уэй С. (Way S.) 420
ИМЕННОЙ УКАЗАТЕЛЬ
873
Фейнберг С. 454, 851 Фельдман М. Р. 845 Феодосьев В. И. 414, 620, 625, 640,
643, 646, 650, 841, 850, 857, 858 Фиников С. П. 428 Фишер Г. (Fischer G.) 855 Флюгге В. (Fliigge W.) 476, 499, 524, 534, 861
Форрей М. (Forray М.) 696, 862 Фридрихе К. О. (Friedrichs К. О.)
418, 620, 850, 857 Фритьоф И. (Fritiof J.) 857 Фриче И. (Fritsche J.) 107, 843 Фын (Fung Y. С.) 649, 775, 780, 851, 858, 865
Хавла И. P. (Chawla J. Р.) 865 Хаймерль Г. И. (Heimerl G.) 397,
849
Хайнс Ф. Д. (Hains F. D.) 865 Халт Дж. A. (Hult J. А.) 846 Хандельман Г. Г. (Handelman G. Н.)
389, 849 Ханджи В. 127
Хантер —Тод Дж. (Hunter-Tod J. Н.) 655, 860
Харрис Л. A. (Harris L. А.) 853, 862 Хачатрян А. А. 863 Хвалла Э. (Chwalla Е.) 107, 843 Хеджпет Дж. М. (Hedgepeth J. М.)
768, 772, 865 Хемп В. С. (Hemp W. S.) 656, 860,
862
Хилл P. (Hill R.) 867 Хопкикс Г. Г. (Hopkins Н. G.) 655, 690, 849, 854, 860 Хофф Н. Дж. (Hoff N. J.) 106, 208, 209, 225, 247, 249, 656, 678, 681,
698, 846, 847, 867, 860—862 Ху Л. В. (Hu L. W.) 846 Хуа Хай-чан (Hu Hai-chang) 845, 857
Хэйс В. Г. (Hayes W. Н.) 759, 865
Цанабони О. (Zanaboni О.) 867 Цзе Бо-минь 845 Циглер Г. (Ziegler Н.) 867 Цолли P. (Zoelly R.) 614, 858 Цук В. (Zuk W.) 698, 700, 862 Цянь Вей-чан (Chien Wei-zung) 459, 470, 851, 857
Цянь Сюэ-сэнь (Tsien Н. S.) 78, 426, 470, 478, 487, 620, 842, 854, 857
Чан (Chang С. С.) 862 Чаусов Н. С. 649, 856, 858 Чебанов В. М. 853 Челомей В. Н. 813, 847, 864 Ченцов Н. Г. 120, 844 Четаев Н. Г. 814 Чудновский В. Г. 197, 841
Шандаров Л. Г. 780 Шаповалов Л. А. 199, 201, 203, 845, 853, 861
Шварц Э. (Schwartz Е.) 536, 854 Швейко Ю. Ю. 863, 864, 865 Шверин Э. (Schwerin Е.) 518, 854 Шевляков Ю. А. 524 Шен С. (Shen S. F.) 865 Шенли Ф. P. (Shanley F. R.) 95,208,
842, 843
Шестериков С. А. 208, 209, 213, 703,
845, 861
Шкалоуд М. С. (Skaloud М.) 867 Шлейхер Ф. (Schleicher F.) 843
Шмитт А. Ф. (Smitt A. F.) 746, 864
Шнелл В. (Schnell W.) 855 Штаерман И. Я. 10, 591, 841, 857 Штейн М. (Stein М.) 305, 656, 687, 690, 861
Штойп Г. (Steup Н.) ИЗ, 197, 841
Штурм Р. Г. (Sturm R. G.) 518, 854
Шютте Е. Г. (Schuette Е. Н.) 849, 859
Эбциоглу И. К.(Ebcioglu J. К.) 862 Эйлер Л. (Euler L.) 18, 123, 842 Элмрот Б. О. (Almroth В. О.) 560 Энгессер Ф. (Engesser F.) 88, 94, 145, 842, 843 Эриксон Б. (Erickson В.) 847 Эринген А. К. (Eringen А. С.) 860 Эшли Г. (Ashley Н.) 759, 865
Юнгблут О. (Jungbluth О.) 857 Юсуфф С. (Yussuff S.) 655, 861
Ямаки Н. (Yamaki N.) 330, 415, 848,
850
Ясинский Ф. С. 24, 86, 88, 842, 843
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 752 Арка круговая 157 Арка-полоска 424 Аэротермоупругость 753
Балка главного направления в стержневом наборе 139 Барьер потенциальный (энергетический) 34, 808 Бимомент 162, 470
Бифуркация равновесных форм 15, 821
Бубнова—Галеркина метод 35, 45, 79
Вес собственный, его влияние на устойчивость 123 Влияние начальных неправильностей на устойчивость оболочек 509, 521, 801
— поперечной силы на критическую нагрузку 144
— сжимаемости материала 383, 393
— температуры на величину модуля упругости 199
на устойчивость 198
— формы сечения стержня на устойчивость 90
Волна, бегущая при флаттере 780
Волнообразование круглой пластинки при радиальном сжатии 413
— прямоугольной пластинки при сжатии 287, 293
при сдвиге 302
Время критическое 198, 225, 228,
234
Выпучивание арки — см. Арка
— «в большом» 75
— «вторичное» круглой пластинки 422
— динамическое 719
— кольца — см. Кольцо •— местное 340
Выпучивание оболочки — см. Оболочка
— пластинки 271; см. также Пластинка
— при ползучести 198, 204
— статическое 752
— стержней — см. Стержень
— температурное 838
Гибкость стержня 25 Гипотеза плоских сечений при исследовании сверхзвукового потока 758
— прямых нормалей в теории оболочек 444
Депланация 159, 470
Дивергенция 752
Длина стержня приведенная 24
Жесткость опоры критическая 139
— переменная 114
Задача бифуркационная 560
— о собственных значениях 19
Изгиб продольный 15
за пределами упругости 86
при ползучести 198, 204
Интенсивность деформаций 357
— напряжений 357
Кармана формула 332 Кирхгофа теорема 818 Колебания параметрические 235, 254, 749
пластинок и оболочек 750
стержней 235, 254
Кольцо круговое 154
при динамическом нагружении
262, 263
Коэффициент динамической перегрузки 734
— приведения длины 24
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
875
Коэффициент редукционный 319 Коэффициенты второй квадратичной формы поверхности 434
— первой квадратичной формы поверхности 431
Кривизна поверхности гауссова 436 средняя 436
Критерий динамический устойчивости в большом 825 в малом 814
— касательно-модульный 209, 210,
232, 233
— критической деформации 209, 232, 233
— начальных неправильностей (несовершенств) 33, 63, 80, 209, 214, 232, 233
— статический устойчивости в большом 826
в малом 816
— устойчивости динамический 32,60, 80, 209, 212, 232, 814, 825
при комбинированной нагрузке 834
при ползучести 209, 212, 232
, его выбор при определении
критической нагрузки стержня за пределами упругости 105
статический 32, 816
энергетический 32, 38, 41, 822,
831
— энергетический устойчивости в большом 831
в малом 822
Круг устойчивости 181 Кручение стесненное 159
Лагранжа — Дирихле теорема 823 Ляпунова теоремы 823
Машины аналоговые (электромоделирующие), их применение к исследованию устойчивости 80, 736
— цифровые электронные, их использование в задачах устойчивости 78, 325, 724
Мембрана хлопающая 635 Мера эксцентриситета 110 Метод Бубнова—Галеркина 35, 45, 79
— возмущений 420
— динамический 78
— интегральных уравнений 56
— коллокации 50
— конечных разностей 47, 79
— последовательных приблйжений 35, 51, 78, 80
Метод проб 35, 55
— Ритца 35, 42, 79
— статистический 781, 839
— степенных рядов 125, 420
— Тимошенко 44
— упругой шарнирной цепи 48
— энергетический 78 Методы вариационные 370
— прямые 51
Моделирование прямое в задачах устойчивости 84 Модуль касательный 88, 356
— приведенный 89
— разгрузки 88
— результирующий 89
— секущий 356
Момент инерции секториальный 161 центробежный 167
Набор стержневой 137 Нагружение динамическое 235, 236, 718, 838
— простое 315, 816
— сложное 817
— ударное 235
Нагрузка касательно-модульная 106
— критическая 15, 105, 271, 816 верхняя 426
, влияние на нее поперечной силы 144
динамическая 719
, ее определение различными
методами — см. название метода нижняя 426, 829
— приведенно-модульная 106
— расчетная 106
— случайная, ее влияние на устойчивость оболочек 807, 812
Напряжения температурные 198 Неправильности начальные, их влияние на устойчивость оболочек 509, 521, 801
Неустойчивость арки, кольца, панели, пластинки, оболочки, стержня — см. Арка, Кольцо, Панель, Пластинка, Оболочка, Стержень
— колебательная 752
— монотонная 752
Обмен устойчивостью 832 Оболочка большого прогиба 458
— коническая под действием внеш него давления 595, 599
кручения 602
осевого сжатия 591
— малого прогиба 444
876
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Оболочка подкрепленная 837
— пологая, обтекаемая сверхзвуковым потоком 761
под действием поперечной нагрузки 633
— при высокой температуре 838
— при динамическом нагружении 838
— при ползучести 702,838
— сферическая под действием внешнего давления 613, 747
динамического нагружения 747
— трехслойная 690, 838
— цилиндрическая в зоне приложения сосредоточенной нагрузки 559
вафельного типа 548
— замкнутая под действием внешнего давления 500. 575
под действием внешнего давления, кручения и изгиба 533 под действием комбинированного нагружения 530
— под действием кручения 515,
576
под действием кручения и
внешнего давления 532
под действием кручения и
внутреннего давления 536 под действием осевого сжатия 471, 478, 569, 742 под действием осевого сжатия и внешнего давления 530
— под действием осевого
сжатия и внутреннего давления 534
под действием поперечного
изгиба 528. под действием чистого изги¬
ба 522
• открытая под действием осе¬
вого сжатия 550, 797
под действием сдвига
554
при динамическом нагружении 720
; характер волнообразования
при сжатии 425
под действием динамического
нагружения всесторонним давлением 729
подкрепленная 541
« под действием осевого сжа¬
тия 544
Оболочка цилиндрическая подкрепленная под действием осевого сжатия и внутреннего давления 547 под действием сосредоточенной нагрузки 560
при высокой температуре
698
Определение критической нагрузки силы различными методами — см. название метода
Панель коническая под действием поперечной нагрузки 642
— плоская, подкрепленная под действием сжатия 340
при высокой температуре
695
— пологая под действием поперечной нагрузки 636
— сферическая под действием поперечной нагрузки 645
— цилиндрическая под действием
динамического сжатия 720
под действием осевого сжатия
550, 579
под действием сдвига 554
при высокой температуре 710
— — трехслойная под действием сжатия 687
Перескок упругой системы из одного положения в другое 77 Пластинка анизотропная 333, 354 приведенная 335
— гибкая 282
— кольцевая 415, 417
— круглая 402, 418
радиально-сжатая 408, 410,412,
418
—, обтекаемая сверхзвуковым потоком 763, 768, 775
— ортотропная 333
— под действием динамического нагружения 718, 720, 728
— подкрепленная 335
—, — системой продольных и поперечных ребер 340
— при ползучести 838
— приведенная 319
— прямоугольная анизотропная 354 под действием комбинированной
нагрузки 311
неравномерного сжатия
308
равномерного сжатия
(растяжения) в одном направлении и сдвига 312
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
877
Пластинка прямоугольная под действием сдвига 300, 302, 306, 348, 351, 381
сжатия 285, 316,372,377,
379, 380, 381, 388 сжатия в двух направлениях 311 й
сжатия в двух направлениях и сдвига 314 сжатия в одном направлении 285, 286, 294, 295, 316, 377, 379, 380, 381, 388
чистого изгиба 308
чистого изгиба и сдвига
315
— с дискретно расположенными ребрами 336
— с искривляющимися кромками 330
— с начальной погибью при высокой температуре 704
— трехслойная 678, 681, 683
с легким заполнителем 657
Плоскость фазовая 825 Плотность вероятности 783, 787 Площадь секториальная 159 Погибь начальная 63 Ползучесть 198, 838
Полоса под действием динамически приложенного момента 265 нагрузки, равномерно распределенной по всей длине 191
поперечного изгиба 186, 187,
189
силы, приложенной на разных расстояниях от опор 193 силы, приложенной посередине пролета 192, 194
чистого изгиба 178
Потеря* устойчивости арки — см Арка
— — в большом 75
в малом 76
динамическая 719
кольца — см. Кольцо
местная 340
оболочки — см. Оболочка
общая 341
панели — см. Панель
пластинки — см. Пластинка
стержня — см. Стержень
Преобразование вероятностей 787,796
— изометрическое 439
Примеры расчета на устойчивость: бак топливный ракеты 539
• башня телевизионная
127
Примеры расчета на устойчивость: винт ходовой токарно-винторезного станка 136
: время критическое для
стержня двутаврового сечения 228, 231
:газопровод внутризаводский 529
: диафрагма коническая
опоры воздушно-реактивного двигателя 594
: диффузор, коническая
часть его внутренней стенки 601
: звено тяги управления к
рулю высоты в самолете 19
: колонна испытательной
машины 25 : крыша цельнометаллического вагона 20 : оболочка стеклопластиковая, сжатая вдоль оси 549 : оболочка цилиндрическая подкрепленная (типа крыла самолета) 306
—: палуба корабля 87
: панель дюралюминовая
при высокой температуре 708, 711
: панель обшивки крыла
самолета 295
: панель, подкрепленная
стрингерами 342, 344 : пластинка дюралюминовая квадратная при высокой температуре 708 : раскос сжатый в конструкции газохранилища 150
— : стержень дюралюмино-
вый при ползучести 217 : стержень с одним защемленным и другим свободным концом 42, 44, 51 •
: стержень тонкостенный
дюралюминовый 170
: стержень, шарнирно
опертый 47, 50, 52, 55, 60 :стрела портального крана 119
: стрингер в фюзеляже 143
Принцип возможных перемещений 36 Прощелкивание 425, 634
Равновесие безразличное 14
— неустойчивое 13, 814, 823, 824, 832
— устойчивое 13, 814, 823, 824, 832 Разветвление равновесных форм 15,
825
878
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Ритца метод 35, 42, 7S Седло (особая точка) 826 Связь поперечная в составном стержне 140
Сжатие стержня внецентренное 65, 66, 67, 68, 107, 110, 791 Сила критическая 18 верхняя 76
, ее определение разными методами— см. вазвание метода
, с помощью аналоговой
машины 80
касательно-модульная 99
нижняя 77
при следящей нагрузке 74
приведенно-модульная 99
— следящая 72
Способность несущая панели подкрепленной 340
пластинки 583
стержня тонкостенного подкрепленного 345 Стеклопластики 333, 353, 838 Стержень двухпролетный 134 —, лежащий на нескольких жестких опорах 134
— многопролетный 135
— на упругой опоре 137
— на упругом основании 141
— наименьшего веса 120
— под действием быстро возрастающей нагрузки 240
внезапно приложенной силы
238
— внецентренного сжатия 65,
66, 67, 68, 107, 110, 791
динамической нагрузки 234,
236, 237
импульсивной нагрузки 252
нагрузки, изменяющейся по
гармоническому закону 259
осевого сжатия и кручения
151, 153
осевой и поперечной нагрузок 69
переменной нагрузки 95, 100
продольной и поперечной нагрузок 69, 70
пульсирующей нагрузки 253
распределенной и сосредоточенной нагрузок 128
скручивающих пар 151
следящей силы 72
только собственного веса 123
центрального осевого сжатия 15, 87, 163, 166, 173, 201, 214
Стержень при нагреве 198, 199,
201
— при ползучести 214, 225, 838
— с жесткостью, непрерывно изменяющейся по длине 116
— с начальной погибью 64, 214, 237,
* 791
— с переменной жесткостью 114, 118
— со ступенчатым изменением поперечного сечения 115, 121
— составной 114, 145 рамного типа 148
с решеткой из диагоналей
146
из диагоналей и стоек
147
— тонкостенный 158
под действием внецентренного
сжатия 179
поперечного изгиба
195
центрального сжатия 163,
166, 173
чистого изгиба 175, 178
Теорема Кирхгофа 818
— Лагранжа — Дирихле 823 Теоремы Ляпунова 823
Теория гибких пластинок 271, 320
— деформаций 355, 383
— жестких пластинок 271
— малых упруго-пластических деформаций 355
— пластичности 353
— старения 207
— течения 355, 389
— упрочнения 207
Точка бифуркации равновесных состояний 59, 821
— коллокации 50
— поверхности гиперболическая 439 параболическая 439
эллиптическая 438
— разветвления равновесных состояний, 59, 821
Траектория фазовая 825
Уравнение изгиба пластинки дифференциальное 274, 276, 404
— непрерывности (совместности) деформаций для гибкой пластинки 282
для цилиндрической оболочки 469
— трех моментов 135 Устойчивость 13д 814
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
879
Устойчивость арки — см. Арка
— асимптотическая 815
— «в большом», 34, 825, 826, 831
— «в малом» 34, 105, 814, 816, 822
— динамическая 235
— за пределами упругости 85, 353, 566
— кольца — см. Кольцо
— неконсервативной системы 72
— оболочки — см. Оболочка
— панели — см. Панель
— пластинки — см. Пластинка
— плоской формы изгиба 158
— при высокой температуре 198
Флаттер 752
— панельный 752 и сл.
Формула Кармана 332
— Эйлера 18, 24, 25
, пределы ее применимости 25
Функция собственная 19, 59
— усилий в срединной поверхности 455
Хлопок оболочки 427, 485
Центр (особая точка) 825
— изгиба 169
Шарнир упругий 49
Ширина пластинки приведенная 319
Эйлера формула 18, 24, 25 Эксперименты, их результаты для оболочек 427, 627, 739 —, и пластинок при вы¬
сокой температуре 714
—, конических 600
—, цилиндрических 491,
505, 537, 572, 574, 744
—, для панелей 649, 650, 652,
714
—, для пластинок прямоуголь¬
ных 397, 398
—, для стержней 86, 91, 248
Эксцентриситет в приложении нагрузки 65, 67
Арнольд Сергеевич Волъцир. Устойчивость упругих систем.
М., Физматгиз, 1963 г., 880 стр. с илл. Редактор Я. К. Снитко.
Техн. редактор К. Ф. Брудно. Корректор О. А. Бутусова.
Сдано в набор 11/IX-1962 г. Подписано
к печати 24/IV 1963 г. Бумага 60x90/16.
Физ. печ. л. 55. Условн. печ. л. 55.
Уч.-изд. л. 53,12. Тираж 7000 экз. Т-04947. Цена книги 2 р. 86 к. Заказ Nfe 704.
Государственное издательство физико-математической литературы. Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой УЦБ и ПП Ленсовнархоза. Ленинград, Измайловский пр., 29.