Автор: Работнов Ю.Н.
Теги: механика деформируемых тел упругость деформация физика теория упругости
Год: 1966
Текст
1 Д+ ft-/"
-
Ю. Н. РАБОТНОВ
ПОЛЗУЧЕСТЬ
ЭЛЕМЕНТОВ
КОНСТРУКЦИЙ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1966
531
Р-13
УДК 539.376
Юрий Николаевич Работное
Ползучесть элементов конструкций
М., 1966 г., 752 стр. с илл.
Редактор Н. И. Малинин
Техн. редактор А. А. Благовещенская
Корректор Т. С. Плетнева
Сдано в набор 8/V 1966 г. Подписано к печати 27/Х 1966 г. Бумага 60x90/Je.
Физ. печ. л. 47. Условн." печ. л. 47. Уч.-изд. л. 44,56.
Тираж 5300 экз. Т-12785. Цена книги 3 р. 06 к. Заказ № 390
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Московская типография № 16 Главполиграфпрома
Комитета по печати при Совете Министров СССР
Москва, Трехпрудный пер., 9
ОГЛАВЛЕНИЕ
Предисловие 9
Введение .... 11
Глава I
Основные понятия механики твердого тела 16
§ 1. Тензоры в трехмерном евклидовом пространстве 17
| 2. Свертывание тензоров. Инварианты 22
§ 3. Взаимный базис. Ковариантные и контравариантные
составляющие тензора 25
§ 4. Дифференциальные операции 30
| 5. Теория деформаций в сплошной среде 36
| 6. Теория напряжений 38
| 7. Декартовы координаты. Определение перемещений 41
| 8. Некоторые дальнейшие свойства тензора напряжений 44
§ 9. Тензор скоростей деформации. Инварианты тензоров
деформации и скоростей деформации 50
§ 10. Упругое тело 54
| 11. Изотропное упругое тело , 58
Глава II
Теория пластичности 62
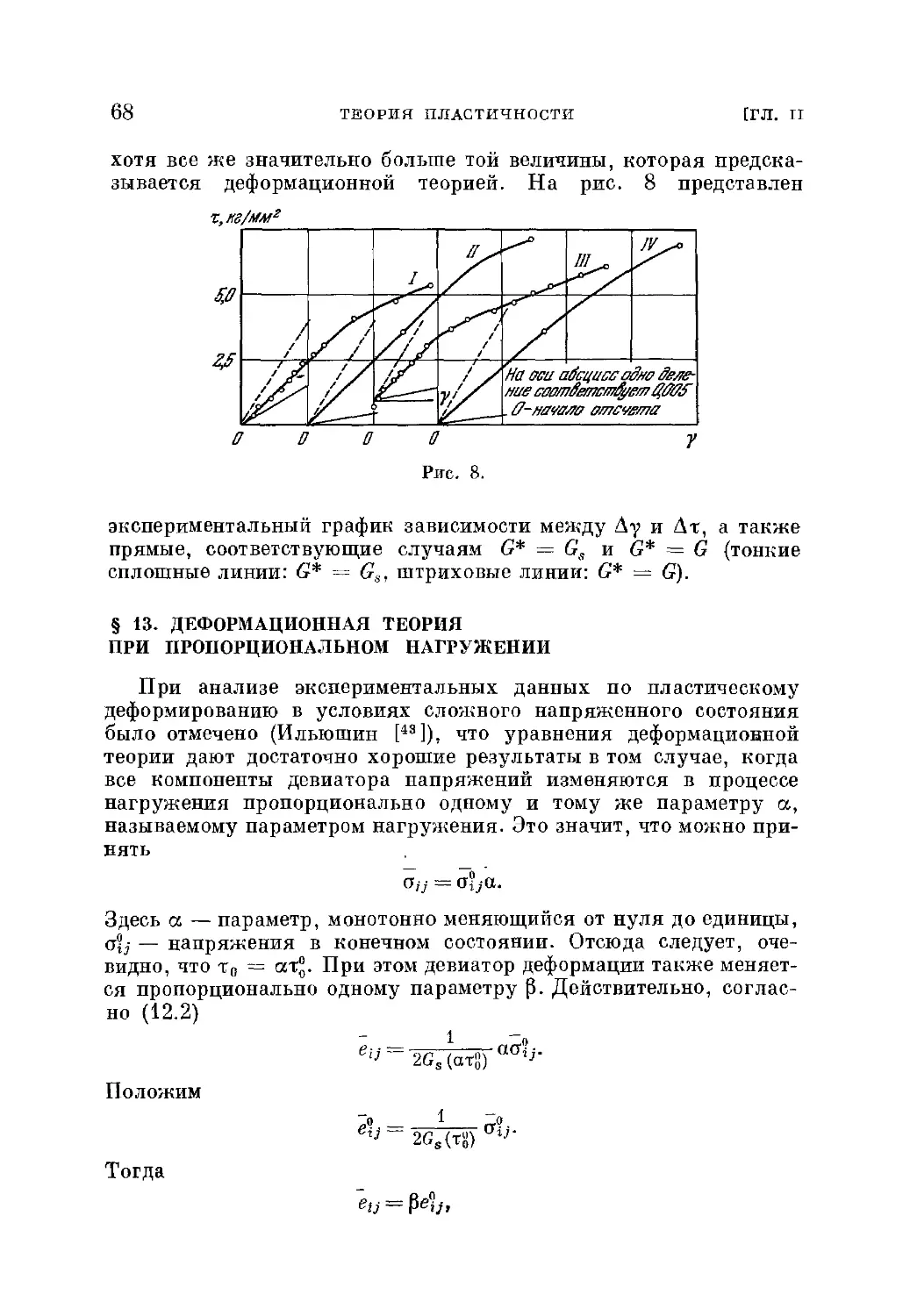
I 12. Деформационная теория пластичности 63
§ 13. Деформационная теория при пропорциональном нагружении 68
§ 14. Постулат упрочнения Друкера 70
I 15. О возможных границах применимости деформационной теории
пластичности 73
§ 16. Двумерная модель упрочняющегося тела 78
§ 17. Теории течения при гладкой поверхности нагружения.
Изотропное упрочнение 86
§ 18. Теории течения с трансляционным упрочнением 89
§ 19. Сингулярные поверхности нагружения 91
§ 20. Теория скольжения 96
§ 21. Модель плоского тела ... . 101
§ 22. Течение с сингулярной поверхностью нагружения 105
Глава III
Линейные вязко-упругие среды .... . 108
§ 23. Простейшие вязко-упругие тела 109
I 24. Дифференциальные законы деформирования более общего вида 114
§ 25. Наследственно-упругое тело 119
4
ОГЛАВЛЕНИЕ
$ 26. Условие замкнутого цикла Вольтерра 122
I 27. Сингулярные ядра наследственности 124
| 28. Экспоненциальные операторы произвольного порядка .... 126
| 29. Теорема умножения для За-операторов 129
§ 30. Асимптотические формулы для Э-функций 132
§ 31. Общая задача теории наследственной упругости. Принцип
Вольтерра 134
§ 32. Применение трансформации Лапласа к задачам теории
наследственной упругости 137
§ 33. Ядра более общего вида 140
§ 34. Линейная ползучесть бетона 144
§ 35. Дальнейшие приложения принципа Вольтерра 147
§ 36. Простейшие динамические задачи 149
§ 37. Комплексные модули 151
§ 38. Функции ползучести и релаксации 153
§ 39. Задачи о подвижной нагрузке. Малые скорости 156
| 40. Движение штампа по границе вязко-упругой среды 159
| 41. Некоторые экспериментальные данные по ползучести пластмасс 162
Глава IV
Ползучесть металлов. Основные опытные факты и феноменологические
теории 166
§ 42. Основные сведения о ползучести 166
§ 43. Эмпирические формулы для кривых ползучести 169
I 44. Подобие кривых ползучести 172
I 45. Температурные зависимости 177
§ 46. Релаксация напряжений 183
§ 47. Простейшие теории ползучести 185
§ 48. Теории старения 190
§ 49. Гипотеза уравнения состояния 196
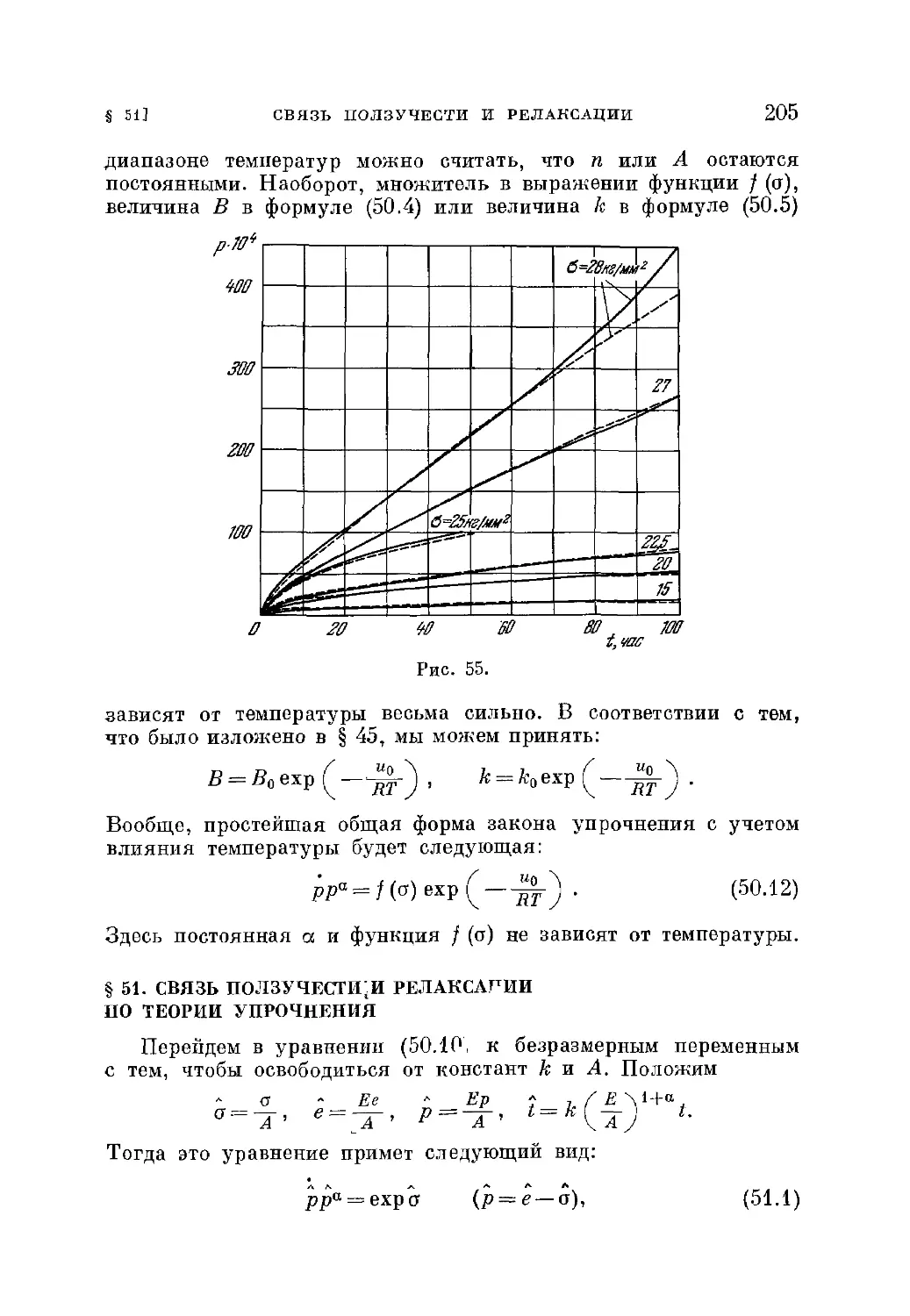
§ 50. Аналитические выражения для закона упрочнения 200
§ 51. Связь ползучести и релаксации по теории упрочнения .... 205
| 52. Наследственная теория ползучести 209
§ 53. Экспериментальная проверка гипотезы упрочнения при
переменных нагрузках 213
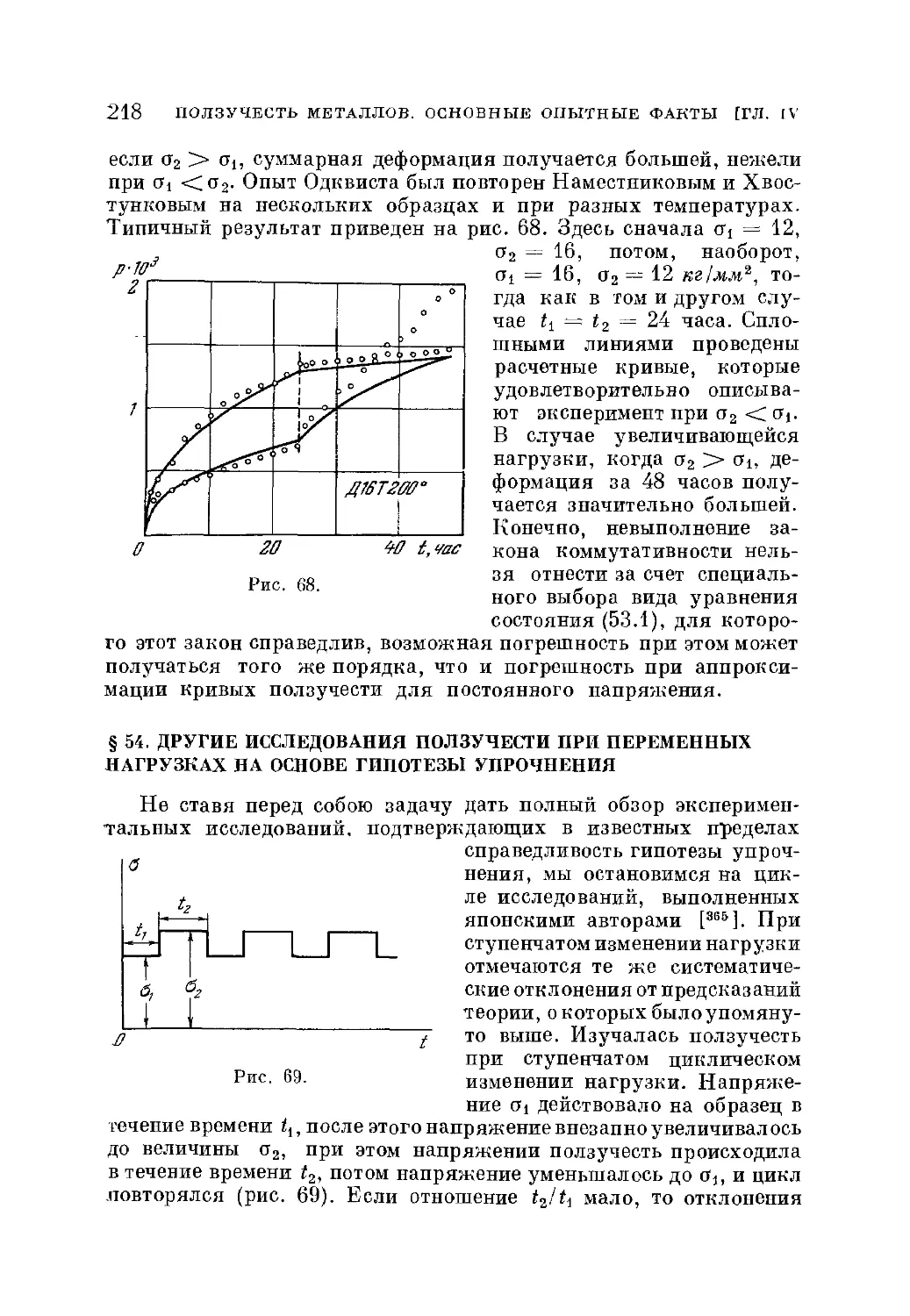
§ 54. Другие исследования ползучести при переменных нагрузках
на основе гипотезы упрочнения 218
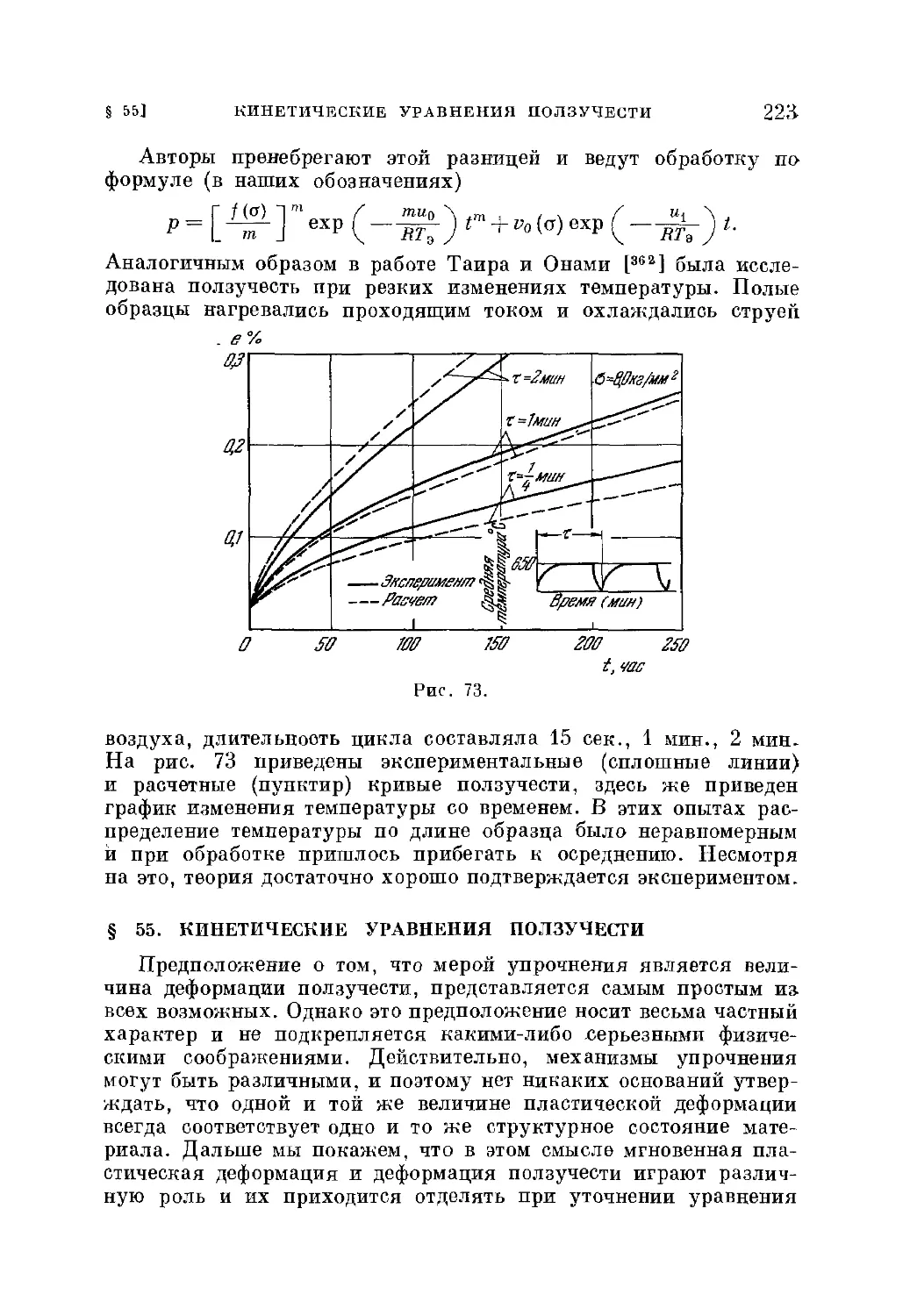
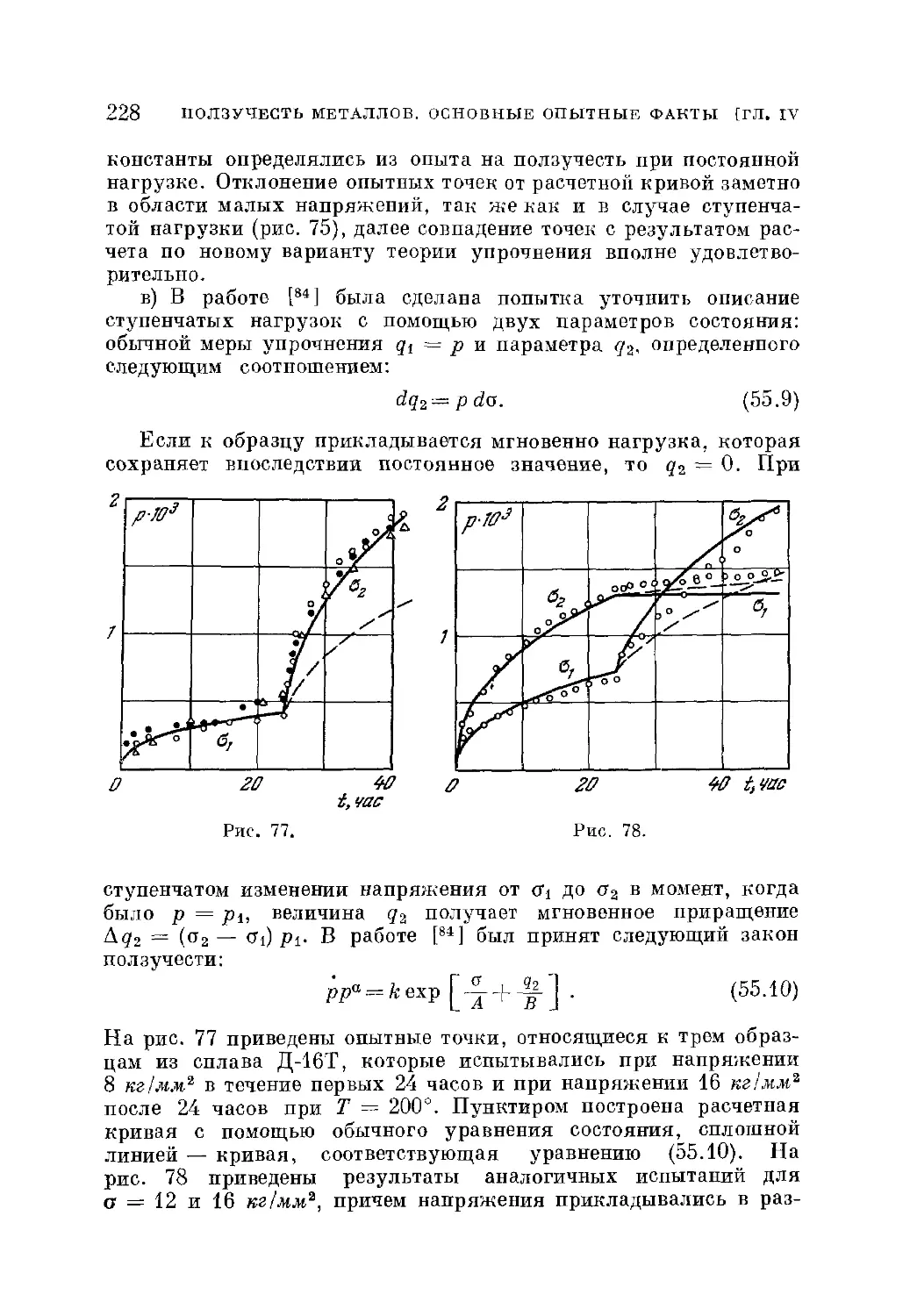
§ 55. Кинетические уравнения ползучести 223
§ 56. Разупрочнение при ползучести 229
§ 57. Ползучесть и мгновенная пластическая деформация 233
§ 58. Кратковременная ползучесть. Основные факты 238
§ 59. Кратковременная ползучесть. Зависимость для скорости . . 243
§ 60. Ползучесть при сжатии. Реверсирование нагрузки .... 246
§ 61. Малые отклонения от основного состояния 249
§ 62. Динамическая ползучесть 252
Глава V
Ползучесть при сложном напряженном состоянии 255
§ 63. Установившаяся ползучесть 256
§ 64. Изотропная ползучесть 258
§ 65. Потенциал ползучести 261
§ 66. Специальные формы закона ползучести 266
§ 67. Обработка опытов на растяжение с кручением 271
§ 68. Квазилинейные уравнения установившейся ползучести . . . 274
§ 69. Анизотропная ползучесть 281
§ 70. Определение параметров анизотропии 286
ОГЛАВЛЕНИЕ
5
§ 71. Неустановившаяся ползучесть .... 288
§ 72. Теории ползучести деформационного типа 291
§ 73. Теории течения 295
§ 74. Обобщение теории упрочнения . . 298
§ 75. Квазиустановившаяся ползучесть 299
§ 76. Экспериментальная проверка теорий ползучести при сложном
напряженном состоянии. Ранние работы 303
§ 77. Ползучесть при сложном напряженном состоянии и
постоянных нагрузках. Опыты Джонсона 306
§ 78. Дальнейший анализ опытов Джонсона 314
§ 79. Экспериментальные исследования ползучести при сложном
напряженном состоянии (продолжение) 325
§ 80. Исследования Наместникова 331
§ 81. Ползучесть при сложном напряженном состоянии и переменных
нагрузках . 334
§ 82. Релаксация напряжений в сложном напряженном состоянии 339
Глава VI
Длительное разрушение при высоких температурах 344
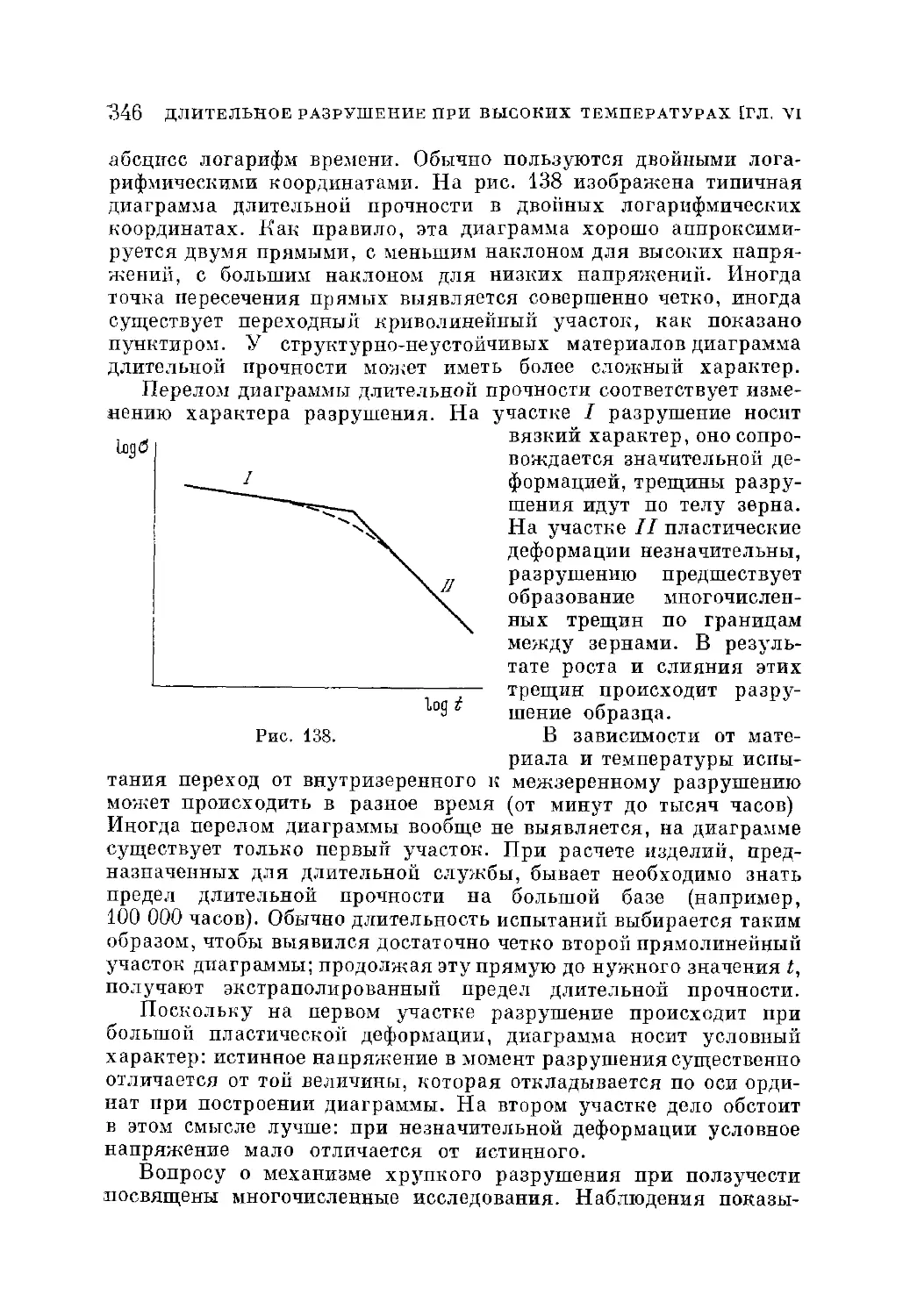
§ 83. Основные сведения о длительной прочности 344
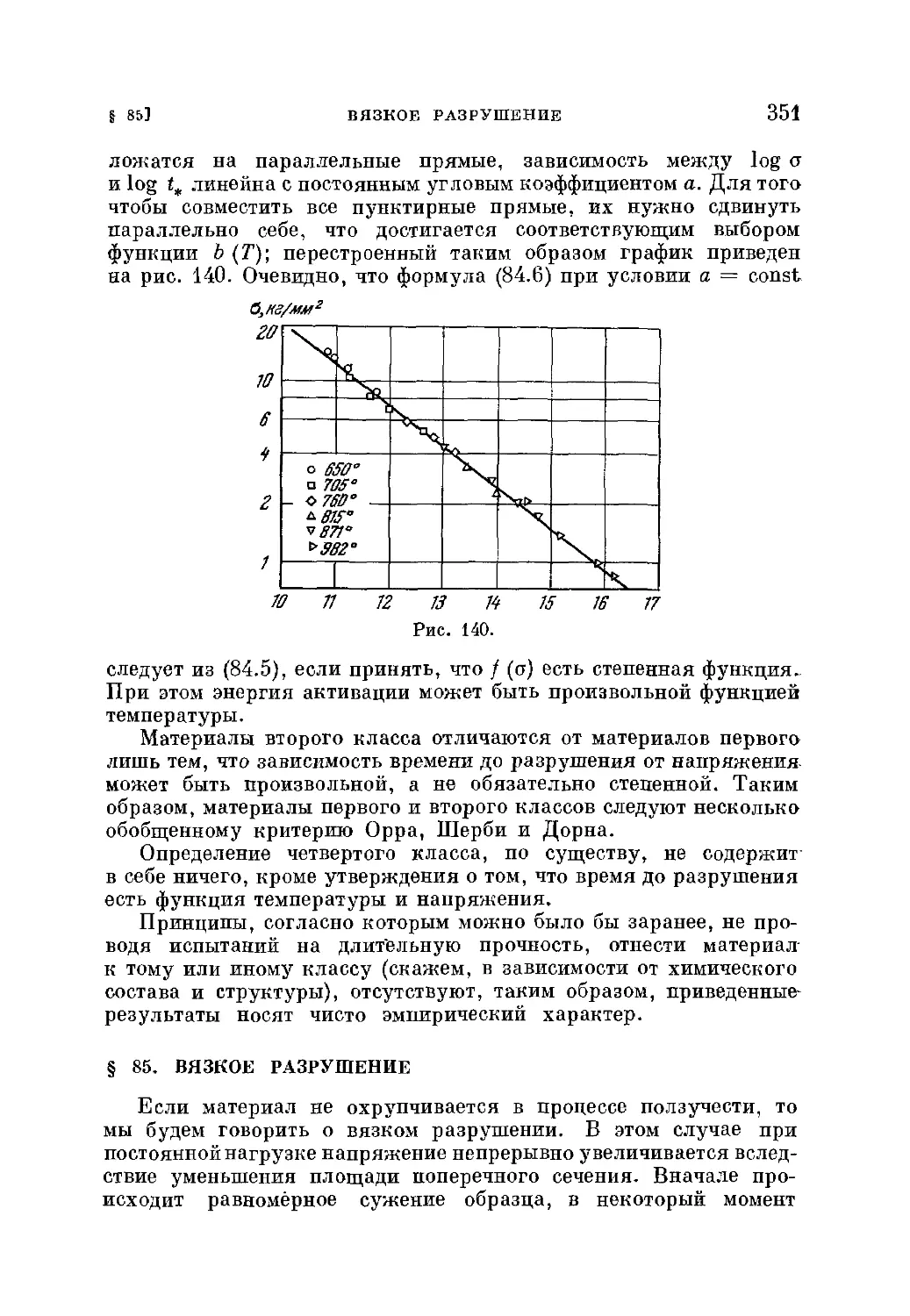
§ 84. Температурно-временные зависимости длительной прочности 347
§ 85. Вязкое разрушение 351
§ 86. Разрушение, сопровождающееся охрупчиванием 357
§ 87. Смешанное разрушение. Гипотеза Качанова 360
§ 88. Более общая гипотеза разрушения. Хрупкий случай .... 363
§ 89. Смешанное разрушение. Кратковременная ползучесть . . . 366
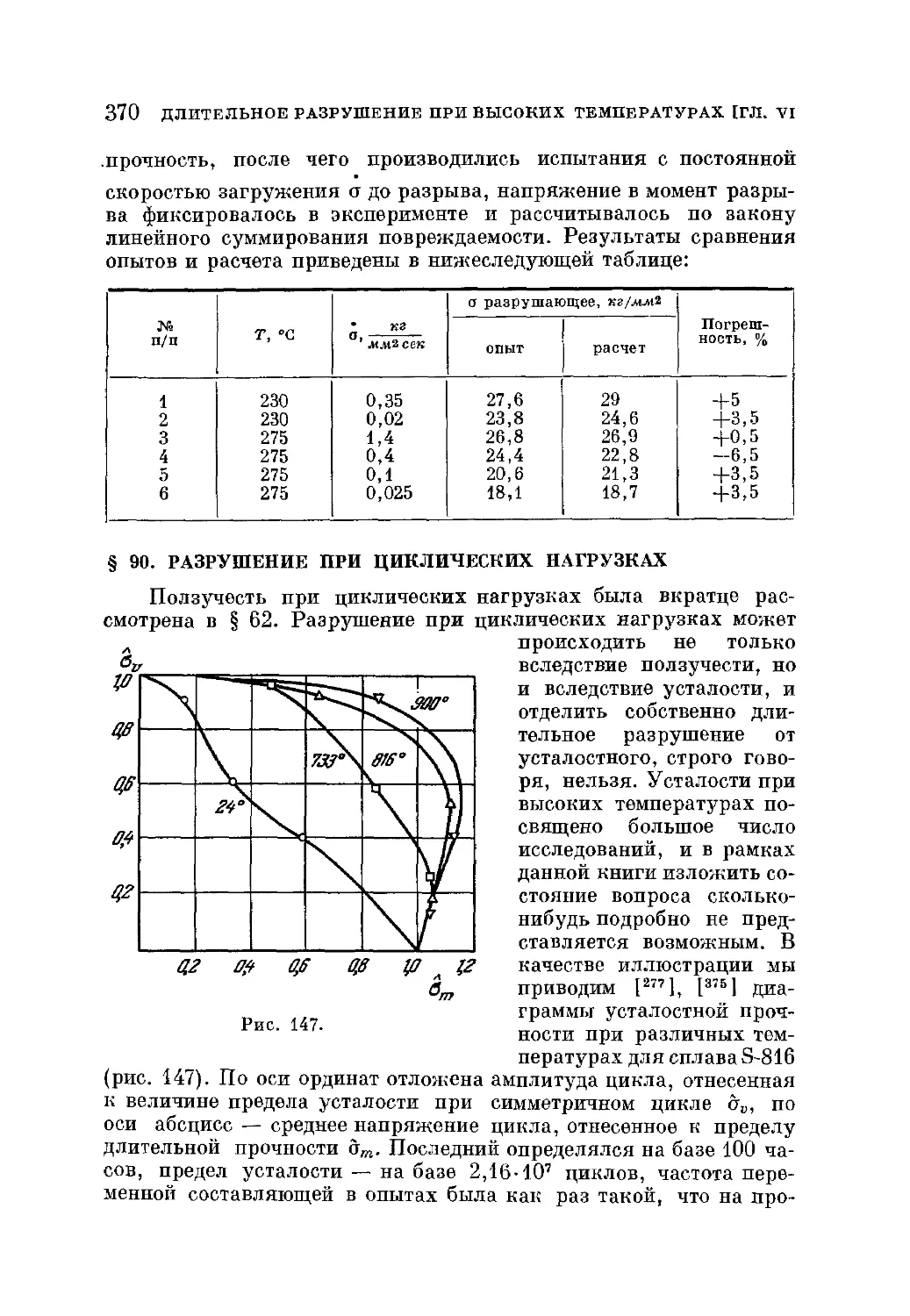
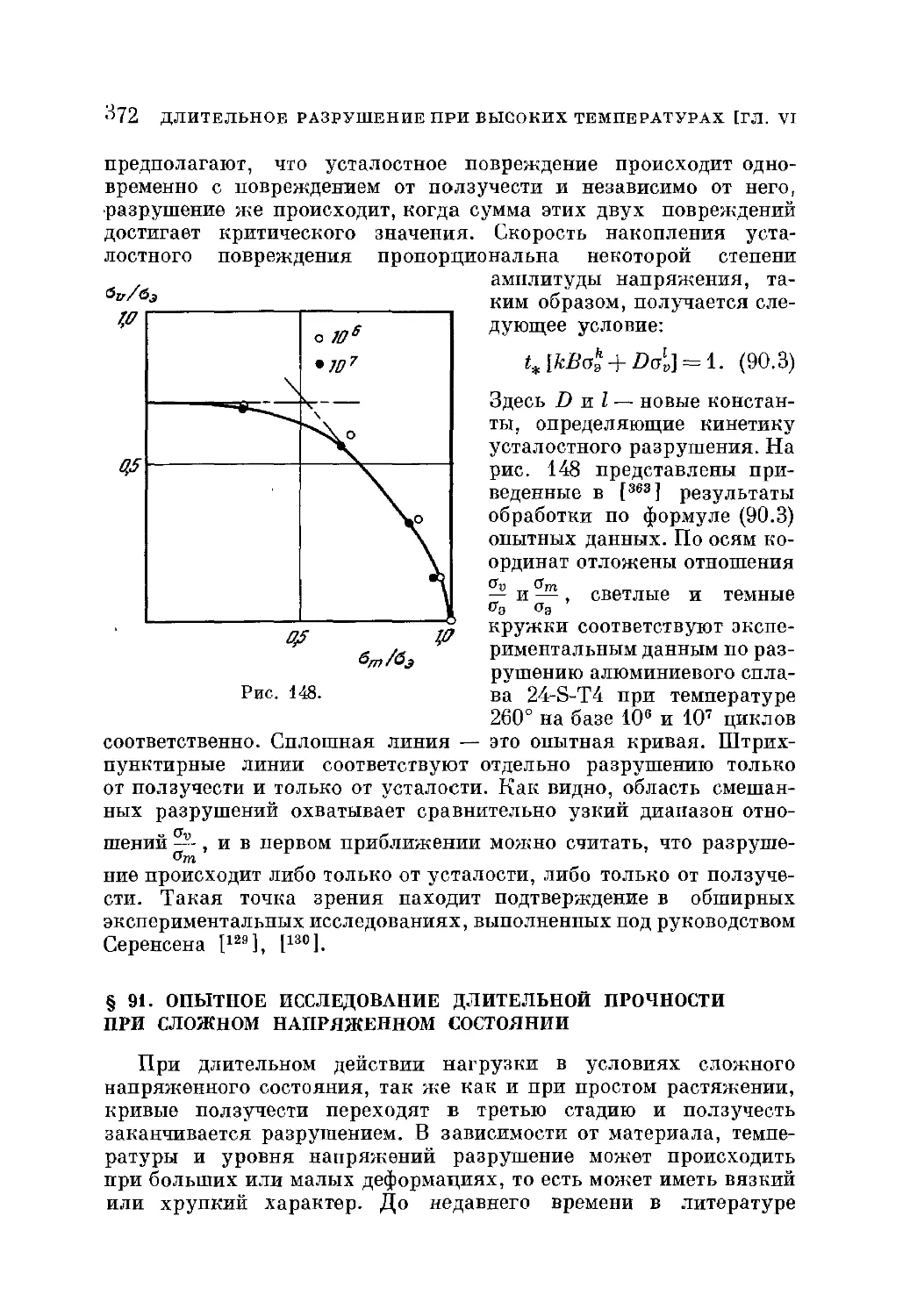
§ 90. Разрушение при циклических нагрузках 370
§ 91. Опытное исследование длительной прочности при сложном
напряженном состоянии 372
§ 92. Простейшие критерии длительной прочности 376
§ 93. Общие представления о длительном разрушении при сложном
напряженном состоянии 379
§ 94. О возможности построения более общей теории длительного
разрушения 383
Глава VII
Установившаяся ползучесть. Общая теория и простейшие задачи 386
§ 95. Единственность в малом и устойчивость 386
§ 96. Вариационный принцип Лагранжа 390
§ 97. Вариационный принцип Кастильяно 392
§ 98. Некоторые следствия вариационных принципов 393
§ 99. Частные формы уравнений установившейся ползучести . . . 396
§ 100. Моделирование установившейся и квазиустановившейся
ползучести 399
§ 101. Степенной закон ползучести. Теорема Кепледайна и Друкера 401
§ 102. Установившаяся ползучесть ферм 405
§ 103. Применение поверхностей постоянной мощности диссипации
к расчету ферм 412
1 104. Кинематический способ расчета ферм. Примеры . . 416
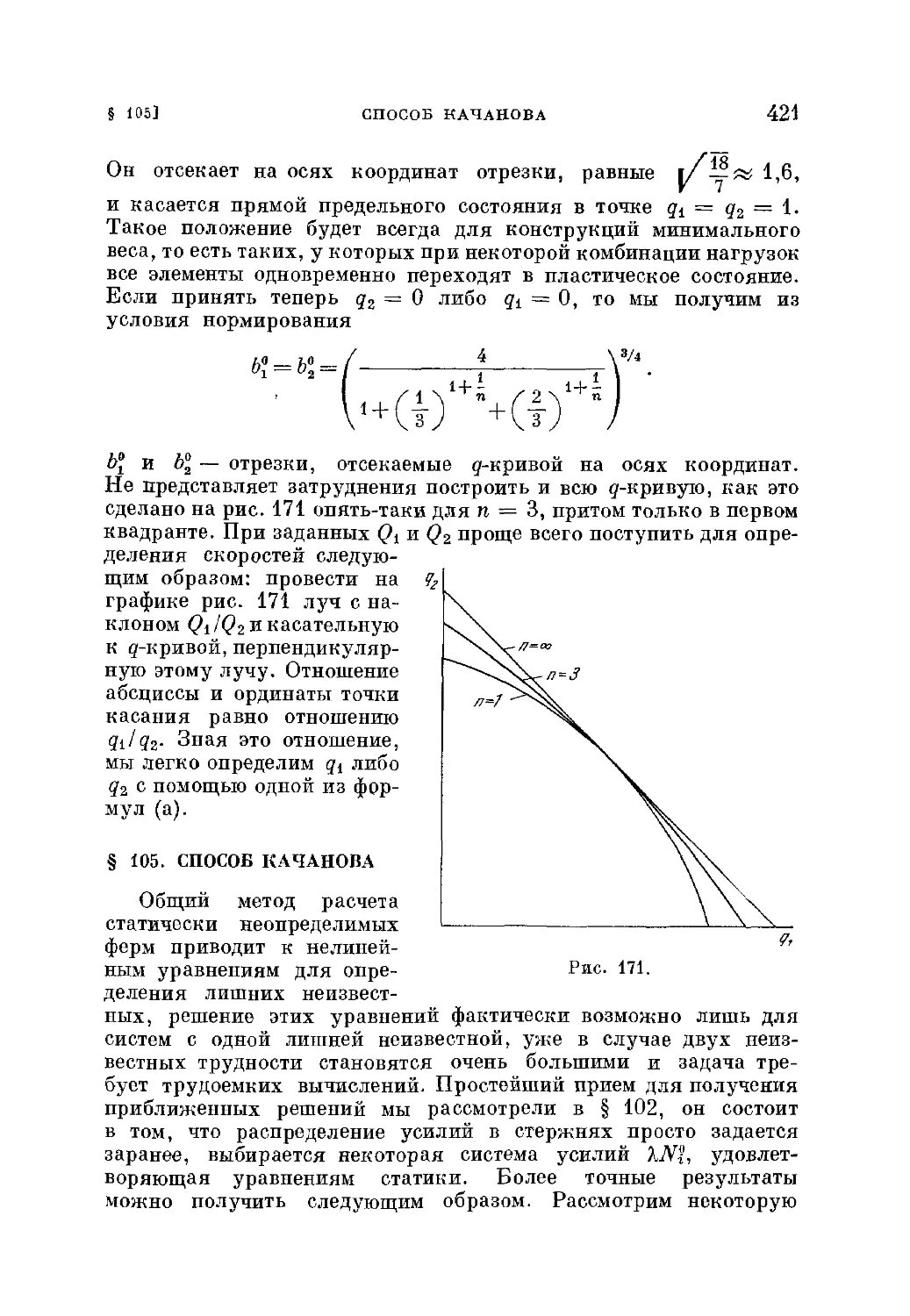
§ 105. Способ Качанова . . 421
Глава VIII
Установившаяся ползучесть. Изгиб и кручение ... ... 423
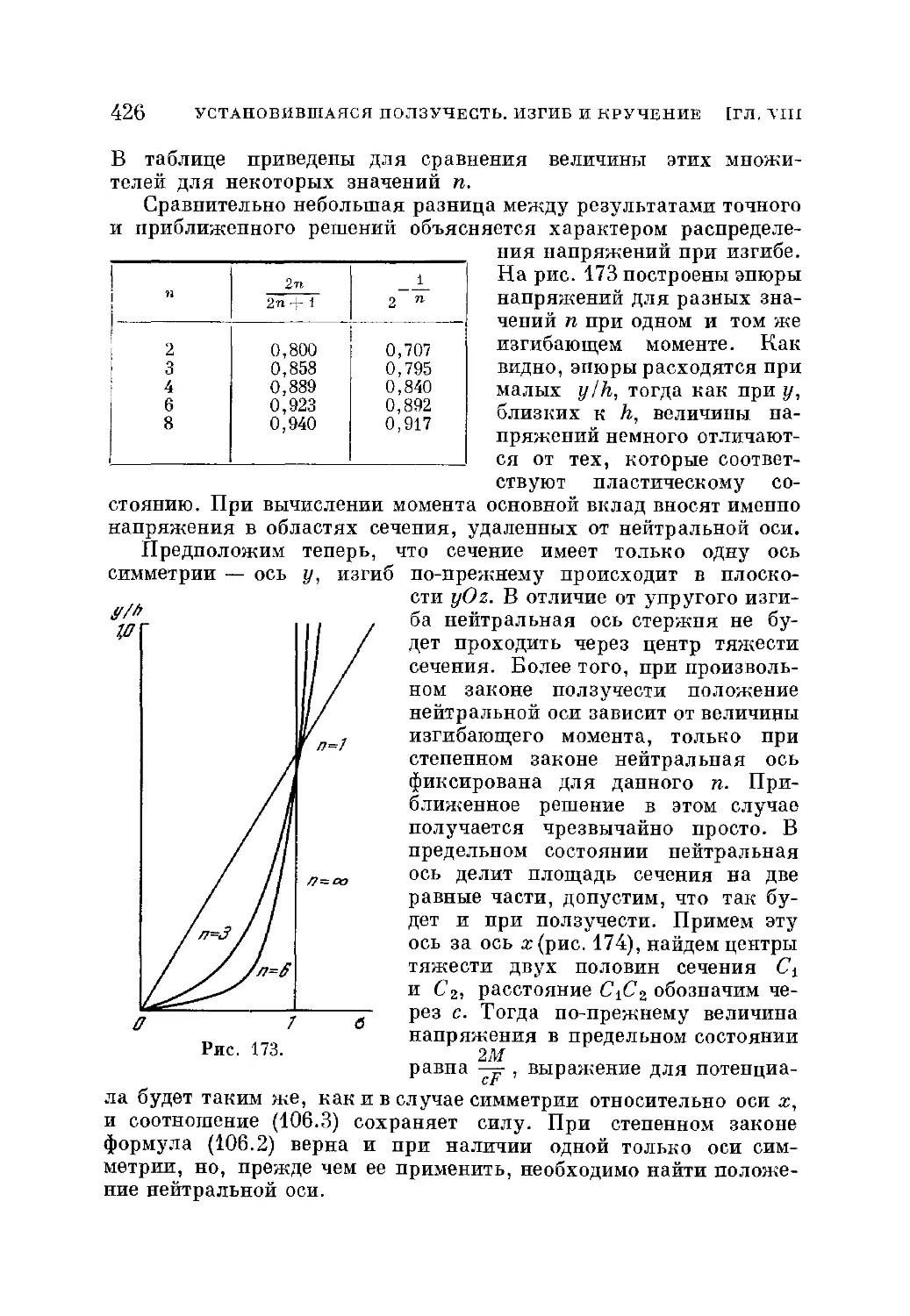
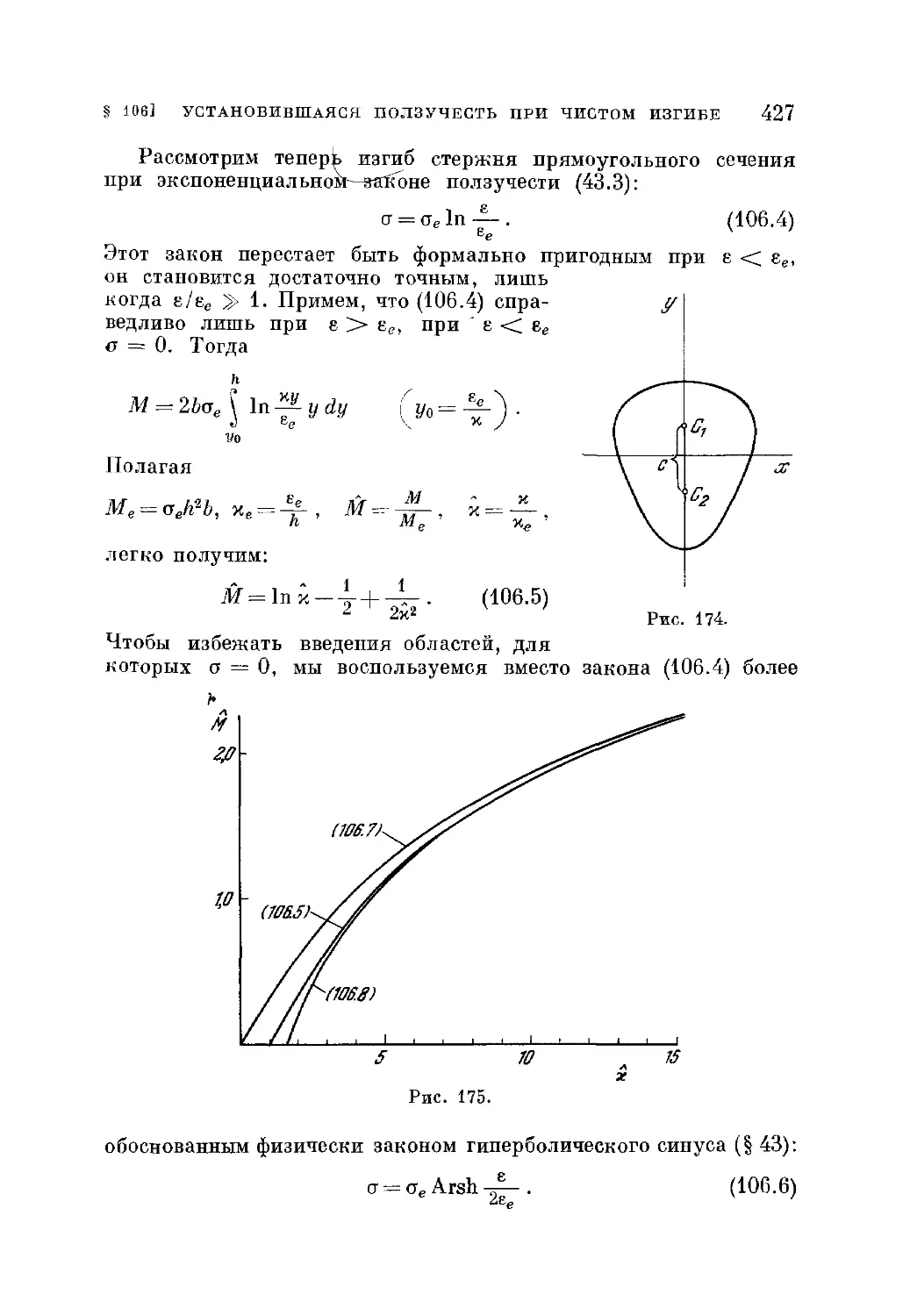
§ 106. Установившаяся ползучесть при чистом изгибе ¦ • 423
§ 107. Общий случай чистого изгиба 429
6
ОГЛАВЛЕНИЕ
§ 108. Тонкостенные стержни открытого профиля 432
§ 109. Приближенный способ исследования изгиба тонкостенных
стержней 437
I 110. Деформация балок и рам при изгибе . 441
§ 111. Ползучесть при кручении 447
| 112. Кручение тонкостенных стержней замкнутого профиля . . . 450
I 113. Кручение тонкостенных стержней открытого профиля . . 454
§ 114. Вариационные методы решения задач о кручении 456
§ 115. Изгиб и кручение тонкостенных стержней замкнутого
профиля 458
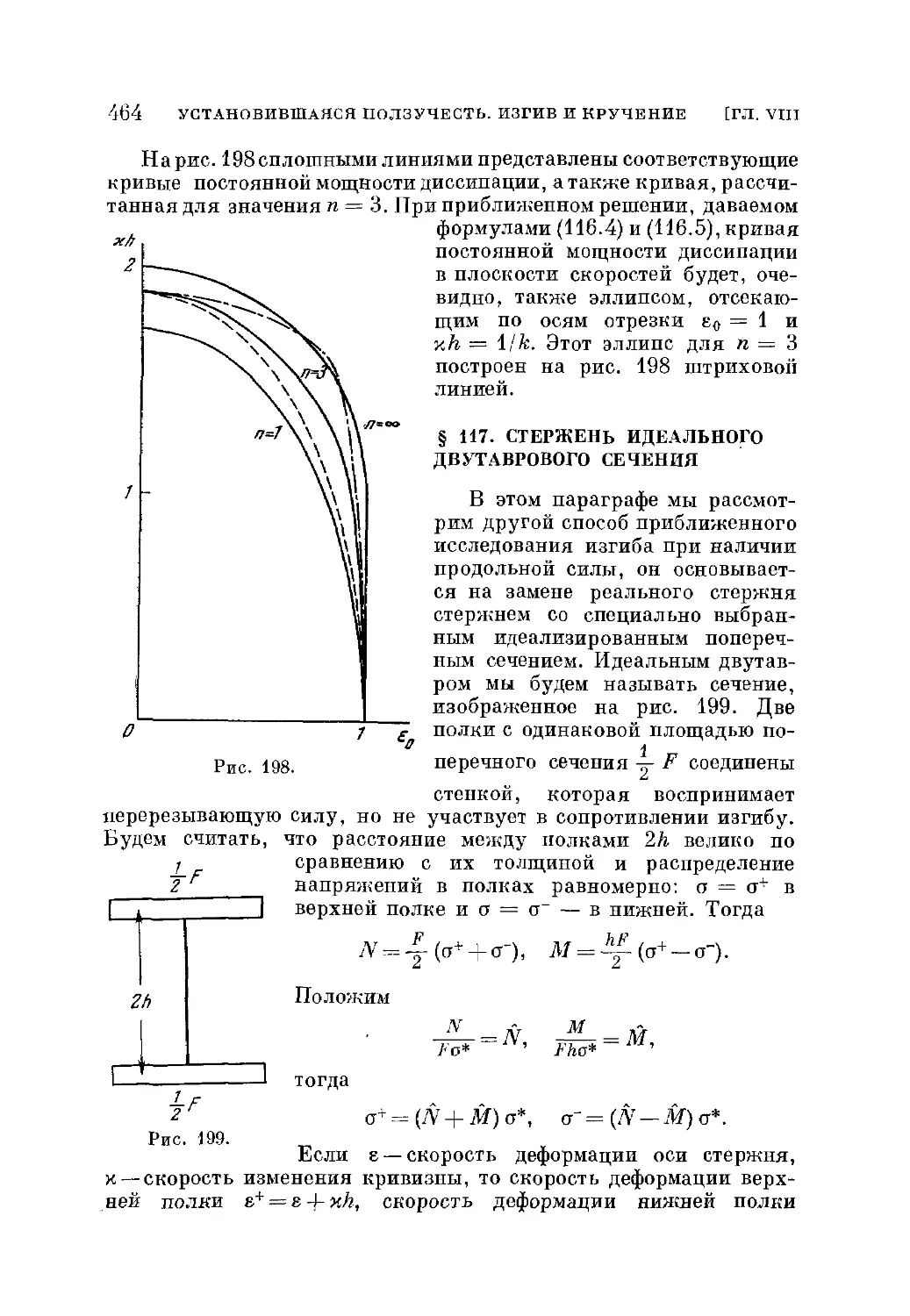
§ 116. Изгиб стержней при наличии продольной силы 461
I 117. Стержень идеального двутаврового сечения 464
| 118. Простейшие задачи продольно-поперечного изгиба .... 466
Глава IX
Плоские осесимметричные задачи теории установившейся ползучести 471
§ 119. Основные уравнения плоской задачи 471
§ 120. Толстостенные трубы 475
§ 121. Чистый изгиб части кругового цилиндра 479
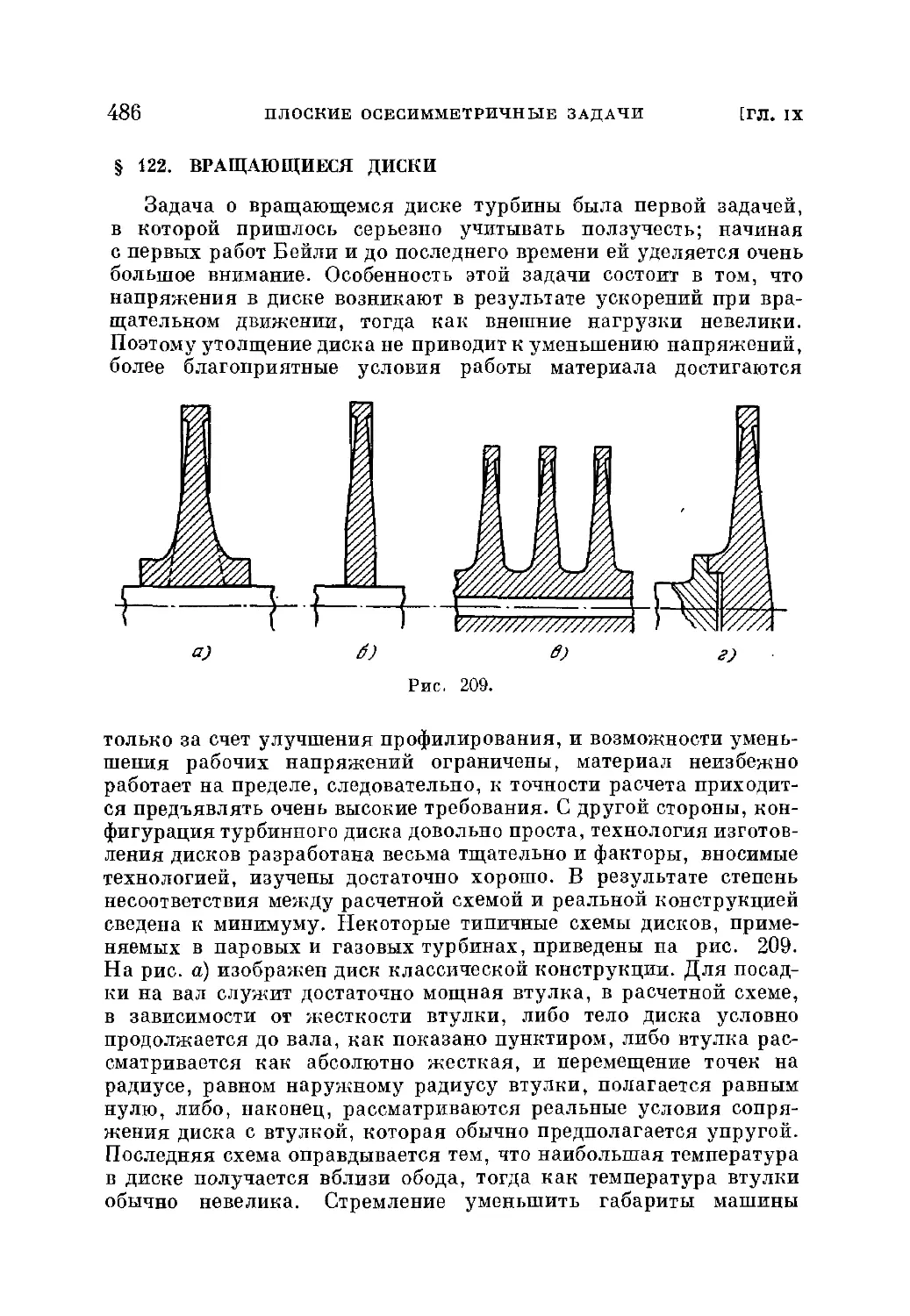
§ 122. Вращающиеся диски 486
§ 123. Ползучесть сплошного диска постоянной толщины 488
§ 124. Ползучесть диска с центральным отверстием 492
§ 125. Прямое численное интегрирование уравнений ползучести
вращающегося диска 494
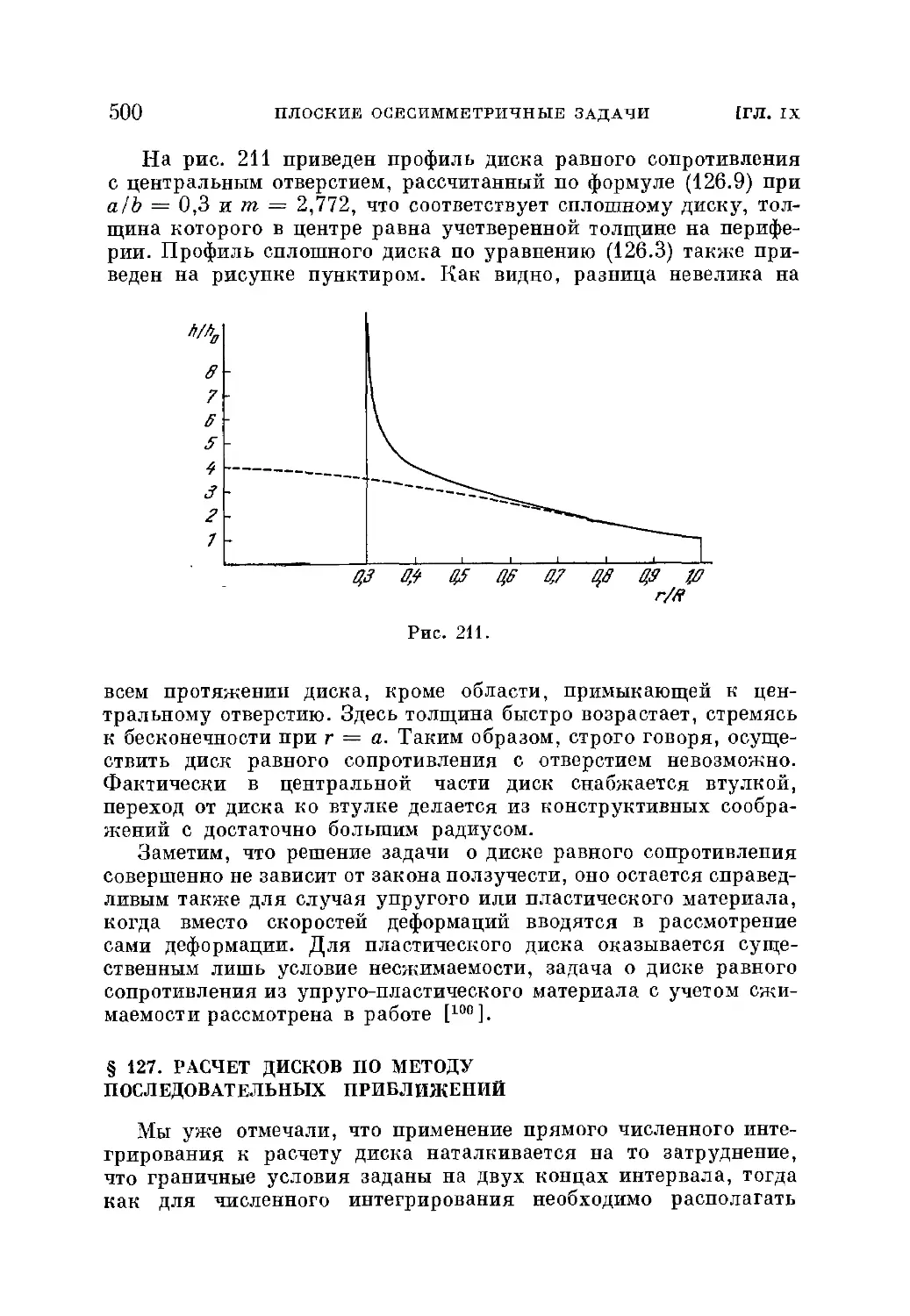
§ 126. Диск равного сопротивления 496
§ 127. Расчет дисков по методу последовательных приближений . . 500
I 128. Другой вариант метода последовательных приближений . . 506
I 129. Концентрация напряжений около отверстия в равномерно
растягиваемой пластинке 509
§ 130. Диск гиперболического профиля, нагруженный радиальными
силами . 515
Глава X
Установившаяся ползучесть пластин и оболочек 517
§ 131. Изгиб пластин. Основные уравнения линейной теории . . . 517
1 132. Потенциал усилий и моментов. Основные уравнения
ползучести пластин 521
§ 133. Частично линеаризированные уравнения ползучести пластин 523
I 134. Ползучесть пластинок при изгибе 526
I 135. Ползучесть круглых пластин по теории типа Мизеса 530
§ 136. Применение вариационных методов к расчету пластин .... 536
§ 137. Расчет пластин на ползучесть при критерии Треска . . 537
§ 138. Более сложные виды нагрузки 542
§ 139. Изгиб пластины распределенной нагрузкой 544
§ 140. Некруглые пластины 547
I 141. Ползучесть оболочек 549
§ 142. Безмоментная теория оболочек 551
§ 143. Безмоментная теория оболочек — определение деформаций
и перемещений 555
§ 144. Безмоментные оболочки вращения 558
I 145. Многослойные оболочки с жестко связанными слоями .... 560
§ 146. Двухслойная модель оболочки 563
§ 147. Уравнения теории оболочек ... • • ... 568
§ 148. Техническая теория оболочек 571
§ 149. Техническая теория ползучести двухслойных оболочек . . 577
ОГЛАВЛЕНИЕ 7
§ 150. Уравнения осесимметричной ползучести круговой
цилиндрической оболочки 581
§ 151. Степенной закон ползучести. Приближенное исследование
краевого эффекта 585
§ 152. Полубесконечная оболочка с шарнирно закрепленным краем 589
§ 153. Пол у бесконечная оболочка с защемленным краем 592
| 154. Распространение технической теории на случай Ги ф 0 ... 595
§ 155. Цилиндрическая оболочка, сжатая осевой силой 597
§ 156. Краевой эффект в цилиндрической оболочке, нагруженной
распределенным давлением и осевой силой 598
§ 157. Приближенные выражения потенциала скоростей для
произвольной оболочки 601
Глава XI
Неустановившаяся ползучесть .... 602
§ 158. Применение гипотезы упрочнения к расчетам на
неустановившуюся ползучесть 602
§ 159. Неустановившаяся ползучесть при изгибе 605
§ 160. Численное решение задачи о неустановившейся ползучести
стержня 608
§ 161. Неустановившаяся ползучесть дисков 613
§ 162. Неустановившаяся ползучесть дисков. Случаи 2, 3, 4 ... . 618
§ 163. Ползучесть вращающегося цилиндра и трубы 621
§ 164. Вариационный принцип Качанова в теории неустановившейся
ползучести 626
§ 165. Вариационный принцип Уанга и Прагера 629
§ 166. Приближенное решение релаксационных задач. Метод Шесте-
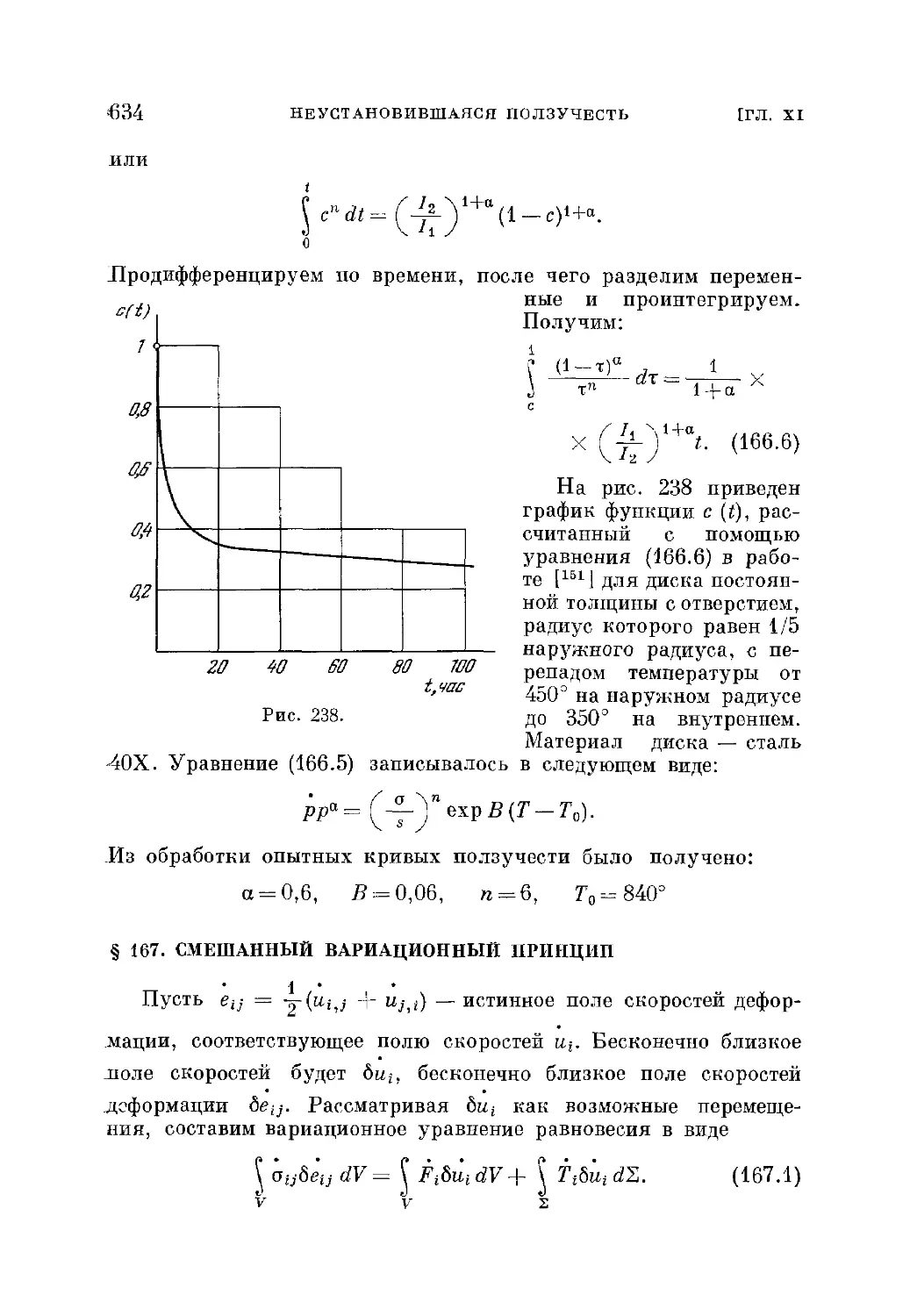
рикова 632
5 167. Смешанный вариационный принцип 634
| 168. Применение смешанного вариационного принципа к задаче
изгиба 637
§ 169. Изгиб стержня при ползучести с упрочнением 640
§ 170. Неустановившаяся ползучесть пластин 643
§ 171. Общий прием исследования неустановившейся ползучести на
основе теории упрочнения 645
§ 172. Применение теории старения к расчетам на
неустановившуюся ползучесть 648
§ 173. Определение времени до разрушения 651
§ 174. Уточненное определение времени хрупкого разрушения
вращающегося диска 654
Глава XII
Геометрически-нелинейные задачи теории ползучести. Критическое
время 660
§ 175. Простейшие геометрически-нелинейные задачи ползучести 660
§ 176. Гибкая нить 662
§ 177. Изгиб балки с шарнирно закрепленными концами 665
§ 178. Критическое время сжатого стержня 670
1 179. Учет мгновенной пластической деформации при определении
критического времени 677
§ 180. Критическое время сжатого стержня. Некоторые дальнейшие
результаты 681
§ 181. Смешанный вариационный принцип в применении к задачам
выпучивания . . 687
8 ОГЛАВЛЕНИЕ
§ 182. Выпучивание сжатого стержня. Применение вариационного
метода 689
| 183. Устойчивость арки 693
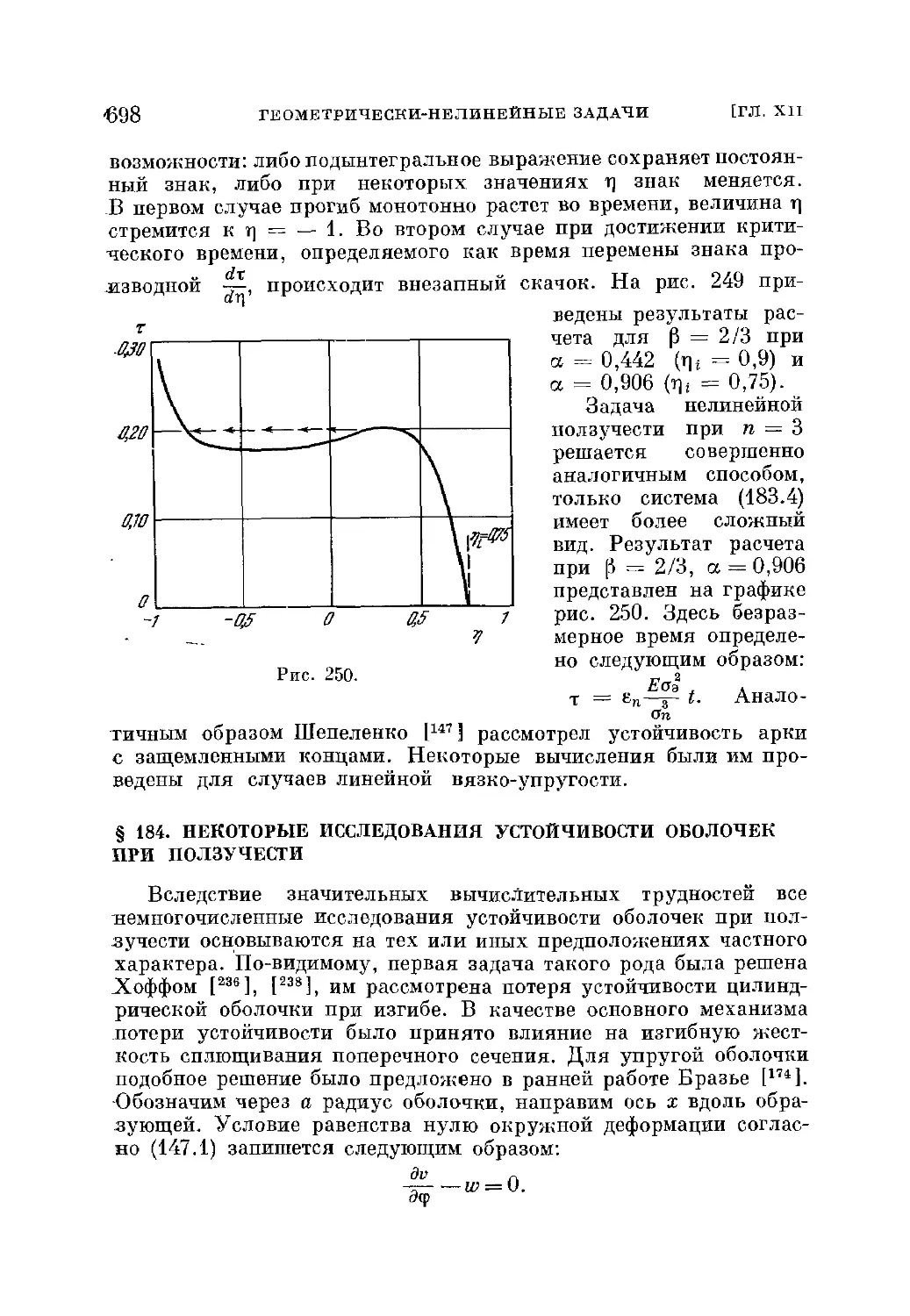
§ 184. Некоторые исследования устойчивости оболочек при ползучести 698
§ 185. Осесимметричное выпучивание коротких цилиндрических
оболочек 701
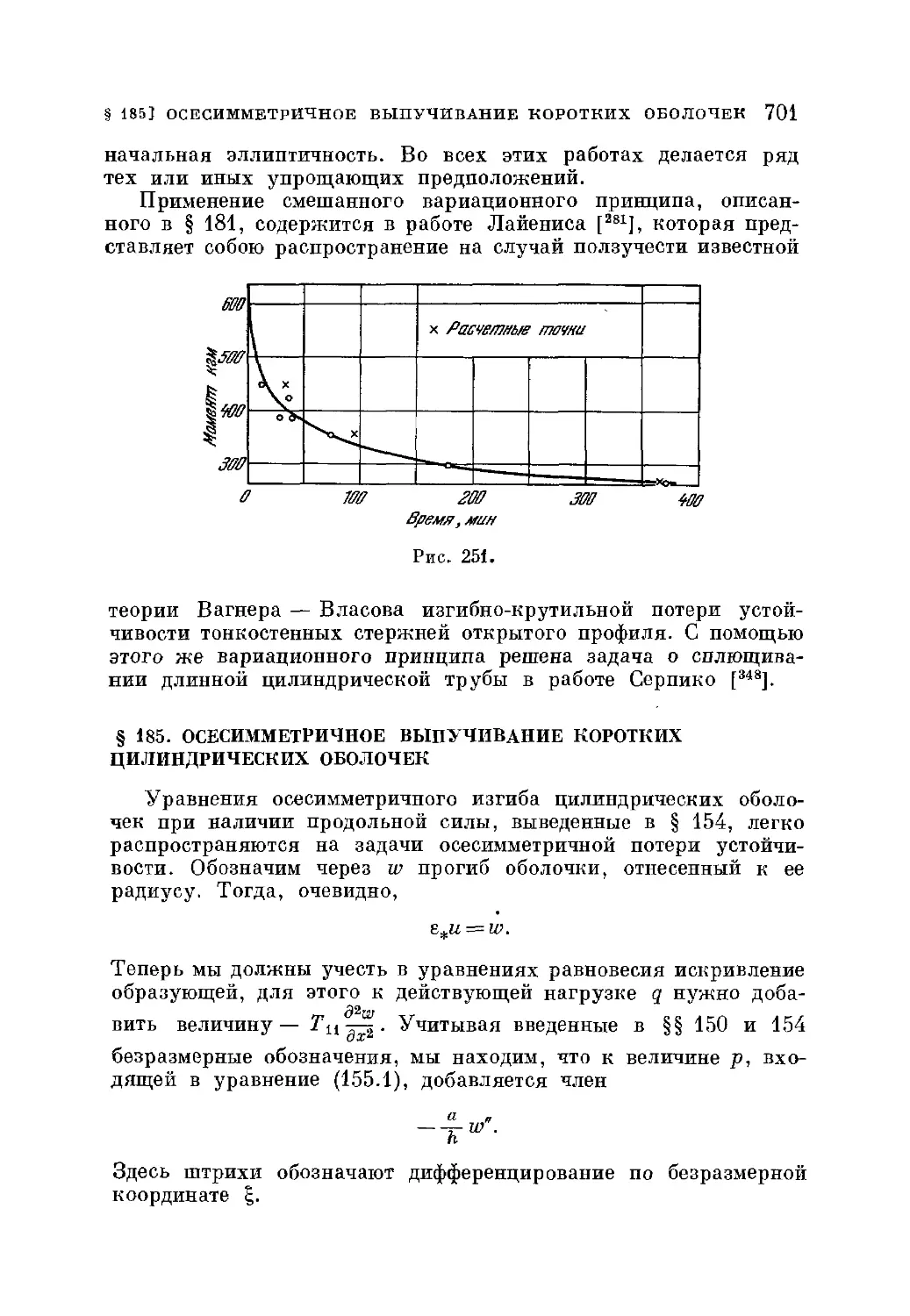
§ 186. Приближенный метод решения задач выпучивания в
нелинейной постановке 704
§ 187. Устойчивость сжатого вязко-упругого стержня 708
§ 188. Устойчивость сжатого стержня, материал которого следует
закону упрочнения 713
§ 189. Условные линеаризированные критерии устойчивости . . . 715
| 190. Применение линеаризированных уравнений к задаче
выпучивания 719
§ 191. Линеаризированные уравнения ползучести с упрочнением 722
§ 192. Выпучивание пластин по линеаризированной теории .... 724
Библиография 727
Указатель имен 743
Предметный указатель 745
ПРЕДИСЛОВИЕ
Теория ползучести — это одна из глав механики
деформируемого твердого тела, сложившаяся в самое последнее время и
занявшая свое место наряду с такими разделами механики, как теория
упругости и теория пластичности. Термином «ползучесть»
(вероятно, не очень удачным, но получившим всеобщее распространение)
мы будем называть всю совокупность явлений, которые можно
объяснить, допустив, что зависимость между напряжениями
и деформациями содержит время, явно или через посредство
некоторых операторов. Свойство ползучести обнаруживают
материалы различной природы: металлы, пластмассы, горные породы^
бетон, естественные и искусственные камни, лед и т. д. Очевидно,
что физические механизмы ползучести у перечисленных
материалов совершенно различны. Более глубокое изучение показывает,
что и внешние формы протекания ползучести сходны лишь на
первый взгляд, различные материалы требуют различных средств
феноменологического описания.
Механика имеет дело именно с феноменологическим описанием
процесса ползучести, те или иные исходные зависимости
формулируются на основе данных макроэксперимента. Физические
представления на современном уровне развития науки приносят
механике скорее косвенную, чем прямую пользу; поэтому
естественно выделение механики ползучести, которая оперирует
с помощью обычных представлений механики сплошной среды,
вводя формальным образом некоторый набор определяющих
параметров. Эти параметры описывают то, что можно назвать
структурным состоянием материала, хотя далеко не всегда мы
можем связать тот или иной параметр с реальными особенностями
структуры, которые фиксируются с помощью физических методов.
Теория ползучести, имея дело со значительно более сложным
комплексом явлений, чем теория упругости и даже теория
пластичности, далеко не достигла такой степени логической
завершенности, как, например, теория упругости и теория идеальной
пластичности. Положение теории ползучести можно сравнить с поло-
10
ПРЕДИСЛОВИЕ
жением теории пластичности упрочняющегося тела; и в той,
и в другой области стремление описать весь комплекс свойств
реального тела, охватив его некоторой единой системой
уравнений, не приводит к достаточно определенным результатам.
Как в пластичности, так и в ползучести оказывается возможным
построить различные упрощенные уравнения, пригодные для
описания ограниченного круга явлений. Имея дело с весьма
разнообразными материалами, свойства которых к тому же
зачастую нестабильны, и будучи вынуждена решать прикладные
задачи, теория'долзучести удовлетворялась построением
приближенных схем, охватывающих явление в общих чертах.
В настоящее время не существует единой теории ползучести,
пригодной для всех материалов, и автор полагает, что такой
теории вообще быть не может. Настоящая книга посвящена
в первую очередь ползучести металлов при высоких
температурах. Соответствующая теория была вызвана к жизни прежде
всего нуждами турбостроения, впоследствии она нашла
применение в атомной энергетике, химическом машиностроении,
авиации, реактивной технике. Выбирая название книги, автор хотел
подчеркнуть, что здесь не будут излагаться физические теории
ползучести. Анализ экспериментальных данных, которому
уделяется относительно большое внимание, имеет целью выявление
возможности применения данного материала для той или иной
конструкции, работающей в определенных условиях. Тот же
опытный материал может быть использован для получения
выводов о причинах, обусловливающих его большую или меньшую
сопротивляемость ползучести, и, в конечном счете,— для
установления путей создания новых материалов, лучших, чем
имеющиеся. Этот аспект здесь совершенно не затрагивается. В то же
время автор не имел возможности изложить достаточно подробно
практические методы расчета на ползучесть и длительную
прочность деталей машин в реальных условиях их эксплуатации, такое
изложение было бы уместным в книге совершенно иного характера.
Две главы имеют косвенное отношение к основному
содержанию книги; одна из этих глав содержит краткий очерк теории
пластичности, вторая — основы теории наследственной упругости
или вязко-упругости. Обе эти теории связаны с теорией
ползучести металлов общностью некоторых идей и аппарата.
Автор считает своим долгом отметить, что многие из
развиваемых здесь точек зрения обсуждались им со своими учениками
и коллегами. Автор особенно благодарен за просмотр разделов
рукописи и ценные замечания Г. В. Иванову, Н. И. Малинину,
С. Т. Милейко, В. С. Наместникову, Ю. В. Немировскому
и С. А. Шестерикову.
ВВЕДЕНИЕ
Для современного развития механики деформируемых твердых
тел характерно стремление к расширению ее физической базы,
к усовершенствованию лежащих в основе теории
феноменологических схем. Задачей механики по-прежнему является
изучение движения реальных тел методами механики
сплошной среды, и эта задача решается путем создания моделей,
воспроизводящих основные, наиболее важные свойства реальных
объектов.
За последние десятилетия получила большое развитие теория
пластичности, изучающая необратимые деформации твердых тел.
Для большей части обычно применяемых в технике металлов при
температурах, допускающих существование живых организмов
и более низких, эти необратимые деформации в первом
приближении зависят только от величины действующих сил и от порядка
их приложения, но не от продолжительности действия их и не
от той скорости, с которой производится нагрузка. Это
утверждение не является точным, уже при нормальных температурах
обнаруживаются некоторые временные эффекты, но они
незначительны, и теория пластичности этими эффектами пренебрегает.
Правда, для теории пластичности небезразлична
последовательность тех или иных производимых на тело воздействий, поэтому
понятия «до» и «после» оказываются необходимыми, в теории,
таким образом, фигурирует время, но это время лишено метрики,
вместо времени можно говорить о любой монотонной функции
времени.
Границы применимости теории пластичности в настоящее время
очерчены достаточно ясно, и нам нет необходимости
рассматривать их сейчас более подробно. В дальнейшем мы вернемся к
вопросу о пластичности, потому что те теории, которые составляют
основной предмет нашего изложения, развивались в тесной связи
с теорией пластичности и многие основные понятия и исходные
точки зрения оказываются общими. Дело в том, что у многих
12
ВВЕДЕНИЕ
материалов в эксплуатационных условиях закон связи между
силами и перемещениями оказывается существенно зависящим
от времени. Эта зависимость проявляется в том, что, например,
при постоянной нагрузке деформации не остаются постоянными,
а растут со временем и достигают недопустимо большой
величины, если нагрузка действует достаточно долго. С другой
стороны, если изделию сообщена принудительная деформация и
наложены связи, удерживающие деформацию неизменной, реакции
связей убывают со временем, таким образом, например,
соединение деталей путем посадки становится неплотным. Все явления
подобного рода мы будем объединять общим термином
«ползучесть», хотя в литературе это слово часто понимается в более
узком смысле.
Пожалуй, наибольший интерес для приложений представляет
ползучесть металлов при повышенных температурах. Такой
материал, как углеродистая сталь, поведение которой при обычных
температурах хорошо описывается теорией упругости, если
напряжения не слишком велики, и теорией пластичности при более
высоких напряжениях, при температуре примерно 450° и выше
ведет себя совершенно иначе. Уже при небольших напряжениях
сталь перестает подчиняться закону Гука, кривая растяжения
ее существенно зависит от той скорости, с которой производится
растяжение, поэтому говорить о кривой
напряжение—деформация, которая в теории пластичности принимается за исходную,
здесь просто не приходится. Под действием постоянной нагрузки
образец продолжает деформироваться, как говорят, «ползет».
Ползучесть наблюдается при любых напряжениях, скорость
ползучести очень сильно зависит от величины напряжения, но
указать какой-то предел ползучести, то есть напряжение, ниже
которого явление ползучести не обнаруживается, невозможно.
Для изделий, работающих в условиях высоких температур,
применяют специальные стали и сплавы, обладающие более высоким
сопротивлением ползучести; однако для любого сплава существует
температура, начиная с которой ползучесть становится
существенной и неизбежно приводит к разрушению изделия после более
или менее длительного срока, в зависимости от уровня
напряжений. Применение сталей аустенитного класса, с высоким
содержанием легирующих элементов — хрома, никеля и других,—
позволяет обеспечить надежную работу конструкций при температурах
порядка 600°. При более высоких температурах применяются
сплавы на основе никеля или кобальта. Дальнейшее повышение
жаропрочности технических сплавов возможно за счет
использования металлов с высокой температурой плавления, как
молибден, вольфрам, ниобий и другие.
Практические задачи расчета на прочность элементов паро
вых, а впоследствии газовых турбин заставили искать пути теоре-
ВВЕДЕНИЕ
13
тического описания процесса ползучести с целью определения
деформаций после определенного времени и установления условий
разрушения. В отличие от обычных расчетов на прочность,
расчеты на ползучесть ставят задачей не обеспечение абсолютной
прочности изделия, а лишь гарантию того, что конструктивная функция
изделия не будет нарушена ранее определенного срока. Таким
образом, всякое изделие, работающее в условиях ползучести,
рассчитано на определенную долговечность, или, как говорят,
ресурс.
На первом этапе, когда техника столкнулась с необходимостью
учета ползучести, этот учет производился следующим образом.
Путем испытаний образцов определялся условный предел
ползучести для данной температуры, то есть такое максимальное
напряжение, при котором деформация ползучести за время, равное
ресурсу изделия, не превзойдет некоторой наперед заданной
условной величины, например 1%. Может случиться, что действующее
напряжение по истечении некоторого времени вызовет
разрушение образца при деформации меньшей, чем заданный допуск.
Тогда необходимо определить предел длительной прочности,
то есть такое максимальное напряжение, которое не вызовет
разрушения образца в течение заданного времени. Далее определяется
допускаемое напряжение, равное одному из названных пределов,
поделенному на запас прочности, и расчет изделия производится
обычным методом по найденному допускаемому напряжению.
Такой способ расчета является грубо приближенным и приводит
к необоснованному завышению запаса прочности. В
действительности к конструкции, работающей в условиях высоких
температур, должны быть предъявлены следующие требования:
1) некоторая суммарная деформация не должна превышать
определенной величины, назначаемой в соответствии с конструктивной
функцией изделия; 2) за время службы не должно произойти
разрушения. Таким образом, задачей теории является разработка
методов определения деформаций в телах, подверженных ползучести,
и методов определения времени до разрушения.
Другая важная область применения теории ползучести —
это высокомолекулярные соединения. Широкое распространение
пластмасс в современной промышленности вызвало к жизни
повышение интереса к их механическим свойствам, а эти свойства
в сильной степени зависят от времени. Пока пластические массы
применялись для деталей, не несущих значительные нагрузки
и не являющихся особо ответственными за прочность конструкции
ft целом, изучение ползучести подобных материалов ставилось
в общем плане исследования их физико-механических свойств
а не имело в виду получение характеристик, необходимых для
предсказания долговечности в эксплуатационных условиях. В то
'Не время ползучесть многих материалов органического происхож-
14
ВВЕДЕНИЕ
дения проявляется заметно при нормальных температурах и сразу
бросаетея в глаза исследователю, занимающемуся их
механическими свойствами; поэтому уже давно этому вопросу посвящается
большое количество исследований, выводы которых носят скорее
качественный характер и оказываются недостаточными для
построения механической теории. Положение с материалами
органического происхождения и полимерными материалами затрудняется
еще тем, что характеристики их малостабильны, они в сильной
степени зависят от способа приготовления материала, от времени
выдержки между получением его и испытанием, от влажности
и от других причин.
Явление ползучести наблюдается в некоторых строительных
материалах, например в бетоне. Ползучесть бетона в сильной
степени зависит от его возраста, со временем происходит так
называемое старение бетона, оно сопровождается усадкой, то есть
изменением объема. Тем не менее в настоящее время существует
теория ползучести бетона, учитывающая названные эффекты.
Аналогичные явления наблюдаются в грунтах, в сооружениях
из льда и в других случаях, которые мы здесь рассматривать
не будем.
Теория ползучести развивалась различными и параллельными
путями, и до сих пор ее трудно рассматривать как единое целое.
В 20-х годах текущего столетия появился термин реология, от
греческого слова рею — теку. Так была названа наука,
призванная описывать всевозможные течения, наблюдаемые в твердых
телах. Основой для нее послужили многочисленные работы физико-
химиков, изучающих течения весьма вязких жидкостей и
дисперсных систем. Как оказалось, закон вязкого течения Ньютона для
таких тел неприменим, силы вязкости зависят от приложенного
напряжения нелинейным образом, и тела, рассматриваемые как
жидкости, обнаруживают некоторые свойства твердых тел,
например упругость и предельное сопротивление сдвигу. Основная
идея при попытках описания подобных сред состояла в том, чтобы
объединить свойства упругости и вязкости и описать их одними
и теми же уравнениями, которые в частных случаях превращаются
в уравнения теории упругости или гидродинамики вязкой
жидкости. Простейшие модели подобного рода предлагались уже
довольно давно Максвеллом, Кельвином, Фохтом и другими
авторами. Впоследствии оказалось, что эти простейшие, модели
не описывают реальных свойств каких-либо материалов, а лишь
качественно иллюстрируют основные наблюдаемые факты. Были
созданы более сложные модели из упругих и вязких элементов,
скомбинированных различным образом. При помощи таких
моделей оказалось возможным удовлетворительно описать поведение
материалов, для которых зависимость между напряжением и
деформацией линейна. В настоящее время можно утверждать, что
ВВЕДКНИЕ
15
для определенного круга материалов при не слишком больших
напряжениях линейная теория дает удовлетворительное первое
приближение; поэтому формальный аппарат линейной теории,
который разработан довольно хорошо и подробно, находит
реальное приложение. Однако область применения линейной теории все
же остается довольно узкой. Для большей части пластмасс с
нелинейными эффектами необходимо считаться, а часто они
оказываются определяющими. Разработка нелинейных теорий началась
в самое последнее время.
Поведение металлов при высоких температурах отличается
довольно существенно от поведения пластиков, и обычные
реологические схемы для металлов заведомо не годятся. В линейных
теориях значительное место занимает так называемая
запаздывающая упругость. Та часть деформации, которая не является
деформацией вязкого течения, оказывается обратимой, то есть
исчезающей при снятии нагрузки по истечении некоторого, достаточно
большого времени. У металлов обратимая часть деформации
относительно мала, и во многих случаях ее можно не учитывать.
Зависимость между деформацией и напряжением у металлов при
ползучести оказывается резко нелинейной. Так, например, если
аппроксимировать зависимость скорости от напряжения степенной
функцией, то показатель степени будет иметь величину от 3 до
12. Очевидно, что никакие линейные аппроксимации здесь
непригодны. Поэтому теория ползучести металлов развивалась
совершенно независимо от реологии, с другой стороны, реологи
оставляли эту область без серьезного внимания. На развитие теории
ползучести металлов скорее повлияла теория пластичности, тем
более, что основополагающие результаты в области теории
ползучести принадлежат ученым, которые работали также и над теорией
пластичности.
ГЛАВА I
ОСНОВНЫЕ ПОНЯТИЯ
МЕХАНИКИ ТВЕРДОГО ТЕЛА
Для описания движения среды в состоянии ползучести
пользуются обычным аппаратом механики сплошной среды, то есть
вводят в рассмотрение тензоры напряжений, деформаций и скоростей
деформации. В общем случае перемещения точек тела могут быть
значительными по сравнению с его первоначальными размерами,
тогда деформации его должны описываться с помощью тензора
конечных деформаций, граничные условия тоже должны быть
заданы на деформированной поверхности тела. Теория конечных
деформаций упругого тела разработана относительно слабо, лишь
недавно были получены основные уравнения этой теории, решение
конкретных задач встречает очень большие трудности. Тем
большие трудности возникают при попытках построения теории
ползучести при конечных деформациях. Поэтому здесь мы будем
рассматривать два типа задач:
а) Деформации тела считаются достаточно малыми, и
квадратами их можно пренебречь. Перемещения малы, и граничные
условия задаются на поверхности недеформированного тела.
б) Деформации тела могут быть сколь угодно велики, но
механическое поведение тела описывается локальными
характеристиками, например соотношениями между напряжениями и
скоростями деформации. Формальный аппарат в том и другом случае
оказывается аналогичным.
В этой главе сообщаются некоторые основные сведения о
тензорах в трехмерном евклидовом пространстве и о тех тензорах,
которые встречаются в механике твердого тела — тензорах
напряжений, деформаций и скоростей деформации. Изложение не
претендует на полноту и строгость, глава представляет собою сводку
определений, терминов и формул, на которые будут делаться
ссылки при дальнейшем изложении. Некоторые дополнительные
сведения из общей теории будут сообщаться в последующих
главах там, где в них возникнет необходимость.
§ 1] ТЕНЗОРЫ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 17
Яэ
е3\
§ 1. ТЕНЗОРЫ В ТРЕХМЕРНОМ
ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Выберем произвольную систему прямоугольных декартовых
координат в трехмерном пространстве, будем обозначать эти
координаты для единообразия Х\, x2, х3- Для определенности будем считать,
что система координат правая, то есть оси расположены так, как
показано на рис. 1. Если смотреть со стороны положительной
оси х3, то переход оси xi в ось х2
кратчайшим путем производится в
результате поворота против часовой стрелки,
то есть в положительном направлении.
Единичные векторы координатных осей
обозначим е1? е2 и е3 соответственно.
Произвольный вектор а, заданный
составляющими aif a2, а3, может быть
представлен следующим образом:
з
<*= 2 aiei-
i=l
Для краткости записи условимся опу- рИс. 1.
екать знак суммы, подразумевая, что
по повторяющемуся индексу производится суммирование от
i — 1 до i = 3. Краткая запись предыдущей формулы будет такой:
а=щег. A.1)
Предположим теперь, что мы хотим от старой системы координат
перейти к новой с осями х[, х2, х'а и соответствующими единичными
векторами е[, е'2, е'3. Составляющие вектора а относительно новых
осей будут а[, а2, а3. В новых осях вектор а может быть
представлен выражением, аналогичным A.1), поэтому можно написать:
а — atei = a'he'k.
Умножим обе части этого равенства на е\. Так как e'ke'i = 0
при 1фк и е\е\ — 1, мы получим:
а\ = ак{е1еъ).
Введем обозначение:
е1ек — PiA-
Искомые формулы преобразования компонент вектора при
повороте осей координат будут иметь следующий вид:
a'i = pihak. A.2)
Точно таким же способом можно выразить компоненты вектора
в старых осях через компоненты в новых осях. В результате
- Ю. Н. Рабоищв
18 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. 1
получим:
ах = ^ма'к. A.3)
Совершенно аналогичным образом единичные векторы
координатных осей новой и старой систем выражаются одни через
другие. Так, вектор е\ всегда может быть представлен
линейной комбинацией векторов е4, е% и е3, следовательно,
Чтобы определить коэффициенты ais, умножим написанное выше
равенство на е^, получим:
aik — e\eh.
Следовательно, aik — §lh и единичные векторы преобразуются
по тем же формулам A.2) и A.3), в которых нужно заменить at
на ег и al на е\.
Для удобства ссылок выпишем формулы преобразования
единичных векторов координатных осей отдельно:
el = piueft, A.4)
ег = Риеь. A.5)
Формулы A.2), A.3) можно принять за определение вектора.
Отвлекаясь от геометрической интерпретации вектора как
направленного отрезка, мы будем понимать под вектором совокупность
трех величин аи а2, а3, связанных с данной системой координат
и преобразующихся при переходе к другой системе по формулам
A.2).
Такое формальное определение, не связанное интуитивными
представлениями, удобно в том отношении, что оно позволяет
естественным образом ввести более общее понятие тензора, которое
нельзя пояснить при помощи простого геометрического образа.
Тензором второго ранга мы будем называть совокупность
величин Ajj, обладающих тем свойством, что если а — произвольный
вектор, то величины Atjaj, или А^а^ в свою очередь являются
составляющими вектора.
Из этого определения легко получить формулы преобразования
составляющих тензора при повороте осей координат. Пусть
составляющие тензора относительно новых осей будут А'ц. По
определению А'цщ суть составляющие относительно новых осей вектора,
составляющие которого для старых осей были A^aj.
Следовательно, эти величины связаны формулами преобразования
компонент вектора A.2):
A'ija'j = p\ft-4ftS<V
Но в свою очередь
§ 1] ТЕНЗОРЫ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 19
Таким образом, мы получили:
Это равенство справедливо для произвольных а$, поэтому из
него следует:
A'ij = №jSAhs. A.6)
Легко показать, что обратное преобразование производится
по формулам
Aij = phiPsjA'hs. A.7)
Можно было сразу определить тензор второго ранга как
совокупность девяти величин Ац, связанных с данной системой
координат и меняющихся при преобразовании координат по формулам
A.6), A.7).
В приложениях часто встречаются симметричные тензоры,
то есть такие, для которых Ац = Ajt.
Установим теперь несколько следствий из определения
тензора второго ранга.
1) Если даны два произвольных вектора а и 6, то выражение
Aijuibj
есть инвариант, то есть величина, не меняющаяся при замене
координат. Действительно, это не что иное, как скалярное
произведение вектора с составляющими Axibj на вектор а или вектора
с составляющими А^а}- на вектор Ь. Обратно, если дана
совокупность величин Aij таких, что Aijuibj есть инвариант, каковы бы
ни были векторы а и Ь, то величины Ац образуют тензор второго
ранга.
2) Если даны два произвольных вектора а и 6, то величины
С; j =
сообразуют тензор второго ранга.
Действительно, возьмем третий произвольный вектор г.
Выражение Cijfj равноaibjTj = a,i (br). Это есть составляющая вектора,
отличающегося от а скалярным множителем (br); таким образом,
по определению, величины C(j являются компонентами тензора.
Образованный таким образом тензор называется
мультипликативным, операция образования мультипликативного тензора
из двух векторов называется их неопределенным или диадным
умножением.
3) Совокупность символов Кронекера образует тензор.
Действительно,
Этот тензор называют единичным. Заметим, что
Oij = &iBj = e}Cj.
2*
20 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
Составляющие единичного тензора не меняются при замене
координат.
4) Если даны два тензора Ai3- и Ви, то величины типа AisBSj
являются компонентами тензора второго ранга. Действительно,
рассмотрим выражение
где cij — составляющие произвольного вектора. Произведение
Bsja.j, в соответствии с определением тензора Btj, есть
составляющая вектора, обозначим ее bs, следовательно,
Но это есть компонента вектора в соответствии с определением
тензора А и, тем самым доказывается тензорный характер
величин A iSBsj. По этому пути можно пойти и дальше, добавив,
например, третий тензор Сц, можно образовать выражения вида
которые в свою очередь являются компонентами тензора второго
ранга, и так далее.
Если А и — тензор второго ранга, то Ajt — также тензор
второго ранга. Очевидно, что сумма или разность компонент
двух тензоров представляет собою тензор. Поэтому величины
1 1
у (Atj + Aji) и -у {А и — Aji) являются составляющими
тензоров. Первый из них симметричен, составляющие его не меняются
от перемены порядка индексов. Второй — антисимметричен, его
составляющие при перестановке индексов меняют знак. Таким
образом, тензор второго ранга всегда можно представить как сумму
симметричного и антисимметричного тензоров:
Aij = ~2 \Aij + Aji) -f- -? \Ац Aji).
Подобно тому как мы определили тензор второго ранга, можно
ввести понятие тензора произвольного ранга п. Так называется
совокупность величин
связанных с данной системой координат и обладающих тем
свойством, что величины
где alk — составляющие произвольного вектора, образуют тензор
ранга п — 1. Точно таким же способом от тензора ранга п — 1
переходим к тензору ранга п — 2 и в конце концов получаем тен-
§ 1] ТЕНЗОРЫ В ТРЕХМЕРНОМ ЕВКЛИДОВОМ ПРОСТРАНТСТВЕ 21
зор первого ранга, то есть вектор. Формулы преобразования
тензора ранга п при замене координат выводятся способом,
совершенно аналогичным тому, который был применен для тензора второго
ранга. Эти формулы имеют следующий вид:
^Н»2- ¦ Лп = PimPiaia ¦ • • Pinin^jih- ¦ -in- \i-°/
Для обратного преобразования нужно, как и в случае тензора
второго ранга, изменить порядок индексов при р\ 3- .
Из определения тензора ранга п следует, что если заданы
произвольные векторы a(i), а<2\ .. ., а(п\ то выражение
М^.. Ana<nafi ¦¦¦ aW есть инвариант. Наоборот, из
инвариантности этого выражения следует, что величины Aili2,_in образуют
тензор.
Если даны два тензора, тензор Aili2,..in ранга п и тензор
Bhh- ш ранга т, то совокупность величин
А- ¦ Я ¦
л'1«2- • •'tnLJ3V2- ¦ -}т
образует тензор ранга п + т, называющийся произведением
тензоров Ailia.,,in и Bhh...jm.
Действительно, возьмем произвольный вектор а^ и образуем
выражения
¦"ilia ¦ . . in-" hh ¦ ¦ . jmais \s^-n)i
зависящие уже от п~\-т — 1 индексов. Чтобы доказать тензорный
характер этих выражений, возьмем новый произвольный вектор
и образуем выражения
Ai1i2...inBhh...jmaua\ (кфз, &<ге, s<«)
либо
Эти величины будут зависеть уже от п-\~т — 2 индексов.
Повторяя эту операцию п-\-т раз, мы получим в конце концов
следующие выражения:
1А- ¦ ¦ п^ п(^>\(П- ¦ ¦ />A) Mmh
Каждая из заключенных в скобки величин представляет собою
скалярный инвариант, что и доказывает высказанное
утверждение.
Операция умножения тензоров приводит к образованию
тензоров более высокого ранга, получение из данного тензора или
совокупности их тензоров низшего ранга будет рассмотрено в
следующем параграфе.
22 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
§ 2. СВЕРТЫВАНИЕ ТЕНЗОРОВ. ИНВАРИАНТЫ
Докажем, что сумма составляющих тензора второго ранга
с одинаковыми индексами
Ац = Aijbij
есть инвариант. Действительно, по формулам преобразования A.6)
A'ii = Pik$uAu.
Но по формулам A.5)
Умножим одно выражение на другое, получим:
ед^г = piftPij = бдг.
Таким образом,
А'ц — &ыАы = Ац.
Операция получения скалярного инварианта тензора подобным
способом называется свертыванием.
Если задан произвольный тензор ранга п, то из него можно
получить тензор ранга п — 2, приняв любые два индекса равными
между собой и просуммировав по этому индексу от единицы до трех.
Действительно, преобразуем тензор к новым осям по формулам
A.8), положим in = in-i и выполним суммирование по этому
индексу. Получим:
¦"*l«i. . .in-2'nin ==PimP»2J2- ' ¦Pinjn-iPinhiAjife. . .in-tin =
= Piij'i- ¦ 'Piji ¦2Jn-i"-3V2 Jn-2}nin>
так как
Pinin-iPinin — °in-lin-
Отсюда следует, что величины
А
образуют тензор ранга п — 2.
Если и — четное число, последовательное свертывание
тензора приведет в конце концов к тому, что мы получим тензор
второго ранга и, при следующем свертывании, инвариант.
Производя эти операции по разным парам индексов, мы, вообще говоря,
будем получать разные инварианты, которые называются
линейными инвариантами. Умножив тензор сам на себя и произведя
свертывание полученного мультипликативного тензора ранга 2п,
мы получим в конце концов систему квадратичных инвариантов
и так далее. Число инвариантов тензора, построенных подобным
образом, может быть сколь угодно велико, но число независимых
S 2]
СВЕРТЫВАНИЕ ТЕНЗОРОВ. ИНВАРИАНТЫ
23
инвариантов конечно. Так, например, если смотреть на вектор at
как на тензор первого ранга, квадратичный инвариант вектора
является линейным инвариантом мультипликативного тензора
aid], это есть квадрат длины вектора atai. Образуя
мультипликативные тензоры сколь угодно высокого четного ранга ataj . . . as
и свертывая по произвольным парам индексов, мы будем при
каждом свертывании получать скалярный множитель atai\ таким
образом, квадрат длины вектора является единственным
независимым инвариантом, все другие инварианты представляют собою
некоторые его степени.
Мы не будем здесь заниматься вопросом о построении полной
системы независимых инвариантов произвольного тензора,
остановимся только на наиболее важном для приложений случае
симметричного тензора второго ранга, для которого существует
три независимых инварианта. Чтобы выяснить это, рассмотрим
задачу о приведении симметричного тензора к главным осям. Будем
искать такое направление, заданное единичным вектором v,
для которого
AijVj = Avi.
Здесь А — скаляр. Запишем эту систему уравнений для
определения неизвестных V/ и А следующим образом;
D„-M)vj = 0. B.1)
Приравняв нулю определитель этой линейной относительно
неизвестных v,- системы уравнений, мы получим кубическое уравнение
для нахождения А. Обозначим три корня этого уравнения АA\
А{2), A{Z). Полагая в B.1) А = А(к\ мы сможем найти
направляющие косинусы Vj '. Величины AW называются главными
значениями тензора, направления v(ft> — главными направлениями.
Предположим сначала, что А^ вещественны и различны.
Первое предположение будет доказано, второе несущественно.
Из B.1) следует:
Умножим обе части на v|J) (/ Ф к) и просуммируем по индексу i.
Получим:
viV^^vJV'. B.2)
^' другой стороны, если отправляться от равенства
24 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
обе части которого умножаются на v\h\ мы получим:
viV^JL^yM4. B.3)
Но AijV^vi^ =AijVj Vi вследствие того, что тензор Ац
симметричен. Поэтому равенства B.2) и B.3) возможны
одновременно только в том случае, когда Ац\) М ) = 0, так как по
предположению A(h) фА{1>. Отсюда следует:
v{kM'> = 0. B.4)
Таким образом, если главные значения различны, главные
направления тензора взаимно ортогональны.
Покажем теперь, что главные значения тензора всегда
действительны. Предположим противное, пусть, например, А<3>
действительно, A(V и Aw — комплексные величины. Будучи корнями
уравнения с действительными коэффициентами, Aw и A{i)
являются комплексно сопряженными. Подставляя АA) и Ai2) в B.1),
мы получим для VjD и vf} также комплексно сопряженные
значения:
Vi2) = ^i— ]/"— 1 m;.
Подставляя в условие ортогональности B.4), получим:
v?442) = S(rc! + m!) = 0.
Но это равенство невозможно, следовательно, главные значения
не могут быть комплексными.
Случай равных корней, как мы уже указывали, не представляет
затруднений. Пусть, например, Аш = A(i). Это значит, Что при
А = АаУ система B.1) содержит лишь одно независимое
уравнение, решение остается неопределенным, и после того, как
использовано условие нормирования V;Vj = 1, мы получаем совокупность
векторов vll>, зависящую от одного параметра. Эти векторы
ортогональны вектору v<3), следовательно, лежат в плоскости,
перпендикулярной к vl3). Любые два взаимно ортогональных вектора
vA> и vB), лежащие в этой плоскости, могут быть приняты за
векторы соответствующих главных направлений. Если, наконец,
Аа) = А<2) = А13\ любые ортогональные оси можно принять
за главные. Это возможно лишь в том случае, если Ац = A8;j.
Такой тензор называется шаровым.
Главные значения тензора являются инвариантами, никаких
других независимых инвариантов симметричный тензор второго
ранга иметь не может, но выбор основной системы независимых
инвариантов может производиться различными способами. Если
отнести тензор к осям, ориентированным по главным направлениям,
§ 3] ВЗАИМНЫЙ БАЗИС. ДОСТАВЛЯЮЩИЕ ТЕНЗОРА 25
то матрица его будет следующей:
Аа> О О
О Ат О .
О О А13)
Первый инвариант тензора Ан будет равен сумме главных
значений Аа) + Ат + Ai3}, второй инвариант АцА^ — сумме
квадратов главных значений и третий инвариант AijAjsAsi —
сумме кубов. Условимся обозначать инварианты теми же
буквами, что и составляющие тензора, с римскими цифрами в индексе,
означающими порядок инварианта. Тогда
А1 = Аи = Аш + Ат + Ат,
Ли = АиАа = (А«У + {А™)* + (А™)',
Аш = АцАиА„ = (А™)* + (А™)* + (А™)*.
Симметричные инварианты различных степеней можно ввести
и другими способами. Так, если к инварианту Ац прибавить
квадрат первого инварианта с любым постоянным множителем, мы
получим другой квадратичный инвариант. К кубическому
инварианту можно добавить любую линейную комбинацию жзА'иА^ц.
Другой естественный путь построения основной системы
инвариантов состоит в следующем. Развертываем определитель B.1),
получаем кубическое уравнение для А. Коэффициент при А в
третьей степени получается равным — 1, коэффициенты при следующих
степенях являются известными симметричными функциями
корней уравнения, то есть инвариантами соответственно первой,
второй и третьей степени.
Запишем это уравнение следующим образом:
A'-W + IuA-Im^O,
по известным формулам теории симметрических функций имеем:
Ii = AIt
hi = -j(Al-An), B.5)
Iin=^(A3l-3AIAu + 2AI11).
§ 3. ВЗАИМНЫЙ БАЗИС. КОВАРИАНТНЫЕ
И КОНТРАВАРИАНТНЫЕ СОСТАВЛЯЮЩИЕ ТЕНЗОРА
Преимущества тензорной символики в механике сплошных
сред в особенности обнаруживаются тогда, когда мы переходим
°т декартовых координат к произвольным, вообще говоря, неорто-
гональным координатам. Зададим направление координатных
26 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
осей тремя некомпланарными векторами еи е2, е3, которые,
вообще говоря, не обязательно являются единичными векторами.
Наряду с основным базисом et введем взаимный базис ег, то есть
тройку векторов, связанных с векторами основного базиса
следующими соотношениями:
в1в} = 8{ C.1)
(мы будем обозначать символы Кронекера 8{). Для этого
достаточно принять:
ei-fsip, в' = ^р, ез = ^р, g = el{e2xe3).
Произвольный вектор а может быть представлен теперь двояким
образом: либо
а = а1еи C.2)
либо
а--=ще\ C.3)
Величины щ называются ковариантными составляющими
вектора, величины а1 — контравариантными составляющими.
Происхождение этих терминов будет ясно из следующего. Произведем
преобразование основного базиса по формулам
е% = alej. C.4)
Здесь а| — произвольная матрица с определителем, отличным
от нуля. Обратное преобразование будет
et = fte'j. C.5)
Матрица |3| является обратной по отношению к а{, элементы
ее являются алгебраическими дополнениями соответствующих
элементов матрицы прямого преобразования, поделенными на
определитель этой матрицы. Выясним теперь, как преобразуются
при этом векторы взаимного базиса. Положим:
e*' = yshek.
Умножим обе части этого равенства на ег. В силу условия C.1)
в правой части останется только одно слагаемое, и мы получим:
-уч = е8 в,.
Воспользуемся теперь формулой преобразования C.5):
у? == pc'e-'ej=pies=p?.
Таким образом, векторы взаимного базиса преобразуются по
формулам
е*' = рУ, C.6)
S 3] ВЗАИМНЫЙ БАЗИС. СОСТАВЛЯЮЩИЕ ТЕНЗОРА 27
и, как легко проверить,
е{ = а)е>'. C.6')
Итак, при преобразовании основного базиса векторы взаимного
базиса получаются по формулам обратного преобразования.
Выясним теперь, как будут преобразовываться ковариантные
и контравариантные составляющие вектора. Из определения
вектора следует:
а = akeh= a1'el.
С помощью соотношений C.5) перепишем это тождество
следующим образом:
ах''е\ = ak$ie's.
Умножим обе части на е1', в результате получим:
ai' = pikah. C.7)
Таким образом, контравариантные составляющие вектора
преобразуются по формулам обратного преобразования базисных
векторов, отсюда и происходит их название. Аналогичным образом
доказывается, что ковариантные составляющие преобразуются
по формулам прямого преобразования базиса, а именно:
а\ = щак. C.8)
Индексы у ковариантных величин принято помещать внизу,
у контравариантных — вверху. Записывая вектор при помощи
тех или иных составляющих, мы каждый раз производили
суммирование по повторяющимся индексам, один из которых является
верхним, другой — нижним. Условимся и в дальнейшем
держаться этого правила, когда мы встретимся с более сложными
выражениями, содержащими по нескольку верхних и нижних индексов.
Удобство, которое получается при одновременном пользовании
основным и взаимным базисами, можно пояснить на следующем
примере. Пусть нам даны два вектора ажЪ:
а —ще1 = alet,
b=biei=biei.
Скалярное произведение их можно построить различным образом.
Если задавать оба вектора ковариантными составляющими, то мы
получим:
ab = aibj€%e}.
Произведения еге' не равны нулю и единице соответственно, как
в случае ортогональных декартовых координат. Аналогичный
результат получится, если оба вектора заданы контравариантны-
ми составляющими. Но если один вектор задан ковариантными
28 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
составляющими, а другой — контравариантными, скалярное
произведение, в силу соотношений C.1), будет иметь наиболее
простой вид:
аЪ — аф1 — albi.
Принимая формулы преобразования C.7) и C.8) за определение
вектора, мы можем ввести понятие о тензоре произвольного ранга.
Так называется совокупность величин А^;;? '",
преобразующихся при изменении базиса по формулам
л;з;;Гь---=а^... p7(t... Ац:!?--\ C.9)
Введенный таким образом тензор Ац.'.а '" является смешанным,
он ковариантный по отношению к индексам i, j, . . . и контра-
вариантный по отношению к индексам а, Ь, . . . Существуют
тензоры чисто ковариантные или контравариантные.
Определяя вектор как некоторый геометрический образ, мы
приходим к понятию о ковариантных и контравариантных
составляющих вектора, то есть о различных формах представления одной
и той же величины. Приведенное определение тензора в силу своего
формального характера еще не содержит принципа, который бы
устанавливал эквивалентность различных форм представления
одного и того же тензора, то есть позволял бы переходить от
ковариантных индексов к контравариантным и наоборот. Чтобы
получить эту возможность, мы пойдем тем же путем, что в § 1.
Определим контравариантный тензор второго ранга А1* как
совокупность величин, обладающих тем свойством, что если а3 —
ковариантные составляющие произвольного вектора», то величины
bl = Aijaj C.10)
представляет собою контравариантные составляющие вектора 6.
Это определение эквивалентно данному выше. Действительно,
при переходе к другому базису
A 'ija • = MAMa]as = Ь\АмаД>\ = Aksasf>\ = b% = bv.
Аналогично определяются ковариантный тензор второго ранга
Ъг = А^ C.11)
и смешанный тензор
bi=Al}aj,bi = Aijai. C.12)
Мы будем говорить, что Ах\ Ац, Аг.) представляют собою
контравариантные, ковариантные и смешанные компоненты одного и того
же тензора, если величины Ьг и Ьг в формулах C.10), C.11), C.12)
§ 3] ВЗАИМНЫЙ БАЗИС. СОСТАВЛЯЮЩИЕ ТЕНЗОРА 29
представляют собою ковариантные и контравариантные
компоненты одного и того же вектора Ъ, каков бы ни был вектор а
с компонентами at или а1. Отсюда мы можем получить формулы
перехода от ковариантных к контравариантным составляющим
тензора и обратно. Воспользуемся, например, формулой C.10)
и первой из формул C.12) и представим вектор Ь следующим
образом:
Ь = А^а}-ег = As!ujes.
Умножим обе части этого равенства на ед. Получим:
Alla,j (е;ей) = A^a,j8sh = A^at.
Введем обозначения
etek = gtk= ght
и приравняем множители при одинаковых aj. Таким образом, мы
получим следующую формулу перехода от контравариантных
составляющих к смешанным составляющим:
Ai! = Akiglh. C.13)
Совершенно так же можно перейти от смешанных составляющих
к ковариантным
Aij = Aikgjh
и от контравариантных к ковариантным
Аи = Aksgihgjs.
Величины gtj определяют так называемый метрический тензор.
Тензорный характер этих величин легко выяснить из их
определения, если воспользоваться формулами преобразования базиса
C.4). С помощью метрического тензора производится операция
«опускания индекса», то есть замены контравариантного индекса
ковариантным. Формула C.13) в этом смысле является общей,
правило опускания индексов состоит в том, что мы умножаем
основной тензор на метрический и свертываем по паре индексов,
в результате ранг тензора сохраняется, но один из индексов
переходит вниз. Для обратного перехода от ковариантных величин
к контравариантным нам понадобятся контравариантные
составляющие метрического тензора glK Разрешая уравнение C.13)
относительно Ak', мы можем написать:
А1'=Ак'л**. C.14)
Здесь glh представляют собою элементы матрицы, обратной
по отношению к g^. Очевидно, что
gi4 = eV.
30 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ 1
Операция поднятия индекса производится по тому же правилу,
что операция опускания индекса, только при помощи контрава-
риантных компонент метрического тензора. Заметим, что
совершенно аналогично преобразуются компоненты вектора, а именно:
a-i = gikdk, a* = gihah.
Связь между основным и взаимным базисом устанавливается
следующим образом:
ej = gih.eh, e{ = giheh.
Наконец, заметим, что операцию опускания или поднятия индекса
можно применить к самому метрическому тензору, а именно:
gi = gtkgih = е^ = б1
Итак, смешанные составляющие метрического тензора образуют
единичный тензор.
Инварианты тензора строятся путем свертывания с
метрическим тензором и могут быть представлены в различных
эквивалентных формах. Так, например, для симметричного тензора второго
ранга
AI = Aijgii = Aiigij = Aig\,
Ли = AihAJsgi}g^ = aUWk =- AihAUgisgv = AuAtJ = MA).
§ 4. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ
Наиболее естественный выбор системы отнесения в трехмерном
пространстве состоит в следующем. Предположим, что радиус-
вектор точки v задан как функция трех параметров х1, ж2, Xs —
криволинейных координат точки. Производные радиуса-вектора
/* по координатам определяют в каждой точке три направления,
которые можно всегда принять за направления осей локального
базиса. Примем за базисные векторы производные от вектора г
ло переменным х1, х2 и х3 соответственно. Будем обозначать эти
производные индексом, соответствующим той координате, по
которой производится дифференцирование, поставленным после
запятой:
Преобразование базиса в данном случае означает переход от
одной системы криволинейных координат хг к другой системе х1',
при этом якобиан преобразования предполагается отличным от
нуля. Радиус-вектор точки, выраженный как функция от новых
координат х1', мы будем обозначать г'. Базисные векторы для
S 4]
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ
31
новой системы координат выражаются следующим образом:
' _ dvL __ ¦
дхг
Считая, что новые координаты являются известными функциями
старых, применим правило дифференцирования сложной функции:
ei = г л = г
3 dxv дх1' ]'
Таким образом, фигурирующие в формуле C.4) коэффициенты
прямого преобразования а\ представляют собою производные от
старых координат по соответствующим новым:
дх>
а3. = —ту .
1 дх1
Коэффициенты обратного преобразования будут соответственно
Rj- дхГ
Возможность обратного преобразования следует из того, что
якобиан отличен от нуля.
Операция дифференцирования по координате, как мы
убедились, приводит к образованию ковариантных величин; с индексом,
поставленным после запятой и обозначающим дифференцирование
по координате, можно поступать, как с обычными ковариантными
индексами.
Запишем теперь выражение для дифференциала радиуса-
вектора dr:
dr — dxlr,i=dxiei. D.2)
Индексы при координатах, а следовательно, и при
дифференциалах координат мы поставили вверху. Формула D.2) показывает,
что dx1 действительно являются контравариантными
составляющими вектора dr. В этом легко убедиться и непосредственной
проверкой. В самом деле,
dxv = -K-j- dx3 = р5 dx3.
Возводя D.2) в квадрат, мы получим в левой части квадрат
линейного элемента, то есть инвариантную величину, определяющую
локальную метрику, а именно:
ds^ — gtj dx1 dx3.
Таким образом, оправдывается название совокупности величин gtj
метрическим тензором:
32 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
Теперь мы можем построить ковариантные составляющие
вектора dr, а именно:
dxi — gij dx1.
Эти величины не являются полными дифференциалами;
следовательно, не существует функций xt, которые можно принять за
координаты точки пространства и приращения которых являются кова-
риантными составляющими dr; переход от контравариантных
величин к ковариантным имеет смысл только для бесконечно малой
окрестности точки.
Рассмотрим теперь произвольный вектор а, являющийся
функцией координат точек пространства, то есть векторное поле. Будем
задавать вектор в каждой точке его контравариантными
составляющими по отношению к локальному базису:
a = alei.
Вычислим дифференциал вектора а, то есть приращение его при
переходе в бесконечно близкую точку г + dr. При
дифференцировании мы должны принять во внимание, что не только величины
аг являются функциями координат, но и базисные векторы также
меняются от точки к точке и должны считаться переменными.
Таким образом,
\ dxi dxi J
Но —^- есть вектор, представляющий собою вторую произ-
dxi
водную вектора г по xh и х1:
деь
Любой вектор в пространстве может быть в свою очередь
представлен как линейная комбинация базисных векторов,
поэтому можно принять
deh _ yip.
Теперь выражение для дифференциала вектора а можно записать
следующим образом:
da=(l± + Tijhak')eidxi.
\ dxi J
Выражения, записанные в скобках, называются ковариантными
производными составляющих вектора а и обозначаются нижним
индексом после запятой:
дх>
§ 4]
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ
33
Выражение для дифференциала da записывается теперь
следующим образом:
da = а]}вг dxj. D.4)
Точно такой вид имел бы дифференциал вектора а, если бы базис
был постоянный, вместо ковариантных производных при этом
в формуле D.4) фигурировали бы обыкновенные производные.
Дифференциал dr может быть произволен, формула D.4)
показывает, что совокупность ковариантных производных от контрава-
риантных составляющих вектора образует смешанный тензор
второго ранга. Если базисные векторы постоянны, то есть
рассмотрение ведется в декартовой системе координат, ковариантные
производные совпадают с обыкновенными.
Осталось определить величины Tjk, называемые символами
Кристоффеля. Необходимо заметить, что, хотя эти величины
характеризуются тремя индексами, они не образуют тензора третьего
ранга, то есть не преобразуются при замене координат по
формулам преобразования составляющих тензора. По определению этих
величин
Умножим обе части этого равенства на es. Получим:
Будем считать формально, что операция опускания индекса при
помощи метрического тензора распространяется и на символы
Кристоффеля. Поэтому сумму в левой части можно обозначить Tkjs.
Правая часть выражается через производные от составляющих
метрического тензора. Для этого выпишем следующие тождества:
dxi dxi
lhjs-lh}gis-Y{~7-+ dxk -J^rJ ¦ D.5)
Теперь легко проверить, что
1 fdghs , Ь%Ы дШ
Эх'
Вспоминая, что g11 представляют собой элементы матрицы,
обратной по отношению к gtj, получим отсюда, в соответствии
с правилом поднятия индексов,
Iy=lW\ D.6)
3 ЮН Работнов
34 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
По определению символы Кристоффеля Vjk представляют собою
контравариантные составляющие вектора . Переходя к кова-
риантным составляющим, можем записать:
Аналогичным образом можно получить формулы для
производных векторов взаимного базиса.
Напишем тождество:
Величины gs равны либо нулю, либо единице, поэтому при
дифференцировании по х1 получим:
дх> дх'
Воспользуемся выражением —- через векторы взаимного базиса.
Получим:
W4^ = o.
0X3
Величина es —- представляет собою ковариантную
составляла^'
дек
ющую вектора —г, следовательно,
дх>
dxi
Теперь мы можем определить операцию ковариантного
дифференцирования ковариантных составляющих вектора.
Действительно, если дано а — а^е1, то
da — ( —^- el + щ —— ) dx •
\ дх> dx' J
или
da= aiijeidx}. D.7)
Здесь
dai _r*aft. D<8)
dxi
Рассмотрим теперь ковариантный тензор второго ранга Atj,
являющийся функцией точки, и произвольный переменный
вектор а. По определению, выражения вида A^ai являются
§ 4]
ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ
35
ковариантнымп составляющими нового вектора Ь:
Ь1 = Аиа?.
Вычислим ковариантные производные от величин bt по
формулам D.8):
bt,a = ^(Аиа>) - Г?а {Аца?) = ^ а' -|- Al} -g, - YUhiaK
Заменим обыкновенную производную -^-g- ковариантной
производной по формуле D.3), а именно:
dai _ J vj „'<
Группируя члены и меняя местами немые индексы к и /,
получим:
Цй - TUkj - T*jAtk) «'' + Аиа^.
Выражение, заключенное в скобках, называется ковариантной
производной составляющей тензора второго ранга Ац и
обозначается
Ац, . = д-?$- rUkj-TUik- D.9)
Для ковариантного дифференцирования составляющих вектора
при этом оказывается справедливым обычное правило
дифференцирования произведения:
bi^^Au^a' + Aija^. D.10)
Если тензор задан смешанными или контравариантными
составляющими, то соответствующие члены, зависящие от символов Кристоф-
феля, появляются с обратным знаком, а именно:
ЗА1-
л\ — L 4- Г1 4^ — Г* А\
D.11)
^j, = -^- + rUhi + rUlh.
Совершенно аналогичным образом определяются ковариантные
производные тензоров сколь угодно высокого ранга.
Заметим, что ковариантные производные от компонент
метрического тензора равны нулю. Действительно, по формуле D.9)
_ dg'J" rh __vk _ dSij v p
gij,s— qxs l isghj L sjgih— qxs * isj L sji-
3*
36 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
Но из формул D.5) непосредственно видно, что правая часть
тождественно равна нулю. Таким образом,
Аналогично
g%-0.
Таким образом, метрический тензор оказывается в известном
смысле постоянным. Пользуясь этим свойством, легко показать,
что поднятие и опускание индексов в выражениях ковариантных
производных вектора или тензора произвольного ранга
осуществляется по общему правилу. Так, например,
ai,j = <*k,jghi, at,j = a^.ghi.
§ 5. ТЕОРИЯ ДЕФОРМАЦИЙ В СПЛОШНОЙ СРЕДЕ
В качестве приложения изложенной выше общей теории
тензоров рассмотрим вопрос о напряженном состоянии в сплошной
среде. Так называется гипотетическая среда, являющаяся
предметом изучения механики и заменяющая в механических моделях
реальные тела — твердые, жидкие и газообразные. Необходимость
введения сплошной среды вместо реального тела связана с тем,
что этим самым открывается возможность рассмотрения
бесконечно малых элементов объема и, следовательно, применения в
механике исчисления бесконечно малых. Имеются многочисленные
попытки более строгого обоснования механики сплошной среды
на основе дискретных представлений, однако вводимые
микрообъекты — материальные точки с некоторыми системами связей —
сами по себе являются абстракциями, лишь весьма условно
воспроизводящими действительное строение материала.
Пусть будут хг — координаты точек тела в его начальном
состоянии, пока к нему не прикладывались никакие внешние силы.
Уточнение определения начального состояния нужно только для
формулировки физических законов, описывающих поведение тела
под нагрузкой, для построения общей теории напряжений и
деформаций любое состояние можно принять за начальное. Радиус-
вектор точки М в начальном состоянии пусть будет г(хг).
Представим себе, что при деформации координатные линии системы хг
остаются материально связанными с телом, так что в одном из
последующих состояний, которое мы будем называть
деформированным, материальная точка М перемещается в точку М'
пространства, радиус-вектор ее становится г', но криволинейные
координаты хг остаются теми же самыми. Разность г' — г = и
называется перемещением точки. Квадрат линейного элемента
в не деформированном состоянии определяется следующим образом:
ds2 = dr2 = gtj dxl dx1'.
§ 5] ТЕОРИЯ ДЕФОРМАЦИЙ В СПЛОШНОЙ СРЕДЕ 37
Квадрат линейного элемента после деформации:
ds'2 —- dr'2 = glj dxl dz}.
Обозначим через е относительное удлинение линейного
элемента вследствие деформации:
ds' — ds
ds
Зная величины gtj и g\j, мы можем вычислить относительное
удлинение любого бесконечно малого отрезка, выходящего из точки М;
поэтому величины g\j можно принять за характеристику
локальной деформации. Тензором деформации ец называют полуразность
между метрическим тензором в деформированном и в начальном
состоянии:
ey = -2-(Sij —gtf)- E-!)
Относительное удлинение элемента ds находится с помощью
тензора деформации из следующего равенства:
ei idx*- dx>
A + ^-1 = 2^-. E.2)
Для конечных деформаций приведенное определение тензора
деформаций не является единственным, различными авторами
развивались различные точки зрения. Общая теория конечных
деформаций для. дальнейшего нам не потребуется, поэтому мы сейчас же
перейдем к тому случаю, когда деформации малы. Физическое
ограничение малости деформаций означает, что относительное
удлинение любого линейного элемента мало по сравнению с
единицей, поэтому в левой части формулы E.2) можно пренебречь
величиной е2 и мы получим:
ejj dxl dx>
ds* "
Предположим теперь, что нам известен вектор перемещения и,
заданный составляющими относительно локального базиса:
и = игег = uie%.
Тогда dr' = dr-\-du. Здесь
dr = €t dxl,
du = Uj^el dx'.
Вычислим теперь квадрат линейного элемента в деформиро-
ванном состоянии:
ds = dr'2 = {dr + duJ = dr2 + 2dr du + du2.
38 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
Внесем сюда значения dr и du, получим:
ds = ds2 + 2^;, j dx1 dx' -\- uft) jKSj jgks dxl dx',
или
2etj dx1 dxj = Bu;, j + "a, !^Sj jgks) dx1 dxK E.3)
Тензор etj — симметричный, тогда как выражения в скобках
в правой части представляют собой составляющие
несимметричного тензора за счет первого члена, поскольку MitJ- ф Uj.j. Однако
квадратичная форма в правой стороне равенства не изменяется,
если заменить тензор его симметричной частью. Приравнивая
коэффициенты двух тождественно равных квадратных форм, мы
можем получить следующие выражения для компонент тензора
конечной деформации:
etj = у {Щ, j + uJt t -f uAj гщ, jg"s). E.4)
Антисимметричная часть тензора, фигурирующего на правой
стороне равенства E.3), называется тензором вращения:
«u = y(wi,j — uhi). E.5)
Особый интерес для приложений представляет случай малых
перемещений. Мы будем называть перемещения малыми, когда
величины utj малы и произведениями их можно пренебречь. В этом
случае выражения для компонент тензора деформаций
упрощаются, мы получим:
Формулы E.5) для тензора вращения одинаковы как при малых,
так и при конечных деформациях.
§ 6. ТЕОРИЯ НАПРЯЖЕНИЙ
Вектором напряжения на площадке, проходящей через
заданную точку и заданной единичным вектором нормали v к этой
площадке, мы называем предел отношения действующей на площадку
силы к площади ее при стягивании площадки в точку. Выбирая
некоторую систему координат, мы тем самым задаем в каждой
точке три плоскости, каждая из которых определяется базисными
векторами et. Нормали к этим площадкам являются векторами
взаимного базиса. Будем нумеровать площадки теми же
индексами, что и нормали к ним. Так, площадку, проходящую через
базисные векторы е2 и е3, будем отмечать индексом 1, поскольку
нормалью к этой площадке является вектор е' взаимного базиса.
Обозначим через S* вектор напряжения на площадке с номером i.
5) 6] ТЕОРИЯ НАПРЯЖЕНИЙ 39
Ыроведем теперь плоскость с нормалью v и рассмотрим тетраэдр,
изображенный на рис. 2. Обозначим площади граней, заключенных
между базисными векторами,
соответственно d(ut, площадь же четвертой грани
обозначим dco, вектор напряжения на этой
грани пусть будет S. Сумма сил,
действующих на тетраэдр, должна быть равна нулю,
поэтому
Sda — ЯГ* c?a>i = 0. F.1)
Векторизированная площадка dca
представляет собою v d(», аналогичным образом,
векторизированная площадка da>t
представляет собою произведение da>i на
единичный вектор, имеющий направление е\ то есть на вектор
—— . Но ele'l = g%l, следовательно, модуль ех равен ]/~gu и
ег |
\
dint — el d(i>i.
У gii
В этой формуле по индексу i суммирование не производится
Сумма векторов площадок, изображающих замкнутый
многогранник, нам известно, равна нулю. Поэтому
(.права здесь стоит сумма по индексу I. Из вышенаписанного
1 Sco; ,.
соотношения следует, что величины ——= -~— представляют собою
У gii tf@
ковариантные составляющие единичного вектора нормали v,
поэтому можно написать;
d(ot = Y~gH Vi da.
Внесем это в условие равновесия F.1) и сократим dot. Получим:
Каждый из векторов S1 может быть задан тремя составляющими
по отношению к ковариантному базису, поэтому мы примем:
\rgTiSi = aueJ.
Предыдущая формула перепишется следующим образом:
8 = au4tej. F.2)
Формула F.2) определяет вектор напряжения на любой площадке,
заданной нормалью v; из структуры этой формулы следует, что
40 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
величины а^ образуют контравариантный тензор, называемый
тензором напряжений. Предположим теперь, что на тело
действуют некоторые поверхностные силы Т и объемные силы F.
Выделим некоторый произвольный объем V, ограниченный
поверхностью 2, и рассмотрим его равновесие. Формула F.2) дает
величину силы на единицу площади поверхности 2, поэтому условие
равенства нулю главного вектора будет следующим:
J FdV + [ a^ejVidJl^O.
Положим временно ollej = t% и преобразуем второй интеграл
по формуле Грина:
\ *Ч<*2= \ fcvtfdV.
Но
di v *' --= t\i = (al'ej\ i = a%j.
Таким образом, условие равенства нулю главного вектора сведется
к следующему:
\ {a%ej + F)dV = 0.
v
Поскольку это условие выполняется для любого объема V,
подынтегральное выражение должно быть равно нулю, и мы
получаем:
о% + Р1=0. F.3)
Найдем теперь главный момент системы сил, действующих
на объем V, и приравняем его нулю:
\ F xrdV + I oi}ejViXrd2 = 0.
V 2
Записывая второй интеграл с помощью векторов tl и применяя
формулу Грина, придем к следующему условию равновесия
моментов:
^ {(F + div tl) xr + t1 xr,i} dV = 0.
v
Но первая скобка под интегралом обращается в нуль вследствие
F.3), остается условие
tixei = ai:iej хег = 0.
Из этого следует а1* = ап, тензор напряжений оказывается
симметричным .
§ 7] ДЕКАРТОВЫ КООРДИНАТЫ. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ 41
§ 7. ДЕКАРТОВЫ КООРДИНАТЫ.
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ
Изложение теории деформаций и напряжений в сплошной
среде в наиболее общей тензорной форме для произвольной системы
криволинейных неортогональных координат оказывается
полезным в теории конечных деформаций, а также в некоторых
специальных разделах механики твердого тела, как, например, теории
оболочек. Выведенные общие формулы позволят нам в дальнейшем
составлять уравнения равновесия в криволинейных координатах
и вычислять компоненты деформации. Однако последовательное
проведение анализа в самом общем виде не всегда целесообразно,
при изложении физических теорий нет смысла вводить лишние
математические осложнения, поэтому мы будем пользоваться
главным образом декартовыми прямоугольными координатами.
В этих координатах основной базис и взаимный базис совпадают,
разница между ковариантными и контравариантными
составляющими векторов и тензоров исчезает. Для определенности мы будем
поэтому в дальнейшем применять одни только нижние индексы
и производить суммирование по нижним индексам тогда, когда
это понадобится.
Индекс после запятой будет обозначать уже не ковариантное,
а совпадающее с ним обыкновенное дифференцирование. Многие
формулы, выведенные для декартовых координат, сохраняют силу
и в общем случае, но это бывает не всегда, и при распространении
формул наобщий случай приходится соблюдать известную
осторожность. Так, например, уравнение равновесия элемента в
декартовых координатах мы можем записать, следуя F.3) и замечанию
об индексах, в виде
<ту,; + ^ = 0. G.1)
Однако, если вывести уравнение G.1) непосредственно в
декартовых координатах, еще не очевидно, как нужно определить
компоненты тензора, чтобы получить уравнения F.3) для контравариант-
ных компонент.
В дальнейшем условимся обозначать декартовы координаты
точек пространства так же, как и криволинейные координаты,
через xt. Это — декартовы координаты материальных точек среды
в недеформированном состоянии и одновременно координаты
точек пространства по отношению к фиксированной системе
координат. Однако при построении теории деформаций мы условились
считать, что координаты материальной точки остаются
неизменными в процессе деформации; поэтому система координатных
линий, которая представляла собою систему взаимно
ортогональных прямых, искривляется и вытягивается в процессе деформации.
Отсюда следует, что координаты хг являются в то же время
42 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
криволинейными координатами точек тела после деформации.
Такая двойная роль декартовых координат не вызывает затруднений
постольку, поскольку мы считаем деформации малыми.
Действительно, когда мы вводили локальный базис в § 5 и определяли
ковариантные и контравариантные составляющие
соответствующих величин, мы исходили из метрики недеформированного тела,
задаваемой тензором gjj. С таким же основанием можно было
выбрать основной базис, связанный с деформированной системой
координат, то есть с метрическим тензором glj. Для теории
конечных деформаций возможен как тот, так и другой подход, и в
разных вариантах теории пользуются разными путями. При
составлении уравнений равновесия, конечно, следует всегда иметь дело
с метрикой деформированной среды.
Если деформации малы и мы пренебрегаем квадратами
производных от перемещений, разница при пользовании той или иной
метрикой оказывается несущественной, поэтому мы фактически
никогда не имеем дело с той криволинейной системой координат,
в которую переходит первоначальная декартова система в
результате деформации. Все величины относятся к первоначальному
базису, заданному тройкой ортогональных единичных векторов
постоянного направления.
Компоненты тензора деформации, определяющие искажения
метрики после деформации, даются теперь следующими формулами:
а компоненты вращения:
шу=-2-(и»,^-«А*)-
Здесь ut —обычные составляющие вектора смещения по осям
координат, индексы после запятой обозначают обычное
дифференцирование по координате.
Пусть теперь компоненты тензора деформации являются
заданными функциями от координат xt; возникает вопрос о том, можно
ли определить перемещения. Заметим прежде всего, что шесть
компонент деформации выражаются через три перемещения,
поэтому они не могут быть независимыми. Геометрически это
означает, что произвольные искажения метрики могут привести
к тому, что это уже не будет метрика евклидова пространства.
Очевидно, что, ставя задачу о нахождении перемещений по
заданной деформации, мы попутно выясним и те условия, которым
должны удовлетворять величины ец.
Предположим на время, что кроме etj мы знаем также тензор
вращения (ои. Тогда
ui,i = eu + ®ij
§ 7] ДЕКАРТОВЫ КООРДИНАТЫ. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ 43
и нахождение перемещений осуществляется путем простого
интегрирования:
иг = \ (еИ + ®И) dxJ-
Нам необходимо избавиться в этом интеграле от величин со^.
Прежде всего несколько уточним запись приведенной формулы.
Пусть в точке М0 величина перемещения uiu известна, известны
также компоненты вращения со^0. Координаты точки М0 пусть
будут xi(l. Будем искать значения перемещения в точке М\ с
координатами Хц. Тогда
Mi Mi
Щ = Що+\ ец dxj + \ ©;; dxj. G.2)
Мо Мо
Интегрирование ведется по произвольной кривой, соединяющей
точки М0 и Mi, Ж; —текущие координаты точек этой кривой.
Координаты Хц точки М{ нужно при этом считать постоянными,
следовательно,
dxj= —d{xn — Xj).
Внесем это в последний интеграл G.2):
Mi Mj
Щ = щ0 + \ etj dxj —\ a>jjd(xn — Xj).
Мо М0
Применим формулу интегрирования по частям. Получим:
Mi Mi
ui = ui0 + J etj dxj — titij (xn — x}) м^ + J {xji — xj) wiJt k dxk.
Mo Mo
Величины C0jy,ft выражаются через производные от компонент
деформации, а именно, как легко проверить, существует
следующее тождество:
aij, k = eih,j — ekj,i-
Таким образом,
Ui = ui0 + сог;о (xJ± — xj0) + \ [eik + (xH — Xj) {elh, j — eft;,,)] dxk. G.3)
м0
Для того чтобы интеграл в формуле G.3) не зависел от пути
интегрирования, необходимо, чтобы стоящее под интегралом
выражение было полным дифференциалом. Это условие приводит к
следующим тождествам:
eik, js + ekj, is = eis, ,h + esii ik. G.4)
44 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ I
Соотношения G.4) представляют собою условия совместности
деформаций Сен-Венана, из них различными оказываются шесть
уравнений. Если условия совместности выполнены, то формулы
G.3) определяют перемещения с точностью до перемещения
твердого тела. Постоянные ui0 определяют поступательное
перемещение, C0;j0 представляют собою жесткий поворот.
§ 8. НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА
ТЕНЗОРА НАПРЯЖЕНИЙ
Общая теория приведения симметричного тензора второго
ранга к главным осям в применении к тензору напряжений
позволяет найти три такие взаимно ортогональные площадки, на
которых действуют только растягивающие или сжимающие
напряжения оь а2 и сг3. Условимся нумеровать главные напряжения так,
чтобы было
oi>a2>o3,
хотя в некоторых случаях нам придется допускать отступление
от этого правила. Эти величины имеют основное значение при
формулировке различных физических соотношений, поэтому во
многих случаях нам будет удобно относить тензор к главным
осям и иметь дело с тремя его главными значениями. Нумеруя
главные оси так же, как и главные значения, мы обозначим е,.
е2 и е3 единичные векторы главных осей. Если задана некоторая
площадка с нормалью v = v;eb то по формуле F.2) напряжение
на этой площадке
8 = GiV^t + 02v2e2 + о^3е3.
Нормальное напряжение на площадке
ач = 8\ = а1\\ + аг\\^а3\\. (8.1)
Из формулы (8.1) следует, что о± является наибольшим, а а3 —
наименьшим значением нормального напряжения на любой
площадке, проходящей через данную точку.
Абсолютная величина касательного напряжения на площадке
с нормалью v равна
T=\rS* — o%,
или
т» = ol (vl - vj) + а\{ v J - vj) + а\ (vj - v J) -
- 2oi02vlv\ - 2a2a3v;^ - Za^vlvl (8.2)
Поставим теперь задачу об отыскании наибольшего касательного
напряжения. Будем искать максимум величины т2 как функции
§ 8] НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ТЕНЗОРА НАПРЯЖЕНИЙ 45
направляющих косинусов нормали v, связанных условием
нормирования:
¦v2 -L va _I_ ^
v» + vj + v| = l.
Применяя способ неопределенных множителей Лагранжа,
лолучим следующие уравнения:
а\ Bvf — ivl) — AOiOzVi-vl — 4a1a3v1 V3 + 2Xvt = 0
или, учитывая (8.1),
[Oi (ai — 2ctv) -f X] vi = 0,
[аг (o2 — 2av) +X] v2 = 0,
[сз (°з — 2av) + X] v3 = 0.
Случай, когда, например, v1 = v2 = 0, интереса не представляет,
мы получаем главное направление, для которого т2 = 0.
Предположим, что Vj^O и хгф0. Исключая из первых двух
уравнений X, получим:
а\ — 2av (о\ — cr2) =-- 0.
_2
Если Oi ^^г. то
а1 + <*2
1
а следовательно, vJ=-Vj = -y, v3—0. Подставляя в формулу
для т, найдем:
Tl2-±—2
для площадки, наклоненной под углом 45° к координатным
плоскостям 13 и 23. Аналогично
х23— ±
2
Тм=± 2 •
Наибольшее касательное напряжение ттах = - 1~ 3.
Найденные таким способом главные касательные напряжения не меняются,
если к тому напряженному состоянию, которое существовало
в теле, добавить всестороннее растяжение или сжатие. При этом
каждое из главных напряжений изменяется на одну и ту же
величину, но разности их останутся неизменными. Опытные данные
и теоретические соображения указывают на то, что характер
протекания необратимой деформации в металлах не меняется при
наложении на основное напряженное состояние гидростатической
46 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
составляющей; поэтому главные касательные напряжения
представляются важной физической характеристикой напряженного
состояния. Следует заметить, что из них независимыми являются
только два в силу очевидного тождества
т12 = т23 = т31 = 0.
При этом в выражениях для т^ нужно брать везде либо верхние,
либо нижние знаки.
Следуя общему правилу, указанному в § 2, мы можем
определить систему инвариантов тензора напряжений, а именно: Sj =
Идея о выделении из напряженного состояния его
гидростатической части, как несущественной для составления физических
соотношений теории пластичности и ползучести, приводит к
понятию о девиаторе тензора напряжений, который определяется
следующим образом:
aij^Oij — auij-
1 1
Здесь а = -^ Si = ~о <Тц. При наложении гидростатического
напряженного состояния девиатор тензора напряжений не меняется.
Действительно, положим
o'ij = Oij + Sup.
Тогда
1 ,
О — J <УЦ — О" + Р-
Следовательно,
в'ц =¦ oi} + Ьцр — 8ij (a+p) = Оц.
Первый инвариант девиатора равен нулю, два других
инварианта представляют для теории пластичности и ползучести
фундаментальную важность, поэтому мы остановимся на них
более подробно. Второй инвариант девиатора определяется
следующим образом:
Su = (аи — dijo) {Oij — 6уа) = (JijOij — 2ао,-Д; + 8и8ио2.
Отсюда
Su = Sn-jSl = Sn-3o*. (8.3)
Если выразить Su через главные напряжения, то мы получим:
Sn = 4 [@i - о2J + (аа - а3J + (а3 - atf]. (8.4)
Простое и наглядное истолкование величины Su было дано
Рошем и Эйхингером. Вычислим напряжение на площадке, равно-
§ 8] НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ТЕНЗОРА НАПРЯЖЕНИЙ 47
наклоненной к трем главным осям, то есть такой, для которой
v4 = v2 = v3= -—— . Будем называть эту площадку октаэдриче-
уЗ
ской площадкой, а напряжения — октаэдрическими напряжениями.
По формуле (8.1) на октаэдрической площадке
1
av = ^-(o-1 + a2 + o-3)-
По формуле (8.2)
^ = 4[(oi-tT2K + (o2-a3J + (a3-a1JJ. (8.5)
Величину т0 мы будем называть октаэдрическим касательным
напряжением. Таким образом,
5„=3т*. (8.6)
Величины о и т0, нормальное и касательное напряжения на
октаэдрической площадке, естественным образом связаны с двумя
первыми инвариантами тензора напряжений; нормальное окта-
эдрическое напряжение равно одной трети первого инварианта,
касательное октаэдрическое напряжение отличается от
квадратного корня из второго инварианта девиатора только постоянным
множителем. Именно такой выбор основной системы инвариантов
оказывается удобным во многих вопросах теории пластичности.
Вместо величины октаэдрического касательного напряжения мы
будем часто пользоваться другой величиной ст0, так называемой
интенсивностью напряжений, которая отличается от т0 только
множителем. Этот множитель подобран таким образом, чтобы
при одноосном растяжении напряжением о величина о0 равнялась
напряжению 0. Для этого нужно, чтобы было
_ У'1
Т0 — —g Of)
и, следовательно,
а^у^п^К^-а^ + ^-аз^ + ^з-о-!J]. (8.7)
Установим теперь связь между третьим инвариантом
девиатора тензора напряжений и инвариантами самого тензора.
По определению
^ш = {от — о6гд) {ahj — e&hj) (о;-г — а&л) =
= oik {Ohj — o-SAj) (ад — odjt) — o6th {ohJ — o8kj) (ал — o8ji) -
Перемножим теперь первые две скобки и заметим, что
множитель 8ik перед вторым произведением скобок можно опустить,
48 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
заменив в скобках к на i. Получим:
^ш = oik [QhjOji — о-(ahi8ji + Oji8h]) -f о28^дп] —
— о {аи — o8ij) (ал — абл) = SIU — 2aSu + За3 — aSn.
Учитывая (8.3), получим окончательно:
Sin — Sin — SiSn — -g SI.
(8.8)
Вместо третьего инварианта тензора напряжений можно
рассмотреть другую величину, которая вместе с а и о полностью
определяет напряженное состояние
с точностью до поворота главных
осей в пространстве, а следовательно,
вместе с о и а0 образует полную
систему инвариантов тензора
напряжений. Приводимый ниже анализ
позволяет ввести эту величину
естественным образом.
Очевидно, что девиатор тензора
напряжений имеет те же главные оси,
что и сам тензор; главные
составляющие девиатора тензора напряжений
будут
ai = a1 — а, о-2 = а2 —а, o3 = ov
•а.
Приложим к телу гидростатическое
напряжение с интенсивностью (—о),
тогда на главных площадках будут действовать напряжения
o"i, o2 и о а, а на октаэдрической площадке нормальное напря~
жение исчезнет, останется только октаэдрическое касательное
напряжение т0- Рассмотрим равновесие тетраэдра, заключенного
между главными плоскостями и октаэдрической плоскостью
(рис. 3). Если площадь грани, принадлежащей октаэдрической
плоскости, есть <о, то площадь каждой из остальных трех граней
Составим уравнение равновесия тетраэдра, получим:
равна
У!
Ог-
^3t0Pi.
Здесь (J — единичный вектор, лежащий в октаэдрической
плоскости и определяющий направление октаэдрического
касательного напряжения. Направление вектора Р может быть задано
при помощи угла между этим вектором и некоторым
фиксированным направлением в октаэдрической плоскости. Проведем,
например, луч из центра октаэдрической площадки в точку пересечения
ее главной осью 1; направление этого луча есть к. Положим рА; =
§ 8] НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ СВОЙСТВА ТЕНЗОРА НАПРЯЖЕНИЙ 49
= cos 0. Из очевидных геометрических соображений следует,
2 1
что к± = —р. , kz — к3 = ——р . Составляющие вектора Р найдут-
уб у6
ся из следующих уравнений:
Pl + P2 + P8 = 0,
2pi-p2-p3 = 1^6cos9.
Первое уравнение — это условие нормирования, второе выражает
тот факт, что вектор Р принадлежит октаэдрической плоскости,
а следовательно, ортогонален вектору нормали, составляющему
одинаковые углы с тремя главными осями. Третье уравнение
получается из условия р& = cos 9.
Решая эти уравнения относительно plt найдем:
Pi^J-0030-
Из соображений симметрии следует, что
p2=/4co8(e-f.),
p3=/!coS(e-f).
Теперь мы можем написать следующие формулы для главных
напряжений:
. 2 q
а1 = а + ^гО cos 6,
о"г = о" +-3 cr0 cos Г 0 ^ J , (8.9)
o-3 = a + -g-CT0cos [Q — ~j .
Угол В называется углом подобия девиаторов тензора
напряжений. Если два тензора имеют одни и те же главные оси и углы 0
для них равны, то девиаторы этих тензоров отличаются лишь
общим множителем.
Вычислим теперь третий инвариант девиатора. В главных осях
Sin = (о, - аK + (о-2 - of + (о3 - of.
С помощью формул (8.9) получим:
Отметим еще одно истолкование величины второго инварианта
девиатора, принадлежащее В. В. Новожилову [89]. Вычислим
4 Ю. Н. Работнов
50 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
среднее квадратичное значение касательного напряжения на
поверхности сферы. Для сферы vt = —, вычисляя \ x2da, где т.
дано формулой (8.2), мы встретимся с интегралами двух типов:
Очевидное преобразование приводит 7t к следующему виду:
так как для сферы \ —|— dco = \ —j— dm. Отсюда следует, что
J T2 da = 1а. (@1 _ а2J + (а2 _ а3J + (аз - стО2}-
Таким образом, октаэдрическое касательное напряжение
отличается от среднего квадратичного касательного напряжения лишь
постоянным множителем.
§ 9. ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ.
ИНВАРИАНТЫ ТЕНЗОРОВ ДЕФОРМАЦИИ
И СКОРОСТЕЙ ДЕФОРМАЦИИ
При формулировке основных физических зависимостей,
характеризующих те или иные реальные твердые тела, наряду с
тензором деформации рассматривают тензор скоростей деформации.
Пусть радиус-вектор материальной точки есть г (хг, t), исходное,
недеформированное состояние соответствует моменту t = 0,
г (х1, 0) = г0. Как и в § 5, криволинейные координаты
материальной точки М остаются неизменными. Составляющие метрического
тензора gtj будут теперь функциями координат и времени, будем
обозначать через gtj0 метрический тензор в исходном, недеформи-
рованном состоянии. Элемент dsa в исходном состоянии имеет
в момент времени t длину ds, в момент времени t -\- dt —длину
ds-\-8ds; -j— есть скорость удлинения отрезка, который в данный
момент имеет длину ds; скорость деформации этого отрезка
б ds
dt ds
Но ds= ds0(i-\-e), —j^- = eds0, поэтому
«=-щт- <9Л>
§ 9] ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ. ИНВАРИАНТЫ 51
Продифференцируем формулу E.2). Получим:
ei,- dx^ dxi
Отсюда
eij dxi- dxj ^
e== d^ (l + <?)a • (9'2>
Величины etj мы будем обозначать ег;- и называть компонентами
тензора скоростей деформации. Вектор г может быть представлен
в виде
r(x\ t) = г0 {х1) + и (х1, t).
Вектор скорости v = и. Дифференцируя соотношения E.4),
получим следующие выражения для компонент тензора скоростей
деформации:
л
eij = y *Vi> J +" VJ> * + ^ iUs> 1 + "a. lV°> J") Sksb (9-3>
В случае малых перемещений
«ij = -2{vi,j + vj,t), (9.4)
то есть компоненты тензора скоростей деформации выражаются
через вектор скорости точно так же, как компоненты тензора
деформаций выражаются через вектор перемещения. Если
производные от перемещений малы, то е < 1 и в формуле (9.2) можно
пренебречь величиной е по сравнению с единицей в знаменателе.
Тогда
е^ dx* dx) eij dxi dxi
E= d& = riP > (9-5)
и аналогия между тензором скоростей и тензором деформаций
становится полной. Одако из предположения о том, что е < 1,
еще не следует, что производные от перемещений малы и что в
формулах (9.3) можно пренебречь членами вида vk^usj.
Система инвариантов тензоров деформаций и скоростей
деформации строится совершенно так же, как система инвариантов
тензора напряжений, все рассуждения § 8 могут быть повторены
применительно к этим двум тензорам. Мы будем обозначать
инварианты тензора деформаций Ег, Еи и EUj, инварианты тензора
скоростей деформации Н\, Нц и Яш. В случае малых деформаций
вводятся величины
e = ytfi и е = у#ь (9.6)
4*
52 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
при этом Ei и Hi представляют собою относительное изменение
объема и скорость относительного изменения объема. То
обстоятельство, что обозначения е и е применялись раньше для
обозначения относительного удлинения и скорости деформации элемента
ds, а теперь применяются для обозначения инвариантов
соответствующих тензоров, не должно приводить к недоразумениям.
Из определения тензора е^ следует, что
е = е.
Совершенно так же, как был определен девиатор тензора
напряжений, вводятся девиаторы тензора деформаций и скоростей
деформации:
&ij — ?ц 60;j, Sij ~ Sjj EOjj.
Вторые инварианты девиаторов определяются по
совершенно аналогичным формуле (8.4):
EII^^[(el-e2y + (e2-e3)' + (e3-ei)i],
tfn=4[(ei-e2J + (e2-e3J + (e3-eiJ].
Однако вместо величины т0, определяемой с помощью формулы
(8.6), мы введем октаэдрический сдвиг у0 и октаэдрическую
скорость сдвига т]0 при помощи соотношений:
Еп = ~у1 //„=4^. (9.8)
Такая разница формул (9.8) по сравнению с (8.6) объясняется тем,
что компоненты тензора деформаций с разноименными индексами
представляют собою не сдвиги, а половины сдвигов. Следуя той
же идее, согласно которой величина т0 была истолкована как
касательное напряжение на октаэдрическои площадке, можно было
бы поставить задачу об определении наибольшего сдвига в
системе осей, одна из которых является нормалью к октаэдрическои
плоскости. Этот наибольший сдвиг и есть октаэдрический сдвиг
7о! направление соответствующей оси, лежащей в октаэдрическои
плоскости, называется направлением октаэдрического сдвига.
В теории напряженного состояния все рассмотрение носило
совершенно наглядный характер, но результаты от этого наглядного
представления не зависят, они выражают некоторые свойства
симметричных тензоров второго ранга безотносительно к их
физической природе. Поэтому теперь мы будем поступать чисто
формально. Наряду с интенсивностью напряжений мы введем
также понятия интенсивности деформаций и интенсивности
скоростей деформации. Так будут называться величины е0 и е0,
отличающиеся от Yo и Ло числовым множителем, подобранным таким
формулам,
(9.7)
§ 9] ТЕНЗОР СКОРОСТЕЙ ДЕФОРМАЦИИ. ИНВАРИАНТЫ 53
образом, что при одноосном растяжении стержня из несжимаемого
материала е0 становится удлинением е, е0 становится скоростью
деформации удлинения е. При одноосном растяжении ei = e,
е2 = е3 = — ув; поставленное условие будет выполнено, если
мы примем
2 - (9-9)
Сравнивая (9.9) с (9.8), находим:
Направление октаэдрической скорости сдвига составляет в окта-
эдрической плоскости угол ф с направлением проекции оси номер
1 на октаэдрическую плоскость. Этот угол играет ту же роль,
что угол 0 в теории напряженного состояния, и выражается через
инварианты Нц и Нщ. По аналогии с (8.9) мы получаем следующие
формулы:
е} =e + e0coscp,
e2 = e + e0cos((p-Hr), (9.10)
s3 = е + е0 cos f ф ^-
Совершенно аналогичные выражения получаются для главных
компонент тензора деформаций еи е2 и е3:
et = е + е0 cos ф,
2я
e2 = e + eacos^ —j ,
Заметим, что е0 и е0 являются однородными функциями первой
степени от компонент соответствующих тензоров, но не
линейными функциями. Поэтому из определения е,7- = etj не следует,
что е0 = е0. Это равенство выполняется только в случае так
называемого пропорционального деформирования, когда еи = atjX (t),
причем а,ц — постоянный тензор. При этом е^- = ацх (t),
следовательно, в каждый момент отношения между компонентами
девиатора скоростей деформации совпадают с отношениями между
компонентами девиатора тензора деформаций:
8И : е22: . ..: e3i — еп.: егг: .. .: e3i.
54 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
До сих пор мы рассматривали случай, когда перемещения
точек тела малы, что дало возможность пренебречь изменениями
метрики в процессе деформации. Однако формальная теория
тензора скоростей деформации сохраняется полностью и в случае сколь
угодно больших деформаций среды, если отказаться от
применения системы координат, связанной с телом и деформирующейся
вместе с ним. Зафиксируем в пространстве систему координат xt
и будем рассматривать поле вектора скорости v (xi), отнесенного
не к данной материальной точке, а к фиксированной точке
пространства, через которое протекает материал. Таким образом, мы
придем к определению тензора скоростей деформации (9.4),
который теперь уже никак не связан с деформациями как таковыми.
Такая точка зрения обычна для гидродинамики.
§ 10. УПРУГОЕ ТЕЛО
Рассмотрим тело, нагруженное поверхностными силами Т
и объемными силами F. Перемещения его точек будут ut. Пусть
внешние силы получили приращения 8Tt и 8Ft, перемещения
точек при этом изменяются на величины биг-. Если б Г/ и 8Ft
бесконечно малы, то работа внешних сил при дополнительном
деформировании выразится следующим образом:
8А = \ Ft6ut dV+[ TMi d2.
V 2
Но поверхностные силы выражаются через значения
компонент тензора напряжений в точках поверхности:
Внося Tj в выражение ЬА и преобразуя поверхностный интеграл
в объемный по формуле Грина, получим:
6А - J IFM + {oiM),,] dV = J [{Fj + oij, j) 6u? + ot№, j] dV.
V V
Вследствие уравнений равновесия круглая скобка обращается
в нуль, и мы получаем:
M=\otj6uttjdV. A0.1)
v
Величины
§ 10]
УПРУГОЕ ТЕЛО
55
представляют собою приращения компонент деформации,
вызванные изменением напряженного состояния при изменении
внешних сил. Вследствие симметрии тензора о"у мы можем переписать
формулу A0.1) следующим образом:
ЬА — \ ацЬец dV.
v
Положим:
aij8eij — 8U.
Рассмотрим теперь два состояния тела: начальное, когда на него
действовали силы Ti0 и Fi0, напряжения были aiJ0, а деформации
ejjo, и конечное, соответствующее силам Tti, Fti, напряжениям
<T;Ji и деформациям etjl. Переход из начального состояния в
конечное может осуществляться разными путями, в зависимости от того,
каким образом мы изменяем внешние силы. Процесс
деформирования каждого элемента удобно представить следующим образом.
Рассмотрим девятимерное пространство, отнесенное к
ортогональной декартовой системе координат. Будем откладывать по осям
координат величины компонент деформации etj, таким образом
тензору деформаций etj ставится в соответствие вектор
девятимерного пространства. Такое представление тензора с помощью
вектора имеет ограниченное значение, оно не инвариантно,
поскольку тому же тензору деформаций, но отнесенному к другим
осям, будет соответствовать другой вектор, правда, той же длины,
поскольку квадрат длины вектора является вторым инвариантом
тензора. Но длина вектора является его единственным
инвариантом, тогда как тензор имеет три инварианта, в этом смысле
представление тензора с помощью многомерного вектора суживает
возможности. Рассматривая вектор etj как радиус-вектор точки
девятимерного пространства, мы изображаем деформированное
состояние элемента точкой N девятимерного пространства;
начальному состоянию соответствует точка 7V0, конечному состоянию —
точка Ni, процесс деформации элемента представляет собою
движение из точки N0 в точку Ni по некоторой кривой. Работа
внешних сил, приходящаяся на единицу объема, выразится при этом
следующим образом:
U=\otJdeiit A0.2)
No
а полная работа
U=\UdV. A0.3)
v
Будем называть упругим такое тело, для которого величина
U не зависит от пути деформирования. Для этого необходимо,
56 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
чтобы выражение под интегралом в формуле A0.2) было полным
дифференциалом, то есть чтобы было
<*„ = ¦?-. A0.4)
Функция U (ец) называется упругим потенциалом.
Одновременно с пространством деформаций мы будем
рассматривать девятимерное пространство напряжений, координаты точек
которого равны составляющим тензора напряжений. Пути
деформирования N0Ni соответствует путь нагружения М9Ми точке N
пути деформирования с координатами е^ соответствует точка М
пути нагружения с координатами Оц. По аналогии с A0.2)
рассмотрим криволинейный интеграл
Ml
Ф=\еХ}дли. (Ю.5)
м„
Оказывается, что если существует упругий потенциал U (ец),
то существует и функция Ф, не зависящая от пути нагружения.
Действительно,
etj dotj =• d {etjOij) — oG deu.
Следовательно,
Ф = еуо-у— ^ Oijdetj.
Поскольку между путем нагружения и путем деформирования
существует однозначное точечное соответствие, интеграл берется
по пути AVV и, следовательно, равен U. Таким образом,
<U = ei3ai}-U. A0.6)
Отсюда следует;
•«-?-• <10-7>
Конечно, при пользовании формулами A0.7) нужно, чтобы Ф
была выражена как функция вц, что всегда возможно, так как
из A0.4) можно найти еи в зависимости от atj и подставить эти
выражения в U (е^) и а^е^. Функция Ф (сггу) называется
дополнительной работой. Происхождение этого названия можно
пояснить на примере нелинейного тела в условиях одноосного
напряженного состояния. Если кривая зависимости напряжения от
деформации будет такой, как показано на рис. 4, то U представляет
собою заштрихованную площадь, а Ф — площадь, дополняющую
§ 10]
УПРУГОЕ ТЕЛО
57
ее до прямоугольника, построенного на абсциссе и ординате
крайних точек.
Простейшее предположение о виде функции U состоит в том,
что это — квадратичная функция от компонент деформации.
Положим
и = ±Е1тецем. (Ю.8>
Величины Ецм образуют тензор четвертого ранга, симметричный
относительно индексов ij и Ы, то есть такой, что Е^ы — Елы*
EijM = Etjih. Будем называть его тензором модулей упругости.
По формулам A0.4)
Ou = EimeM. A0.9)
Здесь учтено, что при
дифференцировании A0.8) одинаковые члены будут
появляться по два раза. Из формул A0.4)
следует, что
d°ij __ doTS
ders ~~ deij
Применяя это соотношение к A0.9),
получим еще одно условие симметрии для
тензора EtjM, а именно: ff e
Eijhi— Ekiij- Рие. 4.
Легко убедиться в том, что число
различных модулей упругости равно 21. Действительно, шесть
компонент напряжения выражены линейным образом через шесть
компонент деформации, общее число коэффициентов равно 36, но-
вследствие симметрии матрицы различных из них остается 21.
В частных случаях наличие так называемой упругой
симметрии позволяет уменьшать число модулей упругости, но это можна
сделать лишь при некотором, совершенно определенном выборе
осей координат.
Разрешая A0.9) относительно etj, мы получим другую форму
закона линейной упругости:
еИ — cijklakh
Величина U может быть теперь представлена следующим образом:
1 1
Для линейного упругого тела дополнительная работа Ф равна
Упругому потенциалу U:
Ф = С7.
58 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
§11. ИЗОТРОПНОЕ УПРУГОЕ ТЕЛО
Изотропным телом называется такое тело, свойства которого
не зависят от ориентировки рассматриваемого элемента. Для
изотропного упругого тела уравнения связи между напряжениями
и деформациями должны иметь один и тот же вид при любом выборе
координатных осей, а следовательно, упругий потенциал должен
зависеть от инвариантов тензора деформаций. Положим:
U = U[Ej, En, Е1и].
Здесь
Ег = еиЬц,
Ец--=еиеи,
Eui = eUejheM-
По формулам A0.4) отсюда следует:
°« = 1ГеТ б" + 2^е;>+3 ЖИГeihehj- A1Л)
Если тело линейно-упруго, то функция U должна быть
квадратичной функцией от компонент деформации в изотропном теле,
она необходимым образом имеет следующий вид:
Соотношения A1.1) принимают следующий вид:
atJ = kE1btj + 2petj. (И -2)
Постоянные к и (х, имеющие размерность напряжения,
называются постоянными Ламе. Образуя первый инвариант от обеих
частей A1.2), получим:
или о"= ЪКе.
Величина
4 Si =f*+!¦(!)?!
К = Х + \у.
называется объемным модулем упругости.
Уравнения A1.2), разрешенные относительно etj, часто
записываются в следующем виде:
1 + у
Е
0«-8и7^Г°] • (И-3)
§ 11]
ИЗОТРОПНОЕ УПРУГОЕ ТЕЛО
59
Модуль упругости Е и коэффициент Пуассона v связаны
с постоянными Ламе следующим образом:
Е = ix (Зк + 2ц)
v = -
или
Ev Е
Х=-
(l+v)(l — 2v) ' r ,2(l+v) '
Заметим также, что
к_ Е
3 A - 2v) '
Возвращаясь к случаю нелинейного упругого материала,
отметим, что в формулах A1.1) нелинейность фигурирует двояким
образом, с одной стороны, -^=г , г^г- , -^— являются функция-
ob\ &Е\\ ^-^III
ми инвариантов, с другой стороны, тензор Оц представляет собою
линейную комбинацию трех тензоров: о^, etl и eikehj.
Для описания поведения'реальных материалов часто
оказывается возможным считать U функцией только двух инвариантов
тензора деформаций, а именно Ег и Ец. При этом компоненты
тензоров напряжений и деформаций оказываются связанными
линейными тензорными соотношениями:
аналогичными соотношениям линейной теории упругости, с той
разницей, что модули упругости оказываются уже не
постоянными, а функциями от инвариантов тензора деформаций.
Вместо второго инварианта тензора деформаций имеет смысл
рассматривать второй инвариант девиатора тензора деформаций:
Еп = Еи-{Е1
3
Вместо A1.4) получаем следующие выражения:
f dU dU 2 „ \ . , „ dU
\dEl дЕц 3 V ' SEn
Отсюда следует:
a*i "+ ая„
Обра зуем первый инвариант от обеих частей этих соотношений.
Получим:
u°=*k*u + 2^h<tJ- A1.5)
60 ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ ТВЕРДОГО ТЕЛА [ГЛ. I
¦«^2^-еу; A1.7)
Уравнение A1.6) выражает закон упругости для объемной
деформации. Связь между вц и e%j можно теперь записать
следующим образом:
эи -
'дЕп
полученные соотношения можно назвать законом упругости для
сдвиговой деформации. Возводя в квадрат A1.7) и свертывая
левую и правую части по г, /, найдем:
или
t0 = ^-Yo. A1-8)
дЕп
Уравнения A1.7) можно переписать следующим образом:
При этом в силу A1.8) a0 = f(e, e0). Используя A1.6), можно
выразить е0 через а0 и а, так что e0 = h(a, cr0); тогда из A1.9)
девиатор деформации выражается через девиатор напряжений
по формулам
- _ 3 «о ~~
Дальнейший шаг по пути упрощения нелинейного закона
упругости состоит в том, что объемная деформация предполагается
не зависящей от сдвиговой, следовательно, в уравнении A1.6)
г=- не зависит от Еп. Тогда упругий потенциал может быть
представлен как сумма двух функций, от Ej и от Ец:
U = U1(Ej) + U2(ElI).
В уравнениях A1.9) а0 = / (е0); таким образом, упругие
свойства материала полностью определяются заданием двух
функций: зависимости интенсивности напряжений от интенсивности
сдвига и зависимости гидростатического напряжения (октаэдри-
ческого нормального напряжения) от относительного изменения
объема.
Для определения функции о = / («о) необходимо поставить
опыт в условиях чисто девиаторного напряженного состояния,
например чистого сдвига.
Особо следует остановиться на случае несжимаемого материала.
Для него Ei = 0, следовательно, U может быть функцией только
инвариантов Ец = Еи и Ет = Еш. Если наложить на данное
§ ii]
ИЗОТРОПНОЕ УПРУГОЕ ТЕЛО
61
напряженное состояние гидростатическое состояние, величина
работы не изменится, поэтому тензор напряжений определяется
с точностью до гидростатической составляющей. Формально
в A1.1) нужно принять -^рг = о, и мы получим:
ац = 2^е„4-3-^-в«в„. A1.10)
Для того чтобы иметь возможность пользоваться формулами
A1.9), мы должны знать либо о0 как функцию е0, либо т0 как
функцию у0, что совершенно безразлично. Если материал несжимаем,
то при чистом растяжении относительное удлинение е равно е0,
растягивающее напряжение а равно о*0 и зависимость о0 от е0
дается непосредственно кривой растяжения. Если материал
сжимаем, то зависимость между а0 и е0 не совпадает с зависимостью а
и е при простом растяжении, для нахождения искомой зависимости
необходим пересчет кривой растяжения. В условиях чистого
сдвига изменения объема не происходит и диаграмма т — 7 ПРИ
чистом сдвиге отличается от диаграммы ст0 — ео только масштабом.
Диаграмма т0 — 7о совершенно совпадает с диаграммой т —у
при чистом сдвиге. Действительно, если о*12, например, равно т,
то е12 = у у, и из A1.9) следует:
Л = 1°
Y Yo "
С этой точки зрения использование в качестве основных
характеристик величин т0 и у0 имеет некоторые преимущества.
В линейной теории упругости
— = u = const.
Yo ^
Вместо обозначения ц для модуля сдвига часто используется
обозначение G. Соотношения A1.9) в линейном случае мы будем
записывать так:
ffy = 2Giy. A1.11)
Отметим, что в линейной теории упругости углы подобия девиа-
торов тензоров напряжений и деформаций равны:
Это следует из сравнения формул (8.9), (9.11) и A1.11).
ГЛАВА II
ТЕОРИЯ ПЛАСТИЧНОСТИ
Теорией пластичности называют механическую теорию,
имеющую своей задачей описать поведение под нагрузкой материалов,
получающих необратимые деформации при условии, что
зависимость между напряжениями и деформациями не содержит времени.
Это верно в первом приближении для обычно употребляемых
в технике металлов при нормальной температуре. Поэтому теория
пластичности фактически занимается описанием поведения сталиг
латуни, алюминиевых сплавов и некоторых других металлов
и сплавов при нормальных и низких температурах. При высоких
температурах часто оказывается, что ползучесть сопровождается
пластической деформацией. Точнее говоря, при изучении
ползучести бывает целесообразно отделять пластическую деформацию
от деформации ползучести.
Развитие теории пластичности предшествовало развитию теории
ползучести, при этом последняя обычно заимствовала основные
принципы из теории пластичности. Поэтому нам кажется
полезным предпослать изложению материала, относящегося
непосредственно к ползучести, краткий очерк современного
состояния теории пластичности применительно к упрочняющемуся
материалу.
Цель этого очерка — изложение идей и методов, лежащих
в основе составления уравнений теории пластичности, а не
приложение этих уравнений в той или иной упрощенной форме к решению
отдельных задач. Поэтому, в частности, мы здесь совершенно не
затрагиваем вопрос об идеальной пластичности.
Элементарные физические факты, которые относятся к
пластичности, а также основные сведения о пластичности при
сложном напряженном состоянии будут предполагаться известными
читателю.
§ 12] ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ 63»
§ 12. ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ
Деформационная теория пластичности Надаи [300] — Хенки [227]
представляет собою распространение на пластическое тело
той связи между напряжениями и деформациями, которая
устанавливается в нелинейной теории упругости. Основными
предположениями, которые обычно принимаются при составлении
уравнений, являются следующие:
1. Объемная деформация подчиняется закону линейной
упругости.
2. Пластический потенциал [/не зависит от третьего инварианта.
Эти предположения не являются строго обязательными, но
они лежат в основе общераспространенного варианта
деформационной теории, названного Ильюшиным [43] теорией малых упруго-
пластических деформаций. Закон линейной упругости для
объемной деформации будет следующим:
а = ЗКе. A2.1>
Соотношения между девиаторами напряжений и деформаций
принимают форму A1.9), а именно:
ffy = 2g;v = 2G,;y. A2.2)
При этом
Gs = Gs (Yo) либо Gs = ?, (т0). A2.3}
Величину Gs можно назвать пластическим модулем сдвига; для
упругого тела формулы A2.2) сохраняют силу, при этом G = \i.
Для дальнейшего развития теории необходимо определить
границы применимости соотношений A2.1) — A2.3), в первую
очередь установить условия, при которых происходит
пластическая деформация, а при которых наступает разгрузка.
Простейший путь заключается при этом в суждении по аналогии.
Действительно, при сделанных ограничениях для задания полных
характеристик пластичности необходимо иметь значения объемного
модуля К и знать функцию A2.3). Проще всего определить вид
этой функции из опыта на чистый сдвиг. Пусть, например, aiz =
= т Ф 0, все остальные компоненты тензора напряжений
обращаются в нуль. Первый инвариант с равен нулю, тензор
напряжений совпадает с его девиатором. По формуле A2.1) е = 0У
следовательно, тензор деформаций совпадает со своим девиатором,
причем из формул A2.2) следует, что единственная отличная or
нуля компонента тензора деформаций будет е^ — ^у. Вычисляя
октаэдрическое касательное напряжение и октаэдрический сдвиг,
64
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
найдем:
то = ]А|т, Yo=/|y-
Зависимость между касательным напряжением и сдвигом по
формуле A2.3) будет следующей:
т. =
/И/10
Обратно, имея опытную кривую зависимости т от у, простым
изменением масштаба мы можем превратить ее в кривую зависимости
То от у0. Диаграмму чистого сдвига можно получить, если
производить, например, опыт над кручением тонкостенных трубок.
Обычным методом изучения механических свойств материала
является испытание на растяжение призматического образца.
Для нахождения функции f(y0) по кривой растяжения
необходимо знать величину объемного модуля К и производить пересчет,
основываясь на уравнениях пластичности. Для несжимаемого
материала при растяжении следует принять:
С
СТц = O-j
?>и =
ледовательно,
! 02 = ОзЗ — °"j2-
еи e2Z = e33= —
1/2
Т0 — -g—Oi,
= 0-23 =
1
Yo =
= o-sl
ei2 =
1
= V2
= U,
= ^23;
et.
a =
= <?31:
J «Ji,
= 0.
Зависимость т0 от Yo b этом случае дается кривой растяжения
с перестроенными соответствующим образом масштабами.
Формулы A2.2) можно представить, как мы видели, также
следующим образом:
aM=|^w. A2.4)
Величины а0 и е0 были определены таким образом, что при чистом
растяжении а0 = ви е0 = е4, если материал несжимаем. Поэтому
уравнения A2.4) представляют некоторые удобства, мы считаем
в них ff0 функцией от е0, причем вид этой функции дается кривой
растяжения непосредственно. Если сжимаемость материала нужно
учитывать, то для получения зависимости а0 от е0 кривая
растяжения должна быть перестроена. Способы такой перестройки
указываются в соответствующей литературе.
Основной опытный факт, наблюдаемый при одноосном нагру-
жении, заключается в следующем. Пока мы движемся по кривой
деформирования от начала координат в направлении, указанном
стрелкой (рис. 5), то есть пока о и е^ возрастают, связь между o"t
§ 12] ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ 65
и ех дается диаграммой пластического деформирования.
Зависимость между напряжением и деформацией является однозначной
в том смысле, что деформирование можно вести быстрее или
медленнее, нельзя только двигаться в обратном направлении, то есть
разгружать образец. При уменьшении напряжения материал
возвращается в упругое состояние; зависимость между
напряжениями и деформацией при разгрузке дается прямой, проходящей
через ту точку кривой деформирования, от которой произведена
разгрузка. Закон упругости при
разгрузке не является точным физическим
законом, эксперимент обнаруживает
систематические отклонения от него. Но всякая
теория пластичности имеет дело с
гипотетической идеальной средой, а не
с реальным телом, поведение которого
всегда описывается лишь в некотором
приближении. Предположим теперь,
следуя Ильюшину [43 ], что в случае сложного
напряженного состояния зависимость
между октаэдрическими напряжениями
и деформациями та же, что и в
одноосном случае, пластическая деформация происходит, когда а0,
а следовательно, е0 возрастают, при убывании интенсивности
напряжения происходит разгрузка и в силу вступает закон
упругости. Таким образом, если для пластической деформации, при
условии da0 > 0, справедливы уравнения A2.1) — A2.3), при
разгрузке, когда do0 < 0, зависимость между напряжениями
и деформациями дается следующими соотношениями:
Qij — a'ij = 2G (etj — е\}),
а — a' = 3if(e— е'), или о — ЗКе.
Штрихами здесь отмечены величины напряжений и деформаций,
достигнутые к моменту начала разгрузки.
Сформулированная подобным образом деформационная теория
пластичности не может считаться истинной физической теорией,
пригодной для всех возможных случаев нагружения. Одно из
ранних возражений против нее состоит в следующем. Предположим,
что мы достигли путем непрерывного пластического
деформирования, то есть такого процесса деформирования, что в каждый
момент было de0 > 0, некоторого состояния, характеризуемого
величинами atj и etj. Произведем теперь бесконечно малое
нейтральное деформирование. Так называется процесс
деформирования, для которого е0 = const и de0 = 0. Приращения
деформаций при этом будут detj, они связаны линейным соотношением:
eijdeij = 0.
5 Ю. H. Работнов
66
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
Приращения девиатора напряжений получаются при этом путем
дифференцирования формул A2.2):
doij = 2Gs{e0)deij.
Поскольку случай rfe0>0 есть случай пластической
деформации, а при de0<cO происходит разгрузка, нейтральное
деформирование, когда de0 = Q, можно рассматривать, с другой стороны,
как предельный случай разгрузки, а для разгрузки
dotj —- 2G detj.
Здесь G — модуль упругости, тогда как в предыдущей формуле
Gs — пластический модуль сдвига, зависящий от е0. Очевидно,
что в действительности переход от пластической деформации
к разгрузке должен происходить непрерывно, таким образом,
полученный результат нельзя считать приемлемым.
Для дальнейшего нам будет удобно воспользоваться
геометрической терминологией. Будем изображать тензор деформации
вектором е в девятимерном пространстве. Составляющие вектора
относительно некоторого ортогонального базиса в этом
пространстве равны компонентам тензора деформаций. Любой процесс
нагружения может быть представлен как движение конца вектора
деформации по некоторой кривой, называемой путем деформации.
Заметим, что вследствие симметрии тензора деформации мы можем
вести рассмотрение в шестимерном пространстве вместо
девятимерного. Более того, предположив, что законы пластичности
выражаются соотношениями между девиаторами, можно
рассматривать определенное тем или иным способом пространство девиато-
ров деформации, однако мы не будем становиться на этот путь.
Через каждую точку М пространства деформации, которой
соответствует определенное значение е„, можно провести
поверхность е0 = const. Будем называть ее поверхностью
деформирования. Если продолжать нагружение из точки М, то могут
представиться три случая:
а) приращение вектора de образует острый угол с
направлением нормали п к поверхности деформирования в точке М,
следовательно, de0>0, происходит дополнительная пластическая
деформация.
б) Угол между de и п больше ^-, происходит разгрузка.
в) Вектор de лежит в касательной плоскости к поверхности
деформирования, произведено нейтральное деформирование.
Все эти три случая схематически показаны на рис. 6.
Рассмотрим одновременно девятимерное пространство напряжений;
вектор а в этом пространстве, называемый вектором напряжения,
имеет своими составляющими компоненты тензора напряжений.
§ 12J ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПЛАСТИЧНОСТИ 67
F) Ш)
iff/ Ш) j
Пути деформирования в пространстве напряжений соответствует
путь нагружения, поверхности деформирования соответствует
поверхность нагружения. Сточки зрения сформулированной
деформационной теории рассмотрение в
пространстве деформаций и в пространстве
напряжений совершенно одинаково, нейтральному
деформированию соответствует нейтральное
нагружение.
Имеются многочисленные опытные
данные, относящиеся к случаю нейтрального
нагружения. Наиболее простая схема опыта
заключается в следующем. Тонкостенный
трубчатый образец растягивается в
пластической области напряжением сг, при
неизменном растягивающем напряя^ешш к нему
прикладывается малый крутящий момент, Рис. (э.
создающий касательное напряжение dr. При
совместном действии растяжения и кручения условие
постоянства октаэдрического напряжения записывается следующим
образом:
ст2 + Зг2 = const.
Поскольку напряженное состояние характеризуется двумя
величинами о и т, пространство нагружения представляет собою
плоскость, поверхности нагружения являются подобными
эллипсами (рис. 7). Путь нагружения при растяжении в данном случае
изображается отрезком ОМ оси
абсцисс; прикладывая касательное
напряжение dx при постоянном о, мы
движемся по бесконечно малому
отрезку дуги эллипса, то есть
совершаем нейтральное нагружение. Угол
закручивания и касательное
напряжение связаны при этом следующим
соотношением:
dx = G*dy.
Рис. 7.
Согласно деформационной теории,
величина G* должна быть равна
0> (То), где 7о — октаэдрический сдвиг для точки М. Если считать,
что нейтральное нагружение сопровождается только упругой
деформацией, то G* = G. Опыты, производившиеся при малой
пластической деформации растяжения, показали, что второе
предположение оправдывается и можно считать с достаточной
степенью точности, что G* — G. Однако опыты, выполненные при
значительной начальной деформации, указывают, что G* < G,
5*
68
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
хотя все же значительно больше той величины, которая
предсказывается деформационной теорией. На рис. 8 представлен
х,иг/ммг
О О В 0 у
Pjtc. 8.
экспериментальный график зависимости между Ду и Дт, а также
прямые, соответствующие случаям G* = Gs и G* = G (тонкие
сплошные линии: G* = Gs, штриховые линии: G* — G).
§ 13. ДЕФОРМАЦИОННАЯ ТЕОРИЯ
ПРИ ПРОПОРЦИОНАЛЬНОМ НАГРУЖЕНИИ
При анализе экспериментальных данных по пластическому
деформированию в условиях сложного напряженного состояния
было отмечено (Ильюшин [43]), что уравнения деформационной
теории дают достаточно хорошие результаты в том случае, когда
все компоненты девиатора напряжений изменяются в процессе
нагружения пропорционально одному и тому же параметру а,
называемому параметром нагружения. Это значит, что можно
принять
oi} = Oija.
Здесь а — параметр, монотонно меняющийся от нуля до единицы,
a\j — напряжения в конечном состоянии. Отсюда следует,
очевидно, что т0 = сст°. При этом девиатор деформации также
меняется пропорционально одному параметру р\ Действительно,
согласно A2.2)
- _ 1 -о
*'¦'' ~ 2GS (atg) a0l>'
Положим
Тогда
etj == PeiJ>
§ 13] ДЕФОРМАЦИОННАЯ ТЕОРИЯ ПРИ ПРОПОРЦИОН. НАГРУЖЕНИИ 69
где
Gs (т0)
р = а
Gs (ат0)
Заметим, что при пропорциональном изменении компонент
тензора напряжений компоненты тензора деформаций (а не девиатора
деформаций) не будут изменяться пропорционально.
Пропорциональное нагружение сравнительно просто
осуществляется на опыте, поэтому законы деформационной теории
пластичности в этих условиях поддаются проверке. Для углеродистой
и низколегированной стали в состоянии отпуска и нормализации
кривые зависимости т0 от у0 при различных видах напряженных
состояний совпадают, однако для других материалов
обнаруживаются некоторые систематические отклонения. Так, для
алюминиевых и магниевых сплавов уже кривые растяжения не совпадают
с кривыми сжатия. Поэтому приходится допустить, что октаэдри-
ческий сдвиг зависит не только от октаэдричеокого напряжения
но также от первого или третьего инварианта тензора
напряжений (см. Ягн [1583, Прагер Е333]).
Вопрос о том, в какой мере справедливы соотношения
деформационной теории пластичности при нагружениях, отличных от
пропорционального, не может считаться решенным. Опытные
данные [31] указывают, что если теория хорошо описывает
процесс пропорционального нагружения, то она дает
удовлетворительные результаты и для нагружения, близкого к
пропорциональному. Сам термин «нагружение, близкое к пропорциональному»
носит чрезвычайно неясный характер, возможный подход к
уточнению этого понятия мы рассмотрим в следующем параграфе,
сейчас же остановимся на вопросе о том, в какой мере может быть
обеспечено условие пропорционального нагружения при
деформировании реального тела внешними силами. Полагая Т — Т'ос,
F = F°a, мы удовлетворим уравнениям равновесия и граничным
условиям, если положим ¦ atj = oij-a, где а — постоянная для
всех точек тела величина. Объемная деформация связана с
гидростатическим напряжением законом Гука, следовательно,
e = TfT a°a = e°a.
- G it®)
С другой стороны, e^ = pe?j, причем ft = а , °0. , поэтому
еу = 6„е»и + еДО = е\$ + е° ф- а) 6У.
Внося эти выражения в уравнения совместности деформации, мы
обнаруживаем, что, вообще говоря, если e\j удовлетворяют
уравнениям совместности, то ец этим уравнениям не удовлетворяют.
Очевидные условия, при которых уравнения совместности будут
70
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
выполнены в процессе деформирования, следующие: во-первых,
р не зависит от координат, и, во-вторых, либо ос = Р, либо е° = 0.
Первое условие будет выполнено, когда Gs (т0) является сте-
пенной функцией от т0. Если Yo = а^. то G* = -^— ,
следовательно, Р = aft. При к = 1 второе условие выполняется для е° ^ 0,
но это тривиальный случай линейно-упругого тела, который нас
не интересует. Если к Ф 1, то необходимо, чтобы было е° = 0,
то есть материал был несжимаемым. Таким образом, достаточные
условия того, чтобы при пропорциональном изменении внешних
сил в теле осуществлялось пропорциональное нагружение, состоят
в следующем:
1. Зависимость между октаэдрическим напряжением и окта-
эдрическим сдвигом — степенная.
2. Материал несжимаем (теорема Ильюшина [43]).
Первое условие является весьма стеснительным, поскольку
требуется степенная зависимость с одним и тем же показателем
во всем диапазоне изменения т0 и у0> а не кусочно-степенная
аппроксимация истинной зависимости. В частности, постановка вопроса
о пропорциональном нагружении лишена смысла для идеально
пластического тела, для которого т9 остается постоянным.
§14. ПОСТУЛАТ УПРОЧНЕНИЯ ДРУКЕРА
Мы убедились, что деформационная теория пластичности не
удовлетворяет условию непрерывности соотношений между
напряжениями и деформациями при переходе от нагрузки к разгрузке.
При анализе этой и других теорий пластичности мы можем
встретиться с подобными же обстоятельствами, когда те или иные
следствия теории покажутся нам противоречивыми или физически
неприемлемыми. Поэтому необходимо иметь некоторый простейший
критерий, удовлетворение которому является минимальным
требованием, предъявляемым к теории пластичности. Попытка
установления такого критерия принадлежит Друкеру [194] — [199].
Постулат упрочнения Друкера состоит в следующем.
Представим себе напряженное состояние crfj, изображаемое в девятимерном
пространстве точкой М* — концом вектора напряжения а*.
Через точку М* проходит замкнутая поверхность нагружения S*,
то есть поверхность, отделяющая область упругих состояний
от области пластических состояний. Это значит, что движение
конца вектора о* за пределы объема, ограниченного поверхностью
S*, соответствует дополнительной пластической деформации.
Рассмотрим наряду с этим второе напряженное состояние otj,
которому соответствует точка М с радиусом-вектором а.
Дополнительное напряжение при переходе из точки М* в точку М есть
<т — а*. Предположим теперь, что мы вышли из точки М* и возвра-
§ 14]
ПОСТУЛАТ УПРОЧНЕНИЯ ДРУКЕРА
71
тились в нее по замкнутому пути, который может частично
выходить за пределы поверхности S*. Приращению напряжения da
всегда соответствует определенное приращение деформации de.
Постулат Друкера утверждает, что работа дополнительных
напряжений на замкнутом пути нагружения неотрицательна:
j(aij-otj)deu>0. A4.1)
Простейшее следствие из постулата Друкера будет следующее.
Рассмотрим замкнутый путь, изображенный на рис. 9. Точка М*,
соответствующая напряженному
состоянию о*, лежит внутри
поверхности S* или в крайнем случае на
этой поверхности, как изображено
на чертеже. Из точки М* можно
прийти в точку Mi, лежащую на S*,
по любой кривой, соединяющей эти
точки и находящейся целиком внутри
поверхности S*. После этого
сообщаем напряжению а' приращение do,
выходящее за пределы поверхности
S*, то есть связанное с пластической
деформацией, таким образом мы
попадем в бесконечно близкую точку
пути нагружения М. Через нее
проходит новая поверхность текучести S, следовательно, возвращение
из М в М* по любому пути, находящемуся внутри S, означает
разгрузку. На участках M*Mt и ММ* деформация является
упругой, на участке MtM она состоит из упругой и
пластической частей:
de = dey + den.
Работа дополнительного напряжения на упругих
перемещениях равна нулю для замкнутого пути нагружения.
Действительно,
(а — a*) dey = $ a de? — o*$ de^.
Первый интеграл представляет собою полную работу, которая
Для замкнутого пути равна нулю в соответствии с определением
упругости, второй интеграл также равен нулю вследствие
однозначности упругих деформаций. Таким образом, необратимая
Работа производится лишь на пластической деформации, и из A4.1)
Следует:
$
(o'ij — otj) defj>0.
A4.2)
72
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
Пусть теперь Сту = a*j, мы выходим из точки М* в бесконечно
близкую точку М, производя все время пластическое
деформирование. Будем называть такой путь активным путем нагружения.
После этого вернемся из точки М в точку М* по произвольному
пути, находящемуся целиком внутри S. Опять-таки необратимая
работа совершается только на пластической со-
/, „ ставляющей деформации, следовательно,
\/ dai}de^>0. A4.3)
I \ Условие A4.2) означает, что вектор а — о*, где
/ \ о* — радиус-вектор любой точки внутри S*, обра-
/ , \ зует острый угол с направлением вектора deu.
I Если поверхность нагружения гладкая и в точ-
/ ке Mi можно провести единственную
касательную гиперплоскость, то вектор dea неизбежно
Рис. 10. должен быть направлен по нормали к
поверхности S* (рис. 10), независимо от величины и
направления da. Поверхность целиком располагается по одну сторону
касательной гиперплоскости и, следовательно, является выпуклой.
Предположение о гладкости поверхности S в точке М не
является обязательным, в некоторых вариантах теории
пластичности принимается, что точка М может
быть угловой точкой. Это значит, что
касательные в точке М поверхности образуют
конус с вершиной в точке М (рис. 11). Из
постулата Друкера (условие A4.2)) следует,
что вектор должен лежать внутри конуса,
образованного нормалями к поверхности S
в окрестности точки М. Никаких других
ограничений направления вектора deu в этом
случае из постулата Друкера не вытекает.
Постулат Друкера, как это
неоднократно подчеркивал сам автор, отнюдь не
вытекает из законов термодинамики и не
является термодинамическим постулатом — Друкер употребляет
термин «квазитермодинамический».
Неравенство A4.1) утверждает, что работа любых
дополнительных воздействий на вызванных ими перемещениях
положительна или равна нулю для замкнутого цикла, тогда как из первого
начала термодинамики следует, что работа полной системы сил,
действующих на тело, неотрицательна. Следовательно,
дополнительными воздействиями нельзя извлечь из системы энергию.
Это свойство характеризует известную устойчивость материала,
что ясно из простого примера диаграммы растяжения. Если da de>
> 0, это значит, что приращению е соответствует приращение о*
того же знака, материал упрочняется. Но если da de < 0, то напря-
§15] О ГРАНИЦАХ ПРИМЕНИМОСТИ ДЕФОРМАЦИОННОЙ ТЕОРИИ 73
жение убывает с ростом удлинения, материал неустойчив в том
смысле, что равновесие стержня, растянутого постоянной силой,
невозможно. Поэтому на требование выполнения постулата
Друкера нужно смотреть как на определение класса устойчивых
материалов.
§ 15. О ВОЗМОЖНЫХ ГРАНИЦАХ ПРИМЕНИМОСТИ
ДЕФОРМАЦИОННОЙ ТЕОРИИ ПЛАСТИЧНОСТИ
Следуя Будянскому [176], выясним, для каких путей нагру-
жения уравнения деформационной теории пластичности не
противоречат требованиям постулата Друкера. Будем считать для
простоты материал несжимаемым, тогда основные уравнения
теории Надаи — Хенки будут следующими:
_ 1 -
Упругие составляющие деформации выражаются аналогичным
образом, только вместо пластического модуля сдвига Gs нужно
будет взять модуль упругости G:
„у
2G
ец = TTF- ot
Вычитая из полных деформаций упругие части, получим
выражения для пластических деформаций:
Вычислим теперь приращение пластической деформации при
заданных приращениях напряжений о^:
^ = К ^~Т) d°U + °" i d (^
Величина Gs является функцией от т0, причем
to
Дифференцируя это соотношение, получим:
dy0=rad (^-?-J+~^d%0.
Отсюда
74
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
Обращаясь к диаграмме зависимости между т0 и у0 (рис. 12),
заметим, что -~ есть угловой коэффициент касательной к кривой
деформирования в точке К(уд, т0). Эту величину называют
касательным модулем сдвига
тогда как величину Gs, угловой коэффициент луча,
проведенного из начала координат в точку К, часто называют секущим
модулем сдвига. Теперь выражение для defj можно переписать
следующим образом:
dt'ii "
-a)daij
Gt
G,
to
dx0. A5.2)
Рис. 12.
В дальнейшем нам будет удобно
пользоваться вместо величины т0
другой величиной, s, представляющей
собою корень квадратный из второго
инварианта девиатора тензора
напряжений:
Вместо изображающего пространства
тензора напряжений atJ- мы будем рассматривать изображающее
пространство девиатора напряжений аи, для простоты мы
сохраним его девятимерным, хотя, поскольку независимых компонент
девиатора всего пять, можно было бы рассматривать, как это
делают некоторые авторы, всего лишь пятимерное пространство.
Мы будем по-прежнему обозначать через а радиус-вектор
точки М в изображающем пространстве, но теперь только
компоненты вектора <г будут не а и, а а^. Величина s имеет простой
геометрический смысл, это есть длина вектора, изображающего
девиатор напряжений. В соотношении A5.2) т0 можно заменить
через s, и мы получим:
1/1 1
акЧ— о 7?
dat
On
— ds.
A5.2')
Проверим выполнение следствия A4.3) из постулата Друкера.
Поскольку материал принят несжимаемым, на перемещении defj
производит работу только девиаторная часть тензора напряжений,
следовательно, должно быть
da-tj defj > 0.
§15] О ГРАНИЦАХ ПРИМЕНИМОСТИ ДЕФОРМАЦИОННОЙ ТЕОРИИ 75
Внесем сюда выражения A5.2'). Получим:
da и defj =
1 ^ г л- ,1^1
1 Л °г/ rfao-
ds.
Но <Jij d<Jij = sds, таким образом,
/" 1 _J_^
ЙО",; rfefj =
С, СУ^^У + К^Г
tfs2
Это выражение положительно, когда G > Gs > (?г, что всегда
выполняется, если материал упрочняется монотонно и кривая
деформирования не имеет точек перегиба.
Таким образом, вытекающие из постулата
Друкера ограничения могут относиться лишь
к виду поверхности нагружения, отделяющей
область активной пластической деформации
от области разгрузки. Прежде всего,
очевидно, что поверхность нагружения не может
быть гладкой. Действительно, для гладкой
поверхности нагружения направление
вектора приращения пластической деформации
зависит только от вектора напряжения а, но
не от da. Второе слагаемое в формуле A5.2')
удовлетворяет этому условию,
действительно, при любом изменении ai} меняется
величина s и соответствующие составляющие
деформации de"j изменяются пропорционально Оц.
вое слагаемое зависит от da и непосредственно, а не через
величину s, поэтому направление вектора den зависит от da. Таким
образом, приходится предположить, что точка М является
угловой точкой поверхности нагружения. Итак, предположим,
что касательные к поверхности нагружения в точке М образуют
конус. Угол между какой-либо образующей конуса и радиусом-
вектором точки М пусть будет р* (рис. 13). Выберем приращения
напряжений такие, чтобы вектор da составлял угол а с вектором
ет, приращение пластической деформации будет составлять с
вектором а угол б. Условие того, что вектор приращения
пластической деформации лежит внутри конуса нормалей к поверхности
нагружения, сводится к выполнению следующего неравенства:
Рис. 13.
Однако пер-
Р + в<^
Положим теперь
a = sp, da — kdq, den—mdr.
A5.3)
A5.4)
76 ТЕОРИЯ ПЛАСТИЧНОСТИ [ГЛ. II
Единичные векторы р, к и т показаны на рис. 13. Полагая
временно
2"(с7~^) = Л' У kg7~~g7)==B'
запишем A5.2') в виде векторного равенства:
de» = Ado-\-B — ds.
s
Внесем сюда выражения A5.4), заметив предварительно, что
s ds = a da = sdq cos а. Получим:
mdr = (fcA-j- pB cosa)dq. A5.5)
Возводя в квадрат обе части равенства A5.5), найдем, что
dq 1
dr ~~ [А* + (В2-\-2АВ) cos2 a]1/2 '
Умножим теперь A5.5) на единичный вектор р. Получим:
cos б dr = (А -+- 7?) cos a dg.
Теперь мы можем написать выражение для cos б, а именно:
cos б = (A + B)cosa
[4а + (й2 4- 2AB) cos3 a]1 '2 '
Положим
А + В
N--
1
с*
1
G7
1
G
1
G
Предыдущая формула перепишется следующим образом:
с N cos а ,. г г>\
cos б = гг- . A5.Ь)
[1 + (JV2 — l)cos2a]1/2
Неравенство A5.3) можно заменить таким неравенством:
cos б > sin p
или
ГУ2 cos2 a . aR
Ц-(ЛГ2 —l)Cos2a >Sln P'
Перепишем последнее неравенство так:
№ _ tg2 p
¦ - ^ —
Отсюда следует:
tga<!p. A5.7)
§15] О ГРАНИЦАХ ПРИМЕНИМОСТИ ДЕФОРМАЦИОННОЙ ТЕОРИИ 77
Неравенство A5.7) не позволяет сделать каких-либо заключений
о виде поверхности нагружения в окрестности точки М, оно только
ограничивает выбор путей нагружения, для которых могут быть
справедливы соотношения деформационной теории. Угол р,
который мы будем называть углом пластичности в точке М, может
зависеть от напряжений а^, а также от истории загружения.
Неравенство A5.7) показывает, что уравнения деформационной
теории не противоречат постулату Друкера тогда, когда вектор
догрузки da направлен в область, ограниченную конусом,
образующие которого составляют угол а с радиусом-вектором точки М.
Если вектор приращения девиатора напряжений da направлен
внутрь поверхности нагружения, то есть внутрь конуса,
образованного касательными к поверхности нагружения, то происходит
упругая разгрузка. Если вектор догрузки выходит в область
пространства, находящуюся вне этих конусов, то закон связи
между приращениями напряжений и приращениями деформаций
должен быть установлен из каких-то дополнительных соображений.
Предположим теперь, что поверхность нагружения, по крайней
мере в окрестности точки М, определяется только координатами
этой точки, то есть вектором а, и не зависит от пути нагружения.
Конус пластичности будет при этом круговым конусом с осью,
проходящей через начало координат, так же как при
пропорциональном нагружении. Это рассуждение не является вполне
строгим. Действительно, формулировка деформационной теории
пластичности такова, что все составляющие изображающего
вектора напряжений совершенно равноправны и никаких элементов,
могущих внести асимметрию, в этих уравнениях не содержится.
Но поверхность нагружения должна быть определена независимым
образом и никаких ограничений на ее вид заранее наложить
нельзя. Поэтому сделанное предположение о том, что конус
пластичности является конусом вращения, не обязательно, хотя и
представляется довольно естественным. Поскольку наша задача состоит
в выявлении возможных границ применимости теории Надаи —
Хенки, тогда как установление истинных границ может
основываться только на данных опыта, и поскольку все равно более
определенные результаты можно получить лишь с помощью тех
или иных гипотез, мы будем вводить гипотезы наиболее простые
и наглядные. Предполагая зависимость поверхности нагружения
от координат точки М непрерывной, рассмотрим две ситуации,
возможные при переходе из точки М пространства девиатора
напряжений в бесконечно близкую точку М'. Конусы
пластичности в точках М и М' повернуты друг относительно друга на
бесконечно малый угол, разница углов пластичности также
бесконечно мала, поэтому можно считать, что образующие этих конусов
параллельны. В первом случае путь нагружения, соответствующий
переходу из М в М', лежит внутри поверхности нагружения для
78
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
точки М', обратный путь из М' в М представляет собою разгрузку.
Во втором случае отрезок ММ' лежит вне конуса пластичности
для точки М\ поэтому путь из М' в М сопровождается
пластической деформацией, что противоречит определению разгрузки.
Итак, если считать, что поверхность пластичности не зависит
от истории нагружения, то возможные пути нагружения следует
ограничить условием, что сс-<р\ Полагая в A5.7) а = р\ мы
найдем значение |50, для которого угол а является наибольшим,
а именно:
tgpo = A'1/2. A5.8)
Предположим теперь, что мы решили какую-то задачу теории
пластичности при помощи уравнений деформационной теории. Это
значит, что для каждой точки тела построен путь нагружения
и известен, следовательно, угол а, между радиусом-вектором точки
в пространстве напряжений (девиаторном) и касательной к пути
нагружения. С другой стороны, в каждой точке известна величина
N. Если а <С ро, причем E0 определяется формулой A5.8), то
применение деформационной теории к данной задаче может считаться
оправданным в том смысле, что требования постулата Друкера
не нарушаются.
§ 16. ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА
Высказанные соображения о возможных границах применения
уравнений деформационной теории пластичности и о
необходимости допущения в этом случае существования угловой точки на
поверхности нагружения имеют под собою и некоторое наглядное
физическое обоснование. Реальный поликристаллический материал
представляет собою конгломерат беспорядочно расположенных
кристаллических зерен, пластическое скольжение развивается
лишь по определенным, неблагоприятно расположенным
системам скольжения и сопровождается упругой деформацией.
Изменение вида напряженного состояния, то есть отклонение от
пропорционального нагружения, связано с тем, что, с одной стороны,
в пластическое состояние переходят новые элементы, с другой —
часть пластически деформированных элементов разгружается,
возвращаясь в упругое состояние. Ниже мы познакомимся с
некоторыми теориями пластичности, учитывающими структуру
материала, сейчас же обратимся к рассмотрению некоторой простой
модели, на которой можно выяснить общие свойства
упруго-пластических систем. По-видимому, эти свойства принадлежат и
упрочняющемуся пластическому телу. В связи с этим следует
напомнить, что свойства упрочняющегося материала при
растяжении могут быть моделированы с помощью стержневой системы,
состоящей из упруго-пластических элементов, материал которых
§ 16] ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 79
не обладает упрочнением. Известный пример такого рода
принадлежит Хенки [227].
В качестве модели упрочняющегося тела мы выбираем
круглую тонкостенную трубу из упруго-пластического материала,
не обладающего упрочнением. Труба изгибается двумя моментами
Мх и Му в перпендикулярных
плоскостях.
Обозначим радиус трубы R,
толщину стенки 6, модуль
упругости материала Е, предел
текучести о*т. Пропорциональным на-
гружением трубы мы будем
называть такое нагружение, когда Мх
и Му изменяются
пропорционально. В этом случае
нейтральная ось сохраняет свое
положение и, очевидно, достаточно
рассматривать изгиб трубы моментом
М = V Ml + Ml, приложенным Рис. 14.
в неизменной плоскости. Не
нарушая общности, можно считать, что действует только момент Мх
в плоскости yOz и нейтральной осью является ось х. Пока
напряжение нигде не превышает предела текучести, кривизна
изогнутой оси зависит от момента следующим образом:
М
к-.
лП3&Е
Пластические деформации возникают прежде всего в наиболее
удаленных от нейтральной оси точках сечения, то есть на оси у,
при увеличении момента образуются симметричные дуговые
пластические зоны, как показано на рис. 14 (зона АВ). Обозначим
через 9 полярный угол границы пластической зоны. Деформация
в точках А и В равна а?/Е, поэтому
кЯ sin 9 = % .
Если определять положение точки окружности полярным
углом 1)з, то в упругой зоне, при t|) < 9,
sini|)
sin 9
A6.1)
Вычислим теперь изгибающий момент в сечении по формуле
Я/2
м
= 4 \ 8а i?2 sin ij) (Щ\
80
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
при этом считаем, что в пластической области о = сгт, в
упругой—напряжение определяется формулой A6.1). После
интегрирования получим:
о9к 20 + sin26
Вместо моментов и изменений кривизн введем соответствующие
безразмерные величины:
М ЕВ., 1
Q =
Шо'г
ER ,
: К =
0™
Зависимость между Q и q будет следующей:
Q = nq в упругой области, при д<1,
Q—BQ^sia2Q)q в упруго-пластической области,
при <7>1.
A6.2)
На рис. 15 приведена диаграмма зависимости между Q ш q,
она очень похожа на диаграмму пластичности для
упрочняющегося материала. Величина Q является
при этом аналогом напряжения или,
лучше, девиаторной части
напряжения, тогда q представляет собою
соответствующую деформацию. Модуль
упругости G при этом равен я,
пластический модуль Gs равен 20+sin 20.
Рассматриваемая модель
соответствует телу с начальной изотропией.
Действительно, соотношения A6.2)
справедливы независимо от того,
в какой плоскости действует
изгибающий момент М; при увеличении
момента изгиб будет всегда происходить в той же плоскости.
Теперь нам легко вернуться к общему случаю, когда изгиб
происходит около произвольной оси и на трубу действуют
пропорционально возрастающие моменты Мх и Му. Соответствующие
кривизны будут кх и ку, при пропорциональном нагружении
всегда кх : ку = Мх : Му. Переходя к соответствующим
безразмерным величинам, мы можем написать:
Qx = Gsqx, Qy = Gsqy. A6.3)
Здесь Gs зависит от величины q — Уq% + q\ или, что то же, от
Q = VQI + Ql, если q < 1 и соответственно Q < я, в формулах
A6.3) нужно принять Gs = G = зт. Соотношения A6.3) являются
аналогами уравнений деформационной теории пластичности На-
даи — Хенки, Q% и q2 соответствуют квадратичным инвариантам
§ 16] ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 81
тензоров напряжений и деформаций, Q и q — аналоги октаэдри-
ческого сдвига и октаэдрического касательного напряжения.
Пространству девиатора напряжений соответствует плоскость.
Если по осям координат откладывать Qx и Qy, условие достижения
пластического состояния
Q=4
определит окружность в этой плоскости, которая соответствует
начальной поверхности текучести (рис. 16). Любой путь
пропорционального нагружения представляет
собою луч, выходящий из начала
координат.
Соотношения A6.3) были выведены
нами для случая пропорционального
нагружения, однако они справедливы
и для некоторых видов нагружения,
отличных от пропорционального.
Предположим, что мы произвели
пропорциональное нагружение до некоторого
значения нагрузки Q > я. Для простоты
предположим, что нагружение
происходило по оси Qx до точки М. Граница
пластической области в трубе при этом
определяется углом 0. Будем производить дальнейшее
нагружение, меняя не только Qx, но и Qy, которое равнялось нулю на
первом этапе нагружения. Нейтральной осью изгиба будет теперь
уже не ось х, а некоторая прямая пп' (рис. 14). В зависимости
от соотношения между Qx и Qv, то есть в зависимости от пути
нагружения, пластическая область АВ (и симметричная с ней
с другой стороны) может непрерывно увеличиваться, а может
произойти частичная разгрузка. В первом случае уравнения A6.3)
деформационной теории будут сохранять силу. Рассмотрим
крайний случай, когда точка А движется по направлению стрелки
в положение А', а точка В остается на месте. Если пластическая
зона стала А 'В, то нейтральная ось пп' должна быть
параллельная хорде А'В, угол между пп' и осью х мы обозначим через р.
Изгибающий момент относительно этой оси найдется по формулам
A6.2), если заменить в них 0 на 6 — р. Таким образом, мы получим:
Рис. 16.
<?* = <?(e-p)cosp, & = (>@-p)sinp.
A6.4)
Уравнения A6.4) представляют собою параметрические
уравнения предельного пути нагружения, выходящего из точки М,
для которого соотношения деформационной теории A6.3) еще
справедливы. Этот предельный путь схематически показан на
рис. 16. Симметричная кривая соответствует движению границы
К пластической области.
Ю. Н. Работнов
82
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ, II
В окрестности точки М
dQ
dQ
A<?*=^cosP(-AP)-<?sinpAp,
A<?„ = -§sinp(-AP) + <?cospAp,
а так как р мало, то
Заметим, что
ДОс=—ЖДР' Д<?» = <?ДР-
d9 _ dg d6- dg ?ctgo.
Величина -p- = 28 — sin 29 представляет собою касательный
модуль Gt на кривой деформирования (рис. 15). Теперь мы можем
записать:
AQX = - Gtq ctg 6 АР, AQy = Gsq Др.
Наклон предельных путей, проходящих через точку М, для
которых остаются справедливыми уравнения деформационной
теории, определяется следующим образом:
AQx _ , G« tgQ
A^-± С*80'
Соответствующий угол а равен -у при 9 = Ож 8 = у , его
минимальное значение, равное 76°28', достигается при 6 = 57°30'.
Выясним теперь условия разгрузки после пропорционального
нагружения. Очевидно, что и здесь упругая разгрузка возможна
не только за счет пропорционального уменьшения моментов,
необходимо, чтобы поворот сечения вследствие разгрузки
происходил относительно некоторой оси, не пересекающей
пластическую область. Назовем эту ось осью разгрузки. Предположим,
что было произведено пропорциональное нагружение по оси х
до величины безразмерного момента Q; в результате
дополнительного поворота относительно оси, составляющей угол ср с осью х.
производится разгрузка. Изменение безразмерных изгибающих
моментов вследствие разгрузки обозначим Q'x и Qy, так что в
процессе разгрузки
QX = Q-Q„ Qv=-Q'u.
Поскольку при разгрузке материал деформируется упруго, Qx
и Q'y являются составляющими момента, направленного по оси
разгрузки; следовательно, можно положить:
Qx— — mocoscp, Q'y—~ ясо sin ср.
I 16] ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 83
Изменение напряжения вследствие разгрузки в точке с
полярным углом if определится при этом следующей формулой:
о' = — соат sin (if — ф).
Если фиксировать значение ф и менять параметр со, то
разгрузка будет происходить по прямой, проходящей через точку М.
Уравнение этой прямой:
QX = Q — ncocostp, Qy=—яю sin ф. A6.5)
Напряжение при этом равно разности напряжения к моменту
разгрузки и напряжения о', а именно:
в = От [1 — со sin (if — ф)] @<а<!л — 0),
"sin4> „„-„л* _„лП m^^fl „ _fl^-m^„\ A6-6)
о =
От [|]^| — u3Sin(l|5 — ф)] (О<ф<0, Л — 0<ф<л).
Для того чтобы упругая разгрузка происходила во всем
сечении, необходимо, чтобы ось разгрузки не пересекала
пластической области, то есть чтобы было ф<10. Предельная прямая
разгрузки соответствует ф = 0 и
составляет угол 0 с осью Qx в точке М. Таким
образом, мы получили
картину,схематически изображенную на рис. 17. Область
I находится внутри контура нагруже-
ния, который заменяет на нашей модели
поверхность нагружения девятимерного
пространства; точка М является точкой
контура нагружения, что соответствует
конической точке гиперповерхности
нагружения. Угол с раствором 2а соответ-
ствует конусу возможных направлений
приращения девиатора напряжений, для
которых сохраняют силу уравнения деформационной теории
(область //). Прямые, проходящие через точку М под углом Р
к оси, образуют границу контура нагружения. Чтобы найти
весь контур, будем рассматривать прямолинейные пути разгрузки
A6.5) при ф < 0. Упругая разгрузка будет продолжаться до тех
пор, пока напряжение в какой-либо точке вновь не достигнет
предела текучести. Предположим, что это произойдет в точке
первоначально пластической области. Наибольшее по абсолютной
величине отрицательное напряжение по первой из формул A6.6)
получается, когда if — ф = у, это напряжение равно стт A —
— со). Приравняем его — ст, получим со = 2. Граница области
упругих деформаций определяется формулами A6.5), где нужно
принять со = 2 и считать ф переменной величиной:
Qx = Q — 2я cos ф, Qy— — 2jtsin<p.
6*
84
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
Это — уравнение окружности с радиусом 2я и центром в точке
М (Q, 0). Выясним теперь возможность появления пластических
деформаций при разгрузке в той области, которая оставалась
Рис. 18.
Рис. 19.
упругой при первом нагружении. Условие достижения
напряжением экстремального значения по второй из формул A6.6)
будет
. !Г со cos(ib —ro) = U.
Приравнивая это напряжение пределу текучести со знаком
минус, получим:
ii5A_(Bsin(lf_e)=_l.
sin 0 vr '
Возводя в квадрат и складывая вышенаписанные равенства,
мы исключим из них угол tj) и придем к соотношению между со,
Ф и 9, а именно:
1 '.Ш2_2(Й^Ф =1.
sin^e
smt
A6.7)
При выполнении этого условия уравнения A6.5) определяют
окружность с радиусом я и центром в точке, имеющей
координаты QX = Q-
sin 6
Qx-Q
, Q„ = 0. Действительно.
¦ЯСОСОЗф-
sin0 ' ' sin I
Qy= —яш sin ф.
Возводя в квадрат и складывая, мы получим, принимая во
внимание A6.7):
§ 16J ДВУМЕРНАЯ МОДЕЛЬ УПРОЧНЯЮЩЕГОСЯ ТЕЛА 85
Таким образом, контур нагружения ограничен двумя прямыми
и дугами одной окружности (первой) при6<43°30' и двух
окружностей при 0 > 43°30". На рис. 18 эти контуры построены для
некоторых значений 0.
Рассмотрим теперь изображающую плоскость деформаций
(рис. 19). Начальная граница пластичности изображается
окружностью g%-{-q\ = \, точке М соответствует точка N, абсцисса
1 г, „ АЧу AQy
которой есть д = -^-Q- . При упругой разгрузке -^- = -щ- ,
следовательно, предельные прямые упругой разгрузки составляют
угол 6 с осью абсцисс и касаются начальной окружности.
Найдем зависимость между приращениями величин qx, qy и Qx, Qy
в области, где справедливы уравнения деформационной теории.
Из A6.3) qx=-j^Qx- Будем считать, что Gs задано как функция
<?=
-VQI + QI
. Тогда
А?* = -
продифференцируем по
но
dq 1
dQ ~ Gf '
dq
lQ
поэтому
dQ \
Gs
+-<?«
— (-
dQ \.<
Q величину q-
1
~ Gs
"с7л
+ Q
1
~ Q
jL(.
dQ К,
а-
57>«
*&¦»
g7J '
~~g~;) •
Получим:
Внося в выражение для Aqx, получим:
Gt Gs J Q*
Аналогично
Aqy=---^AQy+(-L--L^(QxAQx + QyAQy).
В окрестности точки М нужно принять QX = Q и Qy = 0, таким
образом,
Отношение приращений деформаций:
±M = ^L^1L A6.8)
Aqy Gs AQX ¦ ч
Для предельных направлений деформационной теории, когда
86
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ, II
&QX : AQy = — tg 9, мы получим:
Таким образом, уравнения деформационной теории сохраняют
силу тогда, когда приращения деформаций находятся внутри
внешнего угла, образованного касательными к начальной кривой
течения (область // на рис. 19). Некоторые другие выводы,
следующие из рассмотрения приведенной модели, будут сообщены в § 20.
§ 17. ТЕОРИИ ТЕЧЕНИЯ ПРИ ГЛАДКОЙ
ПОВЕРХНОСТИ НАГРУЖЕНИЯ. ИЗОТРОПНОЕ УПРОЧНЕНИЕ
Возможность расширения границ применимости
деформационной теории, вытекающая из исследования Будянского [17в ] и
проиллюстрированная нами с помощью простой модели, выявлена
совсем недавно. Очевидные противоречия, к которым приводит
эта теория, вызвала развитие теорий, основанных на
принципиально ином подходе. Если деформационная теория
пластичности принимает за отправной пункт нелинейную теорию
упругости и представляет собою ее обобщение на случай неупругого
материала, то в теориях течения устанавливаются связи между
приращениями деформаций и напряженным состоянием. Принимая,
что напряженное состояние меняется в зависимости от какого-либо
монотонно возрастающего параметра, можно назвать этот параметр
временем и вводить в рассмотрение скорости деформации; при этом
следует помнить, что выбор масштаба времени для теории
пластичности, в отличие от теории ползучести, никакой роли не играет.
Вводя понятие о поверхности нагружения, мы оставили
совершенно в стороне вопрос о том, каким образом меняется эта
поверхность при пластической деформации. Поверхность, проходящая
через точку М, может зависеть не только от координат этой точки,
то есть от напряжений, но также от деформаций, притом сколь
угодно сложным образом; эта зависимость может учитывать тот
или иной путь нагружения, приводящий в точку М.
Предположим, что уравнение поверхности нагружения,
проходящей через точку М, может быть записано в виде
/(с-о-)-?2 = 0.
Функция / (otj) и постоянная к2 могут зависеть от
деформаций, а также любым сколь угодно сложным образом от путей
нагружения и деформирования. Если напряжения получают
приращения datj, притом такие, что
§ 17]
ТЕОРИИ ТЕЧЕНИЯ
87
то происходит пластическая деформация de^j. В § 14 было
показано, что вектор приращения пластической деформации
направлен по нормали к поверхности нагружения, поэтому можно
написать:
"п л df
eii = Л-^ .
1 Эоц
Здесь мы перешли от приращений к скоростям в соответствии со
сказанным выше. Для того чтобы уточнить вид множителя X,
сделаем предположение о линейной зависимости между defj
и dGjj. Это значит, что мы предполагаем справедливым для малых
приращений напряжений и пластических деформаций принцип
линейной суперпозиции. Друкер [1в6] показал, что эта гипотеза
не является необходимой, а вытекает из постулата пластичности,
однако мы не будем приводить это доказательство. В соответствии
с предложенной гипотезой мы можем разложить приращение
вектора ff на две составляющие: da', направленную по касательной
к поверхности нагружения, и da", направленную по нормали.
Первая составляющая соответствует нейтральному нагружению,
которое не вызывает пластической деформации. Следовательно,
приращение пластической деформации может зависеть только
от нормальной составляющей вектора da, которая
пропорциональна величине —J— da^. Поэтому множитель X должен быть тоже
пропорционален этой величине. В результате получим:
Ъ-Въкш*»' A7Л)
Величина Н в формуле A7.1) может быть функцией напряжений
и деформаций, а также зависеть от путей нагружения и
деформирования, так же как функция /. Заметим, что вместо функции
нагружения / в формулу A7.1) можно ввести любую функцию от /,
поскольку мы располагаем свободой выбора функции Н.
Самое простое из возможных предположений заключается
в том, что функции / и Н зависят только от второго инварианта
девиатора напряжений. В силу сделанного замечания можно
принять
Тогда
fz=Sii = Su—з"^1-
д} =2(ои-о61}) = 2о>
dot
ij-
Выражение -^— a hi представляет собою производную по
времени от /, то есть от Su, или, если перейти к октаэдрическому
88
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
напряжению,
/ = Sn = 6т0т0.
Внося все это в A7.1), мы найдем:
% = Ъф (т0) t0. A7.2)
Уравнения такого типа были предложены Прагером в [зм].
В случае пропорционального загружения мы можем принять
за параметр нагружения или за время в том смысле, в каком
это было разъяснено вначале, величину х0. Условие
пропорционального нагружения состоит в том, что сгу/т0 = const, поэтому
уравнения A7.2) можно проинтегрировать, а именно:
То
«Ъ = о-у •— \ x0h (т0) d%Q,
т^о J
о
Сравнивая эти формулы с уравнениями A5.1)
деформационной теории, мы убеждаемся, что они совпадают, причем
to
1С 1/1 1 \
— ] t0fe(T0)dT0 = T^-g-y .
о
Таким образом, из уравнений A7.2) следует существование
единой диаграммы зависимости между т0 и у0, справедливой для
пропорционального нагружения. Умножая на т0 и
дифференцируя, получим после очевидных преобразований:
^o) = ^(i-4). A7-3)
Таким образом, функция h (т0) легко находится, если известна
диаграмма пластичности, полученная при каком-либо одноосном
деформировании образца из данного материала. Добавляя
упругую деформацию и используя A7.3), мы можем написать
уравнения теории течения следующим образом:
^ = ^Су + з4*6у+%(^-^) • A7.4)
При выводе соотношений A7.1) мы считали, что функция /
сохраняет свой вид в процессе пластического нагружения, тогда как
величина к меняется таким образом, что поверхность нагружения
все время проходит через точку нагружения, изменяясь с
сохранением подобия. Как мы видели в § 15, для несжимаемого
материала, пластическое поведение которого не зависит от первого
инварианта тензора напряжений, вместо пространства напряжений
§ 18] ТЕОРИИ ТЕЧЕНИЯ С ТРАНСЛЯЦИОННЫМ УПРОЧНЕНИЕМ 89
можно рассматривать пространство девиатора напряжений; в этом
пространстве поверхность Sn = к2 представляет собою сферу
с центром в начале координат, радиус которой непрерывно
увеличивается. Пластическое тело, свойства которого описываются
подобным образом, называется телом с изотропным упрочнением.
Если в процессе деформирова~
ния было достигнуто значение
октаэдрического напряжения т'0
и произведена разгрузка, то при
повторном загружении по
любому пути пластическое
состояние будет достигнуто, когда|
октаэдрическое напряжение
станет равным величине т'0. В
частности, растяжение образца
повышает предел текучести при
сжатии. Это следствие из урав- Рис. 20.
нений A7.1) противоречит
наблюдаемому на опыте эффекту, называющемуся эффектом
Баушингера. Этот эффект состоит в том, что повышение предела
текучести при растяжении сопровождается уменьшением предела
текучести при сжатии. Согласно простейшей идеализированной
схеме, предел текучести при сжатии уменьшается настолько,
насколько увеличился предел текучести при растяжении. Желая
построить уравнения теории типа течения, учитывающие
идеальный эффект Баушингера, мы должны допустить, что поверхность
нагружения перемещается параллельно самой себе, следуя за
точкой нагружения. На рис. 20 схематически показаны последующие
поверхности нагружения для случаев изотропного упрочнения (а)
и идеального эффекта Баушингера (б), начальная поверхность
нагружения принята одной и той же.
§ 18. ТЕОРИИ ТЕЧЕНИЯ С ТРАНСЛЯЦИОННЫМ УПРОЧНЕНИЕМ
Упрочнение материала, описываемое при помощи
поступательно перемещающейся поверхности нагружения, сохраняющей свою
форму и размеры, и соответствующее идеальному эффекту
Баушингера, мы будем называть трансляционным упрочнением. Если
уравнение начальной поверхности нагружения было / (atj) =
= к2, то при параллельном переносе уравнение последующей
поверхности нагружения будет
f{°ij-stj) = №. A8.1V
Здесь Sij — тензор, составляющие которого в пространстве
напряжений являются координатами центра поверхности нагружения.
Тензор s^, очевидно, должен быть связан с пластическими дефор-
•90
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
-мациями. Простейшее предположение (Ишлинский [46]) состоит
в том, что считается
stj = a$} A8.2)
и в качестве функции / (а и) принимается второй инвариант девиа-
тора. При одноосном напряженном состоянии уравнение A8.1)
прямо устанавливает линейную зависимость между напряжением
и пластической деформацией; таким образом, это — уравнение
теории пластичности с линейным упрочнением.
Независимо от Ишлинского и одновременно с ним Прагер [ззь)
предложил аналогичную гипотезу, названную гипотезой
кинематического упрочнения, потому что она может быть
проиллюстрирована на простой кинематической модели. Для наглядности
обратимся к двухмерному случаю, тогда поверхности нагружения
соответствует контур нагружения. Представим себе, что по
форме контура нагружения изготовлена рамка, которая может
свободно перемещаться по плоскости напряжений, причем только
поступательно; устроенные каким-либо способом направляющие
предотвращают ее поворот. В плоскости движется палец,
воспроизводящий путь нагружения. Если между пальцем и рамкой нет
трения, то при перемещении пальца в произвольном направлении,
составляющем острый угол с направлением внешней нормали
к контуру рамки, последняя переместится по направлению
нормали; таким образом, перемещение центра рамки будет
направлено так же, как приращение пластической деформации.
Остается предположить, что это перемещение
пропорционально величине приращения пластической деформации, то есть
принять соотношение A8.2). Соображения, развитые для плоской
модели, нужно теперь перенести в девятимерное пространство.
Заметим, что при рассмотрении отдельных частных задач теории
пластичности вместо всего пространства напряжений можно
рассматривать подпространства с меньшим числом измерений. Так,
например, плоское напряженное состояние характеризуется тремя
напряжениями,, следовательно, достаточно рассматривать
трехмерное пространство напряжений, а если иметь дело с главными
напряжениями — то и двухмерное, для которого описанная
кинематическая модель Прагера, казалось бы, может быть
непосредственно применена. Однако при плоском напряженном состоянии
деформация не будет плоской и использование двухмерной
кинематической модели может привести к неверным результатам, как
показал Будянский (см. дискуссию по статье Прагера [335]).
Более детальное исследование вопроса о форме закона
кинематического упрочнения в тех или иных подпространствах
пространства напряжений содержится в статье Шилда и Циглера [351].
Отметим еще один вариант гипотезы трансляционного
упрочнения, предложенный Циглером [зв6]. Тензор stj определяется
§ 19] СИНГУЛЯРНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ 91
по этой гипотезе следующим образом:
Sij = P{<*ij — Sij).
При вц = 0 соответствующее stj также равно нулю, поэтому
кинематическая модель сохраняется в любом подпространстве
пространства напряжений. Более общая точка зрения была
развита Кадашевичем и Новожиловым [48]. Эти авторы принимают, что
тензоры stj и efj связаны соотношениями типа соотношений
деформационной теории пластичности, а именно:
4=2^. A8.3)
Здесь G* — функция инвариантов тензора Sij. При
рассмотрении конкретных примеров авторы считали, как это делается в
теории пластичности Надаи — Хенки, что G* зависит только от
второго инварианта девиатора тензора Sfj.
Существенная нелинейность соотношений A8.3) позволила
авторам гораздо лучше описать поведение реального материала;
сравнение предсказаний теории с некоторыми экспериментами
дало очень хорошее совпадение.
§ 19. СИНГУЛЯРНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ
Выше, при обсуждении границ применимости теории
пластичности, мы убедились в том, что последующие поверхности нагру-
жения могут быть сингулярными; возникновение конических точек
на поверхности нагружения в точке нагружения было
проиллюстрировано с помощью наглядного модельного представления. К
особенностям такого рода приводят некоторые новые теории
пластичности, мы рассмотрим их ниже. Здесь будет идти речь об
особенностях другого рода. Уже начальная поверхность нагружения
может состоять из частей нескольких гладких поверхностей,
образующих при пересечении ребра. На ребрах направление
нормали к поверхности нагружения неопределенно; поэтому
о направлении приращения вектора пластической деформации
можно сказать только то, что он лежит в плоскости, нормальной
к ребру, и заключен между нормалями к поверхностям,
пересечение которых образует ребро. В процессе пластической деформации,
сопровождающейся упрочнением, поверхность напряжения либо
расширяется с сохранением подобия, либо перемещается
параллельно себе. При этом, в отличие от рассмотренного ранее случая,
новые особенности не появляются, гладкие участки поверхности
нагружения остаются гладкими. Наиболее простой и
естественный пример такой сингулярной поверхности нагружения мы
получим, если попытаемся обобщить известную теорию пластичности
Сен-Венана — Треска на случай упрочняющегося материала.
92
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. 11
Критерием достижения пластического состояния в этой теории
является величина наибольшего касательного напряжения. Будем
считать, что величина наибольшего касательного напряжения
определяет и вторичный предел текучести, то есть условие
перехода в пластическое состояние при повторной нагрузке, после
того как были произведены пластическая деформация и разгрузка.
Уравнение поверхности нагружения будет следующим:
lmax — "¦ •
Постоянная к выбирается каждый раз так, чтобы поверхность
проходила через точку нагружения. Выражение наибольшего
касательного напряжения через компоненты тензора напряжения
в общем случае чрезвычайно сложно и практически бесполезно;
теория типа Сен-Венана обнаруживает свои преимущества только
в том случае, когда нам заранее известны главные направления
и вместо девятимерного пространства напряжений можно
рассматривать трехмерное пространство главных напряжений. Если
o"i > 0*2 > о, то тшах = '~ 3 и условие постоянства тшах
записывается так:
01_а3 = ±2А;. A9.1)
Это — уравнение пары плоскостей, параллельных оси 2. В
пространстве главных напряжений мы не можем связывать оси с величинами
ai, о2 и 03» не нарушая неравенства 0!>02>0з; поэтому мы
обозначим главные напряжения Oj, ац и 0^; в разных точках
пространства главных напряжений соотношения между ними
различны, и в соответствии с этим то или иное напряжение должно
быть названо 0\, 02 и 03. Вместо одного условия A9.1) мы получаем
шесть условий:
01 — 0„ = ± 2ft,
огт, — <Ч = ± 2й, A9.2)
о?-ст? = ± 2ft.
Шесть плоскостей, удовлетворяющих уравнениям A9.2), образуют
шестигранную призму, которая и будет поверхностью нагружения.
Предположим, что мы находимся на грани призмы,
соответствующей первому из условий A9.2), когда / = 0| — 0^- Производные
от функции / будут ^=1, ^Г= — 1, ^- = °-По Формуле A7.1)
получаем:
е|[ = Я@| — а„),
е^= — Я@? — 0П),
« = 0.
A9.3)
Естественно предположить, что функция Н зависит в свою очередь
$ 19] СИНГУЛЯРНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ 93
Рис. 21.
от наибольшего касательного напряжения, то есть от величины
Cg — an; тогда соотношения для скоростей пластической
деформации могут быть проинтегрированы, и мы получим:
в5=Л(оЕ — а„),
е?=-й(а6-ач), A9.4)
«? = 0-
Таким образом, хотя в основу были положены соотношения теории
течения, в результате получаются конечные формулы связи между
пластическими деформациями и
напряжениями, как и в деформационной
теории пластичности. Механический смысл
формул A9.4) очень прост и совершенно
очевиден: пластическая деформация
представляет собою чистый сдвиг в
плоскости |<2г], величина этого сдвига при
активной пластической деформации
зависит однозначно от величины
соответствующего касательного напряжения, эта
зависимость сохраняется до тех пор, пока
соблюдается неравенство 0|>стЕ>оГ1.
Как только это неравенство
нарушается, за максимальное и соответственно минимальное напряжение
нужно будет принять другую пару из трех напряжений о-|, <зц
и а?, формулы A9.3) будут справедливы уже для других индексов.
Их опять-таки можно проинтегрировать. Предположим, например,
что мы вышли на грань поверхности нагружения сг? — стг =
= ± 2к. Тогда, интегрируя соотношения, аналогичные
соотношениям A9.3), мы получим:
ef = ft (<xt—at) + ef',
П П'
eT| — ef\ i
e\= — A(at —oc).
Здесь штрихами отмечены пластические деформации,
накопленные в течение того времени, когда точка нагружения находилась
на грани о5 — ап = ±2к, и вычисленные по формулам A9.4).
Особого рассмотрения требует случай, когда точка нагружения
остается на ребре поверхности нагружения. Предположим,
например, что aj = o\,>o"?, тогда одновременно выполняются два
условия: о"| — cTj = ±2к и ст„ — о*? = ± 2к. На рис. 21
показано сечение призмы в окрестности ребра октаэдрической
плоскостью, в этой плоскости лежат нормали к поверхности призмы.
Нормали к граням призмы в точке ребра образуют угол, внутри
94
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
которого лежат возможные направления приращения
пластической деформации. Вектор, лежащий внутри этого угла, может
быть представлен как линейная комбинация из векторов крайних
нормалей с положительными коэффициентами. Скорость
пластической деформации, вектор которой нормален к первой плоскости
°i — ai = + 2fc, будет
Точно так же скорость, нормальная ко второй грани оц—а^=-{-2к,
еп .-_. о, е° = Я2{av — at), еъ= — Н2(ац — <rt).
Складывая эти скорости, получим:
Нх(а% — ot),
Я2К — аг),
_(Я1 + Я2)(а,_а?).
Здесь вместо ап написано сГ|. Величина (Я4 + Я2) должна
рассматриваться как функция cf| — о*?. Действительно, данный
случай, когда о"? = ац, представляет собою, по существу, одноосное
сжатие. Поскольку мы считали, что пластическая деформация
не зависит от гидростатической части тензора напряжения,
приложим к телу всестороннее сжатие интенсивности —о^. Тогда
напряжения по осям ? и т} станут равными нулю, в направлении L
останется сжимающее напряжение — (о*| —- сг?). Деформация в
направлении оси ? будет однозначно зависеть от этого напряжения,
а именно: е? = — h (оч — о*?). Но это соотношение должно
получиться в результате интегрирования последнего из
вышеприведенных уравнений течения. Окончательный результат может быть
записан в следующем виде:
<?с=—й(<** — <*;). ^ = ЯЛ(<г5 —<тс), <г„ = A-Л)й(<г6 —<rt). {19.5)
В соотношениях A9.5) остается неопределенным параметр X.
Значение его состоит в том, что условие в% = an ограничивает
выбор возможных напряженных состояний; для того чтобы при
этих условиях уравнения совместности деформаций были
выполнены, необходимо иметь известную свободу деформации. С другой
стороны, некоторые следствия из вывода о неопределенности
деформаций в сингулярной точке поверхности нагружения
противоречат опыту. Так, при простом растяжении или сжатии поперечные
деформации могут быть какими угодно, лишь бы выполнялось
условие постоянства объема. Этот физически неприемлемый
результат является неизбежным следствием далеко идущей схематизации
п
§ 19] СИНГУЛЯРНЫЕ ПОВЕРХНОСТИ НАГРУЖЕНИЯ 95-
действительного положения дел. Реально можно было бы,
вероятно, говорить о значительной неустойчивости поперечной
деформации при растяжении или сжатии. Это значит, что, прикладывая
малые поперечные напряжения в каком-либо поперечном
направлении, мы достигнем того, что вся поперечная пластическая
деформация будет происходить в том же направлении. Опытов
подобного рода не существует, и нам представляется более правильным
смотреть на теорию течения с кусочно-линейной поверхностью'
нагружения как на аппроксимацию
физически более реальной теории,
основанной на гладкой поверхности
нагружения. Как всегда, можно
указать крайние следствия из принятой
аппроксимации, явно противоречащие
опыту и здравому смыслу, но во
многих случаях результаты расчета
по такой кусочно-линейной теории
достаточно хороши и погрешность их
с избытком окупается несравненной
простотой.
Мы не будем здесь рассматривать
в деталях вопрос о модели
трансляционного упрочнения при
сингулярной поверхности нагружения.
Простая схема, приведенная на рис. 22 (Ходж [22]),
иллюстрирует разницу между кинематическим и изотропным упрочнением
в двухмерном случае. Цифрой 1 отмечена начальная
поверхность нагружения, прямая ОРМ представляет собою путь
нагружения. При изотропном упрочнении шестиугольник,
изображающий поверхность нагружения, равномерно расширяется,
положение точки М при пропорциональном' нагружении остается
неизменным по отношению к вершинам шестиугольника, меняется
только масштаб. Вектор приращения пластической деформации
все время направлен по нормали к той стороне шестиугольника,
на которой находится точка М; таким образом, вектор полной
пластической деформации всегда направлен по оси абсцисс. Если
упрочнение линейно, то величина пластической деформации
пропорциональна изменению линейного размера поверхности
нагружения. В случае трансляционного упрочнения начальная
поверхность нагружения сначала движется вправо до тех пор, пока
точка нагружения не достигнет точки Р. Соответствующее
положение поверхности нагружения показано пунктиром. На
участке ОР пути нагружения предсказания теории изотропного
упрочнения и теории трансляционного упрочнения в отношении
величины и направления вектора пластической деформации совпадают.
На отрезке РМ пути нагружения поверхность нагружения.
96
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
движется в том же направлении таким образом, что вершина
шестиугольника остается все время на пути нагружения. Цифрой 3
отмечено положение поверхности нагружения в точке М. Радиус-
вектор s центра шестиугольника изображает в некотором масштабе
величину пластической деформации, если упрочнение считается
линейным. Мы не будем выводить соответствующие формулы для
пластической деформации, заметим только, что для вычисления
деформаций, например, в случае плоского напряженного
состояния нельзя ограничиться двухмерной моделью, а необходимо
рассматривать движение поверхности нагружения в девятимерном
пространстве, как уже было указано в § 18. Детальное
исследование этого вопроса содержится в статье Хуан Кэ-чжи [144].
Использование в качестве поверхности нагружения призмы
Сен-Венана не является единственным примером применения
кусочно-линейной функции нагружения в теории пластичности. При
решении конкретных задач обычно некоторые из напряжений
можно принять равными нулю, таким образом, нам достаточно
рассматривать подпространство пространства напряжений. Далее,
иногда оказывается возможным заранее предугадать изменения
напряжений, то есть выделить в пространстве напряжений область,
в которой располагаются пути нагружения. Гладкая поверхность
всегда может быть с большей или меньшей степенью точности
аппроксимирована при помощи многоугольника. Общая теория
пластического течения, основанная на такой произвольной
линейной аппроксимации поверхности нагружения, развита
Ходжем [23а].
Следует заметить, что гипотеза трансляционного упрочнения
в случае пропорционального нагружения не приводит к
уравнениям деформационной теории. Эта оговорка необходима в связи
с распространенным мнением об универсальной значимости
деформационной теории для пропорциональных нагружений.
§ 20. ТЕОРИЯ СКОЛЬЖЕНИЯ
Рассмотренные до сих пор теории пластичности основывались
на гипотезах формального характера, реальная структура
металла совершенно не принималась во внимание при выборе этих
гипотез. Такой подход имеет свои преимущества и недостатки.
С одной стороны, общие законы пластичности, сформулированные
для произвольного тела безотносительно к его физической
природе, позволяют охватить единой теорией вопросы пластичности
металлов, предельного равновесия грунтов, хрупкого разрушения
бетонных конструкций и так далее. С другой стороны, при
конкретизации этих общих законов для описания той или иной реальной
среды мы бываем вынуждены пользоваться результатами
макроэксперимента, описывая явление, но не объясняя его. В 1949 г.
^ 20]
ТЕОРИЯ СКОЛЬЖЕНИЯ
97
Батдорфом и Будянским |164] была предложена новая теория
пластичности, названная ими теорией скольжения. Основная
идея этой теории состоит в следующем. Реальный металл
представляет собою конгломерат беспорядочно расположенных
кристаллических зерен. Пластическая деформация единичного кристалла
происходит за счет сдвига в определенной кристаллографической
плоскости в определенном направлении. Пусть п — нормаль
к плоскости скольжения, р — направление скольжения в этой
плоскости. Совокупность двух единичных векторов п и р*
определяет то, что называется системой скольжения. Если касательное
напряжение тпр в плоскости п по направлению р" превышает
напряжение предела текучести, кристалл пластически деформируется,
причем эта деформация представляет собою деформацию чистого
сдвига Y„p. Величина уп$ является совершенно определенной
функцией тпр. В реальных кристаллах всегда имеется несколько
возможных систем скольжения, которым соответствуют плоскости
наиболее плотного расположения атомов и направления, для
которых расстояния между соседними атомами наименьшие. Так,
в кристаллах с кубической гранецентрированной решеткой
имеется 12 систем скольжения. Обычно скольжение происходит
в нескольких системах одновременно, при этом сдвиг,
происшедший в одной системе скольжения, оказывает упрочняющее
действие на другие системы. Таким образом, механизм пластической
деформации, сопровождающейся упрочнением, достаточно
сложен даже для единичного кристалла. Простейшая схема, принятая
Батдорфом и Будянским, состоит в том, что для каждого зерна
предполагается существование только одной системы скольжения.
Если в теле создано некоторое напряженное состояние, то при
достаточно большой величине напряжений в некоторых зернах
касательное напряжение в системе скольжения окажется больше
предельного, и зерно претерпит пластическую деформацию сдвига.
Действительная картина будет достаточно сложной: для того чтобы
деформация могла произойти фактически, нужно, чтобы соседние
зерна этому не препятствовали. Макроскопический эффект
пластической деформации тела в целом будет обнаружен, когда
возникнут цепочки пластически деформированных зерен. На
начальной стадии деформации можно предполагать, что некоторые
блоки останутся в упругом состоянии, перемещаясь и
поворачиваясь как целое. Отсюда — большая неоднородность
пластической деформации, особенно у слабо упрочняющихся материалов,
сопровождаемая локализацией сдвигов в некоторых областях I37].
В теории скольжения эти трудности обходятся путем введения
некоторых простейших гипотез. Зафиксируем по произволу
два взаимно перпендикулярных направления и и р. Если число
кристаллических зерен в рассматриваемом объеме велико, то
всегда найдется некоторое количество зерен, для которых нормаль
7 Ю. Н. Работнов
98
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
к плоскости возможного скольжения (по предположению,
единственной) находится внутри конуса с осью п и телесным углом
dQ (рис. 23). Будем называть эти зерна зернами с плоскостью
скольжения п. Поскольку, если материал первоначально
изотропен, распределение зерен в металле случайно, и никаких
предпочтительных направлений не существует, относительный объем
зерен с плоскостью скольжения п в общем объеме тела, находя
щегося в условиях однородного напряженного
состояния, пропорционален dQ. Если число зе
рен с плоскостью скольжения п в свою очередь
велико, то среди них найдутся такие, у
которых направление скольжения лежит внутри
угла сф с биссектрисой (J, относительный объем
их пропорционален d$. Таким образом, объем
зерен, имеющих систему скольжения п$, про
порционален dQ d$. В системе скольжения ггр
действует касательное напряжение тпр, соответ-
Рие. 23. ствующие зерна претерпевают деформацию
чистого сдвига y?„ = F (tng). Теперь предлагается
гипотеза о том, что деформация зерен с системой скольжения п§
вызывает такую же общую деформацию тела, пропорциональную
относительному объему соответствующих зерен, а именно:
dy^ = F(ln9)dQd$.
Итак, деформация тела в целом представляет собою резуль
тат наложения бесконечно большого числа чистых сдвигов для
всех возможных систем скольжения мр. Чтобы вычислить эту
деформацию, перейдем к составляющим тензора деформации отно
сительно фиксированных осей xt, x2, х3 по формулам преобразо
вания составляющих тензора второго ранга A.7). Принимая
направления п и Р за направления 1 и 2 новой системы координат,
1
мы должны принять все е13 равными нулю, кроме ei2 = у упр-
Тогда
Но Pi; — п-,, р2г = Рь следовательно,
de*. = | (п& + »jpO F (тлР) dQ dp.
Формулы для деформаций будут следующими:
^2
еЪ = т\ \ (л^'+пМFыdQ^-
Q Jit
2
B0.1)
§ 20)
ТЕОРИЯ СКОЛЬЖЕНИЯ
99
Касательное напряжение при этом вычисляется по формуле
¦tnt — otjnfij. B0.2)
Для фактического вычисления деформаций направления п
и Р задаются при помощи эйлеровых углов, по которым и ведется
интегрирование. Основная трудность состоит здесь в том, что*
F {%) отлична от нуля при т > тт, следовательно, интегралы
в формулах B0.1) распространяются не на всю поверхность сферы
единичного радиуса, а на некоторую ее область. В первой статье
Батдорфа и Будянского была решена задача об определении
функции F по заданной кривой растяжения. Считая, что растяжение
происходит вдоль оси 1, мы получим по формуле B0.2) тпр =
= CThWiPj, а так как пластическая деформация происходит тогда,
когда тпр > тт, то должно быть
о и
Это условие определяет область интегрирования. Авторы
предположили, что функция F (т) имеет вид
1
Тогда зависимость пластического удлинения от нормального
напряжения будет
Функции ga были вычислены путем весьма трудоемкого
численного интегрирования для случая N = 5.
Согласно теории скольжения, начало пластической
деформации связано с тем, что в какой-то из систем скольжения будет
достигнут предел текучести; таким образом, начальная
поверхность нагружения соответствует условию максимального
касательного напряжения Треска. Действительно, если ттах = тТ,
то всегда найдется группа кристаллических зерен, для которых
это напряжение будет касательным напряжением в системе
скольжения. Для последующих поверхностей нагружения точка
нагружения будет конической точкой. Исследования, основанные на
уравнениях B0.1), чрезвычайно сложны; Чикала [184] удалось
довести до конца анализ простейшего случая, когда тонкостенный
трубчатый образец сначала растягивается, а потом закручивается.
Не воспроизводя выкладок, которые достаточно трудны, мы
приведем лишь окончательные результаты. Поскольку в опыте
участвуют два напряжения, результаты можно представить в плоскости
7*
400
ТЕОРИЯ ПЛАСТИЧНОСТИ
Ггл. и
с координатами о* и т (рис. 24). Начальная поверхность
нагружения представляет собою эллипс, уравнение которого
о2 + 4т2 = const.
Рассмотрен следующий путь нагружения: по оси абсцисс из
точки О в точку М и далее по лучу, выходящему из точки М.
Оказалось, что касательные к начальному эллипсу, проведенные
из точки М, делят плоскость а — т на 4 области. Если
приращения напряжений таковы, что
точка нагружения попадает в
область /, то происходит
упругая разгрузка. Приращения
пластических деформаций при
приращении напряжений,
соответствующих области //,
определяются по формулам деформа-
р 24 ционной теории пластичности;
наконец, для путей
нагружения, идущих в областях /// и
IV, соотношения между напряжениями и деформациями
получаются по формулам B0.1) в довольно сложном виде.
Законченный результат получен автором для ортогональной догрузки, то
есть такой, когда путь нагружения из точки М направлен
ортогонально к ОМ; это значит, что дополнительное закручивание
происходит при неизменной растягивающей силе. Для этого случая
^-0,-|+»аЛ «у ,20-3)
Сравнение с опытом, которое производилось многими авторами,
показывает, что формула B0.3) дает для G* заниженный
результат РЧ, I1"].
Качественная картина, полученная Чикала, весьма похожа
на ту, которая была найдена нами для модели, рассмотренной
в § 16. Расположение областей, показанное на рис. 24,
совершенно аналогично расположению их на рис. 19; правда, рис. 19
относится к плоскости деформаций; в плоскости напряжений
стороны углов I ш II же являются продолжениями друг друга
и не касаются начальной кривой. Такое сходство качественных
результатов не должно вызывать удивления. Теория Батдорфа —
Будянского, так же как и рассмотренная модель, представляет
тело в виде собрания упруго-пластических элементов, наделенных
простейшими свойствами; в теории скольжения таким элементом
является идеализированное кристаллическое зерно с одной-един-
ственной системой скольжения. Поскольку при активной
пластической деформации касательное напряжение и сдвиг связаны
§ 21J
МОДЕЛЬ ПЛОСКОГО ТЕЛА
101
однозначной функциональной зависимостью, то поведение тела
в целом будет описываться некоторыми уравнениями типа
уравнений деформационной теории до тех пор, пока во всех элементах
будет происходить активная пластическая деформация. При
увеличении напряжения в пластическую деформацию могут
втягиваться новые элементы, но разгрузка тогда происходить
не должна. Такое положение соответствует догрузке внутрь
угла //. При догрузке в областях /// и IV часть элементов
догружается, в пластическую деформацию могут втягиваться новые
элементы, однако некоторые из пластически деформированных
элементов разгружаются и возвращаются в упругое состояние.
Этим определяется сложность анализа для областей III и IV.
Теория скольжения Батдорфа — Будянского, в общем, не
подтвердилась на опыте, что признают и сами авторы [165], хотя она
предсказывает некоторые качественные эффекты, количественные
результаты оказываются не вполне удовлетворительными. Однако
основная идея этой теории в различных формах развивается
рядом авторов. Необходимо отметить, что еще в 1938 г. Тейлор [370]
сделал попытку связать свойства поликристаллического агрегата
со свойствами составляющих его зерен. Основная мысль при
этом состояла в том, что произвольная деформация, не
сопровождающаяся изменением объема, может быть представлена как
результат сдвигов в пяти системах скольжения, а так как число
систем скольжения в кристаллическом зерне больше пяти, то
деформация его может осуществляться различными способами.
Дальнейшее развитие идей Тейлора содержится в работе Бишопа
и Хилла [т], сюда же примыкает вариант теории скольжения,
разработанный Лином I285], I285].
§ 21. МОДЕЛЬ ПЛОСКОГО ТЕЛА
Значительная сложность уравнений теории скольжения B0.1)
почти исключает возможность их практического использования.
Фактическое применение теории к расчетам ограничивалось до сих
пор такими задачами устойчивости, для которых удавалось
выяснить, что соотношения между приращениями напряжений
таковы, что разгрузка нигде не происходит и уравнения теории
скольжения сводятся к уравнениям деформационной теории.
В то же время положенные в основу теории скольжения гипотезы
не настолько достоверны, чтобы имели смысл поиски точных
решений. Для упрощения основных соотношений теории и для
получения более наглядных качественных результатов мы
рассмотрим, следуя Клюшникову [59], некоторую модельную двух-
мерную среду, для которой е33 = 0, а33 = -^ (ан + а22). Тогда
—- , л
а14 = —сг22 = — (а11 — п22), e?i -г ^22 — 0 вследствие условия
102
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
несжимаемости, поэтому можно принять e"i= —ё^г = у (ен — ^"г)-
Будем считать, что этот материал может деформироваться только
за счет сдвигов, происходящих в плоскостях, нормальных к
плоскости Х^Х2-
На некоторой площадке, составляющей с осью Xi угол со,
возникает касательное напряжение
х = у (о"н — о22) sin 2co + 0J2 cos 2co. B1.1)
В тех элементах, для которых т в направлении возможного
скольжения превышает предел текучести тт, произойдет
пластический сдвиг, который участвует в суммарной деформации
объема долей, пропорциональной dco. Таким образом,
dy = F (т) da.
Соответствующие компоненты пластической деформации по осям:
1 11
de^ = — de$t = у (de^ — de^) = у dy sin 2co = у F (r) sin 2co da,
1 1
dej2 = у d j' cos 2ш = у/' (t) cos 2to dco.
Примем за координаты в двухмерном пространстве напряжений
величины @i=y(or1J— ог) и Qz = oi2, соответствующие деформа-
циям qi = у(<?|11 — е?г) и Qr2 = e°2. Начальная поверхность
нагружения изображается в этих координатах окружностью Ql + Ql=const.
Пластические деформации находятся по формулам:
1 !"
<Zi = у \ Р (t) sin 2ш dco,
1 i*
g2 = у \ -F (т) cos 2to dco.
B1.2)
Здесь
T = <?1sin2co + <?2cos2(u. B1.3)
Если из некоторого напряженного состояния производится
догрузка, то
8qi = у \ F' (т) 6т sin 2(o rfco,
1 i1
б^2 =у \ ^" (TNTcos2cod(o.
B1.4)
При этом необходимо иметь в виду, что при догрузке могут
меняться также и пределы интегрирования. Применим соотношения
B1.4) к случаю пропорционального нагружения. Если р — угол,
который составляет луч нагружения с осью Qu то можно принять
C, = (?cosp\ <22 = <>sinp\
J 21]
МОДЕЛЬ ПЛОСКОГО ТЕЛА
103
и, следовательно,
T = <?sinB(o + P).
Вместо разложения вектора q по ортам ii,i2 исходной
координатной системы, введем базис eit е2, связанный с путем
пропорционального нагружения (рис. 25). Равенства B1.2) в векторной
форме выглядят следующим образом:
1 ^
q = у \ F (x) [ii sin 2co + i2 cos 2co] dw.
Но
/1 = e1cos|i — e2sinp\ i2 = ej sinj3-|-e2cosp.
Поэтому
*! sin 2co -+- *2cos 2co =
= e± sin Bo) -f- P) -f e2 cos Bм + P).
Положим теперь
2© + р = ^ + Я.
Получим:
q = ^ \ F(T)(eiC0sX — e2sinX)dX. B1.5) Рис.25.
При этом x~QcosX и интегрирование распространяется на те
значения X, для которых т>тт, то есть
cosA>-^.
Если принять coskl = -^-, то область интегрирования будет
— A j ^ X ^ Л].
Рассмотрим теперь случай догрузки в произвольном
направлении после пропорционального нагружения. Пусть приращение
вектора Q будет направлено под углом а к е2> величина его
пусть будет е. Тогда
A(?! = esin(a — f>), AQ2 = ecos(a — р).
Следовательно,
At =e cos (a — p — 2co) = 6sin (a — X).
Формула для приращения вектора пластической деформации
будет следующей:
1 "
Ад = -^г \ F' (x)sin(a — X) [в! cos A — e2sinA] dX. B1.6)
При пользовании- этой формулой нужно иметь в виду, что при
малой догрузке только те элементы, которые уже были пласти-
104
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
чески деформированы, получают дополнительную пластическую
деформацию, если Ат > 0. Если Дт < 0, то произойдет упругая
разгрузка. Возможные случаи здесь будут следующие:
1. а<:—ки тогда а— к всегда отрицательна, во всей
области —%i < А, < Хи Ат < 0 происходит упругая разгрузка.
Прямые а = —ki определяют угол на кривой нагружения. Легко
проверить, что эти прямые касаются начальной окружности.
2. а > А.4; тогда во всей области разность а — к положительна,
везде происходит догрузка. Соотношение B1.4) получается
из соотношений B1.2), в котором интегрирование предполагается
выполненным, путем варьирования.
3. —kt < а, < kt. В этом случае интегрирование при
вычислении выражения B1.6) производится в пределах —а<;А.<Га.
Заметим, что рассуждения при анализе модели Клюшникова.
которые воспроизводят в сильно упрощенном виде рассуждении
при анализе полной модели Батдорфа — Будянского, совершенно
аналогичны тем, которые мы применяли при исследовании изгиба
упруго-пластической трубы в § 16. Там мы интересовались только
условием р'азгрузки и условием применимости уравнений
деформационной теории; однако не составляет труда выяснить, что
получается при произвольной малой догрузке, следующей за
пропорциональным нагружением. Возвращаясь к рис. 17 и той части
текста § 16, где рассматривается вопрос об упругой разгрузке.
мы предположим, что ось дополнительного поворота при
разгрузке составляет с осью х угол ф > 9 и, таким образом, пересекает
пластическую зону. Дополнительные напряжения упругой
разгрузки & = —cocrT sin AJ5 — ф) появляются только в упругой
области, то есть при —9 <»{|<(рия — 9 < if) <; я + ф.
Вычисляя моменты от этих напряжений, представим результаты в
следующем виде:
\Qx = АЯх Gt(<p) + Gt(Q) + д^ (gii]2 ф _ sin2 9Ь
AQV = Aqx (sin2 ф - sin2 6) + Aqy -а(ф) + С"(9) ,
При этом, очевидно,
- tg9.
B1.7)
Д?ж
Соотношения B1.7) являются довольно сложными нелинейными
соотношениями между приращениями деформаций и напряжений,
поэтому трудно ожидать, чтобы для реальных материалов
аналогичные соотношения оказались простыми. Как теория
скольжения, так и рассмотрение простейшей модели приводят нас к
довольно пессимистическим выводам в отношении возможного
прогресса теории пластичности. Прежде всего, следует заметить, что
Js 22] ТЕЧЕНИЕ С СИНГУЛЯРНОЙ ПОВЕРХНОСТЬЮ НАГРУЖЕНИЯ 105
основная идея теории скольжения, несомненно, правильно
отражает основной механизм пластической деформации
поликристаллического металла; вводимые для получения уравнений гипотезы,
по-видимому, чрезмерно упрощают действительное положение
и, несмотря на это, приводят к сложным выкладкам.
Предложенная модель упруго-пластического тела, как нам кажется,
является наиболее простым примером системы, состоящей из
простейших элементов, притом такой, что механическое поведение ее
определяется возможностью пластической догрузки и упругой
разгрузки этих элементов. Как для теории скольжения, так
и для простейшей модели задача об интегрировании уравнений
пластичности для какого-либо пути нагружения оказывается
трудной, уравнения не позволяют сделать даже какие-либо
качественные выводы о характере изменения поверхности
нагружения при более или менее сложных путях нагружения.
§ 22. ТЕЧЕНИЕ С СИНГУЛЯРНОЙ
ПОВЕРХНОСТЬЮ НАГРУЖЕНИЯ
Выше, при выяснении границ применимости деформационной
теории пластичности, а также при обсуждении теории
скольжения, мы встретились с поверхностями нагружения, имеющими
коническую точку в точке нагружения. С другой стороны, теория
течения основывается на том факте, что вектор приращения
пластической деформации нормален к поверхности нагружения.
Однако в конической точке направление нормали становится
неопределенным, поэтому необходимо формулировать некоторые
дополнительные гипотезы.
Мы уже встречались в § 19 с законами течения,
использующими сингулярные поверхности нагружения, однако там речь
шла о тех ребрах или углах на поверхности нагружения, которые
существовали в исходном состоянии. Последующее изменение
поверхности нагружения представляло собой либо подобное
расширение, либо перенос всей поверхности в целом. В теории
скольжения мы встречаемся с иным типом упрочнения, когда
коническая точка необходимым образом следует за путем нагружения
и геометрия поверхности нагружения существенно изменяется
с развитием пластической деформации. Одна из возможных схем,
позволяющих описать упрочнение подобного рода, принадлежит
Сэндерсу [344]. Отправным пунктом теории Сэндерса является
представление о поверхности текучести, составленной из
плоских граней. Предлагается следующая основная гипотеза. Если
точка нагружения находится на одной из плоскостей,
образующих поверхность нагружения, то по мере нагружения эта и
только эта плоскость перемещается параллельно себе в одном
направлении. Величина приращения пластической деформации пропор-
106
ТЕОРИЯ ПЛАСТИЧНОСТИ
[ГЛ. II
циональна перемещению соответствующей плоскости. Если точка
нагружения попадает на ребро, пересекающиеся плоскости
перемещаются каждая параллельно себе в одном направлении,
приращения пластической деформации вычисляются для каждой
плоскости отдельно и складываются. На рис. 26 схематически
показан случай, когда точка
нагружения находится на ребре.
А' _^-—"^daf/ - Здесь АВ и ВС — плоскости,
принадлежащие поверхности на-
а) ' '"
А
4
Рис. 26.
Рпс. 27.
Рис. 28.
гружения. Если догрузка направлена вне угла, образованного
плоскостями нагружения, то перемещается только одна
плоскость (рис. 26, а). Если вектор догрузки направлен внутрь этого
угла, перемещается как плоскость АВ, так и плоскость ВС
(рис. 26, б). Посмотрим теперь как
изменяется поверхность нагружения, состоящая из
плоскостей, в целом. На рис. 27
изображены начальная поверхность нагружения и
последующая поверхность нагружения для
указанного пути нагружения.
Если начальная поверхность
нагружения является гладкой, ее всегда можно
представить себе как огибающую семейства
плоскостей нагружения; таким образом, получается бесконечное
множество линейных функций нагружения. Воспроизводя
рассуждения для случая поверхности нагружения в форме
многогранника, мы убедимся, что при пропорциональном нагружении
каждая последующая поверхность нагружения будет состоять
из конуса касательных к начальной поверхности из точки
нагружения и части этой поверхности, ограничивающей, вместе с
конусом, выпуклый замкнутый объем (рис. 28).
Нужно заметить, что гипотеза Сэндерса не описывает,
например, эффекта Баушингера. Предположение о том, что плоские
поверхности нагружения перемещаются параллельно себе и
S 22] ТЕЧЕНИЕ С СИНГУЛЯРНОЙ ПОВЕРХНОСТЬЮ НАГРУЖЕНИЯ 107
только тогда, когда точка нагружения попадает на данную
поверхность, является слишком упрощенным.
В работе Сэндерса оговорена возможность взаимодействия
между плоскостями нагружения, однако определенных гипотез,
описывающих это взаимодействие, автор не приводит.
Формулы для приращения пластической деформации при
догрузке для плоского пути нагружения по теории Сэндерса
были даны в работе Клюшникова [68].
В статье [58] Клюшников предложил новый вариант теории
течения, основанный на следующих гипотезах (формулировки
относятся к двухмерной плоскости девятимерного пространства
напряжений):
1. Гипотеза непрерывности. Если расстояние между
соответствующими точками двух путей нагружения меньше 8, то
расстояние между соответствующими точками пути
деформирования меньше чем е (б), причем е ->- 0 при 8 -*- 0.
2. В процессе пластического деформирования кривая
нагружения изменяется непрерывно, в процессе догрузки точки кривой
пластичности в окрестности места догрузки могут перемещаться
только в противоположную началу координат сторону.
3. Связь между векторами da и den определяется только
локальными характеристиками кривой нагружения в
окрестности точки нагружения.
Основной результат теорий Сэндерса и Клюшникова состоит
в том, что при определенных ограничениях, накладываемых
на путь нагружения, дифференциальные соотношения теории
могут быть проинтегрированы, в результате получаются
уравнения деформационного типа, пригодные в той или иной области.
Использование этих теорий для произвольных путей нагружения,
так же как и теории скольжения, встречает почти непреодолимые
трудности.
ГЛАВА HI
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
Теория линейной вязко-упругости представляет собою
естественное обобщение классических направлений механики
сплошной среды — теории упругости, с одной стороны, гидромеханики
вязкой жидкости, с другой. Комбинируя свойства упругости
и вязкости в различных сочетаниях, можно построить большое
количество различных гипотетических сред, поведение которых,
по крайней мере качественно, соответствует поведению реальных
тел, промежуточных между твердыми телами и жидкостями.
При изучении свойств коллоидных растворов, суспензий,
высокомолекулярных соединений реологические модели такого типа
нашли широкое применение, хотя физики и физико-химики,
которые по преимуществу принимали участие в создании теоретической
реологии, были больше заинтересованы в качественном
объяснении наблюдаемых эффектов, чем в их точном количественном
описании. Разработке формального аппарата теории
вязко-упругости посвящено очень большое количество работ, некоторые
направления возникли, по-видимому, не столько из практических
потребностей, сколько из внутренней логики развития науки.
В последнее время интерес к теории вязко-упругости очень
оживился, широкое внедрение в технику полимерных материалов
заставило искать принципы расчета элементов конструкций,
изготовленных из этих материалов. Оказалось, что для
некоторого круга задач приближения линейной теории достаточно,
поэтому уже существующий и разработанный аппарат находит
непосредственные приложения. Многочисленные исследования
последних лет посвящены как разработке общих методов
решения задач вязко-упругости, так и рассмотрению отдельных
более или менее трудных задач; имеющийся материал настолько
велик, что сколько-нибудь полное его изложение должно было бы
служить предметом специальной монографии.
$ 23]
ПРОСТЕЙШИЕ ВЯЗКО-УПРУГИЕ ТЕЛА
109
Линейные теории совершенно неприменимы для описания
ползучести металлов; поскольку в течение долгого времени только
эта область представляла интерес для техники, развитие теории
ползучести шло совершенно другим путем. По существу, первым
серьезным приложением теории линейной вязко-упругости
явилось исследование ползучести бетона. Применение этих же идей
к грунтам, горным породам и некоторым строительным
материалам носило эпизодический характер.
Сейчас круг задач теории линейной вязко-упругости
необычайно расширился, хотя границы ее применимости не
установлены еще достаточно четко. Мы считали полезным посвятить
этой теории одну главу, имея в виду, с одной стороны, осветить
более полно и всесторонне различные принципиальные
подходы к построению теории ползучести и подчеркнуть глубокую
разницу в поведении металлов и полимерных материалов, с
другой — сообщить некоторые сведения о ползучести полимерных
материалов как таковых. Для многих из этих материалов область
линейности оказывается чрезвычайно узкой, и теория должна
быть усовершенствована в направлении учета нелинейной
зависимости между напряжениями и деформациями. Некоторые
сведения о такого рода обобщениях приводятся в следующей главе.
При выборе материала настоящей главы автор ограничился
сообщением сведений самого общего характера, уделив несколько
большее внимание тем вопросам, над которыми он работал лично.
§ 23. ПРОСТЕЙШИЕ ВЯЗКО-УПРУГИЕ ТЕЛА
Явление ползучести, то есть нарастание деформации
нагруженного тела со временем, было известно достаточно давно,
в особенности для материалов органического происхождения.
Однако учет ползучести при расчетах конструкций не вызывался
серьезной необходимостью и первые наблюдения над
ползучестью носили качественный характер. При первом знакомстве
с ползучестью, например, шелковых нитей, применявшихся
в физических приборах, бросается в глаза аналогия с вязким
течением жидкости. Как известно, напряжение и скорость
деформации в вязкой жидкости связаны законом вязкости Ньютона:
ст= Зне.
В упругом материале напряжение и деформация связаны
законом Гуна:
о = Ее.
Первая мысль, которая приходит в голову при попытке
описать деформацию твердого тела, происходящую во времени,
состоит в том, чтобы объединить свойства вязкости и упругости.
110 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. 111
Таким образом, мы приходим к представлению о вязко-упругом
теле Максвелла, для которого связь между напряжениями и
деформациями дается следующим уравнением:
e-TT + ij. B3.1)
Если действующее на тело напряжение постоянно, то деформации
происходит с постоянной скоростью. Предположим теперь, что>
тело растянуто напряжением ст0, после чего деформация е
зафиксирована, так что при t = 0 а = а0, при t > 0 е = 0. Приняв.
Е Т'
получим из B3.1)
о + ± = 0.
Проинтегрируем это уравнение с учетом начального условия.
Получим:
0 = аоехр(--^ . B3.2)
Формула B3.2) дает закон релаксации (ослабления) напряжения
при постоянной деформации. Постоянная т носит название
времени релаксации.
Объединяя свойства упругости и вязкости, можно получить
и уравнение, отличное от B3.1), а именно:
а = Ее + Ъгр = Е{е + хе). B3.3)
Тело, поведение которого описывается уравнением B3.3), мы
будем называть вязко-упругим телом Фохта. В отличие от тела
Максвелла, при постоянной нагрузке тело Фохта не будет
неограниченно деформироваться, его удлинение стремится к величине
а0/Е по закону
[1-ехр(-4-)]. B3.4)
При постоянной деформации тело Фохта не релаксирует,
напряжение в нем остается постоянным. Время т в этом случае мы
будем называть временем запаздывания.
Для того чтобы наглядно представить себе поведение под
нагрузкой тела Максвелла и тела Фохта, обратимся к модели,
составленной из вязкого сопротивления (наполненный маслом
цилиндр с поршнем, имеющим малое отверстие) и пружины.
На рис. 29 изображены два возможных соединения этих элементов:
последовательное и параллельное. Если вязкость цилиндра
с поршнем есть 3ti, жесткость пружины Е, приложенная сила о*
и полное перемещение е, то движение первой модели описывается
6 Е
5 23]
ПРОСТЕЙШИЕ ВЯЗКО-УПРУГИЕ ТЕЛА
111
Рис. 29.
уравнением B3.1), движение второй — уравнением B3.3).
Подобное моделирование всякого рода сред, механическое поведение
которых зависит от времени, применяется очень широко, а сами
модели называются реологическими
моделями; некоторые авторы придают им очень
большое значение и считают задачу описания
свойств той или иной среды решенной тогда,
когда найдена адекватная реологическая
модель. В действительности всякая модель
такого рода является лишь аналогией, но не
средством объяснения явления. В структуре
материала невозможно указать реальных
носителей свойств идеальной упругости или
идеальной вязкости; если иногда и удается
выделить структурные элементы, которым
могут быть приписаны упругие или вязкие
свойства, то их реальные связи и реальное
взаимодействие очень далеки от схем, изображенных
на рис. 29 и им подобных. Правда,
возможность подбора реологической схемы обеспечивает
непротиворечивость описания процесса и гарантирует от таких, например,
результатов, как нарушение закона сохранения энергии системы.
Имея реологическую модель, мы всегда можем выделить упругую
энергию и определить неотрицательную скорость
диссипации энергии.
В природе, вероятно, нельзя указать
материалы, которые подчинялись бы уравнению
B3.1) либо B3.3); идеальная жидкость
Максвелла и идеальное вязко-упругое тело Фохта
представляют собою некоторые воображаемые
модели, свойства которых довольно далеки от свойств
всех без исключения реальных сред. Правда,
до последнего времени не прекращались попытки
применить уравнение Максвелла для описания
свойств грунтов, некоторых пластиков, резино-
подобных материалов и даже металлов. Для
описания рассеяния энергии при упругих
колебаниях неоднократно использовалась модель
Фохта. Эти попытки далеко не всегда
согласуются с опытом.
Комбинируя пружины и вязкие
сопротивления, можно получить схему, поведение которой, по крайней мере
качественно, лучше воспроизводит поведение реальных твердых
тел под нагрузкой. Соответствующая реологическая модель
приведена на рис. 30. Обозначим жесткость пружин Et и Е2
соответственно, вязкость масляной системы пусть будет Зт]. Удлинение
•Z,
37]
Рис. 30.
112
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. JJJ
первой пружины от действия силы а будет
а
Удлинение второй пружины связано с силой
соотношением B3.3), а именно:
а = Е2е2 + 3це2.
Полное удлинение е = е4 -f- е2> исключая et и ег, получим:
V Е± Е2 J ElE2 Е2
Положим
тогда мы получим следующее соотношение между напряжением
и деформацией:
o + Xo = E(e + \ie). B3.5)
Из определения очевидно, что X > ц; это следует из
рассмотренной модели, но это можно показать и непосредственно,
применяя уравнение B3.5) к частным случаям нагружения.
Приложим нагрузку очень быстро, так, чтобы о* было велико. Тогда
е будет тоже велико, а и е можно пренебречь, и мы найдем:
о* = Ее. Величина Е представляет собою мгновенный модуль
упругости. Предположим теперь, что нагрузка действует
достаточно долго, процесс деформирования стал весьма медленным
и производные о и е в B3.5) пренебрежимо малы. Тогда из B3.5)
получаем а = Е~-е- Величину E-j- следует назвать длительным
модулем упругости, она связывает напряжение и деформацию
в предельном состоянии. При внезапном приложении нагрузки,
которая после приложения остается постоянной, сначала
возникает деформация, определяемая мгновенным модулем; эта
деформация растет, стремясь к тому значению, которое соответствует
длительному модулю. Естественно предположить, что при этом
внешняя сила совершает положительную работу. Для этого
необходимо, чтобы было К > ц..
Уравнение B3.5) можно разрешить относительно напряжений
или относительно деформаций. Будем считать, например, что е
есть заданная функция времени. Проинтегрируем получившееся
уравнение для о* (t). Интеграл однороддого уравнения
о = Сехр (— ht).
§ 23] ПРОСТЕЙШИЕ ВЯЗКО-УПРУГИЕ ТЕЛА 113
Применяя способ вариации произвольной постоянной, найдем:
С = Е \ (е-\-\хе) ехр (Хх) dx —
— оо
t
= Е [ е (г) ехр Аг — (X — jx) ? е (т) ехр (Хх) dx 1 .
Таким образом, напряжение выражается через деформацию
следующей формулой:
t
о = Е [е-(Я — u.) J е(т)ехр[ — Я(г — t)]dtl . B3.6)
Совершенно аналогичным образом можно было выразить е
через о. Результат будет следующий:
<? = -g-[c-f-(Л —ц) \ а(т)ехр[ — и,[г — x)]dx~\
B3.7)
Интегральное уравнение типа Вольтерра B3.6) или B3.7)
совершенно эквивалентно
уравнению B3.5) с
соответствующими начальными условиями.
Нижний предел
интегрирования можно принять равным
нулю вместо отрицательной
бесконечности, если при t < О
е = 0 и а = 0.
Применим интегральное
уравнение B3.7) к случаю,
когда на тело действует
постоянная нагрузка,
приложенная в момент времени t = 0.
Тогда с = 0 при t < 0 и ст = 0О = const при t > 0. По
формуле B3.7)
X — [х
е
6р
Е
У^Ёи
/ Е
—
Л бе
I ft Е
1
"""
О
Рис. 31.
е =
= ^L{l+A=iL[i_exp(_^)]}
B3.8)
На рис. 31 приведен график ползучести, описываемый
уравнением B3.8). Предположим теперь, что в момент времени tx
нагрузка снимается, таким образом, 0 = 0 при t>t^. По
формуле B3.7)
{ехр [ — ц (t — *4I - ехр (— ц*)}.
B3.9)
Ю. Н. Работнов
114
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
При t = ti выражение B3.9) дает для е значение,
отличающееся от того, которое следует из формулы B3.8), лишь на величину
мгновенной упругой деформации. При неограниченном
возрастании времени t деформация стремится исчезнуть. Таким образом,
вся деформация ползучести является обратимой, уравнение B3.5)
описывает упругое последействие в воображаемом теле,
называемом телом Кельвина *).
Если сообщить телу Кельвина мгновенную деформацию, то
в нем возникнет напряжение, определяемое по мгновенному
модулю. Это напряжение будет релаксировать до величины,
соответствующей той же деформации при длительном модуле.
Релаксация будет происходить по экспоненциальной кривой
с аргументом —Xt, как легко установить с помощью
интегрального уравнения B3.6).
Детальное рассмотрение свойств тела Кельвина и решение
различных задач для этого тела были выполнены Ишлинским [44],
[45], этим телом занимался также Ржаницын [112].
§ 24. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАКОНЫ
ДЕФОРМИРОВАНИЯ БОЛЕЕ ОБЩЕГО ВИДА
Модель Кельвина описывает свойства тела, обнаруживающего
последействие, при помощи трех констант: мгновенного модуля,
времени запаздывания l/[i и времени релаксации 1/Я.
Количественное соответствие поведения реальных тел модели Кельвина
оказывается, как правило, плохим, кривые ползучести и
релаксации не аппроксимируются с помощью экспоненциальной
функции. Естественный путь обобщения уравнения B3.5) состоит
в том, что как в левой, так и в правой части берутся комбинации
из производных от а и е по времени более высокого порядка.
Положим
, da , , dna , , , ?de , , dme ,„, ..
aoO + aiW+. .. +an — =^ + 6, — + . . . +bm^r . B4.1)
Можно показать, что при некоторых ограничениях среда,
описываемая уравнением B4.1), моделируется с помощью пружин
и вязких сопротивлений, однако мы не будем развивать эту точку
зрения.
Дифференциальные соотношения B4.1) удобно заменить
интегральными соотношениями, подобно тому как это было сделано
в предыдущем параграфе. Для решения дифференциальных
уравнений с постоянными коэффициентами мы применим следующий
способ. Будем отправляться от простейшего дифференциального
*) В литературе можно встретить и другие названия среды,
описываемой уравнением B3.5).
§ 24] ЗАКОНЫ ДЕФОРМИРОВАНИЯ БОЛЕЕ ОБЩЕГО ВИДА 115
уравнения первого порядка:
х + рх = у. B4.2)
Здесь р — константа, ж —искомая функция от t, у — заданная
функция, причем такая, что при t^.0 у — О. Решение этого
уравнения, обращающееся в нуль при t = 0, будет
t <
z = y — $ \ exp[-P(t-x)]y(x)dx= \ ехр[-Р(г — x)]dy(x).
о о
B4.3)
С другой сторовы, проинтегрируем обе части уравнения B4.2)
с учетом начальных условий для х (t) и у (t), получим:
t
х + $ V х(х) dx = у.
о
Введем символическую запись интегрального оператора
следующим образом:
t
\ х (т) dx — Гх.
о
Тогда предыдущее уравнение можно переписать:
{\+$1*)х = у. B4.4)
Решим уравнение B4.4) относительно х формально, поступая
с операторами так же как, с постоянными множителями.
Получим следующую запись:
Дробь, стоящая множителем перед у, напоминает выражение
для суммы бесконечной геометрической прогрессии. Если бы J37*
было числом, меньшим чем единица, то было бы справедливо
тождество
1—р/* + §2/*2—р3/*3+... B4.6)
1 + ря
Предположим, что это тождество справедливо для операторов.
Под степенью п оператора /* мы будем понимать оператор /*,
повторенный п раз; таким образом,
t Xn T2
Т*пУ=\ \ ... I y{Xi)drx ... dxn.
о о
8*
116 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Но по формуле Коши кратный интеграл преобразуется
в обыкновенный, и мы можем написать:
t
7*^ = -(^Т)Т$ (t-xr^y(T)dT (п>1),
о
Формально составленное выражение B4.5), содержащее
оператор /*, расшифровывается теперь следующим образом:
t t
СС = !/-р J y(x)dT + P \ y(X)(t~x)dX-...
или же
х = у — Р ^ ехр[ — Р(< — т)] у(х)йт.
о
Таким образом, в результате чисто формальных операций мы
снова получили формулу B4.3). В отличие от геометрической
прогрессии, ряд операторов в B4.6) сходится при любых
значениях р, поскольку ряд, определяющий экспоненциальную
функцию, сходится всюду. Введем для краткости обозначение
t
Э*(р)у= J ехр[Р(*-т)]р(т)<*т.
о
Соотношение B4.5) устанавливает связь между операторами I*
и Э* (р), а именно:
1
1 + р/*
¦ = 1 —РЭ*(-Р). B4.7)
Соотношение B4.7) позволяет наиболее простым способом
получать решения дифференциальных уравнений с постоянными
коэффициентами при нулевых начальных условиях и при условии, что
правая часть уравнения равна нулю при t ¦< 0. В задачах
механики материалов это предположение означает, что история
материала начинается с некоторого момента времени, существует
исходное состояние, когда материал еще не подвергался никаким
воздействиям.
Изменим немного уравнение B4.2), а именно вместо у в
правой части возьмем просто у, тогда будет
_ I* __ 1 Г ч 1 1
_ i+p/* у р L i+p/* J
у-
§ 24] ЗАКОНЫ ДЕФОРМИРОВАНИЯ БОЛЕЕ ОБЩЕГО ВИДА 117
С помощью формулы B4.7) мы найдем, что в этом случае
Таким образом, мы получили формулу, являющуюся следствием
B4.7) и полезную для приложений:
j*
1 + р/*
¦¦Э*(-Р). B4.8)
Теперь мы в состоянии вернуться к вопросу, поставленному
в начале этого параграфа, а именно к замене
дифференциального соотношения B4.1) интегральным соотношением. Пусть р
есть наибольшее из чисел т и п; умножим обе части B4.1)
на 1*р, получим:
#(/*) а =#(/*) <?• B4'9)
Здесь & и 88—полиномы степени р от /*, а именно:
& = а01*р + Й1/*р-1 + . . . + ап1*р~п,
38 = baI*v + Ь17*р-1 + ... + Ьп1*р~т.
Если п = т и корни полиномов ,#- и 38 действительны и
различны, то уравнение B4.9) можно формально решить относительно е
или относительно с. Разрешим его, например, относительно о.
Получим:
° М{1*)
Частное двух полиномов степени р можно разложить на
простейшие дроби так, что
р т>
= ^ + 2-ТЯ^ = Л(>+2 Л([1-а*Э*(-а?)]. B4.10)
t=i j=i
Следовательно, уравнение B4.1) эквивалентно интегральному
уравнению
t
а = Ае—\ T(t-T)e{x)dx. B4.11)
Здесь
Г(г — т)= 2 Atatexpl — ai(t — т)], 4= 2 ^.
i = l i=0
Функцию Г (< — г) мы будем называть ядром релаксации, а тело,
поведение которого описывается соотношением B4.11), будем
называть наследственно-упругим телом, если т = п, а корни
полиномов & и 38 вещественны, различны и отрицательны.
118 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. Ш
Последнее условие означает, что все at должны быть
положительны, иначе окажется, что при постоянной деформации
напряжение возрастает со временем, вместо того чтобы убывать. При
постоянном е мы получаем:
v
а= {А — 2 Ai{l — ex-p( — a,it)]\ е.
При t = 0 o = Ae, таким образом, A = ^>j А, представляет собой
г=0
мгновенный модуль; при t — oo, a = A0e, следовательно, А0 — это
длительный модуль. Величины 1/ail имеющие размерность
времени, носят название времен релаксации.
Уравнение B4.9) можно решить и относительно деформаций
М {!*)
Разлагая на простейшие дроби, представим частное в
следующем виде:
Ий-Яо+2 Tw=s"+il B([i-p^(-pf)].
i=i i=l
Интегральное соотношение между е и о становится следующим:
t
e = Ba+[K(t-T)o(-v)dT. B4.12)
о
Здесь
K(t-x)= -2 Я«&ехр[-р«(*-т)], В= S Bt.
Функцию K{t — т) мы будем называть ядром ползучести,
ядро релаксации является его резольвентой. При постоянном
напряжении отсюда получается закон ползучести:
e = {B-2?s[l-exp(-P«0]}<*.
Если т -ф п, то положение становится несколько иным; для
выяснения существа дела нам будет достаточно рассмотреть
простейший случай вязко-упругого тела, описываемого уравнением
а — Е(е + те).
Умножая на /*, получим:
1*а = ЕA*е + хе). B4.13)
§ 25]
НАСЛЕДСТВЕННО-УПРУГОЕ ТЕЛО
119
Разрешим это уравнение относительно е:
х + 1* Е '
или, по формуле B4.8),
Если мы теперь будем решать B4.13) относительно а, то
окажется
а = ?(% + -?-/) ,
го есть мы получим исходное уравнение и ничего другого, так
как оператор 1/1* есть оператор дифференцирования. Такое
положение возникает всегда, когда один из полиномов &¦ (/*) или
$ (/*) имеет нулевые корни; наряду с экспоненциальными
операторами остаются операторы дифференцирования. Однако
реальный смысл имеют только такие случаи, когда на наследственно-
упругую деформацию накладывается вязкое течение, а
следовательно, т — п = 1.
§ 25. НАСЛЕДСТВЕННО-УПРУГОЕ ТЕЛО
Соотношения типа B4.1) обычно принимаются в качестве
основных физических соотношений в реологии полимерных
материалов. Если кривые релаксации или кривые ползучести могут
быть аппроксимированы при помощи набора экспоненциальных
функций, то нахождение закона деформирования, то есть
определение коэффициентов ah и bk в соотношении B4.1), сводится
к выполнению алгебраических операций. Действительно, пусть
нам известно уравнение релаксации, это значит — известны
величины А1 и аг. Тогда мы можем написать правую часть
выражения B4.10); приводя к общему знаменателю, мы найдем
полиномы <#- и /Ш, а следовательно, и искомые коэффициенты в B4.1).
Разлагая на простейшие дроби обратное отношение полиномов,
мы можем найти величины Bt и рг, определяющие закон
ползучести.
Однако интегральное уравнение B4.11) или обратное ему
уравнение B4.12) устанавливает связь между напряжением и
деформацией более общую, чем дифференциальное соотношение B4.1),
если понимать под К (t — т) и соответственно Г (t — т) не сумму
конечного числа экспоненциальных функций, а некоторое ядро,
являющееся произвольной функцией t — т, удовлетворяющей
лишь некоторым весьма общим условиям, которые мы сейчас
120
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
выясним. Условимся в дальнейшем записывать закон
наследственности следующим образом:
t
е = 4~[а+ \ ЛГ(г-т)о(т)йт] ,
— оо
B5.1)
о = Е [ е — \ Г (t — т) е (т) dx ] .
Форма закона наследственной упругости B5.1) была введена
Вольтерра [376] на основе следующих соображений. Полная
деформация тела складывается из мгновенной деформации,
которая определяется напряжением, действующим в данный момент
времени, и связана с ним законом Гука, и из наследуемой
деформации. Если в момент времени т было приложено напряжение
о" (г), которое действовало в течение времени dx, то материал
сохраняет воспоминание о действии этого напряжения в виде
некоторой малой деформации de. Величина de пропорциональна
напряжению а (т), продолжительности его действия dx и
зависит от времени, протекшего от момента т, когда было приложено
напряжение, до настоящего момента t, то есть от t — т. Чтобы
учесть эту зависимость, предполагается, что de пропорционально
некоторой функции К (t — т). Таким образом,
de = — o(x) dx K(t — x).
Hi
Интегрируя по т. от — оо до t и добавляя мгновенную упругую
деформацию, получим первое из уравнений B5.1).
Заметим, что функция К (t — x) должна быть убывающей,
«воспоминание» материала стремится изгладиться со временем.
То, что ядро ползучести зависит от разности аргументов t — т,
указывает на неизменность свойств материала во времени; начало
отсчета времени можно изменять по произволу, результаты при
этом остаются одни и те же. Существуют материалы, свойства
которых существенно меняются во времени, например бетон,
который стареет в течение примерно двух лет. Для описания
свойств стареющих материалов ядро должно быть принято
функцией аргументов (нтпо отдельности.
На интегральные зависимости B5.1) можно смотреть как
на предельный случай интегральных зависимостей, рассмотренных
в предыдущем параграфе, когда порядок дифференциальных
соотношений между о" и е стремится к бесконечности. В пределе
сумма, фигурирующая в определении К (t — т) в формуле B4.12),
§ 25]
НАСЛЕДСТВЕННО-УПРУГОЕ ТЕЛО
121
превращается в интеграл
K{t-t)= — ^ |ЗВф)ехр[-р(г-т)]сф.
о
Функция —В (Р) может быть названа спектром ползучести»
Совершенно аналогично
оо
(•
Г (t — т) = \ а4 (а) ехр [ — а ((— т)] da.
о
Функция А (а) представляет собою спектр релаксации. Выше-
написанные формулы показывают, что ядра ползучести и
релаксации представляют собою трансформации Лапласа
соответствующих спектров. Отсюда следует, что спектры могут быть
определены по формулам типа
Y-И00
aA(a) = —— V Г (х) ехр (ах) dx.
у —tOO
Мы показали, что интегральное соотношение типа B5.1)
следует из дифференциального соотношения B4.1), при этом ядра
К (t — т) и Г (I — т) представляют собою суммы
экспоненциальных функций. Нетрудно показать, что справедливо и обратное
заключение. Предположим, что е (t) и a t) связаны интегральной
зависимостью
t
<? = 4~ Гст+ \ K(t — x)o(r)drl .
о
При этом
tf(*-T)=-Jj В,&ехр[-М*-т)].
Запишем интегральное соотношение в символической форме:
Ее = а + 2 В&Э* (- fc) a. B5.2)
г=1
Здесь
t
3*(-P0<r=$ ехр[-М*-т)]ст(т)<*т.
о
Заметим, что
* {a*(-pi)a} = ff-p,5*(-pI)ci.
122 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. Ш
Отсюда следует:
Составляя производные от е по t до порядка р включительно, мы
исключим из этих выражений и равенства B5.2) величины
Э* (—РО с и придем к соотношению вида B4.1), в котором т =
= п = р.
§ 26. УСЛОВИЕ ЗАМКНУТОГО ЦИКЛА ВОЛЬТЕРРА
Еще более общие соотношения между напряжениями и
деформациями, нежели те, которые устанавливаются формулами B5.1),
мы получим, если будем считать, что ядра К и Г зависят от
аргументов (ит произвольным образом, так что, например,
*
е = 1г[о-+ J K(t,T)a(x)dx']. B6.1)
— оо
Свойства тел, описываемых уравнением B6.1), не инвариантны
•относительно изменения начала отсчета времени; в таких телах
происходят процессы старения или, наоборот, разупрочнения.
Типичным примером стареющего материала является бетон.
Для стареющих материалов нет оснований считать и модуль
мгновенной упругости постоянной величиной, поэтому в общем
случае Е = Е (t).
Предположим теперь, что при t <; 0 было о* = 0, в момент
времени t = 0 прикладывается напряжение а, которое является
периодической функцией t с периодом ы, так что о* (t + ю) =
= о (t). Покажем, что если К (t, т) = К (t — т), то величина е,
определяемая уравнением B6.1) (при постоянном Е), будет сколь
угодно мало отличаться от периодической функции, если t
достаточно велико. Действительно, по формуле B6.1)
(+СЙ
Ee(t + &) = a(t)+ [ K(t + a — T;)a(T)dT.
о
Заменим переменную интегрирования на т', положив т =
= т' + ш. Получим:
Ee(t + a,) = o(t)+ \ K(t-x')o{x')di'
S 26]
УСЛОВИЕ ЗАМКНУТОГО ЦИКЛА ВОЛЬТЕРРА
123
или
о
Е [е {t + а) — е {t)\ = [ К {t — т) о (т) dx
— (В
(индекс при т опущен). Применяя теорему о среднем и
обозначая через М максимум абсолютной величины функции o(t),
которая, очевидно, всегда ограничена, получим следующую
оценку:
Е | е (t + со) - е (t) | < MwK (t + со#) @ < ¦& < 1).
Естественно считать, что ядро К (?) стремится к нулю при
неограниченном возрастании аргумента; поэтому разность е (t + со) —
— е (t) стремится к нулю с возрастанием t, что и доказывает
высказанное утверждение.
Если периодическое напряжение начало действовать при
t = — оо, то из прямой теоремы следует строгая периодичность
функции е (t).
Докажем теперь обратную теорему. Предположим, что как
<y(t), так и e{t) являются периодическими функциями с
периодом со. Для момента времени t имеем:
t
Ee(t) = o(t)+ \ K{t,x)a(x)dx,
для момента г + со:
Ее (t Н- со) = о (t + со) -+- \ K(t + и, т) а (х) dx,
а так как e(t -j-co) = e(<), a (t + co) =o (t), то
( (+0)
I K(t,x)o(x)dx = ? K{t + (n, x)o(x)dx.
— ОО —ОО
•Заменив справа переменную интегрирования т на т-fco,
получим:
t t
[ K(t,x)o{x)dx= f K(t + a, x -f со) а (т) dx.
— oo — oo
Отсюда следует, что
K(t, r) = K(t + a, t + co),
а это возможно при произвольном со только тогда, когда ядро К
является функцией разности аргументов t — т.
Теоремы о замкнутом цикле были доказаны Вольтерра.
124
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
§ 27. СИНГУЛЯРНЫЕ ЯДРА НАСЛЕДСТВЕННОСТИ
Как мы видели, интегральные соотношения наследственной
теории упругости эквивалентны линейным дифференциальным
соотношениям с постоянными коэффициентами, если ядро
представляет собою сумму экспоненциальных функций. В то же
время при обработке опытных данных оказывается, что ядра,
содержащие один или несколько экспоненциальных членов,
плохо подходят для описания свойств реальных материалов.
Конечно, вводя спектры ползучести и релаксации, можно
аппроксимировать опытную кривую с любой степенью точности, однако,
по-видимому, набор упругих и вязких элементов не является
подходящей моделью для тел с несовершенной упругостью и для
описания их поведения следует выбирать другие функции.
Еще Больцман [173], впервые сформулировавший принцип
наследственности, предлагал ядро наследственности в виде
K(t-x) = 1^7. B7.1)
При постоянном напряжении отсюда получается
логарифмический закон изменения деформации ползучести во времени,
который неоднократно наблюдался рядом исследователей для
разных материалов. Однако ядро вида B7.1) обладает сильной
особенностью при т= f и интеграл от него расходится. Чтобы
избежать этого, можно видоизменить ядро Больцмана, положив
K(t-x) = -
-т-т-то
Здесь т0 — постоянная, имеющая размерность времени. В
случае ползучести, например, когда напряжение постоянно, в
результате интегрирования получается:
— [4-+^].
Как видно, положить т0 равным нулю в этой формуле нельзя.
При опытах на ползучесть обычно в начале процесса, сейчас
же после приложения нагрузки, скорость ползучести
оказывается весьма большой, настолько большой, что ее измерение
затруднительно и процесс загружения необходимо бывает
рассматривать как динамический процесс. Ядро Больцмана дает
бесконечно большую скорость деформации в момент приложения
нагрузки, однако особенность оказывается слишком сильной,
бесконечно большой становится не только скорость деформации,
но и сама деформация. Этот недостаток устраняется, если
принять за ядро ползучести функцию , где 0 < а < 1. Уравне-
(( — т)а
§27] СИНГУЛЯРНЫЕ ЯДРА НАСЛЕДСТВЕННОСТИ 125
ние кривой ползучести при постоянной нагрузке напишется при
этом следующим образом:
е=*[4-+т^-а]- B7'2>
Полученный степенной закон очень хорошо описывает ползучесть
различных материалов, по крайней мере начальные участки
кривых. С помощью этого закона Дуффинг [20°] интерпретировал
результаты испытаний кожаных приводных ремней, Ержанов [29]
с успехом применял подобную аппроксимацию для кривых
ползучести всевозможных горных пород. Значения показателя а,
для большей части материалов близко к 0,7, хотя Дуффинг дает
для него значение 0,8.
Идея введения в соотношения теории наследственности
интегральных операторов с ядрами типа Абеля, содержащими
слабую особенность, может быть истолкована как некоторое
обобщение идеи вязко-упругости. В § 23 мы начали конструирование
реологических моделей, соединяя вязкие и упругие элементы.
Другой путь построения соотношений между о" и е, содержащих
в себе закон упругости и закон вязкости жидкости как крайние
случаи, состоит в следующем [18]. Положим
o(t) = x-*^K; B7.3)
при а = 0 и х = Е это закон Гука, при а = 1 и и = Зт) мы
получаем закон вязкости Ньютон. Если а — любое число,
заключенное между 0 и 1, то производная дробного порядка в формуле B7.3)
должна пониматься в смысле Лиувилля, а именно уравнение B7.3)
представляет собою символическую запись следующего
интегрального соотношения:
-W = rn^5 S Т%г- <27'4'
В реологических моделях более общего вида элементы типа B7.3)
должны комбинироваться с вязкими элементами (см.,
например, [™Ц).
Интегральные уравнения Вольтерра с ядрами, имеющими
слабую особенность, были применены Вронским [° ] и Слонимским [131 ]
Для описания последействия в резине. Простейшее ядро типа
Абеля хорошо воспроизводит характер поведения материала
Е первое время после приложения нагрузки; однако затухание
скорости деформации иногда происходит быстрее, чем это следует
из B7.2). Стремление объединить свойства ядер со слабой
особенностью и свойства экспоненциальных ядер привело названных
126
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[гл. m
авторов к построению ядра следующего вида:
К(I-т) = const X (t — x)-aexp[ — (t — тI-"]. B7.5)
Резольвенту ядра B7.5) найти не удалось, однако, как показал
Вронский, приближение выражения для резольвенты
представляет собою функцию того же типа, что B7.5).
Несколько иное ядро того же характера было предложено
А. Ржаницыным [т], а именно:
К(t — т) = const х (t — т)-° ехр [ — р (t — %)]. B7.6)
Резольвента этого ядра построена в работе [17].
Мы будем пользоваться другими ядрами, сохраняющими
особенность типа ядра Абеля, но допускающими большую гибкость
при описании свойств реальных материалов,
§ 28. ЭКСПОНЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
ПРОИЗВОЛЬНОГО ПОРЯДКА
Будем обозначать через К* интегральный оператор типа
Вольтерра с ядром К (t — т), зависящим от разности
аргументов. Под умножением оператора на некоторую функцию будем
понимать вычисление интеграла
K*f= [ K(t-T)f{r)dt,
если он существует.
Рассмотрим теперь два интегральных оператора L* и М*
с ядрами L(t — т) и M(t — т) соответственно. Произведением
операторов L* и М* будем называть новый оператор N*, ядро-
которого
t
N(t-T)=*\L(t-$)M(l-T)di. B8.1)
т
Легко убедиться в том, что перемножение операторов
коммутативно:
N* = L*M* = M*L*.
Это значит, что ядро оператора Лг* можно вычислить также
но формуле
N{t-T)=\L(l-x)M{t-l)dl. B8.2)
X
Действительно, замена переменных ? = t -f- т — | переводит одну
формулу в другую.
§28] ЭКСПОНЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ПРОИЗВОЛЬНОГО ПОРЯДКА 127
Квадрат оператора определяется как произведение
оператора самого на себя, ядро оператора К*2 равно
lK(t-t)Ka-r)dt.
т
Но это есть первая итерация ядра К (t — т), то есть Xе2' (t — т).
Продолжая этот процесс, мы определим степень т оператора К*
или К*т как оператор, ядро которого является итерированным
ядром порядка т от ядра исходного оператора.
Запишем теперь интегральное уравнение Вольтерра второго
рода
*
u(t)+ \ K{t — T)u{z)dT = v{t) B8.3)
— оо
следующим образом:
(i + K*)u = v.
Разрешим это уравнение формально относительно и. Получим:
1+К*'
Поступим с выражением .у*» как с обычной дробью, в
которой К* является числом, меньшим единицы, и запишем, опять-
таки формально,
*„ =1 —Г* = 1 — К* + К*2-К*3+ ... B8.4)
Формально решение уравнения B8.3) будет следующим:
и = A —Г*)у, B8.5)
причем
Т* = К* — К**+К*Я—... B8.6)
Полученное решение B8.5) является не только формальным;
действительно, ядро оператора Г*, определенного соотношением
B8.6), представляет собою резольвенту ядра К (t — т), так как
B8.6) является операторной записью известного ряда Неймана
Для резольвенты уравнения Вольтерра:
T{t-T)=:K(t-T)—KW(t-%)+...
Как известно, ряд Неймана сходится при любых значениях
аргумента t — т, в соответствии с этим формальное
разложение B8.6) мы будем считать сходящимся для всей области
определения оператора К*.
128 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Рассмотрим теперь ядро вида [101]
Здесь Г A + а) — гамма-функция. Нас будут интересовать
значения а в интервале —1 <а < 0; уже первая итерация /„' (t — т)
при этом оказывается ограниченной, ряд Неймана для
резольвенты сходится при всех значениях аргумента, и общая теория
сохраняет силу. Будем называть оператор с ядром B8.7)
оператором Абеля. Для операторов Абеля справедлива теорема
умножения, а именно:
It.lt — Ли-p+i- B8.8)
Действительно, ядро оператора 1%1%, по определению, есть
i t
S^c-6)^F-T)rf6=-rA+ttIr(iqFrS(f-e)B(S-T)Pd6-
t т
Подстановка
? —*
t— Т
приводит последний интеграл к виду
1
О
что и доказывает формулу B8.8).
Определим теперь оператор Э% (р) следующим образом:
1 + рЗ*(Р). B8.9)
1-R
Иными словами, ядро оператора За (Р) есть резольвента ядра
1а, то есть
эг (Р)=/s+p/s2+p2/s3 +... B8.Ю)
Применяя формулу B8.8), убеждаемся в том, что ядро
оператора 3J(P) есть
оо
9a(bt-i) = (t-vr%4i^k+W- B8Л1)
о
Ряд B8.11) сходится для всех значений аргумента t — т при
любом р, если —1<а<со.
§ 29] ТЕОРЕМА УМНОЖЕНИЯ ДЛЯ Эа-ОПЕРАТОРОВ 129
§ 29. ТЕОРЕМА УМНОЖЕНИЯ ДЛЯ ^„-ОПЕРАТОРОВ
Если в уравнении Вольтерра второго рода интегральным
оператором является оператор Эа, то есть ядром служит
функция, определенная соотношением B8.10), резольвента
интегрального уравнения тоже будет функцией Эа. В § 24 мы убедились,
что этим свойством обладают экспоненциальные ядра.
Докажем, что
9*(х) — Э*(у)
Э1{х)Э1(у)= g J,/ • B9.1)
Соотношение B9.1) выражает собою теорему умножения для
операторов Эа[101]. Заметим прежде всего, что, если умножить
обе части равенства B8.10) на /ц, мы получим:
вд;(Р)=-р-з?(Р)—f/s.
Умножая еще раз на /?, найдем:
Iа Эа (р) — -р- Эа (р) р- Ia р- 1а
и, наконец,
ПпЭ*а(^ = фгЭШ-ф,П1--^тП2-...-~1Т. B9.2)
Перейдем теперь к доказательству теоремы умножения.
Положим для определенности х < у и запишем:
Э*а (х) Э% {у) = A*а + xlf + x4t + ¦ ¦ ¦) Э* (у) =
= -уЭ*а{у)-
+ -^э*(у)-
+^эш-
т7«+
х Т* х Т"*2 _1_
т2 т% *г2
л т* ¦*• т*2 ¦*¦ т*з 1
Просуммируем правую часть по столбцам, заметив при этом,
что
1 + 4 + -^ +
У У1 У — х
Получим:
Э*а (х) Э*а (у) = -^ [Э* (у) -I*- xl?- хЧ*а°-...].
Таким образом, соотношение B9.1) доказано.
¦* Ю. Н. Работнов
130 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Случай, когда х = у, представляет исключение. Оператор
ЭЭ* (х)
Э*а(*) = -^— B9.3)
имеет своим ядром новую трансцендентную функцию, ряд для
которой получается в результате дифференцирования ряда B8.11)
по параметру р.
Пользуясь теоремой умножения, мы можем разрешить любое
интегральное уравнение, ядром которого является За-функция.
Пусть, например,
A-хэ;(р))и=у.
Отсюда
1
и~ 1-хЭ«(Р) v'
Легко проверить, что
1-хЭ>(Р) =l + *3i(* + P)- B9.4)
Действительно, приводя к общему знаменателю, мы получим:
= da (к + р) да (Р).
Это равенство следует из B9.1). При р = 0 из B9.4)
получается B8.9). В некоторых случаях оператор наследственности
может быть аппроксимирован при помощи линейного агрегата
5а-операторов одного и того же порядка. Возникает вопрос
об обращении подобного оператора, имеющего вид
1-2 x,3S(p,).
t=l
Положим
-1 п
1-S«*9S(P«)
= i+%A,9Z(r.). B9.5)
i=i J s=l
Приведем к общему знаменателю и воспользуемся теоремой
умножения. Мы получим:
2 Авэг (г.) - 2 *,эг (Pi) - 2 2 м. 9"(^I^;(rs) = о.
s i is
Сравнивая коэффициенты при операторах с одинаковым
аргументом, получим две серии равенств:
1+2^=0, 1+2^=°-
s i
§ 29}
ТЕОРЕМА УМНОЖЕНИЯ ДЛЯ Эа-ОПЕРАТОРОВ
131
Второе равенство указывает на то, что величины rs являются
корнями уравнения
1+2-ртЬ-=°.
B9.6)
г=1
Эти корни должны быть вещественными и не равными между
собою. После того как величины rs найдены, коэффициенты As
находятся в результате решения системы линейных уравнений
i + 2
Ая
s=l
Pi
= 0.
B9.7)
В заключение этого параграфа приведены без доказательств
еще две теоремы, принадлежащие Розовскому [ш] и
оказывающиеся полезными при решении задач о ползучести
неоднородных и анизотропных сред.
Теорема 1. Если $хф$2ф ... ф$п, то
-1
II ЗД*)=2 П КР*—Pi)
k=l k=l Li=l
э?(рА)
Теорема 2. Если p\ Ф р2Ф • • • Ф $п, то
1-2лг*Пзз(Р<)
ft=l i=l
-1
= 1+2 акЭ*а (rft).
B9.8)
B9.9)
При этом Гк являются корнями уравнения
т п тл
1+S^7=ok= П <р*—р*)-1 Smp).
fe=i * L j=i J р=й /
а коэффициенты afe определяются в результате решения системы тп
линейных уравнений
m
1+ S ф-г^ад-О, Я*^гА.
ft=i
Первая теорема доказывается путем последовательного
применения основной формулы умножения; фигурирующий во второй
теореме агрегат Эа-операторов, в соответствии с первой
теоремой, превращается в линейную комбинацию этих же операторов,
к которой может быть применена формула B9.5).
В заключение приведем еще одну формулу, полученную
Розовским [122] и представляющую обобщение формулы B9.3), а именно:
5*(п)
ЭГ'(х)-
9п-1 да (х)
(п— 1)! дхп~1
B9.10)
9*
132
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
§ 30. АСИМПТОТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ Э-ФУНКЦИЙ
Ряд B8.11), определяющий функцию Эа (р\ t — г), сходится
довольно медленно, и применение его в практических расчетах
затруднительно. Некоторый интерес для приложений может
представить тот факт, что при а = —1/2 5-функция выражается через
табулированный интеграл вероятностей Ф (х) по следующей
формуле:
Для других значений а таблиц Э-функций не существует. Поэтому
представляет интерес получение приближенных выражений для
функций Э (р, t), а также для функций, получающихся в
результате действия 3-операторов на некоторые простейшие функции.
Если нагрузки постоянны, то при решении конкретных задач
результат представляется обычно в виде произведения <9-опера-
тора на постоянную. Очевидно, достаточно вычислить выражение
t
Э5(-рI= $5>а(-р,г-т)<гт. C0.2)
о
Во всех приложениях аргумент Эа-операторов оказывается
отрицательным, поэтому мы ввели в формулу C0.2) аргумент — р
и будем считать, что р > 0. Выражение C0.2) приводится
к следующему:
9S(-P)l=-p-[l-^i+e(-Pii+e)J. C0.3)
Здесь Ец (х) — функция Миттаг-Леффлера, определенная
следующим рядом:
со
71=0
Свойства функций Миттаг-Леффлера изучены в работе [382].
Для функции Ei+a {x) была предложена следующая
аппроксимация ["8], [ш]:
#i-Hx(-*)«exp(-Y*) (Y = (l + «I+Q)- C0.5)
Теперь формулу C0.3) можно заменить следующей
приближенной формулой:
5S(-p)l^|(l-exp(-Yp<1+a)]. C0.6)
TjpH t _>. оо второй член в скобке стремится к нулю и
выражение C0.6) стремится к предельному значению 1/Р; таким образом,
§ 30] АСИМПТОТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ Э-ФУНКЦИЙ 133"
>Эа-операторы описывают ползучесть, ограниченную при
постоянной нагрузке; неограниченная ползучесть получается лишь в
случае р = 0, когда <9а-оператор превращается в /„-оператор. В этом
смысле ядра, сконструированные из о>а-функций, ведут себя
так же, как ядра Вронского — Слонимского (§ 27).
Дальнейшее исследование асимптотических свойств ,9-опе-
раторов было выполнено Анниным [3] на основе работ [211], [25],
[26], в которых изучались асимптотические свойства некоторых
функций более общего типа, чем функции Миттаг-Леффлера,
а именно функций вида
Яр (г; А)-2 Г(л+ир-1) •
о
Легко убедиться, что
Эаф, f) = <e^j_(P«1+e; 1 + а).
1+а
Для значений а, лежащих в интервале —1<а<1, и
отрицательных значений аргумента асимптотическое представление
5-функции оказывается следующим:
Э (-6 1\ъ-г*У (-РП(РИ+В)-"
Г[A+о)-яA + а)]
n=2
pt2+a Г [ —(l + a)J
+ . . . C0.7)
Для произведения C0.2) получено такое асимптотическое
представление:
Э*Г-ВИ~ 1 /1+о V (-l)"(pt1+°)-n _
n=2
т[1-тпр?рт + -]- (за8>
Приведем еще асимптотическое разложение для произведения
производной 5-оператора на единицу; такое произведение
приходится вычислять, когда в ходе выкладок появляются квадраты
операторов:
аэ?(-рI 1_^Y (-1)"н(Р*1+а)-"
dp ^ р 2л Г[а + 2—иA + а)]:
п=2
Г (—а) рзг1+а + ¦ ¦ * C0.9)
134 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
§ 31. ОБЩАЯ ЗАДАЧА ТЕОРИИ
НАСЛЕДСТВЕННОЙ УПРУГОСТИ. ПРИНЦИП ВОЛЬТЕРРА
Закон наследственной упругости для растяжения — сжатия,
как мы видели, будет следующим:
а = Е(е— С T(t — x)e(x)dx\
или же
е = \ (о + \ K(t — x)a{x)dx
о
Употребив введенные в § 28 символические обозначения, мы
можем написать короче:
o = E(i — Y*)e, e = ±-(l+K*)a.
Далее, обозначим
Тогда
ЕA — Т*) = Ё.
а = Ее. C1.1)
Теперь закон наследственной упругости имеет точно такой же
вид, что и обычный закон Гука, только упругая постоянная
заменена упругим оператором Е. Такая запись является не
только формальной, действительно, уравнение C1.1) можно разрешить
относительно е, а именно:
1
1
Е
е =
1
1—Г*
-з-сг.
Е
ИЛИ
1
Е
A + K*)t
1 ± х i
Оператор — равен -=-, _Tif или — A + К*), как показано
в § 28; таким образом определяется операция деления
постоянной величины на упругий оператор, перемножение двух
различных упругих операторов немедленно вытекает из правила
умножения интегральных операторов, данного в § 28;
следовательно, все алгебраические действия над операторами имеют
определенный смысл.
Закон наследственной упругости для общего случая
пространственного напряженного состояния легко получить из обычного
закона Гука, если заменить упругие константы упругими
операторами образованными так же, как оператор Е. Для изотропного
§ 31] ОБЩАЯ ЗАДАЧА ТЕОРИИ НАСЛЕДСТВЕННОЙ УПРУГОСТИ 135
наследственно-упругого тела
ои = %д + 2реи. C1.2)
Здесь X = Я A + Л*), ]1 = ц, A + М*); операторы Л* и М* —
два различных оператора типа Вольтерра с ядрами Л (t — т)
и М (t — т) соответственно. Закон упругости можно записать в
другой форме, вводя вместо операторов Я и и. иные упругие операторы,
например Е, v, G, соответствующие модулю Юнга, коэффициенту
Пуассона и модулю сдвига соответственно. Соотношения между
различными упругими операторами записываются так же, как
соотношения между упругими константами. Так, например,
G= ^. C1.3)
2(l+v)
Мы уже полагали Е = Е A — Г*), положим v = v A + JV*).
Для расшифровки соотношения C1.3) нужно проделать
следующие операции. Прежде всего заметим, что
1 i 1 i — R*
2(l+v) 2(l + v) _^Л,* 2(l + v) *
"* 1+v
Оператор R* имеет своим ядром резольвенту ядра оператора
V
. , N*; значит, для нахождения R* нужно знать решение
соответствующего интегрального уравнения. После того как R*
найдено, мы получаем:
Все указанные действия выполняются по правилам § 29, если
операторы Г* и N* принадлежат к классу 3-операторов. При
описании наследственных свойств реальных сред наиболее
существенную роль играет сдвиговое последействие, тогда как
объемное последействие, по-видимому, можно считать отсутствующим.
Потребуем, чтобы оператор объёмного сжатия был постоянным.
Это значит, что
1—2v 1—2v
Е Е
Отсюда легко находим:
¦ = const.
*=vA+L2?r*)- C1-4)
При решении статических задач теории наследственной упругости
следует прежде всего заметить, что основные уравнения теории
136 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
упругости сохранят свою форму, только упругие константы будут
заменены упругими операторами. Умножение на Я, или ц, — это
операция интегрирования по времени, тогда как решение задачи
теории упругости связано с интегрированием по координатам.
Эти операции переставимы, поэтому любую статическую задачу
теории наследственной упругости следует решать так же, как
и соответствующую задачу обычной теории упругости, лишь
в окончательном результате нужно заменить упругие константы
упругими операторами.
Этот принцип мы будем называть принципом Вольтерра,
поскольку он был совершенно четко сформулирован этим автором.
Принцип Вольтерра позволяет получить чрезвычайно простые
решения для таких задач теории наследственной упругости,
когда решение задачи обычной теории упругости записывается
как произведение рациональной функции упругих постоянных
на функцию от координат. Если ядра представляют собою
комбинации экспоненциальных функций, обыкновенных или дробного
порядка, или же являются вырожденными, то расшифровка
соответствующих операторов не составляет труда. Так,
например, всевозможные задачи о поперечном изгибе пластинок решают-
ся с помощью двух операторов: D = -^ —=- hv;b плоских задачах
теории упругости для односвязных областей, если на границе
заданы усилия, напряжения оказываются независящими от
времени и такими же, как для упругого тела, в соответствии с
известной теоремой Леви. Однако существуют более сложные задачи,
приводящие к построению новых функций, они будут
рассмотрены в § 35.
Формулируя уравнения пространственной задачи вязко-упру-
гости, мы ограничились рассмотрением изотропного случая.
Более общее предположение состоит в том, что напряжения
и деформации связаны между собою линейными соотношениями
самого общего типа, которые можно записать следующим образом:
вц = Etjki ehl.
Здесь
Eijki = Eijtti A — Tfjki).
Из определения мгновенной упругости и законов термодинамики
следует, что Eim — Eknj, однако требование Г*,м = Г*щ и,
следовательно, Eijhi = EMij, строго говоря, обязательным не
является I225]. Это требование вытекает из некоторого общего
квазитермодинамического принципа, так называемого принципа Онза-
гера (см. [19]).
Общая теория линейной вязко-упругости строится по образцу
обычной теории упругости, для нее доказываются интегральные
§ 32] ПРИМЕНЕНИЕ ТРАНСФОРМАЦИИ ЛАПЛАСА 137
теоремы, аналогичные теореме Бетти, доказывается теорема
единственности при некоторых ограничениях, накладываемых на ядра
операторов. Мы не будем излагать этих результатов,
ограничившись ссылкой на литературу [а25], [175].
§ 32. ПРИМЕНЕНИЕ ТРАНСФОРМАЦИИ ЛАПЛАСА
К ЗАДАЧАМ ТЕОРИИ НАСЛЕДСТВЕННОЙ УПРУГОСТИ
Высказанные соображения, приведшие нас к формулировке-
принципа Вольтерра, могут быть представлены в несколько иной
форме, если применить к уравнениям теории наследственной
упругости преобразование Лапласа. Напомним, что
трансформацией Лапласа функции / (t) называется функция / (р),
определяемая следующим образом:
f(p)=^e-r>4{t)dt.
о
Обращение интеграла Лапласа дается формулой
у+гоо
М = 1тш I nP)eTdP.
у—ioo
Здесь у — положительное число, большее, чем действительная^
часть любого из полюсов функции / (р).
Сверткой двух функций g (t) и h(t) называется функция f{t)Y
определяемая равенством
t t
W)=^ g[t-i)h(i)di= ^g(t)h(t-x)dx.
о о
В операционном исчислении доказывается следующая теорема
о свертках (см., например, {27]):
f(p) = g(P)h(p).
Здесь /(р), g(p) и h(p) — преобразования Лапласа функций
/@> В (t) и М<) соответственно.
Выпишем теперь систему уравнений теории наследственной
упругости:
он, j + Ъ = О,
tij = -2(Ui,J + Uj,i),
аи = Ш?; + 2\Иеи.
138 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Соответствующие траничные условия:
at/vj = Tl на 2Г,
"i = "t на 2И.
Здесь через 2Ti J„ обозначены те части поверхности тела, где
заданы соответственно усилия или смещения. Случай, когда
на части границы заданы смешанные граничные условия, то есть
известны некоторые усилия и некоторые перемещения,
рассматривается совершенно аналогично. Применим к уравнениям
и к граничным условиям трансформацию Лапласа. Получим:
ou,j + Ft = 0, C2.1)
ё«=-j ("''' + "'.')• C2.2)
Выражение вида XQ содержит в себе свертку. Действительно,
хе = яГе+ (л(г-т)9(г)лУ
Трансформация Лапласа от этого выражения равна
А,(ё+лё) = яA + л)ё.
Таким образом, закон наследственности для изображений
принимает форму обычного закона Гука:
ои = К{1 + Л)ёби + р(\ + М)ёц. C2.3)
Соответственно трансформируются и граничные условия:
Oij\>j = Ti на 2Г, щ=щ на 2Ц. C2.4)
При выполнении последнего преобразования было существенно
то обстоятельство, что сама граница тела не меняется в процессе
деформации. Более того, функции Т\(р, хи) и и\ (р, xh) являются
известными функциями только в тех случаях, когда тип
граничных условий остается все время неизменным и граница между
частями поверхности 2Г и 2И также неизменна.
Уравнения C2.1) — C2.3) представляют собою уравнения обычной
теории упругости для изображений функций а и и ut, они содержат
параметр р. В результате решения статической задачи теории
упругости при граничных условиях C2.4) находятся величины
<*и (P. xh) и и, (р, xh), после чего по формуле обращения
отыскиваются оригиналы, то есть функции а-г] (t, х&) и щ (t, агд).
Очевидно, что, по существу, применение прямого символического
§ 32] ПРИМЕНЕНИЕ ТРАНСФОРМАЦИИ ЛАПЛАСА 139
метода, изложенного выше, и применение метода, основанного
на трансформации Лапласа, представляют собою различные формы
записи одних и тех же операций.
Трудности возникают, когда характер граничных условий
меняется со временем. Представим себе, например, что граница
между 2Г и 2и переменна, таким образом, в точке границы
были известны ut при t < ti и Tt при t > it. Для вычисления
Tt (p) нам нужно знать величину Tt не только при t > ?ь но
и при t < tt. Легко наметить схему решения подобной задачи,
если изменение типа граничных условий происходит внезапно
на некотором определенном куске поверхности. Представим себе,
например, что на границу полуплоскости давит штамп, область
контакта есть Q, при t = ti штамп снимается. Тогда приходится
решать последовательно две задачи. Направим для
определенности ось 1 по нормали к границе полупространства. При t < tt
граничные условия будут следующие: Т% = Т% = 0 всюду, Т\ = О
вне Q, щ = и\ (х2, xs) внутри Q. Решая соответствующую задачу,
находим Т\ в области Q, то есть давление под штампом. При
t > ti Т\ = Т\ — Т\ = 0 всюду; применяя трансформацию
Лапласа, мы убеждаемся, что Т\ = Т% = 0 всюду, тогда как
Т\ = 0 только вне области Q; внутри этой области Т\ (р) =
h
= \ Т\ (t) e~pi dt Ф 0. Мы можем фактически вычислить вели-
о _
чину Т\ (р), поскольку давление под штампом при t < ^
известно из решения первой задачи, таким образом, принципиальных
затруднений здесь не возникает. Сложнее обстоит дело в том
случае, когда тип граничных условий меняется непрерывно,
например, когда штамп движется по границе. Подобные задачи
будут рассмотрены далее.
С помощью трансформации Лапласа можно решать также
и динамические задачи теории упругости. Как известно,
преобразование Лапласа производной порядка п от функции / (t) дается
следующей формулой:
со
[ ЦР е-* dt = р»7 (р) - рп~Ч @) - p«-2/i @) - ...
о
В задачах об установившихся колебаниях, которые
представляют наибольший интерес, можно принять значения напряжений,
перемещений и их производных по времени равными нулю для
момента t = 0. Уравнения движения сплошной среды имеют
следующий вид:
Oij,j + Fi — pUi = °-
140
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[гл. ш
Применяя трансформацию Лапласа, получим:
ol},i + Fl-pp4il = 0. C2.5)
Вместе с уравнениями C2.2) и C2.3) мы опять получаем
замкнутую систему для изобржений напряжений и перемещений.
Очевидно, что трансформация Лапласа неприменима для
таких задач, когда ядро наследственности не является функцией
разности аргументов t — т, применение ее затруднительно в
задачах с переменными граничными условиями. Поэтому в
дальнейшем мы будем пользоваться главным образом прямым
символическим методом Вольтерра.
§ 33. ЯДРА БОЛЕЕ ОБЩЕГО ВИДА
Формулировка принципа Вольтерра не связана со
специфическим выбором ядер, для которых справедливо условие
замкнутого цикла, в приложениях иногда появляются ядра более общего
вида, а именно:
K(t, т) = А(т)ф(( —т) C3.1)
или
J?(*,T) = g(*)q><*-T). C3.2)
Ядра вида C3.1) были введены Арутюняном [4] для описания
ползучести бетона. Свойства бетона существенно зависят от его
возраста, то есть от времени, прошедшего с момента укладки;
процесс старения, то есть изменение механических характеристик
во времени, может считаться не зависящим от процесса
деформирования. Вспомним теперь рассуждения, приводящие к
формулировке принципа наследственности для стабильного материала,
приведенные в § 25. Если в интервале времени от т до т + dx
существовало напряжение а (т), то деформация, унаследованная
от этого интервала времени, выражалась следующим образом:
de = -g- а (т) ф (г — т) dr.
Здесь вместо К (t — т) мы написали ф (i — т), этот
множитель характеризует степень «забывания» эффекта воздействия,
относящегося ко времени т, память ослабевает по мере
увеличения расстояния t — т на оси времени. Предположим теперь, что
свойства самого материала меняются со временем. Воспроизводя
приведенное выше рассуждение, будет естественно предположить,
что величина de зависит не только от разности t — т, но также
от состояния материала в момент т, что учитывается при помощи
множителя, зависящего от т. Получаем:
de — -у h (т) ф {t — т) а (т) dx.
§ 33]
ЯДРА БОЛЕЕ ОБЩЕГО ВИДА
141
Таким образом, мы приходим к закону наследственности
с ядром вида C3.1). В теории Арутюняна учитывается также
изменение модуля упругости со временем, вследствие чего вид
ядра несколько усложняется; эта теория рассматривается более
подробно в § 34.
С ядрами типа C3.2) мы встретимся при решении некоторых
задач теории наследственной упругости с граничными условиями,
заданными на переменной границе. Функция g {t) может быть
вынесена из-под интеграла, таким образом, речь идет об
уравнении вида
{l+g(t)K*)u = v. C3.3)
Фактическое решение уравнений с ядрами вида C3.1) или
C3.2) возможно тогда, когда ядра вырождаются; все без
исключения опубликованные результаты относятся к тому случаю,
когда функция ф {t — т) представляется суммой
экспоненциальных функций
п
Ф^ 2 ^*ехр [h{t — x)\.
Рассмотрим в качестве примера решение уравнения C3.3)
при этом предположении. Перепишем это уравнение следующим
образом:
п
" + 2 g(t)At exp {ht) Kt = v. C3.4)
i=i
Здесь
t
Кг = \ exp (— %i%) и (т) dr.
о
Продифференцируем C3.4) по времени. Получим:
n n
и + S At (g + lig) exp {U) Ki + ug @ 2 At = i.
i=l t=l
Повторяя дифференцирование до порядка п включительно, мы
получим систему из п + 1 уравнений, содержащую линейным
образом и, v, производные этих величин до порядка п
включительно и п величин Kt. Исключая эти последние, мы получим
одно дифференциальное соотношение порядка п между и и v,
причем соотношение с переменными коэффициентами. Задавая
одну из функций, и или v, мы всегда получим для другой
функции дифференциальное уравнение с переменными коэффициентами
порядка п. Совершенно аналогичным образом анализируется
случай, когда ядро выражается формулой C3.1).
142
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
В качестве примера рассмотрим задачу, решенную Ли,
Радоном и Вудуордом [2801. Толстостенный цилиндр из материала,
подверженного ползучести, заключен в тонкую металлическую
оболочку (рис. 32). Наружный радиус цилиндра обозначен
через Ь, толщина оболочки — через h.
Внутренний радиус а считается переменным,
он задан как функция от t, причем -т > 0.
При г = a (t) приложено зависящее от
времени давление q (t). Подобная задача была
поставлена в связи с расчетом ракеты на
твердом топливе. Предполагаем, что труба
находится в условиях плоского
деформированного состояния и материал несжи-
рис> 32. маем. Вводим обычные обозначения: о> и
а9— радиальное и окружное напряжения,
/ . du и
и (г) — радиальное перемещение, ег = -г- и е9 = радиальная
и окружная деформации. Дифференциальное уравнение
равновесия в полярных координатах имеет вид:
daT
о г—сге
dr
= 0.
C3.5)
Связь между напряжениями и деформациями для несжимаемого-
материала может быть записана следующим образом:
о"е — о> = 2С (ев — ег).
C3.6)
На внутренней поверхности при г = а о> =—q, на наружной
поверхности аг представляет собою взятое с обратным знаком
давление на оболочку; окружная деформация оболочки
е =
Ь 1— у2
"А Е
ат(Ь).
Здесь Е и v — упругие постоянные материала оболочки.
Второе граничное условие получим, полагая е = <?е (b). Вследствие
несжимаемости материала и отсутствия осевой деформации
ет + ев ¦¦
du
Тг
+ ^- = 0.
Отсюда
и-
.*(*)
ев--
k(t)
г ¦ "г*
Из соотношения C3.6) следует:
сге — от =
е,=
МО
г2
4Gk
§ 33] ЯДРА БОЛЕЕ ОБЩЕГО ВИДА 143
Внесем это выражение в уравнение равновесия C3.5) и
проинтегрируем это уравнение. Получим:
Используем теперь граничные условия. Из первого условия
следует:
Следовательно,
Второе граничное условие приводит к следующему
соотношению:
i_k(t)
с
^^(^-iz)^-!- C3-7>
Здесь для краткости введено обозначение
Ь 1 — у*
Е
= с.
Уравнение C3.7) представляет собою как раз уравнение типа C3.2),
поскольку скобка в правой части является функцией t. Авторы
рассмотрели простейший случай вязко-упругого тела, для которого
Тогда уравнение C3.7) является просто дифференциальным
уравнением для функции к (i), которое имеет следующий вид:
а -Gr$—w)ft+ [P (Jjt)-b)+Wc] k = l(f)-
Очевидно, что это уравнение может быть проинтегрировано^
в квадратурах для любых функций a (t) и q (t). Авторы
проделали вычисления для случая, когда а = . ° и q постоянно,
у\ — ух
в этом случае квадратуры выполняются и решение доводится
до конца. Применяя описанную в предыдущем параграфе
процедуру, можно получить дифференциальное уравнение для
функции к при любом законе вида
144 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
§ 34. ЛИНЕЙНАЯ ПОЛЗУЧЕСТЬ БЕТОНА
Возвращаясь к вопросу о ползучести сред, свойства которых
меняются со временем, выпишем полностью уравнение, которое
предложил Арутюнян [4 ] для описания ползучести бетона и
которое учитывает старение:
tl
На основании обработки опытных данных для функции С (t, г),
названной мерой ползучести, было предложено следующее
выражение:
C(t,T) = <p(T){l-exp[-Y(*-T)]} , C4.2)
Ф(т) = С0 + ф.
Здесь С0, А\, у — константы материала. Константой материала
нужно считать и нижний предел хх интеграла в уравнении C4.1).
Это время, начиная с которого вообще можно говорить о том, что
поведение бетона описывается теорией наследственной упругости.
Дальнейшее уточнение формулы C4.2) может происходить
за счет добавления членов, содержащих последовательные целые
отрицательные степени т в выражении для (ср) т и
экспоненциальные члены в фигурной скобке. Мы не будем
останавливаться на соображениях, которые привели автора к
интегральному уравнению C4.1) и соответствующему выражению C4.2)
для ядра. Существенно отметить, что ядро оказывается
вырожденным, поэтому уравнение C4.1) можно заменить
дифференциальным уравнением. Если е (t) — заданная функция, то величина
е (t) E (t) = o0 (t) представляет собою мгновенное напряжение,
соответствующее заданной деформации, и уравнение C4.1) можно
записать следующим образом:
о0 = A-К*)в.
Здесь ядро оператора К* равно:
К (t, т) - Е (t) А |-*_ + ф (т) [1 _ ехр (- у (t - т))]} . C4.3)
После двукратного дифференцирования интегрального
уравнения по t и некоторых преобразований интегральные члены
исключаются; мы приходим к дифференциальному соотношению
d2<J i d° Г ,\ , г? ч Е' Л
^+ж {yA + ?<p)-t} =
d%o , da0 Г 0?'П YE' f 0 Е' \ . Е" 1 ,Q/ ,.
§ 34] ЛИНЕЙНАЯ ПОЛЗУЧЕСТЬ БЕТОНА 145
Решение этого уравнения при соответствующих начальных
условиях, вытекающих из исходного интегрального уравнения,
после некоторых преобразований приводится к следующему виду:
or (t) = в0 @ - уЕо0 @) ф @) jj ехр [ - ц (т)] dx -
о
t X
— уЕ\. ехр [ — т] (т)] dx \ а'0 (z) ехр [ц (z)] ц> (z) dz. C4.5)
о о
При этом для упрощения выкладок принято E(t) — E = const
и введено обозначение
т!(т) = у$ A+Яф(т))Л.
о
А
Если функция ф (т) имеет вид ф (т) = С0 + —- и мгновенные
напряжения постоянны, то для напряжения а получается
следующая формула:
t
а @ = <т0 [ 1 -уЕ (А + С0) т? ехр (rxj \ вхр{%~ГХ) dx] . C4.6)
Здесь
р = уАЕ, г = у{1+ЕС0).
Величина р, по данным Арутюняна, находится в пределах 0<;
<!р<[1, для большинства бетонов р-<у Материалы, для
которых р близко к нулю, называются быстро стареющими, для
них ядро наследственности мало зависит от возраста. Если р
близко к 0,5 или превышает это значение, бетон является
медленно стареющим. Фигурирующий в формуле C4.6) интеграл
представляет собою неполную гамма-функцию, положим для
краткости
Е
Ф (?,/>) = \ e-^x-Pdx.
о
Используя это обозначение, можно переписать формулу C4.6)
следующим образом:
G = ст0 jl-v^-i (А + с0) т?в"ЧФ(/*, р)-Ф(гхи р)]} . C4.6')
Уравнение C4.6) описывает процесс релаксации в бетонном
стержне, удлинение которого поддерживается постоянным.
10 Ю. Н. Работнов
146 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Очевидно, что уравнение C4.1) может быть представлено в виде
о
а в общем случае пространственной задачи можно использовать
символику, введенную в § 31.
При рассмотрении пространственных задач теории ползучести
важный частный случай будет тот, когда операторы К и (д.
отличаются лишь постоянным множителем. Это значит, что
наследственно-упругие свойства материала определяются только одним
1
размерным оператором, например введенным выше оператором -s=- ,
Е
безразмерные операторы обращаются в константы.
Таким образом, закон Гука, например, можно записать
следующим образом:
аи = ~g (шч + fyeij)-
Здесь К и (х — обычные постоянные Ламе, под е^ в общем
случае можно понимать выражения вида
eij — ~2 \Ut, J ~t~ Uii ') ei3'
При этом e*j — тензор вынужденных деформаций, не связанных
с напряжениями, например температурное расширение или усадка
бетона, то есть объемное изменение, происходящее со временем
независимо от действующих нагрузок. Вообще говоря, этот
тензор не удовлетворяет уравнениям совместности. Уравнения теории
упругости в перемещениях запишутся следующим образом:
¦f [(Л + |1)в,(-ЬцДи, + ^] = 0. C4.7)
Здесь Qi — (Я-}-ji) 8fj + [хАи*. Операторный множитель в
уравнении C4.7) можно опустить, и мы получим обыкновенные
уравнения теории упругости в перемещениях. Если условия задачи
таковы, что граничные условия заданы в перемещениях, которые
являются на границе заданными функциями времени, то решение
уравнения C4.7) будет совпадать с решением обычной задачи
теории упругости, которое может содержать время как параметр,
если граничные условия зависят от времени. Будем называть
эти перемещения, следуя Арутюняну, упруго-мгновенными
перемещениями, соответствующие напряжения, вычисленные по
закону Гука, будут упруго-мгновенными напряжениями от?,-.
Фактические напряжения будут связаны с упруго-мгновенными при
§ 35] ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ ПРИНЦИПА ВОЛЬТЕРРА 147
помощи соотношения
тождественного с соотношением C4.1). Таким образом,
формула C4.5) или следующие из нее дают решения задач
релаксационного типа [4].
§ 35. ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ ПРИНЦИПА ВОЛЬТЕРРА
Возвращаясь опять к ядрам, зависящим от разности
аргументов, остановимся на задачах более сложного характера, когда
решение соответствующей задачи теории упругости таково, что
рациональная функция от упругих постоянных не выделяется
в виде множителя. Один из примеров подобного рода был
рассмотрен самим Вольтерра [376], это задача о равновесии сферы
из наследственно-упругого материала, на поверхности которой
заданы перемещения. Как известно [14°], в этом случае решение
задачи обычной теории упругости может быть представлено так:
Щ = срг + (г2 — а2) ф, t.
Здесь г2 = xtXi, a — радиус сферы, ф, — гармонический вектор,
if — скалярная гармоническая функция, связанная
определенным образом с вектором ф;. При г — а второй член обращается
в нуль, а каждая из составляющих вектора ф; принимает значение,
равное значению соответствующей компоненты перемещения.
Последние считаются по условию задачи известными на
поверхности сферы. Внося ф; в уравнение Ламе, после некоторых
преобразований получим
Здесь принято со = фг>г. Положим
Я + 2Ц н' 2 (Х + 2^) •
В результате интегрирования C5.1) получаем:
*=-А(тУ»%- <35-2>
о
Формулу C5.2) нужно понимать в следующем смысле. По
определению со — гармоническая функция, следовательно, она может
быть представлена в виде ряда, общий член которого есть
произведение некоторой константы на величину rnSn. Здесь Sn —
поверхностная сферическая функция, зависящая от координат
точки на поверхности единичной сферы, например от
географических координат. Подставляя to в C5.2), мы найдем, что функция г|)
10*
148 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
будет представлена рядом, который отличается от ряда для со
тем, что каждый член умножается на —г-= . Отсюда следует, что
функция г|) гармоническая, что и предполагалось вначале.
Предположим теперь, что поведение материала описывается
уравнениями теории наследственности. Тогда постоянные Лир
превращаются в операторы An |3 = f$ -f H*. Положим Аа> = п
и представим ( — ) следующим образом:
Введем, следуя Вольтерра, функцию
V(z, t-T) = zH(t-T) + ~H™(t-r) + z^H™(t-r)+ . . .
Тогда ядро оператора Г — ) будет следующим:
(f.)'[, + r(l.i.,-T)].
и вместо C5.2) получим интегральное соотношение
г t
У=-г~^\ Рр-1 [п+[ л(е. T)v(la-2-, г-тЛ^т] dp. C5.3)
о о
В задачах, подобных рассмотренной, приходится вводить
ядра интегральных операторов, зависящие не только от времени,
но и от координат; как правило, соответствующие операторы
получаются в результате формального разложения в ряды
некоторых трансцендентных функций от операторов и координат,
в результате ядра представляют собою новые трансцендентные
функции. Такое ноложение встречается, например, в задачах
о продольно-поперечном изгибе балки, при изучении изгиба
балки на упругом основании. Несколько иной метод, при котором
искомое решение строится непосредственно в рядах, был
предложен Розовским [120]; мы не будем здесь его рассматривать, отослав
читателя к оригинальной статье. Более простой прием решения
некоторых задач подобного типа состоит в разделении
переменных. В качестве примера рассмотрим задачу о
продольно-поперечном изгибе балки. Уравнение изгиба будет отличаться от
дифференциального уравнения изгиба упругой балки только тем, что
вместо постоянной Е в нем фигурирует оператор Е = Е A — Г*),
в результате получается интегро-дифференциальное уравнение
d-nS + aV-»i. C5.4)
§ 36] ПРОСТЕЙШИЕ ДИНАМИЧЕСКИЕ ЗАДАЧИ 149
Здесь M0(z, t) — изгибающий момент от поперечной нагрузки,
Р
а2 = -щ • При данных граничных условиях существует
последовательность фундаментальных функций vk, каждая из которых
удовлетворяет уравнению
^ + a\vh = 0. C5.5)
При этом а% — фундаментальные числа. Будем искать решение
в виде
Подставим v в уравнение C5.4). Учитывая C5.5), получим:
2 [ - а|A - Г*) Th + a*Th] vh = «фА .
Умножим на vs и проинтегрируем по длине балки. Функции vs
ортогональны, будем считать их нормированными. Введем
обозначение:
jY ] M0 (z, t) vs (z) dz = ms (t).
о
В результате для Ts получается следующее интегральное
уравнение:
(а2-а? + сс!Г*)Г, = т8.
Отсюда
Ts = \ р^ . C5.6)
§ 36. ПРОСТЕЙШИЕ ДИНАМИЧЕСКИЕ ЗАДАЧИ
Задачи о свободных и вынужденных колебаниях упругих
систем решаются также с помощью метода разделения
переменных. В качестве примера рассмотрим вынужденные поперечные
колебания стержня. Для этого в обычном уравнении поперечных
колебаний, следуя общему правилу, заменим модуль упругости
соответствующим упругим оператором. Для стержня постоянного
поперечного сечения F получим:
?/(l-r*)S + pF^=g(Zl0. C6.1)
Главные формы свободных колебаний упругой балки являются
фундаментальными функциями уравнения
150 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
при соответствующих однородных граничных условиях, %% —
фундаментальные числа. Положим v = 2 ^fc @ vk (z) и внесем
в C6.1), воспользовавшись при этом C6.2). Получим:
2 [EH\-V)%\Th+pFTk\vk = q{z, t).
Умножим на vs (z) и проинтегрируем по длине балки. Как
известно, Vh образуют ортогональную систему функций, будем
считать ее нормированной. Введем обозначения:
-zpK = <*>|, fir] Я (z> l) vs B) dz = w>\qs (t).
0
В результате для функции Ts (t) получится следующее интегро-
дифференциальное уравнение:
7;4-<й«A_Г*)Г = <о*? C6.3)
(индекс s опущен).
Величина со, фигурирующая в уравнении C6.3), представляет
собою одну из собственных частот свободных колебаний
упругой балки. Уравнение C6.3) встречается не только в задаче о
поперечных колебаниях балки, а во всех тех случаях, когда
возможно разделение переменных, поэтому исследование его
представляет общий интерес. Особенно просто обстоит дело в том
случае, когда оператор Г* есть сумма экспоненциальных операторов
нулевого порядка. Положим
Г = 2 Asas ехр [ — as (t — т)].
Пусть q(t) = exp(ipt), будем искать функцию Т (t) в виде
71 = аехрг (pf + ф). Подставляя в C6.3), получим:
а{-р» + а,"[1-2^-]}=«о-«Р(-йр).
Отделяя действительную часть от мнимой, найдем:
«=К2^)Ч?-1+2^0Т"" (ЗМ)
и
VI Asas
Zj a2 + р2
Ь9=-Р-Ш L±ZT^- C6-5)
-ZL — IJ-'V s s
йJ 1_rZJ а| + Р2
Вырожденный случай, когда оператор Г* содержит
слагаемые, представляющие операторы дифференцирования, не пред-
§ 37] КОМПЛЕКСНЫЕ МОДУЛИ 151
ставляет каких-либо трудностей. Для примера рассмотрим вязко-
упругое тело, то есть примем (см. § 24)
Уравнение C6.3) сведется к обычному уравнению колебаний
с затуханием, пропорциональным первой степени скорости.
Тот же метод применим в случае, если Г* представляет собою
оператор с произвольным ядром. Считая по-прежнему q =
= exp (ipt), ищем решение в виде Т — а ехр [i (pt + <p)].
Вычислим отдельно величину Г* Г:
t
Т*Т = а ехр (щ)) \ Г (* — t) exp (ipx) dx.
—ос
Положим t — x — z, тогда
t оо
\ Г (t — т) ехр {ipx) dx = ехр (ipt) \ Г (г) ехр ( — ipz) dz =
— х> О
оо оо
= ехр(г>?)Г\ Г (z) cos pzdz — i \ Г (z) sin pzdz .
о о
Подставляя в C6.3), получим:
Здесь
Отсюда
а [ — р2 + и2 — со2 (Г! — гТг)] = о>2 ехр (— мр).
оо оо
Г1== \ Г (г) cos jozrfz, Г2= \ Г (z) sin pz dz.
в=[(-? + 1-г0' + г!] • C6'6)
^ф = -^ • C6-7)
©2
,,-H-ri
§ 37. КОМПЛЕКСНЫЕ МОДУЛИ
Результаты, полученные в предыдущем параграфе, могут быть
представлены в более компактной форме, если ввести понятие
о комплексном модуле упругости. Будем отправляться от
обычного соотношения между напряжением и деформацией при
152 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. Ш
растяжении — сжатии призматического стержня:
а = Ее = ЕA-Г*)е.
Положим e = eQexTp{ipt), тогда, по предыдущему,
оо
а = Ее0 exp {ipt) 1 + \ Г (z) exp (ipz) dz .
о
Введем обозначение:
оо
Е [ 1 + \ Г (z) exp (ipz) <fe ] « Я' + iE"
о
и назовем величину E'-\-iE" комплексным модулем упругости.
Если e — e0exp(ipt), то
o=lE'+iE*]e. C7.1)
Смысл этого равенства состоит в том, что сг представляет собою
также синусоидальную функцию от времени, но со сдвинутой
фазой, так что а = а0 exp [t (р?— ср)], при этом
а0=УЕ'' + Е-е0,
Е"
Величины Е' и Е" выражаются через ядро релаксации
следующим образом:
оо
E'(p) = ECl — ^ T(z)cospzdz^ ,
. ° C7-2)
Е" (р) = Е \ Г (z) sin pz dz.
о
Формулы C6.6) и C6.7) можно теперь переписать в таком виде:
1
§ 38)
ФУНКЦИИ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ
153
Если р достаточно мало по сравнению с со, то есть
циклическое деформирование является практически безынерционным, то
Е . Е"
а = — - , tg ш = —=-=-.
Величины а и <р определяются из опыта как функции
частоты, поэтому Е' и Е" могут быть также вычислены в зависимости
от частоты. После этого ядро релаксации восстанавливается
с помощью обратного преобразования Фурье
оо
о
или
?(t) = ^\^Sinptdp.
о
Совпадение или несовпадение результатов, полученных по этим
двум формулам, может свидетельствовать о пригодности или
непригодности уравнений линейной теории наследственности для
описания колебаний данного материала.
§ 38. ФУНКЦИИ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ
Вместо ядер ползучести и релаксации бывает удобно иметь
дело с функциями
t t
K{t)=[K(t)dt и y(t)=\T{t)dt, C8.1)
о о
которые называются соответственно функциями ползучести и
релаксации. Они могут быть определены непосредственно из опыта
на ползучесть при постоянном напряжении или релаксацию при
постоянной деформации. Действительно, при постоянном
напряжении первая из формул B5.1) дает
е = -|-[1+х@],
при постоянной деформации из второй формулы следует
a = Ee[l — y{t)].
Интегральные соотношения B5.1) могут быть записаны теперь
154
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
в следующей форме:
° C8.2)
a = E[e-ly(t-,)^-dx]
При выводе этих уравнений было произведено интегрирование
по частям и использованы условия: при t = 0 к @) — у @) = О,
а также е @) = а @) = 0. Первое условие вытекает из
определения функции ползучести и функции релаксации, тогда как второе
связано с тем, что в момент начала отсчета времени материал
предполагается находящимся в естественном состоянии.
Положим теперь
x*(t) = x(t)-l,
y*(t) = y(t) + i-
Тогда формулы C8.2) принимают следующий вид:
t
е = 1(и*(г-т) da (г), C8.3)
о
t
Е { y*(t — x)de(t).
о
Такая компактная запись закона наследственности часто
встречается в современной литературе, функции я* и 7* также
называются функциями ползучести и релаксации соответственно.
Чтобы применить, например, уравнения C8.2) к случаю
релаксации при постоянной деформации, нужно рассмотреть два этапа.
Первый этап — это возрастание деформации от нулевого
значения до фиксированного значения е, происходящее за малое
время д. Значение интеграла в правой части, соответствующее этому
этапу, будет следующим:
$„(,_„ <•&*_„(,_,,$??.*.
о о
Здесь | ¦&'' | ¦< 1 Ф | и исчезает вместе с ¦&. Переходя к пределу
при 0 = 0 и выполняя интегрирование, найдем, что интеграл
равен у (t) е. На втором этапе е = const, следовательно, -=- = 0
и соответствующий интеграл обращается в нуль.
В § 25 ядра ползучести и релаксации были представлены
в виде интегралов Лапласа. Соответствующие представления для
S 38] ФУНКЦИИ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ 155
функций ползучести и функций релаксации будут следующими:
оо
x{t)=\ Д(Р)ехр( —pO<fr,
° „ C8.4)
y(t) =¦- — \ A(a)exp(—at)dt.
о
Из того факта, что к (t) и у (t) являются интегралами от ядер
ползучести и последействия соответственно, а одно из ядер
является резольвентой другого, вытекает, что спектры
релаксации и запаздывания связаны между собою. Интегральное
соотношение между А (а) и —В (ее) имеет довольно сложный вид, и мы
его не приводим, отсылая читателя к монографии Гросса [222].
Комплексный модуль выражается через функцию релаксации
по формулам, которые немедленно следуют из C7.2), а именно:
Е' + iE" = Е Г 1 - ip I у (z) ехр (— ipz) dz ] , C8.5)
отсюда
Е' = Е Г 1 + р *\ у (z) sin pz dz 1 ,
о
оо
Е" = — Ер \ у (z) cos pz dz.
о
Воспользовавшись второй из формул C8.4), мы можем выразить
комплексный модуль через спектр релаксации. Подставляя
в C8.5) и меняя порядок интегрирования, получим:
оо
E' + iE" = E[l-ipl A^-da]. C8.6)
о
Разделив действительную и мнимую части, получим:
оо
E' = E[i + \A(a)-^-da],
E" = E\A(aI?±pda.
о
При статических испытаниях на ползучесть или релаксацию
непосредственно определяются функции ползучести и релаксации,
при динамических испытаниях — комплексный динамический
156
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
модуль как функция частоты. Приведенные в этом и предыдущем
параграфе формулы позволяют вычислить динамические
характеристики материала, если известны его статические
характеристики. Решение обратной задачи нахождения статических
характеристик по найденным из опыта динамическим сводится к
обращению соответствующих интегралов Фурье.
При обработке опытных данных в большинстве случаев
стремятся описать вязко-упругое поведение материала с помощью
экспоненциальных ядер, при подборе соответствующих
аппроксимаций оказывается полезным непосредственное определение
спектров запаздывания и релаксации. После того, как спектр
определен, то есть известна, например, функция—В F),
непрерывный спектр заменяется дискретным, это значит, что функция В (В)
определяется следующим образом: она равна нулю всюду, кроме
конечного числа интервалов 6ft — т)<Р<СРй + т], в каждом
из этих интервалов функция —В (В) равна ~- соответственно.
Тогда по формуле C8.4) при ц —v 0 получаем:
x@ = S^exp(-Bft0-
Технике вычислений различных характеристик вязко-упру-
гости посвящена большая литература, с основными идеями можно
познакомиться по упоминавшейся уже монографии Гросса [222].
§ 39. ЗАДАЧИ О ПОДВИЖНОЙ НАГРУЗКЕ.
МАЛЫЕ СКОРОСТИ
Специфические задачи теории наследственной упругости
возникают в тех случаях, когда на тело достаточной протяженности
действует нагрузка, движущаяся с постоянной скоростью
и не меняющая своей конфигурации по отношению к системе
координат, которая движется с той же скоростью. Наиболее
общая постановка будет заключаться в следующем. Тело имеет
форму призмы бесконечной длины. Система координат выбрана
таким образом, что начало координат движется вдоль
образующей со скоростью v, оси хг и х3 расположены в плоскости
поперечного сечения призмы, ось xt параллельна образующей. Наряду
с подвижными осями координат рассмотрим неподвижные оси,
совпадающие с подвижными в момент времени t = 0. Будем
обозначать координаты точек относительно неподвижных осей
соответственно х\. Формулы перехода от одной системы
координат к другой будут следующие:
xl = x'1 — vt, х2 = х'2, х3 = х'3.
Предположим теперь, что внешние силы, как поверхностные,
так и объемные, зависят лишь от координат х%. Будем искать
S 39] ЗАДАЧИ О ПОДВИЖНОЙ НАГРУЗКЕ. МАЛЫЕ СКОРОСТИ 157
стационарные решения, то есть такие напряженные состояния
и такие поля перемещений, которые зависят от координат хь
и не зависят при этом явно от времени. Очевидно, что при этом
нужно предполагать, что движение началось достаточно далеко,
то есть нагрузка приходит из бесконечности. Зависимость
перемещения материальной точки от времени определяется тем, что
ее координата х\ постоянна, тогда как координата xt за время dt
меняется на величину dx^ = —v dt. Поэтому скорость материаль-
г- диь диъ
нои точки в направлении Xft будет ~ = — iij-1, ускорение же ее
-7г-~ = гг -g-f. Будем считать, что скорости достаточно малы
(по сравнению со скоростью распространения упругих волн)
и поэтому силами инерции, происходящими от ускорений, можно
пренебречь.
Основные соотношения теории наследственной упругости
су = Явбу + 2^
относятся к фиксированной материальной точке, то есть к
фиксированному значению координаты х[. Величины etj заданы как
функции координат xt, зависимость их от времени определяется
тем, что Xi (t) = х[ — vt, тогда как в момент времени т для той
же материальной точки было х\ (х) = ?, = х[ — vx.
х t tf?
Отсюда следует, что t — т = — , dx = . Оператор
Л9 принимает следующий вид:
оо
Яв = Я,AЧ-А*)в = я[1+4-jA(l=S-)e(?,iaia;s)dg]. C9.1)
Обозначим новый интегральный оператор через Л**.
Покажем, что при определенных условиях оператор
дифференцирования по координате хх и оператор Л** коммутативны.
Действительно,
оо
X
После дифференцирования и интегрирования по частям
получим:
¦?¦ (Л**Ф) = -Л (оо) и (оо) + Л** -g- . C9.2)
Остается в каждом случае показать, что Л (оо) и (оо) = 0. Для
ограниченных ядер это очевидно, так как и (оо) = 0 является
естественным условием, накладываемым на перемещения при
отыскании решения.
Дальнейшее развитие теории особенно просто в том случае,
когда операторы Лии пропорциональны, то есть когда
158
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. Ill
[X = (х A + Л*). Тогда уравнения закона Гуна приобретают
следующий вид:
ои = (If Л**) (Авбц + 2цеу). C9.3)
Доказанное свойство коммутативности оператора Л** с
оператором -— позволяет ввести трансформированные перемещения
щ = A+Л**)и;. C9.4)
Трансформированные компоненты деформации выражаются через
них по обычным формулам 2е1]-=и1 j + Uj;. Напряжения
связаны с трансформированными деформациями уже обычными
формулами закона Гука, уравнения
равновесия и уравнения совместности
имеют при этом обычный вид, и мы
приходим к постановке задачи
теории упругости, в результате которой
находятся величины Gtj и Ht, после
чего перемещения можно найти па
—j^z^aA
*' формулам
Рис. 33.
1 1 + Л**'
Вопрос об удовлетворении граничным условиям оказывается
очень простым, когда на поверхности тела задана движущаяся
нагрузка. Тогда граничные условия формулируются так же, как
в соответствующей статической задаче теории упругости.
Смешанные задачи представляют значительно большую сложность.
Действительно, рассмотрим, например, вопрос о. движении
жесткого штампа (рис. 33). Задано смещение и2 на отрезке 0<!a;i<;6',
на отрезках х± < 0 и х\ > С величина и2 неизвестна, зато
известно, что 022 = 0. Но для того, чтобы найти и2 при 0<a;i<:CT
необходимо знать функцию и2 не только на этом отрезке, но и при
Xi > С, как это следует из C9.3). Некоторые возможности
решений подобных смешанных задач будут рассмотрены далее.
Для поддержания стационарного состояния, вызванного
движущейся с постоянной скоростью нагрузкой, необходима
некоторая мощность. Величина мощности формоизменения
выражается следующей формулой:
L= — \ OnendV.
= — \ аиеи
v
Но е,-,= — и——. Обозначим щ — —— , тогда
ОХ* ОХ\
- — -р- \Щ, } ~г ui, i) — eij
§ 40] ДВИЖЕНИЕ ШТАМПА ПО ГРАНИЦЕ ВЯЗКО-УПРУГОЙ СРЕДЫ 159
Вследствие симметрии тензора а,7- можно написать:
L = v \ Gije'ij dV = v \ OijUijdV. C9.5)
Преобразуя объемный интеграл в интеграл, распространенный
по поверхности, получим:
Tmidl. C9.6)
Заметим, что если тело является упругим, то oij = Eijflieiti,
Gije'ij =-— , где U -~ у Е^ывцем', следовательно, по формуле C9.5)
V
Интегрируя по объему бесконечной призмы, образующая которой
параллельна оси ж1? и учитывая, что при i) = f oo etj = 0
и, следовательно, U = 0, найдем, что L = 0.
Фактическое построение решений задачи о движущемся
штампе встречает большие трудности. В последние годы этими
задачами заинтересовались английские авторы. В работах [247] и [29в]
для нахождения решения использован метод приведения к
дуальным интегральным уравнениям. Форма получающихся решений
такова, что получение численного результата для конкретных
условий возможно, но какой-либо качественный анализ
затруднителен.
В работе Ивановой [39] для той же задачи был применен
иной метод, основанный на применении аппарата комплексной
переменной. Даже для довольно простых экспоненциальных ядер
получение численного результата связано с вычислительными
трудностями. В следующем параграфе будут рассмотрены идея
этого метода и приложение к вязко-упругой среде, обладающей
простейшими свойствами.
§ 40. ДВИЖЕНИЕ ШТАМПА ПО ГРАНИЦЕ ВЯЗКО-УПРУГОЙ СРЕДЫ
Оператор Л** может быть не только интегральным. Случай
простейшей вязко-упругой среды является вырожденным
случаем, когда Л* = сс-тп-, следовательно, Л**— -аи^- и
трансформированные перемещения определяются следующим образом:
й^щ-аи^. D0.1)
160
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
СГЛ. III
Интегрируя это дифференциальное уравнение относительно щ,
получаем обратное преобразование:
щ==~^\ М?)ехр^-М
D0.2)
Здесь учтено, что моменту времени t = — оо, когда ut = 0,
соответствует значение координаты х^ = оо.
Как пример применения этой теория рассмотрим задачу о
движущемся штампе по границе вязко-упругой полуплоскости. Будем
Рис. 34.
при этом следовать за ходом известного решения Н. И. Мусхели-
швили ["] для соответствующей задачи теории упругости.
Предположим, что штамп имеет круговую форму и трение отсутствует.
Заменяем дугу окружности параболой, тогда уравнение
профиля штампа будет (рис. 34)
f <?> = ¦&•
Вертикальное перемещение точек границы полуплоскости на
участке (а, Ь) следует за профилем штампа, но определение
напряженного состояния в вязко-упругой среде связано с
решением вспомогательной задачи теории упругости, в которой
заданы трансформированные перемещения. В соответствии с этим мы
выбираем трансформированную форму штампа:
С
' 2R
¦O.V
R
Если контакт осуществляется на участке (а, Ъ) границы, то
решение соответственной плоской задачи теории упругости зависит
от нахождения функции комплексной переменной Ф (z),
которая дается формулой (["], стр. 441)
§ 40] ДВИЖЕНИЕ ШТАМПА ПО ГРАНИЦЕ ВЯЗКО-УПРУГОЙ СРЕДЫ 161
Здесь
причем Р—вертикальная сила, действующая на штамп.
Давление р {хх) под штампом выражается следующим образом:
р = Ф+(х1)-Ог(а:1).
В нашем случае вместо / (?) нужно подставить /(C)- Положим
на время
?&) = А? + А0.
Таким образом, нам нужно вычислить интеграл
а
Применяя обычный для вычисления подобных интегралов способ
(["]), найдем, что он равен
го | (AiZ — А0) Y(z — a){b — z) +
+ i[A^+(A0-Ai^y-Al<±^]} .
Не переписывая формулу для Ф(г), приведем сразу выражение
для давления:
p(xi) =
D0.4)
Здесь
Постоянные а и Ь найдутся из условия ограниченности р (х^
при хх = а и при Xi = Ъ. Опуская очевидные выкладки, получаем:
/ 2д 2AJ Аа_ , _ ./2±,Щ_ Л0
а~ V А^ А\ At ' °~ V Л, "Г" А\ Ai •
Возвращаясь к первоначальным обозначениям, заметим, что
А, = -Б-, А0= 5-, следовательно,
а = — Y 2qR + 2 (ayJ + <tv, b = Y2qR+ 2(wJ + av.
И Ю. Н. Работнов
162 ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ [ГЛ. III
Теперь распределение давления будет даваться следующим
выражением:
р {Xi) = ~ JiTWR VW-^aW^)- D0.5)
В заключение вычислим мощность при перемещении штампа
по формуле C9.6). После несложных вычислений получим:
L = va-^P^av*P. D0.6)
Формула D0.6) показывает, что при качении катка по вязко-
упругому основанию приходится преодолевать момент трения
качения, причем коэффициент трения качения равен a v. Таким
образом, результат оказывается чрезвычайно простым. При
качении колеса или скольжении штампа по вязко-упругому
основанию эпюра распределения давлений под штампом оказывается
той же, что и в случае упругого основания. Эта эпюра смещена
в направлении движения на величину av, представляющую собою
плечо пары трения качения.
§ 41. НЕКОТОРЫЕ ЭКСПЕРИМЕНТАЛЬНЫЕ
ДАННЫЕ ПО ПОЛЗУЧЕСТИ ПЛАСТМАСС
Приводимые в этом параграфе данные служат для
иллюстрации того, в какой мере изложенные выше теоретические
соображения применимы для описания свойств реальных материалов.
Многочисленные авторы, анализируя опыты на ползучесть
различных полимерных материалов в стеклообразном состоянии,
приходят к следующим выводам:
1. Кривые ползучести удовлетворительно аппроксимируются
степенными функциями времени.
2. Существует диапазон напряжений, в котором зависимость
деформации, достигаемой по истечении заданного времени, от
нагрузки линейна.
3. Деформация ползучести полностью или почти полностью
обратима.
Степенная зависимость деформации от времени была проверена
на опытах длительностью до 100 000 часов [207], она оказывается
во всех случаях неизмеримо лучшей, чем экспоненциальная или
применявшаяся некоторыми авторами логарифмическая
зависимость. Но это указывает как раз на то, что в качестве оператора
ползучести нужно брать оператор 1~а с ядром ^, _ @ <а < 1),
тогда функция ползучести будет
§ 41] НЕКОТОРЫЕ ДАННЫЕ ПО ПОЛЗУЧЕСТИ ПЛАСТМАСС 163
Что касается линейности зависимости е от а, сошлемся на работы
Финдли [208], который описывает ползучесть разнообразных
пластиков при помощи следующего уравнения:
e=ash— + ft*m sh-
D1.2)
Если принять функцию ползучести в виде D1.1), то окажется,
что а = 1 — т. Выясним, при каких значениях о* можно
заменить гиперболический синус в D1.2) линейной функцией.
Гиперболический синус х отличается от х на 10% тогда, когда х «
«0,77, следовательно, если а < 0,77 ат, то во втором члене
уравнения D1.2) вместо гиперболического синуса можно принять
линейную зависимость от напряжения. В нижеследующей таблице
по данным работы [а09] для 12 материалов приведены значения ее,
ат и 0щ, = 0,77 От — напряжения, начиная с которого
погрешность линейной теории превышает 10%.
Материал
кг/см%
"пр-
кг/см*
1. Стеклотекстолит на меламнновом
связующем "
2. Стеклотекстолит на силиконовом
связующем
3. Слоистый асбестопластик
4. Стеклотекстолит на основе ткани 181
и полиэфирной смолы
5. Тот же материал, что и в 4,
погруженный в воду
6. Армированный пластик на основе стек-
ломата и полиэфирной смолы
7. Стеклотекстолит на основе ткани 181
и эпоксидной смолы
8. Тот же материал, что и в 7,
погруженный в воду
9. Стеклотекстолит на основе ткани № 1000
и полиэфирной смолы
10. Тот же материал, что и в 9,
погруженный в воду
11. Стеклопластик на основе ровничной
ткани и полиэфирной смолы
12. Тот же материал, что п в 11,
погруженный в воду
0,981
0,972
0,733
0,910
0,790
0,810
0,840
0,780
0,900
0,810
0,800
0,770
2460
548
168
980
914
597
3515
773
478
393
1547
2812
1900
420
130
790
705
546
2700
600
370
300
1190
2160
Напряжения, стоящие в последнем столбце, не столь уж
малы, и при длительной службе изделия конструктор бывает
вынужден выбирать допускаемые напряжения в линейной области.
Приложение принципов теории наследственной упругости
к анизотропному конструкционному материалу — стеклопластику
11*
164
ЛИНЕЙНЫЕ ВЯЗКО-УПРУГИЕ СРЕДЫ
[ГЛ. III
АГ4С было произведено Брызгалиным [10]. Материал
представляет собою слои стекловолокна, уложенные в двух взаимно
перпендикулярных направлениях и пропитанные смолой.
Степень армирования в двух направлениях приблизительно
одинакова. Образец, вырезаемый вдоль направления нитей и
поставленный на испытательную машину, под действием постоянной
/
е-70
42
2$
9
г~
f
<р=45°
<р=Ж
tp=15%
<р=0°
" т
о го w ео soJ то
t,vac
Рис. 35.
нагрузки ползет, но через несколько часов эта ползучесть
фактически прекращается, кривая ползучести выходит на
горизонтальную асимптоту. Это и понятно: в первый момент усилие
распределяется между стекловолокном и смолой, но смола релаксирует,
и постепенно вся нагрузка передается на стекловолокно, которое
само по себе при комнатной температуре не ползет. Образец,
вырезаемый из плиты стеклопластика под углом ф = 45° к
направлению нитей, обнаруживает интенсивную незатухающую
ползучесть, которая хорошо описывается при помощи функции
ползучести типа D1.1). На рис. 35 приведены кривые ползучести
для образцов, вырезанных под разными углами ср к направлению
нитей. Обнаруженный характер кривых ползучести
подсказывает следующую модель материала. Будем пренебрегать
ползучестью вдоль стекловолокна; если направить оси х и у вдоль
волокна, то по отношению к действию напряжений ах и ау будем
считать материал упругим; при этом упругие характеристики
соответствуют не мгновенным деформациям, а их предельным
значениям для достаточно большого времени, когда кривая
ползучести практически достигает своей асимптоты. По отношению
к сдвигу будем считать материал наследственно-упругим. Таким
образом, полная система уравнений для плоского напряженного
§ 41] НЕКОТОРЫЕ ДАННЫЕ ПО ПОЛЗУЧЕСТИ ПЛАСТМАСС 165
состояния будет
ex = -^(ax-viay), еу ¦--- -^- (ау — v2ax), Y-"=-=-¦ D1-3)
Уравнения D1.3) не обязательно предполагают одинаковую
степень армирования для направлений х и у, в противном случае
было бы Ei = E2, Vj = v2.
Проверка уравнений D1.3) производилась путем сравнения
деформаций ползучести для образцов, вырезанных под разными
углами. На рис. 36 приведена теоретическая кривая зависимости
деформации ползучести для фиксированного времени согласно
формулам D1.3) и опытные точки.
Величина и представляет собой отношение деформации
ползучести за 100 час. для образца, вырезанного под углом <р к
направлению волокон, к деформации ползучести за то же время
при том же напряжении для образца, вырезанного под углом-45°.
На материалах типа стеклопластиков индивидуальный разброс
данных испытаний обычно велик, поэтому степень совпадения
теории и эксперимента нужно считать хорошей.
ГЛАВА IV
ПОЛЗУЧЕСТЬ МЕТАЛЛОВ.
ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ
И ФЕНОМЕНОЛОГИЧЕСКИЕ ТЕОРИИ
Ползучесть металлов при высоких температурах
характеризуется двумя отличительными особенностями. Во-первых,
большая часть деформации ползучести необратима, возврат после
снятия нагрузки наблюдается только в области относительно
низких температур, и величина восстановленной деформации
составляет лишь незначительную часть общей деформации
ползучести. Во-вторых, зависимость скорости ползучести от
напряжения резко нелинейна, небольшое увеличение напряжения
вызывает сильное возрастание скорости ползучести. Поэтому
рассмотренная в главе III теория наследственной упругости для
металлов неприменима, и теория ползучести металлов строится
на совершенно иных основаниях.
В настоящей главе рассматриваются основные опытные факты,
относящиеся к ползучести при одноосном напряженном
состоянии, а также феноменологические теории, которые описывают
этот простейший случай.
§ 42. ОСНОВНЫЕ СВЕДЕНИЯ О ПОЛЗУЧЕСТИ
Явление ползучести металлов вызвало значительный
интерес со стороны техников, прежде всего, потому, что ползучесть
наблюдалась в деталях паровых турбин — трубопроводах, дисках
и лопатках, работающих при высокой температуре. В диске
и лопатках возникают напряжения от центробежных сил, которые
нельзя уменьшить за счет увеличения толщин; улучшение
конструкции диска путем выбора оптимальной формы профиля
позволяет уменьшить рабочие напряжения лишь незначительно.
Поэтому сразу возникла необходимость оценивать способность
материала сопротивляться ползучести и испытания на ползучесть
получили широкое распространение. В результате оказался
§ 42] ОСНОВНЫЕ СВЕДЕНИЯ О ПОЛЗУЧЕСТИ 167
накопленным огромный опытный материал в виде так называемых
кривых ползучести. Накопление этого материала применительно
к новым сплавам происходит и в настоящее время.
Стандартные испытания на ползучесть производятся по
следующей схеме. Цилиндрический образец помещается в печь и
подвергается действию растягивающей нагрузки, обычно при помощи
рычажного устройства. Печь снабжена регулятором температуры,
обеспечивающим поддержание постоянства температуры с
заданной степенью точности. К образцу крепится экстензометр,
позволяющий регистрировать удлинение образца в фиксированные
моменты времени. В настоящее время существует очень много
конструкций машин для испытания на ползучесть,
принципиальное отличие между ними состоит главным образом в системе
измерения деформации и в методах нагрева и регулирования
температуры. Описание схем такого рода машин не входит в нашу
задачу (см., например, [83], [123]), здесь мы ограничимся некоторыми
замечаниями. Прежде всего, постоянство нагрузки,
обеспечиваемое рычажным устройством машины, не означает постоянства
напряжения. Действительно, в процессе ползучести длина
образца увеличивается, а следовательно, уменьшается площадь его
поперечного сечения. При постоянной силе напряжение растет
в процессе испытания. В начальном периоде исследований
ползучести на отмеченное обстоятельство обращалось большое внимание.
Были предложены различные устройства, позволяющие
поддерживать постоянным именно напряжение. Однако при этом
приходилось исходить из предположения, что объем образца при
ползучести не изменяется и изменение площади сечения можно
определить, зная удлинение образца. В первом приближении эта
гипотеза оправдывается; таким образом, поддержание
относительно постоянного напряжения больших трудностей не встречает,,
но влияние изменения площади сечения сказывается лишь при
достаточно больших деформациях. В реальных конструкциях
обычно бывает можно допустить лишь очень незначительные
деформации ползучести, порядка 1 %; современные жаропрочные сплавы
разрушаются при малом удлинении, поэтому опытное изучение
ползучести в настоящее время ограничивается малыми
деформациями и заботиться о корректировке нагрузки для поддержания
постоянства напряжения не имеет смысла.
Второе замечание относится к системе нагрева. Обычная схема
состоит в том, что образец вместе с захватом помещается в
трубчатую печь с проволочной обмоткой или силитовыми стержнями.
Такая печь обладает большой тепловой инерцией, время
выдержки образца до того момента, когда установится температура и,
следовательно, можно будет начать испытание, составляет
несколько часов D—6). Для структурно-неустойчивых сплавов условия
испытания часто оказываются поэтому отличными от условий
168 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
эксплуатации, когда нагрев происходит за более короткое время.
Поэтому сейчас появились испытательные устройства, в которых
нагрев осуществляется либо с помощью отражательных зеркал,
либо электронным пучком, либо, наконец, проходящим током.
Последний способ наиболее прост, однако для некоторых
материалов свойства при нагреве проходящим током оказываются
отличны от тех, которые обнаруживаются при нагреве с
поверхности.
Результаты испытаний на ползучесть представляются в виде
так называемых кривых ползучести, то есть кривых зависимости
деформации от времени. На рис. 37 схематически изображены
типичные кривые
ползучести для разных
напряжений о-! ¦< 02 •< а3-
Мгновенную
деформацию, возникающую сразу
после приложения
нагрузки, мы обозначим е0 (о),
она может включать в себя
как упругую, так и
пластическую часть. На кривой
ползучести,
соответствующей напряжению ff2,
хорошо видны три участка.
Цифрой / отмечен участок
неустановившейся
ползучести, когда скорость
убывает. На участке // скорость достигает минимального
значения, таким образом, материал ползет с постоянной скоростью
е — е = v (а). Ускорение ползучести на участке /77
предшествует разрушению. Разбивка кривой ползучести на три участка
в значительной мере условна. Прямолинейный участок
установившейся ползучести наблюдается далеко не всегда, на том
же рис. 37 приведена кривая ползучести, соответствующая
большему напряжению сг3, для нее вторым участком можно условно
считать некоторую область вблизи точки перегиба. При меньшем
напряжении cTj за время испытания скорость ползучести еще не
успела достигнуть минимального значения, таким образом,
кривая на рисунке соответствует первому участку.
Определение начальной деформации е0 встречает известные
трудности, связанные с тем, что эта начальная деформация
зависит от способа приложения нагрузки. Чтобы сделать условия
более определенными, в работе [30], например, испытанию на
ползучесть при постоянной нагрузке предшествовало загружение
с постоянной, строго фиксированной скоростью увеличения
напряжения.
Рис. 37.
§ 43] ЭМПИРИЧЕСКИЕ ФОРМУЛЫ ДЛЯ КРИВЫХ ПОЛЗУЧЕСТИ 169
§ 43. ЭМПИРИЧЕСКИЕ ФОРМУЛЫ ДЛЯ КРИВЫХ ПОЛЗУЧЕСТИ
Основная задача, которая ставилась при первых исследованиях
ползучести и сохранила свою актуальность до настоящего
времени,— это задача экстраполяции кривых ползучести на большие
длительности. При испытании образцов из углеродистых и
низколегированных сталей, которые применялись в турбостроении
в 20—30-е годы настоящего столетия, обнаруживался большой
разброс опытных данных, в особенности для начальных участков
кривых ползучести. Более или менее устойчивые результаты
получались только для зависимости скорости установившейся
ползучести v от напряжения. Поэтому усилия исследователей были
направлены на получение именно этой зависимости. Программа
испытаний строилась таким образом, чтобы получить более или
менее надежно прямолинейный участок кривой ползучести, наклон
этого участка и определяет значение v для данного напряжения ст.
Заметим, что, по существу, речь идет лишь о возможности
прямолинейной аппроксимации некоторого участка кривой, выбор
наилучшей аппроксимации зависит от длины этого участка.
Робинсон [342], опубликовавший данные испытаний на ползучесть
длительностью 100 000 часов A2 лет), указывает, что наклон
кривой ползучести в течение всего срока испытания менялся.
Однако, если речь идет об определенном диапазоне длительностей,
величина v (а) может быть определена с достаточной степенью
точности. Различными авторами предлагались различные формулы
для v (о), некоторые из них являются чисто эмпирическими,
некоторые основаны на определенных физических соображениях.
Одно из наиболее ранних исследований ползучести
конструкционных материалов турбин принадлежат Бейли [ш], [162], он
предложил для функции: v (а) следующую зависимость:
е = и(и) = Воп. D3.1)
Показатель п оказывается довольно большим, для сталей он
колеблется от п = 3 до п = 8, а иногда оказывается еще больше. Такая
чрезвычайно сильная нелинейность зависимости скорости
ползучести от напряжения характерна для металлов. Очевидно, что
применение всякого рода линейных теорий, подобных описанным
в третьей главе этой книги, здесь совершенно исключено. Поэтому
развитие теории ползучести металлов шло совершенно иными
путями.
Определение констант В ж п производится чрезвычайно просто,
для этого достаточно нанести точки, соответствующие
измеренным значениям v при заданных значениях сг, в логарифмических
координатах и провести через эти точки прямую.
170 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Соотношение D3.1) мы будем записывать в несколько более
удобном виде, а именно:
i-i-iJ- <43-2>
Здесь гп — константа, имеющая размерность скорости
деформации, 0П — константа, имеющая размерность напряжения.
Очевидно, что
В = епОпП.
Введение двух констант гп и ап вместо одной может показаться
излишним, но при решении задач часто бывает полезным иметь
в своем распоряжении возможность выбора масштаба.
Вообще условимся записывать зависимость скорости
ползучести от напряжения в следующем виде:
е* V а* У
при этом е, и ff„ — надлежащим образом выбранные константы,
знак Д над символом функции обозначает, что эта функция
безразмерна.
Вместо степенной зависимости D3.1) или D3.2) часто
пользуются экспоненциальной зависимостью
? = ехр(?). D3.3)
По-видимому, впервые такая зависимость была введена Люд-
виком [288]; ее широко применяют многие авторы, и она
кажется в некоторых отношениях более удобной, чем степенная
зависимость. Недостаток формулы D3.3) состоит в том, что она дает
отличную от нуля скорость ползучести при а = 0 и,
следовательно, не может давать удовлетворительных результатов при малых а.
Чтобы исправить этот недостаток экспоненциальной формулы,
Надаи [299] предложил заменить экспоненциальную функцию
гиперболическим синусом. Таким образом, по Надаи,
При достаточно больших по сравнению с ое значениях 0
формула D3.4) практически совпадает с D3.3), при малых а
6 ~ 9 а
Закон гиперболического синуса был подвергнут обстоятельной
проверке Мак-Бетти [373]. В результате обработки большого
опытного материала автор заключает, что формула D3.4) дает более
точные результаты, чем степенная формула D3.1).
§ 43] ЭМПИРИЧЕСКИК ФОРМУЛЫ ДЛЯ КРИВЫХ ПОЛЗУЧЕСТИ 171
Более новые данные по этому вопросу приводятся в книге [93],
авторы которой также считают экспоненциальный закон для
скорости ползучести более точным, чем степенной.
Чтобы исправить формулу D3.3) в области малых а, можно
применить и другие способы. Например, Содерберг [355]
предлагает следующее выражение:
при малых значениях a v (а) опять-таки мало отличается от
линейной функции.
Имея в виду построение механической теории ползучести
и применения ее к расчетам, мы не будем придавать существенного
значения тому, в какой форме задана функция v (cr). Для
сравнительно узкого диапазона напряжений в каждой конкретной
задаче может подойти то или иное выражение, и при выборе
между ними мы будем пользоваться главным образом соображениями
удобства.
Имеются многочисленные попытки составления уравнений,
описывающих всю кривую ползучести в целом. Некоторые из этих
уравнений подобраны эмпирическим путем, некоторые следуют
как результат тех или иных физических теорий ползучести.
Рассмотрение физических теорий ползучести не входит в наши задачи,
поэтому мы просто приведем некоторые формулы, достаточно
хорошо описывающие экспериментальные данные.
Первое систематическое исследование ползучести металлов
было выполнено Эндрейдом в 1910 г. [169]. Согласно Эндрейду,
длина образца меняется во времени по следующему закону:
/ = г0A + рг1/з)е"(. D3.6)
Здесь Z0 — начальная длина, р и к — функции от напряжения
и температуры, вид которых не уточнялся. Необходимо заметить,
что автор рассматривал конечные деформации и применял
специальные меры для поддержания напряжения постоянным. Если
ограничиться такими напряжениями, для которых |3 и к достаточно
малы, из закона Эндрейда следует такое уравнение кривой
ползучести:
e = $tlh+kt. D3.7)
Здесь принято, что вся деформация является деформацией
ползучести.
Таким образом, процесс ползучести представляет собою
наложение двух видов течения: <ф-течения» по терминологии Эндрейда,
происходящего с убывающей скоростью, и «^-течения», скорость
которого постоянна.
Это наложение двух видов течения сохраняется и при
конечных деформациях. Действительно, если относить скорость
172 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
деформации к текущей длине образца, то мы получим из D3.6)
-- i dl -Р 1 '-ft.
I dt 3 i2/a-j-p«
Первый член в правой части стремится к нулю при увеличении t,
остается лишь ft-течение, происходящее с постоянной скоростью.
Эндрейд и другие, по преимуществу английские, авторы
производили многочисленные исследования по проверке формулы D3.6)
и по ее уточнению применительно к различным материалам и
условиям испытания (см., например, [160]).
Уравнение D3.7) довольно хорошо воспроизводит
действительные кривые ползучести, более общая форма подобного уравнения*.
p = S(a)tm + v(a)t. D3.8)
Здесь, р — деформация ползучести, р = е — е0.
Показатель т, в общем, оказывается близким к г/3, но для
различных материалов колеблется как в ту, так и в другую сто
рону, достигая значения 0,5 и выше. Для данного материала т
оказывается функцией температуры. Более того, величина т
может зависеть и от напряжения. Функция S (а) аппроксимируется
теми же выражениями, что и v (a).
Во многих случаях нас будет интересовать сравнительно
кратковременная ползучесть, ограниченная первым участком кривой.
Для начальных участков достаточно хорошая аппроксимация
получается, если удержать только первый член в формуле D3.8),
а именно, если принять
p = S(a)tm. D3.9)
Заметим, что формула D3.8) не претендует на роль экстра-
поляционной формулы, которая предсказывает величину
деформации ползучести за большой период времени на основании
данных сравнительно кратковременных испытаний.
Среди других уравнений, описывающих как первый, так и
второй участки кривой ползучести, приведем уравнение Одинга [93]:
? = ТЩ + »(Ф, D3.10)
где С, к — постоянные при данной температуре.
Как сообщает Одинг, это уравнение было проверено на 120
кривых ползучести различных сортов стали.
§ 44. ПОДОБИЕ КРИВЫХ ПОЛЗУЧЕСТИ
При разработке методов расчета на ползучесть и применении
этих методов к исследованию реальных объектов необходимо
считаться с довольно большим разбросом опытных данных по
ползучести. Разница в 20% по деформациям между кривыми ползу-
§ 44]
ПОДОБИЕ КРИВЫХ ПОЛЗУЧЕСТИ
173
чести, снятыми при одном и том же напряжении для данной
температуры на образцах из материала одной плавки, не считается
чрезмерно большой. Чтобы удержаться в этих пределах разброса,
приходится применять специальные меры для строгого контроля
исходного состояния образцов. Поэтому вряд ли стоит стремиться
к очень точному аналитическому описанию кривых ползучести
на всех участках, аппроксимирующие зависимости можно
выбирать такими, чтобы с ними было удобно обращаться в дальнейшем.
Многие авторы, занимавшиеся разработкой механических теорий
ползучести, прибегали к предположению о подобии кривых
ползучести. Это значит, что деформация ползучести может быть
представлена следующим образом:
p = S{a)x(t). D4.1)
Предположение о подобии кривых ползучести достаточно хорошо
оправдывается для начальных участков. Действительно,
формула D3.9), справедливая по крайней мере в некотором диапазоне
напряжений, удовлетворяет этому условию. В более широком
диапазоне напряжений гипотеза подобия может не оправдаться.
Если считать в формуле D3.8) функции S (а) и v (cr)
отличающимися лишь постоянным множителем, то кривые ползучести,
описываемые этой формулой, будут также подобными. В
действительности подобие кривых ползучести с одним множителем
подобия как для первого, так и для второго участка наблюдается далеко
не всегда. Для полных кривых ползучести, включающих третий
участок, никакого подобия вообще не существует, какие-либо
надежные формулы для описания третьего участка отсутствуют.
Начало третьего участка предшествует разрушению, обычно выход
материала на третий участок считают недопустимым, поэтому
при расчетах на ползучесть его не рассматривают. В дальнейшем
мы увидим, что при предсказании времени до разрушения, исходя
из некоторых гипотез, относящихся к процессу разрушения,
можно бывает получить аппроксимацию кривых ползучести до самого
момента разрыва.
Серия кривых ползучести при постоянном напряжении
представляет собою графическое изображение функциональной
зависимости
е = е(<т, *);
при этом по осям координат откладываются переменные е и t,
переменная ст служит пометкой соответствующей кривой. Но
ту же самую функциональную зависимость можно представить
иначе, например, откладывая по осям координат о и е, как это
делается обычно при построении кривых растяжения. Тогда время
t будет пометкой соответствующей кривой. Построенные таким
174 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
образом кривые называются изохронными кривыми ползучести.
Способ перестройки не нуждается в особых пояснениях,
пересечение кривых ползучести с вертикальной прямой, соответствующей
фиксированному значению времени, дает координаты е и о*
соответствующей изохронной кривой. Значению времени t — 0
соответствует кривая мгновенного деформирования.
При обработке большого количества изохронных кривых
ползучести для разных сталей было обнаружено [88], ["], что
изохронные кривые во многих случаях оказываются подобными,
следовательно, уравнение их можно написать следующим образом:
o = cp{e)#(t). D4.2)
Заметим, что условие подобия, выражаемое формулой D4.2),
совершенно отлично от условия подобия D4.1). Они совпадают
только в том случае, когда можно пренебречь упругой деформацией,
то есть считать р а; е, и когда функция S (а) степенная.
Если определить функцию ¦&(() таким образом, что ¦& @) = 1,
то а = ф (е) представляет собою уравнение кривой мгновенного
деформирования. При анализе опубликованных опытных данных
по ползучести обычно оказывается, что сведения о начальных
участках недостоверны, а мгновенная деформация, возникающая
сразу после нагружения, фиксируется с недостаточной точностью.
Поэтому всегда почти оказывается, что кривая, соответствующая
t = 0, а также отличным от нуля, но достаточно малым значением
t, отсутствует. Выбирая подходящую аппроксимацию для
функции Ф (t), можно восстановить кривую о = ф (е) путем
экстраполяции, хотя, конечно, при этом нельзя утверждать, что это будет
действительная кривая мгновенного деформирования. Довольно
хорошая аппроксимация для функции -ё (t) дается следующей
формулой f98], ["]:
0(f)= 1 в ¦ D4.3)
При этом оказывается, что значение fj близко к 0,3.
На рис. 38 представлена серия изохронных кривых ползучести
для хромоникелемолибденовой стали по данным известных
испытаний Робинсона [Зйа] длительностью 100 000 часов (с 27 марта
1931 г. до 8 октября 1942 г.). Выбирая функцию ф (t) в виде D4.3)
при р = 0,3, мы получили приведенную на чертеже кривую о =
= ф (е). Разброс точек, соответствующих отдельным образцам
и перенесенных на эту кривую в соответствии с уравнением D4.2),
не превышает разброса модуля упругости образцов.
Тернер и Блумквист [37а] использовали условие подобия
изохронных кривых ползучести для экстраполяции кривых
ползучести алюминиевого сплава 24S-T3. Для температуры 232°
использовались опытные данные Гварниери [223], в распоряжении авторов
§ 44]
ПОДОБИЕ КРИВЫХ ПОЛЗУЧЕСТИ
175
была кривая растяжения этого материала. Скорость, при
которой производилось растяжение, не указана, однако для данной
температуры ползучесть не настолько интенсивна, чтобы
существенно повлиять на диаграмму растяжения в том диапазоне
скоростей, который осуществляется на разрывных машинах обычного
Рис. 38.
типа. Поэтому кривая растяжения была принята за график
функции ф (е). В формуле D4.3) было принято р = 1/3, постоянная а
определена из того условия, что при напряжении 10,54 кг [мм2
полная деформация, равная 0,5%, была достигнута за 86 часов.
В таблице на стр. 176 приведено время для достижения той
же деформации в 0,5% при разных напряжениях поданным
эксперимента и по формуле D4.2).
При температуре 205° производилась обработка данных Дорна
и Титца [192]. Были взяты две изохронные кривые ползучести,
соответствующие времени 10 часов и 20 часов. По этим кривым
был определен параметр а и восстановлена кривая ф (е).
Сравнение расчета по формуле D4.2) с данными достаточно длительных
176 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. TV
испытаний показало, что если фактически за 1000 часов была
получена деформация в 0,7 % при напряжении 10,54 кг/мж2, то по
расчету, основанному на данных кратковременных испытаний, та же
деформация должна была быть достигнута при напряжении
10,27 кг/мм2.
а, кг/мм%
11,95
14,06
15,46
17,57
21,09
t, час.
опыт
37,0
16,0
6,0
3,5
0,15
расчет
41,1
14,0
6,5
1,9
0,10
Сравнивая расчетные и экспериментальные результаты по
ползучести, всегда нужно иметь в виду, что очень небольшие
изменения напряжения сильно влияют на скорость и, следовательно,
на время, необходимое для достижения заданной деформации.
Незначительные отличия в структуре или химическом составе
образца также сильно влияют на скорость. Поэтому, если мы будем
из опыта определять время для достижения заданной деформации
при фиксированном напряжении, мы получим большой разброс
результатов между отдельными образцами. Если же определять
напряжение, при котором за данное время накапливается данная
деформация, то разброс будет очень небольшим. Поэтому
приведенные в таблице данные, относящиеся к испытаниям при
температуре 232°, нужно считать очень хорошим подтверждением
формулы D4.2), не худшим, чем во втором случае, когда разница
по напряжениям составляет всего 2,7%.
, Однако приведенные опытные данные не следует считать
убедительным подтверждением правила подобия изохронных кривых
ползучести. Нам встречались случаи, когда это подобие явно не
соблюдалось. Там, где оно есть, его можно использовать для
упрощения расчетов.
Более фундаментальная проверка условия подобия
изохронных кривых ползучести была произведена Гольдхоффом [213].
Он обработал данные, полученные в лаборатории Дженерал
Электрик, а также в других лабораториях для следующих материалов:
а) ферритная сталь, содержащая 1% хрома, 1% молибдена,
0,25% ванадия при температуре 562°;
б) сталь с 12% хрома при температурах 427°, 538° и 649°;
в) аустенитная сталь при температурах 649° и 704°;
г) магниевый сплав при температурах 149° и 93°;
д) два сорта пластиков;
е) дисперсионно твердеющая сталь 17-7 при 482°.
S 45]
ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ
177
Для каждого материала значения констант а и р, а также
функция <р (е) находились путем обработки кривых ползучести.
Вычисления производились на электронной машине следующим образом.
Задавались значения р, тогда для а и ср (е) получалась система
линейных уравнений, значения а и ф (е) находились по методу
наименьших квадратов. Вычисления повторялись для других
значений |3 и так до тех пор, пока не была найдена наилучшая
комбинация из а, р и ф (е). Естественно, что рассчитанная таким
образом кривая ф (е) несколько отличалась от кривой растяжения,
хотя разница была не столь велика, значения показателя E также
получались различными. Далее автор произвел расчеты
напряжения, вызывающего данную деформацию за данное время при
р* => 0,33, отправляясь от кривой растяжения и одной изохронной
кривой. Отклонения расчетных значений от экспериментальных
колебались в пределах ±5%, иногда выходя за эти границы.
Исключение составили низколегированная сталь (а) в области
относительно малых деформаций, магниевый сплав в листах (г)
и сталь 17-7 (е). Автор делает вывод, что уравнения D4.2), D4.3)
достаточно хорошо описывают ползучесть структурно-устойчивых
материалов. Показатель р во всех случаях оказался равным 0,33,
кроме пластиков, для которых пришлось принять Р = 0,1.
§ 45. ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ
До сих пор мы рассматривали кривые ползучести при
постоянной температуре. При повышении температуры, как правило,
скорость ползучести увеличивается и та же самая деформация
достигается при том же напряжении за меньшее время. Для
детального описания влияния температуры на кривую ползучести
нужно было бы изучить зависимость от температуры всех
параметров, входящих в какое-либо из уравнений, удовлетворительно
описывающих ход кривой ползучести. К сожалению, таких
уравнений слишком много, а опытные данные слишком разбросаны.
Основное значение физических теорий ползучести, в которых
кривая ползучести получается как результат некоторых
предположений о внутреннем механизме процесса, состоит, пожалуй,
в том, что они могут предсказать и иногда действительно
предсказывают зависимость кривой ползучести от температуры. Во всех
теориях ползучести предполагается, что пластическая деформация
связана с движением некоторых структурных элементов,
вызванных температурными флуктуациями. Каждый из этих элементов
в данный момент времени имеет энергию и, причем распределение
энергий между отдельными элементами подчинено закону
Максвелла.
Пусть р du есть вероятность того, что энергия определенного
элемента в определенный момент времени заключена между и
12 Ю. Н. Работнов
178 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
и и + du. По закону Максвелла
Здесь Д — газовая постоянная.
Множитель -д= перед экспонентой определен из условия, что
оо
о
Если энергия некоторого элемента превысит величину и0,
называемую энергией активации, то этот элемент переместится,
вследствие чего произойдет некоторая деформация. Вероятность
активации элемента или, что то же самое, относительное количество
активированных элементов определяется следующим образом:
оо
^ pdu = exp {—jtfrj ¦
«о
Довольно естественно предположить, что скорость ползучести
пропорциональна количеству активированных структурных
элементов; таким образом, при данном напряжении и данном
структурном состоянии материала
w«exp(--^)/(o). D5.1)
Во всех этих рассуждениях мы сознательно оставили в стороне
вопрос, о каких именно структурных элементах идет речь.
Различные физические теории ползучести конструируют различным
образом эти структурные элементы — гипотетические или реально
наблюдаемые. В соответствии с этим говорят о разных механизмах
ползучести. Величина энергии активации и0 может быть
определена экспериментально; если для одного и того же материала
оказывается, что энергия активации меняется в зависимости от
условий (например, в разных диапазонах изменения нагрузки и
температуры), то делается заключение о том, что преобладает тот
или иной механизм ползучести. Эта точка зрения систематически
развивалась в работах Дорна [192], I193]. Оговорка, что
соотношение D5.1) справедливо при данном структурном состоянии
материала, также принадлежит этому автору. Если материал
структурно-устойчив, это значит, что изменения в нем, приводящие
к уменьшению скорости ползучести (первый участок кривой
ползучести), вызваны накоплением деформации, но не структурными
превращениями, происходящими во времени независимо от
приложенной нагрузки, то из соотношения D5.1) вытекает следующий
вывод. Предположим, что температура меняется в зависимости
§ 45]
ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ
179
от времени, и введем функцию времени
в=$ exp(--^)df. D5.2)
о
Величина Ф может рассматриваться как приведенное время.
Из соотношения D5.1) следует, что скорость ползучести по отно-
de
шению к этому приведенному времени, то есть величина -^ ,
зависит только от напряжения и от структурного состояния,
определяемого величиной накопленной деформации е. Поэтому
кривая ползучести при постоянном напряжении, но переменной
температуре может быть задана зависимостью
е = е(т>). D5.3)
Таким образом, если известна кривая ползучести при
постоянной температуре, то кривая ползучести при переменной температуре
получается в результате соответствующего изменения масштаба
времени. Для подтверждения высказанной точки зрения о том,
что состояние материала, определяющее при данном напряжении
мгновенную скорость ползучести, зависит только от деформации,
а следовательно, в соответствии с уравнением D5.3), от значения
модифицированного времени •&, Дорном были проведены
металлографическое и рентгенографическое исследования образцов,
подвергнутых ползучести, а также испытания этих образцов на
растяжение. Данные этих исследований показали, что,
действительно структура, получающаяся в результате ползучести, зависит
от параметра Ф и практически может считаться одинаковой при
одинаковых значениях ¦&, но разных температурах. Опыты
проводились на чистом алюминии. Прежде всего строилась кривая
ползучести алюминия в координатах е — ¦& для напряжения
14,06 кг/мм2, полученная совмещением трех кривых ползучести
при температурах 422, 478 и 528° по шкале Кельвина. Опытные
точки, отмеченные разными значками, довольно хорошо
укладываются на одну кривую. Для того чтобы проверить справедливость
уравнения D5.3) при переменных температурах, образец из того
же самого чистого алюминия был испытан под тем же напряжением
14,06 кг /мм2, причем температура менялась во время сточасового
испытания довольно причудливым образом примерно от 420 до
480° К. По заданному графику изменения температуры с помощью
D5.2), D5.3) рассчитывалась кривая ползучести и сравнивалась
с опытной, совпадение получилось очень хорошим.
Следует заметить, что опыты Дорна и обработка им данных
других исследователей относились к чистым металлам. Для
сплавов, особенно жаропрочных, температурные зависимости
могут быть более сложными, как мы убедимся далее.
12*
180 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Наряду с простейшей формой температурной зависимости
типа D5.1) другие физические теории приводят к несколько
отличным формулам. Так, ряд авторов [2fi9], [290], отправляясь
от различных гипотетических схем, получает зависимости скорости
ползучести от напряжения и температуры следующего вида:
,«ехр(-Ы?). D5.4)
Здесь и0 — некоторая постоянная энергия активации, у —
структурно-чувствительный коэффициент. Разница по сравнению
с D5.1) состоит в том, что энергия активации процесса зависит
от напряжения. Температурная зависимость типа D5.4)
проводилась на широком круге материалов Журковым с сотрудниками [32 ]
— [36]. По-видимому, формула вида D5.4) даст лучшие
результаты в области умеренных температур, при более высоких
температурах следует пользоваться зависимостью D5.1).
Для области низких температур Моттом и Набарро [2в7 ] была
предложена модель, для которой скорость ползучести
пропорциональна Т2/з- Предполагалось, что кристаллическая решетка
содержит большое количество равномерно рассеянных выделений,
на которых задерживаются дислокации. Вследствие термических
флуктуации отдельные участки линий дислокаций между
препятствиями перебрасываются в положение устойчивого
равновесия. Процесс ползучести оказывается резко затухающим, он
исчерпывается, когда все петли с низкой энергией активации
переходят в устойчивые положения.
С другой стороны, при очень высоких температурах, близких
к температуре плавления, принципиально возможен совершенно
иной механизм ползучести, чисто диффузионного характера.
Направленный поток диффундирующих атомов приводит к
формированию новых атомных плоскостей, а следовательно, к видимой
деформации кристалла. Эта схема была рассмотрена в статьях
[298 ] [229] в работе Лифшица [°8] строится теория диффузионно-
вязкого течения поликристаллических тел, зависимость скорости
от напряжения и температуры оказывается при этом следующего
типа:
е-о^-. D5.5)
Здесь D — коэффициент самодиффузии, который в свою очередь
зависит от температуры следующим образом:
м0
2>-А>ехр^--^
Необходимо помнить, что каждая из приведенных зависимостей
относится к тому или иному определенному механизму, который
предполагается осуществленным в идеальном объекте; для техни-
§ 45]
ТЕМПЕРАТУРНЫЕ ЗАВИСИМОСТИ
181
ческих сплавов, как правило, наблюдаются систематические
отклонения. В то же время прямые опытные данные не всегда
допускают однозначное истолкование. Так, при применении формулы
D5.1) обнаруживается, что она дает достаточно хорошие
результаты, если считать энергию активации и0 функцией температуры.
Изменение функции иа (Т) может служить показателем того, что
в данном диапазоне
преобладающим является тот или иной ме- Щ&\
ханизм; в этом смысле для
физика соответствующая точка
зрения полезна, но ценность
формулы D5.1) как экстрапо-
ляционной или
интерполяционной утрачивается, любая
эмпирическая формула достаточно
простой структуры для техниче- О щ? щ?
ской теории более удобна.
Для установления зависимо- Рис' 39-
сти между данными по
ползучести, полученными при разных температурах, существуют и другие
способы эмпирического или полуэмпирического происхождения.
Различными авторами предлагались температурно-временные
параметры, то есть комбинации из температуры и времени,
принимаемые за независимые переменные при описании ползучести.
Эти параметры в большей мере применялись для экстраполяции
данных по длительной прочности, поэтому они будут рассмотрены
подробно в соответствующей главе.
Применительно к ползучести эмпирические температурно-
временные параметры употребляются главным образом для
определения условного предела ползучести, то есть напряжения а',
при котором за данное время t' будет достигнута данная, условно
выбранная деформация е'. Результаты испытаний на ползучесть
можно представить в следующем виде (рис. 39). По оси ординат
откладывается напряжение, по оси абсцисс — время, по истечении
которого деформация (полная или деформация ползучести)
достигает значения е'. Таким образом, от каждой кривой ползучести
используется только одна точка. Для удобства этот график
строится в логарифмических координатах. Величины V и е' выбираются
в зависимости от условий эксплуатации изделия, е обычно равно
1 %, тогда как t' может меняться от минут до тысяч и десятков
тысяч часов. Очевидно, что каждой температуре будет
соответствовать своя кривая. Опыты конечной продолжительности
позволяют найти предел ползучести так, как показано на чертеже,
только в том случае, когда продолжительность некоторых опытов
больше чем t', в противном случае необходимо экстраполировать
кривую, а это всегда дает ненадежные результаты. Если темпера-
е=е'
182 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IY
турно-временной параметр действительно позволяет описать
процесс ползучести, то, откладывая по оси абсцисс вместо времени
величину этого параметра, мы получим единую кривую для всех
температур. Одно и то же значение параметра соответствует опыту
большой длительности при низкой температуре и опыту малой
длительности при высокой температуре, следовательно,
открывается возможность сокращения срока испытаний за счет повышения
температуры. В качестве температурно-временного параметра
Ларсон и Миллер [27<3 ] предложили принять следующую величину:
(c + \gt)T.
Здесь Т — температура в градусах Кельвина, с — константа,
которую авторы считали одинаковой для всех материалов, а
именно, если измерять время в часах и брать десятичный логарифм
времени, то с = 20. Позднейшие проверки показали, что
экстраполяция пределов ползучести с помощью параметра Ларсона —
Миллера возможна лишь в ограниченном диапазоне температур
и надежных результатов не дает. Несколько лучшие результаты
можно получить, выбирая более подходящее значение константы с.
Параметр Менсона и Хаферда f291] выражается следующим
образом:
т-та
\gt-\gta ¦
Здесь фигурируют уже две константы, Та и ta, поэтому,
естественно, применяя этот критерий, можно добиться лучшей
корреляции результатов.
Вопрос об экстраполяции данных испытаний на другие
длительности и температуры выходит за рамки механической теории
ползучести. При существующем уровне знаний расчет изделия
на ползучесть можно считать надежным только в том случае,
если мы располагаем прямыми опытными данными по ползучести
рассматриваемого материала во всем диапазоне рабочих
напряжений и температур. Формулы, выражающие зависимость
скорости ползучести от температуры, нужны нам не столько для
экстраполяции имеющихся данных, сколько для интерполяции,
притом, как правило, в довольно узком температурном диапазоне.
Поэтому мы вправе отдать предпочтение простой формуле, хотя
бы и не имеющей прямого физического смысла, перед формулой
более обоснованной, но влекущей за собою чисто расчетные
трудности. Неизбежность разброса опытных данных и сложность
поведения технических сплавов, с которыми имеет дело
конструктор, делают такую точку зрения еще более оправданной.
Следует заметить, что физические теории, положенные в основу
вывода приведенных формул, строго говоря, относятся лишь к фазе
установившейся ползучести, на первом участке кривой ползучести
положение еще более осложняется.
3 46]
РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
183
§ 46. РЕЛАКСАЦИЯ НАПРЯЖЕНИИ
Вышеприведенные сведения относились лишь к одному весьма
частному проявлению ползучести — деформации растягиваемого
образца при постоянной силе или постоянном напряжении. Эта
схема осуществляется при стандартном испытании на ползучесть,
однако в реальных условиях приходится иметь дело с явлениями
более сложного характера. Нагрузки, действующие на тело,
меняются со временем; элемент, находящийся в условиях ползучести,
связан с другими элементами, которые могут
деформироваться только упруго; поэтому даже при постоянной
внешней нагрузке усилия между элементами системы
перераспределяются во времени. Последний случай может
быть проиллюстрирован на простой модели. Стержень
единичной длины с единичной площадью поперечного
сечения соединен последовательно с пружиной жесткости
с (рис. 40).
В начальный момент времени стержню сообщено
удлинение е0, причем напряжение в нем равно о0. Удлинение
пружины при этом равно а°,!с. В дальнейшем сумма
удлинений образца и пружины остается постоянной,
следовательно,
е + ~ = е0+-^ = const. D6.1)
Если материал стержня ползет, то удлинение его
сопровождается падением напряжения, так как энергия системы возрастать
не может. Этот процесс падения напряжения со временем
называется релаксацией (лат. relaxatio—отдых, ослабление). Если
жесткость пружины мала, то перемещение ее конца, связанное с
удлинением образца, мало сказывается на величине силы натяжения
пружины, поэтому напряжение в образце остается постоянным
и осуществляется схема испытания на ползучесть. Другой
крайний случай будет тот, когда жесткость очень велика и вторые
члены в левой и правой частях условия D6.1) становятся
пренебрежимо малыми. Полная длина образца остается постоянной, из
D6.1) следует:
е~ const.
Этот случай мы будем называть чистой релаксацией.
Полное удлинение образца е в каждый момент представляет
собою сумму упругого удлинения и удлинения вследствие
ползучести; таким образом, упругость системы, изображенной на
рис. 40, не исчерпывается упругостью изображенной на схеме
пружины, имеется как бы вторая пружина, заключенная в самом
образце, и процесс чистой релаксации представляет собою
ползучесть при убывающем напряжении, которая происходит таким
184 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Рис. 41.
образом, что прирост деформации ползучести компенсирует
уменьшение упругой деформации за счет уменьшения напряжения.
Общая схема, модель которой представлена на рис. 40, очень
часто реализуется в действительности. К ней сводится любая
статически неопределимая система, находящаяся в условиях
ползучести, когда возможность деформирования элемента
ограничена стеснением его со стороны других элементов, остающихся
упругими или перешедшими в состояние ползучести, но
способными одновременно деформироваться упруго. Типичным примером
может служить фланцевое соединение
трубопровода (рис. 41). Болты затягиваются с
некоторым предварительным усилием, которое
ослабевает со временем. Удлинение болта и усилие
в нем связаны условием типа D6.1), поскольку
фланцы не могут считаться абсолютно жесткими.
Определение постоянной жесткости с в этом
случае затруднительно, так как напряжения
сжатия во фланце распределены неравномерно.
Как мы выяснили, общий случай
релаксации, соответствующий условию D6.1),
типичен для условий работы элементов
конструкций, подверженных действию постоянных нагрузок в
течение длительного времени. Поэтому возникает принципиальный
вопрос: можно ли рассчитать процесс релаксации, располагая
характеристиками ползучести, полученными в результате
стандартных испытаний? В случае положительного ответа
необходимо сформулировать теорию одномерной ползучести, то есть
построить такие уравнения, которые могли бы описать ползучесть
при переменных нагрузках. Однако сначала нужно располагать
опытными данными по релаксации напряжений.
Соответствующие эксперименты проводились уже достаточно давно, однако
технические трудности испытаний на релаксацию значительно
больше, чем трудности испытаний на ползучесть, поэтому
испытания на релаксацию не получили широкого распространения.
Задача этих испытаний также менее определенна, чем задача
испытания на ползучесть, характеристики релаксации носят
скорее сравнительный характер и позволяют сделать выбор
между тем или иным материалом, в механических расчетах они
непосредственно не учитываются. Нас эти испытания будут
интересовать только с точки зрения проверки тех или иных теорий
ползучести, поэтому мы не касаемся, например, такого широко
распространенного метода оценки релаксационной стойкости, как метод
кольцевых образцов Одинга [93].
Заметим прежде всего, что осуществление опыта на чистую
релаксацию по схеме, изображенной на рис. 40, для металлов
практически невозможно. Пружина должна служить динамомет-
§ 47]
ПРОСТЕЙШИЕ ТЕОРИИ ПОЛЗУЧЕСТИ
185
ром, следовательно, величина силы может измеряться только
по удлинению пружины, а эта возможность противоречит
требованию, чтобы с было весьма велико. Необходимо, чтобы жесткость
пружины и всех промежуточных звеньев установки, которые не
изображены на схеме, но неизбежны в реальной конструкции,
была много больше, чем жесткость образца. Для испытаний на
релаксацию пластмасс, у которых модуль упругости мал, а
упругая деформация довольно велика, в принципе такую схему
осуществить можно, если не предъявлять слишком высоких
требований к точности выполнения условия е = const; для металлов
это совершенно нереально. В свое время предлагались методы
испытаний на релаксацию, в которых сознательно осуществлялось
условие D6.1) при некоторой фиксированной жесткости с, а не
условие чистой релаксации, но распространения они не получили.
В существующих установках для испытаний на релаксацию
цилиндрических образцов осуществляется другой принцип. Образец
подвергается нагрузке, величина которой может регулироваться
тем или иным способом при помощи сервомотора. На образце
устанавливается экстензометр с контактным устройством,
включающим и выключающим реле, которое управляет сервомотором.
Таким образом, нагрузка все время изменяется, причем
удлинение образца поддерживается постоянным. Фактически контактное
устройство имеет определенную чувствительность A—2 р, в
лучших машинах), поэтому процесс релаксации представляет собою
последовательность процессов ползучести при ступенчато
убывающих нагрузках. Чем меньше ступень, тем лучше приближается
схема опыта к схеме чистой релаксации.
Мы не будем приводить здесь описания кривых релаксации
и различных эмпирических или основанных на тех или иных
теоретических соображениях формул для этих кривых; основной
вопрос, который нас интересует, состоит в возможности
предсказания кривой релаксации с помощью кривых ползучести.
§ 47. ПРОСТЕЙШИЕ ТЕОРИИ ПОЛЗУЧЕСТИ
Задача теории одномерной ползучести состоит в том, чтобы
связать измеряемые величины: напряжения, деформации,
температуру и время — с помощью некоторого уравнения или системы
уравнений, носящей универсальный характер. При этом в
уравнениях могут фигурировать скрытые параметры,
характеризующие состояние материала. Пытаясь построить механическую
теорию, мы должны постулировать принципиальную возможность
существования таких уравнений, изт«>торых внутренние параметры
могут быть исключены и, следовательно, все характеристики
ползучести могут быть найдены в результате макроэксперимента,
186 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
то есть путем измерения механических величин — сил и
деформаций. Можно представить себе теорию, в которой фигурируют
внутренние параметры, не определяемые из макроэксперимента,
например такие характеристики состояния материала, которые могут
быть измерены путем рентгенографии, химического анализа,
оптической или электронной металлографии. Но в механической
теории возможность эта должна быть заранее исключена. Задачу
механической теории следует поставить следующим образом.
Будем считать заданным закон изменения во времени
температуры и одной из механических величин, либо а, либо е.
Требуется определить изменение во времени второй механической
величины. Предположим для определенности, что заданы
функции Т (t) и a (t), ищется функция времени е (t). Поскольку число
экспериментов конечно, то всегда можно сконструировать
выражение для е (t) такое, что при всех заданных Т (t) и a (t) оно
будет правильно описывать экспериментальные данные. Можно
возразить на это, что всегда можно осуществить такой новый
эксперимент, который будет существенно отличаться от
прежних. Можно выбрать такие функции Т (t) и a (t), для которых
найденный способ вычисления е (t) приведет к неверным
результатам. Однако экспериментальные возможности ограничены и круг
практических задач, для решения которых собственно и нужна
теория, довольно узок. Задача исследователя состоит в том, чтобы
остановиться на какой-то определенной ступени приближения
и, основываясь на данных относительно простых и не слишком
разнообразных опытов, выбрать такие средства описания
явления, которые воспроизводят с практически достаточной степенью
точности его основные черты. Под простейшими теориями
ползучести мы будем понимать такие теории, которые черпают все
необходимые данные из описанных выше опытов на ползучесть
при постоянном напряжении.
Наличие участка установившейся ползучести, на котором
скорость ползучести постоянна при заданном напряжении,
подсказывает мысль об отождествлении ползучести металла при
высокой температуре с квазивязким течением жидкости. В
отличие от обычного вязкого течения мы будем называть квазивязким
такое течение, когда скорость зависит от напряжения
нелинейным образом. Такая схема тем более заманчива, что, как мы
видели, наиболее надежные опытные данные получены именно
для участков установившейся ползучести, то есть для
зависимости скорости установившейся ползучести v от напряжения ст.
Итак, пренебрежем упругой деформацией, мгновенной
пластической деформацией и наличием первого участка на кривой
ползучести, будем считать, что е = р, и положим
e = e = v{a,T). D7.1)
S 47]
ПРОСТЕЙШИЕ ТЕОРИИ ПОЛЗУЧЕСТИ
187
Риг. /i2.
Кривые ползучести заменяются, таким образом, прямыми,
проходящими через начало координат (рис. 42).
Теорию ползучести, основанную на уравнении D7.1), мы
будем называть теорией установившейся ползучести.
Применимость этой теории к реальным объектам и реальным материалам
определяется тем, в какой мере
кривые ползучести в
координатах е — t можно
аппроксимировать прямыми. Это оказывается
возможным в двух крайних
случаях. Во-первых, когда речь идет
о весьма больших
длительностях службы изделия и основная
часть деформации происходит с
постоянной скоростью. В
условиях длительной службы многие
материалы оказываются
структурно-неустойчивыми. В них
происходят те или иные внутренние
структурные изменения, которые иногда влияют на ход кривой
ползучести и вызывают аномалии, исключающие возможность
строгого подхода к описанию процесса при современном уровне
понимания его механизма. Разброс результатов испытаний
различных образцов оказывает- ^г
ся при этом довольно боль- 1,5 \
шим. Поэтому уточнение
теории ползучести может
оказаться фиктивным. Проводя
прямую через начало
координат, мы оказываемся в
пределах полосы разброса
индивидуальных кривых,
соответствующих одному и тому
же напряжению. Поскольку
все равно расчет изделия на
ползучесть нужно вести по
определенным
экспериментальным кривым, уравнение
D7.1) может
рассматриваться как осреднение, в принципе не худшее, чем любое другое,
хотя каждая индивидуальная кривая ползучести
аппроксимируется этим уравнением плохо.
Другой крайний случай — это кратковременная ползучесть
при очень высокой температуре и высоком уровне напряжений.
На рис. 43 представлены кривые ползучести алюминиевого
сплава Д-16Т при температуре 250°. Как видно, первый период
W
0,5
й=Щю/мм
/
г
/щ
Ш_,
О
100
Рис. 43.
t.een
200
188 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
ползучести практически отсутствует, деформация происходит
сначала с постоянной, а потом с увеличивающейся скоростью.
Очевидно, что, пользуясь теорией установившейся
ползучести, мы не можем описать процесса релаксации. Поэтому Содер-
берг предложил учитывать начальную упругую деформацию,
то есть заменить уравнение D7.1) следующим:
; = ?. + i; (a, T). D7.2)
Полагая е = const, мы получаем отсюда дифференциальное
уравнение для а, тогда связь между напряжением и временем при
релаксации получается такой:
'--Итетт- <47-3>
Уравнение D7.3), как правило,
плохо подтверждается опытом. Это
понятно, деформация первого
участка ползучести имеет по крайней
мере тот же порядок, что упругая
деформация, а часто значительно
ее превышает. Поэтому быстрое
"ИС- ^ падение напряжения в начальном
периоде релаксации уравнением
D7.3) не описывается. Однако при высоких температурах и
высоких напряжениях, когда кривые кратковременной ползучести
подобны приведенным на рис. 43, уравнение D7.3) довольно
хорошо воспроизводит по крайней мере начальный участок кривой
релаксации, на котором за короткое время происходит
значительное падение напряжения.
По тем же причинам следует с большой осторожностью
применять уравнение D7.2) и для описания ползучести при заданных
нагрузках. Учет упругой деформации при пренебрежении
деформацией неустановившейся ползучести во многих случаях вносит
лишь незначительную поправку, которая не окупает серьезного
усложнения теории, получающегося при распространении
уравнения D7.2) на случай сложного напряженного состояния.
Существенное усовершенствование теории установившейся
ползучести принадлежит Одквисту [314]. Если продолжить
прямую, соответствующую установившемуся участку, до пересечения
с осью е (рис. 44), она отсечет на этой оси отрезок е0\ величина
этого отрезка есть функция от ст. Кривая ползучести заменяется
теперь ломаной ОАВ, причем ОА = е0 (о). Закон ползучести
можно записать следующим образом:
e = e'0{a)a + v(a). D7.4)
5 47]
ПРОСТЕЙШИЕ ТЕОРИИ ПОЛЗУЧЕСТИ
189
Величина е0 состоит из трех частей: она включает в себя упругую
деформацию, мгновенную пластическую деформацию и
деформацию ползучести, соответствующую первому участку кривой.
Третья составляющая объединяется со второй и рассматривается
как начальная пластическая деформация. Обозначим ее g (а),
тогда ей = -у + g (о*). Деформация g (а) необратима, поэтому
корректная запись закона ползучести будет следующей:
e = -%-'o + xg'{a)a + v(o). D7.5)
Множитель х равен единице, если а > 0 и а имеет значение
большее, чем любое из ранее достигнутых значений ст. В противном
случае % = 0. На рис. 45
изображен примерный график измене- <5
ния напряжения во времени,
осуществляемый при некотором
предположительном
эксперименте. На участке О А напряжение
растет, одновременно с
деформацией ползучести происходит
пластическая деформация, равная в
каждый момент g (а). В точке А
достигнуто значение
напряжения Ста, после чего напряжение 1
убывает. Ползучесть
продолжается, но накопленная
пластическая деформация g (aA) остается неизменной, тогда как упругая
деформация уменьшается пропорционально уменьшению
напряжения. Начиная с точки В, напряжение о* снова растет, но х
по-прежнему равно нулю, новый предел текучести стал равен аА,
и дополнительная пластическая деформация появляется, лишь
начиная с точки С, когда становится о* > аА. Такое поведение,
строго говоря, относится лишь к пластической деформации в
прямом смысле, а не к деформации g (а). Мы увидим далее, что опыты
на ползучесть при ступенчатом изменении нагрузки не вполне
•согласуется с введенной гипотезой. Однако вследствие простоты
схемы Одквиста уравнение D7.5) с успехом применяется при
.решении довольно сложных задач, относящихся, например,
к устойчивости стержней в условиях ползучести. Для
функции g (ст) Одквист предложил степенную зависимость с
показателем т + 1, тогда как для функции v (ст) он рекомендует также
степенную зависимость с показателем п. При этом m-\-i <ln.
В качестве примера применения зависимости D7.5) приведем
уравнение, которое использовал Хофф [237 ] для описания
поведения алюминиевого сплава. Поскольку автора интересовали
190 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
задачи изгиба, уравнение записано в такой форме, чтобы его
можно было применять как при растяжении, так и при сжатии,
а именно:
-l+4f)"f+4f)"- <«¦«>
Здесь т и п — целые числа. Так как рассматриваются только
случаи монотонного нагружения, кх и к2 определяются
следующими условиями:
при а> 0, о>0 kt -- 1,
при а > 0, а < 0 /q = 0,
при о < 0, о <; 0 ki—1 для четных т и kt= — 1 для
нечетных т,
при о < 0, о > 0 /q = 0.
Что касается к2, то для четных п к2 = 1 при с > 0 и к2 = — 1
при с < 0, для нечетных и всегда &2 = 1. Численные значения
постоянных, входящих в вышеприведенное уравнение, для
алюминиевого сплава 24S-T4 при температуре 314° следующие:
7тг = 1, га = 3, ? = 5200, jx = 562, A, = 61,5.
При этом о" измеряется в кг/жм2, а время в часах.
Заметим, что распространение закона ползучести,
установленного из опытов на растяжение, на случай сжимающих напряжений
требует специального исследования. Некоторые опытные данные,
относящиеся к этому вопросу, будут рассмотрены далее.
Задача о релаксации напряжения решается по теории Одквиста
так же, как при пользовании уравнением D7.2), так как в D7.6)
при этом следует принять kt = 0.
§ 48. ТЕОРИИ СТАРЕНИЯ
Если уравнение семейства кривых ползучести при данной
температуре записано в виде
e=f(o,t), D8.1)
то самое простое предположение будет состоять в том, чтобы
приписать этому соотношению универсальную значимость, то
есть считать его справедливым не только для ползучести при
постоянном напряжении, но и когда напряжение меняется со
временем. Таким образом, мы приходим к формулировке теории
старения, согласно которой напряжение, деформация и время
связаны конечной зависимостью вида D8.1).
§ 48]
ТЕОРИИ СТАРЕНИЯ
191
Большое удобство теории старения заключается в ее
крайней простоте. При пользовании этой теорией нет необходимости
задаваться каким-либо аналитическим выражением для функции
/ (cr, t), при расчетах можно пользоваться непосредственно
кривыми ползучести, либо построенными в обычных координатах
е — t, либо, что удобнее, изохронными кривыми, способ
построения которых описан в § 44.
Существует и третья возможность построения кривых
ползучести: по осям координат откладывается напряжение и время,
каждая кривая соответствует фиксированному значению
деформации е. Согласно теории старения, перестроенные таким
образом кривые ползучести должны совпадать с кривыми
релаксации.
Для структурно-устойчивых материалов применение
уравнения D8.1) приводит к очевидным противоречиям. Действительно,
это уравнение не инвариантно относительно изменения начала
отсчета времени, деформация ползучести в момент времени' t
не зависит от того, действовала ли нагрузка все время, начиная
с t = О, или же она была приложена в этот самый момент. Для
структурно-неустойчивых материалов можно высказать гипотезу,
что связь между напряжением и деформацией зависит от времени,
причем эта связь определяется структурными изменениями,
зависящими лишь от некоторых внутренних процессов,
протекающих безотносительно к тому, действуют ли на тело нагрузки
и какие оно получает деформации. По-видимому, такие процессы
действительно могут происходить в сплавах. Сфероидизация
цементита в стали, дисперсионное твердение, выпадение
некоторых фаз в сложных сплавах, кажется, не связаны с
деформацией. Однако трудно предположить, чтобы эти процессы
действительно являлись определяющими для ползучести.
Уравнение D8.1) по форме и по существу не является уравнением
ползучести, это закон нелинейной упругости материала, у которого
упругие свойства меняются со временем. Модель подобного
материала можно представить себе следующим образом. Система
упругих элементов — различного рода пружин с нелинейными
характеристиками — находится в агрессивной среде, которая
разъедает эти пружины или растворяет их. В результате
уменьшения поперечных сечений элементов жесткость их уменьшается
и деформация увеличивается при постоянной нагрузке. Внешне
это соответствует ползучести. При постоянной деформации
уменьшается сил.а, происходит релаксация. Но на самом деле
деформация ползучести существенно необратима и аналогия ползучести
металла с поведением рассмотренной системы чисто внешняя.
Легко привести простой пример, показывающий непригодность
уравнения D8.1) для описания ползучести при переменных
нагрузках. Возьмем две кривые ползучести при напряжениях О)
192 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
и сг3 (рис. 46). Пусть вначале напряжение было o"i < о"а; в момент
времени ?ь когда деформация соответствовала точке А,
напряжение было внезапно увеличено до величины о2. Тогда, согласно
уравнению D8.1), произойдет мгновенная деформация на
величину АВ, и ползучесть пойдет по кривой, соответствующей новому
напряжению ста, начиная с точки В. По истечении достаточно
большого времени кривые ползучести для напряжений в± и аа
разойдутся сколь угодно далеко и мгновенная деформация АВ
может быть сколь угодно большой. Ничего подобного на опыте
не наблюдалось. Еще более разительно противоречит всем
известным опытным фактам то обстоятельство, что при уменьшении
напряжения от величины а% до
величины o"i деформация по
формуле D8.1) должна уменьшаться
на тот же отрезок ВА.
На практике при расчетах на
ползучесть частей машин,
работающих в стационарных
условиях, столь резкого изменения
напряжений не происходит.
Типичные условия соответствуют
изображенной на рис. 40 схеме,
для которой крайними случаями
являются чистая ползучесть и
чистая релаксация. Любая теория,
удовлетворительно
предсказывающая кривые релаксации по
кривым ползучести, вероятно, будет пригодна и для промежуточных
состояний. Предсказание кривой релаксации на основании теории
старения получается довольно плохим, но не настолько, чтобы
противоречие с действительностью было резким. Поэтому при
слабо меняющихся нагрузках применение теории старения может
быть оправдано как приближенный прием. Особенно это
относится к тем случаям, когда материал структурно-неустойчив и мы
затрудняемся отнести особенности кривых ползучести за счет
того или иного определенного механизма, применительно к
которому можно было бы сформулировать более точную и логически
совершенную теорию. Возможность непосредственного
использования первичных кривых ползучести со всеми их индивидуальными
особенностями заставляет иногда отдать предпочтение теории
старения перед более обоснованными и более сложными теориями,
поскольку для применения этих теорий необходима та или иная
аналитическая аппроксимация кривых ползучести, неизбежно
искажающая опытные данные.
Другой вариант теории старения состоит в том, что скорость
деформации ползучести считается функцией от напряжения и
Рис. 46.
§ 48]
ТЕОРИИ СТАРЕНИЯ
193
времени. Основное уравнение этой теории следующее:
р = е—|г=/(<т, t). D8.2)
Теперь поведение материала, находящегося в условиях
ползучести, уподобляется поведению нелинейно-вязкой [жидкости,
вязкость которой меняется со временем. Очевидно, что уравнение
D8.2) логически более приемлемо, чем уравнение D8.1).
Деформация ползучести, описываемая уравнением D8.2), оказывается
уже необратимой, мгновенное изменение напряжения не влечет
за собою мгновенного изменения деформации ползучести, меняется
только скорость. Однако и здесь возникает вопрос о возможности
существования механизмов структурных изменений,
определяющих скорость ползучести при данном напряжении и протекающих
вне зависимости от самого процесса ползучести. Современные
физические теории ползучести приводят к выводу о том, что эти
процессы не являются определяющими, этот же результат следует
из прямой экспериментальной проверки теории. В случае оту-
пенчатого изменения напряжения от o"i до а2 положение будет
следующим (рис. 46). Деформация получит приращение АС,
равное °2~Zai в соответствии с законом Гуна; от точки С начнется
ползучесть со скоростью, соответствующей времени (i и
напряжению оа, то есть с той скоростью, с которой происходит
ползучесть при напряжении о2 в точке В. Уравнение D8.2) — первого
порядка, поэтому интеграл его зависит от одной постоянной;
следовательно, кривая ползучести от точки С будет параллельна
верхней кривой, начиная с точки В. Фактически в точке С
скорость ползучести значительно больше, чем в точке В, как это
будет видно из приводимых далее опытных данных.
Предсказание кривой релаксации по кривым ползучести на основании
второй теории старения получается несколько лучшим, чем при
помощи первой теории старения.
Вторая теория старения, иногда называемая теорией течения,
получила довольно большое распространение в связи с
работами Качанова [Б2]; она дает более или менее удовлетворительные
результаты для слабо меняющихся нагрузок. На основе этой
теории разработаны многочисленные расчетные методы. Особенно
удобно ее применение в тех случаях, когда кривые ползучести
подобны, то есть описываются соотношением D4.1). Тогда
уравнение D8.2) принимает следующий вид:
Р = ё—f = S(o)T(*).
Примем за независимую переменную не время t, а функцию
времени x(t). Тогда это уравнение можно записать таким
13 Ю. H. Работнов
194 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
образом:
1 = 5-4-1 = * «О- D8-3)
Мы получили уравнение теории установившейся ползучести
с измененным масштабом времени. Действительно, уравнение D8.3)
по форме совпадает с уравнением D7.2).
Вопрос о релаксации с помощью D8.3) решается весьма просто.
Действительно, полагая е = const, мы получаем:
со
Название этой теории теорией течения оправдывается в том
случае, когда за основное уравнение принимается D8.3).
Упомянем еще об одном варианте теории старения, который
был предложен Малининым I70] в развитие идеи Беляева [6].
Связь между деформацией и напряжением принимается следующей:
е =
•[t+S^*]- <48'5>
Идея Беляева при формулировке этой теории состояла в том,
чтобы сделать уравнения ползучести аналогичными уравнениям
деформационной теории пластичности, которые в свою очередь
представляют собою уравнения теории упругости с переменными
модулями. Выражение, заключенное в скобки в правой
части D8.5), представляют собою величину, обратную модулю
ползучести. Дифференцируя D8.5) по г и исключая интеграл, получим
другую форму записи этого уравнения:
e'=e-^- + S(o). D8.6)
Здесь штрихи обозначают дифференцирование по т. При
пользовании уравнением D8.6), нужно учесть дополнительное
условие, заключающееся в том, что мгновенная деформация
подчинена закону Гука. Это условие следует из D8.5), но не
со
После разделения переменных и интегрирования получаем:
D8.6). В случае релаксации нужно принять е' = 0, е =
во
^-vl^m- D8'7>
Так как — > 1, релаксация по теории Малинина идет
медленнее, чем по теории течения. На рис. 47 приведена эксперимен-
§ 48]
ТЕОРИИ СТАРЕНИЯ
195
рассчитанные Малини-
тальная кривая релаксации для меди при температуре 165°
и начальном напряжении 9,49 кг/мм2 по данным Девиса [189]
(кривая 2), а также кривые релаксации
ным I108] по всем трем
вариантам теории старения (кривая 0,/<г/см2
2 — по уравнению D8.7),
кривая 3 — по уравнению D8.4),
кривая 4 — по гипотезе
старения D8.1).) Чрезвычайно
тщательно поставленные опыты
Девиса до начала 50-х годов
представляли, пожалуй,
единственный надежный материал
для сравнения данных по
ползучести и релаксации. В
Советском Союзе исследования по
механической теории
ползучести начались главным образом
в послевоенные годы (первая
работа Беляева относится к
1943 г.), причем теоретические Рис. 47.
работы предшествовали
экспериментальным, и опыты Девиса широко использовались всеми,
в том числе и автором этой книги, для проверки различных
гипотез. Особенность этих опытов состоит в чрезвычайно большом
воо
еоо
ш
200
\Vbv
^--Z?7
f
3
* 2
tf
..
~~
—--—
О
800 t,«ae
б,лг/см2
2000
1000
'К/
3 2
;—---.
70
20 30
Рис. 48.
W i, vac
внимании, которое уделялось обеспечению однородности
образцов, испытанных на ползучесть и на релаксацию. Из меди
предварительно был удален кислород, влияющий на ее свойства,
и сами испытания проводились в нейтральной атмосфере.
13*
196 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
На рис. 48 представлены экспериментальная кривая
релаксации для стали ЗОХМА при температуре 500° и начальном
напряжении 30,8 кг/мм2, по данным работы [24] (кривая 1), а также
расчетные кривые по уравнениям D8.4) (кривая 3) и D8.7)
(кривая 2).
§ 49. ГИПОТЕЗА УРАВНЕНИЯ СОСТОЯНИЯ
Для структурно-устойчивых материалов, то есть для таких
материалов, структура и свойства которых не меняются в
результате длительного пребывания при температуре испытания без
нагрузки, наиболее естественно предположить, что уменьшение
скорости ползучести на первом участке до минимального
значения, соответствующего второму участку, представляет собою
эффект, аналогичный известному эффекту упрочнения или наклепа
при обычной пластической деформации. В первом приближении
можно считать, что степень упрочнения определяется однозначно
величиной накопленной пластической деформации. Таким
образом, скорость ползучести в каждый момент определяется
величиной действующего напряжения и величиной накопленной
деформации ползучести. Соответствующее уравнение имеет
следующий вид:
Ф(р,о,р,Т) = 0. D9.1)
Оно называется уравнением состояния. Гипотеза уравнения
состояния была впервые, по-видимому, сформулирована
Людвигом [288], потом Надаи [300] и развита в статье Давенпорта I188],
который ввел термин «теория упрочнения» (strain hardening
theory) в отличие от time hardening theory (то есть теории
старения). Этим термином будем и мы пользоваться по
преимуществу. Возвращаясь к изложению точки зрения Дорна в § 45, мы
можем отметить, что, по существу, им формулируется теория
упрочнения, поскольку структурное состояние материала
оказывается зависящим только от величины накопленной деформации
ползучести независимо от температуры и порядка приложения
нагрузки. Это структурное состояние не только определяет
скорость ползучести, но может быть зарегистрировано различными
другими независимыми методами.
Простейшим способом проверки теории упрочнения является
опыт на ползучесть при ступенчатом изменении нагрузки. Такого
рода испытания систематически проводились на разных
материалах в лабораториях Института механики АН СССР,
Московского государственного университета и Института гидродинамики
СО АН СССР. Будучи значительно более простыми, чем испытания
на релаксацию, эти опыты дают более контрастные результаты.
Действительно, как мы убедились на примерах, приведенных
§ 49]
ГИПОТЕЗА УРАВНЕНИЯ СОСТОЯНИЯ
197
в § 48, предсказание кривых релаксации по кривым ползучести
на основе различных теорий старения приводит к результатам,
которые не слишком сильно отличаются от истины. Качественное
предсказание хода кривой релаксации получается по этим
теориям удовлетворительным, количественные же расхождения
всегда могут быть отнесены за счет разброса, связанного с
непостоянством свойств образцов; мы уже неоднократно указывали,
что при испытаниях на ползучесть разброс довольно велик.
Обратимся теперь к испытаниям
на ползучесть со ступенчатым Р
изменением нагрузки. Нам
удобнее будет строить кривые
ползучести в координатах р — t,
где р — деформация ползучести
(дальше мы уточним, в каком
смысле нужно понимать
величину р). На рис. 49
приведены две кривые ползучести при
напряжениях о^ и аг"> а%.
Предположим, что в образце
поддерживается напряжение а±
и ползучесть следует нижней Рис- 49.
кривой. В момент времени t^
мы находимся в точке А этой кривой. Пусть теперь
напряжение внезапно увеличено до а2. Дополнительная упругая
деформация на графике не откладывается, так как р есть только
деформация ползучести; следовательно, кривая ползучести пойдет
из точки А со скоростью, которая, согласно уравнению D9.1),
определяется деформацией рА и напряжением о2. Эта скорость
представляет собою угловой коэффициент касательной к верхней
кривой ползучести в точке В, имеющей ту же ординату, что
и точка А. Поскольку уравнение D9.1) представляет собою
уравнение первого порядка, интеграл его зависит от одной
произвольной постоянной, и кривая ползучести от точки А будет
повторением кривой ползучести при постоянно действующем
напряжении о-2, начиная с точки В. Чтобы получить кривую ползучести,
соответствующую ступенчатому изменению нагрузки, нужно
сдвинуть верхнюю кривую вправо, параллельно себе, до
совпадения точки В с точкой А. По второй теории старения нужно
было бы переносить верхнюю кривую параллельно себе вниз
до совпадения точки С с точкой А. Разница в предсказаниях двух
теорий оказывается чрезвычайно резкой, притом с опытом гораздо
лучше согласуется теория упрочнения. На рис. 50 приведены
результаты из работы [80], кривые ползучести при ступенчатых
нагрузках для меди сопоставляются с предсказаниями теории
упрочнения. Аналогичные данные для сплава Д-16Т по опытам
198 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Наместникова и Хвостункова будут приведены далее. Теория
упрочнения, как видно, дает вполне удовлетворительные
результаты, тогда как теория старения сильно преуменьшает скорость
ползучести после изменения нагрузки.
В то же время предсказания теории упрочнения не являются
вполне точными, обнаруживаются систематические отклонения,
которые особенно проявляются при наличии нескольких ступеней
изменения напряжения. Вопрос о возможных уточнениях
уравнения состояния будет рассмотрен впоследствии более подробно.
Как оказывается, теория упрочнения не описывает некоторых
вторичных эффектов, наблюдаемых при опытах на ползучесть,
Рис. 50.
однако для структурно-устойчивых материалов эта теория может
рассматриваться как надежное средство описания процесса в
первом приближении на основе физически ясной и внутренне
непротиворечивой гипотезы, отражающей основные черты изучаемого
явления.
Гипотеза уравнения состояния, формулируемая при помощи
уравнения D9.1), применялась многими авторами для описания
различных процессов деформирования металлов. При этом обычно
величина р понимается как полная пластическая деформация
и р — как скорость пластической деформации. Если
зафиксировать температуру Т, то уравнение D9.1) можно трактовать как
уравнение поверхности в пространстве с координатами р, р и о;
пересечение этой поверхности с плоскостью р = оо должно дать
кривую мгновенного деформирования. Такая точка зрения, как
мы увидим впоследствии, не оправдывается, и вопрос о
мгновенной пластической деформации должен решаться иначе. Поэтому
мы предположим на время, что мгновенной пластической
деформации нет, существуют только упругая деформация и
деформация ползучести р. Тогда, очевидно, е = — -j- п.
г*
§ 49]
ГИПОТЕЗА УРАВНЕНИЯ СОСТОЯНИЯ
199
Кривая релаксации может быть предсказана, если известны
кривые ползучести, с помощью графического способа, данного
Давенпортом [188]. Пусть задана достаточно густая сетка кривых
ползучести для разных напряжений, построенная в координатах
р — I (рис. 51).
Вместо непрерывного процесса релаксации будем
рассматривать ползучесть при ступенчато меняющихся напряжениях.
Предположим, что в момент времени tt напряжение было at,
значит, мы имеем точку Mt на кривой релаксации (рис. 52). Если
Рис. 51. Рис. 52.
это напряжение удерживается постоянным, то происходит
ползучесть по кривой ползучести, соответствующей напряжению at,
начиная с точки Mt (рис. 51). За время Att накопится деформация
ползучести Apt. Уменьшим теперь напряжение на величину
Act, = E Ари таким образом, общая деформация образца за счет
упругого сокращения вновь примет то же значение, что и в
начальный момент времени tt. Напряжение станет равным at+i =
=¦ at — Дсхг; при этом напряжении будет опять происходить
ползучесть, следуя кривой ползучести для напряжения (Tf+i,
начиная с той точки, где деформация ползучести равна pt+i =
= Pi + Apt. Чтобы найти эту точку, нужно провести
горизонтальную прямую через точку Nt, являющуюся концом участка
ползучести на кривой для напряжения аг. Точкой пересечения
кривой ai+i и этой прямой будет точка Mi+i, которой
соответствует точка на кривой релаксации с координатами сгг+1
и ti+i. Продолжая этот процесс, мы построим кривую релаксации
с любой точностью в зависимости от того, насколько густо
расположены кривые ползучести. Описанный способ расчета
фактически воспроизводит условия эксперимента на
релаксацию (§ 46).
200 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
В действительности сетка кривых ползучести бывает не очень
густой и прямое применение способа Давенпорта затруднительно.
Более надежный численный метод построения кривой релаксации
был развит Поповым [328], который применил его для обработки
уже упоминавшихся опытов Девиса.
§ 50. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ
ДЛЯ ЗАКОНА УПРОЧНЕНИЯ
Уравнение D9.1) может быть задано графически в виде серии
кривых в тех или иных координатах, однако использование его
для расчетов оказывается при этом затруднительным. Более
удобный путь состоит в том, чтобы подобрать для функции
Ф(р, р, с, Т) подходящее аналитическое выражение, которое
было бы достаточно простым и удовлетворительно
воспроизводило, например, кривые ползучести при постоянном напряжении.
Условие подобия кривых ползучести существенно суживает
класс таких возможных представлений уравнения состояния;
при постоянной температуре это уравнение должно необходимым
образом иметь следующий вид:
P-s^F(sW- ECU)
В этом легко убедиться, если представить уравнение кривых
ползучести в виде р = S (а) т (?), продифференцировать и
исключить время. Если функция F является степенной, то мы приходим
к следующему закону упрочнения:
pp«=f{o). E0.2)
Уравнение E0.2) очень хорошо описывает первые участки кривых
ползучести. Действительно, интегрируя его при постоянном о
1
и полагая m = , мы получим:
Как мы видели в § 43, степенная аппроксимация зависимости
от времени для начальных участков дает удовлетворительные
результаты. Функция / (а) может быть также выбрана степенной:
f(a) = Bon, E0.4)
или экспоненциальной:
/(о) = /сехр^-. E0.5)
В первом случае, как это следует из E0.3), должно быть п > 1 +
+ а; в противном случае окажется, что скорость ползучести
§ 50] АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ ЗАКОНА УПРОЧНЕНИЯ 201
пропорциональна напряжению в степени, меньшей чем единица.
Подобные материалы неизвестны, более того, можно привести
убедительные соображения, свидетельствующие о том, что их
не может быть [149]. Выражение E0.5), так же как и
применительно к скорости установившейся ползучести, непригодно для
малых значений напряжений а, однако исправлять его по одному
из способов, описанных в § 43, нельзя. Нужно, чтобы при малых о*
функция / (с) стремилась к нулю, как о*п (п > 1 -\- а), а не как ст.
Одно из возможных уточнений выражения E0.5) будет,
например, следующее:
/(o-) = /cBsh^)n.
Для практических применений это выражение малопригодно,
в то же время область малых напряжений нас обычно не
интересует; в тех задачах, когда приходится рассматривать область
малых напряжений (например, при изгибе около нейтральной
оси), ее можно исключить с помощью искусственного приема,
который будет впоследствии пояснен.
Желая описать при помощи уравнения состояния не толика
начальные участки кривых ползучести, но и установившуюся
ползучесть, мы должны видоизменить уравнение E0.2), например-
заменить его следующим:
ph(p)=f(a). E0.6)
Функция h (p) должна вести себя, как ра, при малых р и
стремиться к постоянному значению с увеличением деформации
ползучести. Шорр [154] предложил определять функцию h (p)
следующим образом:
h{p) = pa (p<Pc), ,507).
h(p) = pac (p>Pc)-
Величина рс зависит от напряжения и температуры, это есть
величина деформации ползучести в момент перехода от первого
участка кривой ползучести ко второму. Граница между участками
кривой ползучести может быть выбрана только условно, но таким
способом можно довольно хорошо аппроксимировать опытные
кривые ползучести.
Для того чтобы получить непрерывный переход к
установившейся ползучести, можно выбрать функцию h (p), например, так;
где с — константа.
202 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Тогда уравнение E0.6) принимает следующий вид:
~^-=E = f{o). E0.8)
•Особенно интересен случай, когда а = 2, следовательно, на
первом участке выполняется закон Эндрейда, и деформация
ползучести пропорциональна времени в степени 1/3. Тогда
уравнение E0.8) легко интегрируется при постоянном напряжении
и мы получаем следующее уравнение кривых ползучести:
рУс — aicig (рУс) = V~cv {о) t. E0.9)
Здесь v (о) — скорость установившейся ползучести. Кривые
ползучести имеют асимптоты, пересекающиеся в одной точке на оси
я
ординат, а именно в точке, отстоящей от начала на расстоянии —-р .
Таким образом, обработка кривых ползучести с помощью E0.9)
производится чрезвычайно просто. Проводятся асимптоты
кривых ползучести, наклон этих асимптот определяет функцию v (а).
Ордината точки пересечения асимптоты с осью р дает
возможность сейчас же найти величину с. Индивидуальные кривые
ползучести укладываются в зависимость E0.9) довольно хорошо,
но при обработке семейства кривых обычно оказывается, что
¦общей точки их пересечения не существует и величина с является
•функцией напряжения. Можно, конечно, считать в E0.8), что
с = с (а), но в таком виде теория становится мало пригодной.
Если же учесть разброс опытных данных и относительно слабую
зависимость величины с от о, то для некоторого узкого диапазона
напряжений применение этого уравнения может быть оправдано.
Несколько иной способ учета неустановившейся ползучести
•состоит в том, что деформация ползучести рассматривается
состоящей из двух частей: деформации неустановившейся
ползучести, описываемой уравнением состояния, и деформации
установившейся ползучести типа квазивязкого течения. Таким
образом, сохраняя уравнение состояния, мы будем понимать
в нем под р величину
t
р = е — е0 (а) — \ v(o) dt.
о
Систематическое развитие этой точки зрения приводит к довольно
сложным результатам даже в простейших случаях, но при
интерпретации некоторых опытных данных она оказывается полезной.
В дальнейшем мы будем пользоваться более простым
уравнением ползучести E0.2), пригодным для описания
неустановившейся ползучести. Функцию / (о) будем принимать по преиму-
§ 50] АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ ЗАКОНА УПРОЧНЕНИЯ 203
ществу в виде E0.5), таким образом, закон упрочнения запишется
следующим образом:
рр^^кехр— (^Р = е-^)- E0.10)
Уравнение кривых ползучести при постоянном напряжении:
*—т-(-=-)"«р(т)«- ("-тяг)- <5011>
Поясним на примере ход определения констант в
уравнении E0.10). На рис. 53 сплошные линии — это кривые
ползучести стали ЗОХМА при температуре 500° [24]. Каждая кривая
О ВО 40 60 3U t^c JOO
Рис. 53.
является результатом осреднения трех экспериментальных
кривых. Перестраивая эти кривые в логарифмических координатах,
мы получаем график, изображенный на рис. 54. Опытные точки,
соответствующие каждому напряжению, достаточно хорошо
укладываются на прямую; наклон прямой сразу дает величину т.
Как видно, т не постоянно, а зависит от напряжения, в
диапазоне от 20 до 25 кг!ммг его можно считать постоянным, при
увеличении напряжения до 27 и 28 кг /мм2 величина т резко
увеличивается.
Отрезок, отсекаемый каждой из прямых рис. 54 на линии,
л л к , От ¦—
соответствующей t = 1, равен т In ^"~Т • ^сли построить
график зависимости этой величины от а, точки расположатся
204 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
на прямой, угловой коэффициент которой есть -^ . Поскольку т
уже известно, А находится. Отрезок, отсекаемый прямой на
оси о\ равен m Id —, следовательно, находится и к. Если
пользоваться средним значением т, то к и А будут постоянными.
В данном случае были найдены
также средние значения:
т = 0,53, /с=2,77.10-101/час,
А = 2,94 кг/мм2.
На рис. 53 пунктиром
проведены расчетные кривые ползучести
по уравнению E0.11) при этих
значениях постоянных. До
напряжения о = 25 кг/мм2 совпадение
расчетных и экспериментальных
кривых вполне удовлетворительно.
При напряжениях 27 и 28 кг/мм*
на кривых явно выражены второй
и третий участки, следовательно,
принятое уравнение заведомо
непригодно. Однако для начальных
участков и здесь совпадение
удовлетворительное. Можно сделать
вывод, что до деформации порядка
1% уравнение E0.10) при
постоянных значениях величин а, к и А
пригодно для описания ползучести
данного материала, хотя опыты
на ползучесть при постоянной
нагрузке не могут рассматриваться
как убедительное доказательство, необходимо проведение
эксперимента в других условиях, хотя бы в условиях чистой
релаксации. Об этом будет сказано в следующем параграфе. Пока
что заметим, что, принимая величины т и А функциями
напряжения, можно добиться значительно лучшего согласования
с опытом. Эти же эксперименты были обработаны в
предположении, что т и А являются линейными функциями от о. На
рис. 55 представлены те же экспериментальные кривые, что и на
рис. 53, а также их аппроксимация на основе высказанного
предположения. Как видно, совпадение получилось очень хорошим.
Постоянные закона ползучести, например величина а, а
также В и п в формуле E0.4) или к и А в E0.5), вообще говоря,
зависят от температуры. Однако зависимость от температуры
величины а, довольно слабая. Также в некотором достаточно узком
Рис. 54.
§ 51]
СВЯЗЬ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ
205
диапазоне температур можно считать, что п или А остаются
постоянными. Наоборот, множитель в выражении функции / (а),
величина В в формуле E0.4) или величина к в формуле E0.5)
р-70*
WO
SOO
too
Jy
^*
в**1
б=2&е/лш2
"*
_—
1 1 /
б=28/<г/ммг /
/У
^j
Z7
20
15
О
ZO
Рис. 55.
t.vac
зависят от температуры весьма сильно. В соответствии с тем,
что было изложено в § 45, мы можем принять:
В = В0 ехр
и0
RT
к = к0 ехр
и0
RT
Вообще, простейшая общая форма закона упрочнения с учетом
влияния температуры будет следующая:
^ = /(a)exp(^--^j . E0.12)
Здесь постоянная а и функция / (о) не зависят от температуры.
§ 51. СВЯЗЬ ПОЛЗУ ЧЕСТИЛИ РЕЛАКСАРИИ
ПО ТЕОРИИ УПРОЧНЕНИЯ
Перейдем в уравнении E0.10, к безразмерным переменным
с тем, чтобы освободиться от констант к ш А. Положим
сг - Ее
а==~А> в==~А
* Ер
Р=-А-.
t-
k(^l+at.
Тогда это уравнение примет следующий вид:
Л. Л А Л Л А
рра = ехра (р = е — а),
E1.1)
206 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
точка обозначает дифференцирование по безразмерному
времени t.
В случае релаксации е—е0 — const, следовательно,
Ро + Оо = Р + о.
Отсюда
а=--0о + ро — р.
Внесем в E1.1) и разделим переменные. Получим:
ра exp p dp =- ехр (о0 + р0) dt. E1.2)
Введем обозначение:
Z
2aexpzdz = x(z).
о
Интегрируя E1.2) при начальном условии р @) = р0, найдем:
X (р) = fexp (a0 + Ро) + X (Ро).
Отсюда
а = о-0 + Я — X ll (Ро) + * ехр (о0 + ро)] E1-3)
(Х-1 —функция, обратная функции х)-
Функция х (р) легко вычисляется и табулируется. В
уравнении E1.3) фигурирует не только начальное напряжение, но
и начальная деформация ползучести р0, таким образом,
рассмотренный случай является самым общим. Дело в том, что к
состоянию начала релаксации материал может быть подведен
различными способами. При обычных испытаниях образец быстро
нагружается до напряжения о0, настолько быстро, что в процессе
нагружения деформация ползучести накопиться не успевает
и можно считать р0 = 0. Тогда уравнение E1.3) существенно
упрощается, мы получаем:
о- = (Т0 —Х_1(?ехра0). E1.4)
В § 50 были приведены данные по обработке кривых
ползучести стали ЗОХМА при 500°; в результате обработки были
найдены средние значения констант т, к и А. При этих значениях
констант были рассчитаны кривые релаксации от начальных
напряжений о*0 = 14,1; 20; 25,92 и 30,8 кг/мм2. Эти кривые
представлены на рис. 56 пунктиром. На том же рисунке нанесены
опытные кривые релаксации сплошными линиями. Как видно,
совпадение получилось достаточно хорошим для всех кривых,
кроме верхней, соответствующей <т0 = 30,8 кг/мм2. Это и понятно,
§ 51]
СВЯЗЬ ПОЛЗУЧЕСТИ И РЕЛАКСАЦИИ
207
мы видели, что для больших напряжений 27 и 28 кг [мм2
уравнение E0.10) становится малопригодным, для напряжений
порядка 30 кг/мм2 оно, вероятно, будет давать совершенно неверный
результат. Важно отметить, что релаксация сопровождается
весьма малой деформацией ползучести, поэтому
удовлетворительная аппроксимация только начальных участков кривых
ползучести при помощи выбранных значений констант
обеспечила хорошее предсказание кривых релаксации. В работе [а*1
б,/ft
30,8
30
?5#2
20
W
к
*/ммг
V-
^-^
52
!=^=^:
s=?=
та
10
?0
30
40
t,vac
50
Рис. 56.
приведены также расчетные кривые релаксации, полученные-
в предположении, что т и А являются функциями а. Как мы
видели (рис. 55), такое усложнение вида уравнения состояния
обеспечило удовлетворительное описание кривых ползучести
в широком интервале напряжений и деформаций, но степень
совпадения расчетных и экспериментальных кривых релаксации
от этого практически не улучшилась. Для проверки общего
уравнения релаксации E1.3) был поставлен следующий опыт. Образец,
подвергался действию постоянной нагрузки в течение 25 часов,
за это время была накоплена деформация ползучести р0.
Достигнутая полная деформация р0 + -§¦ удерживалась постоянной
в течение следующих 75 часов. На рис. 57 приведены кривые
релаксации для неупрочненного образца и для образца,
упрочненного предварительной ползучестью. Тут же нанесены
расчетные кривые по формулам E1.4) и E1.3) соответственно. Для
постоянных ползучести принимались прежние значения,
определенные независимо из опытов на ползучесть при постоянном
208 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
напряжении. Совпадение теории и эксперимента оказалось
исключительно хорошим, тем самым гипотеза упрочнения
получила убедительное подтверждение.
Аналогичные проверки соответствия между опытами на
ползучесть и опытами на релаксацию на основе теории упрочнения
б,яг/ммг
О 10 20 30 W SO
t,vac
Рис. 57.
производились неоднократно на разных материалах. При
небольших продолжительностях испытаний, порядка десятков и сотен
часов, совпадение всегда оказывалось весьма
удовлетворительным. Чуриков [145] произвел таким способом обработку
упомянутых опытов Девиса [189] над медью, соответствующий график
0,мг/ш1г
11
10
3
8
7
6
S
*
3
0 1 г з
1 10 100 1000 t,m
Рис. 58.
представлен на рис. 58 A — опытная кривая, 2 — расчет). Серия
опытов на алюминиевом сплаве Д-16Т была произведена Намест-
никовым и Хвостунковым [85]. Эти опыты производились по более
широкой программе и будут описаны впоследствии. Другие
данные по сравнению ползучести и релаксации на основе гипотезы
упрочнения приводятся, например, в работе [36в].
^~
7
г
L;.
^?5
"^
logf
S 52J
НАСЛЕДСТВЕННАЯ ТЕОРИЯ ПОЛЗУЧЕСТИ
209
§ 52. НАСЛЕДСТВЕННАЯ ТЕОРИЯ ПОЛЗУЧЕСТИ
Рассмотренная нами в третьей главе теория наследственной
упругости Вольтерра описывает существенно обратимые
процессы и предполагает зависимость между напряжениями и
деформациями линейной. Поэтому она совершенно неприменима для
описания ползучести металлов даже в первом, самом грубом
приближении. Однако возможны различные обобщения теории
наследственности, которые делают ее пригодной для изучения
процессов такого рода. Наводящую идею для такого рассмотрения
может дать изучение изохронных кривых подзучести,
произведенное в § 44. Рассмотрим сначала обычное уравнение
наследственной теории упругости:
*
Ее = о+ \ K(t — x)a(x)dx.
о
Если напряжение постоянно, то отсюда получается уравнение
семейства кривых ползучести в следующем виде:
Ee^o[i+G{t)]. E2.1)
Изображая эту зависимость в координатах е — с, мы получим
для фиксированных значений t пучок прямых, проходящих через
начало координат. Эти прямые соответствуют изохронным
кривым ползучести. Прямая Ее = а есть прямая мгновенного
деформирования, она также принадлежит пучку. Для полученных
изохронных кривых ползучести выполняется условие подобия
D4.2), роль функции ft (t) играет - , роль функции ср (е) —
1-\-Ь\1)
линейная функция Ее. Чтобы получить для Ь (t) выражение
вида D4.3), достаточно взять ядро степенным с показателем р* — 1.
Нами было отмечено, что изохронные кривые ползучести для
металлов в большом числе случаев и с достаточной точностью
оказываются подобными. Переписывая соотношение D4.2) в
форме, аналогичной E2.1), получим:
<p(e) = o[l+G(t)J.
Это соответствуй интегральному соотношению
<р(е) = A+*•)<*• E2-2)
Здесь ф (е) — ордината кривой мгновенного деформирования,
К (t — т) — ядро, которое находится по кривым ползучести.
Поскольку, как мы видели, для функции G (t) дает
удовлетворительный результат следующая аппроксимация:
G(t) = alP,
14 ю. Н Работнов
210 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
то ядро ползучести следует принимать таким:
K(t-%) = a${t-xf-i. E2.3)
Но большая часть деформации ползучести необратима, поэтому
применимость уравнения E2.2) ограничена условием того, что
деформация не убывает. Представим себе, что мы достигли
деформации ё, которой соответствует ордината мгновенной кривой
пластичности ср' (рис. 59), после чего произвели разгрузку.
Изменение мгновенной деформации при разгрузке следует закону
упругости. Проведем через точку (ф', ё) прямую, наклон которой
соответствует модулю упругости;
6 ? (м' е') уравнение этой прямой
мгновенной разгрузки будет
ф — Е(е — ё) + ф'.
Внесем это выражение вместо
функции ф (е) в левую часть
уравнения E2.2) и мы получим закон
наследственной ползучести при
разгрузке:
Е{е — ё) + у' = (\. + К*)о.
О е е E2.4)
Рис. 59. Случай релаксации является
крайним в том смысле, что при е — ё
Ф^=ф' и мы остаемся в одной и той же точке кривой
мгновенного деформирования. Закон релаксации получается следующим:
о = [1 — R(t)]oQ. E2.5)
Здесь R (t) — интеграл от резольвенты ядра К, о*0 —
начальное напряжение. Предполагается, что это начальное напряжение
приложено мгновенно и сейчас же зафиксирована длина образца.
Из формулы E2.5) следует, что кривые релаксации для
различных начальных напряжений подобны. На опыте это следствие
из теории наследственности не подтверждается, как и ряд других
следствий, однако теория наследственности качественно
предсказывает некоторые явления, которые не укладываются,
например, в рамки теории упрочнения. В частности, уравнения E2.2)
и E2.4) объясняют эффект восстановления ползучести,
заключающийся в том, что после снятия нагрузки часть деформации
восстанавливается. Действительно, пусть к образцу было приложено
напряжение о; для простоты будем считать, что оно соответствует
упругому участку мгновенной кривой; тогда оно вызывает
мгновенную деформацию a IE (точка А на рис. 60), в течение
времени ti происходит ползучесть по кривой АВ. При t = tx
напряжение снимается, при этом исчезает упругая деформация ВС =
§ 52]
НАСЛЕДСТВЕННАЯ ТЕОРИЯ ПОЛЗУЧЕСТИ
211
= ОА = а1Е. Образец продолжает укорачиваться, зависимость
между удлинением и временем изображается кривой CD; за
время t2, истекшее после снятия нагрузки, восстанавливается
деформация ег (точка D). Проследим этот процесс в плоскости
Ф — е (рис. 61). Мгновенное приложение нагрузки соответствует
движению из точки О в точку А; за время tx растет деформация,
t, <? в/? ег б/?
Рис. 60. Ряс. 61.
что соответствует движению вверх по кривой до точки В. Процесс
ползучести описывается при этом уравнением E2.2), и для
точки В получаем:
ф(ея) = И+(?((,)] а. E2.6)
В результате мгновенной разгрузки мы спускаемся по прямой
разгрузки в точку С на длину отрезка ВС = ОА, восстановление
ползучести соответствует движению по той же прямой до точки D
к моменту времени tt + t2. Чтобы описать восстановление
ползучести, необходимо пользоваться уравнением E2.4), причем под
интегралом в правой части нужно считать а = const при t < t%
и а = 0 при tx < t < tt + t2. Получим:
E(e — eB) + <fB=G(ti + t^ — G(tz). E2.7)
Из чертежа на рис. 61 видно, что
0
ег — ев — — — е.
Комбинируя E2.6) и E2.7), найдем, что
*г = -J- \G (h) + G (t2)-G{t% + t2)]. E2.8)
Линейная зависимость ег от напряжения хорошо подтверждается
опытами Джонсона [253], приблизительно подтверждается также
симметричная форма зависимости величины ег от времен tt и t2.
14*
212 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Для количественной проверки материал, приводимый в этой
работе, недостаточен.
Другие опубликованные данные по восстановлению ползучести
вносят несистематический характер, и обработать их не удается.
Выбранный нами путь обобщения уравнений теории
наследственности на случай нелинейной ползучести, конечно, не
единственный. Арутюнян [4] и Розовский [117] пользуются другим
уравнением, а именно:
е = т|> (о) -l \h{t — x)F [о (т)] dr. E2.9)
(i
Оно обладает несколько большей общностью, поскольку в нем
фигурируют не две, а три функции, подлежащие определению
из эксперимента. Уравнение кривой мгновенного
деформирования здесь будет е = ty (а), и характеристики ползучести не
связаны с этой кривой. Как уже отмечалось, основанием для выбора
более простой зависимости E2.2) послужило подобие
изохронных кривых ползучести и возможность экстраполяции данных
по ползучести с использованием этого подобия. Определение
функций, фигурирующих в E2.2), проще, чем определение
соответствующих функций в уравнении E2.9). Количественные и
качественные результаты, получаемые по каждому из вариантов
наследственной теории, оказываются примерно одинаковыми.
Вопрос о том, в какой мере применимо уравнение типа E2.9)
для процессов, сопровождающихся уменьшением напряжения,
и каким образом оно должно быть в этом случае видоизменено,
насколько нам известно, не рассматривался.
По-видимому, теории ползучести наследственного типа больше
подходят для полимеров, чем для металлов. Обработка -опытов
на ползучесть со ступенчатым изменением нагрузки для
алюминиевого сплава [83] показала, что возврат при разгрузке на самом
деле оказывается меньше, чем это предсказывает теория в любом
из рассмотренных вариантов.
Наряду с описанными вариантами теории нелинейной
наследственности следует упомянуть о более общем уравнении, которое
рассматривалось еще Вольтерра [37е], а именно:
t t t
Ее= ^ v.i(t — x)da{xy) + [ [ ¦nz(t — xl,t — x2)da(xl)da{xi)-t
— ос —оо —со
t t t
f- S J J xs(t~ti,t — x2,t — r3)da(rl)da(t!t)da(x3)+... E2.10)
—-M —OO —OO
Неудобство этого варианта теории состоит в том, что, если
нелинейность зависимости деформации от напряжения сильная, то
§ 53] ЭКСПЕРИМЕНТ. ПРОВЕРКА ГИПОТЕЗЫ УПРОЧНЕНИЯ 213
в ряде E2.10) необходимо удержать довольно много членов, а это
автоматически влечет за собою появление все более и более
сложных ядер наследственности.
В последние годы были предприняты попытки применить
уравнение типа E2.10) для описания поведения полимерных
материалов I218], [301], [279], [3811- Фактическое нахождение
последовательных ядер оказалось затруднительным, экспериментально
подтверждены некоторые качественные следствия из уравнения
E2.10), вытекающие, впрочем, и из E2.2). Действительно,
уравнение E2.2) является частным случаем E2.10). Положим
Щ Ui) = X (ti), Х2 (tt, t2) = Й2Х (*,) X {t2), . . .
.. ., xn(tu t2, .. .,tn) = ann (t{) к (t2) ... x (tn), . . .
Полагая к' {t) — K{t), перепишем E2.10) в следующей форме:
Ее = s + a2s* + a3s3 +...+ ansn +... E2.11)
Здесь
t
s=^a + \ K(t — %)o{x)dx.
Если обозначить через ср обращение ряда, стоящего в правой
части E2.11), то мы придем как раз к уравнению E2.2).
§ 53. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ГИПОТЕЗЫ
УПРОЧНЕНИЯ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ
Мы уже приводили некоторые данные по экспериментальной
проверке гипотезы упрочнения путем сравнения предсказанных
кривых релаксации с экспериментальными. Более простой способ
проверки состоит в испытаниях на ползучесть при ступенчатом
изменении нагрузки. В то же время при ступенчатом изменении
напряжения более резко проявляются отклонения от
предсказаний теории, получаемые результаты более контрастны.
Действительно, как мы видели, расчет кривой релаксации по различным
теориям старения дает тот же качественный результат, что и
расчет по теории упрочнения, и даже кривая, рассчитанная по теории
упрочнения, не всегда бывает ближе к экспериментальной, чем
другие расчетные кривые. Поэтому сопоставление ползучести
и релаксации не дает достаточных данных для того, чтобы
отвергнуть теории старения. В случае ступенчатой нагрузки разница
между предсказаниями различных теорий становится очень
большой и носит уже качественный характер. В то же время для
реальных изделий этот случай является крайним. Теория,
удовлетворительно предсказывающая ход ползучести при резких
изменениях напряженного состояния, будет заведомо хороша в тех
214 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
случаях, когда напряженное состояние меняется плавно и
непрерывно.
Весьма обстоятельная проверка гипотезы упрочнения была
проделана в работе Наместникова и Хвостункова [83]
применительно к алюминиевому сплаву Д-16Т при температурах 150°
и 200°. Продолжительность испытаний составляла во всех
случаях около 100 часов; всего было испытано более 130 образцов,
что обеспечило устранение случайного разброса данных. Образцы
Рис. 62.
изготовлялись из пруткового материала в состоянии поставки,
то есть закаленного и естественно состаренного. Твердость
образцов колебалась в пределах 5 единиц по Роквеллу. Для
обеспечения воспроизводимости результатов режим предварительного
прогрева перед началом испытания был строго регламентирован.
На рис. 62 приведены осредненные кривые ползучести прп
температуре 150°. В логарифмических координатах получились
параллельные прямые, таким образом, величина а оказалась
не зависящей от напряжения. Было найдено, что т = 0,33 в
соответствии с законом Эндрейда. Таким образом, а = 2. Дальнейшая
обработка производилась по уравнению E0.11). Согласно этому
уравнению зависимость между lg p и о при фиксированном
значении времени должна изображаться прямой, в действительности
же получился график, изображенный на рис. 63. Точка пере-
§ 53] ЭКСПЕРИМЕНТ. ПРОВЕРКА ГИПОТЕЗЫ УПРОЧНЕНИЯ 215
сечения двух прямых соответствует значению о = 25,3 «г/ли2,
поэтому для постоянных к и А получились две пары значений:
cr<25,3, fc,= 5,68-10-15, А = 8,77 кг/мм2,
<7>25,3, /с = 5,60-108, А = 2,52кг/мм\
На рис. 62 проведены расчетные кривые ползучести, построенные
по уравнению E0.1) при вышеприведенных значениях констант.
-ЦР
)
с
Г" —
Д70Т1500
t=Wvac
Lo
Sk.
X
w го so
б,яе/мм-
Рис. 63.
Для напряжений, не превышающих 25 кг/мм2, совпадение
получилось очень хорошим. При больших напряжениях кривые
ползучести имеют второй и третий участки, которые заведомо не
описываются формулой E0.11), но для начальных участков
аппроксимация опять-таки вполне удовлетворительна.
Для этого же материала было проведено десять опытов на
релаксацию с начальными напряжениями 20,0; 22,5 (два опыта),
25,0 (два опыта), 26,5; 27,5 (два опыта), 30,0 и 32,0 кг/мм2.
Опытные точки приведены на рис. 64 и 65; на этих же графиках
сплошными линиями построены расчетные кривые по уравнению E1.4),
рассчитанные для приведенных выше значений констант
ползучести, найденных из опыта на ползучесть при постоянном
напряжении. При весьма плавном изменении напряжения, происходящем
в процессе релаксации, гипотеза упрочнения оказывается
достаточно точной. Однако опыт при ступенчатом изменении нагрузки
сразу обнаруживает некоторые систематические отклонения от
предсказаний гипотезы. На рис. 66 изображена кривая
ползучести, соответствующая напряжению 17,5 кг1мм* в течение 45 часов
и напряжению 32 кг [мм2 в течение следующих 27 часов. Здесь
соответствие между опытом и теорией удовлетворительно.
Однако при больших напряжениях, как, например, в опытах, изо~
браженных на рис. 67 вверху, когда напряжение было равно
29,2 кг 1мм2 в течение первых 22 часов и 34 кг!мм2 в течение
следующих 14 часов, ясно видно, что опытные точки ложатся выше
теоретической кривой. Это расхождение между теорией и
экспериментом обнаруяшвается еще более ярко, когда нагрузка меняется
216 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
б^г/мм2
т
20
?»<
Ч°о
¦о-?_
о
'
о
5" ¦
>
о
1
Т=150'\
"
)
>
О 20 40 SO SO ПО
i,vac
Рис. 64.
б,/гг/ммг
3Z
'
27
\
X
Ч
о \
о
^
^
о^*
о
Г-^П ,
о о
т=
?¦
--ш°
-О П
;
0
О О <
¦ "
' ° о
оо 0
ff 20 40 SO
Рис. 65.
80 700
t,wc
7-70
60
ь
/
Lp*
-.И"
\ О
<#*¦
-г
Y"
s°-°
i,
i
jLfffSo
Т=7Ж
О
О 75 32 4В № ВО
t, час
Рис. 66.
§ 53] ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ГИПОТЕЗЫ УПРОЧНЕНИЯ 217
100
SO-
—50
0
f~
T=J50%
f
«**
ОС
о
с*
йS
20
ооо
t,vac
> х
&>-
О
О
О
^
!
60 60
t.vas
несколько раз. На рис. 67 внизу приведена кривая ползучести
для того же материала при температуре 200° для ступеней
напряжения 4, 8 и 12 кг/мм2. На третьей ступени расхождение между
теорией и экспериментом уже очень велико. Общий вывод можно
сформулировать следующим образом. Гипотеза упрочнения
удовлетворительно описывает ползучесть при постоянных и
убывающих нагрузках, при
возрастающих нагрузках пол- p-Ws p-10s
зучесть происходит
несколько быстрее, чем это
следует из теории,
особенно в первые минуты и часы
после изменения нагрузки,
если уровень напряжений
таков, что мгновенная
деформация в основном
упруга. При больших
напряжениях, приложение ко- д 20
торых сопровождается
значительной пластической
деформацией, применение
гипотезы упрочнения
приводит к значительным отклонениям от эксперимента,
фактическая скорость ползучести больше, чем это следует из теории.
Очень наглядная схема эксперимента для выяснения
отмеченного факта была предложена Одквистом I94]. Если уравнение
состояния имеет вид
рА(р) = /(<х), E3.1)
то справедлив закон коммутативности нагружения, состоящий
в следующем. Пусть к образцу прикладывается ступенчато
изменяющаяся нагрузка, напряжение на каждой ступени равно оь
длительность его действия tt. Тогда суммарная деформация
после п ступеней нагрузки не зависит от порядка приложения
нагрузок, лишь бы напряжение и длительность каждой ступени
оставались неизменными. Действительно, разделим переменные
в E3.1) и проинтегрируем. Получим:
р \
J h (p) dp =--- \j / (a) dt = t,f (<т,) J- hf (o2) -f- . . . + tnf {an).
40
Рис. 67.
Левая часть представляет собою однозначную функцию от р,
правая — не зависит от порядка нумерации ступеней нагрузки.
Простейший опыт для проверки закона коммутативности был
произведен Одквистом, который взял всего две ступени
нагружения. Оказалось, что закон коммутативности не выполняется,
218 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
если о2 > ffi, суммарная деформация получается большей, нежели
при а4 <о2- Опыт Одквиста был повторен Наместниковым и Хвос-
тунковым на нескольких образцах и при разных температурах.
Типичный результат приведен на рис. 68. Здесь сначала ai = 12,
о2 = 16, потом, наоборот,
р-10*
ъ8г
^
о ^
6qOO
0
О
О
о
о
)
UogJi
Д75Т2№°
CTi = 16, о2 — 12 кг[мм2,
тогда как в том и другом
случае <i = ?2
24 часа. Спло-
20
Рис. 68.
40 t,vac
шными линиями проведены
расчетные кривые, которые
удовлетворительно
описывают эксперимент при а2 <CQi-
В случае увеличивающейся
нагрузки, когда а2 > о±,
деформация за 48 часов
получается значительно большей.
Конечно, невыполнение
закона коммутативности
нельзя отнести за счет
специального выбора вида уравнения
состояния E3.1), для
которого этот закон справедлив, возможная погрешность при этом может
получаться того же порядка, что и погрешность при
аппроксимации кривых ползучести для постоянного напряжения.
§ 54. ДРУГИЕ ИССЛЕДОВАНИЯ ПОЛЗУЧЕСТИ ПРИ ПЕРЕМЕННЫХ
НАГРУЗКАХ НА ОСНОВЕ ГИПОТЕЗЫ УПРОЧНЕНИЯ
Не ставя перед собою задачу дать полный обзор
экспериментальных исследований, подтверждающих в известных пределах
справедливость гипотезы
упрочнения, мы остановимся на
цикле исследований, выполненных
японскими авторами [365]. При
ступенчатом изменении нагрузки
отмечаются те же
систематические отклонения от предсказаний
теории, окоторых
вышеупомянуто выше. Изучалась ползучесть
при ступенчатом циклическом
изменении нагрузки.
Напряжение Oj действовало на образец в
течение времени ti, после этого напряжение внезапно увеличивал ось
до величины а2, при этом напряжении ползучесть происходила
в течение времени t2, потом напряжение уменьшалось до оь и цикл
повторялся (рис. 69). Если отношение t2lt\ мало, то отклонения
а
4
б, б
\ \
L
?
Рис. 69.
3 54] ДРУГИЕ ИССЛЕДОВАНИЯ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ 219
экспериментальных данных от предсказании теории упрочнения
оказываются существенными, фактическая суммарная
деформация получается большей, чем это следует из гипотезы уравнения
состояния. Типичная кривая, заимствованная из работы [365],
приведена на рис. 70. Автор объясняет это следующим образом.
За время действия меньшего напряжения происходит
восстановление ползучести, сама по себе деформация обратной ползучести
незначительна, основной эффект состоит в том, что при
увеличении напряжения происходит мгновенное увеличение скорости
25 SO
t( бремя под напряжением;
Рис. 70.
7S vac
ползучести, величина которой существенно превышает величину,
определяемую для данного напряжения и данной деформации
уравнением состояния. Если t2 мало, то суммарная деформация
за это время оказывается ощутимо большей, чем следует из
теории.
Эффект быстрого изменения температуры оказывается
аналогичным эффекту изменения напряжения. В работе [309] было
обнаружено, что если во время испытания на ползучесть
температура быстро увеличивается, то деформация в первые моменты
растет быстрее, чем следует из уравнения состояния. Наоборот,
при понижении температуры происходит временная задержка
ползучести. При циклическом изменении температуры оба эти
эффекта взаимно компенсируются и в среднем гипотеза уравнения
состояния оправдывается достаточно хорошо. Соответствующие
данные приводились уже в § 45 при обсуждении исследования
Дорна.
Примем закон ползучести при переменной температуре
в виде E0.12). Как уже было указано, такая простейшая форма
температурной зависимости дает удовлетворительные результаты,
если диапазон изменения температуры достаточно узок. Результат
220 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
интегрирования уравнения
_мо_Л
где о постоянно, а Т есть функция времени, может быть
представлен следующим образом:
Здесь
щ
ехр '
= 4 jexp(--gr)d*. E4.1)
Если Т (t) — периодическая функция времени, то есть если
происходит циклическое изменение температуры, то интеграл
в правой части E4.1) будет содержать член, линейно зависящий
от времени, и ограниченную периодическую часть. При
вычислении эквивалентной температуры мы будем считать, что время t
достаточно велико и влияние второй части несущественно.
Таким образом, более строго:
о
Рассмотрим следующие простые случаи.
1. Температура изменяется по синусоидальному закону Т —
AT
---Т0 -f- AT1 sin at, отношение—=- достаточно мало. В этом случае
ехр f — ~^) ж ехр Г-~^г) ехр (A, sin со*).
Здесь принято
щАТ
ДТ2 '
Таким образом, дело сводится к вычислению интеграла
\ ехр (k sin Ы)
dt.
По предположению к мало по сравнению с единицей. Разложим
экспоненциальную функцию в ряд и проинтегрируем каждый
член по отдельности. Заметим, что J sin2"+1 х dx есть
периодическая функция от х, тогда как I sin2n x dx есть сумма
некоторой периодической функции и неограниченно растущего со
временем члена ^( п )х. Здесь символ (?) обозначает, как обычно
Э 54] ДРУГИЕ ИССЛЕДОВАНИЯ ПРИ ПЕРЕМЕННЫХ НАГРУЗКАХ 221
биномиальный коэффициент. Теперь, как легко видеть,
Нт[|5ехР(^тсо/)^](_ = 2^)!^гB,;)^п.
о
Следовательно, эквивалентная температура определяется
формулой
_L._J ^-ln^— — f2n^kin E4 21
Та ~ Т0 гпщ Ш - Bл)! 22» ^ п J Л ' ^-^
Ряд в формуле E4.2) сходится весьма быстро. Для случая
периодического напряжения результат получается совершенно
аналогично [103], [зв5], при этом ограничение малыми отклонениями
от среднего значения становится ненужным.
2. Температура изменяется ступенями. Продолжительность
каждого цикла есть (t + t2, в течение времени tx температура
равна Ти в течение времени t2 температура есть Тг.
Эквивалентная температура, очевидно, определяется следующим образом:
е*р(—^7)=T:b7['iexp(~^i)+'2exp(_^)] •
E4.3)
Опыты на ползучесть при синусоидальном изменении
температуры были поставлены Ивановой [38] на хромоникелевом сплаве
ЭИ-437Б. Эти опыты относятся к неустановившейся стадии
ползучести, когда кривые ползучести достаточно хорошо
описываются с помощью уравнения состояния E0.10). Специальное
устройство обеспечивало изменение температуры по
синусоидальному закону. Были сняты кривые ползучести при одном
и том же напряжении для верхней и для нижней температуры
цикла, что позволило определить энергию активации иа.
Рассчитанная кривая ползучести при переменной температуре
довольно хорошо совпала с опытными точками (рис. 71). На рис. 71
приведены кривые ползучести при Т = 650° и Т = 700°; при
температуре, меняющейся от 650° и 700° с периодом 30 мин.,
1 час и 2 часа, а также (пунктиром) расчетная кривая для
переменной температуры.
Аналогичные опыты на одной из марок нержавеющей стали
были проделаны Нишихара, Таира, Танака и Онами [310].
Результаты этих опытов представлены на рис. 72, взятом из
упомянутой статьи. Температура менялась в пределах от 575°
до 675° в соответствии с приведенным графиком. Рассчитанная
по формуле E4.1) эквивалентная температура оказалась равной
650°. Светлые точки на графике соответствуют кривой ползучести
при меняющейся температуре, жирные точки — испытанию при
постоянной температуре Т — 650°. Разница между этими
кривыми не выходит за пределы естественного разброса. В этих
222 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. 1\
испытаниях длительность была достаточно большой, и на кривых
ясно обнаруживается установившийся участок.
Авторы воспользовались схемой, упомянутой в § 50, а именно
они рассматривали отдельно деформацию ползучести,
сопровождающуюся упрочнением и подчиняющуюся уравнению состояния.
о zo w so во то
t,vac
Рис. 71.
и деформацию установившейся ползучести, определяемую
выражением \ v (a) dt. Скорость установившейся ползучести или
о гор т еоо воо ш
t,vac
Рис. 72.
квазивязкого течения зависит от температуры так же, как и
функция / (а) в законе упрочнения, то есть
г; = у0 (с) ехр ( — -^J .
Соответствующая энергия активации uj отлична от и0, поэтому
эквивалентная температура, которая может быть и для этого
случая вычислена по формуле E4.1), будет другой.
§ 55] КИНЕТИЧЕСКИЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ 223
Авторы пренебрегают этой разницей и ведут обработку по
формуле (в наших обозначениях)
Аналогичным образом в работе Таира и Онами [362] была
исследована ползучесть при резких изменениях температуры. Полые
образцы нагревались проходящим током и охлаждались струей
i I I i i I
О Sff fffl fSff 200 250
t.vac
Рис. 73.
воздуха, длительность цикла составляла 15 сек., 1 мин., 2 мин.
На рис. 73 приведены экспериментальные (сплошные линии)
и расчетные (пунктир) кривые ползучести, здесь же приведен
график изменения температуры со временем. В этих опытах
распределение температуры по длине образца было неравномерным
и при обработке пришлось прибегать к осреднению. Несмотря
на это, теория достаточно хорошо подтверждается экспериментом.
§ 55. КИНЕТИЧЕСКИЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ
Предположение о том, что мерой упрочнения является
величина деформации ползучести, представляется самым простым из
всех возможных. Однако это предположение носит весьма частный
характер и не подкрепляется какими-либо серьезными
физическими соображениями. Действительно, механизмы упрочнения
могут быть различными, и поэтому нет никаких оснований
утверждать, что одной и той же величине пластической деформации
всегда соответствует одно и то же структурное состояние
материала. Дальше мы покажем, что в этом смысле мгновенная
пластическая деформация и деформация ползучести играют
различную роль и их приходится отделять при уточнении уравнения
224 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
состояния. Кажется довольно очевидным, что структурное
состояние нельзя, вообще говоря, считать однозначно определенным
одной только величиной накопленной деформации ползучести,
безотносительно к тому, каким образом и в какой
последовательности была достигнута эта деформация.
В рамках феноменологической теории мы не можем указать
признаков, характеризующих структурное состояние;
единственное возможное утверждение состоит в том, что существует
некоторое конечное число параметров qu q2, . . ., qn, с помощью
которых это структурное состояние может быть задано. Смысл
этого утверждения состоит в том, что если для двух материалов
все параметры qt равны между собою, то при одинаковых
напряжениях и температурах скорость ползучести для них будет одна
и та же. Подчеркиваем, что здесь речь идет лишь о тех
структурных характеристиках, которые определяют процесс ползучести.
Структурные параметры qt вводятся, таким образом, чисто
формально, вопроса об их физическом значении мы здесь не
затрагиваем, хотя некоторые из приводимых ниже результатов
немедленно переводятся на язык кинетики дислокаций.
Таким образом, более общая гипотеза состоит в том, что
скорость ползучести определяется напряжением, температурой,
а также некоторым числом структурных параметров qi, так что
общее уравнение ползучести будет следующим:
p = f(a, T, qu qz, ..., qn). E5.1)
В ходе ползучести должно происходить изменение структуры,
описываемое изменением параметров qt. Достаточно общее
предположение состоит в том, что это изменение описывается
следующими кинетическими уравнениями:
dqi = aidp + bido + cidt, + UdT. E5.2)
Здесь ah bt, cu ft — некоторые функции от р, a, t, T, а также
qu q2, ¦ • -, qn- Соотношения E5.2), вообще говоря, неинте-
грируемы. Встав на такую точку зрения, мы получаем весьма
широкую свободу для построения сколь угодно сложных и сколь
угодно точных теорий ползучести, однако эта принципиальная
возможность до сих пор использована в очень малой степени.
Рассмотрим некоторые простейшие примеры.
а) Примем п = 1 и положим dq = dp. Отсюда q = p; мы
получаем обычную теорию упрочнения.
б) За меру упрочнения можно принять не величину
деформации ползучести, а, например, работу напряжений, действующих
на деформациях ползучести. Ограничиваясь опять-таки только
одним параметром упрочнения, положим
dq—-a dp,
S 55] КИНЕТИЧЕСКИЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ 225
следовательно,
\ a dp.
E5.3)
Рассмотрим теперь простейший опыт на ползучесть со
ступенчатым изменением нагрузки (рис. 74). Если ползучесть
происходила при постоянном напряжении о^, то к моменту
времени ty была накоплена деформация ползучести pi и величина q
равнялась pi<3i- Если теперь внезапно изменить напряжение,
сделав его равным а2, ползучесть
будет описываться уравнением E5.1),
причем в первый ^момент q = piO"i.
На кривой ползучести,
соответствующей постоянному напряжению <та,
можно указать точку В с ординатой
р2 такой, что
р202 = Pi(I].
Скорость ползучести после
изменения нагрузки будет той же, что на
кривой а2 в точке В, дальнейший ход
кривой будет тем же самым. Таким Рис. 74.
образом, чтобы предсказать ход
ползучести при ступенчатом изменении нагрузки от о*! до о2, в момент,
когда р = pi, следует найти на кривой ползучести при напряжении
= pi —, и перенести правую по
относу точку, для котороир = рг
шению к этой точке часть кривой параллельно самой себе, как
показано на рис. 74. По рассмотренному варианту теории
упрочнения скорость после изменения нагрузки оказывается больше,
чем по обычной теории упрочнения, что соответствует данным
наблюдений, как показано выше.
Выясним теперь возможность предсказания кривой
релаксации по этой теории. Предположим, что серия кривых
ползучести при постоянном напряжении достаточно хорошо
получается из уравнения состояния вида
рра = ап. E5.4)
Здесь масштабы выбраны таким образом, что уравнение не
содержит размерных констант и р — е — а. В случае релаксации
0 = 0О> р — а0 — о и р=—о. Внося E5.4) и разделяя
переменные, получим:
1
h = e-"+"+i J t^^-K. E5.5)
О/Со
15 ю. Н. Работнов
226 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
Выберем теперь вид уравнения E5.1) при q = \ о dp таким
образом, чтобы для постоянных нагрузок оно совпало с E5.4).
Если а = const, то q = ap; исключая из E5.4) р, получим:
p=,q-aan+u. E5.6)
Теперь в случае релаксации
о
q = ^ adp= — \ ada = ^(p\ — a2).
Of)
Внесем в E5.6), разделим переменные и проинтегрируем. Получим:
*п==оГ+-+' \ *Ш?-Ъ- E5-7)
ao/a Ь
Подынтегральное выражение в формуле для tu отличается
от соответствующего выражения в формуле для t\ множителем
Но при Z, < 1 и а > 0 эта величина больше единицы; таким
образом, ?и > h и рассмотренный новый вариант теории
упрочнения предсказывает более медленный ход кривой релаксации,
чем обычная теория.
Вариант теории упрочнения, в котором за меру упрочнения
принимается выражение E5.3), был подвергнут специальной
проверке в работе [1а]. Опыты проводились на материале Д-16АТ
при температуре 150°, плоские образцы вырезались из листа
в направлении проката. На рис. 75 приведены кривые ползучести
при ступенчатом изменении нагрузки. Кривые I ж II
соответствуют ступеням 15 и 25 кг/мм3, кривая /// — ступеням 10, 15
и 20 кг 1мм2. Сплошные линии представляют собою результат
расчета по уравнению E5.6), пунктирные — по уравнению E5.4),
то есть по обычной теории упрочнения. В двух олучаях
совпадение с экспериментом по новой теории оказалось весьма
хорошим, для третьей кривой разница остается заметной. Очевидно,
что без больших затруднений можно добиться очень хорошего
описания опытов при ступенчатых нагрузках, для этого
достаточно принять за меру упрочнения величину
q— \ а {о) dp. E5.8)
Функцию а (о) всегда можно подобрать так, чтобы наилучшим
образом описать ход данного эксперимента, простейшее
выражение E5.3) было принято с тем, чтобы не вносить чрезмерных
§ 55] КИНЕТИЧЕСКИЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ 227
осложнений. Следует помнить, что случай нагрузок, меняющихся
ступенями, является самым острым для выявления отступлений
от теории; при плавно меняющихся нагрузках дело обстоит лучше,
уже обычный вариант теории упрочнения достаточно хорошо
описывает случай
медленно меняющихся на- б,кг/мм2
грузок, с помощью па- 27
раметра вида E5.3)
можно добиться
некоторого уточнения. Так,
на рис. 76 приведены
кривые деформирования
того же алюминиевого
сплава при скорости
возрастания
напряжения 0,002 кг/мм* в
минуту. Максимальное
напряжение не превышает
предела
пропорциональности, поэтому видимая
пластическая
деформация представляет собою
деформацию ползучести
при возрастающей
нагрузке. Сплошными
линиями представлен результат расчета по уравнению E5.6),
пунктирными — по уравнению E5.4). В том и другом случае
15*
р-Т/Г
Рис. 76.
228 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
константы определялись из опыта на ползучесть при постоянной
нагрузке. Отклонение опытных точек от расчетной кривой заметно
в области малых напряжений, так же как и в случае
ступенчатой нагрузки (рис. 75), далее совпадение точек с результатом
расчета по новому варианту теории упрочнения вполне
удовлетворительно.
в) В работе [84] была сделана попытка уточнить описание
ступенчатых нагрузок с помощью двух параметров состояния:
обычной меры упрочнения qi — р и параметра qz, определенного
следующим соотношением:
dqz — pdo. E5.9)
Если к образцу прикладывается мгновенно нагрузка, которая
сохраняет впоследствии постоянное значение, то q2 = 0. При
D 20 40 ?> 20 W t,mc
t,vae
Рис. 77. Рис. 78.
ступенчатом изменении напряжения от o*i до с2 в момент, когда
было р = ри величина да получает мгновенное приращение
Д<?2 = (fa— °"i) Pi.- В работе [м] был принят следующий закон
ползучести:
рр« = кехр [-%¦ + -%-] . E5.10)
На рис. 77 приведены опытные точки, относящиеся к трем
образцам из сплава Д-16Т, которые испытывались при напряжении
8 кг/мм2 в течение первых 24 часов и при напряжении 16 кг 1мм2
после 24 часов при Т = 200°. Пунктиром построена расчетная
кривая с помощью обычного уравнения состояния, сплошной
линией — кривая, соответствующая уравнению E5.10). На
рис. 78 приведены результаты аналогичных испытаний для
о = 12 и 16 кг/мм2, причем напряжения прикладывались в раз-
§ 56]
РАЗУПРОЧНЕНИЕ ПРИ ПОЛЗУЧЕСТИ
229
личной последовательности. Как и прежде, сплошные линии
соответствуют E5.10), пунктир — обычному уравнению
состояния. Следует заметить, что для убывающих нагрузок учет
влияния параметра д2 не улучшает, а ухудшает дело. Расчет кривых
релаксации с помощью уравнения E5.6) приводит к результатам,
которые очень мало отличаются от результатов обычной теории
и не являются лучшими. Поэтому следует считать, что
величина д2 меняется лишь при увеличении напряжения. Таким
образом,
dq2=pdo (do>0), dq2==0 (Ах<0). E5.11)
Наряду с рассмотренными простейшими вариантами
кинетических уравнений ползучести можно делать разнообразные
предположения и получать более или менее сложные варианты теории.
Имеющийся в распоряжении опытный материал еще недостаточен
для выбора наилучшего варианта, однако высказанная точка
зрения позволяет, по крайней мере качественно, объяснить
многие из наблюдаемых фактов и открывает возможности для их
количественного описания.
§ 56. РАЗУПРОЧНЕНИЕ ПРИ ПОЛЗУЧЕСТИ
До сих пор мы рассматривали ползучесть исключительно
структурно-устойчивых материалов. При формулировке закона
упрочнения предполагалось, что состояние упрочнения не может
быть снято в результате выдержки материала при температуре
испытания. В реальных металлах и сплавах диффузионные
процессы, протекающие при повышенных температурах, могут
приводить либо к разупрочнению, либо к упрочнению, которое в этом
случае называется старением. Формальное описание этих
процессов возможно с помощью уравнений E5.1) и E5.2). Еще Бейли
предложил рассматривать ползучесть как результат
одновременного протекания двух процессов — деформационного
упрочнения и температурного разупрочнения. Однако эти рассуждения
не были облечены в корректную математическую форму и
остались лишь качественными соображениями, которые впоследствии
подвергались критике со стороны одной части металлофизиков
и брались под защиту другими [S3]. He касаясь этой стороны
дела, покажем, каким образом можно учесть температурное
разупрочнение. Положим для простоты в уравнении E5.1) га = 1
и примем
dq = dpJ\-c dt.
Коэффициент с, характеризующий скорость разупрочнения,
должен быть отрицательным и увеличиваться по абсолютной
величине с увеличением степени упрочнения; простейшее пред-
230 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
положение состоит в том, что с пропорционально д. Таким образом,
dq = dp- \iqdt. E6.1)
Множитель \х, конечно, в сильной степени зависит от
температуры, при постоянной температуре будем считать его
постоянным. Предположим теперь, что образец полз при напряжении о
до того момента, когда деформация стала равной р}.
Соответствующее значение q есть qi: если р как функция t известно (дана
кривая ползучести); qt можно вычислить, интегрируя E6.1).
Разгрузим образец и будем его выдерживать при той же
температуре, при которой велось испытание. Так как при а = 0 р = 0,
то уравнение E6.1) примет следующий вид:
dq — — \iq dt.
Интегрируем его, считая ( = 0 в момент разгрузки, когда было
р = р4. Получим:
q = qi exp( — \it). E6.2)
Уравнение E6.2) описывает температурное разупрочнение
образца, на который не действует нагрузка. Если теперь вновь создать
в образце напряжение а, то он поползет со скоростью большей,
чем та, которая была в момент, предшествовавший разгрузке.
Постоянная (г имеет размерность единицы, деленной на время.
Таким образом, 1 /ц может рассматриваться как характерное
время разупрочнения. Если это время достаточно велико, то
для первых участков кривых ползучести q « p; следовательно,
уравнение состояния можно принять следующим:
pqa — exjH E6.3)
безразмерные р, о определены, как в § 51, q=—j-
Исключив из E6.1) и E6.3) р, получим:
gga + (igI+a = expa
Интегрируя при условии, что a — const и для t = 0 q — 0,
найдем:
g1+a = ^Р? |4 __ ехр [ _^ A + а) цу E6.4)
V-
Для нахождения р необходима еще одна квадратура, которая
приводит к весьма сложной зависимости р (t), поэтому мы
ограничимся рассмотрением крайних случаев.
§ 56]
РАЗУПРОЧНЕНИЕ1ПРИ ПОЛЗУЧЕСТИ
231
а) Время t мало по сравнению с характерным временем
разупрочнения 1 /ц. Разложим экспоненту в ряд и сохраним два
первых члена разложения. Из E6.4) следует:
9=exp(mo-)(^—J ¦
Интегрируя E6.1), найдем деформацию ползучести:
p^e^(ma)^y[i+r^i]. E6.5)
При малых значениях \it второй член в скобке мал и
формула E6.5) дает результат, совпадающий с E0.3). Постоянная т
может быть найдена из обработки первых участков кривых
ползучести.
б) Время t велико. Величина q, определяемая уравнением
E6.4), стремится к предельному значению q =—Ц±—- , скорость
ползучести становится равной
р = ^1-mexp(wia). E6.6)
Скорость ползучести становится постоянной, когда упрочнение
и разупрочнение взаимно компенсируются; эта идея и была
высказана Бейли, а впоследствии Одингом [91].
Описанная схема не подвергалась серьезной количественной
проверке за недостатком опытного материала, однако факт
разупрочнения в результате выдержки при высокой температуре
в разгруженном состоянии наблюдался. Для иллюстрации
приведем некоторые результаты, полученные на образцах из
технически чистого алюминия А-Д1М при температуре 22,5° в дипломной
работе студента НГУ Петрусева. Образец полз под напряжением
5,61 кг!ммг до момента, когда деформация ползучести становилась
равной 2,45%. После этого образец разгружался, выдерживался
без нагрузки при температуре испытания в течение времени t,
после чего нагружался вновь до того же самого напряжения.
Кривые ползучести при повторном нагружении для разных
значений t приведены на рис. 79, эффект разупрочнения виден очень
отчетливо.
При исследовании ползучести дисперсионно-твердеющих
сплавов выделение упрочняющей фазы может сопутствовать
ползучести, вследствие чего картина явления оказывается чрезвычайно
запутанной. Поэтому, например, результаты испытания образцов
из дюралюминия можно обрабатывать с помощью уравнения
состояния только в тех случаях, когда материал был
предварительно состарен. Поскольку процесс старения в первом
приближении можно считать не зависящим от напряженного состояния,
232 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
для описания свойств стареющего материала удобно ввести два
параметра: д); являющийся мерой деформационного упрочнения
и либо равный деформации ползучести, либо определенный по
одному из способов, изложенных выше, и q2, определяющий
р-Шг
W
?
О / Z 3 4
t,vac
Рис. 79.
степень старения. Если в полностью состаренном состоянии
q2 = q*, то естественно принять
dq2 = K(q* — qz)dt.
Одна из возможных форм записи уравнения состояния
при этом будет
p = qiaq^f(o). E6.7)
В работах японских авторов I307], l3eBl делается попытка
построения теории ползучести на основе некоторых
представлений, развитых в довольно ранней работе Орована [319]. По
существу, эти авторы вводят один параметр упрочнения q, для
которого принимается
^=(?>+(?> E6-8)
Полная скорость пластической деформации считается при этом
функцией напряжения, температуры и параметра q. Величина
до dq
-—- интерпретируется при этом как скорость упрочнения,-^—
§ 57] ПОЛЗУЧЕСТЬ И МГНОВЕННАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ 233
как скорость разупрочнения. Форма записи уравнения E6.8)
неудачна, поскольку существование функции q (е, t) вовсе не
предполагается, величины, обозначаемые через -^- и —-, суть
независимые функции, которые предполагается определять из опыта.
Конечно, такое обобщение уравнения состояния дает возможность
достаточно хорошо описать экспериментальные данные при
переду
менных напряжениях, хотя явных зависимостей параметров -~
и-5~ (в наших обозначениях а^ и С]) от соответствующих аргументов
авторы не приводят.
§ 57. ПОЛЗУЧЕСТЬ И МГНОВЕННАЯ
ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ
В старых работах, рассматривающих уравнение состояния
(см. § 49), не делалось разницы между деформацией ползучести
и мгновенной пластической
деформацией. Обозначая пластическую
деформацию безотносительно к ее
природе через еп, мы должны были
бы записывать уравнение
состояния в виде
Ф(ёп, о, еп, Т)=0. E7.1)
Этому соотношению
приписывался универсальный характер, о J
Так, при еп = 0 уравнение E7.1) Рис. 80.
дает связь между еп и о,
соответствующую растяжению с достаточно малой скоростью.
Многочисленные исследования температурно-временных зависимостей
свойств различных материалов проводились на основе уравнения
E7.1). Однако в области достаточно малых деформаций это
уравнение неверно, в чем можно убедиться путем простого эксперимента.
Приложим к образцу нагрузку, вызывающую в нем
напряжение а такое, что мгновенной пластической деформации не
возникает. Дадим образцу ползти. В некоторый момент времени
деформация ползучести есть рА, мы находимся в точке А кривой
ползучести (рис. 80). Перенесем в точку А начало координат.
Продолжение кривой вправо от точки А есть кривая ползучести
с начальным упрочнением рА. Если уравнение E7.1) справедливо,
то безразлично, каким способом создано начальное упрочнение.
Можно быстро растянуть образец до пластической деформации рА
и подвергнуть действию постоянного напряжения ст. Кривая
ползучести для такого образца должна совпадать с АВ. На самом деле
р1
А
?А
В
f
234 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
кратковременная пластическая деформация не оказывает влияния
на ход ползучести и кривая ползучести деформированного
образца оказывается примерно такой же, как и недеформированного.
На рис. 57 приведены кривые релаксации трех образцов из стали
30 ХМА. Первый образец был из недеформированного материала,
второй подвергался ползучести при о = 20 кг/мм* в течение 25
часов и после этого испытывался на релаксацию, третьему перед
испытанием на релаксацию была сообщена вытяжка при
температуре испытания, в результате чего он получил ту же
пластическую деформацию, которую накопил за время ползучести второй
образец. Как видно, первый и третий образцы релаксируют
совершенно одинаково (с точностью до разброса), второй образец
релаксирует значительно медленнее. Пунктиром проведены
расчетные кривые, построенные с помощью уравнения состояния на
основании характеристик, найденных из опытов на ползучесть при
постоянной нагрузке. Таким образом, мы приходим к выводу, что
кратковременная пластическая деформация не упрочняет материал
по отношению к ползучести и уравнение состояния нужно
записывать в виде
Ф(р, а, р, Г) = 0.
Теперь р определяется следующим образом:
dp = de—р—xg'{a) da. E7.2)
Здесь х = 1, если da > 0, и и = 0, если Jo<0. Уравнение
мгновенной кривой деформирования:
е=-|- + §г(ст).
В формуле E7.2) мы использовали то же обозначение g (о), что
и в § 47 при написании формулы D7.5), хотя здесь это мгновенная
пластическая деформация в прямом смысле, там — некоторая
величина, учитывающая деформацию первого периода ползучести.
Однако формальная роль функции g (а) здесь и там совершенно
одинакова, поэтому мы и не делаем разницы в обозначениях.
Такая трактовка уравнения состояния справедлива лишь в
первом приближении и для достаточно малых мгновенных
пластических деформаций, по-видимому не превышающих 1%. Большие
предварительные пластические деформации существенно влияют
на ползучесть. Детальное обследование влияния предварительной
пластической деформации на вид уравнения состояния для
отожженной меди было произведено Каптелиным [19]. Картина
оказалась чрезвычайно запутанной и сложной. Автору удалось
описать свои эксперименты при помощи некоторых уравнений,
которые вряд ли пригодны для использования их при расчетах.
§ 57] ПОЛЗУЧЕСТЬ И МГНОВЕННАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ 235
Учет упрочнения, вызванного мгновенной пластической
деформацией, возможен в рамках теории, изложенной в § 55.
Действительно, для этого достаточно принять
dq^dp + %' (a) da.
Если функция х (о) совпадает с функцией g (о*), то dq есть
приращение полной пластической деформации, и мы возвращаемся
к уравнению состояния в формулировке E7.1). Вообще говоря,
% (а) — другая функция, которая должна быть найдена из
эксперимента.
Возвращаясь к обычному виду уравнения состояния,
рассмотрим возможности экспериментального определения функции g (a),
то есть нахождения диаграммы мгновенного пластического
деформирования. Доступные схемы опыта здесь следующие:
а) растяжение с постоянной скоростью нагружения,
б) растяжение с постоянной скоростью деформации.
В случае растяжения с постоянной скоростью нагружения
уравнение состояния легко интегрируется, если задаться тем или
иным аналитическим его представлением. Особенно удобно
пользоваться уравнением состояния E5.4), Полагая о = ct и
интегрируя, получим:
Если воспользоваться уравнением E5.6), то результат будет
следующим:
1 т(п + 1) с™ и * W-^
Легко убедиться в том, что численный множитель в правой части
формулы E7.4) всегда больше, чем аналогичный множитель в
формуле E7.3). Зная характеристики ползучести из обработки кривых
кратковременной ползучести, мы можем рассчитать по уравнению
E7.3) или E7.4) деформацию ползучести, накопленную за время
опыта на растяжение, и вычесть ее из измеренной полной
деформации. Именно по этим формулам были построены кривые на
рис. 76. Контролем является то, что восстановленная таким
способом кривая мгновенного деформирования должна получаться
одной и той же, если за отправные кривые деформирования
принимать кривые, снятые при разных скоростях нагружения.
Испытание на растяжение с постоянной скоростью
технически сложнее, чем предыдущее испытание, если ставить задачу
получить постоянную скорость деформации на заданной базе,
а не ограничиться сообщением постоянной скорости одному из
захватов машины. С другой стороны, обработка результатов такого
236 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
испытания значительно труднее, она становится возможной,
только если мы зададимся видом функции g (а); указать какой-
либо достаточно удобный прием для восстановления вида функции
g (а) по данным испытаний с постоянной скоростью растяжения
нам не удалось. Заметим, что кривая растяжения всегда имеет
максимум в отличие от кривой, соответствующей постоянной
скорости нагружения. При этом, конечно, мы не касаемся вопроса
о неустойчивости процесса растяжения и об образовании на
образце шейки. Так как р = v — g' (cr) о, то из уравнения ползучести
следует:
•_v-t(a, p)
g' (a) '
Скорость возрастания напряжения о обращается в нуль, когда
достигается равенство v = f (а, р), то есть когда скорость
растяжения становится равной скорости ползучести при достигнутом
напряжении и достигнутой величине деформации ползучести.
В дальнейшем мы увидим, что вопрос об отделении мгновенной
пластической деформации от деформации ползучести решается
достаточно просто для кратковременной ползучести при высоких
температурах.
Формулировка закона упрочнения, данная в настоящем
параграфе, относится к тем случаям, когда в теле вызвана мгновенная
пластическая деформация небольшой величины (порядка 1%),
а последующая ползучесть протекает при напряжениях меньших,
чем те, которые эту пластическую деформацию создали. Вопрос
о ползучести в собственно пластической области представляется
чрезвычайно запутанным. Прежде всего, мы видели, что с
переходом за предел пропорциональности резко меняются значения
констант в законе ползучести. Это обстоятельство было отмечено
в § 53 для алюминиевого сплава при 150°; напряжение в 25,3 кг/мм2,
при котором происходит пересечение двух прямых на графике
рис. 63, довольно точно соответствует пределу
пропорциональности материала, определенному из опыта на растяжение с
достаточно большой скоростью. Аналогичных данных можно было бы
привести очень много; чтобы не делать это специально, сошлемся
на графики, приводимые в главе V (рис. 107—121), где также
отмечается существенное изменение констант ползучести при переходе
в пластическую область.
Отсутствие упрочняющего действия небольшой мгновенной
пластической деформации можно понять следующим образом.
Мгновенная пластическая деформация происходит за счет
локализованных сдвигов в пачках плоскостей скольжения, которые
сильно упрочняются, в то время как основной объем зерна еще
не деформировался. Деформация ползучести также является
сдвиговой, но эти сдвиги распределены более или менее равно-
§ 57] ПОЛЗУЧЕСТЬ II МГНОВЕННАЯ ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ 237
мерно по объему, поэтому весь объем упрочняется в одинаковой
степени. Если металл получил небольшую мгновенную
пластическую деформацию, то последующая ползучесть идет в основном
по неупрочненному объему.
С другой стороны, нет оснований утверждать, что ползучесть
не оказывает влияния на характеристики мгновенного
деформирования. Кривая мгновенного деформирования сама по себе не
является абсолютной характеристикой материала, при повторных
нагрузках и разгрузках она меняет свой вид в результате
наклепа, сопровождающегося старением. Нужно заметить, что эффект
старения никак не учитывается в обычной теории пластичности;
б,кг/ммг
w - - *
SO
го
w
О & 5 7,5 70 12f
е-Ю*
Рис. 81.
в условиях ползучести дело осложняется тем, что старение
происходит под нагрузкой и сопровождается ползучестью. Не располагая
достаточным материалом для того, чтобы пытаться дать
феноменологическое описание взаимодействия ползучести и пластической
деформации, приведем в целях иллюстрации результаты двух
опытов. На рис. 81 кривая представляет собою кривую
мгновенного деформирования сплава Д-16АТ при 150°, при скоростях
нагружения выше 6 кг1мм2мин диаграммы деформирования
практически не зависят от скорости и могут приниматься за
мгновенные, накопленная в процессе испытания деформация
ползучести пренебрежимо мала. Следующий опыт заключался в том, что
образец нагружался до а = 30 кг /мм2 (точка А) и выдерживался
под нагрузкой. За это время была накоплена деформация
ползучести А А'. При дальнейшем быстром нагружении зависимость
напряжения от деформации изображалась кривой А 'С, а не А 'В',
повторяющей первоначальную кривую деформации АВ; таким
образом, в процессе ползучести произошло упрочнение по
отношению к мгновенному деформированию.
/
в
А'
>V"**
238 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
§ 58. КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ. ОСНОВНЫЕ ФАКТЫ
За последние годы в печати появился ряд работ,
посвященных изучению кратковременной ползучести, то есть ползучести,
приводящей к накоплению значительной деформации за время
нескольких десятков или сотен секунд. В работах [18Б], [206]
изучались магниевые сплавы, в [332], [203], [331], [268] жаропрочные
аустенитные стали, в [2в7] приводятся данные по тугоплавким
металлам. Очевидно, что учет кратковременной ползучести может
представить интерес лишь при высоком уровне температур и
напряжений, то есть в той области, в которой обычно материалы не испы-
тываются. В упомянутых работах, как правило, не приводится
какого-либо анализа кривых ползучести на основе той или иной
теории, в лучшем случае строятся кривые напряжение — время
для фиксированных значений деформации ползучести или же
изохронные кривые ползучести. Но уже при беглом обзоре этих
результатов бросаются в глаза следующие обстоятельства:
1. Первый участок на кривых ползучести выражен слабо,
а зачастую совсем отсутствует. Сначала скорость ползучести
постоянна, потом она увеличивается и продолжает увеличиваться
до момента разрыва.
2. Мгновенная пластическая деформация, происходящая в
момент приложения нагрузки, велика.
Систематическое исследование кратковременной ползучести
ряда конструкционных материалов было выполнено Милейко
[м], [75] в Институте гидродинамики СО АН СССР, дальнейшее
изложение основывается главным образом на результатах,
полученных им путем обработки его собственных экспериментов и
опытов других авторов. На рис. 43 были приведены типичные кривые
ползучести сплава Д-16АТ-2 при 250°. Эта температура для
данного сплава является высокой. Следует обратить внимание на узкий
диапазон напряжений, крайние кривые соответствуют
напряжениям 16,8 и 18,8 кг/мм2; если напряжение несколько уменьшить,
то за время 200 секунд не накопится сколько-нибудь заметная
деформация, при большем напряжении сразу произойдет разрыв.
При а = 16,8 кг/мм2 скорость ползучести строго постоянна,
при а = 17,7 и 18,8 кг/мм2 уже при деформации около 0,5%
начинается третий участок. Первые участки на кривых ползучеоди
отсутствуют. При данной температуре первые участки появились
бы для меньших напряжений, но при этих напряжениях величина
деформации ползучести пренебрежимо мала. Точно так же первые
участки будут появляться при более низких температурах
испытания.
Таким образом, существует некоторая граница температур
и напряжений, начиная с которой ползучесть происходит без
упрочнения.
§ 58] КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ. ОСНОВНЫЕ ФАКТЫ 239
Мы записывали уравнение неустановившейся ползучести в виде
[f(o)t]'
т
1+а
Рис. 82.
ползучесть с постоянной скоростью соответствует а = 0. Опыты
показывают, что а уменьшается с ростом температуры и
напряжения. Чтобы выяснить заранее возможные границы
применимости развиваемой ниже теории кратковременной ползучести,
рассмотрим схематическую диаграмму,
изображенную на рис. 82. По
осям координат отложены
соответственно напряжение и
температура, верхняя кривая
представляет собою кривую
температурной зависимости временного
сопротивления. Очевидно, что
эта кривая служит верхней
границей возможности
использования материала в статических
условиях (при динамических
нагрузках временное
сопротивление может быть превышено).
Область А представляет собою ту область, где ползучесть вообще не
наблюдается. Правая криволинейная граница этой области не очень
определенна, она зависит от допуска на измерение величины
деформации ползучести. Область напряжений и температур,
при которых происходит ползучесть, в свою очередь делится
кривой а = 0 на части В и С. В части В Ползучесть сопровождается
упрочнением, которое, конечно, может закончиться выходом на
установившийся участок. В области С упрочнения не происходит,
этой областью мы и будем сейчас интересоваться. Кривые,
помеченные цифрами 1 и 2, имеют условный смысл. Применительно
к любой технической задаче мы можем указать некоторую
предельную деформацию ползучести р', с которой еще можно не считаться.
Если за срок службы изделия накопленная деформация
ползучести не превышает р, то вообще ползучесть учитывать не нужно,
а следует производить расчет методами теории упругости или
теории пластичности. Кривая 1 на рис. 82 соответствует такой
комбинации напряжения и температуры, которая за длительное время
(скажем, 100 000 часов) вызывает деформацию ползучести р';
область напряжений и температур, при которых необходимо
учитывать ползучесть в условиях длительной службы, расположена
выше кривой 1. Верхняя граница этой области соответствует,
конечно, не временному сопротивлению а , а так называемому
пределу длительной прочности для заданного срока службы.
240 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
в, (г/тг
40
Для нас существенно, что кривая 1 расположена в области В,
поэтому расчеты на ползучесть при длительном действии нагрузок
должны производиться с учетом неустановившейся фазы, то есть
в области упрочнения.
Если изделие находится под нагрузкой непродолжительное
время (несколько минут), то появление за время службы заметных
деформаций ползучести соответствует кривой 2, которая
расположена выше. На схеме она показана целиком в области С. Это
значит, что расчеты на
кратковременную ползучесть производятся
в той области напряжений и
температур, где упрочнение
отсутствует.
Рис. 82 представляет собою
предположительную схему,
фактическое построение
соответствующих кривых и точное
установление границ областей требует
большого количества
экспериментальных данных, которые обычно
отсутствуют. На рис. 83 по данным
работы [167 ] для аустенитной стали
~j N-155 построены кривые о*в (Т), а
также кривые к = 0 и а. = 0,125;
таким образом, частично
определены границы области С, которую
мы будем называть областью кратковременной ползучести.
Основное уравнение, описывающее кратковременную
ползучесть, будет следующее:
30
20 -
10
ос=&25
1000°
Рис. 83.
1Ш°
e = -ir + xg' (a)a+v(a).
E8.1)
Здесь принято, что существует кривая мгновенного
деформирования е = —=r + g (о), тогда как ползучесть происходит с постоянной
скоростью v (о), которая при данной температуре зависит только
от напряжения и не зависит от предыстории деформирования.
Уравнение E8.1) совершенно совпадает по форме с D7.5), но g (a)
представляет здесь мгновенную пластическую деформацию в
прямом смысле.
Если функция v (о) определена из опытов на ползучесть, то
функция g (а), представляющая собою мгновенную пластическую
деформацию, может быть найдена следующим образом.
Произведем серию опытов на растяжение с постоянной скоростью
возрастания нагрузки, так что в каждом опыте о = ct. Применяя
§ 58] КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ. ОСНОВНЫЕ ФАКТЫ 241
к такому опыту уравнение E8.1), найдем:
Величина
и
Р(°") = — \ v{a)da
представляет собою деформацию ползучести, сопровождающую
растяжение. Зная функцию v (о*), мы можем вычислить р (о).
б, яг/ммг 7
ZS
Рис. 84.
W W
Рис. 85.
& 2,0
Вычитая из абсцисс кривой растяжения величину р (а), мы
восстановим кривую мгновенного деформирования е =-^--{- g (а),
как показано схематически на рис. 84. Контролем правильности
исходных гипотез служит то, что, отправляясь от кривых
растяжения с различными скоростями погружения, мы получаем
одну и ту же восстановленную мгновенную кривую. Фактически,
если скорость нагружения такова, что вся кривая деформирования
проходится за время порядка одной секунды, то сопровождающая
растяжение ползучесть невелика и полученная кривая может быть
принята за мгновенную. Контроль правильности исходной
гипотезы теперь можно произвести в обратном порядке, а именно
прибавить к абсциссам мгновенной кривой значения р (о), вычисленные
для различных скоростей нагружения с, и сравнить полученные
расчетом диаграммы растяжения с опытными. На рис. 85 приве-
16 Ю. Н. Работнов
242 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
во.
20
70
дены результаты такой проверки для сплава Д-16АТ при 250°,
верхняя кривая была принята за мгновенную, пунктирные кривые
получены расчетом для различных скоростей нагружения,
измеряемых в кг/мм2 за секунду, здесь же нанесены опытные точки.
Кривая 1 получена для скорости с = 25, кривая 2 для с — 0,289,
кривая 3 для с = 0,063 и
4«^*w' кривая 4 для с = 0,016.
Некоторые авторы
рекомендуют в качестве
основного метода испытаний
для определения
характеристик кратковременной
ползучести испытания с
постоянной скоростью
деформирования. Но
фактически в конструкции
всегда задаются нагрузки,
тогда как скорости
деформации проконтролированы
быть не могут. Имея в
виду расчет определенного
изделия, мы всегда можем
указать реальные пределы
изменения скоростей
нагружения, в которых и
следует определять
механические характеристики.
Указать соответствующие
пределы скоростей
деформации обычно заранее
бывает невозможно. С другой
стороны, имея в
распоряжении кривые деформирования при е = const, мы встретим
серьезные трудности при их обработке, отделение пластической
деформации от деформации ползучести осуществляется при этом нелетко.
Замечание о возможности принять за мгновенную кривую
деформирования при некоторой достаточно большой скорости
нагружения справедливо при не слишком высоких температурах,
в последнем случае приходится восстанавливать мгновенную
кривую описанным способом. На рис. 86 приведены данные для
титанового сплава ВТ-5-1, сплошными линиями проведены
восстановленные мгновенные кривые, штриховой — кривые
деформирования при скорости изменения напряжения 20 кг /мм2 в секунду
и пунктиром — кривые растяжения при постоянной скорости
деформации, соответствующей одному проценту удлинения в
минуту. Последние испытания производились в условиях, когда
/' 600°
'"'/700°
'"J
^^z--~
о
0.4
0,8
1,2
е-7(?г
Рис. 86.
§ 59]
КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ
243
скорость деформации контролировалась непосредственно по
показаниям экстензометра, тогда как в обычных испытательных
машинах задается скорость захватов. Скорость деформации порядка 1%
в минуту примерно соответствует условиям стандартного опыта
на растяжение; сравнение приведенных на рис. 86 кривых
показывает, насколько недостаточные сведения об истинных свойствах
материала при кратковременном нагружении может дать обычная
машинная диаграмма.
§ 59. КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ.
ЗАВИСИМОСТЬ ДЛЯ СКОРОСТИ
В результате обработки данных испытаний пятнадцати
различных материалов в лаборатории Института гидродинамики
Сибирского отделения АН СССР было установлено, что скорость
ползучести в зависимости от напряжения и температуры
достаточно хорошо выражается следующей формулой:
p = feexp(Po + vr). E9.1)
Вид температурной зависимости в формуле E9.1) отличается
от общепринятого в физической литературе, для расчетных целей
такая зависимость представляется несколько более удобной.
Выяснилось, что для некоторых сплавов нужно различать два
интервала температур: умеренные температуры при Т <; Т*
и высокие температуры при Т > Т*. В области умеренных
температур
к = к± = const, p=. Pj = const, v = v1 = const (T<T*). E9.2)
В области высоких температур
fc = &2 = const, р — т , v- = v2= const, E9.3)
TQ = const (T>T*).
На рис. 86 уже были приведены мгновенные кривые
деформирования для титанового сплава ВТ-5-1, приведем для этого же
материала полученные значения констант ползучести. Ползучесть
изучалась в диапазоне температур 600—900°, весь этот диапазон
должен быть отнесен к области высоких температур,
следовательно коэффициенты уравнения E9.1) принимают значения E9.3),
где
fc2 = 7,76-10-11, р2 =. 104, Т0 =1020°, v2 = 0,0140.
При этом напряжение измеряется в кг/лш2, время — в секундах,
температура — в градусах Цельсия.
16*
244 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
30
га
10
I
/ I
/ <\. ?. I
/ //Р '/V
/ лМ /
/ у \ '[б
20
30
to
Рис. 87.
SO 00
t,eg/f
Для других титановых сплавов и аустенитных сталей область
интенсивной кратковременной ползучести принадлежит также
целиком интервалу высоких температур, тогда как у алюминиевых
сплавов значительная ползучесть наблюдается и в области
умеренных температур. Так, для материала Д-16Т (пруток) Т* =
= 270°, для сплава АМГ-6М практически интересный диапазон
150—250° целиком принадлежит интервалу умеренных температур,
тогда как для сплава АМГ-6Н практически важная температурная
область 200-300° должна
g,j?/mm* — е-ш_ быть отнесена к интервалу
высоких температур.
Уравнение E8.1) мы
должны считать
применимым как для случая
постоянных нагрузок и
температур, так и тогда, когда
как нагрузка, так и
температура меняются.
Погрешность, полученная при
расчетах, выполненных в этом
предположении, не
выходит за пределы
естественного разброса опытных
данных. На рис. 87 приведены
результаты испытания на сплаве ВТ-5-1 при температуре 700°.
Напряжение менялось во времени по некоторому довольно
сложному графику, сплошными линиями показана определенная
экспериментально зависимость деформации от времени, пунктирной —
рассчитанная по уравнению E8.1).
При отсутствии первых участков на кривых ползучести расчет
кривой релаксации должен производиться по уравнению D7.3).
На рис. 88 изображены теоретические (сплошные линии) и
экспериментальные (пунктир) кривые релаксации для сплава АМГ-6М
при 227°. Для дополнительной проверки высказанного принципа
независимости скорости ползучести от предыстории нагружения
опыт на одном и том же образце повторялся несколько раз, после
релаксации образец снова подгружался до исходной величины
напряжения и снова релаксировал. Все последовательные кривые
релаксации оказались в точности совпадающими.
Диаграммы мгновенной деформации, как мы видели, также
зависят от температуры, однако температурная зависимость
пластических свойств гораздо более слабая, чем температурная
зависимость характеристик ползучести. Мы будем считать, что
в уравнении E8.1) функция g (о) своя для каждой температуры,
а также что модуль Е есть функция Т. Таким образом, полное
уравнение кратковременной ползучести с учетом температурной
§ 59]
КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ
245
зависимости будет
Е(Т)
¦ Kg' (а, Т)а + к ехр фа + vT).
E9.4)
Для функции g (a, T) мы не пытались подобрать каких-либо
аппроксимирующих выражений, при расчетах следует
непосредственно использовать экспериментально определенную серию
кривых мгновенного деформирования, соответствующих
различным температурам.
В заключение остановимся вкратце на некоторых вопросах
методики испытаний на кратковременную ползучесть.
10
V
Ч ^v
I
о
ffO
Рис. 88.
*Ш
Весьма обстоятельный обзор методов испытаний содержится
в статье [295], кроме упомянутых выше работ этому вопросу
посвящены публикации ["•], [»»], I'94], I347], I384].
Некоторые авторы производили испытания на ползучесть при
сжатии, что представляет непосредственный интерес для
авиационных конструкций.
Милейко была создана специальная установка с
электромагнитным силовозбуждением и автоматической записью
деформации во времени. Установка допускает осуществление нагружения
по заданной программе. В частности, нагрузка может меняться
так, чтобы полная деформация сохранялась постоянной
(релаксация) или чтобы была постоянной скорость деформации. Нагрев
осуществляется радиационным способом, практиковавшийся
некоторыми исследователями нагрев проходящим током рекомендовать
нельзя, так как при этом получаются иные характеристики
ползучести, нежели при радиационном и конвективном нагреве.
Максимальная достигнутая скорость нагрева составляла 40°
в секунду.
246 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
§ 60. ПОЛЗУЧЕСТЬ ПРИ СЖАТИИ.
РЕВЕРСИРОВАНИЕ НАГРУЗКИ
Испытания на ползучесть при сжатии представляют большую
техническую трудность, чем испытания при растяжении. При
использовании длинных образцов существенную роль играют
начальные неправильности и эксцентриситет приложения
нагрузки. При испытании на растяжение влияние эксцентриситета в
процессе испытания уменьшается и результат не очень сильно
зависит от начальных неправильностей и неточности в приложении
нагрузок. Этот вопрос детально выяснен в работе [283]. При
испытании на сжатие начальные прогибы растут, эксцентриситет
приложения нагрузки увеличивается и напряженное состояние
существенно меняется в процессе испытания. Поэтому получение
надежных кривых на сжатие и сопоставление их с данными при
растяжении затруднительно.
Многочисленные и систематические исследования ползучести
при сжатии производил Салли с сотрудниками [ш], [ЗБ7], I358].
Цель этих исследований состояла в разработке упрощенного
метода определения сравнительных характеристик жаропрочности
сплавов. Для этой цели были сконструированы простые машины,
не обеспечивавшие высокой точности измерений, которая,
впрочем, и не была нужна для получения сравнительных данных.
Тем не менее вопросу о соответствии характеристик ползучести
при растяжении и сжатии было уделено большое внимание,
поскольку было необходимо выяснить, могут ли испытания на сжатие
заменить стандартные испытания на растяжение. Большая часть
этих исследований относится к жаропрочным хромоникелевым
сплавам. Общий вывод состоит в том, что при одинаковом
напряжении абсолютная величина скорости установившейся ползучести
при растяжении и при сжатии одинакова в пределах погрешности
эксперимента. На первых участках кривой обнаруживается
разница, которая может быть отнесена за счет экспериментальных
ошибок и неустойчивости характеристик ползучести в первой фазе.
Следует заметить, что третья фаза ползучести наблюдается также
при сжатии, причем начало ее соответствует примерно той же
величине деформации ползучести как при сжатии, так и при
растяжении. Разница в протекании ползучести в третьей фазе состоит
в следующем. При растяжении скорость ползучести непрерывно
увеличивается вплоть до разрыва, при сжатии она сначала
увеличивается, потом несколько уменьшается, потом снова
увеличивается и так далее. В результате получается кривая ползучести
волнообразного характера. Авторы работы [357 ] объясняют
появление третьей фазы атомной перестройкой в наиболее
деформированных участках зерен вблизи границ типа начальной
стадии рекристаллизации. На рис. 89 приведены кривые ползу-
60] ПОЛЗУЧЕСТЬ ПРИ СЖАТИИ. РЕВЕРСИРОВАНИЕ НАГРУЗКИ 247
ш
ом
0,5
Ofi-
Ц2
е-10г
-
' о Сжатие
. Рас/ляжете
О
200
400
800
t, час
чести при растяжении и сжатии хромоникелевого сплава для
одного и того же напряжения а = 1400 кг/см2 и температуры 815°
из упомянутой статьи.
Ползучесть алюминиевого сплава при сжатии изучалась в
работах [182], [183], на первой и второй стадиях кривые ползучести
примерно совпадали, на
третьей обнаруживались
расхождения. Поскольку в
этих работах основное
внимание было уделено третьей
фазе ползучести, Торшенов
[139 ] поставил специальные
исследования по
сравнению кривых ползучести
при растяжении и сжатии
на первом участке
ползучести и при переходе ко
второму. Работа проводилась на
алюминиевом сплаве Д-16Т
при температуре 200°. Для
осуществления сжимающей
нагрузки был
сконструирован специальный
реверсор к машине для
испытаний на растяжение, были
приняты специальные меры для уменьшения эксцентриситета
приложения нагрузки. Было изучено также влияние начального
эксцентриситета на кривую ползучести при сжатии как
теоретически, так и эксперимен- о 0 Л
тально на образцах, у
которых был создан известный
начальный эксцентриситет.
Как показано автором, для
тех опытов, которые пошли
в обработку, влияние
эксцентриситета приложения
нагрузки не выходило за
пределы погрешности измерений.
На рис. 90 приведены
результаты испытаний для
напряжений 8, 12 и 16 кг/мм2,
крестиками отмечены точки
кривой ползучести при растяжении, кружками —при сжатии.
Разница между этими кривыми не выходит за пределы полосы разброса.
Для кратковременной ползучести, понимаемой в том смысле,
как было пояснено в § 58, для большей части материалов,
Рис.
)М
05
p-70s
+!
*+ о '
>-+°+*
-ю
+.*н
•о» о
„ о'
„4.°+
+
о„+„4Х+с
°1
+ + + + +
+ + + +
Ъ о о о t
+++
3 о о о °
+о ° ° °
о
W
20 30
Рис. 90.
4-ff SO
tvac
248 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
б,кг/ммг
-з
по-видимому, поведение при растяжении и сжатии одинаково. На
рис. 91 для того же сплава Д-16Т приведен график зависимости
скорости ползучести от напряжения {дипломная работа студента
НГУ Жигалкина), светлые кружки соответствуют опытам на
растяжение, темные—опытам на сжатие. В полулогарифмических
координатах точки группируются околопрямой, что подтверждает формулу
E9.1), отклонения носят характер случайного разброса. Поведение
магниевых сплавов при сжатии является аномальным. Известно,
что при нормальных температурах
обычные кривые деформирования при
растяжении и сжатии для этих сплавов
существенно различны [109]. Скорости
ползучести при растяжении и сжатии
для одного и того же напряжения также
оказываются существенно различными,
что отмечалось, например, в работе [20в].
Приведем результаты испытаний на
кратковременную ползучесть
магниевого сплава ВМ-65-1 по данным Института
гидродинамики СО АН СССР (рис. 92).
Светлые кружки—растяжение, темные—
сжатие. По осям отложены
напряжение и логарифм скорости ползучести.
При растяжении, как оказывается,
ползучесть идет значительно быстрее, чем
при сжатии.
Малоизученным остается вопрос о
ползучести при переменных нагрузках,
когда меняется знак напряжения.
Некоторые экспериментальные данные,
относящиеся к ползучести при
реверсировании нагрузки, относятся к
знакопеременному кручению [2], [80]. Из этих
работ следует, что деформация в прямом
направлении разупрочняет материал по отношению к ползучести
в противоположном направлении, ползучесть после перемены
знака нагрузки происходит быстрее, чем при первом приложении
нагрузки той же интенсивности. В принципе такое явление может
быть описано с помощью кинетических уравнений § 55, однако
для попыток подобного рода мы еще не располагаем достаточным
опытным материалом.
Некоторая гипотеза, позволяющая оценить эффект упрочнения
при нагрузках, меняющих знак, была высказана Шорром [154],
[168]. Он принимает закон ползучести в виде
/(а)
ЧР
/
1:
4°
of
7»
• /
/ °
/
5
7 Г
Рис. 91.
;;
ph {q) -¦
а.
§ 61] МАЛЫЕ ОТКЛОНЕНИЯ ОТ ОСНОВНОГО СОСТОЯНИЯ 249
Существенно положительная величина q определяется
следующим образом:
q = р+ + %р~ при а > О,
q = p~ + Xp+ при сг<;0.
Здесь р+ — величина деформации, накопленной при растяжении,
р~—величина деформации, накопленной при сжатии; коэффициент X
~3
~4
4 6 8 10 12 П
Рис. 92.
представляет собою константу материала и подлежит определению
из опыта. Экспериментальная проверка этого предположения
и примеры определения величины К нам неизвестны.
§ 61. МАЛЫЕ ОТКЛОНЕНИЯ ОТ ОСНОВНОГО СОСТОЯНИЯ
В некоторых приложениях теории ползучести, например при
рассмотрении задач устойчивости, приходится рассматривать
малые отклонения от некоторого основного состояния ползучести,
например влияние малого увеличения или уменьшения
напряжения на процесс ползучести при постоянной нагрузке. Принимая
за основу любую теорию ползучести, можно написать
линеаризированные уравнения, описывающие малые отклонения от
основного состояния. Предположим, например, что материал
подчиняется уравнению состояния в обычной форме:
р=--ц>(а,р), р = в--|-. F1.1)
В основном состоянии ржа — известные функции времени. Мы
предполагаем, что если, например, задано о как функция времени,
250 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
то уравнение F1.1) проинтегрировано и найдено р в зависимости
от t. Предположим теперь, что в результате изменения внешних
условий напряжение стало а -\- 8а, деформация ползучести р -}-
60
а
6Р
Р
6р. Если — « 1 и — < 1, то из уравнения F1.1) следует
в линейном приближении:
вр = -?вр + ?в0. F1.2)
Величины ~ и -тр представляют собою известные функции
времени. Если нас интересует поведение тела немедленно после
изменения нагрузки, то медленно меняющиеся функции времени
~~ и —5 можно рассматривать как постоянные. Вводя в F1.2)
вместо Ьр изменение полной деформации бе, мы получим:
8а + Х8а = Е(8'е + ц8е). F1.3)
Здесь
''да др ' " др
Уравнение F1.3) совершенно совпадает по форме с уравнением
B3.5) главы III; таким образом, материал, подверженный
ползучести и подчиняющийся уравнению состояния, ведет себя при малых
отклонениях от основного состояния, как упруго-вязкое тело
Кельвина. Мгновенные изменения напряжения и деформации
связаны между собою обычным законом Гука: по истечении
достаточно большого времени (в то же время настолько малого, что
изменением величин Яиц можно пренебречь) напряжение и
деформация остаются пропорциональными, но зависимость между ними
определяется длительным модулем:
Е д1—
да др
Эту величину мы будем называть модулем ползучести. Легко
убедиться, что модуль ползучести представляет собою
касательный модуль кривой деформирования материала при постоянной
скорости деформации ползучести. Следует отметить, что
проведение испытаний при заданной скорости деформации ползучести,
если и возможно в принципе, то во всяком случае представляет
очень большую техническую трудность.
Желая учесть происходящее одновременно квазивязкое
течение, мы примем
¦f-J.o
da.
§ 61] МАЛЫЕ ОТКЛОНЕНИЯ ОТ ОСНОВНОГО СОСТОЯНИЯ 251
Варьируя это соотношение и исключая из F1.2) деформацию
ползучести, получим следующее уравнение:
8о + (Ev' + l)8a + [iv'8a = Е (8е + \i8e). F1.4)
Поскольку уравнение состояния при переменных нагрузках не
дает вполне точных предсказаний, можно ожидать, что
расхождение между данными опыта и предсказаниями линеаризированного
уравнения F1.3) или более общего уравнения F1.4) окажется
большим, чем ошибка, получающаяся при использовании
исходного уравнения F1.1), которое в общем хорошо описывает процесс
накопления суммарной деформации ползучести при переменном
напряжении, но мало пригодно для интервала времени,
непосредственно следующего за моментом резкого изменения нагрузки.
Поэтому представляет интерес непосредственное изучение законов
ползучести при малых изменениях напряженного состояния.
Некоторые данные по этому вопросу содержатся в работе Оната
и Уанга I318]. Эти авторы предположили, что вариации о* и е
связаны линейным дифференциальным соотношением
р28а +pi8(y + p08a = q28e + q18e, F1.5)
которое имеет тот же вид, что F1.4), но величина коэффициентов
остается неконкретизированной. Опыты на ползучесть свинцовой
проволоки при нормальной температуре обнаружили, что, если
изменение напряжения составляет не более 4% от основного
напряжения, величина дополнительной деформации
пропорциональна изменению напряжения, что следует из линейности
уравнения F1.5). Далее, при внезапном изменении напряжения в
момент t = t0 на величину бет, которая в дальнейшем сохраняет
постоянное значение, из F1.5) следует такая зависимость от
времени:
+(f~S-IS0['-«'(-^tO]}*- <61-6»
При этом
11
Опытные кривые достаточно хорошо аппроксимируются
зависимостью подобного типа, однако время запаздывания получается
значительно меньше, чем это следует из уравнения F1.4). В одном
из примеров получилось т = 37,5 минуты, тогда как при
определении этой величины из исходного закона ползучести она
должна равняться 30 часам. Приведенные выше результаты опытов
на ползучесть при переменных нагрузках приводят к убеждению,
252 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
что этого и следовало ожидать. Принимая более общую форму
уравнения состояния, то есть вводя параметры упрочнения qt, мы
получим соответственно более сложные уравнения для вариаций о
и е. Данные Оната и Уанга не дают оснований для выбора более
точной формы уравнения состояния. Можно показать, что
введение параметра упрочнения типа д = \ a (a) dp не улучшает
положения: время запаздывания т остается неизменным, а большая
скорость ползучести получается за счет члена, линейно
зависящего от времени в уравнении F1.6).
§ 62. ДИНАМИЧЕСКАЯ ПОЛЗУЧЕСТЬ
Динамической ползучестью мы будем называть ползучесть,
происходящую в таких условиях, когда на постоянное среднее
напряжение накладывается периодическая переменная
составляющая достаточно высокой частоты. Динамическая ползучесть
наблюдается в различных частях машин, подверженных
переменным нагрузкам, в лопатках турбин и других элементах
конструкций, поэтому изучению динамической ползучести посвящено
довольно большое количество работ. В зависимости от материала
и температуры испытания циклическая составляющая нагрузки
может повышать или, наоборот, понижать скорость ползучести.
Так, в опытах Гринвуда 1аго] на свинце было обнаружено, что
скорость ползучести сильно (до десяти раз) увеличивается при
наложении переменной составляющей напряжения. Как оказалось,
циклическая нагрузка существенно ускоряет процесс
рекристаллизации свинца. Влияние переменной нагрузки на структурные
изменения в материале отмечалось рядом других авторов [236],
[аб11. В работах Гварниери [а23], [224], например, показано, что
у хромоникелевой стали и алюминиевого сплава 24-S-T3
переменная нагрузка ускоряет ползучесть, тогда как у сплава инконель
X скорость остается неизменной, а у сплава N-155 даже
понижается. В этих работах одновременно изучалось изменение
структуры в процессе ползучести при постоянных и переменных
нагрузках. Если ползучесть не сопровождается рекристаллизацией
и фазовыми превращениями, то, по-видимому, никакого
специфического эффекта переменных нагрузок не существует и
деформация ползучести может быть рассчитана с большей или меньшей
точностью по одной из теорий, пригодных для описания
ползучести при медленно меняющихся нагрузках, например с помощью
уравнения состояния в той или иной форме. Так, в наших
неопубликованных опытах 1948 г., выполненных в Институте механики
АН СССР, было обнаружено, что ползучесть свинца при
нормальной температуре и меди при температуре 150° под действием
нагрузки, состоящей из постоянной части и относительно небольшой
§ 62]
ДИНАМИЧЕСКАЯ ПОЛЗУЧЕСТЬ
253
составляющей, изменяющейся по закону синусоиды во времени,
происходит так же, как ползучесть при постоянном напряжении,
несколько превышающем среднее Jg
напряжение цикла, но меньшем,
чем максимальное напряжение.
Опыты были сравнительно
непродолжительными (около суток),
и уровень напряжений, был
невысок, так что, например, у свинца
рекристаллизация не
наблюдалась. Аналогичные результаты
были получены многими другими
авторами [248], [350], I353].
Детальный обзор многочисленных
исследований по динамической
ползучести был составлен Изаксо-
ном [249].
Если
ливость
форме
предположить справед-
уравнения состояния в
ph(p) = f{o)
Ш
V
V
V
04
02
и принять
о = am-{-Gv sin at,
/\
Г
X4V
Щ
/v
/10
j3&
02 О? Off & Q0 W
Рис. 93.
то ползучесть будет
происходить так, как если бы
действовало постоянное эффективное напряжение о~ат-\-а'; при этом
/(am + <j') = lim[y [ /(am + oDsincoO^]t_w • F2Л)
о
Если /(сг)==ееехр—, то из формулы F2.1) следует
<т'=а-1пЕщг^С^)("ё'
2п
F2.2)
Аналогичная формула была получена для случая переменной
температуры (§ 54), в отличие от нее формула F2.2) пригодна при
любых значениях av < ст. При выводе ее предполагалось
только, что напряжение остается положительным. Вопрос о том,
что будет происходить, если напряжение меняет знак в течение
цикла, остается полностью открытым. Соответствующие подсчеты
по теории упрочнения, конечно, возможны, но реальный смысл
их неясен ввиду отсутствия экспериментальных данных.
Для степенного закона ползучести интеграл в формуле F2.1)
может быть вычислен для различных значений п. На рис. 93
254 ПОЛЗУЧЕСТЬ МЕТАЛЛОВ. ОСНОВНЫЕ ОПЫТНЫЕ ФАКТЫ [ГЛ. IV
изображен график из работы [365], позволяющий определить
эквивалентное статическое напряжение ат -j- а', если известны
постоянная слагающая от и переменная слагающая ov. На этом
графике по осям координат отложены отношения ~—; и "—; ,
е %
15
т
?
О 20 40 ВО 80 , 700
Рис. 94.
проведенные из начала координат лучи соответствуют
постоянным отношениям avlam. Кривые построены для п = 7, 9, 11, 15,
21, 31 (в порядке сверху вниз). На рис. 94 приведено сравнение
экспериментальных кривых для углеродистой стали при 450° с
теоретическими (штриховые линии) для случая о*„/о*т = 0,23. В
скобках поставлена величина эквивалентного напряжения о*=ат + а'.
Авторы отмечают, что совпадение эксперимента и теории
оказывается удовлетворительным, если <Jv/om <0,7. При больших
значениях отношения переменной составляющей напряжения к его
среднему значению одновременно с ползучестью происходит
накопление усталостного повреждения, что сказывается как на
скорости ползучести, так и особенно на времени до разрушения.
ГЛАВА V
ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ
НАПРЯЖЕННОМ СОСТОЯНИИ
При расчете большей части инженерных сооружений на
ползучесть приходится иметь дело со сложным напряженным
состоянием. Экспериментальные исследования ползучести при
сложном напряженном состоянии технически трудны, и для получения
более или менее надежных результатов опыты должны быть
поставлены очень тщательно. Поэтому имеющийся опытный
материал невелик и не дает возможности сколько-нибудь надежного
обоснования той или иной теории ползучести, призванной
описывать поведение материала в сложных условиях. К тому же
эксперименты возможны лишь в плоском напряженном состоянии,
если напряженное состояние трехосное, то мы не располагаем
никакими сведениями о закономерностях ползучести.
Примерно такое же положение существует и в теории
пластичности. Действительно, более или менее надежные сведения
получены в отношении поведения материала при пропорциональном
нагружении, тогда как при произвольных путях нагружения
различные теории предсказывают различные результаты, а
опытные данные не доставляют достаточно решительных аргументов
в пользу той или иной из этих теорий.
Подобно теории пластичности, теория ползучести при
сложном напряженном состоянии строится на основе некоторых
умозрительных соображений, лишь частично подтверждаемых опытом.
Наиболее простой случай ползучести это тот, когда напряженное
состояние однородно и удерживается постоянным во времени,
именно к этому случаю относится подавляющее большинство
опытных данных. Описание ползучести такого рода достигается
сравнительно простыми средствами, по внешему протеканию это —
некоторый род вязкого течения. Распространение теории на случай
меняющихся напряженных состояний может быть осуществлено
разными способами, при этом здесь число возможностей много
256 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
больше, чем в теории пластичности. В реальных изделиях
характер напряженного состояния со временем обычно меняется
сравнительно мало, поэтому различные теории приводят к результатам,
не слишком сильно отличающимся между собой.
В настоящей главе излагаются основные представления об
установившейся и квазиустановившейся ползучести как для
изотропных, так и для анизотропных сред. Вводятся потенциалы
скоростей и напряжений при ползучести. Обсуждаются
возможные пути построения теории неустановившейся ползучести. После
этого анализируется почти весь опубликованный до настоящего
времени опытный материал по ползучести. Делается вывод о том,
что квазиустановившаяся ползучесть удовлетворительно
описывается при помощи потенциала скоростей, зависящего только от
второго инварианта девиатора (теория типа Мизеса), иногда
удается обнаружить влияние третьего инварианта, причем
характер этого влияния таков, что истинная поверхность равного
потенциала лежит между цилиндром т0 = const и призмой ттах ==
= const.
§ 63. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
В предыдущей главе мы рассмотрели вопрос о возможностях
описания процесса ползучести при одноосном напряженном
состоянии, причем мы основывались исключительно на данных
опытов при простом растяжении. Это связано с тем, что испытания
на растяжение технически наиболее просты, при этих испытаниях
однородное напряженное состояние осуществляется в достаточно
большом объеме и деформация измеряется на большой базе, что
обеспечивает необходимую точность. Другие способы
осуществления приблизительно однородного напряженного состояния —
опыты на растяжение, сжатие и кручение тонкостенных трубок —
оказываются более трудными и применяются реже. Вопрос о
корреляции данных испытаний на растяжение и, скажем, на кручение
может быть решен только с помощью теории ползучести,
сформулированной для общего случая произвольного напряженного
состояния. Вообще говоря, распространение тех теорий, с
которыми мы имели дело применительно к растяжению в главе IV,
на сложное напряженное состояние может быть осуществлено
различными путями, и можно написать очень большое количество
вариантов уравнений пространственной ползучести, отправляясь
от простейших схем установившейся ползучести, ползучести
с упрочнением и так далее. Возможность экспериментального
осуществления более или менее чистых типов сложного
напряженного состояния и измерения получающихся при этом
деформаций ограничена, поэтому опытная проверка теорий
неизбежным образом оказывается лишь частичной и подтверждение того
§ 63]
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
257
или иного варианта носит косвенный характер. В этой главе мы
рассмотрим с общей точки зрения некоторые достаточно широкие
возможности описания процесса ползучести и сделаем выбор
между этими возможностями, руководствуясь, с одной стороны,
степенью их соответствия с данными опытов, с другой — степенью
относительной простоты и удобства для практических
приложений. На примере ползучести при растяжении мы видели, что самая
простая схема из возможных — это схема установившейся
ползучести, когда при постоянном напряжении скорость ползучести
постоянна. Необходимо различать два случая установившейся
ползучести; в первом — упрочнение отсутствует с самого начала,
во втором — скорость становится постоянной вследствие того,
что материал упрочняется полностью и теряет способность к
дальнейшему упрочнению при продолжающейся деформации. Как мы
видели, упрочнение практически отсутствует при достаточно,
высоком уровне температур и напряжений, это обнаруживается
в опытах на кратковременную ползучесть. При относительно
низких температурах скорость становится постоянной лишь
по истечении достаточно долгого времени, установившейся
ползучести предшествует первая фаза, в течение которой происходит
упрочнение. Разница между двумя случаями установившейся
ползучести обнаруживается при изменении нагрузки. Если
материал не упрочняется, то скорость в данный момент определяется
только действующим в данный момент напряжением и не зависит
от предыстории нагружения; если установившейся ползучести
предшествовала первая фаза, то при ступенчатом изменении
нагрузки в установившейся стадии скорость не сразу достигает
постоянного значения, соответствующего новой величине
напряжения, неустановившийся участок на кривой ползучести как бы
повторяется. Таким образом, область кратковременной
ползучести при высоких температурах — это область, в которой теория
применяется в наиболее чистой форме; исследование ползучести
в этой области представляет особый интерес, не только
практический, но и принципиальный: здесь основные черты явления
проявляются в самом отчетливом виде, не будучи затемнены
побочными осложняющими обстоятельствами.
В сложном напряженном состоянии вопрос о наличии или
отсутствии упрочнения тем более небезразличен. Дело в том,
что упрочнение вследствие ползучести или кратковременной
пластической деформации создает анизотропию материала по отнс
шению к его последующей ползучести. Характеристики
ползучести чрезвычайно чувствительны к степени анизотропии. Так,
например, прокатанный материал — сталь или алюминиевый
сплав — почти не обнаруживает разницы упругих свойств вдоль
и поперек проката. Разница пластических свойств, например
условного предела текучести или временного сопротивления, не
17 ю. Н. Работнов
258 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
превышает 10—15%. Скорости же ползучести, определенные для
образцов, вырезанных вдоль и поперек, при одних и тех же
температурах и напряжениях могут разниться в 2—3 раза. Далее мы
увидим, что анизотропия, создаваемая в процессе ползучести за
счет упрочнения, оказывается еще более резкой.
В первую очередь мы займемся здесь изысканием возможности
описания установившейся ползучести в сложном напряженном
состоянии.
Нам придется различать случаи изотропной и анизотропной
ползучести; при этом анизотропия может определяться
следующими факторами:
1. Исходным состоянием материала, связанным с технологией
изготовления образца или изделия, в первую очередь текстурой,
созданной при обработке металла давлением.
2. Упрочнением или изменением текстуры, вызванным
мгновенной пластической деформацией. Последняя возникает либо
в момент загружения при достаточно больших нагрузках, либо
в процессе ползучести, если напряженное состояние неоднородно
и напряжения перераспределяются (этот случай наиболее труден
для анализа).
3. Упрочнением, происходящим в первой фазе ползучести.
В принципе можно было бы предполагать, что анизотропия
порождается также в процессе установившейся ползучести. Это
значит, что накопление деформации установившейся ползучести
вызывает такие структурные изменения в материале, которые
не обнаруживаются как эффект упрочнения при простейшем
одноосном испытании, но влияют на перераспределение компонент
тензора скоростей деформации ползучести. Эту возможность
мы здесь рассматривать не будем, а будем понимать
установившуюся ползучесть как такую, когда при неизменном напряженном
состоянии все компоненты тензора скоростей ползучести сохраняют
постоянные значения.
§ 64. ИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
Уравнения теории установившейся ползучести представляют
собою зависимости между компонентами тензора скоростей
деформации ползучести Вц и компонентами тензора напряжений atj,
а именно: etj = ftJ- (akl). Вообще, зависимость между
симметричными тензорами xtj = фу {укд является изотропной в том случае,
если она не изменяется при изменении системы отсчета. Пусть
для некоторой новой системы координат компоненты тензоров
будут соответственно х\-} и у'ы-
Тогда, по определению изотропной зависимости,
Xij^Vijiy'hl)-
§ 64]
ИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
259
Этому условию мы удовлетворим, приняв, что tpjj- имеют
следующий вид:
Фи {Уы) = <ро^ + аАи + bBv + cCtj + ... F4.1)
Здесь ф, а, Ъ, с — скаляры, б^ — единичный тензор, А}^
Вц, Cij, ... — произвольные тензоры, имеющие те же главные-
оси, что и тензор уы. Действительно, если бы один из тензоров
Aij, Btj , . . . имел главные оси, отличные от главных осей у^т
то это означало бы, что в среде зафиксированы некоторые
предпочтительные направления, не связанные с видом напряженного
состояния, а характеризующие свойства материала (если
вернуться к поставленной вначале физической задаче).
В разложении F4.1) имеет смысл удерживать лишь линейно-
независимые тензоры Al}-, Btj, . . .; набор же линейно независимых
тензоров ограничен, поскольку число компонент их конечно.
Более того, в данном случае речь идет о тензорах, имеющих
одни и те же главные направления и сконструированных с помощью
тензора уи. Положим Ai} = уи, Btj = yihyhj, Си = yihyhsySf
и так далее, то есть будем вести разложение F4.1) по степеням
тензора ytj. Легко убедиться в том, что это разложение можна
оборвать уже на втором члене. Действительно, пусть xtj
представляет собою третью степень тензора ytj, то есть xtj — ytkyksysj —
= Cij. Покажем, что всегда можно выбрать скаляры ф0, а0 и Ьа
таким образом, чтобы было справедливо раренство
Су = ф0бу + М« + ЬоВ«- F4.2)
Все тензоры, фигурирующие в этом соотношении, соосны, поэтому
можно написать его для главных осей. Получим:
у\ = ф0 + aoVi. + ЬоУЬ
у1 = Чо+аоУг+ЬоУ1,
yl = фо + ЩУз + ЬоУ1-
Это — система трех уравнений для нахождения трех величин:
ф0, а0 и Ь0. Вместо того, чтобы решать непосредственно эту
систему, мы заметим, что yit уг и у3 являются корнями одного и того»
же кубического уравнения, которое может быть записано
следующим образом (§ 2):
у»-/1^ + /пу-/ш = 0. F4.4)
Здесь
11 = У1+У2+Уз,
1п = У1У2 + УгУг + УзУч
hii = У1УъУз-
17*
F4.3»
260 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
В § 2 были приведены формулы, выражающие инварианты /ь
^и и /ш через инварианты, построенные обычным способом.
Сравнивая F4.3) и F4.4), мы убеждаемся, что Ь0 = 1Х, а0 = —
— ^п> фо =^т; поэтому F4.2) может быть записано таким образом:
CiJ-IIBtJ + IllAij-IIIiiiij = 0.
Поскольку Aij, Bij и Ctj — последовательные степени тензора у*;,
то, применяя для степени п тензора уц обозначение у\], мы
получим:
yb-hy% + hiyij-lni&ij = 0. F4.5)
Это тождество называется тождеством Кэли — Гамильтона. Не
составляет труда показать, что любые более высокие степени
тензора i/;j выражаются через сам тензор, его вторую степень и
единичный тензор линейным образом, причем коэффициенты этой
линейной зависимости представляют собою инварианты. Таким
образом, все члены, начиная с члена, имеющего множителем с
в F4.1), следует отбросить, компенсировав это надлежащим
выбором ф, а ж Ъ. Теперь мы можем написать наиболее общую форму
закона изотропной ползучести:
Zij^P&ij + Q'Oij + RoibOkj. F4.6)
Здесь Р, Qf и R — функции инвариантов Si, <S"ir и Sm .
Дальнейшее исследование будет сводиться к разумному ограничению
общности соотношений F4.6), основанному на некоторых физических
или экспериментальных соображениях. Прежде всего заметим,
что как из экспериментальных, так и из физических соображений
следует, что деформация ползучести не сопровождается
изменением объема. В дальнейшем мы приведем некоторые
экспериментальные данные, подтверждающие это обстоятельство, для той
фазы ползучести, когда еще не происходит заметного охрупчива-
ния. В главе VI будет показано, что в третьей фазе ползучести,
предшествующей разрушению, появляются микротрещины.
Раскрытие их, конечно, сопровождается изменением объема, это
изменение объема обнаружено экспериментально.
Считая, что изменения объема на установившейся стадии
ползучести не происходит, умножим F4.6) на дц и свернем.
Получим
ttj6li = SP + S1Q' + SIIR = 0.
Отсюда
P=-oQ'-±SIlR.
Исключим теперь Р из F4.6), формула будет следующей:
еи = <?' (°и — оди) + R Qyikah} — j Sn6ij^j .
§ 65]
ПОТЕНЦИАЛ ПОЛЗУЧЕСТИ
261
Теперь нам будет удобно ввести в рассмотрение компоненты
девиатора тензора напряжений 0У = (г^ —абу. Легко проверить,.
что вторая скобка может быть записана следующим образом:
1 — — 1 — —
OikOkj — -3- SnQij = <yihohf— j Su8tj + 2aOij.
Таким образом,
ец = Qotj + R (oihakj — j Snbij^ . F4.7)
Здесь Q = Q' -f- 2aR и R — функции инвариантов. В
качестве основной системы инвариантов можно выбрать величины
a, ~Sji и Sin, хотя в некоторых случаях может оказаться более
удобным другой выбор. Предположение о несжимаемости часто
дополняется более сильным предположением о том, что
первый инвариант тензора напряжений а не влияет на ползучесть.
Тогда Q и R зависят только от 5ц и 5Ш.
Процесс ползучести представляет собою процесс рассеяния
механической энергии, поэтому целесообразно ввести в
рассмотрение мощность рассеяния:
Тензор напряжений может быть заменен девиатором тензора
вследствие того, что eit = 0 и гидростатическое- напряжение работы
не совершает. С помощью F4.7) находим:
L = QSu + RSUi.
Очевидно, что функции Q и R должны удовлетворять условию,
что L > 0 при любых значениях а^.
§ 65. ПОТЕНЦИАЛ ПОЛЗУЧЕСТИ
Изложим некоторые соображения, делающие гипотезу о
потенциале ползучести вероятной. Прежде всего определим мощность
рассеяния энергии при ползучести:
Полагая L (о*^) = const, мы получим в пространстве напряжений
поверхность постоянной диссипации; для всех напряженных
состояний, изображаемых точками этой поверхности, мощность
диссипации равна к. Очевидно, что поверхности постоянной
диссипации не могут пересекаться, ибо в противном случае мощность
не выражалась бы через напряжения однозначно; эти поверхности
вложены одна в другую, как показано схематически на рис. 95,
при этом /Cj > к*. Рассмотрим теперь некоторый путь нагружения
из точки М* на поверхности L = к* в точку Mi на поверхности
262 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
L = к{. Для определенности будем считать, что этот путь
пересекает каждую из поверхностей постоянной диссипации L = к,
к* <; к *Cki, только один раз, таким образом, в процессе нагру-
жения мощность диссипации не убывает.
Потребуем, чтобы на таком пути нагружения, когда dL >0,
мощность дополнительных воздействий была неотрицательна;
это значит, что для каждой точки М пути М*М±
(au-afj)Bi}>0. F5.1)
В частности, точки М* и М могут лежать на одной поверхности
L — к, тогда путь М*М целиком лежит на этой поверхности и из
F5.1) следует, что вектор скорости
деформации направлен по нормали к
поверхности L (dij) = к. Поэтому
«У = АЮ^. F5-2)
Условие F5.1), по существу, представляет
собою перефразировку постулата Друкера
(§ 14) на случай установившейся
ползучести. Так же, как и в теории пластичности,
условие F5.1) не вытекает из законов
термодинамики и не является
термодинамическим постулатом, это есть
ограничение, которое позволяет выделить класс
материалов, обладающих определенными
свойствами устойчивости; для таких
материалов решение задачи теории ползучести оказывается
единственным, как мы убедимся в главе VII, для них справедливы
некоторые вариационные принципы. Однако вопрос о том, будет ли
условие F5.1) необходимым условием единственности, остается
открытым так же, как и в теории пластичности.
Может случиться, что существует такая функция Ф (о*,;), что
Ф называется потенциалом скоростей ползучести,
F5.2) принимают тогда следующий вид:
дФ
Рис. 95.
Эта функция
соотношения
toij
F5.4)
Условие F5.3) выполняется, в частности, если А(ст^) = Л (L).
Действительно, в этом случае
Q>=\h(L)
dL.
§ 65]
ПОТЕНЦИАЛ ПОЛЗУЧЕСТИ
263
Умножая F5.2) на <ту и свертывая, мы находим:
L = h(au)j?jaiJ- F5-5)
Из F5.5) следует, что вид функции Л(сг^) вполне определен
структурой функции L; определяя h из F5.5) и подставляя
в F5.2), мы найдем:
L дЬ
Gks
dL daij
F5.6)
dOhs
Если L есть однородная функция напряжений степени п + 1,
1 1
то h = ^цтиФ = —7-гL. Если L есть произвольная функция
некоторой однородной функции первой степени s от а и, то h = .,.'
s
и Ф =$?(«) ^-.
о
Итак, мы убедились, что вследствие условия F5.1) при
некоторых довольно широких ограничениях, налагаемых на вид
функции L (Си), для скоростей ползучести справедливы соотношения
F5.3). Из этих соотношений немедленно следуют обратные
формулы; легко установить, что существует функция U (е^) от
компонент тензора скоростей ползучести, при помощи которой
определяются напряжения по формулам
^ = ^г- F5-7)
Действительно, положим
U = виги — Ф = L — Ф.
При этом мы считаем, что напряжения а^ выражены через ейг,
что принципиально всегда возможно, поскольку формулы F5.4)
устанавливают взаимно однозначную зависимость между atj и е^-.
Таким образом, новая функция U зависит от ги.
Продифференцируем обе части вышезаписанного равенства по ?,_,-. Получим:
foij ll hl dei} дам d&ij
Но вследствие F5.4) два последних члена в правой части взаимно
уничтожаются, и мы получаем равенство F5.7).
Функция L (Oij) играет в теории ползучести ту же роль, что
функция течения в теории пластичности. Если условие F5.1)
выполнено, из него следует, что поверхность L = const выпукла.
Точно так же выпуклыми будут поверхности Ф (cFjj) = const
264 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
в пространстве напряжений и U (е,,) = const в пространстве
скоростей деформации.
Очевидно, что потенциал ползучести в изотропной среде может
зависеть только от инвариантов тензора напряжений:
Ф = ФEЬ Su, Sin).
Условие несжимаемости накладывает некоторые ограничения на эту
зависимость. Действительно, из условия несжимаемости и F5.4)
следует:
Это — уравнение в частных производных первого порядка,
эквивалентное следующей системе обыкновенных уравнений:
dcfjj = 6jj da.
Отсюда следует, что потенциал Ф зависит не от компонент тензора
напряжений, а от компонент девиатора ац — аб^-. Таким образом,
можно принять
Ф = ФA„, 5Ш).
Соотношения F5.4) перепишутся теперь следующим образом:
8,7 = 2 W[^ii + *~Sr (<*'*<^—у ^ибу) • F5-8>
Сравнивая с F4.7), мы видим, что Q = 2-^—, R = 3 ¦ _ф .
Учет сжимаемости, если он окажется необходимым, не внесет
каких-либо принципиальных изменений в теорию ползучести,
вопрос состоит лишь в большей или меньшей сложности
получающихся соотношений. Принятие тех или иных частных гипотез
позволяет получить более или менее простые уравнения. Так,
в недавно появившейся работе [324] была развита теория
ползучести, в которой потенциал зависит от некоторого специально
сконструированного инварианта тензора напряжений, а именно от
величины Sn -)- a2iSf, где а — определяемая из опыта константа,
связанная с коэффициентом поперечной деформации при
растяжении, то есть с отношением скорости изменения поперечного
размера растягиваемого образца к скорости его осевого удлинения.
Форма зависимости между напряжениями и скоростями в теории
ползучести, получающаяся из предположения о существовании
потенциала, чрезвычайно напоминает связь между напряжениями
и деформациями в теории нелинейной упругости. В однородном
случае уравнения теории ползучести и теории нелинейной
упругости просто совпадают независимо от гипотезы потенциала,
§ 65]
ПОТЕНЦИАЛ ПОЛЗУЧЕСТИ
265
а следовательно, в теории ползучести справедливы теоремы типа
теорем Лагранжа и Кастильяно. Действительно, рассмотрим
систему, состоящую из одномерных элементов. Это может быть
статически определимая ферма из п стержней. Скорость удлинения
каждого стержня qt есть функция усилия в этом стержне Qt, так
что qt = Vi (Qi). Пусть ферма находится в равновесии под
действием системы внешних сил Ps» число которых равно т. Внешняя
сила Ps производит работу на обобщенном перемещении, скорость
которого us. Составим уравнение равновесия Лагранжа, приняв
за возможные скорости действительные скорости ползучести.
Получим:
¦m n
2^a=2<?^- F5-9>
Рассмотрим бесконечно близкое состояние равновесия,
соответствующее изменению одной из внешних сил Ps на
величину ЬРа. Из F5.9) следует:
п
».=2«'ж- F5Л0)
1
Введем теперь потенциал ползучести следующим образом:
ф= 2 ф* (<?<)•
Здесь функции ф; определены таким образом, что
4>i «?) = »*<<?)•
Продифференцируем Ф по JPS:
= 2м?о-^ = 2*
gps ^J ">w»/ dPs ^*« dPs ¦
Сравнивая с F5.10), убеждаемся, что
• _ дФ
Ms ~~ dPs '
Одномерными элементами системы могут служить не только
растянутые или сжатые стержни, но также стержни, находящиеся
в состоянии изгиба или кручения. Поэтому потенциал ползучести
существует, если тело можно моделировать при помощи
одномерных элементов. Одна из возможных простейших моделей такого
рода была рассмотрена в § 16. Представим себе трубу или
стержень кругового сечения в условиях изгиба. Отдельные «волокна»
266 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. "V
работают либо на растяжение, либо на сжатие, поэтому
вышеприведенный анализ сохраняет силу и уравнения ползучести для
любого направления изгибающего момента могут быть записаны
с помощью потенциала. Приведенные соображения, конечно, не
могут служить доказательством того, что потенциал существует
для пространственного напряженного состояния, однако позволяют
считать это весьма вероятным.
§ 66. СПЕЦИАЛЬНЫЕ ФОРМЫ ЗАКОНА ПОЛЗУЧЕСТИ
Опыты показывают, что зависимость скорости ползучести
от напряжения имеет один и тот же характер для различных типов
напряженного состояния. Так, например, если скорость
ползучести при растяжении пропорциональна растягивающему
напряжению в степени п, то при кручении скорость сдвига будет
пропорциональна касательному напряжению в той же степени. Это
подсказывает некоторый определенный выбор формы зависимости
потенциала от инвариантов Su и 5П1, потенциал должен зависеть
от некоторой однородной функции напряжений. Достаточно общей
формой такой зависимости для несжимаемого материала будет
следующая:
ф-ф[^.(Й)]-
Вместо Su и Sin нам будет удобно ввести следующие величины
{см. § 8):
Тогда потенциал ползучести может рассматриваться как
функция от произведения о0 на g(?), а именно:
Ф = Ф[0О?(О].
Используя очевидные соотношения:
da0 _ 3 dt, _9_j^ dg _ 9 1
dSn ~~ 4o0 ' gsn ~ 4 a<j ' dSIU " 2 ao '
мы можем переписать уравнения F5.8) следующим образом:
- - 2
ew = 4«D'{(*-3te')^- + 9*' ^ }• F6.1)
Если тензор напряжений отнесен к главным осям, то
соотношению F6.1) можно придать иную форму, воспользовавшись
§ 66] СПЕЦИАЛЬНЫЕ ФОРМЫ ЗАКОНА ПОЛЗУЧЕСТИ 267
представлением напряжений с помощью формул (8.9):
2 Q
01 =у OoCOsH,
— 2 fг. 2я
0 = у ° COS f 0 g-
- 2 /Q 4я
о"з = у о"о cos F g-
По формуле (8.8)
Таким образом,
Sm = aj + a23 + of = -L ?? cos 30.
? = cos 30.
Выпишем, например, выражение для ej. Входящий туда
множитель имеет вид
o-iftO-Ai - -| ol = у о; B cos2 0 — 1).
Внося в F6.1) это выражение, а также о{ и ?, после
перегруппировки членов получим:
е1 = ф' {g cos 6 -f 3g' sin 38 sin 6},
e2=O'{gcos@—^-) + 3g'sin3Bsin(e-^-)}, F6.2)
e3 = ф' {^cos (e-^) + 3^'sin30sin (в—у')}.
Две другие формулы получены заменой 0 на 0 —~- и 0 — у
соответственно. При этом sin 39, а также ? = cos 30, аргумент
функции g, не меняются.
Вместо того, чтобы рассматривать функцию g от переменной ?,
будем считать, что g = g @)- Очевидно, что g @) есть периоди-
2ix
ческая функция с периодом у ; до сих пор эта функция была
определена с точностью до произвольного множителя. Будем
считать, что g @) = 1. Тогда при одноосном растяжении аргумент
функции Ф (о*о?) становится равным величине растягивающего
напряжения, а следовательно,
O'(^og) = v(a0g).
Здесь v — функция, дающая зависимость скорости ползучести
при растяжении от растягивающего напряжения. Теперь мы можем
268 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. "V
придать формулам F6.2) следующий более простой вид:
Ej = y |^gcos9 — -^-sinej ,
?2 = v [ g
cos
•-*)
e3
= v[g
COS [ 0
4я
~3~
dg_
sin
sin
0-
9-
Y
2я
4л
T
F6.3)
]
В октаэдрической плоскости вектор интенсивности напряжений
составляет угол 0 с прямой, проходящей через центр
октаэдрической площадки до точки
пересечения ее с осью 1, как показано
на рис. 3 и повторено на рис. 96.
Из формул F6.3) следует, что
вектор интенсивности скоростей
деформации в составляет с той же
прямой угол 0 + ш, причем
Для того чтобы проверить
теорию экспериментально и получить
выражения для функций g @) и
v (a0g), можно поступить
следующим образом. Умножим первое
, третье на
Рис. 96.
из уравнений F6.3) на cos 0, второе на cos ( 0—
cos ( 0—г- J и сложим. Получим:
es = y J81cos0 + e2cos Г0 ?- j + e3cos f 9 ^-j 1
F6.4)
Аналогичным образом
ег = — у 8! sin 0 -f e2 sin ( 9 -
2я
' 3
+ e3 sin ( 0 —
4я
]-
= v(a0g)^
F6.5)
Разделим F6.5) на F6.4). Получим:
е..
g dQ
tgco.
Производя опыты при различных напряженных состояниях, мы
меняем величины 0; по измеренным значениям еь е2 и е3 можно
всегда вычислить е8 и е(; отношение их, таким образом, является
§ 66] СПЕЦИАЛЬНЫЕ ФОРМЫ ЗАКОНА ПОЛЗУЧЕСТИ 269
экспериментально определенной функцией от 0. Тогда вышена-
писанное соотношение представляет собою дифференциальное
уравнение для нахождения функции g @). Обозначим отношение
е^/е^ = к @), здесь мы уже приняли за аргумент переменную 0.
Тогда, очевидно,
е
g @) = ехр { к @) dd. F6.6)
о
При пользовании этой формулой необходимо иметь в виду, что
функция g @) периодическая с периодом -^- , поэтому
\ к @) dQ = 0.
во
Выполнение этого условия для экспериментально определенной
функции и @) есть необходимое условие применимости теории.
Если характеристики ползучести при растяжении и сжатии
одинаковы, то g зависит от модуля 0, следовательно, период g @)
2я я
равен уже не -^ , а -^ .
Постоянная интегрирования в соотношении F6.6) принята
равной единице, чтобы было g @) = 1. Теперь для нахождения
функции v достаточно воспользоваться данными испытаний при
каком-нибудь одном напряженном состоянии, значение g для
этого напряженного состояния уже известно, и в формуле F6.4)
функция v подбирается так, чтобы достичь наилучшего согласия
с опытом. Заметим, что из F6.3) следует, что интенсивность
скоростей деформации
ео = [ 4 еуе„ ]1/a = v (аоё)У?ТГ- F6.7)
Если g = 1, отсюда получается неизменная зависимость между
интенсивностью скоростей ползучести и интенсивностью
напряжений. Если g @) не постоянно, то зависимость для разных
значений 0 будет своя, так же как и зависимость es (o0g) по
формуле F6.4); при обработке опытных данных эта вторая
зависимость кажется более удобной, так как формула F6.4) содержит,
в отличие от F6.7), только функцию g(Q), но не ее производную.
Весьма распространенный способ испытаний на ползучесть
при сложном напряженном состоянии — это испытание
тонкостенных трубчатых образцов на одновременное действие
растяжения и кручения, а также растяжения или сжатия и
внутреннего давления; поэтому нам следует рассмотреть отдельно
случай плоского напряженного состояния. Положим, например, в
270 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
первой из формул (8.9) 01 = 0, тогда о*= — — о*0 cos 9; из двух
следующих формул получим после упрощений:
ао =
Уз
a0sin
т~9
о-3= — —^-o-osin ( —+ 9
F6.8)
а также
-—Г
т/з L
е2 sin [ -у — t
8i = -|[e2cos
+ е3 sin (^-j- + 9^) ] = -^ [ff2e2 + о-3е3],
F6.9)
f-e)-e3coS(f+9)].
Из F6.8) следует, в частности:
<*2 + о"з ~ — 2о"о cos 9 = — За, F6.10)
2
с2 —a3 = r^o-0sinG. F6.11)
Для определения 9 при заданном напряженном состоянии
удобно пользоваться следующей формулой, вытекающей из F6.10)
и F6.11):
l/3ctg9 =
-а3
аг—а3
F6.12)
Осуществляя всевозможные плоские напряженные состояния, мы
2л
пробегаем диапазон углов от 9 = 0 до 9 — -^- . В следующей
таблице приведены некоторые значения отношения сг3/о*2,
соответствующие углы 9, значения ?,, а также cos 9.
03/С2
— со
— 1
0
1/2
1
2
+ со
9
60°
90°
120°
150°
180°
210°
240°
t
—1
0
1
0
—1
0
1
соз $ = Зсг/2со
-1/2
0
1/2
1/3/2
1
1/372
1/2
Заметим, что для установления закона ползучести нам
достаточно располагать опытными данными для диапазона изменения
угла 9 в пределах 120°. Действительно, именно таков период
функции ? (9), а также множителя sin 39 в уравнениях F6.2).
На рис. 97 схематически показана область изменения угла 9.
В октаэдрической плоскости построена окружность, отсчет дуг
§ 67] ОБРАБОТКА ОПЫТОВ НА РАСТЯЖЕНИЕ С КРУЧЕНИЕМ 271
ведется от оси B), символами B) и C) отмечены две другие
главные оси. Цифры, стоящие у соответствующих точек окружности
(через 30°), представляют собою величину ?. Точки, где ? = +1,
соответствуют растяжению, где ? = — 1 — сжатию (на которое
наложено, конечно, произвольное гидростатическое состояние).
Там, где ? = О, получается
напряженное состояние
чистого сдвига (с наложенной
гидростатической
составляющей). Уже было отмечено,
что для определения функции
g (?) достаточно располагать
данными для одного сектора, _
в котором угол меняется в
пределах 120°, совпадение
результатов, получающихся
для других секторов, может
служить критерием для
оценки справедливости теории.
Отклонений можно ожидать
либо за счет анизотропии
материала, либо за счет влияния
гидростатического давления,
что связано с нарушением принципа существования
потенциала ползучести. Строки таблицы 1 следует сопоставлять с
точками сектора, отмеченного стрелкой на рис. 97, причем
направление стрелки соответствует порядку таблицы сверху вниз.
Видно, что лишь первая точкаf в которой ? = 0, соответствует
чистому сдвигу, для двух других точек на чистый сдвиг накла-
1
дывается гидростатическая составляющая, такая, что а = —^ о.
При рассмотрении случая плоского напряженного состояния
мы по произволу положили o*i = 0 и нашли выражения о2 и о*3.
Желая приписать заданным напряжениям другие индексы, мы
можем воспользоваться теми же формулами, изменив начало
отсчета угла 0. Так, если принять а3 = 0, то нужно во все форму-
лы вместо 6 внести 0 + -з- , после такой замены первая из формул
F6.8) будет давать выражение ои вторая формула — выражение а2.
Рис. 97.
§ 67. ОБРАБОТКА ОПЫТОВ НА РАСТЯЖЕНИЕ С КРУЧЕНИЕМ
Осуществление общего случая плоского напряженного
состояния в опытах на ползучесть довольно сложно технически,
особенно трудно измерение окружной деформации тонкостенного
образца, поэтому большая часть опубликованных опытных данных
272 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
относится к одновременному растяжению и кручению. При этом
измеряются относительное удлинение образца е и сдвиг у,
определяемый по углу закручивания. Зная скорости е и у, мы еще
не можем определить главные скорости деформации е2 и е3,
поэтому имеет смысл специально рассмотреть случай растяжения
с кручением. Положим Оц = а, о*12 = oi = т, все остальные
компоненты тензора напряжений равны нулю. Составляющие
девиатора тензора напряжений будут при этом следующие:
- 2 - - 1 - - - п
Оц = j о, о22==о3з = — уО% а12=т, a23 = o3i^=U.
— 2
Второй инвариант девиатора 5'и = -~- (с2 + Зт2), следовательно,
о^а2 + Зт2. F7.1)
Введем для краткости временные обозначения:
— — 1 —
sij = GihGhj — " Sll&iJ-
Получим:
Su=-q02 + jX2, %,= — -g-О2 + 3-Г*, S33 = — -g-O2 — -g-T2,
«12 = у ОТ, S23=S31 = U.
Уравнения F6.1) примут следующий вид:
B"-f»[(f-te')f+iB»'+^*)].
вг2-4" [ ~(f-^')^ + -5F(-CTa + 3l:B)] ¦ <в7'2)
Примем теперь
1
о = о cos а, т = —т= о sin а;
1/3
при этом F7.1) обращается в тождество. Непосредственно
измеряемыми на опыте величинами являются еи и е12, поэтому
мы преобразуем только первое и последнее из уравнений F7.2).
§ 67] ОБРАБОТКА ОПЫТОВ НА РАСТЯЖЕНИЕ С КРУЧЕНИЕМ 273
Получим:
3 Г 2 ~1
еи = у v I "з" 8 cos а + ё' ( — 2? cos а + 1 + cos2a) ,
e12==^|_5z,[-g-gsina + g'( — ? +cos a) sin a] .
Сравнивая выражение для а через о0 и а с формулой F6.10),
находим:
cos9= — ycosa. F7.3)
То, что в формуле F6.10) другие наименования главных осей,
несущественно, перемена наименования осей эквивалентна
сдвигу начала отчета угла 0 на 120°, как было разъяснено
в конце предыдущего параграфа. Теперь мы можем выразить Z,
через а, а именно:
? = cos36 = |-cosa(l — -|-cos2aY F7.4)
Исключив t, из формул для еи и е12, получим следующий
результат:
8ц = у rgcosa + Tg'sm4a] ,
I F7.5)
Уз г . з , . , -1
ei2 = -V"V gsma-yg cosasm^a .
В этих формулах g рассматривается как функция ?. Если
рассматривать g как функцию а, то
но
da
~dl~ ~
Следовательно,
*' 2
6 3 sina(
, dg da dQ
8 ~~da~d~Q~dXs
9 sin0 d9
sin a ' d?
1 dg
3—4sin26) da
1
1
3 sin 36 '
2 1 dg
3 sin3 a da
Уравнениям F7.5) можно теперь придать следующую простую
форму:
e = s11 = v [gcosa — -^-sinal ,
,_ F7.6)
1 • Уз г . , dg ~\
YY:=ei2 = -h2_!; [gsma + -^|cosaJ .
18 Ю. Н. Работнов
274 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖВННОМ СОСТОЯНИИ [ГЛ. V
Образуем следующие комбинации:
es = e cos a + ~^т= У sin a = v (a0g) g,
8t= -esina + —^ycosa = v(o0g)-^-
F7.7)
Поделим второе из соотношений F7.7) на первое. Получим:
1 dg щ -v(a). F7.8)
Отсюда следует:
a
g (а) = ехр \ v (a) da. F7.9)
о
Из формул F7.5) видно, что если напряжения сдвига малы
по сравнению с растягивающими напряжениями, следовательно,
а С 1, то
e = vg,
V= ]/~3vga.
Заметим, что угол а меняется в пределах от а — 0 до a — л,
если опыты проводятся как при растяжении, так и при сжатии.
Косинус угла 9 заключен при этом в пределах от —V2 до +V2,
то есть угол 0 меняется в пределах 60°, например от 120° до 60е.
как показано на рис. 97.
§ 68. КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ
Как мы видели в главе II, учет влияния третьего инварианта
для теории пластичности не очень существен и большая часть
теорий пренебрегает этим влиянием. Опытные данные, которые
будут рассмотрены далее, показывают, что для ползучести во
многих случаях нельзя сделать определенных выводов о
необходимости учитывать третий инвариант, но для ряда материалов при
некоторых условиях влияние его явно невелико. Считая, что
Ф = Ф (ств), мы получаем из F6.1):
6ij'=lyW^' F8.1)
у (а0) = Ф'(<*>)¦
Уравнения F8.1) квазилинейны в том смысле, что соотношения
между компонентами скорости ползучести и напряжения
линейны; вся нелинейность скрыта в множителе, зависящем от инва-
S 68] КВАЗИЛИНЕЙНЫЕ УРАВН. УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ 275
рианта о0. Связывая скорость установившейся ползучести со
вторым инвариантом девиатора тензора напряжений, мы, по
существу, предполагаем, что ползучесть определяется касательными
напряжениями; при этом а0 или 5И является мерой
интенсивности касательных напряжений. Еще более простая гипотеза состоит
в том, что процесс ползучести представляет собою чистый сдвиг,
вызванный наибольшим касательным напряжением. Предположим,
что сг, > ст2 > о"з- Тогда наибольшее касательное напряжение
ттах = -о" (°"i — °з)- Элемент, грани которого параллельны
координатным плоскостям, будет перекашиваться в плоскости 13
без изменения объема; скорость деформации сдвига у = gj — е3,
но е2 = 0, следовательно, ei + е3 = 0, а значит, у = 2е4 = —2е3.
По предположению у должно быть функцией от ттах, вид этой
функции определяется из опыта на простое растяжение,
следовательно,
ei= — 83 = ^@-1— <х3), е2=0. F8.2)
Особого рассмотрения требует тот случай, когда два главных
напряжения равны между собою, например ст2 = о- Наложим
на наше напряженное состояние всестороннее сжатие с
интенсивностью — о2, тогда останется только одно напряжение в
направлении оси 1, равное о4 — о*2, и скорость ползучести в этом
направлении будет
?1 = f(a1 —
соотносительно скоростей е2 и е3 мы уже не можем ничего
утверждать, кроме того, что они удовлетворяют условию
несжимаемости. Примем поэтому
е2= -A*i, вэ--A-Ь)е1. F8.3)
Получающаяся неопределенность является неизбежным
следствием слишком упрощенной гипотезы. На первый взгляд может
показаться, что соображения симметрии заставляют нас поло-
жить А = y , именно этот результат вытекает из
непосредственных наблюдений над ползучестью при растяжении. Однако
такое предположение неминуемо приводит к противоречиям, если
перейти к задачам с неоднородным распределением напряжений.
Условие 02 = о оказывается слишком жестким, и за него
приходится расплачиваться известным произволом кинематической
картины течения.
Соотношения F8.2) вытекают из общих уравнений, если
принять, что потенциал зависит от наибольшей разности главных
18*
276 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
напряжений. Действительно, положим
ф=ф(а1 — а3).
Тогда по формуле F5.4)
8i= —e3 = 0'{cri — a3) = v(ai — a3),
е2 = 0.
Чрезвычайная простота этих соотношений сохраняется лишь до
тех пор, пока мы рассматриваем процесс ползучести в главных
осях. Действительно, в общем случае мы должны выразить
величину о-! — о через инварианты и воспользоваться общими
формулами F5.8). С помощью (8.9) мы находим:
2
<*1 — о3 = 0-J -
¦ ст3 = -о- о"о cos 8 — cos
•-Т-
]-
-^<r,os(|—в)
Но а,— а3 есть аргумент функции Ф, следовательно,
2
*F) =
V3
cos
•?--в
F8.4)
Условие g@)=l при этом выполняется.
Сравним теперь теорию ползучести, соответствующую
уравнению F8.1), и теорию F8.2). Будем называть первую теорией
типа Мизеса, вторую — теорией
типа Сен-Венана. Для теории типа
Мизеса аргумент функции Ф есть
а0, для теории типа Сен-Венана—
o0g (9), где g (б) определяется
формулой F8.4). Полагая а0 — 1, мы
получим в октаэдрической
плоскости окружность, изображенную на
рис. 98, полагая a0g F) = 1 —
хорду с центральным углом 60°,
проходящую через точку 1.
Действительно, высота
изображенного равнобедренного треугольника
Рис. 98.
уз
есть -^- .
из
следует, что ocos ( -^
условия a 0g = 1
Очевидно, что формула F8.4) сохраняет силу лишь до тех пор, пока
о<е<|,
в интервале -^-^б;
,2л
"
следует принять g (б) =
= -р cos ( р—б J и так далее. В принципе мы могли бы теперь
написать общие уравнения ползучести для произвольных осей,
§ 68] КВАЗИЛИНЕЙНЫЕ УРАВН. УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ 277
воспользовавшись формулами F6.1). Решая уравнение
? = cos 39 = 4 cos3 0 — 3 cos 0
относительно cos 6, мы находим 0 как функцию ?, теперь F8.4)
определяет g в зависимости от ?. Получающиеся при этом
формулы чрезвычайно громоздки и вряд ли смогли бы на^ти какие-
либо применения.
Случай одновременного действия растяжения и кручения
на тонкостенный образец, наоборот, рассматривается весьма
просто. Положив Озз = 0, подобно тому как это сделано в § 67, мы
должны принять
?(e) = ^Sm8 = ^f3 + sin2a.
Тогда из формул F7.6) немедленно получаем:
е = еи = У 2>v
ут-
-sin2 a
\ • sin а
Тот же результат может быгь найден совершенно элементарным
способом, если принять во внимание, что при растяжении и
кручении главные оси повернуты на угол 26 по отношению к оси
растяжения, при этом
tg2p=^=wtga-
Главные скорости удлинения равны по величине и
противоположны по знаку:
главные оси деформации совпадают с главными осями тензора
напряжений, поэтому
8ц = е4 cos 2р = УЪь
cos a
V3 + sin2a '
в12 = Et sin 26 = 2v sm a
V3 + sin2a '
Следует отметить, что отношение скорости удлинения к скорости
сдвига в этом случае равно
I еи о -
278 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Согласно теории типа Мизеса это отношение равно
V Зт
Описанный в § 67 способ обработки экспериментальных
данных по ползучести при растяжении и кручении, по существу,
позволяет выявить отклонения реального поведения материала
от предсказаний теории Мизеса. Если материал подчиняется
закону ползучести типа
vrar;
Ц2
0,1
-ш
-аг
¦
7--^___#г
W_ __
к
2
—¦—^ а
Сен-Венана, то
v (а) = —
sin а cos а
Рис. 99.
?<«) = ]/
4 — cos2а
F8.5)
F8.6)
Графики функций v (а) и
g (а) по формулам F8.5)
и F8.6) представлены на рис. 99 и 100. Если нанести на график
рис. 99 опытные точки, то группировка их около оси абсцисс
свидетельствует о справедливости закона течения типа Мизеса,
группировка около кри-
д(а)
U -
вой — о справедливости
закона течения типа Сен-
Венана.
Окружность и
шестиугольник, изображенные
на рис. 98, представляют
собою сечение поверхности
Ф = const октаэдрической
плоскостью. В отличие от
пластичности, мы можем
зафиксировать постоянную
по произволу. Поскольку
при принятых нами
ограничениях аргумент
функции Ф есть a0g (8), мы можем выбрать в качестве стандартной
поверхности равного потенциала ту поверхность, для которой
Oog(Q) = i. F8.7)
Условие g @) = 1 и свойство периодичности функции g F)
фиксируют точки 1, 2 ж 3, предположение об одинаковом законе
ползучести при растяжении и сжатии фиксирует точки Г, 2' и 3';
все они лежат на окружности радиуса, равного единице. Если
функция Ф выпукла, то всевозможные кривые, изображающие
§ 68] КВАЗИЛИНЕЙНЫЕ УРАВН. УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ 279
условие F8.7) в октаэдрической плоскости, будут выпуклыми
кривыми, проходящими через шесть зафиксированных точек.
Очевидно, все эти выпуклые кривые располагаются между двумя
шестиугольниками, вписанным и описанным, как показано
на рис. 101.
Из чертежа видно, что уравнение стороны описанного
шестиугольника, проходящей через точку 1, можно записать в виде
CT0cose = 1.
Следовательно, если
Т<в<1
то
g@) = cosG.
Для других сторон шестиугольника
получим:
g@) = cosF--^-J (ft = 0,l,...,5).
F8.8)
Теперь по формулам F6.3) легко
находим:
= V COS
-2 — к
F8.9)
Если к = 0, то
Рис. 101.
el=v, e2 =
¦v,
6з= — ttV.
F8.1С)
Этот случай реализуется, когда Oi>0 а является наибольшим
по абсолютной величине главным напряжением. Если а3 < 0
и больше по абсолютной величине, чем другие главные
напряжения, то мы оказываемся на стороне ВС изображенного на рис. 101
многоугольника; тогда к = 1 и
•V,
е2=уУ,
Особого рассмотрения требует тот случай, когда два главных
напряжения равны по абсолютной величине и мы находимся
в угловой точке, например в точке В, для которой а3 = —0\. Так
же, как и для закона течения типа Сен-Венана, мы должны
допустить неопределенность в распределении скоростей деформации.
Если г\ есть скорость, определенная из условия, что точка В
принадлежит стороне АВ, а ъ\ — скорость, определенная из
условия, что точка В принадлежит стороне ВС, то
8г = Х,в; + A — К)е\ @<Ж1),
или:
е4 — и
1 + А.
1—2Х
'—2 + Х
280 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ С0СТ0ЯНИИ_[ГЛ. "V
Заметим, что уравнение
Сто cos ( 9 s- J = const
эквивалентно следующему:
max | at | =¦¦ const.
В теории пластичности аналогичное условие текучести было
названо условием наибольшего приведенного напряжения. Пусть
Рис. 102.
наибольшая по абсолютной величине компонента девиатора
тензора напряжений есть оч, тогда
ф = ф [CTl_i-(a2 + a3)] ,
и мы немедленно получаем соотношения F8.10).
Для ползучести критерий наибольшего приведенного
напряжения был использован в работе [86].
Для того чтобы сравнить результаты предсказаний трех
рассмотренных простейших квазилинейных теорий, построим
графики изменения функции к (9) (рис. 102). Выберем интервал
изменения угла 9от9 = уДо9 = -д; обращаясь к схеме рис. 97, мы
убеждаемся, что точка 9 = -=- соответствует растяжению, 9 = -=- —
§ 69]
АНИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
281
кручению. Для этой области по критерию наибольшего
касательного напряжения
g (в)-^= sine,
по критерию наибольшего приведенного напряжения
g(e)=cos(e-f).
Получаем: а) Критерий типа Мизеса:
х = 0.
б) Критерий наибольшего касательного напряжения:
K = ctge=-tg(9--?-).
в) Критерий наибольшего приведенного напряжения:
* = tg(?-e).
Определяя функцию к (9) экспериментально и нанося на график
опытные точки, мы можем сразу сделать качественное
заключение о том, в какой мере поведение материала может быть
описано теорией типа рассмотренной в § 66 и какая из описанных
простейших схем лучше всего его воспроизводит. Если опытные
точки располагаются, группируясь около некоторой плавной
кривой, лежащей целиком между кривыми (б) и (в), например,
так, как показано пунктиром, мы будем называть поведение
материала нормальным, в противном случае поведение будет
характеризоваться как аномальное, связанное либо с
анизотропией, либо со структурными превращениями.
§ 69. АНИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
При испытаниях на ползучесть анизотропия проявляется,
пожалуй, больше, чем при любом другом виде механических
испытаний. Образцы, вырезанные из прокатанного материала или
из поковки, как правило, обнаруживают совершенно
незначительную анизотропию упругих свойств. Анизотропия обычных
характеристик пластичности более заметна, разница в пределах
текучести для образцов из стального проката, вырезанных вдоль
и поперек волокна, может составлять десять — пятнадцать
процентов. Расхождение же в кривых ползучести при одном и том же
напряжении и одинаковой температуре иногда оказывается
огромным, удлинение при одном и том же времени может
изменяться в два-три раза в зависимости от ориентации образца.
У некоторых материалов, например у сталей, как перлитных,
282 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
так и аустенитных, анизотропия полностью устраняется путем
надлежащей термической обработки. У алюминиевых сплавов
анизотропия, связанная с образованием текстуры при
изготовлении прутка или ленты, по-видимому, совершенно неустранима.
Исследование материала турбинных дисков, изготовленных путем
ковки или штамповки, показывает, что стандартная
термообработка, обеспечивающая наилучшие характеристики прочности
материала, не снимает полностью анизотропию, и ее следует
учитывать при уточненных расчетах на ползучесть. Как уже
было оговорено в § 63, анизотропия характеристик ползучести
не обязательно связана с исходным состоянием материала,
кратковременная пластическая деформация, возникающая при нагру-
жении и предшествующая ползучести, уже создает анизотропию.
Анизотропия возникает также на первой стадии ползучести,
сопутствуя упрочнению. Поэтому рассмотрение анизотропной
ползучести должно явиться необходимым элементом для
разработки общей теории ползучести, учитывающей упрочнение.
Вообще говоря, состояние материала, подвергаемого пластической
деформации в окрестности некоторой точки пространства нагру-
жения или находящегося в условиях ползучести, может быть
охарактеризовано целым рядом тензоров различных рангов.
В этом смысле пластическая анизотропия значительно более
сложна, чем упругая анизотропия. Действительно, упругий
анизотропный материал полностью характеризуется заданием
тензора четвертого ранга — тензора упругих постоянных. Число
их в самом общем случае не превышает 21. Говоря об упругой
анизотропии, мы имеем в виду линейную зависимость между
силами и перемещениями и предполагаем обратимость процесса;
в этом смысле свойства элемента материала и свойства
конструкции, состоящей из различных упругих звеньев, совершенно
одинаковы; у нас нет никаких средств для того, чтобы отличить
физическую анизотропию материала от так называемой
конструктивной анизотропии, последняя всегда описывается с помощью
21 константы, причем соображения упругой симметрии
позволяют уменьшить число констант совершенно одинаковым
способом как в том, так и в другом случае. В теории пластичности
положение оказывается гораздо более сложным, примером в этом
отношении может служить работа [87], где рассмотрены условия
предельного равновесия подкрепленных пластин и оболочек.
Возможность перехода в пластическое состояние конструкции
за счет текучести лишь части составляющих ее элементов должна
быть принята во внимание при составлении условия предельного
состояния системы в целом, это приводит к необходимости строить
поверхность текучести по кускам, причем число этих кусков
довольно велико. Рассматривая материал как совокупность
некоторых структурных элементов, мы не должны, в принципе, ожи-
§ 89]
АНИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
283
дать простых соотношений, описывающих пластическую
анизотропию.
Здесь мы не будем рассматривать вопрос во всей общности,
ограничимся лишь теми теориями анизотропной ползучести,
которые приводят к квазилинейным соотношениям между скоростями
и напряжениями. Предполагая и в этом случае существование
потенциала ползучести, мы должны рассматривать его как
функцию совместных инвариантов тензора напряжений и некоторых
тензоров анизотропии. С другой стороны, если тензор напряжений
отнести к главным осям, то потенциал ползучести должен зависеть
только от трех главных напряжений, поэтому число
определяющих инвариантов равно трем. Выбор этих инвариантов и
соответственно тензоров анизотропии в достаточной мере произволен.
Какое-либо исследование общего характера становится при этом
затруднительным, тем более затруднительно применение сложной
теории хотя бы к обработке опытных данных. Аналогичные
трудности возникают в нелинейной теории упругости (см., например,
[2191), поэтому в упомянутой книге избран иной путь
построения теории. Предполагается, что упругий потенциал является
полиномиальной функцией от компонент деформации, после чего
рассматриваются определенные типы упругой симметрии.
Требуя инвариантности потенциала по отношению к тем или иным
группам преобразований, удается показать, что потенциал
должен зависеть от некоторых комбинаций составляющих
деформации.
В теории пластичности анизотропных сред обычно пользуются
более простыми предположениями, которые легко переносятся
на случай ползучести. Будем с самого начала считать материал
несжимаемым и предположим, что потенциал ползучести, по
аналогии со случаем упругости, зависит от одного только
квадратичного инварианта, составленного из компонент тензора
напряжений и компонент некоторого постоянного тензора анизотропии
четвертого ранга. Запишем этот инвариант следующим образом:
S = AtmotJohi. F9.1)
Тензор анизотропии симметричен относительно пар индексов
г/, Ы, а также относительно индексов i и /, к и I, так что
A-ijki = AjiM = Aijik = AkHj.
Если потенциал ползучести Ф зависит от S, то
ец = Ф'(Я)-^- = 2ФМцна«.
Используем теперь условие несжимаемости еу6^
Aijki8ij = Q-
= 0. Получим:
F9.2)
284 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Число коэффициентов анизотропии, учитывая симметрию этих
коэффициентов, равно 21, шесть соотношений F9.2) уменьшают
число независимых коэффициентов до 15, а поскольку функцию
достаточно определить с точностью до произвольного множителя,
для полной характеристики анизотропных свойств при
сделанном предположении о том, что потенциал текучести зависит
от одного лишь квадратичного инварианта, достаточно задать
14 постоянных.
Заметим, что вследствие соотношений F9.2)
S = AijuiOijOki = Aijhl<Jij<jhi.
Аналогично закон ползучести можно записать следующим образом:
B,j = Q>'(SJAimahi. F9.3)
В реальных материалах наличие текстуры, созданной при
обработке, предопределяет тот или иной вид симметрии свойств
ползучести. Наиболее высокая степень симметрии наблюдается
в образцах из пруткового материала или цилиндрических
образцах, упрочненных путем растяжения либо сжатия вдоль оси.
Пусть ось образца является осью 3, тогда следует ожидать, что
при повороте осей 1 и 2 на произвольный угол Р вид инварианта S
не изменится и коэффициенты анизотропии останутся прежними.
При таком преобразовании координат система инвариантов будет
следующей:
СТ33> - °Hi + 0-32> °"ll+02. 0-иСТ22 — 0"i2-
Два последних выражения представляют собою инварианты
плоского тензора (оц, сг22, tfi2); в инвариантности второго
выражения легко убедиться, если заметить, что это есть квадрат
полного касательного напряжения на площадке, перпендикулярной
оси 3. Квадратичная функция, построенная из этих инвариантов,
необходимым образом имеет вид
S = аа%3 + Ьа33 (сг22 + ап) + с (о231 + <4) +
+ d {а\2 + а\х + 2оиа22) + е {апо22 — а\г).
Теперь следует выписать развернутое выражение функции S
по формуле F9.1) и сравнить коэффициенты. В результате
получается:
^4зззз = я, А2222~-Лщ1 — d, 2Aii22 = 2d-\-e — 2f,
2Лгзз = 2Л3311 =• b, 4Л1212 = — е. 4^2323 = 4Л3131 = с,
Ai22z = ^2331 = >43112 = Aiii2 = Aii2S = Ali3l — А2212 —
= А2223 = ^2231 = Ai32l = ^4зз2з — ^3331 == U.
« 691
АНИЗОТРОПНАЯ ПОЛЗУЧЕСТЬ
285
Используя условия F9.2), мы найдем, что коэффициенты
анизотропии должны удовлетворять еще следующим двум
соотношениям:
d + f + ±b = 0,
b + a = 0.
Таким образом, число независимых коэффициентов анизотропии
оказывается равным трем, при этом один из коэффициентов можно
зафиксировать по произволу. Потребуем, например, чтобы для
случая растяжения в направлении оси 3 величина S совпадала
с величиной Su, определенной для изотропного материала. Для
этого нужно, чтобы было
л _ _ 2
^зззз — а — ~т~ ¦
Положим теперь d = -^-B — а), с-
/ = т(-1-
е =
Р ), тогда b=
— — -fa ) . Матрица коэффициентов
анизотропии может быть теперь записана следующим образом:
Мзы I = -q-
2 —a
-1 + a
¦1
О
О
о
¦1 + a -l 0
2_a -l 0
-1
О
О
О
2 О
0|
о о
о о
о
о
о
-ро
о
о
о
о
т-Р°
о 4
F9.4)
При записи матрицы принят следующий порядок чередования пар
индексов: A1), B2), C3), B3), C1), A2). Случай изотропного
материала получится отсюда, если положить а. = р" = 0.
Требование положительной определенности квадратичной
формы S накладывает следующие ограничения на величины а и Р:
_3_
2
а<-
Р<4
В теории пластичности существуют и другие попытки
построения системы уравнений для анизотропного случая, которые
переносятся на ползучесть. Изложенную теорию можно считать
обобщением теории типа Мизеса, использующей квадратичный
инвариант тензора напряжений. С другой стороны, можно было
бы предположить свойства материала для некоторых
фиксированных направлений известными и построить кусочно-линейный
потенциал. Соответствующий критерий ползучести будет являться
286 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
обобщением критерия Треска — Сен-Венана либо критерия
наибольшего приведенного напряжения. Для идеальной
пластичности соответствующие уравнения получены, например, в
работах [41], [346], Р44], для ползучести — в работе [137].
§ 70. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ АНИЗОТРОПИИ
Первый возможный тип испытаний для определения
параметров анизотропии и проверки, существует ли анизотропия на самом
деле и обладает ли она предполагаемыми свойствами симметрии,
заключается в том, что главные оси тензора напряжений
направляются по осям симметрии. Обозначая по-прежнему главные
напряжения а\, сг2, о, запишем:
S -=-- Аймаком =
= { [B-а) о\ - B-а) а| + 2а| + 2 (- 1 г а) fflaa-2a2o3-
-газо,]-^!--Jfaj-aa)*. G0.1)
В этой формуле, очевидно, вместо разности о^ — 02 можно ввести
разность соответствующих компонент девиаторов. Воспользуемся
теперь представлением девиатора напряжений через параметры от,
и 0, как это было сделано в § 66. Получим:
5--|aJ [l-|asin2f'|-9")] .
Положим
и будем считать потенциал ползучести функцией от величины
<т0А(в):
Ф = Ф[а0АF)].
После несложных преобразований мы можем записать
уравнения F9.3) в следующем виде:
Ч = 4 Ф' (о-о/г) -^ [ с, - f (О! - a2) ] ,
ег = А ф' (о-,,/;) -±- [ а2 +1 (ot-o3) ] , G0.2)
§ 70] ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ АНИЗОТРОПИИ 287
или, если перейти к параметрам о0 и 8:
Е) = —г- COS 8 =¦ Sin ( -п С
h L yj V 3
K2 = ^[cos@--f-) + |sin(f-в)],
Ф' /д 4я Л
Образуем из sl5 e2 и е3 те Hie комбинации, что в § 66. Получим:
e,s — -j\ ed cos 8 -f e2 cos ( 8 g- J + e3 cos ( 8 1^ J =
=1ф'[1-4«-(т-е)]- G0-3)
«I = —-g- fi sin 8-f e2sin Г 8 ^- J -fe3sin Г 9 g- J =
А.Ф'айп(^-2е;
Отсюда
x (8) =
2я
es 3—a , fin 2Q
Величина x (8) определяется в результате эксперимента; зная
ее, можно найти а. Действительно, из вышеприведенного
соотношения следует:
— _20Л'.
3 J cosf-^-2eV G0.4)
а ¦& @) V 3
Если изложенная теория справедлива для данного материала, то
правая часть в формуле G0.4) должна быть постоянной. Зная а,
можно найти Ф' (crafe) по любой из формул G0.3).
Отклонения от теории типа Мизеса, обнаруживаемые при
экспериментах, могут быть объяснены либо влиянием третьего
инварианта, либо анизотропией материала. В первом случае
экспериментально определяемая функция к (8) имеет период -а- ,
во втором — период л. Если опыты ведутся в узком диапазоне
углов 6, то обнаружить разницу и сделать определенный вывод
не всегда легко.
Рассмотрим теперь опыт на одновременное действие
растяжения и кручения. Положим а33 = о", о23 = т, все остальные
компоненты тензора напряжений равны нулю. Положим также
288 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ, "НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
е33 = е, е23 = -^-у, еи = е22 = е". Тогда, как легко убедиться,
S* = \[o* + @-2&)i*]. <70-5)
2
.^а — _
3
Скорости ползучести даются следующими простыми выражениями:
в = 4Ф'E)с,
Y = 40'E)C-2P)t, G0.6)
1 •
Отсюда, в частности, следует:
i=C_2p)^. G0.7)
е
Если, например, на опыте будет обнаружено, что -г = 4 — , отсюда
е
можно заключить либо что материал изотропен и подчиняется
закону течения типа Сен-Венана, либо что он анизотропен и р1 =
1 1
= — ^ ¦ Но если (J = — -у , то величина S, определяемая
формулой G0.5), становится пропорциональной квадрату наибольшего
касательного напряжения:
? = |[а2 + 4т2]=4т1ах.
Формулы G0.6) и формулы § 68 делаются при этом
неразличимыми, и опыт на растяжение и кручение не дает возможности
для суждения о том, является ли материал фактически
анизотропным, если не производится измерения деформации в поперечном
направлении. По теории типа Сен-Венана должно быть е22 = —е,
бц = 0, тогда как для анизотропного материала с квадратичным
1 *
потенциалом ползучести е22 = ?зз = ~~ ~2е' ^ы остановились
на этом случае для того, чтобы показать, какие трудности могут
встретиться при интерпретации опытных данных.
§71. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
Теория установившейся ползучести, представляющая собою
обобщение на пространственный случай простейшего
предположения о постоянстве скорости при постоянном напряжении,
оказывается недостаточной для решения большого числа практически
интересных задач. Уже учет упругой деформации приводит
к тому, что напряжения в теле перераспределяются со временем
§ 71]
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
289
от того состояния, которое возникает в начальный момент и
находится методами теории упругости, до предельного состояния
установившейся ползучести, которое не может быть полностью
реализовано за конечное время. Самая простая теория,
позволяющая рассматривать процессы неустановившейся ползучести, будет
состоять в том, что скорость по-прежнему считается зависящей
от напряжения и постоянной при неизменном напряжении, но
упругие деформации не полагаются пренебрежимо малыми.
Соответствующие уравнения можно, конечно, записать для
изотропной среды с учетом зависимости потенциала ползучести
от третьего инварианта, для анизотропной среды, наконец, без
каких-либо предположений о существовании потенциала. Чтобы
не усложнять дело, мы будем отправляться от квазилинейных
уравнений, рассмотренных в § 68. Считая материал упруго-
сжимаемым, причем о = ЗКе, мы найдем, что
1 -
Pi} = eU — -о7Г°
2G
'«/¦
Здесь pij — тензор деформаций ползучести. Скорость
ползучести Zij = рц, поэтому из F2.2) следует:
Уравнения G1.1) с учетом соотношений объемной упругости
можно записать также следующим образом:
еи = 4"[cTl1 ~~ v @22 + °33^ + ~^^~ [ 0ii ~ 4" @22 + 033) ] •
-° ¦ • G1-2)
1 • . о V (On)
Yl2 =-?-0-12+3—~<*12-
Совершенно аналогичным образом можно получить уравнения
теории типа Сен-Венана, если взять за основу F8.2), а именно:
ei = ?г [o-f — v (сг2 + о-3)] + v (o-i —о2),
e2 = xIa2 — v(as + °i)]» G1-3)
Ч = -g- [o-g — v (at + сг2)] — v (o-j — 0-3).
Мгновенная деформация, возникающая при приложении
нагрузки, может быть не только упругой, но и пластической, в этом
случае под тензором рц нужно по-прежнему понимать тензор
19 Ю. Н. Работнов
290 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. \
деформаций ползучести, следовательно,
1 - и
Pij -ец 2G °и еИ'
Для того чтобы объединить уравнения пластичности и
ползучести, можно отправляться от разных теорий пластичности;
простейшее предположение будет состоять в том, что начальная
пластическая деформация сопровождается изотропным
упрочнением, следовательно,
л?Рп _ А 8' (go) - . J„
2 0О
Уравнения, описывающие начальную пластическую
деформацию и ползучесть, будут следующими:
G 2 °° G1.4)
en ==z-2G~au + Yv (ст°) ~^~ ПРИ а°<°-
Совершенно аналогичным образом можно получить уравнения,
в основе которых лежит закон ползучести F8.3); мы их
приводить не будем.
В действительности первый участок на кривых ползучести
отсутствует только при весьма высоких температурах, когда
ползучесть является кратковременной; расчет по
установившейся стадии обычно предполагает, что деформация ползучести
достаточно велика по сравнению с упругой. В тех задачах, в
которых учет упругой деформации необходим, как правило,
пренебрежение первой фазой ползучести вносит погрешность большую,
чем уточнение за счет учета упругой деформации. Поэтому
уравнения G1.1) — G1.4) имеют весьма ограниченную область
применения. Применительно к одномерной задаче этот вопрос был
рассмотрен в § 47, и там же была изложена идея Одквиста [314].
сводящаяся к тому, что деформация первой фазы ползучести
заменяется некоторой эквивалентной мгновенной деформацией.
На уравнения G1.4) можно смотреть точно так же, тогда функция
g (a0) описывает не начальную пластическую деформацию, а дает
поправку на первый участок, именно так была введена функция
g (оо) в § 47.
Изложенная точка зрения оказывается полезной в тех
случаях, когда второй участок на кривых ползучести выражен
достаточно отчетливо и нас интересует поведение конструкции в такие
времена, когда первый участок наверняка пройден. Класс задач,
решаемых по схеме Одквиста, неизбежно ограничен случаями,
когда напряженное состояние существенно не меняется.
§ 72] ТЕОРИИ ПОЛЗУЧЕСТИ ДЕФОРМАЦИОННОГО ТИПА 291
В главе IV мы рассматривали всевозможные теории
одномерной ползучести, устанавливающие связь между величинами р,
о, их производными и временем; любая из этих теорий может
быть распространена на пространственный случай, причем не
единственным способом. Трудность построения системы уравнений^
пространственной ползучести состоит скорее не в недостатке,
а в избытке аналитических средств; вставая па точку зрения
гипотезы упрочнения, старения, наследственности и т. д., мы
можем написать множество систем уравнений, из которых
получаются одинаковые уравнения для одномерного случая.
Очевидное требование инвариантной формулировки теории
наталкивается на затруднение в выборе между очень большим
количеством инвариантов, которые можно образовать, скажем, от двух
тензоров, являющихся функциями времени. При скудности
опытных данных, больших технических трудностях, связанных с
постановкой эксперимента принципиального характера, и
неизбежном разбросе характеристик образцов мы не можем зачастую
отдать решительное предпочтение той или иной теории
ползучести. В некоторой мере спасительным обстоятельством служит то,
что в большинстве случаев условия работы изделий,
подверженных ползучести, оказываются довольно спокойными. Внешние
силы, как правило, либо остаются неизменными, либо меняются
таким образом, что тип напряженного состояния сохраняется;
за счет упругой деформации и первой фазы ползучести происходит
некоторое перераспределение напряжения, но перераспределение
достаточно плавное, обычно не сопровождающееся поворотом
главных осей. Если обратиться к аналогии с теорией
пластичности, то речь будет идти о таких путях нагружения, для которых
учет анизотропии упрочнения не вносит существенного
уточнения по сравнению с расчетом по теории изотропного упрочнения.
Для такого рода задач, по-видимому, наиболее важен вопрос
о том, какой именно принцип полагается в основу теории, с чем
связывается переменность скорости по времени — с самим
временем, с величиной накопленной деформации, с рассеянной
энергией. Различные формулировки уравнений, описывающих
ползучесть на основе этого принципа, не слишком сильно разнятся
между собою, и мы вправе руководствоваться при выборе в
первую очередь соображениями простоты и удобства.
§ 72. ТЕОРИИ ПОЛЗУЧЕСТИ ДЕФОРМАЦИОННОГО ТИПА
Деформационная теория пластичности Надаи — Генки, по
крайней мере принципиально,— наиболее простая из теорий
пластичности, позволяющих учесть упрочнение материала и его
упругие деформации. Имея в виду построение достаточно удобной
технической теории ползучести, Беляев [5] высказал идею, которая.
19*
292 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
легла в основу большого количества различных вариантов
теории. Идея состоит в том, что напряжения и деформации при
ползучести связаны конечными соотношениями, совершенно
аналогичными соотношениям деформационной теории пластичности
(§ 12), а именно:
3 е0 — о
е»,- =
<Уц, е = -цк- G2.1)
11 ~~ 2 о0 ""' Ш ¦
Из G2.1) следует (см. § 12):
^~ у0 ~ 3 о0 ¦
Теперь предполагается, что величины т0 и уо или е0 и о0 связаны
между собою теми же соотношениями, которыми связаны
деформации и напряжения в одноосном случае. Рассмотрим некоторые
получающиеся при этом возможности:
1. Теория старения. Подобно тому, как в одномерной задаче
теория старения предполагает существование зависимости между
деформацией, напряжением и временем, в пространственной
задаче мы будем считать, что е0 = е0 (ст0, t). Эта зависимость
может быть задана изохронными кривыми ползучести [98],
то есть кривыми зависимости е0 — о0 при фиксированных
значениях времени. При этом ед есть интенсивность полной деформации
и в уравнениях G2.1) фигурируют полные деформации, таким
образом, упругая и начальная пластическая деформации
оказываются включенными в рассмотрение автоматически. Уравнения
записываются следующим образом:
ец = у е0 (а0, t) -~ , e=Jx- G2-2)
Это — уравнения деформационной теории пластичности, в
которые время входит как параметр. Если исходные данные
получены из опытов на растяжение, то кривые еа — о0 должны
перестраиваться из кривых е — ос поправкой на сжимаемость.
Обычно такое уточнение не имеет смысла, приближенность теории
старения позволяет принимать К= оо, то есть считать материал
несжимаемым и в упругой области. Расчет по теории старения
сводится, таким образом, к серии расчетов по деформационной
теории пластичности, для каждого момента времени выбирается
соответствующая изохронная кривая, и состояние системы в
данный момент не зависит от ее предшествующих состояний. Мы
видели, что при медленно меняющихся напряжениях теория
старения дает результаты менее грубые, чем это можно было ожидать,
имея в виду явное несовершенство теории. Так, предсказания
релаксации по этой теории оказываются не слишком далекими
от истины (§ 48). Зато отпадают все трудности, связанные с выде-
§ 72] ТЕОРИИ ПОЛЗУЧЕСТИ ДЕФОРМАЦИОННОГО ТИПА 293
лением начальной упругой и пластической деформации, и, что
самое главное, первичные кривые ползучести используются без
какой-либо схематизирующей аппроксимации. Для расчета
изделий из структурно-неустойчивых материалов на большую
длительность, пожалуй, в настоящее время нельзя предложить чего-
либо более разумного, нежели теория старения. Поэтому
изложенный вариант теории старения нашел довольно широкое
распространение в практике расчетов на прочность элементов турбо-
машин (см., например, F3]).
Укажем на одну форму аналитической записи уравнений
теории старения, которая применялась Марином [221]. В главных
осях эти уравнения записываются так:
ei=^-t^ — v(o-2 + o-3)] +
+ ^-1{*1 + Аг[1-ехр(-д01 + *8«} X [at—g-fo + cs)], G2.3)
Очевидно, что это — частный случай уравнений G2.2).
Константы ки к2, кв и q определяют функцию времени, которая
довольно хорошо аппроксимирует действительные кривые
ползучести. Как нетрудно убедиться, уравнения G2.3) соответствуют
тому случаю, когда изохронные кривые ползучести подобны
и зависимость ей от сг0 — степенная с постоянным показателем п.
2. Варианты теории старения. Зависимость между
напряжениями и деформациями, содержащая явно время, может быть
выбрана и более сложным способом. Так, взяв за основу
соотношение D8.2), мы можем принять
1
Если функция в правой части может быть представлена как
произведение функции от напряжения S (о0) на функцию от времени
х (t), то в результате интегрирования получится:
т
*<>=-§-+ $5 (о0)<*т. <72-4>
о
По-видимому, подобная комбинация деформационной теории
пластичности со второй теорией старения никем не
рассматривалась, преимущество ее перед первой теорией сомнительно,
а последовательное проведение точки зрения на ползучесть как
на процесс течения требует, чтобы и тензорные соотношения также
формулировались для скоростей.
3. Теория Беляева. Теория ползучести, предложенная
Беляевым р] и усовершенствованная Малининым I108], применительно
294 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
к одномерному случаю была изложена в § 48. Если переписать
уравнение D8.5) для интенсивностей напряжений и деформаций,
то мы получим:
e^o[^+l^-dr]. G2.5)
о
4. Теория упрочнения. В качестве меры упрочнения можно
выбирать разные инварианты, которые сводятся в одномерном
случае к одной и той же величине — накопленной деформации
ползучести. Следуя идее не вводить иных независимых
инвариантов, кроме е0 и а0, мы должны определить меру упрочнения р0
следующим образом:
р° = е°-ж- G2-6)
Теперь нужно предположить, что величины рд и а0 связаны
уравнением состояния:
Ф(р0,Ро,о0,Т) = 0. G2.7)
Такой вариант теории упрочнения в пространственной задаче
ползучести был развит в работе Чурикова I145]. Нетрудно
убедиться, что величина р0 связана со вторым инвариантом тензора
деформаций ползучести следующим образом:
2 2
5. Теория наследственности. В статье [" ] аналогичным
образом были введены уравнения наследственной теории ползучести.
Зависимость между инвариантами была принята следующей:
t
Ф Ы = ¦$%- + I K(t-x)a0(x)dx. G2.8)
Теории ползучести деформационного типа, если понимать
их как некоторые физические соотношения между напряжениями
и деформациями, вряд ли могут рассматриваться как адекватный
аппарат для описания действительных процессов ползучести
в металлах и представляют теперь скорее исторический интерес.
Однако теория старения, сформулированная уравнениями G2.2),
не потеряла всего значения и в настоящее время, большой опыт,
накопленный в отраслевых исследовательских институтах и на
заводах, позволяет ее рекомендовать для применения в
инженерных расчетах.
§ 73]
ТЕОРИИ ТЕЧЕНИЯ
295
§ 73. ТЕОРИИ ТЕЧЕНИЯ
Теория типа течения устанавливает непосредственную связь
между тензором скоростей деформаций ползучести и тензором
напряжений. Некоторая достаточно общая точка зрения на
ползучесть состоит в том, что и для неустановившейся ползучести
постулируется существование потенциала, так что
• _ дФ
PiJ - doi}
или
PU = B-?L; G3.1)
при этом функции Ф и Н зависят от некоторого числа параметров,
характеризующих состояние материала. Так же как и при
установившейся ползучести, для изотропного материала функция Ф
может зависеть от второго и третьего инвариантов тензора
напряжений, но параметры состояния в свою очередь могут зависеть
от напряжений. Мы вернемся к этому вопросу, когда будем
рассматривать различные варианты гипотезы упрочнения, сейчас же
займемся простейшим случаем. В качестве параметра состояния
может быть выбрано просто время, тогда мы получим некоторый
вариант теории течения. Будем называть соответствующие
уравнения уравнениями теории течения со старением. Если Ф (оц)
может быть представлена как произведение функции
интенсивности напряжений на функцию времени т (t), то
^ = 1-^^@. G3.2)
Уравнения G3.2) широко используются в книге Качанова [52].
Удобство их состоит в том, что они совершенно совпадают с
уравнениями теории установившейся ползучести, только скорости
берутся по отношению к измененному времени х (t). Мы уже
указывали в § 48, что неинвариантность по отношению к
изменению начала отсчета времени делает уравнения теории старения
физически неприемлемыми, однако для медленно меняющихся
напряженных состояний эти уравнения применимы, поскольку
выбор функции т (t) позволяет описать достаточно точно начальные
участки кривых ползучести. При пользовании уравнениями
G3.2) следует учитывать упругие деформации, таким образом
можно описать процесс перераспределения напряжений.
Перейдем теперь к уравнениям, обобщающим гипотезу
упрочнения. Предположим сначала, что единственным параметром
упрочнения является некоторый скалярный инвариант р, который
в случае одноосного растяжения превращается в величину накоп-
296 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. ЛГ
ленной пластической деформации. Тогда Ф = Ф (р, а^}. Здесь
и в дальнейшем мы предполагаем, что зависимость от напряжения
сводится к зависимости от о, то есть уравнения ползучести
являются квазилинейными. Можно сделать более общее
предположение о том, что потенциал зависит от некоторой однородной
функции нулевой степени s(cr^), тогда в рамках тех же
соображений удается рассмотреть закон течения типа Сен-Венана и
законы течения для анизотропных материалов. Мы не будем касаться
сейчас этих обобщений. В качестве инварианта можно ввести
уже использованную в § 72 величину интенсивности деформаций
ползучести
Однако эта возможность не единственна. Интенсивность
скоростей деформаций ползучести, определенная аналогичным образом:
ъ_2_ • -
^о — з PiiPu*
не равна производной от р0 по t, а инвариантная величина
t i
q°= \ ("з pvpvj dt G3-3>
о
может быть выбрана в качестве меры упрочнения вместо р0. Если
рассмотреть девятимерное пространство деформаций ползучести,
то ро есть длина радиуса-вектора изображающей точки, тогда
как q0 — длина дуги ее траектории. Для радиальных путей,
когда все деформации ползучести изменяются в одном и том же
отношении, р0=до- В частности, для одномерного случая всегда
Ро=Яо-
У нас нет сколько-нибудь серьезных оснований для того,
чтобы предпочесть одну меру упрочнения другой, применение
меры упрочнения <?о связано с некоторыми удобствами.
Действительно, если Ф = Ф (а0, q0), то
• _ 3 ЭФ Pij
Р" - 2 Эа0 а0 •
Возведем в квадрат и просуммируем. Получим с учетом G3.3):
ЭФ
«•-ft*'
При одномерной ползучести q0 = р, а0 = о", таким образом,
функция Ф может быть определена. Если закон одномерной ползучести
§ 73]
ТЕОРИИ ТЕЧЕНИЯ
297
можно принять в виде E0.6), то
f(°0)
Яо =
А («о)
p3/MJ^. A3Л)
у,} 2 fe(g0) O0 v '
Уравнение G3.4) дает те же результаты в одномерном случае,
если заменить q0 через р0; в пространственном случае, вообще
говоря, это будут разные уравнения.
Если предположить, что степень упрочнения определяется
тензором деформаций ползучести, то потенциал ползучести
должен быть функцией инваринтов тензора напряжений, тензора
деформаций ползучести и совместных инвариантов. Как известно,
полная система инвариантов будет следующая (см., например, [19]):
о"п, o'ijO-jy, OijGjbabi, pa, PijPtjyPijPjbPhi, рцаи, PuPj^hi, Pu^jk^hi-
Если ввести в рассмотрение тензор скоростей деформации
ползучести, то к этим инвариантам можно добавить интегральные
инварианты; одним из примеров такого инварианта является
определенная выше величина q0. Более общее определение инварианта
подобного рода будет следующее:
¦=\[о^р%т1и^
Здесь а\™\ pfh, pui — соответствующие степени тензоров.
Еще более широкие возможности получаются в том случае, когда
на компоненты тензоров действуют некоторые инвариантные
интегральные операторы. Так, например, можно построить
тензоры вида
ву = л eij, o"ij = i csij,
где К* и Г* — интегральные операторы Вольтерра, и
образовывать инварианты из этих тензоров, при этом получаются
некоторые уравнения теории наследственного типа.
Мы не будем анализировать весьма широкие возможности
построения различных теорий ползучести, которые открываются,
если следовать указанному пути, наша задача скорее состоит
в том, чтобы найти простейшие средства описания явления.
Даже если предположить, что тензор скоростей деформаций
есть функция мгновенных значений тензора напряжений и
тензора деформаций ползучести, то есть не учитывать предыстории
деформирования, тензорно-линейные зависимости оказываются
очень сложными; некоторые примеры сконструированных
подобным образом соотношений можно найти в работе [354].
298 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
§ 74. ОБОБЩЕНИЕ ТЕОРИИ УПРОЧНЕНИЯ
Подобно тому, как это было сделано в одномерном случае
(§ 55), мы будем предполагать, что мгновенное состояние
материала определяется заданием некоторого числа параметров
состояния <7г, так что Ф = Ф (qi7 q2, . . ., qn, atj, T). Для простоты
анализа допустим, что зависимость от напряжений сводится к
зависимости от некоторой однородной функции нулевой степени
s (atj), это может быть интенсивность напряжений, либо
наибольшее касательное напряжение, либо какая-нибудь другая, например
кусочно-линейная, функция напряжений. Параметры состояния
qt мы будем определять при помощи следующих линейных
дифференциальных соотношений [339]:
dqt = а\а dpr$ -J- b\s dars + cldt + dldT. G4.1)
Коэффициенты alrs, blrs, cl, dl могут зависеть от тензоров
напряжений и деформаций ползучести, от времени, температуры и
параметров qt. Достаточно широкие возможности выбора системы
определяющих параметров, заданных соотношениями G4.1),
делают такую точку зрения довольно гибкой. Уравнения течения
могут быть при этом записаны следующим образом:
дф ds дф ,г „, оч
Дополнительные члены, зависящие от b\j, могут описать в
известной мере деформационную анизотропию, а также возврат.
Из соотношений G4.1) и G4.2) следуют известные формы
уравнений теории течения, а также некоторые другие варианты.
В частности, один из параметров qt может быть просто временем,
тогда мы получаем теорию течения со старением. Рассмотрим
некоторые другие возможности:
1. ars — prs, brs = c — d = 0. В этом случае
dg = ptjdpij, q = ^PijPij.
Полагая p\ — ?>q, мы вводим обычную меру упрочнения р0, равную
интенсивности деформаций ползучести.
2. ars = aTS, brs = c = d = 0. При этом
t
dq1 = aTSdprs, qi=\orsdprs. G4.3)
о
Мы уже видели в § 55, что выбор в качестве меры упрочнения
величины рассеянной при ползучести энергии qt имеет некоторые
преимущества перед обычным вариантом теории упрочнения,
S 75]
КВАЗИУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
299
в дальнейшем мы будем пользоваться определенным таким
образом параметром gt.
3. ars=--0, brs = prs, c = d = 0,
л G4-4)
, da r.. '
dq2 = Prsdars, q2 = \ pr
Pij— Яс Ягт. . + Лл„ РЧШ
В одномерном случае введение параметра д2 позволяет хорошо
описать эффекты, наблюдаемые при внезапном изменении нагрузки.
Если сохранить предположение о существовании потенциала,
то уравнения G4.2) принимают следующий вид:
дф ds ЭФ
ds doij dq%
Эти уравнения описывают полный возврат при снятии нагрузки,
что у металлов никогда не наблюдается.
4. Яг8 = Огв1 &rs — Prsi С —и,
dq3 — orsdprs + prsdars, qs = PrSOrS-
Величина qs была предложена в качестве меры упрочнения
в одной из работ Бейли [163], который, впрочем, не обследовал
соответствующие уравнения достаточно подробно и не сопоставил
с экспериментом или результатами других теорий.
5. Выбор в качестве меры упрочнения величины q0,
определенной уравнением G3.3), не укладывается в рассматриваемую
схему. В дальнейшем при рассмотрении конкретных задач
неустановившейся ползучести мы будем принимать в качестве меры
упрочнения либо величину q0, либо в некоторых случаях gt.
Предполагая подобие кривых ползучести и определяя s как
интенсивность напряжений, мы получим:
• _ 3 f(a0) оц п, 5,
Р"-тщ-^- G4-5)
Здесь десть либо qQ, либо qit Совершенно аналогичным образом
получаются уравнения для того случая, когда в качестве
эквивалентного напряжения выбирается наибольшее касательное
напряжение или разность главных напряжений. Мы не будем сейчас
выписывать эти уравнения, а рассмотрим их более подробно
в следующих главах, где они найдут применение для решения
тех или иных задач.
§ 75. КВАЗИУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
Уравнения теории ползучести типа теории течения в
некоторых случаях могут быть проинтегрированы, и из них получаются
конечные зависимости между деформациями, напряжениями и
временем. В случае теории установившейся ползучести это очевидно,
300 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
если напряжения постоянны, то постоянны и скорости
деформации ползучести е^-, следовательно, ptj = &ijt; уравнения
могут быть переписаны в конечном виде следующим образом:
3 и(а0) - ,
Совершенно аналогично будет обстоять дело с уравнениями
теории течения со старением. Когда atj = const, то из G3.2)
немедленно следует:
^=Т^^@- G5Л)
Если в первом случае имеет место установившаяся ползучесть,
то во втором мы будем называть ползучесть квазиустановившейся.
Можно дать общее определение квазиустановившейся
ползучести, а именно: напряжения остаются постоянными, а
деформации пропорциональны одной и той же функции времени х (t).
Строго говоря, квазиустановившаяся ползучесть может быть
реализована, только если напряженное состояние в теле однородно
и, следовательно, для упругих деформаций уравнения
совместности выполняются тождественно. В общем случае тела
произвольной формы, нагруженного внешними силами, упругое
напряженное состояние отлично от напряженного состояния в процессе
ползучести. Таким образом, о квазиустановившейся ползучести
можно говорить лишь тогда, когда упругие деформации
пренебрежимо малы, в частности пренебрежимо мала и объемная
деформация.
Как оказывается, состояние квазиустановившейся ползучести
возможно, опять-таки при пренебрежении упругими
деформациями, также и в теории упрочнения, однако при специальном
выборе функции h (q). Возьмем за основу уравнения G3.4), приняв
в них h (q) = qa, выберем меру упрочнения по Одквисту, то есть
t
положим q = <?0 = ^ Q^PijPuJ /2 dt.
о
Пусть на тело действуют постоянные внешние силы и никакие
внешние кинематические связи не наложены. Тогда уравнения
равновесия будут удовлетворены при предположении, что
напряжения не зависят от времени, atj = const. Деформации
ползучести мы будем искать в виде ptj- = рц т (t), где pi'j — не зависящий
от времени тензор. Тогда q = тр'0, гдер„ — интенсивность тензора
Pi'j. Внесем в G4.5), получим:
ч
LY Гт=Д-У пЛ = ±п'-*Ш-
mJ Кт=Т+Ъ.)' РЧ = -2Р°~
§ 75]
КВАЗИУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
301
Образуя с помощью второго уравнения инвариант р'п, мы получим:
Ро2 — Po~2af2 @o)- Отсюда находится р'0 в зависимости от f(a0),
и мы получаем окончательно:
В случае, когда направление главных осей тензора напряжений
известно, можно получить более простые соотношения на основе
критерия ползучести типа Треска. Для этого мы примем за
функцию s величину <Ti — а3, в качестве же меры упрочнения просто
примем величину наибольшего сдвига, то есть положим
2g = Pi — р3. Тогда из уравнений течения мы получаем:
Pt = — Рз = ф(?, s)> p2 = 0. G5.3)
Функция ф (q, s) определяется так же, как в случае одноосного
растяжения; задаваясь специальным видом закона упрочнения,
мы получим:
Pi=-p3 = q-af(Oi-os), k = 0. G5.4)
Вид правой части в первом уравнении G5.4) определен для условий
опыта на растяжение, когда остается лишь одно главное
напряжение, два других главных напряжения равны нулю. Однако,
когда два главных напряжения равны между собою, условие
текучести типа Треска не позволяет сказать ничего о распределении
деформаций в этих направлениях. Пусть, например, Cj > ст2 — °"з-
Наложив всестороннее сжатие с интенсивностью — ст3, мы получим
одноосное растяжение в направлении. 1, следовательно,
Pi = PTaf(oi-a2l8). G5.5)
Относительно скоростей течения в направлениях 2 и 3 можно
сказать только, что из условия несжимаемости их сумма р2 + Рг
равна — р{. Существенная простота применения теории
упрочнения в соединении с законом течения типа Треска связана с тем,
что мера упрочнения выражается через конечные значения
деформаций. Если напряжения постоянны, то, полагая pt = pi % (t)
и внося в G5.4), получаем:
ri"=-p;=[/(ni-o!,.)r.
Если на границе тела всюду заданы усилия, сохраняющие
постоянную величину, то уравнения равновесия всегда могут быть
удовлетворены в предположении, что напряжения остаются
постоянными. Этим постоянным напряжениям соответствуют постоянные
302 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. \
упругие деформации, но деформации ползучести пропорциональны
совершенно определенной функции времени т (t). Поэтому
уравнения совместности деформаций, вообще говоря, не выполняются.
Состояние квазиустановившейся ползучести может быть
реализовано, когда деформации ползучести достаточно велики и
упругими деформациями можно пренебречь. Таким образом, состояние
квазиустановившейся ползучести для материалов, подчиняющихся
уравнению состояния с изотропным упрочнением, осуществляется
при следующих условиях:
1. Внешние силы постоянны, и на тело не наложены
кинематические связи.
2. Кривые ползучести подобны и описываются степенной
функцией от времени.
3. Упругие деформации пренебрежимо малы.
Заметим, что условия квазиустановившейся ползучести могут
быть реализованы и при иных формах закона упрочнения, например
при q = q% G4.3). Мы не останавливаемся на этом достаточно
очевидном выводе [339]. С другой стороны, возможность
квазиустановившейся ползучести при менее стеснительных
предположениях вытекает и из уравнений наследственной теории
деформационного типа, предложенной ранее автором [9В]. Говоря
точнее, при построении уравнений автор стремился к тому, чтобы
получить возможность нахождения некоторых достаточно простых
и общих классов решений. При этом отправной точкой послужило
отмеченное в § 44 подобие изохронных кривых ползучести.
Уравнения этой теории для пространственного случая (§ 72) имеют
следующий вид:
eiJ~J~^aiJ' е~зк-
При этом е0 зависит от а0 следующим образом*.
A + ?*)со = ф(*о).
Предположим теперь, что материал несжимаем, Оц = а^ц (t),
еи = CijX (t), Oi'j и a'j — тензоры, не зависящие от времени.
Потребуем также, чтобы ф (е0) было степенной функцией с показателем
степени р\ Тогда функции времени ц. (t) и k (t) оказываются
связанными следующим интегральным уравнением:
A + Я*)ц. = ?Л G5.6)
тогда как для сг^и ец мы получаем систему уравнений
деформационной теории пластичности со степенным упрочнением.
По сравнению с предыдущим выводом, основанным на гипотезе
уравнения состояния, мы не должны накладывать ограничений
на вид зависимости деформации ползучести от времени, ядро
К (t — т) — остается произвольным. Упругая деформация, по
§ 76] ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИЙ ПОЛЗУЧЕСТИ 303
существу, здесь также выброшена, поскольку график
функции ф (е0) не может иметь прямолинейного участка. Если
внешние силы постоянны, то |i = const и из G5.6)
определяется X (t). В предыдущем рассмотрении были наложены
ограничения на форму кривых ползучести в зависимости от времени,
тогда как здесь принимается определенная зависимость от
напряжения. Зато теперь ползучесть будет квазиустановившейся не
только при постоянных нагрузках, но и при нагрузках,
изменяющихся со временем в одинаковом отношении. Рассмотрение
этого случая по теории упрочнения возможно лишь тогда, когда
/ (а) есть степенная функция.
По-видимому, расчеты по теории квазиустановившейся
ползучести будут давать удовлетворительные результаты во всех
случаях, когда кривые ползучести можно считать подобными
и упругие деформации пренебрежимо малы.
§ 76. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИЙ ПОЛЗУЧЕСТИ
ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ.
РАННИЕ РАБОТЫ
Количество опубликованных работ, посвященных
экспериментальному исследованию ползучести при* сложном напряженном
состоянии, к настоящему времени довольно велико. Почти все
эти исследования производились на тонкостенных трубках,
подвергавшихся растяжению, кручению и внутреннему давлению
в различных комбинациях. Следует отметить, что из этих опытов
не всегда бывает легко извлечь ясную картину явления. Известно,
что кривые ползучести при растяжении обнаруживают большой
разброс. В сложном напряженном состоянии, конечно,
наблюдается то же самое. Но при опытах на сложное напряженное
состояние многие исследователи не располагали достаточно
большим количеством испытательных машин, поэтому им не
удавалось собрать достаточно полный материал, который бы допускал
надежное осреднение. В ряде работ отсутствуют данные,
подтверждающие изотропию материала в исходном состоянии. При
обработке результатов некоторые авторы рассматривали лишь
зависимость скорости установившейся ползучести от напряжения,
другие же сравнивали кривые ползучести целиком, включая
первые участки.
По-видимому, во всех без исключения работах исходной
гипотезой, подлежащей проверке, была гипотеза о том, что
соотношения между компонентами скорости ползучести и соотношения
между компонентами напряжения связаны между собою
зависимостями теории типа Мизеса, тогда как величины скоростей
определяются вторым инвариантом девиатора тензора
напряжений Sij или интенсивностью напряжений о! таким образом,
304 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
за основу принималось либо соотношение F8.1), либо
аналогичное ему, которое для случая квазиустановившейся ползучести
можно записать следующим образом:
Ру=|*М-^-т@. G6Л)
Обработка с помощью уравнения G6.1), конечно, возможна лишь
тогда, когда кривые ползучести при различных видах
напряженного состояния подобны. Для первых участков кривых
ползучести такое подобие действительно существует, но подобрать
функцию т (t) таким образом, чтобы уравнение G6.1) было
пригодно как для первой, так и для второй фазы ползучести, вряд ли
возможно. Поэтому, строго говоря, результаты обработки данных
кратковременных испытаний с помощью G6.1) и исследования
установившейся ползучести на основании F8.1) нельзя считать
сопоставимыми.
Первые по времени экспериментальные исследования
ползучести в условиях сложного напряженного состояния
принадлежат Бейли [162]. Опыты проводились на свинцовых трубах под
действием внутреннего давления и растяжения или кручения,
а также на стальных образцах из малоуглеродистой стали при
температуре 475° и стали с химическим составом 0,45 С, 0,73 Мп,
0,20 Si, 0,19 Ni, 0,023 Cr, 0,032 S, 0,038 P при 480°. Опыты
доводились до выхода на прямолинейный участок кривой ползучести,
измерялись скорости установившейся ползучести.
Проверка применимости тех или иных уравнений к описанию
опытных данных должна состоять из двух частей: с одной
стороны, проверки закона течения, то есть вытекающей из теории
зависимости между отношениями скоростей и отношениями
напряжений, с другой стороны, проверки зависимости между теми или
иными инвариантами тензоров скоростей и напряжений или
деформаций и напряжений. При испытаниях на растяжение
и кручение, как мы видели в § 68, должно быть
Y о т
е
Опыты над стальными трубами в общем подтвердили этот
результат, хотя в отдельных случаях отклонения были довольно велики.
Следует отметить, что лучшее совпадение с данными теории
получалось при больших значениях напряжений и температур. Для
свинцовых труб результаты оказались, в общем, хуже, чем для
стальных. При сравнении рассчитанных значений скоростей
ползучести с экспериментальными данными обнаружились
довольно существенные отклонения. Чтобы добиться лучшего описания
опытных данных, Бейли предложил довольно сложные уравнения,
§ 7р] ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТЕОРИЙ ПОЛЗУЧЕСТИ 305
а именно:
б1 =-. Ло»-™ [@! - о2)т _ (а3 - CTl)m],
е2 = Ло»-1" [(о2 - о-зГ - (crt - а2 Л - G6.2)
е8 = 4о»-»[(Оз-а1)т-(аг-ая)т].
При т = 1, очевидно, эти уравнения совпадают с G6.1).
Оказывается, что при т = 3 теория Бейли также приводит к
уравнениям G6.1). Действительно, легко убедиться в справедливости
тождества
(<*1 — озK — (оз — °iK =
= -i- Bot - <т2 - ст8) [(o-i - o2J + (aa - a3J + (a8 - 04J].
Очевидно, что, вводя в уравнения лишний параметр т, можно
всегда добиться лучшего описания опытных данных. Однако там,
где отклонения от закона G6.1) значительны, применение
неизмеримо более сложных соотношений G6.2) мало спасает дело. С
другой стороны, теория Бейли представляет собою некоторую частную
форму общих зависимостей F4.7) и выбор именно этой частной
формы особых преимуществ не дает. Некоторые авторы более
поздних работ пытались применить зависимости G6.2) к обработке
своих экспериментальных данных, в настоящее время эти
попытки оставлены; там, где применимы уравнения Бейли, простейшая
теория G6.1) дает также вполне удовлетворительную
аппроксимацию. Не останавливаясь на детальном обзоре соответствующих
результатов, мы упомянем здесь об опытах Ивретта и Кларка [аоа],
в которых проводилось сравнение ползучести при кручении
и при растяжении. Испытанию подвергалась молибденовая сталь,
опыты на кручение производились на тонкостенных трубчатых
образцах, сравнивались скорости установившейся ползучести
со скоростями ползучести, определенными из опытов на
растяжение цилиндрических образцов, прошедших ту же термическую
обработку. Вопрос о степени изотропии исходного материала при
этом остался открытым, неясна роль технологии изготовления
трубчатых образцов. Сравнение результатов испытаний с
предсказаниями теории типа Мизеса обнаружило большое расхождение
[69]; наши попытки обработать данные опытов Ивретта и Кларка
также не привели к положительным результатам, создалось
впечатление, что испытания на кручение дали большой разброс
случайного характера, причина которого не выяснена.
Отметим еще известные и неоднократно обсуждавшиеся [ва],
[и] опыты Нортона I311], а также Нортона и Зодерберга [312].
В этих опытах изучалось поведение труб под действием
внутреннего давления, когда осевое напряжение вдвое меньше окружного.
Обозначая последнее через ait мы найдем, что из уравнений G6.1)
20 ю. Н. Работнов
306 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
следует:
п 1 / dj Уз л
Отметим, что это напряженное состояние отличается от состояния
чистого сдвига только гидростатической составляющей. Действи-
тельно, если а3-=-0 и 02 = -=-сг, го
— 1 — — 1
Oi^-jO, а2 = 0, (т3=-уа.
Опыты Нортона подтвердили достаточно хорошо, что ползучесть
в осевом направлении отсутствует, то есть действительно е2 = 0.
Что касается зависимости скорости окружной ползучести от
напряжения, результаты подтверждают теорию лишь приблизительно.
Значительный разброс экспериментальных точек не дает
возможности основывать на этих опытах какие-либо попытки уточнения
и усовершенствования теории.
Названные экспериментальные исследования, а также другие
работы сделали несомненным одно: для того чтобы исследовать
физические закономерности ползучести при сложном напряженном
состоянии, необходима постановка особо тщательных
экспериментов на материале, который в исходном состоянии заведомо
изотропен, в достаточно широком диапазоне напряжений и температур.
Поскольку структурные превращения, сопровождающие
ползучесть многих сплавов, могут сильно повлиять на наблюдаемые
закономерности, необходимо располагать опытными данными для
достаточно широкого класса материалов. Поведение структурно-
устойчивых материалов, которые приобретают все большее
значение в современной технике, должно рассматриваться как
некоторая норма; при обнаружении отклонений от этой нормы в
индивидуальном поведении тех или иных сплавов при тех или иных
внешних условиях следует искать специфические причины,
обусловливающие эти отклонения. Исследования ползучести при
сложном напряженном состоянии, выполненные в ряде стран в
послевоенные годы, позволяют сформулировать некоторые
определенные выводы; на рассмотрении этих исследований мы остановимся
более подробно.
§ 77. ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ
СОСТОЯНИИ И ПОСТОЯННЫХ НАГРУЗКАХ.
ОПЫТЫ ДЖОНСОНА
Начиная с 1932 г. в Англии сначала в Национальной
физической лаборатории в Лондоне, а с 1952 г. в отделившейся от нее
Национальной инженерной лаборатории (National Engineering
Laboratory) под руководством Джонсона велись систематические
§ 77] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 307
исследования ползучести при сложном напряженном состоянии.
Краткая сводка полученных результатов была недавно
опубликована отдельным изданием [26в]. Обширная программа
экспериментов включала в себя опыты на ползучесть при растяжении и
кручении трубчатых образцов при постоянных и переменных
нагрузках, опыты на релаксацию в сложном напряженном состоянии,
испытания на длительную прочность, а также некоторые
исследования мгновенной пластической деформации. Изучались следующие
материалы:
1. Сталь с содержанием углерода 0,17% при температуре 350°,
450° и 550°.
2. Сталь с содержанием углерода 0,2% при температуре 450°.
3. Молибденовая сталь {0,5% Мо) при 550°.
4. Алюминиевый сплав RR-59 при 150° и 200°.
5. Магниевый сплав B% А1) при 20° и 50°.
6. Хромоникелевый сплав {нимоник 75) при 550° и 650°.
7. Технически чистая медь при 250°.
В первых работах I252], относящихся к исследованию
ползучести углеродистой стали 0,17 С и молибденовой стали, было
установлено подобие кривых ползучести при различных типах
напряженного состояния и возможность аппроксимации
зависимости скорости ползучести от напряжения степенной функцией.
Однако вследствие анизотропии исходного материала сделать
какие-либо четкие выводы о закономерностях ползучести не удалось.
Поэтому мы остановимся более подробно на опубликованном
в 1949 г. исследовании ползучести стали с содержанием углерода
0,17%, выполненном чрезвычайно тщательно, с принятием всех
необходимых мер предосторожности [25Б], а также на последующих
работах, относящихся к другим материалам.
Для того чтобы обеспечить изотропию исходного материала,
образцы вырезались из слитка. Химический состав стали был
следующий: 0,17 С; 0,19 Si; 0,026 S, 0,034 Р, 0,64 Мп. Пробы,
взятые из разных частей слитка, дали одинаковый результат
в пределах точности анализа, таким образом, материал был
химически однородным. Для проверки изотропии материала были
испытаны на ползучесть при температуре 450° и напряжении 945 кг/еж2
цилиндрические образцы, вырезанные в разных направлениях.
Различия в характеристиках ползучести обнаружено не было,
при последующих испытаниях трубчатых образцов также никакого
влияния ориентировки заметить не удалось. Испытания
производились при одновременном действии растяжения и кручения,
трубчатый образец имел внутренний диаметр 1/2 дюйма A2,7 мм),
толщина стенки составляла 0,020 дюйма @,508 мм), допуск на
толщину ±0,0005 дм (~12fi) выдерживался на базе образца,
составлявшей 2 дюйма E0,9 мм). Испытательная машина,
сконструированная и построенная в Национальной физической лаборатории,
20*
308 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Z
в
7
е
5
5
2
7
5S(T
была описана в работе [252]. Всего было испытано около 80
образцов, каждое испытание продолжалось 150 часов. При выбранных
температурах и напряжениях время 150 часов соответствовало
почти всегда первому периоду ползучести, только при 550° для
высоких напряжений кривая ползучести выходила на второй
участок, а иногда даже начиналась третья стадия ползучести.
Для экономии трубчатых образцов испытания на растяжение
производились на обычных цилиндрических образцах,
контрольные опыты на трубчатых образцах заметных отклонений не
обнаружили. При температурах 450° и
550° поверхность образца
окислялась, в результате чего
изменялась эффективная площадь
поперечного сечения. Для выяснения
влияния окисления на изменение
площади было проведено
специальное исследование и при обработке
результатов вносилась
соответствующая поправка. При обработке
данных испытаний в основу был
положен обнаруженный факт
подобия кривых ползучести для
различных уровней напряжений и
различных компонент тензора
деформации при всевозможных
видах напряженного состояния.
Кривые ползучести при кручении
зависят от изменения температуры в процессе испытания
меньше, чем кривые ползучести для других видов напряженного
состояния; поэтому сначала изменением масштаба добивались
того, что все кривые ложились на одну из них, после этого все
другие кривые ползучести перестраивались в измененном
масштабе так, чтобы точки располагались возможно ближе к кривой
кручения. Таким образом была определена функция т (t) в
уравнении G6.1). Графики производной этой функции для трех
температур приведены на рис. 103. Функция т (t) нормировалась
таким образом, что т A50) = 1 при 350° и 450° и т A00) = 1 при
550°, все сопоставление результатов экспериментов ведется по
условным скоростям ползучести в фиксированный момент времени
t = 150 часов для двух меньших температур и ?=100 часов для
температуры 550°, хотя на самом деле производится сравнение
первых участков кривых ползучести в целом; приводимые в статье
значения вовсе не являются скоростями ползучести в данный
момент времени, это некоторые масштабы, использованные для
приведения индивидуальной кривой ползучести к стандартной
кривой при условии наименьшего отклонения на всей длине ее.
50
100
150
Чаш t
Рис. 103.
§ 77] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 309
При более высокой температуре 550° сопоставлялись условные
скорости для времени в 100 часов вместо 150. Это вызвано тем,
что последние 50 часов ползучести сопровождаются появлением
второго и даже третьего участка и подобие кривых нарушается,
тогда как при t < 100 часов подобие соблюдается еще
удовлетворительно. В ходе экспериментов непосредственно измерялись
осевая деформация и угол закручивания; предполагая совпадение
главных осей тензора напряжений и тензора деформаций, а также
пользуясь условием несжимаемости материала, автор вычисляет
главные скорости деформации в определенном выше смысле. Из
условия совпадения главных осей тензора напряжений и тензора
деформаций следует:
2 fa — ey) _ дх
У ~~"
Здесь ех — удлинение в осевом направлении, еу — удлинение
в поперечном направлении, 7 — сдвиг вследствие закручивания,
0Ж — растягивающее напряжение, т — касательное напряжение.
Величины ех и у измеряются непосредственно, из
вышеприведенного уравнения находится еу. После этого вычисляются главные
скорости деформации по формулам
е2,з = —2~ ±уК («x-e^ + Y >
Sj = —83—¦ 63.
G учетом условия совпадения главных осей эти формулы
принимают окончательный вид:
— i + H/H^-S-].
•,-.;.-4[/1ТЩ+?]. G7.D
При комбинации растяжения с кручением одно из главных
напряжений всегда положительно, будем обозначать его а2, второе —
отрицательно, будем обозначать его о3, тогда напряжение в
направлении толщины стенки o"j = 0. Для проверки закона течения
Мизеса, то есть связи между отношениями напряжений и
отношениями скоростей, автор строит график зависимости — от
. Обозначая первое отношение через х, второе через у,
310 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
найдем из G6.1):
Величина х принимает значение, равное нулю при растяжении
и равное 1/2 при кручении. Соответствующие значения у будут
1 /2 и 0. На рис. 104 показана теоретическая кривая зависимости
г/от опытные точки для температуры 350°. Как видно,
существуют некоторые систематические отклонения от предсказаний
ф-
ЦЗ
Ц2
0,1
0,7 Q2 %? Ofi Qf
?з
Рис. 104.
теории; авторы указывают, что эти отклонения увеличиваются
с увеличением интенсивности напряжений. Далее вычислялась
скорость октаэдрического сдвига ^о и строился график
зависимости Yo от т0. На рис. 105 приведен этот график для температуры
350° в двойной логарифмической шкале. Точки достаточно близко
располагаются около одной кривой, несколько неожиданным
кажется то, что точки для чистого кручения, по крайней мере
для невысокого уровня напряжений, все смещены влево примерно
на одинаковую величину, так что через них можно провести
отдельную кривую, показанную пунктиром. В то же время точки,
соответствующие промежуточным между растяжением и
кручением напряженным состояниям, не обнаруживают какой-либо
тенденции расположиться между кривыми для кручения и для
растяжения. Следует отметить, что кривая в двойных
логарифмических координатах может быть аппроксимирована двумя
отрезками прямой, таким образом, степенной закон ползучести для
§ 77] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 311
всего диапазона напряжений не оправдывается. На рис. 106
те же данные представлены в других координатах: по оси абсцисс
отложен логарифм отношения Yo/to, по оси ординат — т0. Точки
группируются около одной прямой, что соответствует зависимости
между уо и т0 вида
7осот0ехр(ст0).
Автор нашел, что для функции v (a0) подходит следующая
аппроксимация:
Отклонения поведения материала от предсказаний теории при
больших значениях интенсивности напряжений Джонсон
объясняет тем, что в момент приложения нагрузки возникает
значительная пластическая деформация, создающая анизотропию
Logv
V
Д75
Ц5
Ц25
350'
/
/
'/
/у
/и
•
Ф
/О
/ у
у
А ^
/У
У
А-
?_
X
• Растяжение
о Иручете
+ б/т=0#
*6/z=0,8
ч б/Г =7,5
о
Рис. 105.
1 W
75
70
О
Л
/У
//"
//
/
#
f
/
•
• Растяжение
о ftpyvmae
* б/Т =0//
+ О/т =Ц8
о а/т =Z5
I
Рис.
106.
щ-%
материала, который в исходном состоянии был изотропен. Для
описания этой анизотропии предполагается, что закон ползучести
имеет следующий вид:
8i = Н (<т0) \А3 (o-j — а2) — А2 (а3 — <Tj)],
е2 = Н (оо) [Ai (a2 — as) - А3 (ai-a2)], G7.3)
е3 = Н (а0) [А2 (сг3 — Oj) — Ai (а2 — с3)].
312 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Коэффициенты анизотропии, вообще говоря, должны определяться
приложенной системой напряжений, то есть зависеть как от типа
напряженного состояния, так и от уровня напряжений. Не
располагая достаточными данными для установления этих
зависимостей, автор подбирал постоянные для каждого типа напряженного
состояния коэффициенты так, чтобы описать опытные данные
наилучшим образом. Оказалось, что можно принять Ах = А3 = 1,
тогда как А2 зависело от отношения напряжений, эта величина
равна единице при чистом кручении и возрастает по мере
приближения напряженного состояния к состоянию одноосного
растяжения. Так, когда т/о = 1,25, найдено, что Аг = 5,75. При
таком характере зависимости А2 от типа напряженного состояния
уравнения G7.3) учитывают фактически только перераспределение
скоростей деформации между направлениями 1 и 3, скорость
ползучести в направлении наибольшего напряжения о2 не
зависит от константы анизотропии, а скорость октаэдрического сдвига
меняется по сравнению с обычным ее значением мало, поэтому
использование соотношений G7.3) практически не нарушает
зависимости между т0 и у0.
Опыты при температурах 450° и 550° обрабатывались
аналогичным образом, во всех случаях зависимость между т0 и у0
оказывалась не зависящей от типа напряженного состояния,
точки более или менее хорошо располагались около одной кривой
в плоскости log у0 — log т0 или log ya — т0. Не удалось
обнаружить какого-либо систематического расслоения опытных точек
в зависимости от отношения т/cr; создается впечатление, что
разброс характеристик индивидуальных образов больше, чем
какие-либо систематические отклонения от предполагаемой
зависимости. Следует отметить, что хотя точки располагаются
достаточно близко к общей кривой в логарифмических координатах,
фактически скорости октаэдрического сдвига при одних и тех
же значениях октаэдрического напряжения могут разниться
в некоторых случаях в 1,5 раза. Значительный разброс опытных
данных, как уже отмечалось, вообще характерен для испытания
на ползучесть.
По-видимому, на трубчатых образцах с малой толщиной
стенки разброс оказывается больше, чем на сплошных образцах.
Действительно, как указывает Джонсон, размер зерна
составлял примерно 1/6 толщины образца, при этих условиях
считать материал однородным можно лишь условно.
Предварительные опыты по выяснению однородности материала
производились на обычных цилиндрических образцах, и на основании этих
опытов было сделано заключение о стабильности характеристик
ползучести, тогда как опыты на трубчатых образцах не
дублировались.
§ 77] -ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 313
В статье [354] приводятся результаты аналогичного
исследования алюминиевого сплава RR-59. Слиток подвергался следующей
термообработке: нагрев при 525° в течение восьми часов с
последующей закалкой в горячую воду, выдержка при нормальной
температуре 24 часа и старение при 170° в течение 16 часов.
Образцы, вырезанные в различных направлениях, обнаружили
достаточно хорошую степень изотропии. Опыты на ползучесть
при растяжении и кручении проводились при температурах 150°
и 200°. Методика обработки экспериментальных данных здесь,
как и в последующих работах, оставалась той же, что и для
стали 0,17 С, в дальнейшем мы это оговаривать не будем.
Совершенно аналогичным образом исследовалась ползучесть
магниевого сплава (98% Mg, 2% Al) [256], подвергнутого
следующей термической обработке: нагрев при 425° в течение 4 часов
и медленное, в течение 10 часов, охлаждение до комнатной
температуры, температура испытаний была принята 20° и 50°. Наконец,,
исследованию при температуре 650° был подвергнут хромонике-
левый сплав нимоник 75 при 650°, образцы вырезались из поковки
турбинного диска. Во всех случаях было отмечено, что
зависимость уо — т0 с точностью до естественного разброса выполняется
при всех температурах и при всех напряжениях. В то же время
условие подобия девиаторов может нарушаться, соотношение
между скоростями е3 и et иногда существенно отличается от тогог
которое следует из теории типа Мизеса. Для стали при
температурах 350° отклонения незначительны; при температуре 450° они
становятся более существенными, при этом материал ведет себя
согласно теории типа Мизеса при малых и средних напряжениях;
существенные отклонения обнаруживаются при больших
напряжениях. Граница между малыми и средними напряжениями
примерно соответствует перелому кривой log у0 — log т0. При
температуре 550° поведение материала становится в сильной степени
аномальным.
Для алюминиевого сплава условие пропорциональности
девиаторов достаточно хорошо выполняется при 150°, однако при
этой температуре опытов с достаточно высоким уровнем
напряжений не производилось. При температуре 200° пропорциональность
девиаторов существует при малых напряжениях и нарушается
при больших, так же как и для стали 0,17 С.
Примерно аналогичные выводы делаются автором для
магниевого сплава [аб8]; наконец, для сплава нимоник 75 [257] отмечено,
что при всех напряжениях закон течения типа Мизеса
оправдывается достаточно хорошо. Следует обратить внимание на то, что
нимоник 75 дал значительно больший разброс точек в координатах
log То — log Тс чеи ДРУгие материалы. Возможно, это связано
с тем, что испытания производились на материале, подвергнутом
314 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
стандартной термообработке, которая дает более крупное зерно.
Для всех материалов требовалось, чтобы размер зерна не
превышал 1/6 толщины стенки, только для нимоника это требование
не было выполнено.
Отклонения в поведении материала от предсказаний теории
типа Мизеса каждый раз характеризуются Джонсоном как
проявление анизотропии и описываются в соответствующих терминах,
а именно при помощи уравнений, подобных G7.3). Конечно, для
каждого индивидуального образца возможно подобрать
константы Аь А2 и А3 так, чтобы добиться удовлетворительного
согласования с опытом, но сами константы при этом оказываются
зависящими от вида напряженного состояния, таким образом,
становится совершенно неясно, какая именно анизотропия возникает
в образце и с чем она связана. Если допустить, что в результате
начальной пластической деформации при нагружении возникает
анизотропия, то, очевидно, далеко не безразлично, каким образом
произведено загружение образца. По-видимому, наиболее чистых
результатов можно ожидать, если нагружать образец
пропорционально, сохраняя постоянное отношение т/а. Совершенно не
очевидно, что возникающая анизотропия оказывается именно
такой, как это предполагает Джонсон, а именно, что в теле
существуют три плоскости симметрии и эти плоскости совпадают
с плоскостями действия главных напряжений. Только при этом
предположении можно считать справедливыми формулы G7.3)
и законным предположение о совпадении главных осей тензора
напряжений и тензора скоростей ползучести. В то же время весьма
систематические и тщательно поставленные опыты Джонсона
представляют собою ценный материал, проливающий свет на
основные закономерности ползучести в сложном напряженном
состоянии, поэтому представляет интерес их более подробный
анализ, что и будет сделано в следующих параграфах.
§ 78. ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА
При обработке своих результатов Джонсон предполагал, что
главные оси тензора напряжений и тензора скоростей деформации
ползучести совпадают. Это возможно либо для изотропной
ползучести, либо для частного вида анизотропной ползучести, а именно
ортогональной изотропии такого типа, когда оси симметрии
ползучести совпадают с главными осями тензора напряжений.
Вторая возможность носит достаточно частный характер, поэтому
мы не будем задаваться целью описать истинную природу
анизотропного поведения материала, ограничимся отысканием тех
условий, при которых соображения анизотропии привлекать
не следует. Будем придерживаться метода, изложенного в § 66.
В опытах на совместное действие растяжения и кручения угол 9
§ 78] ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА 315
меняется в пределах от 6 = -у при чистом кручении до 0 = -~-
при чистом растяжении.
В § 68 было выяснено, что тангенс угла между вектором
октаэдрического касательного напряжения и вектором октаэдри-
ческого сдвига, равный величине к (8), должен заключаться
между значениями х = — tg @ — -„¦ ) ти у, = \% (-^ — 0
если существует потенциал ползучести и если поверхность
постоянного потенциала выпукла. Положенное в основу рассмотрения
предположение об однородности потенциала ползучести как
функции двух инвариантов основывается прежде всего на наблюдении
факта подобия кривых ползучести для различных напряженных
состояний; этот факт был использован для определения
характерных скоростей ползучести, фигурирующих во всех дальнейших
обработках опытов Джонсона. Значения функции g @) должны
быть соответственно заключены в пределах между g @) = —^ sin 0
и g F) = cos f 0 ^ j . Выбрав g @) = 1, мы принимаем за
исходные данные результаты опытов при растяжении, тогда
наибольшее расхождение между предсказаниями зависимости
скорости ползучести от напряжения по различным возможным
вариантам теории будет при чистом сдвиге, когда 0 = -у . В этом
случае по формуле F6.4)
Здесь g* = g ( -Tj- J . В октаэдрических координатах
2
При критерии Сен-Венана g* = —р>1, следовательно, при
[/3
одном и том же октаэдрическом напряжении скорость
октаэдрического сдвига при кручении больше, чем при растяжении. При
1/3
критерии наибольшего приведенного напряжения g* = -—- < 1,
следовательно, при одном и том же октаэдрическом напряжении
скорость октаэдрического сдвига при кручении меньше, чем
при растяжении. Представляя зависимость между у0 и г0,
например, в логарифмических координатах, мы должны получить
единую кривую в том случае, когда потенциал ползучести зависит
от инварианта а0. Если ползучесть подчиняется теории типа
Сен-Венана, то точки расслоятся, кривые для кручения и для
растяжения будут разными, при этом кривая кручения смещена
316 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
в сторону больших скоростей. В случае справедливости критерия
наибольшего приведенного напряжения точки, соответствующие
кручению, смещаются в другую сторону.
На рис. 107—122 приведены графики зависимости величины es
от т0 — ~ в двойных логарифмических координатах по данным,
1/3
приведенным в названных работах Джонсона с сотрудниками,
а также графики зависимости к = — от угла 0. Величина 8^.
представляет собою скорость ползучести, выраженную в
условных единицах, как это было пояснено в § 77.
Бросается в глаза следующая характерная особенность.
Кривые log es — log т0 всегда могут быть аппроксимированы с помощью
двух прямых. Точка пересечения этих прямых отделяет уровень
«высоких» напряжений от уровня «средних и низких»
напряжений. Соответственно те значения и, которые сколько-нибудь
существенно отличаются от нуля, относятся, как правило, именно
к большим напряжениям. Однако характер отклонения величины х
от нулевого значения неодинаков в разных случаях. Рассмотрим
эти кривые более подробно.
Сталь 0,17 С, 350°. На рис. 107 прежде всего бросается в глаза
смещение точек для чистого кручения влево в области низких
ч:а,кг/смг
мии
1ЛЛП
600
400
га?
г
s
/
qS
о
1У*
о
3><
?
г<°
А
о
•
SJ-"
Pat.
fVffl?t?
^
*ше
•
№
Стем ф7Ъ,350°
Рис. 107.
70
100 ес
напряжений. Этот факт в других случаях не повторялся. Точки
на графике к (G) (рис. 108) располагаются достаточно близко от
оси % = 0, причем ниже этой оси х принимает малые
положительные значения. Казалось бы, положительные значения х и
смещение точек, соответствующих кручению, на рис. 107 влево
согласуются между собою и свидетельствуют о том, что истинная кривая
§ 78] ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА 317
ползучести в октаэдрической плоскости располагается между
окружностью и описанным шестиугольником. Но на рис. 107
отслоились только точки, соответствующие чистому кручению,
для всех остальных напряженных состояний точки лежат на
одной прямой, что подтверждает справедливость уравнений типа
Мизеса. Незначительное отклонение величины к от нулевого
значения в области низких напряжений, вероятно, правильнее
отнести за счет погрешности эксперимента и случайных факторов.
¦0,4
02
О
*%г
+0.4
X
~
-
If
-
^
g^l
V
о то ,'
то /'
7320 *W2ff ^
о У
^' О7070
'-' 6/шдг/ан~
i 1 i i
,7,7 '7,3 i 2fl 2J
—
•
Сталь 077 Z J50"
Рис. 108.
При больших г0 положение резко меняется, к становится
отрицательным и растет по абсолютной величине с увеличением 9. Около
соответствующих точек на чертеже указаны значения т0.
Пунктиром проведена кривая х = —tg ( 0 2 ) ' С00тветствУюЩая
теории Сен-Венана. Таким образом, можно сделать следующий
вывод: сталь 0,17 С при 350° достаточно хорошо следует теории
типа Мизеса при напряжениях т0 < 1000 кг /см2, ее поведение
лучше описывается теорией Сен-Венана при т0 > 1000 кг/см2.
Для подтверждения этого вывода следовало бы показать, что
и зависимость между es и т0 включает в себя соответствующую
величину g @), однако малое количество опытных точек в области
больших напряжений и значительный их разброс делают подобную
проверку неубедительной.
Сталь 0,17 С, 450° (рис. 109, 110). Полученные при этой
температуре результаты совершенно подобны результатам при 350°,
обнаруженная картина оказывается даже еще более четкой.
В области малых напряжений зависимость между es и т0
выполняется весьма хорошо, разброс точек относительно невелик
318 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
и носит явно случайный характер, величина к мала, хотя всюду
положительна. При т0 > 600 значения х располагаются
достаточно близко к пунктирной кривой, соответствующей закону
те^<г/слгг
BOO
600
400
100
-
=>
2$
Ж0
о?
о*
/ о
i
о>
э
о ^010^т
5таль Щ7 Z ,Ш
7°
11Г1
ю~-
70''
Рпс. 109.
Ц5
X
Q
у
/
'°800
7020_
У
о BOO
075^
Зрадиан
7,5 1Б
©
"Г" ЗЬТ
2,0
2,7
о/
Сталь Ш7Ь,Ш°
Рис. 110.
течения типа Сен-Венана, в области больших напряжений разброс
значений es становится большим. Обращают на себя внимание
точки 1 ж 2, дающие большие положительные величины х. Для
точки 2, например, было сг2 = Ю80 кг/см2, а3 = —50 kzIcm1.
Естественно ожидать, что отрицательная скорость ползучести будет
§ 78] ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА 319
по абсолютной величине превышать скорость еь поскольку
o*i = 0. Однако приводимые Джонсоном величины скоростей
следующие: е2 = 0,62, е3 = — 0,21, 84 = — 0,41. Такой
результат можно объяснить либо анизотропией, либо какой-то невыяв-
ленной погрешностью эксперимента. Довольно трудно понять»
tB,/<a/cM2
600
400
200
1dO
О
°У
о
О/
о
о/
У о
Стс
-~-з
ml
о"
7/7
С
0^
SSff°
)-""""
-*-о°"'
7 10
Рис. 111.
Ю< ?S
05
х
Q
-л—
IS
©
>—t—
IB
враЗиан
17
f V & 2,0
2,1
Сталь 0,77 1,Ш°
Рис. 112.
каким образом могла возникнуть анизотропия столь странного
характера в результате создания в образце системы напряжений,
близкой к простому растяжению в направлении 2, и почему
появилась столь резкая разница свойств в поперечном направлении.
320 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Точно такой же результат получился для точки 1. Здесь было
а2 = 575 кг/смг, сг3 = — 52 кг/см2, е2 = 0,18, б3 = — 0,07,
gj = — 0,11, значение % получилось почти тем же самым. Если
анизотропия создается первоначальной пластической деформацией
в процессе первоначального загружения, то степень анизотропии
г0,кг/смг
1000
ООО
400
200
,f
/
о
У
1
1
/
Ад
1 °
юминие
Вый с
i/tai
Г, 15
О
0°
10'
70
Рис. 113.
ЦЗ
а?
0,1
о
е
-+*-
врадиан
15 1М 1,7 °tf
е
2ft г;
Av/0Mi/m/efora cmretff, 750°
Рис. 114.
должна зависеть весьма резко от приложенного напряжения,
между тем как в двух этих случаях октаэдрическое напряжение
отличалось в 1,8 раза.
Сталь 0,17 С, 550° (рис. 111, 112). Здесь прежде всего обращает
на себя внимание значительный разброс точек в координатах
log es — log т0, усмотреть в этом разбросе какую-либо систему
трудно. Величина х в общем близка к нулю, только при 6 = 1,9
три точки соответствуют большим положительным значениям х.
Такое поведение материала является аномальным и возможно
лишь при резкой анизотропии свойств в поперечном направлении.
Следует отметить, что и здесь, так же как при 450°, аномалии
§ 78] ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА 321
проявляются тогда, когда напряженное состояние близко к
состоянию одноосного растяжения. Металлографическое исследование
показало, что при 550° ползучесть сопровождается структурными
изменениями. Отмечены сфероидизация цементита и появление
выделений цементита внутри зерен феррита, а также на границах
тд,на/смг
600
т
200
о/
/"
5*
о
Р"
¦—о
о
ор-*^"^
п
*^Ъ
о
Алшмишебьш стаб, 200°
°
10'
W
Рис. 115.
US
О
©
610
S60
-*sso
врадиан
-OI-
#" W 1,7 тд w 2jo г;
© Д/>мми/ше?ый еллаИ, 200°
Рис. 116.
зерен. При больших напряжениях в зернах феррита обнаружена
полигонизация.
За исключением нескольких опытов, все данные
свидетельствуют о том, что наиболее разумное описание процесса
ползучести (если отвлечься от разброса) и здесь может быть произведено
на основе теории типа Мизеса. Заметим, что при высоких
напряжениях никакой тенденции перехода к закону течения Сен-Венана
не обнаруживается.
21 ю. H. Работнов
322 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Алюминиевый сплав, 150° (рис. ИЗ, 114). Как видно из
графиков, для этого материала совпадение данных эксперимента
с теорией исключительно хорошее.
Алюминиевый сплав, 200° (рис. 115, 116). Так же как и сталь,
алюминиевый сплав обнаруживает большой разброс данных при
т0,кг/шг
SOO
№
300
200
700
э о/
So
>
о /
/о
'о
о^-*^1
О
W1
10 е,
Рис. 117.
х
QJ-
0
52
оЗ*0
о 204
Ш
врадиан
15 1fi V W V 20 2J
®
Магяшбый сплав, 20'
Рис. 118.
более высокой температуре. При малых и средних напряжениях
к « 0, при напряжениях, превышающих примерно 500 кг/см2,
меняется характер зависимости es от т0 и закон течения
становится близким к закону течения Сен-Венана. Аномалии
ползучести у алюминиевого сплава не обнаружено.
Магниевый сплав, 20° (рис. 117, 118). При комнатной
температуре поведение магниевого сплава следует считать нормальным
§ 78] ДАЛЬНЕЙШИЙ АНАЛИЗ ОПЫТОВ ДЖОНСОНА 323
в том смысле, что при малых напряжениях справедлив закон
течения Мизеса, при больших напряжениях происходит переход
к закону течения Сен-Венана. Разброс опытных точек в
координатах log es — log To значителен.
та,нг/смг
300
150
100
00
00
W
t
у
f
'о
Ма
'гни
J
*
?вы
^***>
Г
U ?Ш?й
о¦ ,
-
tf, Я?
9
ч^
10~1 7
Рис. 119.
JO ?,
х
-OJ5
0
-\ о—|—
US V
©
и °-t-
Ж
о 2fi0 23
°32в
308
Магниевый сплав, 50°
Рис. 120.
Магниевый сплав, 50° (рис. 119, 120). При малых и средних
напряжениях простейшая теория очень хорошо согласуется
с экспериментом и разброс опытных точек невелик. Существенно
аномальное поведение обнаруживается при больших напряжениях,
21*
324 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
особенно когда напряженное состояние близко к простому
растяжению. Так, например, точка х = — 0,578 соответствует
напряженному состоянию а2 = 411, а3 = — 11. При этом оказалось,
что
е2 = 6,99, е3 = — 0,18, е4 = — 6,81;
таким образом почти все течение в поперечном направлении идет
7000
400
200
W0
/
°)
) /
О /
>
/
Ни
ш
о
7М
ш 7S
о
6SO
О
о
•"—""о
70
Рис. т.
70"
тс
Q3
0
—О—I
1,5
©
Ниш чая 7S, 650°
Рис. 122.
2fl
в
по толщине образца, где не приложено никакого напряжения;
картина течения оказывается прямо противоположной той,
которая следует из теории Сен-Венана.
Нимоник 75, 650° (рис. 121, 122). Здесь х = 0, теория типа
Мизеса справедлива во всем диапазоне напряжений, разброс
довольно значителен, что связано, по-видимому, с выбором
обработки материала и большим зерном.
§ 79] ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПОЛЗУЧЕСТИ 325'
§ 79. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПОЛЗУЧЕСТИ
ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ (ПРОДОЛЖЕНИЕ)
Мы остановились довольно детально на опытах Джонсона,
поскольку в многочисленных публикациях этого автора
содержатся первичные данные, допускающие различную обработку.
Другие статьи содержат, как правило, лишь некоторые
окончательные результаты. Не претендуя на исчерпывающий обзор всех
имеющихся материалов, отметим некоторые результаты.
Работа Нишихара, Танака и Шима I303]. Опыты производились
на специально сконструированной машине, особенность которой
состояла в том, что один и тот же груз создавал как крутящий
момент, так и растягивающую нагрузку. Этим обеспечивалось
пропорциональное загружение. Дополнительный груз на рычаге
приспособления для растяжения перемещался в процессе
испытаний таким образом, чтобы компенсировать изменение площади
поперечного сечения. Крутящий момент, по-видимому, при этом
не корректировался. Испытанию подвергалась сталь с
содержанием углерода 0,10%, трубчатые образцы имели наружный и
внутренний диаметры 10 и 9 мм соответственно, исследована только
одна температура, а именно 450° С. Продолжительность опытов
во всех случаях была невелика — порядка 500 минут, уровень
напряжений был принят достаточно высокий, октаэдрическое
касательное напряжение менялось в пределах от 8,5 до 11,3 кг/мм2,
при этом предел текучести для нормальной температуры
соответствовал величине т0 = 11,3 кг /мм2. Ползучести во всех случаях
предшествовала значительная пластическая деформация (порядка
5%), деформация ползучести за 500 минут была также достаточно
велика, в некоторых опытах суммарная деформация достигала 15%.
Авторы проверяли выполнение следующей зависимости между
октаэдрическим сдвигом и октаэдрическим касательным
напряжением:
Наилучшее совпадение с данными эксперимента было достигнуто
при следующих значениях констант: а = 2,26-Ю-8, р" = 1,17 X
X 10~8, к = 3,16, п = 5,95, т = 0,284; при этом т0 измеряется
в кг/мм2, а время — в минутах. Далее результаты всех испытаний
были представлены в координатах у0 — t и для сравнения
построены кривые по уравнению G6.1). Совпадение во всех случаях
оказалось вполне удовлетворительным, несколько большие
расхождения получались при высоких напряжениях. Проверка
закона течения авторами не производилась, однако по кривым,
приведенным в статье, можно определить отношение у/е и
сравнить с величиной Зт/а(§ 68). Разница между этими величинами
не превышает 10%, причем отклонения идут в ту и другую
сторону. Следует ожидать, что выполнение условий пропорцио-
326 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
нального нагружения исключает эффект анизотропии, вызванной
начальной деформацией. Статья не содержит данных,
позволяющих судить об изотропии материала в начальном состоянии,
по-видимому, образцы делались из прутка. Значительная
пластическая деформация делает влияние начальной анизотропии
несущественным, в этом смысле сопоставление опытов Нишихара
с опытами Джонсона невозможно.
Опыты Кеннеди, Хармса и Дугласа на инконеле [274].
Исследовался жаропрочный сплав номинального состава 80% Ni,
15%Сг, 5% Fe при температуре 812°. Ставилась задача изучения
свойств материала при тех типах напряженных состояний, которые
реализуются в котлах и турбинных дисках, при этом обычно
главные напряжения положительны. Поэтому образцы испытыва-
лись на действие
внутреннего давления и осевой силы.
Образцы изготовлялись из
цельнотянутой трубы
диаметром 3/4", они подвергались
двухчасовому отжигу в
атмосфере водорода при 1060°,
испытания проводились в
аргоне, поскольку в
литературе отмечается влияние
окисляющей среды на
ползучесть и длительную прочность
инконеля. Исследовалась не
только ползучесть, но также
и длительная прочность труб,
соответственно
продолжительность некоторых опытов (при низких напряжениях) достигала
4000 часов. Оказалось, что первые участки на кривых ползучести
отсутствуют и скорость при заданном напряжении остается все
время постоянной, таким образом, данные опытов можно было
обрабатывать по истинным скоростям. В экспериментах
замерялась только осевая деформация, поперечная деформация
определялась после разрушения, на основании чего были сделаны
некоторые выводы о характере деформации в момент,
предшествующий разрушению. К этим выводам мы вернемся позже при
рассмотрении вопроса о длительной прочности. Отсутствие полных
данных о деформациях предопределило программу испытаний
и способ обработки результатов. Проверялись теория типа Мизеса
и теория типа Сен-Венана, однако с законом течения,
ассоциированным с критерием Мизеса. Скорость осевой деформации при
этом выражается следующим образом-
{Щ ф7 бг/бд
Рис. 123.
(У*—
се
§ 79] ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПОЛЗУЧЕСТИ 327
Здесь а2
В первом случае
осевое напряжение, де — окружное напряжение.
s = Ое = У~о1-\- oq — ozOq, во втором s =
в зависимости от соотношений между осевым
— о"тах о"т;п;
напряжением, окружным напряжением и равным нулю
напряжением в направлении толщины стенки в выражении s появляются
разные комбинации. Из опытов на растяжение было установлено,
что зависимость скорости от напряжения степенная с показателем
степени п = 6; таким образом, из любой теории следует:
либо
* = ***(?
Функции /4 и /2 для рассматриваемых теорий легко написать
в явном виде. В каждой серии опытов сохранялось постоянным
Ег % в vac
Рис. 125.
-/ 6z/6g
либо oz, либо о"в, тогда как отношение ог/о& принимало различные
значения. Строились теоретические кривые зависимости ez от
0г/о"е при постоянном az или о*в и наносились опытные точки. На
рис. 123 приведены данные, относящиеся к опытам при
постоянной осевой силе; сплошные линии соответствуют теории типа
Мизеса, пунктирные — теории типа Сен-Венана с законом
течения Мизеса. Цифры рядом с кривыми обозначают величину
осевого напряжения az в кг/см2. На рис. 124 и 125 приводится срав-
328 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
нение теории и результатов испытаний при постоянном окружном
усилии. Опытные точки располагаются достаточно близко к
кривой Мизеса, величины ае указаны около соответствующих кривых.
Заметим, что если воспользоваться критерием Сен-Венана и
ассоциированным законом течения, разница между кривыми
увеличивается. Так, на рис. 123 прямолинейный участок пунктирной
кривой, соответствующий области, когда 0г/ое > 1. станет
горизонтальным.
Авторы приходят к выводу, что теория типа Мизеса достаточно
хорошо оправдывается для рассматриваемого материала в данных
температурных условиях, в то же время допустимо использование
критерия наибольшего касательного напряжения.
Опыты Одинга и Туликова [92]. В отличие от большей части
рассмотренных выше исследований, испытания авторов были
довольно длительными, до 2000 часов. Изучалась аустенитная
сталь 1Х18Н9Т, подвергнутая аустенизации при 1100° с
охлаждением на воздухе. Температура испытаний была 600°, тонкостенные
трубчатые образцы подвергались растяжению с кручением. Для
всех видов напряженных состояний кривые ползучести имели
одинаковый характер, первые участки заканчивались довольно
быстро, большую часть времени скорость ползучести сохраняла
постоянное значение, при высоких напряжениях появлялись
третьи участки. ;
Таким образом, скорость установившейся ползучести
определялась совершенно надежно. Результаты испытаний
представлены в виде кривых зависимости скорости октаэдрическо-
го сдвига от октаэдрического касательного напряжения в
логарифмических и полулогарифмических координатах. Авторы
отмечают, что во втором случае точки лучше укладываются на прямую,
нежели в первом, и делают из этого вывод о преимуществе
экспоненциального закона ползучести перед степенным.
На рис. 126 представлены результаты обработки
экспериментальных данных Одинга и Туликова по описанной выше методике,
в координатах log ss — log a0. Мы выбрали двойные
логарифмические координаты именно потому, что в этих координатах точки
не ложатся на одну прямую и более или менее четко выявляется
граница между областью низких напряжений и областью высоких
напряжений; при обработке опытов Джонсона было установлено,
что при переходе из одной области в другую характер протекания
процесса ползучести меняется. На рис. 127 нанесены значения
величины v (а), найденной по формуле F7.8). Пунктирная кривая
соответствует критерию течения типа Сен-Венана F8.5). Как
видно, разброс опытных данных довольно велик, но все точки,
за исключением двух, соответствуют отрицательным значениям v
и группируются скорее около пунктирной кривой, чем около оси
абсцисс. Таким образом, испытанный материал обнаруживает
§ 79] ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ПОЛЗУЧЕСТИ 329
нормальное поведение, и следует ожидать, что это поведение будет
лучше описано теорией типа Сен-Венана, чем теорией типа Мизеса.
Следует ожидать, что внесение соответствующей поправки в
зависимость между es и о*о должно привести к лучшему совпадению
Рис. 126.
опытных и теоретических данных. На рис. 128 в той же
двойной логарифмической сетке и в том же масштабе построена
Л)
о,г
0,1
0,2
Ц5 7fi 15 и
— г т " *
•
¦
Рис. 127.
зависимость es/g от sg в соответствии с первой из формул F7.7).
При этом функция g (а) определяется формулой F8.6).
Темные кружки относятся к опытам на растяжение, светлые
кружки — к опытам на чистое кручение. Результаты комбиниро-
330 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
ванных испытаний отмечены крестиками. По данным опытов на
растяжение и на кручение проведены кривые 1 и 2.
Кривые растяжения и кручения на рис. 126 разнятся довольно
сильно. Заметим, что аналогичное расслоение получается, если
представлять результаты так, как это делали авторы, в
координатах 7о — т0. Точки, соответствующие комбинированным
испытаниям, располагаются между этими кривыми; те точки, которые
lag \6Bff«xj\
V
Рис. 128.
соответствуют меньшим значениям т/о, больше удаляются от
кривой кручения к кривой растяжения. На рис. 128 все точки
комбинированных испытаний располагаются очень близко к
кривой кручения, при этом отклонение носит не систематический,
а случайный характер. Кривая для чистого растяжения
по-прежнему оказывается изолированной, однако теперь кривые 1 и 2
значительно ближе одна к другой. Одна точка, отмеченная
цифрой 7, резко выпадает, так же как и на предыдущем графике.
Трудно объяснить, почему результаты опытов на чистое
растяжение не ложатся на общую кривую, тогда как точки,
соответствующие малому отношению т/о, то есть явному преобладанию
растяжения, укладываются на нее достаточно хорошо.
В общем, из опытов Одинга и Туликова следует определенный
вывод, что для описания установившейся ползучести данного
материала при данной температуре хорошие результаты дает
теория, принимающая за критерий ползучести величину
наибольшего касательного напряжения.
г^У^
уУ
•
+
§ 80]
ИССЛЕДОВАНИЯ НАМЕСТНИКОВА
331
Опыты Зодерквиста [35в]. Испытанию подвергался
алюминиевый сплав, результаты в общем подтверждают уравнение G6.1).
Особенность работы состояла в том, что образцы имели форму
дисков и растягивались в двух взаимно перпендикулярных
направлениях.
§ 80. ИССЛЕДОВАНИЯ НАМЕСТНИКОВА
Эксперименты Наместникова на аустенитной стали ЭИ-257
при температуре 600° и 500° относятся к периоду неустановившейся
ползучести. Автор ставит своей задачей проверить по отдельности
основные гипотезы теории типа Мизеса, а именно предположение
о подобии девиаторов и связь между октаэдрическим сдвигом,
октаэдрическим напряжением и временем [78]. Сконструированная
и изготовленная в Институте механики АН СССР машина
допускала плавное пропорциональное загружение, грузами служили
баки, в которые через тарированные диафрагмы поступала вода
из резервуара с постоянным уровнем. Меняя диафрагмы, можно
было получить любое соотношение между растягивающей силой
и крутящим моментом. Образцы были изготовлены из пруткового
материала, подвергавшегося отжигу при 1150° с охлаждением
в воде и нормализации в течение десяти часов при 760° с
последующим охлаждением в печи. Всего испытано 24 образца со
средним диаметром 16 мм и толщиной стенки 0,4—0,8 мм. При
температуре 600° было проведено две серии испытаний, при
интенсивности напряжений 17 и 12 кг/мм2, в каждой серии варьировалось
отношение т/cr. При 500° интенсивность напряжений в опытах
была 14 кг/мм2, кроме того, при этой температуре было проведено
три отдельных испытания с большими значениями интенсивности.
По теории типа Мизеса должно быть
е
Определение скоростей на участке неустановившейся
ползучести требует графического дифференцирования, вносящего
погрешность, либо предположения о возможности задать кривую
ползучести аналитически. Но если в процессе ползучести
вышеприведенное условие сохраняет силу в каждый момент, то из него
следует:
?=3?. (80.1)
Именно это соотношение и подвергалось проверке в процессе
испытания. Из него следует:
332 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Левая и правая части (80.2) представляют собою функции от
времени, на рис. 129 представлены графики этих функций для
одного из испытаний. Начиная примерно с 60 часов условие (80.2)
выполняется весьма хорошо. Автор утверждает, что аналогичная
картина получалась и во всех других случаях. В работе [81]
приводится обработка данных, полученных ранее на стали ЭИ-257,
а также новые результаты для сплава Д-16Т при температуре 150°.
Во всех случаях к концу испытания оказывается, что -^ < 3 - ,
причем эта разница при 600° колеблется в пределах от 3,3 до
_
1
1
1
1
\
\\
\>
¦«^^
1 1 !
От» ЗИ-257, 1=000°
Ъ
•
о го w 60 до то
t,vac
Рис. 129.
19,5%, при 500° она достигает даже 28% в одном опыте, только
для сплава Д-16Т равенство — = 3 — соблюдается достаточно
хорошо, с небольшим разбросом в обе стороны. Чтобы объяснить
имеющиеся отклонения, Наместников отказывается от
предположения о несжимаемости материала. Для упругого материала
с коэффициентом Пуассона v
i=2(l + v)?. (80.3)
Если предположить, что в условиях ползучести сохраняется
подобие девиатора полных деформаций и девиатора напряжений,
то уравнение (80.3) будет справедливо и для ползучести, но
величина v будет представлять собою коэффициент поперечной
деформации, который, вообще говоря, меняется с ростом деформации.
В начальный момент v — это коэффициент Пуассона; если
ползучесть происходит без изменения объема, то v стремится к 1/2.
Приняв v = 0,35, автор получил хорошее совпадение
формулы (80.3) с экспериментом.
Кривые ползучести в координатах е0 — t при постоянной
интенсивности напряжений для разных отношений х/а оказались
несовпадающими, при растяжении ползучесть идет быстрее, чем
§ 80]
ИССЛЕДОВАНИЯ НАМБСТНИКОВА
333
при кручении. Типичная серия таких кривых ползучести
представлена на рис. 130. Здесь во всех случаях было о0 = 17 кг/мм2,
нижняя кривая соответствует чистому кручению, следующая
о w го за «о so
t.vac
Рис. 130.
получена при отношении т/о = 1,5, верхняя соответствует
чистому растяжению. Автору удалось подобрать формулу,
позволяющую описать эти результаты, а именно:
Значения констант оказались следующими:
m
к
А
л0
500°
600°
I
0,230 0,341
1,12-10-35 2,27.10-ie
0,258 0,659
0,398 0,578
Единица
измерения
час-1
KZJMM2'
кг/мм2
Пунктирными линиями на рис. 130 проведены кривые по
уравнению (80.4).
Не составляет труда истолковать соотношение (80.4) с общей
точки зрения, развитой в § 66, и получить соответствующий
ассоциированный закон течения, однако степень совпадения
с данными опыта при этом получается худшей, чем для закона
течения Мизеса.
Данные, подтверждающие изотропию материала в исходном
состоянии, были приведены в более поздней публикации
334 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
автора [3°2]. Характерной особенностью полученных результатов
является то, что существование потенциала ползучести не
подтверждается, условие подобия девиаторов не является
ассоциированным с инвариантной зависимостью (80.4).
§ 81. ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ
СОСТОЯНИИ И ПЕРЕМЕННЫХ НАГРУЗКАХ
Как мы видели, вопрос о ползучести в условиях сложного
напряженного состояния при неизменных во времени напряжениях
далеко не прост и до сих пор не нашел исчерпывающего решения.
Понятно поэтому, что при изменении типа напряженного
состояния картина неизмеримо осложняется. Первый принципиальный
вопрос, который здесь возникает, состоит в том, является ли
упрочнение изотропным, это значит — можно ли характеризовать
степень упрочнения заданием некоторого одного инвариантного
параметра. Для того чтобы получить прямой ответ на этот вопрос,
Наместников [7Э] поставил специальные опыты по следующей
схеме. Представим себе два образца, один из которых испыты-
вается на растяжение, другой — на кручение. В периоде
неустановившейся ползучести в том и другом случае происходит
уменьшение скорости ползучести, которое связывается с упрочнением.
Подобие кривых ползучести при растяжении и при кручении
указывает на то, что закон упрочнения в том и другом случае
одинаков; при растяжении мерой упрочнения является
деформация ползучести растяжения, при кручении — деформация
сдвиговой ползучести. Если упрочнение изотропно, то степень
упрочнения, достигнутая при растяжении, характеризует упрочнение
материала по отношению к ползучести при любом напряженном
состоянии. Представим себе теперь, что образец испытывался
на ползучесть при растяжении. В некоторый момент, когда
создалось уже достаточно большое упрочнение, то есть скорость
ползучести значительно уменьшилась по сравнению с той, которая была
вначале, мы снимаем растягивающую нагрузку и прикладываем
крутящий момент. Следует ожидать, что ползучесть при кручении
будет происходить медленнее, чем у образца, который не
подвергался предварительной ползучести при растяжении. Опыты
производились на стали ЭИ-257 при 500° и 600° в тех же
условиях, что и опыты при постоянных нагрузках на этом материале,
описанные в § 80. Каждый образец подвергался ползучести при
одном типе напряженного состояния в течение 50 часов, после
этого разгружался, и к нему прикладывалась новая система
нагрузок с той же интенсивностью, но с другим отношением т/с
Никакого упрочняющего эффекта предварительного растяжения
на последующее кручение и наоборот отмечено не было. Таким
образом, оказалось, что упрочнение при ползучести носит резко
§ 81] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 335
анизотропный характер. Этот результат можно качественно понять
в свете тех идей, которые лежат в основе теории скольжения
в пластичности (§ 20). При данном виде напряженного состояния,
характеризуемом отношением т/ст, ползучесть происходит в тех
зернах и по тем плоскостям, где возникают наибольшие
касательные напряжения. Зависимость скорости ползучести от
напряжения резко нелинейна, поэтому выгодно расположенные по
отношению к главным осям тензора напряжений плоскости
упрочняются очень сильно, тогда как по другим плоскостям практически
нет ни ползучести, ни упрочнения. При повороте главных осей
ff 70 20 30
t,yas
Рис. 131.
на достаточно большой угол вся ползучесть фактически
происходит по другим зернам и другим системам скольжения, где никакого
упрочнения не было. Если провести опыт в менее контрастных
условиях, а именно заставить образец ползти сначала при
отношении напряжений (т/о)ь а потом при отношении напряжений
(т/сгJ, причем эти отношения не слишком разнятся между собою,
то упрочняющий эффект, предшествующий ползучести, будет
заметен. Так, на рис. 131 показаны две кривые ползучести при
500°, о0 = 14 кг/мм2 и т/о = 1,5. По оси ординат отложена
интенсивность деформаций ползучести. Сплошная кривая
относится к недеформированному образцу, пунктирная — к образцу,
который ранее полз в течение 50 часов при той же интенсивности
напряжений, но при т/о = 0,28.
Довольно обширная программа испытаний при сложном
напряженном состоянии и переменных нагрузках была выполнена
Джонсоном с сотрудниками [2621. Испытывались те же материалы,
которые были изучены в условиях постоянных нагрузок (см. § 77),
а именно: алюминиевый сплав RR-59 при 150° и магниевый сплав
при 20° и 50°, а также сталь, содержащая 0,2% углерода, при
температуре 450° (отличная от той, которая ранее изучалась
336 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. У
при постоянных нагрузках). В каждом опыте сначала создавалась
осевая нагрузка, после этого ступенями прикладывался
крутящий момент.
Результаты сравнивались с предсказаниями теории старения
и теории упрочнения. Теория старения принималась в
обычной форме:
P« = yw(oo)-^-t@. (81.1)
Были рассмотрены два варианта теории упрочнения, в обоих
случаях за меру упрочнения принималась величина интенсивности
деформаций ползучести р0 = ( -=- Рцрц ) • Уравнения
выбирались в виде:
б) Р« = |[/Ы-х(Ро)]-^-. (81.3)
Наконец, рассматривались комбинированные уравнения
старения и упрочнения, правые части (81.2) и (81.3) умножались
на некоторую функцию времени, подобно (81.1).
Во всех случаях авторы получили довольно плохое
соответствие теории и эксперимента. Этого и следовало ожидать,
поскольку уравнения (81.1) — (81.3) описывают изотропное упрочнение.
Работа Наместникова [302] ставила перед собою определенную
цель — исследование ползучести при пропорционально
изменяющихся нагрузках. Опыты производились на растяжение и
кручение над сталью ЭИ-257 при 600°, технически чистой медью при
150° и сплавом Д-16Т при 150°. В отличие от предыдущих опытов,
в этой работе была проверена изотропия материала в исходном
состоянии. Была сконструирована и изготовлена специальная
машина для испытаний на ползучесть маленьких образцов с полной
длиной 28 мм. Такие образцы можно было вырезать из прутка
в поперечном направлении. Сталь и медь оказались достаточно
изотропными, на сплаве Д-16Т была замечена ощутимая
анизотропия. Для обработки данных Наместникову нужно было
построить некоторые уравнения теории упрочнения. В новых
опытах условие подобия девнаторов выполнялось весьма хорошо,
отношение
!¦!
е ' а
изменялось от 2,8, что соответствует мгновенной упругой
деформации, до 3 при ползучести. На рис. 132 приведены характерные
31] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 337
примеры. Точки соответствуют опытным значениям у/е, прямая —
величине 3 —. Таким образом, за основу было взято
предположение о подобии девиато-
у/е
V
1,2
О
у/г
12
1,0
т
° «nJOOOOOVcftOOtl
, ь
12
t.vae
„о°°°°
о о
! о о „
и
I
I
0—" Iй и е <
i
а
°о о о«
20
40
.132.
ВО
80
t.vae
ров. Если сохранить
гипотезу существования
потенциала ползучести
при ползучести с
упрочнением, то нужно
считать, что потенциал
зависит от о0.
Расхождение кривых ползучести
в координатах р0 — t
для разных видов
напряженного состояния
при одинаковых с0 автор
относит не за счет вида
напряженного состояния, а за счет вида деформированного
состояния, он вводит безразмерный параметр г, определенный
следующим образом:
4 PijPjhPhi
3 ^3
а также определяет меру упрочнения:
Яз = Pip и
(см. § 74).
Уравнения ползучести принимаются им в следующем виде:
;ц=4Аыв/(вв"-,оу-
(81.4)
да0 а0
Для функций h {q3) и / (а0, г) предлагаются следующие
аппроксимации:
h (q3) = nq^a,
(n + a + i)f (сг„, r) = a«+a+1 exp [a0% (r)].
Для сплава Д-16Т получено: a =1,57, n = 9, к = 2,23-Ю'22,
y (r) = — 2 7 • 10'3 —-—
При этом сила измеряется в килограммах, длины — в
миллиметрах и время — в часах. Из уравнений (81.4) следует
соотношение, которое и использовалось при расчетах:
РоР?= ио- {l + ^?Ti} ехР [<*>Х {г)]. (81.5)
22 Ю. H. Работнов
338 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Мы видели, что аналитические возможности описания
неустановившейся ползучести в сложном напряженном состоянии почти
безграничны, довольно сложные уравнения (81.4) представляют
собою лишь один из возможных вариантов. Для одноосного
напряженного состояния отсюда получается обычное уравнение теории
упрочнения, рассмотренное в главе IV, опыты при сложном
напряженном состоянии и неизменных во времени нагрузках
описываются этим уравнением вполне удовлетворительно. В
опытах со ступенчатым изменением нагрузки оказалось, что при
произвольном фиксированном отношении т/а степень соответствия
р-703
ts\ | | 1
О ГВ 32 43
t,vac
Рис. 133.
теории и эксперимента совершенно такая же, какая получается
при обработке опытов на растяжение со ступенчатой нагрузкой
по теории упрочнения. При внезапном увеличении нагрузки
экспериментальные точки располагаются несколько выше
теоретической кривой, на следующей ступени расхождение
увеличивается. Таким образом, можно сказать, что случай
пропорционально изменяющихся нагрузок описывается уравнением (81.4)
так же хорошо, как и аналогичный одноосный случай. Для более
отчетливого подтверждения этого вывода были поставлены
следующие опыты. Подбирались два таких различных напряженных
состояния, для которых правые части в (81.5) были одинаковы
и одинаково менялись во времени. Строились графики ра — t,
которые оказались совпадающими с точностью до разброса.
На рис. 133 приведены два таких графика для примера.
На кривых указывались номера образцов. Образец 219
подвергался кручению с напряжением 12,7 кг/мм2 на первом участке
и 10,4 кг/мм2 на втором участке. Образец 237 растягивался сначала
напряжением 34 кг/мм2, потом 30,1 кг/мм2. Кривые оказались
практически совпадающими. Аналогичным образом сопостав-
§ 82]
РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
339
ляются результаты испытаний образца 223 на кручение и 244
на совместное действие растяжения и кручения при отношении
х/о = 0,56. Этот эксперимент в меньшей мере связан с частным
выбором закона упрочнения и достаточно убедительно
подтверждает сделанный общий вывод о полной аналогии поведения
материала при пропорциональном нагружении и в одноосном случае.
§ 82. РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ В СЛОЖНОМ
НАПРЯЖЕННОМ СОСТОЯНИИ
Из результатов, изложенных выше, следует, что при
пропорциональном нагружении анизотропия упрочнения обнаружена
быть не может, таким образом, любая достаточно хорошо
подтверждаемая опытом теория ползучести с изотропным
упрочнением в этом случае применима. Близкие условия получаются при
релаксации напряжений. Рассмотрим тело, находящееся в
условиях однородного напряженного состояния; на части поверхности
его 2U заданы перемещения, которые удерживаются постоянными,
остальная часть поверхности 2 т свободна от усилий. В частном
случае 2 т может отсутствовать. Будем говорить соответственно
об общем и специальном случаях релаксации. Примем за основу
уравнения теории упрочнения в виде
Здесь
Pl>-2 h{q0) 0o • (bZ-1}
*2_JL ' ' _" 1 -
<?o— з PijPiji Pij — eij ~2GC'iJ'
Объемная деформация считается упругой и подчиняющейся закону
Гука:
о
е=~м •
Предположим теперь, что в теле создано однородное
напряженное состояние. В специальном случае релаксации, когда
зафиксированы перемещения всех точек поверхности, в начальный
момент возникают упругие деформации еу и упругие напряжен
ния cr*j. Предположим, что деформации e*j сохраняют неизменные
значения и в процессе релаксации. Вследствие закона Гука
гидростатическая составляющая тензора напряжений также
сохраняет постоянное значение о = ЗКе*. Положим a*j = ог*<р (?),
причем ф @) = 1. Внесем эти значения в (82.1). Получим:
\~3GJ
22*
340 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
Величина ст* постоянна вследствие предположения об
однородности напряженного состояния, таким образом, дифференциальное
уравнение (82.2) определяет функцию ф(г). Напряжения
выражаются следующим образом:
Усилия на поверхности:
Tt = (ptw + o8i})vj. (82.3
Как видно, усилия релаксируют не до нуля, а до некоторых
значений, соответствующих предельному гидростатическому
напряженному состоянию в теле.
Найденное решение непригодно для общего случая релаксации.
Действительно, если на 2т величины Tt обращаются в нуль при
t = 0, то в последующие моменты времени, согласно (82.3), они
будут отличны от нуля.
Для несжимаемого материала легко рассмотреть и общий
случай релаксации. Действительно, при К = оо е = 0,
следовательно, а может принимать любые значения. Положим
о" = ст*<р (t), тогда
Релаксация напряжений и усилий на закрепленной части
поверхности тела происходит до нуля, и условия на свободной
поверхности всегда выполняются.
В опытах на релаксацию при сложном напряженном
состоянии всегда фиксируются перемещения на части поверхности
образца, поэтому строгое решение задачи о релаксации с учетом
сжимаемости материала весьма непросто. Использование теории
упрочнения даже в простейших случаях требует численного
интегрирования соответствующих уравнений.
По-видимому, первое экспериментальное исследование
релаксации напряжений при сложном напряженном состоянии
приводится в статье [а21]. Авторы пользуются уравнениями теории
старения в форме G2.3). Опыты производились на образцах из
алюминиевого сплава 3S-0 при комнатной температуре.
Предварительно по кривым ползучести цилиндрических образцов при
растяжении были определены константы в уравнении G2.3).
Опыты на релаксацию были осуществлены: а) при растяжении,
б) при кручении и в) при одновременном действии растяжения
и кручения. В последнем случае поддерживалась неизменной
деформация, крутящий момент изменялся таким образом, что
отношение главных напряжений ог1аг оставалось постоянным.
Теоретические кривые строились с помощью уравнений G2.3),
которые решались применительно к условиям эксперимента
графическим методом. Мы видели (§ 48, гл. IV), что предсказания
§ 82]
РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
341
3,0
2J?
7М
^Sfe
60=27J>'кг/мм
2
Ж
700 t,?ac
кривых релаксации на основе теории старения дают не слишком
большие отклонения от действительности в одноосном случае;
здесь также совпадение получилось вполне удовлетворительным.
На рис. 134 показаны кривая релаксации осевого напряжения
и кривая изменения величины сдвига. Следует отметить, что расчет
кривой релаксации при чистом
кручении дает несколько худ- vZQhs/mm
шее согласие с экспериментом. W
Следующая по времени
работа, посвященная
релаксации в сложном
напряженном состоянии, принадлежит
Джонсону и сотрудникам I263].
Использованная авторами
релаксационная машина была
описана раньше [259];
особенность ее конструкции состоит
в том, что отношение осевой
силы и крутящего момента
остается все время постоянным,
как момент, так и нагрузка
пропорционально
уменьшаются с тем, чтобы угол
закручивания сохранял первоначально
заданное значение. Осевая
деформация при этом остается
неконтролируемой. Авторы
указывают, что фактически она
также сохраняет постоянное
значение, однако более точных данных по этому поводу не
приводится. Для упругого состояния отношение сдвига к осевой
деформации выражается так:
•f-2(l + v)i.
Для деформаций ползучести, происходящих без изменения объема,
справедливо такое же соотношение при v = 1/2. Процесс
релаксации — это процесс перехода упругой деформации в пластическую;
следовательно, если т/а задано и у постоянно, то е постоянным
не будет, изменение е соответствует изменению величины v от
ее значения для упругого состояния до 1/2. Таким образом,
в опытах осуществлялась не чистая релаксация. Объектами для
исследования были выбраны алюминиевый сплав RR-59 при 200°
и магниевый сплав при 50° (см. § 77), причем опыты велись в том
диапазоне напряжений, в котором материал достаточно
изотропен и, следовательно, справедливы уравнения (81.1). Если
?п
7,0
О
so
Рис. 134.
700 t.VOP
342 ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ [ГЛ. V
пренебречь сжимаемостью материала, то для решения задачи
о релаксации можно воспользоваться любой механической
теорией. Авторы сравнивают теорию течения с теорией старения,
теорию упрочнения в обычной формулировке, когда за меру
упрочнения принимается величина октаэдрического сдвига, и
комбинированную теорию. Наилучшее совпадение с опытом в
большинстве случаев было получено по теории старения, хотя в
некоторых опытах теория упрочнения дала одинаковые и даже лучшие
результаты. При температуре испытания было найдено, что
у алюминиевого сплава v = 0,43, а для магниевого v = 0,39;
эти значения мало отличаются от 1/2, поэтому авторы считали,
бе/б0
Z2
W
О 20 40 t,vae
Рис. 135.
что в эксперименте условия релаксации были выполнены. При
расчетах кривых релаксации с помощью теорий старения и
упрочнения упругая сжимаемость учитывалась, однако, не точно.
Наместников в статье [зв2] указывает, что точный расчет кривой
релаксации (при условиях, несколько отличных от тех, которые
осуществлялись в опытах Джонсона и сотрудников) приводит к
результатам, почти не отличающимся от результатов приближенного
решения.
Несколько опытов на образцах из сплава Д-16Т опубликованы
Наместниковым [зоа]. В этой работе поддерживались одновременно
постоянными осевое удлинение и угол закручивания, таким
образом, релаксировали одновременно и сила и момент. При
обработке с самого начала было сделано предположение о возможности
пренебречь сжимаемостью, таким образом, считалось заранее, что
напряжения должны уменьшаться в одном и том же отношении.
В действительности отношение т/а немного менялось в процессе
испытания, оно несколько убывало в первые часы, а потом
оставалось практически постоянным, разница между наибольшим
и наименьшим значением этого отношения не превышала 14%.
На рис. 135 приведены кривые релаксации интенсивности
напряжений, о* — начальное значение интенсивности. Пунктирные
кривые — результат расчета с омощью уравнения (82.1). Для
образца 1 а* = 33 кг[ммг, г*/а* = 0,58; для образца 2 на первом
J^^ /
\^ т-
-—i—
[i
—i
Р*"~
J ^
S 82]
РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
343
этапе было 0* = 18,73 кг/мм2, т*/о* = 1,45, после 26 часов
напряжения были повышены при сохранении неизменного
отношения т/о до о* = 20,4. У образца 3 было а* = 28,1, т*/а* =
= 0,242, при i = 24 часа напряжения были увеличены, и для
следующего этапа а* = 32,2, т*/сг* = 0,214. Как и в опытах
Джонсона, фактически релаксация происходит несколько быстрее,
чем следует из предсказаний теории, однако разница не столь
велика, и совокупность опубликованных данных по
экспериментальному исследованию релаксации при сложном напряженном
состоянии может рассматриваться как серьезное подтверждение
справедливости уравнений течения с упрочнением.
Для большого числа конструкций вопрос о перераспределении
напряжений при ползучести является первостепенным, появление
незначительных деформаций ползучести существенно снижает
пики напряжений, появляющиеся в начальный момент, когда
поведение материала еще упруго. В задачах такого рода
приходится иметь дело с процессами, весьма близкими к процессам
релаксации напряжений, поэтому прямая проверка теории в области
малых деформаций ползучести, сопутствующих релаксации,
представляет непосредственный интерес.
ГЛАВА VI
ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ
ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
При оценке прочности изделий, работающих в условиях
высоких температур, приходится считаться, с одной стороны, с
возможностью недопустимо больших деформаций, с другой — с
возможностью разрушения.
Длительное разрушение металлов и сплавов при высоких
температурах служило предметом многочисленных исследований,
в этой области накоплен большой опытный материал, однако
вопрос об экстраполяции данных по длительной прочности не
может считаться решенным. Здесь сообщаются основные опытные
факты и их феноменологическая интерпретация, а также
излагаются некоторые механические теории, позволяющие
предсказывать время разрушения изделий. Центральная идея этих теорий
состоит в том, что выделяются два основных типа разрушения —
вязкое и хрупкое. В реальных материалах эти типы могут
осуществляться в чистом виде, а могут взаимодействовать между собою,
давая картину смешанного разрушения. Излагается также вопрос
о критериях длительной прочности при сложном напряженном
состоянии.
§ 83. [ОСНОВНЫЕ СВЕДЕНИЯ О ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
Если действующее напряжение достаточно велико, то
ползучесть образца при постоянной нагрузке или постоянном
напряжении заканчивается переходом в третью фазу ползучести и
приводит к разрыву по истечении некоторого времени. Время до
разрушения увеличивается с уменьшением действующего
напряжения. Стандартный метод испытания на длительную прочность
состоит в том, что образец испытывается при постоянной нагрузке,
определяется зависимость времени до разрушения от условного,.
§ 83] ОСНОВНЫЕ СВЕДЕНИЯ О ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 345-
Рис. 136.
отнесенного к начальной площади сечения образца, напряжения.
Результаты испытаний представляются в виде кривых длительной
прочности. Такая кривая схематически показана на рис. 136.
Имея кривую длительной прочности, можно определить так
называемый предел длительной прочности, то есть минимальное
напряжение, при котором разрушение происходит по истечении
заданного времени. Так же как и предел ползучести, предел
длительной прочности представляет собою условную величину;
в зависимости от назначения
изделия предел длительной
прочности определяется для
той или иной долговечности,
от нескольких минут до
десятков тысяч часов.
По-видимому, кривая на рис. 136 не имеет
горизонтальной асимптоты,
поэтому говорить об абсолютном
пределе длительной прочности
вряд ли возможно. При
высоком уровне напряжений
разрушение происходит довольно
быстро и сопровождается значительным удлинением, которое
состоит из мгновенной пластической части и деформации
ползучести. Как правило, при уменьшении напряжения и соответственно
увеличении длительности пребывания образца под нагрузкой до
разрушения деформация к моменту разрыва уменьшается,
характер разрушения становится хрупким.
Многие сплавы, в особенности
жаропрочные сплавы сложной структуры,
разрушаются при длительном
действии нагрузки совершенно хрупко,
без заметной пластической
деформации. На рис. 137 показан примерный
график зависимости удлинения в
момент разрыва от времени
разрушения. У ряда материалов (некоторые
аустенитные стали, технически
чистый молибден) деформация при
разрыве достигает минимума при определенном значении t, более-
длительное разрушение при меньших напряжениях
сопровождается большим удлинением. Соответствующая кривая показана,
схематически на рис. 137 пунктиром.
Незначительные изменения напряжения очень сильно влияют
на величину времени до разрушения, поэтому кривые длительной
прочности удобно строить в логарифмических или
полулогарифмических координатах, во всяком случае, откладывая по оси.
Рис. 137.
46 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
абсцисс логарифм времени. Обычно пользуются двойными
логарифмическими координатами. На рис. 138 изображена типичная
диаграмма длительной прочности в двойных логарифмических
координатах. Как правило, эта диаграмма хорошо
аппроксимируется двумя прямыми, с меньшим наклоном для высоких
напряжений, с большим наклоном для низких напряжений. Иногда
точка пересечения прямых выявляется совершенно четко, иногда
существует переходный криволинейный участок, как показано
пунктиром. У структурно-неустойчивых материалов диаграмма
длительной прочности может иметь более сложный характер.
Перелом диаграммы длительной прочности соответствует
изменению характера разрушения. На участке / разрушение носит
вязкий характер, оно
сопровождается значительной
деформацией, трещины
разрушения идут по телу зерна.
На участке // пластические
деформации незначительны,
разрушению предшествует
образование
многочисленных трещин по границам
между зернами. В
результате роста и слияния этих
трещин происходит разру-
1,09 * шение образца.
Рис. 138. В зависимости от
материала и температуры
испытания переход от внутризеренного к межзеренному разрушению
может происходить в разное время (от минут до тысяч часов)
Иногда перелом диаграммы вообще не выявляется, на диаграмме
существует только первый участок. При расчете изделий,
предназначенных для длительной службы, бывает необходимо знать
предел длительной прочности на большой базе (например,
100 000 часов). Обычно длительность испытании выбирается таким
образом, чтобы выявился достаточно четко второй прямолинейный
участок диаграммы; продолжая эту прямую до нужного значения t,
получают экстраполированный предел длительной прочности.
Поскольку на первом участке разрушение происходит при
большой пластической деформации, диаграмма носит условный
характер: истинное напряжение в момент разрушения существенно
отличается от той величины, которая откладывается по оси
ординат при построении диаграммы. На втором участке дело обстоит
в этом смысле лучше: при незначительной деформации условное
напряжение мало отличается от истинного.
Вопросу о механизме хрупкого разрушения при ползучести
посвящены многочисленные исследования. Наблюдения показы-
I 84] ТЕМПЕРАТУРНО-ВРЕМЕННЫЕ ЗАВИСИМОСТИ 347
вают, что межзеренные трещины могут иметь различное
происхождение. При относительно невысоких температурах существенную
роль играют стыки трех соседних зерен. Вследствие различной
ориентации этих зерен течение металла в окрестности стыка
затруднено, здесь возникает концентрация напряжений, приводящая
к появлению трещины. При более высоких температурах на
границах образуются поры, в результате их слияния возникают
широкие трещины с закругленными концами [187].
Вопрос о связи трещинообразования с ползучестью далеко
не ясен, однако существует некоторый эмпирический факт,
наблюдаемый по крайней мере для некоторых материалов, по
преимуществу чистых металлов и однофазных сплавов: произведение
скорости установившейся ползучести на время до разрушения
оказывается примерно постоянным, не зависящим от напряжения
и температуры [35], [204]. Этот факт дал основание ряду
авторов [33], [зго], I190] использовать одни и те же соотношения для
экстраполяции данных по ползучести и длительной прочности.
§ 84. ТЕМПЕРАТУРНО-ВРЕМЕННЫЕ ЗАВИСИМОСТИ
ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
Получение полных характеристик длительной прочности
материала во всем диапазоне рабочих температур связано с большим
объемом экспериментальных исследований, которые оказываются
просто невыполнимыми, если материал предназначается для
длительной службы. Поэтому совершенно естественны
многочисленные попытки найти какие-либо формулы, которые позволили бы
производить экстраполяцию результатов кратковременных
испытаний пли заменить длительные испытания при низкой
температуре испытаниями меньшей продолжительности при высокой
температуре. Таких универсальных формул, по-видимому, не
существует, различные сплавы ведут себя, в общем, по-разному,
и простые физические модели, которые лежат в основе
соответствующих попыток, относятся к некоторому идеализированному
материалу, а не к реальному техническому сплаву. Литература
по вопросу об экстраполяции данных длительной прочности
чрезвычайно велика, приводимые ниже сведения предназначены
главным образом для того, чтобы проиллюстрировать сложность
проблемы. В § 45 были сообщены некоторые сведения о
температурных зависимостях скорости ползучести, в частности дана
формула D5.4) для зависимости скорости ползучести от
напряжения и температуры. Перепишем эту формулу в более общей форме,
а именно положим:
v _ ехр ( — ^) х const. (84.1)
348 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
Формула D5.4) получается теперь как частный случай, когда
u(cr) = u0 — ус. Как было отмечено в конце § 83, произведение
скорости ползучести v на время до разрушения ^ приблизительно
постоянно, обозначим его через е*, тогда
» = -?-• (84.2)
Из (84.1) и (84.2) следует:
T(c + logQ=F(a). (84.3)
Левая часть уравнения (84.3) называется параметром Ларсона —
Миллера [276]; мы уже ввели этот параметр в § 45. Если
представлять результаты испытаний на длительную прочность,
откладывая по одной из осей напряжение, а по другой — параметр
Ларсона — Миллера, то точки для всех температур и всех
напряжений должны, согласно уравнению (84.3), расположиться на
одной кривой.
Несколько большая гибкость получается при использовании
параметра Мэнсона — Хаферда [219], который был введен чисто
эмпирическим путем. Эти авторы предположили существование
следующего соотношения:
-, ТГ\а r = F{a). (84.4)
log i*—log ta v ' v '
Формула (84.4) содержит уже две константы, Та и ta, поэтому,
конечно, с ее помощью можно добиться лучшего совпадения
с опытом.
Если принять зависимость скорости ползучести от
напряжения и температуры по формуле D5.1), а именно:
то результаты испытаний при различных температурах будут
изображаться одной кривой в координатах о — т}„., где ^ —
приведенное время до разрушения:
t*
%=\exp(^r)dt = F(e). (84.5)
о
Такой способ представления данных по длительной прочности
был предложен в статье Орра, Шерби и Дорна [320].
Возможность предсказания характеристик длительной
прочности с помощью формул (84.3), (84.4), (84.5) и других проверялась
многими авторами на обширном материале [10°], [212], Р16], I250).
Результаты, в общем, оказываются довольно неопределенными.
Авторы отмечают, что, как правило, каждый метод является
§ 84] ТЕМПЕРАТУРНО-ВРЕМЕННЫЕ ЗАВИСИМОСТИ 349
некоторой первой довольно грубой аппроксимацией; с помощью
параметра Мэнсона — Хаферда результаты получаются несколько
лучшие. Для иллюстрации приведем данные по обработке
длительных, до 34 000 часов, испытаний сплавов нимоник 80 и нимо-
ник 90 [169].
Расчетное разрушающее напряжение для фактической долговечности
и ошибка в %
Г, °С
650
700
730
815
870
650
700
750
кг
' Л1Л12
4090
3780
3620
3150
2040
1970
1570
1100
865
630
315
3150
2830
2520
2040
1570
1160
1260
945
630
'*
4110
6440
5370
15290
12090
20400
7590
22160
3340
6830
16292
5270
8170
13390
4840
10900
34060
4490
13090
22660
Формула
(84.3)
%
Нимоник
4090
3900
3960
3540
2440
2230
1570
1260
895
740
284
Н имо
3210
2990
2760
2140
1820
1390
1260
975
835
0
+3
+9
+23
+ 19
+14
0
+14
+4
+18
—10
ник
+2
+6
+10
+5
+16
+26
0
+3
+33
Формула
(84.4)
30
4090
3840
3940
3440
2300
2040
1300
1040
820
645
220
80
3100
2850
2520
2010
1590
ИЗО
1240
880
725
%
0
+2
+9
+9
+12
+4
-5
-6
-5
+2
-30
-1,5
+0,5
0
-1,5
+1
+3
—1
—7
+15
Формула
(84.5)
4160
3940
4060
3630
2470
2230
1600
1210
880
675
236
3220
2980
2770
2180
1820
1370
1240
945
790
%
+2
+4
+12
+15
+21
+14
+2
+10
+2
+8
—25
+1,5
+5
+10
+7
+ 16
+24
—1
0
+25
По формулам (84.3), (84.4), (84.5) рассчитывалось напряжение,
которое соответствует фактически найденному времени до
разрушения. В соответствующих столбцах таблицы приведены величины
этого напряжения и разница по сравнению с фактическим
разрушающим напряжением в процентах.
Имеет смысл более подробно остановиться на работе
Клауса [18в], приводимые в ней данные отчетливо иллюстрируют
трудности, возникающие при применении различных критериев.
На рис. 139 представлена зависимость между напряжением и
параметром Ларсона — Миллера для одной из аустенитных сталей.
350 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
По оси ординат откладывается напряжение в логарифмическом
масштабе^ ло оси абсцисс — параметр Ларсона — Миллера
в условных единицах. Для каждой температуры точки ложатся
на свою прямую, эти прямые приблизительно параллельны, онв
показаны пунктиром. Но можно провести и общую прямую,
показанную сплошной линией, при атом опытные точки
оказываются довольно близко к ней.
б,яг/тг
40 45
Рис. 139.
Если мы имеем опытные
данные для крайних температург
то эту прямую можно
провести и ею можно пользоваться
с известной степенью
приближения для интерполяции. Но-
если мы располагаем
опытными данными при одной только-
температуре или при двух
близких температурах, мы н&
сумеем провести через
соответствующие точки прямую
нужного наклона, если
соединить точки, относящиеся к
одной температуре, и продолжить пунктирную прямую влево»
и вправо, то результат будет грубо ошибочным.
В результате анализа большого экспериментального
материала Клаус приходит к следующим заключениям. Зависимость-
времени до разрушения от напряжения и температуры во всех
случаях удалось записать следующим образом:
log ?* = a log or+ 6 (Г). (84.6)
В зависимости от того, что представляет собою величина аг
исследованные материалы разбиваются на четыре класса:
I. a = const,
II. а = а(а),
III. а = а(Т),
IV. а = а{Т, а).
Для первых трех классов можно указать некоторые простые-
способы представления опытных результатов. В частности,
материалы, поведение которых описывается с помощью критериев
Ларсона — Миллера или Мэнсона — Хаферда ((84.3) и (84.4)),
принадлежат к третьему классу. Аустенитная сталь, для которой
построен график на рис. 139, относится к первому классу, что-
совершенно очевидно. Действительно, при фиксированной
температуре параметр Ларсона — Миллера представляет собою
линейную функцию от log t„ поскольку точки для разных температур
5 85]
ВЯЗКОЕ РАЗРУШЕНИЕ
351
ложатся на параллельные прямые, зависимость между log a
и log tt линейна с постоянным угловым коэффициентом а. Для того
чтобы совместить все пунктирные прямые, их нужно сдвинуть
параллельно себе, что достигается соответствующим выбором
функции Ъ (Т); перестроенный таким образом график приведен
на рис. 140. Очевидно, что формула (84.6) при условии а = const
в, кз/мм г
70 77 72 73 74 75 76 77
Рис. 140.
следует из (84.5), если принять, что / (а) есть степенная функция.
При этом энергия активации может быть произвольной функцией
температуры.
Материалы второго класса отличаются от материалов первого
лишь тем, что зависимость времени до разрушения от напряжения
может быть произвольной, а не обязательно степенной. Таким
образом, материалы первого и второго классов следуют несколько
обобщенному критерию Орра, Шерби и Дорна.
Определение четвертого класса, по существу, не содержит
в себе ничего, кроме утверждения о том, что время до разрушения
есть функция температуры и напряжения.
Принципы, согласно которым можно было бы заранее, не
проводя испытаний на длительную прочность, отнести материал
к тому или иному классу (скажем, в зависимости от химического
состава и структуры), отсутствуют, таким образом, приведенные-
результаты носят чисто эмпирический характер.
§ 85. ВЯЗКОЕ РАЗРУШЕНИЕ
Если материал не охрупчивается в процессе ползучести, то
мы будем говорить о вязком разрушении. В этом случае при
постоянной нагрузке напряжение непрерывно увеличивается
вследствие уменьшения площади поперечного сечения. Вначале
происходит равномерное сужение образца, в некоторый момент
352 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
равномерное течение становится неустойчивым и образуется шейка,
при достаточно большом напряжении в шейке происходит разрыв
того же характера, что и при обычных кратковременных
испытаниях. У некоторых материалов (например, чистый ниобий)
пластичность настолько велика, что сечение в шейке утонынается
до полного исчезновения, половинки разорванного образца
заканчиваются остриями. Время, протекшее от начала образования
шейки до момента разрушения, обычно не слишком велико по
сравнению со всей продолжительностью жизни образца, поэтому
при оценке долговечности процесс образования шейки можно не
рассматривать. Предположим, что равномерное удлинение образца
может достичь сколь угодно большой величины и закон
ползучести, определенный для малых деформаций, остается справедливым
все время. Примем этот закон в виде E0.6):
ph(p) = f(o). (85.1)
Упругая деформация при этом, конечно, несущественна,
следовательно, можно положить
P=e-g{o). (85.2)
Обозначим длину образца в процессе деформации через х,
начальную длину через х0, площади сечения соответственно через F
и F0. За меру конечной деформации примем
е — In — .
хо
Из условия несжимаемости
xF = x0F0.
Отсюда
F = FQe*v(-e).
Поэтому истинное напряжение а связано с номинальным
напряжением а0, отнесенным к первоначальной площади
поперечного сечения, следующим образом:
а = а0ехр(е). (85.3)
Из (85.2) и (85.3) получаем:
Р = 1п -| g(o).
Внесем это выражение для р в (85.1):
o(^-g'(o))h[ln^-~g(a)]^f(a).
« 85]
ВЯЗКОЕ РАЗРУШЕНИЕ
353
Разделяя переменные и интегрируя, придем
результату:
к следующему
*- =
da
с*
)> of (о)
со
[1 - ag' (о-)] h [ In -?- - g](o) ] . (85.4)
Здесь tt — время до разрушения, причем за момент разрушения
принимается момент, когда напряжение а достигает некоторой
величины с*.
Считая в уравнении (85.4) верхний предел интеграла
переменным, мы получим уравнение кривой ползучести, справедливое
для достаточно больших деформаций
и описывающее поведение образца до
момента образования шейки. Эта
кривая схематически показана на рис. 141,
она имеет вертикальную асимптоту.
При о" = о* мы оказываемся в точке
А кривой ползучести; уравнение
перестает быть справедливым при о > о*,
так как растяжение при этом
перестает быть равномерным, на образце
образуется шейка. Однако абсцисса
точки А и абсцисса асимптоты
отличаются между собою мало, кривая
идет после точки А очень круто вверх.
Это дает основание принимать за время
до разрушения время достижения
кривой ползучести ее асимптоты, то есть
принимать в уравнении (85.4) сг^ = оо.
Кривая ползучести будет выглядеть так, как показано на
рис. 141, не всегда, для этого необходимо, чтобы подынтегральное
выражение не меняло знака, то есть чтобы было при любых о
l-ag'(a)>0.
Может оказаться, что при некотором значении о, которое мы
также обозначим 0%., это неравенство окажется нарушенным.
Это значит, что при а—-о^ где о* находится из уравнения
скорость ползучести становится бесконечно большой.
Интегральная кривая, даваемая формулой (85.4), имеет вид кривой,
изображенный на рис. 142. Реальный смысл имеет только участок О А
кривой, при достижении точки А равновесие становится
невозможным и происходит мгновенное разрушение.
Рассмотрим* некоторые частные случаи применения
уравнения (85.4) для оценки длительной прочности.
23 ю. Н. Работнов
Рис. 141.
354 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
а) Вязко-пластическое неупрочняющееся тело. Для него
h (p) =1, / (о) = -х- (а — crj, g (о) = 0. Примем также о** = оо;
таким образом, t есть время, при котором длина вытянутого
образца становится бесконечно
большой, а сечение — бесконечно малым.
Подставляя в (85.4), получим:
= 3^<М
do
— In
Oq
do
г (О — Of) Of °0 — °T
(85.5)
Формула (85.5) была получена Генки
в 1925 г. [228], обобщение для
упрочняющегося вязко-пластического тела
сделано Одквистом [313].
б) Ползучесть без упрочения.
Простейшая оценка времени вязкого
разрушения металлического стержня в
Рис. 142. условиях ползучести при растяжении
была получена Хоффом [233]. Следуя
этому автору, положим а# — оо, h (р) = 1, g (а) = 0. Тогда
уравнение (85.4) приводит к следующему результату:
of {a)
(85.6)
оо
Если f(o) = Aan (в этой главе нам будет удобно пользоваться
именно такой записью степенного закона ползучести вместо
стандартной формы), как полагал Хофф, то
1 (85.7)
t*
AnoS
Если /(а) = ееехр— , то
* 8е V °е
(85.8)
Эти результаты могут быть уточнены, если принять во
внимание мгновенную пластическую деформацию. Соответствующее
решение получено Одквистом [316]. Положим, следуя этому автору,
g = bam
и сохраним остальные предположения Хоффа. Тогда
о*
<Т2 =
Ът
L
-S
do
(l-bmom).
оо
§ 85]
ВЯЗКОЕ РАЗРУШЕНИЕ
355
Заметив, что 6а™ есть начальная пластическая деформация,
соответствующая напряжению oi перепишем эту формулу
следующим образом:
(В оригинальной работе [31в] полагается о# = оо, поэтому
формула для t^ отличается от (85.9) тем, что в правой части отсутствует
третье слагаемое.)
Более простая схема учета возможности пластической
деформации была предложена Розенблюмом [ш]. Считая материал при
мгновенной деформации идеально пластическим (упруго- или
жестко-пластическим, безразлично, поскольку упругая
деформация мала), он заменяет в (85.6) верхний предел интеграла через
предел текучести о"т, считая, что по достижении этого значения
напряжения начинается неограниченная текучесть. При
степенном законе ползучести вместо (85.7) получается:
<.-ж*[4-(-ё-)*]- <85-«»>
Отметим, что при п = \ ползучесть переходит в вязкое течение,
однако схема Розенблюма принципиально отличается от схемы
Генки, поэтому из (85.10) нельзя получить результат (85.5). Если
моделировать соответствующие тела с помощью
упруго-пластических и вязких элементов подобно тому, как это было разъяснено
в § 23, но ввести некоторую обратную связь, изменяющую
характеристики пластичности и вязкости в зависимости от удлинения,
что соответствует изменению площади поперечного сечения
образца, то по схеме Генки элементы должны быть соединены
параллельно, по схеме Розенблюма, как и для уравнения (85.4),—
последовательно.
Возвращаясь к модели Одквиста, которая при частном
предположении о виде функции g (а) приводит к формуле (85.9),
заметим, что функция g (а) может включать в себя как мгновенную-
пластическую деформацию, так и деформацию первого участка.
ползучести. Степенная аппроксимация для функции g (а)
оправдывает себя в области малых деформаций, но совершенно не
очевидно, что в области больших деформаций, когда нужно
пользоваться логарифмической мерой деформации, она будет достаточно-
хороша. В то же время от вида функции g (о) зависит качественный
результат, поскольку эта функция определяет величину at.
Предположим, например, что g есть степенная функция не от
истинного напряжения, а от условного. Для мгновенной
деформации е — g и
g = bo ™ = ?amexp( — mg).
23*
356 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
Дифференцируя обе части по с, найдем:
о *=_?*_<1.
da 1 + mg ^
Таким образом, зависимость о от f всегда будет такой, как
показано на рис. 141.
До сих пор мы предполагали, что действующие на образец
нагрузки постоянны. Будем теперь считать, что а0 есть заданная
функция времени, пренебрежем мгновенной пластической
деформацией и примем, что / (а) — степенная функция. Тогда е ж р
и на основании (85.3)
е = / [«"о ехр (е)] = Aaf exp (пе).
Разделим переменные и проинтегрируем. Получим:
оо t
\ ехр (— пе) de = ~ = ^ Ао% dt. (85.11)
о о
Если бы напряжение о0 было постоянным, по формуле (85.7)
ему соответствовало бы время до разрушения t%, которое мы
обозначимt* (ст0) = -т—я- Теперь формулу (85.11) можно
переписать следующим образом:
t
(' dt
о
= 1. (85.12)
Условие (85.12) выражает так называемый принцип линейного
суммирования повреждаемости. Если в течение времени tt к
образцу было приложено напряжение ah то считается, что образец
приобрел степень поврежденности, которая равна отношению
времени действия напряжения о"?- к времени, необходимому для
разрыва при данном напряжении t% (a>). При переменных
нагрузках поврежденность суммируется; когда величина накопленной
поврежденности достигает значения, равного единице, происходит
разрушение. Этот принцип был высказан Робинсоном [343]. Следует
заметить, что для вязкого разрушения принцип линейного
суммирования вытекает из рассмотренных уравнений лишь при весьма
частном предположении о степенном законе ползучести и о
возможности отбрасывать мгновенную пластическую деформацию.
в) Ползучесть с упрочнением. Если не учитывать мгновенной
пластической деформации, принцип суммирования
повреждаемости будет справедлив и для материала, ползучесть которого
сопровождается упрочнением, если только / (а) — степенная функция.
Действительно, в этом случае уравнение (85.1) дает:
h (е) ехр (— пе) de = Aa^ dt.
§ 86] РАЗРУШЕНИЕ, СОПРОВОЖДАЮЩЕЕСЯ ОХРУПЧИВАНИЕМ 357
Обозначим
h (е) ехр (— ne)de = — .
о
Тогда мы получим:
1= \ n'Aa^dt.
о
Если а? = const, то из этого уравнения получается время до
разрыва:
Это выражение отличается от (85.7) только числовым
множителем. Очевидно, что для переменных нагрузок сохраняет силу
формула (85.11).
§ 86. РАЗРУШЕНИЕ, СОПРОВОЖДАЮЩЕЕСЯ ОХРУПЧИВАНИЕМ
Описанная схема вязкого разрушения реализуется только
для некоторых чистых металлов при малых продолжительностях
испытания. При больших длительностях разрушение, как уже
было отмечено, происходит при значительно меньших
деформациях. Металлографическое исследование показывает, что
разрушению предшествует образование микротрещин, главным образом
на границах зерен. Преимущественное направление этих трещин
перпендикулярно оси действия растягивающего напряжения.
С течением времени трещины растут, в конце концов происходит
разрыв. Разрыву всегда предшествует увеличение скорости
ползучести, то есть образование на кривой ползучести третьего
участка. В § 85 мы видели, что третий участок получается и на
кривой ползучести вполне «вязкого» материала за счет уменьшения
площади поперечного сечения (см. рис. 141); однако на самом
деле третий участок может начаться при очень малых деформациях
и количественный результат, получаемый с помощью
уравнения (85.4), никак не объясняет наблюдаемых экспериментальных
фактов.
Грубо схематическое описание процесса растрескивания может
быть получено следующим образом. Предположим, что в
поперечном сечении стержня появляются круглые трещины таким
образом, что на единицу площади сечения приходится одна трещина
с площадью со = яр2. Скорость распространения фронта трещины
есть функция среднего напряжения и структурного состояния
материала, характеризуемого степенью его упрочнения [1041-
358 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. "VI
Тогда
da n dp -,/—
Величина и равна скорости фронта трещины с точностью
до численного множителя. Если трещина имеет удлиненную форму,
например прямоугольную, и распространяется только в одном
направлении, то
d(i>
В общем случае можно предположить, что
%^и @<Р<1).
Если площадь сечения нерастрескавшегося образца есть F, то
площадь сечения, воспринимающая нагрузку, равна F A — со).
С другой стороны, вследствие ползучести происходит
уменьшение площади поперечного сечения в отношении ехр (— е). Таким
образом, действительная площадь сечения в каждый момент есть
F0{\— со) ехр ( — е),
а истинное напряжение
_ а0 ехр (е)
1—со
Будем называть величину со поврежденностью материала.
Изменение поврежденности со временем описывается следующим
уравнением:
Кроме уравнения (86.1) нам нужно рассматривать уравнение
ползучести
ph(p) = f(a, со). (86.2)
При написании уравнения (86.2) учтена возможность того,
что степень поврежденности материала влияет на ход ползучести.
Относительно функций и и / можно делать различные
предположения, таким образом, открывается широкая возможность описания
различных опытных фактов. Будем считать, например, что
деформация ползучести к моменту разрушения невелика и скорость
распространения трещины зависит только от напряжения. Тогда
нам достаточно рассмотреть одно лишь уравнение (86.1), которое
примет следующий вид:
§ 86] РАЗРУШЕНИЕ, СОПРОВОЖДАЮЩЕЕСЯ ОХРУПЧИВАНИЕМ 359
Если и (а) — степенная функция, так что
u(a) = Boh,
то в (86.3) переменные разделяются, и мы получаем:
A— (o)h«>-fida = Bobdt.
Интегрируя, найдем!
1 t
\ A — co)ftco-Mco= [ Boh0dt.
о о
В левой части интеграл взят от со = 0 до со = 1. Строго говоря,
данная схема предполагает некоторое число зародышевых трещин,
которое остается неизменным. Поэтому в начальный момент
со отлично от нуля. Представляя трещины в виде кругов, нельзя
допустить такого положения, что со = 1, это геометрически
невозможно. С другой стороны, при некотором значении со= со* < 1
происходит отрыв, поэтому верхний предел интеграла должен
быть со,., мы заменяем его единицей из тех же соображений, из
которых в формуле (85.4) верхний предел 0"* заменяется
бесконечностью. Интеграл в левой части всегда представляет собою
конечное число:
5<«-
\k rj ГA + А)ГA — В) 1
.со^со-Мсо^ ^+>^p)W = I_
(при р = 0, Jfe' = ft).
Поэтому условие хрупкого разрушения запишется следующим
образом:
t
[ (l+k')Ba^dt = l. (86.4)
о
Условие (86.4) по виду не отличается от (85.10). Точно так же, если
1
о0 = const, то t% (во) = h — ; к есть время до разруше-
ния при данном напряжении. Если а0 переменно, то условие (86.4)
приводит к закону линейного суммирования повреждаемости,
который оказывается применимым в равной степени как для
чисто вязкого, так и для вполне хрупкого разрушения. В
логарифмических координатах log cr — log t# как (85.10), так и (86.4)
дают прямые с разными наклонами. Мы видели в § 83, что
реальные кривые длительной прочности имеют в логарифмических
координатах два прямолинейных участка. Действительно, первый
участок соответствует транскристаллическому разрушению,
сопровождающемуся значительной пластической деформацией, второй
360 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
участок относится к малым нагрузкам и большим длительностям,
когда разрушение идет по границам зерен и деформация ничтожно
мала. Между этими крайними случаями располагается
промежуточная область смешанных разрушений, для которых
вышеприведенный анализ неприменим и система уравнений (86.1) и (86.2)
должна рассматриваться при более общих предположениях.
§ 87. СМЕШАННОЕ РАЗРУШЕНИЕ. ГИПОТЕЗА КАЧАНОВА
Рассматривая смешанное разрушение, Качанов [51] высказал
предположение о том, что образование трещин не влияет на
процесс ползучести, следовательно, в уравнении (86.2) величина со
не фигурирует и это уравнение интегрируется независимо от
(86.1). В пользу такой гипотезы автор высказал следующие
соображения. Механизм процессов ползучести и разрушения, в общем,
различен, хрупкое разрушение развивается по границам зерен,
а вязкое течение — по телу зерна. С другой стороны, если
влияние трещин на ползучесть имеется, то кривые ползучести, по
которым устанавливаются уравнения ползучести, отражают
суммарный эффект. Ограничиваясь степенным законом ползучести
без упрочнения, запишем (86.2) в следующем виде:
е = Ла"ехр(гее). (87.1)
Отсюда, интегрируя, находим:
ехр (е) = Ц- = A - 1ь4о»*)~1/п.
Заметим, что по формуле (85.7) величина пАа™ равна 1//ь где
tl — время вязкого разрушения для данного напряжения а0-
Вследствие этого можно написать:
exp(e)=fl —iV1/n. (87.2)
Записывая уравнение (86.1), Качанов принимает |3 = 0
и выбирает функцию и в виде степенной функции от одного
только о. Учитывая (87.2), он получает:
ft
dot
i? = JB_L(i_J-) n. (87.3)
Разделяя переменные и интегрируя левую часть от со = 0 до
со = 1, правую от t = 0 до t = t^, представляющего собою время
до разрушения, найдем:
^ = 1_Г1_^_к>-\ (87.4)
§ 87] СМЕШАННОЕ РАЗРУШЕНИЕ. ГИПОТЕЗА КАЧАНОВА 361
Здесь t2 — время хрупкого разрушения при напряжении а0
по формуле (86.4). Формула (87.4) справедлива, когда
определенное ею t^^h, в противном случае произойдет чисто вязкое
разрушение. Если t = tu то
п—к п
Отсюда следует, что уравнение (87.4) действительно при
выполнении условия
1
В k + V
о0<
А п-
= 0„
Рис. 143.
Откладывая, как обычно при построении кривой длительной
прочности, по осям координат log а и log f#, проведем прямые
вязкого разрушения t = tx (а) и хрупкого разрушения t = t2 (о)
(рис. 143). В точке А о=о';
если а > а', то кривая дли- гв9 б
тельной прочности
представляет собою отрезок
прямой t^ = ti слева от
точки А. При меньших
напряжениях это будет
кривая, вписанная в угол
между пересекающимися
прямыми; эту кривую можно
рассчитать с помощью
(87.4); при малых
напряжениях tt (о) > h (о) и
из (87.4) следует t^ & t2-
Качанов особо останавливается на случае, когда п = к.
Соответствующую формулу можно получить предельным переходом
из (87.3), но мы проделаем вывод независимо. Перепишем
уравнения (86.1) и (86.2) следующим образом:
со = 5а™ A — со)"п ехр (пе),
е = А а™ ехр (пе).
Разделим второе уравнение на первое. Получим:
Проинтегрируем это уравнение. Найдем:
362 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
В момент разрушения ш=1, следовательно, е = е* = -^ —г~,т ¦
Итак, если п = к, то хрупкое разрушение происходит всегда
при одной и той же величине деформации. По формуле (87.2)
-? = 1 — ехр ( — e^n) = q = const. (87.5)
н
Итак, охрупчивание уменьшает величину долговечности,
найденную по схеме вязкого разрушения, в постоянном отношении.
Полученный результат в известной мере объясняет тот факт, что
расчет долговечности по схеме Хоффа иногда дает
удовлетворительный количественный результат (хотя бы в примере,
приводимом Хоффом), тогда как исходные гипотезы далеко не
подтверждаются.
Заметим, что при п = к сохраняет силу принцип линейного
суммирования повреждаемости. В этом легко убедиться, если
написать для случая переменной нагрузки вместо (87.1) следующее
выражение:
ехр (пё) = 1 — \ — .
Полагая е = е%, найдем, что \ — = q\ отсюда следует:
J ** (сто)
Здесь ?„., как обычно, время до разрушения при постоянно
действующем напряжении о0.
Дальнейшее уточнение теории Качанова принадлежит Одкви-
сту [31в], который учел мгновенную пластическую деформацию
(или деформацию первой фазы ползучести), поступая следующим
образом. Обозначим ао0 величину напряжения, при котором
происходит разрушение. Из формулы (86.3) следует, что а =
= ехр (е^), где е„. — деформация в момент разрыва. По
формуле (85.4), полагая, как в § 85, / (о) = Аоп, g (о) = bam , h = 1,
получим:
ссоо
'=$т^*-«--?[1 + "'0?-1)]- (87'6>
Здесь t3 — время, определенное по формуле (85.9). Перепишем
теперь уравнение повреждаемости следующим образом:
со A - о)'! = Вок
или
{i—at)hda> = Bah%-do.
« 88] БОЛЕЕ ОБЩАЯ ГИПОТЕЗА РАЗРУШЕНИЯ. ХРУПКИЙ СЛУЧАЙ 363
Но из (87.6)
di _\ — Ьтат
do — 4a"+i -
Поэтому
,. sh , В l — bmam ,
A —а>га(й = —. da.
Проинтегрируем левую часть от со = 0 до со = 1, правую от
<т = сг0 До а = аа0. Получим
после упрощений:
ti \_п— к N >
п~т (\ h\ .,
п — к — т\ *i У
X A - afe+m-n) ] . (87.7)
Исключая из (87.6) и (87.7)
параметр а, получим
кривую длительной прочности.
Проделанное Одквистом Рис. 144.
исследование показало, что
кривая длительной прочности, рассчитанная по уравнениям (87.6)
и (87.7), располагается ниже, чем кривая, рассчитанная по
уравнению Качанова (87.4), как показано на рис. 144.
Некоторые дальнейшие результаты в том же направлении
содержатся в работе [1,а].
§ 88. БОЛЕЕ ОБЩАЯ ГИПОТЕЗА РАЗРУШЕНИЯ.
ХРУПКИЙ СЛУЧАЙ
Введенный в § 86 параметр охрупчивания со для наглядности
можно представлять себе как степень уменьшения эффективной
площади поперечного сечения. Однако такая точка зрения не
обязательна для феноменологической теории. Возвращаясь к общим
представлениям о кинетике процесса ползучести (§ 55), мы можем
рассматривать величину со как один из структурных параметров,
определяющих состояние материала. Эта величина является
некоторой мерой растресканности материала, однако мы не будем
пытаться установить прямую зависимость между количеством
трещин на единицу объема, их размером и ориентацией, с одной
стороны, и величиной параметра со, с другой. Таким образом,
наши предположения сводятся к следующему. Процесс развития
трещин от самого начала до момента разрушения проходит
единообразно. Это значит, что если мы имеем опыты А и Б, в течение
364 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
которых происходит развитие трещин вплоть до разрушения, та
каждому состоянию растресканности в опыте А соответствует
некоторое, точно такое же состояние растресканности в опыте Бг
причем в любом эксперименте эти состояния следуют одно за
другим в той же самой фиксированной последовательности. Это-
дает основание приписать каждому состоянию растресканности
некоторое число со, совершенно условно мы выбираем это число-
в интервале @, 1), при этом со = О соответствует условно
неповрежденному материалу, со = 1 соответствует образованию
макроскопических трещин. Если допустить, что сам процесс
образования и развития трещин происходит неодинаково в разных
условиях, например принять, что существуют трещины двух
родов, то мы будем вынуждены ввести два или больше параметров
охрупчивания. Таким образом, высказанная гипотеза является
самой простой [106].
Предположим теперь, опять-таки для простоты, что величина со
представляет собою единственный структурный параметр, так что,
например, упрочнения не происходит. Тогда, в соответствии
с E5.1), мы должны принять
ё = /(<г, со). (88.1)
Начальной пластической и упругой деформацией мы при этом
пренебрегли. Относительно кинетики изменения со мы также
сделаем простейшее предположение, вытекающее как частный случай
из E5.2):
со = ф(о, со). (88.2)
В зависимости от того, находимся мы в области малых или
больших напряжений, под а можно понимать напряжение о0,
отнесенное к начальной площади сечения, или истинное напряжение
а = о"о ехр (е). Точно так же, если деформации малы, то е
представляет собою обычную деформацию, в противном случае е —
логарифмическая деформация.
При обсуждении более простых схем разрушения мы
аппроксимировали функции, фигурирующие в уравнениях, с помощью
степенных функций. Желая получить обозримые результаты,
поступим так же и в общем случае, а именно примем (88.1) и (88.2)
в следующем виде:
е=аопA -©)-«, со = ссг''A-со)-г. (88.3)
Коэффициенты а ж с будут функциями температуры, при этом
температурная зависимость ползучести и разрушения, в принципе,
может быть различной, эти процессы характеризуются разной
энергией активации.
§ 88] БОЛЕЕ ОБЩАЯ ГИПОТЕЗА РАЗРУШЕНИЯ. ХРУПКИЙ СЛУЧАЙ 365
Случаем чисто хрупкого разрушения мы будем называть такой
случай, когда деформация в момент разрыва невелика и,
следовательно, изменение площади поперечного сечения может не
приниматься во внимание. Положим
в (88.3) а — а0, тогда из второго в'
уравнения системы (88.3) следует:
A-ю)г+1=1-~. (88.4)
h
Здесь t2 — время хрупкого
разрушения, определенное так же, как
в § 86: i
г2 =
с A + 0 о?
Рис. 145.
Заметим, что введение параметра В,
учитывающего форму трещины,
совершенно несущественно для
конечного результата, поэтому мы будем считать 6 = 0 в
соответствии с [61].
Внесем теперь выражение (88.4) для со в первое из
уравнений (88.3) и проинтегрируем его. В результате получим уравнение
кривой ползучести:
п ц L V h
Здесь ti — время вязкого разрушения, определенное в § 85:
¦]¦
(88.5)
U
х=
1-+1
-q + i
Примерный вид кривой ползучести по уравнению (88.5)
приведен на рис. 145. Величина удлинения при разрыве
h
°-ь — „ . —
\-\-r с'а°
¦n—k
(88.6)
Поскольку всегда п > к, то удлинение при разрыве уменьшается
с уменьшением напряжения.
Как видно, использование гипотезы, выражаемой
уравнениями (88.2), не вносит каких-либо изменений в определение времени
хрупкого разрушения, но позволяет описать третий участок
ползучести, предшествующий разрушению. В статически неопределимых
системах учет ускорения ползучести на третьем участке позволяет
более правильно описать перераспределение напряжений в
элементах системы и оценить долговечность более точно.
Для экспериментального определения констант
уравнений (88.3) необходимо иметь данные по ползучести на
установившихся участках, кривую длительной прочности для области
366 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
хрупких разрушений и зависимость удлинения при разрыве от
напряжения. Из обработки кривых ползучести находятся
величины а и и, из обработки кривой длительной прочности константа —
к и произведение с A + г). Далее, если зависимость между е% и о0
укладывается в степенную зависимость с показателем п — к,
то коэффициент X может быть найден, а этот коэффициент
выражается через г и q. Независимое определение величины г
невозможно, поэтому у нас остается некоторый произвол. Положим,
например, г = О, тогда
§ 89. СМЕШАННОЕ РАЗРУШЕНИЕ.
КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ
Если напряжения достаточно высоки, то разрушение
происходит при больших деформациях и учет поперечного сужения
становится необходимым. Положим в (88.3) а = о0 ехр (е), получим:
e=^-exp(ne)(l-(D)-'; ю = —^exp^l-co)-'. (89.1)
Разделим одно уравнение на другое, в результате чего придем
к дифференциальному уравнению для е в функции а, а именно:
? = 1??ехр[<И-*ИA-а,Г'.
Проинтегрируем это уравнение с учетом начального условия
е@)==0. Получим:
e = jr^ln[l—v + v(l —ш)г-«+1]. (89.2)
Здесь
1+г п—к и п—к а „ ъ
V = —¦ — = о
п г—qr + 1 ti г — g-j-1 с °
Теперь мы должны рассмотреть две возможности, а именно:
1. v<l, условие разрушения со = 1 достигается при
некотором конечном значении е = е^, причем
***=-^Ml-v). (89.3)
2. v>l, величина е стремится к бесконечности при
некотором конечном значении (о~щ, причем
1
ю*
= 1-(^-)Г-'+1. (89.4)
§ 89] СМЕШАЙНОЕ РАЗРУШЕНИЕ. КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ 367
Теперь для нахождения времени до разрушения мы внесем
выражение (89.2) для е во второе из уравнений (89.1) и
проинтегрируем его. Результат может быть записан следующим образом:
1
.L = bJ(l_v + v?y?b-»d?. (89.5)
Z*
Здесь введено дополнительное обозначение:
к
Нижний предел интеграла ^ = 0 в первом случае, когда v<l,
и ?„.== во втором случае, когда v>l. Как в том, так
и в другом случае интеграл в формуле (89.5) выражается через
гипергеометрические функции, для этого нужно воспользоваться
известной формулой:
1
\ и' A - иH-"-1 A - uz)~a du = Г (Ь)ГГ((СС)~~ F(a,b;c;z).
о
После несложных преобразований получим:
4 = t2F{-v, 1; 1 + Ь; v) при v<l, (89.6)
f, = f^(l-v, 1;м + 2;4-) ПРИ v>l. (89.7)
Для малых v приближенно получается:
«* = h { 1
/с К *2 \
Особого исследования требует тот случай, когда к = п.
При этом
d-e __ 1 + я t2 ,. фу-q
da> n t± * '
Отсюда
Здесь
Я tn a 1
t- = m = const.
n tj с r-\-\ — g
Внесем найденное значение 1 — со в первое из уравнений (89.1)
и проинтегрируем. Найдем:
\ ехр(-пе)A-^OГ5ТГ^==-2_. (89.8)
368 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
Это есть уравнение кривой ползучести. Интеграл (89.8) можно
вычислить приближенно, если считать, что пе# < 1.
Ограничиваясь двумя членами разложения в подынтегральном
выражении, получим:
-?--*{-<'— 'О-^У-Ш'-О-ОТ}'
(89.9)
Отсюда находим время до разрушения, полагая е = е„.:
или
Кратковременная ползучесть представляет собою особенно
благоприятную область для применения изложенной теории. Как
мы видели в § 58, для кратковременной ползучести характерно
отсутствие упрочнения, таким образом, степень охрупченности
является единственным структурным параметром. У
стабилизированного материала структурные превращения не успевают оказать
существенного влияния на процесс ползучести и разрушения.
При обработке опытов Милейко было принято, что п = к =
= q = г. Условие п = к вытекало из того факта, что в диапазоне
времен от 3 секунд до 3 минут удлинение при разрыве было
примерно постоянным. Условие того, что q — г = п было принято
для простоты, оно является естественным, если считать, что
<в представляет собою уменьшение площади эффективного сечения.
При достаточно малых деформациях из (89.10) следует:
^'«-гтг^тсгт^ {X = n + i)- (89Л1)
Константы а и п находятся в результате обработки начальных
участков кривых ползучести, единственная постоянная, от
которой зависит условие разрушения, есть еч. Мы трактовали эту
величину как удлинение в момент разрыва, но фактическое
определение е% таким образом наталкивается на трудности.
Действительно, с одной стороны, деформация локализуется в местах
разрыва и определение истинной деформации требует
дополнительных предположений, с другой — развитие макротрещин на
последнем этапе разрушения не описывается в рамках изложенной
схемы. Но, зная время до разрушения tm для какого-либо
напряжения, можно найти et из формулы (89.11). Контролем может
служить построение кривой ползучести по уравнению (89.9) или
для малых деформаций по уравнению (88.5), которое принимает
§ 89] СМЕШАННОЕ РАЗРУШЕНИЕ. КРАТКОВРЕМЕННАЯ ПОЛЗУЧЕСТЬ 369
следующий вид:
—•{•-О-гЛ- (8М2>
На рис. 146 нанесены опытные точки кривой ползучести сплава
Д-16АТ при температуре 250° для напряжения 13,6 кг/мм2,
пунктиром построена расчетная кривая по уравнению (89.12).
Константы ползучести определены в результате осреднения
нескольких кривых ползучести, так же как постоянная е%, точки
е-77717
7 2 J 4 5-70*сен
Рис. 146.
относятся к индивидуальному образцу, и полученное
расхождение является типичным для опытов на ползучесть. О том, что
в данном случае расхождение связано с индивидуальным
разбросом, свидетельствует тот факт, что расчетная кривая и опытные
точки не совпадают уже в самом начале, там, где происходит чисто
установившаяся ползучесть. Сплошной линией построена
расчетная кривая для а = 13,8 кг/мм2 при тех же значениях констант,
опытные точки почти совпадают с этой кривой. Приводимый
пример характерен как лишняя иллюстрация того неоднократно
отмечавшегося уже факта, что большой разброс по деформациям
или временам соответствует очень небольшой разнице в
напряжениях (в данном случае всего 1,5%, что составляет погрешность
испытательной машины).
При незначительном влиянии изменения площади
поперечного сечения на разрушение остается справедливым принцип
линейного суммирования повреждаемости, установленный ранее
для чисто хрупкого разрушения. В работе [74] этот принцип был
проверен на опытах при растяжении с постоянной скоростью
нагружения для алюминиевого сплава. Константы ползучести
определялись из опытов на ползучесть при постоянной нагрузке,
среднее значение константы е# находилось из опытов на длительную
24 Ю. Н. Работнов
370 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
прочность, после чего производились испытания с постоянной
скоростью загружения о до разрыва, напряжение в момент
разрыва фиксировалось в эксперименте и рассчитывалось по закону
линейного суммирования повреждаемости. Результаты сравнения
опытов и расчета приведены в нижеследующей таблице:
JN6
п/п
1
2
3
4
5
6
т, °с
230
230
275
275
275
275
кг
' мм% сек
0,35
0,02
1,4
0,4
0,1
0,025
о разрушающее, кг/мм%
опыт
27,6
23,8
26,8
24,4
20,6
18,1
расчет
29
24,6
26,9
22,8
21,3
18,7
Погрешность, %
+5
+3,5
+0,5
-6,5
+3,5
+3,5
§ 90. РАЗРУШЕНИЕ ПРИ ЦИКЛИЧЕСКИХ НАГРУЗКАХ
Ползучесть при циклических нагрузках была вкратце
рассмотрена в § 62. Разрушение при циклических нагрузках может
л происходить не только
W
V
qe
Ц2
вследствие ползучести, но
и вследствие усталости, и
отделить собственно
длительное разрушение от
усталостного, строго
говоря, нельзя. Усталости при
высоких температурах
посвящено большое число
исследований, и в рамках
данной книги изложить
состояние вопроса сколько-
нибудь подробно не
представляется возможным. В
качестве иллюстрации мы
приводим I2"], I3'5]
диаграммы усталостной
прочности при различных
температурах для сплава S-816
(рис. 147). По оси ординат отложена амплитуда цикла, отнесенная
к величине предела усталости при симметричном цикле 6"„, по
оси абсцисс — среднее напряжение цикла, отнесенное к пределу
длительной прочности Ьт. Последний определялся на базе 100
часов, предел усталости — на базе 2,16-107 циклов, частота
переменной составляющей в опытах была как раз такой, что на про-
24*
733\
Г
fffS"
42 a? qp qp p 12
Рис. 147.
S 901 РАЗРУШЕНИЕ ПР1Г ЦИКЛИЧЕСКИХ НАГРУЗКАХ 371
тяжении 100 часов укладывалось 2,16 • 107 циклов. При повышенных
температурах бросается в глаза следующее обстоятельство. Если
о"т< 0,5, то разрушение определяется только переменной
составляющей напряжения, его можно считать чисто усталостным.
Наоборот, если ov <C 0,3, то наложение переменной составляющей мало
влияет на длительную прочность, более того, длительная прочность
увеличивается, вместо того чтобы уменьшаться. Последнее
обстоятельство наблюдается не у всех материалов, оно может быть
отнесено за счет того, что наложение переменной составляющей
ускоряет процесс структурных превращений, действующих в данном
случае упрочняющим образом.
При 733° существует переходная область, в которой
соотношение между д0 и Ьт носит тот же характер, что и при
нормальной температуре; для более высоких температур в первом
приближении можно считать, что либо происходит длительное
разрушение, определенное средним напряжением цикла, либо
усталостное разрушение, зависящее только от амплитуды цикла.
Длительное разрушение при переменных нагрузках можно
рассматривать с точки зрения суммирования повреждаемости.
Если разрушение является хрупким и напряжение меняется
по синусоидальному закону:
o" = crm-f crBsinft>?,
то по формуле (86.4)
**
кВ [ (om + avsmat)hdt=l. (90.1)
о
Разрушение при циклической нагрузке происходит так же, как
при статическом нагружении с напряжением о*э, при этом
о* = lim Г \ К {от + av sin Ы)к dt ] ^. (90.2)
о
Эквивалентное напряжение ползучести и эквивалентное
напряжение разрушения, вообще говоря, отличаются между собою,
поскольку показатель к в формуле (90.2) отличается от
показателя п. Формула (90.2) допускает точно такую же графическую
интерпретацию, как аналогичная формула для ползучести. В
работах японских авторов [М6] предполагалось, что скорость
накопления повреждаемости зависит от абсолютной величины
приложенного напряжения, таким образом, в формуле (90.2) берется
абсолютная величина выражения (am+ с sin at). По их данным,
подобный анализ дает удовлетворительные результаты, если о"„Лхт<;
< 1,5. С увеличением амплитуды цикла по отношению к
среднему напряжению начинает проявляться усталость. Авторы [3631
24*
^72 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
предполагают, что усталостное повреждение происходит
одновременно с повреждением от ползучести и независимо от него,
разрушение же происходит, когда сумма этих двух повреждений
достигает критического значения. Скорость накопления
усталостного повреждения пропорциональна некоторой степени
амплитуды напряжения, та-
jf ким образом, получается сле-
& I I ' I дующее условие:
t„[kBo* + Dolv) = l. (90.3)
Здесь D и I — новые
константы, определяющие кинетику
усталостного разрушения. На
рис. 148 представлены
приведенные в [363] результаты
обработки по формуле (90.3)
опытных данных. По осям
координат отложены отношения
— и
<У3
Ц5
\
о W6
•W7
Х°
светлые и темные
Ц5
Рис. 148.
бт/б.
ГД
соответственно. Сплошная линия
кружки соответствуют
экспериментальным данным по
разрушению алюминиевого
сплава 24-S-T4 при температуре
260° на базе 10е и 107 циклов
это опытная кривая. Штрих-
пунктирные линии соответствуют отдельно разрушению только
от ползучести и только от усталости. Как видно, область
смешанных разрушений охватывает сравнительно узкий диапазон
отношений -,ив первом приближении можно считать, что разруше-
ние происходит либо только от усталости, либо только от
ползучести. Такая точка зрения находит подтверждение в обширных
экспериментальных исследованиях, выполненных под руководством
Серенсена [129], I130].
§ 91. ОПЫТНОЕ ИССЛЕДОВАНИЕ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
При длительном действии нагрузки в условиях сложного
напряженного состояния, так же как и при простом растяжении,
кривые ползучести переходят в третью стадию и ползучесть
заканчивается разрушением. В зависимости от материала,
температуры и уровня напряжений разрушение может происходить
при больших или малых деформациях, то есть может иметь вязкий
или хрупкий характер. До недавнего времени в литературе
§ 91] ОПЫТНОЕ ИССЛЕДОВАНИЕ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 373
отсутствовали какие-либо надежные данные о критерии
разрушения при сложном напряженном состоянии и гипотезы о
характере разрушения носили скорее умозрительный характер. Так,
Зигфрид [352] высказал предположение о том, что при тех
температурах, когда происходит интеркристаллическое разрушение,
критерием разрушения служит гидростатическая составляющая
тензора напряжений, если же разрушение транскристаллическое,
то определяющей величиной является октаэдрическое касательное
напряжение, то есть девиаторная составляющая тензора
напряжений. Такая простая схема не оправдалась, как стало ясно из
данных экспериментов. Прежде чем перейти к описанию имеющихся
в литературе опытных данных, выскажем некоторые общие
соображения, основываясь на аналогии с достаточно хорошо изученным
одноосным случаем. При растяжении можно говорить о времени
вязкого разрушения и времени хрупкого разрушения. Для
стержня время вязкого разрушения определяется по схеме Хоффа.
В условиях сложного напряженного состояния также возможен
расчет времени вязкого разрушения в предположении, что
материал имеет возможность ползти неограниченно, подчиняясь
определенным уравнениям ползучести для конечных деформаций.
Расчет времени вязкого разрушения в каждом случае
представляет собою задачу теории ползучести, решаемую для данной
конструкции, и опыты на образцах могут быть полезны лишь
для проверки и уточнения закона ползучести, но не для
установления критерия разрушения. Область хрупких разрушений
представляет в этом смысле значительно больший интерес.
Действительно, при оценке долговечности конструкции обычно
приходится подходить с двух точек зрения. Во-первых, необходимо
убедиться в том, что деформации конструкции не превосходят
определенного предела, после которого нарушается конструктивная
функция изделия. Обычно эта предельная деформация бывает не столь
большой и срок службы изделия лимитируется именно этой
предельной деформацией, а не возможностью вязкого разрушения
в области значительных деформаций. Во-вторых, нужно
убедиться в том, что прежде достижения предельной допустимой
деформации не произойдет хрупкое разрушение или, в крайнем
случае, разрушение смешанного типа. Что касается критерия
хрупкого разрушения, то представляется логичным предположить
скорость развития трещин связанной прежде всего с величиной
нормальных напряжений на тех плоскостях, где возникают
трещины.
Именно критерий наибольшего нормального напряжения был
использован при обработке опытных данных Джонсоном и
сотрудниками. Авторы исследовали молибденовую сталь при 550°,
медь при 250°, алюминиевый сплав при 200°, магниевый сплав
при 20°, сталь 0,2 % С при 450° и сплав нимоник 75 при 650°
374 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
[258]? [Ш] [26i)? [2бв]_ у ра3ных материалов поведение оказалось
резко различным. Молибденовая сталь, медь и нимоник
обнаружили длительный и заметно выраженный третий период
ползучести — ускоренную ползучесть перед разрушением.
Металлографическое исследование показало, что уже довольно рано в
материале возникают микроскопические трещины, более или менее
равномерно распределенные
&тах>"г/м*1г по объему образца. Для меди,
например, эти трещины были
хорошо заметны в момент
времени, соответствующий
половине полного времени до
разрушения. Джонсон называет
период накопления и
развития внутренних трещин
инкубационным периодом
разрушения; установить нижнюю
границу этого периода
затруднительно, но можно
предполагать, что треящнообразова-
ние сопутствует ползучести с
самого начала. В результате
слияния микротрещин в
одном из сечений образуется
макроскопическая трещина,
которая растет весьма быстро
и приводит к разрушению
образца: время роста
макроскопической трещины
значительно меньше продолжительности инкубационного периода.
Представляя результаты испытаний на длительную прочность
в координатах эквивалентное напряжение — время, авторы нашли,
что точки ложатся на одну кривую, если за эквивалентное
напряжение принять наибольшее нормальное напряжение. На рис. 149
приведена типичная кривая длительной прочности для меди
при 250°, по оси ординат отложено наибольшее нормальное
напряжение, по оси абсцисс — логарифм времени до разрушения;
точки соответствуют различным комбинациям растяжения с
кручением, включая чистое растяжение и чистое кручение. Три точки,
отмеченные буквой С, получены при растяжении сплошных
образцов, через них проведена пунктирная прямая, тогда как все
остальные точки группируются весьма близко около сплошной
прямой.
Третий период на кривых ползучести следует связать с
образованием микротрещин. Это подтверждается следующими
соображениями. Во всех случаях зависимость интенсивности
Рис. 149.
§ 91] ОПЫТНОЕ ИССЛЕДОВАНИЕ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 375
деформаций от времени удалось описать таким уравнением:
Ро = At + Btn + С ехр (Ы).
Для меди можно было принять А = 0. Величина А;,
определяющая скорость ползучести в третьей стадии, оказалась зависящей
только от максимального нормального напряжения а4.
Алюминиевый сплав и углеродистая сталь при 450° обнаружили
совершенно иное поведение. Хотя у них и был явно выраженный
\яй1Тд,лг/лш*
ЩЬ,час
третий период ползучести, но
никакого трещинообразования
в третьем периоде ползучести
заметить не удалось,
разрушение носило локальный
характер. Для алюминиевого сплава,
например, разрушение
происходило при весьма малых
деформациях, порядка 1 % и даже
меньше, поэтому здесь тоже
следует говорить о хрупком
разрушении, однако совершенно
другой природы. Точки
длительной прочности для разных
напряженных состояний
ложились на одну кривую только в
том случае, когда за меру
напряжения принималась
интенсивность напряжений. На рис.
150 приведена в
логарифмических координатах кривая
длительной прочности для алюминиевого сплава, точки
соответствуют различным напряженным состояниям от чистого кручения
до чистого растяжения. Если за меру эквивалентного
напряжения принять величину наибольшего нормального напряжения, как
для материалов первой группы, точки располагаются в беспорядке
и никакой кривой не определяют.
Что касается зависимости интенсивности деформаций от
напряжений в третьем периоде, она сохраняет обычный для ползучести
характер: р0 зависит от о0, но не от других комбинаций из
компонент тензора напряжений. Опытные данные удалось описать
следующей эмпирической зависимостью:
Ро = o»i (A*mi + A2tm*) + oy* (Bit** + B2tm*).
Здесь mi = 0,32, тг = 2,6, Аи А2, Ви В%, пи и2 — константы.
Для углеродистой стали получены аналогичные результаты,
испытания магниевого сплава были немногочисленны и не
позволили сделать определенных выводов.
Рис. 150.
376 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VJ
§ 92. ПРОСТЕЙШИЕ КРИТЕРИИ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
Большая и систематическая программа испытаний на
длительную прочность при сложном напряженном состоянии была
выполнена Сдобыревым [127]. Исследованию подвергался сплав
ЭИ-437Б, образцы изготовлялись из пруткового материала и из
штампованных заготовок для диска газовой турбины. Прутки
были подвергнуты термообработке: закалке при 1080° с
продолжительностью нагрева 8 часов, старению при 750° в течение
16 часов с охлаждением на воздухе. Контрольные испытания
поперечных образцов показали удовлетворительную изотропию.
Было проведено шесть серий испытаний, три серии относились
к образцам из поковки при температурах 700° и 750°, остальные
три — к прутковому материалу при 600°, 650°, 700° и 750°. Часть
образцов, изготовленных из прутка, была испытана в первую
очередь, соответствующие результаты были опубликованы
в статье [126], остальные образцы той же партии из материала
той же плавки были испытаны приблизительно через год.
Оказалось, что длительная выдержка стабилизирует свойства материала,
на выдержанных образцах разброс опытных точек оказался
значительно меньше, чем на образцах, не подвергавшихся выдержке.
Проверка различных критериев длительной прочности привела
Сдобырева к заключению, что среди известных критериев оценка
по наибольшему нормальному напряжению наиболее точна,
однако некоторое систематическое расслоение точек все же
наблюдается. Тогда он задался целью подобрать эмпирически
эквивалентное напряжение, позволяющее наилучшим образом
уложить опытные точки на одну кривую. Поскольку для
разрушения с охрупчиванием критерием длительной прочности служит
o"max> a Для локализованного разрушения а0, естественно принять
стэ = 6ота1 + A-6)а0. (92.1)
Сдобырев полагал 6 = 1/2, таким образом, у него было
СГэ = ?тах±?1_ (92.2)
При обработке опытов оказалось, что во всех случаях в
координатах оэ — log ^, где tm — время до разрушения, опытные
точки располагались очень близко к единой прямой. На рис. 151
показаны результаты для образцов из пруткового материала
при 700°, на рис. 152 — то же для температуры 600° и на рис. 153—
для образцов, вырезанных из диска, при 700°. В последнем случае
разброс оказывается несколько большим.
С помощью критерия (92.2) Сдобырев обработал
многочисленные опытные данные других авторов. Прежде всего, он показал,
что опыты Джонсона^'на молибденовой стали и меди [31° ] подтвер-
§ 92] ПРОСТЕЙШИЕ КРИТЕРИИ ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 377
ждают этот критерий столь же хорошо, как и критерий
наибольшего нормального напряжения. В этих опытах число точек
невелико и разброс данных довольно значителен. Далее, он
проанализировал опыты Каца [53], [м], который испытывал трубчатые
бэ,кг/мм г
40-
©¦"V-
*•
в Растяжение***^
• ffpgve//ue
о Растяжение с
кручением
^^•^
®«
"
30
блнг/ммг
SO
lag t^ (vac)
Рис. 151.
W
в Растяжение
• Кручение
г, Растяжение с
икручением
<
1
3
^^»
-0,5 О 0,5 IP 15
ЩЪ(УЯС)
Рис. 152.
б^яг/мм2
75
50
ъРася
v. в
7яжет
• ft/фШге
о Р&тнжение с
кручением,
If
2fl
2,5
\щ t% (vac)
Рис. 153.
образцы из углеродистой и аустенитной стали на растяжение
и внутреннее давление при температурах 500°, 650° и 700°, опыты
Зверькова для сплава ЭИ-496 при 700° [зв] и опыты Коистра
и др. [275] на углеродистой стали. Во всех случаях наилучшие
результаты получились тогда, когда за эквивалентное напряжение
принималось 0Э по формуле (92.2).
378 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
Следует отметить, что в практически важных случаях
эквивалентное напряжение, по Сдобыреву, при плоском напряженном
состоянии отличается от наибольшего нормального напряжения
довольно мало. Нетрудно подсчитать, что если главные
напряжения одного знака, то минимальное значение аэ равно 0,936 Ощах,
то есть разница составляет всего 6,4%. Поэтому при расчетах
дисков, например, где оба главных напряжения обычно
положительны, безразлично, каким критерием пользоваться.
В заключение этого параграфа мы вернемся еще к данным
Кеннеди и др. [2741, относящимся к инконелю. Данные по
ползучести были рассмотрены в
§ 79; напомним, что каждая
серия испытаний проводилась
при постоянном значении
осевого напряжения az,
менялась величина окружного
напряжения ае. Величина
осевого напряжения была
принята 438, 292 и 219 кг/см2. По
результатам испытаний были
построены кривые
зависимости времени до разрушения
от отношения o$laz, каждая
из кривых соответствует
определенному фиксированному
значению аг. Разброс точек
оказался довольно большим,
поэтому кривые в достаточной
мере условны. Теперь,
пользуясь этими кривыми, можно
построить в плоскости се —
oz линии, соответствующие
нг/см2
Рис. 154.
разрушению по истечении
заданного времени. Этот график воспроизведен на рис. 154, три
кривые соответствуют разрушению соответственно за время 100,
500 и 2000 часов. Существенно отметить, что окружное
напряжение приводит к более быстрому разрушению, чем осевое
напряжение той же величины. Впоследствии мы вернемся к этому
вопросу и покажем, что вязкое разрушение трубки под действием
внутреннего давления происходит быстрее, чем разрушение
стержня, растягиваемого при том же номинальном напряжении; в
стержне рост напряжения при постоянной нагрузке происходит только
за счет уменьшения площади поперечного сечения, в трубке при
постоянном давлении напряжение растет как за счет уменьшения
толщины, так и вследствие увеличения радиуса. Пунктиром
показано условие разрушения за 100 часов по критерию наиболь-
§ 93] ОБЩИЕ ПРЕДСТАВЛЕНИЯ О ДЛИТЕЛЬНОМ РАЗРУШЕНИИ 379
шего нормального напряжения в предположении, что это
напряжение остается постоянным. Разрушение образцов
сопровождалось во всех случаях довольно большой деформацией ползучести,
поэтому интерпретация результатов возможна только с учетом
конечной деформации; качественно условие наибольшего
растягивающего напряжения этими опытами подтверждается.
log^
§ 93. ОБЩИЕ ПРЕДСТАВЛЕНИЯ О ДЛИТЕЛЬНОМ РАЗРУШЕНИИ
ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
Опытные данные, которые были вкратце рассмотрены выше,
позволяют утверждать, что характер разрушения при сложном
напряженном состоянии щ е
существенно зависит от
типа напряженного
состояния. Действительно,
вязкое разрушение является
результатом ползучести и,
следовательно,
определяется интенсивностью
напряжений (или иным
эквивалентным напряжением,
например ттах)- Хрупкое
разрушение прежде всего
зависит от величины
наибольшего нормального
напряжения. Схема,
изображенная на рис. 138, имеет
смысл только применительно к растяжению образца, когда
величина напряжения является единственной характеристикой.
Будем в сложном напряженном состоянии принимать за
величину, определяющую уровень напряженного состояния, величину
интенсивности напряжений о0.
Будем строить диаграмму длительной прочности в
координатах log ff0 — log f„ (рис. 155). Участок вязкого разрушения мы
проведем так же, как на рис. 138, хотя в данном случае это
построение имеет лишь условный смысл. Действительно, при
определении времени вязкого разрушения растянутого образца мы
исходили из определенной геометрической картины деформации,
для других исходных напряженных состояний, хотя бы и
однородных, условие вязкого разрушения приходится
формулировать иначе. Так, в § 92 при обсуждении опытных данных Кеннеди
мы отметили, что разрыв трубки под действием только окружных
усилий происходит быстрее, потому что увеличение напряжений
вызывается не только уменьшением толщины стенки, но л
увеличением диаметра. С другой стороны, при чистом кручении пло-
Рис. 155.
380 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
щадь сечения остается неизменной и вязкое разрушение в смысле
Хоффа вообще невозможно. В действительности оценка
работоспособности конструкции в тех условиях, когда опасность
хрупкого разрушения не возникает, производится по некоторым
суммарным деформациям и допустимость или недопустимость того
или иного состояния можно определять просто по скорости
ползучести, которая не должна превышать определенного предела.
Во всяком случае мы можем фиксировать участок вязкого
разрушения на диаграмме длительной прочности так, чтобы он имел
определенный условный смысл для всех напряженных состояний.
С участком хрупкого разрушения дело обстоит совершенно
иначе, в координатах о0 — t„. мы получим для разных типов
напряженных состояний разные кривые. Примем за характеристику
напряженного состояния величину
j? ___ gmax
Прямой, соответствующей участку хрупкого разрушения на рис.
138, где под сг понимается отах, будет соответствовать серия
параллельных прямых на рис. 155; прямая к = 1 соответствует
растяжению. При к < 1 время, соответствующее переходу от вязкого
разрушения к хрупкому, увеличивается, при к > 1 —
уменьшается. В плоском напряженном состоянии к > 1, если 02 > 0,
поэтому при двухстороннем растяжении хрупкое разрушение
начинается раньше, чем при одностороннем. Наиболее неблаго-
1 2
приятный случай будет тот, когда сг2 =-o"i и к = —-^. В трехосном
^ уз
напряженном состоянии к может быть сколь угодно велико,
поэтому возможны хрупкие разрушения таких материалов,
которые не обнаруживают хрупкого разрушения при растяжении
любой практически доступной длительности. Подобные хрупкие
разрушения наблюдаются в зоне концентрации напряжений.
Миркин и Трунин ['*] исследовали растяжение цилиндрических
образцов с кольцевым надрезом из стали ЭИ-10 перлитного класса
и аустенитной стали ЭИ-257. Было установлено, что в зоне
концентрации напряжений наблюдается интенсивное растрескивание
по границам зерен, при этом трещины образуются от действия
нормальных напряжений, об этом можно судить как по
направлению макроскопической трещины, так и по тому, что зарождение
ее происходит не на поверхности, а на некоторой глубине, где
нормальные напряжения достигают максимума. Отмечено, что
интеркристаллические разрушения начинаются в зоне
концентрации напряжений гораздо раньше, чем у гладких образцов.
Приведем еще некоторые данные, относящиеся к испытанию
медных трубок квадратного сечения. Толщина стенки составляла
около 1 мм, а наружный размер 4 мм. При температуре 650°
§ 93] ОБЩИЕ ПРЕДСТАВЛЕНИЯ О ДЛИТЕЛЬНОМ РАЗРУШЕНИИ 381
Рис. 156.
Рис. 157.
382 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. V]
такая трубка разрушалась от кратковременного приложения
внутреннего давления 150—180 атмосфер, при этом происходила
большая пластическая деформация, квадратное сечение становилось
почти круглым, разрыв происходил в результате местного утонь-
шения стенки. На рис. 156 приведена фотография части сечения
разорванной трубки вблизи угла, начавшееся местное утоныпе-
ние видно отчетливо.
Под действием внутреннего давления 100 атмосфер трубка
держала нагрузку непродолжительное время, после чего происходило
Рис. 158.
разрушение, притом совершенно иного характера, без заметной
пластической деформации. На рис. 157 приведена
микрофотография образца, который разрушился через 30 секунд. Шлиф
изготовлен не для того участка образца, где образовалась сквозная
трещина. Видно интенсивное растрескивание по границам зерен
во всей растянутой зоне и начало образования макроскопической
трещины с внутреннего угла. На рис. 158 приведена
аналогичная фотография, на которой зафиксирован дальнейший этап
развития макроскопической трещины. Эта фотография относится
к другому образцу, который разрушился при тех же условиях
за 60 секунд.
§ 94] О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ БОЛЕЕ ОБЩЕЙ ТЕОРИИ 383
Приведенный пример показывает, насколько относительны
понятия кратковременной и длительной прочности; типичные
длительные разрушения могут быть получены за время, измеряемое
десятками секунд.
§ 94. О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ БОЛЕЕ
ОБЩЕЙ ТЕОРИИ ДЛИТЕЛЬНОГО РАЗРУШЕНИЯ
Высказанные выше общие соображения о длительном
разрушении при сложном напряженном состоянии носят достаточно
схематический характер и позволяют сделать лишь некоторые
качественные заключения о причинах того или иного характера
разрушения в отдельных случаях.
Определение долговечности изделия сложной формы в
условиях сложного и неоднородного напряженного состояния требует,
вообще говоря, построения общей теории ползучести, включающей
в себя описание процесса трещинообразования.
Обычный подход, который широко распространен в настоящее
время в расчетной практике, состоит в следующем. На основе
какой-либо теории ползучести находится распределение
напряжений. Отыскивается величина наибольшего нормального
напряжения. Эта величина сопоставляется с кривой длительной
прочности, найденной в результате испытания цилиндрических
образцов, по кривой длительной прочности находится условное время
до разрушения. Условность такого способа определения
долговечности связана со следующими обстоятельствами. Во-первых, как
мы видели, кривые ползучести' имеют третьи участки, где
скорость ползучести существенно меняется с ростом
трещинообразования. Все описанные выше теории ползучести при сложном
напряженном состоянии не принимают во внимание
трещинообразования и для третьей фазы ползучести непригодны. Поэтому,
рассчитывая напряженное состояние, скажем, по теории
установившейся ползучести, мы не сможем оценить величины
напряжения в момент, предшествующий разрушению. Расчет
напряженного состояния по теории старения с помощью изохронных
кривых, имеет то преимущество, что при этом расчете используются
целиком первичные кривые ползучести для образцов, включая
третьи участки, хотя, конечно, нет оснований считать, что в
сложном напряженном состоянии третья фаза развивается так же,
как и в одноосном случае, и что тензорные соотношения
деформационного типа продолжают иметь некоторый смысл.
Во-вторых, даже если бы мы знали точно распределение
напряжений, определенное по указанному способу время разрушения
было бы лишь временем появления первой трещины в опасной
точке. Для полного разрушения надо, чтобы трещина прошла
через все изделие, разделив его на две части.
384 ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ [ГЛ. VI
Качанов Р2] принимает следующую схему определения
долговечности. Считается, что трещинообразование не влияет на
ползучесть, следовательно, уравнения ползучести берутся в обычной
форме. Предполагается, что трещинообразование происходит
на площадках, перпендикулярных оси наибольшего напряжения
°i> и уравнение кинетики растрескивания записывается
следующим образом:
со = ф(о'1, ©). (94.1)
Если на тело действуют некоторые постоянные нагрузки, то
сначала распределение напряжений остается постоянным, величина со
в каждой точке растет в соответствии с уравнением (94.1), пока
в некоторый момент t = tx в некоторой точке не станет со = 1.
После этого в теле появляются две зоны: зона А, где to < 1,
и зона В, где уже произошло разрушение и материал потерял
способность к сопротивлению.
Граница между зонами А и В — фронт разрушения —
движется таким образом, что на фронте разрушения со = 1 и усилий
со стороны зоны В к зоне А не передается.
Желая учесть влияние трещинообразования на ползучесть,
мы сделаем некоторое крайнее предположение, заключающееся
в том, что трещины образуются только на тех площадках, на
которых действует наибольшее нормальное напряжение а1 и величина
его представляет собою уменьшение площади эффективного
сечения для этого направления. Соответствующее эффективное главное
напряжение будет -——, тогда как два других главных
напряжения остаются неизменными. Принимая, что критерием ползучести
является максимальное касательное напряжение, найдем:
б1=-83 = 1;(т^г-0з), е2 = 0, (94.2)
тогда как изменение величины со по-прежнему описывается
уравнением (94.1).
В случае кратковременной ползучести следует считать, что ср
является степенной функцией от т—~.
Из (94.2) следует, что ползучесть, сопровождаемая
растрескиванием, происходит без изменения объема. На самом деле это
не так, образование трещин всегда сопровождается увеличением
объема, но этот эффект считается несущественным по сравнению
с вызванной наличием трещин интенсификацией сдвиговой
деформации.
Такая простая схема представляется оправданной следующими
соображениями. Когда степень растрескивания значительна,
именно напряжение о-! определяет скорость ползучести и уравнение
§ 94] О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ БОЛЕЕ ОБЩЕЙ ТЕОРИИ 385
(94.2) фактически может быть заменено следующим:
6'=<таг)' (94-3>
что совпадает с первым из уравнений (88.3). Учет величины сг3
вносит лишь незначительную поправку. Фактически в зоне
растрескивания происходит как бы одномерная ползучесть. Там,
где со мало, (94.2) превращаются в обычные уравнения
ползучести; каким образом осуществляется переход от одного крайнего
случая к другому, это не так уже важно. Впоследствии будут
рассмотрены некоторые примеры применения уравнений (94.2) и (94.3).
Вопрос о том, нужно ли учитывать влияние трещинообразова-
ния на скорость ползучести, решается по-разному в
зависимости от того, как именно происходит процесс растрескивания
данного материала.
В некоторых случаях, как уже отмечалось, трещинообразова-
ние идет равномерно по всему объему и не может не влиять на
скорость ползучести. Третий участок на кривых ползучести
связан с равномерным удлинением образца и может быть предсказан
теорией, как это видно из примера, приведенного на рис. 146.
Но существуют материалы, разрушение которых не
сопровождается грещинообразованием во всем объеме. Лишь в некоторых
сечениях возникают трещины или группы трещин, которые
развиваются и приводят к локальному разрушению. У образцов из
подобных материалов тоже могут быть обнаружены третьи участки
на кривых ползучести, но эти третьи участки связаны с
локализованной деформацией вблизи места будущего разрыва,
приложение изложенной выше теории к материалам подобного рода
вряд ли обосновано.
ГЛАВА VII
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ.
ОБЩАЯ ТЕОРИЯ И ПРОСТЕЙШИЕ ЗАДАЧИ
Наиболее простые решения задач ползучести получаются
с помощью теории установившейся ползучести. Как было
показано в главе V, при некоторых предположениях уравнения теории
установившейся ползучести совпадают с уравнениями
нелинейной теории упругости. Для геометрически линейных задач теории
ползучести справедливы вариационные принципы типа Лагран-
жа и Кастильяно. Фактическое решение задач возможно при
произвольном законе ползучести, однако применение степенного
и экспоненциального законов связано с известными
преимуществами. Для степенного закона ползучести при нахождении
приближенных решений оказывается полезной недавно доказанная
теорема Келледайна и Друкера, которая позволяет установить
границы, в которых заключена поверхность постоянного
потенциала, если для тела известны упругое состояние и предельное
пластическое состояние. Далее рассматривается применение
теории к простейшим задачам — расчету ферм. Решение
статически неопределимых задач сводится к решению некоторых
систем нелинейных уравнений, поэтому особую ценность
приобретают разного рода приближенные приемы. Во многих
случаях удовлетворительные результаты можно получить, если
задаться тем же распределением напряжений, которое
реализуется в предельном пластическом состоянии.
§ 95. ЕДИНСТВЕННОСТЬ В МАЛОМ И УСТОЙЧИВОСТЬ
Как мы видели в главе V, предположение о существовании
потенциала ползучести сильно ограничивает класс возможных
видов уравнений теории установившейся ползучести в случае
пространственного напряженного состояния, не являясь строго
необходимым и не вытекая из какого-либо достаточно общего
§ 95] ЕДИНСТВЕННОСТЬ В МАЛОМ И УСТОЙЧИВОСТЬ 387
и надежного механического принципа. Однако принятие этого
предположения позволяет сформулировать для ползучести
вариационные теоремы, совершенно аналогичные известным
вариационным теоремам для нелинейно-упругого тела. Тем самым
открывается возможность развития приближенных методов решения задач
теории ползучести. Итак, предположим, что
Поскольку величины e,j однозначно определяются
напряжениями о>у, мощность диссипации
L = atjetj (95.2)
есть функция либо одних только otj, либо e;j, причем для любых
отличных от нуля значений напряжений или скоростей L > 0.
Введем в рассмотрение новую функцию U {&ц), определяемую
равенством
U = L-$>. (95.3)
Предполагается, что L и Ф являются функциями е^.
Продифференцируем (95.3) по е„:
ди п I, даи ЭФ даы
деи ~"l} l *""'ав,, дам дг1} '
Вследствие (95.1) два последних члена в правой части взаимно
уничтожаются, и мы получаем:
Соотношения (95.1) и (95.4) вполне аналогичны известным
соотношениям нелинейной теории упругости, скоростям деформации
ползучести в нелинейной теории упругости соответствуют
упругие деформации тела. Функция U имеет там совершенно
определенный физический смысл, это — упругая энергия
деформированного тела. Величины L и Ф вводятся уже формально,
последняя называется дополнительной работой. В теории ползучести
сохраняются формальные аналогии, но существо дела становится
совершенно иным. Единственная величина, имеющая отчетливое
физическое значение, — это мощность диссипации L,
представляющая собою работу пластической деформации в единице объема
за единицу времени. В дальнейшем мы будем называть функцию Ф
потенциалом скоростей ползучести, функцию U — потенциалом
напряжений.
Рассмотрим тело, находящееся в состоянии установившейся
ползучести под действием объемных сил Ft и поверхностных
сил Ти приложенных на части поверхности 2Т. На остальной
25*
Я88 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
части поверхности Е„ заданы скорости перемещения точек
поверхности v\. В результате действия сил и сообщения
вынужденных скоростей точкам поверхности в теле возникает
напряженное состояние, определяемое в каждой точке тензором otj,
и поле скоростей vt. Перечислим условия, которым должны
удовлетворять o-jj и vt. Тензор напряжений удовлетворяет
дифференциальным уравнениям равновесия
Ou,j + Fi = 0
и граничным условиям
oryvy = rf на 2Т.
Поле скоростей vt должно быть непрерывным и дифференцируемым,
оно удовлетворяет граничному условию
Vi — vl на 2„.
1
Вычисляя поле скоростей деформации по формулам е^ = -^ (^j; j -\-
+ Vj,i), мы должны потребовать, чтобы atj и ei7- были связаны
соотношениями (95.1) или, что то же, (95.4). Если все
перечисленные условия выполнены, то мы имеем точное решение задачи
установившейся ползучести. Вопрос о существовании решения
достаточно сложен и остается открытым, вопрос о единственности
может быть решен применительно к той или иной частной форме
зависимости между напряжениями и скоростями деформации.
Здесь мы рассмотрим вопрос о единственности в малом.
Предположим, что наряду с известным решением вц, vi существует
другое бесконечно близкое решение Оц + бсг^-, V{-\-&Vi,
удовлетворяющее тем же граничным условиям. Тогда на поверхности
тела Ь<УцУц = 0 на 2Т и бу, = 0 на 2„. Уравнения равновесия
становятся однородными: бсг^ j = 0. Умножим левую часть
уравнения равновесия на бг^, и проинтегрируем по объему тела,
получим:
v
Преобразуем этот интеграл:
V V
= \ batjVjbvidH,— \ 60ijbvitjdV.
2. V
Но поверхностный интеграл равен нулю, так как на 2Г 6o"jjV/ = 0,
на 2„ буг = 0. С другой стороны, баубу^: = бау6еу, что следует
§ 95] ЕДИНСТВЕННОСТЬ В МАЛОМ И УСТОЙЧИВОСТЬ 389
из симметрии тензора 6а^ и определения 6е^. Таким образом,
\ 6aij6eiJdV = 0. (95.5)
v
Теперь можно поступить двояким образом: либо воспользоваться
уравнением (95.1), из которого следует:
либо найти bOij из (95.4), а именно:
В первом случае из (95.5) следует:
? д2Ф
i да1}доы
v
SaijbohldV = Q.
Во втором случае:
V
Эти равенства невозможны при отличных от нуля Ьвц, бе^,
если стоящие под интегралами квадратичные формы знакоопреде-
ленны; в этом случае бесконечно близкое состояние ползучести,
удовлетворяющее тем же граничным условиям, что и основное
состояние, не существует. Покажем, что для того, чтобы основное
состояние было устойчивым, необходимо, чтобы квадратичные
формы были положительно определенны. Действительно, мы
показали, что при условии определенности квадратичных форм
бесконечно близкого состояния ползучести, соответствующего тем же
граничным условиям и тем же массовым силам, не существует.
Но измененным поверхностным силам Т\ + ЬТ\ и измененным
массовым силам Ft -f- 6Ft соответствует измененное движение
Oij + йвц, vt + bvt. Воспроизводя приведенные выше
рассуждения, мы получим вместо (95.5)
\ 671вМ2+ \ bFibvidV= \ дви8Ег}Л?.
2 V V
Левая часть представляет собою мощность, развиваемую
дополнительными силами на дополнительных скоростях. Для
устойчивого материала эта мощность должна быть положительна,
в противном случае, прикладывая внешние воздействия, мы
извлекли бы работу из системы, вместо того чтобы ее затрачивать. Таким
образом, для устойчивого материала
бсг^бву > О,
390 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
или
Условия (95.6) означают, что поверхности Ф = const в
пространстве напряжений и U = const в пространстве деформаций
выпуклы, как было отмечено в § 65.
§ 96. ВАРИАЦИОННЫЙ ПРИНЦИП ЛАГРАНЖА
Пусть, как и в предыдущем параграфе, atj и vtj представляют
собою напряжения и скорости в действительном состоянии,
находимые из уравнений ползучести при заданных граничных
условиях. Материал будем предполагать устойчивым, это значит,
что для него выполняются условия (95.6). Рассмотрим наряду
с действительным полем скоростей vt некоторое воображаемое
поле скоростей v*; мы будем предполагать его непрерывным
и дифференцируемым, так что для него можно определить поле
тензора скоростей деформации sfj. Поскольку внешние силы
Ft и Тг и внутренние силы atj находятся в равновесии, работа сил
на виртуальных скоростях равна нулю. Примем за поле
виртуальных скоростей поле vf, тогда уравнения равновесия
рассматриваемого тела в форме Лагранжа запишутся следующим образом:
\ FtvtdV+ ^ 2>f dS — \ (JijBtjdV = 0. (96.1)
V 2 V
Легко показать, что из (96.1) действительно следуют
дифференциальные уравнения равновесия и граничные условия. Вследствие
симметрии тензора агу- и определения величин Вц = у (vti y + ^-, д
OjjEij = o^v^j. Последний интеграл можно преобразовать
следующим образом:
J atje;t}dV= jj atJvijdV= J I(<tww*)^-ov,^*J<^ =
V V V
= J otjVjVidE— jj OtjjvfdV.
2 V
Внесем преобразованное значение интеграла в (96.1), получим:
\ (Ft + cry, i) vtdV+^ (Ti - wj) vt dZ = 0.
V 2
Но это есть тождество, поскольку первый интеграл обращается
в нуль вследствие уравнений равновесия, второй — вследствие
§ 96]
ВАРИАЦИОННЫЙ ПРИНЦИП ЛАГРАНЖА
391
граничных условий. Рассмотрим теперь некоторые простые
следствия уравнения (96.1).
1. Принцип минимума мощности. Наряду с истинным полем
скоростей vt рассмотрим бесконечно близкое к нему ноле vt -f- &vt,
удовлетворяющее тем же кинематическим условиям, то есть такое,
что 8vt = 0 на 2„. Примем за воображаемое поле скоростей
vt* = 8vt. Подставим в (96.1). Получим:
J FfivtdV+ J Ti6vtd2— [ otflnt,dV = 0. (96.2)
V 2Г V
Здесь второй интеграл распространяется не на всю поверхность
2, а только на часть ее 2Г, для 2„ значение интеграла равно
нулю, поскольку 8vi = 0 на 2„. По формуле (95.4) сгг;8еу =
= -Q—-Ь&и = 8U. Теперь (96.2) можно переписать в виде
Здесь, следуя Качанову, мы примем обозначения:
U= \ UdV.
v
Сумма двух первых интегралов представляет собою мощность,
развиваемую внешними силами. Положим:
\ FividV+\ Tlvtd2 = A.
V 2Т
Тогда мы получаем:
8(U-A) = 0. (96.3)
Условие (96.3) выражает теорему, которую обычно называют
теоремой о минимуме полной мощности, хотя это название в данном
случае некорректно. Действительно, А есть мощность,
развиваемая внешними силами, то есть работа этих сил за единицу времени,
тогда как мощность внутренних сил есть L, а не U. Заметим, что
подобная же неточность существует в названии аналогичной
теоремы для упругого тела. Там U представляет собою
действительно работу внутренних сил, тогда как А вовсе не есть работа
внешних сил, это всего лишь сумма произведений конечных
значений сил на конечные значения перемещений. Но подобно тому,
как в теории упругости вариация величины А при неизменных
внешних силах представляет собою работу на дополнительных
перемещениях, то есть приращение работы, так и в теории
ползучести вариация U — А представляет собою изменение мощности.
392 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Из уравнения (95,1) следует, что в данном случае имеет место
именно минимум U — А.
2. Определение силы, вызывающей заданную скорость
перемещения. Пусть на некоторой части поверхности 2' заданы
скорости перемещений vt, это значит наложены некоторые
кинематические связи. Реакции этих связей будут поверхностными силами
Tt на части поверхности 2'. Положим теперь vt — v\q.
Мощность сил Tt на скоростях Vi есть
. = ^ TxVi dH = q J Ttvt dH = qQ.
X- 2'
Величина q называется обобщенной скоростью, величина
Q — соответствующей обобщенной силой. Выберем теперь
вариации поля скоростей таким образом, чтобы было 6vt = bqvt
на 2'и dv( = 0 на 2 — 2', если Tt Ф 0. На той части оставшейся
поверхности 2 — 2", где Tt = 0, bvt может быть каким угодно.
Будем считать также внешние силы отсутствующими. Тогда
из (96.3) следует:
6д<?-677 = 0,
или
<?=ll- (9б-4)
Очевидно, что для применения этой формулы нужно иметь
выражение для U в функции q.
§ 97. ВАРИАЦИОННЫЙ ПРИНЦИП КАСТИЛЬЯНО
Обозначая по-прежнему через о^, vt действительные
напряжения и скорости, рассмотрим некоторое поле напряжений
afj, удовлетворяющее уравнениям равновесия о,*, 3- + F* = 0,
a*jVj = T* на 2. Поскольку система внешних сил F*, Т*
находится в равновесии с внутренними силами afj, мы можем
составить уравнение равновесия в форме Лагранжа, при этом
в качестве виртуальных скоростей мы выберем истинные скорости
ползучести. Получим:
jj Ftvt dV + \ Tfvt d2 - J ofj-8M dV = 0. (97.1)
V 2 V
Извлечем отсюда некоторые следствия подобно тому, как это было
сделано в предыдущем параграфе.
1. Принцип минимума дополнительного рассеяния. Наряду
с действительным напряженным состоянием atj рассмотрим бес-
5 98] НЕКОТОРЫЕ СЛЕДСТВИЯ ВАРИАЦИОННЫХ ПРИНЦИПОВ 393
конечно близкое к нему статически возможное напряженное
состояние atj + бог^-, то есть такое, которое удовлетворяет тем же
уравнениям равновесия и тем же граничным условиям. Это значит,
что Ьвц образуют самоуравновешенную систему напряжений,
6o"ij, j = 0, bOtjVj = 0 на 2. Положим в (97.1) с*,- = ба^, тогда
Ft* = 0 и Tt* = О, .следовательно,
е,7§о"г7 = 0.
v
Но вследствие (95.1) гц~ —— , еубогу = -jr—-бо^- = 6Ф. Итак,
аа0-' "«""" Э<т„
6Ф = 0. (97.2)
Величина Ф = \ Ф dF называется дополнительным рассеянием.
v
Условие (97.2) выражает принцип минимума дополнительного
рассеяния. Из (95.6) следует, что речь идет именно о минимуме Ф.
2. Теорема Кастильяно. На некоторой части поверхности 2'
действуют силы Т\. Положим Т\ = T\Q. Мощность,
развиваемая этими силами, есть
А =-- J Ttv, d2 = Q J T\Vi dZ = Qq.
2' 2'
Величина Q называется обобщенной силой, q — обобщенной
скоростью. Эти определения совершенно эквивалентны данным
в предыдущем параграфе.
Положим теперь a*j = 6cr^-, причем бегу j — 0, 6оц\; = 0
на 2 — 2' и doijVj = bQT°i на 2'. Из (97.1) получим:
g6Q = 6Ф,
или
дФ
3Q
(97.3)
§ 98. НЕКОТОРЫЕ СЛЕДСТВИЯ ВАРИАЦИОННЫХ ПРИНЦИПОВ
Представим себе тело, нагруженное некоторой совокупностью
внешних сил таким образом, что можно выделить конечное число г
обобщенных сил Qt. Соответствующие обобщенные скорости
будут qt. Мгновенное состояние системы полностью определяется
заданием величин qt либо Qt; таким образом, если решение задачи
теории ползучести известно, то U~ U (д1; . . ., дг), Ф =
= ((?!, . . ., QT). Из теоремы Кастильяно следует, что
___ дФ
394 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Этот результат можно интерпретировать следующим образом.
Уравнение Ф = const представляет собою уравнение
поверхности в r-мерном пространстве, где по осям прямоугольной
декартовой системы координат откладываются величины обобщенных
сил Qt. Будем называть это пространство пространством сил,
а радиус-вектор точки — вектором силы. Тогда вектор скорости
перемещения с компонентами qt всегда направлен по нормали
к поверхности Ф = const. В отличие от теории идеальной
пластичности поверхность Ф = const может быть проведена через любую
точку пространства сил, поэтому существует бесконечное
множество таких поверхностей, соответствующих различным
значениям константы. Будем называть их поверхностями ползучести
в пространстве сил, функцию Ф (<?*) будем называть потенциалом
скоростей. Условие единственности, как показано в § 95,
накладывает ограничение на вид функции Ф (аи), а именно требуется,
чтобы квадратичная форма, коэффициентами которой являются
вторые частные производные от Ф, была положительно
определенной. Но отсюда следует, что аналогичному условию удовлетворяет
и функция Ф ((?;). Действительно, рассмотрим близкое к
основному напряженное состояние а^ + бс^, соответствующее
внешним силам Qi + dQi, то есть представляющее собою решение
задачи ползучести для измененных внешних сил. Тогда, очевидно,
= I {ф^)+-^гб^+4^-&«*^+• • •}dV-
Но если силы и напряжения основной системы удовлетворяют
условиям равновесия, то система дополнительных сил 8Qt и
дополнительных напряжений ба^- также должна удовлетворять
условиям равновесия, следовательно, виртуальная мощность на
кинематически допустимых скоростях равна нулю. За допустимое
поле скоростей мы принимаем поле скоростей основного состоя-
дф дф
ния: qt = -Kfr- и е^ = ~—, следовательно,
V
Таким образом, мы приходим к следующему равенству:
аЦт б<?^ = I Тн^тЬ ^^ dV- (98Л)
§ 98] НЕКОТОРЫЕ СЛЕДСТВИЯ ВАРИАЦИОННЫХ ПРИНЦИПОВ 395
Отсюда следует знакоопределенность квадратичной формы в левой
части (98.1). Геометрически это означает, что поверхность
ползучести в пространстве сил всегда выпуклая.
Совершенно аналогичным образом можно рассмотреть
поверхность ползучести в' пространстве скоростей qt. Уравнение этой
поверхности есть U (qt) = const; вектор силы с проекциями Qs
направлен по нормали к этой поверхности, которая также
выпукла. Функцию U (qi) будем называть потенциалом сил.
Последнее замечание будет относиться к построению
двухсторонних оценок для величины потенциала скоростей. Условие
минимума мощности означает следующее. Выберем некоторое
кинематически возможное поле скоростей деформации е*,
которому соответствуют обобщенные скорости qt*. Вычислим
величину U (ё?}) — Qiqt- Принцип минимума утверждает, что это
выражение будет принимать минимальное значение, если в него
подставить действительные скорости, следовательно,
Qiqt-UtfjXQtqt-UiBtj).
Но Qiqt = L, следовательно, правая часть есть Ф (Qi), таким
образом, мы получаем:
Qiqt-& &})<&№•
С другой стороны, рассмотрим некоторое статически возможное
напряженное состояние, соответствующее заданным внешним
силам Qi, будем обозначать соответствующие напряжения of*.
Величины о** суть известные функции Qt, поэтому, вычисляя
Ф (off), мы получим некоторую функцию от Qi, отличную
от Ф (Qi). Обозначим эту функцию Ф** (Qi). Вследствие
принципа минимума дополнительного рассеяния
<?>(Qi)<&**(Qi)-
Объединяя эти неравенства, мы получаем двухстороннюю оценку
для потенциала скоростей:
Qtqt-U №)<&№<&*•№¦ (98-2)
При составлении этих неравенств мы толковали расширительно
установленные выше свойства относительного минимума функций
U — А и Ф. Действительно, в §§ 96 и 97 было установлено только,
что существует такая точка, для которой эти функции принимают
значение меньшее, чем значения их в любой точке достаточно
малой окрестности. Однако если поверхность ползучести строго
выпукла во всех точках, то этот минимум является абсолютным
и неравенства (98.2) справедливы при любом выборе допустимого
396 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
поля скоростей и допустимого поля напряжений.
Соответствующее доказательство геометрически очевидно для случая функции,
зависящей от одной или двух переменных. Если поверхность
/ (х, у) во всех точках направлена выпуклостью вниз, то она
не может иметь больше одной точки минимума [23°].
§ 99. ЧАСТНЫЕ ФОРМЫ УРАВНЕНИЙ
УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ
В приложениях обычно пользуются только теми вариантами
теории установившейся ползучести, которые приводят к
линейным тензорным зависимостям. Общая формулировка теорий
такого рода может быть следующей. Выберем в качестве
эквивалентного напряжения однородную функцию первой степени
от компонент напряжения s (otj), определенную таким образом,
чтобы при простом растяжении напряжением о было s = о.
Тогда закон ползучести запишется в следующем виде:
Функция v (s) — это та же самая функция, которая дает
зависимости скорости ползучести от напряжения при простом
растяжении, когда е = v (а). Если скорость ползучести определяется
вторым инвариантом девиатора тензора напряжений, то, как
мы видели в § 68,
Если ползучесть определяется наибольшим касательным
напряжением и рассматривается в главных осях, то
ds ds . ds n , , ,
s = cxi-o-2, _=__„i, _ = o (о,Фаг),
s^K(al-a,) + (l-X){G2-a3) (oy = 02), (99.3)
ds _> ds A 1 ds \
dai да2 оо3
Здесь % — произвольная неотрицательная величина, меньшая или
равная единице.
В случае анизотропии типа описанной в § 69 следует принять
s* = с4 - 033 @-22 + о-н) + C - 2р) К + а232) +
+ С1 -т) (°22 + ОиJ + (-3 + 2а) (ацаи-а;,). (99.4)
5 99 ] ЧАСТНЫЕ ФОРМЫ УРАВНЕНИЙ УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ 397
Примем, что. соотношение е == v @) справедливо для ползучести
при растяжении в направлении оси 3. Тогда
ds 1
ds
97 [ — A — а)оц + B — а)о-22—а33],
9ffa2 2s
J (99.5)
ds 1 9s 1 /" 3 \
5^ = -27[-а»-СТ22-2азз]' 5^=27vy-PJa23,
u23
as
a<j
12
1 /3 л a« 1 /-3 Q\
Иногда бывает удобно считать заданными скорости деформации
и по ним определять напряжения. Поскольку s есть однородная
функция первой степени от компонент напряжения, величины
-з— представляют собою однородные функции нулевой степени,
то есть функции пяти отношений величин компонент тензора
напряжений к одной из них. Шесть функций от пяти независимых
неременных должны удовлетворять некоторому тождественному
соотношению, следовательно, существует такая функция F от шести
переменных, что
'О
dOij
= 0.
Следовательно, в силу (99.1)
Bij ^ = 0.
Из этого уравнения находится v как функция &ц. Поскольку
соотношение не меняется при одновременном умножении гц
и »на одно и то же число, функция v есть однородная функция
первой степени от е^. Поскольку v = v (s), то и наоборот.
s = s (v). Умножим обе части (99.1) на ai} и свернем. Получим:
гиаи = vs.
Будем считать в этом равенстве, что v = v (е,;-), a s= s(atj).
Продифференцируем обе части по гьу.
двьг dv , ds dobi
Вследствие (99.1) вторые части слева и справа равны, поэтому
мы получаем:
о« = *(")-^г- (99-6)
398 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VI]
В частном случае, если s2 есть квадратичная функция от КОМ-
ДО*
ds
понент напряжения, s2 = a,^o'jjO"?;, то
dOij
'¦ O-ijhl^kl-
Обозначим через а^ы обратную матрицу, тогда
ds
Если, как это обычно делается в теории ползучести,
предполагается, что ползучесть не сопровождается изменением объема,
то Оц определяется с точностью до шарового тензора и
ds
ds
Этот случай мы и будем рассматривать. Внося сюда -= из (99.1),
получим:
— s ,
Построим квадратичную форму:
№ = ЩыЪцЪы- (99.7)
Очевидно,
, dh
Таким образом,
Умножим на Efj и просуммируем. Заметим при этом, что h —
однородная функция первой степени от гц. Получим:
- sh*
С другой стороны, умножая (99.1) на вц и суммируя, мы
находим, что
ОЦ^И = Oifiij = SV.
Таким образом, мы находим, что
h = v. (99.9)
Введенная при помощи (99.7) величина h = v представляет собою
эквивалентную скорость деформации, зависящую от
эквивалентного напряжения s таким образом, как скорость растяжения
зависит от растягивающего напряжения. Из (99.8) следует, что s= s(v),
где функция s (v) дает зависимость напряжения от скорости
§ 100] МОДЕЛИРОВАНИЕ УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ 399
в одноосном случае. Теперь (99.8) можно переписать следующим
образом:
otJ = s{v)-^. (99.10)
Очевидно, что при растяжении v становится равным скорости
удлинения в направлении растяжения. Если s выражается
формулой (99.2), то
= ]/4#п,
dv 2 е,
v = е0 = "'
d&ij 3 ё0
При использовании закона течения типа Треска эквивалентная
скорость деформации v = -^ (е4 — е3), если ot Ф а2, и v =
= е± + е2 = —е3, если о± = а2.
Функция v (s) может быть совершенно произвольной, однако
в приложениях обычно задаются тем или иным ее аналитическим
выражением. Мы видели, что опытные данные удовлетворительно
описываются степенной зависимостью
y(s)=4i)n
или экспоненциальной
v (s) = se ехр (^—
В аналитическом отношении каждая форма имеет свои
преимущества и недостатки, поэтому в зависимости от конкретного типа
задач следует пользоваться тем или иным выражением.
§ 100. МОДЕЛИРОВАНИЕ УСТАНОВИВШЕЙСЯ
И КВАЗИУСТАНОВИВШЕИСЯ ПОЛЗУЧЕСТИ
Экспоненциальный закон ползучести обладает тем свойством,
что уравнения установившейся и квазиустановившейся
ползучести в том смысле, в каком это понятие было введено в § 75, могут
быть, при соответствующем выборе безразмерных параметров,
приведены к виду, не содержащему каких-либо констант
материала. Рассмотрим сначала уравнения установившейся ползучести,
которые будут иметь следующий вид:
Положим
400 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
тогда
S = S((TU) = —— .
Предыдущее уравнение можно записать в следующем виде:
EU = exp(S)-^. A00.1)
Рассмотрим теперь уравнения квазиустановившейся ползучести
G5.2). В этих уравнениях plj следует рассматривать как скорости
по отношению к измененному времени т = ( — J™. Если / (а) =
— к ехр (-j), то уравнения G0.5) можно переписать следующим
образом:
Полагая
- _ i.m __- та0 да0
в„-« ехр А &
Of/— а , ";/ ,™
мы получим уравнения, буквально совпадающие с A00.1). Если
упругая и мгновенная пластическая деформации могут считаться
пренебрежимо малыми по сравнению с деформацией ползучести,
из изложенного следует весьма широкая возможность
моделирования ползучести металлических изделий при высоких
температурах с помощью моделей из металлов, обнаруживающих
ползучесть при низких температурах, и даже из пластмасс. Конечно,
уравнения теории установившейся и особенно
квазиустановившейся ползучести пригодны лишь для тех задач, когда на тело
действуют неизменные силы и кинематические ограничения
отсутствуют.
Обратимся теперь к случаю степенного закона ползучести.
Ограничимся установившейся ползучестью, квазиустановившаяся
рассматривается совершенно аналогично. Положим
тогда уравнения ползучести будут
е„ = *я-^. A00.2)
ddij
В отличие от A00.1) уравнение A00.2) содержит один
безразмерный параметр п, характеризующий свойства материала.
§ 101] СТЕПЕННОЙ ЗАКОН. ТЕОРЕМА КЕЛЛЕДАЙНА И ДРУКЕРА 401
Перейдем теперь к рассмотрению моделирования ползучести
произвольного тела. Пусть внешние силы растут
пропорционально некоторому параметру Я, и пусть известно решение задачи
теории ползучести для некоторого значения параметра X,
например X = 1. Пусть аи — соответствующие напряжения, vt —
соответствующие скорости. Изменим теперь все внешние силы
в отношении Я. При степенном законе ползучести для значения
параметра нагружения, равного К, напряжения будут Xatj, а
скорости kavt. Действительно, уравнения равновесия, граничные
условия, соотношения A00.2) и условия совместности деформаций
оказываются при этом выполненными.
При экспоненциальном законе ползучести такого простого
результата не получается. Если вц есть решение,
соответствующее некоторой нагрузке, то ка^- вообще не служит решением
уравнений ползучести; это решение существенно зависит от величины
параметра нагружения к, который фигурирует в уравнениях. При
степенном законе параметр к исключается, зато в уравнениях
остается показатель п.
§ 101. СТЕПЕННОЙ ЗАКОН ПОЛЗУЧЕСТИ.
ТЕОРЕМА КЕЛЛЕДАЙНА И ДРУКЕРА
Если v (s) является степенной функцией, например v (s) =
= гп ( — ) (§ 43), то выражения для потенциала ползучести,
диссипативной функции и потенциала напряжений будут
следующими:
а уравнения (99.1) запишутся следующим образом:
s \n ds
&ii — ?n
доц
B;i ~ xjtj
Перейдем к безразмерным переменным, приняв е*; = — , a,-,- = — ,
л S
тогда s = —. Теперь можно написать:
Здесь
дф
А *
Ф- ,
л sn+1.
ге + 1
26 ю. Н. Работнов
A01.1)
A01.2)
402 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Вследствие линейности уравнений равновесия и граничных
условий для напряжений величины напряжений
пропорциональны приложенным силам, поэтому естественно ввести
безразмерные нагрузки Tt = Тц!ап. Если мы сможем вычислить функцию
— г>
Ф = \ Ф^через внешние силы, то мы будем в состоянии найти
с помощью теоремы Кастильяно скорости точек их приложения;
в принципе для нахождения этой функции нужно уметь решать
задачу теории ползучести. Недавно доказанная Келледайном
и Друкером [178], [178] теорема позволяет в некоторых случаях
подобрать приближенные выражения для функции Ф и оценить
получающуюся погрешность.
Рассмотрим тело А, нагруженное силами Т\; материал мы будем
предполагать подчиняющимся уравнениям A01.1), показатель
степени в законе ползучести равен п. Изменяя пропорционально
силы, мы изменяем скорости деформации в том же отношении,
но в степени п; поэтому, если мы нашли решение задачи теории
ползучести для каких-то значений внешних сил, мы получаем
совершенно автоматически решения для сил, пропорционально
увеличенных или уменьшенных. Выберем в качестве стандартной
системы нагрузок такую пропорционально измененную систему Т",
при которой мощность рассеяния принимает некоторое
фиксированное значение, пусть, например, средняя безразмерная мощность
на единицу объема равна единице. Это условие нормирования
запишется следующим образом:
v
Обозначим безразмерные напряжения, соответствующие
нормированной системе нагрузок, через о-, положим sn = s{o). Тогда
условие нормирования можно будет переписать следующим
образом:
.1$ S»+irf7 = l. A01.3)
v
Рассмотрим теперь второе тело В, совершенно такое же, как
тело 4, нагруженное теми же силами Tt. Закон ползучести для
тела В также выражается уравнениями типа A01.1), функция s
определяется точно так же, но показатель степени в формулах
A01.1) равен некоторому числу тпф п. Определим для тела В
нормированную систему нагрузок Г™, подчинив ее условию
4-5c+1dV = l. A01.4)
v
§ 101] СТЕПЕННОЙ ЗАКОН. ТЕОРЕМА КЕЛЛЕДАЙНА И ДРУКЕРА 403
Напряжения а™ удовлетворяют уравнениям равновесия и
граничным условиям, соответствующим нагрузкам Т™. Изменим эти
напряжения в отношении Т^/Т™, то есть рассмотрим систему
напряжений
л* л mi
Оц — Щ^ .
г
Напряжения а*, удовлетворяют уравнениям равновесия и
граничным условиям, соответствующим силам Г", таким образом,
они определяют некоторое статически возможное для тела А
напряженное состояние. По теореме о минимуме
дополнительного рассеяния, используя A01.2), мы получим:
" ч ' -+' dv.
\#1*г<Ш Р:
Разделив на V, мы заметим, что левая часть равна единице
вследствие A01.3), поэтому из выписанного неравенства следует:
mm я+1
г у V
Предположим теперь, что т>и. Интеграл, стоящий в правой
части, может быть записан следующим образом:
I(r) = y- ^xTdV.
V
п 4-1
Здесь г = —~^гт ¦ Очевидно, что 7@)=/A) = 1. Покажем, что
/(г)<1 @<г<;1). Проще всего это сделать, воспользовавшись,
известным неравенством Гельдера (см., например, [ш]):
\ntdv<.(\fdvy(\gdvy
(а>0, р>0, а + р=1).
Положим f = х, g = l, а = г, р = 1— г, тогда получим:
J xTdV<[ [xdvj .
Возвращаясь к исходному неравенству, мы находим:
фт
-^<1 (m>n). A01.5)
тП
26*
404 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Будем считать теперь, что действующие на тело нагрузки
определяются заданием конечного числа обобщенных сил Qs, положим
Qs = — и рассмотрим пространство сил Qs подобно тому, как это
делалось в § 98.
Условие у- \ L dV = 1 определяет некоторую поверхность
в пространстве сил, поверхность постоянной мощности
диссипации, для различных значений п получаются разные поверхности.
Совокупность обобщенных сил Q" соответствует некоторой точке
на поверхности постоянной мощности при показателе п. Усилия
Qm пропорциональны Q'1; следовательно, точка, изображающая
состояние Qm, лежит на луче, проходящем из начала координат
в точку Q*1. При этом, в силу неравенства A01.5), радиус-вектор
точки Qm меньше или равен радиусу-вектору точки Qn. Таким
образом, поверхность постоянной мощности диссипации для
показателя т лежит внутри поверхности, соответствующей
показателю п, если т^> п. Меняя значения п, мы будем получать
серию вложенных друг в друга поверхностей.
Обычно не составляет труда построить поверхность постоянной
диссипации для п = 1; если s= o, например, эта поверхность
соответствует распределению напряжений в упругом несжимаемом
теле. С другой стороны, представим себе, что материал идеально
пластический и условие пластичности имеет вид s ~ 1. Если
условие пластичности выполнено во всех точках тела, то есть тело
находится в состоянии предельного равновесия под действием
некоторой системы сил Q", то условие A01.3) будет выполнено
точно независимо от п, следовательно,
-^г <! 1 при любом п.
Итак, предельная поверхность постоянной диссипации при п -*- оо
есть поверхность текучести в пространстве сил, построенная
в предположении справедливости условия пластичности s = 1.
Заметим, что для данной системы нагрузок состояние предельного
равновесия, для которого s = 1 во всех точках тела, возможно
не всегда, предельное состояние может быть достигнуто с
образованием жестких областей, внутри которых s<l- Пусть силам Q™
соответствует состояние, когда в части тела выполнено условие
s=l, в оставшейся — части s < 1. Распределение напряжений
в жестких частях может быть принято каким угодно, лишь бы оно
не противоречило условиям статики. Обозначим эти
напряжения of}, s<x!<l- Воспроизводя приведенные рассуждения, выберем
в качестве статически возможного состояния для тела А систему
§ 102]
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ФЕРМ
405
О" \
напряжений а** = aTj I -^ I. Тогда получим:
<J sl+idV<l.
Отсюда, так как левая часть равна единице,
Теорема Келледайна и Друкера утверждает, что вся серия
вложенных поверхностей постоянной мощности диссипации будет
заключена между двумя поверхностями для п = 1 и для п = оо.
Будем называть поверхности постоянной мощности диссипации
в пространстве обобщенных сил ^-поверхностями. Заметим, что
при степенном законе упрочнения функции L, Ф и U отличаются
только постоянными множителями, поэтому поверхность Q
является поверхностью Ф = const. Согласно теореме Кастильяно,
,- * дф
обобщенные скорости qt равны я—, значит, вектор скоростей
q (qu . . ., qs) направлен по нормали к (^-поверхности, тогда как
скалярное произведение векторов Q и q, вследствие условия
нормирования, равно объему тела:
Qm = v.
Условию
-и
LdV = i
соответствует также поверхность постоянного рассеяния в
пространстве скоростей qt. Будем называть эти поверхности для
различных п (/-поверхностями. Можно показать [178], что д-поверх-
ности для различных п также располагаются одна внутри другой,
но в обратном порядке: поверхность, соответствующая показателю
т ¦< п, вложена в поверхность, соответствующую показателю п.
В дальнейшем будут рассмотрены некоторые примеры
применения теоремы Келледайна и Друкера для построения
приближенных решений задач теории ползучести.
§ 102. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ФЕРМ
Фермой мы будем называть, как обычно, стержневую систему,
составленную из стержней, находящихся в условиях растяжения
или сжатия. Примеры, когда конструкция типа фермы находится
в условиях ползучести, немногочисленны, и в действительности
406 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
реализуются лишь некоторые простейшие схемы. Поэтому, в
отличие от теории упругих ферм и теории предельного равновесия,
практические приемы расчета более или менее сложных
стержневых систем не разрабатывались. Работы по ползучести ферм имеют
целью скорее иллюстрацию общих принципов и общих теорем,
нежели разработку эффективных расчетных средств. Под этим
же углом зрения мы займемся и здесь установившейся
ползучестью ферм, относящиеся сюда задачи позволяют понять на
простых примерах приложение общих методов для нахождения точных
или приближенных решений. Возможность потери устойчивости
сжатых элементов мы считаем при этом исключенной. Если усилие
в элементе фермы есть Nt, площадь сечения Fu длина Ц, то
потенциал ползучести Ф выражается следующим образом:
г
С помощью уравнений статики усилия в стержнях Nt выражаются
линейно через известные обобщенные силы Qr и «лишние»
неизвестные Х^. Пусть число лишних неизвестных есть р. Тогда
Nt = aiTQr-Y$ihXh.
Суммирование распространено на индексы г, соответствующие
внешним силам, и на индексы к от к = 1 до к = р. Вследствие
принципа минимума дополнительного рассеяния должно быть
Из A02.1) следует:
г
Найдя из этих уравнений лишние неизвестные Хк как функции
внешних сил Qr, мы можем воспользоваться уравнениями A02.1)
для определения обобщенных перемещений. Действительно, по
теореме Кастильяно
i
Как видно, принципиально расчет статически определимых или
статически неопределимых ферм не вызывает никаких затруднений.
Однако если степень статической неопределимости больше
единицы, то фактическое решение системы A02.2) становится очень
сложным. Поэтому разными авторами предлагались различные
приемы для приближенного расчета стержневых систем, элементы
которых работают на растяжение — сжатие. Простейший прием
состоит в том, что распределение усилий в стержнях просто
угадывается заранее. Пусть, например, для пропорционально изме-
§ 102] УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ФЕРМ 407
пенных сил Q0r усилия в стержнях будут N"; если Qr = XQ?,
то Nt = %Nt. Считая Я за обобщенную силу, мы получим по
теореме Кастильяно:
0^ = Ж- = 2''<^К <1°2.4)
Формула A02.4) позволяет весьма просто определить перемещение
для случая, когда на систему действует только одна сила, в
противном случае необходимо еще задаться поверхностью
Ф (<#. Qv • ¦ ¦. Qn) = H (Ql, Ql, ..., Q°n) = const,
дН
тогда qT — fx^-, из уравнения A02.4) находится множитель [х,
после чего скорости легко вычислить. В работе [231]
предлагается в качестве величин N\ принимать усилия,
соответствующие предельному состоянию жестко-пластической системы.
Будем считать для определенности, что предел текучести равен
единице, тогда, если степень статической неопределенности есть р,
то в предельном состоянии для р -f- 1 стержня N° = ± Fit для
остальных — Fi^CNi ¦< Ft. Соответствующие силы Q°
пропорциональны силам, фактически действующим на систему:
Qr — -ttQt- В предельном состоянии си-
л
лы Q° связаны некоторым
соотношением, а именно:
Н (Qr) = const.
Это соотношение нужно нам для
нахождения распределения скоростей, но,
записывая его, мы предполагаем нечто
¦большее по сравнению с тем, что
содержится в A02.4). Для иллюстрации
изложенного рассмотрим некоторые
простые примеры.
Пример 1. Система из трех стержней
одинакового сечения изображена на
рис. 159. Материал стержней одинаков, площади сечения также
одинаковы и равны единице, v (с) = (f1. Обозначая через X
усилие в среднем стержне, находим из уравнения равновесия:
Q-X
N,=
2 cos a
Следовательно, «i= 2cosa ' a2==0> Р* =
нение A02.2) принимает следующий вид:
Q—x
1
2 cos a
, р\> = 1. Урав-
1
cos2 a
2 cos a
+ Z" = 0.
408 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Отсюда
2
* = 7+V' P = 2(cosaI+^-
Теперь по формуле A02.3) находим скорость перемещения точки
приложения силы:
(Заметим, что в данной задаче проще определить q как скорость
удлинения вертикального стержня.)
Решим теперь ту же задачу приближенным способом.
Полагая JVt = N2~l, найдем Q° = 1 + 2 cos а = 1 -+- p0, где р0—
значение р при п = оо. Теперь по формуле A02.4)
Но X = -т^г = т~г^— , окончательно
Q0 1 + ро
q*=l 4 + Ро (_0_у
4 Po(Po+l)Vl + P0y '
Отношение q*/q не стремится к единице при п -*¦ оо, и при
определении скоростей приближенный метод дает большую погрешность,
однако в задачах ползучести следует сравнивать не скорости,
а силы, которые необходимо приложить для того, чтобы получить
одинаковую скорость перемещения. Обозначив силу,
необходимую для сообщения данной скорости перемещения, в точном
решении Q, в приближенном Q*, мы найдем:
Q* ^ 1+Ро ГроA+РоПТ
Q 1 + р L 4 + po J '
На графике рис. 160 представлена зависимость величины 1+р
от п, на графике рис. 161 — отношение Q*/Q. В том и другом
случае было принято a = 60°. Распределение усилий в
стержнях, характеризуемое величиной 1+р, как видно, остается
довольно далеким от того, которое соответствует предельному
состоянию, тогда как отношение сил, создающих заданную
скорость, по точному и приближенному решениям стремится к
единице быстрее. Следует подчеркнуть, что в реальных
конструкциях действующие силы редко бывают известны с большой
точностью, поэтому при определении скоростей возможны очень
большие ошибки. Конструктор, как правило, имеет дело не с
допустимыми скоростями и перемещениями непосредственно, а с
допустимыми нагрузками. Поэтому, если при п — 4, например,
разница между Q и Q* составляет 6,9%, это значит, что при выборе
§ 102]
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ФЕРМ
409
допустимой нагрузки приближенным методом получается
дополнительный запас надежности по нагрузкам и фактический запас
прочности увеличивается на эти 6,9%.
2-
15
1*.
ч.
4 6 8
Рис. 160.
т
г $ s s п п
Рис. 161.
Пример 2. Система из трех стержней, рассмотренная в
примере 1, нагружена двумя силами: вертикальной силой Qt и
горизонтальной силой Q2 (рис. 162). Положим N2 = X. Уравнение
A02.2) оказывается при этом довольно
сложным, а именно:
(Qi-X Q2 у
V 2 cos a ~|-2sinay '
Qi-x Q2
(
2 cos a 2 sin a
2 cos2 aXn.
Если Q2 = 0, то мы получаем
предыдущий пример; если Qi=0, то
очевидное решение есть Х=0; следовательно,
Ni = — N% =9"^— и скорость пере-
мещения узла в направлении силы Qz
42 =
sa U
В общем слу-
sm a cos a \2 sina^
чае, когда Qt и Q2 произвольны, более
удобным оказывается кинематический способ, который будет
изложен в дальнейшем, поэтому мы не будем заниматься поисками
точного решения, а перейдем немедленно к приближенному
способу. Из уравнений равновесия
#,=.?=*-+ 5-2*-, jv3 = ^=^._ «5_, N2 = X.
1 2 cos a ' 2 sin a 2 cos a 2 sin a' **
При направлении сил, показанном на чертеже, в предельном
состоянии возможны следующие комбинации: Ni = N2 = 1
и Ni = -N3 = 1.
410 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ
В первом случае
[ГЛ. VII
$ + #[ctga = l-J-2cosa,
/v; = i, tv» = i, щ^Я^^—;^-
1 2 ' з 2 cos a 2sma
Во втором случае
<?J = 2sina, N1=1, Лт;=-1, №t--
Ql-
Предельное состояние при положительных Ql и QI изображается
двумя прямыми в плоскости Qi, Q2, как показано на рис. 163.
1 1
Рассмотрим сначала первый случай. Внося Ql = t-^?i, Ql ~ j~(?2
в условие предельного состояния, получим к == ??LXv2c %a_
1 ]~ ? COS (X
Составим уравнение A02.4):
*t
2
7
п=7
n=S ^\
/
/
/
/
/
1
/
/
/
/
1
1
/
1
/
//
//
1 /
//
/\
!
)
Jj
cos a v 2 cos a 2 sin a
1 )%n +
kn.
1
Заменяя Ql и Ql через -г- Qi,
1 _
-j- Qz и внося наиденное
выражение к, получим:
f i
х
V.cos a
,'Q4 + Q2 ctg a\«
^ 1+2 cos a У
? ^1+2 cos a
X
X
* 6
X
Рис. 163.
' cos a \Qi + Q2Ctga^
Qtcosa—Q2ctga(l+cos a)\n+l_
cos a A+2 cos a) J
(a)
Из уравнения предельного
состояния следует, что д2 = <7i ctg а, поэтому
QlQi + Окг = ?i (Ql + Ql ctg а) = д. A + 2 cos а).
Перейдем теперь ко второму случаю. Здесь к = -г^- = ^г~^— >
\Jо ^ Sill Ct
Ql = чр = _vi_?lIiiL . Составим уравнение A02.4):
§ 102]
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ФЕРМ
411
Соответствующее предельное условие изображается отрезком
прямой, параллельной оси Qt, поэтому <?i = 0, следовательно,
При Q2 = 0 мы получаем отсюда приближенный результат пре-
дыдущего примера, при^ О д2 = ^-А—^^^у, что совпа-
дает с точным решением. Это и понятно: при Qi = 0 усилие в
стержне 2 равно нулю и система ведет себя, как статически
определимая. Наибольшая погрешность в применении приближенного
метода будет, конечно, около угловой точки на рис. 163, где
QI = 1, QI = 2 sin a. Величина Q\q\ ~r Qllz, определяемая
уравнениями (а) и (б), изменяется при переходе через эту точку
непрерывно, тогда как составляющие скорости qy и q2 по отдельности
внезапно меняют свою величину. Если скорости q± и q2 заданы,
при этом qt Ф 0 и q2 =7^ <?i ctg a, мы неизбежно приходим к тому,
что Qi : Q2 = 1 : 2 sin a.
В действительности, для того чтобы судить о распределении
скоростей, необходимо знать уравнение кривой Ф = const в
плоскости Qi — Q2; примерное расположение этой кривой можно
представить, если воспользоваться теоремой Келледайна и Друкера.
Пример 3. Абсолютно жесткий брус подвешен на четырех
одинаковых тягах (рис. 164). Будем считать Ft = 1 и v = a".
у/////////////м/ЯШ/////////М'/////////////////
Pk
\в
Рис. 164.
9
?
7-
ff
1
Рис.
16
Р
Z
5.
Р
Нагрузка приложена в произвольной точке бруса, мы заменим
ее силами Qx и Q2, приложенными по концам (на рис. 165 Р и Q
соответственно). Положим N± = Хи N2 = X2, тогда
ЛЪ = <?1-
Х2 i-X„ N, = Q2—
1
¦ Xi 3" 2-
_2_ Y 1_
3 2 3 ~и -^z з
Как и в предыдущем примере, уравнение A02.2) оказывается
сложным, и записать решение в явной форме не удается.
Воспользуемся приближенным методом. В предельном состоянии
возможны два случая: либо N\ = №2 = №3 = 1, QI = 2, №t = Qa2 - 1,
412 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
либо N1 = N1 = TV» = 1, Ql = 2, Nl = Ql — l. Условие
предельного состояния в первом квадранте плоскости Qu Q2
изобразится двумя отрезками прямых, параллельных осям Qt и Q2
и отсекающих на этих осях отрезки, равные 2 {рис. 165).
Рассмотрим сначала первый случай. При QI = const должно быть q2 = О,
к =Ks = -5r,(?2=i=-7r- Составим теперь уравнение A02.4):
ei?i+<?272=43fc»+b»(#-i)»+i].
Отсюда
и-тСОТ+С^-'Г']- *-"•
Это уравнение справедливо, если Qt > (J. При (?2 > (?i
сохраняются те же формулы, но (?4 и Q2, <?i и g2 меняются местами.
Если Qi Ф Q2, то жестко-пластическая схема предусматривает
лишь две возможные формы распределения скоростей: всегда
либо qi = 0, либо q2 = 0; значит, один из крайних стержней
сохраняет неизменную длину и брус поворачивается около
соответствующей точки. При Qi = Q2 брус может перемещаться как
угодно, лишь бы qiQi, q2Q2 были положительны. При Qi — Q2
мы получаем:
g1 + ?2=2Z(-|L)".
Из симметрии системы очевидно, что если @i = Q2, то брус должен
перемещаться, оставаясь горизонтальным, при этом усилия в
стержнях одинаковы и легко убедиться, что qx = q2 — I ( -? j .
Если Q2 меньше, чем Qu на сколь угодно малую величину, то
q2 = 0 и qt = 21 ( Щ j ; наоборот, если Q2немного больше, чем Qlr
тогда qi = 0 и q2 = 2/ ( — ) . Такого рода парадоксы возникают
всегда, когда мы ищем приближенное решение задачи ползучести,
отправляясь от распределения усилий при предельном равновесии,
и рассматриваем состояние нагрузки в окрестности угловой точки
предельной поверхности.
§ 103. ПРИМЕНЕНИЕ ПОВЕРХНОСТЕЙ ПОСТОЯННОЙ
МОЩНОСТИ ДИССИПАЦИИ К РАСЧЕТУ ФЕРМ
Если для стержневой системы, находящейся под действием
сил Qr, известен потенциал ползучести, выраженный через
внешние силы, то задача об определении перемещений уже решена,
так как по теореме Кастильяно
_ дФ
* ~ dQT ¦
§ 103] ПОВЕРХНОСТИ ПОСТОЯННОЙ МОЩНОСТИ ДИССИПАЦИИ 413
Для приближенного нахождения потенциала Ф в случае
степенного закона ползучести можно использовать приведенную в § 101
теорему Келледайна и Друкера. Для степенного закона
ползучести диссипативная функция и потенциал ползучести
отличаются лишь множителем, поэтому если известна поверхность
L — const, то известна и функция Ф. Обычно оказывается, что
при некоторой комбинации нагрузок задача ползучести для
системы имеет простое решение. Так, в примере 2 § 102 элементарно
простое решение получалось при Qi = 0 и при Q2 = 0, в примере 3
без всяких затруднений можно было выписать решение для
случая, когда Qt = Q2- Условимся задавать соответствующую
комбинацию нагрузок обобщенной силой Qt. Если увеличить все
нагрузки в X раз, то при степенном законе ползучести с
показателем п мощность диссипации увеличится в A,n+1 раз; отсюда следует,
что мощность диссипации является однородной функцией
степени п + 1 от обобщенных сил. Уравнение поверхности
постоянной диссипации в пространстве сил можно поэтому записать в виде
R (Qu Qz, ¦ ¦ ¦, Qn) = const.
Здесь R — однородная функция первой степени от сил Qr = ~.
Очевидно, что функция В. определена с точностью до множителя;
выберем этот множитель так, чтобы было
Д(<?„ 0, 0,...,0) = &.
Как видно, функция R по отношению к внешним силам играет
ту же роль, что функция s по отношению к напряжениям; если
s есть некоторое приведенное напряжение, то R есть некоторая
приведенная сила. Считая, что основные опытные данные о
ползучести доставляются опытом на растяжение, мы определили
однородную функцию s (ви) так, чтобы при растяжении одним
только напряжением ои было .? = 0"и. Совершенно аналогично,
если считать, что некоторые надежные сведения о поведении
системы имеются, когда действует одна только сила Qt, а
остальные силы равны нулю, мы требуем, чтобы в этом случае было
R = Qi. Теперь константа в уравнении поверхности постоянной
диссипации R = const приобретает определенный смысл: это есть
отрезок, отсекаемый поверхностью на оси Qt. Обозначим этот
отрезок через at и запишем уравнение поверхности постоянной
мощности диссипации следующим образом:
R{Qi,Qb ...IQn) = al. A03.1)
В качестве стандартной поверхности постоянной мощности
диссипации выберем поверхность, нормированную в том смысле,
как было указано в § 101.
414 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. YI1
Условие нормирования имеет следующий вид:
г
Здесь Nt выражены через внешние силы, следовательно, условие
нормирования определяет в пространстве сил поверхность с
координатами Q\, QI, . . ., Q°n. В соответствии с A03.1) мы можем
записать уравнение этой поверхности так:
B0 = R(Ql, Ql,..., Q°n) = a\ = const.
Потенциал ползучести будет функцией от R: Ф = Ф (R);
следовательно,
- _ BФ 8R
to—dR dQz •
Если Q2 =Q3= ...Qn = 0, то Ф= Ф (Qt) и q, = Ц = н;(&).
По предположению, при действии одной только нагрузки Qv
задача ползучести имеет решение, которое можно написать в явной,
форме, поэтому функция w известна. Следовательно,
qx=w(R)W. A03.2)
Пусть в изображающем пространстве усилий вектор Q = Qnf
в изображающем пространстве скоростей вектор q = qv.
Умножая обе части A03.2) на Qt и суммируя, мы найдем:
qQ = w(R)R,
поскольку, по предположению, R есть однородная функция
первой степени. Отсюда получаем:
q= W{R)* A03.3)
Q cos (Qq)
и
Формула A03.3) может быть полезна, когда число обобщенных
сил равно двум и функция R (Qi) задана графически кривой
в плоскости Qu Qz (рис. 166). Если заданы внешние силы Qir
мы строим изображающую точку М в пространстве сил и
проводим в нее луч из начала координат; этот луч пересекает
поверхность постоянной нормированной мощности диссипации в
§ 103] ПОВЕРХНОСТИ ПОСТОЯННОЙ МОЩНОСТИ ДИССИПАЦИИ 41S
точке М0 с координатами Q°. Величина R вследствие A03.1) равна
Я = а'
0_.
на оси Qi и две-
Q0 есть радиус-вектор точки М0, aj — радиус-вектор точки М,
а? — отрезок, отсекаемый поверхностью постоянной
нормированной мощности диссипации на оси аи тогда как вектор q направлен
по нормали к поверхности в точке М0. Для построения
поверхности постоянной нормированной мощности диссипации мы
имеем, по предположению, одну точку Ql
ограничивающие поверхности:
поверхность предельных состояний
и поверхность упругих
состояний. В отдельных задачах обычно
оказывается, что система
допускает точное решение и для
некоторых других комбинаций нагрузок,
например для Q%, Q3. Тогда мы
знаем точки пересечения искомой
поверхности с осями Q2 и Ql, обо-
"о _а Ло „о
значим их Ql = а\, Q9a = а°. За
\"> Q,
Рис. 166.
дача построения поверхности R =
= const становится несколько
более определенной, хотя произвол
все еще весьма велик. Подбор
подходящего аналитического
выражения для функции R (Ql) уже при
п = 2 представляет собою мало благодарную задачу, а при п = 3-
и более совершенно безнадежен; при п = 2 можно рекомендовать
просто провести через заданные точки произвольную кривую на
глаз и отыскивать решение с помощью A03.3), пользуясь
непосредственно чертежом.
Схема построения указана на рис. 166. Предположим, что
мы знаем точки Ql — а\ и Q2 = а\, соответствующие
нормированным точным решениям при <?2 = 0 и 0^ = 0 соответственно.
Проводим через них плавную кривую, заключенную между
предельными кривыми (на чертеже не показаны). Пусть заданы силы Q±
и Q2, требуется определить qx и q2. Строим точку М с
координатами Qi и Q2, проводим луч ОМ, координаты точки М0 будут
Ql и Ql, их следует измерить непосредственно на чертеже. Длина
отрезка ОМ есть модуль вектора усилий Q. Мы
предположили, что при Q2 = 0 решение известно, оно определяется
формулой Qi = w (Qi), значит w — известная функция. Вычисляем-
416 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. "VII
величину R: R = a°1 ^-= а\ ~ = aj -r- , проводим нормаль к кривой
в точке М0 и находим угол я|) между нормалью и осью (^, угол ф
между этой осью и лучом ОМ известен. По формуле A03.3)
w(R\R
q=- — •
Qcos (ф—я|>)
После того, как нашли д, определим qi — qcos^n qz = q sin ty.
§ 104. КИНЕМАТИЧЕСКИЙ СПОСОБ РАСЧЕТА ФЕРМ. ПРИМЕРЫ
Трудность нахождения точных решений задач о ползучести
ферм по способу, изложенному в § 102, состоит в решении
некоторых нелинейных уравнений и связана, по существу, с тем, что
мы хотим найти явные выражения для внутренних сил через
внешние силы и для скоростей через силы. Эту трудность иногда
оказывается возможным обойти, если считать заданными
скорости узлов. Пусть qs — заданные скорости узлов фермы;
составляя кинематические уравнения, мы всегда можем выразить
скорость удлинения каждого стержня v-t линейным образом через
скорости узлов qs, так что
щ = yisqs-
Составим выражение потенциала сил:
U = JjhFtU{vt).
По теореме Лагранжа
<?s = l|r=2 W7'(»*)*. = 2 hFi* ЫЯь)Уи. (Ю4.1)
Функции v и s являются взаимнообратными: если v = v (s),
то s = s (v).
Формулы A04.1) выражают явным образом силы через
скорости узлов фермы; разрешить эти уравнения относительно
перемещений удается далеко не всегда, и в общем случае трудности
кинематического метода остаются теми же, что и трудности
статического метода. Кинематический метод удобно применять тогда,
когда число возможных перемещений узлов невелико, например
для фермы, изображенной на рис. 167. Вследствие симметрии
задачи здесь приходится иметь дело с одной-единственной
скоростью — вертикальной скоростью q точки приложения силы,
поэтому формула A04.1) сразу дает зависимость между О и q,
увеличение степени статической неопределимости, то есть
увеличение числа наклонных стержней, никаких осложнений не вносит.
С другой стороны, для фермы, изображенной на рис. 168, приме-
§ 104] КИНЕМАТИЧЕСКИЙ СПОСОБ РАСЧЕТА ФЕРМ. ПРИМЕРЫ 417
нение кинематического метода не оправдано: здесь приходится
вводить в рассмотрение четыре скорости — две составляющие
скорости точки А и две составляющие скорости точки В. Если нас
интересует только скорость точки приложения силы Q в
направлении ее действия, то три остальные скорости придется исключать
из уравнений.
Рис. 168.
При степенном законе ползучести на основе кинематического
метода можно рассматривать приближенные решения, подобно
тому как это делалось в § 103 применительно к статическому
методу. Примем
/ UN»
положим по-прежнему QT =~- , <?,. = -±г-. Точно таким же
Обрати еп.
зом, как в случае заданных сил, потребуем, чтобы средняя
мощность диссипации на единицу объема равнялась единице,
значит,
2'.4t) "=S№-
Это условие определяет поверхность постоянной мощности
диссипации в пространстве скоростей. Запишем уравнение этой
поверхности в виде
»•(#)=&;.
A04.2)
Здесь однородная функция первой степени г (qs) определена так,
чтобы было г = qu если q2 = q3 = ... = 0. Как мы видели
27 ю. Н. Работнов
418 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. Ml
в § 102, поверхности A04.2) для различных п оказываются
вложенными одна в другую, но порядок здесь обратен тому порядку,
в котором расположены (^-поверхности; внутренняя граничная
^-поверхность соответствует упругому состоянию, то есть п =1,
наружная — предельному жестко-пластическому состоянию,
(^-поверхности и ^-поверхности связаны между собою
соотношениями взаимности. Если в пространстве Q задан вектор ОМ = Q,
то вектор ОМ0= Q0 ему
пропорционален, направление
вектора q совпадает с
направлением нормали к
(^-поверхности в точке М0- Если
теперь построить вектор
ON = q в пространстве
скоростей и пропорциональный
ему вектор ON0, то нормаль
к g-поверхности в точке 7V0
дает направление вектора
Q. Для двух сил, когда
предельная поверхность
превращается в предельную
кривую, отмеченное свойство позволяет построить (^-кривые, если
известны g-кривые, и наоборот (рис. 169),
Вернемся теперь к примерам 2 и 3 § 102 и попытаемся
получить для них более точные результаты.
Пример 2 § 102. Мы выяснили, что в плоскости Qx — Q2
предельное состояние идеальной жестко-пластической системы
изображается двумя прямыми: Ql + Ql ctg а = 1 + 2 cos а и 0°2 = 2 sin а.
Эти прямые при а = 60° построены на рис. 163. В упругом
состоянии
Qi д,- _ Qicosset , Q2
Рис. 169.
лг,=
1+2 cos3 a '
N
1, з
1 4-2 cos3 а — 2 sin а '
Условие нормирования
cos a
(NI + ND
-Ш1-.
21
¦ + 1
приводит к следующему соотношению между QI и 0\:
Qga Ql* _ 2 + cosa
1 + 2 cos3 а 2 sin2 a cos a cos а
Это — уравнение эллипса, для а = 60° эллипс построен на рис. 163.
Все (^-кривые для различных п располагаются между эллипсом
и ломаной и = со, причем величины 0\ и 0\ — отрезки,
отсекаемые этими кривыми на соответствующих осях, —легко
§ 104] КИНЕМАТИЧЕСКИЙ СПОСОБ РАСЧЕТА ФЕРМ. ПРИМЕРЫ 419
находятся. Действительно, решения при Q2 = 0 и ПРИ @i = 0
известны, остается их нормировать (с соответствующим »).
Получим:
1
2 +cos a Y+i
а\ = A + p)«+i
cos а
1
„ с, . /2 + cosa\«+1
При п = 3 соответствующие точки отмечены на чертеже
кружками, при этом а" = 2,16, а° = 1,86. Дальше можно пытаться
угадать, каким образом пройдет Q-кривая через отмеченные
точки, но в данной задаче кинематический метод позволяет
получить точное решение. Сообщим узлу вертикальную скорость
#! и горизонтальную скорость q2, тогда скорости удлинения
стержней будут
cos a , Л qi
г>1,з=—J—(gicosa-j-^2sma), v2 = -j-.
По формуле A04.1) мы получим сразу:
s-, Г cos a , , . n
Qi = —-,— (qi cos a + ?2sm a) cos a +
j_ j_
+ —-j— Wi cos a — q2 sin a) cos a + [ -j5- ) ,
j_
,-. Г cos a , . . . n .
Q2 — —]— № c°s a -j- g2 sni a) sm a —
_i_
Г cos a , • \ П " •
—• —-—((^cosa— (?2sma) sin a.
Таким образом, силы выражены через скорости.
Желая решить обратную задачу, то есть найти скорости при
данных значениях сил, мы должны все-таки построить
^-кривую. Теперь это можно сделать следующим образом. Положим
<?f/<?2 = tg9, qjq2 = tg xp; из найденного решения следует:
— — (sin ibI/"
г81п(г|: + а)]я + [81п(ф-а)]п +л ^—j-
1+
, . . (cos a) "
lg<p = Ctgl|> j ^—^ .
[sin($ + a)]n — [sin(i|3 — a)]"
Рассчитав таблицу или построив график ф от т|), мы будем
отправляться от некоторой заданной точки М0 в плоскости
27*
420 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
Qi — Q2 (рис. 170); радиус-вектор этой точки составляет угол
ф0 с осью абсцисс. Проведем через точку М0 прямую,
которая составляет угол г|з0 (<p0) с осью абсцисс; перпендикуляр к ней
в точке М0 направлен по касательной к (^-кривой. Малый отрезок
М0М\ касательной примем за
элемент дуги, тогда радиус-
вектор OMi будет наклонен
под углом ф!, которому
соответствует угол гр! наклона
нормали; продолжая то же
построение, получим точку
Мг и так далее. Построение
можно сделать и более
точным, но в этом вряд ли есть
необходимость. На рис. 163
д ~п приведена полученная таким
' образом ф-кривая для п = 3.
Рис. 170. Вместо того, чтобы строить
(^-кривые, можно было вести
все рассуждения в пространстве скоростей, мы покажем это
на следующем примере.
Пример 3 § 102. Будем рассматривать этот пример, не
обращаясь к представлению в плоскости сил. Сообщим концам бруса
направленные вниз скорости qx и q2, тогда скорости удлинения
стержней будут: y3 = ?1, Vl = - qi + ± ?2) Vz = 1^ + |. ?2i
vk — 4.%- Но формулам A04.1):
i i I
, i i (a)
n = . 1 / 2 1 \n 2 f 1 ,2 у
Построим теперь соответствующую g-кривую. Условие
нормирования запишется следующим образом:
При п = оо отсюда получается
g,i + ?2 = 2.
При и = 1 ^-кривая будет эллипсом:
7д; + 49,д2 + 7д; = 18.
§ 105]
СПОСОБ КАЧАНОВА
421
Он отсекает на осях координат отрезки, равные i/— л; 1,6,
и касается прямой предельного состояния в точке qt = д2 = 1.
Такое положение будет всегда для конструкций минимального
веса, то есть таких, у которых при некоторой комбинации нагрузок
все элементы одновременно переходят в пластическое состояние.
Если принять теперь q2 = 0 либо #i = 0, то мы получим из
условия нормирования
4 \3А
Ь° и b\ — отрезки, отсекаемые д-кривой на осях координат.
Не представляет затруднения построить и всю g-крнвую, как это
сделано на рис. 171 опять-таки для п = 3, притом только в первом
квадранте. При заданных Qi и Q2 проще всего поступить для
определения скоростей
следующим образом: провести на Ч2
графике рис. 171 луч с
наклоном Qi/Q2 и касательную
к ^-кривой,
перпендикулярную этому лучу. Отношение
абсциссы и ординаты точки
касания равно отношению
qjq2. Зная это отношение,
мы легко определим д4 либо
q2 с помощью одной из
формул (а).
§ 105. СПОСОБ КАЧАНОВА
Общий метод расчета
статически неопределимых
ферм приводит к
нелинейным уравнениям для
определения лишних
неизвестных, решение этих уравнений фактически возможно лишь для
систем с одной лишней неизвестной, уже в случае двух
неизвестных трудности становятся очень большими и задача
требует трудоемких вычислений. Простейший прием для получения
приближенных решений мы рассмотрели в § 102, он состоит
в том, что распределение усилий в стержнях просто задается
заранее, выбирается некоторая система усилий KNt,
удовлетворяющая уравнениям статики. Более точные результаты
можно получить следующим образом. Рассмотрим некоторую
ь\ = К
422 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ОБЩАЯ ТЕОРИЯ [ГЛ. VII
самоуравновешенную систему усилий N1, тогда распределение
усилий X (iV?+ kN'i) будет также удовлетворять уравнениям
статики. Определим параметр к таким образом, чтобы
потенциал скоростей принимал минимальное значение. Подставляя в
A02.1), дифференцируя по к и приравнивая нулю, получим:
При степенном законе ползучести величина К в степени п выходит
множителем за знак суммы и мы приходим к следующему
уравнению для параметра к:
2ЦМ+М)л; = о. (Ю5.1)
Это нелинейное уравнение для к, достаточно сложное, но
единственное, независимо от степени статической неопределенности.
После того, как к найдено, следует поступить обычным способом,
разъясненным в § 102. Заметим, что множитель к определяется
из A05.1) для данной системы нагрузок, при других нагрузках
этот множитель будет другим. Поэтому теорему Кастильяно для
определения перемещений можно применять только в форме A02.4),
в предположении о том, что нагрузки меняются пропорционально.
Качанов предлагает брать в качестве состояния Щ предельное
состояние жестко-пластической фермы при внешних нагрузках
@? = Т> в качестве же состояния N\ — разность между
усилиями, вычисленными для тех же сил Q\ в предположении
упругости материала, и усилиями Nf. Некоторые примеры
применения этого способа приведены в монографии [52], поэтому мы
на них не останавливаемся.
ГЛАВА VIII
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ.
ИЗГИБ И КРУЧЕНИЕ
Общие методы исследования установившейся ползучести,
развитые в главе VII, применяются к теории изгиба и кручения
стержней. Приближенные приемы, основанные на замене
истинного распределения напряжений тем, которое соответствует
предельному состоянию идеально-пластического стержня,
оказываются полезными, они позволяют, в частности, построить
достаточно простую теорию касательных напряжений в тонкостенных
стержнях. Теория кручения тонкостенных стержней открытого
и замкнутого профиля также не встречает трудностей. В
заключение рассматривается вопрос об изгибе при наличии
продольной силы.
§ 106. УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ЧИСТОМ ИЗГИБЕ
Здесь мы рассмотрим ползучесть при чистом изгибе стержня,
сечение которого имеет две оси симметрии х и у, изгибающий
момент действует в плоскости yOz. Высота сечения 2h, ширина Ъ
задана как функция отношения ylh (рис. 172). Примем закон
ползучести в виде а = s (е), сечения стержня остаются при
деформации плоскими, следовательно, е = ху, причем х — скорость
изменения кривизны оси стержня. Если свойства материала при
растяжении и сжатии одинаковы, то изгибающий момент
h
М = 2$ b^ys(xy)dy.
о
Примем за переменную интегрирования величину щ = е,
положим nh = e", тогда
M = fH b(ir)Bs(e)dB.
о
424 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
Введем обозначение:
8'
а
Тогда
M = o*h2b0m(xh).
A06.1)
У
Здесь Ь0 — некоторая характерная ширина, например, при
h = 0, а* — произвольная
константа, имеющая размерность
напряжения. Для степенного закона
ползучести
*(е)
в случае прямоугольного сечения
шириной Ъ и высотой 2h мы
получаем:
2п / xh\n
t
II
.
А \
\ V
^\
} \
0
S
У
X
т =
2n + i Veny
(о* = оп).
Степенной закон ползучести отли-
Рис. 172. чается тем, что зависимость
скорости изменения кривизны от момента
получается также степенной, причем показатель в этой зависи-
1
мости равен п. Действительно, если s (е) = ап ( — J , то
hn F
М =
Обозначим:
У --^
и,1_ h
Тогда
Для прямоугольника
Мп = Ып ^
F
/ М \п
М- - 2п h№a.
У
h
1+1
-f ndF.
A06.2)
2п-\-1
При других законах ползучести функция т (xh) также может
быть вычислена; если квадратуры не выполняются, то построение
функции графическим или численным методом всегда возможно.
§ 106] УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ЧИСТОМ ИЗГИБЕ 425
Чрезвычайно простое приближенное решение о ползучести
при изгибе получается, если принять такое распределение
напряжения, которое соответствует предельному состоянию
пластического стержня. Площадь сечения есть F, и координата центра
тяжести половины сечения, расположенной в области
положительных у, есть -к-; мы :будем считать, что при у > 0 напряжение
имеет постоянную величину а, а при у <; 0 величину —а. Тогда
изгибающий момент
следовательно,
М = ^о,
2М
0 = 7Г
Составим выражение потенциала скоростей для участка балки,
длины, равной единице:
Ф= J 0{a)dF = FOf^f
F
По теореме Кастильяно
и=вм=тЧтг> <106-3>
При степенном законе мы можем привести эту формулу к виду
A06.2), если положим
1
Применим формулу A06.3) к случаю прямоугольного сечения
при степенном законе ползучести. При этом F = 2bh, с =J&,
следовательно,
„ 2гп / М \п
~ ~ h Vb№
Отсюда
_ 1.
т,= 2 п
1
Сравнивая с точным решением для прямоугольника, мы найдем,
что оно отличается от приближенного только множителем.
который был равен ¦ в первом случае и 2 п — во втором.
426 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. YIII
"
2
3
4
6
8
2та
2п+ 1
0,800
0,858
0,889
0,923
0,940
1
2 п
0,707
0,795
0,840
0,892
0,917
В таблице приведены для сравнения величины этих
множителей для некоторых значений п.
Сравнительно небольшая разница между результатами точного
и приближенного решений объясняется характером
распределения напряжений при изгибе.
На рис. 173 построены эпюры
напряжений для разных
значений п при одном и том же
изгибающем моменте. Как
видно, эпюры расходятся при
малых ylh, тогда как при у,
близких к h, величины
напряжений немного
отличаются от тех, которые
соответствуют пластическому
состоянию. При вычислении момента основной вклад вносят именно
напряжения в областях сечения, удаленных от нейтральной оси.
Предположим теперь, что сечение имеет только одну ось
симметрии — ось у, изгиб по-прежнему происходит в
плоскости yOz. В отличие от упругого
изгиба нейтральная ось стержня не
будет проходить через центр тяжести
сечения. Более того, при
произвольном законе ползучести положение
нейтральной оси зависит от величины
изгибающего момента, только при
степенном законе нейтральная ось
фиксирована для данного п.
Приближенное решение в этом случае
получается чрезвычайно просто. В
предельном состоянии нейтральная
ось делит площадь сечения на две
равные части, допустим, что так
будет и при ползучести. Примем эту
ось за ось я (рис. 174), найдем центры
тяжести двух половин сечения С4
и С2, расстояние С^Сг обозначим
через с. Тогда по-прежнему величина
напряжения в предельном состоянии
2М
равна — , выражение для
потенциала будет таким же, как и в случае симметрии относительно оси х,
и соотношение A06.3) сохраняет силу. При степенном законе
формула A06.2) верна и при наличии одной только оси
симметрии, но, прежде чем ее применить, необходимо найти
положение нейтральной оси.
Рис. 173.
106] УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ЧИСТОМ ИЗГИБЕ
427
Рассмотрим теперк изгиб стержня прямоугольного сечения
при экспоненциальном—эакЪне ползучести D3.3):
ст = <гв1п —. A06.4)
Этот закон перестает быть формально пригодным при е < ее,
он становится достаточно точным, лишь
когда г/ге > 1. Примем, что A06.4)
справедливо лишь при е > ее, при " е < ее
<т = 0. Тогда
Ж = 2&ст,
Полагая
1Ь
*/о =
vo
Ме = ое№Ь, ие = -
легко получим:
М -
м
м„
х — ¦
м=1пх-4-+4-
2 2и2
A06.5)
Рис. 174.
Чтобы избежать введения областей, для
которых ст = 0, мы воспользуемся вместо закона A06.4) более
Рис. 175.
обоснованным физически законом гиперболического синуса (§43):
o- = aeArsh^. A06.6)
2е„
428 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
В результате несложных вычислений находим:
М
-0+1
Arsh
2х
A06.7)
На рис. 175 представлены графики зависимости М от к по
формулам A06.5) и A06.7) соответственно. Как видно, при и > 10
разница между этими формулами становится весьма малой. Дело
в том, что область малых на-
б/б,
пряжений находится вблизи
нейтральной оси стержня и эти
малые напряжения
несущественны при вычислении
изгибающего момента.
Использование приема,
заключающегося в том, что
распределение напряжений берется
таким же, как и в пластическом
состоянии, то есть применение
формулы A06.3), при
экспоненциальном законе ползучести
приводит к довольно большой
погрешности.
На рис. 176 построены
эпюры напряжений по сечению для
случая %е = 5 в соответствии:
1) с формулой A06.4) при
сделанной оговорке, 2) с
формулой A06.6) и 3) с формулой
A06.4) без всяких оговорок. В
последнем случае а = — со при
у = 0. Если мы будем вычислять
момент для этой последней эпюры, то величина момента остается
конечной и не будет существенно отличаться от величины,
даваемой формулой A06.5). Если положить нижний предел в
интеграле равным нулю вместо у0, мы получим:
1
Рис. 176.
М = 1пи —
A06.8)
Рассмотрим теперь задачу об изгибе стержня произвольного
поперечного сечения, имеющего ось у осью симметрии, при
экспоненциальном законе ползучести. Приведенный пример убеждает нас
в том, что при достаточно большом изгибающем моменте
обращение напряжения в бесконечность на нейтральной оси практически
не влияет на зависимость между моментом и кривизной, поэтому
нет необходимости принимать специальные меры для улучшения
§ 107]
СШЛЩЙ СЛУЧАЙ ЧИСТОГО ИЗГИБА
429
закона ползучести в области, примыкающей к нейтральной оси.
Вычисляя изгибающий момент от напряжений, заданных
формулой A06.4), получим:
M = o.\ln^\y\dF = a.[\ Inf-\y\dF+\ln^]y\dF]
F " F " F
Здесь h — произвольный линейный размер. Отсюда следует:
М
~ = ^4~- (Ю6.9)
При этом
*е=^ехр[-^-$|У|1пМ^],
р
Me = -|-ovFc,
с — расстояние между центрами тяжести частей сечения,
расположенных выше и ниже нейтральной оси. В несимметричных
сечениях, вообще говоря, с не постоянно, а зависит от к или М.
Приближенно можно принимать с = const.
При больших значениях х разница между A06.5), A06.7)
и A06.8) становится исчезающе малой, поэтому нет нужды
прибегать к искусственному приему исключения зоны малых скоростей
ползучести. На рис. 175 приведена также кривая,
соответствующая. A06.8), она не отличается от кривой A06.5), уже начиная
с х = 5.
§ 107. ОБЩИЙ СЛУЧАЙ ЧИСТОГО ИЗГИБА
Перейдем теперь к общему случаю несимметричного сечения.
Проведем в плоскости сечения произвольные оси х и у, вследствие
закона плоских сечений
е = е0 + %ху — щх.
Для нейтральной оси 8 = 0, следовательно,
ео + кху — КуХ = 0.
Отрезки а и Ъ, отсекаемые нейтральной осью на осях х и у,
будут
а =-*>-, Ь=--*>-.
430 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. Л'Ш
Вычислим теперь продольную силу и изгибающие моменты:
N= J adF = J s(z0-rxxy-xvx)dF,
F F
M*=-J aydF= -J s(e0 + nxy-nyx)ydF, A07.1)
F F
Л/ч = \ az dF — \ s (e0 + xxr/ — х^я) a: u?/1.
F
Потребовав, чтобы было N = 0, мы получим соотношение между
80, их и щ; в случае степенного закона можно вынести е0 из-под
интеграла, тогда условие отсутствия осевой силы будет следующим:
S'O-T-f)^0- A07-2)
F
Составим также отношение моментов Мх и Му:
1---|- )ydF
а Ь ' "
му Г,Л_?_^
A07.3)
4- ) xdF
а
Уравнения A07.2) и A07.3) определяют а и Ъ, таким образом,
при степенном законе ползучести положение нейтральной оси
в сечении зависит от отношения изгибающих моментов, но не от
их абсолютной величины (см. также [326]). Если нейтральная
ось известна, то ее следует принять за ось х, кривизна балки
определится теперь из уравнения
М.
:= — § s(%y)ydF.
Уже для простых форм сечений как нахождение нейтральной оси,
так и последующее вычисление момента в зависимости от
кривизны представляют большие трудности. Приближенный прием,
основанный на замене истинного напряженного состояния тем
состоянием, которое соответствует предельному равновесию
стержня, оказывается полезным и в этом случае. Впервые он был
предложен Бейли [162] для расчета на изгиб турбинных лопаток,
имеющих несимметричное сечение. Предположим, что в сечении
проведены произвольные оси х и у. Разобьем плоскость сечения
на две равновеликие части прямой пп, составляющей угол q>
с осью х (рис. 177), отметим центры тяжести этих частей Ct и Сг.
В предельном состоянии момент должен быть направлен
перпендикулярно прямой С±С2, направление момента составляет угол i|>
107]
ОБЩИЙ СЛУЧАЙ ЧИСТОГО ИЗГИБА
431
с осью х. Поступая точно так же, как в случае симметричного
сечения, мы найдем скорость изменения кривизны балки,
только при применении теоремы Ка-
стильяно нужно иметь в виду, что
обобщенная скорость,
соответствующая моменту М, естьх cos (ф —
— т|э). Таким образом,
2 f 2M \ _r r
с cos (ф — ч|з) V. cF
A07.4)
Основная трудность при
применении изложенного метода состоит в
нахождении зависимости между <р
и ij) или, что то н^е, в построении
зависимости между Мх и Му в
предельном состоянии.
Действительно, если предельная кривая
в плоскости Мх, Mv известна, то
радиус-вектор точки М этой
кривой наклонен к оси Мх под углом
~ty, а нормаль в этой точке наклонена к оси под углом <р.
Абсолютная величина момента пропорциональна с, следовательно, всегда
можно построить предельную
кривую в таком масштабе,
чтобы было ОМ = с.
Рис. 177.
Рис, 178.
Рис. 179.
Пример. Тонкостенный профиль прямоугольного сечения со
сторонами 2а и 2Ь изображен на рис. 178, толщина профиля
432 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
принимается постоянной. Проведем ось пп, обозначим tg ф =
= т) —. Координаты центра тяжести Ct верхней половины
сечения будут
_ аЪ _u2(i_T)a) + 2afe
Величина xQ пропорциональна Му, величина у0
пропорциональна Мх. С точностью до произвольного множителя мы примем
Mx = 2abr\, My=—b*(l-rf) — 2ab @<ti<l).
Если нейтральная ось пересекает горизонтальную сторону, то
есть tg ф > — , то мы обозначим расстояние точки пересечения
от оси у через Zfl и получим:
Мх = аа A - ?2) + 2ab, Му = - 2аЬ?.
Предельная кривая имеет две оси симметрии, поэтому на рис. 179
показана только одна четверть. При построении было принято
а = 1, 6 = 2. Если ф = 0, то с = ~Т а' при заданных а и Ь,
с = 8/3, изменим масштаб чертежа так, чтобы большая полуось
овала равнялась 8/3. Тогда радиус-вектор точки предельной
кривой будет равен с,
§ 108. ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ
В тонкостенных стержнях открытого профиля наряду с
нормальными напряжениями изгиба приходится рассматривать
касательные напряжения, уравновешивающие перерезывающую силу."
Величины этих касательных напряжений сами по себе обычно
бывают невелики, существенно то, что при некоторых условиях
эти напряжения создают неуравновешенную пару сил, которая
вызывает кручение стержня, а жесткость на кручение
тонкостенного профиля мала и напряжения кручения, как мы увидим
впоследствии, могут быть значительными. Величина квадрата
интенсивности напряжений при одновременном действии нормальных
и касательных напряжений равна а2 + Зт2; если т мало по
сравнению с а, то ошибка при замене величины интенсивности
величиной нормального напряжения будет иметь порядок т2/сг2 по
сравнению с единицей. Поэтому обычно в теории пластичности
и ползучести нормальные напряжения в балке определяются
обычным образом, так же, как и при чистом изгибе, а касательные
напряжения находятся независимо из условий статики.
Для выяснения существа дела рассмотрим сначала задачу
об изгибе стержня прямоугольного поперечного сечения. Уравне-
§ 108] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 433
ние равновесия элемента, находящегося в условиях плоского
напряженного состояния, будет следующим:
да , дт п
Отсюда
r=-\^dy + C. A08.1)
Постоянная интегрирования найдется из условия, что т = 0
при у = ± h. При степенном законе а = ап (— J ,
следовательно,
Используя связь между моментом и кривизной по формуле A06.2)
dM n „
для прямоугольного сечения и замечая, что -т— = Q, где Q —
перерезывающая сила, найдем:
r_ Q 2»+l Г, /jV+'
Ш л + 1
[>-(i) »]. A08.2)
Здесь, как и всегда при использовании степенного закона при
напряжениях, меняющих знак, было бы более корректно
записывать выражение а следующим образом:
Тогда формула A08.2) будет иметь такой вид:
т= Q гп±\_ [ л , у [И--1
2bh
2^ + 1 Г, \V_r~Z"]
л + 1 L I A J
Для краткости мы не всегда оговариваем это уточнение записи.
В предельном случае, при м->- оо, мы получаем отсюда линейное
распределение напряжений, а именно:
Такое же линейное распределение касательных напряжений
можно получить, если задаться распределением нормальных
напряжений, соответствующих предельному пластическому состоянию.
Действительно, если а = о (z), то из A08.1) следует:
г, do
28 Ю. Н. Работнов
434 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
Для
= -— , таким образом мы
прямоугольника а = щ , %-ш
сразу получаем формулу A08.3). На рис. 180 приведены эпюры
распределения касательных
напряжений в балке прямоугольного сечения
для некоторых значений п.
Интересно отметить, что линейное
распределение касательных
напряжений получается и при
экспоненциальном законе ползучести. Используя
замечание, сделанное в конце § 106,
мы не будем обращать внимания
на то, что напряжение обращается
в отрицательную бесконечность на
нейтральной оси, логарифмическая
особенность при интегрировании
устраняется. Так как а = а, 7" у
da rflnx Q
dz
Л= со
Г7=3
при у > 0, сле-
Рис. 180.
dz ~ ЪЬ?
довательно, из A08.1) следует снова
формула A08.3).
Совершенно подобным же
способом могут быть найдены
касательные напряжения при изгибе
тонкостенного стержня открытого профиля. Будем предполагать для
простоты, что нейтральная ось,
определенная тем или иным способом, пересекает
среднюю линию профиля только в одной
точке, как показано на рис. 181.
Обозначим переменную в общем случае толщину
профиля б (Z). Тогда из уравнения
равновесия тем же способом, которым была
получена формула A08.1), мы найдем:
T=i[c~S6(Z)J&rf0- A08-4)
Нетрудно убедиться, что результирующая
касательных напряжений в сечении
равна перерезывающей силе.
Действительно, так как a=s{%xy — кух), то
д
31
У-
Рис. 181.
с дв
6lh =
(бт) =
= -bs'(xxy-KBx)(.dz „- dz
Продифференцируем по z, например, вторую из формул A07.1)
х
§ 108] ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПРОФИЛЯ 435
Получим:
Интегрируя по частям и учитывая, что на концах профиля т = 0,
найдем:
<?•"$
6т cos adl.
Здесь а — угол между касательной и средней линии профиля
и осью х. Совершенно аналогичным образом получаем:
<?.= $
8тsin adl.
Если принять за точку приведения начало координат (или
любую другую точку в плоскости сечения), то кроме
результирующей получится еще пара сил с моментом:
М:
= $6тр
dl.
Здесь р — расстояние от точки приведения
до касательной к средней линии профиля,
как показано на рис. 181. Всегда можно
выбрать точку приведения таким образом, •
что момент Мг обращается в нуль. Если
провести через эту точку плоскость,
параллельную плоскости действия изгибающего
момента, то поперечные силы, приложенные в этой
плоскости, будут вызывать только изгиб, но
не кручение стержня. Назовем такую
плоскость плоскостью изгиба, линию
пересечения ее с плоскостью поперечного сечения — Рис. 182.
линией изгиба. Для упругих стержней
доказывается, что все линии изгиба, соответствующие различным
направлениям поперечной нагрузки, пересекаются в одной точке —
центре изгиба. У стержней, находящихся в состоянии ползучести,
центра изгиба не существует. Это было показано Филлипсом [зг6]
на примере стержня полукруглого сечения, изображенного на
рис. 182.
В упомянутой работе получены общие формулы для
нахождения линии изгиба при степенном законе ползучести,
применение их к частным задачам оказывается весьма сложным.
Для того чтобы показать, что не существует точки пересечения
28*
436 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
всех линий изгиба, автор рассмотрел совершенно искусственный
случай, когда п = 1/3, то есть меньше единицы, только для
этого случая ему удалось выполнить все квадратуры и выписать
решение в явном виде. Из этого примера было сделано
заключение, что и при п > 1 центр изгиба существовать не должен. Второй
пример приведен в статьях Пателя и Венкатрамана [322],[323];
он относится к случаю швеллерного сечения постоянной толщины
такого, что Ь = h (рис. 183). Ось х направлена по оси симметрии
профиля, ось у — по оси стенки.
Если изгибающий момент
составляет угол гр с осью х, то
нейтральная ось составляет с
той же осью угол ф и отсекает
на оси у отрезок, равный (—Ь|3).
Точка С на оси хс координатой
(—е) обладает тем свойством,
что если плоскость действия
силы Q проходит через эту
точку, то напряжения кручения
в стержне не возникают. В
нижеследующей таблице
приведены результаты числовых
расчетов при п = 3, а также, для
сравнения, при п — 1 (упругий
случай).
Следует обратить внимание
Рис. 183. на то, что при <р = 45°
нейтральная ось уже пересекает полку,
при меньших значениях ср, когда нейтральная ось полки не
пересекает, величины ij; в случае ползучести очень малы. Это
означает, что малое отклонение вектора момента от оси х
вызывает значительный поворот нейтральной оси. Величина е при
этом меняется очень мало.
ф°
0
15
30
45
60
75
90
71= 1
1|)»
0°
2°25'
5°8'
8°53'
15°8'
30°17'
90°
Р
0
0,067
0,144
0,250
0,433
0,933
е/в
0,3750
0,3750
0,3750
0,3750
0,3750
0,3750
п = 3
¦ф°
0°
0°58'
2°10'
4°4'
12°5'
30°45'
90°
0
0,034
0,072
0,134
0,323
0,670
е/в
0,3500
0,3495
0,3478
0,3420
0,2864
0,2105
§ 109] приближенный: способ исследования изгиба 437
§ 109. ПРИБЛИЖЕННЫЙ СПОСОБ ИССЛЕДОВАНИЯ
ИЗГИБА ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Основная трудность решения задачи изгиба, как мы видели,
состоит в нахождении нейтральной оси. Однако и после этого
определение касательных напряжений требует выполнения
некоторых квадратур и приводит к достаточно громоздким формулам.
Здесь мы воспользуемся приближенным приемом, изложенным
в § 107 и состоящим в том, что нейтральная ось задается так же,
как в предельном состоянии стержня из идеально-пластического
материала. В части стержня, подверженной растяжению, где
0 <С I < k (рис. 181), а = -у , в сжатой части, при — 12 < I <. 0,
гм „
о = у . При этом
h
\ б {sign I) dl = 0.
С помощью A08.4) мы находим:
2<?
Т =
\ 6dl @<1<11),
cdF
J A09.1)
т=^ j 8di (-г2<г<0).
Если б = const, то lt = l2, F = 2^6 и т = -~ ( 1 — у- J при I > 0
и т = —4~A+т~) ПРИ ^<0. Наибольшее касательное
напряжение по формулам A09.1) получается при 1 = 0, оно равно
т --Я-
тах— сб -
Вычислим теперь момент касательных усилий в сечении
относительно некоторого центра приведения О:
М= С xdpdl.
Здесь, в отличие от предыдущего, мы приняли начало отсчета
дуги на одном из концов профиля. Величина р по-прежнему
представляет собою длину перпендикуляра, опущенного из
центра приведения О на касательную к средней линии стержня.
Заметим, что р dl = d(o представляет собою удвоенную площадь
сектора, заключенного между элементом dl и радиусами-векторами
438 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. YIII
концов этого элемента. Интегрируя выражение для М по частям и
учитывая, что т = 0 на концах профиля, получим:
М
= -W
да
dz
dl.
Пусть нейтральная ось пп пересекает несколько раз ось
профиля, как показано на рис. 184. Отрезки 01, 23 находятся в области
сжатия, отрезки 12, 34— в
области растяжения. В области
2М
растяжения о = —=¦, следо-
Лт _ 2Q
dz ~ cF
л do 2<?
в области сжатия -=— = ^,
dz cF
поэтому
м =
_2?
cF
Рис. 184.
{s+J (o6dl-
—S-JoSdA. A09.2)
Символ Б+ показывает, что
суммирование
распространяется на отрезки, находящиеся в области растяжения, 2~ обозначает
сумму интегралов по отрезкам в области сжатия.
Пример 1. Швеллер с постоянной толщиной стенки. Для
простоты будем считать h = Ъ = 1, как и в примере Пателя и Вен-
катрамана, рассмотренном выше. Если нейтральная ось не
пересекает полок, то она проходит через середину стенки,
следовательно, при ф < 45° ч|) = 0 и р = 0. Эпюра секториальных
площадей для полюса О, выбранного в середине стенки, представлена на
рис.185. По формуле A09.2) при ф<45°М = — (Щ, поэтому
расстояние линии изгиба от точки С е = 1 /3. Вспомним, что для
упругого стержня было е = 0,375, при п = 3 е = 0,350. При ф > 45°
из условия равенства площадей, лежащих по обе стороны
нейтральной оси, следует, что последняя пересекает ось у в точке —р
и отсекает от конца верхней полки отрезок, равный р. Отсюда
ЧЧ =
1 + Р
1-р
В результате несложных вычислений находим
координаты центров тяжести половин сечения хи yt и х2, у2,
а именно:
Xi =
#2 :
A-РJ
1+2Р—рг
У±-
3—2р —рз
2/2 =
3—2ft—рз
S 109] ПРИБЛИЖЕННЫЙ СПОСОБ ИССЛЕДОВАНИЯ ИЗГИБА 439
Теперь находим tg -ф и с:
tgl|5 =
х2—х1
У2 — У1
ЗЙй, c=±Vw-pr+(Z-2p-pr-
-2р-р)
Момент касательных усилий относительно точки О находится
по формуле A09.2):
м- 2Q Г A~Р)8 I 1 B~Р)Р
cF
t
]-
2<?
cF
A-РJ
Величины, заключенные в квадратные скобки, представляют
собою площади частей эпюры ю, лежащих по обе стороны оси пп,
взятые с соответствующими знаками.
Разделив М на Q, мы определим
расстояние е* от точки О до линии
действия силы Q, не вызывающей
кручения. Величина е,
представляющая собою абсолютную величину
координаты точки пересечения линии
изгиба с осью х, равна
е =
cos г|)
&>
_L_
Ту
^^^е
/~т
О/
/
1
Результаты вычисления при ф = 60°
и ф = 75° получаются следующие:
при ф = 60° р = 0,267, г|) = 11°,
е = 0,246; при ф = 75° р = 0,578,
1|з = 28°35', е = 0,119. Сравнивая
с результатами точного решения для
п = 3, мы должны отметить, что как
для г[), так и для е при ф = 60°
разница невелика, хотя величины р"
разнятся довольно заметно. При ф = 75°
направления плоскости изгиба для
упругого состояния, состояния пол- Рис. 185.
зучести при п = 3 и состояния
предельного равновесия отличаются довольно мало, тогда как
величина е оказывается существенно различной.
Заметим, что этому же примеру посвящена заметка [ш], где
по данным работы [322] строится кривая постоянной мощности
диссипации для п = 1, 3, оо.
Пример 2. Круглая труба радиуса R разрезана вдоль оси
(рис. 186). Зададим положение нейтральной оси углом ф,
отсчитываемым от диаметра, проходящего через разрез. Для определения
нормальных напряжений наличие резреза значения не имеет,
распределение нормальных напряжений симметрично, и плоскость
изгиба перпендикулярна оси пп. Величина с не зависит от ф,
440 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
с = —. Примем начало отсчета секториальной площади при
а = 0, тогда ш = Л2а. По формуле A09.2)
ф+Я 2Я <р
M = ^[jj ada-\ ada-lada'l^-QIt"^-2^ .
Ф ф+я О
Расстояние ОС от оси трубы до линии изгиба равно
0C==R я(я-2Ф) ^
4
Легко убедиться, что центра
изгиба, то есть точки пересечения
линий изгиба, соответствующих
различным ф, не существует.
На примере стержня
прямоугольного сечения мы видели,
что при экспоненциальном законе
ползучести касательные
напряжения распределены таким же
образом, как и при п = оо. В общем
случае, приняв нейтральную ось
Рис. 186.
за ось х, мы должны положить
o- = creln-^-
ье
Отсюда
да д In х
dz -°e dz
Но
(У>0),
(У>0),
31пх
а а.1п( J)
да a In х
dz ~ °e dz
d In x ^,
(V<0).
(y<0).
dz
dM
Поэтому для момента М будет справедлива формула, совершенно
аналогичная формуле A09.2):
¦<2ае^Шг{ъ+\ oiSdi —2- С ®6dl\. A09.3)
М =
Рассмотрим снова пример 2, но уже при экспоненциальном
законе ползучести и в точной постановке. Расстояние точки
окружности от оси пп равно R sin (а — ф), положим а — ф = Х>
тогда при 0 < % < я
xi? sin х
¦аЛп
Изгибающий момент
М
= 4Д2ае jln^- + ln2-l|-
§ НО] ДЕФОРМАЦИЯ БАЛОК И РАМ ПРИ ИЗГИБЕ 441
Отсюда
d In я _ 1
Применяя формулу A09.3), мы снова приходим к прежнему
результату, таким образом, найденное приближенное решение при
экспоненциальном законе ползучести является точным.
§ 110. ДЕФОРМАЦИЯ БАЛОК И РАМ ПРИ ИЗГИБЕ
Зная зависимость между изгибающим моментом и скоростью
изменения кривизны х = х (М), мы можем определять прогибы
балок путем интегрирования уравнения упругой линии, которое
запишется следующим образом:
-g- = x(M). A10.1)
Здесь v — скорость прогиба балки. Если момент задан как
функция координаты z, интегрирование уравнения A10.1) сводится
к двум квадратурам, которые могут быть выполнены либо в
замкнутом виде, либо путем численного или графического
интегрирования. Те способы интегрирования уравнения изгиба, которые
применяются для упругих балок, целиком переносятся на случай
ползучести. Действительно, уравнение изогнутой оси упругой
балки имеет следующий вид:
d*w _ М
dz* ~ ~Ш '
Здесь w — прогиб балки.
Достаточно принять за эпюру изгибающих моментов,
поделенных на жесткость, эпюру функции х (z), чтобы получить
возможность использовать обычные методы строительной механики.
В частности, на случай ползучести немедленно обобщается
известный графо-аналитический метод. При аналитическом
определении прогиба вся трудность состоит в фактическом выполнении
интегрирования. Таким же способом, очевидно, можно решать
простые статически неопределимые задачи. Когда ставится задача
об определении прогиба в тех или иных отдельных точках балки
или о нахождении величин лишних неизвестных в статически
неопределимых системах, более простой путь состоит в
применении вариационных теорем. Рассматривая х как обобщенную
скорость, а М — как обобщенную силу, мы определим потенциал
скоростей следующим образом:
Ф = \ к (М) dM
442 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
и потенциал напряжений:
Соответственно для балки или рамы в целом:
i i
Ф= [ <b(M)dz, U=[u(x)dz.
= { <S)(M)dz, U=^ U{%)
о о
Выпишем соответствующие формулы для степенного закона
ползучести:
^=iTTr^(?I+i A10-2)
и для экспоненциального закона:
_л, с_,.е_е_
и = хе ехр (-дт-) , Ф = кеМеехр'
Z7 = *.Af..?[ln-?.-l]
A10.3)
Заметим, что при экспоненциальном законе вторая из формул
A10.3) дает отличное от нуля значение Ф при М = 0, однако
если изгибающие моменты в большей части балки достаточно
велики, то вносимая погрешность совершенно несущественна.
Решение статически неопределимых задач, так же как и для
стержневых систем, работающих в условиях растяжения —
сжатия, приводит к некоторым трансцендентным уравнениям для
нахождения лишних неизвестных. Пусть лишние неизвестные
задачи будут Хи Х2, • • -, Хп, обобщенная сила, для которой
ищутся перемещения,— Q. Изгибающие моменты на участках
представляют собою линейные функции от Xs и Q. Если
воспользоваться степенным законом ползучести, то выражение для Ф =
= \ Ф (М) dz может быть всегда представлено в следующем виде:
Здесь §s — безразмерные лишние неизвестные, %s = -^ , Ре —
произвольные величины той же размерности, что Xs, I —
некоторая характерная длина. Величины ?s определяются из условия
минимума функции R: -г?- = 0. После того, как ?s найдены,
§ 110] ДЕФОРМАЦИЯ БАЛОК И РАМ ПРИ ИЗГИБЕ 443
обобщенная скорость, соответствующая силе Q, находится по
теореме Кастилъяно:
ЭФ
8Q
— x„i
М
1 У tiff
52! •
• I Ъп)-
A10.4)
dR
Основная трудность состоит в решении системы -==- = 0; более
простой прием будет состоять в том, что значениями ?s задаются
заранее, принимая, например, те значения лишних неизвестных,
которые получаются для соответствующего упругого случая или
для балки, находящейся в предельном состоянии. Если принять
is = ?*, то соответствующее
значение функции R — R* будет
больше истинного ее значения,
соответствующего выполнению
условия минимума, поэтому
такой прием дает завышенное
значение скорости q* > q.
Обратимся теперь к
рассмотрению простейших примеров.
Пример 1. Статически
неопределимая балка изображена
на рис. 187. Требуется
определить прогиб в точке
приложения силы Q. Примем за лишнюю
неизвестную реакцию опоры X. В точке с координатой Z\
изгибающий момент меняет знак. Разобьем длину балки на три участка,
как показано на рисунке. Абсолютные величины моментов на
участках выражаются следующим образом:
\M\ = Xz @<z<a),
\M\ = Xz — Q(z — a) (a<z<zj),
\М\= — Xz + Q(z — a) (zj<z<2a).
Следовательно,
Рис. 187.
Ф
= Ъ. J \ Xn+1zn+1dz +
+ ll(X-Q)z + Qa]n"dz+l [-(X-Q)z-Qa\n+ldz}.
a Zi
Положим % = -у , выполним интегрирование и представим
444 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. "VIII
результат в виде
Здесь
р^_ 1 A—26)"+» + 5n+1
Теперь нам нужно искать минимум функции R (?). Условие
минимума приводит к довольно сложному уравнению, самый простой
путь состоит в том, чтобы построить график функции R (|) и найти
ее минимальное значение. Для упругой балки % = 5/16 = 0,313;
для балки, находящейся в предельном пластическом состоянии,
Ь, = 1/3 = 0,333; таким образом,
нам достаточно исследовать
функцию R (|) в весьма узком
диапазоне значений аргумента. На
рис. 188 представлен график
функции R (|) при п = 3.
Минимальное значение R достигается при
I = 0,324, R = 0,0487. Таким
образом, по формуле A10.4)
? = 0,0487*„а» (-§!-) \
Если принять распределение мо-
%ЗЯ в$5 <? ментов соответствующим упругому
Рис. 188. состоянию, то следует положить
| = 0,313. Соответствующее
значение R находится из графика, R = 0,492, и скорость
оказывается завышенной на 1,03%. В предельном пластическом
состоянии \ = 0,333 и R = 0,494, при этом ошибка в определении
скорости составит 1,85%.
Такое хорошее совпадение точного решения с двумя
приближениями, одно из которых предполагает распределение моментов
таким же, как и для упругой балки, другое — соответствующим
предельному состоянию упруго-пластической балки, объясняется
тем, что для рассматриваемой системы значения лишней
неизвестной в этих двух крайних случаях разнятся очень мало.
Рассмотрим еще два примера, которые неоднократно разбирались
в литературе [ба], [231], [239]; эти примеры в отношении
применения приближенных методов представляют собою в известном
смысле крайность.
Пример 2. Балка заделана по концам и несет сосредоточенную
нагрузку (рис. 189). Эпюра моментов как в упругом состоянии,
так и в предельном пластическом состоянии одинакова,
изгибающие моменты в заделке и в точке приложения силы равны между
Ц052-
ОШ
OfiW-
§ НО] ДЕФОРМАЦИЯ БАЛОК И РАМ ПРИ ИЗГИБЕ 445
собою и равны -^ . Очевидно, такая же эпюра моментов будет
и при ползучести. В каждом из четырех треугольников, на которые
Oz
разбивается эпюра моментов, \М\ = ~ , если координату
отсчитывать от точки, где М = 0.
Следовательно,
а/г
ф =
4х„
л-и м:
-Ч
9^n+1dz
_ хпа2 / Qa
* 2(» + 1) UMn
Пример 3. Прямоугольная
рама, изображенная на рис. 190, Рис. 189.
загружена двумя силами.
Примем за лишнюю неизвестную величину изгибающего момента
в стойке X. В результате очевидных вычислений находим:
ж у-пМпа ( Qa
^— л + 1 \_Мп
Здесь
11 + 1
Д(Е).
х
Qa
*®=d2[i™+(i-t)n"]+2h'-
-2 I b ' V 2
Если 6 = 0, то мы получаем отсюда:
кпа2 / Qa
n+1 V4M„
то есть удвоенный результат предыдущего примера. Этого и
следовало ожидать, короткие стойки эквивалентны жесткой заделке,
таким образом, изгибаются две
балки с заделанными концами.
Поведение изображенной
рамы в упругом и пластическом
состояниях существенно
различно. Если рама упруга, то
г — т-—-, при Ъ 1а = 0
i + ?a) Рис.190.
1=1/4, при Ь/а->- оо ?-*- 0.
В предельном состоянии идеально жестко-пластической рамы
момент в точке приложения силы равен по абсолютной величине
моменту в стойке и ? =1 /4 независимо от отношения Ыа. Очевидно,
что в состоянии ползучести с увеличением отношения Ыа также
446 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
? будет стремиться к нулю, поэтому трудно ожидать, чтобы
приближенный расчет, основанный на допущении о том, что моменты
распределяются так же, как и в предельном состоянии, дал
удовлетворительные результаты. Действительно, предположим, что
цгг
№
we
Щ2
тп
5 7 3
Рис. 191.
Я -13
п
Ыа > 1, тогда | — малая величина. Легко проверить, что мини-
т> ~ 1 / 2 а V/"
мум R достигается при § = -=-( ——
значение R равно
и соответствующее
При Ыа-^r оо R стремится к пределу
n+i
1-
п+2 '
однако
достаточно медленно, поскольку 1/ге — малая величина. В упругом
состоянии при больших — приближенно 5 я* ^-. Вставляя эту
а
а _г * ~ 2Ь
величину в формулу для R и пренебрегая малыми членами
найдем:
_1 V" Г 2
R =
"[^+D Л
Это выражение стремится к тому же пределу, что и точное
значение, однако гораздо быстрее. Наконец, если принять, как
в предельном пластическом состоянии, \ = 1/4, то мы получим:
R =
Г 1 , Ц1
Lr + 2" 2 a J -
Последнее выражение неограниченно возрастает с увеличением
отношения Ыа и, следовательно, дает совершенно
неудовлетворительную аппроксимацию.
§ ill]
ПОЛЗУЧЕСТЬ ПРИ КРУЧЕНИИ
447
Для квадратной рамы при Ъ = 2а результаты определения
лишней неизвестной при разных значениях п приведены в
работе [127], соответствующий график изображен на рис. 191.
Например, при п = 3 | = 0,175 и R = 0,0098. Приняв значение |,
соответствующее упругому состоянию: | = 0,125, мы получим
завышенное значение R = 0,0128; если же положить | = 0,250т
как для предельного пластического состояния, величина R будет
еще более завышенной, а именно: R = 0,0188.
§ 111. ПОЛЗУЧЕСТЬ ПРИ КРУЧЕНИИ
Теория кручения стержней, находящихся в условиях
установившейся ползучести, строится совершенно таким же образом,
как теория кручения упругих стержней. Направим ось z по оси
стержня, расположим оси хну произвольным образом в плоскости
поперечного сечения и зададимся кинематической картиной
явления, приняв, что здесь, как и для упругого стержня,
и=—xzj/, v = %zx, 1и — щ(х,у).
Здесь и, v и w — скорости течения по направлению осей х, у
и z соответственно, и — угловая скорость закручивания,
отнесенная к единице длины стержня. При таком предположении
оказывается, что все компоненты тензора скоростей деформации
равны нулю, кроме компонент exz и syz, которые выражаются
следующим образом:
Приняв закон течения в соответствии с (99.1) и (99.2), мы найдем,
что все компоненты тензора напряжений, кроме ххг и %уг, нужно
считать равными нулю; для отличных от нуля скоростей
деформации получаем:
Здесь
а20 = 3(т1г + т2уг) = ЗтЛ
Величина т представляет собою модуль вектора касательного
напряжения в плоскости сечения. Для удобства введем следующее
обозначение:
Уз
Тогда
е
хг
y(t) = -^-P(K3t). A11.1)
= т тжг) е{/г =—^—%*• A11.2)
Заметим, что совершенно такие же соотношения получаются
ив том случае, когда в основу положен закон ползучести, исполь-
448 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
-^(^т*0]=2х
A11.3)
зующий критерий наибольшего касательного напряжения.
Конечно, при этом связь между у (т) и функцией v (a0), определяемой
из опытов на ползучесть при растяжении, получается иной,
а именно: у (т) = v Bт).
Продифференцируем первое из уравнений A11.2) по у, второе
по z и вычтем второе из первого. Получим:
Проведем в плоскости поперечного сечения некоторый замкнутый
контур Г, не пересекающий границы, но могущий заключать
внутри себя части границы области сечения. Площадь, ограниченную
этим контуром, обозначим Q.
Проинтегрируем обе части A11.3) по области Q:
?3
Интеграл в левой части преобразуется
по формуле Римана в контурный
интеграл, представляющий собою
циркуляцию касательного напряжения по
контуру Г, и мы получаем:
^y^-ds=2xQ. A11.4)
г
Формула A11.4) является обобщением
известной теоремы Бредта о циркуля-
Ряс 192. цИИ касательного напряжения. Здесь
ts — проекция вектора касательного напряжения в точке контура
Г на касательную к этому контуру, положительное направление
обхода устанавливается против часовой стрелки, в соответствии
с этим выбирается знак xs (рис 192).
К уравнению A11.3) необходимо добавить дифференциальное
уравнение равновесия, имеющее обычный вид:
9тжг
дх
У*
= 0.
Мы удовлетворим
напряжений таким
дх j
+ (f)°
д
дх
дх ' ду
этому уравнению,
образом, что тж2 =
Подставляя в A11.3), получим
- Эх ) + ду К г ду J - **'
если
Эф
ду '
введем
Tf/z =
функцию
^ Т2_
дх ' Т ~
A11.5)
Граничные условия получаются обычным способом. Так же,
как и в теории упругости, на контуре rxz cos vx -J- ryz cos vy = 0.
§ 111]
ПОЛЗУЧЕСТЬ ПРИ КРУЧЕНИИ
449
Внося сюда cos vx —. -—-, cos vy = — -3— и выражения xxz и xyz
через функцию напряжений, мы можем проинтегрировать
граничное условие по каждому из контуров Tt, составляющих границу
поперечного сечейия. Получим:
if=C(- на Г,-.
Если область односвязна, то всегда можно принять Ci = 0;
если область многосвязна, то теорема о циркуляции позволяет
составить недостающие уравнения для нахождения всех констант,
кроме одной, которая фиксируется по произволу.
Совершенно такое же уравнение для кручения стержней из
упрочняющегося материала было получено рядом авторов (см.
["], f52])-
Заметим еще, что, если функция напряжений известна, то
крутящий момент вычисляется следующим образом:
М = J (zxyz - ух„) dF=2^dF.
F F
Интеграл распространяется на площадь поперечного сечения. Что
касается приложений выведенных уравнений, здесь дело обстоит
следующим образом. Точное решение уравнения A11.5) возможно
лишь для стержня круглого сечения (или для трубы), во всех
остальных случаях приходится прибегать к разного рода
приближенным методам. Численное решение уравнения A11.5)
по методу конечных разностей для любой формы контура
поперечного сечения получить сравнительно нетрудно, это уравнение
эллиптического типа второго порядка. Однако автор не встречал
серьезных технических задач, в которых приходилось бы
рассматривать кручение сплошного стержня. Поэтому
соответствующие численные методы развития не получили.
Второй путь получения приближенных решений задачи о
кручении — это применение вариационных принципов Лагранжа
и Кастильяно. Соответствующие функционалы оказываются
довольно простыми, и в этом смысле теория кручения —
чрезвычайно благодарный объект для приложения общих методов и
сравнения различных приемов между собою. Этим вопросам уделено
довольно большое место в книге Качанова [*2], автору книги
принадлежит в этой области ряд эффективных результатов,
поэтому мы коснемся вопроса о применении вариационных методов
к задаче ползучести при кручении лишь вскользь, преследуя
чисто иллюстративные цели. Элементарную же задачу о кручении
круглого стержня мы рассмотрим немедленно как пример
применения уравнения A11.5), хотя в данном простом случае это и не
очень оправдано, задачу следует решать элементарным
методом, подобно тому как это делается для упруго-пластического
29 ю. Н. Работнов
450 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VI11
кручения в курсах сопротивления материалов. Итак, предположим,
что круглый стержень радиуса а закручивается моментом М-
Будем искать функцию напряжений как функцию от радиуса
г = ух2+у2, тогда -^~ = ? -у, -щ; = ? -у > т = — У и
уравнение A11.5) преобразуется к виду
Отсюда, учитывая, что т@) = 0, получим:
у(т) = нг, т = у~г (xr).
Крутящий момент
а
М = 2 [ i|) dF = 4я \ ¦tyrdr.
F О
Интегрируем по частям, учитывая, что ip(a) = 0. Получаем:
а а
М = 2п\ тг2 dr = 2я \ у1 (кг) г2 dr.
о о
Вычисления для конкретных законов ползучести не составляют
труда, мы их здесь не приводим.
§ 112. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
ЗАМКНУТОГО ПРОФИЛЯ
В тонкостенном стержне замкнутого профиля касательные
напряжения следует считать направленными вдоль средней линии
профиля и постоянными по толщине. Поток касательных
напряжений тб постоянен. Это следует из уравнений статики, так же как
и для упругих стержней. Величина крутящего момента для
двухсвязного сечения найдется следующим образом. Усилие ibdl,
приходящееся на участок длины dl средней линии контура, создает
момент относительно точки О на плече р (рис. 193), dM = xbp dl,
следовательно,
М=\ tbpdl.
Но тб = const, p dl есть удвоенная площадь треугольника с
основанием dl и высотой р, то есть da> (§ 109). Тогда
где F — площадь, ограниченная контуром сечения. Отсюда
М
2&F
т = ^. A12.1)
§ 112] КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ЗАМКНУТ. ПРОФИЛЯ 451
Формула A12.1) получена только из условий статики, она
справедлива независимо от физической природы материала. Для
определения угла закручивания необходимо прибегнуть к теореме о
циркуляции. В силу сделанного
предположения т„ = т, следовательно, по формуле
A11.4), вычисляя циркуляцию для средней
линии профиля, мы получим: , . .
\ у (т) dl = 2xF.
г
Внесем сюда выражение т по формуле
A12.1):
М
2&F
dl = Y.F.
A12.2)
Рис. 193.
Уравнение A12.2) представляет собою
искомое уравнение связи между моментом М
и погонной угловой скоростью закручивания к, для получения
дальнейших результатов необходимо конкретизировать вид
функции у (т)-
а) Степенной закон. Функция у отличается только
множителем от функции v, следовательно, можно принять
Y = Y"(^)n'
Тогда
г
б) Экспоненциальный закон. у = Yeexp (-- V В этом случае
X =
Удобной формулы для зависимости между к и М при
экспоненциальном законе ползучести не получилось. Фактически в
реальных задачах б (I)— кусочно-постоянная функция, поэтому
результат оказывается не столь сложным. Действительно, пусть на
участке lt б = бг, тогда
2F
2^р[2-^]-
A12.4)
Как видно, решение задач о кручении двухсвязных профилей
находится элементарно просто и пояснений не требует. Несколько-
сложнее обстоит дело тогда, когда область поперечного сечения
29*
452 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
многосвязна. Такой многосвязный тонкостенный профиль
схематически показан на рис. 194. Обозначим внешнюю область
индексом 0 и занумеруем внутренние области от 1 до к. Будем
обозначать дуги, из которых состоит средняя линия профиля, двумя
индексами, соответствующими тем областям, которые отделяются
данной дугой. Так, дуга АВ будет иметь индекс 01, дуга DC —
индекс 23 и так далее. На каждой дуге
g^ ^ поток касательного напряжения
постоянен, обозначим тб на дуге Ц через ti}.
О / \ 3 \ Тогда момент относительно центра О равен
М
-\
td(a ¦
2 уиЛа>.
A12.5)
Здесь суммирование распространяется на
все дуги ltj, da> =p dl — секториальная
площадь.
Теперь применим теорему о
циркуляции к раз для всевозможных замкнутых
контуров с тем, чтобы все области были
при этом обойдены. Можно, например, обойти каждую из
внутренних областей 1, 2 и 3 по отдельности, можно выбрать и
другие пути обхода. Получим:
dl = 2-nFt.
A12.6)
Кроме того, должны быть выполнены уравнения равновесия
в узлах. Вырезая продольными сечениями какой-либо узел, мы
найдем, что сумма потоков
касательного напряжения в стенках,
сходящихся в данном узле, должна быть равна
нулю. Если в узле сходятся границы
областей г, q, s, . . ., то должно быть
tTq + tq. + tsr+...=0. A12.7)
Таким образом, получается полная
система уравнений для решения
статически неопределимой задачи.
Поясним ход вычислений на
простом примере. Сечение прямоугольной
коробчатой балки с внутренней перегородкой изображено на
рис. 195. Для простоты примем толщину стенки постоянной,
равной б. Не составляет труда проделать вычисления и в том
случае, когда толщина различна на различных участках. На
стенках 01,02 и 12 ttJ сохраняет постоянное значение, при постоянной
толщине касательные напряжения т01, т02 и т12 также постоянны.
§112] КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ЗАМКНУТ. ПРОФИЛЯ 453
Применим теорему о циркуляции в форме A12.6) один раз для
наружного контура, другой — для правого прямоугольника 2.
При степенном законе ползучести получим:
*[(-?)"*+(-?)"••:]-*•¦<"•
V"[(№+G?)=2»'4<"-
Составим теперь уравнение A12.7) для точки \С. Те напряжения,
которые направлены от точки С, будем брать со знаком плюс, те,
которые направлены к точке С,— со знаком минус:
б{т01 + т12— т02) = 0.
Положим т10/т2о = ?. Исключив т12 из полученных уравнений,
мы найдем:
4?п-3A-?)п = 3, A12.8)
* = -S-(-f)BC + 2S-). A12.9)
Дело свелось теперь к решению алгебраического уравнения A12.8).
Предположим, что корень его ? найден. Тогда
Т01 = ?Т02> т12 = A — ?)т02-
Составим уравнение моментов (?12.5), приняв за полюс^точку С.
Тогда интеграл A12.5) примет следующий вид:
М = т01б.4а2 + т02б-8а2 = 4т026а2 B + ?).
Следовательно,
_ М
Внесем это значение т20 в уравнение A12.9), чтобы получить
зависимость между угловой скоростью закручивания и моментом:
»=*0+*»[«зДйв-]"-
Решение уравнения A12.8) для любого п может быть получено
численным методом. В нашем случае очень просто получить
приближенное решение. При п = 1 из A12.8) следует ? = 6/7.
Следует ожидать, что ? > 1 /2 при любом п, следовательно,
A—?)<1/2. С возрастанием п первый член левой части A12.8)
растет значительно быстрее, чем второй, поэтому, если
записать уравнение в виде
К4
1/л[1 + A-СПп,
454 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
то решение его последовательными приближениями должно
сходиться чрезвычайно быстро. Действительно, уже при п = 3
с точностью до третьего знака ? = C/4I^. Другие, несколько
более сложные примеры расчета коробчатых стержней на
кручение приведены в работе [322].
§ 113. КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
ОТКРЫТОГО ПРОФИЛЯ
В тонкостенных стержнях открытого профиля касательные
напряжения в каждом сечении профиля, нормальном к его осевой
линии, направлены параллельно касательной к осевой линии,
распределение их относительно осевой линии обратно симметрично:
если с одной стороны на расстоянии у от осевой линии (рис. 196)
напряжение есть т, то с другой стороны на том же расстоянии оно
равно —т. Две траектории
касательного напряжения замыкаются
на бесконечности; применяя
теорему о циркуляции касательного
напряжения, мы получим (см. [106]):
2у(т) = 2ку.
Следовательно,
Рис. 196. На элемент дуги средней линии
+6/2
приходится момент, равный dl \ rydy, тогда как полный мо-
-6/2
мент для стержня постоянной ширины с длиной средней линии,
равной I, есть
+6/2 +6/2
M = l \ xydy = l jj y-l(xy)ydy.
-6/2 -6/2
Для дальнейшего будет удобно взять некоторый конкретный
закон ползучести, например степенной. Тогда
<г
Положим
Мп —
+6/2
м-' I 4?)"V*
-6/2
Мп = *?гтл1№
б ' ^n~2n + l ln- \2j
S 1133 КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТ. ПРОФИЛЯ 455
Теперь зависимость угловой скорости закручивания от момента
дается следующей формулой:
Если б = б (Z), то формулу A13.1) можно сохранить; при
вычислении xft и Мп вместо б берется некоторая характерная ширина
профиля б0, выбираемая произвольным образом, а вместо I
вводится приведенная длина:
о
Так же, как и в задаче изгиба, простое приближенное решение
можно получить, если принять распределение напряжений
подобным распределению напряжений в идеально-пластическом
стержне, находящемся в предельном состоянии. Вычисления здесь
совершенно аналогичны соответствующим вычислениям в задаче
об изгибе стержня прямоугольного сечения. Если абсолютная
величина т постоянна, то момент, приходящийся на элемент
средней линии стержня, равен
dM = \ xydy=^j62.
-S/2
Полный крутящий момент
М:
^-\d*dl;
AM
следовательно, t = -wt—•
Оо'пр
Здесь приведенная длина /пр определена следующим образом:
о
Потенциал скоростей при чистом кручении определяется так:
При постоянной абсолютной величине т в результате
интегрирования по площади поперечного сечения получим:
456 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
Внося сюда найденное выражение для т через М, получим снова
формулу A13.1), в которой
_ J_
_2Fyn_ м -2 "т I (^°Л2
2v
Для стержня постоянной толщины хп = -—¦. Тогда Ма в точном
- In
и приближенном решениях отличаются множителем „ .- в
первом случае и 2~1/п — во втором. При тг—^-оо эти множители
стремятся к единице, значит, разница между точным и приближенным
решениями исчезает. Но это относится лишь к величине момента,
обеспечивающего заданную скорость; если фиксировать величину
момента и определять соответствующую скорость, то ошибка
приближенного решения может быть довольно значительна, как это
было выяснено в § 106 на примере изгиба стержня
прямоугольного сечения.
§ 114. ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О КРУЧЕНИИ
При исследовании кручения стержней сплошного сечения, как
уже отмечалось, для нахождения приближенных решений с
успехом используются вариационные методы. Один из таких
вариационных приемов уже был применен в предыдущем параграфе.
Потенциал скоростей, отнесенный к единице длины стержня,
определяется, как мы видели, следующим образом:
Ф= JO(t)JF.
Здесь
Ф'(т) = у(т).
При степенном законе
F
или, если ввести функцию напряжений при кручении if,
F
Зададимся некоторым статически возможным распределением
напряжений, то есть определим функцию ф, зависящую от
некоторого набора параметров с?, таким образом, чтобы было т|з = const
на контуре сечения и 2 \ гр dF = М. Если область многосвязна,
то мы можем фиксировать значение г|) на одном из контуров,
значения функции напряжений на других контурах войдут в число
параметров ct. Теперь необходимо минимизировать функцию Ф
§ 114] ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О КРУЧЕНИИ 457
по параметрам ct, это приводит к системе нелинейных уравнений
для ct. Внеся найденные значения ct в выражение для Ф, мы можем
rfO
определить угловую скорость закручивания стержня х = -tj^ .
Очевидно, что при выборе функции \р следует считать г|з
пропорциональной М. Если функция т|) зависит от параметров ct
линейным образом, то выражение для Ф всегда может быть
представлено в виде
Ф_х»Мп ( М у+1 .
ф—V+Г <v^rj Л(с„с2, ...,cftJ.
Здесь ип и Мп — надлежащим образом выбранные константы
(ср. § 110). Очевидно, что точное выражение потенциала скоростей
при степенном законе ползучести может быть представлено в этой
же форме, причем истинная величина R есть некоторая константа.
Истинное значение Ф при заданном М, в силу принципа минимума,
соответствует наименьшему значению R. Минимизируя R по
ограниченному числу параметров, мы всегда получаем для R величину
большую, чем истинная. Соответствующая найденному значению Ф
скорость закручивания
дМ " V М,
в силу вышесказанного, будет всегда больше, чем истинная
скорость; таким образом, применение принципа Кастильяно дает
верхнюю границу для угловой скорости закручивания, жесткость
стержня получается при этом заниженной.
Рассмотрим теперь общую схему применения вариационного
принципа Лагранжа. Потенциал скоростей выражается при
степенном законе ползучести так:
тт п Y "
Вследствие уравнений A11.1)
у2 = х2 [х2 + у2 — 2г/ф, х + 2.гср, у + cpf х + ср? „J.
Таким образом, потенциал сил на единицу длины стержня
Здесь
<? = ЖГ(^)" $1*2 + У2-2г/Ф1* + 2*ср y + tfx + tfvl^dF.
n+i
458 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
Задаем функцию депланации сечения ф в виде линейного
выражения, содержащего некоторое число параметров ct. Минимизация U
по этим параметрам сводится к минимизации величины Q, при
конечном числе параметров найденное значение Q будет больше
истинного или равно ему. Найдя минимальное при заданном
выборе сг значение Q, определяем крутящий момент:
В силу минимального свойства потенциала скоростей и,
следовательно, функционала Q найденное значение М будет больше
истинного или в крайнем случае равно ему. Если же разрешить A14.3)
относительно и, то для угловой скорости кручения получается
оценка сверху. Одновременное применение решения с помощью
вариационного принципа Лагранжа и Кастильяно позволяет
получить двухсторонние оценки для скорости закручивания.
Соответствующие теоремы для упругого кручения хорошо известны
[67], для упрочняющихся пластических сред и для ползучести
они были доказаны Качановым [62], примеры их применения
указаны в упомянутой книге.
§ 115. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
ЗАМКНУТОГО ПРОФИЛЯ
Рассмотрим задачу об одновременном изгибе и кручении
стержня в предположении, что касательные напряжения малы по
сравнению с нормальными напряжениями изгиба, поэтому можно
считать, что
а0 = (а2 + 3т2I/а»а.
Тогда из уравнений ползучести следует:
e = v(a), y = 3v(o)l. A15.1)
Здесь у — скорость сдвига. Поскольку в зависимость между е
и о не входят касательные напряжения и сдвиги, задача изгиба
решается отдельно, после чего рассматривается вопрос о
кручении. Возвращаясь к выводу, сделанному в § 111, мы должны
считать, что величина у в уравнениях A12.2) и следующих
уравнениях определяется второй из формул A15.1). Тогда
уравнение A11.4) приводится к следующему:
3 f ^T,dZ = 2xQ. A15.2)
г
§ 115] ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 459
Совершенно аналогично записывается условие теоремы о
циркуляции для упругого стержня с переменным модулем сдвига
Перейдем теперь к рассмотрению совместного изгиба и
кручения тонкостенных стержней замкнутого профиля.
Для стержня замкнутого профиля касательные напряжения
находятся по формуле A08.4), то есть так же, как и для стержней
открытого профиля, но константа С остается пока
неопределенной. Перепишем формулу A08.4) следующим образом:
x = \{C-t).
Здесь
о
По теореме о циркуляции
\ v-fxdl= С J \v-^dl- \ ±v-fdl=^xQ. A15.3)
г г г
Теперь можно вычислить крутящий момент относительно
произвольной оси, пересекающей плоскость поперечного сечения
в точке Q:
MK=\xdpdl=CQ-\tda>. A15.4)
г г
Здесь, как обычно, р — длина перпендикуляра, опущенного из
точки О на касательную к средней линии профиля, р dl = dco,
причем со — секториальная площадь. Если стержень изгибается
силами, плоскость действия которых находится на расстоянии е
от точки О, то Mw = Qe; из формулы A15.4) находится величина С
и подставляется в A15.3), в результате получается скорость
изменения угла закручивания стержня в зависимости от
перерезывающей силы, расстояния е и изгибающего момента в сечении.
Для степенного закона ползучести уравнения A15.3) и A15.4)
принимают следующий вид:
г о
Применение этих формул к решению задач весьма просто, хотя
вычисления довольно громоздки. Простота связана с тем, что
460 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
зависимость скорости сдвига от касательного напряжения
получилась линейной, задача эквивалентна задаче теории упругости с
переменным, известным заранее модулем сдвига; для таких
задач справедлив принцип суперпозиции, поэтому лишняя
неизвестная С вышла из формулы линейным образом и необходимость
решать обычные в теории ползучести нелинейные уравнения
отпадает.
Еще более простые результаты мы получим, если
воспользуемся приближенной теорией, в основе которой лежит
предположение о том, что напряжения распределяются так же, как в
пластическом предельном состоянии. Нейтральная ось пп при этом
делит площадь поперечного сечения на две равновеликие части.
Будем отсчитывать дугу средней линии поперечного сечения от
точки О, где средняя линия пересекается нейтральной осью, длина
дуги верхней половины контура есть 1и длина дуги нижней
половины есть 12- При этом
h 0
\ 6dl= \ &dl = ~F.
о -Л 2
По формулам A09.1)
h
i
i
т=|[с + -|г \ bdi] _/2<г<о.
-%
Величина —— постоянна для данного сечения, при этом а =
2М „
-—jr. 1еорема о циркуляции дает следующий результат:
c\f+^[\dlhdi+ \dl 16dZM*Q^- .
г о с -1г -h
Выражение в квадратных скобках можно преобразовать,
окончательный результат записывается следующим образом:
clf+Jlhdl-ilbdl]=ixQ^k- A15'5)
Г 0 -1г
Напишем теперь выражение для крутящего момента:
Мк=\х&й<й = Са — Щ-\(лЬй1. A15.6)
§ 116] ИЗГИБ СТЕРЖНЕЙ ПРИ НАЛИЧИИ ПРОДОЛЬНОЙ СИЛЫ 461
§ 116. ИЗГИБ СТЕРЖНЕЙ ПРИ НАЛИЧИИ ПРОДОЛЬНОЙ СИЛЫ
Задача об изгибе стержня при наличии осевой силы имеет
особое значение в связи с теорией устойчивости в условиях
ползучести. Эта теория будет рассмотрена особо впоследствии, здесь
же мы коснемся лишь некоторых простых задач. Возвращаясь
к выводу общих уравнений теории изгиба в §§ 106 и 107, заметим,
что рассуждения не изменяются и при наличии осевой силы,
только условие N = 0 нужно заменить условием, что N равно
заданной силе. Фактические вычисления оказываются при этом
довольно громоздкими; чтобы пояснить существо дел«, мы рассмотрим
здесь задачу об одновременном изгибе и растяжении стержня
прямоугольного сечения. Предполагая, что изгиб происходит в
плоскости симметрии стержня, мы заменим уравнения A07.1)
следующими:
N= {s(e0 + xy)dF,
A16.1)
Mx=-\js(ea + щ) у dF.
При вычислении интегралов, взятых по площади прямоугольника
с высотой 2/i и шириной Ъ, следует иметь в виду, что на
нейтральной оси при у = у0 е0 + ху0 = 0. Величина у0 может быть
по абсолютной величине меньше или больше h, то есть
нейтральная ось может пересекать сечение и может целиком лежать за его
пределами. Как в том, так и в другом случае для степенного
закона ползучести результат получается следующим:
A16.2)
Эти уравнения невозможно разрешить относительно xh и е0,
поэтому использование их при расчетах затруднительно.
Для преодоления возникающих трудностей можно предложить
различные пути. Один из них состоит в том, что подбирается
некоторая аппроксимирующая функция для потенциала скоростей
ползучести, который представляется в виде Ф = Ф (R). При этом
под Ф понимается потенциал, приходящийся на единицу длины
стержня, тогда как R — некоторая функция от М и N,
подобранная таким образом, чтобы при N = 0 было R = М- Тогда
_^Ф^^Д_ _ dO> 8R
к~~ йв. ам ' 8° ~ dR dN '
462 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
A16.3)
Если N = 0, то по формуле A06.2)
_ ( м
Но при этом, как мы условились, М — R. Следовательно,
Для подбора функции R воспользуемся теоремой Келледайна
и Друкера, подобно тому как
это было показано в § 103 для
ферм. В предельном состоянии
стержня прямоугольного
сечения, нагруженного изгибающим
моментом и продольной силой,.
сила и момент связаны
следующим соотношением (см. [105]):
Рис. 197.
При этом М =
M + iV2-=l.
М
С другой стороны, в упругом состоянии а
ляя условие нормирования:
Ь№от '
N 3 My
2bh~^~ 2 ЪЬ?
N--
- N
2bkaT
Состав-
Ъ \ ст2 dy -.
-ft
¦-F = 2bh,
получим:
M2 + /V2=l.
В координатах М — N условие предельного состояния
изображается параболой, условие нормирования мощности диссипации
при п = 1 — эллипсом (рис. 197).
Очевидно, что все кривые постоянной мощности диссипации
пройдут через одну и ту же точку A, 0) на оси N. Чтобы найти
точку пересечения кривой, соответствующей заданному п, с осью М,
вычислим мощность диссипации при чистом изгибе и подчиним
ее условию нормирования. Получим:
Отсюда
М-
м
Ъ№оп
= 2
п+1
2п
2л-И
п + 1
§ 1163 ИЗГИБ СТЕРЖНЕЙ ПРИ НАЛИЧИИ ПРОДОЛЬНОЙ СИЛЫ 463-
Таким образом, все кривые постоянной мощности диссипации,
пересекают ось М на отрезке от М=1 до М = -—=.. По теореме
Келледайна и Друкера все эти кривые с возрастанием п
оказываются вложенными одна в другую, все они расположены между
эллипсом, соответствующим случаю п = 1, и параболой для п = оо.
Предположим, что эти кривые — эллипсы:
.?)'+*-'¦
Здесь
к =
2я+1,
Тогда следует принять
R2 = M2 + k2h2N2. A16.4).
Скорости изменения кривизны и удлинения запишутся
следующим образом:
e°=^G?r)nirw'
\1ум_ A1б-5>
Легко проверить, что эти формулы дают правильный результат
при N = 0 и при М = О, то есть при чистом изгибе и при чистом
растяжении. Сопоставление формул A16.4) и A16.5) с точным
решением затруднительно, поскольку написать явное выражение
потенциала Ф через М и N невозможно. Однако, если
рассматривать пространство скоростей, точные формулы A16.2) позволяют
построить кривую постоянной мощности диссипации. Условие
нормирования мощности будет следующим:
M'x + Te0 = F = 2bh.
С помощью формул A16.2) получаем соотношение между е0 и xh:
T2^Ii{leo + ^r+1M-ho-x/?!^1^} = l. A16.6)
При ге=1 отсюда следует:
4-(хАJ + е;=1.
При га=оо -—-г [(ккJ-\-г20] = 1, если х/г>е0. и е0 — 1, если х!г<с
< е0. Видно, что кривые A16.6) пересекают ось е0 в точке е0 = 1
и ось xh в точке xh
-i<
464 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
На рис. 198 сплошными линиями представлены соответствующие
кривые постоянной мощности диссипации, а также кривая,
рассчитанная для значения п = 3. При приближенном решении, даваемом
формулами A16.4) и A16.5), кривая
постоянной мощности диссипации
в плоскости скоростей будет,
очевидно, также эллипсом,
отсекающим по осям отрезки е0 = 1 и
xh — i/k. Этот эллипс для п = 3
построен на рис. 198 штриховой
линией.
§ 117. СТЕРЖЕНЬ ИДЕАЛЬНОГО
ДВУТАВРОВОГО СЕЧЕНИЯ
В этом параграфе мы
рассмотрим другой способ приближенного
исследования изгиба при наличии
продольной силы, он
основывается на замене реального стержня
стержнем со специально
выбранным идеализированным
поперечным сечением. Идеальным
двутавром мы будем называть сечение,
изображенное на рис. 199. Две
полки с одинаковой площадью по-
перечного сечения у- F соединены
стенкой, которая воспринимает
перерезывающую силу, но не участвует в сопротивлении изгибу.
Будем считать, что расстояние между полками 2h велико по
сравнению с их толщиной и распределение
напряжений в полках равномерно: а = о+ в
верхней полке и а = а~ — в нижней. Тогда
Рис. 198.
*'
Zh
i'
N--
Положим
тогда
-f(a+ + a-), M = 4f @-+-0-).
N
Fo*
= N,
M
Fha*
= M,
a+=GV + M)o-*, a- = {/V —M)c*.
Рис. 199.
Если s — скорость деформации оси стержня,
к — скорость изменения кривизны, то скорость деформации
верхней полки е+= ? + и/г, скорость деформации нижней полки
§ 117] СТЕРЖЕНЬ ИДЕАЛЬНОГО ДВУТАВРОВОГО СЕЧЕНИЯ 465
е~ = е — xh, при этом
е+ = у{о+), E~~v(a')
или
a+=--s(e+), o- = s(e_).
Отсюда следует:
в = 1{у [(# + Jlf) a*] +1; [{N-M) о*]},
nh=Y{v[(ft + &)o*] — v[(ft — M)o*]},
или
^ = 2a*"{s(e + KA) + s(E — xh))>
1
M = -^r {s (e + х/г) — s (& — xA)}.
При степенном законе ползучести
e = — = ^-l\N + N[\n^{N + i^) + \N — M\n--4N — ]&)],
x = — = l[|iY + M|n-1GV + M)-|iV-M|'1-1(/V-M)],
или
. 1 - . J--1 ~ . . . J--1 „ .
iV = y[|e + x|" (в + х) + |в-хГ (e-x)],
—-l —-i
M = i[;e + «|" (e + x) —|e — и |n (e — x)].
A17.1)
A17.2)
A17.3)
A17.4)
Нам осталось связать характеристики идеального двутавра с
характеристиками реального стержня. Если принять Травной
площади поперечного сечения реального стержня, то при отсутствии изгиба
о+ == о- = — = No*, из A17.1) следует е = v (No*), таким
образом, идеальный стержень ведет себя совершенно подобно
реальному. Подберем теперь размер h таким образом, чтобы
при отсутствии продольной силы зависимость между моментом
и кривизной для идеального двутавра совпадала с этой же
зависимостью для реального стержня. Будем предполагать последний
имеющим две оси симметрии, тогда зависимость между моментом
30 Ю. H. Работнов
466 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
и кривизной дается для степенного закона ползучести формулой
A06.2):
F
Здесь Н — высота реального сечения, входящая в выражение
для Мп. С другой стороны, при 8 = 0 из A17.4) следует:
xh _ / М \п
"^Г ~~ Ч Fhan J
Сравнивая, находим, что
А_ f2hH Лп
Я~Ч F 1) ¦
Для прямоугольного сечения
п
А _ ( п \ n+1
Условие постоянства мощности диссипации запишется в новых
обозначениях следующим образом:
7Уе + М>с = 4-[|е + к|1+7Г + |е-и11+""] = 1. A17.5)
На рис. 198 штрих-пунктирной линией изображена кривая,
соответствующая уравнению A17.5) при п = 3.
Выбор параметров модельной балки таким образом, чтобы при
чистом растяжении и при изгибе поведение ее было
тождественным с поведением реальной балки, возможен только при
степенном законе ползучести. В других случаях отношение hlH
оказывается зависящим от величины момента или кривизны. Заметим,
что для рассмотрения задач об изгибе и растяжении или сжатии
стержней, имеющих только одну плоскость симметрии, может
быть сконструирована модель в виде идеального двутаврового
профиля е неравными площадями полок.
§18. ПРОСТЕЙШИЕ ЗАДАЧИ
ПРОДОЛЬНО-ПОПЕРЕЧНОГО ИЗГИБА
Простейшими задачами об изгибе при наличии продольной
силы являются такие задачи, в которых нет необходимости
учитывать изгибающий момент от продольной силы и величина этой
силы известна заранее, она сохраняет все время постоянное
значение. Рассмотрим в качестве примера следующую задачу. Балка
§ 118] ПРОСТЕЙШИЕ ЗАДАЧИ ПРОДОЛЬНО-ПОПЕРЕЧНОГО ИЗГИБА 467
длины 21 несет равномернораспределенную нагрузку д, концы
балки закреплены таким образом, что они не могут перемещаться
в вертикальном направлении и поворачиваться, но осевое
перемещение не исключено, длина балки в процессе изгиба меняется
(рис. 200). Будем ре-
Ч
lit
и.
21
—*-
N
Рис. 200.
шать эту задачу для
сечения в форме
идеального двутавра; как мы
увидим, аппроксимация
A16.5) в данном случае
приводит к совершенно
аналогичным
выкладкам. Сначала мы найдем точное решение для частного значения
п = 3, для других целых значений п вычисления становятся
соответственно более громоздкими, но принципиальный ход решения
остается тем же самым. Обозначим неизвестный изгибающий
момент в заделке М0, тогда в сечении с координатой х
M^M0-qlx + ^f.
Здесь мы не приняли во внимание изгибающего момента от
продольной силы, возникающего тогда, когда прогиб отличен от
нуля, что собственно и составляет специфику
продольно-поперечного изгиба. Такие более сложные задачи рассматриваются в
главе XII.
Введем обозначения:
2М0
qP
= ?,
ql
г
2Fho,
х r
¦=р> т = ?
Тогда, переходя к введенным в § 117 безразмерным величинам,
найдем:
Положим, далее,
2Nh
= Я.
ql*
Следовательно,
Если обозначить прогиб балки u?(|, t)
кривизны
d2w 1 d2w
то скорость изменения
и =
(Э*2 Р ?|2
= -?-*(?),
поэтому
Совершенно
d*w
еЛ*
*(?)•
9|а h
аналогичным образом скорость относительной
30*
468 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
деформации оси балки г=гпг(?,). При п = д уравнения A17.3)
приводятся к следующим:
х = C№ + М*)М,
8 =GV2 + 3M2)./V.
Внесем сюда выражения для М и N, получим:
x = j^[3^ + (?-2g + S2J] (?_2g + g»),
A18.1)
После раскрытия скобок в первой формуле справа получается
полином шестой степени относительно |, во второй формуле —
полином четвертой степени. Но % пропорциональна второй
производной от прогиба. При I — 0 w = -я? = 0, вследствие симметрии
—y = 0 также в середине балки, при ? = 1. Интегрируя
выражение для к один раз и используя это условие, получим уравнение
для нахождения лишней неизвестной ?:
Заметим, что при отсутствии осевой силы, то есть при % = О,
решение для балки с защемленными концами дано в работе [317],
там приведено вычисленное значение действительного корня
кубического уравнения, а именно: Z, = 0,6041. Следует отметить
вывод, сделанный в этой статье. Если прогиб в середине упругой
балки с защемленными концами в пять раз меньше, чем прогиб
такой же свободно опертой балки, то в условиях ползучести при
п — 3 защемление концов уменьшает скорость прогиба в 24,5 раза.
Интегрируя вторично и полагая | == 1, найдем скорость
прогиба в середине балки:
* /J4 е„гз f ql* V
Здесь
Теперь мы можем определить изменение длины балки от
действия осевой силы. Обозначив это удлинение через Д, найдем:
21 1
Д = \ ?dz = enl \ e (?) dg.
о о
§ 118] ПРОСТЕЙШИЕ ЗАДАЧИ ПРОДОЛЬНО-ПОПЕРЕЧНОГО ИЗГИБА 469
Подставим сюда значение е (|), даваемое вторым уравнением
A18.1), получим:
ql* \з_
A = e„ZA,
2Fhan
Р-
Здесь
Р = 6С2-8? + 2^ + ^-.
Найденные формулы позволяют решить, например, следующую
задачу. Квадратная рама нагружена внутренним давлением
(рис. 201), требуется определить скорость изменения размера с,
показанного на чертеже.
Очевидно, что каждая из сторон рамы находится в условиях
балки предыдущей задачи, при этом N = ql, следовательно,
к = -у . Скорость изменения искомой
величины с:
с= 2ц>A)~|- Д = 2е»
Р
X
Л K2Fhan
Рис. 201.
Приведенное решение могло быть
доведено до конца благодаря тому, что
мы приняли п = 3. Совершенно
очевидно, как нужно поступать в случае, когда
п — любое целое число. Однако, как
мы видели, показатель п определяется из опыта и может
принимать любые значения. В общем случае произвольного п для
решения подобных задач следует рекомендовать численный метод.
Сохраняя те же обозначения, мы найдем, что при любом п
-^т-ИЬ+М"-1^-
-uMA.-jil'-Hb-li)],
A18.2)
8
7
-Г| Л.Н-И- j~-i (А.-ЬМ) Ч- i Л, — fi |"-* (Л. — |Л>].
м
Здесь и. = и. (?) = — , в нашей задаче ц = ?, — 2? 4- ?2, в других
примерах это может быть другая функция от ?, содержащая
линейным образом лишнюю неизвестную ?. Задаваясь произвольным
значением ?, мы можем построить эпюру функции к!рп, то есть
правой части первого из уравнений A18.2). Применяя обычные
соображения графо-аналитического метода теории изгиба
балок, мы можем всегда установить, выполнено ли при данном
470 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ. ИЗГИБ И КРУЧЕНИЕ [ГЛ. VIII
значении Z, поставленное кинематическое условие. В
рассмотренном примере это кинематическое условие приводит к тому, что
2
к (|) d? = 0, следовательно, площадь эпюры должна равняться
о
нулю. Повторяя вычисления для нескольких значений ?, мы легко
подберем нужное значение неизвестной. После того, как Z, найдено,
эпюра к/рп позволяет определить коэффициент прогиба в
середине балки; величина а представляет собою изгибающий момент
в среднем сечении от фиктивной нагрузки к, в соответствии с
известным правилом для балки с заделанными концами фиктивные
реакции и реактивные моменты равны нулю. Теперь мы можем
написать:
Совершенно таким же способом находится скорость осевого
удлинения:
Множитель Хр равен площади эпюры правой части второго из
уравнений A18.2), то есть функции е/рп. При построении этой
эпюры, конечно, нужно пользоваться ранее найденным
значением ?.
Мы уже упоминали о том, что аппроксимация A16.5) приводит
к аналогичным вычислениям. Действительно, при нечетном п,
если подставить в A16.5) выражения для момента М, то окажется,
что е будет полиномом степени п — 1 относительно М и степени
2 (п — 1) относительно х, тогда как х — полином степени п
относительно М и степени 2п — 1 относительно х. Второе уравнение
интегрируется один раз для нахождения угла наклона, второй
раз — для нахождения прогиба, условие горизонтальности
касательной в середине пролета приводит к алгебраическому
уравнению степени п для неизвестного реактивного момента М0. При
четных значениях п аналитическое решение становится более
сложным, однако во всех случаях описанная выше процедура
получения численного решения применяется без каких-либо
принципиальных изменений.
ГЛАВА IX
ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ
ТЕОРИИ УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ
Плоские осесимметричные задачи теории ползучести являются
одномерными, решение их сводится к интегрированию некоторых
систем обыкновенных нелинейных дифференциальных уравнений.
Естественно, что на эти задачи было обращено большое внимание
и число посвященных им работ велико. В то же время они
представляют определенный технический интерес — расчет
толстостенных труб под действием внутреннего давления и расчет
вращающегося диска относятся именно к этому кругу задач. Особенно
большая литература имеется по вопросу о ползучести
вращающихся дисков, разработка практически удобных методов расчета
дисков является заслугой прежде всего советских ученых и
инженеров. Применительно к реальным конструкциям теория
установившейся ползучести не всегда бывает достаточной, поэтому
в практике заводов и конструкторских бюро обычно пользуются
теорией старения, позволяющей использовать первичные кривые
ползучести материала со всем их своеобразием. Расчеты по
теории старения производятся совершенно так же, как по теории
установившейся ползучести, поэтому изложенные здесь методы
найдут применение в главе XI. С другой стороны, для прикидоч-
ных расчетов и для нахождения предельного состояния, которое
устанавливается по истечении достаточно большого времени,
теория установившейся ползучести оказывается достаточной.
§ 119. ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ЗАДАЧИ
Для удобства ссылок приведем вначале основные уравнения
теории ползучести для плоской задачи.
Плоское деформированное состояние. Так называется
состояние, реализуемое в цилиндрическом теле при условии, что если
за ось х3 принять ось цилиндра, то составляющая скорости »3 = 0.
472 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
Сохранение индексных обозначений при рассмотрении плоских
задач не очень оправдано, поэтому мы назовем осями х и у оси,
расположенные в плоскости сечения, перпендикулярного оси
цилиндра z. Поскольку ez = 0, то из условий несжимаемости
следует:
вх + гу = 0.
Рассмотрим теперь различные критерии ползучести:
а) Квадратичный критерий ползучести (типа Мизеса). Из
уравнений F8.1) следует:
_ 3 v (о0) - _п
е33 — гг— ~2 ^ 3 — и;
следовательно, 033 = о"г = О и
<Уг = -2-{(Ух + Оу).
Исключая в выражении ст0 напряжение аг, получим:
eu = ^-V{ex-Oyf + № A19.1)
или для главных осей:
о-о-^-<о-1-о-2). A19.2)
Вычислим теперь величину е0, учитывая, что ez = 0:
2
Уз
г0 = ~\/гх + г1-вхгу + ^у^ = -^=- j/eJ + ^Y2 A19.3)
и для главных осей:
e°=wei=~w82- A19-4)
Теперь уравнения течения будут следующими:
_ 3 p(g„) - _ 3 v (о0) . ,
&х~ 2 а0 °х~ 4 о0 {-°х а^'
о v(aa)
Y <*о
б) Критерий ползучести типа Треска. Поскольку скорость
ползучести в направлении оси z равна нулю, эта ось является
осью среднего напряжения, тогда наибольшее касательное напря-
жение всегда будет у (Oj — ст2), при этом оси 1 и 2 лежат в
плоскости х, у. Таким образом,
5 = 04-0-2 A19.6)
§ 119] ОСНОВНЫЕ УРАВНЕНИЯ ПЛОСКОЙ ЗАДАЧИ
473
или
s = V(ex-<yyJ + W. (И9.7)
Уравнения течения оказываются такими:
гх=-ву = ^(ах-ау), ? = 4^т A19.8)
или для главных осей:
ei = — е2 = v (ofj — a2). A19.9)
в) Критерий приведенного напряжения. Положим
s=l [o-j |-@2 + о-з)]+[А [сга —4-(а1 + °з)] • ("9-Ю)
Отсюда
et = y(s) Гя,—у nj , e2 = v(s)(—g-^ + nJ ,
e3=v(s)(—j A,—jl*) •
Потребуем, чтобы было е3 = 0, тогда [1=—А; из условия, что
при о2 = о"з = 0 s = Cj, нужно принять Х = 2/3. Теперь
s = 0j —а2, 81 = у(с1 —а2), е2= —у(а4 —о2).
Мы получили в точности тот же результат, что и по критерию
наибольшего касательного напряжения.
Плоское напряженное состояние. Так называется состояние
в тонком листе, нагруженном силами, действующими в его
плоскости. Направляя ось z по нормали к плоскости листа, получим,
что az = 0.
а) Квадратичный критерий ползучести:
ао=К°1 + <-о^ + Зт2. A19.11)
С помощью условия несжимаемости исключим ez из выражения
для е0. Найдем:
е0 = ^/e|f 4 + 8*8,+JL?2- A19.12)
Закон течения:
Часто бывает нужно выразить напряжения через деформации.
Это осуществляется по формулам:
4 *(е0) („ , 1 о ^ п _ 4 »(80) („ ,1_
77ы- с ^ ' <»"*>
ах~Т~Е^\.В* + ~2вч)' СТу~~ 3 е0 (чеи+28*
Т: 3 е0
474 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
б) Критерий наибольшего касательного напряжения. Условие
Tmax = const в плоскости главных напряжений изображается
шестиугольником (рис. 202). Соответственно значения величины s
и закон течения будут следующими:
s = au ei = v(s), е2 = 0,
Ез=— u(s) (стороны FA и CD),
s = o2, ei = 0, ez = v(s),
e3 = — v (s) (стороны В А и DE), A19-15)
s = Oi — a2, ei = v(s), ez=—v(s),
83 = 0 (стороны ВС и EF).
Остается рассмотреть состояния, изображаемые угловыми
точками:
s = kOi + A — Я) о2 = Oi,
el = kv(s), е2=A — X)v(s), e3=—v(s),
0<Я,<1 (точки А и D),
s = % (а, — а2) + A + Я) <?2 = Рг,
st = b(s), 8j = p(s), вя=-A+Х)и(з), A19.16)
0<Л<1 (точки В и Е),
s= — A,(ai —а2) + A+^)сг1 = о-1,
e^vfs), e2 = ?u>(s), е3 = — A +Я,) v (s),
— 1<Я<0 (точки i? и С).
в) Критерий приведенного напряжения. Условие Oi = const в
плоскости главных напряжений cfj — о2 изображается
шестиугольником, приведенным на рис. 203. На сторонах шестиугольника
§ 120]
ТОЛСТОСТЕННЫЕ ТРУБЫ
475
условия будут следующие:
1
е1 = е2 = уУ
83= — v(s) (стороны АВ и DE),
1 1
s = y(o"i + o2), E1 = e2 = yy(s)
s = oi — Ta2, et = v(s),
2
e_ —- .
2
1
82= —«-y(s) = e3 (стороны AF и Z)C),
A19.17)
1 1
s = <*2 —yffi, e1 = e3= —yi;(s),
e2 = f(s) (стороны С В и ?F).
Для состояний, соответствующих вершинам:
s = y(ori + o-2) + (l —X) (ot — yCTaJ =-^-0-,,
ei=(^l — yjf (s), e2 = D — -jjv(s), e3= ±— y(s),
0<Я<1 (точки ^ и Z)),
s= —T (^ + 02) +A-Я) Гог — 4-сгЛ =-7-о2)
e1=(X-i-)y(s), e2=(l-A^(s)i es= _*+*„(,), (Ц9.18)
0<Я<1 (точки В и Е),
s = % ^о"! —y02J—A —X) (^а2 — уаЛ= —CTl,
bi = —2-v{s), б2=—2-J—y(s), e3 = —2— u(s),
0<Л<1 (точки ^ и С).
§ 120. ТОЛСТОСТЕННЫЕ ТРУБЫ
Труба, находящаяся под действием внутреннего давления,
наряду с турбинным диском, была первым объектом для
применения теорий ползучести; количество публикаций, посвященных
ползучести толстостенных труб, к настоящему времени стало
совершенно необозримо. Принципиальный интерес этой задачи
состоит в том, что она является простейшей из возможных
одномерных задач, в которой напряженное состояние трехосное и ни
одно из главных напряжений в нуль не обращается. Поэтому,
совершенно естественно, случай толстостенной трубы под
действием внутреннего давления служил пробным камнем для оценки
и сравнения различных теорий ползучести, начиная с простейших
и кончая весьма сложными.
476 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
Особенно просто решение этой задачи ползучести, когда
на концах трубы имеются донья и внутреннее давление вызывает
осевую растягивающую силу. Как оказывается, при этом в трубе
осуществляется плоская деформация. Самый простой путь
решения будет заключаться в том, что мы заранее предположим
деформацию плоской, а потом вычислим осевую силу и убедимся в том,
что она имеет требуемую величину. Итак, предположим, что
равномерно нагретая труба нагружена внутренним давлением q,
внутренний радиус ее есть а, наружный — Ъ. Направив ось zno оси
трубы, примем ег = 0, тогда как еэ = - , гг = -г- , если и (г) —
скорость радиального перемещения. Из условия несжимаемости
и , du „
е9 + 8г = 7- + ж = 0,
отсюда
_ Уз _с_ _ Уз" _с_ _ Уз _с_
и~ 2 г ' 8г— 2 г2 ' ее~ 2 г*
Здесь с — постоянная интегрирования, множитель -^— введен
для удобства.
Вычислим теперь е0 по формуле A19.4). Найдем, что е0 = с/г2.
Из закона ползучести A19.5) следует:
4 * (8л) r,
Се —^ = -д-^^ее, qz — о = 0.
Отсюда
Уравнение равновесия элемента в цилиндрических
координатах будет
daT orr— с9 _ q
dr ' г
Воспользовавшись первым из уравнений A20.1), получим:
,_ 2 / с \ dr 1 s (у) , / с
ааг = —7= s -»¦ — = т= —5-i- «у у = е0 = -=-
]/3 V'V ' УЗ v \ ° /-а
Интегрируем это уравнение при начальном условии о> (а) = — q:
s (v) dv
Уз
va
\ siv)vav . A20.2)
§ 120]
ТОЛСТОСТЕННЫЕ ТРУБЫ
477
Теперь легко находим о9 и azi
i= —q-
аг= —q-
)dv
Уз
Уз
f i_H
dv
Уз
l
Уз
rs(p),
s(v).
A20.3)
A20.4)
Величина » содержит неизвестную константу с, которая должна
быть определена из граничного условия аг (Ь) = 0, что приводит
к уравнению
-г-W?-^-0- A20-5)
а
В общем случае, если s (v) — какая-либо функция, заданная
графически, таблично или аналитически в неудобной для
вычислений форме, то можно рекомендовать
следующую процедуру расчета.
Определим функцию
!>(*)= \
s (х) dx
Этот интеграл будет сходящимся при
любых разумных законах
ползучести, надлежащим образом
описывающих область малых х. Тогда
уравнение A20.5) будет следующим:
чУ~Ъ = ЪЫ-ЪЫ. A20.6)
Рис. 204.
С другой стороны, va=c/a2, vb—clb2,
поэтому г>ь/г?а=а2/62. Если построен
график функции if> (х), то без всяких затруднений чисто
графическим путем строится серия кривых зависимости между q и va
для разных значений alb. Действительно, так как
то, фиксируя значение а2/Ь2, мы устанавливаем
пропорциональный циркуль так, чтобы отношение измеряемых отрезков
равнялось заданному а2/Ь2. Меряя ординату (рис. 204),
соответствующую любому va, мы немедленно меряем ординату,
соответствующую абсциссе j^va; разность этих ординат есть q УЗ, таким
478 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
образом, строится график q от va при заданном отношении
радиусов.
При степенном законе ползучести все формулы выписываются
в замкнутом виде. Положим s=an (—) , тогда i|j (х)=пап (—) »
следовательно,
1/в_ дУз"
_ |- / а\2/п1 • A20.7)
ч4-Ст; J
По формулам A20.2), A20.3) и A20.4) легко получаем:
- = -^к--['-0-|)AГ]. («0.8,
0\ =
6 > 2/n
1
а
[К'+ЖтЛ
Проверим теперь высказанное утверждение о том, чю
найденное распределение напряжений соответствует трубе с доньями.
Вычислим осевую силу:
ь \ъ
Р = 2л \ a2r dr= — пс \ oz -?¦.
a va
Внося сюда выражение для аг по формуле A20.4), заметим, что
при интегрировании первого члена в правой части, равного — д,
нет необходимости переходить к переменной интегрирования vT
этот член дает составляющую в интеграле, равную —nq (b2 — а2).
Результат интегрирования оставшейся части будет следующим:
vb
dv
$?^*-$«м!
"а
Таким образом,
Р = — л? (б2 — а2) + щЪ* = яда2,
что и доказывает сделанное заранее предположение.
Приведенное элементарное решение, как видно, представляет собою про-
§ 121] ЧИСТЫЙ ИЗГИБ ЧАСТИ КРУГОВОГО ЦИЛИНДРА 479
стую перефразировку задачи о пластических деформациях трубы,
решаемой на основе деформационной теории пластичности.
Рассмотрение более сложных случаев, когда осевая сила равна нулю
(открытая труба) или задана каким-либо иным способом, в
принципе проводится точно так же, но осевая скорость деформации
принимается отличной от нуля. Решение этой задачи в общем
виде приведено в книге [43], а также в различных формах
получалось другими авторами.
В заключение посмотрим, какие результаты можно получить,
если воспользоваться критерием Треска. Если сг9 > az > °7> то
нужно принять 0е — ar = s (е9 — ег), вся разница сведется
к значению константы с, это значит, что при том же законе
ползучести для растяжения численное значение скорости ползучести
получится другим. Распределение напряжений по-прежнему будет
определяться формулами A20.2) и A20.3), но осевое напряжение
az никак не фиксируется, оно может принимать произвольное
значение, заключенное между о"е и аг. Эта неопределенность
мгновенно устраняется, если допустить, что наряду е деформацией
ползучести существует упругая деформация, в рамках же теории
установившейся ползучести приходится удовлетвориться
сделанным замечанием.
§ 121. ЧИСТЫЙ ИЗГИБ ЧАСТИ КРУГОВОГО ЦИЛИНДРА
Представим себе часть кругового цилиндра, вырезанную двумя
меридиональными сечениями и загруженную равномерно
распределенными вдоль образующих моментами в плоскости,
перпендикулярной оси. Для упругого случая это задача о чистом изгибе
кривого бруса, в условиях ползучести разница между плоским
напряженным и плоским деформированным состояниями существенна
и задача уже не может быть названа задачей о кривом брусе.
Последняя задача для пластичности и ползучести рассматривалась
рядом авторов при обычных допущениях приближенной теории
(см., например, [62]); в условиях плоской деформации, то есть для
цилиндра достаточно большой длины, ход вычислений, конечно,
тот же самый и окончательные формулы получаются
аналогичными. Однако, эта задача допускает и весьма простое точное
решение, аналогичное известному решению Головина для изгиба
упругого стержня прямоугольного поперечного сечения. При
этом выявляются некоторые качественные особенности,
отсутствующие в приближенном решении. Пусть будет а — внутренний
радиус цилиндра, Ъ — наружный радиус. Для определенности
считаем, что изгибающий момент разгибает брус (рис. 205). Будем
искать такое напряженное состояние, которое не зависит от угла 9.
Перемещения при этом, конечно, остаются функциями как г,
так и 0. Считая напряженное состояние не зависящим от 0, мы
480 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧЕ [ГЛ. IX
должны принять равным нулю касательное напряжение т,
следовательно, оставшиеся напряжения о> и о*9 удовлетворяют точно
такому же уравнению равновесия, как и для осесимметричнои
деформации трубы:
dar . ar—oq
dr
- = 0.
A21.1)
Общие выражения для компонент деформации в полярных
координатах будут следующие:
е,=
ди
~дУ
_ и 1 ди
ее-у + у-ёё"'
1 ди
ди
Ч г дВ "¦" дг г "
Из условия несжимаемости при
е2 = 0 следует:
8г + ее = 0-
С другой стороны, разность
напряжений ое — аг как при
критерии Мизеса, так и при
критерии Сен-Венана есть функция разности скоростей деформации
ее — ег, поэтому ее — ег должно зависеть только от г. Поэтому
можно положить
Бе — ег = 2<р'(/-).
Принимая во внимание условие несжимаемости, найдем:
Рис. 205.
ди , . ,
ег = -^г= —ф (г),
е9 =
1 ди
г дв
:-г+^-?г = ф'(г)-
Проинтегрируем первое уравнение, получим:
и= —<р(г) + А'(в).
Внесем найденное значение и во второе и найдем функцию v:
v = Q[r<('(r) + y(r)]-h(Q) + g(r).
Подставим теперь найденные выражения для и и v в
формулу для у и воспользуемся условием у = 0. Получим:
0.
1[/г"(9) + /г@)] + е[,ф"(г) + ф'и—?]+г»—^-
Отсюда следует:
А"(9)+ А(9) = СО, Ф*(г) + -21—^-+§- = 0. A21.2)
Постоянную С можно положить равной нулю, так как для
определения напряжений достаточно знать функцию ф (г) с точностью
§ 121J ЧИСТЫЙ ИЗГИБ ЧАСТИ КРУГОВОГО ЦИЛИНДРА 481
до аддитивной постоянной. Интегрируя A21.2), найдем:
Следовательно,
2Ф» = #-А
8е-е, = -|— А. A21.3)
Для дальнейшего решения мы воспользуемся критерием
наибольшего касательного напряжения и положим
/'га — 8Л1/В
Учитывая A21.3), можем переписать это соотношение следующим
образом:
aa — or = onen -it—A ^
Последняя формула справедлива до тех пор, пока ее — ег>>0.
Так будет в растянутой области, примыкающей к поверхности
г = а. При некотором значении г — с величина ее — ег обращается
в нуль, и мы имеем:
-?-* = *¦
Отсюда В = Ас2. Таким образом, в растянутой области
а6-ог = оя(-) (тт,) ¦ A21-4)
В сжатой области е9 — ег<;0, следовательно, мы должны принять
ae-oT=-aa(—) A-75-; ¦ A21.5)
Напишем уравнение равновесия для растянутой области,
подставив A21.4) в A21.1), получим:
Здесь мы обозначили:
Сделаем замену переменной, положив
Получим:
31 Ю. Н. Работнов
т = ^5-ГАу/п. A21.7)
г2
и71
dar = — m j——z, du.
1 + un
482 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
При г —с и = 0, при r~a ua=(a —1I/п, где а = -^->1; таким
образом,
A21.8)
2m. , * ? ип du
о
Здесь через о* обозначена величина радиального напряжения
с> при г = с.
Для сжатой зоны вычисления производятся совершенно
аналогично, уравнение равновесия записывается следующим образом:
dr nr \ г2 у
Теперь мы положим
1-^г = »п
и придем к следующим выражениям для напряжений:
A21-9)
о
При r = cu = 0, при r=b иъ = (\ — РI/п, где р = -?г<1. При
выполнении расчетов по этим формулам можно поступать
следующим образом. Введем обозначения:
, , \ ип du
о
Напряжение ог обращается в нуль при г=а и г-—Ь,
следовательно, при и-=иа и и — иъ. По формулам A21.8) и A21.9)
получим:
о* — тщ (иа) — о* — ли|) (ць) = О-
§ 121] ЧИСТЫЙ ИЗГИБ ЧАСТИ КРУГОВОГО ЦИЛИНДРА 483
Отсюда следует, что
*
фЫ=^Ы = —¦
т
Строятся графики функций ср (и) и ij> (и) и отмечаются те
значения иа и иь, которые соответствуют одинаковым величинам
ординат обеих кривых, каждая такая ордината есть о*/т. Таким
образом, каждому значению а*/т ставится в соответствие пара
,1/л /¦ . с8 М*
62
исключая
чисел иа и щ. Но иа = { —%—-1 ) , Щ = ( 1
отсюда с, найдем, что данная величина о*/т соответствует
определенному отношению b/а, а именно:
*-«?
Таким образом, мы нашли а* как некоторую функцию от к:
о* — тС (к). Теперь формулы для напряжений можно переписать
следующим образом:
растянутая зона
с
т С(к)-<?(и), ^=^ + С(^-фН A21.10)
сжатая зона:
% = С(К)-Ъ(и), % = -1и + С(к)-у{и).
Функции ф (и) и г|з (и) при целых п легко выписываются в
замкнутом виде, однако получающиеся выражения не очень удобны
для расчетов, поэтому при рассмотрении конкретного примера
для ге = 3 оказалось удобнее пользоваться численным
интегрированием, выделив предварительно некоторые члены. Так, было
принято
и
f" du
о
1 1 /Л' ч , 1 С 2 + и ,
t=_u__ln(l_u)+_^TT-F-3du.
о
На рис. 206 представлены графики функций <р (и) и \|; (и). По
этим графикам с помощью описанной выше процедуры была
определена зависимость функции С от к = b/а, эта зависимость
приведена на рис. 207; здесь же приведено отношение с/а в зависимости
от к. Эпюры напряжений ав и аг для к--^А показаны на рис.208.
Интересно отметить, что максимум напряжения сг9 достигается
не при г = а, как это было бы для упругого случая и как это
всегда получается по приближенной теории, а в некоторой
внутренней точке. Этот результат нельзя считать неожиданным.
31*
484
ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ
[гл. IX
Действительно, с увеличением п распределение напряжений
стремится к распределению напряжений в теле из
идеально-пластического материала. Для случая идеальной пластичности
соответствующее решение получается немедленно. Полагая о"е — OV = от
Щ
ф
Q3 0,4 Ц5 Ofi 0J
>Щ ЦР 10 р & & # &
а
Рис. 206.
в растянутой области и о9 — аг = —от в сжатой области, мы
немедленно находим, что в первой области
<тг = схт In-^-, ae = 0T(l + ln-^-
В сжатой области
0"9= —СТТ (l + ln-?-
Or= — CrTln-?- ,
Из условия непрерывности аг на границе областей при г = с
§ 121] ЧИСТЫЙ ИЗГИБ ЧАСТИ КРУГОВОГО ЦИЛИНДРА 485
получаем:
с = У^аЬ.
Величина изгибающего момента вычисляется элементарно.
На рис. 208 пунктиром показано распределение напряжений при
п = оо для той же величины изгибающего момента, что и при п = 3.
Рис. 208.
Найдем теперь значение радиуса г, для которого <ув достигает
максимума. Дифференцируя вторую из формул A21.8) по г и
приравнивая производную нулю, получим:
Отсюда
U ~ i* 1 ~ п-2 '
или
f=Y5- A21Л1)
Из A21.11) следует прежде всего, что максимум существует лишь
для п > 2. При выполнении этого условия максимум напряжения
будет во внутренней точке, когда значение г, даваемое
формулой A21.11), окажется больше, чем а, то есть для случая
достаточно большой кривизны. Так, при п = 3 мы получаем с/г = 1,73,
из графика рис. 207 видно, что это соответствует X = 3,33.
Полученные результаты интересны в том отношении, что, как
оказывается, при изгибе подобного рода цилиндрических
элементов область больших растягивающих напряжений проникает
на значительную глубину, вследствие чего может происходить
интенсивное трещинообразование.
486 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
§ 122. ВРАЩАЮЩИЕСЯ ДИСКИ
Задача о вращающемся диске турбины была первой задачей,
в которой пришлось серьезно учитывать ползучесть; начиная
с первых работ Бейли и до последнего времени ей уделяется очень
большое внимание. Особенность этой задачи состоит в том, что
напряжения в диске возникают в результате ускорений при
вращательном движении, тогда как внешние нагрузки невелики.
Поэтому утолщение диска не приводит к уменьшению напряжений,
более благоприятные условия работы материала достигаются
а) б) в) г)
Рис. 209.
только за счет улучшения профилирования, и возможности
уменьшения рабочих напряжений ограничены, материал неизбежно
работает на пределе, следовательно, к точности расчета
приходится предъявлять очень высокие требования. С другой стороны,
конфигурация турбинного диска довольно проста, технология
изготовления дисков разработана весьма тщательно и факторы, вносимые
технологией, изучены достаточно хорошо. В результате степень
несоответствия между расчетной схемой и реальной конструкцией
сведена к минимуму. Некоторые типичные схемы дисков,
применяемых в паровых и газовых турбинах, приведены на рис. 209.
На рис. а) изображен диск классической конструкции. Для
посадки на вал служит достаточно мощная втулка, в расчетной схеме,
в зависимости от жесткости втулки, либо тело диска условно
продолжается до вала, как показано пунктиром, либо втулка
рассматривается как абсолютно жесткая, и перемещение точек на
радиусе, равном наружному радиусу втулки, полагается равным
нулю, либо, наконец, рассматриваются реальные условия
сопряжения диска с втулкой, которая обычно предполагается упругой.
Последняя схема оправдывается тем, что наибольшая температура
в диске получается вблизи обода, тогда как температура втулки
обычно невелика. Стремление уменьшить габариты машины
§ 122]
ВРАЩАЮЩИЕСЯ ДИСКИ
487
и улучшить систему уплотнения заставляет искать путей отказа
от длинных втулок. На рис. б) приведена схема конструкции,
иногда применяемой на паровых турбинах небольшой мощности,
диск непосредственно сажается на вал с натягом. Для получения
возможности увеличить натяг в диске предварительно создаются
начальные напряжения путем пластического деформирования
(автофреттирование дисков).
На рис. (?) изображена часть цельнокованого ротора, диски
составляют одно целое с валом. Обычно при этом вал имеет осевую
расточку, этим несколько повышаются рабочие напряжения, зато
появляется возможность проконтролировать отсутствие дефектов
в металле ротора в его центральной части, где эти дефекты
наиболее вероятны в связи с условиями технологии. Наконец, на
рис. г) приведена схема сплошного диска, укрепляемого консольно
на фланце вала.
На периферии диска всегда имеется утолщенная часть — обод,
к которому тем или иным способом крепятся лопатки. Силы
инерции лопаток создают на ободе распределенную радиальную
нагрузку. Обод иногда рассматривается как кольцо, тогда
приходится отдельно составлять условия ползучести для диска под
действием неизвестной нагрузки, передаваемой от обода, и для
обода, рассматриваемого как вращающееся кольцо, на которое
действует изнутри реакция со стороны диска и снаружи
лопаточная нагрузка. Более простой путь состоит в том, что несущей
способностью обода пренебрегают и считают диск загруженным на
периферии известными центробежными силами инерции обода
и лопаток.
В рамках теории установившейся ползучести корректная
формулировка граничных условий для приведенных схем возможна
не всегда. Так, в случае а) рассмотрение взаимодействия упругой
втулки и ползущего диска имеет смысл только в том случае,
если мы учитываем упругие деформации самого диска, то есть
имеем дело с неустановившейся ползучестью. В случае б) плотная
посадка диска на вал обеспечивается упругими деформациями
диска и задача расчета состоит не столько в оценке прочности диска
или определении его деформаций по истечении заданного
времени, сколько в исследовании релаксации натяга, то есть
определении того времени, когда величина контактного давления
перестанет обеспечивать надежность посадок. Случай г) является,
пожалуй, наиболее чистым из всех приведенных в отношении
применимости к нему представления об установившейся ползучести.
Выбор профиля диска существенно влияет на распределение
напряжений в упругом диске, и раньше, когда расчеты на
ползучесть не производились, вопросу об оптимальном профилировании
уделялось очень большое внимание. Ползучесть приводит к
выравниванию напряжений, поэтому влияние профилировки в условиях
488 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
ползучести становится не столь существенным и современные
диски обычно имеют довольно простой профиль, по большей части
конический, что связано с технологическими преимуществами.
Распределение температур в дисках, как правило,
неравномерно: обод нагрет значительно больше, чем центральная часть,
и учет неравномерности температур существен.
При расчете диска в большинстве случаев конструктор имеет
дело с хорошо изученными материалами, для которых
существуют кривые ползучести в достаточно широком диапазоне времени
для разных температур и напряжений. Применение всякого рода
аналитических зависимостей скорости ползучести от напряжения
и температуры связано с неизбежным искажением опытных
данных; в то же время все более или менее сложные реальные задачи
приходится решать численными методами. При использовании
численных методов преимущества простых законов ползучести —
степенного или экспоненциального — оказываются уже не столь
большими, поэтому наибольшую ценность представляют те
численные методы, которые используют непосредственно найденные
по кривым ползучести зависимости скорости от напряжения
и температуры. Это замечание в особенности важно в связи с тем,
что расчет неустановившейся ползучести дисков на основе теории
старения с использованием изохронных кривых строится
совершенно так же, как расчет на установившуюся ползучесть, только
вместо скоростей рассматриваются деформации, вместо
зависимости скорости деформации от напряжения — зависимость
деформации от напряжения для данного времени (см. гл. XI).
Большое количество предложенных методов расчета дисков
можно разбить на следующие группы:
а) точные решения дифференциальных уравнений (в
замкнутой форме или путем численного интегрирования);
б) методы последовательных приближений в различных
вариантах.
Методы второй группы получили большее распространение
в практике проектирования, при ручном счете они оказываются
более простыми и удобными. Возрастающее применение
электронных машин делает перспективными также и методы первой
группы.
§ 123. ПОЛЗУЧЕСТЬ СПЛОШНОГО ДИСКА
ПОСТОЯННОЙ ТОЛЩИНЫ
В серии работ Валя [377], [3781, I379] был развит метод расчета
вращающихся дисков как постоянной, так и переменной толщины
с помощью условия Треска и ассоциированного закона течения.
Довольно детальное изложение этих решений содержится в
книге [52], поэтому мы не будем повторять изложение и с единствен-
§ 123] ПОЛЗУЧЕСТЬ СПЛОШНОГО ДИСКА ПОСТОЯННОЙ ТОЛЩИНЫ 489
нои целью проиллюстрировать ход рассуждений рассмотрим
некоторые достаточно простые задачи, пользуясь
экспоненциальным законом ползучести, а не степенным, который был принят
Валем. Некоторое преимущество экспоненциального закона, как
мы видели, состоит в том, что уравнения, представленные в
безразмерной форме, не содержат никаких опытных констант и
найденные решения вполне универсальны. Рассмотрим сначала
сплошной диск радиуса Ъ вращающийся с угловой скоростью со.
Лопаточная нагрузка создает радиальные напряжения ar (b) на контуре
диска, при этом or (b) пропорционально со2. Уравнение равновесия
элемента диска будет следующее:
If (™т) — о0 + pcoV2 = 0.
Здесь р — плотность материала диска. Поскольку мы будем
пользоваться экспоненциальным законом ползучести
е = ееехр(-^
определим безразмерные напряжения следующим образом:
"Ог (То
Введем также безразмерный радиус ? = т!Ъ, вместо скорости
радиального перемещения точек диска будем рассматривать без-
размерную скорость и = т— . Уравнение равновесия перепишется
08 е
следующим образом:
~($6r)-Se+ml* = 0. A23.1)
Здесь т = — . Вследствие сделанного замечания о том, что
лопаточная нагрузка пропорциональна со2, мы всегда можем
принять о, (b) = mqoe, поэтому граничное условие при | = 1
будет ar(l) = mq.
ирмации ея, = —
деляются следующим образом
Безразмерные скорости деформации ее = —— и гТ——^ опре-
?е 8в
А и ' du,
89- у, ег--^|-.
В центре диска о@ = ог, следовательно, в области, окружающей
центр, может быть либо 00 > 0Г > 0, либо ог > 06 > 0, либо
0е = 0Г- Вторая возможность отпадает сразу. Действительно, в этом
случае должно быть е9 = 0, следовательно, и = 0 на конечном
490 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
отрезке, но тогда на этом отрезке и — = гт — 0 и никакой
ползучести не происходит. По той же причине отпадает и первая
du ~ п "
возможность: если на конечном отрезке — = ег = и, то величина и
также равна нулю, поскольку и @) = 0, а значит, и гв = 0.
Остается допустить, что в области 0 <! ?, <; а ое = вг — а-
Из уравнения равновесия немедленно следует:
а = С \-rnl*. A23.2)
В случае равенства двух главных напряжений, как было
показано в § 119, закон ползучести нужно принять следующим:
?е + ег = у (а).
Для экспоненциального закона в безразмерных переменных мы
получим следующий результат:
~з|- + -|-=ехро' = ехр6-ехр ( т- ) • A23.3)
Проинтегрируем это дифференциальное уравнение для
перемещения и(|), полагая и@) = 0. Найдем:
«=-LexpC-i-[l-exp(-^fi)]. A23.4)
Вычислим теперь скорость радиальной деформации:
^ = ^ = е-^{"^[1-ехР(-^)] + >пехр(-^)}.
A23.5)
Граница области, в которой о"е = о>, определится из условия
обращения в нуль гг при ? = а, тогда при ?>а сохранится
ег = 0, а значит, будет ов>ог. Полагая в A23.5) ? = аи ег = 0,
придем к следующему уравнению:
ехря0 = 1 +2х0. A23.6)
г_> та2
одесь хй=—^—.
Корень этого уравнения легко вычисляется, а именно: а;0 =
= 1,256, таким образом,
та? = 2,512.
Теперь мы должны различать два случая:
1. т<.2х0= 2,512. Напряжения равны между собою во
всем диске при 0<?<;1, постоянная С в формуле A23.2)
§ 123] ПОЛЗУЧЕСТЬ СПЛОШНОГО ДИСКА ПОСТОЯННОЙ ТОЛЩИНЫ 491
определяется из условия ov (l) = m.g, следовательно,
Г , 1—g2
or = ae = m [g + —^J •
2 512
2. пг>2ж0 = 2,512, следовательно, а2 = ——<1. При ?>а
л л л л. л.
должно быть о"е>огг>*0! еГ = 0, следовательно, и = ы(а) и ее =
= ~-^. Величина и (а) определится из условия непрерывности
перемещения при | = а, то есть из формулы A23.4) при | = а,
а именно:
^Р = ехр(С — х0).
При этом было учтено условие A23.6).
Теперь скорость окружной деформации при ? > а выразится
следующим образом:
В соответствии с законом ползучести ее зависит только от 09,
а именно: ее = ехр0е, поэтому
а9 = С ~ х0 + In у .
Внесем найденное выражение для с9 в уравнение равновесия
A23.1) и проинтегрируем. Получим:
аг = С — ж0 + 1п-|- + 1 — -j- + -|- ¦
Для определения постоянных интегрирования С к D
используем условие непрерывности напряжения аг при ? = а и
граничное условие при |=1. Из первого условия следует:
D= —a fl—jx0
Из второго условия:
Сг-а^ = С = т (? + -!-)-l + a(l-^)-lna =
= m (д + -|Л — 1+ 0,164a — In a.
Теперь формулы для напряжений можно переписать следующим
образом:
При К а
от = 6в = С + 1,256 (l _|i) ; A23.7)
492 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫВ ЗАДАЧИ [ГЛ. IX
при |>а
o, = C'-ln4+(l--i-)+0,836(f-?), A23.8)
ae = C'-lni-.
Проверим выполнение условия Ов>о"г. Разность ат — ов =
= A—~j 1 ~(l + — + \-) ¦ Это выражение
отрицательно при любом ?><х.
§ 124. ПОЛЗУЧЕСТЬ ДИСКА С ЦЕНТРАЛЬНЫМ ОТВЕРСТИЕМ
Рассмотрим теперь задачу о ползучести диска постоянной
толщины с центральным отверстием. Сохраняя те же безразмерные
обозначения, которые были использованы применительно к
сплошному диску, будем понимать под а относительный внутренний
радиус диска, при | = а радиальное напряжение мы примем
равным нулю, тогда как при ? = 1 по-прежнему ar = mq.
Предположим, что во всем диске, то есть при a <! | <; 1, ав > о> > 0.
Тогда решение запишется совершенно так же, как и для
сплошного диска в области | > а, а именно:
(те = С + In ~ ,
o-r = C + ln-! + l-^L-il.
Выписывая эти выражения, мы несущественно изменили
обозначения. Из граничных условий ог(а) = 0 и or(l) = mq находим
константы:
/-»_ m Г» i l+a + a3'] 4 In a
6~l-aL? + ~~3 J 1-a'
м , ч п i 124.2)
г. Га. a(l+a)l a In a v '
D = m \ q . —- -^—-' — -. .
L 1 —a ' 3 J 1 —a
Осталось выяснить пределы применимости найденного решения.
По предположению должно быть
Or — ae=l ^—у< °-
Это неравенство может быть нарушено либо на границе, либо
в области а<|<1- В первом случае оно сводится к
следующим условиям:
D>i-f, D>l-%.
§ 124] ПОЛЗУЧЕСТЬ ДИСКА С ЦЕНТРАЛЬНЫМ ОТВЕРСТИЕМ 493
Если подставить сюда выражение A24.2) для D, то мы убедимся,
что первое неравенство выполняется всегда, тогда как второе
накладывает некоторое ограничение на то и д. При q = 0
величина D принимает минимальное значение, поэтому мы
ограничимся выяснением того, начиная с каких значений т
справедливо найденное решение при отсутствии лопаточной
нагрузки; наличие этой нагрузки уменьшает нижнюю границу для т.
Получим:
. a In a
т>гт+^- A24-3)
Предположим теперь, что максимальное значение аг — 06
достигается в области а < ? < 1, и потребуем, чтобы это значение
оставалось отрицательным. В результате мы придем к следующему
условию:
аA+а)т а 1п а 2
"* ЗТА
В диапазоне значений а до 0,30 определяющим оказывается
условие A24.4). В нижеследующей таблице приведены минимальные
значения т, при которых решение A24.1) остается справедливым,
для некоторых величин а:
а 0,05 0,10 0,15 0,20 0,25 0,30
т 6,28 3,22 2,17 1,65 1,27 1,05
Приведенные примеры наглядно показывают преимущества и
недостатки применения критерия ползучести Треска к задачам о
вращающихся дисках. При некоторых условиях решения получаются
простыми, однако выяснение границ применимости этих простых
решений связано с довольно громоздким исследованием,
требующим вычислительной работы. В других случаях может оказаться,
что диск разбивается на области, напряженное состояние в
каждой области соответствует какой-либо стороне или вершине
шестиугольника Треска. Для каждой такой области решение, то
есть формулы для напряжений и скоростей, содержащие
некоторые константы, может быть написано. Однако границы областей
заранее неизвестны, они находятся вместе с константами
интегрирования из граничных условий сопряжения, в результате
получаются достаточно сложные нелинейные уравнения, которые
приходится решать численно.
Весьма подробное исследование подобного рода
применительно к степенному закону ползучести было проведено Валем
в цитированных работах. Кроме диска постоянной толщины
там рассмотрены диски с толщиной, меняющейся по закону
494 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫВ ЗАДАЧИ [ГЛ. IX
h = h^. Интегрирование и в этом случае выполняется в
конечном виде. Однако профили реальных дисков, несмотря на
современную тенденцию к их упрощению, все же остаются более
сложными, чем те, для которых построены графики и таблицы.
§ 125. ПРЯМОЕ ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ
ПОЛЗУЧЕСТИ ВРАЩАЮЩЕГОСЯ ДИСКА
Уравнения ползучести вращающегося диска приводятся к
квазилинейной, то есть линейной относительно производных искомых
функций, системе второго порядка, довольно удобной для
численного интегрирования. Этот прием был применен к задаче о
пластическом состоянии вращающегося диска Соколовским [1331
и к задаче о ползучести — Малининым [69]. Как выяснится,
неудобство метода состоит в том, что краевые условия заданы на
двух границах интервала, поэтому одно из начальных условий
заранее неизвестно, расчет приходится вести путем попыток
либо же рассчитывать серию однотипных дисков. С появлением
электронных быстродействующих машин эти трудности
оказываются легко преодолимыми, и метод может быть, безусловно,
рекомендован для практического использования.
В самом общем случае будем предполагать, что диск с
внешним радиусом Ъ имеет переменную толщину h = h (r),
распределение температуры по радиусу будем тоже считать в общем случае
переменным. Как обычно при расчете дисков, мы предполагаем,
что напряженное состояние является обобщенным плоским. Для
осесимметричной задачи это означает, что напряжения о"е = а4
и а,. = а2 равномерно распределены по толщине диска, тогда
как а3 = 0. Воспользуемся представлением напряжений по
формулам (8.9), исключим а с помощью условия а3 = 0 и для
удобства примем
После элементарных преобразований .получим:
ar = -|=r<ro9in(\p —-f-)» ав = -да08т(\р + ^ . A25.1)
Вычислим теперь компоненты скорости деформации по теории
типа Мизеса, а именно:
ег= — -g-vcos С 9 +-J- ) > B9 = yycos Гф — -|- J . A25.2)
При 0О = const формулы A25.1) определяют в плоскости ог — о9
эллипс, каждой точке которого соответствует определенное
значение ф. На рис. 210 изображена часть этого эллипса с пометками
значений ф против соответствующих точек, этот рисунок окажет-
5 125] ПРЯМОЕ ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ
495
ся полезным при определении области изменения ф в различных
частных задачах.
Уравнение равновесия элемента диска будет следующее:
-*(*,,) +Л-0'"*
рсо^йг = 0.
A25.3)
dr ч '' ' г
Удобно принять за независимую переменную величину
?=1п-?- = 1п?.
Вместо толщины h мы будем иметь дело с функцией т] (?), причем
Л0 — произвольная константа, имеющая размерность длины
(характерная толщина диска). Внесем в
A25.3) выражения A25.1) для
напряжений. После несложных преобразований
получим следующее уравнение:
^-соз(ч)—J) +
Уз
¦созф + т-^-ехрB? — -ф) =0. A25.4)
Здесь
¦ф = 1п
сто
т-
РШ2Ь2
Рис. 210.
от — произвольная константа, имеющая
размерность напряжения.
Зи du
аметим теперь, что, поскольку ее = —, гг = -г-, скорости
е9 и гг удовлетворяют следующему уравнению совместности:
dee , ее —ег
dr
0.
A25.5)
Положим s = In—, где е* — произвольная константа, имеющая
размерность lit. Внесем в A25.5) значения гТ и гв по формулам
A25.2). Получим:
dm .
dz
Jcos (m—IL\—Y3 cos ф = 0. A25.6)
Таким образом, задача свелась к интегрированию относительно
простой нелинейной системы A25.4) — A25.6). Величина z,
фигурирующая в уравнении A25.6), является функцией от г];. При
496
ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
степенном законе ползучести
' Со
v = e
Положим ещ = еп, о# — ап, тогда
г = Щ. A25.7)
При экспоненциальном законе ползучести
а
v = ееехр— .
Положим е* = ее, а* — ае, тогда
z =--^ = ехр ф. A25.8)
Теперь в уравнениях A25.4) и A25.5) удобно удержать одну
переменную z, исключив г|з из A25.4) с помощью A25.8) и -jjr = — -4 •
Конечно, численное интегрирование возможно и тогда, когда z
есть произвольная, заданная таблицей или графически функция
от г|э.
Остановимся еще на вопросе учета переменности температуры.
Как было показано в § 45, простейшее предположение состоит
в том, что е„. есть функция температуры, а следовательно, радиуса.
Итак, е, = е# (?)— известная функция. Пусть теперь в*,. —
произвольная константа, имеющая размерность скорости деформации,
г = Ь^,х@ = 1п(Е-^).ТоГда
dt, е* tf? "T" dt,
и уравнение A25.6) нужно заменить следующим:
-^-sin (ф—?¦) - (^|+^|) cos (ф-f )-Vr3cos4. = 0.
A25.9)
Для сплошного диска точке г = 0 соответствует ? = —оо,
что влечет за собой неудобство при численном интегрировании.
В этом случае следует вернуться к переменной Ъ, = ехр ?.
§ 126. ДИСК РАВНОГО СОПРОТИВЛЕНИЯ
Диском равного сопротивления мы будем называть диск,
у которого величина о*0 одинакова для всех точек, следовательно,
v также постоянно. Задача состоит в определении профиля такого
диска, то есть нахождении функции h (г). Полагая в A25.4) и
§ 126]
ДИСК РАВНОГО СОПРОТИВЛЕНИЯ
497
A25.6) ij; = const и z = const, получим:
/ я \ dr\ . f л, \ dw
Sin (^ф-т j — + COS ^Ф-Т; -% ~С08ф +
4^-ехрB?-ф) = 0, A26.1)
sin(^9—J-")-^.—1ЛЗсозф = 0. A26.2)
Прежде всего отметим существование тривиального решения
Ф = -2-для уравнения A26.2). Подставляя в A26.1), получим:
4f=— ™ехрB?—if).
Не нарушая общности, мы можем принять -кр = 0, это значит о0 = о-*.
Тогда, интегрируя, находим:
Отсюда
А = ехр ( —Ё|^Л х const. A26.3)
Это — известное решение задачи о диске равного сопротивления,
которое совершенно не зависит от физической природы материала
диска; зная, например, нагрузку, приложенную на наружном
контуре, мы определяем постоянный множитель в A26.3) и
находим профиль сплошного диска равного сопротивления.
Если же диск имеет отверстие, на контуре которого приложена
другая нагрузка, то мы не можем построить по этому способу
профиль равного сопротивления, так как формула A26.3) не
содержит достаточного числа констант. Поэтому мы возвращаемся
к уравнениям A26.1) и A26.2). Второе уравнение интегрируется,
а именно мы получаем:
'-•"Чч'^Р-ТТгО-т)- <«">
Для определенности мы приняли, что на контуре отверстия при
г = а и ? = 1п-г-=1па радиальное напряжение обращается
в нуль, и, следовательно, как это видно на схеме рис. 210, ф = -g-.
Выражение A26.4) можно переписать следующим образом:
32 Ю. Н. Работнов
498 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
Видно, что г стремится к бесконечности при ф = ^ , таким образом,
диапазон изменения угла ф будет от ф = ^ , до некоторого значе-
п
ния ф*<^- Обратимся теперь к уравнению A26.1). Примем за
независимую переменную угол ф, исключим ? с помощью A26.2)
и A26.4). Получим следующее дифференциальное уравнение:
ехр
Ч> —
dr\ , ( л \ . 1 ,1/3 \ УЗ /
-г~— —ctg ф J- ) А у=г — та2-!, i ^L L .
<?Ф б \Т 6 J ' -у2, 4 cos2cp
Прежде чем записывать интеграл этого уравнения, выясним
граничные условия. Из A26.4) прежде всего мы можем найти
значение ф* в зависимости от а. Легко убедиться в том, что для
реальных значений а < 0,3 величина ф* очень близка к я/2.
Поэтому мы сделаем замену переменной интегрирования, приняв
Рл
= -г-Ф.
Уравнение A26.5) перепишется теперь следующим образом:
rW^exp(-^)^exp(JL).
Когда г = Ъ, ф = ф*, р = 6* = —ф*. Если Ъ > г, то мы можем
ограничиться первыми степенями р в разложении правой части.
Получим:
p* = ^V3exP(-^-)«0,473|i. A26.6)
Теперь нам будет удобно записать уравнение A26.5) в
следующей форме:
&ГехР^- A26.7)
б2 sin р * "]/з
Вернемся к тому дифференциальному уравнению, которое было
получено из A26.1). Примем здесь также |3 за независимую
переменную и введем вместо комбинации постоянных в последнем
члене правой части новую постоянную |5*, определенную по
формуле A26.6). Получим:
Р
ехр —^—
^(f-lO-Tk+^-ai^- <>26-8>
§ 126]
ДИСК РАВНОГО СОПРОТИВЛЕНИЯ
499
В области малых р существен только последний член,
обращающийся в бесконечность при р = О, поэтому при малых Р
Т|:
т Р*
2 р
2№
Отсюда получаем снова результат A26.3) для сплошного диска.
Будем считать, что при г = b h= h0 и, следовательно, tj = 0.
Действительно,,на контуре диска задано радиальное напряжение
(лопаточная нагрузка), поэтому величину й0 можно выбрать
таким образом, чтобы напряжение принимало заданное
значение а*. Теперь мы запишем интеграл уравнения A26.8) следующим
образом:
Р
ц = In
з1п(т~р0
sin ( -= Р
г ехр
Р^* , ^Р?
1/3 + 2 J sii
Уз
sin^p
dp.
При вычислении интеграла удобно выделить ту часть, которая
неограниченно возрастает при р* -*¦ 0, поэтому мы представим
окончательный результат в таком виде:
т] = In
(т-f
Р-Р*
Уз
+ 5|![gr(P)-ff(P*)-ctgp + -^- + ^-lnAtgI]. A26.9)
Здесь
¦»>=$[
ехр
Уз
1
sin р~| rfp
Уз
J sin2
p
— функция, не имеющая особенности при р = 0. Значения этой
функции приведены в нижеследующей таблице:
р
<Г(Р)
. р
«<р>
0,1
0,0175
0,7
0,1588
0,2
0,0365
0,8
0,1905
0,3
0,0571
0,9
0,2260
0,4
0,0794
1,0
0,2654
0,5
0,1036
я/3
0,2846
0,6
0,1301
;
32*
500 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
На рис. 211 приведен профиль диска равного сопротивления
с центральным отверстием, рассчитанный по формуле A26.9) при
alb = 0,3 и т = 2,772, что соответствует сплошному диску,
толщина которого в центре равна учетверенной толщине на
периферии. Профиль сплошного диска по уравнению A26.3) также
приведен на рисунке пунктиром. Как видно, разница невелика на
Щ |
в -
в - у
* ^^\_
цз ot & це а7 qs ip tff
Рис. 211.
всем протяжении диска, кроме области, примыкающей к
центральному отверстию. Здесь толщина быстро возрастает, стремясь
к бесконечности при г — а. Таким образом, строго говоря,
осуществить диск равного сопротивления с отверстием невозможно.
Фактически в центральной части диск снабжается втулкой,
переход от диска ко втулке делается из конструктивных
соображений с достаточно большим радиусом.
Заметим, что решение задачи о диске равного сопротивления
совершенно не зависит от закона ползучести, оно остается
справедливым также для случая упругого или пластического материала,
когда вместо скоростей деформаций вводятся в рассмотрение
сами деформации. Для пластического диска оказывается
существенным лишь условие несжимаемости, задача о диске равного
сопротивления из упруго-пластического материала с учетом
сжимаемости рассмотрена в работе [10°].
§ 127. РАСЧЕТ ДИСКОВ ПО МЕТОДУ
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Мы уже отмечали, что применение прямого численного
интегрирования к расчету диска наталкивается на то затруднение,
что граничные условия заданы на двух концах интервала, тогда
как для численного интегрирования необходимо располагать
§ 127]
РАСЧЕТ ДИСКОВ
501
значениями двух констант на одном конце интервала. Поэтому
в практике расчетов получили распространение в большей мере
различные варианты метода последовательных приближений.
Один из таких вариантов был впервые предложен Бейли [162], он
был усовершенствован Поповым [329] и потом подвергался
дальнейшим улучшениям в работах Богуславского [7], Костюка [61],
Малинина [72], [108J и других. В результате последовательных
видоизменений метода, сопровождавшихся конкретными
расчетами, удалось достичь весьма быстрой сходимости процесса.
Запишем уравнение равновесия для диска, который в общем
случае предполагается имеющим переменную толщину {125.3),
в несколько иной форме, а именно:
^(hlor)-hoe + mhl2 = 0. A27.1)
Здесь мы ввели безразмерный радиус | = -г- , но оставили
величины аг, а9, а также h размерными. Поэтому
т= рш2Ь2.
Будем считать в общем случае, что диск имеет центральное
отверстие радиуса а, радиальное напряжение при ? = alb = а задано
и равно тр, тогда как при | = 1 or = mq. Проинтегрируем A27.1),
считая о"е заданной функцией от ?. Получим:
<Уг = щ jj heedl — щ [ ^ ЩЧ% — />аА(а)] .
а а
Второй интеграл в формуле представляет собою момент инерции
относительно оси части площади сечения, заключенной между
радиусами а и |; обозначим его через / (|), это всегда известная
функция. Перепишем найденный результат следующим образом:
I
Ог = ^[ \ hoedl—mI + mpah(a)'\ . A27.2)
а
Соотношение A27.2) представляет собою первое уравнение,
которое используется во всех вариантах метода последовательных
приближений типа Бейли. Второе уравнение получается из
условия совместности, притом различными способами у разных авторов.
Запишем уравнение совместности:
^ + ^9^ = 0. A27.3)
Для определенности примем обычный закон ползучести типа
Мизеса A19.13):
—'-^O'-t-O- '--'-S'O'-т''О. <127-4>
502 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫВ ЗАДАЧИ [ГЛ. IX
хотя аналогичный ход вычислений возможен и при других
законах. Наша задача будет теперь состоять в том, чтобы заменить
уравнение A27.3) при условиях A27.4) некоторым интегральным
соотношением типа
06 = F(|, от, о„, С). A27.5)
Здесь F — функционал того или иного вида, зависящий от сг, Ое, ?
и константы интегрирования С. Температура предполагается
известной функцией от радиуса, поэтому явно в функционал не входит.
Очевидно, что построить функционал типа A27.5) можно самыми
различными способами, в процессе преобразований можно
использовать также уравнения равновесия A27.1). В работе [61] автор
заменяет в A27.3) скорости деформаций через напряжения по
формулам A27.4), исключает с помощью A27.1) производную -^f
и интегрирует получившееся уравнение. Ход выкладок при этом
следующий. Внося значения ег и ее согласно A27.4) в уравнение
совместности, получаем:
doe i daT _ d In со f J \ 3 ag— 0r
o"e — ?di
dl 2 d% ~~ d\ V. 2 2 |
Здесь <о = —.
V
С другой стороны, так как v = v(o0, T), то
d In (О 1 д In ы Г f 1 Л dar . f 1 \ doe, I , д In ш dT
Исключаем из первого уравнения —-^-- , перегруппировываем
члены и исключаем -— с помощью A27.1). Результат
получается такой:
1 In со dT ( _i^
дТ d\ V°6
3 агад\
ae —т-o-r ) • A27.6)
Здесь принято:
А =
Таким образом,
= fi(l-
4i)- в=о(
Q=_a]n»
да0
1
oB = C+^Hd\
J
A27.7)
§ 127]
РАСЧЕТ ДИСКОВ
503
где
*-rb{-A-i")afs-'-T<'+«)(»t+.^) +
. д In ю dT f l \ I
Для определения константы С служит второе граничное
условие для о>, а именно: ov(l) = mq. По формуле A27.2) мы
получим:
1
- [ haBdl — I(i) = qh(l) — pah(a). A27.8)
а
Процесс последовательных приближений заключается в
следующем. Задаемся некоторым предположительным
распределением Ое Для первого приближения, например полагаем сте = const.
Величина Ое первого приближения найдется с помощью A27.8).
Вставляем это значение о*9 в формулу A27.2) и находим
соответствующее распределение радиального напряжения аг для первого
приближения. Теперь, используя значения аг и ое первого
приближения, рассчитываем функцию Н (?) и находим ав второго
приближения с помощью формулы A27.7). Постоянная С
находится из условия A27.8), по формуле A27.2) отыскивается
распределение радиальных напряжений во втором приближении. Весь
процесс повторяется до тех пор, пока два последовательных
приближения не окажутся практически совпадающими. Автор
указывает, что почти во всех случаях третье приближение дает
приемлемую точность. Оригинальный метод Бейли и другие его
модификации требуют обычно пяти или шести приближений.
При большом градиенте температур член -^ в выражении
для Н оказывается наиболее существенным. Как показали
расчеты Костюка, в этом случае сходимость процесса
последовательных приближений ухудшается, поэтому метод подвергается
некоторой модификации. Положим
1 dlnwdT __ Т
1+А дТ d\~ ¦
Тогда уравнение A27.6) можно записать в следующем виде:
d-^ + Loe = H + Lee.
Интеграл этого линейного уравнения будет следующим:
I
ae = ~[C+^(H + La&)Rdl]. A27.9)
а
504 ПЛОСКИЕ ОСЕСИММВТРИЧНЫБ ЗАДАЧИ [ГЛ. IX
Здесь
I
i? = exp \ Ld\.
а
Весь процесс последовательных приближений остается тем же,
только вместо A27.7) следует пользоваться A27.9).
Для сплошного диска применение указанного метода связано
с некоторыми неудобствами. Действительно, в выражении для И
имеются члены, содержащие | в знаменателе, и если не
потребовать дополнительного выполнения условия аг @) = сге @), то
интеграл для Ое окажется расходящимся. Чтобы обойти эту
трудность, выделим некоторую область 0 <; ? <; а, где а —
достаточно малая величина, и будем искать решение для этой области
в виде рядов
0", = о @)A + а,?я +...), ав = а@)A + Ь^+...). A27.10)
Предположим также, что вблизи точки ? = 0 толщину диска
и температуру можно представить аналогичным образом:
h = h0{l-e^+...), T = T0 + Til*+...
Подставляя эти ряды в дифференциальные уравнения A27.1)
и A27.6), найдем:
«.= -4ТГЬ5-){6 + <1 + ЗД(^-2е0-2''(^)Е=о}'
»¦= -ГЯТВ5 {6-<1 + а'> Gw-2") -Т' №).-} '
A27.11)
Здесь принято fi0 = й @). Теперь в области 0 << | <; а
напряжения вычисляются по формулам A27!9), а в области а < ? < 1 —
по способу последовательных приближений, так же, как и для
диска с отверстием.
Метод Костюка особенно удобен в том случае, когда функция
v (o*o» T) задана численно или графически.
При степенном законе ползучести более простой способ был
предложен Малининым [72]. Положим v = еп ( —- J , при этом
будем считать ап постоянной величиной, е„ — известной
функцией от температуры, а следовательно, известной функцией
от радиуса. Разделим уравнение совместности на ее, получим:
d In Be 1 f ъг л
ее
§ 127] РАСЧЕТ ДИСКОВ 505
Проинтегрируем это уравнение:
I
е6 = Сехр$ (^-l)|. A27.12)
а
Обозначим отношение — через р\ тогда а0 = A + Р2 — РI/2 сте
и, в соответствии с принятым законом ползучести,
и = гпA){2) (l + f^-P)
Скорости деформации выразятся следующим образом:
Отсюда следует, что
86 2 — р
Теперь A27.12) перепишется так:
о
Положим
¦ ГО-Ш-Р-И^ A-|р)'"Мр L -I j И|] ¦
о
Тогда
сх9 = <Тп(?I/ГЧШ. A27.13)
Теперь по способу последовательных приближений решаются
уравнения A27.2) и A27.13). Для определения константы С
по-прежнему используется уравнение A27.7), которое приводится
к следующему виду:
1
a
В работе [,2] рекомендуется в качестве исходного приближения
принимать то распределение напряжений, которое соответствует
упругому состоянию диска. Очевидно, что можно поступать
506 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
и иначе, например задаться в начале предположительным
распределением величины Р по радиусу. Так, для сплошного диска,
свободного от контурной нагрузки, всегда р* @) = 1 и р A) = 0,
поэтому кривая типа параболы будет служить
удовлетворительным приближением. За дальнейшими деталями, касающимися
метода последовательных приближений, отсылаем читателя
к оригинальным работам. Там же содержатся примеры расчетов,
которые мы здесь не воспроизводим.
§ 128. ДРУГОЙ ВАРИАНТ МЕТОДА
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Подобно тому, как это делается обычно при расчетах дисков
из упругого материала, систему уравнений равновесия и
совместности можно заменить одним уравнением второго порядка,
которое теперь будет нелинейным. Для решения этого уравнения
можно опять-таки воспользоваться методами последовательных
приближений. Один из вариантов такого расчета, предложенный
в работе [98], излагается ниже.
Для того чтобы удовлетворить уравнению равновесия A27.1),
введем функцию напряжений z (?) таким образом, что
йае = гоЛ?* + ^, har = j. A28.1)
Положим
Тогда скорости деформаций выразятся следующим образом:
ег = ехр(-х) [1_^_1тЛ|»] ,
ее = ехр( — и) [щ + mhf — у-|-] .
Внеся эти выражения в уравнение совместности деформаций,
после несложных преобразований получим следующее
дифференциальное уравнение для z (?):
(iO'-f =-^аE+Л'О+к'/гК09_^(Тг)' A28-2)
Рассмотрим для определенности следующие граничные условия:
сгг (а) =/rap, or(i) — mq.
Обозначим правую часть уравнения A28.2) через то/ (?) и будем
решать это уравнение при заданных граничных условиях по
способу вариации произвольных постоянных. Получим, следуя
§ 128] ДРУГОЙ ВАРИАНТ МЕТОДА ПОСЛЕДОВ. ПРИБЛИЖЕНИЙ 507
известной процедуре:
z(l) = mllCi + fi^)]+^[C2-f2{l)].
Здесь Ci и С2 — постоянные, подлежащие нахождению из
граничных условий, функции /i (|) и /2 (I) определены следующим
образом:
Мб) =4 $ ^ dl, h (I) =* у J / (S) I rf?- A28.3)
a 0
Теперь по формулам A28.1) мы найдем напряжения:
Лае = тГл?я + А + /1<Е)-& + *#1 ,
г С U(l)i <128-4>
har = m[cl + fi(l) + ^-t^1] ¦
Воспользовавшись граничными условиями, мы определим
постоянные Cj и С2, которые выражаются следующими
формулами:
Ci=I^fllh(i)q-a>h(a)p]-r^[fi(l)-U(l)],
Cz=-^lh(l)q--h(a)p} + T^[fi(l)-f2(i)l
В нашем случае / {?) состоит из двух слагаемых:
A28.5)
Положим
1/г + П = Я(|), x'hfaQ—g-(rr)=g(E).
Соответственно постоянные С1! и С2 состоят каждая из двух
частей, одна из них зависит от известной функции Я {?) и
граничных значений ar, другая зависит от неизвестной
функции g(|). Выделим эти известные части, положив в формулах
для Ct и Сг /(!)= —?2Я(?). Введем при этом обозначения:
S 1
яле)=4 $H{i)idi, #2(Е)=4 5ff(g)g»dg.
a a
По формулам A28.3) получим:
Сю = Г^5[ЛA)г-а"А(о)р]+г^5[Я1A)-ЯаA)],
С2о = 14^[/гA)?-/г(а)рЦ-г^[Я1A)-Я2A)].
A28.6)
508 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
Точно так же выделим из решения, даваемого формулами A28.4),
ту часть, которая соответствует случаю /(?) = —%Н(?,) и
неоднородным граничным условиям задачи. Введем обозначения:
(hoe)* = т [h? + Cl0-C-§—«i (I)~^Нг (I) ]
(Ла^т^о + ^-Я.Ш + ^/Ы!)] •
Положим, наконец,
а а
Теперь формулы для напряжений A28.4) могут быть
переписаны, после несложных преобразований, следующим образом:
1гав = (hoe)* - ^±§г} [gi A) - g2 A)J + gi (I) + p gz (?),
har = (hary + ~jff~ t^i A) - ?2 A)] + gi (I) - ~ §2 (I).
Для численных расчетов удобно ввести новые неизвестные,
а именно:
2а = о"е + о*г, 2т = о"е — ог.
Тогда по формулам A28.6) получим:
(ha)> = m[±h!* + Cl(i-Hl(l)'\ ,
(Ы)* = т [ 1 /г|2 - i (C20 + Я2 (|)) ] .
Из формул A28.7) следует:
/га = (Аа)*-^ [^ A) -ife A)] + ffi (g),
1,т /Ьт\* 1 gl(l)—g2(l) 82 (I) ^ "^
В новых переменных функция g (|) принимает вид
g(l) = ~H'h(a + 3x).
При этом Од = а2 + ЗтА В случае сплошного диска формулы
несколько упрощаются, они получаются из вышеприведенных
формул, если положить С10 = 0 в A28.6), а во всех остальных
случаях принять а = 0.
Заметим, что левая часть уравнения A28.2) представляет собою
оператор типа Штурма — Лиувилля. Обозначим его L (z). Если
A28.8)
§ 129J КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЯ 509
определить z* как функцию, удовлетворяющую уравнению
L (г*) = — т^Н (I)
и неоднородным граничным условиям, то уравнение может быть
заменено следующим интегральным уравнением:
i
2 = Z*+ $<?(?, t)tg{t)dt.
а
Здесь G (|, t)— функция Грина, определенная при
соответствующих однородных граничных условиях. Так была изложена идея
метода в статье I98]. Очевидно, что если проделать все выкладки,
мы придем к результату, приведенному выше.
В качестве исходного приближения можно взять величины
а* и т*, расчет состоит в том, что значения о и т каждого
последующего приближения вычисляются по формулам A28.9), где
функция g находится через выражения о и х предыдущего
приближения.
§ 129. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЯ
В РАВНОМЕРНО РАСТЯГИВАЕМОЙ ПЛАСТИНКЕ
Одна из немногих плоских задач теории ползучести,
допускающих точное решение,— это задача о концентрации напряжений
около круглого отверстия в пластинке, находящейся в условиях
равномерного растяжения. Применительно к деформационной
теории пластичности при степенном законе упрочнения
соответствующий результат был получен Винцером и Прагером [8831, он
может быть получен как частный случай из решения более общей
задачи, найденного Костюком [60]. Позже вопрос о концентрации
напряжений около круглого отверстия был изучен при более
общих предположениях о законе упрочнения в работе [17?].
Определение коэффициента концентрации напряжений может быть
при этом получено достаточно простыми средствами, нахождение
распределения напряжений приводит к довольно громоздким
формулам, поэтому здесь мы ограничимся только первой задачей,
а именно задачей о концентрации напряжений, в дальнейшем же
приведем в качестве независимого результата общее решение
более сложной задачи, данное в статье [60].
Итак, мы рассматриваем бесконечную плоскость с отверстием
радиуса а. Начало полярных координат мы помещаем в центре
отверстия, вводим безразмерную координату ? = In — , остальные
обозначения будут те же, что в § 125. На бесконечности оТ = а$ =
= (Ti, на контуре отверстия при ? = 0, от @) = 0. Из
формул A25.1) следует, что при ?=оо ф = я/2, при ?, = 0 ф = — ,
510 ПЛОСКИЕ ОСЕСИММВТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
следовательно, а0 (оо) = а, и а9 @) = —~±-t sin —- = а0 @). Коэф-
фициент концентрации ЛГ определится следующим образом:
* = ^ = ^=«Р1*<0)-Ф(»I-
Соответствующим выбором размерной константы а# мы всегда
можем добиться того, что а0 (оо) = 1 и ф (оо) = 0, следовательно,
Я = ехрф@). A29.1)
Уравнения A25.4) и A25.6), выведенные для вращающегося
диска, сохраняют силу и в нашем случае, в них нужно положить
т = 0 и tj = 0, так как рассматривается пластинка постоянной
толщины. Входящая во второе уравнение величина z есть
известная функция от ф, поэтому j? = z* ("Ф) jF" • Перепишем
уравнения A25.4) и A25.6) с отмеченными упрощениями. Получим:
A29.2)
-^ cos (ср — -^-J + -jjt- sin (q> - ^ J — cos ф = 0,
-^-sin^ — -f-^)— -z''7f"C0S((P — If)- K3cos9 = 0.
Умножим первое уравнение на l/З и вычтем второе. При этом
получившееся уравнение будет однородно относительно
производных, оно не содержит величины ?, следовательно, связывает
функции ф и ф. Это уравнение можно представить следующим
образом:
2созФ-^-+/38т(ф—5-)ч-2'(*)со8(ф—5-)=0. A29.3)
При ф = у ф = 0; интегрируя уравнения A29.3) до точки ф = -д- >
мы найдем соответствующую величину ф @) и, следовательно,
коэффициент концентрации по формуле A29.1). Очевидно, что
численное интегрирование возможно при любом законе
ползучести. Для степенного закона ползучести интегрирование
выполняется в конечном виде. Действительно, при степенном законе z—nxp
и z' = п.
Положим теперь
. я
Ф = ш-г-т —у-
Если выбрать угол у таким образом, чтобы было
W^C0SY' W = sinv'
§ 129] КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЯ 511
то сумма второго и третьего членов в уравнении A29.3) примет
вид cos у |/~3 + я2 и уравнение, в котором за независимую
переменную принято « вместо ф, перепишется следующим образом:
dty
rfoo
(•
я \
ь V
1/3 +«а
S1I1 (О
При (р = я/2, @ =
-q-+Y» ^ = 0, при ф —л/3 со = у, г|з = ф@);
в результате интегрирования получаем:
ч>@)=.
У3 + п2
cos
sin
ln-
я
- + Y
sin у
¦sin
--Y
Я =
Отсюда, исключая угол у, найдем следующее выражение для
коэффициента концентрации
напряжений: <?/>
2" ) 6XPV 1/3 3+«а
A29.4)
Эта формула получена в работе I1"].
Рассмотрим теперь ту же задачу,
но на основе кусочно-линейных
критериев ползучести. Будем применять те
же обозначения, что в §§ 123, 124,
положим ав = од1ап, Ът = ог1оп, Ъ = г/а, м = —
ся критерием типа Треска [115], то мы должны допустить, что на
бесконечности реализуется состояние, соответствующее точке А
(рис. 212), а при 5 = 1— точке F. К контуру отверстия
примыкает область, соответствующая стороне AF шестиугольника
Треска, так что в этой области ае > о*г > 0, следовательно, ег =
и и = const. Скорость окружной деформации ее =
Рис. 212.
Если воспользовать-
= -*L = 0
rfS
\i/n
= u/?, поэтому оге = (и/|) и уравнение равновесия получается
следующим:
Интеграл его:
п С и М/п , С
512
ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ
[ГЛ. IX
При некотором значении | = а неравенство о9 > ог обращается
в равенство, мы получаем:
Из этих условий находятся постоянные Спи, после чего формулы
для напряжений принимают следующий вид:
A29.5)
се= о-!
Теперь мы определяем радиус зоны а из условия (Тг A) = 0.
Получаем:
,n-i
а — п"
Коэффициент концентрации, согласно второй из формул A29.5),
1
К^а^п = пп'К
A29.6)
Эта простая формула приводит к значениям коэффициента
концентрации большим, чем формула A29.4). Так, при п = 1 по
формуле A29.4) мы получаем К = 2,
по формуле A26.9) К = е (если
раскрыть неопределенность).
Мы привели в § 119
уравнения, основанные на недавно
предложенном кусочно-линейном
критерии ползучести или
пластичности, получившем название
критерия наибольшего приведенного
&д напряжения, однако нигде ими
фактически не пользовались.
Задача о концентрации напряжений
около отверстия была решена при
помощи этого критерия Немиро-
вским [86], это решение мы воспроизводим ниже. Так как на
контуре аг = 0, то вблизи контура будет осуществляться
состояние, изображаемое отрезком AF на рис. 213, для этого состояния:
2?P + e"9 = 2i|+i- = 0.
Отсюда, интегрируя, находим:
,". Хп Е—1/г о 7гп Е—3Л
Через от мы обозначили константу интегрирования, смысл именно
такого обозначения константы выяснится, как только мы перейдем
Рис. 213.
% 129] КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ОКОЛО ОТВЕРСТИЯ 513
к определению напряжений. Для отрезка AF мы имеем:
s = oe-±-or = e? = omt 2™. A29.7)
С помощью этого соотношения исключим о"е из уравнения
равновесия и проинтегрируем его, учитывая граничное условие сг A) = 0.
Получим:
Ог = отТ^Тч1~~цН1-1) (v = |). A29.8)
Из A29.7) следует, что при | = 1 ае = от; таким образом, от
и есть максимальное значение ае на краю отверстия, которое
нужно определить.
При некотором значении | = а выполняется равенство
а9 = 2ог, то есть достигается точка А шестиугольника,
изображенного на рис. 213. Значение а находится из этого условия
с помощью A29.7) и A29.8), а именно:
Формулы A29.7) и A29.8) справедливы при условии 0 < | < а,
далее возникает некоторая зона, соответствующая точке А шести-
угольника, то есть такая зона, в которой о*е = 2сгг. Для
определения напряжений в этой зоне достаточно одного уравнения
равновесия, из которого следует:
аТ = А1, ов = 2АЪ A29.10)
Из условия непрерывности ог при | = а найдем:
A^^2T^a~3h- (ШЛ1)
Решение A29.10) непригодно для того, чтобы удовлетворить
условию на бесконечности, так как напряжения по этим
формулам растут неограниченно с ростом ?, следовательно, точке А
шестиугольника соответствует некоторая конечная область
а <С \ <С р. В этой области связь между напряжениями и
скоростями деформации будет следующей:
2ее + ег
или
du . 2и
33 Ю. Н. Работнов
(
3 - \™
та9
Ki^y
514 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
Проинтегрируем с учетом непрерывности и при | = а. Получим:
"=Cf
n-f-l An g3—а3 ~n a
При g > p реализуется состояние, изображаемое стороной АВ,
для которого е6 —ег = 0 или -^ 1- = 0. Отсюда следует, что
й = Вп\.
Константа Вп найдется из условия непрерывности при | = р,
а именно:
*" = Гт
3 >п+1 Л™
, 7
Jh
A29.13)
«+3V Р3 J ' "'"' Р3
Связь между напряжениями и скоростями в этой области будет
такой:
от + Oq = 2 (ег + ee)v.
Выражая отсюда Ое, внося в
уравнение равновесия, полагая
гг = гв = Вп и интегрируя,
получим:
o^-l-^-P^ + Ap»],
1
Л
\
\
G23.5)
"Ч
"-•—.
Г""-
"•¦7-
G2S.7L
У
G22.4)
"¦"¦,
ае = w [а4 (Б* + ря) — Лр»].
Рис. 214.
A29.14)
/7
Здесь принято
о\ = 2V?
и учтено условие непрерывности ат при | = р. Как видно, ах
представляет собою напряжение на бесконечности. Теперь
осталось определить величину р. Требуя, чтобы напряжения,
задаваемые формулами A29.14), соответствовали точке А для ? = Р,
получим:
Р = |§-. A29.15)
Теперь из уравнения A29.13) можно исключить все величины,
кроме ат и at. Действительно, В отличается от at лишь
множителем, А по формуле A29.11) выражается через ат, Р исключается
с помощью A29.15), а —известное число. После всех
исключений для коэффициента концентрации К = ат/а1 получается
§ 130]
ДИСК ГИПЕРБОЛИЧЕСКОГО ПРОФИЛЯ
515
следующая формула:
Я=C)^[^±3] 9-п* _ A29Л6)
На рис. 214 построен график зависимости величины К от
показателя п по всем трем формулам: A29.4), A29.6) и A29.16). Нужно
отметить, что разница получается довольно значительной,
особенно велика она при п = 1, когда первая формула дает К = 2,
это известное решение теории упругости, по второй формуле
получается К = е = 2,718, по третьей, наконец, К = 1,438.
§ 130. ДИСК ГИПЕРБОЛИЧЕСКОГО ПРОФИЛЯ,
НАГРУЖЕННЫЙ РАДИАЛЬНЫМИ СИЛАМИ
Наиболее общее решение плоской осесимметрической задачи
теории ползучести при степенном законе удалось получить
Костюку [60]. Он рассмотрел диск гиперболического профиля
с наружным радиусом Ъ и внутренним радиусом а, при этом
безразмерный радиус ? = г 1а. Толщина пластинки есть степенная
функция радиуса h= h0l,~~ . Уравнения равновесия и совместности
деформаций будут следующие:
^(Г^г) + (о-г-ае)Г1_^ = 0, A30.1)
^ + ??=?г = 0. A30.2)
Будем считать, как и прежде, что безразмерные напряжения
и скорости деформаций определены таким образом, что при
простом растяжении е = ап или а = ev, следовательно,
ее = оо ' (oe + yovj , бг=Оо ' fov + уаЛ . A30.3)
годится
A30.1) следует:
Далее вводится новая переменная ю = —— . Тогда из уравнения
Действительно, A30.1) можно переписать следующим образом:
^ln(rWo)-^ = 0,
откуда и получается A30.4).
Совершенно аналогичным образом, если ввести в A30.2)
напряжения вместо скоростей деформации по формулам A30.3)
33*
516 ПЛОСКИЕ ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ [ГЛ. IX
и ввести параметр да, то из уравнения A30.2) следует:
1-V
Сте=д {LJr е*К-3у\-2^т)- (m5)
Приравнивая правые части A30.5) и A30.4), мы получим
некоторое интегральное соотношение для определения со; взяв от обеих
частей этого равенства логарифмические производные, получим
следующее дифференциальное уравнение:
1 d\ _ 1 (ш-2J + Зусо2 /140f^
% da, 2A —X—3v)(l—и + со2)(ш—Pl)(co—p2) " K^v.vf
Здесь
_3A —v)—2Я j;l/9v2 + 6v(i+A) + (l—Яр
Р^'— 2 A-Я—Зу)
Уравнение A30.6) интегрируется, таким образом мы получаем
зависимость радиуса | от параметра со:
| = X(l_(B + lD»)«|<a_p1|P|(B_pa]VeXp^fiaictg2^i^ A30-7)
Здесь А — постоянная интегрирования, остальные константы
имеют следующие значения:
3(l-v)(l-2X-3y) R (Р1-2J + Зу/>1
4ДA-Х-ЗуJ ' Р 2(l-J.-3v)(pi-p2)(l-p1+jpi)'
(р2— 2J + 3vp| o_3"l/3 1 — у2
Y 2A-А-Зг-)(Л~й)A-й+;»1)' _ 2 ДA-Л-ЗуJ-
A=(l-Pl + Pl2)(l-p2 + ^).
Теперь в соотношении A30.4) либо A30.5) мы можем заменить
-^- с помощью A30.6) через некоторую функцию со, умноженную
на с/со. В результате выполнения квадратур получаем
представление о9 через со, а именно:
o-e = 5(l-co + co2)*|co-/p1|!|co-/72rexp(?arctg2^=i). A30.8)
Здесь В — постоянная интегрирования, тогда как
1-уГ1 3 М2Х-1) + 6у(у + ХП /=_6ГХ + Зг^^1
*" 2 L 2 ДA_Х-Зу2) J' *~ Р L^^-^V ^_2 J ,
.. Г* i д.. Рг-i "I „ ЗУЗ A-у)(Х + 2у)
m=-YL?i + 3v^—2J, д= 2~ТA-Х-ЗуJ •
Таким образом, формулы A30.7) и A30.8) дают общее решение
поставленной задачи, представленное в параметрической форме,
о"е, 0г = соо"е и ? выражены как функции параметра и.
ГЛАВА X
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
ПЛАСТИН И ОБОЛОЧЕК
В этой главе рассмотрена общая теория ползучести пластин
с учетом усилий, действующих в срединной плоскости, свойства
соответствующих потенциалов ползучести и возможность частичной
линеаризации уравнений. Далее разбираются задачи о
симметрично загруженных круглых пластинах, допускающих
относительно простое численное решение, а в некоторых случаях
решаемые в замкнутом виде.
При изложении теории оболочек автор ограничился безмо-
ментными оболочками, в том числе многослойными, а также
развитием приближенной теории, основанной на замене
реальной оболочки двухслойной моделью. Для осесимметричных
цилиндрических оболочек, в частности, эта приближенная теория
позволяет получить достаточно простые уравнения, являющиеся
уравнениями Эйлера некоторого функционала.
§ 131. ИЗГИБ ПЛАСТИН.
ОСНОВНЫЕ УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ
Как обычно, пластиной мы будем называть тело,
ограниченное двумя параллельными плоскостями и нормальной к ним
цилиндрической поверхностью. Расстояние между плоскостями,
называемое толщиной пластины, обозначим 2/г. Предполагается,
что толщина мала по сравнению с наименьшим линейным
размером той фигуры, которая образуется в пересечении граничного
цилиндра и граничной плоскости. Назовем срединной плоскостью
пластины плоскость, равноотстоящую от граничных плоскостей,
выберем прямоугольные декартовы оси координат таким образом,
чтобы плоскость хОу совпадала со срединной плоскостью. Тогда
z = ± h есть уравнение граничных плоскостей и F (х, у) = 0 —
уравнение граничной цилиндрической поверхности. Вместо
518 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
обозначений х и у примем обозначения хх и х2 в соответствии с общей
системой, но сохраним для третьей координаты обозначение z
ввиду ее особой роли. Единичные векторы, направленные вдоль
координатных осей, обозначим еи е2, к соответственно. Радиус-
вектор любой точки М пластины может быть записан так:
r — xlel + x2e2 + zk. A31.1)
Положим q = Хув^ -\- х2е2. Точка Р, радиус-вектор которой
есть q, является проекцией точки М на срединную плоскость,
она отстоит от точки М на расстоянии z. Предположим теперь,
что пластина изгибается и растягивается, но перемещения ее
точек малы в том смысле, в каком это понимается в линейной
теории упругости, это значит, что производные от перемещений
по координатам пренебрежимо малы по сравнению с единицей.
Гипотеза Кирхгофа, обычно принимаемая в теории изгиба
пластин, означает, что взаимное расположение точек Р и М
сохраняется в процессе деформации. Отрезок РМ, нормальный к
срединной плоскости пластины до деформации, остается нормальным
к той поверхности, в которую переходит срединная плоскость,
и сохраняет при этом неизменную длину z. Обозначим
положения точек РжМпосле деформации соответственно Р' и М'. Радиус-
вектор точки Р'
Q' = (#i + Щ) ei + (х2 + щ) e2 + wk.
Здесь через щ, и2 и w обозначены перемещения точек срединной
поверхности, являющиеся функциями х1 и х2. Вследствие
гипотезы Кирхгофа радиус-вектор точки М' будет
г' — q' + zn.
Здесь п — вектор единичной нормали к деформированной средней
поверхности. Линии xt = const и х2 = const определяют
координатную сетку на деформированной средней поверхности,
касательные к этим линиям векторы образуют базис
Здесь, как обычно, индексы после запятой обозначают
дифференцирование по соответствующей координате xt. Имеем:
е[ = A + «J, i) €i + u2i ±е2 + ш, tfc,
е2 = щ,2е% + A + "г, г) е2 + w, 2k.
A31.2)
Единичный вектор нормали ортогонален векторам е± и е2,
следовательно,
п= eiXe2
I «i X е2 | '
§ 131] ИЗГИБ ПЛАСТИН. УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ. 519
Опять-таки с точностью до малых величин второго порядка
малости получим:
п = — w, i^! — wt 2е2 + к.
Теперь мы можем написать выражение для г':
г' = (xi + щ — zw, j) в! + (х2 + u2 — zw, 2) е2 + (г + ы>) &•
Величины U! — ги?^, u2 — zu>j2, w представляют собою
компоненты перемещения произвольной точки М по отношению к
исходной системе декартовых координат хи хг, z, следовательно, по
обычным формулам мы можем вычислить компоненты
деформации:
ец = Щ,1 — ®в,и, e22 = u2,2—zwj22,
1 / , ч п A31-3)
ei2 = y(^i,2 + W2,i) — ZU7,i2, eJ3 = е23 = е33 = 0.
В условиях ползучести нас будут интересовать скорости
деформации, которые получаются немедленно дифференцированием
соотношений A31.3), а именно:
еи =Щ i — ZWn, 822 = U2,2—ZM>,22.
! . . • A31.4)
8l2 = у ("i,2 + «2,l) — 210,12.
Вследствие линейности A31.3) оказывается, что скорости
деформации выражаются через скорости перемещений точно так же,
как деформации — через перемещения. Мы подчеркиваем это
обстоятельство потому, что в нелинейной теории положение
существенно меняется, там скорости деформации зависят не
только от скоростей перемещений, но и от самих величин
перемещений.
Однако даже в геометрически линейной постановке задача
о ползучести пластин остается достаточно сложной. Следующий
шаг будет заключаться в том, чтобы ввести усилия и моменты
и использовать условия равновесия.
Как обычно, напишем уравнения равновесия:
0"ll,l + 0-12,2 +013,3 = 0.
О1,1 + О-22J + О-23K = 0. A31.5)
СТ31,1 + СТ32,2 + а33,3 = О-
При этом мы считаем объемные силы отсутствующими и
граничные плоскости свободными от касательных напряжений,
действующие на них нормальные нагрузки равны q+ и q~
соответственно, так что о33 (h) = q+, сг3з (—Щ — — Ч~-
Проинтегрируем уравнения равновесия A31.5) по z в пределах от —А до
520 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
-\-h. Введем при этом обозначения:
TtJ= \ audz (i,j = l, 2).
-л.
Первые два уравнения дадут
^11,1 + ^12,2= 0, 7'M,l + 2,22,2 = 0. A31.6)
Интегрируя по z члены вида а13,3! мы получим выражение
°13 (+ Л) — о а (— /г) и второе аналогичное. Эти выражения
обращаются в нуль вследствие сделанного допущения о том, что
граничные плоскости несут только нормальную нагрузку.
Положим, далее,
+л
jj a3idz = Ni.
-h
Тогда из третьего уравнения равновесия следует:
Nui + q = 0. A31.7)
Здесь q = q+ + q~ — полная поперечная нагрузка на пластину.
Величины Tij мы будем называть усилиями, величины Nt —
перерезывающими силами.
Введем теперь моменты Мц, определив их следующим образом:
+л
M,j = — jj zav dz.
-h
Чтобы получить уравнения моментов, умножим каждое из
уравнений A31.5) на г и проинтегрируем по толщине. В первом
уравнении, например, первый и второй члены будут производными
от соответствующих моментов по координатам, тогда как третий
член придется интегрировать по частям, а именно:
-Н +л
\ ff13,3z dz = <r13z _h — \ al3dz= —JVd.
-h -h
Точно таким же образом мы поступаем со вторым уравнением,
в результате получим:
Mu,i + M12,2 + A'i = 0,
^2.,'l + M22,2 + iV2 = 0. A3L8)
Рассмотрение третьего уравнения равновесия, получающегося
таким образом, уже излишне. Действительно, при этом мы должны
-Hi +h
будем ввести новые характеристики типа \ cr31z dz и \ cr33 dz.
-h -h
§ 132]
ПОТЕНЦИАЛ УСИЛИЙ И МОМЕНТОВ
521
§ 132. ПОТЕНЦИАЛ УСИЛИЙ И МОМЕНТОВ.
ОСНОВНЫЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ ПЛАСТИН
Как следует из определения, величины Тц и Мц представляют
собою двухмерные симметричные тензоры второго ранга, число
их компонент равно шести. Соответственно состояние ползучести
пластины описывается при помощи трех компонент скорости
деформации срединной поверхности и трех величин wtiJ, которые
характеризуют изменение кривизны. Обозначим скорости
деформации срединной поверхности через e°j, так что
e?J = T(»U + "J,0 (i,/ = 1,2). A32.1)
Соответственно назовем величины w^j скоростями изменения
кривизн и положим
*ij = ut,ti. A32.2)
Введение этих обозначений имеет тот смысл, что все дальнейшее
будет справедливо не только по отношению к выбранной нами
первоначально из соображений простоты системе декартовых
ортогональных координат, но и для произвольных компонент
соответствующих тензоров, выражения же этих компонент через
соответствующие векторы перемещения будут, вообще, другие.
В линейной теории формально они будут записываться точно,
так же, но индексы после запятой нужно будет понимать как
символ ковариантного дифференцирования. В нелинейной теории
формулы придется заменить другими, однако связь между
тензорами 8°;, Xjj, с одной стороны, Tij и Мц, с другой стороны,
остается неизменной, если деформации предполагать малыми.
Теперь ги = efj — zx^, если i, f = 1, 2, гц = 0, если один
из индексов равен трем.
Задать закон установившейся ползучести для материала —
это значит задать потенциал напряжений U (е,;), таким образом,
функция U предполагается известной. Напряжения выражаются
при этом следующим образом:
dU(eu)
Но отличные от нуля компоненты скорости имеют вид е?;-— zxy*
следовательно, функцию U можно рассматривать как функцию-
от &\j и Kij, содержащую z как параметр. Очевидно, что
дЦ __ &U_ _ dU J_
522 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Напишем теперь
_ дЦ
aiJ~ ^ь
и проинтегрируем обе части этого равенства по z в пределах
от —h до -}-h. Получим:
—a ft
Здесь С7*= \ U dz. С другой стороны, напишем
1 dU
Умножим обе части этого равенства на —z и проинтегрируем.
Получим:
-h
В дальнейшем мы не будем отмечать функцию U звездочкой,
а для деформаций средней поверхности примем обозначение ег/,
функция U (ey, %ij) может быть названа потенциалом усилий
и моментов для пластины, так как
Г« = -^-'^ = "^- A32-3>
Заметим, что из A32.3) следует существование взаимных
формул:
ЭФ дФ ..„„ /ч
Здесь Ф(Тц, Mtj) — потенциал скоростей деформации средней
поверхности и изменений кривизны. При этом
0 = TTaera + MTtxr,-U. A32.5)
Действительно, продифференцируем A32.5) по Тц, получим:
дФ _, d&TS . м d-aTS dU ders dU dxrs
¦ eij -r Irs W7T + m r
dTtj "» ' ™ dTtj ' " dTtj dzrs 8TtJ dxrs dTu •
Все члены в правой части, кроме первого, взаимно уничтожаются
попарно вследствие A32.3), таким образом доказывается первая
из формул A32.4). Доказательство второй формулы совершенно
.аналогично. Легко убедиться в том, что выражение
Ь = Тиви + Михи
§ 133] ЧАСТИЧНО ЛИНЕАРИЗИРОВАННЫЕ УРАВНЕНИЯ 523
представляет собою мощность диссипации энергии при
ползучести. Соотношения между усилиями и моментами, с одной
стороны, скоростями деформации и изменения кривизны, с другой
стороны, по форме совершенно аналогичны соотношениям между
напряжениями и скоростями деформации при ползучести, поэтому
можно назвать эти величины соответственно обобщенными
напряжениями и обобщенными скоростями деформации, все общие
теоремы теории установившейся ползучести допускают при этом
простую перефразировку. Фактическое нахождение потенциала
усилий и моментов, то есть функции U (etj, хц) затруднительно,
при каждом конкретном законе ползучести необходимо вычислить
соответствующие интегралы. Еще более сложно записать в явном
виде функцию Ф (Т ц, Ми). В дальнейшем мы обратимся к
рассмотрению частных случаев закона ползучести, пока что
продолжим исследование в общей постановке.
Заметим прежде всего, что с помощью уравнений § 131 и
формул A32.3) мы можем получить полную систему уравнений для
нахождения трех неизвестных скоростей: ui и w. Два первых
уравнения мы получим непосредственно, если подставим
выражения Тij по формулам A32.3) в уравнения равновесия A31.6)
и заменим гц и к^ через производные от перемещений с помощью
A32.1) и A32.2). Далее, из A31.8) следует:
Nt=-MtJlJ.
Подставляя в A31.7), получим:
MtJlt)-q=0. A32.6)
Внеся сюда выражение Мц через потенциал и заменяя еу и ху
через производные от перемещений, найдем третье уравнение.
В отличие от упругой пластины уравнения изгиба и
уравнения, описывающие деформацию срединной плоскости, не
распадаются на две независимые системы. Мы не будем выписывать
эти уравнения, поскольку использевать их фактически все равно
не сумеем, в общем случае мы рассмотрим лишь такие задачи,
в которых они допускают частичную линеаризацию.
§ 133. ЧАСТИЧНО ЛИНЕАРИЗИРОВАННЫЕ УРАВНЕНИЯ
ПОЛЗУЧЕСТИ ПЛАСТИН
Здесь мы рассмотрим две частные возможности, которые могут
возникнуть при решении определенных классов задач.
а) Основное напряженное состояние пластины есть плоское
напряженное состояние с равномерным распределением
напряжений по толщине, напряжения изгиба малы по сравнению
с основными напряжениями. Потенциал напряжений зависит от
524 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
аргументов гц — гх,ц. Считая, что | г&ц \ <С | Ъц \, разложим
в ряд по zxu функцию U0(sij — zXij), ограничившись первыми
степенями Kij. (Мы употребили обозначение U0 для потенциала
напряжений, поскольку условились в этой главе обозначать
через U потенциал усилий и моментов)
dU0
U = U0 (?tj) — ZX
rs
де
rs
Здесь U0 зависит только от е^. Теперь напряжения определятся
следующим образом:
--"' -,^%-- ASS.1)
"" дги "ге деи ders
Проинтегрируем обе части этого равенства по толщине. Получим:
Умножим обе части равенства A33.1) на z и проинтегрируем
по толщине. Получим:
2й3 dW0
М
13 3 дги deTS
Будем называть потенциалом усилий U (e?j) функцию U0 (г^),
умноженную на 2h. Введем еще обозначения:
3 d&ij ders
Тогда мы получим формулы:
г« = -Щ7' MiJ = ?>""Хм- A33-2)
Уравнения A31.6) после подстановки в них величин Гу примут '
следующий вид:
Т д2и с .-О
Il^J- двиде„ E™>J~U
или же
flyr*,,j = 0. A33.3)
Этой системы уравнений достаточно для определения скоростей
деформации срединной поверхности, которые находятся
независимо от прогиба.
Теперь мы должны подставить выражения для моментов
в A32.6) и получим следующее уравнение для функции w:
{DUrW,r.),t}-q = 0. A33.4)
§ 133] ЧАСТИЧНО ЛИНЕАРИЗИРОВАННЫЕ УРАВНЕНИЯ 52&
Это линейное уравнение четвертого порядка с переменными
коэффициентами, которые являются известными функциями
координат, поскольку решение первой задачи о нахождении плоского
напряженного состояния в пластине считается известным.
Нетрудно убедиться, что уравнение A33.4) является
условием минимума следующего функционала:
1 = \ \ [~2D^klW'i^W'kl —1W~] dxi dx*-
Это замечание позволяет искать приближенные решения
уравнения A33.4) с помощью вариационного метода.
Уравнение A33.4) совершенно совпадает с уравнением изгиба
упругой анизотропной пластины, величины DijM играют роль
коэффициентов анизотропии.
б) Основное напряженное состояние есть состояние изгиба,
скорости деформации точек срединной поверхности малы по
сравнению со скоростями деформации точек, принадлежащих
граничным плоскостям z = ± h, то есть | е^ | <С | zxjj | . Разложение
для потенциала напряжений получается следующим:
U0=U0(- ZKtJ) — y -Щ- 8у.
Следовательно,
1 ди0 1 дЮ0
Оц= —
z дЩ] z2 dy,ij dx.TS
Здесь Uо рассматривается как функция аргументов — гху.
Проинтегрируем обе части по толщине, получим:
+h +h
—л —л.
Умножим теперь обе части выражения для Оц на z и
проинтегрируем. Получим:
-ft -ft
Теперь для нас будет существенно, одинаков ли закон
ползучести при растяжении и сжатии. Мы ограничимся при
дальнейшем исследовании тем случаем, когда этот закон одинаков,
следовательно, [/(—zxij) = U(zXij). Тогда, очевидно, первый интеграл
в выражении Ttj и второй интеграл в формуле для Мц
исчезнут. Назовем величину
U = \ U0 (— z%ij) dz
-л
526 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
потенциалом моментов, положим также
+h
п °2 ? тт I \dz
-h
Тогда
MtJ = -gL, Ttl = Cmi4l. A33.5)
Теперь уравнение A32.6) приводится к следующему:
Это уравнение содержит одну независимую функцию и>. Вторая
группа уравнений A33.5) выражает усилия через скорости
деформации по формулам, которые совершенно аналогичны формулам
связи между усилиями и деформациями в линейно-упругой
анизотропной пластине, причем коэффициенты анизотропии являются
известными функциями координат.
§ 134. ПОЛЗУЧЕСТЬ ПЛАСТИН ПРИ ИЗГИБЕ
Если граничные условия задачи таковы, что на контуре
пластины отсутствуют силы, расположенные в ее плоскости, то
усилия Tjj тождественно равны нулю (пока мы ограничиваемся
линейным приближением) и ползучесть при изгибе полностью
описывается уравнением A33.6). Уточним теперь вид закона
ползучести, а именно примем, как в § 99, что потенциал
ползучести зависит от некоторой инвариантной функции v первой
степени от компонент тензора скоростей деформации егу. Если
&и = — zxtj, то v = zk вследствие однородности и к
представляет собою выражение, образованное точно таким же способом
из компонент х^, как v было образовано из е^-.
Теперь потенциал моментов будет определяться следующим
образом:
+hh hh
U{k) = -^ \и0{1)й\ = ^-\и0{1)^. A34.1>
-hk 0
Второе выражение написано в силу того, что ползучесть при
растяжении и при сжатии предполагается следующей
одинаковому закону. В противном случае, как мы видели в § 133, изгиб
будет сопровождаться деформацией средней поверхности, и эти
два вида деформации необходимо рассматривать одновременно,
усилия в средней поверхности возникнут и при соответствующих
нулевых граничных условиях. Теперь выражения для моментов.
§ 1341 ПОЛЗУЧЕСТЬ ПЛАСТИН ПРИ ИЗГИБЕ 527
перепишутся следующим образом:
Mu = U'{k)-^. A34.2).
Не составляет труда написать и обратные формулы. Поступая,
так же, как в § 99, мы определим однородную функцию первой
степени т {Ми), которая выражается через к. Потенциал
скоростей изменения кривизн
Ф = V (к) к — U (к) = Ф (т).
Следовательно,
Щ} = ф'{т)^-. A34.3).
Выпишем формулы связи между моментами и кривизнами для
критериев ползучести типа Мизеса и типа Треска при степенном
и экспоненциальном законах ползучести,
а) Критерий типа Мизеса. Положим
т2 = М\ = Ml + Ml - МпМ22 + -| (Ml, + Mlh
к2 = *\ = у [ «L + >4 + «11*22 + у (*?, + О ] •
Тогда получим следующие формулы:
2 U'(K0)
3 х0
м12=4^-^>с
Подставляя в выражение для М\, найдем, что
U'(xo) = M0. A34.4>
В некотором отношении более удобной является следующая,
запись вышеприведенных формул:
4 Мо<*0) /' , 1 Л м _AMo(*o) Л ,1
Mll="^^~DXll+2"X2V' ^22-у—^— ^ ^22+2 *П
A34.5>
„ _ 2 М0 (хр)
Обращение формул A34.5) будет следующим:
xq(Mq) ( м 1 м \ _ хр (Afp) / м 1 м \
3 хр (М0) м
Xl2=T М0 Ml2'
A34.6)
528 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Вычислим функцию М0 (х0) для степенного закона ползучести.
В этом случае
1+4-
г7о(е) = -^рг(Т'«е™
п [ г
Вычисляя по формуле A34.1) U (х0), найдем следующее
выражение:
В этой формуле принято
Отсюда следует на основании A34.4):
?-(-?)"¦ <134-8»
Соотношение A34.8) совершенно совпадает с основным
уравнением, связывающим момент и скорость изменения кривизны
при изгибе балки, а выражения для Мп и кп получаются теми
же, что для балки прямоугольного сечения с высотой 2А и
шириной, равное единице. Это и естественно, при рассмотрении изгиба
узкой полоски, вырезанной из пластины, Мц и х0 становятся
¦соответственно изгибающим моментом и скоростью изменения
кривизны в плоскости изгиба.
Теперь для экспоненциального закона ползучести мы можем
просто взять то соотношение между моментом и скоростью
кривизны, которое было найдено для балки в § 106. Как уже
выяснено, особенность экспоненциального закона для области малых
напряжений, то есть малых z, не сказывается существенно на
зависимости между М и х, поэтому мы воспользуемся
формулой A06.8):
Ме V хе J 2 ¦
Здесь A34.9)
Me^aeh2, не = -^-.
б) Критерий типа Треска. Применение этого критерия
приводит к простым результатам лишь тогда, когда нам заранее
известны главные направления. Соответствующие изгибающие
моменты будут Л/\ и М2, скорости изменения кривизн и, и х2.
§ 134]
ПОЛЗУЧЕСТЬ ПЛАСТИН ПРИ ИЗГИБЕ
529
м2
в
с/
в
\
у
/F М,
?
Рис. 215.
Скорости деформации в точке с координатами хи х2, z будут
e-i = — zxj, е2 = — zx2. Этим скоростям деформации
соответствуют напряжения, распределение
которых определяется
распределением скоростей в соответствии с
рис. 215, представляющим собою
шестиугольник Треска для
моментов. Разберем все возможные при
этом случаи поочередно:
1. и1>0,х2>0, г± >0, е2>0
при z<0, et<;0, е2<С0 при z>0.
Обе скорости одновременно
положительны тогда и только тогда,
когда напряженное состояние
изображается точкой А
шестиугольника Треска, следовательно, а1=сг2>0
при z <Z 0. Области
положительных z точно так же соответствует точка D. Скорости ползучести
связываются при этом следующим условием {§ 119):
?j + s2 = y(a1) или cr1 = 02 = s(E1 + e2).
Это соотношение справедливо как для точки А, так и для точки D,
поэтому всюду по толщине пластинки
О"! = <Х2 — S [ — Z (X! + Х2)].
Умножая на z и интегрируя, находим:
М^Мг=т{щ + щ). A34.10)
Здесь функция s та же, что функция, определяющая закон пол-
/ \ dUn т->
зучести при одномерном растяжении, то есть s (е) = -=— . Ь
результате интегрирования мы получаем функцию U (к), и,
следовательно, т (к) = V (к), как и в предыдущем случае A34.4). Закон
ползучести можно теперь записать либо в форме A34.10), либо
в форме
.Xf-MtMi), nz = {l—k)k{Ml), 0<Д,<1. A34.11)
2. и2 = 0, щ > 0, е2 = 0, Si < 0 при z > 0 и Et > 0 при
z <Г 0. Напряженное состояние изображается сторонами AF
и CD шестиугольника Треска, и мы легко получим:
М, = ш(х1), щ = к(М^. A34.12)
3. xt > 0, х2 <С 0. Напряженное состояние соответствует
точкам F и С либо В и Е шестиугольника Треска, в первом случае
Мг = 0, тогда как
Ml~m(Ki),xi = k(Mi). A34.13)
34 Ю. Н. Работнов
530 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Величина х2 остается при этом неопределенной. Во втором случае
М2 = т(к2), к2 = к(М2); A34.14)
неопределенной остается величина щ.
4. щ=—х2. Напряженное состояние соответствует
сторонам СВ и EF,
Mi — Af2 = m(x1 — х2), щ — х2 = к (Mt — М2). A34.15)
Совершенно подобным образом можно было бы рассмотреть
ползучесть пластин по критерию наибольшего приведенного
напряжения.
§ 135. ПОЛЗУЧЕСТЬ КРУГЛЫХ ПЛАСТИН
ПО ТЕОРИИ ТИПА МИЗЕСА
Задачи о ползучести круглых, осесимметрично загруженных
пластин изучены лучше всего. Эти задачи являются одномерными,
поэтому получающиеся дифференциальные уравнения могут быть
проинтегрированы, по крайней мере численно. При
использовании квадратичного критерия ползучести вообще возможны только
численные решения, метод получения таких решений мы здесь
и рассмотрим.
Для осесимметричной деформации круглой пластины
радиуса Ъ мы обозначим через Мг и Me соответственно радиальный
и окружной момент, через хг и %% — соответствующие скорости
изменения кривизн. При этом по формулам A34.5) предыдущего
параграфа
М9=4^(х6 + 1хг), A35.1)
«S ^= у («* + «§ +«г«е)-
Скорости изменения кривизн найдутся по формулам A32.2),
в которых нужно теперь понимать дифференцирование прогиба w
как ковариантное дифференцирование.
Учитывая, что единственной независимой переменной является
радиус г, получим:
d2w 1 dw
Исключая из этих соотношений w, мы найдем следующее
уравнение совместности скоростей изменения кривизн:
* (гхе)-хг=0. A35.2)
§ 135]
ПОЛЗУЧЕСТЬ КРУГЛЫХ ПЛАСТИН
531
Уравнение A35.2) совершенно аналогично уравнению
совместности скоростей A25.5) для осесимметричной деформации.
Далее, запишем уравнения равновесия A31.8) в полярных
координатах. Второе из них выполняется тождественно (если
индекс г отождествить с индексом 1), первое же примет
следующий вид:
-^(rMT)-MQ + rNr = 0. A35.3)
Кроме того, вследствие A31.7)
-L(rlVT) + rq = 0. A35.4)
При решении конкретных задач удобно бывает иметь дело
непосредственно с системой A35.2) — A35.4), не производя
исключения неизвестных и приведения системы к одному уравнению
второго порядка. Применяя ту же идею, которая была реализована
для дисков в § 125, мы положим:
Mr = ^M0sin(cp-f), Me = ^=-Mosin(q> + -5-). A35.5)
Из этих тождеств по формулам A35.1) следует:
3
хт— 2
к0 cos Г ср + -j-j , щ = -j к0 cos ( ф — -j-j . A35.6)
Теперь мы вносим выражения A35.5) для моментов в уравнение
равновесия A35.3) и выражения A35.6) для скоростей изменения
кривизн в A35.2). Получим:
9'Jifcos(\p —-^Л+ЛЗГ'вшЛр—-g-")-yCoscp-f-# = 0,
-.л- (I35-7)
Ф к sin ( ф g- 1 — к cos ( ф „- 1 — к ~- cos ф = 0.
Здесь
lCt—M± i-i^SL /V-^5— ?-— id'—^2.
Мх ии,- произвольные константы, имеющие размерности
силы и скорости изменения кривизны соответственно, выбранные
таким образом, чтобы связь между М0 и х0 можно было записать
в виде и = х (М). Уравнения A35.7) весьма сходны с
уравнениями A25.4) и A25.6) для диска в случае постоянной толщины,
разница состоит лишь в последнем члене левой части первого
уравнения, соответствующего нагрузке на пластину. Эти
уравнения написаны в несколько иной форме* сейчас мы не
вводили в качестве независимой переменной логарифм радиуса и в
34*
532 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
качестве одной из искомых функций In m, подобно тому как это
было сделано в § 125. Для целей численного интегрирования
практически безразлично, какой из этих форм пользоваться.
Перерезывающая сила N для сплошной пластины находится
немедленно из A35.4). Действительно,
г
о
Для случая сосредоточенной силы Р, приложенной в центре,
лт Р лт Р h УЗ Р
Для распределенной нагрузки
Nr^=-^-, N = q%, здесь q = ±?^-.
В самом общем случае всегда можно принять
# = ?!>(&).
где я|з (?) — известная функция от |, q — некоторый
безразмерный параметр нагрузки. В зависимости от условий закрепления
функция я|> (|) может содержать некоторое количество
неопределенных констант.
Перепишем уравнения A35.7) следующим образом:
dtp = 1 Дф_(ф, М, I)
dl ^«р.л.в' A35.8)
dM _ 1 Рм (у, М, I)
dl I D(q>,M, |) ¦
Здесь
В=~^^С082(Ф~^)_5;81П2(Ф_^)'
Dv = (JV? — М cos ф) —^- cos ( ф —у )—V3 х cos ф sin (ф —-|-
DM = 2Mx cos2 ф + i^Vx sin (ф —g-
Предположим, что решение этих уравнений найдено, то есть
известны Миф как функции |. После этого прогиб находится
с помощью квадратуры. Действительно,
1 й 3 f л
rdr =*е=2-*0соз,т 6
§ 135]
ПОЛЗУЧЕСТЬ КРУГЛЫХ ПЛАСТИН
533
Введем безразмерную скорость прогиба
ь2** •
Тогда
w = ~2 \ ^cos Гф—g-J|d|. A35.9)
При фактическом интегрировании системы A35.8) бывает
несколько удобнее принять за независимую переменную угол ф.
Тогда система будет следующая:
^!__?_D_ dM __g DM
Лр ~ fe ?>ф ' йф — ё Dv '
При ручном счете преимущество состоит в том, что область
интегрирования по ф разбивается на равные интервалы и значения
тригонометрических функций от угла ф, входящих в
выражения D, Dv и DM, вычисляются заранее, после чего нахождение
этих величин на каждом этапе численного расчета требует
выполнения очень простых и нетрудоемких операций.
Если мы рассчитываем, например, пластину, свободно опертую
на наружном контуре, то граничные условия будут следующие:
Мт@) = Мв@), МГA) = 0.
Мы можем принять
Ф@) = -?, ФA) = ?.
Для пластины, защемленной по контуру, к$ A) = 0,
следовательно,
<p@) = 4L, фA)=_^.
При выполнении расчета мы задаемся значением функции М (?)
в той точке, от которой начинается счет, для сплошной
пластины—в точке | = 0. Положим М @) = и. и зададимся некоторой
величиной \i =[х4. Будем вести численное интегрирование от
? = 0 до тех пор, пока угол ф не примет то значение, которое
он должен иметь на второй границе. Конечно, это случится не
при |=1, как было бы, если бы мы точно угадали начальное
значение \к, а при некотором \ = gj. Это означает, что мы нашли
при данном значении параметра нагрузки решение задачи об
изгибе пластины, радиус которой равен не Ь, a fej = ?4Ь. Но
величина радиуса не входит явно в уравнения, она содержится
лишь в параметре нагрузки и безразмерной скорости прогиба.
Предположим для определенности, что мы рассматриваем задачу
534 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
о равномерно распределенной нагрузке. Тогда найденное
решение соответствует безразмерной нагрузке
Яг
УЗ qb*
4 ??М*'
и по формуле A35.9) мы нашли безразмерную скорость прогиба:
Wi =
иг
Повторяя расчет для различных значений цъ мы можем построить
график зависимости wt от qu являющийся универсальным графиком
для расчета пластин подобного
рода при данном законе
ползучести.
Экспоненциальный закон
ползучести обладает тем
преимуществом, что он не содержит
никаких констант материала,
кроме ае и ее, поэтому
построенный вышеуказанным способом
график является вполне
универсальным. В качестве
примера на рис. 216 приведен график
зависимости прогиба при ? = О
от q для сплошной пластины,
опертой по контуру и
нагруженной равномерно
распределенной нагрузкой ["]. При экспоненциальном законе следует
принять М* = Ме = oeh2, и* = хе = eJh, поэтому
5
4
3
2
1
О
2 3 4
Рис. 216.
Уз #з
4 оЛ2
w =
гиЪ
гЛ*
При степенном законе ползучести решение будет зависеть
от показателя степени п, однако здесь возникают другие
упрощения. Действительно, пусть будет
Предположим, что мы нашли с помощью вышеописанной
процедуры решение для какого-то произвольного значения М @) =
= ja±. Соответствующая величина параметра нагрузки есть qit
соответствующая скорость прогиба в центре "w±. Увеличим
параметр нагрузки в К раз. Первое уравнение A35.7) будет
удовлетворено, если мы примем, что величина момента М также увели-
§ 135]
ПОЛЗУЧЕСТЬ КРУГЛЫХ ПЛАСТИН
535
чится в К раз. Соответствующая скорость изменения кривизны
увеличится в отношении №, следовательно, второе уравнение
A35.7) также будет удовлетворено. Отсюда следует, что при
увеличении нагрузки в отношении К распределение изгибающих
моментов остается неизменным, величины их изменяются также
в отношении Я, скорости же прогибов изменяются в
отношении №. Получаем:
Й = Й1D-'), ш = щ(^У. A35.10)
V qi У \ 9l J
Таким образом, при данном значении показателя п достаточно
произвести только один расчет, отправляясь от произвольного
значения момента М в центре пластины. Для каждого
значения п, конечно, расчет нужно производить заново. Это свойство
степенного закона ползучести уже отмечалось в § 100 и
использовалось при доказательстве теоремы § 101.
Построение подобного рода универсальных решений для
круглых пластин при простейших граничных условиях имеет
смысл постольку, поскольку, например, круглая, свободно
опертая пластина под действием равномерно распределенной нагрузки
при равномерно распределенной температуре уже представляет
собою довольно распространенный конструктивный элемент.
В случае вращающегося диска положение совершенно иное:
сплошной диск постоянной толщины, свободный от нагрузки
на наружном крае и вращающийся при постоянном
температурном поле, встречается как элемент конструкции исключительно
редко, поэтому задачи, допускающие построение некоторых
универсальных графиков, в теории ползучести дисков носят по
преимуществу модельный характер и большого реального смысла
не имеют.
Численное интегрирование уравнений теории пластичности
для пластин при степенном законе упрочнения и деформационной
теории пластичности было развито Соколовским [134], эти
результаты немедленно переносятся на случай ползучести. Так, для
свободно опертой пластины, несущей равномерно распределенную
нагрузку, при п = 3 Соколовским получен следующий результат:
^ = 0,87-10-3 Qg-K. A35.11)
Для пластин с центральным отверстием, например, решение
будет зависеть еще от одного параметра — от отношения
радиусов, и для построения каких-либо безразмерных графиков или
таблиц, позволяющих рассчитывать всевозможные пластины
подобного типа, необходимо проделать большой объем
вычислительной работы.
536 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
§ 136. ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ
К РАСЧЕТУ ПЛАСТИН
В отличие от расчета дисков на ползучесть расчет пластин
на ползучесть заключается в первую очередь в определении
скорости прогибов, для большинства технических приложений
лимитирующим является максимальный достигнутый прогиб, а не
максимальные напряжения. Поэтому основные усилия были
направлены именно на отыскание перемещений, а не на
распределение моментов. Для определения скоростей прогибов
достаточно хорошие результаты дает метод Ритца или метод Галеркина,
при вынужденном однопараметрическом представлении
искомого решения разница между этими двумя методами
незначительна. Метод Ритца в применении к задачам изгиба пластин был
развит Качановым [82]. Соответствующее вариационное уравнение
Лагранжа на основании (96.3) запишется следующим образом:
ь ь
\ U(щ)гйг— \ q(r)w(r)rdr— min. A36.1)
а а
Здесь Ь и а — наружный и внутренний радиусы пластины
соответственно. Для фактического нахождения решения по методу
Ритца мы должны задаться прогибом в виде
w (г) = с,щ (г) + с2ф2 {г)+ .. .
Здесь функции ф; (г) удовлетворяют геометрическим граничным
условиям. Вычисляя х0, подставляем результат в A36.1); левая
часть этого уравнения будет некоторой функцией от констант сь;
минимизируя эту функцию по аргументам ct, мы найдем
наилучшее приближение в смысле Ритца.
Наиболее простая форма применения метода Ритца в подобных
задачах заключается в том, что мы принимаем за функцию q>j (г)
прогиб в соответствующей задаче теории упругости и
удерживаем в разложении w (г) только один член. Особенно удобно
строить такие приближенные решения для степенного закона
ползучести. Действительно, х0 пропорциональна си если в
выражении прогиба взят только один член, функция U0
пропорциональна х™-1, следовательно, первый член A36.1) может быть
представлен в виде c^+lIi, второй член имеет вид ctql2- Здесь 1±
и /2 — постоянные числа, которые вычисляются, как интегралы
от заданных и вполне определенных функций, тогда как q —
безразмерная нагрузка, введенная тем или иным способом.
Уравнение A36.1) принимает вид
Ci Ii—qcil2 = m\n.
137] РАСЧЕТ ПЛАСТИН ПРИ КРИТЕРИИ ТРЕСКА 537
Отсюда следует:
1/п
= ( *т* у
Качанов, пользуясь этим методом, произвел расчеты для
сплошной круглой пластины, опертой по контуру или
защемленной по контуру, под действием равномерного давления. Для
пластины, опертой по контуру, при п = 3 результат отличается
от результата, даваемого формулой A35.11), множителем 0,85
вместо 0,87.
Малинин [71] применил для решения этих задач метод Галер-
кина. Внося в уравнение равновесия A35.3) выражения моментов
через скорости изменения кривизн A35.1), он получил
дифференциальное уравнение второго порядка для одной неизвестной
функции ¦§ (г) = -=-. При степенном законе ползучести и одно-
параметрическом задании функции # (г) параметр q всюду входит
множителем, то есть возникает та же ситуация, которая была
разъяснена выше применительно к методу Ритца. Дело сводится
каждый раз к вычислению некоторых стандартных интегралов
от неизвестных функций. Для четырех простейших случаев —
сплошной круглой пластины, опертой или защемленной на
наружном краю и несущей равномерно распределенную нагрузку или
сосредоточенную силу в центре,— подсчитана зависимость
скорости прогиба в центре от величины нагрузки при различных
значениях показателя п. Очевидно, что результат всегда может
быть представлен в виде
w = kqn или w = kPn;
график зависимости коэффициента к от п для названных случаев
приведен в III томе справочника [108]. Там же дано решение
задачи о кольцевой пластине с внутренним радиусом а и
наружным радиусом Ь; пластина оперта на внутреннем контуре и
нагружена распределенной линейной нагрузкой Q на наружном
контуре. Это решение протабулировано по двум параметрам: п и
а —а/Ь.
§ 137. РАСЧЕТ ПЛАСТИН НА ПОЛЗУЧЕСТЬ
ПРИ КРИТЕРИИ ТРЕСКА
Как мы уже убедились в § 134, при использовании критерия
Треска соотношения между скоростями изменения кривизн
и изгибающими моментами получаются в точности такие же, как
соотношения между главными скоростями деформации и глав-
538 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
ными напряжениями в плоском напряженном состоянии. Если
дана точка в плоскости Мт, М$, изображающая состояние изгиба
элемента пластины, то всегда можно построить такой
шестиугольник Треска, что эта точка лежит либо на одной из сторон
шестиугольника, либо в одной из его вершин. В зависимости
от ее положения связь между моментами и скоростями изменения
кривизн будет выражаться той или иной формулой (см. § 134
и рис. 215). Таким образом, задача об изгибе пластин решается
аналогично задаче о ползучести диска, с той разницей, что в
пластинах нагрузки и граничные условия более разнообразны.
Соответственно для простых задач удается получить простые и
практически приемлемые решения. Для более сложных задач
применение критерия типа Треска снимает те трудности, которые
встречались нам при использовании квадратичного критерия
ползучести, но приводит к новым трудностям, преодолеть
которые иногда оказывается не проще. Чтобы выяснить существо дела,
рассмотрим несколько примеров. Характер внешней нагрузки
при этом оказывается существенным, в соответствии с этим мы
группируем примеры по возрастающей степени сложности. При
решении этих задач мы будем непосредственно отправляться от
уравнения равновесия; так как для каждой стороны
шестиугольника Треска кинематическая свобода деформации сильно
ограничена, то параметры изменения кривизны могут быть
представлены как известные функции от радиуса, содержащие лишь
небольшое число постоянных. Пусть, как и прежде, наружный
и внутренний радиусы диска будут Ъ и а соответственно,
положим | = rib, a = alb, определим безразмерные моменты Мг —
= МТ1М*, М% = Mq/M# и безразмерные скорости изменения
кривизны иг = «г/и,,, Ив = —- . При этом М% ии* выбираются
таким образом, чтобы соотношения между моментом и
соответствующей скоростью искривления имели вид М = m (к), где
функция, стоящая в правой части, не содержит размерных
констант ж имеет простейшую возможную форму. Так, при степенном
законе ползучести мы потребуем, чтобы было и = Ма.
Безразмерную перерезывающую силу N мы определим соотношением
N = -тт- ; в отличие от § 135 мы не вводим в это определение
Уз"
множитель -^2~. Соответственно безразмерные силы Р и
нагрузка q, определенные в том же параграфе, этого множителя не
содержат. Таким образом, уравнение равновесия мы запишем
в следующем виде:
±(tMr)-Me + lN = Q. A37.1)
§ 137] РАСЧЕТ ПЛАСТИН ПРИ КРИТЕРИИ ТРЕСКА 539
Пластина нагружена моментам, распределенным по контуру.
Предположим, что Же > Мг>0, тогда хг = -^ = 0. Здесь w
определяется так же, как в § 135; ^ = -р—• Пластина
деформируется таким образом, что —^ = •& = const. Поскольку при
нагрузке моментом перерезывающая сила равна нулю,
уравнение A37.1) принимает следующий вид:
а(|мг)=Ч!
При степенном законе
*№*,>-(?)* 0-4)-
Интегрируя, находим:
Рассмотрим частные случаи краевых условий.
а) Пластина нагружена моментом на наружном контуре,
внутренний контур свободен (рис. 217), Тогда из условия, что
JVfr(l) = u., Йг{а)=0, найдем: i
^вA _*)_?._. A37.2) Т^Ш-Х^^Щ)
При ЭТОМ ^- [ g"^ ft ,_ *
Мг^^^^-^П ри,217.
Мы предположили, что М9 = { -=- J <CMT. Проверим условия,
при которых это предположение выполняется. Получим:
g-v > _L_ [|-v _ ai-^g-1]
или
Отсюда следует, что должно быть
:тГ>*
Это неравенство прежде всего нарушается при ? = 1, таким
образом, найденное решение справедливо, если
540 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Если условие A37.3) не выполнено, то при некотором значении
| = C становится Же = Мг. Предположим, что условие Mq = Мт
выполняется в области р <С ? < 1. Для этой области уравнение
равновесия будет следующим:
Ф = 0. A37.4)
Отсюда Мт = const = \i¦= Мд, щ + хг = \in.
Для определения прогиба мы можем по произволу считать
опертым наружный или внутренний край, безразлично. Положим,
например, w (а) = 0. Тогда в области а<^<р» = #(^ — а),
где Ф определяется формулой A37.2). В наружной области
Р<?<1
cfiw 1 dw n
Отсюда
w = ^l* + Clnl + D. A37.5)
Постоянные С и D определятся из условий непрерывности
прогиба при ? = р. В результате полное решение задачи
записывается следующим образом [32S]:
*-=М»AГ-*]-'
Ме = (х(|I/И, а<?-<р,
Mr = Me = fi, Р<6<1,
uJ = -^-[-l-3p2 + 2p»lnp + 4pEI, a<?<p,
^ = -f [P'-l + 2palng], Р<?<1-
n-l
Здесь (|) и =1.
б) Пластина нагружена моментом на наружном контуре,
внутренний контур защемлен. В этом случае существует только
такое решение, в котором МТ = Же = V- Полагая w (а) =
= w' (а) = 0, найдем по формуле A37.5):
ю = -?[(Б»-а«)-2а»1п4]
Последний пример также рассмотрен в упомянутой статье Пателя
и Венкатрамана [32я].
§ 137] РАСЧЕТ ПЛАСТИН ПРИ КРИТЕРИИ ТРЕСКА 541
Как мы убедились, использование кусочно-линейного
критерия ползучести чрезвычайно упрощает интегрирование
уравнений равновесия по участкам, но зато возникает новая задача —
сопряжение найденных кусочных решений на границах областей,
которые заранее неизвестны. В рассмотренных простейших
задачах соответствующих трудностей не возникает, в примере а)
величина р — радиус неизвестной границы — определяется весьма
просто. Однако при усложнении нагрузки соответствующие
трудности возрастают.
Возвращаясь к примеру а), мы вцдим, что, по существу, это
задача о закручивании кольца равномерно распределенным по
окружности моментом, величина
которого, отнесенная к единице длины
наружного контура и измеренная в
соответствующих единицах, есть (х. Пока
выполняется условие A37.3),
соответствующая деформация носит
чрезвычайно простой характер, каждое сечение рис. 218.
кольца поворачивается, сохраняя
прямоугольную форму. Элементарная теория подобного рода
деформации закрученного кольца хорошо известна (см., например [в9]),
зависимость скорости угла закручивания от момента д. по этой
теории дается формулой A37.2), что и следовало ожидать. Но в
элементарной теории способ приложения крутящего момента никак не
оговаривается. При решении задачи на основе теории изгиба
пластинок способ приложения момента существен и формула
A37.2) применима только в том случае, если действительно во
всей пластинке Me > Мт > 0. Предположим, например, что
распределенный крутящий момент приложен не на наружном,
а на внутреннем контуре пластинки (рис. 218). Интенсивность
этого распределенного момента в безразмерных величинах пусть
будет (х/сс, тогда нагрузки на пластины, изображенные на рис. 217
и 218, будут эквивалентны в том смысле, что элементарная
теория дает для угла поворота одно и то же значение. В отличие
от предыдущего случая здесь средняя поверхность пластины
деформируется в поверхность отрицательной кривизны, поэтому,
если Мт >0, то Мв < 0, и мы находимся на стороне ВС
шестиугольника Треска (рис. 215, Мв — Мь Мт = М2),
следовательно, мы имеем:
. - 1 dw , d2w л
Интегрируя, найдем:
542 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Теперь
Mr-Me = (xe-KP)v=^j
к \v
Внесем в уравнение равновесия и проинтегрируем. Получим:
1
Мт
i[~n
к
О-
Постоянная С найдется из условия на свободном крае,
константа к —us условия на загруженном контуре, а именно:
&!/« =
2A
МГ =
апA-а-2/п)
а а-2/«_1 -
Это решение остается справедливым при любых ее. В отличие от
предыдущего случая, когда радиус срединной поверхности
оставался прямолинейным, теперь он искривится.
Р
м:.±:
§ 138. БОЛЕЕ СЛОЖНЫЕ ВИДЫ НАГРУЗКИ
Анализ ползучести круглых пластин на основе критерия
типа Треска существенно осложняется, если пластина несет
поперечную нагрузку. Рассмотрим прежде всего задачу,
представляющую собою другой вариант
решенной выше задачи о
закручивании пластины распределенными
моментами. Пусть пластинка будет
загружена силами, распределенными по
наружному и внутреннему контурам
(рис. 219). Для того чтобы она
находилась в равновесии, нужно, чтобы
силы, приложенные к каждому из
контуров, были одинаковы. Обозначая величину силы через Р,
найдем: N = Р 1\. Предположим, что мы остаемся на стороне AF
шестиугольника' Треска, тогда -j=- = ¦& = const и уравнение A37.1)
принимает следующий вид:
F
[Рис. 219.J
d
Отсюда
в*,>-(*)*-*.
*.-ЫтУ-р+$-
§ 138]
БОЛЕЕ СЛОЖНЫЕ ВИДЫ НАГРУЗКИ
543
Теперь if,, (а) = Мг A) = 0, из этих условий находятся 9иС,
мы получаем:
tiv=(l-v) /~Х%Р A38.1)
1—a v
И
Й -р\ 1~а ?-* 1 а ct~V~1 1
Me = P(l-v)-b^-v.
1 —a1 v
Заметим, что изображенная нагрузка дает момент на единицу
длины наружного контура, равный Р A — а). Положив Р ( 1 —
— а) = (л, мы убедимся, что формулы A38.1) и A37.2) дают
совершенно одинаковую зависимость угла # от момента в
соответствии с результатом элементарной теории, однако в последнем
случае пределы применимости решения будут другими, притом
выяснение этих пределов более сложно. Сравнивая выражения,
Me и Мт согласно A38.2), мы убеждаемся, что если Me > Мт, то
b ^ 1—a ~ 1—a I •
Соответствующее предельное значение а найдется из условия,
что если заменить здесь знак неравенства на знак равенства,
то получившееся уравнение относительно | будет иметь
двойной корень. Проделав соответствующие выкладки, мы убеждаемся,
что решение A38.1), A38.2) справедливо, если а удовлетворяет
следующему неравенству:
V
Неравенство A38.3) довольно неудобно, для того чтобы
определить из него минимальное значение а при заданном v,
приходится прибегать к численному решению.
Эту и другие подобные ей задачи можно решать при
экспоненциальном законе ползучести. Исследование границ
применимости решений в некоторых случаях оказывается более простым,
в других — сложность примерно одинакова со степенным законом.
Ход расчета при этом совершенно аналогичен тому, который был
применен в задаче о вращающемся диске (§ 124), поэтому мы
не приводим соответствующих решений.
A38.2)
544 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
§ 139. ИЗГИБ ПЛАСТИНЫ РАСПРЕДЕЛЕННОЙ НАГРУЗКОЙ
Задача об изгибе пластины распределенной нагрузкой
совершенно тождественна с задачей о вращающемся диске постоянной
толщины. Действительно, при распределенной нагрузке N == д|.
Подставляя в уравнение равновесия A37.4), мы получим
уравнение, точно совпадающее с уравнением A23.1) для диска
постоянной толщины, только напряжения оказываются заменены
моментами и вместо постоянной т фигурирует постоянная q.
Условие опирания по контуру пластины соответствует
условию равенства нулю радиального напряжения на контуре диска,
то есть отсутствию лопаточной нагрузки.
Для свободно опертой пластины, так же как и для диска,
мы получим две зоны. При 0 < ? <С а, МТ = Mq = М, тогда как
скорости изменения кривизн могут принимать различные
положительные значения, притом такие, что сумма их есть заданная
функция от момента. Для первой зоны уравнение равновесия
будет следующее:
Скорость изменения угла наклона Ф определится при этом из
уравнения
«е + х, = -|"^-(??) = х(Л*). A39.2)
Во второй зоне при а < | < 1 становится Me > Mr > О, следо-
вательно, хг = Ь' — 0 и •& = const = f>i, поэтому щ = -у-. Изги-
бающий момент Мт есть функция от щ, таким образом,
уравнение равновесия приводится к следующему виду:
-±{lMr)=m(^-^-ql\ A39.3)
В § 123 мы рассмотрели задачу о диске при экспоненциальном
законе ползучести, все это решение буквально переносится на
пластину. Рассмотрим здесь задачу об изгибе плиты при
степенном законе, как это сделал Валь [3,э] для случая диска.
Проинтегрируем уравнение A39.1) для первой области. Получим:
ifr = C[l-'l-i-?*]. A39.4)
Внесем найденное значение момента в уравнение A39.2) и
проинтегрируем с учетом условия Ф @) = 0. Результат будет
§ 139] ИЗГИБ ПЛАСТИНЫ РАСПРЕДЕЛЕННОЙ НАГРУЗКОЙ 545
следующий:
и+1 9S L V 2 С S ) J ¦
Теперь нам нужно определить границу первой зоны. Вычислим
производную -та-и приравняем ее нулю, положив при этом \ = а.
Если ввести обозначение
-|-§-a2 = z, A39.5)
то для z получится следующее уравнение:
Bга + 1) A -z)n+1- 2 (и+1) A -z)n + 1=0. A39.6)
Таким образом, величина z зависит только от п и может быть
вычислена для любого га.
Теперь мы можем переписать выражения для М и для #
следующим образом:
M==Mr = Me = c[l-z-|-],
# <^!«?Г1_A_Я4У4Ч. A39'7)
2(л + 1) г | L V а2 У J
Переходим ко второй зоне. Здесь ¦& = fl-j = const, причем
должно быть выполнено условие непрерывности ¦& при ? = а,
поэтому величина ^ найдется по второй из формул A39.7), если
положить в ней ? = а. Учитывая A39.6), получим для bt
следующее выражение:
^l = OCn(i—Z)n.
Уравнение A39.3) запишется теперь так:
^(EJfrr) = C(i-z)(D1'"-gp.
Проинтегрировав его, найдем:
Момент Мг должен удовлетворять условию сопряжения при
? = а, а также условию свободного опирания МгA) = 0,
следовательно,
C(l-z)=c7(l-Z)^-f + §,
п q
VJ = ^ IX ? I -
V ' П
35 Ю. Н. Работнов
°=сA-г).-+т-| + д-
546 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Учитывая A39.5), из второго уравнения находим:
Подставив в первое граничное условие, получим следующее
уравнение для нахождения неизвестной а:
Отсюда находится величина а, а следовательно, и С по
формуле
Ь~И ¦
Теперь мы находим Мг и М% по первой из формул A39.7)
при 0 < ? < а и по формулам:
*„_C(l-»)(f)'\
b-cfav-Kiy-SW* (i39'9)
+ [S-„-f«A-')»""-']l}
при а<|<1.
Угол поворота ¦& определяется формулой A39.7) в первой зоне,
он сохраняет ^постоянное значение т}4 = аСаA — z)" во второй
зоне; для нахождения прогиба нужно выполнить еще
квадратуру, результат которой при произвольном п через элементарные
функции не выражается.
Приведенный пример характерен для решения задач о
пластинах с помощью кусочно-линейных критериев ползучести. Даже
в такой простой задаче, как пластина, опертая по контуру, мы
встретились с необходимостью последовательно решать
алгебраические уравнения A39.6) и A39.8), что можно выполнить
только численно. Построение формы упругой поверхности опять-
таки требует численного интегрирования. Поэтому мы
решительно отдаем предпочтение общему методу, изложенному в § 135.
где численное решение получается в результате прямого счета по
стандартной программе. В этом случае расчет пластины, скажем,
защемленной по контуру, производится точно так же, никаких
дополнительных затруднений при этом не возникает. Решение
задачи о защемленной пластине с помощью критерия типа Треска
принципиально, конечно, возможно, но вряд ли целесообразно,
выражения получаются чрезвычайно громоздкими, и преодоление
чисто алгебраических трудностей элементарного, по существу,
характера может представить только спортивный интерес.
§ 140]
НЕКРУГЛЫЕ ПЛАСТИНЫ
547
К расчету пластин с успехом применяются также методы
последовательных приближений, особенно целесообразные тогда,
когда функция т (и) задана графически или численно. Мы не
будем на них останавливаться специально, поскольку методы,
применимые для вращающихся дисков, немедленно переносятся
на пластины.
§ 140. НЕКРУГЛЫЕ ПЛАСТИНЫ
Рассмотренные примеры относились к пластинам, имеющим
форму круга, закрепленным симметричным образом и несущим
осесимметричную нагрузку. Для пластин другой формы мы
отметим некоторые элементарные решения.
а) Чистый изгиб пластины. Если пластина, имеющая
произвольную форму в плане, нагружена по контуру всюду
одинаковыми изгибающими моментами, то уравнения статики будут
удовлетворены, если принять Мц = М22 = M, Mi2 = 0. Тогда
М0 = М, из A34.6) следует, что
б) Цилиндрический изгиб. Положим х22 = >Ч2 = 0, хи = х,
тогда по формулам A34.5)
М11 = 2МВ=М, ^и = х0(^м) A40.2)
либо
?* = м.(Щ.
в) Чистое кручение. До сих пор мы не рассматривали
специально вопрос о граничных условиях, в изученных простейших
задачах они были совершенно очевидными. В общем случае,
как известно из теории упругих пластин, одно из статических
условий на краю может оказаться лишним. Так, для свободного
края можно было бы потребовать условия равенства нулю
изгибающего момента, крутящего момента и перерезывающей силы.
Поставленная таким образом задача оказывается
переопределенной, построение решения бигармонического уравнения,
удовлетворяющего трем контурным условиям, вообще говоря,
невозможно. Как хорошо известно (см., например [138]), выход из
противоречия заключается в том, что, следуя Кирхгофу, вместо
требования равенства нулю крутящего момента Н и
перерезывающей силы N записывают одно граничное условие:
d-? + N = 0. A40.3)
35*
548 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Здесь s — дуга контура пластинки. Это следует из того факта,
что распределение крутящего момента на дуге А В статически
эквивалентно распределению линейной нагрузки интенсивности
ЛИ"
-д- , к которой добавляются сосредоточенные силы в точках А я В,
численно равные величинам момента НА и Нв в этих точках.
Очевидно, что эти соображения, носящие чисто статический
характер, полностью сохраняют силу и в теории ползучести,
поэтому, по аналогии с
соответствующей задачей теории изгиба
упругих пластин, мы можем
рассмотреть чистое кручение
пластины в условиях ползучести.
Положим Мц = М2 = 0, Mi2 = Н.
Предположим, что пластина имеет
прямоугольную форму, тогда на
контуре мы получаем всюду
крутящий момент, равный Н. Но
-д— = и, таким ооразом, контурная нагрузка статически
эквивалентна четырем силам величиной 2# каждая, приложенным
в углах пластины так, как это показано на рис. 220. Теперь,
в силу формул § 134,
*12 = у= Щ {Я УЩ = W, 12-
Так же, как и в упругом случае, поверхность пластины
представляет собою гиперболоид, прямые, параллельные осям 1 и 2,
становятся прямолинейными образующими гиперболоида.
Расчет на ползучесть пластин, находящихся в более сложных
условиях, пока что производится только с помощью
вариационных методов. Следуя методу Ритца, мы должны аппроксимировать
подходящим образом прогиб пластины. Если выбирать в качестве
аппроксимирующей функции прогиб для упругой пластины, то
решение получается чрезвычайно сложным, поэтому обычно
просто подбирают некоторые выражения, удовлетворяющие
кинематическим граничным условиям, например первый член
двойного ряда Фурье, представляющего решение для упругого случая,
либо некоторый полином. Далее применяется уравнение Лагран-
жа точно так же, как это было разъяснено в § 136 для круглой
пластины; зависимость функции ц>1 уже не от одной, а от двух
переменных никаких принципиальных осложнений не вносит.
Совершенно аналогичным образом можно задаться
распределением изгибающих моментов, которое удовлетворяло бы
статическим граничным условиям и уравнению равновесия A32.6).
Пусть это распределение есть М°ц (xk). Найдем второе
распределение моментов, удовлетворяющее уравнению равновесия при
Рис. 220.
дИ „
§ 141]
ПОЛЗУЧЕСТЬ ОБОЛОЧЕК
549
отсутствии внешних сил и нулевых граничных условиях М™ (#а)-
Очевидно, что
Mij^Ml + cMTi
представляет собою статически возможное состояние пластины,
какова бы ни была постоянная с. Теперь мы составляем
функционал Кастильяно и минимизируем его по параметру с. Примеры
применения вариационных принципов к расчету прямоугольных
пластин содержатся в книге [52].
§ 141. ПОЛЗУЧЕСТЬ ОБОЛОЧЕК
Общие уравнения установившейся ползучести пластин и
оболочек могут быть выведены тем же путем, что и аналогичные
уравнения теории упругих оболочек. На этом пути возникают
те же хорошо известные из теории упругости затруднения,
связанные с необходимостью удерживать лишь ограниченное число
членов в разложениях различных встречающихся функций по
степеням переменной, меняющейся в направлении толщины
оболочки. Соответственно могут быть построены различные
варианты основных уравнений, отличающиеся между собою
учетом или неучетом тех или иных малых членов. Однако задачи
ползучести оболочек настолько сложны, что в настоящее время
имеются решения или попытки решения лишь для простейших
случаев, поэтому исследование общего характера могло бы в
лучшем случае открыть некоторые перспективы, не подсказывая
каких-либо путей для реализации намечающихся возможностей.
Действительно, в наиболее простом и общепринятом варианте
теории упругих оболочек связь между усилиями и моментами,
с одной стороны, скоростями деформации срединной поверхности
и скоростями изменения кривизн, с другой стороны, сохраняется
той же, что и в теории пластин. Для упругих оболочек усилия
связаны с деформациями, а моменты — с изменениями
кривизн, тогда как для оболочек в состоянии ползучести мы должны
принять соотношения A32.3) или обратные им A32.4). Таким
образом, первая и основная трудность в теории оболочек
заключается в том, чтобы найти выражение потенциала усилий и
моментов или потенциала соответствующих скоростей. Это удается
сделать для немногих лишь случаев достаточно простых
оболочек. В частности, в оболочках могут возникать состояния без-
моментные и чисто моментные. В безмоментном состоянии усилия
определяются из условий статики, если соответствующие
граничные условия заданы для усилий. Если граничные условия
содержат ограничения, налагаемые на перемещения, то в некоторых
случаях оказывается возможной формулировка статически
неопределимых задач безмоментной теории оболочек, решение которых
550 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
в принципе мало отличается от решения соответствующих задач
теории упругих оболочек. Примерами таких статически
неопределимых задач могут служить задачи о ползучести слоистых
оболочек при различных предположениях о характере связи
между слоями.
Чисто моментное состояние оболочки мы будем понимать
в том смысле, что усилия в срединной поверхности определены
заранее, то есть находятся из уравнений равновесия и граничных
условий независимо от изгиба. Для изгибающих же моментов
и скоростей изменения кривизн получается независимая система
уравнений.
Наличие усилий в срединной поверхности, хотя бы и
заранее известных, серьезно осложняет зависимости между
моментами и скоростями изменения кривизн. С трудностями
подобного рода мы встречались при рассмотрении задач об изгибе
балок при наличии продольной силы. Фактически решаемые
задачи о чисто моментном состоянии оболочек носят такой же
характер, это — задачи об изгибе бесконечно длинной
цилиндрической оболочки силами, распределенными одинаковым
образом во всех поперечных сечениях.
Условия существования безмоментного и чисто моментного
состояний в упругих оболочках выяснены достаточно хорошо [13],
[20], однако мы не будем ссылаться на эти общие результаты
или пытаться провести аналогичный анализ для случая
ползучести, рассматриваемые ниже случаи достаточно просты и
очевидны. Как мы уже имели случай убедиться, эффект
концентрации напряжений при ползучести существенно меньше, чем в
упругом состоянии. Поэтому следует ожидать, что краевой эффект
в оболочках при ползучести выражен менее отчетливо, нежели
в упругих оболочках, роль его не столь значительна и уравнения
безмоментной теории можно применять с большим основанием.
Этот факт будет выяснен ниже на некоторых примерах,
относящихся к осесимметричной деформации цилиндрических
оболочек.
Задача об осесимметричной деформации цилиндрических
оболочек принадлежит к числу немногих задач, для которых
возможны по крайней мере численные решения. Существенным
обстоятельством здесь служит то, что продольное усилие сразу
находится из условий статики, тогда как в поперечном
направлении отсутствует изменение кривизны. В этом смысле напряженное
состояние цилиндрической оболочки сохраняет некоторые черты
безмоментного и чисто моментного состояний. Подобное
обстоятельство с известной степенью приближения встречается и в
некоторых других задачах теории оболочек, возникающие при этом
упрощения положены в основу приближенной теории упругих
цилиндрических оболочек средней длины, подвергнутых дей-
§ 142]
БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
551
ствию несимметричной нагрузки [гз], [88]. В теории ползучести
оболочек соответствующие предположения также вносят
существенное упрощение, основанный на них вариант теории мы
будем называть технической теорией оболочек.
§ 142. БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
Напомним основные факты из безмоментной теории оболочек.
Пусть поверхность отнесена к криволинейной системе координат
и1, и%, так что радиус-вектор ее точек есть г (их, и2). Векторы r,t,
где индекс после запятой при векторной величине обозначает
дифференцирование, образует ковариантный базис на
поверхности, вектор единичной нормали к поверхности мы обозначим
через п. Ковариантный метрический тензор есть gtj = r,iv,j,
коэффициенты второй квадратичной формы суть Ъ tj = r tJ ri =
= riiW.<j. Напомним деривационные формулы Гаусса и Вейн-
гартена [110]:
/r,ij = G*jrih + bijn, n, ,= —b\r,j.
Здесь G^. — символ Кристоффеля для поверхности. Контрава-
риантный тензор усилий в оболочке Тг] может быть введен
формально следующим образом. Будем рассматривать
оболочку как нерастяжимую поверхность. Это значит, что если
точка поверхности получает перемещение w, то деформации
равны нулю. Радиус-вектор изогнутой оболочки есть г + w,
условие нерастяжимости можно записать следующим образом:
dr dw = 0
или
w,ir,! = 0, w7!»«, 2 + w,2r,i = 0, wJr,2 = 0. A42.1)
Рассмотрим часть оболочки S, ограниченную контуром Г. На
единицу площади действует сила q, на контуре приложено
усилие Т на единицу длины линии контура. Приравняем нулю
виртуальную работу всех сил, действующих на выделенную часть
оболочки, имея в виду, что возможные перемещения подчинены
условиям связи A42.1). Для этого нам нужно ввести множители
Лагранжа, которые мы обозначим Г11, Г12 и Г22. Если считать,
что Т12 = Т21, то условия связи A42.1) запишутся следующим
образом:
T'l!w i r , = 0.
Приравнивая нулю виртуальную работу всех сил, получим
с учетом уравнений связи:
\ \ [qw - Tijw,, r, j] dS+\ Twds = 0. A42.2)
552 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Пусть v — вектор нормали к контуру Г в касательной
плоскости, так что v = vkek = vhgskrtS. Преобразуя поверхностный
интеграл, приведем уравнение A42.2) к следующему виду:
J \ [Q + Т)\ г,} + Tijbun] w dS + J [T— Tijrt jv,j w ds = 0. A42.3)
s г
Отсюда следует:
T% + qj = 0, Г% + д„ = 0, Г = ГЧ- A42.4)
В первом соотношении индекс после запятой обозначает ковариант-
ную производную тензора 21".
Развернутая запись первого из уравнений A42.4) может быть
получена в более простой и симметричной форме. Положим
Ttj = TijY^g. Тогда, используя известные соотношения:
придем к следующему результату:
Ш + dS-+G"fn + 2G?2^+G|2r22+^ ]Tg = 0, A42.5)
ТЩп + 2ТЩ12 + T"b22 + qnY~g = 0.
Величины Тгз не образуют контравариантного тензора; если
изменить порядок индексов, то их можно рассматривать как
смешанный тензор. Действительно, процесс образования величин
Т1} представляет собою результат свертывания контравариантного
тензора Tlj с дискриминантным тензором (см., например, [*']).
Дальнейшее преобразование формул A42.5) получится, если
принять за компоненты усилий величины Tl,g. Умножение
компонент контравариантного тензора на величину g эквивалентно
двукратному опусканию индекса с помощью, дискриминантного
тензора, поэтому в результате мы получаем ковариантный
тензор, компоненты которого суть
Su = gT**, Si2=-gT™, S22 = gT*.
Уравнения равновесия для тензора усилий Stj запишутся еле
дующим образом:
^-Sr-'S'"G2i+^2(Gl1-Gf2) + (S22G?1+^ = 0,
т~Ш + 5"G22 + Si2 (Gf2 - G\ 2) - S22Gf2 + qlg = 0, A42.6)
S\ i b22 + S22b ii — 2Si2bi2 — q n ¦
§ 142]
БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
553
Уравнения безмоментной теории в форме A42.6) были получены
в работе [97], введение компонент Sij тензора усилий удобно
в том отношении, что оно позволяет естественным путем ввести
функцию напряжений, позволяющую удовлетворить первым двум
из уравнений A42.6). Вернемся для этого к уравнению A42.2)
и будем преобразовывать поверхностный интеграл путем
интегрирования по частям. Заметим при этом, что элемент площади
dS = Y~8 du^du2. Этот поверхностный интеграл может быть
переписан в следующем виде:
\ \ [Vlqw - {VgTUr, j) w, t] du1 du* =
[\rgqw~(V~gTiirjjw),t + (VgTijr>j),iw]duldu\
11
Интеграл от второго члена в подынтегральном выражении
преобразуется в контурный. Положим:
«1 = rV i]/'g=^=[5lir,2-512r,I],
S2 = - ГУ iV"g = ^ [Snr, 2 - Sztr,,].
A42.7)
Тогда условие равновесия примет следующий вид:
S-g + ffV^-O, A42.8)
а граничное условие:
Tds = Sidu1 + S2du2. A42.9)
Уравнение A42.8) представляет собою векторную запись
системы A42.6), с помощью деривационных формул Гаусса из A42.8)
легко получаются уравнения A42.6). Пусть S* и 8* — некоторое
частное решение A42.8), соответствующие компоненты усилий
будут S*j. Очевидно, мы получим общее решение, если прибавим
к частному решению S* решение однородного уравнения,
получающегося из A42.8), если положить д = О, а именно:
^-Э=°- A42Л0>
Мы удовлетворим последнему уравнению, приняв Si = at 4
и $2 = аJ, где а — произвольный вектор:
a = aV, t + tyn.
Теперь
«, J = SJ = (a! i - #') ^i+ltj" a%) n
554 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Так как Sj, а следовательно, и a,j лежат в касательной
плоскости, то
i|), j — albij = 0.
Отсюда
a1 = g-D\abi2-4>, 1622), «2= -^0Ми-Ч>,Ф12). A42.11)
Здесь К — гауссова кривизна поверхности. Поскольку Stj —
-симметричный тензор, то Sjel = Q или а^ег=0. Отсюда
Записывая явно выражения ковариантных производных и
пользуясь для упрощения тождеством — У = G\h, получим
следующее уравнение:
i (^ VI)+?* («2 VI) -yfVe (Pi + ъ\) = о.
Внося сюда выражения A42.11), получим окончательное
уравнение для функции напряжений "ф:
5Г.A!^^) + ^A,У?|^) + *^№1 + ^ = 0. A42.12)
Теперь величины усилий можно записать при помощи
следующих симметричных выражений:
Sij=-^+ckGhij-(oikbl A42.13)
Здесь
Ci=-Vga2
:?y=W\2bii-l|\ib12).
«11 = «22 = 0, С012= — Ы21 = ,ФК^-
Приведенный анализ неприменим для случая
развертывающейся поверхности, однако если К = 0, то, как легко проверить,
мы можем ввести функцию напряжений обычным для плоской
-задачи способом, а именно принять:
Sij = %ij. A42.14)
§ 143
БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
555
§ 143. БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК —
ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЙ
Введенные формальным образом компоненты тензора усилий
Sij имеют простой механический смысл. Положим в
формуле A42.9) du2 = О, это значит, что мы принимаем за ds элемент
дуги линии и1, ds = Ygudu1. Тогда из A42.7) и A42.10) следует:
Векторы гJ и гу1 направлены по касательным к линиям и2 и и1
соответственно, длины их ]/g22 и У gu, тогда как вектор Т есть
вектор усилия, действующего на единицу длины линии и1. Из
вышеприведенного соотношения следует, что величины
Su
Уё22
-S
12
Vg
представляют собою «физические» составляющие усилия,
действующего на единицу длины линии и1 и разложенного по
направлениям линий и1 и и2.
Совершенно аналогично
а 1
'21
У~8
представляют собою физические компоненты усилия на единицу
длины линии и2. На рис. 221 изображен бесконечно малый
элемент поверхности со
сторонами Vgn du1 и Yg2zdu2
и показаны действующие
усилия.
Если поверхность
отнесена к ортогональным
координатам, например к
линиям кривизны, как это
обычно делается, то
линейный элемент ее часто
принимают в виде ds2 = A2 (du1J + В2 (du2J, следовательно,
gH = A2, gz2 = В2 и физические компоненты усилия будут
Рис. 221.
1 <?
За * п.
В*
1
АВ'
1
Заметим, что -^-^п есть нормальное усилие в направлении и2,
тогда как -s^Szz — нормальное усилие в направлении и1.
556 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Если принять для физических компонент усилий в
ортогональных координатах обычные обозначения: Nit N2 и Ni2, то мы
получим:
iV, = pS22, Nz = ±Sllt Ni2=-±Si2. A43.1)
Потенциал скоростей для оболочки выражается следующим
образом:
Ф(Г**) = 1фBАа");
при этом в правой части фигурирует потенциал скоростей
ползучести, выраженный через контравариантные составляющие
тензора напряжений. Составляющие скорости деформации е^,
выражаются через потенциал следующим образом:
дф
6,-;=—~ ¦
J дТ1>
Переходя к тензору Sy, получим:
6« = ^ЖГ' ъ*=8щ:' «H*=-*as-- A43.2)
В ортогональных координатах, когда gu = A2, g22 = 52, gi2 = О,
скорости относительных удлинений 8lt e2 и скорость сдвига у
выражаются через Еу следующим образом:
р _ _!У_ р _ е22 У __ Ё12
Ч- А , е2_ в , -2--уЖ*
В физических компонентах напряжений и скоростей деформации
соотношения A43.2) заменяются соответственно более простыми,
которые буквально совпадают с выражениями скоростей через
напряжения в декартовых координатах для плоского
напряженного состояния.
Однако в теории оболочек выбор линий кривизны или иной
ортогональной сетки в качестве системы отнесения не всегда
оказывается наивыгоднейшим.
Если принять закон ползучести типа Мизеса, то потенциал
будет функцией от интенсивности усилий, которая выражается
в общих координатах следующим образом:
Следовательно,
е„ = —?$- [3T»gihgn -{Thlghl) glj).
§ 143]
БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК
557
Перейдем от составляющих усилий 7113 к величинам Sa. После
прямых вычислений получим следующую форму записи закона
ползучести:
ео- = -^ [(>W) Ifu—|Sy] • A43.3)
Здесь
Разрешая A43.3) относительно Sij, найдем:
Stj = 1^)" [2 Ы8Ы) gij-Btj].
С другой стороны, Ф' (Го) = v (Т0) и, наоборот, Т0 = s (v),
функции s и v те же самые, что в основном законе ползучести.
Поэтому мы перепишем последнее уравнение так:
После того как усилия в оболочке найдены, по формулам A43.4)
находятся скорости деформации, скорости перемещений
оболочки по заданным скоростям деформации всегда могут быть
определены. Действительно, пусть вектор скорости
перемещения задан следующим образом:
w — wlr7i + wn. A43.5)
Тогда компоненты скорости деформации определяются так:
Вычислим производные от вектора w, заданного выражением
A43.5), используя при этом деривационные формулы Гаусса
и Вейнгартена. В результате получим:
еи = f (wi, J + v>u i) — wbi}. A43.6)
Как показано в работе [97], нахождение перемещений зависит
от нахождения решения уравнений той же формы, что A42.12),
но с известной отличной от нуля правой частью; после того как
это решение найдено, формулы для перемещений записываются
в виде квадратур. Мы не приводим здесь описания этого метода,
поскольку в дальнейшем будут рассматриваться относительно
простые задачи.
558 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
§ 144. ВЕЗМОМЕНТНЫЕ ОБОЛОЧКИ ВРАЩЕНИЯ
Оболочка вращения, несущая осесимметричную нагрузку,
представляет собою наиболее простой объект приложения общей
теории, в то же время
имеющий наибольший
практический интерес. На
рис. 222 изображен
меридиан такой оболочки, в
качестве координатных
параметров мы выберем дугу ?
меридиана для направле-
ния 1 и угол ф между
соседними
меридиональными сечениями
(географическую долготу) для
направления 2. Будем считать, что радиус точки М задан как функция
дуги \\г = т (|). Элемент дуги поверхности оболочки выражается
следующим образом:
Таким образом, gtl = i, g22 = g = r2, gi2 = 0. Символы Кри-
стоффеля (см. [110]) будут
Рис. 222.
G\1 = 0,
GJ1 = 0,
G12
О,
1 dr
p2 1 ar SIn I
12" T ~Ж = ~~T
— r sin 9,
GL-0.
Коэффициенты второй квадратичной формы:
Hi
Дя
6.2 = 0.
Здесь Bt =
радиус кривизны меридиана, R2
jfj ^"A^J^ "^лиолиишл bu,jiiiHiiuuu, it-,; COS G
радиус кривизны нормального сечения, проведенного через
параллель. При осесимметричной нагрузке усилия не зависят от ф
и Si2 = 0, поэтому первое из уравнений A42.6) удовлетворяется
тождественно, тогда как второе дает
dS,
dl
-sin 8
r^ii — у ^22
+-?!>¦'= 0.
Третье уравнение приводится к виду
г2 1
^11 -ТГ + "-*> 22 -ТГ + ЯпГ2 = 0.
§ 144] БЕЗМОМЕНТНЫЕ ОБОЛОЧКИ ВРАЩЕНИЯ 559
В рассматриваемом простом случае удобно перейти к
физическим компонентам усилий:
Тогда получим:
^1 = ^22, ^2 = ^,,.
dNl • "^iw-*,) + * = о,
Система A44.1) имеет хорошо известное решение:
N2= —^^-Я2дп.
A44.2)
Компоненты скорости деформации по формулам A43.6) найдутся
следующим образом:
'dw, w / ¦ г, m
бц = -^г д~ > е22 ^=/• (г^ sm 9 — wcos9).
Физические компоненты скорости деформации:
dwl w
82 = if- = i(a)lSin9- wcos9). A44.3)
г
Соотношения между скоростями деформации и усилиями мы
можем теперь написать в обычной форме, так же как и для
пластинки. При квадратичном критерии ползучести
N0
Здесь
Если основной закон ползучести задан в виде е = г% v( — ) , то
теперь v = у(дг)> гДе N* = 2AoV
После того как скорости деформации вычислены, перемещения
точек оболочки находятся из A44.2) квадратурами, а именно:
Wi = COS 9 \ С 6i — -д2- 82
dl
cose ' A44.5)
w = Wi tg6— /?2e2.
560 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ, X
§ 145. МНОГОСЛОЙНЫЕ ОБОЛОЧКИ
С ЖЕСТКО СВЯЗАННЫМИ СЛОЯМИ
Слоистые оболочки, составленные из материалов с
различными характеристиками ползучести, встречаются довольно часто
как элементы конструкций. С другой стороны, однородная
оболочка, неравномерно нагретая по толщине, может быть
моделирована многослойной оболочкой. При этом считается, что в
пределах каждого слоя температура, а следовательно, и
характеристики ползучести неизменны. Мы будем считать, что общая
толщина оболочки мала по сравнению с ее радиусами кривизны,
поэтому для всех слоев коэффициенты
первой и второй квадратичных форм
принимаются одинаковыми. Схема
такой многослойной оболочки показана
на рис. 223; слой номер к имеет
толщину бд, общая толщина оболочки по-
прежнему остается 2h. Рассматривая
оболочку как целое, мы находим по
безмоментной теории величины усилий
Stj, поскольку применение
безмоментной теории не связано с какими-либо
предположениями о строении и
физических свойствах оболочки.
Компоненты напряжений в каждом слое мы обозначим а%. Здесь а и не есть
обычный ковариантный тензор напряжений, а тензор,
полученный из контравариантного тензора напряжений двукратным
опусканием индексов с помощью дискриминантного тензора; величины
о*;, связаны с о13 так же, как 5 у связаны с Tli. Каждый слой
можно рассматривать как отдельную оболочку, находящуюся
в безмоментном состоянии. Поэтому по формулам A43.4)
а*А = | -^ 6* [2 (гт$П gtJ - ги].
С другой стороны, очевидно,
k
Следовательно,
Мы предположили, что слои жестко связаны между собою, их
взаимное проскальзывание невозможно, поэтому величины ец,
а следовательно, инвариант v для всех слоев одни и те же. Таким
образом, связь между усилиями и скоростями деформации
§ 145] МНОГОСЛОЙНЫЕ ОБОЛОЧКИ С ЖЕСТКО СВЯЗАННЫМИ СЛОЯМИ 561
по-прежнему дается формулами A43.4), в которых
*H = S°>ftH- A45.1)
Положим
_ Sksk (v)
2] V; (t>)
Тогда
4 = -^-^- A45.2)
Если все слои следуют степенному закону ползучести с одним
и тем же показателем п, так что
то
Здесь
<Ь
Как всегда, в выборе величин sn и vn остаетсяпроизвол. Теперь
В этом случае величины щ постоянные, во всех других
случаях rift есть функция v. Заметим, что из A45.2) следует:
r\k = bk^. A45.3)
Здесь oj и So — любые инварианты первой степени, составленные
одинаковым образом из тензоров ац и Бц, в частности, о\ может
быть интенсивностью напряжений в слое, S0 — интенсивностью
усилий. Поскольку метрика в каждом слое считается одинаковой
и тождественной с метрикой оболочки в целом, физические
компоненты напряжения также выражаются через физические
компоненты усилия по формулам A45.2).
Если понимать под д по-прежнему вектор усилия,
приходящегося на единицу площади поверхности оболочки, то для того;
чтобы рассмотреть взаимодействие между слоями, мы должны
уточнить способ приложения этих усилий. Будем считать, что
на единицу площади каждого слоя действет усилие qh, так что
36 ю. H. Работнов
562 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Кроме усилий qh при деформации оболочки на каждый слой будет
действовать усилие рк, представляющее собою реакцию
примыкающих слоев. Каждый слой мы можем рассматривать как
отдельную безмоментную оболочку и составить для него условия
равновесия. Введем для этого обозначения:
/ A45.4)
<*2 = -y=r @i2r,2 — 022»*,l)-
Теперь уравнение равновесия можно записать в форме
уравнения A42.8), а именно:
-^ (8А<) - -А- (б***) + (qh + Pk) VJ = 0. A45.5)
Вследствие A45.2) a^—^S^ <т? = -тр- Sz, внесем эти выражения
в A45.5). Получим:
<j dt\h g dr\k ( dSl dSz\ h , .г— Q
Отсюда, с учетом A42.8),
р -пня—я —у- {*>!-№ «г ди1
или, в проекциях на оси,
Й = ад2-^-^(^н|^-^2^) , A45.6)
Здесь рц /32j ?i> ?2 — физические составляющие вектора усилия
по направлениям касательных к координатным линиям и1 и и2.
Для симметрично загруженной оболочки вращения формулы A45.6)
принимают вид
Р?=*ив1-д?--^г^1, р* = ти«»-#. A45.7)
В большинстве случаев оболочка бывает загружена только
нормальным давлением qn, приложенным к одному из наружных
слоев оболочки. Тогда q{ = q2 = q\ — q\ = 0, q\ — О при
к Ф 1 и q^ = ^„. Тем не менее, по формулам A45.6), каждый слой
испытывает касательные усилия со стороны соседних слоев,
§ 146] ДВУХСЛОЙНАЯ МОДЕЛЬ ОБОЛОЧКИ 563
а также воспринимает часть нормальной нагрузки; формулы
A45.6) дают в этом случае:
Pi р- ^22-зйГ —«^ja-^rj ,
„ft _ Vg22_ f с дг\к „ drift \ /ЧЛс: оч
р.-—— v "i^ ""^"J ' A45-8)
Рп = (щ —l)9n, P« = T]ft?n (кф\).
На поверхности соединения соседних слоев возникают
касательные напряжения, которые мы условимся обозначать следующим
образом. Пусть %\ есть физическая составляющая по
направлению вектора r)S касательного уси- ^я
лия, действующего между слоями
номер к и к + 1 (рис. 224). Тогда,
очевидно, р\ = %\— Tj-, отсюда
получается следующая формула для
подсчета %Ъ\
h
Тг = 2 Р|. РИС. 224.
s=l
Знание величины т? позволяет, во-первых, оценивать прочность
соединения между слоями, во-вторых, судить о границах
применимости теории, так как по толщине слоя возникают
касательные напряжения, меняющиеся от %Ь—1 до т*. Эти напряжения
должны быть невелики по сравнению с нормальными
напряжениями, в противном случае мы должны были бы принять во
внимание сдвиг, происходящий в слое. Гипотеза о работе
оболочки как единого целого и о постоянстве тензора во всех слоях
будет неверна, если величины т* значительны. Так обстоит дело,
если свойства слоев сильно отличаются, например, если мы имеем
дело с оболочкой типа сандвич, когда металлические листы
связаны между собою слоем легкого заполнителя, мало
сопротивляющегося ползучести.
Заметим, что если все слои следуют степенному закону
ползучести с одним и тем же показателем п, то величины nfe
постоянны, следовательно, р% =р\ = 0, касательные напряжения в
оболочке не возникают.
§ 146. ДВУХСЛОЙНАЯ МОДЕЛЬ ОБОЛОЧКИ
Построение общей теории ползучести тонких оболочек с учетом
как растяжения, так и изгиба наталкивается на чрезвычайные
трудности. Применяя гипотезу Кирхгофа — Лява о прямых
нормалях, уже в первом приближении мы придем к соотношениям
36*
564 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
между моментами и усилиями, с одной стороны, скоростями
деформации и изменения кривизн, с другой стороны, которые будут
повторять соответствующие соотношения, найденные для пластин
в § 132. Поэтому буквально все известные до сих пор, кстати
весьма немногочисленные, решения задач о ползучести оболочек с
учетом изгиба основываются на тех или иных упрощениях
частного характера. Смысл этих упрощений, в конце концов, состоит
в следующем. Потенциал скоростей или потенциал усилий и
моментов представляет собою каждый функцию шести переменных: М ц
и Ttj или ttj и Ktj (см. §147). Условие U = const либо Ф = const
определяет поверхность в соответствующем шестимерном
пространстве, нормаль к поверхности в каждой точке изображает
распределение скоростей для заданных усилий или, наоборот,
распределение усилий при заданных скоростях. Фактическое
построение этих поверхностей затруднительно: они всегда состоят
из некоторых отдельных кусков аналитических поверхностей
с более или менее сложными границами. Реальные результаты
удается получить лишь в частных случаях для некоторых
подпространств с меньшим числом измерений. Однако некоторые
точки этих поверхностей, соответствующие простейшим
напряженным состояниям, могут быть получены достаточно просто.
Не зная истинной формы поверхности постоянного потенциала,
мы проводим через известные точки подходящую поверхность,
которая служит более или менее удачной аппроксимацией
истинной поверхности.
Некоторое обоснование подобного способа может быть сделано
на основе следующих рассуждений, общих как для теории
ползучести, так и для теории пластичности. Условие пластичности,
связывающее величины напряжений в предельном состоянии,
по существу не есть выражение некоторого определенного
физического факта, а всего лишь более или менее условный способ
приближенного описания реального поведения некоторой
совокупности образцов при достаточно определенных условиях
эксперимента. В простейшем опыте на растяжение мы получим для
различных образцов, вообще говоря, некоторый пучок диаграмм
деформирования, который заменяется для целей расчета средней
кривой.
В качестве такой средней диаграммы можно принять, в
частности, и диаграмму идеальной пластичности без упрочнения,
это один из возможных выборов, который отнюдь не является
наилучшим для большей части материалов, но зато допускает
совершенно определенную постановку задачи о предельном
равновесии. Теперь, рассматривая, например, изгиб стержня, мы
можем рассчитывать диаграмму зависимости кривизны от
изгибающего момента, основываясь на ранее принятой идеализации
диаграммы деформирования в однородном напряженном состоя-
§ 146]
ДВУХСЛОЙНАЯ МОДЕЛЬ ОБОЛОЧКИ
565
нии. G другой стороны, можно представить себе, что мы строим
диаграмму изгиба для индивидуальных образцов путем расчета
или находим ее из эксперимента, а потом производим осреднение,
руководствуясь при этом соображениями наибольшей простоты
последующего рассмотрения задачи изгиба. В числе других
возможна и такая аппроксимация, когда постоянному предельному
моменту соответствует какая угодно кривизна. Этот путь
используется при построении теории жестко-пластических балок, чтобы
логически связать идеализацию диаграммы изгиба с
представлением об идеальной диаграмме о* — е;
реальная балка подменяется моделью,
либо упруго-пластический материал
заменяется жестко-пластическим,
либо действительное сечение балки
заменяется сечением в форме
идеального двутавра. 2h
Совершенно такое же положение
возникает в теории ползучести,
элементарные законы ползучести
представляют собою лишь более или менее
удовлетворительную аппроксимацию
истинных кривых ползучести для
большого числа образцов, которые Ржс- 225.
довольно сильно разнятся между
собою, по крайней мере для технических сплавов, когда не
приняты специальные меры для стабилизации свойств материала.
При рассмотрении элементов, находящихся в условиях сложного
напряженного состояния, сюда добавляется еще одно
дополнительное обстоятельство. Простейшие законы установившейся
ползучести, полагаемые в основу теории, справедливы лишь при
постоянных или пропорционально меняющихся нагрузках. Эти условия
далеко не всегда выполняются в реальных конструкциях.
Поэтому, если бы мы даже сумели построить потенциальную
поверхность для оболочки, отправляясь от того или иного закона
ползучести, совершенно точным образом, реальное значение этого
результата не следовало бы переоценивать.
Для построения упрощенной теории оболочки мы будем
заменять реальную оболочку двухслойной моделью, которая
аналогична известной модели идеального двутавра для балки.
Представим себе оболочку состоящей из двух слоев
толщиной 6 каждый, расстояние между серединами слоев пусть будет
2ft (рис. 225). Будем считать сначала, что б < h. Слои считаются
связанными между собою таким образом, что связь или
заполнитель передает сдвигающее усилие, но не принимает участия в
восприятии растягивающих усилий и изгибающих моментов, таким
образом, деформация слоев происходит в соответствии с гипотезой
^с^т
О1
566 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Кирхгофа — Лява. За поверхность отнесения мы будем принимать
поверхность, находящуюся посередине между слоями. В силу
малости толщины каждого слоя мы можем пренебречь следующим
из гипотезы прямых нормалей изменением деформаций по толщине
и, следовательно, считать напряжения равномерно
распределенными в пределах толщины каждого слоя.
Изображенная на рис. 225 двухслойная оболочка служит
моделью сплошной оболочки толщины 2Н. Предполагая, что
свойства материала реальной оболочки и модельной оболочки
одни и те же, подберем параметры модели б и h таким образом,
чтобы поведение реальной и модельной оболочек совпадало в двух
случаях: при безмоментном напряженном состоянии и при
цилиндрическом изгибе.
По формулам § 119 в плоском напряженном состоянии
_ 4 *(во) / , 1 >|
При безмоментном напряженном состоянии величины е^
постоянны по толщине в реальной оболочке, одинаковы для верхнего
и нижнего слоя в модельной оболочке. Усилия в реальной оболочке
поэтому равны
Усилия в модельной оболочке
Сравнивая эти два выражения, мы заключаем, что
6 = Я. A46.1)
Рассмотрим теперь состояние изгиба оболочки, не
сопровождающееся деформацией средней поверхности. Вследствие гипотезы
прямых нормалей мы получаем совершенно так же, как и для
пластины при изгибе, что Ец — кц z; здесь щ^ — соответствующая
скорость изменения кривизны. В этом случае е0 = x0z, где х0 —
инвариант, составленный из скоростей изменения кривизн точно
так же, как е0 составляется из е^-. Для простоты все рассуждения
ведутся относительно физических компонент усилий, моментов,
скоростей деформаций и кривизн в ортогональной системе
координат, результаты немедленно переносятся на случай
произвольной системы отнесения. Теперь а0 = s (x0z). Для реальной
оболочки изгибающий момент, например Мп, выражается следующим
§ 146]
ДВУХСЛОЙНАЯ МОДЕЛЬ ОБОЛОЧКИ
567
образом:
+н я
Мц= ^ auz dz = -^(^x±l + Y'>izzJ—\is{ii0z)zdz.
-я о
У модельной оболочки деформации каждого слоя одинаковы по
величине и противоположны по знаку, в середине слоя ег;- =
= -? h%ij, соответствующие напряжения, которые считаются
равномерно распределенными по толщине каждого слоя, равны
Следовательно, изгибающий момент
M,1 = 2o116fe = y (xji+y^J — s (x0h) 8k.
Сравнивая два выражения для Ми, мы находим:
н
Ш (щ!г) = f s (x0z) z dz. A46.2)
о
В частности, при степенном законе ползучести
1+2л
Отсюда, учитывая A46.2), получаем:
1+2га
n+1 H. A46.3)
При и = 1 h = —— /7 « 0,577ЛГ, при и = оо, то есть в случае
у 3
идеальной пластичности, Л = Я/2. На первый взгляд может
показаться, что найденные для б и Н значения таковы, что
исходные предположения нарушены. Действительно, мы считаем, что
6 < h, тогда как на самом деле это величины одного порядка.
Но мы для удобства полагали закон ползучести для материала
модели и натурной оболочки одним и тем же. На самом деле мы
получим совершенно тот же результат, если в законе ползучести
* V.e*
мы сохраним для модели и для реальной оболочки одно и то же
значение константы е*, но увеличим в произвольном отношении
константу а* для модели, уменьшив в том же отношении
величину б. Очевидно, что таким образом можно сделать б сколь угодно
568 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
малым по сравнению с h. Для удобства мы будем пользоваться
действительными характеристиками материала, не обращая
внимания на то, что неравенство 6 < /г грубо нарушается.
Заметим, что формула A46.2) устанавливает зависимость h
от Н, которая вообще содержит величину и0, только при степенном
законе получается неизменное соотношение между h и Н. Так,
при экспоненциальном законе ползучести в зависимости от
величины х0 отношение hlH меняется в некоторых пределах, стремясь
к значению 1/2 с увеличением кривизны.
§ 147. УРАВНЕНИЯ ТЕОРИИ ОБОЛОЧЕК
Упрощения, связанные с заменой истинной оболочки
двухслойной моделью, не столь уж велики, чтобы можно было говорить
о построении общих уравнений в такой форме, когда отыскание
общих методов их решений становится в какой-то мере реальным.
Нужно сказать, что и теория упругих оболочек развивается
главным образом в направлении исследования некоторых
приближенных систем уравнений, описывающих определенные классы
оболочек и определенные типы возникающих в них
деформированных и напряженных состояний. Выделение соответствующих
упрощенных вариантов уравнений теории оболочек в случае
упругой оболочки основывается на соображениях, которые в общих
чертах состоят в следующем. Делаются определенные
предположения о характере убывания тех или иных величин,
характеризующих напряженное и деформированное состояния оболочки
вдоль тех или иных линий на поверхности, которые обычно
принимаются за координатные линии. Анализ порядка величины
членов в уравнениях теории оболочек с неизбежностью приводит
к тому, что если мы желаем ограничиться некоторой разумной
степенью точности (например, пренебречь членами порядка h/R,
где R — радиус кривизны, по сравнению с членами порядка
единицы или, в более грубом приближении, членами порядка
(h/R)a @ < а < 1), то ряд этих членов должен быть из
уравнений выброшен.
Мы не будем здесь излагать подробно этот анализ (см.,
например, [20]), заметим только, что наряду с точными уравнениями
теории оболочек рядом авторов предлагались те или иные
приближенные варианты, основанные на упрощениях и
предположениях скорее интуитивного характера. Последующие более строгие
исследования обычно подтверждали с той или иной степенью
точности законность введенных гипотез. Применительно к
оболочкам, находящимся в условиях ползучести или пластичности,
подобных строгих исследований до сих пор не имеется, поэтому
здесь мы рассмотрим некоторые варианты приближенных
уравнений теории, построенные по аналогии с соответствующими вариан-
§ 147]
УРАВНЕНИЯ ТЕОРИИ ОБОЛОЧЕК
569
хами теории упругих оболочек, которые достаточно хорошо
оправдали себя.
Будем, как это обычно делается, относить оболочку к линиям
кривизны ее срединной поверхности. Положим
Через Ri и R2 обозначим главные радиусы кривизны. Введем
физические компоненты усилий и моментов: Ti, Т2 и Ti2, Mu М2
и Mi2, а также физические компоненты скорости деформации:
6i, ё2! у Y' х1> И2И т. Вектор скорости перемещения будем опять-
таки задавать физическими компонентами и, vvi wm> направлению
координатных линий ^ и ?2 и нормали к поверхности
соответственно. Выпишем основные уравнения теории оболочек,
следуя [88].
а) Выражения скоростей деформации через скорости
перемещений:
1 ди , v дА w
А % ¦ АВ Э%2 Ri
i dv и дБ w 1\1Л \\
— JL JL fJL\ л- — -А— (—
Y~ А д\х ^bJ+~B д\2 \А
1 д f I dw i и \ , 1 &А f 1 dw , v
"I л at. I ~л at. г~тГ~ I ~T '
A47.2)
&iL V A dli ' Ri J ' AB d\2 V В д\2 ' R2
*2~ В dl2 \B д\г + R2) + AB dU\A dl, + Rt
1 / d*w 1 ЭА dw I dB dw
ab V d\t ai2 a aii di± в dii &I2
+
, 1 /J_ ди _i*_ ЭА ~\ , 1 / 1 _5u_ v dB
б) Уравнения равновесия:
Ш^+ъ^+ж^-ъ^-ъ+q^0' A47-3)
i[4(i?^+4(^)+ilM-"fM2]+iV^0' A474)
1
AB
570 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
В строгой и последовательной теории оболочек мы должны
были бы различать величины Г12 и Т%и М& и M2i- Действительно,
вычисляя усилия на единицу длины средней поверхности, мы
должны считаться с тем, что нормали к поверхности не
параллельны, поэтому, например,
+п
—к
+h
Та=\ aiz(l+^)dz
и Т12ФТ21.
Вопросу о построении последовательной теории упругих
оболочек на основе гипотезы Кирхгофа — Лява уделялось довольно
много внимания в литературе, различными авторами предлагались
различные системы уравнений, мало разнящиеся между собою.
Если принять выражения для усилий в форме A47.5) и для
моментов в аналогичной форме, то уже для упругой оболочки
получаются достаточно сложные выражения этих величин через
деформации, которые для приложений упрощаются. В теории
ползучести мы сразу пренебрегаем членами вида zIR в формулах A47.5)
и аналогичных для Мц\ при этом оказывается, что Тц и Мц
выражаются точно так же, как и для пластины, а именно:
+h +h
Tl}= \ Uijdz, Mu= \ Oijzdz. A47.6)
Заметим, что в нашей работе [9в] величины Тц и Mi} были введены
непосредственно как параметры, характеризующие напряженное
состояние оболочки, которые не рассматриваются как усилия
и моменты, эти величины вообще не фигурируют в теории. Тогда
уравнения равновесия элемента оболочки оказываются не
совпадающими с A47.3), A47.4), а имеющими более сложную
структуру i упрощение теории заключается в последовательном
отбрасывании некоторых членов в уравнениях равновесия.
Известно, что если принять выражения для усилий и моментов
по формулам A47.6), то окажется невыполненным еще одно,
шестое уравнение равновесия, которое мы не выписали, но это
противоречие, как было показано многими авторами,
несущественно. Итак, в теории ползучести оболочек мы считаем, что
усилия и моменты даются формулами A47.6) и, следовательно,
к написанным уравнениям нужно добавить закон ползучести,
получающийся точно так же, как и для пластин (см. § 132),
A47.5)
§ 148]
ТЕХНИЧЕСКАЯ ТЕОРИЯ ОБОЛОЧЕК
571
а именно:
Г" = 1^' М" = -Щ7 A47)
или
80=адг-. Щ! = дЩГ (Ш-8)
§ 148. ТЕХНИЧЕСКАЯ ТЕОРИЯ ОБОЛОЧЕК
Общим условным названием «техническая теория оболочек»
мы будем объединять различные упрощенные системы
уравнений оболочек, для которых по отношению к координатной системе,
образованной линиями кривизны, выполняются следующие
условия:
1) усилие Тц = 0;
2) скорость изменения кривизны х2г = 0;
3) отсутствуют касательные усилия и крутящие моменты:
712 = 0, М12 = 0.
Перечисленные условия могут выполняться либо точно, либо
приближенно. В последнем случае существенно то, что,
ограничиваясь определенной степенью точности, мы можем пренебрегать
соответствующими членами в основных уравнениях задачи.
К технической теории относятся следующие вопросы:
а) Теория осесимметричной деформации круговой
цилиндрической оболочки. В цилиндрической оболочке мы направим ось 1
по образующей, соответствующая координата будет х, тогда как
за координату у мы примем дугу контура поперечного сечения.
При этом А = В ~ I, Ri = оо, R2 = а. В осесимметричном
случае существуют две компоненты перемещения и и ш, е12 = х12 = 0,
Ti2 = М12 = 0, остальные величины зависят только от х.
Из A47.1) и A47.2) следует:
Из уравнений равновесия A47.3) и A47.4) получаем:
dTU J_„ -Г) dJVl J. Г22 , _ Л Ш
1й- + ?! = 0, ^ + 4^+^ = 0, ^ + ^ = 0. A48.2)
Первое из уравнений A48.2) сразу интегрируется, таким образом,
Тп — известная функция от х. Если qt = 0, то Ttl = const, эта
постоянная обращается в нуль тогда, когда на торце оболочки
отсутствует осевая сила. В этом случае выполняются все
предположения технической теории. Исключив из выражений для
е22 и xii по формулам A48.1) величину w, мы получим следующее
572 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
уравнение совместности:
^+^11 = 0. A48.3)
Теперь исключим iVj из второго и третьего уравнений системы
A48.2). В результате получается:
^-|г»-?п = 0. A48.4)
Уравнение совместности и уравнение равновесия оказываются
построенными симметричным образом, это обстоятельство
существенно для технической теории.
б) Теория длинных цилиндрических оболочек. В длинных
цилиндрических оболочках реализуются напряженные
состояния, довольно медленно меняющиеся по длине. Продольные
изгибающие моменты, крутящие моменты, и усилия в
поперечном направлении при этом незначительны, основные
факторы, которые определяют состояние оболочки,— это
продольные силы и поперечные моменты. Касательные усилия
существуют и фигурируют в уравнениях равновесия, но сами по себе
они невелики, и поэтому связанный с ними сдвиг пренебрежимо
мал. Теория таких длинных цилиндрических оболочек строилась
разными авторами на основе различных подходов [21], [881: либо
как результат исследования свойств некоторых решений полной
системы уравнений теории оболочек, либо с помощью явно
сформулированных гипотез. Первый путь, реализованный для упругих
оболочек, требует в случае ползучести самостоятельного
исследования, второй приведет нас к цели быстрее, поэтому мы изложим
здесь вывод основных уравнений теории длинных цилиндрических
оболочек, иногда называемой полубезмоментной теорией, следуя
Власову. Мы выберем систему координат так же, как и в
предыдущем случае при рассмотрении осесимметричных деформаций
цилиндрической оболочки. Разница будет состоять в том, что
цилиндр уже не предполагается круговым, поэтому i?2 = R (у)-
Перепишем выражения для е^ и х,;- по формулам A47.1) для
цилиндрической оболочки:
ди dv w п dv . ди
32iw д / dw . v \ /л /о с\
_ d^w 1 dv
Кинематические гипотезы Власова состоят в том, что
поперечное удлинение е22 и сдвиг е12 считаются равными нулю.
Таким образом, к A48.5) нужно добавить следующие условия:
е22 = 0, в„ = 0. A48.6)
§ 148]
ТЕХНИЧЕСКАЯ ТЕОРИЯ ОБОЛОЧЕК
573
Смысл второго из условий A48.6) заключается в том, что, хотя
сдвигающее усилие Г12, от которого в первую очередь зависит е12,
и нельзя считать равным нулю (позже мы увидим, что
производные от Г12 будут фигурировать в уравнениях равновесия), но это
усилие мало по сравнению с основным усилием Ги, следовательно,
деформация сдвига мала по сравнению с продольной
деформацией еи. Аналогичное положение возникает в элементарной теории
изгиба балок. Касательные напряжения изгиба фигурируют
в уравнениях статики, результирующая их для данного сечения
есть перерезывающая сила, которую нельзя положить равной
нулю. Тем не менее при рассмотрении характера распределения
основных, то есть нормальных, напряжений изгиба мы пользуемся
гипотезой плоских сечений, следовательно, не принимаем во
внимание связанную с касательными напряжениями деформацию
сдвига.
Первое условие носит не столь ясный характер. Действительно,
мы вправе предположить, что Г22 <€. Гц, но из этого не следует,
что е22 С 6ц, эти величины имеют одинаковый порядок. В
упругой оболочке 822 будет исчезающе мало только в том случае, когда
равен нулю коэффициент Пуассона, именно в этом предположении
и развивалась Власовым теория длинных цилиндрических
оболочек. Последующие исследования показали, что первое из
условий A48.6) может быть отброшено, при этом, конечный результат
изменяется весьма мало и уравнения остаются справедливыми
с той же степенью точности также при v =^= 0. Мы сохраняем
условие Власова в целях простоты изложения.
Из A48.5) с учетом A48.6) можно получить уравнение
совместности, которое связывает скорость деформации еп и скорость
изменения кривизны х22-
Это уравнение имеет следующий вид:
Qe11 + ^ = 0. A48.7)
Здесь дифференциальный оператор Q определяется так:
Заметим, что при сделанных предположениях
*«=-**/•
Следовательно, первый член в уравнении A48.7) представляет
собою —~. Всякие уравнения приближенной теории имеют
смысл, когда в них удерживаются члены одинакового порядка.
Теория длинных цилиндрических оболочек должна описывать
такие напряженные состояния, которые меняются медленно по
574 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
длине оболочки и относительно быстро в поперечном направлении.
Характерная длина, на которой происходит изменение той или
иной переменной от наибольшего до наименьшего значения в
поперечном направлении, есть характерный радиус кривизны
поперечного сечения а; характерную длину оболочки, для которой теория
применима, мы обозначим через I. Предполагается, что а < L
Порядок первого члена в уравнении A48.7) есть Хц/й2, порядок
последнего x22/Z2, а так как эти порядки должны быть одинаковы
(в противном случае соответствующий член в уравнении
отбрасывается), то
О'
2
¦Лц ~ -р- Х22.
Итак, мы нашли, что искривление образующей мало по
сравнению с искривлением поперечного сечения оболочки, и мы можем
принять
хи = 0. A48.9)
Следует подчеркнуть, что условие A48.9) можно использовать
при нахождении усилий и моментов из закона ползучести;
получающаяся в результате погрешность будет невелика, но
производные от ии в том направлении, в котором хи меняется быстро,
могут быть значительны и пренебрежение этими производными,
как мы видели, недопустимо.
Переходим теперь к уравнениям равновесия. Выпишем сначала
полную систему уравнений для цилиндрической оболочки:
дГи , dTi2 _п дТа , 0Т22 N2 _ п
дх ' ду ' дх ду R
дх ду дх ду
При написании уравнений равновесия принято, что на оболочку
действует только нормальная нагрузка д„. Поскольку мы
установили, что хи < х22, то следует ожидать, что моменты Мц и М2г
одного порядка, скажем М. Тогда из четвертого уравнения
следует оценка порядков Nt и М12:
tfi~4' M12~-fM.
Если принять последнюю оценку для Mi2, то есть допустить, что
в четвертом уравнении производная от Mi2 существенна, то
окажется, что в пятом уравнении порядок первого члена есть
Ма/l2, порядок второго М/а, следовательно, первым членом
можно пренебречь с ошибкой а2/Is по сравнению с единицей.
§ 148]
ТЕХНИЧЕСКАЯ ТЕОРИЯ ОБОЛОЧЕК
575
Это уравнение перепишется следующим образом:
^ + N2 = 0. A48.11)
Отсюда следует оценка для N2:
a L a
Переходим теперь к третьему уравнению^ системы A48.10).
Отправляясь от найденных оценок порядков^Л^ и N2, получим, что
порядок первого члена есть МП2, тогда как порядок второго М 1а?,
следовательно, первый член пренебрежимо мал, и мы
переписываем уравнение в упрощенной форме:
dN2 т22
ду
f R +«» = °- A48.12)
Оставшиеся уравнения мы перепишем без изменения:
дТп dTi2 n dTi2 дТ22 N2 _ п /ЛАЯ.ЛЧ\
Предполагая, что все члены в этих уравнениях одного порядка,
мы находим, что усилия Тп являются основными, усилия Тхг
по сравнению с ними представляют малые величины порядка all,
усилия Т22 — малые величины порядка а2Н2, таким образом,
оправдывается гипотеза об отсутствии сдвига, зависящего прежде
всего от TiZ, и можно приближенно положить
7,22 = 0. A48.14)
Условия A48.9) и A48.14) вместе с условиями отсутствия сдвига
и малости момента М12 по сравнению с М22 представляют собою
сформулированные в начале параграфа условия принадлежности
рассматриваемого варианта к технической теории оболочек.
Исключим теперь из уравнений равновесия A48.11) — A48.13)
NL, Ti2 и Т22- Получим:
ЯАГИ + ^—Jr (Rqn) = 0. A48.15)
Сравнивая уравнения A48.7) и A48.15), мы обнаруживаем ту же
симметрию, что и в случае осесимметричного нагружения
цилиндрической оболочки.
в) Чистый изгиб криволинейной трубы. Решению этой задачи
для трубы из упругого материала посвящена обширная
литература (см. I111]). Приближенное решение задачи ползучести
содержится в"[52]. Здесь приводится несколько иной вариант основных
уравнений задачи [1021.
576 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Пусть радиус трубы есть R, радиус сечения — а, выбор
системы координат ф = |j и 9 = |2 ясен из Рис- 226. Очевидно, что
А^Л + acosQ, В = а, R2 = a, Ri =
Д+а
cos в
A48.16)
В дальнейшем мы будем считать, что а -С R, поэтому вместо
выражений A48.16) можно принять:
R
A = R, В=а, Л4 = -
Д, = а.
A48.17)
Однако там, где, например, величину А придется
дифференцировать по 6, мы должны
будем воспользоваться
точным выражением A48.16).
Если труба
подвергается чистому изгибу и
сечение ее сохраняет круговую
форму, то все параметры
изменения кривизны и все
скорости деформации
равны нулю, кроме в± =
= с cos 6. В
действительности появляются
дополнительные деформации, связанные со сплющиванием трубы. Обо-
.значим через v (9) и w @) дополнительные скорости перемещений.
По формулам A47.1) и A47.2) получим:
Рис. 226.
е., =-
гг-
п v sin Q-\-w cos 0 w"-\-v'
R
Так как, по предположению, а < R, то для того, чтобы е2 и ei
¦были одного порядка, необходимо, чтобы числитель в
выражении е2 был малой величиной. Одинаковость порядков величин
е2 и 8j нужна для того, чтобы было возможно поставить условие
Т2 ¦€ ?V Таким образом,
w
Итак,
e1 = ccos6— — (f sin 9 +у'cos G),
Kz=~(V" + v').
Исключив отсюда v, придем к следующему уравнению
совместности:
ei" + Ч + -w [(>«2 cos 9)' — х2 sin 9].
Д2
A48.18)
§ 149] ТЕОРИЯ ПОЛЗУЧЕСТИ ДВУХСЛОЙНЫХ ОБОЛОЧЕК 577
Уравнения равновесия A47.3) и A47.4) приводятся теперь к
следующей системе:
ir;+A.r2sine-iiv2=o, 1m;+tv2=o,
В результате исключения Т2 и 7V2 получим:
ДГ»_М; —-J [(Г4 cos 9)' — Z\ sin 81 = 0. A48.19)
Опять-таки, как и в предыдущих случаях, уравнение совместности
и уравнение равновесия оказываются симметричными. В [ш]
аналогичные уравнения получены в несколько иной форме.
§ 149. ТЕХНИЧЕСКАЯ ТЕОРИЯ ПОЛЗУЧЕСТИ
ДВУХСЛОЙНЫХ ОБОЛОЧЕК
Рассмотрим теперь двухслойную модель оболочки в
предположениях, сформулированных в начале § 148. Элемент
оболочки, вырезанный вдоль линий кривизны, изображен на рис. 225,
толщины б слоев и расстояния 2/г между их серединами выбраны
в соответствии с формулами § 146. Выберем за поверхность
отнесения поверхность, расположенную посередине между слоями,
будем обозначать величины, относящиеся к верхнему слою,
знаком + , величины, относящиеся к нижнему слою, знаком —.
Пусть будут ei и е2 скорости удлинения средней поверхности,
к1 — скорость изменения кривизны в направлении 1, и2 = 0 по
предположению.
Вследствие гипотезы прямых нормалей
8n = 8j -f- щп, eu = ei — %Ji, e22 = e22 = e22.
Напряжения в слоях выражаются через скорости деформации
следующим образом:
+ 4 s+ г ,1 1 и
A49.1)
(S = CT0, V = ?0).
Теперь должно быть выполнено условие Tit = 0, это значит,
что о*ц= —(Гц. Из формул для напряжений видно, что так будет,
37 Ю. Н. Работнов
578 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
если
е4-уЕ2Г~° A49.2)
и, кроме того,
S+ S"
[)+ Ь'~
Поскольку материал слоев предполагается одинаковым и s = s (v),
то должно быть v+ = v~. Мы убедимся сейчас, что это второе
условие является следствием A49.2). Действительно, если A49.2)
выполнено, то формулы для напряжений перепишутся следующим
образом:
<2 = 7F [g2-f у«1/г] 1 <T22 = -^r [e2 — уМ]
A49.3)
Внесем теперь значения о^ и оп в выражение
,2_
В результате получим:
s2 = cr^j-г о-22 — о-ио-22.
(y+)«==e*4-|xj/j*. A49.4)
Напряжения в нижнем слое выражаются теми же формулами, что
и в верхнем слое, с заменой h на —/г, но выражение A49.4) не
изменяется при замене h на —h, следовательно, v+ — V и s+ =
= s~. В дальнейшем мы не будем ставить значок у величин v и s.
Вычислим усилие Ггг и изгибающий момент Мцт.
Тгг = S «2 + о22) = 26 — б2,
Мн = 6/г (а^ — a~j) = ^- б i- jq/г2.
Введем следующие безразмерные величины:
а = Ш-, и=-^, m = Vl*bL. A49.5)
Здесь и^не^ — произвольные константы, имеющие соответственно
размерность напряжения и скорости деформации. Теперь
Тг2=2Ьот?, ^Н = ^ф-г^п(о. A49.6)
Первая из формул A49.5) определяет со как функцию v;
обратно, можно представить v как функцию параметра к>, тогда
§ 149] ТЕОРИЯ ПОЛЗУЧЕСТИ ДВУХСЛОЙНЫХ ОБОЛОЧЕК 579
соотношение A49.4) примет следующий вид
у2 (со) = и2 + тасо2. A49.7)
Для каждого частного закона ползучести функция v (со) известна,
поэтому уравнение A49.7) позволяет определить величину со
как функцию безразмерных переменных т и и. Некоторое
неудобство состоит в том, что со задана как неявная
функция т и и.
Следующий шаг будет заключаться в том, чтобы исключить
из уравнений совместности и уравнений равновесия с помощью
A49.5) и A49.6) все другие переменные, кроме и и т. Этим мы
займемся в следующем параграфе, а пока обратимся к более
подробному рассмотрению уравнения A49.7).
В дальнейшем нам понадобятся частные производные от со
по т и и. Дифференцируя A49.7), мы получим для них
следующие формулы:
($'-2m*)^ = ^-t (ф'-2т«)^ = 2та). A49.8)
Функция 'ф(со) определяется таким выражением:
¦-iS^- <"»¦•>
Штрихи в формулах A49.8) обозначают дифференцирование по
параметру со.
Рассмотрим теперь частные случаи закона ползучести.
а) Степенной закон в — е% ( — J . Уравнение A49.7)
принимает вид
2п
со"-1 = и2 + те2ш2. A49.10)
На рис. 227 приведена номограмма уравнения A49.10).
Функция я|>, определенная формулой A49.9), при степенном законе
ползучести будет следующей:
^JjLjbi. A49.11)
б) Закон гиперболического синуса. При использовании
степенного закона ползучести для исследования оболочек иногда
возникают известные затруднения, которые будут разъяснены
впоследствии. Они связаны с тем обстоятельством, что производная —
обращается в бесконечность при s = 0. Закон гиперболического
синуса свободен от указанного недостатка и для численного счета
37*
580 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
т
7
qss
0J9
Ц85
0,7S
07
q/55
Ц55
?
ф5
77fi
Q3S
Ф
$25
Ц2
Ц75
Ц7
Vs
у&
tic Л\
V и
W
V \ Щ A Q7S
7,ffS \ \
1 \
\0,7
\\ А 4&
W \\о/ \
_
—
-
-
«AV*
77,7 \\п
W
= <? \ф5
77 =2,j\ \1Щ \
7щ\\
4*\
77SS
Рис. 227.
\f \*
\о& \^ss
\ \0 \
\ у \G3
\ \ Л qzs
' Ц7
§ 150] УРАВНЕНИЯ ПОЛЗУЧЕСТИ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 581
является, пожалуй, наиболее подходящим. Заменяя его
экспоненциальным законом, мы вынуждены особо выделять области
малых напряжений, что мало удобно при вычислениях, если
стремиться придать им стандартную форму и использовать
счетные машины. Уравнение A49.7) имеет при этом вид
фа (о) = и2 + пг2<й2.
Здесь функция ср является обращением следующего
соотношения:
Ф
СО =
Arshcp
A49.12)
При этом мы считаем
<V
= 28„
ое и ге — константы экспоненциального закона.
На рис. 228 приведен график функции ср (со) для закона
гиперболического синуса. Напомним, что при законе гиперболического
Рис. 228.
синуса, так же как и при экспоненциальном законе, толщина
модельной оболочки определяется неоднозначно.
§ 150. УРАВНЕНИЯ ОСЕСИММЕТРИЧНОИ ПОЛЗУЧЕСТИ
КРУГОВОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Будем предполагать, что оболочка несет только нормальную
нагрузку qn. Перейдем в уравнениях A48.3) и A48.4) к
переменным и и т, введенным выше. Получим следующую систему:
и" + 2пиа = 0,
со ^
A50.1)
A50.2)
582 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Здесь
Р - 26<х* '
штрихи обозначают дифференцирование по безразмерной
переменной | = х/Ь, где Ъг = —-= ah. Функция со (и, т), фигурирую-
1/3
щая в уравнениях A50.1) и A50.2), определяется
соотношением A49.6).
Для решения полученной системы можно применять
различные методы численного интегрирования, в работе I103], где
аналогичная система была получена для упруго-пластических
оболочек, указан путь ее приближенного решения по методу Галеркина.
Другая возможность состоит в использовании вариационных
методов. Оказывается, что уравнения A50.1) и A50.2) выражают
условие стационарности некоторого функционала, таким образом,
к решению задач теории оболочек оказывается возможным
применить прямые методы вариационного исчисления. В
уравнениях A50.1), A50.2) фигурируют две функции: и (?) и т (?),
мы будем их варьировать, считая независимыми между собою;
поэтому новый вариационный принцип не является следствием
принципа Лагранжа или принципа Кастильяно, наоборот, каждый
из этих принципов следует из нового принципа при определенных
частных предположениях. Поэтому мы не будем обращаться
к общим принципам теории ползучести, а постараемся подобрать
функционал, для которого A50.1) и A50.2) служат уравнениями
Эйлера. Это будет следующий функционал:
N
= t [и'т' + г|> (со) - 2пАо — 2ра] сЦ. A50.3)
Здесь tf (со) — функция, введенная соотношением A49.8).
Вычислим вариацию функционала N, используя при этом формулы
A49.7) для производных ~^— и -=— . Получим:
6ЛГ = (и'6т + т'бв)< +
i
+ \ \(~-m" + ^- — 2p\bu-{u" + 2mcoNт 1 dg.
о
Таким образом, 6iV = 0, если выполнены уравнения A50.1)
и A50.2) и естественные граничные условия, вытекающие
из равенства
(rt'6m+m'fiw)J = 0. A50.4)
§ 150] УРАВНЕНИЯ ПОЛЗУЧЕСТИ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 583
Формуле A50.3) можно придать более симметричный вид, если
проинтегрировать выражение для if по частям:
Y 4 со ,) V ш У
Положим
-iD,4i> $*> = *(»>;
тогда, учитывая A49.7), получим:
Ф —-^-+»»*© +х(<»).
Выражение функционала N примет следующий вид:
i
N=[ [н'мЧл(о)) + ~т2со-2ри]й|. A50.5)
о
Покажем теперь, что из вариационного уравнения 67V = 0
следуют вариационные принципы Лагранжа и Кастильяно.
Предположим, что уравнение совместности A50.1)
удовлетворено заранее. Это значит, что мы задаемся по произволу
функцией и (?), которая и варьируется; функция т (?) при этом
определена единственным образом с помощью A50.1) и A49.7).
Преобразуем функционал A50.3), проинтегрировав по частям первый
член подынтегрального выражения:
i
N = mu'\l0+<i l — mu" + ty — 2m*a> — 2pu]dl.
о
Вследствие A50.1) это выражение приводится к следующему:
i
N=mu'\l0+ \ (y — 2pu)d?,.
о
Выясним теперь механический смысл величины ар (со). Это не что
иное, как удвоенный потенциал напряжений на единицу объема,
выраженный в безразмерных единицах. Действительно,
^="р" \ -Уа^=Л-\sdv-
Поэтому выражение для N при условии выполнения уравнения
A50.1) можно записать следующим образом:
N = 2{U~A) + mu'\[. A50.6)
Это не что иное, как функционал Лагранжа. Действительно,
U есть потенциал напряжений, А = \ ри dl, — работа внешних
584 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
сил на соответствующем перемещении, последний член
представляет собою работу приложенных на краях моментов. Но
вариация 67V обращается в нуль, если выполнено условие A50.4).
Проварьируем A50.6) с учетом этого условия, получим:
26{U — A) = (—m'8u + mGu')l0. A50.7)
Уравнение A50.7) представляет собою вариационное
уравнение Лагранжа. Если функции сравнения выбираются так, что при
варьировании их внешние силы, приложенные к торцам оболочки,
не совершают работы, то уравнение A50.7) сводится к следующему:
8(U-A) = 0. A50.8)
Для фактического вычисления функционала U — А мы будем
поступать следующим образом. Соотношение A49.7) выражает
to как функцию аргумента и2 + щ2со2, поэтому -«- г|з (ю) =
= U (u3+ яг2со2), но мы предположили выполненным
уравнение A50.1), из которого m2w2=f yj . Таким образом,
i
U-A= J [и(и* + ^?Л— pu'jdl A50.9)
о
Предположим теперь, что выполнено уравнение
равновесия A50.2), мы задаемся функцией т (?) и находим из этого
уравнения функцию и. Поступая точно таким же способом, как и ранее,
преобразуем функционал A50.3) путем интегрирования по частям
к следующему виду:
о
При преобразовании было учтено выполнение уравнения A50.2)
и использовано соотношение A49.7). Фигурирующая под
интегралом величина
^-JS=i4-П^-Н = -г!-\vds (l50-l0>
представляет собою удвоенный безразмерный потенциал
скоростей, отнесенный к единице объема, следовательно,
N = um' и-2Ф. A50.11)
Если сравнивать статически возможные состояния, отвечающие
заданным нагрузкам, то при варьировании A50.1) члены,
зависящие от условий на торцах оболочки, исчезнут, и мы получим
§ 151] СТЕПЕННОЙ ЗАКОН ПОЛЗУЧЕСТИ 585
вариационное уравнение Кастильяно:
6Ф=0. A50.12)
Величина —^——^^р(а) есть функция ш, следовательно, ее можно
считать функцией аргумента —^--fm2:
Но из A50.2) следует:
± = {{т" + 2Р).
Поэтому функционал Кастильяно может быть вычислен по
следующей формуле:
i
ф= \ ф Гто2 + 1-(т." + 2рJ] d\. A50.13)
§ 151. СТЕПЕННОЙ ЗАКОН ПОЛЗУЧЕСТИ.
ПРИБЛИЖЕННОЕ ИССЛЕДОВАНИЕ КРАЕВОГО ЭФФЕКТА
По формулам A49.10) и A49.11) при степенном законе
ползучести
tb = ——г со"-1 = —j-r - лг2ы .
г п + 1 п-\-1 L и J
Поэтому выражение A50.3) для функционала N становится
следующим:
N=l [м'т'+п-тг^-4тт2@-2^1^ A511)
о
Эта форма более удобна, поскольку она не содержит функции \р.
Чтобы составить функционал Лагранжа, заметим, что
Поэтому
I Ц±1
G = ^a\ (WxmJ"^- <151'2>
о
С другой стороны, из равенства
со«-1 = и2 + то2й2
586 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
следует:
Теперь
у2
в|и
Следовательно,
1 гЬ-
2 гр"
п+1 2 П+J
1+1 И+1Х '
( п+1
о
Рассмотрим полубесконечную цилиндрическую оболочку,
нагруженную равномерно распределенным давлением и
закрепленную на торце. Будем различать два случая:
а) Край оболочки свободно оперт, следовательно, если
поместить начало координат на конце оболочки, то
»@) = т@) = 0.
б) Край оболочки жестко защемлен, следовательно,
«@) = и'@) = 0.
На достаточно большом расстоянии от торца оболочка
находится в безмоментном состоянии. Будем считать, что при \ = оо
т = 0, и = и*, со = со*. Из A50.2) следует:
а из A49.10)
Отсюда
и*
<а* Р'
2п
= рп, со* = рп~х
A51.4)
Введем функции U и V, удовлетворяющие следующей системе
линейных уравнений:
G" + 2иУ=0, V — 2k{U — u*)-Q A51.5)
и граничным условиям нашей задачи; U @) == V @) в случае а)
и U[0) = U'@) в случае б). Здесь X и ц —не определенные пока
константы. Исключив из A51.5) функцию V, мы придем к
следующему уравнению:
C/IV + 4a4(^-w*) = 0.
§ 151J- СТЕПЕННОЙ ЗАКОН ПОЛЗУЧЕСТИ 587
Здесь a* = A,[i. Найдем решение этого уравнения,
удовлетворяющее условию ?/(оо) = и*:
U = и* + е~а% (я cos a| -f- Ь sin а?).
Теперь с помощью первого из уравнений A51.5) получим:
V — у — е_а? (b cos а? — а sin а?).
Константы а и 6 определяются так, чтобы удовлетворить
граничным условиям на закрепленном крае. Введем дополнительно
обозначение
]/?«• = P(u*)i/h
н положим
U-^u*U0(al), V=P(u*)i/nV0{a?). A51.6)
Функции U0 и V0 определяются следующим образом:
в случае а)
U0 — l — e_a^cosag, F0 = e~a^ sin a?;
в случае б)
U0 = l— e-°?(cosa?-f sinag), F0= —e-a?(cosa? — sin ct?).
Будем искать приближенное решение задачи в виде
u = U, m = V;
при этом параметрами аир мы будем распоряжаться таким
образом, чтобы функционал принимал стационарное значение.
Положим, кроме того,
п-1
со = й>*о,)о = {и*) п со0. A51.7)
Внесем выражения A51.6) и A51.7) в уравнение A49.10). Заметим,
что множитель, зависящий от и*, сократится, и мы получим:
df^Ul + pvWo. A51.8)
Теперь мы должны вычислить функционал A51.1). Для
бесконечной области интеграл будет расходящимся, поскольку
величина и2/а вследствие A51.4) стремится при | = оо к значению
(и*) п , произведение ри стремится к тому же значению.
Подставим в A51.1) выражения A51.6) и A51.7) и заменим р через
(м*I/'1 на основании A51.4), добавив под интегралом постоянные
588 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
члены, необходимые для обеспечения его сходимости. Получим:
"-егЧГ^+ЗтСЗ-О-
о
-JTFlP8^- 2(tfo-l)]dE-
Перейдем от переменной | к переменной z — <х?, теперь штрихи
будут обозначать дифференцирование по этой переменной. Поло-
жим также N = (и*) п JV0 (a, §). Получим:
оо
N„ = a$[ U'0V'0dx +
о
И [.-TlS-O-^i^b-2^-!)]^ A51-9)
a
о
Очевидно, что при принятом выборе функций сравнения
граничные условия A50.4) будут выполнены как для свободно опертого,
так и для защемленного края. Следовательно, N0,
рассматриваемое как функция от а и р\ должно принимать стационарное
значение. Обозначим:
оо
[ U'€U'0dx = A,
о
A51.10)
оо
о
Тогда
N0 = a$A + ±BW).
Условия экстремума будут следующие
Отсюда
М-^-Д(Р) = 0, аА + ±-Ц-0.
-|-B?Р) = 0,- а? = ^. A51.11)
Величина А вычисляется немедленно, в случае а) А = — 1/4,
в случае б) А = 1/2. Теперь мы должны подобрать параметр р\
при котором выполняется первое из условий A51.11). Для этого
§ 152]
ПОЛУБЕСКОНЕЧНАЯ ОБОЛОЧКА
589
нужно вычислить В (|3) для ряда значений р" по второй из
формул A51.10) и найти то значение, при котором р*В достигает
минимума.
В случае упругой оболочки все рассуждения сохраняют силу,
только слова «скорость деформации» заменяются словом
«деформация», во всех вышеприведенных формулах следует положить
п = 1. Выражение для В ф) становится следующим:
Положим:
Тогда
В=\ l{U0-\y-FVl]dx.
о
со оо
J (U0-l)*dx = C, \>Vldx = D.
B = C-^D.
Из первого условия A51.11) получаем:
V 3D •
Интегралы, обозначенные через С и D, легко вычисляются.
Так, для случая а) мы имеем:
Г—— Л——
Поэтому р2 = 1. Если принять р= —1, то по второй из формул
A51.11) а=1.
§ 152. ПОЛУБЕСКОНЕЧНАЯ ОБОЛОЧКА
С ШАРНИРНО ЗАКРЕПЛЕННЫМ КРАЕМ
Графики функций U0 (х) и V0 (x) для опертого края построены
на рис. 229. Величина V0 значительно меньше, чем U0, особенно
при достаточно больших х; при х = 0 по формуле A51.8)
величина со0 = 0, следовательно, при малых х со0 мала. Таким образом,
в правой части уравнения A51.8) первый член всегда значительно
больше второго. Поэтому мы можем принять
Щ = и0п A + 6),
где б < 1. Подставляя в A51.8) и ограничиваясь первой
степенью 5, найдем:
6 = -^p2F^2/n. A52.1)
590
УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Фиксируем теперь некоторое значение х = с, начиная с которого
) и0 — 1 ) < р> причем р < 1. Представим интеграл, дающий
выражение В (Р), в виде суммы двух интегралов: от х = 0 до
х — с, который мы обозначим через Въ и от ,т = с до х — оо,
который мы обозначим В2. По второй из формул A51.10),
учитывая принятое приближенное выражение для <л0 и
пренебрегая членами порядка б2, найдем:
о о
Величина В2 вычисляется по той же формуле при других
пределах интегрирования, но мы будем пренебрегать членами
порядка р по сравнению с
единицей, поэтому
1
2Д>-
^\v\dx.
Последний интеграл flerKo>
вычисляется, а именно:
\ v;d*=$
е 2Х sin2 х dx —
= jr e~2c D+cos 2c + sin 2c).
Приведем результаты вычислений для некоторых значений п.
При этом было принято с — я, поэтому В2 — — р20,0009Л.
Выражение для В представим в следующем виде:
В(Р) = 2/1-р»/2.
Здесь
п-1
/2= J V2aU0n da;+ 0,00093.
Теперь из условия
мы находим:
i<№=°
Р-&
§ 152] ПОЛУБЕСКОНЕЧНАЯ ОБОЛОЧКА 591
и по второй из формул A51.11)
а«=-4(^-/2р).
В нижеследующей таблице приведены значения а и р в
зависимости от п:
п
1
2
3
4
5
6
Р
-1
—0,840
—0,728
—0,643
—0,598
-0,540
а
1
0,860
0,763
0,718
0,678
0,646
Для больших значений п приближение, полученное в
предположении о том, что прогибы и изгибающие моменты
распределяются так же, как в упругой
оболочке, не может считаться надежным. °
Более того, формулировка задачи об
оболочке, нагруженной давлением и
шарнирно опертой на торце, при
степенном законе ползучести приводит к
противоречию. Действительно, при х = 0
прогиб и момент равны нулю, следо- ^
вательно, также со=0, и решения урав- '
нений A50.1) и A50.2) в окрестности
точки х = 0, удовлетворяющего
условиям и @) = т @) = 0, не существует.
Это легко понять из следующих
соображений. Представим себе оболочку из
жестко-пластического упрочняющегося
материала, следующего диаграмме, изображенной на рис. 230.
При о<<тг пластический модуль равен бесконечности, а со
представляет собою величину, которая соответствует обратному
значению пластического модуля. Если край такой
жестко-пластической оболочки не нагружен и при х = 0 все напряжения равны
нулю, то напряжения будут оставаться меньше предела текучести
в некоторой области 0 < х < б, а следовательно, часть оболочки
длины б будет вести себя, как жесткое кольцо.
Оставшаяся часть оболочки находится в пластическом
состоянии, но при х = 6 выполняются условия жесткого
защемления.
592 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Диаграмма о — е при степенном законе пластичности
касается оси а в начале координат, в этой точке пластический модуль
равен бесконечности, поэтому, хотя б стремится к нулю, все же
жесткое кольцо, хотя и бесконечно малой длины, сохраняется,
и непрерывное решение невозможно.
§ 153. ПОЛУВЕСКОНЕЧНАЯ ОБОЛОЧКА
С ЗАЩЕМЛЕННЫМ КРАЕМ
В этом случае, как мы видели в § 151, функции U0 и Vo
выбираются следующим образом:
U0 = 1 — е~х (cos х -\-sin х),
V0— —e_3:(cosx — sin ж).
Очевидно, что упрощения, связанные с относительной малостью
VQ, в случае опертого края здесь не появляются.
Представим выражение A51.10) для В ((J) следующем виде:
T*(P) = 'i—^-Ъ. A53.1)
Здесь
со оо
о о
Для фактического вычисления этих интегралов поступим так же,
как и раньше: выберем некоторое значение х = с такое, что при
х> с \иа — 1 I < р, причем р < 1. Тогда по-прежнему при
п—1
х > с шо = U о A + б), причем б определяется формулой A52.1).
Пренебрегая малыми более высокого порядка, получаем:
о
Здесь
ОО
Я= \ VUx. A53.3)
о
Точно так же
с
/2== ? Vl(o0dx + K. A53.4)
о
§ 153] ПОЛУБЕСКОНЕЧНАЯ ОБОЛОЧКА С ЗАЩЕМЛЕННЫМ КРАЕМ 593
Вычислим теперь производную -^~. Произведем
дифференцирование под знаком интеграла, с другой стороны,
продифференцируем по р уравнение A51.8), в результате чего получим:
(nUl + FVX)^L- = (n-l)VVy0.
ар
дщ
Исключив с помощью этого соотношения производную ° под
знаком интеграла, найдем:
1 дБ
2 ар
¦р/2. A53.5)
Теперь первое из условий A51.11) приводится к следующему:
Ji-Ps-?±f/2 = 0. A53.6)
Величина К вычисляется непосредственно, а именно:
К = -1 е"ас B - sin 2с - cos 2c).
Так, при с = я, что было принято при вычислениях, /Г = — ея =
= 0,00093.
Вычисления производятся следующим образом. Величины ^
и /2 определяются для нескольких значений C, выбранных в
предположительной области, где следует искать истинное значение.
Результаты предыдущего параграфа могут быть использованы
при этом для некоторой ориентации. После этого графически
находится корень уравнения A53.6), вычисляется В по формуле
A53.1) и находится а по второй из формул A51.11), причем
А = ill.
При фактических вычислениях положение оказывается
следующим. В отличие от случая опертой оболочки величина р
сравнительно мало отличается от единицы, соответствующей упругой
оболочке. Действительно, величина изгибающего момента в
реальной оболочке пропорциональна величине h, которая связана
с действительной толщиной Н формулой A46.3). Поэтому,
принимая C = 1, мы найдем, что момент в заделке
мп-' - ^n+i
1+2л
Отношение величины момента в предельном состоянии при п — оо
к величине момента при п = 1 по этой формуле получается
равным у 3/2. Но при п = оо в оболочке реализуется предельное
38 ю. н. Работнов
594 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК;! [ГЛ. X
состояние, при этом, если предельное напряжение есть о^,
то р — —1. В заделке возникает шарнирная окружность,
изгибающий момент равен предельному, но в предельном состоянии
т/3
т = ~- , что следует из определения величины Мп при
ojj = —oi = °V Произведенный для случая п = 3 расчет
показал, что величина В, определенная уравнением A53.6),
действительно весьма близка к единице. Полагая 6 = 1 и производя
вычисления, находим, что при п = 3 а = 0,716.
О qZ0<ft$>
л=7
т/ги*/А
Рис. 231.
Заметим, что в работе [17°] эта же самая задача решалась при
помощи вариационного уравнения Лагранжа. Для упрощения
было принято, что изгибающий момент зависит только от
изменения кривизны, а окружные усилия — только от деформации,
поэтому вместо функционала A50.9) варьировался некоторый
более простой функционал. Форма прогиба задавалась так же,
как в нашем случае, и отыскивался параметр а, величина
момента вычислялась по прогибу. Результаты оказались близкими,
для п = 3 получено а = 0,659. О степени достоверности
полученного распределения момента судить трудно, как это бывает
всегда, если варьируются скорости. Задача о краевом эффекте
в полубесконечной защемленной оболочке была рассмотрена также
Волчковым [14], который непосредственно интегрировал
уравнения A50.1), A50.2) методом последовательных приближений. Идея
метода состояла в том, что в этих уравнениях выделялась
линейная часть, нелинейные члены переносились вправо. Зная
функции и и т в приближении номер к, можно было вычислить
правую часть уравнений, в левой же части оставались линейные
§ 154]
РАСПРОСТРАНЕНИЕ НА СЛУЧАЙ Гп ф О
595
операторы, интегрирование получившихся линейных уравнений
позволяло найти функции и и т в приближении номер к + 1.
Вычисления производились на электронной счетной машине, пятое-
приближение практически не отличалось от четвертого. На рис. 231
приведены графики функции и и т для п — 1, 3 и 5 (сплошные-
линии). Полученный вариационным методом для п — Ъ
результат, заключающийся в том," что 8 = 1, подтверждается с очень
хорошей точностью как для п = 3, так и для п — 5. Пунктиром
для сравнения построены графики « (?) и т(?), соответствующие-
приведенному выше приближенному решению.
Возвращаясь к атому решению, посмотрим, как можно
применить его для оценки напряжений в реальной оболочке. Зная,
величины U0 и V0 как функции аргумента х, мы можем вычислить
напряжения по формулам § 149. За напряжения в оболочке мы
будем принимать напряжения, определенные для слоев модели.
Можно поступить более точно, а именно получить формулы для
напряжений в реальной оболочке по заданным величинам и и m,
которые были вычислены для модели. Приближенный характер
исследования делает такие уточнения бесполезными. Нетрудно
убедиться, что формулы для напряжений имеют следующий вид:
^ = ,^РП№ ^. = р[!Ь±^мы)]. (Ш.7)
Величина р представляет собою безразмерное окружное
напряжение на бесконечности:
§ 154. РАСПРОСТРАНЕНИЕ ТЕХНИЧЕСКОЙ ТЕОРИИ
НА СЛУЧАЙ Тц Ф О
Указанное обобщение вышеизложенной теории не встречает
существенных затруднений. Мы будем следовать изложению § 149
и ссылаться на соответствующие формулы, внося по ходу дела
необходимые изменения. Приведенные в начале параграфа
выражения для деформаций и формулы для напряжений A49.3)
сохраняют силу, но условие A49.2) уже не выполняется. Псь
прежнему
но
Ти = б(сЪ + <Га).
Отсюда следует:
_+ . Mn+hTn _ _ Mu-hTu
°ii- 26Л ' °"~ ж • A54.1)
38?
596 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
С другой стороны, Ojj и о~г выражаются через деформации по
формулам A49.1), поэтому
Здесь, как и раньше, ю± = —-——. Введем теперь следующие
е* s±
обозначения:
Уз ми =т J/3_Jji_ = t Л2.=ц
4 6Ла* ' 4 6а* ' е*
Обозначения для т и и совпадают с принятыми в § 149. Теперь
формулу A54.2) можно переписать следующим образом:
— (е1±х1А) = -^(т±т)<в±— ±-и. A54.3)
Для интенсивности скоростей деформации выражение будет таким:
(И' = 4 [ е* + (е* ± к'йJ + 8* (8i ± **й) ] •
Учитывая A54.3) и введенные выше обозначения, получим:
У± V = а3 + (т ± тJ (ю±J. A54.4)
Соотношение A54.4) в точности соответствует
соотношению A49.7), v+ есть функция со+, V есть функция и-; для
нахождения со+ и со" применяется та же самая номограмма, которая
используется для нахождения со, только величину момента нужно
изменять на известную величину + т соответственно.
Вычислим теперь усилие Т22-
С помощью A54.3) приведем это выражение к следующему:
Т»=6°.[»AГ + 4=-)+^]. A54.5)
Теперь нам осталось выписать выражение для скорости
изменения кривизны, которое немедленно следует из A54.3):
и1 = У^-^-1(т + г)(о+ + (т — г) со~]. A54.6)
§ 155] ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА, СЖАТАЯ ОСЕВОЙ СИЛОЙ 597
§ 155. ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА, СЖАТАЯ ОСЕВОЙ СИЛОЙ
Здесь мы будем принимать во внимание только влияние
осевой силы на ползучесть оболочки, но не роль ее в создании
изгибающего момента. Если учесть осевое усилие в уравнении
равновесия, туда придется ввести кривизну образующей и задача
станет существенно нестационарной; к рассмотрению
подобного рода задач мы обратимся в главе XII. Пока что мы сохраняем
уравнения A48.3) и A48.4) для осесимметрической деформации
цилиндрической оболочки. Подставляя в эти уравнения
найденные выше выражения для Г22 и щ, а также заменяя е2 и Мн их
выражениями через и и иг, мы придем к следующим уравнениям:
т'-ц(-^ + -^)-^гт + 2р = 0, A55.1)
к" + (т + т)<й+ + (т — х)©- = 0. A55.2)
Дифференцирование производится по безразмерной
координате |, определенной так же, как в § 150, величина р сохраняет
то же значение.
Следуя методу, изложенному в § 150, нетрудно показать,
что уравнения A55.1) и A55.2) представляют собою уравнения
Эйлера для следующего функционала:
N= J [u'm' + yiHco+) + yiMa)-)-(m + TJco+-
о
— (m —т)*сг + 2 (-4=— Р^)и] dl- A55.3)
При степенном законе ползучести этот функционал можно
записать в иной, более удобной форме, а именно:
i
N=[ Ги'т'Н ?т-ияГ-4г + — ^ тт-Х
J L n + l Ч,со+ ' а>~ J л-f-l
о
X {(т + тJ й+ + (т-тJсо-} + 2 (^~ р) и] dg, A55.4)
что соответствует выражению A51.1) для случая отсутствия
осевой силы.
Мы не будем доказывать высказанное утверждение, это
доказательство ничем не отличается от того, которое было проведено
в § 150, естественные граничные условия, при которых
обращение в нуль вариации функционала A55.3) эквивалентно
выполнению уравнений A55.1) и A55.2), остаются теми же самыми,
что и при отсутствии осевой силы.
598 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Если предположить выполненным уравнение равновесия A55.1)
или уравнение совместности A55.2), то требование стационарности
функционала N эквивалентно условию стационарности
функционала Кастильяно или Лагранжа соответственно. Однако, в
отличие от рассмотренного ранее более простого случая, явное
выражение этих функционалов записать не удается. Действительно,
предположим, что выполнено уравнение A55.1). Интегрируя по
частям первый член A55.3) и учитывая A55.1), получим:
Здесь
*- И1*м4*м-Н(-50ЧЯ2]Н <155-5>
о
Это выражение представляет собою функционал Кастильяно, если
выполнены статические граничные условия, то 6N = 0
эквивалентно 6Ф = 0. Однако теперь составить для Ф простое
выражение через функцию т(|), подобное выражению A50.13), уже
нельзя. Действительно, при степенном, например, законе
ползучести формула A55.5) переписывается так:
I п+1 п+1
ф=тЬг$ [<»+)п-1+(<Оп-1]<*?.
о
Из уравнения A55.1) следует:
Теиерь мы должны подставить найденное выражение для и
в уравнение A54.4), в результате получится система двух
уравнений, решение которых определяет со+ и со- в зависимости от
функции т(?); найденные значения следует внести в формулу
для Ф. Однако явные выражения для ю+ и аГ не получаются.
Совершенно аналогичные трудности возникают при переходе к
вариационному принципу Лагранжа.
§ 156. КРАЕВОЙ ЭФФЕКТ В ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКЕ,
НАГРУЖЕННОЙ РАСПРЕДЕЛЕННЫМ ДАВЛЕНИЕМ
И ОСЕВОЙ СИЛОЙ
Схема решения этой задачи при помощи вариационного
уравнения при степенном законе ползучести, по существу, не
отличается от схемы, развитой в § 151. Положим:
т = стс1/", u = ycU0, m = ^nV0, u)± = c1-1-©^. A56.1)
§ 156] КРАЕВОЙ ЭФФЕКТ В ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКЕ 599
Здесь U0 — функция, удовлетворяющая граничным условиям
для прогиба и равная единице на бесконечности, V0 — функция,
удовлетворяющая граничным условиям для момента и
исчезающая на бесконечности. Естественно выбрать эти функции так же,
как в § 151, тогда они будут функциями аргумента а|; величина а,
определяющая быстроту затухания краевого эффекта, является
одним из подлежащих варьированию параметров, вторым таким
параметром служит величина |3. На достаточном удалении от края
величина т становится пренебрежимо малой, поэтому значения
<о+ и со~ стремятся к одному и тому же пределу при | -*- до.
Потребуем, чтобы было
<в+(оо) = ш-(оо) = 1.
Из уравнения A54,4) при этом следует, что
1 = у* + а*. A56.2)
Кроме того, при § = оо из A55.1) получим:
р = сш(ч+^у A56.3)
Поскольку величина т задана, первое из соотношений A56.1)
и уравнения A56.2) и A56.3) позволяют определить значения
всех введенных параметров, а именно:
?_ L_
i х УЗ ,/п г
<У-= , Y = , ci'a = —.
/*+(*-тг)' V'^-^ff
A56.4)
Внесем теперь выражения A56.1) в уравнение A54.4),
ваписанное для случая степенного закона ползучести. Получим:
К±OГГГ = y*Ul + (рТ0 ± <*)а К*)8- A56.5)
Постоянная с при этом сократится. Эта постоянная в степени
' ' 1
1 Н выносится также множителем из-под интеграла в
выражении для N, и задача сводится к отысканию стационарного
значения следующей функции от переменных а и В:
N0 = t$A+±.B$).
600 УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН И ОБОЛОЧЕК [ГЛ. X
Здесь
оо
А = у \ ^о^» dx,
о
о
-^~T№o + o)Za: + (pV0-o)z<*--2oZ]-2y2(CfQ-l)}dx. A56.6)
Здесь, как и в § 151, UQ и F0 являются функциями аргумента х
и под интегралом добавлены слагаемые, обеспечивающие его
сходимость. Условия стационарности по параметрам аир
буквально совпадают в этом случае с условиями A51.11), и ход
вычислений остается тем же самым. При выборе предположительной
области, в которой отыскивается значение C, может оказаться
полезным следующее замечание. Положим ге=1, что
соответствует линейно-вязкой оболочке или оболочке из
упруго-несжимаемого материала, если вместо скоростей рассматривать
перемещения. В этом случае <oJ = шй —1 и функция В (р) принимает
следующий простой вид:
оо
#(Р)= I h4U0-l)* + FVl\dx.
о
Рассмотрим, например, случай свободно опертого края, тогда,
как мы видели,
U0 = 1 — е~х cos х, F0 = e_a:sina;,
Оо оо
J (t/0-lJ^ = -jj-, J Vldx = ±-,
о о
и, следовательно,
Минимальное значение величины В$ достигает при р = у. В
условиях ползучести при п > 1 изгибающие моменты будут меньше,
поэтому искомое значение Р всегда меньше по абсолютной
величине, чем у.
Заметим, что если pl% = l/j/^З, у = 0 и никакого изгиба
не происходит. Легко убедиться, что в этом случае осевое
напряжение аи вдвое больше, чем окружное напряжение аг2, поэтому
скорость ползучести в окружном направлении равна нулю и
закрепление края никакого действия на оболочку не оказывает.
§ 157] ПРИБЛИЖЕННЫЕ ВЫРАЖЕНИЯ ПОТЕНЦИАЛА СКОРОСТЕЙ 601
§ 157. ПРИБЛИЖЕННЫЕ ВЫРАЖЕНИЯ ПОТЕНЦИАЛА
СКОРОСТЕЙ ДЛЯ ПРОИЗВОЛЬНОЙ ОБОЛОЧКИ
Как мы убедились, основная трудность в теории ползучести
оболочки состоит в том, что потенциал скоростей в общем случае
явно выписать не удается, поэтому все вышеприведенные
результаты относились к частным случаям и были получены с помощью
тех или иных упрощающих предположений.
Некоторый разумный способ получения приближенного
выражения потенциала состоит в том, чтобы следовать для оболочки
той же идее, которая была осуществлена в § 116 для
сжато-изогнутого стержня. Предположим, что
-Ф = Ф(Д),
где
Д2 = Мо2 + аг71,
м; = м1\+м^-лг11м22+4(м*1+аг;1), (i57.i>
Tl^K + Ttt-TuTv + ^iTl + Tl).
Отсюда следует:
гП — а д I -Ml — "J-* 22 )¦> ?22— « ^ I ^22_ у ^11
о _ Q„l Ф' (Д) Т
42 — оа ^ L 12i
Хи=*Ш(м„-±м»у к^^(м22-±миу A57'2)
_ о Ф' (Я) .,
^12 — ° д М 12-
Для степенного закона ползучести
так как при Т0 = 0 R = М0. Требуя, чтобы формулы A57.2)
давали правильный результат также и при чисто безмоментном
напряженном состоянии, мы должны принять, как и в § 116,
, / П \ 1+1
ГЛАВА XI
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
Расчеты неустановившейся ползучести на основе теории
упрочнения встречают значительные трудности. Наиболее
эффективным, но достаточно трудоемким методом является численный
метод расчета шагами по времени, который иллюстрируется на
некоторых одномерных задачах, относящихся к изгибу стержней,
к вращающимся дискам и цилиндрам.
Применение вариационных принципов позволяет получить
некоторые приближенные решения задач неустановившейся
ползучести, однако возможности их эффективного использования
ограничиваются относительно простыми случаями. В то же время
в расчетной практике получили широкое распространение методы
расчета неустановившейся ползучести на основе теории старения,
отличающиеся неизмеримо большей простотой.
К области неустановившейся ползучести следует отнести
та такие задачи, когда ищется время до разрушения с учетом
трещинообразования и влияния трещинообразования на
перераспределение скоростей, а следовательно напряжений. Одна
такая задача рассмотрена в конце главы.
§ 158. ПРИМЕНЕНИЕ ГИПОТЕЗЫ УПРОЧНЕНИЯ
К РАСЧЕТАМ НА НЕУСТАНОВИВШУЮСЯ ПОЛЗУЧЕСТЬ
В этой главе мы будем рассматривать такие задачи теории
лолзучести, при решении которых предположение об
установившейся или квазиустановившейся ползучести не может считаться
оправданным и вопрос о перераспределении напряжений в
процессе ползучести является существенным. Прежде всего это
относится к тем задачам, в которых рассматриваются
сравнительно небольшие деформации ползучести, имеющие тот же порядок
величины, что и упругая деформация. Но, учитывая упругую
§ 158] ПРИМЕНЕНИЕ ГИПОТЕЗЫ УПРОЧНЕНИЯ 603
Л5
деформацию, мы, как правило, не можем пренебрегать первым
участком кривой ползучести, а поскольку напряжение меняется
во времени, мы должны пользоваться теорией ползучести,
пригодной для случая переменных напряжений. В главе IV было
показано, что гипотеза упрочнения в ее простейшем варианте
удовлетворительно описывает ползучесть при переменных
напряжениях, если напряжения меняются достаточно плавно. Применение
уточненных кинетических уравнений здесь вряд ли оправдано,
эти уточнения покупаются слишком дорогой ценой, и мы увидим
далее, что даже простейший вариант тео- у/ у-,
рии упрочнения в приложении к реаль- "^ "^
ным задачам приводит к очень большим
трудностям. Поэтому в настоящее
время решения, основанные на теории
упрочнения, очень немногочисленны,
они достигаются путем громоздких
вычислений. В практике расчетов
применяются, как правило, более простые
теории неустановившейся
ползучести, хотя они и не имеют под собой дос- Рис. 232.
таточного физического обоснования.
Для выяснения существа дела мы рассмотрим схематически
простой пример стержневой системы, изображенной на рис. 232.
Уравнение равновесия для этой системы:
а1 + 2а2 = о-.
Уравнение совместности деформаций:
е2 = 2е.[.
Здесь а1; оz, о* — выбранные соответствующим образом
безразмерные напряжения, е2 и et — деформации с точностью до
некоторого множителя пропорциональности, закон ползучести при
этом записывается так:
Степенная зависимости от а принята нами для определенности.
Решение полученной системы весьма затруднительно, однако
о характере решения можно сделать некоторые заключения.
Действительно, в начальный момент времени t = 0 pi = р2 ~ 0,
следовательно, а± = еи о2 = е2, и мы находим:
o-i@) = TC a2@) = -|a.
С другой стороны, когда время t. достаточно велико, р± л; еи
р2»е2, напряжения практически не изменяются, поэтому
604
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
pi — ei, P2 = e2> следовательно,
ИЛИ
1+а
сг2 = ог12 " .
Теперь из уравнения равновесия следует:
1+а
3 3'2 ™
°i = ^1±^а' ff2== ^Ш~-
1+2 п 1+2 п
Так, если -у—— = 3, то а4 = 0,854а, ст2 = 1,076с
Итак, в процессе ползучести напряжение о^ возрастает от
начального значения о4 = 0,600а, приближаясь к пределу, равному
0,854а, тогда как напряжение а2 убывает от начальной
величины 1,200а, стремясь к пределу 1,076с Предельное состояние
соответствует квазиустановившейся ползучести и находится
достаточно просто, в общем случае для этого применяются все методы,
которые были изложены в главе VII. Исследование
неустановившейся ползучести должно состоять в том, чтобы найти Oj и а2
как функции времени. Если нас интересуют перемещения точек
системы, например перемещение точки приложения внешней
силы, то в первый момент величина этого перемещения будет
определяться упругими деформациями стержней, далее
перемещение будет изменяться в функции времени.
Даже для приведенного чрезвычайно простого примера
решение в замкнутом виде получить не удается, приходится прибегать
к численным методам. Наиболее простой и естественный метод
заключается в том, что расчет ведется конечными разностями
по времени. Пусть в момент tk напряжения в стержнях были o1)ft
и а2,й, а деформации e1)fe и e2,ft, соответственно деформации
ползучести Pi^ и p2,ft- Тогда для близкого момента времени
h+i — h + &h
Pi, A+i = Pi, h + (pTacft),h &th. A58.1)
Теперь мы решаем совместно систему уравнений
01, u+i + 2o2j ft+i = a,
ei, ft+1 — °"l, ft+l = Pi, h+iJ
eZ fc+1 — °2, fi+1 = P2, ft+l>
находим значения a,- и et для момента th+i и продолжаем процесс.
§ 159] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ИЗГИБЕ 605
Некоторая модификация указанного приема будет состоять
в следующем. Проинтегрируем уравнение ползучести. Получим:
„1+а я
-гт— = \ стП dL
1+а J
Для интервала Atk получим отсюда:
(Pft+i)^" - Ы1+а + (»ft)n A*a (! + <»)• A58.2)
Преимущество формулы A58.2) заключается в следующем.
Мы должны начинать счет с момента t = 0, когда пластическая
деформация еще отсутствует. Но в правой части формулы A58.1)
величина р стоит в отрицательной степени, поэтому для первого
шага она непригодна. Формула A58.2) свободна от этого
недостатка.
Мы не будем проводить фактических вычислений для этого
примера, который сам по себе малоинтересен, совершенно
аналогичный способ будет применен в дальнейшем для других задач.
§ 159. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ИЗГИБЕ
Простейшая задача о неустановившейся ползучести стержня
прямоугольного сечения при чистом изгибе не допускает
замкнутого решения на основе теории упрочнения. По-видимому, первой
работой, посвященной этому вопросу, было исследование I16'].
Автор пользовался следующим законом ползучести:
р — ра(ехрв — 1).
Решение строилось в рядах, при этом оказалось, что вблизи
нейтральной оси а меняет знак. Это получается вследствие того,
что исходное уравнение непригодно для малых о, как было
показано в § 50, правая часть при малых о должна иметь вид
const X а", где п > 1 + а.
В работе [157] было внесено некоторое исправление в
уравнение, которое устраняло отмеченную особенность. Заслуживает
внимания использованный в этой работе прием линеаризации
исходного уравнения ползучести, который позволяет построить
решение в рядах и доказать их сходимость.
Этому же вопросу посвящена более поздняя работа [24в].
В отличие от [157] закон ползучести принимается степенным,
а именно:
р = р-а0п A59.1)
Рассматривается стержень произвольного сечения, имеющий две
оси симметрии, плоскость действия изгибающей пары
принимается совпадающей с одной из главных плоскостей, например
плоскостью yOz.
606
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Положим е = х (t) у и \ а (у, t)y dF = М. Изгибающий момент
прикладывается внезапно при t = 0 и сохраняет постоянное
значение, поэтому х @) = 0.
Будем обозначать через Is момент порядка s площади сечения
относительно оси х:
/.= \\y\sdF.
F
Тогда, как известно, напряжение в упругом состоянии сразу
после приложения изгибающей пары
а(У^)=-^-у.
Будем искать решение для напряжений в виде
оо
a(y,t) = ^-y[l + ^iFT(y)trm]. A59.2)
r=i
Так как 0 (—у, t) = а (у, t), то все функции Fr (у) должны быть
четными, или
Fr(y) = FT{\y\).
Из условия равновесия следует:
со
2*m \FT(y)y*dF = 0,
1 F
и так как это равенство справедливо для любых t, то
\FT{y)y*dF = b. A59.3)
F
Теперь автор подставляет выражение A59.2) в уравнение
ползучести A59.1) и записывает результат следующим образом:
со
1
Ц1+а)(^)',г/«[1 + ^Г + (^^ + ^)Р+...].
Это уравнение интегрируется при начальном условии р (у, 0) = 0,
1
ряд в правой части возводится в степень . , , и для р
§ 159] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПРИ ИЗГИБЕ 607
получается следующее разложение:
i
+ ••• [гЬг2^й(т^+/,2
2Ta + l)^(™+TF-^]"+I^+---}- A59-4>
_ а rfi ™ 1 ,2т+
2(а + 1J (га
Здесь
v = -
1+а ' V'/
Кривизна теперь может быть определена следующим образом:
е в + р
«== = —
Здесь сг выражается формулой A59.2), а р — формулой A59.4)_
Но и не должна зависеть от у, отсюда следует, что
т-
1+а
и
^Л+1(^)>-^гЛ = С„ A59.5>
где Ci, C2, ... — константы.
Для определения этих констант следует воспользоваться
условием A59.3), умножаем каждое из соотношений A59.5) на у*
и интегрируем по площади. Учитывая A59.3), получим:
Г -is /~ M yv-2 „ „Cm+8)-(m+2)a /-/$+1 2/2v/v+1 J3v_i
3 W2^ 2 (m + 3)(m+2J К^ Ц 1\ + /2
Теперь
x = Xo + Ci*m + C3?2m+... A59.7>
608
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Здесь
М
После того, как константы Ch найдены, из соотношений A59.5)
можно получить явные выражения для функций Fk и, таким
образом, записать формулу для напряжения в зависимости от
у и от t. Мы не приводим эти громоздкие формулы. Необходимо
заметить, что автор ограничился только тремя членами
разложения; выписать формулы для С4, С5, ... и соответственно для
Fi7 F5, . ¦ ,конечно, возможно, но с возрастанием номера
выражения становятся все более и более сложными, а выписать общий
член ряда не удается. Вопрос о сходимости полученных рядов
остается открытым.
Практическое значение изложенных здесь попыток решения
задачи о чистом изгибе по теории упрочнения невелико,
численное решение, основанное на реализации того же приема, который
был рассмотрен в § 158, приводит к цели быстрее.
§ 160. ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ
О НЕУСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ СТЕРЖНЯ
Будем считать сечение стержня имеющим две оси симметрии,
направим ось z по оси стержня, пусть плоскость действия
изгибающей пары совпадает с плоскостью yOz. Пусть в начальный
момент а = а0 (у), эти напряжения могут быть упругими или могут
быть связаны с мгновенной пластической деформацией. Будем
считать, что при этом р = 0. Примем закон ползучести в виде
{51.1), а именно:
рра = ехро. A60.1)
Здесь р и о определены формулами § 51. Будем вести все
рассмотрение в безразмерных переменных, тогда безразмерный
изгибающий момент
M = ^[aydF.
При этом F — площадь поперечного сечения, h — любой
линейный размер (высота сечения), интеграл распространен на
половину площади сечения у > 0.
Вследствие закона плоских сечений е = ку, здесь к —
кривизна изогнутой оси; при t = 0, когда о = а0 (г/), мы считаем
к = 0.
Упругая деформация есть е — р, поэтому
а = ку 4- о-0 — р.
§ 160] ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ 609
Внесем это выражение в уравнение A60.1) и разделим
переменные. Получим:
рраехр р — ехр(ку-\-а0). A60.2)
Если изгибающий момент постоянен, то
^ oydF=\ a0y dF,
а следовательно,
к
k = ^\pydF- A60.3)
о
Здесь / — момент инерции площади поперечного сечения.
Уравнение A60.1) пригодно лишь при достаточно больших а. Как
было оговорено в § 50, мы должны считать, что если рр°<;1,
то а = 0. Поэтому, строго говоря, интеграл в A60.3) должен
вычисляться в пределах от ув до А, где у0 определяется из условия
рра — 1. В § 106 было показано, что учет этого обстоятельства
при вычислении изгибающего момента дает лишь
незначительную поправку.
Положим теперь
Л
Р
%(Р)=\ p°exppdp.
о
Тогда уравнение A60.2) может быть численно проинтегрировано
по следующим формулам:
%(Рт)- %(Рт-1) = ехр(кт_1у + о0) (tm — L-0- A60.4)
После каждого шага численного интегрирования находится
распределение рт, по формуле A60.3) вычисляется кт, и процесс
повторяется.
В работе Шорра [156 ] развит метод численного интегрирования
уравнений неустановившейся ползучести при изгибе в более
общих предположениях. Сечение стержня считается совершенно
произвольным, стержень нагружен изгибающими моментами Мх
и Му и растягивающей силой N, распределение температуры по
сечению может быть также произвольным. Вследствие гипотезы
плоских сечений
е = е0 + кху — кух.
С другой стороны,
е = ^+уТ + ем + еп.
39 Ю. H. Работает
610 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. ¦ XI
Здесь у— коэффициент теплового расширения,. Г — температура,
ем — мгновенная пластическая деформация, еп — деформация
ползучести. Комбинируя написанные выше выражения, найдем, что
o = E[e0 + kxy-kyX-yT-eM-en). A60.5)
В этой формуле нужно считать Е зависящим от координат я ж у.
Уравнения равновесия стержня выписаны в § 107, перепишем
их еще раз:
N=\odF, Мх= -\aydF, My=[<sxdF.
F F F
Внесем сюда выражение A60.5). До сих пор выбор осей х и у
не был подчинен условиям, потребуем теперь, чтобы было
\ ExdF = [ EydF = [ ExydF^Q.
F F F
Если Е постоянно, то оси х и у являются главными
центральными осями инерции сечения.
ьВ результате находим:
e° = ^r(N+l E4TdF + \ EeNdF+ J EeadF^j ,
° F F F
Хх=щт^(~Мх+\ EyTydF + SEe*ydF + \ Ee°ydF)• A60-6)
F F F
¦Ky = ^j~(—Mv— ^ EyTxdF— J EeuxdF— J EenxdF
У F F F
Здесь введены следующие обозначения:
E^—^EdF, Ix = ±^Ey*dF, 1у = -^^ЕхЫЕ.
F F F
Теперь формула A60.5) для напряжений может быть
переписана следующим образом:
а = а^Я(Ееа). A60.7)
Здесь
о1=* ("** + »&.)+R(EyT) + R (Ееj
и оператор R определен таким соотношением:
RM = ?(i-\fdF + tl fydF + ^y\f^F). A60.8)
Если внешние силы и температурное поле остаются неизменными,
то величина (Tj может меняться только вследствие того, что ползу-
§ 160]
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ
611
честь сопровождается мгновенной пластической деформацией.
В принципе такое положение возможно. В процессе
перераспределения напряжений в одной части сечения напряжения растут
и происходит дополнительная пластическая деформация.
Фактически дело обстоит так, что в той области, где напряжения велики,
они релаксируют; увеличение напряжений происходит в той
части сечения, где они были относительно малы и, следовательно,
вызывали лишь упругую мгновенную деформацию. Во всяком
случае, автор рекомендует
считать величину ot
постоянной и равной начальному
значению напряжения при
* = 0.
Таким образом, расчет на
ползучесть сводится к
определению изменения во
времени величины еп, которая
должна рассматриваться как
функция х, у и t.
Мы ввели обозначение еп
для деформации ползучести
с тем, чтобы сохранить
обозначение р для
существенно положительной величины,
характеризующей меру упрочнения
напряжения р = \еп\,
Рис. 233.
При постоянном знаке
но в процессе ползучести при изгибе
в отдельных точках напряжение может менять знак, в соответствии
с этим скорость ползучести также меняет знак. Соответствующая
гипотеза Шорра была изложена в § 60, мы не будем здесь
рассматривать общий случай, ограничимся простейшим предположением
о том, что ползучесть при растяжении не оказывает никакого
упрочняющего действия на ползучесть при последующем сжатии,
и наоборот (в формулах § 60 следует принять к = 0). Таким
образом, р представляет собою абсолютную величину
пластической деформации, накопленной за период растяжения, если
а > 0, и абсолютную величину пластической деформации за
период сжатия, если а < 0. На рис. 233 приведен примерный
график изменения величин е„ и р. На первом участке а > О
и р = еп, точка А соответствует моменту изменения знака
напряжения, как только стало а < 0, упрочнение нужно считать
исчезнувшим; на втором участке р представляет собою величину
накопленной деформации сжатия, то есть р = рА — еп. Это соотношение
справедливо до момента достижения точки В, когда снова
становится о" < 0. Упрочнение, накопленное в период сжатия,
перестает действовать, но деформация растяжения, в первом периоде
равная р', вносит свой вклад в упрочнение по отношению
39*
612
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
к действию растягивающих напряжении; это упрочнение
увеличивается за счет возрастающей деформации, поэтому на третьем
участке р = рА + (еп — епВ).
Закон ползучести записывается теперь в следующем виде:
pA(p) = fcexp( —p) [expiji-l]. A60.9)
Как видно, функция от \а\ в правой части выбрана так, чтобы
избежать необходимости исключения зон малой напряженности
вблизи нейтральной оси. Уже было замечено (§ 50), что такой
выбор функции от | а | не вполне корректен, однако при численном
интегрировании область весьма малых напряжений фактически
исключается и никаких затруднений, подобных тем, которые
встречались в работе [167], не возникает. Величина f5 в уравнении A60.9)
есть функция от температуры, вид этой функции безразличен,
обычно принимают Р = Т~г X const. Функция h (p) выбирается
в виде
"<Нй 111 {шм)
с тем чтобы описать как первые, так и вторые участки на кривых
ползучести (§ 50). Величина рс есть функция напряжения и
температуры, определяемая непосредственно по кривым ползучести.
В случае, если окажется, что с изменением а величина рс
убывает с течением времени, автор предлагает определять h (pc)
по ранее достигнутой наибольшей величине рс, притом отдельно
для а>0и для а < 0.
Промежуток времени от t = 0 разбивается на участки Att
от f;_j до tt, так что Att = ti — ?,_!¦ Теперь численное решение
можно вести разными способами. Один из них заключается в
следующем. Положим
р
H(p)=^h(p)dp. A60.11)
о
Если функция h(p) определена соотношениями A60.10), то
Я(р)= + A60.12)
[ Н(рс) + рс(р~рс), р>рс.
Будем считать, что величина | а | меняется в интервале от ^_4
до tt по линейному закону, так что
MH^-il + ^tf-'i-i).
§ 161] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ 613
Здесь
A\oi\ = \e(ti)\ — \o(ti-i)\ .
Интегрируя A60.9) в указанном интервале и учитывая A60.11),
получим:
Я (р,) = #(/>,_,)+А ехр(-Р)
Д
i i ехР
ехр]^
г А кА\а,
ехр-у^--1
Att.
A60.13)
Если за время Att знак напряжения не меняется, то по
определению р получаем:
бпг = <?Пг-1 + (Pi—Pi-l) Sign OVj. A60.14)
Теперь по формуле A60.7) находится напряжение of.
oi = o1 + R(Eeni).
Если интервалы времени Att достаточно малы и соответственно
малы приращения Даг, то правая часть A60.13) может быть
упрощена, а именно это соотношение можно заменить следующим:
Н (Pi) = Я (p,_t) + к ехр (- р) [ ехр 1^ -1 ] At,. A60.15)
Счет с помощью формулы A60.15) оказывается чрезвычайно
простым, поскольку в правой части фигурируют известные величины
0Vj, найденные в приближении номер i — 1, однако интервалы
Att следует при этом выбирать достаточно малыми. При
пользовании полной формулой A60.13) интервалы А/, можно брать
значительно большими, однако Aat приходится искать методом
последовательных приближений. Аналогичный способ применим и тогда,
когда нагрузки меняются во времени, притом достаточно плавно.
При этсм величина Oj является заданной функцией времени,,
в остальном же процедура остается неизменной. Не составляет
принципиальной трудности и распространение метода на случай
переменной во времени температуры.
§ 161. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ
Наиболее простая гипотеза неустановившейся ползучести при
сложном напряженном состоянии состоит в том, что деформация
ползучести представляет собою чистый сдвиг, вызванный
действием наибольшего касательного напряжения ттах. Скорость
сдвига Ymax зависит от величины сдвига ушах и от касательного
напряжения тшм. Если главные напряжения суть at > а2 > <т3,
то это предположение означает, что
Р\= —Рз, Рг
= 0.
614
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Величину s = 2тшах — at — а3 мы выбираем в качестве
эквивалентного напряжения; в качестве эквивалентной деформации
мы выберем величину р = pd = —р3, при простом растяжении s
есть растягивающее напряжение, р есть удлинение, поэтому s
и р связаны между собою так же, как а и р при растяжении.
Принимая закон упрочнения в виде G5.4), мы перейдем к
безразмерным величинам, полагая, как это было сделано в § 51,
л —flL ; _ Eeii п _ EpiJ 7 — и ( Е Y+a /
aU— А . еИ~ А - Pii-~~A~' 1-к\^) 1-
В дальнейшем мы будем опускать значки безразмерных величин,
таким образом, основное уравнение ползучести записывается
следующим образом:
ppa = exp(s — p). A61.1)
Если два главных напряжения, например а± и а2, равны между
собою и положительны, то напряженное состояние элемента
представляет собою сжатие в третьем главном направлении
сжимающим напряжением ог — а3, на которое наложено
гидростатическое всестороннее растяжение с интенсивностью а4.
Скорость сжатия в направлении оси о определяется величиной
o*i — a3, ее и нужно принять за р; скорости деформаций в
направлениях Oj и о2 неопределенны и подчинены только условию
несжимаемости. Таким образом, к уравнению A61.1) нужно добавить
следующие соотношения:
Р± = Р, Рз=—Р, />2 = 0 (o-i>a2>a3),
Рз=—Р, Р\ = Ьр, p2=(i — X)p (ai = a2>a3). (
Уравнения A61.2) записаны в проинтегрированном виде. Такая
запись возможна только в том случае, если знаки неравенств
между главными напряжениями не нарушаются в процессе
ползучести. Но может случиться, что в течение некоторого времени
было, например, а± > а2, в какой-то момент эти напряжения
сравнялись, после чего стало а2 > а4. Это означает, что ползучесть
стала совершаться за счет скольжения в других плоскостях,
и вопрос о том, сохраняет ли силу упрочнение, приобретенное
на первом этапе, остается неясным. Мы будем предполагать
для простоты, что упрочнение целиком аддитивно независимо от
того, в каких системах происходит сдвиг, приводящий к
накоплению упрочняющей деформации ползучести. В литературе имеются
некоторые данные, свидетельствующие о том, что у кристаллов
сдвиг в одной системе скольжения упрочняет не только данную
систему скольжения, но и все другие. Таким образом, в общем
случае уравнения A61.2) следует записывать для скоростей
и интегрировать их по этапам.
§ 161) НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ 615
Перейдем теперь к задаче о вращающемся диске,
безразмерные напряжения в нем будут ат и 09. Предположим, что в исходном
состоянии в диске существовали начальные напряжения о°г и Oq,
а также начальные распределения упрочняющей деформации
ползучести р0. Если а° и og связаны с мгновенной пластической
деформацией, то нужно считать р0 = 0. Будем рассматривать
следующие возможности:
1) ае>0>аг, s = a9 —аг, 2(р — р0) = е9п—ern, ezn=^0;
2) ст6>о-г>0, s = a&, 2(p — po) = eea — eza, ern = 0;
3) аг>а9>0, s = or, 2 (р — р0) = ern —ezn, e9n = 0;
4) ае = аг>0, s = 06 = o-r, 2(р — р0) = евп— еш.
Будем записывать уравнение равновесия элемента диска
следующим образом:
Здесь | = -г-, где г — текущий радиус, a b — наружный радиус
диска, лг= Положим:
1 ?2
ar = z—ута§2,
при этом уравнение равновесия будет удовлетворено тождественно.
Обозначим через и величину радиального перемещения, поде-
ЪА du
ленную на характерный линейный размер -== , тогда -^ = еГ)
Y = «е> или
| = а9 — var — @9 — vo?) + е6п + (ср — tp0).
dl A61'4>
-щг = о> - vo9 — (а? — voe1) + <?гп + (ср — <р0).
Здесь ф представляет собою температурную деформацию:
Рассмотрим теперь последовательно возможные частные случаи.
Случай 1. Положим в A61.4) е9п = (р — Ро), ега= — {р— р0),
внесем вместо о9 и ог выражения A61.3) и исключим
перемещение и. Получим следующее уравнение для функции z (?):
J?2 I ? rt% — "l \L V t I
d^^ I dl --^ У' I V d\ 1 I J \ dl
616 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Здесь р* = р — р0 — (сте — <*?)• В результате интегрирования найдем:
Теперь выпишем формулы для напряжений:
Cv = 0?-P(?)-^mg2—J,- J ?(ф-фо)« + В--^- ,
Св = о8-р-Р(?)-±±^тЕ«—(ч>-фо)+ A61-5)
Здесь принято
рш=5 ^rfg.
Величина s выражается следующим образом:
s = s*-i° + -f-- (I61'6)
Здесь s* — известная функция координаты и времени, а именно:
8* = а&-а0,-р0-(ф-фо) + ^5&(ф-ф„)^ + ^=^-^.
Теперь мы должны внести выражения A61.6) в уравнение
ползучести A61.1), после разделения переменных оно примет
следующий вид:
рра ехр (р) = ехр (V + -— - р) .
Это уравнение интегрируется численно совершенно так же, как
в случае изгиба в § 160; опять-таки вводится функция % (р),
уже введенная в § 51 для решения задачи о релаксации
напряжений, формулы для расчета последовательных шагов записываются
следующим образом:
хЫ = Х(^-1) + ехр (st-i +^r-1-P«-i) (ti-tt-i)- A61.7)
После каждой ступени необходимо производить вычисление
константы Ci при помощи некоторого интегрального соотношения,
вытекающего из граничных условий. Рассмотрим некоторые
примеры.
а) Диск с внутренним относительным радиусом а посажен
на жесткий вал с натягом. За начальное состояние принимается
состояние диска, посаженного на вал, но не приведенного во
S 161] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ 617
вращение и не нагретого. Граничные условия будут следующие:
о> A) = 0, ит (а) = 0.
С помощью A61.4) и A61.5) находим:
С={_РA)-3-+-^ + ф^-5|(ф-фо)^}:{1+^^},
а
1
Д = С + РA)+^т+$6(Ф-<ро)<*Е.
а
б) Диск с внутренним относительным радиусом а посажен
на упругий вал. Обычно температура вала и примыкающей к валу
части диска незначительна и ползучесть этой части диска не
играет сколько-нибудь существенной роли, перераспределение
напряжений происходит за счет ползучести периферийной части
диска. Заменим, как это обычно делается, вал цилиндром конечной
- длины, превышающей толщину диска в 1 /к раз .Значениях
приводятся, например, в I108]. Условие аТ A) = 0 сохраняется, не составляет
труда заменить его условием того, что ог A) равно заданному
напряжению, возникающему от лопаточной нагрузки. Обозначим через
q0 начальное значение давления посадки, тогда второе условие
запишется следующим образом:
c=_{«[C+v)E^+1)_(,j±j]+pA)+
а
Величина В находится так же, как и в предыдущем случае.
в) Диск ступенчатого профиля. В этом случае формулы A61.5),
A61.6) и A61.7) сохраняют силу, но на каждом участке
константы В и С имеют различные значения. Если на границе двух
участков толщина меняется внезапно в т) раз, то кроме граничных
условий необходимо заботиться о выполнении условий
сопряжения, а именно, если относительный радиус границы между
участками есть с, то
а'г (с) = ца'г (с), и' (с) = и" (с).
Одним и двумя штрихами соответственно отмечены значения
напряжений и перемещений для граничащих участков.
Присоединяя сюда граничные условия, мы можем получить общие
формулы для определения постоянных В и С на каждом участке,
однако они оказываются столь громоздкими, что практически
следует решать получающуюся систему уравнений каждый раз
численно для конкретных значений входящих параметров.
618
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
§ 162. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ. СЛУЧАИ 2, 3, 4
Случай 2. Рассмотренный в § 161 случай, когда ое > 0 > аг,
реализуется в диске с отверстием, посаженном с натягом на вал.
В свободном диске при однородном температурном поле
осуществляется второй случай, когда од > аг > 0. При этом ползучесть
в радиальном направлении отсутствует и в формулах A61.4)
следует принять е9п = (р — Po)i ?гп = 0. Поступая точно так же,
как и выше, мы получим следующее дифференциальное уравнение
для функции z (?):
d2z , 3 dz ,. ч 1 d ,*. , ., ,
-d%r + j-dt^m(i-v)-^liZ&(p-Po)} +
+ |3 dl te ^°e °г>> I d%
Интеграл этого уравнения
+ o°r—^-$Е(ф-фо)<*5 + В—p-.
Формулы для напряжений получаются следующими:
ar = o-°r -Р^-Ур^--!- J ito-^di + в—^- ,
a9 = (Jg _p_Pa(g)_l+^m|»_(»p_V(,)+ A62.1)
+ -^- Jg(9-4)o)d? + B +
^2~
Здесь
Положим
з* = оЪ- Ц^ mg2 - (ф - фо) + ± \% (Ф - ф0) dg - Рг {?). A62.2)
Тогда уравнение ползучести будет следующим:
pp°exp(p) = exp(s*+ ? + -?¦-?) A62.3)
и численный расчет ведется по формуле
X (Pi) = X (Pi-i) + exp (*?-i + В,-! + ^p- — Pt-i) (tt — *i-i).
§ 162] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДИСКОВ. СЛУЧАИ 2, 3, 4 619
Большая трудоемкость расчета в этом случае по сравнению
с предыдущим зависит от того, что после каждой ступени
должна еще вычисляться величина s* по формуле A62.2).
Константы В ж С также определяются из граничных условий для
каждого этапа. Например, если диск свободен, то
ог(а) = агA) = 0.
С помощью первой из формул A62.1) находим:
1
C=3±vma8+_^_j-pA)+^.J 5(ф_ф0)^],
о
B=i*+-irma-
Случай 3. Если диск снабжен тяжелым ободом, то может
оказаться, что с> > о"е > 0. Поступая так же, как и ранее,
найдем для этого случая:
ов = о&+Л<?)-^т?' + -р-$ Н<Р-фо)^- A62.4)
— (ф —фо) + ^+-р-.
Вообще говоря, в одном и том же диске могут возникнуть зоны
с различными соотношениями между главными напряжениями,
тогда появляются дополнительные трудности, связанные с
установлением границ между этими зонами. Типичным примером может
служить здесь сплошной диск. В упругом состоянии при
однородном поле температур всюду а9 > ог > 0> лишь в центре диска
выполняется условие се = <тг, которое не нарушается и в процессе
ползучести. Мы видели в § 123, что если решать задачу о ползучести
сплошного диска с помощью критерия типа Сен-Венана, то
приходится допустить справедливость равенства о*е = о*г в некоторой
конечной области, примыкающей к центру. Совершенно такое же
положение будет и при неустановившейся ползучести: область,
в которой главные напряжения равны между собою, постепенно
расширяется, стремясь к некоторому предельному положению,
которое может быть найдено, если решать задачу квазиустано-
вившейся ползучести так, как это было сделано в § 123.
Случай 4. Случай сплошного диска был рассмотрен в
работе [135].
В центральной области 0< |<с, о*г = о"е = о% из формул
A61.3) следует, что z = const = Z, таким образом,
a = Z — -i-ml2. A62.5)
620
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Так как az = 0, то s = а, етп = кр, e$n = A — к) р. С другой
стороны,
er = ~ = (l — v)o + kp,
A62.6)
ee = ^ = (l-v)o + (l-X)p.
Складывая, получим:
^. + ^. = 2(l-v)(r + p = 2(l-v)Z-(l-v)m6» + p.
Интегрируя, находим:
u = Z(l-v)g-b^m?« + |Jp?dE. A62.7)
I
1
Постоянная интегрирования принята равной нулю, поскольку
и @) = 0. При |>с равенство напряжений нарушается и
становится Сто > о> > 0, следовательно, егп = 0. Для обеспечения
непрерывности перемещений нужно, чтобы и во внутренней области
при I = с было егп = 0, а следовательно, А, = 0. С помощью
первого из соотношений A62.6) находим, что при | = с
du .. .
•5g=(l-v)a
или, учитывая A62.5) и A62,7),
с
р (с) с"-~ шЦ = J Pi dl. A62.8)
о
В наружной части диска при ? > с всюду остается о"е > Яп
а следовательно, справедливы формулы A62.1) для напряжений,
которые содержат две константы В и С. Обозначая одним
штрихом величины, относящиеся к области 0 <; I < с, и двумя
штрихами величины, относящиеся к области с < | < 1, мы найдем, что
в первой области численно интегрируется уравнение
рра = exp ( Z — у т?2
тогда как во второй области интегрируется уравнение A62.3).
Константы после каждого шага интегрирования определяются
из граничных условий и условий сопряжения, а именно:
u'(c) = u"(c), o-'r(c) = ov(c), a"r(i) = q.
На рис. 234 приведен график из работы [135]. Рассчитывался
диск постоянной толщины диаметром 900 мм из стали 40Н при
температуре 400° С, делающий 3000 оборотов в минуту. Лопаточ-
§ 163] ПОЛЗУЧЕСТЬ ВРАЩАЮЩЕГОСЯ ЦИЛИНДРА И ТРУБЫ 621
ная нагрузка принята равной 4 кг 1мм. Мы привели только три
кривые аг и се: Для начального состояния, для времени 1 час и для
установившегося состояния. В последнем случае расчет
производился по формулам § 123.
Несколько отличный метод численного решения задач
неустановившейся ползучести на основе того же варианта уравнений
теории упрочнения развивается в работе !136]. При этом, в отличие от
б,кг/ммг
изложенного выше метода, составляются дифференциальные
уравнения для функции и (|). Как это сделать, принципиально
совершенно ясно: из A61.4) находятся напряжения и подставляются
в уравнения равновесия. Толщина диска, температура и упругие
константы рассматриваются как функции радиуса и задаются
в виде степенных рядов, решение также ищется в виде степенного
ряда, коэффициенты которого являются функциями времени.
§ 163. ПОЛЗУЧЕСТЬ ВРАЩАЮЩЕГОСЯ ЦИЛИНДРА И ТРУБЫ
Во вращающемся цилиндре или толстостенной трубе все три
главных напряжения отличны от нуля. Положим:
?еп = 2А., е2П = ц — %, егп=—ц. — X.
Сохраняя обозначения § 161, получим:
ее = х = сге — v (or + oz) + (ср — ф0) + 2А,,
ег = сг — v ((те + а г) + (q> — cp0) — Я, + р.
622 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Здесь для простоты мы посчитали, что начальные напряжения
отсутствуют.
Принимая, что сечение ротора останется плоским, мы должны
считать, что ez зависит только от времени t. Исключим аг из двух
первых уравнений A63.1) и составим условие совместности. При
этом Се и о"г мы выразим через функцию z (?, t) по формулам
A61.3), которые сохраняют силу, поскольку уравнение
равновесия остается тем же, что и для диска. В результате получается
следующее дифференциальное уравнение:
d^z , 3 tfz_l — 2-v ra62 1 1 d(y — Фо) 2 —v 1 d%
- + Т^Г = Т7-^т^
dg2 ' | dl 1 —v b 1— v % й\ 1—v2 I dt,
_ 1 — v2 I dl ~~1 — v2 \W^"WJ ~
Мы выпишем интеграл этого уравнения для несжимаемого
материала, когда v = l/2:
Формулы для напряжений получаются при этом следующие:
ffr= -ymg2- -^ J (Ф —Фо)?аб—J J ^~
kdl , -г, С_
I2 ¦
.2 J ^ + i?
i г i r 1 A632)
с9 = —Tmg2 —2 [(Ф— фо) — -р~ )) (ф —фо) I <*Е J -
as= -1j»?»-2 (Ф - фо)--1 Bji + J ^)-2 J ^+В+е»@-
Теперь можно рассматривать различные частные случаи,
а именно:
1) аг ;> 0е > аг, s = ar — az, евп--0, следовательно, Х = 0;
егп=—егп = р, следовательно, и,= —р.
2) сте > стГ > стг, s = (Те — аг, еГП = 0, следовательно, (х + ^ = 0;
1 1
ееп=—?zn = Р> следовательно, Х = -^р, ц. =—у р.
3) ae>o-z>ar, s = a9 — aT, eZII = 0, следовательно, ц — Я = 0;
е8п =—егп = р, следовательно, A, = [i=yj9.
163] ПОЛЗУЧЕСТЬ ВРАЩАЮЩЕГОСЯ ЦИЛИНДРА И ТРУБЫ Ч 623
Совершенно аналогично находятся формулы для трех
случаев, которые получаются из рассмотренных путем изменения
знака неравенств.
Численное интегрирование выполняется здесь совершенно
так же, как и в задаче о ползучести диска.
С помощью формул A63.2) можно рассмотреть также задачу
о толстостенной трубе под действием внутреннего давления.
Полагая ги = 0, ф=^ф0, Ое>о>аг, мы должны принять, что
в трубе реализуется третий случаи и, следовательно, А, = р, = -^ ,
s = Oq — от. По формулам A63.2) получим:
<гр=~1/> + В—?, A63.3)
az=-^p-~P + B + ez(t).
Здесь
Р®={^
Граничные условия будут ar (a) — —q, стгA) = 0, следовательно,
q=-B+^, 0=-±РA)+В-С. {163.4)
Если концы трубы закрыты, то уравнение равновесия в осевом
направлении будет следующим:
1
а
Преобразуя интегрированием по 'частям входящий сюда
интеграл \ %Р (?) d|, найдем, что вследствие A63.4) ez (t) = 0. Заме-
тим, что при этом условии из A63.3)"следует:
CTz = -({Te + o-J.).
Таким образом, предположенное неравенство между главными
напряжениями всегда выполняется.
Теперь величина s будет следующей:
8=-*р + Ц, A63.5)
624 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
при этом из A63.4) следует:
С--
*+№)?,¦
[ГЛ. XJ
A63.6)
Внесем A63.5) в уравнения ползучести, разделим в нем
переменные. Получим:
рраехр^ = ехр(ж — Р
ti+j
Рис. 235.
A63.7)
Таким образом, мы должны численно интегрировать A63.7) при
условии A63.6).
Ход вычисления можно
пояснить следующей
схемой (рис. 235). Разобьем
радиус а < | < 1 на ряд
интервалов, обозначим
границы интервалов |',
отметим также границы
интервалов времени tt.
Пусть для момента
времени tt известно значение
константы Ct, известны
также значения р для
различных значений ?', обозначим эти величины pi. Теперь
определится величина р| для всевозможных значений индекса / по
формуле
2Cj__
Здесь
_3 \1+а
4
Теперь численным интегрированием находится функция Р(|)
по следующим формулам:
рШ = И+1 + Яи-|(^+1-?').
Возвращаясь к общему случаю вращающегося цилиндра, мы
замечаем, что во всех трех перечисленных выше случаях из
формул A63.2) следует:
4
%i(Pji+i)-%i И = ехр ( ^L— p, ) (ti+i-tt).
Xi(p) = J exp (—p^po-dp--
'х(т/0'
s = s*
P-
В первом случае
5*=-2(ф-ф0) + -|г \ (ф—q3o)?dE + -p- + ^Wt
§ 163] ПОЛЗУЧЕСТЬ ВРАЩАЮЩЕГОСЯ ЦИЛИНДРА И ТРУБЫ 625
во втором
и в третьем
S* = -p" ^ (ф —<Po)?d| + ^- —ez(«),
бд,/(г/ммг
ЗО -
5* = 2(ф-ф0)+-|-$ (ф-Фо)Б<*6 +
бz, кг/ммг
гс
7мин
2 мим
ЗЯмш
-20
Рис. 236.
Рис. 237.
Таким образом, всегда приходится интегрировать уравнение
ppaexp-^- = exp(s*-p). A63.8)
Если ат (а) = аг A) = 0, то
i
х 1
+ -|.$-|-d?+2"\-|-d?, A63.9)
С=— ^ma4 + Cia2
40 Ю. Н. Работнов
626 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Величина ег (t) находится из условия равенства нулю
равнодействующей осевых напряжений, а именно:
1 1
ez(o=4-m(i+a2)+i^[4S (<p-4>o)s^+-|-j ц^+
a a
15 IE
+ A JgdgJ-tdg + 4 JgrfgJ -jd?,~]-B. A63.10)
a a a a
На рис. 236 и 237 приведены графики распределения
напряжений Ое и огв процессе пуска ротора, полученные Даниловой [23].
Принималось, что пусковой период продолжается 7 минут, за это
время угловая скорость возрастает по линейному закону,
температура омывающего газа также растет по линейному закону от
180° до 550°.
§ 164. ВАРИАЦИОННЫЙ ПРИНЦИП КАЧАНОВА В ТЕОРИИ
НЕУСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ
Предположим в самом общем случае, что деформация тела
состоит из мгновенной деформации, включающей упругую и
пластические части, и деформации ползучести. Будем принимать для
простоты, что мгновенная деформация подчиняется уравнению
деформационной теории, следовательно,
Скорость деформации ползучести определяется потенциалом
скоростей Ф, так что
• _ ЭФ
Pij" dotj ¦
Потенциал скоростей может зависеть от любого числа структурных
параметров, в частности от компонент тензора деформации
ползучести Pij. Скорость полной деформации определяется следующим
образом:
Теперь мы воспроизводим вывод вариационного принципа
Кастильяно, данный в § 97. Предположим, что на тело действуют
поверхностные силы Т% и объемные силы Ft, в нем возникают
система напряжений oti и поле скоростей vit определяющее поле
тензора скоростей деформации еи. Наряду с основным
напряженным состоянием рассмотрим бесконечно близкое статически
возможное напряженное состояние, соответствующее тем же объемным
§ 164] ВАРИАЦИОННЫЙ ПРИНЦИП КАЧАНОВА 627
силам и тем же поверхностным силам на той части поверхности,
где эти силы заданы. Тогда величины бо,,- образуют
самоуравновешенную систему напряжений, при этом 6Тг = 0 на части
поверхности 2Г. Составим уравнение равновесия в форме Лагранжа
для этого самоуравновешенного состояния, при этом в качестве
возможных скоростей выберем действительные скорости,
реализуемые в теле. Получим:
Поверхностный интеграл обращается в нуль на 2Т, где 8Т{ = 0;
внося выражения A64.1) для е^ в объемный интеграл, получим:
J 67>?d2-oJ ('¦^- + O~)dV = 0. A64.2)
Это и есть вариационное уравнение неустановившейся ползучести,
полученное Качановым [52]. Необходимо подчеркнуть, что
варьируются только напряжения, но не скорости их изменения;
структурные параметры, входящие в выражение для Ф, не варьируются.
Таким образом, вариационное уравнение A64.2) остается
справедливым для любой теории ползучести. Вывод этого уравнения
для теории упрочнения принадлежит Шестерикову [11в]. Однако
при применении вариационного уравнения введение параемтров
упрочнения связано с серьезными затруднениями и эффективные
результаты получить практически не удается. Если потенциал Ф
зависит только от напряжений, то есть скорость ползучести при
постоянных напряжениях постоянна и ползучесть оказывается
неустановившейся только вследствие того, что она сопровождается
упругой деформацией, то уравнение A64.2) позволяет развить
эффективные методы приближенного исследования различных
задач.
Заметим, что совершенно аналогичное положение возникает
и в том случае, если мы становимся на точку зрения теории
течения Качанова: если считать функцию Ф зависящей от времени
как от параметра, то никаких принципиальных трудностей не
возникает. Когда кривые ползучести подобны, мы видели в § 73, что
явную зависимость от времени можно исключить
соответствующим выбором масштаба. Если в уравнение A64.2) ввести вместо t
некоторую функцию т (t) и считать Ф зависящим только от
напряжений, то мы получим формулировку вариационного принципа
применительно к уравнениям теории течения Качанова;
многочисленные приложения этого принципа содержатся в книге [5а].
В приложениях уравнения A64.2) обычно поступают следующим
образом. Задаются некоторым статически возможным
распределениям напряжений, содержащим к произвольных параметров
40*
628
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
cs(t). Обычно эти параметры входят в выражения для
напряжений линейным образом. Теперь <р = ф (cs) и Ф = Ф (cs). По
формуле A64.2) функционал равен
$(а+ф)^=|ц,+ф.
При варьировании этого выражения мы считаем, что мгновенно
изменяются величины напряжений, но не скорости их
изменения, поэтому
v
Мы предположили, что граничные условия для напряжений
выполняются независимо от значений параметров с„, поэтому вариация
первого члена A64.2) равна нулю и функции cs (t) определяются
лз следующих уравнений:
Так, в книге [62] большое количество задач рассматривается
следующим способом. Пусть а", — начальное упругое распределение
напряжений, &?. — распределение напряжений при
установившейся ползучести. Положим
oij = 4 + с @ (оЗ -4)- A64.4)
Функция с (t) определяется из одного-единственного уравнения
вида A64.3), очевидно, что должно быть с @) = 0, с (со) = 1.
Вариационное уравнение A64.2) применимо в тех случаях,
когда ползучесть сопровождается мгновенной упругой
деформацией, тогда ф (o*jj) есть квадратичная функция — упругий
потенциал. Если ползучесть сопровождается пластической
деформацией, то мы вынуждены необходимым образом считать, что эта
мгновенная пластическая деформация описывается уравнениями
теории деформационного типа, для которых существует
потенциал ф (o"jj). В этом случае приведенный выше анализ неполон,
так как наряду с зонами активной пластической деформации
необходимо рассматривать также области разгрузки. Это
обстоятельство не вызывает принципиальных затруднений, в области
нагрузки функция ф будет пластическим потенциалом
деформационной теории, в области разгрузки — упругим потенциалом.
Соответствующее рассмотрение приведено в книге [62], мы его
здесь не воспроизводим.
Заметим, наконец, что с помощью уравнения A64.2) мы можем
производить исследование неустановившейся ползучести по схеме
Одквиста (§ 47), рассматривая участки установившейся ползу-
§ 165] ВАРИАЦИОННЫЙ ПРИНЦИП УАНГА И ПРАГЕРА 629
чести и учитывая первую фазу ползучести как мгновенную
начальную пластическую деформацию. Правда, здесь можно выдвинуть
то возражение, что, трактуя установившуюся ползучесть как
процесс течения, будет нелогичным рассчитывать состояние,
соответствующее завершению первой фазы, с помощью уравнений
деформационного типа.
§ 165. ВАРИАЦИОННЫЙ ПРИНЦИП УАНГА И ПРАГЕРА
Если мгновенная пластическая деформация подчиняется
уравнениям типа уравнений теории течения, то формулировка
вариационного принципа, подобного тому, который был приведен
в § 164, становится невозможной. Однако в теории
неустановившейся ползучести возможности составления вариационных
уравнений более широки, чем в теории установившейся ползучести
и нелинейной теории упругости, так как кроме тензоров Оц и гц
в уравнениях фигурируют тензоры atj и etj. Здесь мы рассмотрим
некоторые новые вариационные принципы, полученные
относительно недавно и основанные на варьировании тензоров скоростей
изменения напряжений и деформаций. Продифференцируем по
времени уравнения равновесия и граничные условия. Получим:
°tj,j + Fi=0, Vijvj^ft. A65.1)
Вид этих уравнений указывает на то, что скорости изменения
напряжений Оц могут рассматриваться как напряжения,
вызванные объемными силами Ft и поверхностными силами 7Y
Деформация состоит из мгновенной деформации б™,
включающей упругую и пластическую часть, и деформации ползучести
Ри, так что
еи = е"+ри.
Вставая на точку зрения теории пластичности типа теории
течения, мы получим следующие соотношения между
приращениями мгновенной деформации и приращениями напряжений:
defj = a.ijki doM;
при этом aijki — dkuj. Действительно, если мгновенная
деформация упруга, то aljhi являются упругими константами. Если
мгновенная пластическая деформация следует теории течения, то,
вследствие A7.1),
Симметрия тензора ailU относительно двух пар индексов
усматривается здесь непосредственно, этот тензор зависит от напря-
630 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
жений и, может быть, от предшествующего деформирования, но
не зависит от приращений datj. Будем вести дальнейшее
рассмотрение в скоростях, поэтому запишем:
ец = ат1аы. A65.2)
Скорости деформации ползучести ру в свою очередь зависят
только от напряжений и параметров упрочнения, но не зависят от
скоростей изменения напряжений.
Наряду с действительным полем скоростей напряжений Оу
рассмотрим бесконечно близкое статически возможное поле
otj + бегу. Эти величины будут удовлетворять уравнениям A65.1)
при измененных значениях скоростей изменения поверхностных
и объемных сил 8F; и 6 Г;, так что
&ту^ + 6>, = 0, 6ayvj = 62V
Рассматривая величины 6Ft и бГг как внешние силы, а величины
двц как напряжения, применим к ним начало возможных
перемещений, приняв за поле возможных скоростей поле истинных
скоростей, реализуемое в теле. Получим:
\ бауву dV = \ 6Ftut dV + \ 6Г,и, dL. A65.3)
v
В правой части знак вариации может быть вынесен из-под
интеграла, в левой части этого сделать нельзя, если не преобразовать
ее соответствующим образом. Для простоты записи мы будем
представлять тензоры векторами в девятимерном пространстве;
векторы с, еы, р, е имеют своими компонентами ay, ef., py, е,7-
соответственно, и подынтегральное выражение в левой части A65.3)
может быть записано как боге.
Рассмотрим следующее выражение:
а(е+р).
Вычислим вариацию от этого выражения, считая, что варьируются
скорости изменения напряжения а и, следовательно, зависящие
от них скорости полной деформации е, но не скорости ползучести р,
которые зависят от напряжений, но не от скоростей их изменения.
Получим:
6 [а (е +р)] = Ьае -f- Sap -f- в8е = бае + да (р + е — е) + обе =
= 2б<ге — 6с (е —р) + обе.
•g 165J ВАРИАЦИОННЫЙ ПРИНЦИП УАНГА И ПРАГЕРА 631
Величина 8а (е—р) есть 8о*ем=6а;^. Вследствие A65.2) находим:
6а (е —р) = amiohl8oij.
Точно так же
обе = а8еы — aij8efj = aijklaijdaki.
Эти выражения равны между собою, поэтому
во&ц = уб [аг} (etj + ptJ)]. A65.4)
Теперь мы можем переписать уравнение A65.3) следующим
•образом:
б 4" J '°u{eu + Pi})dV = b [ J ЛМ7+ J 7>^2 ]. A65.5)
Уравнение A65.5) выражает первый вариационный принцип,
установленный в работе Уанга и Прагера [3S0]. Необходимость
варьирования скоростей изменения напряжений вц, а не самих
напряжений, как это делается при варьировании функционала A64.2),
вызвана тем, что при выводе A65.5) сделано более общее
предположение о законе пластичности для мгновенной деформации.
Если мы будем по-прежнему считать, что
м Зф
то пользование вариационными уравнениями A64.2) и A65.5)
приводит к совершенно тождественным выкладкам.
Действительно, положим
Ojj = a?j +aijCft.
Для простоты будем считать, что оц образуют
самоуравновешивающиеся системы напряжений, поэтому при варьировании с^
внешние силы не варьируются.
Применим сначала вариационный принцип A64.2).
Функционал может быть записан следующим образом:
Будем теперь варьировать ck, оставляя скорости ch
неизменными. Получим:
6/1 = \ [ d^k. ^ + J^ ] ac*dV = °-
632 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Поскольку bci произвольны и независимы, условие 6It = 0
распадается на систему следующих уравнений:
Воспользуемся теперь вариационным уравнением A65.5).
Перепишем фигурирующий в левой части функционал так:
h = Woij(efi + ipl3)dV.
Н° e'i = dOtjdOr, Р"С" Р11 = 1*ГГ П°ЭТ0МУ
Проварьируем скорости ck. Получим:
6/2=К *5ч7 ст'^+5-) а^с* dV=°-
Отсюда следует:
И Щк, "'•'¦+ ^"'мЛ'-О. A65.7,
Уравнения A65.6) и A65.7) полностью тождественны.
§ 166. ПРИБЛИЖЕННОЕ РЕШЕНИЕ РЕЛАКСАЦИОННЫХ ЗАДАЧ.
МЕТОД ШЕСТЕРИКОВА
Шестериков в работе [151] предложил приближенный метод
решения задач о релаксации напряжений с помощью
вариационного уравнения A64.2). Здесь под релаксационными задачами мы
будем понимать такие задачи, для которых в предположении
установившейся ползучести существует единственное решение oTj = 0.
Пусть начальное упругое распределение есть o*j, мы будем искать
приближенное решение в виде
au = c(t)at}. A66.1)
Считая мгновенную деформацию упругой, мы должны принять
в A64.2)
Вследствие A66.1) получим:
Ф = с2ф*. A66.2)
с*2 3
Здесь ф* = -^р- + ~y Ко*2.
Заменим здесь -^— через q0 согласно A66.3) и проинтегрируем
аа0
§ 166] ПРИБЛИЖЕННОЕ РЕШЕНИЕ РЕЛАКСАЦИОННЫХ ЗАДАЧ 633
Будем теперь считать, что потенциал ползучести Ф =
= Ф(а0, qe), при этом д0 определено формулой G3.3). Тогда,
как показано в § 73,
?о = Ц- A66-3)
Составим функционал A64.2):
/= С [2cc<f* + <b]dV.
Вариация этого функционала:
ЭФ
по t. Получим
\ [2(c-l)<p* + q0G%]dV = Q. A66.4)
Решение функционального уравнения A66.4) возможно лишь
при определенных частных предположениях о законе
ползучести. Положим, например, что в одноосном случае
рр* = Аап. A66.5)
Заменив здесь р на q0 и а на ст0, мы получим частный вид
соотношения A66.3). Полагая а0 = о%с (i), проинтегрируем A66.5).
Найдем:
о
Внесем в A66.4). Получим:
t
2(с-1) J q>*dV+f^-Y[\ cndtY \ °imn+idV=0-
V О V
Положим:
v
2 \ <p*dV--=I2.
Тогда предыдущее уравнение запишется так:
t ¦
/, l^cndt]m = I2(l-c)
634
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
ИЛИ
сп dt -
1+а
A_сI+а.
Продифференцируем по времени, после чего разделим
переменные и проинтегрируем.
Получим:
A-т)а
dr = -
1+а
X
X
1+а
~) t. A66.6)
80 700
t,vac
Ha рис. 238 приведен
график функции с \t),
рассчитанный с помощью
уравнения A66.6) в
работе [151] для диска
постоянной толщины с отверстием,
радиус которого равен 1/5
наружного радиуса, с
перепадом температуры от
450° на наружном радиусе
до 350° на внутреннем.
Материал диска — сталь
40 60
Рис. 238.
-40Х. Уравнение A66.5) записывалось в следующем виде:
№а=(^-)ПехрВ(Г-Г0).
Из обработки опытных кривых ползучести было получено:
а = 0,6, 5 = 0,06, «= 6, Г0-840°
§ 167. СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП
Пусть etj = y^uUi + Ujti) — истинное поле скоростей
деформации, соответствующее полю скоростей ut. Бесконечно близкое
лоле скоростей будет Ьщ, бесконечно близкое поле скоростей
деформации 8etj. Рассматривая 6ut как возможные
перемещения, составим вариационное уравнение равновесия в виде
Ft6uidV+[tt&Uid2. A67.1)
yotMjdV= J Л
§ 167] СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП 635
Левую часть этого уравнения теперь уже не удается представить
как вариацию некоторого функционала, так как стг-7- не
выражаются через скорости полной деформации. Поэтому уравнение A67.1)
не содержит в себе какого-либо принципа, позволяющего
отобрать среди различных кинематически возможных полей
скоростей то поле, которое наилучшим образом аппроксимирует
истинное; извлекаемая с помощью этого уравнения информация
относительно невелика. В работе Сэндерса, Мак-Комба и Шлехте [345]
¦был сформулирован новый вариационный принцип для
ползучести, основанный на одновременном варьировании поля скоростей
ползучести и поля скоростей напряжений; к изложению этого
принципа мы и перейдем.
Авторы указывают, что при выводе вариационного уравнения
для ползучести они отправлялись, с одной стороны, от
вариационного принципа Рейснера в теории упругости, а с другой — от
приведенной в § 165 теоремы Уанга и Прагера. Поэтому мы начнем
с изложения идей Рейснера I340], [341].
Предположим, что на части поверхности 2U заданы смещения
щ, на части поверхности 2Т заданы усилия Т\. Массовые силы
лредполагаем отсутствующими. Составим функционал:
К = J [(ту<?и - Ф (сту)] clV - J FiUt dV ~
V V
- \ Tt (Ui —14) dl, — \ Т[щ d2. A67.2)
Найдем вариацию этого функционала в предположении, что
величины Oij и ut варьируются независимо, при этом еу=
= -rr(Ui,j + uj,i)- Получим:
дК=1 [ (*у _ йтОЬаи+aiMi ]dv ~
v 3
— [ 6Ti(ui — u,i)d2+- С TiduidZ— \ 2f6wjrfS.
Преобразуем, как обычно, объемный интеграл от о-^Ьец:
\ aijbeijdV— \ -ciijbu^}dV= \ о^ч^щйИ,— \ aihJbuidV.
636 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Получим:
&К = \ [ (*" ~ ^ ) 6(Гу ~~ а"'j8Ui ~}dV~
v ' lJ
Таким образом, выполнение условия
8К^=0 A67.3)
dw
эквивалентно выполнению уравнении связи eij—^~ t
уравнений равновесия a,J; j = 0, а также граничных условий щ = и\
на 2„ и (Tjj-v; = Т\ на 2Т.
Перейдем теперь к случаю ползучести. Функционал Уанга
и Прагера играет роль, подобную роли функционала Кастильяно,
это обстоятельство подсказывает выбор выражения К для
ползучести, а именно:
К - J [ аиеи - -j- D + 2/>у) аи ] c?F -
v
- [ ft(Ui — u\)dZ— { r?i*idS. A67.4)
Здесь предполагается, что на части поверхности 2И заданы
скорости перемещения ее точек, на части поверхности 2Г заданы
скорости изменения поверхностных нагрузок.
Будем считать в выражении A67.4) а^ и и, независимыми пере-
менными, etj = у (к;, у — it;, г), тогда как ец зависит от а^
и CTjj-, a /?jj зависит от а и и, возможно, от некоторых параметров
упрочнения. Вычислим вариацию функционала A67.4). Получим:
V
\ 2« гт
Заметив, что ч
§ 168] ПРИМЕНЕНИЕ СМЕШАННОГО ВАРИАЦИОННОГО ПРИНЦИПА 637
перепишем выражение 8К следующим образом:
v v
-\8Ti{ii — it)dl,— ^Ti6Uidl>-\ Г? &*, dZ.
При варьировании скоростей перемещений мы должны
потребовать, чтобы выполнялись граничные условия, то есть было 6uj = О
на 2U.
При варьировании напряжений мы не нарушаем граничного
условия Г; = Т\ на 2Г, следовательно, bTt = 0 на 2Г. Первый
интеграл тождественно обращается в нуль, так как ец =
= efj + ptj. Преобразуем второй интеграл обычным способом,
получим:
6Х=~5 cry, jfiiii d7 + J [а«^-Г4]6М2 -J 6r,(uj-uJ)d2.
V 2 2
Обращение в нуль вариации 6i? эквивалентно выполнению
уравнений равновесия и граничных условий для ац, если вариации &ut
и боц подчинены сформулированным выше ограничениям.
§ 168. ПРИМЕНЕНИЕ СМЕШАННОГО ВАРИАЦИОННОГО ПРИНЦИПА
К ЗАДАЧЕ ИЗГИБА
В качестве простейшего примера рассмотрим задачу об изгибе
стержня, сечение которого имеет две оси симметрии. Рассмотрим
сначала более простой случай неупрочняющегося материала,
для которого
e = g' (a)a + v (a).
Вследствие закона плоских сечений е = щ. Зададимся линейным
распределением напряжений по сечению стержня, то есть положим
a = pi/. Составим теперь функционал A67.2) для элемента стержня
единичной длины, находящегося в условиях чистого изгиба
моментом М:
K = fc\ yW-l-P2^ g'iMy'dF-'fi I v(fy)ydF-Mx.
A68.1)
Приравняем нулю вариацию &К, вычисленную в предположении,
638 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
что варьируются только Р и к, притом независимо:
ЬК =-- / FJ3x + рбх) - рбр J g' фу) i/2 df -
-брЧ » (ру) г/JF- if би = 0.
Здесь / — момент инерции площади сечения. Отсюда следует:
x=pi-J g'(ps)j,»dif + ^J v{$y)ydF.
Положим
^$g(Py)^dF==x0(P) = Xo(^).
Величина и0 (р) представляет собою мгновенную кривизну
стержня, вызванную приложением изгибающего момента; если
начальная деформация упруга, то х0 (Р) есть точное значение кривизны;
если существует мгновенная пластическая деформация, то х0 (Р)
представляет собою приближенное значение кривизны,
вызванной этой мгновенной пластической деформацией. Теперь мы можем
переписать соотношение между кривизной и изгибающим
моментом следующим образом:
«=*to+T I v^y)«dF- A68-2>
Очевидно, что здесь, как и в других аналогичных случаях,
функция g (о) и соответственно х0 ( -у J могут соответствовать либо
начальной пластической деформации, либо первому периоду
ползучести по схеме Одквиста.
Будем теперь считать, что мгновенная деформация упруга,
а ползучесть следует степенному закону. Тогда из A68.2) следует:
*-.?-+-(?)¦¦ <№3>
Здесь
хп = % , Мп = <jnI: {y\\v i"+1 dF} иП- (ШЛ>
F
Приняв линейное распределение напряжений, мы, естественног
допустили некоторую погрешность. Для установившейся
ползучести из A68.3) следует соотношение, которое по форме
совершенно совпадает с точным соотношением A06.2), разница состоит
§ 168] ПРИМЕНЕНИЕ СМЕШАННОГО ВАРИАЦИОННОГО ПРИНЦИПА 639
лишь в определении величины Мп. Так, для стержня
прямоугольного сечения шириной Ъ и высотой 2/г в § 106 было получено такое
выражение:
По формуле A68.4) мы получаем:
Погрешность определения величины М„ по формуле A68.4)
в зависимости от величины п видна из следующей таблицы:
п
М'
мп
х' /х
1
1
1
2
0,963
1,08
3
0,921
1,28
4
0,894
1,57
5
0,869
2,04
6
0,849
2,69
Если принять за единицу величину момента, необходимого
для получения заданной скорости ползучести, то приведенные
во второй строке цифры будут представлять собою приближенное
значение момента для получения той же скорости, найденное
в предположении о линейном законе распределения напряжений.
Приведенные в третьей строке цифры представляют собою
приближенные значения скорости установившейся ползучести
при заданном моменте, если истинное значение скорости для
этой величины момента принять равным единице. Ошибка при
определении момента, соответствующего данной скорости,
относительно невелика, тогда как ошибка в определении скорости
при заданном моменте значительна и резко возрастает с
увеличением п. Аналогичное положение встретилось нам при анализе
примера 1 § 102.
Возвращаясь к уравнению A68.3), заметим, что применение
вариационного принципа привело нас к определенной структуре
этого уравнения, аналогичного исходному соотношению между е
и а. Действительно, записывая это соотношение в виде
о /¦ а \п
мы убеждаемся, что обобщенное перемещение к и обобщенная
сила М в уравнении A68.3) связаны между собою так же, как
деформация и напряжение. Вследствие сделанного предположения
о линейном законе распределения напряжений первый член
640
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
в правой части A68.3) дает величину мгновенной упругой
деформации совершенно точно, зато второй член, соответствующий
установившейся ползучести, является приближенным, при этом
степень погрешности нами выяснена. Если теперь мы будем
пользоваться для нахождения Мп не формулой A68.4), а
приведенной в § 106 точной формулой
M„ = Aa„J \\ ndF, A68.5)
F
то уравнение A68.4) будет давать точный результат и для
установившейся ползучести, именно так и следует применять это
уравнение.
§ 169. ИЗГИБ СТЕРЖНЯ ПРИ ПОЛЗУЧЕСТИ С УПРОЧНЕНИЕМ
Сформулированный в § 167 смешанный вариационный
принцип применим и тогда, когда ползучесть сопровождается
упрочнением, при этом закон упрочнения безразличен, существенно
лишь то, что скорость ползучести не должна зависеть от скорости
изменения напряжения. Предположим, например, что закон
упрочнения задан уравнением
рра = Аоп.
1 1
Положим А = -г-ц — , будем обозначать точкой дифференци-
рование по безразмерному времени t — tit^, положим также а =
= а/ст#. Тогда основное уравнение ползучести перепишется так:
Из A69.1) находим:
и, следовательно,
P=[jand*]T
1
о
Положим теперь:
ХМ
Заметим, что здесь обозначения несколько изменены по
сравнению с § 168; произвольная величина h, имеющая размерность
§ 169] ИЗГИБ СТЕРЖНЯ ПРИ ПОЛЗУЧЕСТИ С УПРОЧНЕНИЕМ 641
длины, введена для того, чтобы сделать к и р безразмерными.
Внося выражения для о в A69.2), найдем:
i a
1+а
p=yi+aTT^^[\^ndtJ
о
Составим теперь функционал К. С точностью до постоянного
множителя
• ' а
jjr = xp-i-p*-^--T-jL-pn Г [ pn&]~1+e R — &U. A69.3)
о
Здесь
F
Приравнивая нулю вариацию функционала A69.3), придем к
следующим уравнениям:
Р = М' A69.5)
Здесь р~- представляет собою упругое изменение кривизны,
поэтому величина
хп = и — р-^-
является изменением кривизны, накопленным в процессе
ползучести. Перепишем второе соотношение A69.5) следующим
образом:
t a
** = j^&n [\ Mndt~] i+a. A69.6)
о
Положим временно
t
о
Отсюда
Mn=(.l-{-a)qaq.
Подставляя в A69.6), находим, что
• *
41 Ю. Н. Работнов
642
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
и, следовательно,
9 = -R~
Теперь мы можем исключить из A69.6) интегральный
множитель, в результате получим:
R
1+а
xn*eS = jT5-M". A69.7)
Уравнение A69.7) по структуре совершенно такое же, как
исходный закон упрочнения A69.1). Приближенность этого
уравнения связана с тем, что при его выводе мы пренебрегали
перераспределением напряжений по поперечному сечению
стержня, считая, что закон распределения напряжений остается все
время линейным. Это справедливо для первого момента после
приложения нагрузки, поэтому выражение для мгновенной
деформации является точным, однако с течением времени роль упругой
деформации становится исчезающе малой и распределение
напряжений стремится к стационарному распределению,
соответствующему квазиустановившейся ползучести. Значение
множителя R в формуле A69.7) таково, что точного значения скорости
квазиустановившейся ползучести не получается. Найти
соответствующую поправку нетрудно. Считая, что е ~ р, заменим
исходное уравнение ползучести следующим:
' а 1 /" а
1+а V о*
П1ЛЦ
оложим по-прежнему е = -~, найдем из вышеприведенного
уравнения а и вычислим момент. В результате мы получим
следующее соотношение между кривизной и моментом:
XKa=jj—Ml. A69.8)
Уравнение A69.8) можно рассматривать как предельный случай
уравнения A69.7), когда упругая деформация изгиба My
становится исчезающе малой по сравнению с х, однако, в отличие
от A69.7), уравнение A69.8) является совершенно точным и
соответственно величина Bt в этом уравнении определяется не
формулой A69.4), а следующей формулой:
Й1 = 1:[^^|Х|1+^]^. A69.9)
F
Если теперь при пользовании уравнением A69.7) определять В
соотношением A69.9), то уравнение будет давать точные резуль-
§ 170] НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН 643
таты для крайних случаев: для начального момента времени,
когда деформация чисто упруга, и для достаточно большого
времени, когда упругая деформация может не приниматься во
внимание по сравнению с деформацией ползучести.
§ 170. НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ПЛАСТИН
Приближенная теория неустановившейся ползучести пластин
может быть построена точно таким же образом. Запишем основной
закон ползучести при степенном упрочнении и степенной
зависимости скорости от напряжения следующим образом (§ 74):
¦ ^-та'-(-?;),4г- <170-1»
Здесь
Р= \ (^-РиРи) *dt,
о
хотя аналогичный результат можно получить и при другом
выборе меры упрочнения.
Из A70.1) следует:
или
1
р=[$о?л],+в. A70-2>
Здесь принято оу = ¦ . Предположим, что напряжения рас-
пределены линейным образом по толщине, так что
ац = &„-?-. A70.3)
Изгибающие и крутящие моменты в пластине выражаются так:
ДГу = -§-офА«*у. A70.4)
В соответствии с гипотезой Кирхгофа
^ = ^1 • A70.5)
Здесь
причем w — безразмерный прогиб, «; = — .
41*
644 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Составим выражение функционала К. С точностью до
множителя
к= \ [titjij -Ц1-^- (йу^у-^- йа$й8Л _
F
t a
i^-jtf-J-i Q ЛЗГ?Л) 1+а MtJtitJ-wq ] dxdy. A70.6)
2
Здесь
Mij=Mu-\6uMss q = -~, R =
3"""*" « о,' 2J n
1 + а
Проварьируем это выражение, считая ЬМг} независимыми
и §y,n — bw^j. Получим:
\){iiijw^-wq)dxdy = Q, A70.7)
F
ij = A + v) -J- [ jfry - -^ 8.Д. ] +
( «L.
+ -2ТТТ^^г1 [ \ mdt] ^ М* A70-8)
о
Из A70.7) обычным способом получаются уравнение равновесия
и граничные условия, тогда как уравнение A70.8) можно
преобразовать подобно тому, как это было сделано в случае изгиба
балки. Положим
«5 = «v + A + v) -J- [М«--у^ btJM3s]
и образуем инвариант
И0 = -yKl + «L + Иц«22+ ««]•
С помощью A70.8) найдем:
о
Структура этого уравнения совершенно подобна структуре
уравнения A70.6), поэтому из него следует:
t
\M«dt = ^-.
о
§ 171]
ОБЩИЙ ПРИЕМ ИССЛЕДОВАНИЯ
645
Теперь мы можем записать A70.8) в следующем виде:
к = sniTij ^)"a йГ1ми. A70.9)
Отсюда следует:
Уравнения A70.9) по структуре совершенно подобны исходным
соотношениям закона упрочнения A70.1).
Предположение о линейном законе распределения
напряжений по сечению предопределило структуру этих уравнений, но
внесло некоторое искажение. В случае исчезающе малой упругой
деформации уравнения A70.9) должны совпасть с уравнениями
квазиустановившейся ползучести, в этом случае гипотеза
нормальных элементов приводит к совершенно определенному
нелинейному распределению напряжений по толщине пластины.
Полагая и?,- « и;7-, мы легко придем к формулам, отличающимся
от A70.9) только значением R, а именно:
^=4-B+^)- <170-10>
Поэтому мы будем получать более точные результаты, пользуясь
скорректированными формулами A70.9), в которых R
определяется выражением A70.10).
§ 171. ОБЩИЙ ПРИЕМ ИССЛЕДОВАНИЯ НЕУСТАНОВИВШЕЙСЯ
ПОЛЗУЧЕСТИ НА ОСНОВЕ ТЕОРИИ УПРОЧНЕНИЯ
Отправляясь от смешанного вариационного принципа и
задаваясь некоторым неизменным распределением напряжений, мы
получили для случая изгиба балки и пластины соотношения,
связывающие непосредственно пластические деформации, скорости
пластических деформаций и изгибающие моменты. Найденные
соотношения были прокорректированы таким образом, чтобы они
были справедливы в предельном случае больших деформаций
ползучести. Аналогичный прием можно распространить на
произвольные системы, находящиеся в состоянии неустановившиеися
ползучести.
Рассмотрим тело, находящееся под действием обобщенных
сил Qi (I = 1, 2, . . ., к). Соответствующие обобщенные
перемещения пусть будут qb. Упругие перемещения выражаются через
силы линейным образом, поэтому
qf = hiQi- A71.1)
Положим
Pi = qi-$uQu A71-2)
646 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
величины pi представляют собою перемещения вследствие
ползучести. Если pi = qt и Qi = const, то при степенном законе
упрочнения в теле реализуется состояние квазиустановившейся
ползучести; это значит, что распределение напряжений остается
неизменным, таким же, как при установившейся ползучести, тогда
как перемещениярг изменяются пропорционально tm ( т = -г—г— ).
Построим соответствующие зависимости между pi и Qi.
Рассмотрим сначала состояние установившейся ползучести, причем для
определенности выберем степенной закон ползучести с
показателем г, так что
Ф = ^—sr+1-
r-j-1
Здесь s — однородная функция первой степени от напряжений.
Предположим, что соответствующая задача об установившейся
ползучести решена, напряжения выражены в зависимости от
внешних сил следующим образом:
(по индексу I произведено суммирование). Потенциал скоростей
для всего тела выразится следующим образом:
ф=$ф(с^)^.
Продифференцируем это выражение по Qt:
дФ f дФ
¦=l -^-o'tdV.
Умножим на Qi и просуммируем по индексу I. Получим:
Таким образом, Ф является однородной функцией степени 1 -j- r
от Qi, которую всегда можно представить в виде
Ф = 7Т^<?Г+1- A71'3)
Здесь Q — однородная функция первой степени от Q,. По
определению потенциала скоростей
Величины ~- представляют собой однородные функции
нулевой степени от Qi; таким образом, к величин -~ выражаются
§ 171] ОБЩИЙ ПРИЕМ ИССЛЕДОВАНИЯ 647
л •• <?1 <?2
через А;—1 отношении, например: ^~-, ~-, ..., следовательно,
между ними существует тождественное соотношение:
'Ж-о-
С помощью A71.4) убеждаемся, что величина Qr должна быть
функцией pt:
<?г=фЫ; A71.5)
при этом ф (pi) — однородная функция первой степени. Положим
t
р= \ q>(pi)dt.
о
Подставляя в A71.5) выражение pi по формулам A71.4), находим:
Ф (-§>!• A71.6)
Предположим теперь, что деформации ползучести, скорости
ползучести и силы связаны следующими соотношениями:
л-тЬ-^Ж- A71J)
Вследствие A71.6) отсюда получается:
1 + а
Если действующие на тело силы неизменны, то A71.8) можно
проинтегрировать; в результате находим:
п 1
И
dQ
Pi=pwr
Найденное решение соответствует квазиустановившейся
ползучести, распределение напряжений при этом получается так же,
как при установившейся ползучести с показателем г = ;г7Г~'
это значение показателя и нужно выбирать при построении
функции Q. Если закон упрочнения выбран в виде A70.1), то
константа о> в законе ползучести, принятом для решения
вспомогательной задачи установившейся ползучести, должна быть принята
равной константе а* в A70.1).
648
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Положение значительно упрощается, если ползучесть
происходит без упрочнения. Тогда вместо A71.7) мы получим:
gz-M?« = en-jg-. A71.9)
Желая воспроизвести действительную форму первичных
кривых ползучести, мы должны, вставая на точку зрения теории
течения, вместо времени t ввести измененное время т. Таким
способом были получены уравнения ползучести оболочки в работе [11в].
Если внешние силы постоянны, то уравнения A71.7), как мы
уже видели, дают сразу квазиустановившуюся ползучесть,
которая сопровождает мгновенно возникшую упругую деформацию.
В этом, конечно, состоит противоречивость уравнений, дело
обстоит так, как если бы после упругой деформации произошло
мгновенное перераспределение напряжения, притом не
вызывающее дополнительных упругих перемещений. В то же время
с помощью этих уравнений можно находить вполне
удовлетворительные приближенные решения задач о релаксации реакций
внешних связей, о перераспределении реакций в статически
неопределимых системах, подвергнутых действию нагрузок, хотя
фактическое отыскание решений может быть выполнено лишь
численными методами.
§ 172. ПРИМЕНЕНИЕ ТЕОРИИ СТАРЕНИЯ К РАСЧЕТАМ
НА НЕУСТАНОВИВШУЮСЯ ПОЛЗУЧЕСТЬ
В предыдущих параграфах этой главы мы рассмотрели
некоторые численные методы решения задач неустановившейся
ползучести, а также применение к этим задачам вариационных
принципов. Рассмотренные примеры носили достаточно простой
характер, изучение неустановившейся ползучести более сложных
систем в принципе может производиться аналогичным образом,
но объем вычислений становится очень большим. Принцип этих
вычислений должен быть понятен из вышеизложенного; расчет
ведется шагами по времени, величина деформации ползучести,
добавляющейся на каждом шаге, определяется скоростью
ползучести, вычисленной по величинам напряжений и накопленных
деформаций ползучести для предыдущего шага. Общая схема
этих вычислений была приведена в работе [62], примеры
применения к задачам о пластинах и оболочках содержатся в статьях [287 ],
рзо]_ -рем не менее вряд ли приходится рассчитывать на то, что
расчеты неустановившейся ползучести по теории упрочнения
найдут в ближайшее время сколько-нибудь широкое
распространение в практике проектирования, если не говорить о
релаксационных задачах. Действительно, общая схема работы
конструкции в условиях неустановившейся ползучести под действием
§ 172]
ПРИМЕНЕНИЕ ТЕОРИИ СТАРЕНИЯ
64?
заданных нагрузок состоит в том, что первоначальное
распределение напряжений, определяемое упругими и мгновенными
пластическими свойствами, постепенно меняется, приближаясь к
состоянию установившейся или квазиустановившейся ползучести.
Точное описание процесса перераспределения напряжений обычно
бывает не столь уж важно. Зависимость перемещений от времени,,
конечно, в известной мере обусловливается процессом
перераспределения напряжений, но это влияние не очень велико.
Поэтому при нахождении суммарных перемещений точек системы
обычно бывает достаточно пользоваться уравнениями
установившейся или квазиустановившейся ползучести. Другое дело —
релаксационные задачи, когда именно ход перераспределения
напряжений и соответственно уменьшение со временем реакций
связей интересуют нас в первую очередь.
Учитывая, что разброс опытных данных делает бесполезным
стремление к получению точных решений, нужно считать
оправданным широкое распространение расчетов на неустановившуюся
ползучесть при помощи теории старения. Для чисто
релаксационных задач ошибка при применении этой теории будет наибольшей,
однако и здесь ею можно пользоваться для приблизительных
оценок. Как было указано в § 72, расчеты на ползучесть по теориа
старения выполняются совершенно так же, как расчеты по теории
пластичности деформационного типа; изохронные кривые
ползучести, построенные в координатах а0 — е0, соответствуют диаграмме-
пластичности, расчет повторяется для каждого момента времени..
Мы не будем здесь излагать различные способы расчета на
ползучесть по теории старения, это было бы простой перефразировкой
соответствующих решений в теории пластичности, последней же
посвящена большая литература. Особенность этих расчетов состоит
в том, что, как правило, изохронные кривые ползучести
используются для решения непосредственно, без каких бы то ни было
аналитических аппроксимаций. Такая возможность составляет
очень серьезное преимущество теории старения, неизбежная
ошибка при подгонке экспериментальных данных под то или
иное аналитическое выражение часто сводит на нет
преимущества более физически обоснованной и внутренне
непротиворечивой теории ползучести.
Специфика методов расчета на ползучесть по сравнению
с расчетами методами теории пластичности определяется не
существом дела, а выбором объектов. Большая часть работ в этой
области относится к элементам турбин: трубопроводам, дискам,
диафрагмам. Для дисков широко распространен метод
последовательных приближений в разных вариантах, один из этих
вариантов описан в § 127 применительно к установившейся ползучести,,
он переносится на неустановившуюся ползучесть по теории
упрочнения без каких-либо изменений, если под величинами ее
€50
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
и ег понимать не скорости деформации, а сами деформации,
а в качестве функции v (o0) взять функцию е0 (?, ст0),
фигурирующую в уравнении изохронной кривой ползучести для времени t:
e0 = e0(t, a0).
Если при расчете учитывается также температура, то мы должны
располагать серией изохронных кривых для различных
температур:
e0 = e0(t, (Т0. Т).
Другой способ расчета дисков был предложен в работе [М- Идея
способа состоит в том, что составляется дифференциальное
уравнение для радиального перемещения. Это — уравнение второго
порядка, его можно записать в форме линейного уравнения,
хотя на самом деле коэффициенты зависят достаточно сложным
и нелинейным образом от искомой функции. При вычислении
каждого последующего приближения эти коэффициенты
выражаются через функцию, найденную в предыдущем приближении,
таким образом, каждый раз приходится интегрировать линейное
уравнение с переменными коэффициентами. Указанный процесс
сходится довольно медленно, и при ручном счете метод вряд ли
можно было бы отнести к числу лучших, однако автор работы I1]
разработал программу счета применительно к машине «Стрела»,
программа оказалась достаточно удобной, и ею пользуется
в настоящее время ряд организаций.
Расчет турбинных диафрагм путем последовательных
приближений предложил Богуславский [7].
Этими краткими замечаниями мы и ограничим изложение
вопроса о применении теории старения к расчетам
неустановившейся ползучести. Заметим, что результаты расчетов
неоднократно сравнивались с экспериментом, при этом совпадение
получалось вполне удовлетворительным. Здесь мы упомянем
об одном экспериментальном исследовании I11], в котором
изучался вопрос о возможности моделирования ползучести на основе
теории старения. Согласно этой теории, желая отыскать
напряженное и деформированное состояние тела в момент времени t,
мы должны иметь в своем распоряжении одну только изохронную
кривую, соответствующую данному времени t; распределение
напряжений и перемещений оказывается совершенно не
зависящим от предшествующей истории. Предположим теперь, что для
двух различных материалов изохронные кривые ползучести
при времени ^ для первого материала и при времени t2 для
второго материала оказываются подобными. Тогда для
геометрически подобных и подобно загруженных моделей из этих материалов
перемещения в момент времени tt для первого материала и в
момент времени t2 для второго материала будут находиться между
§ 173] ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ДО РАЗРУШЕНИЯ 651
собою в определенном отношении, которое легко находится из
условий подобия. Оказалось, что кривая а0 — е0 для стали 20
при 480° и при ti = 300 часов подобна такой же кривой для
меди при 250° и t2 — 150 часов, тогда как для других моментов
времени условие подобия кривых не выполняется.
Были испытаны кольцевые пластины, полукольца, модели
сопловых диафрагм, пружины. Для пластин отношение прогибов
медной пластины при 150° и стальной при 300° (с учетом масштаба)
составляло 0,96, для полуколец то же отношение было в
среднем 0,75—0,76, для моделей диафрагм 1,20 и для пружин 0,82.
Как видно, наилучшее совпадение получилось для пластин —
образцов наиболее простой геометрической формы, однако и на
других моделях совпадение нужно считать
удовлетворительным, разброс свойств индивидуальных образцов имеет тот же
порядок.
Приведенные результаты служат косвенным подтверждением
приемлемости теории старения для практических расчетов.
Конечно, упомянутый вывод о независимости состояния
в момент времени t от всех предшествующих состояний,
вытекающий из гипотезы старения, приемлем лишь постольку, поскольку
речь идет о достаточно плавных и монотонных процессах.
§ 173. ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ДО РАЗРУШЕНИЯ
Как было показано в главе VI, разрушение вследствие
ползучести в зависимости от материала, уровня напряжений и
температур может либо иметь хрупкий характер и происходить при
весьма малых деформациях ползучести, либо быть вязким, то
есть сопровождаться существенным изменением формы и
размеров изделия. Подобно тому, как определялось время вязкого
разрушения стержня по схеме § 85, для любого тела,
находящегося в условиях ползучести, можно ставить вопрос об отыскании
такого состояния, когда равновесие становится неустойчивым
и, следовательно, происходит разрушение тела. Некоторые задачи
подобного рода будут рассмотрены в главе XII, в этих задачах
необходимо рассматривать конечные деформации и учитывать
геометрическую нелинейность. Практическая значимость
подобного рода расчетов ограничена; как правило, конструктивная
функция изделия нарушается, если деформации превышают
определенную величину, назначаемую в зависимости от
конструктивной функции изделия. Для современных материалов,
используемых в турбостроении, характерны малая величина
деформации к моменту разрушения и хрупкий характер разрушения.
Поэтому оценка прочности, например, турбинного диска должна
состоять из двух элементов. Во-первых, деформация, в данном
случае изменение наружного диаметра, не должна превышать
652
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
некоторого разумного предела, во-вторых, должна быть гарантия
от разрушения в прямом смысле слова. Простейшая схема расчета
изделия на длительную прочность будет состоять в том, что
с помощью той или иной теории ползучести вычисляется
наибольшее нормальное напряжение, которое сравнивается с пределом
длительной прочности для времени работы диска, определенным
путем испытания образцов. Для турбинного диска такая схема
тем более приемлема, так как оба главных напряжения
положительны и, следовательно, критерий наибольшего нормального
напряжения совпадает с критерием наибольшего касательного
напряжения, который приблизительно справедлив для оценки
возможности вязкого разрушения.
Найденное в результате расчета наибольшее нормальное
напряжение изменяется во времени, поэтому сравнивать с
пределом длительной прочности приходится эквивалентное
напряжение, определяемое при помощи принципа суммирования
повреждаемости, а именно:
a3=(l(afe^I/ft. A73.1)
о
Заметим, что при этом нет необходимости требовать очень
строгого соблюдения прямолинейности диаграммы длительной
прочности в координатах log о — log t, мы будем сравнивать
величину о"э с истинной кривой длительной прочности, тогда как
в формуле A73.1) величина к находится путем достаточно грубого
спрямления диаграммы на интересующем нас участке. Для дисков
стационарных турбин, как мы видели, процесс
перераспределения напряжений происходит довольно быстро и величина оэ
отличается от величины а, соответствующей установившемуся
состоянию, всего на несколько процентов. Поэтому неточность
в определении показателя к мало существенна.
С целью проверки описанной схемы предсказания
долговечности дисков было предпринято экспериментальное исследование
I95] на моделях дисков из четырех материалов, широко
применяемых в турбостроении: перлитной стали Р-3 при температуре 575°,
аустенитных сталей ЭИ-405 и ЭИ-572 при 650° и жаропрочного
сплава ЭИ-437Б при 700°. Выбор температур испытания
определялся желанием приблизиться к типичным эксплуатационным
условиям. Все материалы были подвергнуты стандартной
термической обработке, сталь Р-3, кроме того, испытывалась в охрупчен-
ном состоянии.
Испытания проводились в разгонной установке ЦНИИТМАШ,
модели дисков были плоские, с центральным отверстием.
Наружный диаметр моделей был 280 мм, часть моделей была надрезана
на ободе; этим имитировалась лопаточная нагрузка.
§ J73] ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ДО РАЗРУШЕНИЯ 653
Испытания периодически прерывались для замера деформации
наружного диаметра; большая часть моделей доводилась до
разрушения, часть снималась с испытаний и разрезалась для
определения остаточных напряжений. По величине остаточных
напряжений можно было вычислять величины напряжений в условиях
ползучести и сравнивать их с данными расчета. Всего было
испытано 25 дисков, длительность испытаний была в диапазоне от
нескольких часов до двух тысяч часов. Одновременно было
испытано на ползучесть около 200 образцов из различных поковок
в различных зонах по разным направлениям, что позволило
получить достаточно надежные средние изохронные кривые ползучести.
Расчет дисков производился по этим изохронным кривым на
основе теории старения. Этот расчет показал, что действительно
перераспределение напряжений заканчивается очень быстро,
в течение большей части времени жизни диска напряжения
остаются неизменными. Величина сгэ, вычисленная по формуле A73.1),
отличалась от напряжения в установившемся состоянии не больше,
чем на 3%. Расчетные значения остаточных напряжений хорошо
совпали со значениями, определенными из опыта, разница между
расчетными и экспериментальными величинами деформации на
наружном и внутреннем радиусах диска не выходила за пределы
экспериментального разброса.
Результаты определения времени до разрушения
обрабатывались следующим образом. Для каждого диска определялось время
до разрушения, для этого времени по кривой длительной
прочности, полученной в результате испытания стандартных
цилиндрических образцов, находилось разрушающее напряжение о*д. После
этого путем расчета определялась величина наибольшего
нормального напряжения в диске crmax и вычислялось отношение о"тах /о"я.
Величина отах находилась тремя различными способами:
1. В предположении, что материал до момента разрушения
ведет себя упруго.
2. В предположении, что распределение напряжений подобно
распределению напряжений в идеально-пластическом диске, то
есть о"е = const.
3. С учетом ползучести на основе теории старения.
Первый способ заведомо неправилен, однако в практике
конструкторских бюро еще до недавнего времени влияние ползучести
на перераспределение напряжений не учитывалось.
Представлялось интересным оценить величину дополнительного запаса
прочности, который вносит этот способ расчета.
Второе предположение соответствует цредельному случаю
степенного закона ползучести при п->- оо. Такого рода
аппроксимация неоднократно использовалась в главе VI, для больших
значений п она дает не слишком плохой результат. Соответствующий
метод расчета подкупает своей крайней простотой.
654 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ [ГЛ. XI
Результаты испытаний до разрушения приведены в следующей
таблице:
Материал
Сталь Р-3
стандартн.
термообработка
Сталь Р-3
охрупченная
Сталь ЭИ-405
<тшах/ад
. ! 2
1
1,78
1,85
1,67
1,32
1,35
1,33
1,33
1,89
1,92
0,89
0,92
0,83
0,72
0,74
0,73
0,73
0,93
0,96
3
0,95
1,00
0,94
0,96
0,98
0,97
0,97
1,03
1,05
Материал
Сталь ЭИ-405
Сталь ЭИ-572
Сплав ЭИ-437Б
атах/°д
1
1,92
1,83
1,87
1,52
1,57
1,38
1,44
1,52
1,58
2
0,96
0,94
0,96
0,81
0,82
0,72
0,82
0,86
0,89
3
1,05
1,04 >
1,06 [
0,95 ¦
1,02
0,93
0,95
0,97
1,01
Из таблицы видно, что расчет с учетом ползучести дает вполне
удовлетворительное согласие с опытом. Для стали ЭИ-405 расчет
по второму способу дает примерно тот же процент ошибки (в
другую сторону), что и расчет с учетом ползучести. Но диски из
этой стали разрушаются при большой деформации (порядка 12%),
когда, с одной стороны, уравнения теории ползучести типа теории
старения, выведенные в предположении малости деформаций,
перестают быть точными, с другой — характер разрушения вряд
ли может считаться хрупким. Для таких материалов расчет по.
среднему напряжению дает удовлетворительную оценку.
§ 174. УТОЧНЕННОЕ ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ХРУПКОГО
РАЗРУШЕНИЯ ВРАЩАЮЩЕГОСЯ ДИСКА
Обычная схема расчета на прочность в условиях ползучести
не принимает во внимание того обстоятельства, что разрушению
предшествует трещинообразование, в свою очередь влияющее
на скорость ползучести и приводящее к перераспределению
напряжений (§ 88). При расчетах по теории старения это частично
учитывается тем, что для построения изохронных кривых
используются кривые ползучести целиком, включая третий участок.
Исходя из тех соображений, которые были высказаны в § 94,
можно наметить схему расчета долговечности изделия, в которой
отмеченное обстоятельство учитывается целиком. Реализация
этой схемы встречает определенные затруднения, приводимый
ниже пример носит скорее характер иллюстрации постановки
задачи, которую в данном случае удается решить до конца.
Следуя изложению § 94, запишем для вращающегося диска в пред-
§ 174] УТОЧНЕННОЕ ОПРЕДЕЛЕНИЕ ВРЕМЕНИ РАЗРУШЕНИЯ 65S
положении ад > ог > 0 уравнения ползучести:
ee=-'ez-^A(j^)'\ ег = 0 A74.1)
и уравнение охрупчивания:
»=(тЗг)"- <174-2>
При этом единица измерения для напряжений выбрана так, что-
с = 1, это значит, что напряжения отнесены к величине с1/™,
о- == а/с1/".
Введем безразмерный радиус диска % таким образом, что
на контуре отверстия | == а, на периферии 1 = 1. Обозначим
через Ь наружный радиус диска, через и — радиальное
перемещение и примем
и
и—АЬ
Тогда из A74.1) следует:
Второе уравнение показывает, что и есть функция времени;
сравнивая первое с A74.2), замечаем, что
и
так как при t = Q и ~ 0, со = 0. Теперь из первого
уравнения A74.3) следует:
и \ С и \
ту ktJ
1/п
Уравнение равновесия элемента диска:
-щ (|о>) = <ге — ml2 (т = ри*с). A74.4)
Здесь р — плотность материала, v — окружная скорость диска.
Внесем в уравнение равновесия A74.4) выражение для о"е и
проинтегрируем. Получим:
i. = i"*[i?rr,*+»«t-,-±]-^?-+f
Используем теперь граничные условия оу A) = аг (а) = 0.
Исключая постоянную, получим следующее* дифференциальное
656 НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ГГЛ. XI
уравнение для функции u(t):
-тк}а) Y. A74.5)
1 — up (а) У
¦Здесь
fc(a) =
р(а) =
1
' 3
(п
n — i
п
-1)
1
а
1 —
1
— а
1
п
1-
аз
п
-1
1
Проинтегрируем A74.5) при начальном условии и @) = 0.
Результат будет следующий:
Здесь принято
-^ = р(а)[тк(а)ГA + п).
В некоторый момент времени tt на контуре отверстия при ? = а
¦становится <о = 1 и, следовательно, й = а. Из A74.6) находим:
г* = т[1-A-ар)"+Ч.
Легко убедиться непосредственно, что ра<1,если а<1.
Учитывая A74.5), мы можем теперь написать формулы для напряжений;
тк f. и \ t-l/n
Ов~- — [ 1
1—ир . - .
A74.7)
л_1 | \ ь > ^ w 1_цр
тогда как величина й в зависимости от ? дается формулой A74.6).
В формулах A74.7) принято р = р (а), к — к (а). Решение,
даваемое этими формулами, пригодно тогда, когда выполняется
исходное предположение jzz~-> °V Известно, что в случае
ползучести без охрупчивания соответствующее решение, полученное
в предположении сге > о>, справедливо при а > 0,25 и при любых
п I378]. В нашей задаче такое распределение напряжений
получается при t = 0, когда охрупчивания еще нет. Есть основание
«читать, что требуемое неравенство будет выполняться и в
последующие моменты времени. На рис. 239 приведены эпюры
распределения напряжений при п = 3 и а = 0,3 для значений и — 0;
§ 174] УТОЧНЕННОЕ ОПРЕДЕЛЕНИЕ ВРЕМЕНИ РАЗРУШЕНИЯ 657
ОД; 0,2; 0,3. В момент, когда становится и = а, = 0,3,
следовательно t = t^, напряжение о"е на расточке падает до нуля в
соответствии с тем, что при этом становится со = 1.
6s/m, Or//n
W
W
ф
G
/
k
^
>-~
°в
-й=0-
\Д2^
ИЗ
¦=к
~w
у
R2
бг
^^
&
ф Off
Рис. 239.
ф-
При t > t% в диске образуются три области. В области I,
примыкающей к краю отверстия, при а <С ? < У произошло
полное радиальное растрескивание, со = 1, и ав = 0. Из уравнения
равновесия A74.4) и граничного условия о> (ее) = 0 следует:
°v = ^r -it —
ае = 0. о<?<у.
A74.8)
Поскольку при i = Y ог<.0, будет существовать кольцевая
область II при Y<?<P- в которой ое>0, ог < 0;
следовательно, в этой области ед= —еТ, отсюда
ди и
= 0,
№@
Уравнение ползучести будет при этом следующее:
ее = — ег = А
св
-0"г
Но величина со во второй области близка к единице, поэтому
первый член в скобке является преобладающим и приближенно
можно принять:
ее = — ет~А
1— ы
)*
42 Ю. Н. Работнов
658
НЕУСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ
[ГЛ. XI
Отсюда, учитывая полученное выражение для и во второй
области, получим:
<*о
1 —ш
— О).
При t = t4 мы должны считать w = 0, в этот момент со = у ,
поэтому
w , а
Теперь напряжение а0 выражается следующим образом:
Внесем выражение A74.9) в уравнение равновесия A74.4) и
проинтегрируем его, учитывая граничные условия:
M?) = f (f-/)'Mp)==0-
В результате мы получим следующее дифференциальное
уравнение для функции w (t):
;-(тЗ?)" <174-,0>
Здесь
1 gs-p;
,з
О 2 2
^.(Y^^_p1_^)+^(Y-2/n_p-2/n)
2
^ " y'^^^1
и + 2 i_A i_i_
^2-(Y "-P n)+~-(Y-2/n-p-2/")
В области III при р" < !¦ < 1 опять о> = 0, поэтому решение
сохраняет тот же вид, что в первой фазе разрушения, только
граничное условие о"г = 0 выполняется при | = [5. Следовательно,
функция й (t) определяется в этой области уравнением A74.5),
в котором нужно заменить постоянную величину а функцией
времени f$, а именно:
--(т^Йг)"- <174-">
Выпишем теперь условия на границах областей. При I = у
должно быть со = 1, следовательно,
w = f — ay. A74.12)
§ 174] УТОЧНЕННОЕ ОПРЕДЕЛЕНИЕ ВРЕМЕНИ РАЗРУШЕНИЯ 659
При | = Р окружная деформация, а следовательно, и со
непрерывны, поэтому
й = а+у. A74.13)
Таким образом, мы получили систему четырех уравнений A74.10)—
A74.13) для определения четырех функций времени: и (t), w (t),
у (t) и р (t). При Р (t) = 1 третья зона исчезает, следовательно,
остаются только уравнения A74.10) и A74.12); в первом из них
нужно положить р = 1. Момент, когда у (t) = 1, является
моментом разрушения диска, при этом становится всюду со = 1.
Приближенная оценка времени до разрушения может быть
произведена следующим образом. Пренебрежем размером второй
зоны, то есть положим Р = у. Тогда из A74.12) и A74.13) следует
и = р, и остается только уравнение A74.11), изкоторого
продолжительность второй фазы разрушения определяется следующим
образом:
а
Для случая п = 3, а = 0,3, к которому относятся эпюры на
на рис. 239, было подсчитано:
2,32 t 2,22 ч 0,144'
т3 ' * то3 ' ** т3
Как и следовало ожидать, продолжительность второй фазы
разрушения невелика, после того как стало со = 1 на расточке,
разрушение идет катастрофически быстро.
42*
ГЛАВА.XII
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ
ТЕОРИИ ПОЛЗУЧЕСТИ. КРИТИЧЕСКОЕ ВРЕМЯ
Подобно тому, как упругая или упруго-пластическая система
при некоторых значениях внешних нагрузок может терять
устойчивость, то есть получать весьма большие перемещения в
результате незначительного изменения параметров системы, у тел,
находящихся в условиях ползучести, при определенных обстоятельствах
скорости перемещений могут стать недопустимо большими.
Критическое состояние, понимаемое в указанном выше смысле, может
наступить по истечении некоторого времени пребывания тела под
нагрузкой, поэтому в теории ползучести вводится понятие
критического времени.
В настоящей главе рассматриваются некоторые простейшие
задачи принципиального характера, на которых выясняется существо
проблемы, а также намечаются пути решения более сложных задач.
§ 175. ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ
ПОЛЗУЧЕСТИ
В этой главе мы будем рассматривать такие задачи
ползучести, в которых перемещения нельзя считать малыми и изменение
геометрии тела в процессе ползучести должно быть принято во
внимание. Ползучесть металлов не ограничена в том смысле, что
при сколь угодно малом напряжении за достаточно большое время
деформация достигает сколь угодно большой величины, поэтому
любая система, находящаяся в условиях ползучести,
неустойчива. Изменение геометрических размеров, связанное с
ползучестью, приводит к изменению действующих напряжений при
неизменных внешних силах, в результате чего происходит увеличение
скорости ползучести такое, что либо перемещения, либо
скорости перемещений стремятся к бесконечности в конечное время.
Это время называется (критическим временем.
§ 175] ПРОСТЕЙШИЕ ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ 661
При анализе схемы вязкого разрушения в § 85 мы
встретились с примером определения критического времени растянутого
стержня; аналогичным образом могут быть рассмотрены другие
простые задачи, например задачи об определении критического
времени для тонкостенных труб. При этом, так же как в § 85,
мы будем считать закон установившейся ползучести справедливым
при любых сколь угодно больших деформациях, это
предположение приводит нас необходимым образом к использованию
логарифмической меры деформации.
Положим, что в начальном состоянии длина трубки была
равна 10, радиус г0, толщина стенки 6„; в процессе деформации
те же величины мы будем обозначать г, гиб.
Из условия несжимаемости
1гЬ = 10г0б0.
Логарифмические деформации по длине, по окружности и в
направлении толщины мы будем обозначать:
ez = \n1-, ее=1п—, ег = 1п-т-.
h ro °о
Рассмотрим по отдельности следующие случаи:
1. Действует внутреннее давление д; в осевом направлении
трубка разгружена, следовательно, Ое = ~т- > сгг = 0. Положим
Ое = -j-, тогда а& = о§ ехр (^е — ег). Поскольку аг = аТ = О,
скорости ползучести еГ и ez равны между собой. Из условия несжи-
3
маемостии отмеченного равенства ет = ez следует, что ев — ег==у ее;
таким образом, о"е = сё ехр -|^ . Внесем это значение
напряжения в закон ползучести, который мы будем предполагать
степенным:
Разделяя переменные и интегрируя от е9 = О до ее
время до разрушения:
1 3 / ое Лп
Оказывается, что время до разрушения трубы в полтора раза
меньше, чем время до разрушения стержня при том же
номинальном напряжении.
оо, найдем
A75.1)
662 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
2. Действует осевая сила, создающая номинальное
напряжение сг°. Время до разрушения определяется по формуле Хоффа:
В этом случае рост напряжения происходит только за счет утонь-
шения стенки, тогда как в первой задаче наряду с утоньшением
стенки играет роль увеличение радиуса. Это обстоятельство
необходимо иметь в виду при интерпретации данных по разрушению
трубчатых образцов. В существующих конструкциях
испытательных машин окружное усилие создается ^внутренним давлением,
а осевое — комбинацией внутреннего давления и независимо
действующей осевой силы.
3. Трубка снабжена доньями и нагружена внутренним
давлением. Рассуждения, подобные приведенным для случая 1,
убеждают нас в том, что
ае = 0-9 ехрBе9 + ег),
az^=ozexpBe& + ez),
„о ч?а _о 1 «""о
Вследствие закона ползучести
ев = еп ("J)" -щ (°° "~Та0 ехр 1га B<?е + е*I'
ez=e,n (¦^)П-^о- (°"° —~2а^ ехр[«Bее + е2)],
следовательно, ег — О, и первое уравнение принимает вид
Уз / ?г0Уз л" 0
ee=__eIv^-25-5-j ехр2пео.
Интегрируя, находим:
^-^дау-^-с*)-- с75-3»
Случай толстостенной трубы рассматривался рядом авторов [52],
[55], мы не будем на нем останавливаться.
§ 176. ГИБКАЯ НИТЬ
Пусть гибкая нить, натянутая между двумя опорами,
подвергается действию постоянной нормальной нагрузки q. Очевидно,
что после деформации нить примет форму дуги окружности.
Начальная длина нити 10 = 2р sin ф, текущая длина I — 2рср
§ 176]
ГИБКАЯ НИТЬ
663
(рис. 240), поэтому логарифмическая деформация
е — In -7— = In
sm<p
A76.1)
Растягивающее нить напряжение в каждый момент есть
9Р
F
Но р = -9 .° , FI — FQl0, следовательно, F = F0-f- = Fi
sin <р
2sin9
поэтому
а =
9^0 ф
2F0 sin2 ф
A76.2)
Вычислим из A76.1) скорость
ползучести:
sin Ф — Ф cos m
е = -—~ — ю,
cpsiuip т
Рис. 240.
и внесем это выражение е, а
также значение A76.2) для а в формулу степенного закона
ползучести. Получим:
втф—ф cos ф /'втЗф'Ч"
<Р
ф Sin ф
ф
V
= enq
A76.3)
Здесь
qh
' 2F0on
Интегрируя A76.3), найдем:
snqnt = \
sin ф—ф cos ф
ф вШф
!H^)"dcp.
A76.4)
Когда ф = я, радиус нити становится бесконечно большим;
поэтому, полагая в формуле A76.4) верхний предел интеграла ср = я,
мы получим критическое время, которое всегда конечно. На
рис. 241 представлена зависимость между безразмерным прогибом
л 04 А Pf)S CD Л Л
/ = -!- = -^и безразмерным временем t= ernqnt, найденная
численным интегрированием A76.4) при п = 3. Критическое время
оказалось tKP = 0,1973.
Из графика видно, что вначале прогиб растет чрезвычайно
быстро и при оценке реальной несущей способности конструкции,
включающей в себя элемент рассмотренного типа, величина
664
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
критического времени не является показательной, долговечность
конструкции должна оцениваться по допустимому прогибу,
который обычно невелик. При относительно небольших прогибах
J— zf
можно получить более простое решение. Будем пользоваться
обычной мерой деформации вместо логарифмической, положим
sm ф « ф — у, cos ф
тогда из A76.1) следует:
и из A76.2):
а;
1-*-.
1Г
2F0 Ф '
Внесем в уравнение ползучести. Получим:
ФФ = Зе„<7яф-п-
Отсюда, интегрируя, находим:
1 1
<p=[3(B + 2)]»+2(gnft!n)»+2.
Безразмерный прогиб / = -?-, следовательно,
/ = ±[3(я + 2)г>+2.
A76.5)
Соответствующая кривая показана на рис. 241 пунктиром.
§ 177] ИЗГИБ БАЛКИ С ШАРНИРНО ЗАКРЕПЛЕННЫМИ КОНЦАМИ 665
Заметим, что найденные решения пригодны также для
мембраны в форме вытянутого прямоугольника, нагруженной
равномерным давлением; при этом несколько изменяется значение констант
в определении безразмерных параметров. Соответствующий вывод
совершенно очевиден, и мы его не приводим.
§ 177. ИЗГИБ БАЛКИ С ШАРНИРНО ЗАКРЕПЛЕННЫМИ КОНЦАМИ
Полученные в предыдущем параграфе решения относятся к
весьма тонкому стержню, когда можно пренебречь изгибной жесткостью.
Задача о балке, концы которой закреплены и не могут смещаться,
оказывается значительно более сложной. Пусть длина балки 1Г
интенсивность распределенной нагрузки q. В основу расчета
мы положим модель балки в виде идеального двутавра и проведем
анализ для случая п = 3. Для других целых значений п
вычисления аналогичны. Итак, полагая п = 3, из A17.3) мы получаем:
e = ^r = N(N* + m*), Z = ±?g = M{3N* + M*). A77Л)
При этом мы воспользуемся тем обстоятельством, что в степенном
законе ползучести остается известный произвол в выборе
констант еп и ап, вместо них можно ввести две другие константы
г'п и а'п, лишь бы было
Дополнительное условие, делающее выбор констант определенным,,
мы введем дальше. Введем безразмерную координату ? = x/hr
безразмерный прогиб ш = -г- и безразмерное осевое перемещение
и = у . Тогда
- 1 d2ir ~ 1 / ди . dw dw \
Будем искать прогиб w в виде
w= — csin Ц.
Jt/i
Здесь с — функция времени, Я. = —т~ , ? меняется в пределах
от нуля до l/h.
Изгибающий момент в балке
М = МГ + Nw,
666 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
где Мх — изгибающий момент от нагрузки q. Отсюда следует:
M = Mi + Nw, Mi
Mi
Изгибающий момент от поперечной нагрузки выражается
формулой
Mi = qlx-?f.
Заменим функцию Mt (x) первым членом ее разложения в ряд
Фурье:
Следовательно,
Mi « ^g ql* sin -r
M^§i&Sin^-
Выберем теперь постоянную а'п таким образом, чтобы
множитель при sinX§ обратился в единицу, то есть положим
°ИН?- <177-2)
Теперь мы можем написать:
M^asmll, a = l-cN. A77.3)
Вносим значения е, и, М в A77.1), получаем следующую
систему уравнений:
14 sin XI = г'па C#2 + a2 sin2 Щ sin Ц,
|| + Pec cos2 Я? = е;Л' (N2 + За2 sin2 Л?).
Первому уравнению мы удовлетворим в среднем, для этого
умножим обе части на sin Я| и проинтегрируем. Получим:
¦КЧ = г'па (ъ$г + \сА ¦ A77.4)
Заметив, что вследствие условия закрепления концов и (?)
обращается в нуль на концах балки, проинтегрируем второе
уравнение от ? = 0 до b, = l/h. Получим:
Л»сс'=е;#B#« + 3а»). A77.5)
$ 177] ИЗГИБ БАЛКИ С ШАРНИРНО ЗАКРЕПЛЕННЫМИ КОНЦАМИ 667
Теперь нам остается только изменить масштаб времени, чтобы
уравнения не содержали никаких параметров. Положим
I? Я2Л2 ^ „3 Fh0n J l-
Исключим из A77.4) и A77.5) с, тогда получившееся уравнение
вместе с A77.3) позволит выразить а и N через с, а именно:
если ? (с) есть корень кубического уравнения
?-^? + Ч-~ = 0, A77.6)
то
c-t-S(c)' с + ?(с) '
и дело сводится к интегрированию уравнения
dc Го тОго , 3
dt
= а [ЗУУ2 + |-а2] A77.8)
при начальном условии с @) = 0. В начальный момент N @) = 0,
а@) = 1. Если прогибы достаточно велики, то ? мало, из A77.6)
следует ? «-gj , отсюда, пренебрегая малыми членами, получаем:
dt ~~ с4 '
Отсюда
с « A0ГI/б.
Подставляя сюда выражение для ? и переходя к прогибу,
найдем, что прогиб посредине равен
тогда как формула A76.5) при и—-3 дает
Разница порядка 3,5% в коэффициентах связана с тем, что как
в том, так и в другом случае речь идет о приближенном решении,
хотя принципы получения этих приближенных решений
совершенно различны. На рис. 242 и 243 представлены кривые,
изображающие функции с (t), a (t),N (t), и кривая, полученная путем
численного интегрирования уравнения A77.8). При этом из
A77.6) находилось с в зависимости от ?; для различных значе-
668
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
ний ? вычислялись N ша, а также правая часть A77.8). На рис. 243
пунктиром нанесена также кривая зависимости прогиба от
времени по приближенной формуле с = A0}I/&. Видно, что, начиная
с, a
v>
7JJ
up
a -s. /
Г 1
у/С
1 1
2
Рис. 242.
N
Ф
Л
t
/''' ^^*
V /
Д /
' 1/
i т
"/L- л
п N
1 ^**^~~— о
i i i
—" ~
1
•
¦
-
^
_
-
л
4*
W
У?
V
#7
Ф
44Г
в»
4?
Ц2
"ч
70
Zff 3ff
Рис. 243.
W
Sff
примерно с с = 3, роль изгиба становится совершенно
незначительной, изгибающий момент а делается весьма малым и ошибка
в определении прогиба по асимптотической формуле при с = 3
составляет примерно 7%. Таким образом, при рассмотрении задач
S 177] ИЗГИБ БАЛКИ С ШАРНИРНО ЗАКРЕПЛЕННЫМИ КОНЦАМИ 669
подобного рода учет изгиба не очень существен, основные черты
поведения элемента могут быть выяснены, если считать его гибким
и не сопротивляющимся изгибу, тем более, что решение задачи
о продольно-поперечном изгибе является приближенным и
основанным на довольно грубых допущениях. Здесь мы взяли выражения
скорости удлинения и изменения кривизны в зависимости от
усилия и момента такими, которые получаются для идеального
двутавра. Мы видели в § 116, что возможны и другие
аппроксимации этих зависимостей, соответственно и приведенное здесь
решение допускает различные модификации. Мы вернемся к этому
вопросу при изложении вариационных принципов в нелинейных
задачах теории ползучести д рассмотрим в качестве примера
другой способ решения этой же задачи.
Изгиб стержня с закрепленными концами изучался также
Одквистом в статье [317]. Приведенное в этой работе решение
относится только к начальной стадии изгиба, когда продольная
сила невелика, автор составляет уравнения типа A77.1) для
произвольного п, вносит туда выражение для М, содержащее
член Nw, и разлагает правые части по N, ограничиваясь первой
степенью N. Прогиб w разлагается в ряд Фурье по косинусам
нечетных аргументов (начало координат берется в середине балки),
в правых частях уравнений фигурируют функции М™ и М™'1,
которые также разлагаются в ряды по косинусам; для
коэффициентов Фурье выражения прогиба получается бесконечная
система обыкновенных дифференциальных уравнений, которая
потом укорачивается. Система оказывается все же слишком
сложной, поэтому автор в конце концов ограничивается одним
членом ряда Фурье и получает приближенное решение, которое
сводится к следующему ("в наших обозначениях):
Коэффициент с^п> зависит от п\ значения этого коэффициента
приведены в следующей таблице:
п
1
0
1,273
1
1,032
2
0,891
3
0,796
4
0,726
5
0,672
6
0,628
7
0,626
Приближенное решение уравнения A77.9) ищется в виде
ряда типа
c—Cot-j- Cji3 + ...
670
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Если ограничиться первым членом ряда, то мы получим случай
изгиба одной поперечной нагрузкой без продольной силы. Решение
Одквиста при п = 3 получается следующим:
с = °'323жB?;K'> A77.Ю)
тогда как точное решение этой задачи дает коэффициент 0,332.
Случай отсутствия продольной силы получается и из наших
уравнений, если положить в них N = 0 и, следовательно, а — 1.
Тогда из A77.9) следует:
с — -г-1.
4
Приводя результат к виду A77.10), мы находим, что численный
коэффициент оказывается равным 0,331, что почти не отличается
от точного решения. Таким образом, мы проверили, что
найденное методом численного интегрирования приближенное решение
задачи о балки под действием поперечной нагрузки при
неизменном расстоянии между концами весьма мало отличается от
точного решения как при весьма малых, так и при достаточно больших
прогибах.
§ 178. КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ
Сжатый стержень из материала, обладающего свойством
ползучести, абсолютно неустойчив в смысле, разъясненном в начале
§ 175. Последовательные состояния такого стержня изображены
примерно на рис. 244. Если принимать за меру деформации прогиб
стержня, то есть наибольшее расстояние оси стержня от линии
действия сил, то, очевидно, прогиб будет сначала возрастать,
потом убывать, в большей части стержня сжатие сменится
растяжением и в некоторый момент времени произойдет разрушение
вследствие утоныпения стержня. Соответствующее время
является критическим временем в строгом смысле слова, задача
определения критического времени в указанной постановке слишком
сложна, и решение ее вряд ли имело бы практическую ценность.
При оценке реальной несущей способности сжатых стержней мы
должны потребовать, чтобы боковой прогиб не выходил за
некоторые достаточно узкие пределы, поэтому реальным предельным
временем эксплуатации нужно считать время, за которое
начальный прогиб с0 увеличивается до некоторого предписанного
значения с4. Однако поведение сжатого стержня при ползучести
отличается той особенностью, что под действием сжимающей силы
начальный прогиб возрастает сначала относительно медленно,
но начиная с некоторого момента времени этот рост становится
катастрофически быстрым. Если воспользоваться линеаризиро-
§ 178] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 671
ванным уравнением изогнутой оси стержня, то оказывается, что
прогиб стремится к бесконечности в конечное время, которое
и принято называть критическим временем.
Как мы увидим, в некоторых случаях оказывается, что скорость
прогиба становится бесконечно большой, хотя сам прогиб остается
конечным. Время, когда это происходит, мы будем также называть
критическим. Необходимо иметь в виду, что определенное таким
способом критическое время, строго говоря, механического смысла
Рис. 244.
не имеет, линеаризированные уравнения пригодны лишь для
достаточно малых прогибов. Рис. 244 убеждает нас в том, что
в действительности ни о каких бесконечных прогибах речи быть
не может. Однако, определяя критическое время указанным
способом, мы не ставим себя в зависимость от величины заданного
допустимого прогиба и получаем некоторую объективную, хотя
и условную оценку реальной долговечности стержня.
Существование критического времени в указанном смысле было впервые,
по-видимому, обнаружено Фрейденталем [21°], который допустил
ошибку, считая, что критическое время существует и для стержня
из линейного вязко-упругого материала. Эта ошибка исправлена
в работе [271]. Здесь мы рассмотрим вопрос о критическом времени
на простейших примерах, считая материал следующим закону
установившейся ползучести и пренебрегая упругой деформацией,
а) Модель Шенли. Явление потери устойчивости неупругой
системой проще всего иллюстрируется на модели, предложенной
Шенли [349]. Жесткий блок длины I прикреплен к двум стержням,
длины а и площади F12, материал которых обладает свойством
ползучести (рис. 245). Обозначим е+ и е_ относительные
укорочения стержней, сг+ и сг_ напряжения в стержнях; будем считать,
672
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ
[ГЛ. XII
что е = v (а). Из уравнений равновесия следует:
Отсюда
С другой стороны,
или
a+ = a(l + w),
а_ = стA — w),
w —
w-
f
la
1№
F *
(е+ — е_),
w--
la
2Д2
{v[o(l + w)]-v[a(i-w))}.
A78.1)
Интегрируя A78.1), мы найдем критическое время, когда прогиб
обращается в бесконечность. Существование
критического времени легко усматривается
при степенном законе ползучести, когда
v(o) = Rn — — .
Подставляя в A78.1) и разделяя переменные,
найдем:
dw
eja f a\nt
(l+w)n~\l—w\n-i(l—w) 2№ \anJ Kp"
Введем обозначение:
2h?
al _"э-
Смысл этого обозначения будет виден из
дальнейшего. Заметим, что
о Л»
t = P,
где р представляет собою накопленную за время t дефор-
гмацию ползучести основного состояния сжатия. Поэтому
§ 178] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 673
вышеприведенную формулу можно переписать так:
со
Ркр = бэ ) A + *)»-| i-w\»-i(i-w) ¦ A78.2)
wo
При любом /г>1 интеграл в формуле A78.2) конечен. Так,
при п = 3 этот иг
п — Ъ получается:
при п = 3 этот интеграл равен T^ln^-r^-a. Следовательно, для
1Z О -j— W?q
В приведенном анализе мы не учитывали упругой деформации.
Будем теперь считать, что
e± = ^-o± + v{e±) = ± ^w + v[o{l±w)\.
Теперь вместо A78.1) мы имеем:
ш-М?И = жИаA + ^)]-^<тA-ф A78.3)
Пусть начальный, до приложения нагрузки, прогиб был w00;
если нагрузка прикладывается за достаточно короткое время,
то правая сторона в уравнении A78.3) пренебрежимо мала и мы
получаем:
ala n
w0 — w00 — -j^ w0 = 0.
Отсюда
т-
, ala
2EW
Знаменатель в этой формуле обращается в нуль тогда, когда
_ 2Е№
la.
Но это есть упругая потеря устойчивости в смысле Эйлера.
Величина
2Е1&
°* = -[а-
представляет для модели Шенли эйлерово критическое напря-
жение, а величина ед = — упругую деформацию,
соответствующую эйлерову критическому напряжению. Положим
а Р
43 Ю. Н Работнон
674 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Тогда
w0 = ^L. A78.4)
Теперь мы должны интегрировать уравнение A78.3), положив
в нем а = 0, при начальном условии w = w0- Легко влдеть, что
результат будет отличаться от результата A78.2) только
множителем A — со), а именно:
оо
ркр = еа A - со) J {Х+а))П_^ш]П-Х{1_ю) ¦ A78-5)
Wo
Необходимо помнить, что нижний предел интегрирования ц>0
теперь определяется с помощью A78.4).
б) Стержень идеального двутаврового сечения. Степенной
закон. Предполагая сечение стержня идеальным двутавровым,
рассмотрим случай, когда оба конца шарнирно защемлены и
длина стержня равна I [272]. Подставим во вторую из формул A17.3)
N = —, М = — 2^-, и = -^щ, получим следующее
дифференциальное уравнение:
h д3ш
en dz^dt
-т(?Ж»+т)Ч'-т
п-1 f . W
Введем безразмерный прогиб w = -г- и безразмерную координату
\ = zlh, тогда уравнение перепишется следующим образом:
d*w 1 / а
a? dt- 2-nKan/[(l+wr-\l-wr^(i-w)]. A78.6)
Здесь а = P1F. Для приближенного решения этого уравнения
применяются различные приемы, наиболее простой случай
соответствует значению п = 3, рассмотрением его мы и ограничимся.
При ге = 3 из A78.6) следует:
д3» _8пЛ?.у[3? + ^]. A78.7)
д& at "п V а„
Будем искать решение в виде
. . . nhl
w — c(t) sin —-—- .
Подставив в A78.7), получим:
(J^2csin^i = en (^-K [3csin4l + c»sm»^i] . A78.8)
Дальше можно поступать по-разному. Можно потребовать,
чтобы уравнение A78.8) выполнялось в одной точке, а именно
§ 178] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 675
посередине балки, когда ^ = -пГ"- Тогда получим:
ЯН J \ О;
Разделим переменные и проинтегрируем. Найдем:
Здесь с0—начальный безразмерный прогиб. Критическое время
мы получаем отсюда, полагая с = оо, а именно:
^-тС*)'^- <"8-»>
С другой стороны, можно было потребовать выполнения
уравнения A78.8) в среднем, для этого нужно умножить обе части
его на sin —у5- и проинтегрировать по длине, в результате
вместо A78.5) получается следующее уравнение:
«=e-(isrJ(i)'Ce+l-c')' A78Л2)
и формула для критического времени принимает вид
вЛ— *кр = 7Г(-г) Ь-54. A78.13)
_ о„ J кр 6 V « у -о
Для других значений п вычисления приведены в работе [27°].
Аналогичные решения содержатся в статьях [234], [238].
в) Стержень идеального двутаврового сечения. Закон
гиперболического синуса. Положив в формулах A17.1) v = 2ге sh alae,
по второй из этих формул получим:
В нашем случае N = aF, М= —.oFkw, следовательно,
•*-^i=''{,lhU<1-i>]-*[^1+i»]}-
= -в.сЬ^Л™. A78.14)
Опять-таки примем w = с (t) sin -у- и потребуем, чтобы
уравнение A78.14) выполнялось в середине балки. Получим:
'яйДя •_ _ , а .,_ ас
О
-г , с = ге ch — sh — .
43*
676 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Разделим переменные и проинтегрируем. Получим:
,/oV /лЛ\20е1 Г 1
th?5
A78.15)
Заметим, что во всех случаях формула для критического времени
может быть записана в более компактной форме. Для идеального
n2Z?i<7i2 /я/г"\2
двутавра эйлерова сила Рэ =—-^—, поэтому множитель ( — )
представляет собою упругую деформацию, соответствующую
эйлеровой силе. Обозначим ее еэ. При степенном законе ползучести
величина е„( — ) iKp, фигурирующая в левой части A78.13),
представляет собою деформацию ползучести при равномерном
сжатии стержня силой Р за время tKp; назовем эту величину
критической деформацией и обозначим ркр. Тогда формула A78.14)
примет следующий вид:
Аф = §1п^. A78.16)
Формула A78.15) не приводится к столь простой форме, однако
следует заметить, что при напряжениях, при которых ползучесть
ощутима, сп— мало отличается от sh —, поэтому можно при-
ближенно принять
pBp=.-_^-lnth^-. A78.17)
Здесь а = а/ае.
Решения, подобные вышеприведенным, как уже было
отмечено, находились различными авторами. Незначительная разница
в результатах объясняется тем, что для приближенного
интегрирования уравнений A78.6) или A78.14) можно применять разные
приемы. Способ удовлетворения уравнению в одной точке
является простейшим и самым грубым. Более точные результаты
получатся, если задать прогиб в виде ряда Фурье и искать
коэффициенты по методу Галеркина. Количество работ, содержащих
подобного рода уточнения, довольно велико, однако мы не будем
на них останавливаться.
Стержень идеального двутаврового сечения является
статически определимым, поскольку напряжение в полках определяется
по формулам A17.3) через сжимающую силу и прогиб единственным
образом. Поэтому учет начальной упругой или
упруго-пластической деформации в рамках приведенной схемы не вызывает каких
бы то ни было затруднений. Действительно, предположим, что
мгновенная деформация стержня упруга. Если начальный
прогиб был Соо, то сейчас же после приложения нагрузки прогиб
§ 179] УЧЕТ МГНОВЕННОЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ 677
становится равным с0, причем
г - с-°°_ (л - Р
" 1—0) Рд
Здесь Рэ — эйлерова критическая сила. Деформации
ползучести определяются через действующие напряжения так же, как
и выше, однако деформация ползучести сопровождается
увеличением упругой деформации, как это было выяснено на примере
модели Шенли. Аналогичное исследование легко проделать
и в общем случае, различие будет состоять в том, что во все
полученные формулы для критического времени нужно будет ввести
еще множитель A — со). Поэтому формулы настоящего параграфа
для критического времени сохраняют силу, если только мы
предполагаем упругость стержня неограниченной. Если материал
стержня может пластически деформироваться, то положение
оказывается несколько более сложным.
§ 179. УЧЕТ МГНОВЕННОЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ
ПРИ ОПРЕДЕЛЕНИИ КРИТИЧЕСКОГО ВРЕМЕНИ
Для выяснения существа дела мы обратимся прежде всего
к рассмотрению простейшей модели Шенли.
Сначала будем предполагать материал стержней просто
пластическим, таким, что е = е0 (а). Функция е0 (а) предполагается
определенной таким образом, чтобы описывать как активную
пластическую деформацию, так и разгрузку. Воспроизводя
рассуждения предыдущего параграфа, найдем, что связь между
усилием и прогибом выражается следующим соотношением:
w-w0 = ^{e0la(l+w)]-e0[a(l-w))}. A79.1)
Приведенная запись имеет условный характер, поскольку мы
должны еще установить, имеет место нагрузка или разгрузка
в каждом из стержней. Так или иначе, уравнение A79.1)
определяет кривую зависимости о от w; при некотором значении w сила
достигает максимального значения, следовательно, —— = 0.
Продифференцируем A79.1) по w, полагая -=— = 0. Получим:
1 = 0i К1° A +«01 + < [о A - »)]}• A79.2)
Уравнение A79.2) определяет критическое состояние стержня,
то есть такой максимальный прогиб, при котором стержень
выдерживает сжимающую нагрузку а или ту минимальную
силу, которую выдерживает система при заданном прогибе.
Для фактической оценки устойчивости или неустойчивости
678 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
системы мы должны решать совместно уравнения A79.1) и A79.2);
исключая из этих уравнений w, мы находим соотношение
между силой а и начальным прогибом wq, соответствующее
критическому состоянию. Предположим теперь, что мгновенная
упруго-пластическая деформация сопровождается ползучестью.
В результате ползучести прогиб растет и в некоторый момент
времени достигает значения, определенного при данной силе
соотношением A79.2). Тогда равновесие системы станет
невозможным и произойдет мгновенное выпучивание. Критическое
время стержня есть время достижения конечного критического
прогиба, скорость выпучивания становится при достижении
критического времени бесконечно большой.
Высказанные интуитивно очевидные соображения легко
проверить. Предположим, что мгновенная деформация
сопровождается ползучестью и справедливо уравнение D7.4):
e = e'a(a)o+v(o).
Прогиб w (t) будет удовлетворять следующему
дифференциальному уравнению:
w {l-?L[e'0(a (l + w)) + e-0(o(l-w))]} =
= ^{v[o(l+w)]~v[c(l-w)]}. A79.3)
При выполнении условия A79.2) множитель при w обращается
в нуль и, следовательно, w = оо.
Отмеченный простой результат, состоящий в том, что за
критическое время для стержня с сечением в форме идеального
двутавра нужно принимать время достижения критического прогиба,
величина которого определяется только упруго-пластическими
свойствами материала, но не характеристиками ползучести, был
сформулирован Веубеком [374] в результате анализа решения,
найденного Хоффом [237]. Это решение мы сейчас приведем.
Автор рассматривает стержень идеального двутаврового сечения
с шарнирно опертыми концами, качественная сторона дела
остается той же, что и для рассмотренной выше стержневой модели
Шенли. В основу полагается следующее соотношение между
напряжением и деформацией (см. § 47):
Здесь /cj может принимать значения —1, 0, +1; кг принимает
значения —1, +1, как указано в § 47. Если п целое нечетное,
то к% = + 1. При увеличении напряжения о" следует принять
ki = + 1, при разгрузке ki = 0. Хофф принимал при
вычислениях п = 3 и т — 1.
§ 179] УЧЕТ МГНОВЕННОЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ 679
Уравнение A79.4) было предложено, как мы уже указывали,
Одквистом, который применил его также и к задачам
устойчивости [3151. Второй член в правой части A79.4) с одинаковым
успехом может отражать как мгновенную пластическую
деформацию, так и деформацию первой фазы ползучести. При тех же
предположениях, которые были сделаны в § 178, мы получим
следующее дифференциальное уравнение продольного изгиба:
-Й-т<^-^+т[* (frt-
Сюда нужно подставить:
a+ = a(l + w), а- = а A — w).
Если w мало, то а+ и а_ имеют одинаковый знак; будем считать
сжимающие напряжения положительными, как это часто делается
в задачах продольного изгиба. С увеличением w напряжение с+
растет, тогда как 0_ убывает. Поэтому к* = 1, /е~ = 0.
Величины Щ и к~ равны между собою и равны единице. Внося
выражения а+ и а_ в уравнение A79.5), получим:
d&dt E ^ 2 V^y \х^ш'
+ i(^yi(U-wr-(l-wy). A79.6)
Предполагается, что начальное искривление оси балки после
приложения нагрузки может быть представлено с помощью одной
полуволны синусоиды:
w0 = c0 sm -~ .
Прогиб ищется также в виде
w = c sin —р ,
где с — функция от времени.
В дальнейших вычислениях принимается т = 1, п = 3, что
соответствует, как указывает Хофф, поведению алюминиевого
сплава 24-S-T4 при 314°. Выражение для w подставляется в A79.6),
все нелинейные члены разлагаются в ряды Фурье по синусам,
и коэффициент при sin —~ приравнивается нулю. В результате
получается следующее уравнение для функции с (t):
tj '-j'tvsv y^3ij^"ys;j \-^хс
680 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Величина (-г), как мы видели, представляет собою упругую
деформацию еэ, соответствующую эйлеровой силе. Перепишем
дифференциальное уравнение следующим образом:
'[*-W(?),(>+?)]--(?),(>+t<0- AЯ.7)
Это уравнение интегрируется, результат получается следующий:
—-кш^ [та-и'-ызё?-]} ¦
A79.8)
Здесь
Л = еэ-?—-^(jf-J . 5 = зн(-|г) •
Множитель при с в левой части уравнения A79.7) обращается
в нуль при некотором значении с = скр; эта величина
находится по формуле
Когда с = скр, скорость прогиба, в соответствии с A79.7),
становится бесконечной, поэтому критическое время tap определяется
по формуле A79.8), в которой нужно положить с = скр. Однако
этот анализ справедлив лишь в том случае, когда по
формуле A79.9) получается скр<;1. Действительно, при составлении
уравнения A79.6) мы существенным образом предполагаем, что
обе полки находятся в состоянии сжатия. Если условие скр <; 1
не выполняется, то приходится рассматривать два этапа
процесса. Обозначим через ^ время достижения значения с = 1.
величина tt находится с помощью уравнения A79.8), в котором
нужно положить с = 1. При t > <i на некотором участке,
примыкающем к середине пролета, напряжение о"_ становится
растягивающим, поэтому следует принять для этого участка к~ = 1,
тогда как для остальной части балки по-прежнему к^ = 0. В такой
пос ановке получить относительно простое приближенное
решение подобное тому, которое получается в случае скр < 1,
оказывается невозможным. Автор предлагает находить верхнюю и
нижнюю оценки для критического времени. Верхняя оценка
получается, если не обращать внимания на перемену знака напряжения
в одной из полок и считать решение A79.8) справедливым также
и тогда, когда с>\. Пренебрегая пластической деформацией
растяжения полки, мы завышаем жесткость балки, следовательно,
увеличиваем критическое время. Нижняя оценка для
критического времени получается, если принять к~ = 1 для всей балки,
§ 180] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 681
а не только для ее центральной части. Уравнение A79.7)
заменяется при этом следующим уравнением:
Из условия обращения в нуль множителя при с находится
критический прогиб:
«*-?(?)'[*-*]• <"••">
Теперь критическое время равно ?Кр= ti-\-t2. Здесь t2 — время,
за которое прогиб изменяется от с = 1 до с = скр,
определенного формулой A79.11). Интегрируя A79.10), находим:
A79.12)
Хофф приводит в статье [237] пример расчета критического
времени для стержня из алюминиевого сплава. Было принято l/h =
= 50, сс = 0,15. Для критического времени описанным способом
были найдены следующие оценки:
15,85 < ?Кр< 16,3 мин.
При этом оказалось tx ~ 11,95 мин.
Величина с0 представляет собою стрелу прогиба стержня сразу
после приложения нагрузок. Фактически заданным бывает
начальное искривление стержня, стрелу начального искривления мы
будем обозначать с00. Величина с0 ищется в результате решения
задачи пластичности. Если сО0 достаточно мало и сжимающая сила
не слишком велика, то св <; 1, в первый момент после приложения
нагрузки обе полки сжаты и вышеприведенный анализ справедлив.
Однако может случиться, что начальный эксцентриситет настолько
велик, что уже сразу после приложения нагрузки в одной из полок
возникают растягивающие напряжения. За деталями,
относящимися к нахождению величины с0 и рассмотрению всех
возможностей, которые могут при этом представиться, отсылаем читателя
к оригинальной статье.
§ 180. КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ.
НЕКОТОРЫЕ ДАЛЬНЕЙШИЕ РЕЗУЛЬТАТЫ
Как было замечено, величина критической деформации, при
которой скорость прогиба становится бесконечной, определяется
только мгновенными упруго-пластическими свойствами материала
стержня. Этот вывод, полученный для стержня идеального
двутаврового сечения, строго говоря, не может быть распространен
682
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
на реальные стержни. Дело в том, что в идеальном двутавре
распределение напряжений в полках для данного прогиба и
данной величины сжимающей силы определяется единственным
образом, поэтому мгновенная потеря устойчивости при данном
значении прогиба происходит одинаковым образом, независимо от
того, каким образом был достигнут этот прогиб. В реальных
стержнях при одном и том же прогибе
распределение напряжений по сечению мо-
1 жет быть различным, а критическое со-
г ¦ I 1— стояние определяется не только величиной
<?'\ I j прогиба, но и распределением напряжений
h в сечении. Таким образом, величина кри-
±
К
±
тического прогиба будет зависеть от
протекания процесса ползучести. Это
обстоятельство было проиллюстрировано
Шестериковым [1б3 i на модельном стержне, состо-
| I I ящем из трех полок (рис. 246). Толщина
/ ^|—1— каждой из полок б считается малой по
сравнению с h, напряжения в каждой пол-
Рис. 246.
ке предполагаются распределенными
равномерно. Такой стержень статически
неопределим, распределение напряжений
между полками при одних и тех же
значениях сжимающей силы и изгибающего момента может быть
различным. В зависимости от этого критическое состояние подобного
стержня реализуется при различных величинах прогиба. Даже
для такой простой модели анализ оказывается довольно сложным
и замкнутого решения получить не удается.
Однако некоторые экспериментальные данные указывают на то,
что критический прогиб у реальных стержней меняется в довольно
узких пределах. Ссылка на эти данные приводится в работе [238].
Так, по данным [321], отношение критического прогиба к радиусу
инерции поперечного сечения менялось'в пределах от 0,49 до 0,63,
тогда как отношение начального прогиба к радиусу инерции
изменялось от 0,035 до 0,131. Аналогичный результат был получен
в работе [182], внезапный рост прогиба у стержней с одинаковой
гибкостью при одинаковой сжимающей силе начинался после
достижения примерно одинакового прогиба.
Мгновенные пластические свойства материала, вообще говоря,
зависят от предшествующей ползучести (см. § 57), поэтому
определение критического состояния с помощью мгновенной диаграммы
сжатия не вполне точно.
Основываясь на замечании, сделанном в начале этого
параграфа, Хофф рекомендует процедуру определения критического
. времени для сжатого стержня, основанную на замене его сечения
идеальным двутавром [238], [2411- Выбор размеров приведенного
§ 180] КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ 683
двутаврового сечения был пояснен в § 117. Сохраняя обозначения
§ 179, напишем дифференциальное уравнение изгиба сжатого
стержня следующим образом:
+ aw{e'0[a(l+w)]+e'0[(T(l-w)]} +
+ {D[o(l + v>)]—vio[l—w)]}. A80.1)
Здесь к—кривизна оси стержня, w — безразмерный прогиб.
Положим
к = hw", w = cV.
В отличие от § 179 здесь штрихи обозначают дифференцирование
по координате z, a V есть первая фундаментальная функция
уравнения
EIV" + PV = 0.
Соответствующее фундаментальное число определяет Эйлерову
силу Рв. Для идеального двутавра 1~F№, следовательно,
рэ _ °э = еэ
EI ~~ Е№ № '
Внося в A80.1), получим:
2еэ'с = а {A + w) е, [а A + и>)] - A - w) ей [а A - w)}} +
+ ow {е'0 [а A + и?)) + е; [а A -w)]} + {v [о A + w)]-v [a (i-w)]}.
A80.2)
Приближенное решение уравнения A80.2) можно теперь получать
разными способами. Простейший способ будет состоять в том,
что мы требуем выполнения уравнения A80.2) в одном только
сечении z = z*. Очевидно, за это сечение нужно принимать то
сечение, где действует наибольший изгибающий момент.
Функцию V (z) всегда можно определить таким образом, чтобы было
?-{г,) = 1. Тогда уравнение A80.2) дает следующее обыкновенное
дифференциальное уравнение для функции с (t):
2eBc = o{(l + c)e'1,[o(i + c)]-{i-c)e'0[o(l-c)]} +
- ос {e„la (I+c)] + е0 [о (i - с)}}+ {v [a A +с)]-и [о (I-с)]}.
A80.3)
Другая возможность состоит в том, что уравнение A80.2)
умножается на V (z) и интегрируется по длине балки. Этот способ был
684 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
пояснен в § 178. Вычисления, естественно, оказываются
значительно более сложными.
Рассмотрим сначала процесс нагружения стержня.
Предположим, что сжимающая сила прикладывается в течение достаточно
короткого времени, так что в A80.3) члены, содержащие
производные по времени, велики по сравнению с остальными членами.
Интегрируем A80.3), не обращая внимания на часть, зависящую
от скорости ползучести v. Получаем:
2e0(c0 — cm) = e0la(i+c)]-e0[a(l-c)]. A80.4)
Решая уравнение A80.4), мы находим величину прогиба с0,
которую нужно принять за начальную величину для анализа
последующей ползучести.
В большинстве случаев определение начального прогиба
можно производить, предполагая материал упругим, а
следовательно, по формуле
с01 а
с0 = . о) = — .
и 1—со аэ
Начальная пластическая деформация может быть допущена только
у стержней с весьма малой продолжительностью жизни. Если учет
начальной пластической деформации необходим, то при
использовании формулы A80.4) необходимо иметь в виду, что в полке,
находящейся с выпуклой стороны, напряжение будет сначала
возрастать, а потом убывать. Поэтому функция е0 [о A — с)]
сначала соответствует нагружению, а потом — разгрузке. Может
оказаться более удобным вместо конечного уравнения A80.4)
пользоваться дифференциальным уравнением, которое следует
из A80.3), если удержать в этом последнем уравнении только
члены, содержащие производные, и принять за независимую
переменную напряжение о. Введем для краткости обозначения:
~- = е'0[вA+с)], ^- = е;[огA-с)],
?* 2 V?+ ?-У ~ 2?+?_ -
Тогда получим:
О-г.) ?-?+*(?-?)• <т5)
В зависимости от того, происходит нагружение или разгрузка
в менее нагруженной полке, величина Е может быть касательным
модулем на диаграмме пластичности либо равняться модулю
упругости. Напряжение о_ = о A — с) с увеличением о сначала
возрастает, потом начинает убывать с момента, когда выполняется
§ 180]
КРИТИЧЕСКОЕ ВРЕМЯ СЖАТОГО СТЕРЖНЯ
685
условие
da Vi "' " da
do_ ,. ч dc „
= (l_c)_„ =0
я, следовательно,
dc 1—с
da ~~ a
Внося в A80.5), получим следующее условие перемены знака
da_
У -do-'
±A_е)(в8_?)=? + ^(?_?) . A80.6)
Убедиться в том, что перемена знака действительно происходит,
можно на примере упругого стержня. Полагая Е+ = Е- = Е,
а/аэ = со, находим, что A80.6) вы/юлняется при условии
C = l-i©.
Но для упругого стержня
t"_l-0) '
таким образом, условие перемены знака есть
со = 1 — Кс00.
Имея диаграмму сжатия материала, мы можем построить график
функции е0 (о) и, следовательно, определить величины Е+ и Е~
для любых значений а ж с; таким образом, численное
интегрирование уравнения A80.5) труда не составляет.
Если с > 1, то о. > 0 и величина Е- должна рассчитываться
по диаграмме растяжения, следующего за разгрузкой, при учете
эффекта Баушингера в той или иной форме. По причинам,
которые будут разъяснены далее, этот случай детально не
рассматривается.
Итак, предположим, что величина с3 найдена. Дальнейшее
движение стержня описывается уравнением A80.3), в котором
нужно положить а=0. Следовательно, мы имеем:
2(e6—j?-)c = vlo(l+c)]-vl<T(i-c)]. A80.7)
Отсюда
tKP = 2еэ ^ j,[<j(i + c)]-y['<T(i-c)] йс- A80.8)
В формуле A80.8) при вычислении Еш всегда нужно принимать
Е- = Е. Действительно, при с = const а_ = — ос < 0. Верхний
686 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
предел интеграла в формуле A80.8) представляет то значение с,
при котором числитель подынтегрального выражения обращается
в нуль, то есть происходит мгновенная потеря устойчивости,
как это уже было выяснено и что видно уже из уравнения A80.5).
Интеграл в формуле A80.8) вычисляется в замкнутом виде лишь
при простейших предположениях о законе ползучести и форме
кривой мгновенного деформирования; рассмотренный в § 179
пример относится к такому частному случаю. В принципе
формула A80.8) применима при любых значениях сА, однако при
с > 1 необходимо учитывать изменение знака напряжения а_
и выбирать соответствующим образом величину Е— Но большие
прогибы в стержнях, являющихся элементами конструкций,
недопустимы сами по себе; поэтому, если величина оказывается
большой, будет разумно ограничить время службы стержня не
условием достижения критического состояния, а условием достижения
прогибом некоторой величины, фиксированной из тех или иных
соображений, например с = ck = 1, что соответствует прогибу,
равному половине толщины стержня (Розенблюм [52]). Итак, если
числитель подынтегрального выражения в формуле A80.8)
обращается в нуль при с = ck < 1, эту величину ck мы будем
принимать в качестве верхнего предела интеграла. Если критическое
состояние достигается при с > 1, мы примем в этой формуле
ck = 1.
Хофф в работе [241] рекомендует еще более простую процедуру
определения критического времени, а именно предлагает разбить
задачу на две самостоятельные и независимые части. Сначала
ищется критический прогиб из условия
-?- = 1,
после этого приближенно вычисляется время достижения
критического прогиба. При этом не обращают внимания на изменение
пластической деформации, сопутствующее ползучести, и находят
прогиб так, как это было сделано в § 178, то есть полагают
в подынтегральном выражении формулы A80.8) числитель равным
единице. Очевидно, таким способом получаются завышенные
значения критического времени. Опытные данные, приводимые
в упомянутой работе, дают критическое время меньше расчетного,
хотя трудно сказать, может ли эта разница быть отнесена целиком
за счет отмеченного допущения.
Смысл такой чрезвычайно упрощенной схемы заключается
в следующем. При решении задачи выпучивания в полной
постановке мы сталкиваемся с большими трудностями и можем довести
решение до конца лишь при очень простых и грубых
предположениях. Определение критического прогиба упруго-пластического
стержня при заданной диаграмме деформирования может быть
§181] СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП 687
произведено с большой точностью, этому вопросу посвящена
обширная литература Iе], I166]. Для решения задачи о продольном
изгибе при ползучести также можно применить численные методы,
которые позволяют решать эту задачу, не связывая себя слишком
большой идеализацией закона ползучести реального материала;
поскольку напряжения меняются монотонно, расчет на основе
теории старения с помощью действительных кривых ползучести
приведет к достаточно точному результату.
Попытки более точного определения критического времени
за счет менее стеснительных предположений о форме поперечного
сечения и об исходном законе ползучести предпринимались в ряде
работ. Так, в работах [282], [283], определяется критическое время
по теории упрочнения в форме рра = к ехр а /А, в первой работе
для стержня с сечением в форме идеального двутавра. При этом
предполагалось, что стержень, шарнирно опертый на двух
концах, изгибается по синусоиде, уравнение равновесия
удовлетворяется в среднем сечении стержня, как и в примерах,
рассмотренных выше. Вторая работа относится к выпучиванию стержня
прямоугольного поперечного сечения, решение получено путем
численного интегрирования. Другие решения приводятся в
работах ["•], [284Ь
§ 181. СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП
В ПРИМЕНЕНИИ К ЗАДАЧАМ ВЫПУЧИВАНИЯ
В § 167 был рассмотрен недавно предложенный смешанный
вариационный принцип, позволяющий независимо задавать
предположительные поля напряжений и перемещений. Однако в
задачах устойчивости бывает недостаточно считать производные от
перемещений малыми и удерживать только линейные члены в
выражениях для компонент деформации через перемещения. Мы будем
пользоваться точными выражениями для компонент
деформации (§ 5), а именно в декартовых координатах:
*»./= 2" ["'-../ + ^М+ "*.»""*,/]• A81.1)
Теперь и уравнения равновесия, строго говоря, уже нельзя писать
в первоначальной метрике, необходимо учитывать, что задание
поля перемещений определяет в теле некоторую криволинейную
систему координат. Наиболее простой способ получения
уточненной системы уравнений равновесия заключается в следующем.
Предположим, что на тело действуют поверхностные силы Г;,
тогда вариационное уравнение равновесия будет следующим:
V 2
688
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Но по формуле A81.1)
feij = ~2 №ui, j + 8ujt i + ий, fiuh, j + uh: }8uh, t] =
= у KUy + «ft, j) SUA, j + (бАг + Eift> ,•) 8«ftj j].
Здесь 6fts — единичный тензор.
Введем несимметричный тензор:
Ski=Oij(8hJ + u^j). A81.2)
Теперь вариационное уравнение равновесия запишется
следующим образом:
j ^ ski8uhj i dV + у \ skjSuktj dV — jj ГА6ий d2 = 0.
v v i
Преобразуя объемные интегралы обычным способом, получим:
stj,j = 0, A81.3)
su\1 = Ti на S. A81.4)
Если в функционале if, определенном формулой A67.4), понимать
под ец выражение A81.1), то для того, чтобы получить из
вариационного уравнения условие равновесия A81.3) и граничные
условия A81.4), необходимо добавить еще некоторые члены.
В цитированной работе [345] это было сделано; для нелинейных
задач выражение функционала оказывается следующим:
V
-J Ti(ut-u\)dl-\ T&idZ. A81.5)
Все обозначения остаются здесь теми же, что и в § 167,
варьируются считающиеся независимыми величины щ и а^, при этом
производные от компонент деформации по времени вычисляются
с помощью A81.1), а именно:
еи = у (мг, j + и}, i 4- «ft, j "a, j + uk, j "й, О-
Доказательство того, что обращение в нуль вариации
функционала К эквивалентно выполнению уравнений равновесия,
граничных условий и условий связи между скоростями деформации,
напряжениями и скоростями изменения напряжений,
производится совершенно так же, как в § 167. Дополнительные члены
в A81.5) не содержат скоростей изменения напряжений, поэтому
§ 182] ВЫПУЧИВАНИЕ СЖАТОГО СТЕРЖНЯ 689
разница будет состоять только в той части 6К, которая
соответствует изменению поля скоростей. Обозначим эту часть через ЬК',
получим:
Р г * 1 * * * *
ЬК' = ^ [ (Ту у (SUj, } + бид i + Ид, г6иА, ^ + Uft> j6l/ft> ,-) +
V
+ у о-у (uft,{6uft, j + Mfttj-6wft);) J dF — ^ Tkbuh d^—\ Tehbuhdl> =
V V Zu 2T
Преобразуя объемные интегралы, найдем, что из условия ЬК' = О
следует:
si;,; = 0, SijVj = Ti на 2.
Эти уравнения получаются в результате дифференцирования по
времени A81.3) и A81.4).
§ 182. ВЫПУЧИВАНИЕ СЖАТОГО СТЕРЖНЯ.
ПРИМЕНЕНИЕ ВАРИАЦИОННОГО МЕТОДА
Для иллюстрации применения вариационного принципа,
изложенного в § 181, мы рассмотрим уже изученную нами задачу
об устойчивости при ползучести сжатого стержня, имеющего
начальное искривление. Обозначая через и я w соответственно
осевое перемещение и прогиб, получим:
1 2
e = w,z+yW,2— yw,zz.
Предположим, что к торцу стержня приложена сила N, кроме
того, существует поперечная нагрузка д. Выражение
функционала К запишется следующим образом:
i
К=\ \ [o(u,z + w:Zw,z — ywjZZ) + jow2z — po'jdFdz —
О F
I
\'qwdz—N[u{l)-u@)\. A82.1)
Внутренний интеграл распространен по площади поперечного
сечения. Заметим, что
\ cdF = N, \'oydF=M.
44 Ю. Н. Работнов
690 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Здесь М — изгибающий момент в сечении стержня. Скорость
ползучести выражается через потенциал ползучести по формуле
Произведение
ЭФ
дФ • йф
Pa = -toa = -dt
поэтому соответствующий интеграл в A82.1) принимает вид
F F
Но интеграл от Ф по площади представляет собою потенциал
ползучести на единицу длины стержня, то есть функцию от N
и М:
Следовательно,
\ Q>dF = <b(M,N).
• • , р дФ •, , дФ ,\
Выполнив таким образом интегрирование по площади в A82.1)
и проинтегрировав первый член по 2, найдем следующее
выражение для функционала К:
i
о
A82.2)
Вопрос о ползучести при совместном действии изгиба и
растяжения или сжатия был рассмотрен в § 116, в частности, было
показано, что для потенциала ползучести может быть принята
эллиптическая аппроксимация, а именно:
Ф = Ф(Я), Яа = М2 + Л7!№.
Тогда
Функция к (R) определяется таким образом, что при R — M
к (М) есть скорость изменения кривизны.
§ 182] ВЫПУЧИВАНИЕ СЖАТОГО СТЕРЖНЯ 691
Положим теперь
w = he (t) sin —р , М = hb (t) sin —?- ;
при этом h—некоторый характерный поперечный размер,
например половина высоты сечения. Подставляя в A82.2), найдем:
К^ (J^y j[~Ncc-Nc* + Ъс\ — NNkW \ ^-dz-
- bbh* J -^i sin3 -^- dz - ch \'q sin -^i dz. A82.4)
При решении задачи о выпучивании мы будем считать N —
¦¦¦= const = —Р и д = 0, поэтому соответствующие члены в A82.4)
выпадают. Варьированию теперь подлежат только параметры
с и Ь.
В результате получаем следующую систему уравнений:
i
Рс + 6=0, с + Ь^ J ^-^-sin2^dz = 0. A82.5)
о
Из первого уравнения следует:
Рс=— Ъ,
а второе принимает вид
i
с = ~Ра^ ^Ш- sin2 -H. ^2. A82.6)
о
Правая часть представляет собою функцию от с и Р, так как
R* = р«л» [ &2 + с2 sin2 -25-] .
Численное определение критического времени с помощью
уравнения A82.6) возможно при любом законе ползучести; степенной
закон, как обычно, приводит к наиболее простым результатам.
Положим
i
/(<0 = т$ [k2 + c2smi~Y'1smi~dz.
о
После несложных преобразований мы получаем отсюда
следующее выражение для критической деформации ползучести:
оо
со
44*
692 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
При ге = 3 получается следующий результат:
4
^P = -l6-D-rJ ln cl •
Способ определения величины к был разъяснен в § 116, для
идеального двутавра к = 1, и последнюю формулу можно
сравнить с A78.11) либо A78.13).
Посмотрим теперь, каким образом можно использовать
вариационные уравнения для решения задачи об изгибе балки с
закрепленными концами, рассмотренной в § 177. Зададимся теми же
приближенными выражениями для прогиба и изгибающего
момента, для функционала К мы получим опять выражение A82.4),
но теперь N Ф 0 и подлежит варьированию. В результате
варьирования по трем параметрам получим следующие уравнения:
-Nc-Nc + b-^- [ qs,m~dz = 0,
c + b§\^f-Sin^dz=0,
Первое уравнение сразу интегрируется, из него следует:
b-Nc + Q.Q-^-lqan^-ds.
Из двух других уравнений теперь получается следующая система
для с и N:
cc=—N^-k*\2yp-dz. A82.8)
Правые части в 'этих уравнениях — известные функции от с и N,
их можно выразить в явном виде при степенном законе ползучести
с нечетным целым показателем. Разделив одно уравнение на
другое, мы получим конечное соотношение между с и N, после чего
всегда можно проинтегрировать любое из уравнений A82.8)
численно; ход вычислений здесь получается весьма близким
к тому, который был осуществлен в § 177, когда эта же самая
задача решалась другим методом.
Заметим, что в работе I3*5] применение смешанного
вариационного принципа иллюстрируется также на примере выпучивания
сжатого стержня. Однако в этой работе принимается линейный
закон распределения по толщине стержня. Окончательная
формула, полученная для п = 3, имеет ту же структуру, что и приве-
§ 183]
УСТОЙЧИВОСТЬ АРКИ
693
денная выше, однако числовые значения получаются несколько
отличными. В § 168 этот прием был пояснен применительно
к задаче о поперечном изгибе стержня, распространение его на
случай выпучивания под действием продольной силы очевидно
и специальных разъяснений не требует. Следует указать, что
Розенблюм решал задачу о выпучивании сжатого стержня на
основе теории течения с помощью несколько иного вариационного
метода, также задаваясь при этом линейным распределением
напряжений по сечению. Эта работа детально изложена в книге [521.
Рис. 247.
§ 183. УСТОЙЧИВОСТЬ АРКИ
Примером более сложной задачи устойчивости, решаемой
с помощью вышеописанного вариационного метода, служит задача
об устойчивости пологой арки,
нагруженной равномерно
распределенным давлением. В
конструкциях подобного типа
наблюдается потеря устойчивости
типа «хлопка», что можно
обнаружить, только если учитывать
геометрическую нелинейность.
Приводимое ниже решение [327]
интересно также и в том
отношении, что оно в известной мере
иллюстрирует трудности, встречающиеся при решении задач
устойчивости тонких оболочек, хотя для оболочек эти
трудности оказываются неизмеримо более серьезными. Итак,
рассматривается изображенная на рис. 247 арка, шарнирно опертая
на двух концах, имеющая пролет I и высоту с0. Предполагается,
что ось арки образована дугой синусоиды:
w0 = cs'm —j- .
Арка несет равномерно распределенную вертикальную нагрузку
интенсивности q. Обозначая через у расстояние некоторой точки
оси арки по нормали, вследствие закона плоских сечений имеем:
е = и,г + у [w% — wl,z] — у [и;,гг — и>0,г2],
и функционал A81.5) приводится к следующему виду:
+h I
К=Ъ^\ [<т(и,г + ы?,ги>)Г — ywitz)+-
- aw", —
-k О
Ш-**(±У]*У*'- A83.1)
694
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Здесь принято, что мгновенная деформация упруга, ползучесть
следует степенному закону. Сечение арки предполагается
прямоугольным с высотой 2/г и шириной Ъ. Естественно предположить,
что в процессе деформации ось арки сохраняет синусоидальную
форму, а также принять синусоидальный закон распределения
момента по длине арки. Что касается распределения напряжений
по толщине, автор принимает его линейным. Таким образом,
71Z . Я2
V) = С Sill —j- = T]C0 Sin —j- ,
и=0 A83.2)
а =сгэ [ao + Oi-^-sin
2у ^.п nz
Т
Здесь о"э = —щ ¦ критическое эйлерово напряжение для балки
длиной I, таким образом, т), о0 и ot — безразмерные параметры.
Дальнейший ход вычислений состоит в том, что выражения
A83.2) подставляются в A83.1) и функционал К находится как
функция от т), а0, а1 и производных этих параметров по времени.
• • •
Далее К варьируется по т), а0 и а±, в результате чего получается
система трех уравнений. Опуская элементарные выкладки,
приведем сразу эти уравнения для случаев п = 1 и п = 3.
Для п = 1
¦w) n-^i-nr*. •!>=<>, A83-3)
(-
^ ) ад + 4г о\ + (^-) о-от] = 0.
Для п = 3
со V • • Eal Y з
8 J '
^)ц-^о,^^(<^ + ^)=0, A83.4)
со \ • , 1 • ,Y c0
Начальные условия для уравнений A83.3) или A83.4) мы запишем
следующим образом:
Т1@) = Т)Ь а0@) = аог, 01(O) = CTii.
Величины r\t, o0t, о1{ представляют собою значения
соответствующих параметров немедленно после приложения нагрузки. Если
§ 183]
УСТОЙЧИВОСТЬ АРКИ
695
считать, что мгновенная деформация упруга, то для определения
искомых параметров естественно применить вариационный метод
Рейснера (см. § 167), задавшись тем же предположительным
распределением напряжений и перемещений, что и при анализе
ползучести, то есть представив w и а формулами A83.2).
Функционал Рейснера принимает в нашем случае следующий вид:
-\-h I
К = Ъ ^ ^ jo [yw2z — Yw^z-y(w,zz — w0,zz) ] — -Trg-j dydz +
-h 0
I
+ ^qwdz. A83.5)
0
Вычисляя этот функциионал и варьируя его по г];, а0; и ati,
получим следующую систему:
°" = 12(ж)(Ч*-1). <^ = 3 (-§-)* (г,?-1),
( со Л , ! , 4 ?г4 1 п
Исключая отсюда ct0j и Оц, приходим к следующему
алгебраическому уравнению для y\f.
3(^-J(T,?-nO + M»-l) + a = 0 A83.6)
Здесь
_ 4 ql*- i
я5 EI с0
Из A83.6) следует, что а как функция т]г принимает
экстремальное значение при
/'
-fO-V-1
ri, = т],кр = ± -^ ^4? . A83.7)
о
2fc
Если ( of ) < "г5 то прогиб растет монотонно с изменением
нагрузки; если ( ?т ) > "o-i то при достижении критического
значения параметра нагрузки акр происходит хлопок, прогиб
мгновенно изменяется на конечную величину, как показано
стрелками на рис. 248. Величина критической нагрузки находится
по формуле A83.6), если внести в нее значение т);кр, даваемое
696 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
формулой A83.7). Рассмотрение вопроса об устойчивости при
ползучести имеет смысл, когда действующая нагрузка меньше
критической. В этом случае следует определить т); как
наибольший корень уравнения A83.6), после чего находятся aoi и olt;
-2
В'
А'\
\ s
Г
т —
в \
шч
—
Mil
W4
а
V
Ц5
1_
_J_
&
о
W
'-%
2Д
~&
Рис. 248.
эти величины служат начальными значениями
соответствующих переменных при интегрировании системы A83.3) или
A83.4).
Случай линейной ползучести, очевидно, представляет лишь
очень ограниченный практический интерес. Тем не менее
рассмотрению устойчивости для линейных вязко-упругих тел посвящено
довольно много работ, вычисления при этом оказываются
относительно простыми, и можно рассчитывать на доведение их до конца.
Так, из A83.3) путем исключения Oj можно получить следующую
§ 1833
УСТОЙЧИВОСТЬ АРКИ
697
систему:
da0
oq
dn =Рл+^-A + »о + Рт|'),
dr[
dx
= _ a . A83.8)
l + Oo + РЛ2 V '
Здесь p = 6 ( ^Л , т = e„
t.
Первое уравнение системы A83.8) не имеет замкнутого
решения, его приходится интегрировать численно. После того, как
г
Sfl
а)
V
\ 1
\ 1
-&
*)
о
-7
-Ц5 О
Рис. 249.
Off
rjiS^.
---р;
It-f
05 J
V
из этого уравнения найдено а0 (т]), безразмерное время % для
достижения прогиба ц определяется по формуле
—S
i+qoOD+N'
dy\.
A83.9)
При определении функции % (ц) могут представиться две
698 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
возможности: либо подынтегральное выражение сохраняет
постоянный знак, либо при некоторых значениях т) знак меняется.
В первом случае прогиб монотонно растет во времени, величина г|
стремится к г) = — 1. Во втором случае при достижении
критического времени, определяемого как время перемены знака про-
dx
-изводной -^, происходит внезапный скачок. На рис. 249 при-
rfTl'
г
430
Ц20
0,10
^ ^
\,
\ф&
-US
OJ
Рис. 250.
ведены результаты
расчета для р = 2/3 при
а = 0,442 (Tjt = 0,9) и
а = 0,906 {г,; = 0,75).
Задача нелинейной
ползучести при п = 3
решается совершенно
аналогичным способом,
только система A83.4)
имеет более сложный
вид. Результат расчета
при р = 2/3, а = 0,906
представлен на графике
рис. 250. Здесь
безразмерное время
определено следующим образом:
т = е„
Gn
t. Анало-
тичным образом Шепеленко I147] рассмотрел устойчивость арки
с защемленными концами. Некоторые вычисления были им
проведены для случаев линейной вязко-упругости.
§ 184. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ ОБОЛОЧЕК
ПРИ ПОЛЗУЧЕСТИ
Вследствие значительных вычислительных трудностей все
немногочисленные исследования устойчивости оболочек при
ползучести основываются на тех или иных предположениях частного
характера. По-видимому, первая задача такого рода была решена
Хоффом [23в], [238], им рассмотрена потеря устойчивости
цилиндрической оболочки при изгибе. В качестве основного механизма
потери устойчивости было принято влияние на изгибную
жесткость сплющивания поперечного сечения. Для упругой оболочки
подобное решение было предложено в ранней работе Бразье [т].
Обозначим через а радиус оболочки, направим ось х вдоль
образующей. Условие равенства нулю окружной деформации
согласно A47.1) запишется следующим образом:
-я— —W = 0.
Оф
§ 184] НЕКОТОРЫЕ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ ОБОЛОЧЕК 699
Этому условию можно удовлетворить, приняв
w — ccos2(p, t> = ysin2cp. A84.1)
Круговое сечение оболочки переходит при этом в эллиптическое
с полуосями a -j- с. Изменение кривизны в окружном направлении
, 1 / d2w , dv \ Зс п /л о/ о\
^=^-С^^^^; = -^со82(р- <184-2)
Существенное упрощение, принятое при рассмотрении данной
задачи, состоит в том, что напряжения в направлении образующей
считаются связанными только со скоростями деформации в этом
направлении, тогда как скорость изменения кривизны /сф
связывается только с поперечными изгибающими моментами, а именно:
-«.С*)"- *.-•(?)'• A84.3)
Такое предположение будет близко к истине для оболочек,
подкрепленных набором, когда в продольной деформации участвуют
стрингеры, а в поперечной — шпангоуты, работающие
независимо. Формулы A84.3) относятся к некоторой приведенной
оболочке, жесткость набора в них включена. При пользовании
первой из этих формул нужно считать, что напряжение а
распределено по некоторой приведенной толщине 2h.
До деформации расстояние точки срединной поверхности
оболочки от оси изгиба было у = a cos ф, после деформации
у = a cos ср — w cos ф — v sin cp
или
у = a cos ф 1 —— cos2 cp
Обозначая через к изменение кривизны оси оболочки вследствие
изгиба моментом М, мы найдем, что
е = ку = каcos ф М —-со82ф]. A84.4)
Для составления условия равновесия оболочки применим
начало возможных перемещений. Будем варьировать только
параметр с, сохраняя неизменным величину момента М.
Уравнение равновесия запишется следующим образом:
Я/2 я/4
h J обеЛр + 2 j М<РбА;(рйф = 0. A84.5)
о о
Здесь е и kv определяются формулами A84.4) и A84.2), тогда
как а и Мф должны быть определены из A84.3). В уравнении
700
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
A84.5) будут фигурировать параметры с, к, а также их
производные с и к. Второе уравнение получится, если приравнять
момент от напряжений а в поперечном сечении постоянному
приложенному моменту М:
Я/2
¦Aha \ оу dtp. A84.6)
М--
В результате очевидных вычислений для неизвестных функций
к (t) и с (t) получается следующая система из двух
дифференциальных уравнений:
?_е* ( м Л
« 1 /ЛГЛ\Р
J Зге
1 f_(i+a)_^L
"« ^Зп
З-'тЛр i
Jl±Li-f I.
Здесь
Я/2
я + 1
ftn+1
A84.7)
A84.8)
Ас Г -——-
Z = —, 1кп = ^ \ (COS<p) п d(Q
кс i
Система A84.7) — A84.8) может быть проинтегрирована
численно. Автором работы [236j это было сделано для случая гладкой
оболочки, когда п = р. Определение критического времени,
то есть такого времени, когда скорость сплющивания становится
бесконечно большой, не связано с заданием начального
сплющивания. Действительно, система A84.7) — A84.8) имеет
решение, удовлетворяющее начальным условиям к @) = с @) = 0
вида
с = c0tp+1 + ..., k = k0t+ ...
Результаты расчета критического времени для гладкой оболочки
из алюминиевого сплава обнаружили весьма удовлетворительное
совпадение с данными эксперимента (рис. 251).
Не останавливаясь подробно на других, впрочем
немногочисленных, работах, посвященных выпучиванию оболочек в
условиях ползучести, отметим некоторые из них.
Сундстрем [3591 исследует устойчивость оболочек при сжатии
и внешнем давлении, рассматривая такие возможные
перемещения, при которых срединная поверхность не деформируется;
в работах Хоффа, Джасмана и Нахбара [240], а также Тхейн
Ван [371] рассматривается поведение круговых цилиндрических
оболочек при внешнем давлении. Предполагается, что имеется
§ 185] ОСЕСИММЕТРИЧНОЕ ВЫПУЧИВАНИЕ КОРОТКИХ ОБОЛОЧЕК 701
начальная эллиптичность. Во всех этих работах делается ряд
тех или иных упрощающих предположений.
Применение смешанного вариационного принципа,
описанного в § 181, содержится в работе Лайениса [281], которая
представляет собою распространение на случай ползучести известной
о гоо МО зов ш
Время, мин
Рис. 251.
теории Вагнера — Власова изгибно-крутильной потери
устойчивости тонкостенных стержней открытого профиля. С помощью
этого же вариационного принципа решена задача о
сплющивании длинной цилиндрической трубы в работе Серпико [348].
§ 185. ОСЕСИММЕТРИЧНОЕ ВЫПУЧИВАНИЕ КОРОТКИХ
ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Уравнения осесимметричного изгиба цилиндрических
оболочек при наличии продольной силы, выведенные в § 154, легко
распространяются на задачи осесимметричной потери
устойчивости. Обозначим через w прогиб оболочки, отнесенный к ее
радиусу. Тогда, очевидно,
е,.и = w.
Теперь мы должны учесть в уравнениях равновесия искривление
образующей, для этого к действующей нагрузке q нужно
добавить величину— Гцт-j. Учитывая введенные в §§ 150 и 154
безразмерные обозначения, мы находим, что к величине р,
входящей в уравнение A55.1), добавляется член
п
Здесь штрихи обозначают дифференцирование по безразмерной
координате ?.
702 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Очевидно, что вариационное уравнение сохраняет силу,
функционал A55.4) для задачи устойчивости переписывается
следующим образом:
i
N = \ \и'т' +-?гги*(-±-т—") ^{(т + тKсо+ +
J L ' ra-f 1 V «+ r / ra + 1 ' ' '
(т-т)»<»-} + 2т(-^- + х w"\u]dl. A85.1)
\V3
Применение вариационного уравнения к исследованию
выпучивания короткой цилиндрической оболочки, шарнирно опертой
на концах, содержится в работе Волчкова [14]; эти результаты
и будут здесь вкратце изложены.
Подобно тому, как это делалось в § 152, мы будем считать,
что и больше, чем т и т, а так как со < 1, в уравнении
2п
(и*)"-1 =. и2 + (т ± if (co±J A85.2)
второй член в правой части мал по сравнению с первым. Так же,
как в § 152, положим
п-1
(В±=И " A + в±),
где б± < 1. Подставляя в A85.2) и удерживая первые степени 6,
найдем:
б± = ~ и~2'п (т ± тJ.
Подставим теперь приближенное выражение для со* в формулу
A85.1) и удержим в этой формуле члены, содержащие (mj-x)
в степени не выше второй. Получим:
К=^ |u'm'+^lW1+--(^ + T>1^ + 2(-iI + -f u,»)-ro}dg.
о
A85.3)
Для достаточно короткой оболочки можно принять:
* . я? о . яЕ я?
и = a sin -р , т = р sm -р , и> = е„.а sm -j2- .
Подставляя в A85.3), мы получим следующее выражение для
функционала К:
га+1 п—1 п—1 , ,
Я = ^[ар + Жх~—Вр«а~—Ст«а » +?>та —?аа] -
§ 185] ОСЕСИММЕТРИЧНОЕ ВЫПУЧИВАНИЕ КОРОТКИХ ОБОЛОЧЕК 703-
Здесь А, В, С, D — интегралы от некоторых степеней sin ^.
Варьируя параметры а и р\ получим следующую систему:
Р-
ПЛ±А^!п_
-1
5Д2а-
1/п.
—- Ct2a-i/n _ Dx - 4 а = 0,
n-i
а —2Вра " =0.
Исключая отсюда JJ, придем к следующему дифференциальному
уравнению для функции a (t):
М1/п-М-1/п-ха + D = 0.
A85.4>
Здесь /q и &2 — некоторые комбинации констант А, В та. С.
Решение уравнения A85.4) может быть представлено в
параметрическом виде:
h
\Кя.
1/п.
1/п
п — 1
k2q-Vnj_Dh
„-1/п
A85.5>
n + i J g
При этом безразмерное время t = fs^x", константа
интегрирования представляет собою критическое время, когда а стремится
к бесконечности. Действительно, первое из уравнений A85.5)
при q = оо дает а = оо, но при q = со из второго уравнения
? = ?кр. Чтобы определить критическое время, нужно
использовать начальные условия: при t = 0, а = 0, q = q0. Из первого
уравнения, полагая а = 0, находим q0 и подставляем это
значение во второе уравнение, в котором следует принять t = 0.
Величина критического времени зависит от длины оболочки,,
некоторые результаты расчетов приведены в нижеследующих
таблицах:
ге = 3
1
? й
КР h
1
83,2
1,5
8,41
2
2,73
2,5
1,85
3
1,78
3,5
2,16
4
2,43
5
3,42
1
1 а
"Р h
2,8
1,51
2,9
1,48
3
1,48
п-
3,1
1,47
= 5
3,2
1,49
3,3
1,49
3,4
1,54
704 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Как и должно быть, критическое время убывает с увеличением
длины оболочки и достигает некоторого минимального значения.
Рост критического времени при дальнейшем увеличении длины,
конечно, не отражает какого-либо механического факта, а связан
с недостаточностью аппроксимации кривой прогиба синусоидой.
Действительно, у достаточно длинных оболочек проявляется
краевой эффект и критическое время не зависит от длины.
Определенные выше минимальные значения критического времени,
4Р = 1,78— для п = 3 и tKp = 1,47— для п = 5,
по-видимому, можно считать за некоторую реальную оценку для
критического времени длинных оболочек при условии, что форма
потери устойчивости осесимметрична.
§ 186. ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ
ВЫПУЧИВАНИЯ В НЕЛИНЕЙНОЙ ПОСТАНОВКЕ
В § 180 было отмечено, что для некоторых систем задача
выпучивания распадается на две отдельные задачи: определение
некоторого критического для
данной нагрузки прогиба и
определение времени достижения
этого критического прогиба в
результате ползучести. На
примере сжатого стержня
оказалось, что сама потеря
устойчивости определяется мгновенными
характеристиками системы, в
рассмотренном примере — ее
упруго-пластическими характеристиками; роль ползучести
сводится к такому изменению геометрии, которое приводит стержень
в критическое состояние. Условие для того, чтобы предлагаемая
схема расчета была вполне строгой; состоит в том, что система
должна быть статически определимой. Это значит, распределение
напряжений в элементах системы определяется единственным
образом, если заданы внешние силы и перемещения. В
геометрически нелинейных системах положение может быть совершенно
аналогичным: если система статически определима, то роль
ползучести сводится к тому, что изменяются геометрические размеры
до тех пор, пока не наступит критическое состояние, при котором
происходит мгновенная потеря устойчивости. Простейший
пример, позволяющий выяснить существо дела,— это так
называемая ферма Мизеса (рис. 252). Подробное исследование поведения
такой стержневой системы в условиях линейной ползучести
содержится в работе [246], мы ограничимся здесь более простым
^анализом. Будем считать, что стержни могут сжиматься, но не
186] (ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ВЫПУЧИВАНИЯ 705
могут терять устойчивость вследствие изгиба. Пунктиром
изображено первоначальное положение стержней, каждый из
которых составляет угол #0 с горизонтом; под действием силы Р
стержни укорачиваются, и угол их наклона равен ¦&. Легко
подсчитать, что относительное укорочение
ei=I(#2-fl2). A86.1)
Сжимающее напряжение в каждом стержне есть
_ Р
0 ~~ 2F О -
Мы считаем углы Ф и г% достаточно малыми, так что sin ¦& ft; $,
COS XT ft! 1 ^ •
Рассмотрим сначала поведение системы в предположении
упругости материала, то есть будем считать о = Ее. Положим
Р
q = — , тогда
? = 0@;-#«). A86.2)
Можно найти значение ®, при котором ~ = 0. Это будет, когда
и, следовательно, ¦& = дкр = ~= . Соответствующее значение пара-
метра нагрузки будет максимальным, дальнейшее уменьшение
угла ¦& происходит при убывающей нагрузке. Момент, когда
достигается значение Ф = 'Окр, является моментом потери
устойчивости системы; критическое значение параметра нагрузки
?кр = 2а;р. A86.3)
Предположим теперь, что материал стержня ползет, при этом
закон ползучести совершенно безразличен, существенно лишь
то, что всегда существует упругая деформация, связанная с
действующим в данный момент напряжением законом Гука. Тогда
связь между напряжением и деформацией будет следующая:
е-^ + р.
Величина р зависит от а и любых параметров, но не от е и не
от о. Подставляя выражения для е и а, найдем:
(-2Р—fl')* = P- <186-4>
45 Ю. Н. Работнов
706
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Скорость ползучести Ь становится бесконечно большой, когда
обращается в нуль скобка:
2#2 о _ и.
Таким образом, мы снова приходим к условию A86.3)
совершенно независимо от закона ползучести. Теперь это условие
нужно понимать следующим образом. Любая нагрузка q может
стать критической в тот момент, когда угол наклона стержня
достигает значения, определяемого в зависимости от q
формулой A86.3). Критическое время есть время достижения
вследствие ползучести прогиба, критического для данной нагрузки.
Фактическое определение критического времени требует
интегрирования уравнения A86.4), поэтому сделанное замечание
о том, что критическое состояние определяется геометрией и
упругими характеристиками, может показаться бесполезным. В
действительности, определяя зависимость деформации от времени
в условиях ползучести для более или менее сложных систем, мы
вынуждены пользоваться теми или иными приближенными
приемами, и в приближенных уравнениях особенность, ведущая к
бесконечно большому значению скорости, явно видная в
уравнении A86.4), может не усматриваться. Всякого рода процессы
численного интегрирования становятся затруднительными вблизи
тех значений независимой переменной, когда производная от
искомой функции неограниченно возрастает. Поэтому имеет
смысл формулировать задачу устойчивости как задачу
определения времени, необходимого для достижения прогибом заранее
известного критического значения.
Возвращаясь к уравнению A86.4), предположим, что закон
ползучести, то есть зависимость р от a, t и других параметров,
может быть любым. В течение короткого промежутка времени At
напряжения в стержнях существенно не меняются,
следовательно, величина Ар « р At может быть вычислена. В результате
уравнение A86.4) заменяется следующим разностным
уравнением:
М = ^Р__. A86.5)
Л $
С помощью формулы A86.5) можно вести расчет
последовательными ступенями, определяя каждый раз напряжение по
формуле о* = о"? • Формуле A86.5) можно придать несколько иное
истолкование. Влияние деформации ползучести Ар, происшедшей
за время At, совершенно эквивалентно влиянию изменения
начального угла ¦§¦(,, причем из A86.1) следует, что эквивалентное
§ 186] ПРИБЛИЖЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ВЫПУЧИВАНИЯ 707
изменение Ф0 есть
Дво=-^. A86.6)
Теперь, предполагая систему упругой, из A86.2) при q = const
мы найдем, что изменение Фо вызывает изменение угла ¦&, которое
выражается следующим образом:
ДА _ АрААр
2d"
А-*
Внося сюда выражение ДФо из A86.6), мы опять придем к
соотношению A86.5).
Использованный прием, состоящий в том, что деформация
системы ищется по формулам, относящимся к случаю упругости,
а роль ползучести сводится к изменению начального прогиба,
является совершенно строгим для данного примера, в котором
распределение усилий полностью определяется заданием внешней
силы и прогиба; в общем случае такой прием, конечно, не будет
приводить к точному результату. Однако для приближенного
определения критического времени для сложных систем его
можно использовать.
В работах Вольмира и Зыкина [16], [15] дается
приближенное решение задачи о выпучивании цилиндрической панели,
опертой по контуру и сжатой вдоль образующей. Метод решения
состоит в следующем. Для прогиба w и функции усилий в
срединной поверхности Ф в предположении упругости оболочки
получается известная система двух нелинейных
дифференциальных уравнений. Предполагается, что
w = en sin — sin -— ,
а Ь A86.7)
, . Пх . Яу % '
Wn ~ С0П S1U Sin -~ .
и а о
Одно из уравнений теперь интегрируется, и находится
выражение функции Ф, другое — удовлетворяется приближенно
в смысле метода Галеркина. В результате получается
зависимость сжимающего усилия от с и с0:
Р = р(с, с0). A86.8)
Кривая зависимости р от с при заданном с0 имеет максимум,
соответствующий верхней критической нагрузке, и минимум,
соответствующий нижней критической нагрузке. Для данных
значений р и са теперь могут быть вычислены усилия в
срединной поверхности T;j и моменты Mtj. Найденным усилиям и
моментам соответствует определенная скорость ползучести, следова-
45*
708 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
тельно, за время At происходит некоторая деформация
ползучести. Очевидно, что при нелинейном законе ползучести
происходящая деформация ползучести неизбежно исказит форму
поверхности панели, заданную уравнением A86.7).
Приближенно полагается, что вид функции w(x,'y) сохраняется,
изменение прогиба рассчитывается по величинам деформации
ползучести в центре панели. Это изменение прогиба считается
эквивалентным изменению начального прогиба с0 на величину Ас0.
Теперь расчет повторяется, но в качестве начального прогиба
принимается с'0 = с0 + Ас0. Так, последовательными шагами
по времени расчет доводится до момента хлопка. Условие
наступления хлопка определяется уравнением A86.8), так как при
любом р можно найти такое значение с, что -^ = 0, если р
выражается через с и с0 по формуле A86.8).
§ 187. УСТОЙЧИВОСТЬ СЖАТОГО ВЯЗКО-УПРУГОГО СТЕРЖНЯ
Задачи, рассмотренные выше, по своему характеру близки
к тем задачам, которые называются в теории упругости или
пластичности задачами устойчивости, однако мы избегали употреблять
термин «устойчивость», потому что все рассмотренные примеры
относились к системам, неустойчивым в смысле классического
определения. Речь шла поэтому не об устойчивости сжатого
стержня, а о характере нарастания его прогибов со временем
и об установлении того момента, когда эти прогибы становятся
в известном смысле недопустимыми. Для вязко-упругих
стержней, изготовленных из материала с ограниченной ползучестью,
возможна постановка задачи устойчивости в прямом и строгом
смысле слова. Будем считать, что связь между напряжением
и деформацией устанавливается уравнением B3.5), а именно:
a + K(y = E(e + \ie). A87.1)
Устойчивость сжатого стержня из такого материала была
впервые рассмотрена Ржаницыным [11а]. Напомним, что в
уравнении A87.1) Е представляет собою мгновенный модуль упругости.
Это значит, что при мгновенном приложении напряжения о
«мгновенно» (если отвлечься от динамических эффектов)
возникает деформация е = a IE. Если постоянное напряжение а
действует в течение длительного времени, то деформация е
стремится к значению, определяемому формулой е = а/Ея. Здесь
Ел — длительный модуль упругости, Ед = Е у . Очевидно, как
было разъяснено в § 23, что \i <i К.
Предположим теперь, что стержень изгибается в главной
плоскости нагрузкой, которой соответствует распределение изги-
§ 187] УСТОЙЧИВОСТЬ СЖАТОГО ВЯЗКО-УПРУГОГО СТЕРЖНЯ 709
бающего момента М0 (t, z); начальное искривление стержня
в этой же главной плоскости задано некоторой функцией v0 (z).
Положим е = ку, внесем в A87.1), умножим обе части на у и
проинтегрируем по площади сечения. Получим:
М + Ш = Е1{к + рк). A87.2)
Здесь М — изгибающий момент, / — момент инерции площади
сечения. Если сжимающая сила есть Р и v — прогиб, то
М=— Pv + M0, k = v"{z) — v{z).
Теперь уравнение A87.2) примет следующий вид:
— Pv — P{v + ku) + М0 + Ш0 = EI {v" + ]w")-EIv—\iEIv. A87.3)
Пусть Vk (z) — фундаментальная функция задачи об
устойчивости упругого стержня, то есть функция, удовлетворяющая
уравнению
EIVk(z) + PhVh{z) = 0
и однородным граничным условиям задачи. Величины Рк
представляют собою фундаментальные числа, то есть критические
силы. Как известно, функции v (z) и г?0 (z) можно разложить
в ряды по фундаментальным функциям. Представим формально
в виде такого же ряда функцию М0 (z), а именно:
v (t, z) = 2 Tft @ Vh (z), v0 (z) = 2 chVh (z),
M0(t,z)=-^mh(t)Vk(z)Pk. A87.4)
Предположим теперь, что начальное искривление и внешняя
нагрузка таковы, что в рядах для v0 (z) и М (t, z) сохраняются
лишь первые члены: v0 = с^Уи М0 = — m^VJ*^, тогда и в
выражении для v достаточно удержать первый член v = tjFj. Здесь
Vi — первая фундаментальная функция, определяющая форму
потери устойчивости упругого стержня при приложении силы,
равной первой эйлеровой силе. Такое рассмотрение, по
существу, не нарушает общности; следуя обычному методу, не
составит труда построить решение и для общего случая, когда
начальный прогиб и момент заданы рядами A87.4). В дальнейшем мы
будем опускать индексы у Tj, с±, т^ и Vi, тогда как вместо Pt
будем писать Рэ. При сделанных предположениях из A87.3)
следует такое дифференциальное уравнение для функции т:
• • ¦
— сот+ т A — и) + (ц — соЯ)т = |хс + (^1 + ^та), A87.5)
Р
710
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. Х1Г
Предположим теперь, что продольная сила возрастает по
произвольному закону от нуля до своего конечного значения за
некоторое достаточно малое время ?4, после чего остается
постоянной. Внешний изгибающий момент за время tt меняется
достаточно мало. При t = 0 было х = с. В промежутке времени
О < t < fj производные «вит весьма велики; поэтому в
уравнении A87.5) нужно удержать только члены, содержащие эти
производные; получим:
т — ют — шт = 0. A87.6)
Проинтегрируем A87.6) в пределах от t = 0 до t = ti, учитывая,
что Р@) = 0 и т@) = с. Результат будет следующий:
т —с = шт.
Отсюда
*о = ~- A87-7)
Здесь через т0 обозначена величина т при t = t^. В пределе,
устремляя Ъ\ к нулю, мы найдем, что при постоянной силе Р
нужно интегрировать уравнение A87.5), где принято со = 0;
начальное условие для этого уравнения будет т @) = т0,
причем т0 определяется формулой A87.7).
Величина Ра пропорциональна модулю упругости материала Е;
таким образом, Рэ есть критическая сила, соответствующая
мгновенному модулю. Можно определить критическую силу,
соответствующую длительному модулю:
Р'-Р I^L- V- p
Г3-ГЭ Е -уП.
Таким образом, отношение -у- представляет собою критическое
значение безразмерной силы Р1РЬ, вычисленное по отношению
к длительному модулю. Положим
Тогда уравнение A87.5) при со = 0 перепишется следующим
образом:
i + fr^j^llic + m + Xm]. A87.8)
Здесь В = к "'~ю и т @) = т-^— .
" ^ 1 — СО v ' 1 — (й
Заметим, что
6>0 при ю<о)',
6<0 при со'<со<1.
S 187] УСТОЙЧИВОСТЬ СЖАТОГО ВЯЗКО-УПРУГОГО СТЕРЖНЯ 711
Члены в правой части уравнения A87.8) представляют собою
возмущения. Происхождение этих возмущений двоякое: с — это
начальный прогиб, т — приложенный момент. Имеет смысл
рассмотреть действие возмущений по отдельности, имея в виду
различие их природы. Начальный прогиб с был создан в стержне
до приложения нагрузки, и после того, как сила приложена,
мы не имеем никакой возможности его изменить, это возмущение
является постоянно действующим возмущением. Поперечная
нагрузка, создающая момент т, прикладывается извне и задается
как функция времени; этой функцией можно управлять по
произволу. Итак, предположим сначала, что т = 0. Тогда
решение A87.8), удовлетворяющее начальному условию для т, будет
т = е
A87.9)
Если р" > 0, т стремится с увеличением времени к пределу
Это есть значение прогиба, которое получается в предположении
упругости материала при длительном модуле. Если (J > 0, то
решение, определяемое уравнением A87.9), устойчиво в том
смысле, что малое изменение Ас величины начального прогиба с
вызывает малое изменение Ат величины т, причем, каково бы ни
было положительное число т), всегда можно найти такое
положительное число е, что если | Ас | < е, то | Ат| < т] для любых
значений t. Это и есть классическое определение устойчивости
в смысле Ляпунова. При f$ <C 0 и, следовательно, со > со'
величина т, определяемая формулой A87.9), растет неограниченно;
неограниченно растет также величина |Ат|, сколь бы ни было
мало | Ас [. При to > 1 опять становится Р > 0. Однако из этого
не следует устойчивости стержня, в этом случае потеря
устойчивости происходит мгновенно. Действительно, формула A87.7),
полученная в результате интегрирования A87.6), справедлива
для процесса нагружения стержня достаточно быстро
возрастающей силой. При ю —*- 1 величина т0, определяемая этой формулой,
стремится к бесконечности; таким образом, при to >> 1
формула A87.7) не имеет смысла.
Рассмотрим теперь действие возмущения, созданного
поперечной нагрузкой. Положим в A87.8) с = 0, будем считать, что
т — заданная функция от t. He нарушая общности, мы можем
принять т @) = 0. Действительно, если нагрузка
прикладывается внезапно, то мы всегда вправе предположить, что это
712 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
происходит не в момент t = 0, а в момент t = е, где е — любая
сколь угодно малая положительная величина. Тогда решение
уравнения A87.8) представится следующим образом:
<
Т = Т35- + (Г=^<Н"$ rn{t)e^dt. A87.10)
о
Будем считать для определенности, что т (t) ф 0 при 0 < t < t2,
тогда как при t> tz m (t) = 0. Тогда интеграл в правой части
A87.10) при t > t2 сохраняет постоянное значение, и мы имеем:
г=е_Р* X const.
При Р > 1 прогиб, созданный нагрузкой, после прекращения
действия нагрузки убывает, стремясь к нулю при t -> оо. Если
Р < 1, прогиб неограниченно возрастает, хотя действие
возмущения уже прекратилось.
Рассмотренный пример показывает, что суждение об
устойчивости и неустойчивости стержня из материала, свойства
которого описываются уравнением A87.1), производится чрезвычайно
просто. Стержень устойчив тогда, когда сжимающая сила меньше,
чем эйлерова сила, определенная по длительному модулю. Если
сжимающая сила больше, чем длительная эйлерова сила, но
меньше, чем мгновенная эйлерова сила, то стержень неустойчив, любое
возмущение приводит к неограниченному росту прогиба со
временем. Наконец, если сжимающая сила больше мгновенной
эйлеровой силы, то происходит мгновенная потеря устойчивости. Этот
результат остается справедливым и для линейного вязко-упругого
тела, описываемого при помощи соотношений линейной теории
наследственности. Если ядро ползучести не ограничено,
стержень всегда неустойчив; если ядро ограничено, то суждение об
устойчивости или неустойчивости можно произвести так же, как
для упругого стержня, заменив мгновенный модуль длительным
модулем [1S1].
Если положить в A87.1) и. = 0, то мы получим вязко-упругое
тело с неограниченной ползучестью, скорость которой постоянна
при постоянном напряжении. Сжатый стержень из такого
материала всегда неустойчив, для него ю' = 0 и р < 0. Поэтому для
суждения о возможности использования сжатых элементов из
подобного материала нужно непосредственно определять прогибы
по формуле A87.9), если известен начальный прогиб, или по
формуле A87.10), если задана поперечная нагрузка, и находить время,
по истечении которого прогиб начинает превышать некоторое
значение, выбранное из тех или иных соображений.
§ 188] СЛУЧАЙ МАТЕРИАЛА, СЛЕДУЮЩЕГО ЗАКОНУ УПРОЧНЕНИЯ 713
§ 188. УСТОЙЧИВОСТЬ СЖАТОГО СТЕРЖНЯ,
МАТЕРИАЛ КОТОРОГО СЛЕДУЕТ ЗАКОНУ УПРОЧНЕНИЯ
Предположим, что материал стержня ползет, следуя закону
упрочнения
Ф{р,р,о) = 0, Р = е-±. A88.1)
Основным состоянием стержня является состояние равномерного
сжатия, когда а = const = PIF; будем считать, что для основного-
состояния уравнение A88.1) проинтегрировано; это значит, что
р известно как функция от t. Будем рассматривать достаточно
малые отклонения от основного состояния; тогда величины бе
и ба, связанные с изгибом, удовлетворяют уравнению,
получающемуся в результате линеаризации A88.1) около основного
состояния. Это уравнение было приведено в § 61, а именно:
(El — ii)Sa~vSa + E(ii8e + vSe) = 0. A88.2)
„ . дф ЗФ дф v
Здесь л = д— , ц. = — , v = —; известные функции времени^
da dp д'р
Положим, как и в § 187, Ье = ку, подставим в A88.2), умножим
на у и проинтегрируем по площади поперечного сечения. Получим:
(El -\i)M-vM-} EI (jift + vie) = 0. A88.3)
Отличие уравнения A88.3) от уравнения A87.3) состоит в томг
что коэффициенты A88.3) переменные — известные функции
времени. Положим, как и в предыдущем параграфе,
M=M0 — Pv, k = v"-v.
Тогда уравнение A88.3) примет следующий вид:
(El — |д) Мо — vM0 — Р [El - ц) v + v (Pv + Pv) +
+ EI bxv" — \w'0 + w") = 0.
Пусть теперь
M0= -P3m(t)V(z), v = j(t)V, v0==cV.
Здесь функция V есть первая фундаментальная функция
уравнения
EIV" = -PV,
а Рэ — соответствующее фундаментальное число.
Внося выражения М0, v и v0 в уравнение продольного
изгиба, найдем, что функция т (t) удовлетворяет следующему
714 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XIT
дифференциальному уравнению:
со (Ек — и.) т — v (сот -f тш) + (?Х — ц) т — vm -f от — u^ + vt = 0.
A88.4)
При t = 0 должно быть т = с. Предположим, что продольная
сжимающая сила прикладывается в течение весьма малого
промежутка времени. Тогда в уравнении A88.4) следует удержать
только члены, содержащие т и со, а именно:
— сот — тсо + т = 0.
Интегрируя, получим, что мгновенный прогиб после приложения
силы будет
с
Теперь, если сжимающая сила постоянна, то мы должны
рассматривать уравнение A88.4), в котором принято со = 0.
Начальное условие для интегрирования этого уравнения будет т @) = т0.
Запишем уравнение для функции х (t) следующим образом:
;+v[f^+»]-T^[--^»+S«]- <188-5>
Для дальнейшего следует задаться каким-либо определенным
видом закона упрочнения. Положим
Ф(р,р,а) = рр*-Аоп.
Тогда
v = />a, ц = ара~1, Я = — пАа4'1 = — — рра.
Если внести эти выражения в A88.5) и принять за независимую
переменную величину, пропорциональную деформации
ползучести основного состояния сжатия, а именно:
g _ nE со
то уравнение A88.5) преобразуется к следующему виду:
Aт {, a \ 1 ( dm f 1—ш , a Л _ . ас Л ,,occ,
Члены в правой части, зависящие от т, представляют собою
возмущение от внешних нагрузок; член, содержащий
множителем с, является постоянно действующим возмущением;
рассмотрим действие этих возмущений по отдельности.
а) Постоянно действующее возмущение. Если т = 0, то
решение уравнения A88.6), удовлетворяющее начальному условию
§ 189] УСЛОВНЫЕ ЛИНЕАРИЗИРОВАННЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ 715
т@)- 1.1@ ' бУДет следующее:
I
r=^re^>~ale~l^d^ <188-7)
о
Уравнение A88.7) всегда определяет возрастающую функцию |,
таким образом, движение стержня неустойчиво.
б) Возмущение типа внешней нагрузки. Если с = О, то
интеграл уравнения A88.6) будет следующий:
I
т = т + ± Гае1 \ т (?) ^«Г6 dg A88.8)
о
(в работе [338] эта формула приведена с ошибкой в коэффициенте,
которая не влияет на качественный результат).
§ 189. УСЛОВНЫЕ ЛИНЕАРИЗИРОВАННЫЕ КРИТЕРИИ
УСТОЙЧИВОСТИ
Мы убедились в том, что движение сжатого стержня в
условиях ползучести всегда неустойчиво, формулы A88.7) и A88.8)
дают величину прогиба, стремящуюся со временем к
бесконечности. Поэтому реальный результат, который можно получить
с помощью этих формул, состоит в определении времени (или
деформации сжатия), при котором прогиб достигает некоторой заданной
величины. Если начальное возмущение достаточно мало и
допускаемый прогиб также выбран достаточно малым, то
линеаризированное уравнение будет давать достаточно хорошее
приближение. Однако поведение функций, заданных соотношениями
A88.7) и A88.8), отличается некоторыми особенностями, на кривых
зависимости т (t) можно бывает указать характерные точки, в
которых поведение функции меняется в том или ином смысле. Время
достижения этих точек можно условно назвать критическим
временем. В зависимости от типа возмущения условное критическое
время будет определяться по-разному.
1. Квазистатический критерий. Если отвлечься от действия
возмущений, то есть рассматривать уравнение A88.5) без правой
части, то функция х (t), определяемая этим уравнением, будет
убывающей или возрастающей в зависимости от знака множителя при
т. Назовем в первом случае состояние устойчивым, во втором —
неустойчивым. Граница устойчивости определится из условия
^Г + ц^О. A89.1)
716 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XI]
При степенном законе упрочнения, использованном в
предыдущем параграфе, это условие приводится к виду
E = ?i = a. A89.2)
Это условие получается сразу, если приравнять нулю
множитель при т в уравнении A88.6). Критерий устойчивости A89.1)
был введен в работах [ззв], [10г]. В этих работах оставалась
некоторая неясность в истолковании смысла критерия A89.1); дело в томт
что для уравнения A88.5) без правой части нельзя поставить
начального условия, отклоненный от прямолинейного состояния
стержень не будет находиться в равновесии. Однако если
рассматривать действие на стержень некоторой системы возмущений,,
то критерий A89.1) приобретает совершенно определенный смысл,
как это показано в [338]. Предположим, что некоторая нагрузка
действовала в течение времени t*, после чего нагрузка снимается,
и мы следим за дальнейшим движением стержня. Роль времени
у нас теперь играет параметр ?, пропорциональный деформации
ползучести основного состояния; времени t* соответствует
значение ?* этого параметра. При ? > ?* т (|) = 0, следовательно,
интеграл в A88.8) сводится к константе, и формула A88.8)
записывается следующим образом:
т = 1-ае5 х const.
Отсюда следует:
Если | < а, то ^| < 0; если Ь, > а, то -^ > 0. Изменение
прогиба в зависимости от ? схематически изображено на рис. 253.
При ? < |*, пока действовала поперечная нагрузка, величина т
менялась в соответствии с законом изменения нагрузки, то есть
в зависимости от функции т (|) согласно A88.8). Если нагрузка
снята до достижения критической деформации ti = и, то есть
если ?* •< ii, как показано на рис. 253, а, прогиб, достигнутый
к моменту ? = ?*, уменьшается: достигает минимального
значения при | = %i, после чего неограниченно растет. Если нагрузка
снята после достижения критической деформации |4 = а, прогиб
сразу начинает возрастать (рис. 253, б).
В упомянутых работах [107], [ззе] была дана также
динамическая трактовка критерия A89.1). Следует подчеркнуть, что
динамический подход к задаче устойчивости в данном случае вовсе
не означает, что закон упрочнения в той же форме, в какой он
применяется для описания медленных процессов, считается
физически верным законом и для описания колебательных процессов.
Рассмотрение динамической постановки задачи устойчивости
имеет в данном случае чисто формальный смысл, речь идет о выяс-
$ 189] УСЛОВНЫЕ ЛИНЕАРИЗИРОВАННЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ 717
нении всех возможных следствий из принятого закона ползучести.
Конечно, в действительности потеря устойчивости носит
квазистатический характер, и
рассмотрение динамических
эффектов может представить интерес
лишь в специальных случаях.
Выясненное здесь довольно
¦странное и неожиданное
поведение сжатого стержня,
материал которого следует закону
упрочнения, послужило
предметом детального исследования в
работе Хоффа [2i2].
2. Критерий Куршина. В
работах Куршина [вз], [6i\ было
рассмотрено поведение стержня
под действием возмущений типа
внешней нагрузки, но
несколько иного вида. Предполагается,
что стержень сохраняет
прямолинейную форму до тех пор,
пока параметр \ не достигнет
-значения | = |2. В этот момент
времени внезапно
прикладывается нагрузка, которой
соответствует изгибающий момент
т. Для простоты будем считать т постоянным. Исследуется
движение стержня в течение весьма малого промежутка времени,
•следующего за моментом приложения нагрузки.
По формуле A88.8) получим:
Если
(Л Ъ \
?2 мало, то можно принять
у-Ъ
dl.
^т + ^Ш <*-ь<Б-Ь>
Вычислим производную
(I
-](i
е?-Ь.
A89.3)
Полагая здесь ?=|2> найдем ту скорость, с которой будет
прогибаться стержень тотчас же после приложения нагрузки:
718
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Величина т', конечно, не является скоростью, так как | есть
функция от времени. Для нас существенно то, что при любом
значении %2 т\ а следовательно, и т положительны.
Однако вторая производная от т по времени т, как мы увидим,
может быть либо положительна, либо отрицательна. Поскольку
параметр % пропорционален f
т —
-U'
, то, как легко убедиться,
A89.4)
Дифференцируя A89.3) еще раз по ?, найдем:
, 2 ... . , 1 f I
[О-f > ?«-*>+О-f )«-"К?Г'
Л-Ъ
При| = ^т"(Ы=^^-^
Вследствие A89.4) условие
т = 0 приводится к
следующему виду:
2а
= 0.
Отсюда
ёг = 2а.
A89.5)
Величине ?2 соответствует
время t2, которое и принимается
за критическое. Если нагрузка
прикладывается при t < t2,
движение будет замедленным, как
показано на рис. 254, а. Если
нагрузка приложена при t >• tz,
движение является ускоренным; примерный график функции
т (t) изображен на рис. 254, б.
3. Критерий Шестерикова. Наиболее реальным будет тот
случай, когда стержень имеет начальный прогиб или начальный
эксцентриситет и движение описывается уравнением A88.6).
Интеграл в A88.7) представляет собою неполную гамма-функциюТ
он табулирован, следовательно, т (?) всегда можно построить.
Скорость прогиба оказывается при этом положительной, однако
при некотором значении ? = ?3 ускорение меняет знак. Точка
I = ?3 условно отделяет область медленного роста прогиба от
области быстрого его роста и принимается за точку критического
состояния. Для вычисления величины ?3 необходимо вычислить
функцию т (|); в работе [150j это было сделано для некоторых
§ 190] ПРИМЕНЕНИЕ ЛИНЕАРИЗИРОВАННЫХ УРАВНЕНИЙ 719
целых значении а, результаты оказались следующие:
а= 1 2 3
|s=i,36 3,10 4,98
Все три рассмотренных критерия определяют критическое
состояние стержня как состояние, при котором параметр ?
достигает некоторого критического значения |й, являющегося
той или иной функцией от а. Возвращаясь к определению
параметра |, получим, что в критическом состоянии
1Т-Т^-Р = Ыо). (Ш.6)
Но р = е — =-, со = Р/Рэ = а/аа. Будем обозначать в
дальнейшем безразмерное напряжение сг/аэ = со через о. Точно так же
будем обозначать через е величину
Тогда условие A89.6) может быть
приведено к следующему виду:
Ik
п
е_Е
е~
л 6fe
п
о. A89.7)
Уравнение A89.7) определяет в
координатах о" — е прямую, проходящую
через точку A,1) и отсекающую отрезок
?й/га на оси абсцисс (рис. 255).
Биссектриса координатного угла о = е
представляет собою линию мгновенной
деформации. При приложении некоторого Рис. 255.
напряжения а < стэ такого, что о
изображается отрезком О А на рис. 255, происходит мгновенная упругая,
деформация, изображаемая отрезком е = АВ. Вследствие
ползучести деформация продолжается, и критическое состояние наступает,
когда к упругой деформации, изображаемой отрезком АВ,
добавляется деформация ползучести, изображаемая отрезком ВС.
§ 190. ПРИМЕНЕНИЕ ЛИНЕАРИЗИРОВАННЫХ УРАВНЕНИЙ
К ЗАДАЧЕ ВЫПУЧИВАНИЯ
Как показывает сравнение с экспериментом, условные
критерии устойчивости, описанные выше, дают чрезвычайно
заниженную величину критического времени. Это само собою очевидно,
поскольку фиксируемые этими критериями качественные
изменения в ходе кривой ползучести незначительны и фактический рост
прогибов происходит довольно медленно. Так, если
предположить характер возмущения соответствующим квазистатическому
720
ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
критерию, прогиб достигает минимального значения при \ —
= ^ = а. При увеличении параметра | в два раза и при а = 2
{закон ползучести Эндрейда) прогиб увеличивается на 84%, то
есть примерно удваивается. Если п = 3, то это увеличение
прогиба происходит за время, превышающее критическое время в 8 раз.
Такие изменения прогиба в эксперименте не фиксируются, на
опыте определяется фактически время полного исчерпания
несущей способности стержня или время появления весьма больших
прогибов. С другой стороны, мы видели, что определение
критического времени как такого времени, когда прогиб становится
равным бесконечности, также лишено смысла. Фактически за
критическое время следует принимать время достижения
определенного прогиба, который либо сам по себе считается недопустимым,
либо соответствует мгновенной упруго-пластической потере
устойчивости. Величина этого прогиба, отнесенная к половине толщины
стержня, может быть оценена порядком с « 1, если при с <С 1
не происходит мгновенной потери устойчивости. Представляет
интерес выяснить, какова будет точность, если вместо полных
уравнений ползучести пользоваться для определения этого
прогиба линеаризированным уравнением. Предположим для
определенности, что упрочнение отсутствует и закон ползучести
следующий:
Проварьируем уравнение A90.1). Получим:
Ge=-j6o + lp6a. A90.2)
Здесь р = еп I — J —скорость ползучести в основном состоянии.
Полагая е--ку, умножая на у и интегрируя, найдем следующее
уравнение связи между моментом и кривизной:
dp dp О
Положим, как и выше, к = v" — v"Q, M = —Pv, v = cV, где
V — первая фундаментальная функция задачи об устойчивости
упругого стержня. В результате приходим к следующему
уравнению для с (р):
Начальное условие при t = 0 с @) = с0 = °° . Интегрируя
A90.3), получим:
P==(l_m)-J.lnf. A90.4)
п с0
§ 19A] ПРИМЕНЕНИЕ ЛИНЕАРИЗИРОВАННЫХ УРАВНЕНИЙ 721
Формула A90.4) является для линеаризированного закона
ползучести совершенно точной независимо от показателя п и формы
поперечного сечения стержня. Исходя из точного уравнения
ползучести, в § 178 мы смогли решить эту задачу только для сечения
в форме идеального двутавра, и то приближенным методом. Явное
выражение для критического времени, даже при указанных
ограничениях, можно получить, если п — целое. Сравним формулу
A90.4) с формулой A78.10):
p = (l-«)f 1п-Ц^4, A90.5)
полученной при п — 3. Для этого значения п формула A90.4) дает
p = (l_coLf-]n-f . A90.6)
Конечно, существенное различие между A90.6) и A90.5)
заключается в том, что из формулы A90.5) при с = оо получается
конечная критическая деформация, тогда как по формуле A90.6) при
с = со р = со. Однако если считать с0 С 1 и с порядка единицы,
то разница между результатами, полученными по формулам A90.5)
и A90.6), оказывается небольшой. Действительно, считая с*0 < 3
и с = 1, найдем, что в формуле A90.5) под логарифмом будет
величина
с0 V 4 '
что соответствует увеличению начального прогиба с0 в
приближенной формуле A90.6) в отношении 2/у'З = 1,15. Конечно, величина
начального прогиба с точностью 15% никогда не известна. Более
того, способ вывода формулы A90.5) таков, что достоверной
является лишь структура формулы, но не фигурирующие в ней числа.
Действительно, в § 178 эта формула была получена двумя
способами и числа оказались различными. В § 182 эта же задача
решалась при помощи вариационного метода, результат опять-таки
получился отличным. Поэтому применение линеаризированного
закона ползучести для определения условного времени
выпучивания в указанном выше смысле может считаться вполне
оправданным. Преимущество такого способа заключается в том, что
линеаризированное уравнение допускает совершенно точное
решение независимо от формы сечения, граничных условий и закона
ползучести. В частности, используя формулу A88.7), мы можем
решать задачи выпучивания и при ползучести,
сопровождающейся упрочнением.
46 ю. Н. Работнов
722 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
§ 191. ЛИНЕАРИЗИРОВАННЫЕ УРАВНЕНИЯ ПОЛЗУЧЕСТИ
С УПРОЧНЕНИЕМ
Для того чтобы иметь возможность распространить
линеаризированную теорию на задачи выпучивания пластинок и оболочек,
нужно прежде всего выписать систему уравнений, связывающих
вариации напряжений и вариации деформаций, для материала,
следующего закону ползучести с упрочнением. В одномерном
случае эта задача оказалась простой, для произвольного
напряженного состояния соотношения оказались не столь простыми.
В работе [107] эти соотношения были выведены в предположении
о том, что параметры, характеризующие основное состояние.
могут считаться постоянными. Для одномерного случая это
означает, что в уравнении A88.2) величины К, |х и v рассматриваются
как постоянные. Такое рассмотрение достаточно для того, чтобы
изучать движение в течение некоторого достаточно короткого
времени, следующего за возмущением, но не для определения
фактической зависимости прогиба от времени. Приводимые ниже
уравнения были получены в работе [152], эти уравнения были
применены к задаче о выпучивании пластинки. Одновременно
и независимо линеаризированные уравнения изгиба пластинки
получены в работе [63].
Будем отправляться от степенного закона упрочнения
3 . „ 71— 1"
р = Ар-ао™, A91.1)
2 " 3 — —
Р2 = РчРи = сто = У аИ°и-
Предположим, что в основном напряженном состоянии
напряжения либо постоянны, либо меняются пропорционально одному
и тому же параметру, так что
Здесь ац — постоянный тензор, причем а^а^ = 2/3. Проварьируем
второе уравнение A91.1). Получим:
8р= —аАр-^оъ&р + Ар-япв^-1 ба0
или же
бр= — iLp6p + -J-p6a0.
Р сг0
Теперь нам удобно принять за независимую переменную
величину р в основном состоянии. Обозначая штрихом производную
§191] ЛИНЕАРИЗИРОВАННЫЕ УР-НИЯ ПОЛЗУЧЕСТИ С УПРОЧНЕНИЕМ 723
по этой переменной, получим:
6р'=—^6p + -i-6<r0. A91.2)
С другой стороны, из определения р следует:
2 •
pbp = -jPijSpij.
Разделим обе части на р2 и заметим, что
PU 3 <*ij з
Р
вследствие A91.1), тогда как б/5?/ = бе^ —^^ 6cr;J. Следовательно,
2 <тп ~ 2 °iJ
— 1 —
бр' = ац be\j — -^г aij &о'ц.
^з 2G
2G
Положим
q = Еаиеи.
Заметим, что из определения а0 следует:
3 — — 3 — —
вог0 = -^- Gtj бои = у atj 6ati.
Теперь выражение для бр' может быть переписано следующим
образом:
или, после интегрирования,
Sp = ~Fg-6a0). A91.3),
Исключая бр из A91.2) и A91.3), приходим к следующему диф--
ференциальному соотношению между 8q и ба0:
6^+(J + pNa0 = 6g4f б?- A91-4)»
Здесь введено обозначение:
Интегрируя A91.4), найдем:
v
бай = бд —рр-"е-РР \ рае^ 8q dp. A91.5)
о
46*
724 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Проварьируем теперь первое уравнение A91.1). Получим
в результате:
бо'и + у6ои=1беи + аи [y6?-(y+(P-Y)°V)]. A91.6)
Здесь
__ Е
У ~ °о '
Теперь нужно внести в A91.6) выражение 8ас по формуле A91.5)
и проинтегрировать получившееся уравнение относительно 5ст^-.
При этом интегрированием по частям удается избавиться от
двукратного интегрального оператора, и окончательный результат
записывается в следующем виде:
р
бац = 2G 6ег; + "Уе_№ \ ечг> [ау 8q — 2G 8etj] dp —
— au$p-ae-Vp:ipaefiP8qdp. .A91.7)
§ 192. ВЫПУЧИВАНИЕ ПЛАСТИН
ПО ЛИНЕАРИЗОВАННОЙ ТЕОРИИ
Применим уравнение A91.7) к задаче о выпучивании
пластины. Считая напряженное состояние плоским и материал
несжимаемым, положим, как обычно,
+h
ei} = kijZ, Ми= \ OijZdz (i, 7 = 1,2).
«J
-h
Тогда из A91.7) следует:
MU = D{ (wiU + - u>j22) - ye-™ J eVP (wtil + i и^) dp +
+ -|a" [уе~ур { eWmdp — Pp-be-VP f p*e№mdp~\ \ . A92.1)
or. r. 8?fe3
одесь D— цилиндрическая жесткость D =—„—,
т = аиш?11 + a22wJ2 + 2a12wjl2.
Введем дифференциальный оператор
D в* I д* I О д*
F ~ Qii ~W + °22 ~W + 12 ~d^f '
тогда
m = P(w).
§ 192] ВЫПУЧИВАНИЕ ПЛАСТИН ПО ЛИНЕАРИЗИРОВАН. ТЕОРИИ 725
Уравнение равновесия для выпученной пластины под действием
усилий Tij в средней поверхности и поперечной нагрузки q
будет следующее:
Ми,ц + Тии;,и + д = 0. A92.2)
При этом Tij = 2haij = 2ha.ij<ja.
Будем предполагать, что пластина имеет начальный прогиб w0,
тогда в уравнении A92.1) следует в правой части брать вместо
w величину w — wu, тогда как в уравнении A92.2) остается w.
После несложных преобразований получается следующее интегро-
дифференциальное уравнение для прогиба пластины:
A92.3)
Здесь интегральные операторы R* и R* определены следующим
образом:
v
R*f = y \ ехр (— у (р — х)} f (х) их,
I A92.4)
ДЯ7 = Р \ (?)""ехр[-Р(р-*)]/(*)<**,
о
Е а Еп
В общем случае переменные в уравнении A92.3) не разделяются,
однако можно указать частные случаи, когда разделение
переменных возможно. Так, если пластина произвольного очертания
равномерно сжата, то Р (w) = — Aw. При q = 0 уравнение A92.3)
примет следующий вид:
A-Д*)ДД(ы>-ы?о)-^Ди> = 0. A92.5)
Здесь
Рассмотрим уравнение упругой потери устойчивости:
AAw-^Aw = 0.
При данных граничных условиях это уравнение определяет
интенсивность первого критического напряжения о"оэ и
соответствующую фундаментальную функцию W{. Положим w = с (t) W^.
726 ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫЕ ЗАДАЧИ [ГЛ. XII
Будем считать также, что w0 = с0 W\. Тогда из A92.5) следует:
A —Д*)(с —с0) —<ас=0. A92.6)
Здесь, как и выше, ы = — .
Решение интегрального уравнения A92.6) может быть
записано в символическом виде:
СК1+Т=?=Ж>' A92.7)
Фактическое его решение затруднительно; исключая
интегральные операторы, мы приходим к дифференциальному уравнению
второго порядка с переменными коэффициентами, сводящемуся
к уравнению Уиттекера.
Б работе [152] проведено исследование поведения прогиба
на основе условных критериев, описанных в § 189, а именно
квазистатического критерия и критерия обращения в нуль
второй производной прогиба по времени; это исследование оказалось
возможным только для тех случаев, когда ш либо мало по
сравнению с единицей, либо близко к единице. В работе [63] устойчивость
пластины исследована с помощью критерия Куршина. Имея в виду
условность названных критериев, мы не приводим здесь этих
результатов, значение уравнения A92.3) заключается в том, что
оно позволяет производить вычисление фактической зависимости
прогиба от времени, если начальный прогиб известен. Можно
ожидать, что и для пластин применение линеаризированной
теории будет давать удовлетворительные результаты, если
прогибы невелики (порядка толщины пластины).
БИБЛИОГРАФИЯ
1. Амельяпчик А. В., Расчет на прочность дисков турбомашин
на математической машине, Изв. АН СССР, ОТН, Механика и
машиностроение, № 1, 1959.
2. Андраде да К., Представление о ползучести, сб. «Ползучесть
и возврат», Металлургиздат, Москва, 1961.
3. Аннин Б. Д., Асимптотическое разложение экспоненциальной
функции дробного порядка, ПММ, т. XXV, вып. 4, 1961.
4. Арутюнян Н. X., Некоторые вопросы теории ползучести, Гостех-
издат, Москва, 1952.
¦5. Беляев Н. М., Применение теории пластических деформаций
к расчетам на ползучесть деталей при высоких температурах, Изв.
АН СССР, ОТН, № 7, 1943.
<з. Б л е й х Ф., Устойчивость металлических конструкций, Физматгиз,
Москва, 1959.
7. Богуславский П. Я., Исследование ползучести элементов
турбин, Тезисы докладов на Всесоюзном совещании по теории упругости,
строительной механике и теории пластичности 7—10 декабря 1950 г.,
Изд-во АН СССР, 1950.
8. Б о й ч е н к о Г. А., Сопротивление перекатывания наследственно-
упругих тел, Изв. АН СССР, ОТН, № 9, 1955.
9. Б р о н с к и й А. П., Явление последействия в твердом теле, ПММ,
т. V, вып. 1, 1941.
10. Б р ы з г а л и н Г. И., К описанию анизотропной ползучести
стеклопластиков, ПМТФ, № 6, 1963. .
11. Варшавский Д. П., Богуславский П. Я., Полу-
мордвинова И. Г., Моделирование деформированного состояния
деталей сложной формы в условиях ползучести, Теплоэнергетика, № 5,
1955.
12. В и л е с о в а Н. С, Н а м е с т н и к о в В. С, Об одном параметре
упрочнения, ПМТФ, № 3, 1964.
13. В л а с о в В. 3., Общая теория оболочек, Гостехиздат, Москва,
1949.
14. В олчков Ю. М., Осесимметричные задачи ползучести круговых
цилиндрических оболочек, Изв. АН СССР, Механика, № 5, 1965.
15. В о л ь м и р А. С, Устойчивость упругих систем, Физматгиз, Москва,
1963.
16. В о л ь м и р А. С, 3 ы к и н П. Г., Устойчивость в большом
цилиндрических оболочек при ползучести, сб. «Тепловые напряжения в
элементах турбомашин», вып. 2, Киев, 1962.
728
БИБЛИОГРАФИЯ
17. В у л ь ф с о н С. 3., К вопросу линейной теории ползучести, Тр. Центр,
н. и. ин-та строит, конструкций Акад. стр-ва и архитект. СССР, вып. 4.
1961.
18. Герасимов А. Н., Обобщение линейных законов деформирования
и его применение к задачам внутреннего трения, ПММ, т. XII, вып. 3,
1948.
19. Г о л ь д е н б л а т И. И., Некоторые вопросы механики
деформируемых сред, Гостехиздат, Москва, 1955.
20. Гольденвейзер А. Л., Общая теория оболочек, Гостехиздат.
Москва, 1949.
21. Гольденвейзер А.Л., О теории тонкостенных стержней, ПММ ,
т. XIII, вып. 6, 1949.
22. Гудьер Дж. Н., Ходж Ф. Г., Упругость и пластичность, ИЛ,
Москва, 1960.
23. Данилова И. Н., К расчету напряженного состояния в роторе
при неустановившейся ползучести, Изв. АН СССР, ОТН, Механика
и машиностроение, № 5, 1959.
24. Даниловская В. И., Иванова Г. М., Работнов Ю. Н.,
Ползучесть и релаксация хромомолибденовой стали, Изв. АН СССР,
ОТН, № 5, 1955.
25. Джрбашян М. М., Об интегральном представлении функций,
непрерывных на нескольких лучах, Изв. АН СССР, серия матем, т. 18,
№ 5, 1954.
26. Джрбашян М. М., Об одном новом интегральном преобразовании
и его применении в теории целых функций, Изв. АН СССР, серия
матем, т. 19, № 2, 1955.
27. Д и т к и н В. А., Прудников А. П., Интегральные
преобразования и операционное исчисление, Физматгиз, Москва, 1961.
28. Ержанов Ж. С, Об оценке напряженного состояния горного
массива, сб. «Математические методы в горном деле», т. 2, Изд-во
СО АН СССР, Новосибирск, 1963.
29. Ержанов Ж. С, Теория ползучести горных пород и ее
приложения, Изд-во «Наука», Алма-Ата, 1964.
30. Жуков А. М., Работнов Ю. Н., Чуриков Ф. С,
Экспериментальная проверка некоторых теорий ползучести, Инженерный
сборник, т. XVII, Изд-во АН СССР, Москва, 1953.
31. Ж у к о в А. М., О пластических деформациях изотропного металла
при сложном нагружении, Изв. АН СССР, ОТН, № 12, 1956.
32. Журков С. Н., Нарзуллаев Б. Н., Временная зависимость
прочности твердых тел, ЖТФ, т. 23, № 10; 1953.
33. Ж у р к о в С. Н., Санфирова Т. П., Температурно-временная
зависимость прочности чистых металлов, ДАН СССР, т. 101, № 2, 1955.
34. Ж у р к о в С. Н., Проблема прочности твердых тел, Вестник АН СССР,
№ 11, 1957.
35. Ж у р к о в С. Н., Санфирова Т. П., Связь между прочностью
и ползучестью металлов и сплавов, ЖТФ, т. 28, № 8, 1958.
36. Зверьков Б. В., Длительная прочность труб при сложных
нагрузках, Теплоэнергетика, № 3, 1958.
37. И в а н о в а В. С, О природе деформации на площадке текучести
металлов, ДАН СССР, т. 94, № 2, 1954.
38. Иванова Г.М., Ползучесть сплава ЭИ-437Б при переменных
температурах, Изв. АН СССР, ОТН, № 4, 1958.
39. И в а н о в а Р. Я., Качение вязко-упругого цилиндра по основанию
из того же материала, ПМТФ, № 3, 1964.
40. Иванов Г. В., Ш е п е л е н к о В. Н., Выпучивание и хлопок
сжатой вдоль образующей квадратной цилиндрической панели в условиях
ползучести, Инж. журн. Механика твердого тела, № 3, 1966.
БИБЛИОГРАФИЯ
729
41. Ивлев Д. Д., К теории идеальной пластической анизотропии,
ПММ, т. XXIII, вып. 6, 1959.
42. Ивлев Д. Д., О свойствах соотношений закона анизотропного
упрочнения пластического материала, ПММ, т. XXIV, вып. 1, 1960.
43. И л ь ю ш и н А. А., Пластичность, Гостехиздат, Москва, 1948.
44. Ишлинский А. Ю., Продольные колебания стержня при
наличии линейного закона последействия и релаксации, ПММ, т. IV, вып. ] ,
1940.
45. Ишлинский А. Ю., Об уравнениях пространственного
деформирования не вполне упругих и вязко-пластических тел, Изв. АН СССР,
ОТН, № 3, 1945.
46. Ишлинский А. Ю., Общая теория пластичности с линейным
упрочнением, Украинский математический журнал, № 3, 1954.
47. Каган В. Ф., Основы теории поверхностей в тензорном изложении,
т. 1, Гостехиздат, Москва, 1947.
48. Кадашевич Ю. И., Новожилов В. В., Теория
пластичности, учитывающая остаточные микронапряжения, ПММ, т. XXII,
вып. 1, 1958.
49. К а п т е л и н Ю. П., Урттт"тптр состояния для ползучести
наклепанной меди, Сборник трудов ЛИИЖТ, вып. 192, 1962.
50. К а р п и н Е. Б., Из опыта автофретирования турбинных дисков.
Энергомашиностроение, № 1, 1959.
51. К а ч а н о в Л. М., О времени разрушения в условиях ползучести,
Изв. АН СССР, ОТН, № 8, 1958.
52. Качанов Л. М., Теория ползучести, Физматгиз, Москва, 1960.
53. К ац Ш. Н., Исследование длительной прочности углеродистых труб.
Теплоэнергетика, № 11, 1955.
54. К а ц Ш. Н., Разрушение аустенитных труб под действием
внутреннего давления в условиях ползучести, Энергомашиностроение, № 2,
1957.
55. К ац Ш. Н., Ползучесть и разрушение труб под действием
внутреннего давления, Изв. АН СССР, ОТН, № 10, 1957.
56. Кеннеди А. Дж., Влияние переменных нагрузок на ползучесть-
и отдых, сб. «Усталость металлов», ИЛ, Москва, 1961.
57. К л ю ш н и к о в В. Д., О законах пластичности для материалов
с упрочнением, ПММ, т. XXII, вып. 1, 1958.
58. Клюшников В. Д., О возможном пути построения соотношений
пластичности, ПММ, т. XXIII, вып. 2, 1959.
59. Клюшников В.Д., Новые представления в пластичности и
деформационная теория, ПММ, т. XXIII, вып. 4, 1959.
60. К о с т ю к А. Г., О равновесии кольцевой пластинки при степенном
законе упрочнения, ПММ, т. XIV, вып. 3, 1950.
61. К ост ю к А. Г., Напряжения во. вращающемся диске при
ползучести, Инженерный сборник, т. XV, Изд-во АН СССР, 1953.
62. Куратов П. С, Розенблюм В. И., Об интегрировании
уравнений неустановившейся ползучести твердых тел, ПММ, т. XXIV, вып. 1,
1960.
63. К у р ш и н Л. М., Об устойчивости стержней и пластин в условиях
ползучести, ДАН СССР, № 3, 140, 1961.
64. Куршин Л. М., Устойчивость стержней в условиях ползучести,
ПМТФ, № 6, 1961.
65. Куршин Л. М., Об одном возможном подходе к задаче устойчивости
стержней в условиях ползучести, сб. «Ползучесть и длительная
прочность», Изд-во СО АН СССР, Новосибирск, 1963.
66. Кузнецов А. П., Решение задачи устойчивости сжатой оболочки
в условиях ползучести по гипотезе упрочнения, ПМТФ, № 2,
1964.
730
БИБЛИОГРАФИЯ
67. Лейбензон Л. С, Вариационные методы решения задач теории
упругости, ОГИЗ, ГТТИ, Москва, 1933.
68. Л ифшиц И. М., К теории диффузионно-вязкого течения
поликристаллических тел, ЖЭТФ, т. 44, вып. 4, 1963.
€9. Малинин Н, Н., Основы расчетов на ползучесть, Машгиз, Москва,
1948.
70. Малинин Н. Н., Некоторые одномерные задачи неустановившейся
ползучести, Инженерный сборник, т. X, Изд-во АН СССР, 1951.
71. Малинин Н. Н., Установившаяся ползучесть круглых симметрично
нагруженных пластин, сб. «Расчеты на прочность, жесткость и пол-
аучесть элементов машиностроительных конструкций*, Машгиз, 1952.
72. Малинин Н. Н., Расчет на ползучесть вращающихся
неравномерно нагретых дисков переменной толщины, сб. «Вопросы прочности
материалов и конструкций, Изд-во АН СССР, Москва, 1959.
73. Малинин Н. Н., Прочность турбомашин, Машгиз, Москва, 1962.
74. Милейко С. Т., Теленков В. И., Кратковременная
ползучесть алюминиевых сплавов, ПМТФ, № 5, 1962.
75. Милейко С. Т., Кратковременная ползучесть при переменных
напряжениях, сб, «Ползучесть и длительная прочность», Изд-во СО
АН СССР, Новосибирск, 1963.
/6. М и р к и н И. Л., Т р у н и н И. И., Исследование ползучести и
разрушения стали в зоне концентрации напряжений, сб. «Прочность
металлов», Изд-во АН СССР, Москва, 1956.
77. Мусхелишвили Н. И., Некоторые основные задачи
математической теории упругости, изд. 4, Изд-во АН СССР, Москва, 1954.
78. Наместников В. С., О ползучести при постоянных нагрузках
в условиях сложного напряженного состояния, Изв. АН СССР, ОТН,
№ 4, 1957.
79. Наместников В. С, О ползучести при переменных нагрузках
в условиях сложного напряженного состояния, Изв. АН СССР, ОТН,
№ 10, 1957.
80. Наместников В. С, Прямое и обратное кручение в условиях
ползучести, ПМТФ, № 1, 1960.
81. Наместников В. С, Об одной гипотезе в теории трехосной
ползучести, Изв. СО АН СССР, № 2, 1960.
82. Наместников В. С, О ползучести алюминиевого сплава при
переменных нагрузках, ПМТФ, № 4, 1960.
83. Наместников В. С, Работнов Ю. Н., О наследственных
теориях ползучести, ПМТФ, № 4, 1961.
84. Наместников В. С..Работ но в'Ю. Н., О гипотезе уравнения
состояния при ползучести, ПМТФ, № 3, 1961.
85. Наместников В.С.,Хвостунков А. А., Ползучесть дура-
люмина при постоянных и переменных нагрузках, ПМТФ, № 4, 1960.
86. Немировский Ю. В., Об уравнениях ползучести, основанных
на критерии максимального приведенного напряжения, Изв. АН СССР,
Механика и машиностроение, № 3, 1964.
87. Немировский Ю. В., Работнов Ю. Н., Предельное
равновесие подкрепленных цилиндрических оболочек, Изв. АН СССР, ОТН,
Механика и машиностроение, № 3, 1963.
88. Новожилов В. В., Теория тонких оболочек, Судпромгиз,
Ленинград, 1962.
89. Новожилов В. В., О физическом смысле инвариантов
напряжения, ПММ, т. XV, вып. 2, 1951.
90. Н о в о ж и л о в В. В., Теория упругости, Судпромгиз, Ленинград,
1958.
91. Од инг И. А., Механизм ползучести (сгеер'а) металлов, Металлург,
№ 1, 1934.
БИБЛИОГРАФИЯ
731
92. Одинг И. А., Туляков Г. А., Ползучесть аустенитной стали
при сложно-напряженном состоянии, Изв. АН СССР, ОТН, № 1, 1958.
93. Одинг И. А. и др., Теория ползучести и длительной прочности
металлов, Металлургиздат, Москва, 1959.
94. Одквист Ф., Технические теории ползучести, «Механика», сб.
перев. и обз. ин. период, лит., № 2, 1959.
95. Работнов Ю. Н., Рабинович В. П., О прочности дисков
в условиях ползучести, Изв. АН СССР, ОТН, Механика и
машиностроение, № 4, 1959.
96. Работнов Ю.Н., Основные уравнения теории оболочек, ДАН СССР,
т. XVII, № 2, 1945.
97. Работнов Ю. Н., Некоторые решения безмоментной теории
оболочек, ПММ, т. X, вып. 5—6, 1946.
98. Работнов Ю. Н., Расчет деталей машин на ползучесть, Изв.
АН СССР, ОТН, № 6, 1948.
99. Работнов Ю. Н., Некоторые вопросы теории ползучести, Вестник
МГУ, № 10, 1948.
100. Работнов Ю. Н., О диске равного сопротивления, ПММ, т. XII,
№ 4, 1948.
101. Работнов Ю. Н., Равновесие упругой среды с последействием,
ПММ, т. XII, № 1, 1948.
102. Работнов Ю. Н., Приближенная техническая теория упруго-
пластических оболочек, ПММ, т. XV, вып. 2, 1951.
103. Работнов Ю. Н., О некоторых возможностях описания
неустановившейся ползучести с приложением к исследованию ползучести
роторов, Изв. АН СССР, ОТН, № 5, 1957.
104. Работнов Ю. Н., О механизме длительного разрушения, Сб.
«Вопросы прочности материалов и конструкций», Изд-во АН СССР, Москва,
1959.
105. Работнов Ю. Н., Сопротивление материалов, Физматгиз, Москва,
1962.
106. Работнов Ю. Н., О разрушении вследствие ползучести, ПМТФ,
№ 2, 1963.
107. Работнов Ю. Н., Шестериков С. А., Устойчивость
стержней и пластинок в условиях ползучести, ПММ, т. XXI, вып. 3, 1957.
108. Пономарев С. Д. и др., Расчеты на прочность в машиностроении,
Машгиз, Москва, 1958.
109. Ратнер С. И., Прочность и пластичность металлов, Оборонгиз,
Москва, 1949.
110. Рашевский П. К., Курс дифференциальной геометрии, ОНТИ,
Москва, 1938.
111. Рейс нер Э., Кларк Р., Изгиб труб с криволинейной осью,
сб. «Проблемы механики», ИЛ, Москва, 1955.
112. Ржаницын А. Р., Некоторые вопросы механики систем,
деформирующихся во времени, Гостехиздат, Москва, 1949.
ИЗ. Розенблюм В. И., Время до разрушения вращающегося диска
в условиях ползучести, ПММ, т. 2, № 3, 1957.
114. Розенблюм В. И., Влияние пластических деформаций на время
разрушения при ползучести, сб. «Ползучесть и длительная прочность»,
Изд-во СО АН СССР, Новосибирск, 1963.
115. Розенблюм В. И., О приближенных уравнениях ползучести,
Изв. АН СССР, ОТН, Механика и машиностроение, № 5, 1959.
116. Розенблюм В. И., Приближенный анализ неустановившейся
ползучести пластин и оболочек, сб. «Исследования по упругости и
пластичности», сб. 3, Изд-во ЛГУ, 1964.
117. Розовский М. И., Ползуч-есть и длительное разрушение
материалов, ЖТФ, т. ХХГ, № И, 1951.
732
БИБЛИОГРАФИЯ
118. Розовский М. И., О некоторых особенностях
упруго-наследственных сред, Изв. АН СССР, Механика и машиностроение, № 2, 1961
119. Розовский М. И., Нелинейные интегрально-операторные
уравнения ползучести и задача о кручении цилиндра при больших углах
крутки, Изв. АН СССР, ОТН, Механика и машиностроение, JV» 5, 1959.
120. Розовский М. И., Полусимволический способ решения некоторых
задач теории ползучести, Изв. АН АрмССР, Физ., мат., естеств. и техк.
науки, т. IX, № 5, 1956.
121. Розовский М. И., Некоторые свойства специальных операторов,
применяемых в теории ползучести, ПММ, т. XXIII, вып. 5, 1959.
122. Розовский М. И., Об одном свойстве степени специального
оператора и его приложении к решению динамических задач, сб.
«Ползучесть и длительная прочность», Изд-во СО АН СССР, Новосибирск.
1963.
123. Сазонова Н. Д., Испытание жаропрочных материалов на
ползучесть и длительную прочность, Изд-во «Машиностроение», Москва,
1965.
124. Салли А., Ползучесть металлов и жаропрочные сплавы, Оборониш,
Москва, 1953.
125. Свешникова В. А., О пластическом деформировании
упрочняющихся металлов, Изв. АН СССР, ОТН, № 1, 1956.
126. С д о б ы р е в В. П., Длительная прочность сплава ЭИ-437Б при
сложном напряженном состоянии, Изв. АН СССР, ОТН, № 4, 1958.
127. Сдобы рев В. П., Критерий длительной прочности для некоторых
жаропрочных сплавов при сложном напряженном состоянии, Изв.
АН СССР, ОТН, Механика и машиностроение, № 6, 1959.
128. Сервисен С. В., Вопросы прочности в машиностроении, Вестник
АН СССР, № 4, 1951.
129. Серенсен С. В., Козлов Я. А., Несущая способность и расчет
на прочность деталей при статических и переменных напряжениях.
Вестник машиностроения, № 12, 1953.
130. Серенсен С. В. и др., Прочность при нестационарном режиме
нагрузки, Изд-во АН УССР, Киев, 1961.
131. Слонимский Г. Л., О законах деформации реальных материалов,
ЖТФ, т. 9, № 20, 1939.
132. Слонимский Г. Л., О законе деформации высокоэластичных
полимерных тел, ДАН СССР, т. 140, № 2, 1961.
133. Соколовский В. В., Пластическое напряженное состояние
вращающегося диска, ПММ, т. XII, вып. 1, 1948.
134. Соколовский В. В., Теория пластичности, Гостехиздат, Москва.
1950.
135. С о с н и н О. В., Перераспределение напряжений в сплошном
вращающемся диске в первой стадии ползучести, ПМТФ, № 2, 1960.
136. Соснин О. В., Неустановившаяся ползучесть вращающихся дисков,
сб. «Ползучесть и длительная прочность», Изд-во СО АН СССР,
Новосибирск, 1963.
137. Соснин О. В., Установившаяся анизотропная ползучесть дисков,
ПМТФ, № 4, 1963.
138. Тимошенко С. П., Пластинки и оболочки, Гостехиздат, Москва,
1948.
139. Торшенов Н. Г., Ползучесть алюминиевого сплава Д-J6Т при
сжатии, ПМТФ, № 6, 1961.
140. Т р е ф ф ц Е., Математическая теория упругости, ГТТИ, Москва, 1934.
141. Уиттекер Е. Т., В а т с о н Г. Н., Курс современного анализа,
ГТТИ, Москва, 1934.
142. Харди Г. Г., Л и т т л в у д Дж., Полна Г., Неравенства, ИЛ,
Москва, 1948.
БИБЛИОГРАФИЯ
733
143. Хил л Г., Математическая теория пластичности, Гостехиздат,
Москва, 1956.
144. X у а и К э - ч ж и, Об упрочнении жестко-пластического материала,
ПММ, т. XXII, вып. 4, 1958.
145. Чуриков Ф. С, К вопросу о напряжениях и деформациях при
высокой температуре, Вестник МГУ, № 2, 1949.
146. Шенли Ф. Р., Анализ веса и прочность самолетных конструкций,
Оборонгиз, Москва, 1957.
J47. Шепеленко В. Н., Устойчивость бесконечно длинной
цилиндрической панели, защемленной по краю, Изв. АН СССР, Механика,
№ 6, 1965.
148. Шестериков С. А., Об одном вариационном принципе в теории
ползучести, Изв. АН СССР, ОТН, № 2, 1957.
149. Шестериков С. А., Об одном условии для законов ползучести,
Изв. АН СССР, ОТН, № 1, 1959.
150. Шестериков С. А., О критерии устойчивости при ползучести,
ПММ, т. XXIII, вып. 6, 1959.
151. Шестериков С. А., Расчет дисков на релаксацию, ПМТФ, № 1,
1960.
152. Шестериков С. А., Устойчивость пластинок при ползучести
по теории течения, ПМТФ, № 5, 1961.
153. Шестериков С. А., Выпучивание при ползучести с учетом
мгновенных пластических деформаций, ПМТФ, № 2, 1963.
154. Ш о р р Б. Ф., Влияние неравномерного нагрева в условиях
ползучести на изменение напряженного состояния, ДАН СССР, т. 123, № 5, 1958
155. Ш о р р Б. Ф., К расчету на неустановившуюся ползучесть
неравномерно нагретых стержней произвольного поперечного сечения, Изв.
АН СССР, ОТН, Механика и машиностроение, № 1, 1959.
156. Штаерман И. Я., Пиковский А. А., Методы расчета
конструкций на устойчивость, Гос. изд. местн. пром., Киев, 1938.
157. Щетинин Н. Н., Чистый изгиб стержней в условиях ползучести,
Изв. АН СССР, ОТН, № 8, 1956.
158. Ягн Ю. И., Виноградова И. Н., Влияние вида девиатора
напряжений на сопротивление металлов пластической деформации,
ДАН СССР, т. 96, вып. 3, 1954.
159. Andrade E. N., da С, On the viscous flow of metals and allied
phenomena, Proc. Roy. Soc. (А), т. 84, № A567, Lond., 1910.
160. A n d г a d e E. N. da C, The validity of the t1/s law of flow of metals,
Phil. Mag., т. 7, № 84, 1962.
161. Bailey R. W., Creep of steel under simple and compound stresses
and the use of high initial temperature in steam power plant, Transactions
Tokyo Sectional Meeting of the World Power Conference, Oct.—Nov.,
Tokyo, 1929.
162. В a i 1 e у R. W., The utilisation of creep test data in engineering design,
Proc. Inst. Mech. Engrs.,T. 131, Nov.—Dec. 1935.
163. Bailey R. W., Creep relationships and their applications to pipes,
tubes and cylindrical parts under internal pressure, Proc. Inst. Mech.
Engrs., т. 164, 1951.
164. Batdorf S. В., Budiansky В., A mathematical theory of
plasticity based on the concept of slip, NACA, T.N. 1871, 1949.
165. Batdorf S. В., Budiansky В., Polyaxial stress-strain relations
of a strain hardening metal, Journ. Appl. Mech., т. 21, 1954.
166. Bernett E. C, Short-time, elevated temperature stress-strain
behaviour of tensile, compressive and column members properties, Wright Air
Dev. Center, Techn. Rep. 59-484, Ohio, 1959.
167. Bernett E. C, Tensile and short-time creep properties of N-155
alloy sheet, Trans. ASME, B-82, № 4, 1960.
734
БИБЛИОГРАФИЯ
168. В е s s e I i n g J. F., A theory of elastic, plastic and creep deformations
of an initially isotropic material showing anisotropic strain hardening,,
creep recovery and secondary creep, Journ. Appl. Mech., т. 25, № 4, 1958.
169. Betteridge W., The extrapolation of the stress-rupture properties-
of the nimonic alloys, Journ. Inst, of Metals, January, 1958.
170. Bieniek M. P., Freudenthal A. M., Creep deformation and
stresses in pressurized, long cylindrical shell, JAS, т. 27, № 10, 1960.
171. Bishop J. F. W., Hill R., A theoretical derivation of the plastic
properties of a polycrystalline face centered metal, Phil, Mag., Ser. 7r
т. XLII, 1951.
172. В on t de R. A., A special case of uniaxial creep, including rupture.
Institutionen for Hallfesthetslara Kungl. Tekniska Hogskolan, Publ.
№ 37, Stockholm, 1962.
173. Boltzmann L., Zur Theorie der elastischen Nachwirkung, Annaleii
der Physik und Chemie, Erg. Bd. 7, 1876.
174. Brazier L. G., The flexure of thin cylindrical shells and other «thin*
sections, A.R.S.R. and M., № 1081, London, 1927.
175. Breuer S., Onat E. Т., On uniqueness in linear viscoelasticity,
Quart. Appl. Math., т. XIX, № 4, 1962.
176. Budiansky В.,A reassessment of deformation theories of plasticity,
Journ. Appl. Mech., т. 26, № 2, 1959.
177. Budiansky В., M a n g a s a r i a n' 0. L., Plastic stress
concentration at a circular hole in an infinite sheet subjected to equal biaxial
tension, Journ. Appl. Mech., т. 27, № 1, 1960.
178. Calladine С R., D r u с к e r D. C, Nesting surfaces of constant
rate of energy dissipation in creep, Quart. Appl. Math., т. XX, № 1, 1962.
179. Calladine C. R., Drucker D. C, A bound method for creep
analysis of structures: direct use of solutions in elasticity and plasticity r
Journ. Mech. Eng. Sci., т. 4, № 1, 1962.
180. Calladine C. R., Edge-load response of a thin cylindrical shell
in creep, Non classical shell problems, Proc. IASS Sympos., North Holland
Publ. CO-PWN, 1964.
181. Calladine C. R.,A note on the bending of beams made of nonlinear
material, Journ. Royal Aeronaut. Soc, т. 67, № 626, Febr. 1963.
182. Carlson R. L., Manning G. K., Investigation of compressive
creep properties of aluminium columns at elevated temperaturesr
Wright Air Dev. Center, Techn. Rep. 52-231, ч. 2 A954), ч. З A955),
ч. 4 A955).
183. Carlson R. L.,BodineE. G.,An experimental study of
compressive creep behaviour at elevated temperatures, Proc. ASTM, т. 57, 1957.
184. Cicala P., Sulle deformazione plastiche, Ace. dei Lincei, Rendiconti,
т. 5, вып. 6, 1950.
185. Clapper R. В., Isochronous stress-strain curves for some magnesium
alloys showing the effect of varying exposure times on their creep
resistance, Proc. ASTM, т. 58, 1958—1959.
186. С 1 a u s F. L., An examination of high temperature stress-rupture
correlating parameters, Proc. ASTM, т. 60, 1960.
187. Cottrell A. H., Dislocations and plastic flow in crystals, Oxford,
1953. (Русск. пер.: Котгрелл А. X., Дислокации и пластическое
течение в кристаллах, Металлургиздат, Москва, 1958.)
188. Davenport С. С, Correlation of creep and relaxation properties
of copper, Journ. Appl. Mech., т. 60, p. A-56, June 1938.
189. Davis E. A., Creep and relaxation of oxygen-free copper, Journ. Appl.
Mech., т. 10, № 2, 1943. (См. также: Теория пластичности ИЛГ
Москва, 1948, стр. 336—363.)
190. Davies P. E., Wil shire В., An interpretation of the relationship
between creep and fracture, Spec. Rep. Iron and Steel Inst., № 70, 1961.
БИБЛИОГРАФИЯ
735
191. DiStefano J. N., Sulla stabilita in regime visco-elastico a compor-
tamento lineare, Ace. dei Lincei. Rendiconti, Ser. VIII, т. XXVII, вып.
56, 1959.
192. D orn J. E., Tietz Т. Е., Creep and stress-rupture investigation^
on some aluminium alloy sheet metals, Proc. ASTM, т. 49, 1949.
193. D о r n J. E., Some fundamental experiments on high-temperature creep,
Journ. Mech. Phys. Solids, т. 3, № 2, стр. 85, Jan. 1955.
194. D r u с к e r D. C, Coulomb friction, plasticity and limit loads, Journ.
Appl. Mech., т. 21, № 1, 1954.
195. Drucker D. C, Some implications of -work hardening and ideal
plasticity, Quart. Appl. Math., т. VII, № 4, Jan. 1950.
196. Drucker D. C, Plasticity, сб. «Structural Mechanics», Pergamon
Press, 1960.
197. Drucker D. C, On uniqueness In the theory of plasticity, Quart.
Appl. Math., т. XIV, № 1, 1956.
198. Drucker D. C, Stockton E. D., Instrumentation and
fundamental experiments in plasticity, Proc. Soc. Exper. Stress Analysis,
т. X, № 2.
199. Drucker D. C, A more fundamental approach to plastic stress-
strain relations, Proc. First USA National Congr. Appl. Mech.,
1952.
200. Duffing G., Elastizitat und Reibung beim Riementrieb, Forschung
auf dem Gebiete des Ingenieurwesens, т. 2, № 3, 1931.
201. Dushman S.,Dunbar L.,Huthsteiner H., Creep of metals,
Journ. Appl. Phys., т. 15, 1944.
202. Everett F. L., Clark С L., Report on torsion creep tests for
comparison -with tension creep tests on a carbonmolybdenum steel, Proc.
ASTM., т. 39, 1939.
203. Faure G.,Touski A., Determination de la Vitesse de fluage etabli
d 'un acier refractaire fluant tres rapidement a haute temperature, La
recherche aeronautique, № 85, 1961.
204. Feltham P., M e а к i n J. D., On the representation and
extrapolation of creep data of metals and technical alloys, Rheol. Acta, т. 1, № 2—3,
1958.
205. Fenn R. W., Gusak J. A., Effect of strain rate and temperature
on the strength of magnesium alloys, Proc. ASTM, № 58, 1958.
206. Fenn R. W., Compression testing of sheet magnesium utilising rapid
heating, Proc. ASTM, т. 60, 1960—1961.
207. Fi nd ley W. N., Peterson D. В., Prediction of long-time creep
¦with ten years creep data on four plastic laminates, Proc. ASTM, т. 58,
1958.
208. Findley W. N., Creep and stress relaxation of plastics, сб. «High
temperature effects in aircraft structures», Pergamon Press, 1958. (Русск.
пер.: Влияние высоких температур на авиационные конструкции,
Оборонгиз, Москва, 1961.)
209. Findley W. N., The effect of temperature and combined stress on
creep of plastics, Proc. Second Intern. Reinforced Plastics Conference,
London, Dec. 1960.
210. Freudeuthal A, M., The inelastic behavior of engineering
materials and structures, John Wiley, N.Y., 1950.
211. Fry С G., Huches H. K., Asymptotic developments of certain
integral functions, Duke Mathem. Journ., т. 9, 1942.
212. G ar of a 1 о F., Smith G. W., R oyl e B. V., Validity of time
compensated temperature parameters for correlating creep and creep-
rupture data, Trans. ASME, т. 78, № 7, 1956.
213. Goldhoff R. M., The application of Rabotnov's creep parameter,
Proc. ASTM, т. 61, 1961.
736
БИБЛИОГРАФИЯ
214. Goldhoff R.M., Comparison of parameter methods for extrapolating
high temperature date, Pap. Amer. Soc. Mech. Eng., A-121, 1958.
215. Gomez M. P., Correlation and extrapolation methods of creep data,
Trend. Eng. Univ. Wash., т. 11, № 3. 1959.
216. Graham A., Numerical regularities in uniaxial deformation, Proc.
IX Intern. Congress Appl. Mech., т. 8, Brussels, 1957.
217. Grant N. J., В u с к 1 i n G., On the extrapolation of short time
stress-rupture data, Trans. Amer. Soc. for Metals, т. 42, 1950.
218. Green A. E., R i vlin R. S., The mechanics of non-linear materials
with memory, Arch. Rat. Mechanics, т. 1, 1957.
219. Green A. E., A d к i n s J.E., Large elastic deformations and
non-linear continuum mechanics, Oxford, Clarendon Press, 1960. (Русск. пер.:
Грин А., Адкинс Дж., Большие упругие деформации и нелинейная
механика сплошной среды, Изд-во «Мир», Москва, 1965).
220. Greenwood J. N., The influence of vibration on the creep of lead,
Proc. ASTM, т. 49, 1949.
221. Griffith I. E., Marin J., Creep relaxation for combined stress,
Journ. Mech. Phys. Solids, т. 4, № 4, 1956.
222. Gross В., Mathematical structure of the theories of viscoelasticity,
Hermann, Paris, 1953.
223. G u a r n i e г i G. I., Intermittent stressing and heating tests of aircraft
structural metals, Wright Air Dev. Center, Techn. Rep. 53-24, 1954.
224. G u a r n i e r i C. I., The creep-rupture properties of aircraft sheet alloys
subjected to intermittent load and temperature, ASTM, Spec. Techn.
Puhl., № 165, Baltimore, 1954.
225. GurtinM. E., Sternberg E., On the linear theory of
viscoelasticity, Archiv for Rational Mechanics and Analysis, т. 11, № 4, 1962.
226. Hanstock R. F., The effect of vibration on a precipitation hardened
aluminium alloy, Journ. Inst, of Metals, т. 74, стр. 469—492, 1948.
227. H e n с k у H., Zur Theorie plastischer Verformungen und der hierdurch
im Material hervorgerufenen Nachspannungen, ZAMM, т. 4, № 4, 1924.
(Русск. пер.: Теория пластичности, ИЛ, Москва, 1948, стр. 114—135.)
228. Hencky H., Ueher langsame stationgre Stromungen in plastischen
Massen mit Riicksicht auf die Vorgange beim Walzen, Pressen und Ziehen
von Metallen, ZAMM, т. 5, 1925. (Русск. пер.: Теория пластичности,
ИЛ, Москва, 1948, стр. 136—156.)
229. Herring С, Diffusional viscosity of a polycrystalline solid, Journ.
Appl. Phys., т. 21, № 5, 1950.
230. Hill R., On uniqueness and stability in the theory of finite elastic
strain, Journ. Mech. Phys. Solids, т. 5, № 4, 1957.
231. Hodge P., Venkatraman В., Approximate solitions of some
probleme in steady creep. Memorie di symposium sulla plasticita nella
scienza delle costruzioni in onore di A. Danusso, Bologna, 1956.
232. Hodge P. C, Piecewise linear plasticity, Proc. IX Intern. Congress
Appl. Mech., 1957.
233. H о f f N. J., The necking and rupture of rods subjected to constant tensile
loads, Journ. Appl. Mech., т. 20, 1953.
234. H о f f N. J., Buckling and stability, Forty-first Wilbur Wright Memorial
Lecture, Journ. Roy. Aeronaut Soc, т. 58, Jan. 1954.
235. H о f f N. J., Approximate analysis of structures in the presence of
moderately large creep deformations, Quart. Appl. Math., т. 12, № 1, 1954.
236. Hoff N. J., Creep bending and buckling of thin circular cylindrical
shells, PIBAL Report № 555, July 1956.
237. Hoff N. J., Creep buckling, The Aeronautical Quarterly, т. VII, Febr.
1956.
238. Hoff N. J., Buckling at high temperature, Journ. Roy. Aeronaut. Soc,
т. 61, № 563, 1957.
БИБЛИОГРАФИЯ
737
239. Hoff N. J., Stress distribution in the presence of creep, сб. «High
temperature effects in aircraft structures», Pergamon Press, 1958. (Русск.
пер.: Влияние высоких температур на авиационные конструкции,
Оборонгиз, Москва, 1961.)
240. Hoff N. J., J ahsm an W. E., N a chb a r W. A., A study of creep
collapse of a long circular cylindrical shell under uniform external
pressure, JASS, № 10, 1952.
241. Hoff N. J., Structure and materials for finite lifetime, Advances in
Aeronaut. Sciences, т. 2, Pergamon Press, 1959.
242. Hoff N. J., Reversed creep: a remark to the creep buckling theory
of Rabotnov and Shesterikov, Journ. Mech. Phys. Solids, т. 12, № 2, 1964.
243. Howe P. W. H., Mathematical techniques applying to the thermal
fatigue behaviour of high temperature alloys, The Aeronautical Quarterly,
т. XIII, 1962.
244. Hu L. W., Marin J., Anisotropic loading functions for combined
stresses in the plastic range, Journ. Appl. Mech., т. 22, 1, 1955.
245. Hult J., Oil canning problems in creep, сб. «Creep in structures»,
Springer, 1962.
246. H u 1 t J., Mechanics of a beam subject to primary creep, Chalmers
Tekniska Hogskolans handlingar, № 236, 1962.
247. Hunter S. C, The rolling contact of a rigid cylinder with a visco-
elastic half space, Journ. Appl. Mech., т. 28, № 4, 1961.
248. Inverkan av intermittent uppvarming pa hallfastheten for lattmetall,
3526-3-FFA Rapport № HU-568, 1957.
249. Isaksson A., Kryptning vid variabel spanning ogh temperatur,
Institutionen for Hallfasthetslara, Kungl. Tekniska Hogskolans Public.
№ 116, Juni 1957.
250. Jenkinson E.A., Smith A. I.,Hopkin M.T., The long time
creep properties of an 18% Cr, 12% Ni, 1% Nb steel steam pipe and
superheater tube, Journ. of the Iron and Steel Inst., т. 200, 1962.
251. Johannson A., Fatigue of steels at constant strain amplitude and
elevated temperature, Proc. ШТАМ Coll. on Fatigue, Stockholm, 1955;
Berlin, 1956.
252. Johnson A. E., Tapsell H. J., Creep under combined tension
and torsion, Engineering, т. 150, № 3887, 3889, 3892, 3894, 1940.
253. Johnson A. E., The creep recovery of a 0,17 per cent carbon steel,
Inst, of Mech. Eng. Journ. Proc, т. 145, 5, 1941.
254. Johnson A. E., The creep of a nominally isotropic aluminium alloy
under combined stress systems at elevated temperatures, Metallurgia,
т. 40 B37), 1949.
255. Johnson A. E., Behaviour of cast steel at elevated temperatures,
Engineer, bond., т. 188, № 4879, 4880, 4881, 4882, 1949.
256. Johnson A. E., The creep of a nominally isotropic magnesium alloy
atnormaland elevated temperatures under complex stress systems,
Metallurgia, т. 42, № 252, 1950.
257. Johnson A. E., Creep under complex stress systems at high
temperatures, Proc. Inst. Mech. Engrs., т. 164, № 4, 1951.
258. Johnson A. E., Frost N. E., Fracture under combined stress
creep conditions of a 0,5 per cent Mo steel, Engineer, т. 191, 1955.
259. Johnson A. E., Frost N. E.,A tension and torsion machine for
relaxation tests, Engineer, т. 193, № 5160, 1954.
260. Johnson A. E., Frost N. E., Note on the fracture under complex
stress creep conditions of a 0,5 per cent Mo steel at 550Q and a commercially
pure copper at 250a, Creep and fracture of metals at high temperatures,
London, H. M. Stationary Office, 1956.
261. Johnson A. E., Henderson J.,Mathur V. D., The complex
stress creep fracture of a commercial copper at 250a, Engineer, т. 202, 1956.
47 ю. Н. Работнов
738
БИБЛИОГРАФИЯ
262. Johnson A. E., Henderson J., Mathur V. D., Creep under
changing complex creep systems, Engineer, т. 206, 1958.
263. Johnson A. E., Henderson J., Mathur V. D., Complex
stress creep relaxation at elevated temperatures, Aircr. Eng. т. 31, 1959.
264. Johnson A. E., Henderson J., Mathur V. D., Complex
stress creep fracture of an aluminium alloy, Aircr. Eng. т. 32, 1960.
265. Johnson A. E., Complex stress creep of metals, Metallurgical Reviews,
т. 5, № 20, 1960.
266. Johnson A. E., Henderson J., Khan B. Complex stress
creep, relaxation, and fracture of metallic alloys, Edinburgh, H. M.
Stationary Office (Department of scientific and industrial research, National
Engineering Laboratory), 1962.
267. Kattus J. R., High temperature structural materials for missiles,
Jet Propulsion, т. 27, № 6, 1957.
268. Kattus J. R., M с D о w e 1 1 D. W., Strength of structural alloys
under rapid heating and loading, Proc. ASTM, т. 60, 1960—1961.
269. К a u z m a n W., Flow of solid metals from the standpoint of the
chemical rate theory, Trans. AIME, т. 143, 1941.
270. Kempner J.,Patel A., Creep buckling of columns, NACA T. N..
3138, Jan. 1954.
271. Kempner J. E., Pohle F. V., On the non-existence of a finite
critical time for linear viscoelastic columns, JAS,t. 20, № 8, Aug. 1953.
272. Kempner J.E., Creep bending and buckling of nonlinearly
viscoelastic columns, NACA T. N., 3137, Jan. 1954.
273. Kennedy A. J., The creep of metals under interrupting stressing,
Proc. Roy. Soc, т. А213, 1952.
274. Kennedy С R., H а г m s W. O., D о u g 1 a s D. A., Multiaxial
creep studies on inconel at 15004 F, ASME Paper, № 58-A-193, 1958.
275. К о о i s t r a L. ?., В 1 a z er H.U.Jucker J. Т., High
temperature stress rupture testing, Trans. ASME, т. 74, № 5, 1952.
276. Larson F. R., Miller J., A time-temperature relationship for
rupture and creep stress, Trans. ASME, т. 74, № 5, 1952.
277. Lazan B. J., Fatigue of structural materials at high temperatures,
сб. «High temperature effects in aircraft structures», Pergamon Press,
1958. (Русск. пер.: Влияние высоких температур на авиационные
конструкции, Оборонгиз, Москва, 1961.)
278. Leaderman Н., Elastic and creep properties of filamentous and other
high polymers, Textile Foundation, Washington, 1943.
279. Leaderman H., McCrackin F., N a k a d a O., Large
longitudinal retarded elastic deformation of fubberlike network polymers,
Trans. Soc. Rheol., т. VII, 1963.
280. Lee E. H., R a d о k J. R. M., W о о d w a r d W. В., Stress analysis
for linear viscoelastic materials, Trans. Soc. Rheol., т. Ill, 1959.
281. L i a n i s C, Torsional creep buckling of open tubes having arbitrary
cross-section, School of Aeronaut., Eng. Purdue Univ., Rep. № S-59-1,
Dec. 1959.
., Creep buckling of columns, JAS, N° 7, 1952.
., Creep buckling analysis of rectangular section columns,
№ 2956, Washington, D. C, 1953.
Creep stresses and deflections of columns, Journ. Appl.
№ 2, 1958.
A proposed theory of plasticity based on slip, Proc. 2nd
Congr. Appl. Mech., N.Y., 1954.
, On stress-strain relations based on slips, Proc. 3rd U. S. Nat.
Congr. Appl. Mech., N. Y., 1958.
287. Lin Т. Н., Bending of a plate with non-linear strain hardening creep,
сб. «Creep in structures», Springer, 1962.
282.
283.
284.
285.
286.
L i b о v e C.
L i b о v e C.
NACA T. N.
Lin Т. Н.,
Mech., т. 25,
L in Т. Н.,
U. S. Nat. Ci
Lin Т.Н., С
БИБЛИОГРАФИЯ
739
288. Ludvik P., Elemente der technologtschen Mechanik, Berlin, 1908.
289. Ma В. М., A further creep analysis for rotating solid discs of variable
thickness, Journ. Franklin Inst., № 5, 1960.
290. Machlin E., Nowick A., Stress rupture of heat resisting alloys,
Trans. AIME, т. 172, 1947.
291. M a n s о n S. S., Haierd A. M., A linear time—temperature relation
for extrapolation of creep and stress rupture data, NACA TN2890,
Washington, D. C, March 1953.
292. Marin I., PaoJoh-Han, An analytical theory of the creep
deformation of materials, Journ. Appl. Mech., т. 20, № 2, 1953.
293. Mellgren A., Measuring accuracy in creep test, Institutionen for
Hallfasthetslara, Kungl. Tekniska Hogskolans, № 125, Stockholm, 1958.
294. Michalko R. E., Short-time, rapid heating, elevated temperature
testing, Journ. of Metals, т. 12, № 8, 1960.
295. Moon D. P., Simmons W. F., Methods for conducting short-time
tensile, creep and creep-rupture tests under conditions of rapid heating,
Battelle Memor. Inst. DMIC Report, JY° 121, 1959.
296. Morland L.W.,A plan problem of rolling contact in linear viscoela-
sticity theory, Journ. Appl. Mech., т. 29, № 2, 1962.
297. Mott N. F., N а Ь а г г о F. R.N., Dislocation theory and transient
creep. Report of Conference on Strength of Solids, Phys. Soc. London, 1948.
298. Nabarro F. R. N., Deformation of crystals by the motion of single
ions. Report of the Conference on Strength of Solids, Phys. Soc. London, 1948.
299. N ad a i A., On the creep of solids at elevated temperatures, Journ.
Appl. Phys. т. 8, № 6, 1937.
300. N a d a i A., Plasticity, McGraw-Hill Book Co., N. Y. — London, 1931.
(Русск. пер.: Надаи А., Пластичность, ОНТИ, Москва, 1937.)
301. N a k a d а О., Theory of non-linear responses, Journ. Phys. Soc. Japan,
т. 15, № 12, 1960.
302. Namestnikov V. S., Combined-stress creep under changing loads,
Proc. of the Joint Intern. Conference on Creep, 1963.
303. Nishihara Т., Tanaka K., Shim a, Creep under tension and
torsion, Proc. 5th Japan Nat. Congr. Appl. Mech. 1955, Tokyo, 1956.
304. Nishihara Т., Taira S., Tanaka K., Effect of unloading
on the creep test of steel, Proc. 5th Japan Nat. Congr. Appl. Mech. 1955,
Tokyo, 1956.
305. Nishihara Т., Taira S., Tanaka K., Creep of mild steel,
Techn. Rep. Eng. Res. Inst. Kyoto Univ., т. VI, № 6, 1956.
306. Nishihara Т., Tanaka K., Tension and creep test on mild
steel, Proc. 5th Japan Nat. Congr. Appl. Mech. 1955, Tokyo, 1956.
307. Nishihara Т., Taira S., Tanaka К., О h j i K., Creep
of low carbon steel under interrupted stressing, Techn. Rep. Eng. Res.
Inst. KyotfrUniv., т. VI, № 7, 1956.
308. Nishihara Т., Taira S., T a n a k а К., О h j i K., On the
creep of low carbon steel under fluctuating stress, Proc. 7th Japan Nat.
Congr. Appl. Mech. 1957, Tokyo, 1958.
309. Nishihara Т., T a i r a S., Tanaka K., Ohnami M.,
Creep of low carbon steel under varying temperatures, Proc. 1st Japan
Congr. Testing Mater. Kyoto, 1958.
310. Nishihara Т., Taira S., Tanaka K., Ohnami M.,
Experimental study on the relationship between creep rate determining factors
of low carbon steel, Techn. Rep. Eng. Res. Inst. Kyoto Univ., т. 8, 2
A958) (Rep. № 42).
311. N о r t о n F. H., Creep in tubular pressure vessels, Transactions ASME,
т. 61, 1939.
312. Norton F. H., Soderberg С R., Report on tubular creep tests
of 0,5% Mo, С steel, Trans. ASME, т. 64, № 8, 1942.
47*
740
БИБЛИОГРАФИЯ
313. О d qui st F. К. G., Verfestigung von flusseisenahnlichen Korpern,
ZAMM, т. 13, 1933. (Русск. пер.: Теория пластичности, ИЛ, Москва,
1948, стр. 283—290.)
314. О d q u i s t F. K. G., Influence of primary creep on stresses in structural
parts, Transactions of the Roy. Inst, of Technology, № 66, Stockholm,
1953.
315. О d q u i s t F. K. G., Influence of primary creep on column buckling,
Journ. Appl. Mech., т. 21, № 3, 1954.
316. Od quist F. K. G., On theories of creep rupture, Institutionen for
Hallfasthetslara, Kungl. Tekniska Hogskolan. Public. № 136, Stockholm,
1961.
317. О d q u i s t F. K. G., Applicability of the elastic analogue to creep
problems of plates, membranes and beams, сб. «Creep in structures», Springer,
1962.
318. Onat E. Т., Wang Т. Т., The effect of incremental loading on creep
behaviour of metals, сб. «Creep in structures», Springer, 1962.
319. О г о w an E., Creep in metallic and non-metallic materials, Proc. 1st U. S.
Nat. Congr. Appl. Mech. 1952.
320. О г г R.L., Sherby O. D., D о r n J. D., Correlation of rupture data
for metals at elevated temperatures, Trans. Amer. Soc. for Metals, т. 46,
1954.
321. Pa tel S. A., Kempner J., Correlation of creep-buckling tests
with theory, PIBAL Report № 285, 1955.
322. P a tel S. A., P a n d a 1 a i K. A. V., Venkatraman В., Creep
stress analysis of thin walled structures, Journ. Royal Aeronaut. Soc,
т. 64, November 1960.
323. P a t e 1 S. A., Venkatraman В., On the creep stress analysis
of some structures, сб. «Creep in structures», Springer, 1962.
324. Patel S. А., С о z z a r e 1 1 i F. A., Venkatraman В., Creep
of compressible circular plates, Intern. Journ. of Mech. ScL, т. 5, № 1, 1963.
325. Perzyna P., The constitutive equations for rate sensitive plastic
materials, Quart. Appl. Math., т. XX, № 4, 1963.
326. Phillips Aris, The shear center in creep of beams of thin-walled
open cross section, сб. «Creep in structures», Springer, 1962.
327. P i a n Т. Н. H., Creep buckling of curved beam under lateral loading,
Proc. 3rd U. S. Nat. Congr. Appl. Mech., N. Y., 1958.
328. Popov E. P., Correlation of tension tests with relaxation tests, Journ.
Appl. Mech., т. 14, № 2, 1947.
329. Popov E. P., Stresses in turbine disks at high temperatures, Journ.
Franklin Inst., т. 243, № 5, 1947.
330. Poritsky H., Effect of creep on stresses in cylindrical shells, сб. «Creep
in structures», Springer, 1962.
331. Poulignier J., Fluage periodique rapide. Cas du nicral D-alliage
refractaire Fe—Ni—Cr, La recherche aeronautique, № 83, 1961.
332. Poulignier J., Fluage rapide de l'alliage refractaire Fe — Ni — Cr,
nicral D, La recherche aeronautique, № 81, 1961.
333. Prager W., Strain hardening under combined stress, Journ. Appl.
Phys., т. 16, N° 12, 1945. (Русск. пер.: Теория пластичности, ИЛ,
Москва, 1948, стр. 325—335.)
334. Prager W., Recent developments in the mathematical theory of
plasticity, Journ. Appl. Phys., т. 20, 235—241, 1949.
335. Prager W., A new method of analyzing stress and strains in work-
hardening plastic solids, Journ. Appl. Mech., т. 23, 1956.
336. Rabotnov Yu. N., Shesterikov S. A., Creep stability of
columns and plates, Journ. Mech. Phys. Solids, т. 6, 1957.
337. Rabotnov Yu. N., Pelzanie metali i ohliczanie pelzania, Rozprawy
inzynierskie, CLVIII, т. VIII, № 3, I960.
БИБЛИОГРАФИЯ
741
338. Rabotnov Yu. N., The theory of creep and its applications, сб.
«Plasticity», Pergamon Press, 1960.
339. Rabotnov Yu. N., On the equations of state for creep, сб. «Progress
in Applied Mechanics», Galley, N.Y., 1963.
340. R e i s s n e r E., On a variational theorem in elasticity, Journ. Math.
and Phys., т. 29, № 2, 1950.
341. Reissner E., On a variational theorem for finite elastic
deformations, Journ. Math, and Phys., т. 32, № 2—3, 1953.
342. Robinson E. L., 100 000 hour creep test, Mech. Engineering, 1943.
343. Robinson E. L., Effect of temperature variation on the long time
rupture strength of steels, Trans. ASME, т. 74, № 5, 1952.
344. Sanders I.L., Plastic stress-strain relations based on linear loading
functions, Proc. 2nd U. S. Nat. Cong, of Appl. Mech., N.Y., 1954.
345. Sanders J.L.,McComb H. G., S с h 1 e с h t e P. R., A
variational theorem for creep with applications to plates and columns, NACA,
Rep. № 1342, 1957.
346. S a w с z u к A., Linear theory of plasticity of anisotropic bodies and
its applications to problems of limit analysis, Archivum mechaniki sto-
sowanej, т. XI, № 5, 1959.
347. Schwartzberg F. R., Effects of high strain rates and rapid heating
on the tensile properties of titanium alloys, Light Metal Age, т. 17, № 1—2,
1959.
348. Serpico J. C, A study of creep collapse of a long cylindrical shell
under various distributed stress systems, JAS, т. 29, № 11, 1962.
349. Shanley Г. К., Inelastic column theory, JAS, т. 14, № 5, 1947.
350. Shepard D. A.,Starr С D., Wiseman C. D.,Dorn J.E.,
The creep properties of metals under intermittent stressing and heating
conditions, Wright Air Dev. Center, Tech. Rep. № 53-336, 1954.
351. Shield R. Т., Ziegler H., On Prager's hardening rule, Z. ang.
Math, und Phys., т. 9а, 1958.
352. Siegfried W., Failure from creep as influenced by the state of stress,
Journ. Appl. Mech., т. 10, № 4, 1943.
353. Simmons W. F., CrossH.S., Constant and cyclic-load creep tests
of several materials, ASTM Spec. Techn. Publ., № 165, Baltimore, 1954.
354. Sobotka Z., Some problems of non-linear rheology, Int. Symp.
on second-order effects in elasticity, plasticity and fluid dynamics, Haifa,
Apr. 21—29, 1962, preprint.
355. Soderberg C.R., The interpretation of creep tests for machine design,
Trans. ASME, т. 58, № 8, 1936.
356. Soderquist В., An experimental study of creep under biaxial
tension, Institut for Hallfesthetslara, Kungl. Tekniska Hogskolan, Publ.
№ 142, Stockholm, 1963.
357. Sully A. H., С a 1 e G. N„ W illoughby G., Creep of metals
subjected to compression stress, Nature, № 162, Sept. 1948.
358. Sully A. N., Creep testing in compression for simple creep assesment,
Product Engineering, т. 24, № 4, 1953.
359. Sundstrom В., Creep buckling of cylindrical shells, Trans, of the
Roy. Inst, of Technology, Stockholm, № 115, 1957.
360. Taira S., T a n а к а К., О h j i K., Creep deformation under varying
stresses, Proc. 8th Japan Nat. Congr. Appl. Mech., Tokyo, 1959.
361. Taira S., Tanaka K., Koterazawa R., Dynamic creep
characterictics of low carbon steel at eleveted temperature, Proc. 2nd
Japan Congr. Testing Mater. Kyoto, Japan, 1959.
362. Taira S., Ohnami M., Creep under rapid cycling temperatures,
Proc. 3rd Japan Congr. Testing Mater. Kyoto, 1960.
363. Taira S., Koterazawa R., Dynamic creep and fatigue of an
18—8 Mo—Cr steel at elevated temperature, Bull. JSME, t. 5, № 17, 1962.
742
БИБЛИОГРАФИЯ
364. Taira S.,Tanaka К., О h j i К., A mechanism of deformation
of metals at high temperatures with special reference to the creep after
a sudden change in stress, Bull. JSME, т. 4, № 13, 1961.
365. Taira S., Lifetime of structures subjected to varying load and
temperature, сб. «Creep in structures», Springer, 1962.
366. Taira S., Koterazawa R., Some experiments and analysis
of dynamic compression creep, Proc. 5th Japan Congr. Testing Mater.
Kyoto, 1962.
367. Taira S., Ohnami M., S а к a t о М., Influence of temperature
history on creep, Bull. JSME, т. 5, № 17, 1962.
368. Taira S., Ohnami M., Sugioka S., Creep under stepwise
temperature cycling, Bull. JSME", т. 5, № 17, 1962.
369. Taira S., Suzuki F., Relaxation and stepdown tests of metals
at high temperature, Proc. 4th Japan Congr. Testing Mater. Kyoto, 1961.
370. Taylor G. I., Analysis of plastic strain in a cubic crystal, Timoshenko
Anniversary Volume, Macmillan Co., 1938.
371. T h e i n Wan, Creep collapse of cylindrical shells, Journ. Franklin Inst.,
т. 272, № 1, 1961.
372. Turner F. H.,Blomquist K. E.,A study of the applicability
of Rabotnov's creep parameter for aluminium alloy, JAS, т. 23, № 12,
1956.
373. McVettyP. G., Creep of metals at elevated temperatures. The
hyperbolic sine relation between stress and creep rate, Trans. ASME, т. 65,
1943.
374. De Veubeke Fraeijs В., Creep buckling, сб. «High temperature
effects in aircraft structures», Pergamon Press, 1958. (Русск. пер.:
Влияние высоких температур на авиационные конструкции, Оборонгиз,
Москва, 1961.)
375. Vitovec F. H., Lazan В. J., Fatigue, creep and rupture
properties of heat resisting materials, Wright Air Dev. Center, Techn. Rep.
№ 36-181. '
376. Volterra V., Fonctions de Hgnes, Gauthier-Villard, Paris, 1913.
377. Wahl A. M., Analysis of creep in rotating disks based on the Tresca
criterion and associated flow rule, Journ. Appl. Mech., т. 23, № 2, 1956.
378. Wahl A. M., Stress distribution in rotating disks subjected to creep
including effects of variable thickness and temperature, Journ. Appl. Mech.,
т. 24, № 2, 1957.
379. Wahl A. M., Further studies of stress distribution in rotating disks
and cylinders under elevated temperature creep conditions, Journ. Appl.
Mech., т. 25, № 2, 1958.
380. Wang A. J.,PragerW., Thermal and creep effects in work hardening
elastic-plastic solids, JAS, т. 21, № 5, 1954.
381. Ward J. M., О n a t E. Т., Non-linear mechanical behaviour of
oriented polypropylene, Journ. Mech. Phys. Solids, т. 11, 1963.
382. W i m e n G., Ober den Fundamentalsatz in der Theorie der Funktionen
Ел(х), Acta Math, т. 29, 1905.
383. Winzer A., Prager W., On the use of power laws in stress analysis
beyond the elastic range, Journ. Appl. Mech., т. 14, № 4, 1947.
384. Yerkovich L. A., Investigation of the compressive, bearing and
shear creep rupture properties of aircraft structural metals and joints
at eleveted temperatures, Wright Air Dev. Center, Techn. Rep. 34-279
(ч. 3), 1958-
385. Z i e g 1 e r H., A modification of Prager's hardening rule, Quart. Appl.
Math., т. 17, 1959.
УКАЗАТЕЛЬ ИМЕН
Аннин Б. Д. 133
Арутюнян Н. X. 140, 141, 144 — 146, 212
Батдорф (Batdorf S. В.) 97, 99 — 101, 104
Баушингер (Bauschinger) 89, 106, 685
Бейпи (Baily R. W.) 169, 231, 299, 305,
430, 481, 501, 503
Беляев Н. М. 194, 195, 291, 293, 304
Бишоп (Bishop H. W.) 101
Блумквист (Blomquist К. Е.) 174
Богуславский П. Я. 501, 650
Больдман (Boltzmann L.) 124
Бразье (Brazier L. G.) 698
Бронекий А. П. 125, 126, 133
Брыэгалин Г. И. 164
Вагнер В. И. 701
Валь (Wahl A. M.) 488, 489, 544
Венкатраман (Venkatraman В.) 436, 438,
540
Веубек (De Veubeke F. В.) 678
Винцер (Winzer A.) 509
Власов В. 3. 572, 701
Волчков Ю. М. 594, 702
Вольмир А. С. 707
Вольтерра (Volterra V.) 113, 120, 122—
129, 134—137, 140, 147, 148, 209,
212 297
Вудуорд (Woodward W. В.) 142
Гуарньери (Guarnieri G. 1.) 174, 252
Гольдхофф (Goldhoff В. М.) 176
Гринвуд (Greenwood J. N.) 252
Гросс (Gross В.) 155
Давенпорт (Davenport С. С.) 196, 198
Джасман (.Talisman W. Е.) 700
Джонсон (Johnson A. E.) 211, 306, 311,
314, 316,319,325,328,335, 341,343,376
Дорн (Dorn J. E.) 175, 178, 179, 196, 219,
348, 351
Друкер (Drucker D. С.) 70, 75, 77, 78, 87,
262,386,401,402, 405, 411, 413,462,463
Дуглас (Douglas D. А.) 326
Дуффинг (Duffing G.) 125
Дэвис (Davis E. А.) 195, 200, 208
Ержанов Ж. С. 125
Журков С. Н. 180
Зверьков Б. В. 377
Зигфрид (Siegfreed W.) 373
Зодерберг (Soderberg В.) 171, 305
Зодерквист (Soderquist В.) 331
Зыкин П. Г. 707
Иванов Г. В. 10
Иванова Г. М. 221
Иванова Р. Я. 159
Ивретт (Everett F..L.) 305
Изаксон (lsaksson A.) 253
Ильюшин А. А. 63, 68, 70
Ишлинский А. Ю. 90, 114
Каптелин Ю. П. 234
Кац Ш. Н. 317
Качанов П. М. 193, 295, 360—362, 384,
421, 422, 449, 537, 626, 627
Келледайн (Calladine С. R.) 386, 401,
402, 405, 411, 413, 462, 463
Кельвин (Kelvin W. J.) 14, 114, 179, 250
Кеннеди (Kennedy A. J.) 326, 378
Кларк (Clark L. L.) 305
Клаус (Claus Г. L.) 349, 350
Клюшников В. Д. 101, 104, 107
Коистра (Kooistra L. F.) 377
Костюк А. Ф. 501, 503, 504, 509, 515
Куршин Л. М. 717, 726
Лайенис (Lianis G.) 701
Ларсон (Larson F. R.) 348—350
Ли (Lee E. Н.) 142
Лин (Lin Т. N.) 101
Лифшиц И. М. 180
Людвик (Ludwik) 170. 196
Мак-Ветти (MeVetty P. G.) 170
Мак-Комб (McComb H. G.) 635
Малинин Н. Н, 194, 195, 293, 494, 501,
504, 537
Мизес (Mises В..) 256, 276, 278, 281, 285,
305, 313, 314, 317, 321 — 333, 472, 480,
491, 501, 527, 530, 556, 704
Милейко С. Т. 10, 194, 245, 368
Миллер (Miller J.) 182, 348—350
744
УКАЗАТЕЛЬ ИМЕН
Миркин И. Л. 380
Мэнсон (Manson S. S.) 182, 348—350
Набарро (Nabarro F. R. N.) 180
Надаи (Nadai A.) 63, 73, 77, 91, 170, 291,
300
Наместников В. С. 10, 198, 218, 331, 334,
336, 342
Нахбар (Nachbar W. А.) 700
Немировский Ю. В. 10, 512
Нишихара (Nishihara Т.) 221, 325
Новожилов В. В. 49, 91
Нортон (Norton F. Н.) 305
Одинг И. А. 172, 184, 327, 330
Одквист (Odquist F. К. С.) 188, 189, 217,
218, 290, 354, 355, 362, 363, 628, 636
Онами (Olmami E.) 221, 223
Онат (Onat E. Т.) 251, 252
Opp (Orr R. L.) 348, 351
Патель (Patel Sh. A.) 436, 438, 540
Радок (Radok J. R. M.) 142
Рейснер (Reissner E.) 635, 695
Ржаницын А. Р. 114, 126, 708
Робинсон (Robinson E. L.) 174, 356
Розенблюм В. И. 355, 686
Розовский М. И. 131, 148, 212
Салли (Sully A.) 246
Сдобырев В. П. 376, 378
Серенсен С. В. 372
Серпико (Serpico J. G.) 701
Слонимский Г. Л. 125, 133
Содерберг (Soderberg С. В.) 171, 305
Соколовский В. В. 494, 533
Сундстрем (Sundstrom В.) 700
Сэндерс (Sanders J. L.) 105, 107, 635
Таира (Taira S.) 223
Танака (TanaJca К.) 221, 325
Тейлор (Taylor в. F.) 101
Тернер (Turner F. H.) 174
Титц (Tietz Т. В.) 175
Торшенов Н. Г. 247
Трунин И. И. 380
Туляков Г. А. 327, 330
Тхейн Ван 700
Уанг (Wang- A. 3.) 251, 252, 629, 631, 635,
636
Филлипс (Phillips A.) 435
Финдли (Findley W. N.) 163
Фрейденталь (Freudenthal A. M.) 671
Хармс (Harms W. О.) 326
Хаферд (Halerd A. M.) 182, 348, 350
Хвостунков А. А. 198, 218
Хенки (Hencky H.) 63, 73, 77, 91, 291,
354, 355
Хилл (Hill R.) 101
Ходж (Hodge P. С.) 9 5, 96
Хофф (Hoft N. J.) 189, 354, 362, 373, 380,
678, 679, 682, 686
Хуан Кэ-чжи 96
Циглер (Ziegler H.) 90
Чикала (Cicala P.) 99, 100
Чуриков Ф. С. 208, 294
Шенли (Shanly F. К.) 671, 673, 677, 678
Шепеленко В. Н. 698
Шерби (Sherby О. D.) 348, 351
Шестериков С. А. 627, 632, 682, 718
Шилд (Shield R. Т.) 90
Шима 325
Шлехте (Schlechte F. R.) 635
Шорр Б. Ф. 201, 248, 609, 611
Эндрейд (Andrade da С.) 171, 420
Ягн Ю. И. 69
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алюминий (сплав) 208, 214, 247, 313,
375
Анизотропия деформационная 298,
311
— ползучести 278, 281, 282,
287
— упрочнения 257, 258, 339
Арка 693
—, устойчивость 693, 698
Базис взаимный 25, 41
— локальный 37, 42
— основной 41
Балка, деформация изгиба 441
— на упругом основании 148
— с закрепленными концами 444,
669, 692
— с шарнирными концами 665
— статически неопределимая 443
Бетон, ползучесть 14, 109, 122, 140,
144
Вектор 17, 18, 21, 28
— взаимного базиса 26
— девиаторов деформации 66
— — скоростей деформации 268
— напряжения 38, 39, 66
—, преобразование составляющих
17, 27
Возврат 298
Время
— до разрушения 13, 254, 353, 602,
651, 654
— — — приведенное 348
— запаздывания 110
— критическое 660, 670, 677, 681,
686, 719
— — сжатого стержня 670
— приведенное 179
— релаксации 110, 118
Выпучивание 678, 687, 689, 719, 724
— мгновенное 678
— оболочек 701, 722
— осесимметричное коротких
цилиндров 701
— пластин 722
Вязкость 108, 125
Вязко-упругость 108, 109, 698
Гипотеза (теория) Качанова 360
— Кирхгоффа — Лява 518, 563, 570,
643
— потенциала ползучести 337
— упрочнения 295, 602
кинематического(Ишлинского—
Прагера) 90, 214, 217, 218
— уравнения состояния 196, 219
Девиатор деформаций 68
— напряжений 46, 47, 48, 68
Депланация сечения 458
Деформация балок и рам при изгибе
441
— конечная 16, 38, 41
'— критическая 691
— логарифмическая 661
— малая 16, 37
— мгновенная упругая 114, 168
— необратимая 11, 62
— обратимая 15, 114
— пластическая 62, 65, 237, 311
— — мгновенная 233, 362, 611,
671
— ползучести 12, 13, 62, 114
— — как мера упрочнения 223
— — критическая 691
— — необратимая 192, 687
— сдвиговая 60, 236
— упругая 67, 83
—, условия совместности 44, 69
746
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Диаграмма длительной прочности
346, 652
Диск (вращающийся) 471, 486
—, автофреттирование 487
—, выбор профиля 486, 487
— гиперболического профиля 515
—, интегрирование уравнений
ползучести 494, 500, 506
—, лопаточная нагрузка 493
— на жестком вале 616
— на упругом вале 617
—, ползучесть 488, 492
—, профилирование 486
— равного сопротивления 496
—, разрушение хрупкое 654
—, релаксация натяга 487
-- с тяжелым ободом 619
— с цельнокованым ротором 487
— с центральным отверстием 492
— сплошной 488
— ступенчатого профиля 617
Диссипация энергии при ползучести
261, 298
Дифференцирование ковариантное 35
Диффузия 180, 229
Долговечность дисков 652
— материалов 362, 383, 671
— сооружений 13
Жаропрочность технических сплавов
12, 179, 238, 246
Жидкость нелинейно-вязкая 193
Задача общая теории наследственной
упругости 134, 137, 156
— с переменными граничными
условиями 140
Задачи выпучивания 687
— динамические 149
— геометрически нелинейные теории
ползучести 660
— плоские осесимметричные 471
— пространственные 146
— релаксационные, метод Шестери-
кова 632
— статически неопределенные 386,
442
— устойчивости 101, 249, 679
— — в нелинейной постановке 704
— — для подвижной нагрузки 156
Закон вязкости Ньютона 109, 125
— Гука 12, 109, 125, 134, 146, 158,
193, 194, 250
— коммутативности нагружения 217
— наследственности 120
— ползучести 118, 284
— — для оболочек 557
Закон ползучести изотропной 260
— — логарифмический 120
— — при переменной температуре
219
— —, специальные формы 266
степенной 125, 253, 310, 401,
422, 585
— — экспоненциальный 399, 401
Эндрейда 202, 720
— релаксации 210
— течения типа Сен-Венана 296
— упрочнения 200, 203, 205, 713
— упругости для сдвиговой
деформации 60
— — линейной 57
— — нелинейной 60, 191
— — при разгрузке 65
Зоны пластические 79
Изгиб балок 441, 665
— стержней 423, 424, 427, 429
— — продольно-поперечный 466
— — произвольного сечения 428
— — с защемленными концами 660
— — тонкостенных 437
— турбинных лопаток 430
Изотропия упрочнения (проверка)
334, 336
Инвариант 19, 21, 22
— девиатора 49
— квадратичный 22
— линейный 22
— тензора деформации 50
— — скорости деформации 50
Индексы тензоров — поднятие,
опускание 29, 30
Интенсивность деформации 52
— — ползучести 298, 336
— — — как мера упрочнения 336
— касательных напряжений 275
— напряжения 47, 60, 268
— скоростей деформации 52, 268,
269
Искривление начальное 679, 689
История нагружения 77, 78
Исследования Арутюняна 140, 144
— Бейли 169, 231, 299, 304
— Беляева 194, 291
— Беляева — Малинина 293
— Брызгалина 164
— Будянского 73
— Гварниери 174, 252
— Гольдхоффа 176
— Гринвуда 256
— Девиса 195
— деформирования пластического 68
— Джонсона 211, 306, 314, 374
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
747
Исследования длительной
прочности 372
— до разрушения материала 651
— Дорна 174, 178, 179
— Друкера 70, 87
— Дуффинга 125
— Зодерквиста 331
— Ивановой 221
— Ивретт — Кларка 305
— Ишлинского 114
— Каптелина 234
— Каца 377
— Качанова 360, 361, 362
— Кеннеди, Хармса, Дугласа 326
— Клауса 349, 350
— Клюшникова 101, 104
— кратковременной ползучести 245
— кручения 271
— Лифшица 180
— методом колец Одинга 184
— Милейко 245
— Надай 170
— Наместникова 331, 336, 342
— Нишихары, Танаки, Шимы 325
— Нортона 305
— Одинга 72, 231
— Одквиста 354, 362
— ползучести при сжатии 245
— Попова 200
— при сложном напряженном
состоянии 306
— при циклических изменениях
нагрузки 196, 225
— растяжения 235, 271
— Ржаницына 114
— Робинсона 169
— Розенблюма 358
— Салли 246
— Сдобырева 376
— Содерберга 171, 305
— сплавов 242, 244, 307, 313, 349
— ступенчатого изменения нагрузки
196, 225
— Торшенова 247
— Филлипса 435
— Хенки 354, 355
— Ходжа 95
— Хоффа 354, 362, 373
— Эндрейда 171, 202, 214
— экспериментальные 68, 108, 155,
— 156, 162, 166, 169, 184, 195, 208,
213, 214, 252, 269, 303
История нагружения 77, 78
Кольцо жесткое 591
Компоненты (составляющие) вектора
17, 27
Контур нагружения 83, 85
Конус пластичности 77, 78
Концентрация напряжений 347
— — у отверстия в пластинке 509
Координаты декартовы 17, 41
— криволинейные 30, 41
— неортогональные 25, 41
Коэффициент концентрации
напряжений 512
— Пуассона 59, 135
Кривая длительной прочности 345,
363
— мгновенного деформирования 174,
198, 235, 237, 241
— ползучести 167, 168, 191, 281, 353,
365, 368
— —, влияние температуры 177
изохронная 174, 191, 206, 649,
653
, их подобие 172, 308
— — кратковременной 188
— —, экстраполяция 169
— —, эмпирические формулы 109
— релаксации 210
— — опытная 206
— —, предсказание по кривым
ползучести 185, 199, 225
Критерии длительной прочности 376
— устойчивости 715
Критерий пластического состояния
92
— ползучести, квадратичный (Ми-
зеса) 472, 473
— — наибольшего касательного
напряжения 281, 473, 474
— — обобщенный типа Треска, Сен-
Венана 285, 301, 472, 479, 493,
527, 546
— — приведенного напряжения
281, 285, 483, 484
типа Мизеса 281, 472, 527
Кручение стержней 423
— — тонкостенных замкнутого
профиля 450
— труб тонкостенных 64, 67, 269, 271
— — — двухсвязного сечения 451
— — — многосвязного профиля 452
— — — открытого профиля 454
Линеаризация исходного уравнения
ползучести 249, 605
Матрица коэффициентов
анизотропии 285
Мембрана 664
Мера деформации логарифмическая
661
748
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Мера ползучести 144
— растресканности 363
— упрочнения 224, 226, 296, 298,
301, 334—337
Металлы, их ползучесть 166, 238,
320—339
Метод вариационный 634
— Галеркина 537, 582, 676, 707
— Рейснера 635, 695
— смешанный 634, 687, 689, 692
Моделирование 11, 91
— оболочек 566
— ползучести 399
Модель двумерная (упругого тела) 78,
100
— Кельвина 114
— кинематическая 90
— нелинейного упругого материала
191
— плоского тела 101
— реологическая 108, 111, 125
— упруго-пластической системы 78,
79
— Шенли 671
Модули упругости, их число 57
Модуль касательный 74, 82, 250
— пластический 63, 66, 73, 80
— ползучести 250
— сдвига 61, 135
— секущий 74
— упругости 57, 59
— — длительный 112, 250, 711
— — комплексный 151
мгновенный 112, 122, 708
— — объемный 58, 63, 64
— Юнга 13, 135
Нагружение динамическое 124
— нейтральное 67
—, параметр 68
— переменное 218
— по программе 245
— пропорциональное 68, 79, 81, 331
—, скорость его 241
— ступенчатое 196, 213, 217
Нагрузка лопаточная 653
— переменная 213
— подвижная 156
— реверсивная 246
—, ступенчато изменяющаяся 213
— циклическая 252
Наклеп 196, 267
Направление октаэдрического
сдвига 52
Напряжение 9, 38 39, 40, 44, 189
— главное 45, 49
— допускаемое 13
Напряжение, интенсивность его 47
— истинное 352
— касательное 44, 67
— номинальное 352
— нормальное 44
— обобщенное 523
— октаэдрическое 373
—, условие постоянства 67
Наследственность 209, 210, 212
— нелинейная 212
Нимоник (сплав) 307, 313
Нить гибкая 662
Оболочка 549, 551
— безмоментная 551, 555, 558
— вращения безмоментная 5."j8
—, гипотеза Власова 572
— гладкая 700
— двухслойная, модель 563
—, деформации и перемещения 555
— круговая цилиндрическая 571,
581, 597
— — —, краевой эффект 598
— — —, осесимметричная
ползучесть 581
— многослойная 560
—, ползучесть 517, 549, 581
— полубезмоментная 572
— полубесконечная 586
— — с защемленным краем 589
— — с шарнирно укрепленным
краем 592
—, потенциал скоростей 601
—, сплющивание 698, 700
—, техническая теория 551, 571,
568, 577, 595
Оператор Абеля 128
— Вольтерра 135
— наследственности 130
— упругий 134, 135
Операторы интегральные 297
—, умножение их 129
— формулы асимптотические 132
Ось нейтральная (в неупругом
изгибе) 426, 430, 436, 437
Отклонения малые (от состояния
ползучести) 249
Охрупчивание 351, 357, 363, 655
Параметр Ларсона — Миллера 182,
348
— Мэнсона — Хаферда 348
— нагружения 68, 88
Параметры анизотропии 286
— деформационного упрочнения 232
— охрупчивания 363, 364
— состояния 298
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
749
Параметры структурные 224, 363
— температурно-временные 181, 182
— упрочнения 252
Перемещение 42
—, жесткий поворот 44
— поступательное 44
— упруго-мгновенное 146
Пластина 136, 536
—, вариационные методы (Галерки-
на, Лагранжа, Ритца) 536
—, изгиб распределенной нагрузкой
544
— круглая, ползучесть по теории
типа Мизеса 530
, Треска 537
— не круглая 547
—, ползучесть при изгибе 526
—, скорость прогиба 536
—, уравнения ползучести 523
Площадка октаэдрическая 47
Поверхность деформирования 66
— нагружения 67, 72, 75, 77, 86,
91, 92, 95, 96, 105
— постоянной диссипации 361, 404,
405, 412, 417
— текучести 81, 105
Повреждаемость 356, 359, 362
Повреждение усталостное 372
Повреяеденность 356
Подобие кривых ползучести 172
Поле векторное 32
Ползучесть 9, 12, 205, 287, 386, 645,
648
— анизотропная 258, 281, 314
— без упрочнения 288, 354
— бетона 9, 109, 140, 144
—, влияние высоких температур 10,
12
— горных пород 9, 125
— динамическая 252
— диска 471, 486, 605, 613, 615, 618
— — при кручении 423
— — при чистом изгибе 423
— диффузионный процесс 180
— изотропная 258
— квазиустановившаяся 256, 299,
300, 645
— кратковременная 187, 188, 236,
238, 243, 257, 366, 368
— линейная 696
— металлов 9, 10, 12, 109, 166, 186,
209, 212, 307
— наследственная 209
— — при разгрузке 210
— неустановившаяся 168, 202, 239,
256, 288, 602, 613, 618, 621
— оболочек 517
Ползучесть, определение времени до
разрушения 651
— пластин 517, 643
— пластмасс (полимерных
материалов) 9, 108, 162, 212, 213
— при кручении 447
— при переменных нагрузках 334
— при постоянных нагрузках 306
— при растяжении 241
— при сжатии 246
— при сложном напряженном
состоянии 255, 306, 334
— при ступенчатом изменении
нагрузки 196, 213
— стержня 608, 689
— — с упрочнением 640
— установившаяся 168, 182, 186,
188, 201, 202, 256, 386, 396, 405,
423, 471, 517
— цилиндра 621
Последействие объемное 135
— сдвиговое 135
— упругое 114
Постоянное Ламе 58, 59
Постулат упрочнения Друкера 70,
77, 78, 262
Потенциал кусочно линейный 285
— моментов 526
— напряжений 387, 521
— ползучести 261, 265, 271, 284,
295, 297, 334, 337, 386
— сил 395
— скоростей ползучести 262, 387,
422, 441, 461, 556
— — — для оболочек 556
— упругий 56, 60, 283
— усилий и моментов 521
Потеря устойчивости неупругой
системой 671, 701, 720
Предел длительной прочности 13,
239, 345
— ползучести 12
— — условный 13, 181, 345
— текучести 89
— — вторичной 92
Принцип вариационный 386, 390,
393, 449, 456, 602
— — в задаче изгиба 637
Галеркина Б. Г. 537, 582, 676,
701
Кастильяно 265, 386, 392, 449,
457, 458, 582
— — Качанова 628
Лагранжа 265, 386, 390, 449,
457, 458, 582
Ритца 536, 537, 548
— — смешанный 634, 687
750
предметный указатель
Принцип вариационный Уанга —
Прагера 629
— Вольтерра 134, 147
— линейного суммирования
повреждаемости 356, 359, 362, 652
— линейной суперпозиции 87
— минимума дополнительного
рассеяния 392
— — мощности 391
— Онзагера 136
Прогиб критический 678, 682
Пространство девятимерное 55
— деформаций 56, 66
— нагружения 67
— напряжений 56, 67, 261
— обобщенных сил 394
— скоростей
— — деформации 264
Профиль тонкостенный 431
Прочность длительная 344, 347, 348,
372, 383
— —, критерий 344
— кратковременная 383
Работа дополнительная 56, 71
Разброс опытных данных 312
Разгрузка 65, 70, 78, 83, 210
— мгновенная 211
— упругая 77, 83
Разрушение вязкое 344, 351, 361,
379, 661
— длительное 344, 370, 379
— — при сложном напряженном
состоянии 372, 379
—, общая теория 383
— при циклических нагрузках 370
— с охрупчиванием 357
— смешанное 344, 360, 366
— усталостное 370
— —, зависимость от амплитуд
цикла 371
— хрупкое 344, 346, 355, 361, 363,
379
Разупрочнение 122, 229, 248
—, скорость его 229
— температурное 229, 230
Рама, изгиб 441
— квадратная 469
— прямоугольная 445
Распределение напряжений
линейное 433
Растяжение 64, 235
— с кручением 303
Реверсирование нагрузки 246
Релаксация НО, 117, 145, 183, 192,
205, 210, 339, 632
Ресурс 13
Свертывание тензоров 22
Сдвиг 60, 63, 64
— октаэдрический 52, 67
— —, его скорость 52
Символы Кристоффеля 33, 34, 35,
558
— Кронекера 19, 26
Скольжение 96, 97
— пластическое 78
Скорость выпучивания 678
— деформации обобщенная 523
— — срединной поверхности 521
— изменения кривизны 441, 521
— нагружения 241
— накопления усталостного
повреждения 372
— октаэдрического сдвига 52, 312
— перемещения обобщенного 392
— ползучести 12, 168, 177, 202,
222, 231, 243, 309, 353
— распространения фронта трещин
257
— сдвига 277
Состояние деформированное 36
— — плоское 471
— критическое 704
— напряженное 36, 64, 379, 380,,
473
Спектр ползучести 121
— релаксации 121
Сплавы 242, 244, 307, 313
Сплющивание оболочек 698, 700, 701
Способ Качанова 421
— кинематический в расчете ферм
416
Среда анизотропная 256, 283
— вязко-упругая линейная 108
— изотропная 256
— сплошная 36
Сталь 12, 62, 69, 238, 240, 307, 32а
Старение 190, 229, 232, 237
— бетона 14, 120, 122, 140, 144, 145
Стержень 432, 458, 459, 461, 633,
670, 681, 689, 692
— идеально пластический 423
— идеального двутаврового сечения
464, 675, 678
— тонкостенный 423, 432
Тело вязко-упругое 108, 109, 117, 119,
696
— — Максвелла 110
Фохта 14, 110, 111, 114, 250
— идеально пластическое 70
— изотропное 58
— — наследственно-упругое 135
— линейно-упругое 58
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
751
Тело нелинейное 56
— пластическое 18, 89
— упругое 54, 55
Температура: влияние на временное
сопротивление 239
— : — на скорость ползучести 177,
229
—, ее быстрое изменение 219, 220,
221 223
Тензор 16, 17, 18, 19, 20, 22, 25,
28
— анизотропии 283
— деформации 37, 42
— — конечной 38
— единичный 19
—, компоненты его 20
— метрический 29, 31
— напряжений 40, 44, 46, 295
—, преобразования 18
— скоростей деформации 50
— — ползучести 295
— упругих постоянных 252
— шаровой 24
Теорема Бетти 137
— Бредта о циркуляции
касательного напряжения 448, 451
— Кастильяно 393, 405, 406, 407,
412, 422, 425, 431, 443
— Келледайна — Друкера 401, 411,
413
— Лагранжа 416
— Леви 136
Теории ползучести 303
— — квазилинейные 280
— — при сложном напряженном
состоянии 303
— — физические 171, 178
Теория вязко-упругости 108, 109,
117, 119, 136, 696
— деформаций конечных 41
— наследственности 108, 109, 210,
254, 712
— оболочек 411
— пластичности 9, 11, 47, 62, 63,
65, 70, 75, 86
— — анизотропных сред 283
— — Ватдорфа, Будянского 97, 121
— — деформационная 63, 65, 70, 86,
91, 292
— — Ильюшина 63
Надаи — Хенки 63, 77, 91, 291
— — Сен-Венана — Треска 91, 92
— ползучести 9, 10, 13, 61, 62, 182,
185, 186, 188, 195, 256, 291, 386,
388, 471
Бейли 304, 305
— — Беляева 293
Теория ползучести, геометрически
нелинейные задачи 660
— — диффузионная 180, 229
Качанова 360, 362
— — типа Мизеса 256, 276
Сен-Венана 276, 289, 296,
315, 317, 318, 321, 324, 326, 329,
480
физическая 9, 171, 178, 180
— разрушения 363
— скольжения (Ватдорфа,
Будянского) 91, 97, 101
— старения 190, 193, 194, 196, 198г
292, 293, 294, 383, 471, 602, 648
Качанова 193, 293
— течения 86, 88, 193, 295
— — с трансляционным
упрочнением 89
— упрочнения 196, 198, 205, 208г
224, 226, 294, 298, 336, 602, 627
— упругости 9, 86, 209, 386, 387
— — наследственной 10,119,134,157
Течение вязкое 119, 255
— квазивязкое 186, 202, 250
Тождество Кэли — Гамильтона 260
Трансформация (преобразование)
Лапласа 121, 137, 140
Трещинообразование 347, 374, 383,
384
Труба криволинейная, чистый изгиб
575
— толстостенная 471, 475, 662
— тонкостенная 64, 67, 79, 260, 303,
305, 377, 439, 661
— упруго пластическая 79, 104
Удлинение при разрыве 365
Умножение диадное 19
Упрочнение 79, 196, 291
— деформационное 229, 232
— изотропное 86, 95, 336
— кинематическое 90, 95
—, мера его 298, 299, 301, 336
— при переменных нагрузках 213,
248
— трансляционное 89, 95
Упругость линейная 57
— наследственная 15, 134, 137
Уравнение интегральное типа Воль-
терра 113
— — второго рода 127
— кривой кратковременной
ползучести 244
— мгновенной кривой
деформирования 234
— Одинга 172
— ползучести 194, 224, 239
752
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнение состояния 196, 201, 202,
217, 233, 234, 251, 253
Уравнения деформационной теории
пластичности 86, 194
— ползучести 194, 223, 224, 239, 248,
274, 295, 396, 722
— — пластин 523
— совместности деформаций 69
— теории наследственной упругости
136, 145, 157, 212
— — пластичности 62
— — старения 295
— — упругости 146, 194
течения 88, 295
Условие совместности деформаций
Сен-Венана 44
— хрупкого разрушения 359
Усталость 370
Устойчивость 386, 671, 677, 678, 708,
711, 712
— в смысле Ляпунова 711
—, критерии условные 711, 715,
716
—, критерий Куршина 717
—, — Шестерикова 718
— линейного вязко-упругого тела
696, 708
— и неустойчивость системы 677,
678, 712
— оболочек 698
— стержней 708, 713
— цилиндрической панели 707
Фермы, расчет ферм 265, 386, 405,
406, 412, 416, 421
Формула Грина 54, 509
— Коши 116
Формулы деривационные Гаусса-
Вейнгартена 551, 557
— эмпирические кривых ползучести
169
Функции Миттаг-Леффлера 132
— ползучести 153
— релаксации 153
Хлопок 695, 708
Цикл замкнутый Вольтерра 122, 140
Цилиндр толстостенный 142, 479
Швеллер со стенкой постоянной
толщины 438
Штамп жесткий — его движение 159,
160
Экстраполяция кривых ползучести
169
Энергия активации 178, 364
— диссипации (рассеяния) 261, 298
— упругая деформированного тела
387
Эффект Баушингера 89, 685
— краевой оболочки 550, 588, 598
Ядро Абеля 125, 126
— Вронского — Слонимского 125
— интегрального уравнения 119,
120
— наследственности (сингулярное)
124, 145
— — Больцмана 124
— — общего типа 140
— ползучести 118, 121, 153, 712
— релаксации 117, 121, 153