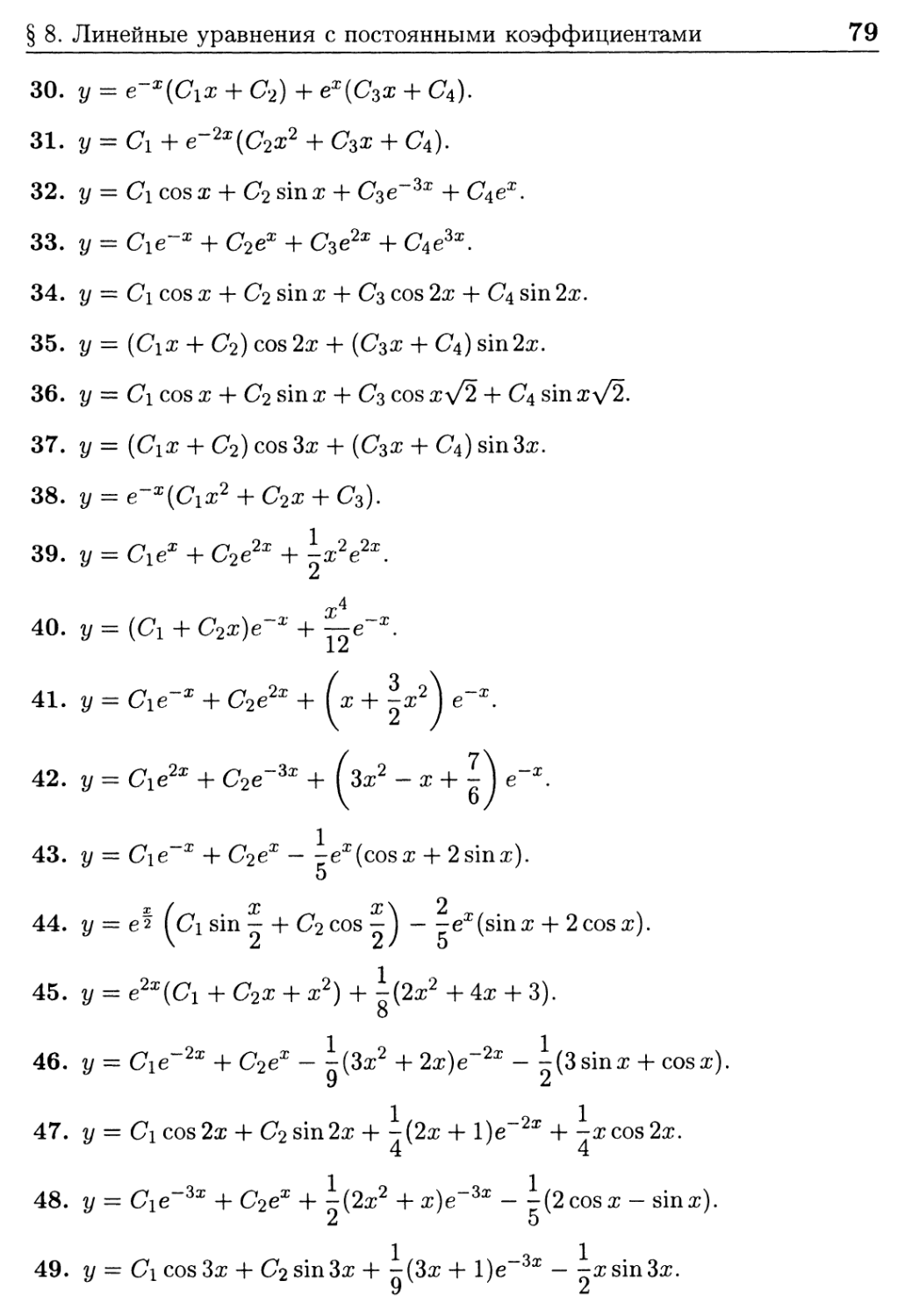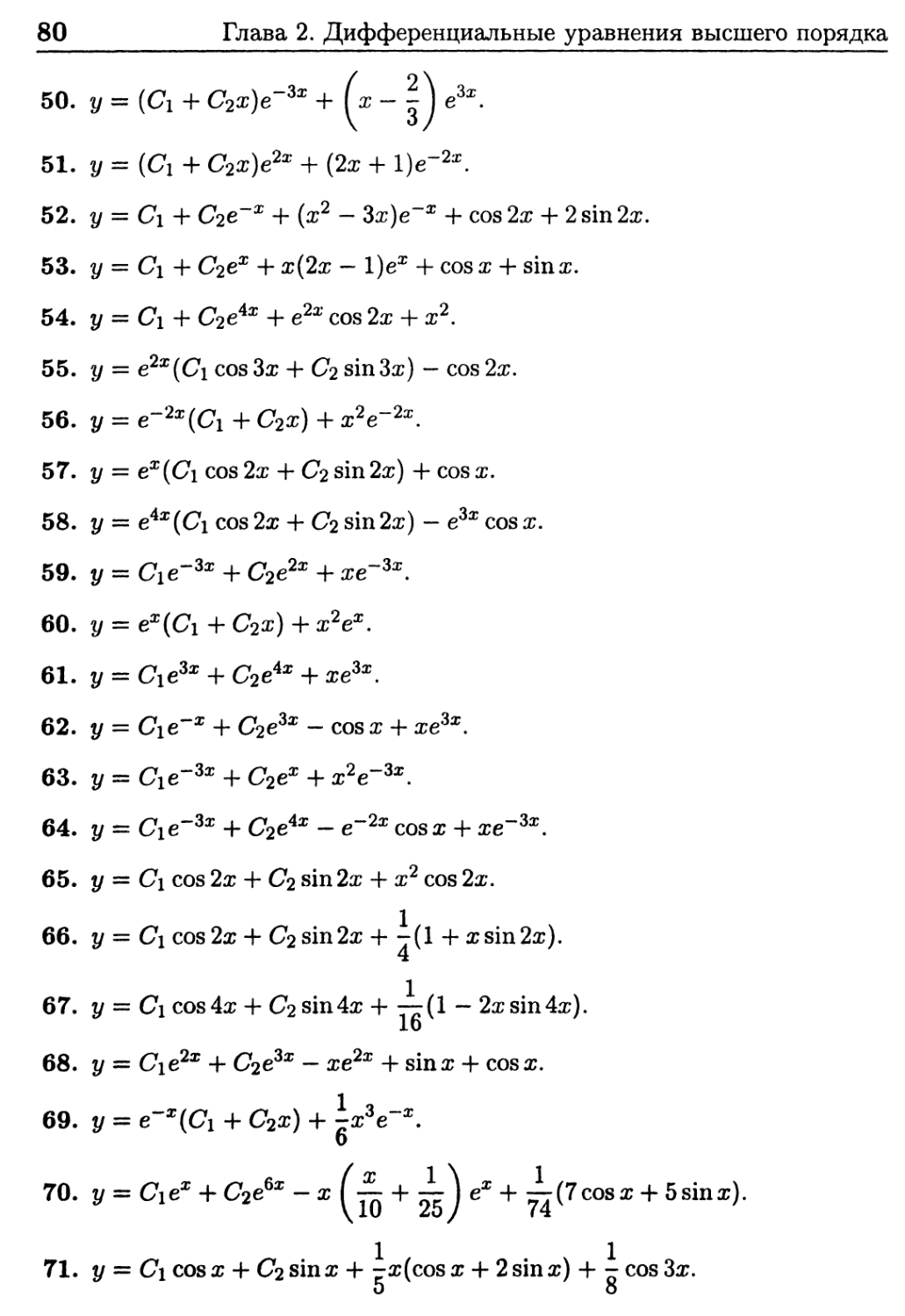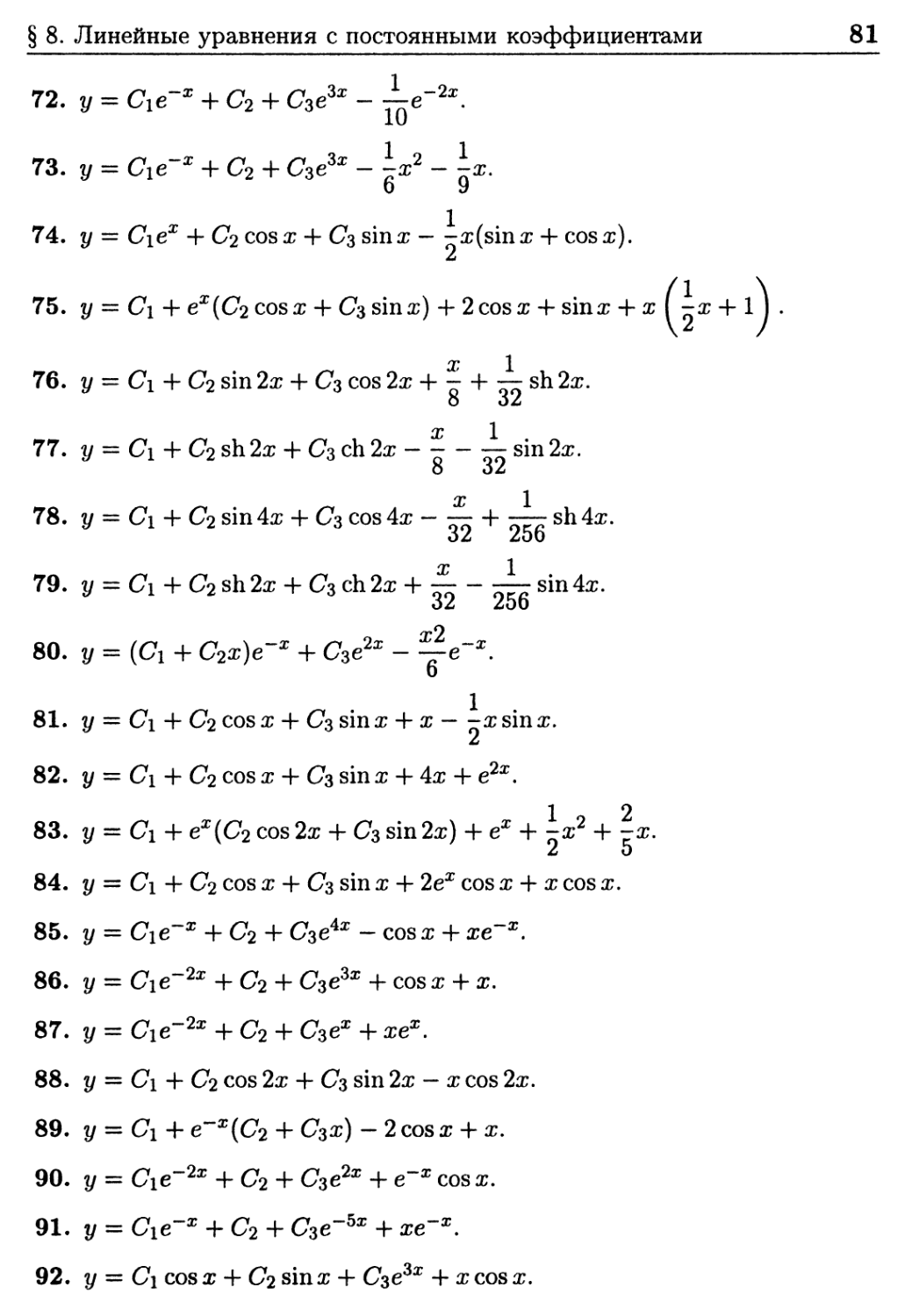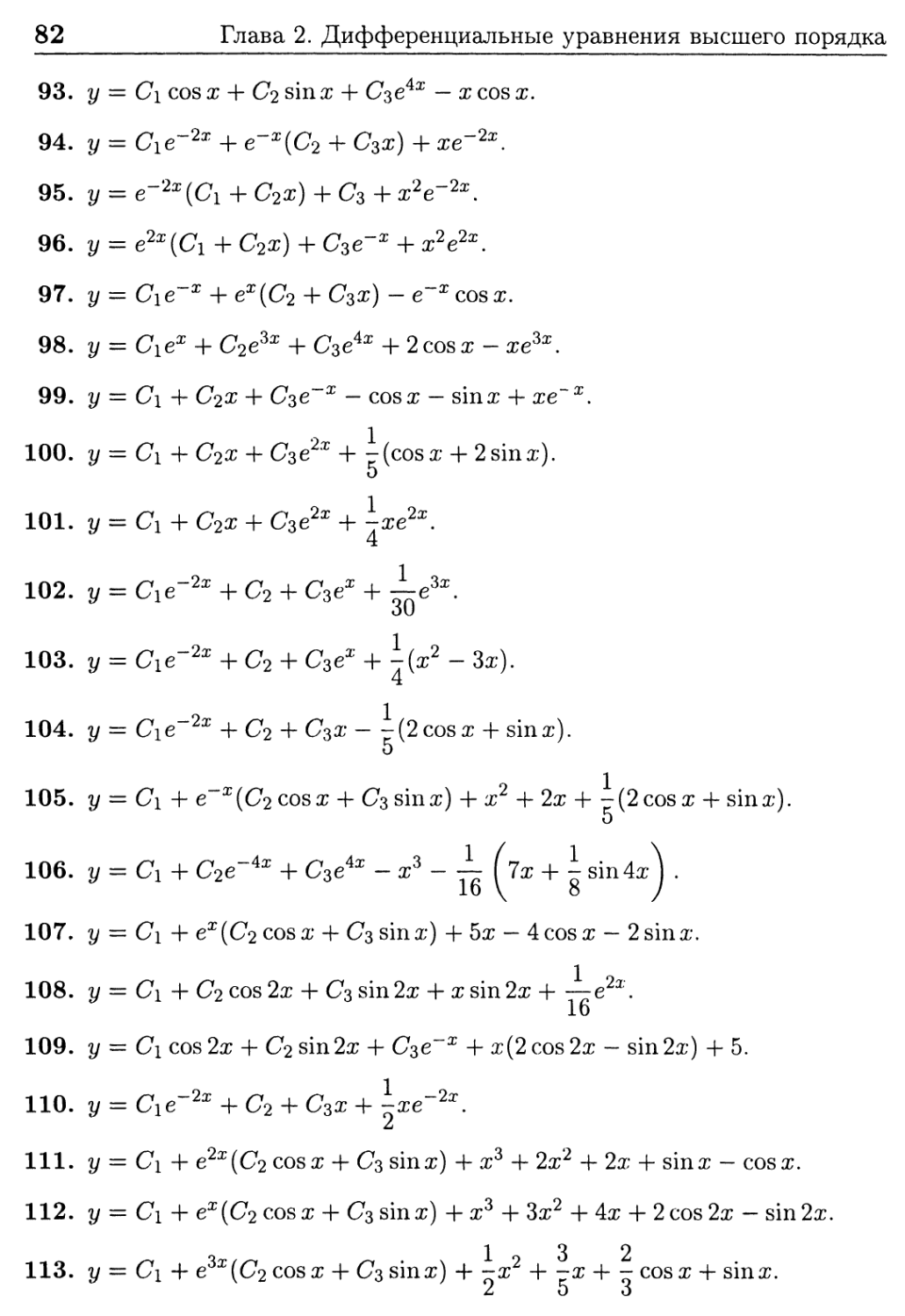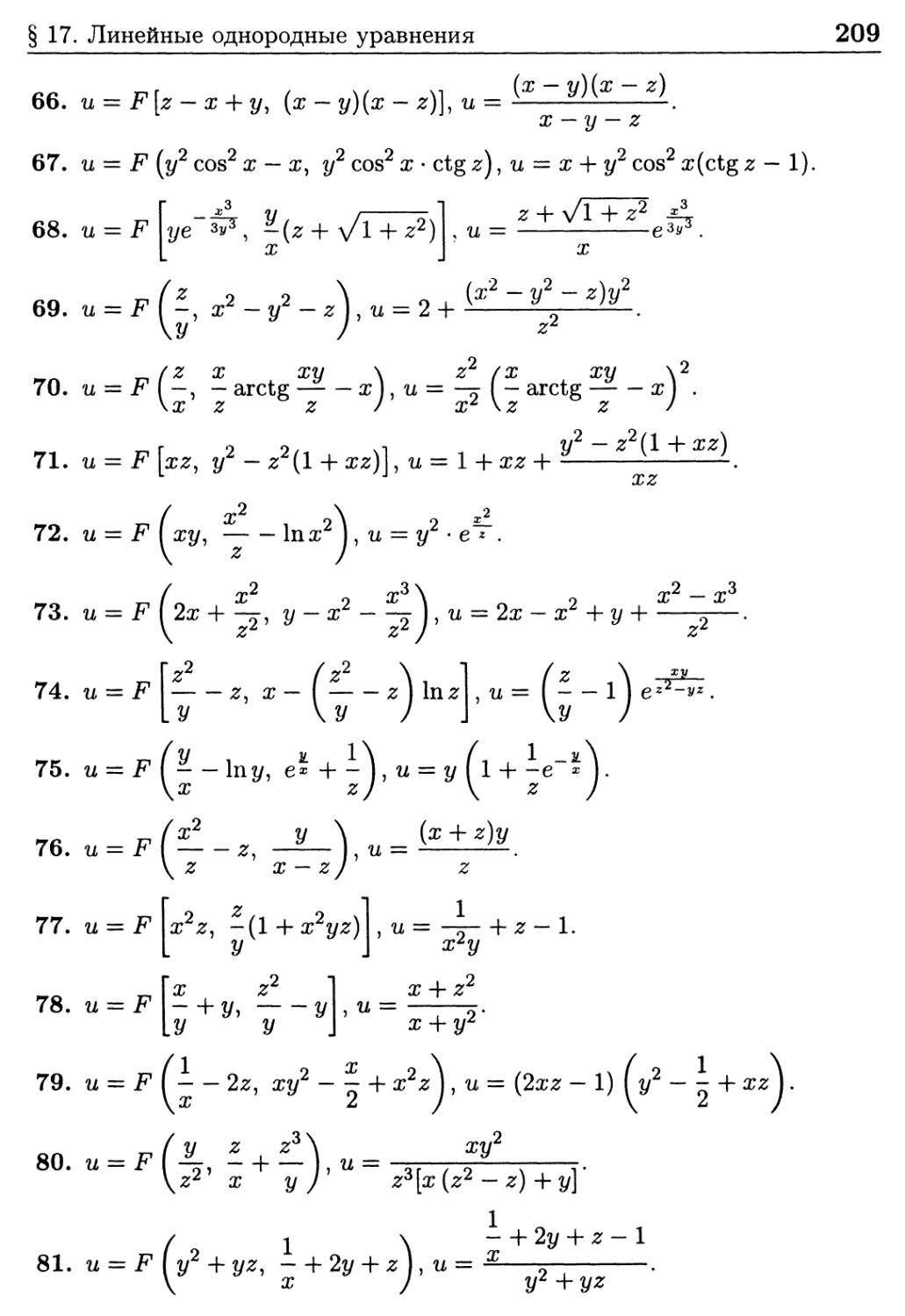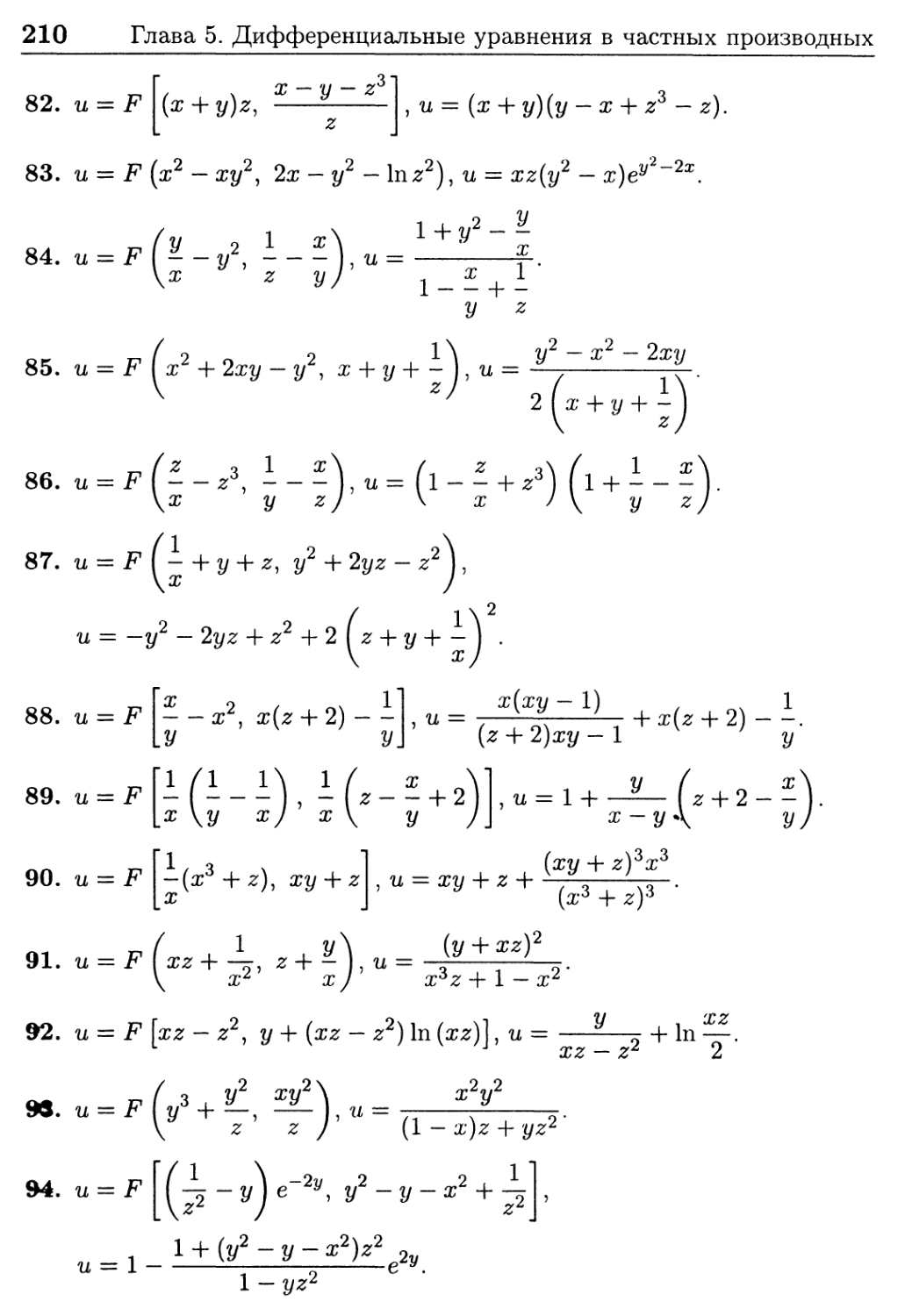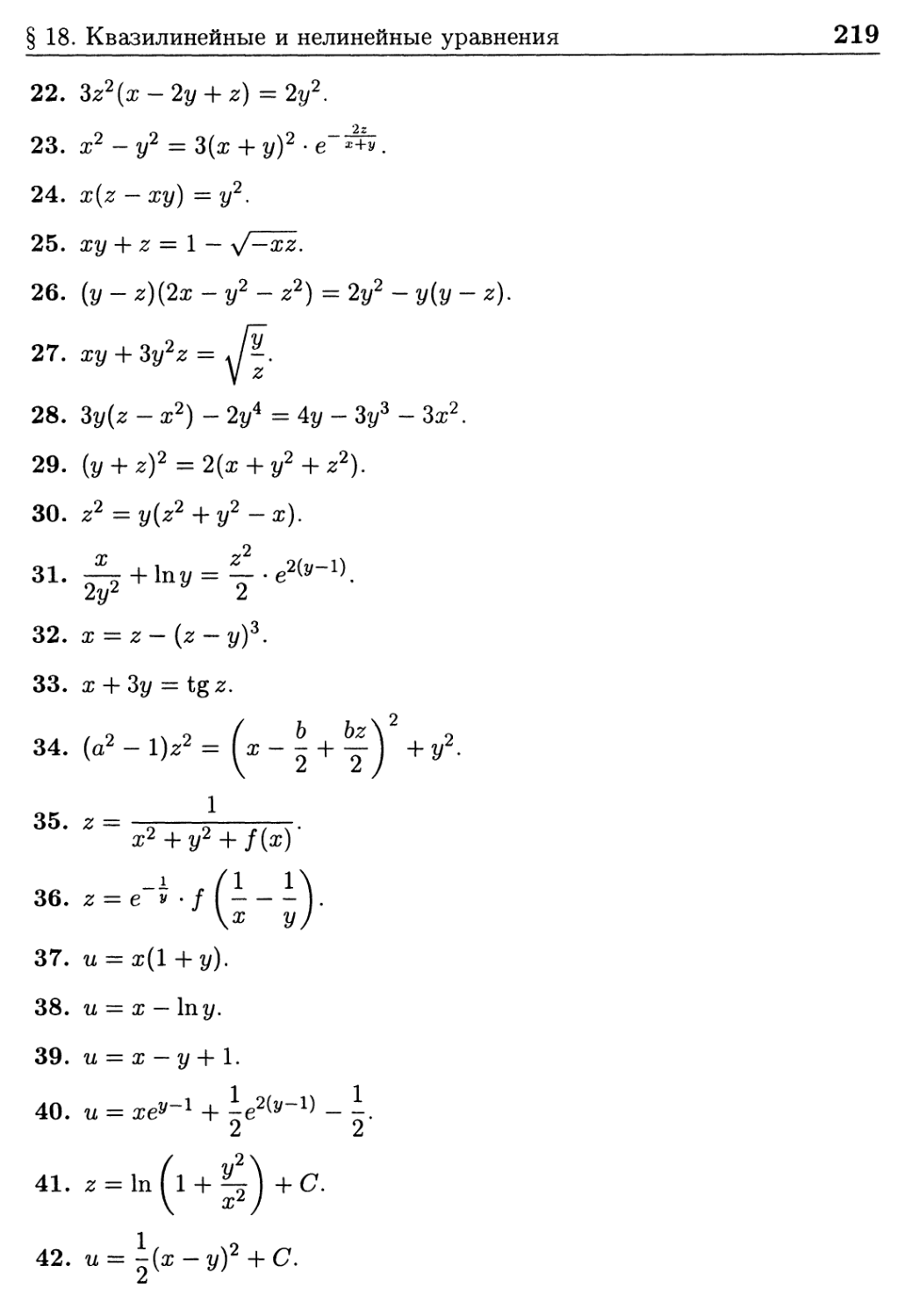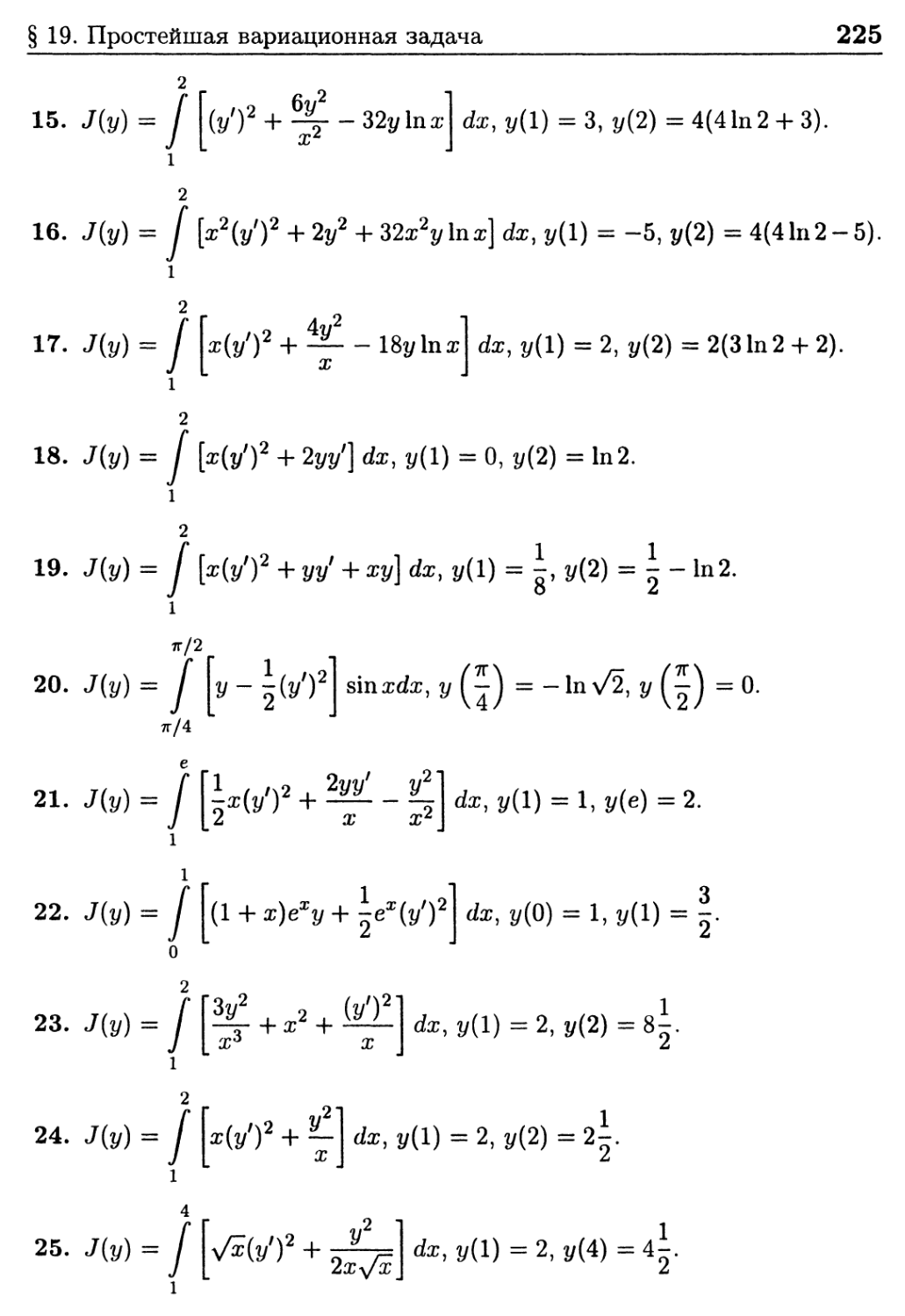Текст
технический тш университет
!|8.
в. к. Романко, Н. X. Агаханов, В.В.Власов, Л.И.Коваленко
СБОРНИК ЗАДАЧ ПО
ДИФФЕРЕНЦИАЛЬНЫМ
уравнениям
ВАРИАЦИОННОМУ
исчислению
Под редакцией В. К. РОМАНКО
%
Москва
Лаборатория Базовых Знаний
ЮНИМЕДИАСТАЙЛ
ФИЗМАТЛИТ
2 00 2
УДК 517.9
ББК 517.2
Р69
Под редакцией В. К. Романко
Романко В. К.
Р 69 Сборник задач.по дифференциальным уравнениям и вариационному
исчислению/В. К. Романко, Н. X. Агаханов, В. В. Власов, Л. И. Коваленко. —
М.: ЮНИМЕДИАСТАЙЛ, 2002. - 256 с: ил.
ISBN 5-93208-120-1
Задачник обеспечивает практические занятия по курсу «Дифференциальные
уравнения и вариационные исчисления». В начале каждого параграфа приводятся
решения типовых задач. Ко всем задачам даны ответы.
Для студентов физико-математических, инженерно-физических и
экономических специальностей.
УДК 517.9
ББК 517.2
Серия «Технический университет»
Учебное издание
Романко Василий Кириллович
Сборник задач по дифференциальным уравнениям
и вариационному исчислению
Художественный редактор Н. Лозинская
Технический редактор Т. Бленцева
Оригинал-макет подготовлен в пакете LAT^X 2^
с использованием кириллических шрифтов семейства LH
Гарнитура Computer Modem
Лицензия на издательскую деятельность № 066140
от 12 октября 1998 г.
Подписано в печать 13.03.02. Формат 70x100'/,^. Бумага офсетная.
Печать офсетная. Усл. печ. л. 20,64. Тираж 5000 экз. Заказ 1374
000 Издательство «Лаборатория Базовых Знаний»
Адрес для переписки: 103473, Москва, а/я 9
Телефон @95)955-0398. E-mail: lbz@aha.ru
Гигиеническое заключение 77.99.2.953.П.9816.3.00 от 22.03.2000 г.
Отпечатано с готовых диапозитивов в полифафической фирме
«Полиграфист*. 160001, г. Вологда, ул. Челюскинцев, 3.
© Романко В. К., Агаханов Н.Х.,
Власов В.В., Коваленко Л.И., 2002
ISBN 5-93208-120-1 © ЮНИМЕДИАСТАЙЛ, 2002
ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Дифференциальные уравнения первого порядка 6
§ 1. Составление уравнений заданного семейства плоских кривых.
Приближенное изображение интегральных кривых уравнений ... 6
Ответы к задачам §1 9
§ 2. Уравнения с разделяющимися переменными. Ортогональные
траектории. Однородные уравнения 10
Ответы к задачам § 2 16
§ 3. Линейные уравнения первого порядка. Уравнения Бернулли и
уравнения Риккати 19
Ответы к задачам § 3 24
§ 4. Уравнения в полных дифференциалах. Интегрирующий
множитель. Замена переменных 27
Ответы к задачам § 4 31
§ 5. Исследование задачи Коши 32
Ответы к задачам § 5 42
§ 6. Уравнения первого порядка, не разрешенные относительно
производной. Особые решения 44
Ответы к задачам § 6.. * 48
Глава 2. Дифференциальные уравнения высшего порядка 52
§ 7. Основные типы уравнений, допускающие понижение порядка
уравнения 52
Ответы к задачам § 7 62
§ 8. Методы решения линейных уравнений с постоянными
коэффициентами. Уравнения Эйлера 65
Ответы к задачам § 8 78
§ 9. Методы решения линейных уравнений второго порядка с
переменными коэффициентами 88
Ответы к задачам § 9 96
§ 10. Теорема Штурма. Граничные задачи 101
Ответы к задачам § 10 107
Глава 3. Линейные системы дифференциальных уравнений 109
§ 11. Методы решения линейных систем уравнений с постоянными ко-
4
эффициентами 109
Ответы к задачам § 11 127
§ 12. Линейные системы уравнений с переменными коэффициентами .. 150
Ответы к задачам § 12 154
Глава 4. Автономные системы дифференциальных уравнений 156
§ 13. Поведение фазовых траекторий в окрестности грубых положений
равновесия 156
Ответы к задачам § 13 164
§ 14. Поведение фазовых траекторий в окрестности негрубых
положений равновесия и на всей фазовой плоскости 173
Ответы к задачам § 14 177
§ 15. Устойчивость по Ляпунову положений равновесия 180
Ответы к задачам § 15 185
§ 16. Первые интегралы 186
Ответы к задачам § 16 191
Глава 5. Дифференциальные уравнения в частных производных
первого порядка 194
§ 17. Линейные однородные уравнения 194
Ответы к задачам § 17 204
§ 18. Квазилинейные и нелинейные уравнения 211
Ответы к задачам § 18 218
Глава 6. Элементы вариационного исчисления 220
§ 19. Простейшая вариационная задача 220
Ответы к задачам § 19 234
§ 20. Обобщения простейшей вариационной задачи 237
Ответы к задачам п. 1 § 20 241
Ответы к задачам п. 2 § 20 245
Ответы к задачам п. 3 § 20 248
§ 21. Изопериметрическая задача 248
Ответы к задачам § 21 252
§ 22. Достаточные условия строгого слабого локального экстремума в
простейшей вариационной задаче 253
Ответы к задачам § 22 255
Список литературы 256
ПРЕДИСЛОВИЕ
Настоящий сборник составлен на основании многолетнего опыта
преподавания курса обыкновенных дифференциальных уравнений в
Московском физико-техническом институте (государственном университете).
В сборнике содержится большое число оригинальных задач,
составленных преподавателями кафедры высшей математики МФТИ. Значительная
часть задач сборника подготовлена авторами. Н. X. Агаханов
укомплектовал задачами §6 и §13 сборника, В.В.Власов совместно с В.К.Романко
подобрали задачи §8 и §11 сборника, Л.И.Коваленко составила задачи
§7 и совместно с В.К.Романко подобрала задачи §§2—4 и §9 сборника.
Подбор задач остальных параграфов сборника и общая редакция сборника
осуществлены В.К.Романко.
В начале каждого параграфа сборника помещены примеры решений
типовых задач. Начало решения задачи отмечается значком Л, а конец
решения — значком А. В конце каждого параграфа приведены ответы к
задачам параграфа.
В сборнике предлагается большое количество задач по основным
темам программы курса обыкновенных дифференциальных уравнений. Это
позволяет использовать сборник преподавателями для аудиторной работы,
для домашних заданий, для составления контрольных работ, а студентами
для самостоятельной работы.
Авторы сборника выражают глубокую благодарность коллективу
кафедры высшей математики МФТИ, чья многолетняя творческая
деятельность способствовала появлению этого сборника. Авторы сборника
особенно благодарны профессору Г. Н. Яковлеву и профессору М. И. Шабунину
за помощь при написании сборника.
Глава 1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
§ 1. Составление уравнений заданного семейства
плоских кривых. Приблилсенное изобралсение
интегральных кривых уравнений
Пусть семейство плоских непрерывно дифференцируемых кривых
задано уравнением Ф{х,у,С) = О, где у неявная функция :/; при каждом
•значении параметра С. Если система уравнений
аФ 9Ф ,_
дх ду
^ Ф{х,у,С) = 0
позволяет исключить параметр С, то получается дифференциальное
уравнение заданного семейства кривых.
В случае, когда семейство кривых задано уравнением Ф(.7;,у,С1,С2) =
= О, зависящим от двух параметров С\ и С2, исключение параметров Сь
С2 и получение дифференциального уравнения семейства кривых
достигается с помощью нахождения второй производной от Ф по х.
Пример 1. Составить дифференциальное уравнение семейства кривых
tgy = Ce-^\
Л Продифференцируем по х заданное соотношение, считая у неявной
функцией х:
-V- = -2хСе-'\
cos^ у
Подставляя сюда найденное из заданного соотношения С = е^ tgy,
получаем искомое уравнение
у' Н- xs\n2y = 0. А
Чтобы приближенно построить интегральные кривые
дифференциального уравнения у' = f{x,y), необходимо рассмотреть несколько изоклин
§ 1. Составление уравнений заданного семейства плоских кривых 7
уравнения и найти линии, на которых могут находиться точки экстремума
и точки перегиба интегральных кривых.
Пример 2. Построить приближенно интегральные кривые уравнения
у =у - Зх.
Д Правая часть уравнения удовлетворяет условиям теоремы
существования и единственности решения задачи Коши на всей плоскости (ж,у).
Поэтому интегральные кривые не могут ни пересекаться, ни касаться.
Изоклины уравнения имеют вид у — Зх = А:, где А: = const. При А: = О изоклина
у = Зх делит плоскость на две части. Слева от прямой у = Зх у' > О и,
значит, интегральные кривые там возрастают, а справа от прямой у = Зх
у' < О и, значит, интегральные кривые там убывают. Следовательно, на
прямой у = Зх находятся точки максимума интегральных кривых.
Возьмем eni;e две изоклины. Изоклина у = Зх +1 пересекает
интегральные кривые в точках, в которых касательные к ним образуют с осью Ох
углы —. Изоклина у = Зх — 1 пересекает интегральные кривые в точках, в
которых касательные к ним образуют с осью Ох углы ----.
Из уравнения найдем у" = у' — 3 = у — Зх -- 3. Прямая у = Зх + 3
делит плоскость на две части. Слева от прямой у = Зх -h 3 у" > О и,
8
Глава 1. Дифференциальные уравнения первого порядка
значит, интегральные кривые выпуклые вниз, а справа от этой прямой
у" < О и, значит, интегральные кривые выпуклые вверх. Прямая у = Зж + 3
является интегральной кривой, в чем можно убедиться подстановкой в
уравнение. Поэтому интегральные кривые не пересекают эту прямую и,
следовательно, они не имеют точек перегиба.
Проведенное исследование позволяет приближенно построить
интегральные кривые заданного уравнения (см. рис.). А
Составить дифференциальные уравнения семейства кривых A—18):
1. у = Сх^ - X.
3. у = (х-СJ.
5. (х->СJ + у2=:1.
7. 2п:2 + Су2 = 1.
9. х2 + 2х - (у - Cf = 2.
11. Сх = sin Су.
13. х'^ = {С + у)еУ.
15. у = Acos(a;-Ь у?).
17. у = — + С2Х.
X
2. у = х^ + Сх.
4. (у - Cf = 2х.
6. х2 + (у-СJ = 1.
8. (y-C)^ = i.
10. y = tg{x + C).
12. Cy = tgCx.
14. у2 + 2Сху -Ь х^ + 2х = 0.
16. y = (Ci + C2x)e^\
18. у2 = Cix2 + С2Ж.
Построить приближенно интегральные кривые уравнений A9—38):
19.
21.
23.
25.
27.
29.
"''7^1-
, 1-Х
У = Г-
у-1
, 1-У
У = •
X
у' = {х- 1)у.
, 2х + у
V = •
х-2у
у' = 2х + 2у + 1.
20.
22.
24.
26.
28.
30.
" х + 1
, х + 1
У =-. •
1-у
/ У
у' = х(у + 1).
, _ у-2х
^ ~ 2у + х'
у' = 2х-2у- 1.
§ 1. Составление уравнений заданного семейства плоских кривых 9
31. у'= у-х^-2х-2, 32. у' = у-х^ ^2х,
33. у' = -х2-^. 34. у' = ^+х2.
X X
35. у' = у-х^. 36. у' = 2жу-2.
37. у' = ж^ + у2 - 1. 38. у' = ж^ - у2 - 1.
39. Пусть задано уравнение у' = f{x,y) с непрерывной функцией f{x,y)
на всей плоскости (ж,у). Показать, что если это уравнение имеет
периодическое решение периода Т, то необходимо /(ж, у) является
периодической функцией х периода Т.
40. Пусть у = ip{x) — решение уравнения у' = f{x,y) с непрерывной
функцией f{x,y) на всей плоскости (ж,у). Показать, что:
а) при fi—x^y) = —f{x,y) функция у = </?(—ж) также решение
уравнения,
б) при f(x,—y) = —f{x,y) функция у = —(pix) также решение
уравнения,
в) при /(—ж,—у) = f{x,y) функция у = —(/?(—ж) также решение
уравнения.
41. Пусть f{x,y) — непрерывно дифференцируемая функция на всей
плоскости (ж, у) и пусть f{x,y) — периодическая функция по х пе-
риода Т и ^Ф^ > 0.
ду
Доказать, что уравнение у' = f{x,y) не может иметь более одного
периодического решения.
Ответы к задачам § 1
1. ху' ~ 2у = ж. 2. ху' — у = а:^.
3. у'^ = 4у. 4. 2ху'^ = 1.
5. у2(у'2+ 1) = 1. 6. A-0:2) у'^^: 0:2.
7. Bx2 - 1) у'= 2ху. 8.4x^ = 1.
9. (а:2 + 2х~2)у'2 = (х + 1J. 10.у' = 1+у2
10 Глава 1. Дифференциальные уравнения первого порядка
1 V\/v'^ — 1 . о X\/v' — 1
11. ~ = cos ^^.^ ^. . 12. y'cos^-^^f- = 1.
у' \^у\ \у\
13. (ж2 + е^/) у' = 2х. 14. X (у^ - х^ - 2х) у' = у (у^ - х^).
15. у" + у = 0. 16. у" - 2у' + у = 0.
17. х2у" + ху' - у = 0. 18. х2 (уу" + у'2) = уBху' - у).
§ 2. Уравнения с разделяющимися переменными.
Ортогональные траектории. Однородные уравнения
Для решения уравнения с разделяющимися переменными
Р(х, y)dx + Q(x, y)dy = О
необходимо уравнение сначала умножить или разделить на такое
выражение, чтобы в результате получилось уравнение, одна часть которого
содержит только dx и некоторую функцию х, а другая часть содержит
только dy и некоторую функцию у. При делении уравнения надо следить,
чтобы не потерять решений уравнения.
Пример 1. Решить уравнение
(х + 2) A + у2) dx + (х + l)y'^dy = 0.
Л Разделив уравнение на (х + 1) A + у^), получаем уравнение с
разделенными переменными
^dx + -^dy = 0.
Х+1 1 + у2
При делении на (х + 1) можно потерять решение х = — 1. Подстановка
X = — 1 в заданное уравнение показывает, что х = —1 действительно
является решением уравнения.
Далее имеем
■Чу
/ -dx + / -^—^ = С,
J х + 1 У И-у2
где С — произвольная постоянная. Найдя интегралы, получаем
ж + уЧ-1п|ж + 1| — arctg у = С.
§ 2. Уравнения с разделяюш;имися переменными 11
(-^)-
Для получения ортогональных траекторий заданного семейства
плоских кривых нужно сначала составить дифференциальное уравнение
семейства кривых F(x,y,y') = 0. Затем заменить в этом уравнении у' на
Это дает дифференциальное уравнение искомых ортогональных
траекторий.
Пример 2. Найти ортогональные траектории семейства кривых
у = tg(lnCx).
Д Сначала составим дифференциальное уравнение заданного семейства
кривых. Дифференцируя по х уравнение заданного семейства и исключая
параметр С, получаем уравнение
Заменяя в этом уравнении у' на ( —- ], находим дифференциальное урав-
\ У J
нение ортогональных траекторий
-X = A 4- у^) у'.
Заменив у' на — и решив полученное уравнение с разделенными перемен-
ными, находим уравнение ортогональных траекторий Зж^4-2у^4-6у = С А
Однородные уравнения P{x,y)dx-hQ{x^y)dy = О решаются с помощью
замены у = ж • z, приводяп;ей их к уравнениям с разделяюп;имися
переменными.
Пример 3. Решить уравнение 2xydx = (х^ 4- у^) dy.
Д Замена у = xz приводит заданное уравнение к уравнению с
разделяющимися переменными
ж A 4- z^) dz + z (г^ - 1) dx = 0.
Заметим, что z = О, ±1 -- решения этого уравнения. Тогда из замены
следует, что у = О и у = ±х — решения исходного уравнения. При z ^ О, ±1
уравнение с разделяющимися переменными можно записать в виде
— ( ^^ Md
X \г2 — 1 zj
12 Глава 1. Дифференциальные уравнения первого порядка
_ у
Решив это уравнение и использовав замену г = ~, получаем решения
X
заданного уравнения:
х^ - 2/2 = Су, 2/ = 0. А
Уравнение вида {aix4-biy + ci)dx + {а2Х-hЬ2У + C2)dy = О в том случае,
когда прямые aix-hbiy+ci = О и a2X-hb22/+C2 = О пересекаются, приводится
к однородному уравнению с помощью переноса начала координат в точку
пересечения прямых.
Решить уравнения A—23):
1. у' = у2 - у. 2. (^2 4- х) 2/' - {2х Ч- 1J/ = 0.
3. ж2/'со8 2/4-sin2/= sin2 2/- 4. у^cosx'hy{l-h y)smx = 0.
5. 2xydx = (l — ж^) dy. 6. x^ydy = {x — l)dx.
7. 2/2/'cos ж = A - y)sinx, 8. ж (l - 2/^) у' = У {^ + У^)•
9. (ж^ - l) г/йж = ж (ж^ 4-1) dy. 10. жB/ + 1)^2/ = (l - 2/^) cfx.
11. жу' 4- у2 ( - ~ Зж j = 0. 12. A - ж2)^ уу' 4- ж = 0.
13. (ж 4- 1)у' 4- у{у 4-1) = 0. 14. A 4- у2) у^ж = ж (l 4- 2у'^) dy.
15. ж^ (ж^ 4- 4) 2/' = cos^ у. 16. 2/' tg^ ж — ctg у = 0.
17. A 4- cos х)уу' = A 4- у^) sin ж. 18. ye^dy 4- же^' с^ж = 0.
19. жA 4-у)у'4-(л/i 4-1пж)A 4-у2) =0.
20. (ж - 1)уу' 4- (ж2 4-1) (у 4-1J = 0. 21. x^dx 4- (l 4- х^) ./T^^dy = 0.
, sm^ ж
22. yVl - х^ 4- ж A 4- 62^) = 0. 23. 2/' 4- e-^^vTTe^ = 0.
cos ж
с помощью линейной замены переменных привести уравнения к
уравнению с разделяющимися переменными и решить их B4—27):
24. Bж 4- у 4- 2)бгж - Dж + 2у + 9)dy = 0.
25. D - ж - 2y)dx - 2A 4- ж 4- 2y)dy = 0.
26. Bу - ж 4- 1)бгж 4- D2/ - 2ж 4- G)dy = 0.
§ 2. Уравнения с разделяюищмися переменными 13
27. (у - Зж + 2)dx + (Зж - у - l)dy - 0.
Найти решение уравнений, удовлетворяющее заданному начальному
условию B8—39):
28. 2у A + у2) Ax-Vx (Зу2 + у + З) dy = О, уA) = 1.
29. жBу - 1)у' + 4у2 = О, у(-1) = -1.
30. жA-|-у)у' = у2, уA) = 1.
31. Ъх{х + 1)у' = (ж + 2)у, уA) = -1.
32. (у + 2)у' = sin 2а:, у@) = 1.
33. {е + 1J у' + {е2^ - 1) у = О, у@) = ^.
34. {э? + ж) у' - (ж2 + X + 1) у = О, уA) = |.
35. (жЗ + ж) у' - (Зж2 - 1) у = О, у(-1) = -4.
36. y' + 3y2 = 3y,y@) = i.
37. y'=(y + y'^)thж, у@) = 1.
38. жу' + уA + у) зтж = О, у@) = 1.
39. 2у' = (у2-2у)е^',у@) = 1.
Найти ортогональные траектории для заданных семейств плоских кривых
D0-50):
40. у = С(ж + 1)е-^. 41. у2 = Ce^'+s/'.
42. (Се-^' - l) у = 2. 43. у = Сзтж - 2.
44. у A + Се==) = 1. 45. у = Ссо8ж + 2.
46. e^ = C(l-e-J'). 47. 1 + ег' = СA + ж2).
48. у2 = Ce-(^+J'). 49. жу = Се".
50. 2ж + у - 1 = Се^з'-^.
51. Найти ортогональные траектории семейства эллипсов, имеющих
общую большую ось.
14 Глава 1. Дифференциальные уравнения первого порядка
52. Найти ортогональные траектории семейства гипербол, имеющих
общую мнимую ось.
53. Семейство кривых задано в полярных координатах уравнением
г{(р) = Cf{(p), где /((^) — непрерывно дифференцируемая функция.
Составить дифференциальное уравнение ортогональных траекторий.
Найти ортогональные траектории семейства кривых г = Се^.
54. Семейство кривых в полярных координатах задается уравнением
г'{(р) = rf{(p)^ где /((/?) — непрерывная функция. Составить
дифференциальное уравнение семейства ортогональных траекторий. Найти
ортогональные траектории семейства кривых г = С cos (р.
55. Доказать, что решение задачи Коши существует и единственно при
любых начальных данных для уравнения у' = а{х)-Ь(у), где а(х), Ь{у)
заданные и непрерывные соответственно на интервалах (а,у9), G>^)
функции, причем Ь{у) Ф 0.
56. Пусть функции /(х), д{у) непрерывны на всей числовой оси, причем
l/HI^(l^j^|)i+e' 0<5(у)<5A + |у|),
где Л, В, е — положительные постоянные.
Доказать, что при любых хо, уо существует единственное,
определенное при — со < ж < 4-оо решение уравнения
удовлетворяющее условию у(хо) = уо и имеющее конечные lim у(х),
ж—>—оо
lim у{х),
ж-->+оо
х^ Л-у^
Решить уравнения E7—78):
57. ху' = у f 1 -fin ^У 58. ху' =
\ х) X + у
59. xdy = (у 4- \/ж2 4- у2 j dx. 60. xydx = (ж^ - у^) dy.
61. xdy = (у - \/х2 + у2) dx. 62. (х 4- 2y)dx + ydy = 0.
§ 2. Уравнения с разделяющимися переменными 15
63. {ху + у2) у' = у2 g4, Bа; + у)у' = х + 2у.
65. {х^ + уЗ) у' = а;2у. 66. {х + 2у)у' + у = 0.
67. (у - а;)у' = ж + у. 68. ж^у' = 2у^ - жу.
69. ж^у' = у2 + 2жу. 70. 2жуу' + ж^ - у2 = 0.
71. (Зж^у — ydx) (ж^ + у2) 4- x'^ydy — xy'^dx = 0.
72. (ж + у + l)dx + (ж - у + 3)dy = 0.
73. Bж - у - 2)dx + (ж + у - 4)dy = 0.
74. (ж + 2у - 5)dx + {у-х-4)dy = 0.
75. (ж - 1)у' + Зж + 2у + 3 = 0. 76. (ж + у - 2)у' + ж - у = 0.
77. Bж + у - 3)у' + у + 1 = 0. 78. (ж + 2у)у' + 2ж + 5у - 1 = 0.
Найти решения уравнений, удовлетворяющие заданному начальному
условию G9-83):
X — 1у X -\- 2.у
81. B/2 ~ 3x2) у' 4- ху = О, уA) = V6.
82. хуу' = (х ~ 2уJ, уA) = 2. 83. (х ~ у)У = 4ху, у(~1) = 2.
Решить уравнения, приведя их с помоп;ью замены вида у = г"^ к
однородным уравнениям (84—87):
84. Dx2 ^ у4) ^у _ 2xydx = 0. 85. (Зх2у2 -f l) у' 4- Зху^ = 0.
86. у' = 4x2 _ У 87. у/ = д; ^ ^.
х4 у
88. Найти интегральные кривые уравнения
ху' = 2 (у 4- \/у2 - х4) ,
проходяп;ие через а) точку B,5), б) точку A,1).
89. Найти ортогональные траектории семейства окружностей, проходя-
ш,их через начало координат, центры которых лежат на оси абсцисс.
16 Глава 1. Дифференциальные уравнения первого порядка
90. Составить дифференциальное уравнение траекторий, пересекающих
под углом V^ = 7 параболы с общей вершиной и общей осью.
91. а) Составить дифференциальное уравнение ортогональных
траекторий семейства кривых
/ 2 , 2\2 2
б) Найти ортогональные траектории семейства кривых
t 2 , 2\2 2
[х 4- у ) = а'^ху.
Указание. Перейти к полярным координатам.
92. Составить дифференциальное уравнение семейства окружностей,
имеющих центр на прямой у = х и проходящих через начало
координат.
Ответы к задачам § 2
1. у A + Се^) = 1, у = 0. 2. у = С (х2 4- а:).
С cos X
3. xsiny = СA - siny). 4. у = , у = -1.
1 — и COS X
5. (x2-l)j/ = C. 6. у2 = ^--+С, а: = 0.
7. (у - 1)еУ = С cos X. 8. х (у^ + l) =Су,у = 0.
9. у2 = С(ж2 - 1)^е=^', а; = 0. 10. х{у - 1) = С, у = -1.
11. i + - = С - Зж, у = 0. 12. у2 + —L- = С.
уж 1 - ж^
13. (х + 1)у = С{у + 1), у = -1. 14. а;2 = Су^ (l + у^), у = 0.
1 1 /г ffr
15. tgy = -— - - arctg - + С, у = - + А;7г, А; € Z.
7Г
16. In I COS у I - ctg Ж ~ Ж = С, у = ~ + кп, к е Z.
17. A + у2)(Ц-со8а;J = С. 18. е"^* + 2(ж + 1)е-* = С.
19. 4v/i + In^X + 2arctgy + In (l + y^) = C.
§ 2. Уравнения с разделяющимися переменными 17
20. — 4- а; + In (х ~ 1)^ 4- In |у 4-1| + = С, у = -1.
Z 1 4" 2/
21. arctgx-v^(l ~2жK = С. 22. - arcsina;^4-2/-ln(l 4-е^^) = С.
23. 2л/ГТё!^ - ^^ = С. 24. у + 2а: + 4 = Ce^-^J/.
sinx
25. (ж + 2уJ - Зж + 4у = С. 26. 2у - ж + 2 = Се^^+^у
27. 2у - 6ж + 1 = Се^У-"^^. 28. In ж^ + 3 In у + arctg У = j-
29. In (ж''у2) + 1 + 1 = 0. 30. In - + - = 1.
У У У
31. 2ж2 + (ж + 1)уЗ = 0. 32. у2 + 4у + cos 2ж = 6.
33- у = Го- 34. у
A + е^Г ^ + 1
= -^^ -■ 36. у = —-^
ж 1 + е
f^dt
37. у\/2-сЬЗж = сЬж. 38. уBео ' - 1) = 1-
39. уA + ео ) = 2. 40. ж^ = Се'' ^.
41. ж2 + Су2 = С. 42. же^'+зУ" = С.
43. Сезз/^+з» ^ РОЗ д. 44. ж = iy^ - iy^ + С.
45. e^y-s»'. зтж = С. 46. е" - у + ж = С.
47. ж2 + In (ж2) + 4 (у - е-") = С. 48. (у + 2J6^-" = С.
49. (у - 1)е»+5«* = С. 50. Bж + уJ - 6ж + 2у = С.
51. ж2 + у2 = 2а2 In Сх. 52. ж^ + у2 + 26^ In Су = 0.
53. /'. г' + / • г = О, г = Ce-'f. 54. / • г' + г = О, г = Csinv?.
57. у = хе^"". 58. Сж = (у - жJех.
59. у + ^/ж2 + у2 = Gа;2^ д. = 0. 60. у = Се 5;^.
18
Глава 1. Дифференциальные уравнения первого порядка
61.
63.
65.
67.
69.
71. In
у + \/х^ + у2 = С, Ж = 0.
ж = Су + у1п\у\, у = 0.
у = Се^.
х^ + 2ху -у^ = С.
х"^ + ху = Су, у = 0.
У
62. X + у = Се ^+1'.
64. (у - х)^ = С{у + х),у = -X.
66. у^ + ху = С.
68. ж - у = Сх'^у, у = 0.
70. х"^ + у^ = Сх.
Л -i- 0^„ _ ».2
+ arctg - = С, X = О, у = 0. 72. ж^ + 2жу - у^ + 2ж + 6у = С.
ж
73.
74.
75.
76.
77.
79.
81.
83.
85.
87.
88.
89.
91.
у2 + 2ж2 - 4у - 8ж + 12 = Се^*'"'^ 0^^.
х^Л-у^^ху-х-ЬуЛ-1 = сё^"^"""'^ f^^.
ж + у + 2 = С{х - 1)е^^, ж = 1.
ж2 + у2 - 2ж - 2у + 2 = Ce-2^*='s Н.
(у+1)(ж-2K = С(ЗжН-у-5).
ж2 + у2 = е*^^'81
78. ж2+2у2+3жу+2у = С
80. (ж2 + у2)е^^"8^ =1.
а^ + 2у
ж + у + 1'
уЗ = Зл/б-УУ^-2а:2.
2(у + жK(у-3ж)=5у.
у2^3х^у^ = С.
(у-ж2JBу + ж2)=С.
2-2х
82. Зу — ж = 5(у — ж) • е 2 .
84. у2 = Се^.
86. ж^ (у - ж') = С (у + 4жЗ).
ж^
ж^'ч-!
а) У = Y + 1' б) У = ^^' 2/ = 2 ■
у = С(ж2 + у2). 90. (ж - 2у)у'= ж + 2у.
а) ж (Зу2 - ж2) ЙЖ = у (Зж2 - у2) dy, б) у2 - ж2 = С (ж2 + у2J.
ж2 + 2жу — у2
92. у' =
ж2 — 2жу — у
-,/2-
§ 3. Линейные уравнения первого порядка 19
§ 3. Линейные уравнения первого порядка.
Уравнения Бернулли и уравнения Риккати
Для нахождения общего решения линейного неоднородного уравнения
у' 4- а{х)у = /(ж) необходимо сначала найти общее решение
соответствующего линейного однородного уравнения, а затем применить метод
вариации постоянной.
Пример 1. Найти общее решение уравнения
ху' ^ у — 2х .
Л Найдем общее решение линейного однородного уравнения ху' = у. Для
этого, положив 2/' = ~- и разделив переменные, получаем уравнение
ах
dy dx
У X '
При делении переменных потеряно решение у = 0. Отсюда находим общее
решение однородного уравнения у = Сж, где С — произвольная
постоянная.
Для получения общего решения заданного уравнения применим
метод вариации постоянной, т. е. ищем решение заданного уравнения в виде
у = С{х) • ж, где С{х) — неизвестная пока непрерывно
дифференцируемая функция. Для определения функции С{х) подставим у = С{х) • х в
исходное уравнение. Имеем
х[С'{х) • X 4- С{х)] = С{х)' X - 2ж2,
С'{х) = -2,
С{х) = -2х 4- А,
где А — произвольная постоянная. Следовательно, общее решение
заданного уравнения имеет вид
у = Ах-2х^. А
Уравнение Бернулли у' -\-а{х)у = Ь{х)у^ заменой z = у^~^ приводится
к линейному уравнению.
20 Глава 1. Дифференциальные уравнения первого порядка
Пример 2. Решить уравнение жу' 4- 4у = Зжу^.
Д Очевидно, что у = О ~ решение. При у ф Q, разделив уравнение на у^
и положив г = -, получаем линейное уравнение xz' — 4г 4- Зж = 0. Решив
У
это уравнение методом вариации постоянной, находим z = Сх^ 4- ж, где
С — произвольная постоянная. Следовательно, у = О и - = Сх'^ + х — все
У
множество решений заданного уравнения. А
Если известно какое-нибудь решение Уо{х) уравнения Риккати
у' 4- а{х)у'^ 4- Ь{х)у 4- с[х) = О, то заменой у = z Л- уо{х) оно сводится к
уравнению Бернулли.
Пример 3. Решить уравнение ж^y' 4- 2ж^у^ — бжу 4-4 = 0.
Д Проверкой можно убедиться, что уо{х) = - является решением задан-
ж
ного уравнения. После замены у = г 4— получаем уравнение Бернулли
ж
г' = 2г^. Замена w = - при z ф^ дает линейное уравнение п' 4- - = 2,
ж ;гг ж
Метод вариации постоянной для этого уравнения дает решение
(J
и = h ж, где С — произвольная постоянная. Отсюда получаем решение
ж
заданного уравнения
ж 1
С 4- ж^ ж
Найти обп;ее решение уравнений A—31):
1. у' 4- у = 2е^. 2. жу' = у - 2ж2.
G-)
3. у^йж 4- (жу - l)dy = 0. 4. 2убгж 4- ( ж ) dy = О
5. ж D - ж^) у' = 2ж^у 4-1. 6. жу' = ж^ 4- у.
У
7. у' = ж. 8. (ж 4- у)^ж = xdy.
X
9. 2ж^у' = 2ж2у - 3. 10. ydx - (ж 4- у^) dy = 0.
11. убгж = (Зж - у2) dy. 12. у' = у 4- 2же^.
13. (ж 4- у^ cos у) dy = уб{ж. 14. жу' = ж^ 4- у .
ж
15. у' = - - 2ж^. 16. ж^йу = B - х^у) dx.
X
§ 3. Линейные уравнения первого порядка 21
17. ydx = {2у - x)dy. 18. dx = {2х + е^^) dy.
19. х^у^ 4- 2ж^у = 2 In ж. 20. (sin ж — 1)у' Ч- у cos ж = sin х,
21. у' 4- 2ху = 2 A -Ь 2ж2). 22. ху' -2у = 2х^,
23. ж^у' -Ь 2ж^у = 1. 24. жV + 2жу = 1.
25. жу' - Зу = 4ж2. 26. ж^у' + ж^у = ж^ - 1.
27. 4у' -Ь 12ж2у = Зж^. 28. жу' + (l + ж^) у + ж = 0.
29. ж (у - yj\ + хЛ огж + A + ж^) dy = 0.
30. у' + у tg ж = е^ cos X. 31. (l + у^) йж + (жу - у^) dy = 0.
Уравнения C2—35) искусственным приемом решаются короче, чем
методом вариации постоянной.
32. жу' — у = ж^. 33. (у + ж^ cos ж) dx — xdy = 0.
34. ж^у' + жу + 1 = 0. 35. A + у2) dx + Bжу - l)dy = 0.
Найти решения уравнений, удовлетворяюш,ие заданному начальному
условию C6—45):
36. жу' + 2у = Зж, у(-1) = 1. 37. ж^у' = 5жу + 6, уA) = 1.
38. жу' = 7у -h ж^ уA) = --. 39. жу' = 5у -h Зж^, у(-1) = -1.
40. A + ж^) у' = 2жу - 2ж, у@) = 2. 41. у' - у tgж = sin ж, у@) = 0.
42. (ж^ -f- ж) у' - (д;2 + ж -Ы) у -Ь Ж^ = О, уA) = 1.
43. жу' = Зу -Ь 2ж^ у(-1) = 1. 44. жу' ~ 2у = 2ж^ уA) = 1.
45. ж2у' + ?/ = 4, у(-1) = 5.
46. Найти ортогональные траектории семейства кривых у-Ьж = Се"^ Ч-1.
Решить уравнения D7—72):
47. 4жу' + Dж + 1)у2 - 4у = 0. 48. 2жу' -Ь 2у = ж^у^.
49. у' = жу2 -ь -. 50. 2жу' = Зу - 4жу^.
ж
22 Глава 1. Дифференциальные уравнения первого порядка
51. ху' -у + 2ху^ 1пж = 0. 52. 2ху' + 2ху^ = у.
53. 2ж2у' + ху = 2у^. 54. ху' + 4у = Зжу^.
55. у' ~ - = у^ 56. жу' = 2у - 4а;2у2.
ж
57. у^ -у + 2ху^ = 0. 58. жу' + Зжу2 = 2у.
59. ху' -уЛ- 4у^ = 0. 60. у' + у tg ж + 4y^ sin ж = 0.
61. жу' + Зу = 4ж2у2. 62. жу' + 2жу^ = Зу.
63. у(у + l)dx + (ж + \)dy = 0. 64. у' cos ж + у sin ж + Зу^ cos ж = 0.
65. 5жу^у' = у^ + 4. 66. у Dжу2 ~ З) йж + 2жогу = 0.
67. 8у' + Зж^у (у2 - 4) = 0. 68. уогж -Ь Bж^у - Зж) dy = 0.
69. Зж^йж - (ж^ -Ь у + 1) dy = 0. 70. y'^dx -Ь (ж^ In у - жу^) dy = 0.
71. ydx + Dж^ - ж) dy = 0.
72. (у2 - 1) йж - у [ж + (y^ - 1) у/х] dy = 0.
73. Найти решение уравнения 4жуу' — Зy^ + ж^ = О, удовлетворяюш;ее
начальному условию уA) = 1.
74. Найти интегральную кривую уравнения ydx — ^{x + y^y/x)dy = О,
проходящую через точку @,1).
75. Найти интегральную кривую уравнения ^ж — жу A Ч- жу^) dy = О,
пересекающую биссектрисы обоих координатных углов при ж = 1.
Уравнения задач G6—81) искусственным приемом решаются короче, чем
методом сведения к линейному уравнению.
76. жу' - у + жу^ = 0. 77. ж^у' - ж^у - у^ = 0.
78. у^ж - ж (жу^ + l) dy = 0. 79. 4жу' + 4жу^ = 4у - у^.
80. Найти решение уравнения sin^ж(y'sinж — у cos ж) = у^созж, удовле-
творяющ,ее условию у f — j = 1.
81. Найти решение уравнения со8^ж(у'со8ж + у sin ж) + y^sinж = О, удо-
влетворяюш;ее условию у@) = 1.
§ 3. Линейные уравнения первого порядка 23
С помощью подбора какого-либо решения найти общее решение уравнений
(82-95):
82. 2ж2у' + х'^у^ -f 4 = 2ху. 83. ж^у' + х'^у'^ + 2ху = 2.
4
84. 4у' = у2 + _, 85. ху' = у'^ + 2{х + 1)у + х^ + х,
86. ж^у' = ж^у^ + Зжу -Ь 3. 87. ж'^у' = у^ + 2жу - 2ж2.
88. у' ^у'^ ^ 2жу 4- ж^. 89. у' = у'^ - 2жу + ж^ - 3.
90. у' -Ь е-^у2 -Ь у = Зе^. 91. у' - е^у^ Н- Зу = е"^.
92. у' = у"^ — 2у sin ж -Ь cos ж Ч- sin^ ж.
93. у' + у^ — 2у cos ж -Ь sin ж -Ь cos^ ж = 0.
94. ж^у' - 5жу + ж^у^ -Ь 8 = 0.
95. (Зж^ + 2у) A + y)dx + Bж - ж^) dy = 0.
96. Доказать, что уравнение у' = ку + /(ж), где к = const т^ О, /(ж) —
непрерывная и периодическая функция, имеет только одно
периодическое решение. Найти его.
97. Доказать, что у уравнения жу' -{- ау = /(ж), ж > О, где а = const ^ О,
/(ж) — непрерывная ограниченная функция, существует только одно
решение, ограниченное при ж > 0.
98. Доказать, что у уравнения жу' Н- ау = /(ж), О < ж < а, где а =
= const > О, а > О, /(ж) — непрерывная функция при О < ж ^ а и
lim /(ж) = /3, существует только одно решение, ограниченное при
о < ж < а и имеющее предел при ж -> Ч-О. Найти этот предел.
99. Доказать, что у уравнения у' = а(ж)у Ч- Ь(ж), О < ж < -Ьоо, где а(ж),
Ь{х) ~ непрерывные при О ^ ж < Ч-сю функции, Ь(ж) — ограничена,
а(ж) ^ ао = const > О, существует только одно решение, ограниченное
при О < ж < Ч-оо.
100. Пусть а(ж), Ь(ж) — непрерывные при О < ж < Ч-оо функции,
имеющие конечные lim а(х) = А > О, lim Ь(ж) = В, Доказать, что
существует единственное решение уо{х) уравнения у' = С1(ж)у Ч- Ь(ж),
О < ж < Ч-оо, имеющее конечный предел при ж —> Ч-оо.
24
Глава 1. Дифференциальные уравнения первого порядка
Найти lim уо{х).
X—>-Ьоо
Указание. Рассмотреть ограниченное решение и доказать, что оно
имеет конечный предел при х -> Ч-оо. Можно воспользоваться
правилом Лопиталя.
101. Пусть а(ж), Ь{х) — непрерывные при О < ж < +оо функции, причем
существует конечный lim а(х) = А > О и lim жЬ(ж) = 1. Пусть
ж—>-Ьоо ж->-Ьоо
уо{х) — решение уравнения у' = а{х)у + Ь(ж), О < ж < +оо, имеющее
конечный предел при ж —> +оо. Найти lim уо{х).
х—>-Ьоо
Ответы к задачам § 3
1. у = Се-^-|-е^.
3. ху = С + 1п\у1у = 0.
С + In |ж|
4 - ж^
7. у =^Сх- ж^.
11. ж = СуЗ + у2, у = 0.
13. X = у(С + sin у), у = 0.
15. у = Сх- х^.
17. ху-у^=^ С.
С \п^х
19. у - ;:2 -^ ^
21. у = Се^^ + 2х.
С X
23- У-^-З-
25. у = Сх^- 4x2.
2. у = Сж - 2ж2.
4. а; = С^+-.
У
6. у = Сх + ж2.
8. у = Сж + ж In \х\, X = 0.
10. ж = Су + у2, у = 0.
12. у= (С7 + ж2)е='.
14. у = Сж + ж^ + --.
2ж
,^ С- 1
16. у = г, Ж = 0.
ж Ж"*
18. ж = Се^" - е".
С — cos ж
20. у = -.
зтж — 1
22. у = -^+ж1
х^
24. у = + -.
Х^ X
26. у= - + 1 + -^.
X
Ж*
§ 3. Линейные уравнения первого порядка 25
3 1 С х2 1
27. у = Се-^ + 4- 28. у = ^e'T - -.
4 ж ж
С + ж^
29. у= —===. 30. у= (С + е^)со8ж.
31. (Зж -1/2 + 2) x/lTy2 = С. 32. у = Сж + ж2.
33. у = Сж Ч- ж^ sin ж + ж cos ж, ж = 0. 34. ху Ч- In |ж| = С.
2
35. ж A + 1/2) = у -I- С. 36. у = ж Ч- -2 •
ж
37. у = 2ж^--. 38. 1/ = -^ж^
ж 3
39. у = -ж^. 40. у = ж2ч-2,
1-С08 2ж
41. у = . 42. у = X.
cos ж
43. у = -2ж^ + ж^. 44. у = ж^.
45. у = е^^ Ч- 4. 46. (ж Ч- у Ч- 1)е-У = С.
^^ 1 С 2ж + 1 ^о 1 ^ 1 2
47. - = — ч- —:—. 48. ~ = Сж - -ж"^.
у X А у 2
.^ 1 С' 1 2 .^ 1 С'
49. - = -х\ 50. -^ = -^ Ч- ж.
ухо у^ х^
.. 1 С' , 1 .о 1 С'
51. - = Нжшж ж. 52. --Г = h ж.
ух 2 у^ X
53. — = Сж Ч- -. 54. - = Сж^ Ч- ж.
у^ ж у
55. - = -. 56. - = -1г Ч- ж^.
у ж 2 у х^
57. -^ = Се-2^ + 2ж - 1. 58. ~ = -^ -Ь ж.
у^ у ж^
.^ 1 С' , .^ 1 С' ^
59. — = — Ч-4. 60. - = 2со8ж.
у^ х^ у cos ж
61. - = Сх^ + Ах\ 62. - = -^ + |.
У у Ж'=* 2
63. (ж Ч-1 - С)у = С. 64. C81пж Ч- С)у = cos ж, у = 0.
26 Глава 1. Дифференциальные уравнения первого порядка
65. у^ + 4 = Сх. 66. у2 (а;4 + С)= х^, у = 0.
67. у2 ^е-:=з + (^7) = 4С. 68. ж (у'' + 1) = 2Су^, у = 0.
69. а;3 + у + 2 = Се". 70. г/ = х^ (in^у + С), ж = 0.
71. а;2 Dу2 + С) = у^, а; = 0.
72. 3Vi = y2-l + CJy2-l|^a; = 0, у = ±1.
у2ж2 — х^.
— л,Л 1г,2,
73. у = у2ж2-ж2. 74. а; = 4у^In-*у.
75. ж B - у2) = 1. 76. у (Сж2 + 1) = 2Сж.
77. ж^еТ^ = С, у = 0. 78. ж (Су^ + 1) = ЗСу, у = 0.
79. у Bж2 + ж + С) = 4ж, у = 0. 80. у = sin^ ж.
2 2
81. у = cos^ ж. 82. у = - +
ж С7жЧ-ж1п(ж|
о„ 1 16 о. 2 1
83. у = - + ^„4. .„ .• 84. у = -- +
ж Се4=^ - 4ж - 1 ■ ■ '^ ж ж(С - In |ж|)'
2С7ж2 „„ 1 2ж
Зж* 2Се^^
87. у = ж + т. 88. у = ж + 1 +
89. у = ж - 2 + , . ^ . ■ 90. у = е^ +
1 + Се^^ ■ • г/ ' ^g3i _ g-i •
е-^ 1
91. у = е ^ + -г . 92. у = 8шж + -:; .
о — ж G — ж
1 «.2 2ж
93. у = cos ж + — . 94. у = —h
С-х' -^ ж ж2 + С'
95. СA + у) = Bу + ж2) ж.
96. у = / e''^''-^^f{t)dt, fc > 0; у = / e''^^-*^f{t)dt, к<0.
+00 —(X)
98. -. 100. ~. 101. 0.
а А
§ 4. Уравнения в полных дифференциалах 27
§ 4. Уравнения в полных дифференциалах.
Интегрирующий мнолситель. Замена переменных
Дифференциальное уравнение P{x,y)dx Ч- Q[x^y)dy = О, заданное в
области D, называется уравнением в полных дифференциалах, если
найдется такая непрерывно дифференцируемая в D функция и{х,у), что
du{x,y) = P{x,y)dx + Q{x,y)dy. Для такого уравнения решения задаются
формулой и{х,у) = С, где С — произвольная постоянная. Функция и{х,у)
ди „, . ди ^, .
находится из системы уравнений тг- = Р\Х->у), тг- = ЧК^^У)-
их оу
Если D — односвязная область и -^г—, -;г непрерывны в D, то до-
ох оу
статочным условием того, что уравнение является уравнением в полных
дифференциалах, служит равенство |3 = 1^.
ОХ оу
Пример 1. Решить уравнение
(Зж^ + y-l)dx+[x + Zy'^ - 1) dy = 0.
Д Заданное уравнение является уравнением в полных дифференциалах,
/ ^ dQ дР , ^
поскольку оно задано на всей плоскости (ж, у) и -т— = -^— = 1. Функцию
ох оу
и{х,у) находим из системы уравнений
ди о
ди с 9 .
ду
Из первого уравнения получаем и{х,у) = х^+х{у — 1) + (р{у), где (р{у) —
произвольная непрерывно дифференцируемая функция у. Подставляя
выражение для и{х^у) во второе уравнение системы, получаем уравнение
(р'{у) = Зу^ — 1. Отсюда находим <^(у), а, значит, и функцию и(х^у). В
данном примере можно взять и(х^у) = х^-\-у^^-ху — х — у. Следовательно,
решения заданного уравнения задаются формулой
х^ + ху + у^ -х-у = С. к
Если уравнение не является уравнением в полных дифференциалах,
то можно пытаться найти его интегрируюш;ий множитель. Обш,его
метода отыскания интегрируюш;его множителя не существует. В некоторых
28 Глава 1. Дифференциальные уравнения первого порядка
случаях удается решить уравнение, применяя метод выделения полных
дифференциалов некоторых выражений и замену переменных.
Пример 2. Решить уравнение {у — 4:ху^) dx = Bж^y^ + х) dy.
Д Заметим сначала, что у == О — решение уравнения. Пусть у ф 0.
Уравнение запишем в следуюш,ем виде
ydx — xdy = 2у^ {x^dy + 2xydx) .
Если разделить уравнение на у^, то уравнение примет вид
d(^)=2d(x2y).
Получили уравнение в полных дифференциалах, из которого находим,
что X = 2xhj^ + Су, где С — произвольная постоянная. Отметим, что
интегрируюш,им множителем заданного уравнения служит функция —^,
Таким образом, все множество решений заданного уравнения
описывается формулами X — 2ж^y^ Ч- Су, у = 0. А
Решить уравнения A—18):
1. A - Ъх^ -y)dx= {х- Зу2) dy.
2. {у2 - 2х^) dx + 2xydy = 0.
3. [{х — у)^ — х] dx -{- [у — {х - у)^] dy = 0.
4. (у — sinx)dx + {х -h еУ) dy = 0.
5. (у - x)dx + {х + 2е^У) dy = 0.
6. (ж + y)dy = {2е^^ ~ у) dx.
7. (у -I- sin x)dx + {х + cos y)dy => 0.
8. {2х -Ь у^) dx + Зжу^йу = 0.
9. (у^ — 2а:) йж -|- Bжу — siny)dy = 0.
10. (у - За:^ -\-1) dx-\-(х-\- lny)dy = 0.
11. (у^ Ч-In ж) da; + Bжу — In y)dy = 0.
12. (е^ -Ь у) da; + (ж -Ь 2у cos y^) dy = 0.
§ 4. Уравнения в полных дифференциалах 29
13. A + Зж^Ыу) dx + (Зу2 + —]dy = 0.
14. B.-'Jp.y^+By+'^yy = 0.
i5-(i^ + ;)<'--(^ + i + 2!,)<;v = o.
16. е- (l --\dx+(l + e^) dy = 0.
17. -dx + [1 + In {xy)]dy = 0,x>0,y>0.
f 2x\ (\ Зж2\
Найдя интегрирующий множитель или сделав подходящую замену
переменных, решить уравнения A9—60):
19. Ixydx + (у2 - ж^) dy = 0.
20. 2xydx = (ж^ - 2у^) dy.
21. (З^ж — у — 2ж) dx = {^у/х — у — 2у) dy.
22. [у - Зж^у^) б/ж - (ж + ж^у2) dy = 0.
23. Bжу^ -Ь у) б/ж - (ж^у + 2ж) dy = 0.
24. ус!ж = (ж - 2у^) dy.
25. ж^йу -Ь 2 (у - ж'^) ydx = 0.
26. 7/йж = Bу - е^) dy.
27. жйу = у A — уе^) йж.
28. у' = ~-Ь2ж2.
ж
29. x'^dy = (жу + у^) dx.
30. у^йж = жBу — x)dy.
31. ж^dy = (жу — 2ж^y^) йж.
32. xdy = уB + 3xy)dx.
30 Глава 1. Дифференциальные уравнения первого порядка
/1 \ 1
33. у ] dx = -dy.
\^ J У
34. {2х^у + а;2у4) dx + (ж^ + х^у^) dy = 0.
35. (Зж^у + 7у^) dx - {2х^ + 5ху) dy = 0.
36. Bу - ж^у^) dx = [х^у - х) dy.
37. Dж^у + Зy^) йж - Bж^ + жу) dy = 0.
38. (Зжйу - ydx) [х^ + у^) 4- x'^ydy - жу^йж = 0.
39. (Зж2 -ь 2у) A + y)dx + Bж - ж^) dy = 0.
40. (жу^ + 2у) dx+ {х- ж^у^) dy = 0.
41. Зжс/у Ч- ус^ж + xy^{xdy Ч- у^ж) = 0.
42. xy'^dx Ч- (ж^у — ж) dy = 0.
43. ж (ж^ Ч- у^) dy Ч- у(уйж — жф) = 0.
44. (жу^ Ч- у) йж Ч- Bж Ч- ж^y^) dy = 0.
45. 2ж^(жйж Ч- ydy) Ч- (ж^ + y^)^ (жйу - Зуйж) = 0.
46. y{2ydx — xdy) Ч- x'^{ydx Ч- 2жс(у) = 0.
47. (у2 - Зж^) dy + xydx = 0.
48. xdy — ydx = ж\/ж2н-у^• с/ж.
49. xdy — 2уйж Ч- жy^Bжdy Ч- уйж) = 0.
50. x'^y^dx + (ж^у^ Ч- ж) dy = 0.
51. 5жйу Ч- у</ж Ч- xy^{xdy — у^ж) = 0.
52. жс/у Ч- у</ж Ч- xy'^{xdy — 5у^ж) = О, ж > О, у > 0.
53. 2жс/у Ч- уйж Ч- xy^{xdy Ч- 2ус(ж) = 0.
54. (у^ Ч- у) йж Ч- (жу Ч- 2ж + - J dy = 0.
55. [(Зж^ Ч- 2) у Ч- Зж] dx Ч- Bж - ж^) dy = 0.
56. жу' — у = 2ж^е~х.
§ 4. Уравнения в полных дифференциалах 31
57. 2xy^dx -f x'^y'^dy = (l - y^) dy.
58. Ba;y^ - y) dx-\- (y^ Iny -f ж - y) dy = 0.
59. x'^yy' -f ж^ = (ж^ -f y^)^.
60. Ax'^y'^dx -f a;^By ~ l)dy = 0.
61. Найти интегральную кривую уравнения (l — х^у) dx-\'X^{y — x)dy = О,
1
пересекающую прямую ж = - под прямым углом.
Ответы к задачам § 4
С х^
1. у^ - х^ - ху + х = С. 2. у^ = h -тг, ж = 0.
X 2
3. 2(у - ж)^ = 3 (у2 - а;2) + С. 4. ху -f cos х -f е^^ = С.
5. а;2 + С = 2а;у -f ге^з^. 6. у^ -f 2ху = 26^^ + С.
(J
7. жу ~ cos а; + siny = С 8. у^ = х, х = 0.
а;
9. жу^ -x^-f cosy = С 10. a;(y-f 1) - х^ -f уAпу- 1) = С.
11. а;у2 -f а;Aпа; -- 1) + уA - Iny) = С, 12. е^ + жу -f siny^ = С.
13. хЧп у -f а; + уЗ = С. 14. а;^ + у^ -f ^^^-^ = С.
15. ~ - ^ ~ у2 = С. 16. у-^хе^ = С.
У X
17. у In (ху) = С. 18. а; -f -т = С'.
У^ У
19. а;2 -f у^ = Су, у = 0. 20. х^ = Су - у^, у = 0.
21. х^ -у^ ^ 2(а; - у)§ -f С. 22. а; - х^у^ =:Су,у = 0.
23. а; -f a;V = Су^, у = 0. 24. а; = Су - у^, у = 0.
25. а:^ ~ 2у 1п|а;| = Су, а; = О, у = 0. 26. y^e'^ = у + С.
27. а; = уе^ -f Су, а; = О, у = 0. 28. у = Сх + х
Г.2
,3
а;"
29. ^ + 2ж = С, у = 0. 30. у^ -ху = Сх, а; = 0.
32
Глава 1. Дифференциальные уравнения первого порядка
31. X — х^у = Су, г/ = 0.
33.
^-^ = а
2 у
х^ Зж^ ^
-6 + -5" = <^. У = О-
37. х^ = Су- 62^5, а; = о, у = 0.
35. -fi+—г
32. х^у + х'^ = Су,у = 0.
34. x'^y'^ {7х + 4уЗ) = с.
^ = С, а,- = О, у = 0.
36. жуе
у!
X
38. In
2/
- arctg - = С, а; = О, J/ = 0.
а;
39.
1 + У
1
41. ху = Се^, а; = О, у = 0.
43. а;е2' = С^/а;2 +у2, у = 0.
45. ^ -^ ^ = ^ -f С, а; = 0.
х'' -f у'' а;"^
47. - - - = Су, у = 0.
X у
49. уе^"' = Са;2, ж = 0.
1
51. у = Схе^, а; = О, у = 0.
53. а:5у10 = С A + 5а;у^)
1 ^
40. -^ -f ^ = С, ж = О, у = 0.
х^у X
42. ху - In \у\ = С, х = 0,у
44. ху = Се^, а; = О, у = 0.
46. ху'^ = Се^, а; = 0.
= 0.
48. хё
= c(y-f v^^2-:r7).
57. у = С (ж2 + 1) у2 + С.
50. у^е^""' = С, ж = 0.
52. (жу)Ч = СA1жу2-1)^
54. Су(жу+1) =у + 1.
е^ = ж2 + С.
55. {4жу + 3)С = B - x^f, ж = 0. 56. е-
^ " ~ 58. ж2 + уAпу-1)-1пу-- = С.
V
59. (ж2 + у2) (Сж + 2) = ж
г2 + 8+-.
ж
60. жУе^ =С, у = 0.
61. у = ж + л/ж-
Исследование задачи Коши
§5
Важную роль в исследовании задачи Коши играет условие Липшица.
Говорят, что функция f{x,y) удовлетворяет условию Липшица по у
равномерно по а; в некоторой области G плоскости Rhy)^ если
найдется такое число L > О, называемое постоянной Липшица, что для любых
§ 5. Исследование задачи Коши 33
{x,yi) е G и {х,у2) Е G выполняется неравенство
Следующий пример дает удобные для практики достаточные условия на
f{x,y)^ обеспечивающие выполнение условия Липшица по у равномерно
по X на компакте (ограниченной замкнутой области) плоскости -R? ч.
dfix v)
Пример 1. Доказать, что если функции /(ж, у) и —-^— непрерывны в
области G плоскости i?? ч, то /(ж, у) удовлетворяет условию Липшица по
у равномерно по х на каждом компакте К С G.
Д Рассуждаем от противного. Пусть утверждение неверно. Тогда
найдутся компакт Ко С G и последовательности {Ln}^i, Ln > О, Vn € N,
{(^п,Уп)}^=1 С Ко, {(^п,Уп)}^=1 С Ко такие, что
\f{Xn,y'n)-'f{Xn.yn)\>Ln\y'n-ynl
Так как Ко — компакт, то из последовательностей точек {х^Уп) и
(хп^Уп) можно выбрать сходящиеся подпоследовательности (ж„^,у{^^) -^
-> (^о,Уо) ^ ^0, (a^njb,ynj -> Ы,Уо) ^ Ко при fc -> 00. Рассмотрим
функцию
у - у
в достаточно малой окрестности точки (жо,Уо,Уо)- Если j/q т^ Уо» "^^ ^^
непрерывности /(ж,у) следует ограниченность функции F(x^y\y") в этой
_ - .. dflx,y)
окрестности. Если же уд = Уо = уо, то из непрерывности —
следует выполнение условия Липшица по у равномерно по а; в окрестности
точки {хо,уо)у что означает ограниченность F{x,y\y") и в этом случае.
Но ограниченность F{x^y',y") противоречит нашему предположению о
компакте Ко при достаточно больших rik. Это доказывает утверждение
примера 1. А
Пример 2. Выполнено ли условие Липшица по у равномерно по х для
функции f{x,y) в полукруге ж^ + у^ < В?, у > О, i? > О, если:
а)/(ж, у) = а;2 sin а:-fy^, б)/(а;,у) = х-f |у|, в)/(а;,у) = а;-f >/у ?
34 Глава 1. Дифференциальные уравнения первого порядка
Д В случае а) для любых двух точек {x,yi) и {х,у2) из полукруга имеем:
\f{x,yi) - Лх,у2)\ = \у1 - у1\ = \У1 - У2\ • \у1 + У1У2 + у1\ ^
<.\{у1 + У2)\У1-У2\<.Ш^\У1-У2\.
Значит в случае а) условие Липшица выполнено. В случае б) условие
Липшица тоже выполнено, так как
|/(а:,У1)-/(ж,У2)| = ||У1|-|У2|| ^ \У1 - У21
Покажем, что в случае в) условие Липшица не выполняется.
Рассуждаем от противного. Пусть это условие выполнено в полукруге с некоторой
постоянной Липшица L > 0. Тогда для точек @,1) и (О,у), где О < у < е,
е > О и достаточно мало, имеем
|/@,j/)-/@,l)| = |V^-lKL|y-l|.
Отсюда L{y/y Л- 1) ^ 1, что невозможно при достаточно малых у > 0.
Противоречие. Условие Липшица не имеет места. А
Пример 3. Указать какой-либо отрезок, на котором супхествует решение
задачи Коши, если:
а) у' = у'^-^х'^, у@) = О, \х\ ^ 1, |у| ^ 1, б) у' = x-fsin(.T2 + у), у@) = О,
\х\ ^ 1, в) у' = \х\ -f siny^ -f cosy^, y@) = 0.
Д Известно, что решение задачи Коши у' = f{x^y)^ у{хо) = Уо? где f{x^y)
dfix^y) T-r г/ \ I I I
и —-г непрерывны в прямоугольнике П = \\Хту) : \х — xol ^ ol^ \у—
ду
—Уо| ^ у9}, всегда суш^ествует на [хо — 5, жо + 5], где 5 = min ( а, — J, М =
= max \f{x, у)\ при (ж, у) G П.
В случае а) имеем а = у8 = 1,М = 2и, значит, решение существует
при \х\ ^ -.
В случае б) имеем а = 1,^ = оо, М = 2и, значит, решение суш,ествует
при \х\ ^ 1.
В случае в) для всех \х\ ^ а при любом а > О имеем а = а, /3 = оо,
М = 2. Следовательно, решение суш,ествует для \х\ ^ а при любом а > О,
т. е. для всех х G (—оо, -f оо). А
§ 5. Исследование задачи Коши
35
Пример 4. Методом последовательных приближений найти решение
задачи Коши: у' -f у = х + 1, j/@) = 0.
Л В нашем случае последовательные приближения задаются формулами
2/0
X
(х)=0, Ук{х) = j[i + l-yk-i{0]di, А; = 1,2,3,.
Методом математической индукции можно проверить, что Ук{х) =
= X -h (—1)^, /с = 1,2,3,... Отсюда следует, что при \х\ ^ а для любого
0'> О Ук{х) при /с -> оо равномерно стремится к х. Значит, у = х является
решением задачи Коши. А
Пример 5. Доказать, что последовательность функций Уп{х),
определяемая соотношениями
уо{х) = О, уп{х) = 2
1-х
X
\ j yl-x{t)dt,
п
1, Z, о, . . . ,
сходится равномерно на [1,2] и не сходится равномерно на [1,8].
Л Заданная последовательность функций служит последовательными
приближениями решения задачи Коши вида
9 '
уA)=0.
Рассмотрим сначала эту задачу в области G = {(а;,у) : а; G [1,2]
^ Ь, Ь > 0}. В этой области G max
62
М < 2 + — И max
, \У
df
ду
й
max
_2jt
9
, "а;2 9
Из теоремы существования решения задачи Коши следует, что
последовательные приближения сходятся равномерно на [1,1 + 5], где число
S > О одновременно удовлетворяет двум оценкам: 6 <
М
2 + f
5 <
N 26
. Выбирая число 6 так, чтобы обе оценки совпали, получаем
6 = 3V^, 5< —7=. Ясно, ЧТО E = 1 удовлетворяет этому неравенству.
2\/2
36 Глава 1. Дифференциальные уравнения первого порядка
3 3
Решая на [1,8] уравнение Риккати, получаем у = —I ^, Из на-
^ х + Схз
чального условия С = — 2. При х -^ 8 получаем у -> сю, что противоречит
равномерной сходимости. А
При исследовании зависимости решения задачи Коши от параметров
и начальных данных используются уравнения в вариациях.
Пример 6. Найти —^ от решения у = (^(ж, 1,уо) задачи Коши
дуо
у' = 2у + х^^ - xV, уA) = уо.
Л Очевидно, что решением заданного уравнения при начальном условии
уA) = О является у = (р{х^ 1,0) = 0.
Известно, что искомая функция и = —— должна быть решением урав-
оуо
нения в вариациях по уо
^ = [2 + 2х'у - 3xV]u,
где у = (р{х, 1,0) = О, при начальном условии и |xo=i= 1-
dip
Другими словами, для нахождения функции и = —— необходимо ре-
оуо
шить задачу Коши вида
g = 2u, u(l) = l.
Искомым решением является и = е^^^~^К А
„ „ __ д(р(х,1^0) / ^ч
Пример 7. Найти ;г от решения у = (р[х^хо^1) задачи Коши
OXQ
у' = у ~ 1 -f 2а;у2(у2 - 1), у{хо) = 1.
Д Очевидно, что решением заданного уравнения при начальном условии
у@) = 1 является у = (р{х^О, 1) = 1.
д(р
Известно, что искомая функция v = —— должна быть решением урав-
охо
нения в вариациях по xq
-£='[1 + 8ху^ -4xy]v,
где коэффициент при v берется при значении у = 1 и при начальном
условии V |х=о= -[у ~ 1 + 2а;у^(у^ - l)]U=o = 0.
§ 5. Исследование задачи Коши 37
Следовательно, для нахождения функции v нужно решить задачу
Коши вида
dv
— = A + 4x)v, v{0) = 0.
CfX
Отсюда искомое решение v = 0. А
1. Выполнено ли условие Липшица для функции f{y), если:
а) f{y) = У^, \у\ <:а, а>0,
б) /Ы = |у|, \у\ ^а, а>0,
в) /(у) = VWl \У\ < а, « > О?
2. Доказать, что из выполнения условия Липшица для функции f{y) на
[а,у8] следует непрерывность f{y) на [а,у8].
3. Выполнено ли условие Липшица по у равномерно по х для функции
/(ж, у) в круге ж^ -f у^ ^ -R^, i? > О, если
а) f{x,y) = a;2-fi/^,
б) f{x,y) =х- \у\,
в) fix,у) = ху/\у\?
4. Доказать, что если функция f{x^y) непрерывна по а; в области G
и удовлетворяет в G условию Липшица по у равномерно по ж, то
f{x^y) — непрерывна в G.
5. Показать, что не дифференцируемые по у при у = О функции
fi{x,y) = |y|(l-fsina;) и /2{х,у) = |y|(l-fcosa;) удовлетворяют условию
Липшица по у равномерно по х на всей плоскости i?? ч.
6. Показать, что функция f{x,y) = а{х)у -f b{x) удовлетворяет условию
Липшица по у равномерно по х в полосе \х\ ^ а, а > О, если только
а{х) и Ь{х) — непрерывные функции при \х\ ^ а.
7. Показать, что функция f{x,y) = [И-а^(а;)]у^, где а{х) — непрерывная
функция при |а;| ^ а, а > О, не удовлетворяет условию Липшица по
у равномерно по гг в полосе \х\ ^ а.
8. Доказать, что функция f{x,y) = Р{х) -f Q{smy,cosy), где Р{х) и
Q{u,v) -— многочлены, удовлетворяет условию Липшица по у
равномерно по X на всей плоскости Щ^у)-
38 Глава 1. Дифференциальные уравнения первого порядка
9. Доказать, что функция f{x,y) = х -у не удовлетворяет условию
Липшица по у равномерно по х на всей плоскости Л? ,..
10. Методом последовательных приближений найти решение задачи
Коти, если:
а) у' -f у = гг -М, 2/@) = 1, б) у' -f у = 2е^, у{0) = 1,
в) у' ~ у = 1 - X, у@) = 1, г) у' - у = e2^ у@) = 1.
11. Методом последовательных приближений найти приближения уо(^),
yi{^)i У2{х) к решению задачи Коши, если:
а) у' = у^- X, у@) = 1, б) y' = f-h х\ у@) = О,
в) у' = 2у2 + X, у@) = 1, г) у' = п:2 - 2у2, у@) = 0.
12. Оценить погрешность, получаемую при замене решения у{х) задачи
Коши его последовательным приближением yz{^)^ если:
а) у'= у2 + 2х, у@) = О, |х|^1, |у| ^ 1,
б)у' = у2 + х2,у@)=0, Irrl^l, |у|^1.
13. Доказать, что последовательность функций Уп{х), определяемая
соотношениями
Уо{х) = О,
X
Уп{х) = е-^ + ^е-2^ - ^ + / [22/П-1 (Ое-' - yLi@]d^, п = 1,2,3,...
о
сходится равномерно на [0,0.2] и не сходится равномерно на [0,1].
14. Доказать, что последовательность функций yn(^), определяемая
соотношениями
Уо{х) =0,
X
Уп{х) = ^A ~ ^^) + / ^[B^ -^ 1)Уп-1@ ~ Уп-1 W]rf^, п = 1,2,3,...
1
сходится равномерно на [1,1.1] и не сходится равномерно на [1,2].
15. Доказать, что последовательность функций Уп{х)^ определяемая
соотношениями
Уо(^) = О,
§ 5. Исследование задачи Коши 39
X
Уп{х) = COSX — 2 — sint[yп-1{t) — COSt]^dt^ n= 1,2,3,...
0
сходится равномерно на [0,0.1] и не сходится равномерно на О, -- .
16. Доказать, что последовательность функций Уп{х), определяемая
соотношениями
Уо{х) = 0,
X
Уп{х) = гг -f 2 / COS (з; - t)yn-i{t)dt, п= 1,2,3,...
о
сходится равномерно на любом отрезке и найти ее предел.
17. Доказать, что последовательность функций Уп{х), определяемая
соотношениями
Уо{х) = О,
X
Уп{х) = 5cosrr-4-f2/ {1 - e^-'')yn-i{t)dt, n = 1,2,3,...
о
сходится равномерно на любом отрезке и найти ее предел.
18. Доказать, что последовательность функций Уп{х)^ определяемая
соотношениями
Уо{х) =0,
X
Уп{х) = 4 -f 5 / sin (х - t)yn-i{t)dt, n = 1,2,3,...
о
сходится равномерно на любом отрезке и найти ее предел.
19. Доказать, что последовательность функций Уп{х)^ определяемая
соотношениями
Уо{х) = О,
X
Уп{х) = 5(cosrr-fsinx) + / [1 + 2(х - t)]yn-i{t)dt, п = 1,2,3,...
о
сходится равномерно на любом отрезке и найти ее предел.
20. Используя какое-либо достаточное условие единственности решения
задачи Коши, указать области, через каждую точку которых прохо-
40 Глава 1. Дифференциальные уравнения первого порядка
дит единственная интегральная кривая уравнения:
а) у' = У^ -^ ж^, б) у' = а; -f ^у-х, в) у' = у^ ^ у/хТу,
г) {х + у)у' = жЬу, д) жу' = е^ + ctgy, е) у' = у + \/у-х2,
ж)у' = (у +1)(у-1I.
21. Найти значения вещественных параметров а, р и линии на плоскости,
в каждой точке которых нарушается единственность решения
уравнения:
а) у' = у-A ~ y)^ б) у' = у" 1п^ -, в) уЧпу = у-A - yf.
У
22. При каких начальных данных жо, уо, Ух задача Коши у" = f{x^y,y')^
у{хо) = Уо, у'(^о) = 2/1 имеет единственное решение, если:
а) f{x,y,y') = -(y'-f х/у-1)» б) fix,у,у') = —yln(xy-l),
в) fix,у,у') = —^у-х, г) fix,у,у') = -(cosy'-fx^ In у'),
1 2
Д) fi^^y^y') = -ix- \/у' -у), е) fix,у,у') = х^еУ -{-smiy' -х'^у.
У
23. Показать, что уравнение у" = 3(у')з при начальных условиях у@) =
= у'@) = О имеет два решения. Почему это не противоречит теореме
существования и единственности решения задачи Коши?
24. Показать, что уравнение у" = 2^/\уГ\ при начальных условиях у@) =
= у'@) = О имеет два решения. Почему это не противоречит теореме
существования и единственности решения задачи Коши?
25. Могут ли две интегральные кривые уравнения пересекаться в
некоторой точке (а;о,Уо)-
а) для уравнения у' = ж^ -f у^? б) для уравнения у" = х^ -f у^?
26. Могут ли две интегральные кривые уравнения касаться друг друга в
некоторой точке ixo^yo)'-
а) для уравнения у' = х^ -\- у^1 б) для уравнения у" = ж^ -f у^?
в) для уравнения у'" = х"^ -\-у^1
27. Сколько существует решений уравнения у^*^) = х^ -{-у^^ при п = 1, 2,3,
удовлетворяющих одновременно двум условиям у@) = 1, у'@) = О?
§ 5. Исследование задачи Коши 41
28. При каких п G N уравнение у^^^ = f{x^y), где f{x,y) и —^
оу
непрерывны на всей плоскости Я?^ ч, могут иметь среди своих
решений две функции:
а) у1 = ж, у2 = ж + х'^? б) у1 = 1 ~ cos ж, у2 = -ж^?
29. Найти производную по параметру А при А = О от решения у = (^(ж, А)
задачи Коши:
а) у' = у + А(ж2 + у2), у@) = О, б) у' = ~у + А(а: + у^), у@) = О,
в) у' = 2у + А(у2 - ж2), у@) = О, г) у' = ~3у + А(у2 - х), у@) = О,
Д) у' = У - У^ + А(ж + уЗ), у@) = О, е) у' = у2 ~ у + А(у^ - ж), у@) = О,
ж) у' = 2жу + А(у^ + 2х), у@) = О, з) у' = ~2жу + Х{у^ ~ 2ж), у@) = 0.
«л тт d(p(x,XQ.yo) ^ , .
30. Найти —^-7г при уо = О от решения у = ср(ж,жо,уо) задачи
5уо
Коши у' = /(ж,у), у(жо) = Уо, если:
а) у' = 2у + ж2у2 ~ y^ у@) = УО, б) у' = у + 2ху'^ + y^ у@) = уо,
в) у' = -2у + 2ж2у2 + y^ у@) = Уо, г) у' =-у ^ у'^ ^ ж2y^ у@) = уо-
31. Показать, что т-^—^— = О для решения у = (р{х, жо, 0) задачи Коши
ажо
у' = /(ж,у), у(жо) = О, если:
а) у' = у + ж(уЗ + у2), у@) = О, б) у' = -у + 2ж(уЗ ~ у2), у@) = О,
в) у' = 2у ~ ж(у2 + у^), у@) = О, г) у' = -2у - х^у{у^ + 2у), у@) = 0.
32. Найти с точностью до 0(x, A^) решение задачи Коши:
а) у' = 2жу + АBж + у^), у@) = О, б) у' = ~2жу + А(у2 ~ 2х), у@) = О,
в) у' = у2 + у + АA + ж), у@) = О, г) у' = у2 ~ у + Аж, у@) = О,
Д) у' = -у^ + У + Аж, у@) = О, е) у'=-у^ - у + Ах, у@) = 0.
33. Пусть у = (^(ж, А) решение задачи Коши у' = у + sin у, у@) = А. Найти
аА "" аА2 •
34. Пусть у = (^(ж, А) решение задачи Коши у' = АA — д:) Ч-у — у^, у@) = 0.
35. Пусть у = ip{x^a^l3) решение задачи Коши у" = ау — у^, у@) = 1,
42 Глава 1. Дифференциальные уравнения первого порядка
у @) = ^. Найти —д^— и g^ ■
36. Пусть у = (р{х,а,Р) решение задачи Коши у" = у + 3siny, у@) = а,
у @) = ^. Найти —д^— и ^^ •
37. Пусть у{х) при х ^ О удовлетворяет уравнению у' = 1 + х + 100 sin у и
начальному условию у@) = 0. Доказать, что у{х) > О для всех х > 0.
38. Функция у{х) при X ^ О удовлетворяет уравнению у' = 2 + д;^ + sin'^ у
и начальному условию у@) = 0. Имеет ли нули у{х) при х > О?
39. Функция у{х) при х ^ О удовлетворяет уравнению у' = х -{- cosy.
Имеет ли у{х) асимптоту при х -> 4-оо?
40. Функция у(х) при X ^ О удовлетворяет уравнению у' = х + тт.
1 -f у^
Существует ли конечный lim у{х)?
41. Доказать, что каждое решение уравнения у' = ^г определено
1 -f х^ + у^
при ~оо<д:<4-оои имеет конечные пределы при х -> — оо и при
X -> +00.
Ответы к задачам § 5
1. а) Да. б) Да. в) Нет.
3. а) Да. б) Да. в) Нет.
10. а) у = х + е~^. б) у = е^. в) у = х + е^". г) у = e^^.
11. а) уо{х) = 1, yi(a;) = 1 + х - у, угН = ^ + ^ + Y " 1 0 '
4 4 9
б) уо(ж) = О, yi{x) = —, у2{х) = Y "^ 144 ■
в) уо{х) = 1, уИх) = 1 + 2а: + у , у2{х) = ^ + Y'^~3~'^^^'^10'
X X 2ж
г) уо{х) = о, yi(a;) = у, У2(а;) = у - ^ •
12. а) \у{х) - уз{х)\ ^ ^ (J\ el .
§ 5. Исследование задачи Коши 43
б)\у{х)-уг{х)\^^.
16. у = 2{х-1)е=' + х + 2.
17. у = 2cosa;+ sina; — е^.
18. у = I (е2- + е-2-) - 1 .
19. у = 4e^^ + cos х + 2 sin ж.
20. а) Вся плоскость (х,у). б) у т^ ж. в) х т^ О, у > —х.
т) X ф -у, у > 0. д) ж 7^ О, у 7^ /стг, /с G Z. е) у > ж^. ж) у 7^ 1.
21. а) а < 1, у = О и ^ < 1, у = 1. б) а < 1, у = О и /3 < 1, у = 1.
в) а < 1, у = 0 и ^5 < 2, у = 1.
22. а) жо 7^ О, уо 7^ 1, yi — любое, б) хоуо > 1, уо т^ О, yi 7^ 0.
в) Уо 7^ 3^0, 2/1 7^ 0. г) хо — любое, уо 7^ О, yi > 0.
д) хо — любое, уо 7^ О, у1 7^ Уо. е) ж§ 7^ уь уо - любое.
25. а) Нет. б) Да.
26. а) Да. б) Нет. в) Да.
27. При п = 1 нет решений, при п = 2 одно решение, при п = 3 бесконечно
много решений.
28. а) п ^ 3, б) п ^ 5.
29. а)^^ = 2в^-а:^~2а:-2.б)^^^е- + х-1.
ил ил
Эу(ж,0) _ _1 _зх _ ^ , 1
^ ал ~ 9 3^9-
ж) ^^ -е 1.3) ^д -е 1.
30. а) e^^, б) ё", в) е-2^, г) е"^.
44 Глава 1. Дифференциальные уравнения первого порядка
32. а) у = А(е^' - 1) + 0{х, А^), б) у = Л(е-^^ - 1) + 0{х, А2),
в)у = АBе^-ж-2) + А2[4е2^ + 2е^C-2ж-а;2)-ж2-6а:-10] + О(а;,А2),
г)у = А(е-^ + а;-1) + А2[(ж2-2а:-4)е-^-е-2^ + а;2-4а; + 5] + 0(ж,А2),
д) у = А(е^ - ж - 1) + А2[(ж2 + 2а: - 4)е^ - е'^^ + ж2 + 4а; + 5] + 0(ж, А^),
е) у = А(е-^ + ж-1) + А2[D + 2а:-ж2)е-^ + е-2^-ж2+4а:-5] + 0(а;,А2).
ау(ж,0) _о. 2х ,ч аУ(х,0) _
34. ^ ' = ж, ^\; ' = -4е^ + 2а;2 + 4а; + 4.
35. Щ^ = 1 - cosa;, Щ^^ = sina;.
да др 4
38. Нет.
39. Нет.
40. Нет.
§ 6. Уравнения первого порядка,
не разреп1енные относительно производной.
Особые репхения
Основным методом решений таких уравнений является метод введения
параметра. Кандидаты в особые решения находятся с помощью дискри-
минантных кривых, а затем для них проверяется определение особых
решений.
Пример. Найти все решения, исследовать особые решения и нарисовать
качественную картину поведения интегральных кривых уравнения
Д Введем параметр р = у'. Тогда заданное уравнение эквивалентно
системе уравнений
1 д:^[p^ - р] + 2хур + у^ = 0.
§ 6. Уравнения первого порядка. Особые решения 45
Разрешив второе уравнение системы относительно у, получаем, что
у = —хр ± Ху/р^ где р ^ 0. Найдя отсюда dy и подставив его в равенство
dy = pdx^ получаем уравнение
B^/р q= l){2pdx + xdp) = 0.
Первая скобка может обраш,аться в нуль лишь при у/р = -. Подставив
у/р = - в формулу для у, получаем решение у = -х. При этом было
учтено, что в формуле для у нужно брать только знак «плюс».
Приравнивая нулю выражение второй скобки, получаем уравнение
с разделяюш,имися переменными. Все его решения задаются формулой
pд:^ = С, где G^0. Подставляя р = —г^ в формулу для у, в которой
С
берется только знак «плюс», получаем решение у = h vC • sign ж, где
X
X ф О, С > 0. Кроме того, при р = О имеем решение у = 0.
Дискриминантные кривые находятся из системы уравнений
у = -хр ± Ху/р,
О = -x± ,
2ч/р'
где второе уравнение получается дифференцированием по р первого
уравнения. Исключая из этой системы параметр р, находим, что у = -х задает
дискриминантную кривую. Это единственный кандидат в особые решения
нашего уравнения. Поскольку , = ix - решение уравнения, то ос^я
ДЛЯ него проверить выполнение определения особого решения. Для этого
составляем систему уравнений относительно С:
1 С
-тх = h VC • signx, X 7^ О,
4 X
4 ^ ж2*
Легко видеть, что найденное из второго уравнения С = jx
удовлетворяет и первому уравнению при х ^ 0. Следовательно, оба луча прямой
у = -j-x, получаемые при х т^ О, являются особыми решениями заданного
уравнения.
46
Глава 1. Дифференциальные уравнения первого порядка
Качественная картина поведения интегральных кривых уравнения
показана на рисунке. Из рисунка, в частности, видно, как из найденных
решений уравнения можно получать составные решения уравнения. А
Найти все решения, исследовать особые решения и нарисовать
качественную картину поведения интегральных кривых уравнений A—66):
1. у'^ ~ Ахуу' + 8у2 = 0. 2. ?у2 + 2х^у' - Ах'^у = 0.
3. 8ху'^ = уA2у'2 _ 9). 4. х^у'2 - 4х{у + 2)у' + 4у{у + 2) = 0.
5. x^y'2 + х'^уу' + 1 = 0. 6. у'^ - Зхугу' -h 9у3 = 0.
7. у'^ - Зх'^у' + Аху = 0. 8. y^y'2 + 2хуу' ~ у2 + 1 = 0.
9. у' = In —^. 10. ху'2 ~ 2уу' + 2у = 0.
11. ж^у'2 - 4ж2уу' + 4xy2 + 4у' = 0. 12. Sy'^y'^ ~ Зу + 6{х ~ 2)у' = 0.
13. 5xy'2 + 1 = уу'A + уу'). 14. ж^y^y'^ ~ 2х'^у^у' + ху^ + 2уу' =: 0.
16. у'2 - 8xy' + 8x2 ^ 4у = 0.
18. 2у2у'2 - 2xy'2 -f 4уу' + 1 = 0.
20. x^y'2 + ху' + у = 0.
22. A ~ x2)y'2 + 2xyy' + 2;2 = 0.
24. yy'iyy' - 1) = ж-у2.
15. -у
/2
у' + У = 2х - 3.
17. у'2 + а:у2у' + у^ = 0.
19. у'2 - 2уу' + 4е2^ = 0.
21. 4у'2 + Зж^у' = 9х*у.
23. у = у' + -(а:-1пу')
4
X \ 3
§ 6. Уравнения первого порядка. Особые решения 47
25. Цху' - 2у) = 4x2 _ у/2 26. 2уу'^ + х^{у'^ + 1) + 2ху' = 0.
27. 3 (^1 - у - ^у'^^ = (^х + ^у'^ . 28. 2ху = х^у' + Зг/ (^^^
29. у' = у^е у . 30. у = у'-— - y'^-2-•
sh X sh а;
31. уу'2 - 2ху' + у = 0. 32. 12уу' = 9a:y'^ + 4^.
33. у + у^^ cos"^ X = y'sinrrcosx, |х| < •-. 34. (у — ху'J = у' + 1.
35. 4уЗу'2 - 4а;у' + у = 0. 36. 2а:у2у'2 - у^у' + 1 = 0.
37. жу'З - уу'2 +4 = 0. 38. 8а;у'^ + 12уу'2 - 9у^ = 0.
39. х^у'З + а:'*уу'2 -1 = 0. 40. у'^ - ху' + у = 0.
41. у'2 + 4е-з^у' + бе-зху = о. 42. Зу'2 - 4е2^у' + 4уе2^ = 0.
43. 4уу' = ху'2 + х^. 44. у' = f ^-^^^ .
45. буу'2 = 2жу'3 + Зж! 46. (жу' + уJ = -у^у'.
47. (у + xf = -у'ЦЗу' + 5J. 48. {х - yf = у'^^Ьу' - if.
49. у' — In у' = у — ж. 50. 1 + уу' + у' In у' = ху'.
51. 4у'3 - Зж2у' + 4а:у = 0. 52. 4уу'2 - 2ху'^ - х^ = 0.
53. 4а,-уу'2 - 8ж2у'3 = 1. 54. 2х-уу'2 = Ах^ + {х"^ + 1)у'3.
55. 2уу' + 2у - Зж = а:у'2. 56. 4а:2у + у'2 = 2ж(ж2 + 1)у'.
57. ^ + 1пу' = 1. 58. ху' = уA + 1пу').
ху'
59. а:у'2 = у' - ^е'^У. 60. 4а:^у - х'^у' + ^у'2 = 0.
4 8
61. ^у'^ - Зж^у' + бх^у = 0. 62. {ху' + уJ + 20а:2у' = 0.
63. х^ + 5ху' + у'2 = 5у + Ах^ + 2ж\'. 64. ху'^у' + Зу^ + y"^ = 0.
65. ху'^ + Зуу'2 + 27y'^ = 0. 66. х^ + Зжу' + у'2 = Зу + 2х^ + 2а:2у'.
48 Глава 1. Дифференциальные уравнения первого порядка
Ответы к задачам § 6
1. у = С{х — С)^, 27у = 4ж^ — особое решение.
2. у = Сх'^ + C^, у = —-т^^ — особое решение.
B 3 \^ 3
-х Н- —:; I , у = ±-ж — особые решения.
4. у = ~2 + 2(Сж + l)^, у = ~2 — особое решение.
С' 1 2 .
5. у = h ~, ху^ = 4 — особые решения.
6
- j — особое решение.
о
4 .^^Q , Х^
7. у = ЗСхз ~ 16С , у = ±— особые решения.
8. у^ ^ С'^ Л- 2Сх + 1, у = ±л/1 - ж^ — особые решения.
9. у = (ж + С)[In(ж + С) — 1], у = —1 — особое решение.
10. 4у^ = СCх — С)^, у = X — особое решение при х ^ 0.
11. у = С — -C^x^, 2ж^у = 1 — особое решение.
12. у = О, X = 2 + —; - ~С^у^, 4(x - 2)^ + 9у^ = О — особое решение.
13. X = —у^ — Су — 7^^^ 4д: = у^ — особое решение.
о
14. 2у^ + С^х^ = 2С, ху = ±~7= ~ особые решения.
v2
15. у = —(х — С)^ + 2С — 3, у = 2x — 2 ~ особое решение.
16. у = д:^ + Сх C^, у = 2х^ — особое решение.
17. у = О, Cy(x - С) = 1, х^у = 4 — особое решение.
18. X = —-у^ — Су + ;^C'^, х + y^ = О — особое решение.
19. у = Се^^ + ~, у = ±2е^ — особые решения.
G
§ 6. Уравнения первого порядка. Особые решения 49
20. у = C^, 4д:^y = 1 — особое решение.
X
21. у — Сх^ + 4C^, у — ~тгх^ — особое решение.
16
22. У = л ( ^^^ "^ С' ~ ~ I, у = ±\/1 — x2 — особые решения.
23. у = е^"^^ - ^С, у = -(х + 1 + 1п2) — особое решение.
24. {х ~ C^)^ + y^ = C^, х = у^ — j — особое решение.
25. у = х^ + Сгг + qC^, у = —3:^ — особое решение.
о
26. д:^ + ( у + -C^ I = С^, 2у = 1 ~ д:^ ~ особое решение.
27. у = 1 ~ д:^ + Сх — ^C'^, у = 1 - --д:^ ~ особое решение.
28. у = 2C^д:^ + ^т^, х = ±y^ — особые решения при у ^ 0.
29. у = Се^^, С ^ О, еху = — 1 — особое решение.
30. у = С ch х — C^,y= -- ch^ х — особое решение.
31. у = О, х = Cy^ + -—, X = ±у — особые решения при у т^ 0.
40
14 2
32. у = jp^x^ + С^ у = ±х^ ~ особые решения при х ^ 0.
4G
33. у = Сtgх — C^, у = - tg^ ж — особое решение.
34. у = (C^ — 1)х + С, у = —X — особое решение.
4д:
35. у = О, х = Су"* + —^, X = ±y^ — особые решения при у т^ 0.
40
36. X = Су'^ ~ 2C^, 8а: = у^ — особое решение.
4 2
37. у = Сх + -^, у = 3x3 — особые решения при ж т^ 0.
50 Глава 1. Дифференциальные уравнения первого порядка
/ ЗС \^ 2
38. у = ± { -г——- , ху = ±- ~ особые решения.
\C — 3xJ 3
С 1
39. у = 1- 7^5 4:х'^У^ = 27 — особое решение.
X С^
40. у — Сх — С^, 27у^ = Ах^ — особое решение.
3 2
41. у = 4Се~2^ - 6С^, у = ;^е~^^ — особое решение.
о
3
42. у = Се^ С^, Зу = е^^ — особое решение.
111
43. у = тС'д^^ 4- -г^, у = ^о^^ ~ особое решение.
44. у = С -^, у = ж ± 2 — особые решения.
X — О
45. у = Сх^ Н—^7^, 2у = v^a;^ — особое решение.
18G
46. у = 7^, у = —4д: — особое решение.
X ~ С
fx + C\^
47. у = С ~ 3 I —-— I , у = —X ± 2 — особые решения.
48. (у + С)^7'^ = 5^{х + су, у = х±2 — особые решения.
49. у = е^^^ ~С, у = д: + 1— особое решение.
50. у = In (х + С) + С, у = х — 1 — особое решение.
3 4 д;^
51. у = т^'з^з — С^, у = ±— особые решения.
rt ^
52. у = Cж^ + 77777, 4у = Зхз — особое решерше.
53. X = С(у — C)^, 27x = 4у^ — особое решение.
1 2
54. у = C(д:^ + 1) + г-^, 2у = 3(a:^ + 1)з — особое решение.
55. у = Cд:^ — х + -р::;,у = хиу = —Зх — особые решения при у ^ 0.
56. у = C(д:^ + 1) - C^, у = -(х^ + l)^ — особое решение.
§ 6. Уравнения первого порядка. Особые решения 51
X
57. у = С + С\п—,у = х — особое решение.
G
58. у = —е^^~\ у = X —- особые решения при х ф^.
О
59. X = 2СеУ + 20^, Зх = е^У — особое решение.
60. у = 2Сх^ — 2С^, у = -х^ —- особое решение.
3
61. у = -Сх'^ — 2С^, 2у = ±х^ — особые решения.
ill
62. у = V \^С, у — —Ьх —- особое решение.
X
63. у — -х^ + Сх + -С^^ у = -х^ — -х'^ — особое решение.
5 5 5 4
64. у = О, уС{х + С)^ = -27, х^у = 256 — особое решение.
65. {х + С)^у = -С, 27х'^у = ~4 — особое решение.
1 1 3 '^ 1 •
66. у == -х^ + Сх + ^С^, у = --7^^ + Q^"^ ~~ особое решение.
о о 4 о
Глава 2
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВЫСШЕГО ПОРЯДКА
§ 7. Основные типы уравнений,
допускающие понилсение порядка уравнения
В § 7 рассматриваются уравнения вида
F(x,y,y',...,yW)-0,
где у{х) — искомая функция, х — независимая переменная, п ^ 2.
1. Простые случаи понижения порядка уравнения. Порядок
уравнения легко понижается, если его можно преобразовать в равенство
полных производных по X от некоторых выражений.
Пример 1. Решить уравнение
Д Заметим, что у = С — решение уравнения. Пусть далее у ф С. Перенеся
У2/'^ в левую часть уравнения, разделим обе его части на у^. Получаем
у2
у^' \у) \уЧ
Отсюда
у г/^
в случае С = О имеем
уу' = 1, {у^У = 2, у^ = 2х + С.
В случае С ^0 получаем
§ 7. Основные типы уравнений 53
Последнюю формулу можно преобразовать к виду
2х
y' = Ci+C2e-^i, CiT^O.
2х
Ответ, у = С, у^ = 2х + С, y^ = Ci +С2е~^, где С, Сь Сг — произвольные
постоянные, при этом Ci Ф 0. А
В случае, когда уравнение не содержит у, порядок уравнения
понижается, если сделать замену, взяв за новую неизвестную функцию
производную от у наименьшего порядка, входяшую в уравнение.
Пример 2. Решить уравнение
Л Сделаем замену у" = гг. Тогда у'" = 2г' и уравнение преобразуется к виду
1 ^ 1С
х^2г' + 2xz = -^. Отсюда {x'^z)' = ( — j ,
x'^z = -- + С, z = —^ + -^.
Возвращаясь к у, имеем
Ответ, у = Ciln|x| + С2Х + Сз — тг"» ^Д^ Ci, С2, С3 — произвольные
2х
постоянные. А
Когда уравнение не содержит х, порядок уравнения понижается, если
за новую независимую переменную взять у и ввести новую неизвестную
функцию z{y) = у'. При этом у" = z{y) • z\y).
Пример 3. Решить уравнение
y"{y-l)+y'{y-lf = y'\
Д Заметим, что у = С — решение уравнения. Пусть далее у ф С. Положив
у — 1 = U, получим уравнение
Возьмем и за новую независимую переменную и положим и'{х) = z{u).
Тогда и"(х) = Z • z'{u) и уравнение примет вид uz • z' + u^z = z'^.
Заметим, что z ф О, так как случай z = О дает у — С.
54 Глава 2. Дифференциальные уравнения высшего порядка
Сократив уравнение на z, получаем
, 2 uz' — Z ^ (z\' ^ о ^
UZ — Z = —и \ 5— = ~1? ~ — ~? ^ == ~'^^ + С^'^'
Отсюда и'{х) = —v? + Си.
В случае С = О w — —-, а в случае С Ф ^ — In
X -f Со С
= X + Со.
\С -и\
Полагая гл = у — 1 и упростив полученное выражение, получаем ответ:
х + С ^ l + Cie^^^'
где С, Ci, С2 — произвольные постоянные. А
При решении задач с начальными условиями целесообразно
использовать заданные условия в самом процессе решения.
Пример 4. Решить задачу Коши
2(у + х)/ + у^^ + 2уЧ , ^^ ,, ^0, y(^/2)-l-v^, y'(^/2) - ^/2 - 1.
Л Положив и — уЛ-х^ преобразуем уравнение к виду
2W -f и'2 - 1 + -^ = 0.
Так как это уравнение не содержит х, то положим w'(x) = z[u). При этом
и" — Z • z'iu) и уравнение примет вид 2wzz' + z^ — 1 Н—5" — О-
Это уравнение Бернулли. Положив w = z^., получаем uw' -\-w = \ г,
11 1 G
(ш/;)' = 1 7^, UW = и-\ \- С, W = и''^ — 1-\—^Н .
и"^ и и^ и
Учитывая начальные данные и равенство и' = у' -f 1, находим, что
и'(\/2) = \/2, u{V2) - 1, Тогда С - О, и'^ - 1 + Д., и' = у!±±]^^
w^ и
у/1 + у? = X + с. Из условия w(\/2) = 1 следует, что С = 0. Тогда
>/l + (у + х)^ = X. Учитывая начальные данные для у, получаем отсюда
ответ, у = \/х2 — 1 — X. А
Пример 5. Решить задачу Коши
г/у" = (у" + у") thy, у@) = 1, ?/'@) = -1.
§ 7. Основные типы уравнений 55
Д Заметим, что у = С — решения уравнения, но среди них нет решений
задачи Коши, так как у' = 0. Пусть далее у ф С.
Полагаем у' — z{y). Тогда у" = zz' и после сокраш,ения на z т^ О
уравнение примет вид
yz' =^z{z^ ^l)thy.
Заметим, что z = —1 — решение этого уравнения. Из замены тогда имеем
у' =.^1,у = -х + С.
Используя начальные условия, получаем решение задачи Коши
у = 1 — X. Других решений задача Коши не имеет, поскольку при у ф Q
для рассматриваемой задачи Коши выполняется теорема единственности
решения. А
Решить уравнения A—17):
1. ху" -f ху'^ -f у' := О, .т ^ 0. 2. у"^ + у'^ = {у" + у')у"у'^'
3. / = ^1п^ + ^. 4.4у"^У = 1-
XXX
5. уу" - у'2 = у'у2. 6. Зуу'у" = у'З + 2.
7. 5уу'3у" = у'5 + 4. 8. уу" = 7у'2 + у^у'.
9. уу" = 2у'2 - 4у2у'3. 10. (уЗ + у) у" - (Зу^ - 1) у'^ = 0.
11. уу"' - у'у" = 0. 12. уу" = 2у' + 2у'2.
13. A + у2) у" + 2уу'2 = у'. 14. A + у2) у" = у (у'2 - 1).
15. 4а:у" - у = 4(у' + 1). 16. 2A - у)у" = у'^ + 1.
17. 2уу'у"-у=у'3.
Найти решение уравнения, удовлетворяющее заданным начальным
условиям A8—38):
18. y"s{n^x- (y'sm-^aj + y'2)cosa; = 0, у(|) = О, у'(|) = 1.
19. у" cos^ ж + (у' cos^ а; + у'^) sin ж = О, у@) = О, у'@) = 1.
20. (а;-|-1)у(") = у("-1), п > 2, у("-2-'=)@) = (n-2-A;)!, А; = 0,1,... ,п-2,
у("-1)@) = 0.
56 Глава 2. Дифференциальные уравнения высшего порядка
21. ху^"^^ = у("-1), п > 2, ?/("-2-'=)@) = {п-2-к)\, к = 0,1,... ,п - 2,
у(п-1)@) =0.
22. у" = Ъу^, г/@) = 1, у'{0) = -2.
23. у" = у'2 + A - у)у', у{1) = у'A) = 1.
24. у" + у'2 = y'e^ у@) = О, у'@) = \.
25. уу" - у'2 + 2 = О, у@) = 1, у'@) = 0.
26. уу" = уУ + у'2, у@) = 1, у'@) = -3.
27. Зу'у" = e^ у(-3) = О, у'(-З) = 1.
28. 2уу" = у'2 C - 4уу'2), у{4) = 1, у'D) = -1.
29. уу" - у'2 = у\ уA) = 2, у'{1) = -4.
30. уу" = 5у'2 + Зу2у', уA) = 1, у'A) = -1.
31. уу" = Dу'4 - у'2) еУ, у@) = 1, у'@) = -\.
32. 2у2у" = 2у'4 - уу'2, уA) = у'A) = 1.
33. 2у2у" + у'2 = 4, у@) = 1, у'@) = -2.
34. Зу'у" - у'З - у + 2 = О, у{0) = О, у'@) = 1.
35. 2 (у2 + у) у" - (у2 + у + 1) у'2 + уЗ = о, уB) = 1, у'B) = -1.
36. 2 {еУ + 1J у" + {е^У - 1) у'^ + 1 = О, уA) = О, у'A) = ^.
37. у" + B + 4у2) у'З - 2уу'2 = О, у{0) = 1, у'@) = ^.
38. уУ + у'" In у - у-'у'^ = О, у@) = у'@) = е.
2. Случаи однородного и однородного в обобщенном смысле
УРАВНЕНИЙ. Если уравнение является однородным относительно у и всех
производных от у, т. е. уравнение не меняется при одновременной замене
у на Ау, у(*^^ на Ау(*\ А т^ О, А; = 1,2,..., п, то порядок уравнения можно
понизить на единицу, если ввести новую неизвестную функцию z{x) по
правилу у' = yz. При такой замене у" = y{z' + z^).
§ 7. Основные типы уравнений 57
Пример 6. Решить уравнение
2:^yy" - Ьхуу' - x^y'^ = 6y^, х ^^ 0.
Д Заметим сначала, что у = О — решение уравнения. Пусть далее у Ф
Ф 0. Убедившись в однородности по у, у', у" заданного уравнения, вводим
новую функцию Z с помощью равенства у^ — yz. После сокращения на
у ф^ получаем уравнение x^2r' — Ъхх = 6.
Общим решением этого линейного уравнения первого порядка является
Z = Сх^ . Отсюда и из замены находим, что
X
У X
Решая это уравнение, получаем ответ:
у=^iв^-^
X
где Ci и С2 — произвольные постоянные. А
Пример 7. Решить уравнение
хуу'' + xy'^ = Зуу', X 7^ 0.
Д Данное уравнения является однородным по у, у', у" и его можно решить,
понизив порядок уравнения с помощью рекомендуемой замены.
Однако уравнение можно решить и по-другому. Заметим, что у = С —
решение уравнения. Пусть далее у Ф С. Если иметь ввиду, что
{хуу'У = хуу" + ху^ + уу\
то заданное уравнение можно записать в виде
{хуу'У = Ауу' или {хуу'У = By^)^
Отсюда
хуу' = 2у^ + С или {ху'^У = 4у2 -Ь 2С.
Полагая у'^ ^ и, получаем уравнение с разделяющимися переменными
хи' = 4w 4- 2С.
58 Глава 2. Дифференциальные уравнения высшего порядка
Интегрируя его, получаем ответ, у^ = Cix'* -f С2, где Ci и С2 —
произвольные постоянные. А
Пусть теперь уравнение является однородным в обобщенном смысле,
т. е. существует такое число 5, что уравнение не меняется при
одновременной замене х на Ах, у на Х^у, у^^^ на У~^у^^\ где А т^ О, к = 1,2,... ,п.
При X > О вводим новую независимую переменную t и новую
неизвестную функцию z{t) с помощью замены
X = е^, у = ze^K
Тогда уравнение приводится к виду, в который не входит t. Следовательно,
порядок уравнения понижается по правилу, изложенному в п. 1.
При X < О полагаем х = —е^.
Пример 8. Решить задачу Коши
х^{у" + 2уу') + 2ху^-2у = 0, уA) - 3, у'{1) = -3.
Л Подставив в уравнение Хх вместо х, Х^у вместо у, А^"^у' вместо у'
и Х^~'^у" вместо у", потребуем, чтобы параметр А входил в одинаковой
степени во все слагаемые. Если это возможно, то после сокращения на
множитель с такой степенью А получим опять то же уравнение. Для
определения числа S имеем равенства
2 + ,9-2 = 2 + 5 + 5-1 = 1 + 25 = 5,
которые выполняются при 5 = — 1. Полагая х = е^, у = z{t)e~^^ находим,
что
у'(х) = [z{t)e-^y • е-^ = {z' - z)e-^\
у"{х) = [{z' - z)e-2^]' . е-^ = {z" - 3z' + 2z)e-^K
После подстановки в уравнение выражений для х, у, у', у'' и сокраще-
ение
z" - 3z' + 2zz' = О,
ния на е ^, получаем уравнение
в которое не входит t.
Заметим, что z = С — решение этого уравнения. Из замены следует, что
С
у = решение исходного уравнения. При С — 3 такое решение удовле-
X
творяет заданным начальным условиям. В силу теоремы единственности
§ 7. Основные типы уравнений 59
решения задачи Коши, которая в нашем случае выполняется при х ф О,
других решений заданная задача Коши не имеет.
Ответ, у = —. А
X
Решить уравнения C9—53):
39. хуу'' - {х + 1)уу' = ху'^, хф{).
40. уу" — у''^ + у^ sin а; = 0.
41. уу"-!-^-/^ = 0.
X
42. хуу" + уу' = ху''^ + г/,хфО.
43. у2?/' - Зуу'у" + 2у'^ + у^ sinx = 0.
44. х'^угУ^ = {хУ + yf, X фО.
45. хуу'' ~ уу' = 1ху'^, X ф 0.
46. yy" + yy'tgx + 2y'^ = Q.
47. yy" + yy'tgx = 2y'^,
48. уу" - ^f- = 2у'\
X + 1
49. хуу" + 2ху'^ = 2уу', хфО.
50. хуу" + ху'^ + уу' = {)^хф 0.
51. y^y"-yy'U+y) + iy'^^Q.
\ Х/ X
52.уу'у"-^-у"=х'у\
X
53. {х + 1)уу" + уу' = ху'^, X ф -1.
Найти решение уравнения при заданных начальных условиях E4—67):
54. уу" = {1-х)у'2,уA) = 1,у'A) = 2.
55. (уу" - у'2) sina; + у^ = (sina; - cosx)yy', у \^-j = у' (^-j = 1.
56. хуу" - ху'^ + у'{у' + у) sina; = О, уA) = 1, у'A) = -1-
57. 4хуу" - 4уу' + у'2 = О, у(-1) = 1, у'{-1) = -4.
60 Глава 2. Дифференциальные уравнения высшего порядка
58. хуу" - 4ху'^ + Ауу' = О, у{1) = 1, у'{1) = 2.
59. 2жу2у" - 2ху2/'2 + 2ху'^ = у'у^, у{1) = у'{1) = -1.
60. A - smx)yy" + уу'COSX = у'^, у{0) = 2, у'{0) = 1.
61. уЦу" - у') = у'Ну - 2ху'), у{1) = у'A) = е.
62. хуу" + хB1пх - 1)у'2 = уу', уA) = 1, у'{1) = -2.
63. хуу" + A + х^) уу' + ху^ = а;у'2, уA) = 1, у'A) = -1.
64. у2у" - ^xVy' + l^y' - уу'^ = О, уA) = 1, у'A) = -2.
65. х^у" + 2а:2уу' + 2ху^ - 2у = О, а) уA) = 2, у'A) = О, б) уA) = -1,
У'A) = 1-
66. х^" - хуу' + 2 (у - х2) у = О, у{1) - 1, у'A) = ^.
67. а;4у" - а;2уу'2 + 2xyV = у\ уB) = 2, у'B) = 1.
3. Разные задачи. Все задачи этого пункта можно решать методами,
изложенными в п. 1 и п. 2.
68. С помощью подстановки у — z^ решить уравнение
2х^уу" + 4у2 = х2у'2 + 2а;у(у' + ^у), хф{).
Решить уравнения F9—87):
69. уу" - 2у'2 = 0. 70. (у2 + у) у" - Bу + 1)у'2 = 0.
71. Зуу" - 5у'2 = 0. 72. 4уу'2у" = у'" + 3.
73. х'^у" = 2у'(у - .х), ж 7^ 0. 74. ху" = у' + 2х^уу', хфО.
75. уу" + 4у' = у'2. 76. у" = (^) + 2^.
77. 2у(жу" + у') = а;(а; + 2)у'2, а; / 0. 78. ж^уу" = {ху' - 2у)'^, хфО.
79. уу" = (уЗ + у') у'. 80. уу" + 2у'2 = Зуу'.
81. (у + 1)у" + -4т = У'^- 82. 2а:2уу" + 4у2 = х2у'2 + 2а;уу', х ф 0.
у + 1
§ 7. Основные типы уравнений 61
83. х'^уу" + а;2у'2 - Ъхуу' + Ау"^ = О, х ^ 0.
84. х'^у" - х'^{ху' - у) - {ху' - уK = О, ж ^ 0.
85. у'у'" = у - (^^) . 86. у'у'" = Зу.
87. х^у'у'" - а;2у ^y^^ = {s,xф 0.
Найти решение уравнения при заданных начальных условиях (88—95):
88. хуу" + у2 = а;у'2 + {х - \)уу\ уA) = у'A) = 2.
89. A + у)у" + ху'2 = О, уA) = О, у'A) = ^.
90. у{у" + у') = у'2 (ху2 - 1), у@) = у'@) = 1.
91. (у + 2)у" + у'2 = cos2x, у@) = -2, у'@) = 1.
92. 2 (уу" - у'2) = (у'2 - 2у'у) е\ у@) = 1, у'@) = 2.
93. а; {уу" - у'2) = уу'In ^, уA) = у'A) = 1.
94. ху'" - у" = 0:2 ,„3 X, у (|) = О, у' (|) = 1, у" (f) = |.
95. Зу"у"' - 2у = 16, уA) = 2, у'A) = О, у"A) = -2.
Найти интегральные кривые, а) касающиеся прямой у = 1, б)
пересекающие прямую у = 1 под углом V = -г или (^ = —, для уравнений (96—97):
96. 2 {уу" - у'2) + Зуу'4 = 0.
97. уA - 1пу)у" + A + 1пу)у'2 = 0.
98. Для уравнения A -1- у'2) у'" = Зу'у найти интегральные кривые,
пересекающие ось ординат под прямым углом и имеющие в точке
пересечения кривизну, равную а) нулю, б) единице.
Найти решение уравнения при заданных условиях (99—102):
99. у" + 2A - у)у< = О, у\х) ^ О в (х, 1).
100. уу" - 2у'2 = 2у\', уB) = У7B) ф 0.
62
Глава 2. Дифференциальные уравнения высшего порядка
101. 2уу" - у'2 4- 2уу'^ = О, уA) • /^A) = 1.
102. уу" + yy'tgx = A - sinx)y'2, у@) • у'@) < 0.
Ответы к задачам § 7
1. еУ = Ci\n{C2x),y = C.
2. е^а: + Сх) = Сч, (у + Сх){С2 - а;) = 4, у = С..
3. 2у = 3:2 + (о^ у@2 ^ е^1Х(@^^ _ ^^ ^ ^^^
4. 4(^+Ci)i-12Gi(Vy + <:?i)^=C2±3a;.
5. уA + С2е^>^)=Сьу(С-а;) = 1.
(^
Cia; + C2 +2, у = G-а;^.
6. уСх
7. yCi = ( ^Схх + CsV + 4, у = С - a;i5^.
8. уЗ
И-Сзе
c^i(-;^)
Ci.
9. y'' + Ci=yCx + C72),y = C.
10. (l + y2)(Ci:r + G2) = l.
11. у + vV+^ = С2е^зх_ У = ^^sin{Cix + Сз), у = Схх + Сг-
12. у (l - СгеЩ = Ci (l + Сае^), arctg (Ciy) + Ci,t = С?, у + .т = С.
13. (у - CiJ + (Cf + 1) In (у + Cxf = 2а,' + (^2, у = С.
14. у + yr+TTCf = G26^1, у = v'Cf^sin ( ^ + <^2
у = ±а; + С.
15. у = Схх^ - С1х - а; 4- С2, Зу = з;3 - Зж + С.
16. 2х = CiBf + sin2<) + С2, у = 1 - Сх cos^ «.
17. 2у = С2е'^'^ + Ci, у(з; + С) 4- 2 = 0. 18. 4у = 2ж - тг - sin 2х.
19. 4у = 2а; + sin2a;. 20. у = а;"-^ + ^.п-з ^ ... + j
§ 7. Основные типы уравнений 63
21. у = Сх" + а;"-2 + а;"-^ + ••• + !. 22. у{х + 2)'^ = 16.
23. у = е^-1. 24. B-а;)е!/ = 2.
25. у = cos {xs/2).
27. хЗе!' + 27 = 0.
29. уBх - 1) = 2.
31. 2у = 2 - ж.
33. у = 1 - 2х.
35. 4у = (а; - 4J.
26.
28.
30.
32.
34.
36.
У =
у =
ху-
iy-.
У =
^1
('
= 1.
= {х
1-
у + еУ =
-9х.
3 ^
+ 1J
(-
: X.
2
Г
2 ^
3^
3
г
37. у = у/х + 1. 38. 1пу = ч/2ж+Т.
39. 1п(С2у) = CiC; - 1)е^, у = 0. 40. 1п(С2у) = Ci^ + sina;, у = 0.
41. у = Ci|a;|^2. 42. у = Cie^|a;|^2.
43. In (Сзу) = С2а;2 + Cix - cos ж, у = 0. 44. In (С2У'^) = Cix^, у = О
45. y(Ci + С2х2) = 1, у = 0. 46. у = ^Ci + C2sina;.
47. y(Ci + С2 sina;) = 1, у = Q. 48. у [Ci + G2(а; + 1)^] = 1, у = 0.
49. у = ^Cia;^ + С2. 50. у^ = Ci In |ж| + С2.
51. In (С2у2) = ±^а;2 + Сь у = С. 52. In (Сзу^) = ± (х^ + Ci)^ у = 0.
53. ylCia; + Ci + 1|^ = Сг, у = Ce'^ у = С. 54. ж1пу = 2(а; - 1).
X
55. у = tg —. 56. Iny = I — X.
57. у = Bз; + 1J. 58. yv^2-a;3 = a;.
59. In(-y) = 2(v/x-1). 60. Iny = ln(l+ cosa;)+ tg-.
61. Iny = sj2x - 1. 62. у = 1 - 21na;.
63. xy = l. 64. Iny = 2A-a;)-
65. a) у A + 2a;^) = 6a;2, 6) a;y + 1 = 0. 66. у (l + 5a;^) = 6a;2.
64
Глава 2. Дифференциальные уравнения высшего порядка
67. у = X. 68. 16у = ж2 (In^ |а;| + Cj In |а;| + Сг) ,у = 0.
69. y{Cix + С2) = 1, у = 0. 70. A - С2е<^1^) у = С^е^^"".
71. у|а; + С2|5= 6-1,^ = 0.
73.
72. Ciy = ( \Cix + С2У + 3.
74.
75.
76.
Схх ■ arctg(Ciy) = С2Х - 1, у(^С2е х - ij = Ci (^Сае ^ +lj,
^" 1 + Са:'
2Ciajctg(Ciy) = х2 + С2, y(l-C2e^i^') = Ci A + Сге^'^'),
у{С-х^)=2.
Сгу + 4 = C2e^^^ у = 4ж + С, у = 0.
2у + х2 = 2Cix - 2С\ In |х + Cil + С2, у = С.
1
77. у = С2
а;
x-2Ci
у = Сех, у = С.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
4 £l
у = С2ХЗ • е'^.
у2 A - Сге^!^) = ClC2e^^^ у2(С - х) = 1, у = С.
у = ^Cie3^ + С2.
Ci(y + 1J = Сзе^!^ - 1, (у + 1)^ = а; + С.
y = Cix2(C2 + ln|x|J,y = Cx2.
у = Cix ± х-\/С2 — Inx''', у = Сх.
у = ^26^1 (х - ^) + Сз, у = CiХ2 + С2.
(у + Сх? = Сга: + Сз, У = Cjx + С2.
у = C2e^i^(Cix - 1) + Сз, у = Gix2 + С2.
у = 2х.
(х + 1Iп(у + 1) =х-1.
У=^/1п(х + 1J + 1.
§ 8. Линейные уравнения с постоянными коэффициентами
65
91. у = sin а; — 2.
92. у = е^^.
93. у
— ^Х-1
7Г
94. у = -г — о; sin ж — 2 cos ж.
^ 2
95. у = 2а; - з;2 + 1.
96. аJ/ = 1, б)у= (^^x + cV.
1
97. а) у = 1, б) 1пу = 1 ±
х + С
98. а) у = С, б) у = С ± \/Г^^ж2.
99. Ci arctg [Ci(y - 1)] = х + Сг, A - у){х + С) = 1, у = 1.
100. у^Зж + С + 1 = 0.
101. у={^х + Су.
102. у = ^2
sin а; — Ci
sin X + Ci
§ 8. Методы решения линейных уравнений
с постоянными коэффициентами. Уравнения Эйлера
Для решения линейного однородного уравнения с постоянными
(вещественными) коэффициентами необходимо составить характеристическое
уравнение, найти его корни и по ним написать общее вещественное
решение заданного уравнения.
Пример 1. Решить следующие линейные однородные уравнения:
а) у"^ - 6у"' + 8у" + 6у' - 9у = О,
б) у^^ + 6у"' 4- 13у" -1- 12у' + 4у = О,
в) г/^ - Зу'" + 5у" - у' - 10у = 0.
Д а) Составляем характеристическое уравнение
Л^ - 6А^ -1- 8А2 + 6А - 9 = 0.
66 Глава 2. Дифференциальные уравнения высшего порядка
Легко видеть, что его корнями являются Ai == — 1, Л2 = 1. Чтобы найти
остальные корни, достаточно разделить левую часть характеристического
уравнения на (Л^ — 1). Тогда уравнение можно разложить на множители
следующего вида
(Л2 - 1)(Л2 - 6Л + 9) = (Л^ - 1)(Л - 3J - 0.
Таким образом получаем еще один корень Лз = 3 кратности два.
Следовательно, общее решение заданного уравнения имеет вид
у = Cie-^ + С2е^ + (Сз + C4x)e^^
где Ci, С2, Сз, С4 — произвольные постоянные.
б) Нетрудно проверить, что Ai — — 1 и Л2 — —2 являются корнями
характеристического уравнения
Л^ + 6Л^ -f 13Л'2 + 12Л + 4 = 0.
В таком случае это уравнение можно представить в виде
(Л + 1J(Л + 2J-0.
Отсюда видно, что оба корня Ai = — 1, Л2 = —2 кратности два. Значит,
общее решение заданного уравнения имеет вид
у = (Ci + С2х)е-'' + (Сз + C4a;)e-^^
где Ci, С2, Сз, С4 — произвольные постоянные.
в) Характеристическое уравнение
Л'^ - ЗЛ^ + 5Л2 - Л - 10 - О
имеет корни Ai = — 1, Л2 = 2. Разделив левую часть этого уравнения на
(Л + 1)(Л — 2), получаем следующее представление характеристического
уравнения
(Л-f 1)(Л-2)(л2-2Л + 5) = 0.
Это дает еще два комплексно сопряженные корнр! Лз = 1 — 2г, Л4 = 1 Ч- 2г.
Сдедовательно, общее решение заданного уравнения имеет вид
у = Cie-"-' + С2е2^' + е^(Сз cos2.x- + С4 sin2а.-),
§ 8. Линейные уравнения с постоянными коэффициентами 67
где Ci, С2, С35 С4 — произвольные (веш^ественные) постоянные. А
Для решения линейных неоднородных уравнений с постоянными
коэффициентами используются чаще всего метод неопределенных
коэффициентов и принцип суперпозиции.
Пример 2. Решить линейное неоднородное уравнение
/' _ у" - 4у' + 4у = -8(cos2a; -f 2sin2a.') - Зе^.
Л Сначала составляем характеристическое уравнение
Л^'^ - Л^ - 4Л + 4 = 0.
Его корнями являются Ai = —2, Л2 = 1, Л3 = 2. Поэтому общее решение
соответствующего линейного однородного уравнения имеет вид
где Сь С2, Сз — произвольные постоянные.
Чтобы получить общее решение заданного уравнения, необходимо
найти какое-либо его решение yi{x) и прибавить к уже найденному общему
решению уо{х) линейного однородного уравнения. Согласно принципу
суперпозиции решение yi{x) =^ У2{^') + Уз(^)) вде У2(^) " какое-либо решение
уравнения
у" - у" - 4у' + 4у -: -8(cos2a; -f 2sin2a;),
а 'уз(^') — какое-либо решение уравнения
/'- у" - 4у'+ 4у =-Зе^
Решение У2{х) ищем в виде
У2{^) — а cos 2а: -Ь 6sin2x,
а решение уз(^) ищем в виде
Уз (а;) = схе^,
где коэффициенты а, Ь, с находим подстановкой У2{х) и уз(^) в
соответствующие уравнения. Подстановка У2[.х) и уз(^) в уравнения дает а = — 1,
68
Глава 2. Дифференциальные уравнения высшего порядка
Ь = О, с = 1. Таким образом, yi{x) = — со8 2з: 4- хе^ — решение исходного
уравнения. Общее решение заданного уравнения у{х) = уо(^) + yi(^)- А
Другим методом решения линейных неоднородных уравнений с
постоянными коэффициентами является метод вариации постоянных.
Пример 3. Методом вариации постоянных решить уравнение
1
У"+У =
cos^x
л Поскольку характеристическое уравнение А^ 4- 1 = О имеет корни Ai =
= —2\ А2 = i, то общее решение линейного однородного уравнения у"+у — О
имеет вид
у = Ci cos ж -f С2 sinx,
где Ci и Сг — произвольные постоянные.
Общее решение заданного уравнения ищем в виде
у = Ci{x) cosX -{- C2{x)smx,
где Ci{x) и С2{х) -— неизвестные пока непрерывно дифференцируемые
функции. Согласно методу вариации постоянных для их нахождения
составим систему уравнений
C[{x)cosx + C2{x)smx = О,
—C[{x)smx + C2{x)cosx =
1
COS^ X
Отсюда находим, что С[{х)
получаем
/* cos xdx
cosa:
, С2{х) = 2~- Интегрируя,
C0s2 X
^ , . г dx I cos xdx С dsinx 1 ,
САх) = / = / 5— — I о~ = :;:: In
у cos ж J cos^ X J I - sur X 2
sinx + 1
J cos^ X J
dcosx
cos^x
1
cos ж
sin ж — 1
+ B,
+ A,
где A и В — произвольные постоянные. Подставляя найденные значения
Ci{x) и С2{х) в выражение для у, найдем общее решение заданного
уравнения
1 I cin 'Г* -I- 1
cosx —tgo;. А
у = А cos X + Bsinx -^ - In
sin X + 1
smx
1
§ 8. Линейные уравнения с постоянными коэффициентами 69
Еще один метод решения линейных уравнений с постоянными
коэффициентами основан на использовании преобразования Лапласа. Этод метод
называют операционным.
Пример 4. Операционным методом решить задачу Коши
у" - 4у' + Зу = 2{е' 4- е^^), t ^ О, у@) = -1, у'@) = 1.
Д Будем считать, что при t < О y(t) = О и правая часть
уравнения тождественный нуль. Тогда так продолженные на всю числовую ось
t G (—оо, Н-оо) решение и правая часть уравнения являются оригиналами.
Если y{t) = Y{p), то в силу свойств преобразования Лапласа и начальных
условий y'{t) .= pY{p) + 1, y"{t) = p'^Y{p) + p — 1. Продолженная нулем
при t < О правая часть уравнения имеет своим преобразованием Лапласа
функцию 2 { г Н г 1. Переходя в исходном уравнении к преобра-
зованию Лапласа, т. е. умножая его на е"*^* и интегрируя по t от нуля до
бесконечности, получаем алгебраическое уравнение для нахождения У{р)
p'Yip) +Р-1- A\pY{p) + 1] + ЗУ(р) = 2 (^ + ^) .
Если считать комплексный параметр р таким, что Rep > 3, то из
алгебраического уравнения находим
Y{p) =
(р-1)(р-3)
+ о-Р+^
р — 1 р — 3
Разложим правую часть на простые дроби
А В С D
У(Р) = Z—T + IZ—^ + Z-^ +
p-l ' (p-lJ p-3 (p-3J"
Приравнивая выражения для Y{p), находим
A = ^2, Б = -1, C=l, D = l,
Переходя к оригиналам, получаем искомое решение
y{t) = {t + l)e^'-{t^2)eK
70 Глава 2. Дифференциальные уравнения высшего порядка
Уравнение Эйлера а^х^у" + aixy' + а2у = f{x), х > О, заменой х — е^
сводится к линейному уравнению с постоянными коэффициентами.
Пример 5. Решить при х > О уравнение Эйлера
х'^у" -ху' -Зу=-Ах^.
Л Если положить X — е^, то у' — е~^у[, у'' — е~'^^{у[[ — у[). Подставляя
выражения для х^ у'^ у" ъ заданное уравнение, получаем
у"-2у' -Чу = Ае''.
Характеристическое уравнение Л'^ — 2Л — 3 = О имеет корни Ai =^ — 1,
Л2 = 3. Следовательно, общее решение полученного уравнения с
постоянными коэффициентами имеет вид
y{t) = Cie~^ Л-С2е^^ Л-ate^\
где Ci и С2 — произвольные постоянные, а коэффициент а находится
подстановкой функции ate^^ в уравнение. Подстановка в уравнение дает
а = I. Сделав обратную замену t = \пх, получаем общее решение
заданного уравнения Эйлера
С*
у[х) = — Л- С2Х^ + х^ 1пх. А
X
Решить линейные однородные уравнения A—38):
1. у" - Ау' + Зу - 0. 2. у" - 6у' + 8у = 0.
3. у" -f Зу' + 2у = 0. 4. / - у' - 2у - 0.
5. г/ + Ьу' 4- бу -= 0. 6. у" - 4у' -f 8у = 0.
7. у" - 6у' + 18у -: 0. 8. у" - 2у' + Юу - 0.
9. у" + 2у' + 5у - 0. 10. у" 4- 2у' + 2у = 0.
11. у" - Ау' + 4у = 0. 12. г/ - 6у' + 9у = 0.
13. у'' - 8у' 4- 16у = 0. 14. у'" + 4у" - у' - 4у = 0.
15. у''' + Зу" - у' - Зу - 0. 16. у'" - 7у" + 14у' - 8у - 0.
§ 8. Линейные уравнения с постоянными коэффициентами 71
17. у"' + Ау" + 5у' + 2у = 0. 18. у'" + Зу" - 4у = 0.
19. у'" - Зу" + Ту' - 5у = 0. 20. у'" + у" + 4у' + 4у = 0.
21. у'" + Зу" + 4у' + 2у = 0. 22. у'" - у" + у' - .у = 0.
23. у^^ - у'" + 2у' = 0. 24. у^^ - Ту'" + 14у" - 8у' = 0.
25. у^^ - 5у"' + 1у" - Зу' = 0. 26. y^^' - 6у"' + 9у" + 4у' - 12у = 0.
27. у^^ + 5у"' + 9у" + Ту' + 2у = 0. 28. у^*^ + 2у"' + 2у" + 2у' + у = 0.
29. у^^ - 2у"' + 2у" - 2у' + у = 0. 30. у^'^ - 2у" + у = 0.
31. у^^ + 6у"' + 12у" + 8у' = 0. 32. у^^ + 2у"' - 2у" + 2у' - Зу = 0.
33. у^^ - 5у"' + 5у" + 5у' - 6у = 0. 34. y^^' + 5у" + 4у = 0.
35. у^^' + 8у" + 16у = 0. 36. у^*^ + Зу" + 2у = 0.
37. у^^ + 18у" + 81у = 0. 38. у'" + Зу" + Зу' + у = 0.
Решить линейные неоднородные уравнения C9—151):
39. у" - Зу' + 2у = A + ж)е2^. 40. у" + 2у' + у = х^е"^.
41. у" - у' - 2у = -9хе-^. 42. у" + у' - 6у = -ISx^e"^.
43. у" — у = е^ COSX. 44. у" — у' + -у = е^ sinx.
45. у" - 4у' + 4у = х^ + 2е2^. 46. у" + у' - 2у = 2xe-2i- + 5sinх.
47. у" + 4у = 4хе-2^ - sin2х. 48. у" + 2у' - Зу = 2 cos х - Sxe'^^.
49. у" + 9у = бхе-^'^ - 3 cos Зх. 50. у" + 6у' + 9у = Збхе^^.
51. у" - Ау' + 4у == 32хе-2^. 52. у" + у' = E - 2х)е-^ - 10sin2x.
53. у" - у' = Dх + 3)е^ - 2 cos х. 54. у" - 4у' = -8e^^ cos 2х - 8х + 2.
55. у" - 4у' + 13у = -9cos2x - 8sin2x. 56. у" 4- 4у' + 4у = 2е-2^.
57. у" - 2у' + 5у = А cos х + 2 sin х.
58. у" - 8у' + 20у ^ -26^^BcosX + sinx). 59. у" + у' - 6у = -5е
60. у" - 2у' + у = 2е^. 61. у" - Ту' + 12у = -е
.Зх
72 Глава 2. Дифференциальные уравнения высшего порядка
62. у"-2у' + 3у = 4 cos а;-2 sin а;+ 46^^. 63. у" + 2у'-3у = B-8ж)р-з^.
64. у" -у' - 12у = e-2^Gcosx - 5sina;) - Те"^^'.
65. у" + 4у = 2 cos 2а; - 8а; sin 2а;. 66. у" + 4у = 2 cos^ х.
67. у" + 16у = 2 sin^ X. 68. у" - 5у' + by = 10 sin х + е^^.
69. у" + 2у' + у = а;е~^. 70. у" - Ту' + 6у = sinx + хе^'.
71. у" + у = 2sinX • sin2х. 72. у'" - 2у" - Зу' = е'^^.
73. у'" - 2у" - Зу' = X + 1. 74. у'" - у" + у' - у = 2 cos х.
75. у'" - 2у" + 2у' = 5 cos х + 2х. 76. у'" + 4у' = ch^ х.
77. у'" - 4у' = cos^ X. 78. у'" + 16у' = sh^ 2х.
79. у'" - 16у' = sin2 2х. 80. у'" - Зу' - 2у = 6"=^.
81. у'" + у' = 1 + sinx. 82. у'" + у' = 4 + 10e^^.
83. у'" - 2у" + 5у' = 5х + 4е^. 84. у'" + у' = -2e^(cosх + 3sinх) - 2 cos х.
85. у'" - Зу" - 4у' = -3C0SX - 5sinx + 5е"^.
86. у'" - у" - 6у' = cos X + 7 sin X - 6. 87. у'" + у" - 2у' = Зе^'.
88. у'" + 4у' = 8 cos 2х. 89. у'" + 2у" + у' = 4 cosх + 1.
90. у'" - 4у' = 2e-^Ccosx + sinx). 91. у'" + 6у" + 5у' = -4е-^.
92. у'" - Зу" + у' - Зу = 6 sin X - 2 cos X.
93. у'" - 4у" + у' - 4у = 2 cos X - 8 sin х.
94. у'" + 4у" + 5у' + 2у = e"'-^^'. 95. у'" + 4у" + 4у' = -4в-2^'.
96. у'" - Зу" + 4у = бе^^. 97. у'" - у" - у' + у = е-='C sin х - 4 cos х).
98. у'" - 8у" + 19у' - 12у = 2е^^ - 8cosх - 36sinx.
99. у'" + у" = е-^ + 2 cos х. 100. у'" - 2у" = sin х.
101. у'" - 2у" = e^^. 102. у'" + у" - 2у' = е^^.
103. у'" + у" - 2у' = 2 - X. 104. у'" + 2у" = cos х.
105. у'" - 2у" + 2у' = 4х + cos х. 106. у'" - 16у' = 48x2 + 2 cos^ 2х.
§ 8. Линейные уравнения с постоянными коэффициентами 73
107. у'" - 2у" + 2у' = 20 sin^ |. 108. у'" + 4у' = е^^ - 8 sin 2х.
109. у'" + у" + 4у' + 4у = 40sin^ х. 110. у'" + 2у" = 2е-2^.
111. у'" - 4у" + 5у' = 15ж2 - 4ж + 8 sin ж.
112. у'" - 2у" + 2у' = 6x2 + 2 + 20 cos 1х.
113. у'" - 6у" + 10у' = 13 cos X + Юж.
114. у'" + 2у" + 5у' = 2ж - 17sin2x.
115. у'" - 2у" + у' = 2ж + 2 cos ж. 116. у'" - 2у" = lбsin2ж - 12ж.
117. у'" -у" ^у< -у = 4же^ + 4. 118. у'" + у" + у' + у = 4же-^ + 4.
119. у'" - у" + 4у' - 4у = 40 cos2 ж. 120. у^^ - 2у" + у = 1 + ж^.
121. у^^-у = е^со8ж. 122. y^^ + 2y" + y = ж^ + 9sin2ж.
123. у^^ + 8у" + 16у = 1бж2 + 9 sin ж.
124. у^^ + 18у" + 81у = 64 cos ж - вХж^.
125. у^^ + 50у" + б25у = 576 cos ж + 625ж2.
126. у^^ - 4у"' + 5у" = 6A + 5ж) + е2==.
127. у^'^ + 2у" + у = ж + cos 2ж. 128. у^^ - 16у" = 64 sin^ 2ж.
129. у^^ + Зу" - 4у = 10sin2x + бе^^. 130. у^^ + у" = sin2 '
о ж
г —.
2
131. у^^ - у" - 2у = 12sinЗжcos2ж - б(е-2^ +sin5x).
132. 4у^^ - у" = 12ж sh2 I + 3(8 - же"^). 133. у^^ - 4у" = 16 ch^ ж - 8.
134. у^^ - 2у"' + 2у" = 10cos2 ж + 5(же^ - 1).
135. у^^ - 2у"' - Зу" = 8 8Ьж + Юже^.
136. у^^ + 2у" + у = 18sin2ж + 3sin2x + ж^.
137. у^^ - 2у" + у = 8 ch2 I + ж2 - 2е-^
ли
138. у^^ + у'" - 2у" = Зе^ + 32е2^. 139. у^^ + у" = 8cos^ ^.
140. у^^ - Зу" - 4у = 24со8 2ж + 20е2^. 141. у^^ + Зу"' - 4у" = Ьь\хх.
74
Глава 2. Дифференциальные уравнения высшего порядка
142. у^^' -у = -8(cosa; + 3sina;)e^^' - 4е~^.
143. у'^ - у" = 4а; cos а; + 12 sin ж - 2е^.
144. у^^ - Ау'" + Зу" = 4 cos ж + 8 sin а; + 6.
145. /^ + 7у"' + 16у" + 10у' = -5е-^.
146. у''^ - Зу'" + 4у' = - COSX + 7sinx + 4.
147. у^^ + Зу'" + Зу" + у' = 2(sina; - cosx) + 2а; + 6.
148. у^^ - 2у" + у = 8е=^ - 4 cos х.
149. у'^ - у'" - у" -у' -2у = -6е-^.
150. у^^ - у'" - Зу" + у' + 2у = -5(cosa; + sina;)e-^.
151. у^^ - 2у"' - 2у" = 4cha;.
Методом вариации постоянных решить уравнения A52—171):
152. у" + у = -г4-- 153. у"-3у' + 2у = -^.
154. у'
156. у'
158. у
160. у'
162. у'
166.
168.
170.
У
у'
е^' — е
-Зу' + 2у = -4-^. 155.у"-у=^—-^_^.
- 2?/' = 5C - Ах)у/^. 157. / - 27/' + Ю^/ = —.
cos3x
- Ay' + 8у = 4G - 21 j: + ISx^) ^. 159. у" ^у = - ctg^ а
- 4у = A5 - 16a;2)v^. 161. у" + 4у' + 4у = .
X +1
2р2^
163. у"-4у' + 4у = -—^.
1 + а:'^
+ 3у' =
За;-1
х'
164. у" + у' = 7D + 3х)^.
+ 2у = 2-4a;^sina;^.
165. у" + 2у'+ 2у = -.—.
sin а;
167. у" + 2у' + 5у = -^^.
COS 1Х
— —2 — 4x^cosx^.
+ 2^/4 2/ = (х + 2) (лпх 4- Н • 169. у" - 2у
171. у" -2у' = i-21n(ex)
2/"-1/
/ _
хЛ- 1
х"^
§ 8. Линейные уравнения с постоянными коэффициентами 75
Операционным методом решить при t ^ О задачу Коши A72—183):
172. у" - Зу' + 2у = е-\ у@) = О, у'{0) = 1.
173. у" - у' - 2у = Zte\ у@) = у'@) = 0.
174. у" - 5у' + 4у = (lOi + l)e-S у@) = у'@) = 0.
175. у" 4- 5у' + 6у = е-2', у@) = -1, у'@) = 0.
176. у" - 2у' + у = 2е*, у@) - у'@) = 1.
177. у" + 2у' + у = (< + 2)е-*, у@) = 1, у'@) = -1.
178. у" - 2у' - Зу = 4еЗ* - Ае'^ у@) = 2, у'@) = 0.
179. у" + у = 4cosi, у@) = 1, у'@) = -1.
180. у' + у = 5te^', у@) = О, у'@) = 1.
181. у" + 9у = 6 cos 3< + 9 sin 3i, у@) = 1, у'@) = 0.
182. у" + 4у = 4(cos2t + sin2i), у@) = О, у'@) = 1.
183. у" + у = 2(cosi-sini), у@) = 1, у'@) = 2.
Решить при X > О уравнения Эйлера A84--207):
184. х'^у" + 2ху' - 12у = 0. 185. 2а-2у" - ху' - 2у = 0.
186. 4а;2у" - Зу = 0. 187. х'^у" - 2ху' - 4у = 0.
188. х'^у" + 5ху' + 8у = 0. 189. 2х'^у" - Зху' + Зу = 0.
190. х'^у" - 6у = 0. 191. 2а;2у" + 5ху' - 2у = 0.
192. х'^у" + Зху' - Зу = -■^. 193. 4а;2у" - 4ху' - 5у = -4^/х.
194. х'^у" - 2у = -2ж^ 195. х'^у" - Зху' + 4у = 4а:^
196. х'^у" +ху' + у = Юж^. 197. х'^у" + Зху' + у = -.
198. а;2у" + ху' + у =-2 sin (In ж). 199. х^у" - 4а;у'+ 6у = 22:^-
200. a;^y" + 2а;у' - 2у = Ых. 201. ж^у" - 6у = -IGx^
202. а;2у" + ху' - 4у = -ЭжЫге. 203. ж^у" - 20у = 10х^.
76 Глава 2. Дифференциальные уравнения высшего порядка
3
204. ж^у" + Зху' - Зу = —^. 205. ж^у" ~ ху' - 8у = Пх^ Ina:.
х^
X Х^
206. 2х2у" + ху' - у = --. 207. х^у" - 2у = ■^.
Решить каким-либо способом задачу Коши B08—236):
208. у" + у = -2 sin ж, у@) = О, у'@) = 1.
209. у" - у' - 2у = -18а;е-=^, уA) = 5е-\ у'A) = Зе-Ч
210. 9у" + у = 6sin|, уC7г) = О, у'C7г) = 1.
211. у" + у = cos (х - 1), у@) = у'@) = 0.
212. 4у" + у = 4cos |, уGг) = О, у'Gг) = |.
5l3. у" + у = 2 sin (а; + 1), у@) = у'@) = 0.
214. у" - 2у' + у = 2e^ уA) = О, у'A) = -е.
215. у" - Зу' + 2у = 2хе\ уA) = е, у'A) = 5е.
216. у" - 4у' = -8е2^ cos 2а; - 8а; + 2, у@) = 5, у'@) = -6.
217. у" + Зу' + 2у = -2cos 2а; - 6sin 2а; - е'^^^, у@) = 3, у'@) = -7.
218. у" - 2у' - Зу = 4 cos а; - 2 sin а; + Ае^"", у@) = 5, у'@) = 7.
219. у" + у = sin {х-1), у@) = у'@) = 0.
220. у" + у = -^, у@) = О, у'@) = 1.
COS Ж
221. у" + 2у' + у = -e-^ уA) = у'A) = 0.
X
222. у" - 2у' + у = -e^ уA) = у'A) = 0.
X
224. a;V' + 2а:у' - 2у = -—, уA) = О, у'A) = 1.
223. у^^ - 2у" + у = 1 + а;2, у@) = у'@) = у"@) = у"'@) = 0.
а;^
225. а;2у" + 2а;у' - 6у = а;^, уA) = О, у'A) = ^
о
226. хУ + ху'-у = Ых, уA) = 2, у'A) = 1.
§ 8. Линейные уравнения с постоянными коэффициентами 77
227. 4х^у" - Зу = 5а;2, уA) = 1, у'A) = 2.
228. а;2у" + ху'- у = 2х, уA) = О, у'A) = 1.
229. у'" + у' = 2а;, у@) = О, у'@) = 1, у"@) = 2.
230. у'" - у' = 6 - 3x2, уA) = уA) = О, у"A) = 3.
231. у^^ + 2у" + у = О, у@) = у"@) = О, у'@) = 2, у"'@) = -4.
232. у'" + 6у" + Ну' + 6у = х2 + X + 1, у@) = у'@) = у"@) = 0.
233. у'" - 6у" + Ну' - 6у = 1, у@) = у'@) = у"@) = 0.
234. у^^ - 2у"' + 2у" - 2у' + у = I + 4cosx, у@) = |, у'@) = 1, у"@) = О,
У"'@) = -3.
235. у(8) + 2у(«) - 2у" - у = О, у@) = у"@) = уD)@) = у(б)@) = О, у'@) = 2,
у"'@) = 2,уE)@) = -1,уG){0) = Н.
236. у(8) - у = О, у@) = 1, у'@) = у"@) = у"'@) = yW@) = уE)@) =
= уF)@)=уG)@)=0.
237. Найти решение уравнения у"^ — Зу' — 2у = хе"^, ограниченное при
X --> +00 и удовлетворяющее условиям у@) = 1, у'@) = 0.
238. Составить линейное однородное уравнение наименьшего порядка
Ly = О с постоянными веш^ественными коэффициентами, имеюш;ее
решения у\{х) и 1/2(^)) и решить неоднородное уравнение Ly = /(а;),
если:
а) yi{x) - sinx, у2{х) = е"^, f{x) = х-h 2е"^,
б) yi{x) = X, у2{х) = е^, f{x) = 2 sin ж - 2,
в) yi{x) = cos ж, у2(^) = е^, /(ж) = 2е^ - ж,
г) у1(ж) = X, у2{х) = е~^, f{x) = 2 - 2со8ж.
239. Доказать, что любое решение уравнения
уУ _ у1У _ 9у"' + у" + 20у' + 12 = О
однозначно представимо в виде суммы решений уравнений у'" — у"—
-5у' -Зу = 0иу"-Ау = 0.
78 Глава 2. Дифференциальные уравнения высшего порядка
240. Верно ли, что каждое решение уравнения у" — у' — 2у = О
удовлетворяет уравнению
У^ - Зу^^' - у'" + 7у" - 4у = О?
Ответы к задачам § 8
1. у = Cie^ + Сге^^. 2. у = de^^ + Сзе"*^.
3. у = Cie-2^ + Сге--^. 4. у = Схв"^' + Сге^^.
5. у = Cie-3^ + С2е-2^. 6. у = ^^^(C'l cos 2а; + C2sin2a:).
7. у = е^^(С] cosЗх + Сг sinЗж). 8. у = е^{Сх cos Зх + Сг sinЗ.г).
9. у = e~^(Ci cos2x + C2sin2a;). 10. у = e~^(Ci cos а; + C2sina;).
11. у = e2^(Cia; + C2). 12. у = e^^ldx + C2).
13. у = e4^(Cia; + C2). 14. у = Cie'-'^^ + C'le''' + Сзе^
15. у = Cie-3^ + C2e-^- + Сзе^. 16. у = de^ + Cse^^ + Сзе^^.
17. у = Cie-2^ + е-^(С2Ж + Сз). 18. у = 6-2^@10; + d) + de^
19. у = Cie^ + е^(С2 cos 2а- + Сз sin 2а;).
20. у = Cie-^ + С2 cos 2х + Сз sin 2а;.
21. у = Cie~^+ e~^(C2COsa; + C3sina;).
22. у = Ci cos ж + C2 sin x + C^e^.
23. у = Cie"^ + C2 + е^(Сз cosx + C4 sin a;).
24. у = Ci + Сзе^ + Сзе2^- + C4e^^.
25. у = Ci + e*(C2a; + C3) + CAe^"".
26. у = Cie-^ + e2^(C2a; + C3) + de^^.
27. у = Cie-2^ + e-^(C2x2 + Сза; + C4).
28. у = e~^(Cia; + C2) + C3 cos a; + C4 sin a;.
29. у = Ci cosa; + C2 sin a; + е*(Сза; + C4).
§ 8. Линейные уравнения с постоянными коэффициентами 79
30. у = e-^{Cix + С-г) 4- е^(Сзх + С^).
31. y = Ci + e-2^(C2a;^ + С^х + d).
32. у = Ci cos ж + С2 sin а; + Сзе-^^ + С4е^.
33. у = Cie-^ + Сге^ + Сзе^^ + ^46^^.
34. у = Ci cos X + С2 sin а; + Сз cos 2х + С^ sin 22:.
35. у = (Cia; + С2) cos 22; + (С32; + С4) sin2x.
36. у = Ci cos 2; + C2 sin 2; + C3 cos 2;\/2 + C4 sin хл/2.
37. у = {Cix + C2) COS32; + (C3X + C4) sin32;.
38. у = е-^(С712;2 + С2Х + Сз).
39. у = Cie^ + C2e2^ + ^ж^е^^.
40. y = (Ci + C22;)e-- + ^e-^
41. у = Cie-^ + C2e2^ + Гж + ^жЛ 6"^
42. у = Cie2^ + Сге-^^ + (^Зж^ - о; + ^"j е'^
43. у = Cie""^ + С2е^ - -е^(со8ж + 2sinx).
5
44. у = 6 2 (Ci sin — + C2COS •-) e^(sinx + 2cosx).
\ 2 2/5
45. у = e2^(Ci + С2Ж + ж2) + ^Bж2 + 4ж + 3).
О
46. у = Cie^ + Сге^ - ^(Зж^ + 2ж)е-2^ - ^Csinж + cos ж).
47. у = CiCOs2x + C2sin2j: + -Bх + 1)е~^''+-:rcos2x.
48. у - Cie-^^ + С2е^ + ^B^2 + х)е-^^ - iBcosx - sinx).
2 5
49. у = Ci cos Зх + С2 sin Зх + qCx + 1)е"^^ - -xsin3x.
80 Глава 2. Дифференциальные уравнения высшего порядка
50. у = (Ci + С2х)е~^^ "^ (^ "" ^) ^^'''
51. у = (Ci + С2х)е2^' + {2х + 1)е-2^.
52. у = Ci + Сге"^ 4- (ж^ - Зх)е-^ + cos 2д: + 2 sin 2х.
53. у = Ci + С2е^ + х{2х — 1)е^ + cosx + sin ж.
54. у = Ci + С2е^^ + е^^' cos 2х + ж^.
55. у = e^^(Cl cos Зге + Сг sin3x) - cos 2х.
56. у = e~2^(Ci + С2х) + гг2е-2^.
57. у = e^(Ci cos 2ж + С2 sin 2я;) + cos х.
58. у = e^^(Ci cos 2ж + С2 sin 2х) — е^^ cos х.
59. у = Cie-3^ + С2е2^ + аге-^^.
60. у = e^(Ci + С2Ж) + х^е"^,
61. у = Cie^^ + С2е^^ + гсе^^.
62. у = Cie-^ + С2е^^ - cos ж + же^^.
63. у = Cie-3^ + С2е^ + х'^е"^'^.
64. у = Cie-3^ + Сге^^ - е-"^^ cosx + гсе~^^.
65. у = Ci cos 2rc + С2 sin 2ж + ж^ cos 2x.
66. у = Ci cos 2a; + C2sin2a; + -(l +a;sin2rc).
67. у = C\ cos4a; + C2sin4rc + —A — 2a; sin4a;).
16
68. у = Cie^^ + Сге^^ - xe^"^ + sina; + cos a;.
69. у = e-^(Ci + C2X) + ^a;^e"*^.
0
70. у = Cie^ + C2e^^ - ^ ( :^ + ;^) e^ + ;^G cos a; + 5 sinx).
\1U 25 / 74
71. у = Cicosa; + C72sina; + -a;(cosx + 2 sin a;) + -cos 3a;.
5 8
§ 8. Линейные уравнения с постоянными коэффициентами 81
72. у = Cie-^ + С2 + СзеЗ- - ^е'^^
73. у = Cie-^^ + Сг + Сзе^^ - ^ж^ - ].х.
6 9
74. у = С\е^ + Сгсозж + Сзsina; — -a;(sina; + cosa;).
75. у = Ci + e^(G2COsrr + Casina;) Ч- 2 cos ж 4-sin^ + ж ( -ж + 1J .
ж 1
76. у = Ci + C2 sin2ж + Сз cos 2ж + - + — sh2ж.
о 32
ж 1
77. у = Ci + С2 sh2ж + Сз ch 2ж - ~ - — sin2ж.
о 32
ж 1
78. у = Ci + С2 sin4ж + Сз cos 4ж ~ — + -— sh4ж.
61 zoo
ж 1
79. у = Ci + С28Ь2ж + СзсЬ2ж + — - -— smAx.
32 256
80. у = (Ci + С72а:)е-^ + Сзе^^ - ^е'^
О
81. у = Ci + С2С08ж + Сз81пж + ж —-Ж81пж.
82. у = Ci + С2 COS ж + Сз 8шж + 4ж + е^^.
1 2
83. у = Ci + е^(С2 со8 2ж + Сз 8т2ж) + е^ + -ж^ + -ж.
2 5
84. у = Ci + С2 COS ж + Сз sin ж + 2е^ cos ж + ж cos ж.
85. у = Cie"^ + С2 + Сзе^^ ~ созж + же"^.
86. у = Cie--2^ + С2 4- Сзе^^ + cos ж -h ж.
87. у = Cie-2^ + С2 + Сзе^ + же^.
88. у = Ci + С2 cos 2ж + Сз sin 2ж — ж cos 2ж.
89. у = Ci + е~^(С2 4- Сзж) - 2со8ж -h ж.
90. у = Cie~2^ + С2 4- Сзе^^ + е~^ cos ж.
91. у = Cie"^ + С2 + Сзе"^^ -h же""^.
92. у = Ci cos ж + С2 sin ж + Сзе^^ 4- ж cos ж.
82
Глава 2. Дифференциальные уравнения высшего порядка
^Зх
93. у = Ci cosa; 4-C2sina; 4-Сзе"^^ — a;cosa;.
94. у = Cie-2^ 4- е-^(С2 4- Сза;) 4- а;е-2^.
95. у = e-'^^(Ci 4- С2а;) 4- Сз 4- x^e'^"^.
96. у = e2^(Ci 4- С2а;) 4- C^e'^ 4- а;2е2^
97. у = Cie-^4-e^(C2 4-C3a;)-e-^cosa;.
98. у = Cie^ 4- С2е^^ 4- Сзе^^ 4- 2 cos а; - хе^
99. у = Ci 4- С2а; 4- С^е~^ — cos а; — sina: 4- хе~^.
100. у = Ci 4-С2а; 4-Сзе^"^ 4- -(cos а,-4-2 sin а,-).
5
101. у = Ci 4- С2а; 4- Cзe^^ + ^хе'^''.
102. у = Cie-2^ 4- С2 4- Сзе^ 4- ^е^^
103. у = Cie-2^ 4- С2 4- Сзе^" 4- ^(а;^ - Зх).
104. у = Cie"^^ 4-С2 4-Сза,-- -B cos а: 4-sina:).
5
105. у = Ci 4- e~^(C2C0sa; 4- C3sina;) 4- а;^ 4- 2а; 4- -B cos а; 4- sina;).
о
106. у = Ci 4- С2е-^^ 4- Сзе^^ "" ^^ ~ ]^ (^^ "^ ^ ^^''^^') '
107. у = Ci 4- e^(C2COsa; 4- C3sina:) 4- 5а; — 4 cos а; — 2 sin а,'.
108. у = Ci 4-С2 cos 2а: 4-Сз sin 2а; 4-а; sin 2а; 4- —е^^\
16
109. у = CiCOs2a;4-C2sin2a;4-C3e~^ 4-xBcos2a: -sin 2а,-) 4-5.
110. у = Cie-2^ 4- С2 4- Сза: 4- ^^^^
111. у = Ci 4- e2^(C2COsa; 4- C3sina;) 4- a;*^ 4- 2a;''^ 4- 2a; 4- sina: - cos a;.
112. у = Ci 4-e''(C2COsa;4-C3sina;) 4-a;^ 4-За;^ 4-4a; 4-2 cos 2a; -sin 2a:.
13 2
113. у = Ci 4- e^^(C2COsa; 4- C3sina;) 4- -x'^ + 7^ + 7: cos a; 4- sina;.
2 5 3
§ 8. Линейные уравнения с постоянными коэффициентами
83
114. y = Ci'\-e ^(C2COs2a; 4-C3sin2a;) 4--а;'^ - —a;-b2sin2a; +-cos2a;.
о 25 2
115. у = Ci + (C2 + Сза-)е^ + a;^ + 4a; + cos a;.
116. у = Ci + C2.T + Cзe^^ + x^ + -x^ + sin 2x + cos 2a;.
117. у = Cie^ + C2 cosa; + C3 sin a; + (x^ - 2a;)e^ - 4.
118. y=^ Cie-^ -\- C2COSX + Сзз'тх -^ (x^ + 2a;)e-^ + 4.
119. у = C\e^ 4- C2 cos 2a; -f- C3 sin 2x — xB cos 2a; 4- sin2x) — 5.
120. у - e^(Ci 4- C2a;) 4- е-^(Сз 4- C4a;) 4- a;^ 4- 5.
121. у =^ Cie~^ 4-C2e^ 4- C3 sin a; 4-C4 cos a; - -e^cosa;.
5
122. у = (Ci 4- C2a:) cos x 4- (C3 4- C4a;) sin x 4- sin 2a: 4- a;^ - 4.
123. у =:= (Ci 4- C2a;) cos 2a; + (C3 + C4X) sin 2a; 4- a;^ - 1 4- sin x.
4
124. у = (Ci 4- C2a;)cos3a; 4- (C3 4- C4a;)sin3x 4-cosx - ^'"^ + q •
4
125. у — (Ci 4- C2a;) cos5x 4- (C3 4- C4a;) sin 5a; 4- cos a: 4- a;^ — --.
25
126. у = Ci 4-C2a;4-e^^(C3COsa;4-C4sinx) 4-a;^C 4-a;) 4- -e^^.
127. у = (Ci 4- C2a;)cosa; 4~ (C3 4- C4a;)sina; 4- a; 4- -cos2a;.
128. у - Ci 4- C2a; 4- Сзе"^^ 4- C4e^^ - a;^ - -^ cos 4x.
16
129. у := Cie'"" 4- C2e'' 4- C3 cos 2a; 4- C4 sin 2a; 4- -e^"" 4- -x cos 2a;.
130. у = Ci 4- C2a; 4- C3COsa; 4- C4 sina; 4- т^(^ + sinx).
о
131. у = Ci cosX + C2 sinrc + Сзе~^^ + C^e'^'^ + xcos x - re~^^.
5
132. y = Ci+C2X + Cset + C4e-f + (^ " у ) e"" + x^{x - 12).
133. y^Ci + C2X + Сзе^^ + C4e-2^ + ia;sh2x.
Глава 2. Дифференциальные уравнения высшего порядка
84
134. у
135. y = Ci + C2X + Сзе-^ + G46^^ +
Ci + С2Х + е^(Сз cos X + С4 sin х) + - (cos 2а; + 2 sin 2х).
8
(-Н
е^ + а;е""^.
1
136. у = (Ci + С22;) cosrr + (Сз + С4х) sinx - cos 2ж Ч- ^ sin2а; + а;^ - 12а; + 9.
137. у :
138. у:
139. у:
140. у:
141. у.
142. у :
143. у
144. у :
145. у.
146. у:
147. у ^
148. у ^
149. у
150. у
151. у
(Ci + С2а;)е-^ + (Сз + С4х)е'= + -х^е" + х^ + 8.
Ci + С2Х + Сзе^ + С4е-2^ + же^ + 2е^='.
С\ + Сга: + Сз cos а; + С4 sin ж + 2а;'^ — 2х sin х.
С\ cos а; + С2 sin а; + С^е^^ + С4е~^^ + cos 2х + хе^^.
Ci + С2Х + Сзе^ + de-^^ + ia;e^ + ^е"^.
Cie~^ + Сге^ + Сз cos а; + С4 sin а; + е^^ cos а; + хе~^.
Ci + С2Х + Сзе^ + С4е-^ + 2а; cos х - хё^.
Ci + Сга; + Сзе^ + С4е^^ - 2 cos а; + а;^.
Ci + Сге"^ + е"''^(Сз cos а; + С4 sin ж) + хе~^.
Сх + Сге-^ + е2^(Сз + С4а;) - cos а; + х.
Ci + е~^(С2 + Сза; + С4а;2) + cos а; + х^.
e-^(Ci + Сгж) + е^(Сз + С4а;) + х^е"" - cos а;.
Cie~^ + Сге-^^ + Сз cos а; + С4 sin а; + хе~^.
e-^(Ci + Сга;) + Сзе^ + С4е2^ + е"^ cos х.
Ci + Сга; + Сзе^^"^)^ + С4е(^+^)^ - \е' + 2е-^
«5
1
152. у = Ci cos а; + С2 sina; + 1 + ^ In
1 +sina;
1 — sin a;
153. у = Cie^ + Сге^^ + (e^ + e2^)[x - In A + e^)] + e^ + ^.
154. у
155. у
Cie^ + Сге^^ + (e^ - e2^)[x - In A + e^)] - ^
Cie-"" + Сге^ + 2 arctge^ • chж - 1.
§ 8. Линейные уравнения с постоянными коэффициентами
85
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
170.
172.
174.
176.
178.
180.
у = Ci + Сге^^ + 4а;2у^.
у = e^(Ci cos Зх + Ci sin Ъх) + e^(ln | cos Ъх\ cos За; + Ъх sin Зж).
у = e2^(Ci cos 2х + С2 sin 2х) + Эж^ ^.
1 11 ~Ь cos XI
у = Ci cos ж + Сг sin ж + 2 — - In cos х.
2 11 — cos XI
у = Cie-2^ + Сге^^ + 4х'^^.
у = e-2^(Ci + Cix) + е-^^[{х + 1) In |ж + 1| - х].
y = Cie-3^ + C2 + ln|x|.
у = e2^(Ci + Сгж) + е2^[2а; arctg ж - In A + ж^)].
у = С1е-^ + С2 + 9ж2^.
у = e~^(Ci cosж + С2 81пж) + e~^(ln|sinж|sinж — жсо8ж).
у — С\ cos {хл/2) + С^ sin (жу^) + sinж^.
у = e~^(Ci cos 2ж + Сг sin2ж) + е~^ ( ж sin2ж + - In | cos 2ж| cos 2ж 1 .
у = e-^(Ci + С2ж) + ж1пж. 169. у = Cie-^^ + С2е=^^ + cosx^.
171. у = С1+С2е2^ + ж1пж.
173. y = -ie-' + e2*-^(l + 2t)e*.
у = С1+С2е=^ + 1п|ж|.
2t
у = -е* + ie"* + (^ + <) е-*. 175. у = Зе-З' + (t - 4)е
177. у = (l+f2 + ^f4e-t
179. у = cos Л- Bf - 1) sini
у = (f2 + l)e*.
у= B + t)e-* + <e3*.
у = -(cost + 2sin<) + I * — 7 I ^
(l-^t)cos3t+(i + l)
181.
182. у = (l + t)sin2f-fcos2f. 183. у = A+ f)(cosi + sint).
86
184. у
186. у
188. у
189. у
191. у
193. у
195. у
196. у
197. у
198. у :
199. у :
201. у :
203. у ■■
205. у:
207. у
209. у
211. у
213. у
215. у
Глава 2. Дифференциальные уравнения высшего порядка
■ CiX^-^C2X-\
■■ —p=z + С^Ху/х.
у/х
^[С\ cos B Inх) + С2 sin
185. у = Cix^ + -L.
187. у = Cix^ + ^.
B In а,-)].
= CixJx + С2л/х. 190. у = Cix^ + ^.
: Cla.•2^/5 + ^ + 1^. 194. у = Cix^ + — - ^
V.T 2 ж 2
Г^ 2
192. у= -4 + С2а; + ^=.
91 -1.»
a;2(Ci+C2lna;) + x^
: Ci COS (In a;) + C^ sin (In x) + 2a;^
7^1n':r.
2 о 1 ,
— - sin (Inж) cos (Ins) +
^■-3
C2 - - COS B1nx)
sin
(Inx).
^ 200. у = Cix + ^ - ^
C2 1 , 1
-I2 -ol"^•-7•
Cla;^ + C^x^ + 2a;^ Ina; - —-.
Ax
^ + С2а;^ + а,'2D1пж + 3).
ж*
^ + ^22;^ - ^^х^{ЪЫх + 4). 206. у = Cix + -^ - -.
Х'"^ 25 V'x X
202. у = Схх"^ + ^ + жC1пх + 2).
Х^
204. y = Cix=* + ^ + ^.
X Х^
^^+c,x■'^\.
X Ж^
(За;2+2а;)е-^.
: - sin 1 sin а; + -а; sin (а; — 1). 212. у
208. у — а; cos .т.
210. у ^ C7г-а:)со8^
о
. ^ , X
= [Х — 27Г) COS —
^ ' 2
: COS Isinx — xcos (х + 1),
;8е2^-1-(х2 + 2х + 4)е^. 216. у
= е^(х2-Зх + 2).
214. у
= 6-2e''^ + e2^cos2x + x2.
§ 8. Линейные уравнения с постоянными коэффициентами 87
217. у = (а; + 6)е-2^ - 4е-^ + cos 2а;. 218. у = {х-^ 3)е^^ + Зе"^ - cos х.
219. у = -cos 1 sin а; —-а; cos {х — 1). 220. у = (а;4-1) sina;4-cosa;ln| cosa;|.
221. у = {\ - X-V x\vLx)e~'^, 222. у = A - a; + a;lna;)e^.
223. y = .^ + 5-ь(^.-^)e^- (^.4-06-
224. y = -:rlna;. 225. у =-a;^(a: - 1).
x^ ^6
226. у = 2a; - \vlx, Til. у = x^.
228. y = a;lna;. 229. у = a;^ + sina;.
230. у = a;^ + 2-3e^-^ 231. у = a; cos a; + sin a;.
^^^- ^4 Э'^^б'^ ^2' ' 2?" •
233. У = ^ (-9a;^ - 42a; + lOSe"^ - 5462"^ + 14e^^ - 68) .
7Г
234. у = a; cos a; + —.
9 3
235. у = e^ - e~^ 4- -a; cos a; 4- -(a;^ - 3)sina;.
8 8
la; a; 1 1
236. у = - ch —pz cos —= + T ch a; + - cos a;.
^ 2 У2 ч/2 4 4
237. y=(l-^x)[\-'^e-\
238. a) y'" + y" + y' + у = 0, у = Ci cosa; + C2 sina; + Сзе"^ + a; - 1 + a;e~^,
б) y'" - y" = 0, у = Ci + C2X + Сзе'' + sina; + cosx - a;^,
в) у'" - у" + у' - у = О, у = Ci cos a; + С2 sina; + Сзе^ -Ь a; + 1 + а;е^,
г) у'" Ч- у" = О, у = Ci -Ь С2Х + Сзе"^ -Ь sina; + cosa; + а;^.
240. Да.
88 Глава 2. Дифференциальные уравнения высшего порядка
§ 9. Методы решения линейных уравнений второго порядка
с переменными коэффициентами
Для получения обш^его решения линейного неоднородного уравнения
второго порядка с переменными коэффициентами наиболее часто
применяется следуюш;ий метод. Сначала путем подбора находят какое-нибудь
решение соответствуюш^его линейного однородного уравнения и с помощью
формулы Лиувилля-Остроградского получают обп^ее решение линейного
однородного уравнения. Затем методом вариации постоянных находят об-
ш,ее решение заданного линейного неоднородного уравнения.
Пример 1. Найти обш^ее решение уравнения
а;/ - A + х)у' -Ь 2A - х)у = 9a;^e^^, х > 0.
Л Рассмотрим однородное уравнение
ху" - A+ х)у' -f 2A - а;)у = О
и попробуем найти его решение вида е^^. Подставив е^^ в это
уравнение, находим а = 2. Следовательно, е^^ — решение. Запишем формулу
Лиувилля-Остроградского для однородного уравнения:
е2^ у
2е2^
= Се/^^^ = Са;е^
Отсюда е^^у' — 2е^^у = Схе^. При делении обеих частей этого уравнения
на е^^ получаем уравнение
Отсюда находим обш,ее решение однородного уравнения
y = Cie2^-hC2(l + 3a;)e^^,
где Ci и С2 — произвольные постоянные.
Чтобы найти обш,ее решение заданного уравнения, применим метод
вариации постоянных. Иш,ем решение неоднородного уравнения в таком
же виде, как обш,ее решение однородного уравнения, но считаем Ci и С2
§ 9. Линейные уравнения второго порядка 89
не произвольными постоянными, а некоторыми непрерывно
дифференцируемыми функциями. Для их нахождения составляем линейную систему
уравнений для С[{х) и Cl^ix) следующего вида:
[ 2С[{х)е^'^ + С'2{х){2 - За;)е-^ = дхе'^'^.
Из этой системы находим, что С[{х) = 1 Ч-Зх, O^ix) — —е'^^'.
Следовательно, Ci{x) = А -\- X -\- •тх'^, С2{х) = JB — -е^^, где А и В ~ произвольные
постоянные.
Таким образом, общее решение заданного уравнения имеет вид
у = е2^ f Л + о; + ^хА +A4- Зх)е-^ (в ^ ^е^Л =
= Ле2^ + ВA + Зх)е-^ + ( L2 - М е^^
и 4)
^2
Другим распространенным методом решения линейных уравнений с
переменными коэффициентами является метод замены переменных.
Пример 2. Найти общее решение уравнения
хУ' + 2х\' -у = -у^^, а; > О,
ех —1
1
с помощью замены а; = —.
А После замены уравнение принимает вид
и ^
е ^ — 1
Решая это уравнение методом вариации постоянных, находим, что
у«) = е'(л-1е-Ч^1п^)+е-'(в+iln(l-е*)) ,
где Аи В — произвольные постоянные. Полагая t = —, после приведения
X
подобных членов отсюда получаем общее решение заданного уравнения
у = Ае~'^ + Ве^ — -;: ^ тг"^"^ -f sh { - 1 In {1 — е~^ ). А
2 2а; \xj \ /
Найти общее решение уравнений A—66):
90 Глава 2. Дифференциальные уравнения высшего порядка
1. {2х^ + Ъх) у" - 6(а; + \)у' + 6у - х[2х + З)^, х > 0.
2. а;(а; + 4)у" - {2х + 4)у' + 2у = а; + 4, а; > 0.
3. {2х - а;2) у" + (а;2 - 2) у' + B - 2а;) = {2х - x^f.
ХпхЛ-! „ 1 , 1 ,, _2
5. а;A + 2х)у" + 2A + х)у' - 2у = A + 2xf smx, а; > 0.
6. A - \пх)у" + iy' - -3-у = A - Ina;)^
X Х^
х^
7. ху" - A + а;)у' + у = ——, х > 0.
1 +а;
8. xV - 2гA + а,-)у' + 2A + х)у = 2a,'3e2'\
9. Bх + 1)у" + Dа,' - 2)у' - 8у = 4Bж + 1)^
10. 2а;у" + Dа; + 1)у' + Bа; + 1)у = е"^, а; > 0.
11. а;у" - Fа; + 2)у' + (9х + 6)у = 12а;-''еЗ^.
12. (а; - 1)у" - ху' + у = (х - Xfe''.
13. ху" - Bх + 1)у' + 2у = IGx^e^^.
14. х2у" - х(х + 2)у' + (х + 2)у = ж^е^.
15. (х2 - Зх) у" + F - х2) у' + (Зх - 6)у = (х - 3)^.
16. ху" - Bх + 1)у' + (х + 1)у = 2х2е2^.
17. (х - 1)у" - (х + 1)у' + 2у = (х - 1)^е-^.
18. хBх + 1)у" + 2 A - 2х^) у' - 4(х + 1)у = Bх + 1)'^ х > 0.
19. х(х + 3)у" + A2 - х2) у' - 3(х + 4)у = (х + 3J, х > 0.
20. 2х(х - 2)у" + (х^ - 8) у' + (х - 4)у = (х - 2)^, х > 2.
21. х(х - 2)у" + (х2 - 6) у' + 2(х - 3)у = (х - 2)^, х > 2.
22. х^у" - X (х^ + З) у' + (х^ + 3) у = Юх^ sinx2.
23. (х - 1)у" + A - 2х)у' + ху = ^(х - 1J.
§ 9. Линейные уравнения второго порядка 91
24. х^(х - 1)у" + 2ху' - 2у - х^е^.
25. ху" + B - 2х)у' + (х - 2)у = е^^, х > 0.
26. A - х2) у" + 2у' - -^у = A - хJA + х)е-^
X + 1
27. х(х + 1)у" + 2у' ^у = (х + 1Jе2^, х > 0.
X + Г
28. хCх + 2)у" + 3 B - 3x2) yi _ щ^ ^ ^у^ ^ ^Зх + 2)^ х > 0.
29. 2х(х + 2)у" + (8 - х^) у' - (х + 4)у = (х + 2)^, х > 0.
30. хCх - 2)у" + 3 Cx2 _ 2) у' + 18(х - 1)у = (Зх - 2)^, х > ^.
31. Aпх)у" - -у' + -^у = \г? X.
X Х^
х^
32. 2ху" - (х + 2)у' + у = ——, X > 0.
X + Z
33. ху" - Dх - 2)у' + 4(х - 1)у = е}^ cosx.
7Г
34. x^ij^ Ч-х(—2 Н- xtg j:)y' Ч- B - xtgx)'y = x^e-^'cosx, О < х < -.
35. A - х)у" + B - 4х)у' - 4ху = е"^-^ sin х.
36. (х + 1O/ + (х - 1)у' - 2у = е-^(х + 1)^
37. Bх - х2) у" + 2у' - -у = B - хJхе-^.
' X
38. (х - 1Jу" - (х2 - 1) у' + (х + 1)у = (х - 1KCх - 2)е^.
39. (х + 1Jу" - 2 (х2 + Зх + 2) у' + 2(х + 2)у = -2х(х + ife^""-.
40. х(х + 1Jу" + 2(х + 1)у' - 2у = (х + 1)^6^, х > 0.
41. ху" + 2(х + 1)у' + (х + 2)у = 2chx, х > 0.
42. (х - 1Jу" - 2х(х - 1)у' + 2ху = (х - 1I
43. 2ху" + Dх + 1)у' + Bх + 1)у = -е"''lux.
X
44. Зху" + Fх + 1)у' + (Зх + 1)у = х'^е-^.
45. х2Aпх — 1)у" — ху' + у = хAпх — 1J.
92 Глава 2. Дифференциальные уравнения высшего порядка
46. ly" - Dа; + 2)у' + [Ах + 4)у = ж^е^^, а; > 0.
47. у" - Зу' ctg ж + ( —5 2 ) у = 2 sin^ х, О < а; < тг.
\sm а; /
48. (а;1па;)у" + (Ina; + 1)у' ^ = ^^, а; > 1.
а;1па; х
а;2
49. (Ц-х2)у" + а;у'-у = -—-^.
^ ' 1 + а;''
50. а;2у" + а;(а; - 2)у' + B - а;)у = х'^е'''.
51. а;у" - 2(а; + 1)у' + (а; + 2)у = За;е^.
52. х{х - 1)у" + Dа; - 2)у' + 2у = е"^.
53. а;(а; + 1)у" + Dа; + 2)у' + 2у = 6(а; + 1).
54. (ж - 1)у" - 2а;у' + (а; + 1)у = Зе^.
55. ху" - 2{Ах - 1)у' + 8Bа; - 1)у = 2е2^.
56. Bа; + 3)у" - 2у' - —у = 3Bа; + 3)^.
_6^
а;2
57. Bа; + 1)у" - 2у' - Bа; + 3)у = 3Bа; + 1J • е1.
58. 2а;у" - (а; + 4)у' + f 1 + ^ j у = а;^
59. ху" + Bа; - 1)у' + (а; - 1)у = 8а;2е^, а; > 0.
60. а;(а; - 1Jу" - 2(а; - 1)у' + 2у = а;(а; - ife-"", х > 1.
61. (а; - 2)у" - Dа; - 7)у' + {Ах - 6)у = Ах{х - ife^"", х > 2.
62. а;2(а; + 1)у" + а; (а;^ - 2а; - 2) у' - 2 (а;^ - х - 1) у = х'^{х + 1)^, х > 0.
63. а;2у" - а;(х + 3)у' + Bх + 3)у = х1
64. а;2(а; - 3)у" - х'^{х - 2)у' + 2 (х^ - Зх + З) у = (ж - З)^.
65. х2(х - 1)у" + ж B - 4х + ж2) у' - 2(х - 1Jу = ^^(ж - 1J.
66. х^{х - А)у" - ж2(х - 2Jу' + 2х (х2 - 5х + 8) у = (ж - 4J, X > 0.
67. Найти обш,ее решение уравнения, если известны два его решения У1(ж)
и у2(ж):
§ 9. Линейные уравнения второго порядка 93
а) у" -y'tgx + 2y = 2tgx + —г~, О < а; < ~,
cos*' X Z
yi = tgx, у2 = tga; + 2sina;.
б) у" + Аху' + Dа:2 + 2) у = [Ах'^ + 4д; + З) е^,
У1 =е^, У2 = e^^-e'"^^
в) жу" - Bа: + 1)у' + (ж -f 1)у = (х - 1N^^, х > О,
У1 =е^^, у2 = е^^ -е^.
г) ху" + 2у' - жу = 2 - х^, X > О,
У1 =з;, У2 = жН .
X
д) xBa; + 1)у" + 2(а; + 1)у' ~ 2у = Зх^ + Зх + 1, х > О,
У1 = 2(:^ + 1J,У2 = -(х2~-1).
68. Составить и решить линейное дифференциальное уравнение второго
порядка, если известны его правая часть f{x) и фундаментальная
система решений yi{x) и У2(з:) соответствующего линейного
однородного уравнения:
а) f{x) = 1 ~ х^, у1 = X, 7/2 = ^2 + 1.
б) f{x) = 1, у1 = X, у2^х'^ - 1.
в) /(ж) = COS2х, у1 = sin^ х, у2 = cos^ ж.
69. Решить уравнение
A-а;2)у"-ху' + у = ~\/l-x2, 0<х< 1,
7Г
С ПОМОЩЬЮ замены х = cost, О < t < —.
70. Решить уравнение
ex — 1
1
с помощью замены х = —,
71. Решить уравнение
2ху" '\-у' = 2(y + thx)
с помощью замены а; = -—, t > 0.
94 Глава 2. Дифференциальные уравнения высшего порядка
72. Решить уравнение
у" +у' tgx — 4:[у + cos^ х) cos^ X, О < X < —
с помош,ью замены t — sinx.
Приведением к виду z" + a{x)z — f{x) решить уравнения G3—76):
73. х'^у" + ху' + (х^--]у = 2xie^.
74. у" + -у' + 'У - 2.
75. A + х2)^ у" -f 2х A -f х2) у' -f у - 1 + х2.
77. Пусть функция р{х) определена и непрерывна при х ^ О и пусть yi(x),
У2{х) ~~ решения уравнения у" + р{х)у = О, причем Ит Уг{х) — О,
производные у[{х) ограничены при х ^ О, г — 1, 2. Доказать, что yi(x)
и У2(^) линейно зависимы при х ^ 0.
78. Пусть yi(x), У2(^) ~ два линейно незавр1симые решения уравнения
y(ri) _^p^^j.>iy{ri-i) _^,,. _^р^(^^Уу — Q Указать подстановку, приводящую
к линейному уравнению порядка п — 2.
79. Пусть решение у{х) уравнения х'^у" + xij + (х^ — п^) у — О, п > О,
X > О, положительно при манных х > О и у{-\-0) = О, Доказать, что
точка первого положительного максимума этого решения находится
от нуля на расстоянии, которое не меньше чем п.
80. Пусть а(х) ~ непрерывная функция при х ^ 0. Доказать, что если
уравнение у" -{-а{х)у ~ О имеет решение у{х) такое, что lim у'{х) —
= -hoo, то ОНО имеет также нетривиальное решение, стремящееся к
нулю при X --)' Н-ос.
81. Пусть функции а(х) и Ь{х) непрерывны на всей оси, причем а(х) —
нечетная, а Ь(х) — четная. Доказать, что решение уравнения у"н-
-\-а{х)у' + Ь{х)у = О, удовлетворяющее условию у'@) = О, есть четная
функция.
§ 9. Линейные уравнения второго порядка 95
82. Пусть функция q{x) непрерывна на всей оси и периодична с периодом
1. Доказать, что если нетривиальное решение уравнения у" -\-q{x)y —
= О, удовлетворяет условиям у@) = у[1) = О, то у[х -\- I) — Су{х),
С — const.
83. Найти два линейно независимые решения в виде степенного ряда
уравнения у" -Ь 4ху — 0.
84. а) Найти решение уравнения ху" — у' ~ 4х^у = О в виде степенного
ряда при условиях у@) = 1, y"{Q) = 0. Определить радиус сходимости
ряда.
у'
б) Решить уравнение у" А.х у = 0.
X
Указание. Найти сумму ряда в п. а).
85. а) Найти решение уравнения ху" — 2у' Н- 9х^у == О в виде степенного
ряда при условиях ?/@) = О, y"'[Q) ~ 6. Определить радиус сходимости
ряда.
2
б) Решить уравнение у" у' + ^х^у — 0.
X
Указание. Найти сумму ряда в п. а).
86. Проинтегрировать при х > О с помош,ью ряда по степеням х уравнение
Аху" Ч- 2у' -Му = 0.
Указание. Для отыскания решения уравнения, линейно
независимого в решением, пред ставимым степенным рядом, сделать в уравнении
замену у — у/х • z.
87. Найти при О < х < 1 общее решение уравнения 2хA — х)у" -f A —
—х)у' + Зу = О в виде ряда по степеням х.
Указание. Воспользоваться указанием к задаче 86.
88. а) Найти при решение уравнения
Bх Ч- х^) у" - у' - бху =- О
в виде степенного ряда по х. Определить радиус сходимости ряда,
б) Найти обш^ее решение заданного уравнения в виде ряда по степеням
X.
96
Глава 2. Дифференциальные уравнения высшего порядка
пачам 8 9
Ответы к задачам § 9
1. y = Cl{X'{'l)'{'C2X^-\-X^\nX-'-x\
'• ^ ^ "^^ (^' ~ ^ "^ ^ ^'^ ^) + ^"^ "^ ^^^^^ - In (х + 4)).
4. у = С\х Л- С2Х^ \пх -\- х^ In^ X - ж^ -f а:^ In^ х.
5. 2/ = h С2[х + 1) (sinx + 2cosx) - 2sinx.
х а;
6. у = Cix 4- С2 In ж + a;^ — -ж^ 1пх.
7. у = Ci(l + х) + Сге^ - A + а;) InA + ж) - 1.
8. у = Cia; + Сгже^^ + | ж^ - -х j е^^.
9. у = Cie-2^ + Сг Dа;2 + 1) + Ьх^ - 2ж + 2.
10. у = (Ci + Сгч/^ + а;)е-^.
11. у=(С1+С2Ж^ + За;^)е^^.
12. у = Cix + Сге"^ + f -^2 - а; ] <
13. у = Cie^^ + С2Bх + 1) - е"^.
14. y = a;(Ci + C2e^)+a;2e^.
15. у = Схе" Л- Cix^ + -ж - 1.
16. у = (Ci + С2а;2) е^ + JBx - 1)б
17. у = Схё" + Сг (а;2 + 1) + ^^а;^ - х^ - ^ е".
18. y = Cie2^ + ^-^(x + l).
X L
19. y = Cie^ + ^-ix-l.
х*^ 4
,3ж
§ 9. Линейные уравнения второго порядка
97
20. y = Cie-t + —+ ^ж-2.
X 2
21. у = Cie-^ + ^ + ix - 1.
22. у = а; (Ci + С2е^^\ +x(cosa;2 -2sma;^).
23. у = Cie'' + С2 {х^ - 2х) е" + ^х.
25. y = e^fci + ^ + -e^.
\ X X )
27.!,= (х+1)(с. + | + 1в-).
28. !, = Cie" + %-!(! + 1).
X Оо 1
29. у = Cie2 +-i--x-2.
X 2
30. у = С,е-^^ + Щ + \{х-1).
X о
31. у = Cix + С2Aпх + 1) + -х^A - 1пх).
32. у = Ci(a; + 2) + Сге^ + (ж + 2) [ln(a; + 2)^ - or - 2]
33. у= {Ci + —+ 2sina; + -cosa; le^"".
\ X X )
34. у = x{C\ + C2sina;) + -a;(cosx + sina;)e^.
Zi
35. у = f Ci + -^ + -i- sinx^ e-2^
\ a; — 1 a; — 1 /
36. у = Cie-^ + C2 [x^ + 1) - ( ^ж^ + or^ + X J e-^.
98 Глава 2. Дифференциальные уравнения высшего порядка
37. y = Cix + Сг^^ + (- -х] е'"".
X \Х J
38. у = (х - 1) (С*1 + С^е") + {х-1) (^х^ - Ъх\ е".
39. у = {х + 1) (Ci + Сзе^^) -\{х^ + 1) е^^.
40. у = (х + 1) f Ci + ^) + ^i^e^
\ X J X
41.y = e-^(c.4-^)-biB. + i)e^
42. у = (х - 1) (Ci + С2е2^) - ^х(а; - l)^.
43. у = (Ci + С2л/5)е-^ - ЬпжAпх + 4N"^.
44. у = (ci + C2xi + ^хЛ e-^
45. у = Cix + C2lna; + ж1пх ( ~ Inx--1 I.
46. у = (Ci + Сзх^) е^^ + \х^е^^ Апх - ^).
47. у = Ci sinx + C2sin2a; + 2sin^x(l - xcosx).
48. у = Ci 1пж + -^ + ~ In^ X.
\nx 3
49. у = Cix + C2 V 1 + ж^ — X arctg ж — 2.
50. у = ж (Ci -f C2e-^) ~ ^x2(x + 2)e-^.
.y = e-(c,+C2x3-|x2).
;. у = _ Cl + —^ + .
X\ X — 1 X— 1/
51
52
§ 9. Линейные уравнения второго порядка
99
54.
55
2х
56. у = Cix2 + Ca^i^ + 2х^ + Зх^ Ь\х\.
X
57. у = Cie-^ + С*2хе^ + (^ - 8^) «^ ■
58. у = х (Ci + С2е^) -х(-х'^ + 2х J.
59. у = е-^ (Ci + Сгх^) + Bа; - 1)е^.
60. у = (х - 1) f Ci + ^ V ^^е-^
\ X J X
61. у = Сге^^ + С2(х - 2Jе2- + Qx^ - ^х^) ,
62. у = Cix^ + Сгже"^ + а;^ + х^ In ж.
.. у = Ci (х^ + х) + Сгхе^ - х^.
,2ж
63 ,
е^ 1 1
64. у = Cix^ + Сз— + ;г - -
X 2 X
65. у = Ci (х^ - 2х) + Сахе"^ + х
66. у = С1х2 + С24 + ~-Л
Х'^ ох Х'^
67 _ .
б) у = (Ci + С2х)е-^' + ,
,2х
(х- 1J.
5. y = Cix^ + C2-^ + ±.-'.
х^ ох х^
, , ^ . ^ (^ . , l + smx\
Г. а) у = Ci smx + С2 2 - sinx • In :— + tgx.
\ 1 —sinx/
6) у = (С, + Cox)e-^' + e^.
б) у = (Ci + C2x)e-^' +
в) у = (С, + C2x2) e^ + e^^
r) у = i (Cie^ + C2e-^) + x.
д)у = С1(х + 1) + ^ + 1(х + 1)
x 2
д)у = С1(х + 1) + -^ + -(х + 1J.
68. a) (x^ - 1) y" - 2xy' + 2y = 1 - x^,
у = X (^Ci + x + ln||^h + (x2 + 1) [c^ - ^ln|x2 - 1|^
100 Глава 2. Дифференциальные уравнения высшего порядка
б) (x2 + l)y"~-2xy'-f22/-l,
y = Cix-hC2{x^-l) + ^.
в) у" sin 2х — 2у' cos 2х = — cos 2х,
у = Ci sin^ X + С2 cos'^ X -Ь -X.
1 . l + vT^^
69. y = CiVn^ + C2a;--a;ln ^ ^.
•u 1 — vl — ж^
70. у = Cie~^ Ч-Сгех - 1 e"^ +2sh | - ) Inll -e'^l.
X \xj I I
71. у = Cie^^ + Сге"^^ + 2y/^e'^^ - 2 sh Bv/^) In (l + e^^).
72. у = Cie^^'"^ + C2e-2^'"^ + sin2 x - i
1 1 ж — 1
73. у = —y={Ci COS! + C2 sinx) + -л/хсозЗх H 7=^e^.
\/x 2 yjx
74. у = —(Ci sino; + Сгсозж) + 2.
X
75. у = , - 1 + , In hr + V1 + a;2 .
76. у = a;^(CiCOSx + Сгзтх).
78. 2
^ / y'yi-yy'i У
\У1У2-У1У2/ '
83. У1 - 1 + Z. 2.3.5.6...Cn-lKn'
y2-a; + 2^2^g^ 3nCn + 1)"
n=l ^ ^
n=0 ^ ^*
6) у = Clcha;^ + C2shx^.
6) у = Ci sinx^ + C2Cosx^.
§ 10. Теорема Штурма. Граничные задачи 101
86. у = Сш + С2У2,У1 = 1 + ^^„^ 3.3-5-4-7...пBп-1)'
П=1 ^
-М-^л^ '-"""
6 ^3-2"-2-5-3-7...п(п + 1) Г
87. у = Cm + С2У2, У1 = 1 - Эх + х^ + f; [^" ~ ^jl'x",
У2 = A - а;) V^.
88. а) „ = 1 + Зх^ + 5,. + 3 £(-1Г^ P"."DnU)-"- « = ~-
п=3
б) У = C'lyi + С2У2, У1 см. в п. а),
^Л 3 2 оТ^/ ,4n-il-5...Dn-7) 2п\
J/2 = х. (^1 + -х2 + 3 5:(-1)" 8"-п! ^ J •
§ 10. Теорема Штурма. Граничные задачи
При решении задач на теорему Штурма необходимо заданное уравнение
привести сначала к двучленному уравнению. Затем сравнить количество
нулей нетривиальных решений полученного уравнения с количеством
нулей нетривиальных решений соответствующим образом подобранного
линейного уравнения с постоянными коэффициентами или уравнения
Эйлера.
Пример 1. Доказать, что любое нетривиальное решение уравнения
у" + 2ху' + 5?/ = О на интервале (—оо, +оо) имеет не более 6 нулей.
л Заменой у = е '^ • z заданное уравнение приводится к виду
z" 4- {A — x'^)z = 0. При \х\ ^ 2 всякое нетривиальное решение полученного
уравнения имеет не более одного нуля. При \х\ ^ 2 имеем 4 — x^ ^ 4.
Поскольку любое нетривиальное решение уравнения z^' + 4z = О на
отрезке [—2,2] имеет не более трех нулей, то по теореме Штурма любое
нетривиальное решение уравнения z" + D — x'^)z = О имеет на [—2,2]
тоже не более трех нулей. Так как число нулей любого нетривиального
решения заданного уравнения в силу замены совпадает с числом нулей
нетривиальных решений уравнения z" + {A — x'^)z = О, то задача решена. А
Решение граничной задачи, собственные значения и собственные функ-
102 Глава 2. Дифференциальные уравнения высшего порядка
ции граничной задачи находятся подстановкой обш,его решения уравнения
в заданные граничные условия.
Пример 2. Найти решение граничной задачи
у"Л-у = Зсоз2х, у@) = -1, у'{7г)=0.
Л Обш,им решением заданного уравнения является у = С\ cosx-\-C2 sinx-—
— cos 2а;. Подставляя это решение в граничные условия, получаем систему
для нахождения постоянных С\ и С2:
{
-С2 = 0.
Отсюда Ci = С2 = О и, значит, решением граничной задачи является
у = — cos2x. А
Пример 3. Найти собственные значения и собственные функции
граничной задачи у" = Лг/, х G [0,1], у{0) = у{1) = 0.
Д Нетрудно видеть, что при Л ^ О граничная задача имеет лишь
тривиальное решение, т. е. никакое Л ^ О не может быть собственным значением
граничной задачи. Пусть Л < 0. Тогда обш,им решением уравнения
является у = Ci cos х\/—Л + С2 sina;\/^ и подстановка его в граничные условия
дает уравнения для нахождения постоянных Ci и С2'
Ci =C2smV^ = 0.
Так как собственными функциями являются нетривиальные решения
граничной задачи, то С2 ф 0. Значит, sin\/^ = 0. Отсюда находим, что
собственными значениями задачи являются числа Л^ = —n^7г^, а соответ-
ствуюш,ими им собственными функциями являются Уп(^) = CnSinnTTx,
где п = 1,2,3,..., а Сп ~ произвольная постоянная, отличная от нуля. А
Для нахождения функции Грина граничной задачи следует
воспользоваться ее определением.
1. Доказать, что каждое нетривиальное решение уравнения г/"Н-
_j_-j —у = о имеет на интервале (О,+оо) бесконечное множество
1 + yjx
нулей.
§ 10. Теорема Штурма. Граничные задачи 103
2. Доказать, что каждое нетривиальное решение уравнения у"+
Н-7Г~2—г\У ^ ^ имеет на промежутке [О,Н-оо) лишь конечное число
нулей.
3. Доказать, что каждое нетривиальное решение уравнения у"-\-
Л-" 2^ ~ ^ имеет на промежутке [О, +оо) бесконечное число нулей.
4. Доказать, что любое нетривиальное решение уравнения у'^—ху^+у = О
на интервале (—ос,+оо) имеет не более пяти нулей.
5. Доказать, что любое нетривиальное решение уравнения г/"—(ж—3)^г/'4-
-\-{х + 1)у = о на интервале (—оо, +оо) имеет не более шести нулей.
6. Доказать, что любое нетривиальное решение уравнения у" 4- х'^у'Л-
4-(ж 4- 4)у = О на интервале (—оо, 4-оо) имеет не более шести нулей.
7. Доказать, что решение Jo(^) уравнения Бесселя ху" -f у' 4- ж?/ = О при
0.1 < ж < 10 имеет не менее трех нулей.
8. Доказать, что нетривиальное решение г/а (ж) уравнения ху"Л-
4-(- — ж}?/' — ау = 0 при любом значении вещественного параметра
а имеет на интервале A,4-оо) лишь конечное число нулей.
9. Доказать, что решение Ji{x) уравнения Бесселя ж^y-жy'4-(ж^ —1J/ =
= О имеет один из нулей на интервале C,7).
10. Доказать, что каждое нетривиальное решение уравнения у" Н—у'л-
X
Л-е^у = О на промежутке [1,4-оо) имеет бесконечно много нулей xi <
< Ж2 < ... < Жп < ... и при этом lim \хп — Xn-i\ = 0.
n-4-fOO
11. Доказать, что каждое нетривиальное решение уравнения х^у^Л-
Л-2х^у' 4- 1 -zx^ — 2 11/ = О на интервале @,4-оо) имеет не более одного
нуля.
Найти решение граничной задачи A2—24):
12. У'-У = 2е2-,У@) = 2,уA) = е2.
13. y"-~y = 2sinx,y@)=y(|)=0.
104 Глава 2. Дифференциальные уравнения высшего порядка
14. у" + у' = 2, у@) = О, уA) = 2.
15. 2;2у" + 2жу' - 12у = О, уA) = 1, у{х) = О (^j при х ^ +оо.
16. y"-y = e^^y@) = ^,y(l) = ^e2.
17. у"-4у = 4, у@) = -1,уA) = 0.
18. у" + у = О, у@) = у'@), у (I) + у' (I) = 0.
19.
у" + у = О, у@) = у'@), у (I) = у' (I) + 2.
20. х^у" + 2ху' = -, уA) = 1, у(е) = 0.
X
21. ж^у" + 2а;у' - бу = ж^, уB;) = 0{х^) при а; -> О, уA) = 1.
22. х^у" + ху'-у = 2х, уA) = О, уB) = 21п2.
23. у" + 7г2у = 1, у@) = уA) = 0.
24. у" + 7г2у = 37r2sin27ra;, у@) = уA) = 0.
Найти собственные значения и собственные функции граничной задачи
B5-34):
25. у" = Ау, у@) = у'A) = 0.
26. у" = Ау, у'@) = уA) = 0.
27. у" = Ау, у'@) = у'A) = 0.
28. у" = Ау,у@)=уA), у'@)=у'A).
29. у" = Ау, у@) = О, у(а;) = 0A) при х -^ +оо.
30. у" = Ау, уB;) = 0A) при х -> —оо и при а; -> +оо.
31. х^у" -ху' + у = Ау, уA) = уB) = 0.
32. х^у" -ху' + у = Ау, у{х) -)■ О при х -^ О, уA) = 0.
33. х'^у" — ху' + у = Ау, уA) = О, у{х) = 0A) при х -> +оо.
34. a;^y" + Зху' + у — Ау, уA) = О, у{х) -^ О при х —> +оо.
§ 10. Теорема Штурма. Граничные задачи 105
35. Доказать, что всякое вещественное число А является собственным
значением граничной задачи у" = Ау, у{0) = уA), у'{0) = —у'{^)-
36. При каких значениях вещественного параметра А граничная задача
у" + Х^у = О, у{0) = О, у'{1) = Ху{1) имеет нетривиальные решения?
Найти эти решения.
37. Рассматривается граничная задача на собственные значения
-у" + q{x)y = Ху, у{х) ф О,
у @) cos а + у'@) sin а = у A) cos ^0 + у'A) sin ^0 = О,
где q{x) — заданная непрерывная функция на [0,1], а и ^0 —
заданные числа. Доказать, что: а) собственные значения граничной задачи
вещественны, б) собственные функции у[х, Х\) и у{х, Х^)
соответствующие различным собственным значениям Ai и А2 ортогональны, т. е.
1
I-
у{х, Ai) • у{х, X2)dx = О, Ai 7^ А2.
о
38. Рассматривается граничная задача вида
-у" -\-q{x)y = Ху-^ fix),
y{0)cosa -f y'@)sina = y(l)cos^0 + y'(l)sin^ = 0,
где q{x), f{x) — заданные непрерывные функции на [0,1], а и ^ —
заданные числа. Доказать, что а) если параметр А не совпадает ни с
одним собственным значением граничной задачи, то граничная
задача имеет единственное решение, б) если же А ~ некоторое собственное
значение граничной задачи и ему соответствует собственная функция
у(х,А), то граничная задача разрешима только в том случае, когда
1
f{x)y{x,X)dx = 0.
о
39. Показать, что все собственные функции граничной задачи —у" = Ау,
у'{0) = у'Gг) = О обладают следующими свойствами: а) п-я
собственная функция на [0,7г] имеет ровно п нулей, б) нули п-й и (п -f 1)-й
собственных функций перемежаются.
1
/■
106 Глава 2. Дифференциальные уравнения высшего порядка
Найти функцию Грина G{xX) граничной задачи D0—50):
40. у" + ?/ = /(ж),у@) = у'A)=0.
41. y" + 4y = f{x),y'{0)=y{l) = 0.
42. у" - 4у = fix), у'@) = О, 2уA) = у'A).
43. у" -у' = fix), 2/@) = О, уA) = у'A).
44. у"-у = fix), у@) = уA) = 0.
45. х2у" + Зжу' - Зу = /(х), уA) = О, уB) = 2у'B).
46. (ж2 + 1)у" + 2а;у' = fix), у@) = у'A) = 0.
47. а;у" + у' = /(х),уA)=уB)=0.
48. ж2у" + ху'-у = fix), уA) = у'B) = 0.
49. х^у" - ху' - Зу = fix), у@) = О, yix) = о(-] при а; -> +оо.
50. х'^у" + 2ху' - 12у = fix), у@) = О, yix) = 0A) при х ->• +оо.
51. Пусть р(ж) — непрерывная функция на [а, Ь] и р* = maxpix) > О при
X 6 [о, 6]. Доказать, что граничная задача у" +pix)y = /(ж), у(а) = А,
у F) = В имеет единственное решение при всех А и В и для любой
7Г
непрерывной /(ж) на [а, Ь], если выполнено условие F — а) < —=:.
VP*
52. Пусть а(ж) — непрерывно дифференцируемая положительная
функция на всей оси и пусть yi{x), У2{х) — линейно независимые решения
уравнения у" + а{х)у = 0. Доказать, что нули у[{х) и У2{х)
перемежаются.
Указание. Показать, что ух и г/2 удовлетворяют соотношению
У2У1 - У1У2 = О-
53. Пусть на множестве D = {О ^ х ^ I, -оо < у < +ос} функц]
ИИ
л/ л df{x,y) df{x,y) .f.jj
fix, у), —т; непрерывны и — ^ и. Доказать, что граничная
ду ду
задача у" = /(ж, у), у{0) = уA) = О может иметь только одно решение.
Указание. Рассмотреть какому уравнению удовлетворяет разность
двух решений.
§ 10. Теорема Штурма. Граничные задачи 107
Ответы к задачам § 10
12. е2^ 13. ^-siux. 14.2а;.
shf
15. 1. 16. 1е2^ 17. ^ - 1.
а;4 3 sh2
18. C{cosx + sina;), С ~ произвольная постоянная.
1 — In ж 1
19. cosx-f sinx. 20. . 21. -{х^-х^).
X о
22. ж In ж. 23. Нет решений.
24. Сз'ттгх — sin27ra;, С — произвольная постоянная.
25. An = -fn+-j 7г2, уп(а;) = Спsin fn+2 j^ra;, Сп 7^0, п = 0,1,2,...
26. Хп = -\пЛ-'Л 7г2,?/п(а;) = Cncos (п+2 JTTX, Сп 7^0, п = 0,1,2,...
27. Хп — —г?т:^, Уп{х) = Спсозптгх, Сп т^ О, п = 0,1,2,...
28. An = -Ап^п^, Уп{х) = CinCos2n7rx + C2nsin2n7ra;, |Cin| + |C2n| > О,
n = 0,l,2,...
29. любое A < О, y{x,X) = Csmx\/^, С ^ 0.
30. любое A ^ О, y{x,X) = Cicosx\/^ +C2smxy/^, \Ci\ + IC2I > 0.
—j , уп{х) = CnXsinl ^^2 j, Спт^О, n= 1,2,3,...
32. любое A G (—00,1). Для A G (-00,0) j/(x, A) = Ca;sin(\/^lnx), С ^ 0,
для A = 0 у (ж. A) = Cxlnx, Ct^O, и для A G @,1) y{x,X) = Сж(а;^-
-ж-^), C^O.
33. Нет собственных значений.
34. любое А G (—00,1). Для А G (—оо,0) у(ж,А) = — sin(\/^lnx), для
X
А = О у{х, А) = С—, для А G @,1) у(а;. А) = ~(х^ - х"^), С ^ 0.
36. An = — + 2п7г, Уп(^) = CnSinAn^, Сп 7^ О, п = О, ±1,±2,...
108
Глава 2. Дифференциальные уравнения высшего порядка
1
40. G{x,0
41. G{x,0
42. Gix,0 =
43. G{x,0 =
44. G{x,0 =
45. G{x,0 =
46. Gix,0 =
47. G{x,0
48. G(x,C) =
49. G(x,C) = -
50. G(a;,C) = -y<
1 j sina;cos A — C), 0 ^ a; ^ Ci
cos 1 1 cos(l — a;)sinC, С ^ з; ^ 1.
1 f cos 22; sin BC-2), 0 ^ x ^ C,
2 cos 2 1 sin {2x - 2) cos 2C, С < a; ^ 1.
Г e^'^ch2a;, 0 ^ a; ^ C,
I e2^ch2C, C<a;^ 1.
\ e^(e-^-l), C<2;^1.
]_ f sha;sh(l - C), 0 ^ ж ^ C,
~shll shCsh(l-a;), C^x^l.
4" VC2
l^a;^C,
-СЧ, C^a:^2.
— arctgx, 0 ^ ж ^ C)
— arctgC, С ^ з; ^ 1.
1
йГ2
10C2
In a; In-, I ^x ^ C,,
lnCln|, С ^2; ^2.
^4, O^x^C,
С ^ a; < +00.
-4, 0^2;^C,
-T, C^a;<+oo.
Глава 3
ЛИНЕЙНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
§ 11. Методы рехпения линейных систем уравнений
с постоянными коэффициентами
Для решения линейных систем второго порядка уравнений с
постоянными коэффициентами, как правило, удобным является метод исключения
неизвестных.
Пример 1. Найти общее решение линейной системы уравнений
{X = X — 2у — 2te*,
y = 5x-y-{2t-{-6)e^.
Л Продифференцируем первое уравнение системы:
x = x-2y-2{t-{-l)eK
В полученное выражение подставим выражение у из второго уравнения
системы:
x = x-2{t-{- 1)е* - Юж + 2у + 2{2t 4- 6)е* = х - 10х-{-2у-j- Bt + 10)е^
Подставив сюда выражение 2у из первого уравнения системы, получаем
уравнение для x{t):
х-{-9х = 10е*.
Его решением является x{t) = CiCos3t + C2sin3^ + е*, где Ci и С2 —
произвольные постоянные. Подставив x{t) в первое уравнение системы,
находим y{t) = -(Ci -3C2)cos3t+ -(ЗС1 -i-C2)sm3t - teK
Zi Zt
Таким образом, общее решение заданной системы уравнений имеет вид
x{i) = Cicos3t + C2sin3^ + eS
110
Глава 3. Линейные системы дифференциальных уравнений
y{t) = i(Ci ~ ЗСз) cos 3t + ^CCi + С2) siuSt - te\ A
Для решения линейных систем третьего порядка с постоянными
коэффициентами удобным является метод, использующий нахождение
собственных значений, собственных и присоединенных векторов матрицы
системы.
Пример 2. Найти общее решение линейной системы уравнений
у = -2х + Зу - Z,
i = 4а; + 5г.
Д Для матрицы системы
из уравнения det {А — ХЕ) = О, где Е ■— единичная матрица третьего
порядка, находим собственное значение Л = 3 кратности три. Из линейной
алгебраической системы уравнений {А — \E)h = О, где вектор Л т^ О имеет
три компоненты, находим два линейно независимые собственные векторы
Л1 =
/12 =
Из системы уравнений {А — XE)hs = /12 находим присоединенный вектор
Лз к вектору h2'-
{ о
/13 =
V
Следовательно, искомое общее решение имеет вид
X
§ 11. Линейные системы уравнений с постоянными коэффициентами 111
где Ci, С2, Сз — произвольные постоянные. А
Линейные системы уравнений можно решать с помои;ью матричной
экспоненты.
Пример 3. С помош;ью матричной экспоненты решить систему уравнений
fx = x + y,
у = -х + Зу.
Д Для матрицы системы -А = I ^1 находим собственное значение
Л = 2 кратности два. Ему соответствуют собственный вектор /ii = ( 1 и
присоединенный вектор /i2 = I . 1 • В базисе из векторов /ii, /12 матрица А
„ри^маег нормальную жорданову форму . = (^ ')• Из онред^вняя
матричной экспоненты нгьходим, что
Если через Н обозначить матрицу, у которой первый столбец hi и второй
столбец /i2, то
\-t 1 + tJ
Общее решение заданной системы имеет вид
где Ci и С2 — произвольные постоянные. А
Линейные неоднородные системы уравнений можно решать методом
вариации постоянных.
Пример 4. Методом вариации постоянных решить систему уравнений
i = а; — 2у,
1
у — X — у -\- -—:—.
112 Глава 3. Линейные системы дифференциальных уравнений
А тг 1 i = ГС — 2?/,
Л Линейную однородную систему < . решаем методом исклю-
[ у^х-у,
чения. Ее решение имеет вид
ж = Ci cos t + C2 sin t,
У = ^[(Ci - C2)cost + {Ci + C2)smtl
где Ci и C2 — произвольные постоянные.
Решение заданной линейной неоднородной системы уравнений ищем в
виде
X = Ci (t) cos ^ -f G2 {t) sin t^
У - \[{Ci{t) - C2{t))cost + (Ci(t) + C2{t))smtl
где Ci{t) и C2{t) — некоторые непрерывно дифференцируемые функции,
которые находятся подстановкой хиу в заданную систему уравнений.
Подстановка X и у в заданную систему уравнений дает следующую линейную
алгебраическую систему для Ci{t) и G2(^I
Ci{t)cost + C2{t)sint=^0,
Ci{t)smt-'C2{t)cost
s'mt
Отсюда находим Ci{t) = 1, C2{t) — — ctg^ и, значит, Ci(t) — t + Ci,
C2{t) = — In I sin^l -h C2, где Ci и C2 — произвольные постоянные.
Подставляя найденные значения Ci{t) и C2(t), получим общее решение заданной
системы уравнений
ж = Ci cost + C2sin^ + tcost — sinHn|sin^|,
у = -[(Ci-G2)cost-h(Ci-hG2)sini + (t-f ln|sinit|)cost + (^-ln|sin^|)sin^].
к
Линейные системы уравнений можно также решать операционным
методом, т. е. методом, использующим преобразование Лапласа.
Пример 5. Операционным методом решить задачу Коши при ^ ^ 0:
{X = 3a;-?/ + 4e^S
у = 4а;~у-8еЗ^ а;@) = 1, 2/@) - 0.
§ 11. Линейные системы уравнений с постоянными коэффициентами 113
Д Положим при ^ < О решение x{t), y{t) системы и свободные члены
системы тождественно равными нулю. Тогда так продолженные на всю
числовую ось t G (—оо, -f оо) решение и свободные члены системы
являются оригиналами. Пусть x{t) ==' Х(р), y{t) == Y{p). Тогда x{t) = рХ{р) — 1,
y{t)=pY{p).
Переходя в заданной системе уравнений к преобразованиям Лапласа,
т. е. умножая каждое уравнение системы на е~^* и интегрируя его по t
от нуля до бесконечности, получаем линейную алгебраическую систему
уравнений для нахождения Х{р) и Y{p)
{p-Z)X{p)+Y{p) = l+ ^
4Xip) + {p + l)Y{p) = -.
р-3
Если считать комплексный параметр р таким, что Rep > 3, то из
полученной системы уравнений находим
(р-3)(р-1J ' >"' (р-3)(р-1J-
Разлагая выражения для Х{р) и Y{p) на простые дроби, имеем
Y( \ ^ 5 6 v^ ^ 4 4 12
р-3 р-1 (р-1J' '"^^ р-3 р-1 (р-1J'
Переходя к оригиналам, получаем искомое решение
x{t) = 6е^* - E + 6t)e\ y(t) = 4е^* - 4A -f 3^)е^
Решить линейные однородные системы второго порядка A—14):
1.
X = —5х — бу, о J ^ ~ -^^^ "" ^^'
у = 8а; -f 9?/. * | у = 18а; - Ну.
i = —6а; -f 8у, л ] ^ ~ "^^ ~ ^^'
у = —4а; -f 6у. ' 1 у = 6а; -f 7у.
i = —5а; — 4у, ( i = 5а; — 6у,
6. <
у = 10х -f 7у. у = За; - у.
114
Глава 3. Линейные системы дифференциальных уравнений
9.
11.
13.
{X = -12а; - 8у,
у = 20х + 12у.
{X = —2х — 4у,
у = 2х + 2у.
{X = 6х + у,
у = -16а; - 2у.
{X = -2х + у,
у = -Ах + 2у.
10.
12.
14.
= —5а; — 10у,
= 5x4- 5у.
{X = 5х -\- 4у,
у = -9а; - 7у.
{X = —5х -f 4у,
у = -ж - у.
{X = —5а; + 4у,
у = -9а; + 7у.
Решить линейные однородные системы уравнений третьего порядка A5-
116):
X = —5а; - 2у - 2г,
15. I у = Юх + 4у + 2^:,
i = 2а; -f у -f Зг.
X = —2а; -f 6у — 4г,
17. < у = 9а; - 5у Ч- 6^:,
i = 15а; - 18у + 15г.
i = 5а; -f у — г,
19. I у = а; Ч- Зу + г,
i = 7а; + Зу + 2:.
i = 5а; Ч- 2у + 2г,
21. «^ у = х + 6у + 2г,
г = —5а; — 7у - Зг.
о; = а; -f 2у — г,
23. I у = 9а;-6у + 3г,
i = 20х - 20у + Юг.
i = 8а; - 2у + 2z,
25. -^ у = 8а; - Зу + 4г,
i = -2а; - 2у + Зг.
16.
18.
20.
22.
24.
26.
X =
У =
Z =
X =
у =
i =
X =
2/ =
i =
-а; -f 2у - 4г,
-8а; - Зу Ч- 2г,
—2х — 4у + 6г.
-2а; + 2у - г,
—6а; + 2у — 2г,
—6а; — 2у — г.
x-y-z,
-2х + 2у Ч- г,
4а; Ч- 2у + Зг.
X = —а; Ч- 2у — Зг,
у = -ж + 4у - г,
i = 4а; — 2у + 6г.
i = а; Ч- 4у + 4г,
у = а; Ч- Зу - г,
i = -За; + 4у Ч- 8г.
i = хЧ-у- г,
у = а;-у + г,
i = а; — Зу + Зг.
§11. Линейные системы уравнений с постоянными коэффициентами 115
: = ~2а; + 8у + 6г,
27. I у = -Ах + 10у -f 6г,
; = 4а: ~ 8у — 4z.
; = ж -f 2у + Зг,
29. ^ ?/ = 2а; + 4у + 6г,
i; = Зж -f бу -f 9г.
i: = ж + 2?/ + 2г,
31. I y = 2x + y + 2z,
i: = 2а; -f 2у + г.
к = 2а: -f у ~ 2г,
33. < у = -х^- Z,
\^2хЛ-2у- Z,
с; = За: — Зу + г,
35. ^ у = За: - 2у -f 2z,
i = —а: + 2у.
х = х-у,
37. < y = a: + z,
Z = X -{- Z.
i = а: — 6у -f Зг,
39. ^ v = ~8y + 6z,
j = Зх ~ 12у -f 7z.
b = ~5у + Зг,
41. < у =-а:-бу-f 5г,
j = а: — 9у + 6г.
с = За: — у + 2г,
43. ^ у = 2а: - 5у + 2г,
Z = ~2а: — 4у — г.
i = а: + 2у + 2г,
45. I у = -^у^ 2г,
г = уЧ-г.
i = 2а: — у -f Зг,
28, I у = -2а: + у + 5г,
i = —а: — у + 6г.
i = 2а: + 2у - 2г,
30. ^ у = 2а; + 5у - 4г,
i = —2х — 4у + 5г.
i = 5а: — Зу + 2г,
32. ^ у = 6ж - 4у + 4г,
Z = Ах — 4у + 5г.
i = 2ж — 4у,
34. < у = X + 2у Ч- г,
г = Зу + 2г.
i = а; + 2у — г,
36. ^ у = -2х Ч- у ~ 2г,
г = X Ч- 2у Ч- г.
X = —X — у — г,
38. ^ у = Зх ~ 7у Ч- г,
г = 5х — 5у — Зг.
X = —2х — Зу + г,
40. I у = х~8уЧ-Зг,
i = Эх - 7у.
X = —5х — у Ч- Зг,
42. I у= ~5х - Зу + 5г,
г = ~х — Зу Ч- г.
X = X Ч- у,
44. < у = -а: Ч- г,
i = -ж — у Ч- 2г.
X = 7х — 4у + г,
46. I у = 7х~ЗуЧ-г,
г = 4х ~ 2у + 2г.
116
Глава 3. Линейные системы дифференциальных уравнений
i = Зж — 8у -f г,
47. I y = x-2y-\'Z,
Z = Зх — 12у — 5z.
X = —X — 4?/,
49. < у = X — у -{- z,
Z — Зу — Z,
х-=: -у- Z,
51. < у = х-\-у,
Z = Ах + у-\' 2z.
X — —Зх -f г,
53. I y = -3y-^2z,
z = 3x-2y- 3z.
X = X -\- 2г,
55. < у =^2х - у -^2z,
Z = X — у + Z.
X = —Зх — г,
57. I у = -4а; -2у- 3z,
i = Ax-\-2y-\- 3z.
b = X -\-5у — 2z,
59. I y = x + 2y-z,
z = 3x + 9y - 4г.
X = 7x - lOy - 4г,
61. < у =^ Ax -7y - Az,
z = —6x -f 7?/ -f г.
b = 2x — 3y,
63. < y = x-2z,
2: = -y + 2z.
Ь = -Зж + ?/ - 2г,
65. I у = Ах + у,
z — Ах -{■ z.
X = 3х -{■ 2z^
48. I y = x-\'2y-\'Z,
z = -X- y.
X — 3x — 2y -\' 2г,
50. < y = 2x-{-z,
z = -2x -\'2y- 2z,
x = y- z,
52. { y = -y-\'Z,
z = x — z.
X = ~5x — 4y + 9z,
54. I у = Юж + 9y- lOz,
z = X -\-y -\'3z.
X — Ax — ly — z^
56. < у = 2x — 3y — z^
z = -2x -\-2y-\- 3z.
x — —x — у + 2z,
58. I у = -Ьх -y-\'2z,
z = —7x — 3y + 6z.
X = X — у — Az^
60. I y = -2x + 2y + 12г,
z z=z X — у — 5z.
X = 7x -{- 8y — 2z^
62. I у = -Ьх -7y Л- z,
i = 6rc + 8?/ — 2:.
X = —2x + ?/,
64. < у = 3x — г,
i = 4y - 2z.
i = 2a; + ?/,
66. I у = Ax-\'2y-\' Az,
z = —2x — у — z.
§ 11. Линейные системы уравнений с постоянными коэффициентами 117
X = —6х + Зу — 5г,
67. \ у =" —X — у — Z,
Z = Зх — 2у -{- 2г.
\ X = -Зу + 3z,
69. \ у = —X — 4?/ -f 6zj
z = -2у -f 2г.
X = —2у — 2г,
71. ^ y = 3x + 5y-\'3z,
Z = —ж — 2у — Z.
X = 2х + 12у - Зг,
73. <^ у = -ж - 5у -f г,
Z = —X — 12у + Az.
X = Qx — 7у + Az,
75. < y = x-\'Z,
z = —2x + Зу.
X = —2x — у -^ z,
77. I у = 2x-'5y-\' 2г,
z = 3x — 2y — 2z.
X = Ax — у + z,
79. I у = -2x -f 3y - г,
i = —бж -^ Ay — z.
i = Зж — у + Зг,
81. < у = -бж -f у - 5г,
i = —Зж -f 2?/ — 4г.
X = —2а; — у — Z,
83. ^ у = -4а; -f 2у - г,
i = 16а; -f 4у -f 6г.
i = Зж + 2у - 4г,
85. I y = x + Ay-z,
г = Зж -f 6у — 4г.
X — —2х -\-у — z^
68. I у = -6х -Ау + Зг,
г = —2а; + 2у — Зг.
i = 7а; + 8у - 2г,
70. < у = -5х - 7у -f г,
г = 6а; + 8у — г.
i = 4а; — Зу — г,
72. ^ у = -з: + 2у + г,
г = 4а; — 4у — г.
X = 2х — Ъу - 8г,
74. I у = 7х- Ну - 17г,
г = -За: -f 4у + 6г.
X = —2а; -f г,
76. ^ у = -2^ - 2у + Зг,
г = -у + г.
i = 2а; + у — г,
78. -{ у = 7х + 4у - г,
г = 13а; + 7у — Зг.
i = о; + у - г,
80. <^ у = -X + 4у - 2г,
г = —2а; -f 5у — 2г.
о; = —X + 2у + г,
82. < у = 2;-у + г,
г = —2а; — Зу — 4г.
X = —2а; + у — г,
84. ^ у = 4а; + 2у - 2г,
г = 6а; + 7у - 6г.
о; = а; + 5у — 2г,
86. I у = -х + 5у- 2г,
г = —2а; + 15у — 6г.
118
Глава 3. Линейные системы дифференциальных уравнений
: = 2х + 6у - 15г,
87. I y = x-\-y-5z,
: = X + 2У — Qz.
: = -Ay,
89. I у^х-Ау,
': = X — 2y — 2z.
Ь = 12a; — 6y — 2г,
91. I y= I8x - 9t/ - Зг,
z = 18ж — 9y — 3z.
i = Зж + 2y — Зг,
93. ^ ?/ = 4a; + lOy - 12z,
j: = 3a; -f 6y — 7г.
95. -^ V = -0; + Ay,
i = -2х + ?/ + 2г.
fc = 6a; + y + г,
97. ^ V = -5a; + у - г,
i = -За; - у -f 2г.
t; = 4a; + 2y — г,
99. I y = -2x + y + z,
i = 2a; + 3y + г.
i = a; — 2y + 2г,
101. I j/ =-За; + 2у-3г,
i = -6a; + 8y — 8г.
a; = 2a; + 3y — г,
103. I y = -6a; - 6y + г,
z = ~4a; - 2y - 2г.
X = —ж — 5y -f г,
105. ^ у = -а; + 3у-г,
г = 4a; -f 5y + 2г.
i = 9a; — 6y — 2г,
88. I y = 18a; - 12y - Зг,
z = 18ж — 9j/ — 6г.
i = 4a; -f 6y — 15г,
90. < у = з; + 3y - 5г,
г = a; + 2y — 4г.
a; = 6a; -f 6y — 15г,
92. ^ у = ж + 5y - 5г,
г = X + 2y — 2г.
i = a; + у — г,
94. ^ у = -Зж - Зу + Зг,
г = -2а; - 2у -f 2г.
а; = 7а; -f 4у — г,
96. ^ у = -7а; - 4у + 2г,
г = —9а; — 9у -f 6г.
X = —2а; -{-у — Z,
98. I у = 2х-2у- г,
г = За; + 2у — 5г.
i = 4а; — у — 2г,
100. I у = 2а; -f у - Зг,
г = 2а; — у -f г.
i = —ж — 2у -f 2г,
102. I у = -Ах - 2у - Зг,
i = —За; + Зу — 6г.
I а; = —За; — у — г,
104. < у = 5а; -f Зу + г,
I г = 16а; -f 4у + 5г.
X = —За; — Зу — 2г,
106. I у = 6а; + 6у + 2г,
г = 7а; + 4у + 5г.
§ 11. Линейные системы уравнений с постоянными коэффициентами 119
107.
109.
111.
113.
115.
X = —8а; -f 6у — 4г,
у = -8ж + 14у - 4г,
i = 4а; + 13у + 2г.
X = —5ж -f 2у — 2г,
у = ж - Зу + г,
I i = 7а; — 5у + Зг.
X = —8а; -f у — 5г,
у = 18а; - у + Юг,
i = 11а;-7уЧ- Юг.
а; = —За; -f 2у — г,
у = 8а; + 4у + 4г,
i = 6а; — 6у + 2г.
а; = 2а; + 4у — 4г,
у = 4а; — 6у + 12г,
Z = —8а; — 8у + 6г.
а; = 5а; — у + 2г,
108. I y = -x + 3y-z,
Z = —4а; + 2у — г.
i = 2а; -f 4у — г,
110. I у =-2а;-7уЧ-4г,
Z = —5а; — 10у + 4г.
i = 2а; -f 5у + г,
112. { у = 8а; + Зу + 4г,
г = -14а;- 18у -7г.
i = 2а; -f у + г,
114. I у = 3а;-6у + 3г,
г = 4а; — 16у + 5г.
а; = 6а; — Зу + 7г,
116. { у = -Зх-2уЧ-г,
г = —7а; — у — 4г.
С помощью матричной экспоненты решить линейные однородные системы
уравнений A17—136):
117.
119.
121.
123.
125.
127.
а; = 2а; + у,
у = а; -f 2у.
X = -Зж + у,
у = а; - Зу.
i = 2а; — у,
у = -4а; + 2у.
а; = За; — у,
у = х + у.
X = х + у,
у = -х-у.
X = х + у,
у = -5а; - Зу.
118.
120.
122.
124.
126.
128.
i = а; + 2у,
у = 2а; + у.
а; = -а; + у,
у = 2х - 2у.
а; = За; + у,
У = -х-\- 5у.
а; = 2а; — у,
у = а; + 4у.
а; = X — 2у,
у = х-у.
X = 2х — Зу,
у = За; -f 2у.
120
Глава 3. Линейные системы дифференциальных уравнений
129.
131.
133.
135.
X = —X + у,
у = -5х + Ъу.
X = —X — 2у,
y-x-Zy.
X = X + у,
у = 2х + 2у,
Z = Зг.
130.
132. < у =
134.
136.
X
у
X
у
Z
X
у
Z
X
у
Z
= X
= z,
= 2/.
= 0.
= Z
= X
= —
= Z,
= X
= 0.
+ У,
2х + Зу.
+ 2/,
-у,
X — Z.
-y + z,
Решить линейные неоднородные системы уравнений A37—168):
137.
139.
141.
143.
145.
147.
149.
X = —2х — у + 37 sin t,
у = —Ах — Ъу,
X = -2х -у-\' 36t,
у = —Ах — 5у.
x = Qx-3y + 30e\
у = 15х-6у-\' АЫ.
X = 5х + Ау + 7е^\
у = -9х - 7?/ + ^^ -f 1.
х = у,
у = X + е^ -{- е~^
X = -6х- 10у-f 4sin2^,
у = Ах -{- 6у.
X = —Зх — Зу + t -f 1,
у = бж + 6у -f 2t.
138.
140.
142.
144.
146.
148.
150.
X = Зх — 5у — 2е^
у = х-у - еК
X = Их - 8у + Ае^\
у = 20х- 13у.
X = —5х — ?/,
у = X - Зу - 9е^К
X = Зх '\'2у — е~*,
у = —2х — 2у — е~^
X = -Ах - 4?/ -f 2e^S
у = бж + бу -f 2t.
X ^ -7х + 2у-^е~\
у — —15а: -f- Ay.
X = —Зх + 2/ — е~^,
у = -Ах + у.
§ 11. Линейные системы уравнений с постоянными коэффициентами 121
151.
153.
155.
157. <
159.
161. <
163.
165.
167. <
х = Зх-\-2у'- 2e^
у = -Зх -2у- 2еК
X = у -\- cos 2t — 2 sin 2t,
у = -x-\-2y-\-2sin2t-^3cos2t.
152.
154.
X = X -\-y,
y = 3y-2x-2{t + l)eK
X = 2x -\-y -\-5,
у = x-\-2y-i- z,
z = -2y + 2z.
156.
158. <
X = —3x — 4y -\- Az -j- sint -^ cos t,
у z=:z Sx -\- Ay — 5z — sin t — cos t, 160.
z = X -j- у — 2z.
x = 2x — y-\-z-\- cos t,
у = 5x-4y + 3z-\- sint, 162.
z = 4x — Ay -\- 3z -\- 2s'mt — 2cos t.
X = 2x-^ у - 3z-\-2e^\
у = 3x-2y-3z - 2e^\ 164.
i = a: + у — 2;г.
X = Ax — y^
ij = a; + 2г/-h 2e^^
f i = a;-27/-2^eS
I y = 5a:-7^-Bt + 6)e^
i = 5a: — у H- 5sint,
у = 4a; H- г/ H- 3 sin it — cos t.
X — Ax -\-'iy — iz,
у — —Ъх — 2y + 3;г,
i = За: + Зу - 2;г + 26"*.
i = —5х + у - 2;г Н- cht,
у = -X - у Н- 2 sh t Н- ch t,
i=: 6a:-2y + 2z-2cht.
д; = д; + ;г — 2cht + 3sh^,
у = -2a: + 2y+ 22; + 4sht,
i = 3x — 2y H- ;г — sh t.
a: = x — 2y — ;г — 2e*,
t
X —
y =
z —
X =
y =
z =
-9x + 3y + 7;г + 2,
X -\-y - z -\-A,
-11а: + 3г/ + 9;г.
-x-y-^t'^,
-y-z + 2t,
-z-\-t.
у = -x-hy-\-z + 2e%
z = X — z — e^.
x = 2x — y-hz — 2e~S
166. { y = x-{-2y-z-e-^,
z = x-y-+'2z'- 3e~^
168. <
X = 2x — 3y -\-t^
y=^x-2z- 3t2,
-y + 2z + 3t - 2.
Методом вариации постоянных решить линейные неоднородные системы
уравнений A69—186):
-2х + 4у +
1
169.
у = —2х Н- 4у
1 + е^'
1
а; = -X - у +
170. <
1 + е^'
l + e
г
у = 2а; + 2у +
l + e
t'
122
Глава 3. Линейные системы дифференциальных уравнений
171.
173.
175. <
177.
179.
181. <
183. <
185.
X =
X
У
4x-8y + tg4^,
Ах — 4у.
Зх - 4у + -7
2а:-у.
i = Зж + у,
У = ~4х - у +
i = —X — 4у +
у = 2х + 5у.
X = —6х + 8у,
у = —4х + 6у
ж = 5ж — 6у +
У = Зх - у.
i = Зх + 2у ~
у = ~3х - 2у -
sin 2t'
2V^'
o3t
l + e^*'
ch2t'
3e2'
cos^St'
1
1
1 + e-
-f
i = —8x — 4y,
у = 20x + 8y-4ctg4t
1
172. <
174.
176.
cos3 3i'
i = 3x — 6y +
у = 3a; - 3y.
i = —3x + y,
y = -4a; + y+^.
X = 2x + у — Int,
у = —4x — 2y + In t.
o2t
178. <
180.
182. <
184.
186.
1 + e*'
= -За; - 2y +
I у = 10a; + 6y.
x = —Ix + 2y,
у = -15a; + 4y +
X = 10a; — 6y,
y = 18.-lly-^^3^.
X = —2x -\-y -\-tlnt,
у = -Ax -^ 2y -h 2t\nt.
X = Ax — 2y,
у = 8x - Ay + Vi.
e
1 +
3e*
Zl
e2(
Решить операционным методом задачу Коши при f^ О A87—197):
187.
189.
а; = 2ж — у,
у = Зх - 2у,
х@) = у@) = 1.
о2<
Ж = X + у + е-",
у = -2х + 4у + е^',
х@) = 1, у@) = 2.
I х = х + у,
188. I у = -2х - у,
х@) = 1, у@) = -1.
j х = -х-2у + 2е~',
190. I у = Зх + 4у + е~*,
х@) = у@) = -1.
§ 11. Линейные системы уравнений с постоянными коэффициентами 123
{X = 3х - 4у + е *■,
у = х-2у + е-\
х{0) = -1, у@) = 1.
{ж = 4ж — у + е*,
у = х + 2у + Ze\
х{0) = у{0) = 1.
{X = X — 2у + t,
у = х-у + 2,
х@) = у@) = 0.
{X = 4х + 5у + 4,
у = -4х - 4у + it,
х@) = О, у@) = 3.
I х = х + у + 3< + 6,
195. [ у = -10х - у + 6* + 3,
х@) = у@) = 0.
,2t
I X = —X — у + е
196. [ у = 2х + 2у + 2е2*,
х@) = у@) = 1.
ix = Зх + у + е*,
у = -4х - 2у + te\
х{0) = у@) = 0.
Решить каким-либо методом задачу Коши A98—224):
..{
X = Зх + у + е',
198. I у =-4x-2y-|-te',
х@) = у@) = 0.
200.
202.
X = 7х - 2у + Sfe"',
у = 8х - у,
х@) = О, у@) = \.
{X = Их - 2у +
у = 18х - у,
12<е-
х@) = --, у@)=0.
Г x = -i
—2х — у + 6t,
204. I у = —4х - 5у,
х@) = 2, у@) = 3.
199.
201.
203.
205.
х = 2х + -у,
у = -18х - 4у + 18fe2',
^@) = \, У@) = 2.
X = 5х + Зу,
у = -Зх - у + Qfe^S
т = \, У@) = 0.
X = -5х - 2у + 24е*,
у = -Зх - 4у,
х@)=0, у@) = 2.
X = —5х — у,
у = X - Зу - Збе^*,
х@) = 1, у@) = -6.
124
Глава 3. Линейные системы дифференциальных уравнений
206.
208.
210.
212.
214.
216.
218.
220.
X = Ах — у,
у = х + 2у + 2е^К
х{0) = 1, у{0) = 2.
x = Zx + 2y + {l- 4t)e-\
у = -2х -2у + 2te~\
х@)=у@) = -1.
i = 2у — 2г,
у = х-у - Z,
Z = —X — у — Z,
х@) = 3, у@) = О, z{0) = 1.
х = у- Z,
y=-y + Z,
Z = X — Z,
х@) = у@) = о, z{0) = 1.
х = х-у,
у = х + Z,
Z = X + Z,
х@) = о, у@) = г@) = 1.
X = X — Зу + Z,
у = х-2у,
z = y- Z,
х@) = 1, у@) = О, ziO) = -1
X = -2у + 2z,
у = X - у + Z,
z = y- Z,
х@) = г@) = О, у@) = 1.
х = 2х — y + z + 8,
y = y + z,
z = —X + у + z,
х@) = у@) = г@) = 0.
207.
209.
211.
213.
215.
217.
219.
221.
X = —2х — у + 37 sin t,
у = -4х - 5у,
х@) = 0, у@) = -1.
X = Зх — 5у — 2е',
у = х-у-е*,
х@) = 2, у@) = 1.
X =z X — У -\- Z^
у = у -х + Z,
Z = 3z — X — у,
х{0) = 3, у{0) = О, ^@) = 1.
y = y-j-z,
Z = —X — у — Z^
х@)=у@) = 1, z{0) = -l.
X = X — 2у -\- Z,
у = -у -f 2,
Z = X — у — Z^
а:@) = 2/@) = о, z{0) = L
X — 2у -\- Z,
y^x-i-z,
z = -у- Z,
а:@)=0, у@) = 1, z@) =-1.
т — X — 2у.
y=^-x-y-2z,
z^yA-z,
а:@)=0, 2/@)--1, z{0) = l.
х = 2х — y-i-z-hl — е~^,
у = 2а; — у — 2;г Н- 1,
i = -а:+ 2/+ 22; - 1 + e~S
а;@) = у@) = z{0) = 0.
§ 11. Линейные системы уравнений с постоянными коэффициентами 125
222.
224.
225.
226.
227.
228.
X = 2х — у + 2z, lx = x — 2y — z + l,
y = x + 2z, 223 I ^^'~^'^^'^^'
z = —2x + y — z + 1, I z = X — z + I,
x@) = y@) = ^@) = 0. х{0) = z@) = 1, y{0) = 0.
X = 2x + y + e^',
у = 2y + Az — 4e~*,
Z — X — Z,
a:@) = 0, y@) = -1, ^@) = 1.
Найти все решения системы, стремящиеся к нулю при ^ —> — оо:
i = Зх Н- у — 3;г,
у = -7х - 2у + 9z,
Z = —2х — у -\- 4г.
Найти все решения системы, ограниченные при t —> Н-оо:
Xl = —Xi -f 2X2 + ^3 — ^'4,
Х2 = -4xi + 4x2 + 2x3 - ^4,
хз = —4xi + 2x2 + 4x3 — ^4?
Х4 = —^1 Н- 2x2 Н- з:з — Х4.
Показать, что решение системы уравнений xi = —а^Х2, Х2 = ^i при
каждом из граничных условий: 1) xi@) = О, xi(T) = Ь, 2) xi@) =
= О, Х2(Т) = Ь, 3) Х2@) = О, xi(T) = Ь, 4) Х2@) = О, Х2(Т) = b в
зависимости от выбора параметров а, Ь и Т > О либо существует и
единственно, либо существует и неединственно, либо не существует.
Найти решение системы
X — 8х + л/бу = О,
у-у/ёх + 2у = О,
1,у@)=у@)=х@)
I
229.
удовлетворяющее начальному условию х@)
= 0.
Найти решение системы
X — ^ Н- i — 4х — 2у — 2;г = sin2^,
2х - у -\- Z -\- Зу - Az = О,
X -\- Z — 2х — у — Az = О,
126 Глава 3. Линейные системы дифференциальных уравненш!
удовлетворяющее начальному условию а;@) = i;@) = у@) = у{0) =
= z{0) = i@) = 0.
230. Пусть А=( " ^ V Доказать, что е^^ = в"' ( ^^^f ^^"^' ] .
\ -р а 1 \ - sin pt cos pt J
231. Пусть квадратная матрица второго порядка А имеет собственные
значения Ai, Л2 и Ai 7^ Лг- Доказать, что тогда
Аг - Ai
где Е — единичная матрица второго порядка.
232. Пусть квадратная порядка п матрица А имеет собственное значение
Ао кратности п. Доказать, что тогда
gtA ^ gAot
£^+^(А-Ао£;) + |(А-Ао£;J + ..
где Е — единичная матрица порядка п.
233. Пусть А — собственное значение квадратной матрицы А и пусть h —
соответствующий ему собственный вектор А, Доказать, что тогда
е^ — собственное значение матрицы е"^, а /i -~ соответствующий ему
собственный вектор е^.
234. Пусть Ai, А2,..., Ау1 — собственные значения квадратной матрицы А
(с учетом их кратности). Доказать, что определитель |е*^| матрицы
е*^ удовлетворяет равенству |е*^| = е{'^1+'^2+-н-Лп)«
235. Доказать, что матричные ряды для sin Л и cos Л
\к °5. (_л\к
сходятся для любой квадратной матрицы А.
2к
§ 11. Линейные системы уравнений с постоянными коэффициентами 127
Ответы к задачам § 11
1.
Се- -М+св' -'
;]-0,.'{1).С.е-^-{1
;----'•>-<
^1
Cie^' I / 1 + Сзе*
5. fM^CieM"''''^'^'^''^'Uc2eM~'''^''^'^''^'
\yj y2cos2t-^sm2tl \^cos2^ - 2sin2^^
yyy ^^ (^ sin3^ / ^^ \ ^^^^^ /
/xA _ /—cos4< —sin4A /~cos4t + sin4A
\^yy ^2cos4t + sin4^y "^ ^ \^cos4t - 2sin4ty
(x\_ /cosSt + sinSA /cos5t —sinSA
I у у \ —cosbt J I sin 5t у *
^ /^A ^ /cos2t + sin2A ^ /'cos2t ~sin2A
10.
11.
12.
13.
-2'
Cie-4 J'\+C2e-'
X
X
.у,
Сге^Ч Л+C2e2'
Cie-^Mj +С2е-з*
'-/Ь?
'-;ь-/
'^ь:
с, J+C2
i\V{\
128
Глава 3. Линейные системы дифференциальных уравнений
14.
\1
X
16. \у
.Z ,
17.
CieM 1+С2е*
'зЬГ
Cie' 4
Л
i
У
C7ie-2* I 2
.1/
+ С2е'
2f
1
V-V
л
■Л
+ Сзе-* I 2
О
+ Сге' I 3
+ Сзе
3t
/xN
у
v^^
= Cie^*
/-2\
3
wy
-2^
+ С2е'\ 3 I + Сзе^'
18.
' X
19. I у
^0\
= Cie-2* I 1
Cie^' I 3
/-1'
+ C2
2
\2У
/-1
1
V
1 I + СзеЧ 0
4 / I Зу
4i
/.
20.
V
'x\
21. I У
7
22. I у
1/
- Cie2' I -3
-1^
+ C2e
+ ^26*
1
VV
/o
-i\
+ Сзе'' 2
1 I + Cгe^^
0
V
/-1
= C7ie* I -1 +C2e4* 1 | + Сзе^*
V
2
Cxe
3t
1 I + ^26^*
/l\
1
V-V
/
+ Сзе2Ч
\
23.
-C7ie2* I 3 I +C2
1 I + Сзе
\2
3^
§ 11. Линейные системы уравнений с постоянными коэффициентами 129
/ 2sint + cost
— sint
2sint
130
Глава 3. Линейные системы дифференциальных уравнений
34.
\
35. L
vJ
36. L
Cie2*| О I +С2е2*
/ 4cosf
V-
-3cost
/-4sint^
cost
3sint
Cie-
l\
V
/cos t — sin t\
+ C2e*
V
cost
sint
/cost + sint\
+ Сзе*
/
v
sint
- cost
/
/ 4cos3t-3sin3t
-2cos3t~6sin3t I +
У 5 cos 3t
/ 4sin3t + 3cos3t
+ Сзе^
—2sin3t H- 6cos3t
5 sin 3t
— sin Л
37.
38.
cost
+ Сзе* I sint I .
sin t,
1
VJ
cos 2t \
+ C2e-^^ I cos2t + sin2t
2 cos 2t + sin 2ty
+
/
-4t
39.
+ Сзе
/ cos 3t
cos3t-hsin3t I +
\2 cos 3t + sin 3t^
sin2t
\
sin 2t — cos 2t
y2sin2t-cos2ty
/
-hCse'
sin3t
sin 3t — cos 3t
\^2 sin 3t - cos 3t^
1^
cos2t
\
40.
= Cie-4*
1 +C2e-^* cos2t + sin2f
1/ y2cos2t + sin2ty
+
§ 11. Линейные системы уравнений с постоянными коэффициентами 131
(sin2t \
sin 2^-cos 2^ .
2 sin 2t - cos 2tJ
X
41. \y
= C
le
-2t
/l\ / cos2t
1 +C2e^ cos2t + sin2t | -f
\lj y2cos2^ + sin2t^
+Сзе^
/ sin2t \
sin 2t — cos 2t
\2sin2t - cos 2tJ
X
cos 2t -f 3 sin 2t \
42. U =Cie-34l +C2e
3-2t
5sin2t
+
^3 cos 2^ + 4 sin 2t)
-2t
'x\
43. I у
Cie*
+Сзе
—3cosi + sinA
4 cos t + 2 sin <
10 cos t J
I 3cos2f-sin2f \
5 cos 2t
^4 cos 2t - 3 sin 2y
+
— cos t — 3 sin <
+Сзе-2' I -2cos< + 4sin<
10 sin t
44.
(x\
У
Л
45. I у
= Cie*
-n.^t
in Л
sin
+ Сге' I cos t
cost J
+ Сзе*
Cie'
46.
/A
0
VV
/l\ / 2 cost \
0 + C2 -2 cos f
У0 / \ cos t — sin tj
/—cos Л
sin t
у sint J
2s'mt
+ C3 I -2sinf
cos t + sin f,
- Cie2* I 2 I + C2e2«
/ cos t — sin t \
2 cos t — sin t
2 cost
V
COS t + sin t \
+ Сзе'^^ I cost + 2sint
2sint J
132
Глава 3. Линейные системы дифференциальных уравнений
47.
- п., ^-2t
= Cie
2\
-V
^4 cost -3 sin Л
+ С2е~^ I 2 cos ^ - sint
—3cos^
-Ь
3cost -Ь 4sint
Ч-Сзе"^ I cosi + 2sint
—3sint
i\
48. I
V
(x\
49. у
\z}
I
50.
51.
= Cie* 0
■1
/cos i — sin t
+ C2e
2t
cost. I +Сзе2*
— cosi
l\
= Cie-* 0
.-V
4cost \
+ C2e~^ I sint
-3cost У
cost + smt\
sint
— sint
-4sint\
+ C^e ^ \ cost
3sint
-l\ / -2sint \ / 2 cost \
Cie'^ \ 0 +С2еЧ 2 cost-sint +СзеЧ cost 4-2 sint
2 I \ cos t + sin t I \ sin t — cos t I
Cie^
/o\
\1/
-f C2e^
/ -2sin2t
cos2t I +
\^3 cos 2t -f 2 sin 2t^
+Сзе^
/ 2 cos 2t \
sin2t
y5sin2t-2cos2ty
— cost
— sint
-fC2e~^| cost +Сзе-Ч sint |.
— sint/ \ cost
cos
t\
+ C2e-^^ 2 cost
sin
int \
sin
V
+ Cze-^'- \2smt
cost
+ С2ё
At
0 I + Сзе^'
§ 11. Линейные системы уравнений с постоянными коэффициентами 133
55. \у\= Cie
(l\
1
\v
+ Сзе*
t
(Л
м^
о;
/о\1
0
1
\2/\
134
Глава 3. Линейные системы дифференциальных уравнений
65.
§ 11. Линейные системы уравнений с постоянными коэффициентами 135
+Сзе-'
*1
2
/1
2| +
/5^
75. \у\ =Cie24 О I +С2е2*
Г
г
(Л
oU
f'^il
1
[ v-iy Voyj
+Сзе2'
|;f;i
v-v
+
^2\
+ i I 1
.0/
+ 1-2
'l\
76. \y\= Cie-' 2
+ C2e
-t
/l\
L VV
+Сзе-'
/l^
1
WJ
+
t'
77.
VV
= C,e-3*
'l\
.V
+ C2e-3*
'
f
Л\
2
Ml
+ i;o
[ w VJ\
+Сзе-з*
Ч
2
L \
'l\
.V
+
/l\
*lll +
.0
0
\0у
ж
78. I у I = Сге'
3
+ C2e*
■l\
t I 3
X '
-l\
79. I у I = Cie2' I 1
+Сзе'
/-1
+ 1-1
-Л
<^
/
+
+ t\-l\ +
2
0
+ C2e
2t
1 1 +
V3
/-A
1
\2/
+
136
Глава 3. Линейные системы дифференциальных уравнений
+Сзе
2t
-1
-1
1 \+t\ 1 +
О
\1
80. \у\
(Л
е' 1
W
+ С2е«
t
(Л
1
v)
+
/з\1
2
WJ
+
+Сзе*
/А
1
VV
+ t
/з\
2
VV
+
/6\
2
V-V
81.
у
= Ci
/-2\
3
+ С2
-2\ /-1\
i I 3 + 2 I +
/-2\
+Сз
i^
3
+ ^
' ■) • (■ ^
X'
82. 1у
-Се
-2t
О
V-V
+ С2е-2*
i I О
-V
+
1
+
+Сяе-2«
f^
83.
/х\
VJ
= Cie
2t
0 I +C2e2*
0
-V
/-Л /o
/i
0
+
L \4/
+Сзе2*
+ i
+
-jn"f
f2
2
/-l'
'o\
0 +Ч 1
4} \0J
■l\
+ \ 1
3
/J
84.
= Cie
-2t
2 1 + C2e-2*
H 2 I +
0
VV
+
§ 11. Линейные системы уравнений с постоянными коэффициентами 137
+Сзе-
-2t
-i\
i\
+
и,
85.
86.
\t
(-2\
1
[ч
+
("М
ч
W
/-А
1
\2/
+
+Сз
f
2
+ t
1
\2/
+
2
\
+ С2е-'
/
/з\
1
Iv
+ Сзе-'
i
/з\
1
Iv
(Л]
А'\\
W
+ Сзе
+ Сзе
х\
90. I у
91.
= Cie'
О + С2еЧ 1 I + Сзе'
W U
/х\
у
\^^
= Ci
л\
0
1^;
[ (')
\t 6
[ W
+
/l\l
1
WJ
92.
У
v)
- Cie3' I О I + C2e^^
/з\
1
v)
+ СзеЗ'
[ (Л
til
w
+
Ml
0
wJ
138
Глава 3. Линейные системы дифференциальных уравнений
/.
93.
= Cie'
2t
94.
/х
У
(х\
95. у
v)
96. \у
/з\
О
VV
'Л
Ci |0
+ С2е2' 4
VV
+ Сге
2t
'Л
+
+ С2
-3
2t
Cie
= Cie3*
h
О +C2e2*
VV
+ Сз
M4
/ 1 \ /l\
0
-3
+
0
2 I + Сзе2'
\1,
+
-1
+ C2e'
зг
И -11 +
+СзеЗ*
i^
'Л
П 2
V
/-1
2
^ 3
-1 I +t
О
+
/-А
2
/-1^
+
' X
97. |у
-г,
/1
= Cie
3t
-2 I + Cse^*
1
+
+Cze
zt
-2\ +t
/l\
-1
V-v
^-i\
+ 1 2
98.
У
= Cxe
-at
1 I + C2e-3*
Vi.
/0>
11 +
/l^
Vb
+
+Сзе
-3«
/0\
1
VV
+ t
(:)•(■)
99. I у
= Cie2* I 0
+ C2e'
2t
'l\
По
2/
^0\
+ |1
.2/J
+
§ 11. Линейные системы уравнений с постоянными коэффициентами 139
+Сзе'
2«
'о\
о +н 1
+
kV
(-i\
\Ч\
'х\
100. I у
Z
= Cie2' I 2 I + С2е2'
X
101. I у
z
= Cie-
+ С2е
102. \у
,z
/-2'
\^-3t
Cie
1 I + Сге-з*
\3
/о\
1
ч
+
(-Л]
"
U;
Cie-2* I О I + СзеЗ'
-1
V-V
140
Глава 3. Линейные системы дифференциальных уравнений
110.
X
111. I у
112. I у I
Z
= Ci
= Сх
I cosSt \ / sin3t \ /-Л
cos 3^ +sin 3^ М"^^ cos3t-sin3t + Сзе-Ч 1
у2 cos 3t -f sin 3tJ ycos 3t-2 sin 3tJ \l J
:os 5t \
cos
^ ' ) ( 1
2sin5i И"^Ч 2cos5i +^36^
\^cos 5t + 2 sin 5^ / \ 2 cos bt — sin 5w
/ -cos4t \ / sin4t \
/-1^
V
= Cie
-t
I
sin4t
\^3cos4t - sin4ty
sin4t
+ C2e~^ cos4i
~ cos 4^-3 sin Mj
+
113.
= Cie'
2t
/ -cos2i \ / sin2t
-cos2^ + sin2t Л-С^е^^ cos2t + sin2i | -f
y 3cos2t у у -3sin2t
{Л
+Сзе-' О
\2/
11. Линейные системы уравнений с постоянными коэффициентами 141
114.
115.
/
У
V/
— COS 3^ \
sin 3t
\^2 cos 3^ + 2 sin 3tJ
( - cos 4t \
sin3t
+ C2 cos3t
2 cos 3^ — 2 sin 3t /
Л-Съе' I 0
Cie
2t
2cos4t+ sin4t
\ 2 cos 4t /
/
+ C2e
at
sin4t
\
cos4i - 2sin4t
-2sin4i
+
/
116.
117.
118.
119.
120.
121.
122.
123.
= Cie-
/ - cos At \
sm4i
у cos 4i + sin At J
+ C2e
-t
+Сге
\
-2t
2
1
sin4i
cos4<
\ cos At — sin At I
+
+Cse
уУ)
^yj
<yj
X
кУу
^Уу
^x'
1 / e* + e^* e^* - e*
2 \ e"** - e' e'^' + e
3t
C2.
2 1 еЗ« - е-* еЗ' + e"*
C2.
,C2,
-3i
3t'
2 + e-"" 1 - e
2 - 2e-3* 1 + e-3«
'C7i
,C2,
1 / 2 + 26^* 1 - e^*
4 \ 4 - 4e^* 2 + 26^**
o4t
=,2t
1 -t t '
^1 + f -t ^
< 1 -t.
142
Глава 3. Линейные системы дифференциальных уравнений
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
= еЗ«
1 -t -t
t l + t,
C2,
l + t t
-t 1-t
Ci.
cost + sin^ -2sin^ \ [С\
sin^ cost — s'mt I \C2
.-t
cos t -\-2smt
s'mt
= e2*
I 5 sin t cos t — 2 sin t
cos3t — sin3t\ I Ci\
Сг
C2.
\ sin Zt cos 3t
cos ^ — 2 sin t
—5sint
/ cos t — sin i
[Czj'
sint
cos t + 2 sin t
Сг
C2.
= e
—2sini
cos t + sin t
sint
sint
cost -f sint
—2sint
cos t — sin t
Сг'
'c:
C2.
1 0 л
0 e* 0
0 0 l)
I (^Л
1 ka
' \4
/e^* + 2 e^'-l 0 \
2e3* - 2 2e3* + 1 0
0 0 3e3«
1
1-e-
r.-t
-* 1 + te-^ l-(t + l)e-'
1 (H-«)e-*-l (t + 2)e-'-iy
(Сг\
\C,J
\l + t)e^ 0 -te^
1-е* 1 e* - 1
te* 0 (l-<)e*
§ 11. Линейные системы уравнений с постоянными коэффициентами 143
136.
/ 1 О А
1 - е-* е-* t
^ О Q l)
\у ' U/ 1-1/ \-10sm< + 14cost
138.
139.
X
X
' ^t
С\е
2 cos t — sin f
cosi
+ 0-26*
= Cie
-6t
+ C2e
-t
-1
+
cos t + 2smt
sini
^30< - 29\
28 - 24i ] ■
+
140.
a;\ _ _^ I sm4i —cos4i \ ^ _W sm4t + cos4t \ /e
.y)~ ^^ lsm4<-2cos4J ^^ I cos4t + 2sin4i / U
,^, (a;\ _/ sm3< \ ^ I cos3t \
141. = Ci + <^2 +
\y I \ 2sin3t — cos3t I \2cos3< + sin3t I
+
21e' - 15t
, 45e* - 30t + 5 ,
142.
a;
Cie-« _M + C2e-4*
'UbU
-r^-'r.
143.
Cie-M ^]+C2e-'
^1И-:
+
7e2* + 4<2 - 16t + 28
-7e2< - 5^2 + 22f - 39 ,
144.
a;
Cie
2t
+ C2e-* „ + e-*
l-2<
145.
X
= Cie4\ +C2e
-t
1 \ 1
t(e* - e-')
-1/ 2 U* + l)e'+ (t - l)e
-«
146.
144
Глава 3. Линейные системы дифференциальных уравнений
\у1~ 4sin2^-3cos2iJ "^ ^ \^3 sin 2i - cos 2у "^
At cos 2t
+ 12 2
-(l + 2i)sin2i--(l + 6i)cos2i
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
Cie-
-2t
r
+ Сге-* I : 1 + е-'
-I5t
^'^"r:h<:hnrj
""^ Cie-MM+C2e-'
'^Al
+ e
-t
'e-t'
2f ,
cJ-:).c.,-;)..-zr
C7ie3* r + СгеЗ'
'CbJ
— e
зг
i2 + 2i + 2^
= C7ie4 l+Cae*
'lb"
Cl
2 cos 3t
cos 3^ + 3 sin 3^ ^
+ C2
+ cos 2t
2 sin 3^
^ sin 3t — 3 cos 3^ ,
4-e^
у I \cost — sint I {cost -\- smt I \ 1
'Шч:
-Л
Cie'' 0
+ C2e'
2i
/ COS t \
— sint
y—2 cost J
+ C'se
+
t ^2t
— sint
cost
sm
t \
cost
-2suit I
+
/-3\
1
\4
11. Линейные системы уравнений с постоянными коэффициентами 145
'х\
158. I у
Z
' X
-Л
159. \у\= Cie* 1
+ С2е'
+ С2е-
160.
У
vl
= Cie
-2t
1
v-v
+ C2e
Л
161. I у
Ч
(x\
у
VJ
/x\
У
VJ
' ^-t
C\e
h
I
v)
+ Cae'
/Л
1
[v
+ Сзе*
[ (Л
til
w
+
/o\l
1
wJ
+ smt 0
162.
163.
'l\
= Cie'^ 1
.V
+ C2e' I 2 cos i I +Сзе*
sin t
l\
= Cie-'' -1
+ Сге-
Л
164. у
165.
(Л
у
V/
Cie
- г, ^-2t
Cie
1
/A
0
+ C2
+ C2e*
/A
1
VV
/l\
/o
+ Сзе
2t
+
\2/
\1/
146
Глава 3. Линейные системы дифференциальных уравнений
166.
167.
Ч-Сге'
+ C2e-^
168.
169.
170.
х\
у
У
= С7ге2'
/2\
0
v)
X
X
+Сзе-*
+ С2е* I 1 I +Сзе^ |f I 1 I + I -1
'^i^ - 20t - 79\
+ I 6*2 - 19t - 46
^if - 16t - 30y
M /Л /Ce2*-4)ln(H-e-*)-3e' + |^
С\П+^2в2* +
VV VV \^(Зе2'--2IпA+е-')-Зе* + |У
^'' I 2 )+^4 1 ) + l-4e4n(H-e-*)-31n(l + e'))-
171.
X
/cos4t+ sin4*\ / cos4i - sin4< \
/
+ :
(sin4t - cos4t)ln
v
COS 4t • In I
1
1 + sin4t
1 - sin4t
1 Ч- sin 4t
-2
1 - sin 4t
/
172. д: = (Ci + C2) cos 3^ + (Ci - C2) sin3t + :^—[2sin3t + cos 6t(sin3^
6 cos^ 3t
cos 6t
~ COS 3^)], у = Ci sin 3t + C2 cos 3t —
173. X
6 cos 3t
Cie^(cos2t + sin 2^) + C2e\cos2t - sin 2^) + te^(sin2^-
§11. Линейные системы уравнений с постоянными коэффициентами 147
-cos2t)-h ~e^(cos2t+ sin2t)ln|sm2t|, у = e^(Ci sin2t-f C2 cos2t)-f
H-~e4in2tln|sin2t] - te^cos2t.
174. a; = (Ci + Cit)e-^ + te-*(ln|f| - 1), у = CiBf + l)e-* + 2026"'+
+e-'Biln|t| + ln|t|-20-
175. X = -Ci(f + l)e' - Cae* + ^<\/<e', у = CiBt + l)e* + 2С2еЧ
О
+ (^V^-^f\/<je'.
176. ж = -Ci[t + 1) - C72 + f + ^<^ - U + )f\ \nt,y = Ci{2t + 1) + 2C2-
3
-t- -t"^ + {t + t'^)lnt.
177. a; = 2Cie'-C2e3* + e4n(l + е2*) + ^е^*1пA + e'^'), у = -C7ie4C2e^*-
-ie*ln(l + e^*) - ^e3*ln(l +e-2*).
178. X = -2Cie2* - C2e* + 5еПпA + е') + 4e2*ln(l + e"'), у = SCie^^
+2C2e* - lOe* In A + e*) - lOe^* In A + e"*).
179. ж = 2Cie-2* + C2e^^ + 2e-2* In A + e^*) + 26^* In A + e"'"), у = ^е-'^Ч
+C2e2* + e-2* In A + e^*) + 26^' In A + e-^').
180. X = 2Cie-2' + C2e-' - 2e-2* - e-24n(l + e-^*) - 2e-*arctge',
у = 5Cie-2* + ЗСге-' - бе-^' - ^e'^' In A + e'^') - бе"' arctg e'.
181. .-E = (Ci + C2)e^'cosЗ^ + (Ci - C2)e^*siпЗi + e^HgZt{s\nZt + cos3t)+
6 e COS 6^
+ 7^^ ^r—(sm3f-cos3t), у = C]e2*sin3< + C2e^'cos3< —.
2cos'^3< cos3t
182. X = 2C7ie4C2e-244e'-arctg еЗ*-2е-2' ln(l + e'^'), у = 3Cie'+2C2e-2*+
+6e' arctg e^* - 4e-2* In A + e*^').
183. a; = -2Ci - C2e' + 41n(l + e*) + 5e4n(l + e-'), у = 3Ci + Сге'-
-61n A +e*) - 5еЧп A +е-*).
184. a; = Ci + Сз* + jt'^{2\nt - 1), у = 2Ci + C2{2t + 1) + ^<2B1п< - 1).
148
Глава 3. Линейные системы дифференциальных уравнений
185. X = -Cicos4t - C2sin4^ - sinSt - - In
1 -h cos 4t
1 - cos 4t
1
+C2)cos4t+ BC2 -Ci)sin4t + cos8^ + 2sin8^- -In
+2sin4t).
sin 4^, у = BCi +
1 + cos 4t I
1 - cos 4t
(cos 4^4-
16 5 2 3
12 -f -t2.
15 3
186. x = Ci-\-C2t- —tl, y = 2Ci-\-C2(t-^
187. x = y = еК
188. X — cos t, у = — cos t — sin t.
189. x = e^^ -\- te^\ у -: 2e^* + te^^
190. re =: 2e^^ - e^ - 2e-S t/ = e^ + e"^ - Зе^^
191. у - JEe-^ - Se^^) + te-^ t/ - \{Ъе-^ - 2e^^) + te'K
192. ГС = B - t)e^^ -e\y = {3- t)e^^ - 2eK
193. X = 3 cos t — sintH-^ — 3, t/==2 cos t -\- sint -\-1 — 2.
194. x==^4 + 5t-4cos2t + 7sin2^, у = 6cos 2^ - 4sin2t - 3 -At.
5 4 7 19
195. X = -sin3t+ -A -cos3t) -\-t,y = -sin3t-f- —(cos3t~ 1) -At.
196. a; = 1 + e* - e^', у = -i - 2e* + 46^'.
197. a; = ^e^* + le"' - ^e* - ^te', у = -^e^* - ^e'^ + 2e* + te^
2 ' " 3 3
198. X = le-' - iBt + 7)e* + fe^*, у = -^e"* + (t + 2)e' - |
12
e^K
199. re = Ci + l)e-* + (^ - I) e^*, у = -IS^e"* + 2e2'.
200. a; = ^e"* + (* ' I) ^''' У = D* + 2N"' + Bt - ^-] e^K
201. х = {Ш- 2)e^' ~ ( 4< + Q ) ^^'' У = e^' - A + 4<)e2*.
202. a; = Je"' - B^ + l)e'\ у = Fi + 2) (e"* - e^*).
О
203. ж = -e-^* - 4e-2* + Ъе\ у = -e"'^' + 6e-2* - 3e'.
§ 11. Линейные системы уравнений с постоянными коэффициентами 149
31 et 29 t , 29 62 .^ 29 , , 14
30 5 5 15 5 3
205. а; = e^' - te'^^, У = {t + 1)е-4* - 7е^К
206. x={l-t- f)e^^, y = {2 + t- t'^)e^K
207. X = 15e~' - 15cosi + 16sin<, у = -15e~'+ 14cos<- lOsint.
208. x = {t + l)e-* - 2e2', у = e^* - 26"'.
209. X — e'(cos< — 3sin< + 1), у = e'(cosi — sint).
210. rr = e2* + 2е-2', у = ^(e^* - e'^'), z - ^(-e^' + Зе-^*).
211. x = 2e^-\- e2^ 'i/ - 2(e* - e^*), ^ - 2e^ - e^^
212. X = —e~^sint, у = e~^ sint, z = e~*cost.
213. x = {l-\- t)e\ y=-{l- t)e\ z = -еК
214. X = —e^ sint, у = e^ cos t, z = e^ cos t.
215. X = te-\ у = te~\ z = e~^
216. X = e~^ (cos t + sin t), t/ = e~^ sin t, 2г = e~^ cos t.
217. X -: te-S у = e-\ z = -{t-\- l)e-^
218. X = -2e~* sin t, у = e~^ cos t, 2г = e~^ sin t.
219. X == 2te\ у = -e\ z = {I - t)e^.
220. X = 8te\ у = 4{2te^ - e^^ + 1), ^ - 4Be* - e^^ - 1).
221. x = z = 0,y = l -e-^
222. X = у = 2{1 — cost), 2Г — cost + sint - 1.
223. x = z = t-\-l,y = 0.
224. a; = 0, t/ = -e^S 2г === e~^
225. X - -C2e2^ - Caters у = 3Cie' + 4026^^ + СзD^ - l)e2^ ;^ = Cie4
+C2e2^ + Cзte2^
226. a;i = 072 = 2:3 = C, 0:4 =^ 2C.
150 Глава 3. Линейные системы дифференциальных уравнений
228. X ^ ~{3ch2t - cos2t), у = Ve{ch2t - cos2t).
-|(cos2( + sm2<),z = ie-'-ie-"-le^' + iGsi„2(-9cos2().
§ 12. Линейные системы уравнений
с переменными коэффициентами
По заданной фундаментальной матрице Ф{х) линейной однородной
системы у'{х) = А{х)у[х) с непрерывной на промежутке / и квадратной порядка
п матрицей А{х) всегда можно однозначно определить матрицу А{х)^ т. е.
построить линейную однородную систему.
Пример 1. По заданной фундаментальной матрице
(cos X sin X \
составить линейную однородную систему.
— sin X cos X I
Л Неизвестная матрица А{х) находится из условия, что Ф{х) — решение
матричного уравнения Y'{x) — A{x)Y{x). Отсюда А{х) = Ф'{х) • Ф~^{х) =
= 1 1. Искомая система имеет вид
y'l =У2, У2 = -У1' А
Формула Л иу вилл я-Остроградского позволяет по заданному решению
линейной однородной системы найти общее решение этой системы.
[х\
Пример 2. Известно, что вектор-функция I 1 — решение системы
{/ оч . Найти обш,ее решение системы.
{1-\-х^)у'^ = -2у1-^2ху2.
Л Пусть решением системы является вектор-функция с компонентами
У1 = (p{x)j у2 = ф{х), причем (^@) = 1, '0@) = 0. По формуле Лиувилля-
Остроградского имеем:
^{х) X
ф{х) 1
1 о
О 1
г 2<Ж
§ 12, Линейные системы уравнений с переменными коэффициентами 151
Отсюда (р{х) — хф{х) = 1 -h ж^. Подставляя выражение для (р{х) во второе
уравнение системы, получаем задачу Коши для ^{х)
ф\х) = -2, ^@) = 0.
Следовательрю, ф[х) — ~2х, (р{х) = 1 — ж"^.
Тогда обш,ее решение заданной системы имеет вид
Пример 3. Может ли система < , . J^ иметь два огра-
[ У2 = ж У1 + е^У2
ничейных на (~оо,+оо) линейно независимые решения?
Л Ответ на поставленный вопрос отрицательный, поскольку допустив
противное, получаем, что определитель Вронского этих решений является
ограниченной на (—оо, +оо) функцией и отличен от нуля. С другой
стороны первообразная следа матрицы системы
X
I
о
4
4
является неограниченной на (—оо, -|-оо) функцией. Это противоречит
формуле Лиувилля-Остроградского. А
1. Пусть задана линейная система у'{х) = (р{х)Ау{х), где (р{х) —
непрерывная на промежутке / функция и А — чиатовая квадратная мат-
X
рица порядка п. Доказать, что замена t = J V^(C)^C Д21ет линейную
хо
систему y'{t) = Ay{t).
2. Пусть Ф{х) — фундаментальная матрица линейной системы
z'{x) = B{x)z{x), где В{х) — квадратная порядка и и непрерывная
на промежутке / матрица. Показать, что замена у[х) — Ф{х)г[х)
в линейной системе у\х) — А{х)у{х) с квадратной порядка п
и непрерывной на / матрицей А{х) дает линейную систему вида
z'[x) = ф-\х)[А{х) - В{х)]Ф{х)г{х).
152
Глава 3. Линейные системы дифференциальных уравнений
В задачах C—9) исследовать линейную заврюимость вектор-функций на
(-оо,+оо):
sh ж \ I chx
ch ж /' \ sh а:
2х'
2х
5. е^
cos ж
smx
— sin X
COSX'
— sin 2х
—2 cos 2х.
В задачах A0—18) по заданной фундаментальной матрице Ф{х) найти
матрицу А{х) линейной однородной системы у'{х) = А{х)у{х).
10. Ф{х) =
12. Ф{х) =
14. Ф(ж) =
16. Ф{х) =
18. Ф{х) =
1 -х\
X 1 j
е" О
е cos з; — sin х
е sin X cos ж
и. Ф(х) = L',. f
13. Ф(ж)
15. Ф(х')
хе^ ё^'^
ch X sh ж
, sh ж ch ж ,
ж ж^
1 2ж
, ж > 0.
17.Фм= ;, М,х.>о.
е ^ + X 1
же
В задачах A9—23) но заданному решению у{х) линейной однородной
системы найти фундаментальную матрицу Ф(х) этой системы:
1
19. у{х)
IX
у[
У'2
1+ж4
1
1+ж4
Bж'^У1-2жу2),
Bжу1 +2х^у2).
§ 12. Линейные системы уравнений с переменными коэффициентами 153
20. у{х) =
21. у{х) =
22. у{х) =
23. у{х) =
X
1 /
е- \ f ^1--Bх + 1)ш+2у2,
^е-A + х)у ' \ у1, - (-2Х-2 - 2х + 1)у1 + Bх + 1)у2-
' е--- \ Г у; - A - 2:с)ш - 2^2,
^е-^-A - •^•)У ' 1 ^2 ^ B:^'^ ~ 2х- - 1)ш + [2х - 1)у2.
— sinxM J ^j — 'У1 cos"^ X + (sinxcosa: — 1)у2,
cos .т у ' I ^2 ~ (^^^ ^' ^^^^ ^ + 1)У1 + ^2 sin^ X.
24. Пусть квадратная порядка п матрица А{х) непрерывна на
промежутке / и при всех X G / перестановочна со своей первообразной,
X X
т. е. А{х) • ^ A{QdC, — ^ A[QdQ-A[x), где хо Е /. Доказать, что
XQ ХО
тогда фундаментальной матрицей Ф(х) линейной однородной системы
у'[х) — А(.т)у(а:) является матрица
ф(х) =: е^о
25. Пусть квадратная порядка п и непрерывная на промежутке / матрица
А{х) = HJ{x)H~^^ где J(x) — жорданова и nenpepi^iBna на / матрица,
а Я ~ числовая невырожденная порядка п матрица. Доказать, что
матрица А{х) перестановочна со своей первообразной на промел<утке
/ и что на / фундаментальной матрицей системы у'{х) — А{х)у{х)
является матрица
Ф{х) = Яе^о Я~\ XQ е L
Используя результат предыдущей задачи, в задачах B6—37) найти
фундаментальные матрицы Ф(ж) линейных однородных систем.
I '^2 == ~У1 + Bх- + 1)у2- I ^2 ^ -У1 + A - 2хJУ2.
154
Глава 3. Линейные системы дифференциальных уравнений
28.
30.
32.
34.
36.
y'l = Bх + 1)у1 + у2,
У2 = -У1 + Bа; - 1)У2-
у[ = -B + sina;)yi + 4у2,
У2 = -У1 -yasinx.
y'l = A -sma;)yi +у2,
У2 = -У1 - A + 8тж)у2.
y'l =yicosa;-y2sinx,
У'2
-yi sin а: + у2С08Х.
y'l
-2ху2,
У2 = -2ху1-
29.
31.
33.
35.
37.
у[ = (со8х-2)у1 + 4у2,
У2 = (-ЗУ1 +5у2)с08Х-.
y'l = B + cosx)yi +У2,
У2 = -У1 + (С08Ж- 1)у2.
y'l =yismx -у2С08х,
'У2
-7/1 COSX + ?/2sinx.
У1 = yis'mx + y2Cosx,
У2 = У1 COS а: + у2^\пх.
у\ = Зх'^У2,
у2 ^Зж^уь
38. Может ли система y'l
У1
+ A + xfy2, У2 = У\ In \х\ - Ау2 иметь
1+ж2
два ограниченных на (—оо, 0) линейно независимые решения?
yi
39. Может ли система yi = 5" — ^У27 Уо ~ У1 ^g^ + Зу2 иметь два
1 — х^
ограниченных на (—1,1) линейно независимые реи1ения?
40. Пусть Ф{х) — фундаментальная матрица линейной системы
у'{х) — А{х)у{х)^ где А{х) — квадратная порядка п матрица с
непрерывными на (—оо,+оо) элементами aij{x), причем aij{x-}-w) ~ aij[x),
W
J aij{x)dx = aij^ i^j = l,n, г^; > 0. Доказать, что
x->-|-oo X
Ответы к задачам § 12
3. Линейно независимы.
5. Линейно независимы.
7. Линейно зависимы.
9. Линейно независимы.
1 1 "'
lim - In I det Ф(х)| = — У^ ац.
->-|-оо X W ^^-^
г=1
4. Линейно зависимы.
6. Линейно зависимы.
8. Линейно независимы.
10.
1
X
1 + Ж^ \ 1 X
§ 12. Линейные системы уравнений с переменными коэффициентами 155
^^- 1 + а.-4 -2х 2x4'
13.
15.
17.
19.
21.
23.
е^A + а;) же ^
cos^ X sin о; cos ж — 1
sin X cos X + 1 sin'^ x
14.
16.
18.
20.
22.
26. e^
28. e^
29. eSinJl-2- 4x 30. e(—1)^-2^ '^
У -X 1 + 2x / \^ -X 1 + 2x^
32. e(cosx-i)(^ + l X \
\ —X 1 — Xj
33. g(i-cosx) Z' ch(sinx) -sh(sinx)\
I—sh(sinx) ch(sinx) J
34. gsinx /^ ch(l-cosx) -sh(l-cosx)y
\—sh(l~cosx) ch(l—cosx) /
35. g(i-cosx) Ah(sinx) sh(sinx)\
\ sh (sin x) ch (sin x) у
I chx^ -shx^\ fchx^ shx^\
\—shx^ chx^ / ' Ishx^ chx^j
38. He может. 39. He может.
Глава 4
АВТОНОМНЫЕ СИСТЕМЫ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 13. Поведение фазовых траекторий
в окрестности грубых пололсений равновесия
Для автономной системы второго порядка
i X = fi{x,y),
с непрерывно дифференцируемыми fi{x,y), /2@;,?/) в некоторой области
G С Rfj^y) положение равновесия (ai,a2) называется грубым положением
равновесия, если матрица линеаризованной в точке (ai,a2) системы имеет
такие собственные значения Ai, Л2, для которых Ai т^ А2 и ReAi ф О,
ReA2 7^0.
В окрестности грубого положения равновесия автономной системы
поведение фазовых траекторий качественно одинаково с поведением
фазовых траекторий линеаризованной в этой точке системы.
Пример 1. Найти положения равновесия, определить их характер и
нарисовать фазовые траектории линеаризованных систем в окрестности
положений равновесия для автономной системы
Г X = х-у'^,
[ у = х^Л-г/ -2.
Л Приравнивая правые части системы нулю, находим положения
равновесия A,1) и A, —1).
Рассмотрим сначала точку A,1). Для дальнейшего удобно ее
преобразовать в начало координат. С этой целью сделаем замену переменных
§ 13. Траектории в окрестности грубых положений равновесия
157
X — 1=и, у — l=VB заданной системе. Система примет вид
и = и — 2v — v^^
для которой точка @,0) ~ положение равновесия. Линеаризованная в
точке @,0) система имеет вид
й — и — 2v^
V = 2и + 2v.
Находим собственные значения матрицы этой системы
1 -2
2 2
из уравнения
1-А -2
2 2-Л
А^ - ЗА + 6 - 0.
Так как собственные значения Ai^2 — -C±i\/i^), то положение равновесия
является неустойчивым фокусом. Следовательно, кроме положения
равновесия @,0), остальными траекториями являются спирали. Для
определения направления движения по спиралям при t -> +оо достаточно найти
вектор фазовой скорости а линеаризованной системы в какой-нибудь
точке. Например, в точке A,0) вектор скорости а имеет координаты A,2),
Следовательно, при t —> +оо движение по спиралям направлено против
часовой стрелки. Поведение фазовых траекторий в этом случае
схематически показано на следуюш,ем рисунке.
158
Глава 4. Автономные системы дифференциальных уравнений
Для другого положения равновесия A,-1) замена переменных х — 1 =
= и, у -\- I = V дает систему вида
и
V ■
u + 2v
2и -2v Л-и^ Л-v^.
Линеаризация этой системы в точке @,0) имеет вид
й — и Л- 2v^
V — 2и — 2v.
Собственные значения матрицы этой системы
находим из уравнения
ll
2
-2-А
- А^ + А - 6 = 0.
Получаем Ai = — 3, А2 = 2. Так как Ai и А2 разных знаков, то положение
равновесия @,0) является седлом. Для того, чтобы нарисовать картину
поведения фазовых траекторий, осталось найти линейно независимые
собственные векторы hi и /i2 для Ai и А2. Для Ai = —3 собственный вектор
§ 13. Траектории в окрестности грубых положений равновесия
159
/ii = ( j, а для А2 = 2 собственный вектор /^2 = I 1 • Известно, что
в случае седла траекториями являются гиперболы, для которых прямЕ^ю,
определяемые векторами /ii и /i2, служат асимптотами. Лучи этих прямых
тоже траектории.
Поведение фазовых траекторий в этом случае схематически показано
на следующем рисунке, где стрелки указывают направление движения по
траекториям при t —> +со.
Пример 2. Для уравнения х-\-х^ — е~~ = О найти положения равновесия,
определить их характер и нарисовать фазовые траектории
линеаризованного уравнения в окрестности положений равновесия.
Л Введя обозначение .т = у, преобразуем уравнение к системе
По определению положениями равновесия и фазовыми траекториями
заданного уравнения являются соответственно положения равновесия и
фазовые траектории этой системы. Приравнивая нулю правые части
системы, находим пололчение равновесия A,0). Перенося начало координат в
160 Глава 4. Автономные системы дифференциальных уравнений
положение равновесия A,0) с помощью замены х = и-{-1, у = v, получаем
автономную систему
и — v^
о 4и
i) z=. -(n+ 1)*^ +е ^^+i
Разлагая правую часть системы по формуле Тейлора в окрестности (О, 0)
и ограничиваясь лишь линейными членами разлол<:ения, получаем
линеаризованную систему вида
Матрица этой системы 1 имеет собственные значения Ai —
= — 1, Л2 — — 3. Соответствующие им линейно независимыми
собственными векторами являются
hi
Положение равновесия @,0) линеаризованной системы ~ устойчивый
узел. Поведение фазовых траекторий схематически показано на
следующем рисунке, где стрелки указывают направление движения по
траекториям при t -> +00.
13. Траектории в окрестности грубых положений равновесия
161
Найти положения равновесия, определить их характер и нарисовать
фазовые траектории линеаризованных систем в окрестности положений
равновесия для автономных систем A—52):
1.
У = arccos {х — х^) —
2.
i =:1пA -у),
У = ^х — 4у -\- X — 2.
3. <
х = In A -Ь х/1 + 4у - у^) - In 2,
2 4.
у — — arctg {х Н- ЗуOг -Ь 2 — у.
7Г
i==lnE-2x-2y),
у - е-^ - 1.
5.
i == sh(y — x^ — х),
у = Зх — х^ — у.
6.
х = 2x + y^ — 1,
у = sinx — y^ + 1.
7.
.т == 1п(х Н- у),
у = х^ Н-у^ - 1.
8.
X = Зх^ - ху Н- 2,
у = х^ — X — 2.
162
Глава 4. Автономные системы дифференциальных уравнений
X
У
X
У
X
У
^Ji
х^ + х-^2у^ - 2,
х-{-у^.
= е
—4х _ 1
i = ж^ - у,
у = 1пCа;2~1)~1п2.
у = 1п(ж^ -1-2/) ~3у.
X
у
у{х-2у-6),
\п{х-2у).
= arcsin (ж^ — 2ж — у),
= ln(l-x4)-
а; =
arctg (ж^ - х + у),
1пA -|-ж2-|-За;~у).
i = shy,
у = е^-
1.
X
у
sh(x~y),
-{^
2/^ - J/ - 2,
у = -ху - Зу2 - 2.
12.
i = 2а; — J/ — ж^,
у = х/ГТ1^ - v'l + 2ж + 2у2.
Ч:
с = -3 + 2а; + у,
arctg (а;J/).
i = 4 - а;Cу + 2) - 9у\
16. < . , 1 + а;
у = In-
18.
I:
1-2а;
= За;у,
20. <
22.
X = Ьх — 8у + 3,
2/ = In-.
j.^g-sh(i+y) _2^
у = 2ху + X - у.
24.
{:
- = е^ -у- 1,
= ж4-1пA 4-у).
( х = 1пA-|-д,'-|-4у),
I у = arcsm I ж -|- у ——• I.
28.
у = arctgl 4ж~у- — 1.
27Г -h arcsin (y^ + 8 -I- sin x) -f
2y -I- 4 — Ssinx.
i = 7Г -I- arctg (ж^ - 8 - tg y) - y,
у = 2x-|-12tgy-4.
i = In {x^ - 1 - 6e^) ~ y,
у = 4ж — 4e^ ~ 4.
= >/y^ — 1 — 6x2 _ дг.^
^ = v/2y'^=^ - V2x^ ~ 1.
§ 13. Траектории в окрестности грубых положений равновесия
163
33.
35.
37.
39.
41.
43.
45.
{
47. <
49.
51.
X = shBa; + у — ж^),
у = 1пA + 3ж -ж^).
i = 1пB - ж -h у),
у = X — у — е^^^ ~^К
х = 4д: 4- 22/ — 4,
2/ = —2ж — ху.
i = 8 -h 42/ - 2x2/,
у = х^ — 4у^,
X = ei-2^-32/ 4- ж,
2/ = arctg (ж'^ — 1).
а; = е а: — X,
у = arctg (.т^ — х).
х = д/1 -h 2ж - 52/ - 1,
(ж 3 о г. \
i = a:^ — 2/?
2/=^ In Bx^-1).
i = 2 - 2vTTxTy,
2/
i = arcsin 2 f ^
2/ = 1 - 4a; -I- З2/.
').
34.
36.
38.
40.
42.
44.
46.
48.
50.
52.
X = arctg (a; - 2/ "" 4),
y = 2x-2y- 4v^x2 - 1.
i = 1 ~ 2ж — 2/^,
2/ = -1 - 6ж -f 2/^.
i = ж^ — 42/^,
2/ = 2 - 22/.
i = ^7ж -I- 2/ + 2/ - 2,
2/ = "-ln(l -I- a;).
i= -д/4-б2/-4уЗ - 1,
2/ = In (ж^ - 7y) + 2y.
2/ = th{2-{-x-x^).
X = arctg (ж — 2/ ~ 1)?
y= ^Зж2 + Зу-2~-1.
ж = ж — 2/ ,
у = arctg A ~у2).
X = 1 - х/ГГ2у,
2/ = sin(Vi-y - 1).
X = 2{у/х-у- 1),
2/ = sh(a;-|-y - 1).
Найти положения равновесия, определить их характер и нарисовать
фазовые траектории линеаризованного уравнения в окрестности положений
равновесия для уравнений E3—82):
53. i -h i = In A - Зж -4- ж^ - i). 54. ж -I- i -I-1 = ^1 -h x -h ж^ - i.
55. i-l-ж? = e"""^. 56. i-h3i = ln(i + x^).
57. x + 2x + x-2x'^ + 1=^0. 58. i - 4i -I- 2^2 - x - 3 = 0.
164 Глава 4. Автономные системы дифференциальных уравнений
59. ж - A Ч- i)^ + ж^ = 0. 60. ж - е^^ - ж^ = 0.
61. 2i + 5sini-h л/1 Ч-4ж- 1 =0.
62. X — arcsin {х — 2i) -|- 71п A — ж) = 0.
63. X cos i — 4 tg xyj\ — sinx -f Зж = 0.
64. i~e^^-^^-|-21n(l-x)-|-l = 0.
65. £-|-tgBa:-|-6i) ~31n(l-a:) = 0.
66. i + ж^[1 + In A -I- 2x)\ = A -I- 2iJ.
67. ж -f 2e^ - x^ cosi = 3. 68. x + B -f .т)^ arctg.T + x? = 1.
69. i = 5 arctg {x - 1) + 4e^ sini. 70. i = Ci ~ 2x)e^ .
71. i -I- Di -I- 3x)e^' = 0. 72. ж - (i -I- 4x)^ + 2i -f 1 - 0.
73. i-i~x[arctgDi)-2] = 1. 74. 3i-|-3(x-3) sin Bi)-5x^4-5 = 0.
75. X -I- 4i - In [ i - 2x -I- - J = 0. 76. x -I- In A - 2x) -h 2 arctg x = 0.
77. X -I- \/5x + 5x -I- cos x = 0. 78. x == 3 arcsin x - 2 In
1 + x
3 — X
79. X + 3x - 4x -I- 2x2 = 0. 80. x - 5x - 6x -I- Зх^ = 0.
81. X + 5x -I- 6x -I- 2x2 = 0. 82. x - 3x -I- 4x - 4x2 == 0.
Ответы к задачам § 13
Примечание. В ответах даны координаты положений равновесия и их
тип. В случаях узла и седла указаны собственные значения Ai и Л2 и
соответствующие им линейно независимые собственные векторы /ii и /i2
для матрицы линеаризованных систем. В случае фокуса знак О означает
движение против часовой стрелки по траекториям при t -> +00, а знак О
означает движение по часовой стрелке по траекториям при t -> -Ьоо.
Данных ответов достаточно для изображения фазовых траекторий
линеаризованных уравнений и систем в окрестности положений равновесия.
1. (-1,1) — седло, Ai =: -1, Л2 = 4, /ii = ( J, /гз = ( J.
§ 13. Траектории в окрестности грубых положений равновесия 165
2. A,0) — устойчивый фокус, О.
3. (—6,2) — неустойчивый узел, Ai == 1, А2 = 4, /ii = I 1 Ь ^2 = I ^ ) •
4. @,2) — устойчивый фокус. О;
B,0) - седло, Ai = -2, А2 = 2, /11 - Г j, /12 = f М.
5. (О,0)-седло, Ai--x/3-l, А2-\/3-1,/ii- ( ^-J,/i2- ( J^J;
A,2) — устойчивый узел, Ai = -2+\/2, А2 = -2-\/2, hi = i ^ J,
/12
l-x/2 •
6. @,-1) — неустойчивый фокус. О;
((у /r \ /9-1- /r\
1 , /i2 = ( ^ 1 •
7. @,1) — неустойчивый узел, Ai = 1, А2 == 3, /ii = I п Г ^^ ~ \ о )'
A,0) -седло, Ai - ^A - х/13), А2 - ^A + \/l3), /ii - I ^\^\
8. (—1,-5) — устойчивый фокус. О;
B, 7) — неустойчивый узел, Ai = 2, А2 = 3, /ii = I r> Ь ^2 == I . 1 •
9. (—1, —1) — устойчивый фокус, О;
(-1,1) — седло, Ai = -2, А2 = 3, /ii == I _i 1' ^2 ^ [ i I •
10. E,-1) — неустойчивый фокус. О;
166 Глава 4. Автономные системы дифференциальных уравнений
(—7,2) — устойчивый узел, Ai = —2, А2 = -3, hi = i j,
11. @,0) — устойчивый узел, Ai = —1, А2 = —3, /ii = I 1 I' ^2 = I ^ );
A, -1) — седло, Ai = -e, A2 = e, /ii = ( 1, /i2 = ( J.
12. @,0) — неустойчивый узел, Ai = 1, A2 = 3, /ii = I j, /i2 = I I;
A,1) — седло, Ai = --T^, A2 = -^, hi= I ^ I' ^^г = I _^ I •
13. @,-1) — устойчивый фокус, О; @,1) — седло, Ai = -4, А2 = 2,
14. @,3) - седло, Ai = ~1, А2 = 3, /ii = ( М, /i2 = ( J j;
( 2'^) ~ неустойчивый узел, Ai = -, A2 = 2, /ii = ( _-. 1 > ^2 = ( ^ 1 •
15. A,1)— неустойчивый фокус, О;
(-1,1) — седло, Ai = -3, А2 = 1, /ii = ( 1 )' ^2 = ( _i 1 •
(«•!)
16. I 0, - 1 — устойчивый фокус, О;
(О, -- j - седло, Ai = -6, Аз = 6, /ii = I ^ j, /12 =
-1/ \1
17. A,0) - седло, Ai = -3, Аг = 1, /ii = f _g j, /i2 = ( J
§ 13. Траектории в окрестности грубых положений равновесия 167
18. A,0) — устойчивый узел, Ai = —1, А2 = —3, /ii = 1 1 Ь ^2 = I ., 1 •
19. A,0) — устойчивый фокус, О.
20. A,1) — неустойчивый узел, Ai = 1, А2 = 3, /ii = 1 1, /i2 = I 1.
21. @,0) - седло, Ai = -\/2 - 1, A2 = v/2 ~ 1, /ц = [J_X ^2 =
B — \/з\
22. @,0) — устойчивый фокус, О;
A, -1) — седло, Ai = -\/2, Л2 = \/2, /ii = ( ^ _ ^ 1 > ^2 = ( ^ , j ) •
23. (-1,-2) — устойчивый узел, Ai = -2 + \/2, Аг = -2 - \/2, hi =
(О,0)-седло, А1 = -ч/3-1, А2 = л/3-1,/11= l\A,h2= l^V
24. @,0) — неустойчивый фокус, О.
25. @,0) - седло, Ai = -1, А2 = 1, /ц = ( М, /12 = ( J
'■('-i)-"
26. ( 3, — - ) — неустойчивый фокус, О;
@,0) — седло, Ai = -1, А2 = 3, /ii = { I, /i2 = 1
27. @,0) — неустойчивый фокус, О;
168 Глава 4. Автономные системы дифференциальных уравнений
(-1,-1) - седло, Ai = -\/2, Л2 = \/2, /ii = { i + х/2 )'
'■('■D-
28. ( 3, 7 1 ~ устойчивый фокус. О;
0,0) - седло, Ai = -5, Л2 = 3, /ii = { ], /i2 = ( |.
—27Г, —2) — неустойчивый фокус, О.
2,0)-седло, Ai = -2, А2 = 10,/11- B)'''2- ]1у
2,7г) — неустойчивый фокус. О-
1.2) — устойчивый узел, Ai = —1, А2 = —5, hi = \ \ ^ h2 = \
VJ VJ
0,0) — седло, Ai = -1, Л2 = 3, /гх = ( 1, /i2 = I 1;
3.3) — устойчивый узел, Ai = — 1, Аг = —3, /i.i = I « 1 > ^2 = I
3,-7) — устойчивый фокус, О;
3, -1) — седло, Ai = -2, А2 = 1, Л,1 = ( о )' ^2 "^ ( п )"
1,0) — устойчивый фокус, О;
-1, -2) - седло, Ai = -4, А2 = 2, /ii = [_ j, /гз = I 1.
29.
30.
31.
32.
33.
34.
35.
36.
37.
0,-1) — устойчивый фокус, О;
;0,1) - седло, Ai = -4, А2 = 4, /ii = ( J, /12 = I _^
0,2) — неустойчивый фокус. О;
§ 13. Траектории в окрестности грубых положений равновесия 169
B,-2) - седло, Ai --2, Л2 = 4,/11 = f _М,/i2 - (М.
38. (—2,1) — устойчивый узел, Ai — —2, А2 — —4, /ii == 1 1 )' ^2 ~ I п )'
B.1) - седло, Ai = -2, А2 - 4, /ii = f J, /i2 - L ].
39. (—2,-1) ~ неустойчивый фокус, О;
D.2) — устойчивый узел, Ai = -8, А2 == -12, hi = ( J, /12 = ( 1.
40. @,1) — неустойчивый узел, Ai =: 1, А2 == -, /ii == [ _i I' ^^2 ^ I -3 I'
41. (-1,1)-седло, А1--З, A2-2,/ii- (з)'^^"^ (_\)-
42. A,0) — устойчивый узел, Ai = --, A2 = --, hi = i У h2 = I I.
43. A, —1) — устойчивый фокус, О.
44. (-1,1) — седло, Xi = -1^ Х2 = 3, hi= i \ h2 = I 1;
B,4) — устойчивый узел, Ai == -1, A2 = -3, /ii = f j, /12 = I I.
45. ( :t? 7 ) — устойчивый фокус. О;
@,0) - седло, Ai = --, Х2 = -, hi= i\h2= ( J.
46. A,0) ~ неустойчивый фокус, О;
(-2, -3) - седло, Ai = -1, А2 = 3, /ii = f J, /12 == 1 -2 )'
47. A,1) — неустойчивый фокус. О;
170 Глава 4. Автономные системы дифференциальных уравнений
(-1,1) — седло, Лх = ~3, Л2 = 1, /ii = ( 1 )' ^2 = ( -3 ) *
48. A, —1) — неустойчивый узел, Лх = 1, Л2 = 2, /ix = I 1, /i2 = 1 1;
A,1) - седло, Лх = -2, Л2 = 1, /ix = ( 3 )' ^2 = ( ^ J •
49. ( Т) "т 1 "~ устойчивый фокус. О;
\4 4;
@,0) -седло, Лх = --, Л2 = -, /ix = ( _Л) ^2 = [А-
50. A,0) — устойчивый фокус, О.
51. A,1) — седло, Лх = -1, Л2 = 5, /ix = A)' ^2 = ( „9 ) *
52. A,0) — неустойчивый фокус. О-
53. @,0) — устойчивый фокус. О;
C,0) — седло, Лх = -3, Л2 = 1, /гх = [ ^о )' '^'^ "^ ( 1 ) *
1 /з\
54. (—1,0) — устойчивый узел, Лх = --, Л2 = —1, /ix = I - 1, ^,2 =
:}■
@,0) - седло, Лх = ^(-2 - ч/7), Аз = ^(-2 + л/7), /ц = L_^^^\
55. A,0) — устойчивый узел, Ai = —1, А2 = —3, /ii = I I, /12 = I „ )•
56. A,0) - седло, Ai = -3, Aa = 1, /ii = I _М , /i2 = ( J ] •
§ 13. Траектории в окрестности грубых положений равновесия 171
{-»
57. ( —-?0 ) — устойчивый фокус, О;
A,0) — седло, Ai = -3, А2 = 1, /ii = ( 1, /i2 = I - I.
/3 \
58. ( ;^?0 I — неустойчивый фокус. О;
-1,0) ~ седло, Ai = -1, A2 = 5, /ii = ( __-. J' ^^'^ = ( ^
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
1,0) — неустойчивый фокус, О.
— 1,0) — неустойчивый фокус, О.
0,0) — устойчивый узел, Ai = --, А2 = -2, /ii = ( |, /12 = I
0,0) - седло, Ai = -4, А2 = 2, /ii = ( ^ J, /i2 = L
0,0) — неустойчивый узел, Ai = 1, А2 = 3, /ii = ( j, /i2 = I ^
0,0) — седло, Ai = -5, A2 = 1, /ii = ( _r )' '^з = [А-
0,0) ~ устойчивый узел, Ai = —1, A2 = —5, /ii = I J, /^2 = I
1,0) — неустойчивый фокус, О.
-1,0) — седло, Ai = -3, А2 = 1, /ii = I ^3 )» ^^2 = [ Л.
1,0) — устойчивый узел, Ai = —1, А2 = —3, /ii = I ), ^2 = I
1,0) ~ седло, Ai = -1, A2 = 5, /ii = ( _j 1 ^ ^^2 = ( ^
172 Глава 4. Автономные системы дифференциальных уравнений
70. @,0) ~ неустойчивый узел, Ai = 1, Аг = 2, /ii = [ 1, /i2 = I 1 •
71. @,0) — устойчивый узел, Ai = —1, А2 = —3, /ii = j 1, /^2 == I I •
72. Q,0J -седло, Ai =-3, A2 = 4,/ц = f M,/i2 = f J.
73. ( 2'^) ~ неустойчивый узел, Ai ^ 1, A2 = 2, /?4 =: I j, /13 = I 1.
74. A,0) - седло, Ai = -1, A2 = 5, /ii = ( _ J ^ /^2 = f ^ J •
75. ( ^,0 j — устойчивый узел, Ai = ~1, A2 = —2, hi =^ I J, /12 ==
-2
1\ , /1
76. @,0) — неустойчивый фокус, О.
77. ( -~7?0 j — устойчивый фокус, О.
78. A,0) — неустойчивый узел, Ai = 1, А2 = 2, /ii = ( j, /12 = I
79. B,0) — устойчивый фокус. О;
@,0) - седло, Ai = -4, А2 = 1, /ii = ( ^ J, /12 = L J •
80. @,0) -седло, Ai =-1, Аз = 6,/ii = f М ,/i2 = f ^ J;
B,0) — неустойчивый узел, Ai = 2, Аг = 3, /ii = j j, /12 = j j
81. (-3,0)-седло, Ai = -6, A2 = l,/11= ( _M ,/12 = ( ];
§ 14. Траектории в окрестности негрубых положений равновесия 173
@,0) — устойчивый узел, Ai == —2, А2 — ~3, hi —
82. @,0) — неустойчивый фокус, О;
-2
§ 14. Поведение фазовых траекторий
в окрестности негрубых полож:ений равновесия
и на всей фазовой плоскости
Для автономной системы второго порядка
{ х = fi{x,y),
С непрерывно дифференцируемыми /i(a;,y), /2C:,у) в некоторой области
G С Rfxy) положение равновесия (ai,a2) называется негрубым
положением равновесия системы, если матрица линеаризованной в точке (ai,a2)
системы имеет такие собственные значения Ai, А2, для которых либо Ai = А2,
либо ReAi = О, либо ReA2 = 0. В окрестности негрубого положения
равновесия фазовые траектории нелинейной автономной системы и ее
линеаризации могут себя вести принципиально по-разному.
Пример 1. Исследовать при всех значениях вещественного параметра а
поведение фазовых траекторий в окрестности положения равновесия @,0)
для системы
у = х-\-ау{х^ Л-у'^).
Л Точка @,0) является центром для линеаризованной системы в точке
@,0) при а = О
1 i = -у,
поскольку матрица линеаризации имеет собственные значения А = ±г.
Чтобы исследовать поведение фазовых траекторий заданной системы
при а Ф О, перейдем к полярным координатам x{t) = r(t) cos(/9(t), y{t) =
174 Глава 4. Автономные системы дифференциальных уравнений
= г(t) sin (p{t). Получаем систему вида
{г cos (р — гфзтср = —г sin ср -h аг^ cos (^,
rsm(p + гф cos (р = г cos ср + аг^ sin (^,
откуда находим
{г = аг^,
гф = г.
При г = О имеем положение равновесия. При r>0(p = t + CH(p-^ -hoc
при t —> +СЮ, а f < О при а < О и г > О при а > 0.
Отсюда следует, что при г > О траекториями системы служат спирали,
движение по которым идет против часовой стрелки, причем при а < О
спирали закручиваются вокруг @,0) при t —^ +сю, а при а > О спирали
раскручиваются вокруг @,0) при t -> -l-oo. А
При исследовании поведения фазовых траекторий на всей фазовой
плоскости необходимо находить не только положения равновесия системы,
но и предельные циклы.
Пример 2. Исследовать при всех значениях вещественного параметра а
поведение фазовых траекторий на всей фазовой плоскости для системы
{X = -у + ах{х^ 4- y^ - 1),
у = х + ау{х'^ -f-y^ - 1).
Л При а = О имеем линейную систему, для которой начало координат
является центром. Пусть а ^ 0. После перехода к полярным координатам
x{t) = r(^)cos<^(^), y{t) = г(t) sin (p{t) получаем систему уравнений
{
г = ar{r'^ — 1),
гф = г.
г = о дает положение равновесия @,0), а г = 1 является решением. При
г > О, г 7^ 1, траекториями являются спирали. Если а < О, то г > О при
О < г < 1 и, значит спирали раскручиваются вокруг г = О против часовой
стрелки при t —> +00 и стремятся изнутри к окружности г = 1. При а < О и
г > 1 имеем г < 0. Спирали против часовой стрелки извне накручиваются
на окружность г = 1 при t -> +сю. Таким образом, при а < О окружность
г = 1 является устойчивым предельным циклом.
§ 14. Траектории в окрестности негрубых положений равновесия 175
Если а > О, то при О < г < 1 спирали закручиваются вокруг г = О
при t -^ +СЮ, а при г > 1 спирали раскручиваются вокруг окружности
при t -^ +00 против часовой стрелки, так как (р -¥ +оо при t -¥ -{-оо. В
этом случае окружность г = 1 является неустойчивым предельным циклом
системы. А
Исследовать при всех значениях вещественного параметра а
поведение фазовых траекторий в окрестности положения равновесия @,0) для
систем A—11):
(
X = ~2у -f аху/х^ 4-у^, j х = у-{- ах{х'^ + у^),
у = 2ж -f ayyjx^ + у2. 1 у = -ж -f ау{х^ + у^).
i = 4у -f аж v'x^+y^, Г i = -Зу -f аж(ж^ + у^)^,
у = ~4х 4- ау^х^ -\гу^. \ у = Зж 4- ay(ж^ + y^)^.
i = 2у4-аж(ж^+ у^)^, J i = ~ау4-ж(х^-hy^),
у = ~2ж 4- ay(ж^ + y^)^. [ у^ахЛ- y(a;^ + у^).
х^-у-аху^, Гж = у~ажу2,
9 ^' 1 . 9
У = Ж + ах^у, I У = -~з; 4- аж^у.
X = -у{х'^ + у'^ -а), ( х = у{-а 4- ж^ 4- у^),
{i = у(-а4-
у = -ж(-а
11.
у = х(а:^ 4- y^ — а). [ У = —х{—а 4- ж^ 4- у^).
X = ~у(х^ 4-y^ 4-a^),
у = х(ж^4-у^ 4-а2).
Исследовать при всех значениях веш,ественного параметра а поведение
фазовых траекторий на всей фазовой плоскости для систем A2—21):
i = у 4- ах{х'^ 4- y^ - 2),
у = -ж 4- ayix'^ 4- у^ - 2).
12.
13.
14.
X = -2у 4- ах{л/х^1^ - 1)B - \/ж2Ту2),
у = 2а; + ау{у/х^ + у^ - 1)B - у/х^Ту^).
i = 2у 4- ахA - Vx2 + y2)B - х/ж^Ту^),
у = -2:г 4- ауA ~ у/х^Ту^){2 - v^a;2-f у2).
176
Глава 4. Автономные системы дифференциальных уравнений
15.
16.
17.
18.
19.
20.
21.
X
У
Ь = —ау -h хух^^Л-у^ • sin
7Г
= ах + у\1х^ 4- у^ •
7Г
Sin
\Jx^ 4- у2
i = [-у 4- ад;(а;2 4- у^ ~ 1)](^^ 4- у^ - 1),
у = [ж 4- ау(а;2 + у^ - \)\{х^ Л-у^ ~ 1).
7Г
i = 2?/ 4- axyjx^ 4- у^ • sin^
у = -2ж 4- ауу/х^^Ту^ • sin^ . ^
л/д;^ 4- у^
i = [у 4- аа;(ж2 4- у^ - 2)]{х'^ 4- у^ - 2),
у = [-Ж -f ау{х^ 4- у2 ~ 2)](:г2 4- у^ - 2).
X = -ауЛ'х{х'^ 4-у^ -2),
у == аж4-у(ж2 4-у^ - 2).
i = ~ау 4- х{^х'^ Лгу^ - 1),
у = ад: 4- у{\/х^~Т^ - 1).
i = -у 4-аж(\/жМ^~ 1)^,
у = х + ау{у/х'^ 4-у2 ~ 1)^.
На всей фазовой плоскости нарисовать схематически фазовые траектории
систем B2—45):
22.
24.
26.
28.
30.
X = Х^,
У = У-
У^у'^'
X = ху,
у = Х^ -f у2.
X = 2{х -у2),
у = у(ж-у2).
X = у,
-2х\
23.
25.
27.
29.
31.
X = Х"^,
У = -У^-
X = -2ху{х'^ 4-у^),
у = ^2 4-у^.
ж
-ж,
У = У^'
ж = у2,
у = жу.
§ 14. Траектории в окрестности негрубых положений равновесия 177
32.
34.
36.
38.
40.
42.
44.
У = -ху.
X = sin а;,
у = ycosx.
2
X = Ж ,
у = у^- 2ху.
X = ху,
у ■
X
у ■
X 4-у^.
X = Зх^ — у^^
У = ху,
X = хеУ^
У = уеУ.
33.
35.
37.
39.
41.
43.
45.
ж 4-1,
-ху.
X — X,
у = у-у'^
X
У
х^ -\-у^.
х = 2у,
у = Зх^.
X = у^ -\- 2ху — х^
7у г= x^ 4- 2ху — у^
X = 2ху^
у = х-\-2у'^.
X = х{у — х^),
у =^у{у-х^)'
Ответы к задачам § 14
1. При а -- О начало координат — центр. При а < О спирали против
часовой стрелки закручиваются вокруг @,0), а при а > О они
раскручиваются от @,0) при t -^ -I-00.
2. @,0) — центр при а = 0. При а < О спирали по часовой стрелке
закручиваются вокруг @,0) при t —> 4-00, а при а > О они раскручиваются
от @,0) при t —> 4-00.
3. @,0) — центр при а = 0. При а < О спирали по часовой стрелке
закручиваются вокруг @,0) при t —> 4-00, а при а > О они раскручиваются
от @,0) при t —> 4-00.
4. @,0) — центр при а = 0. При а < О спирали против часовой стрелки
закручиваются вокруг @,0) при t -^ 4-оо, а при а > О они
раскручиваются от @,0) при t —> 4-00.
178 Глава 4. Автономные системы дифференциальных уравнений
5. @,0) — центр при а = 0. При а < О спирали по часовой стрелке
закручиваются вокруг @,0) при t -> -fcx), а при а > О они раскручиваются
от @,0) при t -> +00.
6. При а = О траекториями являются радиальные лучи, по которым
движение направлено от @,0) при t -> -f-oo. При а < О спирали по
часовой стрелке раскручиваются вокруг @,0) при t -> -l-oo, а при
а > О они раскручиваются вокруг @,0) при t -> -l-oo против часовой
стрелки.
7. @,0) — центр при а = 0. При а т^ О @,0) — положение равновесия и
аху = — 1 — линия положений равновесия, являющаяся траекторией.
Остальные траектории — окружности в окрестности @,0).
8. @,0) — центр при а = 0. При а у^ О @,0) — положение равновесия и
аху = 1 — линия положений равновесия, являющаяся траекторией.
Остальные траектории — окружности в окрестности @,0).
9. @,0) — положение равновесия при любых а и х^ + у^ = а — линия
положений равновесия, являющаяся траекторией, при а > 0. Другие
траектории представляют собой окружности при всех а.
10. @,0) — положение равновесия при всех а. Траектории
представляют собой окружности при всех а. При а > О х^ + у^ = а является
траекторией, все точки которой являются положениями равновесия.
11. При любых а @,0) является положением равновесия, а траектории
представляют собой окружности с направлением обхода против
часовой стрелки.
12. @,0) — центр при а = 0. При а т^ О траекториями являются
спирали с направлением движения по часовой стрелке при t -^ 4-ос.
Окружность ж^ -h у^ = 2 — устойчивый предельный цикл при а < О и
неустойчивый предельный цикл при а > 0.
13. @,0) — центр при а = 0. При а т^ О траектории — спирали с
направлением движения против часовой стрелки при ^ -> -Нею. Окружность
а;2 -I- у^ = 1 — предельный цикл, который является неустойчивым
при а > О и полу устойчивым при а < 0. Окружность х^ + у^ = 2 —
§ 14. Траектории в окрестности негрубых положений равновесия 179
предельный цикл, который является устойчивым при а > О и
полуустойчивым при а < 0.
14. @,0) — центр при а = 0. При а ^ О траектории — спирали с
направлением движения по часовой стрелке при t -> -Нею. Окружность
х^ 4- ?/^ = 1 — предельный цикл, который устойчивый при а > О и
неустойчивый при а < 0. Окружность х'^ -{- у'^ = 2 ~ предельный
цикл, который неустойчивый при а > О и пол у устойчивый при а < 0.
15. Окружности х^ -{• у^ =^ —;т, п £ N, служат при а ф О предельными
циклами, причем они устойчивы при нечетном п Е N и неустойчивы
при четном п Е N. Начало координат @,0) — положение равновесия.
Остальные траектории при а ^ О спирали, по которым движение идет
против часовой стрелки при а > О и по часовой стрелке при а < 0.
16. @,0) — центр при а = 0. При а ^ О окружность ж^ -Ь у^ = 1
является полу устойчивым предельным циклом. Траектории — спирали,
по которым движение идет по часовой стрелке, если они находятся
внутри круга ж^■fy^ ^ 1, и по которым движение идет против часовой
стрелки, если они находятся вне круга х'^ -{- у'^ ^ 1. Точка @,0) —
положение равновесия.
17. @,0) — центр при а = 0. При а^О окружности х^ +у'^ = -^^ п £ N,
служат предельными циклами, которые являются пол у устойчивыми,
а @,0) — положение равновесия. Траекториями являются спирали с
направлением движения против часовой стрелки при t -> -l-oo.
18. @,0) — центр при а = 0. При афО точка @,0) — положение
равновесия и окружность ж^ 4- у^ = 2 является полуустойчивым предельным
циклом. Траектории — спирали, по которым движение идет по
часовой стрелке, если они находятся внутри круга ж'^ + y^ ^ 2, и по
которым движение идет против часовой стрелки, если они находятся
вне круга ж^ -h y^ ^ 2.
19. @,0) — положение равновесия при всех а. При а ф {) окружность
a;2-f у2 = 2 — неустойчивый предельный цикл. Траектории — спирали,
по которым движение идет против часовой стрелки при а > О и по
часовой стрелке при а < 0.
180 Глава 4. Автономные системы дифференциальных уравнений
20. @,0) — положение равновесия при всех а. При а ^ О окружность
х^-^-у^ = 1 — неустойчивый предельный цикл. Траектории — спирали,
по которым движение идет против часовой стрелки при а > О и по
часовой стрелке при а < 0.
21. @,0) — центр при а = 0. При а ^ О точка @,0) — положение
равновесия и окружность ж^ 4-у^ = 1 — пол у устойчивый предельный цикл.
Траектории — спирали с движением по ним против часовой стрелки
при t -^ 4-00.
§ 15. Устойчивость по Ляпунову полож:ений равновесия
Пусть в области f2 евклидова пространства Щ задана автономная система
уравнений
x{t) = f{x),
где f{x) — непрерывно дифференцируемая в ft вектор-функция с п
компонентами, и пусть О Е: ft является положением равновесия автономной
системы. Разложим f{x) в окрестности д: = О по формуле Тейлора с
остаточным членом в форме Пеано
f{x) = Ax + o{\x\),
где матрица
1^@)
А =
dxj
, ij = l,n, о{\х\) ->0, \х\ = yjxl + --^xl -^
Линейная автономная система
X — Ах
называется линеаризацией системы хA) = f{x) в точке х = О или системой
первого приближения для x{t) = /(ж).
Из теорем Ляпунова следует, что в случае, когда все собственные
значения А имеют отрицательные вещественные части, х = О является
асимптотически устойчивым положением равновесия для системы х — f{x). Если
же хотя бы одно собственное значение А имеет положительную
вещественную часть, то ж = О является неустойчивым положением равновесия для
системы X = f{x).
§ 15. Устойчивость по Ляпунову положений равновесия 181
Для линейной автономной системы х — Ах эти результаты можно
уточнить.
Пример 1. Исследовать устойчивость положений равновесия с помощью
системы первого приближения автономной системы
fx = 1 — 2х — у'^,
у = е-4^ - 1.
Д Найдем сначала положения равновесия системы. Для этого необходимо
решить систему уравнений
f 1 - 2ж - у2 - О,
I е-4^ -1 = 0.
Получаем два положения равновесия: @,1) и @,-1).
Исследуем устойчивость положения равновесия @,1). С этой целью в
автономной системе сделаем замену у — 1 = yi и правые части
полученной системы разложим по формуле Тейлора в окрестности точки @,0),
являющейся положением равновесия новой системы. Имеем
1 i - 1 - 2х - A + ш)^ = -2а: - 2yi - yl
\ yi — —4ж + о{х).
Матрица
имеет собственные значения Ai = 2, Л2 = —4. Следовательно, положение
равновесия @,1) является неустойчивым.
Для исследования устойчивости второго положения равновесия @,-1)
в заданной системе сделаем замену уН-1 = yi. Тогда точка (О, —1) перейдет
в точку @,0) и можно в окрестности @,0) разложить по формуле Тейлора
правые части новой системы. Получаем
1 i = 1 - 2х - (у1 - 1J = -2х + 2ш - у1
\ У1 = -Ах + о{х).
Матрица
182 Глава 4. Автономные системы дифференциальных уравнений
имеет собственные значения Ai = — l+i\/7, А2 = — 1~г\/7. Следовательно,
положение равновесия (О, ~1) является асимптотически устойчивым. А
В тех случаях, когда вещественные части всех собственных значений
матрицы А неположительны, причем хотя бы одно собственное значение
А имеет вещественную часть равную нулю, исследование устойчивости
положений равновесия нелинейной автономной системы с помощью системы
первого приближения, как правило невозможно, так как начинают влиять
нелинейные члены. В таких случаях используют метод функций Ляпунова
(второй метод Ляпунова).
Пример 2. Исследовать устойчивость положений равновесия автономной
системы
у у = -ху-у^.
Л Единственным положением равновесия является точка @,0). В этом
случае матрица
не позволяет воспользоваться теоремой Ляпунова об устойчивости по
первому приближению. Применим второй метод Ляпунова. Если взять в
качестве функции Ляпунова функцию V{x,y) = ж^ + у^, то ее производная
в силу автономной системы
v{x, у) = -^(-ж + у^) + -Q^i-^y"- у^) = М^^ + у^) + Ы-ху - 2/^) =
= -2(а;2 + у^)^0,
причем V{x^y) = О лишь при а; = у = 0. По теореме Ляпунова отсюда
следует, что точка @,0) является асимптотически устойчивым положением
равновесия системы. ▲
Исследовать устойчивость положений равновесия с помощью системы
первого приближения A—15):
ж = —3 + 2а; + у, ^ \ ^ = ^^ -^У-,
* I у = arctg {ху). "' I у = In (Зж^ — 1) — In2.
'■{:-
§ 15. Устойчивость по Ляпунову положений равновесия 183
3.
9.
11.
13.
15
1-2а;"
1 4- Ж 4. л
у = 1п- —. у = 1п{х^+у)-3у.
X = Sh(x — у), ^ . . , /, „ 9-4
^ ^2ху+х+у- 1. 6.Х + Х = In A _ ЗХ + х2 - Х).
У
.2 ( i = 5а; - 8у + 3,
^=^~У' 8 < X
X = е^^+^У + х, Г ж = е^г' + у2 _ 3,
/ чч тг 10. < . .ж
у = arccos (х - х'^) — —. \ У = arctg -.
Z \ у
х = \п{х + у), по I ^ = ^^ + У^ - 3,
у = Ж"" + у' - 1. У = 4arctg -г.
^5-
у = -Х'-2у- у'^.
X = 2х — у — х'^,
14. ж + i + 1 = v^l + а; + а;2 - i.
16. При каких значениях вещественного параметра а система
(
X = —X + ау,
у = х-у.
имеет асимптотически устойчивое положение равновесия @,0)?
17. При каких значениях вещественных параметров а и b система
{
X = ах + by,
у = bx + ay.
имеет устойчивое по Ляпунову положение равновесия @,0)?
Исследовать устойчивость положения равновесия @,0,0) для линейных
систем A8—27):
184
Глава 4. Автономные системы дифференциальных уравнений
X = 2х — Зу,
18. I у = х- 2z,
Z = —у -j- 2z.
20. <
22. <
24. <
26. <
X = Зх -i- 2z,
y=^x-\-2y-\-z,
z — —X — у.
X = y- z,
у = -y-j-Z,
Z = X ~ Z.
X = 7x — lOy — Az^
у — 4x — 7y — 4z,
z = —dx -\-7y -\- z.
X == -Зж -\-2y-\- 2z,
у = -3x -уЛ- z,
z = —X + 2y.
X ■= —x — 4^/,
21. ^ у = x-y-i- z,
z — 'iy ~ z.
X = 3X — %y •\- Z^
23. ^ y^x-2y + z,
z = 3x — 12y — 5z.
X = 7x — 4y -^ z^
25. < у — 7x — 3y -\- z^
z = 4x - 2y -i- 2z.
X — —X H- z,
27. { y = -y~z,
z = y- z.
С помощью функции Ляпунова вида V{x^ у) = ax'^-j-by'^ исследовать
устойчивость точки @,0) для автономных систем B8—36):
28.
30.
32.
34.
36.
X = —2у — ж^,
у = х-у^.
X —
у
у = ху - х^у.
X = —ху'^^
у = -4а;у2 - 2у^.
X = 2у+ ж^,
У = -х-Ьу^.
29.
31.
33.
35.
X = у — 2х^,
У = -2х-у^.
X ==z -ху\
У^ -у- 2х2у.
ж = ж — у^,
у = хуЛ-у^.
X = -у-\- 2х^,
у = 2х-\-у^.
X
у
Лх^у - 2х^,
-х'^у.
37. Рассмотрим уравнения х = — gradF(a:), описывающие движение
некоторых механических систем. Здесь х = {xi^... ^Хп) и V{x) — по-
§ 15. Устойчивость по Ляпунову положений равновесия 185
тенциальная энергия механической системы, имеющая минимум при
ж = 0. Взяв V{x) в качестве функции Ляпунова, показать, что х = О
является устойчивым положением равновесия системы.
38. Показать, что есди функция Ляпунова V{x)^ х — {х\^... ^х^^ для
автономной системы х — f{x) определяет асимптотически
устойчивое положение равновесия ж = О, то V(x) для системы х — —}'{х)
определяет неустойчивое положение равновесия ж = 0.
39. Пусть А — матрица квадратичной формы в п-мерном
вещественном евклидовом пространстве. С помощью функции Ляпунова
п
V{x) — YIj ^f показать, что х — О для системы х — Ах является
асимптотически устойчивым положением равновесия, если
квадратичная форма отрицательно определенная, и ж = О является
неустойчивым положением равновесия, если квадратичная форма
положительно определенная.
Ответы к задачам § 15
1. @,3) и ( -?0 ) ~" неустойчивые положения равновесия.
2. A,1) и (—1,1) — неустойчивые полол<ения равновесия.
( 2\
3. I О, - I — асимптотически устойчивое положение равновесия,
О, — - 1 — неустойчивое положение равновесия.
4. A,0) — неустойчивое положение равновесия.
5. @,0) и (—1,-1) — неустойчивые положения равновесия.
6. @,0) — асимптотически устойчивое положение равновесия,
C,0) — неустойчивое положение равновесия.
7. A,1) и A,-1) — неустойчивые положения равновесия.
8. A,1) — неустойчивое положение равновесия.
9. (—1,1) — неустойчивое положение равновесия.
186
Глава 4. Автономные системы дифференциальных уравнений
10. (О, —л/2) — асимптотически устойчивое положение равновесия,
(О, л/2) — неустойчивое положение равновесия.
11. @,1) и A,0) — неустойчивые положения равновесия.
12. (О, л/^) и (О, —л/^) — неустойчивые положения равновесия.
13. @,0) — асимптотически устойчивое положение равновесия,
A,-1) — неустойчивое положение равновесия.
14. @,0) ~ неустойчивое положение равновесия,
A,0) -— асимптотически устойчивое положение равновесия.
15. @,0) и A,1) — неустойчивые положения равновесия.
16. а < 1.
18. Неустойчивое.
20. Неустойчивое.
22. Устойчивое.
24. Неустойчивое.
26. Асимптотически устойчивое.
28. Асимптотически устойчивое.
30. Устойчивое.
32. Устойчивое.
34. Неустойчивое,
36. Устойчивое.
17. а + |Ь| < 0.
19. Асимптотически устойчивое.
21. Асимптотически устойчивое.
23. Асимптотически устойчивое.
25. Неустойчивое.
27. Асимптотически устойчивое.
29. Асимптотически устойчивое.
31. Устойчивое.
33. Неустойчивое.
35. Неустойчивое.
§ 16. Первые интегралы
Пусть задана автономная система х = /(ж), где f{x) — непрерывно
дифференцируемая вектор-функция с п компонентами /i(x),..., fn{x) в
некоторой области G евклидова пространства Щ с декартовыми
прямоугольными координатами жь Х2,..., Жп-
§ 16. Первые интегралы
187
Для того, чтобы непрерывно дифференцируемая функция и{х), х Е G,
была первым интегралом системы i = /(ж), необходимо и достаточно, что-
бы ее производная в силу системы й{х) = (gradix(a;),/(a;)) = Y1 fi{^)'^— ==
г=1 ^^г
= О В области G.
Первые интегралы ui{x)^,.. ,щ{х), 1 ^ к < п, автономной системы
называются независимыми в области Go С G, если ранг матрицы Якоби
дщ{х)
dx-i
, г = 1,А;, j = 1,п,
равен к для всех точек а; Е Go-
Зная к {1 ^ к < п) независимых первых интегралов в Go, можно в
области Go понизить порядок автономной системы до (п—А:), что позволяет
либо найти решение нелинейной автономной системы при п ^ 2, либо во
всяком случае облегчить нахождение решения системы.
Знание первого интеграла и{х) автономной системы при п = 2
позволяет нарисовать глобальный фазовый портрет системы на фазовой
плоскости, поскольку каждая линия уровня функции и{х) является
объединением непересекающихся фазовых траекторий системы. Кроме того, с
помощью и{х) можно определить центр для нелинейных автономных
систем.
Пример 1. Проверить, что функция u{x,y,z) = -B:^-hy^ + г^) при х ^0
X
является первым интегралом системы
X = 2xz,
У = 2yz,
i = 2Г^ — Х^ ~ у^.
Д Достаточно установить, что u{x^y^z) = О при х ^ 0. Имеем
u = 2xz ~ -h2yz- — + [z^ - а;2 - у2) . —
Х^ X X
= ~[;г(a;^ - у^ ~ z'^) + 2y^z + z{z^ - х^ - у'^)] = 0.
X
Пример 2. Показать что функции ui{x,y,z) = -(ж + у + z ),
X
188
Глава 4. Автономные системы дифференциальных уравнений
У
U2{x^y^z) = — являются независимыми первыми интегралами при ж > О,
X
Z > О для автономной системы примера 1.
Д Сначала проверим, что U2 ~ первый интеграл системы примера 1.
Имеем
U2 = 2xz- (-^) -\-2yz- =0.
Итак, ui, 1^2 ~ первые интегралы системы примера 1. Они являются
независимыми при X > О, Z > О, так как матрица Якоби
ж^
-у'-
х^
_У_
-^2
X
1
2z
X
0
имеет ранг 2 при а; > О, z > 0. В самом деле, при ж > О, z > О определитель
из элементов второго и третьего столбцов матрицы Якоби
2у
X
X
2£
X
о
2г , г.
Пример 3. Найдя первый интеграл, решить систему при ж > О, z > О
Д Перемножая крест-накрест первое и третье уравнения, получаем zx —
— —XZ. Отбрасывая dt, находим отсюда, что xz — С\. Значит, и — xz —
первый интеграл. Из третьего уравнения находим z = C\t -\- €2- Тогда
X — — —-. Подставляя найденные ж, z во второе уравнение системы,
С\1 Л- С2
получаем уравнение для у\
У =
CiV
-2(Cit + C2)^
Cit^C2
Это линейное уравнение первого порядка, обш,им решением которого
является
y = {Cit + C2){C3-Cit''-2C2t).
§ 16. Первые интегралы 189
Пример 4. Найдя два независимые первые интегралы системы, решить
при X > z > О, у > О систему
X — Х^ -\- Z^,
y = y{x-z),
z = 2xz.
Д Умножая крест-накрест первое и третье уравнения и отбрасывая dt,
получим уравнение
2xzdx — [рР' 4- z^^dz^
(х^\ х^
которое можно записать в виде d\ — ) — dz. Отсюда z — С\. Значит,
\z ) Z
^^
ui — Z — первый интеграл системы. Вычтем из первого уравнения
третье уравнение и рассмотрим полученное уравнение со вторым
уравнением системы. Имеем
{X — Z — {х — г)^,
y = y{x-z).
Перемножая крест-накрест эти два уравнения, сокраш,ая на ж — 2: т^ О и
отбрасывая di, получаем yd{;x — ^) == (ж — z)dy. Отсюда ж — z = С2У и,
X — Z
значит, U2 — первый интеграл системы. Можно проверить, что
У
при ж>г>0, у>0 первые интегралы u\, U2 являются независимыми.
Подставляя х — z — С2У во второе уравнение исходной системы, по-
^9/-ч /ч 1 тт \ X — Z = С2У-,
лучаем у — С2У - Отсюда y[t) — — ——. Из системы < о о ^
Съ - C2t 1 х"^ - z"^ = Ciz
CW г. Cly' т.
находим Z — ——^———, X — 02V + т^—^г;^—• Подставляя в эти формулы
Ci - 2С2У ^ Ci - 2С2У
выражение для y{t)^ получаем, что
z{t) - ^"^
x{t)
{Сз - C2t)iCiC3 - CxC^t - 2С2)'
C2{CiCs — CiC2t — C2)
(Сз - C2<)(CiC3 - CiC2t - 2C2) ■
Найдя первый интеграл, решить системы A—17) в указанных областях:
190
Глава 4. Автономные системы дифференциальных уравнений
X =
1.
{х + уУ'
У
{Х + уJ
^2
, (ж > О, у > 0).
X =
3. <; у
у = х, {х>0, у> 0).
5. <
у = ^, {х>0, у> 0).
X
^ I х = у-ху,
\ У = -у + ху, {у
2.
4.
6.
х = х у,
у = а;у2, (х > О, у > 0).
а;
X =
X — у
у=—^, (а;>у>0).
ж-у
X = X — ху,
у = -X + ху, (х > о, X + у > 1)
X
X =
(у>0, х + у>1). I у = ._L_^, (х > О, у > 0).
х^ + у^
х'^ + у^
1
Z = -у, I Z = -,
у2 10.
у = ^, (ж > о, у > о, ху < 2).
X
у = 2_, (х > о, у > 0).
X = ху — X ,
11- < У = У\
[ z = z"^ + 2yz, (х > 0, у > 0,
12. <
( • 2
х = у^,
i = -z^, (у > 0, z > 0).
z>0).
13. I
i = 1 + 2Г,
14. ^ г/ = у2е^^,
i = (l+2rJ, (y>^Q^ 2Г>~1).
16. <
I i = a;By+ 2г),
i = -By + 2r), (a;>0).
у = xy-2z'^,
z = жг, (х- > 0).
i = (l~.т)^
15. < y={x^l)\
z = z^e-^y, {x >1, z> 0).
X = X — у2,
17. < y = y,
z = X + y'^ -b z, (y > 0).
Найдя два независимые первые интегралы системы, решить системы A8-
26) в указанных областях:
§ 16. Первые интегралы
191
X = Х^у — ж,
,2
X = Z"^
у',
18. .{ у = -ху^, 19. <
i = г, (ж > О, у > О, г > 0).
i = х{х + у),
20. ^ у = -у{х + у),
[ Z = -z{x - у), (ж > о, у > о, Z > 0).
i = a;(y-2),
21. -! у = -у(у + гг),
i = z(y + z), (ж > О, у > О, Z > 0).
22. ^ у = 2у(у-гг2),
Z = -г^, (а; > О, у > О, z> 0).
i = ху,
23. I у = у, 24.
i = же"!* + Z, (у > 0).
25. ^ J/= Зж^у'^;^, 26.
i = г, (ж > О, у > О, z>0).
^^ -у, {у> z> 0).
у = ж Ч- у^,
i = -2^2, (г > 0).
2
Ж = Ж ,
У = 2х^ — ху — z^
z = xz-2x^, (ж > 0).
27. С помощью первого интеграла убедиться в том, что положение
равновесия @,0) является центром для систем
а) ^--У-^^У
I у = ж + iC'y,
б)
X = ж^у Ч-у^,
у = —жу^ — ж^.
Ответы к задачам § 16
1
1. ж =
V2t + C2{l + Ci)\ у =
Ci
2. ж = Ci(C2 - 2Cit)-\ у = {С2- 2Cit)-K
3. а; = CiCae^'S у = С72е^»'.
л/2* + 02A+С,J.
192
Глава 4. Автономные системы дифференциальных уравнений
5. X =
6. X =
7. X
8. х =
9. X
10. X
11. X
12. X
13. X
14. а;
15. X
1 „-Cit ,1 „. _ /-.„Ct 1
С2С2
+ —, y = C2e^'i' + ^^.
Ci-1
(Ci - l)C2e(^i-i)' + 1
, 2/ = Ci
Ci-1
y =
(Ci-l)C2e(^i-i)« + l
Ci-1
(Ci-l)C2e(i-^i)i + i' -^ (Ci-l)C2e(i-^0i + i-
VCi + C2e«, у = ^e'WCi + C2eK
Ci
v/C2 - 2Cit, y =
1
Г' у
VC2-2Cit
1
, 2
l + Ci(C72-<)' " C2-^' ^-С2 + Сз(^-С2J
1
3Ci
{Clt + C2f + C3, y = Clt + C2, Z =
Cx
Cit + C2
Ci
Cit + C2
, y = {Cit + C2){Cz-Cif-2C2t), z = Cit + C2.
I fn г-л 2Ci{C2-Cxt)^ Cx{t + 1)-C2
-ln(C2 - Cit), у = ^r^IT^^^T^ ^^-^ 7, Z -
2CiCs{C2 - Cit)^ - I
1 + Ci{C2 - 3Cff)~5, y = -^ ln(C2 - 3Cfi),
1
C2 - Cii
16. ж
17. X
18. re
19. X
z
1-2Сг + щ{С2-ЗфI
@^g-{2Ci-C2e4C3e-')_ у = C2e* - Ci, ^ = 2Ci - C2e* + Сзе-*.
C7iC72e' - С|е2*, у = C2e\ z = {C2t + Сз)еК
c,.-,
c.
cz , у = e
-Ci-^e
£2.p-t
z = Сзе*.
i[Ci -C2- sm2{t + Сз)], у = VU^siuit + C3),
= v/Crcos(t + C3).
§ 16. Первые интегралы 193
20. X = VClcig л/СГ(Сз - t), у = v/CTtg у/С[{Сг - t),
^ = ^sin2^/cГ(Cз-t).
21. x = -%.sm2^/c'iiCs-t), y = ^/CГtg^/CГ(C7з-t),
z = VC~ictgVC'i{C3-t).
23. x = Cie'^2^', у = C2e\ z = Сзе' - d.
24. X = Cit + Сз, у = ;^(Cit + C3){Cit + C2 + Сз), z ^^
^^v-i -.A-i -. -./. Cii + Сз'
26. a; = —^,y = C2(Ci-t)-Ci + —-^, z "^^ ^
Ci-f" ^' ' ' ^ (Ci-tJ' Ci-< {Cx-tf
Глава 5
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
ПЕРВОГО ПОРЯДКА
§ 17. Линейные однородные уравнения
Пусть Л — непустая область пространства Л'^. Линейное однородное
уравнение в частных производных первого порядка в области Л имеет вид
aiix.y.z)— '\-a2{x,y,z)— -{-asix.y.z)— =0. A)
В уравнении A) коэффициенты ai(a;,y,z), a2{x,y^z) и asix.y.z) -
заданные непрерывно дифференцируемые функции в области Q, а
и = u{x^y^z) — искомая непрерывно дифференцируемая в Л функция.
Автономная система уравнений
x{t) =ai{x,y,z),
y{t) =a2{x,y,z), B)
z{t) = asix.y.z)
называется характеристической системой для уравнения A). Чтобы
решить уравнение A), необходимо сначала найти два независимых первых
интеграла характеристической системы B) ui{x^y,z), U2{x^y,z). Общим
решением уравнения A) называется
u{x,y,z) = F[ui{x,y,z),U2{x,y,z)],
где F[ui^U2] — произвольная непрерывно дифференцируемая функция.
Если 5 обозначает заданную уравнением д{х^ y^z) = О гладкую
поверхность в области ft и (р{х^ у, z) — заданная на S гладкая функция, то задача
нахождения решения уравнения A), удовлетворяюш,его начальному
условию
u\s = fp{x,y,z), C)
§ 17. Линейные однородные уравнения 195
называется задачей Коши для уравнения A).
Чтобы решить задачу Коши A), C), необходимо из системы уравнений
f g{x,y,z) =0,
ui{x,y,z) = Ci,
U2{x,y,z) = C2
выразить Xj у, z через ui^U2 и подставить найденные выражения для ж, у,
Z в начальную функцию (p{x^y^z). В найденное таким образом выражение
вида Ф(гА1,и2) подставляем ui{x^y,z) и U2{Xjyjz). Тогда функция
и=: Ф[ul{x,y,z),U2{x,y,z)]
является искомым решением задачи Коши A), C).
Пример 1. При х > О, z > О найти обш,ее решение уравнения
И решить для этого уравнения задачу Коши с начальным условием и =
4.3 1
= X + XZ при у = —.
X
Д Найдем независимые первые интегралы характеристической системы
для заданного уравнения
I x{t) = Зжyz^,
y{t) = 3y^z^
Перемножив крест-накрест первых два уравнения этой системы, имеем
3y^z^x{t) = 3xyz^y{t).
Сократив на Зyz^ и отбросив dt, получаем
ydx = xdy.
У
Отсюда у = Cix и, значит, ui = первый интеграл.
х
Подставив найденное значение у =^ Cix в первое и третье уравнения
характеристической системы, имеем
f i = ЗCl:r^z2,
196 Глава 5. Дифференциальные уравнения в частных производных
Перемножая крест-накрест эти уравнения, сокращая на а: и отбрасывая
dt, получаем
-{2х + Ciz^)dx = 3Cixz'^dz.
Полагая Ciz^ = t, отсюда для t находим линейное уравнение первого
порядка
— = ---2,
dx X
общим решением которого служит t = х. Подставляя Ciz^ вместо t
X
и — вместо С*1, находим еще один первый интеграл U2=^ х'^ '\- yz^.
X
Общим решением заданного уравнения является
= Fg,x2 + yz3),
где F(u\^U2) — произвольная непрерывно дифференцируемая функция.
Чтобы решить задачу Коши, рассматриваем систему уравнений
1
X
У
X
U2 = :r^ '\-yz'^.
Из этой системы уравнений находим, что
Х^ -\-Xz'^ =: .
Ui
Следовательно, решением задачи Коши является
и = -(:г^ + yz^) = h xz'^.
У У
Пример 2. При ж < О, z > О найти общее решение уравнения
ху— Ч- {2х^у Ч- Г)^ - (ж Ч- 2x^z ч- уг)— = О
§ 17. Линейные однородные уравнения 197
у
и решить для этого уравнения задачу Коши с начальным условием i/ = —
при 2х Л- yz =^ 0.
Д Составляем характеристическую систему
x(t) = ху,
1^ z{t) = -{х + 2x^z Ч- yz).
Перемножая крест-накрест первые два уравнения системы, сокращая на у
и отбрасывая dt, получаем для у линейное уравнение первого порядка
xdy = {2х^ -f y)dx,
общим решением которого является у = Cix -{- х^. Значит, первым инте-
У 9
гралом является щ = х .
Умножая „ерзое ,р1„е„„е харак«р„„„,еско« с„с.е„ь, „а 1, ..оро.
У
Z
уравнение на - и складывая полученные выражения с третьим
уравнением, находим, ^о
X Z
--{--y-^z = 0.
У У
Отбрасывая dt, отсюда dx-hzdy-^-ydz = О или dx'{-d{yz) = 0.
Следовательно, а:-fyz = С2, значит, U2 = X'\-yz — первый интеграл характеристической
системы.
Общим решением заданного уравнения является
F^^-x^.x-^yz^
и
<х
где F{ui,U2) ~- произвольная непрерывно дифференцируемая функция.
Для решения задачи Коши составляем систему уравнений
Г 2:r-fyz = 0,
У 2
щ = X
X
{ U2 — X -\-yZ.
Из этой системы находим, что
У 9
— = щ -{■ щ.
X
198 Глава 5. Дифференциальные уравнения в частных производных
Следовательно, решением задачи Коши является
и = X +(х + yz) = —h 2xyz -h y^z . A
X X
Найти обш,ее решение уравнения и решить задачу Коши с указанным
начальным условием A—100):
ди I ди . А 2\9и ^ 2z — х^
ди ( х^\ ди ^ ди ^ yz^ - 1
2. х—+(у+ — )— + 2z— = О, U = при XZ = 1.
ох \ Z J оу OZ z'
^ Z ди ^ ди . ^ ^ ^.ди ^ 1 9 .
3. 2yz-^ Ч- (г^ Ч- 2ху - 1)-^ = О, 1/ = жу - - при жу + г^ = 1.
у ох оу OZ 2
^ , о о.ди ^, -х.ди ^ ди ^ у z'^ 9 9^
4. ix^ Л- z^)-^ Л-2{ху - xz^)t- ^-2xz^- = О, i/ = - - — при rr^ - z^ == 2.
аж ay az z 2
ди ди 2( о ^ди :r^
5. х-^ Ч- у-^ Ч- г^(а; - Зу)-^ = О, и = — при 3yz = 1.
ох оу OZ у
^ / г. о^ди ^ о ди суди ^ 4z^ — х^ ^
6. (у Ч- 2;г:2)— __ 2x^z— Ч- гг^— = О, i/ = при y-^z^+yz = 0.
7. ху""-^ Ч- :с 2г^7г- + у 2г—- = о, 1/ = у^ при жг*^ = 1.
ох оу OZ
^ ди , .ди ди ^ ^
8. Х-— Ч- (:гг Ч- у)-г- Ч- 2Г-—- = О, 1/ = 1 - ж при ж Ч- у - 2г = 0.
аж ау az
9. xix^- z)-Tr- Л-укх - zj-TT z[x'\- z^-^r- =0 и = x-\-y при г = 1, a; > 0
ox dy OZ
o^du 24^*^ ^"^ 2
10. 2у(ж - у )^ (:г; - у )^ ^y^'s~ = 0,u = xy при 2: = 1.
-.-< / ^9^ r 4^"^ / \du ^ 2 2
11. ж(жЧ-у)^ y\x^y)-^ ^(ж-yj—= 0, 1/= ж Ч-у приг = 1.
.^ / \ди , .ди , ^ди ^ 9
12. ж(у - z)- yiy^ z)— Ч- z[y Ч- г)— = О, и = у - ж при г = 1,
9и ^ ди ,_ 9 ^9'i^ ^ 2г
2
2
13. 2xz—- + 2у2;^- + {2х^ + у^-^ = О, и = — при у = ж
аж ау OZ у
§ 17. Линейные однородные уравнения 199
ди , , ди ди
. ди , , ди ди л
14. (z^-2x- 2у)-— -{-(z-2x-{-2y)- 2z—- = О, i/ = xz^ при х + у = 0.
ди ди . о о.ди ^ (z\
15. xz- yz— Л-[х уЛ-х )— = О, и = 1-1 при у ^ х.
.ди . .ди ди Ау
16. [z - X Л- Ъу)-— -^ [z Л- X - Ъу)- 2z—- = О, и = — при х = Зу.
ох ау OZ z
^^ ди ^ ди , о ^дu ^ о
17. :г-г- + 2у7г- Л- (х у -^г z)-pr- = О, и = х^ при z = х.
ох ду OZ
t с^ ди оди ди ^ 9 9
18. ху- X ——(- yz-;— — \), и = X при Z — х"^ Л- у .
ох ду OZ
^^ ^ ди . , (ди ди\ (У\^ 9
19. 2x- + (y + z)(^- + -j=0,.= (^) прих = .^
20. (х^ + У )^ + ^w "^ ^^az ^ ^'" "^ (ту "Р" ^ "^ ■^-
21. B:rz - x)-^ Ч- Bуг - y)-^ + Cz^ - 3;г; - y^)•^ = О, и = xz при у = z.
ox оу OZ
«^ /.л 9 9 ^дu , , о , 9l/ / , с» , 9l/ ^ 9
22. Bx'^z'^ + х)-к Uxyz"^ -у)-7: i^xz^ - z)-— = О, и ^ yz"^ при х = z.
ох оу OZ
23. х^'у^ + :г^ + О/ - Згг^у'^ — + {x^y^z + г — = О, п = ж'^г при у = х.
ох оу OZ
^. / 9 ^ ^ди . п .ди , ^ ^ди ^ 1
дх оу OZ у
при X — у.
ГУН {/И {/И 11
25. :r^— + B:гу - y^)— + B:rz ~ yz)— = О, i/ = — при :г = 2у.
9а: 5у 5z
^^ ^ ди . ^ г,Ви ^ ди ^ 2
26. 2:г7г- + Bу - 3:гг^)т- - Зг-тг- = О, и = у - - при xz = 2.
дх ду dz X
^^ ди . г, г,8иди^ у 9 9
27. Х-— + (:г^ + у + г^)-^ + г-:г- = О, i/ = - при :г^ + z^ = z.
дх ду dz X
^^ /^ о^ди ди , о^ди ^ 9 ^9
28. (За: - у^)— + у^ + (;^ + :г - у^)— = О, 1/ = Z - у^ при д; = Зу^
ди ^ ди , .ди ^ Z
)— - 2у— Л-{х-у Л- z)— = О, 1/ = -
дх ду dz у
29. (ж Ч- у -f z)- 2у— Л-[х-у Л- z)— = О, i/ = - при :г = z.
200 Глава 5. Дифференциальные уравнения в частных производных
. ди , , ди , , ди
30. {х - 2z)— Ч- Bz - у)— + (у - х)— = О, и = :г при у = О, Z > 0.
31. ^xz-^ Ч- 2(z'^ - zy)-^ Ч- (у - ^ )^-- = О, 1/ = :rz при у = О, Z > 0.
ох Оу UZ
32. о; ^- Ч- y[z - х)- Z —- = 0, и = у при х^ z,
ох оу OZ
ди , о ^ 'х.ди ^ ди ^ z^
33. жу^- Ч- (у - Зг*")-^ 2у;г;-^ = О, i/ = -^ при у = х.
ох оу OZ ж^
^. ди ,^ у .ди ди ^ л
34. х-^ Ч- Bze^ Ч- у)^- Л- -г- ^Q,u^ z при ж = у.
дх ду dz
^^ ^ди ^, о. ди оди ^ о у
35. жг^тг- Ч- 2(у - z^)y- z-^TT- = О, г/ = х^е' при у = г, z < 0.
аж ау OZ
оди .^ ...ди пди ^ (z-x)'^
36. х^— Ч- {2z - е^^)— Ч- г^тг- = О, 1/ = -^ :г-^ при у = Ьж.
аж ау OZ а;^
37. (^ + ^)^ + (?^ + ^)^ + (^ + ?/)^ = о, U = (lЧ-г)(l-2z)^ при д;Ч-у = 1.
ди . ^ .ди ди ^ Or.
38. ху-^— Ч- (ж - 2;г;)-г- Ч- у^^тг- = 0, и = х при у^ = 2ж.
ох оу OZ
о ди о ди , sdu ^ _zi
39. ж^^тг" Ч- у z-r- Ч- (ж Ч- у)тг- = О, гл = е 2 при х = 2у.
аж оу OZ
40. A + z)|^ + у2^3х|1 ^ {1 + zf^ = 0,и = е2^ при у = 2{1 + z)e-^\
ОХ оу OZ
.. , 9 \ди ди ди ^ 3;г;^ ^ . г,
41. г(жЧ-у со8уOг-Ч-у2Г7г-Ч-усо8у-7г~ = О, u = —- при X — 2ysmy^yz^
ох оу OZ I
ди ди ди
42. ZCOSX-T—\- z{l — ysin^JTT" + A "" ^) sin^TT- = О, 1/ = е [z — 1) при у =
ох оу OZ
= 1 Ч-зшж fo < ж < ^У
43. 1 - х)^— Ч- 1 - х^— Ч- г^е 2/ = о, U = — при z =
дх ду dz [х - ly
= -?=(^-1Jе2, {х> 1).
§ 17. Линейные однородные уравнения 201
/fQI /ill X /mQ I I
44. {xy + y'^)-^-- + y'^ -r- + {yz + ev )-^ =0,u = l + - при ж = ylnz, у > 0.
ox ay az у
ди ди ди
45. xzigz- V (у — х)-т ;гг7г- = О, и = cosz - sin;2r при х = yz
ох оу OZ
(°<-D-
.^ / с. ди ^ди , и. .ди ^ у . ^
46. {ху-х^)-^Л-у''-^ + {е^ +У^)-К- = 0, ?i= —— приу = a;lnz, у > 0.
дх ду dz 1 + у
,^ ди , .ди . ди ^
47. х-—^ (Z — у)-—h xzctgx-T- = О, и = smx + cos а; при z = жу,
от ау dz
(о<.<^).
^1А ^1А ^1А
48. {х + 2ze^)—- + (а; - у)-рг- + г(а; - у)-7г- = О, и = е^ при ж = 2у, z > 0.
дх ду dz
^^ / о ^ .ди ди ^ди ^ о 9
49. (о; + у^ + 2;гг)-~ + у—- + у^—- = О, п = жу - у" при ;гг = у^
аж ду dz
ди ди ди
50. х{2у + z)^- + {хе"^ + у)— - {2у + z)— = О, и = z npuy + z = О, х > 0.
ах оу az
г\ ^ i^
51. {х + у)-^ + {2ze' - у)^ + {х + y)z-^ = О, ?i = ;гг^ при 2а; + у = О,
z>0.
ди ди , _,, .ди ^ о / ч _,/
52. хутг- + у-7т~ + {хе У + z)-^ = О, гл = ж^ при z = [у - х)е у.
дх ду dz
2/Ч .ди xzdu ,^ .ди ^ о .. л
53. oj'^fl + xzOr- Н тг + A + 2^2:)—■ = О, гл = ху"^ при а;;гг = 1, ж > 0.
аж у ду dz
^ ^ 1 ди I ди I ди ^
54. -^- + --— + —■ —- =0,и = х при z = 0.
у dx X dy X -i-yz dz
ди idu , о 1 2\ди ^ о r^
55. ху— + у^— + {х^ + y^)-Q^ = О, ?i = у^ при ;г = 0.
ди 9 ди 9 ди
56. а;A~а;уOг- + 2;у -;г- + '2^(^г/ +^У"-1)-^ = О, гл = xz{x-l) при у = жг;,
аж ау OZ
ж > О, у < 0.
57. х{у ~ zey)-^ + у-г- + 2:A - ^e^JTT" =Q,u = x при y^z,[x> 0).
аж ау а2:
^г. г. л , о ^лди 2у ди ^ ди ^ 9 1 , / 2 \ /-
58. [1-1п(а;^у)]- ^ — +xy'^z— = 0,и = гс^уН-- ln(rr:^y) при z = Ху/у.
202 Глава 5. Дифференциальные уравнения в частных производных
59. же^-т; 2у^ -Б" + \^У ~ ^)^~ =0,и = ~-^ при у = -х.
ах оу oz х'^
60. 2хе^'-^ -2е^^тг-+а: 1 -1/Ьг = О, и = ( -+у ] е ^ при z = 0.
ах ду oz \х J
ди ди . .ди ^ . / 9 . \
61. XQOSZ— tgy • COSZ——h xitgy — у)-7г- = О, u = xsiiix (х + 81пг)
ох оу OZ ^ ^
ириу = х\^0<у<-, о < Z < -j.
^^ ди . .ди пди ^ 2
62. XZ—- -i- [х + yz)-T ^ -77- = о, и = ху - х^ при Z = 1.
дх оу dz
63. [х^ + У )-7г + 2ху-— + е -^ =: О, и == е^ при а: = 2у, х > у > 0.
ах оу OZ
^. / хди . .ди ди ^ . -
64. (х + у - г)^ + A + г)^ + ^ - О, U = уA + X + у) при г - 0.
oSu . ч\ди пди
65. ж^— + {2ху - у )— + z''— z=zO,u = yz~y-z при х := yz.
ди ди ди
66. {у - z)— л-[х- z)— Л-[у- х)— = Q, и ■= 2{х - у) upw X - Z = 2у.
^ ^ о ди .^ 1 . с^ ^ди ^m2z ди
67. 2ycos а;-^:—h A + у sin2a;)-;r—| -— = [), и = х - I Л- cigz при
дх ду у dz
y^cos^x = 1, (о < ж < ^, О < г < jV
^^ г -х '\^ди о ди у^\/1 Л- z^ ди ^ г г о
68. [х^ + у^)-^ + '^ У-^ + -^ - О, U = Z + Vl + z^ при х^
= Зу^1па;.
/^9 sdu ^ ди ^ ди ^ х'^ 9
69. Bу^ + ;ггOг- + Зз^у-тг" + 2х;гг7г =- О, и = — при ?/ -- z.
дх ду dz Z
оди , су су су^ди ди ^ 9
70. х^-^ + (з: у + 2;"^)-;— + xz-^ = 0,u = z'^ при у = О, жг > 0.
от ду dz
ди , о о.ди ди ^ /У\2
iSu о ди _, о , Su
^ / -^ 9ч ^^ ди ^ /У^^
71. жу^! [xz^ + ^ )^ - У^^ =0,и= \^~j при Z = о;.
72. х^- х'^Утг- + 2(a;^ - z)z-^ =0 и = y^e'^ при z = х.
дх ду dz
суди х^ ди , -ххди ^
73. х^— -i- ——'i-ixz'i-z'^)— =0,и = 1-{-у при х = 1.
§17. Линейные однородные уравнения 203
74. z^{z - у)— Л- y^{2z - у)— + yz^— =0,и = ег при у = -, ^ > 0.
эп^ / s9u оди о иди ^ . _и.. ^ ^
75. ж(у - ж)— + ?у^— + уг^еа^ — := О, и = у(Ц- е -) при г; = 1, у > 0.
э^^ / 9 9ч ^'^^ / \9и ^ ди ^
76. (х^ + ^ )-7Г- + У(^ - ^)тг + Зж^г-тг" = О, U = ж 4- Z при у = Z.
ах ду oz
^^ хди . о .ди ди ^ 9 ^
78. 2г ж - у^)— + 2уг— + Г + ^ Ь" - О, и = х + 2г^ при у^ = 1 - х.
аж ду OZ
^^ ^ ди . г> ^ ^ди у ди ^ 1 о 9
79. 2ху— + 1 - у^ - 2xz)— - ^— = О, U = - - у2 при у2 + a;z = 1.
ох ду X dz 2
80. \х-\ тг- + 2у—- 4- Z—- =0^ и = ху при z = 1.
\ у J ох ду dz
^^ о ди ди . ^ди ^ ^1
81. X Z- у— + Bу + z)— =Q^u=l-\ при у-\- z = 1.
«^ / •^^дu , о.ди ди ^ 9 9
82. (у - ^ )^ + (^ + ^ )^ - Z— = О, U = у2 - ж2 при ;гг = 1.
9и , о, ди о ди о о о
83. 2ху— + {2х - У^Ь- + У^-^ - О, U - а;^^^ при у^ - 2а;.
аж ду dz
, 9 ч ди ди 9 9 9*^^ 9
84. (х - 2х^у)-^ + у—- + 2х'^г'^-7г- = О, и = y^z при х - у = 0.
arc ay dz
ди ди 9 ^'^^ 9
85. (у - х)— + (х + у)— + 2yz — = О, и == X г при ж + у = 0.
^^ / г. 9 9^ди ^ о О ди ди ^ z^
86. (х - 3a;^z^)-7~ + Zx^y^z-:^ Л- ^тг- = О, и == — при х = z.
дх ду dz у
Г.Ш, .. 9 ди , о^ди , 9^ди ^ / ч9 1 л
87. 2х2^г— + (уг " Г )^ + (^^ + у)^ - О, и = (г - у)^ при z + - = 0.
88. х^-— + (а;у - 2а;^у^)-г^ hrz+~-;r- = 0, и==2а; при z = -1.
So; Sy \ у) dz у
с^ ^ди . С) .ди ( х^\ ди ^ X
89. х^— + 2у2 - ху)— + hrz + — ^ = О, U - - при Z = -1.
So; ду \ у ) dz у
204 Глава 5. Дифференциальные уравнения в частных производных
90. х^-— + Bх'^ -ху- z)—- + (xz - 2x^)^r- = О, u = z + гж"^ при у = х^.
ох ду ' oz
А ди , л "х ч ди , о ^ ди , о
91. x^-^ + {x^z + x'^y-2x)-^ + {2-x'^z)-p- = О, ?i = (у + 1) при а;^; = 1.
ох ду oz
ди о ди ди у
92. xBz — х)"^- '\-2z [z — х)-;-- + xz-j— = О, гл = ^ при xz = 2,xz> 0.
ox ду oz 2 — z^
ди ди ди о
93. 3xyz-p-- + утг + ^B + 3yz)-r- =0, и = ху" при ж = yz, xz < 0.
с/ж ду dz
ди о 5^ 'i. о Оч S'ti о о
94. 2тг- + 2ж;г^7г- + xz^Byz^ - 2 - z^)-^ = О, и = x^z^ при ?у = 0.
дх ду dz
ди ди ди X
95. х-^- + уC + 4а;уOг- + 4а;у2:7г-- = О, и = — при z = ху, х > О, у > О,
ох Оу OZ у
z>0.
^^ ди о /. .ди ди ^ 9
96. yz— + y^z{l - xy)-Q- + -^ = 0,u = yz при X = 0.
^^ / п.ди ди , 1 ^ди ^ Z су
97. {х - У )^ + y-Q- + B^ + У + z)— = О, U = ^ при ГС = ту^ ту > 0.
^« /^ 9 ^ди ди , ^ о.ди ^ X — еУ о
98. Bа; + у^ + ;гг)—+ ^ + (;гг-2у + Г)^ =0,и = —2— приг = а;-у2.
^^ оди . .ди оди ^ ^ Z
99. ж^тг- + УB^ - У)тг + ^ тг- = О, и = 1 - - при ;гг = 22;.
дх ду dz у
100. [(. + y-.Ly-z-2]- + (. + l)- + (y-l)- = 0,. = ^:^;^^
при ;гг = 1, у > 1.
Решить уравнение, преобразовав его к указанным новым независимым
переменным A01—102):
dz dz
101. —■ + -— = Q^u = x + y,v = x-y.
дх ду
^^^ dw dw dw ^
102. -—- = -—- + —-' = 0^и = х, у = хЛ-у, t = x + z.
дх ду dz
Ответы к задачам § 17
1. u = F (ху^, ^ - \^V), ^ = ^У^B^ - 2;V).
§ 17. Линейные однородные уравнения
205
^ f Z у х^\
2. u = F[-^, У.^ — \и
\Х^ X Z J
xyz — х"^
u^F\2x--, ху^Л-yz^ -^yYu = {2ху-1) (^У + '^г^--).
_/;гr^-ж^ у ;гr^^ у z^ 4z^
/а; 1 + xz — 3yz\ х{1-i-xz — 3yz)
\y ^ )
u = Fly + z^, 3 +yz\,u =
yz
Az^ -x^
+ y + z^-{-yz.
7. u = F (-, y^ - a;^;гr^ j, и
8. u = f(^, ^-z),u
\X X /
2^2
y^ ~ x^z^ +
X
X + у — XZ
9. u = F I XZ
2 -a;2
' r^2
(a;^ + а;;ггJ
I, u = a;z + ;^(x;^ + l)~^-~e (^ V.
/ x + z
10. u = F[x^- y^, ;^(у2 -x)],u = ^[{x + у2J - z'^iy'' - a;J].
11. и = F [xy, {x + у);гг], u = ;гr^(rc + j/)^ - 2rry.
12. ^ = F [y^, x{y + z)lu = y'z' ""^^^^
1+yz
x^{z^ — x^ — y)
^5
+ 2.
13. 'a = F(~, ;^2~a;2~yl, n
14. u = F [ж + у + ;гг, (s - y)z^\ ,u = -{x- y)z^{x + у + ;гr)^.
I-. г 2 2/-. xl . z'^ - x'^(l +Xy)
15. u = F [жу, ;гг^ - х^{1 + жу)], u = 14- а;у + ^^ —.
\х + у -i- Z,
ху
16. u = F
X — Зу Л- Z
{x-\-y + z){x-3y + z)
, и = 5 1.
Ъх'^ + п:^у - Zxz
17. U = F ( -~, жу ), U =
\х^ X J у
\ ХУ Z
206 Глава 5. Дифференциальные уравнения в частных производных
19. - "' - - " < --1 . J'
ух^-у^ у J
\х у
^2 \ а;2 - '(у2
21. n = F|^, - + ^-^Yu "'^^
у^ / ?y^ + Z — г^
22. и = F -, 2а;^2; , и -
\у Z ) 2z^
23. ii = F ( - - х'^у, -|,ii = z( +х^?у
\У ^) \^ У
_ ( X Х^\ X Х^
24. и = F 1 XZ, -тт-\ ], и = XZ -{- -7^ -\ .
\ У^ У J У^ У
(х'^-ху у\ х?-ху
25. и=- F \ , - , U = -
2z
2>
26
т^ (^ y-x^-z^\ уЛ-z-x^-z^
XX) X
28. и = ^Г^, 2г^;:^+_у^\ Bг-хЧ-Л^
29. п = F [гг + у - ^, у(гг + ^)], п = ^^^ip^-^.
30. и=^ F {хЛ-уЛ- z^ ху Л- z^^.u — хЛ-уЛ- Z — ужу + г^.
32. u = F(l + i, хугУи=^(^ + ")
2 _
■ z"-
2
33. u = F ( ж2^, у2^ - ^гЛ , u = 2 f 1 - 4 + ""^
2 7' V a;2 ' 2x2
34. u = F (же""'', ye~^ - z^), u = (ze"'' - ye"'' + z^)^.
§ 17. Линейные однородные уравнения
207
35. и = F [xz, 21n|z| ], и = х^еу .
36. u = f(---, z'^e-y-z\
Z е У - z],ti = -—
X
37. u = F
X + у + z
, {2z - X - y){ij - х)
[ {x - уJ
г./^ 2 г. . \ x(y'^-2x + Az)
\х I 4z
1 1
, и = (х + у + z){x + у - 2z)'^.
38
39. u^F
X у
, (х-у)е 2
2(у-хУ z2
ху
40. и = F
У
, u = -е Н • е .
2 г/
3J \ Т 2^
41. U — F ( г"^ — 2siny, sin?y ], ?i = —\- —— 2 sin у.
У J У ^
42. u = F
43. U = F
г-1
cos а;
_ y — smx
• е^, I, г^ =
cosa-
{z - l)e'
y — smx
- ^\'^P^y
{х-1)еУ, е'У-^-^^—^
и =
{х - \)еУ 1
-П2-
(гг-1)
44. U -: F —-, —-—F \,и= -^z-e у.
V У yz-\-eyl У
45. u=^F{ , yz — xigz], и
\ cos z J
46. u = F I ^
yz
cosz — smz.
1 u.
и —
'i/e^
yz Л- г^
47. u=:F{-: , xy Л-ZQXgx\.u=^
\s\nx J
xysiiix -h jsrcosa;
ж"
ж"
ay
еУ
48. u = F ( ;ге~^, xy-'^ Л-zeyyu^e^y Л-
A9.u = F[z- \y\ ^JLEyM^^j, ^ = iB^ _ ^2)(^ _ 3^2 ^ 3^)
2 У J У
208 Глава 5. Дифференциальные уравнения в частных производных
50. и
51. и
52. и
53. и
F (хе\ y^ + yz + xze'), u = z+ У^У±^.
хе^
F [ze'"", 2ху + у^ - 2ze''), и = z'^ - --{2х Л- y)yze~
V у ) \x + zeyj
I ^ J 1
X ' X 2y2 2x{xz + l)\^
и =
{xz + 1)
.4^''2^
8x
1 ^
2x(xz + l)J
X J
54. и
55. и
56. гл
57. гл
58. и
59. U
60. и
61. гл
62. ?i
63. и
64. U
65. и
F[|,.-arctg(f)],n = g(.-arctgf)
F(rr:y-ln|y|, y-ln|a;z|), ?i = (ж - l)y + ln
\.г I ;гг I / V z J z
xz
У
[ у ' ln(a;2y)
о Inix'^y) • ln>г:^
У
= F {x'^y, x + y + e''),u
X Л-у + e^
x'^y
F[xey,xy + e'^%u=^^y±^.
F{xsiny, xy + svu.z),u = Xsiny{xy + sinz).
F{xz, yz — x), u = xz{yz — x).
= F
x + y
+ e%
,z a;2 - у2
У
, и
x-2y
x^ — y^
+ e'
y-z-—, {x + y + l)e ''\,u = {x + y + l){y-z-—\
V^^ ^ У / y^
§ 17, Линейные однородные уравнения
209
66. и = F[z — X + у^ {х — у){х — z)], и =
{x-y){x-z)
X — у — Z
67. и = F {у^ cos^ х — х^ у^ cos^ х • ctgz), и = х -\-у^ cos^ a;(ctgz — 1).
,.3
68. u = F
ye
"^, ^{z+Vl + z^)
, и =
+ \/ГТг2 ^
e'^.
69. u = F(^, a;^ - y^ - z ), u = 2 4-
(a;'^ -y'^ - z)y'^
70. и = F (—. — arctg a; , u = —;r -- arctg x] ,
\x z z J x^ \z z J
71. u^F \xz, y^ - z^(\ + xz)\ ,u^\^-xz+ У ~ ^ ^ + ^^)
"" ■" XZ
72. u = Flxy, Inx^ j, u =: y^ • e^.
^^\ о 2
2;|ln;2r,u= ( 1)
У J \ \y J
73. u = F [2x-{- -^, y-x
a;^ - x^
74. u = F
75
z^ X
~T~^—
^z^—yz ^
r?(y Л ^ ^Л л . 1 -Л
. u = F \ my, e^ Л- - Uu — у [ХЛ- -e ^ \
76. u = F[ z,
Z X — Z
у \ __{x-\- z)y
1 '^ —
77. u = F
78. u^F
x'^z, -A -hx'^yz)
у
z
1
x^y
+ Z--1,
X Z
Ly у
, n =
ж + ^гг^
79. u = F [ 2z, 2;y^ - I + x^z J, и = Bх';г - 1) { y"^
Z^ X у J Z'^IX [Z^ — Z) + y\
i + xz).
81. и
-(
y^ + yz, - + 2y + z
- + 2y + z - 1
+ уг
210 Глава 5. Дифференциальные уравнения в частных производных
82. и
83. и
= F
(ж + у)^,
х-у - z^
и = {x-i- у){у -хЛ-z'^-z).
F [х'^ - жу^, 2х-у'^ - Inz'^), и = xz{y^ - a:)e^^~^'^.
„2 У
84. u = F{^-i/, --- ].и
^х Z у ^
1 + Г
х
1-^ + Г
У Z
85. u = F [х^ •^2ху-г/, х Л-у Л- -\ и = ^ , ^
86. и
87. и
F[:^-z\ ---
^х у Z
>'-f-')(-J-f
р1-+у + г, y'^ + 2yz-zA,
= -у^ -2yz + z^ + 2\z + y +
88. u = F
89. u = F
90. u = F
x^, xiz'\-2) - -
У У
и
IX \y xj X \ у
xjxy - 1)
{z + 2)xy -
u = l +
1/ 3 x
-{x'' + г), xy-i-z
X
u = xy Л- z Л-
[xy + zyx
- + x(z + 2)--.
z + 2
X - у -V у
3^3
(а-з ч- г)'^
91. и
92. U
98. U
„ / 1 у\ (у + a;z)^
F[xz^-—, ^+-Ь^-"Т^—т-Ц-
\ а*^ X/ x'^z 4- 1 — х^
F [х;гг — ;гr^, у 4- (a;z — z^) In {xz)\, u
^ +ln^.
xz — ;гr^
F(„3 у! V\ A?
94. u = F
i"^)
e ^^, y^ -y-x'^ + -^
z^
и =
^ \ 2 ^ •
1 -y^:^
§ 18. Квазилинейные и нелинейные уравнения
211
95. и = F [х^ -\ , ],и = ж* Н
\ У У J У \ У У J
96. u = F
97. u = F
а; + 1 ) е^, z'^ -\ х^
z' +
X
u = -2 +
- д: + 1 е^ - 1
X Z ~ {х -\- у'^) \пу
- + У,
У У
Z х + у
и = т: + ш
2 . ^\2 _ (п,2
98. u = F [{у' + z)e-y, (х + у^ + z)e-'y], ^ = (У + ^) " (У + ^)в^
99. u = F[ , z],u = '-^ ^.
\z X у J ху
100. и = F
{y-lf-{z + lf,
1
X + у — Z
+ 1п|у + г|
и^ 1_ +\n\y + z\-l\n[{y-lf-{z + lf].
X \~ у Z Zd
101. z-=^F{x-y),
102. w = F(a; + y,a: + ^).
§ 18. Квазилинейные и нелинейные уравнения
Если Л — некоторая область пространства Л*^, то квазилинейное уравнение
в частных производных первого порядка в области Л имеет вид
A)
В уравнении A) коэффициенты a{x^y^z)^ b{x^y^z) и c{x^y^z) -~ заданные
непрерывно дифференцируемые в области Л функции, д. z ■= z{x,y) —
искомая непрерывно дифференцируемая функция. Эта функция задает
в Л некоторую поверхность, называемую интегральной поверхностью A).
Автономная система уравнений
x{t) =a{x,y,z),
y{t) = b{x,y,z),
z{t) = c{x,y,z)
B)
212 Глава 5. Дифференциальные уравнения в частных производных
называется характеристической системой уравнения A).
Если ui{x,yjz), U2{x,y,z) -~ два независимые первые интегралы
системы B), то общее решение уравнения A) записывается в неявном виде
F[ui{x,y,z),U2{x,y,z)] =0,
где F{ui^U2) — произвольная непрерывно дифференцируемая функция,
допускающая нахождение z — z[x^y) как неявной функции.
Пусть 7 ~ некоторая гладкая кривая в области 11. Задачей Коти для
уравнения A) называется задача нахождения интегральной поверхности
уравнения A), проходящей через заданную кривую 7-
Пусть гладкая кривая 7 задается как пересечение двух поверхностей:
Г ^i{x,y,z) =0,
[ Ф2(ж,у,2г) =0.
Чтобы в этом случае решить задачу Коши, необходимо из системы
уравнений
' ^i{x,y,z) = 0,
Ф2(ж,у,^) =0,
Ul{x,y,z) =1^1,
U2{x,y,z) =U2
исключить X, у, z и найти связь между г^х, U2. Если эта связь вида
Ф(^ь^2) = 0) то уравнение Ф[lll{x^y^z),U2{x,y,z)] = О дает решение
задачи Коши для уравнения A).
Пример 1. Найти общее решение уравнения
/ sdz , .dz
и ту интегральную поверхность этого уравнения, которая проходит через
прямую X = 1у у = Z.
Л Характеристическая система имеет вид
x{t) =z-y,
y(t) =x-z,
z{t) =y-x.
§ 18. Квазилинейные и нелинейные уравнения
213
Сложив первые два уравнения, рассмотрим систему
I х-\-у = х~у,
у z = y-x.
Отсюда X -\-у -\- Z = О или dx -\- dy -\- dz = О, что дает первый интеграл
1^1 = X -\- у -\- Z.
Если первое уравнение характеристической системы умножить на ж,
второе уравнение умножить на у, третье уравнение умножить на ;г: и сложить,
то получаем хх -\- уу -\- zz = О или xdx + ydy + zdz = 0. Отсюда находим
еще один первый интеграл
2,2,2
U2 = X -\-у -\- Z .
Общее решение уравнения задается формулой
где F{ui,U2) — произвольная непрерывно дифференцируемая функция.
Для решения задачи Коши, исключая ж, у, z из системы
ж = 1, у = Z,
щ = X -\-у -\- Z,
U2 = Ж^ +у^ -\-z'^,
находим, что U2 = I -\- -{их — 1)^. Следовательно, решение задачи Коши
задает функция
х'^ ^у'^ ^-z^ = l^-{x^y-\-z- \f.
Если кривая 7 задана параметрически
ж = V^iW, У = 4>2{г), z = (рз(г),
то из системы уравнений
X = (pi{r), у = (р2{г), Z = (рз(т),
1^1 =ui{x,y,z),
U2 =U2{x,y,z)
214 Глава 5. Дифференциальные уравнения в частных производных
находим связь Ф{и1,и2) = 0. Тогда уравнение Ф[и1{х,у,г),и2{х,у,г)] = О
задает искомую интегральную поверхность, проходящую через кривую 7-
Пример 2. Найти интегральную поверхность уравнения
dz dz r-iz X ^
x-Q- + у-д- = z- \Jx^ Л-у^ Л- z^,
проходящую черех кривую ж = т,у = т^,;г: = 0.
Л Составим характеристическую систему
x(t) = X,
y{t) = У,
z{t) = z ~ yjx^ Л-у^ Л- z^.
Перемножая крест-накрест первые два уравнения системы и отбрасывая
у
dt, находим, что ydx = xdy. Отсюда ui = первый интеграл. Умножая
X
первое уравнение на х, второе — на у, третье — на 2: и складывая, имеем
XX -\- уу -\- ZZ = х^ Л- у'^ -\- z^ — zyx^ + у^ + z^.
Перемножая крест-накрест это выражение с третьим уравнением системы,
получаем после отбрасывания di
{z — \/х^ + у^ + z^){xdx Л- ydy Ч- zdz) — [х^ + у^ Л- z^ ~ z\Jх^ Ч- у'^ Ч- z^)dz.
Отсюда
d{x? + у2 + z^) = -2x/^2Ty2T^d;^.
Значит, U2 = \Jx^ -\-у^ -\- z^ + z.
Из системы уравнений
X -
их
= г, у =
- у.
X
-т\
Z -
= 0,
U2 = \/х^ Л-у^ Л- z^ л- Z
находим, что 1^2 — "^1 +^i- Тогда искомая интегральная поверхность
задается уравнением
Х^ Х^
В задачах A-~33) найти интегральную поверхность уравнения,
проходящую через заданную линию.
z.
§ 18. Квазилинейные и нелинейные уравнения 215
OZ OZ 9 9 9 9-. 9 1
1, X—- л- у— -^z-x^ ~у\ х^ + г = 1, 2: = х^ - 1.
ах ау
г. / 2 2\ ^-2: dz
2, (х -у )— + ху— Л- xyz = 0, Z = х,у = 1.
л UZ л OZ 9 9 9 1
3, XZ W- +yz -^ = х^у^, Z = х% у = -.
ох оу X
л ( 2 \9z 2^^ 1
4, [х у - х)— -ху — = Z, Z = х,у = 1.
^ . 2 9ч ^-2: ^ 9z
5, (х + у )— + 2ху— == XZ, у == 1, 2: = X.
7. (у^ + 2:^ - х^)- 2ху-— + 2x2: =:= О, х == О, 2; = у^.
ох ' оу
^ dz dz г, г, ^
9. Х2:—- + У2:—- + х^ + у^ = О, х = 1, у = 2:.
ох оу
/9 9 9\ 9z dz
10. (х - у - 2: JTT- + 2ху- 2x2: = О, х == О, у = sinr, 2: = cost.
ox оу
- - / \dz , .dz
11. (X — yJT; h (X + y)— 2: = 0, X — COST, у — SHIT, Z = T.
dx dy
12. y'^z- xy^z-— + x(x^ + y^) = 0, X = л/т, у = 1^ z = \Jt^ + т.
ax ay
13. (x^ - 7/^ + z^)-— + 2xy-- = 2x2:, x = 1, у = сЬт, 2: = shT.
dx dy
. / 9ч^^ 9^^ 9 ^
14. (xy - x^)— + r ^ = 2:^ + 27/2:, у - 1, 2: = 2x.
15. xD - x^)-^ + Bx^y + 1)-^ ^x,x^\,y^-z.
dx dy
16. 2x^-^ + yBx^-y2)-^ = l + z^, x = 1, y = arctg2:.
ax dy
17. Bx + v)| + (x + 2ri(|-l)
1 = 0, X == 0, z = 2y.
216 Глава 5. Дифференциальные уравнения в частных производных
2dz dz _ 2
18. Г—- + yz— = -z\ x-y = 0,x-yz = l.
ox ay
19. {z - y)^-Q-^ + ^^-g- = xy^ X = 0,y = 0.
^^ dz dz у ^ 9
20. y—-^z— = ^,x = l,z = y^.
ox oy X
21. {xz + y)-^ -{-{x-^yz)-^ = l-z^,z = 2,2x = 3y.
dz dz
22. {2y-z)—+y— = z,y = 3^2, x + z-4y = 0.
dz dz
23. y— + X— = x-{-y-{-z,x-h2y = 0,z = 0.
dx dy
^, dz dz 9 ^
24. Х-— + y-^ = жу + ;г:, у = ж^, ^ = 2ху.
ox oy
25. —ж^"r—h (ж?/ — 2г^Oг- = xz^ xy = 1, x -\- z = Q,
dx dy
26. {2x + y^ + 2:^)-^ + 2y-^ = 2^:, у - 2: + 1 = 0, 2: = 2ж.
ox oy
27. ~(ж + 3y^)^ + y^ = ^, ж + 2y^ = 0, yz = 1.
28. BуЗ - a;2)^ - 2хуу + 2x^ =Q, у = z = 1.
29. {z'^-y'^)—+ z~+y = 0,x = 0, у = z.
, 9 2ч 9z dz
30. {x + y^ + z^)— +y— = z,x = y = l.
„^ , 9 2sdz dz
31. (ж^ - У )^ + a;y J- + жуг = 0, z = ж, у = 1.
32. 2ж^ + (у + z)^ = у + z, ж = уЗ, z = 0.
33. 3y— + (ж + 2?/)— = 3cos2 ^ . ^g^^ ^ ^ 3^ ^ 1 ,. ^ ^ (^0 < ;г: < -j.
34. Найти поверхность, проходящую через окружность ж^ + y^ + г^ = а^,
г = 1 и ортогональную к семейству сфер х'^ Л-у'^ -\- z'^ = bx.
§ 18. Квазилинейные и нелинейные уравнения 217
35. Решить уравнение
dz dz 2
преобразовав его к новым независимым переменным и = х^ Л- 'у^.
V = X,
36. Решить уравнение
2dz 2^^ _
дх ду
преобразовав его к новым независимым переменным и = ,г? = у.
X у
В задачах C7—40) найти решение нелинейного уравнения,
удовлетворяющего указанному начальному условию.
ди ди ди
ди
(ди\
38. (—j +y—=Q^u = x,y = l,
ду
ди _ ди (д'^\
2
ди (ди\ ди
41. Определить функцию z = z{x,y), удовлетворяюи;ую одновременно
двум уравнениям
dz dz ^^ dz ^ dz 2у^
дх ду ' дх ду ж^ + у^ *
42. Определить функцию и — и{х^у), удовлетворяющую одновременно
двум уравнениям
ди ди ^ f ди\ f ди\ ^, ,з
7Г + ^==0' \1г] -\-^] -2(х-у)^
дх ду ^ \дх) \дуJ
218 Глава 5. Дифференциальные уравнения в частных производных
Ответы к задачам § 18
1. (х2+у2J-(х2+у2 + ;^J=х4.
2. 2\ny-h-^ = z'^e'^y-^.
3. 4z^ ~ bxS^ =:^-Ъ.
уЪ
4. xyz = {ху — 1пуJ.
5. х'^ — у'^ -\-у = z^.
6. {x-y-z)^ = А{х^ Л-у^).
7. у^{х^ + у2 + z^) = y'^z + z^.
8. {х -\-у -\- zf' = 3{xy -i- xz -\- yz).
9. ж^ + 2у2 = х^{х^ Л-у^ Л- z^).
10. [х^^у^Л-z^Y^y^^z^.
11. ж = e'^cos (^ + г), у = e'^sin(^ Ч- г), 2: = ^е'^
12. Ц-:г2 + ^ = (а;2 + у2J.
13. (a;2 + y2_z2J = 4(y2-^2)
^^•7 + ^4(^ + 1-^)-
15. 1D-а;2)у + 4^ + 1п(^)=^1пИ.
1 1 У
16. —5-+arctg2: = - +
4а;2 ^ 4 ^а;2-у2 1па;'
17. (у-жK = (а; + у)(у-2;J.
18. уЗ _ зжуг = {yz + 1K - 3(уг + 1J + 3(у2 + 1).
19. ^2 - у2 = а;2 + (г - уJ.
20. у2 + z(l - 2а:) +-х'2 + Bа; - х^ - 1Iпх = -.
Zi Zi
21. 3(а; + y)(z - 1) = Ь{х - y){z + 1).
§ 18. Квазилинейные и нелинейные уравнения
пп 0-.2/- п.. , .л г. 2
219
22. 32:2(а;-2у + 2) = 2y^.
23. х^ -у^ = Z{x + уJ • е~^.
24. а;(г — а;у) = y^.
25. жу + 2: = 1 — \/—xz.
26. (у - z)Ba; - у^ - г;^) = 2у2 - у{у - z).
27. ху + 3y2z = j|.
28. ЗуB - х2) - 2у^ = 4у - ЗуЗ - Zx^.
29. (y + zJ = 2(a; + y2 + z2).
30. z^ = уB;2 + у2 -ж).
32. x^z- {z-yf.
33. ж + Зу = tg;?:.
34. (a2-V=(a;-^ + |y + y2.
^^' '^^а;2 + у2 + /(х)-
36. 2 = e"i •/ (--iУ
Va; уУ
37. u = a;(l + y).
38. u = X — Iny.
39. u = a;-y + 1.
40. u = хеУ-^ + ^e2B'-i) - ^.
41. ^ = ln(l + ^)+C.
42. u=^(a;-yJ + C.
Глава 6
ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
§ 19. Простейшая вариационная задача
Рассмотрим
b
J{y) = / F[x,y{x),y'{x)]dx,
а
где а и b {а < b) заданные числа, F{x,y^p) — заданная вещественнознач-
ная дважды непрерывно дифференцируемая функция при всех х Е [а,Ь],
у е (-00, +оо), р е (~оо, +оо).
Пусть М обозначает множество всех непрерывно дифференцируемых
функций у{х), заданных на [а, Ь] и удовлетворяющим граничным условиям
у{а) = А, у{Ь) = В,
где AvL В — заданные числа.
Простейшей вариационной задачей называется задача нахождения
слабого экстремума J{y) в классе функций у{х) G М.
Если дважды непрерывно дифференцируемая на [а, 6] функция у{х)
является решением простейшей вариационной задачи, то она на [а, Ь]
необходимо удовлетворяет уравнению Эйлера.
ду dx ду'
Всякое решение уравнения Эйлера называется экстремалью. Экстремаль,
удовлетворяюш,ая заданным граничным условиям, будем называть
допустимой экстремалью.
о
В этом параграфе через С^[а, Ъ] обозначается множество всех тех
непрерывно дифференцируемых на [а, Ь] функций г]{х), которые удовлетворяют
нулевым граничным условиям г]{а) = ri{b) = 0.
§ 19. Простейшая вариационная задача 221
Пример 1. Решить простейшую вариационную задачу, если
1
J{y) = I W + '^^У + A + ^^){у'?Мх. 2/@) = О, 2/A) = 1.
о
Л Уравнение Эйлера имеет вид
[(l+a;V]' = 0.
Экстремали задаются равенством у = Ciarctgx + С2, где Ci и С2 —
произвольные постоянные. Используя граничные условия, получаем до-
4
пустимую экстремаль у{х) = — arctgx. Проверим, действительно ли на
7Г
о
у{х) достигается экстремум J {у). Для любой ri{x) G С^[0,1] имеем
1
AJ{y) = J{y + г?) - J{y) = J{x{y + r]f + ж2(у + г]){у' + V) +
о
+ A Ч- х'){у' + ri'f - xf - хЦу' + A Ч- x'){y'f]dx -
1 1
= / [2xy + x^y]r]dx-{- I [ж^у+ ж^г? + 2A+ ж^)y']Vdx+
0 о
1
Ч- Axr?^ + (l+x^)(r?')^]dx.
о
Во втором интеграле проинтегрируем по частям. Получаем
1
[[х'^у + х^г] + 2A + х^)уУAх = [ж2у + 2A + х'^)у']г]{х)\1^^ +
о
1 1^ }
+ -ж^r?^(ж) - / {[ж^y + 2A + х'^)у]'г) Ч- жr?^}dж =
1
= - [{[хЦ + 2A + х^)у']'г1 + .xr?2}dx,
222 Глава 6. Элементы вариационного исчисления
так как проинтегрированная часть обращается в нуль, поскольку г]{х)
обращается в нуль на концах [0,1]. Подставляя найденное выражение второго
слагаемого в AJ(^), находим
1 i
AJ{y)= I{2ху-h х'^у' - [х'^у-h 2{1-h x'^)y']}r]dx-{■ I {1 + x^){r]'fdx
0 0
1 1 1
= - /^2[A + x'^)y'yr)dx + /A + х^){г)')Чх = [{1 + x^)(V)^dж > 0.
Здесь был использован тот факт, что у{х) — экстремаль и, значит,
1
ЛA + x^)y'yridx = 0.
о
Таким образом, допустимая экстремаль у{х) дает абсолютный
минимум в заданной простейшей вариационной задаче. А
Пример 2. Решить простейшую вариационную задачу, если
2
J{y) = I [6y^ + х\у')^ + 12x^y]dx, у{1) = 1, уB) = 8.
1
Л Уравнение Эйлера
x^2/" + 2ху' -6у = 6х^
определяет семейство экстремалей
у = -4 + C2X^ + ж^
где Ci и С2 — произвольные постоянные. Используя граничные условия,
о
находим допустимую экстремаль у{х) = х^. Для всякой ri{x) G С^[1,2]
§ 19. Простейшая вариационная задача 223
имеем
AJ{y) - J{y + г?) - J{y) = |{6(у + гуJ + х\у' + ri'f + 12хНу + г?)-
1
2
- 6у2 - ж^(^')^ - I2x^i/}dx = Абг/2 + x^(V)^]dx+
1
2 2
М12^ + 12x^)r]dx + 2 I x'^iyyri'dx.
i 1
Проинтегрируем по частям в последнем интеграле и воспользуемся тем,
что 77A) — 77B) = 0. Тогда получаем
2 2
1х.
' ^ dx' ^ " '
1 1
Но выражение в квадратных скобках во втором интеграле
AJ{y) = f[6ri'^ + x'^{ri'f]dx + Al2^ + 12x^ - ^{2x'^y')]r]da
12y + 12x^ - -^{2x'^y') = -2{x^f + 2х^Ц - 6y - 6x^) = 0
dx
на [1,2], так как y{x) — решение уравнения Эйлера. Следовательно,
2
AJ{y) = Абг?2 + x'^{r]'y^]dx > 0.
1
Это значит, что у{х) дает абсолютный минимум.
Решить простейшую вариационную задачу A—90):
1
J{y) = l{y-hy'fdx,y{0)=0,y{l) = l,^
1
1
о
е
2. J(y) = у [^ + уу'+ XV)^
1
3
dx, уA) = 1, у(е) = 0.
3. J{y) = f[2y- уу' + х{у')^] dx, уA) = 1, уC) = 4.
224
Глава 6. Элементы вариационного исчисления
4. J(y)
5. Jiy)
6. J{y)
7. J{y)
8. Jiy)
9. J(y)
10. J(y)
11. J{y)
12. J(y)
13. J{y)
= j [4y2 + [y'f + 8y] da;, y@) = -1, у (^) = 0.
0
1
= / [{y'f + y' + 2e'^y] do;, y@) = i, y(l) = \e\
0
7г/2
= у* [{у? + V + 2ycosx] dx, 2/@) - ^, 2/ (^) = e\
0
-1
= / [^\y'? + 12y'] do;, y(-2) = ^, y(-l) = 1.
-2
2
/ [22/ + yy' + x^B/'J] d:r, y(l) = 0, 2/B) = 1 + lii2.
1
2
|[:.y + 2/]^dx,y(l) = l,yB) = i.
1
7Г
/ [(?/' + y? + 22/sinx] dx, 2/@) = 0, 2/Gг) = 1.
0
1
j \x' + \y' + 2(y'JT
dx, y@) = 0, y(l) = 2.
-I
1
2
, ,,9 y^ 2ylna;
2;(y') +- +
x x
dx,y(l) = 0, yB) = l-ln2.
H h 02/
x*^ ж
dx, y(l)=0, уB)=81п2.
14. J[y)
= |UyT + ^ + 4y
dx, y(l) = 0, yB) = 21n2.
§ 19. Простейшая вариационная задача
225
15. J{y) = J ^{у'
1
2
dx, 2/A) = 3,2/B) =4DIn2 + 3).
16. J{y)= /[2;2B/')^ + 2y2 + 32x2yln2;]d2;,y(l) = -5,yB)=4D1ri2-5).
1
2
17. J{y) = I L(iyJ + ^ - 18y\nx\ dx, 2/A) = 2, 2/B) = 2C1n2 -f 2).
1
2
18. J(y) = I [x{y'f + 2yy'] dx, y(l) = 0, yB) = In2.
1
2
19. J(y) = I [x{y')^ + yy' + xy] dx, y(l) = ^, yB) = ^ - ln2.
7Г/2
20. J{y) = I [y-\{y'
7Г/4
sina;da;, у (-j = -ln\/2, у (-j = 0.
21
.Лу) = /
k„r + 2-«^-''-'
22.
i
x x^
r.x„. , ^^x/„.f\2
{1 + х)е^у + -еЦу'У
dx, y(l) = 1, y(e) = 2.
dx, y@) = 1, y(l) =
23. J{y)
/[¥-
2 ^ iy')
-П21
dx, y(l) = 2, yB) = 8-.
2
24. J(y) = |[x(y'J + ^
dx, y(l) = 2, yB) = 2-.
25.
4
J{y) = I [Л{у')
2 ^ 1
2x-v/xJ
dx,y(l)=2,yD)=4-.
226
Глава 6. Элементы вариационного исчисления
26. J{y)
27. J{y)
/
1
2
-I
{у')' у'
у/х Х^^/х
dx, уA) = 2, уD) = 16-.
-х{у')'^ + хуу + -у^
dx, уA) = о, уB) = 1.
— 1
28. J{y) = I [2уу' - х^{уУ] dx, у(-2) = ^, у(-1) = 2.
-2
1
29. J(y) = У [хуу' - 2B/')'] dx', у@) = 1, уA) = ch ^.
о
7г/2
30. J(y)
31. J(y) =
J [{y'f + 2yy' + 4y'] dx, y@) = 0, у (^) = shvr.
0
1/2
2y2
32. J{y)
1/4
2
[(ж-1J a;(x--lKj
da;,y(M=l,y(i)=2.
, ,.2 Д. V ^ 8y
dx, y(l) = 1, yB)
^^2|d^,y@) = l, У(^2'=^•
34. Jiy)
— i
-2
а:3(уГ + Зху2-^^
dx, y(-2) = -, y(-l) = 1.
тг/З
35. J(y) = J [{y'f - Gysinx] cos'^xdx, у (-^) = у (^) = 1.
-тг/З
§ 19. Простейшая вариационная задача
227
1/2
J[y) = I [{х' - Щу'Г - ix'y' - 4у] dx, у (-0 =у{1)= \-
36.
-1/2
1
37. J{y) = J [еЦу' - xf + 2у] dx, у{0) = 1, уA) = i.
38.
1
J{y) = J [(у') V4 - n-2 - 2у] dx, y@) = 2, y(l) = ч/З.
— 1
39. J{y) = У [i'(v')' + Зх!,^) dx. !/(-2) = ^, v(-l) = 0^
-2
2
40. Jiy) = J [(y'
1
41. J(y)=ri^+ '
dx, y(l) = 0, yB) = -.
cos X cos^ X
dx
n\ 1
х,у{0) = 0,у{^) = -.
42. J(y) = J [{xy' + yJ + A + x^)y'] dx, y(l) = -i, yB) = 1.
1
7Г/4
43. J{y) = f [{y'f cos2 X + .x'^yy' + жу2 - 2y' cos^ i] dx, y@) = 0, у (J) =
- J_
~ V2-
2
44. J(y) = I
1
, ^ + 2^yy'+-4= - 2v/^y'
dx, y(l) = 2, yB) = 5.
1
45.
«^(y) = / A+ж^)(у')^-4a;y' + yy'sin^a; +-y^sin2x
dx, y@) = 0,
y(l) =ln2.
228
Глава 6. Элементы вариационного исчисления
46. J{y) -.
47. J{y) -.
48. J{y) -.
49. J{y) -.
50. J{y) =
51. J{y) =
52. J{y) :
-I
0
2
Ч
0
2
0
7Г
= /
0
1
0
7Г
0
7Г
53. J{y)
1
= /
(y'J + у2 _ 23.yj c(x-, y@) = 1, y(l) = 1 + e.
4(y')^ + y^ - бе^у'] dar, y@) = 2, yB) = e"! + e^.
4(y')^ + y^ + 4xy] da;, y@) = 1, yB) = e - 4.
{y'Y + 8y' sin^ a; + 4y] dx, y@) = 0, y(ir) = n\
{y'Y + у2 + x'^y'] dx, y@) = 1, y(l) = 1 + e-\
{y'f + y^ - 4ysinx] da;, y@) = 1, уGг) = ё^.
[y'f + y^ + 10y'(a; + sin^ x)] dx, y@) = 6, y{ir) = 5 + e"'^.
4a;yy' - {y'Y - 4y^ + A2a;2 - 4)y] da;, y@) = 0, y(l) = 1.
54. J(y) = / (y')^ + 2yy'sina; + f cosa; + —y^ + 20a;*y j
dx, y(l) = -1,
yB) = 0.
4
55. J{y) = 1
1
2
56. J(y) = У
M _ V _ (y'J - ^1
a; a;-'
da;, y(l) = yD) = 4.
1 da;, y(l) = 2, yB) =
4 ■
§ 19. Простейшая вариационная задача
229
57. J{y) = j [24х% - уу' - х^{у')^] dx, уA) = 1, уB) = -7.
58.
J{y) = j [x''{y^f + уу' + Пху] dx, уA) = 1, уB) = 5.
59. J{y) = / I ( i - А ) у2 ^ 2уу' \пх - A{y'f - lOy
X Х'-
dx, уA) = -1,
60
УD) = 0.
3 (х^
{y'f + хуу' + т2/^ + тг - 6 1 у
4" V 2
da;, у@) = 5, уB) = е.
61. J(y) = у [l2a;y - ^^уу' - 3(y')^
1
X
dx, уA) = -, уB) = 0.
62.
1
J{y) = f [{у'? - 2уу' cos а; + D + sma;)y2 + 4Bа;2 - 3)у] dx, у@) = 2,
УA) = е2.
2
63. J(y) = y"e3-[(y'J + 4y2]da;,y@)
ei"-l,yB)=0.
--«=/©'4^
1/2
1
d^,y(^) = §,y(i) = o.
65. J{y) = У" e^ [(y'J + 6у2] dx, y(-l) = 0, y(l) = e^ -
e-3.
66.
2
^(y) = / [(y')^ + 6 (I)'] dx, y(l) = 0, yB) =
31.
4 '
230
Глава 6. Элементы вариационного исчисления
1
67. J{y) = y"|i(y')^ + y2/'tgx+f2+2-^^jy-^ + 3ychx
dx, у{0)
= -1,уA) =2sh2-chl.
7г/4
^2 , у
уу' arctg х - (у') + ^ _^2) ~ '^У + ^^У ^^•'^
dx, у@)
. т = /
1
. J{y) = J [бжу' - ^у2 - ж2^(у'J] dx, у ('i') = -1, уA) = 1.
1/4
2
70. J{y) = [ \-{y'f + \уу' - Щ^ dx, уA) = -1 уB) = 0.
J \Х X J
3
71. J(y) = / [2v^(yr + 4= - ^
У [ ху/х х-Ух
dx, уA) = -2, уC) = 2.
72.
4
J(y) = /" [l5V^.y + Ъх'^уу' - x\y'f\ dx, уA) = 1, уD) = -3.
73
74.
75.
76.
31
'l6'
1
J[y) = У [4а;3(у'J - бх^уу' - Зу] dx, у Q^ = i, уA) = ^.
1/3
2
J{y) = j [Ахуу' - x\y'f + 4ж2у] с/х, у Q") = уB) = i.
1/2
1
J{y) = I [Ъх'у - уу' + x\y'f] dx, у Q) = ^, уA) = 1.
1/2
§ 19. Простейшая вариационная задача
231
2
2„ / „3/ /ч2 , %
77. J(y)= / \Ъх'уу'- х\уГ +
dx, уA) = О, уB)
•-""' = /
1
3
.Л») = /
1
3
■■'«=/
1
4
2
е
1
1
е
1
е
1
2
87. J(y) = I
79
80
81
82
83
84
85.
2а;у2 + 2х'^уу' + x''{y'f + 12х2у] dx, уA) = 2, уB) = 5.
%ху - х2(у'J - х^уу' -{х + 6)у2] dx, уA) = О, уC) = -6.
a;^(y')^ + х^уу' + жу^ + 4а;у] dx, уA) = уC) = 4.
х'^уу' + 8а;2у - а;2(у'J + (х - 2)у2] dx, уB) = О, уD) = -8.
а;^(у')^ + 6y^ + lOOyx^lnx] dx, уA) = О, у(е) = Зе^.
х''(у')^ + 18х2у2 + ЭОх^у + 16х^у'] dx, уA) = О, у(е) = бе^.
x^(y')^ + 8ху2 + 72ух^ 1пх] dx, уA) = 1, у(е) = Ъе^.
Зх5(у')^ + 15х^у2 + 36х\ - 14х%'] dx, уA) = 1, у(е) = 2е2.
Zx\y'f - ЪАх^у' + Зх2у2 - 84хЗу] dx, уA) = 2, уB) = 10.
x2(y')^ - Юхуу' - Зу2 - 4у] dx, уA) = 4, уB) = 7.
232
Глава 6. Элементы вариационного исчисления
88. J{y) = [ [x^iy'f - Пх'^уу' - 3x2/2 - Юх^у] dx, у{1) = 3, уB) = 10.
1
2
89. J{y) = J [а;2(у'J - Uxyy' -у^ - ^ху\ dx, уA) = 2, уB) = 6.
90. J{y)
1
^'^ir^y'
dx, уA) = 1, уD) = 8.
Найти значения вещественного параметра а, при которых на допустимой
экстремали достигается минимум (91—93):
1
91
о
1
92
о
1
93
о
Найти допустимые экстремали (94—101):
1
94
о
1
95
о
7г/2
96. J{y) = J [{y'fsmx + 2ycosx]dx,y{^^^ = ^'^ (D = i*
7г/4
1 г
1
Ау) = I [у ~ 2у' + а(уТ] dx, у@) = О, уA) = 1.
о
1
. J{y) = 1 [(уТ + axiy'f] dx, у@) = О, уA) = In |1 + а|.
о
1
J{y) = J[x^x^^y'^ a(y')^] dx, у@) = О, уA) = 1.
о
?и допустимые экстремали (94—101):
1
Лу) = |у"(уТй^, у@) = О, уA) = 1.
о
1
Ау) = I [уЧу')'' + 9у2] dx, у@) = О, уA) = -5.
97.
Лу) = | (^) -^ху'^у
dx,y{0) = l,y{l) = e-\
§ 19. Простейшая вариационная задача
233
J{y) = 1 [Inу' - Зуу' - ху'] dx, у{1) = -1п2, 2/B) = 0.
98.
99. Jiy)
1/2
у + ху' --{y'f
dx,y{0) = ly(\ V2-
100. J{y) = I [у'еУ + x\y'f] dx, y(l) = 3, yB) = 2.
2
101. J{y) = J\^y'siny+^{y')A
dx, y{l) = 0, yB) = 3.
В задачах A02—105) показать, что допустимая экстремаль не дает
экстремум функционала:
тг
■ т-1
О
[у) - уу +2ysma;
dx, у@) = О, уGг) =
Уз
{уГ - У + 18у
dx, у@) = 4, уGг) = 0.
104. J{y)
105. J{y)
= / [(V)^ -
О
7Г
25
Г + 68е^у
)^ - ттг/^ + бОжу
10
dx, у@) = 9, уGг) = 9е^.
dx, у@) = О, уGг) = 1б7г.
Показать, что простейшие вариационные задачи A06—107) не имеют
смысла:
1
106. J{y) = j [х^у' + 2ху] dx, у@) = О, уA) = 1.
о
2
107. J{y) = I ^ [ху' - у] dx, уA) = О, уB) = 2.
234
Глава 6. Элементы вариационного исчисления
Ответы к задачам § 19
Примечание. В ответах у{х) обозначает допустимую экстремаль,
абсолютный минимум обозначается абс. min, а абсолютный максимум
обозначается абс. max.
1. у{х
3. у{х
5. у{х
7. у{х
9. у{х
11. у{х
13. у{х
15. у{х
17. у{х
19. у{х
21. у{х
23. у{х
25. у{х
27. у{х
29. у(д;
sha;
she
, абс. min.
Ino; ^
= о; + :;—-, абс. mm.
1пЗ
= -е^^, абс. min.
о
= —г, абс. min.
х^
= —, абс. min.
X
2sh|
= 7^, абс. min.
^ ж^ In о;, абс. min.
2. у(а;
4. у(а;
6. у{х
8.у{х
10. у(^
12. у{х
14. у(а;
= a;^D1na; + 3), абс. min. 16. у{х
= a;^C1na; + 2), абс. min. 18. у{х
= —— In ж, абс. min.
8
= Ino; + 1, абс. min.
3 1 ^ .
= X -\—, абс. mm.
X
1 .
= X -\—;=, абс. mm.
у/х
\пх
Ы2
, абс. min.
= eh-, абс. max.
20. у{х
22. у{х
24. у{х
26. у{х
28. у{х
30. у(а;
1 — In ж
абс. min.
sh2x
—^r^— 1, абс. mm.
o2x
1
= e — - cos a;, абс. min.
In a; h 2, абс. min.
X
shx 1
shTT 2
sin a;, абс. min.
Л(.-1,-...с....
= x\nx, абс. min.
= д:^D1na; — 5), абс. min.
= In a;, абс. min.
= In sin a;, абс. mcix.
= I + —^ абс. min.
1 ,
= Ж H—, абс. mm.
X
2 1 ^ .
= ж H—-=z, абс. mm.
= 1 , абс. max.
X
= sh2a;, абс. min.
§ 19. Простейшая вариационная задача
235
31.
32.
33.
35.
36.
38.
40.
41.
42.
44.
46.
48.
50.
52.
53.
55.
57.
59.
61.
63.
у{х]
у{х]
у{х)
У{х]
У{х]
У{х]
у{х]
У{х]
у{х
У{х]
У{х.
У{х.
у{х
у{х
у{х
у{х
у{х
у{х
у{х
у{х
— 4х, абс. min.
= l4i" -^J+^'"^'^
9 За; ^ ^
= о;" + — + 1, абс. max.
= —-tgx -г sin о; + 1, абс.
— x•^, абс. max.
= v 4 — а;2, абс. min.
2 1 ^ .
= X , абс. mm.
х
) = -(sinо; - COSX + 1), абс.
1 2
1 = -о; + 1 , абс. min.
2 X
' = a;^ + 1, абс. min.
1 = о; -f е^, абс. min.
X
1 = е2 — 2х, абс. min.
1 — X + е~^, абс. min.
. min.
34. у{х)
min.
37. у(х)
39. у[х)
min.
43. у{х)
45. у{х\
47. у{х)
49. у(а;]
51. у(х)
1 = е"^ -f 5 -f sin2x, абс. min.
\ — х^, абс. max.
4 з; X
1 — —^ -^ абс. max.
о; 4 4
3 2 .
1 = —о; Н—, абс. mcLX.
X
2 "^
) — X — 2а;2, абс. max.
) = a;^ — -о;^, абс. max.
) = ^10-42^ _ е^^ абс. min.
54. у(а;'
56. у{х\
58. у(а;)
60. у(а;^
62. у[х)
64. у(а;'
= 1, абс. шал.
= A — х)е~'^ + -а;^, абс. min.
= sin о;, абс. min.
= In A + х^), абс. min.
= е~2 + е^, абс. min.
= sin 2а; + 2a;^ — тго;, абс. min.
— е^ •\' sin о;, абс. min.
— х^ — 2а;^, абс. min.
2 1 ^ .
= о; Н—^, абс. mm.
х^
2
= За; , абс. min.
X
= 62 + 4 - a;^, абс. min.
= e^^ — а;^ -f 1, абс. min.
= х^, абс. min.
X
236
Глава 6. Элементы вариационного исчисления
65. у{х)
67. у{х)
69. у{х)
71. у{х)
73. у{х)
75. у{х)
77. у{х)
79. у{х)
81. у(а;)
83. у{х)
84. у(а;)
85. у(а;)
86. у{х)
88. у(а;)
90. у{х)
92. у(д;)
94. у(а:)
96. у{х)
98. у(д;)
2sh2a; — chx, абс. min. 68. y{x
Ay/x — 3, абс. max. 70. y(a;
a; , абс. min.
X
= -77 — y/x, абс. max.
5x x'^
= -j —, абс. max.
= —о Tj ^6c. max.
«2
72. y{x
74. y(a;
76. y{x
78. y(a;
80. y(a;
82. y{x
X — X , абс. max.
2x — x^j абс. max.
5x^A — ж + xlno;), абс. min.
a;^(l + 31n^a; — In a;), абс. min.
x{2x — 1 + In a:), абс. min.
3 1 ^ .
= X :r, aoc. mm.
x"^
= 2 sh Зж 4- sh X, абс. max.
= --x'2 — X 2 абс. mm.
2
2 ^
= —ж H—7=, абс. max.
л/х
= -—, абс. min.
ox
x + 1
, абс. min.
X 4-1, абс. min.
a; H—, абс. min.
X
= E1na; — 2)a;^lna;, абс. min.
= X + X, абс. min.
= 2x^ + ж, абс. min.
= x\/x, абс. min.
= ln|l + ax\, a > 0.
= |.„[l+(e!-lL
87. y{x) =
89. y{x) =
91. у{х)
Зж + 1, абс. min.
a; + ж, абс. min.
= a; +
a;*^ — a;
4o
o>0.
7Г
= a; —
1 ^
93. y{x) =
95. у{х)
97. y(a;)
99. y(a:)
sh-7=
, a^O.
sh
•\/a
-\/9а:2 + 16х.
1
v/1 + (e2 - l)a
-(xH-lJ.
§ 20. Обобщения простейшей вариационной задачи 237
100. у{х) = 1 + -. 101. у{х) = ж^ - 1.
X
§ 20, Обобщения простейшей вариационной задачи
1. Задача со свободным концом и задача вез ограничений.
Рассматривается
J{y) = / F[x,y{x),y{x)]dx,
где функция F{x,y,p) удовлетворяет тем же условиям, что и в
предыдущем параграфе. В отличие от предыдущего § 1 функция у{х) должна
удовлетворять лишь одному граничному условию у{а) = А,
Задачей со свободным концом {х = Ь) называется задача нахождения
слабого экстремума J{y) в классе непрерывно дифференцируемых
функций j/(x), удовлетворяющих условию у (а) = А.
Если дважды непрерывно дифференцируемая функция у{х) является
решением задачи со свободным концом, то необходимо она удовлетворяет
уравнению Эйлера
ар ^_d_aF _
ду dx ду'
и граничному условию вида
dF[x,y{x),y'{x)]
ду'
= 0.
х=Ь
Решение уравнения Эйлера, удовлетворяющее условию j/(a) = Л и
указанному условию при X = bj называется допустимой экстремалью задачи
со свободным концом.
Задачей без ограничений называется задача нахождения слабого
экстремума J (у) в классе непрерывно дифференцируемых функций j/(x), не
удовлетворяющих каким-либо граничным условиям при х = а и х = Ь.
Дважды непрерывно дифференцируемое решение у{х) задачи без
ограничений необходимо удовлетворяет уравнению Эйлера и граничным
условиям вида
дР[х,у{х),у'{х)]
ду'
дР[х,у{х),у'{х)]
ду'
= 0.
х=Ь
238
Глава 6. Элементы вариационного исчисления
Пример 1. Решить задачу со свободным концом
2
Лу) = 1
""^ "yy'-{yV + Sxy'
X
dx, уA) - 0.
Л Уравнение Эйлера имеет вид
Экстремали задаются формулой
С*
у{х) = -^ + С2х'^ -х^.
х^
Граничное условие при х — 2 находим из уравнения
ар
ду'
х=2
6ж - Г2
X
у~2у' + 8х
= -2у'B) + 16 = 0.
х=2
Отсюда j/'B) = 8. Это условие вместе с условием уA) = О определяют
допустимую экстремаль у{х) = х^ — х'^.
Пусть г]{х) — произвольная непрерывно дифференцируемая на [1,2]
функция, для которой 7^A) =0. Тогда
AJ(y) = J(y + r/)-J(y)
•2
-1{
6ж-12
X
{У + Гт' + 'П')-{У'^-П'?+
бх — 12 1
+ Ъх{у' + V) — уу' + {у'У - Ъху' \dx =
2
Лба; — 12 1
— (то' + уг]' + щ') - 2ijri - [rlf + bxrl I dx.
1
Если проинтегрировать по частям слагаемые в этом интеграле,
содержащие ту', воспользоваться уравнением Эйлера для у{х) и условиями
у'B) = 8, 7?A) = О, то получим
Д7(у) = -|
W + -,^'
dx < 0.
х^
§ 20. Обобщения простейшей вариационной задачи 239
Значит, допустима51 экстрема^ль у{х) в рассматриваемой задаче дает
абсолютный максимум. А
Пример 2. Решить задачу без ограничений, если
1
Jiy) = l[{y'f + y' + 2ye-]dx.
О
л Уравнение Эйлера у" ~ у — е^ дает множество экстремалей задачи
у{х) = Cie~^ + С2е^ + т:^^^- Граничными условиями для у{х) являются:
у'{0) = у'A) = 0. Определив Cj и Сг из этих граничных з'словий, находим
допустимую экстремаль
^^ ^ A - 2е2) е^ - е2-^ 1 ^
^(") = W^) ^2"'-
Для всякой непрерывно дифференцируемой на [0,1] функции ri{x) имеем
i
^J{y) = J{y + г])- J{y) = l[2y'r/ + {r]'f + 2уг] + г]^ + 2e^r]]dx =
о
1 1
= 2у'{х)ф)\1^^ + 1Фу + 2е- - 2y"]dx + ^[(V)^ + rj"] =
О о
1
= jlirir + ri'Vx,
о
так как проинтегрированная часть обращается в нуль в силу граничных
условий у'@) = у'A) = О и первый интеграл равен нулю в силу того,
что у{х) удовлетворяет уравнению Эйлера. Поскольку из полученного
равенства следует А J {у) > О для всех рассматриваемых г?(х), то у{х) дает
абсолютный минимум. А
Решить задачу со свободным концом A—10):
2
1-
о
J{y) = l[2xy + {yT]dx,yiO)=0.
240
Глава 6. Элементы вариационного исчисления
1
2. Ну) = J[2y + Qy' + ivT] dx, y(o) = 0.
0
2
3. J{y) = I [x^y'f + 6y2 + 2x'y] dx, y(l) = ^.
1
1
4. J{y) := f[y + xy' + {y'f] dx, y@) = 0.
0
2
5. J{y) = J [x^yf + 12?/^] dx, y(l) = 97.
-<v)=/F-!^
dx, y{2) = -.
7. J{y) = J [xHy'f + W] dx, yB) =
49
24'
г.
8. J{y) = y^ \x^{y'f - ^{x^ - x)yy' + 4y2 + Sx'^y'] dx, yB) = -7.
1
3
9. J(y) = / [Syy'lnx - xiy'f + бжу'] <^a;, yC) = 15.
1
Решить задачу без ограничений A1—12):
т/г
11. Jiy) = I [4у2 + (у'J + 2усо8ж] dx.
dx, уB) = 10.
§ 20. Обобщения простейшей вариационной задачи
241
12.
Л.) = /
, ;.9 V^ 2у1пх
^B/0^ + — +
X X
dx.
Найти допустимые экстремали в задаче без ограничений A3—15):
13. J{y) = J[2y + уу' + хНу')^] dx.
14.
J{y) = J [^У- уу' + <У'?] dx.
15.
1
J{y) = j[2yy'^-{y'f]dx.
Ответы к задачам п. 1 § 20
1. у = — 2а;, абс. min.
6
^•^=2^б-^У'^^'-^^^-
3 96 ,
5. у = X Н—J, абс. mm.
х^
7. у = X + г-^, абс. mm.
6Х^
2. у = —За;, абс. min.
X
4. у = —-, абс. min.
6. у = х Н—, абс. min.
X
8. у = 1 — 2а;^, абс. min.
10. у = х^ + х, абс. min.
mm.
9. у = 2х^ — X, абс. max.
^^ . 1 /2ch2x Л ^
11. у = ~- I —; hcosx 1, абс
5 \ 8П7Г /
1 / в \ X
12. у = [х j — Inx, абс. min. 13. у = In— —
Inx + 2
14. у = X + 1 + -j^. 15. у = 0.
X In 4 + 4
-6.
2. Функционалы, зависящие от двух функций. Рассматривается
242 Глава 6. Элементы вариационного исчисления
задача нахождения слабого экстремума
J{yuy2) = / F[x,yi{x),y2{x),y[{x),y2{x)]dx,
а
где F — заданная дважды непрерывно дифференцируемая функция своих
аргументов, в классе непрерывно дифференцируемых пар функций yi{x),
У2{х) на [а, Ь], удовлетворяющих граничным условиям
yi{a) = Ль У2{а) = ^2, уЛЬ) = Bi, У2{Ь) = ^2,
где ^1, ^2, ^1, ^2 ~ заданные числа.
Если дважды непрерывно дифференцируемая на [а, Ь] пара функций
2/1 (х) J 2/2 (х) дает экстремум рассматриваемому функционалу, то
необходимо yi{x), 2/2(х) на [а,6] удовлетворяют системе уравнений Эйлера
ду1 dxdy[ ' ду2 dx ду2
Всякая пара функций, удовлетворяющая системе уравнений Эйлера,
называется экстремалью. Экстремаль, удовлетворяющая заданным граничным
условиям, называется допустимой экстремалью.
Пример. Исследовать на экстремум функционал, если
2
JB/b2/2) = J[6y^i+x\y[L{y'2?]dx, 2/i(l) = 2/2A) = 1, 2/1 B) = 4, 2/2B) = 2.
1
Д Система уравнений Эйлера имеет вид
f 12у1 - [2х^у[]' = О,
Отсюда находим экстремали yi{x) = Cix'^ -\—з", 2/2(^) = Cix -f С2.
Подставляя 2/1 (^) J 2/2(^) в заданные граничные условия, получаем допустимую
экстремаль yi{x) = х^, у2(^) = ^•
Покажем, что на допустимой экстремали заданный функционал имеет
о о
абсолютный минимум. Пусть (см. §1) rii{x) € С^[1,2], г]2{х) € С^[1,2].
§ 20. Обобщения простейшей вариационной задачи 243
Тогда
^Jim^m) = J {ill +г?1,у2 + Г/2) - Jivum) =
2
- |[6Bу1Г?1 + 'пЬ + х'{2у[г,[ ~Ь G?;J) + {2у^2 + Ш^)]с1х.
1
Интегрируя по частям слагаемые, содержащие г][ и 772, и учитывая, что
7/1 A) = rjiB) = rj2(l) = rj2B) = О, отсюда находим
2 2
AJiyum) = f[12yi - {2х%У]7пс1х - 2 f гУ^г]2с1хА-
1 1
2
1
Первые два интеграла равны нулю, так как yi{x) и У2{х) удовлетворяют
системе уравнений Эйлера. Поскольку последний интеграл
неотрицательный, то AJ(yi,y2) > О при всех рассматриваемых rji{x) и г]2{х). Значит,
пара функций yi{x), У2{х) дает абсолютный минимум функционала. А
Исследовать на экстремум функционал, если:
1
1. J{yuy2) = j[{y[? + {y2?]dx, ш@) = У2@) - о, yi(l) = У2{1) = 1.
о
1
2. 7(уьу2) = j[yl + {У\? + {У2?¥х. yi@) - о, у2@) = 1, шA) = 1,
о
У2A) = е.
1
3. 7(уьУ2) = |Ь? 4- У2^ + (у1)^ + [y'2?]dx. ш@) = У2@) - 1, шA) =
о
= У2A) = е.
2
4. ^(Ш,У2) = j[ny\ + У2^ + x^iy'i? + {У2?¥х, yi{l) = 1, ^2A) = е,
yiB)-8, У2B)=е2.
244 Глава 6. Элементы вариационного исчисления
Найти допустимые экстремали E—11):
7г/2
5. Дуиу2) = Jliy'if + (у^J - 2yiy2]dx, yi@) = 1, 2/2@) = --1, ш (I) =
О
1
6. АуиУ2) = У^[2у1+у1 + (у1)Ч(у^J]^х,ш@) =0,2/2@) = 1,2/1A) = ^,
о
.-1
2/2A) = е-
7Г/2
7. J(yi,2/2) = У^[2У1У2 + (Уl)^ + {y2?]dx, 2/1 @) = У2@) = 1, уг (^) =
о
= У2(|)=е1.
1
8. J{y\,y2) = / [У1У2 + у1У2]б(х, yi@) = 2/2@) = 1, yi(l) = 2/2A) = е.
о
7г/2
9. J{yi,y2) = / [у1у2 - ШЫ^^» Ш@) = У2@) = О, у1 (^) = у2 (I) = 1.
О
1
10. 7(уьУ2) = j[2yl + 2у1У2 + {y[f - {y'2?]dx, yi@) - У2@) = о, у1A)
о
= 2she, у2A) = -2she.
7г/2
п. 7(уьу2) = |[2ylУ2-2y^ + (yl)^-(y^)^]dx,yl@) =У2@) =0,у1 (|)
12. Показать, что задача на экстремум при
1
^(УЬУ2) = J[yiy2 + y2y[]dx, yi@) = у2@) = о, yi(l) = У2A) = 1
о
не имеет смысла.
§ 20. Обобщения простейшей вариационной задачи
245
Ответы к задачам п. 2 § 20
1. yi{x) = У2(^) = ^, 2i6c. min.
3. yi{x) = У2{х) = е^, абс. min.
5. yi{x) = е^, у2{х) = -е"^.
7. yi(x) =У2(^) = е^.
9. yi(^) = У2{х) = sinx.
11. yi{x) = xcosx + sinx, У2{х) = жсозж — sino;.
3. Функционалы, содержащие производные второго
порядка. Рассматривается задача нахождения слабого экстремума
b
2. yi{x)
4. yi{x)
6. yi{x)
8. yi{x)
10. yi(x)
= X, У2{х) = e^, 2i6c. min.
= x^, У2(^) = e^, 2i6c. min.
д;2
= У2(ж) = e^.
= 2shx, У2(^) = ~2shx.
J{y) = j F[x,y{x),y'[x),y"[x)]dx,
где F — заданная трижды дифференцируемая функция своих аргументов,
в классе дважды непрерывно дифференцируемых функций у{х) на [а^Ь]^
удовлетворяющих граничным условиям
у{а) = Аи у'{а) = ^2, у{Ь) = Ви у\Ь) = ^2,
где Лх, ^2, Bi, jB2 — заданные числа.
Если четырежды непрерывно дифференцируемая на [а^Ь] функция
у{х) дает экстремум рассматриваемому функционалу, то у{х) необходимо
на [а, Ь] удовлетворяет уравнению Эйлера-Пуассона
дР d дР d^ дР
= 0.
ду dx ду' (ix^ ду"
Всякое решение этого уравнения называется экстремалью. Экстремаль,
удовлетворяющая заданным граничным условиям, называется допустимой
экстремалью.
Пример. Исследовать на экстремум функционал, если
1
J{y) = f[{y'? + {y"?]dx, у@) = у'@) = О, уA) = е - 2, у'{1) = е - 1.
246 Глава 6. Элементы вариационного исчисления
Л Уравнение Эйлера-Пуассона имеет вид
-2y" + 2y^^^=0.
Экстремали задаются формулой
у = Cie^' + C'ze-'^ + С^х + С4.
Используя граничные условия, получаем допустимую экстремаль
у[х) — е^ - X - \.
Покажем, что у{х) дает абсолютный минимум функционала.
Для всякой дважды непрерывно дифференцируемой на [0,1] функции
?7(х), удовлетворяющей граничным условиям
7?@)=V@)=r/(l)=r?'(l) = 0,
имеем
1
ДJ(y) = J{y + П)- J{y) = jWn' + {ri'? + 2yV + {7i"?]dx.
0
Проинтегрируем no частям первое слагаемое один раз, а третье слагаемое
дважды. В силу граничных условий для 7]{х) проинтегрированная часть
обратится в нуль и получаем
1 1
^J{y) = j\-2f + 2y''']rjdx + j[{n'f + {n"?]dx.
0 0
Так как y{x) удовлетворяет уравнению Эйлера-Пуассона, то первый
интеграл равен нулю. Поэтому
1
о
Значит, у{х) дает абсолютный минимум функционала.
Исследовать функционал на экстремум, если:
§ 20. Обобщения простейшей вариационной задачи 247
1
1. J{y) = j[^2xy + {y"?]dx, у@) = y'{Q) - О, у{\) = i, у'{1) = ^.
о
1
2. J{y) = j[2e-y - {y"f]dx, у@) = у'@) - 1, уA) = е, у'A) = 2е.
о
7г/2
3. J(y) =: j[2y^mx-\-{y"f]dx, у@) - О, у'@) - -1, у (|) - -1,
1
4. J(y) = |[4(у'J + (y"?]dx, у@) = у'@) = О, уA) = ^(е^ - 3), у'A) =
= ^(e^-l).
2
1
о
1
J {у) = /[У^ + 2{y'f + {y'T]dx, у@) = у'@) = О, уA) = 2she, у'A) =
2е.
7r/2V^
6
J(y) = I [16у2 + (у"J]йа:, у@) = у'@) = у (^) = О, у' (^) =
о
-2\/2shf.
Найти допустимые экстремали G—9):
7г/2
о
7г/4
8
о
Лу) = / Ну"? - {y'?]dx, у@) = у'@) = у (I) = о, у' (I) = 2 -1.
^(у) = 1[{у'Г-ЧуГ¥х, у(о) = у'@) = о, у (^) = |-2, у' (^) = 0.
248
Глава 6. Элементы вариационного исчисления
7г/2
J{y) = fiy^- 2B/')^ + iy"f]dx, у@) = у'{0) = О, у (|) = ^, у' (|)
О
= 1.
10. Показать, что задача на экстремум при
1
Ау) = J[xy" + 2уу' + y']dx, у@) = у'@) = О, уA) = у'A) = 1,
не имеет смысла.
Ответы к задачам п. 3 § 20
1. у{х
2. у{х
3. у{х
4. у{х
5. у{х
6. у{х
7. у{х
8. у(х
9. у(а;
х^ + х^ — x^ 1, абс. min.
4! \5
= е^ + е (х — X ), абс. max
= —sinx + х
7ГХ"
, абс. min.
= - (e^^ - 2х - l), абс. min.
= 2х • shx, абс. min.
= 2sh f x\/2j • cos (xV2V абс. min.
= X — sinx + A — — ) A — cosx).
= cos 2x — sin 2x + 2x — 1.
= xsinx.
§ 21. Изопериметрическая задача
Изопериметрической задачей называется задача исследования слабого
экстремума функционала
о
J{y) = jF[x,y{x),y'{x)]da
§ 21. Изопериметрическая задача 249
в классе непрерывно дифференцируемых функций у{х) на [а,Ь],
удовлетворяющих граничным условиям у{а) = А, у{Ъ) = В и условиям связи
вида
ь
Kj{y) = / Gj[x,y{x),y'{x)]dx = Ij, j = T7n,
a
где A, jB, /j, j = l,n — заданные числа. Здесь F и Gj — заданные дважды
непрерывно дифференцируемые функции, j = 1,п.
Пусть задано лишь одно условие связи
о
К{у) = j G[x,y{x),y'[x)]dx^
L
Введем в рассмотрение функцию
L{x,y,y',X) = F{x,y,y') Л-\С{х,у,у'),
называемую лагранжианом, где параметр А G i? называется
неопределенным множителем Лагранжа.
Если дважды непрерывно дифференцируемая на [а^Ь] функция у{х)
является решением изопериметрической задачи и при этом первая вариа-
о
ция SK[y[x),r]{x)] ^ о для всех г]{х) G С^[а,Ь], то у{х) необходимо на [а,Ь]
удовлетворяет при некотором значении А уравнению Эйлера вида
ду dx ду'
Решения этого уравнения называются экстремалями. Экстремали,
удовлетворяющие граничным условиям и условию связи, называются
допустимыми.
Пример. Решить изопериметрическую задачу, если
J{y) = / {y'fdx, у{0) = 1, уGг) = -1, / ycosxdx = -.
о о
Л Уравнение Эйлера для лагранжиана L = {у')^ + Xycosx имеет вид
2у" = Acosx.
250 Глава 6. Элементы вариационного исчисления
Экстремали задаются формулой у{х) = Cix -\- С2 — --cosx. Используя
граничные условия и условия связи, получаем допустимую экстремаль
у{х) = COSX. Покажем, что на ней изопериметрическая задача имеет
абсолютный минимум.
7Г
Возьмем любую rj{x) G С^[0,7г], для которой / rjcosxdx = 0. Тогда на
о
у{х) 4- г]{х) определен функционал J{y) и можно рассмотреть
7Г
AJ{y) = J(y + rj)- J{y) = I [2y'v' + Wf] dx.
0
Интегрируя no частям первое слагаемое и учитывая, что г/@) = //(тг) = О,
получаем
AJ{y)=^-2 Ifvdx^ ji'n'fdx.
о о
в силу уравнения Эйлера и условия связи для 'q{x)
7Г 7Г
/ y"r]dx = X Tf cos xdx = 0.
о о
Следовательно,
А^(У) = 1Ы
fdx > О
о
и, значит, у{х) дает абсолютный минимум.
Решить изопериметрическую задачу A—10):
7Г 7Г
1. J{y) = / {y'fdx, у{0) = О, у{7г) = 7г, / ysinxdx = 0.
о о
1 1
2. J{y) = J {y'fdx, у@) = О, у{1) = е - 3, У уеЧх = 0.
о о
1 1
3. J{y) = [{y'fdx, у@) = 2е + 1, у{1) = 2, / e'^ydr =
е.
§ 21. Изопериметрическая задача 251
1 1
4. J{y) - j{y'?dx, у@) = О, у{1) = 2, Jxydx = 1.
о о
5. Ау) = 1[у' + (уТ] dx, у@) = О, уA) = -1, 1уе-Чх = ^^^^.
о о
1 1
6. J{y) = 1[У^ + {У'Л dx, у{0) = О, уA) = 4е, |ye^dx = 1 +
е\
1 i
Г. J(y) = / [2ху + {у')^] dx, у{0) = О, 1/A) - 3, /*:rydx = 1.
о о
1 1
7.
0 о
2 2
8. J{y) = J xiy'fdx, у{1) = О, уB) = 12, / xydx = 9.
1 1
9.
о о
7Г 7Г
10. J(y) = / [{y'f Ч-у'^ + 2ycosj:] da.\ у@) = 2, уGг) = -2, / ycosxdx =
о о
= 7Г.
7Г 7Г
J{y) = 1 [2у-\- Зу' + (у')^] dx, у@) = О, уGг) = тг^, fysmxdx = tt^-L
Найти допустимые экстремали изопериметрической задачи A1—14):
1 1
11. J{y) = I [2уу' + (уТ] dx, у@) - уA) = О, J[Axy' + yy']dx = 4.
о о
1 1
12. J{y) = j[yy' + 4V](i:i^, У@) - уA) = О, У [2уу' + [y'f] dx = 4.
о о
1 1
13. J{y) = j [уу' + 2(у')^] dx, у@) = уA) = О, j[yy' - %xy']dx = 8.
о о
252
Глава 6. Элементы вариационного исчисления
i 1
14. J{y) = Jlyy' - 8xy']dx, y{0) = y(l) = 0, y* [yy' + 2{y'f] dx = 8.
0 0
7Г 7Г
Найти минимум J (у) = / (y')^dx, если y@) = ^(тг) = О, / y^dx = 1.
15
1
. Найти минимум J{y) = / [j/^ + (у)^] dx^ если у@) = у{1) = О,
о
1
fy^dx=: 1.
Ответы к задачам § 21
1. у{х
2. у{х
3. у{х
4. у(а;
5. у{х
6. ^(ж
7. ^(ж
8. у{х
9. у(а;
10. у{х
11. у(а;
12. ^(ж
13. у{х
7Г"
= Ж —-- sinx, абс. min.
о
2(е^~1) , ^, ^
= — \- [е — 1)х, абс. mm.
1 — е
= 2е^""^ — X + 1, абс. min.
9х - 5х^ ^
= а,бс. mm.
2
= —хе^~^, абс. min.
= 4x6^, абс. min.
= Зж, абс. min.
= 4 (ж^ — l), абс. min.
X тгх 2
= — + -— Н— sinx, абс. min.
2 2 7г
= 2cosx, абс. min.
= Q{x^ -х).
= ±2\/3(ж-х2).
= б(а;-а;2).
§ 22. Строгий слабый локальный экстремум
253
14. у{х) = ±2^3 {х'^ - х).
15. -1.
16. 1 + 7г2.
§ 22. Достаточные условия строгого слабого локального
экстремума в простейшей вариационной задаче
Рассмотрим простейшую вариационную задачу:
6
Jiy) = / F[x,y{x),y'{x)]dx, у{а) = А, у{Ь) = В,
а
где функция F является трижды непрерывно дифференцируемой при всех
X Е [а^Ь] и всех (у,р) € В?[у,р). Если у[х) — допустимая экстремаль
(см. § 1) этой задачи, то положим
Р(х) =
д'т
ду
/2
у=у(х)
, Q{X) =
d^F d d'^F 1
[ ду'^ dx дуду' J
y=y(^)
Говорят, что выполнено усиленное условие Лежандра, если Р{х) ф О для
всех X Е \а^\}\.
На [а, Ь] рассмотрим задачу для уравнения Якоби:
Р(х)
с?гл(а;)
dx
- Q(a;)^(a;) = О, и{а) = 0.
Если каждое нетривиальное решение и{х) этой задачи не имеет нулей на
(а, Ь], то говорят, что выполнено усиленное условие Якоби.
Теорема. Если: 1) у{х) — допустимая экстремаль, 2) выполнено
усиленное условие Лежандра, 3) выполнено усиленное условие Якоби, то при
Р{х) > О на [а, Ь] у{х) дает строгий слабый локальный минимум J(y), а
при Р{х) < О на [а, Ь] у{х) дает строгий слабый локальный максимум J(y).
Пример. Исследовать на слабый экстремум, если
7г/2
J{y) = I [у'-(у')']^^' 2/@) = О' у(f) = 1-
254 Глава 6. Элементы вариационного исчисления
Л Для нашего примера уравнение Эйлера
2у-^[-2у'] = у" + у = 0
дает экстремали у = Cicosa; -h C2sinx. Граничные условия выделяют
допустимую экстремаль у{х) — sinx.
Усиленное условие Лежандра выполнено, поскольку Р — -—-рг = — 2 <
ду'^
< 0. Уравнение Якоби имеет вид
- 2и = 0.
dx
-2 —
dx
Нетривиальные решения этого уравнения, удовлетворяющие условию
и{0) = О, имеют вид и{х) = Csinx и не обращаются в нуль при всех
х Е @?";7 • Следовательно, выполнено усиленное условие Якоби. Значит,
у{х) = sin .х- дает строгий слабый локальный максимум. А
Исследовать на экстремум A—9):
1. J{y) = [{y'fdx, 7/@) = О, уGг) = атг, а ^ 0.
о
1
2. J[y) = j [{yf + ^{y'f -f у'] dx, y@) - 0, 'y(l) - 1.
0
1
3. J(y) = |^,y@) = 0,y(l)=:l.
0
2
1
2
5. J(y) = y^^,y(l) = l,j/B)=4.
1
2
6. J(y) = Jx^y'fdx, y{l) = 0, yB) = ln2.
§ 22. Строгий слабый локальный экстремум 255
• J{y) = JyHy'fdx, уA) = 2, у{2) = 2ч^.
1
. J{y) = / ^da;, у@) = 1, уA) = е.
О
2
. J{y) = I е-'^ [{y^f - у'] dx, у{\) = е, уB) =
Ответы к задачам § 22
1. у{х) = ах дает строгий min при а > О и строгий шах при а < 0.
2. у(х) = X дает строгий min. 3. у(х) = ж дает строгий min.
4. у(х) = ~х^ дает строгий min. 5. у{х) = х^ дает строгий min.
6. у{х) = In ж дает строгий min. 7. ^(х) = 2>/х дает строгий min.
8. у(^х) = е^ дает строгий min. 9. у{х) = е^ дает строгий min.
список ЛИТЕРАТУРЫ
1. Беклемишев Д. В. Курс аналитической геометрии и линейной
алгебры. — М.: Наука, 1984.
2. Владимиров B.C. Уравнения математической физики. — М.: Наука,
1976.
3. Галеев Э.М., Тихомиров В. М. Краткий курс экстремальных задач.—
М.: Издательство МГУ, 1989.
4. Гюнтер Н.М., Кузьмин Р. О. Сборник задач по высшей математике.—
М.: Физматгиз, 1958, т. 1; 1959, т. 2.
5. Дезин А. А. Общие вопросы теории граничных задач. — М.: Наука,
1980.
6. Краснов М.Л., Киселев А. И., Макаренко Г. И. Сборник задач по
обыкновенным дифференциальным уравнениям. — М.: Высшая
школа, 1978.
7. Кудрявцев Л. Д. Курс математического анализа. — М.: Высшая
школа, 1981, т. 1,2.
8. Немыцкий В. В., Степанов В. В. Качественная теория
дифференциальных уравнений. — М.; Л.: Гостехиздат, 1949.
9. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. — М.:
Наука, 1982.
10. Романко В. К. Курс дифференциальных уравнений и вариационного
исчисления. — М.: Лаборатория Базовых Знаний, 2000.
11. Сидоров Ю.В.,Федорюк М.В., Шабунин Н.И. Лекции по теории
функций комплексного переменного. — М.: Наука, 1982.
12. Степанов В. В. Курс дифференциальных уравнений. — М.: Физматгиз,
1959.
13. Тер-Крикоров A.M., Шабунин М.И. Курс математического
анализа. — М.: Наука, 1988.
14. Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. —
М.: Наука, 1992.