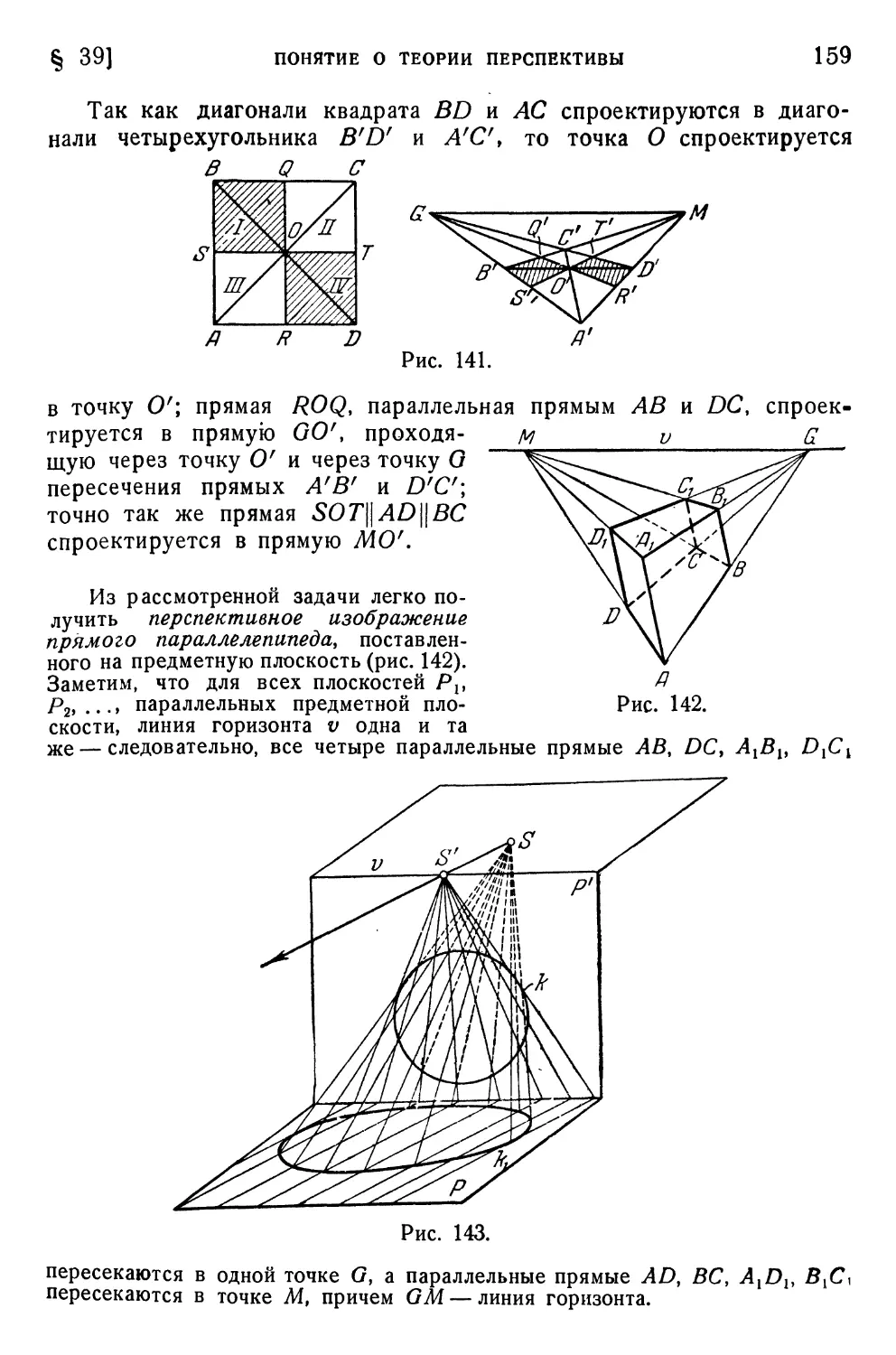
Текст
ФИЗИКО-МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА ИНЖЕНЕРА
Я. Л. ГЕРОНИМУС
ГЕОМЕТРИЧЕСКИЙ АППАРАТ
ТЕОРИИ СИНТЕЗА
ПЛОСКИХ МЕХАНИЗМОВ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1962
ОГЛАВЛЕНИЕ
Предисловие 6
часть I
ЭЛЕМЕНТЫ ТЕОРИИ АЛГЕБРАИЧЕСКИХ КРИВЫХ
И ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Глава I. Несобственные и мнимые элементы в аналитической
геометрии 9
§ 1. Бесконечно удаленная точка прямой . 9
§ 2. Бесконечно удаленная прямая плоскости 12
§ 3. Примеры, иллюстрирующие применение несобственных
элементов 14
§ 4. Пересечение алгебраических кривых 18
§ 5. Пересечение алгебраической кривой с бесконечно удаленной
прямой 22
§ 6. Введение мнимых элементов 25
§ 7. Изотропные прямые 27
§ 8. Циклические точки 29
§ 9. Нахождение асимптот алгебраических кривых 31
§ 10. Некоторые примеры на исследование кривых 33
§ 11. Понятие о классе алгебраической кривой . . . • 36
Глава II. Ряды точек и пучки прямых 38
§ 12. Свойства дробно-линейной функции 38
§ 13. Ангармоническое отношение четырех точек 41
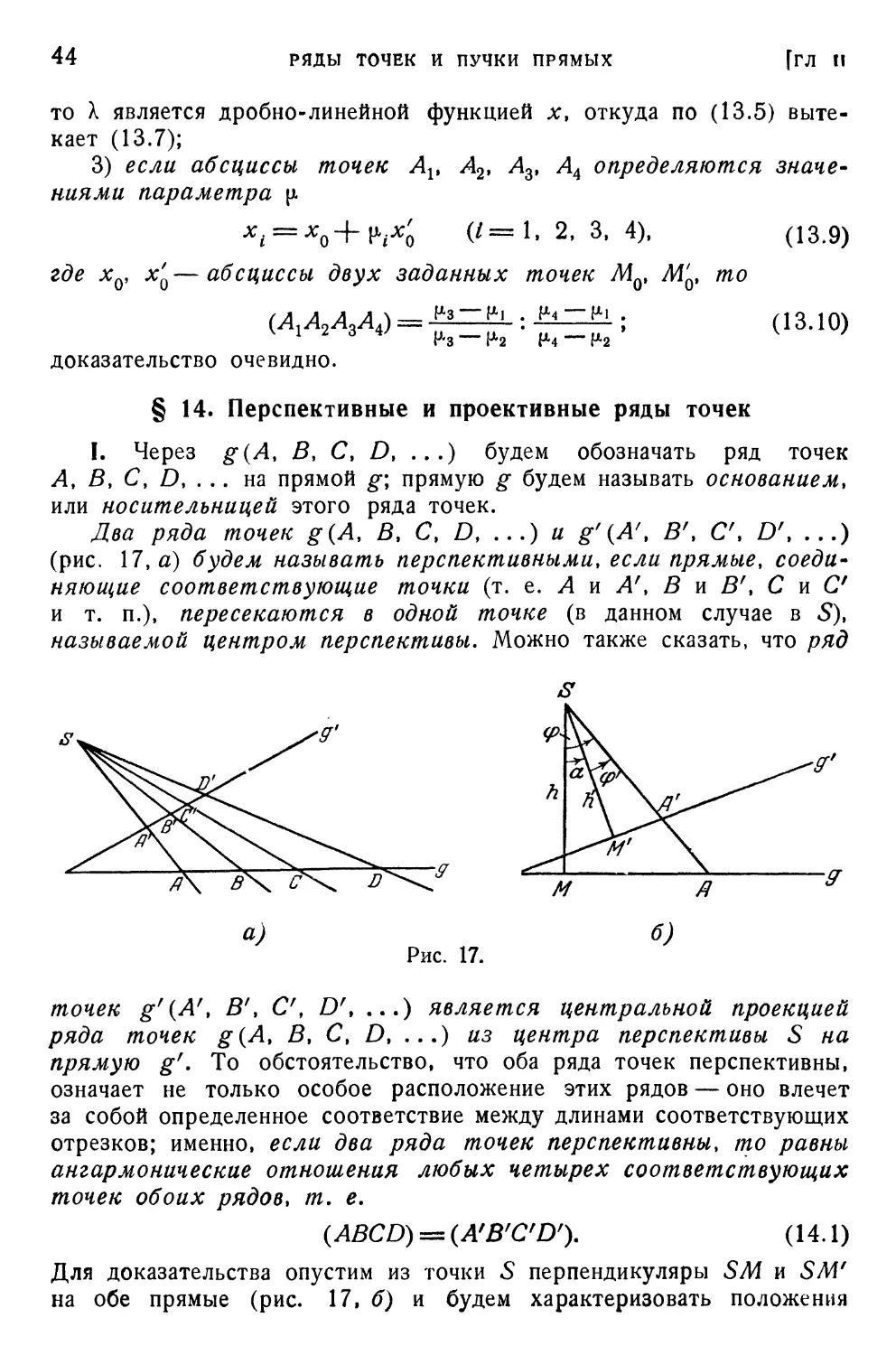
§ 14. Перспективные и проективные ряды точек 44
§ 15. Проективное соответствие на одном основании; понятие об
инволюции 47
§ 16. Пучки прямых. Сокращенные обозначения 54
§ 17. Ангармоническое отношение четырех прямых пучка 56
§ 18. Перспективные и проективные пучки прямых 59
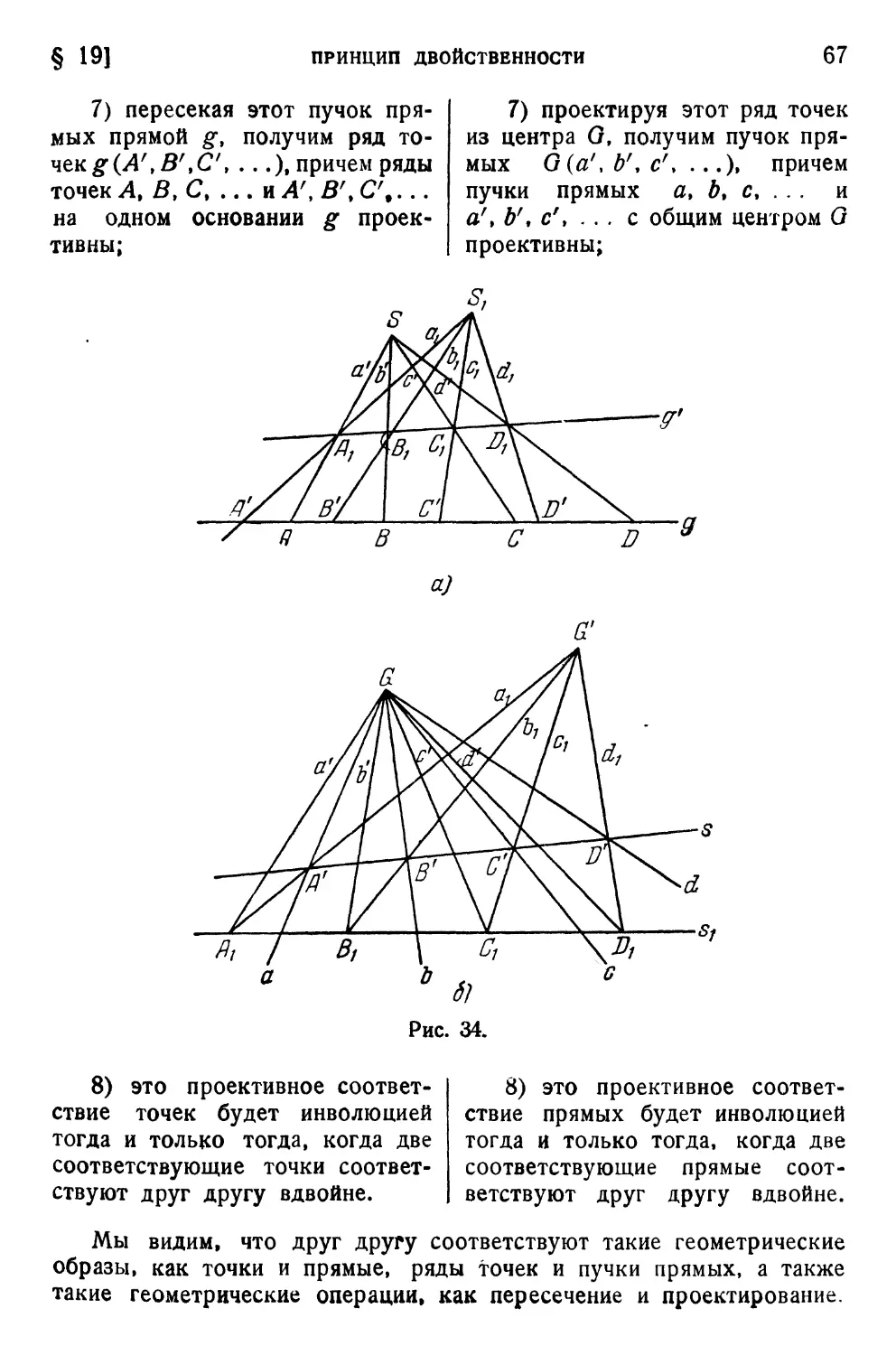
§ 19. Принцип двойственности • 65
Глава III. Образование геометрических форм высших порядков 71
§ 20. Пучки кривых 71
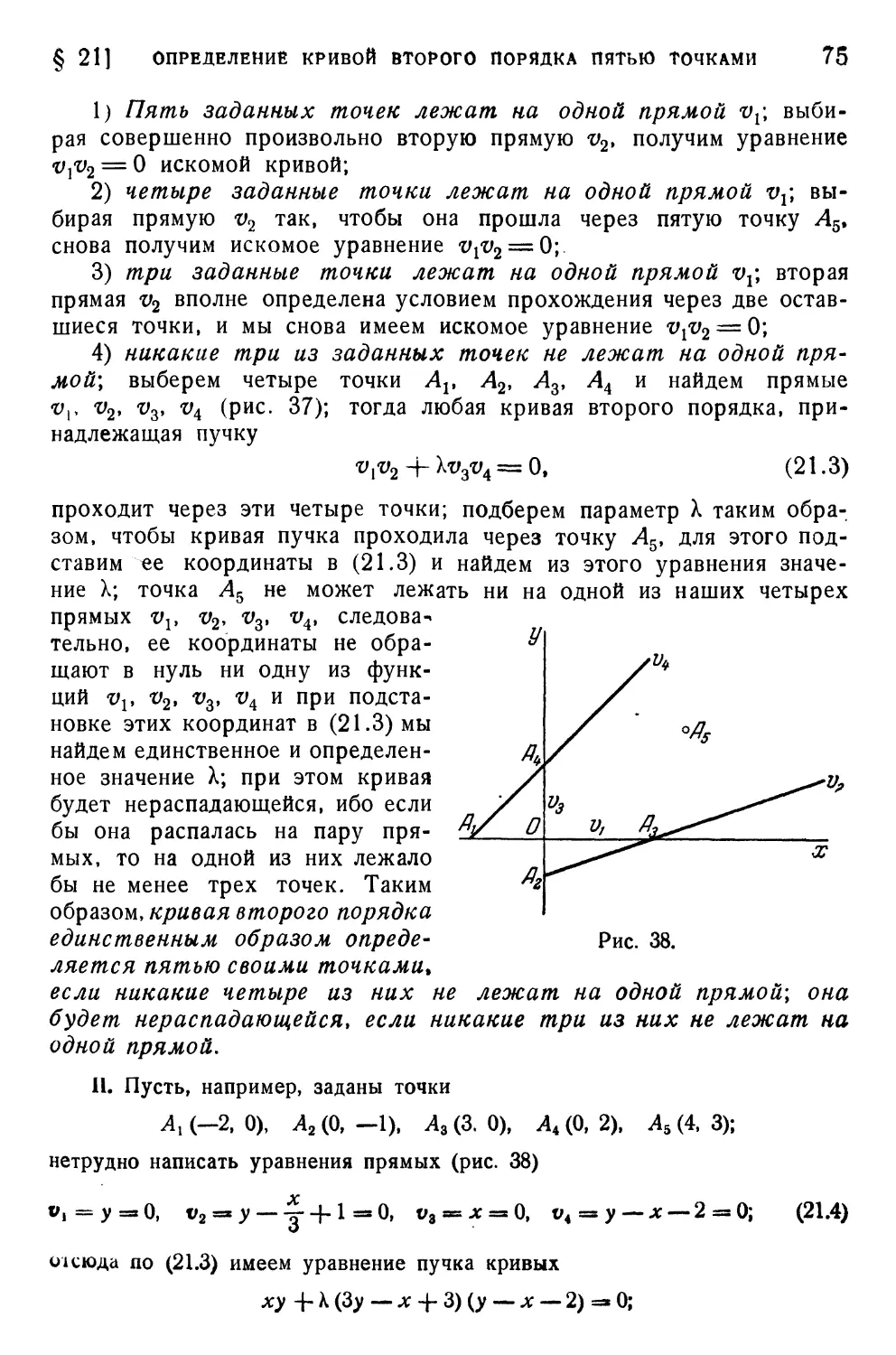
§ 21. Определение кривой второго порядка пятью точками .... 74
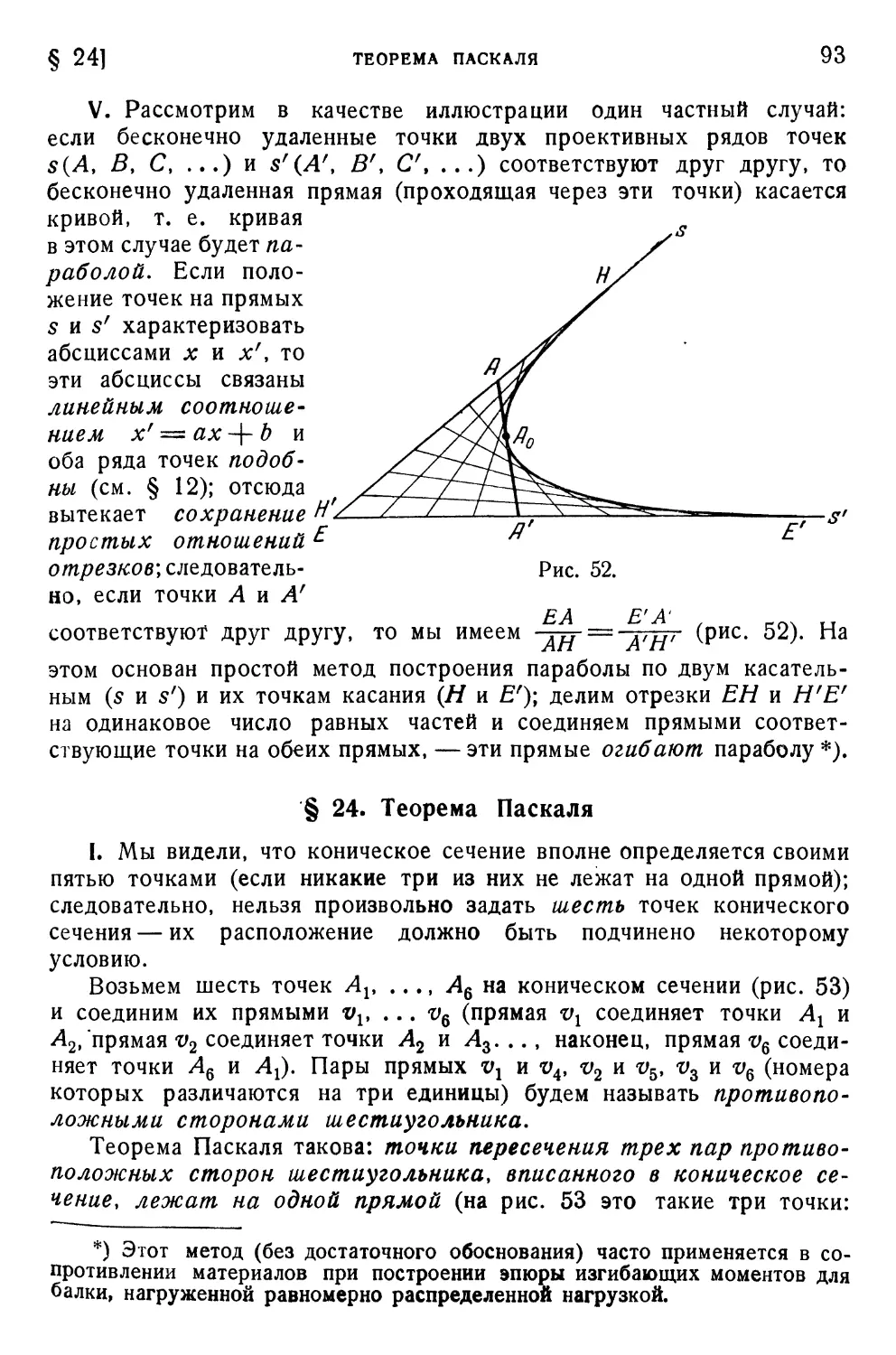
§ 22. Теорема Штейнера 78
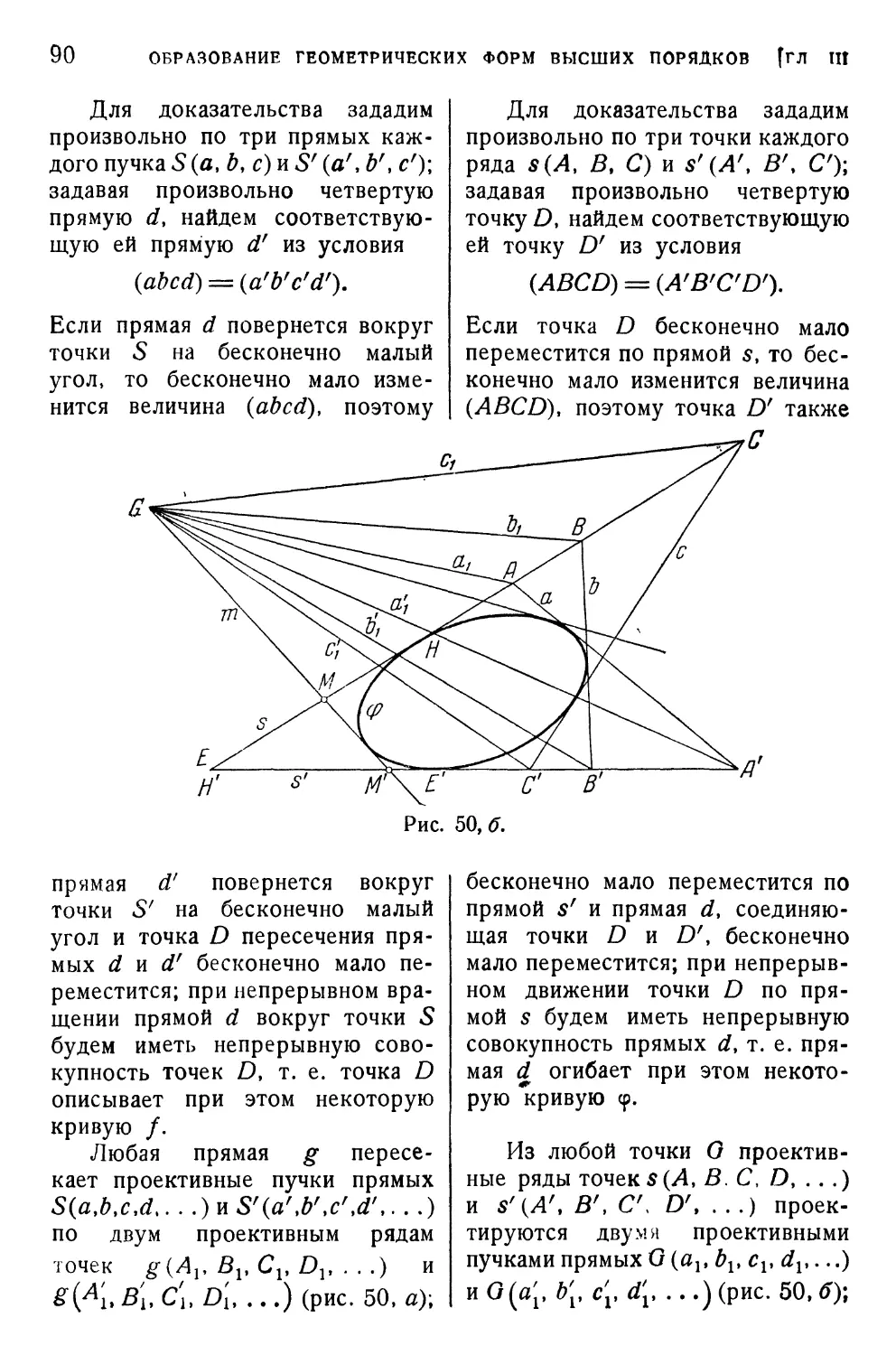
§ 23. Два метода образования кривых 83
§ 24. Теорема Паскаля ' 93
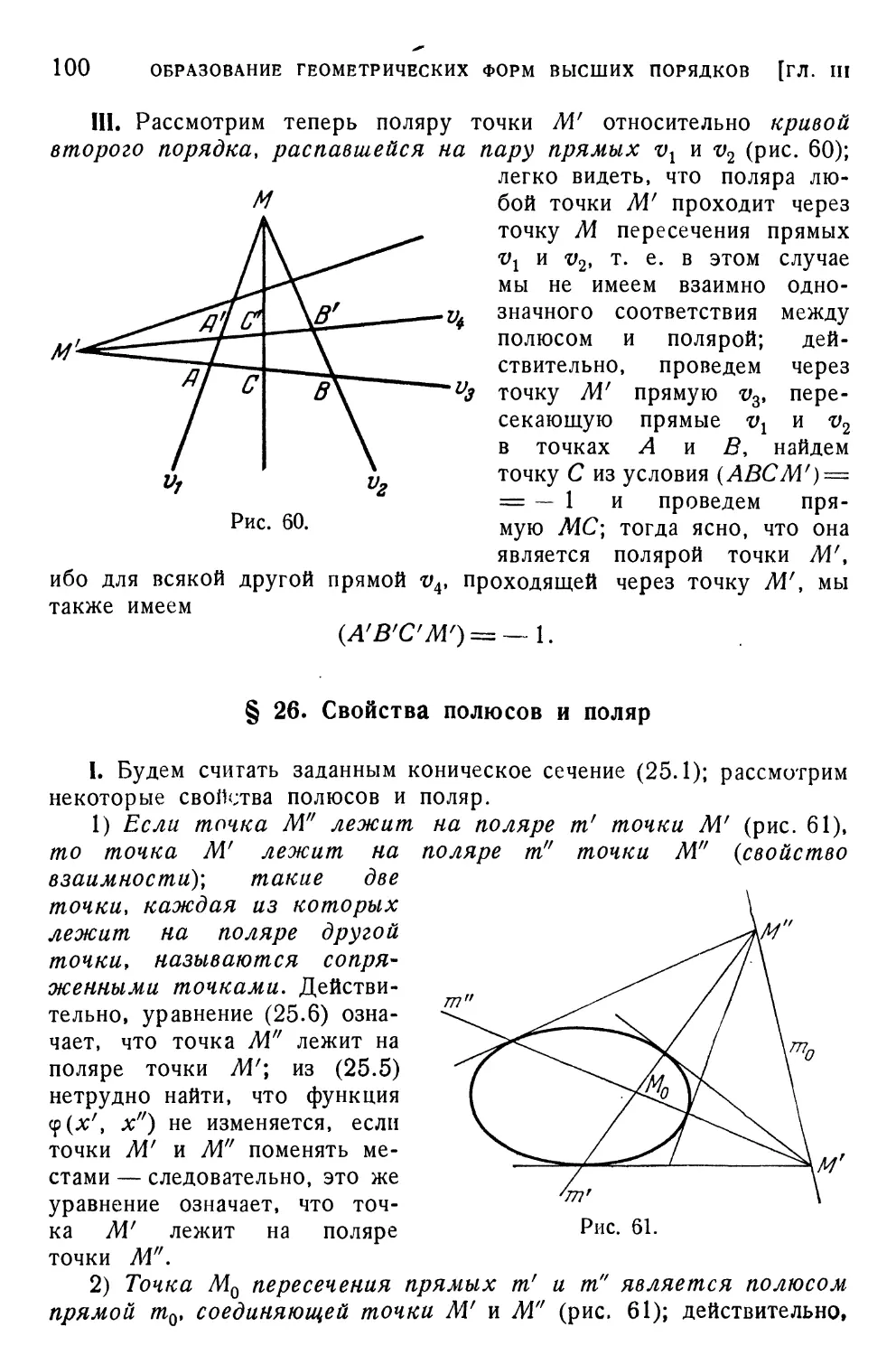
§ 25. Теория полярного соответствия 97
§ 26. Свойства полюсов и поляр 100
4 ОГЛАВЛЕНИЕ
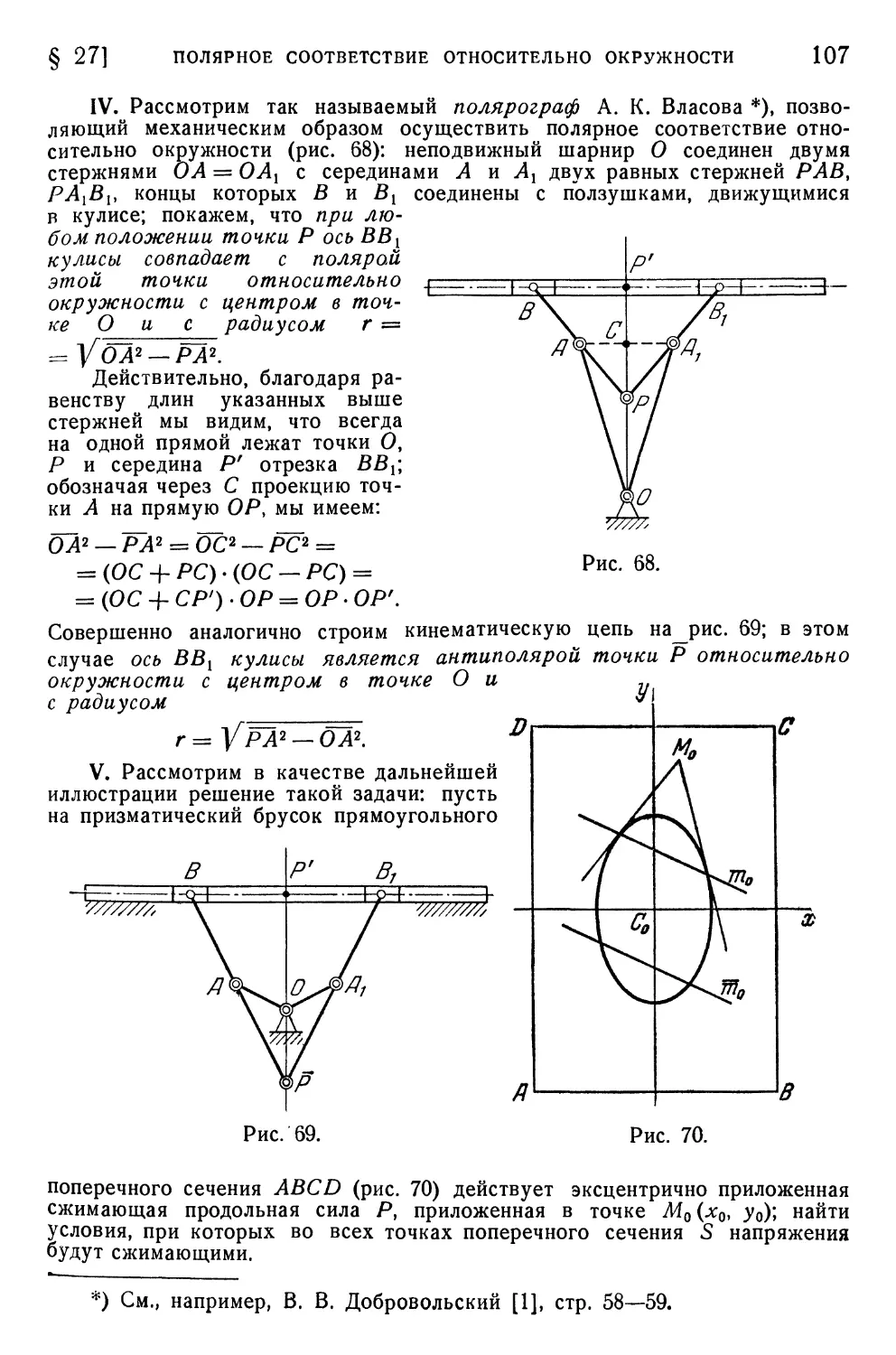
§ 27. Полярное соответствие относительно окружности 105
§ 28. Инволюция сопряженных прямых 109
§ 29. Определение кривой второго класса пятью касательными.
Теорема Брианшона 114
Глава IV. Некоторые свойства конических сечений 121
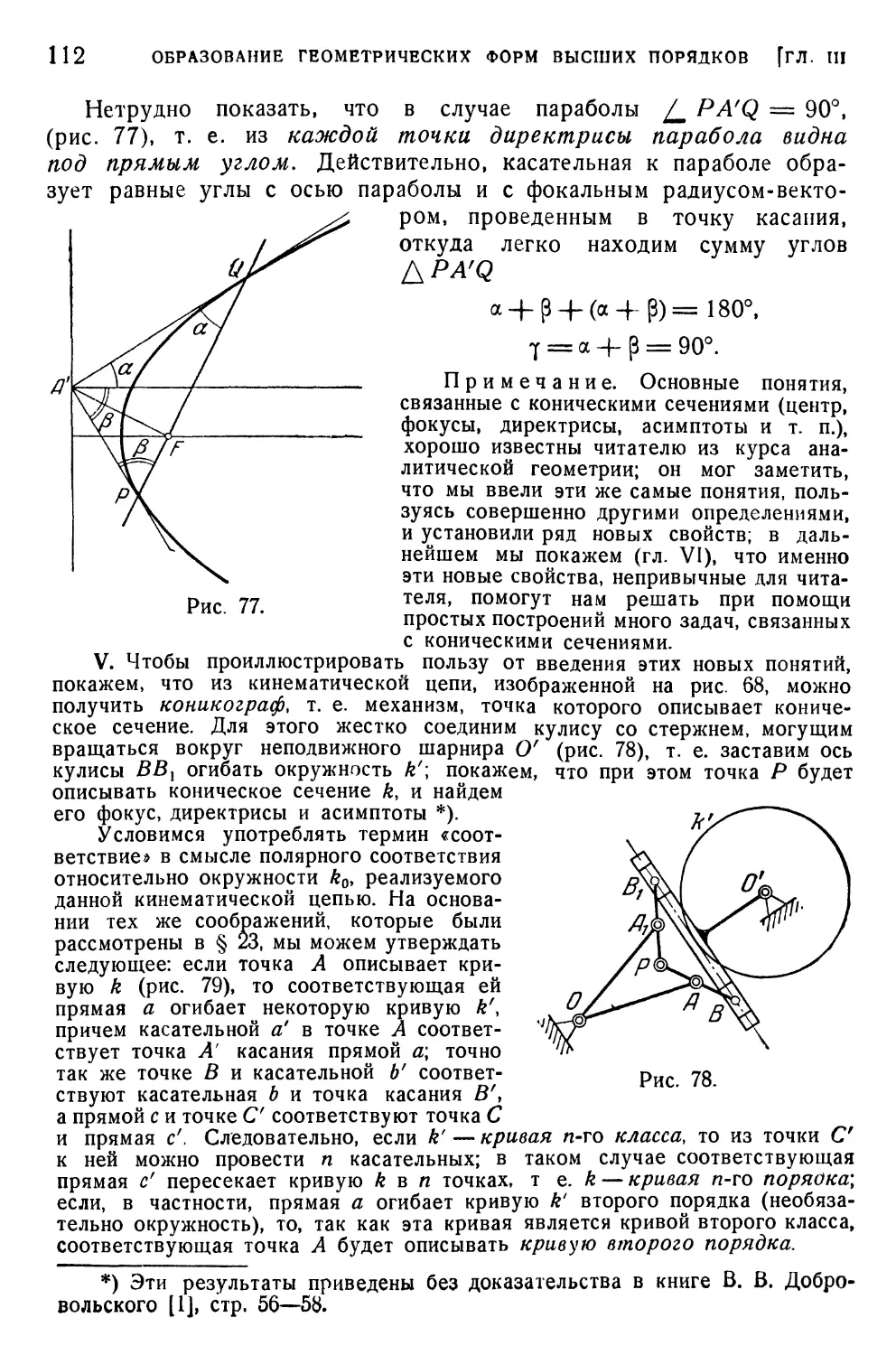
§ 30. Свойства касательных ' 121
§ 31. Свойства касательных к центральным коническим сечениям . . 123
§ 32. Свойства касательных к параболе 125
§ 33. Свойства окружности, описанной вокруг треугольника .... 129
§ 34. Степень точки относительно окружности; радикальная ось
и радикальный центр 132
§ 35. Пучки окружностей 135
Глава V. Преобразования координат 145
§ 36. Простейшие точечные преобразования 145
§ 37. Основные свойства проективного преобразования 149
§ 38. Геометрический смысл проективного и аффинного
преобразований 151
§ 39. Понятие о теории перспективы 155
§ 40. Классификация геометрических дисциплин 161
§ 41. Квадратичное соответствие 165
§ 42. Некоторые механизмы для установления квадратичного
соответствия 172
Глава VI. Конструктивные методы проективной геометрии ... 176
§ 43. Проективные и перспективные ряды точек и пучки прямых 176
§ 44. Построение двойных элементов 179
§ 45. Гармонические свойства полного четырехугольника и полного
четырехсторонника 183
§ 46. Построение конического сечения по пяти касательным или
пяти точкам 190
§ 47. Построение полюса и поляры 196
§ 48. Примеры построения кривых 198
Глава VII. Некоторые свойства циркулярных кривых третьего
порядка 201
§ 49. Общие теоремы 201
§ 50. Каноническая форма уравнения циркулярной кривой третьего
порядка 203
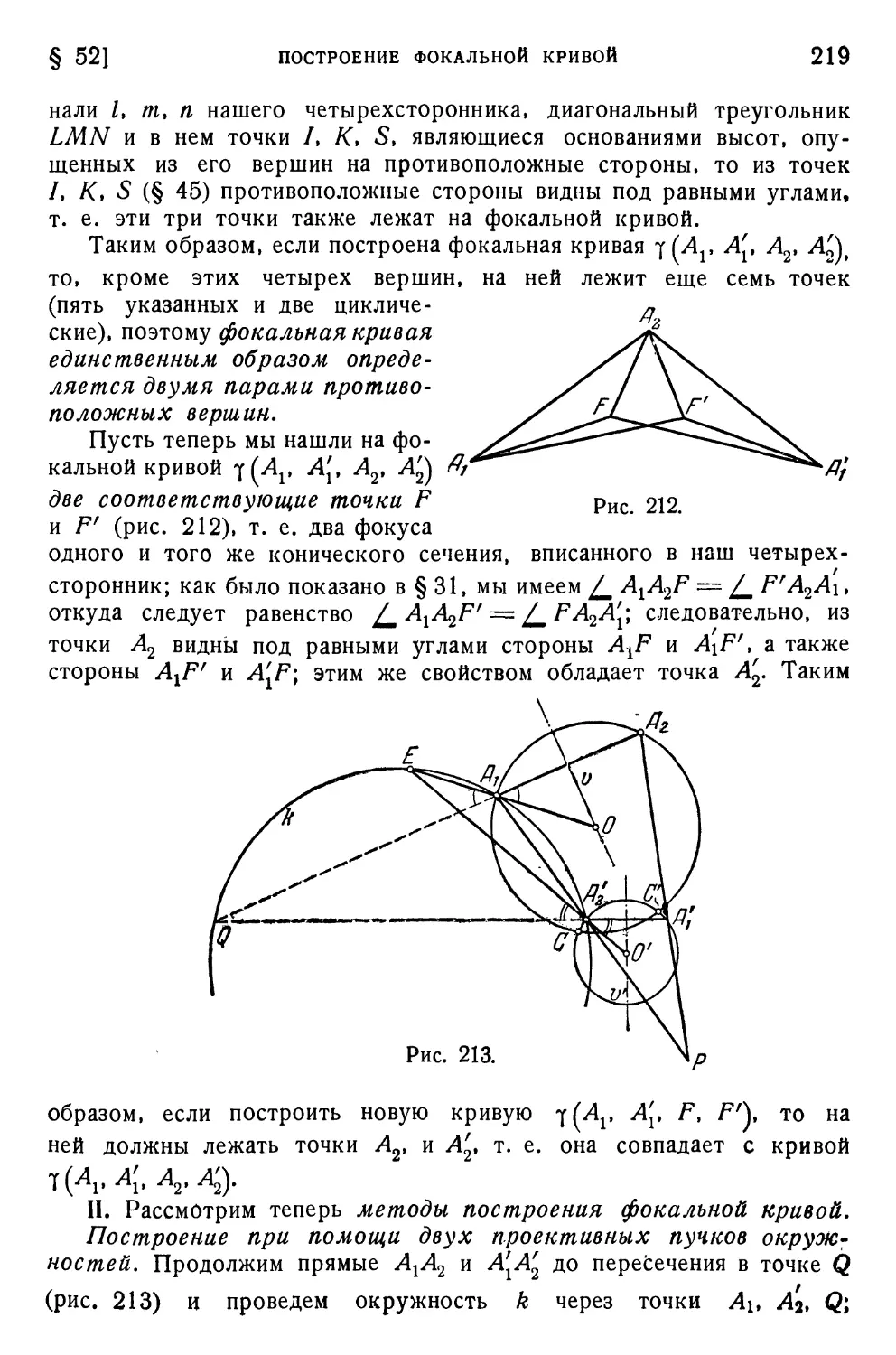
§ 51. Фокальная кривая 207
§ 52. Построение фокальной кривой 218
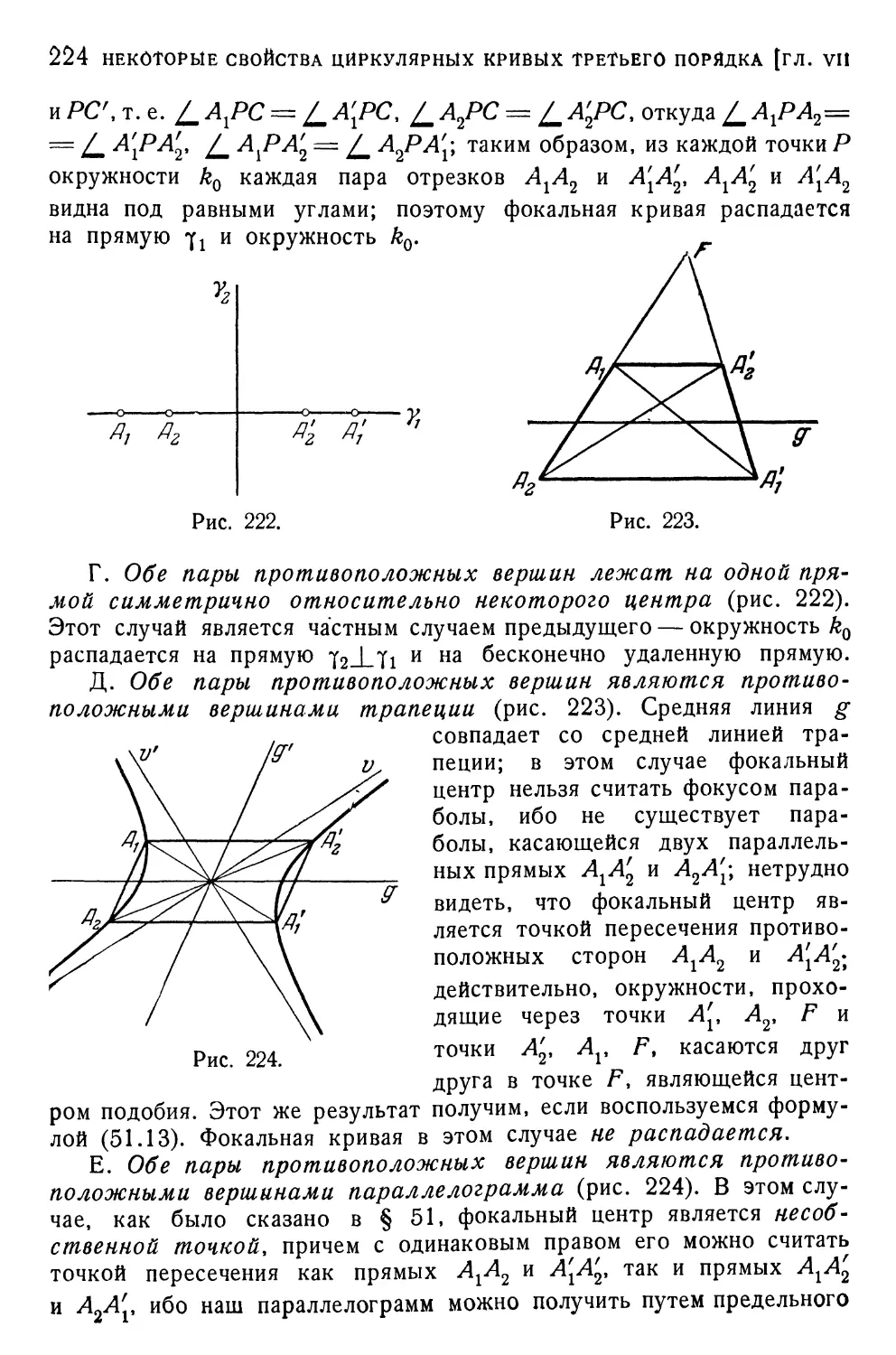
§ 53. Некоторые особые случаи расположения вершин,
определяющих фокальную кривую 222
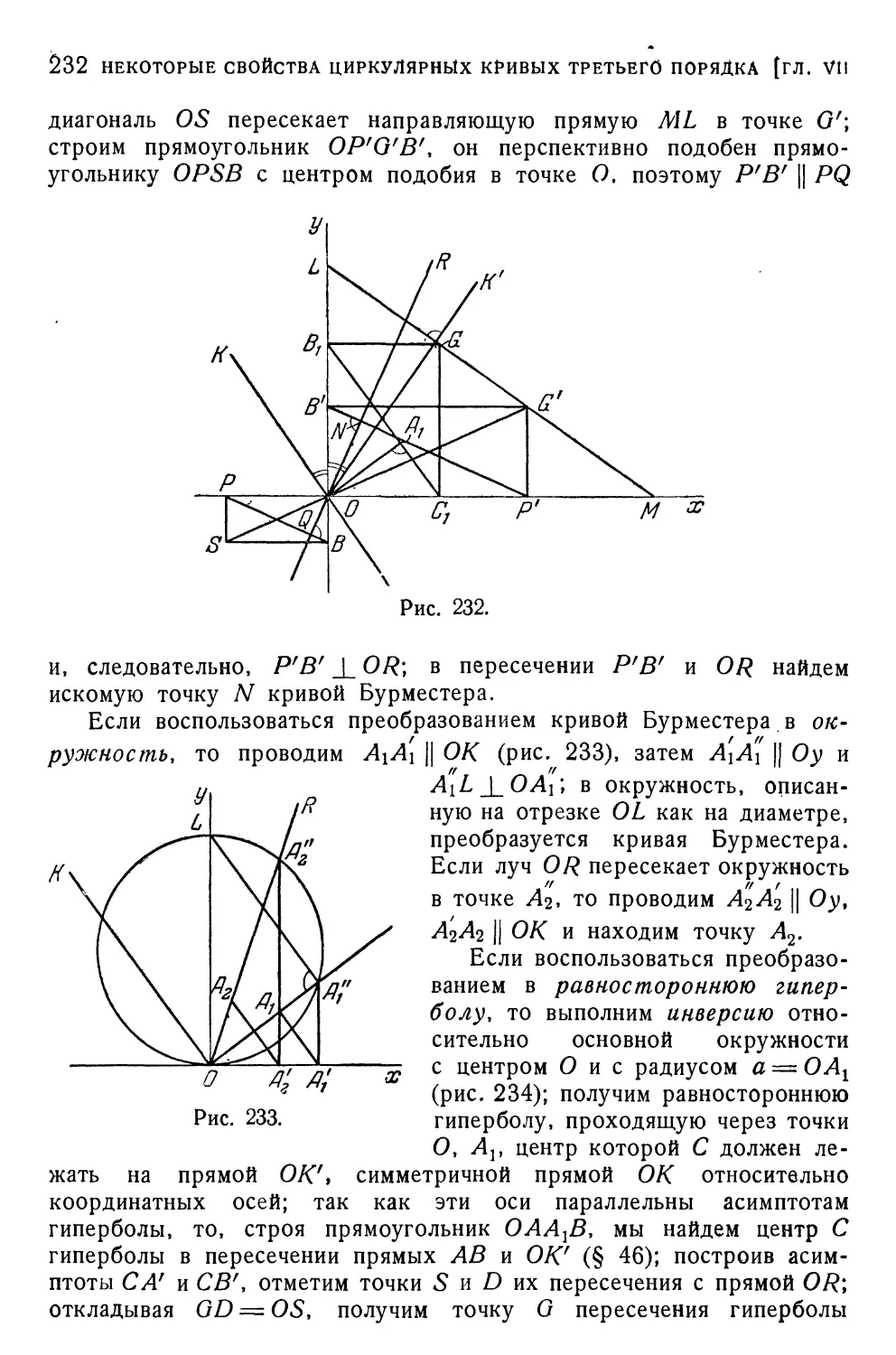
§ 54. Кривая Бурместера 226
§ 55. Аналитическое и графическое определение кривой Бурместера
по различным данным 231
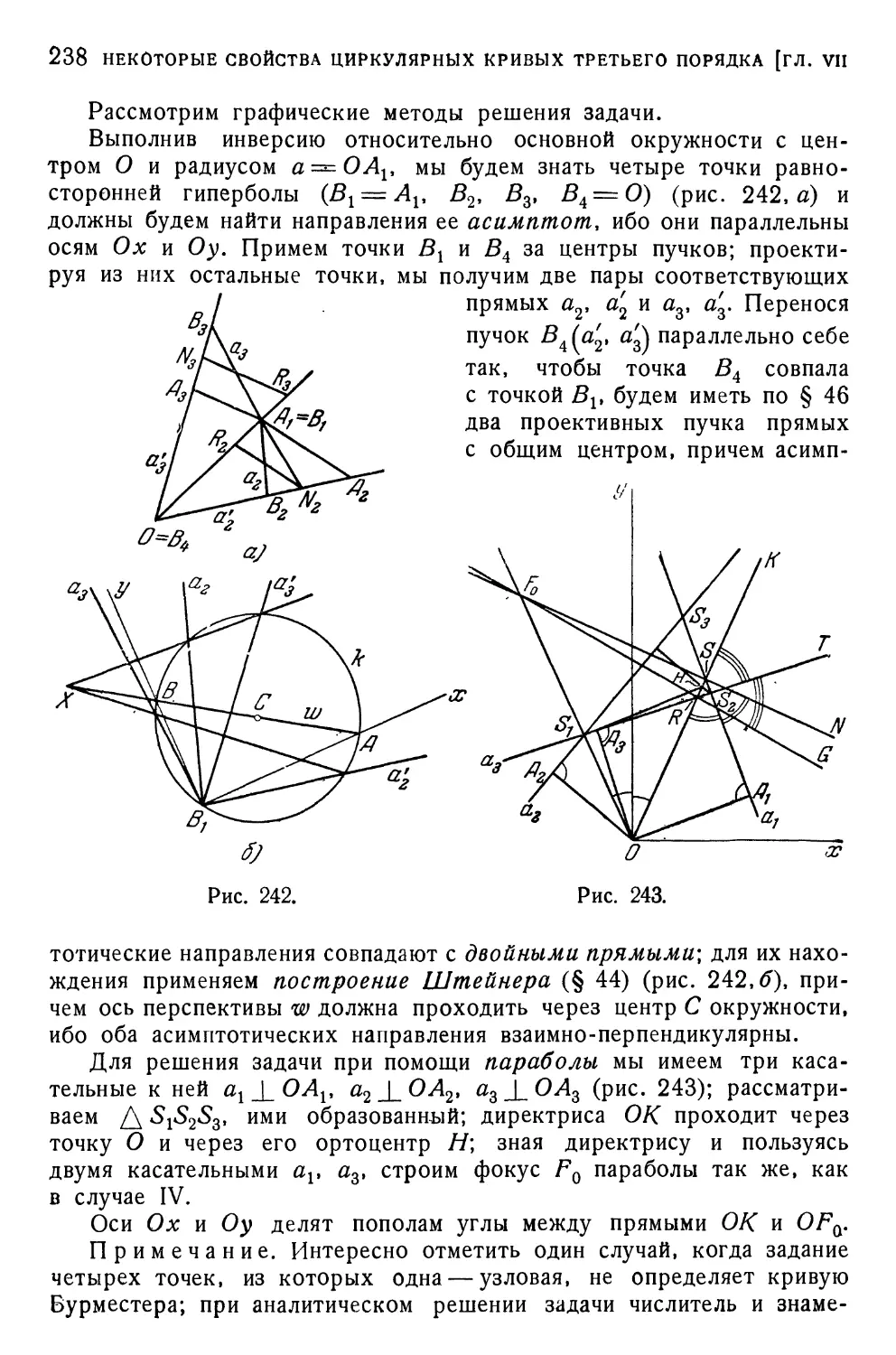
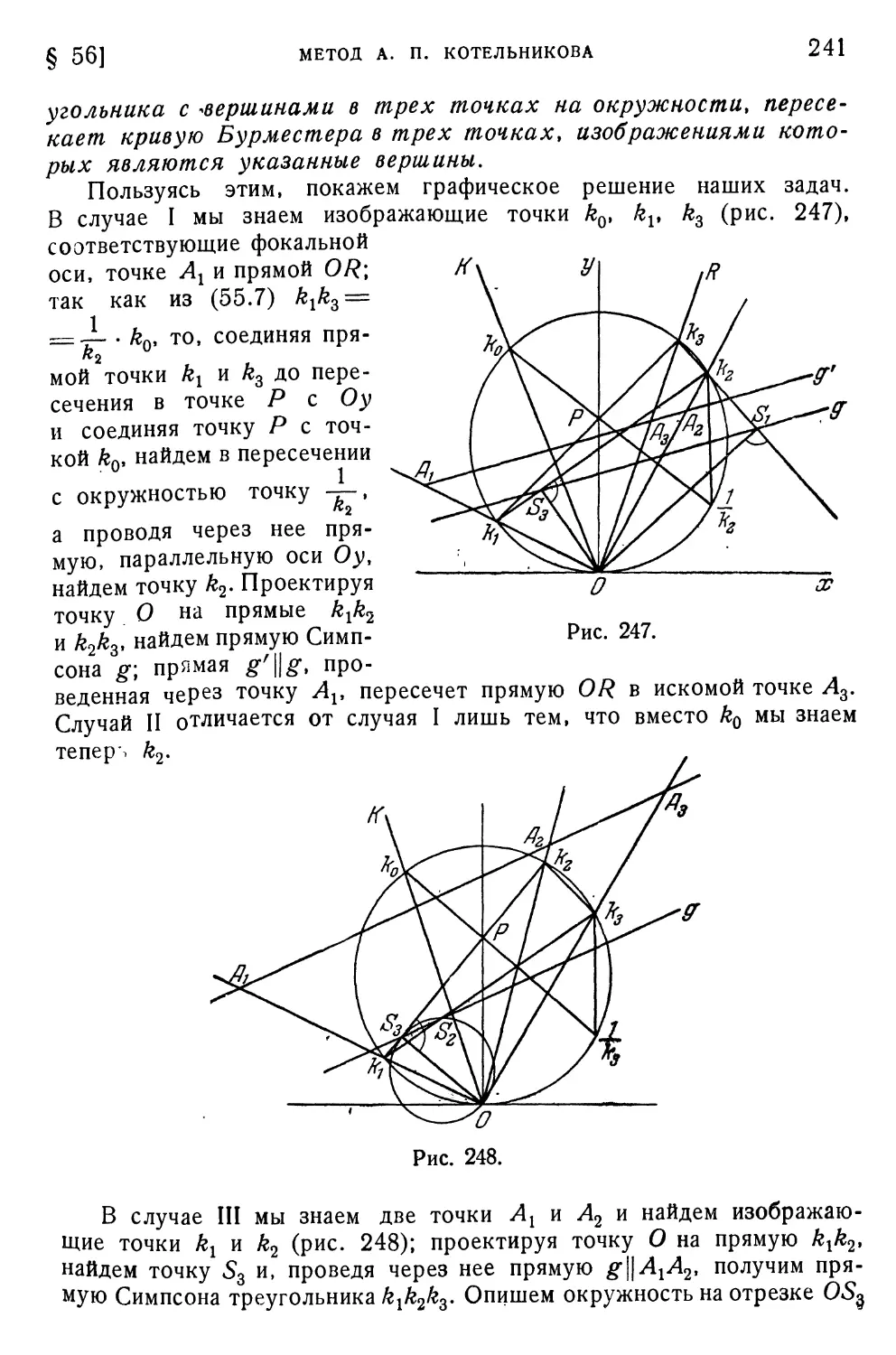
§ 56. Метод А. П. Котельникова 239
ЧАСТЬ II
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
Глава VIII. Соприкосновение плоских кривых 243
§ 57. Порядок соприкосновения плоских кривых 243
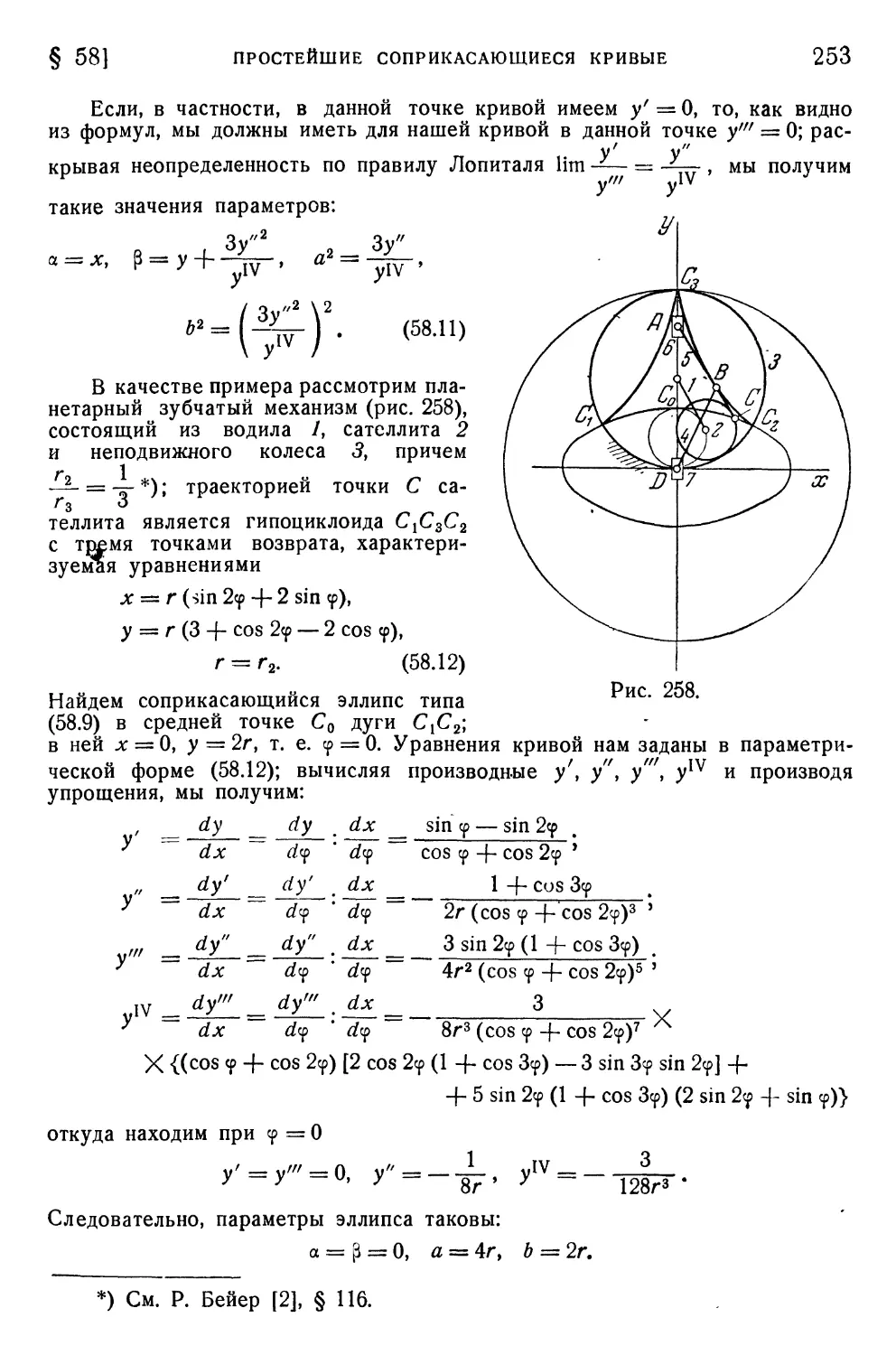
§ 58. Простейшие соприкасающиеся кривые 248
§ 59. Естественное уравнение кривой 254
ОГЛАВЛЕНИЕ 5
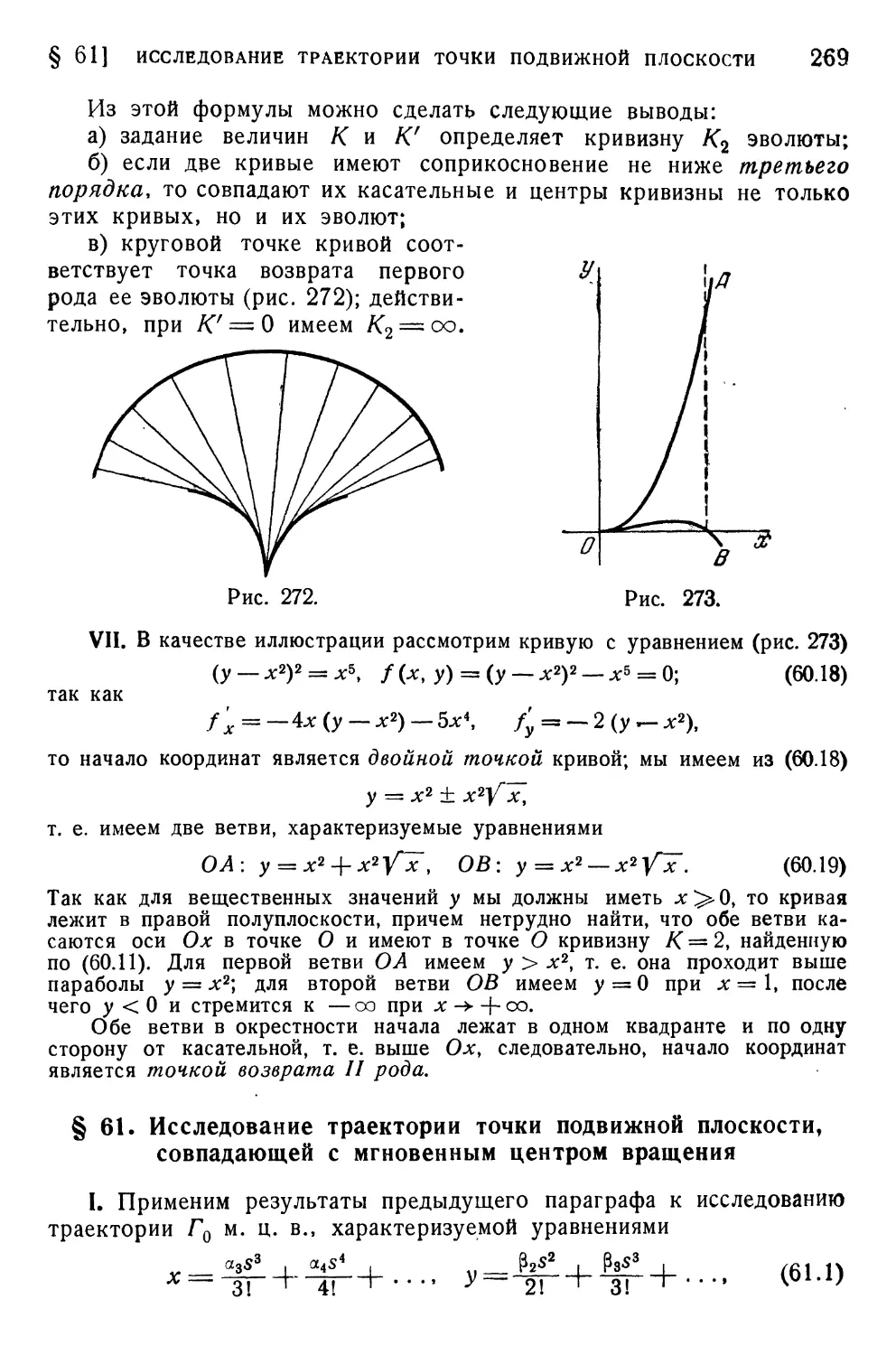
§ 60. Особые точки кривой 261
§ 61 Исследование траектории точки подвижной плоскости,
совпадающей с мгновенным центром вращения 269
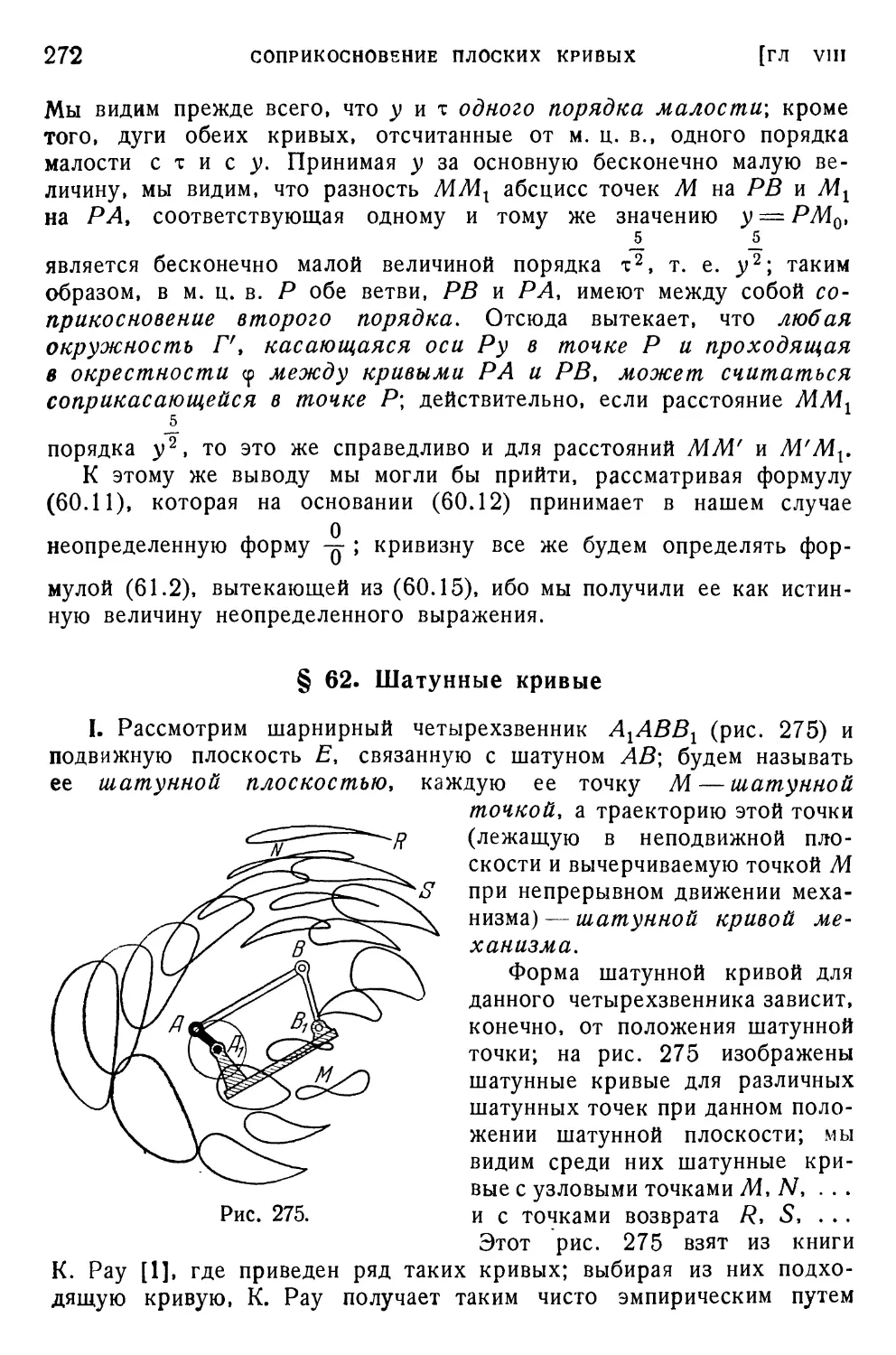
§ 62. Шатунные кривые . . . 272
§ 63. Однопараметрическое семейство плоских кривых.
Характеристические точки и огибающая 277
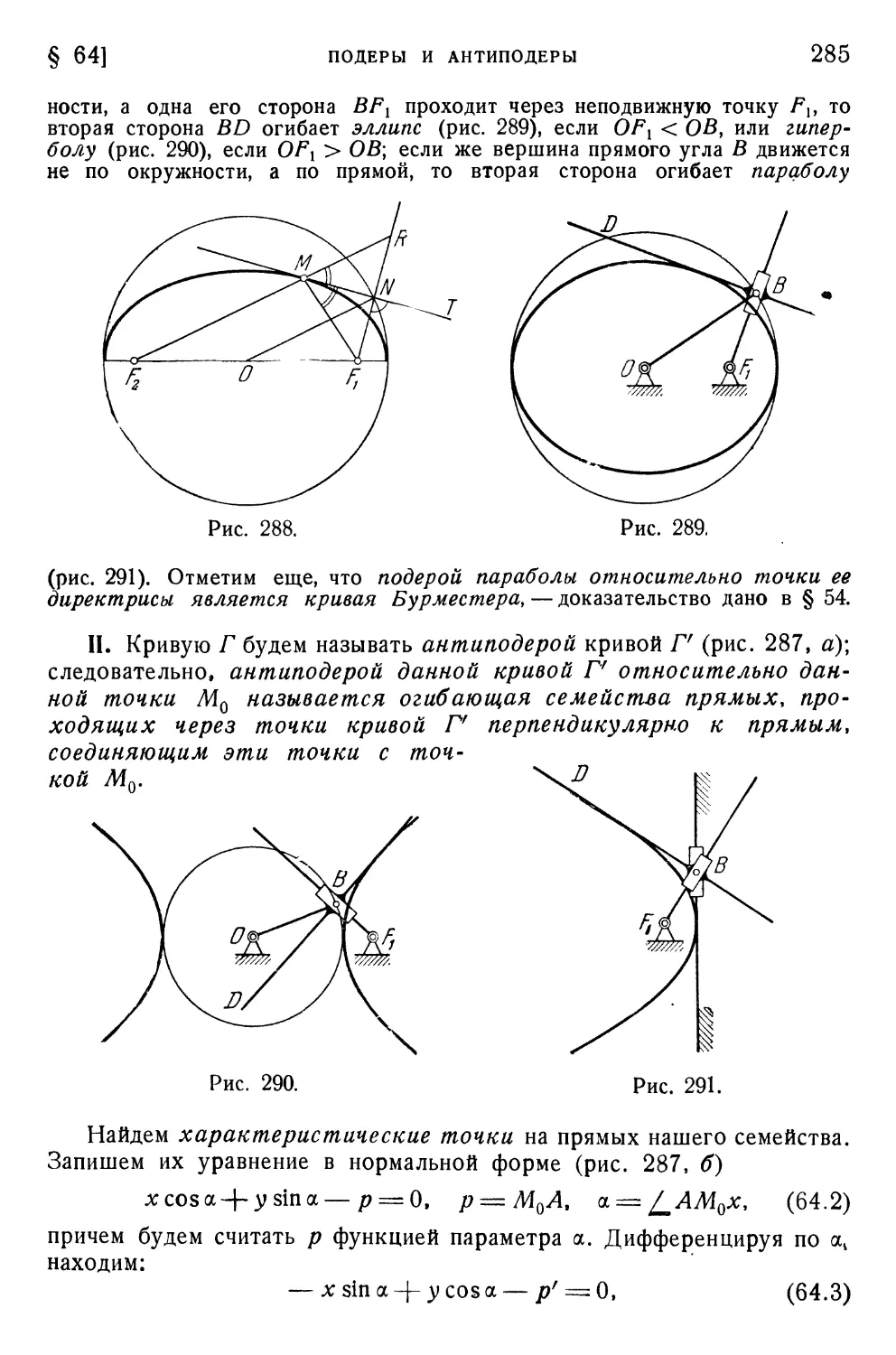
§ 64. Подеры и антиподеры Р . . . . 283
ЧАСТЬ III
ЭЛЕМЕНТЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
Глава IX. Два и три бесконечно близких положения
подвижной плоскости 289
§ 65. Общие замечания 289
§ 66. Скорость перекатывания центроид, полюс поворота и
поворотная окружность 291
§ 67. Формула Эйлера; теорема Бобиллье 296
§ 68. Геометрические построения 301
§ 69. Уравнение Эйлера — Савари; кривизна сопряженных рулетт . 306
§ 70. Ускорения точек подвижной плоскости; редуцированные
ускорения 312
Глава X. Четыре бесконечно близких положения подвижной'
плоскости 318
§ 71. Кривая круговых точек и кривая центров 318
§ 72. Точка Болла 323
§ 73. Распадение кривых Бурместера 325
§ 74. Построение обеих кривых Бурместера 329
Глава XI. Пять бесконечно близких положений подвижной
плоскости 335
§ 75. Вспомогательные формулы 335
§ 76. Точки и центры Бурместера 339
§ 77. Распадение кривых; случай Чебышева и точка Чебышева . . 345
§ 78. Применение к задачам анализа и синтеза 349
Глава XII. Шесть бесконечно близких положений подвижной
плоскости 356
§ 79. Точки Бурместера пятого порядка; случай Чебышева пятого
порядка 356
§ 80. Понятие о синтезе передаточных механизмов 360
Глава XIII. Соседние положения подвижной плоскости 369
§ 81. Два и три соседних положения подвижной плоскости .... 369
§ 82. Четыре и пять соседних положений подвижной плоскости . . 374
§ 83. Различные методы, применяемые в задачах синтеза
механизмов 382
Литература 389
I. Алфавитный список 389
II. Литература по отдельным вопросам 392
Именной указатель 394
Предметный указатель , , , , , . 395
ПРЕДИСЛОВИЕ
Развитие автомато- и приборостроения вызвало за последние
два-три десятилетия повышенный интерес как к теории, так и
к решению конкретных задач синтеза механизмов — доказательством
тому является хотя бы большое количество монографий и
журнальных статей в отечественной и зарубежной литературе, посвященных
задачам синтеза механизмов*).
В теории синтеза механизмов имеется два основных направления:
применение аналитических или геометрических методов**).
Основоположником аналитического метода синтеза механизмов
является знаменитый русский ученый П. Л. Чебышев; в своих
работах, начиная с 1853 г., он рассмотрел ряд задач синтеза конкретных
механизмов и создал для решения этих задач новый математический
аппарат — теорию наилучшего приближения заданной функции при
помощи некоторых простейших функций.
Замечательные идеи и методы П. Л. Чебышева на протяжении
многих лет лежали под спудом — конструкторы не могли ими
пользоваться, ибо не владели необходимым для этого математическим
аппаратом.
Советские ученые проделали большую работу по ознакомлению
широких кругов работников техники с идеями П. Л. Чебышева и
с их применениями к решению, новых задач синтеза — в первую
очередь следует указать работы 3. Ш. Блоха [1], [2], [3], а затем
Н. И. Левитского [1] и др.
Многие доклады на II Всесоюзном совещании по основным
проблемам теории механизмов и машин (1958 г.) и на Всесоюзном съезде
по механике (1960 г.) с неопровержимой ясностью показали, что
широкие слои научных работников и работников техники овладели
методами П. Л. Чебышева и успешно применяют их к решению
новых задач синтеза.
Основоположником геометрических методов синтеза
механизмов является немецкий ученый Л. Бурместер; он разработал метод
геометрических мест, основанный на построении некоторых кривых
*) См. литературу по синтезу механизмов, приведенную в конце книги.
**) Подробный исторический очерк развития методов синтеза читатель
найдет в гл. II книги С. А. Черкудинова [1].
ПРЕДИСЛОВИЕ
7
третьего порядка, на которых, в частности, должны лежать все
неподвижные и, соответственно, подвижные шарниры. Методы Бур-
местера получили дальнейшее развитие и применение в трудах ряда
немецких ученых, в первую очередь X. Альта, Р. Мюллера, В. Лих-
тенхельдта, Р. Бейера, Р. Крауса и др.; достижения немецкой
научной школы синтеза механизмов подытожены в монографии Р.
Бейера [2].
Геометрические методы синтеза плоских механизмов в некоторых
случаях проще, чем аналитические — они часто позволяют при помощи
весьма легких и наглядных построений получить целый ряд решений;
из них можно выбрать наиболее подходящее, которое можно затем
уточнить при помощи аналитических методов. Кроме того, многие
формулы, которые применяются при аналитических методах
решения, выводятся при помощи соображений геометрического характера.
Таким образом, геометрический и аналитический методы решения
задач синтеза плоских механизмов не противопоставляются друг
другу, не исключают, а дополняют один другой.
В качестве иллюстрации можно привести задачу, решенную
В. Лихтенхельдтом и рассмотренную нами в § 74 — он решал ее
чисто геометрическими методами, а мы рассматриваем оба метода
решения этой задачи — графический и аналитический *).
Следует сказать, что геометрические методы синтеза требуют
основательного знания многих положений геометрии, которые
совершенно неизвестны инженеру, ибо значительно выходят за пределы
того курса высшей математики, который изучается во втузах.
Поэтому, хотя многие монографии по синтезу механизмов — в
частности, вышеупомянутая книга Р. Бейера [2] — предназначены для
конструктора, однако именно конструктору они недоступны, причем
он даже не знает, где найти необходимые сведения, которых ему
не хватает; Р. Бейер, а также другие авторы (В. В. Добровольский
[1], С. В. Вяхирев [2] и др.), чтобы выйти из этого положения,
приводят многие геометрические теоремы и построения без вывода,
преподнося построения в виде некоего «рецепта» без всякого
обоснования. Однако при таком изложении читатель не сможет разумно
и сознательно воспользоваться данным построением и, конечно, не
овладеет методами геометрического исследования настолько, чтобы
применить их и в других случаях, отличающихся от рассмотренного.
Таким образом, налицо большой разрыв между уровнем
подготовки конструктора в области геометрии и тем геометрическим
аппаратом, которым приходится пользоваться при решении задач
синтеза геометрическими методами.
*) Заметим, что в недавно вышедшей в свет книге В. Лихтенхельдта [2]
применяются исключительно геометрические методы решения задач синтеза
плоских механизмов.
8
ПРЕДИСЛОВИЕ
Мы поставили себе целью ликвидировать этот разрыв, аналогично
тому, как это было сделано для ознакомления конструкторов с
аналитическим методом. Считая известными лишь те сведения из области
анализа, геометрии, кинематики и кинематики механизмов, которые
будущий инженер получает во втузе, мы в систематической форме
разрабатываем тот геометрический аппарат, который применяется
при решении задач синтеза, приводя и некоторые из этих задач
в качестве иллюстрации.
Читатель, внимательно проработавший настоящую книгу, не
встретит никаких затруднений при изучении книг и журнальных
статей, где применяются геометрические методы синтеза механизмов
по Бурместеру.
Особо отметим весьма содержательное, ставшее классическим
исследование А. П. Котельникова [1], посвященное кривым и точкам
Бурместера. Оно является подлинной сокровищницей оригинальных
методов и глубоких идей, которые могут иметь прямое и
непосредственное применение в задачах синтеза. Хотя все авторы упоминают
об этой работе, однако нигде в литературе мы не встречали ее
применений; основной причиной этого является то обстоятельство,
что работа носит сугубо математический характер и отнюдь не
рассчитана на конструктора.
Мы показываем в настоящей книге основные методы А. П.
Котельникова (преобразование строфоиды в окружность; инволюция
изображающих точек на окружности и т. п.) и их применение к решению
конкретных задач синтеза механизмов (например, к решению задачи
В. Лихтенхельдта); мы ставили себе целью приобщить широкие
круги научных работников и конструкторов к этой замечательной
работе, изучение которой после проработки настоящей книги
не представит трудностей.
В конце книги приведен алфавитный список авторов; для
читателей, желающих более углубленно познакомиться с тем или иным
вопросом, приведена дополнительная литература по отдельным
вопросам.
Не нам судить о том, в какой мере мы достигли поставленной
нами цели; во всяком случае мы будем весьма признательны за
всякие указания недостатков, которые неизбежны, ибо настоящая
книга является первой попыткой собрать в едином систематическом
изложении весь необходимый материал.
ЧАСТЬ I
ЭЛЕМЕНТЫ ТЕОРИИ АЛГЕБРАИЧЕСКИХ КРИВЫХ
И ПРОЕКТИВНОЙ ГЕОМЕТРИИ
ГЛАВА I
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Весьма многие положения и утверждения аналитической
геометрии значительно выигрывают в общности, если мы расширим те
элементарные понятия о точках, прямых и кривых, которые даются
в обычных учебниках аналитической геометрии для втузов; кроме
того, без этого расширения невозможно было бы ввести
рассмотрение основных положений так называемой проективной геометрии.
Начнем с введения понятия о бесконечно удаленных или
несобственных точках,
§ 1. Бесконечно удаленная точка прямой
I. Пусть на прямой g (рис. 1) заданы две точки Мх и М2 своими
абсциссами x'l% х'2, т. е. величинами направленных отрезков
х[ = ОМх К = ОМ2\
положение всякой точки М этой прямой можно характеризовать
величиной отношения направленных от-
резков —J—тпгм—9
М,М ' г
Х = М; (1.1)
М2М Рис. 1.
для точек правее точки М2 это отношение больше единицы, ибо
для таких точек МХМ> М2М одного знака и МгМ > М2М; для
точек левее точки Мх оно положительно, но меньше единицы, ибо
для таких точек МгМ < М2М; наконец, для точек, лежащих между
Мх и М2% это отношение отрицательно; точкам Мх и М2
соответствуют значения Х = 0 и Х = оо. Если х = ОМ — абсцисса точки М,
то отношение (1.1) имеет такую величину
/
X Хл
1 Г". (1-2)
х — х<>
10 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. I
откуда легко находим искомую абсциссу
X л —— КХп
х{\—\) = х'1 — 1х'2. X = ' _
(1.3)
Каждой точке М нашей прямой соответствует определенное
значение отношения X, но обратное утверждение было бы неверно;
каждому значению Хф\ соответствует определенная точка нашей
прямой; нам приходится делать оговорку Х=£1 не только по
формальным соображениям (ибо в (1.3) при делении на 1—X мы обязаны
предположить, что Х=£1), но и по существу дела: как было
указано выше, на прямой g не существует ни одной точки, для которой
мы имели бы Х=1, т. е. МХМ = М2М. Из (1.3) мы видим, что
при приближении X к единице абсцисса точки М безгранично
возрастает по модулю; это дает нам основание ввести следующей
определение: будем считать, что значению отношения Х=1
соответствует несобственная или бесконечно удаленная точка
нашей прямой. Мы считаем таким образом, что на каждой прямой
имеется единственная бесконечно удаленная точка. При этом
соглашении, пополнив нашу прямую бесконечно удаленной точкой, мы
сможем утверждать, что каждому значению отношения X
соответствует одна определенная точка, и наоборот, каждой точке М
прямой соответствует одно
определенное значение отношения X.
Мы пришли бы к тому же
заключению о необходимости пополнить
нашу прямую бесконечно удаленной
точкой, если бы взяли точку 5 вне
прямой g (рис. 2) и построили бы
так называемый пучок прямых
с центром 5, т. е. совокупность
прямых, проходящих через точку 5.
Если мы соединим точку 5 прямыми
с точками Л, В, С, ... прямой g, то мы можем сказать,
что каждой точке прямой g соответствует прямая пучка,
соединяющая эту точку с точкой S; нельзя утверждать, однако, что каждой
прямой пучка соответствует определенная точка ее пересечения
с прямой g, ибо прямая g'\\g не пересекается с прямой g и
никакая точка прямой g ей не соответствует. Если же мы пополним
нашу прямую указанным способом, то бесконечно удаленной точке
прямой g соответствует прямая g't и мы будем иметь взаимно
однозначное соответствие между точками прямой g и прямыми
пучка с центром 5.
Прямую, пополненную бесконечно удаленной точкой, будем
называть проективной прямой; так как она имеет одну бесконечно
удаленную точку, то ее следует считать замкнутой; действительно,
Рис. 2.
а, Ъ, с,
§1]
БЕСКОНЕЧНО УДАЛЕННАЯ ТОЧКА ПРЯМОЙ
11
если вращать прямую вокруг точки 5 против часовой стрелки, то,
пока угол ср (рис. 2) удовлетворяет неравенству 0 <^ ср <; -^-, точка
пересечения этой прямой с прямой g пробегает полупрямую в
направлении, показанном стрелкой; значению 9 =-у соответствует, как
было сказано, бесконечно удаленная точка прямой g\ при
дальнейшем вращении, когда угол ср удовлетворяет неравенству -к-<Сср^тс,
точка пересечения пробегает левую полупрямую в направлении,
показанном стрелкой.
II. Положение точки на прямой можно характеризовать еще при
помощи так называемых однородных координат xv х2% причем
абсцисса х равна их отношению
*\ .
* = -
х2
(1.4)
при этом предполагается, что хх и х2 не равны нулю одновременно
и что величинам kxv kx2 при любом k Ф 0 соответствует одна
и та же точка прямой; мы могли бы,
например, положить в (1.4), (1.3) х?\
х\ — х\'
Ч-
*2=1 —X.
При д;2—>0 будем иметь х-+оо;
поэтому будем считать, что
бесконечно удаленной точке прямой
соответствует значение х2 = 0.
Для того чтобы яснее представить
себе однородные координаты и произ*
вол в выборе числа k, будем
рассматривать хь х2 как декартовы коорди- р о
наты точки плоскости; рассмотрим пря- ' *
мую g с уравнением х2 = 1 (рис. 3).
В таком случае х = хх является абсциссой некоторой точки М на этой
прямой. Если провести луч из начала координат через точку М, то все точки Мь
Mv м'[9... на этом луче проектируются в точку М; так как для всех этих
точек мы имеем
/ п
Хл Х\ Хл
то положение точки М на прямой g можно характеризовать отношением
или равным ему отношением —-» причем хх = kxv х2 = kx2; коэффициент
х2
k Ф 0 совершенно произволен, ибо в качестве характеристики можно взять
любую точку этого луча; значение k = 0 надо исключить, так как в этом
случае мы получили бы х[ =з х2 = 0, т. е. начало координат 0% и вместо двух
12
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
[ГЛ. f
точек О, Мх, определяющих луч ОМ, мы имели бы только одну точку О.
Таким образом, однородные координаты хь х2 точки М на данной прямой g
являются декартовыми координатами любой точки прямой пучка с центром
в начале координат, проектирующей точку М\ бесконечно удаленной точке
прямой g соответствует в качестве проектирующего луча ось Охх, т. е.
прямая с уравнением х2 = 0.
В отличие от бесконечно удаленной точки будем называть все
остальные точки прямой собственными.
§ 2. Бесконечно удаленная прямая плоскости
I. Рассмотрим теперь точки М(х, у), лежащие в плоскости.
Хорошо известно, что уравнение
а1д: + л2у+^з = 0
(2.1)
является уравнением прямой при условии, что коэффициенты а1% а2
не равны нулю одновременно; две прямые, характеризуемые
уравнениями
#1*+#2У+Яз = 0' *1* + #2:У+#з=0, (2-2)
пересекаются, т. е. имеют общую точку, только тогда, когда
ах а2
Ь\ Ь2
Ф0.
(2.3)
Таким образом, если не ввести понятия бесконечно удаленных точек,
то в ряде случаев нам
придется делать оговорки и наши
утверждения не будут общими.
Введем снова однородные
координаты точки (xlt х2, хг),
причем положим
* = -?• *=-?• <2-4>
Предполагаем, что они не равны
одновременно нулю и что числа
kxv kx2y kx3 при любом k Ф 0
определяют одну и ту же
точку М.
Для ясности мы
рассмотрим трехмерное пространство
(рис. 4) и будем считать (xv xv хг) декартовыми координатами
точки в этом пространстве; в плоскости Е, характеризуемой
уравнением х3=1, имеем точку М с координатами x = xv у = х2- Про-
Рис. 4.
§ 2] БЕСКОНЕЧНО УДАЛЕННАЯ ПРЯМАЯ ПЛОСКОСТИ 13
водим луч ОМ и берем ряд точек Ми М[, Мх, ... на этом луче;
для этих точек имеем:
X j Х2 ЛСд иС| Х2 <Лд
т. е. мы можем положить x[ = kxv х'2 = kx2, х'г — kxv где к Ф 0 —
любое число, ибо для определения положения точки М на плоскости Е
мы можем взять любую точку на луче ОМ. При дг3 = 0 выбранная
точка лежит в плоскости Оххх2 и прямая, соединяющая ее с началом
координат, не пересекает плоскости Е.
II. Если рассмотреть точки прямой g на плоскости Е, то им
соответствует плоский пучок лучей, проектирующих эти точки из
точки О, причем по предыдущему бесконечно удаленной точке
прямой g соответствует прямая g'\\gt лежащая в плоскости Ох^С^ эта
прямая характеризуется уравнениями
*3 = 0, **. = !. = —lL. (2.5)
d хх х а2
Мы считаем, что на каждой прямой плоскости, характеризуемой
уравнением
«1*1 + я2*2 + аз*з = °- (2 -6)
имеется одна несобственная, т. е. бесконечно удаленная точка,
характеризуемая условием дго = 0 и направлением — = L;
для двух параллельных, но не совпадающих прямых
аххх + а2х2 + агхг = 0, Ьгхг + Ъ2х2 + Ьгхг = 0, (2.7)
имеем:
Ь. = Ь.фЬ., _£L = _*L, (2.8)
а{ а2 а3 а2 о2
т. е. бесконечно удаленные точки параллельных прямых
совпадают.
Если рассмотреть все прямые, лежащие в плоскости Et и их
бесконечно удаленные точки, то общим условием, характеризующим
бесконечно удаленные точки всех прямых, является хг = 0, ибо
направления для непараллельных прямых различны; таким образом,
*з = 0 является уравнением геометрического места бесконечно
удаленных точек всех прямых плоскости. Поскольку оно первой
степени, будем называть его уравнением несобственной, т. е.
бесконечно удаленной прямой плоскости; в отличие от нее все
остальные прямые плоскости будем называть собственными.
Плоскость, дополненную бесконечно удаленной прямой, будем
называть проективной плоскостью; в проективной плоскости всякое
уравнение первой степени (2.6), связывающее однородные координаты,
14 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. I
является уравнением прямой; если av а2 не равны нулю
одновременно, то это — собственная прямая; если же а1 = а2 = 0,
#з Ф О» то это — несобственная прямая; можно также сказать, что
любые две прямые плоскости (2.7) всегда имеют общую точку:
собственную точку, если —Ф-£-% и несобственную, при усло-
вии (2.8). Можно считать, что любая прямая плоскости
параллельна бесконечно удаленной прямой; действительно, две прямые
параллельны, если они имеют общую несобственную точку, — это
как раз имеет место, если одна из прямых — несобственная; это
следует из условия параллельности (2.8), ибо для бесконечно удаленной
прямой имеем:
Ьг = 0, £2 = 0, ЬгфО.
III. Примечание. Мы условились считать, что на каждой прямой
есть своя бесконечно удаленная точка, а геометрическим местом таких точек
является бесконечно удаленная прямая;
Р возможны и другие подходы к введению
несобственных элементов.
Например, в теории функций комп-
, лексного переменного рассматривается
/ плоскость (рис. 5), причем каждой ее
/ точке М (х, у) ставится в соответствие
/ комплексное число z = х + /у, / = V—1 •
/ Построим сферу произвольного радиуса,
/ касательную к нашей плоскости в начале
/ координат; каждую точку М плоскости
J проектируем на сферу в точку М' из
точки Р сферы, диаметрально
противоположной точке О. Тогда каждой точке
нашей плоскости соответствует точка М'
на сфере, но обратное утверждение не верно: точке Р сферы не соответствует
ни одна точка плоскости. Если расстояние ОМ неограниченно возрастает,
то расстояние РМ' стремится к нулю; мы говорим поэтому, что точке Р
сферы соответствует несобственная, т. е. бесконечно удаленная точка
плоскости; при таком введении бесконечно удаленной точки, отличающемся
от нашего, надо считать, что бесконечно удаленная точка плоскости
единственна.
§ 3. Примеры, иллюстрирующие применение несобственных
элементов
I. Рассмотрим в качестве первого примера нахождение мгновенного
центра вращения (м. ц. в.) в плоском движении.
Пусть известны векторная скорость v. полюса А и угловая скорость о>
(рис. 6). Если со Ф 0, то м. ц. в. Р существует и лежит на прямой ЛВ, про-
v А
ходящей через точку А перпендикулярно к скорости v , причем РА = ■ ;
если же о> = 0, то скорости всех точек фигуры геометрически равны
§ 31 ПРИМЕРЫ ПРИМЕНЕНИЯ НЕСОБСТВЕННЫХ ЭЛЕМЕНТОВ 15
в этом случае м. ц. в. как точка подвижной плоскости, скорость которой
равна нулю, не существует — скорости всех точек либо все равны нулю,
либо ни одна из них не равна нулю. Так как мы имеем
lim РА = lim
► о I Ч
• = оо,
(3.1)
то мы можем сказать, что м. ц. в. является бесконечно удаленной точкой
прямой АВ\ мы говорим также, что м. ц. е. ушел в бесконечность по на-
правлению АВ, перпендикулярному к скорости полюса v.. Если в этом
случае нам надо соединить некоторую
точку С с м. ц. в., мы проводим через
точку С прямую CD || АВ, ибо две
параллельные прямые имеют общую бесконечно
удаленную точку.
И. В качестве иллюстрации рассмотрим
еще известную теорему Кеннеди — Арон-
гольда: пусть Раь является полюсом,
т. е. м. ц. в. в относительном движении
двух звеньев a, b плоского механизма *);
тогда для трех любых звеньев а, Ь, с
точки РаЬ, Рас, РЪс лежат на одной
прямой. рис б /
В случае шарнирного четырехзвен-
ника /, 2, 3, 4 (рис. 7) сразу находим
точки Р12, Я2з. ^34. Р*\\ точка Р31 лежит в пересечении прямых Pi2P2z
и Р41Рз4, а точка Р24— в пересечении прямых Р12Р41 и ^23^34-
В случае кривошипно-шатунного механизма (рис. 8)---сразу находим
точки Р12, Я23, Ръ\\ звено 4 (ползун) движется относительно стойки /
поступательно, следовательно, для него о> = 0 и м. ц. в. Р41 ушел в бесконечность
в направлении, показанном стрелкой, перпендикулярном к скорости точки Р34,
Рис. 8.
т. е. является бесконечно удаленной точкой прямой РЪ4А. Точка Р31 лежит
в пересечении прямых Р23Р12 и ^34^41» точку Р2А надо найти в пересечении
прямой Р23Р34 с прямой, соединяющей точку Р12 с точкой Р4Х> поэтому
проводим через точку Р12 прямую Я12Я24||Р34^-
III. Покажем также, как вывести свойства параболы из
соответствующих свойств эллипса и гиперболы при помощи несобственных
*) Точку Раь можно назвать и Р^а.
и
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
[ГЛ. I
элементов Рассмотрим эллипс (рис. 9, а) с уравнением
а2
+V-»
(3.2)
и перенесем начало координат в его вершину О, т. е. выполним
преобразование координат
х' = х — а. у' = у. (3.3)
Мы получим тогда уравнение эллипса в новой системе координат
yi = 2px-£x\ Р = -^. (3.4)
Для гиперболы с уравнением
У—
Ь2
1
аналогичное преобразование приводит к уравнению
(3.5)
(3.6)
Будем неограниченно увеличивать а и Ь> но так, чтобы вели'
Ь2 „ Ь2
чина отношения — оставалась неизменной, — = /? (например,
Рис. 9.
если увеличить а в п раз, то надо увеличить Ь в Yn Раз)» в таком
случае мы получим из (3.4), (3.6) после предельного перехода
уравнение параболы
у2=2рд:. (3.7)
Таким образом, параболу можно рассматривать как предел
эллипса и гиперболы при условии
Ь2
lim а === lim £ = оо, — = /?. (3.8)
§ 3] ПРИМЕРЫ ПРИМЕНЕНИЯ НЕСОБСТВЕННЫХ ЭЛЕМЕНТОВ 17
Пользуясь этим, можно вывести все основные свойства параболы.
Найдем расстояние фокуса Fx эллипса от его вершины О; так как
е =
0'FX = ае,
У а2 — Ь2
00'= a, OFx = a(\ — е)9
(3.9)
где е — эксцентриситет, а а — большая полуось эллипса, то после
предельного перехода получим:
а (1-е2) __ ,. р _р
lim е=1, lim OFx= lim "V м= lim . —9.
л-Voo а-±оо я-Уоо 1 т~ # а->► оо *• ~Ге *
(3.10)
Таким образом, левый фокус Fx эллипса переходит в фокус F
параболы, находящийся от вершины на конечном
расстоянии -7Г, а центр О' и правый фокус F2 эллипса уходят в
бесконечность в направлении большой оси OFx эллипса, которая
переходит в ось параболы.
IV. Известно, что геометрическим местом середин параллельных хорд
эллипса (рис. 9, а) является прямая, проходящая через центр эллипса и
называемая его диаметром; таким образом, диаметры эллипса образуют пучок
прямых с центром в центре О' эллипса; касательная к эллипсу в точке его
пересечения с данным диаметром параллельна тем хордам, которые делятся
этим диаметром пополам. После
предельного перехода мы получим
параболу, причем центр эллипса
переходит в бесконечно удаленную точку ее д
Рис. 10.
оси; поэтому диаметры параболы образуют пучок прямых с центром в
бесконечно удаленной точке оси параболы, т. е. они все параллельны этой оси.
Касательная к любой точке параболы, как и в случае эллипса, параллельна
тем хордам, которые делятся пополам диаметром, проведенным в точку
касания (рис. 9, б).
Мы могли бы убедиться в правильности наших утверждений и чисто
аналитическим путем: если хорды имеют угловой коэффициент к, то
диаметр эллипса, делящий их пополам, имеет уравнение
18 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. I
Пользуясь преобразованием (3.3), получим:
'-*-£• »>•>
Выполняя предельный переход а->оо, получим уравнение диаметра
параболы у = ±г, делящего пополам хорды с угловым коэффициентом k.
Известно также, что нормаль AN в каждой точке А эллипса (рис. 10, а)
является биссектрисой между фокальными радиусами-векторами F{A} F2A,
Проведенными в точку касания; в случае параболы фокус F2 является
бесконечно удаленной точкой ее оси и поэтому прямая AF2, соединяющая
точку А с фокусом F2, пойдет параллельно оси параболы; следовательно,
нормаль в каждой точке параболы является биссектрисой угла между
фокальным радиусом-вектором FA и диаметром AF2, проведенными в точку
касания (рис. 10, б).
Совершенно аналогично можно было бы получить и все остальные
свойства параболы; кроме того, можно было бы их получить посредством
предельного перехода, исходя из свойств гиперболы, а не эллипса.
§ 4. Пересечение алгебраических кривых
I. Напомним, что кривая называется алгебраической, если
в ее уравнении
/(*. 30 = 0
функция f(x, у) является многочленом как относительно х,
так и относительно у; в противном случае кривая называется
трансцендентной.
Из определения вытекает, что уравнение алгебраической кривой
должно иметь такой вид
fix. y) = ^akTxky\ (4.1)
где akr—некоторые коэффициенты, а показатели &, г—целые
неотрицательные числа.
Порядком алгебраической кривой называется наибольшая
сумма показателей при х и у в ее уравнении; следовательно,
если кривая с уравнением (4.1) имеет порядок п% то k-\-r^n,
причем хоть для одного члена имеет место равенство.
Нетрудно видеть, что порядок алгебраической кривой не
изменяется при повороте и переносе координатных осей;
действительно, при таком преобразовании имеем:
х = хх cos а — ух sin а -|- а, У = хг sin а -f- У\ cos а -|- Ь, (4.2)
т. е. мы перенесли начало координат в точку Ol(at b) и повернули
оси на угол а; уравнение (4.1) примет в новых координатах такой
вид:
ср (xv ух)=2 akr (х\cos а—Ухsin а + °)k ix\sin а+Уicos а ~Н bf =
= 2 «/Wi;
§ 4] ПЕРЕСЕЧЕНИЕ АЛГЕБРАИЧЕСКИХ КРИВЫХ 19
если выполнить все перемножения, то ясно, что сумма показателей
при хх и ух не превзойдет п, т. е. порядок п! в новых
координатах удовлетворяет неравенству п' <^ п. Выполняя обратное
преобразование
хх = х cos a -f- у sin а — а, ух = — х sin а -|- у cos а — Ь, (4.3)
мы снова не сможем повысить порядок кривой, т. е. будем иметь
п^Сп', откуда п' = п*).
II. Общий вид уравнения алгебраической кривой первого
порядка таков:
а1х + а2у-\-аг = 0, (4.4)
т. е. это — прямая) для кривой второго порядка имеем общий вид
уравнения
апх2 + 2а12ху + а22у2 + 2а1гх + 2я23у + я3з = °> <*** = аы- (4-5)
Покажем важное геометрическое значение порядка алгебраической
кривой: любая прямая может пересечь алгебраическую кривую
п-го порядка не более чем в п точках (кратная точка считается
при этом столько раз, какова ее кратность).
Действительно, для нахождения точек пересечения кривой (4.1)
и прямой с уравнением у = тх-{-Ь мы должны совместно решить
их уравнения; исключая из них у, мы должны найти "абсциссы-точек
пересечения как корни уравнения ч
/(*. mx + b) = 2iakrxk(mx + b)r = Anxn+An_lxn~1+ ...
... + Агх + Ао = 0. (4.6)
Представив левую часть этого алгебраического уравнения в виде
произведения линейных множителей
An*n+An-i*n-l+ ••• +Лхх + А^
= Ап(х — хх) {х — х2)...{х — хп) = 0, (4.7)
мы видим, что оно имеет п корней — вещественных, или
комплексных, простых или кратных; даже если бы все корни были
вещественными и простыми, уравнение дало бы п точек пересечения.
Отметим одно обстоятельство, весьма существенное для
последующего изложения: если прямая имеет с алгебраической кривой
п-го порядка более п общих точек, то все точки прямой
принадлежат кривой, т. е. она распадается на эту прямую, и на
кривую (п—1)-го порядка. Доказательство вытекает из того, что если
*) В дальнейшем будет показано, что порядок не изменяется и при
более общих преобразованиях координат (§ 37).
20 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. !
уравнение (4.7) имеет более п корней, то все его коэффициенты
равны нулю и оно обращается в тождество, т. е.
удовлетворяется при всех значениях х.
III. В качестве иллюстрации рассмотрим алгебраическую кривую третьего
порядка, характеризуемую уравнением
/ (х, у) = Ъх2у — Sxy2 — 2х3 + 5уs _ дХу + 6х2 + Зу2 — 2у + 2х = 0; (4.8)
прямым вычислением убеждаемся в том, что четыре точки
AM0.0), М2(-1, -1), Af8(l, 1), Af4(2f 2)
лежат на кривой; но эти же четыре точки лежат на прямой с уравнением
у — х = 0; следовательно, все точки этой прямой принадлежат кривой,
которая распадается на эту прямую и кривую второго порядка. Для
нахождения ее делим левую часть (4.8) на у — х; легко найдем:
/(х, у) = (у — х) (2х2 — Зху + 5у2 — 6х + Зу — 2) = 0;
приравнивая нулю первый множитель, найдем у — х = 0, т. е. уравнение
прямой; приравнивая нулю второй множитель, найдем:
2х2 — Зху + 5у2 — 6* + Зу — 2 = 0,
т. е. уравнение кривой второго порядка; все точки прямой и этой кривой
лежат на заданной кривой (4.8), ибо их координаты удовлетворяют ее
уравнению.
IVi Оставляя в стороне общий вопрос о распадении
алгебраической кривой любого порядка, выведем условие, необходимое
и достаточное для распадения кривой второго порядка (4.5):
для этого должен равняться нулю определитель из
коэффициентов
|#11 #12 #13 I
Д = Uai #22 #23 = 0. (4.9)
I #31 #32 #33 |
Положим сперва а22 Ф 0; поделив на этот коэффициент
уравнение (4.5)
у2 1 2 у a*2* + a23 1 gn*2 + 2ai8-* + fl88_Q
#22 #22
и решив его относительно у, мы получим:
У = ~ й12Ха~12 й2Ъ ± -^ V(al2x + д23)2 - а22 (апх* + 2а1гх + агз);
(4.10)
из этого решения ясно, что у может быть линейной функцией х
тогда и только тогда, когда подрадикальное выражение
(а2и — ацАгг) х2 + 2х (а^агэ — #22^13) + #23 — #22#зз (4.11)
§41
ПЕРЕСЕЧЕНИЕ АЛГЕБРАИЧЕСКИХ КРИВЫХ
21
будет полным квадратом, т. е. при выполнении условия
(#12#23 — #22#1з) = (#12 #11#22) (#23 #22#3з)',
иначе говоря, после сокращения на а22 мы должны иметь:
2 2 2
#11#22#33 #11#23 #12#33+ 2#12#23#13 — #22#13 = О,
что совпадает с условием (4.9).
Предполагая, что а22 = 0, поделим на ап и решим относительно х\
если же предположить, что оба коэффициента равны нулю
#11 = а22 = 0, #12 Ф О,
/ (*, у) = 2а12ху + 2а1гх + 2а2гу + я33 = О,
(4.12)
то находим отсюда
2ахъх + а3з .
у 2(а12х + а2з)'
так как а12 Ф О, то у может быть линейной функцией д: тогда
и только тогда, когда коэффициенты в числителе и знаменателе
пропорциональны
о,
(4.13)
2а,
. 2зз __ \,
#23
при этом условии
2а1гх -|- я33 = X (а12х + я23)
и мы будем иметь из (4.12)
/ (*, у) = 2 (а12* + а23) у + 2я13д; + #23 == {а12х + я23) (2у + X) = О,
(4.14)
т. е. левая часть уравнения является произведением двух линейных
множителей.
Из (4.13) имеем ап = -^а12% #33 = Х#23; подставляя эти значения
в определитель (4.9), найдем, что он равен нулю
А=#?о
• 4
О я23
а23 Х#оя
= 0.
Случай, когда #n = #i2= #22 = 0, будет рассмотрен в дальнейшем
V. Мы рассматривали пересечение кривой с прямой; более общий
результат дает теорема Безу: число точек пересечения двух
алгебраических кривых порядков т и п не превышает тп;
22 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. I
если же оно больше, чем тп% то таких точек бесчисленное
множество и кривые имеют общую компоненту *).
VI. Примечание. Сделаем несколько замечаний о решении
алгебраического уравнения (4.7) степени п.
. 1. Если среди линейных множителей
есть равные, то соответствующий корень называется кратным»
причем его кратность равна числу равных корней.
2. Если уравнение с вещественными коэффициентами имеет
комплексный корень а-(-/[}, то оно имеет и комплексный
сопряженный корень а — /р той же кратности; действительно, если хх =
= <х -f- /(5, то произведение (х — хх) (х — х2) будет вещественным
числом тогда и только тогда, когда х2 = &— /[}, ибо в этом случае
имеем:
(х — хх) (х — х2) = (х — <х — /р) (х — а + /р) = (х — а)2 + рз.
3. Уравнение нечетной степени с вещественными
коэффициентами всегда имеет хоть один вещественный корень; действительно,
комплексные корни всегда входят попарно.
4. Стремление к нулю старшего коэффициента Ап уравнения (4.7)
эквивалентно безграничному возрастанию одного из корней; для
доказательства положим х = —; мы будем иметь:
yn(Anx* + An_xx"-i+ ... +Агх + А^ =
= i40y»+^iyl,-1+ ... + \_xy + An = 0; (4.15)
если д:1->оо, то ух-+0; так как хх является корнем (4.7), то ух
является корнем уравнения (4.15), а при у1 = 0 мы имеем:
ля = о.
5. Стремление к нулю старших коэффициентов Ап% An_v ...
.... An_k+X уравнения (4.7) эквивалентно безграничному
возрастанию k его корней.
§ б. Пересечение алгебраической кривой с бесконечно
удаленной прямой
I. Рассмотрим уравнение алгебраической кривой п-то порядка
•*) Доказательство можно найти, например, у Р. Уокера [1], стр. 72, 127»
§ 5] ПЕРЕСЕЧЕНИЕ АЛГЕБР. КРИВОЙ С БЕСКОНЕЧНО УДАЛЕННОЙ ПРЯМОЙ 23
вводя однородные координаты x = — t y = ~^t получим уравнение
х^ х$
[ Х\ хЛ vi ххх2
умножая обе его части на х%, получим уравнение в однородных
координатах
<р(*ь Х2. *3) = *з/(§. ^ = ^акгх\хГ2Х^к'г = 0. (5.2)
причем <f(xv х2, хг) является однородным многочленом порядка п
относительно xv х2, хг, ибо сумма показателей при них в любом
члене равна k-\-r-\-{n— к — г) = п. Умножая (5.2) на х^ мы
считали хг ф 0; условимся считать несобственные точки
принадлежащими кривой (5.1) в том случае, если их однородные
координаты удовлетворяют уравнению (5.2).
Полагая в (5.2) хг = 0, мы получим некоторый однородный
многочлен порядка п относительно xv х2% ибо все члены (5.1), для
которых & + r<Ai, содержали хг и обратились в нули; деля этот
многочлен на xnv мы получим уравнение /г-й степени для
нахождения отношения — =&
хх
1/+^.^+ ... +<ц*+«о=о; (5.3)
если kv k2, ..., kn — его корни, то точки пересечения кривой (5.1)
с бесконечно удаленной прямой характеризуются
координатами *)
*3 = 0, £ = ft, (5=1, 2 /г); (5.4)
найденные угловые коэффициенты kv k2, ..., kn характеризуют так
называемые асимптотические направления; если это уравнение
имеет кратные корни, то будем говорить, что бесконечно
удаленная прямая касается данной кривой.
II. В качестве иллюстрации рассмотрим пересечение кривой
второго порядка с бесконечно удаленной прямой; вводя однородные
координаты, мы получим:
апх\ + 2а]2х1х2 + а22х22 + 2а1гхгхг + 2а2гх2хг + аггх1 = 0; (5.5)
полагая д:3=0, — = & и деля на х\, придем к квадратному уравне-
Х\
нию для нахождения k
#22^2 + 2#12& + ап = 0. (5.6)
*) Некоторые из этих корней могут оказаться мнимыми; этот случай
рассмотрен в § 6.
24 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. Т
8 =
#i2> а21 = а12. (5.7)
Рассмотрим все возможные случаи в зависимости от знака величины
#11 #12
l#2i a22\ — aua™~aUt и2\ — "п-
1) Пусть сперва 8 < 0, т. е. кривая принадлежит к
гиперболическому типу; уравнение (5.6) имеет при а22 Ф 0 два
вещественных различных корня
Ь2_ #^ * (5,8)
т. е. кривая гиперболического типа пересекает бесконечно
удаленную прямую в двух точках
х3 = 0, % = k1; х3 = 0, % = k2; (5.9)
если же #22 = 0, ап Ф О, то ищем отношение — из уравнения
х2
ЧйУ + ЧйН'
откуда находим два корня —1 = 0, -i = — —-^, т. е.
А1 = оо, й2 = -2^2; (5.10)
наконец, при ап = а22 = 0 корни таковы: /г1 = оо, /г2 = 0.
2) Пусть теперь 8 = 0, т. е. кривая принадлежит к
параболическому типу; если а22 Ф 0, то из (5.6) находим два
вещественных равных корня
*i=*»=-2: (5Л1)
если же #22 = 0, а следовательно, и #12 = 0, ап Ф 0, то ищем об-
ратное отношение — из уравнения ап[ — \ =0, откуда снова
находим два равных корня — = 0, т. е. kx = k2 = oo. Таким образом,
х2
кривая параболического типа касается бесконечно удаленной
прямой.
3) Пусть, наконец, 8 > 0, т. е. кривая принадлежит к
эллиптическому типу; в этом случае имеем:
*12±V=±-9 yZJb = iyb,
1,2 #22
т. е. кривая эллиптического типа не пересекается с бесконечно
удаленной прямой, или, как можно еще сказать, пересекает ее
д двух мнимых точках.
§ 6]
ВВЕДЕНИЕ МНИМЫХ ЭЛЕМЕНТОВ
25
Мы предполагали до сих пор, что из трех коэффициентов alv
#12» #22 хоть °ДИН не равен нулю; если же ап = а12 = а22 = 0, то
фактически мы имеем по (4.5) кривую не второго порядка, а
первого, т. е. прямую. Однако, если мы рассматривали кривые
второго порядка (4.5) с любыми коэффициентами aik и если все три
коэффициента ап, #12, а22 обратились в нули, то по (5.5)
уравнение нашей кривой таково:
хз (2#i3*i i 2#2з*2 т" ^зз-^з)= О»
так как мы рассматриваем кривые второго порядка, то в этом
частном случае будем говорить, что кривая распалась на две
параллельные прямые
д:3 = 0, 2al3xl~f- 2а2ъх2-\- ^зз-^з= О»
одна из которых — бесконечно удаленная прямая д:3 = 0; в этом
случае, как легко видеть, § = 0, т. е. наша распадающаяся кривая
второго порядка принадлежит к параболическому типу.
§ 6. Введение мнимых элементов
I. Хорошо известно, какую пользу принесло введение мнимых
чисел в алгебре, — без них нам пришлось бы считать, что даже
квадратное уравнение не всегда имеет решение.
Для достижения наибольшей общности во всех наших
рассуждениях мы введем мнимые элементы в аналитическую геометрию.
Мы будем говорить, что уравнение первой степени
а1х-\-а2у-+-а3 = 0 (6.1)
с комплексными коэффициентами является уравнением мнимой
прямой; две мнимые прямые
а1х-^га2у-\-аг = 0ш bxx-\-b2y -f-^3 = 0 (6.2)
будем называть параллельными при условии
и пересекающимися при условии
й{ =/= а* • /А А\
'\
координатами их точки пересечения будем называть числа (х, у),
являющиеся корнями обоих уравнений (6.2).
Если соответствующие коэффициенты двух мнимых прямых (6.2)
являются комплексными сопряженными числами, то прямые
называются сопряженными; две мнимые сопряженные прямые
26 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. t
пересекаются в вещественной точке\ действительно, из (6.2) имеем:
у ^з^г — "2#з #з^1 —ахЬг щ •о рг\
ахЬ2—а2Ь{ * У ахЬ2— а2Ьх * \ • )
если bx = av b2 = a2, Ьг = аг, то
х _ а2а3 — а2а3 ^ __ а%ах — агах ^ g g
Л\Л2 — clxcl2 a{a2 — #i#_
Каждый числитель и знаменатель являются чисто мнимыми числами
как разность двух комплексных сопряженных чисел, поэтому х и у
вещественны.
Координатами точек пересечения мнимой прямой (6.1) с кривой
будем называть общие корни их уравнений; в случае кратных
корней будем говорить, что прямая касается кривой.
II. Вернемся снова к кривым второго порядка.
1) При 8 < 0 кривая гиперболического типа может быть
гиперболой или же при выполнении условия (4.9) распадаться на пару
вещественных пересекающихся прямых; так как при этом подради-
кальное выражение (4.11) будет полным квадратом, то будем иметь:
— §*2 + 2 х (а12 а23 — а22аи) + я_3 — а22агг =
_. g / х #12#23 #22#13 \2
и таким образом, при а22Ф0 найдем из (4.10)
_____ #12* + #23 + У~~Ь (х #12#23 —#22#13 \ .
У а22 ~ а22 \ —5 /'
уравнение кривой приобретает такой вид:
i-(а12х + а22у + а23 + * f=Т + *"*»=**» ) X
X (а12х + а22у + а2г-х V=* - fl"^Zf^» ) = 0; (6.7)
аналогичное решение получим при #22—=0, ап Ф 0; если же ап =
= #22 = 0, то имеем (4.14).
2) При 8 = 0 кривая может быть параболой или при
выполнении условия (4.9) может распадаться на пару прямых; при 8 = 0
ясно из (4.10), (4.11), что у будет линейной функцией х лишь при
условии а12а2г = а22а1г, т. е. мы должны иметь:
#11 __ ___ #13 . (g Q\
#12 #22 #23
следовательно, при а22Ф0 найдем' из (4.10), (4.11)
#22 #23
аих ■+ а22у -\- #23 ± "У^— Ьг =0, 8Х =
#32 #33
(6.9)
§ 7] ИЗОТРОПНЫЕ ПРЯМЫЕ 27
т. е. левая часть уравнения (4.5) такова:
—- {а12х + а22у + я23 -f l/11^") {al2x -f я22у + я23 — У— Ьх) = 0;
обе прямые параллельны, ибо их уравнения различаются лишь
свободными членами; аналогичное решение получим при #22 = #12 = 0,
ап Ф 0. Таким образом, кривая параболического типа при условии
(4.9) распадается на пару параллельных прямых; при Ьх < 0 они
вещественны и различны, при ^ — 0 они вещественны и совпадают,
при \ > 0 они мнимые сопряженные.
3) Пусть, наконец, 8 > 0; кривая эллиптического типа может быть
эллипсом или мнимым геометрическим местом; в последнем
случае уравнение приводится к форме
£ + -р-+1=0, (6.11)
откуда ясно, что левая часть не может обратиться в нуль ни при
каких вещественных значениях координат.
При выполнении условия (4.9) имеем (6.7), где на этот раз
У— 8 является мнимой величиной; следовательно, при условии (4.9)
кривая эллиптического типа распадается на пару мнимых
сопряженных прямых, имеющих вещественную точку пересечения.
Таким образом, кривая второго порядка может распадаться на
пару прямых, может быть мнимым геометрическим местом и,
наконец, может быть коническим сечением, т. е. эллипсом, параболой
или гиперболой.
§ 7. Изотропные прямые
I. Рассмотрим один частный случай мнимых прямых, так
называемые изотропные прямые.
Мнимая прямая называется изотропной, если ее угловой
коэффициент равен ± /, т. е. уравнение изотропной прямой имеет
следующий вид:
у= ± /АГ + а + /р, (7.1)
где а, р — вещественные числа; две сопряженные изотропные
прямые
у =/i-fa "HP' у = — tx~{-a — /[)
пересекаются, как было показано выше, в вещественной точке с
координатами л: = — р, у = а.
Для того чтобы показать, что с изотропными (и вообще с мнимыми)
прямыми нельзя связывать никаких наглядных геометрических представлений,
рассмотрим некоторые свойства изотропных прямых.
28 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. I
1) Изотропная прямая сама себе перпендикулярна-, действительно,
условие перпендикулярности двух прямых kxk2 =— 1 удовлетворяется при
kl = k2=±L
2) Изотропная прямая образует один и тот же угол со всеми
прямыми. Мы имеем, полагая k2 == /, угол между прямыми с угловыми
коэффициентами ku i
т. е. результат не зависит от углового.коэффициента kx первой прямой.
3) Расстояние от любой точки плоскости до изотропной прямой
бесконечно велико. Известно, что расстояние d от точки М0 (х0> у0) до
прямой с уравнением у = kx + Ь выражается формулой
rf =
у0 — kx0 — b
при k = ± / получим d = оо.
4) Расстояние между любыми двумя точками изотропной прямой
равно нулю *). Мы имеем следующую формулу для расстояния d между
точками Мх (хь у{), М2 (х2, у2)\
Уравнение изотропной прямой, проходящей через точку Ми таково:
у — yl=si(x — х{); условие того, чтобы точка М2 лежала на этой прямой,
приводит к соотношению у2 — у1 = Цх2— хх), откуда
d = /<*2--*i)2<l+/2) =0.
П. Покажем одно применение изотропных прямых, важное для
понимания дальнейшего.
Хорошо известны фокальные свойства конических сечений; однако
эти свойства являются специфическими именно для конических сече?
ний и другие кривые этими свойствами не обладают. Вместе с тем
нам придется встречаться с другими кривыми, для которых также
вводится понятие фокуса; поэтому мы дадим новое определение
фокуса, правда, весьма формальное, но зато имеющее смысл для
любой кривой: фокусом алгебраической кривой называется точка,
обладающая тем свойством, что касательные, проведенные из
нее к кривой, являются изотропными прямыми.
Мы будем рассматривать лишь вещественные фокусы и поэтому
ограничимся рассмотрением точек пересечения лишь сопряженных
изотропных прямых.
Докажем, что известные нам фокусы конического сечения
обладают указанным свойством; пусть М0 (х0, у0) — фокус конического
сечения, а соответствующая директриса пусть характеризуется
уравнением
Ах+Ву -f С = 0;
*) Благодаря этому свойству немцы называют изотропные прямые ну-»
левыми линиями (Nuiiinien).
$ 81 ЦИКЛИЧЕСКИЕ точки 29
обозначая через dud' расстояния точки М(х, у) от фокуса и от
директрисы, мы имеем:
Ах + Ву + С
а = у(х-Х(у+(у-у0у*9 d' =
Va2 + в2
так как по основному свойству конических сечений отношение этих
расстояний постоянно и равно эксцентриситету е, то мы имеем:
(х - *0)2 + (У - Уо)2 - e4AXilyBtC? = 0. (7.2)
Проведем через точку М0 прямую с уравнением
У — Уо = к(х — х0)
и будем искать те значения &, при которых обе точки пересечения
прямой и кривой совпадут, т. е. прямая будет касаться кривой; мы
имеем:
(x-x0)*(l + k*) = Af+B2 [x(A + Bk) + B(y0-kx0) + C]*,
откуда
(7.3)
корни этого уравнения будут равны между собой тогда и только
тогда, когда l-f-&2 = 0, т. е. к = ± /.
§ 8. Циклические точки
I. Известно, что коническое сечение определяется пятью
точками *), однако окружность, являющаяся частным случаем
конического сечения, определяется лишь тремя точками; кроме того,
два конических сечения пересекаются по теореме Безу в четырех
точках, причем все четыре могут быть вещественными; если же
рассмотреть совместно уравнения двух окружностей
(x-atf + ty-btf-r*^, (х-а2у + (у-1>2у-г1 = 0, (8.1)
то, исключая из них х2-\-у2ь мы придем к уравнению первой
степени
2x(a1-a2)+2y(b1-b2) + al + bl-rl-a\-b\ + rl = 0, (8.2)
и, решая его совместно с уравнением любой из наших окружностей,
мы найдем лишь две точки пересечения, вещественные или мнимые.
*) Подробнее об этом см. в § 21.
30
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
[ГЛ. Г
Для достижения наибольшей общности мы введем новое понятие,
связывающее бесконечно удаленную прямую, рассмотренную в § 2,
и изотропные прямые, рассмотренные в § 7.
Циклическими точками плоскости называются точки
пересечения изотропных прямых с бесконечно удаленной прямой)
таким образом, мы имеем две циклические точки, характеризуемые
однородными координатами
:0,
х%
: /; х, = 0, -^ = -
(8.3)
Циркулярной кривой называется кривая, проходящая через
циклические точки] если циклические точки являются двойными, то кривая
называется бициркулярной, если тройными — трициркулярной, и т. п.
II. Рассмотрим снова в качестве иллюстрации кривые второго
порядка (5.5) и их пересечение с бесконечно удаленной прямой;
уравнение (5.6) может удовлетворяться при
k = ± / тогда и только тогда, когда
а2212 + 2а12/ + Яц = а\\ — а22 + 2fli2/ = 0,
откуда ап = а22, #12 = 0, что характеризует
окружность; таким образом, циркулярными
кривыми второго порядка являются
только окружности. Все окружности про-
х ходят через циклические точки, поэтому
окружность определяется пятью точками, как
и любое коническое сечение; так как две
из них — циклические, то для определения
окружности достаточно знать три ее
вещественные точки.
Циклические точки играют важную роль
при подсчете (по теореме Безу) числа точек
пересечения циркулярных кривых; например, две окружности, как
и любые два конических сечения, пересекаются в четырех точках,
но так как две из них—циклические, то вещественных точек
пересечения не больше двух.
III. В качестве второго примера рассмотрим так называемую
кривую Бурместера*) (рис. 11), характеризуемую уравнением
(х2 + у2) (тх + 1у) — Imxy *= 0; (8.4)
вводя однородные координаты, мы получим уравнение
[х\ 4- лф(тхх + /*2) — 1т ххх2хъ = 0;
Рис. 11.
*) Эта кривая играет большую роль в синтезе механизмов (см. §§ 54—55).
Кривой Бурместера ее называет А. П. Котельников в своем классическом
исследовании [1].
§ 9] НАХОЖДЕНИЕ АСИМПТОТ АЛГЕБРАИЧЕСКИХ КРИВЫХ 31
полагая затем х3 = 0, — = k, придем к уравнению для нахождения k
(l+A52)(£/+m) = 0;
отсюда находим все три корня
kl = /, k2 = — /i &з = Г" (8-5)
Таким образом, кривая Бурместера является циркулярной кривой;
поскольку она третьего порядка, то она пересекается с окружностью
в шести точках; так как две из них — циклические, то кривая
Бурместера не может пересекаться с окружностью более чем
в четырех вещественных точках *).
§ 9. Нахождение асимптот алгебраических кривых
Известно, что асимптотой кривой, имеющей бесконечную ветвь,
называется прямая, обладающая тем свойством, что расстояние от нее
до точки кривой, безгранично удаляющейся по бесконечной ветви,
стремится к нулю. Если уравнение кривой задано в форме у = f (х)>
то для существования асимптоты у = kx -\- Ъ, не параллельной оси Оу,
необходимо и достаточно существование двух пределов
lim i^- = kb lim [f(x) — kx] = b; (9.1)
*-> OO X X -> oo
для существования асимптоты x = a, параллельной оси Оу,
необходимо и достаточно существование такого значения а аргумента х,
при котором lim/(#) = оо.
Известно также следующее: если при безграничном удалении точки
по бесконечной ветви кривой касательная в этой точке стремится
к некоторому предельному положению, то эта предельная прямая
является асимптотой **).
Если кривая — трансцендентная, то асимптота может
существовать, хотя касательная не стремится ни к какому предельному
положению: например, если у = sn\x.) f т0 |у|^— и цт у = 0,
Х ' •* I X -> оо
т. е. ось Ох является асимптотой; если же написать уравнение
касательной в точке (Xi, уО . 9Ч
sin(jq)
У —yi = 3>i(* —*i), )>! = 2 cos (*2) i^,
то при xx—>oo величина cos(a:^ не стремится ни к какому пределу.
Для алгебраической кривой такой случай невозможен —
асимптота алгебраической кривой всегда является предельным
*) Эти простые рассуждения позволят нам установить наибольший
порядок соприкосновения кривой со своей окружностью кривизны (см. § 58).
**) См., например, Н. Н. Лузин [1], §§ 160—162.
32 НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ [ГЛ. X
положением касательной и поэтому может быть названа касатель^
ной в бесконечности. Это свойство асимптот алгебраической кривой'
облегчает их нахождение. Для нахождения асимптот алгебраической
кривой с уравнением f(x, у) —О мы должны найти абсциссы точек
пересечения этой кривой с прямой y=.kx~\-b (которую, таким
образом, сперва предполагаем не параллельной оси Оу); они находятся
из уравнения
/(х, kx + b) = 0, (9.2)
которое должно иметь два бесконечных корня, ибо искомая прямая
должна касаться в бесконечности нашей кривой; для этого
необходимо и достаточно (в соответствии с примечанием § 4), чтобы два
старших коэффициента уравнения (9.2) обратились в нуль; из этих
двух условий находим две неизвестные величины k и Ъ. Если же
ищется асимптота, параллельная оси Оу, с уравнением х = а, то,
подставляя х = а в уравнение кривой, получим уравнение /(а, у) = 0
для нахождения ординат точек пересечения; если расположить это
уравнение по степеням у
/(a, у) = а0уп+а1(а)уя-* + ••. + *„-i (*)У + Ма) = 0, (9.3)
где аг(<х) — многочлен степени не выше г относительно а, то
возможны два случая: 1) если а0 Ф 0, то, поскольку это константа,
старший коэффициент не может обратиться в нуль — кривая не имеет
асимптоты, параллельной оси Оу; 2) если же а0 = 0 и отсутствуют
члены с У1""1, уп~2, ..., yn~k+l, т. е.
/(^.y) = ^Wr4%iWrH1+ ...
... +*„-i(*)y+M*) = 0. (9.4)
то, подставляя х=а и приравнивая старший коэффициент нулю,
получим уравнение ak (а) = 0 для нахождения а.
Если найденные числа /г, Ъ или а окажутся мнимыми, то мы
говорим о мнимых асимптотах; если мнимыми асимптотами
окажутся изотропные прямые, то точка их пересечения на-
зывается фокальным центром, или особым фокусом кривой:
ограничиваясь случаем вещественного фокального центра, мы будем
рассматривать лишь точки пересечения сопряженных изотропных
асимптот.
Сходство между фокусом и фокальным центром в том, что
в обоих случаях это — точка пересечения изотропных сопряженных
прямых, касательных к кривой; различие в том, что точки касания
не являются бесконечно удаленными в случае фокуса и являются
таковыми в случае фокального центра.
Так как бесконечно удаленные точки изотропных прямых—это
циклические точки, то фокальные центры могут быть только у кри--
§ 10] НЕКОТОРЫЕ ПРИМЕРЫ НА ИССЛЕДОВАНИЕ КРИВЫХ 33
вых, проходящих через циклические точки, т. е. у циркулярных
кривых *).
Примечание. Приравнивая нулю старший коэффициент в
уравнении (9.2), мы найдем лишь асимптотические направления,
которые мы могли бы найти в случае кривых второго порядка и из
уравнения (5.6); это еще не значит, что существуют асимптоты с такими
направлениями. Например, для параболы у2 = 2рх мы получаем
асимптотические направления — = 0, но парабола не имеет асимптоты;
действительно, написав уравнение параболы в виде у = \2рх и
воспользовавшись (9.1), мы видим, что существует лишь первый
предел и не существует второго.
§ 10. Некоторые примеры на исследование кривых
I. В § 7 мы показали, что фокус конического сечения является
точкой пересечения двух сопряженных изотропных прямых,
касательных к нему; если коническое сечение не является окружностью,
то оно не может быть циркулярной кривой и фокус не может быть
фокальным центром, — это видно из формулы (7.3), определяющей
при k = I конечные абсциссы точек касания.
Рассмотрим особо случай окружности; подставляя y = kx-\-b
в ее уравнение
(*-а)2 + (у_Р)2-г2=0, (ЮЛ)
получим:
д:2(1 -Ь^2)+ 2х [k ф — Р) — а] + а2 + ф — Ь? — г2 = 0; (10.2)
приравнивая нулю его два старших коэффициента
#2-f 1=о, k{b — р) — <х = 0.
найдем & ~ ±/, & = Pq:/a. Таким образом, сопряженные изотропные
прямые
у = /л; + р — /а, у = — /ДГ+Р -На, (Ю.З)
пересекающиеся в точке д; = а, у = р, т. е. в центре окружности,
являются ее асимптотами**), — следовательно, центр окружности
является ее фокальным центром.
II. В качестве второго примера рассмотрим кривую с уравнением
2х (х2 + у2) = а (Зх2 — у2) (10.4)
и найдем ее вещественные фокусы; она является, как легко видеть,
циркулярной кривой третьего порядка.
*) Все эти понятия нам понадобятся в дальнейшем при исследовании
некоторых кривых, имеющих применение в синтезе механизмов (см гл. VII).
**) Благодаря этому свойству изотропных прямых их часто называют
круговыми асимптотами.
34
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
[гл. Ц
Для нахождения асимптот и фокальных центров положим в (10.4) у =ri
= kx + Ь\ мы получим уравнение
2л:3 (1 + к2) + х2 (4bk -f ak2 — За) -f 2bx (b -f ak) + ab2 = 0; (10.5)
приравнивая нулю его два старших коэффициента, найдем:
£2+1^0, Л=»±/; 4*£-f-я*2 — Зд = 0, &=+ш;
таким образом, кривая не имеет вещественных асимптот; ее мнимые
асимптоты — это сопряженные изотропные прямые
у =zix — ai> у
- ix + ai;
(10.6)
1 t
\ V
' N. \
У////Ш&,
У
7////У//Л
точка их пересечения Fx (а, 0) является фокальным центром; поскольку
ее координаты не удовлетворяют уравнению кривой, то она не лежит на
кривой.
Для нахождения фокуса положим в (10.5) k = /; получим квадратное
уравнение для нахождения абсцисс точек пересечения
4л:2 (Ы — а) 4- 2bx (Ь + ai) + ab2 = 0; (10.7)
для того чтобы изотропная прямая у = ix 4- b касалась кривой, это
уравнение должно иметь равные корни, для чего
должно выполняться условие
b2 (Ь -Ь ai)2 = 4ab2 (bi — а) = 4ab2i (b + at),
откуда
6, = 62 == 0, 63 = 3ш\ Ь4 =— ai;
таким образом, изотропные прямые
у = ix, у = — ix; у = ix + За/,
у = — /дг — За/ (10.8)
касаются нашей кривой; корень 64 = — ai
мы отбросили, ибо ему соответствует х = оо
и по (10.6) мы видим, что в этом случае
& получим фокальный центр; окончательно
рис 12. кривая имеет фокусы
F2 (0, 0), Fz (— За, 0).
III. Найдем фокальный центр кривой четвертого порядка (рис. 12)
с уравнением
а\х2 + у2 + /2_г2)2_ 4а/ (дг—*) (д: cos 7 —У sin т)(а:2 + )'2 + '2—^2) 4~
-+- 4/2 (л:2 + у2) (лг — ef — 4а2/2 (л: sin т + У cos ?)2 = 0, (10.9)
являющейся траекторией точки М шатунной плоскости криво-
шипно-шатунного механизма; все обозначения понятны из рис. 12.
Подставляя в (10.9) y = kx-\-b и собирая члены с х* и х3, получим:
х4 [а2 (1 + &2)2 — 4а/ (1 + &2^cos т — k sin т) + 4/2 (1 4~ k2)] +
+ х3 \4a2bk (1 + k2) — 4а/ \2bk (cos 7 — k sin T) — (1 + k2) ф sin T 4-
+ *cosT — ^sinT)] + 4/2[2^— 2*0 4-ft2)]} 4" ..- (10.10)
где многоточием обозначены члены с х1% х1, х°.
§ 101
НЕКОТОРЫЕ ПРИМЕРЫ НА ИССЛЕДОВАНИЕ КРИВЫХ
35
Приравнивая нулю первый коэффициент, получим:
(1 + k2) [а2 (1 + к2) — Ш (cos 7 — k sin т) + it2] = 0,
откуда найдем четыре корня
/vi —— 1% /vo ' '» Ко
-— 2t sin f 4- / (а — 2t cos -у)
, — 2t sin 7 — / (я — 2£ cos f)
*4 ;
кривая, конечно, не имеет вещественных асимптот, ибо она не имеет
бесконечных ветвей. Так как нас интересует лишь фокальный центр,
то рассмотрим лишь те мнимые асимптоты, которые являются
изотропными прямыми, т. е. рассмотрим лишь корни к = ±L Полагая
k = / и приравнивая нулю коэффициент
при л;3, получим:
ЫЫ [t — a (cos 7 — / sin 7)] = 0,
откуда £ = 0; таким образом,
сопряженные изотропные прямые у = ±tx являются
асимптотами, а точка F(G, 0) их
пересечения является фокальным центром,
причем в данном случае он не лежит на
кривой.
IV. Рассмотрим теперь кривую,
определяемую как геометрическое место
точек С и С пересечения окружностей
с, проходящих через две заданные точки А и В, с прямыми,
соединяющими центры окружностей с третьей заданной точкой О
(рис. 13). Если третья точка — собственная, то, не нарушая общности,
возьмем в ней начало координат, а ось Ох выберем параллельной
прямой, проходящей через две заданные точки Л (а, с) и В(Ь, с).
Мы имеем уравнение окружности с центром в точке Dy-—^—, d\
(рис. 13)
х2 — (a + b)x + y2 — 2dy-\-ab + 2cd — с2 = 0 (10.11)
и уравнение прямой OD
2d
О
\ °у>
\" S
yzN-
^х'
/ V
■^с
X
Рис. 13.
У —
а + Ь
х\
(10.12)
исключая из этих уравнений параметр d, получим после простых
преобразований
(х2 + у2)(х-а — b) + (ab — с2)х +c(a + b)y = 0; (10.13)
таким образом, искомым геометрическим местом является
циркулярная кривая третьего порядка *).
*) Она будет детально изучена в гл. VII; она изображена на рис. 203.
36
НЕСОБСТВЕННЫЕ И МНИМЫЕ ЭЛЕМЕНТЫ
[ГЛ. |
Так как в ее уравнении отсутствует член с у6, то для
нахождения ее асимптот положим х = ту-\-п\ приравнивая нулю два
старших коэффициента в уравнении
т(\ + т2)У* + [2т2Аг + (1 + т2)(Аг— а — Ь)]у2+ ... =0,
будем иметь:
m(l-\- т2) = 0, mx = l, т2 —— /, w3 = 0;
(1 + т2) (а + Ь) л , ,
Следовательно, кривая имеет сопряженные изотропные асимптоты
у= ±1х\ точка их пересечения, т. е. фокальный центр, совпадает
с заданной точкой, лежащей в начале координат, и в данном случае
лежит на кривой; вещественная асимптота х = а-\-Ь параллельна
прямой, на которой лежат центры окружностей, и проходит через
точку, симметричную с фокальным центром относительно этой прямой.
Если же третья точка несобственная, то возьмем начало
координат в середине отрезка АВ\ все прямые, проходящие через
несобственную точку, параллельны между собой, — пусть они
характеризуются угловым коэффициентом k. Мы имеем уравнение
окружности с центром в точке D(0, d)
Х2+ у2 _ 2dy - (-^-)2 = 0
и уравнение прямой у == kx -\- d, проходящей через ее центр;
исключая из этих уравнений параметр d, получим:
x2 — y2+2kxy = (^^j\ (10.14)
т. е. в этом случае кривая является равносторонней гиперболой,
центр которой лежит в середине отрезка между двумя заданными
точками.'
Примечание. Хотя мы определили фокальный центр чисто
формально — как точку пересечения изотропных сопряженных
асимптот, тем не менее он играет большую роль в дальнейшем; при
рассмотрении некоторых циркулярных кривых третьего порядка (гл. VII),
играющих важную роль в задачах синтеза, знание фокального центра
позволяет построить эти кривые по точкам.
§11. Понятие о классе алгебраической кривой
I. При подсчете числа фокусов (вещественных, или мнимых, но
не фокальных центров) нам приходится решать такую задачу: найти
число касательных, которые можно провести к данной кривой
через циклическую точку; действительно, мы ищем изотропные
§ И] ПОНЯТИЕ О КЛАССЕ АЛГЕБРАИЧЕСКОЙ КРИВОЙ . 37
прямые, касательные к данной кривой, а все изотропные прямые
проходят через циклические точки.
Мы приходим к основному понятию теории алгебраических кривых:
классом алгебраической кривой называется число касательных *),
которые можно провести к кривой через произвольную точку
плоскости. В некоторых простейших случаях класс нетрудно найти;
например, для того чтобы прямая с уравнением у — y0 = k(x— х0)
касалась кривой второго порядка (4.5), необходимо и достаточно,
чтобы уравнение для нахождения абсцисс точек пересечения
апх2 Н- 2я12 (kx + У0 — kxQ) х + а22 (kx + у0 — kxQ)2 + 2а1гх +
+ 2 я23 (kx +у0 — kx0) -+- я3з = ° (ИЛ)
имело равные корни; так как уравнение — квадратное, то это
условие таково:
КУО — kX0) (а12 + *<*22> + «13 + ^«2з12 =
= (<*22*2 + 2«12^ + а\\) 1^22 (Уо — kxof + 2«23 (Уо ~ kxo) + «Зз1 • (l 1 «2)
Нетрудно проверить, что члены с &4 и &3 сокращаются и остается
уравнение второго порядка для нахождения k\ следовательно, кривая
второго порядка одновременно является кривой второго класса.
II. Приведем без доказательства простые формулы Плюккера**),
связывающие порядок и класс алгебраической кривой: если кривая n-го
порядка имеет k двойных (т. е. узловых) точек и g точек возврата, то ее
класс т дается формулой
т = п (п — 1) — 2k — Zg. (11.3)
Кривая второго порядка не имеет ни двойных точек, ни точек возврата, т. е.
для нее п = 2, k — g — О, откуда т = 2. Кривая Бурместера (рис. 11) имеет
одну двойную точку, т. е. для нее п = 3, k = 1, g = 0, откуда т = 4.
Обратно, если кривая имеет / касательных, касающихся ее в двух точках,
и г точек перегиба, то порядок выражается через класс следующей
формулой:
п = т (т — 1) — 2/ — Зг. (11.4)
В § 23 мы еще вернемся к классу кривой.
*) Вещественных или мнимых.
**) См., например, Р. Уокер [1], гл. IV, §6, В. В Добровольский [1], гл. II.
ГЛАВА II
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
§ 12. Свойства дробно-линейной функции
Для всего дальнейшего нам необходимо сделать небольшое
отступление чисто алгебраического характера — ознакомиться со
свойствами так называемой дробно-линейной функции.
I. Функция f (х) называется дробно-линейной, если она
является дробью, числитель и знаменатель которой являются
линейными функциями, т. е.
/(*) = т£±Т' I? ЬИ\==аа-ЬсфО; (12.1)
сх + d ' \с а
оговорка ad—ЬсфО существенна, так как если ad = be, то — = — = А,
т. е. а = сХ, Ь = d\t откуда
J v ' cx + d
Рассмотрим свойства дробно-линейной функции; пусть две
переменные х' и х связаны дробно-линейным соотношением
1) Функция, обратная дробно-линейной, также
дробно-линейна; действительно, из (12.2) найдем:
dx' — b \ d —£1 , , , л /in о\
х=-сх'+а> \-с a\ = ad-bc+Q; (12.3)
2) дробно-линейная функция от дробно-линейной есть также
дробно-линейная; действительно, если дано, что
о*' + Р ~/ _ ах + Ь
X
а ко.
то мы имеем:
'_ а (ал -+ 6) + Р (сх + d) _ Ах + В
ФО,
х' —
1(ах + Ь) + Ъ (сх + d) Cx + D '
§ 121 СВОЙСТВА ДРОБНО-ЛИНЕЙНОЙ ФУНКЦИИ. 39
где мы положили
А=*аа + фс, B = ab + $d, С — уа^Ьс, D = ib + bd,
причем
\А В\ \а 81 \а Ь\
А В
С D
а р
7 *
a b
с d
3) каждому значению х соответствует одно и только одно
значение х1\ и наоборот, значению х = соответствует
х' = оо, а значению х' = — соответствует х = оо; таким
образом, бесконечно большому значению одной величины
соответствует конечное значение другой;
4) для нахождения коэффициентов дробно-линейной функции
(12.2) надо знать три значения xv х2, хг и три
соответствующих значения х[, х'г х'3; дальнейшие значения х1 можно
находить по соответствующим значениям х по формуле
xz-
Xе-
X ~—~~ Хо
х$ — Х\
Х$ --"~" х2
(12.4)
Действительно, формула (12.2) содержит четыре коэффициента; деля
на один из них, мы получим три параметра, для нахождения
которых надо задать три условия, т. е. три пары значений х и х\ Мы
имеем:
^, v, ax + b ax{ + b (ad — bc)(x — xx)
i ex + d
, ax -f- b
X<>— cx + d
cxx + d (ex -f- d) (cxx ■+• d) *
ax2 -\-b (ad — be) (x — x2)
(ex ■+• d) (cx2 + d) *
4
X Хг
cx2 +d
cx2 + d
x ~-~ Xn jc m—mm x2 ex j ~j— a
Точно так же, полагая х'
х'—х
Ч
3, мы получим:
х3 — хх сх2 -f- d
лп —• Хп х$~~~ х2 СХ\ —\— а
откуда делением найдем (12.4);
5) если переменные х% х' связаны соотношением (12.4), то
справедливо (12.2). Обозначая через t общее значение обоих
отношений в левой и правой частях (12.4), мы видим, что t является
дробно-линейной функцией х'\ тогда по свойству 1) х' является
дробно-линейной функцией /; но / является дробно - линейной
функцией х\ отсюда по свойству 2) х' является дробно-линейной
функцией х.
40
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
•Уз — ■
X-
Не исключена возможность того, что одна из величин xv х2, xz,
или х[9 x'v х'г обращается в бесконечность; в таком случае ту дробь,
в числитель и знаменатель которой входит эта величина, полагаем
равной единице; пусть, например, л;2 = оо; в таком случае мы имеем:
l=L*l = (*L— l):(— — l), lim *1=*L=U
< — x2 \x2 J \ x2 J Xi_+ qo x — x2
II. Рассмотрим теперь свойства линейной функции
x' = ax + b; (12.5)
ее можно считать частным случаем дробно-линейной функции при
с = 0, d=l;
1) функция, обратная линейной, также линейна;
2) линейная функция от линейной функции также линейна;
эти два свойства аналогичны свойствам дробно-линейной функции;
3) каждому значению х соответствует одно и только одно
значение х!, и наоборот; значению х = оо соответствует
значение х! = оо; таким образом, в отличие от дробно-линейной функции
в случае линейной функции бесконечно большие значения обеих
переменных соответствуют друг другу;
4) для нахождения коэффициентов линейной функции (12.5)
надо знать два значения хх, х2 и два соответствующих
значения x'v х'2; дальнейшие значения xf можно находить по
соответствующим значениям х по формуле
X —— Хл X "-"• Х\
X •-—" х2
(12.6)
5) если переменные х, х' связаны соотношением (12.6), то
справедливо (12.5).
III. Отметим в заключение следующее важное обстоятельство:
если переменные связаны дробно-линейной зависимостью и если
бесконечно большие значения обеих переменных соответствуют
друг другу, то дробно-линейная зависимость вырождается в ли*
нейную х' = ъх-\- (5; действительно, мы имеем л;' = оо при х = ,
Л , ах + Ь , Л
откуда вытекает, что с = 0 и, следовательно, х' = —^— — ajt-f-p;
такие два ряда точек называем подобными, ибо по (12.6) имеем
пропорциональность соответствующих отрезков; при а=1 оба ряда
тождественны, ибо различаются только сдвигом.
Если точки х = сю, х' = оо и л; = 0, х' = 0 соответствуют друг
другу, то, очевидно, имеем х' = <*х.
Все рассмотренные условия, которым должны удовлетворять
коэффициенты для того или иного характера соответствия точек, являются
не только достаточными, но, как легко видеть, и необходимыми.
§ 13] АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ ЧЕТЫРЕХ ТОЧЕК 41
§ 13. Ангармоническое отношение четырех точек
I. Рассмотрим на прямой g четыре точки Av А2, Л3, Л4 и введем
новое понятие, весьма простое, но играющее важную роль во всем
дальнейшем: ангармоническим отношением четырех точек прямой
называется величина
■^2^*3 А%А\
если одна из точек бесконечно удаленная, то, аналогично тому, как
мы делали в § 12, полагаем равной единице ту дробь, в числителе
и знаменателе которой фигурирует данная точка.
Если в соответствии с § 1 выбрать точки Av А2 за основные,
а положения точек Av Л4 характеризовать отношениями их
расстояний от этих двух точек
Л7Л
|Х==
A<lA\
то, очевидно, ангармоническое отношение четырех точек равно
отношению этих величин —, — поэтому его часто называют сложным»
или двойным отношением.
II. В том частном случае, когда {АхА2АгА4) =—1, говорят, что
эти точки образуют гармоническую группу (или являются
гармонически сопряженными); в частности, гармоническую группу образуют
концы Аг и А2 отрезка, его
середина Аъ и бесконечно удаленная
точка Л4, ибо мы имеем:
А[А3 ..
А2Ай ' ЛАГ
Наоборот если четыре точки
образуют гармоническую группу
и одна из них несобственная, то из остальных точек одна является
серединой отрезка, образованного двумя основными точками.
Мы встречаемся с гармоническими группами точек уже в
элементарной геометрии: на каждой стороне треугольника имеем
гармоническую группу точек, образованную двумя вершинами
треугольника и точками пересечения этой стороны с биссектрисами
внутреннего и внешнего угла при противоположной вершине
(рис. 14); действительно, мы имеем по свойству биссектрисы
Л^___АО АР __ AG
ВС BG\ ~BD~ BG%
откуда вытекает {ABCD)— ~ 1.
42
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. и
Покажем построение четвертой точки D, образующей на прямой g
гармоническую группу с тремя заданными точками А, В, С (рис. 15);
через точки А и В проводим произвольные параллельные прямые а
и Ь, через точку С проводим произвольную прямую с, пересекающую
прямые а и Ъ в точках Р и Q; откладываем BQf = BQ и
проводим PQ' до пересечения в точке D с прямой g; мы имеем *):
АС
ВС
АР
QB
AD
BD
АР
Q'B
АР
QB
(ABCD) = —l.
III. Рассмотрим некоторые простейшие свойства ангармонического
отношения.
1) Ангармоническое отношение четырех точек, три из
которых даны, единственным образом определяет положение
четвертой точки, т. е. может служить
ее координатой; действительно, если
точки Av А2, Аъ даны, то из (13.1)
находим:
А\АА
А2А4
А\Аъ
АоАъ
(АХА2АЪАА) = X;
(13.2)
так как все величины в правой части
известны, то мы можем найти
параметр X, который в соответствии
с § 1 определяет положение точки АА\
2) ангармоническое
отношение четырех точек может
иметь любое значение, кроме единицы**); действительно, если
(АХА2АЪАА) = 1, то по (13.1) мы имели бы
Рис. 15.
А{А3 _ AjAa. ^
А^А^ ■"2'М
что невозможно;
3) легко видеть, что (АхА2АгАА) < 0 тогда и только тогда, когда
одна из точек Л3, АА лежит внутри отрезка [Av А2\, а другая —
вне его (рис. 16, а); в этом случае мы говорим, что обе пары
точек Ах, А2 и Аъ% Л4 взаимно разделяются, ибо при переходе
от Ах к А2 по конечному или бесконечному пути надо перейти
через одну из точек Аг, АА\ точно так же (АХА2АЪА^ > 0 тогда и
только тогда, когда обе точки Л3, А4 лежат или вне, или внутри
*) Другой способ построения будет рассмотрен в § 45.
**) Четыре точки Ах, А2, Аъ, АА предполагаются различными; поэтому
их ангармоническое отношение не может равняться ни нулю, не
бесконечности.
§ 13] АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ ЧЕТЫРЕХ ТОЧЕК 43
отрезка [Av А2\ (рис. 16, б% в)\ в этом случае обе пары точек Av А2
и Av А4 не разделяют друг друга;
4) ангармоническое отношение не изменяется, если две основ-
ные точки А1% А2 поменять местами с двумя другими
точками Л3, Л4, т. е.
(А1А2А^А^) = (Л3Л4Л1/12);
если же поменять местами точки Av А2, или точки Л3, Л4,
то величина ангармонического отношения заменится своей
обратной величиной
(А2АхАгА4) = (АхА2А4Аг) =
1 ' (13.3)
—о——
я,
А,
——О-—0 О
а)
Аг Я3 До
б)
~ {А{А2А,А,) '
таким образом, мы имеем;
(А1А2АгА4) = (АгААА1А2) = (А2А1АААг) = Л, Л3 Л, Л2
= (АААгА2А1); (13.4) #
Рис. 16.
доказательство вытекает из (13.1).
IV* Покажем теперь вычисление ангармонического отношения
четырех точек при различных способах задания положения точки.
1) Если положения точек Av А2, Л3, АА на прямой g
определяются их абсциссами xv x9t
(A.AJLA.) = х%~Хх : х'~Хх ; (13.5)
v ' i 3 *' хг— хг ХА—хг v '
2) если положения точек Ах, А2, А3, А4 определяются
отношениями их расстояний от заданных точек М0, М0, с
абсциссами х0, х'0
М0А
\ = ^Ш- (/=1, 2. 3. 4). (13.6)
M'0At
то
X, —X
^i^A) = -x^:^rg-: (13>7)
действительно, полагая в (12.4) х'= х'4, х = хг мы получим
соотношение
Хо •*■-"" Х\ Хд ~~~ Хл JCo ■—* Хл Хл •—■ Хл
JCn ™""" Хп им ™""" Ло «о ~~~"* лп Л* -""""" Хп
(13.8)
справедливое для любых двух величин х>', х, связанных дробно-
линейной зависимостью; так как по (1.2) имеем
-\ X — Xq
44
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл и
то X является дробно-линейной функцией х% откуда по (13.5)
вытекает (13.7);
3) если абсциссы точек Av А2, Л3, Л4 определяются
значениями параметра ц
xi = xo+V4x'o ('=1. 2> 3» 4>' (13.9)
где xQ, х'0—абсциссы двух заданных точек MQ, M'Q% то
(А1Л2ЛгЛ,)= ^^ -iiizzJil; (13.10)
доказательство очевидно.
§ 14. Перспективные и проективные ряды точек
I. Через g(A, В, С, D, ...) будем обозначать ряд точек
Л, Б, С, D, . .. на прямой g\ прямую g будем называть основанием,
или носительницей этого ряда точек.
Два ряда точек g(At В, С, D, ...) и g'(A't В\ С, D', ...)
(рис. 17, а) будем называть перспективными, если прямые,
соединяющие соответствующие точки (т. е. А и А', В и В'% С и С
и т. п.), пересекаются в одной точке (в данном случае в S),
называемой центром перспективы. Можно также сказать, что ряд
а)
Рис. 17.
б)
точек g'(A't В', С, D\ ...) является центральной проекцией
ряда точек g(A, В, С% D, ...) из центра перспективы S на
прямую g\ То обстоятельство, что оба ряда точек перспективны,
означает не только особое расположение этих рядов — оно влечет
за собой определенное соответствие между длинами соответствующих
отрезков; именно, если два ряда точек перспективны, то равны
ангармонические отношения любых четырех соответствующих
точек обоих рядов, /п. е.
(ABCD) = {A'B'C'D'). (14.1)
Для доказательства опустим из точки 5 перпендикуляры SM и SM'
на обе прямые (рис. 17, б) и будем характеризовать положения
§ 14] ПЕРСПЕКТИВНЫЕ И ПРОЕКТИВНЫЕ РЯДЫ ТОЧЕК 45
точек на прямых абсциссами х и х', отсчитанными от точек М и VT;
мы имеем:
x = MA = htg<f, *' = MM' = /*'tg(p'. h = SM. h' = SM',
причем cp — cp' = a = /_ MSMf — постоянная величина; отсюда
*' = /z'tg(cp-
и окончательно
-a)
_ «./ tg? —tga _ и, . fttg <p — /Hg a
1+ tgcptga
cr = hrX-higa
h 4- X tg a
A'
A -b A tg 9 tg a
(H.2)
т. е. переменные x a xf связаны дробно-линейной зависимостью;
отсюда вытекает (13.8) и из (13.5) следует наше утверждение.
II. Чтобы лучше понять его значение, рассмотрим сперва
частный случай, когда точка 5 уходит в бесконечность, т. е
лучи SA\Ai, 5Л2Л2, . .. параллельны между собой (рис
известно из геометрии, эти прямые
отсекают на пересекающихся
прямых g и g' пропорциональные
отрезки, т. е.
тот
все
как
А4з
А А
(И.З)
таким образом, при параллельной
проекции простые отношения
отрезков (14.3) остаются
неизменными; в общем случае
центральной проекции простые отношения Рис. 18.
(14.3) уже не будут неизменными —
при центральной проекции неизменными остаются не простые,
а двойные, т. е. ангармонические отношения
Уз
v»
А{А3
А А
следовательно, доказанное утверждение можно рассматривать как
обобщение на случай центральной проекции указанной теоремы
геометрии, справедливой для параллельной проекции.
Представим тепер.ь, что мы перенесли прямую gf с рядом точек
А\ В', С, D', . .. (рис. 17) в другое положение в той же плоскости;
перспективность расположения нарушится, т. е. прямые, соединяющие
соответствующие точки, уже не будут пересекаться в одной точке»
но равенство ангармонических отношений (14.1) не нарушится.
46
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
Ггл. «
III. Введем новое понятие: два ряда точек g(A, В, С, D, ...)
и g'(A', В\ С, D', ...) называются проективными (или
находящимися в проективном соответствии), если равны ангармонические
отношения любых четверок соответствующих точек обоих
рядов. Таким образом, два перспективных ряда точек всегда
проективны, если же один из них перенесем, то нарушится
перспективность расположения, но проективность останется.
Совершенно аналогичную картину мы имеем в элементарной геометрии
(рис. 19); пусть треугольники ABC и А'В'С перспективно расположены,
т. е. лучи АА\ ВВ', СС пересекаются в одной точке S, а прямые АВ и А'В\
ВС и В'С', АС и А'С параллельны между собой; отсюда вытекает
равенство углов и пропорциональность сторон,
т. е. наши треугольники перспективно
подобны; если же треугольник А'В'С
переместить в положение А"В"С'\ то
перспективность расположения
нарушится, но подобие останется; обратно,
два подобных треугольника всегда можно
сделать перспективно расположенными.
Возникает естественный вопрос;
можно ли всякие два проективных
Рис. 19 ряда точек g (Л, В, С, D, . . .) и
gf {А'> В',С, Df,...) считать
получившимися из двух перспективных рядов за счет перемещения одного
из них, т. е. можно ли всякие два проективных ряда точек сделать
перспективными^ В § 43 мы покажем, что это можно сделать
при помощи простых геометрических построений.
Примечание. На основании свойств ангармонического
отношения, рассмотренных в § 13, и свойств дробно-линейной функции (§ 12)
можно утверждать следующее: для того чтобы два ряда точек
были проективны, необходимо и достаточно условие, которое
в зависимости от того, каким образом задано положение точек,
имеет следующий вид:
1) если положение точек характеризуется их абсциссами х
и х', то условие таково:
у/ _ ах + b .
х — cx-j-d '
это вытекает из (13.5), (13.8) и свойства 5) дробно-линейной функции;
2) если положение точек характеризуется параметрами X, X'
(13.б>/ то условие таково:
\, flA + P.
3) если положение точек характеризуется параметрами [х, р/
(13.9), то условие таково-
/ - А* + в
? —Ct + D*
§ 15] ПРОЕКТИВНОЕ СООТВЕТСТВИЕ НА ОДНОМ ОСНОВАНИИ 47
Во всех случаях можно произвольно задать три пары
соответствующих точек двух проективных рядов; задавая после этого произвольно
четвертую точку первого ряда, мы найдем соответствующую вполне
определенную точку второго ряда из условия равенства
ангармонического отношения, которое при трех известных точках однозначно
определяет четвертую; в § 43 мы покажем чисто графический метод
нахождения соответствующих точек двух проективных рядов, не
требующий никаких вычислений.
§ 15. Проективное соответствие на одном основании;
понятие об инволюции
I. Мы до сих пор предполагали основания g и gf наших
проективных рядов точек различными; в том случае, когда оснований,
двух проективных рядов точек совпадают, мы будем говорить
о проективном соответствии рядов точек на одном основании.
Например (рис. 20), ряды точек g(A, В, С, ...) и gx(Av Вх, Cv ...)
перспективны с центром перспективы 5, а следовательно, и
проективны; но ряды точек gi(Av Bv Cv .. .) и g(A', В', С, . . .)
перспективны с центром перспективы S\ т. е. проективны; поэтому
два ряда точек А, В, С, ...
и А'', В', С, ... на одном осно-'
вании g проективны *).
Если некоторой точке D
первого ряда соответствует
точка D' второго ряда,
совпадающая с D, то такая
точка называется двойной
точкой проективного
соответствия на одном
основании; покажем, что таких точек
не больше двух.
Действительно, обозначая
через х и х' абсциссы
соответствующих точек наших двух рядов, отсчитанные от общего начала,
мы знаем, что эти абсциссы связаны дробно-линейным соотношением
ах + Ь
х' ==-
(15.1)
cx + d '
для того чтобы точка была двойной, надо, чтобы х' = х> и для
нахождения д; имеем квадратное уравнение
сх2 + (d — а)х — Ь = 0,
*) Для ясности точки первого ряда обозначаем буквами сверху, а
второго— буквами снизу.
48
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[ГЛ. II
получающееся из (15.1) при х' = д;; если оно имеет два
вещественных различных корня, то имеем две двойные точки; если корни
равны, то скажем, что две двойные точки совпали; в случае
комплексных сопряженных корней скажем, что двойные точки — мнимые *).
В частности, если е = 0, то один из корней обращается в
бесконечность, т. е. бесконечно удаленная точка является двойной, и мы
имеем х' = ад; -j- р; если, кроме того, а = 1, т. е. а — d, то обе
двойные точки совпали в бесконечно удаленной точке; наконец, если
р = 0, то х' = ад;, и двойными точками являются точки д; = 0, д; = оо.
И. Рассмотрим теперь один частный случай проективного
соответствия на одном основании (рис. 21); пусть точке А первого ряда
соответствует точка А' второго ряда;
- D Д С В точку первого ряда, совпадающую с А\
С Q* jjr д* обозначим через В и будем искать
соответствующую ей точку В' второго ряда;
Рис. 21 если случится, что точка В' совпадает
с точкой Л, то мы скажем, что точки А
и А вдвойне соответствуют друг другу: если одну из них
рассматривать как точку одного ряда, то вторая будет в обоих
случаях соответствующей точкой другого ряда.
Покажем следующее: если два ряда точек на одном основании
проективны и если две точки соответствуют друг другу вдвойне,
то все пары соответствующих точек обладают этим свойством.
Пусть точки А и А' вдвойне соответствуют друг другу (рис. 21),
возьмем еще две соответствующие точки С и О; пусть точке С,
рассматриваемой как точка D' второго ряда, соответствует точка D
первого ряда; надо доказать, что D = C'**).
Так как наши ряды проективны, то имеем:
{ABCD) = {A'B'C'D');
так как А = В', В —A', C = D\ то мы имеем, пользуясь (13.4),
(ABCD) = {В АС С) = (АВСС).
откуда С = D, ибо ангармоническое отношение при заданных трех
точках однозначно определяет четвертую точку.
Введем следующее определение: точечной инволюцией (или
инволюционным соответствием) называется такое проективное
соответствие двух рядов точек на одном основании, при котором
каждые две соответствующие точки соответствуют друг другу
вдвойне; для этого необходимо и достаточно, чтобы этим свойством
обладала одна пара соответствующих точек.
*) В § 44 будет показано простое графическое построение для
нахождения двойных точек.
**) Запись D = С означает, что две точки D и С совпадают.
§ 15] ПРОЕКТИВНОЕ СООТВЕТСТВИЕ НА ОДНОМ ОСНОВАНИИ 49
Из соотношения (15.1) имеем:
схх' + dx — ax' — b = 0', (15.2)
для того чтобы в этом соотношении можно было бы поменять
местами х и х\ необходимо и достаточно, чтобы d = — я, т. е.
в случае инволюционного соответствия формула (15.1) должна иметь
такой вид:
_ ах + b схх, _ _ ъ =
сх — a vi/ \ /
откуда легко находим, что х выражается через xf этой же формулой
х=аУ-М (15.4)
сх' — a v J
если х' принять за абсциссу точки первого ряда, то абсциссой точки
второго ряда будет х, т. е. точки поменяются местами. Так как
в формуле (15.3) фигурируют лишь три коэффициента, на один
из которых можно поделить остальные, то инволюционное
соответствие вполне характеризуется двумя парами соответствующих
точек. Двойные точки инволюции находим посредством решения
квадратного уравнения
сх2~2ах — £ = 0, х = ——. (15.5)
Ш. Точку С с абсциссой хс, соответствующую бесконечно
удаленной точке С прямой g, называем центром инволюции; легко
видеть из (15.3), что хс — —. Если абсциссы всех точек отсчитывать
от центра инволюции, т. е. положить
то из (15.3) найдем:
z = x , г' = х'
с с
а2 + Ьс
, , а ах 4- Ь а ' с а А * а2 + Ьс
Z ~Х " — ~7 а~\~Т~ cz ~~Т~7' с2 •
е\х-т)
т. е. будем иметь такое простое соотношение
zz* = \. (15.6)
Этот результат можно получить еще проще: если абсциссы
отсчитывать от центра инволюции, то значению z = 0 должно соответствовать
значение z' = oo, т. е. из (15.3) вытекает а = 0, ^= const. При
X > 0 соответствующие точки расположены по одну сторону от центра
инволюции и двойные точки вещественны; такая инволюция
называется гиперболической; при А < 0 соответствующие точки
расположены по разные стороны от центра инволюции и двойные точки —
50
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
мнимые; такая инволюция называется эллиптической-, наконец, при
X —0 имеем из (15.4) х' = — независимо от х, т. е. любой точке
первого ряда соответствует одна и та же точка второго; в этом
случае обе двойные точки совпали в центре инволюции; такую
инволюцию называем параболической.
IV. Во всех предыдущих рассуждениях мы считали центр
инволюции собственной точкой, т. е. полагали с Ф 0; если же с = 0,
то центр инволюции является несобственной точкой прямой, т. е.
совпадает с одной из двойных точек, ибо он соответствует
бесконечно удаленной точке; вторая двойная точка, как видно из (15.5),
при с = 0 имеет абсциссу х0 —— у-, причем по (15.4) имеем
х + xf = 2х0, т. е. в этом случае соответствующие точки
симметричны относительно двойной точки.
Покажем следующее: если в инволюции точек две пары
соответствующих точек симметричны относительно некоторой
точки, то центр инволюции ушел в бесконечность и инволюция
сводится к симметрии относительно указанной точки.
Действительно, пусть мы имеем две пары соответствующих
точек А и А', Б и В', характеризуемые абсциссами х и х\ у и у\
и пусть дано, что х + хг = у -f- у' = 2х0, где х0 — абсцисса центра
симметрии; мы имеем по (15.4)
cxxf — а (х + х') — Ь = 0, сууг — а (у + У') — Ь = 09
откуда с(ххг— yyf) = 0; равенство xxf = yyf невозможно, ибо при
его выполнении обе пары точек совпадали бы; следовательно, с = 0,
т. е. центр инволюции ушел в бесконечность и инволюция сводится
к симметрии.
V. Рассмотрим в качестве примера плоскую фигуру (рис. 22) и
положения центра подвеса А и соответствующего центра качания А' на любой
прямой, проходящей через центр тяжести С
фигуры; если эти точки характеризовать
абсциссами х = С А, х' = С А', то по известной
теореме Гюйгенса имеем:
2
** «-PJ. х = — , (15.7)
где рг — центральный радиус инерции фигуры;
мы видим, что два ряда точек на этой пря-
р лл мой — центры подвеса и соответствующие
Рис* гг' центры качания — проективны, ибо х и х'
связаны дробно-линейным соотношением; более
того, мы имеем в данном случае инволюцию, ибо соотношение,
связывающее х и х\ не изменится при их перестановке; физически это означает,
что центр подвеса и соответствующий центр качания можно поменять
местами: если сделать новым центром подвеса старый центр качания, то
§ 15] ПРОЕКТИВНОЕ СООТВЕТСТВИЕ НА ОДНОМ ОСНОВАНИИ 51
новым центром качания будет старый центр подвеса; легко видеть также,
что в данном случае центром инволюции является центр тяжести фигуры
и инволюция — эллиптическая, т. е. двойные точки — мнимые, ибо уравне-
ние х2 = — р^ не имеет вещественных корней. Если вместо (15.7) взять
соотношение хх' = а2, то точки А, А' соответствуют друг другу по принципу
инверсии *); мы имеем гиперболическую инволюцию с двумя
вещественными двойными точками ± а.
VI. Рассмотрим еще пример (рис. 23): если Р — мгновенный центр
вращения подвижной плоскости, Рх — касательная к центроидам и
если на луче, проведенном через Р под углом ср
к оси Рх взята точка М и через Мх
обозначен центр кривизны ее траектории в точке М,
то радиусы-векторы г, гх точек М, Мх связаны
соотношением **)
У
sin
*(т-7г) = Т'
(15.8)
1
где -jr — разность кривизн обеих центроид
в точке Р; отсюда м,к
- - rd sin ср
1 d sin ср — г '
таким образом, мы имеем два ряда точек М,.
эЛ/
\Ф
а:
(15.9)
Рис. 23.
М', М", .
М\, Мь Mi, ,.. на одной прямой, причем эти ряды проективны,
ибо /*i связано с г дробно-линейным соотношением (15.9); точка Р
является двойной, ибо при г = 0 имеем т^ —0, причем надо считать,
что обе двойные точки совпали в Я, ибо при г = гх получим г2 = 0.
Рассматриваемое проективное соответствие на одном основании не
является инволюционным, ибо из (15.8) ясно, что г и гх нельзя
поменять местами ***).
VII. Во всех рассмотренных примерах мы исходили из формулы,
связывающей координаты точек обоих рядов и по виду этой
формулы устанавливали характер соответствия; в следующем примере
мы будем исходить из геометрических соображений и лишь потом
установим формулу.
Рассмотрим так называемое преобразование Котельникова ****)-.
пусть заданы оси Ох, Оу (рис. 24) и направление OR\ для каждой
точки А на луче g, не совпадающем ни с OR, ни с Оу, проводим
прямую AA0\\OR до пересечения с осью Ох, а через точку А0
*) Об инверсии см. § 41.
**) Оно будет выведено и исследовано в § 67.
***) Это возможно было бы сделать, если бы одновременно изменить
знак у d\ в § 69 будет показано, что это соответствует обращению
движения, т. е. перемене ролей подвижной и неподвижной центроид.
****) В § 41 будут рассмотрены применения преобразования Котельникова.
52
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
прямую Л0Л'||Оу до пересечения в точке Л' с лучом ОА\ точка А
преобразуется таким образом в точку А' на том же луче. Ясно, что
два ряда точек g(A, В% С, ...) и gf(Л0, В0, С0, ...) проективны,
ибо они перспективны с центром перспективы в бесконечно
удаленной точке; но этим же свойством обладают и два ряда точек
g'(A0,B0tC0t ...) и #-(Л',£',С, ...); поэтому ряды точек g (Л, В, С, ...)
и g(A't В', С, ...) проективны на одном основании; это
проективное соответствие не является инволюцией, — если точку А'
принять за точку первого ряда и к ней применить то же
преобразование, указанное на рис. 24 пунктиром, то мы получим точку Л",
нг совпадающую с А. Ясно,
что точка О переходит сама
в себя—она является
точкой, в которой совпали обе
двойные точки; ясно также,
что бесконечно удаленной
точке первого ряда
соответствует бесконечно удаленная
точка второго ряда, т. е. мы
должны иметь г' = Х/\ где
коэффициент X изменяется
при переходе от одного луча
к другому.
Если подойти к вопросу
аналитически и обозначить
через k0 угловой коэффициент прямой OR, а через (xv ух) координаты
точки А, то уравнение прямой АА0 таково: у— ух=.к0(х— хг),
откуда легко найти координаты (x'v у'Л точки А'\
У
О
/
/ L
са ь
/ 1 /
/ f '
/ 1 /
/ '/
'о А
7>
1о
fi^ff
ff'
X
Рис. 24.
Mi —yi
У\
(Mi —yi)yi
Mi
(15.10)
Если через k=~- обозначить угловой коэффициент прямой gt то
I —Л
мы
торы
имеем
г\ г
хх — х
связаны
1 kQ
-• Уг =
соотношением
-о-
■■Уг
k
k0
k0
>•
Т.
радиусы-век-
(15.11)
VIII. Рассмотрим теперь следующую задачу: пусть даны две
точки MQ, Mo; будем каждой точке М на прямой М0М0 ставить в
соответствие некоторую точку Mf этой же прямой таким образом, чтобы
ангармоническое отношение заданных точек Ж0, Mq и двух соответ-
§ 15] ПРОЕКТИВНОЕ СООТВЕТСТВИЕ НА ОДНОМ ОСНОВАНИИ 53
ствующих точек М, М' имело заданную величину X =£ 1; надо
исследовать характер соответствия между точками М и М' *).
Обозначая через х0, x'Qt х, xf абсциссы точек Mq, Mo, М, М ,
мы имеем: / лл'ля ляг\ х — xQ х' — xQ *
[МоМоММ ) — 2-: —, 2- = X,
откуда легко находим:
, х[х0 — \х0) — х0х0 (1 — X) ^
дг(1—А) — (*о — Ц))
так как л;' является дробно-линейной функцией х, то ряды точек М,
Mv М2» •.. и м', М\% М% .. . проективны, причем точки М0 и Мо
являются двойными точками, ибо при х — х0 имеем л*' = х0 и
при д: = д:^ имеем xf = x'Q; это проективное соответствие на одном
основании будет по (15.4) инволюцией при условии х0 — Хд:^ =
= х'0 — Хл:0, откуда Х =—1; следовательно, если две точки даны
и к каждой точке М мы ищем соответствующую точку М' как
четвертую гармоническую, то ряды точек М, Mv М2, ... и
М, М\, Мъ ... находятся в инволюционном соответствии,
а данные две точки являются двойными точками инволюции.
Справедливо и обратное утверждение: если в двух
проективных рядах точек на одном основании принять двойные точки
за основные, то ангармоническое отношение этих двойных точек
и двух любых соответствующих точек всегда одно и то же;
в случае инволюции оно равно —1.
Для доказательства достаточно записать равенство
(МоМоММг) = (МоМоМ'м[),
I г
X "™~" Хг\ X-t "—~" Хг\ X "~~" лл Х-у "—-" лл
/ г >
Хл — Хг\
откуда легко находим:
X ~~™ Хг\ X ■—■
X —-* Хг\
(МоМоММ') = (MoMoMiM
в случае инволюции соотношение
: const,
) = X == const;
X —~ Xq ^ X -"— Xq ^^ -\ X —~* Xq \ X —— Xq **
7" • —7 Г Л» 7 Л—7 Г = V
X Хг\ X ""■"■" Xi\
не должно измениться, если х и хг поменяются местами, откуда
вытекает X == — 1.
*) Своеобразие этой задачи в том, что в ангармоническое отношение
входят точки не из одного ряда, как раньше, а из обоих рядов.
54
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
§ 16. Пучки прямых. Сокращенные обозначения
I. Рассмотрим две прямые sx и $2, характеризуемые уравнениями
ахх -+- Ьху + сх = О, а2х + b2y 4~ с2 = 0; (16.1)
будем всегда обозначать одними и теми же буквами и прямую,
и левую часть ее уравнения, т. е. в данном случае
sx = axx + bxy + *i. *2 = а2х + ьтУ + <V (I6-2)
Рассмотрим уравнение
$ = $14-Ц8 = 0, (16.3)
где X—произвольный вещественный параметр; если ввести
однородные координаты (xv дг2, лг3), то мы имеем:
5 = аххх 4- Ьхх24- сххг 4- X (а2хх 4- *2*2 + ^2*з) = °» 0 6-4)
поскольку 5 является линейной функцией (jtlf д;2, дг3), то мы имеем
уравнение первой степени относительно однородных координат,
которое соответствует некоторой прямой; единственный
исключительный случай может представиться тогда, когда все три
коэффициента одновременно равны нулю, т. е.
ах 4т Х#2 = *i ""b ^2 == с1 + ^2 = 0»
но в этом случае коэффициенты обеих прямых пропорциональны
ах Ьх С\
&2 V2 ^2
т. е. обе прямые совпадают.
Уравнение (16.3) называется уравнением пучка прямых,
проходящих через точку 5 пересечения двух данных прямых sx и $2;
действительно, две прямые sv s2 с уравнениями (16.4) всегда имеют
общую точку (хх, х'2% х'Л (собственную или несобственную);
подставляя эти значения координат в левую часть уравнения (16.4), получим:
(ахх[ 4- Ъгх'2 + схх'ъ) + X (а2х\ + Ь2х'2 + с2х$
так как каждая скобка в отдельности равна нулю, то при любом
значении параметра X уравнение (16.4) удовлетворяется при xx = x,v
х2 = х2, хг = х'3, т. е. прямая (16.4) проходит через точку
пересечения прямых sx и s2.
Отсюда вытекает, что если левые части уравнений трех
прямых sv 52, 53 связаны соотношением
\sx 4- X2s2 4" hss — °»
§ 161
ПУЧКИ ПРЯМЫХ. СОКРАЩЕННЫЕ ОБОЗНАЧЕНИЯ
55
справедливым при всех значениях xv х2 и xv причем из трех
множителей \v Х^ Х3 хоть один не равен нулю, то все три
прямые проходят через одну и ту же точку; действительно,
если, например, Х3 ф О, то, деля на Х3, получим:
:— -^-S
К
•So,
что подходит под тип (16.3).
П. Легко видеть, что значению параметра
Х = 0 в (16.3) соответствует прямая s2; если
же поделить (16.3) на X
^ + *2
:0
и положить затем X = со, то получим прямую s2.
Если уравнения обеих прямых написаны
в нормальной форме
Sj = х cos а2 -f- у sin а2 — Р\ — О,
52 = х cos а2 -f- у sin а2 — р2 = О,
(16.5)
то параметр X, характеризующий прямую s, имеет простой
геометрический смысл (рис. 25)
X = -jl = -sins's, • (16.6)
а2 sin s2s v 7
где c?ls d2—расстояние любой точки М0 прямой 5 от прямых sv s2,
a sts — угол между прямыми st и s. Действительно, если точка -М0
имеет координаты (jc0, у0), то,
как известно,
dx = д:0 cos ъх -+ у0 s^n ai — Pi»
flf2 = х0 cos а2 -f- у0 sin а2 — /?2,
откуда на основании (16.3) нахо-
дим Х = ~-\ мы имеем из чер*
а2
тежа
dl=M0S • sin^s, d2 = M0Ssins2s,
откуда вытекает (16.6).
III. Чтобы проиллюстрировать
пользу сокращенных обозначений,
покажем, что три высоты треугольника пересекаются в одной точке
(называемой ортоцентром треугольника).
Пусть (рис. 26) Si = 0, s2 = 0, s3 = 0 — уравнения сторон
треугольника в нормальной форме; тогда по (16.6) для высоты s3> опущенной
56
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
Ггл. и
на сторону s3> имеем такое значение параметра л
sin 5^з cos А2
sin s2s3 COS Л j
и уравнение прямой, по которой идет эта высота, таково:
53 = 5! + Xs2 = s1 cos Ах — s2 cos A2 = 0;
совершенно аналогично получаем для двух остальных высот
Sj = s2 cos А2 — s3 cos A6 = 0, s2 = s3 cos A6 — s1 cos A1 = 0,
откуда sx + s2 + 53 = 0; следовательно, Sj = — s2 — s3, т. е. прямая s[
проходит через точку H пересечения прямых s2, s3.
Еще проще доказывается, что три биссектрисы углов треугольника
пересекаются в одной точке; по (16.6) уравнения трех прямых, по
которым идут три биссектрисы, таковы:
// // f
53 == 51 — s2> sl =s s2 — 53> S2 == 53 51>
откуда снова имеем:
H + 4 + sz = °-
§ 17. Ангармоническое отношение четырех прямых пучка
I. Через G(#, Ъ, с, d, ...) будем обозначать пучок
прямых а, Ь, с, d, ... с центром в точке G (рис. 27, а); пусть сперва
G— собственная точка) в § 14 доказано, что в этом случае любые
две прямые g, gf пересекают прямые нашего пучка в точках Л, В,
С, D, . .. и А', В\ С, D\ .... ангармонические отношения которых
равны между собой (ABCD) = (A'B'C'D'); если G — несобственная
точка, то все прямые а,
Ь% ct d параллельны между
собой (рис. 27, б) и снова
справедливо это же
равенство. Поэтому мы
можем ввести
следующее определение:
ангармоническим
отношением (abed) четырех
прямых пучка G(a, Ь,
с, d) называется
ангармоническое отношение
четырех точек, в которых любая прямая пересекает прямые
пучка; отсюда вытекает весьма важное свойство ангармонического
отношения: ангармоническое отношение не изменяется ни при
пересечении, ни при проектировании. Действительно, если пучок
§ 17] АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ ЧЕТЫРЕХ ПРЯМЫХ ПУЧКА 57
прямых G (а, Ь, с, d) проектирует ряд точек g(A, В, С, D), то по
определению имеем:
(abed) = (ABCD)\
таким образом, величина (ABCD) не изменилась при
проектировании. Пересекая пучок О (а, Ь% с, d) прямой g', получим новый ряд
точек g'(A\ В'. С, D'). причем {A'B'C'D') = {abcd) = (ABCD)% т. е.
ангармоническое отношение не изменилось и при пересечении.
В том частном случае, когда (abcd) =—1, прямые я, Ь> с, d
образуют гармоническую группу; примером могут служить две
прямые а% b и две биссектрисы с% d углов между ними (рис. 14);
наоборот» если четыре прямые образуют гармоническую группу и
две основные прямые взаимно-перпендикулярны, то две другие
прямые расположены симметрично относительно основных; для
доказательства достаточно пересечь эти четыре прямые прямой gt
перпендикулярной к прямой с, и рассмотреть точки Л, В, С и
бесконечно удаленную точку прямой g.
II. Рассмотрим теперь различные способы вычисления
ангармонического отношения четырех прямых пучка в зависимости от способов
задания этих прямых.
1) Если выбраны две основные прямые sv s2 (16.2) и прямые
пучка характеризуются значениями параметра X в (16.3)
я, = sx + Х,$2 = 0 (/=1,2,3,4), (17.1)
то
(,iW4)==^l: Wl. (17.2)
Действительно, прямая пучка v = sl-\-\s2 = Q пересекает ось Ох
в точке с абсциссой
сх + Хс2
л, + \а2 '
т. е. х является дробно-линейной функцией X; на основании (13.8)
имеем:
xs — х{ t хА — хх _ Х3 — \х ш Х4 — \ . (\ч *\\
Х$ — Х2 ХА — Х2 Х3 — А.2 ^4 — ^2
левая часть является ангармоническим отношением четырех точек,
в которых ось Ох пересекает прямые пучка, — по определению оно
равно (vxv2vzv^.
2) Если центр пучка — собственная точка и если прямые пучка
характеризуются угловыми коэффициентами kv k2, А3, kA% то
(W4) = ^ = ^. (17.4)
38
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
Для доказательства заметим, что прямая пучка v = sl -|-Xs2 = 0 имеет
угловой коэффициент
#1 + ^#2
k = -
bx+U2 '
т. е. k является дробно-линейной функцией X; отсюда на
основании (13.8), (17.2) вытекает наше утверждение.
3) Если центр пучка — собственная точка, то
ангармоническое отношение четырех прямых vv v2% vv vA пучка таково:
(vxv2vzvA) =
sin vxvb
= ±-
sin I/,v4
sin v2v3
Рис. 28.
sin v2v4
(17.5)
Мы говорим, что пары
прямых vv v2 и v3, vA
разделяют друг друга, если vx
и v2 нельзя совместить
вращением, не переходя через vs
или vA% и не разделяют друг
друга, если указанное
совмещение возможно; правая часть (17.5) берется с отрицательным или
с положительным знаком в зависимости от того, разделяют пары
прямых vv v2 и vv v4 друг друга или не разделяют (рис. 28, а, б).
Для доказательства примем за основные прямые пучка две прямые
vx — ахх + Ъху + сг = 0, v2 — а2х + Ь2у + с2 = 0, (17.6)
и пусть
Ъ = ^1 + ^2 = 0, vA = vx -h \Av2 = 0;
таким образом, мы должны положить Хх = 0, Х2 = оо, и по (17.3)
найдем: \
(vxv2vuv^ = ^. (17.7)
Л4
С другой стороны, если привести уравнения (17.6) к нормальной
форме, то аналогично (16.6) мы имеем:
1 d2 ' у 4+bl
Sin ViV.
lv3
i
Л? + «
4 + bi
^ _ sin v^ -ш/ a\ + b\
4 sin v2vA \f c?2-\-b\
III.
Рассмотрим пучок прямых, в котором в качестве прямых vlt v2
взяты изотропные прямые, т. е. положим в (17.4) £,=*/, k2 = — /; будем
иметь:
-'' + *8_. --< + *4 = — * + tg?8 . — ^ + tgу4
* + *а ' * + Л4 * + tg?e ' * + tgcp4 '
Л = (f 1V2V3V4) = -
§ 18] ПЕРСПЕКТИВНЫЕ И ПРОЕКТИВНЫЕ ПУЧКИ ПРЯМЫХ 59
где мы положили k3 = tg ср3, kA = tg ср4; отсюда легко находим, пользуясь
формулой Эйлера,
х ^ cos ср3 + i sin ср3 # cos ср4 -f / sin ср4 = ?*>з . *'?« = ^« ((р3-W
cos ср3 — / sin cpg cos cp4 — / sin cp4 e~if*' e~i<fA
и окончательно ^
«W = ?з — ?4 == "27- In X, (17.8)
т. е. угол между двумя прямыми может быть выражен через
ангармоническое отношение пары изотропных прямых и пары данных
прямых *).
§ 18. Перспективные и проективные пучки прямых
I. Два пучка прямых G(a, Ь, с, d, . . .) и G' (af, b\ с\ d', .. .)
будем называть перспективными, если точки пересечения
соответствующих прямых (т. е. прямых а и а', Ь и Ь\ с и с' и т. п.)
лежат на одной прямой s,
называемой осью перспективы (рис. 29).
Из предыдущего ясно, что
(abed) — (ABCD) = (a'b'c'd'),
т. е. перспективность обоих пучков
означает не только особое их
расположение, но и то, что равны
ангармонические отношения
любых четверок соответствующих
прямых обоих пучков; это
последнее свойство сохранится и в том случае, если мы нарушим
перспективность расположения обоих пучков, перенеся один из них в другое
положение в той же плоскости.
Введем следующее определение: два пучка прямых G(a, ЬУ с%
d, ...) и Gf{ar, b>\ с', df, ...) называются проективными, если
равны ангармонические отношения любых четверок
соответствующих прямых обоих пучков\ в частности, два
перспективных пучка прямых всегда проективны.
II. Найдем необходимые и достаточные условия
проективности двух пучков прямых в зависимости от способа задания
прямых.
1) Если имеем два пучка прямых
*Х + Ц=:0, $; + }/$; = 0, (18.1)
где прямые характеризуются параметрами X и \', то
*) Формула (17.8) имеет большое принципиальное значение в геометрии.
60
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
доказательство вытекает из (17.2) и из свойства 5) дробно-линейной
функции (§ 12).
2) Если центры пучков — собственные точки и если прямые
характеризуются угловыми коэффициентами k и k', то
Доказательство вытекает из (17.4).
3) Если центры пучков О {а, Ъ, с, d, ...) и О'(#', Ь\ с', d't...) —
собственные точки, то
sin ас sin ad sin а'с' sin a'd'
sin be ' sin bd sin b'c' ' sin b''d' '
(18.4)
доказательство вытекает из (17.5).
Во всех случаях можно произвольно задать по три пары
соответствующих прямых обоих пучков; задавая после этого
Произвольно четвертую прямую первого пучка, мы найдем
соответствующую ей вполне определенную прямую второго пучка из условия
равенства ангармонических отношений, ибо при известных трех
прямых и известном ангармоническом отношении четвертая прямая
определится однозначно; в § 43 мы покажем чисто графический метод
построения соответствующих прямых двух проективных пучков, не
требующий никаких вычислений.
III. Мы предполагали до сих пор центры О и О' наших пучков
различными; в том случае, когда центры двух проективных
пучков прямых совпадают, будем говорить о проективном
соответствии на одном основании.
Совершенно аналогично тому, как показано в § 15, можно
показать, что в рассматриваемом соответствии может быть не больше
двух двойных прямых; их угловые коэффициенты по (18.3) найдем
как корни квадратного уравнения
Ttf + (8_<x)* —р = 0. (18>5)
Проективное соответствие прямых двух пучков с общим
центром назовем инволюцией прямых, если каждые две
соответствующие прямые соответствуют друг другу вдвойне, т. е. если
одну из них рассматривать как прямую одного пучка, то вторая
в обоих случаях будет соответствующей прямой другого пучка; для
этого необходимо и достаточно, чтобы две прямые соответствовали
друг другу вдвойне.
В случае инволюции прямых мы должны иметь в (18.2) d —— a,
а в (18.3) 5 = —а; таким образом, инволюция прямых
характеризуется двумя парами соответствующих прямых.
Отметим также следующее свойство пучка прямых с общим
центром: если две прямые пучка mQ> m'Q принять за основные и каждой
§ 18] ПЕРСПЕКТИВНЫЕ И ПРОЕКТИВНЫЕ ПУЧКИ ПРЯМЫХ 61
прямой т пучка ставить в соответствие прямую т' пучка таким
образом, чтобы ангармоническое отношение двух заданных прямых
m0, m'Q и двух соответствующих прямых т, т' имело заданную
величину \ф\, то пучки прямых т, тх, т2, ... и т\ т[, т'2, ...
проективны, причем т0 и m'Q—двойные прямые; при Х =— 1 имеем
инволюцию прямых. Справедливо и обратное утверждение: если
в двух проективных пучках прямых с общим центром принять
двойные прямые за основные, то ангармоническое отношение
этих двойных прямых и двух любых соответствующих прямых
всегда одно и то же\ в случае инволюции оно равно —1.
Докажем, что в инволюции прямых всегда есть одна пара
соответствующих взаимно - перпендикулярных прямых; если
таких пар больше одной, то этим свойством обладают все
соответствующие пары, т. е. в этом случае каждой прямой
пучка соответствует другая, повернутая относительно нее
на 90°.
Мы имеем из (18.3) при 8 = — а и при k' = — -j-
1 _ ak + Р
k ~ ik — а '
откуда
а*2 + (Р+7)*-а = 0. »„,= "№ + т> ± %Р +Jtt».. (18.6)
так как подкоренное выражение положительно, то мы имеем два
вещественных корня kx, k2, причем kxk2 ——1; если бы таких пар
взаимно-перпендикулярных прямых было больше одной, то
квадратное уравнение имело бы больше двух корней, т. е. все его
коэффициенты были бы равны нулю, а = 0, (5 = — f, откуда мы имели бы
k' = —-г для любой пары соответствующих прямых.
Если отсчитывать углы от одной из двух
взаимно-перпендикулярных прямых, то значению k = 0 должно соответствовать
значение kf = со\ из (18.3) ясно, что это возможно только при 7 = 0,
т. е. мы имеем kkf = \. При Х>0 имеем гиперболическую
инволюцию с двумя двойными прямыми, характеризуемыми угловыми
коэффициентами &=± "j/'X; при Х<0 имеем эллиптическую
инволюцию с мнимыми двойными прямыми; при Х = 0 имеем
параболическую инволюцию: kr — 0 при любом значении k.
IV. Рассмотрим теперь два проективных пучка прямых с общим
центром, двойными прямыми которого являются изотропные
прямые; уравнение (18.5) должно удовлетворяться при & = /, откуда
_ 1 -J-/(8 —а) — Р = 0. 8 = а, т = — р; (18.7)
62
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
таким образом (18.3) приобретает следующий вид:
*+1
*' =
аЛ + Р
-РЛ + а
1-^Л
гак как к, к' — угловые коэффициенты прямых, то к ■= tgcp, ft' -- tgcp';
положив также
:tg<|>, получим:
^ = т¥^ = *(*+Ф>.
р.
1—tgcplg^
откуда срг == ср —[— ф; в случае инволюции имеем Ь = а = — а, у
т. е. & = а^0, tg<]> = oo, ф = 90°.
Таким образом, если двойными прямыми двух проективных
пучков прямых с общим центром являются изотропные прямые,
то прямые второго пучка получаются из прямых первого пучка
поворотом на один и тот же угол ф; в случае инволюции
прямых имеем ф = 90°, т. е. в этом случае все соответствующие
прямые взаимно-перпендикулярны;
отсюда вытекает, что две взаимно-
перпендикулярные прямые образуют
гармоническую группу с двумя
изотропными прямыми.
Справедливы также и обратные
утверждения.
V. Рассмотрим теперь одно свойство
окружности, играющее важную роль
в дальнейшем: из двух любых
точек 5, 5' окружности (рис. 30) все
ее точки Л, В, С, D, ...
проектируются двумя проективными
пучками прямых S(a, b, с, d, ...)
и S'(а\ Ь', с', d', .. .). Действительно,
мы видим, что углы между двумя соответствующими прямыми обоих
пучков или равны, или дополняют друг друга до 180°; в данном
случае имеем:
ас = а'с', b.c = b'c', ad + a'd1 = 180°, bd + b'd' = 180°,
sin ac = sin a'c'% sin be = sin Vc'% sin ad = sin a'd', sin bd = sin b'd'.
Кроме того, ясно, что пары прямых a, b и с, d, с одной стороны,
и а', Ь' и с', d', с другой стороны, одновременно разделяют или
не разделяют друг друга; поэтому по (18.4) имеем (abcd) = (a'b'c'W).
§ 18]
ПЕРСПЕКТИВНЫЕ И ПРОЕКТИВНЫЕ ПУЧКИ ПРЯМЫХ
63
Мы можем, таким образом, ввести следующее определение:
ангармоническим отношением (ABCD) четырех точек Л, В, С, D
окружности называется ангармоническое отношение четырех
прямых, проектирующих эти
точки из любого центра на
этой окружности', мы можем
говорить также о проективном
соответствии двух рядов точек
на окружности и об
инволюции.
Докажем, что два
перспективных ряда точек на
окружности образуют
инволюцию *).
Для доказательства возьмем
окружность с уравнением **)
х2Л-У1 — d0y = 0 (18.8)
М(х0,Уо)
Рис. 31.
и на ней две точки Ax[xv y^t
A[(xv У\) (Рис- 31),
характеризуемые полярными углами срг cpj или угловыми коэффициентами
kv k\ соответствующих лучей ОАи ОА'х\ очевидно, -имеем:
хх = d0 sin cpt cos cplf у{ = d0 sin2 cplt
x[ = d0 sin <f[ cos <f'v y[ = dQ sin2 <f'v
и уравнение прямой uv проходящей через точки А\ и А\% таково:
У — ^osin Ti
2fn —.
• 2 '
sin Cpj ■
- sin2^!
sin cpj cos cpj — sin cpj cos cpj
(x — d0 sin cpj coscp!);
так как
sin2 cp^ — sin2cp1
cos 2cpj —- cos 2cpj
icpt
cos cpj — sin cpj cos cpj sin 2cpt — sin 2cpt
2sin(cPl + cp/1)sin(cp/1 — cp1) __ *i + *j
2 cos (b + ,[) sin (cp[ - 9l) ~ tg № + '0 ~ 1 - ^ '
*) Этой теоремой широко пользуется А. П. Котельников в своих
классических исследованиях [1] точек Бурмёстера; в § 40 мы приведем ее
обобщение.
**) Общность результата, конечно, не уменьшилась оттого, что
специальным образом выбраны координатные оси в уравнении (18.8).
64
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. и
то мы имеем:
аг^ч-*;)+у (*!*;—1)—tf0sin?1[coscPl(&1 + &l) — sin ?1(i—*!*;)]=
= х (kx 4- *i)+ У (*!*i — 1) — d0 sin cpt f sin cpj + Л^ cos cpx —
-sin *+*; IsfJr)=*(*i+*o+у (*i*; - о - w;->
окончательно прямая Л^1 характеризуется уравнением
Ui = x(ki + *i)+y(*i*i — I) —dofti*i = 0. (18.9)
Если прямая проходит через заданную точку Л1(л;0, у0), которую
примем за центр перспективы, то угловые коэффициенты прямых,
проектирующих точки Ль А[
из точки О окружности,
связаны соотношением
Wo-do) +
+(А1 + А'1)х0-у0 = 0; (18.10)
следовательно, эти прямые
с общим центром О образуют
инволюцию; отсюда на
основании данного определения
вытекает, что перспективные
ряды точек Ль Л2, Л3, ...
и Ль Л2, Лз, ... на окруж-
Рис. 32. ности с центром
перспективы М образуют инволюцию.
VI. Пользуясь (18.9), выведем еще одно свойство окружности:
проекции любой точки окружности на три стороны вписанного
в эту окружность треугольника лежат на одной прямой (рис. 32),
называемой прямой Симпсона *).
Действительно, прямая #2, проведенная через точку О
перпендикулярно к прямой uv характеризуется уравнением
u2 = (kik[— l)x — (fti + *i)y = 0. (18.11)
Рассмотрим прямую и, принадлежащую пучку прямых, проходящих
через точку пересечения В" прямых их и и2, являющуюся
проекцией точки О на прямую А\Х\\ параметр пучка подберем
специальным образом, именно, положим:
U = k\U\ -f- «2 = X {k\k\ -+- k\k"\ -f- k\k\ — l) +
+ y{k\k[k[ — kx — k\ — k[) — dQkik[kl = 0, (18.12)
*) См. А. П. Котельников [1], § 27.
§ 19]
ПРИНЦИП ДВОЙСТВЕННОСТИ
65
где к\ —угловой коэффициент прямой ОА\. Так как уравнение (18.12)
не изменится, если k\, k[, k\ поменять местами, то прямая и
проходит и через точки В', В, являющиеся проекциями точки О на
стороны А\А\, A[Ai. Из (18.12) вытекает *): если угловые
коэффициенты ku k[, k'[ прямых ОАи OA'i, О А", где Au а[, А\—три точки
окружности (18.8), являются корнями кубического уравнения
А^+^ + ^ + Рз^0» (18.13)
ir f
то прямая Симпсона треугольника А\А\А\, соответствующая
точке О, характеризуется уравнением
(р2_1)* + (А — Рг)У + <*оРз = 0. (18.14)
Действительно, мы имеем:
&+р^+p2k+ps={k - а,)(k - й;)(ft - ft;),
откуда легко найдем:
flj&j&j = /?3, k{kl -f- klkl -f- kikl = pv kl -f- kx -j- #j = —- /7^
отсюда на основании (18.12) следует (18.14).
Примечание. Отметим в заключение, что А. П. Котельников
в своем исследовании [1] вводит понятие об инволюции прямых,
понимая под этим следующее:
пусть на каждой из двух
заданных прямых gx и g2 имеем
инволюцию точек: Аи Bv
Cv . . . и Ль Bi, Сь... на
прямой gx и А2, В2, С2, ... и A'v
В2, С2, ... на прямой g2;
проведем произвольную прямую g
(рис. 33), пересекающую
прямые gx и g2 в точках Dx
и D2; возьмем на прямой g{
точку Du соответствующую
точке Dv а на прямой g2 — точку D2, соответствующую точке Z>2,
и проведем через них прямую g'\ совокупность прямых таких, как
g и g\ называется у Котельникова инволюцией прямых.
§ 19. Принцип двойственности
I. Читатель мог заметить, что при рассмотрении свойств пучков
прямых О (a, b, ct d, . . .) мы почти дословно повторили тс же
рассуждения, которые мы применяли при рассмотрении свойств рядов
*) См. А, П. Котельников [1], § 27.
66
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
точек g(A, В, С, D, ...); эта аналогия не поверхностна и не
случайна, а имеет весьма глубокое значение.
Мы знаем, что две точки Л, В определяют прямую gt
проходящую через них; точно так же две прямые a, b определяют точку О
пересечения (собственную или несобственную); мы в этих двух
случаях употребили различные термины (прямая проходит через точку,
точка лежит на прямой), но аналогия будет гораздо отчетливее, если
мы будем пользоваться единым термином ^инцидентностью,
имеющим следующее значение: говорим, что точка инцидентна
некоторой прямой, если она лежит на этой прямой; говорим, что
прямая инцидентна некоторой точке, если она проходит через
эту точку.
Пользуясь этим термином, мы можем утверждать следующее:
существует одна и только одна прямая, инцидентная двум
точкам, и существует одна и только одна точка, инцидентная
двум прямым.
II. Рассмотрим для ясности несколько примеров взаимных свойств
точек и прямых. Для записи дальнейшего текста разделим страницу
на две половины, причем правая половина будет соответствовать
левой по некоторому вполне определенному принципу, который мы
в дальнейшем сформулируем.
1) Рассмотрим прямую g и
точки Л, В, С, ..., инцидентные
с прямой gt т. е. ряд точек
g(A, В, С, ...) (рис. 34а);
2) рассмотрим точку S и
построим прямые а\ Ь', с', ...,
инцидентные точкам «S и Л, 5 и В,
и т. д.;
3) в результате этой
операции проектирования ряда точек
g(A, В, С, ...) из центра
5получим пучок прямых 5(а\Ь',с\...);
4) пересекая пучок прямых
S(a\ b\ с', ...) прямой g't
получим ряд точек g' (Alt Bv Cv ...);
5) ряды точек g(Ay Bt С, ...)
и g' (Av BVCV ...)
перспективны;
6) проектируя ряд точек
g'(Alt BltCv ...) из центра Sv
получим пучок прямых
Sx(altbvcv ...);
1) Рассмотрим точку О и пря*
мые а, Ь, с, ... инцидентные
с точкой О, т. е. пучок прямых
G(a, Ь, с, ...) (рис. 34,б);
2) рассмотрим прямую 5 и
построим точки Л', В', С, . . .,
инцидентные прямым 5 и а, 5 и bt
и т. д.;
3) в результате этой
операции пересечения пучка прямых
G(a, bt ct ...) прямой s получим
ряд точек s(A\ В\ С, ...);
4) проектируя ряд точек
s(A\ В', С, ...) из точки О',
получим пучок прямых
0'(av bv cv ...)\
5) пучки прямых G(atb>c, ...)
и G'(av bv cv ...)
перспективны;
6) пересекая пучок прямых
О' (av bv cv ...) прямой sv
получим ряд точек st (A VBVCV ...);
§ 19]
ПРИНЦИП ДВОЙСТВЕННОСТИ
67
7) пересекая этот пучок
прямых прямой g, получим ряд
точек g(A'tB'tС', ...). причем ряды
точек Л, В, С, ... и А\ В\ С\...
на одном основании g проек-
тивны;
7) проектируя этот ряд точек
из центра О, получим пучок
прямых 0(а\ Ь', с\ ...), причем
пучки прямых а, Ь, с, . . . и
а', Ь', с', ... с общим центром О
проективны;
8) это проективное
соответствие точек будет инволюцией
тогда и только тогда, когда две
соответствующие точки
соответствуют друг другу вдвойне.
8) это проективное
соответствие прямых будет инволюцией
тогда й только тогда, когда две
соответствующие прямые
соответствуют друг другу вдвойне.
Мы видим, что друг другу соответствуют такие геометрические
образы, как точки и прямые, ряды точек и пучки прямых, а также
такие геометрические операции, как пересечение и проектирование.
68
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. тт
III. Мы рассмотрели эти образы и операции с чисто
геометрической точки зрения; рассмотрим теперь уравнение
«1*1+ «2*2+«3*3 = °'
1) Задавая величины xv х2, хг
(или их отношения), мы
определим некоторую точку О; поэтому
мы назвали величины xv х2, хг
однородными координатами
точки G;
2) если заданы однородные
координаты uv и2, иг прямой gt
а величины xv х2,
хг—переменные, то уравнение (19.1) является
уравнением прямой g в
однородных координатах точки
xv х2, xz\ это значит, что, зада-
вая произвольно отношение —L,
мы сможем найти из (19.1) от-
х2
ношение —- и найти, таким обра-
хъ
зом, точку, инцидентную этой
прямой; таких точек
бесчисленное множество, ибо отношение—-
х3
взято произвольно;
3) например, при
и
и0: Uo
2: 1
1
^4*2-^3 — — а. ж. — х (19.2)
получим уравнение
— 2хг + х2 — :;3 = 0 (19.3)
прямой gt характеризуемой
однородными координатами (19.2);
х\ л
полагая, в частности, —- = 4,
хъ
найдем из (19.3) величины
х1:х2: х3=4 : 9 : 1, (19.4)
являющиеся однородными
координатами одной из точек Ж,
инцидентных прямой g; найдем еще
(19.1)
1) Задавая величины uv и2, иъ
(или их отношения), мы
определим некоторую прямую g\
поэтому мы назовем величины uv и2, иг
однородными координатами
прямой g;
2) если заданы однородные
координаты xv х2, хг точки О,
а величины uv и2, иъ —
переменные, то уравнение (19.1) назовем
уравнением точки G в
однородных координатах прямой
uv и2, иъ\ это значит, что, зада-
и,
вая произвольно отношение —-*-,
и3
мы сможем найти из (19.1)
отношение — и найти, таким об-
и3
разом, прямую, инцидентную этой
точке; таких прямых
бесчисленное множество, ибо отноше-
ние —L взято произвольно;
3) например, при
*!: х2: *3 = 4 : 9 : 1 (19.2)
получим уравнение
4и1+9^2-|-^з=0 (19.3х)
точки О, характеризуемой
однородными кординатами (19.2');
полагая, в частности, -^- = 2,
и3
найдем из (19.30 величины
а1:а2:а3= -- 2 : 1 :— 1, (19.40
являющиеся однородными
координатами одной из прямых т,
инцидентных точке О; найдем
§ 19]
ПРИНЦИП ДВОЙСТВЕННОСТИ
69
одну такую точку М' с
координатами
х\ : х'2\ *3= 1 : 1 : — 1 (19.5)
и т. д. *);
4) если заданы три точки УИ,
Ж', М" своими однородными
координатами
M(xv х2% а:3), M'(x'v x'v *3),
М»[х\, х:2.х"6)9
то для того, чтобы они были
инцидентны одной прямой,
необходимо и достаточно условие
Х\ Х2 Х3
хх х2 х3
Х\ Х2 Х3
= 0; (19.6)
действительно, оно эквивалентно
тому, что система уравнений
«i*i + Чхч + агхг = 0,
и{х[ + и2х'2 + иъх'ъ = 0. (i9.7j
vi'+s^ + v^0
имеет решение, отличное от
решения и
0;
5) если заданы две точки
М\ N[" своими однородными
координатами, то любая точка М
такая, что три точки М, Mf', М"
еше одну такую прямую т/
с координатами
а[: и'2: и'.6 = 3 : - 1 :
3 (19.50
и т. д. *);
4) если заданы три прямые тч
т\ т" своими однородными
координатами
m(uv и2, я3), т!(и\ш u'v u'^t
т" (u"v и'2\ и3')»
то для того, чтобы они были
инцидентны одной точке,
необходимо и достаточно условие
#i U0 Uo
= 0; (19.60
действительно, оно эквивалентно
тому, что система уравнений
и1х1 + и2х2 4~ uzx3 = 0,
и\хх + и2х2 + «з^з = °- (19.70
^Ч+^Ч + ^зЧ^0
имеет решение, отличное от
решения хх =. х2 = xz = 0;
5) если заданы две прямые
т\ т!' своими однородными
координатами, то любая прямая т.
такая, что три прямые т, т!% т!г
*> Мы имеем, таким образом, по (19.1), (19.40, (19.50
т = — 2хх+х2 — хъ вз 0, т' = Зхх — х2 — Зх% =я 0:
по этим уравнениям построены обе прямые т% т' (рис. 35), причем
70
РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ
[гл. II
инцидентны одной прямой,
характеризуется координатами
Х^ = Xj -j- AXj, Л?2 = ЛГ2 —\~ Х^2,
(19.8)
инцидентны одной точке,
характеризуется координатами
их = и[ -+- ^i, и2 = и'2-\- \и\,
(19.80
я3 = Яз+Хлз»
действительно, при этом выпол- действительно, при этом
выполняется условие (19.7). I няется условие (19.70-
IV. Рассмотренные нами примеры
являются иллюстрацией общего принципа,
называемого принципом двойственности
(или взаимности): из любой теоремы
геометрии, в которой идет речь о
взаимном расположении точек и прямых,
можно получить новую теорему, если
-£ заменить всюду слово «точка» словом
«прямая», а слово «прямая» — словом
«точка».
Принцип двойственности дает весьма
эффективный и плодотворный метод
получения новых теорем геометрии, как будет
показано в следующих главах; его строгое
обоснование, требующее детального
анализа аксиом геометрии, выходит за
пределы нашей монографии, —читатель может найти его в книге
Н. В. Ефимова [1], §§ 154—156.
Рис. 35.
ГЛАВА HI
ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
ВЫСШИХ ПОРЯДКОВ
Мы рассмотрели в главе II простейшие геометрические образы
первого порядка — ряды точек на прямой и пучки прямых; покажем,
как при помощи этих простейших форм можно образовать более
сложные формы, в первую очередь формы второго порядка.
§ 20. Пучки кривых
I. По аналогии с пучком прямых будем называть пучком
кривых семейство кривых, линейно зависящее от одного параметра;
обозначая через / кривую и одновременно левую часть ее
уравнения f(x, у) = 0, мы видим, что уравнение пучка кривых,
определяемого двумя основными кривыми / и ср, таково:
F = / + Xcp^0; (20.1)
при Х = 0 получим кривую /; деля на X, полагая у = Iх» получим
{л/ -)- ср = 0, откуда при |х = 0, т. е. при X = оо, будем иметь
кривую ср.
Все кривые пучка проходят через точки пересечения
основных кривых f и ср, ибо для этих точек функции / и ср обращаются
в нуль и, следовательно, и F обращается в нуль при любом
значении параметра X.
Два пучка кривых
/-f-Xcp = 0, /' + ху = 0 (20.2)
называются проективными, если их параметры связаны дробно-
линейным соотношением
В частности, если обе кривые / и ср — алгебраические порядков п
и т, то, очевидно, и кривая F будет алгебраической кривой
порядка v, где \—большее из двух чисел пит. Полагая для опре-
72
Образована геометрических форм высших порядков (гл- ш
деленности п^т и переходя к однородным координатам, мы
получим по (6.2), после умножения на х$, уравнение
/1-f->^-mcpi = 0, (20.4)
где fv срх — однородные многочлены порядков пит относительно
обобщенных координат
/,(*,, х2. х3) = х"г/[^, -g), ъ(*1' х» **) = *?<? ($•-§•)•
При Х = 0 получим кривую пучка с уравнением fx = 0, а при \=оо
кривая пучка распадается на кривую т-го порядка с уравнением
<Pi = 0 и на бесконечно удаленную
прямую, повторенную п—т раз;
аналогичный результат получим при п^т.
II. Рассмотрим в качестве
иллюстрации эллипс, вписанный в окружность
(рис. 36); если уравнения этих кривых
~а2
/2
Ь2
~2-4-45- = 1. -*" + У'=я2 (20.5)
преобразовать, как в (3.3), перенося
начало координат в точку О (— а, 0), то
получим по (3.4)
Рис 36.
у2 == 2/7JC — -^- JC2,
J r а
х2 + у2 — 2ах = 0;
при а->оо, £->оо, — = р эллипс, как было показано в § 3, перейдет
в параболу; наш пучок окружностей
х2 + у2 — 2ах = 0, (20.6)
зависящий от параметра а, после перехода к однородным координатам таков:
х\ + х2
2а
■ хххг = 0;
при а = оо окружность, в которую вписан эллипс, распадается на две
прямые с уравнениями
^ = 0, х3 = 0, (20.7)
т. е. на ось Оу и на бесконечно удаленную прямую; мы еще раз убедились,
таким образом, в том, что парабола касается бесконечно удаленной
прямой (см. § 5); кроме того, из свойств эллипса, связанных с описанной
вокруг него окружностью, можно получить путем предельного перехода
свойства параболы, связанные с касательной в ее вершине.
III. Рассмотрим теперь более подробно пучок кривых второго
порядка. Если / = 0 и ср = 0 — уравнения кривых второго порядка,
где
/ = апх'2 + 2а12ху +- а22у2 + 2а13* + 2я23у + % = 0,
ср = bnx* + 2bvlxy + b22y2 + 2b13x -f- 2b23y + b33 = 0,
(20.8)
§ 20]
ПУЧКИ КРИВЫХ
73
то уравнение
,Р = / -Н Хер = 0 (20.9)
характеризует, как было сказано, пучок кривых второго порядка;
интересно отметить, что всякий пучок кривых второго порядка
содержит одну распадающуюся кривую, но не более трех таких
кривых; действительно, по (4.9) условие распадения кривой F таково:
а\\ + Щ\ а\2 + М>12 аП + ^13 I
а2\ + 1Ь2\ а22 + Х^22 а22> + Щг = °> (2®Л °)
#31 + Щ\ #32 + ^32 #33 ~+~ ^33 I
причем это уравнение, кубическое относительно X, имеет или один,
или три вещественных корня, среди которых могут быть равные.
IV. Рассмотрим теперь кривые второго порядка, построенные
при помощи двух основных кривых, каждая из которых распадается
на пару прямых. Если vv v2— две прямые, то уравнение
vxv2 = 0 (20 Л1)
является уравнением кривой второго порядка, распадающейся на пару
прямых с уравнениями vx = 0, v2 = 0 (рис. 37); если же взять две пары
прямых vv v2% vv г;4, то уравнение
vlv2 + \vzvA = 0 (20.12)
характеризует пучок кривых
второго порядка, причем все кривые
этого пучка проходят через
четыре точки Av Л2, Л3, Л4
пересечения прямых vx и v3, vx и <у4,
v2 и v^ v2 и vz.
Докажем теорему: любая прямая
пересекает пучок кривых второго
порядка по двум рядам точек,
образующих инволюцию.
Не уменьшая общности, мы
всегда можем преобразовать
координаты таким образом, чтобы наша прямая имела уравнение у = 0;
пользуясь (20.9) и (20.8), мы должны найти абсциссы хх и х2 точек
пересечения из уравнения
апх2 + 2а13х + я33 + X фпх2 + 2ЬХзх + Ьгз) = 0,
откуда по теореме Виета находим:
2iai8+^ie) ^ „ _ аЛЪ+\Ьм .
Рис. 37.
(20.13)
х\ П~ х2
ХлХ
(20.14)
аи+1Ьи ' -1-2— д-.+Х*,;
на основании свойств дробно-линейной функции (§ 12) отсюда
вытекает, что величины х, -\-xi и ххх% связаны дробно-линеЯниЯ
74 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ, III
зависимостью, и даже линейной, ибо бесконечно большие значения
обеих величин соответствуют друг другу (при X——-г^]> таким
образом, мы имеем хгх2 = a (xl-\- х2)-{-Ь, что подходит под тип (15.3).
В частности, пучок кривых второго порядка (20.12),
проходящих через заданные четыре точки, содержит две кривые,
распадающиеся на пары прямых: vxv2 = 0 при X —0 и vzv4 = 0 при Х = оо;
следовательно, находя точки пересечения нашей прямой с прямыми
vv .... vA мы найдем две пары соответствующих точек А и А\
В и В', которые полностью определяют инволюцию; в этом случае
существует и третья кривая пучка, распадающаяся на пару прямых —
именно, на прямые v5 и v6, проходящие через те же четыре точки
Лр Л2, Л3, Л4.
§ 21. Определение кривой второго порядка пятью точками
I. Кривая второго порядка характеризуется уравнением
апх2 + 2al2xy -f- а22у2 + %а1гх + 2а2гу -f-.Язз = 0, (21.1)
содержащим шесть коэффициентов] так как на один из них можно
поделить, то остается пять параметров, для определения
которых нужно пять условий; если задано пять точек
Mxf Уд (*=1. 2» •••■ 5)'
через которые должна пройти кривая, то из пяти уравнений
апх\+ 2а12х{у{ + а22у\ ■+ 2а13хх + 2о23у1 + а^ = 0,
(21.2)
апх\ + 2а12д:5у5 + а22у| + 2a13*5 + 2а2гу5 + ^ = 0
мы должны найти отношения пяти коэффициентов к шестому; при
решении этой системы уравнений может представиться два случая:
1) пять уравнений (21.2) независимы между собой; в таком
случае мы найдем вполне определенные значения для отношений
коэффициентов и получим единственную кривую второго порядка,
проходящую через пять заданных точек; 2) хоть одно из уравнений —
например, пятое — является следствием остальных уравнений;
в таком случае имеется бесчисленное множество решений и любая
кривая второго порядка, проходящая через точки Av Л2, Л3, Л4,
пройдет и через точку Л5.
Эти случаи можно было бы распознать чисто алгебраическими
методами по заданным числам (xlt yt) (/=1, ..., 5); однако гораздо
проще и нагляднее провести геометрическое исследование, исходящее
из расположения пяти заданных трчек»
§21] ОПРЕДЕЛЕНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА ПЯТЬЮ ТОЧКАМИ 75
1) Пять заданных точек лежат на одной прямой vx\
выбирая совершенно произвольно вторую прямую v2, получим уравнение
v}v2 = 0 искомой кривой;
2) четыре заданные точки лежат на одной прямой vx\
выбирая прямую v2 так, чтобы она прошла через пятую точку Л5,
снова получим искомое уравнение <р1<р2 = 0;.
3) три заданные точки лежат на одной прямой юг\ вторая
прямая v2 вполне определена условием прохождения через две
оставшиеся точки, и мы снова имеем искомое уравнение vxv2 = 0\
4) никакие три из заданных точек не лежат на одной
прямой', выберем четыре точки Av А2, Av АА и найдем прямые
vv v2, v3, v4 (рис. 37); тогда любая кривая второго порядка,
принадлежащая пучку
vxv2 + \v3vA — 0, (21.3)
проходит через эти четыре точки; подберем параметр X таким
образом, чтобы кривая пучка проходила через точку Л5, для этого
подставим «е координаты в (21.3) и найдем из этого уравнения
значение X; точка А5 не может лежать ни на одной из наших четырех
прямых vv v2, vz% t/4, следова-»
тельно, ее координаты не
обращают в нуль ни одну из
функций vv v2% vv tj4 и при
подстановке этих координат в (21.3) мы
найдем единственное и
определенное значение X; при этом кривая
будет нераспадающейся, ибо если
бы она распалась на пару
прямых, то на одной из них лежало
бы не менее трех точек. Таким
образом, кривая второго порядка
единственным образом
определяется пятью своими точками%
если никакие четыре из них не лежат на одной прямой; она
будет нераспадающейся, если никакие три из них не лежат на
одной прямой.
II. Пусть, например, заданы точки
Ах (-2,0), Л2(0, -1), Л3(3. 0), Л4(0, 2), Л5(4, 3);
нетрудно написать уравнения прямых (рис. 38)
Рис. 38.
р, = у = 0, v2:
.- + 1^0, *,.
:0, ^«у-л-2-0; (21.4)
01 сюда по (21.3) имеем уравнение пучка кривых
xy+k(3y-x + 3)(y--x-2)~0;
76 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
подставляя координаты точки А5> найдем:
3.4 +А (9 — 4 + 3) (3 — 4 — 2) = О, К = у,
и уравнение искомой кривой второго порядка таково:
х2 — 2ху +3y2 — jc-~3y—6 = 0;
мы могли бы найти этот результат и решением системы уравнений (21.2).
III. Рассмотрим, в частности, определение кривой второго
порядка по четырем точкам при наличии дополнительного условия:
асимптотические направления (определяемые формулой (5.6)),
должны быть взаимно-перпендикулярны или совпадать. В
первом случае имеем kxk2 = —— = — 1, откуда
#22
а11 + а22 = 0; (21.5)
кривая будет по (5.7) принадлежать гиперболическому типу, т. е.
будет равносторонней гиперболой или парой
взаимно-перпендикулярных прямых; во втором случае будем иметь:
ail^22-~ai2 = 0' (21.6)
и кривая будет принадлежать параболическому типу, т. е. будет
параболой или парой параллельных прямых.
Если все четыре точки лежат на одной прямой vv то
искомое уравнение таково: у^2 = 0, где произвольная прямая v2
подчинена условию v2 J_ vx в первом случае и условию v2\\vl во втором
случае; если три точки лежат на одной прямой vv то прямая v2
полностью определяется добавочным условием—проходить через
четвертую точку; если никакие три точки не лежат на одной
прямой, то в отличие от задания пяти точек кривая все же может
распадаться, если эти точки лежат на двух прямых, перпендикулярных
или параллельных друг другу.
Покажем, что кривая гиперболического типа со
взаимно-перпендикулярными асимптотическими направлениями определяется
четырьмя точками, если через них нельзя провести двух
различных кривых, обладающих указанными свойствами.
Действительно, пользуясь (20.8) и (20.9), имеем уравнение
первого порядка для нахождения X
*п + я22 + х (*п + *22) = 0; (21.7)
оно будет тождеством лишь при условиях ап +- а22 = 0, Ьп +~ Ь22 = 0,
которые означают, что обе основные кривые / и ср обладают
указанными свойствами.
Отсюда можно сделать следующий вывод: все равносторонние
гиперболы, проходящие через три вершины треугольника,
проходят и через его ортоцентр.
§21] ОПРЕДЕЛЕНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА ПЯТЬЮ ТОЧКАМИ 77
Действительно, пусть через вершины Л, В, С (рис. 39)
проведена равносторонняя гипербола, пересекающая высоту BD в точке Н\
через эти же четыре точки Л, В, С, Н проходит и кривая,
распадающаяся на пару взаимно-перпендикулярных прямых АС и ВН\
следовательно, все кривые пучка, определяемого двумя основными
кривыми, являются равносторонними
гиперболами или распадаются на пару
взаимно-перпендикулярных прямых,
поэтому прямые ВС и АН должны быть
взаимно-перпендикулярны, т. е. точка
И — ортоцентр треугольника.
IV. Покажем теперь, что через
заданные четыре точки можно
провести не более двух кривых
параболического типа.
Действительно, мы имеем в данном
случае такое условие для X:
I #11+^11 #12+^12 I _ Q /2| Q)
I #21 + ^2]. #22 + ^22 I ' РИС 39.
дающее не более двух вещественных значений X; оно может быть
тождеством лишь при выполнении условий
flllfl22 - *?2 = 0« ^1А2 - Ъ\ = °' V22 + Vll = 2ai2b\2'
первые два показывают, что члены второго порядка таковы:
/ = (а1х+р1у)2+ .... <Р = (а2* + Р2У>2 + -.-I
из третьего условия вытекает (ахр2 — ol2$1)2 = Q1 т. е. — = —- = ^,
ai Pi
откуда
/ = (*i*+M2+«... <? = ь2(*1* + Ш+ .-.; (21-9)
решая совместно эти два уравнения, мы видим, что в этом случае
все кривые пучка проходят лишь через две вещественные точки.
Например, если заданные четыре точки являются вершинами
трапеции, то через них можно провести, во-первых, кривую
параболического типа, распадающуюся на пару противоположных
параллельных сторон трапеции, и, во-вторых, одну параболу; если же
заданные четыре точки являются вершинами параллелограмма, то
единственными кривыми параболического типа, проходящими через них,
являются те две, каждая из которых распадается на пару
противоположных сторон параллелограмма.
78 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. Ill
§ 22. Теорема Штейнера
I. Докажем следующую основную теорему Штейнера:
геометрическим местом точек пересечения соответствующих прямых
двух проективных пучков является кривая второго порядка,
проходящая через центры обоих пучков; если прямая,
соединяющая центры пучков, соответствует сама себе, то кривая
распадается на пару прямых, одной ив которых является эта
прямая.
Пусть заданы два пучка прямых (рис. 40) S(a, b, с, ...) и
S'(а\ Ъ', с', ...); пусть в первом пучке за основные прямые
взяты а, Ь и каждая прямая пучка характеризуется параметром \
c = a-fW = 0, (22.1)
и аналогично для второго пучка
(22.2)
Рис. 40.
так как по условию наши пучки прямых проективны, то по (18.2)
мы должны иметь:
находя X и V из (22.1), (22.2),
получим:
а' _—ал + Ъ$
У ~ —ai-i ЬЬ '
откуда окончательно найдем:
Ьа'Ь — чаа' + Щ' — *аЬ' = 0.
(22.4)
Все четыре функции а, Ь% а\ V
линейны относительно х, у, поэтому
левая часть (22.4) содержит члены второго порядка, т. е. (22.4)
является уравнением кривой второго порядка. Для центра 5 имеем
а = £ = 0, а для центра S' имеем а' = Ь' = 0; в обоих случаях
уравнение (22.4) удовлетворяется. Нетрудно также видеть, что
прямой SS', рассматриваемой как прямая d первого пучка,
соответствует некоторая прямая d' второго пучка, касательная к кривой
в точке S'\ точно так же прямой S'S, рассматриваемой как
прямая е/ второго пучка, соответствует прямая е первого пучка,
касательная к кривой в точке 5. Для доказательства достаточно
рассмотреть соответствующие прямые / и /', бесконечно близкие к d
и df\ точка F их пересечения бесконечно близка к точке S', и
предельным положением секущей S'F является прямая df, касательная
к кривой в точке 5.
§ 22]
ТЕОРЕМА ШТЕЙНЕРА
79
Пусть теперь прямой SS', рассматриваемой, например, как
прямая а первого пучка, соответствует эта же самая прямая как
прямая а' второго пучка, т. е. функции а, а/ различаются лишь
постоянным множителем а'ч=вка\ из (22.1), (22.2) ясно, что
значению Х = 0 соответствует прямая а, а значению У==0 соответствует
прямая а\ совпадающая с а\ таким образом, значения параметров
X = 0 и \' = 0 должны соответствовать друг другу, т. е. мы должны
иметь в (22.3) Р = 0; при этом из (22.4) найдем:
а (Ш — k^a — ab') = О,
т. е. кривая распадается на две прямые с уравнениями
а = 0, № — k*(a — ab' = 0; (22.5)
первая из них проходит через центры пучков 5 и S', а вторая
является осью перспективы, ибо на ней лежат точки пересечения Bv
Cv ... соответствующих прямых обоих пучков b и bf, с и с' и т. д.
Н. Справедливо и обратное утверждение: из двух любых точек
кривой второго порядка остальные ее точки проектируются
посредством двух проективных пучков прямых *).
Пусть сперва кривая — нераспадающаяся-, взяв на ней пять
точек Ах Аъ (рис. 41) и приняв точки Av А2 за центры
пучков, мы найдем по три прямые Ах{а, Ь, с) и А2(а', Ь', с') каждого
из пучков; возьмем на кривой
произвольную точку Лб, проведем в нее
прямые d, df и докажем, что
(abcd) = (a'b'c'd'). (22.6)
Действительно для прямой d первого
пучка найдем соответствующую
прямую d" второго пучка из условия
(abcd) = (a'Vc'd")\ (22.7)
точка пересечения прямых d и d" Рис. 41,
по теореме Штейнера должна лежать
на кривой; если она не совпадала бы с Аб, то прямая d
пересекала бы кривую в трех точках, что невозможно; поэтому d"
совпадает с df и из (22.7) следует (22.6).
Если же кривая второго порядка распадается на пару
прямых uv и2 (рис. 42), то, взяв центры 5, S' на прямой их и
проектируя из них точки А, В, С мы получим перспективные,
а следовательно, и проективные пучки прямых S(a, b% с, ...) и
S'(a\ Ь\ с\ ...).
*) Для частного случая окружности это утверждение доказано в § 18,
80 . ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
III. Рассмотрим несколько простых примеров, иллюстрирующих теорему
Штейнера.
Рассмотрим механизм коникографа для вычерчивания конических
сечений; он состоит (рис, 43) из двух жестких углов со сторонами /, 2 и /', 2',
вращающихся вокруг своих вершин 5 и S';
стержни / и /' входят в поступательные пары
со звеньями 3 и 4 двухповодковой группы,
причем звенья 3 и 4 входят во вращательную
пару М; аналогичная картина для звеньев 2
и 2' и звеньев 5 и 6, входящих во
вращательную пару М'\ тогда, если вести точку М
по некоторой прямой, то точка М' опишет
коническое сечение *) (которое при
продолжении прошло бы через точки 5, S').
Действительно, пучки прямых S (а, Ь, с, ...)**) и
5' (а', Ь', с', ...)» проектирующие точку М из
центров S и S', перспективны, ибо точка М
движется по прямой, а следовательно, и про-
ективны\ пучки прямых S (а, Ь, с, ...) и
5 (ах, Ьь си ...) также проективны на
основании (18.4), ибо прямые аъ Ьъ сь ... получены
из прямых а, Ь, с, ... поворотом на один и
тот же угол; по этой же причине
проективны и пучки прямых S' (а\ Ь', с',...) и
.^следовательно, пучки прямых 5 (ах, bv сх,...) и 5 (a'v bx, cx,...)
а поэтому геометрическим местом точки М' пересечения соот-
прямых этих пучков является коническое сечение. Для того
чтобы оно прошло через пять заданных точек, выбираем центры
неподвижных шарниров в двух точках 5, S' из этих пяти точек; поставим
механизм в такое положение, чтобы
прямые SM и S'M совпали;
если при этом точка М' будет
совпадать с третьей заданной
точкой Alt то этим
определятся величины жестких углов
механизма:
/ M'SM = / S'SAU
£ М'S'М = £ SS'Ах.
Поставив механизм в такое
положение, чтобы точка М'
совпала с четвёртой заданной
точкой Аъ мы найдем
соответствующее положение точки М; используя пятую заданную точку А3, мы
таким же образом найдем второе соответствующее положение точки М, чем
вполне определится та прямая, по которой должна двигаться точка М.
IV. Рассмотрим еще такую задачу: найти траекторию ортоцентра Н
треугольника, две вершины которого А, В даны, а третья вершина С
движется по заданной прямой и (рис. 44).
S'{a[,b[,
проективны,
ветствующих
Рис. 43.
*) В. В. Добровольский ([1], стр. 43) подчеркивает, что идея этого
механизма была указана еще И. Ньютоном.
**) Чтобы не усложнять чертеж, мы указали только одну прямую этого
дучка.
§ 22]
ТЕОРЕМА ШТЕЙНЕРА
81
Пучки прямых А {а, ах, аь ...) и В{Ь, Ьх, Ь2, ...) перспективны, а
следовательно, проективны; пучок А (а , а[, а2, . . .) проективен пучку
В (b, bx, Ь2, ...), ибо их соответствующие прямые взаимно-перпендикулярны;
это же справедливо в отношении пучков A (a, av а2, ...) и B(b\ b[, b2, ...);
таким образом, пучки А(а', а[, а2, ...) и B(b'', b[, Ь2,...^ проективны, а
поэтому точка И пересечения соответствующих прямых этих пучков описывает
коническое сечение, если только прямая
их = АВ не соответствует сама себе.
Этот исключительный случай имеет
место лишь тогда, когда и ±их — в этом
случае точка И движется по прямой и,
которая является осью перспективы,
а кривая распадается на пару прямых и
и их. Отбрасывая этот случаи, мы видим,
что, когда точка С уходит в
бесконечность, прямые АС и ВС становятся
параллельными и точка И уходит в
бесконечность по направлению,
перпендикулярному к и (рис. 45, а); когда точка С
совпадает с точкой пересечения
прямых и, их, точка Н уходит в
бесконечность по направлению,
перпендикулярному к их (рис. 45, б). Таким образом, если прямые и и их не
параллельны, то траекторией является гипербола, асимптоты которой
перпендикулярны к прямым и и их. Если же и\\их, то оба асимптотических
направления совпадают и траекторией является парабола, ось которой
перпендикулярна к прямым и, их.
Рис. 44.
Рис. 45.
V. В качестве последнего примера рассмотрим решение такой простой
задачи: даны две прямые а и Ь (рис. 46), точка Р пересечения которых
недоступна', через заданную точку М провести прямую, которая
проходила бы через точку Р.
Проведем через точку М две произвольные прямые с, d, пересекающие
прямые а и b в точках G, Н и F, Е; проведем прямые k и / через точки G, Е
и f, Я до пересечения в точке Q и проведем через эту точку новую
прямую s, пересекающую прямые а и Ь в точках N и /; проведем, наконец,
прямые т и г через точки F, I и Н, N и назовем через Т их точку
пересечения; тогда прямая МТ проходит через точку Р,
82 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
Действительно, отметим прежде всего, что два ряда точек a (G, F, N, Р)
и Ь(Е,Н,1,Р) перспективны, а следовательно, и проективны; проектируя
их из центров F и //, получим два проективных пучка прямых F(d, 1\т, а)
и Н(с, I, г, Ь)у причем прямая /, соединяющая центры пучков, соответствует
сама себе; поэтому точки М, Т, Р пересечения соответствующих прямых
(d и с, m и г, а и Ь) лежат на одной прямой, являющейся осью перспективы.
■ Рис. 46.
Пользуясь принципом двойственности, отсюда легко получить решение
такой задачи: даны две точки А и В и прямая т (рис. 47). Найти на
прямой т точку, которая лежала бы вместе с точками А и В на одной
Рис. 47.
прямой р. Построение на рис. 47 отличается от построения рис. 46 заменой
точек прямыми, а прямых— точками; для ясности те точки и прямые,
которые заменяют друг друга, обозначены одинаковыми буквами (точки —
большими, прямые—малыми).
§23]
ДВА МЕТОДА ОБРАЗОВАНИЯ КРИВЫХ
83
§ 23. Два метода образования кривых
I. В § 19 мы говорили о принципе двойственности в
применении лишь к простейшим геометрическим объектам — точкам и прямым,
рядам точек и пучкам прямых; рассмотрим теперь вопрос об
образовании кривых линий с точки зрения принципа двойственности.
Если за основной
геометрический элемент принять точку,
то кривая может быть образована
непрерывной совокупностью
точек (рис. 48, слева); точка при
этом описывает кривую. Точка
Если за основной
геометрический элемент принять прямую,
то кривая может быть образована
непрерывной совокупностью
прямых, касающихся ее (рис. 48,
справа); прямая при этом огибает
Рис. 48.
называется инцидентной этой
кривой, если она лежит на ней.
Две точки, лежащие на кривой,
определяют проходящую через
них (т. е. инцидентную им)
прямую; если вторая точка стремится
к совпадению с первой, то
предельным положением этой
секущей является касательная в
первой точке.
Если любая прямая пересекает
кривую в п точках (вещественных
кривую *). Прямая называется
инцидентной этой кривой, если
она касается ее. Две прямые,
касающиеся кривой, определяют
точку их пересечения, т. е.
инцидентную им точку; если вторая
прямая стремится к совпадению
с первой, то предельным
положением этой точки пересечения
является точка касания первой
прямой.
Если из любой точки можно
провести к кривой п касательных
) Например, рабочий профиль кулачка для толкателя с плоской тарелкой
является огибающей различных положений этой тарелки; профиль зубца на
зубчатом колесе, сцепляющемся с зубчатой рейкой с прямолинейным
профилем зубца, является огибающей различных положений этого
прямолинейного профиля.
84 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ (гл. III
или мнимых), т. е. если
существует п точек, инцидентных
прямой ^ кривой,'то кривая будет
п-го порядка.
Уравнение
f(xv xv дг3) = 0 (23.2)
является уравнением кривой /
в однородных координатах
точки xv х2, дг3, или иначе
в точечных координатах; точка
M(xv х2, хг) инцидентна кривой/
(т. е. лежит на ней), если ее
координаты удовлетворяют
уравнению кривой (23.2).
Задавая произвольно хх и лг3,
мы сможем найти из (23.2)
величину х2 и найти, таким образом,
точки, инцидентные этой кривой;
таких точек бесчисленное
множество, ибо величины xv хг взяты
произвольно.
Если /—алгебраическая
функция, то кривая называется
алгебраической, а наибольшая сумма
показателей при xv х2, хг
называется порядком алгебраической
кривой.
В случае кривой п-то порядка
уравнение (23.1) прямой g (при
фиксированных uv uv #3) и
уравнение кривой (23.2) имеют п общих
корней (вещественных или
мнимых), т. е. существует п точек,
инцидентных прямой gи кривой/.
Таким образом, задавая прямую £,
(вещественных или мнимых), т. е.
если существует п прямых,
инцидентных точке и кривой, то
кривая будет /1-го класса.
Уравнение
<f(uv и2, иг) = 0 (23.20
называется уравнением кривой ср
в однородных координатах
прямой uv и2, иг, или иначе в
тангенциальных координатах;
прямая m(uv и2, иг) инцидентна
кривой ср (т. е. касается ее), если ее
координаты удовлетворяют
уравнению кривой (23.2').
Задавая произвольно их и #3»
мы сможем найти из (23.2')
величину и2 и найти, таким образом,
прямые, инцидентные данной
кривой; таких прямых бесчисленное
множество, ибо величины uv иг
взяты произвольно.
Еслиср — алгебраическая
функция, то кривая называется
алгебраической, а наибольшая сумма
показателей при uv и2, иг
называется классом алгебраической
кривой.
В случае кривой п-то класса
уравнение (23.1) точки G (при
фиксированных xv х2, хг) и
уравнение кривой (23.2') имеют п
общих корней (вещественных или
мнимых), т. е. существует п
прямых, инцидентных точке G и
кривой ср. Таким образом, задавая
Эти соображения чисто геометрического характера дополним
рассмотрением уравнения
ulxl + и2х2 -f- игх3 = 0 (23.1)
(которое при фиксированных значениях величин uv и2, иг является
уравнением прямой, а при фиксированных значениях величин xv xv хг
является уравнением точки) и уравнений более общего типа.
§ 23]
ДВА МЕТОДА ОБРАЗОВАНИЯ КРИВЫХ
85
мы найдем п точек ее
пересечения с кривой /.
Например, если дана прямая g
с координатами
а{ = 1, и2 = 1, и3 = —2
то, решая совместно уравнение
прямой g
с уравнением кривой второго порядка
в точечных координатах
х\ + *2 — ^х2хъ — 4^j^3 +
+ Аххх2 = 0, (23.3)
найдем координаты точек пересечения
Л4,(1, 1- 1). ^2 (0, 2, 1).
точку О, мы найдем /г
касательных, проведенных из нее к
кривой ср.
Например, если дана точка С
с координатами
__ 5 к _i
Хх — -jr , ^2 == — ^»- -*3 — 1»
то, решая совместно уравнение
точки G
5
-^•^ — 5^2 +и3 =0
с уравнением кривой второго класса
в тангенциальных координатах
31^ + \2и\ — 32*4 — 68^ —
— 48и,!*8 4- 40и2и3 = 0, (23.30
найдем координаты прямой
/я, (6, 1, —10), /я2(2, 1, 0);
следовательно, через точку G
проходят две прямые
6*! + х2 — Ю^з = 0, 2^j + л:2 = 0,
касательные к кривой (23.3х).
II. Рассмотрим коническое сечение с уравнением в точечных
координатах
/ = / С*. У) = Яц*2 +- 2а12ху + а22у2 + 2a13*4- 2а23у-~Мзз = 0 (23.4)
и покажем, как найти уравнение этой кривой в тангенциальных
координатах.
Уравнение касательной к нашей кривой в точке М' (х\ у') таково:
■^-(*-*')+-^г (У-/) =
= (х - х') (апх' + а12у' + а13) + (у — у') (а21х' + я22/ + «23) = 0;
воспользовавшись тем, что точка М' лежит на кривой, получим:
(аих' + а12у' + а13)х + (а21х' + а^у'+a23)y+a31x'-\-a32y'-j-a33 = 0,
или в однородных координатах
{auxi + «12*2 + ахбх'б)х1 + К*! + «аз^г-Ь а23*з)*2 +
■+ («а*! + а*А + ааз*з) хг = °; С23-5)
86 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
сравнивая с уравнением (23.1), найдем:
а21х[ + а22х'2 + а2гх'3 = 9и2, (23.6)
х Л31^ + ^2Л:2+аЗЗД:3 = Р^
где р — некоторый коэффициент пропорциональности; если кривая —
нераспадающаяся, то условие (4.9) не выполняется и мы можем
разрешить эту систему уравнений относительно х'у х'2, х'3:
х[ = р (р.иих + <х12я2 + <*13tf3),
*2 = р (02i«i -+ а22и2 + а23й3), (23.7)
Хз = р (азЛ + а32«2 + а33я3).
Так как точка Ж' лежит на кривой, то ее координаты удовлетворяют
уравнению кривой, что можно записать таким образом:
х\{апх[ + al2xf2+ a13*3)+ *J(«2i*I + "22*2 + а2з*з) +
■+ ^з(а31^ + вза^+азз^з) = °- <23'8)
Чтобы получить искомое уравнение в тангенциальных координатах,
нам надо подставить вместо x'v x'v х'3 их значения (23.7); мы
получим, пользуясь (23.6):
«1 (а11«1 + а12^2 + а13%) + U2 (а2 А + а22^2 + *23из) +
-+- Ч (а3 А + а32^2 + а33^з) = 0.
и окончательно уравнение конического сечения в
тангенциальных координатах таково:
F = апи\ + 2a12w^2 + а^а\ + 2а13^1й3 + 2а23я2и3 + а^и\ = 0. (23.9)
Таким образом, если дано уравнение (23.4) конического сечения
в точечных координатах (т. е. не выполняется условие (4.9) и левая
часть уравнения не является произведением двух множителей), то,
решая уравнения (23.6) и находя коэффициенты aik в формулах (23.7),
мы получим уравнение (23.9) той же кривой в тангенциальных
координатах.
Обозначая через а\п алгебраическое дополнение элемента aik
в определителе Д формулы (4.9), мы получим решение системы (23.6):
^i=fKitti + a2itt2 + a3itt3)'
Х3 = 1 (а>1 + V2 + Л33"3>
§ 23]
ДВА МЕТОДА ОБРАЗОВАНИЯ КРИВЫХ
87
так как уравнение (23.9) не изменится, если все коэффициенты aik
умножить на произвольный общий множитель, то, сопоставляя (23.10)
с (23.7), находим:
"<* = PiV (23.11)
где рх — произвольный множитель.
Так как формулы (23.7) найдены посредством решения системы
уравнений (23.6) при условии Д Ф 0, то, решая в свою очередь
систему уравнений (23.7), мы должны прийти к исходным формулам
(23.6); отсюда вытекает, что
Д' =
аи
«21
а31
а12
а22
а32
а13
а23
а33
=£0, (23.12)
ибо в противном случае система уравнений (23.7) была бы либо
несовместной, либо неопределенной *).
Пусть теперь дано уравнение конического сечения в
тангенциальных координатах (23.9), причем Д' Ф 0 (т. е. левая часть
уравнения не является произведением двух множителей и кривая — невы-
рождающаяся); решая систему уравнений (23.7), мы найдем по (23.6)
коэффициенты aik и сможем написать уравнение *той же кривой
в точечных координатах (23.4); так как все коэффициенты можно
умножить на произвольный общий множитель, то их можно найти по
формуле а/Л==р2а^, где р2 — произвольный множитель, а а^. —
алгебраическое дополнение элемента akl в определителе Д'. Таким
образом, нераспадающаяся кривая второго порядка является невы-
рождающейся кривой второго класса, и наоборот.
Например, в случае кривой с уравнением (23.3), решая систему
уравнений
х\ + 2*2 — 2л:3 = pwr ^x'i -f- х'2 — х3 = ри2, — 2х\ — х2 = ри3»
мы найдем:
х\ =* -J (— и\ + 2w2). 4Я{ (2Wl ~*4"2~~ 3wsj)' х'ъ ~ "з (~~3"2 ~~3w^'
и уравнение этой же кривой в тангенциальных координатах таково:
— и j + 4utw2 — 4^ — 6u2w3 — За3 = 0.
III. Пусть теперь справедливо (4.9), т. е. левая часть уравнения
(23.4) такова:
/ = / J2 = (axi + bx2 + схг) (лхг + р*2Н- Тдг3) = 0; (23.13)
*) В теории определителей выводится формула р^Д' = Д2, откуда ясно,
что определители Аи А' одновременно равны или не равны нулю.
88
ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ ТП
в этом случае кривая распадается на пару прямых fY и /2, не совпа-
а Ь с
дающих друг с другом, если не имеет места равенство —
из (23.13) находим определитель
2асс ар + Ъъ (ц-\- со.
а$ + Ьа 2Ь$ bf + c$ | = 0.
ay + col b-{ + c$ 2cy
A =
(23.14)
Мы не можем решить систему уравнений (23.6), ибо Д = 0, но мы
можем найти коэффициенты aik по формуле blk = a'fcr откуда
ап = (*Т — СР)2' а12 = (с<х — аЧ) (*Т — СР)' а22 = (^а — ят)2'
<*13 = (*Т —*P)(flP —**)• ^23 = ^ —flT)(flP —**)• азз = («Р — И2;
подставляя эти значения aik в (23.9), найдем окончательно:
К*Т — фиг + (са — ач)и2 + (а§ — Ьа)и3]2 = 0. (23.15)
С другой стороны, координаты точки M0(xv х2, хг) пересечения
прямых fx и /2 найдем, решая два уравнения /г = 0 и /2 = 0, откуда
хх = Ь-\ — сф, х2 = са — #-[• хг = аф—Ьа.
Уравнение (23.15) примет следующий вид: (и1х1~\~ щх2-\- игхг)2 — 0;
следовательно, кривой второго порядка, распадающейся на пару
прямых,, соответствует
кривая второго класса,
вырождающаяся в две точки,
совпадающие с точкой
пересечения прямых; к этому
результату можно прийти и
без вычислений: всякая
прямая g (рис. 49, а),
пересекающая прямые /х и /2, на
которые распалась кривая /,
является секущей, а
прямая g0, проходящая через
точку М0, пересекает
кривую / в двух совпадающих
точках, т. е. ее следует
считать касательной к распадающейся кривой /; всевозможные ее
положения проходят через точку MQ, которую следует считать
огибающей касательных.
Совершенно аналогично получим взаимную теорему: если задана
кривая второго класса в тангенциальных координатах (23.9) и
Рис. 49.
§ 23]
ДВА МЕТОДА ОБРАЗОВАНИЯ КРИВЫХ
если А'= 0, то левая часть уравнения распадается на два
множителя
F = FlF2 = (lul-\- ти2 + пиг) (\их + ця 2 + шг) — 0,
т. е. кривая вырождается в две точки FX{1, т, п) и F2(k, |х, v)
(рис. 49, б)\ соответствующая кривая второго порядка
распадается на пару прямых, совпадающих с прямой FXF2.
Действительно, если взять произвольную точку О вне прямой т0, то прямые
QFX и OF2 следует считать двумя касательными, проведенными из
точки О к кривой F, выродившейся в пару точек Fx и F2\ если же
точка G0 лежит на прямой т0, то обе касательные совпадают, а
следовательно, точку G0 следует считать лежащей на кривой F, откуда
вытекает наше утверждение.
IV. В качестве весьма важных применений теории рассмотрим
чисто геометрическое доказательство теоремы Штейнера и попутно,
пользуясь принципом двойственности, докажем новую теорему о
свойствах конических сечений.
Точки
пересечения
соответствующих прямых двух
проективных
пучков S (а, Ь, с, ...)
и S'(a't b', с', ...)
(рис. 50, а) лежат
на кривой
второго порядка /,
которая проходит
через центры
пучков S и S'\ если
прямую,
соединяющую центры
пучков S и S\
рассматривать как
прямую е первого
пучка, то ей
соответствует во
втором пучке
прямая е'',
касательная к f в точке Sf\
если же ее
рассматривать как
прямую h' второго
пучка, то ей соответствует
в первом пучке прямая h,
касательная к / в точке S.
Рис. 50, а.
первом ряде
прямой s с
Прямые,
соединяющие
соответствующие точки
двух проективных
рядов s (Л, В, С,...)
и s'.{A', Вг, С',...)
(рис. 50, б),
огибают кривую
второго класса ср,
которая касается
прямых s и sr\
если точку
пересечения прямых
s и s'
рассматривать как точку Е
первого ряда, то
ей соответствует
во втором ряде
точка Е'
касания прямой s'
с ср; если же
ее рассматривать
как точку Н!
второго ряда, то ей
соответствует в
точка Н касания
90 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ III
Для доказательства зададим
произвольно по три прямых
каждого пучка 5 (а, Ь, с) и S' (а\ Ь', с')\
задавая произвольно четвертую
прямую d, найдем
соответствующую ей прямую dr из условия
(abed) = (a'b'c'd').
Если прямая d повернется вокруг
точки S на бесконечно малый
угол, то бесконечно мало
изменится величина (abed), поэтому
Для доказательства зададим
произвольно по три точки каждого
ряда s(A, В, С) и s'(A', В\ С);
задавая произвольно четвертую
точку D, найдем соответствующую
ей точку Df из условия
(ABCD) = (A'B'C'D'Y
Если точка D бесконечно мало
переместится по прямой $, то
бесконечно мало изменится величина
(ABCD), поэтому точка D' также
С
Рис. 50, б.
прямая d' повернется вокруг
точки S' на бесконечно малый
угол и точка D пересечения
прямых d и d' бесконечно мало
переместится; при непрерывном
вращении прямой d вокруг точки S
будем иметь непрерывную
совокупность точек D, т. е. точка D
описывает при этом некоторую
кривую /.
Любая прямая g
пересекает проективные пучки прямых
S(a,b,c,dt...)nS'(a',b\c',d',...)
по двум проективным рядам
точек g(Av Bv Cv Dv . . .) и
«■(^l.ai.Ci, Dl, ...)(рис. 50, я);
бесконечно мало переместится по
прямой sf и прямая d,
соединяющая точки D и D', бесконечно
мало переместится; при
непрерывном движении точки D по
прямой s будем иметь непрерывную
совокупность прямых d, т. е.
прямая d огибает при этом
некоторую кривую ср.
Из любой точки О
проективные ряды точек 5 (Л, BCD,...)
и s'(Л\ В', С D', . . .)
проектируются двумя проективными
пучками прямых О (av bv cv dv...)
и G(a'v b'v c'v d'v ...) (рис. 50, 6)\
§23] ДВА МЕТОДА ОБР
очевидно, точки пересечения
прямой g с кривой / являются
двойными точками этого проективного
соответствия на одном основании,
ибо обе соответствующие прямые
т и т\ проектирующие точку
пересечения М из центров 5 и S\
пересекают прямую g в одной и
той же точке; так как таких
двойных точек не более двух, то
никакая прямая не может иметь
более двух точек, инцидентных с /,
поэтому / является кривой
второго порядка, а следовательно,
и второго класса.
Прямые е и е', а. также h и h'
соответствуют друг другу,
следовательно, точки 5 и Sf их
пересечения также лежат на кривой /.
Каждая прямая а, Ъ, с, ...
первого пучка пересекает
кривую /, кроме точки 5, еще в одной
точке А, В, С, . . . своего
пересечения с соответствующей прямой
второго пучка; но прямая h не
имеет общих точек с /, кроме
точки 5, следовательно, она
касается кривой / в точке 5.
Примечание 1. Если бы
прямая SS' соответствовала сама
себе (т. е. прямые е и eft h и h'
совпали), то оба рассмотренных
пучка прямых были бы
перспективны, а кривая / распалась бы
на пару прямых.
Примечание 2.
Справедлива обратная теорема: из двух
любых точек на коническом
сечении f все остальные точки
проектируются посредством
двух проективных пучков
прямых.
ования кривых 91
очевидно, прямые, проходящие
через точку G и касающиеся
кривой ср, являются двойными
прямыми этих проективных
пучков с общим центром, ибо обе
точки М и М' пересечения
касательной прямой т с прямыми
s и sf лежат на одной прямой т
с точкой О; так как таких двойных
прямых не более двух, то ни из
какой точки нельзя провести
более двух прямых, инцидентных
с ср; поэтому ср является кривой
второго класса, а следовательно,
и второго порядка.
Точки Е и Е\ а также Н и Н'
соответствуют друг другу,
следовательно, соединяющие их
прямые s и s' также касаются
кривой ср.
Из каждой точки А, В, С, ...
первого ряда можно провести,
кроме st еще одну прямую а, Ь,
с, . . ., которая касается кривой ср
и соединяет указанные точки
с соответствующими точками А',
В', С, ... второго ряда; но из
точки Н нельзя провести к ср
другой касательной, кроме s,
следовательно, Н является точкой
касания прямой s с кривой ср.
Примечание 1. Если бы
точка пересечения s и s'
соответствовала сама себе (т. е. точки Е
и Е', Я и Н1 совпали), то оба
рассмотренных ряда точек были бы
перспективны, а кривая ср
свелась бы к двум точкам.
Примечание 2.
Справедлива обратная теорема: все
касательные к коническому
сечению ср пересекают две любые
касательные по двум
проективным рядам точек.
92 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
Действительно, возьмем на /
шесть точек S, S', Л, В, С, D
(рис. 51, а); спроектировав точки
Л, В, С, D из центров 5 и S',
получим пучки прямых 5 (а, Ь, с, d)
uS'(a't b't с\ d')\ построим
прямую d" второго пучка по условию
(abcd) = (a'b'c'd").
Пусть прямая d" пересекает
прямую d в точке D'\ точки Л, В,
С, D' пересечения
соответствующих прямых двух
проективных пучков должны лежать вместе
с точками S и S' на коническом
сечении fv которое должно
совпадать с /, ибо оно имеет с ним
пять общих точек 5, S', Л, В, С;
следовательно, точки D и D'
совпадают, прямые d' и d"
совпадают, откуда
{abed) = (a'b'c'd').
Действительно, возьмем шесть
прямых s, s't a, bt с, d,
касательных к ср (рис. 51, б); прямые
я, Ь, с, d пересекают прямые 5
и s' в точках 5(Л, В, С, D) и
s'(A', В\ С, D'); построим
точку D" второго ряда по условию
(ABCD) = (A'B'C'D").
Пусть прямая d' соединяет
точки D и ЕУ'\ прямые я, Ь, с, d'y
соединяющие соответствующие
точки двух проективных рядов
точек, а также прямые s и s'
должны касаться некоторого
конического сечения <plf которое
должно совпадать с ср, ибо имеет
с ним пять общих касательных s,
$', я, ЬУ с; следовательно,
прямые d и d' совпадают, точки D"
и D' совпадают, откуда
{ABCD) = (A'B'C'D').
D'
Рис. 51, а.
§ 24]
ТЕОРЕМА ПАСКАЛЯ
93
V. Рассмотрим в качестве иллюстрации один частный случай:
если бесконечно удаленные точки двух проективных рядов точек
s(A, В, С, ...) и s'(A', В', С, ...) соответствуют друг другу, то
бесконечно удаленная прямая (проходящая через эти точки) касается
кривой, т. е. кривая
в этом случае будет
параболой. Если
положение точек на прямых
s н s' характеризовать
абсциссами х и х\ то
эти абсциссы связаны
линейным
соотношением х'=-ах~\-Ь и
оба ряда точек
подобны (см. § 12); отсюда f
вытекает сохранение Hr^_Zl
простых отношений Е
отрезков;
следовательно, если точки А и А'
ЕА Е'А'
соответствуют друг другу, то мы имеем -трг~' А'Н' ^ис* ^* ^а
этом основан простой метод построения параболы по двум
касательным (s и s') и их точкам касания {Н и Е'); делим отрезки ЕН и Н'Е'
на одинаковое число равных частей и соединяем прямыми
соответствующие точки на обеих прямых, — эти прямые огибают параболу *).
§ 24. Теорема Паскаля
I. Мы видели, что коническое сечение вполне определяется своими
пятью точками (если никакие три из них не лежат на одной прямой);
следовательно, нельзя произвольно задать шесть точек конического
сечения — их расположение должно быть подчинено некоторому
условию.
Возьмем шесть точек Av ..., А6 на коническом сечении (рис. 53)
и соединим их прямыми vv ... v6 (прямая vx соединяет точки Ах и
Л2, прямая v2 соединяет точки Л2 и Л3. .., наконец, прямая vQ
соединяет точки А6 и Ах). Пары прямых vx и гг4, v2 и vb, vs и v6 (номера
которых различаются на три единицы) будем называть
противоположными сторонами шестиугольника.
Теорема Паскаля такова: точки пересечения трех пар
противоположных сторон шестиугольника, вписанного в коническое
сечение, лежат на одной прямой (на рис. 53 это такие три точки:
*) Этот метод (без достаточного обоснования) часто применяется в
сопротивлении материалов при построении эпюры изгибающих моментов для
балки, нагруженной равномерно распределенной нагрузкой.
94 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. Ill
точка Хг пересечения v} и v4, точка Х2 пересечения v2 и v5, точка Хъ
пересечения vz и v6).
Для доказательства обозначим через v прямую, соединяющую
точки А2 и Л5; так как наша кривая должна проходить через точки
Av Л2, Л5, Л6, то по § 20 она должна принадлежать пучку
vlv5~\-lw6 = 0 (24.1)
при некотором значении параметра X. Но эта же кривая должна
пройти и через точки Л2, Л3. Л4, Л5, следовательно, она должна
принадлежать и пучку ггЛ + рот3 = 0 (24.2)
при некотором значении параметра [а. Так как уравнения (24.1), (24.2)
соответствуют одной и той же кривой, то их левые части могут
различаться лишь постоянным
множителем, т. е. мы должны иметь:
vxvb + Хот6 зз С (v2v4 +- jxwa).
откуда
vivs — ^v2vA =з vat
и = —Xve •+- Cjjw3. (24.3)
Левая часть этого равенства
обращается в нуль при подстановке
координат точек пересечения следующих
прямых: 1) г»! и v2 (точка А2)\ 2) vx
и vA (точка Л^); 3)v4nv5 (точка Л5);
4) v2 и ^5 (точка Х2); следова-
же координат должна обратиться
в нуль и правая часть. Точки Л2, Аъ лежат на прямой г/,
следовательно, при подстановке их координат имеем ^ = 0; точки Хх и Х2
не могут лежать на прямой v—если бы, например, точка Хх лежала
на прямой v, то прямые v и vx совпали бы и на них лежали бы три
точки Ах% Л2, Л5, что невозможно, ибо кривая нераспадающаяся.
Таким образом, точки Хх и Х2 лежат на прямой и\ но из формулы
(24.3) видно, что и точка Хг пересечения прямых vz и vQ лежит на
прямой и\ таким образом, все три точки Хх% Х2, Хъ лежат на
одной прямой и *).
Справедлива и теорема, обратная теореме Паскаля: если три
точки пересечения трех пар противоположных сторон
шестиугольника лежат на одной прямой, то его можно вписать в
коническое сечение.
Рис. 53.
тельно, при подстановке этих
*) Мы доказали теорему Паскаля для случая конического сечения, т. е.
нераспадающейся кривой второго порядка; теорема верна и в том случае,
когда кривая второго порядка распадается на пару прямых, если точки А19
Аъ, Аь лежат на одной, а то*ши A2t А4, Лв на другой прямой (см. § 40).
§ 24]
ТЕОРЕМА ПАСКАЛЯ
95
Пусть Av .... Aq — заданный шестиугольник, vl и v4, v2 и v5,
v% и Vq — его противоположные стороны, пересекающиеся в точках
Xv Xv Хъ прямой и\ проведем коническое сечение через пять точек
Ах Л5, и пусть оно не проходит через точку Л6, а пересекает
прямую Vq в точке А'6 (рис. 53), причем через v's обозначена прямая,
соединяющая точки А5 и А'6. Все прямые, кроме v5, остались неиз*
менными; применяя теорему Паскаля к шестиугольнику Ах Л5, Л^
мы видим, что прямая v'b должна пройти через те же точки А5 и Xv
что и прямая #5, т. е. А'6= А6 и коническое сечение проходит и
через шестую вершину Лб.
II. Рассмотрим несколько частных случаев теоремы Паскаля. Если
точка А2 стремится к совпадению с точкой Av то секущая прямая vx
стремится к своему предельному положению, которым является
касательная к кривой в точке Ах; следовательно, при совпадении двух
точек кривой мы знаем касательную в этой точке. Таким образом,
коническое сечение, которое мы определяли пятью точками, можно
Рис. 54. Рис. 55.
определить еще иначе: четырьмя точками и касательной в одной из
них или тремя точками и касательными в двух из них. В
соответствии с этим можно в теореме Паскаля рассматривать не
шестиугольник, а пятиугольник (считая, что две вершины совпали), или
четырехугольник (считая, что две пары вершин совпали), или
треугольник (считая, что три пары вершин совпали); мы получим, таким
образом, следующие частные случаи:
1) вписанный пятиугольник, причем задана касательная в одной
из вершин (рис. 54);
2) вписанный четырехугольник, причем заданы касательные в двух
вершинах (рис. 55);
96 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. II!
3) вписанный треугольник, причем заданы касательные во всех
трех вершинах (рис. 56).
Во всех случаях на рисунках показаны все стороны и все вершины,
причем две буквы,
соответствующие одной и той же
точке, означают, что эту
точку рассматриваем как две
совпавших точки; например,
в случае 3) можно
сформулировать так теорему
Паскаля: если в коническое
сечение вписан треугольник,
то три точки пересечения
касательных в вершинах
треугольника с его
противоположными
сторонами лежат на одной
прямой.
III. Рассмотрим две
простые задачи, решение которых
опирается на теорему Паскаля.
Коническое сечение задано
пятью точками Аи .... Л5
Рис. 56.
ресечения с заданной прямой
чая через Ле искомую точку
(рис. 57); найти точку его пе-
проходящей через точку А{.
Обогнана заданной прямой ve, мы можем по-
v3t vA и найти точки л{ (в пересечении v{ с vA) и
Х3 (в пересечении vz с v6); две точки Хх и Х3 определяют прямую Паскаля и,
на которой должна лежать и точка Хц пересечения v2 с v5\ так как прямая
строить прямые vx, v2,
Рис. 58.
v2 известна, то в пересечении ее с и находим точку Х2\ но прямая v5 должна
проходить через точки Аь, А6, Х3, поэтому, проведя через точки А5, Х2
прямую, мы найдем точку А6 в ее пересечении с прямой v6.
При тех же условиях найти касательную к коническому сечению
в точке Ах (рис. 58). Будем считать точку Лб совпавшей с^; в таком
§ 25]
ТЕОРИЯ ПОЛЯРНОГО СООТВЕТСТВИЯ
97
случае соединяющая их прямая ve является искомой касательной. Зная точки
j4|, ..., А6, мы можем построить прямые vit ..., vs, найти точки Хх (в
пересечении г/, с г/4) и Х2 (в пересечении v2 с vb) и прямую Паскаля ХХХ2\
прямая г/3 пересекает ее в точке Хъ\ соединяя прямой точки Ах и Х3, найдем
искомую касательную vQ. В обеих задачах вместо пяти точек коническое
сечение можно было бы задать посредством четырех точек и касательной
в одной из них, или трех точек и касательной в двух из них; при всех этих
видах задания мы можем построить сколь угодно новых точек конического
сечения и касательные в них.
§ 26. Теория полярного соответствия
I. Пусть нам дана кривая второго порядка (рис. 59),
характеризуемая уравнением в однородных координатах
/ = апх\ ~f- 2а12хгх2 + а22х\ + 2а{3х{х3 + 2а23х2х3 + а^х\ = 0.
(25.1)
Возьмем точку М'{х\, х'т х'Л не на кривой, проведем через нее
прямую и, пересекающую
кривую в точках А и В, и
найдем на этой прямой точку
М" {х\, x"v дГз)' образующую /i ч . и^^\В
гармоническую группу с
точками Л, £, М\ т. е.
(АВМ'М") = 1. (25.2) Mrt
Фиксируя точку М' и проводя
через нее пучок, прямых, рас- Р с 59
смотрим геометрическое место
точек М".
Координаты любой точки на прямой М'М" могут быть выражены
по (1.3) формулой
1+х
Хп ———
Т+Т~
1+ь
(25.3)
причем точке М' соответствует значение параметра Х = 0, а точке
М" — значение Х = оо. Так как точки Л, В лежат на этой прямой
и на коническом сечении, то они соответствуют таким значениям
параметра X, при которых координаты (25.3) удовлетворяют уравнению
(4
+ kxv х2 + ^х2 хя + ^*э
+ х
1+Х
1+Х
.)-..
98 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
Нетрудно видеть, что, умножая на (1+Х)2 и группируя члены по
степеням X, мы получим:
/ Хл + X-Ki х9 + \х9 Хо + \хп \
= /(*;, 4 xQ-b2XT(x'. х") + ^2/«. х2\ <) = 0. (25.4)
где сокращенное обозначение ср(лг', л;") имеет следующий смысл:
т (х'. х") = anx\xl + а12(*;*£ + *£<) + а22х^' +
+ «13 «*з + «) + «23 (*2*з + «) + азз*з<- (25-5)
Легко видеть, как получается эта функция из функции (25.1): там,
где мы имеем член с квадратом, например апх^ = апх1Ху мы
заменяем один множитель хх на х\ а второй множитель хх на х'[\ там,
где мы имеем удвоенное произведение, например 2а12х1х2 —
— а\2 (х\х2 Ч~ хгх2)ъ мы заменяем в первом слагаемом хх на х[ и х2
на ATg» а во втором слагаемом хх на х"х и д:2 на д^. Пусть Хх, Х2 —
корни квадратного уравнения (25.4), соответствующие точкам А и В\
так как мы имеем для точек М' и М" Х3 = 0 и Х4 = сх>, то по (13.7)
и (25.2) находим:
(АВМ'М")= \*~\1 : \А~~\1 =-Ь-= —1, Х1 + Х2 = 0.
откуда получаем условие
<р(лг', лг") = 0. (25.6)
Если точка М' фиксирована, а точка М" — переменная, то,
обозначая для простоты через (xv х2, х3) координаты точки М'\ получим
из (25.6):
апх[х1 + а12(х[х2+ хгх'2)+ а22х'2х2 + a13(*'i*3 + ХА) +
+ а2г(х2Х*+ х2хг)+ азг х'ъх* = °- (25-7)
что можно записать еще таким образом:
ulxl -f- и2х2 -f- и3хг = 0, (25.8)
где мы положили
ai = flll*i + fl12*2+fl13*3'
и2 = а21х[ + я22*2+ *2з*з- ^25-9>
^з === ^31*1 "Т" #32*2 ~Ь азЛ-
Мы можем записать эти формулы в таком виде:
1
■Ш- <-ЖУ- ■.={©' <»«»
§ 25] ТЕОРИЯ ПОЛЯРНОГО СООТВЕТСТВИЯ 99
где штрих показывает, что после дифференцирования функции
f (xv х2, ■%) (25.1) надо вместо хх, х2, хг подставить x'v х'т х'^
Так как мы получили уравнение первой степени относительно
координат {хх, х2, хг), то искомым геометрическим местом является
прямая линия.
Мы пришли к следующему результату: если заданную точку
М'(x'v x'v х'Л принять за центр пучка прямых и на каждой
из них найти точку, образующую гармоническую группу с
центром пучка и с точками пересечения прямой с заданной кривой
второго порядка, то геометрическим местом таких точек
является прямая линия, однородные координаты которой {их,
и2, и3) выражаются формулами (25.9).
II. Заданная точка М' называется полюсом, а найденная прямая —
ее полярой относительно заданной кривой второго порядка (25.1);
таким образом, каждому полюсу М'(x'v х'2, х'Л соответствует
определенная поляра т' с уравнением (25.8), где (их, и2, иг) даются
формулами (25.9) *).
Если кривая — нераспадающаяся (т. е. не выполнено условие
(4.9)), то мы сможем разрешить систему уравнений (25.9)
относительно х[, х'2, х'3\ решая ее по известным правилам, мы получим,
так же как в § 23,
*i = aiitfi + ai2tf2-+ai3tf3- -
*2 = a21tfl + a22tf2 + a23tf3' (25.11)
*3 = a31tfl + a32tf2 + a33tf3'
таким образом, при заданном коническом сечении (25.1) каждой
поляре с уравнением (25.8) соответствует определенный полюс
с координатами (25.11).
Например, если задано коническое сечение
х\ + Ахх х2 + Ъх\ + \0хх хг — 16х2 хг — 4x1 = О»
то: 1) полюсу М (2, —1, 1) соответствует поляра т
т = 5х{ — 9х2 + 14*3 = О,
ибо по (25.9)
w1==5, и2 =— 9, иг = 14;
2) поляре т!
т' = — \0х{ — 5х2 + 33*з = О
соответствует полюс М' (1, —3, —1), как легко найти, решая систему
уравнений
х[ + 1х'2 + 5*з = и1 = — 10, 2хх + 5^2 — 8-*з = w2 ~ — 5,
Ъхх — 8*2 — 4^з = w3 = 33.
*) Обозначаем полюсы большими буквами, а их поляры —
соответствующими малыми буквами.
100 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
III. Рассмотрим теперь поляру точки М! относительно кривой
второго порядка, распавшейся на пару прямых vx и v2 (рис. 60);
легко видеть, что поляра
любой точки М' проходит через
точку М пересечения прямых
vx и v2, т. е. в этом случае
мы не имеем взаимно
однозначного соответствия между
полюсом и полярой;
действительно, проведем через
точку М' прямую v3,
пересекающую прямые vx и v2
в точках А и В, найдем
точку С из условия (АВСМ') =
= — 1 и проведем
прямую МС\ тогда ясно, что она
является полярой точки М\
ибо для всякой другой прямой v4, проходящей через точку ЛГ, мы
также имеем
(А'В,С'М/) = —1.
§ 26. Свойства полюсов и поляр
I. Будем считать заданным коническое сечение (25.1); рассмотрим
некоторые свойства полюсов и поляр.
1) Если точка М" лежит на поляре т' точки М' (рис. 61),
то точка М' лежит на поляре т!' точки М" {свойство
взаимности); такие две
точки, каждая из которых
лежит на поляре другой
точки, называются
сопряженными точками.
Действительно, уравнение (25.6)
означает, что точка М" лежит на
поляре точки М'\ из (25.5)
нетрудно найти, что функция
cp(jc/, х") не изменяется, если
точки М' и №' поменять
местами — следовательно, это же
уравнение означает, что
точка М' лежит на поляре Рис. 61.
точки М".
2) Точка М0 пересечения прямых т! и т" является полюсом
прямой т0, соединяющей точки М' и М" (рис. 61); действительно,
»1 v2
Рис. 60.
§ 26]
СВОЙСТВА ПОЛЮСОВ И ПОЛЯР
101
являющихся полярами
Рис. 62.
точка М0 лежит на обеих прямых т\
полюсов АГ, М" —
следовательно, ее поляра т0 должна
проходить через точки AT, М".
3) Если полюс движется по
некоторой прямой т0, то его
поляра вращается вокруг
точки М0, являющейся полюсом
прямой т0 (рис. 62); при этом
ряд полюсов m0(Mv М2, Мг, . . .)
и пучок их поляр M0(mv т2,
тг, ...) проективны, т. е. мы
имеем:
(МгМ2МгМА) = (mlm2m3mA)t
(26.1)
Действительно, по (25.3)
положение точки M(xv xv хг) на
прямой М'М" (рис. 59) характеризуется параметром X; если т
т" — поляры точек М, М' и М"\ причем
т' = и'ххх -f- и'2х2 -f- и'^Хр т" = и[хх + и2х2-{- и"ъ лг3,
т ^^z u-tX-t —— UnXn —|— UoXoi
то из (25.8), (25.9), (25.10) находим:
ап (х\ + \х[) + д12 ( х2 + \х2) + д13(*з + **з ) _и\ + 1и\
иг— 1+Х — 1+х '
а2\ ( *1 + 1х1 ) + Д22 ( Х2 + Х*2 ) + а23 ( *3 + Хх1) __ U2 + Хц2
^2— 1+Х — 1+Х '
Д31 ( х\ + **Q + аЪ2 ( 4 + Х*2 ) + Д33 ( *3 + 1х1) _ Ч + >^3
w3— 1+Х — 1+х »
т. е. поляра т точки Ж характеризуется уравнением
т = т' + Х/я" = 0;
отсюда на основании (17.2), (13.10) следует (26.1).
4) Полюс лежит на соответствующей ему поляре тогда и
только тогда, когда он лежит на коническом сечении.
Действительно, подставляя в (25.7) x{ = x'v х2 = х'г хг~х'г, мы получим:
/(*;. к- *з)=0-
5) Если полюс лежит на коническом сечении, то полярой
является касательная в этой точке кривой; обратно, полюсом
т' и
(26.2)
102 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
касательной к коническому сечению является точка касания;
мы имеем из (25.4) при f (х[, х'г *з) = 0
2Ц{х', ^) + Х2/«. <. <) = 0.
Если точка М" (х'[, х"2, х^ сопряжена с точкой M'(x[t х'2, x£)t то
: 0 и мы имеем
0; так как
по (25.7) ср(АГ/, *") =
*7«.
<з)
Рис. 63.
точке М' соответствует корень
Х= 0, то второй корень также будет
равен нулю, т. е. сопряженные
точки М' и М" совпадают; так как
поляра точки М', проходящая через
точку М', должна по свойству
взаимности пройти через точку М"', то
она совпадает с касательной к
кривой в точке М'\ обратно, если
прямая а, касающаяся кривой в точке Л,
имела бы полюсом некоторую точку В, не совпадающую с Л, то она
была бы полярой для двух точек Л и В, что невозможно.
6) Если полюс М лежит вне конического сечения (рис. 63),
то, проводя из него две касательные a, b к кривой и проводя
прямую через точки касания А, В, мы получим поляру т\
действительно, так как касательные
а, Ъ являются полярами точек Л,
В и так как точка М лежит на
обеих этих полярах, то ее
поляра т должна пройти через обе
точки Л, В.
7) Если полюс М лежит
внутри конического сечения
(рис. 64), то проводим через
него две произвольные прямые
a, b и строим указанным
способом их полюсы Л, В; по
свойству взаимности поляра т
точки М должна пройти через
точки А и В.
II. Теория полярного соответствия приводит к понятию диаметра
конического сечения. Пусть в рассуждениях § 25 точка М' —
бесконечно удаленная (рис. 65), т. е. мы имеем пучок параллельных
прямых; в таком случае точка М" (§ 13) совпадает с серединой
хорды; таким образом, полярой точки, ушедшей в бесконечность
по данному направлению, является прямая, делящая пополам
все хорды этого направления; поляру бесконечно удаленной точки
Рис. 64.
§26]
СВОЙСТВА ПОЛЮСОВ И ПОЛЯР
103
назовем диаметром конического сечения. Если все полюсы лежат
на одной прямой, то по свойству 3) их поляры принадлежат одному
пучку, центр которого является полюсом этой прямой; поэтому все
диаметры, т. е. поляры всех точек бесконечно удаленной прямой,
принадлежат одному пучку прямых, центр которого является полюсом
бесконечно удаленной прямой;
назовем центром конического сечения
полюс бесконечно удаленной
прямой] в таком случае центр кривой
является центром пучка ее
диаметров.
В случае параболы бесконечно
удаленная прямая является ее
касательной, следовательно, центр
параболы, т. е. полюс бесконечно
удаленной прямой, лежит на этой прямой;
таким образом, центр параболы
является несобственной точкой
и все диаметры параболы
параллельны между собой. Эллипс и
гипербола называются
центральными кривыми—для них центр
является собственной точкой.
С аналитической точки зрения, подставляя в (25.9) ^ = 0,
получим: / /
ul а\\х\ ~т~ а\2х2
Рис. 65.
а2\х\ ~Ь а22Хс1
обозначая через k = -4- угловой коэффициент хорд, а через
k' = L угловой коэффициент поляры, полюсом которой служит
и2
бесконечно удаленная точка этих прямых, т. е. диаметр,
соответствующий этим хордам, мы получим основное соотношение
аи +kal2 и
а2х + ka22
(26.3)
если 8 = я11Д22 — а\ч = 0, то, как было показано в §12, будем
иметь k'' = ^-; таким образом, все диаметры параболы парал-
#22
лельны между собой и имеют направление ее оси (5.11), т. е.
прямой, по которой ушли в бесконечность центр и второй фокус
эллипса или гиперболы при предельном переходе, рассмотренном в § 3.
III. Рассмотрим теперь некоторые полярные свойства пучка
кривых второго порядка у —J— Хер = 0: поляры заданной точки
104 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
относительно всех кривых пучка образуют пучок прямых, про-
ективный пучку кривых.
Для доказательства заметим, что по (25.10) поляра данной точки
AV(x'{, x'v х'Л имеет однородные координаты
(26.4)
откуда на основании (19.80 вытекает наше утверждение. В
частности, если М' — бесконечно удаленная точка некоторой прямой, то
ее полярой является диаметр, сопряженный с этим направлением;
'V*
т' f
ул^
'V*
Z^N'
,£'
Щ
^vs
Nq'
"^С
V*
Рис. 66.
поэтому диаметры всех кривых пучка, сопряженные с данным
направлением, образуют пучок прямых, проективный пучку
кривых.
IV. Найдем теперь точки, поляры которых относительно
всех кривых данного пучка не зависят от выбора кривой (т. е.
от величины X); из формулы (26.4) ясно, что это возможно лишь
в случае
( д<? V —fJSLY —(A-Y—о
\dxj ~\dxj —\dxj ~~~U'
т. е. при обозначениях (20.8) при условиях
W + ^+V^0-
V<i + *22*2 + *23*3 = 0'
§ 27] ПОЛЯРНОЕ СООТВЕТСТВИЕ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ 105
для того чтобы эта система имела решение, отличное от решения
х\ = х'2 = х'г = 0, необходимо и достаточно равенство нулю
определителя, составленного из коэффициентов, т. е. по (4.9) кривая ср
должна распадаться на пару прямых; точка М' в этом случае
является точкой пересечения этих прямых. Таким образом, если
ср — кривая, распадающаяся на пару прямых vx и v2 (рис. 66), то
поляра точки М' пересечения этих прямых относительно всех
кривых пучка одна и та же; для кривых yl = v3v4 и ср2 = т>5'У6
(распавшихся на пары прямых v3 и v4 или vb и v6) эта поляра должна
проходить через точку Z/, или соответственно через точку N'\
следовательно, прямая L'Nf является полярой точки Mf
относительно всех кривых пучка; этим же свойством обладает
прямая M'N' (поляра точки L') и прямая LfMf (поляра точки N').
§ 27. Полярное соответствие относительно окружности
I. Рассмотрим несколько подробнее тот простой случай полярного
соответствия, когда коническое сечение является окружностью; если
она задана уравнением в однородных координатах
х\+х\ — гЧ1 = Ъ, (27.1)
то по (25.10) точке М'(x'v, x'v х^ соответствует поляра с
уравнением
х{х\ -4- х2х'2 — r2*3*j = 0; (27.2)
следовательно, каждой точке М'(х[, х'у х'Л соответствует ее
поляра т', т. е. прямая с уравнением
аххг -Ь и2х2 -f игхг = 0, (27.3)
где ах~== х[, и2=х'2> иг= — г2х'3; наоборот, каждой прямой тг
с уравнением (27.3) соответствует ее полюс ЛГ, т. е. точка с
координатами
x[ = uv х'2 = иг 4 = —-pf-. (27.4)
При пользовании неоднородными координатами уравнение поляры
точки M'(je', у') относительно окружности с уравнением х2-\-у2 —
—- г2 = 0 таково:
**/ + у/ — г2 = 0. (27.5)
Покажем, что полярами циклических точек являются
сопряженные изотропные прямые, проходящие через центр окружности^
действительно, для циклических точек мы имеем
x's = 0, х\ = ± 1х'х
Ц по (27.2) подучим х] ± ix%=^0..
106 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
II. Покажем построение полюса и поляры относительно
окружности *); если точка М лежит вне окружности (рис. 67), то по
общей теории проводим через точку М две касательные си>к
окружности; прямая т, проходящая через точки А и В их касания
с окружностью, является полярой точки М. Отметив точку М'
пересечения этой поляры с лучом ОМ, мы видим, что
6М-ОМ'==г2, (27.6)
т. е. на каждом луче, проходящем через центр окружности, мы имеем
гиперболическую инволюцию, образованную полюсами М и
точками Mf пересечения их поляр с этим лучом. Так как поляра т
точки М проходит через
точку М!, то по свойству
взаимности поляра т! точки М'
должна пройти через точку М,
г? причем она должна быть
перпендикулярна к лучу ОМ, ибо
из (27.5) ее угловой коэф-
х'
фициент равен г; мы
построили, таким образом, по-
Рис. 67. ляру т' точки М' лежащей
внутри окружности) поляра
точки, лежащей на окружности, совпадает с касательной к
окружности в этой точке.
III. В синтезе механизмов пользуются антиполюсом и
антиполярой, определяемыми следующим образом **): антиполюсом
данной прямой т относительно окружности называется точка М,
симметричная с полюсом М этой прямой относительно центра
окружности-, точно так же антиполярой данной точки М
относительно окружности называется прямая т, симметричная
с полярой т этой точки относительно центра окружности',
антиполюс и антиполяра указаны на рис. 67.
Формально антиполюс и антиполяру можно рассматривать как
полюс и поляру относительно мнимой окружности с радиусом гх = ir\
при этом мы будем иметь из (27.6)
ОМ' .0М = — г2, (27.7)
т. е. на каждом луче будем иметь эллиптическую инволюцию.
Уравнение антиполяры, соответствующей полюсу М'(х', у'),
очевидно, таково:
хх' + уу'-+-г2 = 0. (27.8)
*) Для произвольного конического сечения построение приведено
в § 47.
**) См. Р. Бейер [2], § 85; В. В. Добровольский [1], стр. 57—59.
§ 27]
ПОЛЯРНОЕ СООТВЕТСТВИЕ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ
107
IV. Рассмотрим так называемый полярограф А. К. Власова *),
позволяющий механическим образом осуществить полярное соответствие
относительно окружности (рис. 68): неподвижный шарнир О соединен двумя
стержнями О А = ОА{ с серединами А и Ах двух равных стержней РАВ,
РАХВ{, концы которых В и В{ соединены с ползушками, движущимися
в кулисе; покажем, что при
любом положении точки Р ось ВВ{
кулисы совпадает с полярой
этой точки относительно
окружности с центром в
точке О и с радиусом г =
= V0A2 — РА2-
Действительно, благодаря
равенству длин указанных выше
стержней мы видим, что всегда
на одной прямой лежат точки О,
Р и середина Р' отрезка ВВ{\
обозначая через С проекцию
точки А на прямую ОР, мы имеем:
ОА2 — РА2 = ОС2 — PC2 =
= (ОС + PC). (ОС — PC) =
= (ОС + СР') -ОР = ОР- ОР'.
Совершенно аналогично строим кинематическую цепь на_рис. 69; в этом
случае ось ВВ{ кулисы является антиполярой точки Р относительно
окружности с центром в точке О и
с радиусом
г = УГРА2 — ОА2. Dx
V. Рассмотрим в качестве дальнейшей
иллюстрации решение такой задачи: пусть
на призматический брусок прямоугольного
Рис. 68.
Рис. 70.
поперечного сечения ABCD (рис. 70) действует эксцентрично приложенная
сжимающая продольная сила Р, приложенная в точке М0 (х0, у0); найти
условия, при которых во всех точках поперечного сечения S напряжения
будут сжимающими.
*) См., например, В. В. Добровольский [1], стр. 58—59.
108 образование геометрических форм высших порядков [гл. ти
Строим центральный эллипс инерции для S с уравнением
гх, г у — радиусы инерции S относительно осей С0х, С0у, где С0 центр
тяжести 5; напряжение р в любой точке М (х, у) сечения S выражается, как
известно, формулой
р = Ц1 + ^+шу (27.10)
где F — площадь S; геометрическое место точек М, для которых р = 0,
называется нейтральной линией S; оно, очевидно, характеризуется уравнением
££L+i^L + l=0; (27.11)
Г г
'у 'X
по аналогии с (27.8) мы можем сказать, что нейтральная линия 5,
соответствующая данной точке MQ (х0, у0) приложения нагрузки, является
антиполярой этой точки относительно эллипса инерции (на рис. 70
построены поляра т0 и антиполяра т0 точки М0).
Если нейтральная линия пересекает S, то она делит 5 на две части
с напряжениями различных знаков, как видно из (27.10); следовательно,
в нашей задаче крайними положениями нейтральной линии являются
стороны контура ABCD. На рис. 71 построены антиполяры с, 7, F, b точек
Рис. 7L Рис. 72. Рис. 73.
Л, С, В, D; заштрихованный ромб, ими образованный, называется ядром
сечения S; таким образом, напряжения во всех точках S будут
сжимающими, если точка приложения нагрузки не выходит за пределы ядра
сечения.
Аналогично решается задача и в том случае, когда сечение S
ограничено любым п-угольным выпуклым контуром: ядро сечения будет также
п-угольником, вершины которого являются антиполярами сторон данного
контура; если же сечение 5 ограничено выпуклым криволинейным
контуром Г, то заставим прямую огибать эту кривую; тогда антиполюс этой
прямой опишет контур, ограничивающий ядро сечения.
Если многоугольный или криволинейный контур Г, ограничивающий
сечение S, не является выпуклым (т. е. сечение S не лежит с одной сто-
§ 28]
ИНВОЛЮЦИЯ СОПРЯЖЕННЫХ ПРЯМЫХ
109
роны от каждой из касательных к контуру), то контур Г надо
предварительно заменить наименьшим выпуклым контуром Г0, за пределы которого
не выходит сечение S (рис. 72); например, в случае двутаврового сечения
балки (рис. 73) контуром Г0 является прямоугольник ABCD, и поэтому ядром
сечения будет заштрихованная часть ромба.
§ 28. Инволюция сопряженных прямых
I. Если задано коническое сечение, то две прямые, каждая из
которых проходит через полюс другой, называются
сопряженными (относительно этого конического сечения).
Возьмем точку 5 (рис. 74), не лежащую на коническом сечении,
за общий центр двух пучков прямых, причем в качестве
соответствующих прямых обоих пучков возьмем сопряженные прямые
(такие, как а и а'); нетрудно
видеть, что сопряженные прямые
образуют инволюцию, двойными
прямыми которой являются
касательные к коническому
сечению, проведенные из данной
точки.
Действительно, пересекая оба
пучка прямых прямой s, мы
имеем *):
(ABCD) = {abed).
(A'B/C'D') = (a'b'c'd')
по основному свойству 3)
полюсов и поляр; кроме того, рис 74.
(ABCD) = (a'b'c'd')
благодаря перспективности ряда точек s(A, В, С, D) и пучка
прямых S(a', b', с'', df)\ отсюда (abed) = (a'b'c'd').
Сопряженность прямых является взаимным свойством, т. е.
если а/ считать прямой первого пучка, то соответствующей прямой
второго пучка будет а; отсюда ясно, что рассматриваемое
проективное соответствие является инволюцией. Если бы прямая а была
двойной, т. е. совпала бы с а', то полюс А прямой а совпал бы
с точкой А', т. е. лежал бы на прямой а\ в таком случае прямая а
касалась бы кривой в точке А.
II. В качестве центра обоих пучков выберем сперва центр
кривой (эллипса или гиперболы); так как каждая прямая пучка, т. е.
диаметр кривой, является полярой бесконечно удаленной точки, то
бесконечно удаленная точка одного из диаметров является полюсом
*) На рис. 74 показаны лишь прямые а, а'.
110 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
другого, сопряженного с ним, причем сопряженные диаметры
обладают тем свойством, что каждый из них делит пополам хорды,
параллельные другому. Двойными прямыми этой инволюции прямых
являются касательные к кривой, проведенные из ее центра; в случае
эллипса они — мнимые; так как полюс касательной лежит на ней,
а полюсом диаметра является бесконечно удаленная точка
сопряженного диаметра, совпадающего в случае двойной прямой с данным
диаметром, то двойными сопряженными диаметрами гиперболы
являются ее диаметры, касающиеся ее в бесконечно удаленных точках,
т. е. асимптоты; следовательно,
по § 18 две асимптоты
гиперболы и два ее
сопряженных диаметра образуют
гармоническую группу. В
случае равносторонней гиперболы
асимптоты
взаимно-перпендикулярны, поэтому по § 17 два
ее сопряженных диаметра
симметричны относительно
асимптот.
В инволюции сопряженных
диаметров есть одна пара
взаимно-перпендикулярных
сопряженных диаметров (§ 18)—
это главные оси, т. е. оси
симметрии центрального конического сечения. Отметим одно
важное свойство конических сечений (рис. 75): если полюс
соединить с серединой отрезка соответствующей поляры
(определяемого пересечением поляры с коническим сечением), то эта
прямая является диаметром, сопряженным с направлением
поляры. Действительно, если точка Р является полюсом прямой р,
то по свойству взаимности поляра любой точки, взятой на прямой /?,
пройдет через точку Р\ бесконечно удаленной точке М прямой р
соответствует диаметр т, сопряженный с направлением р\ он
должен разделить отрезок АВ пополам и в то же время пройти через
точку Р.
III. С аналитической точки зрения угловые коэффициенты &, k'
двух сопряженных диаметров связаны соотношением (26.3), откуда
можно вывести их свойства: в случае центральной кривой*
направляя оси координат по осям симметрии, будем иметь а12 = 0 и,
таким образом, kk' = — = const; в случае эллипса ап = —т>
а22 = -и2~ и мы имеем эллиптическую инволюцию kk' = g~;
в случае гиперболы ап = — > а22 = р- и мы имеем гиперболи-
§ 28] ИНВОЛЮЦИЯ СОПРЯЖЕННЫХ ПРЯМЫХ 111
Ь2
ческую инволюцию kkr = — ; в случае параболы мы имеем & = 0,
k' = — независимо от k% т. е. мы имеем параболическую ин-
волюцию.
IV. Выберем теперь в качестве центра обоих пучков фокус
конического сечения; по § 7 касательные, проведенные из него к
коническому сечению, являются изотропными прямыми] но по § 18,
если в инволюции прямых двойные прямые изотропны, то
соответствующие прямые обоих пучков взаимно-перпендикулярны;
следовательно, фокус конического сечения является центром пучка
сопряженных взаимно-перпендикулярных прямых.
Для вывода некоторых свойств фокуса докажем сперва, что
полярой фокуса является соответствующая директриса.
Действительно, полагая в (7.2) для простоты л;0 = у0 = 0 и вводя
однородные координаты, получим:
х\ (А2 + В2 — А2е2) + х2 {А2 + В2 — В2е2) — 2е2АВххх2 —
2е2АСх1х3 -
2е2ВСх2х3 -
е2С2х2--
О;
:0, лГд=1, мы найдем:
полагая в (25.9) х[ = х'2
Ul=- e2ACt и2 = — е2ВС, иъ = ~ е2С2,
и полярой фокуса является прямая
иххх + и2х2 -)- игхг = Ахх -f- Вх2 -\- Схг = О,
т. е. директриса.
На основании доказанного выше свойства фокуса F проведем
через него произвольную прямую а (рис. 76) и отметим точку А'
ее пересечения с директрисой /;
прямая а', сопряженная с а, должна
быть перпендикулярна к а, причем
по доказанному свойству точки А
и А' являются полюсами прямых а
и а' и лежат на директрисе /. Если
прямая а' пересекает кривую в
точках Р, Q, то прямые АГР и A'Q
являются касательными к кривой,
проведенными из точки А!\
следовательно, если из точки на
директрисе проведены две касательные
к коническому сечению, то
прямая, соединяющая их точки каса- Рис. 76.
ния> проходит через фокус и
перпендикулярна к прямой, соединяющей фокус с данной точкой
директрисы. Таким образом, фокус конического сечения является
проекцией любой точки директрисы на поляру этой точки.
112 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
Рис. 77.
Нетрудно показать, что в случае параболы ^ PA'Q = 90°,
(рис. 77), т. е. из каждой точки директрисы парабола видна
под прямым углом. Действительно, касательная к параболе
образует равные углы с осью параболы и с фокальным
радиусом-вектором, проведенным в точку касания,
откуда легко находим сумму углов
а + р + (« + Р)=180°.
т = a + р = 90°.
Примечание. Основные понятия,
связанные с коническими сечениями (центр,
фокусы, директрисы, асимптоты и т. п.),
хорошо известны читателю из курса
аналитической геометрии; он мог заметить,
что мы ввели эти же самые понятия,
пользуясь совершенно другими определениями,
и установили ряд новых свойств; в
дальнейшем мы покажем (гл. VI), что именно
эти новые свойства, непривычные для
читателя, помогут нам решать при помощи
простых построений много задач, связанных
с коническими сечениями.
V. Чтобы проиллюстрировать пользу от введения этих новых понятий,
покажем, что из кинематической цепи, изображенной на рис. 68, можно
получить коникограф, т. е. механизм, точка которого описывает
коническое сечение. Для этого жестко соединим кулису со стержнем, могущим
вращаться вокруг неподвижного шарнира О' (рис. 78), т. е. заставим ось
кулисы ВВ1 огибать окружность k'\ покажем, что при этом точка Р будет
описывать коническое сечение k, и найдем
его фокус, директрисы и асимптоты *).
Условимся употреблять термин
«соответствие» в смысле полярного соответствия
относительно окружности k0, реализуемого
данной кинематической цепью. На
основании тех же соображений, которые были
рассмотрены в § 23, мы можем утверждать
следующее: если точка А описывает
кривую k (рис. 79), то соответствующая ей
прямая а огибает некоторую кривую kf,
причем касательной а' в точке А
соответствует точка А' касания прямой а\ точно
так же точке В и касательной Ь'
соответствуют касательная Ь и точка касания В',
а прямой с и точке С соответствуют точка С
и прямая с''. Следовательно, если k' — кривая п-го класса, то из точки С
к ней можно провести п касательных; в таком случае соответствующая
прямая с' пересекает кривую k в п точках, т е. k — кривая n-го поряока;
если, в частности, прямая а огибает кривую k' второго порядка
(необязательно окружность), то, так как эта кривая является кривой второго класса,
соответствующая точка А будет описывать кривую второго порядка.
*) Эти результаты приведены без доказательства в книге В. В.
Добровольского [1], стр. 56—58.
Рис. 78.
§ 28]
ИНВОЛЮЦИЯ СОПРЯЖЕННЫХ ПРЯМЫХ
из
Из рис. 79 можно также сделать следующий вывод: возьмем
произвольную точку С, найдем соответствующую ей прямую с, построим полюс С
прямой с относительно конического сечения k' и найдем прямую с',
соответствующую точке С; тогда найденная прямая с' является полярой
заданной точки С относительно конического
сечения k.
Пусть теперь даны окружность k0 с
центром О и радиусом г и окружность k' с
центром О' и радиусом г' (рис. 80). Если в
качестве точки С взять точку О, то ей
соответствует в качестве прямой с бесконечно
удаленная прямая, которая пересекает
окружность k' в циклических точках (играющих
роль точек А' и В')\ этим точкам
соответствуют изотропные прямые, пересекающиеся
в точке О (играющие роль касательных а'
и Ъ')\ следовательно, касательными,
проведенными из точки О к кривой k, являются
сопряженные изотропные прямые, т. е. по § 7
точка О является фокусом конического сече- Рис. 79.
ния k. Так как с — бесконечно удаленная
прямая, то ее полюсом С относительно
окружности k' является ее центр 0'\ точке О' соответствует прямая с\
которую легко построим как поляру точки О' относительно окружности kQ;
тогда прямая с' является полярой точки О относительно конического
сечения &, т. е. его директрисой.
Найдем центр D конического сечения k\ если он играет роль точки С
(рис. 79), то его полярой с1 относительно k является бесконечно удаленная
прямая, которой соответствует точка О (играющая роль точки С ); строим
Рис. 80.
прямую сх, являющуюся полярой точки О относительно окружности k'
(рис. 80), и строим точку D (играющую роль точки С), соответствующую
прямой с,.
Для построения асимптот конического сечения k отметим прежде
всего, что бесконечно удаленной точке любой прямой соответствует прямая,
проходящая через точку О перпендикулярно к этому направлению; поэтому
114 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
кривая k имеет вещественные асимптоты только в том случае, когда
касательная к окружности k' может пройти через точку О; таким образом,
кривая k является гиперболой, параболой или эллипсом в зависимости
от того, лежит ли точка О вне, на или внутри окружности k'.
На рис. 80 рассмотрен первый из этих случаев: из точки О проведены
две касательные а и b к окружности k'; асимптоты а' и Ь' перпендикулярны
к ним и проходят через центр Д найденный вышеуказанным способом;
можно было бы показать также, на чем мы не будем останавливаться, что
00'
эксцентриситет е выражается отношением е = —у— .
§ 29. Определение кривой второго класса пятью касательными.
Теорема Брианшона
I. Мы нашли, что кривая ф второго класса характеризуется
уравнением (23.9) в тангенциальных координатах; деля все
коэффициенты на один из них, мы видим, что оно содержит пять
параметров, для нахождения которых нужно пять условий', например,
если заданы пять касательных своими уравнениями в точечных
координатах
u^xx + ufx2+ufx^ = Q (/=1, 2, .... 5), (29.1)
то мы знаем пять троек координат прямой Ш{\ uifK и^\ подставляя
которые в (23.9), получим пять уравнений для нахождения
коэффициентов.
Кривая будет невырождающейся, если из заданных пяти
касательных никакие три не проходят через одну точку; в противном
случае кривая вырождается в две точки и левая часть ее уравнения
является произведением двух множителей
ф = WXW2,
Wx — ахих-f- а2и2 + azuv W2 = blul-\-b2u2 + bzuv
причем:
1) если три касательные проходят через одну точку Wv а две
другие — через точку W2, то кривая вполне определена, ибо мы
знаем величины av а2, av bv b2, Ьъ\
2) если четыре касательные проходят через точку Wv то точку W2
берем произвольно на пятой заданной касательной; ,
3) если все пять касательных проходят через точку Wv то
точку W2 берем совершенно произвольно.
Пусть имеем две кривые второго класса с уравнениями
а = antf2+ 2аииги2+ *22и\+ 2a13«i«3+ 2а23^з + агги1 = °-
Р = М+2МЛ+М+2Р1з"Л+2М2вз+ Рзз«| = 0; ( '2)
§ 29] ОПРЕДЕЛЕНИЕ КРИВОЙ ВТОРОГО КЛАССА ПЯТЬЮ КАСАТЕЛЬНЫМИ 115
семейством кривых второго класса называем совокупность
кривых, характеризуемую уравнением в тангенциальных
координатах
т = а + Хр = 0. (29.3)
При любом значении параметра X это будет некоторая кривая
второго класса.
По теореме Безу уравнения а = 0 и {3 = 0 имеют четыре
решения; поэтому существуют четыре касательные (вещественные или
мнимые), касающиеся кривых а и (3; так как при этих решениях
обращается в нуль и функция -[ независимо от значения параметра X,
то уравнение (29.3) определяет семейство кривых второго класса,
касающихся чеггырех заданных прямых.
Если ищется та кривая семейства, которая будет касаться и
пятой прямой, заданной уравнением и1х1~\-и2х2~\- игх3 = 0 (причем
никакие три касательные не пересекаются в одной точке), то при
подстановке в (29.3) значений uv и2, иъ ни одна из функций аир
не обратится в нуль и мы сможем найти значение параметра X, при
котором функция -[ обратится в нуль; мы показали аналитический
метод определения кривой второго класса по пяти касательным,
вполне аналогичный тому методу,
каким мы определяли кривую
второго порядка по пяти точкам.
В частности, если мы хотим
найти параболу, принадлежащую
нашему семейству, то пятой
касательной должна быть бесконечно
удаленная прямая с уравнением
хг = 0, т. е. мы должны положить
их — и2 = 0; подставляя в (29.3),
получим а33+Хрзз = 0, Х = —-^.
Рзз
И. Если заданы четыре прямые а, Ъ, с, d (рис. 81), которых
должны касаться кривые семейства, то находим координаты точек
Wv W2, Wv W4 попарного пересечения этих прямых и находим
уравнения этих точек в тангенциальных координатах (например,
если, решая совместно уравнения прямых а и Ъ, мы получили
координаты х^К х21\ х^ точки Wv то уравнение этой точки таково:
Мы можем рассматривать точки Wx и W2 или точки Ws и WA как
выродившиеся кривые второго класса; в таком случае уравнение
нашего семейства таково:
т = WXW2 + \W3WA = 0. (29.4)
Рис. 81.
116 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
В §§ 20—26 мы рассмотрели некоторые свойства пучка кривых
второго порядка; пользуясь принципом двойственности, мы
получим из них соответствующие теоремы для семейства кривых
второго класса: 1) если из любой точки провести касательные
к кривым семейства, то получим инволюцию прямых; 2) полюсы
произвольной прямой относительно кривых семейства лежат
на одной прямой и образуют на ней ряд точек, проективный
семейству кривых *).
Если свойство 2) применить к бесконечно удаленной прямой,
полюсами которой являются центры кривых, то получим следующее:
центры всех кривых семейства лежат на одной прямой и
образуют на ней ряд точек, проективный семейству кривых.
III. Формулируя принцип двойственности в § 19, мы только
утверждали возможность получения из каждой теоремы геометрии
положения новой теоремы путем замены точек — прямыми, а
прямых—точками; при этом, однако, мы не указывали конкретного
способа осуществления такой замены. Теория полярного
соответствия, рассмотренная в §§ 25—27, позволяет по-новому подойти
к этому вопросу и указывает, как можно эту замену осуществить.
Возьмем некоторое коническое сечение k, характеризуемое
уравнением (25.1), и проделаем следующее: каждой точке А поставим
в соответствие ее поляру а относительно k, а каждой
прямой Ь — ее полюс В относительно k\ ряду точек s(A, В, С, ...)
будет соответствовать пучок их поляр S(a, Ъ, с, . . .), а пучку
прямых F(a\ b'\ с\ ...) — ряд их полюсов f{Af, В', С, ...);
при этом одинаковы ангармонические отношения ряда точек и
соответствующих поляр пучка или пучка прямых и
соответствующих точек ряда.
В качестве иллюстрации применения этого метода рассмотрим
теорему Брианшона, взаимную по отношению к теореме Паскаля
и имеющую многочисленные применения.
Рассмотрим шесть прямых av #2, . . ., #6, касающихся
конического сечения, и будем говорить о шестистороннике, описанном
вокруг конического сечения &** (рис. 82); обозначим через
Vv . . ., Vq точки пересечения наших прямых (Vx — точка пересечения
ах и #2, V2 — точка пересечения а2 и av ..., наконец, V6 — точка
пересечения а6 и а{)\ пары точек Vx и V4, V2 и V5, Vz и V6 (номера
которых различаются на три единицы), будем называть
противоположными вершинами шестисторонника. Теорема Брианшона
*) Это означает, что параметр X в уравнении семейства и параметр
или координата, характеризующие положение точки ряда, связаны дробно-
линейным соотношением.
**) Это совсем не значит, что коническое сечение лежит целиком внутри
этого шестисторонника; кроме того, считаем, что никакие три из сторон
не пересекаются в одной точке.
§ 29] ОПРЕДЕЛЕНИЕ КРИВОЙ ВТОРОГО КЛАССА ПЯТЬЮ КАСАТЕЛЬНЫМИ 117
утверждает: три прямые, соединяющие три пары
противоположных вершин шестисторонника, описанного вокруг конического
сечения, пересекаются в одной точке (на рис. 82 это такие
прямые: прямая xv соединяющая точки Vx и V4, прямая х2,
соединяющая точки V2 и V5, и прямая хг, соединяющая точки Vz и V6).
Для доказательства заменим прямые av . .., #6 их полюсами, т. е.
точками касания Ах, .. ., Л6,
а точки Vx V6—их
полярами vx Vq, точка Хх
пересечения прямых vx и v4
лежит на этих прямых, поэтому
ее поляра хх проходит через
точки Vx, VA\ точно так же
точки Х2 и Хг являются
полюсами прямых х2 и хг. По
теореме Паскаля точки Xv
Х2, Хг лежат на одной
прямой р, следовательно, их по- ^
ляры xv х2, хг пересекаются
в одной точке Р.
Так же, как для теоремы
Паскаля, для теоремы Бриан-
шона справедлива обратная
теорема: если в шестисто-
роннике три прямые,
соединяющие противоположные
вершины, пересекаются в
одной точке, то в него можно
вписать коническое сечение.
Отметим, что мы могли
бы доказать теорему Бриан-
шона независимо от теоремы
Паскаля— для этого надо
воспользоваться (29.4).
IV. Рассмотрим несколько частных случаев теоремы Брианшона.
Пусть прямая а2 стремится к совпадению с прямой ах —тогда
предельным положением их точки пересечения явится точка касания Vx
прямой ах\ таким образом, вместо шести касательных можно
рассматривать пять касательных и точку касания на одной из них
(рис. 83) или четыре касательные и точки касания на двух из них
(рис. 84), или, наконец, три касательные и их точки касания (рис. 85);
во всех случаях на фигурах показаны все стороны и все вершины,
причем две буквы на одной стороне показывают, что эту прямую
рассматриваем как две совпавшие касательные и знаем их точку
касания.
118 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
В качестве примера сформулируем теорему Брианшона для случая,
изображенного на рис. 85: три прямые, соединяющие вершины
трех сторонника, описанного вокруг конического сечения, с
точками касания противоположных сторон, пересекаются в одной
точке.
Рис. 83. Рис. 84.
V. Рассмотрим несколько простых задач, решение которых опирается
на теорему Брианшона.
Зная пять касательных ах, ..., аъ к коническому сечению (рис. 86),
найти вторую касательную к нему, проходящую через точку, взятую
на одной из касательных. Обозначая через а6 искомую касательную,
проходящую через заданную точку V6 на прямой ах, мы можем построить
точки Vx, V2, V3, У4 и найти прямые хх (через точки Ух и VA) и хг (через
Рис. 85. Рис. 86.
точки V3 и V6); в пересечении хх и хъ найдем точку Брианшона Р; так как
прямая х2 должна пройти через точки Р, V2, V5, то в пересечении ее
с прямой а5 найдем точку V5, а, соединяя точки V5 и Ve, найдем искомую
касательную а6. В частности, если V6 — бесконечно удаленная точка
прямой ах,- то мы получим решение следующей задачи: зная пять
касательных к коническому сечению, провести касательную, параллельную одной
из заданных', построение указано на рис. 87, причем ах \\ хъ || а6.
§ 29] ОПРЕДЕЛЕНИЕ КРИВОЙ ВТОРОГО КЛАССА ПЯТЬЮ КАСАТЕЛЬНЫМИ 119
Пусть снова задано пять касательных alf ..., аъ к коническому
сечению (рис. 88); найти точку касания на касательной а{. Будем
считать прямые а6 и а{ совпавшими, тогда точка Ve явится искомой точкой
касания. Снова находим точки Vv V2, К3, V4 и точку V5 в пересечении
Рис. 88.
прямых аъ и а6, а затем находим прямые хх и х2 и точку Брианшона Р в их
пересечении; прямая хъ должна пройти через точки V3, Р и V6.
Даны четыре касательные к параболе; построить точку касания на
одной из них. Обозначая эти касательные через ах, ..., а4 (рис. 89), будем
искать точку касания V6 на прямой а1У т. е. будем считать прямые а{ и Ощ
совпавшими; так как парабола касается бесконечно удаленной прямой, то эту
последнюю примем за касательную аъ.
Мы можем построить точки Vu V2, V3; точки 'VA и Vb — это точки
пересечения прямых аА и а6 с бесконечно удаленной прямой, т. е.
бесконечно удаленные точки прямых аА и а6. Прямая xv соединяющая точки Vx
и VA, направлена параллельно
прямой а4, а прямая х2, соединяющая
точки V2 и V5, параллельна
прямой а6; в их пересечении
получим точку Брианшона Р, а
прямая лг3, проходящая через точки
V3, Р, пересекает прямую ах
в искомой точке V6.
При тех же условиях по-
строить касательную,
параллельную данной прямой Ь
(рис. 90). Обозначим снова через
#i, ...,#4 заданные касательные,
через аъ\\Ь искомую касательную
и через а6 бесконечно удаленную
прямую; легко находим точки V{,
^2> ^з> причем точки V5, Vb — это
бесконечно удаленные точки
прямых Ь и ах. Через точку V2
проводим х2\\Ь, а через точку V3 проводим ^с3II^i
и хъ находим точку Брианшона Р. Соединяя Р с Vlt находим прямую xlt на
которой должна лежать точка V4 пересечения прямых аА и а5; найдя точку V4
в пересечении прямых х{ и а4, проводим через нее прямую а51| Ь.
При тех же условиях найти бесконечно удаленную точку параболы,
т. е. направление ее оси. Мы должны теперь найти точку касания V5 на
в пересечении прямых х2
120 ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ ВЫСШИХ ПОРЯДКОВ [ГЛ. III
бесконечно удаленной прямой, которую назовем аъ, а6; строим точки V„ V2, И3
(рис. 91); точки V4 и V6 — это бесконечно удаленные точки прямых а4 и ах.
Рис. 90. Рис. 91.
Проводим через точку V, прямую xx\\aAi а через точку V3 прямую х3\\ах
и находим в их пересечении точку Брианшона Р; тогда прямая *2.
соединяющая точки V2 и Р, должна пройти через точку Vb на бесконечно
удаленной прямой — ось параболы параллельна прямой х2*).
*) Другой способ рассмотрен в § 45.
ГЛАВА IV
НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ
В этой главе мы рассмотрим некоторые свойства конических
сечений, часто встречающиеся при решении задач синтеза
механизмов; в основном — это свойства фокусов и касательных,
§ 30. Свойства касательных
I. Пусть к коническому сечению (рис. 92) в точках А и В
проведены касательные а к Ь, пересекающиеся в точке 5; всякая новая
касательная с% d, е, ... пересекает заданные касательные в точках
С, D, Е, ... и С, D', Е\ ...;
докажем следующую теорему: отрезок
любой касательной к коническому
сечению, отсекаемый на ней двумя
заданными касательными, виден из
фокуса под одним и тем же углом
при любом положении этой
касательной, т. е.
l^CFC■ = l_DFD' = /_EFE' = ...
(30.1)
По теореме, взаимной теореме Штей-
нера (§ 23), ряды точек а (S, Е,
АС. А, ...) и b(B, Е', D', С\ 5,...)
проективны, причем точке 5 прямой а
соответствует точка касания В прямой Ь,
а точке 5 прямой Ъ — точка касания А
прямой а. Спроектировав эти два ряда
точек из произвольного центра G, мы
получим два проективных пучка прямых с общим центром О; двойные
прямые, очевидно, будем иметь в том случае, когда прямая, соединяющая
соответствующие точки обоих рядов, будет касаться кривой; таким
образом, двойными прямыми являются касательные к коническому
сечению, проведенные из точки О. Если точка О совпадает с
фокусом Ft то по определению фокуса (§ 7) касательные, проведенные
122 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
из него к коническому сечению, являются изотропными прямыми;
как показано в § 18, если в проективном соответствии двух пучков
с общим центром двойными прямыми являются изотропные прямые,
то каждая прямая второго пучка получается из соответствующей
прямой первого пучка поворотом ее на
d один и тот же угол, откуда
следует (30.1).
Так как точкам В, S прямой Ъ
соответствуют точки 5, А прямой а,
то £_ BFS = l_ SFA; таким образом,
постоянный угол, о котором шла речь
в доказанной теореме, равен половине
угла между фокальными радиусами-
векторами, проведенными в точки
касания заданных двух касательных.
II. Рассмотрим теперь
четырехсторонник а, Ъ, с, d, описанный
вокруг конического сечения (рис. 93); так как для полного
определения конического сечения необходимо задать пять касательных,
то существует бесчисленное множество конических сечений,
касающихся четырех заданных прямых, и, следовательно, будем иметь
бесчисленное множество их фокусов; однако по доказанной теореме
из каждого положения фокуса две противоположные стороны а и с
четырехсторонника видны под равными углами или под углами,
дополняющими друг друга до 180°. Мы пришли к результату,
имеющему весьма важное значение в задачах синтеза (см. §§51, 82):
геометрическое место точек,
из которых две
противоположные стороны данного
четырехсторонника видны
под равными углами или под
углами, дополняющими друг р
друга до 180°, является в то
же время геометрическим
местом фокусов конических
сечений, касающихся
сторон данного
четырехсторонника.
III. Пусть теперь к коническому сечению проведены две
касательные а и Ъ (рис. 94) и точки А и В их касания соединены
прямой с\ докажем, что для любой прямой с'\\с имеем равенство
отрезков А]С1 = DXBV отсекаемых на ней кривой и
касательными.
Так как точка Р пересечения касательных является полюсом
прямой с, то прямая PL, соединяющая точку Р с серединой L
§31] СВОЙСТВА КАСАТЕЛЬНЫХ К ЦЕНТРАЛЬНЫМ КОНИЧЕСКИМ СЕЧЕНИЯМ 123
хорды АВ, является диаметром конического сечения (§ 28), поэтому
и хорда ClDl || АВ делится пополам в точке Lx своего пересечения
с PL\ так как CXLX = LlDl и, кроме того,
AlLl = LlBv то AlCl = DlBv
В случае гиперболы (рис. 95) мы
можем в качестве прямых а и Ъ
рассмотреть касательные в бесконечно
удаленных точках, т. е. асимптоты
гиперболы; в этом случае прямая с будет
бесконечно удаленной и всякую другую
прямую можно считать параллельной
прямой с\ поэтому на любой прямой,
пересекающей гиперболу, асимптоты и
гипербола отсекает равные отрезки; зная
обе асимптоты и одну точку М гиперболы, можно построить сколько
угодно ее точек Р, Q, /?, ..., пользуясь равенствами Р0Р1 = РМ,
Q0Ql = QM, RqR^RM, ...
Рис. 95.
§31. Свойства касательных к центральным коническим сечениям
I. Докажем следующее свойство касательных к центральным
коническим сечениям: произведение расстояний от обоих фокусов
до любой касательной является
постоянной величиной (рис. 96).
Рассмотрим уравнение
v;2
_
О*
(31.1)
где е == —(— 1 в случае эллипса и е = — 1
в случае гиперболы; уравнение
касательной в точке Ml(xv уг) таково:
*Х\ | , УУ\
Рис. 96.
Ь2
= 1;
(31.2)
так как фокусы имеют координаты (±ае, 0), то легко найти
расстояния hv h2 от обоих фокусов до касательной
-+1
Vi
h2 —
+
Л.
*4
V а4 ' <?4
откуда
1-
еЧ\
hxh2 = -L-j
а* ^ ЬА
124 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
Из (31.1) находим:
Ъ* е а2Ь2 ' я4 ~"~ b* ~~ а*Ъ2
причем в обоих случаях Ь2— га2 =— еа2е2, откуда имеем:
а' ~^~ b* ~~ b2 \ 1 а2 )'
и таким образом,
hxh2 = b2. (31.3)
П. Из этого свойства касательной вытекает свойство двух
касательных: если из некоторой точки проведены две касательные
к центральному коническому сечению и эта точка соединена
прямыми с обоими фокусами, то эти прямые образуют с
касательными углы, равные по величине, но противоположные по
Рис. 97. Рис. 98.
направлению, т. е. а — ^ (Рис- 97)- Мы имеем по предыдущему
hx h2
hxh2 = h[h2, откуда вытекает — = —-. Обозначая через 8 угол
hx h2
между заданными касательными, мы имеем:
hx = FXP sin a, h[ = FXP sin (8 — а),
h2 = F2P sin (8 — y), h'2 = F2P sin T,
откуда
sin (5 — a) sin (5 — 7)
sin a sin 7
и таким образом a=='f.
III. Рассмотрим в качестве иллюстрации следующую задачу: зная
один фокус конического сечения, касающегося трех заданных
прямых, найти его второй фокус (рис. 98). Зная фокус Fv нахо-
§ 32] СВОЙСТВА КАСАТЕЛЬНЫХ К ПАРАБОЛЕ 125
дим углы срх = /_ FXSXS2, <р2 —Z. F^S^ проводим через точку St
луч под углом срх к прямой 5^3, а через точку S2 луч под углом ср2
к прямой 5253; в пересечении этих лучей находим второй фокус F2.
Предположим теперь, что фокус /^ описывает прямую g\
тогда фокус F2 опишет коническое сечение. Действительно, пучки
прямых Sx (а, Ь, с, . ..) и S2(a\ bf, с\ ...) перспективны, ибо
точка Fx движется по прямой, а потому проективны; пучки прямых
Sx(a, b, с, ...) и Sl(av bv cv ...)
также проективны, ибо для них в
формуле (17.5) ab=a'b' для любых двух
пар соответствующих прямых; по этой
же причине проективны пучки прямых
S2(a\ Ь\ с',...) и S2(a'v b'v c'v . . .).
Таким образом, пучки прямых
S^a^ bv cv . ..) и S2.(a'v b'v c'v ...)
проективны, а тогда по теореме Штей-
нера геометрическим местом точки F2
пересечения соответствующих прямых
этих двух пучков является коническое
сечение.
Рассмотрим механизм (рис. 99), в котором соосные редукторы с
передаточным числом / = — 1 имеют своими осями оси шарниров Su S2, причем
пусть в начальном положении механизма звенья SXM и S2M направлены
по стороне SxS2j звено SXM'— по стороне S:S3t а звено S2M'— по стороне
S2S3; если центр ролика М будет двигаться прямолинейно, то центр
ролика Ш опишет коническое сечение.
§ 32. Свойства касательных к параболе
I. Рассматривая параболу как предел эллипса и гиперболы (§ 3),
мы должны считать, что на рис. 97 фокус F2 ушел в бесконечность
по направлению оси FXF2, а прямая PF2 стала параллельной оси
параболы (рис. 100); таким образом, из теоремы предыдущего
параграфа получаем: если точка пересечения двух касательных
к параболе соединена прямой с ее фокусом, то первая
касательная образует с этой прямой такой же угол, как ось
параболы со второй касательной.
Отсюда вытекает такое свойство: касательная к параболе
является биссектрисой угла между ее директрисой и прямой,
соединяющей фокус с точкой пересечения касательной с
директрисой (рис. 101). Для доказательства достаточно взять точку Р
на директрисе, рассмотреть рис. 77, воспользоваться результатом § 28
и только что доказанным свойством; мы имеем очевидное равенство
2a-f-T = 90°, a-+ Т = 90° — a = p.
Рис. 99.
126 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
Отсюда, в частности, вытекает, что две касательные к параболе
не могут быть параллельны — если бы это было так, то по
предыдущему фокус параболы ушел бы в бесконечность.
Рис. 100.
П. Рассмотрим дальнейшие свойства двух касательных к
параболе: в четырехугольнике, образованном двумя касательными
к параболе и двумя фокальными радиусами-векторами,
проведенными в точки касания, угол между радиусами-векторами
дополняет до 360° удвоенный угол между касательными (рис. 102).
Действительно, касательная к параболе образует равные углы с осью
параболы и с фокальным
радиусом-вектором,
проведенным в точку касания;
поэтому
l_ AFx = 2ol = 2^ APF,
l_ BFx = 2p = 2 /. BPxx,
откуда *)
/mmAFx + lmBFx =
= 2(а + Р) = 2^ЛР2£,
l + 2/_AP2B =
= T + 2a-f 2(3 = 360°.
Из доказанных свойств вытекает свойство трех касательных,
имеющее частые применения в задачах синтеза: если даны три
касательные к параболе (рис. 103), то треугольник,
образованный точками их пересечения, обладает следующими свойствами:
1) фокус параболы лежит на окружности, описанной вокруг
Рис. 102.
*) Аналогичное доказательство в том случае, когда обе точки касания
лежат по одну сторону от оси параболы.
§ 32] СВОЙСТВА КАСАТЕЛЬНЫХ К ПАРАБОЛЕ 127
этого треугольника; 2) прямой Симпсона (см. § 18) этого
треугольника относительно фокуса является вершинная
касательная параболы; 3) директриса параболы проходит через
ортоцентр этого треугольника.
Для доказательства свойства 1) рассмотрим три касательные а,
Ъ, с, образованный ими треугольник ЛВС и точки касания Е и D
касательных с и Ъ\ применим результаты § 28; мы получим по
предыдущему свойству
£mCFB = ±/_EFD -
= 180° — l_EAD%
т. е. в четырехугольнике FCAB
суммы противоположных углов
равны 180°, а поэтому вокруг
него можно описать окружность.
III. Прежде чем доказать
свойство 2), покажем следующее
свойство: две касательные к
параболе отсекают на любой
касательной к ней такой отрезок, рис юз.
что треугольник, образованный
его концами и фокусом, остается подобным себе при всех
положениях касательной. Действительно, описав окружность вокруг
четырехугольника ABFC (рис. 103), мы имеем:
£ CBF = ЦСАЕ, 1_ ВСЕ = ^ В AF.
Отсюда вытекает новое свойство: если угол постоянной величины
движется так, что его вершина движется по заданной прямой,
а одна сторона проходит через заданную точку, то вторая
сторона огибает параболу, для которой заданная точка
является фокусом, а заданная прямая—касательной. Для
доказательства достаточно рассмотреть /_FBC (рис. 103) — точка В
движется по прямой АЕ, касательной к параболе, сторона BF
проходит через ее фокус, а сторона ВС касается параболы; в частности,
если угол прямой £_ FBC = 90°, то мы видим, что геометрическим
местом проекций фокуса параболы на касательные является
вершинная касательная (рис. 104). Для доказательства достаточно
заметить, что все касательные располагаются симметрично
относительно прямой FL, проходящей через фокус F перпендикулярно
к прямой АВ, следовательно прямая АВ является вершинной
касательной.
Теперь мы сможем доказать ранее сформулированное свойство
2): проекции фокуса на три касательные а, Ь, с к параболе, т. е.
на три стороны описанного треугольника АВС% лежат на вершинной
128 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
касательной, которая является, таким образом, прямой Симпсона
треугольника ABC относительно фокуса F (рис. 105). Свойство 3)
мы докажем в следующем параграфе.
Из свойств параболы можно сделать следующий вывод: если
из четырех данных прямых образовать четыре треугольника, беря
Рис. 104.
все четыре комбинации по три прямых, то: 1) четыре
окружности, описанные вокруг этих треугольников, проходят через одну
точку; 2) ортоцентры всех четырех треугольников лежат на
одной прямой.
\\. Пользуясь найденными свойствами, рассмотрим решение такой
задачи кинематики: найти огибающие направлений скоростей и
ускорений точек отрезка прямой. Пусть точка Р(рис. 106) — мгновенный
центр вращения подвижной плоскости,
движение которой характеризуется
движением отрезка АВ\ так как скорость vc
Рис. 105. Рис. 106.
каждой точки С прямой перпендикулярна к соответствующей
прямой PC, то мы имеем прямой угол, вершина которого движется
по прямой, а одна сторона всегда проходит через точку Р —
огибающей различных положений второй стороны угла, т. е. скоростей
§ 33] СВОЙСТВА ОКРУЖНОСТИ, ОПИСАННОЙ ВОКРУГ ТРЕУГОЛЬНИКА 129
Рис. 107.
различных точек прямой, является парабола, для которой
мгновенный центр вращения Р служит фокусом, а заданная прямая АВ —
вершинной касательной.
Пусть теперь точка R (рис. 107) является мгновенным центром
ускорений подвижной плоскости; так как ускорение wc любой
точки С прямой образует с
соответствующей прямой RC угол
а = arctg -Ш-» одинаковый для всех
точек, то мы имеем постоянный угол,
вершина которого движется по
прямой АВ, а одна сторона всегда
проходит через точку R; тогда
огибающей различных положений второй
стороны, т. е. ускорений различных
точек прямой, является снова парабола, для которой мгновенный
центр ускорений служит фокусом, а заданная прямая — касательной *).
V. Докажем теперь свойство, обратное доказанному в § 18:
если проекции точки на три стороны треугольника лежат
на одной прямой, то эта
точка лежит на
окружности, описанной вокруг
этого треугольника.
Пусть точка Р
спроектирована на стороны /\АВС
в точки L, М, N, лежащие
на одной прямой (рис. 108);
так как /_ ANP = 2. AMP =
= 90°, то точка Р лежит на
окружности, описанной вокруг
Д AMN, и точно так же на
окружностях, описанных вокруг
треугольников BNL и CLM\ но
тогда через точку Р должна
проходить и четвертая
окружность, описанная вокруг Д ABC, ибо все эти четыре треугольника
образованы четырьмя прямыми ANB, АМС, NML, BCL.
§ 33. Свойства окружности, описанной вокруг треугольника
I. В этом параграфе мы рассмотрим некоторые весьма
элементарные свойства окружности, описанной вокруг треугольника,
связанные с ортоцентром этого треугольника. Покажем прежде всего
Рис. 108.
*) Эту параболу можно построить, ибо мы можем построить сколько
угодно касательных к ней.
130 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
Рис. 109.
следующее: точки, зеркальные с ортоцентром треугольника
относительно его сторон* лежат на окружности, описанной
вокруг треугольника*). Пусть точка И (рис. 109) является
ортоцентром треугольника АВС\ продолжим
прямую BHD до пересечения с
окружностью в точке Е\ мы имеем /_ЕАС =
= /_DBC, как вписанные углы,
опирающиеся на одну и ту, же дугу ЕС, а кроме
того, [_ ВВС = 1_ НАС, ибо их
стороны взаимно-перпендикулярны; отсюда
l^HAD = l_DAE, т. е. HD = DE.
Отсюда вытекает следующее свойство:
если вокруг треугольника описана
окружность, то три окружности,
зеркальные с ней относительно сторон
этого треугольника, проходят через его
ортоцентр. Действительно, если
окружность k проходит через точку Е,
зеркальную с ортоцентром Н относительно
стороны АС, то окружность kf, зеркальная с k относительно стороны АС,
проходит через точку Н\ можно сказать еще иначе: если построить
три окружности, каждая из которых проходит через две
вершины треугольника и через точку, зеркальную с третьей
вершиной относительно противоположной ей стороны, то все три
окружности проходят через
ортоцентр треугольника.
II. Докажем теперь такое простое
свойство, имеющее применение в
синтезе механизмов **): три вершины
треугольника и три центра
окружностей, зеркальных с описанной
вокруг него окружностью, образуют
шестиугольник, вокруг которого
можно описать коническое сечение
(рис. ПО).
Действительно, обозначая через
Рис. ПО.
Мг, М2, Ж3 центры окружностей,
зеркальных с описанной вокруг Д АгА2Аг, т. е. точки,
зеркальные с центром О описанной окружности, мы видим, что
четырехугольники ОА2М1Аг, ОАгМ2Аг и ОАгМгА2 являются ромбами, а
поэтому в шестиугольнике А1М2А3М1А2Мг противоположные стороны
*) «Зеркальный относительно прямой» означает «симметричный
относительно этой прямой».
**) См., например, Р. Бейер [2], § 14.
§ 33] СВОЙСТВА ОКРУЖНОСТИ, ОПИСАННОЙ ВОКРУГ ТРЕУГОЛЬНИКА 131
МХА2 и АХМ2, MXAZ и M3Alt M2AZ и МгА2 параллельны, т. е;
точки их пересечения лежат на бесконечно удаленной прямой; на
основании теоремы, обратной теореме Паскаля, вокруг него можно
описать коническое сечение.
III. Рассмотрим еще одно свойство ортоцентра треугольника: три
точки, зеркальные с произвольной точкой окружности
относительно трех сторон вписанного в нее треугольника, лежат
на одной прямой, проходящей
через ортоцентр треугольника.
Пусть вокруг треугольника ABC
(рис. 111) описана окружность k
и на ней взята точка D; пусть
точки Ах, Bv Сх являются
проекциями точки D на стороны ВС,
AC, АВ, а точки А2, В2, С2
зеркальны с точкой D относительно
этих сторон; так как три точки Av
Рис. 111. Рис. 112.
Bv Сх лежат на прямой Симпсона, то, принимая точку D за центр
перспективного подобия с отношением
РА2 _ РВ2 _ РС2 _ 0
DAX ~~ DB{ — DC{ ~Zi
мы видим, что точки А2, В2, С2 также лежат на одной прямой.
Проведя AQ_\_BC, докажем, что точка Н пересечения прямых AQ
и А2В2С2 является ортоцентром треугольника ABC. Мы видим, что
точки Ах, Сх лежат на окружности, диаметром которой служит
отрезок DB, откуда имеем /_ DAlCl = ^ ОВСг = 2. DBA\ но
/emDBA = l_DQA, ибо они оба опираются на дугу AD, a /^DQA^sk
= l^ A2DQ, как внутренние накрест лежащие углы при параллельных
132 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
прямых; отсюда /^ DA2C2 = £_ A2DQ, т. е. QL — LH\ таким
образом, точка Q, зеркальная с И относительно стороны ВС, лежит
на окружности k\ следовательно, точка Н является ортоцентром
треугольника ABC.
IV. Теперь мы сможем доказать свойство 3), сформулированное
в предыдущем параграфе. Проекции Ах, Bv Cv ... фокуса F
параболы (рис. 112) на касательные а, Ъ, с, . . . к ней лежат на
вершинной касательной; точки А2, В2, С2, . . ., зеркальные с точкой F
относительно касательных а, Ъ, с, . . ., лежат на директрисе, ибо
мы снова имеем перспективное подобие с центром F и с
отношением
FA2 _ FB2 _ FC2 __ 0
FA, — FBX ~ FC{ ~~~ Z>
но фокус параболы лежит на окружности, описанной вокруг
треугольника ABC, образованного пересечением касательных а, Ъ, с;
следовательно, точки, зеркальные с фокусом относительно трех
сторон треугольника ABC, должны лежать на директрисе и в то же
время должны лежать на прямой, проходящей через ортоцентр
треугольника.
§ 34. Степень точки относительно окружности;
радикальная ось и радикальный центр
I. Рассмотрим окружность ср, характеризуемую уравнением
ср = ср(д:, у) = (Х-а)2 + (у-№-г* = 0, (34.1)
и точку М0(х0, у0)\ степенью точки относительно окружности
будем называть число ср(д:0, у0), т. е. результат подстановки
координат этой точки в левую часть уравнения окружности, записанного
в нормальной форме (34.1).
Вводя расстояние с1=У(х0 — a)2 -f- (у0 — (З)2 от точки М0 до
центра С (a, (J) окружности, находим
?(*<>. Уо) = ^-г^ (34.2)
отсюда вытекает геометрическое значение степени точки
относительно окружности при различных случаях их взаимного
расположения:
1) для точек, лежащих на окружности, степень равна нулю;
2) для точек, лежащих вне окружности, степень положительна
(ибо d > г) и равна квадрату длины касательной М0Т,
проведенной из данной точки к окружности (рис. 113, а);
3) для точек, лежащих внутри окружности, степень
отрицательна (ибо d < г) и ее модуль равен квадрату длины
полухорды М0Т этой окружности, проведенной через данную точку
§ 34] степень точки относительно окружности; радикальная ось 133
перпендикулярно к прямой, соединяющей эту точку с центром
окружности (рис. 113,5).
II. Рассмотрим теперь две окружности срх и ср2, характеризуемые
уравнениями
ср1 = (х-а1)2 + (У-Р1)2-'-? = 0. -
ъ={х_^+{у-Ы-г1
:0.
Найдем геометрическое место точек М(х, у), степени которых
относительно обеих окружностей равны между собой. Мы должны
иметь
<Pi(*. У) = Ъ(*> У} (34-4) М&
откуда, после сокращения членов второго порядка,
найдем:
2х(а1-а2) + 2у(р1-р2) +
+ Г2_г2_а2_р2 + а2 + р2 = 0; (34.5)
переходя к однородным координатам, получим:
2х1(а1-а2)+2х2(^1-р2) +
+('-;-i-a?-p?+^+Pi)*3=o- <34-б>
Так как мы пришли к уравнению первого порядка,
то геометрическим местом точек, имеющих
равные степени относительно двух данных
окружностей, является прямая линия,
характеризуемая уравнением (34.6); эта прямая
называется радикальной осью двух данных
окружностей.
III. Рассмотрим некоторые свойства
радикальной оси.
1) Если две данные окружности концентричны, то их
радикальная ось является бесконечно удаленной прямой; для двух
неконцентрических окружностей радикальная ось — собственная прямая;
действительно» из (34.6) имеем (г\—r|)^3=t) при а1 = а2, рх = Рд.
т. е. лг3 = 0; если же (аг — a2)2+(pj — р2)2 > 0, то (34.6) является
уравнением собственной прямой;
2) радикальная ось двух неконцентрических окружностей
перпендикулярна к их линии центров; для доказательства
достаточно рассмотреть угловые коэффициенты kx и k2 радикальной оси
и линии центров
ftt =
а2 — а,
k9 =
02-Pi
{kxk2
l); (34.7)
134 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
3) радикальная ось двух окружностей проходит через точки,
общие обеим окружностям] действительно, в этих точках имеем
одновременно срх = 0, ср2 = 0, и, следовательно, срх = с^.
Рассмотрим все три возможных случая относительного
расположения двух окружностей:
1) окружности пересекаются в двух точках (рис. 114, а) —
радикальная ось АВ проходит через эти точки пересечения;
2) окружности касаются друг
друга (рис. 114,5) извне или
изнутри — радикальная ось АВ
совпадает с их общей касательной;
3) окружности не имеют общих
точек (т. е. пересекаются в двух
мнимых точках (рис. 114, в)) —
радикальная ось проходит через эти же мнимые
точки, т. е. не имеет вещественных
точек пересечения с окружностями.
IV. В случае трех окружностей cplf
ср2, фз мы имеем три радикальные оси
vv v2, v3 с уравнениями
*1 = ?2 — ?3=0'
^2 = ?з —?i = 0, (34.8)
*з = <Р1 —<Ра = °;
так как
^1 + ^2 + ^3 = °'
то все три радикальные оси проходят
через одну точку (собственную или
несобственную); эта точка называется
радикальным центром трех
окружностей и обладает тем свойством, что
ее степени относительно всех трех
окружностей равны между собой.
V. Покажем построение
радикальной оси двух окружностей cplf ср2
(рис. 114, б), не имеющих общих точек:
проведем произвольную окружность ср3,
пересекающую обе данные окружности ср2, ср2, и построим
радикальные оси v2 (окружностей ср3 и <pi) и v\ (окружностей ср2 и ср3); точка их
пересечения О является радикальным центром всех трех
окружностей срр ср2, ср3; следовательно, искомая радикальная ось v3
окружностей cpj, ср2 проходит через точку О перпендикулярно к линии
центров СгС2 этих двух окружностей.
а)
\В
Рис. 114.
§ 35]
ПУЧКИ ОКРУЖНОСТЕЙ
135
§ 35. Пучки окружностей
I. В § 20 мы дали общее определение пучка кривых,
определяемого двумя основными кривыми срх, ср2, и рассмотрели, в
частности, пучки конических сечений; так как после прямой простейшей
линией является окружность, то рассмотрим несколько подробнее
пучок окружностей
<P = <Pi + *<h = 0f (35.1)
определяемый двумя основными окружностями срх и ср2 с
уравнениями (34.3).
Переходя к однородным координатам, мы получим:
ср = [х\ + xl) (1 + X) - 2хгхг (аг + Ха2) — 2х2хг (^ + Ц2) +
+ [а2 + р2_г2 + Х(а2 + р2_г2)^2_0, (35.2)
откуда видно, что при Х =—1 кривая пучка распадается на бес-
конечно удаленную прямую лг3 = 0 и на прямую (34.6),
являющуюся радикальной осью двух основных окружностей срх и ср2;
следовательно, радикальную ось двух окружностей можно
рассматривать как ту из окружностей пучка» которая имеет
бесконечно большой радиус.
При X Ф — 1 мы легко приводим уравнение
? _ ?1+Ч2 _ ^2 , 4>2 «1 + Хоа 9 Pi + Хр2 ,
«1 + р1-г1+Ч4 + $-4)
1+Х
к такому виду:
?1 + М>2 _
(,_^^ + (,-ii*)-p» = 0.
1 + Х
, {Л + lrl) (1 + X) - X [(а, - а2)* + (Р, - Р2)2]
Р2 = (Г+хр ; <35-3)
следовательно, для значений X, удовлетворяющих неравенству
x2i-4(ai-a2)2+(Pi-P2)2-i-i]+'?>°- (35-4)
кривая ср пучка является окружностью с центром
«1 + Xa2 Pi+^2 \ ,ор; кч
+!"• 1 + х j ^D-0)
я с радиусом р. Таким образом, величина —X имеет следующее
значение: центр Сх делит отрезок СХС2 между центрами основных
окружностей в отношении — X; кроме того, отношение степеней
каждой точки окружности ср относительно окружностей срх и ср2
равно —X.
/ «г
Л 1
136
НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ
[ГЛ. IV
Если в (35.3) р2 = 0, то окружность вырождается в точку; если же
р2 < 0, то кривая пучка является мнимым геометрическим местом.
II. Рассмотрим некоторые свойства пучка окружностей.
1) Любые две окружности лучка (35.1) имеют одну и ту же
радикальную осъ\ действительно, пусть имеем две окружности пучка
<Р — 14-Х' ' ? ^
1+Х'
1 + Х"
X', Х"=£ —1, X' ф\";
их радикальная ось определяется уравнением ср = ср , т. е.
?! + *'?2 _ ?1 +^?2
Рис. 115.
1+Х' ~~ 1 + X"
откуда
(X" —X')(<pi —<Р2) = 0;
таким образом, радикальные
оси окружностей ср' и ср" и
окружностей cpj и ср2
совпадают;
2) центры всех
окружностей пучка лежат на одной
прямой; действительно, линия
центров каждой пары окружностей пучка должна быть
перпендикулярна к радикальной оси;
3) радикальная ось и линия центров пучка окружностей
являются его осями симметрии;
4) пучок окружностей вполне определяется заданием одной
окружности пучка и радикальной оси; действительно, (35.1) можно
записать таким образом:
ср = срj -f- Хср2 = срх — ср2 + (X -f- 1) ср2 = 0;
вволя обозначения
¥l — СР2=5' X-f 1=Х'. jr = ^
мы можем записать наше уравнение пучка в одной из форм
= 0,
где 5 — радикальная ось пучка.
III. Рассмотрим .подробнее основные типы пучков окружностей.
1) Пусть сперва
(35.6)
\ri — r2\< VVi - *2)2 + (Pi - Р2)2 < гг + г2.
\2) равна расстоянию между
Так как величина Y(ai — аг)2 Н~ (Pi — Р2)2
центрами основных окружностей срх и ср2, то в этом случае эти
последние пересекаются в двух точках А и В (рис. 115) и все окруж-
§ 35]
ПУЧКИ ОКРУЖНОСТЕЙ
137
ности пучка проходят через эти две точки; такой пучок окружностей
называется эллиптическим. Так как в этом случае справедливы
неравенства
- 2гхг2 < (а, - а2)2 + (Р, - р2)* - г\ - r\ < 2r/a,
то для квадратного трехчлена (35.4) имеем:
" [(«i - *2)2 + (Pi - hf -Л- i]2 > 0; (35.7)
L = Ar\r\-
следовательно, этот трехчлен имеет комплексные сопряженные корни,
а поэтому неравенство (35.4) выполняется при всех значениях X;
поэтому в случае эллиптического пучка уравнение cp1-j-Xcp2 = 0
выражает окружность при всех
вещественных значениях X. ~
2) Пусть теперь справедливо
одно из равенств
^(а! — a2)2 + (Pi — Р2)2 = /"I Ч-/-2.
V^i-^ + CPr
-W=
Г,—Л
21»
(35.8)
Рис. 116.
т. е. основные окружности
касаются друг друга извне или
изнутри (рис. 116); в этом случае все окружности пучка касаются друг
друга в одной и той же точке А\ такой пучок окружностей называется
параболическим, В этом случае имеем Л = 0 и неравенство (35.4)
справедливо при условии
Хф
(«1 - «2)2+(Pi - р2)2 - Л - Л Л + Л± 2г\гг —Л—Л
1г\
24
+ и
(35.9)
значению параметра X = —- (в случае касания извне) или X = -
(в случае касания изнутри) соответствует окружность нулевого
радиуса, т. е. точка касания всех окружностей пучка.
3) Пусть, наконец, справедливо одно из неравенств
V(*i - <*2)2 + (Pi - Р2)2 > гх + г2,
l/^-a2)2-KPi-p2)2 < | r,-r21,
(35.10)
т. е. основные окружности не имеют общих точек и находятся одна
вне другой или внутри другой (рис. 117); такой пучок называется
гиперболическим.
138
НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ
[ГЛ. IV
Так как в этом случае А < 0, то трехчлен (35.4) обращается
в нуль при двух вещественных различных значениях X, именно при
X = Xj и Х = Х2, где
, _И 2) -riHi W 1—2 г ^ Х2 > Х2; (35.11)
4,2"
2г\
поэтому в случае гиперболического пучка уравнение <рг +- Хср2 = О
выражает окружность
лишь при выполнении
одного из неравенств
Х>Х1§ Х<Х2; (35.12)
при Х = Х2 и Х = Х2 по-
.лучим две окружности
нулевого радиуса, т. е.
точки М0 и iV0, причем
из определения радикаль-
Рис. 117. ной оси вытекает, что она
является осью симметрии
отрезка M0N0; при Х2 < X < Xj получим мнимое геометрическое
место (см. § 6).
В качестве иллюстрации положим:
9l = (^-l)2 + (>' + 2)2-4 = 0,
?2 = С* + 4)2 + (У + 1)2-С) = 0;
так как в этом случае имеем
/(«i-«2)2 + (§i-p2)2 = /26» Ъ+г^Б, \rx-r2\ = h
то пучок — гиперболический; так как А =*= — 25, то по (35.11) имеем Xj = 1,
А
\2 — -q\ по формуле (35.5) находим координаты точек М0 и N0:
(35.13)
М{
\ 2 ' 2)' N°\ 13' 1з)"
Мы получим тот же пучок окружностей, если в качестве основных примем
не окружности (35.13), а окружности нулевого радиуса ср3 и ср4 с центрами
в точках М0 и N0, т. е.
„»(,+4),+(,+1),=о.
"=(*+п)'+(>'+п)'=0:
уравнение пучка окружностей запишем в таком виде:
"" 1+1*
(,+4)4(y + »y+F[(,+&)r+(,+gyi
l+i*
= 0.
§ 35]
ПУЧКИ ОКРУЖНОСТЕЙ
139
Нетрудно видеть, что окружности ср х и ср2 соответствуют таким значениям
13 13
параметра: ^ == — -^, ^2 = — ~.
IV. Рассмотрим теперь построение окружности, принадлежащей
данному пучку, если известны одна из его окружностей и
радикальная ось.
1) Окружность пересекает радикальную ось в двух точках А
а В (рис. 118) — пучок, очевидно, будет эллиптическим и все
окружности пучка пройдут через точки А и В\ задавая произвольно
центр С на прямой, проходящей через
центр Сх заданной окружности
перпендикулярно к радикальной оси MN, мы
легко найдем радиус СА = СВ этой
окружности пучка. Так же легко
построить окружность пучка, проходящую
через заданную точку D. Возьмем на
радикальной оси произвольную точку
/С—степень этой точки относительно
всех окружностей пучка равна КТ2 =
= К А • KB = КО2 — ЛО2, откуда
ЛТ< /СО; если построить окружность ф
с центром в точке /Сие радиусом КТ,
то этот радиус является длиной
касательной из точки /С к любой
окружности ср нашего пучка; следовательно,
окружность ф пересекает произвольную окружность ср пучка
ортогонально (т. е. под прямым углом); выбирая новую точку К\
на радикальной оси, получим новую окружность ф2, обладающую
тем же свойством. Так как CT—CTV то линия центров ССг
данного пучка окружностей является радикальной осью окружностей ф
и фр а радикальная ось MN данного пучка является линией центров
окружностей ф и фх. Таким образом, с данным эллиптическим
пучком окружностей связан новый пучок окружностей, называемый
сопряженным с ним, причем любая окружность одного из пучков
ортогональна ко всем окружностям сопряженного пучка; линия
центров и радикальная ось одного из пучков являются радикальной осью
и линией центров сопряженного пучка; наконец, точки Л, В
пересечения окружностей данного эллиптического пучка являются
окружностями нулевого радиуса сопряженного пучка, который, таким
образом, будет гиперболическим; действительно, благодаря неравенству
АТ</СО все окружности второго пучка не пересекают его
радикальной оси.
2) Окружность не имеет общих точек с радикальной осью
(рис. 119) — пучок, очевидно, будет гиперболическим. Беря снова
Рис. 118.
140 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
Рис. 119.
произвольную точку К на радикальной оси, получим КТ2 — КС2—
— С{Р > КС2 — Cfl2 > КО2, т. е. КТ>КО; проводим снова
окружность ф с центром в точке /Сие радиусом К Г; она ортогональна
ко всем окружностям ср
данного пучка и, следовательно,
проходит через его
окружности нулевого радиуса, т. е.
через точки М0 и N0 ее
пересечения с линией
центров; таким образом, пучок,
сопряженный с
гиперболическим, является
эллиптическим, и окружности
нулевого радиуса
гиперболического пучка являются
точками пересечения
окружностей сопряженного
эллиптического пучка *).
Для построения
окружности пучка с центром
в точке С строим окружность на отрезке КС как на диаметре и
находим точку L ее пересечения с окружностью ф; тогда CL является
искомым радиусом окружности пучка с центром в точке С.
Если нужно построить окружность, принадлежащую
гиперболическому пучку и проходящую через заданную точку D% причем
известны окружности нулевого
радиуса М0 и N0 (рис. 120), то
строим ось симметрии g
отрезка DMQt соединяем точку К
ее пересечения с радикальной
осью с точкой D и проводим
прямую n±_KD\ точка С ее
пересечения с линией центров
является центром искомой
окружности; действительно, окружность
с центром /Сие радиусом
КМ0 = KN0 = KD принадлежит
глиптическому пучку
окружностей, сопряженному с данным
гиперболическим, а поэтому искомая окружность с центром Сие
радиусом DC ей ортогональна.
77 \/
£_(__
А А£Ч
_к
Vo_
м
м
\
\
")
/N„
Рис. 120.
*) Рис 119 может быть получен из рис. 118 поворотом этого
последнего вокруг точки О на 90°.
§ 35]
ПУЧКИ ОКРУЖНОСТЕЙ
141
3) Окружность касается радикальной оси (рис. 121) — данный
пучок и сопряженный с ним являются параболическими; построение
новых окружностей пучка не вызывает затруднений.
Отметим, что во всех трех случаях пучок окружностей вполне
характеризуется линией центров, радикальной осью и степенью т
точки О их пересечения
относительно всех
окружностей пучка; действительно,
если т < 0, то пучок
эллиптический и расстояния точек
А и В от точки О таковы.
О А = ОВ = У—т; если
т > 0, то пучок
гиперболический и величина Ym равна
расстоянию точки О от
окружностей нулевого радиуса М0
и iV0; наконец, если т = 0,
то пучок параболический.
V. В качестве иллюстрации рассмотрим такую задачу: найти
геометрическое место точек, для которых отношение расстояний от двух
данных точек является постоянным; таким образом, ищутся точки М (х, у),
для которых МАХ : МА2 = А, где
A C*i» У\), А2(х2, у2)— заданные точки
(рис. 122); мы имеем:
(*-*,)» +(у-уQ»
■у2У
■ = х»,
(X-
(х-х2у + (у-
-*,)2 + (y-yi)2-
-^2[(^-^)2 + (у-у2)2]-0;
искомым геометрическим местом
является, очевидно, окружность,
называемая окружностью Аполлония; она
принадлежит гиперболическому пучку
окружностей, для которого точки Ах
и А2 являются окружностями нулевого
Рис. 122. радиуса, прямая АХА2 — линией
центров, а ось симметрии g отрезка АХА2—
радикальной осью; если известна точка В, которая должна лежать на этой
окружности, т. е. если дано, что ВАх\ВА2 — \, то строим вышеуказанным
способом окружность ср гиперболического пучка, проходящую через точку Б.
Ввиду того, что окружность Аполлония встречается в задачах синтеза *),
приведем и геометрическое решение задачи (рис. 123). Найдем на прямой Ах А2
две точки А3 и Л4, удовлетворяющие условиям АЪАХ: А3А2 = ВАХ: BA2t
АААХ: ААА2 = В А, : ВА2. Для точки М имеем
МАХ
<™3^1 -^4-^1
МА0
А<хА2
А,А2
прямые МАг и МАА являются биссектрисами углов с вершиной М; так как
*) См. Р. Бейер [2], § 40.
142 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
они взаимно-перпендикулярны, то из точки М отрезок АЪАА должен быть
виден под прямым углом, т. е. искомое геометрическое место является
окружностью с диаметром АЪАА\ отме-
В тим, что заданные точки Ах и А2 и
найденные концы диаметра As и АА
образуют гармоническую группу.
VI. Рассмотрим теперь
применение пучка окружностей к теории
инволюционного соответствия (§ 15),
важное для дальнейшего.
Докажем сперва следующее:
окружности, принадлежащие
некоторому пучку, пересекают любую прямую в двух рядах точек,
образующих инволюцию *).
Действительно, пусть радикальная ось v пучка окружностей
пересекает прямую g в некоторой точке С (рис. 124); так как
радикальная* ось одна и та же для двух любых окружностей пучка, то
степени точки С относительно всех окружностей пучка одинаковы, т. е.
Рис. 124.
для любых двух пар точек пересечения Л, А' и В, В' мы имеем:
С А -СА' = СВ -СВ'. (35.14)
Следовательно, абсциссы х и хг соответствующих точек,
отсчитанные от точки С, связаны соотношением хх' = const, которое
подходит под тип (15.4) или (15.6); двойными точками инволюции
являются точки касания D и Df прямой g с двумя
окружностями пучка. Так как для \ = —1 окружность пучка (35.1) рас-
*) Эта теорема является частным случаем теоремы, доказанной в § 20;
мы приводим простое геометрическое доказательство для этого частного
случая, ибо оно полезно для дальнейших геометрических построений.
§ 35]
ПУЧКИ ОКРУЖНОСТЕЙ
143
падается на радикальную ось пучка и на бесконечно удаленную
прямую, то и эта окружность пересекает нашу прямую в двух
соответствующих точках: в центре инволюции Сив бесконечно удаленной
точке С.
Инволюция будет гиперболической, эллиптической или
параболической в зависимости от того, лежит ли центр инволюции вне,
внутри или на окружности пучка (рис. 124—126).
Рис. 125.
Рис. 126.
Покажем справедливость обратного утверждения: если на прямой
заданы два ряда точек, находящихся в инволюционном
соответствии, то эти два ряда точек можно рассматривать как точки
пересечения прямой с окружностями некоторого пучка.
Пусть инволюция задана двумя парами соответствующих
точек А, Аг и В, В! (рис. 127); возьмем произвольную точку Р вне
Д
я
Д'
д' в
а)
В Д'
8)
Д,В
В'
В'
В'
Рис. 127.
9)
Рис. 128.
прямой g, проведем две окружности через точки А, А'', Р и В, В', Р
и приме,м их за основные окружности пучка; тогда по доказанному
все окружности этого пучка пересекут прямую g в двух рядах точек,
образующих инволюцию, которая не может отличаться от заданной
инволюции, ибо у них совпадают две пары соответствующих точек,
144 НЕКОТОРЫЕ СВОЙСТВА КОНИЧЕСКИХ СЕЧЕНИЙ [ГЛ. IV
Если теперь нужно найти точку D', соответствующую данной точке D,
то проводим окружность пучка через точку D; второй точкой ее
пересечения с прямой g является точка D''.
Отметим, что по заданным двум парам точек можно сказать,
какого типа будет инволюция, не строя ее центра: инволюция будет
гиперболической (рис. 128, я), если две заданные пары точек Л, А'
и В, В' не разделяют друг друга, эллиптической (рис. 128, б),
если разделяют, и параболической (рис. 128, в), если А совпадает
с В или А' совпадает с В'.
ГЛАВА V
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
§ 36. Простейшие точечные преобразования
I. Рассмотрим в плоскости Р некоторую область В, и пусть
функции fi(x, у) и f2(x, у) однозначны и непрерывны, когда точка
М(х, у) лежит в этой области.
Пусть декартовы координаты некоторой точки Mf другой
плоскости Р' выражаются формулами
*' = /i(*. У). У = /2(*. У)\ (36.1)
тогда каждой точке М плоскости Р ставится в соответствие
некоторая точка Мг плоскости Р', причем двум бесконечно близким
точкам первой плоскости соответствуют две бесконечно близкие точки
второй.
Если уравнения (36.1) можно разрешить относительно х и у
* = <Pi(*'. У). У = %(*'. У). (36.2)
где <?i(xf, У) и ср2(д;/' У)—некоторые однозначные и непрерывные
функции в некоторой области В' плоскости Р', то соответствие
между точками обеих плоскостей взаимно однозначно, т. е. каждой
точке одной плоскости соответствует одна и только одна точка другой.
Мы говорим, что посредством формул (36.1) осуществляется
некоторое точечное преобразование, или, иначе, некоторое
преобразование координат.
Если в плоскости Р дана некоторая фигура Е, то
преобразование (36.1) переведет каждую ее точку в некоторую новую точку
плоскости Р', а вся фигура Е, преобразуется в некоторую новую
фигуру Е' плоскости Р'. Возникает вопрос о тех свойствах фигуры,
которые при этом преобразовании останутся неизменными, или,
как говорят в математике, являются инвариантными по
отношению к этому преобразованию.
II. Мы рассмотрим несколько основных типов таких
преобразований.
146 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [ГЛ. V
1) Преобразование
х' = х cos а + у sin а + х0, у' = — х sin а -|~ у cos а + у0, (36.3)
О < а < 2тс,
называется изометрическим; нетрудно видеть, что обратное
преобразование
х = xr cos а — у* sin а — л;0, у = х' sin а + у' cos а — у0 (36.4)
также является изометрическим, ибо получается из него
изменением знака or, х0 и у0.
Если две точки AfjOtfj, у^ и М2(лг2» у2) преобразуются в точки
Afj(Xj, у() и M'2(x'v Уг)» то мы имеем:
*2 — *( = (*2 ~~ х\) cos а + (Уг ~ Уi) sin а»
у; — у; = — (*2 — Д^) sin а + (У2 — Ух) cos а,
откуда МiM2 = Af 1М2» ибо
(4 - *02+$ - *02=& - *02+(у2 - Уд2- (36.5)
Если взять еще третью точку Мг(х%, у3). которая преобразуется
в точку М'г(х'г, Уд), то все три стороны треугольника МхМ^М^
равны соответствующим сторонам треугольника MXM2MZ, откуда
вытекает равенство соответствующих углов. Таким образом, при изо*
метрическом преобразовании все метрические свойства фигуры
(т. е. длины отрезков, величины углов)
остаются неизменными *); поэтому
преобразованная фигура Ef
конгруэнтна фигуре Е (т. е. может быть
с нею совмещена путем наложения).
В аналитической геометрии
формулы (36.4) рассматриваются как
формулы преобразования координат
путем переноса начала О в точку
О
с2г О'(—xQt —у0) и поворота всей коор-
Рис. 129. динатной системы на угол а (рис. 129);
при этом фигура Е' совпадет с
фигурой Е\ если же оси О'х'у' совместить с осями Оху, то фигура Е\
конгруэнтная фигуре £, отличается от нее только положением в
плоскости; поэтому изометрическое преобразование называют также
преобразованием движения, ибо оно соответствует перемещению плоской
фигуры в своей плоскости как твердого тела.
2) Более общее преобразование
х' — alx-\-bly-{-cv yf = а2х-]-Ь2у-\~с2 (36.6)
*) Отсюда название «изометрическое», т. е. обладающее равной метрикой.
§ 36]
ПРОСТЕЙШИЕ ТОЧЕЧНЫЕ ПРЕОБРАЗОВАНИЯ
147
а
называется аффинным; если I ~1 "* \Ф О, то уравнение (36.6) можно
разрешить относительно л; и у, ,т. е. обратное преобразование
х = агх' + №+ъ. У = «2^, + Р2У, + Т2 (36-7)
также является аффинным.
Изометрическое преобразование является частным случаем
аффинного— оно соответствует тому случаю, когда коэффициенты
преобразования связаны соотношениями
ai + #i = #2 + ^2= 1» ala2-\-blb2 = 0.
(36.8)
Рассмотрим еще такие частные случаи аффинного преобразования
(оси О'х'у' совместим с осями Оху):
2а)
х' = \х% у' = \у.
(36.9)
Это — случай перспективного подобия с центром в точке О и с.
коэффициентом подобия I (рис. 130); в книгах И. И. Артоболевского [3] (§ 6)
Р. Бейера [2] (§ 105) и В. А. Юдина [1]
(стр. 182—184) читатель найдет так „ „*
называемые пантографы, т. е. кине- *' & I
матические цепи, посредством
которых можно осуществить
преобразование 2а) с последующим поворотом
на некоторый угол.
26) х' = рх9 у' = у. (36.10)
Это — случай равномерного сжатия
или растяжения фигуры в
направлении оси х в ц раз; например, при
таком преобразовании окружность
с уравнением х2 + У2 = г2 преобра-
Л"
n/'p/^
/у^м
р'
Ум'
-о'
я%х'
зуется в эллипс
fxV2
1.
Рис. 130.
В книге В. Мейера цур Капел-
лена [1] (стр. 154—156) читатель найдет так называемые аффиннографы, т. е
кинематические цепи, позволяющие осуществить преобразование 26).
Рассмотрим основное свойство аффинного преобразования:
из (36.6) ясно, что точка с координатами х = оо, у = оо
преобразуется в точку с координатами х' — схэ, у = оо, т. е. аффинное
преобразование оставляет неизменной бесконечно удаленную
прямую плоскости*) — все собственные точки плоскости Р
преобразуются в собственные точки плоскости Р', а несобственные
точки — в несобственные.
*) Название «аффинный» произошло от латинских слов «ad finem», что
значит «к концу»; аффинное преобразование оставляет неизменными
бесконечно удаленные точки, т. е., так сказать, концы пространства.
148 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [рл. V
3) Еще более общее преобразование
, _ alx + bly + cl , _ а2х + Ь2у + с2
Х — аъх + Ъъу + съ ' У — аъх + Ъъу + съ (*ЬЛ1)
называется проективным преобразованием; если в обеих плоскостях
ввести однородные координаты, то будем иметь:
аххг + Ьхх2 + с^з х2 а2хх + Ь2х2 + с2хг
(36.12)
*3 Vl+V2 + ¥3 Ч ^3^1 + V2 + C3^3
откуда
px[ = alxl-i-blx2-+clx3t
рх'2 = а2хх + b2x2+c2xv (36Л 3)
где р — некоторый множитель пропорциональности. Если
| а\ Ьх сх
ФО, (36.14)
а2 Ъ2 с2
аг Ьг с3
то эту систему можно разрешить относительно xv х2 и хг и мы
получим:
Х2 = Р(а2Х,1 + $2Х2+ЪХг)> (36.15)
-з-РМ + Рз^ + ТзО
^о = 1
Возвращаясь к неоднородным координатам, будем иметь:
^ _ «i^ + Piy'+Ti „ _ а2*' + fey' + 72
(36.16)
— «а*' + РзУ' + 7з ' У W + РзУ/ + 7з '
т. е. обратное преобразование также является проективным.
Легко видеть, что аффинное преобразование является частным
случаем проективного—оно соответствует тому случаю, когда аг = Ьг = О,
сг=\. В отличие от аффинного преобразования при проективном
пре о образовании бесконечно удаленная прямая плоскости не
остается неизменной; из формулы (36.13) ясно, что собственная прямая
плоскости Р
агх -+-Ьгу-{-сг = 0 (36.17)
преобразуется в бесконечно удаленную прямую х'г = 0 плоскости Р'\
а собственная прямая плоскости Р'
а3*' + р3У' + Тз = 0 (36Л8>
преобразуется в бесконечно удаленную прямую лг3 = 0 плоскости Р.
§ 37] ОСНОВНЫЕ СВОЙСТВА ПРОЕКТИВНОГО ПРЕОБРАЗОВАНИЯ 149
§ 37. Основные свойства проективного преобразования
I. Рассмотрим некоторые свойства проективного преобразования,
которыми, следовательно, будут обладать и его частные случаи —
аффинное и изометрическое преобразования.
Покажем, что при проективном преобразовании алгебраическая
кривая п-го порядка преобразуется в алгебраическую же кривую
того же порядка.
Действительно, по (5.2) уравнение алгебраической кривой ср
Ai-ro порядка в однородных координатах таково:
ЪнАхГ2хГк-г=ь. (37.1)
Пользуясь (36.15), получим после преобразования уравнение
кривой ср' в однородных координатах
х(а3*;+Рз^-Из*;Г*-г=°; (37-2)
так как левая часть является многочленом относительно всех трех
координат x'v x'v x'v то кривая ср' также алгебраическая', если
раскрыть все скобки, то сумма п! показателей при х'у х'г х'г во всех
членах, очевидно, удовлетворяет неравенству п' ^ п\ если
предположить, что пг < п, то, применяя к кривой ср' Обратное
преобразование (36.13), мы получим алгебраическую кривую порядка не
выше п'\ но мы должны при этом вернуться к кривой ср порядка п,
т. е. должны будем иметь п4^п\ откуда nf = п.
II. Рассмотрим подробнее случаи п=\ и п = 2.
При проективном преобразовании прямая преобразуется
в прямую *); пучок прямых преобразуется в пучок прямых, но
параллельность прямых при этом не сохраняется; пучок параллельных
прямых с центром в несобственной точке плоскости Р преобразуется
в пучок прямых плоскости Р', с центром в собственной точке,
лежащей на прямой (36.18); в частном случае аффинного преобразования
параллельность прямых сохраняется.
Кроме того, при проективном преобразовании не изменяется
ангармоническое отношение четырех любых точек, лежащих на
одной прямой, т. е.
(м[м'2МгМ[) = {МхМ2МъМь)\ (37.3)
следовательно, при этом первоначальный и преобразованный ряды
точек проективны, так же как первоначальный и преобразованный
*) Можно показать, что проективное преобразование является наиболее
общим взаимно однозначным преобразованием, преобразующим прямую
в прямую; оно называется также коллинеацией.
150 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [ГЛ. V
пучки прямых. Для доказательства рассмотрим две точки М\(х\\
х2\ х^) и М2(х¥\ х2\ *з2)) плоскости Р\ любая точка М на
прямой М1М2 имеет координаты
Xl = xP + \xf\ х2 = x2l)+ lx(22\ *3=*?) + **?); (37.4)
по формулам (36.13) найдем координаты соответствующих точек
М[(х(;\ х$\ За4) и М2(х?\ xf, xf>) плоскости Р'
рх*/' = сцх^ + Ьгхф + cix$\ рхф = a2x(i) + b2x2l) + c2x$\
рЗё?» = atx[l) + hx2l) + c34K
PX(i2) = Oi*? > + *l42) + Cl42), P*22) = fl242> + Ы(22) + C2xf\
px? = a3xi2) + hxf + c3x32);
точке M с координатами (37.4) будет соответствовать точка М'
с координатами
pxi = aiXi -|- &iX2 + CiX3, рх2 = а2Х\ -\- b2x2 -\- с2х3,
рх3 = azxi + bsx2 + с3х3)
т. е. мы имеем:
x[=W+lxf\ х'2 = хУ+1х%\ x',= xf+llcf;
отсюда по § 13 следует (37.3).
В частном случае аффинного преобразования мы можем принять
в качестве Ж4 и Ж4 соответствующие друг другу бесконечно уда-
ленные точки обеих прямых; в таком случае получим из (37.3)
МЛМ9 МЖ
-^ = -==*' (37.5)
m2mz м2мг
таким образом, при изометрическом преобразовании сохраняются
длины отрезков, при аффинном — их простые отношения, при
проективном — их двойные отношения.
III. При проективном преобразовании кривая второго порядка
преобразуется в кривую второго порядка, причем распадающаяся
кривая преобразуется в распадающуюся же, а нераспадающаяся,
т. е. коническое сечение, преобразуется в коническое сечение;
однако, так как бесконечно удаленная точка одной плоскости
преобразуется в собственную точку другой, то коническое сечение, не
имеющее бесконечно удаленных точек (эллипс, окружность), может
преобразоваться в коническое сечение, имеющее такие точки
(парабола, гипербола); в частном случае аффинного преобразования беско-
§ 38] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОЕКТ. И АФФИН. ПРЕОБРАЗОВАНИЙ 15!
нечно удаленные точки сохраняются и каждое коническое сечение
преобразуется в одноименное с ним, за исключением окружности и
эллипса, которые могут переходить одно в другое.
В качестве иллюстрации рассмотрим окружность с уравнением
х2 + у2 = г2;
проективное преобразование
преобразует ее в гиперболу с уравнением
г2*'2-у'2 = 1;
аффинное преобразование
х = \х', у = у-у'
преобразует ее в эллипс
х'2 v'2
XV2 ^ \х2г2
§ 38. Геометрический смысл проективного
и аффинного преобразований
I. Мы определили проективное преобразование, устанавливающее
соответствие между точками двух плоскостей чисто аналитическим
путем — при помощи формул (36.11), позволяющих вычислить
координаты точки М', если
теперь весьма простой
геометрической метод,
посредством которого мы
установим то же самое
соответствие между
точками обеих плоскостей.
Пусть даны две
непараллельные плоскости
Р и Р' и точка 5 вне их
(рис. 131); рассмотрим
центральную проекцию
плоскости Р на
плоскость Р;, т. е. каждую
точку М плоскости Р
соединим прямой с
центром 5 и поставим ей в
луча с плоскостью Р'.
координатных осей Оху
проекции одной плоскости на другую координаты соответствую-
щих точек обеих плоскостей связаны проективным преобразо-
известны координаты точки М\ покажем
Рис. 131.
соответствие точку Mf пересечения этого
Введем в каждой из плоскостей систему
и Огх'у'\ докажем, что при центральной
152
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
[ГЛ. V
ванием (36.11); коэффициенты av blt сх
Ло, bv с* зависят от
положения плоскости Р', точки S и осей О'у'х* относительно
плоскости Р.
Действительно, пусть оси О'х' и О'у' плоскости Р' преобразуются при
центральной проекции в прямые и{ и и2 плоскости Р (рис. 131). Проводя
через центр S плоскость Р"\\Р', мы найдем в ее пересечении с
плоскостью Р прямую и3, которая, очевидно, преобразуется при центральной
проекции в бесконечно удаленную прямую плоскости Р *).
Рассмотрим треугольник М0М3МА (рис. 132), образованный прямыми ии
и2, и3 (при условии (36.14) они не пересекаются в одной точке); возьмем
точку М (х, у) и проведем через нее прямую М0ММ{; пусть точка М{
переходит при центральной проекции в некоторую точку Мг оси О'х', причем
У
,0
щ
W
у*
MfHZ,
лмч
,и.
Зз\М
^\
У'\
х
Здг
"г
м;
Рис. 132.
х' = OfM[; возьмем на этой оси еще точки М2, Мг, М4, характеризуемые
абсциссами х2=1, хг = 0, х\ ^ °°» ПРИ центральной проекции мы получим
на прямой иг перспективный, а следовательно, и проективный ряд точек
М2, М3, М4; так как мы имеем
(м'гМ'2МъМ% =
Хо ~~~" Хл
: X =
Хо х9
= (М{М2М3М4) = (v{v2u2u3)t (38.1)
где прямые vx и v2 проектируют точки Л^ и М2 из центра М0, то отсюда
вытекает равенство х' = {yxv2u2u%). Записав уравнение пучка прямых,
определяемого основными прямыми и2 и и3» в виде
и2 -f- ли3 = О,
(38.2)
мы видим, что этим основным прямым соответствуют значения параметра
Х3 = 0, л4 = оо; таким образом, мы имеем:
х' = (vlv2u2us) = -
• Aj Л4 — Aj
- Х2 л4 — Х2
х2
(38.3)
*) Плоскость Р" не показана на рис. 131, чтобы не усложнять его.
§ 38] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОЕКТ. И АФФИН. ПРЕОБРАЗОВАНИЙ 153
где значения Хи Х2 параметра X соответствуют прямым vu v2. Так как для
всех точек прямой vlt в частности для точки М, имеем \{ = —
(38.2), (38.3) находим:
и2
X —■ С 1 • ,
где Сх — постоянный множитель; совершенно аналогично имеем:
= С2
то из
(38.4)
(38.5)
т. е. мы пришли к формулам типа (36.11).
II. Примечание. Проективное преобразование (36.11)
характеризуется восемью коэффициентами, ибо на один из коэффициентов
можно поделить числители и знаменатели, обеих дробей; для их
нахождения достаточны четыре условия: четырем произвольно
выбранным точкам Mv М2, Мг, М4 первой плоскости должны
соответствовать четыре произвольно выбранные точки Ми М2>
Мз, М$ второй плоскости *) (рис. 133). Действительно, задание
У\
о
м,<
а$
■"■«^
^аз
й£ч
л5
\м*
fk
~~VU
У
п'
t
м'Ь
Л7,
°'5/
/у
/щ\
^1 \
а'г
*<
' к
м
•
Рис. 133.
х'
одной пары соответствующих точек дает два соотношения между
коэффициентами. Поэтому если задано проективное
преобразование (36.11) при условии (36,14), то можно найти такие
положения плоскости Р! и центра S, чтобы соответствующие
точки обеих плоскостей получались друг из друга путем
центральной проекции из центра S.
Так как для определения положения плоскости Р' относительна
фиксированной плоскости Р нужны три параметра, для центра 5 —
еще три и для положения осей О'х'у' в плоскости Р'— еще три,,
то мы должны определить девять параметров из восьми условий».
*) Никакие три точки из каждой четверки не должны лежать на одной
прямой.
154 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [ГЛ. V
поэтому один из параметров можно взять произвольно, и задача
имеет бесчисленное множество решений.
Покажем теперь, как, зная четыре пары точек Мх М4 и
Ми . . ., Ж4, соответствующих друг другу при проективном
преобразовании (36.11), найти точку Ms, если задана соответствующая ей
точка Мъ (рис. 133).
1) Если найти положение плоскости Р' и центра перспективы 5,
то, проектируя точку М5 из центра перспективы 5 на плоскость Р'',
получим точку М$.
2) Чисто аналитическое решение задачи таково: подставим
координаты заданных точек в уравнения (36.11), решим полученные восемь
уравнений относительно параметров, после чего сможем по заданным
координатам точки Ж5 найти координаты точки М$.
3) Чисто геометрическое решение таково: так как пучки прямых
Mx{ar av а4, аЛ и MUary a'v а'г а'Л должны быть проективны,
то находим прямую а'5 из условия Ы2ага4аЛ = (а'2а'га'Аа'Л\ пользуясь
проективностью пучков прямых М2(Ьг, br Ь5, аЛ и М'2(Ь'2, Ъ\, Ь'5, а'Л
находим из условия (ЬъЬ^ЬБаЛ = (Ьф'/р'ъа'Л прямую Ь'5, которая пере-
сечет прямую #5 в искомой точке М$.
III. Предположим теперь, что центр проекции S на рис. 131,
уходит в бесконечность, т. е. центральная проекция
вырождается в параллельную (рис. 134); плоскости Р и Р' будем
считать непараллельными. В этом случае бесконечно удаленная прямая
первой плоскости должна преобразоваться в бесконечно удаленную
прямую второй плоскости, т. е. по (36.17)
мы должны иметь аг = Ьг — 0, с3Ф0,
и формулы (36.11) принимают вид
формул (36.6). Следовательно, при
параллельной проекции одной плоскости на
? другую координаты соответствующих
точек обеих плоскостей связаны
аффинным преобразованием (36.6). Чтобы
показать справедливость обратного
утверждения, заметим прежде всего, что
аффинное преобразование (36.6)
характеризуется шестью коэффициентами
(например, оно вполне определяется заданием
трех пар соответствующих точек обеих
плоскостей). С другой стороны,
положение плоскости Pf относительно плоскости Р, положение осей О'х'у'
и направление лучей при параллельной проекции определяются
в общей сложности восемью параметрами; выбирая произвольно
два из них, мы можем найти остальные шесть по заданным шести
§ 39]
ПОНЯТИЕ О ТЕОРИИ ПЕРСПЕКТИВЫ
155
коэффициентам аффинного преобразования; поэтому если задано
аффинное преобразование (36.6), то можно найти такие
положения плоскости Р' и такое направление, чтобы соответствую*
щие точки обеих плоскостей получались друг из друга путем
параллельной проекции параллельно этому направлению.
IV. Рассмотрим теперь случай, который мы исключили: пусть
плоскости Р' и Р параллельны (рис. 135); так как в этом случае
бесконечно удаленные прямые обеих плоскостей соответствуют друг
другу, то проективное преобразование вырождается в аффинное;
более того, при центральном проектировании фигуры Е и$
центра S мы получим
фигуру Е', перспективно
подобную фигуре Е. Действительно,
выберем произвольные точки
А', В! плоскости Р'',
проектирующиеся в точки Л, В
плоскости Р, и произведем
параллельное проектирование
плоскости Pf в направлении А'А\
тогда точка В' спроектируется
в точку В[ на прямой АВ и мы
будем иметь:
АВг = А В ,
АВ\
SA'
Рис. 135.
АВ
SA
т. е. мы получим фигуру Ег в плоскости Р, конгруэнтную фигуре Ег
и перспективно подобную фигуре Е с центром подобия Лис
коэффициентом подобия k\ точно так же при параллельности плоскостей
Р' и Р мы получим в результате параллельного проектирования
фигуру, конгруэнтную данной.
§ 39. Понятие о теории перспективы
I. На рис. 136 изображен разрез глаза вертикальной плоскостью
проходящей через так называемый оптический центр 5*); лучи*
исходящие от различных точек рассматриваемого предмета
(необязательно плоского), проходят через центр 5 и попадают на сетчатую
оболочку, которую в первом приближении считаем плоской;
аналогичную картину имеем при фотографировании — в этом случае S
это центр линзы объектива, а роль сетчатой оболочки играет
светочувствительная пластинка.
*) См. Н. Ф. Четверухин [1], стр. 49.
156
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
[ГЛ. V
Рис. 136.
Если мы пересечем плоскостью Р' пучок лучей, соединяющих
точку 5 со всеми точками рассматриваемого предмета, то получим
в пересечении некоторую плоскую фигуру Е\ являющуюся его
центральной проекцией на плоскость Р'\ если точка 5 совпадает с
оптическим центром глаза, то глаз получит
от рассмотрения фигуры Е' такое же
впечатление, как и от рассмотрения
данного предмета, ибо все
проектирующие лучи в данном случае
одинаковы. Фигура Е', т. е. центральная
проекция данного предмета на
плоскость Р', называется его
перспективным изображением, или перспектив
вой, центр проекции 5 называется
точкой зрения, а плоскость Р' называется картинной; перспективное
изображение данного предмета зависит от положения картинной
плоскости и точки зрения.
Теория перспективы, рассматривающая общие методы построения
перспективных изображений, является основой для живописи,
архитектурного черчения, фотограммометрии и т. п. *); ее основы были
заложены в трудах великих итальянских архитекторов и живописцев
эпохи Возрождения.
В случае перспективного
изображения плоских фигур
мы имеем центральную
проекцию одной плоскости на
другую, которая эквивалентна
проективному преобразованию
координат, поэтому все
свойства такого перспективного
изображения вытекают из
рассмотренных нами свойств
проективного преобразования.
II. Рассмотрим
перспективные изображения некоторых
простейших геометрических
образов, нужные для
дальнейшего.
Пусть картинная плоскость Р' перпендикулярна к плоскости Р,
которую будем называть предметной — их, очевидно, можно
поменять местами. Проведем через точку зрения 5 (рис. 137) плоскость Pv
параллельную плоскости Р\ прямую пересечения плоскости Рг с кар-
Рис. 137.
*) См., например, Г. А. Владимирский [1]; см. также Н. Ф. Четверухин,
[1], гл. III, VI.
§ 39]
ПОНЯТИЕ О ТЕОРИИ ПЕРСПЕКТИВЫ
157
я
/s//\ v
/ &ч
/ w \
/Р
/V
м\/
в/
тинной плоскостью Р' назовем линией горизонта v\ все лучи,
проектирующие из точки 5 различные точки А0, В0, С0, ... линии
горизонта, параллельны плоскости Р, т. е. пересекают ее в ее бесконечно
удаленных точках; так как при центральном проектировании каждая
прямая проектируется в прямую, то мы приходим к весьма важному
выводу: линия горизонта v картинной плоскости Р!
соответствует бесконечно удаленной прямой предметной плоскости Р\
отсюда происходит ее название: если предметная плоскость Р является
плоскостью, касательной к земной поверхности, то при изображении
некоторого ландшафта на картине или на фотографическом снимке
прямая v действительно будет
являться изображением линии
горизонта, рассматриваемой как
бесконечно удаленная прямая предметной
плоскости.
Покажем теперь, как построить
точку М' на картинной плоскости Р\
соответствующую заданной точке М
на предметной плоскости Р, если
задан центр перспективы 5 и найдена
линия горизонта v (рис. 138).
Проведем через точку 5 произвольную
прямую SS', параллельную
предметной плоскости, до пересечения
в точке S' с линией горизонта v\
соединим точку 5 с заданной точкой М, проведем прямую MM0\\SS'
до пересечения в точке М0 с линией* пересечения плоскостей v0 и
проведем прямую S'M0,—легко видеть, что она пересечет
прямую SM в искомой точке М''. Пользуясь этим методом, легко
построить по точкам перспективное изображение любой фигуры,
заданной в предметной плоскости.
Например, прямая и предметной плоскости спроектируется в
некоторую прямую и' картинной плоскости, которую найдем следующим
образом: если прямая и проходит через точку Ж, то прямая и'
пройдет через точку М'\ если прямая и пересекает прямую v0
в точке М0, то эта точка спроектируется сама в себя, т. е. искомая
прямая и! проходит через точки М и Mq. Если же прямая w
проходит через точку М и параллельна прямой v0, то она
спроектируется в прямую w't проходящую через точку М' параллельно
прямой v0.
Рассмотрим теперь две параллельные прямые а и аг (рис. 137),
лежащие в предметной плоскости; так как прямая проектируется
в прямую и определяется двумя своими точками, то нам надо найти
по две точки каждой из прямых в картинной плоскости. Прямые а
Рис. 138.
158
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
[ГЛ. V
и аг пересекают в точках Аг и А[ прямую v0, являющуюся линией
пересечения плоскостей Р' и Р\ эти точки при проектировании
переходят сами в себя; прямые а и ах пересекаются в бесконечно
удаленной точке А^ плоскости Р\ луч, проектирующий эту точку А^
Рис. 139.
из центра 5, параллелен обеим прямым и пересекает линию гори-'
зонта v в точке А0\ таким образом, параллельные прямые а и аг
предметной плоскости проектируются в прямые а! и а[
картинной плоскости, пересекающиеся на линии горизонта. Только
прямые, параллельные линии vQ
пересечения плоскостей Р и Р\ проектируются
в параллельные прямые.
Рассмотрим теперь параллелограмм
ABCD (рис. 139), лежащий в предметной
плоскости; мы видим, что прямые АВ
и CD проектируются в прямые А0А'
и А0А[, где SA0\\AB\\CD, а прямые AD
f г , и ВС проектируются в прямые В0В'
в' в1 л л1 и В0В{, где SB0\\AD\\BC; таким обра-
Рис. 140. зом, перспективным изображением па-*
раллелограмма ABCD является
четырехугольник A'0B'0C'0D'0, противоположные стороны которого
пересекаются на линии горизонта (рис. НО).
Рассмотрим еще такую задачу: зная перспективное
изображение A'B'C'D' квадрата ABCD (рис. 141), найти перспективное
изображение четырех малых квадратов /, //, ///, IV.
I 39]
ПОНЯТИЕ О ТЕОРИИ ПЕРСПЕКТИВЫ
159
Так как диагонали квадрата BD и АС спроектируются в
диагонали четырехугольника B'D' и А'С', то точка О спроектируется
Л R D Л'
Рис. 141.
в точку О'; прямая ROQ, параллельная прямым AS и DC,
спроектируется в прямую GO', проходя- м v а
щую через точку О' и через точку О
пересечения прямых А'В' и DrC'\
точно так же прямая SOT\\AD\\BC
спроектируется в прямую МО'.
Из рассмотренной задачи легко
получить перспективное изображение
прямого параллелепипеда,
поставленного на предметную плоскость (рис. 142).
Заметим, что для всех плоскостей Pv Л
Р2,..., параллельных предметной пло- Рис. 142.
скости, линия горизонта v одна и та
же —следовательно, все четыре параллельные прямые АВ, DC, АХВХ, DlCl
Рис. 143.
пересекаются в одной точке G, а параллельные прямые AD, ВС, A{DU ВхСу
пересекаются в точке М, причем GM — линия горизонта.
160 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [ГЛ. V
Пр имечание. Перспективное изображение предмета на данной
картинной плоскости весьма существенно зависит от положения точки зрения;
в живописи эту точку стараются выбрать таким образом, чтобы она
соответствовала естественному положению зрителя, стоящего перед картиной.
Рис. 144.
III. Рассмотрим теперь задачу о перспективном изображении
окружности, играющем важную роль в теории конических сечений.
Пусть в картинной плоскости Р' дана окружность k и построена
линия горизонта v\ будем различать три случая в зависимости от их
относительного расположения.
1) Окружность не имеет общих точек с линией горизонта-,
ее перспективным изображением на плоскость Р является коническое
сечение, не имеющее общих
точек с бесконечно удаленной
прямой, т. е. эллипс kx (рис. 143).
2) Окружность пересекает
линию горизонта-, ее
перспективным изображением является
коническое сечение, имеющее две
общие точки с бесконечно
удаленной прямой, т. е. гипербола k2
(рис. 144). Касательные а'у а'2
к окружности в точках ее
пересечения с линией горизонта про-
Рис. 145. ектируются в касательные av а2
к гиперболе в ее бесконечно
удаленных точках, т. е. в ее асимптоты. Если точка описывает
непрерывным движением окружность, то ее проекция описывает
непрерывным движением гиперболу; частям окружности, лежащим ниже или выше
линии горизонта, соответствуют ветви гиперболы, лежащие перед или
за картинной плоскостью Р'.
§ 40] КЛАССИФИКАЦИЯ ГЕОМЕТРИЧЕСКИХ ДИСЦИПЛИН 161
3) Окружность касается линии горизонта-, в этом случае обе
касательные av а2 сливаются в одну, совпадающую с линией
горизонта V) перспективным изображением окружности является
коническое сечение, касающееся бесконечно удаленной прямой, т. е.
парабола къ (рис. 145).
§ 4). Классификация геометрических дисциплин
I. Мы будем называть метрическими, или аффинными, или проективными,
свойствами фигуры те ее свойства, которые остаются неизменными
соответственно при изометрическом, или аффинном, или проективном преобразовании,
1) Проективными свойствами, остающимися неизменными при
центральном проектировании, являются, например, такие: свойство линии быть
алгебраической кривой заданного порядка — в частности, быть прямой линией или
коническим сечением; ангармоническое отношение четырех точек прямой или
четырех прямых пучка; проективное соответствие рядов точек или пучков
прямых — в частном случае инволюция.
2) Аффинными свойствами, остающимися неизменными при
параллельном проектировании, являются, кроме перечисленных в 1), следующие:
свойства точек быть собственными или несобственными; параллельность прямых;
простое отношение двух отрезков прямой.
3) Метрическими свойствами, остающимися неизменными при
движении фигуры как твердого тела, являются, кроме перечисленных в 1) и 2),
следующие: длины отрезков, углы между прямыми.
Очевидно, метрические свойства фигуры являются наименее стойкими —
они сохраняются лишь при ее движении как твердого тела, но утрачиваются
уже при параллельной проекции; аффинные свойства являются более
стойкими, чем метрические, но менее стойкими, чем проективные, —они
сохраняются при параллельной проекции, но утрачиваются при центральной;
наконец, проективные свойства фигуры, сохраняющиеся и при центральной
проекции, являются наиболее стойкими и, следовательно, наиболее общими,
ибо сохраняются при более общем преобразовании.
В зависимости от того, какие свойства фигуры рассматриваются,
различают геометрию метрическую, геометрию аффинную и геометрию
проективную. Например, в аналитической геометрии, изучающейся во
втузах, рассматривают лишь метрические свойства и пользуются исключительно
изометрическим преобразованием (36.3); это же относится и к кинематике.
В теории упругости при рассмотрении бесконечно малых деформаций
пользуются аффинным преобразованием (36.6), т. е. аффинные свойства фигур
сохраняются при указанной деформации.
В § 5 мы классифицировали конические, сечения в зависимости от их
расположения относительно бесконечно удаленной прямой; эти вопросы
относятся к аффинной геометрии, ибо с точки зрения проективной
геометрии бесконечно удаленная прямая не играет исключительной роли и ничем
не отличается от собственной прямой, в которую она преобразуется при
проективном преобразовании.
Свойства полюсов и поляр конических сечений являются проективными,
ибо связаны с гармоническими группами, т. е. с величиной ангармонического
отношения, не изменяющейся при проективном преобразовании; свойства
центров, фокусов, директрис, сопряженных диаметров и осей симметрии
конических сечений, рассмотренные в § 28, тоже являются проективными,
так же как и свойства, выражаемые теоремами Паскаля и Брианшона *).
*) Весьма большое значение для геометрии имеет формула (17.8),
выражающая чисто геометрическое понятие — угол между двумя прямыми — через
ангармоническое отношение четырех прямых.
162
Преобразования координат
[гл. v
ъ
>
£
к\
Q
К
О
W
\уу\[/
/с а
\ \ /т т\ i
Q
г
S
*■'
>' J
II. Мы рассмотрели в предыдущих главах ряд теорем проективной
геометрии, но доказывали их преимущественно аналитическим путем;
геометрическое значение проективного преобразования, рассмотренное в § 36*,
дает ключ к их новому истолкованию и к выводу новых теорем; изучив
проективные свойства простейших фигур (например, параллелограмма,
окружности и т. п.), мы будем знать проективные свойства гораздо
более сложных фигур, являющихся их центральными проекциями
(например, произвольный четырехугольник, коническое сечение и т. п.).
Например, при построении перспективных изображений квадратов /, ...,1V
(рис. 141), мы не можем пользоваться тем, что прямые RQ и TS взаимно-
перпендикулярны, а диагонали АС и BD взаимно-перпендикулярны и делят
углы квадрата пополам (ибо это метрические свойства), ни тем, что
диагонали делятся в точке О пополам, а отрезки RQ и TS делят друг друга и
стороны квадрата пополам, причем RQ\\AB\\DC и ST\\AD\\BC (ибо это
аффинное свойство); мы
воспользовались проективным свойством: точка
пересечения двух прямых проектируется
в точку пересечения соответствующих
прямых, причем это верно как для
собственных, так и для несобственных точек.
В качестве дальнейшего примера
рассмотрим решение такой задачи: даны
две параллельные прямые а и b и
точка М на равных расстояниях от
них (рис. 146); провести через
точку М прямую, параллельную данным
прямым.
Проведем через точку М две
произвольные прямые с и d,
пересекающие прямые а и b в точках Я, G
и £, F; прямые k и /, соединяющие
точки Е, G и F, Я, очевидно, параллельны, т. е. пересекаются в несобственной
точке Q; проводим произвольную прямую s||£||/, отмечаем ее точки
пересечения J и N с прямыми а и b и проводим прямые гит через точки Я,
N и F, J; искомая прямая МТ проходит через точку их пересечения Т.
При центральной проекции прямые k, I, s, а также прямые a, b, МТ
пересекутся в собственных точках Q и Р и мы придем к рис. 46, т. е. решение
задачи, рассмотренной в § 22, сразу вытекает из решения гораздо более
легкой задачи настоящего параграфа.
Если провести еще прямые EJ и GN и обозначить через Alt АЪу А3, АА,
А2, А6 точки Е, Я, /, G, F, N, а затем применить к рис. 146 центральную
проекцию, при которой прямые а и b перейдут в пересекающиеся прямые а7
и b', то мы придем к теореме Паскаля для кривой второго порядка,
распавшейся на пару прямых а' и Ь'.
III. Рассмотрим теперь некоторые теоремы о центральной проекции
окружности. Мы доказали в § 18 теорему Штейнера для окружности при
помощи простых геометрических рассуждений — после центральной проекции
окружность спроектируется в коническое сечение, а два проективных пучка
прямых — в два проективных пучка прямых, откуда вытекает справедливость
теоремы Штейнера для любого конического сечения. Точно так же, доказав
теоремы Паскаля и Брианшона для окружности и применяя центральную
проекцию, мы покажем справедливость этих теорем для любого конического
сечения *).
а
F
А/
-*^Р
Рис. 146.
*) См., например, А. А. Смогоржевский [1], § 10.
§ 40] КЛАССИФИКАЦИЯ ГЕОМЕТРИЧЕСКИХ дисииплин 163
Рассмотрим теперь такую задачу: найти перспективное изображение
окружности k с центром С, лежащей в предметной плоскости (рис. 147).
На основании § 37 окружность k спроектируется в коническое сечение к',
однако при этом проекция С центра С не будет совпадать с центром С0
кривой kf. Для нахождения точки С мы не можем воспользоваться тем,
что точка С равноудалена от всех точек окружности k (ибо это
—метрическое свойство), ни тем, что любая хорда окружности, проходящая через С,
рг/
1
V
x^^^v
" Y
в
'-а /
SM
_р\
делится в этой точке пополам (ибо это —аффинное свойство); мьГдолжны
воспользоваться проективным свойством центра окружности, ибо только
оно сохраняется при центральной проекции.
В § 26 мы дали проективное определение центра: центр любого
конического сечения является полюсом бесконечно удаленной прямой- так как
окружность k проектируется в коническое сечение k','a бесконечно
удаленная прямая предметной плоскости проектируется в линию горизонта v то
при центральной проекции окружности k '
ее центр С проектируется в точку С,
являющуюся полюсом линии горизонта
относительно того конического сечения k'', в
которое^проектируется окружность; полюс
прямой v относительно конического сечения k'
строим методом, указанным на рис. 64.
Рассмотрим теперь окружность k (рис. 148)
и два пучка параллельных прямых а, Ь, ..., е
и #i, Ьь ..., ех, перпендикулярных между
собой. При параллельной проекции
перпендикулярность этих прямых, являющаяся
метрическим свойством, не сохраняется, но
сохраняется параллельность прямых и то свойство,
что каждый из диаметров сие, делит
пополам хорды, параллельные другому, ибо это —
аффинное свойство; мы получим, таким
образом, после параллельной проекции рис. 148,
эллипс &', вписанный в параллелограмм
(рис. 149), причем центр О окружности спроектируется в центр О' эллипса
а диаметры с и сх окружности-в сопряженные диаметры с' и с[ эллипса'
(оис 15оГп?,и1ТеПерЬ' ЧТ° П0ЛУЧИТСЯ в Результате центральной проекции
(рис. 150), пучки параллельных прямых а, Ь, ..., е и al9 *,,..., ех спроекти-
руются в пучки пересекающихся прямых S(a"t b", е")и S (a" b" е\
касательные а, е, ах, ех к окружности спроектируются в 'касательные
Рис. 148.
164
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
[ГЛ. V
а >..., е и flj ^ к коническому сечению. Несобственная точка
пересечения прямых я, 6,..., е является полюсом прямой си следовательно,
точка S является полюсом прямой clf а точка S{ — полюсом прямой с"
относительно конического сечения k"\ в таком случае точка О" пересечения
прямых с и СрВ которую
проектируется центр О окружности,
является полюсом прямой SSU
в которую спроектируется
бесконечно удаленная прямая плоскости
окружности k.
Благодаря симметрии ясно,
что из точки N (рис. 148) точки
L, Р, Н, ... и точки G, Q, F, ...
проектируются посредством двух
проективных пучков прямых; из
свойств окружности,
рассмотренных в § 18, вытекает, что это
же заключение справедливо, если
точку N заменить любой другой
точкой окружности, т. е. парал-
пересекают окружность в двух рядах точек,
образующих инволюцию; после центрального проектирования точки L"
и G , Р" и Q", Н" и F", ... образуют инволюцию; таким образом,
свойство, установленное сперва для окружности, является общим свойством
всех конических сечений: два перспективных ряда точек на коническом
сечении образуют инволюцию (при этом под ангармоническим отношением
Рис. 149.
лельные прямые Ь, с, d,
Рис. 150.
четырех точек на коническом сечении понимается ангармоническое
отношение четырех прямых, проектирующих эти точки из любой точки конического
сечения).
Примечание. Интересно отметить, что эта теорема нам уже известна
для того частного случая, когда кривая второго порядка распадается на
пару прямых; действительно, рассмотрим два перспективных, а следовательно,
§41]
КВАДРАТИЧНОЕ СООТВЕТСТВИЕ
165
и проективных ряда точек g (А, В, С, ...) и g' (А', В\ С, ...) (рис. 151)
на двух прямых g и g''. Будем считать эти обе прямые составными частями
одной кривой второго порядка k с уравнением gg' = 0; тогда оба ряда
точек перспективны, лежат на одном основании k и не только проективны,
но и образуют инволюцию, ибо, если точку А заменить соответствующей
ей точкой А', то этой последней будет
соответствовать точка А, т. е. каждые две
точки, лежащие на одном и том же луче,
соответствуют друг другу вдвойне. ——-^JZl \д'
§ 41. Квадратичное соответствие
I. Как было сказано в § 37,
наиболее общее взаимно однозначное
соответствие между точками двух
плоскостей, преобразующее прямую в
прямую, осуществляется проективным Рис. 151.
преобразованием (36.11); поэтому
простейшим преобразованием после проективного является так
называемое квадратичное преобразование (или соответствие), которое
каждой прямой одной плоскости ставит в соответствие коническое
сечение второй плоскости.
Пусть
х, _ А (*. У) ' v/_ /а(*. У) /41 П
где все функции fv ..., /4 не выше второго порядка (типа левой
части уравнения (5.5)) подчинены следующим условиям:
а) если все функции fv . .., /4 не выше первого порядка, то
знаменатели /2 и /4 не совпадают;
б) если хоть одна из функций /г /4 второго порядка, то
знаменатели /2 и /4 совпадают.
Мы имеем в случае а)
Ах' + Ву' + С= ЛА/*+ В/// + С/гЛ ,
J2JA
а в случае б)
мы видим, что в обоих случаях прямой с уравнением
Ах' + Ву'-\-С = 0 (41.2)
соответствует кривая второго порядка; следовательно,
преобразование (41.1) при наших условиях осуществляет квадратичное
соответствие между точками обеих плоскостей.
Следует, однако, отметить, что в рассматриваемом общем случае
это соответствие не будет взаимно однозначным, ибо, решая (41.1)
относительно х и у, мы не получим единственного решения^
166 ПРЕОБРАЗОВАНИЯ КООРДИНАТ [ГЛ. V
рассмотрим поэтому несколько частных случаев квадратичного
соответствия, являющегося взаимно однозначным.
II. Преобразование Котелъникова. Мы рассмотрели в § 15
преобразование Котельникова
(М — У)х ,_ (k0x — y)y
k0x * У kQ>
xlz=W-y)Xt у1=аУ^-У)У t (4L3)
KnX /CnX
подходящее под тип (41.1); обратное преобразование
ko* — У k0x' — yf v '
также является однозначным и подходит под этот же тип; прямая
(41.2) преобразуется в гиперболу
Ak0x2~i-(Bk0 —А)ху — By2-}-Ck0x = 0. (41.5)
Применяя преобразование Котельникова к кривой Бурместера (8.4),
мы получим:
(а:2 -f- У2) (тх + 1у) — 1т ху =*
= (kjf-yy [/ео (т х> + у') (*'* + у'2) - ту' <*о*' - У'] ] '
если положить k0 = т-, то кривая Бурместера преобразуется
в окружность с уравнением
*'2-f у'2 — /у' = 0. (41.6)
III. Соотношение (15.9) между радиусами-векторами г и г'
точек подвижной плоскости и центров кривизны их траекторий.
Умножая (15.9) на coscp и на sin ср, получим квадратичное
преобразование
"- dXy— *->'£-«• (4Ь7)
dy — x2 — y2' у dy — x2 — у2
Обратное преобразование
*_ **V v *£ (418)
также является однозначным и квадратичным. Прямой (41.2)
соответствует коническое сечение
A dxy -f В dy2 + С (dy — х2 — у2) = 0, (41.9)
касающееся оси Ох в начале координат. Бесконечно удаленной
прямой плоскости О'х'у' соответствует в плоскости Оху окружность
x* + ? — dy = Q. (41.10)
§ 4Ц
КВАДРАТИЧНОЕ СООТВЕТСТВИЕ
167
IV. Инверсия, или преобразование при помощи обратных
радиусов-векторов. Пусть каждой точке М(х> у) плоскости Оху
соответствует точка М'(х\ у') на том же луче ОМ (рис. 152),
причем
ОМ -ОМ' = /?2;
мы скажем, что точка М' получена из точки М посредством
инверсии относительно основной окружности с центром в точке О
и радиусом R *); если
радиус основной окружности
считать мнимым R^iRv
то получим ОМ • ОМ' =
= — /?2, т. е. в этом случае
точки М и М' лежат на
одной прямой, проходящей
через центр основной
окружности, но по разные
стороны от него. Нетрудно
видеть, что координаты
точек Мг и М связаны
соотношением
R*x
у' =
лг2 + у2
R2y
(41.11)
х* + у*
Рис. 152.
подходящим под тип (41.1); обратное преобразование выражается
такими же самыми формулами
х =
R2x'
х'2 + У'2
RY
*'2+у'2
(41.12)
прямая (41.2) преобразуется в окружность
С(х2 + у*) + Афх + Вфу = 09 (41.13)
проходящую через начало координат.
Нетрудно видеть, что окружность
(x — a)2 + (y — b)2 — r2^x2 + y2 — 2ax~2by + a2-{-b2—r2==0
преобразуется в новую окружность
(а2 + Ъ2 — г2) (х'2 + У'*) — 2/?2 (ах' + by') — R* = 0.
*) Точки М и М' называются также симметричными относительно
основной окружности.
1 бв Преобразования координат (гл. V
Если же данная окружность ср проходит через центр основной
окружности ср0 (рис. 153), то а2 + #2 — г2 = 0 и новая окружность
распадается на бесконечно удаленную прямую и на прямую v с
уравнением
2(ax'-)-by')-{-R2 = 0. (41.14)
Легко видеть, что инверсия преобразует точки внутри основной
окружности в точки вне ее, и наоборот; точки на основной
окружности преобразуются сами в себя.
V. Мы уже встречались с инверсией в предыдущем изложении.
В § 15 было показано, что всякая инволюция, центром которой
является собственная точка, сводится
к инверсии относительно основной
окружности (с вещественным или
мнимым радиусом), причем центр
основной окружности совпадает
с центром инволюции, а
вещественные двойные точки инволюции лежат
в пересечении основной окружности
с прямой, на которой лежат два
ряда точек в инволюции.
В § 27 при рассмотрении
полярного соответствия относительно
Рис. 153. окружности k0 показано, что любой
полюс М и точка М' пересечения
его поляры с лучом ОМ, проведенным через центр
окружности kQt соответствуют друг другу по принципу инверсии; при
этом основная окружность инверсии совпадает с k0; отсюда вытекает
метод построения точки М' по точке Mt указанный на рис. 67;
укажем еще два метода такого построения:
а) если точка N лежит на основной окружности (рис. 152), то
имеем ОМ - OMf = ON2, т. е ОМ : ON= ON: ОМ'; так как у
треугольников ONM' и ONM общий угол при точке О, то они по*
добны, поэтому точку Мг можно найти, строя
£ ONM' = £ OMN;
б) проводим N'M0\\MN и строим ОМ' = ОМ0.
Отметим, что во всех рассмотренных случаях (41.3), (41.7),
(41.11) мы имеем у' : х' = у : х, и, таким образом, любая прямая,
проходящая через центр основной окружности, преобразуется сама
в себя (если совместить обе плоскости).
VI. Если точка M(xt у) описывает кривую Г с уравнением
f(x, y) = Q, то точка М' (x't у'), полученная преобразованием
инверсии, опишет кривую Г\ называемую инверсией кривой Г относи-
§ 41]
КВАДРАТИЧНОЕ СООТВЕТСТВИЕ
169
тельно основной окружности и характеризуемую по (41.12)
уравнением
/ R2x' R*y' \ _
(41.15)
На рис. 154 показана кривая, являющаяся инверсией параболы,
причем указано несколько пар соответствующих точек;* С. А, Чаплы*
гин изучал крылья самолета с такой
формой поперечного сечения.
Рассмотрим теперь инверсию
кривой Бурместера(8Л); мы имеем:
(х2 + у2) (тх + 1у) — Imxy =
__ R6 (тх' + ly') ImR^x'y'
~~~ ix'2+y'2)2 U'2+y/2)2 '
и, таким образом, инверсией кри-
вой Бурместера относительно Рис. 154.
основной окружности с центром
в двойной точке является равносторонняя гипербола (рис. 155),
проходящая через начало координат и характеризуемая
уравнением
R2(mx' + ly') — lmx'y'=:0. (41.16)
Следовательно, если надо найти точки пересечения кривой
Бурместера с заданной прямой, то,
применив преобразование инверсии, мы
придем к более легкой задаче: найти
точки пересечения равносторонней
гиперболы (41.16) с окружностью,
проходящей через начало
координат.
Из (41.16) находим координаты
центра С гиперболы
*с = кг» Ус = — • (4Ы7)
Наконец, из (41.16) находим по
(5.6) угловые коэффициенты
асимптот гиперболы kx = оо, k2 = 0, т. е.
асимптоты гиперболы
параллельны координатным осям.
VII. Преобразование ъгиперболизмъ. Гиперболизмом называется
преобразование
. \
У
О
с
ч
\
а:
Рис. 155.
х' =х,
, ху
> = «'
(41.18)
170
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
[ГЛ. V
(41.19)
подходящее под тип (41.1); обратное преобразование также будет
однозначным и квадратичным
ау'
х = х\ у = -£г,
но уже не будет гиперболизмом.
Гиперболизм преобразует прямую (41.2) в гиперболу *)
Аах + Вху + Са = 0.
(41.20)
Гиперболизмом данной кривой Г с уравнением f(x, у)=0 является
новая кривая Г' с уравнением fix', —4-) = 0.
VIII. Мы установили квадратичное соответствие чисто
аналитическим путем — посредством формулы (41.1); покажем теперь
геометрический метод установления такого соответствия.
Рассмотрим в плоскости Р (рис. 156) два пучка прямых
Sx{av bv dx) и S2(#2, ^2» ^г)> пусть в плоскости Р' первому
соответствует проективный пучок S\{a\, b\t d\)t а второму —
проективный пучок S2(#2, ^2. ^2); обращаем внимание на то обстоятельство,
Рис. 156.
что прямой 5^2, рассматриваемой как прямая Ьх пучка с центром Sv
соответствует прямая Ь\, а этой же прямой 5j52, рассматриваемой
как прямая £2 пучка с центром в точке 52, соответствует прямая £2»
не совпадающая с Ь\.
Возьмем в первой плоскости точку М и построим прямые ех и е2
обоих пучков; соответствующие прямые е'х и е'2 пучков второй
плоскости найдем из условия
в пересечении прямых е'х и е'2 найдем точку М'> соответствующую
точке М.
*) Этим объясняется термин «гиперболизм», введенный еще И.
Ньютоном при рассмотрении кривых третьего порядка.
§ 411
КВАДРАТИЧНОЕ СООТВЕТСТВИЕ
171
Точки S[, S2 и точка S'3 пересечения прямых Ь{ и Ь2 называются
главными точками, а прямые S^S^ SjSg» ^2^3 — главными прямыми
квадратичного соответствия. Точно так же, пусть при обратном преобразовании
прямой S[S2, рассматриваемой как прямая Д пучка с центром S[,
соответствует прямая /, а прямой S^, рассматриваемой как прямая /2 пучка
с центром S2, пусть соответствует прямая /, пересекающая прямую f{
в точке S3; точки S{, S2, S3 называются главными точками, а прямые SjS2,
Si53, 52S3 — главными прямыми квадратичного соответствия.
Пусть точка пересечения М соответствующих прямых пучков с
центрами в точках Sx и S2 движется по прямой g, т. е. эти пучки перспективны,
а следовательно, и проективны; пучки прямых с центрами в точках SY и S2
проективны указанным пучкам, а поэтому проективны друг другу; если бы
прямые Ьх и Ь2 совпали, то у этих проективных пучков прямая SXS2
соответствовала бы сама себе; но в таком случае эти пучки были бы перепек-
тивны,. т. е. прямая преобразовалась бы в прямую и мы имели бы не
квадратичное, а проективное соответствие, рассмотренное на рис. 133.
Пусть сперва прямая g не проходит через главную точку, по
теореме Штейнера точка пересечения М соответствующих прямых проективных
пучков с центрами Sx и 52 описывает кривую второго порядка е — в
данном случае коническое сечение, проходящее через главные точки Sv S2, S3.
Пусть теперь прямая g проходит через главную точку, но не
является главной прямой (рис. 157); любой ее точке М, не совпадающей
с точкой Slt соответствует точка М' пересечения прямых g' и т2,
соответствующих прямым g и т2\ однако точке Sx первой плоскости не
соответствует никакая определенная точка второй — ей соответствует любая
Рис. 157.
точка К' прямой Ь2, действительно, точка к! лежит в пересечении прямых Ъ2
и k', которым соответствуют прямые Ь2 и k, пересекающиеся в точке S^
следовательно, если точка первой плоскости описывает прямую, проходящую
через главную точку, но не являющуюся главной прямой, то кривая £
распадается на пару прямых, одна из которых проходит через одноименную
главную точку, а вторая совпадает с противоположной ей главной прямой
(в данном случае эти прямые gr и ь'Л.
Пусть, наконец, прямая g совпадает с главной прямой', в этом случае
кривая е распадается на пару других главных прямых (рис. 158);
172
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
(гл. $
действительно, любой точке М' на прямой b[t или точке N' на прямой Ь2
соответствует точка на прямой SiS2.
Частным случаем квадратичного соответствия, установленного
геометрическим путем, является соответствие фокусов Fx и F2 конического
сечения, касающегося трех прямых, рассмотренное в § 31 (рис. 98); легко
видеть, что в данном случае точки S{ и S2 совпадают с точками S[ и Sf2;
значению cpj = 0 соответствует в первом пучке прямая SXS2, а во втором —
прямая 5^3; следовательно, и точки S3 и S3 совпадают.
Рассмотрим тот частный случай, когда g — бесконечно удаленная
прямая; покажем, что в этом случае второй фокус F2 описывает окружности
проходящую через главные точки
Si, S2, S3; действительно, если
Fx — бесконечно удаленная точка
(рис. 159), то прямые SXFX, S2FX
и Sg/7! параллельны и, кроме того,
срх = ср2; так как из точек Sx и S2
отрезок F2S3
углами, то
окружности,
ляется F2Sz
виден под равными
эти точки лежат на
хордой которой яв-
таким образом, вокруг
треугольника,
четырехугольника SYS2SSF2 можно
описать окружность, и поэтому
точка F2 лежит на окружности,
описанной вокруг треугольника SlS2Ss.
Так как фокус Fx —
несобственная точка, то он может
принадлежать только параболе; мы
доказали другим путем, что фокус
параболы лежит на окружности,
образованного тремя касательными
описанной вокруг
к ней (§ 32).
Отметим, что на рис. 159 показано решение такой задачи: найти фокус
параболы, касающейся трех заданных прямых, если известно направление
ее оси.
§ 42. Некоторые механизмы для установления квадратичного
соответствия
I. Любой коникограф *), в котором движение точки по коническому
сечению вызывается движением некоторой другой точки по прямой, уста-
*) Большое количество коникографов читатель найдет в книгах
И. И. Артоболевского ЦЗ], гл. IV, В. В. Добровольского [1], гл. I и
В. А. Юдина [1], гл. IV.
§ 42] МЕХАНИЗМЫ ДЛЯ УСТАНОВЛЕНИЯ КВАДРАТИЧНОГО СООТВЕТСТВИЯ 173
навливает механическим путем квадратичное соответствие между точками;
примером могут служить коникографы, рассмотренные в §§ 22, 31.
В качестве дальнейшего примера рассмотрим гиперболограф Верхов-
ского (рис. 160): стержни 2 и 3, вращающиеся вокруг неподвижных
шарниров А и В, соединены двухповодковой группой, которая состоит из звеньев
4 и 5, входящих во вращательную пару М\ при помощи зубчатой передачи
с передаточным числом 2: 1 (она не показана на рис. 160) стержень 6
вращается вокруг неподвижного шарнира В вдвое быстрее, чем стержень 3;
стержни 2 и 6 соединены двухповодковой группой, которая состоит из
звеньев 7 и 8, входящих во вращательную пару Mf.
Покажем, что при движении точки М по любой прямой g точка М'
описывает коническое сечение с фокусом В, директрисой g и с эксцен-
триситетом е = —г- , где d —
расстояние от неподвижного шарнира А до
прямой g.
Действительно, обозначим через d'
расстояние от точки М' до прямой g\
так как прямая MB является биссектрисой
угла В треугольника АВМ', то мы имеем
d' М'М М'В М'В АВ
Ч-^ЧАА--Ж^ОТК^-^---а-
= £ = const.
Верховский выбирает прямую g
перпендикулярной к прямой АВ и проходящей
между точками А и В; в этом случае
АВ > d, т. е. е > 1, и кривая является
гиперболой.
Примечание. Описывая этот
механизм В. Мейер Цур Капеллен ([1], стр. 163) Рис. 160.
говорит: ... «... прибор Верховского для
вычерчивания гиперболу основан на
проективном построении гиперболы с помощью двух пучков лучей» — эта
утверждение неверно: так как точка М движется по прямой g, то пучки
прямых (таких, как 2 и 3), проектирующих ее из центров А и В,
перспективны, а следовательно, и проективны, но два пучка прямых (таких,
как 3 и 6) с центром В не проективны, ибо угловые коэффициенты
&з = — tg 7, k6 = — tg 2? прямых 3 и 6 связаны соотношением k6 ■■
2k,
\-ki
не являющимся дробно-линейным; поэтому точка Мг не является точкой
пересечения соответствующих прямых двух проективных пучков и теорема
Штейнера неприменима.
II. Рассмотрим теперь такой механизм (рис. 161): по стержню 2,
который вращается вокруг неподвижного центра О, движется ползушка 3,
входящая во вращательную пару с жестким прямым углом со сторонами 4
и 4Г\ сторона 4 движется поступательно в направляющих /. Вдоль стержня 2
движется еще одна ползушка 5, входящая во вращательную пару со
стержнем 6, который вместе со второй стороной 4' прямого угла входит в
поступательную пару с крестообразным ползуном 7, прорезы которого взаимно-
перпендикулярны.
Покажем, что если точка С движется по некоторой кривой Г, то
точка D (являющаяся центром крестообразного ползуна 7), описывает
кривую Г', являющуюся гиперболизмом кривой Г; при этом роль константы а
в (41.18) играет расстояние от шарнира О до оси стержня 4.
174
Преобразований координат^
[гл. V
Действительно, для точек С (х, у) и D (х', у') имеем:
ON ау_
OK ^ х
х' = х = ОК, у' = DK = BN = CK-
Совершенно аналогично можно доказать, что координаты точек С (х, у)
У\
Рис. 161,
Рис. 162.
и D (х\ yf) механизма, изображенного на рис. 162, связаны квадратичным
соответствием *)
х' = х, у' = —. (42.1)
III. Рассмотрим теперь инверсор, т. е. механизм, осуществляющий
инверсию.
Пусть равные стержни 2 и 3 (рис. 163), могущие вращаться вокруг
неподвижного центра О, шарнирно соединены в точках А и В с шарнирным
ромбом АМВМ\ образованным стерж-
д нями 4, 5, 6, 7.
Треугольники ОАМ и ОВМ равны
^^^ . . по трем сторонам, следовательно, точ-
^^^^ 4/ \5 ка М лежит на биссектрисе угла AOBt
'/л О ^*^^ \М/ \М/ гак же как и точка -М'; поэтому точки О,
^3Z^r М n М' всегда лежат на одной
прямой. Опишем окружность k0 с
центром А, проходящую через точки М
и М'; тогда будем иметь ОМ • ОМ' =
= ОТ2, где ОТ — отрезок касательной
к окружности k0 из точки О; так как
ОТ2 = UA2 — AM2, то окончательно
Рис. 163.
ОМ-ОМ' = R2, R=VOA2 — AM2;
таким образом, рассматриваемый механизм осуществляет инверсию,
причем центр основной окружности находится в точке О, а радиус
равен R.
*) См. И. И. Артоболевский [3], § 9.
§ 42] МЕХАНИЗМЫ ДЛЯ УСТАНОВЛЕНИЯ КВАДРАТИЧНОГО СООТВЕТСТВИЯ 175
Этот инверсор был впервые построен французским артиллеристом По-
селье (1864 г.), а затем, независимо от него, русским студентом Липкиным
(1871 г.), слушателем лекций П. Л. Чебышева *).
Если в инверсоре заставить точку М двигаться по окружности k,
проходящей через точку О, то по рис. 153 точка М' будет двигаться строго
прямолинейно; следовательно, если
ввести добавочный кривошип 8
(рис. 164), причем О'М = -^ ОМ, то
мы получим так называемый
точный прямолинейно-направляющий
механизм, или, короче, точное
прямило; если же центр О'
немного сместить, то точка М' будет
описывать дугу окружности очень
большого радиуса.
В книгах И. И.
Артоболевского [3] (§ 12), В. А. Юдина [1],
гл. 1 и Р. Бейера [3] (§§ 103,
104, 106) читатель найдет целый ряд
точных и приближенных прямил,
П. Л. Чебышева», т. II, он сможет ознакомиться с методами,
ными указанным ученым для построения приближенных прямил.
Рис. 164.
а в сборнике «Научное наследие
разработан-
*) В книге И. И. Артоболевского [3], §§ 7, 10 читатель найдет
некоторые другие типы инверсоров.
ГЛАВА VI
КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
В предыдущих главах мы рассмотрели ряд основных понятий и
теорем проективной геометрии, причем доказательства мы проводили
по преимуществу аналитическими методами; теперь мы покажем
графические методы, позволяющие решать основные задачи
проективной геометрии при помощи простых построений посредством
циркуля и линейки.
§ 43. Проективные и перспективные ряды точек и пучки прямых
I. Пользуясь принципом двойственности, будем рассматривать
одновременно ряды точек и пучки прямых.
Для того чтобы два
проективных ряда точек s {А, В,
С, ...), s'(A\ В', С, ...) были
перспективны, необходимо и
Для того чтобы два
проективных пучка прямых S(a,
Ъ, с, ...), S'(a', V, с', ...)
были перспективны, необходимо
S
Ну
Рис. 165.
достаточно, чтобы точка
пересечения прямых s и s'
соответствовала сама себе.
Если оба ряда точек
перспективны с центром перспективы 5
(рис. 165, а) и если точку пере-
и достаточно, чтобы прямая,
соединяющая точки S и S',
соответствовала сама себе.
Если оба пучка прямых
перспективны с осью перспективы s
(рис. 165, б) и если прямую, со-
§ 43] ПРОЕКТИВНЫЕ И ПЕРСПЕКТИВНЫЕ РЯДЫ ТОЧЕК И ПУЧКИ ПРЯМЫХ 177
сечения прямых s и s' обозначим
через X в первом ряде и через
Хг во втором, то прямые SX и
SX' совпадают, точка
пересечения соответствует сама себе, т. е.
указанное условие необходимо.
Докажем достаточность;
пусть дано, что точка X
соответствует точке А"7; соединим
соответствующие точки А и А'', В и В'
прямыми а и Ъ и точку их
пересечения обозначим через 5.
Проведем прямую с через точки 5 и С,
и пусть она пересечет прямую sf
в точке С"; так как ряды
точек
s(X, А, В, С) и s' (X', А', В', С")
перспективны, то
(ХАВС) = (Х'А'В'С);
но по условию имеем:
(ХАВС) = (Х'А'В'С).
откуда видно, что точка С"
совпадает с точкой С и оба ряда
точек перспективны.
Если даны два ряда точек
& (Л, £, С, ...)us'(A',B\C',...),
проективных, но не
перспективных, то всегда можно найти
третий ряд точек,
перспективный обоим заданным рядам.
Обозначим через а прямую,
соединяющую точки А и А'
(рис. 166, а); проектируя оба за-
единяющую точки 5 и Sf,
обозначим через х в первом пучке
и через х! во втором, то точки
пересечения прямых х и 5 и
прямых хг и sf совпадают,
прямая SS' соответствует сама себе,
т. е. указанное условие
необходимо.
Докажем достаточность;
пусть дано, что прямая х
соответствует прямой х'\ найдем точки
пересечения А и В соответствующих
прямых а и а', Ъ и Ъ' и через
точки А и В проведем прямую 5.
Найдем точку С пересечения
прямых с и 5, и пусть прямая с"
проектирует ее из центра S'; так
как пучки прямых
5(дг. a, ft, с) и S'(x\ а', Ь\ с')
перспективны, то
(xabc) = (х'а'Ь'с");
но по условию имеем:
{xabc) = (х' а'Ь' с'),
откуда видно, что прямая с"
совпадает с прямой с' и оба пучка
прямых перспективны.
Если даны два пучка
прямых S(a, b, с, ...) и S' (а\ Ь!,
с', ...), проективных, но не
перспективных, то всегда
можно найти третий пучок
прямых, перспективный обоим
заданным пучкам.
Обозначим через А точку
пересечения прямых а и а' (рис. 166,5);
пересекая оба заданных пучка
II. Рассмотрим теперь теорему, которая позволит нам весьма
просто строить соответствующие элементы двух проективных рядов
точек или пучков прямых, не прибегая к вычислению ангармони*
ческого отношения, как мы это делали до сих пор.
178 КОНСТРУКТИВНЫЕ МЕТОДЫ
ПРОЕКТИВНОЙ ГЕОМЕТРИИ [ГЛ VI
данных ряда точек из
произвольных центров 5 и S', взятых на
прямой я, мы получим два
проективных пучка прямых S(a, Ъ,
с, ...) и S'(a\ Ь\ с', ...); так
как при этом прямая а
соответствует сама себе, то эти пучки
прямых перспективны, причем
ось перспективы s0 проходит
через точки В0 и С0 пересечения
прямых Ь и Ь\ с и с';
найденный ряд точек s0(A0, В0, С0, . ..)
перспективен ряду точек s(А, В,
С, ...) с центром перспективы 5
и ряду точек s'(A\ В\ С, ...)
с центром перспективы S\
Построив ось перспективы по
трем заданным парам
соответствующих точек, мы сможем для
любой точки D первого ряда
построить соответствующую
точку D' второго ряда; для этого
проектируем точку D из центра 5
в точку Ь0 оси перспективы
посредством прямой d> а точку D0
проектируем из центра S' в
точку Df прямой sr посредством
прямой d\
прямых произвольными прямыми S
и s\ проведенными через точку Л,
мы получим два проективных
ряда точек s(A, В, С, ...) и
sf (А\ В', С', . . .); так как при
этом точка А соответствует сама
себе, то эти ряды точек пер-
спективны, причем центр
перспективы S0 лежит в точке
пересечения прямых Ь0 и с0, соеди-
■S,
няющих точки В и В\ С и С'\
найденный пучок прямых S0(a0,
b0, с0, ...) перспективен пучку
S(a, b, с,...) с осью
перспективы 5 и пучку прямых Sr (a'% V %
с\ . ..) с осью перспективы s\
Построив центр перспективы
по трем заданным парам
соответствующих прямых, мы сможем
для любой прямой d первого
пучка построить соответствующую
прямую d' второго пучка; для
этого находим точку D
пересечения прямых d и 5, проектируем
точку D из точки S0 в точку D'
прямой s' посредством прямой d6,
а точку U проектируем из
центра S' посредством прямой d'f
Рис. 166.
s
§ 44] ПОСТРОЕНИЕ ДВОЙНЫХ ЭЛЕМЕНТОВ 179
Мы покажем в дальнейшем (§§ 46, 48), что указанные
построения можно упростить за счет специального выбора точек 5 и S', или
прямых 5 и sf.
§ 44. Построение двойных элементов
I. При рассмотрении проективного соответствия на одном
основании (два р!да точек в § 15, два пучка прямых с общим центром
в § 18) мы ввели понятие о двойных элементах такого
соответствия; в ряде дальнейших теорем мы встречались с двойными
точками и двойными прямыми; покажем теперь построение Штейнера,
позволяющее найти их графическим путем.
Пусть на прямой g даны два проективных ряда точек
g(A, В, С, ...) и g(Af, В', С, ...) (рис. 167); проектируя их из
любого центра 5, мы получим два проективных пучка прямых
у Л ЛВС В' С" У Л'
Рис. 167.
S(a, b, с,...) и S(a\ b', с',...) с общим центром 5; ясно, что
прямые, проектирующие искомые двойные точки, являются в то же
время двойными прямыми.
Проведем произвольную окружность k через точку 5 и отметим
точки Av Bv Cv Аъ В\, С\ ее пересечения с проективными пучками
прямых; спроектируем из точки Ах точки А'у В'у С'х прямыми av рх, fi
и спроектируем из точки А!х точки Av Bv Сх прямыми <х|, (5|, Y\> на
основании свойства окружности, рассмотренного в § 18 (или на основании
180 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИЙ [гл. VI
теоремы Штейнера, §§ 22, 23), мы имеем проективные пучки прямых
^i(ai' Pi' Ti*---) и 5(a> *» с,...)» а также Ax(av plf ^. .. .) и
£(#', &', с',...); следовательно, пучки прямых Ax(a.v fyv 7i» • • •)
и -4j(aJ, р|, Yi» ...) проективны; так как при этом прямая ах,
соединяющая центры пучков А\ и А\, соответствует сама себе, то эти
пучки перспективны, причем ось перспективы s проходит через
точки В0 и С0 пересечения прямых (5Х и (3|, fi и Тг
Если взять произвольную точку на оси перспективы,
спроектировать ее на окружность из центров Ах и A'v а полученные точки на
окружности спроектировать на прямую g из центра S, то получим
на прямой g пару соответствующих точек; но если взять точку Х0
пересечения оси перспективы с окружностью, то она спроектируется
на окружность из центров А\ и А\ сама в себя, т. е. обе точки на
окружности сливаются в одну; поэтому прямая SX0 и точка X—
двойная прямая и двойная точка нашего проективного соответствия;
этим же свойством обладают прямая SY0 и точка К, где К0—вторая
точка пересечения оси
перспективы с окружностью.
Если ось перспективы
касается окружности, то обе
двойные точки совпадают,
если же она не имеет с
окружностью общих точек, то
двойные точки — мнимые.
II. Рассмотрим теперь
нахождение двойных элементов
инволюции (§§ 15, 18); пусть
инволюция точек на прямой g
задана двумя парами соответ-
Рис. 168. ствующих точек А и А', В
и В! (рис. 168); как было
показано в § 35, мы можем их рассматривать как точки пересечения
прямой с пучком окружностей; этот пучок вполне определяется
заданием двух окружностей е и е', которые мы получим, проводя их
через точки Л, А', Р и В, В\ Р, где Р—произвольная точка вне
прямой g. Очевидно, двойные точки инволюции соответствуют
точкам касания окружностей пучка с прямой g. Если заданные пары
точек не разделяют друг друга, как на рис. 168, то радикальная
ось PQ пучка пересекает прямую g в центре инволюции С, лежащем
вне окружностей пучка; проводя из точки С касательную СТ
к окружности е и откладывая CM = CN = CT, мы получим на
основании свойств радикальной оси двойные точки М и N нашей
гиперболической инволюции. Если заданные пары точек разделяют
§ 44] ПОСТРОЕНИЕ ДВОЙНЫХ ЭЛЕМЕНТОВ 181
друг друга (рис. 169), то центр инволюции С лежит внутри
окружностей пучка, из него нельзя провести к ним касательной и двойные
точки этой эллиптической инволюции — мнимые; наконец, если центр
инволюции С совпадает со второй точкой Q пересечения окружно-
Рис. 169. Рис. 170.
стей (рис. 170), то обе двойные точки этой параболической
инволюции совпадают с точкой С.
Если имеем инволюцию прямых с центром 5, то для
нахождения двойных прямых пересекаем прямые пучка некоторой прямой gt
не проходящей через центр 5, — получим на ней инволюцию точек;
найдя двойные точки этой инволюции и соединяя* их с центром S,
получим двойные прямые.
Рис. 171.
III. Покажем еще построение двух взаимно-перпендикулярных
соответствующих прямых, имеющихся в каждой инволюции
прямых (§ 18); пусть инволюция прямых с центром 5 задана двумя
парами соответствующих прямых а и а', Ъ и Ь' (рис. 171); проводя
снова прямую g, получим на ней инволюцию точек, определяемую
двумя парами точек А к А', В к В'. Проводим окружности е и е'
182 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [гл. VI
Рис. 172.
точками Ах, А2, Аг, Л4
через точки А, А'\ S и Б, В\ S; так как они определяют пучок
окружностей, центры которых лежат на одной прямой (§ 35), то,
соединяя прямой центры Е и Е' окружностей е и е'\ мы получим
в ее пересечении с прямой g точку Н. Окружность е0 с центром Н
и радиусом HS принадлежит
пучку; она пересекает
прямую g в двух точках X й Х\
соответствующих друг другу,
поэтому прямые х и х',
соединяющие эти точки с
центром 5, соответствуют друг
другу и в то же время взаимно-
перпендикулярны .
IV. В качестве иллюстрации
рассмотрим решение такой задачи
(рис. 172): построить коническое
сечение, определяемое четырьмя
(из которых никакие три не лежат на одной
прямой) и касательной и (не проходящей ни через одну из этих точек).
На основании теоремы Паскаля (§ 24) задача будет решена, если мы
найдем точку касания Аъ касательной и. Через заданные четыре точки можно
провести пучок кривых второго порядка (§ 20), который в пересечении
с прямой и дает инволюцию точек; если кривая, принадлежащая пучку,
касается прямой и, то точка касания является двойной точкой инволюции;
следовательно, наша задача сводится к нахождению двойных точек
инволюции, определяемой пересечением прямой и с пучком. Рассмотрим
кривую пучка, распадающуюся на пару прямых а и а', соединяющих
точки Ах и А4, А2 и Аъ; она пересекает прямую и в точках А и А'; точно
так же находим точки В и В' пересечения прямой и с прямыми bub',
соединяющими точки Ах и А2, Агп А4.
Имея две пары соответствующих
точек, находим двойные точки
инволюции X и Х'\ на рис. 172
изображен тот случай, когда они
вещественны и задача имеет два решения,
ибо любую из них можно принять за
точку А5; в случае совпавших
двойных точек имеем одно решение, в
случае мнимых— ни одного.
Совершенно аналогично решается
задача, взаимная рассмотренной
(рис. 173): построить коническое
сечение, касающееся четырех
заданных прямых ах, а2, а3, аА (из которых
никакие три не проходят через одну
точку) и проходящее через заданную точку U (не лежащую ни на одной
из этих прямых). Действительно, на основании теоремы Брианшона (§ 29)
задача будет решена, если мы найдем пятую касательную аъ, проходящую
через точку U; касательные ко всем кривым семейства, проведенные из
точки U, образуют инволюцию прямых (§ 29), двойные прямые которой
соответствуют двум совпавшим касательным, что может быть только в том
случае, когда точка U лежит на кривой семейства. Инволюция прямых
Рис. 173.
§ 45] ГАРМОНИЧЕСКИЕ СВОЙСТВА ПОЛНОГО ЧЕТЫРЕХУГОЧЬНИКА 183
вполне определена двумя парами прямых а и а\ b и Ь\ которые
соответствуют двум кривым семейства, выродившимся в пары точек А и А', В
и В'\ так как в данном случае эти пары прямых разделяют друг друга, то
имеем эллиптическую инволюцию с мнимыми двойными прямыми, т. е.
задача не имеет решения.
V. Рассмотрим еще такую задачу: даны две пары сопряженных
диаметров а и а'', Ь и Ъ' центрального конического сечения; найти его оси
симметрии и асимптоты (в случае гиперболы).
Сопряженные диаметры центрального конического сечения образуют
инволюцию прямых (§ 28), причем оси симметрии являются
соответствующими взаимно-перпендикулярными прямыми этой инволюции
прямых, определенной двумя парами прямых. Их легко найти при помощи
построения, показанного на рис. 171.
Асимптоты являются двойными прямыми этой инволюции прямых
(§ 28); они будут вещественными лишь в случае гиперболической
инволюции, при которой заданные пары прямых а и а', b и br не разделяют друг
друга. Их нетрудно найти при помощи построения Штейнера, показанного
на рис. 167.
§ 45. Гармонические свойства полного четырехугольника
и полного четырехсторонника
I. Полным четырехугольником называется фигура,
образованная четырьмя точками (вершинами), из которых никакие три
не лежат на одной прямой, и шестью прямыми (сторонами), яро-
ходящими через эти точки] на рис. 174 имеем четыре вершины
Рис. 174.
А, В, С, D и шесть сторон vv ..., v6; пара сторон, на которых
лежат все четыре вершины, называется парой противоположных
сторон {vx и v2> vz и vv v5 и v6); каждая пара противоположных
сторон пересекается в точке, не являющейся вершиной и называемой
184 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [ГЛ. VI
диагональной точкой (L, М и N); прямые, соединяющие
диагональные точки, называются диагоналями (I, т, п) *).
Докажем, что полный четырехугольник обладает следующими
свойствами: 1) любая прямая пересекает три пары
противоположных сторон по трем парам точек, образующих инволюцию]
2) на каждой диагонали имеем гармоническую группу,
образованную двумя диагональными точками и двумя точками
пересечения этой диагонали с третьей парой противоположных
сторон, т. е.
(LNSQ) = (MNGP) = (LMKT) = — 1; (45.1)
3) на каждой стороне имеем гармоническую группу,
образованную двумя вершинами, диагональной точкой и точкой
пересечения стороны с диагональю, соединяющей две другие
диагональные точки, т. е.
(ADLP) = (ABMS) = (ВСЮ) = (DCMQ) =
= (BDKN) = (ACTN) = — 1. (45.2)
Для доказательства 1) достаточно вспомнить теорему § 20 о
пересечении прямой с пучком кривых второго порядка и применить
ее к трем кривым пучка, распадающимся на прямые vx и v2, v3 и v4,
v5 и v6\ свойство 2) получим, применяя свойство 1) к диагоналям;
диагональные точки в этом случае являются двойными точками
инволюции; беря, например, точки L и N диагонали т за основные
точки при нахождении ангармонического отношения, мы имеем по
§ 15 (LNSQ) =— 1; для доказательства свойства 3) обратим
внимание на то, что ряды точек v2(A, D, L, Р), m(S, Q, L, N) и
vx(B, С, L, О) перспективны с центром перспективы М, откуда
по (13.4)
(ADLP) = (ВСЮ) = (SQLN) = (LNSQ) = — 1.
II. Из доказанной теоремы вытекает способ построения четвертой
точки D, образующей с заданными точками А, В, С гармоническую группу;
проведем через точку С произ-
2) J) D вольную прямую (рис. 176),
возьмем на ней две произвольные
точки Е и F\ соединяя эти точки
с точками А к В получим четы-
«/ \ л/ \ д А\ рехугольник EHFG с диагональ-
** ^ * ^ * V \ \ ными точками А, В, К', обозна-
*) Мы называем
четырехугольник полным потому, что мы
рассматриваем не только четыре
прямые, как в геометрии, а шесть;
кроме того, полный
четырехугольник содержит три четырехугольника в обычном смысле этого
£ЛОв3 __ АВСР ADBC, АСОВ (рис 175).
§ 45] ГАРМОНИЧЕСКИЕ СВОЙСТВА ПОЛНОГО ЧЕТЫРЕХУГОЛЬНИКА
185
чая через D точку пересечения прямых GH и АВ, мы имеем на основании
свойства 2) диагонали равенство (ABCD) = —1 *).
Примечание 1. Свойство 3) сторон полного четырехугольника
можно вывести также следующим образом (рис. 177): рассмотрим
параллелограмм A0B0C0D0, у которого диагональные точки М0 и LQ ушли в
бесконечность, a S0Q0 и G0P0 — прямые,
проведенные через центр N0
параллельно соответствующим сторонам; так
как концы отрезка, его середина
Мп
Рис. 177.
и бесконечно удаленная точка образуют гармоническую группу, то мы имеем
для каждой стороны
{A0DQL0P0) = (B0CQL0G0) = (A0B0M0S0) = (DQC0M0Q0) =
= (A0C0T0N0)=z(B0Q0K0N0) = —}t (45.3)
где Т0 и Ко — бесконечно удаленные точки прямых А0С0 и B0D0. При
центральной проекции бесконечно удаленная прямая L0M0 преобразуется
в прямую LM рис. 174, параллелограмм A0BQC0D'0 — в
четырехугольник ABCD; соотношение (45.3) перейдет в (45.2), ибо при центральной
проекции ангармоническое отношение
остается неизменным.
Примечание 2. Если даны
прямые vx и v2 и точка М
(рис. 174), то из равенств
(A BSM) = (PGNM) = (DCQM) =
= — 1 мы видим, что прямая m
является полярой точки М
относительно кривой второго
порядка, распавшейся на пару
прямых vx и v2\ для ее построения
совсем не нужно находить точки
как четвертые гармонические:
проводим через точку М (рис. 178) две произвольные прямые
т>з и v^ пересекающие прямые vx и t/2 в точках Л, В, С, D,
и находим точку N пересечения прямых АС и BD, — искомая прямая
проходит через точки L и N; если точка L недоступна, то
Рис. 178.
*) Этот метод построения требует лишь проведения прямых линий,
т. е. может быть выполнен при помощи одной линейки, в отличие от метода
построения § 13, для выполнения которого нужны линейка и циркуль.
186 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [гл. VI
проведем через точку М еще одну прямую v', пересекающую
прямые vx и v2 в точках F и Е, и находим точку R пересечения
прямых BF и ЕА,— прямая NR должна пройти через точку Z,*).
Отметим также, что из § 26 вытекает следующее свойство
четырехугольника, вписанного в коническое сечение: каждая диагональ
является полярой соответствующей диагональной точки
относительно всех кривых
второго порядка, проходящих
через его вершины.
III. Введем теперь такое
определение: полным
четырехсторонником называется
фигура, образованная
четырьмя прямыми
{сторонами) и шестью точками их
пересечения (вершинами); на
рис: 179 имеем четыре стороны
а, Ъ, с, d и шесть вершин
Vv . . ., V6; пара вершин, через
Ц которые проходят все четыре
^ М /£ стороны, называется парой
рис 179 противоположных вершин
{V, и V2, V3 и V4, V5 и V6);
через каждую пару противоположных вершин проходит прямая, не
являющаяся стороной и называемая диагональю (/, т, п)\ точки
пересечения диагоналей называются диагональными точками (L, М, N).
Пользуясь принципом двойственности, легко находим свойства
полного четырехсторонника, аналогичные свойствам полного
четырехугольника: 1) три пары прямых, соединяющих любую точку
с тремя парами противоположных вершин, образуют
инволюцию (например, GVX и GV2, GV3 и GK4, GV5 и СУ6); 2) через
каждую диагональную точку проходят четыре прямые, образующие
гармоническую группу, две диагонали и две прямые,
соединяющие эту точку с третьей парой противоположных вершин, т. е.
(lnsq) = (mngp) = (lmkt)=z—1; (45.4)
3) через каждую вершину проходят четыре прямые,
образующие гармоническую группу: две стороны, диагональ и прямая,
соединяющая вершину с диагональной точкой, в которой
пересекаются две другие диагонали, т. е.
(adlp) = (abms) = (bclg) = (dcmq) = (bdkn) = (actn) = —1. (45.5)
*) Мы пришли из совершенно других соображений к тому же
построению, которое было рассмотрено в § 22 для проведения прямой через
заданную точку и недоступную точку пересечения двух прямых.
§ 45] ГАРМОНИЧЕСКИЕ СВОЙСТВА ПОЛНОГО ЧЕТЫРЕХУГОЛЬНИКА 187
Рис. 180.
Применим свойство 2) к диагональной точке S и покажем, как
построить прямую d, образующую с данными прямыми а, Ь, с гармоническую
группу (рис. 180): возьмем на прямой с произвольную точку V2 и проведем
через нее две произвольные прямые е и /; находя их точки пересечения
с прямыми а и Ь, получим четырехсторонник ehfg с диагоналями a, Ь, k\
обозначая через d прямую,
соединяющую точки пересечения V, и S
прямых g и h, а и Ь, имеем {abed) =
IV. Мы можем получить
некоторые свойства полного
четырехсторонника а, Ъ, с, d (рис. 179),
если рассмотрим семейство
кривых второго класса, вписанных
в этот четырехсторонник (§ 29);
пары противоположных вершин
^ и l/2, V3 и V4, V5 и V6 будем
считать тремя кривыми семейства,
выродившимися в пары точек.
Свойство 1) полного четырехсторонника вытекает из того, что
мы получим инволюцию прямых, если из произвольной точки
проведем касательные к кривым семейства (§ 29); эти
касательные вырождаются в прямые, соединяющие выбранную точку с
парами противоположных
вершин.
Докажем теперь теорему
Гаусса: середины трех
отрезков, образованных тремя
парами противоположных
вершин полного
четырехсторонника, лежат на одной
прямой (рис. 181).
Мы доказали в § 29, что
центры всех кривых семейства
лежат на одной прямой; для
наших выродившихся кривых
^центрами являются точки X,
Y, Z — середины отрезков
VXV2, V3VA и V5V6.
Отсюда следует теорема Ньютона: если парабола вписана в
четырехсторонник, то прямая, фигурирующая в теореме Гаусса,
параллельна оси параболы.
Действительно, среди кривых семейства найдется, как показано,
одна парабола, центр который, являющийся бесконечно удаленной
точкой ее оси, должен лежать на найденной прямой, следовательно,
эта прямая параллельна оси параболы.
Рис. 181.
188 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [гл. VI
V. Рассмотрим еще одну простую теорему, в которой фигурируют
и четырехсторонник, и четырехугольник: если четырехсторонник, описан*
ный вокруг конического сечения е, является параллелограммом, то
вписанный в е четырехугольник, вершинами которого являются точки
касания, также является
параллелограммом, причем центры обоих
параллелограммов совпадают с цен*
тром е и диагонали каждого из них
параллельны сторонам другого.
Пусть прямые а\\Ь и c\\d
касаются е *), а А, В, С, D — точки
касания, являющиеся вершинами
вписанного четырехугольника (рис. 182).
Точки касания двух
параллельных касательных лежат на диаметре,
сопряженном с направлением этих
касательных, следовательно, CD и АВ
являются диаметрами е, точка О их
пересечения является центром е, причем отрезки CD и АВ делятся в точке О
пополам; поэтому фигура ACBD — параллелограмм.
Так как а и d — касательные к £ в точках А и D, то прямая AD
является полярой точки Р, а прямая С В — полярой точки М; по свойству
взаимности прямая РМ является полярой точки пересечения прямых AD
и СВ, т. е. бесконечно удаленной точки; по § 26 прямая РМ, так же как
и прямая NQ, является диаметром е, т. е. проходит через его центр **).
Касательные а и b параллельны диаметру CD, сопряженному с
диаметром АВ; точно так же касательные с и d параллельны диаметру АВ.
С другой стороны, диаметр РМ делит
пополам хорды AD и ВС, т. е. он должен быть щ С о М
параллелен сторонам АС и BD, а диаметр
NQ — параллелен сторонам AD и ВС.
Примечание 3. В случае эллипса
теорему можно доказать проще: рассмотрим а
квадраты (рис. 183) а, Ь, с, d и ABCD,
описанный вокруг окружности и вписанный в нее
с центрами в центре окружности; при аффин- Д к —"Ж ъВ
ном преобразовании (т. е. параллельном
проектировании) получим рис. 182.
VI. В качестве иллюстрации свойств
четырехугольника и четырехсторонника рассмотрим
шарнирный четырехзвенник со звеньями ах,
#2» аг> аь (Рис- 184). Его можно рассматривать
как полный четырехсторонник, образованный
d D
Рис. 183.
прямыми д„ а2, аъ, #4 с вершинами Р12, Лз»
Р\а> ^23» р2\> рм> каждая из вершин Pik
является полюсом, т. е. мгновенным центром
вращения в относительном движении звеньев с
ными вершинами являются Р12 и РЪА, Р13 и Р24, Рм и Р23; такие пары
называются в синтезе механизмов парами противополюсов.
номерами /, k; противополож-
*) Наличие параллельных касательных исключает случай параболы (§ 32)
т. е. е—центральное коническое сечение.
**) Значение этой теоремы в том, что она позволяет найти центр
конического сечения по двум парам параллельных касательных.
§ 45] ГАРМОНИЧЕСКИЕ СВОЙСТВА ПОЛНОГО ЧЕТЫРЕХУГОЛЬНИКА
189
Пусть звено а4 является стойкой; по известной теореме Виллиса легко
найти передаточное число k = —-, где o>j, о>3— угловые скорости звеньев ах
и #3; мы имеем k = ■
^14^13.
P**Pi
; проводя прямую Р2АР через точку
пересечения N ПРЯМЫХ Р\2РгА И ^23^14»
мы имеем по (45.2)
(P14P34^P13) :
РцР. РцР\з
РмР РмР\,
■■-1,
откуда вытекает другой способ
нахождения передаточного числа
£ =
Р14Р
РЯз
(45.6)
^
Рассмотрим еще . одно свойство
полного четырехугольника: если р ^
/я/?и полюса в движении трех
звеньев относительно
четвертого лежат на одной прямой, то на ней лежат и все шесть полюсов
в движении всех четырех звеньев друг относительно друга, причем эти
три пары точек образуют инволюцию *).
Рассмотрим пять звеньев 1, ..., 5 и пусть полюсы Р12, Р\& Ри лежат
на прямой g (рис. 185); рассмотрим четыре полюса Ру5, Р45, Р25, Рзь — по
теореме Кеннеди — Аронгольда (§ 3) полюсы Р34, ^24» Аз лежат в
пересечении прямой g с прямыми РАЪРЪЪ, ^гбАб» ^25^35- Прямая g пересекает
три пары противоположных
р сторон полного четырехуголь-
1S ника, определяемого
вершинами Pl5, Р45» Р25> Р*5 В Трех
парах точек Pl2 и Р34, ^24 и
Р13, Рн и Р23, образующих
инволюцию; четыре звена,
о которых идет речь в
теореме,— это звенья 1, 2, 3, 4.
VII. Рассмотрим еще
я одно свойство полного
четырехсторонника, имеющее
применение в теории синтеза
механизмов: в диагональном
треугольнике полного четырехсторонника проекция каждой
вершины на противоположную сторону обладает следующим
свойством: из нее отрезки, соединяющие смежные вершины
четырехсторонника, видны под одинаковыми углами**).
Рис. 185.
*) Л. Бурместер [1], § 185.
**) См. Л. Бурместер [1], § 251.
пользуемся этим результатом в § 52.
См. также Р. Бейер [2], § 48. Мы вое-
190 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [ГЛ. VI
Пусть дан четырехсторонник я, Ъ, с, d (рис. 186) с парами
противоположных вершин Vx и V2, V3 и V4, V5 и V6, с диагоналями 1%
т, п и с диагональными точками Z, Ж, N. На основании
свойства 3) полного
четырехугольника ^з^5^4^б имеем
(V3VANL) — — 1; проектируя эти
четыре точки из центра У,
являющегося проекцией точки N
на прямую п, получим (efgn) —
= —1; так как g J_ п% то на
основании § 17 имеем ^mV^JN=
— l_ VAJN. Совершенно
аналогично получим для другой пары
вершин^ VlJN=/mm V^JN, откуда,
складывая и вычитая, найдем:
LV3jv^^v2jv,.
Аналогичными свойствами обладают точки К и S.
§ 46. Построение конического сечения по пяти
касательным или пяти точкам*)
I. Поставленную задачу легко решить при помощи теоремы
Штейнера и взаимной с ней теоремы на основании построений § 43.
Если даны пять касательных
av ..., %. то, выбирая в
качестве прямых 5 и s'
касательные ах и #2 (рис. 187, я), будем
иметь, изменяя обозначения, еще
три касательные а, Ь, с,
пересекающие прямые 5 и s' в точках
5 (Л, В, С) и s'(A\ В', С).
Выбираем вспомогательные точки 5
и Sf на прямой а и строим ось
перспективы s0 при помощи
построения рис. 166, а\ чтобы
построить новую касательную d,
проходящую через произвольную
Если даны пять точек Av ...
. . ., Л5, то, выбирая в качестве
центров пучков 5 и Sf (рис. 187,tf)
точки Ах и Л2, будем иметь,
изменяя обозначения, еще три
точки Л, В, С; проектируя их из
центров 5 и S', получим два
пучка прямых S(a, Ъ, с) и
S' (а\ Ь\ с'). Выбираем
вспомогательные прямые 5 и s'
проходящими через точку А и строим
центр перспективы S0 при
помощи построения рис. 166, б;
чтобы построить новую точку D,
*) Предполагается, что никакие три точки не лежат на одной прямой
Л никакие три касательные не проходят через одну точку.
§ 46] ПОСТРОЕНИЕ КОНИЧЕСКОГО СЕЧЕНИЯ ПО ПЯТИ КАСАТЕЛЬНЫМ 191
Рис. 187.
192 КОНСТРУКТИВНЫЕ МЕТОДЫ проективной геометрии [гл. vt
точку D первого ряда, строим,
как показано в § 43,
соответствующую ей точку Df второго
ряда; прямая d, соединяющая
точки D и Df, касается
конического сечения.
Для нахождения точек касания
прямых s и s' поступаем
следующим образом: рассматривая точку
пересечения прямых s и sf как
точку Е первого ряда,
проектируем ее из центра 5 в точку Е0
оси перспективы; проектируя
точку Е0 из центра S' на
прямую sf, получим точку Е'\ точно
так же точке пересечения
прямых s и sf как точке F' второго
ряда соответствует в первом ряде
точка F\ в частности, если
вспомогательные точки S и Sf
выбрани совпадающими с двумя
соответствующими точками
А! и А на заданных
касательных, то ось перспективы
является полярой точки
пересечения этих касательных-,
действительно, в этом частном
случае точки касания на
касательных 5 и sf лежат на оси
перспективы 50.
лежащую на прямой d,
проходящую через точку 5, строим, как
показано в § 43,
соответствующую ей прямую d' второго пучка;
точка D пересечения прямых d
и d' лежит на коническом
сечении.
Для нахождения касательных
в точках S и У поступаем
следующим образом: рассматривая
прямую SS' как прямую е
первого пучка, находим точку ее
пересечения с прямой s и
проектируем эту точку из центра
перспективы на прямую $';
получим прямую е'\ точно так же
прямой SS' как прямой /'
второго пучка соответствует в
первом пучке прямая /; в
частности, если вспомогательные
прямые s и sf выбраны
совпадающими с двумя
соответствующими прямыми а' и а
обоих пучков, то центр
перспективы является полюсом
прямой, соединяющей центры
этих пучков, действительно,
в этом частном случае
касательные в точках S и Sf проходят
через центр перспективы SQ.
Покажем еще один способ выбора вспомогательных прямых при
построении конического сечения по пяти точкам 5, S', А, В, С\
в качестве прямых s и sf выберем прямые АС и АВ\ на рис. 188
построен соответствующий центр перспективы 50. Для прямой d
первого пучка построим соответствующую прямую d' второго пучка,
причем точка D пересечения этих прямых лежит на коническом
сечении; если перенумеровать вершины так, как показано на рис. 188,
то мы видим, что три точки S0, X, Y пересечения трех пар
противоположных сторон {АХА2 и АААЪ, A2AZ и АЬА6, АгАА и АеАх)
лежат на одной прямой; таким образом, из теоремы Штейнера мы
получили новое, чисто геометрическое доказательство теоремы
Паскаля; совершенно аналогично можно доказать и теорему Бриан-
шона.
§ 4б] ПОСТРОЕНИЕ КОНИЧЕСКОГО СЕЧЕНИЯ ПО ПЯТИ КАСАТЕЛЬНЫМ 193
На рис. 189 изображен механизм *), который можно рассматривать как
материализацию рис. 188: точка М описывает коническое сечение,
проходящее через заданные пять точек; S, S\ S0 — центры неподвижных шарниров,
точки В и С лежат в пересечении осей направляющих прямых с
прямыми SS0 и S'S0; А — точка
пересечения этих осей.
Примечание. Мы считаем
заданными пять точек и строим
лучи, проектирующие три из них
из двух центров; пусть теперь
заданы четыре точки S, S\ А В,
а пятая точка С является точкой
пересечения прямых с и с',
вышедшей за пределы чертежа
(рис. 190); строим центр
перспективы SQ так же, как на рис. 188;
для этого надо знать прямую BS
и прямую, соединяющую точки
пересечения прямых с и s, с' и s'\
после этого произвольно
выбираем прямую d, строим
соответствующую ей прямую df и
точку Д которую можно принять
за пятую точку вместо точки С **).
Л=/?£
s-л.
и=д>
В=А,
Рис. 188.
II. Мы можем построить
указанным способом сколько
угодно новых касательных и найти их точки касания, или новых точек
и найти касательные в них (см. §§ 24, 29); так как коническое сечение
Рис. 189.
вполне определяется пятью элементами (точками или касательными), то
*) См. В. В. Добровольский [1], стр. 23.
**) См., например, И. И. Артоболевский, 3. Ш. Блох, В. В.
Добровольский [1], фиг. 294; точка те на этой фигуре — центр перспективы.
194 конструктивные методы проективной геометрий (гл. VI
надо по этим элементам распознать, будет ли оно эллипсом,
параболой или гиперболой, и в последних двух случаях найти его
асимптотические направления, т. е. бесконечно удаленные точки.
Если коническое сечение имеет бесконечно удаленную точку К,
то проходящие через нее прямые k и k' обоих пучков будут
параллельны между собой;
поэтому если задано пять точек
конического сечения S, S't
А, В, С (рис. 191, а), то
строим два пучка прямых
S(a, ft, с) и S'(af, V, с') и
через центр 5 проводим
прямые а"\\а', ft"||ft', с"\\с'\ мы
получим два проективных
пучка прямых с общим
центром S, определяемых тремя
парами соответствующих
прямых а и а"% ft и ft", с
и с" (рис. 191, б); искомые
асимптотические
направления являются двойными
прямыми, которые мы легко
найдем по построению Штей-
нера (§ 43); если ось
перспективы пересечет
окружность в двух точках, то будем иметь две вещественные двойные
прямые, т. е. два асимптотических направления, и кривая является
гиперболой, для которой мы нашли направления асимптот; если ось
Рис. 191.
перспективы касается окружности, то двойные прямые совпадают,
т. е. будем иметь одно асимптотическое направление — кривая
будет параболой, для которой мы нашли направление оси; если ось
§ 46] ПОСТРОЕНИЕ КОНИЧЕСКОГО СЕЧЕНИЯ ПО ПЯТИ КАСАТЕЛЬНЫМ 195
перспективы лежит вне окружности, то двойные прямые — мнимые,
т. е. кривая является эллипсом.
III. Рассмотрим два частных случая, в которых коэффициенты
в общем уравнении (25.1) связаны одним соотношением и,
следовательно, кривая определяется четырьмя точками; в построении
Штейнера мы будем иметь лишь две пары соответствующих
прямых и сможем построить лишь одну точку оси перспективы, но
дополнительное соотношение даст нам дополнительные сведения о
положении оси перспективы.
а) Если известно, что кривая является равносторонней
гиперболой, то по (21.5) имеем соотношение ап + а22 — 0, означающее
взаимную перпендикулярность асимптот; следовательно, двойные
прямые должны быть взаимно-перпендикулярны, т. е. ось
перспективы должна пройти через центр окружности; если же
найденная точка оси перспективы совпадает с центром окружности, то осей
перспективы можно построить бесчисленное множество; в этом случае
через заданные четыре точки можно провести пучок кривых
гиперболического типа со взаимно-перпендикулярными асимптотическими
направлениями.
б) Если известно, что кривая является параболой, то по (21.6)
имеем соотношение апа22 — tf^2 = 0, означающее совпадение обоих
асимптотических направлений; следовательно, в этом случае двойные
прямые должны совпадать, т. е. ось
перспективы должна касаться окружности. Если
найденная точка оси перспективы лежит вне
окружности, то из нее можно провести
к окружности две касательные, т. е. задача
имеет два решения — через заданные четыре
точки можно провести две параболы (рис. 192);
если точка лежит на окружности, то
касательная одна и решение одно; если точка
внутри окружности, то касательной нельзя
провести — через заданные четыре точки Рис. 192.
нельзя провести параболу*).
IV. Рассмотрим некоторые примеры построения гиперболы и параболы%
причем в качестве центров пучков будем брать бесконечно удаленные точки.
Пусть даны три точки А, В, С гиперболы (рис. 193) и прямые d
и е, параллельные ее асимптотам (т. е. будем считать заданными
бесконечно удаленные точки D и Е этих прямых).
Примем точки D и Е за центры S и Sf пучков; так же как в § 43,
проведем через точку А прямые s\\e и s'\\d (т. е. прямые s, s' совпадают
с прямыми а\ а); проведя через точку В прямые b\\s' и b'\\s, а через
точку С прямые с || s' и с' || s, найдем точки В0 и В'0, С0 и С'0 — в пересечении
прямых В0В'0 и С0С'0 найдем центр перспективы S0; он должен являться полюсом
*) К этим же выводам мы пришли в § 21 аналитическим путем.
196 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [ГЛ. VI
прямой, соединяющей центры пучков, т. е. бесконечно удаленной
прямой поэтому найденный центр перспективы является центром гиперболы.
Так как А, В, С — произвольные точки гиперболы, то из указанного
построения вытекает следующее свойство центра гиперболы: если через две
точки гиперболы провести прямые, параллельные ее асимптотам, то
центр гиперболы лежит на диагонали полученного параллелограмма, не
проходящей через эти точки.
Пусть теперь даны две точки 5 и Л параболы (рис. 194),
касательная е в точке S и прямая /, параллельная оси параболы.
Рис. 193. Рис. 194.
Примем за центры пучков точку S и бесконечно удаленную точку S'
прямой /; центр перспективы S0 должен быть полюсом прямой SS'; так как
прямая е касается параболы в точке S, то точка S0 должна быть бесконечно
удаленной точкой прямой е.
Проведем через точку А прямые а и а', проектирующие ее из
центров S и S', и возьмем эти прямые в качестве вспомогательных прямых s'
и s; проводя через центр 5 произвольную прямую d, находим точку р0 ее
пересечения с прямой s, проектируем точку D0 из центра S0 в точку D'0
прямой s' посредством прямой d0 и проектируем точку Dq из центра 5
посредством прямой d'\ точка D пересечения прямых dud' лежит на параболе.
§ 47. Построение полюса и поляры
Рассмотрим полный четырехугольник АгА2ВгВ2, вписанный в
коническое сечение е (рис. 195). В § 26 мы показали (рис. 66), что
каждая диагональная точка является полярой диагонали, сое-
диняющей две другие диагональные точки (т. е. точки L, М, N
являются полюсами прямых /, т, п), причем полярное
соответствие можно рассматривать не только относительно конического
сечения е, а относительно любой кривой второго порядка,
проходящей через четыре точки Av А2, Вх, В2.
Если через точку L провести произвольную прямую, пересекающую
коническое сечение е в точках Сх и С2, прямые АгВх и А2В2 в
точках С[, С2 и прямые АХВ2 и А2ВХ в точках С" и с£. то во всех
случаях будем иметь:
{Cf2RL) = (C[C2RL) = {cldRL) = -1.
§47]
ПОСТРОЕНИЕ ПОЛЮСА И ПОЛЯРЫ
197
Отсюда вытекает способ построения поляры по данному полюсу Р
(рис. 196): проводим через полюс две произвольные прямые, пере-
Рис. 195.
Рис. 196.
секающие коническое сечение в четырех точках А{, Л2, Bv В2, строим
соответствующий полный четырехугольник, в котором заданная точка Р
будет диагональной; ее поляра р
проходит через две другие
диагональные точки Ж, N.
Вместо одного полного
четырехугольника, мы можем для по-
Рис. 197.
Рис. 198.
строения поляры внешней точки построить два обычных
четырехугольника (рис. 197): проведем через заданную точку три прямые,
198 КОНСТРУКТИВНЫЕ МЕТОДЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ [гл. VI
пересекающие коническое сечение в шести точках, построим два
четырехугольника и проведем их диагонали — поляра проходит через
две точки пересечения диагоналей R и N. Прямые Л1В1 и А2В2,
а также В^СХ и В2С2, которых мы можем в данном случае не строить,
пересекаются в точках, лежащих на поляре /?, как это следует из
рис. 196; это вытекает и из теоремы Паскаля, если соответствующим
образом перенумеровать наши шесть вершин.
Пользуясь свойством взаимности, легко найти полюс Р по
заданной поляре р: возьмем на прямой р две произвольные точки А и В
и построим их поляры а и bt — точка С пересечения этих поляр
является полюсом прямой р.
Мы можем, таким образом, решить задачу, поставленную в § 40:
если при центральной проекции окружность спроектировалась в
эллипс е и если прямая р является линией горизонта, то, построив
указанным способом ее полюс Я, мы найдем этим ту точку, в
которую спроектируется центр окружности.
Примечание. Рис. 197 можно рассматривать как центральную
проекцию рис. 198, следовательно, построение полюса и поляры
в случае любого конического сечения вытекает из аналогичного
построения для окружности.
§ 43. Примеры построения кривых
Рассмотрим сперва графическое решение некоторых задач, относящихся
к построению конических сечений по заданным элементам.
I. Найти точки пересечения дан- I Найти касательные,
проведенной прямой g с коническим сече- ные из данной точки G к кони-
нием, заданным пятью точками ческому сечению, заданному пятью
Alt ...» А5 (Рис- 199, а). Выбирая касательными аи .. ,,я5 (рис. 199, б).
Рис. 199.
центры пучков в точках А{ и А4 I Выбирая две касательные ах и а4
и проектируя из них все остальные и находя их точки пересечения
точки, получим два проективных | с остальными, получим два проектив-
§ 48]
ПРИМЕРЫ ПОСТРОЕНИЯ КРИВЫХ
199
пучка прямых Ах (а2, а3, аъ) и АА (Ь21
b3, b5); прямая g пересекает эти два
пучка по двум проективным рядам
точек g(A'2, А# Л5) и g (В'2, Б3, Я5)
(на одном основании g). Искомые
точки пересечения прямой g с
коническим сечением являются двойными
точками и могут быть найдены при
помощи построения Штейнера (§ 44).
ных ряда точек ах (А2, А3, Аъ) и аА (B2t
В3, В5); проектируя их из точки G,
получим два проективных пучка
прямых G (а2, #з> аъ) и б (^2» ^з' ^б) (с °б-
вдим центром G). Искомые
касательные к коническому сечению,
проходящие через точку G, являются
двойными прямыми и могут быть
найдены при помощи построения
Штейнера (§ 44).
Примечание I. Рассмотрим тот частный случай, когда прямая g
проходит через одну из заданных точек (например, Ах)\ вторую точку
пересечения можно найти при помощи теоремы Паскаля (как это
сделано в § 24) или при помощи следующих соображений: прямая g
пересекает все кривые второго порядка, проходящие через точки А2, А3,
А4, А5, по двум рядам точек, образующим инволюцию (§ 20); кривые,
распадающиеся на пары прямых А2АЬ и А3АА, а также А2АА и АЪАЪ,
пересекают прямую g в двух парах точек
А и А', В и £' (рис. 200), которые
полностью определяют эту инволюцию; нам
надо найти точку, соответствующую
точке Ах\ это легко сделать так же, как
в § 35.
II. Рассмотрим решение такой
задачи: для конического сечения, опре-
?' А\
\/
ъ
х
7*К
Рис. 200.
у
J
vi*M
Рис. 201.
деляемого пятью точками А{,...,АЪ, найти диаметр, сопряженный
с направлением, параллельным заданной прямой g (рис. 201).
Рассмотрим пучок кривых второго порядка, проходящих через четыре
точки Ах, А2, А3, А4, и выделим две кривые ср1} ср2 этого пучка, распавшиеся
на пары прямых vx и v2, а также vz и v4; пересекая прямые v{ и v2
прямой g'\\g и соединяя точку М их пересечения с серединой N отрезка CD,
мы получим диаметр sx распавшейся кривой ср1} сопряженный с данным
направлением; аналогично строим диаметр s2 распавшейся кривой ср2; прямые s{
и s2 пересекаются в точке X, через которую должны проходить диаметры
всех кривых пучка, сопряженные с данным направлением (§ 26); рассмотрим
теперь точки Ах, А2, А3, Аъ; совершенно аналогично можно найти точку X',
причем прямая XX' явится искомым диаметром.
Пользуясь решением этой задачи, можно решить такую задачу: найти
центр и оси симметрии конического сечения, заданного пятью
точками Ах, ..., Аъ. Выбираем произвольно две прямые g и / и указанным
способом строим диаметры g' и /', сопряженные с направлениями этих
200 конструктивные методы Проективной геометрии [гл. VI
прямых; точка пересечения прямых g' и /' является центром конического
сечения. Так как мы знаем две пары сопряженных диаметров gf и g", f и f'%
где прямые g" и f проведены через центр С параллельно прямым g и /,
то в инволюции прямых мы знаем две пары соответствующих прямых;
пользуясь построением § 44, мы найдем пару взаимно-перпендикулярных
соответствующих прямых, которые и будут искомыми осями симметрии; если
двойные прямые окажутся вещественными, то коническое сечение будет
гиперболой и они служат ее
асимптотами.
Рассмотрим также задачу:
найти центр конического се-
чения, заданного пятью
касательными а{1 ..., аь.
Выберем касательные ах
и а2\ пользуясь теоремой Бриан-
шона, мы сможем построить
касательные ах и а2>
параллельные ах и а2 (§ 29). На
основании § 45 центр лежит
в точке пересечения диагоналей
Рис 202 четырехсторонника,
образованного касательными av а2, av а^-
Рассмотрим решение такой задачи *): построить коническое сечение,
если даны три его точки Аь А2, А3, диаметр е и прямая /, параллельная
диаметру е', сопряженному с е (рис. 202).
Зная направление диаметра е', проводим через точки Alt А2, А3 прямые,
параллельные е', и откладываем отрезки ААВХ = ВХА{, АЪВ2 = В2А2, А6В3 «=
= В3А3\ ясно, что точки АА, А5, А6 также лежат на коническом сечении; мы
знаем шесть его точек, и задача сводится к предыдущим; нетрудно также
найти точки пересечения данного диаметра е с коническим сечением.
•) См. Р. Бейер [2], § 113.
ГЛАВА VII
НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ
ТРЕТЬЕГО ПОРЯДКА
Графические и аналитические методы исследования простейших
кривых — конических сечений — позволят нам исследовать и более
сложные кривые третьего порядка, имеющие применение в синтезе
механизмов.
§ 49. Общие теоремы
I. Общее уравнение алгебраической кривой третьего порядка
f = ал:3 + $х2у + ^ху2 + 5у3 + агх2 +
+ 2а2ху + azy2 + 2а4х + 2а'ъу + а6 = 0 (49.1)
содержит девять параметров, ибо на один из коэффициентов можно
поделить; однако по теореме Безу две кривые третьего порядка
пересекаются в девяти точках; следовательно, задание девяти
точек не определяет единственной кривой третьего порядка; но если
две кривые третьего порядка имеют десять общих точек, то они
совпадают.
Отметим также следующее: все кривые третьего порядка, про-
ходящие через восемь заданных точек, проходят через одну и
ту же девятую точку. Действительно, пусть кривые /г и /2
проходят через восемь заданных точек; тогда все кривые пучка / =
= /1-|-Х/2 = 0 также проходят через эти же точки; если девятая
точка не является точкой пересечения кривых /г и /2, то,
подставляя ее координаты в уравнение пучка, мы получим единственное
значение X; если же она является точкой пересечения кривых /х и /2,
то при подстановке ее координат в уравнение пучка получим / = 0
независимо от X.
II, Мы показали в § 22, что кривую второго порядка можно
образовать как геометрическое место точек пересечения
соответствующих прямых двух проективных пучков; совершенно аналогично
можно образовать кривые высших порядков при помощи
проективных пучков кривых низших порядков.
202 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
Покажем, что геометрическим местом точек пересечения двух
соответствующих линий пучка кривых второго порядка и
проективного ему пучка прямых является кривая третьего
порядка, проходящая через четыре точки пересечения кривых
пучка и точку пересечения прямых; обратно, любую кривую
третьего порядка можно получить указанным способом.
Действительно, пусть /г и /2 — две кривые второго порядка,
a vx и v2— две прямые. Так как по условию два пучка
проективны, то мы имеем Х'= . ~Т ; находя значения X и X'
из уравнений пучков, получим:
Vl {cfl _ df2) + „2 (fl/l _ bh) = о. (49.2)
Мы получили уравнение третьего порядка, причем простой
подстановкой можем убедиться в том, что оно удовлетворяется, если
одновременно v1 — v2 = 0 или /1 = /2 = 0. Четыре коэффициента
а, Ь, с, d и 18 коэффициентов в уравнениях для vv v2% fv f2 можно
бесчисленным множеством способов подобрать из тех девяти условий,
чтобы коэффициенты в уравнениях (49.1) и (49.2) совпадали.
III. Рассмотрим теперь циркулярные кривые третьего порядка,
т. е. кривые, проходящие через циклические точки; вводя
однородные координаты, имеем:
/ = ах\ + §х\х2 + 7*1*! + Ьх* +
—j— Хо i а~[Х.. —|— j,a2x-iX2 —|— а*Хп —|— лалХ-iXo j л,асХ2Хо j а^х^j —— и.
При подстановке координат циклических точек (лг3==0, х2 —±ixx)
получим а±/р — ^Т^"^^' 0ТКУДа следует а = *{, р = 8. Таким
образом, общее уравнение циркулярных кривых третьего порядка
таково:
/ = (** + у2) (ал: + ру) + агх* + 2а2ху + а^ +
+ 2аАх + 2а5у + а6 = 0. (49.3)
По доказанному ясно, что циркулярную кривую третьего
порядка можно получить при помощи пучка окружностей и
проективного ему пучка прямых.
Рассмотрим возможность ее получения при помощи двух
проективных пучков окружностей; если эти пучки таковы: s1-j-^2 = 0,
53 + X/s4 = 0, то аналогично (49.2) получим уравнение
5з (csi — ds2) + 54 (asi — *5г) = 0»
§ 50] КАНОНИЧЕСКАЯ ФОРМА УР-НИЯ ЦИРКУЛЯРНОЙ КРИВОЙ 3-ГО ПОРЯДКА 203
характеризующее циркулярную кривую четвертого порядка. Легко
видеть, в каком случае коэффициент при члене (х^-\-у2)2 обратится
в нуль: если все четыре функции sv s2, s3, s4 второго порядка, то мы
должны иметь
a-\-c = b + d\ (49.4)
если же функции sv s3 второго порядка, а функции s2, 54—первого,
то мы должны иметь с = 0; при этих условиях геометрическим
местом точек пересечения соответствующих окружностей двух
проективных пучков является циркулярная кривая третьего
порядка.
Рассмотрим еще один метод получения этих кривых: циркулярная кривая
третьего порядка является инверсией конического сечения, причем центр
основной окружности инверсии должен находиться на коническом
сечении и касательная в этой точке параллельна асимптоте циркулярной
кривой *).
Действительно, полагая в (4.5) azz = 0 и пользуясь формулами (41.12)
_ а2х' __ а2у'
Х- х'2 + у'2% У~ *'»+/" '
получим:
а* («„*'* +2апх'у' + а22у'2) + 2(х'2 + у'2)(а1гх'+ а23у') = 0. (49.5)
Любая прямая, проходящая через начало координат, преобразуется при
инверсии сама в себя, а начало координат — в бесконечно удаленную точку
этой прямой; следовательно, эта прямая после преобразования будет иметь
с циркулярной кривой общую несобственную точку, т. е. она дает
асимптотическое направление этой кривой.
Отметим, что в общей теории кривых третьего порядка циркулярные
кривые играют ту же роль, какую играют окружности в общей теории
кривых второго порядка: любую кривую третьего порядка можно получить
при помощи проективного преобразования, т. е. при помощи
центральной проекции циркулярной кривой третьего порядка. Действительно,
всегда можно так подобрать восемь коэффициентов в уравнении
циркулярной кривой (49.3) и восемь коэффициентов, характеризующих проективное
преобразование (36.11), чтобы получить после преобразования заданные
значения десяти коэффициентов (49.1).
§ 50. Каноническая форма уравнения циркулярной
кривой третьего порядка
I. Приведем уравнение (49.3) к некоторой простейшей
канонической форме. Предположим сперва, что коэффициенты а и р
одновременно не равны нулю; найдем в этом случае асимптоты;
полагая 'у = kx-\-п, имеем:
(1 + k2) (а+ Щ л:3+ [2Лл(а + р*) +
+ (\ + k2)$n+al + 2a2k + a2k2\x2 + ... =0;
*) С частным случаем этой теоремы мы уже познакомились в § 41.
204 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА (ГЛ. VII
приравнивая нулю коэффициенты при л:3 и л:2, найдем:
ь 2l h 4- /• п йх "^ 2д2& ~^~Дз^2
к\— р» ^2,3—-'» п— 2£(а + р£) + (1+£2)р '
_ а$* — 2д2оф + л3а2 „ _ + , ax—ab±2a2i
Я1— р (а* + р») • Я2,3— ^' 2(а±ф) • <0иЛ'
Таким образом, кривая имеет вещественную асимптоту с
уравнением
ах + ^+а^-ур + й'а8=0 (50.2)
и две сопряженные изотропные асимптоты
*,_ 4- ... i Р fa — дз) — 2ада ± г [2рд2 + а(а1 — az)\
у—Т.1Х^ 2(а2 + р2) •
пересекающиеся в фокальном центре F с координатами
2pa2 + a(ai— да) tI _ Р fa — Да) — 2<*Д2 ,гП оч
•*> — 2(а2 + р2) > Ур — 2(а2 + р2) • Wv.o;
Перенесем начало координат в фокальный центр. Полагая хг = х—xF%
ух = у — yF, найдем уравнение в новых координатах:
(50.4)
так как изотропные асимптоты теперь таковы: у1=±/д;1, то при
подстановке в (50.4) получим:
x\(bl±2ibi-b,)+ ... =0.
т. е. мы должны иметь bx — b3, Ь2 = 0, и уравнение примет форму
(х\ + У\) (ах1 + РЗ»! + Т) + 2 Vi + 2^1 + h = 0- (50-5)
При этом вещественная асимптота имеет уравнение oixl-\-fyyl-{-*i = Qt
ибо при подстановке уг = —аХх„|*~ ^ в уравнение (50.5) коэффициенты
при х\ и х\ будут равны нулю.
Повернем теперь координатные оси таким образом, чтобы новая
ось Fy2 стала параллельна вещественной асимптоте; так как
при повороте осей имеем х\-\-у\ = х\-\-у\, то в новых координатах
будем иметь
(*2+ $(*2+т0+ rf*2+ «y2-t-/=о.
ибо теперь уравнение вещественной асимптоты должно быть таким:
х2-\-С = 0; окончательно, отбрасывая значки, имеем каноническое
уравнение циркулярной кривой третьего порядка
(*2 -f у2) (* + т) + ** + *У + / = 0, (50.6)
§ 50] КАНОНИЧЕСКАЯ ФОРМА УР-НИЯ ЦИРКУЛЯРНОЙ КРИВОЙ 3-ГО ПОРЯДКА 205
причем начало координат совпадает с фокальным центром, а
ось Fy параллельна асимптоте кривой.
Прямую с уравнением х = —\ , параллельную асимптоте х = —f
и проходящую через середину отрезка, являющегося кратчайшим
расстоянием асимптоты от фокального центра, будем называть
средней линией циркулярной кривой третьего порядка.
II. Сопоставляя найденное каноническое уравнение с
уравнением (10.13), приходим к следующему выводу: всякая циркулярная
кривая третьего порядка, проходящая через свой фокальный
центр, может быть получена единственным образом как
геометрическое место точек пересечения соответствующих линий
пучка окружностей и пучка прямых, проходящих через центры
соответствующих окружностей; если кривая задана каноническим
уравнением (50.6) при / = 0, то по коэффициентам ^, d, е можем
найти координаты точек (а, с) и (Ь, с), через которые проходят
все окружности пучка
с = -у. а + Ь = -Ъ aft =</+-£. (50.7)
Линией центров пучка окружностей является средняя линия, ибо
х = |- =—n—i а центром пучка прямых — фокальный центр.
Так как результаты § 10, очевидно, справедливы для любого пучка
окружностей (гиперболического, параболического или эллиптического),
то вместо двух точек А и В, которые могут быть мнимыми, будем
его характеризовать радикальной осью пучка \У = ——)• линией
центров пучка (х = — -^-j и степенью т0 точки их пересечения,
т. е. m0 = d — X-f—-, ибо
«.~(^У~Ш+
ab.
III. Из рассмотренной теории вытекают простые геометрические
методы построения циркулярной кривой третьего порядка,
проходящей через свой фокальный центр, если известны: фокальный центр F,
линия центров и, радикальная ось v и степень т0 точки О их
пересечения.
Рассмотрим три случая.
а) Эллиптический пучок, т. е. т0 < 0; откладывая от точки О
отрезки О А = ОВ = У — т0, получим точки А и В (рис. 203) и
сможем построить кривую; в данном случае она состоит из двух
ветвей: замкнутого овала, на котором лежит фокальный центр, как
это видно из построения, и незамкнутой ветви, имеющей асимптоту,
206 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
а
й 1 1 i\[ UsJ
^ —— /
^Г\\
&
ч___^/
8
S
а,
§51] ФОКАЛЬНАЯ КРИВАЯ 207
причем обе ветви расположены по разные стороны от средней линии и\
в этом случае а и Ъ — вещественные числа,
б) параболический пучок, т. е. т0 = 0; обе точки А и В
совпадают с точкой О и все окружности касаются друг друга в точке О
(рис. 204); в этом случае имеем а = Ь = — у, кривая состоит
из одной ветви и имеет в О узловую
точку;
в) гиперболический пучок, т. е.
т0 > 0; обе точки А и В — мнимые
(рис. 205), причем в этом случае имеем
а = — ^ — 1Ущ, Ъ = ~\ + l Ут&
описывая окружность с центром в точке О
и радиусом У~Щ и восставляя в концах
этих радиусов перпендикуляры к ним до
пересечения с линией центров, мы
получим центры окружностей пучка, радиусы
которых равны длинам указанных
перпендикуляров; в этом случае кривая
состоит из одной ветви; точки М и
N — окружности нулевых радиусов пучка.
Мы рассмотрели тот случай, когда
а2-\-ф2Ф0 и фокальный центр является
собственной точкой] пусть теперь имеем а = р = 0. Вводя
однородные координаты, мы можем записать уравнение (49.3) в таком виде:
+ *з [ аА + 2а2*!*2 + аъх\ + 2аАхгхг + 2а5х2х3 + а6х*\ = 0.
Таким образом, если фокальный центр — несобственная точка, то
наша циркулярная кривая третьего порядка распадается на
бесконечно удаленную прямую xz = 0 и на коническое сечение
агх2 -\- 2а2ху + агу2 + 2а4х -\- 2аьу + а6 = 0. (50.8)
§ 51. Фокальная кривая
I. Рассмотрим такую задачу: найти геометрическое место
фокусов кривых второго класса, вписанных в данный
четырехсторонник а, Ъ, с, d (рис. 206); эта кривая называется фокальной кривой.
Будем рассматривать лишь две пары противоположных вершин
А\ и Ль A<i и Аъ нашего четырехсторонника; в таком случае
208 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VI
можно говорить и о четырехугольнике А1А2А1А2, в котором АХА2
и AiA2, а также А\А^ и A\A<i являются двумя парами
противоположных сторон.
Введем координаты всех четырех вершин AAxv уХ A[(x'v у'\
А2(ху у2), А'2(хгу у'^ и напишем уравнение (29.4) кривых семейства
второго класса, касающихся четырех заданных прямых
(игхг+ и2ух+ иг)(игх[ + и2у[+ и3) +
+ Ци1Х2+ ЗД + Uz)(UlX2 + «2^2 + из) = °> (51Л)
сравнивая с (23.9), найдем значения всех коэффициентов
ап = Х1Х[ + \Х2Х/21 ^^Х^ + Х^^Цх^ + х'^),
а22 = У1У1Ч- ХУ2 У Г 2а13 = *1 + *1 + * (*2 + К} (5 ! -2)
2а23= ^i + ^l-T-^C^-b^)' аЗЗ=1+Х-
Если ввести комплексные числа *)
zl = xl + iyv z2 = x2 + iy2, z[ = x[ + iy'v z'2 = x'2-+-iyry (51.3)
то будем иметь:
аП — a22+2/ai2 = ^— У1У[+1{ХхУ[ + Х[Ух) +
-\-\[Х2х'2— У2У2+ /(^2+^2)] = ^+ XZ2ZV
2(а13+/а2з) = ^1+< + Х(2:2 + 4> (51-4)
Найдем фокусы кривых нашего семейства; по определению, данному
в § 7, изотропная прямая с уравнением
у — Уо = 1(х — х0), где (*0, ^ —
координаты фокуса, должна касаться кривой
(23.9); записав ее уравнение в такой
форме —/*-[-у + Ц> = 0» где го=хо^г
-\- iy0, мы находим координаты этой
прямой иг = — /, и2=\, u3 = izQt причем
они должны удовлетворять уравнению
(23.9), ибо прямая должна касаться
кривой; после подстановки получим:
«27
-2/a12 + a224-
Рис. 206. ~" и,'оГ . • ч ^ п
+- 2 (а13 + ia23) z0 — азз^о = 0,
или, если воспользоваться (51.4), будем иметь, опуская значок
(l + ^zt-fa + z^ + ^ + z'^z+z^ + Xz/^O. (51.5)
*) Комплексные числа весьма удобны при рассмотрении многих задач
синтеза; см. работы 3. Ш. Блоха [1], [3], К. Зикера [1], [2] и др.;
см. также И. И. Артоболевский, Н. И. Левитский, С. А. Черкудинов [1],
§ 32,
§ 51]
ФОКАЛЬНАЯ КРИВАЯ
209
П. Пусть сперва \Ф—1; в этом случае уравнение имеет два
корня С и С, соответствующих двум фокусам конического сечения;
будем называть такие две точки соответствующими друг другу.
Из (51.5) имеем:
гЛ + Z'\ + ^ (Z9 + z'o) „„ ZiZi-\-\z9z'<)
С+С^ l^ 7+х ' сс/= 1 + х ' (5L6)
Отсюда легко найдем центр С конического сечения
zc=i±^ = ^ ^ . (51.7)
Таким образом, центры всех кривых семейства лежат на прямой,
соединяющей середины отрезков между противоположными
вершинами, причем ряд центров проективен семейству кривых *).
Положив в (51.1) Х = 0, получим кривую, вырождающуюся в пару
точек Wv W2\ мы видим из (51.6), (51.7), что в этом случае
фокусы можно считать
совпадающими с этими точками, а центр —
серединой отрезка между ними.
Пусть теперь Х = —1, т. е.
а33 = 0; в этом случае уравнение
(23.9) удовлетворяется при их —
= и2 = 0, но при этом прямая
и\х\ Ч~ #2*2 + игхг = 0 становится
бесконечно удаленной прямой
хъ = 0, т. е. наша кривая касается Рис* 207-
бесконечно удаленной прямой и
поэтому принадлежит к параболическому типу. При Х = —1 один
фокус уходит в бесконечность, а второй, как видно из (51.5),
определяется формулой
zo = ■? /• (51.8)
^1 —^2 + ^1 —^2
Он является несобственной точкой лишь при условии zl-\-z[ =
= z2-\-z2, при котором наш четырехсторонник становится
параллелограммом (рис. 207); следовательно, если zx -f- z[ ф z2 -\- z2, то
формула (51.8) дает фокус единственной параболы, имеющейся
среди кривых нашего семейства.
Пусть F — фокус конического сечения, вписанного в данный
четырехсторонник (рис. 206); по § 30 две касательные bud
отсекают на двух других касательных а и с отрезки AiA2 и AiAy
*) Это свойство было доказано другим методом в § 29,
210 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
которые должны быть видны из точки F под углами, равными или
дополнительными до 180°; этим же свойством должны обладать и
отрезки A\A% и А^Ау
Таким образом, фокальная кривая является геометрическим
местом точек, из которых каждые две противоположные
стороны четырехугольника видны под углами или равными, или
дополнительными до 180°*).
III. Выведем теперь уравнение фокальной кривой; пусть
М(х, у) — точка фокальной кривой и z—x-\-iy; вводя обозначения
для вещественной й мнимой
частей комплексного числа
а = a -f- /р
Re (а) = ос, 1т(а) = р,
покажем, что уравнение
фокальной кривой в
комплексной форме таково:
Im
^■=0. (51.9)
Из формулы (51.5) имеем:
г2 — *(*i + *i)+2ri2ri
— X
^-*(*a+*a+v;
Рис. 208.
Так как мы рассматриваем лишь вещественные кривые семейства,
то параметр X должен быть вещественным, откуда вытекает (51.9).
Покажем, что доказанное свойство фокальной кривой вытекает
***'/*• *-4=';'"*.
из (51.9). Введем обозначения: z
(/5=1, 2), где rk, r'k — модули, а ср^, ср^ — аргументы комплексных
чисел z — zk, z — z'k (рис. 208).
Если комплексным числам z, zk, zfk соответствуют точки М, Ak, A'k,
то числам z — zk, z — z'k соответствуют векторы AkM, A'kM
(рис. 208). Мы имеем:
z—г2
ei (<pi-<fc)f
г-
г-
*± = !1.А*1-ъ).
*) Именно это свойство фокальной кривой оказывается исключительно
важным в задачах синтеза; см. § 82.
§51] ФОКАЛЬНАЯ КРИВАЯ 211
вводя обозначение срх— <р2 = 8 и отсчитывая угол 8 в пределах от О
до 180°, мы видим, что 8 является тем углом, на который нужно
повернуть вокруг точки М прямую ЖЛ2, чтобы совместить ее
с прямой МЛг *); аналогичное значение имеет угол 87 = ср| — ср^.
Применяя формулу Эйлера, мы имеем:
г (Z~zi)(z~~zi) riri Аъ-ъ+ъ-ъ)
Im -7 тг = —г# ч / =
(Z-Z2)(2-22) Г2Г2
j-t А*(ъ-ъ + 9[-<&) = Т7sin (8 + 8,) = 0,
ГпГо 'о'о
Г1Г1
7
Г2Г2 '2'2
откуда 8 = — 8', или 8 4-8'=180°; таким образом, из точки М
отрезки А\А2 и А\А2 видны под углами, либо равными, либо дающими
в сумме 180°; аналогичное свойство имеем для отрезков А\А2 и А2А\.
IV. Покажем, как найти уравнение фокальной кривой в
декартовых координатах. Мы имеем:
im <*~*i>(*~*p =im (g"li)(l"g;)(;"[2)(;-^ =
(*-Z2)(Z-Z2) (*-*2)(*-4)(*-*2)(5-"г2)
^ im {(g - Zi) (z—«;) (^ - ;2) (; -;;)}
где a = oc— /p означает комплексное число, сопряженное с а,
причем аа = (а-|- /[}) (а — ф) = | а|2; следовательно, наше уравнение
можно записать в такой форме:
1т[{г—гг){г—г[)(г—12)(г—72)) = 0, (51.10)
откуда ясно, что все четыре вершины нашего четырехугольника
лежат на кривой] мы имеем, далее,
1Ш {(*_ Zi){z- *;)(z-z2)(z-4)}
= im {[*»-*(*,+*;)+*,*;] • p-zfa+q+z^q) =
= Im||z|4+Jz|2[(z1 + z^2 + 4)-^2+^)-^(z1 + ^)] +
+ A^+^Vl — z{zx + z;)^ — z(z2 4- z2) z,z; 4- ZjZ^} = 0.
Заменяя в этом уравнении
z — x-4-ly, z = x— ty, z2=x2 — y2A-2ixy,
_ (51.11)
z2 = x2 — y2— 2/xy, |z|2 = x2-)-y2,
*) Положительные углы соответствуют повороту против стрелки часов.
212 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
и производя приведение подобных членов, мы видим, что фокальная
кривая является циркулярной кривой третьего порядка,
характеризуемой уравнением (49.3), коэффициенты которого имеют
следующие значения:
а = Im [zx + z[ — Z2 — z'2),
P=-Re fr+s;-*,-2Q.
fl2 = Re(*1*; —v0._ _ (51.12)
fla = — Im [(гг + z[)(z2 + ?2) — ^ + s^],
2a4 = Im [ft + *;)y; + & + 4) v^
2a5= Re[(^ + ^24-(I2 + 4)^].
ae = —Im(2r/12r2^).
Мы видим, что фокальная кривая полностью определяется
двумя парами противоположных вершин А\ и Ль А2 и А2, по
которым она построена; поэтому будем ее обозначать f (Ль Ль Л2, А2)\
обе пары вершин можно поменять местами, ибо для всякой дроби ~
имеем:
Im£= Im j~ = -~ Im {ab\
и, таким образом, эквивалентны оба условия:
r (z — zA (z — г'Л (z — zAfz — z',))
(z-z2)\z-z2) (z-zi){z-zi)
Отметим также следующее свойство фокальной кривой: если на
фокальной кривой т(^ь Д» Л2, А2) найдена пара
соответствующих точек Dx и DJ, то кривые т(Ль а[, А2% Л2), f(Du D[, A2t Л2)
и T(Db Db Ль А[) совпадают, т. е. пару соответствующих точек
можно принять за новую пару противоположных вершин; мы имеем
из (51.6):
(* —C)(s — С') = 22 — 2(С + С') + СС' =
_ г2(1 + X) — z [zx + г[ +1 (г2 + 4)] + г1*1 + Хг2*2 _
~ 1+Х " ~
- - 1+1 •
§ 51] ФОКАЛЬНАЯ КРИВАЯ 213
откуда
lme-o(x-co i_ .lm(«-«,)(«-*0
Таким образом, обращение в нуль одной из частей равенства влечет
за собой обращение в нуль другой, т. е. кривые f (D\, D\, А2, Л2)
и т(^1' А\, A<i> Лг) совпадают.
V. Найдем по формулам (50.3) фокальный центр. Мы имеем:
zF = xF + iyF = - " ~Д+^2 ' (51ЛЗ)
Так как по (51.12)
a+/p = [Im(z1 + 2Q-/Re(2?1+<)] + [-Im(^+^
= —t(zl + *1) + l(z2 + 2Q = —i(zl + Jl — z2 — J2).
аг — а3 = — 21m (zxz[ — z2zT^, ia2 = i Re (zxz[ — z2z2),
то окончательно фокальному центру соответствует комплексное
число
zP= Z/)~ZA ,. (51.14)
Он будет несобственной точкой лишь при условии zx ~\-z[=^z2-j-z2,
которое означает, что наш четырехугольник — параллелограмм
(рис. 207).
Сравнивая эту формулу с формулой (51.8), приходим к весьма
важному результату: фокальный центр фокальной кривой
совпадает с фокусом параболы, касающейся данных четырех прямых.
В случае, когда фокальный центр — собственная точка, мы
имеем:
__ (*i-*2)(*i —*г) 9 9 _(*2-*i)(*2 —*Q
Zp Z\ — ■ -, г» Zp *2 — ; / г»
г1 + г1 — Z2 — г2 *1 + zl — z2 — г2
откуда легко находим:
Imfa-«i)(«^
(*> — *2) fa ^ г2) (*2 - *l) (*2 - *l) {Z2 - *l) (*2 - Zl)
Таким образом фокальный центр лежит на кривой; поэтому,
приведя ее уравнение к каноническому виду (50.6), мы сможем
построить ее при помощи методов §§ 10, 50. Отсюда вытекает также,
что любая циркулярная кривая третьего порядка, проходящая
через свой фокальный центр, является фокальной кривой.
VI. Так как выбор координатных осей для нахождения координат
заданных вершин совершенно произволен, то гдля упрощения всех
214 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. уП
вычислений выберем начало координат в середине отрезка,
соединяющего точки z и z'v а ось Оу направим так, чтобы она прошла
через середину отрезка, соединяющего точки z2 и z2 (рис. 209);
при этих условиях будем иметь:
z[ = —zv z2 + z'2 = 2tg, g>0,
(51.15)
и формулы (51.12) примут более простой
вид:
a=—2g, р = 0,
а2=-Щх\+гА)> (51.16)
a6=lm(z\z2?2).
Легко видеть, что в этом случае фокальный центр имеет координаты
х р —
2*'
yF = 2vr> перенося в эту точку начало координат, т. е.
полагая х = xf + o~L> У —У+тр» мы получим из уравнения (49.3)
после упрощений
(*'Ч/)(*' + ^-)+а'- а1~^ ^ + ^^-/=0; (51-17)
аха± -f- а2я>ь ,
g/ ' 4#2 ~ ' 2#
легко проверить вычислением, что свободный член
g
равен нулю: полагая z^ = \i-\-h, z2z2 = %-{-ie, мы находим
аг = — а3 = v + s. а2 = — (^ + 8).
04 = № а5 = ^, Г 2 =[^ —v8,
а6 = Im [([х -f /v) (8 — is)] = v8 — jie.
Сравнивая это уравнение с уравнением (50.6), мы можем найти все
характеристики нашей кривой: средняя линия, являющаяся линией
центров пучка окружностей, имеет уравнение х' = — тр-, или в
первоначальной системе координат х = 0; таким образом, средняя линия
кривой проходит через середины отрезков, соединяющих
противоположные вершины, т. е. через середины отрезков А\АХ и Л2Л2;
радикальная ось пучка окружностей имеет уравнение у' = , или
у=^; наконец, степень точки их пересечения относительно
§51] ФОКАЛЬНАЯ КРИВАЯ 215
всех окружностей выражается по § 50 формулой
2 2
- 5 ' 2 5 —. (51.18)
Таким образом, не производя построения кривой, мы можем найти
коэффициенты av а2, av а4, а5, g по формулам (51.16), — кривая
будет состоять из двух ветвей (как на рис. 203), если т0 < 0,
она будет иметь узловую точку (как на рис. 204), если т0 = 0,
она будет состоять из одной ветви (как на рис. 205), если т0 > 0.
VII. Покажем теперь, что среди кривых второго класса,
касающихся четырех заданных прямых, всегда имеется одна кривая,
у которой одна из осей симметрии совпадает со средней линией;
при наличии двух таких кривых фокальная кривая распадается
на среднюю линию и на окружность. Действительно, по (51.6)
и (51.15) мы имеем для двух соответствующих точек
Вводя обозначение С= a-\-ic, U = a'-\-ic', мы имеем:
С + С = £* + £*' + /(£? + £?'). ХЦ = аа' — cc' + i(ac' + afc),
Re (С + СО = а + а' = 0, Im (СС) = ас' -\-а'с = а (С — с).
Произведение К' может быть вещественным числом лишь в случаях
c = crt или а —0, т. е.
£—а + /с, £' = — a-\-tc, или t = /c, X' = ic'.
В первом из них обе соответствующие точки симметричны
относительно средней линии, а во втором — лежат на ней. Мы должны
таким образом, иметь:
1ш(г?)
Im(tt') = Im(— *? + Ц^) = 0, Х= ; i;v (51.20)
Im (£2г2)
Предполагаем сперва, что числитель и знаменатель не
обращаются в нуль одновременно.
Так как в этом случае мы получаем одно определенное значение
параметра X, то существует единственная кривая семейства,
обладающая указанным свойством.
Пользуясь (51.16), находим Х = —, после чего находим
из (51.19)
2 ах gax v • ;
Мы видим, что центр рассматриваемой кривой, характеризующийся
С + С
комплексным числом —к—, лежит на радикальной оси пучка ок-
216 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
ружностей; далее, мы имеем по (51.18)
-(^-НМ^Ь ^-*р«*» ^ (51.22)
Мы видим, что при т0 < 0 имеем (С — С')2 > 0; в этом случае С — (.' —
вещественное число, т. е. оба фокуса симметричны относительно
средней линии; при т0 > 0 имеем (t — С')2 < 0; в этом случае С — С —
чисто мнимое число, т. е. оба фокуса лежат на средней линии;
наконец, при т0 = 0 имеем С = С, т. е. оба фокуса совпадают.
Пользуясь этим, мы сможем дополнить аналитический критерий,
позволяющий по знаку т0 распознать характер фокальной кривой,
чисто геометрическим критерием.
1) Если в заданной четырехсторонник можно вписать коническое
сечение, фокусы которого симметричны относительно средней
линии, то они будут общими точками всех окружностей эллиптического
пучка и фокальная кривая состоит из двух ветвей, как на рис. 203.
2) Если в заданный четырехсторонник можно вписать коническое
сечение, фокусы которого лежат на средней линии, то они будут
окружностями нулевых радиусов гиперболического пучка
окружностей и фокальная кривая состоит из одной ветви, как на рис. 205.
3) Если в заданный четырехсторонник можно вписать окружность,
то через ее центр будут проходить все окружности параболического
пучка и фокальная кривая имеет в этой точке узловую точку,
как на рис. 204*).
VIII. Рассмотрим теперь исключительный случай:
Im (**) = 0, Im (224) = 0. (51.23)
Геометрический смысл этих условий таков: каждые две
противоположные вершины или симметричны относительно средней
линии, или лежат на ней (рис. 219—222); во всех этих случаях
можно считать, что каждые две противоположные вершины
являются частями выродившейся кривой второго класса.
Так как в этом случае по (51.16) мы имеем аг = а3 = а5 — 0,
то по (51.17) уравнение фокальной кривой таково:
*' \х' +У' 4р—/ =0,
откуда следует ее распадение на ось Oyf и на окружность.
IX. В качестве иллюстрации рассмотрим такие вершины (рис. 210):
Ах (1, 0), Л[(—1,0), А2(2, — 1), Л2(—2, 2), т. е. наши комплексные числа
таковы: ^j = 1, z[ = —1, z2 = 2 — /, z2 = —2 + 2/, z2 + z2 = i, g=-^-9
*) Если числитель и знаменатель в (51.20) не равны нулю одновременно,
то для заданного четырехсторонника всегда имеет место один из
рассмотренных трех случаев.
§ 51]
ФОКАЛЬНАЯ КРИВАЯ
217
тач как средняя линия совпадает с мнимой осью, а соответствующие
точки Ах и Ах расположены симметрично относительно этой оси, то без
всяких вычислений ясно, что точки Аг и Ах можно считать фокусами
выродившейся кривой нашего семейства, причем через эти точки пройдут все
Рис. 210.
окружности эллиптического пучка; так как по (51.16) имеем я, = б, а2 = 1,
то фокальный центр F имеет координаты хр = 6, ур = 1; уравнение нашей
кривой таково:
О'2 + /2) (х' + 12) + 34*' + 12/ = 0;
чтобы получить его в данной координатной системе, надо положить
х = х'+Ъ, у = / + 1.
Кривая построена на рис. 210.
218 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
§ 52. Построение фокальной кривой
I. В предыдущем параграфе мы исследовали фокальную кривую
аналитическими методами: мы показали, что она является
циркулярной кривой третьего порядка, проходящей через свой фокальный
центр, и полностью определяется заданием двух пар
противоположных вершин четырехсторонника; мы нашли все характеристики,
позволяющие выяснить ее тип, а затем построить ее по точкам. Ввиду
той большой роли, которую играет фокальная кривая при решении
различных задач синтеза, мы покажем еще
чисто геометрические методы ее
исследования и построения.
Пусть коническое сечение касается трех
прямых а, Ъ, с (рис. 211); если его фокус Fx
описывает прямую v, то, как показано
в § 31, второй фокус F2 описывает
коническое сечение е, проходящее через точки
Л, В, С; если же коническое сечение
касается прямых a, ct d и точка Fx описывает
Рис- 211. прямую v, то точка F2 описывает коническое
сечение ev проходящее через точки D, С, Е\
следовательно, если коническое сечение касается всех четырех
прямых а, Ъ% с, d и точка Fx находится на прямой v, то
соответствующая точка F2 может находиться лишь в точке пересечения двух
конических сечений е и Sjj они могут пересекаться в четырех
точках, одной из которых является точка С; поэтому на произвольной
прямой v может быть лишь три точки фокальной кривой, т. е.
она является алгебраической кривой третьего порядка.
Фокальную кривую можно построить как геометрическое место
точек пересечения окружностей с хордами АХА2 и А'ХА2 (рис. 213),
причем дуги окружностей должны образовывать с этими хордами
равные углы; из обеих точек пересечения оба отрезка АХА2 и А[А2
видны под углами или равными, или дополнительными до 180°; так
как все окружности имеют общие циклические точки, то и фокальная
кривая проходит через них, т. е. является циркулярной кривой.
В семействе кривых второго класса, касающихся заданного
четырехсторонника, есть кривые, распадающиеся на пары
противоположных вершин Ах и A'v А2 и А'2, следовательно, эти четыре точки,
которые, как показано, можно считать фокусами выродившихся
кривых, также должны лежать на фокальной кривой (см. рис. 186, где
VX = AV V2 = A[, VQ=A2, V4 = A2y Если рассмотреть третью пару
противоположных вершин D и D' (т. е. У5 и У6 на рис. 186), то
по тем же соображениям они являются соответствующими точками
и должны лежать на нашей кривой; наконец, если построить диато-
§ 52]
ПОСТРОЕНИЕ ФОКАЛЬНОЙ КРИВОЙ
219
нали /, m, п нашего четырехсторонника, диагональный треугольник
LMN и в нем точки /, К, S, являющиеся основаниями высот,
опущенных из его вершин на противоположные стороны, то из точек
/, К, S (§ 45) противоположные стороны видны под равными углами,
т. е. эти три точки также лежат на фокальной кривой.
Таким образом, если построена фокальная кривая "[{Av Afv Ау А'0\
то, кроме этих четырех вершин, на ней лежит еще семь точек
(пять указанных и две цикличе- д
ские), поэтому фокальная кривая
единственным образом
определяется двумя парами
противоположных вершин.
Пусть теперь мы нашли на
фокальной кривой f(Av Arv Av Л0 #/
две соответствующие точки F рис 212.
и F' (рис. 212), т. е. два фокуса
одного и того же конического сечения, вписанного в наш
четырехсторонник; как было показано в § 31, мы имеем /_ AXA2F — £_ FfA2A\t
откуда следует равенство /mAlA2F/ = /emFA2A[') следовательно, из
точки А2 видны под равными углами стороны A{F и A\F'', а также
стороны AXF' и AXF\ этим же свойством обладает точка А'у Таким
\
fj
Г
л;
Рис. 213.
образом, если построить новую кривую f(^i' A'v ^» ^')' то на
ней должны лежать точки Ау и Afv т. е. она совпадает с кривой
II. Рассмотрим теперь методы построения фокальной кривой.
Построение при помощи двух проективных пучков
окружностей. Продолжим прямые АХА2 и АТХА'2 до пересечения в точке Q
(рис. 213) и проведем окружность k через точки А\, Л2. Ql
220 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
построим оси симметрии v и vf отрезков АХА2 и а[Х2\ взяв
произвольную точку Е на окружности k, соединим ее с точками Ах
и А'2 прямыми, пересекающими прямые v и v' в точках О и О'.
Опишем две окружности: с центром О и радиусом ОАх = ОА2 и
с центром О' и радиусом 0'А'г = 0'А^ точки их пересечения С
и С лежат на фокальной кривой. Изменяя положение точки Е
на окружности k, можем построить сколько угодно точек нашей
кривой.
Для доказательства достаточно заметить равенство углов
£mEA1Q = ^OAlA2 = $, LE41Q = LO%A[ = $%
откуда вытекает, что из точки С отрезки АХА2 и А[А2 видны под
углами 90°—р и 90°+ р; нетрудно видеть, что из точки С оба
отрезка АХА2 и А'ХА'2 видны под равными углами.
III. Построение при помощи пучка окружностей и
проективного пучка прямых. Найдем фокус F параболы, касающейся
нашего четырехсторонника АХА2А[А2 (рис. 214); по теореме § 32 он
лежит в точке пересечения окружностей kx и &2, описанных вокруг
треугольников A[A2D и А[А'2Е\ найдем
среднюю линию v кривых нашего
семейства; по теоремам §§ 29, 45 она
проходит через середины отрезков
АгА[ и А2А'2 и параллельна оси
параболы; поэтому бесконечно удаленную
точку F' этой прямой можно считать
вторым (несобственным) фокусом
параболы, и таким образом, F и Ff — пара
соответствующих точек; отсюда
следует, что кривые i(Av А[, Ау А£)
и tMi» Л[, Ft Ff\ совпадают.
Отметим, что фокальный центр можно найти
другим способом: зная линию
центров, т. е. направление оси параболы, мы
можем найти фокальный центр при по-
Рис. 214. мощи одной описанной окружности, если
воспользуемся построением рис. 159.
Рассмотрим теперь четырехсторонник (рис. 215) со сторонами
AXF, A[Ft AXF', A[F' и двумя парами противоположных вершин
Аг и А[, F и Ff\ точки С и С пересечения прямых AXF' и A[F,
A[Ff и A\F также лежат на кривой и являются соответствующими, ибо
9Т0—третья пара противоположных вершин; отсюда следует, что кривые
Т (Av Afv F, Ff) и f (С, С, Ft Ff) совпадают. Окружности, опи*
§ 52]
ПОСТРОЕНИЕ ФОКАЛЬНОЙ КРИВОЙ
221
санные на отрезках А^С и АхО как на диаметрах (рис. 216),
пересекаются в точках D и D', лежащих на кривой и являющихся парой
соответствующих точек, симметричных относительно средней линии,
следовательно, кривые ? (С, С, F, Ff) и f(D,
D'', F, F') совпадают. Проведем окружность
через точки D и D' с произвольным. центром К
на средней линии, и пусть прямая FK
пересекает ее в точках М и N (рис. 217); мы имеем
£ MDD' + 21 MND' = 180°, откуда (90° +
+ L DMS) + (90° — L D'MN) = 180°. Таким
образом, найденная нами точка М обладает свой-
СТВ01И
21 DMF' = 21 D'MF, (52.1)
т. е. точка М — и точно так же точка N—лежат
на фокальной кривой.
Мы пришли к построению § 10, но теперь Рис. 215.
оно приобрело совершенно другой смысл: мы
строим точки М из условия (52.1); мы видим, что фокус параболы
является фокальным центром кривой; применяя построение § 10,
мы можем построить сколько угодно точек кривой *).
Мы рассмотрели тот случай, когда точки D и D'
вещественны, т. е. пучок окружностей — эллиптический; е.сли окружности
VF'
л'
I
S
м
[/■'
( t
в
,г
<
V 1
1
F ,
Рис. 216.
Рис. 217.
с диаметрами С'АХ и СА'г не пересекаются и мы имеем
гиперболический пучок окружностей, то строим радикальную ось этих двух
*) Любопытно отметить, что все авторы приписывают это построение
Бурместеру, однако сам Бурместер приписывает его своим
предшественникам.
222 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
окружностей, после чего легко построить окружности нулевого радиуса и
любые новые окружности пучка методами, рассмотренными в §§ 33, 34.
Примечание. Мы видели, что для построения фокальной
кривой надо сперва построить фокальный центр и среднюю линию, а
затем найти характеристики пучка
окружностей; для проверки можно
воспользоваться результатами § 51.
IV. Покажем в частности,
нахождение точки /?',
соответствующей заданной точке R
(рис. 218). Мы исходим из двух
ьд' заданных пар произвольных вер-
2 шин Аг и А[, Л2 и А'2, полностью
определяющих фокальную кривую,
и предполагаем, что каким бы то
Рис. 218. ни было способом мы нашли
некоторую точку R этой кривой.
Строим прямую v'\\v, расстояние которой от средней линии v такое
же, как и расстояние точки /?. Точка /?', очевидно, должна лежать
на прямой vr. В соответствии с § 31 строим /_ МАгА2 = ^mA2AlR;
искомая точка R' лежит в пересечении прямых МАг и v'.
§ 53. Некоторые особые случаи расположения вершин,
определяющих фокальную кривую
Если 5 = 0 — уравнение окружности, а г> = 0 — уравнение прямой,
проходящей через ее центр, то уравнение sv = 0 характеризует
распадающуюся циркулярную кривую третьего порядка,
проходящую через свой фокальный центр, ибо фокальный центр
окружности совпадает с ее центром. Фокальная кривая полностью
определяется заданием двух пар противоположных вершин — если эти
вершины соответствуют исключительному случаю, рассмотренному
в § 51, то фокальная кривая распадается на окружность и на
прямую, проходящую через ее центр. Рассмотрим несколько частных
случаев расположения вершин.
А. Обе пары противоположных вершин симметричны
относительно некоторой прямой. Средней линией является прямая fi
(рис. 219); кривая распадается на прямую fi и на окружность ^2,
причем на кривой лежит и третья пара противоположных вершин С
и С.
Б. Две противоположные вершины симметричны относительно
прямой, соединяющей две другие вершины (рис. 220). Средней
линией является прямая ^г\ на кривой должна лежать и третья пара
противоположных вершин С и С'\ если поменять местами пары то-
§ 53] НЕКОТОРЫЕ ОСОБЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ВЕРШИН 223
чек С, С и Av Arv то рис. 220 ничем не будет отличаться от
рис. 219; фокальная кривая распадается на окружность у2 и ПРЯ"
мую Yi« проходящую через ее центр.
В. Обе пары противоположных вершин лежат на одной
прямой (рис. 221). Определим инволюцию точек на прямой ^i двумя
Рис. 219.
Рис. 220.
парами соответствующих точек Av А[ и Av А'2\ . построим
окружность k на отрезке АХА[ как на диаметре и проведем произвольную
окружность W через точки А2 и А'2; эти две окружности определяют пучок,
радикальная ось которого пересекает прямую fi в центре
инволюции F (§ 35). Проведя из точки F касательную FT к окружности k
и построив окружность k0
с центром F и радиусом FT,
мы получим в ее
пересечении с прямой ух двойные
точки инволюции С и С.
Действительно, именно в
этих точках окружности
пучка касаются прямой fi»
ибо степень точки F
относительно всех окружностей
пучка равна FT2 = FC2.
Если спроектировать точки
прямой Yi из произвольной
точки Р окружности k0, то получим инволюцию прямых с
центром Р, причем двойные прямые инволюции PC и PC взаимно-
перпендикулярны; поэтому на основании §§ 17, 18 каждые две
соответствующие прямые симметричны относительно прямых PC
Рис. 221.
224 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
иРС'.т.е./. АХРС = /_ А[РС, /_ А2РС = /_ А'2РСЛ откуда £ АгРА2=
= l_ А[РА'2, l_ А{РА2 = 2. ^V^r таким образом, из каждой точки Р
окружности k0 каждая пара отрезков АХА2 и А[А'Г АХА2 и А[А2
видна под равными углами; поэтому фокальная кривая распадается
на прямую 7i и окружность k0.
4 Яг
Я г 4
Рис. 222.
Рис. 223.
Г. Обе пары противоположных вершин лежат на одной
прямой симметрично относительно некоторого центра (рис. 222).
Этот случай является частным случаем предыдущего — окружность &0
распадается на прямую 72_LTi и на бесконечно удаленную прямую.
Д. Обе пары противоположных вершин являются
противоположными вершинами трапеции (рис. 223). Средняя линия g
совпадает со средней линией
трапеции; в этом случае фокальный
центр нельзя считать фокусом
параболы, ибо не существует
параболы, касающейся двух
параллельных прямых АХА2 и А2А[\ нетрудно
видеть, что фокальный центр
является точкой пересечения
противоположных сторон АХА2 и A[A'2-t
действительно, окружности,
проходящие через точки A'v Ау F и
точки A!v Av F, касаются друг
друга в точке /\ являющейся
центром подобия. Этот же результат получим, если воспользуемся
формулой (51.13). Фокальная кривая в этом случае не распадается.
Е. Обе пары противоположных вершин являются
противоположными вершинами параллелограмма (рис. 224). В этом
случае, как было сказано в § 51, фокальный центр является
несобственной точкой, причем с одинаковым правом его можно считать
точкой пересечения как прямых АгА2 и А[А2, так и прямых АгА'2
и А2А[, ибо наш параллелограмм можно получить путем предельного
Рис. 224.
§ 53] НЕКОТОРЫЕ ОСОБЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ВЕРШИН 225
перехода либо из трапеции на рис. 223, когда станут параллельными
прямые ЛгА2 и А[А2, либо из трапеции рис. 225, когда станут
параллельными прямые АХА2 и А2Агу Как сказано в § 50, в этом
случае наша фокальная кривая распадается на бесконечно удаленную
прямую и на коническое сечение (50.8);
беря начало координат в центре
параллелограмма, будем иметь z[ = —zv z2 = —z2
и по (51.12) найдем ах = — ~ а3, а4=а5 = 0;
поэтому уравнение конического сечения
таково:
аг (х2 — у2) -f- 2а2ху —(— а6 = 0,
т. е. оно является равносторонней
гиперболой с центром в центре параллелограмма. Рис. 225.
Так как каждая из прямых g и gf,
проведенных через центр гиперболы параллельно сторонам
параллелограмма, делит пополам хорды, параллельные другой, то эти прямые
являются сопряженными диаметрами гиперболы; из § 28
вытекает, что асимптоты гиперболы v и vf являются
биссектрисами углов между прямыми g и gf.
В частном случае ромба, направляя оси координат по диагоналям,
будем иметь Im (z2\ = Im (z2} = ax = a6 = 0, a2 Ф 0; следовательно,
в этом случае равносторонняя
гипербола распадается на две взаимно-
перпендикулярные прямые, идущие по
диагоналям ромба.
Ж. Прямая, соединяющая две
противоположные вершины, делит
пополам отрезок между двумя другими
(рис. 226). (Предполагается, что середины
отрезков АХА'Х и А2А2 не совпадают, как
в случае Е, и что отрезки АХА'Х и А2А2
не перпендикулярны, как в случае Б.)
Средняя линия v совпадает с
прямой АХА'{> так как соответствующие
точки Аг и А'х лежат на средней линии,
то они являются окружностями
нулевого радиуса гиперболического пучка
окружностей, радикальную ось
которого g найдем как ось симметрии
отрезка АхАу Применяя указанное в § 35 построение окружности,
принадлежащей гиперболическому пучку и проходящей через точку Л2,
находим прямую и, на которой должен лежать центр окружности
Рис. 226.
226 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
пучка, а следовательно, и фокальный центр F\ применив то же по*
строение к точке А'г найдем вторую прямую и', которая пересечет
прямую и в точке F. Фокальная кривая в этом случае не распадается.
§ 54. Кривая Бурместера
I. Рассмотрим более детально тот тип фокальной кривой,
который соответствует параболическому пучку окружностей, т. е.
кривую с узловой точкой, изображенную на рис. 204; будем
называть ее кривой Бурместера, а ее среднюю линию — фокальной осью.
Рассмотрим простой механизм для вычерчивания этой кривой *): пусть
прямая v — фокальная ось, точка F—фокальный центр, Р—узловая точка
(рис. 227); построим произвольную окружность с центром С на фокальной
оси, проходящую через узловую точку Р\ прямая CF пересечет эту
окружность в точках Мк М' кривой. Построим £ FMD = /_ FPD, тогда Д CFP =
= Д CMD по стороне и двум
углам, откуда MD = PF = const
и /_ FMD = const; поэтому, если
жесткий угол с вершиной М
движется так, что точка D на одной
его стороне движется по прямой g
благодаря ползушке D, а вторая
сторона проходит через пол-
v зушку D', вращающуюся вокруг
;/////ш неподвижной точки F, то точка М
опишет кривую Бурместера.
II. Покажем теперь, что ее
Рис. 227. уравнение можно привести
к форме (8.4). Воспользуемся
(10.13), где Ь—а, и перенесем начало координат в узловую точку
Р(а, с), т. е. положим х = х' -\-а, у — у'-\-с\ мы получим:
(х'2 + у'2) (х' — а) + 2ах/2 + 2сх'у' = 0;
повернем теперь координатные оси на некоторый угол а, т. е.
положим
х' = хг cos а — уг sin а, у' = хг sin а -|- уг cos а;
наше уравнение примет форму
(х\ + у2) (хг cos а — уг sin а) -f- (х\ — yf) (a cos 2а + с sin 2а) —
— 2хгуг (a sin 2а — с cos 2а) = 0.
Полагая tg2a~ — —, получим:
а2 4- с2
(х\ + У\) (хг cos a — уг sin a) + 2ххух cos 2a —±-— = 0.
*) См. В. В. Добровольский [1], стр. 66.
§ 54]
КРИВАЯ БУРМЕСТЕРА
227
Умножим все члены уравнения на некоторый множитель X и введем
новые обозначения X cos а = яг, Xsina =— /; подберем X таким
образом, чтобы коэффициент при хгуг стал равным —ml, т. е.
— ml = X2 cos a sin a = 2X cos 2a ——,
с
откуда
Наше уравнение примет форму
(л:2 + у2) (тх + /у) — mlxy = 0. (54.1)
Это уравнение мы уже рассматривали в §§ 8, 41; оно зависит от
двух параметров, как и уравнение (10.13) при Ь — а. Эта кривая
в геометрии называется строфоидой (точнее, косой строфоидой, ибо
обычная, или прямая
строфоида соответствует случаю ^1
т = /). KVr ^
III. Рассмотрим некоторые
свойства кривой Бурместера
(рис. 228). Координатные оси
являются касательными
в узловой точке: ось Ох
касается дуги ЛОВ, а ось
Оу — дуги COD *).
Фокальный центр F по
(50.3) имеет координаты
ml2
XF— 2(т2 + I2) '
тц Рис. 228.
у^= 2(/я2 +12) ' (54-2)
Вещественная асимптота vf по (50.2) характеризуется уравнением
га2/2
^ + /у + -^^пр7г = 0. (54.3)
а фокальная ось v имеет уравнение
т
у — j-x, тх-\-1у = 0.
(54.4)
Из сопоставления (54.2) с (54.4) вытекает, что фокальная ось и
прямая, соединяющая узловую точку с фокальным центром,
расположены симметрично относительно осей координат*
*) Это будет доказано в § 60.
228 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
IV. Отметим случаи распадения кривой Бурместера.
А. Если т = 0, то кривая распадается на ось Ох и на две
изотропные прямые у = ± 1х\ аналогичный результат при / = 0.
Б. Если т = оэ, то кривая распадается на ось Оу и на
окружность
*2 + У2 —/у = 0
(54.5)
с центром на этой оси; точно так же, если / = оо, то кривая
распадается на ось Ох и на окружность
х2-\-у2 — тх = 0.
(54.6)
Для доказательства делим все члены (54.1) на т и полагаем т->оо.
В. Если т = 1 = оо, то кривая распадается на бесконечно
удаленную прямую и на оси координат; действительно, деля (54.1)
на ml и вводя однородные координаты, имеем:
{Х\ + Xl) (^- + -£) — *3*1*2 = °-
При т = 1 = оо получим xzxxx2 — Q, откуда л;3 = 0, или хх = 0,
или х2 = 0.
Г. Если кривая проходит через точку на оси Ох, отличную от
начала координат, то она распадается на ось Ох и на
окружность (54.6); аналогичный результат, если точка лежит на оси Оу.
V. Рассмотрим теперь способы построения кривой Бурместера.
1) Построение при помощи пучка окружностей и
проективного пучка прямых. Так как кривая Бурместера является частным
случаем фокальной кривой, то по §§ 10, 50, 51 она является
геометрическим местом точек пересечения окружностей, проходящих
через узловую точку и
имеющих центры на фокальной оси,
с прямыми, проходящими через
фокальный центр и центры
окружностей.
2) Построение при
помощи двух проективных
пучков окружностей. Построим
прямую с уравнением
в
<
о
L
KJ
Е
^ч/У
Д \л?
- + f=l;
(54.7)
Рис. 229.
спроектируем произвольную
точку G (\i, X) этой прямой на
оси Ох и Оу (рис. 229) и на отрезках ОА и ОБ как на
диаметрах построим окружности 7 и Y> т°чк>а Q #* пересечения лежит
на кривой.
§ 54]
КРИВАЯ БУРМЕСТЕРА
229
Действительно, окружности т
х2-\-у2 — рх = 0,
причем
[ ^ имеют уравнения
х2 + у2 — Ху = 0,
т
+т =
1. и =
/я/— тк
(54.8)
(54.9)
т. е. мы имеем два проективных пучка окружностей (ибо
параметры пучков |х и X связаны линейным соотношением (54.9));
находя |х и X из уравнений пучков и подставляя в (54.9),
получим (54.1).
VI. Рассмотрим теперь различные способы преобразования кривой
Бурместера в более простые кривые.
Преобразование кривой Бурместера в прямую. Прямую с
уравнением (54.7) назовем направляющей прямой (рис. 229); она
пересекает оси Ох и О}) в точках М и L, причем т—ОМ, l=OL.
Проектируя снова ее произвольную точку G на оси координат,
соединяем эти проекции А к В прямой АВ и проектируем на нее
начало координат в точку Q — эта точка лежит на кривой;
наоборот, если в каждой точке Q кривой провести перпендикуляр АВ
к прямой OQ и восставить в точках А и В перпендикуляры к
координатным осям, то они пересекутся в точке G, лежащей на
направляющей прямой, т. е. при помощи этого построения мы
преобразовываем кривую в направляющую прямую. Для доказательства
XV
напишем уравнение Ьу = 1 прямой АВ, где (х и X связаны
соотношением (54.9); прямая OQ _]_ АВ характеризуется уравнением
y—-t-xt и координаты точки Q таковы: х— У* , у =
откуда [л
х2 + у2
Х =
х2 + у2
под-
х у
ставляя в (54.9), получим (54.1).
Преобразование кривой Бурместера Ч^
в окружность. В §§ 15, 41 мы
рассмотрели преобразование Котельникова;
пользуясь (54.9), мы видим, что если
через каждую точку М кривой Бурместера
провести прямую ММ\ параллельную
фокальной оси v (рис. 230), до пересечения
с осью Ox, 2l из точки пересечения М'
провести прямую М'М'\ параллельную
оси Оу, до пересечения с лучом нашей
точки, то полученные точки М" лежат на
окружности (54.5).
Преобразование кривой Бурместера в равностороннюю
гиперболу. Если произвести инверсию относительно окружности любого
радиуса с центром в узловой точке, то по § 41 получим равносто-
Рис. 230.
230 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
роннюю гиперболу, асимптоты которой параллельны осям
координат; центр гиперболы С лежит на прямой, соединяющей узловую
точку О с фокальным центром, причем если через С назвать точку,
являющуюся инверсией точки С, то легко видеть- из (54.2), (41.17),
что фокальный центр кривой Бурместера является серединой
отрезка ОС; касательная к гиперболе в узловой точке совпадает
с фокальной осью (см. рис. 155).
Преобразование кривой Бурместера в параболу. Прямая АВ
(рис. 229) пересекает оси Ох и Оу в точках А и В с
координатами ([л, О) и (О, X); так как параметры |i и X, определяющие
положение точек на прямых Ох и Оу, связаны линейным
соотношением (54.9), то мы имеем два проективных ряда точек на осях
Ох и Оу, следовательно, по теореме § 23, взаимной теореме Штей-
нера, такие прямые, как АВ, огибают некоторое коническое сече-
ние\ из (54.9) видно, что при (л = оо имеем Х = оо, т. е.
бесконечно удаленные точки осей Ох и Оу соответствуют друг другу,
а поэтому бесконечно удаленная прямая касается нашего конического
сечения — следовательно, оно является параболой.
Из (54.9) видим, что при |х = 0 имеем Х==/, а при Х = 0 имеем
jx = //г; таким образом, точке О, рассматриваемой как точка оси Ох,
соответствует точка L оси Оу, а точке О, рассматриваемой как
точка оси Оу, соответствует точка М оси Ох; поэтому точки М и L
являются точками касания прямых Ох и Оу с параболой, а
направляющая прямая ML является полярой начала координат
относительно параболы. По § 28 проекция F0 точки О на прямую ML
является фокусом параболы,—
находя его координаты и
сравнивая с (54.2), видим, что фокус
параболы Р0 лежит на том же
луче, что и фокальный центр F
кривой Бурместера, но вдвое
дальше от начала координат
(рис. 231). Наконец?, директриса
параболы должна проходить через
начало координат, ибо только из
точек директрисы парабола видна
под прямым углом, и должна
совпадать с фокальной осью кривой Бурместера; действительно,
с одной стороны прямая OF0 и директриса параболы должны быть
симметричными относительно прямых Ох и Оу, касающихся параболы,
а с другой стороны, прямая OF и фокальная ось v кривой
Бурместера должны быть симметричны относительно осей координат.
Таким образом, кривая Бурместера является геометрическим
местом оснований перпендикуляров, опущенных на касательные
к параболе из точки на ее директрисе; наоборот, если в каждой
Рис. 231.
§ 55] АНАЛИТИЧЕСКОЕ И ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КРИВОЙ БУРМЕСТЕРА 231
точке кривой Бурместера восставить перпендикуляр к ее лучу,
то полученные прямые огибают параболу. Фокус и директриса
параболы связаны с фокальным центром и фокальной осью кривой
Бурместера простыми соотношениями.
§ 55. Аналитическое и графическое определение кривой
Бурместера по различным данным
I. Заданы оси Ох и Оу, фокальная ось ОК и одна точка Аг
кривой; найти точку ее пересечения с заданным лучом OR.
Из (54.1) вытекает уравнение кривой Бурместера в полярных
координатах (г, ср)
1 " ' Р - ' 3=4. (55.1)
Sin ср
COS ср
а=т
Обозначая через k0= — угловой коэффициент фокальной оси, мы
имеем k0 — g-, а-|~р&0=0; следовательно, если (rv cpt) —
полярные координаты заданной точки Av то мы имеем:
1 , п, а , 0 _1_
г
Sill Cpj
COS Ср!
а + Р*о = 0'
Sin ср
COS ср
Так как эти три уравнения с двумя неизвестными аир должны
быть совместными, то, приравнивая нулю определитель этой системы
1
1
Sin ср
1
COS ср
1
= 0,
(55.2)
sin cpj COS Cpj г\
1 k0 о
получим уравнение кривой в полярных координатах
г —г sin2cP(feocos <Pi ~~sin <Pl)
1 sin 2cp! (&0 cos cp — sin cp)
Подставляя cp = cp2, где cp2 — угол, соответствующий данному лучу OR,
найдем радиус-вектор г2 точки пересечения.
Покажем теперь графические методы решения задачи.
Зная точку Ах (рис. 232), проводим BlC1 _\_OAv затем
проводим Cfi || Оу, BXG || Ох — точка G лежит на направляющей прямой;
далее строим прямую ОК', симметричную с фокальной осью ОК
относительно осей координат; так как на ней должен лежать
фокальный центр, то направляющая прямая MGL проходит через точку G
перпендикулярно к прямой ОК'.
Возьмем теперь на заданном луче OR произвольную точку Q и
проведем PQB J_ OR; построим прямоугольник OPSB, и пусть его
232 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
диагональ OS пересекает направляющую прямую AIL в точке G'\
строим прямоугольник OP'G'B', он перспективно подобен
прямоугольнику OPSB с центром подобия в точке О, поэтому Р'В' || PQ
Рис. 232.
и, следовательно, Р'В' _[_ OR; в пересечении Р'В' и OR найдем
искомую точку N кривой Бурместера.
Если воспользоваться преобразованием кривой Бурместера в
окружность, то проводим A\A\ || OK (рис. 233), затем А\А\ \\ Оу и
ML \_ОА\\ в окружность,
описанную на отрезке OL как на диаметре,
преобразуется кривая Бурместера.
Если луч OR пересекает окружность
tf ft г
в точке А2, то проводим А2А2 \\ Оу,
А2А2 || ОК и находим точку А2.
Если воспользоваться
преобразованием в равностороннюю
гиперболу, то выполним инверсию
относительно основной окружности
с центром О и с радиусом а = ОАг
(рис. 234); получим равностороннюю
гиперболу, проходящую через точки
О, Av центр которой С должен
лежать на прямой ОК', симметричной прямой ОК относительно
координатных осей; так как эти оси параллельны асимптотам
гиперболы, то, строя прямоугольник ОААгВ, мы найдем центр С
гиперболы в пересечении прямых АВ и ОК' (§ 46); построив
асимптоты С А' и CB't отметим точки 5 и D их пересечения с прямой OR;
откладывая GD — 05, получим точку G пересечения гиперболы
4' <
Рис. 233.
§ 55] АНАЛИТИЧЕСКОЕ И ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КРИВОЙ БУРМЕСТЕРА 233
с прямой OR (§ 30); остается перейти от точки О к точке TV
на том же луче посредством инверсии, как это показано в § 41
(рис. 152).
При преобразовании кривой Бур-
местера в параболу мы знаем ее
директрису, совпадающую с фокальной
осью ОК> и три касательные к
параболе (Ox, Оу, SAfi _[_ ОАг)
(рис. 235); фокус F0 параболы
должен лежать в пересечении
окружности, описанной вокруг Д OSC,
с прямой ОК', симметричной с
прямой ОК относительно
координатных осей. Мы должны найти
такую точку N на луче OR, чтобы
прямая ANB _[_ OR, касательная
к параболе, пересекала директрису ОК в точке G, для которой мы
имели бы /_F0GA = /_AGO (§ 32); для этого проводим прямую
F0D || OR и строим ось симметрии АВ отрезка F0D.
II. Заданы оси Ох и Оу и две точки Аг и А2 кривой Бурме-
стера; найти ее фокальную ось и точку пересечения с заданным
лучом OR.
При аналитическом решении мы имеем три уравнения:
Рис. 234.
Sin ср
COS ср
Sin cpj
а
COS cpi
Sin cp2
COS<p2
откуда находим уравнение кривой
Бурместера в полярных координатах
Рис. 235.
1
1
Sin ср
1
sin cpt
1
COS ср
1
COS ср,
1
Sin ср2 COS ср2
Г
J_
r2
= 0. (55.3)
Из (55.2) можно найти угловой коэффициент фокальной оси
r2 sin ср2 sin 2cpt — rx sin у, sin 2cp2
r2 cos cp2 sin 2cpi — /*! cos cpj sin 2cp2
(55.4)
234 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
При графическом решении задачи мы строим направляющую
прямую LM по двум точкам Ах и А2 указанным выше способом (рис. 236);
фокальную ось ОК найдем как
прямую, симметричную
относительно координатных осей с
прямой OK' ±_ML.
Если воспользоваться
равносторонней гиперболой, то,
выполняя инверсию, мы будем знать
три точки гиперболы (В\ = О,
В2 = А[, Вг = А2) (рис. 237)
и направления ее асимптот, т. е.
мы знаем бесконечно удаленную
точку В4 оси Ох и бесконечно
удаленную точку В5 оси Оу, также
лежащие на гиперболе; точку
пересечения гиперболы, заданной
пятью точками, с заданной
прямой легче всего найдем при
помощи теоремы Паскаля (§ 24);
найдя точку В6, мы найдем иско-
Рис. 236. мую точку N на луче OR,
выполнив инверсию.
Если воспользоваться параболой (рис. 238), то мы знаем четыре
касательных к ней (Ох, Оу, ААгВ _]__ OAv CA2D J_ ОА2), и нужно
Рис. 237. Рис. 238.
построить пятую касательную, параллельную заданному
направлению, т. е. перпендикулярную к прямой OR; это легче всего сделать
при помощи теоремы Брианшона (§ 29), причем аг, а2, аг, а4 —
§ 55] АНАЛИТИЧЕСКОЕ И ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КРИВОЙ БУРМЕСТЕРА 235
данные четыре касательные (рис. 239), а пятая касательная а5 должна
быть параллельной заданной прямой а"ъ J_ OR *); искомая точка N
является проекцией точки О на прямую as. Нетрудно найти
фокальную ось ОК—она проходит через ортоцентр Н треугольника BDS
(рис. 238), образованного тремя касательными SB, CD, Оу.
III. Заданы оси Ох и Оу а две точки Ах и А2 кривой Бурже-
стера\ найти третью точку Аъ ее пересечения с прямой АгА2.
Если мы ищем точку
пересечения кривой Бурместера с прямой
и = Ах-\-Ву-\-С = 0,
то положим у = kx и будем искать
угловые коэффициенты k лучей,
соответствующих точкам
пересечения; мы имеем:
л:3 (1 + ft2) (т + Ik) — Imkx2 = О,
лг(Л + ВА) + С = 0; (55.5)
исключая отсюда х, получим
искомое уравнение для k:
4-*(1+4?) + т = °-
Обозначая через k{, k2,
корни, мы находим:
(55.6)
его
(55.7)
Рис. 239.
Для двух данных точек Аг и А2 мы знаем ft1 = tgcp1, k2 = tgy2 и
можем найти kQ по формуле (55.4); после этого легко найдем:
r2 cos cpt —rx cos <
(55.8)
3 tg<p,.tg<p2 Г2 SHI <pj — Tj Sill cp2
Так как прямая и должна проходить через точки Аг и А2, то из ее
У2 — У1
(х — хг) находим А — у2 — yv В = хх-
уравнения); — );!:
-*2 х\
С — угх2 — хгу2 и по (55.9) можем найти координаты точки
пересечения
_С _ klk2(xly2 — x2yl) y = kx
X=z
A + Bk3 klk2(y2 — yl) — k0(x2 — xl) '
где k0 дается формулой (55.4).
(55.9)
*) P — точка Брианшона; мы воспроизвели построение рис. 90.
236 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
Для графического решения задачи воспользуемся преобразованием
в параболу; так как три точки Av А2, Аг пересечения прямой и
с кривой Бурместера должны лежать на одной прямой, то прямые
aiA-OAv а2±_ОА2, az±_OAz (рис. 240), касательные к параболе,
обладают следующим свойством: проекции на них точки О должны
лежать на одной прямой; следовательно, если рассмотреть
треугольник SXS2S3, образованный
касательными av а2% а3, то по § 32
точка О должна лежать на
окружности, описанной вокруг него,
а прямая и должна быть его
прямой Симпсона относительно
точки О (§ 18). Так как из трех
вершин Sv S2, S3 мы знаем
только *S3, то воспользуемся тем,
что на указанной окружности
должен лежать и фокус F0
параболы (§ 32); поэтому описываем
окружности вокруг
треугольников ОВгСг и ОВ2С2, в их
пересечении находим фокус F0 и
проводим окружность через точки
прямая^
Симпсона
Рис. 240.
О, Fq и Sz; в ее пересечении
с прямыми ах и а2 найдем точки
соединяя их прямой,
с прямой АгА2 найдем третью точку пересече-
найдем третью касательную а3;
Sj и S2
в ее пересечении
ния Л3.
IV. Заданы фокальная ось и три точки кривой Бурместера,
из которых одна узловая; найти касательные в узловой точке,
т. е. оси Ох и Оу.
Введем оси Охх и Оух и обозначим через ф неизвестный угол
между осями Охг и Ох; обозначая также через ср0 заданный угол
фокальной оси с осью Oxv мы имеем k0 = у— == tg* (ср0 —|— ф). Мы
можем воспользоваться уравнением (55.2), в котором надо заменить
срх и ср на cpj-f-ф и ср2 —|— Ц>, а г—на г2. Мы получим:
r2 _ sin 2 (уя + ф) [tg (у0 + ф) cos (у t + ф) — sin (у t + Ф)] _
г, sin 2 (cPl + ф) [tg (ср0 + ф) cos (у2 + ф) — sin (у2 + ф)]
_ sin 2 (у2 + ф) sin (ср0 — у,) _ (sin 2у2 + cos 2у2 tg 2ф) sin (у0 — yQ
sin 2 (у, -f Ф) sin (у0 — у2) (sin 2у, + cos 2^ tg 2ф) sin (у0 — у2) '
откуда легко найдем:
. r2 sin 2cpt sin (ср0 -
tg2^:
■Ъ)-~г1 sin2yasin(y0 —yQ
Г! cos 2у2 sin (у0 — у!) — г2 cos 2у, sin (у0 — у2)
(55.10)
§ 55] АНАЛИТИЧЕСКОЕ И ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КРИВОЙ БУРМЁСТЕРА 237
Зная (rv cpj), (г2, ср2) и ср0, мы можем найти угол 2ф,
щий неравенству 0<;2ф<180°, и задача имеет
ф и 90° + ф.
Если воспользоваться преобразованием
мы будем знать директрису, совпадающую
две касательные аг J_ OAv а2 J_ ОА2 (рис.
пересекает директрису ОК в точке Sv
то строим равные углы Z.^>iai =
= l^ axSxKi, на прямой SXKX должен
лежать фокус F0 параболы (§ 32).
Проделывая то же построение- для второй
касательной а2, найдем фокус FQ в
пересечении прямых KiSx и K2S2, искомые оси
координат, касательные к параболе, делят
пополам углы между прямыми ОК и OF0.
V. Заданы четыре точки кривой
Бурместера, из которых одна —
узловая', найти касательные в этой точке,
т. е. оси Ох и Оу.
Зная полярные координаты (rv срх).
(г2, ср2), (г3, ср3) точек Av А>, Л3, мы
воспользуемся (55.3), где заменим срг и ср2 на
удовлетворяю-
два решения:
в параболу, то для нее
с фокальной осью ОК, и
241); если касательная ах
ним г, ср на г3, фзН~Ф- Будем иметь:
cpj-f-ф и ср2 + ф и заме-
1
1
sin (ср! + ф)
1
sin (ср2 + ф)
1
COS^+Ф)
1
COS (ср2 + ф)
1
sin (ерз + Ф) cos (ср3 + Ф)
_1_
= 0.
Раскрывая этот определитель по элементам последнего столбца,
получим:
sin (уз
2)
rx sin 2 (ср2 + ф) sin 2 (ъ + ф)
+
sin (?!--уз) .
r2 sin 2 (ср! + Ф) sin 2 (ср3 + Ф) '
I sin(cp2 —cpQ
1 r3 sin 2 (ср! + ф) sin 2 (ср2 + ф)
Предполагая, что sin 2 (ср1 -f- ф) sin 2 (ср2 -f- ф) sin 2 (ср3 + ф) Ф 0, и
умножая все члены на это произведение, получим после простых
преобразований
tg 2ф == -
Задача снова имеет два решения: ф и 90° + ф*
sin (ср3 — ср2) sin 2cpt
Г\
sin (ср3 — ср2) cos 2^
, sin (<fi
1
■ sin (cpt
— ср3) sin 2ср2
r2
— ерз) cos 2ср2
sin (ср2 — cpt) sin2cp3
r3
1 sin (cp2 — cPl)cos2cp3
(55.11)
238 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
Рассмотрим графические методы решения задачи.
Выполнив инверсию относительно основной окружности с
центром О и радиусом a=^OAv мы будем знать четыре точки
равносторонней гиперболы (В1 = А1, В2, В3, £4 = 0) (рис. 242, а) и
должны будем найти направления ее асимптот, ибо они параллельны
осям Ох и Оу. Примем точки Вх и ВА за центры пучков;
проектируя из них остальные точки, мы получим две пары соответствующих
прямых ау а'2 и а3, а'ъ. Перенося
пучок BAa'v а'Л параллельно себе
так, чтобы точка ВА совпала
с точкой Bv будем иметь по § 46
два проективных пучка прямых
с общим центром, причем асимп-
7* aj
6J О 07
Рис. 242. Рис. 243.
тотические направления совпадают с двойными прямыми; для их
нахождения применяем построение Штейнера (§ 44) (рис. 242, <f),
причем ось перспективы w должна проходить через центр С окружности,
ибо оба асимптотических направления взаимно-перпендикулярны.
Для решения задачи при помощи параболы мы имеем три
касательные к ней ax±_OAv а2±_ОА2% а3 J_ ОЛ3 (рис. 243);
рассматриваем Д SxS2Sfr ими образованный; директриса ОК проходит через
точку О и через его ортоцентр Н\ зная директрису и пользуясь
двумя касательными av а3, строим фокус F0 параболы так же, как
в случае IV.
Оси Ох и Оу делят пополам углы между прямыми ОК и OFa.
Примечание. Интересно отметить один случай, когда задание
четырех точек, из которых одна — узловая, не определяет кривую
Бурместера; при аналитическом решении задачи числитель и знаме-
§ 56]
МЕТОД А. П. КОТЕЛЬНИКОВА
239
натель в (55.11) должны быть нулями; при графическом — четыре
точки, полученные после инверсии, таковы, что одна из них
является ортоцентром треугольника с вершинами в трех остальных
точках (§ 21).
§ 58. Метод А. П. Котельникова
I. При решении задач I, II, III предыдущего параграфа весьма
полезен метод Котельникова, который в дальнейшем будет
применен к решению и более сложных задач.
Так же как в § 18, рассмотрим
окружность (18.8) и каждому лучу y = kx
сопоставим точку его пересечения с окружностью;
будем ее называть изображающей точкой
и обозначать той же буквой k.
Легко видеть (рис. 244), что точки k
и — k симметричны относительно оси Оу%
1
точки k и — -j симметричны относительно
1 О <2Г
центра окружности, точки я и -г- лежат
-к
/\
к
У
Л
^*Х }<
/1
L-S к
О
Рис. 244.
на прямой, параллельной оси Оу.
Мы показали в § 18, что прямые некоторога пучка пересекают
окружность по двум рядам точек, образующим инволюцию;
рассмотрим некоторые случаи расположения пучка (рис. 245).
1) Если центр Sx пучка лежит на оси Оу, то для каждой пары
соответствующих прямых имеем hkf = const; действительно, в этом
случае прямая OSxT пересекает
окружность в точках О и Г, которым
соответствуют значения k = 0 и &7 = оо;
так как эти точки лежат на одной
прямой, проходящей через центр пучка,
то k = 0 и k' = со должны
соответствовать друг другу; поэтому из
формулы (18.3) при условии 5 = — а будем
иметь kk' =з const.
2) Если центр S2 пучка лежит на
"в касательной к окружности,
параллельной оси Ох, то для каждой
пары соответствующих прямых имеем
k-{-k' = const; действительно, в этом
случае двойными прямыми являются касательные S2T и S2TX к
окружности, причем первой из них соответствует значение & = со; на
основании § 4 и уравнения (18.6) имеем 7 = 0, после чего
уравнение (18.3) при 7 = 0, Ь = — а даст k-\- k' = const.
240 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [ГЛ. VII
3) Если центр 53 пучка лежит на оси Ох, то для каждой пары
соответствующих прямых имеем -т-+тг = const. Действительно,
пучку прямых с центром 53 на оси Ох соответствует пучок,
симметричный с ним относительно прямой у = -£-, причем каждой
1
точке к соответствует точка у,
т. е. мы приходим к случаю 2).
Отметим, что все рассмотренные
случаи можно получить из (18.10),
полагая в ней х0 = 0, или y0 = d0,
или у0 = 0.
Пользуясь этими соображениями,
рассмотрим нахождение двух
неизвестных изображающих точек
х и у из двух уравнений
х-\-у = a-\-b, xy = cd,
причем изображающие точки а, Ъ,
с, d известны (рис. 246).
Пусть прямая, соединяющая изображающие точки а и £*),
пересекает касательную в точке Р\ через эту же точку должна пройти
прямая, соединяющая точки х к у; пусть прямая, соединяющая
точки с и d, пересекает ось Оу в точке Q; через эту же точку
должна пройти прямая, соединяющая точки х к у; следовательно,
прямая PQ пересекает окружность в искомых точках и у.
II. Рассмотрим теперь кривую Бурместера; если прямая
пересекает кривую Бурместера в трех точках и построен
треугольник с вершинами в трех изображающих точках, то его
прямая Симпсона относительно точки О параллельна данной
прямой**).
Для доказательства сравним (18.13) и (55.6); мы имеем:
т . Вт 1 . Am т
Pi = —-\ —» Р2= *+-£""' Pz~T'
и по (18.14) прямая Симпсона имеет уравнение
Am , Вт
-с~х+-с~у
:0, Лх + Яу-Ь
Cd0
0,
т. е. параллельна прямой Ах-\~Ву-±-С = 0 ***); справедливо и
обратное утверждение: прямая, параллельная прямой Симпсона тре-
*) Такую прямую будем обозначать аЬ или (а, Ь).
**) См. А. П. Котельников [1], § 30.
***) Очевидно, при d0 = I обе прямые не только параллельны, но
совпадают.
§ 56]
МЕТОД А. П. КОТЕЛЬНИКОВА
241
задач.
247),
угольника с вершинами в трех точках на окружности,
пересекает кривую Бурместера в трех точках, изображениями
которых являются указанные вершины.
Пользуясь этим, покажем графическое решение наших
В случае I мы знаем изображающие точки kQt kv k3 (рис
соответствующие фокальной
оси, точке Лг и прямой О/?;
так как из (55.7) &1&3 =
== J_ . &0, то, соединяя пря-
мой точки kx и &з до
пересечения в точке Р с Оу
и соединяя точку Р с
точкой k0, найдем в пересечении
с окружностью точку у-,
а проводя через нее
прямую, параллельную оси Оу,
найдем точку k2. Проектируя
точку О на прямые kxk2
и k2kv найдем прямую Симп-
сона g\ прямая g'\\g, про-
веденная через точку Av пересечет прямую OR в искомой точке Л3.
Случай II отличается от случая I лишь тем, что вместо kQ мы знаем
теперь &2.
и А2 и найдем изображаю-
В случае III мы знаем две точки Ах
щие точки kx и k2 (рис. 248); проектируя точку О на прямую kxk2
найдем точку 53 и, проведя через нее прямую ^||ЛХЛ2, получим
прямую Симпсона треугольника kxk2kz. Опишем окружность на отрезке 05§
242 НЕКОТОРЫЕ СВОЙСТВА ЦИРКУЛЯРНЫХ КРИВЫХ ТРЕТЬЕГО ПОРЯДКА [гл. VII
как на диаметре — она пересечет прямую Симпсона в точке 52.
Проводя прямую через точки кх и 52, получим в ее
пересечении с окружностью точку &3; прямая Okz пересечет прямую ЛгА2
в точке Л3.
Проводя прямую через точки kx и k2 до пересечения в точке Р
с осью Оу и соединяя точки Р и -г-, найдем в пересечении с
окружностью точку k0, а соединяя эту последнюю с точкой О,
получим фокальную ось О/С. После этого случай II сведется
к случаю I.
ЧАСТЬ II
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ
ГЛАВА VIII
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
§ 57. Порядок соприкосновения плоских кривых
I. Рассмотрим две плоские кривые Г и Гг с общей точкой М0
(рис. 249), которую считаем обыкновенной, т. е. неособой точкой
обеих кривых*). Отложим от точки М0 по обеим кривым в одну
сторону равные дуги <иМ0М = 1иМ0Мг = /±8 и рассмотрим
величину MMV характеризующую близость обеих кривых друг к другу
в окрестности точки Ж0; оценим
порядок ее малости относительно /ц ^
бесконечно малой величины As.
Если выполняется условие
lim
ММ,
As"
= 0,
(57.1)
Рис. 249.
где п — целое положительное число,
то будем говорить, что кривые Г и Гх имеют в точке М0
соприкосновение не ниже п-го порядка; если же п является
наибольшим целым числом, для которого выполняется (57.1), то будем
говорить о соприкосновении п-го порядка.
Данное нами определение удобно тем, что является чисто
геометрическим и не зависит от какой бы то ни было системы
координат; однако оно еще не дает удобного для практики критерия,
позволяющего судить о порядке соприкосновения.
Пусть теперь кривые Г и Гг характеризуются уравнениями
x = fi(t).
у = <Pi (0.
(57.2)
где t — некоторый параметр, а все четыре функции предполагаются
дифференцируемыми на некотором отрезке [tv t2]\ пусть точке М0
соответствует значение параметра tQt причем tx < t0 < t2\ мы имеем
*) Об этом подробнее в § 60.
244 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
для обеих кривых
* = K/,fW + T,f('o)*. ds = yrff1\t0) + v[\tQ)dt. (57.3)
Поэтому если оба подрадикальных выражения отличны от нуля, то
величины ds и dt являются бесконечно малыми величинами одного
порядка малости и в условии (57.1) можно заменить Д$ на Д/.
II. Предположим, что все четыре функции имеют на отрезке [tv t2]
непрерывные производные первых /г-f- 1 порядков. Полагая
ф(0 = /(0 —/i(0. <■>(') = <р (0 —<Pi(0. &t = t-t0
и применяя формулу Тейлора, получим:
<K*) = «K*o)+f адД' + ••• +Ф(л)('о)^+Г+1КП(^гтя.
ш(0 = ш ад + «/ ад Д^ + • • • + *W (t0) ~ + m<»+i) (П ~щ,
(57.4)
где точки t', t" лежат между t0 и t. Если точки М и Мх
соответствуют одному и тому же значению параметра t, то мы имеем:
мм, = Vi/W-AWP+ItW-tiC)]2 = Ww + ^W-
Для выполнения условия
Ит**1. = 0 (57.5)
А/-» О АГ
необходимы и достаточны условия
/ ад = Л ад. /' Со) = /i Co) /п) ('о) = //" Оо):
т ад=ь ад. ?' ад=?! ад ?№ ад=?iB) ад- (57.6)
Достаточность их очевидна, ибо при их выполнении мы имеем:
/ (0 - /, (0 = Ф<"+1> (О (^ • ? (О - «Pi (0 = «>(л+1) (О ^л •
Для доказательства необходимости предположим, что хоть одно из
равенств (57.6) не выполнено, например, что
/W ('о)-/№)=£ О, k<n;
мы имели бы тогда
/ю-/,<о=[/*Ч'о)-/1* (*»)]-£+....
откуда вытекало бы, что
ШЩ.Ф0, k<n,
ы-ю (АО*
т. е. не выполнялось бы (57.5).
§ 57] порядок соприкосновения плоских кривых 245
Если при условиях (57.6) имеем
[/-+1,Ы-/У+1) WF+r"W-»r" № > о,
то порядок соприкосновения равен п, ибо предельное соотношение
(57.5) уже не выполнится, если п заменить на п-\-\.
Легко видеть, что при п = 0 кривые только пересекаются, но
не касаются друг друга, ибо угловые коэффициенты касательных
различны; при я>Л кривые имеют
общую касательную, т. е. касаются
друг друга.
Простейший случай получим,
выбирая в качестве параметра t
абсциссу х (в предположении, что
касательная к кривым не
параллельна оси Оу), т. е. пусть
уравнения наших кривых таковы:
Г: y = F(x); Гг: y = Fx(x). (57.7)
Величина ММХ является в данном
случае разностью ординат, ибо
точки М и Мг должны иметь одинаковые абсциссы хд (рис. 250);
условия соприкосновения порядка не ниже п таковы:
F(x0) = Fl(xQ), F'(x0) = F'i(xJt
F{n){x0) = F[n)(xQ). (57.8)
Если при этом F{n+1) (х0) Ф F[n+l) (х0), т0 порядок соприкосновения
равен п.
"!'/'
ИГ
а
W"
U —
ML _М^
а
м]
? а
j
г./
Рис. 252.
Отметим одно свойство соприкасающихся кривых: если
соприкосновение нечетного порядка, то в окрестности данной точки одна
кривая лежит внутри другой (рис. 251); в случае четного порядка
соприкосновения кривые в данной точке не только касаются, но и
пересекают друг друга (рис. 252).
246 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
Действительно, пусть обе функции F(x), Fx(x) имеют на
некотором отрезке [xv х2], хг < х0 < х2, непрерывные производные
первых п-\- 1 порядков; так как функция F{n+l) (х)—Fin'il)(x)
непрерывна на этом отрезке и не обращается в нуль в точке х0, то
всегда можно подобрать настолько малый внутренний отрезок [лг3, х4],
х\ < хг < хо < х4 < х2» чт°бы во всех его точках эта функция была
одного и того же знака.
Аналогично (57.4) имеем:
F (х) - Fx (х) = [F (х0) - Fx (х0)] + [pf (х0) - р[ (х0)] Дх + . ..
...+[^Vo)-/fV0)]^
ШС ^^ JC "^fi>
где л:7 лежит между х и дг0. На основании (57.8) имеем:
MM, = />(*)- F, (х) = [F<"+1>(*')_ М"+1)(*')] ^j • (57.9)
Величина хг зависит от выбора х на отрезке \xv Jt4], т. е. от
величины Алг, но так как квадратная скобка имеет один и тот же знак
при любом выборе х на отрезке [xv дг4], то в случае нечетного п
правая часть имеет один и тот же знак при Дл: > 0 и при Длс < О,
т. е. мы имеем расположение кривых, указанное на рис. 251; если же
п—четное число, то при Дл; > О и Дл: < О эти знаки различны
(см. рис. 252).
III. Пусть теперь кривая Гх зависит от т параметров
у = РЛх; С, Ст),
т. е. мы имеем не одну кривую Г, а целое семейство таких
кривых; выберем из них кривую, соприкасающуюся с кривой Г
в точке MQt т. е. подберем т параметров таким образом, чтобы
кривая семейства Гх имела с кривой Г соприкосновение наиболее
высокого порядка, какой только возможен для кривых данного
семейства; для этого надо подчинить т параметров п-\-\ условиям
(57.8), т. е. кривая Гх, зависящая от т параметров, может
быть подобрана таким образом, чтобы иметь в данной точке
кривой Г соприкосновение с ней не ниже (т—1)-го порядка;
в некоторых отдельных точках кривой Г, как будет показано ниже,
порядок соприкосновения может повыситься.
IV, К понятию соприкасающейся кривой можно прийти из других
соображений. На кривой Г выберем т произвольных точек Pv
Р2> ..., Рт с абсциссами xv х2, .... хт (рис. 253) и подберем
такие значения Cv С2 С^ наших параметров, чтобы и кривая Гх
§ 57]
ПОРЯДОК СОПРИКОСНОВЕНИЯ ПЛОСКИХ КРИВЫХ
217
проходила через эти же т точек; для этого параметры должны
удовлетворять условиям
/7(х1) = /?1(х1). F(x2) = Fl(x2), ..., F(xm) = F1(xm). (57.10)
Рассмотрим функцию ср (х) = F (х) — Fx (х)\ так как
<Р (*l) = <Р (*2> = . . . = ср (ATJ = О,
то по теореме Ролля будем иметь:
«р'(*</>)=,,'(4>)= •
*i < хф <х2< .
Применяя снова теорему Ролля к функции у'(х), получим:
Т"(42>)=?"(42))=--- =«г(^_з) = о.
Продолжая этот процесс, получим, наконец:
^-2) ^(m-2)) = ^(m-2) ^(т-2)) = ^ ^(т-1) ^(т-1)) = ^
х{т-2) < х{т-\) < х^п-2)^
(57.11)
(57.12)
(57.13)
(57.14)
причем все точки являются внутренними точками отрезка [xv хт].
Пусть теперь все точки Pv Р2,
Рт кривой Г стремятся
к одной ее точке М0, т. е. пусть lim хг = lim хт = х0; будем
предполагать, что при этом предельном переходе параметры Cv С2,
.... Ст стремятся к некоторым пре- у
дельным значениям Сг, С2 Ст.
Так как отрезок [xv хт] стягивается
в точку, то все введенные нами
абсциссы стремятся к х0\ мы будем
иметь из (57.11) —(57.14)
ср (л:0) = ^(х0) = . .. = срС*-1) (х0),
«г.
£2
Рис. 253.
Хт «27
т. е. мы пришли к условиям (57.8).
Таким образом,
соприкасающуюся кривую, зависящую от т
параметров и имеющую соприкосновение (т—\)-го порядка
с данной кривой, можно рассматривать как кривую,
проходящую через т бесконечно близких точек данной кривой (точнее,
как предельное положение такой кривой, когда все точки стремятся
к совпадению с данной точкой).
Из этих же соображений вытекает весьма простой способ оценки
порядка соприкосновения алгебраических кривых: две алгебраиче-
248 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
f л-четное
ские кривые порядков тип могут иметь друг с другом
соприкосновение не выше (тп—1)-го порядка; действительно, по
теореме Безу они пересекаются в тп точках, т. е. одна из них может
проходить не более чем через тп бесконечно близких точек другой.
§ 58. Простейшие соприкасающиеся кривые
а) Соприкасающаяся прямая. Так как в случае прямой, не
параллельной Оу, имеем у = С^л;-f-С2 и т = 2, то соприкасающаяся
прямая имеет в данной точке кривой соприкосновение с ней не ниже
первого порядка, т. е. является ее
касательной, ибо из условий (57.8) имеем:
Cxx0-i-C2 = y0 = F(x0),
Ci = y'0= F' (х0),
у = Уо(* —*0) + Уо-
Будем называть точками распрямления
кривой такие ее точки, в которых она имеет
соприкосновение не ниже второго порядка
со своей касательной; для прямой, не
параллельной Оу, имеем у" — 0; поэтому те
точки кривой у = F(x), в которых F"(х)
обращается в нуль, являются ее точками
распрямления — в окрестности такой точки
кривая теснее прилегает к своей
касательной, чем в окрестности обыкновенной точки *).
В качестве иллюстрации рассмотрим
параболу п-го порядка у = хп (где я >- 3 —
целое число); так как мы имеем при х = 0
у = у' = у" = ... =у(л-1)_о, у(п) ф 0,
а)
У\
х
1л-нечетное
б)
Рис. 254.
то начало координат является точкой распрямления, в которой
кривая имеет со своей касательной соприкосновение (п—1)-го
порядка.
Интересно отметить, что точка перегиба является точкой рас*
прямления, но точка распрямления может и не быть точкой
перегиба; в рассматриваемом случае начало координат будет точкой
перегиба лишь при нечетном п (рис. 254, а, б).
Отметим, что касательная в обыкновенной точке кривой проходит
через две ее бесконечно близкие точки, а в точке распрямления —
по крайней мере через три.
*) Если касательная параллельна оси Оу, то записываем уравнение
кривой в форме х = Ф (у) — точка распрямления характеризуется условием
Ф" (у) = 0.
§ 58]
ПРОСТЕЙШИЕ СОПРИКАСАЮЩИЕСЯ КРИВЫЕ
249
Отметим также, что алгебраическая кривая я-го порядка может
иметь со своей касательной соприкосновение не выше (п—1)-го
порядка; например, кривая (10.9), являющаяся траекторией точки
шатунной плоскости кривошипно-шатунного механизма, имеет
соприкосновение не выше третьего порядка с любой из своих касательных.
б) Соприкасающаяся окружность. Для окружности
(х — а)2+(>> — bf— /?2 = 0 (58.1)
имеем т —3, поэтому соприкасающаяся окружность имеет в данной
точке кривой соприкосновение с ней не ниже второго порядка;
находя из (58.1) первые две производные по правилам
дифференцирования неявных функций, получим:
(х —а) + (у —*)у' = 0. i + y'2 + (y_ft)y" = o, (58.2)
причем по условиям (57.8) мы должны положить y = F(xQ),
y' = F'(x0), y" = F"(x0). Из (58.1), (58.2) легко находим центр С (а, Ь)
и радиус R соприкасающейся окружности в точке М(х, у) кривой
а = х-
(! + /')/
Ь = у-
R
•. (58.3)
К этим же формулам мы пришли бы рассматривая вопрос о кривизне
в данной точке кривой; из определения средней кривизны Кср
и кривизны К в данной точке кривой
(рис. 255)
.. Да ,, *• rs- 1- &а da
aS As-»0 As->0 AS aS
мы имеем для кривой, заданной
уравнением у= F (х),
y"dx
a = arctgy', da =
i + y'2
ds = Vl+y'*dx,
(58.4)
Рис. 255.
К-
(58.40
откуда вытекают известные формулы для кривизны К и радиуса
кривизны р
У" 1 _(1 + /2)%
(1 + У)*' ?~К~ У" '
Сопоставляя (58.4) и (58.3), мы видим, что в данной точке кривой
соприкасающаяся окружность совпадает с ее окруэюностью
кривизны (т. е. с окружностью, которая проходит через данную точку,
имеет радиус, равный радиусу кривизны, а центр ее, называемый
центром кривизны, лежит на нормали к кривой).
250 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ (гл. VIII
Пользуясь понятием кривизны, мы можем дать определение точек
распрямления и перегиба: точка распрямления характеризуется
условием К=0 (т. е. в этой точке соприкасающаяся окружность
выродилась в соприкасающуюся прямую); точка перегиба
характеризуется тем, что в ней кривизна К изменяет свой знак.
Если представить себе точку, движущуюся по данной кривой, то
при этом касательная к кривой непрерывно вращается; точка
перегиба характеризуется тем, что при переходе через нее направление
этого вращения изменяется на прямо противоположное.
Так как соприкасающаяся окружность имеет с кривой
соприкосновение не ниже второго порядка, то можно считать ее проходящей
через три бесконечно близкие точки кривой; те точки кривой,
в которых соприкасающаяся окружность имеет с ней
соприкосновение не ниже третьего порядка, будем называть круговыми
точками кривой (в этом случае соприкасающаяся окружность
проходит, по крайней мере, через четыре бесконечно близкие точки
кривой, т. е. круговая точка и три точки кривой, бесконечно к ней
близкие, лежат на одной окружности).
Нетрудно показать, что круговая точка характеризуется
условием dK — 0. Действительно, из (57.8) при лг ^= 3 вытекает равенство
ординат и первых трех производных для кривой и для окружности,
т. е. по формуле (58.4) равенство кривизн и их первых производных,
ибо ясно, что третью производную нетрудно выразить через первую
производную от кривизны; так как для
окружности К' = 0, то в круговой точке
мы должны иметь и для нашей кривой
К' = 0, dK=0.
Отсюда можно сделать такой вывод:
точки кривой, в которых кривизна
достигает экстремума, являются
С круговыми точками; действительно,
в таких точках мы должны иметь
dK=0.
В качестве иллюстрации рассмотрим
коническое сечение; так как оно может
пересекаться с окружностью не более
чем в четырех вещественных точках, то
оно может иметь соприкосновение не
выше третьего порядка со своей соприкасающейся окружностью;
в точках, отличных от вершин, имеем соприкосновение второго
порядка и соприкасающаяся окружность касается кривой и в то же время
пересекает ее (рис. 256); в вершинах кривизна достигает экстремума
и мы имеем соприкосновение третьего порядка — в этих точках
соприкасающаяся окружность лежит целиком внутри (рис. 257, а) или
целиком вне кривой (рис. 257, б).
§ 58] ПРОСТЕЙШИЕ СОПРИКАСАЮЩИЕСЯ КРИВЫЕ 251
Кривая Бурместера (54.1) (рис. 228) имеет с окружностью ЗХ 2 = 6
точек пересечения, из которых две — циклические, т. е. не более
четырех вещественных точек пересечения; в той точке петли, где
кривизна наибольшая, имеем соприкосновение третьего порядка
кривой со своей соприкасающейся окружностью, в остальных точках —
второго порядка.
в) Соприкасающаяся парабола. Рассматривая параболу с осью,
параллельной Оу,
у = С1-\-С2х-\-Съх'2% (58.5)
мы видим, что в этом случае m — 3 и, таким образом,
соприкасающаяся парабола имеет с кривой соприкосновение не ниже второго
Рис. 257.
порядка, причем коэффициенты уравнения находятся из условий (57.8)
Ci + C2x0 + Cbxl = F(x0)t C2+2Csx0=F'(x0), 2С3= F"(*o); (58.6)
в частном случае, если х0 = F (х0) — F' (л;0) = 0 (т. е. начало
координат взято в данной точке, а ось Ох совпадает с касательной), то
из (58.4), (58.5) имеем:
У = -ТГ- (58.7)
Воспользуемся этой формулой для нахождения кривизны в начале координат
той дуги ЛОВ кривой Бурместера, которая касается Ох (рис. 228); введем
обозначение у = ах2 + А» где у — ордината кривой Бурместера, а ах2 —
ордината соприкасающейся параболы, причем параметр а надо подобрать таким
образом, чтобы иметь Игл —г- = 0.
* Х-+0 х2
Мы имеем, пользуясь (54.1),
(х2 + а2х* + 2ax2L + ...)(тх + lax2 + / Д) — Imax* — xlmb =
= тх* (1 — la) + lax" + Д (— Imx + lx2 + ...) = 0.
Если положить а = —, то Д будет бесконечно малой величиной третьего
порядка малости относительно х, т. е. К = -г и радиус кривизны равен
I т ^
р =-о-', точно так же находим р, =-сг Для тои дуги, которая касается Ох
252 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
в точке О. Таким образом, окружности с диаметрами ОМ и OL (рис. 229)
являются соприкасающимися в узловой точке.
Это можно доказать и чисто геометрическим путем: любая окружность -у
(рис. 229), касающаяся Оу в точке О, пересекает кривую в двух бесконечно
близких точках, совпавших в точке О, и еще в некоторой точке Q; для
окружности с диаметром ОМ точка Q совпадает с точкой О и эта окружность
проходит через три бесконечно близкие точки кривой.
г) Соприкасающееся коническое сечение *). Этот случай
представляет интерес потому, что он является обобщением всех
предыдущих случаев, а, кроме того, коническое сечение является
простейшей кривой после окружности.
Так как коническое сечение можно провести через пять точек
кривой, то соприкасающееся коническое сечение имеет с кривой
соприкосновение не ниже четвертого порядка] для его нахождения
надо для простоты перенести начало координат в данную точку и
поделить (4.5) на один из коэффициентов, например на а23. Мы
получим уравнение
Ах2-+2Вху-+-Су2-+-2Ох-{-2у = 0. (58.8)
Дифференцируя 4 раза и пользуясь (57.8) при п = 4, найдем все
коэффициенты Л, В, С, D.
Если же рассмотреть эллипс с осями, параллельными координатным осям
("^^)2 + (^Т^")2==1, t>2(x — a)2 + a2(y — $)2 — a2b2 = 0f (58.9)
то т = 4 и соприкасающийся эллипс такого типа имеет с кривой
соприкосновение не ниже третьего порядка; дифференцируя (58.9) трижды, найдем:
Ь2 (х — а) + а2 (у — $)у' = О, Ь2 + а2у/2 + а2 (у — р) у" = О,
Зу/Г + (У-Р)У,,, = 0,
откуда вытекает:
Ь2 ,2 , , йч „ у'(уУ"-Зу"2)
--аТ^У +(У —Р)Г= у,„ •
Окончательно параметры соприкасающегося эллипса таковы.
= У-
*У'У" B = v4-^
Ъу" —у'ут
Уу'у"* Ьо_ Яу'2у"А
ут (3/'2 _ уу")2 ' у»2 (Зу"2 — //")
(58.10)
*) См. Р. Бейер [2], гл. IX.
§ 58}
ПРОСТЕЙШИЕ СОПРИКАСАЮЩИЕСЯ КРИВЫЕ
253
Если, в частности, в данной точке кривой имеем у' = 0, то, как видно
из формул, мы должны иметь для нашей кривой в данной точке ут = 0; рас-
у/ v"
крывая неопределенность по правилу Лопиталя Hm -1— = -^-
IV
мы получим
такие значения параметров:
а = х.
= у-
Ь2
З/'2
wIV
а
2_3у"
ylV
-(*)
(58.11)
В качестве примера рассмотрим
планетарный зубчатый механизм (рис. 258),
состоящий из водила /, сателлита 2
и неподвижного колеса 3, причем
точки С
са-
г 1
— = — *); траекторией
/*з о
теллита является гипоциклоида С{С3С2
с тр£мя точками возврата,
характерная
зуема
уравнениями
х = г (sin 2<р + 2 sin ср),
у = г (3 + cos 2<р — 2 cos ср),
г = г2. (58.12)
Рис. 258.
Найдем соприкасающийся эллипс типа
(58.9) в средней точке С0 дуги С{С2;
в ней х = 0, у = 2г, т. е. ср = 0. Уравнения кривой нам заданы в параметри-
У =
ческой форме (58.12); вычисляя производные у', /', у
упрощения, мы получим:
dx ___ sin ср — sin 2ср
rfcp ~~ cos ср 4- cos 2ср '
dx ___ 1 + cos Зср
rfcp "~" 2r (cos ср + cos 2cp)3 '
dx _ 3 sin 2cp (1 -f- cos Зср)
rfcp ~~ 4r2 (cos cp 4- cos 2cp)5 '
dx 3
uIV
и производя
dy
dx
dx
„ __ df
dx
IV_^T
rfy
flfcp
_ dy'
dy
dy"
dy
dyr"
y'" =
X
7 dx rfcp rfcp 8r3 (cos cp 4- cos 2cp)7
X {(cos cp 4- cos 2cp) [2 cos 2cp (1 4- cos Зср) — 3 sin Зср sin 2cp] +
4- 5 sin 2cp (1 + cos Зср) (2 sin 2<p 4 sin cp)}
откуда находим при cp = 0
:y'" = 0, y" = —
,iv = .
128/*
Следовательно, параметры эллипса таковы:
а = р = 0, а = 4г, 6 = 2г.
*) См. Р. Бейер [2], § 116.
254 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
Если построить кривошипно-шатунный механизм ABD (рис. 258), у
которого АВ = BD = Зг, ВС = г, то при неподвижной точке D точка С опишет
эллипс с полуосями а = 4г, 6 = 2г; если же точку D освободить, а точку С
вести строго по этому эллипсу, то точка D останется неподвижной; если же
точка С будет двигаться по дуге СХС2 гипоциклоиды, близкой к этому эллипсу,
то точка D будет иметь лишь приближенный выстой. Если ее сделать
центром ползуна, могущего перемещаться вдоль оси Оу, то этот ползун будет
иметь приближенный выстой, когда точка С описывает дугу гипоциклоиды,
близкую к ее средней точке. Следовательно, если к звеньям /, 2, 3
присоединить стержни 4, 5 и ползуны 6, 7, могущие двигаться в вертикальных
направляющих, то при небольших отклонениях водила / от вертикали (от —30°
до 30°) ползун 7 имеет приближенный выстой *).
§ 69. Естественное уравнение кривой
I. Естественным уравнением кривой будем называть уравнение
K = f(s), выражающее кривизну К в каждой точке кривой Г через
дуговую координату $, определяющую положение этой точки на
кривой Г**); в частности, для окружности естественное уравнение
K=z const, а для прямой /С=0. **
Если кривая задана уравнением у = F (х) в декартовых координатах, то
из (58.4), (58.40 имеем:
X
s= fVl + y'2 dx, К=. У" y = F(x), (59.1)
т. е. обе величины, К и 5, выражены как функции абсциссы х> играющей
роль параметра; исключая этот параметр из обоих уравнений, получим
естественное уравнение кривой. Наоборот, если дано естественное уравнение, то
мы имеем:
S
-g = /< = /(*), a = a0 + ff(s)ds = y(s), (59.2)
о
где ср (s) — некоторая вполне определенная функция s, а а0 — угол наклона
касательной в начальной точке М0 (х0, у0); из формул
dx . ч dy • / ч
-т— = COS а = cos ср (s), -т^- = sin а = sin ср (s)
вытекают уравнения кривой в параметрической форме
5 S
х = х0+ Г cos ср (s) ds, у = Уо + Г sin ср (s) ds. (59.3)
о о
II. Пользуясь естественным уравнением кривой, найдем
разложения в ряд Маклорена (по степеням s) радиуса-вектора г, идущего
*) См. Р. Бейер [2], § 116.
**) Уравнение называется естественным потому, что не связано ни с
какой системой координат и является соотношением между величинами К и $,
естественно связанными с кривой.
§ 59] ЕСТЕСТВЕННОЕ УРАВНЕНИЕ КРИВОЙ * 255
из точки М0, от которой отсчитываем дуговую координату s, в
некоторую точку М кривой Г (рис. 259). Из кинематики известны формулы
ds
d2r
ds2 р
dr =
ds
где т, п — орты касательной и
нормали в точке М0. Мы можем
представить орт п в таком виде п==
= ky^t, где орт k направлен
перпендикулярно к плоскости чертежа
на нас; дифференцируя по s, найдем
£ = kx£ = K(kXn) =
■Кч.
ds ds
Пользуясь формулами
*L = -&.{№ А) рис-259.
мы сможем найти все производные радиуса-вектора по дуге
dx „
ds
dr
ds"
= т,
d2r
dz
ds2
ds
■Kn,
d4
dn
ds3
dsA ds ds
К'п + К-^г==К'п-К2ч,
- ЗАГАГ'т+(К"- AT3) п.
d5r ■=(—ж'2 — ъкк")ъ — мае £-+цс" — т2к')п+ (59,5)
ds5
+ (К* — К3) ^ = (КА — 4КК" — ЗК'2) т + (К"' — 6К2К') я,
Подставляя 5 = 0, мы найдем все производные в точке М0. Пользуясь
найденными производными, мы находим искомое разложение
r = s% + ^Kn + ^(K,n — K2%) + ^[(K,f — K^n — 3KK^]-\'
+ ^[(K'" — 6K2K')n + (K* — 4KK" — ZK'2)>t]+ .... (59.6)
где многоточием обозначены члены, содержащие s6, s7, ...
Для дальнейшего нам удобно сопоставить каждому вектору
А — ъАг-\-пА2 комплексное число 2 = Ax-\-iA2, причем
вещественная и мнимая оси совпадают, соответственно, с касательной и
нормалью к кривой в точке Ж0.
б таком случае радиусу-вектору г соответствует комплексное число
- - ■ iK$2 + (- _ К2 + ОС) 4-+[- ЪКК' + / (К" - К3)} -J +
2| г v - i "v у з! ' l v v ' vv v " 4!
■+- [К4 — 4KK" — Ж'2 +1 {К'" — 6К2К')] !]-+••• (59.7)
256'
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
(гл. VHt
Дифференцируя по s, получим новое комплексное число zr>
соответствующее орту касательной т' в точке М,
+ [КА— 4КК"-\-ЗК'*-\-1(К'" — 6K2/0]-fJ-+ ... (59.8)
Найдем еще разложение в ряд Маклорена (по степеням дуги s) угла а,
характеризующего наклон касательной в точке М\ так как -^-=К>
то
dna dn'lK
ds
dsn
dsn~l
(n=l, 2, ...), и таким образом, имеем:
К'$2
K"s*
K'"s*
2!
3!
4!
(59.9)
В формулах (59.6) — (59.9) кривизна и все ее производные найдены
для 5 = 0, т. е. для точки М0*).
III. Из формулы (59.6) можно сделать следующий вывод: наряду
с нашей кривой Г рассмотрим касательную к ней окружность Г0
с кривизной /С0; полагая в (59.6) для окружности r = r0, К — К0,
К' = К" = . . . =0 и вычитая полученный результат из (59.6), найдем:
+ 4г {{К -K3 + Kl)n- ЪКК'ч] +
4!
Если s->0, то мы будем иметь соприкосновение не ниже второго
порядка, если К = К0; не ниже третьего порядка, если, кроме
того, К' = 0, и т. д. В общем случае
кривая будет иметь соприкосновение
не ниже п-го порядка со своей
соприкасающейся окружностью, если
К' = К"= ... =K(n~V = 0t п>2.
(59.10)
Для соприкосновения не ниже п-го
порядка с касательной надо еще
добавить условие К=0.
IV, Рассмотрим теперь решение
такой задачи, играющей важную роль
в кинематической геометрии: пусть даны естественные
уравнения обеих центроид Г и Гг (рис. 260); найти параметрические
уравнения траектории точки подвижной плоскости,
совпадающей с м. ц. в. Р.
*) Все производные в этих формулах взяты по дуге s (при 5 = 0).
§ 591 ECTFCTBEHHOE УРАВНЕНИЕ КРИВОЙ 257
Направим ось Ру по нормали к центроидам в сторону вогнутости
неподвижной центроиды Г, а ось Рх направим по общей касательной
к центроидам в такую сторону, чтобы вращение от оси Рх к оси Ру
происходило против стрелки часов; в таком случае кривизна Кг
неподвижной центроиды всегда положительна.
Построим радиусы-векторы г и гг точек М и Мг и орты т' и %'х
касательных в этих точках; векторам гг и х[ соответствуют
комплексные числа
гг = s -\- a2s2 + a3s3 + a4s4 + • • •»
z[ = l + 2a25 + 3a352 + 4a453+ ....
(59.11)
причем
-iq + tKx
24
векторам гит соответствуют комплексные числа
z = s^rb2s2-+-b^ + b^+ ....
г' = \ +-2£2$+3£3*2Ч-4£4$3+ ...
(59.12)
(59.1Г)
причем
" 1К
■K2 + iK'
bA
.$KK' + i(K"-K*)
24
(59.120
в этих формулах /С, К\ К'\ ...—кривизна подвижной центроиды
и ее производные, найденные для м. ц. в. Pt а К\, K'v К[, ... —
кривизна неподвижной центроиды и ее
производные, найденные для м. ц. в. Р.
Так как подвижная центроида
катится по неподвижной без
скольжения, то дуги обеих центроид,
отсчитанные от точки Р, равны. Пусть
подвижная центроида Г перекатилась по
неподвижной центроиде Гг на дугу i^-
s = ^j РМ = о PMV т. е. точка М
совпала с точкой Mv а орт т' — с
ортом xj (рис. 261); пусть при этом
бывший полюс Р перешел в
положение Р', характеризуемое комплексным
числом С, которое надо найти.
Так как z\=zf • -\, то для совмещения вектора т' с вектором т{
надо соответствующее ему комплексное число zf умножить на ком-
Рис. 261.
плексное число —Т; при этом и комплексное число z умножится на
258 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
этот же множитель, ибо все векторы в подвижной плоскости
повернулись на один и тот же угол, и мы будем иметь:
^ + Z'— = zv (,z/ = z/z1 — z[z. (59.13)
Записывая разложение Маклорена для С с неопределенными
коэффициентами
^=То+Т1*+Т2«2 + Тз*3Ч-Т4«4+ •••• (59Л4)
мы должны найти их из соотношения
(7о+Т1* + Т2*2+Тз«3+Т454Ч- • • .)(l+2V + 3*3s2+4V+ .. .)==
= (1 + 2V + 3V2+4V+ ...Ke + e^+V+e^-b •••)-
— (l + 2a2s-4-3a3s2+4a4s3+ _..) (s + ^s2 + &3s3 + ^s4 + ...).
Приравнивая коэффициенты при одинаковых степенях s в обеих
частях равенства, мы получим:
То= Ti = 0, ъ = Ь2 — л,, Ь = 2(Ь3— Оз) + 2*а(о, — b2), gg
Т4 = 3 (Ь4 — а4) — 7*2*3 + 4fl2*3 + Щ<*з ~ Abl (а2 — *г).
Подставляя сюда значения коэффициентов (59.12), (59.12').
полагая t, = x-\-iy и выделяя вещественную и мнимую части, получим
разложения координат м. ц. в. по степеням дуги
x = (K-2K1)(K-Kl)~+(9K1Ki-\-^K'SKlK'-6KK[)^r-j- ....
У = {К-К1)^- + 2(К'-К'1)^- +
+ [3 (К"-К\)-{К-К,){ък\- гккх + /с2)]-£■Ч (59.16)
V, Найдем аналогичное разложение для угла ср, на который
повернулась подвижная плоскость при перекатывании центроид на дугу s;
обозначая через а и аг углы наклона ортов *ъ' и xj к оси Рх, мы,
очевидно, имеем <р = ах — а (рис. 261), причем по (59.9) a = /Cs-f-
KiS + -^r-4 ^—h • • - оконча-
г 2! ^ 3! "Г"" ^1 — 'Ч*-г 2! ^ 3!
тельно искомое разложение таково:
9 = (^1_/C)s + (/c1'-/C')^4-(^-/C")|-+ ••• (59-17)
Пользуясь этой формулой, найдем еще разложения в ряд
Маклорена (по степеням угла поворота ср) координат точки подвижной
плоскости, которая при ср = 0 совпадала с м. ц. в. Р. Обозначая
точками производные по углу ср (в отличие от производных по дуге s,
§ 59] ЕСТЕСТВЕННОЕ УРАВНЕНИЕ КРИВОЙ 259
обозначенных штрихами), мы имеем для любой функции дуги а = и ($)
такие формулы для производных по углу ср:
<р' ср'3
откуда легко находим:
Пользуясь разложением (59.17), находим при s = cp = 0:
^=кг —к. f = K[—K,^{kl—k)^,=-(kl—k){Kx — Kh
и, таким образом, при ср = s — 0 связь между производными такова:
fl/=«(/C1 —/С), u,f = u{Kl — Kf + u(Kl — k){Kl — K). (59.18)
Если записать (59.16) в таком виде:
•^ —-3Г + -4Г+. ••• ^—"2Г + ~зГ~1—41—•"•"•, ^УЛЬ>
и заменить по (59.18) производные по дуге 5 при 5 = 0
производными по углу ср при ср = 0, то мы легко найдем:
а3 = (2/С1-/С)(/С1-/С).
а4 = (Кг — К) (?Кгкг + ЬКК — ШХК — 6/САГх). . . /
fc = -(*i-*). Рз = -2(а:1-Ю(/с1-/С).
р4={-3(^1-Ю(/С1-/С)-3(/С1-Ю2 +
+ 3/Ci — 3/С/С! + /С2} (Кх —К),. . .
Положим
Л^ Л^ _ Я2<р2 Дз(р3 /^4
*— 31 "^ 4! "Г"--' У— 2! "Т" 3! "^ 4! "^ * * '
и найдем коэффициенты этих разложений. Пользуясь (59.18), мы
имеем из (59.17)
<р «(*,-*){« + (*!-AT) £ +
+l(*i-tf) (а:,-/о+ (й-кЯ-щ-Ч- ...};
подставляя это разложение в разложение для х и группируя члены
с s3, s4, .... получим:
_ аз£^ а^ _ Лз(К,-АУ „з
* — з! "Г 4! "i" 31 S ^~
Г Л, (У.-К)» 3 д, ^ , Л№-К)П„д , .
+ L з1 -2^1 — К>-\ J! р4+-.-;
260
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
[гл. VIU
приравнивая друг другу коэффициенты при s3, s4,. .. в обеих частях
равенства, найдем, пользуясь (59.16').
z~(Kl — K)2' 4~ (К, — кг
проделывая аналогичные вычисления для разложения у, найдем:
„_ 2К, —/С у» , АКЛ-КК-ЖхКх ?4
(Ki-K)2 3!
1
(Ki-Kf
4!
■+....
Г
К,-К
Ki — K 2! ' (Ki—K)2 3!
+
(59.19)
+
(Ki-K){kl-k)-2(kl-k)2+з/с?—зкк,+к2 ?
(Kt-K)3
4!
VI. Откладывая детальное исследование траектории точки
подвижной плоскости, совпадавшей при ср = 0 с м. ц. в., до следующего
параграфа, сделаем пока несколько замечаний.
Рис. 262.
1) Рассмотрим величину К\ — К при всех случаях взаимного
расположения центроид (рис. 262, а, б, в); введем обозначение
т = *-*1-
(59.20)
Ясно, что КхфК, ибо иначе центроиды не смогли бы перекатываться
друг по другу; будем считать также, что во всех точках обеих
центроид кривизна имеет конечное значение, определяемое из
естественного уравнения кривой; в таком случае величина d имеет всегда
конечное, отличное от нуля значение.
В случае, изображенном на рис. 262, а, мы имеем:
1 1 1 ^0 К- 1
§ 60]
ОСОБЫЕ ТОЧКИ КРИВОЙ
261
В случаях, изображенных на рис. 262, б и в> мы имеем;
±__1 L к-±-
d— R Rx ' А ~ R '
причем на рис. 262, б имеем d > 0, а на рис. 262, в d < 0 *).
2) Если дуга 5, на которую перекатились центроиды, бесконечно
мала, то, как видно из (59.17), угол ср поворота подвижной
плоскости является бесконечно малой величиной того же порядка малости,
как и s\ бесконечно малое перемещение 5 любой точки М
подвижной плоскости, отличной от точки Р, выражается формулой 5 = MP - с#,
т. е. является бесконечно малой величиной первого порядка
малости относительно угла ср или дуги s; в то же время
формула (59.16) показывает, что перемещение м. ц. в. является
бесконечно малой величиной второго порядка малости сравнительно
с дугой sy а, следовательно, и сравнительно с перемещением S
любой точки плоскости, отличной от м. ц. в.
Пусть, например, плоская фигура S (рис. 263) катится без скольжения но
неподвижной шероховатой фигуре S{; если к ее точкам, отличным от
полюса, приложены силы F{, F2, ..., то,
вычисляя алгебраическую сумму их
элементарных работ по формуле ^Fb cos (F, 5),
мы видим, что все эти работы будут
бесконечно малыми величинами первого
порядка относительно 5, т. е. относительно <р
или s. В точке касания Р приложена
нормальная реакция N и сила трения
скольжения F, но элементарная работа этих сил
будет бесконечно малой величиной
второго порядка малости сравнительно
с s, а следовательно, и сравнительно с 5
и сравнительно с суммой работ всех
остальных сил; поэтому она может быть отброшена, и мы можем считать
идеальной связь, которая принуждает катиться без скольжения шероховатую
поверхность одного тела по такой же поверхности другого тела.
§ 60. Особые точки кривой
I. Рассмотрим функцию F(x), однозначную, непрерывную и
дифференцируемую на некотором отрезке [а, Ь]\ если положим y = F(x),
то посредством этой формулы точкам отрезка [а, Ь] ставятся в
соответствие точки некоторого геометрического места, которое будем
называть простым отрезком кривой; для нахождения касательной
к ней в точке с абсциссой х = х0, где а < х0 < Ъ, мы должны, как
известно, найти производную у'0 = F' (х0), равную угловому
коэффициенту касательной.
*) Геометрическое и кинематическое значение величины d будет
указано в §§ 66, 70.
262 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
Пусть теперь кривая определена уравнением f(xt у) = 0; если
предположим, что на некотором отрезке [а, Ь], внутри которого
лежит х0, наша кривая имеет вид простого отрезка кривой, то,
подставляя y=F{x) в уравнение f(x, у) — 0, мы получим тождество
f[x, F(x)] = 0] дифференцируя его по х, найдем:
/;+/;/=о- (бол)
Мы сможем отсюда найти у'0 в каждой точке х0, в которой обе
производные fx и /' не обращаются в нуль одновременно *).
Такие точки называются обыкновенными; если же
/;=/;=о, (60.2)
то (60.1) обращается в тождество и из него нельзя найти у'\ точка,
в которой выполняется (60.2), называется особой точкой кривой.
Предположим существование непрерывных частных производных
второго порядка fxx, f" % f" в данной точке; дифференцируя наше
тождество дважды, получим:
{гхх+гХУу')+(/;*+/;>о у+/;/'=о. (бо.з>
Подставляя координаты данной особой точки М0, видим» что /у = 0,
а у'0 находится как корень квадратного уравнения
А + 2Ву'0 + Су'02 = 0, (60.4)
где мы положили для простоты
А = {ГХХ)М, В = (/:у)м, С = (Г„)м.. (60.40
Предположим сперва, что эти три числа не равны нулю
одновременно; в таком случае точка называется двойной и
уравнение (60.4) дает два направления касательных в двойной точке.
В частном случае, когда С = 0, один из угловых коэффициентов
касательной становится бесконечно большим, а при В — С = 0 оба
угловых коэффициента обладают этим свойством (§ 4) — это
означает лишь то, что соответствующие касательные параллельны оси Оу.
II. Будем различать три случая в зависимости от характера
корней (60.4).
1) Если В2 — АС > 0, то уравнение (60.4) имеет два
вещественных различных корня, т. е. абсциссе х0 соответствует точка М0
*) Если /у = 0, то можно найти -з— из уравнения / -\-/х ~л— = 0> от"
куда -т— = 0, т. е. —~- = оо. В этом случае касательная параллельна оси Оу.
§ 60]
ОСОБЫЕ ТОЧКИ КРИВОЙ
263
кривой с двумя направлениями касательных (рис. 264); такая
точка называется узловой.
2) Если В2 — ЛС < 0, то имеем два комплексных сопряженных
корня, т. е. две мнимые сопряженные касательные с вещественной
точкой касания; такая точка называется
изолированной.
3) Если В2—ЛС = 0, то имеем два
вещественных равных корня, т. е. две
совпавших касательных) такая точка
называется точкой возврата (рис. 265) или
точкой самоприкосновения (рис. 266).
Если точка движется по нашей кривой,
то при переходе через точку возврата ее
скорость должна мгновенно изменить свое
направление на прямо противоположное;
при переходе через точку
самоприкосновения этого не происходит, ибо, перейдя точку М0, движущаяся
точка описывает затем петлю М0АВМ0 и только после этого снова
приходит в точку М0 со скоростью противоположного направления.
Рис. 264.
Рис. 265. Рис. 266.
Если А = В = С = 0, то (60.4) обращается в тождество, из
которого нельзя найти у'0; дифференцируя еще раз (60.3), получим:
[(C+/V)+(/^+/:;y/)/+/;yy"] + {г;хх + оо у +
+(/;v+О'2) у+(fU+/;у) у"+
+(С+/;>о у"+/>"'=0; <60-5)
подставляя координаты точки М0 и пользуясь тем, что в этой точке
имеем
/'=/' = f = Г = /" = о,
J х J у J хх J ху J уу *
получим кубическое уравнение для нахождения у'0
D+3£^+3/^2 + G< = 0,
D = \fxxx)M09 E — (fxxy)M0' /7 = (/^уу)ж0* 0 = (Луу)мо*
Если D, Е, F, G не равны нулю одновременно, то имеем тройную
точку, в противном случае дифференцируем еще раз и т. д.
264
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
[ГЛ. VIII
Для вычисления кривизны в двойной точке по формуле (58.4')
находим сперва значение у' из (60.4), а затем по нему
соответствующее значение у" из (60.5) *).
III. Рассмотрим в качестве первого примера кривую Бурместера (54.1);
мы имеем для нее
/х = Зтх2 + 21ху + ту2 — 1ту, /у = 3/у2 + 2тху + Ix2 — Imx
и точка (0, 0) является особой. Так как
fxX = 6mx + 2ly, /jy = 2lx + 2my — lm, /уу = 61у+2тх,
то, подставляя х = у = 0, получим по (60.4), (60.4') уравнение — /ту^ = 0,
т. е. наши два корня таковы: у0 = 0, у0 = со; следовательно, оси Ох и Оу
являются касательными к кривой
Бурместера в ее узловой точке (рис. 228).
Рассмотрим теперь кривую с уравнением
у* == -Ах2 + х\ f = у2 + \х2 — л:4 = 0. (60.6)
Мы имеем:
/х=*9х-4л*. /у=2у /;, = 8-12Л
/*У=о, /;у=2,
откуда ясно, что начало координат является
особой точкой, притом изолированной, ибо
при х = у = 0 имеем по (60.4')
А = 8, В = 0, С = 2, #2__лС==—1б<0.
Для того чтобы лучше представить себе
изолированную точку, запишем уравнение (60.6)
в таком виде: у2 = х2(х2— 4); так как левая
часть неотрицательна при всех вещественных значениях у, то такой же
должна быть и правая часть, т. е. мы должны иметь х2 > 4, что возможно
лишь при л:>2 и при лг<!—2; кривая состоит, таким образом, из двух
ветвей (рис. 267), причем в области —2 < х< 2 нет вещественных точек кривой
(ибо х2—4 < 0), кроме точки х = у = 0, — эта точка является
изолированной, ибо в ее окрестности нет других вещественных точек кривой.
IV. Для того чтобы подробнее исследовать точки возврата,
предположим, что кривая задана уравнениями в параметрической форме:
* = /(*)> у = <р(0.
где t — некоторый параметр, а обе функции f(t) и ср(^)
предполагаются однозначными, непрерывными и дифференцируемыми на не-
Рис. 267.
*) Если у' = оо и, следовательно, у" = оо, то пишем уравнение кривой
в форме х = Ф (у) и находим кривизну по формуле
d2x_
~dy2 '
К =
(1+*'2)'"
dy
§ 601 ОСОБЫЕ ТОЧКИ КРИВОЙ 265
котором отрезке [tv /2]. В таком случае снова будем говорить
о простом отрезке кривой.
Угловой коэффициент касательной в точке, соответствующей
некоторому значению параметра t0, (tx <t0<C t2), найдем по формуле
Мы не сможем его найти в случае
f'(t0) = y'(t0) = 0t (60.7)
ибо в этом случае наша дробь для нахождения k приобретает
неопределенную форму; таким образом, эти равенства являются
условием того, что точка — особая; очевидно, в особой точке нарушено
то условие, при котором величины As и А/ являются бесконечно
малыми одного порядка.
Пусть в окрестности точки t0 координаты х и у разложены
в ряды Тейлора
(60.8)
так как при t = t0 мы должны иметь х' = у' = 0, то, очевидно,
а1 = ф1 = 0; перенося начало координат в особую точку, будем иметь
а0 = ро = 0. Предположим, что оба разложения имеют такой вид:
(t — t0)n , (* — t0)n+l ,
/2! ' л+1 (n + 1)! ' • • •'
(60.9)
где ал, pm—первые не равные нулю коэффициенты в разложениях х
и у. Мы имеем в таком случае
(t-t0)m-1 , д (t-t0)m
dy__dy_.dx__ Pm (m — l)\ "rPm+1 ml "*" '" .
dx dt ' dt a /\л-1
a.
(^-^о)л"1 , „ <'-'о)л
я (л—1)1 Г n+l Ж
полагая t~>t0, мы видим, что дробь стремится к нулю при m > п,
к бесконечности при m < п и к конечному, отличному от нуля
пределу -^- при т = п\ таким образом, раскрывая неопределенность
266 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
при помощи рядов, мы находим угловой коэффициент
касательной по формуле
( 0, т > п,
k0 = } оо, т < я, п, т^2. (60.10)
V. Воспользуемся известной формулой для вычисления кривизны
К= Х'У''~КХ1 . (60.11)
(x'2+y'2)'h '
где производные взяты по параметру /; так как мы имеем
неопределенность при t = t0, то снова раскрываем ее при помощи
разложения числителя и знаменателя в ряды; мы имеем:
(* —'о)""1 , / о (t — t0)m-1
(П— 1)! "Г • • •» ^ —^т (т_1)!
(60.12)
л (п — 2)! ^•••» ^ — Ym (т — 2)\ п~.-..
откуда
*.'*•" \»'у" (/У2 я) апрт ( п+т-$ /ел inn
*у —ух —(n_1)I(m_1)|V — 'о) +... (Ь0.12)
Для вычисления суммы х'2-\-у'2 сделаем сперва предположение,
что п > т; в таком случае
* +У = (m-l)l' •-•••• (6°ЛЗ)
причем при t—>t0 все выписанные нами члены являются главными
частями соответствующих бесконечно малых величин. По (60.11) —
(60.13) имеем:
■■{"'Ч'-цГ' +■■■}■ <60Л4>
При t->t0 эта дробь стремится: к нулю при п > 2т, к бесконечности
при п < 2т и к конечному, отличному от нуля пределу при я=2т;
таким образом, при я > т кривизна в особой точке выражается
формулой
( 0, п> 2т,
АГ={ оо, п< 2т, (60.15)
| + тап(т-\)\* п=2т
I -Рт1Ря.1(2т-1)!' П Zm"
При п > 2т особая точка является точкой распрямления.
§ 60]
ОСОБЫЕ ТОЧКИ КРИВОЙ
267
Случай п < т вполне аналогичен рассмотренному случаю п > т\
если же п—т, то, как легко видеть, имеем:
x'f — у'х" --
«п$п+1 — ап+1$п,£ ^ ч2л-2 ,
п\(п — 1)!
и таким образом,
К = \ п\(п-\)\ ('"'о) +"•)'
I (а2 _L 82V 2
;\ (я-цр K-^r+.-l: (60.16)
,3л-3
следовательно, при п — т имеем К=оз, за исключением того част-
= ft^+1 ; в этом случае надо знать дальнейшие
ного случая, когда ~- = -^-^
члены разложения числителя.
VI. Предположим теперь, что параметр t стремится к значению /0
монотонно, т. е. оставаясь все время меньше или больше его.
Пусть сперва я > т\ в таком случае по (60.10) в особой точке,
совпадающей с началом координат, кривая касается
оси Оу. Будем различать четыре случая.
1) Оба числа п и т — четные (рис. 268). Мы
видим по (60.9), что абсцисса х одного и того
же знака при бесконечно малых значениях t —1$
как положительных, так и отрицательных (ибо
знак зависит от членов наинизшего порядка
малости); этим же свойством обладает и ордината у\
следовательно, когда t стремится к t0, оставаясь
меньше него, точка опишет ветвь АО кривой,
касающуюся Оу в точке О, которая соответствует
t = t0; если же t стремится к t0, оставаясь больше
него, то точка опишет ветвь ВО, также
касающуюся Оу в точке О; обе ветви в точке О
имеют общую касательную (т. е. касаются друг
друга) и одинаковую кривизну. В рассматриваемом случае обе ветви
лежат в одном и том же квадранте (который зависит от знаков ап
и рт) и по одну сторону касательной; такая точка называется
точкой возврата II рода.
2) п — нечетное, т — четное (рис. 269). Повторяя те же
рассуждения, мы видим, что в этом случае ветви АО и ВО лежат по
разные стороны от касательной, такая точка называется точкой
возврата I рода.
3) п— четное, т — нечетное (рис. 270). В этом случае ветви АО
и ВО имеют общую касательную в точке О и при непрерывном
изменении параметра / точка описывает дугу АОВ без изменения
268 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [гл. VIII
Рис. 269,
направления скорости на прямо противоположное при прохождении
точки О; в этом случае О — обыкновенная точка кривой.
4) Оба числа п и т — нечетные (рис. 271). Обе ветви АО и ВО
расположены в двух несмежных квадрантах по разные стороны как
от касательной Оу, так и от
нормали Ох\ точка О является точкой
перегиба, ибо при переходе через
нее кривизна изменяет свой знак;
это может произойти как при
переходе через нулевое, так и при
переходе через бесконечно большое
значение кривизны.
Примечание 1. Из
формулы (60.14) видно, что кривизна К
изменяет свой знак при переходе
через точку О в том случае, когда
п~\-т является четным числом;
однако в случае, когда пят — четные
числа (рис. 268), может показаться,
что кривизны обеих ветвей ОА
и ОБ в окрестности точки О одного знака. Это будет верно,
если мы будем рассматривать обе эти ветви как две
самостоятельные кривые, пробегаемые в направлениях ОА и ОВ\ но в данном
случае мы рассматриваем обе эти кривые как
ветви одной и той же кривой, которая при
непрерывном возрастании параметра t
пробегается в направлении АОВ\ при этом в
случаях, изображенных на рис. 268, 271,
направление вращения касательной изменяется на прямо
противоположное при переходе через точку О.
Примечание 2. Если через ds2
обозначить элементарную дугу эволюты Г2 кривой Г,
то кривизна К2 эволюты выразится формулой
K2=-rL, ибо касательная к Г2, т. е. нормаль
US2
к Г, повернется на тот же угол da, что и
касательная к Г\ по известному свойству
эволюты имеем:
„ da ', da , da dp
к2- • •
ds2 = ±dp,
da
dSo
d9
ds
K2
ds
Рис. 271.
так как-т- = /С, ^=~й7\~]() = — ~Ш» то окончательно кривизна
эволюты связана с кривизной данной кривой Г соотношением
К'
К2= +
(60.17)
§61] ИССЛЕДОВАНИЕ ТРАЕКТОРИИ точки подвижной плоскости 269
Из этой формулы можно сделать следующие выводы:
а) задание величин К и К' определяет кривизну К2 эволюты;
б) если две кривые имеют соприкосновение не ниже третьего
порядка, то совпадают их касательные и центры кривизны не только
этих кривых, но и их эволют;
в) круговой точке кривой
соответствует точка возврата первого У\ \
рода ее эволюты (рис. 272);
действительно, при К' = О имеем К2 = оо.
Рис. 272.
VII. В качестве иллюстрации рассмотрим кривую с уравнением (рис. 273)
(y—X2)2==x5t /(л:> у) = (у— ЛГ2)2_ЛГ5==0; (60.18)
так как
/ ; = - 4х (у - х2) _ б**, /у =, _ 2 (у .- х2),
то начало координат является двойной точкой кривой; мы имеем из (60.18)
у = х2 ± х2Ух~,
т. е. имеем две ветви, характеризуемые уравнениями
О А: у = х2 + х2У^, OB: у = х2 — х2УТ. (60.19)
Так как для вещественных значений у мы должны иметь х > 0, то кривая
лежит в правой полуплоскости, причем нетрудно найти, что обе ветви
касаются оси Ох в точке О и имеют в точке О кривизну К = 2, найденную
по (60.11). Для первой ветви О А имеем у > х2, т. е. она проходит выше
параболы у = х2\ для второй ветви ОВ имеем у = 0 при х = 1, после
чего у < 0 и стремится к —оо при х -> +оо.
Обе ветви в окрестности начала лежат в одном квадранте и по одну
сторону от касательной, т. е. выше Ох, следовательно, начало координат
является точкой возврата II рода.
§ 61. Исследование траектории точки подвижной плоскости,
совпадающей с мгновенным центром вращения
I. Применим результаты предыдущего параграфа к исследованию
траектории Г0 м. ц. в., характеризуемой уравнениями
270 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
причем коэффициенты этих разложений имеют значения, указанные
в (59.16). Отметим, что из (59.20) вытекает условие f^^O-
На основании (60.10), где в данном случае /г^З, /я —2, имеем
Л"«, = оо, т. е. ось Ру— нормаль к центроидам — является
касательной в м. ц. в. к его траектории.
Так как т — четное число, то по рис. 268, 269 траектория
м. ц. в. имеет в этой точке точку возврата (I рода при п
нечетном и II рода при п четном).
Легко видеть, что м. ц. в. является единственной точкой
подвижной плоскости, траектория которой имеет в этой точке
точку возврата; действительно, при переходе через точку возврата
скорость точки подвижной плоскости должна изменить свое
направление на прямо противоположное, а это (благодаря непрерывному
изменению скорости) возможно лишь при обращении скорости в нуль.
Для нахождения кривизны К0 траектории м. ц. в. применяем (59.16),
(60.15) и получаем следующий результат:
1) если 2КхфК, то я = 3, К0 = оо и м. ц. в. является точкой
возврата I рода кривой Г0;
2) если 2Кг = К, но Ж\ф2К', то п=4 и
^о=±—^ : (61-2)
в этом случае м. ц. в. является точкой возврата II рода кривой Г0;
3) если 2К1 = К, З/Ci = 2/С , то /г>-5, /С0 = 0, причем м. ц. в.
является точкой распрямления и, кроме того, точкой возврата
(I рода при п нечетном и II рода при п четном).
Для доказательства достаточно заметить, что
р2 = К — Kv а3 = (2Кг — К)(КХ — К),
а4 = 9/Ci/Ci + ЬКК' — 8КгК' — 6КК[\
при а3=0, т. е. при К=2Кг, имеем а4 = Лг1(2Лг' — 3/Ci).
II. Рассмотрим еще вопрос о порядке соприкосновения
траектории м. ц. в. Р в этой точке со своей касательной или с
соприкасающейся окружностью.
В случае 3) соприкасающаяся окружность вырождается в
касательную; по (61.1) у является бесконечно малой величиной порядка s2\
если у принять за основную бесконечно малую величину, то s будет
1 п
порядка у2, а х — порядка у2 ; следовательно, задавая бесконечно
малое значение у, мы видим, что х (т. е. расстояние точки на
кривой Г0 от касательной Ру) является бесконечно мглой величиной по-
п
рядка у2; таким образом, если разложение (61.1) для х начи-
§ 61] ИССЛЕДОВАНИЕ ТРАЕКТОРИИ точки подвижной плоскости 271
нается членом с sn (п^>5), то траектория м. ц. в. в этой точке
имеет соприкосновение со своей касательной порядка v, причем
| ft,
' = U-1.
если п -
если п -
= 2А+1.
:2ft.
(61.3)
Действительно, при п нечетном можем положить n = 2k-\-\> т. е.
п — Ь_|_1
при п четном полагаем п-
2ft, -j = ft, т. е. в этом
: 0, равно ft —1.
случае наибольшее целое число, при котором lim —
у-»о У4
Интересно отметить, что такой же порядок соприкосновения будет
между кривой Г0 и любой окружностью,
касающейся оси Ру в точке Р и проходящей между
этой осью и ветвью кривой; действительно,
разность абсцисс точек этих кривых для одной
и той же ординаты также имеет порядок);2;
в частности, соприкасающаяся окружность
(при п^Ъ) становится неопределенной.
Рассмотрим теперь случай 2). При
перекатывании подвижной центроиды в таком
направлении, при котором точка касания центроид
перемещается в положительном направлении
оси Рх, мы считаем s > 0 и м. ц. в.
описывает ветвь РВ (рис. 274); при
перекатывании в противоположном направлении мы
считаем s < О и м. ц. в. описывает ветвь РА.
Введем новый параметр X по формуле s=X для ветви РВ и
s~—X для ветви РА\ мы получим:
Рис. 274.
(
х ■■
аА1*
«Б*Б
РВ:
|,_
4!
№2
5!
(U3
РА:
2!
3!
«4Х4
4!
Ml.
2!
«5Х5
5!
3!
Будем рассматривать обе ветви как две самостоятельные кривые,
пробегаемые в направлениях РВ и РА, т. е. для обеих кривых при
этом Х^О. Полагая теперь Х2 = т, получим:
272 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ VIII
Мы видим прежде всего, что у и т одного порядка малости; кроме
того, дуги обеих кривых, отсчитанные от м. ц. в., одного порядка
малости с т и с у. Принимая у за основную бесконечно малую
величину, мы видим, что разность ММХ абсцисс точек М на РВ и Мх
на РА, соответствующая одному и тому же значению у = РМ0,
1 1
является бесконечно малой величиной порядка т2, т. е. у2; таким
образом, в м. ц. в. Р обе ветви, РВ и РА, имеют между собой
соприкосновение второго порядка. Отсюда вытекает, что любая
окружность Г', касающаяся оси Ру в точке Р и проходящая
в окрестности ср между кривыми РА и РВ, может считаться
соприкасающейся в точке Р\ действительно, если расстояние ММХ
порядка у2, то это же справедливо и для расстояний ММ' и М'МХ.
К этому же выводу мы могли бы прийти, рассматривая формулу
(60.11), которая на основании (60.12) принимает в нашем случае
неопределенную форму -^ ; кривизну все же будем определять
формулой (61.2), вытекающей из (60.15), ибо мы получили ее как
истинную величину неопределенного выражения.
§ 62. Шатунные кривые
I. Рассмотрим шарнирный четырехзвенник АХАВВХ (рис. 275) и
подвижную плоскость Е, связанную с шатуном АВ\ будем называть
ее шатунной плоскостью, каждую ее точку М — шатунной
точкой, а траекторию этой точки
(лежащую в неподвижной
плоскости и вычерчиваемую точкой М
при непрерывном движении
механизма) — шатунной кривой
механизма.
Форма шатунной кривой для
данного четырехзвенника зависит,
конечно, от положения шатунной
точки; на рис. 275 изображены
шатунные кривые для различных
шатунных точек при данном
положении шатунной плоскости; мы
видим среди них шатунные
кривые с узловыми точками М, N, ...
Рис. 275. и с точками возврата /?, 5, ...
Этот рис. 275 взят из книги
К. Pay [1], где приведен ряд таких кривых; выбирая из них
подходящую кривую, К. Pay получает таким чисто эмпирическим путем
§ 62]
ШАТУННЫЕ КРИВЫЕ
273
механизм, в котором точка на рабочем органе описывает эту кривую
(например, механизм тестомесильной машины, изображенный на
рис. 276)*).
II. Исследуем двойные точки шатунной кривой, сперва
геометрическими, а затем аналитическими методами.
Пусть механизм будет в положении АХАВВХ (рис. 277); пусть
точка М является двойной точкой своей траектории, т. е. пусть
шатунная точка М
проходит через рассматриваемое
положение при двух
различных положениях
механизма А1АВВ1 и А1А'В'В1
(рис. 277). Очевидно, при
конечном перемещении
шатунного треугольника из
начального положения АМВ
в конечное положение Af MB'
точка М является центром
конечного вращения, откуда
вытекает равенство углов
/_ AMAf = l_ ВМВ'. Так как треугольник АМВ — жесткий, то
£АМВ = £яА'МВ'. Мы имеем, таким образом, ^АМВ = /ттАМА'-\-
+ L А'мв = L А'мв + L вмв' = L л'мв' = т.
Следовательно, двойная точка М шатунной плоскости в дан-
ном положении АХАВВХ механизма характеризуется тем, что
Рис. 277.
из нее шатун АВ и стойка АХВХ видны под одинаковыми углами
(или под углами, дополнительными до 180°, если точка М лежит
внутри четырехугольника АХАВВХ).
В соответствии с § 51 имеем: в данном положении шатунной
плоскости геометрическим местом двойных точек шатунных
*) Читатель найдет ряд шатунных кривых в т. IV полного собрания
сочинений П. Л. Чебышева (стр. 190, 196, 198, 205 и др.); см. также Р. Бейер [2],
гл. VIII.
274 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
кривых является фокальная кривая fx (построенная для
четырехугольника АХАВВХ, в котором Ах к В, А к Вх— две пары
противоположных вершин).
Этот вывод относился к тому случаю, когда угол ^ не задан;
если же он задан, то таких точек всего две; опишем окружность Г,
из которой отрезок АХВХ должен быть виден под углом f —
очевидно, двойные точки должны лежать на этой окружности; для
их нахождения воспользуемся методом построения фокальной
кривой, изображенным на рис. 213, С и С7 —искомые двойные
точки.
III. Рассмотрим теперь точку самоприкосновения (рис. 278);
можно считать ее двумя слившимися двойными точками; если
угол -у задан, то обе эти двойные
точки лежат на окружности Г и
соответствующая шатунная кривая должна
проходить через две бесконечно
близкие точки окружности Г, т. е. касаться
ее. Если Р и Р'— м. ц. в. в обоих
положениях механизма,
соответствующих двойной точке, то обе
касательные в двойной точке М совпадут лишь
в том случае, когда все три точки Р,
Р' и М лежат на одной прямой;
следовательно, если угол -у задан и
построена окружность Л то, соединяя
м. ц. в. Р с ее центром С, мы получим
Рис. 278. в пересечении прямой PC с
окружностью Г две точки Ж, М2, шатунные
кривые которых будут в этих точках касаться окружности Г. Если
угол -у не задан, то проводим пучок окружностей через точки Ах и Вх и
находим две точки пересечения каждой из них с прямой,
соединяющей центр этой окружности с точкой Р\ на основании § 10 и гл. VII
геометрическим местом таких точек является фокальная
кривая /2, для которой точка Р является фокальным центром,
а пучок окружностей определяется точками Ах и Вх. Эта кривая
является геометрическим местом шатунных точек в данном положении
шатунной плоскости, обладающих следующим свойством: из каждой
такой точки и из бесконечно близкой к ней точки шатунной
кривой отрезок АХВХ должен быть виден под одинаковыми
углами.
Фокальные кривые fx и /2 пересекаются в девяти точках, но
из них две точки — циклические, а три точки — это Av Вх и Р\
следовательно, кроме этих точек, они пересекаются в четырех
точках, которые являются точками самоприкосновения шатунных кривых
в данном положении шатунной плоскости.
§ 62]
ШАТУННЫЕ КРИВЫЕ
275
Чх.у)
Отметим, что острие, т. е. точка возврата, может быть в каждом
положении шатунной плоскости лишь у шатунной кривой точки,
совпадающей в данном положении с
полюсом *).
IV. Для исследования шатунной
кривой аналитическим методом выведем ее
уравнение (рис. 279). Выражаем
координаты точек В и С через координаты
шатунной точки М(х, у)
Хг.
■ х — ^cosX, хс — х — acos(X-f--]f)' д&
yB = y — ts\n X, ус:
'.у — asin(X-j-'y)'
(62.1)
Рис. 279.
Исключая из этих соотношений координаты точек В и С при
помощи формул
4 + У| = г2, (xc-df.+ y% = b\ (62.2)
получим:
2tx cos X -f- 2ty sin X = x2 -f- y2 +t2 — r2,
2a(x—d)cos(X + T) + 2aysin(X+ T) = (x—d)2 + y2-\-a2—b2\ (62.3)
так как
cos (X + f) = cos X cos 7 — sin X sin 7,
sin (X -f- 7) = cos X sin y + sin X cos 7,
то из этих уравнений (62.3) можем найти:
sinX:
JJ_
cosX =
W '
(62.4)
b2\,
где мы положили для краткости
U = а[(х — d) cos 7 + у sin 7] (х2 -+- У2 +12 — г2) —
— tx[(x — d)2-+-у2 + а*-
V =а[(х — tf)sinT — усо$ч]{х2 + у2 + Р — r2)+ (62.5)
+ ty[{x — d)2 + у2 + a2 — £2],
№ = 2a^sin ч[х(х — d)-+-y2— dyctg^].
Исключая sinX и cosX, находим окончательно уравнение шатунной
кривой шарнирного четырехзвенника
U2-\~V2 = W2. (62.6)
*) У Р. Бейера [2], § 99 читатель найдет применения шатунных кривых
с остриями к некоторым задачам синтеза механизмов.
276 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [гл. VIII
Мы видим прежде всего, что она является алгебраической кривой
шестого порядка. Если ввести однородные координаты, умножить
обе части (62.6) на х^ и затем положить лг3=:0 (в соответствии
с § 5), то мы получим (jc^-f- х|)3 = 0, т. е. циклические точки
являются тройными точками шатунной кривой, которая, таким
образом, является трициркулярной (§ 8).
Для нахождения ее двойных точек выясним сперва их количество:
шатунная кривая пересекается окружностью Г в 6X2 = 12
точках, из которых шесть точек—циклические; следовательно, кроме
них, остается шесть точек пересечения, т. е. три двойные точки
(ибо каждую из них следует считать за две).
Для нахождения координат этих точек воспользуемся
условием (60.2). Полагая /= U2-\-V2— W2, получим:
UU'x-\-W'x—WW'x=0, UUy-\-VVy — WWy = 0.
Легко видеть, что уравнение
r=(^-4)2+(y-4d^)2-(-2lrr)s=-0 <62-7>
является уравнением окружности Г, из точек которой отрезок Л1В1
виден под углом *у; отсюда по (62.6) вытекают уравнения для
координат двойных точек *)
U = 0, V = 0. W = 0. (62.8)
Отметим, что в уравнение шатунной кривой (62.6) входит шесть
параметров (а, Ъ, г, t, d, 7) — следовательно, при заданных
неподвижных шарнирах можно построить такой шарнирный четырехзвенник,
чтобы шатунная кривая некоторой его точки пришла бы через пять
заданных точек; если же неподвижные шарниры не заданы, то число
заданных точек можно увеличить до девяти.
V. Покажем нахождение шатунной, кривой для кривошипно-
шатунного механизма (рис. 12). Полагая в (62.5) d = e-\-R, где е
является проекцией отрезка DC на Ах, получим, переходя к
однородным координатам
xlU = U0-Rx3Ul, xlV = V0-RxsVv x^ = WQ-Rx^v
где мы положили:
Ux = a cos т [х\ -+- х\ -+- х2 (t2 — г2)] — 2txx {хх — ехъ),
Vx=a sin т [х\ + х2 + х\ (t2 - г2)] + 2tx2 {хх - ехг),
Wx = 2atxz (хх sin 7 -j- х2 cos 7),
а величины UQt V0, WQ содержат лишь разность Ъ2 — /?2, остающуюся
ограниченной при /?->оо; действительно, при безграничном удалении
*) На основании (62.6) любые два из них влекут за собою третье.
§ 63] ОДНОПАРАМЕТРИЧЕСКОЕ СЕМЕЙСТВО ПЛОСКИХ КРИВЫХ 277
точки D будем иметь CD = #->оо, причем b2 — R2~y2c. Отсюда
находим:
XQ{U2+V2_W2) =
-ф-^.у+ф-^ОГ-ф-х.г.у-о.
и при /?->оо получим:
x\{u\ + V\ — x\w\) = 0. (62.9)
Следовательно, в случае кривошипно-шатунного механизма
шатунная кривая (62.6) распадается на дважды взятую бесконечно
удаленную прямую и на кривую с уравнением
U\ + У\ — хЬг\ = 0, (62.10)
являющуюся бициркулярной кривой четвертого порядка *).
§ 63. Однопараметрическое семейство плоских кривых.
Характеристические точки и огибающая
I. Рассмотрим уравнение
f(x, у, Х) = 0, (63.1)
зависящее от параметра X; предполагается, что функция f(xy у, X)
имеет непрерывные частные производные по х, у, X.
Фиксируя значение параметра X, мы получим вполне определенную
кривую; если же X непрерывно изменяется, то получим целое
семейство кривых, зависящее от одного параметра X. Характеристической
точкой кривой семейства назовем
предельное положение точки пересечения
этой кривой с соседней кривой семей- \ з \ J JR+JA
ства, когда эта последняя стремится
к совпадению с данной кривой. Таким
образом, фиксируя значение X, мы "-
должны найти точки пересечения
кривых семейства с уравнениями / (х, у, X)— Рис. 280.
= 0, / (х, у, X -(- ДХ) = 0 и затем найти
предельное положение этих точек при ДХ->0 (рис. 280). Из этих
уравнений вытекает равносильная им система уравнений
fix, у.х)=о. /^уД+^)-туД)=01
*) Ее уравнение легко привести к виду (10.9), если положить в (62.9),
(62 10) х3 = 1, хх = х-, х2 = у.
278 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
откуда получим при ДХ->0
/(x.y.X)=0. lim /1*>УЛ + *к)-/(х,уЛ) ,
Таким образом, характеристические точки кривой семейства
(которая соответствует фиксированному значению параметра X) найдем,
решая совместно два уравнения:
f(x, у, Х) = 0, /£(*, у, Х) = 0, (63.2)
откуда найдем координаты (дг, у) этих точек, выраженные через X,
х = ср1(Х), у = ср2(Х). (63.3)
При непрерывном изменении параметра X уравнения можно
рассматривать как параметрические уравнения некоторой кривой. Ее
уравнение F(x, у) = 0 можно также получить, исключая X из двух
уравнений (63.2). Кривую, уравнение которой получено последним способом,
называем дискриминантной кривой данного семейства.
Следовательно, характеристические точки всех кривых семейства лежат
на дискриминантной кривой.
Из второго уравнения системы (63.2) можно выразить X через
координаты (х, у) характеристической точки Х = ф(х, у), т. е. найти
ту кривую семейства, которая проходит через данную
характеристическую точку. Таким образом, уравнение (63.1) при фиксированном
значении X является уравнением кривой семейства, а при
Х = ф(лг, у) — уравнением дискриминантной кривой.
Из (63.1) имеем, находя полный дифференциал,
f'xdx + f'ydy + f'xdk = Q. (63.4)
причем это равенство имеет место в обоих указанных случаях, ибо,
как известно из анализа, выражение для полного дифференциала
сохраняет свою форму независимо от того, будет X независимым
переменным, или будет функцией некоторых аргументов. Нетрудно
видеть, что последний член f'xd\ в обоих случаях равен нулю: для
кривой семейства, ибо вдоль нее Х = const, и для дискриминантной
кривой, ибо для нее /^^0; таким образом, в каждой
характеристической точке имеем:
f'xdx + f'ydy = 0. (63.5)
Если кривые семейства не имеют особых точек, то f'x -\~/'у ^0 и
мы находим у'=--У- = — f'jc'-f'* следовательно, в каждой
характеристической точке совпадают касательные к дискриминантной кривой
и к кривой семейства, проходящей через эту точку.
§ 63] ОДНОПАРАМЕТРИЧЕСКОЕ СЕМЕЙСТВО ПЛОСКИХ КРИВЫХ 279
Назовем огибающей семейства кривых (63.1) кривую, которая
в каждой своей точке касается кривой нашего семейства;
следовательно, если кривые семейства не имеют особых точек, то дискри-
минантная кривая является огибающей.
Но уравнение (63.5), справедливое для дискриминантной кривой,
удовлетворяется и в особых точках кривых семейства, ибо в этих
точках /^ = /'=0; таким образом, в состав дискриминантной
кривой может входить не только огибающая, но и
геометрическое место особых точек кривой семейства*).
II. Рассмотрим несколько примеров. Семейство полукубических парабол
характеризуется уравнением (рис. 281)
у2 = (лг — X)3. (63.6)
Находя производную по X, получим х — X = 0, причем дискриминантная
кривая имеет уравнение у = 0, т. е. совпадает с осью Ох; она в каждой своей
точке касается параболы, т. е. является огибающей, и в то же время она
Рис. 281. Рис. 282. Рис. 283.
является геометрическим местом точек возврата; характеристические точки
в данном случае мнимые, ибо кривые семейства не имеют общих точек.
Для аналогичного семейства с уравнением (рис. 282)
(у — Х)2 = л:3 (63.7)
дискриминантной кривой будет ось Оу; она является геометрическим местом
точек возврата, которые совпадают в данном случае с характеристическими
точками; огибающей данное семейство не имеет.
Рассмотрим, наконец, такое семейство кривых (рис. 283):
(у - X)2 = (х — Х)з. (63.8)
*) Мы считаем, что параметр X не входит линейно, ибо в этом случае
/ = /1+Х/2, т. е. мы имеем пучок кривых, —дискриминантная кривая
вырождается в точки пересечения кривых fx и /2, определяющих пучок.
280 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
Дифференцируя по X, найдем:
у-Х = !(*-Х)2.
9
Подставляя в (63.8), получим -j (х — X)4 — (х — X)3 = 0, откуда находим два
решения:
} У =х;
4
т. е. дискриминантная кривая состоит из двух прямых: прямая у = х является
не огибающей, а геометрическим местом точек возврата парабол; прямая
у = х — iy=- является огибающей.
III. В кинематической геометрии огибающая семейства кривых
встречается весьма часто и играет важную роль *).
Отметим сперва несколько простых случаев нахождения
огибающей и характеристических точек в геометрических задачах.
А. Каждую кривую можно рассматривать как огибающую
семейства своих касательных, причем характеристической точкой каждой
касательной является точка ее касания**).
Б. Огибающей семейства нормалей кривой является ее эволюта,
причем характеристической точкой на каждой нормали является центр
кривизны кривой. Действительно, так как угловой коэффициент
касательной к кривой у = / (х) в точке (х, у) равен k = y', то
угловой коэффициент нормали будет г и уравнение нормали таково:
X—x-+-y'(Y — y) = 0,
где (X, Y) — текущие координаты точек нормали; параметром X
в данном случае является абсцисса х\ дифференцируя по нему имеем:
-1 + у"(К-у)-У2 = 0.
Из этих двух уравнений находим координаты (X, Y)
характеристической точки
У = у + 1±£, Х=х-У'{1+У'2); (63.9)
-* ' у" у
сравнивая с (58.3), находим Х= a, Y — b, где (а, Ь) — координаты
центра кривизны. Эволюта кривой, как известно, является геометри-
*) См., например, гл. IX.
**) В § 23 мы специально рассмотрели образование кривой как
огибающей семейства прямых.
§ 63] ОДНОПАРАМЕТРИЧЕСКОЕ СЕМЕЙСТВО ПЛОСКИХ КРИВЫХ 281
ческим местом ее центров кривизны — следовательно, она будет
геометрическим местом характеристических точек нормалей, т. е. их
огибающей.
В. Найдем, например, точку касания А0 на каждой касательной АА'
к параболе (рис. 52); мы могли бы это сделать на основании теоремы Бриан-
АА НА Н' А'
шона, как в § 29, но мы сделаем проще: докажем, что л л°/ ==~af'== А'Р' '
Действительно, обозначая касательные НЕ, Н'Е'', АА' цифрами I, II, III,
НА И'А'
мы имеем по § 23
•ггрг > причем Н и Е' — точки касания касатель-
АЕ А'Е'
ных I и II, Е — точка их пересечения, А и А' — точки их пересечения с
касательной III. Назовем теперь прямую АА' касательной II, а прямую Н'Е'
касательной III; в таком случае роль точек Е'', Н' Е, А будут играть точки
НА Н' А' НЕ А А'
А0, А, А, Е к вместо пропорции -^ = .,-,- мы будем иметь -=-т- = ., . ,
НА АА
откуда находим производную пропорцию -гр- = ,*•.
В частности, если точки А и А' являются серединами отрезков НЕ и
Н'Е', то точка А0 является серединой отрезка АА'.
IV. Рассмотрим теперь нахождение характеристических точек семейства
окружностей постоянного радиуса
(X — x)2 + (Y— у)2 — г2 = 0;
(63.10)
их центры С (х, у) находятся на заданной кривой Г0 (рис. 284), для которой
x=fl(s), y=/2(s), где s—длина дуги Г0. Для нахождения
характеристических точек дифференцируем (63.10) по s
(X — x)x' + (Y— у)у' =0;
полученное уравнение означает, что векторы
z = ix'+jy' и Ш = 1(Х—х) + ЦУ — у)
взаимно-перпендикулярны; так как вектор х
направлен по касательной С Т и кривой Г0, то
вектор МС должен быть направлен по
нормали MCN, следовательно,
характеристический точки М и N каждой окружности
семейства лежат в ее пересечении с
нормалью CMD к кривой Г0. Эта же прямая-будет
нормалью и для огибающих Гх и Г2, ибо они
касаются окружности в характеристических
точках М и N. Так как у кривых Г0, Ги Г2
совпадают нормали, то им соответствует
одна и та же эволюта Г', но если р0 = CD
является радиусом кривизны кривой Г0, то для кривых Гх и
кривизны таковы:
Pl = MD = Ро — г, Р2 = ND = Ро + г.
Кривые Г0, Гу, Г2 называются равноотстоящими по нормалям, или
эквидистантными; это является естественным обобщением понятия о
параллельных прямых.
Г2 радиусы
282
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
[ГЛ. VIII
Рассмотрим некоторые применения этой теории в задачах синтеза
механизмов *).
Пусть кулачок, равномерно вращающийся вокруг центра с угловой
скоростью о) (рис. 285), приводит в движение поступательно движущийся
толкатель с роликом; предположим, что мы исходим из диаграммы (v, t)
скоростей толкателя, и путем графического интегрирования построим диаграмму
его перемещений (s, t).
Строим обычным образом кривую центров Г0, т. е. теоретический
профиль кулачка; если он повернулся на угол ср = а>/, то, откладывая
я = АО' 1_иА, получим точку О' теоретического профиля; для нахождения
соответствующей точки М касания ролика с рабочим
профилем кулачка, т. е. с огибающей Гъ находим
нормаль О'К при помощи такого построения: если аир
масштабные коэффициенты для s и v, т. е. s = ay,
v = рг, то откладываем отрезок
О В = z • -i-, проводим OD±_00'
0CG)
и ВС j_ OD\ прямая О'С является
искомой нормалью, и, откладывая
отрезок О'М, равный радиусу
ролика, получим искомую точку М.
Действительно, из равенства v =
ds ds 0
= —— = —г—. © = Зг вытекает,
dt dy
ds
что —г— — olx, х = OB. Таким об-
разом, отрезки АО' и ОВ
выражают s и -г— в одном масштабе;
Г/
О'
'/ S
аЛ
\м
—г0
-V
В
из построения имеем
и, таким образом, г' = ОС • а =
кает гг
т. е. ОС =
ОВ-АС
SS'
00'
, ибо из равенства
аг
,г=а-00',
г2 = s2 + а2 выте-
Из рис. 285 мы видим, что tgcp = tg / ОСО' = —-; как известно,
тангенс угла касательной с радиусом-вектором выражается этой формулой,
т. е. О'С — нормаль в точке О к кривой центров.
В том частном случае, когда а = О, построение можно упростить:
откладываем на OD ±ООг отрезок OC = z-—\ О'С является нормалью.
асо
V. Рассмотрим нахождение характеристических точек семейства
окружностей переменного радиуса, касающихся заданной кривой Г0
(рис. 286); мы снова имеем (63.10), причем теперь
х = % — г sin a, y = r\-\-r cos а,
(63.11)
*) Читатель,найдет множество примеров такого рода в книге И. И.
Артоболевского [1], гл. X. Мы хотим показать уточненный метод построения
огибающей, основанный на нахождении точек ее касания с каждой
окружностью семейства.
§ 64]
ПОДЕРЫ И АНТИПОДЕРЫ
283
где г, а и координаты (£, у\) точки касания М являются функциями
ДЛИНЫ ДуГИ 5.
Мы имеем, дифференцируя (63.10) по s,
(X— £ -f- г sin а) (г cos аа' -|- г' sin а — £') +
+ (К — т] — г cos а) (г sin аа' — г7 cos а — ч\') — rrf = 0.
Так как £' = cosa, 7)':= sin а, а' = К, где К — кривизна кривой Г0
в точке Ж, то после упрощений
получим:
У — У] cos а (гК — 1) + rf sin a
X — £ cos a • г' — sin a (r/C — 1)
r/C —1
tg<
1—tgc
где мы положили
rK— 1
_£_ = tg(a + 8), (63.12)
tgS:
8 = arctg
r/C—1
Рис. 286.
r ° r'
(63.13)
Следовательно, характеристические точки каждой окружности
рассматриваемого семейства лежат в ее пересечении с прямой,
проходящей через ее точку касания с кривой Г0 под углом 8
к касательной; одной из этих точек является точка касания.
§ 64. Подеры и антиподеры
I. Будем называть подерой кривой Г относительно заданной
точки M0(xQt у0) (рис. 287, а) новую кривую Г\ являющуюся
геометрическим местом проекций точки М0 на касательные
к кривой Г*).
Если уравнение кривой Г задано в параметрической форме
x = fx{t)i у = /2(0« то уравнение касательной в точке М{х> у)
кривой таково:
Y-y = ^r(X—x).
Уравнение прямой, проходящей через точку М0 перпендикулярно
к касательной, таково:
У — Уо = — у-(х~ *<>)•
*) Подера иначе называется «подошвенной кривой».
284
СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ
[ГЛ. VIII
Из этих двух уравнений находим координаты ХУ Y точки
пересечения этих двух прямых:
у _ / С*/ — ух') + х' (х0х' + у0у')
х,2+у2 .
— х' (ху' — ух') + У' {XqX' + УоУ')
(64.1)
х'2+у'2
Так как х, у, х\ у' являются известными функциями параметра t,
а.
Рис. 287.
то мы получили уравнение подери Г кривой Г в
параметрической форме.
Рассмотрим несколько примеров.
Подерой эллипса и гиперболи
± —г- == 1 относительно фокуса
а2 - Ь2
является окружность х2 + у2 = а2, касающаяся этих кривых в вершинах;
в случае параболы она вырождается в касательную в вершине (§ 32).
Мы могли бы доказать это, пользуясь формулами (64.1); покажем это
чисто геометрическим методом.
Рассмотрим для примера эллипс (рис. 288), касательную МТ и точку N
подеры; продолжая прямые F{N и F2M до пересечения в точке R и
пользуясь тем, что касательная МТ делит пополам £.FXMR, видим, что MR =
— MFV и таким образом, по основному свойству эллипса имеем RF2 = RM +
-f MF2 = MFX + MF2 — 2a\ соединяя точки N и О— середины отрезков FXR
и FxF2i — находим N0 = а = const, откуда вытекает наше утверждение.
Аналогичное доказательство — для гиперболы.
Пользуясь этими свойствами, получаем простые механизмы для огибания
конических сечений *): если вершина В прямого угла движется по окруж-
*) См. И. И. Артоболевский [2], § 14.
§ 64] ПОДЕРЫ И АНТИПОДЕРЫ 285
ности, а одна его сторона BFX проходит через неподвижную точку Fu то
вторая сторона BD огибает эллипс (рис. 289), если OF{ < OB, или
гиперболу (рис. 290), если OFx > ОВ\ если же вершина прямого угла В движется
не по окружности, а по прямой, то вторая сторона огибает параболу
Рис. 288. Рис. 289.
(рис. 291). Отметим еще, что подерой параболы относительно точки ее
директрисы является кривая Бурместера, — доказательство дано в § 54.
II. Кривую Г будем называть антиподерой кривой Г (рис. 287, а)\
следовательно, антиподерой данной кривой Г* относительно
данной точки М0 называется огибающая семейства прямых,
проходящих через точки кривой Г' перпендикулярно к прямым,
соединяющим эти точки с точ-
Рис. 290. Рис. 291.
Найдем характеристические точки на прямых нашего семейства.
Запишем их уравнение в нормальной форме (рис. 287, б)
хcosа + У sin а— /7 = 0. р = М0А, а = £ЛЖ0л:, (64.2)
причем будем считать р функцией параметра а. Дифференцируя по а,
находим:
— х sin a -f- у cos а — р' = 0, (64.3)
286 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
л
/s
О
J
-s' М
^Р
-s'
^у^ <
\s
В/
S"
Н
X
откуда получаем координаты характеристической точки М на прямой а
х = р cos а — р' sin а, у = р sin а + р' cos а. (64.4)
Легко видеть, что характеристическую точку М на прямой а
найдем, откладывая на ней от точки А отрезок AM = р''.
Восставим в точке М перпендикуляр а' к прямой а, это б^дет
нормаль к кривой Г. Проведем M0N\\AM. Рассмотрим огибающую
семейства прямых а', т. е. эволюту кривой Г; характеристической
точкой прямой а' является центр
кривизны кривой Г. Прямая а' отличается
от прямой а тем, что а и р надо
заменить на a-f--n- и р'\ следовательно,
откладывая отрезок NK=prr от
точки N по прямой а', мы получим
искомый центр кривизны.
Следовательно, если кривая Г'
задана уравнением в полярных
координатах г = р = /(а), то радиус
кривизны ее антиподеры Г в
соответствующей точке выражается формулой
р=р+-ё-- (64-5>
III. Рассмотрим применения этой
формулы к задачам синтеза кулачковых
механизмов с плоским толкателем,
заканчивающийся плоской тарелкой,
движется поступательно (рис. 292). Пусть кулачок повернется на
угол ср против стрелки часов; считая закон движения толкателя
известным s = /(cp), мы можем найти его подъем, т. е. расстояние
точки О от нового положения тарелки; поворачивая тарелку с
толкателем на угол ср по стрелке часов в положение CD, мы видим,
что рабочий профиль кулачка является огибающей семейства
прямых CD, для которых в (64.3) надо положить ^ = ^—ср. p = s.
—Р- = Д-, то, откладывая от точки А отрезок ЛМ —
da dy
, получим точку касания М.
d2v d2s
~ = -j-f, откуда вытекает простая формула *)
л- —
"г" ay »
Рис. 292.
Пусть сперва толкатель,
Так как
ds
Мы имеем, далее,
da*
dy2
(64.6)
*) Она впервые получена автором [1] другим путем.
§ 64]
ПОДЕРЫ И АНТИПОДЕРЫ
287
позволяющая найти радиус кривизны кулачка по закону движения
толкателн\ неравенство
5 + ^г>°
(64.7)
позволяет найти наименьший радиус кулачка из того условия, чтобы
рабочий профиль кулачка был во всех точках выпуклым.
Пусть теперь плоский толкатель вращается вокруг оси Ох
(рис. 293); пусть кулачок повернется на угол ср против стрелки
часов, тогда толкатель повернется на угол ф, который мы найдем
по заданному закону движения толкателя ф = /(ср). Повернув линию
центров OOl вокруг точки О на угол ср по стрелке часов и затем
повернув толкатель вокруг точки Ох так, чтобы иметь /_ х'0[С — ф,
мы видим, что рабочий профиль кулачка является огибающей
семейства прямых 0[С, для которых в (64.3) надо положить
а = ф— ср — у, /7 = ^/ sin ф, где d=OOv
Мы имеем:
dp dp da dp ,., ,
и, таким образом, для нахождения точки касания М надо отложить
отрезок
СМ
d cos ф . ф' гп ф'
ф'-1 — — !' ф'-1
Далее находим:
d2p __ d2p
dy2
dp
da2
(f — О' + ^Ф'^^созф.ф" —^пф.ф'
288 СОПРИКОСНОВЕНИЕ ПЛОСКИХ КРИВЫХ [ГЛ. VIII
откуда
<РР__ срзф.ф" — ^пф-ф'2 (1 —фО .
da2 ~ й ' (1 —ф/)3
окончательно по (64.5) радиус кривизны рабочего профиля кулачка
таков *):
р = ^5тф(1-ф0а-2у + со8ф-ф^ (648)
Отсюда нетрудно найти условия выпуклости всего рабочего профиля
кулачка.
*) Эта формула впервые получена С. Н. Кожевниковым ([1], § 47) другим
путем.
ЧАСТЬ III
ЭЛЕМЕНТЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
ГЛАВА IX
ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ
ПОДВИЖНОЙ ПЛОСКОСТИ
§ 65. Общие замечания
I. Рассмотрим некоторую точку М подвижной плоскости; кривую
Г, вычерчиваемую этой точкой в неподвижной плоскости при
непрерывном движении подвижной плоскости, будем называть рулеттой
этой точки *).
Рассмотрим п бесконечно близких положений Ev Е2, .... Еп
подвижной плоскости; отметив в положении Ех некоторую точку Mv
мы сможем найти ее новые положения М2, Mv .... Мп, когда
подвижная плоскость будет занимать положение Е2, Ег Еп\ мы
будем знать, таким образом, п бесконечно близких точек Мх, М2, .. .
.... Мп на рулетте точки Мг. Проводя через эти п точек кривую,
уравнение которой зависит от п параметров, мы получим после
предельного перехода соприкасающуюся кривую, имеющую с нашей
рулеттой в точке Мг соприкосновение не ниже (п—1)-го порядка
(§ 57); таким образом, во всех вопросах и задачах, в которых
рассматривается п бесконечно близких положений подвижной
плоскости, мы можем заменить элементарную дугу нашей
кривой в бесконечно малой окрестности точки М элементарной
дугой любой другой кривой, имеющей в точке М с данной
кривой соприкосновение не ниже (п—\)-го порядка. В частности, при
п — 2 мы можем любую кривую заменить ее касательной в данной
точке, а при п = 3 — ее соприкасающейся окружностью, т. е. ее
окружностью кривизны в данной точке.
II. От этих геометрических соображений мы можем перейти
к кинематическим. Будем рассматривать точку М, движущуюся по
кривой Г по закону s = f(t) и находящуюся в данный момент
времени tx в точке Mv При п=2 мы сможем находить лишь скорости
*) Если подвижная плоскость Е связана с шатуном шарнирного четырех-
звенника или кривошйпно-шатунного механизма, то рулетта некоторой точки
является ее шатунной кривой.
290 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ IX
ds
всех точек подвижной плоскости, причем формула <р = т-^-
показывает, что во всех задачах нахождения скоростей можно заменить
точку М точкой М', движущейся по касательной к кривой Г
в точке Мх по закону s = f1(t), если только
/id)=/('i). fi(ti)=f'(ti).
Задание двух бесконечно близких положений подвижной
плоскости эквивалентно заданию мгновенного центра вращения Р.
При п = 3 мы можем находить не только скорости, но и
ускорения всех точек подвижной плоскости; формула
dv , v2 d2s . „(dsV
показывает, что во всех задачах нахождения ускорений можно
заменить точку М точкой М", движущейся по окружности,
соприкасающейся с кривой Г в точке Mv по закону s = f2 (t), если только
Отсюда можно сделать вывод, весьма важный по своим
практическим применениям: во всех задачах кинематики (в которых
фигурируют скорости и ускорения точек) можно заменить
подвижную и неподвижную кривые,
касающиеся друг друга в некоторой точке,
их окружностями кривизны в этой
точке и рассматривать отрезок
прямой между центрами кривизны этих
кривых как твердый стержень.
На этом основана замена высших пар
низшими, которая весьма часто
применяется в теории механизмов *).
В качестве иллюстрации рассмотрим
неподвижную и подвижную центроиды Цг
и Ц с центрами кривизны Сх и С (рис. 294)
и кривую Г подвижной плоскости,
катящуюся по кривой Гг, неподвижной плоскости;
очевидно, кривая Гг, является огибающей
всех положений кривой Г\ такие две
кривые называем взаимно огибающими
кривыми, или сопряженными рулеттами.
Если они касаются друг друга в точке А то скорость этой
точки на подвижной плоскости, перпендикулярная к прямой АР,
должна быть направлена по касательной AT к обеим кривым;
следовательно, общая нормаль двух сопряженных рулетт всегда
проходит через мгновенный центр вращения.
*) См., например, Р. Бейер [2], § 29.
§ 66] СКОРОСТЬ ПЕРЕКАТЫВАНИЯ ЦЕНТРОИД, ПОЛЮС ПОВОРОТА 291
Если D и Dx — центры кривизны кривых Г и Г1 в точке
касания Л, то отрезки CD и CXDX неизменны, ибо соединяют точки,
лежащие в одной и той же плоскости; отрезки ССХ и DDV как
было сказано, можем считать неизменными; таким образом, при
нахождении ускорений точек подвижной плоскости и кривизны их
рулетт можно считать подвижную плоскость шатунной
плоскостью заменяющего шарнирного четырехзвенника ClCDDl со
стойкой ClDl и с шатуном CD.
III. Положение точки в подвижной плоскости характеризуется
координатами (?, т)). Если мы ищем точки подвижной плоскости,
подчиненные некоторым дополнительным условиям, то при наличии г
таких условий координаты (£, т}) будут связаны г соотношениями;
если г=1, то геометрическим местом таких точек является
некоторая кривая в подвижной плоскости; при г =2 будем иметь
конечное число точек пересечения двух кривых; при г ^> 3 условия могут
оказаться несовместными.
Отсюда можно сделать следующий вывод: 1) геометрическим
местом точек подвижной плоскости, являющихся точками
распрямления своих рулетт, является некоторая кривая; 2) имеется лишь
конечное число точек подвижной плоскости, рулетты которых имеют
в этих точках соприкосновение не ниже третьего порядка со
своими касательными; 3) не во всяком положении подвижной
плоскости найдутся точки, рулетты которых имеют в этих точках
соприкосновение не ниже четвертого порядка со своими
касательными.
Действительно, по § 59 для выполнения 1) имеем одно
условие /е=0, для выполнения 2) — два условия /С = /<г/ = 0.
Совершенно аналогично получим: 1) геометрическим местом точек
подвижной плоскости, являющихся круговыми точками своих рулетт,
является некоторая кривая; 2) имеется лишь конечное число точек
подвижной плоскости, рулетты которых имеют в этих точках
соприкосновение не ниже четвертого порядка со своими окружностями
кривизны; 3) не во всяком положении подвижной плоскости найдутся
точки, рулетты которых имеют в этих точках соприкосновение не
ниже пятого порядка со своими окружностями кривизны.
Действительно, по § 59 для выполнения 1) имеем одно
условие Дг/ = 0, для выполнения 2) — два условия /С/ = Аг// = 0.
Эти кривые и точки будут рассмотрены в дальнейших параграфах.
§ 66. Скорость перекатывания центроид, полюс поворота
и поворотная окружность
I. Касательную и нормаль к обеим центроидам в точке их
касания, т. е. в м. ц. в., будем называть полюсными касательной и
нормалью.
292
ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
Мы имеем по формуле (59.17)
К — Кх =
(66.1)
так как 5 — дуга, на которую перекатились друг по другу обе
ds
центроиды, то величина # = — является скоростью
перекатывания центроид, т. е. скоростью перемещения по каждой из центроид
точки их касания — мгновенного
центра вращения.
Дифференцируя (66.1) по t и
полагая затем ср = 5 = 0, получим
соотношение между скоростью
перекатывания центроид и
угловой скоростью подвижной
плоскости
и = — da,
ds
ИГ
dy
~df'
(66.2)
Рис. 295.
Если ввести векторную скорость #,
то она, очевидно, будет
направлена по полюсной касательной в сторону возрастания дуги 5,
т. е. и = чи; точно так же <о = £а), где k — орт оси Pz. Так
как т = «Х^ где, как было сказано, орт п направлен по полюсной
нормали в сторону вогнутости неподвижной центроиды, то
а = iu = и(п X k) = — du>(п X k) == — d(п X *«>) (66.3)
и окончательно векторная скорость перекатывания центроид
такова:
u = — d(nX«>). (66.4)
Точку W подвижной плоскости, характеризуемую
радиусом-вектором
rw = dn,
будем называть полюсом поворота-
полюсной нормали; так как
она, очевидно, лежит на
u = (i>Xdn = toXr
w*
(66.5)
то, применяя формулу Эйлера, видим, что полюс поворота является
той точкой подвижной плоскости, векторная скорость
которой геометрически равна векторной скорости перекатывания
центроид (рис. 295). Это свойство полюса поворота удобно тем
что не зависит от выбора координатных осей.
§ 66] СКОРОСТЬ ПЕРЕКАТЫВАНИЯ ЦЕНТРОИД, ПОЛЮС ПОВОРОТА 293
Так как положение полюса поворота определяется полюсной
касательной и нормалью и величиной d, причем все эти элементы
зависят только от положения центроид в точке Р и от разности их
кривизн, то полюс поворота является чисто геометрическим
понятием— его положение не зависит от того, по какому закону
подвижная центроида будет двигаться по неподвижной; например,
если отрезок АВ неизменной длины движется своими концами А к В
по двум заданным кривым ГА и Гв, то этим вполне определяются
обе центроиды (которые легко можно построить по точкам), а
следовательно, и полюс поворота в каждом положении подвижной
плоскости, связанной с отрезком АВ.
II. Для графического нахождения скорости перекатывания
центроид и полюса поворота применим метод дополнительных групп *).
Рассмотрим шарнирный четырехзвенник
АХАВВХ (рис. 296), продолжим звенья
/ и 3 и присоединим двухповодковую
группу, состоящую из звеньев 5 и 6,
входящих в поступательные пары со
звеньями / и 3 и во вращательную
пару Р друг с другом. Так как точка
Р является мгновенным центром
вращения, то при неподвижном звене 4
она опишет неподвижную центроиду Цх\
если же неподвижным сделать звено 2,
то та же точка Р опишет подвижную
центроиду Ц**). Этот результат имеет
место, очевидно, лишь для шарнирного
четырехзвенника AlABBv звенья
которого при любом его перемещении Рис. 296.
имеют постоянные длины, но методы
нахождения скоростей и ускорений, которые мы сейчас рассмотрим,
верны и для любого заменяющего четырехзвенника (рис. 297).
Обозначая через Рг точку звена /, совпадающую в данный
момент с точкой Р, мы, очевидно, имеем по теореме о сложении
скоростей
t>/,= n = t>Pi + V (66.6)
где vp — переносная скорость точки Р, a cof — относительная
скорость, т. е. скорость скольжения ползунка 5 вдоль звена 1 (рис. 296);
точно так же
*P = » = *Pt-|-V (66.7)
*) См., например, И. И. Артоболевский [1].
с*) Этот механизм называется поэтому центроидографом.
294 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ IX
Выбираем точку Р за полюс плана скоростей, повернутого на 90°;
мы имеем vA = РА • со, vB = РВ • со, где со — угловая скорость
шатуна, которую для определенности будем, например, считать
положительной; так как точки Рг и А находятся на одном твердом теле
У, вращающемся вокруг неподвижной точки Av то скорости этих
точек пропорциональны их
^ Р и ^ расстояниям от этой точки.
Мы имеем, таким образом,
*я=^
РА,
РА.РАХ
АА,
PB-PBi
со,
— ВВ{
Построим отрезки
РА-РА{
РА,
Рис. 297.
РВ0 =
ААХ
РВ-РВ,
ВВ,
(66.8)
восставив в точках А0, В0 перпендикуляры к РА0 и PBQ, мы
получим в их пересечении точку «S; как легко видеть,
PS = PA0+A£, PS = PB0+B^S,
т. е. мы имеем:
vp=\u\ = PS'<»=\d\ -со, \d\=P5.
vf = AQS • со, v = B0S • со.
(66.9)
Следовательно, мы нашли \d\ и полюсные касательную Pt и
нормаль Рп.
Мы считали со > 0 и скорость точки А выразили вектором РА,
т. е. мы ее повернули на 90° по стрелке часов, следовательно,
направление векторной скорости и перекатывания центроид получим,
поворачивая вектор PS на 90° против стрелки часов, — ясно, что
полюс поворота W совпадает с найденной точкой 5, ибо его
векторная скорость геометрически равна а.
III. Окружность, для которой диаметром является отрезок PW,
назовем поворотной окружностью; она, очевидно, характеризуется
уравнением
x2+y2 — dy = 0. (66.10)
§ бб] СКОРОСТЬ ПЕРЕКАТЫВАНИЯ ЦЕНТРОИД, ПОЛЮС ПОПОРОТА 295
Обе найденные точки А0, Б0 лежат на поворотной окружности.
Из (66.8) вытекает равенство
ААп = РАп — РА =
РА-РАХ
ААХ
-РА-.
РА(РАХ—ААХ) .
АА{
окончательно имеем:
ААп
РА2
АА,
RR - РВ*
(66.11)
т. е. расстояние каждой точки подвижной плоскости от м. ц. е.
является среднегеометрическим между радиусом кривизны ру-
летты этой точки и расстоянием этой точки от поворотной
окружности (считаемым по лучу этой точки).
IV. Из формулы (66.11) можно сделать такой вывод: задание
трех бесконечно близких положений подвижной плес сости
эквивалентно заданию мгновенного центра вращения Р и полюса
поворота W.
Действительно, при задании трех бесконечно близких положений
подвижной плоскости мы будем знать по три бесконечно близких
точки на рулетте каждой точки, т. е. будем знать соприкасающуюся
окружность в данной точке рулетты; выбирая две точки А к В
подвижной плоскости и зная, таким образом, центры 'кривизны Ах и В1
их рулетт в этих точках, мы сможем найти м. ц. в. Р в пересечении
прямых АХА и ВХВ и построить
точку W указанным способом.
Наоборот, зная точки Р и W, мы
можем построить поворотную
окружность, а затем для любой точки А
подвижной плоскости найти точку А0
пересечения ее луча с этой
окружностью; зная точки Р, А, А0, мы
сможем по (66.11) вычислить
отрезок AAV
Покажем еще простое
геометрическое построение, позволяющее без
построения поворотной окружности
найти точку Alt если заданы точки
Р, W и выбрана точка А (рис. 298): строим окружность с
центром А и радиусом РА и строим поляру w точки W относительно
этой окружности; искомая точка Ах лежит в пересечении прямой w
с лучом РА данной точки. Действительно, если AL_\_w, то мы
имеем:
Рис. 298.
АР2 = AL- AW = ААг cos а - AW = ААг - АА0.
296 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ IX
§ 67. Формула Эйлера; теорема Бобиллье
I. Из формул (66.11) вытекает соотношение, играющее основную
роль во всем дальнейшем.
Обозначим через г и г{ радиусы-векторы точек А и Аь а через ср—
угол луча РААХ с полюсной касательной (рис. 299); мы имеем:
РА = г, РАг = гг, AAl = rl — r,
РА0 = PW sin ср = d sin ср,
АА0 = РА0 — РА = d sin ср — г;
из (66.11) вытекает:
dsmy—r= г _г ,
гг d sin ср — rdsin ср = rrv (67.1)
и мы приходим к основной формуле
Эйлера
связывающей радиусы-векторы точек подвижной плоскости и
их центров кривизны. Из этой формулы вытекает, что при r = tf sincp
имеем /-j = oo, т. е. для точек, лежащих на поворотной окружности,
радиусы кривизны их рулетт бесконечно велики; отсюда вытекает, что
поворотная окружность — это геометрическое место точек
подвижной плоскости, являющихся точками распрямления их
рулетт. Единственным исключением может явиться мгновенный центр
вращения Р, ибо, как показано в § 61, он не всегда будет точкой
распрямления своей рулетты.
Поворотную окружность часто называют окружностью перегибов;
$то название не точно, ибо мы можем утверждать лишь то, что в ее
точках рулетты этих точек имеют со своими касательными
соприкосновение не ниже второго порядка*). Мы покажем в § 72, что
на поворотной окружности имеется одна точка, в которой
соприкосновение будет третьего порядка — в этой точке перегиба нет.
Примечание 1. Покажем, что рулетты всех точек,
лежащих на полюсной касательной, имеют центр кривизны в м.ц.в.\
действительно, полагая в (67.1) sin ср = 0, получим ггх = 0, т. е. при
г Ф О имеем гг = 0.
II. Пр имечание 2. Мы вывели формулу (67.2) из (66.11) и
рис. 299, считая, что поворотная окружность и обе точки А и Аг
лежат по одну сторону от м. ц. в. Я; нетрудно показать (§ 75), что
*) В § 58 приведен пример, в котором точка распрямления не является
точкой перегиба.
§ 67]
формула Эйлера; теорема бобиллье
297
Рис. 300.
она справедлива при любом расположении этих точек, причем для
точек, лежащих по другую сторону от Р, надо считать
радиусы-векторы отрицательными.
На рис. 300 показана равносторонняя гипербола, являющаяся
графиком зависимости (67.2) на данной прямой, причем x — rt y = rv
Мы можем сделать следующие
выводы: 1) расположение обеих точек,
А и Av по одну сторону м. ц. в. Р,
причем РА*< PAV возможно тогда
и только тогда, когда поворотная
окружность и обе точки лежат по
одну сторону полюсной
касательной; при этом точка А лежит внутри
окружности; 2) расположение точек
А и Аг по разные стороны м. ц. в. Р
возможно тогда и только тогда,
когда поворотная окружность и
точка А лежат по одну сторону
полюсной касательной, причем точка А
лежит вне окружности; 3)
расположение обеих точек, Ли Alt по одну
сторону м. ц. в. Я, причем /М>РЛ1,
возможно тогда и только тогда, когда поворотная окружность и
обе точки лежат по разные стороны полюсной касательной.
На рис. 301 изображены подвижная и неподвижная плоскости и
размечены соответствующие области для точек А и Аг *).
Случай 1) соответствует областям
/, //; случай 2) — области ///,
случай 3) — областям IV, V\
7о — поворотная окружность.
III. В некоторых вопросах
статики поворотную окружность
называют окружностью
устойчивости; разъясним смысл этого
термина на примере:
рассматривается поверхность,
образованная вращением кривой -у
вокруг вертикальной оси и
однородный горизонтальный
стержень АВ длиной 2/ лежащий
своими концами на этой
поверхности (рис. 302); считая
поверхность идеально гладкой, найти
достаточное условие устойчивости равновесия стержня. Проведем
нормали к кривой 1 в точках А и В; в их пересечении получим точку Р — м. ц. в.
Л
#4.
ш /Т
\ш
Ш^;
Л
Ул
ijy
IF J
^ Ш
точка Л
точка Л1
Рис. 301.
*) См. Р. Бейер [2], § 33,
298
ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
стержня; через Ах и Вх обозначим центры кривизны кривой f в точках А
и В; при бесконечно малом перемещении стержня мы рассмотрим
заменяющий шарнирный четырехзвенник А1АВВ1 со стойкой АХВХ и шатуном АВ:
Построим поворотную окружность 7о>
по (66.11)
Q-AA{\ рис.
ствует случаю 2).
причем
= АА
имеем РА2 =
302 соответ-
Рис. 302.
Рис. 303.
Известно, что для устойчивости равновесия тяжелого тела достаточно,
чтобы его центр тяжести С занимал наинизшее положение; для этого
траектория точки С должна быть обращена в точке С вогнутостью вверх, т. е.
центр кривизны Сх траектории должен лежать выше тонки С — это
возможно только тогда, когда
точка С лежит вне
поворотной окружности, т. е. при
условии
РА*
АА0 = . . ■ > АА' = / cos а,
о= < РАС;
следовательно, равновесие
стержня АВ будет
устойчивым, если радиус кривизны
р = ААХ кривой в точке А
удовлетворяет неравенству
р < / sec3 а.
Если в наинизшей точке
'^/кривой радиус кривизны
наибольший (рис. 303), то ее
эволюта обращена острием кверху,
радиус кривизны меньше длины
нормали АА{ < ДР, т. е. мы
имеем случай 3) — поворотная окружность лежит выше полюсной
касательной и центр кривизны Сх лежит выше точки С, т. е. в этом случае условие
устойчивости всегда выполнено.
IV. Покажем простое геометрическое построение точек Л0, В0 по
формуле (66.11), а следовательно, и построение поворотной
окружности, если известны две точки А и В подвижной плоскости
и центры кривизны Ах и В^ их рулетт в этих точках (рис. 304),
Рис. 304.
§ 67] формула Эйлера; теорема бобилльв 299
Построим м. ц. в. Р и найдем точку Q пересечения прямых АВ
и А\ВХ\ через точку Р проведем прямую PR\\A1B1 до пересечения
в точке R с прямой АВ, а через точку R проведем прямую RK\\PQ*
которая пересечет прямые АРАХ и ВРВХ в искомых точках А0 и В0.
Действительно, ДPЛQ—Д АЛ/?, откуда вытекает пропорция
PA QA
- . = —гр-; кроме того, Д PRA ~ Д Q/^Л, откуда следует новая
СМ ЛЛ РА АА
пропорция -^тр-= -pjr; из этих двух пропорций следует -дТ~=~~рТ»
т. е. (66.11). Из приведенного
построения вытекает одна простая
геометрическая теорема, весьма
полезная в задачах синтеза
механизмов.
Рассмотрим снова шарнирный
четырехзвенник А1АВВ1(рис. 305);
если перенумеровать звенья, то,
по терминологии § 45, мы имеем
три пары противополюсов (Р14 и
Р23' Р12 И Р34' РЪ\ И Р2А>* И3 К0"
торых только последние два,
Р31 и Я24, не являются шарни- Рис. 305.
рами. Прямая РиР2^
соединяющая два противополюса шарнирного четырехзвенника, не
являющиеся шарнирами, называется осью коллинеации.
Пользуясь этим понятием, докажем теперь теорему Бобиллье:
ось коллинеации образует с одним из вращающихся звеньев
шарнирного четырехзвенника такой же угол, какой второе
вращающееся звено образует с полюсной касательной.
Мы должны доказать, таким образом, равенство углов <х = р
(рис. 304), где а = ^QPAq, $ = /B0Pt, причем Pt — полюсная ка-
РВ
сательная; угол р и ^В0А0Р = а измеряются дугой ^ ■■ ° .
V. Мы рассматривали шарнирный четырехзвенник, но все наши
рассуждения остаются в силе и для заменяющего шарнирного
четырехзвенника, т. е. они применимы к любым двум прямым
подвижной плоскости, проходящим через м. ц. в., если на каждой из них
мы знаем точку и центр кривизны ее рулетты в этой точке. Такие
две точки будем называть соответствующими точками.
Из формулы (67.2) имеем:
rd sin ср
d sin <р -
(67.3)
т, е. величины г и rv определяющие положения соответствующих
точек на данной прямой, связаны дробно-линейным соотношением;
следовательно, пары соответствующих точек на каждой прямой
300 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
образуют два проективных ряда точек на одном основании (§ 15),
причем, как было сказано, обе двойные точки на каждой прямой
совпадают с м. ц. в. и указанное проективное соответствие не
является инволюцией. Обычно проективное соответствие двух рядов
точек на прямой задается тремя парами соответствующих точек,
но в частном случае (67.3) мы имеем лишь один параметр ^ sin ср
для каждой прямой, причем точке, для которой г = ^ sin ср,
соответствует бесконечно удаленная точка.
VI. В задачах кинематического анализа мы знаем точки Р и W
и, следовательно, полюсные касательную и нормаль, поворотную
окружность и величину d. Выбирая произвольно точку А на прямой а
(рис. 306), мы сразу найдем
по формуле (67.3) (или при
помощи указанного
построения) соответствующую ей
точку Аг. Выбрав эти две
точки за центры двух пучков
прямых, будем
проектировать из центра А точки В,
В', В"\ . . . подвижной
плоскости, лежащие на
прямой Ь, и из центра Аг —
соответствующие точки Bv Ви
В\, ... неподвижной
плоскости. Мы получим два
проективных пучка
прямых, но обе прямые 5 и sv проектирующие двойную точку Р,
совпадают, поэтому наши два пучка прямых перспективны (§ 43), т. е.
прямые, проектирующие соответствующие точки прямой Ь из центров
А и Av пересекаются на некоторой оси перспективы s0; ее легко
построить, зная, кроме центров пучков А и Av одну пару
соответствующих точек В и Вг; ось перспективы s0 проходит через точку Р
и через точку С пересечения прямых АВ и АгВг; если теперь взять
новое положение В' точки подвижной плоскости, то, проводя прямую
АВ' до пересечения в точке С с осью перспективы и соединяя Ах
с С', мы получим в пересечении прямых АХС и Ъ точку В\ и т. п.
Мы видим, что при заданной паре соответствующих точек А и
Аг на прямой а (центров пучков) положение оси перспективы не
зависит от выбора пары соответствующих точек на прямой Ь.
Если теперь выбрать центры пучков в точках В и Вх и из них
проектировать соответствующие точки на прямой а, то получим ту
же самую ось перспективы и можем повторить то же самое
рассуждение. Мы приходим к следующему выводу: для двух любых
заданных прямых а и b всегда можно построить ось коллинеации,
§ 68]
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
301
т. е. ось перспективы для двух пучков прямых, имеющих
центры в двух соответствующих точках одной прямой и
проектирующих соответствующие точки другой прямой; направление
этой оси параллельно прямой, соединяющей точки'пересечения
поворотной окружности с этими двумя прямыми *).
VII. В задачах кинематического синтеза мы, вообще говоря,
не знаем заранее ни Р, ни W, ни поворотной окружности. Если
дана прямая, проходящая через заданный м. ц. в., то мы можем
произвольно задать на ней одну пару соответствующих точек,
чем уже определится величина fi?sincp, а следовательно, и точка
пересечения этой прямой с поворотной окружностью, после чего для
каждой новой точки А мы сможем найти соответствующую точку Ау
Если же м. ц. в. на этой прямой не задан, то на ней произвольно
можно задать две пары соответствующих точек и по ним найти
м. ц. в., как будет показано дальше.
Если даны две прямые, проходящие через м. ц. в., то он
определяется их пересечением, причем на каждой из этих прямых можно
произвольно задать по одной паре соответствующих точек; этим
определятся две точки пересечения этих прямых с поворотной
окружностью, которая проходит через эти точки и м. ц. в., а
следовательно, и ось коллинеации и полюсная касательная; после этого на
каждой новой прямой, проходящей через м. ц. в., проективное
соответствие точек полностью определено.
§ 68. Геометрические построения
I. Рассмотрим так называемое построение Гартмана (рис. 307),
позволяющее найти скорость перекатывания центроид и, если
известны скорость vA некоторой точки А подвижной плоскости,
соответствующая ей точка Ах и м. ц. в. Р. Соединим точки А и Ах
отрезком АХА, который будем рассматривать как твердый стержень /,
вращающийся вокруг неподвижной точки Av Введем два звена 2,
5, входящих во вращательную пару Р друг с другом; звено 2
входит в поступательную пару со звеном /, а звено 3 — с неподвижным
звеном 4, направленным по полюсной касательной; обозначим через
Рх точку стержня /, совпадающую с Р; ее скорость vp можно
найти, соединяя конец вектора vA с точкой Ах и пользуясь тем,
что скорости точек стержня / изменяются по линейному закону.
Из теоремы о сложении скоростей vp = и — vPl -\- vr, зная
направление всех трех скоростей и модуль vp % находим скорость и;
восставляя в конце вектора <ор перпендикуляр к vp до пересечения
с полюсной касательной, получим конец векторной скорости и.
*) На рис. 304 имеем AQB0\\PQ. Направление оси коллинеации можно
найти по теореме Бобиллье.
302 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
Наоборот, зная скорость перекатывания центроид я, мы можем найти
вектор юр, а следовательно, и vA.
II. Пусть теперь дан м. ц. в. Р (рис. 308) и на прямой а,
проходящей через него, дана пара соответствующих точек А и Ах\
требуется найти на этой
прямой точку А\, соответствующую
точке А'.
Рис. 307.
Рис. 308.
Проведем через м. ц. в. Р произвольную прямую Ь, выберем на
ней произвольные точки В и Вх за центры пучков, спроектируем из
них точки А и Ах и проведем через точку Р и через точку С
пересечения прямых АВ и АгВг ось коллинеации PS для двух прямых
а и Ь, т. е. ось перспективы для наших двух пучков прямых. Про-
, ектируя точку А' из центра В,
о 21 о с7 а нах°Дим точку С на оси
коллинеации; проектируя точку С из
В В с В' В' центра Вх на прямую а, получим
~° °" о о—с искомую точку Ль
Рис. 309. В частности, если мы хотим
найти точку А0 пересечения
прямой а с поворотной окружностью, то этой точке подвижной
плоскости соответствует в неподвижной плоскости бесконечно удаленная
точка прямой а; проводя через центр Вг прямую ВхС0\\а,
проектирующую эту бесконечно удаленную точку в точку С0 оси коллинеации,
и проектируя точку С0 из центра В на прямую я, получим искомую
точку А0.
III. Пусть теперь на прямой а, проходящей через м. ц. в., произвольно
заданы две пары соответствующих точек А и Аи А' и А[ (рис. 309) и
требуется найти м. ц. в.
§ 68] ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ 303
Мы имеем:
да
1
г
1 _ 1
гх г'
-L+-U
1 1
/■' d sin ср '
г, + г' '
(68.1)
если принять за соответствующие точки А и Av Ах и А' и если через г и
г' назвать абсциссы соответствующих точек, то будем иметь:
Выполняя инверсию относительно точки Р, являющейся началом отсчета
радиусов-векторов, введем новые точки В и Blf В' и Bv характеризуемые
абсциссами
Л — — , Хл — —у » Л1 » «*- т" >
г Г\ Г\ Г
причем по (68.1) имеем:
х + х[ == хх + х\ (68.2)
Определим точечную инволюцию двумя парами соответствующих точек В
и В[, Вх и В'\ мы видим из (68.2), что середины отрезков ВВ{ и В{В'
совпадают в некоторой точке С, откуда вытекает (§ 15), что рассматриваемая
инволюция сводится к симметрии относительно точки С, т. е. абсциссы v и vf
двух соответствующих точек связаны соотношением
v + vf = с = const.
с
Точка С с абсциссой -~- является двойной точкой этой инволюции, а вторая
двойная точка, совпавшая с центром инволюции, ушла в бесконечность.
Выполним снова инверсию, необходимую для обратного перехода от точек В,
В[, Ви В' к точкам Д A'v Аь А'\ из соотношения (68.2), вводя величины
1 , 1
о = — , о' = —г , имеем:
i + -L = c р'--^. (вел)
т. е. точки А и Лр А{ и Л' также являются соответствующими точками
некоторой точечной инволюции; ее двойные точки характеризуются условиями
2
р = 0, или р = —; мы приходим к следующему выводу: если задать на
прямой а точечную инволюцию двумя парами соответствующих точек А
и Av Ах и А', то в качестве м. ц. в. может быть взята любая из двойных
точек этой инволюции *).
Таким образом, мы сможем найти вещественный м. ц. в. лишь в том
случае, когда указанные две пары соответствующих точек не разделяют
друг друга.
*) Их можно найти построением, указанным в § 44,
304 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
IV. Покажем на простом примере, почему поставленная задача может
иметь два решения.
Рассмотрим в мертвом положении шарнирный четырехзвенник А1АВВ1
(рис. 310), длины звеньев которого удовлетворяют условию
АХА + АВ = АВХ + ВХВ.
Такой механизм называется предельным; он характеризуется тем, что оба
вращающихся звена АХА и ВхВ одновременно находятся в мертвом
положении; будем искать в этом мерт-
Л Л Р В В Р вом положении м- Ч- в- Р шатуна.
<£ <§>—<Д—@£ @ «/ , Так как обе пары
соответствующих точек А и Ви Ах и В не
Рис. 310. разделяют друг друга, то
существуют две вещественные двойные
точки Рх и Р2 этой инволюции.
Если механизм выйдет из мертвого положения в положение АХА'В'ВХ
(рис. 311, а), то м. ц. в. в этом новом положении будет в точке Р{, а его
предельным положением будет точка Рх; если же механизм выйдет из
мертвого положения в положение АХА"В"ВХ (рис. 311, б\ то м. ц. в. в этом
положении будет в точке Р'2, а его предельным положением будет точка Р2.
В частности, если АХАВВХ — шарнирный параллелограмм, то точки А
и ВХ) Ах и В симметричны относительно середины С отрезка АВХ\ двойными
б)
Рис. 311.
точками инволюции будут бесконечно удаленная точка и точка С; если
механизм выйдет из мертвого положения, оставаясь параллелограммом
(рис. 312, а), то будем иметь первый случай, если же он станет
антипараллелограммом (рис. 312, б) — второй*).
V. Пусть теперь даны две пары соответствующих точек А
и Av В и Вх (рис. 313), и надо найти точку Cv
соответствующую заданной точке С.
*) Во втором случае неподвижной центроидой является гипербола с
фокусами в точках Ах и Вх, у которой расстояние между вершинами равно АХА;
точка С является точкой пересечения правой ветви этой гиперболы с
прямой АХВХ.
§ 68] ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ 305
Найдем точку 5 пересечения прямых АВ и АХВХ и построим ось
коллинеации PSQ для прямых а и Ь\ по теореме Бобиллье имеем
а=р. Построим прямую g, образующую с прямой с угол ^ = а = Р;
ясно, что прямая g является осью коллинеации для прямых а и с.
Рис. 312.
Проводя прямую АС до пересечения с прямой g в точке D,
проводим прямую AXD, которая пересечет прямую с в искомой точке Cv
Пользуясь аналогичными построениями, решим следующую задачу: дана
кривая второго порядка у, касающаяся полюсной касательной Pt
в точке Р; найти геометрическое место fi точек Ах, если точки А
лежат на 7 (рис. 314).
Пусть точка Ах соответствует точке А\ возьмем на f произвольную
точку В, построим ось коллинеации Ь' для прямых АР и ВР и проведем
через точки А п В прямую Ъ"
до пересечения в точке В'
с осью коллинеации; найдем
геометрическое место точек В',
если будем повторять это
построение для точек С, А...
кривой 7-
Пучки прямых А (Ь", с"',
d", ...) и Р (Ьу с, d, ...) проек-
тивны, ибо проектируют точки
В, С, D, ... конического
сечения из двух центров А и Я,
лежащих на нем (§22); пучки
прямых Р(Ь, с, d, ...) и
Р(b', c'yd'i...) также проек-
тивны, ибо получены друг из друга поворотом всех прямых на один и тот
же угол; следовательно, пучки прямых Р (b'f с', d',...) и А (Ь", с", d", ...)
проективны, а поэтому геометрическим местом точек В'у С, D', ...
пересечения соответствующих прямых этих пучков является некоторая кривая
второго порядка У (§ 23). Если точку В взять совпавшей с точкой Я, то
прямая Ь совпадает с полюсной касательной Pt, прямая Ъ' совпадает с РА,
прямая Ь" — с АР; следовательно, прямая АР, соединяющая центры обоих;
Ъ Q
Рис. 313.
306 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
проективных пучков, соответствует сама себе и эти пучки перспективны
(§ 43), т. е. кривая второго порядка т' распадается на прямую АР и на
ось перспективы gx, являющуюся геометрическим местом точек В'.
Проектируя точки В', С, D', ... из центра Ах, получим пучок прямых
Ах {Ъ'", сш, dm, ...), перспективный пучку прямых Р (b', c'f d', ...). На
основании всего вышесказанного пучки прямых Ах {Ьш, ст\ dm, ...) и Р (b, c,d, ...)
проективны и геометрическим местом точек Ах, Blf Сх, Dx, ... является
коническое сечение fi, проходящее через точки Ах и Р; если точка В
совпадает с точкой Р, то, как было сказано, прямые Ь" и Ь совпадают с АР
и с Pt, прямая Ьш также совпадает с АХР\ таким образом, прямой АХАР,
рассматриваемой как прямая первого пучка, соответствует во втором пучке
прямая Pt — поэтому fi касается в точке Р полюсной касательной (§ 23).
При этом, если из тдчек А и Ах проектировать все остальные пары
соответствующих точек, то все соответствующие прямые пересекутся на одной
Прямой — оси перспективы. В частности, если кривая f распадается на
полюсную касательную Pt и на прямую g, не проходящую через Р, то
геометрическим местом точек Ах, соответствующих точкам А на прямой g,
является по-прежнему коническое сечение fi *)• Если прямая g не имеет
общих точек с поворотной окружностью, то кривая не будет иметь бесконечно
удаленных точек, т. е. будет эллипсом; если прямая g пересекает
поворотную окружность в двух точках М и N, то кривая fi будет гиперболой,
причем прямые РМ и PN параллельны ее асимптотам; наконец, если
прямая g касается поворотной окружности в точке М, то кривая fi будет
параболой, ось которой параллельна прямой РМ.
Если рассмотрим еще одну прямую g', то получим еще одно коническое
сечение fi» касающееся fi в точке Р; если прямые g и g' пересекаются
в точке А, то fi и Ti пересекаются в соответствующей точке Ах и больше
не могут иметь общих точек, ибо в противном случае прямые g и g'
имели бы больше одной общей точки. Следовательно, обе кривые ^х и Yi»
имеют в Р три бесконечно близкие общие точки, т. е. имеют
соприкосновение второго порядка.
Возьмем в качестве прямой g' бесконечно удаленную прямую подвижной
плоскости; из формулы (67.2) при г = оо имеем гх = — d sin ср, т. е.
соответствующие точки в неподвижной плоскости лежат на так называемой
окружности возврата, симметричной с поворотной относительно полюсной
касательной; следовательно, коническое сечение fi имеет в точке Р
соприкосновение второго порядка с окружностью' возврата, которая является, таким
образом, окружностью кривизны в м. ц. в. для всех указанных конических
сечений.
§ 69. Уравнение Эйлера —Савари; кривизна
сопряженных рулетт
I. Рассмотрим две сопряженные рулетты (подвижную и
неподвижную), их центры кривизны В и Вг и обе центроиды Ц и Цх с
центрами кривизны С и Сг (рис. 315). Введем снова заменяющий четы-
рехзвенник СХВХВС со стойкой СгВг и шатуном ВС; он точно такой же,
как если бы мы заменили подвижную рулетту ? ее центром кри-
*) В § 41 мы доказали это утверждение аналитическим путем; из наших
рассуждений настоящего параграфа вытекает метод построения конического
Сечения fj.
§69] УРАВНЕНИЕ ЭЙЛЕРА — савари; КРИВИЗНА СОПРЯЖЕННЫХ РУЛЕТТ 307
визны В, а неподвижную рулетту ?i заменили кривой ^j»
вычерчиваемой точкой В\ в точке В прямая ВР является нормалью к ее ру-
летте Yi» ибо скорость точки В перпендикулярна к ВР\ если через
р = АР обозначить отрезок общей нормали к рулеттам и через р = АВ
и р1 = АВ1 их радиусы кривизны,
то мы видим, что можно применить
формулу (67.2), полагая в ней
r = PB = ? + p,rl = PBl = pl — p.
Мы придем к формуле Эйлера —
Савари
—} J_ =_!— , (69.1)
?+Р ?i—P dsm<? к >
связывающей кривизны сопряжен-
ных рулетт с кривизнами
центроид (ибо -j — К — /(Л.
Поскольку в формулу входит лишь
величина -г — К — К\, т. е. разность
кривизн центроид, а не каждая из
них в отдельности, то при нахожде- рис 315
нии кривизн рулетт ничто не из- -
менится, если мы заменим наши центроиды Ц и Цг другими
центроидами— окружностью Ц0 и прямой Ц10 с той же разностью кривизн
1
= К — К1=К(
-Къ
Кп,
(69.2)
где К0 — кривизна прямой — равна нулю; окружность Ц0 называется
окружностью катания; ее радиус равен диаметру поворотной
окружности (как видно из формулы |/f0| = __-j и она лежит с нею по
одну сторону полюсной касательной.
II. Рассмотрим теоремы Аронгольда о сопряженных рулеттах —
их доказательство вытекает из (69.1).
а) Если неподвижная рулетта — прямая, то р1==оо и р-\-р =
— РВ = d sin ср, т. е. центры кривизны подвижных рулетт,
огибающими которых являются прямые неподвижной плоскости,
лежат на поворотной окружности (рис. 316).
б) Если подвижная рулетта — прямая, то р = оо, pt— р==РВ1 —
= — й? sin ср, т. е. центры кривизны неподвижных рулетт,
огибаемых прямыми подвижной плоскости, лежат на окружности
возврата*) (рис. 317).
*) Окружность возврата симметрична с поворотной окружностью
относительно полюсной касательной.
308 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
в) Если назвать полюсом возврата точку R окружности возврата,
диаметрально противоположную м. ц. в., то каждая прямая а
подвижной плоскости, проходящая через полюс возврата, огибает
Рис. 316.
неподвижную рулетту, имеющую точку возврата в точке
пересечения прямой а с окружностью возврата (рис. 318);
действительно, точка касания обеих рулетт должна совпадать с точкой А, ибо
их общая нормаль должна пройти через м. ц. в. Р\ по б)
неподвижная рулетта должна иметь свой центр кривизны в точке А,
следовательно, радиус кривизны неподвижной рулетты в точке А равен нулю.
Таким образом, окружность возврата является геометрическим
местом точек возврата кривых неподвижной плоскости,
огибаемых прямыми подвижной плоскости,
причем эти прямые проходят через полюс
возврата.
III. Рассмотрим так называемое
обращенное движение, т. е. поменяем ролями обе
центроиды; при этом м. ц. в. Р не
изменится, а две сопряженные рулетты также
поменяются местами; в частности, если
точка М подвижной плоскости описывала
кривую Y! неподвижной плоскости, то при
обращенном движении эта кривая fi будет
при своем движении постоянно проходить
через неподвижную точку Ж.
Из (59.20) ясно, что при обращении
движения величина d изменит свой знак,
следовательно, окружность и полюс возврата являются поворотной
окружностью и полюсом поворота в обращенном движении.
С этой точки зрения случай б) получим из случая а); точно так же
справедливы два утверждения г) и д), получающиеся друг из друга
при обращении движения:
Рис. 318.
§69] уравнение эйлера — савари; КРИВИЗНА СОПРЯЖЕННЫХ РУЛЕТТ 309
г) Все точки подвижной плоскости, описывающие прямые
линии, лежат на поворотной окружности, причем все эти
прямые должны проходить через полюс поворота (рис. 319).
Рис. 319.
Рис. 320.
Рис. 321.
д) Все прямые подвижной плоскости, огибающие в процессе
своего движения неподвижные точки, проходят через полюс
возврата, а эти точки лежат на окружности возврата (рис. 320).
Пользуясь г), мы можем, например, легко построить поворотную
окружность для кривошипно-шатунного механизма (рис. 321); строим
м. ц. в. Р, ось коллинеации PQ,
полюсную касательную Pt по
теореме Бобиллье; полюс поворота W
лежит в пересечении полюсной
нормали Рп с линией движения центра
ползуна.
IV. В качестве иллюстрации
формулы Эйлера — Савари рассмотрим
пример.
Если мы знаем обе центроиды и
произвольно выберем подвижную ру-
летту, то этим полностью определится
неподвижная рулетта как огибающая
всевозможных положений подвижной
рулетты.
В относительном движении
круглых цилиндрических зубчатых колес
(рис. 322) центроидами являются
начальные окружности радиусов R и Rx\
проведем через точку Р прямую под
углом ср к полюсной касательной,
опустим на нее из центров С и С{ перпендикуляры CD иСД и построим
новые окружности Цг и Цх с центрами Си^и радиусами г и ду, построим
эвольвен?ы Э и Эх этих окружностей и докажем, что они будут
сопряженными рулеттами (т. е. что для них будет выполняться формула Эйлера —
Савари).
Мы имеем в (69.1)
p-=DA р=РА, ^ = DXA,
Рис. 322.
310 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
причем величину р{—р = PD{ = R{ sin ср следует считать положительной,
а величину p-j-/? = PD = — R sin ср — отрицательной, ибо точка D лежит
по другую сторону от Р\ мы имеем:
1
1
1
1
9+Р
Рг
R sin ср R{ sin ср
ncp \R^ R')'
sin ср
с другой стороны, по (59.20) имеем:
1
= /< — /<! = — -д —
т. е. правая часть равна
1
*).
d sin ср
Покажем еще при помощи теоремы Аронгольда следующее: если
выбрать прямолинейный профиль зубца на рейке, то профилем зубца на
колесе будет эвольвента (рис. 323).
В относительном движении рейки по колесу подвижной центроидой
является прямая Z/, а неподвижной — окружность Цх\ следовательно, -т = К—
— Ki =— Кь т. е. полюс возврата R совпадает с центром окружности //,;
на основании б) центр кривизны Вх неподвижной рулетты (т. е. профиля
зубца на колесе) должен лежать на окружности возврата в точке N ее
пересечения с прямой PL; строя
окружность Цх с центром R и с
радиусом RN, касающуюся, таким образом,
прямой PL, мы видим, что она должна
являться геометрическим местом
центров кривизны профиля зубца, т. е.
его эволютой — профиль является
'Ь эвольвентой окружности Z/r
V, Формула Эйлера — Савари
связывает между собой радиусы
кривизны двух сопряженных ру-
летт; покажем простое
построение, позволяющее найти центр
кривизны одной из них.
Докажем следующую простую
теорему: если центры кривизны
обеих центроид взять за центры двух пучков прямых и
проектировать из этих центров центры кривизны сопряженных рулетт,
лежащие на некоторой прямой, проходящей через м. ц. е., то эти
два пучка прямых перспективны и осью перспективы является
прямая, проходящая через м. ц. в. перпендикулярно к общей нор-
мали к рулеттам. *
Рис. 323.
*) Этим методом Л. Эйлер теоретически обосновал в 1767 г.
возможность использования эвольвент окружностей в качестве профилей зубчатых
колес.
§ 69] УРАВНЕНИЕ ЭЙЛЕРА САВАРИ; КРИВИЗНА СОПРЯЖЕННЫХ РУЯЕТТ 311
Действительно, рассмотрим снова заменяющий шарнирный четырех-
звенник СгВгВС (рис. 324); по теореме Бобиллье ось коллинеации
для двух прямых ССг и ВВг (т. е. осью перспективы для указанных
пучков прямых) является прямая
PQ±_BBV
Построение можно еще более
упростить, если заменить цент- \Ф^1 *^-^ Q
роиды Ц и Цг окружностью
катания Ц0 и прямой Ц10 (рис. 325);
так как центр окружности катания
совпадает с полюсом поворота W,
то построение таково: центр
кривизны В подвижной рулетты
соединяем прямой с полюсом
поворота W и находим ее точку
пересечения Bf с прямой PQ _|_ РВ\
через точку В' проводим прямую
параллельно полюсной нормали,
она пересечет прямую РВ в
искомой точке Bv являющейся центром
кривизны неподвижной рулетты; если подвижная рулетта
стягивается в точку В, то Вг является центром кривизны ее траектории.
Это построение осуществляется механизмом *) (рис. 326), в котором
звенья / и 2 вращаются вокруг неподвижных центров Р и W, а звено 3
в\^
у4
4
п
mw^^
tffr/p
с,
с
v/%
F
7/
%Ui
Рис. 324.
Рис. 326.
движется поступательно, причем ось его кулисы параллельна полюсной
нормали PW; если ролик В находится в центре кривизны подвижной рулетты,
то ролик В{ будет в центре кривизны неподвижной рулетты.
VI. Мы видим, что центры кривизны рулетт находятся чрезвычайно просто
(особенно легко это сделать в тех случаях, когда центроидами являются
*) См. В. В. Добровольский [1], стр. 52.
312 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ плоскости [гл. тх
окружности и прямые); возникает вопрос: можно ли произвольную кривую
считать рулеттой}
Покажем, что если задана произвольная кривая Yi и произвольная
неподвижная центроида Ц{, то всегда можно • найти подвижную
центроиду Ц и точку М0 подвижной
плоскости так, чтобы при качении без
скольжения Ц по Ц{ точка М0 описала
кривую Yi (рис. 327). Будем отсчитывать
дугу s = о Р0Р неподвижной центроиды
от некоторой ее точки Р0; проведем через
t точку Р нормаль РМ к заданной
кривой Yi; ее можно построить как
касательную из точки Р к эволюте ?2 кривой
Yi—пусть касание произойдет в точке М{.
Проводя в точке Р касательную к цен-
троиде Ци мы будем знать угол <р, г = РМ%
/•j = РМи т. е. из формульЦ67.2) сможем
Уг найти d\ так как К = К\-\- -т , причем кри-
Рис. 327. визна К\ центроиды Ц1 в точке Р известна,
то мы найдем отсюда К в функции 5, т. е.
найдем естественное уравнение
подвижной центроиды; точка Р0 задана, и известна полюсная касательная в этой
точке — по § 59 подвижная центроида будет полностью определена;
проводя через точку Р0 нормаль к кривой Yi. найдем на ней точку М0.
§ 70. Ускорения точек подвижной плоскости; редуцированные
ускорения
Во всех параграфах этой главы мы рассматривали чисто
геометрические задачи (за исключением задачи о нахождении скорости
перекатывания центроид); в настоящем параграфе мы рассмотрим
кинематические задачи, для решения которых надо знать со и е,
т. е. угловые скорость и ускорение подвижной плоскости.
I. Редуцированным ускорением jA точки А подвижной плоскости
w А
назовем вектор, геометрически равный ул = —-, где wA —
векторное ускорение точки Л*).
Рассмотрим следующие свойства редуцированных ускорений.
а) Концы редуцированных ускорений двух точек отрезка лежат
на прямой, перпендикулярной к этому отрезку.
б) Мгновенный центр ускорений Q лежит на каждой окружности,
описанной на редуцированном ускорении любой точки как на диаметре.
в) Редуцированное ускорение м. ц. в. Р таково:
jp = d = PWt (70.1)
где вектор d определяется формулой tf = — dn,
*) См. Д. П. Котельников [1], гл. Ц.
§ 70]
УСКОРЕНИЯ ТОЧЕК подвижной плоскости
313
г) Редуцированное ускорение полюса поворота W таково:
Jw~-
(70.2)
где е = -
did
, векторное угловое ускорение подвижной плоскости.
д) В пересечении окружностей, описанных как на диаметрах на
векторах jp и jw, получим мгновенный центр ускорений Q, причем
для его нахождения достаточно пересечь поворотную окружность
лучом, образующим с полюсной нормалью угол а-
arctg-ij-
для
нахождения этого луча надо повернуть вектор PW вокруг точки Р
на угол а против стрелки часов
если s < 0. Мгновенный центр
ускорений совпадает с полюсом
поворота W, если а)^=0, s = 0>
и с м. ц. в. Р, если а) = 0, ефО
если s > 0, и по стрелке часов,
С
в Л
Рис. 328.
Действительно, для двух точек Л, В отрезка имеем (рис. 328):
*>z = wA + wBA = wA + wBA + wBA,
причем wBA = В А • о)2, a WBA±_AB\ отсюда, деля на ш2, находим:
Jb=Ja + BA +
w
ВА
из рис. 329,а имеем:
BD = BA-\-AC-{-CD.
то CD
w
ВА
Следовательно, если jB = BD, jA = AC,
В частности, если В — мгновенный центр ускорений, то wB
= BD = 0, т. е. l_ ABC =90° (рис. 329, б).
Для нахождения ускорения м. ц. в. wp напишем:
dx dx^ ds_ d2x d2x ( ds\2 . dx_ d*s_
dt ' dt2 ~~ ds2 \ dt ) •" ds ' dt2 '
ds d2y d2y ( ds\* , dy d2s
ds2 \ dt J ~T~ ~ds
1_AB.
= /* =
dt
dy_
dt
ds
ds
dt
d2y
dt2
dt2
314 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ плоскости [гл. IX
Из (59.16), (59.20) имеем при 5 = 0
d2y
ds2
dx-
ds
ds
d2x
ds2
0, »L = K-Kv
d *
ds
dt
= // = — da),
и таким образом находим:
wx = 0, wy = d^t jx = 0, jy = d, j = d= — dn.
Так как ускорение м. ц. в. Р направлено по полюсной нормали,
которая является касательной к его траектории (§ 61), то это
ускорение м. ц. в. является касательным.
Для точки W имеем:
JW Jp\Wr^\JwP JWP 0)2 (i)2 '
II. Для любой точки А подвижной плоскости мы имеем (рис. 330):
^л = ^р + ^лр^^лр + ^р + ^лр = ^,ш2 + ^,ш2 + ^лр^
= AW • о)2+ WfAp= AW • ©2 + e X PA. (70.3)
Следовательно, ускорение каждой точки подвижной плоскости
имеет две составляющие: первая соответствует вращению
вокруг полюса поворота W при
условиях е = 0, о)=£0, а вторая —
вращению вокруг м. ц. в. Р при
условиях (о = 0, ефО.
Так как вторая из этих
составляющих перпендикулярна к АР,
а проекция вектора AW на
направление АР равна АА0, то
редуцированное нормальное ускорение
каждой точки А подвижной
плоскости выражается
вектором АА0, где А0 — точка
пересечения прямой АР с поворотной
окружностью. Отсюда ясно, что
поворотная окружность является
геометрическим местом точек
подвижной плоскости, нормальные ускорения которых равны
нулю, т. е. АГ == 0 —мы показали другим способом, что поворотная
окружность является геометрическим местом точек распрямления.
III. Найдем теперь касательное ускорение w*A; проектируя
векторы в обеих частях (70.3) на касательную AN, получим:
wAt = е . РА + A0W • о)2 = s [РА + d С08* ' ^ ].. (70.4)
§ 70] УСКОРЕНИЯ ТОЧЕК подвижной плоскости 315
Откладывая по полюсной касательной отрезок PWX ■
d<o2
(рис. 331),
назовем точку Wx тангенциальным полюсом; он, очевидно,
характеризуется тем, что при вращении вокруг м. ц. в. Р при условиях
u) = 0, вфО он имеет ускорение, равное и противоположное
ускорению полюса в действительном движении; легко также видеть, что
вектор PW{ направлен параллельно векторному ускорению полюса
поворота W и в одну сторону
с ним.
Построим на отрезке PWX
как на диаметре окружность,
которую будем называть
окружностью перемени; мы получим
d cos <рсо2 r,.v/ ~,
1— = PWX • coscp = PL
AP + PL=AL;
окончательно имеем:
Wa = AL • e,
(70.5)
т. е. касательное ускорение
каждой точки подвижной
плоскости таково, как если бы она
вращалась при условиях (0 = 0,
ефО вокруг точки L, в которой прямая АР пересекает окружность
перемены; таким образом, окружность перемены является
геометрическим местом точек подвижной плоскости, касательные
г-» * dv Л
ускорения которых равны нулю. В частности, условие wt = — — 0
удовлетворяется в тех точках, в которых скорость достигает
экстремума и ее возрастание сменяется убыванием, или наоборот*).
IV. Поворотная окружность и окружность перемены пересекаются
в двух точках (рис. 331); одной из них является м. ц. в. Р, а
другой — мгновенный центр ускорений Q; так как он лежит на o6ei х
окружностях, то не имеет ни касательного, ни нормального
ускорения; из рис. 331 имеем:
tg/_WWxP =
PW
PW*
= ^ = tga.
Если е = 0, то окружность перемены распадается на бесконечно
удаленную прямую и на полюсную нормаль, причем в этом случае
мгновенный центр ускорений совпадает с полюсом поворота.
*) Этим объясняется название «окружность перемены»; ее иногда
называют также окружностью Бресса (Bresse, 1853 г.); поворотную окружность
иногда называют окружностью Лягира (de 1а Hire, 1706 г.).
316 ДВА И ТРИ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. IX
V. Рассмотрим несколько простых примеров нахождения мгновенного
центра ускорений Q.
Пусть дана поворотная окружность и направление AS ускорения
точки А подвижной плоскости (рис. 332); проведем через полюс поворота W
прямую WL || AS до пересечения с окружностью в точке L\ прямая LA
пересечет поворотную окружность в искомой точке Q; действительно, как известно
из кинематики, векторы wp и w. должны образовывать с прямыми PQ и AQ
равные углы а; мы как раз и имеем в данном случае
/ LAS = £ ALW = Z WPQ.
Пусть даны направления ускорений AS и BG двух точек А и В
подвижной плоскости (рис. 333). Найдем точку Т пересечения данных
Рис. 332. Рис. 333.
прямых AS и BG и проведем окружность f через точки А, В и Т\ какую бы
точку N мы ни взяли на ней, мы имеем /_NAS = /_ NBT, т. е. искомая
точка Q должна лежать на этой окружности.
Для ее нахождения нужно дополнительное условие, —например, пусть
W А
дано отношение ускорений —— = X; из кинематики известно, что
«д _ AQ
wB - BQ -Л'
т. е. отношение расстояний точки Q от данных точек А и В равно данной
величине X. Мы показали в § 33, что геометрическим местом таких точек
является окружность Аполлония fil она пересекает окружность f в двух
точках X и Y (рис. 334); мы имеем:
£_ ХА Т = Z. Хвт> L Y&S = !80° — L YB(J>
т. е. мгновенным центром ускорений является точка X.
В частности, если даны векторные ускорения wA и «л двух точек А
и В (рис. 335), то снова строим окружность у через точки А, В и Т\ вместо
§ 70] УСКОРЕНИЯ ТОЧЕК подвижной плоскости 317
окружности Аполлония построим окружность 7i через точку Т и концы Ах
и Вх векторов w. и wR; окружности 7Х и Т пересекутся в точке Г и в
искомой точке Q; действительно, как показано, /. QAT~ /_ QBT и, кроме того,
Рис. 334. Рис. 335.
^ QAXT— /Q517,) ибо оба угла опираются на одну дугу; отсюда следует
Д AQAX ^ Д BQBb и поэтому мы имеем нужное нам соотношение
ААХ В'ВХ
AQ ~~ BQ '
ГЛАВА X
ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ
ПОДВИЖНОЙ ПЛОСКОСТИ
§ 71. Кривая круговых точек и кривая центров
I. В соответствии с тем, что сказано в § 65, найдем
геометрическое место круговых точек подвижной плоскости; будем его
называть кривой круговых точек. Оно
характеризуется условием К' = 0, где
К= кривизна рулетты, а произ-
г
водная взята по дуге s центроиды.
Мы имеем р = /*! — г; из (67.1)
находим: *
YP 1 d sin ср -
д = — =-
dy
— г*
x = rcosy,
у = г sin ср,
где А (х, у) — точка подвижной плоскости. Отсюда
■р, _ г (d'y + dy' — 2rr') — 3r' (dy — r2) _ r(d'y + dy'+rr') — bdr'y
(71.1)
и нам нужно найти производные у' и г*'. Введем вектор (рис. 336)
г2 = АР=— г, r = tx + ny = PA
и найдем векторную производную по 5 (при фиксированной точке Л),
пользуясь (59.4),
^ = % = — %х' — пу' — %'х — п'у = *(!<у—х') — п(у'+Кх).
откуда
х'=Ку—1, у'=-Кх, гг' = хх' + уу'=—х. /■'=—7' (71,2)
§ 71] КРИВАЯ КРУГОВЫХ ТОЧЕК И КРИВАЯ ЦЕНТРОВ 319
Эти производные характеризуют изменение координат точки
подвижной плоскости, происшедшее благодаря тому, что при перекатывании
подвижной центроиды по неподвижной начало координат Р
переместилось по подвижной центроиде и оси координат (т. е. полюсные
касательная и нормаль) повернулись.
Подставляя в (71.1), найдем:
/?' _ _ (*2 + У2) ИМ + 1) х - d'y] - 3 dxy .
К' =
г
3d
умножая числитель и знаменатель на , (Kd, 14 и полагая
3d , 3d ,- л 0
т^-^г, / = ЖТТ> (71-3)
мы получим:
у/ — К*2 + У2) ("** + 1У) - Irnxy] d' (Kd + 1)
Условие К' = 0 эквивалентно уравнению
(х2 + у2) (тх -f- ly) — Irnxy = 0. (71.4)
Следовательно, кривая круговых точек уг является кривой Бур-
местера, изображенной на рис. 228, свойства которой были изучены
в §§ 54—50. Параметры /я, / выражаются по (59.20) формулами
3(/C-/d) /= 3 в (715}
К-К\ 2К-Кх
Переходя к полярным координатам, получим'из (71.4):
г /sincp ' /И COS ср
По формуле Эйлера (67.2) найдем:
11 1 /1 1\ 1 , 1
(71.6)
JL_ = (1_±\JL
sin ср \ / d J sin <
Г] г d sin ср \ / d ) sin ср ' т cos ср
Если ввести новый параметр 1г по формуле
1__L —1
/ Z, d
(71.7)
(71.8)
то получим уравнение в полярных координатах
1 _ * | '
rx lx sin ср ' т cos ср '
вполне аналогичное (71.6); в декартовых координатах получим:
(*2 + У2) (тх + 1ху) — 1хтху = 0. (71.9)
320 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ плоскости [гл. X
Эта кривая, называемая кривой центров f2> также является кривой
Бурместера, ибо отличается от (71.4) только заменой / на lv
II. Рассмотрим данное положение Е подвижной плоскости и три
других Ef, Еп\ Еш, бесконечно близких к Е, и для каждой точки А
положения Е найдем соответствующие три точки А', А", Аш в
положениях Е', Е", Еш. Кривая круговых точек является
геометрическим местом точек А положения Е, которые вместе с тремя
точками А', Af, Ат лежат на одной окружности, а кривая
центров является геометрическим местом центров этих
окружностей. Можно также сказать, что кривая круговых точек является
геометрическим местом точек подвижной плоскости, рулетты которых
имеют в данных точках соприкосновение не ниже третьего порядка
со своими соприкасающимися окружностями, а кривая центров
является геометрическим местом центров этих окружностей.
Отсюда ясно значение этих кривых в синтезе механизмов: если
какая-нибудь шатунная точка движется строго по окружности
(например, палец кривошипа), то ее траектория совпадает со своей
соприкасающейся окружностью и, можно считать, имеет с ней
соприкосновение сколь угодно высокого порядка —такая точка должна
лежать на кривой круговых точек, а неподвижный шарнир, т. е.
центр соприкасающейся окружности, должен лежать на кривой
центров.
Кривую центров можно получить еще и таким путем: из (71.5),
(71.7) имеем:
т= 3<*'~*> , /1Я= ? . (71.10)
Рассматривая обращенное движение, при котором обе центроиды
поменялись своими ролями, а следовательно, К и Кг следует
поменять местами, мы видим, что при этом обе кривые Бурместера -\\
и ^2 меняются своими ролями.
Направляющая прямая кривой круговых точек пересекает оси Pt
и Рп в точках М и L, причем т = РМ, 1 — PL (§ 54), а
направляющая прямая кривой центров — в точках М и Lv причем 1г = PLX\
следовательно, направляющие прямые обеих кривых Бурместера
пересекаются на полюсной касательной.
III. В уравнение кривой круговых точек входят два параметра т, I,
выражающиеся по (71.5). через кривизны центроид и их производные
в м. ц. в. Р —этих величин в задачах синтеза мы обычно не знаем;
однако если мы знаем полюсные касательную и нормаль и две точки,
которые должны лежать на кривой круговых точек, то мы сможем
найти оба параметра при помощи простых геометрических построений.
Рассмотрим, например, шарнирный четырехзвенник АгАВВг
(рис. 337); построив точки Р, Q и ось коллинеации PQ, находим
по теореме Бобиллье полюсные касательную Pt и нормаль Рп\ точки А
§71] КРИВАЯ КРУГОВЫХ ТОЧЕК И КРИВАЯ ЦЕНТРОВ 321
и В должны лежать на кривой круговых точек, причем мы знаем ее
узловую точку Р и касательные в ней Pt и Рп\ следовательно, мы
должны построить кривую круговых точек по двум ее точкам;
получив по этим данным направляющую прямую (§ 54), мы найдем, как
было указано, параметры т и /; аналогично строится кривая центров.
На рис. 337 построены обе кривые Бур-
местера для шарнирного четырехзвенника.
IV. Во всех задачах предыдущей главы
фигурировала только величина (1 = -^—-гг,
i\ — ai
а не кривизна каждой центроиды в
отдельности; если мы нашли величины / и lv то из
(71.5), (71.10) имеем:
1 _2к 1 ^ Х —2 к 1 К
откуда находим кривизны обеих центроид
к-1Н
Kv
- + 1
/ I /
(71.11)
Если через С и Сх обозначить центры кривизны центроид, то на
полюсной нормали имеем (рис. 338):
1 2.1 1 2,1
PC
PL
PLX РСХ
PL,
PL
Введем в рассмотрение точки L* и Z,*,
симметричные с точками L и Lx
относительно м. ц. в. Р; мы имеем:
1
PL
2
Щ
Покажем, что
(pll[c) =
PC
--^--f
рсх '
(PL^Q
PL\
1
PL*
= —
•
i
(71.12)
(71.13)
т. е. искомые центры кривизны С и Сх
центроид являются четвертыми
гармоническими точками к точкам Р, Z,, L*
и Р, Lv L*. Для доказательства (71.13) обозначим через yv у2, Уз» У а
ординаты точек Р, Z,, L*t С; мы имеем:
PL = y2 — yv PC = y4 — yv PL* = Уз— yv
322
ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ
[ГЛ. X
и первое из равенств (71.12) запишется следующим образом:
2 1,1
Отсюда находим:
(у2-
Уа — Уг-
и окончательно
У2 — У\ У* — У\
У\)(Уъ — У\)
У г —Ух
2У;
з — Уг — Ух
У4 — У2:
(У 2 — Ух)(Уъ — У2)
2у3 — У 2 — Ух
Уъ — Ух . У а — Ух
Уз — У2 У4 —Уг
1.
Построим поляру точки L\ относительно окружности с диаметром PL
(рис. 338); легко видеть что эта поляра пересечет полюсную
нормаль в точке С; аналогично можем найти точку Сг *).
V. Рассмотрим один частный случай, приводящий к весьма простым
геометрическим построениям для обеих кривых Бурместера. Мы видели,
что два рода соответствующих точек (рис. 339) а (А, А\ А'\ ...) и
а( Al% Av -dj,...) проективны,
так же точно как и два ряда
точек Ь(В, В', В", ...) и
ь{в1%в[%в°1%...).
Рассмотрим тот частный
случай, когда оба параметра
кривой круговых точек
связаны дробно-лине иным
соотношением
1 =
am
(71.14)
Pm + 7'
Из (71.4) имеем:
(*2 + у2)(т* + «:у) +
+ тх [(х* + у2) р — ау] = О,
(71.15)
откуда ясно, что в этом случае все кривые круговых точек образуют пучок
характеризуемый параметром т.
Если прямые а и Ь характеризуются углами <р и ср', то, записав (71.15)
в полярных координатах, имеем для каждой из этих прямых
Рис. 339.
г =
та sin <р cos <р
та sin ср cos <р
mp cos <р + (y cos <р -j- ol sin <p) '
mp cos <p' + (y cos <p' -f- a sin <p') "
Исключая отсюда параметр m, найдем, что радиусы-векторы гиг'
связаны дробно-линейным соотношением
г' =
<*!/*
Pi'+ 7i
(71.16)
*) См. Р. Мюллер [1], стр. 51; несколько иное построение указывает
Р. Бейер [2], § 85.
§ 72]
ТОЧКА БОЛЛА
323
коэффициенты которого нетрудно найти; следовательно, два ряда точек
а {А, А', А", ...) и Ь(В, В', В", ...) проективны\ так как точка Р
соответствует сама себе (ибо при г = О имеем г' = 0), то оба ряда точек
перспективны с некоторым центром перспективы S.
Из формулы (71.7) находим:
. dam
'i- W^a)m + dl' (7U7>
Таким образом, кривая центров также обладает указанными свойствами
т. е. оба ряда точек а[Ах, А[, Аг, ...) и b(Bv В[, в[, ...) также
перспективны с некоторым центром перспективы Sx.
Прямые, проектирующие точки А, А'', А", ... из центра S и точки Ах,
A'v А'[, ... из центра Su пересекаются на оси перспективы (являющейся
осью коллинеации) — следовательно, эти пучки прямых перспективны, а
поэтому прямая SS{ должна соответствовать сама себе, т. е. точки S, S{ и Р
должны лежать на одной прямой. Таким образом, при выполнении
условия (71.14) мы имеем пучок кривых круговых точек и кривых центров;
для каждых двух прямых, проходящих через м. ц. в., существуют такие
два центра перспективы 5 и S, (лежащие на одной прямой с точкой Р)
и такая ось перспективы, что задание одной точки А одной из кривых
Бурместера определяет точки Alt В, Вх с помощью весьма простого
геометрического построения (указанного на рис. 339).
§ 72. Точка Болла
I. Мы нашли поворотную окружность как геометрическое место
точек распрямления, для которых /С —0, и нашл-и кривую круговых
точек как геометрическое место точек, для которых К' = 0; точки
их пересечения характеризуются
условиями К = К' = 0.
Рассматривая совместно (66.10),
(71.4) и исключая
мы найдем:
из них х2 + у2
у [dly — т (/ — d) х] = 0;
у = 0 имеем х = 0,
(72.1)
при у = и имеем х = [), т. е. одной
точкой пересечения является м. ц. в. Р,
который в общем случае следует
исключить из рассмотрения, ибо он
может не являться точкой
распрямления. Пользуясь (71.7), имеем из (72.1):
т
у = — — х.
(72.2)
Рис. 340.
Точка U пересечения поворотной окружности с этим лучом
называется точкой Болла (рис. 340); рассмотрим ее свойства:
а) в общем случае точка Болла является единственной точкой
подвижной плоскости, рулетта которой имеет в этой точке
соприкосновение не ниже третьего порядка со своей касательной-,
324 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
б) точка Болла лежит на фокальной оси кривой центров
и является проекцией полюса поворота на эту ось — это
вытекает из формулы (54.4), в которой надо заменить / на 1Х\
в) луч, идущий в точку Болла из м. ц. в., характеризуется
угловым коэффициентом
__ (/С — /С,)(/С —2/Q .
tgcp:
(72.3)
это вытекает из формул (71.5), (71.10);
г) точка Болла является характеристической точкой на
каждой из поворотных окружностей; действительно, заменяя
d 1
в (63.13) S на ср, а г на у = -п
tg<P =
dK — 2
(]Г-Г/Г)' получим:
_ </С —/С,)(/С —2/СО
/с-/с;
II. Наше последнее утверждение вытекает из простых
геометрических соображений: рассмотрим положение подвижной плоскости Е
и еще три положения, бесконечно к нему близкие, и пусть точка А
положения £ и те точки А', А", А!"% в которых она находится
в положениях Е', Е"% Е"\ лежат на одной прямой. Из того факта, что
точки Л, А'% А' лежат на одной прямой, вытекает, что в точке А ее
Рис. 341.
рулетта имеет соприкосновение не ниже второго порядка со своей
касательной, т. е. А — точка распрямления своей рулетты и поэтому
лежит на поворотной окружности f для положений Е, Е', Е"
подвижной плоскости. Совершенно аналогично из того, что точки Л,
А", А/г/ лежат на одной прямой, .вытекает, что точка А должна
лежать и на поворотной окружности для положений Е, Е"\ Еш
подвижной плоскости, т. е. точка Болла является предельной точкой
пересечения двух бесконечно близких поворотных окружностей.
§ 73]
РАСПАДЕНИЕ КРИВЫХ БУРМЕСТЕРА
325
Отсюда вытекает простой способ Н. И. Мерцалова *) для
приближенного нахождения точки Болла. Рассмотрим шарнирный четы-
рехзвенник А1АВВ1 (рис. 341) и в трех положениях АВ, А'В', А'В"
шатуна построим поворотные окружности f» т'» т" методом,
указанным в § 67; скопировав на кальку Y и ^" вместе с А'В' и А'В",
наложим их на исходное положение так, чтобы отрезки А'В' и
А'В" совпали с АВ\ три точки попарногб пересечения наших
окружностей лежат вблизи м. ц. в. Р, а три другие—-вблизи точки Болла U.
§ 73. Распадение кривых Бурместера
I. На основании § 54 имеем геометрический критерий
распадения: если кривая Бурместера должна пройти через точку,
лежащую на полюсной касательной или нормали (отличную от
м. ц. в.). то она распадается на эту прямую и на окружность
с центром на этой прямой] с другой стороны, формулы (71.5),
(71.10) дают в некоторых случаях аналитический критерий
распадения.
Рассмотрим все возможные случаи.
а) Одновременное распадение обеих кривых Бурместера
эквивалентно тому, что одна из них должна проходить через
точку на полюсной нормали; обе кривые распадаются на
полюсную нормаль и на окружности (/) и (1г) с уравнениями
*2 + У2 — 1у = 0, х2 + У2 — 1гу = 0; (73.1)
это одновременное распадение эквивалентно условию т = оо, т. е.
условию К =К\\ в частности, оно имеет место, если м. ц. в.
является круговой точкой обеих центроид (например, если в этой
точке кривизны обеих центроид достигают экстремальных значений
и поэтому К ==К[ = О).
Указанное одновременное распадение эквивалентно тому, что
точка Болла совпадает с полюсом поворота, ибо при этом
. т
Отметим также, что одновременное распадение обеих кривых
Бурместера имеет место и тогда, когда траектории всех точек
подвижной плоскости симметричны относительно полюсной
нормали.
б) Распадение одной кривой круговых точек эквивалентно
тому, что она должна проходить через точку на полюсной
касательной; она распадается на полюсную касательную и на
окружность (т) с уравнением
х2-\-у2 — тх = 0, (73.2)
*) См. Н. И. Мерцалов [1], § 44.
326 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
Это распадение эквивалентно условию / = оо, т. е. 2K — KV
в) Распадение одной кривой центров эквивалентно тому, что
она должна проходить через точку на полюсной касательной;
она распадается при этом на полюсную касательную и на
окружность (т)\ это распадение эквивалентно условию 1Х = оо, т. е.
условию 2Кг = АГ, а также тому, что точка Болла должна совпадать
с м. ц. в. Р, ибо при этом tgcp= — — = 0; однако, как вытекает
м
из § 61, м. ц. в. Р при условии 2КХ = К может и не быть точкой
распрямления; в этом случае точка Болла не существует.
II. В качестве применения рассмотрим шарнирный четырехзвен-
ник АХАВВХ\ так как задание положения механизма полностью
определяет обе кривые Бурместера, то распадение их может иметь
место лишь в некоторых особых его положениях.
Покажем прежде всего, как впервые нашел Роденберг, что
одновременное распадение обеих кривых Бурместера имеет место в двух
случаях: 1) ось коллинеации перпендикулярна к вращающемуся
звену, 2) шатун и стойка параллельны между собой.
Действительно, в случае 1), как видно из рис. 342, мы находим
на основании теоремы Боббилье, что полюсная нормаль должна
совпадать с одним из вращающихся звеньев, например АХА\ так как
Рис. 342. Рис. 343.
точка А (соответственно, точка Аг) должна лежать на кривой
круговых точек (соответственно, на кривой центров), то мы имеем
случай а).
В случае 2) (рис. 343) находим ось коллинеации, параллельную
стойке, и полюсную касательную по теореме Бобиллье; кривая
круговых точек т полностью определяется двумя своими точками А и В
и может быть построена. Построим кривую ?', перспективно
подобную т относительно точки Р, причем отношение подобия пусть будет
§ 73]
РАСПАДЕНИЕ КРИВЫХ БУРМЕСТЕРА
327
РЛХ
рвх
л, — -pj- — -ртг> она пРойдет' очевидно, через точки Ах и Вх и
должна совпасть с кривой центров, которая полностью определена
своими двумя точками Ах и Вх. Из перспективного подобия обеих
кривых Бурместера с центром подобия в узловой точке вытекает
,сл л\ mm
совпадение их фокальных осей, т. е. по (54.4) равенство — = у-,
которое возможно лишь при т = оо, ибо ни одна из величин т,
/, 1Х не может быть равна нулю. / Rр
Д /
дЩ
'
\ \
м
£
f У
\t
Рис. 345.
Покажем теперь, что распадение кривой круговых точек
(соответственно, кривой центров) имеет место в том положении
механизма, в котором ось коллинеации перпендикулярна к шатуну
(соответственно, стойке) (рис. 344).
Действительно, в случае распадения точки А и В лежат на
окружности с центром О на полюсной касательной, причем
l^PBA = 90°-|-а, ибо он измеряется половиной дуги РМВ\ так как
/tmPQB = 1_РВА — р == 90° —[— а — Р» то наше утверждение вытекает
из теоремы Бобиллье.
Рассмотрим еще мертвое положение механизма-, пусть звено АХА
и шатун АВ вытянулись в одну прямую (рис. 345); м. ц. в. Р,
лежащий в пересечении прямых АХА и ВХВ, совпадает с точкой В,
точка Q, лежащая в пересечении прямых АВ и АХВХ, совпадает
с точкой Av а ось коллинеации PQ — с прямой АВ. По теореме
Бобиллье полюсная касательная должна совпадать с ВВХ\ так как
на ней должна лежать точка Вх, то кривая центров распадается
на окружность ^ и прямую ^ (случай в)); кривая круговых точек fi
не распадается.
Так как точка Ах должна лежать на кривой центров — именно,
на окружности у'2—то центр этой окружности (являющийся фокальным
328 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
центром кривой центров) лежит в точке F2 пересечения
полюсной касательной Pt с осью симметрии отрезка РАХ\ окружность ^
пересекает Pt в точке Ж, причем РМ — т. Зная одну точку А
кривой круговых точек fi» строим обычным образом точку А'
направляющей прямой; так как она должна пройти и через точку Ж,
то этим она полностью определена и пересекает полюсную
нормаль Рп в точке L, причем PL = l\ зная направляющую прямую
кривой круговых точек, мы сможем построить сколько угодно ее
точек.
/1==:оо, мы имеем из (71.7) l = d, т. е.
с поворотной окружностью, а точка L —
с полюсом поворота W.
Аналогичную картину распадения кривой
центров имеем в другом мертвом
положении (рис. 346).
Мы рассмотрели случай
совпадения осей кривошипа и шатуна;
Благодаря тому, что
окружность (/) совпадает
Рис. 346.
Рис. 347.
пусть теперь совпадают оси кривошипа и стойки (рис. 347).
В этом случае точки Р и Q, являющиеся точками пересечения
прямых АХА и ВХВ, АВ и А1В1 совпадают с точками Вх и Л, ось кол-
линеации совпадает с прямой ААХВХ и полюсная касательная Pt —
с прямой ВХВ.
Таким образом, кривая круговых точек fi должна проходить
через точку В на полюсной касательной (случай б)); она
распадается на окружность у[ с центром в точке Fx и полюсную
касательную Tj'; кривая центров, проходящая через неподвижный
шарнир Av не распадается, и ее направляющую прямую найдем точно так
же, как в предыдущем случае.
§ 74] ПОСТРОЕНИЕ ОБЕИХ КРИВЫХ БУРМЕСТЕРА 329
§ 74. Построение обеих кривых Бурместера
I. Если м. ц. в. известен, то кривые Бурместера
характеризуются четырьмя параметрами: величинами т, I, 1г и углом,
определяющим положение полюсной касательной; для их определения
необходимы, таким образом, четыре условия.
Так как неподвижный шарнир должен лежать на кривой центров,
а подвижный — на кривой круговых точек, то задание одного из
шарниров эквивалентно одному условию. Задание прямой, на которой
лежит точка Болла (т. е. задание фокальной оси кривой центров),
эквивалентно одному условию, а задание самой точки Болла — двум условиям.
В частности, точкой Болла является точка подвижной
плоскости, движущаяся прямолинейно. Если же прямая подвижной
плоскости всегда проходит через неподвижную точку, то эта последняя
является точкой Болла обращенного движения.
Построение кривой Бурместера по трем условиям, полностью
ее определяющим, приведено в § 55; мы рассмотрим те случаи,
когда условия, наложенные на каждую кривую в отдельности, ее
не определяют, но совокупность условий, наложенных на обе
кривые, определяет эти последние.
II. Рассмотрим в качестве примера задачу, решенную В. Лихтенхельд-
том [1]; он рассмотрел задачу синтеза подъемного крана системы Демаг
или гоночного механизма ткацкого станка и в обоих случаях пришел
к такой задаче (рис. 348): зная две
прямые а и Ь, вдоль которых должны
идти оси двух вращающихся звеньев
шарнирного четыре хзвенника,
построить его таким образом, чтобы
рулетта заданной шатунной точки U
возможно ближе подходила в этой
точке к заданной прямой и.
Мы знаем, таким образом, м. ц. в. Р,
в котором пересекаются прямые а и Ь,
и точку U, которая, очевидно, должна
быть точкой Болла; мы имеем два
условия и можем наложить произвольно
еще два условия.
Рассмотрим сперва аналитический
метод решения задачи. Так как
фокальная ось PU кривой центров известна, а полюсная касательная Pt
неизвестна, то, отсчитывая угол ф по часовой стрелке от PU к Pt, мы будем
иметь по (54.4) условие
tg«|,«£, ф= -<Р, (74.1)
причем будем полагать — 90°<ф<90°; так как известна точка Болла
Uy то по (71.7) мы можем выразить все параметры через /, и ф
Рис. 348.
■■ /i tg ф,
d =
/ = -
Ph
г, P = PU.
(74.2)
sin ф ' ' ' p — lx sin ф'
Отсчитывая угол p от оси PU и вводя полярные координаты (г, р —+),
330 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
мы имеем, пользуясь (71.6) и (74.2), уравнения кривой круговых точек
г = /?/isin2(p —ф)8Шф
2 [р sin р — /, sin^ cos (р — ф)] *'*'°'
и кривой центров
__ /15Шф5Ш2(р —ф)
Г* 2slFp * (/4Л)
Рассмотрим некоторые дополнительные условия:
А. Задан угол ф и один из шарниров *). Если задан шарнир Л, то
мы имеем для прямой а, полагая р = рь
/A sin 2(3, — ф) . гч
»• — ^- ^ -^ , А = /j sin ф, (74.5)
2 [/? sin р, — A sin ф cos ($х — ф)]
откуда легко находим:
1 = Prsin^ . (746)
cos (р, — ф) [р sin (р, — ф) + г sin ф] к }
После этого легко найти /,, а следовательно, и гх для шарнира Л] на
прямой а, а также г' и г' для шарниров В и Вх на прямой ft, для которой
положим в (74.3), (74.4) р = р\
Если бы был задан шарнир Alt то по (74.4) мы имели бы еще более
простую формулу:
9r.cln н.
(74.7)
2r1sing1
sin2(P, —ф) *
Б. Заданы оба неподвижных шарнира Ах и В{. Мы имеем по
предыдущей формуле
2r,sinp, 2r'sinp'
* = — == • 0L—-тт • (74-8)
sin 2 (р, — ф) sin2(pi— ф)
Зная величины гх, г' и углы р„ р' обеих прямых а и b с осью PU, мы
легко найдем отсюда
rx sin Pj sin 2р' — г' sin р' sin 2pj
tg 2^ = r, sin p, cos 2P' — r' sin p' cos2 p, * (74,9)
Мы получим отсюда два значения ф, различающиеся на 90°, что сводится
к тому, что оси Pt и Рп поменяются местами.
В. Заданы два шарнира А, Ах одного вращающегося звена. Мы имеем
по (74.4), (74.3)
2r,sinp, __ 2pr sin$x
sin 2 (р, — ф) р sin 2 (р! — ф) + 2r sin ф cos (р, — ф)
откуда находим решения
. (74.10)
w=«*h+ „^^ +-*+£••>. (74.И)
*) Хотя задание угла ф полюсной касательной с осью PU не имеет
непосредственного кинематического смысла, этот случай важен тем, что
к нему мы будем сводить некоторые другие случаи задания.
**) При ф = Pi +-0- имеем распадение обеих кривых Бурместера (§73, а).
§ 74] ПОСТРОЕНИЕ ОБЕИХ КРИВЫХ БУРМЕСТЕРА 331
Г. Заданы два подвижных шарнира А и В. Мы имеем по (74.6)
pr sinf^
Х =
cos (р! — ф) [г sin ф -f-/7 sin (Pi — ф)]
pr' sin p J
откуда находим:
tg 2ф = />.
co8(p; —ф)[г'мпф+^8т(р; —ф)]
rsin^sin2^ — r'sinpj sin2p,
rr'sin (p' —pi) +/?[r sin p!cos 2p^ —r'sin pj cos 2p,]
(74.12)
(74.13)
Задача снова имеет два решения, различающихся на 90°.
III. Рассмотрим теперь геометрические методы решения задачи.
А. Задан угол ф. Зная угол ф, мы можем построить полюсные
касательную Pt и нормаль Рп (рис. 349); так как точка Болла U лежит на
поворотной окружности, то, восставляя в точке U перпендикуляр к PU,
мы найдем в его пересечении с Рп полюс поворота W, построим
поворотную окружность, найдем точки А0 и В0 ее пересечения с прямыми а и b
и построим для них ось коллинеации
PQ НАД).
Так как условие (74.1) при
заданном угле ф подходит под тип (71.14)
или (71.17), то мы сможем по одному
параметру найти три остальных, если
построим два центра перспективы S
и S, (§ 71).
Из (74.4) ясно, что все кривые
центров, соответствующие различным
значениям параметра 1и перспективно
подобны друг другу с центром
подобия в Р\ следовательно, все прямые,
соединяющие неподвижные шарниры,
параллельны друг другу, т. е. центр
перспективы Sx ушел в
бесконечность по направлению, которое
нетрудно найти: зная координатные оси
и фокальную ось кривой центров
и произвольно задавая неподвижный
шарнир Аи мы можем применить
преобразование Котельникова (§§ 54, 55) и найти неподвижный шарнир Вх
(рис. 350). Следовательно, S, — несобственная точка прямой АХВХ.
Соединяя точки А0 и В0, получим прямую, на которой должен лежать центр
перспективы S — он лежит в ее пересечении с прямой PS, проведенной
через Р параллельно АХВХ. Следовательно, при задании угла ф легко
найти оба центра перспективы и ось коллинеации, после чего по одному
Рис. 349.
заданному шарниру легко найти три остальных.
Б. Заданы оба неподвижных шарнира Ах и Вх. Мы знаем, таким
образом, фокальную ось и три точки Ах, Вх, Р кривой центров, из
которых одна — узловая, и мы должны найти касательные к ней в узловой
точке, — эта задача решена в § 55; мы пришли к случаю А.
332 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
В. Заданы два шарнира А и Ах на одном вращающемся звене
(рис. 351). Зная точки А и Ах прямой а, мы можем построить точку А0 ее
пересечения с поворотной окружностью (§ 68) и провести эту окружность
через три точки Р, {], А0;
прямая, проходящая через ее центр
и точку Р, является полюсной
нормалью, и мы снова
приходим к случаю А.
Г. Заданы два подвижных
шарнира А и В. Мы знаем,
таким образом, четыре точки
А, В, U, Р кривой круговых
точек, из которых одна —
узловая; нахождение касательных
к ней в узловой точке
рассмотрено в § 55.
IV. Поскольку в
рассматриваемой задаче мы можем
выбрать два параметра
произвольно, то желательно выбрать
их таким образом, чтобы
получить наиболее простое
решение. В. Лихтенхельдт при
решении своей задачи требует,
чтобы заданный неподвижный
шарнир Ах был фокальным
центром кривой центров;
в таком случае координатные
оси, т. е. полюсные
касательная и нормаль, являются
биссектрисами углов между прямыми PU и РАХ, т. е. его условие
эквивалентно заданию угла ф; он получает оо1 решений, ибо при его условии можно
произвольно выбрать лишь один неподвижный шарнир Ах; мы показали, что
задача имеет оо2 решений, ибо можно и угол ф
выбирать совершенно произвольно, причем
построение на рис. 350 получилось не намного
сложнее, чем построение, найденное В. Лихтен-
хельдтом для его частного случая.
Мы получим еще более простое построение,
если выберем угол ф таким образом, чтобы иметь
одновременное распадение обеих кривых Бур-
местера — это будет иметь место, если точка
Болла будет совпадать с полюсом поворота, т. е.
если полюсная нормаль Рп будет совпадать
с фокальной осью PU кривой центров; обе
кривые распадаются на полюсную нормаль и на
окружности (/) и (1Х), причем прямые АВ и АХВХ
параллельны прямой А0В0 (рис. 352). Отложим
от м. ц. в. Р отрезок PR, равный и параллельный
отрезку WA0. Выбирая произвольно неподвижный
шарнир Ах, находим второй неподвижный
шарнир Вх, проводя прямую АХВХ\\А0В0;
проектная точку Ах из центра R в точку L полюсной нормали и проводя прямую
А || WAQ, получим подвижный шарнир А, а проводя АВ || А0В0, найдем
второй подвижный шарнир В.
Рис 350.
Рис. 351.
I
§ 74] ПОСТРОЕНИЕ ОБЕИХ КРИВЫХ БУРМЕСТЕРА 333
Для доказательства нам надо проверить, что точки L и L, получились
такими, что выполняется (71.7). т. е. надо доказать выполнение равенства
1
1
1
PL
PL г
(74.14)
Оно вытекает из подобия треугольников PL А и PWA0, PRAX и LAAX,
LXAXP и LAP, ибо мы имеем:
PL LA LA АА, ААХ
РА,
PW ~ WAQ
АА±
PR~~ РА,
LLX
PLX>
откуда вытекает равенство
1 _ LLX
PW
PL,—PL
PL • PLX
PL-PL,
PL
PL,
V. В качестве дальнейшего примера рассмотрим построение кривых
Бурместера для механизма, изображенного на рис. 353. Точка В шатунной
плоскости движется по прямой b и является, таким образом, точкой Болла
и должна лежать на поворотной
окружности-, прямая т шатунной плоскости во
все время своего движения проходит через
неподвижную точку М, которая является
точкой Болла обращенного движения
и должна лежать на окружности
возврата-, по этим двум точкам Болла
(прямого и обращенного движений) мы должны
построить обе кривые Бурместера.
Рис. 352.
Проведем в точках В и М прямые b'±Ь и т'±т (рис. 354), в их
пересечении найдем м. ц. в. Р. Воспользуемся тем, что обе окружности должны
быть симметрично расположены относительно полюсной касательной.
Пусть прямые bum пересекаются в точке G; проведем прямую GP,
отложим отрезок G'P = GP и построим параллелограмм с центром Р и
со сторонами b и т\ его диагональ PQ является искомой полюсной
нормалью; действительно, проводя окружности через точки Р, В, Q и Я, М, Q',
мы видим, что они будут поворотной окружностью и окружностью возврата,
ибо их центры лежат на прямой, проходящей через точку Р, на равных
расстояниях от нее; следовательно, точки Q и Q' являются полюсом
поворота и полюсом возврата.
Для каждой из кривых Бурместера мы знаем полюсные касательную
и нормаль, фокальную ось и одну точку; кривую можно найти по этим
данным, как показано в § 55.
334 ЧЕТЫРЕ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЯ ПЛОСКОСТИ [ГЛ. X
VI. Заканчивая главу, отметим, что задание четырех бесконечно
близких положений подвижной плоскости эквивалентно заданию
м. ц. в. Р, полюса поворота W и фокального центра кривой
круговых точек.
Рис. 354.
Действительно, не зная координат фокального центра, мы могли
найти величину d, и по формуле (59.17) нашли бы -£- = — (К — Кг) =
= — —, т. е. мы смогли бы лишь найти при перекатывании
центроид на бесконечно малую дугу ds новые положения точки Р и
полюсных касательной и нормали, но в этом новом положении мы
не знали бы величину d\ зная фокальный центр F, мы сможем по
формулам (54.2) найти параметры т и /, а затем по формуле (71.3)
найти dr — это позволит нам найти полюс поворота в новом
положении подвижной плоскости.
ГЛАВА XI
ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ
ПОДВИЖНОЙ ПЛОСКОСТИ
§ 75. Вспомогательные формулы
I. Введем две системы координат: 02х2у2 в неподвижной
плоскости и Оху— в подвижной (рис. 355); для любой точки М
подвижной плоскости ее координаты (х, у) и (х2, у2) в этих двух
системах связаны соотношениями
х2 = х0 + х cos ср — у sin ср,
у2 — yQ -}- л: sin ср -|- У cos ср, (75.1)
где ср — угол поворота подвижной
плоскости относительно неподвижной,
а (х0, у0) — координаты начала О.
Дифференцируя по углу ср, мы
имеем:
02
-*ь
Х2 — ^О"
■ х sin ср — ycoscf,
Рис. 355.
^2= У'о + х cos Т — У sin ?• (75-2)
причем координаты (х, у) постоянны, ибо точка М жестко связана
с подвижной плоскостью; пользуясь (75.1), получим:
Х2^Х0-{У2-Уо)> У 2 = Уо + (*2—*о):
отсюда легко находим дальнейшие производные по углу ср
(75.3)
■ х0 -(л
<о>
Х2 — ^0 "Т" \Х2 Х0Г
У* =Уо —(У2~УоУ
■у!? + (»>-Уо)'
< = < + (У2-Уо).
Х2=Х0-(У2-Уо)'
(75.4)
у?-
У1
= $+(*,
<0>
Для упрощения вычислений найдем все производные, совместив
точки О и 02 с м. ц. в. Р и совместив оси 02х2 и Ох с полюсной
касательной, а оси 02у2 и Оу с полюсной нормалью. Для упрощения
336 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
записи напишем разложения координат (х0, у0) м. ц. в. Р по
степеням угла ср в такой форме:
хо — ло~1- л1Т-1- 2! ^г з! ^ 4! ^ 5!
V -В -4-Ясс . ^ . _^ . А^-^-
где на основании (59.19) имеем:
А0 = Щ = Аг = Вг = А2 = О,
B*^d, А:к = -П?—-гг^г, В,
(75.5)
(75.6)
(К-Кд2' 3~~ (К-К,)2
причем штрихами обозначены производные, взятые по углу ср *)
(при ср = 0).
Пользуясь этим, получим из (75.2), (75.3)
х2 = х.
х;=-х.
х?=АА-\-х,
У2 =У.
У; =d-y,
х2= — у.
х? = А3 + у,
х*=А6-у.
у'2 =х.
У2=В3-х,
,75.7)
У\У = В,+ у, у]=В5 + х.
II. Рассмотрим теперь рулетту f точки Ж, причем уравнение f
в параметрической форме таково:
*2 = /i (<р). У2 = Л (<Р).
и окружность Yo с уравнением
(*2 - *i)2 + (У2 - Ух)2 - Я2 = 0. (75.8)
Дифференцируя по ср, получим:
Если потребовать, чтобы при ср = 0 первые производные для
окружности То были такими же, как для кривой ?, то кривые будут
*) В § 59 мы обозначали производные по углу точками, чтобы отличить
их от производных по дуге; так как обозначение производных высших
порядков точками неудобно, то мы возвращаемся к обычному обозначению
производных: при помощи штрихов для производных не выше третьего
порядка и при помощи римских цифр для производных, начиная с четвертого
порядка.
§ 75]
ВСПОМОГАТЕЛЬНЫЕ ФОРМУЛЫ
337
иметь соприкосновение не ниже первого порядка; пользуясь (75.7),
получим:
— у (х — хх) + х (у — ух) == 0, хгу = угх, (75.10)
т. е. центр Mx(xv уг) окружности лежит на одной прямой с
точками Ж и Р. Дифференцируя (75.9) снова по ср, найдем:
-^2 (^2 — -^l) + ^2 (^2 — ^l) "Г" ^22 + ^^ = °^ (75.11)
если потребовать, чтобы при ср = 0 производные первых двух
порядков для кривых Y и То были соответственно равны, то кривые
будут иметь соприкосновение не ниже второго порядка, т. е. fo
будет окружностью кривизны и из (75.8), (75.9), (75.11) мы получим
формулы, аналогичные (58.3), но в параметрической форме.
Пользуясь (75.7), будем иметь:
— х (х — хг) + ((1 — у)(у —Ух) + *2 + У2 = 0. (75.12)
Решая (75.10), (75.12), получим:
ф = г2 — dy, г2 = х2-\- у2,
откуда легко найдем величины
(75.13)
Ч-' Ъ — Ч-- (76-14)
Мы имеем по (41.7) квадратичное соответствие между (х, у) и
(xv ух)\ из него вытекает формула Эйлера (67.2), которую мы
доказали теперь аналитическим методом независимо от расположения
точек М и Mv
Из (75.14) мы снова видим, что поворотная окружность с
уравнением ф = 0 является геометрическим местом точек подвижной
плоскости, для которых соответствующие точки неподвижной
плоскости ушли в бесконечность. Дифференцируем (75.11) еще раз по ср
х2 (х2 ~ хг) + Я (У2 - У,) + 3 (4** + УУ2) = 0. (75.15)
Если потребовать, чтобы при ср = 0 производные первых трех
порядков для кривых То и Т были соответственно равны, то кривая ?
будет иметь со своей соприкасающейся окружностью
соприкосновение не ниже третьего порядка. Пользуясь (75.7), получим:
(Л3 + у) (х - хг) + (В, -х)(у- уг) + Sdx = 0. (75.16)
Исключая х — хх и у — ух из уравнений (75.10), (75.12) и (75.16),
получим:
— у х 0
— Х d — y л;2 + у2 | = 0,
13 + у В3 — х Ых
338 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
откуда находим
(*2 + У2) [(Л3+ 3<0 * + язУ1 — м2 ХУ = °- (75.17)
Деля обе части равенства на ^ 3 ~t ■—— и вводя обозначение
т^1ъ> / = -лгрзг- (75Л8)
мы снова придем к уравнению кривой круговых точек (71.4);
легко видеть, что эти формулы для т и / совпадают с (71.5).
Действительно, по (59.19), (59.20), (59.16'). (75.6)
л ± м Жх — К , 3 2K — Ki 3d2 3
(K-Kt)2^ К-Кх (K — KiV A3 + 3d — 2K — Ki '
HI. Из (75.14) легко найдем:
Ф^^ + yf + rfy,—^1. x^ = ^L, (75.19)
откуда находим формулы, аналогичные (75.14):
dxxyx dy\
ir* y=~t' (75-20)
Подставляя эти значения х, у в (75.17), найдем уравнение кривой
центров
(х\ + у?) (А3хх + Вгух) - ЪсРх^ = 0. (75.21)
А В
Деля все его члены на JL3, приведем его к виду (71.9), причем
Zl — Л * / /, ~~ 3tf2 3tf2 — d ' (75.22)
Угловой коэффициент луча, идущего в точку Болла, в новых
обозначениях по (72.2), (75.18), (75.22) таков:
k = -f = -±; (75.23)
его легко найти и непосредственно из (75.21).
Таким образом, применяя аналитический метод исследования,
разработанный А. П. Котельниковым [1], мы вновь нашли все те
результаты для трех и четырех положений подвижной плоскости,
которые мы получили раньше геометрическим методом.
§ 76]
ТОЧКИ И ЦЕНТРЫ БУРМЕСТЕРА
339
§ 76. Точки и центры Бурместера
I. Дифференцируя (75.15) по ср, найдем:
(76.1)
Если потребовать, чтобы при ср = 0 производные первых четырех
порядков для кривых 7 и То были соответственно равны, то кривая f
будет иметь со своей соприкасающейся окружностью
соприкосновение не ниже четвертого порядка.
Пользуясь (75.7), получим уравнение геометрического места точек,
обладающих этим свойством:
(Л4 + х) (х - хг) + (В4 + у) (у — У0 - *АзУ +
+ 4Bzx — r2-{-3d2 — 6dy = 0. (76.2)
Подставляя вместо х — хг и у — уг их значения (75.13), получим
после упрощений уравнение третьей степени
г2 (А4х + ВАу + dy) + ф (4£3Jt — 4Л3у + 3d2 — 6 rfy) = 0. (76.3)
Решаем его совместно с уравнением (75.17) кривой круговых точек,
которое можно записать в таком виде:
г2(А3х+Вгу)-{-Ц4х = 0. ' (76.4)
г2
Исключая из этих двух уравнений отношение -г-, найдем кривую
второго порядка
yx — 3dx (А4х -f- В4у -\- dy) —
— (Агх + Bzy) [4Вгх — (4Л3 + 60) у + 3d2] = 0. (76.5)
Эта кривая пересекает кривую круговых точек ? в шести точках;
так как она проходит через начало координат, являющееся двойной
точкой, то остаются четыре точки, называемые точками
Бурмастера; таким образом, в каждом положении подвижной плоскости
имеется четыре точки Бурместера, определяемые пересечением
кривой круговых точек с кривой срх *); рулетты этих точек
имеют в этих точках соприкосновение не ниже четвертого по-
рядка со своими соприкасающимися окружностями.
Назовем через L0(0, /0) точку пересечения кривой срг с полюсной
нормалью Рп\ полагая х = 0, найдем по (75.18)
*) Две из них, или все четыре могут оказаться мнимыми.
340 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
если воспользоваться тем, что по (75.22)
Покажем также, что кривая срх касается в м. ц. в. Р фокальной
оси кривой центров; мы имеем при х = у = 0
и на основании (60.1) имеем:
ft1 = -^ = --i = - —. (76.7)
II. Если в (76.5) подставить значения х и у из (75.20) и
воспользоваться (75.21), то получим кривую второго порядка
ср2 = 3^^1 [ААхх + (В4 + <0 У1 — 3d2] —
—(Л3хх + В3Л) [4^i ~ (4Л3 + 6d) ^ + 3d2] = 0; (76.8)
она пересечет кривую центров в четырех точках, называемых
центрами Бурместера и являющихся центрами тех соприкасающихся
окружностей, о которых шла речь выше (т. е. центрами кривизны
рулетт точек Бурместера в этих точках). Кривая ср2 также
проходит через точку LQ и касается в м. ц. в. Р фокальной оси
кривой круговых точек; мы имеем при хг — уг = 0
откуда по (60.1)
Ъх, A„ + 3d т
k2 = -?p-=--±- = -. (76.9)
ЪУх я3 1
III. Для нахождения точек Бурместера положим у = kx и будем
искать угловые коэффициенты лучей этих точек. Подставляя в (75.17)
и (76.5), получим:
. х (k2 + 1) (Д3* + А> +- 3d) — Sd2k = 0,
3 dx [(В4 + d) k + АА] — (fi3* + ^з) [3d2-\-x (4В3 — 4 Л36 — Ш)] = 0.
Находя л: из обоих уравнений и приравнивая друг другу, найдем:
3d2k
х =
(k* + l)(kB3 + A3 + 3d)
_j 3d2(B3k + A3) .
3d ЦВА + d)k + A4] + (Bzk + A3) [(4i48 + 6rf) k - 4B3] '
§ 76]
ТОЧКИ И ЦЕНТРЫ БУРМЕСТЕРА
341
отсюда получаем уравнение четвертой степени для нахождения
угловых коэффициентов лучей, на которых лежат точки Бур-
местера:
B2zkA — (2 Л3 + 3d) 53/г3 + (5В§ — ЗЛз — 3d2 — W4d — SA3d) k2 +
+ (6Л3В3 + 3dfi3 ~~ 3rfi44) * + Лз(Лз 4- 3d) = 0. (76.10)
IV. Рассмотрим еще геометрический метод нахождения точек
Бурместера. Если ввести обозначение (рис. 356)
v, =х,
v2 = AAx + (BA + d)y,
4Вгх-
(4Л3 + 6й?)>;4-3^2,
(76.11)
vz = A3x-+-B3y, v
то по (76.5) имеем:
?1 = bdvxv2 — v3v4 = 0. (76.12)
Таким образом, кривая ср2 является геометрическим местом
точек пересечения соответствующих прямых двух проективных
пучков прямых
tr1 + Xtr4 = 0> tf2 + |W,=
(76.13)
Рис. 356.
с центрами в точках £0(0, /0) #
Р(0, 0); отметим при этом, что от
параметров Л4, £4 зависит только
прямая v2, прямая v3 касается кривой ср2
в точке Р и на ней лежит точка Болла.
Если параметры Л4, ВА известны,
то, зная две пары соответствующих
прямых (vx и v3, v4 и v2) и придавая X произвольное значение, мы
найдем третью пару соответствующих прямых; на основании
теоремы Штейнера (§ 23) и графического построения § 46, мы можем
по точкам построить кривую срх. Совершенно аналогично имеем
по (76.8) для кривой ср2
ср2 = Mvxv'2 — v3v4 = 0, (76.14)
где vv v3, vA имеют те же значения, а
г£ = v2 — 3d2 = А4х + (Я4 + d) у — 3d2. (76.15)
V. Рассмотрим теперь тот случай, когда две точки
Бурместера Ох и 02 известны — например, заданы два подвижных
шарнира шарнирного четырехзвенника. Отметим, что коэффициенты
при kz и свободный член уравнения (76.10) не зависят от Л4, В4;
342 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
если корни этого уравнения назвать kv k2, к3, &4, то левую часть
уравнения можно записать в таком виде:
В\ (к — кг) (к — k2) (к — *3) (* — *4) =
= Bllk2 — (kl + k2)k + k1k2][k2 — (k3+ k4)k + kzk4)] = 0. (76.100
Приравнивая друг другу коэффициенты при kz и свободные члены,
2A3B3 + 3dB3 _ 2А3 + 3d
mлучим:
*1 + *2+*3 + *4 ='
в\
в„
#с1#с2#с3/с4 D2
В2
Обозначая через k0 и k10 угловые коэффициенты фокальных осей
наших кривых Бурместера, имеющие по (76.7), (76.9) следующие
значения:
т Az-\~3d , т Аъ
К
(Г
/
В*
(76.16)
получим окончательно следующие соотношения:
#1 + &2 + &3 + ^4 :
kxk2kzkA = k0kl0. (76.160
Таким образом, если известны обе кривые Бурместера (т. е.
величины k0 и kl0) и две точки Бурместера Gx и G2, то две
остальные точки Бурместера
G3, G4 можно найти по этим
формулам.
Если воспользоваться
геометрическим методом (рис. 357), то для
кривой срх мы будем знать четыре
точки (Я, L0, Gv G2) и
касательную 1>з в точке Р—по этим
данным ее можно построить (§ 46),
после чего придется искать точки
ее пересечения с кривой круговых
точек.
VI. Значительно проще графическое решение этой задачи по
методу А. П. Котельникова (§ 56).
Рис. 357.
Введем обозначения
k\k2
1
*1 + k2 + К = ~ д>
(76.17)
*о с
где величины с, д будут найдены; в таком случае, очевидно, имеем:
кю
'• С* *^з"~| 4 l~ ^
10'
(76.18)
§ 76]
ТОЧКИ И ЦЕНТРЫ БУРМЕСТЕРА
343
Построим произвольную окружность (рис. 358), касающуюся
полюсной касательной в м. ц. в. Р, и касательную а к ней, параллельную
полюсной касательной; найдем на окружности изображающие точки
kv k2, k0, k10 (в ее пересечении с лучами, характеризуемыми этими
угловыми коэффициентами). Пусть прямая kxk2 пересекает ось Ру
в точке А — тогда прямая k0A пересечет окружность в точке —,
а точку с найдем, проводя через точку — прямую, параллельную
полюсной нормали; если
прямая kxk2 пересекла
касательную а в точке В,
то, соединяя ее с
точкой — k0, получим в
пересечении с окружностью
точку — д, а проведя
через эту последнюю
прямую, параллельную
полюсной касательной,
найдем точку д.
Пусть теперь
прямая ck10 пересечет ось Ру
в точке Ах, а прямая
d, — kl0 пересечет
касательную а в точке
Вх — тогда прямая А1В1
пересечет окружность в
искомых точках k3, kA. Соответствующие точки Бурместера
являются точками пересечения лучей Pk3 и Pk4 с кривой Бурместера
и могут быть найдены методами § 55.
Сравнивая (76.17), (76.18) с (55.7), мы видим, что
изображающая точка с соответствует третьей точке С пересечения
кривой круговых точек с прямой GXG2\ если ввести изображающую
точку сх по формуле
*1 = -7Г-. <76-19>
то из (76.18) ясно, что она соответствует третьей точке Сг
пересечения кривой круговых точек с прямой GZGA.
Из (76.19) вытекает cc1kl0 = k0\ так как k10 является
изображающей точкой для точки Болла, тр эта последняя лежит на одной
прямой с точками С и Cv Из (76.17), (76.19) вытекает, что прямые
kxk2, lk0, —J и kxocx пересекаются в одной точке на оси Ру\
аналогичным свойством обладают и прямые kzkA, lk0, —) и kl0c; отсюда
Рис. 358.
344 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
вытекает теорема А. П. Котельникова ([1], § 36): ось Ру является
прямой Паскаля для шестиугольника, вписанного в окружность
и имеющего вершины в точках
kq, с , ct kl0,
1
Си -•
Если известна только кривая круговых точек, то величина kl0 остается
неопределенной; исключая ее из (76.1 б7),
получим:
*l*2*aVK*l + *2+*3+ *4) *о+ *?=0.
(76.20)
Следовательно, если известны
изображающие точки k0, kv k2, то точки
ks, kA образуют на окружности
инволюцию; сравнивая эту формулу
с (18.10), которую запишем в виде
*з*4 (Уо — do) + (*з + *4> хо — Уо = 0.
мы находим координаты (х0, у0) центра
перспективы 5
Уо — d0 Хо Уо
kxk2
откуда
Хс\ — ■
(&1 + ^2 + ^о) К
d0k0
Рис. 359. _ rf0M*o + *i+*2) (7R 91 ^
Любая прямая, проведенная через центр перспективы 5, пересекает
окружность в двух точках къ и kA. Покажем построение этого центра
перспективы *); для этого достаточно знать две пары
соответствующих изображающих точек (хг, уг) и (х2, У2У, найдем их из условий
(— *i) + (— У г) = К + К (— *i) ' (— У г) = ko'(~r)'
(— *2) + (— У2) = К + К (— *2) ' (— У2) = *о (— kl)'
При этом легко видеть, что (76.20) удовлетворено, если положить
kz— xv kA — yx или k3 = x2, k4=±y2. Обозначим через Л и Аг
(рис. 359) точки пересечения касательной а с прямыми k0kx и k0k2,
а через В и Вх — точки пересечения оси Ру с прямыми (k0, — ^-j
•) См. А, П. Котельников [1], § 38.
§ 77] распадение кривых; случай чебышева и точка чебышева 345
и (k0, —-t-j; тогда прямые АВ и Л1В1 пересекают окружность
в точках (—xv —ух) и (—х2, —у2) и поэтому точка пересечения V
прямых АВ и АХВХ будет симметрична с искомой точкой 5
относительно оси Ру.
§ 77. Распадение кривых; случай Чебышева
и точка Чебышева
Из (76.12) ясно, что кривая второго порядка срх распадается на
пару прямых в тех двух случаях, когда прямая vs совпадает или
с прямой vv или с прямой v2\ рассмотрим эти случаи.
А. Случай Вг = 0.
Так как по (75.18) равенство это эквивалентно равенству т — оо,
то, как было сказано, при этом обе кривые Бурместера распадаются
на полюсную нормаль и на окружности (/) и (1Х). Мы имеем при этом
vz = Ajuv срх = vx (3 dv2 — Asv4) = 0, (77.1)
т. е. кривая срх распадается на полюсную нормаль и на прямую
3 dAAx +у [3 </(Д4+ </)■+ 4Лз + 6 dAs] — 3 d2Az = О, (77.2)
проходящую через точку R пересечения прямых v2 и v4 (причем
прямая v4 имеет уравнение у = 10). Так как полюсная нормаль
является составной частью как кривой круговых точек fi» так и
кривой срр то точки Бурместера, лежащие на полюсной нормали, мы
найдем из уравнения (76.3), полагая в нем х = 0, т. е.
y*(BA + d) — (y-d)[(4Az +6d)y —3</2] = 0. (77.3)
Следовательно, в рассматриваемом случае две точки Бурместера Gx
и G2 лежат на окружности (I) в ее пересечении с прямой (77.2),
а две остальные точки Бурместера G3 и G4 лежат на
полюсной нормали и их ординаты являются корнями квадратного
уравнения (77.3).
Обозначая через у0 ординату точки пересечения прямой (77.2)
с полюсной нормалью, мы имеем:
y0[3d(B4-+-d)-i-4Al+6dA3] — 3<fU3 = 0;
умножая на у2, исключим из этого уравнения и из (77.3) параметр В4
3d (ВА + d) у0у2 = (М2Аг — 4А23у0 - 6dA3y0) у2 =
= 3dy0(у-d)[(4Аг +Щу- 3^] = О,
откуда
y^3A,-2y0[^ + ^ + 9)^3y0y(4A3--{-9d)~9yQd^ = 0.
346 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
Подставляя по (71.7), (75.22) d —
Hi л _Jl%
2 и производя
упрощения, мы найдем окончательно
У> [/* - 2у0 (/ +1,)] + yl (I + Щ Уо - Р1гУо = °- (77-4)
Отсюда вытекает следующее соотношение между ординатами уг, у4
точек Бурместера G3, G4, независящее от у0:
Z + 3Z,
//,
(77.5)
Следовательно, если рассмотреть точку V (0, -jtj—-) полюсной
нормали, то точки —, — симметричны относительно точки Z/; выбирая
произвольно одну из них, легко
найдем вторую; выполняя инверсию,
мы найдем у3 и у4, г по ним можно
найти Уо- Так как в (77.4) входят
не уг и у2, а только у0, то, построив
по этой ординате точку G0
пересечения прямой Gfiz с осью Ру, мы
можем как угодно поворачивать
прямую G{G2 вокруг точки G0 (рис. 360),
мы найдем таким образом точки
Бурместера Сг и С2, Dx и D2, ... на
окружности (/) и соответствующие
центры Бурместера С\ и С2, D'{
и D2, ... на окружности (1г). Если
известны величины /, у0 и
ордината Уз одной из точек Бурместера на полюсной нормали, то из (77.4)
можем найти параметр 1г
/Уз[Уо(/-2у3) + /Уз] .
U
(77.6)
Уо</-У8)</-2у8) '
его нетрудно найти графическим путем *). Справедливо и обратное
заключение: если точка Бурместера лежит на полюсной
нормали, то Вг = 0; действительно, при этом условии, как было
показано, яг = сю. Отметим, что в рассматриваемом случае и кривая ср2
распадается на полюсную нормаль и на прямую с уравнением
ЫААх + [(Я4 + d) 3d + 4Лз + 6dAs] у — 9й?3 — ЗЛ3й?2 = 0. (77.7)
Б. Случай ~г =
А, _ B4 + d
А3
с прямой vz, ибо
#3
. При этом условии прямая v2 совпадает
срх = v3 (3dAAvx — AzvA) = 0,
*) См. Я. Л. Геронимус [4].
§ 77] распадение кривых; случай чебышева и точка чебышева 347
т. е. в этом случае кривая срх распадается на прямую, идущую
из м. ц. в. Р в точку Болла, и на прямую с уравнением
(SA4d — 4Я3Л3) x-\-Az (4Л3 + 6d) у — 3 Аг d2 = 0; (77.8)
первая прямая проходит через м. ц. в. и пересекает кривую
круговых точек в точке Болла, следовательно, в рассматриваемом
случае одна из точек Бурместера совпала с точкой Болла; этот
случай, следуя А. П. Котельникову, будем называть случаем
Чебышева, а точку Болла, совпавшую с точкой Бурместера, назовем
точкой Чебышева; в этой
точке ее рулетта имеет со
своей касательной
соприкосновение не ниже
четвертого порядка.
Остальные три точки
Бурместера лежат в случае
Чебышева на одной прямой
с уравнением (77.8).
Справедливо и обратное
заключение: если три
точки Бурместера Gv
G2, G3 лежат на одной
прямой, то четвертая
точка G4 является точкой
Чебышева; действительно,
по (55.7) мы должны иметь kxk2kz= k0; в сопоставлении с (76.160
получим k4 = k1Q; отсюда вытекает также, что случай Чебышева
возможен только при условии Б.
Докажем следующее (рис. 361): если в случае Чебышева
известна точка Болла U и угловой коэффициент kx луча точки
Бурместера Gv то все прямые, соединяющие изображающие точки k2
и къ точек Бурместера G2 и G3, проходят через точку S'
пересечения прямых и и v, где *)
и = у — kxx — d0 = 0, v = y + kmx — ^ = 0. (77.9)
Мы имеем из (76.16), полагая k4 — k10 и исключая kQ:
*i + *2 + kz + *1*2*з = — 2*io- (77-1 °)
Следовательно, при фиксированных kx и kl0 изображающие точки k2
и kz на окружности образуют инволюцию; если мы подберем две
пары соответствующих точек, то прямые, соединяющие
соответствующие точки, пересекутся в центре перспективы S'. Прямая и пересекает
Рис. 361.
*) А. П. Котельников [1], § 40.
348 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
окружность в изображающих точках хг = со, у1 = ~—-. Подстав-
1
ляя в уравнение (77.10) &2 = со, &3 = ——, мы видим, что оно
удовлетворяется, ибо, деля все члены на k2 и полагая &2->оо,
получим:
14-^3=0.
Если ввести обозначение k1Q = tga, то прямая v пересекает
окружность в точках х2 и у2, причем ^ tPx2 = ~ — у, ^ tPy2 = ~ — ~;
следовательно,
i-tgf l + tg-S-
x2 = tg£mtPx2^= -, y2 = tg£mtPy2 = -
и, таким образом,
1+tgTjr 1-tg-i
a
l-tgy l+tg-g" 4tgT
^2+У2 = -= - = —2tga=-2ft10.
1+tg-J 1—tg-f- l-tg2J
Полагая &2 = л;2, &3 —y2 и подставляя в уравнение (77.10), мы видим,
что оно удовлетворяется.
В. Случай Л3-+ 3^ = 0.
Так как это условие эквивалентно условию / = со, то оно
эквивалентно также распадению кривой круговых точек на полюсную
касательную и на окружность (т).
Кривая срх (76.5) пересекает полюсную касательную в м. ц. в. Р
и в точке Бурместера с абсциссой
Х - М2А* - М2 П1 114
Соответствующий ей центр кривизны совпадает с м. ц. в. Р\ три
остальные точки Бурместера лежат на окружности (т). Докажем
еще, что в рассматриваемом случае прямые kxk2 и k3kl0
пересекают касательную а в точках, симметричных относительно
ови Рп\ действительно, по (18.10) прямые kxk2 и kskl0 пересекают
касательную а с уравнением у = d0 в точках с абсциссами
d0 .. d
хЛ
kx-\-k2* 2 ^3 + ^11
причем в рассматриваемом случае &4=&0 = 0, и по (76.160 имеем
kx-\-k2 =— &3— k10. Кроме того, покажем, что в данном случае
справедливо соотношение
W3 = *io(l-]T0). <77Л2)
§ 78] ПРИМЕНЕНИЕ К ЗАДАЧАМ АНАЛИЗА И СИНТЕЗА 349
связывающее угловые коэффициенты трех точек Бурместера на
окружности с абсциссой четвертой точки *).
из (76.10)
Действительно,
находим:
^1^2% ~"
из (77.11) имеем АА
3dA4 — 6ЛВ3 -
«2
-3dB3
—
-4£3
Ы-^
Xq
+ 5Д3
В2
Подставляя найденное значение АА и пользуясь (75.18), (76.16),
найдем (77.12)
Г. Случай Л3 = 0.
Так как это условие эквивалентно условию 1г = оо, то оно
эквивалентно также распадению кривой центров на полюсную
касательную и окружность (т).
Кривая ср2 (76.8) пересекает полюсную касательную в м. ц. в. Р
и в центре Бурместера с абсциссой # = --=-; так как кривая круго-
вых точек в рассматриваемом случае не распадается, то точка
Бурместера, соответствующая этому центру, должна совпадать с м. ц. в, Р,
однако это последнее утверждение надо понимать условно: как
показано в § 61, мы не можем утверждать в общем случае, что рулетта
точки Р имеет со своей соприкасающейся окружностью нужный
порядок* соприкосновения.
Отметим также, что в рассматриваемом случае прямые kxk2
и k3k0 пересекают касательную а в точках, симметричных
относительно оси Ру — доказательство такое же, как в случае В.
Рассмотрим еще случай бесконечно удаленной точки Бурместера; если
это точка Gv то ее луч должен быть параллелен асимптоте, т. е. должен
совпадать с фокальной осью кривой круговых точек; полагая k4 = k0, имеем
из (76.16') k{k2k3 = kl0 — следовательно, если одна из точек Бурместера
бесконечно удалена, то центры Бурместера, соответствующие трем
остальным точкам, лежат на одной прямой', случай бесконечно
удаленного центра Бурместера является случаем Чебышева и был уже рассмотрен.
В случае одновременного распадения обеих кривых Бурместера мы имеем
по (77.5) при у4 = оо равенство у3 = у ъ/ > так как уравнение (77.4)
/ —j— о/1
должно иметь бесконечный корень, то коэффициент при у2 должен обра-
щаться в нуль, откуда у0 = 0 ; следовательно, при заданных / и / {
и при условии у4 = оо легко можем найти у0, у3.
§ 78. Применение к задачам анализа и синтеза
I. В качестве первого примера рассмотрим шарнирный четырехзвен-
ник А{АВВ{ (рис. 362) в том его положении, когда три точки Alt А, В лежат
на одной прямой; при этом АВ = ВВХ. Найдем кривые и точки Бурместера
и точку Болла.
*) См. А. П. Котельников [1], § 55.
350 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ XI
Повторяя рассуждения § 73, мы видим, что точка Р совпадает с £,,
а полюсная касательная Pt с прямой ВВХ (рис. 363). Так как подвижный
шарнир В лежит на полюсной
касательной Pt, то кривая круговых точек
распадается на Pt и на окружность (т)
с центром на Pt; на ней должен лежать
и второй подвижный шарнир А, поэтому
ее центром является точка В.
Неподвижный шарнир А{ должен лежать на
кривой центров; методом, указанным в § 54,
строим точку А' ее направляющей
прямой; так как эта последняя должна
пройти через точку М, то она этим
полностью определена; она пересекает
полюсную нормаль Рп в точке Llf причем
РА1=/1;в данном случае / = оо и из
■d, что дает возможность найти полюс поворота W
Рис. 362.
(71.7) находим 1Х =_-_
из условия PL{ +^W= о.
Точка Болла U лежит в пересечении поворотной окружности и
окружности (т); лучу PU соответствует угловой коэффициент kxo.
Рис. 363.
Найдем теперь точки Бурместера; одна нз них В лежит на полюсной
т
касательной, причем в формуле (77.12) — =2; вторая точка А, луч которой
имеет угловой коэффициент &3> лежит на окружности (т). Построим на
поворотной окружности изображающие точки &3 и ^iq« соответствующие
§ 78] ПРИМЕНЕНИЕ К ЗАДАЧАМ АНАЛИЗА И СИНТЕЗА 351
прямым РА и PU, и точку г-. Из (77.12) имеем для угловых коэффи-
циентов k{ и k2
k{k2kb = k{Q\A — —J = — kl0, k{k2 = kl0-l jjA- (781)
Пусть прямая lkl0, ^-j пересечет Pn в точке С\, а прямая kl0k3 пусть
пересечет касательную а в точке D{\ построим точку D2, симметричную
с точкой D{ относительно полюсной нормали, и проводим прямую D2Cl —
она пересечет окружность в искомых точках kXt k2, а прямые Pklt Pk2
пересекут окружность (т) в искомых точках Бурместера Glt G2.
Наметим путь аналитического решения задачи *). Так как мы знаем
полюсные касательную и нормаль, то для нахождения обеих кривых
Бурместера надо знать три параметра, например Аг, Въ, d\ так как кривая
круговых точек должна проходить через точку А, а кривая центров через точку А{,
то, подставив их координаты соответственно в (75.17) и (75.21), получим два
условия; третье условие Аъ = — 3d является условием распадения кривой
центров.
Для нахождения точек и центров Бурместера надо знать еще два
параметра АА и ВА\ мы их найдем, подставив координаты точек В и А в (76.5).
II. Рассмотрим снова задачу Лихтенхельдта (§ 74) с дополнительным
условием: точка Болла U должна быть точкой Чебышева, т. е. мы
должны иметь случай Чебышева. В этом случае три остальные точки Бурместера,
в число которых входят два подвижных шарнира А и В, должны лежать
на одной прямой.
Мы имеем по (76.16')
kxk2k% = k0, k{ + k2 + &з = — 2kl0 — k0; (78.2)
исключая kz, получим:
*, + fc,+ M1fe+M,) +2*10=0. (78.3)
Пользуясь (76.7), (76.9)
Aj__ f„, u _ A3 + 3d _ 3d
*..=—Sj—tg+. *, = T^ = -B7 + *.o-
находим:
*'+*-ii£4-*»+£)+2*'o-*
B* M' M2(*l+*2) + *10(l+3M2) ' (78'4)
Отсюда легко находим Аъ = — kl0B3 и
k{k2 (k{ + k2) + 2kXQkxk2
A3 + 3d = 3d •
klk2(kl + k2) + kl0(l+3klk2) '
*) В книге И. И. Артоболевского, Н. И. Левитского и С. А. Черкуди-
нова [1] (§ 52) эта задача решена аналитическим методом.
352 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
Пользуясь (75.18), (75.22), находим параметры кривых Бурместера
m = d
l = d
kxk2 (k{ + k2) + kl0 (1 + %k{k2)
1 + k{k2
k{k2 (k{ + k2) -\~ kl0 (1 -f- 3k{k2)
L =—d
klk2(kl + k2) + 2kl0klk2
k{k2 (k{ + k2) + kl0 (1 + 3k{k2)
(78.5)
Так как
d = -
kl0(l + k{k2)
sin ф
, Л10==—tg4;f *I=tg(pI-+)f ^2 = tg (p; — ф), (78.6)
то, зная угол ф, мы можем сперва найти т, /, 1и а затем по формулам (74.3),
(74.4) найти радиусы-векторы всех шарниров (полагая <р = Pi— ф, а
затем <р = (5 J — ф).
Все вычисления значительно упростятся, если выбрать угол ф = —90°,
т. е. совместить полюсную нормаль Рп с прямой PU (рис. 364); как было
сказано в § 74, обе кривые Бурместера
распадутся на полюсную нормаль и на
окружности (/) и (1Х)\ так как в этом случае kl0 = оо,
то, деля на kl0 и полагая затем &10->оо,
получим:
;-,/ 1+ЗМ2 _ 1+ЗМя
L~'a"~2kJ2~i х" l + k,k2 '
(78.7)
Так как в данном случае по (78.6) имеем:
</=/,, *!= —ctgplf Ля = —ctgPj. (78.8)
то окончательно найдем:
з+tgPitgp;
/=/?.
Рис. 364.
/,=—/> •-
З+tgPitgp
(78.9)
l + tgp,tgpi
В пересечении окружностей (/) и (1{) с прямыми а и Ь найдем подвижные
и неподЕИЖные шарниры.
Пусть, в частности, точка U лежит на биссектрисе угла между
прямыми а и Ь (рис. 365); мы будем иметь в этом случае
tgPi = —Ctga, tg Pi == Ctg a.
Если ввести обозначение h = PC, hl =PCU то из (78.9) найдем*)
1 h Ctg»a-1 _ h±_
hx
2(h + h{)
(78.10)
Мы можем утверждать, что шатунная кривая точки U имеет со своей
касательной в точке U соприкосновение не ниже четвертого порядка, но бла-
*) Этот направляющий механизм найден П. Л. Чебышевым [1], а затем
другим методом Н. Е. Жуковским [1].
§ 78] ПРИМЕНЕНИЕ К ЗАДАЧАМ АНАЛИЗА И СИНТЕЗА 353
годаря симметрии всего механизма относительно оси Рпу эта кривая не может
иметь в U точки перегиба — следовательно, порядок соприкосновения должен
быть нечетным числом, т. е. мы имеем соприкосновение пятого порядка
(шатунная кривая шарнирного четырех-
звенника является алгебраической
кривой шестого порядка (§ 62), число ее
точек пересечения с прямой равно шести
и даже если все они совпадут, то будем
иметь соприкосновение лишь пятого по-
рядка, как в рассматриваемом частном
случае).
III. Рассмотрим графический метод
решения задачи Лихтенхельдта (рис. 366).
Построив поворотную окружность,
как в § 56, мы будем знать на ней
изображающие точки kl0, k]y k2 и найдем
еще точку — &10; проведем через полюс
поворота W прямую и параллельно
прямой Pku а через центр окружности
прямую v, параллельную (Р, — kl0).
Прямая, соединяющая точку S' их
пересечения с точкой k2, пересечет поворотную
окружность в точке k3. Строим
треугольник k}k2ks, проектируем на его
стороны точку Р и строим прямую
Симпсона s этого треугольника — на
основании § 56 прямая s параллельна
прямой, соединяющей подвижные шарниры А
мы могли бы закончить задачу методом § 74-
вести через центр перспективы S прямую s,
Рис. 365.
Проведем
прямые а и
ляры а' и Ь'
и В. Найдя эту прямую s,
для этого достаточно про-
s, которая пересечет прямые а
и Ь в искомых точках А и В\
однако можно решить задачу
еще проще, не строя центра
перспективы.
Если бы была дана не точка
Болла, а только прямая PU,
и известно, что мы должны
иметь случай Чебышева, то
рассмотрим пучок кривых
круговых точек, перспективна
подобных друг другу с центром
подобия в точке Р; если
искомую кривую прямая s, j|s
пересекает в точках Бурместера,
лежащих на прямых а и Ь, то
этим же свойством будет
обладать любая кривая пучка,
соответствующая коэффициенту
подобия I, причем роль прямой s1
будет играть прямая s2\\slt
полученная из s{
преобразованием подобия с
коэффициентом А.
произвольную прямую s' |j s (рис. 367) и пусть она пересекает
b в точках А' и В'\ восставляя в этих точках перпендику-
к прямым а и Ь, мы будем знать четыре касательных (Pt, Рп,
Рис. 366.
354 ПЯТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖНОЙ ПЛОСКОСТИ [ГЛ. XI
а', br) к параболе (§ 54); пользуясь теоремой Брианшона и построением
рис. 90, мы найдем пятую касательную wr±PLf данного направления,
пересекающую прямую PU в точке U\ отличной от W; точки А и В,
построенные на прямых а и Ь по
~t условиям
PA РВ PU
РА'
РВ'
PU'
являются искомыми
подвижными шарнирами.
IV. Покажем применение
точек и центров Бурместера
в задачах синтеза механизмов
с остановками. Пусть мы
нашли точку Бурместера Gx
и соответствующий центр
Бурместера R{\ если ввести двух-
поводковую группу SlRlGl
(рис. 368), то при прохождении
Рис 367 шатунной плоскости через пять
бесконечно близких положений
точка (7, будет находиться на
окружности с центром Ru точка R{ будет неподвижна так же, как и
коромысло SiRi\ следовательно, при небольших перемещениях точки Gx
коромысло SlRl имеет приближенный выстой.
Если дан шарнирный четырехзвенник, то точки Бурместера его
шатунной плоскости нетрудно найти лищь в случаях распадения кривых
Бурместера или кривой второго порядка ^ — эти случаи были рассмотрены
в §§ 73, 77; но, как было
сказано, они могут иметь место
лишь в некоторых особых
положениях заданного шарнирно- y<^<XVV^4—' 1
Рис. 368.
го четырехзвенника. Поэтому предположим, что заданы только точка Р,
точка С{ (которая должна иметь приближенный выстой), а также
прямые а и Ь, по которым должны идти оси звеньев А{А и ВХВ (рис. 369).
Направим полюсную нормаль Рп по прямой а — в таком случае обе
кривые Бурместера распадаются на полюсную нормаль и на окружности (/)
и (/,); построим окружность (1Х) с центром на оси Рп, проходящую через
центр Бурместера Cf, в ее пересечении с прямой b получим центр Бурме
стера Вх. Прямая В{С{ пересекает ось Рп
Произвольно выберем неподвижный шарнир,
в некоторой точке В0 (0, у0).
т. е. центр Бурместера А{
§ 78] ПРИМЕНЕНИЕ К ЗАДАЧАМ АНАЛИЗА И СИНТЕЗА 355
на прямой а\ зная величины у0, 1Х, мы можем найти / по уравнению (77.6),
в котором надо поменять местами / и 1Х и положить у == РАХ; окружность (/)
пересечет прямую b в неподвижном шарнире В, а прямую РСХ в точке
Бурместера С, которую примем за подвижный шарнир. Так как легко найти
ось коллинеации PQ±_b, то, зная В, Вх и Ах,
находим Л.
Пусть теперь даны оба неподвижных
шарнира Ах и Вх и центр Бурместера Сх
(рис. 370). Так как все эти три точки должны
быть центрами Бурместера, то они играют
одинаковую роль; будем считать, например, что
точка Ах лежит на диаметре окружности,
проходящей через заданные точки Вх и Сх
и неизвестную точку Р, как в предыдущем
случае. Построим пучок окружностей,
проходящих через точки Вх и С,, центры которых
лежат, очевидно, на оси симметрии отрезка
В{СХ\ соединяя третью точку А{ с центром
каждой окружности, мы получим в
пересечении этой прямой с окружностью две точки Рх
и Р2 — каждая из них может быть принята за
м. ц. в. Р. Рассматриваемая окружность пучка может быть принята за ок*
ружность (1Х), и мы приходим к предыдущей задаче; мы получаем, таким
образом, бесчисленное множество решений.
На рис. 371 построена кривая у0, являющаяся геометрическим местом
м. ц. в. Р (т. е. точек Рх и Р2 каждой окружности); на основании §§ 10, 50
Рис. 371.
она является фокальной кривой (состоящей из двух ветвей), причем точка Л|
является ее фокальным центром, а пучок окружностей определяется точ*
ками Вх и Сх.
ГЛАВА XII
ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ
ПОДВИЖНОЙ ПЛОСКОСТИ
§ 79. Точки Бурместера пятого порядка; случай Чебышева
пятого порядка
I. Продифференцировав (76.1) по <р, получим:
4 (*2 - *i) + У? <Л - Л) -Н 5 (х?х'2 + ^v У2) +
+ 10(44'-^2У2")=0- (79-п
Если потребовать, чтобы при ? = 0 производные первых пяти
порядков для кривой y и окружности *уо были соответственно равны,
то кривая ^ будет иметь cq своей соприкасающейся окружностью
соприкосновение не ниже пятого порядка. Такие точки будем
называть точками Бурместера пятого порядка.
Пользуясь (75.7), получим уравнение геометрического места точек,
обладающих этим свойством:
(Аь—у)(х — х{)+(Въ+х)(у — ул)-\-Ь\—{АА+х)у-+-
+ {В4+у)х]-^\01—х{Аг + у) + ^ — у)(В3—х)) = 0.
Производя упрощение и пользуясь (75.13), получим:
г2 (Аъх + Въу) + 5ф [ (В4 — 2 Л3 — 2*) х — (Л4 + 2£3) у + 2Ва<Ч = 0.
(79.2)
Исключая f2 и ф из этого уравнения и из (76.4), получим кривую
второго порядка
Ьг = Sdx (А5х -+- В5у) — 5 (А3х -+ Въу){ (В4 — 2Л3 — 2d) х —
_(Л4 + 2£3)уЧ 2Б3^1 = 0. (79.3)
Следовательно, те и только те точки Бурместера будут пятого
порядка, которые лежат в пересечении кривой круговых точек
с кривой второго порядка уг и в то же время лежат на кривой
второго порядка bv Кривые cpi (76.5) и Ьх проходят через м. ц. в. Р
и касаются в этой точке одной и той же прямой (с уравне-
§ 79] ТОЧКИ RVPMECTHPA пятого ПОРЯДКА 357
нием А3х-{- Вгу — О, идущей в точку Болла) — следовательно, они
могут иметь еще две общие точки, а при наличии трех общих
точек — совпадают; таким образом, если три точки Бурместера
пятого порядка, то этим же свойством обладает и четвертая
точка Бурместера. Кривые срг и \ пересекают ось Рп в точках
с ординатами
— м* — 2Вза по А\
Следовательно, их равенство, т. е. условие
3dA4 = 2Вг (4Л3 + 3d), (79.5)
эквивалентно тому, чтобы, при наличии двух точек Бурместера
пятого порядка, две остальные точки Бурместера были также
пятого порядка; в частности, в случае шарнирного четырехзвен-
ника это условие эквивалентно тому, что две точки Бурместера,
не являющиеся подвижными шарнирами, будут пятого порядка.
Нетрудно видеть, что при условии (79.5) коэффициенты при &3
и при k в (76.10) становятся равными друг другу — следовательно,
по (76.10') будем иметь:
*1 -Н ^2+^3 + ^4 =
~j~ K-iKoKa ~"i RrnKoRiA)
это равенство можно записать
еще и таким образом:
(*1 + *2) + (*8+*4) =
=*1*2(*3+*4)-+- *3*4(*1 + ^)'
откуда
kx + k2
£з + &4
= 0.
1 — k}k2 1 — k3k4
(79.6)
обозначение kt -
Рис. 372.
очевидно,
Если ввести обозначение kt = tgcp/(/= 1, ..., 4), то,
имеем tg(cp1 + cp2) + tg(cp34-cp4) = 0, откуда «Pj-fft-f- cp3-fcp4 = 0,
или тс; пользуясь рис. 372, где р = ср1 (как углы, измеряющиеся
половиной одной и той же дуги), мы видим, что срг —|— ср2 == X;
следовательно, условие (79.5) эквивалентно тому, что прямые kxk2 и
k3k4 образуют с осями Pt и Рп равные углы.
Таким образом, если kx и k2 известны и построен центр 5 (рис. 359),
то при условии (79.5) прямая k3k4 должна не только проходить
через 5, но и иметь вполне определенное направление.
П. Пусть теперь выполняется условие
А* _ B4-hd
Вя
(79.7)
358 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ подвиж. плоскости [гл. XII
т. е. мы имеем случай Чебышева) и одновременно выполняется
условие
ZdAA=2Bz(AAz + M). (79.8)
В этом случае одна из точек Бурместера совпадает с точкой Болла,
(т. е. является точкой Чебышева), а три остальные лежат на одной
прямой; если две точки Бурместера пятого порядка, то и две
другие будут пятого порядка. Этот случай одновременного выполнения
условий (79.7) и (79.8) будем называть случаем Чебышева пятого
порядка.
Полагая в (76.160 k4 = km и исключая величину kQt мы видим,
что в случае Чебышева пятого порядка угловые коэффициенты
трех точек Бурместера и точки Чебышева связаны
соотношениями
К + &> + Цъ + *1*2*з = — 2А10,
(79.9)
(1— M2)(^3 + ^io) + (l— *з*10)(*1 + *2) = 0.
Второе из них имеет простой геометрический смысл: прямая kxk2
перпендикулярна к прямой (-т—, —кЛ . Действительно, по (18.9)
угловые коэффициенты этих двух прямых выражаются формулами
kx + k2 -^ + (—^з) =i — *10fea
1 —Мг ' 1 1 / и ч ^ю + ^з
Покажем также, что в случае Чебышева пятого порядка три
точки Бурместера лежат па прямой с уравнением
у = -£- + 10. (79.10)
Действительно, подставляя в (77.8) значение 3dA4 из (79.8) и
пользуясь (76.6), (76.16), получим (79.10).
III. Рассмотрим случай Вг = 0; мы видели, что при этом две
точки Бурместера лежат на окружности (/) в ее пересечении с
прямой (77.2), а две другие — на оси Рп и их ординаты являются
корнями (77.4).
Полагая в (79.2) л; = 0, получим:
Bsy — 5(y — d)A4 = 0;
обе точки Бурместера, лежащие на оси Рп, будут пятого порядка
лишь при выполнении этого условия; так как это уравнение первого
порядка должно иметь, таким образом, два корня, то оно должно
быть тождеством и его коэффициенты должны быть нулями, откуда
Л4 = Я5 = 0. (79.11)
§ 79] ТОЧКИ БУРМЕСТЕРА ПЯТОГО ПОРЯДКА 359
Находя при этих условиях точки пересечения кривой (79.2) с
окружностью (/) (для которой г2 — 1у), мы придем к уравнению
х [1А5 — 5(l — d) (2Л3 + 2d — ВА) ] = 0;
следовательно, если обе точки Бурместера, лежащие на полюсной
нормали, будут пятого порядка, то обе точки Бурместера, лежащие
на окружности (/), также обладают этим свойством при условии
1АЬ = 5(1 — d)(2A3+2d — ВА). (79.12)
Если это равенство не выполнено, то или мы должны иметь х = 0,
т. е. две точки Бурместера, лежащие на окружности (/) должны
совпадать с точкой L(0, /), или же, если это невозможно, то обе
точки Бурместера, лежащие на полюсной нормали, одновременно
не могут быть пятого порядка. Наоборот, если при одновременном
распадении обеих кривых Бурместера обе точки Бурместера,
лежащие на окружности, будут пятого порядка и если они
лежат на прямой, параллельной полюсной касательной, то и
две точки Бурместера, лежащие на полюсной нормали, также
будут пятого порядка.
Действительно, прямая (77.2) параллельна оси Pt лишь при
условии Л4=0.
Совершенно аналогично можно рассмотреть случай распадения
одной из кривых Бурместера*).
IV. Рассмотрим снова в качестве иллюстрации задачу В. Лихтенхельдта
(§§ 74, 78); так как искомые подвижные шарниры являются точками
Бурместера пятого порядка, то для случая Чебышева пятого порядка
прямая АВ должна иметь уравнение (79.10) или, на основании (76.16), (76.6),
уравнение
l>x+my=imhj- <7913>
Пользуясь (74.2), имеем:
р\
х cos ф + У sin ф = 2 _ , X = /,sin^.
Условие того, что точки А и В с координатами
| х = г, cos (р, — ф), Ь= r[ cos (pj — ф),
А < В <
( у = г, sin (р, — ф), ( у = r[ sin (pj — ф)
лежат на этой прямой, приводит к уравнениям
г, cos (р, - Ц) = r\ cos (р; - 2ф) = 2(2^Х_Х) ,
*) Детальное исследование всех этих случаев, а также случая бесконечно
удаленного м. ц. в. читатель найдет у А. П. Котельникова [1], гл. V,
360 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖ. ПЛОСКОСТИ [ГЛ XII
откуда, пользуясь (74.5), найдем:
sin 2 (р, — ф) cos (р, — 2ф) sin 2 (р( — ф) cos (р( — 2ф) 1
/? sin р,—A sin ф cos (Р,—ф) psinPj — X sin ф cos (pj— ф) 2p — A
>шая эти ур
\ = /, sin ф =
Решая эти уравнения относительно А
2/7 sin (Зр, — 4ф) 2р sin (зр j — 4ф)
sin (Зр, — 4ф) + sin (Р, — 2ф) sin (Зр| — 4ф) + sin (р[ — 2ф) '
(79.14)
мы приходим к уравнению для нахождения ф
sin 2 (р, + Pi — Зф) — 2 cos (р; — Pj) sin (pt + Pi — 2ф) = 0. (79.15)
2
Вводя новую переменную ф! —-^-(pj + PJ)— 2ф, будем иметь:
sin Зф1 = 3sin^j соэ2ф1 — sin^ = 2 cos (pj — pj) sin ( -^—--|-ф, ) .
Полагая
* = tg фг = tg [|- (p, + P,') - 2ф] , (79.16)
получим кубическое уравнение для х
ах* + р*2 4- tx + Р = 0, (79.17)
причем коэффициенты имеют следующие значения:
Pi + Pi / / ч Pi + Pi
а = l + 2 cos (р; — pi) cos * * , p = 2 cos (pj — pj) sin * * , (79.18)
Y = a — 4.
Каждому корню соответствует по (79.16) значение tg 2ф, по которому
найдем два значения ф, различающиеся на 90°; после этого по (79.14) найдем к,
а затем по (74.5), (74.7) радиусы-векторы всех шарниров.
Задача имеет или два, или шесть решений.
§ 80. Понятие о синтезе передаточных механизмов
I. Во всех формулах глав XI — XII фигурировали коэффициенты
разложений (75.5); мы рассматривали задачи геометрического
синтеза, причем эти коэффициенты нам не были известны *), а вместо
этого мы знали подвижные шарниры, или точку Болла и т. п.;
поэтому особо важную роль играли такие соотношения, в которые не
входили эти коэффициенты.
Мы рассмотрим теперь решение некоторых задач
кинематического синтеза, в которых нам придется находить указанные
коэффициенты.
*) Мы исключаем тот случай, когда мы знаем центроиды, тогда все
параметры выражаются через их кривизны по формулам (59.19).
§ 80] ПОНЯТИЕ О СИНТЕЗЕ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 361
Рассмотрим шарнирный четырехзвенник А1АВВ1 (рис. 373);
пусть Л1В1 — его стойка, Р — м. ц. в. шатуна АВ, PQ — ось кол-
линеации, o)j и оо3 — угловые скорости кривошипа / и звена 3,
9\ и Н—их Углы поворота
относительно стойки 4\
введем обозначения
(k=l, 2
(ft».
Л+i
.) (80.1)
Рис. 373.
для передаточного
отношения v и его производных
по углу срх; будем считать q
—^-=1, т. е. пусть
кривошип вращается
равномерно -с единичной угловой скоростью, тогда передаточное
отношение v является угловой скоростью звена 3, v'— его угловое
ускорение, а дальнейшие производные являются угловыми ускорениями
высших порядков.
Задача синтеза передаточного механизма (в данном случае
шарнирного четырехзвенника) заключается в нахождении его
Рис. 374.
параметров по заданным величинам v, v', v", . .. (при заданных
неподвижных шарнирах Аг и Вх)*).
Сообщим всей системе вращение с угловой скоростью — со3
вокруг точки Вх\ мы получим новый шарнирный четырехзвенный
механизм (рис. 374) со стойкой 3, относительно которой звено 4
вращается с угловой скоростью — со3; звено / теперь будет шатуном —
оно вращается вокруг точки Q, являющейся м. ц. в. шатуна /
нового механизма, с угловой скоростью о) = а^— со3=1—со3; во всем
*) См. С. А. Черкудинов и Н. В. Сперанский [1].
362 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ подвиж. плоскости [гл. хп
дальнейшем мы будем рассматривать этот новый механизм, для
которого мы знаем подвижный и неподвижный шарниры Лг и Bv
лежащие на одном луче QAXBV
II. Задание передаточного отношения v позволяет найти
точку Q на прямой BXAV ибо по известной теореме Виллиса мы
имеем при r = QAv r1 = QBl*)
Покажем, что задание v,v' определит полюс поворота W,
задание v, v', v"—обе кривые Бурместера, задание v, v', v", v'"—
точки и центры Бурместера.
Рассмотрим шатунную плоскость и в ней две точки Q и Av
Введем в неподвижной плоскости систему координат Оху, начало
которой О совпадает с м. ц. в. Q в данном положении, а ось Од:
направлена по касательной к центроидам, причем по теореме Бо-
биллье
d = /_xOA1 = /_BQP.
В гл. XI, пользуясь формулами (75.3), (75.4), мы выражали
производные от координат любой точки подвижной плоскости через
соответствующие производные от координат точки О. В той задаче,
которую мы теперь рассматриваем, будем, наоборот, выражать
производные от координат точки О через соответствующие
производные от координат точки Av ибо эта последняя лежит на звене 4,
вращающемся вокруг точки Вг.
Если, как обычно, через ср обозначен угол поворота плоскости,
связанной с шатуном /, то мы имеем:
Д?ср3 <о3 оз v atyi <»i 1_
flfcp (О О), С03 1 V rfcp (Oj —со3 1 —
(80.3)
Вводя для удобства записи новую величину
f* = T^V 1+»1 = Т^7' (80-4>
мы имеем:
Так как звено 4 длиною 8 вращается вокруг неподвижного центра Вх
с угловой скоростью — (о3, то точке Ах соответствует в системе
координат Вхху комплексное число
г = ЪеСа, -5—=—(Do,
*) Рис. 373 соответствует положительному знаку v.
. Liz ua . . d2a Г / da\2 . . d?2a "1
(80.70
§ 80] ПОНЯТИЕ О СИНТЕЗЕ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 363
причем в том положении, которое изображено на рис. 374, имеем:
a = e + 7r, z = — beib. (80.6)
Дифференцируя z по ср, получим:
£="»"1Н*1г; (80-7)
пользуясь этой формулой, найдем дальнейшие производные
d2z dz_ da
dy2 dy dy
d*z _ 1 .Г/ flfaX3 d4 I ate </»g )
Мы имеем, обозначая штрихами производные по углу срх:
пользуясь этой формулой, легко найдем производные а по ср
dot da dyx /1 . ч d2a * ./1 . ч
^ = _!x"(l+lx)2-tl'2(H-tl), (80.9)
*£ = ц'" (1 + ц)3 - V|x" (1 + Ц)* -ц'э (1 + p).
Мы обозначили через 2 комплексное число, характеризующее
положение точки Ах относительно системы координат Вхху\ если через
z2 = х2-f- iy2 обозначить комплексное число, характеризующее
положение той же точки Ах относительно системы координат Оху,
то, очевидно, имеем:
z2 = rxeib -\-z = el* {rx — 8) = pie*. (80.10)
Формулы (75.7), вводя комплексное число z0 = х0-\-iy0, можно
записать в таком виде:
d2° — л -J- /я — _^£
d^o _ Л , ,r> __^£2 , ,„ _"^0
i^^ + Ifl^-^ ^ = Л2 + /Б2 = ^+.2,
-^Г — ~3 "Г ^3 — rf?3 "I" '*2' rfcp4 — ЛА -h Ш4 — rf(p4 *2-
III. Так как мы ввели неподвижную систему координат Оху,
то 22 отличается от z лишь на постоянную величину; поэтому,
364 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ подвиж. плоскости [гл. XII
пользуясь (80.11), (80.7), (80.9), (80.10), найдем:
Аг + tBl = iz^ — iz2 = t\ibe" — /ji8*'e = 0.
Этот результат мы и должны были получить на основании (75.5).
(75.6); наоборот, исходя из этого результата, мы получили бы
теорему Виллиса. Далее мы имеем:
откуда
Aj = 8(l -f-j*)(jxcos6 — |t' sin 9). fi2 = 8(l + p.)(Kcos6+ ii sin8);
так как по (75.6) A2 = 0, то отсюда легко находим:
Ctge=-£l, 81116=: -=£=-. COS6 =-—£=-; (80.12)
возвращаясь к передаточному отношению v, имеем *):
v 0-у)
с<е6 = „/1_,л' sin
~V> / /V2 + V2(1_v)2 •
cos 6 == -— v/ (80.13)
yV2+ V2(l_v)2 '
Пользуясь (75.6), находим
d = Б2 = 8 (1 -+- |i) (|i/ cos 6 + |i sin 6) = 8(1 + |i) Vy/2 + (a2,
или окончательно
И^2 + ^(1-^ (80.14)
Таким образом, зная величины v, v\ мы сможем найти по (80.13)
угол 6, т. е. положения полюсной касательной и нормали, а затем,
зная d, сможем найти полюс поворота W.
IV. Мы имеем из (80.11), (80.70
л I -о I -П da V d4 1 i о da d2a . . }
= 8*"{/[— ^+^(1+^)2+ ^2(1 +11)]+з№Ч1 + ^+Ы =
откуда
i43 = 8(l+|i){3|iK.4ose —[ji(l—|i) + |i^(l-f |i)4-K./2]slne}t
B3 = 8(l+|i){3|4i'sin9 + [|i(l —^-4-^(1 +|i) + ^2]cos6>;
*) Эта формула найдена впервые Ф. Фрейденштейном [1J; см. также
У. Картер [1].
§ 80] понятие о синтезе передаточных механизмов 365
возвращаясь к передаточному отношению v и подставляя значения
sin б, cos 6, получим:
Лч —6 Чу(1-^)(2у-1)-Л
(1— V)3Kv/2 +-V2(1—V)2
*з-
В =Ъ v Ь (1 — ^)2(!+**) + *" О — v) + ЗУ2]
(l__v)5|/v/24-v2(l— V)2
По формулам (76.7), (75.18), (75.22) легко найдем:
v(l-v)2[v» + v(l-2v)(l-v)]
^ю ■
(80.15)
v'[V
(1 —
'(1-
■V)2
-v)4-3v'
[vv" — 3v,:
2 4-
2
v(l-
*8(1-
-v)!(l + v)]
-v)(2-v)]
(80.16)
k
0 v [V (1 — v) + 3v'2 4- v (1 — v)2 (1 + v)]
а также параметры кривых Бурместера
35{v'24-v2(l — v)2}3/2
m =
v' (I — v) [V (1 — v) + 3v/2 4- * 0 — ^)2 (1 + \)1
Z - 35|у24-^2(1-у)2ГЧ гяо 16/v
/ = 35{У24-^2(1~^)2Г/?
(1 _ v)3 [_ w + 3v/2 4- V2 (l — >) (2 — v)] "
Следовательно, задание величин v, v', v" полностью определяет обе
кривые Бурместера.
Совершенно аналогично, находя АА и В4, видим, что задание
величин v, v', v", V" определяет точки и центры Бурместера.
V. Пользуясь этими результатами, рассмотрим решение некоторых
задач кинематического синтеза.
А. Для четырехзвенника рис. 373 задано положение ведомого звена 3
и величины v, v', v".
Мы можем найти по формулам (80.13), (80.16') угол 8 и параметр 1Х и
построить окружность (/,); на ней будем строить изображающие точки kh
k2, k3 (рис. 375), соответствующие лучам точек ее пересечения с заданной
прямой ВХВ, которая должна быть прямой Симпсона для треугольника kxk2k%
(§ 56). Так как мы знаем пока только один луч QBX, то имеем только одну
точку kx. Опишем на отрезке Qkx как на диаметре окружность и пусть она
пересечет прямую ВВХ в точках М и N) проведем прямые kxM и kxN и
пусть они пересекут окружность (1Х) в точках k2 и kb\ тогда на лучах Qk2
и Qk3 лежат две другие точки Н2 и Нъ пересечения прямой ВВХ с кривой
центров — любую из них можно принять за шарнир В.
Для чисто аналитического решения задачи воспользуемся
уравнением (55.6) (с заменой / на 1Х), дающим значения ku k2t къ\ мы имеем из него
Ma*s = *ю> *i + *2 + *з =» — т (j- + -pj , (80.17)
366 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ПОДВИЖ. ПЛОСКОСТИ [ГЛ. XII
откуда
&2&3-:
&10
, k2 + ks = — kx — m (j~ + -^-J.
(80.18)
Так как величины kx, kxo, m, /, могут быть найдены, a Ax -f By + С = 0
является уравнением заданной прямой £#!, то &2 и ^з можно найти как
корни квадратного уравнения.
Б. Для четырехзвенника рис. 373
задано положение ведущего звена 1
и величины v, v', v".
Задача решается точно так же, но
вместо кривой центров надо
рассмотреть кривую круговых точек.
В. Для четы ре хзвенника рис. 373
задано положение шатуна и
величины v, v', v".
В этом случае мы должны будем
найти точку пересечения одной из
кривых Бурместера с заданным лучом.
Г. Для четыре хзвенника рис. 373
заданы величины v, */, v", */".
Мы сможем вычислить, как было
указано, параметры d, Аъ, В3, АА, ВА\
зная один луч QAXBX, на котором лежит
точка Бурместера и деля левую часть
уравнения (76.10) на k — kx, получим
кубическое уравнение; любой из трех
его корней можно принять за угловой
коэффициент луча, в пересечении
которого с кривыми Бурместера получим
оба шарнира А и В.
Д. Для четыре хзвенника рис. 373
даны положение обоих звеньев 1 и 3
и величины v, v'.
В их пересечении найдем точку Р; соединяя ее с точкой Q, найдем ось
коллинеации PQ; по формуле (80.13) найдем угол 8 и проведем прямую QAB
под углом 0 к PQ.
VI. Найдем в заключение величину -тг . т. е. угловую скорость
вращения оси коллинеации относительно шатуна*).
По теореме Бобиллье она равна и противоположна по знаку
угловой скорости вращения полюсной касательной Qx относительно
звена Аф^ таким «образом, имеем:
db db_
dt dyx
где u)0—абсолютная угловая скорость полюсной касательной. Если
точка Q переместилась на величину ds по неподвижной центроиде,
da
ds
Рис. 375.
— шо"
■(—а)з)=а)о + а)з«
то касательная повернулась на угол da, причем
(80.19)
:/d; следова-
*) В. Картер [1] рассматривал эту задачу, но его решение можно
применить только в задачах анализа (когда механизм уже известен), но не
синтеза.
§ 80] ПОНЯТИЕ О СИНТЕЗЕ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 367
тельно, по (66.2)
da da ds Tyr J* , ,s , / ч
и, таким образом, из (80.19) находим:
— -ft = ~ Кх d (о)! — о>3) + со3 = (Кх d + 1) 0)3 — #i ^1 =
= Kdu>2> — Кг diax = d(Kv — Кг).
Если воспользоваться формулами (71.11), (71.7), то мы легко найдем
db _
формулу, выражающую -тт- через параметры кривых Бур-
местера
_^^2v-l+3rf(r1)=2 — + 2&F&. (80.20)
Если из (80.13) найти
v/ = (v _ v2) ctg 6 (80.21)
и продифференцировать по срх, то мы найдем, пользуясь (80.21) и
(80.20):
v" = v' (1 — 2v) ctg 0 — (v — v2) cosec2 0 • ^ =
_V2(l_2v) У2 + у2(1_,)2 r ' 3^ (v — 1) 1
— v(l—v) "Г" v(l-v) Г 1_^ /1 J'
откуда легко найдем формулу для lv совпадающую с (80.160.
Воспользуемся формулой Эйлера (67.2), в которой (рис. 373) по (80.2)
1 I 1 —v 1
r = vru
v г гх чгх rf sin в '
_ W24-v2(l—v)2
гх (1 — v) sin 0 (1— v)2
Если записать уравнение кривой центров в таком виде:
_L=_J_+_L_
/*! /j sin 6 ' т cos 6 '
и умножить все его члены на lv то, воспользовавшись (80.2) и
соотношениями (80.13), получим:
h = /i(l-v) = 1 , U = 1 L
»- й cin fl I *yi nr\a ft oiti ft h r»/->
sin 6 kl0 COS 6
= VV+V2(1_v)2 J V ( 1 V) ^— \ ,
откуда легко найдем формулу для kl0, совпадающую с (80.16).
368 ШЕСТЬ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ подвиж. плоскости [гл. XII
VII. Рассмотрим такой числовой пример: пусть
5 = 0,6, v = 0,5, V = 0,3, v" = 0,4.
В. Картер [1], у которого мы заимствовали этот пример, решает задачу
синтеза таким образом: он строит угол I = /_ AQAX через каждые 5е (в
пределах от 0 до 40°), находит —г- и путем проб подбирает положение точки Р
на оси коллинеации и строит для каждого значения к свой шарнирный
четырехзвенник — как мы видим, это совершенно ненужно: мы имеем по (80.2)
г1 = -^ = 1,2; далее, по (80.13) находим о = 39,8"; формулы (80.16') дают:
»~2g"M*-H»7. / = 11-61^3,33,
/, = — 0,009 • 61!/2 = — 4,288; k0 = — 0,326, kl0 = 0,253.
Этими данными полностью определяются обе кривые Бурместера- проводя
любой луч, мы легко найдем точки его пересечения с обеими кривыми
Бурместера, являющимися геометрическими местами шарниров Л и В.
ГЛАВА XIII
СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости
§ 81. Два и три соседних положения подвижной плоскости
I. В гл. IX—XII мы рассматривали бесконечно близкие
положения подвижной плоскости; в настоящей главе мы рассмотрим
положения, находящиеся уже на конечном расстоянии друг от друга;
будем их называть соседними положениями.
Если даны два положения Ех и Е2 подвижной плоскости
(рис. 376), характеризуемые положениями Л1В1 и А2В2 отрезка АВ,
то, как известно из кинематики,
переход из положения / в
положение 2 можно осуществить одним
поворотом; центр поворота, который
мы будем называть полюсом Р12,
является точкой неподвижной
плоскости, в которой пересекаются оси
симметрии а и Ъ отрезков АХА2
и ВХВ2\ при этом любая прямая
подвижной плоскостиповернетсяна один
и тот же угол, который мы
обозначим ср12 *); в данном случае
<Ри = L А\р\гА<1 = L В1Р\2В2-
При перемещении из положения 2 Рис. 376»
в положение / полюс останется
прежним (т. е. точка Р21 совпадает с Р12), но угол изменит знак
(т. е. ср21 = — ср12). В случае п соседних положений подвижной
плоскости Ev Е2,
из п по 2, т. е.
Еп число полюсов будет равно числу сочетаний
п(п— 1)
Зная два положения подвижной плоскости, мы сможем найти
полюс Р12 и угол ср12; наоборот, если даны полюс Р12 и угол ср12,
*) Угол поворота всегда берем не превосходящим по модулю 180°; угол
считаем положительным, если при этом поворот произошел против
часовой стрелки.
370 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. XIII
то каждой точке Сх положения / можно найти гомологичную
точку С2 в положении 2, т. е. ту точку С2, в которую она перейдет
после поворота; для этого соединим Сг с Р12, повернем луч Рг2Сг
вокруг точки Р12 на угол ср12 и отложим Рг2С2 = Pyfii.
П. В случае трех положений подвижной плоскости мы имеем
3 ■ 2
-у-=3 полюса Р12, Р13, Р23 (рис. 377); треугольник с вершинами
в этих точках будем называть полюсным*треугольником *). Докажем
основную для всего дальнейшего
теорему о полюсном
треугольнике, позволяющую найти углы
поворота: угол при каждом
полюсе полюсного треугольника
равен половине угла вращения
вокруг этого полюса.
Рис. 377.
Действительно, рассмотрим точку Аг положения /, совпадающую
с Р12 — очевидно, при переходе в положение 2 она останется
неподвижной, т. е. А2 совпадет с Аг. При переходе из положения /
в положение 3 точка Аг перемещается по дуге окружности с
центром Р13 и радиусом Pi2P13. а при перемещении из положения 2
в положение 3 — по дуге окружности с центром Р23 и радиусом P23Pi2;
в пересечении этих двух дуг найдем точку Л3, причем легко
видеть, что
1_ АъРпАх = ?23 = 2 L РгЛгРп-
Покажем, как при помощи полюсного треугольника мы можем, зная
точку Ах положения /, найти гомологичные точки А2, Аг
положений 2 и 3 (рис. 378). Найдем точку А0, зеркальную с точкой Ах
*) Теорема Кеннеди — Аронгольда (§ 3) неприменима, ибо в данном
случае Р12, Р13, Р2з являются центрами конечных поворотов, а не м. ц. в.
§ 81] ДВА И ТРИ СОСЕДНИХ ПОЛОЖЕНИЯ подвижной плоскости 371
относительно стороны Р12 Р13 полюсного треугольника *)— будем
называть ее основной точкой] точки Л2 и Л3, зеркальные с основной
точкой Л0 относительно сторон Р12^2з и ^13^23 полюсного
треугольника, гомологичны с точкой Av
Для доказательства рассмотрим, например, точку Л2; мы видим,
что /^Л2Р12А1 = 2^Р2гР12Р1г и Pl2A2 = Pl2Av Опишем окружность,
проходящую через три гомологичные точки Av А2, Л3, соединим
прямыми ее центр Ло с точками Av А2, Л3, и пусть эти прямые
пересекают стороны полюсного треугольника в точках Bv В2, В%.
Мы имеем:
А0Вг + А0Вг = АгВг -+ А0В1 = A0AV
А0В2 -+- А0В2 = А2В2 + А0В2 = А0А2, (81.1)
А0Вг + А'0Вг = Л3£3 + А0Вг = Л0Л3.
Таким образом, если для трех гомологичных точек построить
основную точку и центр описанной окружности, то эти две
точки являются фокусами центрального конического сечения,
вписанного в полюсный треугольник, причем радиус описанной
окружности равен 2а**). Мы имеем, таким образом, определенное
соответствие между точками А0 и Л0: если задана точка А0, то
легко построить зеркальные точки Аг, А2, Л3 относительно сторон
полюсного треугольника, провести через них окружность и найти
ее центр Ло.
В соответствии с §§ 31, 41 это — квадратичное соответствие,
причем, зная точку А0, мы можем найти точку Ло, пользуясь
равенством углов
^Л4> = L^PoPk- АЛзЛгЛ = LA'oPA
Таким образом, если точка А0 описывает прямую, не проходящую
через полюс, то точка Ло описывает коническое сечение, проходящее
через все три полюса; аналогичный вывод справедлив, если прямую
описывает точка А1% ибо тогда и точка Л0 опишет прямую.
III. Рассмотрим теперь наибольшее и наименьшее значения
радиуса окружности, проходящей через три гомологичные точки.
Наибольшее значение, очевидно, равно бесконечности; найдем
геометрическое место точек Аг плоскости Ег, которые вместе
*) Берем ту сторону, в обозначении которой дважды повторяется индекс
данной точки.
**) Коническое сечение будет эллипсом или гиперболой в зависимости
от того, лежат ли обе точки А0 и Л0 по одну сторону от стороны Pi2P \з
полюсного треугольника или по разные стороны; в этом последнем случае
в формулах (81.1) будут не суммы, а разности.
372 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. XIII
с двумя гомологичными точками А2, Л3 лежат на одной
прямой g\ в этом случае точка Ло уходит в бесконечность и
коническое сечение, вписанное в полюсный треугольник, обратится в
параболу с фокусом Л0; так как точки Av А2, А3 зеркальны с
фокусом А0 относительно трех сторон полюсного треугольника, в
который вписана парабола, то по §§ 32, 33 точка А0 должна лежать на
окружности, описанной вокруг него, а прямая g должна проходить
через его ортоцентр И (рис. 379); так как точка А1 зеркальна с
точкой А0 относительно стороны Я12Я13, то она, очевидно, лежит на
окружности, проходящей через
точки Р12, Р13 и Я, ибо эта
окружность зеркальна
относительно стороны P12Pi3 с
окружностью, описанной вокруг
полюсного треугольника.
Рис. 379. Рис. 380.
Совершенно аналогично находим окружности, на которых лежат
точки А2 и Л3. Центры Cv С2, С3 этих окружностей и точки Р12,
Р13, Р23 лежат на одном коническом сечении (рис. ПО, § 33).
Если произвольно выбрать точку Аг на своей окружности и
соединить ее прямой с ортоцентром И полюсного треугольника, то
в пересечении этой прямой с соответствующими окружностями
найдем точки А2 и Л3.
Рассмотрим теперь наименьший радиус окружности,
проходящей через три гомологичные точки (рис. 380); если обозначим
через г0 радиус окружности, вписанной в полюсный треугольник, то
ясно, что эллипс, у которого большая полуось не более г0, не
выходит за пределы этой окружности и не может касаться полюсного
треугольника в трех точках; следовательно, радиус окружности*
проходящей через три гомологичные точки, не меньше диаметра
окружности, вписанной в полюсный треугольник.
Мы рассмотрим наибольший и наименьший радиусы окружности,
проходящей через три гомологичные точки; укажем, что Альт [1]
нашел геометрическое место точек положения /, которые вместе
§81] ДВА И ТРИ СОСЕДНИХ ПОЛОЖЕНИЯ подвижной плоскости 373
с двумя гомологичными точками лежат на окружности, заданного
радиуса, а также геометрическое место центров этих окружностей *).
VI. В качестве иллюстрации рассмотрим решение такой задачи
синтеза**) (рис. 381): построить шарнирный четырехзвенник, зная
неподвижные шарниры АхиВх и зная три
положения кривошипа Ахтх, Ахт2, Ахтъ и три
соответствующих положения коромысла
Вхпх% Bxn2i Вупг.
Найдем положения кривошипа
относительно коромысла Вхпх— для этого повернем
фигуры п2ВхАхт2 и пъВхАхтъ (как твердые
тела) вокруг точки Вх до совпадения Вхп2
и Вхп3 с Вхпх\ получим три положения
подвижной плоскости (рис. 382), определяемые
прямыми Ахтх, А2т2, Агт3, причем, очевидно
точки Ах, А2, Аъ лежат на окружности с
центром в тбчке Вх. Возьмем на прямой Ахтх про- рис 381.
извольную точку Мх и найдем гомологичные
точки М2, М3 на прямых А2т2, Агт'г; зная три положения отрезка АхМу*
найдем все три полюса Р12, Лз» ^гз относительного вращения и центр Мх
окружности, проходящей через точки Мъ М2, М3. Возьмем еще точку В на
Рис. 382.
прямой Ахтх и обозначим через В' центр окружности, проведенной через
точку В и две гомологичные точки; так как точки Alt Мх, В лежат на одной
*) См. X. Альт [1], Р. Бейер [2], § 12.
**) См. И. И. Артоболевский, 3. Ш. Блох, В. В. Добровольский [1], § 39.
'4
т.
"/ ш
374 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. хщ
прямой, то соответствующие центры окружностей Ви М' и В' должны
лежать на коническом сечении, которое вполне определяется пятью
точками (Р12, Лз> ^гз» #i> ЛГ); выберем в качестве точки В' точку его
пересечения с лучом В{пь которую можно найти по теореме Паскаля (§ 24);
принимая точки В и В' за подвижные шарниры, найдем искомый четырехзвен-
ник АХВВ'ВХ.
§ 82. Четыре и пять соседних положений подвижной плоскости
I. Мы видели, что в случае трех положений подвижной плоскости
все три полюса Р12, Р13. ^23 можно было выбрать совершенно
произвольно — этим определялся полюсный треугольник и соответствующие
углы поворота; в случае четырех положений подвижной плоскости
4-3 а
имеем —о- = о полюсов
М2» "l3« ™14» ™23» ^24» "з4»
их можно сгруппировать так, чтобы иметь три пары противопо-
люсов (§ 45):
Рп и Р^ pi3 и Р^ Ри и Р23. (82.1)
Бурместер показал следующее: если выбрать произвольно две пары
противополюсов, то два остальных полюса должны лежать на
так называемой полюсной кривой, проходящей через заданные
четыре полюса; один из них можно выбрать произвольно на этой
кривой, а последний полюс этим вполне
определится.
Для доказательства рассмотрим полюс Pik
(где /, k, г, 5 — любые два неравные между
собою числа из чисел 1, 2, 3, 4); этот полюс
входит в два полюсных треугольника PikPirPkr
и PikPiSPks (рис. 383). Так как угол при
вершине Рш полюсного треугольника равен
половине угла поворота при переходе из
положения / в положение k, то мы имеем *):
LPirPikPkr = LpisPmpks> (82.2)
Рис. 383. т. е. из точки Pik отрезки PirPkr и PisPks
видны под углами или равными, или
дополнительными до 180°; следовательно, если две пары противополюсов
Ри И Pkr- Plr И Р^ .
принять за противоположные вершины четырехугольника, то из
пятого полюса Pik противоположные стороны этого четырехугольника
видны или под равными углами, или под углами, дополнительными
*) Эти углы могут быть не равными, но дополнительными до 180°,
§ 82] ЧЕТЫРЕ И ПЯТЬ СОСЕДНИХ ПОЛОЖЕНИЙ подвижной плоскости 375
до 180°. На основании §§ 51, 52 геометрическим местом полюса Pik
является фокальная кривая -f (Pis, Pkr\ Plr, Pks), т. е. полюсная
кривая Бурместера для данных четырех соседних положений
подвижной плоскости является фокальной кривой, определяемой
четырехсторонником, для которого противоположными
вершинами являются две пары противополюсов (рис. 384).
Так как все три пары противополюсов играют одинаковую роль
и две пары (82.1) являются парами соответствующих точек, то и
противополюсы Pik и Prs являются парами соответствующих точек,
т. е. фокусами одного и того же конического сечения, вписанного
Рис. 384.
в данный четырехсторонник, поэтому мы получим ту же самую
фокальную кривую, если одну пару противополюсов заменим парой
противополюсов Рш и Prs\ таким образом, все три фокальные кривые
Т ^12' ^34' ^13» ^24)» Т (^12» ^34' ^14' ^2з)' Т (^13' ^24' ^14' ^2з)
совпадают и могут быть названы полюсной кривой "f1234 для
заданных четырех соседних положений подвижной плоскости *).
П. Рассмотрим точку Ах плоскости Ег и три гомологичных
точки А2, Az, Л4; точку Ах будем называть круговой точкой для
четырех соседних положений подвижной плоскости, если она
и три гомологичных точки лежат на одной окружности.
Для четырех соседних положений подвижной плоскости назовем
кривой круговых точек геометрическое место круговых точек (в
плоскости Е^), а кривой центров — геометрическое место центров
указанных окружностей (в неподвижной плоскости). Докажем, что
кривая центров для четырех соседних положений подвижной пло-
*) Мы можем, таким образом, применить к полюсной кривой всю теорию,
ассмотренную в гл. VII; она может иметь форму, приведенную на рис. 203,
04, 205.
376 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. XIII
скости совпадает с полюсной кривой Бурместера ^12м и
является, таким образом, фокальной кривой, для которой двумя
парами противоположных вершин служат две пары противо-
полюсов.
Действительно, пусть четыре точки Ar Ak, Ar, As лежат на
окружности с центром в точке Ло (рис. 385); каждый полюс,
например Pir, лежит на оси симметрии соответствующего отрезка А{АТ\
поэтому мы имеем:
L Ptr^Pkr = L PtMr+L Ал'оР.г =
_ Z.AiAoAr + Z ArAoAk _ L AiA'oAk
~~ 2 ~ 2
так как этот результат не зависит от
положения точки Ат, то мы имеем,
заменяя г на 5, равенство
LPuAoPks = —^, (82.3)
т. е. точка Aq удовлетворяет^ условию
LPirA°P*r= LPutens- (82.4)
такому же, как точка Pik, ибо оно совпадает с условием (82.2).
III. Найдем теперь кривую круговых точек для четырех
соседних положений подвижной плоскости; мы имеем из рис. 386
L PlrArAo = L BxfxrAr - L BlrA^Ar.
LA'oA,Pkr = L ArPk,BkT - L ArA'oBkr,
где Blk — середина дуги AtAk; так как
L B\rPUAr = \L AlPlrAr = \ Til-
А^ЛАг=т LArPkrAk = j ?,*.
то находим:
^ИЛг=£^ИЛ-+ LA'oArPkr =
_ Vir + Vrk _ £AiAoAr+£ArAoAk _ ylfe — £AxXQAk
— 2 2 — 2 '
Так как этот результат зависит только от индексов 1, k и не
зависит от г, то имеем, заменяя г на s:
Ч\ь— /АхАпАь
LPlsAsPks = ^-^^± = £ PuArPkr (82.5)
Рис. 385.
§ 821 четыре и пять соседних положений гюдвижной плоскости 377
Повернем Д ArPlTPkr вокруг полюса Р1г так, чтобы точка Аг
совместилась с точкой А{\ при этом точка Р1г останется неподвижной,
а полюс Pkr перейдет в точку, которую мы обозначим Р\г. Легко
видеть, что точка Р^т зеркальна с точкой Pkr относительно прямой
PirPik> Для этого достаточно заметить, что
/тА1Р1гАг = 91, = 2£Р1кР1гРЛг
Точка Р\г является той точкой положения /, которая в положении k,
т. е. после поворота вокруг полюса Plk, перейдет в полюс PkT\ при
Рис. 386.
переходе в положение г она останется неподвижной — следовательно,
Pkr является той точкой положения 1, которая в
положениях k и г совпадает с точкой Pkr.
Повернув Д AsPlsPks вокруг точки Ри так, чтобы точка As
совпала с Av получим Д AxPlsPlks. На основании (82.5) будем иметь:
Из точки Ах видны под одинаковыми углами противоположные
стороны четырехзвенника с парами противоположных вершин
Ри и P\r% Р1г и PL; . (82.7)
поэтому геометрическое место круговых точек Av т. е. кривая
круговых точек для четырех соседних положений подвижной
плоскости, является фокальной кривой -j (Pls, p\r\ Plr Plks)t для
378 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл XIII
которой двумя парами противоположных веригин служат точки
(82.7). Ясно, что парой соответствующих точек является третья пара
точек Plk и Pis, которой можно заменить одну из пар (82.7). Мы
видим, таким образом, что для построения полюсной кривой, или
совпадающей с ней кривой центров, надо знать две пары противо-
полюсов из трех пар (82.1); для построения кривей круговых точек
надо знать две пары противоположных вершин из трех пар
Р12 и Р\А\ Р13 и Pi,; Ри и Pit,
причем точка Plik, где in k не равны единице, зеркальна с
полюсом Plk относительно прямой РиРгк. При решении задач надо иметь
в виду при рассмотрении вращающихся звеньев, что неподвижные
шарниры должны лежать на кривой центров, а подвижные — на
кривой круговых точек. Особый интерес представляют те случаи, когда
фокальная кривая распадается на более простые кривые (§ 53) *).
IV. В случае пяти соседних положений подвижной плоскости мы
5 • 4
имеем —g- = Ю полюсов
^12» ^13' ^14' ^15» ^23' ^24' ^25' ^34' ^35' ^45*
Для пяти соседних положений подвижной плоскости назовем
точками Бурместера точки Ах плоскости Ev которые вместе
с четырьмя гомологичными точками Л2, Л3, Л4> А5 лежат на одной
окружности, а центрами Бурместера — центры этих окружностей.
Рассмотрим сперва кривую круговых точек 81234 для положений
7, 2, 5, 4\ она будет проходить через точки
™12» ™13' ™14' ™23' ™24' "з4*
те и только те из ее точек могут быть точками Бурместера,
которые одновременно лежат и на кривой круговых точек 81235 для
положений J, 2, 3, 5, проходящей через точки
^12' ^13' ^15» ^23* ™25* ^35*
Так как кривые 81234 и 81235 пересекаются в девяти точках, из
которых две циклические, а три точки — это Р12, Р13, Р12г, то имеем
четыре точки Бурместера в пересечении кривых 81234 и 81235
(рис. 387); ясно, что и кривые 81245 и 82345 пересекут кривую 81234
в этих четырех точках. Точно так же, кривая центров 81234
проходит через точки
^12» ™13» ™14' ^23» ™24' ™34'
*) Читатель найдет решение целого ряда задач синтеза механизмов
на основе теории этой главы в книгах: И. И. Артоболевский, 3. Ш. Блох,
8. В. Добровольский [1], гл. VII; Р. Бейер [2], гл. II, IV, V; С. В. Вяхирев
[1], гл. IV, V; С. В. Вяхирев [2], гл. XII — XIII; С. А. Черкудинов [1].
§ 82] ЧЕТЫРЕ И ПЯТЬ СОСЕДНИХ ПОЛОЖЕНИЙ подвижной плоскости 379
а кривая центров fms — через точки
23'
25'
35*
Эти две кривые имеют две общие циклические точки и три общие
точки Р12, Р13, Р23 — следовательно, все четыре кривые
Tl234' Tl235' Tl245» Т2345
пересекутся в одних и тех же четырех центрах Бурместера*).
V. Покажем еще аналитический вывод уравнений кривых
круговых точек и центров **).
Рассмотрим подвижную плоскость Ех и неподвижную плоскость
Ег (рис. 388); положения точки в подвижной плоскости будем
характеризовать комплексным
числом z = х-\- iy, а в
неподвижной—комплексным числом
C = £-|-nj. Мы имеем основное
V,
У\Е,
V/
^А ^^
/ лк^^а
^л
/Уо
Рис. 388.
Рис. 387.
равенство С —7 + Х2, где комплексное число f характеризует
положение точки О, a\ = eta, ибо вектор, соответствующий комплексному
числу z, повернут на угол а.
Четырем гомологичным точкам Av Л2, Л3, Л4 соответствуют
числа
С* = Т* + М (А=1 4), (82.8)
где z во всех случаях одно и то же, ибо изменяется только
положение подвижной плоскости, а точка в ней все время одна и та же.
Полюс Pkr найдем из условия
отсюда легко найдем
z= — }k~~lr; (82.10)
*) С. А. Черкудинов ([1], гл. III) приводит формулы, позволяющие
вычислить координаты точек и центров Бурместера, как корни некоторых
уравнений четвертой степени.
**) См. Э. Хакмюллер [1].
380
СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости
[гл. XIII
если обозначить через ккг комплексное число, соответствующее
в неподвижной плоскости полюсу Pkr то, подставляя найденное
значение z в (82.8), будем иметь:
lkr-
__ hb — Klk
(ft, r= 1, 2, 3, 4).
(82.11)
ч — К
Этой точке неподвижной плоскости соответствует в подвижной
плоскости точка, характеризуемая комплексным числом (82.10),
которое обозначим:
U — Тг
Pkr =
^k — ^r
причем, конечно, имеем
(ft, г=1, 2, 3, 4), (82.12)
*kr = Т* "Г hPkr = Tr + Ur
(ft, r=l, 2, 3, 4).
(82.120
Если ft = 1, или r = 1, то комплексное число /?fer
соответствует полюсу Pftr> лежащему и в непо-
Рис. 389. движной плоскости, и в плоскости Ех\ если же
k Ф1, г Ф1, то число pkr соответствует той точке
плоскости Ev для которой гомологичными точками в плоскостях Ek и Ет
явится точка Pkr—следовательно, в этом случае pkr соответствует
точке Plkr плоскости Ev Пусть точка Лг плоскости Ег и гомологичные
точки Л2, Л3, АА лежат на одной окружности неподвижной плоскости
(рис. 389); покажем, что в этом случае выполняется условие *)
Im \^^р-: ^=^4 = 0. (82.13)
Действительно, повторяя рассуждение § 51, мы видим, что
Im
U3-c2 • с4-с2)
SlflCP! р2> = 0.
ибо р!~р2 или рх — р2 = тт. Из (82.8), (82.12) мы имеем:
С* — ^г = Т* ~ 1г + (К — K)Z = (Х* — Хг) (* — Лг)-
Oi \ да находим:
(С3 — Ct) (С4 — С2) = (Х3 — Xt) (Х4 — Х2) (z — pl3)(z—p24)
«3 - С2) (С4 - С,) (Х3 —Х2)(К4 —Х0 '(* —/,„)(* _ /?14) "
Так как все четыре точки, соответствующие комплексным числам
Хх, Х2» Х3, Х4, лежат на окружности единичного радиуса, ибо
rk\= \^l<Xk\ = 1, то первая дробь в правой части удовлетворяет
*) Интересно отметить, что выражение в фигурных скобках аналогично
выражению (13.5) для ангармонического отношения четырех точек.
§ 82] ЧЕТЫРЕ И ПЯТЬ СОСЕДНИХ ПОЛОЖЕНИЙ подвижной плоскости 381
(82.13), т. е. имеет вещественное значение; поэтому условие (82.13)
эквивалентно условию
Iml^-^ii^^H^O. (82.14)
К* — />2з)(г— Pu)\ V '
Это уравнение совпадает с (51.9), если положить
Zl = P\V Z\ = Р24> Z2 = PlV Z2 == Pw
Следовательно, мы снова видим, что кривая круговых точек
плоскости Ех совпадает с фокальной кривой, для которой парами
противоположных вершин являются точки
^13 И ^24' ^14 И ^23*
Обозначим через Ах точку плоскости Ev являющуюся центром
окружности, на которой лежат гомологичные точки Av ..., Л4; если
положения £2, Я3, £4 подвижной плоскости совместить с положением
Ev то точки А2, Л3> Л4 совпадут с точкой Ах\ при этом плоскость
Ег займет некоторые положения Е2, Ег, £4, а точка A
Y—положения Л2, Л3, А4 (рис. 390), причем все четыре точки Av . . ., Л4
Рис. 390.
должны лежать на окружности с центром Av ибо их расстояния
от этой точки равны между собой. Обозначим через w комплексное
число, соответствующее точке Ах в плоскости Ev ъ через zv
z2, z%, zA — комплексные числа, соответствующие точкам Av . . ., А4
в плоскости Ег. Мы имеем по (82.8)
* = Т* + М*. ^ = iT^=(^-T*)\; (82Л5)
отсюда легко находим по (82.11)
^ —2rr = (w-Tft)Ift—(« —Тг)Хг = да(Хй—Xr)-(g-b) =
w(\T — lk) — faXr — blk) __ lr — \k
hK
h^r
(w — izkr) = (Xk— \r) (w — izkr).
(82.16)
382 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. хш
Так как точки Av . . ., Л4 должны лежать на одной окружности,
то по (82.13) будем иметь:
Im
llF^'lF^^0' (82.17)
Подставляя значение (82.16), найдем:
(г3 — гх) (г4 — z2) _ (w — ic13) (w — n2A) (T3 — K{) (\ —12) #
(^з — ^2) (^4 —^1) (w — «гаИ» — «u) ' (Tg — Xa) (I4 — I,) *
Вторая дробь в правой части имеет вещественное ^значение, ибо
четыре точки, соответствующие комплексным числам \v . . ., Х4
лежат на единичной окружности; следовательно, условие (82.17)
эквивалентно условию
Im 4<ш — те»> <ш — ^>1 = 0, (82.18)
Таким образом, сопоставляя с (51.9), снова видим, что
геометрическим местом в неподвижной плоскости Ьх центров окружностей,
на которых лежат четыре гомологичных точки, т. е. кривой
центров является фокальная кривая, для которой двумя парами
противоположных вершин являются две пары противополюсов
Р\2> U ^24' ™23 U £*№
Заметим в заключение, что вычисление комплексных чисел pkr
и izkr соответствующих точкам Plkr и Pkr по формулам (82.12),
(82.11), позволяет применить в дальнейшем аналитические формулы
§ 51 для нахождения всех характеристик фокальной кривой.
§ 83. Различные методы, применяемые в задачах синтеза
механизмов *)
I. Рассмотрим в заключение некоторые общие положения,
позволяющие сравнить между собой различные методы, применяющиеся
при решении задач синтеза механизмов.
Мы рассмотрели в настоящей главе п соседних положений
подвижной плоскости — рассмотрим теперь предельный переход, при
котором £2, Ev .. ., Еп стремятся в положение Ev При п = 2
предельным положением полюса Р12 является, как известно из
кинематики, м. ц. в. Р. При п = 3 мы нашли, что геометрическим местом
точек А] плоскости Ev которые вместе с гомологичными точками
А2 и Л3 лежат на одной прямой, является окружность (§ 81), ее
предельным положением является поворотная окружность.
*) См. С. А. Черкудинов и Н. В. Сперанский [1].
§ 83] МЕТОДЫ, ПРИМЕНЯЕМЫЕ В ЗАДАЧАХ СИНТЕЗА МЕХАНИЗМОВ 383
При п — 4 найдем полюсы Р12, Р23, Р34, затем Р13 и Р14 и,
наконец, Р*3 и Р\А (рис. 391); при повороте вокруг точки Р12 на
угол ср12 точка Р12 останется неподвижной, а точка Р*3 совпадет
с точкой Р23; при повороте вокруг точки Р23 на угол ср23 точка Р23
останется неподвижной, а точка Р*4 совпадет с точкой Р34; при
предельном переходе ломаная Р12 Р23 Р34 перейдет в дугу
неподвижной центроиды, а ломаная Р12 Р*3 Р*4— в равную ей дугу
подвижной центроиды; кривые круговых
точек и центров для четырех соседних
положений перейдут в кривые того же
названия для четырех бесконечно близких
положений, т. е. в кривые Бурместера.
При п = 5 точки и центры Бурместера
для пяти соседних положений подвижной
плоскости перейдут в точки того же
названия для пяти бесконечно близких
положений *).
Мы рассмотрели два крайних случая,
когда все положения соседние, или все
бесконечно близкие; С. А. Черкудинов [1]
рассмотрел и все промежуточные случаи,
когда дано несколько соседних и несколько бесконечно близких
положений подвижной плоскости.
Рис. 391.
Рис. 392.
П. Рассмотрим в качестве простейшего примера шарнирный
четырехзвенник А1АВВ1 (рис. 392) с длинами звеньев а, Ь, с, d=l
и с углами поворота вращающихся звеньев ср и ф, отсчитанными
от стойки. Мы имеем из рис. 392
хА= a cos ср, хв = d-\- с cosф,
У а — а sin Ъ У в ~с sin Ф»
*) Р. Бейер [2] систематически получает соотношения для случая
бесконечно близких положений подвижной плоскости путем указанного
предельного перехода из аналогичных соотношений для соседних положений.
384 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости ! [гл. XIII
откуда находим:
= {a cos ср — d — с cos ф)2 -f- (a sin ср — с sin ф)2.
Следовательно, мы приходим к уравнению
F(y, ty) — a2-\-c2-\-d2 — b<1 — 2ассо5(ф— ср) —
— 2adcos[ -|-2а/а)§ф = 0, (83.1)
определяющему угол ф как некоторую неявную функцию углх ср:
ф = ф (ср) = ф (ср; а, Ь. с), (83.2)
зависящую от трех параметров а, Ъ, с.
III. Предположим, что нам нужно построить механизм, в
котором ведомое звено для а ^ ср ^ (J вращалось бы по некоторому
заданному закону ф = Ф0(ср) (рис. 393). Мы видим, что при
помощи простейшего механизма—шарнирного четырехзвенника — мы не
V
о
ащ
Фп
Ф
Рис. 393.
ч
/3
-<р
сможем осуществить точно заданный закон движения, ибо заданная
функция Ф(ср) может не совпадать ни при каком выборе параметров
а, Ь, с ни с одной функцией семейства (83.2); следовательно,
пользуясь шарнирным четырехзвенником, мы не сможем точно
осуществить заданный закон; задачей приближенного синтеза
механизмов является такой подбор параметров а, Ь, с, при котср)м
значение функции Ф(ср;а, Ъ> с) будет в каком-то смысле
близким к значениям заданной функции Ф0(ср), т. е. функция Ф(ср)
будет являться каким-то приближением к функции Ф0(ср) на задан-
§ 83] МЕТОДЫ, ПРИМЕНЯЕМЫЕ В ЗАДАЧАХ СИНТЕЗА МЕХАНИЗМОВ 385
ном отрезке [а, р]; рассмотрим несколько способов такого
приближения.
А. Интерполирование с простыми узлами.
Так как функция (83.2) содержит три параметра а, Ъ, с, то для
их нахождения можно ее подчинить трем условиям', потребуем,
чтобы при трех заданных значениях срр ср2, ср3 угла ср угол ф имел
заданные значения фР ф2, Фз» т- е* потребуем выполнения равенств
Ф(срА; а, Ь, с) = Ф^к) = % (k=l, 2, 3),
а<ср1<ср2<ср3<р. (83.3)
Геометрически это означает, что при значениях ср ===== ср1ж ср2, ср3,
называемых узлами интерполирования, обе кривые ф = Ф0(ср) и
ф = Ф (ср) пересекаются (рис. 393).
Мы показали в § 81 решение этой задачи методом
геометрических мест] ее можно решить и чисто аналитическим.методом —
найти три параметра а, Ъ, с из трех уравнений (83.3). Совершенно
аналогично рассмотрим такую задачу: построить шарнирный
четырехзвенник А1АВВ1 с заданными неподвижными
шарнирами Av Bv для которого некоторая шатунная точка С
проходила бы через пять заданных точек С, Cv С2, С3, С4, лежа*
щих на одной заданной прямой g.
Мы видели в § 62, что при данных неподвижных шарнирах
шатунная кривая характеризуется пятью параметрами; требуя,
чтобы она проходила через пять заданных точек, мы снова имеем
интерполирование с пятью простыми узлами, ибо в точках С,
C'v .... С4 шатунная кривая должна пересекать данную прямую.
Таким образом, методы гл. XIII (т. е. рассмотрение соседних
положений подвижной плоскости) соответствуют интерполированию
с простыми узлами.
Б. Интерполирование с одним кратным узлом.
Предположим т п рь, что все три точней срх, ср2, ср3 (рис. 393)
совпали; в этом случае мы будем иметь при ср == сра один узел
третьей кратности, т. е. обе кривые ф = ф(ср)и ф = Ф0(ср) имеют
при ср = epj соприко уновение не ниже второго порядка (§ 57)
(рис. 394); это значит, что при ср = ср1 должны совпадать значения
этих обеих функций и их производных первых двух порядков, т. е.
Ф(ср1; а, Ь, с) = Ф0(ср1) = ф1,
Ф' (?1; а, Ь, с) = Ф'0 (срх) = ф; == v,
Ф" fa; а, Ь, с) = Ф0' (?1) = <|>;' = v',
386 СОСЕДНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. XIII
ибо передаточное число v и его производная v' определяются
формулами
:Ф'' / = 4^' = *,/ при ^ = cPi'
Мы пришли к задаче, рассмотренной в § 80: зная положение обоих
вращающихся звеньев, мы легко можем найти м. ц. в. Р\ число v
позволит найти точку Q, а число v'— угол между искомым
шатуном АВ и осью коллинеации PQ.
V
О
а
9}
А
<Р
Рис. 394.
Задачу можно решить и аналитически по формулам (83.1); так
как уравнение (83.1) определяет ф как неявную функцию ср, то
дифференцируем (83.1)
подставляя ср == срх. ф = фх, ф' = ф| = v, ф" = ф" = v', получим три
уравнения с тремя неизвестными а, Ъ% с. Совершенно аналогичную
картину мы имеем в задаче Лихтенхельдта (§ 79): шатунная
кривая должна иметь в данной точке соприкосновение пятого
порядка со своей касательной.
Так как в данной задаче ни один из шарниров не дан, но
известны прямые, на которых они лежат, то положение каждогЬ
шарнира определяется одним параметром, а положение точки
в шатунной плоскости — двумя параметрами) эти шесть
параметров находим из шести условий, обеспечивающих равенство в данной
точке ординат шатунной кривой и данной прямой и равенство нулю
первых пяти производных ординаты шатунной кривой по абсциссе.
Если же заданы три положения шатунной точки и направления
касательных в двух из них, то мы имеем задачу интерполирования
с тремя узлами, из которых один простой, а два двойных.
§ 83] МЕТОДЫ, ПРИМЕНЯЕМЫЕ В ЗАДАЧАХ СИНТЕЗА МЕХАНИЗМОВ 387
Таким образом, рассмотрение бесконечно близких положений
подвижной плоскости (т. е. методы гл. IX-XI) соответствует
интерполированию с кратными узлами.
В. Методы приближения Чебышева.
Метод интерполирования с простыми узлами обеспечивает
совпадение значений обеих функций в заданных узлах; при одном
кратном узле обе кривые весьма близко примыкают друг к другу
лишь в малой окрестности этого узла, однако в обоих случаях
мы не можем утверждать, что разность между функциями
Ф(ср) и Ф0(ср) будет на всем отрезке [а, (3] малой.
Назовем эту разность Дф = ф(ср)— Ф0(ср) и найдем ее максимум
Д на отрезке [а, р], т. е. максимальную погрешность при замене
функции Ф0(ср) функцией Ф(ср); она, конечно, зависит от того, какие
мы взяли значения параметров а, Ь, с\ подберем теперь такие
значения а*, Ь*, с* этих параметров, чтобы сделать величину Д
минимальной. Если теперь построить функцию Ф(ср; а*, Ь*, с*) с этими
значениями параметров и сравнить ее значения на отрезке [а, [3]
со значениями функции Ф(ср; а, Ъ% с) при любом другом подборе
параметров, то мы можем утверждать, что на отрезке [а, (3]
тах|Ф(ср; а*, £*, с*) |<тах| Ф (ср; а, Ъ, с)\,
т. е. максимальная погрешность приближения на отрезке [а, [3]
заданной функции Ф0 (ср) посредством функции Ф(ср; а*, Ь*, с)
меньше, чем та же максимальная погрешность при приближении
посредством любой другой функции Ф(ср; а, Ъ, с) этого семейства.
Функция Ф(ср; а*, Ь*, с*) называется наилучшим (в смысле Чебышева)
приближением функции Ф0(ср) на всем отрезке [а, (3] *) Это
приближение в окрестности каждой точки дает погрешность большую,
чем интерполяционное приближение с кратным узлом, но
максимальная погрешность на всем отрезке при наилучшем приближении
меньше, чем при любом другом приближении. Однако, к сожалению,
задача нахождения наилучшего приближения часто представляет
непреодолимые математические трудности.
Гораздо проще находить наилучшее среднее приближение —
под этим понимается такой подбор параметров, при котором
обращается в минимум так называемая средняя квадратическая
погрешность
*) В работе 3. Ш. Блоха и Н. Н. Иващенко [1] читатель найдет
решение задачи синтеза крана Демаг по методу наилучшего приближения.
388 СОЕДИНЕНИЕ ПОЛОЖЕНИЯ подвижной плоскости [гл. XIII
Дифференцируя это выражение по всем параметрам и приравнивая
производные нулю, мы получим столько уравнений, сколько имеем
параметров.
Эти два метода приближения являются чисто аналитическими;
их применение к синтезу механизмов разработаны советскими
учеными 3. Ш. Блохом, Н. И. Левитским, Г. Г. Барановым,
С. А. Черкудиновым и др.
Автор применил эти методы Чебышева к задаче
уравновешивания механизмов.
ЛИТЕРАТУРА
I. Алфавитный список
Альт X. (Alt Н.)
1. Zur Synthese der ebenen Mechanismen, Zeitschr. fur angew. Math, und
Mech., 1921.
Артоболевский И. И.
1. Геометрические методы решения некоторых задач теории плоских
механизмов, Труды семинара по ТММ, 1947, т. 1, вып. 3.
2. Теория механизмов и машин, ГТТИ, 1953.
3. Теория механизмов для воспроизведения плоских кривых, Изд-во
АН СССР, 1959.
Артоболевский И. И., Блох 3. Ш., Добровольский В. В.
1. Синтез механизмов, ГТТИ, 1944.
Артоболевский И. И., Левитский Н. И., Черкудинов С. А.
1. Синтез плоских механизмов, Физматгиз, 1959.
Бейер P. (Beyer R.)
1. Technische Kinematik, Leipzig, 1931.
2. Кинематический синтез механизмов, Машгиз, 1959.
Блашке В., Мюллер Г. (Blaschke W., Muller Н. R.)
1. Ebene Kinematik, Munchen, 1956.
Блох 3. Ш.
1. Проектирование плоских механизмов с низшими парами, Москва, 1941 #
2. Основные результаты работ П. Л. Чебышева по метрическому син-*
тезу плоских механизмов, «Научное наследие Чебышева», II, Изд-во
АН СССР, 1945.
3. Приближенный синтез механизмов, Машгиз, 1948.
Блох 3. Ш. и Иващенко Н. Н.
1. Применение метода Чебышева к расчету поворотных кранов с
уравнительным полиспастом, Сборник «Регулирование машин и синтез
механизмов», Машгиз, 1950.
Бурместер Л. (Burmester L.)
I. Lehrbuch der Kinematik. Leipzig, 1888.
Владимирский Г. A.
1. Перспектива, Учпедгиз, 1958.
390
ЛИТЕРАТУРА
Вольберг О.
1. Основные идеи проективной геометрии, ОНТИ, 1935.
Вяхирев С. В.
1. Кинематика механизмов (отд. IV), ОНТИ, 1935.
2. Автоматы и полуавтоматы (ч. 1), ГНТИ, 1939.
Геронимус Я. Л.
1. Нахождение профиля кулачка по заданному закону движения
толкателя, Техника воздушного флота, № 3, 1933.
2. О применении методов Чебышева к задаче уравновешивания
механизмов, ГТТИ, 1948.
3. Динамический синтез механизмов по Чебышеву, Изд. Харьк. гос.
университета, 1958.
4. О нахождении точек Бурместера в случае распадения обеих кривых
Бурместера, Труды семинара по ТММ, т. XXII, вып. 85—86, 1961.
Гиршвальд Л. Я.
1. Проективная геометрия, ГНТИУ, 1935.
Гроше Г. (Grosche G.)
1. Projektive Geometrie, I, II части, Leipzig, 1957.
Делeман K.
1. Проективная геометрия в синтетическом изложении, Харьков, 1908.
Дзиобек О.
1. Курс аналитической геометрии, ч. I, Одесса, 1911.
Добровольский В. В.
1. Теория механизмов для образования плоских кривых, Изд-во АН СССР,
1953.
Дыдырко В. К.
1. Циркулярные кривые 3-го порядка, Працы БДУ, № 17—18, Минск,
1928.
Ефимов Н. В.
1. Высшая геометрия, ГТТИ, 1953.
Жуковский Н. Е.
1. Приложение теории центров ускорений высших порядков к
направляющему механизму Чебышева, Собр. соч., т. I, 1948.
Зикер К. (Sieker К. Н.)
1. Zur algebraischen Mafisynthese ebener Kurbelgetriebe, Ingr. Arch,
т. XXIV, вып. 3, 4, 1956.
Картер У. (Carter W.)
1. Kinematic analysis and synthesis using collineation-axis equation, Trans,
ASME, NF-4, 1956.
ЛИТЕРАТУРА
391
Клейн Ф.
1. Элементарная математика с точки зрения высшей, т. II, ОНТИ, 1934.
Кожевников С. Н. _.
1. Теория механизмов и машин. Машгиз, 1954.
Кокстер X. С. М.
1. Действительная проективная плоскость, Физматгиз, 1959.
Котельников А. П.
1. Точки Бурместера, их свойства и построение, Матем. сб., 1927, т. 34,
205—348.
Левитский Н. Н.
1. Синтез механизмов по Чебышеву, Изд-во АН СССР, 1946.
2. Проектирование плоских механизмов с низшими парами, Изд-во
АН СССР, 1950.
Лихтенхельдт В. (Lichtenheldt W.)
1. Konstruktionstafeln fur Lenkergeradefuhrungen, Wiss. Zeitschr. Techn.
Hochsch. Dresden, 7, 1957—1958.
2. Konstruktionslehre der Getriebe, Berlin, 1961.
Лориа Дж. (Loria Gino)
1. Spezielle algebraische und transzendente ebene Kurven, (Глава II),
Leipzig, 1902.
Лузин H. H.
1. Дифференциальное исчисление, M., Советская наука, 1949.
Мейер Цур Капеллен В.
1. Математические инструменты, ИЛ, 1950.
Мерцалов Н. И.
1. Кинематика механизмов, М., 1916.
Мусхелишвили Н. И.
1. Курс аналитической геометрии, ГТТИ, 1947.
Мюллер P. (Muller R.)
1. Einfuhrung in die theoretische Kinematlk, Berlin, 1932.
Пёшль Т. (Poschl Т.)
1. Einfuhrung in die ebene Getriebelehre, Berlin, 1932.
Pау К. (Rauh K.)
1. Praktische Getriebelehre, Berlin, 1931.
Рашевский П. К.
1. Курс дифференциальной геометрии (гл. I—III), ГТТИ, 1956.
Сальмон Г. (Salmon G.)
1. Analytische Geometrie der Kegelschnitte (I, II части), Teubner, 1907.
392 ЛИТЕРАТУРА
СмогоржевскийА. А.
1. Линейка в геометрических построениях, ГТТИ, 1957.
Уокер Р.
1. Алгебраические кривые, ИЛ, 1952.
Фрейденштейн Ф. (Freudenstein F.)
1. On the maximum and minimum velocities and the accelerations in four-
link mechanisms, Trans. ASME, 78, 1956.
Хакмюллер Э. (Hackmuller E.)
1. Eine analytisch durchgefuhrte Ableitung der Kreispunkts-und Mittel-
punktskurve, Zeitschr. fur angew. Math, und Mech., 1938.
Чебышев П. Л.
1. О простейших параллелограммах, симметрических около одной оси,
Поли. собр. соч., т. IV, 1948.
Чезаро Э.
1. Элементарный учебник алгебраического анализа и исчисления
бесконечно малых, Одесса, 1914.
Черкудинов С. А.
1. Синтез плоских шарнирно-рычажных механизмов, Изд-во АН СССР.
1959.
Черкудинов С. А. и Сперанский Н. В.
1. Синтез четырехзвенных передаточных механизмов посредством
интерполяционного приближения с одним узлом высокой кратности, Труды
семинара по ТММ, 1957, т. XVII, вып. 67.
Четверухин Н. Ф.
1. Введение в высшую геометрию, Учпедгиз, 1934.
Юдин В. А.
1. Механизмы приборов, Машгиз, 1949.
II. Литература по отдельным вопросам
Общие вопросы геометрии
Ефимов [1]; Клейн [1].
Аналитическая геометрия
Дзиобек [1]; Мусхелишвили [1]; Сальмон [1].
Проективная геометрия
Вольберг [1]; Гиршвальд [1]; Гроше [1]; Делеман [1]; Кокстер [1]; Четве-
рухин [1].
Дифференциальная геометрия
Рашевский [!}; Чезаро [1].
ЛИТЕРАТУРА 393
Алгебраические кривые
Дыдырко [1]; Лориа [1]; Уокер [1].
Кинематика
Бейер [1]; Блашке и Мюллер [1]; Бурместер [1]; Мюллер [1].
Кинематика механизмов
Артоболевский [1], [2]; Добровольский [1]; Мерцалов [1]; Пёшль [1].
Синтез механизмов
Артоболевский, Блох, Добровольский [1]; Артоболевский, Левитский,
Черкудинов [1]; Бейер [2]; Блох [1], [2], [3]; Вяхирев [1], [2]; Герони-
мус [2], [3]; Левитский [1], [2]; Pay [1]; Черкудинов [1].
ИМЕННОЙ
Альт X . (Alt Н . ) 7 , 373 , 388
Артоболевский И . И . 147 , 172 , 174 ,
175 , 193 , 208 , 282 , 284 , 293 , 351 , 373 ,
378 , 388 , 392
Баранов Г . Г . 387
Бейер P . (Beyer R . ) 7 , 106 , 130 , 141 ,
147 , 175 , 189 , 252 — 254 , 273 , 275 ,
290 , 297 , 322 , 373 , 378 , 383 , 388 , 392
Блашке В . (Blaschke W . ) 388 , 392
Блох 3 . Ш . 6 , 193 , 208 , 373 , 378 ,
386 — 388 , 392
Бурместер Л . 6 , 7 , 30 , 189 , 221
Владимирский Г . А . 156 , 388
Власов А . К . 107
Вольберг О . 389 , 391
Вяхирев С . В . 7 , 378 , 389 , 392
Геронимус Я . Л . 346 , 389 , 392
Гиршвальд Л . Я . 389 , 391
Гроше Г . (Grosche G . ) 389 , 391
Делеман К . 389 , 391
Дзиобек О . 389 , 391
Добровольский В . В . 7 , 37 , 80 , 106 ,
107 , 112 , 172 , 193 , 226 , 311 , 373 , 378 ,
388 , 389 , 392
Дыдырко В . К . 389 , 392
Ефимов Н . В . 389 , 391
Жуковский Н . Е . 352
Зикер К . (Siker К . Н . ) 208 , 389
Иващенко Н . Н . 386 , 388
Картер У . (Carter W . ) 346 , 366 , 389
Клейн Ф . (Klein F . ) 390 , 391
Кожевников С . Н . 288 , 390
Кокстер X . С . М . 390 , 391
Котельников А . П . 7 , 8 , 30 , 63 , 65 ,
240 , 312 , 338 , 342 , 344 , 347 , 349 , 359 ,
390
Краус Р . 7
УКАЗАТЕЛЬ
Левитский Н . И . 6 , 208 , 351 , 387 , 388 ,
390 , 392
Липкин 175
Лихтенхельдт В . (Lichtenheldt W . J
7 , 8 , 329 , 390
Лориа Дж . (Loria Gino) 390 , 392
Лузин Н . Н . 31
Мейер Цур Капеллен В . 147 , 173 ,
390
Мерцалов Н . И . 325 , 390 , 392
Мусхелишвили Н . И . 390 , 391
Мюллер Г . (Muller Н . R . ) 7 , 322 , 388 ,
390 , 392
Ньютон И . (Newton I . ) 80 , 170
Пёшль Т . (Poschl Т . ) 390 , 392
Pay К . (Rauh К . ) 272 , 390 , 392
Рашевский П . К . 390 , 391
Роденберг 326
Сальмон Г . (Salmon G . ) 390 , 391
Смогоржевский А . А . 162 , 391
Сперанский Н . В . 361 , 382 , 391
Уокер Р . 22 , 37 , 391 , 392
Фрейденштейн Ф . (Freudenstein F . )
364 , 391
Хакмюллер Э . (Hackmuller Е . ) 379 ,
391
Чаплыгин С . А . 169
Чебышев П . Л . 6 , 175 , 273 , 359 , 391
Чезаро Э . (Cesaro Е . ) 391
Черкудинов С . А . 6 , 208 , 351 , 361 ,
378 , 379 , 382 , 383 , 387 , 388 , 391 ,
392
Четверухин Н . Ф . 155 , 156 , 392
Эйлер Л . (Euler L . ) 310
Юдин В . А . 147 , 172 , 175 , 391
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Антипараллелограмм шарнирный 304
Антиподера 285
Антиполюс 106
Антиполяра 106
Асимптота 31
— кривой Бурместера вещественная
227
— круговая 33
— мнимая 32
Асимптоты гиперболы 110 , 113 , 123
— кривой третьего порядка
циркулярной 203 , 204
Аффинографы 147
Вершины , определяющие фокальную
кривую 223 и д .
— противоположные полного
четырехсторонника 186
Геометрия аффинная 161
— метрическая 161
— проективная 9 , 161
Гипербола 26 , 103 , 110 , 194 , 195
Гиперголограф Верховского 173
Группа прямых гармоническая 57
— точек гармоническая 41
Движение обращенное 308
Диагональ полного
четырехсторонника 186
четырехугольника 184
Диаметр конического сечения 103
Директриса конического сечения 111 ,
113
Задача Лихтенхельдта 329 , 351 , 353 ,
359
Изображение перспективное 156 , 160
окружности 160
Инверсия 167 , 168
— кривой Бурместера 169
— параболы 169
Инверсор 174
Инволюция 48 , 60 , 65
Инволюция гиперболическая 49 , 61 ,
106 , 110 , 143
— параболическая 50 , 61 , 111 ,
143
— эллиптическая 50 , 61 , 106 , 110 , 143
Интерполирование с одним кратным
узлом 385
— с простыми узлами 384
Инцидентность прямой и точки 66
Касательная к алгебраической
кривой в бесконечности 32
— к коническому сечению 121 и д .
— к центроиде полюсная 291
Касательные к параболе 125
— к центральным кривым 123
Класс алгебраической кривой 37 , 84
Коникограф 80 , 112 , 172
Координаты однородные 11
Кривая алгебраическая 18 , 84
второго порядка 19 , 26 , 75 — 77
первого порядка 19
, порядок ее 18
— бициркулярная 30
— Бурместера 30 , 166 , 226 и д . , 230 ,
264
— гиперболического типа 24
— дискриминантная однопараметри -
ческого семейства 278
— круговых точек 318
— параболического типа 24
— соприкасающаяся 247
— трансцендентная 18
— третьего порядка 201
циркулярная 202
параболического типа 209
, уравнение каноническое
204
1— общее 204
— трициркулярная 30
— фокальная 207 , 210
— центров 320
— циркулярная 30
— шатунная механизма 272
— эллиптического типа 24
Кривизна кривой 249
в особой точке 266
396
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Кривизна сопряженных рулетт 310
— эволюты 268
Кривые взаимно огибающие 290
— эквидистантные 281
Линия горизонта 157
— нейтральная 108
— нулевая 28
— средняя кривой третьего порядка
циркулярной 205
фокальной кривой 214
Метод аналитический построения
кривых Бурместера 329
— дополнительных групп 293
— Котельникова графического
определения кривой Бурместера 240 ,
241
— синтеза механизмов
аналитический 6
геометрический 6
Методы геометрические построения
кривых Бурместера 231 , 331
фокальной кривой 218 и д .
— приближения Чебышева при
синтезе механизмов 386
Механизм зубчатый планетарный 253
— коникографа 80 , 112 , 172
— кривошипно - шатунный 15 , 272 ,
276
— кулачковый с плоским толкателем
286 и д .
— пантографа 147
— передаточный 360 и д
— поляриографа 107
— с остановками 354
— центроидографа 293
— шарнирного антипараллелограмма
304
параллелограмма 304
четырехзвенника 15 , 188 , 275 ,
299 , 326 , 349 , 354 , 373
предельный 304
Направление асимптотическое
алгебраической кривой 23
Нахождение мгновенного центра
вращения 14
Нормаль центроиды полюсная 291
Огибающая семейства кривых 279
Окружность Аполлония 141 , 316
— , описанная вокруг треугольника
129 и д .
Окружность перемены (окружность
Бресса) 315
— поворотная (окружность Лягира)
294 , 296
— соприкасающаяся 249
— устойчивости 297
Определение кривой Бурместера
аналитическое 231 ид .
геометрическое
второго класса пятью
касательными 114 и д .
порядка пятью точками 74
и д .
Ортоцентр треугольника 55 , 130 , 131
Основание ряда точек 44
Ось коллинеации 299 , 300
— радикальная двух окружностей
loo
концентрических 133
неконцентрических 133
— симметрии центрального
конического сечения 110
— фокальная 226
кривой Бурместера 227
Отношение ангармоническое четырех
прямых 56
точек 41 , 43
окружности 63
Отрезок кривой простой 261
Пантограф 147
Парабола 103 , 125 и д . , 194 , 195
— соприкасающаяся 251
Пара противоположных сторон
полного четырехугольника 183
— - противополюсов 188
Параллелограмм шарнирный 304
Пары прямых , не разделяющие друг
друга 58
, разделяющие друг друга 58
— точек , не разделяющие друг
друга 43
, разделяющие друг друга 42
Пересечение алгебраических кривых
19 , 21
— алгебраической кривой с
бесконечно удаленной прямой 23
с мнимой прямой 26
— кривой второго порядка с
бесконечно удаленной прямой 24
Перспектива 156
Плоскость картинная 156
— предметная 157
— проективная 13
— шатунная 272
Подера 283
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
397
Под ер а гиперболы 284
— параболы 285
— эллипса 284
Положения подвижной плоскости
соседние 349
Поляра 99
Полюс 99 , 188
— поворота 292
— тангенциальный 315
Поляриограф 107
Порядок алгебраической кривой 18 ,
84
— соприкосновения плоских кривых
243 , 245
Построение Гартмана скорости
перекатывания центроид 301 ид .
— гиперболы 194 , 195
— конического сечения 182 , 198 и д .
по пяти касательным 190
■ по пяти точкам 190
— кривой Бурместера 231 и д . , 329
и д .
при помощи двух
проективных пучков окружностей 228
пучка окружностей и
проективного пучка прямых 228
— окружности , принадлежащей
данному пучку 139
— параболы 194 , 195
— поворотной окружности 298
— полюса 196
— поляры 196
— фокальной кривой 219
при помощи двух
проективных пучков окружностей 219
пучка окружностей и
проективного пучка прямых 220
— циркулярной кривой третьего
порядка 205
— эллипса 194
Преобразование «гиперболизм» 169
— Котельникова 51 , 165 , 166 , 229
— кривой Бурместера в окружность
229
в параболу 230
в прямую 229
в равностороннюю
гиперболу 229
— проективное 148 , 150 , 153
— точечное 145
аффинное 147 , 150 , 154
движения 146
изометрическое 146 , 150
Принцип двойственности в геометрии
70 , 88
Проектирование параллельное 155
Проекция параллельная 45
— центральная 45 , 151
Прямая бесконечно удаленная — см .
Прямая несобственная
— изотропная 27 , 28
— мнимая 25
— направляющая преобразования
кривой Бурместера в прямую 229
— несобственная 13
— проективная 10
— Симпсона 64
— собственная 13
— соприкасающаяся 248
Прямые главные квадратичного
соответствия 171
— двойные 179 и д .
— мнимые сопряженные 25
Пучки кривых проективные 71
— прямых перспективные 59 , 176 и д .
проективные 59 , 176 и д .
Пучок кривых 71
второго порядка 72
, свойства полярные 103
, основные кривые 71
— окружностей 137
параболический 137
, сопряженный с данным 139 ,
140 , 141
эллиптический 137
— прямых 10
Радиус кривизны 249
Распадение алгебраической кривой 19
второго порядка 20 , 26 , 27
— кривой Бурместера 228 , 325 и д . ,
345
, случай Чебышева 347
фокальной 215
на бесконечно удаленную
прямую и равностороннюю
гиперболу 225
на прямую и бесконечно
удаленную прямую 224
на прямую и окружность
222
Рулетта 289 , 312
— , сопряженные рулетты 290
Ряды точек перспективные 44 , 176
и д .
подобные 40 -
проективные 46 , 176 и д .
Свойства ангармонического
отношения четырех прямых 58
точек 42
— аффинные 161
398
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Свойства дробно - линейной функции
38
— линейной функции 40
— метрические 161
— полного четырехсторонника 186
и д . , 189
четырехугольника 184 и д . , 189
— полярные пучка кривых второго
порядка 103
— проективные 161
— пучка окружностей 136
— фокальной кривой 218 , 223
Сечения конические 15 — 17 , 27 , 123
Синтез механизмов ,
интерполирование с одним кратным углом 385
с простыми узлами 384
кулачковых с плоским
толкателем 286 и д .
, метод приближения Чебышева
386
• передаточных 360 и д .
с остановками 354
Скорость перекатывания центроид
292 , 301 ид .
Случай Чебышева пятого порядка
358
Соответствие инволюционное 48 , 142
и д .
— квадратичное 165
, геометрический метод 170
— полярное 99
— проективное пучков на одном
основании 60
рядов точек на одном
основании 47
— точек взаимно однозначное 145
Соприкосновение кривых 243 , 248
Степень точки относительно
окружности 132
Строфоида косая 227
— прямая 227
Теорема Безу 21
— Бобиллье 299
— Брианшона 116 , 117
— Гаусса 187
— Кеннеди — Аронгольда 15
— Котельникова 344
— Ньютона 187
— Паскаля 93 , 94
— Штейнера 78
Теоремы Аронгольда 307 , 308
Теория перспективы 156 и д .
Точка бесконечно удаленная — см .
Точка несобственная
Точка Болла 323 , 324 , 329
— возврата I рода 267
II рода 267
— диагональная полного
четырехугольника 184
— зрения 156
— кривой двойная 262
изолированная 263
круговая 250
несобственная 9 , 10 , 23
особая 262 , 265
— — узловая 263
— несобственная кривой 23
плоскости 14
~ прямой 9 , 10
— перегиба 248 , 250 , 268
— проективного соответствия двои -
ная 47
мнимая 48
— распрямления 248 , 250
— самоприкосновения 263
— собственная прямой 12
— характеристическая однопарамет -
рического семейства кривых 277 ,
278
— циклическая плоскости 30
— Чебышева 347
— шатунная 272
Точки Бурместера 339 , 378
пятого порядка 356
— , гармонически сопряженные 41
— главные квадратичного
соответствия 171
— двойные 179 и д .
— диагональные полного
четырехсторонника 186
— инволюции двойные 49
— , соответствующие друг другу
вдвойне 48
шарнирного четырехзвенника
299
— сопряженные 100
Треугольник полюсный 370
Угол между двумя прямыми 59
Уравнение алгебраической кривой в
однородных координатах 23
— конического сечения в
тангенциальных координатах 86
в точечных координатах 86
— кривой естественное 254
— подеры 284
— прямой 13
— пучка прямых 54
Уравнение фокальной кривой 211
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
399
Уравнение фокальной кривой в
комплексной форме 210
— шатунной кривой шарнирного че -
тырехзвенника 275
Ускорение точки подвижной
плоскости 314
касательное 314 , 315
редуцированное 312
Условие перспективности
проективных пучков прямых 176
рядов точек 176
Фокус конического сечения 111
— кривой 28
— особый 32
Формула Эйлера 296
— Эйлера . — Савари 307
Формулы Плюккера 37
Функция дробно - линейная 38
— линейная 40
Центр инволюции 49
— конического сечения 103 , 113
Центр кривой Бурместера 227
третьего порядка
циркулярной 204
— оптический 155
— перспективы 44
— радикальный трех окружностей 134
— ускорений мгновенный 315
— фокальный 32 , 213
Центроида неподвижная 290 и д .
— подвижная 290 и д .
Центроидограф 293
Центры Бурместера 340 , 378
Четырехсторонник полный 186 и д .
Четырехугольник полный 183 и д .
Шестисторонник , описанный вокруг
конического сечения 116
Эллипс 103 , 195
— соприкасающийся 252
Геронамус Яков Лазаревич.
Геометрический аппарат теории синтеза
плоских механизмов.
М„ Физматгиз, 1962 г., 400 стр. с илл.
(Серия «Физико-математическая библиотека
инженера»)
Редактор Сперанский Н. В.
Техн. редактор Мурашова Н. #.
Корректор Серкина А. Ф.
Сдано в набор 23/Н 1962 г. Подписано к
печати 16/VI 1962 г. Бумага 60x90Vi«.
Физ. печ. л. 25. Условн. печ. л. 25.
Уч.-изд. л. 24,66. Тираж 5000 экз. Т-02795.
Цена 1 р. 38 к. Заказ № 217.
Государственное издательство физико-
математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой
УПП Ленсовнархоза.
Ленинград, Измайловский пр., 29.