Автор: Артоболевский И.И. Левитский Н.И. Черкудинов С.А.
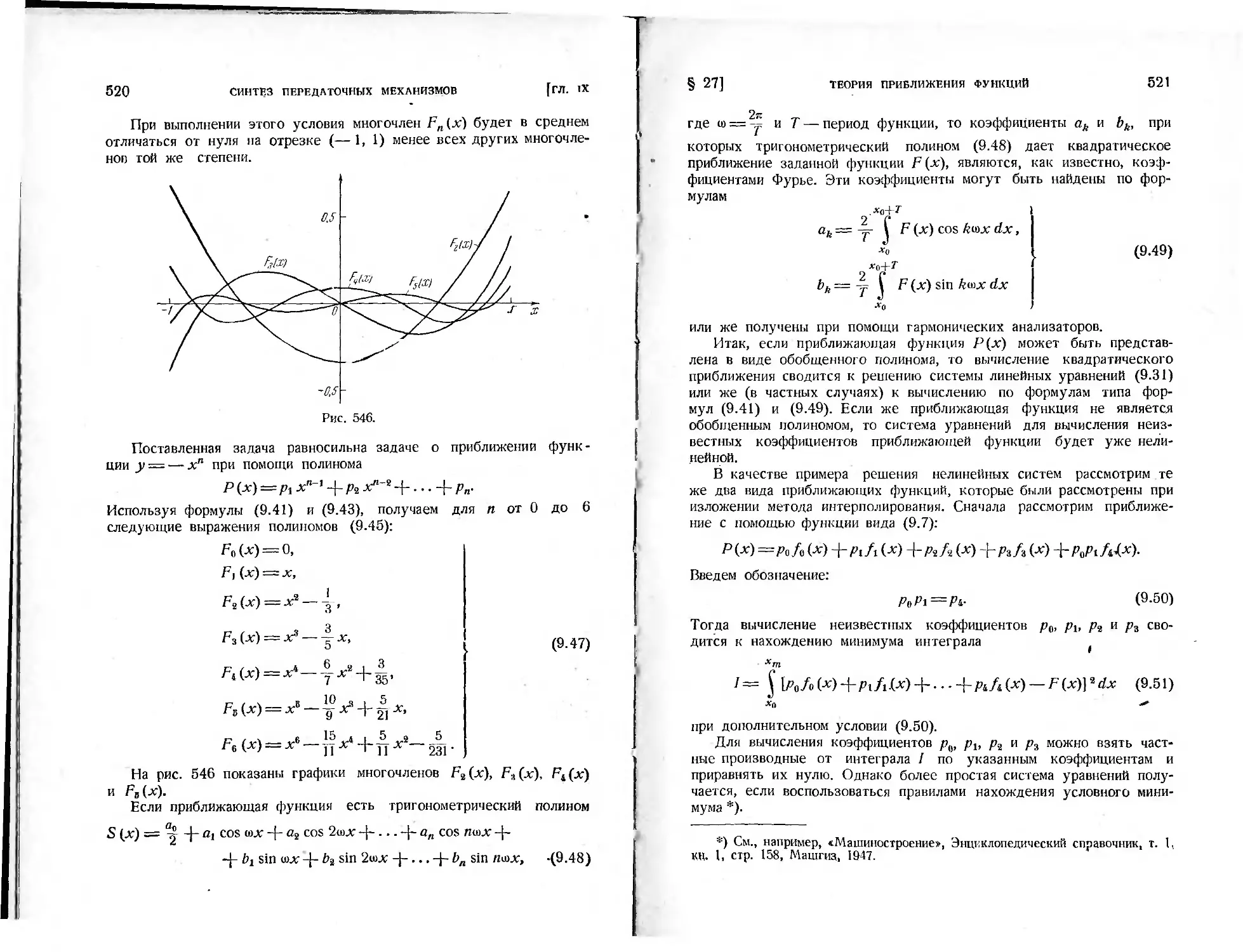
Теги: машиностроение механика кинематика синтез плоские механизмы
Год: 1959
Текст
34 рбОк.
и4АЖРКУ,ДДП0В
ДИ.Й.АРТОБОЛЕБСКИЙ,Ш1.ЛЁБИТСКИЙ
ни.левигскии
11С.АЧ1 рщино;
г
№
К* •
-1
СИНТЕЗ
lc> irn-'.З’ .
I ';b 11ЦТАОСК ИХ МЕХАНИЗ?10В
X7 НИ J>t
195',
И. И. АРТОБОЛЕВСКИЙ,
Н. И. ЛЕВИТСКИЙ, С. А. ЧЕРКУДИНОВ
СИНТЕЗ
ПЛОСКИХ МЕХАНИЗМОВ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА-1959
12-5-4
Артоболевский Иван Иванович, Левитский Нико гай Иванович,
Черкудинов Сергей Александрович
Синтез плоских механизмов
Редактор Кобринский А. Е.
Тех. редактор Муратова Н. Я. Корректор Бакулова А. С.
Сдано в набор 10/XII 1958 г. Подписано к печати 4/V1 1959 г. Бумага 60X921/16* Физ. печ.
л. 67,75. Условн. печ. л. 67,75. Уч.-изд. л. 65,84. Тираж 10000. Г-06314. Цена книги 34руб. 90 коп.
Заказ № 577
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградский Совет народного хозяйства. Управление полиграфической промышленности.
Типография № 1 «Печатный Двор» имени А. М. Горького. Ленинград, Гатчинская, 26.
ОГЛАВЛЕНИЕ
Предисловие..................................................... 6
Введение...................................................... 11
ЧАСТЬ первая
НЕКОТОРЫЕ СВЕДЕНИЯ ПО ТЕОРИИ СТРУКТУРЫ
И КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ МЕХАНИЗМОВ
Глава 1. Основные виды плоских механизмов и их структура ... 27
§ 1. Трехзвенные механизмы................................. 27
§ 2. Четырехзвенные механизмы................................ 44
§ 3. Пятизвенные механизмы................................... 62
§ 4. Шестизвенные механизмы.................................. 67
Глава И. Введение в кинематическую геометрию механизмов .... 70
§ 5. Некоторые сведения по кинематической геометрии на плоскости . . 70
§ 6. Метод дополнительных групп в решении задач кинематической гео-
метрии механизмов............................................ 87
часть вторая
ТЕОРИЯ ТОЧНЫХ МЕТОДОВ СИНТЕЗА МЕХАНИЗМОВ
Глава III. Синтез трехзвенных центроидных механизмов..........117
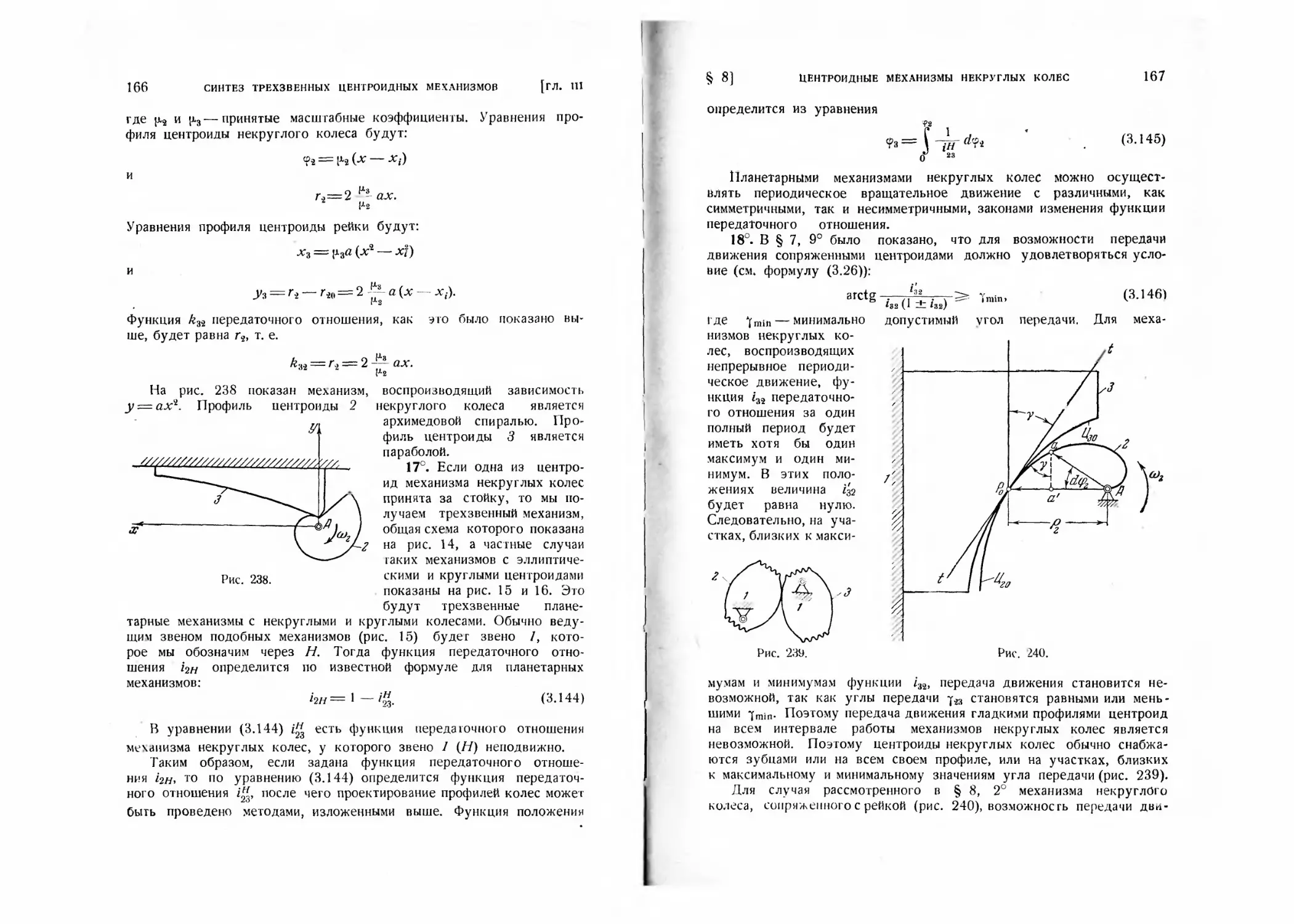
§ 7. Общий случай центроидного механизма................... 117
§ 8. Центроидные механизмы некруглых колес................. 134
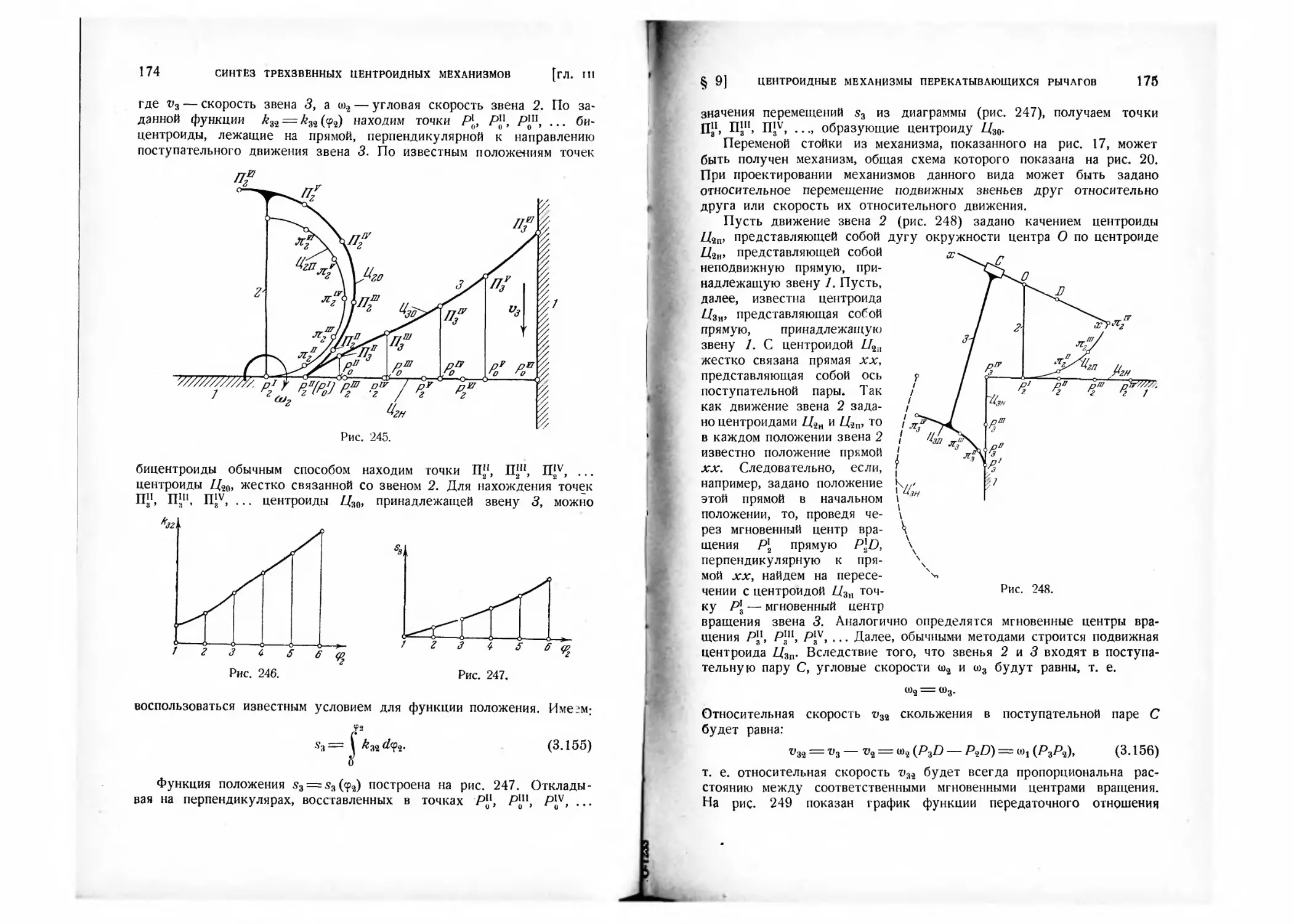
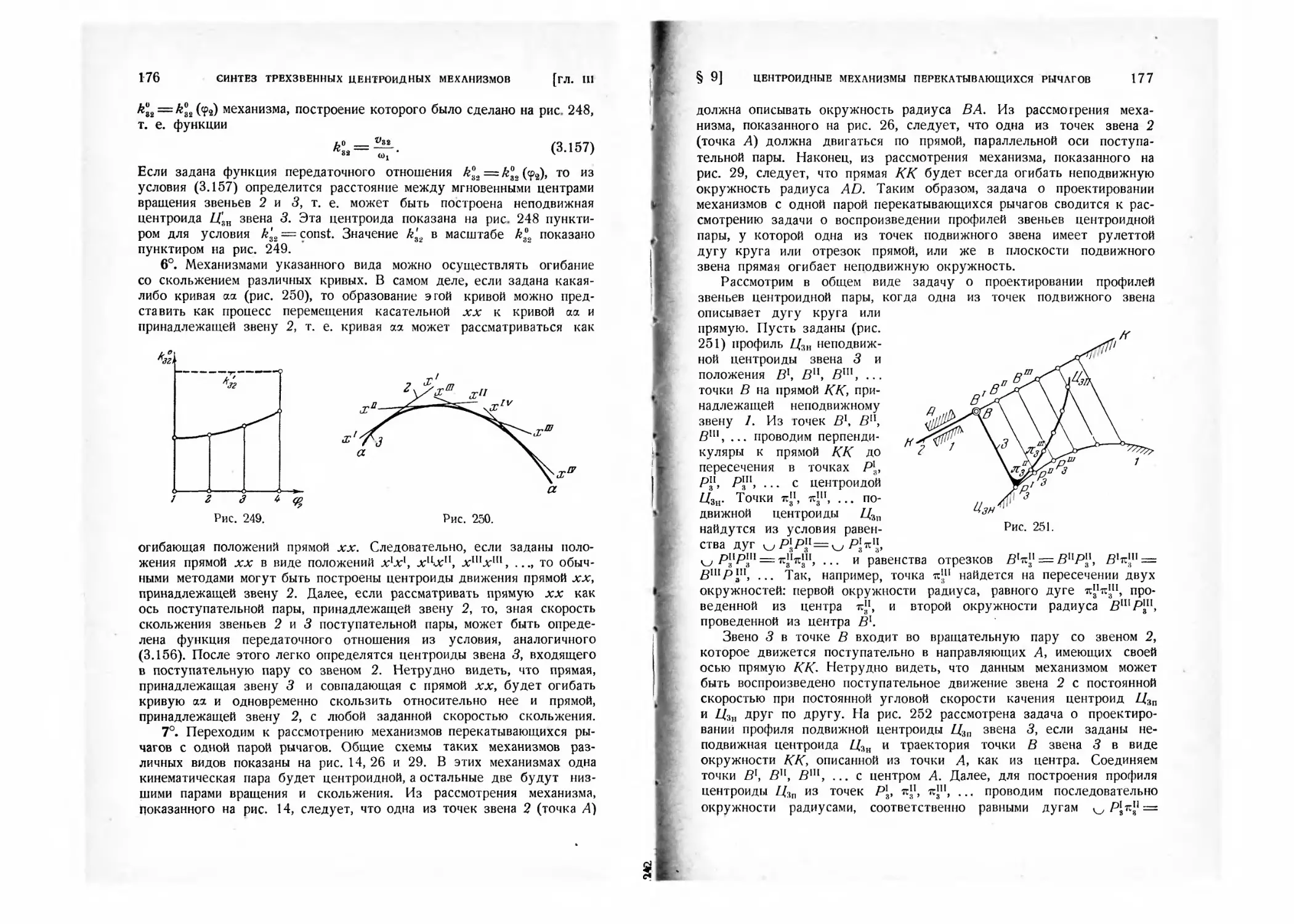
§ 9. Центроидные механизмы перекатывающихся рычагов........ 169
Глава IV. Синтез трехзвенных механизмов с центроидной парой
и парой качения и скольжения................................. 182
§ 10. Механизмы с одной и двумя центроидными парами.........182
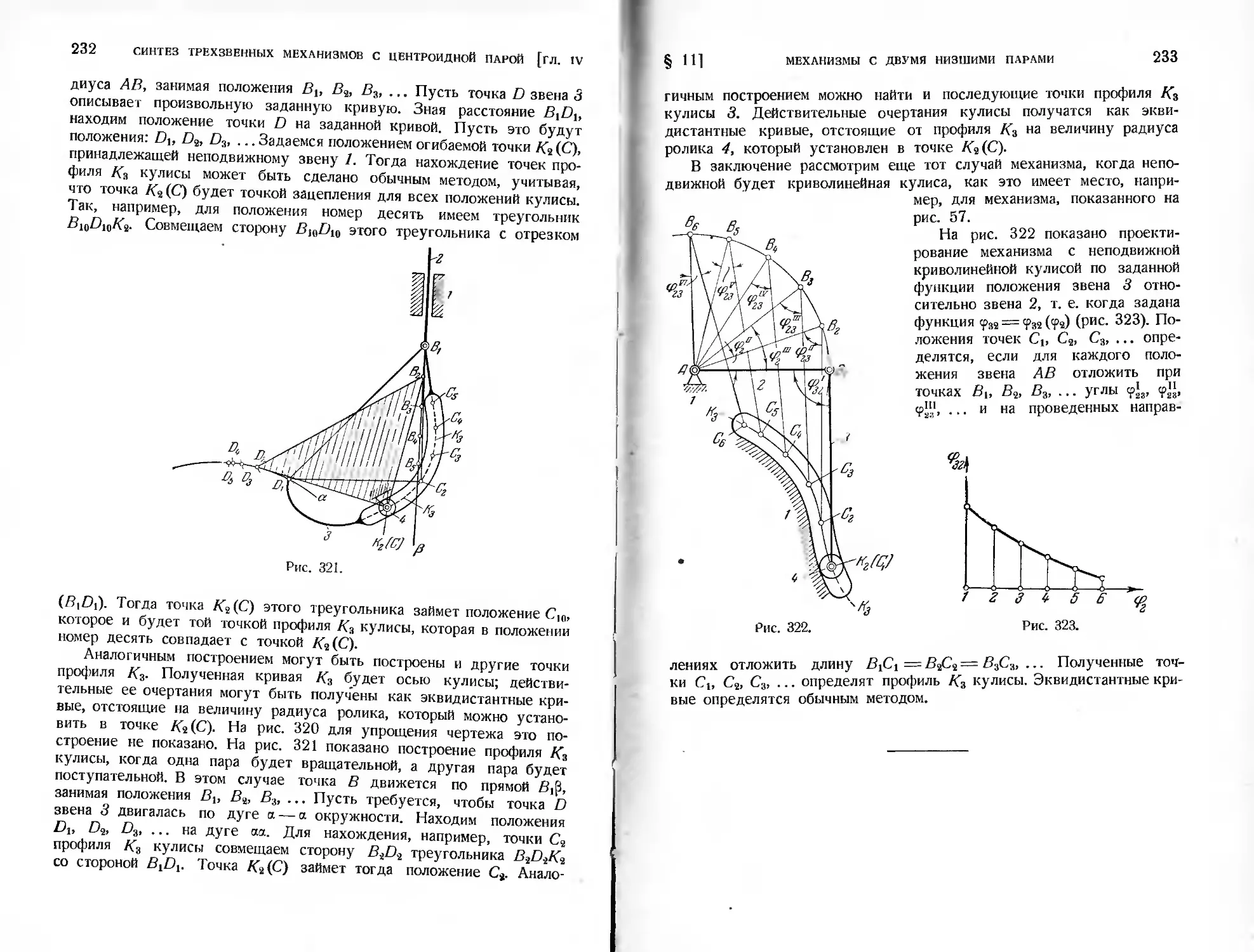
§ 11. Механизмы с двумя низшими парами......................196
Глава V. Синтез многозвенных механизмов с центроидными парами
и парами качения и скольжения................................ 234
§ 12. Четырехзвенные механизмы с центроидными парами........234
§ 13. Четырехзвенные механизмы с парами качения и скольжения .... 236
§ 14. Пятизвенные механизмы с парами качения и скольжения...241
Глава VI. Некоторые задачи синтеза механизмов с низшими парами
для точного воспроизведения кривых .............................260
§ 15. Общие методы решения.....................................260
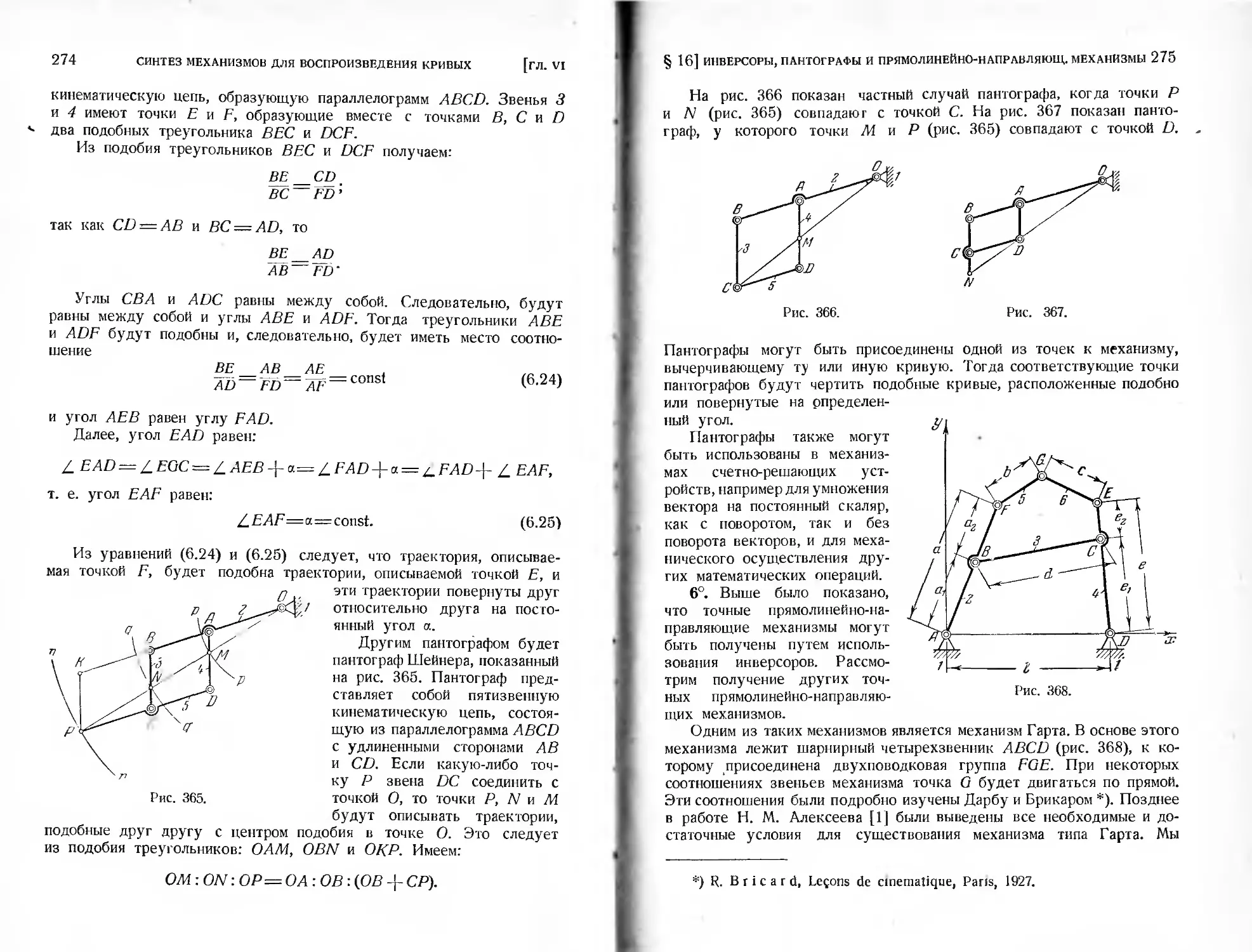
§ 16. Инверсоры, пантографы и точные прямолинейно-направляющие ме-
ханизмы .......................................................265
4
ОГЛАВЛЕНИЕ
& 17 Механизмы для черчения и огибания конических сечении....277
§ 18 * Механизмы для черчения и огибания некоторых кривых высших
порядков ....................................... ........... 300
§ 19. Механизмы для воспроизведения различных функциональных зави-
симостей ...................................................319
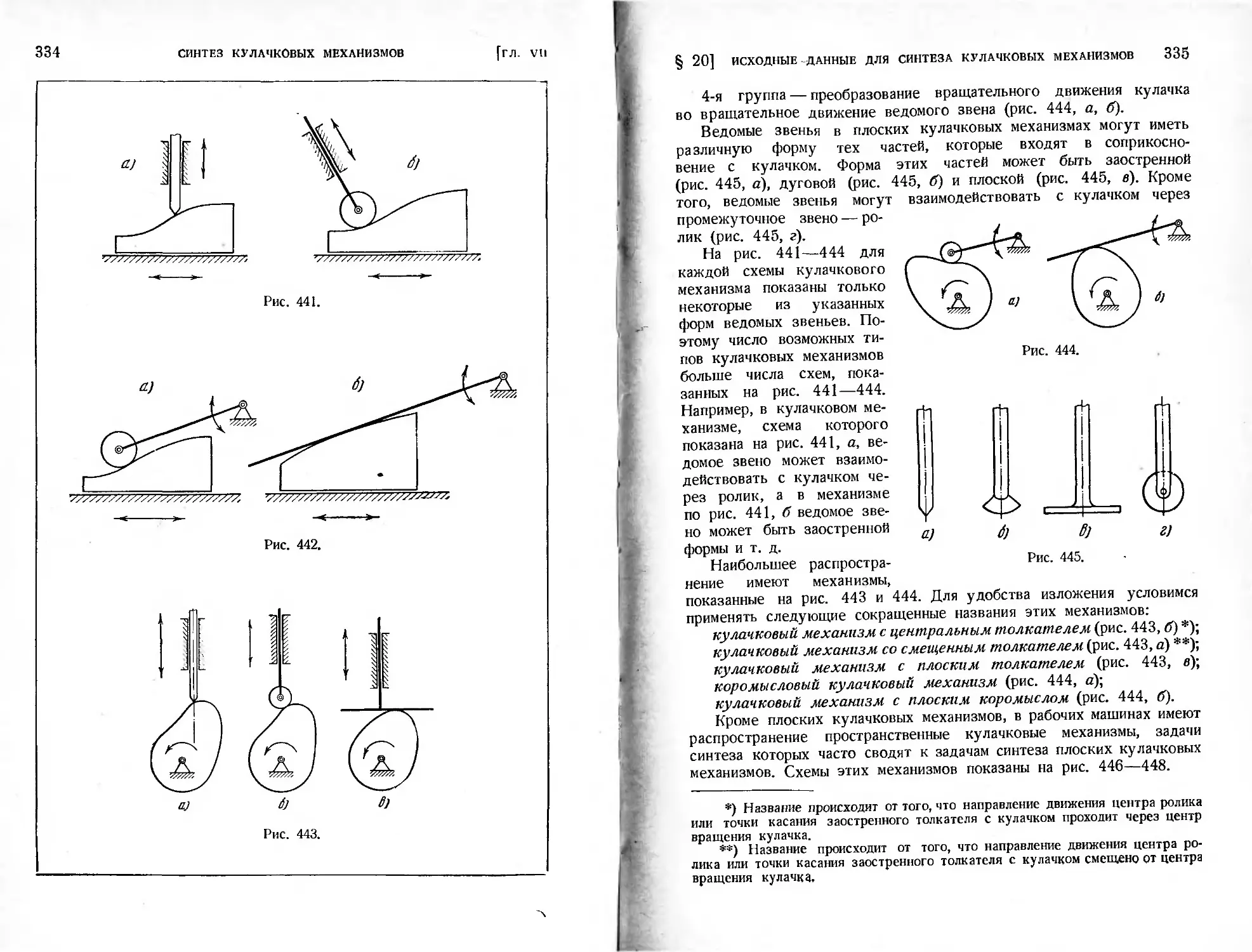
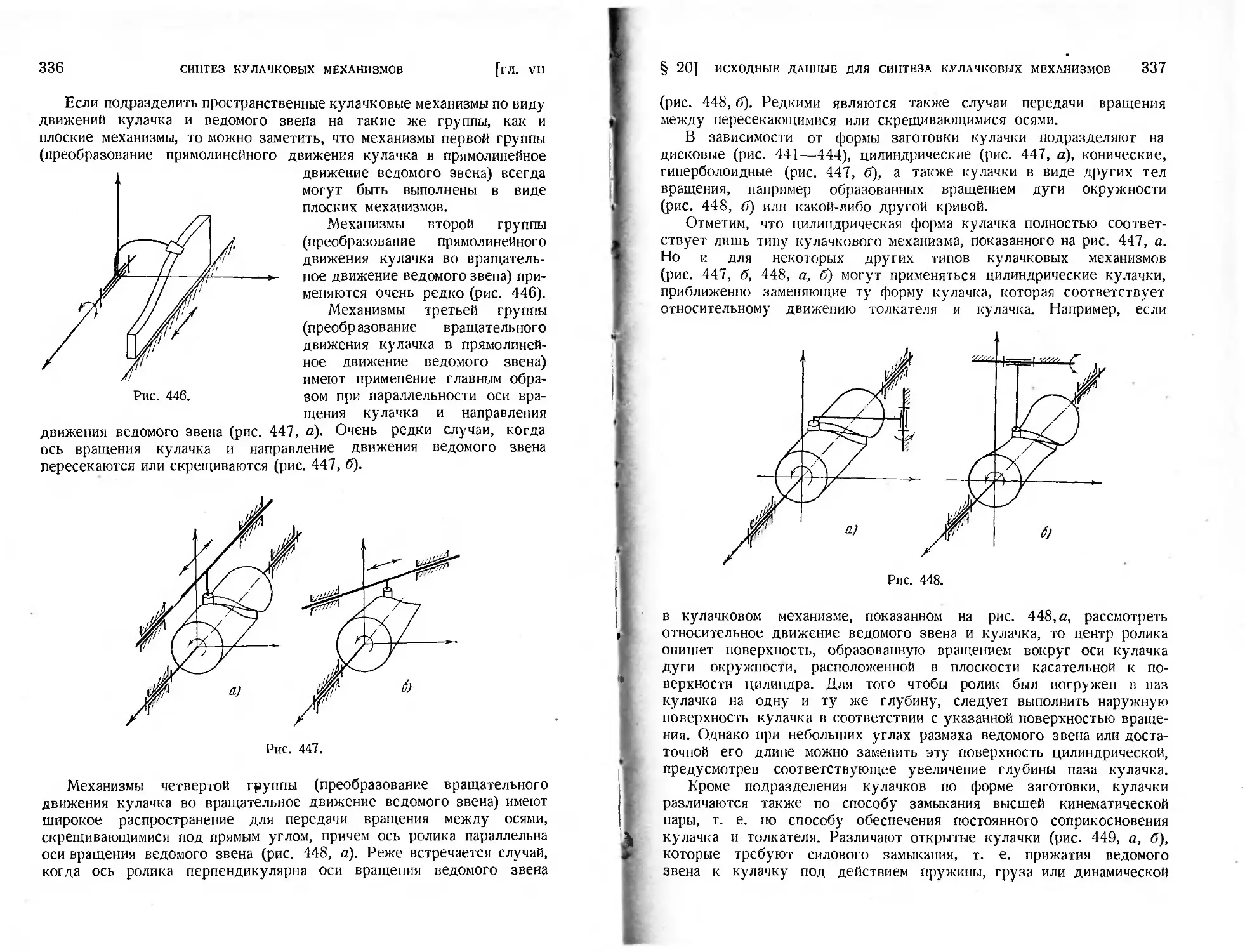
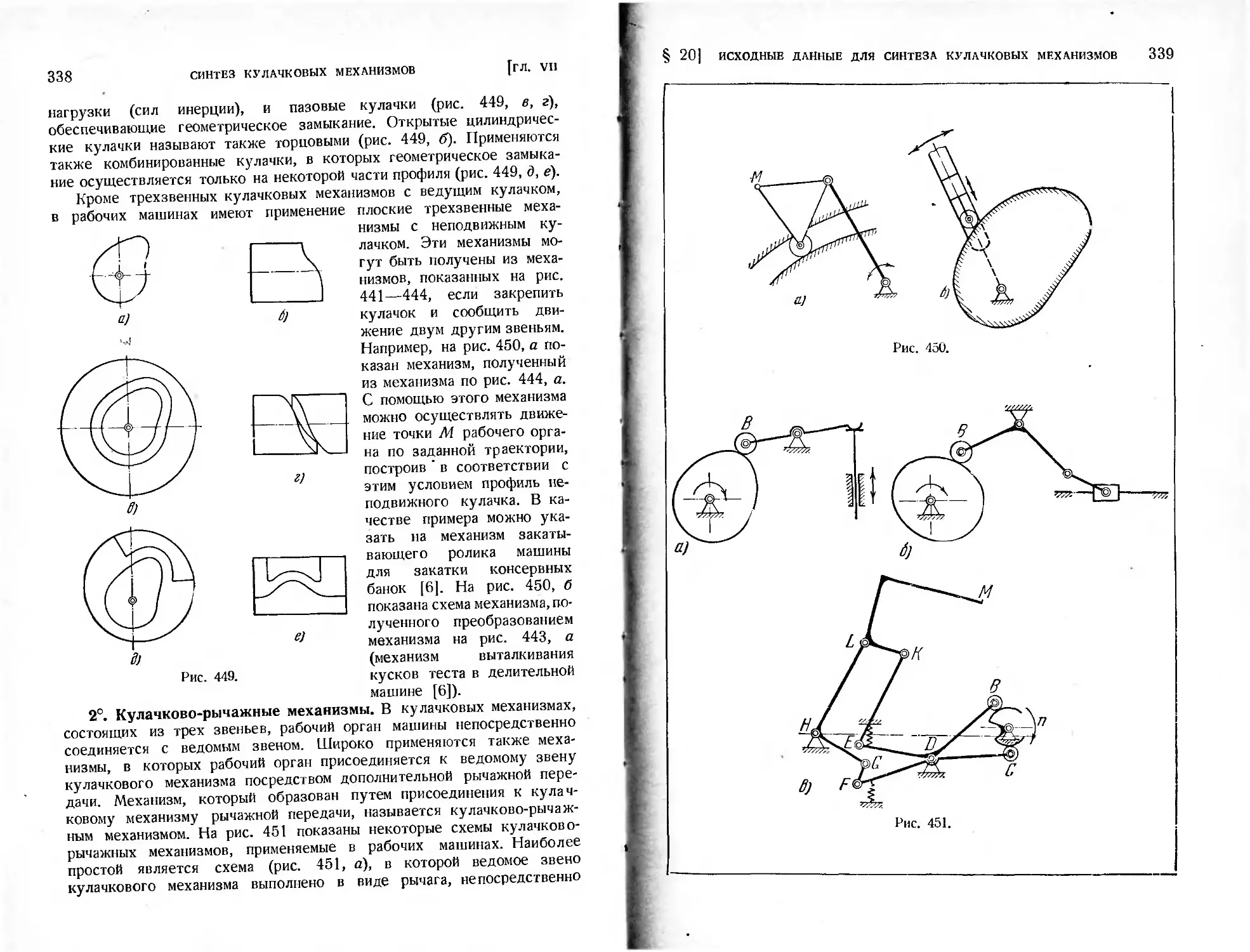
Глава VII. Синтез кулачковых механизмов.....................333
§ 20. Исходные данные для синтеза кулачковых механизмов......333
§ 21. Выбор закона движения ведомого звена...................343
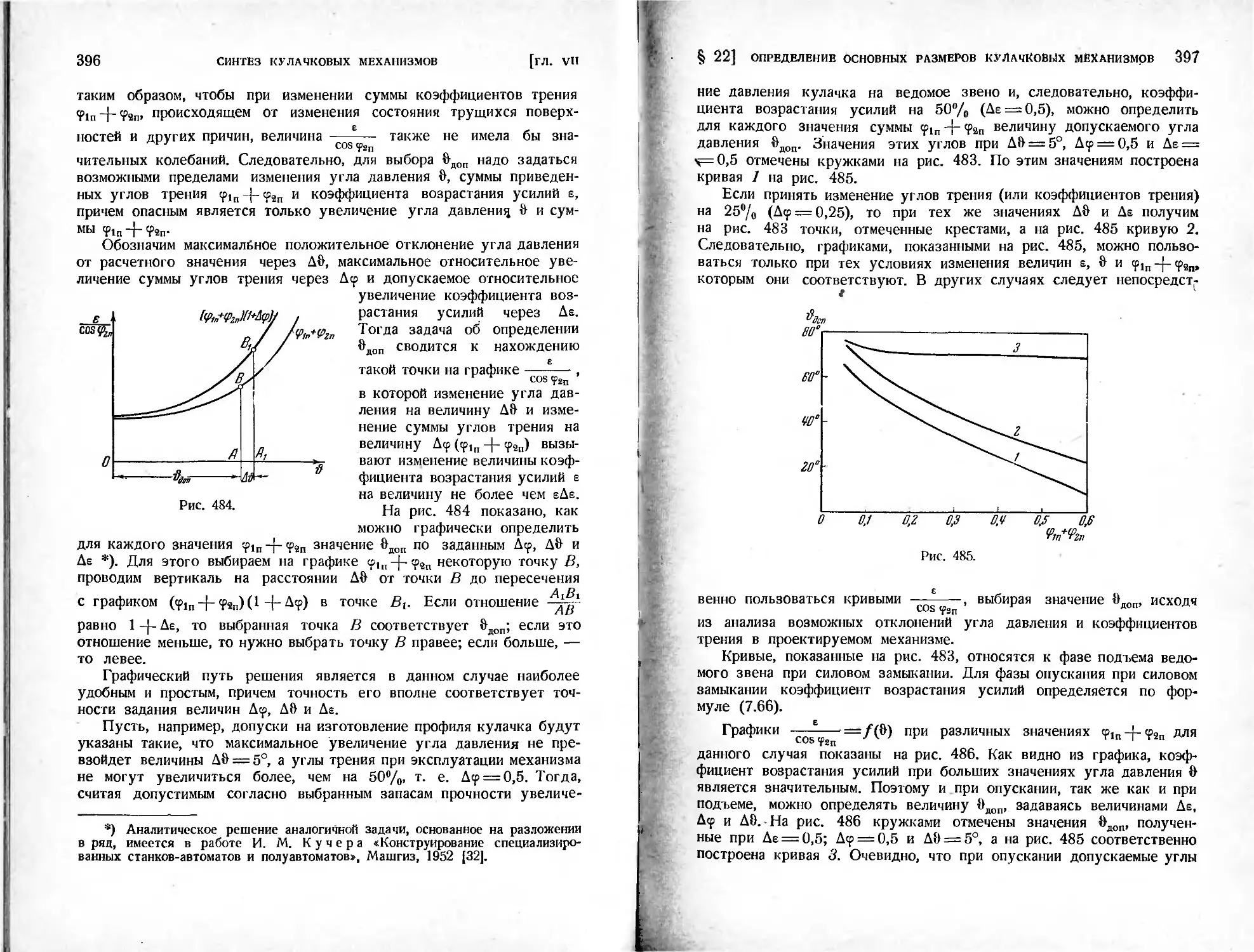
§ 22. Определение основных размеров кулачковых механизмов...373
§ 23. Определение профиля кулачка по заданному закону движения ве-
домого звена................................................409
Глава VIII. Синтез мальтийских механизмов....................428
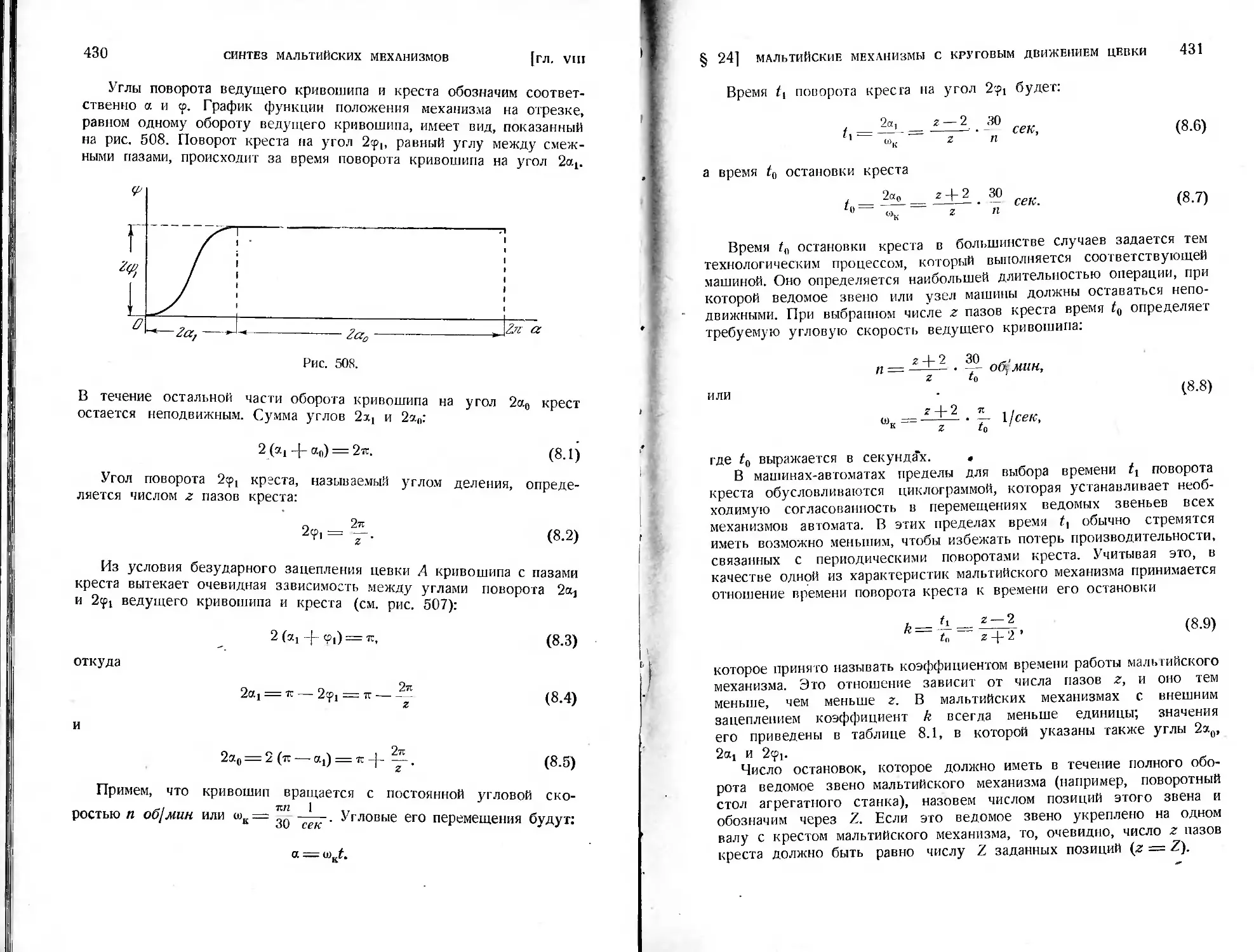
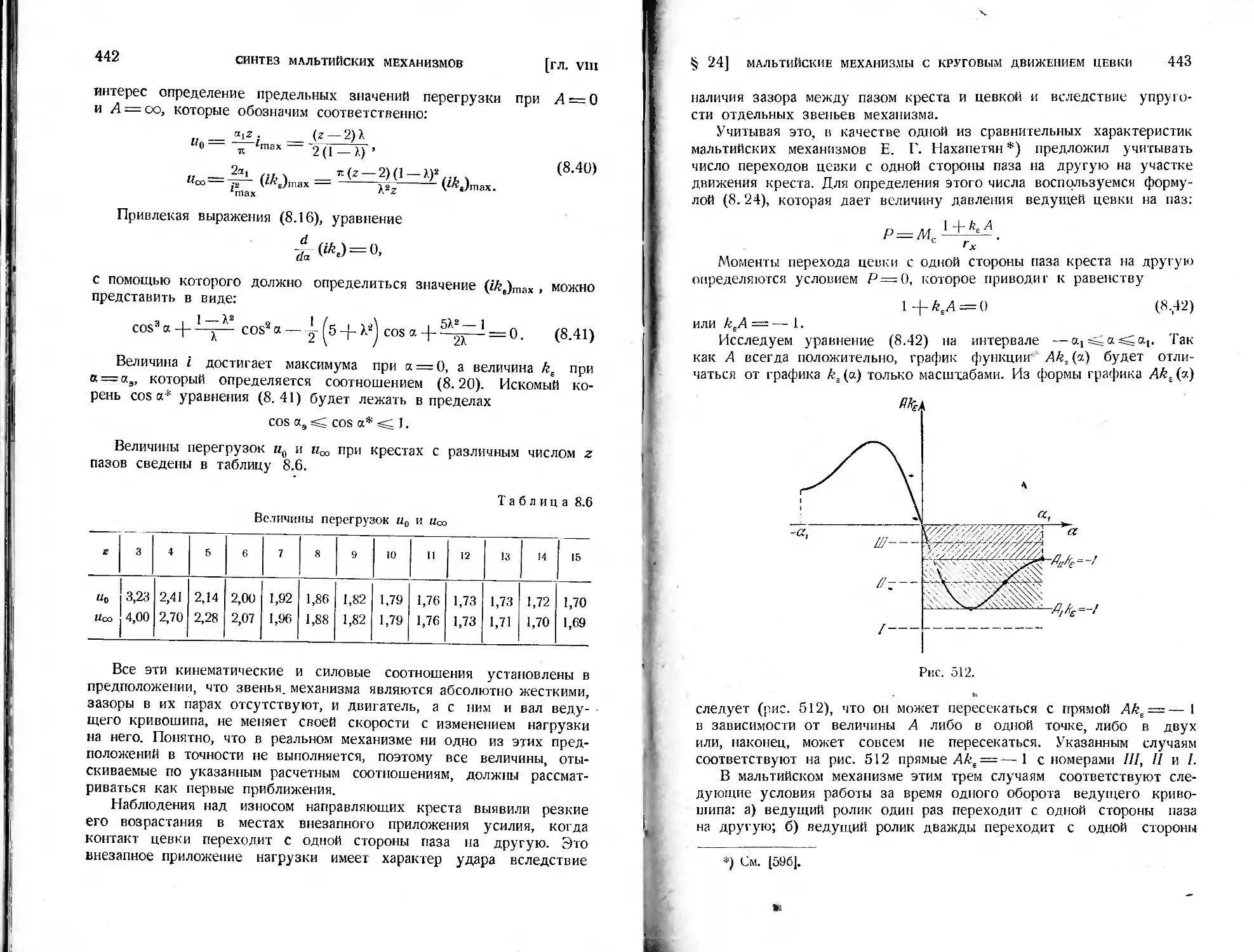
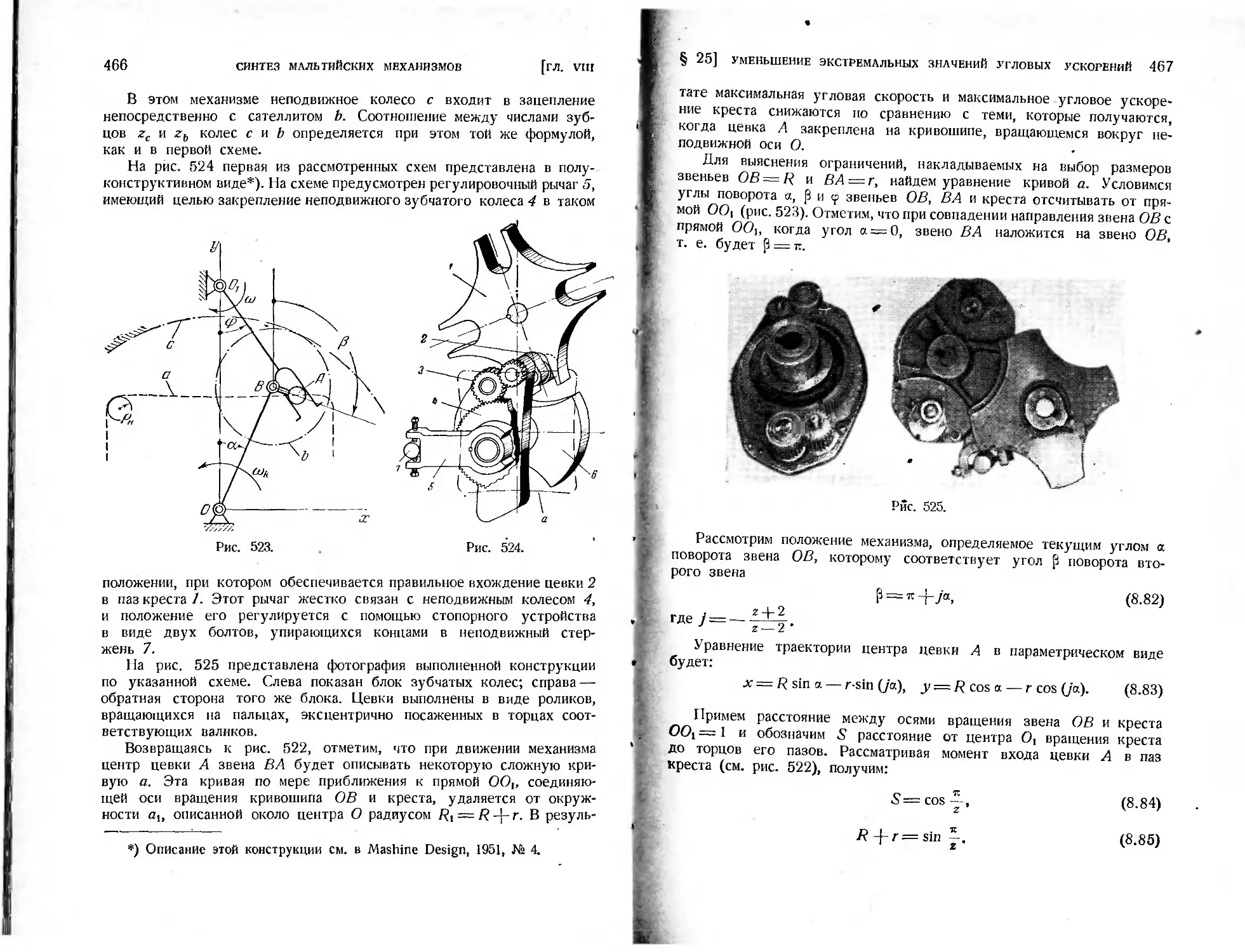
§ 24. Схемы мальтийских механизмов с круговым равномерным движе-
нием цевки .................................................428
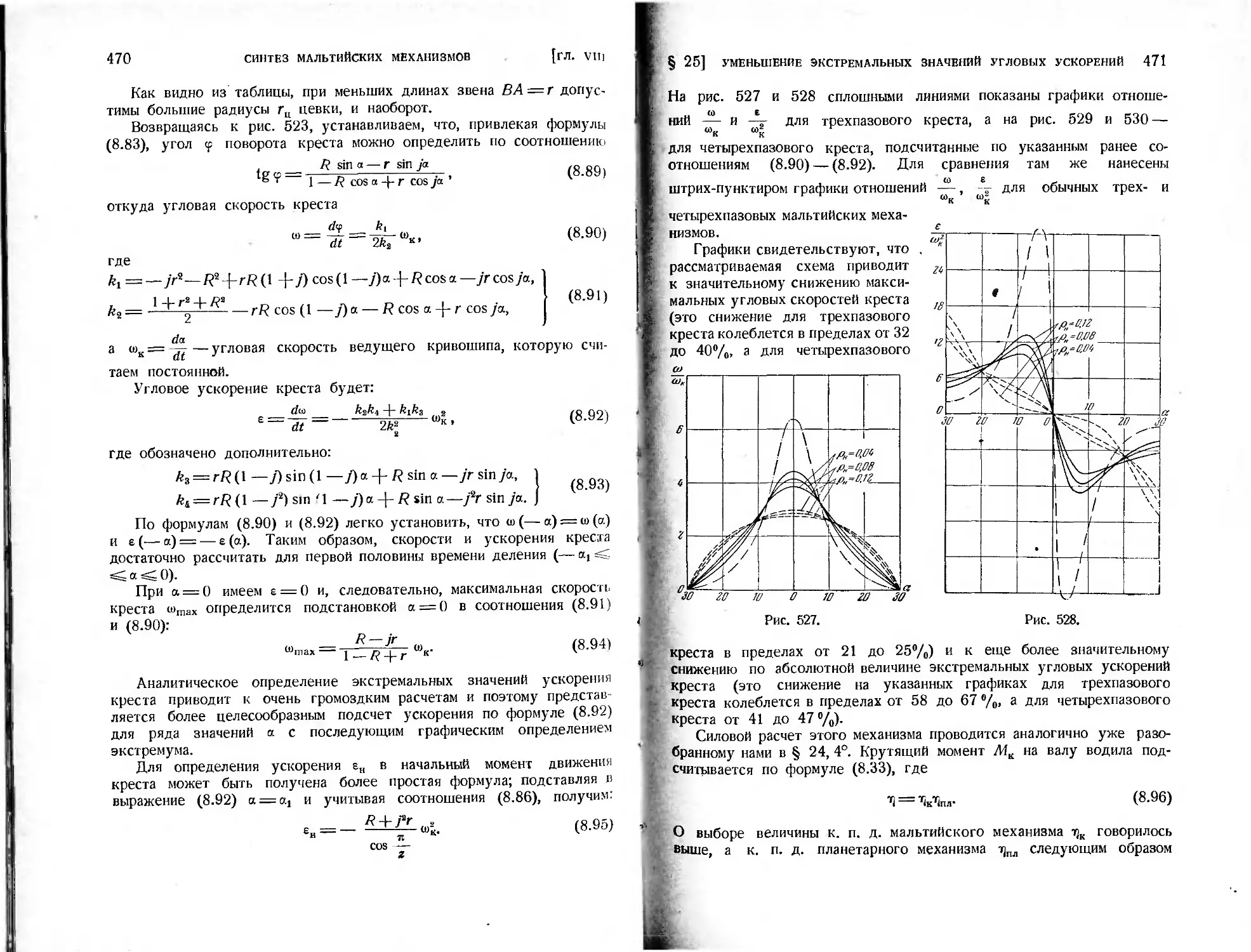
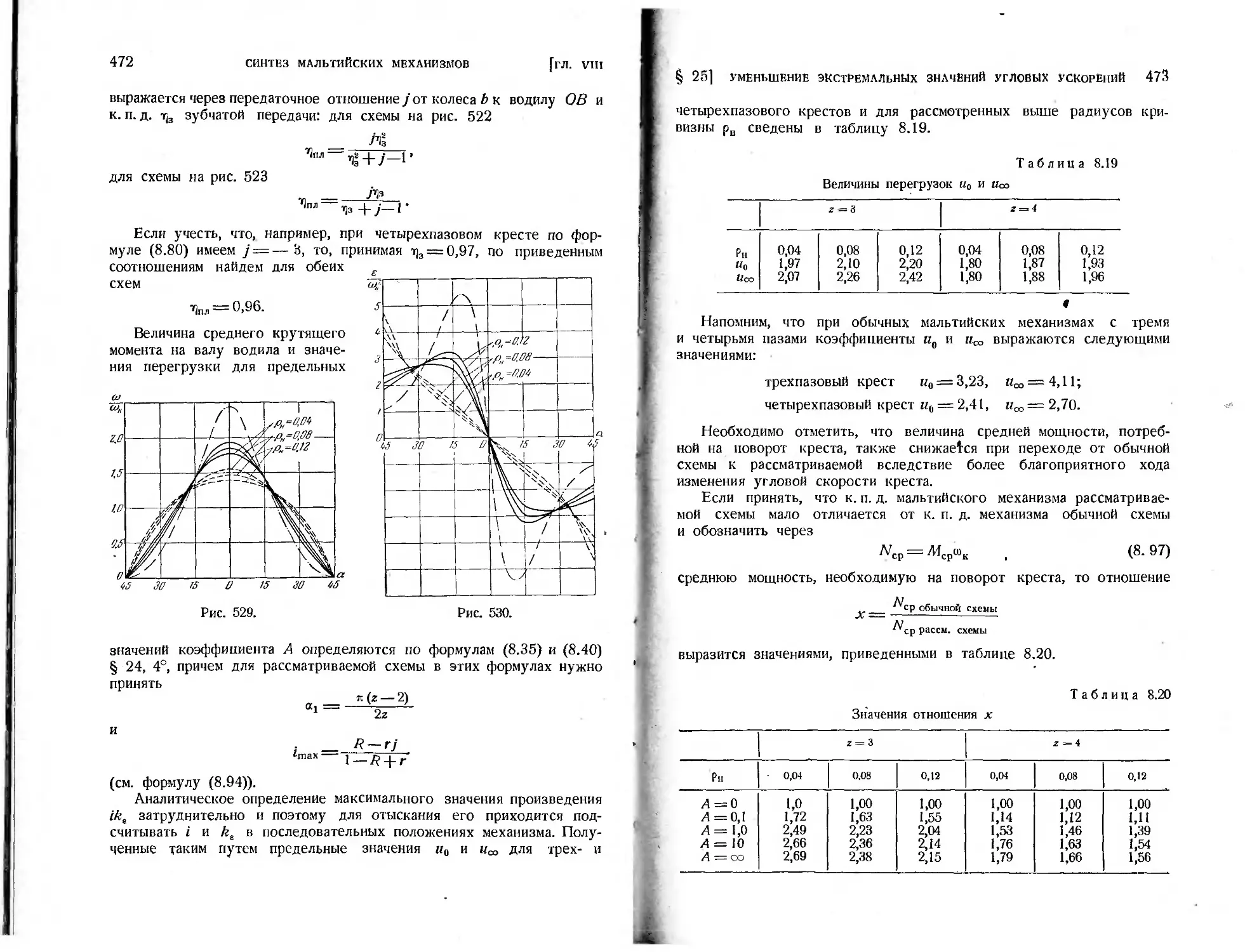
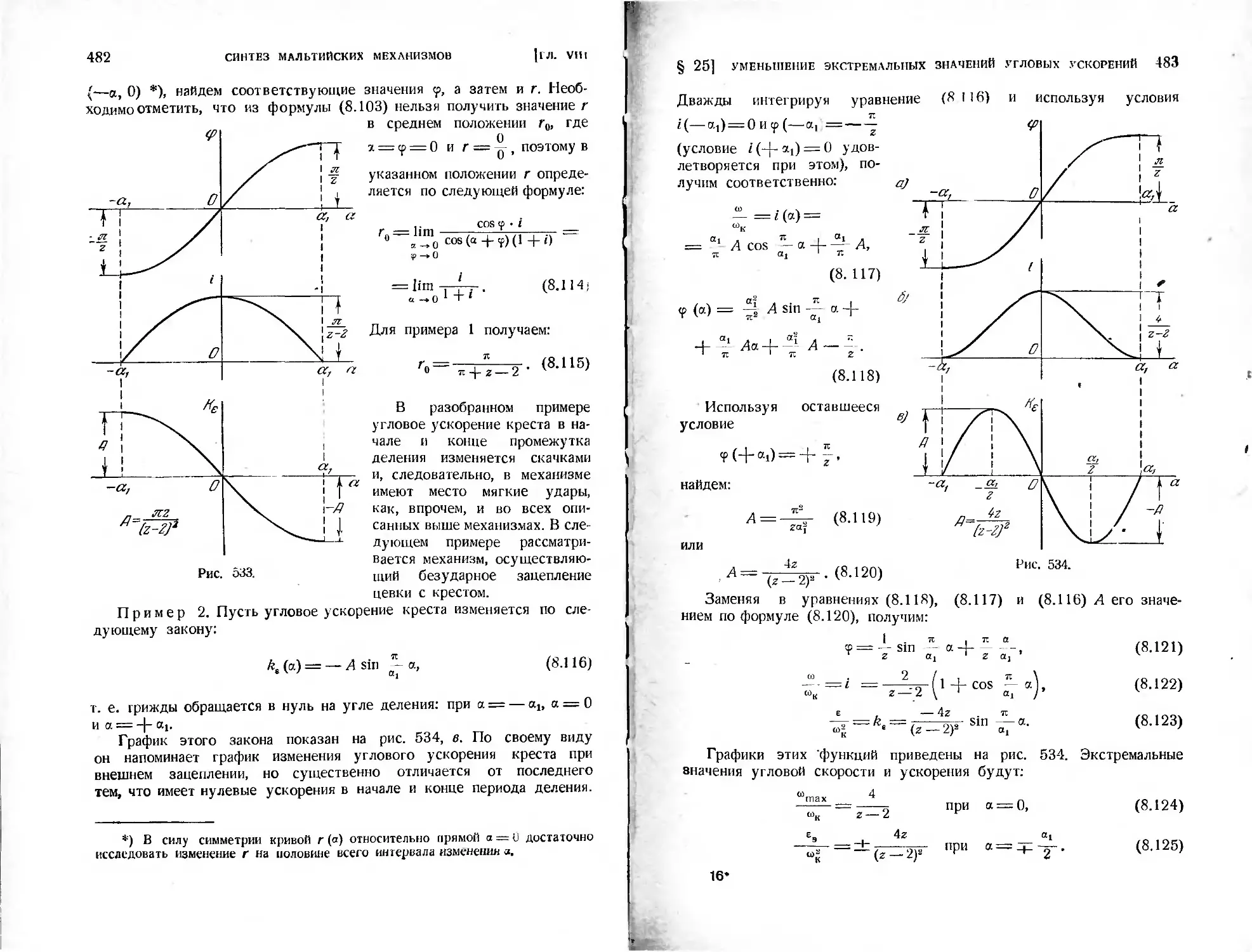
§ 25. Схемы мальтийских механизмов, позволяющие уменьшить экстремаль-
ные значения угловых ускорений креста ..................... 462
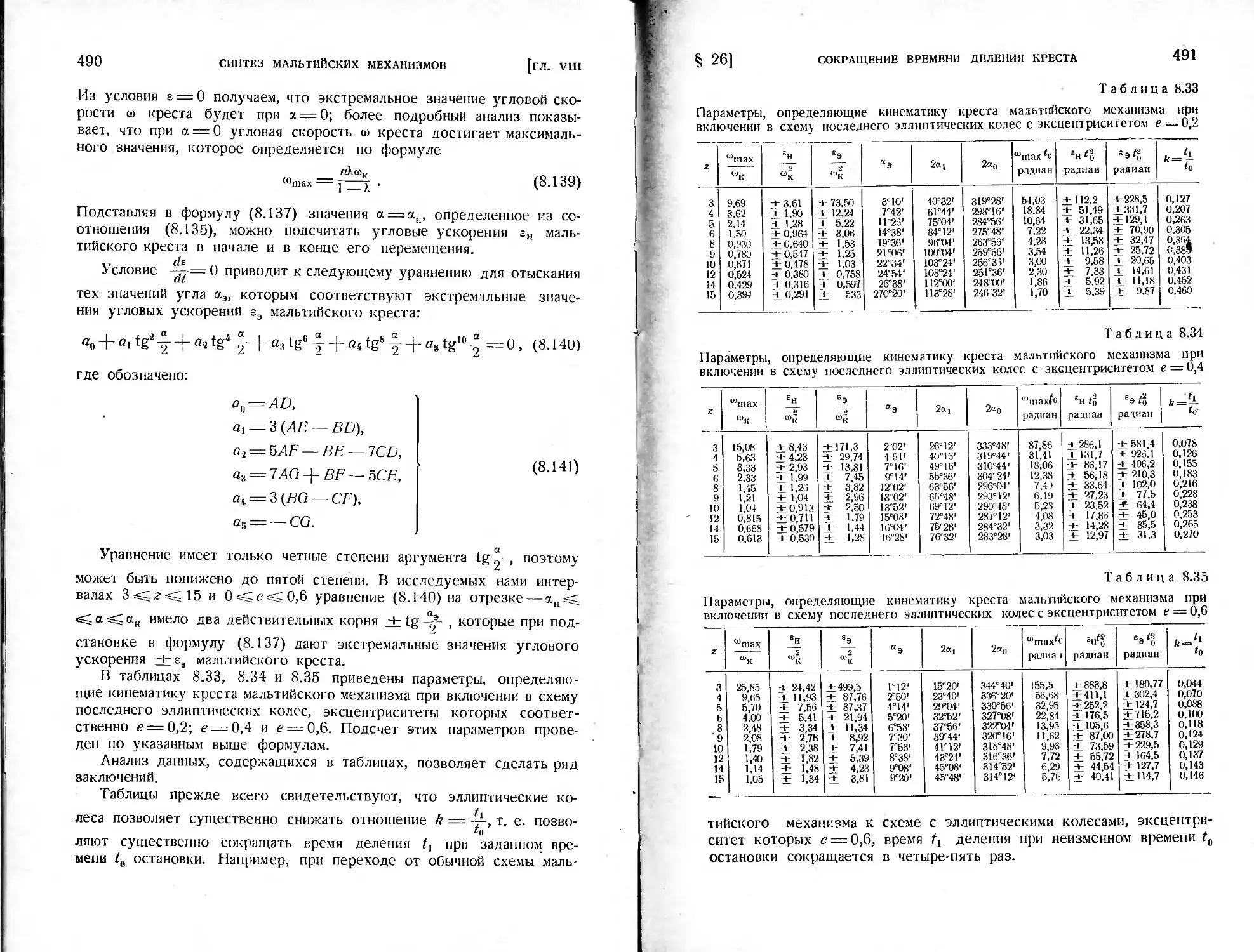
§ 26. Схемы мальтийских механизмов, позволяющие сократить время
деления креста..............................................485
ЧАСТЬ ТРЕТЬЯ
ТЕОРИЯ ПРИБЛИЖЕННЫХ МЕТОДОВ СИНТЕЗА МЕХАНИЗМОВ
А. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ
Глава IX. Синтез передаточных механизмов......................501
§ 27. Теория приближения функций и связь ее с задачами приближен-
ного синтеза механизмов ................................... 501
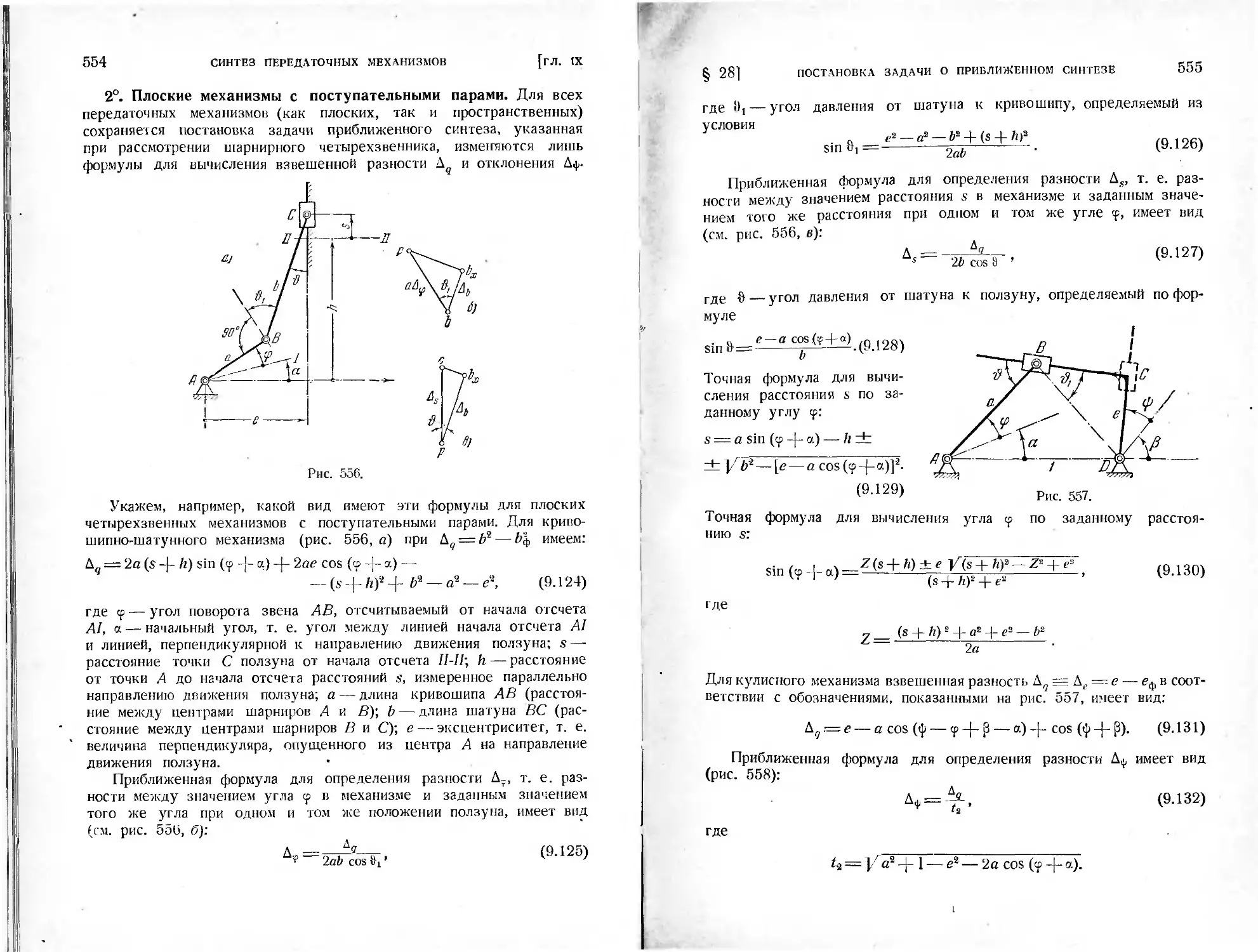
§ 28. Постановка задачи о приближенном синтезе передаточных меха-
низмов и аналитические выражения отклонения от заданной функ-
ции для некоторых механизмов................................547
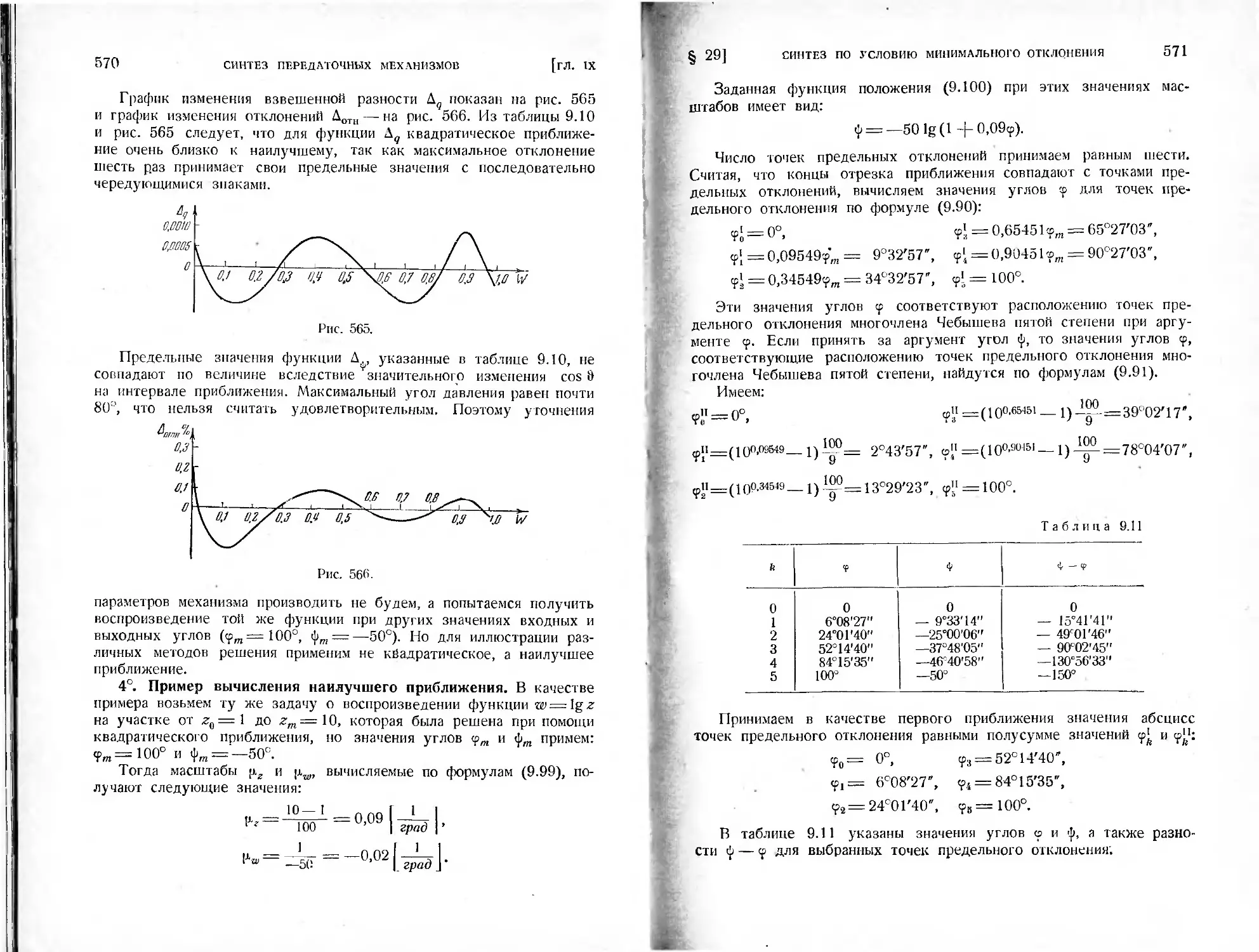
§ 29. Синтез передаточных механизмов по условию минимального откло-
нения от заданной функции...................................558
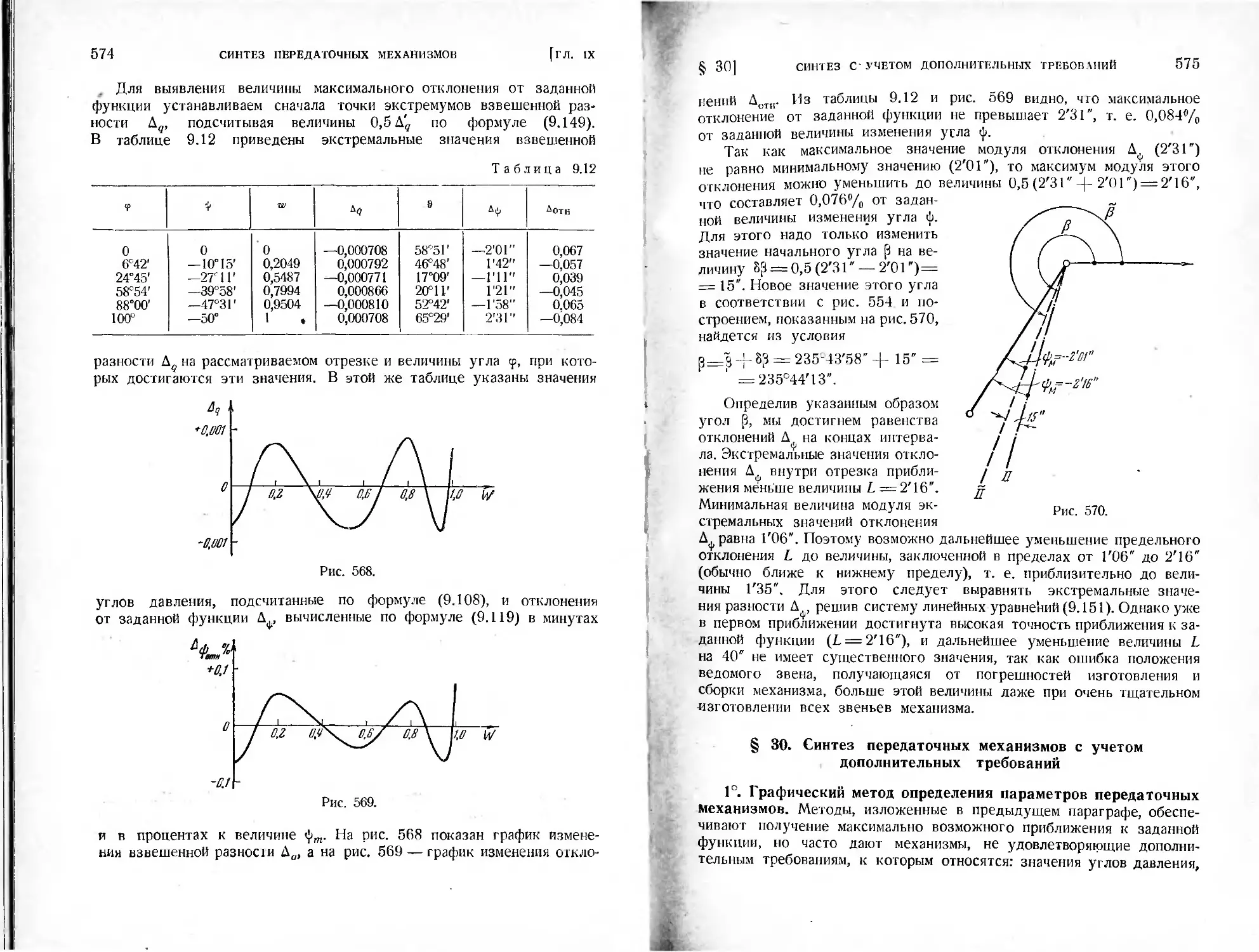
§ 30. Синтез передаточных механизмов с учетом дополнительных требо-
ваний ......................................................575
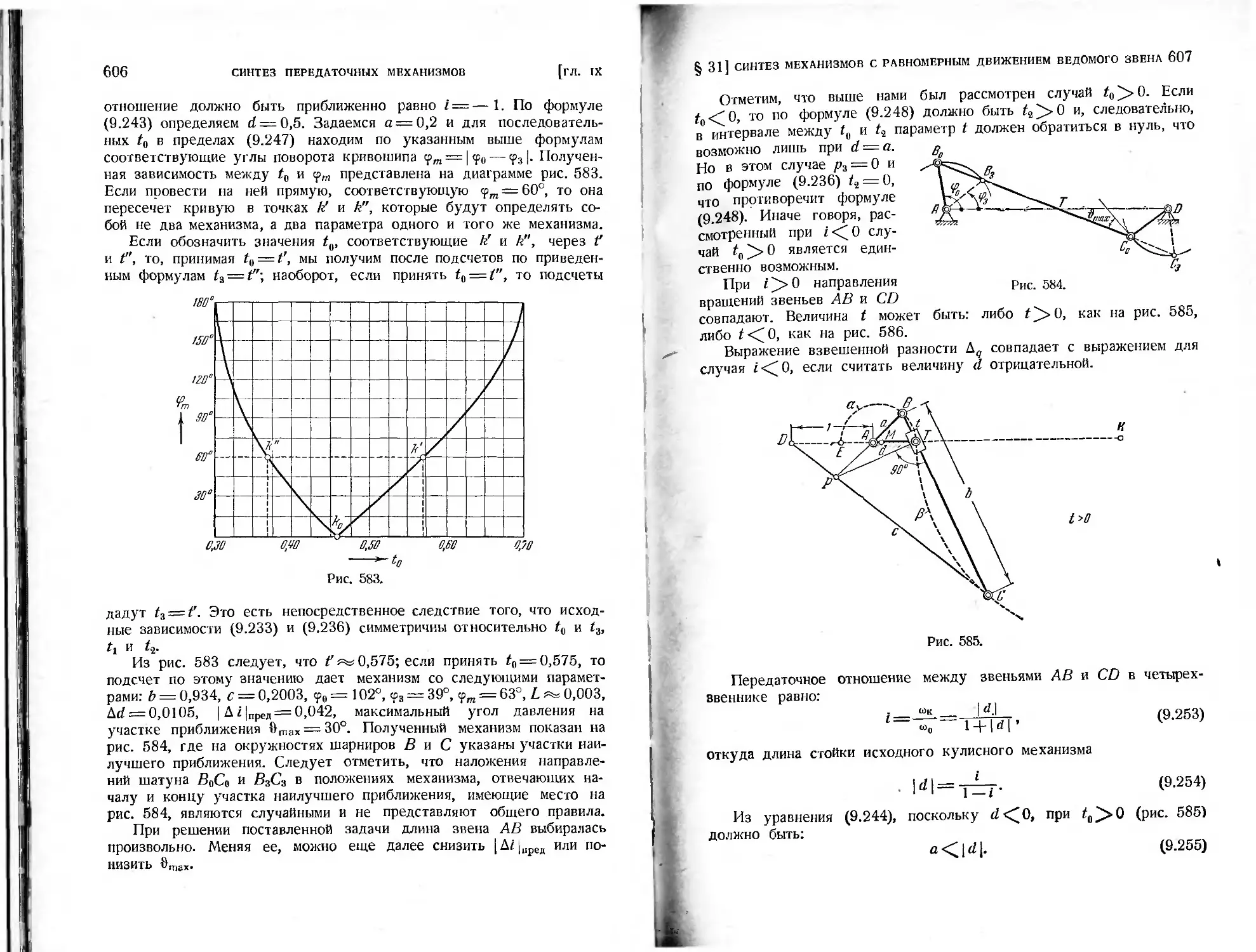
§ 31. Синтез механизмов с равномерным движением ведомого звена. . . 600
§ 32. Применение метода комплексных чисел к синтезу передаточных
механизмов..................................................638
Глава X. Синтез приближенных направляющих механизмов......648
§ 33. Шатунные кривые..................................... 648
§ 34. Синтез направляющих механизмов по условию минимального от-
клонения от заданной функции...............................675
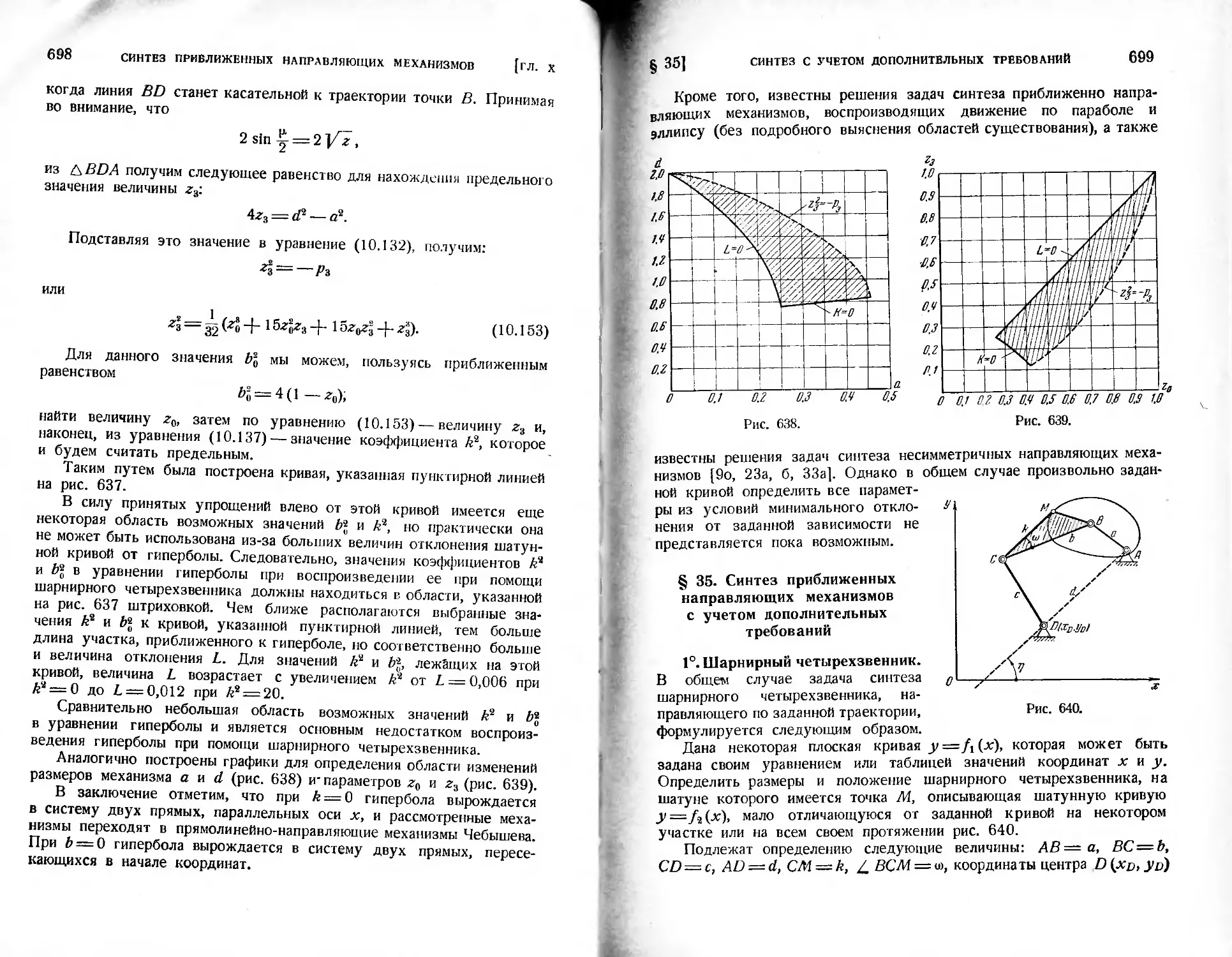
§ 35. Синтез приближенных направляющих механизмов с учетом допол-
нительных требований.......................................699
Б. МЕТОДЫ, ОСНОВАННЫЕ НА КИНЕМАТИЧЕСКОЙ
ГЕОМЕТРИИ
Глава XI. Кинематическая геометрия конечно удаленных положе-
ний плоской фигуры ........................................ 727
§ 36. Два и три положения плоской фигуры....................727
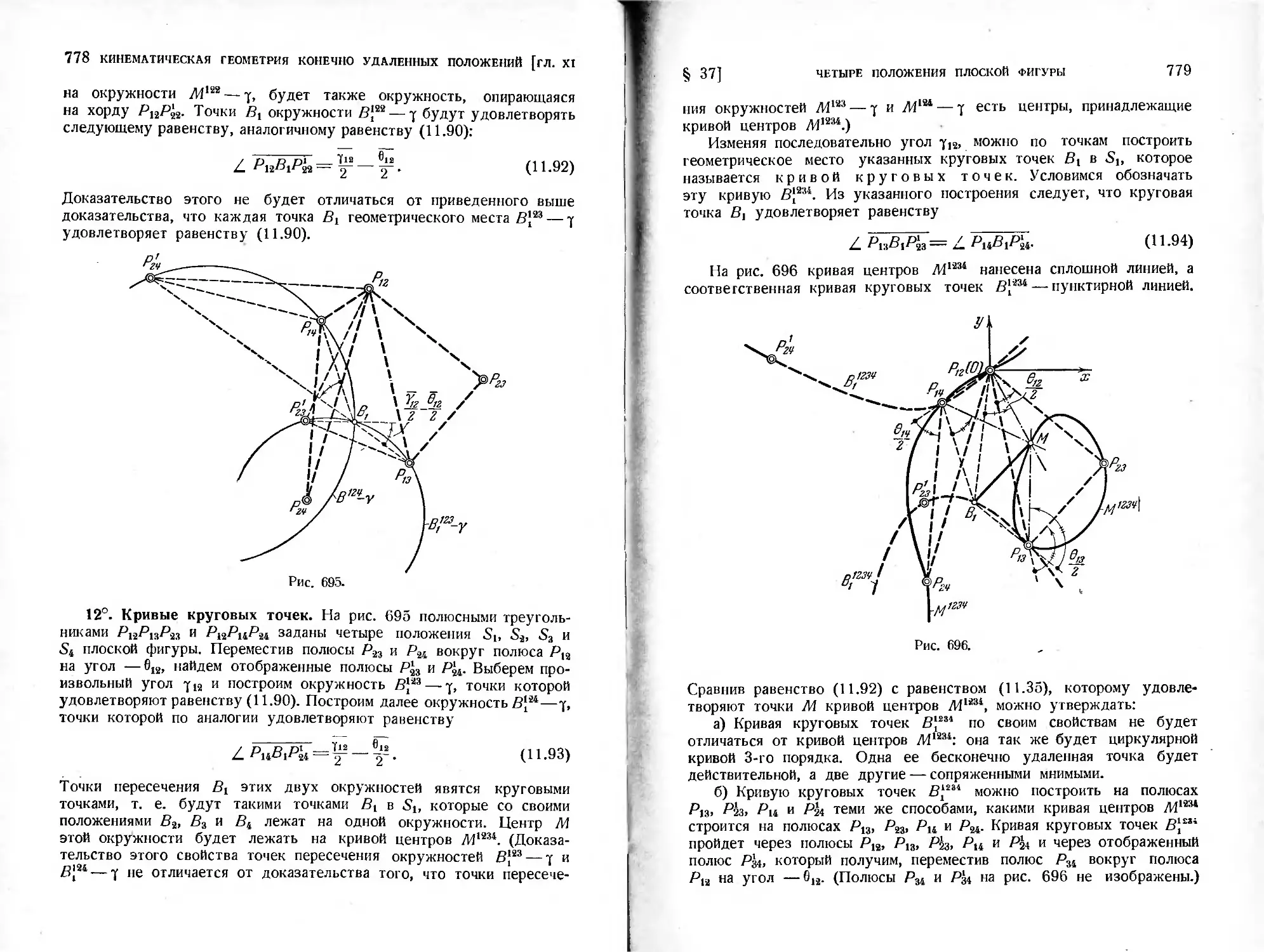
§ 37. Четыре положения плоской фигуры ......................745
§ 38. Пять положений плоской фигуры ........................789
ОГЛАВЛЕНИЕ
5
Глава XII. Синтез механизмов по положениям звеньев...............806
§ 39. Синтез шарнирного четырехзвенника по двум и трем положениям 803
§ 40. Синтез шарнирного четырехзвенника по четырем и пяти положе-
ниям ..........................................................821
§ 41. Синтез кривошипно-шатунного механизма и кулисного механизма
по положениям..................................................834
Глава XIII. Синтез передаточных механизмов по методу интерполи-
рования ........................................................ 842
§ 42. Интерполяционное приближение с двукратными узлами........842
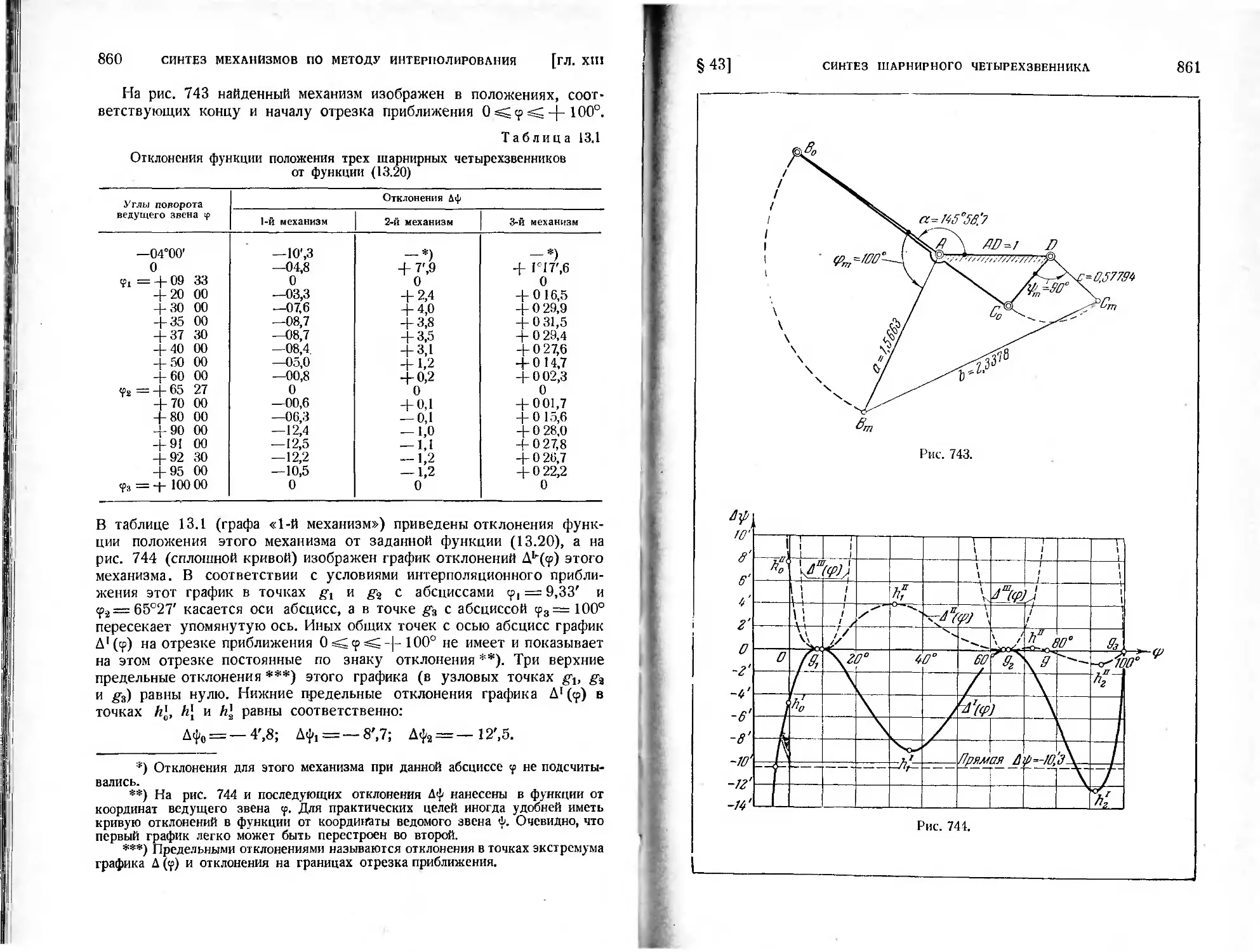
§ 43. Синтез шарнирного четырехзвенника по полному числу парамет-
ров схемы .....................................................850
§ 44. Синтез кривошипно-шатунного и кулисного механизмов по пол-
ному числу параметров схемы....................................880
Г лава XIV. Синтез передаточных механизмов по методу наилуч-
шего приближения.................................................916
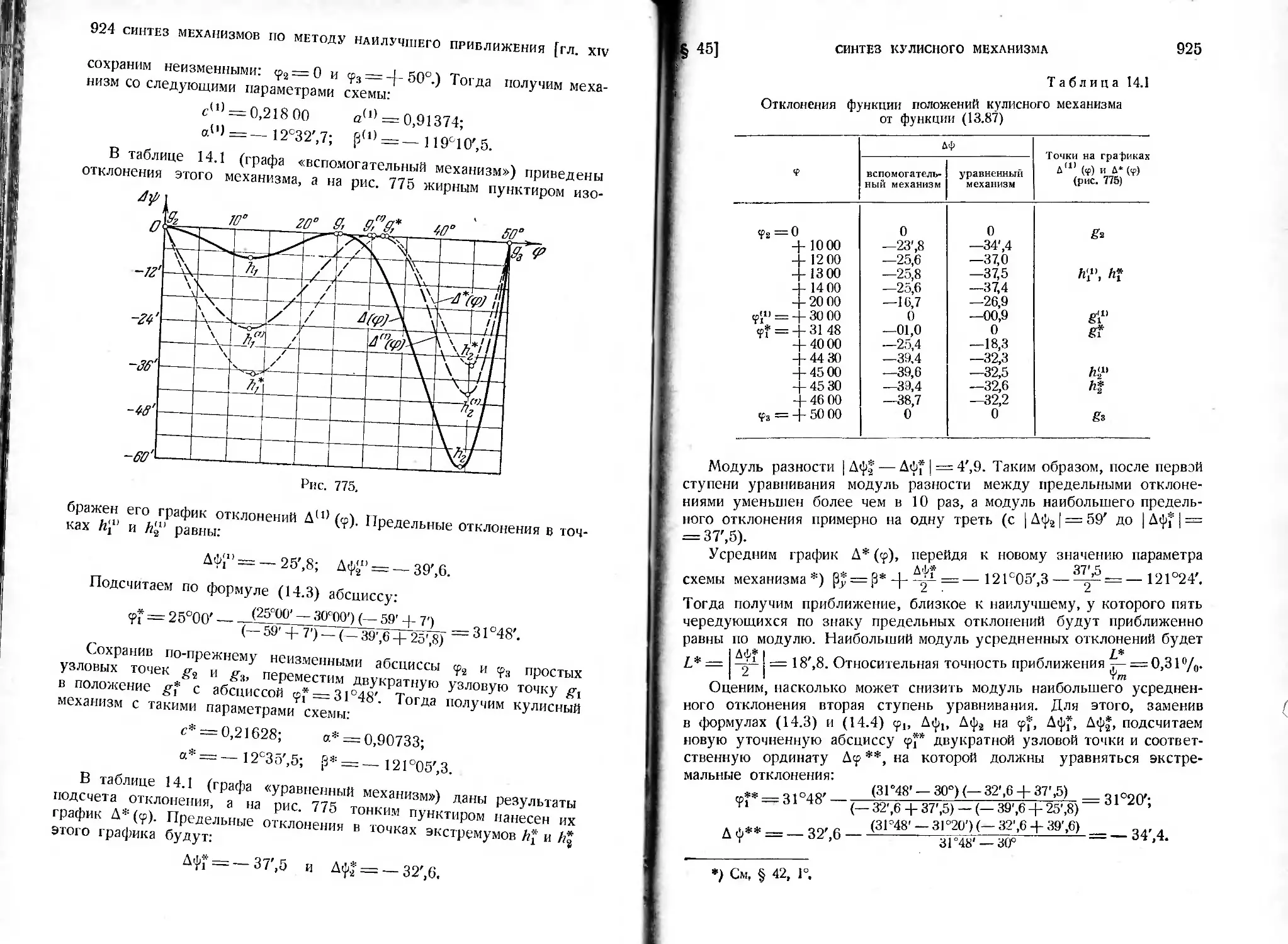
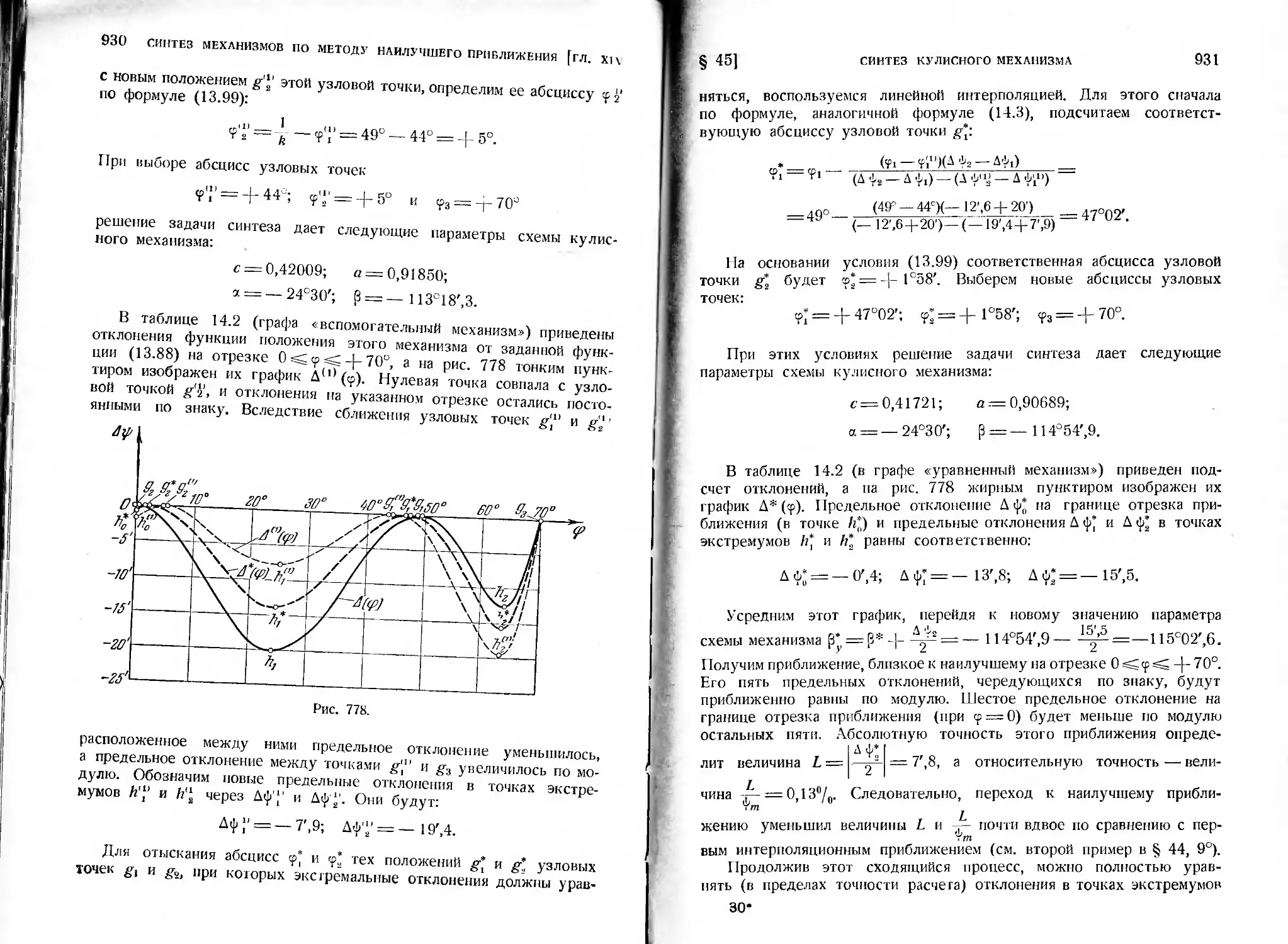
§ 45. Отыскание наилучшего приближения в задаче синтеза кулисного
механизма......................................................916
§ 46. Отыскание наилучшего приближения в задаче синтеза шарнирного
четырехзвенника и кривошипно-шатунного механизма...............950
Глава XV. Синтез механизмов с остановками........................986
§ 47. Механизмы с остановкой, у которых ведомая диада присоединена
к шатуну основного механизма ............................ 986
§ 48. Преобразование шатунных кривых...........................998
§ 49. Механизмы с остановкой, получаемые последовательным соедине-
нием четырехзвенных механизмов................................1005
Глава XVI. Кинематическая геометрия бесконечно близких поло-
жений плоской фигуры и ее использование в синтезе механизмов 1017
§ 50. Основы кинематической геометрии бесконечно близких положений
плоской фигуры, движущейся в своей плоскости.............1017
§ 51. Синтез четырехзвенных передаточных механизмов...........1033
§ 52. Синтез четырехзвенных направляющих механизмов...........1054
Литература.................................................... 1069
Именной указатель...............................................1073
Предметный указатель............................................1031
ПРЕДИСЛОВИЕ
Генеральной линией в развитии современной техники являются
комплексная механизация и автоматизация производственных про-
цессов.
Автоматизация и механизация производственных процессов осу-
ществляются многими средствами. Важнейшим средством автомати-
зации производственных процессов является создание машин и меха-
низмов автоматического действия, т. е. так называемых машин-авто-
матов. Не менее важным является создание приборов и устройств
автоматического действия, регулирующих и контролирующих
производственные процессы. Наконец, в последние годы важнейшим
средством автоматизации является использование математических
машин и устройств для управления производственными процессами.
Развитие различных средств автоматизации идет параллельно,
и в современном производстве мы являемся свидетелями комплекс-
ного использования всех вышеуказанных средств для решения раз-
личных задач автоматизации производственных процессов.
Но основной проблемой, которая всегда стоит перед конструкто-
ром, решающим задачу об автоматизации того или иного производ-
ственного процесса, будет проблема создания той машины автома-
тического действия, которая должна выполнять заданный технологи-
ческий процесс. Процесс конструирования машин-автоматов является
очень сложным и трудным, особенно если учесть, что в современных
машинах-автоматах используются механические, гидравлические, радио-
технические и другие виды устройств. Все это требует от конструк-
торов и инженеров глубокого знания теории и методов расчета и
проектирования подобных устройств. В связи с этим в последние
десятилетия в теории машин и механизмов стали развиваться раз-
личные новые разделы, посвященные исследованию и методам про-
ектирования устройств различных видов. В частности, большое раз-
витие получили методы проектирования механизмов машин-автоматов.
Раздел теории механизмов, изучающий методы их проектирования,
получил название «синтез механизмов». Задачей синтеза меха-
низмов является создание таких методов проектирования механизмов,
которые позволили бы конструкторам быстро и рационально
проектировать механизмы, удовлетворяющие высоким требованиям
ПРЕДИСЛОВИЕ
7
современной техники. Этого можно достичь только в том случае,
если инженеры будут в совершенстве владеть теорией и на базе
теории развивать практические приемы проектирования.
При решении прикладных задач синтеза большую пользу кон-
структорам могут оказать справочники по механизмам, эксперимен-
тальные модели механизмов и т. д. Составление таких пособий по
проектированию механизмов требует глубокого знания обшей теории
механизмов и в первую очередь методов синтеза механизмов.
Мощным орудием в решении практических задач проектирования
механизмов должны явиться также методы прикладной математики,
в частности: таблицы, номограммы, графики, позволяющие упрощать
решение задач синтеза механизмов. Важнейшая роль в решении
задач синтеза механизмов в ближайшие годы будет принадлежать
математическим машинам. Использование средств вычислительной тех-
ники — счетно-решающих машин и устройств — потребует дальнейшего
развития в первую очередь алгебраических методов, позволяющих
в более удобной форме составлять вычислительные программы для
этих машин.
Таким образом, практические методы проектирования механизмов
могут успешно развиваться только на базе глубокого знания теории
вопроса. Этим объясняется тот факт, что за последние годы как
у нас, так и за рубежом появилось большое количество статей,
монографий и справочных материалов, посвященных синтезу меха-
низмов. В этих работах дается решение задач синтеза различных
видов механизмов с помощью самых разнообразных приемов и мето-
дов. Появление этих работ способствовало внедрению современных
методов синтеза механизмов в инженерную практику. Важное значе-
ние в этом деле принадлежит сводным монографиям, подводящим
итоги развития науки за тот или иной, достаточно продолжительный
период времени.
К таким монографиям относятся опубликованные в Германии
монографии Р. Бейера «Technische Kinematik» (1931 г.) и «Kinema-
tische Getriebesynthese» (1953 г.) и монография Р. Крауса «Getriebe
Aufbau» (1952 г.)
В СССР коллективом авторов в составе: И. И. Артоболевского,
3. Ш. Блоха и В. В. Добровольского была опубликована сводная
монография «Синтез механизмов» (1944 г.).
С момента издания последней монографии прошло четырнадцать
лет. За это время в СССР и за рубежом были значительно развиты
различные методы синтеза механизмов, получены новые крупные
научные результаты. Поэтому назрела необходимость составления
новой монографии, в которой нашли бы свое отражение научные
результаты, полученные и за последние годы. Задачу составления
такой монографии взяли на себя авторы этого труда.
Предлагаемая монография, посвященная синтезу механических
устройств, рассчитана в основном на инженеров, конструкторов,
8
ПРЕДИСЛОВИЕ
научных работников, преподавателей втузов и студентов старших
курсов, г. е. на лиц, знающих основы теории механизмов. Авторы
стремились к тому, чтобы книга содержала все основные методы
синтеза механизмов, которыми могли бы воспользоваться конструк-
торы в своей практической работе. С целью облегчения пользования
книгой в первой ее части (главы I и II) излагаются необходимые сведе-
ния по теории структуры и кинематической геометрии с тем, чтобы
читатель мог не обращаться за необходимыми сведениями по этим
вопросам к общим и специальным источникам.
Изложение основ структуры механизмов сделано не в общей,
а в прикладной форме, увязанной с теми задачами синтеза, которые
рассмотрены в монографии, и имеет своей целью только установле-
ние и систематизацию объектов, подвергнутых исследованию в дан-
ной книге.
Кинематическая геометрия, лежащая в основе методов анализа
механизмов, широко используется в решении различных задач син-
теза механизмов. Поэтому изложение общих положений кинематиче-
ской геометрии должно подготовить читателя к изучению некоторых
методов синтеза механизмов, основанных на использовании кинемати-
ческой геометрии.
Как известно, в синтезе механизмов применяются как точные,
так и приближенные методы решения задач. Эти методы существенно
различны. Поэтому главы III — XVI монографии делятся на две части.
В главах III — VIII излагаются точные методы синтеза механизмов,
в главах IX — XVI излагаются приближенные методы синтеза меха-
низмов. Эти последние главы монографии подразделены на два раз-
дела в соответствии с применяемыми методами синтеза. Отдельно
излагаются задачи синтеза, решаемые с помощью алгебраических ме-
тодов, и отдельно — задачи синтеза, решаемые с помощью геометри-
ческих методов.
Вопрос о точном в кинематическом смысле воспроизведении
алгебраических и трансцендентных плоских кривых с помощью меха-
низмов представляет большой и самостоятельный раздел теории
механизмов. Достаточно полное изложение этого вопроса в настоя-
щей монографии не могло быть сделано. Поэтому в главе VI авторы
ограничились изложением только отдельных задач теории этих меха-
низмов. При этом был применен геометро-алгебраический метод реше-
ния задач синтеза, особенностью которого является синтетическое
использование геометрических свойств кривых, связанных с их по-
строением и видом уравнений этих кривых. Как показывает опыт
советских и зарубежных исследователей, при таком методе могут быть
получены механизмы с наименьшим количеством звеньев. Таким об-
разом, глава VI монографии является в некотором смысле иллюстра-
тивной и не претендующей на исчерпывающее изложение проблемы.
В монографии излагаются методы синтеза плоских механизмов,
и только в отдельных случаях даны указания на возможность рас-
ПРЕДИСЛОВИЕ
9
пространения излагаемых методов на пространственные механизмы
некоторых частных видов.
Основой современной теории синтеза механизмов являются фун-
даментальные работы П. Л. Чебышева и Л. Бурместера, опублико-
ванные во второй половине XIX века. Работами этих ученых опре-
делились два основных направления в синтезе механизмов, получивших
свое развитие в последующие годы. Последователи П. Л. Чебышева
развивали в основном алгебраические методы синтеза механизмов,
а последователи Л. Бурместера — геометрические методы синтеза
механизмов.
В последние десятилетия мы являемся свидетелями значительного
развития теории синтеза механизмов, при этом как советские, так и
зарубежные ученые используют и геометрические и алгебраические
методы синтеза, но наметилось направление, соединяющее в себе
оба метода, позволяющее сочетать изящество и простоту геометри-
ческих построений с точностью и глубиной алгебраических исследо-
ваний. Можно предполагать, что и в дальнейшем развитие методов
синтеза будет идти в основном в направлении создания комплексных
методов, использующих геометрические и аналитические приемы
решения задач проектирования механизмов.
Естественно, что авторы не могли полностью изложить все много-
образие предложенных и развитых методов синтеза. В основном
авторы стремились изложить те методы, которые по их мнению
позволяют в наиболее простом и удобном виде получать реше-
ния конкретных задач синтеза механизмов, возникающих в практике
конструирования современных механизмов приборов и машин-авто-
матов.
Применение общих методов синтеза показано на конкретных
примерах механизмов. Так, рассмотрены задачи проектирования цен-
троидных механизмов, шарнирно-рычажных механизмов, кулачковых
механизмов, механизмов мальтийских крестов, механизмов с низшими
парами для воспроизведения плоских кривых и г. д. Проектирование
профилей зубьев зубчатых колес рассмотрено только в общем виде,
так как этот вопрос достаточно полно рассмотрен в специальной
литературе. Вопрос синтеза механизмов с учетом динамических фак-
торов в монографии не рассматривается, так как этот вопрос, если
он поставлен во всей своей полноте, связан >с рассмотрением гео-
метрии масс звеньев, режимов движения механизмов, сил трения и
сил упругости, зазоров в кинематических парах и т. л. Динамические
факторы учитываются только в тех случаях, когда они органически
увязываются с методами метрического синтеза как дополнительные
условия при воспроизведении заданных форм движения.
Монография содержит список основной литературы, опубликован-
ной за последние годы по 1957 г. включительно. Более ранняя лите-
ратура в этом списке не приводится, кроме фундаментальных работ,
так как подробный список литературы по синтезу механизмов
16
ПРЕДИСЛОВИЕ
имеется в вышеуказанной монографии 1944 г. В необходимых слу-
чаях ссылки на литературу даются в тексте книги.
Введение содержит историко-библиографические сведения по раз-
витию теории синтеза механизмов, которые, конечно, не претендуют
на исчерпывающую полноту.
Главы 1, II, III, IV, V и VI написаны И. И. Артоболевским,
главы VII, IX и X Н. И. Левигским, главы VIII, XI, XII, XIII, XIV,
XV и XVI С. А. Черкудиновым, причем в написании глав VIII и XVI
принял участие Н. В. Сперанский. Введение и список литературы
были написаны и подготовлены авторами совместно.
Авторы приносят свою глубокую благодарность доктору физ.-
матем. наук, проф. Я. Л. Геронимусу и доктору техн, наук
А. Е. Кобринскому за исключительно ценные критические замечания,
подавляющее большинство которых было учтено авторами при дора-
ботке рукописи.
Авторы обращаются с просьбой ко всем читателям направлять
критические замечания по настоящей книге в Государственное изда-
тельство физико-математической литературы.
ВВЕДЕНИЕ
1°. Научные основы теории проектирования механизмов, зало-
женные в конце XVIII и начале XIX веков в работах выдающихся
геометров и механиков: Эйлера, Ломоносова, Монжа, Понселе и др.,
получили значительное развитие во второй половине XIX века в ра-
ботах русских и зарубежных ученых. Это научное направление в
теории механизмов называется в настоящее время синтезом механиз-
мов. Под синтезом механизмов понимается проектирование кинемати-
ческой схемы механизма, удовлетворяющей заданнььм законам движе-
ния его звеньев и заданной структуре механизма. Таким образом,
синтез механизмов состоит в решении двух основных задач. Первая
задача — это задача структурного синтеза, т. е. установление пра-
вильного строения механизма с точки зрения числа кинематических
пар, из которых образован механизм, класса этих пар и их геометри-
ческих характеристик.
Если установлена принципиальная структурная схема механизма,
то вторая задача синтеза будет состоять в установлении форм
и размеров звеньев, удовлетворяющих тем движениям, которые должны
осуществлять звенья механизма. Эта задача может быть названа зада-
чей метрического синтеза механизмов.
Совершенно очевидно, что первая задача, как правило, предшест-
вует второй, так как, только установив структуру механизма, можно
переходить к определению размеров звеньев механизма по требуемым
законам движения звеньев.
С точки зрения методов решения задач синтеза эти методы доста-
точно четко могут быть разделены на две группы методов: точные
методы синтеза и приближенные методы синтеза. В решении задач
синтеза как точными* так и приближенными методами могут быть ши-
роко использованы геометрические и алгебраические методы или
синтетические методы, в которых приемы кинематической геометрии
сочетаются с использованием различных методов алгебраического
анализа и теории функций.
Ниже дается краткий обзор работ по синтезу механизмов, в основ-
ном тех, которые представляют собой фундаментальные исследования
или же были использованы авторами. Учитывая, что в монографии
И. И. Артоболевского, 3. Ш. Блоха и В. В. Добровольского
12
ВВЕДЕНИЕ
«Синтез механизмов*, изд. 1944 г., имеется подробный список лите-
ратуры по синтезу механизмов, авторы стремились в первую очередь
отразить в настоящем обзоре работы, опубликованные после 1944 г.,
и только в случае необходимости отражают в нем более ранние
работы.
Последовательность изложения материала соответствует принципу
построения монографии, т. е. вначале излагается литература по
точным методам синтеза. После этого излагается литература по при-
ближенным методам синтеза с подразделением на алгебраические
и геометрические методы.
Как было указано в предисловии, первые две главы монографии
являются вводными, содержащими необходимые сведения по струк-
туре рассматриваемых в монографии механизмов и по основам кине-
матической геометрии. Поэтому в настоящем введении авторы не
дают обзора литературы по этим вопросам, отсылая интересующихся
к таким работам, как монография А. Манхейма [91]*), Р. Бейера [63а],
В. Блашке и Мюллера [64] и др.
2°. Точные методы решения задач синтеза механизмов, в общем
случае задания движения, приводят к необходимости построения меха-
низмов, структурная схема которых будет включать в себя как
низшие, так и высшие пары.
Как известно, в основу синтеза механизмов с высшими парами
положены методы кинематической геометрии, разработанные приме-
нительно к построению центроид и взаимоогибаемых кривых.
Вопрос о нахождении сопряженных взаимоогибаемых кривых рас-
сматривался рядом ученых. Еще в 1733 г. Л. Камус [68] показал,
что сопряженные профили могут быть получены качением вспомога-
тельной центроиды по двум основным.
Вопросы построения сопряженных профилей, очерченных по эволь-
вентам и циклическим кривым были подробно рассмотрены Г. Пон-
селе [100] и Ф. Рело [102]. Важные вопросы о кривизне сопряжен-
ных профилей и связи их кривизны с кривизной центроид были
рассмотрены Л. Эйлером [70] и обобщены Савари [109]. Методы
определения центров кривизны сопряженных профилей получили
изящное геометрическое решение в работе Е. Бобилье [65].
В работах Н. И. Мерцалова [38], В. Гартмана [78], Р. Бейера [63а]
и др. для изучения кривизны сопряженных профилей была использо-
вана теория поворотных кругов. И. И. Артоболевский [Зе] для ре-
шения этих вопросов пользовался методом аналогов поворотных
кругов и методом дополнительно присоединяемых групп. Весьма
важное значение в теории проектирования механизмов с высшими
парами имела работа К. Виллиса [116], которым была установлена
основная зависимость между угловыми скоростями звеньев, входящих
*) Здесь и далее цифрами в квадратных скобках даны ссылки на список
литературы, помещенный в конце книги.
ВВЕДЕНИЕ
13
в высшую пару. Синтезу центр шдных механизмов были посвящены
работы многих авторов. Синтезу механизмов некруглых колес посвя-
щены работы Л. Бурместера [676], В. Яра, П. Кнехтеля [82]
и Д. С. Зернова [21], Ф. Л. Литвина [36]. Синтезу механизмов пе-
рекатывающихся рычагов была посвящена работа Г. Гольцера [80].
Общая теория синтеза центроидных механизмов и механизмов
с парами качения и скольжения была развита в работах Н. И. Мер-
цалова [38] и И. И. Артоболевского [3], А. М. Антовиля [2], кото-
рые использовали метод бицентроид для построения центроид в отно-
сительном движении. Большое количество различных задач по проек-
тированию механизмов с высшими парами рассмотрено в монографиях
И. И. Артоболевского, 3. Ш. Блоха и В. В. Добровольского [4],
Р. Крауса [85е], К. Хайна [766] и М. Никеза [96], а также в многочис-
ленных работах советских и зарубежных исследователей.
3°. Значительную группу механизмов с высшими парами представ-
ляют собой кулачковые механизмы.
Основными вопросами при решении задач синтеза кулачковых
механизмов с одной степенью свободы являются выбор закона дви-
жения ведомого звена и определение основных размеров механизма
с учетом углов давления.
Описание различных законов движения и сравнение их по основ-
ным характеристикам можно найти в работах X. Финкельнбурга (71 а],
X. Уэйда и Шостера [114], С. И. Артоболевского [6], Н. И. Левит-
ского [ЗЗи] и К. В. Тира [52в].
Кроме традиционных законов движения, получивших широкое
распространение (закон постоянной скорости, закон постоянного уско*
рения, законы с изменениями ускорения по трапеции, по синусоиде
и по косинусоиде), в работах К. В. Тира [52а, б, в, г], Я. Л. Геро-
нимуса [14в, г] и Зауэра [108] указывались законы движения с иными
характеристиками. Изучались также законы движения кулачков, про-
филь которых выбирался из условия получения простой схемы обра-
ботки, т. е. законы движения кулачков, очерченных по дугам окруж-
ностей и по растянутой эвольвенте. Методы проектирования этих
кулачков рассматривались в работах М. М. Тишина [53а] и Л. Н. Реше-
това [476].
В связи с повышением быстроходности кулачковых механизмов
особое внимание в работах С. Н. Кожевникова [28а], А. Е. Кобрин-
ского [26в] и Д. Митчела [93] было обращено на те законы движе-
ния, которые обеспечивают отсутствие скачков ускорения.
По исследованиям Зауэра [108] и А. Е. Кобринского [26г] среди
этих законов движения одним из лучших является закон движения
с ускорением, изменяющимся по наклонной синусоиде. Исследовались
также в работах X. Финкельнбурга [716], А. Е. Кобринского [26г]
и О. С. Езикашвили [19] способы обработки кулачков по методу
обкатки в приспособлениях с целью повышения точности образования
профиля кулачка.
14
ВВЕДЕНИЕ
При решении задачи об определении основных размеров кулачко-
вых механизмов наиболее важным вопросом является выбор допускае-
мого угла давления. В первых исследованиях К. А. Флокке [726]
и В. А. Юдина [60], посвященных решению задачи об определении
основных размеров, величину допускаемого угла давления рекомен-
довалось принимать: 60° для прямолинейно движущегося ведомого
звена и 45° для качающегося ведомого звена. В последующих иссле-
дованиях Г. А. Шаумяна [59а], Б. В. Шаскольского [58], И. М. Кучера [32]
и Н. И. Левитского [ЗЗи] были даны более обоснованные рекоменда-
ции для выбора допускаемого угла давления в зависимости от-мате-
риала и состояния трущихся поверхностей, а также предполагаемой
обработки профиля. Обстоятельной монографией, посвященной кине-
матике, динамике и некоторым вопросам точности, явилась опублико-
ванная в 1956 г. монография X. Ротбарта [107].
Основные вопросы проектирования обыкновенных мальтийских меха-
низмов изложены в работах Н. С. Ачеркана [7] и Г. А. Шаумяна [596].
Теории отдельных типов мальтийских механизмов посвящены работы
Ю. Н. Герасимова [13], Н. В. Сперанского [50а, б] и С. А. Черку-
динова и Н. В. Сперанского [576].
Большая литература посвящена задачам синтеза зубчатых меха-
низмов. Методы синтеза сопряженных профилей зубцов основываются
< на общих принципах построения взаимоогибаемых кривых. Мы не даем
обзора работ по вопросам проектирования схем зубчатых редукторов,
методов проектирования профилей зубцов в связи с процессом их
нарезания и г. д., так как эти вопросы не затронуты в настоящей
монографии.
4°. Точные методы синтеза механизмов с одними только низшими
парами получили свое развитие применительно к задачам воспроизве-
дения траекторий точек звеньев, являющихся прямыми и алгебраиче-
скими или трансцендентными кривыми.
Точные методы синтеза механизмов для образования плоских кри-
вых получили особое развитие во второй половине XIX века в связи
с задачами преобразования вращательного движения в поступательное
с помощью рычажных механизмов и задачами черчения кривых вто-
рого и более высоких порядков.
Теории точных прямолинейно-направляющих механизмов во второй
половине XIX века и начале XX века были посвящены работы:
А. Поселье [97], Л. Липкина [90], Г. Гарта [77], А. Кемпе [83],
В. Лигина [89], Н. И. Мерцалова [38] и др.*)
Теории механизмов для образования кривых второго и более высо-
ких порядков были посвящены работы: В. Г. фон Бооль [11], Н. Б. Де-
*) Мы указываем далеко не полный перечень работ этих авторов. Желаю-
щих более подробно ознакомиться с работами этих авторов отсылаем к книге
«Синтез механизмов» И. И. Артоболевского, 3. Ш. Блоха и В. В. Доброволь-
ского, Гостехиздат, 1944, стр. 375 — 384.
ВВЕДЕНИЕ
15
лоне [17а, б], П. О. Сомова [49]. В этих работах дается теория
различных механизмов: для черчения конических сечений, для черче-
ния некоторых кривых более высоких порядков и для преобразования
с помощью шарнирных механизмов вращательного движения во вра-
щательное с различными знаками и величинами передаточных отно-
шений.
В последние годы интерес к задачам проектирования механизмов
для воспроизведения теоретически точных законов движения значи-
тельно повысился в связи с развитием счетно-решающих устройств
и машин для математических операций, а также в связи с зада-
чами, связанными с обработкой профилей изделий, имеющих сложные
очертания.
Весьма полное описание различных механизмов для выполнения
математических операций и для черчения кривых различных порядков
имеется в работах Н. Г. Бруевича [126], В. Мейер-цур-Капеллен [92],
Ф. Виллерса [115], Н. Е. Кобринского [27], С. А. Гершгорина,
Н. И. Алексеева [1] и ряда других ученых.
Теории новых видов коникографов посвящены работы: В. П. Камин-
ского [24], И. И. Артоболевского [Зд, ж, з], В. Крауфорда [69] и др.
Теории механизмов для образования плоских кривых высших
порядков посвящены работы: Г. Л. Полыновского [45], В. В. Добро-
вольского [18е], Н. А. Никулина [39], И. И. Артоболевского [Зи, к, л,
м, н, о], Л. С. Поккера [99] и других ученых. В этих работах изла-
гаются различные методы синтеза механизмов для образования кривых
в основном третьего и четвертого порядков. Эти механизмы содержат
как вращательные, так и поступательные пары и могут быть исполь-
зованы для воспроизведения некоторых функций, представленных в ана-
литическом виде.
5°. Методы синтеза механизмов с одними низшими парами можно
подразделить на две группы. К первой группе относятся методы,
позволяющие создавать механизмы, теоретически точно воспроизводя-
щие заданную траекторию или заданную зависимость между переме-
щением звеньев *). Обзор литературы по этим методам был нами дан
выше. Ко второй группе относятся методы, позволяющие создавать
механизмы, воспроизводящие заданную форму движения лишь при-
ближенно, но с достаточной для практики точностью. Появление
и развитие методов второй группы, т. е. приближенных методов син-
теза механизмов, объясняются тем, что во многих случаях нельзя
получить практически удобного механизма для теоретически точного
воспроизведения заданной траектории или заданной зависимости между
перемещениями звеньев. Кроме того, с помощью приближенных
*) При теоретически точном воспроизведении заданной траектории или задан-
ной зависимости между перемещениями звеньев предполагается отсутствие
погрешностей, зависящих от неточности изготовления звеньев, хпругости звеньев
и условий работы механизмов и т. д.
16
ВВЕДЕНИЕ
методов можно в ряде случаев вместо теоретически точных много-
звенных механизмов получить воспроизведение тех же траекторий
или зависимостей между пеоемещениями звеньев при помощи простей-
ших четырехзвенных механизмов, которые вследствие меньшего влия-
ния погрешностей изготовления и упругости звеньев будут прак-
тически более точными, чем теоретически точные многозвенные ме-
ханизмы.
Основные методы приближенного синтеза механизмов в свою оче-
редь можно подразделить на две подгруппы. К первой подгруппе
относятся методы, основанные на том, что для данного механизма
составляется точное или приближенное аналитическое выражение от-
клонения от заданной функции и затем при помощи методов прибли-
жения функций вычисляются такие значения параметров, входящих
в это аналитическое выражение, при которых отклонение от заданной
функции мало отличается от нуля на заданном отрезке изменения
аргумента. Основным в этой группе методов является получение
достаточно простых для вычислений аналитических выражений откло-
нения от заданной функции. В дальнейшем эти методы будем назы-
вать алгебраическими. Ко второй подгруппе относятся методы, осно-
ванные на применении кинематической геометрии. В этих методах
аналитическое выражение отклонения от заданной функции исполь-
зуется лишь для подсчета отклонений после нахождения параметров,
определяющих кинематическую схему механизма. Решение же самих
задач синтеза механизмов выполняется графическим или аналитическим
путем на основании положений, вытекающих из основных теорем
кинематической геометрии. Эти методы в дальнейшем будем называть
методами, основанными на использовании кинематической геометрии,
или, кратко, геометрическими методами.
В соответствии с указанным подразделением методов синтеза
механизмов с одними низшими парами обзор основных работ по
приближенным методам синтеза этих механизмов будет построен в
следующем порядке. В начале будут рассмотрены работы по алгебраи-
ческим методам приближенного синтеза механизмов, а потом работы
по методам, основанным на кинематической геометрии.
6°. Алгебраические методы приближенного синтеза механизмов
применяются для решения следующей задачи. Дана непрерывная функ-
ция y = F(x), которую нужно воспроизвести при помощи механизма.
Переменные х и у представляют собой в задачах синтеза направляю-
щих ’ механизмов координаты точек заданной траектории, в задачах
синтеза передаточных механизмов — углы поворота ведущего и ведо-
мого звеньев и т. д. Заданная функция у — F(x) в большинстве
случаев не может быть воспроизведена механизмом точно. Обозначим
ту функцию, которую можно воспроизвести механизмом через
v = FM(x, г.2, • •• , гп), где г2, , гп — параметры кинема-
тической схемы механизма, т. е. длины звеньев и другие величины,
входящие в кинематическую схему. Требуется так подобрать пара-
ВВЕДЕНИЕ
17
метры гь г2, ... , гп, чтобы функция j/ = FM(x, г{, гъ\.. , rfl) воз-
можно мало отличалась от заданной функции y = F(x).
Первые работы по алгебраическим методам приближенного синтеза
механизмов принадлежат П. Л. Чебышеву [55а—п]. В своих работах
по теории механизмов Чебышев дал образцы применения двух соз-
данных им методов приближенного синтеза механизмов.
Первый метод состоит в том, что на основании условий наилуч-
шего приближения функций выводятся соотношения между парамет-
рами кинематической схемы, необходимые цля получения малой ве-
личины отклонения функции у — FmП, г.2, ... , гп) от заданной
функции y = F(x). При выводе этих соотношений основным являет-
ся получение достаточно простого аналитического выражения для
отклонения от заданной функции.
В простейших случаях можно использован^ непосредственно раз-
ность
A=Fjf(x) —
Так была решена Чебышевым задача об определении параметров ки-
нематической схемы симметричного шарнирного четырехзвенника, в ко-
тором шатунная кривая приближена к прямой линии [55е, и, к, л].
При решении более общей задачи о приближении шатунной кри-
вой симметричного шарнирного четырехзвенника к дуге окружно-
сти Чебышев (55о, п) принимает в качестве отклонения от заданной
функции величину
Дл = /?ж— 7?,
где R — радиус окружности, к которой должна быть приближена
шатунная кривая; Rm — переменное расстояние от центра этой окруж-
ности до точек шатунной кривой.
Величина RM, а следовательно и Дп, являются функцией парамет-
ров кинематической схемы, но использовать аналитическое выражение
функции Дп для определения искомых параметров не представляется
возможным ввиду его сложности. Поэтому Чебышев вводит другую
функцию
Д7== Rm —R>
которая связана с отклонением Дл зависимостью
Д^ — (R R Д/г
Функция Д7 также зависит от искомых параметров кинематической
схемы, но аналитическое выражение ее значительно проще, чем
выражение Дп. Если мала величина Дд, то соответственно мала и ве-
личина отклонения Дп. На этом основании Чебышев вычисляет иско-
мые параметры из условий получения малых величин Д^ на рассматри-
ваемом отрезке изменения аргумента. При Дд, равном нулю, Дл также
равно нулю. Поэтому в результате вычислений находятся такие соот-
ношения между параметрами кинематической схемы механизма, при
18
ВВЕДЕНИЕ
которых шатунная кривая оказывается на некотором участке, заклю-
ченной между двумя близкими концентрическими окружностями с
радиусами R и Rm.
Характерной особенностью первого метода Чебышева является то,
что число получаемых соотношений между параметрами кинематической
схемы обычно меньше числа этих параметров. Поэтому задача может
считаться полностью решенной только после установления областей
существования механизма, а также тех областей изменения парамет-
ров кинематической схемы, в которых отклонение от заданной функ-
ции будет малым.
По второму методу Чебышева решение задачи приближенного
синтеза механизмов разделяется на два этапа. Первый этап состоит
в предварительном определении параметров кинематической схемы
механизма при помощи способов, которые дают простую схему ре-
шения, но не обеспечивают получения минимального отклонения от
заданной функции. Второй этап состоит в уточнении параметров
кинематической схемы с целью уменьшения величины отклонения от
заданной функции.
На первом этапе Чебышев использует разложение в степенной
ряд отклонения от заданной функции. Искомые соотношения между
параметрами кинематической схемы получаются, если приравнять ну-
лю коэффициенты нескольких первых членов ряда.
На втором этапе Чебышев определяет поправки к вычисленным
параметрам из условий наилучшего приближения.
Второй метод Чебышев применяет в тех случаях, когда первый
метод оказывается неприменимым ввиду сложности получаемых ана-
литических выражений, характеризующих отклонение от заданной
зависимости. Используя разложение в ряд, но без вычисления попра-
вок, Чебышев решает задачу о синтезе несимметричных и много-
звенных прямолинейно-направляющих механизмов [55в, г, ж, м, н].
Вычисление поправок к параметрам кинематической схемы, т. е. вы-
полнение второго этапа, было дано Чебышевым только при решении
задачи о профилировании зубчатых колес, зубья которых очерчены
по дугам окружностей [55з]. Способ вычисления поправок при ре-
шении задачи синтеза четырехзвенного прямолинейно-направляющего
механизма Уатта был впоследствии показан в работе И. И. Артобо-
левского и Н. И. Левитского [5в] *).
Еще при жизни Чебышева разработанные им методы были раз-
виты в работах Н. Леоте [86а, б, в, г, д], который решал задачи о
приближении к дугам окружности, циклоиды и эвольвенты шатунной
кривой несимметричного шарнирного четырехзвенника. Леоте исполь-
зует преимущественно разложение в ряды, причем применяет не
*) Более подробные сведения о работах П. Л. Чебышева можно найти
в статьях И. И. Артоболевского, В. В. Добровольского и Н. И, Левитского [Зг,
5а, б, в, 186].
ВВЕДЕНИЕ
19
только степенные, но и тригонометрические ряды. В дальнейшем
неоднократно в литературе указываются новые способы вывода фор-
мул Чебышева для симметричных прямолинейно-направляющих меха-
низмов [20].
Однако новые механизмы, полученные по методу Чебышева, ста-
ли описываться в отечественной литературе только, начиная с 1940 г.,
когда появились статьи 3. Ш. Блоха [9е, ж, з, и, к, л, м, н], объеди-
ненные им впоследствии в монографию [9о]. В работах 3. Ш. Блоха
были восстановлены все промежуточные выкладки и доказательства,
которые были опущены Чебышевым при рассмотрении задач синтеза
механизмов. Кроме того, были решены по методу Чебышева ряд но-
вых задач, из которых отметим задачи о приближении шатунной
кривой центрального кривошипно-шатунного и кулисного механизмов
к прямой линии и дуге окружности, а также задачи о воспроизведе-
нии приближенно равномерного движения с помощью шарнирного
четырехзвенника и кривошипно-шатунного механизма.
При решении этих задач для вычисления искомых параметров
кинематической схемы 3. Ш. Блох использует следующий метод.
Для механизма с одной степенью свободы можно установить сис-
тему уравнений:
-V = cp, (£, ГЬ гг, .... г„),
= г„ г4, .... г„),
определяющую связь между любыми его двумя переменными парамет-
рами х и у через вспомогательный параметр f, причем в эти ура-
внения входят искомые параметры кинематической схемы гь г2, ...» гп.
Если механизм предназначен для воспроизведения функции, предста-
вленной в неявном виде
F(x, д/) = 0,
то, подставляя в это уравнение значения х и у, выраженные через
аргумент t, получим функцию 9 = F(£, rb r2, , rrt), которая зави-
сит от аргумента t и параметров кинематической схемы. Эти пара-
метры выбираются из условий наилучшего приближения так, чтобы
величины 6 (t, rlt r.2, ... , гп) были малы на рассматриваемом отрезке
изменения аргумента Л
Аналогично решается задача, если заданная функция представле-
на в явном виде
y = F(x),
а связь между переменными х и у в механизме представлена в виде
уравнения
/(JC, У, П, .... г„) = о.
Подставляя в это уравнение величины заданной функции, полу-
чаем функцию
9=/[f (*)> X, rt, гъ ..., гп].
20
ВВЕДЕНИЕ
Искомые параметры кинематической схемы определяются в этом
случае из условий получения малых величин 6 на рассматриваемом
отрезке изменения аргумента х.
Границы применимости этого метода были уточнены в работах
Н. И. Левитского [33а] и С. А. Черкудинова [56м].
7 . В монографии Н. И. Левитского [33а| было показано, что
можно получать аналитические выражения функции, связанной с откло-
нением от заданной зависимости, в удобном для вычислений виде,
если принимать в качестве этой функции взвешенную разность, т. е.
выражение вида
где А — отклонение от заданной функции, измеренное по определен-
ному направлению; q — параметрической вес, т. е. произвольная не-
прерывная функция, содержащая искомые параметры кинематической
схемы и удовлетворяющая на рассматриваемом отрезке изменения
аргумента неравенству
Если пределы т и М в этом неравенстве достаточно близки между
собою, т. е. вес q незначительно отличается от постоянной величины,
то условия наименьшего отклонения от нуля функции Д^ практически
совпадают с условиями наименьшего отклонения функции А.
Произвольность выбора веса q (с указанным ограничением) дает
возможность значительно изменять вид функции Д^. Поэтому если
непосредственное определение параметров кинематической схемы из
условий наименьшего отклонения от нуля разности А практически
невозможно, то соответствующим выбором веса можно в некоторых
случаях получить искомое решение из условия наименьшего откло-
нения от нуля взвешенной разности.
Применение взвешенного приближения с параметрическим весом
дало возможность расширить круг задач синтеза механизмов, решае-
мых аналитическими методами.
К взвешенному приближению с параметрическим весом приводит
в общем случае также метод С. А. Черкудинова [56м]. Получаемое
при этом решение отличается ясной геометрической картиной прибли-
жения (приближающая кривая заключена между двумя граничными
кривыми).
Несмотря на применение взвешенного приближения, круг задач,
решаемых непосредственно с помощью метода Чебышева, оставался еще
очень ограниченным. В основном можно было считать решенными
только задачи о приближении шатунных кривых четырехзвенных меха-
низмов к прямой линии [8в, 9е, ж, з, к, л, м, о, 23а, б, 33а], сим-
метричных шатунных кривых — к кривым второго порядка [9к, о, 33а,
56м] и задачи синтеза механизмов для воспроизведения равномерного
движения [9н, о, 33а, 56и, л, о]. Поэтому дальнейшие усилия иссле-
ВВЕДЕНИЕ
21
дователей, развивающих аналитические методы приближенного синтеза
шарнирно-рычажных механизмов, были направлены на разработку
таких методов синтеза, которые давали бы возможность решать
задачи о воспроизведении любых законов движения или любых тра-
екторий, если только они могут быть воспроизведены с некоторым
приближением при помощи механизмов с одними низшими парами. С этой
целью, кроме наилучшего приближения, предлагалось использовать
другие виды приближения функций: интерполирование и квадратичес-
кое приближение, а также изыскивались способы наиболее простого
представления функции, характеризующей отклонение от заданной за-
висимости.
Интерполирование при решении задач синтеза механизмов с низ-
шими парами использовалось сначала в геометрической форме *). В виде
аналитического или графоаналитического способа оно применялось
в работах М. В. Семенова [48а], 3. Ш. Блоха [4, 9а, б], В. А. Зиновь-
ева [22а], Е. П. Новодворского [40| и Ф. Фрюдепштейпа [73а, б, в]
и К. Зикера [1 Иг]. Квадратическое приближение предлагалось в рабо-
тах Г. Г. Баранова [8а] и Н. И. Левитского [ЗЗв, г].
8< Однако решающую роль в распространении методов синтеза
механизмов с низшими парами на любые заданные зависимости сыгра-
ли те исследования, в которых предлагались новые способы аналити-
ческого представления функций, связанных с отклонением от задан-
ной функции.
М. В. Семеновым [486] было предложено использовать методы
гармонического анализа при уточнении параметров механизма, вос-
производящего заданную траекторию.
А. Свобода [112] при синтезе шарнирного четырехзвенника и кри-
вошипно-шатунного механизма раскладывает в ряд аналитическое
выражение отклонения от заданной функции, рассматривая эго вы-
ражение как функцию нескольких переменных. Если принять в каче-
стве этих переменных параметры кинематической схемы и удержать в раз-
ложении только первые члены, то получается приближенное выражение
отклонения от заданной функции, которое является линейным относи-
тельно искомых параметров кинематической схемы. Аналогичный спо-
соб был предложен И. Ш. Пинскером [44а].
Использование приближенного выражения, предложенного в рабо-
тах А. Свободы и И. Ш. Пинскера, предполагает, что предварительно
были найдены параметры кинематической схемы механизма, дающего
некоторое приближение к заданной функции, и, следовательно, это
выражение служит лишь для вычисления поправок, уточняющих зна-
чения параметров кинематической схемы. В дальнейшем было показано
[ЗЗз, стр. 83], что получаемые по этому методу поправки могут ухуд-
шать приближение к заданной функции, если первое приближение
не было достаточно близко к окончательному.
*) См. далее стр. 23.
22
ВВЕДЕНИЕ
Другой путь получения простых аналитических выражений для
отклонения от заданной функции был предложен Н. И. Левитским
в ряде статей [33г, ж, 34], обобщенных затем в монографию [ЗЗз].
По методу Н. И. Левитского в тех случаях, когда нельзя полу-
чить достаточно простое аналитическое выражение отклонения от задан-
ной функции, предлагается использовать взвешенную разность с пара-
метрическим весом, причем эта разность ищется в первую очередь
в виде обобщенного полинома
Д (?) = Л [/70/0 (?) + Pi/i (?) + •. + pnfn (?) — F (?)],
где А, р{}, ри...,рп — постоянные коэффициенты, зависящие от
искомых параметров кинематической схемы; F(ср), /0(ср), /1(ср), ...,
А(?) — функции обобщенной координаты механизма (например, угла
поворота ведущего звена), не содержащие искомых параметров.
Для получения этого выражения применительно к плоским четы-
рехзвенным механизмам был предложен прием, состоящий в том, что
сначала составляется аналитическое выражение взвешенной разности
путем определения разности между постоянной величиной одного из
параметров кинематической схемы и переменной величиной того же
параметра (или квадратов этих величин), если путем удаления одной
из связей превратить рассматриваемый механизм в систему с двумя
степенями свободы. После составления взвешенной разности находится
точное или приближенное выражение параметрического веса, и сле-
довательно, получается аналитическое выражение (точное или прибли-
женное) для отклонения от заданной функции. Взвешенная разность
с параметрическим весом может иметь и более сложный вид.
Например,
А (?) = A [p0f0 (?) (?) + •• • +Рп?я(?) (?) — F (?)!•
Для вычисления искомых параметров в работах Н. И. Левитского [33г, ж,
з, 35а] использовались квадратическое приближение, интерполирование
и наилучшее приближение, причем для вычисления наилучшего при-
ближения к произвольно заданной функции был использован метод по-
следовательных приближений, состоящий в уравнивании максимальных
отклонений *). Следовательно, если удается получить отклонение от
заданной функции или взвешенную разность с параметрическим весом
в виде обобщенного полинома или сходной по форме функции, то в
настоящее время мы можем применить любой из трех указанных видов
приближения функций, выбирая из них тот, который соответствует
заданным условиям приближения **).
*) В задачах уравновешивания механизмов этот метод был использован
Я. Л. Геронимусом [146].
**) Под наилучшим приближением здесь понимается то приближение, кото-
рое получается путем уравнивания максимумов при максимально возможном
числе точек предельного отклонения. Строго говоря, оно не является наилучшим,
но во многих практических случаях весьма близко к нему.
ВВЕДЕНИЕ
23
Вскоре после появления работы [ЗЗз] предлагаемые в ней методы
были распространены Н. И. Левитским, Б. И. Степановым и К. X. Шах-
базяном на пространственные механизмы [Зоб, 51]. Кроме того, Б. И. Сте-
пановым (совместно с Н. И. Левитским) был предложен графический
метод, позволяющий находить конструктивно приемлемые решения,
если механизм, полученный из условия минимального отклонения от
заданной функции, не удовлетворяет конструктивным требованиям [34].
С этой же целью Е. П. Новодворским и И. Ш. Пинскером предла-
галось учитывать при аналитическом решении задач синтеза механиз-
мов угол передачи [41], и рядом ученых составлялись атласы зависи-
мостей, которые могут быть воспроизведены с помощью простейших
механизмов [36, 446, 81].
При решении задачи о воспроизведении заданной траектории при
помощи шарнирных механизмов необходимо всегда иметь в виду
возможности преобразования механизмов, причем эги преобразования
могут быть точными или приближенными. К точным преобразованиям
относится преобразование Робертса [103]. Согласно этому преобразо-
ванию шатунная кривая шарнирного четырехзвенника может быть
воспроизведена в общем случае тремя различными четырехзвенниками.
Преобразование Робертса было впоследствии распространено Н. И. Ле-
витским на шарнирные механизмы с любым числом звеньев [336].
К приближенным преобразованиям относится преобразование Чебышева
[55м], предложенное им для прямолинейно-направляющих механизмов,
и преобразование С. А. Черкудинова [56п] для механизмов, направ-
ляющих по дугам окружностей. Приближенные преобразования дают
механизмы с различными шатунными кривыми, но имеющими один и
тот же порядок приближения к заданной траектории.
9°. Вопросы синтеза механизмов с низшими парами с применением
геометрических методов начали разрабатываться во второй половине
XIX века.
В 1870 г. печатаются в переводе на немецкий язык первые работы
Чебышева по синтезу механизмов с комментариями Ф. Рело *). Как
известный отклик на них в 1876 — 1877 гг. появляется капитальное
исследование немецкого ученого Л. Бурместера [67 а, б], в котором
отмечается сложность, по мнению автора, аналитических методов
Чебышева и дается обоснование наглядного геометрического метода
решения задачи синтеза направляющих механизмов. Бурместер в этом
исследовании разрабатывает новый раздел кинематической геометрии,
а именно кинематическую геометрию конечно удаленных положений
плоской фигуры, совершающей движение в своей плоскости, и уста-
навливает две важнейшие кривые геометрического синтеза: кривую
круговых точек и кривую центров. Кривая круговых точек это — гео-
метрическое место таких точек плоской фигуры, четыре положения
Рг В CM^Verhandlungen des Vereins zur Beford erung des GewerbefleiBes in
24
ВВЕДЕНИЕ
которых лежат на одной окружности, а кривая центров — геометри-
ческое место центров этих окружностей. С помощью указанных
кривых Бурместер дал решение задачи об интерполяционном при-
ближении с четырьмя, пятью и шестью узлами шатунной кривой
четырехзвенных механизмов к прямой линии. В отличие от Чебышева
Бурместер не ставит вопроса о численной оценке полученных откло-
нений шатунной кривой от прямой линии.
Метод Бурместера подобно методам Чебышева долгое время
не находил отражения в литературе по теории механизмов.
В 1917 г. М. Грюблер [746] показывает простое геометрическое
решение задачи синтеза шарнирного четырехзвенника как передаточ-
ного механизма по двум и трем положениям его ведущего и ведо-
мого звеньев. В 1921 г. Г. Альт [61а], применив теорию Бурместера,
распространяет решение Грюблера на четыре и пять заданных поло-
жений и показывает, что задача синтеза шарнирного четырехзвенника
и кривошипно-шатунного механизма по пяти положениям может иметь
до трех решений.
Упомянутые работы Бурместера и Альта положили начало основ-
ному направлению в немецкой школе приближенного синтеза меха-
низмов с низшими парами, которое характеризуется следующими
моментами: а) в качестве метода приближения используется интер-
полирование; б) единственным средством повышения точности при-
ближения считается увеличение числа узлов на заданном отрезке;
в) форма решения задач синтеза чисто геометрическая. В последую-
щих работах Г. Альт дал решение задачи о предельных положениях
механизма [616, к, л], рассмотрел некоторые задачи синтеза меха-
низмов с остановками [61 ж, о], исследовал кривые центров и кривые
круговых точек в случаях, когда некоторые положения плоской
фигуры оказываются бесконечно близкими [61м] или параллельными
друг другу [61з, и, к], указал на ряд решающих преимуществ шар-
нирных механизмов над кулачковыми в практике эксплуатации машин-
автоматов [61 в, д]. Дальнейшей разработкой этого направления
занимались в Германии В. Лихтенхельдт [88а, б, в, г, д, е, ж, з],
К. флокке [72а], Р. Краус [85а, б, в, г, д, е], Г. Кипер [84], И. Мюл-
лер [94а, б], Е. Хаккмюллер [75а, б, в], К. Шнарбах [110а, б],
Р. Бейер [636, в, г, д, е] и Рёснер [106]. В работах этих авторов
указаны решения задач синтеза шарнирно-рычажных механизмов с
числом заданных положений, большим чем пять, решения отдельных
задач распространены на многозвенные механизмы второго и высшего
классов. Обобщающая монография по методу Бурместера принадле-
жит Бейеру [63д].
Развитию геометрического направления в приближенном синтезе
шарнирно-рычажных механизмов уделялось внимание и в отечествен-
ной литературе. Г. Г. Баранов [86] предложил простой вывод усло-
вий, определяющих кривую центров и кривую круговых точек. В ра-
ботах Н. Г. Бруевича [12а] и А. Б. Парницкого [43] геометрическим
ВВЕДЕНИЕ,
25
методом Бурместера решены задачи синтеза механизма с прицепным
шатуном и механизма крапа с укосиной. Ряд других задач рассмот-
рен в работах В. В. Добровольского [4, 18в] и С. Л. Черкудинова
[56а, б, в, г, ж, р]. В частности, Добровольским 118в] теория Бур-
местера была перенесена на сферу и на последней изучены кривые,
аналогичные кривым Бурместера на плоскости.
Оригинальные интерполяционные методы приближенного синтеза
механизмов с низшими парами, чисто геометрические по форме,
разработаны К. Хайном [766]. Эти методы во многих случаях поз-
воляют использовать большее число параметров схемы, чем аналити-
ческие методы и геометрические методы, основанные на теории
Бурместера.
М. Грюблер [74а], К. Родеиберг [104] и Р. Мюллер [95а, б] иссле-
довали кривые Бурместера (кривую центров и кривую круговых
точек), относящиеся к случаю четырех бесконечно близких положений
плоской фигуры, совершающей движение в своей плоскости. С помо-
щью этих кривых ими дано геометрическое решение задачи об интер-
поляционном приближении шатунной кривой четырехзвенника к прямой
линии с одним узлом, кратность которого может быть равна четырем,
пяти и шести. Примеры применения этих результатов для решения
других задач синтеза механизмов указаны Г. Альтом |61е] и Лихтен-
хельдтом [88в].
В работе А. П. Котельникова [31] установлены общие аналити-
ческие условия соприкосновения кривых, и на их основе дана ана-
литическая теория кривой центров и кривой круговых точек для
случая бесконечно близких положений плоской фигуры. Котельников
установил ряд новых свойств этих кривых и дал примеры их при-
менения в синтезе направляющих механизмов. Дальнейшие примеры
в этом направлении принадлежат В. В. Добровольскому [4]. В ра-
боте С. А. Черкудинова и Н. В. Сперанского [57в, г] содержатся не-
которые обобщения теории Котельникова, которые позволили приме-
нить эту теорию к решению задач синтеза передаточных механизмов.
Во всех указанных выше исследованиях, начиная с работы самого
Бурместера, решения отдельных задач имеют чисто геометрическую
форму. Последняя не обеспечивает необходимой точности в опреде-
лении параметров схемы механизма и не позволяет выявлять все
имеющиеся р'ешения. Однако начавшаяся разработка аналитических
решений, основанных на теории Бурместера, открывает реальные
перспективы внедрения в конструкторскую практику того широкого
круга задач синтеза механизмов с низшими парами, которые решены
геометрическими методами. Первой попыткой в этом направлении
является работа С. А. Черкудинова [56р], в которой дан аналитиче-
ский метод подсчета пяти параметров шарнирного четырехзвенника,
оснсвзппый на теории Бурместера. Подсчет этих параметров ведется
из условия интерполяционного приближения с двукратными узлами.
В работе С. А. Черкудинова и Н. В. Сперанского [57а] указано
26
ВВЕДЕНИЕ
аналитическое решение задачи синтеза шарнирного шестизвенника
с остановками, основанное на теории Бурместера. В работах К. Зи-
кера [1116] и Р. Крауса [85д] показан аналитический подсчет четырех
параметров шарнирного четырехзвенника с помощью кривых Бурме-
стера.
Успешное внедрение в конструкторскую практику методов при-
ближенного синтеза механизмов с низшими парами немыслимо без
углубленного изучения свойств и возможностей отдельных схем этих
механизмов и создания соответствующих справочных материалов в
форме вспомогательных графиков, таблиц и т. д. Работа в этом
отношении еще только начата. Упомянем здесь многотомный справоч-
ник по механизмам И. И. Артоболевского [Зп], атлас шатунных
кривых шарнирного четырехзвенника Хронса и Нельсона [81], ат-
лас по кинематическому расчету кривошипно-шатунных механизмов
И. И. Артоболевского [36], номограммы по расчету четырехзвенных
механизмов 3. LLL Блоха и Е. Б. Карпина [10], работу Г. Альта [61н],
в которой дана вспомогательная диаграмма для проектирования шар-
нирного четырехзвенника по предельным положениям, работу Лих-
тенхельдта [88д], содержащую диаграммы для проектирования одной
из схем шестизвенника с выстоем.
Сюда же могут быть отнесены работы И. И. Артоболевского и
Н. И. Левитского [5а], 3. Ш. Блоха [96], Н. И. Колчина [29],
С. А. Черкудинова [56д] и Ф. Фрейдештина [73в] по исследованию
частных свойств отдельных схем шарнирно-рычажных механизмов,
а также работы С. А. Черкудинова [56к] и Р. Крауса [856] по выявле-
нию числа независимых параметров, определяющих кинематическую
схему механизма.
ЧАСТЬ ПЕРВАЯ
НЕКОТОРЫЕ СВЕДЕНИЯ ПО ТЕОРИИ СТРУКТУРЫ
И КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ МЕХАНИЗМОВ
ГЛАВА [
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ
* И ИХ СТРУКТУРА
§ 1. Трехзвенные механизмы
1°. Простейшими плоскими механизмами являются трехзвенные
механизмы, образованные из замкнутой кинематической цепи, состоя-
щей из трех звеньев, входящих последовательно в три кинемати-
ческие пары. Кинематические пары, которыми образованы эти меха-
Рис. 1.
низмы, могут быть парами IV и V классов. К парам IV класса отно-
сится высшая пара (рис. 1, а), обеспечивающая качение со скольжением
одного элемента пары относительно другого. К парам V класса
относятся: низшие вращательная (рис. 1, б) и поступательная пары
(рис. 1, в), а также высшая центроидная пара (рис. 1, г), обеспечи-
вающая перекатывание без скольжения одного элемента пары отно-
сительно другого. К высшим парам V класса также относится пара
(рис. 1, д), состоящая из двух попарно сопряженных элементов:
28
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУР X
[гл. I
п — п’ и гп— гп'. Эту пару будем называть сложной или траектор-
ной, так как подбором очертаний профилей элементов //, /г', т и т'
можно осуществить движение точек звеньев по различным траекториям.
2е. Трехзвенные плоские механизмы могут быть механизмами
третьего и четвертого семейства [Зр]. Рассмотрим механизмы четвер-
того семейства. Структурная формула механизмов этого семейства,
как известно, имеет следующий вид:
w — 2п — /?3,
(1.1)
где w — число степеней подвижности, равное для рассматриваемых
далее механизмов w=l; п — число подвижных звеньев, равное для
рассматриваемых механизмов п = 2; рГ1 — число пар V класса.
Из уравнения (1.1) следует, что число пар равно трем.
Рис. 2.
Рис. 3.
Таким образом, трехзвенные плоские механизмы четвертого се-
мейства могут иметь в своем составе только пары, показанные на
рис. 1, б, в, г и д. Пары IV класса, показанные на рис. 1, а, в со-
став механизмов этого семейства входить не могут.
3°. Первым видом трехзвенных плоских механизмов четвертого
семейства будут так называемые ценпгроидные механизмы. Центро-
идным механизмом называется механизм четвертого семейства, все
высшие кинематические пары которого являются только центроидными
нарами, т. е. парами вида, показанного на рис. 1, г.
На рис. 2 показана принципиальная кинематическая схема цен-
троидного механизма, образованного тремя центроидными парами.
Точки А, С и В соприкосновения звеньев 7, 2 и 3 должны лежать
на одной общей прямой, так как они являются мгновенными центрами
вращения А21, и Р31. Перекатывание звеньев 7, 2 и 3 друг по
другу происходит без скольжения, т. е. каждая пара соприкасаю-
щихся кривых должна быть сопряженными центроидами. На рис. 3
§ 1]
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
29
показан пример центроидного механизма, образованного тремя ценгро-
идными парами. Звено 2 представляет собой окружность а, перека-
тывающуюся без скольжения по прямой Ох. С этой окружностью
жестко связан некруглый сектор а. Звено 3 представляет собой
окружность Ь, перекатывающуюся без скольжения по прямой Оу.
С этой окружностью жестко связан некруглый сектор р. Секторы
аир перекатываются без скольжения друг по другу. На рис. 4, а
показан один из возможных видов планетарного центроидного меха-
низма с круглыми цилиндрическими колесами, воспроизводящий по-
Рис. 4.
з
стоянное передаточное отношение Радиусы колес /, 2 и 3
равны между собой. Радиус колеса Г равен четырем радиусам ко-
леса 1. Радиусы колес 2' и 3' соответственно равны и з 4/д радиу-
са ’ колеса /. При этих условиях бицентроидой в относительном
движении колес 2 и 3 будет окружность радиуса ОС. и точки Д,
С и В будут всегда лежать на одной общей прямой. Это позво-
ляет установить дополнительно поводок Н, который будет обеспе-
чивать кинематическое замыкание всего механизма. На рис. 4, б по-
водок Н, как накладывающий на механизм пассивные связи, показан
пунктиром.
4°. Если одна из центроидных пар заменена парой вращательной,
го мы получаем центроидный механизм, принципиальная схема кото-
рого показана на рис. 5. На рис. 6 показан пример центроидного
механизма с одной вращательной парой — планетарный механизм с
30
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА |ГЛ. I
эллиптическими гладкими колесами. Колесо 2 обегает неподвижное
колесо 1. При этом жестко связанное с колесом 2 колесо 2' пере-
катывается без скольжения по колесу 3, которое вращается около
оси В, Поводок /7, показанный на рис. 6, б пунктиром, накладывая
пассивные связи, обеспечивает кинематическое замыкание всего ме-
ханизма. Частным случаем механизма будет планетарный механизм с
круглыми цилиндрическими колесами, один из возможных вариантов
которого показан на рис. 7. Вариантом механизма, показанного на
рис. 5, будет центроидный механизм, полученный путем перемены
стойки; его принципиальная кинематическая схема показана на рис. 8.
§ И
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
31
На рис. 9 показан пример центроидного механизма указанного вида.
Некруглый сектор 3 входит во вращательную пару В с круглым
цилиндрическим колесом /. При качении колеса 1 по неподвижной
прямой хх некруглый сектор 3 перекатывается по неподвижной
кривой qq, являющейся центроидой в движении сектора 3 относи-
тельно неподвижного звена 2. Одним из частных случаев такого
Рис. 10.
механизма будет планетарный механизм на рис. 10, состоящий из двух
круглых цилиндрических колес 1 и 3, перекатывающихся по непо-
движным колесам 2 и 2'. Колеса 1 и 3 входят во вращательную пару В,
Так же как и в выше рассмотренных планетарных механизмах, поводок И9
показанный на рис. 10, б обеспечивает кинематическое замыкание
механизма.
32 ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. [
§
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
33
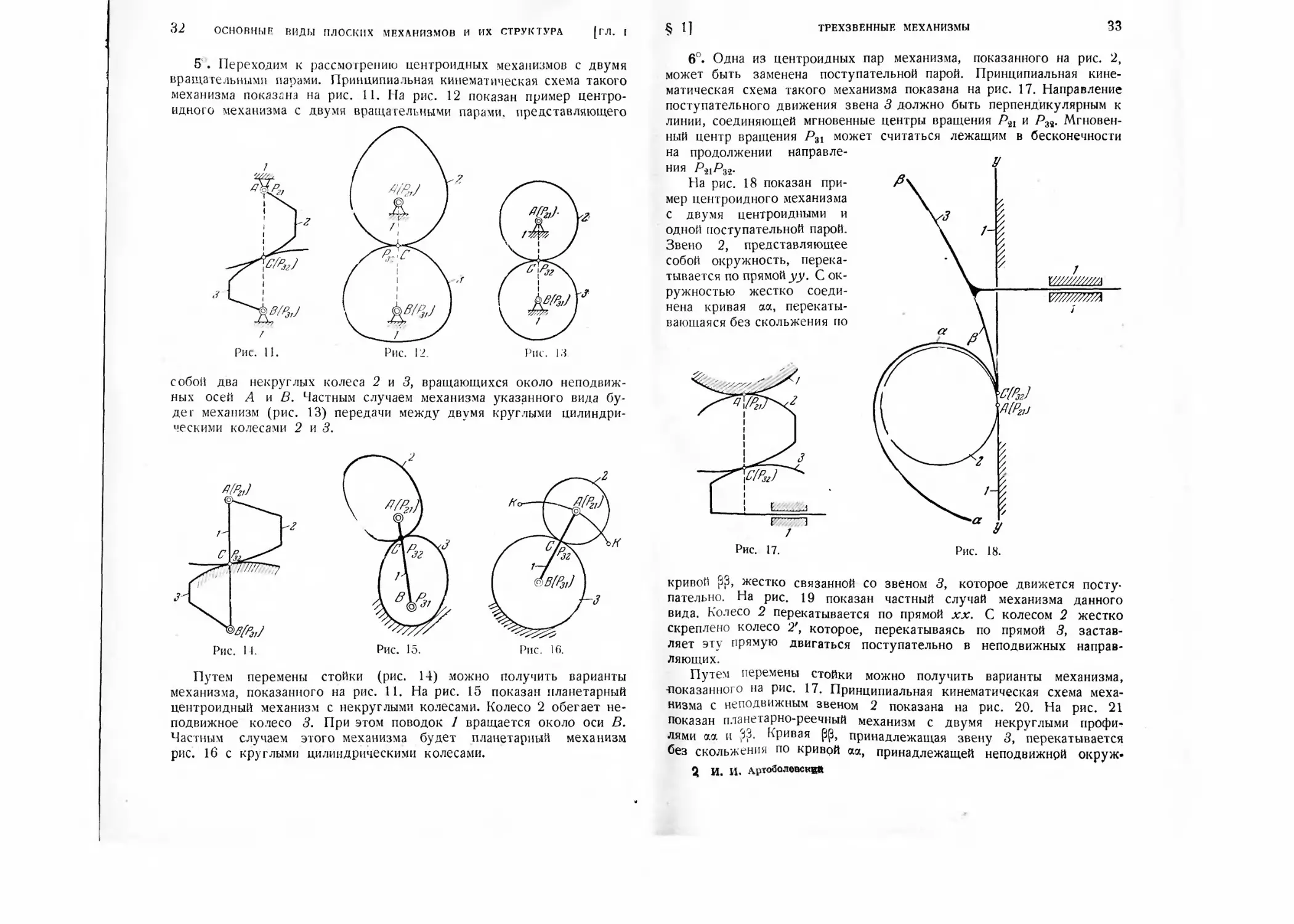
5'. Переходим к рассмотрению центроидных механизмов с двумя
вращательными парами. Принципиальная кинематическая схема такого
механизма показана на рис. 11. На рис. 12 показан пример центро-
идного механизма с двумя вращательными парами, представляющего
6°. Одна из центроидных пар механизма, показанного на рис. 2,
может быть заменена поступательной парой. Принципиальная кине-
матическая схема такого механизма показана на рис. 17. Направление
поступательного движения звена 3 должно быть перпендикулярным к
линии, соединяющей мгновенные центры вращения Р21 и Р32. Мгновен-
ный центр вращения Р31 может считаться лежащим в бесконечности
на продолжении направле-
НИЯ РиРзг.
На рис. 18 показан при-
мер центроидного механизма
с двумя центроидными и
одной поступательной парой.
Звено 2, представляющее
собой окружность, перека-
тывается по прямой уу. С ок-
ружностью жестко соеди-
нена кривая аа, перекаты-
вающаяся без скольжения по
собой два некруглых колеса 2 и 3, вращающихся около неподвиж-
ных осей А и В. Частным случаем механизма указанного вида бу-
дет механизм (рис. 13) передачи между двумя круглыми цилиндри-
ческими колесами 2 и 3.
Рис. 17.
Путем перемены стойки (рис. 14) можно получить варианты
механизма, показанного на рис. 11. На рис. 15 показан планетарный
центроидный механизм с некруглыми колесами. Колесо 2 обегает не-
подвижное колесо 3. При этОхМ поводок / вращается около оси В.
Частным случаем этого механизма будет планетарный механизм
рис. 16 с круглыми цилиндрическими колесами.
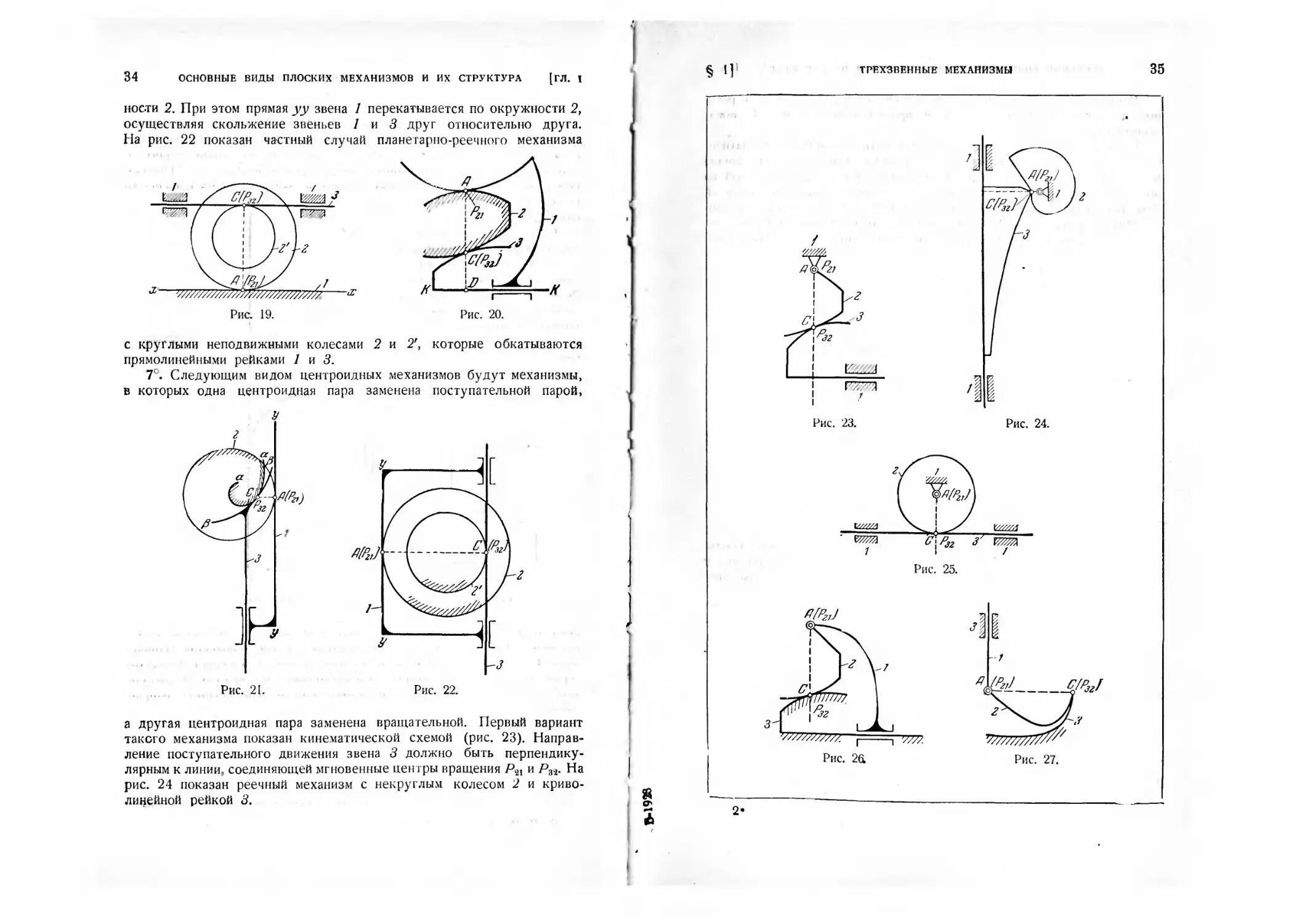
кривой ^3, жестко связанной со звеном 5, которое движется посту-
пательно. На рис. 19 показан частный случай механизма данного
вида. Колесо 2 перекатывается по прямой хх. С колесом 2 жестко
скреплено колесо 2', которое, перекатываясь по прямой 3, застав-
ляет эту прямую двигаться поступательно в неподвижных направ-
ляющих.
Путем перемены стойки можно получить варианты механизма,
-показанного на рис. 17. Принципиальная кинематическая схема меха-
низма с неподвижным звеном 2 показана на рис. 20. На рис. 21
показан планетарно-реечный механизм с двумя некруглыми профи-?
лями аа и ^3. Кривая рр, принадлежащая звену 3, перекатывается
без скольжения по кривой аа, принадлежащей неподвижной окруж*
Я И. И. Артоболевский
34 ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл. I
ности 2. При этом прямая уу звена 1 перекатывается по окружности 2,
осуществляя скольжение звеньев 1 и 3 друг относительно друга.
На рис. 22 показан частный случай планетарно-реечного механизма
с круглыми неподвижными колесами 2 и 2', которые обкатываются
прямолинейными рейками 1 и 3.
7°. Следующим видом центроидных механизмов будут механизмы,
в которых одна центроидная пара заменена поступательной парой,
а другая центроидная пара заменена вращательной. Первый вариант
такого механизма показан кинематической схемой (рис. 23). Направ-
ление поступательного движения звена 3 должно быть перпендику-
лярным к линии, соединяющей мгновенные центры вращения Р21 и Р32. На
рис. 24 показан реечный механизм с некруглым колесом 2 и криво-
линейной рейкой 3.
§ И’
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
35
36 основные виды плоских механизмов и их структура [гл. [
Частным случаем механизма, показанного на рис. 24, будет рееч-
ный механизм круглого колеса 2 и прямолинейной рейки 3, пока-
занный на рис. 25.
Сделав стойкой звено 3, можно получить механизм, кинематиче-
ская схема которого дана на рис. 26. Примером подобного механизма
может служить механизм перекатывающихся рычагов, показанный на
рис. 27. Звено 2 перекатывается без скольжения по звену 3.
При этом точка Л, принадлежащая звеньям 2 и /, движется прямо-
линейно-поступательно. Частным случаем этого механизма будет ме-
ханизм кардановых кругов (рис. 28). Окружность 2 с диаметром,
равным половине диаметра окружности 3, перекатываясь без сколь-
жения по окружности 3, воспроизводит прямолинейно-поступательное
движение звена 1. Звено 1 входит во вращательную пару со зве-
ном 2 в точке А.
Сделав стойкой звено 2, можно получить механизм, кинематиче-
ская схема которого показана на рис. 29. Примером этого механизма
может служить обращенный механизм кардановых кругов, показан-
ный на рис. 30. Окружность 3 обкатывает без скольжения неподвиж-
ную окружность 2, диаметр которой равен половине диаметра ок-
ружности 3. Звено 1 при этом вращается около неподвижной оси А,
лежащей на окружности 2.
Частным случаем механизма вида, показанного на рис. 29, будет
реечно-планетарный механизм (рис. 31). Прямая уу, обкатывая без
скольжения окружность 2, сообщает звену 1 вращательное движение
около оси А.
Другие варианты центроидных механизмов, методом замены центро-
идных пар двумя парами V класса, получены быть не могу г, так
§ U
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
37
как при замене двух центроидных пар поступательными парами
третья пара не может быть центроидной.
К трехзвенным механизмам четвертого семейства также относятся
так называемые клиновые механизмы, образованные тремя поступа-
тельными парами. Кинематическая схема клинового механизма пока-
зана на рис. 32, а один из примеров этого вида механизма показан
на рис. 33.
Рис. 32. Рис. 33.
8°. Переходим к рассмотрению трехзвенных механизмов третьего
семейства. Структурная формула этих механизмов будет иметь вид:
= 3 п — — р^. (1.2)
Для трехзвенных механизмов должно удовлетворяться условие:
Рз“Г/?4=3, . , (1.3)
38
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [|Л. X
так как наибольшее число возможных сочетаний из трех элементов
(звеньев) по два равно трем. .<> ? n in кр-
«т и Для рассматриваемых механизмов число степеней подвижности
равняется те>=:1, а число подвижных звеньев равно и = 2. ьм in
Следовательно, уравнения (1.2) и (1.3) удовлетворяются только
при числе ' пар V класса, равном р% = 2, и числе пар IV клас*
са, равном jp4 = 1.
Пары V класса могут быть всех четырех видов (рис. 1 б, в, г
и д'). Пара’IV класса будет только одна (рис. 1, а).
Сочетанием из различных пар может быть получено десять ви-
дов механизмов. Эти вйды сведены в нижеследующую таблицу.
Так как сложная или траекторная кинематическая пара редко
встречается в конструкциях механизмов, то остановимся на рассмот-
рении первых шести видов Механизмов.
9°. На рис. 34 показан пример механизма с двумя центроидными
и одной парой, образованной взаймоогибаемыми кривыми ’К2 и
Окружности а и b перекатываются без скольжения по прямым Ох и
Оу. На рис. 35 показан механизм, образованный одной центроидной,
одной вращательной и одной парой, образуемой взаимоогибаемыми
точкой и кривой Окружность 3 перекатывается без скольже-
ния по прямой хх. Примером механизма, образованного одной цент-
роидной, одной поступательной и одной парой, представляющей со-
(Х5бЙ ‘ вЗйиМЬЬгйбйемые кривую и прямую К& может служит# ме-
ханизм/ показанный на рис. 36. Окружность 2 перекатывается бее
^<скс|льжения по окружности 1. Жестко скрепленная с окружностью 2
окружность воздействуя на прямую принадлежащую звену 3,
приводит это звено в поступательное движение. . |JHII
В рассмотренных примерах взаимоогибаемыми элементами были
(точка, прямая и кривая. Очевидно, что, варьируя эти элементы, их
§ 1]
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
39
расположение и форму, можно получить бесчисленное количество
механизмов, выполняющих самые различные формы движения. ло.-о.
10°. Следующим видом механизма будет
двумя вращательными парами и одной парой,
механизм, образованный
образованной взаимооги-
Рис. 36.
Рис. 37.
баемыми кривыми. Механизмы этого вида чрезвычайно разнообразны
и широко используются в технике. К этим механизмам в первую
очередь относятся механизмы плоских зубчатых передач (рис. 37).
Профили зубцов очерчены по взаимоогибаемым кривым К* ц К*
40 ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл. I
К механизмам этого же вида относятся кулачковые ^механизмы с
качающимся толкателем. На рис. 38 взаимоогибаемыми элементами
являются точка и профиль кулачка К %. На рис. 39 взаимоогибае-
мыми элементами являются прямая Кз и профиль кулачка /С2- На
рис. 40 показана другая разновидность
Взаимоогибаемыми элементами являются
криволинейная кулиса
этого же вида механизмов,
цилиндрический шип /<2 и
Рис. 40.
К этим же механизмам относятся цевочные и звездчатые (рис. 41)
механизмы. Если кулиса 3 (рис. 40) будет прямолинейной, то мы
получаем механизм мальтийского креста (рис. 42).
Методом перемены стойки могут быть получены и другие разно-
видности механизмов данного вида. Если один из взаимоогибаемых
элементов принадлежит сгойке (рис. 43), то мы получаем механизм
перекатывающихся рычагов. Кривая принадлежащая звену 3, пе-
§ Я
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
41
рекатывается со скольжением по прямой
движному звену 2.
Другим примером механизма того же вида может служить пла-
нетарный зубчатый механизм, показанный на рис. 44. Кривые и
Л”3 представляют собой профили зубцов. Если один из взаимооги-
баемых элементов будет цилиндрическим
шипом, то может быть получен кулисный
механизм (рис. 45) с криволинейной кули-
сой 3, имеющей сложное движение.
Вариантом последнего механизма будет
механизм, показанный на рис. 46, у кото-
рого кулиса 3 является прямолинейной.
11°. Широкое использование в технике
получили механизмы, образованные одной
принадлежащей непо-
Рис. 44.
Рис. 43.
вращательной парой, одной поступательной парой и одной парой, об-
разуемой двумя взаимоогибаемыми элементами.
К этим механизмам относится реечное зубчатое зацепление
(рис. 47). Если одним из взаимоогибаемых элеменов будет точка К*
(рис. 48), то может быть получен реечно-цевочный механизм.
К этому же виду механизмов относятся кулачковые механизмы с
поступательно движущимися толкателями. На рис. 49 показан ку-
лачковый механизм, у которого один из взаимоогибаемых элементов
будет точка На рис. 50 показан кулачковый механизм, у кото-
рого один из взаимоогибаемых элементов будет прямая /С3. Если
взаимоогибаемый элемент в виде точки (рис. 51) будет принад-
лежать звену 2, входящему во вращательную пару со стойкой /, то
может быть получен механизм поступательно движущейся кулисы 3
с криволинейным пазом Если паз К$ будет прямолинейным, то
42 ОСНОВНЫЕ виды плоских МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл; 1
механизм, ’показанный на рис. 51, переходит в механизм прямолиней-
ной поступательно движущейся кулисы (рис. 52).
Рис. 49. Рис. 50. Рис. 51.
Рис., 52. Рис. 53» Рис. 54.
Методом перемены стойки могут быть получены различные видо-
изменения рассмотренного вида механизмов. Так, например, (рис. 53),
если один из взаимоогибаемых элементов будет жестко связан со
Стойкой 2, то может быть получен механизм перекатывающихся ры-
§ м
ТРЕХЗВЕННЫЕ МЕХАНИЗМЫ
43
чагов. Кривая Къ перекатывается со скольжением по кривой К*.
Другой механизм перекатывающихся рычагов показан на рис. 54-
Кривая 7f3 перекатывается со скольжением по кривой Если один
из огибаемых элементов будет точкой, связанной со стойкой, то могут
Рис. 55. Рис. 56.
быть получены кулачковые механизмы, показанные на рис. 55 и 56. Если
со стойкой связана кулиса, то может быть получен механизм вида,
показанного на рис. 57.
Очевидно, что, варьируя последовательность расположения пар
и форму взаимоогибаемых элементов, можно получить и другие
видоизменения рассмотренного типа механизмов.
12°. Переходим к тому виду механизмов, который содержит две
поступательные пары и одну пару, образованную взаимоогибаемыми
элементами. К этим механизмам должны быть отнесены клинчатые
механизмы с одной высшей парой (рис. 58). Звено 2 скользит вдоль
направляющих Ох, а звено 3 — вдоль направляющих Оу. Кулисные
механизмы с двумя, поступательными парами показаны на рис. 59,. a нб*
44
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. I
Методом перемены стойки могут быть получены и другие разно-
видности механизмов этого вида. Так, на рис. 60 показан механизм
перекатывающихся рычагов. Кривая /С3 скользит по кривой К* На
рис. 61 показан кулисный механизм с кулисой 7<3, скользящей по
ролику Къ принадлежащем звену 2. Совершенно очевидно, что и для
этого вида механизма могут быть получены различные видоизмене-
ния путем изменения стойки, выбора профилей взаимоогибаемых
кривых и т. д.
§ 2. Четырехзвенные механизмы
1°. Четырехзвенные плоские механизмы могут быть механизмами
третьего и четвертого семейств.
К механизмам четвертого семейства будут относиться центроидные
механизмы.
Из формулы (1.1) следует, что указанные механизмы будут
всегда образованы четырьмя звеньями, входящими в пять пар V класса.
Примером такого механизма может служить планетарный механизм,
§ 2] ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ 45
показанный на рис. 62, полученный из механизма на рис. 1 путем
присоединения одного звена, состоящего из двух жестко связанных
между собой окружностей 4 и 4'. Окружности 4 и 7' равны окруж-
ностям 2 и 2' и перекатываются без скольжения по окружностям
1 и 3. Такой планетарный механизм с несколькими сателлитными
колесами широко применяется на практике. Путем введения в кон-
струкцию механизма дополнительных колес могут быть получены и
многозвенные планетарные центроидные механизмы.
На рис. 63 показана более общая схема планетарного редуктора,
состоящего из четырех звеньев, из которых два звена являются сател-
литными. Поводки Н и 77', накладывая пассивные связи, обеспечи-
вают кинематическое замыкание механизма.
Рис. 62.
Из рассмотренных примеров следует, что каждый четырехзвенный
центроидный механизм с точки зрения его структуры можно всегда
рассматривать как трехзвенный центроидный механизм, к которому
дополнительно присоединено одно звено, входящее в две пары
V класса.
Таким образом, класс и порядок класса при переходе от трех-
звенного механизма к четырехзвенному механизму остаются без из-
менения.
Четырехзвенные механизмы четвертого семейства с одними по-
ступательными парами, так же как и центроидные механизмы, могут
рассматриваться как образованные путем присоединения к трехзвен-
ному механизму одного звена, входящего в две поступательные пары
V-ro, класса.
2 . Четырехзвенные механизмы третьего семейства являются весьма
разнообразными по своей структуре, так как эти механизмы могут
быть образованы как парами V класса, так и парами IV класса. Каж-
дое звено этих механизмов может входить с другим звеном только
46
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. I
в одну кинематическую пару IV или V классов, так как если одно
из звеньев будет входить в две кинематические пары IV класса, то
мы получим сложную пару V класса, показанную на рис. 1, д. Та-
ким образом, наименьшее число кинематических пар IV и V классов
будет равно четырем, а наибольшее будет равно шести, так как наи-
большее число сочетаний из четырех элементов (звеньев) по два
будет равно шести. Имеем:
1 23 - 4_
w! (л — т)\ 1 - 2 • 1 • 2
Из структурной формулы для четырехзвенных механизмов треть-
его семейства (1.2) имеем условие
2ps + Pt = 8.
(1-4)
Кроме того, на основании вышеизложенных соображений . сумма
пар IV и V классов должна удовлетворять
условию:
/ Ръ~\~Рь = (Ь С1-5)
/& где <? = 4, 5, 6.
¥ / Для q — \ получаем из уравнений (1.4)
и (1.5), что число пар V класса будет
"у* равно р3 = 4, а число р4 пар IV класса равно
7 7 ^=0.
Рис. 64. Соответственно для q = 5 число р§ пар
V класса будет равно рв = 3, а число р4
пар IV класса будет равно р4 = 2. Наконец, для <? = 6 число р$ будет
равно р8 = 2, а число р^ будет равно р4 = 4.
Механизмы, удовлетворяющие условию <7 = 4, будут четырех-
звенными механизмами, образованными одними парами V класса, т. е.
вращательными парами, поступательными парами, центроидными парами
и сложными парами в различных их комбинациях.
Учитывая, что число таких комбинаций достаточно велико, в даль-
нейшем рассмотрим только те типовые механизмы, которые получили
применение в современных машинах и приборах.
3°. Широко используется в технике механиз1ч шарнирного четырех-
звенника, т. е. механизм, образованный четырьмя вращательными
парами (рис. 64). В зависимости от соотношений длин его звеньев
могут быть получены механизмы, ведомые и ведущие звенья которых
будут иметь различные движения.
Все шарнирные четырехзвенники распределяются по трем груп-
пам: к первой относятся те, у которых сумма наименьшего и наиболь-
шего звеньев меньше суммы двух других звеньев, ко второй —
те, у которых эта сумма больше суммы двух других звеньев, к
третьей — те, у которых эти суммы равны. Это положение впер-
§ 21
ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ
•47
вые было сформулировано Грасгофом и носит название «теорема
Грасгофа» *).
Механизмы первой группы при неподвижном наименьшем звене
представляют двухкривошипные механизмы; при постановке на звено,
смежное с
шипно-коромысловые
наименьшим, — криво-
механизмы,
причем кривошипом является наименьшее звено, и при постановке на
звено, противоположное наименьшему, — двухкоромысловые механизмы.
Механизмы второй группы будут всегда двухкоромыслбвые неза-
висимо от того, какие из звеньев будут неподвижными. Наконец,
Рис. 67.
Рис. 68.
Рис. 69.
механизмы третьей группы могут занимать такое положение, пере-
ходя через которое они обращаются в механизмы первой или второй
группы [18 и].
На рис. 65 показан кривошипно-коромысловый механизм. Криво-
шип 2 совершает полный оборот, а коромысло 4 качается на неко-
торый угол. На рис. 66 показан двухкривошипный механизм. Криво-
шипы 2 и 4 совершают полные обороты. На рис. 67 показан двух-
коромысловый механизм, у которого коромысла 2 и 4 качаются на
некоторые углы. На рис. 68 показан частный случай двухкривошип-
ного механизма, у которого длины смежных звеньев попарно равны,
т. е. AB = AD и ВС—CD. На рис. 69 показан механизм шарнир-
*) F. Grashof, Theoretische Maschinenlehre, Berlin* 1883.
48
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. I
ного параллелограмма. В этом механизме противоположные звенья
равны и параллельны, т. е. AB = DC и BC = AD. На рис. 70 пока-
зан механизм шарнирного антипараллелограмма. В этом механизме
противоположные звенья равны, но не параллельны.
Частным случаем механизма шарнирного параллелограмма будет
механизм шарнирного ромба, показанный на рис. 71, у которого
зун 4 имеет возвратно-поступательное
длины всех звеньев равны
между собой, т. е.
AB — BC — CD = DA.
4°. Переходим к рассмо-
трению четырехзвенных ме-
ханизмов с тремя вращатель-
ными и одной поступатель-
ной парой (рис. 72). Первым
видом этих механизмов бу-
дет кривошипно-шатунный
механизм, показанный на
рис. 73. Кривошип 2 совер-
шает полный оборот. Пол-
движение в неподвижных на-
правляющих.
Другими видами этих механизмов будут кулисные механизмы,
показанные на рис. 74—76.
На рис. 74 показан кулисный механизм качающейся кулисы. Кри-
вошип 2 совершает полный оборот, а кулиса 4 качается на некото-
рый угол. На рис. 75 показан кулисный механизм вращающейся
§ 2]
ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ
49
кулисы. Кривошип 2 и кулиса 4 совершают полный оборот. На рис. 76
показан кулисный механизм качающегося ползуна. Кривошип 2 совер-
шает полный оборот, а ползун 4 качается около неподвижной
точки С. На рис. 77 показан коромыслово-шатунный механизм.
Коромысло 2 качается на некоторый угол. Звено 4 совершает воз-
вратно-поступательное движение.
Рис. 76.
5°. Следующей разновидностью четырехзвенных механизмов будут
механизмы с двумя вращательными и двумя поступательными парами.
Здесь может быть два вида механизмов.
В первом виде две поступательные и две вращательные пары
являются смежными (рис. 78). Из этого вида механизмов следует
отметить механизм поступательно-движущейся кулисы (рис. 79). Кри-
вошип 2 совершает полный оборот. Звено 4 движется возвратно-
поступательно. На рис. 80 показан другой.механизм того же вида —
механизм эллипсографа. Ползуны 2 и 4 двигаются возвратно-поступа-
тельно. Каждая точка звена 3 описывает эллипс, откуда и получил
свое название этот механизм. На рис. 81 показан механизм кресто-
вой муфты. Звенья 2 и 4 могут совершать полные обороты около
точек А и В.
Во втором виде рассматриваемых механизмов вращательные и по-
ступательные пары чередуются (рис. 82). Примером этого вида механиз-
мов может служить кулисный механизм, показанный на рис. 83. Кулиса 2
качается на некоторый угол. Звено 4 движется возвратно-поступа-
тельно в неподвижных направляющих.
50
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл. I
6°. В состав четырехзвенных механизмов с одними парами V класса
могут входить не только вращательные или поступательные пары, но
и центроидные пары. На рис. 84 показан общий случай такого меха-
низма с тремя вращательными и одной центроидной парой, предста-
вляющей собой кривые аа и рр, перекатывающиеся друг по другу
без скольжения. Такие механизмы нашли себе использование в ряде
машин и носят название четырех-
звенных механизмов перекатываю-
щихся рычагов. На рис. 85 пока-
зан пример механизма перекатываю-
щихся рычагов, воспроизводящий знакопеременное качение без
скольжения цилиндра 4 по неподвижной плоскости, принадлежащей
звену 7. На рис. 86 показан механизм перекатывающихся рычагов
для воспроизведения движения точки Е, принадлежащей звену 4,
по прямой уу. Для этого кривые аа и рр должны быть двумя окруж-
ностями, радиусы R и г которых удовлетворяют условию R^=2r,
§ 2]
ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ
51
Любая из вращательных пар механизма вида, показанного на
рис. 84, может быть заменена поступательной парой. На рис. 87
показан четырехзвенный планетарный зубчатый или фрикционно-
рычажный механизм с одной центроидной, двумя вращательными и
одной поступательной парой. Окружность 2 перекатывается без сколь-
жения по неподвижной окружности, принадлежащей звену 1. Окруж-
ность 2 входит во вращательную пару с шатуном 5, который в свою
очередь входит во вращательную пару с ползуном 4. Механизм
предназначен для сообщения движения ползуну 4 по различным
законам, в зависимости от соотношения радиусов перекатывающихся
Окружностей. В частности, с помощью механизмов
с подобной кинематической схемой может быть
осуществлено движение ползуна 4 с остановкой.
На рис. 88 показана общая кинематиче-
ская схема механизма, который может быть
получен из механизма, показанного на рис. 84,
если стойкой сделать звено 2. Подвижная кривая аа перекатывается
без скольжения по подвижной кривой
Призером механизма такого вида может служить механизм, пока-
занный на рис. 89. Эллиптическое колесо 1 перекатывается без
скольжения по эллиптическому колесу 4. С колесом 4 входит во
вращательную пару коромысло 3, качающееся около точки В. Меха-
низм воспроизводит сложный закон качания коромысла 3.
52
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. Т
На рис. 90 показан механизм, воспроизводящий возвратно-враща-
тельное движение цилиндра 1 около оси А посредством прямой аа,
принадлежащей звену 4. При вра-
щении кривошипа 3 прямая аа пе-
рекатывается без скольжения по
окружности
На рис. 91 показана общая
кинематическая схема четырех-
звенного механизма, образован-
ного двумя центроидными парами и
двумя вращательными парами. Кривые аа и уу перекатываются без сколь-
жения но сопряженным кривым и 88. На рис. 92 показан механизм
подобного вида, представляющий собой планетарный зубчато- или
фрикционно-рычажный механизм. Окружность аа перекатывается по
неподвижной окружности [Зр и шатуном 3, входящим во вращатель-
ные пары со звеньями 2 и 4, передает движение звену 4. При этом
окружность перекатывается без скольжения по прямой 88. На
рис. 93 показана общая кинематическая схема механизма, который
может быть получен из механизма, показанного на рис. 91, если
стойкой сделать звено 2. На рис. 94 показан пример механизма
§ 2]
ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ
53
данного вида. Кривошип 3 входит во вращательную пару с круго-
вым сектором 4. Окружность уу, принадлежащая звену 4, перекаты-
вается без скольжения по окружности /. В свою очередь окруж-
ность 1 перекатывается без скольжения по неподвижной прямой аа,
принадлежащей звену 2. Кривые и совпадают, образуя общую
окружность /. Механизм предназначен для сообщения цилиндру 1
знакопеременного качения по плоскости аа.
Структуру четырехзвенных механизмов, в составе которых имеются
и сложные пары V класса, мы не рассматриваем, так как подобные
механизмы мало используются в технике.
7°. Переходим к рассмотрению четырехзвенных механизмов, для
которых в уравнении (1.5) число q равняется q = b. Как было пока-
зано выше, для этих механизмов число /?5 пар V класса должно рав-
няться /7Й = 3, а число рь пар IV класса должно равняться />4=2.
Как известно, с точки зрения структуры высших кинематических
пар IV класса каждая такая пара эквивалентна звену, входящему
в две кинематические пары V класса. Следовательно, для числа
пар IV класса, равного /?4 = 2, будем иметь два эквивалентных звена,
входящих в четыре пары V класса, заменяющих две пары IV класса.
Тогда общее число звеньев цепи после введения в нее замещающих
звеньев будет равно шести, а число пар V класса — семи, т. е. после
замены высших пар цепями с низшими парами, полученная цепь
должна быть шестизвенной, образованной семью парами V класса.
Шестизвенные цепи могут быть образованы путем присоединения
к стойке и кривошипу двух групп II класса или одной группы
III класса 3-го порядка, или одной группы IV класса 2-го порядка.
Таким путем могут быть получены две шестизвенные цепи, показан-
ные на рис. 95 и 96. Первая цепь (рис. 95) при любых звеньях,
выбранных за стойку и кривошип, будет образовывать механизмы
II класса.
Вторая цепь при неподвижных звеньях 2 или 5 и кривошипах 1
или 6 будет также образовывать механизмы II класса. То же самое
оудет иметь место при неподвижных звеньях 1 и 6 и кривошипах 2
54
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. Г
и 5. При неподвижных звеньях 2 или 5 и соответственно кривоши-
пах 3 или 4 цепь будет образовывать механизмы III класса 3-го порядка.
При неподвижных звеньях 3 или 4 и кривошипах 2 или 5 цепь
будет также образовывать механизмы III класса 3-го порядка. Нако-
нец, при неподвижных звеньях 3 или 4 и соответственно кривошипах
4 или 3 цепь образовывает механизмы IV класса 2-го порядка.
Рис. 95.
Рис. 96.
8°. На рис. 97 изображена кинематическая схема механизма
с двумя парами IV класса, полученная из шестизвенной цепи на рис. 95,
если в последней звенья ВС и DE являются заменяющими пары
IV класса и стойкой будет звено AGF. Примером механизма это-
го вида может служить кулачковый механизм клапанного распределе-
ния, показанный на рис. 98. Ролик а как на этой схеме, так и на по-
следующих схемах не должен входить в структурное уравнение Mexat
низмов и указывается как обычная конструктивная деталь толкателей
кулачковых механизмов. Следующий вид механизма (рис. 99) может
быть получен из цепи, показанной на рис. 95, если заменяющими
звеньями будут звенья АВ и FE и стойкой — звено AQF. Примером
механизма этого вида может служить кулачковый механизм ротацион-
ного насоса, показанный на рис. 100. Корпус 3 вращается около
оси G. Штоки 2 и 4 входят с корпусом 3 в поступательные пары,
§ 2]
ЧЕ ТЫРЕХ 3 ВЕН Н Ы Е МЕХ А Н И ЗМЫ
55
а с круговыми неподвижными эксцентриками, принадлежащими
звену /,— в высшие пары IV класса К и L, Следующий вид меха-
низма (рис. 101) может быть получен из цепи, показанной на рис. 95,
если заменяющими звеньями будут звенья ВС и FE, а стойкой —
звено AGF. Пример механизма этого вида показан на рис. 102, а.
Кулачок 3 вращается около оси А,
Толкатель 2 движется в непо-
движных направляющих G. Тол-
катель 4 движется в направляю-
щих принадлежащих кулачку 3.
Движение толкателя 4 в направ-
Рис. 100.
Рис. 9У.
ляющих D осуществляется качением круглого ролика а по неподвиж-
ному круглому эксцентрику, принадлежащему звену I. Другим при-
мером механизма того же вида может служить планетарный зубчатый
механизм (рис. 102, б).
Если стойкой механизма, полученного из основной цепи, показанной на
рис. 95, будет одно из двухпарных зве-
ньев, например звено ВС, а заменяющи-
ми звеньями будут звенья АВ и EF, то
мы получим механизм, кинематическая
схема которого показана на рис. 103.
На рис. 104 показан пример ме-
ханизма данного вида. Звено 4
оканчивается двумя роликами а,
скользящими в криволинейных па-
зах, принадлежащих звеньям 1 и 3,
образуя две высшие кинематические пары IV класса с этими звеньями.
Если при той же стойке заменяющими звеньями будут звенья АВ
и ЙЕ, то мы получим механизм, кинематическая схема которого
показана на рис. 105. Пример механизма данного вида показан на
рис. Ю6. Кулачок 2 входит в высшую пару Е с толкателем 3.
Звено 4 входит в две вращательные пары со звеньями 2 и 3 и
в одну высшую пару IV класса Л, представляющую собой ролик а,
скользящий в неподвижном пазу, принадлежащем звену
56
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. I
§ 2]
ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ
57
9°. Переходим к рассмотрению механизмов, которые могут быть
получены из кинематической цепи, показанной на рис. 96. На рис. 107
дана кинематическая схема механизма, который может быть получен
из цепи, показанной на рис. 96, если неподвижным будет одно из
трехпарных звеньев, в данном случае звено 5, а заменяющими
Рис. 108.
звеньями — звенья АВ и ED. Пример механизма данного вида пока-
зан на рис. 108. Звенья 2 и 4 входят в высшие пары IV класса К
и L, представляющие собой ролики а, скользящие в неподвижных
пазах, принадлежащих звену 7. Если стойкой будет звено 5, а заме-
няющими звеньями будут звенья АВ и CD (рис. 96), то мы получим
механизм, кинематическая схема которого
показана на рис. 109. Примером механизма
этого вида может служить кулачковый ме-
ханизм, показанный на рис. 110. Толкатель 3
имеет сложное движение, обусловленное
его вхождением в высшие пары IV класса К и L со звеньями 1
и 4 и во вращательную пару Q со звеном 2.
На рис. 111 дана кинематическая схема механизма, полученная
из цепи, показанной на рис. 96, если стойкой будет звено 7, а заме-
няющими звеньями — звенья FG и CD. Примером механизма подоб-
ного вида может служить кулачковый механизм (рис. 112), у кото-
рого два жестко связанных друг с другом кулачка 3 и 3' входят
в высшие пары IV класса К и L со звеньями 2 и 4. На рис. 113
дана кинематическая схема механизма, у которого стойкой является
58 ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл. I
звено 4 (рис. 96), а заменяющими звеньями АВ и CD. На рис. 114
показан пример механизма данного вида. Толкатель 3, входящий
в две высшие пары IV класса К и L и одну вращательную пару G,
имеет сложное движение. Другие комбинации стойки и заменяющих
звеньев в кинематической цепи, показанной на рис. 96, не дают
кинематических схем механизмов, принципиально отличных от рас-
смотренных выше.
10°. Если в уравнении (1.5) число q будет равно 7 = 6, то
число пар V класса будет равно = а число р^ пар IV класса
будет *равно /?4 = 4. Если заменить все пары IV класса цепями и
парами V класса, г. е ввести вместо четырех пар IV класса четыре
заменяющих звена, входящих каждое в две пары V класса, то кине-
матическая цепь после этой замены должна быть восьмизвенной и
состоять из десяти пар V класса.
Полученные после замены цепи должны еще обладать некоторыми
особенностями. Так как каждое действительное звено основного
четырехзвенного механизма с высшими парами должно входить в три
кинематические пары, то в получаемой после замены цепи должно
быть четыре трехпарных звена. Таким образом, искомые кинематиче-
ские цепи имеют четыре трехпарных и четыре двухпарных звена.
Далее, в пары V класса могут входить только два соседних трех-
!§ 2]|
ЧЕТЫРВХЗВЕННЫЕ МЕХАНИЗМЫ
‘ПЛР "• *11 н >
59
парных звена. Наконец, каждое трехпарное звено может быть соеди-
нено с другим трехпарным звеном только одним двухпарным звеном.
Указанным условиям удовлетворяют кинематические цепи, показанные
на рис. 115 и 116. Если в цепи, показанной на рис. 115, за стойку
выбрать любое из звеньев /, 2 или 3, то мы получаем механизм
Рис. 116.
Рис. 1,15.
III класса, образованный одной двухповодковой и одной трехповодг
новой группой. Если в цепи, показанной на рис. 116, выбрать любое
трехпарное звено за стойку, то мы получим механизм IV класса,
образованный одной четырехповодковой группой, Кривошипами во
всех случаях могут быть выбраны только трехпарные звенья, вхо-
дящие в пару V класса со стойкой. Если в цепи, показанной на
рис. 115, стойкой сделать звено /, то мы получим механизм, схема
которого дана на рис. 117. Примером механизма данного вида может
служить кулачковый механизм, показанный на рис, 118... Жестко,свя-
занные между собой кулачки 2 образуют высшие цары JV кдарра 4
п К с толкателями 3 и 4. Толкатель 4 входит в три рысщие пары
IV класса К, N и Ж. Пары N и М представляют собой ролцкн я,
Скользящие р криволинейных пазах, принадлежащих толкателю^ *
60 ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И их СТРУКТУРА [гл. I
Если в кинематической цепи, показанной на рис. 115. в качестве
стойки выбрать звено 2, а в каяестве кривошипа — звено /, то мы по-
лучим механизм, кинематическая схема которого показана на рис. 119.
Примером механизма указанного вида может служить механизм,
показанный на рис. 120. Толкатель 4 этого механизма входит
в три высшие кинематические пары IV класса К, N и М. Толка-
тель 3 входит в две высшие кинематические пары IV класса N \\ L
и одну вращательную пару Н. Пары N и L представляют собой
ролики а, скользящие в криволинейных пазах, принадлежащих
звеньям 2 и 4.
11°. Из кинематической цепи, показанной на рис. 116 при любом
трехпарном звене, принятом за стойку, и любом соседнем трехпарном
звене, принятом за кривошип, мы получим механизм, кинематическая
схема которого показана на рис. 121. Примером механизма данного
вида может служить кулачковый механизм, показанный на рис. 122.
Жестко связанные между собой кулачки 2 входят в высшие кинема-
тические пары IV класса К и L с толкателями 3 и 4, Толкатели 3
? § 2] ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ 61
и 4 входят каждый в две высшие кинематические пары IV класса и
одну вращательную пару. Пары N и Л4 представляют собой ролики а,
скользящие в криволинейных пазах, принадлежащих стойке /.
12°. В рассмотренных кинематических схемах общих случаев
механизмов (рис. 97, 99, 101 и т. д.) условно все пары V класса
были показаны как вращательные, а высшие кинематические пары
IV класса — в форме двух взаимоогибающих кривых. В конкретных
примерах кроме вращательных пар встречаются и поступательные
пары (рис. 98, 100 и т. д.). Точно так же в качестве взаимоогибаемых
встречаются: точка и кривая, точка и прямая и т. д. Построение
различных видов механизмов и воспроизведение ими различных форм
движения могут быть осуществлены методом соответствующих соче-
таний кинематических пар, их элементов и размеров. В частности,
при рассмотрении четырехзвенных механизмов с высшими парами
IV класса (рис. 95—122) мы не использовали центроидные пары
V класса. Очевидно, что при их использовании можно также полу-
чить новые виды механизмов. Так, например, на рис. 123 показан
пример механизма с одной центроидной парой. В этом механизме
пара, в которую входят звенья 7 и 2, выполнена как центроидная
пара и представляет собой окружность 2, перекатывающуюся по
неподвижной окружности, принадлежащей звену 7. Круглый ролик а
через двуплечий рычаг 3 передает движение толкателю 4, двигаю-
щемуся в неподвижных направляющих, принадлежащих звену 1. При
проектировании четырехзвенных механизмов с центроидными и посту-
пательными парами нельзя допускать, чтобы в состав механизмов
входило более двух центроидных или поступательных пар, так как
три последовательно расположенные поступательные или центроидные
пары представляют цепь с одной степенью подвижности и могут
образовывать механизм четвертого семейства.
62
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [!гл. I
§ 3, Пятизвенные механизмы
1°. Пятизвенные механизмы четвертого семейства, т. е. центроид-
механизмы с одними поступательными парами,
вые механизмы и
Рис. 124.
степенью подвижности
могут рассматриваться как образованные пу-
тем присоединения к четырехзвенным меха-
низмам одного звена, входящего в две цен-
троидные или соответственно в две посту-
пательные пары. Таким образом, с точки
зрения структуры пятизвенные механизмы
этого семейства будут того же класса, как
трехзвенные или четырехзвенные.
Переходим к рассмотрению пятизвенных
механизмов третьего семейства. Так как
число возможных видов этих механизмов
очень велико, то остановимся только на типо-
вых примерах. Из структурного уравнения (1.2)
следует, что для пятизвенных механизмов со
w=l всегда должно удовлетворяться условие
— 11*
(1.6)
2°. Первым видом механизма может быть механизм, состоящий
и одной пары IV класса. Также как и в рас-
из пяти пар V класса
смотренных примерах, пары V класса мо-
гут быть вращательными, поступательными,
центроидными и сложными, а пары IV
класса — взаимоогибаемыми кривыми. После
замены пары IV класса звеном, входящим
в две пары V класса, общее число звеньев
структурной схемы такого механизма бу-
дет равно шести, т. е. в основе механиз-
мов рассматриваемого вида лежат шести-
звенные кинематические цепи, схемы кото-
рых показаны на рис. 95 и 96^ На
рис. 124 показан пример пятизвенного ку-
лачкового механизма, в основе которого
•лежит кинематическая цепь, показанная
на рис. 95.
он 3Q. Из кинематической цепи, показанной
на рис. 96, может быть получено большое
количество различных механизмов в зависи
мосте от выбора того или иного звена за стойку и кривошип и соответ-
ствующих двухпарных звеньев за звенья, заменяющие пару IV класса.
На рис. -125 показан механизм мальтийского креста с приводом от
шатуна 3 шарнирного четырехзвенника. Для поворота мальтийского
креста 5 используется участок шатунной кривой, описываемой центром
§ 3]
ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ
63
цевки А. На рис. 126 показан кулачковый механизм, полученный из
схемы цепи, показанной на рис. 96. Кулачок 5 входит в высшую
пару К со звеном 3 посредством промежуточного круглого ролика 6У
свободно поворачивающегося относительно звена 3. Звену 3 принад-
лежит кулиса, скользящая вдоль ползуна 4, который входит во вра-
щательную пару со стойкой 1.
Из схемы цепи, показанной на рис. 96, могут быть получены
пятизвенные механизмы с двумя круглыми зубчатыми колесами,
Рис. 129.
используемые в различных машинах. Первый пример подобного меха-
низма показан на рис. 127. Если вращательные пары Е и D совпадут,
то мы получим механизм, показанный на рис. 128, у которого
колесо 5 вращается около той же оси, что и звено 4,
К этому же виду механизмов относится рычажно-планетарный
механизм, показанный на рис. 129.
64
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ ГЛ. 1
4°. Вторым видом пятизвенного механизма может быть механизм,
состоящий из четырех пар V класса и трех пар IV класса. После
замены пар IV класса звеньями, входящими в пары V класса.
структурная схема кинематической цепи,
лежащей в основе механиз-
Рис. 130.
ный механизм, показанный на рис.
мов данного вида, будет восьми-
звенной. Не рассматривая всех
вариантов восьми звенных цепей,
которые могут лежать в основе
механизмов данного вида, остано-
вимся только на тех цепях, в со-
став которых входят трехповод-
ковые или четырехповодковые
группы III класса, т. е. цепи,
структурные схемы которых по-
казаны на рис. 115 и 116.
Примером механизма, образо-
ванного из цепи, показанной на
рис. 115, будет кулачково-рычаж-
130. Криволинейная кулиса, при-
надлежащая звену 4, имеет сложное движение, обусловленное ее под-
весом на рычаге 5 и скольжением вдоль одного неподвижного и
одного подвижного роликов а. Примером механизма, образованного из
цепи, показанной на рис. 116, будет планетарный механизм зубчатого
колеса, показанный на рис. 131. Жестко скрепленные колеса 2 и 2'
через промежуточные колеса 3 и 4 и неподвижное колесо / сообщают
движение поводку 5.
5°. Третьим видом пятизвенного механизма может быть механизм,
состоящий из трех пар V класса и пяти пар IV класса. После замены
высших пар IV класса звеньями, входящими в пары V класса,
структурная схема кинематической цепи, лежащей в основе механиз-
§ 3]
ПЯТИЗВЕННЫЁ МЕХАНИЗМЫ
65
мов данного вида, будет десятизвенной,
смотрим только один вариант этой цепи,
В этой цепи все пять двухпарных звеньев
В качестве примера рас-
показанный на рис. 132.
эквивалентны пяти парам
Рис. 132.
Рис. 133.
IV класса. На рис. 133 показан кулачковый механизм, в основе кото-
рого лежит цепь, показанная на рис. 132. На оси В вращаются два
жестко скрепленных друг с другом кулачка 2 и 2'. Сложное движе-
ние звена 3 обусловливается
скольжением роликов а в криволи-
нейных кулисах, принадлежащих
звеньям 4 и 5.
Рис. 135.
Рис. 134.
6°. Четвертым видом пятизвенного механизма может быть меха-
низм, состоящий из двух пар V класса и семи пар IV класса.
Схема кинематической цепи, лежащей в основе механизмов этого
вида, должна быть двенадцатизвенной. На рис. 134 показан пример
такой цепи, а на рис. 135 — пример кулачкового механизма, в основе
которого лежит цепь, показанная на рис. 134. На оси А вращаются
3 И. II. Артоболевский
66
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [ГЛ. I
два жестко скрепленных друг с другом кулачка 2 и 2Г. Сложное
движение звеньев 4 и 5 обусловливается скольжением роликов а
Рассмотрение пятизвенных
преследует цель показать, каь
в криволинейных кулисах, принад-
лежащих звеньям /, 3 и 4,
Последним видом пятизвенного
механизма может быть механизм, со-
стоящий из одной пары V класса и
девяти пар IV класса. Четырнадцати-
звенная кинематическая цепь, лежа-
щая в основе этих механизмов, по-
казана на рис. 136. Пример кулач-
кового механизма, соответствующего
цепи, показанной на рис. 136, дан на
рис. 137. Кулачок 2 сообщает слож-
ное движение звеньям 3, 4 и 5,
каждому из которых принадлежит
по две криволинейных кулисы.
механизмов со сложной структурой
м многообразием форм движения обла-
дают эти механизмы. Многие из рассмотренных нами схем находят
себе использование в различных машинах: текстильных, сельскохо-
зяйственных, пищевых, полиграфических и др. При этом проектиро-
вание их, как правило, ведется эмпирически. Между тем системати-
ческий подход к их синтезу, начиная с изучения структуры этих
§ 4]
ШЕСТЙЗВЕННЫЕ МЕХАНИЗМЫ
67
механизмов, позволяет установить методы их синтеза и получить
новые виды механизмов, ранее не использовавшиеся на практике.
Таким образом, как в этом параграфе, так и в последующем рас-
сматривается, возможно более широко, все многообразие механизмов,
могущих быть использованными в практике конструирования совре-
менных машин и приборов.
§ 4. Шестизвенные механизмы
1°. Так же как и для пятизвенных механизмов, образование ше-
стизвенных механизмов четвертого семейства может быть сделано путем
присоединения к пятизвенному
механизму одного звена, входя-
щего или в две центроидные
или в две поступательные пары.
Таким образом, с точки зрения
структуры шестизвенные меха-
низмы четвертого семейства
будут того же класса, как
и ранее рассмотренные.
Для шестизвенных меха-
низмов третьего семейства со
степенью подвижности w = 1
должно удовлетворяться усло-
вие
2^+р4=14. (1.7)
Из уравнения (1.7) следует, что шестизвенные механизмы с парами
V и IV классов должны иметь число пар, соответственно равное
р< = 0, Ра — Ч, Pi = i...... Pi =12,
Ръ — Т, Ръ — ^, ps = 5,..., ps= 1.
Нетрудно видеть, что условию (1.7) могут удовлетворить различные
сочетания пар V и IV классов. Соответственно с этим могут быть
получены и механизмы различных видов.
2°. Широкое распространение в различных машинах и приборах
имеют шестизвенные механизмы с одними парами V класса. В основе
этих механизмов лежат шестизвенные кинематические цепи, показан-
ные на рис. 95 и 96. На рис. 138 показан пример механизма с дли-
тельной остановкой звена 6. Механизм представляет собой шесги-
звенный .механизм, образованный вращательными парами V класса.
1очка Е описывает шатунную кривую аа, которая на значительном
участке может быть заменена дугой а'а' окружности, описанной из
точки F как центра. Тогда при движении точки Е по участку своей
траектории, приближенной к дуге а'а', звено 6 с весьма большим
3*
68
ОСНОВНЫЕ ВИДЫ ПЛОСКИХ МЕХАНИЗМОВ И ИХ СТРУКТУРА [гл. I
приближением будет неподвижным. На рис. 139 показан другой ше-
стизвенный механизм с длительной остановкой звена 6. В этом меха-
низме имеется одна поступательная пара. На рис. 140 показан
шестизвенный кулисный механизм с двумя поступательными парами.
Ползун 6 имеет различные периоды времени прямого и обратного
хода. На рис. 141 показан шестизвенный кулисный механизм с тремя
поступательными парами, предназначенный, так же как и механизм
на рис. 140, сообщать ползуну движение с различными периодами
времени прямого и обратного ходов. Наконец, на рис. 142 показан
шестизвенный механизм с четырьмя поступательными парами. Много-
образные варианты шестизвенных механизмов с парами V класса могут
быть получены путем различных сочетаний вращательных и поступа-
тельных пар, изменением стойки и ведущего кривошипа и введением
в схему центроидных пар.
Механизмы с сочетанием пар /?4 = 2, р3 = 6 в своей основе имеют
восьмизвенные кинематические цепи вида, показанного на рис. 115
и 116, которые были положены в основу пятизвенных механизмов
§ 4]
ШЕСТИЗВЕННЫЕ МЕХАНИЗМЫ
69
с числом пар />в = 4 и /?4 = 3. Шестизвенные механизмы могут быть
получены путем замены двух двухпарных звеньев цепи (рис. 115) двумя
парами IV класса. Так, например, можно из пятизвенного механизма,
показанного на рис. 130, получить шестизвенный путем замены одной
из пар IV класса — Л", L или N—звеном, входящим в две пары
V класса. В механизме, показанном на рис. 143, такая замена
произведена для пары N. По-
добным же преобразованием
могут быть получены и дру-
гие виды механизмов с числом
пар: /?4 = 4, /?5=5, /?4 = 6,
Ръ — 4, ... и т. д. соответствен-
но из десятизвенных, двена-
дцатизвенных и т. д. кинемати-
ческих цепей.
Мы не будем рассматри-
вать шестизвенные механизмы
всех этих видов, так как метод
их структурного образования
будет аналогичен ранее рассмотренным механизмам. При этом естест-
венно, что при увеличении числа звеньев механизма увеличивается и
число возможных его видоизменений. Практика машиностроения исполь-
зует в основном механизмы, включающие не более шести звеньев, хотя
в некоторых случаях возможно применение механизмов и с большим
числом звеньев. Получение таких многозвенных механизмов и их син-
тез представляют самостоятельную задачу, при решении которой
могут быть использованы методы, применяющиеся для решения задач
синтеза многозвенных механизмов.
ГЛАВА II
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ
§ 5. Некоторые сведения по кинематической геометрии
на плоскости
1°. Плоско-параллельное движение плоской фигуры 1 (рис. 144)
может быть воспроизведено качением без скольжения подвижной
центроиды Ц\ЦЪ принадлежащей этой фигуре, по неподвижной цен-
троиде принадлежащей той неподвижной плоскости 2, относи-
тельно которой рассматривается движение фигуры /. Движение фи-
гуры 1 в каждый рассматриваемый
момент времени с точки зрения
скоростей точек фигуры может быть
сведено к ее вращению около
Рис. 145.
Рис. 144.
мгновенного центра вращения Ро с мгновенной угловой скоро-
стью со.
Задание подвижной и неподвижной центроид и мгновенных угловых
скоростей для каждого положения подвижной центроиды полностью
определяет движение фигуры 1 относительно неподвижной пло-
скости 2. В самом деле, рассмотрим движение произвольной точки А
(рис. 145), принадлежащей фигуре /. Перекатываем центроиду ЦХЦ\
в положение Ц\Ц[. Так как дуги PQP'2 и Р0Р, равны, т. е.
Р0Р'= РцР'1> то, откладывая по центроиде Ц[ дугу P'tP'^ равную
§ 5]
НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
71
РХо = о = находим
совпадает с мгновенным центром вран
центроид Ц^Ц\ и UtU* Положение А‘
центроиды Цх на дугу Р^Р[ найдется,
фигуру Р^Р^А\ равную фигуре
Р[Р0Д. Таким образом, может быть
всегда по точкам построена траекто-
рия К\К\ точки А. Скорость кд
(рис. 146) точки А в каждом рас-
сматриваемом положении найдется
из условия
vA = | О) I (Р0Д), (2.1)
где (о — мгновенная угловая ско-
рость; РпА — расстояние точки А от
мгновенного центра вращения Ро.
2°. Пусть далее, на плоскости,
принадлежащей фигуре 1 (рис. 147),
выбрана произвольная кривая К\К\.
в положения Ц\Ц\> И”И'^ Щ Цг, ..
последовательно положения: К
статочно близкие положения кривой 1
положение точки Р'(], которая
;ния Ро в начальном положении
точки А после перекатывания
если на дуге P2Pq построить
Перекатываем центроиду ГЦ
Тогда кривая К\К\ займет
Xi> ... Если взять до-
СХ1, то мы получаем семейство
Рис. 147.
этих кривых, к которым
можно провести огибающую
кривую принадлежа-
щую неподвижной плоско-
сти 2. Кривые KiKi и
будут взаимоогибаемыми
кривыми. Движение кривой
К\К\ по кривой будет
сводиться к качению кри-
вой К\К\ по кривой КъКъ со
скольжением. Следователь-
но, кривые К\К\ и будут
представлять собой кинема-
тическую пару IV класса,
накладывающую на относи-
тельное движение ее эле-
ментов одно условие связи.
Если теперь кроме кривой К\К\ выбрать на плоскости, принад-
лежащей фигуре /, еще другую произвольную кривую KXKX (рис. 148),
то аналогичным построением может быть получена огибающая ЛпЛп,
принадлежащая плоскости 2. Кривые К\К\ и /СцАТи будут также
представлять собой кинематическую пару IV класса, накладывающую
на относительное движение ее элементов одно условие связи, а со-
вокупность кривых /СХ1, и К\К\, К\\К\\ представит собой одну
72
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [гЛ. И
кинематическую сложную (траекторную) пару V класса (рис. /, д),
накладывающую на движение фигуры 1 относительно плоскости 2
два условия связи.
Движение фигуры 1 относительно плоскости 2 может быть теперь
воспроизведено не качением центроид и Друг по другу,
Рис. 148. Рис. 149,
а качением со скольжением кривых KJK\ и К\К\ по сопряженным
кривым К^Кг и К\\К\\ (рис. 149). При этом фигура 1 будет вращаться
в каждый рассматриваемый момент около мгновенного центра вра-
щения с мгновенной угловой скоростью (О.
Из изложенного следует, что если фигуру 1 (рис. 149) рассма-
тривать как звено механизма, то движение этого звена будет вполне
Рис. 150.
на 1 может быть найден
определенным, если на звене
выбрать два элемента, каждый
из которых, входя в кинемати-
ческую пару с сопряженным
ему элементом, принадлежа-
щим неподвижной плоскости и
неподвижному звену, будет
накладывать на относительное
движение подвижного звена
одну связь. В качестве таких
элементов могут быть выбра-
ны кривые, прямые и точки.
Для каждого положения зве-
149)
мгновенный центр вращения Ро (рис.
на пересечении нормалей, проведенных через точки касания А и В
кривых К\К\ и К\К\ с кривыми К%Къ и К\\Кп- Следовательно, могут
быть построены подвижная и неподвижная центроиды.
3°. Как эго было указано выше, в качестве огибаемой может быть
выбрана точка. Пусть точка А (рис. 150) выбрана в качестве огибае-
мой Тогда траектория АГ2/С2 точки при качении центроиды LIM\
§ 5] НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ 73
по центроиде будет огибающей кривой. Эта кривая носит также
название рулетты. Согласно изложенному выше (§ 5, 2°), зная ру-
летты двух точек звена, всегда можно построить центроиды его
движения. Всякую линию, описываемую какой-либо из точек звена
при плоско-параллельном его движении можно рассматривать как
рулетту этой точки. Эта рулетта может быть получена при помощи
бесчисленного количества различных пар центроид. Пусть задана
рулетта KyJK* (рис. 151) точки А. В качестве неподвижной центроиды
выберем произвольную кривую Z/2Z/2. Тогда подвижная центроида UxLh
может быть построена следующим образом. Отметим на рулетте
точку Д', бесконечно близкую к точке А, и проведем в этой точке
нормаль N'N' к кривой Тогда точка Р2 пересечения этой нор-
мали с центроидой UzUi будет мгновенным центром вращения в сле-
дующем бесконечно близком поло-
жении подвижного звена. Дуга
Р0Р2 будет той дугой, на кото-
рую перекатилась подвижная цен- Цг
троида Z/iZ/i по неподвижной ЦД2
при переходе точки А в поло-
жение А'. Эта дуга должна рав-
няться дуге Р^Р[ подвижной цен-
троиды ЦГЦ\. С другой стороны,
расстояние Д'Р2 должно равнять-
ся расстоянию АР[. Следователь-
но, точка Р[ центроиды Ц\Ц\
может быть найдена на пересе-
чении дуг окружностей радиусов
Р0Р2 и ДР^==Д'Р2, проведенных
из точек Ро и Д. Аналогичным по-
строением можно найти и другие
точки подвижной центроиды Таким образом, мы видим, что,
задавшись рулеттой одной из точек подвижного звена, мы можем
одну из центроид выбрать произвольно, лишь бы нормали в после-
довательных точках этой рулетты пересекались с ценгроидой и шли
в том же порядке, как и точки, выбранные на рулетге. Тогда всегда,
может быть построена сопряженная центроида. Так как указанные
выше условия могут быть удовлетворены в бесчисленно большом
количестве вариантов, то, следовательно, можно построить бесчислен-
ное количество пар центроид, воспроизводящих движение одной из
точек подвижного звена по заданной кривой.
4 • Переходим к рассмотрению различных приемов построения
огибающей кривой по заданной огибаемой кривой.
Выше (§ 5, 2°) было дано построение огибающей кривой путем
нахождения семейства огибаемых, получаемого при перекатывании
центроид друг по другу. Этот прием, будучи вполне общим, является
достаточно трудоемким. Удобнее использовать следующие приемы
74 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. И
построения огибающей, не требующие перекатывания центроид друг
по другу.
Пусть задана огибаемая К\ (рис.
и требуется построить огибающую
Рис. 152.
152), принадлежащая звену /,
Къ принадлежащую звену 2.
Наметим на кривой ряд
точек: а, Ь, с, ... , достаточно
близких друг к другу, и че-
рез эти точки проведем нор-
мали к кривой /Ср Пусть точ-
ками пересечения этих норма-
лей с центроидой UxUx будут
точки Ро, PJ, Р}1, Р|и, ...
Откладываем далее на цен-
троиде дуги: P0Pj,
kJ Р^Р", kJ P^Pl11, ...» соот-
ветственно равные дугам:
kj Р0Р}» kj Р[Р\\ • • •
Нормаль к огибаемой и оги-
бающей в точке их соприкосно-
соответствующий
центроид ЦХЦХ и
вения должна проходить через
мгновенный центр вращения. При перекатывании
ДРУГ п0 ДРУГУ соприкосновение будет про-
исходить последовательно в
точках Р{ и Pj, Р}1 и Р*1, Р}11
и Р*п и т. д. и нормали яР0,
ЬР\, сРхх, dPxxx будут проходить
через точки Ро, Р\, РХХ, Рхх\ ...
Расстояния от точек Ро,
Р*, Р’1, pi11, ... до огибающей
будут, очевидно, равны
отрезкам аР0, ЬР\, сРхх, dPxxx,...
Из точек Ро, Р*, Р“, Р|п, ...
проводим окружности радиу-
сов, равных отрезкам яР0,
bPxv сРхх, dPxxx, ... Огибающая
всех проведенных окружно-
стей и будет искомой кривой
/С2, принадлежащей звену 2.
Если требуется построить
кривую /СзА'а по точкам, тО в
Рис. 153.
точках Р{, Р}1, Р*и, ... прово-
дим нормали к центроиде Ц\И\ (рис. 153). Эти нормали образуют с
прямыми ЬР\, сРхху dPxxx, ... углы ср1, ср11, ср111,... Тогда, проведя в
точках Рх, Рхх, Р”1, ... нормали к центроиде и отложив при
этих нормалях углы, равные ср1, срн, ср111,..., получим направления
нормалей к искомой кривой К* Отложив на этих нормалях отрезки,
§ 5] НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ 75
равные ЬР\, сР^, dP™,..., получим точки а, р, у, 8..., принад-
лежащие кривой К*
5°. Рассмотрим еще один метод образования двух взаимоогибаемых
профилей. Пусть движение звеньев 1 и 2 задано качением центроид
UiU\ и UzUi (рис. 154). Пусть некоторая, произвольно выбранная
нами кривая S катится без скольжения последовательно по центроидам
Ц\Ц\ и ЩЦ* При этом точка Л, жестко связанная с кривой S,
описывает траектории и /С2. Кривые и К* будут взаимоогибае-
мыми кривыми, так как они могут быть образованы как огибающие
двух семейств окружностей. Для этого на кривой S, намечаем доста-
точно близкие точки a, b, с, d, ... и откладываем на центроидах
и дуги, соответствен-
но равные дугам ab, Ьс,
cd, т. е.
^Р.Р\= ^P.Pl=^abt
^Р\Р"=^Ьс,
pup\u = ^pupn\=^cd
Соединяем точку А с
точками a, b, с, d, ... Кри-
вая К\ может быть теперь
получена как огибающая се-
мейства окружностей, прове-
денных из точек Р}, Р}1,
PJ11, ... радиусами, равными
Ab, Ac, Ad, ... Точно так
же кривая К2 может быть
получена как огибающая семейства окружностей, проведенных из то-
чек Р\, Р^, PJ11, ... теми же радиусами, равными Ab, Ac, Ad, ... ,
т. е. образование кривых К\ и К* сводится к рассмотренному в § 5,
4° построению.
Так как вспомогательных кривых S может быть выбрано сколь
угодно много, то один и тот же закон движения звена может быть
воспроизведен бесчисленным количеством пар сопряженных взаимо-
огибаемых кривых.
6°. Рассмотрим вопрос о связи между кривизной центроид и взаимо-
огибаемых кривых. Для этого предварительно необходимо рассмотреть
вопрос об ускорениях точек звена плоского механизма. Как известно
из теоретической механики, ускорение любой точки звена механизма
может быть определено с помощью мгновенного центра ускорений.
Пусть, например, даны звено ВС (рис. 155, а) и его план уско-
рений bcTz (рис. 155, 6). Из свойств плана ускорений следует, что
точка звена П, ускорение которой равно нулю, будет изображаться
плане ускорений вектором, равным нулю, т. е. вектором, совпадающим
7 б ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. П
с точкой тс плана. Поэтому, для того чтобы определить на звене ВС
точку, не имеющую ускорения, нужно на нем построить фигуру 5СП,
подобную фигуре Ьск плана. Полученная точка П (рис. 155, а) и
будет мгновенным центром ускорений, так как вследствие подобия
треугольников ВСП и Ьс~ ускорение точки П равно нулю, т. е.
= 0.
Построение подобной фигуры ВСП можно сделать по углам ср и ф,
полученным в плане ускорений (рис. 155, б). Для этого при точке В
на отрезке ВС строим угол, равный <р, а при точке С строим угол,
равный ф. Точка пересечения П прямых /Ш и СП будет мгновенным
центром ускорений. При обходе контуров треугольников 23СП и Ьс~
в одном и том же направлении
порядок букв должен быть одина-
ковым.
Как известно, вектор относи-
тельного ускорения асв повернут
относительно звена ВС на угол
(т, определеямый из уравне-
ния
= (2.2)
где е есть угловое ускорение
звена ВС, а со — его угловая ско-
рость. Таким образом, сторона Ьс
треугольника Ьс~ образует со сто-
роной ВС угол Вследствие подо-
бия треугольников Ьс~ и ВСП
стороны ~Ь и tzc образуют со
сторонами ПВ и ПС тот же угол рь,
т. е. вектор ав образует угол р.
со стороной £Ш, а вектор —
угол со стороной СП. Векторы абсолютных ускорений любых других
точек звена наклонены под тем же углом к радиусам-векторам,
соединяющим эти точки с точкой П.
Ускорение любой точки может быть всегда выражено через уско-
рение переносного поступательного движения с ускорением точки П
и ускорение относительного движения около этой точки. Так, на-
пример, вектор а в ускорения точки В может быть представлен в виде
следующей геометрической суммы:
. п I t П \ t
^В—^Т£ авП I ~ aBTL 1 аВТЪ
так как ап — 0.
Вектор ускорения адп направлен от точки В к точке П, а вектор
ускорения адп перпендикулярен к отрезку ВП (рис. 155, а).
§ 5]
НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
77
и
Так как
Йвп = wVfin
ввп = | е | /вл,
то модуль полного ускорения точки В равен:
Дв = /вп]^0)4 + = ^вп-
Точно так же модуль ускорения точки С будет равен:
— ^сп]40/1 £г =
(2.3)
(2.4)
где £ =
Таким образом, полные
нальны расстояниям этих
ний.
Очевидно, что движение
ускорения всех точек звена пропорцио-
точек от мгновенного центра ускоре*
точки звена, совпадающей с центром П,
как не имеющей ускорения, может быть с точностью до
малых 3-го порядка принято
за равномерное прямолиней-
ное.
7°. Пусть в рассматри-
ваемом положении звена
его мгновенный центр вра-
щения находится в точке Р
(рис. 156), а его мгновенный
центр ускорений — в точке
П. Соединяем точки Р и П
прямой и при точке Р откла-
дываем угол определя-
емый уравнением (2.2) в
направлении, удовлетворяю-
щем заданному направлению
углового ускорения е. Да-
лее, в точке П восстав-
ляем перпендикуляр к отрез-
ку РП и продолжаем его до
пересечения в точке К
с прямой, проведенной через
точку Р под углом {л к от-
резку РП. Тогда отрезок РК
Центром в точке О, проходящей
теперь скорость* и ускорение ам какой-либо точки 7И, произвольно
выбранной на этой окружности. Скорость фм имеет величину
= (2-6)
и направлена по прямой, проходящей через точку К»
бесконечно
/И
Рис. 156.
Pi
диаметром d
окружности с
будет
через точки Ру П и К. Рассмотрим
78 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. П
Ускорение ам точки М. должно составить угол с направлением
МП. Из чертежа следует, что вектор ам также направлен по пря-
мой, проходящей через точку К, т. е. направление полного ускоре-
ния ам точки М совпадает с направлением скорости Фм точки М
или ему противоположно. Следовательно, полное ускорение ам точки
М есть ускорение тангенциальное. Так как точка М была выбрана
на построенной нами окружности произвольно, отсюда следует, что
любая точка звена, лежащая на этой окружности, обладает только
тангенциальным ускорением. Построенная окружность с диаметром РК
называется поворотным кругом.
Если какая-либо точка звена обладает только тангенциальным
ускорением, то, очевидно, она или движется по прямой линии или же
находится на перегибе своей траектории *). Вот почему поворотный
круг называется также кругом перегибов. Точка К поворотного круга
называется полюсом поворота. Из построения (рис. 156) следует,
что векторы скоростей всех точек, принадлежащих поворотному кругу,
направлены по прямым, проходящим через полюс поворота.
8°. Продолжаем прямую /<11 до пересечения в точке L с перпен-
дикуляром, восставленным в точке Р к диаметру РК поворотного
круга, и на отрезке (РА), как на диаметре, строим окружность с
центром в точке О.. Нетрудно видеть, что угол ПАР равен углу р..
Рассмотрим, далее, скорость ф^ и ускорение какой-либо
точки 7V, произвольно выбранной на только что построенной окруж-
ности. Скорость ф^ равна по величине
фу = । w | ZpjV (2.6)
и направлена по прямой, проходящей через точку А.
Ускорение ау точки N образует угол р. с направлением ДАЛ. Из
построения (рис. 156) видно, что вектор ау направлен по прямой,
проходящей через точку Р. Таким образом, полное ускорение а у
точки W перпендикулярно к скорости Фу, а следовательно, есть
ускорение нормальное.
Так как точка W нами была выбрана на окружности центра Oj
произвольно, отсюда следует, что любая точка звена, лежащая на
окружности с центром Оь обладает только нормальным ускорением.
Эта окружность называется кругом перемены. Нетрудно видеть, что
продолжения векторов скоростей всех точек звена, лежащих на
круге перемены, проходят через точку А.
9°. Из рис. 156 видно, что поворотный круг и круг перемены
пересекаются в двух точках: Р и II. Точка звена, находящаяся
в данный момент в мгновенном центре ускорений П, имеет ускоре-
ние ац, равное нулю, и скорость 27п, равную по величине фп =
= |(о|/РП. Точка звена, находящаяся в данный момент в мгновенном
*) Имеется в виду соприкосновение касательной с траекторией точки 2-го
или 4-го порядка.
§ 5]
НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
79
центре скоростей Р, имеет скорость Vp, равную нулю, и ускорение
арг равное по величине
ар — 1рц со4 —|— е2. (2.7)
Из рис. 156 имеем:
Zpn — Z/v<cos [i. (2.8)
Далее,
1 гпч Н. (2.9)
Wo [J- < V 1 + tg3 |Х
или так как
tgp.=y. (2.10)
то, следовательно,
со3 ГПС fJL (2.U)
Vwo " — ~ е
Подставляя выражения из уравнений (2.8) (2.7), получаем: и (2.11) в уравнение
аР = IpKtf? — dco2, (2.1,2)
где а — диаметр поворотного круга.
Из построения и условия (2.12) следует, что прямая РК нор-
мальна к подвижной и неподвижной центроидам звена в точке Р.
10°. Пусть мгновенный центр вращения звена занимает последо-
вательно положения Ръ Р.2, Р3) ... на неподвижной центроиде ЦЦ
(рис. 157). Обозначим скорость его
перемещения через и в отличие от
Vp—скорости точки звена, в кото-
рой в данный момент времени нахо-
дится мгновенный центр вращения
и которая равна нулю. Пусть за бес-
конечно малый промежуток времени
di мгновенный центр вращения Р
перемещается из положения Рх в
положение Р2. Если обозначить
Рис. 157.
угловую
путь, пройденный центром Рь через ds, мгновенную
скорость вращения около центра Р\ — через <d, а около центра
Р<2—через со<7со, то приращение dvp скорости vP будет равно по
величине
| dvP\ = ds | со -1- dco
(2.13)
или с точностью до бесконечно малых 2-го порядка
| dvP\ = | со | ds. (2-14)
Ускорение ар мгновенного центра вращения равно по величине
(2.12):
= (2.15)
80 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
Подставляя в уравнение (2.15) значение
имея в виду, что величина скорости и равна
из уравнения (2.14) и
получаем:
ds
dt
(2.16)
(2.17)
Из уравнений (2.15) и (2.17) следует, что диаметр d поворотного
круга может быть всегда определен через величины со, и и ар.
Имеем:
и ар
GO I СО3
(2.18)
11°. Переходим к вопросу о кривизне сопряженных элементов
взаимоогибаемых кривых и кривизне траекторий, описываемых отдель-
ными точками звеньев механизмов.
Начнем с рассмотрения вопроса об определении радиуса криви-
зны траектории К (рулетты), описываемой некоторой точкой Д1 (рис. 158),
неизменно связанной с центроидой Ц\Ц\
при качении последней по центроиде
Z/2Z72. В точке Р проводим нормаль NN
к центроидам Ц}Ц\ и Центр кри-
визны О траектории точки М должен
лежать на прямой, соединяющей точку
М с точкой Р, т. е. на нормали ОМ к
траектории КК точки М. Пусть эта
нормаль образует с нормалью Д/Л/
угол ср, а центр кривизны траектории
Л7С лежит в точке О. Обозначим отрезки
РМ и ОР через г и гь тогда радиус
кривизны р в точке М будет равен:
Р = г4-Гр (2.19)
В течение бесконечно малого про-
межутка времени dt точка М перейдет
в положение М' и мгновенный центр
в положении Р. Так как центр кривизны
есть пересечение бесконечно близких нормалей кривой, то, очевидно,
нормаль ОМ' будет проходить через центр Р. Из точки Р опустим
на прямую ОМ' перпендикуляр PQ. Тогда, учитывая, что угол между
нормалями ОМ и ОМ' есть бесконечно малый угол dy, из рис. 158
получаем:
/Г
Рис. 158.
вращения будет находиться
ММ__г + и
PQ
(2.20)
и =
§ 5]
НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
81
Далее, имеем:
ММ = \<*>\rdt, (2.21)
PQ = PP cosy. (2.22)
Так как
pp = udt,
где и — скорость перемещения мгновенного центра вращения, то,
следовательно:
PQ = и cos ср dt. (2.23)
Подставляя величины из (2.21) и (2.23) в уравнение (2.20), по-
лучаем:
| со | г = r + ri_ р (2 24)
и COS ср dt ГI * v • 7
и далее:
(-F + ^)costP = Ti> (2-25)
или
(7 + 7^7)^?=-^. (“б)
Мы рассмотрели тот случай, когда точка М и центр кривизны О
расположены по разным сторонам от центра Р. В случае их распо-
ложения по одну сторону от центра Р знаки у величин г и 1\
в формуле (2.25) будут разными.
Из уравнения (2.17) следует, что
где d — диаметр поворотного круга, и уравнение (2.26) принимает
вид:
(7 + тМ «»Т = 7- <228>
Из уравнения (2.28) может быть определен радиус кривизны р
траектории точки М, если известны диаметр d поворотного круга,
длина г радиуса-вектора точки М относительно мгновенного центра
вращения Р и угол ср, который этот радиус-вектор образует с нор-
малью к центроидам.
12°. Переходим теперь к выводу условия, связывающего радиусы
кривизны р! и р2 взаимоогибаемых. кривых и (рис. 159). Пусть
Центры кривизны этих кривых находятся соответственно в точках
и О2. При своем перемещении центр кривизны Oj описывает траек-
торию OiOp которую можно рассматривать как рулетту этой точки.
Так как прямые РМ и РМ одновременно нормальны к кривым Ki
и в точках М и М' и к траектории OxOj точки Оь то центром
82 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. И
кривизны рулетты ОХО\ будет точка О*. Для нахождения этого
центра кривизны воспользуемся уравнениями (2.25) и (2.27). Полу-
чаем:
(± + ±)eos,P = M = l (2.29)
где р = РО{ и pi — О.гР.
Если обозначить расстояние точки /И до центра
(рис. 159), то получаем:
P = Pi + r и р{ = ^ — г.
Тогда уравнение (2.29) перепишется так:
/ 1 । 1 \ I со | I
---7-----------cos ср =------L = -у .
\Р1 + г 1 Рз — Г т и d
Р через г
(2.30)
Сопряженные центроиды Ц\Ц\ и ЩЦ? (рис. 160) можно рассма-
тривать как частные случаи двух взаимоогибаемых кривых и /С2,
у которых угол ср и расстояние г равны нулю. Обозначая радиусы
кривизны центроид соответственно через и /?2 и применяя к ним
уравнение (2.30), получаем:
— 4-ts- = —=4-. (2.31)
Уравнение (2.31) дает связь между радиусами и /?2 кривизны
центроид UiU\ и угловой скоростью со, скоростью и и диа-
метром d поворотного круга.
Из сопоставления уравнений (2.30) и (2.31) получаем:
(—J— + —— ') cos <р = j+ъ-. (2.32)
\Р1+г 1 Ра — Г/ т Ri 1 R* 7
§ 5] НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ 83
Мы рассмотрели тот случай, когда центры Oj и 0.2 лежат по раз-
ные стороны от центра Р. Если центры и О,2 лежат по одну и ту
же сторону от центра Р, то величине — в формуле (2.29) надо при-
давать знак минус.
Уравнение (2.32), связывающее радиусы кривизны взаимоогибаемых
кривых и центроид, было впервые получено академиком Российской
Академии наук Л. Эйлером в 1765 г. и развито Савари. Поэтому
уравнение (2.32) носит название уравнения Эйлера — Савари.
13°. Центр кривизны траектории любой точки движущегося звена
может быть также определен, если построен
метром PK=d (рис. 161). Пусть требуется
визны р траектории какой-либо точки А. Сое-
диняем точку А с мгновенным центром враще-
ния Р. Пусть точкой пересечения прямой РА
с поворотным кругом будет точка 7И. Уско-
рение ад точки А может быть всегда пред-
ставлено так:
аА = ам + а(АМ-}-апАЛ1. (2.33)
Точка /И, как лежащая на поворотном
круге, имеет только тангенциальное уско-
рение а*м. Следовательно:
4“ аАМ 4“ аАМ‘ (2.34)
поворотный круг с диа-
определить радиус кри-
Параллельные векторы и а\м, очевидно, в сумме дают тангенци-
альное ускорение точки А. Поэтому уравнение (2.34) получает
вид:
аА = а‘А+а"АМ.
Ускорение ад иначе может быть представлено так:
aA = atA+a".
Сравнивая между собой два последних выражения для Яд, полу-
аА 4~ аАМ = аА 4" аА- (2.35)
Из уравнения (2.35) следует, что нормальные ускорения апА и
Равны между собой. Тогда, так как
где <оА — скорость точки Аир — радиус кривизны траектории этой
точки и
ап — tn2/
иАМ —
84 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. П
где <0 — мгновенная угловая скорость звена и 1^А — расстояние от
точки /И до точки А, получаем:
V2.
— = ш^МА,
или так как vA = | <о ' 1РА, то, следовательно:
Р=А'.
1М.А
(2.36)
(2.37)
Так определится величина р радиуса кривизны траектории точки А.
14°. Уравнение (2.32) позволяет определить радиус кривизны
одной из взаимоогибаемых кривых, если известны радиусы кривизны
которая и будет искомым
центроид и радиус кривизны другой
взаимоогибаемой кривой. В некото-
рых случаях удобно пользоваться
графическим методом определения
радиуса кривизны одной из взаимо-
огибаемых кривых. Предположим
(рис. 162), что известны центро-
иды UiUi и ЦчЦъ их радиусы кри-
визны OiP=Ri и O^P — Rz. Далее
известен радиус кривизны O[C = pi
огибаемой КуКь Требуется опреде-
лить центр кривизны О' и радиуср2
огибающей К2КЪ Для этого восста-
навливаем в точке Р перпендикуляр
к нормали NN, проведенной в точке С
к кривым К\К\ и К2К± Далее,
соединяем центры О' и Oi и нахо-
дим точку пересечения D прямой О\ Oj
с перпендикуляром, восстановленным
из точки Рк прямой PC. Полученную
точку D соединяем с точкой 0.2 и
на пересечении прямой DO2 с
нормалью AW находим точку О',
)ом кривизны кривой Для до-
казательства опустим из точек Ot и 0.2 перпендикуляры О^Е и O.2F.
Тогда из подобия треугольников 0'iPD и 0.2F0.2 имеем:
PD _ FO3
РО'2~ ео’2-
Обозначая РС = г и имея в виду, что FCh = R.2 sin ср, РО2 =
= О2С — г и FO2 = PF — Р0'2 = R2 cos ср — (О2С — г), получаем:
пП __ R* sin т (О2с — г)
R2 cos? — (O'2C — r) •
(2.38)
§ 5]
НЕКОТОРЫЕ СВЕДЕНИЯ ПО КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
85
Далее, из подобия треугольников O^PD и O[EOh имеем:
PD _ЕСЕ
РО[ ~ ЕО[ ’
или так как ЕО{ = sin ср, РО{ = рt-]- г, ЕО[ = РО1 — РЕ =
— (р 1 + г) — cos ср, то, следовательно:
pD _ Pi sin у (pt + г)
(Pi + г) — cos у *
(2.39)
Из уравнений (2.38) и (2.39) следует:
R2 (О'2С — г) — (pt + г)
R2 cos у — (О'2С — г) (pi + г) — Ri cos у ’
откуда после несложных преобразований получаем уравнение Эйлера —
Савари:
1 , 1 f 1 . 1 \
Rt ~ Vpi+r +o;c-r ;cosc?’
(2.40)
т. е. отрезок О\С представляет собой радиус кривизны р,2 огибаю-
щей К^Къ а точка есть ЦентР кривизны этой кривой в точке С.
Если вместо взаимоогибаемых кривых заданы точка С (рис. 163)
и ее рулетта КК, то центр кривизны О* кривой КК может
быть найден аналогичным ранее рас-
смотренному построением с учетом,
что огибаемая кривая превратилась в
точку С и, следовательно, центр кри-
визны будет совпадать с точкой С.
Из рассмотренных построений так-
же следует, что линии, соединяющие
центры кривизны неподвижных кривых
(неподвижной центроиды и огибающей),
и центры кривизны подвижных • кри-
вых (подвижной центроиды и огиба-
емой) пересекаются на перпендикуляре,
восставленном из мгновенного центра
вращения к общей нормали к взаимо-
огибаемым кривым.
15°. Из рассмотрения уравнения
Эйлера — Савари следует, что кривизна
взаимоогибаемых кривых зависит не от
Л
Рис. 163.
общей формы центроид, а лишь от их
кривизны в точке касания.
Поэтому в каждый рассматриваемый момент времени сопряженную пару
действительных центроид можно заменить парой других кривых,
удовлетворяющих условию, чтобы сумма кривизн этих кривых была
бы равна сумме кривизн действительных центроид, т. е. чтобы
удовлетворялась правая часть уравнения (2.32).
86
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. И
В частности, можно в качестве заменяющих центроид выбрать
окружность Ц'( и прямую Щ (рис. 164), касающиеся в той же точке Р.
Тогда если радиус окружности Ц[ обозначить через /?0, то величина
этого радиуса найдется из условия
±+J_= ’-ф t
СО * 7?0 ' Р2 ’
(2.41)
где Ri и Д2— радиусы кривизны действительных центроид. Из урав-
нения (2.41) получаем:
(2.42)
Окружность Щ радиуса /?0 называется кругом катания.
С помощью круга катания легко определяется центр кривизны
одной из взаимоогибаемых кривых, если известен центр кривизны
другой.
Пусть центр кривизны кривой лежит в точке О{. Соединяем
точку с точкой К — центром круга катания и продолжаем
прямую О[К до пересечения
в точке D с перпендикуля-
ром, восставленным в точке Р
к общей нормали AW к
кривым К\К\ и /С2/<2 в точке
их касания С. Так как центр
кривизны прямой Ц* лежит
в бесконечности, то из точ-
ки D проводим перпендику-
ляр к прямой Ц*. Точка О2
пересечения этого перпен-
дикуляра с нормалью NN
и будет центром кривизны
кривой
Построим на отрезке РК,
как на диаметре, окружность
с центром в точке О. Не-
трудно показать, что эта
Рис. 164.
окружность будет поворотным кругом, а точка К — полюсом пово-
рота. В самом деле, точка К должна принадлежать поворотному
кругу, как имеющая прямолинейное движение. Далее, поворотный
круг должен проходить через мгновенный центр вращения Р. Сопо-
ставляя уравнения (2.42) и (2.31), имеем:
/^о — d,
т. е. радиус /?0 круга катания равняется диаметру d поворотного
круга. Следовательно, отрезок РК есть диаметр поворотного круга,
а точка К есть полюс поворота. Из изложенного следует, что кри-
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
87
§ 61
визна взаимоогибаемых кривых может быть всегда определена, если
построен поворотный круг и найден полюс поворота К.
Из построения (рис. 164) также следует, что если центр кри-
визны кривой KiKi будет находиться в точке О'[, лежащей на по-
воротном круге, то центр кривизны кривой будет находиться
в бесконечности, т. е. эта кривая будет иметь в рассматриваемом
положении точку перегиба *).
Мы рассмотрели плоско-параллельное движение звена относи-
тельно неподвижной плоскости, но все полученные выводы могут
быть распространены и на относительное движение двух сопряженных
звеньев.
§ 6. Метод дополнительных групп в решении задач
кинематической геометрии механизмов
1°. Изучение кинематической геометр
общих положениях, изложенных нами в
использованы некоторые особые свойства
которых случаях позволяющие значи-
тельно упростить решение и расширить
круг задач об исследовании механизмов
и изучении их кинематической геомет-
рии. В частности, может быть исполь-
зован метод присоединения к исследуе-
мому механизму дополнительных групп,
сущность которого будет изложена
ниже на конкретных механизмах [Зе].
2°. Начнем с задачи об определении
центроид.
Пусть задан механизм шарнирного
четырехзвенника ABCD (рис. 165).
Мгновенный центр вращения Р24 звена 2
относительно стойки 4 найдется на пе-
ресечении направлений АВ и CD. Тогда
для нахождения неподвижной центроиды звена 2 можно применить
следующий прием. Продолжаем звенья 1 и 3 и присоединяем к ним
двухповодковую группу, состоящую из звеньев 5 и 6, входящих в по-
ступательные пары со звеньями 1 и 3 и во вращательную пару Е
друг с другом.
Нетрудно видеть, что при движении этого нового механизма его
точка Е опишет траекторию, совпадающую с неподвижной центрои-
дой ZZ2h звена 2.
>ии механизмов основано на
§ 5. При этом могут быть
кинематических цепей, в не-
Рис. 165.
*) Имеется в виду соприкосновение второго или, вообще, четного порядка
касательной с кривой.
88
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. И
Таким образом, если в точке Е было бы установлено перо или
карандаш, то это перо при движении всего механизма начертило бы
на неподвижной плоскости очертание неподвижной центроиды звена 2.
Наоборот, для получения очертания подвижной центроиды Т/2п звена 2
необходимо было бы обратить движение, т. е. остановить звено 2
Рис. 166.
(сделать его стойкой), и тогда
траектория точки Е будет сов-
падать с неподвижной цен-
троидой звена 4 или с подвиж-
ной центроидой Ц2п звена 2.
Центроиды относительного
движения звеньев 1 и 3 могут
быть найдены аналогичным прие-
мом. Для этого продолжаем
звенья 2 и 4 (рис. 166) и
присоединяем к ним такую же
двухповодковую группу, как
и в ранее рассмотренном случае. Делая последовательно стойкой
звенья 1 и 3 и двигая механизм, получим две траектории точки Е,
одна из которых будет совпадать с центроидой, принадлежащей
звену 7, а другая — с центроидой, принадлежащей звену 3. Закрепив
полученные центроиды со звеньями 7 и 3, получим передачу движе-
ния между звеньями 7 и 3 по закону шарнирного четырехзвенника
ABCD.
В кривошипно-шатунном механизме АВС (рис. 167) двухповодко-
вая группа, состоящая из звеньев 5 и 6, присоединяется к криво-
шипу 7 и ползуну 3. Траектория точки Е будет совпадать с по-
движной и неподвижной центроидами в движении звена 2 относительно
звена 4, если стойками будут сделаны последовательно звенья 2 и 4.
В кулисном механизме АСВ (рис. 168) аналогичная группа должна
быть присоединена к кривошипу 7 и к коромыслу 3.
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
89
В механизме АСВ качающегося ползуна (рис. 169) группа присо-
единяется к кривошипу 1 и к качающемуся ползуну 3.
В механизме эллипсографа АВ (рис. 170) двухповодковая груп-
па присоединяется к ползунам 1 и 3. В этом механизме вследствие
Рис. 169.
постоянства угла а между направляющими ползунов 5 и 6 можно
было бы не вводить звенья 5 и 6 во вращательную пару Е, но ее
фиксация на чертеже необходима для построения ее траекторий в
прямом и обращенном движениях.
Для механизма крестовой муфты (рис. 171) двухповодковая группа
присоединяется к ползунам 1 и 3.
В кулисном механизме, показанном на рис. 172, двух поводковая
группа присоединяется к кулисе 1 и ползуну 3.
90
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [гл. II
Рассмотренными примерами охватываются все основные виды
четырехзвенных плоских механизмов, а также, в чем мы встретим не-
обходимость далее, и те кулачковые механизмы, которые приводятся
после замены высших пар цепями с низшими парами к этим видам
механизмов.
Вышеуказанный прием может быть распространен на более слож-
ные механизмы. Пусть, например, задан шесгизвенный механизм
(рис. 173), образованный путем присоединения к четырехзвенному
механизму ABCD двухповодковой группы NFH, состоящей из звеньев
5 и 6. Если бы для данного механизма потребовалось, например,
J (J
Рис. 173.
построить подвижную и неподвижную центроиды в движении звена 5
относительно стойки 4, то эта задача могла бы быть разрешена при
помощи следующего механизма. Присоединяем к звеньям 2 и 6 двух-
поводковую группу, состоящую из звеньев 7 и 8, аналогичную по
структуре ранее разобранной. Такую же группу, состоящую из
звеньев 9 и 10, присоединяем к звеньям 1 и 3. Точки L и R этих
групп будут всегда совпадать с соответствующими мгновенными
центрами вращения Р63 и Р24. Далее, к стойке 4 присоединяем звено И,
входящее во вращательную пару D со стойкой и в поступатель-
ную пару со звеном /2. Звено 12 в свою очередь входит во враща-
тельную пару со звеном 7 или 8. Аналогичную группу, состоящую
из звеньев 13 и 14, присоединяем к звену 2 и к звеньям 9 и 10.
Точка Е пересечения осей DL и Д/Р звеньев 11 и 13 будет всегда
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
91
Рис. 174.
совпадать с мгновенным центром вращения Р54, и следовательно,
если к звеньям 11 и 13 присоединить еще одну двухповодковую
группу, состоящую из звеньев 15 и 16, то точка Е вращательной
кинематической пары этой группы будет при движении всего меха-
низма описывать траекторию, совпадающую с неподвижной центрои-
дой звена 5. При обращенном движении та же точка опишет траек-
торию, совпадающую с подвижной центроидой звена 5.
Мы не останавливаемся на рассмотрении более сложных механиз-
мов, так как общий метод решения задачи из рассмотренных приме-
ров является совершенно ясным.
3°. Как было показано выше (§ 5, 10°), задача об определении
скорости и перемены мгновенных центров вращения обычно решается
путем исследования законов качения непо-
движной и подвижной центроид или же при
помощи построения поворотного круга. Как
известно (см. формулу (2.17)), диаметр d
поворотного круга связан с угловой скоро-
стью со звена и скоростью и условием
и = | со | d.
Следовательно, определив угловую ско-
рость и найдя диаметр поворотного круга,
можно всегда найти и скорость и перемены
мгновенных центров вращения.
Покажем, что эта задача может быть ре-
шена непосредственно, без нахождения диа-
метра d поворотного круга. Для этого вос-
пользуемся соображениями, установленными
нами в § 6, 2°.
Если точки Е всех рассмотренных в
§ 6, 2° механизмов имеют траектории, сов-
падающие с соответствующими профилями
центроид, то, очевидно, что для нахождения
мгновенных центров вращения необходимо и
рость ггд точки Е механизма. Найденная скорость Ve будет равна
скорости w, т. е.
tvE = u. (2.43)
скорости и перемены
достаточно найти ско-
Последнее легко может быть сделано при помощи плана скоро-
стей. На рис. 174 показано определение скорости и для механизма
шарнирного четырехзвенника ABCD. Построение повернутого плана
скоростей ведем в масштабе угловой скорости tOi ведущего звена АВ
(в масштабе кривошипа, отложенного в натуральную величину). Ско-
рость <Ve точки Е будет равна:
92
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
или так как Ve — u, то
«=I <011 (ре).
(2.44)
Из построения непосредственно следует, что концы векторов ско-
ростей фе> ®еех и ЯЕЕу лежат на окружности центра О, диаметр ко-
торой равен отрезку (ре). Так как точка ех плана совпадает с цен-
тром то очевидно, что для определения скорости <vE = u надо
провести окружность, проходящую через точки /?, Р24 и ev. Диаметр
этой окружности и определяет вектор скорости и, повёрнутый на
90°. Данное свойство является общим для двухповодковой группы,
состоящей из звеньев, входящих во вращательную пару и имеющей
две крайние поступательные пары. Из построенного повернутого плана
175, б) следует, что отрезки рех и реу, представляю-
щие собой абсолютные скорости точек Ех и Еу,
принадлежащих направляющим хх иуу (рис. 175, а),
всегда параллельны этим направляющим, так как
последние являются действительными или фиктив-
ными звеньями, проходящими через соответствую-
щие центры мгновенного вращения в абсолютном
движении. Отрезки ехе и еуе, как представляющие
скорости Veex и ФЕЕу> перпендикулярны к направ-
ляющим хх и уу. Следовательно, отрезок ре, пред-
ставляющий собой скорость Ve* будет диаметром
круга, проведенного через точки р, ех и еу.
4°. Решение задачи об определении радиусов
кривизны центроид механизмов может быть сде-
лано аналитически общими приемами. Состав-
ляется уравнение центроиды в декартовых или
полярных координатах. Далее, по получен-
ному уравнению г = г(у) определяются вели-
чины г иг. Радиус кривизны р центроиды будет тогда равен:
2
_(г2 + г2) з~
Р f2-|-2r2 — г г *
Нетрудно видеть, что данный путь решения задачи хотя и является
общим, но отличается большой громоздкостью. Поэтому ниже изла-
гается графоаналитический метод, который может быть использован
при исследовании тех простейших видов механизмов, синтезу которых
будут посвящены последующие главы.
Покажем, что радиус кривизны р центроиды может быть определен
непосредственно, используя положения, изложенные в § 6, 2° и 3°.
В качестве примера рассмотрим механизм шарнирного четырехзвен-
ника ABCD (рис. 176, а). Строим обычными приемами план ускорений
механизма (в масштабе кривошипа, отложенного в натуральную вели-
чину) (рис. 176, б) и находим в нем отрезок (тсе), представляющий
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
93
в масштабе угловой скорости иц кривошипа АВ полное ускорение ад
точки Е, присоединенной группы, т. е.
Ускорение на основании вышеизложенного будет равно полному
ускорению су перемены мгновенного центра вращения, т. е. а£=су.
Полученный вектор ускорения откладываем от точки Е механизма
(рис. 176, а) и проводим через эту точку направление нормали NN
к центроиде, параллельное отрезку (ре) ранее построенного плана
скоростей (см. рис. 174). Вектор СУ разлагаем на направление NN и
перпендикулярное к нему. Тогда определится вектор чя)п нормального
ускорения перемены мгновенного центра вращения.
Радиус кривизны рн неподвижной центроиды в движении звена 2
относительно 4 определится из уравнения
Так как
и
_ а2
Рн---wn •
и1 = со| (ре)2
(2.440
Ф = W cos а,
94 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
где а — угол, образованный направлениями отрезков (ре) (рис. 174) и
(~е) (рис. 176, б), то
рн = = (ОНЕ). (2.45)
гн (не) cos a v н 7 v 7
Отложив в масштабе чертежа (рис. 176, а) полученный отрезок
(ОиЕ) на нормали NN в сторону направления ускорения wn, найдем
точку Он — центр кривизны неподвижной центроиды. Для определе-
ния радиуса кривизны рп и центра кривизны Оп подвижной центро-
иды надо обратить движение, т. е. рассмотреть движение звена 4
относительно звена 2 и привести аналогичные построения.
Можно также радиус кривизны рп определить и из известного
соотношения между радиусами кривизны центроид, скоростью и и
угловой скоростью <о. Имеем
откуда
_ «Рн
Pn wPh — ii-
Так как
-=-(ю). <2-47’
где (Ьс) — отрезок плана скоростей, изображающий скорость фСв
(рис. 174), то, используя условия (2.45) и (2.47), окончательно полу-
чаем:
_ (ре)* (ВС)
Рп — (Ьс) (ре) — (ВС) (не) cos а * v }
Так определяются по известным величинам соответствующих от-
резков и углу а радиусы кривизны центроид.
Указанный метод определения радиусов кривизны центроид
может быть распространен и на более сложные механизмы. Для
этого надо использовать дополнительно присоединяемые группы
(см. § 6, 2е).
5°. Переходим к рассмотрению задачи о построении поворотных
кругов и кругов перемены. Построение поворотного круга обычно
сводится к нахождению трех точек: Р, Мх и М2 (рис. 177), через
которые проходит поворотный круг с центром О. Одной из точек будет
всегда мгновенный центр вращения Р. Остальные точки Mi и М2
находятся из условия, что если известны траектории каких-либо двух
точек А и В звена АВ и центры кривизны 01 и 0.2 этих траекто-
рий, то точки Му и М2 звена АВ, принадлежащие поворотному кругу,
будут лежать на направлениях POi и Р02 и будут всегда согласно
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
95
уравнению (2.37) удовлетворять соотношениям:
л м (АРУ
АМ'~ AOt ’
RM
ВМг — -во^ .
(2.49)
Из условий (2.49) следует, что для нахождения точек поворот-
ного круга необходимо знать радиусы кривизны траекторий двух
точек звена. В простейших механизмах задача о нахождении радиу-
сов кривизны траекторий не представляет больших затруднений.
В более сложных механизмах, как,
ном на рис. 173, при построении
поворотного круга для звена 5
необходимо было бы определить
радиусы кривизны точек F и N,
что потребовало бы полного ис-
следования ускорений звена FN.
Покажем, что эта задача может
быть решена иначе — при помощи
только планов скоростей, не при-
бегая к исследованию ускорений
звена. В § 6, 3° нами было дано
решение задачи об определении
скорости и перемены мгновенных
центров вращения. Диаметр d по-
воротного круга будет равен:
d=^. (2.50)
Тогда решение задачи о нахо-
ждении диаметра d поворотного
например, в механизме, показан-
круга может быть сделано следующим образом. Пусть требуется
найти поворотный круг звена ВС механизма шарнирного четырех-
звенника ABCD (рис. 178). Пользуясь построением, показанным на
рис. 174, строим повернутый план скоростей механизма в масштабе
угловой скорости cot кривошипа АВ, отложенного в натуральную
величину (рис. 178). Отрезок (ре) и будет в масштабе <Oj предста-
влять собой повернутую скорость и, т. е.
и = ^(ре). (2.51)
Так как угловая скорость со мгновенного вращения звена ВС равна:
“^^(W)’ (2.52)
где (Ьс) — отрезок плана скоростей, то, следовательно, диаметр d
поворотного круга будет равен:
d = ^(BC)==(EK). (2.53)
Р6
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. П
Далее, так как направление диаметра d поворотного круга, про-
ходящего через центр мгновенного вращения Р, совпадает с нормалью
к центроидам, то очевидно, что отрезок (ре) плана скоростей, пред-
ставляющий собой повернутую скорость и, определит направление
указанного диаметра. Проведя через точку Л24 (£) направление, па-
раллельное отрезку (ре), и отложив на этом направлении отрезок (ЕК)
(рис. 178), равный
(ВД=$§•<«:).
находим точку К — полюс поворота. Окружность, построенная на
отрезке (ЕК), и будет поворотным кругом звена ВС. Между пово-
ротным кругом и кругом перемены имеется существенное различие.
Диаметр поворотного круга, как это следует из формулы (2.31),
может быть определен, если известны радиусы кривизны центроид,
т. е. этот круг является чисто геометрическим понятием и его раз-
§ 6] МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП 97
меры не зависят от закона движения ведущего звена механизма.
Диаметр круга перемены зависит от величины углового ускорения
ведущего звена. В дальнейшем рассмотрено построение круга
перемены только для тех случаев, когда движение ведущего звена
принято равномерным. Для построения круга перемены для
случая постоянной угловой скорости кривошипа 1 через точку Р^{Е)
проводим перпендикуляр к отрезку {ЕК). Этот перпендикуляр будет
касательной tt к поворотному кругу. На этой касательной и должен
лежать центр О2 круга перемены. Так как этот круг должен еще
пройти через точки В и Р24, то, восставив в середине Т отрезка
(Р24Т?) перпендикуляр, находим в пересечении проведенных прямых
точку О2 — центр круга перемены. Проведя круг перемены, находим
в пересечении его с поворотным кругом точку G, представляющую
собой центр ускорений звена ВС. Величины полных ускорений всех
точек звена ВС будут пропорциональны расстояниям до центра уско-
рений G, а направления полных ускорений будут образовывать по-
стоянный угол с этими расстояниями, тангенс которого равен:
tg!x = y, (2.54)-
где е-—угловое ускорение звена ВС. Нетрудно из рис. 178 видеть,
что угол EBG и будет углом р,.
Величина тангенса этого угла может быть также, как известно,
определена из условия
(2-55>
Из уравнений (2.54), (2.55) и (2.52) следует, что угловое ускоре-
ние е звена ВС будет равно:
Центр ускорений G может быть найден и без построения круга
перемены. Для этого продолжаем направление BE до пересечения
в точке F с поворотным кругом. Точку F соединяем с центром Oi
и продолжаем направление FOj до пересечения в точке Q с пово-
ротным кругом. Соединив точку Q с точкой В и продолжив напра-
вление BQ, получаем в точке пересечения G этого направления с по-
воротным кругом положение центра ускорений.
Очевидность этого построения следует из следующих условий.
Как было показано выше,
/ GEK= LEBG=
Таким образом, если задано направление ускорения ав точки В,
совпадающее с прямой BE, и построен диаметр d поворотного круга,
то задача сводится к нахождению на окружности поворотного круга
точки, в данном случае точки G, выходящие из которой радиусы-
4 И. II. Артоболевский
98 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ { ГЛ. И
векторы, соединяющие точку G с точками В и Е, образуют с на-
правлениями BE и ЕК равные углы. Соединим точку К с точкой Q.
Углы Z, EO^F и Z, QO\K равны между собой. Следовательно, тре-
угольники Д E01F и д QO{K также равны между собой и отре-
зок (QK) параллелен отрезку (BE). Кроме того, Д KEG = L KQG,
как опирающиеся на дугу KG, и следовательно, полученная точка
G и будет той точкой, выходящие из которой радиусы-векторы об-
разуют с направлениями BE и ЕК равные углы, т. е. эта точка и
есть центр ускорений звена ВС.
Нахождение точек Q и G может быть сделано и проще. Так как
Д QEF = 90°, как опирающийся на диаметр круга, то для нахожде-
ния точки Q достаточно в точке Е восставить перпендикуляр к от-
резку (BE). Точка Q пересечения этого перпендикуляра с поворотным
кругом и определит направление прямой BQ, в точке встречи кото-
рой с поворотным кругом и будет находиться центр ускорений G
звена ВС.
Отметим здесь, что могущий возникнуть при построении пово-
ротного круга вопрос о том, в каком направлении от точки Е откла-
дывать найденный по формуле (2.53) отрезок (ЕК), решается чрез-
вычайно просто при помощи следующего правила. Если точка В веду-
щего кривошипа лежит вне отрезка (АЕ) = (pP%i), то отрезок (ЕК)
следует откладывать от точки Е в направлении, совпадающем с на-
правлением повернутой скорости и. Если же точка В будет лежать
внутри отрезка (А£) = (pP<KF т0 отрезок (ЕК) должен откладываться
от точки Е в направлении, обратном направлению повернутой ско-
рости и.
Мы не останавливаемся на рассмотрении других видов механизмов,
так как метод решения задачи является совершенно аналогичным.
6°. К числу трудностей, связанных с построением кругов поворота
и перемены, обычно относят то, что в большинстве случаев очертания
этих кругов выходят за пределы чертежа. Это, конечно, затрудняет
выполнение всех требуемых построений. Покажем, что все ранее
разобранные задачи могут быть разрешены при помощи других кругов,
представляющих аналоги кругам поворота и перемены. В § 6, 3° было
показано (рис. 175, б), что для двухповодковой группы модификации,
показанной на рис. 175, а, точки р, ех, ev и е лежат на одной окруж-
ности диаметра, равного отрезку (ре). Так как по предыдущему ско-
рость и может быть найдена путем присоединения двухповодковой
группы указанной модификации, то, очевидно, для нахождения век-
тора скорости и в плане скоростей (рис. 179) достаточно найти
точки ех и еу, представляющие собой в плане скоростей концы век-
торов скоростей точек Еу и Ех звеньев АВ и CD, совпадающих для
рассматриваемого положения механизма с мгновенным центрОхМ вра-
щения Р24. Тогда диаметр (ре) окружности, проведенной через точки
р, ех и еу, и будет представлять собой отрезок, изображающий
в плане скоростей повернутую скорость и.
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
99
Так как построение плана скоростей нами ведется в масштабе
кривошипа, то очевидно, что точка еу всегда будет совпадать с мгно-
венным центром вращения Таким образом, две точки р(А) и
через которые проходит искомая окружность, будут всегда
известны, остается только найти третью точку ех. Ее нахождение не
представляет никаких трудностей, если воспользоваться условием
(рис, 179), что
{pc) (CD) *
4
100
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
откуда
(рех)=(рс){-^. (2.57)
Последнее отношение может быть легко построено графически.
Для этого продолжаем направления сторон ВС и AD до их пересе-
чения в точке Р13 — мгновенном центре вращения звена / относи-
тельно звена 3.
Далее соединяем точку Р13 с точкой Р24 и продолжаем отрезок (рс)
плана скоростей до пересечения в точке ех с направлением Р^Р^.
Таким образом, находим положение точки ех и отрезок (рех), удо-
влетворяющий условию (2.57). Через полученные точки р(А), еу(Ры)
и ех проводим окружность центра
Проведенная окружность центра ох представляет собой изображе-
ние поворотного круга звена ВС в плане скоростей, т. е. каждая
точка проведенной окружности изображает в плане скоростей соответ-
ствующую точку поворотного круга. Так, точка ех изображает одно-
временно и точку Mi поворотного круга (рис. 179), точка ev —
точку ТИ2, точка е — точку К и т. д.
Для доказательства найдем изображение в плане скоростей точки Mi
(рис. 179). Из условия (2.49) следует, что
(СР24) (СМ.) (СР) (СРа.) (2.58)
или, так как (СР) _ (рс)
(СР*) (сех)
то, следовательно, (СР3.) _ (см.) (рс) (сех)’ (2.59)
т. е. точка изображающая точку Mf звена ВС, совпадает с точ-
кой ех, изображающей точку Ех звена CD. Аналогично можно пока-
зать, что точка /п2, изображающая точку М.2 звена ВС, совпадает
с точкой еу, изображающей точку Еу звена АВ, и т. д.
Выведенное свойство подобия точек круга, построенного в плане
скоростей, точкам поворотного круга позволяет использовать его для
решения всех задач, связанных с теорией поворотного круга, применяя
для этого аналог этому кругу в плане скоростей.
На рис. 179 показано также построение аналога круга перемены
в плане скоростей для случая, когда угловая скорость кривошипа I
принята постоянной. Этот круг с центром в точке о2, лежащей на
касательной к аналогу поворотного круга, пересекает аналог пово-
ротного круга в точках р и g, подобных точкам Р и О поворотного
круга. Точка g, лежащая на пересечении обоих кругов, изображает
в плане скоростей центр ускорения G звена ВС. Для сравнения полу-
ченных аналогов кругов с действительными кругами поворота и пере-
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
101
мены на рис. 179 показаны эти круги: первый с центром в точке Oj
и второй в точке 0.2. Нетрудно видеть, что аналоги кругов намного
меньше действительных кругов, т. е. они гораздо удобнее для реше-
ния различных задач, связанных с этими кругами.
Модуль полного ускорения ав точки В будет пропорционален от-
резку (gb) плана скоростей; модуль полного ускорения ас точки С
будет пропорционален отрезку (gc) плана скоростей и т. д.
Угол рь, образуемый векторами полных ускорений точек звена ВС
и радиусами-векторами, соединяющими эти точки с центром ускоре-
ний, определяется из условия
6 r (pg)
(2.60)
Угловое ускорение е звена ВС будет равно:
е = о)
'kg\( Ьс~ V
.pg) \вс) •
(2.61)
2
1
Определение положения точки g может быть сделано теми же
приемами, которые были изложены в § 6, 5°. Соединяем точку Р24
с центром Oj круга до пересечения в точке q с кругом. Соединив
точку В(Ь) с точкой q и продолжив это направление до пересечения
с кругом, получаем точку g. Угол /, pbg будет углом, равным углу
|л. Точку g можно также определить, восставив в точке р перпен-
дикуляр к звену АВ. Точка пересечения этого перпендикуляра с кру-
гом будет точкой q. Соединив точку В с точкой qt находим на пере-
сечении этого направления с кругом точку g.
7°. Изложенные выше методы могут быть использованы для опре-
деления центров кривизны траекторий, описываемых точками звеньев
механизма и нахождения эволют этих траекторий [Зс].
Пусть требуется определить центр кривизны Он и радиус кри-
визны рн точки Н произвольного звена I механизма, входящего в ки-
нематические пары со звеньями п и т (рис. 180). Движение звена I
может быть представлено как движение шатуна ВС некоторого услов-
ного четырехзвенника ABCD, у которого точки А и D будут мгно-
венными центрами вращения Рх1 и Ру1 дополнительно присоединяемых
звеньев х и у относительно неподвижного звена I. Присоединим
в точке Н к шатуну ВС дополнительное звено г, один конец кото-
рого входит во вращательную пару Н с шатуном, а другой конец
будет всегда проходить через точку Е — шарнир, дополнительно при-
соединяемый к звеньям х и у группы, что может быть легко осуще-
ствлено постановкой дополнительной ползушки q с шарниром в точке Е
(рис. 180, а).
При движении всего механизма центр кривизны Он будет всегда
совпадать с мгновенным центром вращения Рг1 звена z. Для нахождения
точки Он построим план скоростей pbc механизма ABCD (рис. 180, б)
и проведем в нем указанную нами окружность центра Q. Согласно
102
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. И
уравнению Эйлера — Савари (2.32) между угловой скоростью со- звена г,
скоростью и перемены мгновенных центров вращения, расстоянием
(РцН), углом (р (рис. 180, б) и радиусом р// имеет место следующая
зависимость:
"S' = ~ с<* ?’ (2,62)
откуда
Р„=—(2.ез>
‘ « COS + «i (РцН) v
Так как ^i(PilH) — VH = ^v(ph)) где vH—скорость точки Н,
a — масштаб плана скоростей и и cos <р = (pk) cos ф = (pez)
(рис. 180, б), то, следовательно:
=татв® =вд <р“"’=(0"Е’- ,2-64'
Из условия (2.64) следует, что для нахождения центра кривизны Он
и радиуса кривизны р# необходимо отрезок (НЕ) звена z разделить
на части, пропорциональные отрезкам (ph) и (pez) плана скоростей.
Рис. 180.
Так как отрезки (ph) и (рег) пропорциональны скоростям точек Н
и Ег звена z, то, следовательно, это деление сводится к нахождению
на звене z точки, совпадающей с мгновенным центром вращения Pzt
звена z. Таким образом, центр кривизны Он траектории точки Н
в каждом положении механизма будет совпадать с положением мгно-
венного центра вращения дополнительно присоединяемого звена z,
т. е. задача о нахождении центра кривизны сводится к задаче о на-
§ 6|
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
103
хождении мгновенного центра вращения, что всегда может быть сде-
лано с помощью построения обычного плана скоростей.
Геометрический прием нахождения центров кривизны для различ-
ных точек шатуна ВС механизма шарнирного четырехзвенника показан
на рис. 181. Для нахождения центра кривизны О/И траектории точки М
строим окружность центра О и соединяем точку М с точкой Е (Р24).
Через точку А(р) проводим прямую те'. параллельную прямой ME,
до пересечения в точке е' с окружностью центра О. Соединив точки Е
и е' прямой, продолжаем ее до пересечения с направлением оси ВС
шатуна в точке Точку /' соединяем с точкой А(р) и продолжаем
ее до пересечения в точке Ом с ранее проведенной
построения непосредственно следует, что
__рт
°мЕ ~ре"
прямой ME. Из
т. е. точка Ом будет совпадать с мгновенным центром вращения
звена ME и, следовательно, будет центром кривизны траектории
точки М в рассматриваемом положении механизма. Отрезок (ОмМ)
будет радиусом кривизны р^. Для нахождения центра кривизны 0^
траектории какой-либо другой точки, например точки N, аналогичным
построением находим точки п, е" и Соединив точку /" с точкой
А(р), находим на пересечении этой прямой с прямой NE искомый
центр кривизны Оу и т. д.
Доказанное свойство позволяет сделать следующее обобщение:
эволюта траектории любой точки звена механизма, описывающей
шатунную кривую, может быть представлена как неподвижная цен-
троида некоторого звена, дополнительно присоединяемого к основ-
ному механизму. На рис. 182 показан шарнирный четырехзвенник ABCD,
104 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. П
точка М которого описывает шатунную кривую аа. Геометрическое
место мгновенных центров вращения дополнительно присоединяемого
звена ME образует неподвижную центроиду ЦиЦп, которая и будет
эволютой кривой аа. При этом подвижной центроидой ЦпЦп будет
само звено ME. Таким образом, при движении точки М по ее траек-
тории аа звено ME будет перекатываться без скольжения по кри-
вой ЦДН.
8°. Рассмотрим на нескольких примерах, как могут быть опреде-
лены радиусы кривизны траекторий точек звеньев механизмов. На
рис. 183 показан механизм шарнирного четырехзвенника ABCD,
у которого требуется найти величину р/? радиуса кривизны и центр Of
" шатуна, лежащей вне его оси. Присоединяем
к основному механизму ABCD двухповодковую
группу, состоящую из ползушек 4 и 5, вхо-
дящих во вращательную пару Е. Далее в точке F
присоединяем звено 6, которое входит во вращательную пару с
шатуном 2. Звено 6 должно скользить в ползушке, вращаю-
щейся около точки Е. (На рис. 183 эта ползушка, чтобы не затем-
нять чертежа, не показана.) Центр кривизны Or точки F согласно
предыдущему может быть найден как мгновенный центр вращения
звена 6. Для отыскания мгновенного центра вращения OF можно
использовать аналог поворотного круга для шатуна 2 (§ 6, 6°).
Находим (рис. 184) мгновенные центры вращения Рп и Р31 и соеди-
няем их. Далее через точку А проводим прямую, параллельную DC,
до пересечения в точке ev с прямой Р24Р31. Аналог поворотного
круга согласно § 6, 3° проходит через точки А, Е и еу. Это будет
окружность центра О. Через точку А проводим линию, параллель-
ную FE. Точка f пересечения с направлением BF, будет концом
вектора скорости v? точки F звена 6 (рис. 183). Точка ez пересече-
ния с аналогом поворотного круга будет концом вектора скорости
точки Ez звена 6 (рис. 183). Таким образом, отрезки (/?/) и (рег)
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
105
Рис. 185.
§ 6]
будут представлять собой скорости двух точек F и Ez звена 6. Для
нахождения мгновенного центра вращения этого звена необходимо
разделить отрезок (FE) (рис. 184) в отношении
(р/)__
(pez) (OfE) •
где Op — мгновенный центр вращения звена 6 и он же центр кри-
визны точки F. Деление отрезка (FE) в указанном отношении про-
водим графически. Для этого находим точку G пересечения напра-
влений FB и Eez. Соединив точку О с точкой А и продолжив это
направление до пересечения с прямой FE, находим точку Ор. От-
резок (OpF) будет радиусом кри-
визны р/7 точки F.
Существуют и другие методы опре-
деления радиусов кривизны простей-
ших четырехзвенных механизмов. В ка-
честве примера можно указать на ме-
тод, предложенный Р. Мюллером [956],
сущность которого изложена в моно-
графии [4].
Рассмотрим задачу о нахождении
центра кривизны и радиуса кривизны
траектории какой-либо точки механизма
с высшей парой. Пусть требуется опре-
делить центр кривизны Ор точки F
зубчатого колеса 3 планетарного трех-
звенного механизма (рис. 185). Присое-
диняем к механизму двухповодковую
группу, состоящую из звеньев 4 и 5.
Звено 4 скользит в ползушке 5, вхо-
дящей во вращательную пару Е с
поводком 2. Нетрудно видеть, что
точка Е в каждом положении будет совпадать с мгновенным цент-
ром вращения колес 3 и 1. Выбираем точку В за полюс р повернутого
плана скоростей. Далее строим в масштабе поводка 2 план скоростей
механизма. Отрезки (р/) и (ре^ будут представлять собой соот-
ветственно скорости <0р и Vpz точек F и Ez звена 4.
Для графического построения требуемого отношения
(Р/) _ (OfF)
(Ptz) (pFE)
находим точку G пересечения направления fA и ezE. Соединив точку
G с точкой В, находим в пересечении направлений ОВ с направле-
нием FE точку Of — центр кривизны траектории точки F. Отре-
зок OpF будет радиусом кривизны траектории точки F. Нетрудно
106 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
видеть, что построение, показанное на рис. 185, может быть сделано
и непосредственно по способу, изложенному в § 5, 15° и показан-
ному на рис. 163.
На рис. 186, а показан прием определения центра кривизны Of
траектории точки F зубчатого колеса 3 как мгновенного центра
вращения звена 4 с помощью построения эпюры скоростей этого
звена. Зубчатое колесо 3 вращается около оси А, принадлежащей
ползуну 2, двигающемуся в прямолинейных направляющих, принад-
лежащих неподвижному звену 7. Колесо 3 перекатывается по непо-
движной зубчатой рейке 7. Присоединим к механизму звено 4 и пол-
зу шку 5. Звено 4 входит с колесом 3 во вращательную пару и
Рис. 186.
скользит в ползушке 5, которая
входит во вращательную пару Е
со звеном 2. Строим план скоро-
стей механизма (рис. 186, б). От-
резки (pf) и плана будут со-
ответственно представлять собой
скорости и Vez точек F и Ег
звена 4. Откладываем эти отрезки
в точках F и Ег (рис. 186, а);
соединяем концы векторов Vf и Vez
прямой и продолжаем эту прямую
до пересечения в точке Of с пря-
мой FE. Точка Of будет центром
кривизны траектории точки F, а
отрезок OfF будет радиусом кри-
визны траектории этой точки. Не-
трудно видеть, что нахождение
точки Of может быть также сде-
лано приемом, изложенным в § 5,
15° и показанным на рис. 164.
Если требуется определить эволюту траектории точек F звеньев
механизмов, показанных на рис. 183, 185 и 186, то это может быть
сделано путем построения огибающих кривых к прямым FE, при-
нимаемым за огибаемые, как это было показано выше (§ 6, 7°) при-
менительно к механизму шарнирного четырехзвенника (рис. 182).
На рис. 187 показано построение эволюты аа эпициклоиды ээу по-
лученной как траектория точки F при качении окружности 3 по не-
подвижной окружности 7. В точке F окружность 3 входит в кине-
матическую пару со звеном 4У скользящим в ползуне 5, который качается
около точки Д совпадающей в каждом положении механизма с мгно-
венным центром вращения, Р31. Прямая Fm обкатывает без скольже-
ния эволюту аа. Нетрудно видеть, что эволюта аа представляет со-
бой также эпициклоиду, уменьшенную в отношении
1_ г_ — 1
Г + 2Z? “ 3 '
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
107
так как г = R, и повернутую относительно эпициклоиды на
угол тс.
На рис. 188 показано кинематическое исследование четырехзвен-
ного шарнирного механизма ABCD. Порядок исследования будет
такой. Находим точку PiA пересечения прямых ВС и AD. Далее
находим точку Р24 пересечения прямых АВ и DC. Соединяем точки
Р13 и Ли- Через точку А проводим параллель прямой DC до пере-
сечения в точках с и ех с прямыми ВС и Р\$Ри> В точках ех и А
восставляем перпендикуляры к прямым АВ и Р13Р24. Точка пересе-
чения q этих перпендикуляров определит диаметр qP^ аналога по-
воротного круга и центр Ov этого круга, проходящего через точки
Л, ех, Р24 и q. Соединив точку В с точкой q, продолжаем прямую
Bq до пересечения в точке g с построенным кругом.
Модуль скорости Vb точки В будет равен:
108
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
Модуль скорости <ос точки С будет равен:
®с = |^ (рс).
В будет равно:
Ускорение ав точки
an = ^a{gb\
Ускорение ас точки С
будет равно:
где и — масштабы
скоростей и ускорений.
Направление векторов
ускорений ав и ас будет
определяться углом |i, рав-
ным
Рис. 189.
BG=
Z z pbg.
Если по условиям зада-
чи необходимо найти истин-
ный центр ускорений Q зве-
на ВС, то он может быть
найден на продолжении пря-
мой bg (рис. 179) из условия:
(2.65)
В кривошипно-шатунном
механизме (рис. 189) аналог
поворотного круга проходит
через точки р, с и Р24.
Точка q будет лежать на
противоположном конце диа-
метра круга, проведенного
через точку Р24. Соединив
точку q с точкой В и про-
должив это направление до
пересечения с кругом, на-
ходим точку g. Так как
точка В ведущего звена на-
ходится внутри отрезка рР^,
то угол (л будет добавочным
до 180°, т. е. векторы пол-
ных ускорений точек звена
ВС будут образовывать с
этих точек в плане скоростей
соединяющими изображения
g, углы, равные 180° —|±. Величины этих ускорений будут
прямыми,
с точкой
пропорциональны отрезкам, соединяющим изображения соответствую-
§ 6]
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
109
тих точек в плане скоростей с точкой g. Для наглядности на рис. 189
показаны часть действительного поворотного круга и положение на
нем центра ускорения G.
На рис. 190 показано построение аналога поворотного круга для
кулисного механизма. Аналог поворотного круга проходит через
точки р, ех и Рп, Положение точки ех, представляющей собой в
плане скоростей точку Ех кулисы, совпадающую в рассматриваемом
Рис. 190.
положении с точкой Р24, найдется в пересечении прямой схех, парал-
лельной прямой АС, с прямой рех, параллельной прямой ВР^. Про-
ведя аналог поворотного круга, соединяем точку Р24 с центром
круга и находим точку q пересечения направления P240i с кругом.
Точка g найдется на пересечении прямой Cq с кругом. На рис. 190
показана часть действительного поворотного круга.
На рис. 191 показано построение аналога поворотного круга для
звена ЕЕ шестизвенного механизма.
Рассмотрим в заключение тот случай, который может иметь место
при исследовании механизма, когда мгновенные центры вращения Р13
и ^24 (рис. 188) один или оба находятся вне пределов чертежа.
Покажем, что и в этом случае задача может быть решена при по-
мощи простейших геометрических построений. Пусть мгновенные
по
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [гл. U
Рис. 192.
§ 6] МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП 111
центры вращения Р13 и Р24 (см. рис. 188) механизма A BCD (рис. 192)
не могут быть построены в пределах чертежа и требуется построить
аналог поворотного круга.
Строим план скоростей pbc механизма ABCD. Проводим далее
диагонали АС и BD в четырехзвеннике ABCD. Затем через точку D
проводим прямую, параллельную диагонали АС, до пересечения в
точке f с продолжением стороны АВ. Через точку f проводим пря-
мую, параллельную стороне AD, до пересечения в точке h с прямой
Dh, параллельной стороне ВС.
Аналогично через точку А проводим прямую, параллельную диа-
гонали BD, до пересечения в точке k с продолжением стороны CD.
Через точку k проводим прямую, параллельную стороне AD,
до пересечения в точке т с прямой Ат, параллельной стороне ВС.
Соединив полученные точки h и т прямой и продолжив направ-
ление прямой рс до пересечения с прямой hm, получим искомую
точку ех, изображающую в плане скоростей точку Ех звена
CD, совпадающую с мгновенным центром вращения Р24. Аналог по-
воротного круга должен проходить через две точки: р и ех. Третья
точка, через которую должен проходить круг, определится, если в
точках р и ех восставить перпендикуляры к прямым АВ и mh и
найти их точку пересечения q. Таким образом определятся три точки:
р, ех и q. Проведя через эти три точки окружность и соединив
точку q с точкой В, находим на пересечении продолжения прямой Bq
с проведенной окружностью точку g, изображающую центр ускоре-
ний звена ВС в плане скоростей.
Доказательство правильности'указанного построения следует не-
посредственно из условия подобия получаемых при этом построении
треугольников.
9°. Использование метода дополнительных групп и аналогов по-
воротных кругов дает весьма изящное решение задач кинематики
кулачковых механизмов. На рис. 193 показано построение аналога
поворотного круга для кулачкового механизма с поступательно дви-
жущейся штангой 3. Для этого кулачкового механизма заменяющим
механизмом с низшими парами в рассматриваемом положении будет
кривошипно-шатунный механизм АВС. Строим план скоростей меха-
низма АВС и находим мгновенный центр вращения Р24. Аналог пово-
ротного круга пройдет через точки р, с и Р24. Точка g определится
общим приемом, изложенным выше (рис. 189).
На рис. 194 показано построение аналога поворотного круга для
кулачкового механизма с качающейся штангой 3.
Для этого кулачкового механизма заменяющим механизмом с низ-
шими парами в рассматриваемом положении будет четырехзвенный
шарнирный механизм ABCD. Находим мгновенный центр вращения Р24.
Далее строим план скоростей механизма и находим в нем точку ех,
изображающую точку Ех звена 3, совпадающую для рассматриваемого
положения механизма с мгновенным центром вращения Р24. Анало!
112
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ |гл. II
Рис. 195.
§ 6] МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП 113
поворотного круга пройдет через точки р, ех и Р24. Точка g опре-
делится приемом, изложенным выше (рис. 188).
На рис. 195 показано построение аналога поворотного круга для
кулачкового механизма с качающейся штангой 3, плоскость сопри-
косновения которой касательна к профилю кулачка. Для этого меха-
низма заменяющим механизмом в рассматриваемом положении будет
кулисный механизм АВС. Находим мгновенный центр вращения Р24.
Рис. 196.
Далее строим план скоростей механизма и находим в нем точку ех,
изображающую точку Ех звена 3, совпадающую в рассматриваемом
положении с мгновенным центром вращения Рп. Аналог поворотного
круга пройдет через точки pt ех и Р24. Точка g определится при-
емом, указанным выше (рис. 190).
10°. Укажем далее на другую возможность решения задачи об опре-
делении ускорений механизмов с помощью метода дополнительных групп
без построения плана ускорений, пользуясь только планом скоростей.
Пусть требуется определить ускорение точки С кривошипно-ша-
тунного механизма АВС (рис. 196, а), если угловая скорость ш,
кривошипа АВ принята постоянной. Строим повернутый план скоро-
114 ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. II
стей pbc механизма. Далее продолжаем звено ВС и присоединяем
к нему и к стойке 4 двухповодковую группу модификации, анало-
гичной показанной на рис. 175, а, состоящую из звеньев -5 и 6,
входящих во вращательную пару К (рис. 196). Находим далее в
плане скоростей скорость точки К- Скорость точки К будет
пропорциональна отрезку (kp) плана (рис. 196, а).
Нетрудно теперь показать, что этот же отрезок (kp) в масштабе
кривошипа изображает ускорение ас точки С. В самом деле, отре-
зок (bkx), изображающий скорость vKxB точки Кх звена ВС относи-
тельно точки/?, находится из пропорции
(bkx) __ (ВКХ) _ (be)
(be) (ВС) (ВС) ’
откуда
г. е. отрезок (bkx) представляет собой не что иное, как нормальное
ускорение а"в в движении точки С относительно точки В. Относи-
тельная скорость ^ккх< изображенная в плане скоростей в виде от-
резка (kxk), будет перпендикулярна к звену ВС. Тогда точка k
пересечения отрезка (kxk) с прямой АС и определит начало вектора
ас полного ускорения точки С.
Нетрудно видеть, что присоединение дополнительной двухповод-
ковой группы к основному механизму должно удовлетворять условию,
чтобы точка К присоединяемой группы всегда совпадала с концом С
вектора Vc точки С и следовала за этой точкой во всех положениях
основного механизма. Тогда ускорение ас точки С, представляющее
приращение вектора скорости vc точки С, будет равно вектору
скорости точки К-
В четырехзвенном шарнирном механизме ABCD (рис. 196, б)
ускорение точки С может быть найдено, если присоединить к меха-
низму в точках F и А двухповодковую группу FEA, у которой
стороны соответственно равны: AE=DF и EF = AD. Продолжив
звено ЕА за точку А, получим, что при движении такого механизма
звено ЕАу будет всегда параллельно звену CD, и, следовательно,
направление повернутого вектора Фс скорости точки С будет всегда
совпадать с осью звена ЕАу. Конец вектора Фс (точка С) будет всегда
находиться в точке пересечения осей звеньев ВС и ЕАу. Для определе-
ния приращения этого вектора присоединяем к механизму двухпо-
водковую группу, состоящую из звеньев 6 и 7, и находим скорость
точки К этой группы. Отрезок (/:/?) будет пропорционален вектору ф«
скорости точки К и одновременно с этим пропорционален вектору
ас ускорения точки С.
В самом деле, из построенного плана скоростей следует:
(bk,y (Z>c)
W ~ (ВС)
МЕТОД ДОПОЛНИТЕЛЬНЫХ ГРУПП
115
§ 61
Откуда
(bk \
т. е. отрезок (bkf) представляет собой не что иное, как нормальное
ускорение а^в точки С и ее движение около точки В. Далее имеем:
(fd) _ (FD)
(de) (DC)’
или так как (fd) == (ре) и (de) -
то. следовательно, (ре) _(FD)
(рс) (DC) ’
откуда (ре) = < х FD) (DC)
С другой стороны,
(pky) (AKy)
(ре) (AE) ’
или так как (АКу) = (ре) и (AE)
то, следовательно, (pky) (pc)
(ре) (FD) ’
откуда (pky) (pe)
(ре) ~ (FD)
(рс)>
==(FD),
(2.66)
Подставляя в последнее уравнение вместо отрезка (ре) его выра-
жение из (2.66), получаем:
(Pfe.y) _ (Рс)
(pc) (DC)’
откуда
(2.67)
('^~(DC)
Таким образом, отрезок (pky) представляет собой не что иное,
как нормальное ускорение точки С в ее движении около точки D.
Направления (kxk) и (kyk) относительных скоростей ч>ккх и ^кк у
будут совпадать с тангенциальными ускорениями ассв и ассо> и, сле-
довательно, точка k плана скоростей будет одновременно концом
вектора скорости точки К и началом вектора полного ускоре-
ния ас точки С. Полное ускорение ас точки С представится отрез-
ком (kp) плана скоростей.
На рис. 197, а и б показано аналогичное решение задачи для
кулисных механизмов. Для определения ускорения аСх точки Сх
116
ВВЕДЕНИЕ В КИНЕМАТИЧЕСКУЮ ГЕОМЕТРИЮ МЕХАНИЗМОВ [ГЛ. Н
кулисы 3 механизма (рис. 197, а) с одной поступательной парой
необходимо присоединить двухповодковую группу EDAy и двух-
поводковую группу, состоящую из звеньев 7 и 8. Вектор скорости
точки К механизма будет представлять собой одновременно и вектор
ускорения точки Сх.
Необходимо только заметить, что так как для кулисных меха-
низмов вектор скорости <vKzC будет изображать собой одновременно
и ускорение Кориолиса а£с в движении точки С относительно точки Сх,
Рис. 197.
имеющее коэффициент 2, то полученный отрезок (ckz) надо увели-
чить в два раза (точка k'z на рис. 197, а). Остальные построения
будут обычными.
На рис. 197, б показано нахождение полного ускорения ас точки С
кулисного механизма с двумя поступательными парами методом пла-
нов скоростей путем присоединения двухповодковой группы, состоя-
щей из звеньев 5 и 6. Вектор скорости <ок точки К будет одновре-
менно и вектором полного ускорения ас точки С. Необходимо, так же
как и в выше рассмотренном примере кулисного механизма, учесть
наличие ускорения Кориолиса и увеличить отрезок (cxk) вдвое (точка kv
на рис. 197, б).
На этом мы заканчиваем изложение основ кинематической гео-
метрии плоских механизмов и ее применение к решению задач кине-
матического исследования механизмов.
ЧАСТЬ ВТОРАЯ
ТЕОРИЯ ТОЧНЫХ МЕТОДОВ СИНТЕЗА МЕХАНИЗМОВ
ГЛАВА III
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
§ 7. Общий случай центроидного механизма
1°. Общим случаем трехзвенного центроидного механизма является
трехзвенный механизм, образованный тремя
(рис. 198). Общая кинематическая схема
такого механизма была показана ранее на
рис. 2, а пример механизма этого вида
был показан на рис. 3.
Рассмотрим, в какой форме может
быть задано движение подвижных звеньев
этого механизма (рис. 198).
Пусть ведущим звеном будет звено 2,
а ведомым звено 3. Если текущие углы
поворота звеньев 2 и 3 относительно
неподвижного звена 1 обозначить соот-
ветственно через и ср31, то уравнение
движения звеньев 2 и 3 в общей форме
может быть записано в виде следующих
уравнений:
(3.1)
и
центроидными парами
Рис. 198.
<Рз1 = ?31 (О-
Исключая из уравнений (3.1) время f, получаем:
?31----?31 (?21)*
(3.2)
Зависимость (3.2) носит название функции положения, так как
она определяет положение ведомого звена 3 в зависимости от поло-
жения ведущего звена 2. Дифференцируя уравнение (3.2) по углу
118 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
поворота <p2i, получаем:
(3.3)
Так как
<*?81
</^21 “21
ИГ
где w2i и u).u — угловые скорости звеньев 2 и 3 относительно непо-
движного звена 1 и /32 — передаточное отношение звеньев 2 и 3, то
уравнение (3.3) в окончательном виде перепишется так:
= (<рг1). (3.4)
“si
Зависимость (3.4) носит название функции передаточного отно-
шения Соответственно величина
носит название функции передаточного числа. Функция положе-
ния (3.2) является геометрической характеристикой механизма, гак
как не включает в себя параметр времени. Функция передаточного
отношения (3.4) или функция передаточного числа (3.5) представляет
собой также геометрическую характеристику механизма, но записанную
в дифференциальной форме. Очевидно, что общая связь между ними
может быть представлена как в дифференциальной форме в виде урав-
нения (3.3), так и в интегральной форме в виде уравнения
4>21 ?21 -Р31 J
?31 = J ?31 (Т21) ^21 = j W^-21 = -21 ^21- (3.6)
Таким образом, при решении задач проектирования задание дви,-
жения может быть осуществлено в любой форме или как функция
положения, или как функция передаточного отношения, или, наконец,
как функция передаточного числа.
2°. Связь между угловыми скоростями звеньев механизма и основ-
ными их: размерами может быть установлена на основании известного
соотношения между угловыми скоростями и расстояниями между
мгновенными центрами вращения. Обозначая мгновенные центры
(рис. 198) соответственно через Р.2Ъ Р32 и Р31, имеем:
___“31 ____(Рsi^*3s)
“si (Cai Р за)
Далее, для скоростей ю2), ю31 и ю32 имеем условие
шза — ц>и ш31.
(3.7)
(3.8)
§ 7] ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА 119
Так как сообщив всему механизму общую угловую скорость,
равную и обратную по знаку угловой скорости звена 2, мы
можем рассматривать движение звена 3 с угловой скоростью ш34
относительно звена 2 как происходящее с угловой скоростью равной
сумме угловых скоростей щ21. и щ-ц. Наконец, из условия, что мгно-
венные центры вращения Р21, Рц и Р32 должны всегда лежать на
одной общей прямой, получаем:
(РцРзд + (PaiPat) — (РМ- (3.9)
3°. Основная задача проекгирования механизмов состоит в том,
чтобы при заданном движении ведущего звена механизма обеспечить
заданное движение ведомого звена. Требуемое движение может быть
задано в виде функции положений или в виде функции передаточ-
ного отношения, или передаточного числа. Применительно к трех-
звенному центроидному механизму это будут соответственно уравне-
ния (3.2), (3.4) и (3.5). Так как уравнения (3.4) и (3.5) могут быть
всегда получены путем дифференцирования уравнения (3.2), а ура-
внение (3.2), если известны начальные положения звеньев, может быть
получено путем интегрирования уравнений (3.4) или (3.5) согласно
условию (3.6), то, очевидно, исходными зависимостями, которыми мы
будем в дальнейшем пользоваться, будут следующие:
фз = <Рз (<Рй) (3.10)
или
В уравнениях (3.10) и (3.11), как и в последующих, для упро-
щения записания уравнений второй индекс у угловых скоростей ю31
и ю21 и мгновенных центров вращения P3i и Р.21 будем опускать,
считая, что во всех случаях неподвижным будет звено 1. Точно
так же мгновенный центр вращения в относительном движении Р33
будем обозначать через Ро.
Условие (3.10) для центроидного механизма (рис. 198) будет
означать, что для каждого заданного положения звена 2 мы имеем
вполне определенное заданное положение звена 3. Последовательные
положения звеньев 2 и 3 полностью определяются качением соответ-
ствующих подвижных центроид Ц.2п и Ц3п по неподвижным Ц2н и
Ц3н (рис. 198). Очевидно, что для воспроизведения заданного дви-
жения по условиям (3.10) и (3.11) надо найти соответствующие очер-
тания центроид Ц20 и Z/30 в относительном движении звеньев 2 и 3.
К методике решения этой задачи мы и переходим.
4°. Пусть мгновенный центр вращения звена 2 (рис. 199) в пер-
вый момент времени находится в точке Р', мгновенный центр вра-
щения звена 3 в тот же момент времени находится в точке PJ и
мгновенные угловые скорости систем будут wj, и <й*. Определим
положение мгновенного центра вращения Р* в движении звена 2
120
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. Ill
относительно звена 3. Для этого сообщим обоим звеньям общую
мгновенную угловую скорость, равную со’, но обратную по знаку.
Тогда звено 3, как имеющее две равные и противоположные ско-
рости, будет как бы неподвижным, а звено 2 будет двигаться с сум-
марной мгновенной угловой скоростью равной согласно (3.8)
<°o = 4 + w,3-
Угловая скорость будет мгновенной
в движении звена 2 относительно звена 3.
относительной скоростью
Мгновенный центр враще-
ния в этом относительном движении
Рис. 199.
будет лежать в точке Р’о, лежа-
щей на прямой Р\Р\. Поло-
жение точки Р* определится
согласно (3.7) из отношения
б «I pi pi
<ol pi pi ’
2 3 0
т. е. мгновенный центр вра-
щения Р{ делит отрезок Р’Р’
на части, обратно пропор-
циональные угловым скоро-
стям.
Переместим, далее, по-
движные центроиды Цгп и Цзв
в положения, соответствую-
щие какому-либо второму,
третьему и т. д. моментам
времени. Пусть мгновенным центром вращения звена 2 для второго
момента времени будет точка Р*1, а мгновенным центром вращения
звена 3 точка Р’1. Соответственно мгновенные угловые скорости дви-
жения звеньев 2 и 3 будут о)” и tuj'. Положение мгновенного центра
вращения Р” в относительном движении определится на прямой рнр’1
из уравнения
шп рпрп
3 2 О
иП pilpil
2 3 0
Повторяя подобные построения для ряда последовательных поло-
жений звеньев 2 и 3, получим на неподвижной плоскости ряд точек
Р’, Р’1, Р1}*,... , которые образуют бицентроиду.
Построив бицентроиду, можно перейти к построению центроид отно-
сительного движения звеньев 2 и 3 (рис. 200). В самом деле, так
как мгновенными центрами вращения в относительном движении звеньев 2
и 3 будут точки Р’, рн, рн*, ... , го, для того чтобы построить
центроиду Ц10, принадлежащую звену 2, необходимо найти геометри-
ческое место точек плоскости, принадлежащей звену 2, последова-
тельно совпадающих с точками Р\, PJ,1, Р’п, ... Точно так же, для
того чтобы построить центроиду Цм, принадлежащую звену 3, надо
§ 7]
ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА
121
найти геометрическое место точек плоскости, принадлежащей звену 3,
последовательно совпадающих с теми же точками Р', Р'1, Р[ц, ...
Для нахождения указанных геометрических мест поступаем сле-
дующим образом.
Отмечаем на неподвижной центроиде Z/3h ряд точек Р\, Р“, Р'п, ...
(рис. 200). Далее, имея в виду, что подвижная центроида катится
по неподвижной без скольжения, отмечаем на подвижной центроиде
Ц3п ряд точек к*, те” it'11, ... , которые последовательно будут сов-
падать с точками Р\, Р*1, Р'11, ... Для этого достаточно соблюдать
условия,
равны:
чтобы дуги перекатывающихся центроид были соответственно
, PJP**= Ф"
Р«РП> =
Пусть мгновенный центр вращения в относительном движении нахо-
дится в начальный момент времени в точке Р* бицентроиды Б и пусть
с точкой Р\ совпадает в этот момент точка к’ подвижной центроиды
в положении Д(*п. Перемещаем подвижную центроиду в следующее
положение. Пусть это будет положение Z/Jln. Тогда точка it’1 совпа-
дет с точкой Р*1, а точка л', ранее совпадающая с точкой Р*8, займет
на центроиде /Д’ новое положение, определяемое равенством
Р’Р>>= ^х1-
В данном положении подвижной центроиды мгновенный центр вра-
щения в относительном движении звеньев 2 и 3 пусть будет лежать
на бицентроиде Б в точке Р”. Какая-то точка П*1 подвижной центроиды
в этом положении будет совпадать с точкой Р”. Для того чтобы
найти положение этой точки в начальном положении Ц\п подвижной
122 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ |гл. Ill
центроиды, соединяем точки л* и л’1, принадлежащие центроиде ZZ''n,
с точкой Р’1. Тогда получаем фигуру которую и переносим
на начальное положение подвижной центроиды, для чего на
дуге центроиды Ц[п строим фигуру равную фигуре
и с тем же порядком букв по контуру. Положение точки П'1
определится простыми засечками из точек Р’ и тс'1. Таким образом
определится положение точки ГЦ1, принадлежащей звену 3 и совпа-
дающей с мгновенным центром вращения Р’1 в тот момент, когда
подвижная центроида приходит в положение ZZ*'n. Точно таким же
образом может быть определена точка ГЦ11, совпадающая с мгновен-
ным центром вращения Р*п в тот момент, когда подвижная центроида
приходит в положение Z/Ц’. Для этого перемещаем подвижную цен-
троиду в положение Находим на положении Ц™. центроиды
Рис. 201.
с точкой Р*и. Далее, на начальном
положении Ц\п подвижной центроиды
строим фигуру Р'П'11^11, равную фи-
гуре it’PjnP’H. Соединив все полу-
ченные точки 1Г8, П*1, ГЦ11, ... плав-
ной кривой Ц9й, получим центроиду
относительного движения, принадле-
жащую звену 3. Аналогично может
быть построена центроида Ц№ отно-
сительного движения, принадлежа-
щая звену 2. Соединив жестко полу-
ченные центроиды со звеньями 2 и 3
и воздействуя центроидой Ц№ на цен-
троиду Цж или наоборот, получим
воспроизведение заданного движе-
ния звеньев (рис. 201).
Таким образом, для центроидно-
го механизма задача о воспроизве-
дении заданного движения его звеньев сводится к построению двух
центроид в относительном движении этих звеньев. Решение задачи
не изменится, если число подвижных звеньев центроидного механизма
будет больше двух, т. е. будут проектироваться трехзвенные
четырехзвенные, и т. д. механизмы.
5°. В качестве примера спроектируем следующий механизм (рис. 202).
Окружность 2 катится без скольжения по неподвижной прямой Цги
с постоянной угловой скоростью ю2. Окружность 3 катится без
скольжения по неподвижной окружности Цзп с постоянной угловой
скоростью ш3. Требуется воспроизвести указанные движения звеньев 2
и 3 воздействием одного звена на другое, если отношение угловых
скоростей равно : ш3 — 2 : 1 = const, а углы поворота <р2 и <р3 окруж-
ностей 2 и 3 заданы в виде последовательности мгновенных центров
вращения Р1’, и т. д„ которым соответствует последователь-
ность центров Р!в, Р[', Р[11 и т. д.
§ 7|
ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА
123
Так как окружности 2 и 3 катятся без скольжения по прямой Ц2а
и окружности Цйк, то, очевидно, что эти окружности будут подвиж-
ными центроидами звеньев 2 и 3, а прямая USH и окружность Ц3п
будут неподвижными центроидами. Тогда точки Р\, Р]}, ... и Р’, Р^, ...
представят собой мгновенные центры вращения звеньев 2 и 3. Для
построения бицентроиды соединяем точки Р' и Р’ прямой и делим
ее согласно заданию в отношении
иа pi pi
» so
124
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. Ш
Получаем первую точку Р* бицентроиды. Аналогичным построением
получаем точки Р“, Р^1, ... Соединив все полученные точки плавной
кривой, получаем бицентроиду Б.
Так как угловые скорости <о2 и <о3 по заданию противоположны
по знаку, то точки /*, Р”, ... делят отрезки Р\Р\, Р^Р^, ... внутрен-
ним образом. При одинаковом направлении угловых скоростей точки Р\,
рп, ... будут делить те же отрезки внешним образом.
Далее, строим центроиды относительного движения. Найдем, на-
пример, точку Пу, принадлежащую центроиде Д[20 звена 2. Для этого
находим на подвижной центроиде в положении 1Дп точку соответ-
ствующую мгновенному центру вращения Р\ для начального положе-
ния ££п подвижной центроиды. Положение точки определится из
условия, что отрезок Р*РУ должен равняться дуге Р[«у. Соединив
далее точки Ру и ^у с точкой Ру, получаем треугольник ^2vP0vPy.
Если подвижную центроиду из i
положения вернуть в исходное
положение 1Дп, то очевидно, что
точка тгу совпадает с точкой Р\.
Положение точки в исходном по-
ложении Ц\п подвижной центроиды
найдется из условия, что дуга Р*^
должна равняться дуге Р\Р^. Для
определения положения точки Пу
строим на отрезке Р[Р^ треуголь-
ник Р'РУПу, равный треугольнику
^УРУРУ- Из чертежа можно ви-
деть, что при движении треуголь-
ника Р'Рупу вместе с окружно-
стью 2 точка Пу треугольника в
совпадает с точкой Ру бицентроиды.
пятом положении действительно
Подобным же образом могут быть построены и все остальные
точки обеих центроид. Соединив центроиду Ц№ жестко со звеном 2,
а центроиду Ц-м жестко со звеном 3, можно заданные движения
воспроизвести качением центроид Z/so и Ц30 друг по другу без сколь-
жения. Перекатывание без скольжения может быть осуществлено,
если, например, между перекатывающимися системами будет создана
достаточная сила трения путем нажатия одной системы на другую.
6е. Выше нами было рассмотрено графическое решение задачи
о построении сопряженных профилей центроид. В некоторых случаях
для получения точного очертания профилей центроид удобно восполь-
зоваться аналитическим методом построения центроид.
Рассмотрим, как могут быть получены уравнения центроид в абсо-
лютном и относительном движениях.
Пусть задано движение звена 2 центроидной пары (рис. 203).
Система координат Оху принадлежит неподвижному звену 1. Система
координат О'?т] жестко соединена со звеном 2. Тогда движение звена 2
будет полностью определяться вектором q и углом поворота а системы
§ 7] ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА 125
координат (7^ относительно оси, перпендикулярной к плоскости
движения звена. Выбираем на звене 2 какую-либо точку А. Для
точки А можем написать следующее векторное уравнение:
Г=? + П, (3.12)
где г, есть вектор постоянного модуля, соединяющий точку А с точ-
кой О'. Так как r=r(t), q — q{t) и ^ = ^(0, то, дифференцируя
уравнение (3.12) по времени, получаем:
__dq । dr____dq H 19 1
где w есть вектор мгновенной угловой скорости звена 2.
Если точка А совпадет с мгновенным центром вращения, то ско-
рость ее равна нулю, т. е.
1=0,
откуда
^ + -»Хг. = о.
Умножая правую и левую части полученного уравнения на единич-
ный вектор ю°, имеем:
X + [w X П] X «>0 = О,
откуда получаем:
Так как
dq dq da dq
dt da dt da’
Если в уравнении (3.13) вектор гх задан в функции угла а, то
это будет уравнение подвижной центроиды. Уравнение неподвижной
центроиды получится, если подставить выражение для вектора и из
уравнения (3.13) в уравнение (3.12). Получаем:
г=9 + <о«Х^. (3.14)
В уравнения (3.13) и (3.14) входят векторы г, q и если один
из них задан в функции угла а, то остальные могут быть легко оп-
ределены. Таким образом, аналитическое решение задачи о построении
центроид сводится к решению уравнений (3.13) и (3.14).
Уравнения подвижной и неподвижной центроид могут быть пред-
ставлены и в координатной форме. Для этого обозначим координаты
126 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
точек О' и А (рис. 203) через х0, _v0 и х, у. Тогда координаты хР
и уР мгновенного центра вращения будут:
и
(3.15)
Координаты и мгновенного центра вращения, принадлежа-
щие подвижной центроиде, в координатной системе ОТ-ц будут равны:
с Х0 Sin а —COS а
----------
а
Л'о COS а + V sin а
--------
(3.16)
а
Так как функции х0 = х0(£), _yo=_Vo (О и a = a(t) являются задан-
ными, то по уравнениям (3.15) могут быть построены неподвижная и
подвижная центроиды, т. е. аналитически разрешена задача о центроидах
в абсолютном движении звена 2 центроидной пары относительно звена 1.
7°. Переходим к выводу уравнений центроид в относительном
движении [2]. Пусть задано движение звеньев 2 и 3 (рис. 204).
Выберем систему координат Оху за неподвижную, т. е. принадлежа-
щую неподвижному звену 1 механизма. Пусть, далее, система коор-
динат связана жестко со звеном 2, а система координат O'T"V' —
со звеном 3. Движение звена 2 будет определяться вектором q' и
углом поворота а', а движение звена 3— вектором q" и углом по-
ворота а". Для составления уравнений центроид в относительном
движении найдем уравнение бицентроиды, для чего рассмотрим отно-
сительное движение звена 3 относительно звена 2. На звене 3 вы-
берем произвольную точку А3. Для этой точки имеем (рис. 204):
r* = q" 4
§ 7|
ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА
127
Дифференцируя это уравнение по времени, получим уравнение,
определяющее скорость точки А3:
dr:: dq" dr"
dt dt "T" dt
lit + W:<X Г”’
где w3 есть вектор мгновенной угловой скорости звена 3. Так как
dr3 dq"
dt=*X И ~ЗГ
>
ГО
®ЛЬ = »АО11
(3.17)
Сообщим звеньям 2 и 3 общую угловую скорость около оси
О' равную и обратную угловой скорости ю2. Тогда звено 2 будет
как бы неподвижным, а звено 3 получит кроме угловой скорости о)(
дополнительную угловую скорость — В этом движении точка А3
звена 3 будет иметь скорость
®АзАа — ^As ' (3.18)
где vAi есть скорость точки Л2, принадлежащей звену 2.
Вектор г2, определяющий точку на звене 2, равен:
следовательно.
dr а do', ...
df = -> + ^XK
Так как
dr2 do'
и W = ®o-,
ТО
= V(y + X г'. (3 19)
Подставляя в уравнение (3.18) выражения для г»д3 и ч)Аз из урав-
нений (3.17) и (3.19), получим:
vAsas = Do„ Ц- X г” — ©0, — и>2 X г’. (3.20)
Имея в виду, что
®о" = &'• г^ = гз^= О
т”=г—</' и г' —г — qf,
перепишем уравнение (3.20) в следующем виде:
®АзА2 + (9" — «Э4-«>3X (/—9") —
ИЛИ
ЯДзАа = W — V) -+ (<О3 — Ю2) X Г — (W3 X ?" — «>2 X Q'\
Если точка А3 есть мгновенный центр вращения в относительном
движении звеньев пары, то ©дзЛа=:0, и, следовательно, уравнение
(9" — 9') + (шз — w>) X г — (w3 X <Г ~ w2 X = 0 (3.21)
есть уравнение бицентроиды.
128
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. III
В координатной форме уравнение бицентроиды имеет вид:
(х0„ — х0,) — К — “«) J + (шаУ0" ~ =0>
(у0„ —.У o') + (“з — <"2) * —(w3xoi,—<d3xo,)=0,
где хну — текущие координаты бицентроиды, а Х(', уо и х('', у о" —
координаты точек О' и О". Отсюда легко получаем параметрические
уравнения бицентроиды
(“з^о" — “so') 4* O'o" Уо') \ too toq . »1 г 1 } (3.22) (“зУо" — “«Уо') 4* (x O" — x0') I у = . 1 “3 “2 I
Для нахождения уравнения центроид, связанных со звеньями 2 и 3,
необходимо в уравнениях (3.22) координаты х и у выразить через коор-
динаты if и nj", принадлежащие координатным осям ОТт/ и
Как известно, формулы преобразования координат имеют следую-
щий вид: E' = (x —Xo>) cos a' (y—Уог) sin a', | . , 4 r z \ . • ( (3.23) if = (y —Уо*) cos a' —(x —Xo>) sin a\ |
Подставляя в уравнение (3.23) значения х и у из уравнения (3.22),
получим параметрические уравнения центроиды звена 2:
(xo„ — xo,) IQ3 — (y0„ — y0,) 1 C, ! r~ — LUs 1Л 1 to3 — cos 1 (Уо'< —Уо>) “з 4- <У'О" — х0') . , 4 sin a. I ‘ too — to2 p . . ... . . (3.24) , (Ус —Уо1) “a 4" (хон — xo') , tf= cos a — Gig — tog (xo" —x0')“a — (Уои —Уо') . , sin a. tog tog
Параметрические уравнения центроиды, принадлежащей звену 3.
имеют аналогичный вид.
Имея уравнения центроид звеньев 2 и 3, профили элементов
высшей пары можно построить по точкам, так как известны законы
движения звеньев:
Xq,—Уо:—у Qi (0> а —а (О»
Xqu == XQU{t), У0н —У()п(Р)’ °- —а (О
и, следовательно, могут быть определены величины:
dx6 . dyo ,
хо'=~аГ> yO'=-dF и
dxo". dyo"
XO" dt ’ dt И
da'
~ dt ’
da"
^—dt‘
§ 7]
ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА
129
В некоторых случаях удобнее пользоваться уравнениями центроид
в полярной системе координат. Прямоугольные координаты xQ<, у0<,
хо"’ У о" связаны с радиусами-векторами q', q" и углами р и -у (рис. 204)
следующими соотношениями:
х0, = q' cos р, у0> = q' sin р, х0« =q" cos у, Уо"— q" sin 7.
Подставляя значения xQ<, уо>, х0», _у0„ и их производных в урав-
нения (3.23) и (3.24), получим параметрические уравнения центроиды
звена 2 в полярных координатах, а исключая из этих уравнений время,
получим полярное уравнение центроиды звена 2. Уравнение центро-
иды звена 3 найдется с помощью аналогичных рассуждений.
8°. В качестве примера рассмотрим построение профилей центроид
в относительном движении для центроидного механизма, показан-
ного на рис. 205.
5 И. И. Артоболевский
130 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
Движение звена 2 задано качением подвижной центроиды Ц2п по
неподвижной центроиде //2н с постоянной угловой скоростью ш2.
Движение звена 3 задано качением подвижной центроиды Ц3п по
неподвижной центроиде Ц3я с постоянной угловой скоростью ш3.
Центроиды Ц2н и Ц3н представляют собой две взаимно-перпендику-
лярные прямые. Отношение ii3 угловых скоростей <и2 и и>3 равно:
Бицентроида Б представляет собой прямую, проходящую через
точку пересечения неподвижных центроид. Положения точек Р*, Р”,
РП0, ... определяются из заданного отношения т23. Точки II],, П’*, П”1,
... и П>, П”, П*п, ... пентроид Ц20 и Цзо определятся, если для
каждого положения звеньев 2 и 3 найти точки, принадлежащие этим
звеньям и последовательно совпадающие с точками Р^, Р^, Р"1, ...
бицентроиды. На рис. 205 показано определение точки
Пу центроиды Ц20. Для определения точки 1LV перекатываем
центроиду Ц2п в то положение, в котором мгновенным центром
вращения является точка Р^. При этом точка центроиды Ц2п, совпа-
дающая в первоначальном положении центроиды с мгновенным цент-
ром Pj, переместится в положение Р. Соединив точку Р с точками
pv и Ру, получим треугольник РР^ Р^. Возвращаем, далее, центроиду
в первоначальное ее положение. Тогда треугольник РР^Р^ зай-
мет положение и тем самым определится положение точки П^.
С помощью аналогичных построений определятся остальные точки
центроид Ц2о и Цзо. Кривые ПуП'рТ” ... и П'П'р!”1 ... будут пред-
ставлять собой профили элементов высшей пары, принадлежащие
звеньям 2 и 3. Соединив первый профиль жестко с окружностью Ц2п,
а второй профиль с окружностью Ц3п, можно воспроизвести заданное
движение звеньев 2 и 3 воздействием друг на друга построенных
профилей.
Та же задача может быть решена аналитически. Найдем уравне-
ния бицентроиды Б и центроид Ц.1О и Ц3о для случая передачи дви-
жения, изображенного на рис. 205. Выберем оси координат Оху,
O'Sj'-rf и О"^"п" так, как показано на рис, 206. Тогда координаты
точек О' и О" будут:
xoi = r'a.', уо< = ^, xQ< =— Г" и Уо" = — Г"а.",
где г* и г" суть радиусы центроид Ц211 и Ц3п, а а' и а" — углы их по-
ворота. Так как по заданию
г' — г" = г и а' = а" = а,
то
Хо' = га. уо. = —г, хоп = — г, уо"=га.
§ 7] ОБЩИЙ СЛУЧАЙ ЦЕНТРОИДНОГО МЕХАНИЗМА 131
Следовательно,
• da • п
хо' = гТ1=гш’ Уо' = °’
л . da
х0- = °, yo„ = rTt = r^.
Подставляя полученные выражения в уравнения (3.22) для бицент-
роиды, найдем:
га га
Х=2’ У=2‘
Исключая параметр а, получим:
х—у,
т. е. бицентроида Б представляет собой прямую (рис. 206), прохо-
* Рис. 206.
128S/-O
дящую через начало осей координат Оху и образующую угол в 45°
с осями х и у.
Для определения уравнений центроиды Z/2o подставляем значения
х, у, х0, у0 и а' в уравнения (3.23). Получаем:
Е' — — у [a cos а —|— (а —2) sin а]
и
V = — [(а 2) cos а —а sin а].
Аналогично определятся параметрические уравнения для цен-
троиды USo.
9°. Возможность передачи движения центроидными механизмами
зависит от того, будут ли в механизме обеспечены соответствующие
б*
132
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. III
значения углов передачи, при которых возможно воспроизведение
заданного закона движения ведущего и ведомого звена механизма.
Рассмотрим вопрос об определении угла передачи для общего
случая центроидного механизма (рис. 207), когда движение звеньев
2 и 3 воспроизводится посредством центроид в относительном дви-
жении. Так как обе центроиды в точке соприкосновения имеют общую
скорость 1>р0, то угол у будет у них общим и равным независимо
от того, какая из центроид является ведущей. Переменные расстояния
точек Ро от мгновенных центров вращения звеньев 2 и 3 обозначим
через р2 и р3. Пусть за бесконечно малый промежуток времени цен-
троида Lfon повернулась около
центра Р2 на угол На центрои-
де Ц20 отложим из точки Ро бес-
конечно малую дугу Роа и из точ-
ки а опустим на направление
перпендикуляр aav Тогда ^.а^аР^
будет с точностью до бесконечно
малых второго порядка равен углу
давления у и, следовательно,
PpCi
aat
Так как с точностью до беско-
нечно малых высших порядков
можно положить, что
= фГ
ТО
и аах == р2с/ср2,
tg I
Из условия передаточного отношения следует:
Фа
фа
И
• ________^2 __________Рз
23 <*>3 р2с
Кроме того,
РцРз — Ра 4~ Рз — I-
Отсюда определяем
Ра = ^
С02
। ^3
‘ (О2
Так как
§ 7]
ОБЩИЙ СЛУЧАЙ ЦЕИТРОИДНОГО МЕХАНИЗМА
133
где <р3 и <р2 — углы поворота центроид, то предыдущее равенство
принимает вид:
d^3
п — /
o<fi
Тогда
d-'f3 dtfa
,Ал_ z^7
dy8
d<fl. 1 dl
d<?2 \ d'fi)
откуда
В рассмотренном случае воспроизведения движения угловые ско-
роста о>2 и <о3 были различными по знаку. В том случае, когда угловые
скорости ш2 и <о3 имеют одинаковые знаки, последнее уравнение
принимает следующий вид:
d\3
У___________d<f2_______I___1_
f 1 _ ^f»\ 1 fy* ’
dcp2 dtps/
Производные, которые входят в указанные уравнения
и определяются либо графически, либо аналитически, в зависи-
мости от характера задания величин ср3 = ср3 (ср2) и I = I (ср2). Центроиды
будут работать без заклинивания только на тех участках, где все
значения полученного угла передачи -у будут больше некоторого ми-
нимального значения ?пиП, рекомендуемого для данного вида центроид-
ной пары. Величины угла ут1п, допускаемые в этих парах, различны
и зависят от коэффициента трения в парах и конструкции самих пар.
На тех участках профилей, где угол у меньше угла пара рабо-
тать не будет; здесь необходима замена центроид взаимоогибаемыми
кривыми, т. е. необходима установка дополнительных зубцов, кулис
и т. д.
Таким образом, условием возможной передачи движения в центроид-
ном механизме общего вида будет условие
d*<p8
_______d^fl____
d'fa /. dcfg\
d<?a \ — dtfS;
I 1 dZ ,
(3.25)
134
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. III
Величина представляет собой
ханизма (см. § 7, 1°).
Следовательно, уравнение (3.25)
передаточную функцию г32 не-
окончательно перепишется так:
arctg
^32
1з2 (1 — Isa)
L d_L
I d<fs
Tmin-
(3.26)
Из неравенства (3.26) следует, что при задании передаточной
функции г32, равной i32 = const, производная i32 от передаточной
функции по углу поворота будет равна нулю, и условие (3.26) пере-
ходит в условие
arctgT^^Tmin’ (3-27)
При постоянном расстоянии I между мгновенными центрами вра-
щения ведущего и ведомого звеньев, т. е. при I— const, неравенство
(3.26) принимает вид.-
arctg
1за)^Тт’п-
В этом случае возможность передачи движения обусловливается
только передаточной функцией, а не размерами механизма.
§ 8. Центроидные механизмы некруглых колес
1 . Переходим к рассмотрению вопроса о проектировании трех
звенных центроидных механизмов, образованных одной центроидной
парой и двумя низшими парами. К этим механизмам относятся меха-
низмы прямых и прямых колес (рис. 12 и 13), механизмы кривых
(рис. 24) и прямых (рис. 25) реек, механизмы перекатывающихся
рычагов (рис. 27) и др.
Механизмы некруглых колес и реек получают широкое распро-
странение в современном приборостроении и общем машиностроении
вследствие возможности воспроизведения ими большего числа разно-
образных функций передаточного отношения. Рассмотрим геометри-
ческий метод решения задачи о построении центроид этих механизмов.
Как было показано выше (§ 7, 1°), требуемый закон движения веду-
щего и ведомого звена может быть задан или в виде функции поло-
жений или функции передаточного отношения. Предположим, что нам
заданы в виде графиков угловые скорости <о2 и ведущего и ведо-
мого звеньев (рис. 208, б) в функции угла поворота <р2 ведущего
звена 2 и задано расстояние АВ между осями вращения звеньев 2 и 3
(рис. 208, а). Так как <о2 = ю2 (<р2) нами принята постоянной (рис. 208, б),
то функция передаточного отношения г32 = Z32 (<р2) будет представлена
на рис. 208, б в виде кривой, совпадающей с кривой <о3 = <о3 (<р2).
Если за начальные положения сопряженных центроид принять поло-
жения. при которых углы поворота центроид, отсчитываемые от на-
§ Я]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
135
правления АВ равны нулю, то функция положений <р3 = ср3 (ср2) (рис. 209)
может быть легко получена из условия (3.6). Имеем:
Ч>2
0
Для этого производим графическое интегрирование графика
ht = hi (?«) (Рис. 208, б).
Имея функцию передаточного отношения (рис. 208, <5) и функцию
положений (рис. 209), переходим к графическому построению сопря-
женных цецтроид, принадлежащих звеньям 2 и 3. Пусть угловые
скорости о>2 и ш3 противоположны по знаку. Тогда положение мгно-
136
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. in
венных центров вращения (рис. 208, а) в относительном движении
звеньев 2 и 3 будет определяться из условия (3.7). Имеем:
. A Ро АЗ — ВР0
ВРй
(3.28)
Таким образом, расстояние АВ вследствие противоположности
знаков угловых скоростей ю2 и w3 должно быть разделено внутренним
образом согласно условию (3.28). Полученные из условия (3.28) по-
ложения мгновенных центров вращения Р\, Р”, Р™, ... (рис. 208, а)
образуют бицентроиду. Для построения профилей центроид находим
точки, принадлежащие звеньям 2 и 3, приходящие последовательно
в совпадение в точках Р°, Р”, Р’11, ... бицентроиды. Для этого от
направления АВ (рис 208, а) откладываем углы <р2 и <р3. Углы <р2
поворота центроиды 2 между двумя соседними положениями (рис. 209)
являются равными. Поэтому из точки А (рис. 208, а) проводим лучи
А2, АЗ, ... под равными друг другу углами <р2. Углы <р3 поворота
центроиды 3 между двумя соседними положениями будут переменными.
Поэтому из точки В проводим лучи: В2, ВЗ, ... под углами <р3, <р3,
<р3", ... , полученными из графика (рис. 209). Из точки А (рис. 208, а)
радиусами АР”, АР”1, ... проводим дуги до пересечения в точках 2",
3", 4", ... с соответственными лучами .42, АЗ, А4, .... Соединив
плавной кривой полученные точки Р\, 2", 3", ..., получим профиль
центроиды, принадлежащей звену 2. Точно так же, из точки В про-
водим дуги радиусами PPJ1, ВР™, ... д.о пересечения в точках 2"',
3"', 4'",... с соответственными лучами В2, ВЗ, В4, ... Соединив
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС 137
плавной кривой точки Р[, 2"', 3"', , получим профиль сопряженной
центроиды, принадлежащей звену 3. Нетрудно видеть, что для воз-
можности передачи непрерывного периодического движения длины
профилей центроид должны быть равны и, следовательно, полные
углы поворота Ф2 и Ф3 (рис. 209) сопряженных центроид должны
быть равны между собой и за полный угол движения давать угол,
равный Ф2 = Ф3 = 2те. Возможны профили центроид с разными углами
поворота за полный цикл движения, но при этом эти углы должны
быть кратны целому числу; профили центроид должны иметь сим-
метрию, для чего необходимо, чтобы была обеспечена и симметрия
в графике кривой, изображающей передаточную функцию. Из изло-
женного следует, что для случая среднего передаточного отношения,
равного (г32) ср = — 1 за один оборот ведущего и ведомого звена,
как это имеет место для рассматриваемого механизма (рис. 208, б),
необходимым условием должно быть равенство углов Ф2 = Ф3. Это
условие требует, чтобы площади, ограниченные кривыми <о2 = <о2 (<р2)
и u>3 = ю3 (<р2) (рис. 208, б) были бы равцы между собой, т. е. чтобы
всегда удовлетворялось условие:
Фд Фд
С <o2(Z<p2 = f w3(Z(p2.
о о
(3.29)
2°. Переходим к рассмотрению геометрического метода решения
задачи о проектировании профилей сопряженных центроид для случая
механизма некруглого колеса, сопряженного с рейкой (рис. 24). Пусть
некруглое колесо 2 вращается с постоянной угловой скоростью и>2,
а рейка 3 должна двигаться поступательно со скоростью vs, заданной
графиком = v3 (<р2) (рис. 210). Пусть, далее, полный угол пово-
4
рота Ф2 колеса 2 равен Ф2 = у тг и задано положение оси вращения А
колеса 2 и направление хх перемещения рейки (рис. 211).
138
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. III
Мгновенные центры вращения Р', Р},11, ... в относительном
движении будут лежать на направлении Ау. Положение этих точек
определится из условия:
ds3
AP9 = ^=-^ = dS3=k^. (3.30)
U>2 Cltfs d<f2 ’
clt
Условимся величину /г32, хотя и имеющую размерность, называть
Рис. 211.
передаточной функцией для случая передачи поступательного движе-
ния от некруглого колеса к рейке.
Из уравнения (3.30) следует:
х3
<РЗ
J ^32^2-
О
(3.31)
Так как угловая скорость ю2 звена 2 нами принята постоянной,
то график. (ср.2) (рис. 210) будет и графиком Аза = /г32 (<р2). Для
§ 8]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
139
получения графика s3 —s3(c?2) (рис. 212) производим графическое
интегрирование графика k32 = ks2 (<р2), принимая за начальное 1-е по-
ложение рейки положение, совпадающее с прямой Ау. Ордината S3
в крайнем 10-м положении (рис. 212) определит полное перемещение S3
рейки 3. Далее, на направлении Ау (рис. 211) откладываем отрезки:
ДР’1, АР™, АР™, ... , определяемые графиком = k32 (ср2) (рис. 210).
Таким образом определится по-
ложение точек Р’, Р’1, Р™, ...
бицентроиды. Далее, из точки А
проводим лучи А2, АЗ, А4,...
под равными друг другу угла-
ми ср2. Из точки А радиусами
ДР'1, ДР’”, ДР{У, .. • проводим
дуги до пересечения в точках 2",
3", 4", ... с соответственными
лучами А2, АЗ, А4, ... Соеди-
нив плавной кривой точки Р’,
2", 3", 4", ... , получим про-
филь центроиды некруглого
колеса. Для получения профиля
центроиды, принадлежащей рей-
ке, проводим из точек Р’’, Р’”, P’v, ... прямые Р’’2, Р’”3, Р™4, ... ,
параллельные направлению хх, и откладываем на этих прямых ве-
личины перемещений s3 рейки, определяемые графиком s3 = s3 (ср2)
(рис. 212). Соединив полученные точки 2"', 3'", 4"', ... плавной кривой,
— I-----
Рис. 213.
получим профиль сопряжен-
ной центроиды, принадлежащей
звену 3.
3°. Мы рассмотрели выше
геометрические методы по-
строения профилей центроид
некруглых колес. В большин-
стве случаев при проектирова-
нии некруглых колес для полу-
чения большей точности расче-
тов применяются аналитические
методы. Аналитические методы
проектирования вследствие их сложности применяются только к оп-
ределенным типам некруглых колес, наиболее широко применяющихся
на практике. Аналитическая теория некруглых колес наиболее подроб-
но развита в работе [36]. Некоторые вопросы преобразования профилей
изложены в работах других советских ученых (см., например, [21]).
В дальнейшем изложении мы будем следовать этим работам. Рассмот-
рим вопрос об уравнениях профилей центроид, сопряженных для
случая внешнего зацепления. Обозначим (рис. 213) расстояние между
осями А и В через I, радиусы профилей центроид 2 и 3 через г2 и
140 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [гл. III
г3 и углы поворота центроид через у.2 и <р3. Ведущим принимаем
звено 2. Тогда на основании соотношения даточного числа (3. 5) имеем для пере-
W2 Г3 23 «3 Г2 d<?s 1 (3.32)
И
Га~(--Гз = А (3.33)
Из уравнений (3.32) и (3.33) получаем:
r‘2_“Z 1-i-i 1 "т г23 (3.34)
И
1 "Г г23 (3.35)
Уравнения (3.34) и (3.35) будут уравнениями центроид в поляр-
ной системе координат. Угол срг, образуемый радиусом-вектором г8,
является независимой переменной, а угол <р3, образуемый радиусом-
вектором г3, определится из условия
^2 <Р2
<р3= I /32rf(p2= I - (3.36)
J J *23
О о
Уравнения (3.34), (3.35), (3.36) будут уравнениями сопряженных
центроид в параметрической форме.
Из формулы (3.32) следует:
r2(Z®8 = r3tZ<p3. (3.37)
Из очевидных геометрических условий также следует, что при-
ращения радиусов-векторов профилей центроид всегда удовлетво-
ряют условию
dr8 = —<7г3. (3.38)
Разделив уравнения (3.37) и (3.38) друг на друга, получим:
d<fs
Как известно из дифференциальной геометрии, отношения, входя-
щие в левую и правую части уравнения (3.39), представляют собой
тангенсы углов [т2 и р3 (рис. 213), образованных касательной к про-
филям центроид с радиусами-векторами этих профилей. Следовательно,
получаем:
tg {*-2= — tgp3.
Согласно условию соприкосновение профилей сопряженных цен-
троид происходит в точке Ро бицентроиды. Точка Ро лежит на на-
правлении АВ. Следовательно,
На + На — (3.40)
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРГТЛЫХ КОЛЕС 141
Выведенные соотношения вполне определяют основные геомет-
рические параметры профилей сопряженных центроид в аналитичес-
кой форме.
4°. Если некруглыми колесами должно передаваться непрерывное
вращательное движение, то профили сопряженных центроид должны
представлять собой замкнутые кривые. Рассмотрим условия, обеспе-
чивающие замкнутость профилей центроид.
Как было показано выше для заданной функции передаточного числа
/23 уравнение профиля центроиды 2 (рис. 213), принятой за ведущую,
будет (3.34):
Г2==/пгТ^==гиср'2)- (ЗЛ1)
Для обеспечения замкнутости профиля центроиды ведущего ко-
леса необходимо, чтобы функция г23 передаточного числа, входящего
в уравнение (3.41), была периодической функцией с периодом
равным f2 = —, где Ф2 — полный угол поворота центроиды 2, а
п2
пг — число оборотов центроиды 2, равное целому числу, т. е. и2 =
= 1, 2, 3,... В этом случае функция г2 = г2(ср2) будет периодичной
Фа
с тем же периодом, равным —, т. е. значения радиуса-вектора г2
Zig
совпадут при значениях угла ср2, равных ср2 = 0 и ср2 = 2 тг. Для
ведомой центроиды имеем следующие уравнения ее профиля (3.35)
и (3.36):
Гз = ^-Н!т-=Гз(^) (3.42)
1 Т *23
И
«₽2
<р3= \ т-с?ср2 = ср3(<р2). (3.43)
J *23
О
Функция г3 = г3(ср2) является периодической, так как функция
/23 передаточного числа была принята периодической. Кроме того,
Ф
период t3 функции r3 = ra (ср2), равный t3 = —, где Ф3 — полный
угол поворота центроиды 3, а п3 — ее число оборотов, равное п3 —
= 1, 2, 3,..., должен равняться периоду f2 функции г2 = г2(ср2).
Таким образом, для замкнутости профилей центроид некруглых
колес необходимо, чтобы функция передаточного числа была пе-
риодической с периодом, равным периоду целой части одного обо-
рота как ведущей, так и ведомой центроиды, т. е. период Т функ-
ции г23 передаточного числа должен быть связан с периодами <2 и t3
оборотов колес 2 и 3 соотношениями:
где л2 и п3— целые числа.
142
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. III
б°. Переходим к рассмотрению вопроса о кривизне профилей
центроид. Если уравнения профилей центроид заданы в полярной си-
стеме координат, то радиус кривизны р в каждой точке профиля мо-
жет быть определен из известного выражения для радиуса кривизны:
(3.45)
Для ведущего звена 2 (рис. 213) имеем:
1 _L( > * “Г *23 (3.46)
dt2 j Xgg d^~ (14-123)2 (3.47)
и rf2r2 d<fl Z (1 4~ *2s) *23 (*2з)8 ~ (14-*2з)3 (3.48)
Подставляя выражения (3.46), (3.47) и (3.48) в уравнение (3.45)
получим после несложных преобразований:
3
п — / 1(1 4- *~23)8 4- (*"8з)8] 2 (1 4" *2з)3 (1 4" *23 4~ *2з) ' (3.49)
Соответственно для профиля центроиды 3 будем иметь:
г 1 *88 ‘ 3 * 1 I ! 1 1 "Т~ 123 (3.50)
dr& _ drs ^8 ; 7 fgg ; (3.51)
d<fz dsrt d *??3 rf?2 23 (1 4- *23>8 83 ’ / rfr3 \ _ rf / dra \ 1 = \ d<fs ) d<fs d<fg \ d<i>3 ) 23 4~ *2з) ](*2з)8 4~ *23*2'3] 2*2» (*2з)8 • (1+«2з)3 23 ’
d^'i dy% (3.52)
Подставляя выражения (3.50), (3.51) и (3.52) в уравнение (3.45),
получим после несложных преобразований:
з
0 ____j *23 [(1 4~ 4з)а 4~ Раз)8] 2________
3 (1 4~ *2з)3 |1 4“ *23 4’ (*2з)8 - *23*2’3]
(3.53)
Таким образом, радиусы кривизны профилей центроид могут
быть всегда определены, если будут известны функция передаточ-
ного числа =/«а (<р4) и расстояние Z между осями вращения центроид.
С точки зрения обработки профилей центроид и профилей зуб-
цов некруглых колес весьма важно исследовать вопрос о том, бу-
дут ли профили центроид на всех участках выпуклыми или на не-
которых участках они будут выпуклыми, а на других вогнутыми.
§
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
143
В первом случае обработка профилей центроид может быть произ-
ведена методом обката инструментальной рейкой. Во втором случае
вогнутые участки профилей могут быть обработаны только с помо-
щью долбяка. При переходе от выпуклого участка профиля к во-
гнутому радиус кривизны профиля в точке перегиба будет равняться
бесконечности. Следовательно, в выражениях (3.49) и (3.53) знаме-
натели будут равны нулю. Так как
выражение 1 -f- /23, стоящее в знаме-
нателе, может равняться нулю только
при частном значении z23 =—1, то
условие наличия точки перегиба про-
филя для центроиды 2 будет опре-
деляться выражением
1 Ч- 4з “Ни = 0, (3.54)
а для профиля центроиды 3 — выра-
жением
1 ~|~4з4“(*2з)2—W23—0- (3.55)
Следовательно, для того чтобы
профили центроид были на всех
участках выпуклыми, должны всегда
профиля центроиды 2
Рис. 214.
удовлетворяться условия: для
(3.56)
и для профиля центроиды 3
1 Ч-4зЧ“(*2з)--
(3.57)
Из выражений (3.56) и (3.57) следует, что выпуклость или во-
гнутость профилей центроид зависит только от функции z23 = z23 (<р2)
передаточного числа.
6е. В некоторых случаях необходимо определить радиус кри-
визны р3 одной из центроид, если известны: радиус кривизны р2
сопряженной центроиды, передаточное отношение z’23 центроид и угол ср,
образованный нормалью к центроидам в точке соприкосновения с
линией центров. Для этого воспользуемся связью между радиусами
кривизны р2 и р3 центроид, выраженной с помощью теоремы Эйлера—
Савари (§ 5, 15°), — формула (2.40).
Для этого рассмотрим движение центроиды 3 относительно цен-
троиды 2 (рис. 214). Для этого сообщаем механизму общую угло-
вую скорость, равную и противоположную угловой скорости ю2.
Тогда центроида 2 будет неподвижной, а центроида 3 будет пере-
катываться по центроиде 2. При этом точка В центроиды 3 опишет
дугу kk окружности радиуса АВ. Кривая kk будет рулеттой точки В.
Следовательно, точка В будет огибаемой, а кривая kk — огибающей.
144 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [гл. III
Тогда на основании уравнения (2.40) можно написать:
(3-58)
откуда получаем:
Рз = ~п-------А----------. (3.59)
Ps v+v с08?—1
\ Г2 Г 3
Подставляя в уравнение (3.59) значения для г2 и г3 из уравнений
(3.46) и (3.50), получаем:
Таким образом, если известна функция /23 = /23 (ср2) передаточного
числа, радиус кривизны профиля одной из центроид и направление
нормали к профилям центроид, то легко определяется радиус кри-
визны профиля второй центроиды. Для определения радиуса кри-
визны р3 (рис. 214) можно также использовать графическое построе-
ние, изложенное в § 5, 15°. Из точки Ро восстанавливаем перпен-
дикуляр к направлению АВ. Далее, соединяем точку А с центром
кривизны О2 профиля центроиды 2 и продолжаем это направление до
пересечения в точке D с перпендикуляром к прямой АВ. Соединив
точку D с точкой В и продолжив направление DB до пересечения в
точке О3 с прямой О2Р0, находим положение центра кривизны О3
профиля центроиды 3. Радиусы кривизны р2 и р3 будут соответст-
венно равны р2 = О2Р0 и р3 = ОЛР{}.
7°. Рассмотрим вопрос о проектировании профилей сопряженных
центроид для воспроизведения заданной функции y=f(x). При этом
предполагается, что воспроизводимая функция в заданном интервале
xk х непрерывна и дифференцируема.
Пусть центроида 2 вращается пропорционально изменению неза-
висимого переменного х, т. е. угол ср2 поворота центроиды будет
равен:
<р2 = р.2 (х — х;), (3.61)
где — масштабный коэффициент. Тогда угол поворота с?3 центро-
иды 3 может быть представлен как:
?з = Нз (У — Уд = Из —/(X;)], (3.62)
где р-з — масштабный коэффициент.
Начало отсчета углов поворота центроид определится значениями
x = xt и /(х)=/(хД Функция /32 =/32 (ср2) передаточного отноше-
ния будет равна:
. ctys б?тз dx
*32 dy2 dx dy2 *
(3.63)
§ 8]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
145
Из уравнения (3.62) получаем:
Из уравнения (3.61) имеем:
dx 1 1
d^f>2 (tyz P'S
dx
d-Чъ dx rn r
Подставляя выражения для и в уравнение (3.63), полу-
чаем:
i3i = ^f'(x). (3.64)
Р-2
Полярное уравнение профиля центроиды 2 определится из урав-
нений (3.34) и (3.61). Имеем:
1 i г/,(х) ’
г^ = 1т^г = 1т^-=1—--------------
1 -р
*23 1 ~Г *32 1 I № Р / И
1+^/(хЬ (3.65)
И
Ъ — Р-2 (-* — J
где I—расстояние между осями вращения центроид.
Полярное уравнение профиля центроиды 3 определится из урав-
нений (3.35) и (3.62). Имеем:
r3=z = = /------!----]
1+/23 1+«з2 X+^f'(x) I (3.66)
И р-2 I
?» = М/(•*)—/(*.•)]• *
Функция y=f(x) может быть задана различно. Если она задана
аналитически, то решение задачи о воспроизведении этой функции
механизмом некруглых колес может быть сделано с любой требуемой
степенью точности. Если функция задана в табличной форме, то
для нахождения ее производной можно воспользоваться методом таб-
личного дифференцирования или другими методами численного
дифференцирования. Изложенное проиллюстрируем примером нахожде-
ния уравнений профилей центроид для воспроизведения квадратичной
зависимости вида:
у = ах\
где а — постоянный коэффициент.
146 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
Пусть для начального значения х, равного хг- углы поворота
<р.2 = <р3 = 0. Тогда на основании уравнения (3.64) функции z32 пере-
даточного отношения будет иметь следующий вид:
^ = ?/'(х) = ^2ал:,
Р2 Р<2
где |i2 и |х3 — масштабные коэффициенты.
Полярные уравнения профиля центроиды 2 получим согласно
уравнению (3.65):
1 4- 2ах
Н
и
(р2 = (х — Xi),
Полярные уравнения профиля центроиды 3 получим из уравнений
(3.66). Имеем:
гз=:/—'
1 + 2ах
Р-2
И
?з = (Мг(х2 — xi\
Очертание профилей центроид может быть легко построено, если заданы
функция у = ах2, интервал ее изменения, масштабные коэффициенты и..
и р-з и расстояние I между осями вращения центроид. На рис. 215 по-
казан один из вариантов механизма для воспроизведения зависимости
у == ах2,
8°. Для передачи непрерывного вращательного движения между
двумя осями применяются эллиптические, овальные, логарифмические
колеса и колеса, одна из центроид которых представляет собой
окружность с эксцентрично расположенной осью вращения. Рассмот-
рим общие вопросы, связанные с проектированием таких колес.
Рассмотрим случай эллиптических колес. На рис. 216 представ-
лено эллиптическое колесо 2 с осью вращения в точке А, совпадаю-
щей с фокусом эллипса. Если обозначить длину большой оси эллипса
§ 8]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
147
через 2а, длину малой оси эллипса через 2/?, длину хорды, прове-
денной через фокус эллипса перпендикулярно к его большой оси,
через 2/?, расстояние между фокусами эллипса через 2с, то эксцен-
триситет е эллипса будет равен е = а уравнение эллипса в по-
лярной форме относительно полярной оси Ах будет иметь вид:
г.>=-.---£----. (3.67)
1 — е cos ср2 47
Примем колесо 2 за ведущее. Как было показано выше (§ 8, 4°),
для воспроизведения непрерывного вращения колес профили центроид
должны быть замкнутыми кривыми, функция передаточного числа
должна быть периодической с периодом, равным 2тс, и должно удов-
летворяться условие (3.44), т. е. чтобы при повороте ведущей
центроиды 2 на полный угол поворота Ф2 = 2тс полный угол поворота
2?t
Ф3 ведомой центроиды 3 был бы равен Ф3 =—, где д3—целое число.
Из
Функция Z23 передаточного числа будет равна:
Подставляя значение для г2 из уравнения (3.67), получаем:
4з = -- (1 — е cos <pg) — 1, (3.68)
где I—расстояние между осями вращения центроид. Из уравнения
(3.36) имеем, что угол с?3 поворота центроиды 3 от положения, когда
ср2 = <р3 = 0, будет равен:
с?2
с 1 , 2р
= I т~ “Чъ — ~г—' arctg
J у(1 — р)2 — 12е2
^\1-рУ-^ tg
/(1 — е) — р 2
(3.69)
При полном угле поворота <р2 центроиды 2, равном Ф2 = 2тс, пол-
27:
ный угол поворота <р3 центроиды 3 будет равен Ф3 = —. Тогда
уравнение (3.69) будет иметь следующий вид:
«3 ]Л(/—рУ — /2с2 К /(1— е) — р ®2
откуда получаем:
_К(/-р)2-/2е*
По --------------.
(3.70)
(3-71)
Из уравнения (3.71) определится величина расстояния I между
осями вращения центроид. Имеем:
Г-Ь Ь + 1 И" 1)(1—е£)]. (3.72)
148
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. Ш
Уравнение профиля центроиды 3 имеет вид:
г3 = I — г± = 1 — -г----------------
d z 1 — е cos?-
(3.73)
В уравнение (3.73) входят величины I и cos <р2. Величина I может
быть взята из уравнения (3.72), а величину cos ср2 можно определить
из уравнения (3.69). Для этого представим уравнение (3.69) в форме
tg?2
g 2р / (1 — е) — р 2 *
(3.74)
Учитывая выражение (3.71) для значения пл, получаем:
или
_ К(Z-p)2-/2e2tg ?2
2 — /(1— е) — р 2
tg^ = ^tg^, (3.76)
l/~(l_ п)2_ ре2
где k = —-— — постоянная, содержащая основные пара-
метры эллиптического профиля
ведущей центроиды. Величи-
на coscp2 будет равна:
cos <р2 =------— =
1 + tg2^
1 - fe2 tg2
1+Л2 tg2^
(3.77)
cos ср2 из уравнений
Подставляя выражения для I и
(3.77) в уравнение (3.73), после преобразований получаем:
(3.72) и
pnl
Гз У1+(п|— 1)(1 — е2)-Н cosw3<p3 *
(3.78)
Уравнение (3.78) будет уравнением профиля центроиды 3 в по-
лярной форме. При и3 = 1 профиль центроиды 3 будет идентичен
профилю центроиды 2.
9°. В различных машинах и устройствах широко используются
эллиптические колеса со средним передаточным числом (4з)ср=1>
т. е. колеса, у которых п3=1, и, следовательно, за один оборот
ведущего колеса ведомое колесо делает также один оборот (рис. 217).
Для этих колес расстояние I между осями их вращения определится
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС 149
из уравнения (3.72). Имеем:
/=1^. (3.79)
Как известно из аналитической геометрии, величина 2р (рис. 216)
равна:
2/2 = 2а (1 — е~). (3.80)
Следовательно, расстояние I будет равно:
/=2а,
т. е. центрами вращения центроид будут фокусы А и В (рис. 217)
эллипсов.
Передаточное число z.23 из уравнения (3.68) получим равным
2а х . I—2г cos <р2 + г2 оп
ггз = а(1—— ecos^) — 1=---------------1 - • (3.81)
Максимального значения передаточное число z,23 достигает при <р2 = те,
а минимального значения при ср,2 = О. Следовательно, передаточное
число z23 механизма будет меняться в пределах:
(^2з)пнп ^23 (4з)тах
ИЛИ
L ' <382>
Уравнение профиля центроиды 2 получим из условия (3.34):
Г2 = /у-^ = 2а-------=---Д------. (3.83)
1 + z23 i-i-l — 2г cos ср2 -|~ г2 1 — е cos <р2 v ’
' 1 — г2
Соответственно из условия (3.35) получим уравнение профиля
центроиды 3. Имеем:
1 — 2г cos <р2 4-
Г —I *2» _о 1—е2 _ а(1 —2ecos<p2 + e2)
3 l+t2S . , 1 — 2е cos ^>2 + е2 — l-ecos?2 ’
+ 1 — е2
Функцию <р3 — ср3 (с?.2) положений получим из уравнения (3.69).
Имеем:
<р2
С 1 , 2а (1— г2) . |а(1—- г2) х ср9 I
= ) ^^=a-(i-e2) arctg|4r^tgT.| =
— 2 arct£ | fg у 1 • (3l85)
10°. Рассмотрим, далее, вопрос о проектировании сопряженных
центроид некруглых колес, когда одна из центроид будет окруж-
ностью (рис. 218) радиуса а с осью вращения в точке А Обозна-
чаем эксцентриситет через е, радиус вектор центроиды через г2 и угол,
образованный радиусом вектором л2 с полярной осью Ах, через
150
СИНТЕЗ ТРЕХЗВЕННЫХ 11ЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. Ш
Тогда уравнение профиля центроиды 2 будет иметь вид:
г.2 = ]/а2 — е2 sin2 ср,2 — е cos <р2. (3.86)
Функция z.23 передаточного числа будет равна:
I — г 2 _____________________/______________________
а2 — е2 sin2 — е cos
(3.87)
где I—расстояние
между
Рис. 218.
осями вращения центроид. Угол поворота <р3
центроиды 3, отсчитываемый от
жения, когда <р2 = <р3 = 0, будет
поло-
равен:
е2 sin2 ср2— £Cos
____________ d^.
— У а2 — е2 sin2 е cos ^>2
(3.88)
Ф. Л.
Как показало исследование
Литвина [36], точное решение уравне-
необходимости использования эллиптиче-
_ _ „ _ и третьего родов^ им был предложен спо-
приближенного вычисления интеграла уравнения (3.88). Если
(3.88) мо-
(3.88) приводит к
интегралов первого
НИЯ
ских
соб
обозначить отношения — = т
а
жет быть приведено к виду:
и А — е, то уравнение
а
о
___ С 1 — £2 —тг COS Ш 1 — £2 sin2 Cfa j
J (ш2 —£2 — 1)Ч~ cos
о
(3.89)
1
Раскладывая величину (1—s2sin2<?2)2 в ряд Фурье и ограничи-
ваясь ввиду быстрой сходимости ряда двумя первыми членами ряда,
получаем после преобразований:
<Рз b arctg (и • tg +/><р4 — q Sin
(3.90)
где
. 1 Г ('» + 1 + О ('» +1—0 Д2 v
°— у (т_ 1 _ е)(т — 1 + о те2 л
[Дм — 1 — е) («; — 1 + о (/« + 1 + е) (/И + 1 — е) ’
„ _ 1 /Дт—1—о (ш-1 -!-О~
“—У (m+l-e)(m+l + e) >
'>-2. ’=?•
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС 151
Величины Bq, В.2, В^ ... представляют собой коэффициенты чле-
нов ряда Фурье, расположенные по косинусам углов, кратных 2сра,
т. е. полученные из разложения
1
(1 — е2 sin2 ср.2)2 = Bq Bi cos + Вц cos 4<р2 -[”••• >
где
50—1 4 е2 64 ®4 256е6
= !б е* + 512ев + --”
Bi ( 64 s4~^ 256 £<:+
Для определения межосевого расстояния Z, при котором обеспе-
чивается замкнутость центроиды колеса 3, имеем уравнение
2~ 2л
= fС I------------------ . -------------1|<% (3.91)
«з о *23 *) М — — £2 sin2 <р2 + е cos <ps -I
Z e
где tn — — и е = —.
а а !
После разложения выражения (1—£2sin2cp2)2 в ряд Фурье и
ряда преобразований и упрощений *) можно получить для tn следую-
щее приближенное уравнение:
(« + 1)[1 - . (3.92)
Из выражения (3.92) может быть получено известное приближен-
ное уравнение для относительного расстояния т, данное Бурместе-
ром [676], если пренебречь в уравнении (3.92) членами, содержащими
е4. Имеем:
OT^(w+l)_ .(»_+1H”-2) е«. (3.93)
Уравнение профиля центроиды колеса 3 будет иметь следующий
вид:
г3 — Z — г2 = та — г% = а(\ — ]/1 — е2 sin2ср2 -J-е cos ср2). (3.94)
Угол <р2 в этом уравнении может быть выражен через угол <р3,
если воспользоваться уравнением (3.89) или приближенным уравне-
нием (3.90). Вследствие сложности этого уравнения для построения
сопряженного профиля центроиды колеса 3 можно воспользоваться
графическим приближенным построением, указанным на рис. 219. На
*) См. вышеуказанные работы Ф. Л. Литвина.
152 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. HI
рис. 219 показано графическое определение профиля центроиды ко-
о 1 2
леса о, если величина п3 = 1, а величина е = -д-.
Окружность центроиды 2 разбиваем на двенадцать равных дуг и
проводим лучи; А1, Д2, АЗ, ... Из точки А откладываем расстояние
АВ = 1 = та, определяемое из уравнения (3.92) или (3.93). Далее,
из точки А проводим дуги, радиусами Al, А2, АЗ, ... до пересече-
ния с направлением АВ. Точки Ро, Ръ ... и т. д. будут точками
бицентроиды. Из точки В проводим дуги радиусами: ВРЪ ВР%,
ВР%, ... Так как сопряженные центроиды перекатываются без сколь-
жения друг по другу, то, очевидно, что дуги
1 2 = о 1'2', 2 3 = 2'3' ... Следовательно, положение точки Г
найдется, если из точки Ро сделать засечку радиусом, равным дуге
Ро1, на проведенной дуге радиуса BPt. Если, далее, из полученной
точки Г сделать засечку радиусом, равным дуге 12 на проведенной
дуге радиуса ВР%, то мы получим точку 2' профиля центроиды ко-
леса 3 и т. д. Соединив полученные точки плавной кривой, получим
профиль центроиды колеса 3, сопряженный с круглым профилем ко-
леса 2. Так как при этом построении практически профиль сопря-
женной центроиды строится по хордам, то для получения большей
точности построения желательно разбивать профиль центроиды ко-
леса 2 на возможно большее число равных дуг. На рис. 220 пока-
p. 1
зано аналогичное построение для случая, когда п — 2 и е =
Наконец, на рис. 221 показано построение для случая, когда
п = 3 и е = Функция передаточного отношения /32 механизмов
некруглых колес указанного вида будет меняться в пределах:
G*32)min ^32 G3‘2)max;
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС 153
где
z> \ 1 - Е (' \ ___ 1 "Т е
(Winin = ,„_(1 и (Wmax--------m_(1+^y.
11°. В качестве сопряженных профилей центроид могут быть
также выбраны центроиды, профили которых очерчены по логариф-
мическим спиралям. На рис. 222 показана логарифмическая спираль.
Уравнение такой спирали относительно полярной
оси Ох будет:
г = ает?у (3.95)
где пг — постоянная величина, равная т = ctg р..
Рис. 22 L
При угле ср, равном ср = 0, величина г равняется г = ОК — а.
Таким образом, логарифмическая спираль полностью определяется
заданием двух ее параметров. Логарифмическая спираль характери-
зуется тем, что угол [х между касательной ft (рис. 222) и радиусом-
154 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. HI
вектором г в любой точке М спирали постоянен. В самом деле,
из дифференциальной геометрии имеем:
<з.эб)
dy
Из уравнения (3.95) имеем:
dr
= атет<?. (3.97)
Подставляя в уравнение (3.96) значение для г из уравнения
(3.95)
получаем:
и для ~ из уравнения (3.97),
, aemf 1 /о ло\
tgii = —- = —. (3.98)
& 1 атет$ т v f
Пусть центроиды двух сопря-
женных некруглых колес очерче-
ны по логарифмическим спиралям
(рис. 223), полярные уравнения
которых соответственно будут:
г2 = агет^
и
г3 =
(3.99)
где <р2 и (р3 — углы, образованные радиусами-векторами г2 и г3 с по-
лярной осью.
При этом вращение центроид происходит в разном направлении.
Из уравнений (3.98) и (3.96) следует:
^1Х2 = Г2 ~2 = — и tg|i3=r3^3 = —- - , (3.100)
ь 1 - dr 2 т ь ‘ л d dr-A т 9 4 7
т. е. всегда удовлетворяется условие
= 180°.
Следовательно, касательные к центроидам в точках соприкосно-
вения центроид совпадают.
Нетрудно показать, что рассмотренные профили, очерченные по
логарифмическим спиралям, действительно будут перекатываться без
скольжения. Элементарная дуга ds% профиля центроиды 2 будет, как
известно из дифференциальной геометрии, равна:
(^,)2 = W +(г,//%)’ = (dr2)e + (^y = (rfr2)2[l 4- (3.101)
Соответственно элементарная дуга профиля центроиды 3 будет
равна:
(ds^ = (dr3y J- (r3 d'ftf = (drtf + = (drtf (1 + , (3.102)
§ 81
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
155
т. е. элементарные дуги ds.2 и ds3 всегда равны между собой, когда
равны элементарные приращения dr2 =— dr* и когда расстояние
между осями вращения центроид является постоянным, т. е.
/ = г2 r3 = const.
Так как логарифмическая спираль представляет собой незамкну-
тую кривую, го для воспроизведения среднего передаточного отно-
шения (z32)cp=—1 за один полный оборот необходимо, чтобы каж-
дая центроида была образова-
на не менее чем двумя ветвя-
ми логарифмической спирали
(рис. 224). Тогда период / функ-
ции передаточного отношения
/32 будет равен/ = тс. Функция
/32 передаточного отношения
будет равна:
г г рГП'И
/32 = , (3.103)
3 /-ro2^ v 7
так как при ср2 = ср3 = 0 по-
стоянные и соответствен-
но равны а2 = г02 и а\\ —
(рис. 224), и уравнения профилей центроид 2 и 3 при 180°
имеют следующий вид:
г.2 = г08 ет^ >
и
= Гоз )
Функция <р3=<р3(ср2) положения определяется из уравнения
С. F Г.,ет^
?3 -- \ *32 ~
о о 1~г^-е
(3.104)
— — 1п|---------ет*Т (3.105)
W I Го2 J
12°. Для воспроизведения среднего передаточного отношения
(/32)ср =—1 могут быть использованы профили центроид, состоящие
из нескольких участков логарифмической спирали. Так, например,
если период t функции передаточного отношения равен / =
то для построения профилей центроид можно применить следующий
прием. Возьмем два равных квадрата (рис. 225) со сторонами, рав-
ными 2Л. Тогда расстояние I между "Осями А и В вращения центроид
2 и 3, совпадающими с центрами квадратов, будет равно:
l = k(\ -ф- ] г2).
Стороны квадрата заменяем на каждом участке, равном Л, дугой
логарифмической спирали, началом которой являются соответственно
точка А или точка В. Сопряженные участки профилей: Роа.2 и
156 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
а2Ь2 и а3&3; Ь2с2 и &3с3; ... и т. д. имеют уравнения, аналогичные
уравнениям (3.104):
(--1п2)<р —ср.,
г2 == r02 ет^ = kem'^ =ke^K 7 = k2 *
и
— (— Itl 2^ CDq ---— СРч.
r3 = r03 ет'^ = ke™'^ = ke v 7 = k2 к
так как
2
^02 = ^03 = ^ и т = — In 2.
к
Из рис. 225 непосредственно следует, что передаточное отноше-
ние /32 для указанных колес изменяется в пределах:
z32 (^32)шах,
где
•р/ 2 ___
feOmin = ~2~ И G*32)max = l 2.
При этом передаточная функция четыре раза переходит через макси-
мум и минимум. Рассмотренный прием построения симметричных колес
с профилями центроид, ограниченными по логарифмическим спиралям,
может быть распространен и на другие случаи, когда среднее пере-
даточное отношение fe)cp должно равняться (Z:V2)cp = —1, но
требуется другая периодичность изменения функции передаточного
отношения. Образование таких колес можно представить как замену
сторон, соответствующих правильных многоугольников, врашаюшихся
вокруг своих центров, участками логарифмических спиралей.
13°. Переходим к рассмотрению вопроса о проектировании профи-
лей центроид некруглых колес, полученных как производные кривые
от основных профилей.
Пусть профили сопряженных центроид 2 и 3 заданы в виде
двух кривых аа и (рис. 226). Находим точки: Ро, Рь Р2, ...
бицентроиды и соответствующие им точки а.2, Ь2, ... и а3, Ь3,...
профилей центроид 2 и 3, Обозначим углы, образованные радиусами-
§ 8]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
157
Рис. 226.
векторами с линией центров, соответственно через: <р2, ... и
<рз, <рз, ... Далее, на прямой, соединяющей точки А и В (рис. 227),
наметим точки бицентроиды: Ро, Ръ Р*> • • на том же расстоянии
от точек А и В, как и для случая, показанного на рис. 226. Из
точек А и В (рис. 227) про-
ведем лучи под углами: ,
F / f М
CD Q Ср О Ср О
— , . . . и —, , ... ,где т—
т т,т
некоторая произвольная по-
стоянная, и находим на этих
лучах сопряженные точки: а2,
... и а3, />3, ... профилей
центроид. Соединив эти точ-
ки плавными кривыми, по-
лучим профили сопряженных
центроид в виде кривых апап
и рпрп (рис. 227), представляю-
щих собой производные про-
фили от профилей аа и [ф (рис. 226).
ственно следует, что приращения dp3
производных профилей равны приращениям
ров основных профилей, т. е. dpv — dr^ и dp% = dr3) а следовательно,
всегда удовлетворяется условие (3.41):
Из построения непосред-
и б/р3 радиусов-векторов
dr% и dr% радиусов-векто-
^Рз — dr-2 -drз — 0.
(3.106)
Кроме того, р.2 = г2 и Рз = гз и, далее, р^ -|— р3 = г.2 —Н = Z. Тогда
Рис. 227.
условие перекатывания для
основных профилей в форме
для производных профилей на-
пишется так:
<зл07)
Производные профили бу-
дут обеспечивать вращение
центроид с передаточным отношением, имеющим период в т раз
меньший периода центроид с основными профилями. Если преобра-
зованные центроиды представляют собой замкнутые кривые, то число т
должно быть целым и больше единицы.
14°. Указанный метод преобразования центроид используется для
получения из эллиптических центроид так называемых «овальных»
центроид. Пусть имеется механизм эллиптических центроид (рис. 217).
Разделим все полярные углы центроид на постоянное целое число т.
158 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. И!
Тогда уравнения производных профилей центроид будут иметь вид
(см. уравнения (3.83) и (3.84)):
ra = .g(1~c8) (3.108)
L 1 — е cos mw2 v 7
и
г — 2gCOSffl(f2 +g2) /3 109Ч
3 1 — е cos tny2 ’ < • /
Функция /.23 передаточного числа будет равна (см. уравнение (3.81)):
^=1-2g;°^+f3-, (злю)
и функция <р3 = <р3 (<р2) положения примет вид (см. уравнение (3.85)):
?3=^rctg(^tg^). (3.111)
Этими уравнениями определяются все параметры овальных центроид.
На рис. 228 показан механизм овальных центроид для значения
т = 2 и е= %, а на рис. 229 — для значений /?г = 2 и е==~.
Нетрудно видеть, что оба эти механизма будут иметь период функ-
ции передаточного отношения в два раза меньший, чем период
основных центроид. Профили центроид, показанных на рис. 228,
имеют выпуклые и вогнутые участки, а профили центроид, показан-
ных на рис. 229, являются выпуклыми на всем своем очертании.
Выясним предельное значение эксцентриситета е основной эллипти-
ческой центроиды, при котором будет иметь место переход от только
выпуклого профиля к профилю, имеющему выпуклые и вогнутые
участки.
Условие обращения в нуль кривизны профиля центроиды ведущего
колеса имеет вид (см. уравнение (3.54)):
1+^ + '2з = 0. (3.112)
§ 8]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
159
Для рассматриваемого вида овальных колес т — 2. Следовательно,
функция z23 передаточного числа будет равна:
1 — 2с cos 2^>о + е2 /о 1 1 1 е2 • (0.110)
Тогда (3.114)
и уравнение (3.112) примет вид: 1 | 1 — 2ec°s2<f2 + g2 । 8е cos 2?2 __ Q (3 115)
откуда получаем:
1 -ф- Зе cos 2<р3 = 0. (3.116)
Значение Зе cos 2<р2 изменяется в пределах ± Зе, Уравнение
(3.116) может удовлетворяться только при значениях е^^. Следо-
вательно, овальные колеса указанного вида не будут иметь вогну-
тых участков при значениях
На рис. 229 показан
предельный случай центро-
ид, для которых т = 2 и
1
е~ 3'
На рис. 230 показаны
центроиды, полученные пу-
тем сокращения углов элли-
птических профилей с ко-
эффициентом т = 3.
Аналогично могут быть
построены центроиды, про-
фили которых будут образованы
Рис. 230.
из основных профилей путем
сокращения углов в четыре, пять и т. д. раз.
Для получения некруглых колес с разным числом оборотов веду-
щего и ведомого колес необходимо на профилях основных центроид
выбрать равные дуги, стягиваемые углами, находящимися в заданном
отношении числа оборотов. Например, пусть требуется из профилей
эллиптических ценгроид 2 и 3 (рис. 231) получить производные про-
фили овальных колес, у которых отношение полных чисел оборотов
за весь период движения равнялся бы 3 :2. Выбираем равные дуги
Р0а2 = PqG3j стягиваемые углами <р2 и ср3, находящимися в задан-
ном отношении 3:2. Сокращаем далее каждый из этих углов так,
чтобы в пределах угла, равного 2тг, уложить целое число периодов
изменения радиуса вектора центроиды. Как видно из рис. 231, на
ведущем колесе профиль центроиды имеет четыре симметрично рас-
положенных и равных участка, а на ведомом колесе профиль имеет
160
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. И!
шесть симметрично расположенных и равных участка. Очевидно, что
указанный метод преобразования профилей ценгроид может быть
применен к любым начальным профилям центроид.
15°. Выше мы рассмотрели те случаи преобразования эллиптиче-
колеса имеют симметричные
ских центроид, когда преобразованные
Рис. 231.
участки профилей и симме-
тричное изменение функции
передаточного отношения.
В практике весьма часто
ставятся задачи о получении
несимметричного передаточ-
ного отношения за один
полный оборот механизма.
Так, с целью уменьшения
времени холостых ходов и
увеличения производитель-
ности машины часто тре-
буется, чтобы на участках
движения, соответствующих
холостому ходу, вращение
ведомого колеса происходило быстрее, чем на участке, соответствующем
рабочему ходу. Для решения таких задач можно использовать, как
это было указано Ф. Л. Литвиным, механизмы некруглых колес
с эллиптическими профилями
центроид, с несимметричными
учас гками профилей центроид
и, следовательно, с несимме-
тричным изменением функции
передаточного отношения [36в].
Пусть задано отноше-
$ (^s)max
ние о = .— максимального
v32)mjn
fe)max И минимального (/3s)tnin
значений функции z32 переда-
точного отношения, соответ-
ствующие значениям углов <р2,
равным ср2 = 0 и <р2 = 2тс для
значения (/32)тах и <?ъ=
для значения (z32)min. Примерный харак-
тер такого изменения функции передаточного отношения Z32 = z32(cp2)
показан на рис. 232. Среднее передаточное отношение (£32)ср равно
(/32)ср = п, где п — целое число оборотов ведущего колеса.
Из условия (3.82) следует
0з2)тпах
1-е/ •
(3.117)
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
161
Из уравнения (3.117) определяется величина е, равная где
с — расстояние от центра эллипса до его фокуса А (рис. 233), около
которого происходит вращение. Имеем:
Расстояние между фокусами сопряженных эллипсов равно задан-
ному расстоянию I между осями вращения центроид, т. е.
1= 2а.
Следовательно, величина с определится из уравнения (3.118) через
расстояние I как
I ]/& — 1
С 2 F& +1
(3.119)
Так определятся все необходимые параметры исходного эллипса,
уравнение которого будет:
г = а(у-е)*
2 1 — е cos ср2
(3.120)
Применим к этому эллипсу метод преобразования, изложенный
выше (§ 8, 13°). Сохраняя радиусы-векторы основного эллипса, будем
уменьшать полярный угол на интервале от ^2 = 0 до <р2 = —
mi
6 И. И. АртоболеескШ
162 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [гл. Itl
в т\ раз, а на участке от фй= — - до 2л в т\\ раз. Из рис. 232
т\
легко видно, что
-4- -=2л, (3.121)
тх 1 ти
откуда получаем соотношение между коэффициентами т\ и гп\\.
Имеем:
= ‘ЗЛ22>
На рис. 233 показано построение участка abc профиля путем
уменьшения угла <р.2 на величину коэффициента тх. Для этого каждый
радиус вектор г.2, направленный под углом поворачиваем около
точки А до совпадения с лучом, проведенным из точки А под
углом —. Аналогично может быть построен участок cda профиля
77? I
путем увеличения угла <?.2 на величину так как коэффициент ni\\
выбран /тгц<^1.
Функции передаточного числа на отдельных участках профилей
центроид на основании уравнения (3.81) будут иметь вид:
1 1 — COS 777^2 +
(3.123)
п___ 1 1 — 2^cos[mn (2 л — ?2)|+<?2
~ п Г=7«
(3.124)
Для замкнутости сопряженной центроиды необходимо, чтобы
удовлетворялось условие
и
"7 2тс
О тс
(3.125)
Уравнение профилей участков центроид будут иметь следующий
вид: для ведущей центроиды 2
_ g2(l — gp
1 —С2 COS (tn ff2)
_______fl2 (1 — el)______
1 — e2 cos |/77 ц (2 л —cp2)]
(3.126)
(3.127)
и для ведомой центроиды 3
g3(l-gl)
1 -f- es cos (nm^2)
(3.128)
и
§ 8]
и
ЦЕНТРОИДНЫХ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
163
(1 —
ГИ =___________________________________
3 1 + е3 cos [тп (2к — п<р2)] *
(3.129)
В уравнениях (3.126) — (3.129) аъ еъ а3, ел— параметры исходных
эллипсов, которые преобразуются в несимметричные овалы, п— сред-
нее передаточное число и пц, т\\ — коэффициенты преобразования
углов радиусов векторов. Параметры эллипсов связаны между собой
условиями:
3 /1+(яз_1)(1_₽|)
и
а3 = /1+(л2—1)(1 — d).' (3.131)
Нетрудно видеть, что при л, равном /7—1, центроида ведомого
колеса имеет такие же очертания профиля, как и центроида веду-
щего колеса.
Таким же образом, если участок одной из центроид представляет
собой преобразованный эллипс с коэффициентом преобразования,
равным //г, то соответствующий участок сопряженной центроиды будет
также преобразованным эллипсом с коэффициентом преобразования,
равным пт, где п — среднее передаточное число. На рис. 234 изобра-
1 3
жены сопряженные центроиды для случая, когда п=\, =
3
и тп=—. На рис. 235 изображены сопряженные центроиды для
О 3 3
случая, когда п = 2, т\—^ и =
Примем в уравнениях (3.126) — (3.129) коэффициенты т\ и тц
равными /^1 = /77п=1. Тогда ведущая центроида будет правильным
эллипсом, а ведомая центроида будет правильным эллипсом, равным
ведущему эллипсу при значении п, равном и=1. При и, не равном
единице, ведомая центроида будет преобразованным эллипсом с коэф-
6*
164 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. Ill
фициентом преобразования, равным п. На рис. 236 изображены сопря-
женные центроиды, когда п равно п = 2, а на рис. 237 — сопряжен-
ные центроиды при и, равном л = 3. Центроиды 2 в обоих случаях
являются правильными эллипсами.
16°. Выше (§ 8, 2°) мы рассмотрели геометрический метод проек-
тирования профилей центроид некруглого колеса и рейки. Эта же
задача может быть разрешена и в аналитической форме. Обозначим
перемещения ведомой рейки 3 через s3> а углы поворота ведущего
колеса 2 через ср2. Тогда функция положения будет иметь вид:
$з = $з(ср2). (3.132)
Функцией передаточного отношения /г3.2 мы назовем отношение ско-
рости т>3 рейки 3 к угловой скорости о>2 колеса 2 (см. уравне-
ние (3.30)), т. е.
*>»=;!=S=s«<»>- <3133>
Нетрудно видеть (рис. 211), что радиусы-векторы центроиды 2
определяются непосредственно из уравнения (3.133), т. е. уравнение
профиля центроиды 2 будет иметь вид:
= (3.134)
где углы <р2 должны отсчитываться от полярной оси центроиды 2.
На рис. 211 эта полярная ось совпадает с осью Ау.
Уравнение профиля рейки в параметрической форме будет иметь
вид (рис. 211):
x=\r^d^ и у = г^~ г20, (3.135)
о
где г20— радиус-вектор центроиды 2 при <зр2 = О.
Рассмотрим вопрос о проектировании профилей сопряженных
центроид колеса и рейки для воспроизведения заданной функции
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС 165
y=f(x). Предположим, что воспроизводимая функция в заданном
интервале, от положения / до положения k, непрерывна и диффе-
ренцируема и
(3.136)
Пусть центроида 2 некруглого колеса вращается пропорцио-
нально изменению независимого переменного х, т. е. угол <р2 пово-
рота центроиды 2 будет равен:
<p2 = [i2(x —хД (3.137)
где р..2— масштабный коэффициент (см. § 8, 6°). Тогда перемеще-
ние $3 центроиды 3 рейки может быть представлено так:
«3 = Из О' —Ji) = Из [/(*) — /(-*,•)]• (3.138)
Уравнения (3.137) и (3.138) являются уравнениями функции по-
ложения в параметрическом виде.
Функция Л32 передаточного отношения будет иметь вид:
^ = -g£ = ^L/,(x). (3.139)
^Т2 Г-2
Уравнение профиля центроиды некруглого колеса в параметриче-
ской форме будет иметь вид:
г4=^/'(х) (3.140)
и
<р2 = На (х — хД (3.141)
Уравнения профиля центроиды рейки будут иметь следующий вид
в прямоугольной системе координат:
х3 = М/(х)-/(хД (3.142)
И
Js = г.2 - Г4О = [/' (X) (х,.)1, (3.143)
где г20 — радиус центроиды 2 при значении х, равном х — хг. .
В качестве примера определим уравнения профилей центроид
колеса и рейки для воспроизведения зависимости:
у = ЯХ2,
где а — постоянный коэффициент. Функция у = ах2 задана в ин-
тервале xk^x^Xi, Тогда на основании уравнений (3.137) и (3.138)
для функции положения получаем следующие уравнения:
= [Х2 (х — х;)
и
«3 = Нз« (** — Xi ).
166 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. Ш
где и |i3—принятые масштабные коэффициенты. Уравнения про-
филя центроиды некруглого колеса будут:
С*---Xi)
И
г.2=2 ах.
Р2
Уравнения профиля центроиды рейки будут:
х3 = да (х* — х;)
и
Уз — r.2 — ri0 = 2 а (х — х,).
г 2
Функция передаточного отношения, как это было показано вы-
ше, будет равна г2, т. е.
kAi = г.г = 2 — ах.
Р-2
На рис. 238 показан механизм,
у = ах2. Профиль пентроиды 2
воспроизводящий зависимость
некруглого колеса является
архимедовой спиралью. Про-
филь центроиды 3 является
параболой.
17°. Если одна из центро-
ид механизма некруглых колес
принята за стойку, то мы по-
лучаем трехзвенный механизм,
общая схема которого показана
на рис. 14, а частные случаи
таких механизмов с эллиптиче-
скими и круглыми центроидами
показаны на рис. 15 и 16. Это
тарные механизмы с некруглыми и
щим звеном подобных механизмов
будут трехзвенные плане-
круглыми колесами. Обычно веду-
(рис. 15) будет звено 7, кото-
рое мы обозначим через Н. Тогда функция передаточного отно-
шения определится по известной формуле для планетарных
механизмов:
Ьн = 1 — ^23’
(3.144)
В уравнении (3.144) 1% есть функция передаточного отношения
механизма некруглых колес, у которого звено 7 (И) неподвижно.
Таким образом, если задана функция передаточного отноше-
ния то по уравнению (3.144) определится функция передаточ-
ного отношения г**, после чего проектирование профилей колес может
быть проведено методами, изложенными выше. Функция положения
§ 8] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ НЕКРУГЛЫХ КОЛЕС
167
определится из уравнения
(3.145)
Планетарными механизмами некруглых колес можно осущест-
влять периодическое вращательное движение с различными, как
симметричными, так и несимметричными, законами изменения функции
передаточного отношения.
18°. В § 7, 9° было показано, что для возможности передачи
движения сопряженными центроидами должно удовлетворяться усло-
вие (см* формулу (3.26)):
arctg
г де 7 тш — минимально
низмов некруглых ко-
лес, воспроизводящих
непрерывное периоди-
ческое движение, фу-
нкция передаточно-
го отношения за один
полный период будет
иметь хотя бы один
максимум и один ми-
нимум. В этих поло-
жениях величина /32
будет равна нулю.
Следовательно, на уча-
стках, близких к макси-
(3.146)
Для меха-
______*32_______
*32 (1 — Z32)
Train»
допустимый угол передачи.
Рис. 239.
мумам и минимумам функции /32, передача движения становится не-
возможной, так как углы передачи у23 становятся равными или мень-
шими 7min. Поэтому передача движения гладкими профилями центроид
на всем интервале работы механизмов некруглых колес является
невозможной. Поэтому центроиды некруглых колес обычно снабжа-
ются зубцами или на всем своем профиле, или на участках, близких
к максимальному и минимальному значениям угла передачи(рис. 239).
Для случая рассмотренного в § 8, 2° механизма некруглОго
колеса, сопряженного с рейкой (рис. 240), возможность передачи два-
168
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. Ill
что угол передачи у не зависит от того,
ведущим. Обозначим радиус-вектор АР$
Пусть центроида Ц.2О повернулась на бес-
Отложим на центроиде бесконечно малую
опустим перпендикуляр аа' на направле-
жения определяется условием, чтобы углы передачи у на всем ин-
тервале движения механизма были бы больше некоторого заданного
угла Yrain.
По рис. 240 следует,
какое из звеньев будет
центроиды Ц.2О через р2.
конечно малый угол
дугу Р^а и из точки а
.ние ЛР0. Тогда угол Р^аа’ с точностью до бесконечно малых вто-
рого порядка будет равен углу у и, следовательно:
, Ро^'
Роа
Так как с точностью до бесконечно малых высших порядков
и аа' = р.2 d<?it
то можно написать:
tty 2
t61=^
(3.147)
Величина р.2 равна:
„ ____ v3
р2 —
<о2
ds,
dt ds, _______
dt
где — скорость звена
Тогда
3, а ш.2 — угловая скорость колеса 2.
др2
d3S3 К’ ( \
Подставляя полученные значения и р2 в уравнение (3.147),
получим:
d^
__ __ S3 (?з) __ ^32 (?a)
ds% S' (t2) &32 Cfs)
(3.148)
б?<?2
Из уравнения (3.148) следует, что угол у не зависит от размеров
центроид. Для того чтобы механизм работал без заклинивания, не-
обходимо, чтобы
^3
min*
Из уравнения (3.148) видно, что когда функция
принимает максимальное или минимальное значения, ^’32 — ^32 (^)
равно нулю и, следовательно, угол передачи равен нулю.
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 169
Таким образом, в общем случае передача движения является
невозможной в положениях, когда значения у равны или близки
к нулю. Поэтому при воспроизведении возвратно-поступательного
движения передача центроидами может быть осуществлена не на
полном обороте колеса.
Мы не рассматриваем вопрос о проектировании профилей зубцов
некруглых зубчатых колес, т. е. этот вопрос связан непосредственно
с процессом нарезания зубцов этих колес на специальных станках
и приспособлениях. При наличии у профилей центроид только вы-
пуклых участков зубцы на колесах могут быть нарезаны методом
обката. При наличии вогнутых участков профилей нарезание зубцов
может происходить по методу, когда используется в качестве ин-
струмента долбяк. Подробно вопрос о нарезании зубцов некруглых
колес, методах исследования и расчета их профилей и приспособле-
ниях для их нарезания рассмотрен в цитированной выше моногра-
фии Ф. Л. Литвина [36а].
§ 9. Центроидные механизмы перекатывающихся рычагов
1°. Как было указано выше (§ 8, 1°), к трехзвенным центроид-
ным механизмам относятся механизмы перекатывающихся рычагов.
Отличие механизмов перекатывающихся рычагов от механизмов пере-
катывающихся колес заключается не в отличии их структуры, которая
является общей у этих механизмов, а в отличии их назначения.
Если механизмы перекатывающихся колес обычно имеют своей зада-
чей воспроизведение непрерывного периодического движения с за-
данным передаточным отношением и в этих случаях профили их
центроид являются замкнутыми, то механизмы перекатывающихся
рычагов обычно имеют незамкнутые профили центроид, что позво-
ляет этим механизмам воспроизведение только возвратно-вращатель-
ного или возвратно-поступательного движения как звеньев, так и
отдельных точек этих звеньев. Кроме того, у этих механизмов одна
из центроид неподвижна.
Общие кинематические схемы механизмов перекатывающихся
рычагов с различными сочетаниями кинематических пар и стоек
показаны на рис. 5, 8, 14, 17, 20, 26 и 29. На рис. 5, 8 и 20
механизмы имеют по две центроидных пары, на остальных рисунках
механизмы имеют одну центроидную пару. Механизмы со схемами,
показанными на рис. 5, 8 и 20, представляют собой механизмы
с двумя парами перекатывающихся рычагов. Остальные механизмы
будут механизмами с одной парой перекатывающихся рычагов.
2°. Механизмы с двумя перекатывающимися рычагами показаны
на рис. 5, 8 и 20. Рассмотрим вопрос о проектировании механизма
вида, показанного на рис. 5, когда задано движение звеньев 2 и 3,
т. е. задана функция положений
?8 = ?3 (?2)
170
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[гл. III
или функция передаточного отношения
*32 — *32 (?*)•
Общее решение такой задачи может быть сделано геометриче-
ским приемом, приложенным в § 7, 4°. Рассмотрим решение этой
задачи на примере механизма, показанного на рис. 241.
Окружность Z/2n, принадлежащая звену 2, катится без скольже-
ния с постоянной угловой
скоростью со2 по непод-
вижной прямой * Т/гн»
принадлежащей звену I.
Звено 3 вращается около
оси В с постоянной угловой
скоростью ю3, равной и про-
тивоположной угловой ско-
рости со2. Заданным значе-
ниям ф*, ср11, ср*1*, ... угла
поворота звена 3 соответ-
ствуют. положения: Р\у Р*1,
Р***, ... мгновенного центра
вращения окружности Ц,2[1У
полученные поворотом ок-
ружности на углы: ср*, ср**,
ср***, ... равные и противо-
положные углам поворота
звена 3. Бицентроидой этого
механизма будет прямая Б,
параллельная прямой Ц2иу
гак как передаточное отно-
шение Z32 равно:
/32 = -— = — 1 = const.
Положение точек Р[у Р**, Р*11, .,. бицентроиды
. _Р1'Р1' _ _
32 BPI врч ВР‘"
а о о о
найдется из условия
.. = const.
Далее строим профили центроид Ц.2О и 7/30 в относительном движе-
нии звеньев 2 и 3. Соответственные точки П*, П**, П*п, ... и
П‘, П'1, Щ", ... этих центроид найдутся как точки плоскостей,
принадлежащих звеньям 2 и 3 последовательно, приходящие в со-
прикосновение друг с другом в точках Р*, Р**, Р*и, ... бицентроиды.
Построение таких профилей по точкам было изложено выше (§ 7, 4е).
Спроектированный механизм (рис. 241) будет механизмом, состоя-
щим из двух пар перекатывающихся рычагов: окружности Ц2п и
прямой Ц2пУ кривой Ц.щ и кривой
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 171
3°. Переходим к рассмотрению задачи о проектировании профилей
для механизмов перекатывающихся рычагов со схемой, показанной
на рис. 8. Пусть профили двух перекатывающихся рычагов,
принадлежащих звеньям 1 и 2 (рис. 242) будут представлять собой
дуги окружностей, описанных из то-
чек О и А1. Это будут соответствен-
но неподвижная центроида Ц*п и под-
вижная центроида Т/2п. Требуется по-
строить профили рычагов, принадлежа-
щих звеньям 7 и 3, если задана функ-
ция передаточного числа z23 = /23 (ср2)
(рис. 243). Рычаги 2 и 3 входят в
точке А1 во вращательную пару. Из
условия
___ О)2 _____ APs
'-3 ~ — ~АРз
(3.149)
где Р2 и Р3— мгновенные центры вращения звеньев 2 и 3, прини-
мающие положения (рис. 242) Р», Р|п, ... и Р\, PJ1, Р*11, ... 9
имеем:
АР3 = АР* = 1*3 АР*. (3.150)
сод
Так как АР* нам известно и равно
APt = А'Р\ = = ...== const,
172 СИНТЕЗ ТРЕХЗВЕННЫХ ПЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ, Ш
то из уравнения (3.150) для каждого значения /23 (рис. 243) опре-
делится и соответствующее положение мгновенного центра враще-
ния Р3. Точки Р\, Р\[, ... должны лежать на направлениях,
соединяющих точки А’, А”, А’1’, ... с точками Р’, Р\1, Р’”, ...
Откладывая на направлениях А{Р\, АиР2, А”1Р’”, ... отрезки А’Р’,
А”Р’’, AHIPju, ... , находим точки Р\, Р^, Р\[{, ... Соединив эти
точки плавной кривой, получим профиль неподвижной центроиды ЦЛн
звена 3. Построение профиля подвижной центроиды может быть
сделано различно. Углы поворота <р2 звена 2 нам известны. Тогда
из условия
Ф2
(3.151)
J *23
О
находим графическим интегрированием заданной функции =/(ср2)
*23
значения углов поворота звена 3, принимая за начало отсчетов
углов ср2 и срз прямую Ох. Далее, из точки А1 проводим ряд лучей
под углами ср’’, ср*п, ... к прямой Ох и откладываем на этих
лучах соответственно отрезки А’тс’’= А”Р’’, А’тс’” = А’”Р’”,
A’tc’v — A’VP’V, ... Соединив полученные точки Р^, тс”, тс’”, tc’v, ...
плавной кривой, получим профиль центроиды /73п, принадлежащей
звену 3. Приближенно точки тс”, тс’”, tc’v, ... могут быть также
получены, если из точки А’ провести дуги, соответственно равные
отрезкам А’Р’”, А’Р-”, A’P^V, ... , и на этих дугах делать засечки
радиусами, приближенно равными длинам дуг Р’Р”, о
P”’P’V, ... Вследствие очевидности этих построений они не пока-
заны на рис. 242.
В некоторых случаях в задании на проектирование могут
быть заданы угловая скорость w2 звена 2 и относительная угловая
скорость со32 звена 3 относительно звена 2 или углы поворота звена 3
относительно звена 2.
При заданном направлении вращения звеньев 2 и 3 угловая ско-
рость о)32 будет равна:
<о32 — со3 — и)2 — —;—-— to2, (3.152)
*23
откуда
Таким образом, зная угловые скорости ю2 и (п32, с помощью усло-
вия (3.153) определяем функцию передаточного числа Z23, после чего
решение задачи будет таким же, как и выше рассмотренное.
4°. Механизмами с двумя парами перекатывающихся рычагов может
быть легко разрешена задача о движении точки по заданной кривой.
Пусть точка А (рис. 244) должна двигаться по кривой КК, принад-
лежащей неподвижной плоскости, занимая последовательно положе-
§ 9]
ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ
173
ния А1, Аи, А111, Если не заданы дополнительные условия о за-
конах движения звеньев 2 и 3, то можно задаться очертаниями двух
неподвижных центроид £/2н и ^зн- Проводим, далее, нормали к кри-
вой КК в точках А1, Аи, А111, ... до пересечения в точках Р\,
Р’п, ... и PJ, рн, ЯД ... с неподвижными центроидами Т/2н и Z/3h.
Далее, одним из ранее указанных методов находим центроиды Z/2n
и Z/3n. Соединив эти центроиды в точке А во вращательную пару,
получаем искомый механизм. Если, кроме условия движения точки А
по кривой ЛХ, была бы задана функция передаточного отношения /32,
то, задаваясь одной из неподвижных центроид, например центроидой
£42н, легко получить точки неподвижной центроиды 7/зн путем
Рис. 244.
деления отрезков АТД АИР|1, АИ1РД ... в отношении, определяемом
заданным передаточным отношением /32. На рис. 244 показано пунк-
тиром очертание неподвижной центроиды Ц'н при передаточном отно-
шении /32, равном /32 — 2.
5°. Если подвижные звенья 1 и 3 входят в поступательную пару,
то мы получаем механизмы, общие схемы которых показаны на
рис. 17 и 20.
Пусть заданы профили Z/2h и Ц%п перекатывающихся рычагов
(рис. 245), представляющие собой полуокружность 2, перекатываю-
щуюся по неподвижной прямой, принадлежащей звену /. Требуется
построить сопряженные центроиды Z/20 и Ц30, если заданная пере-
даточная функция &з2 = £з2(?-2) (рис. 246) равна:
^32 --- -------^32 (?2)»
ш2
(3.154)
174 синтез трехзвенных центроидных механизмов [гл. HI
где г/3 — скорость звена 3, а их2 — угловая скорость звена 2. По за-
данной функции Л32 = Л32(ср2) находим точки pi, PJ1, рр1, ... би-
центроиды, лежащие на прямой, перпендикулярной к направлению
поступательного движения звена 3. По известным положениям точек
бицентроиды обычным способом находим точки Пр, П|п, ..
центроиды Т/20, жестко связанной со звеном 2. Для нахождения точек
Щ1, Пр1, . центроиды Z/30, принадлежащей звену 3, можно
воспользоваться известным условием
для функции положения. Имеэм:
(3.155)
Функция положения 53 = 53(<р2) построена на рис. 247. Отклады-
вая на перпендикулярах, восставленных в точках Рр, Ppi, P*v, ...
дугу окружности центра и по центроиде
Рис. 248.
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 175
значения перемещений s3 из диаграммы (рис. 247), получаем точки
Щ1, njn, njv, ..образующие центроиду 7/30.
Переменой стойки из механизма, показанного на рис. 17, может
быть получен механизм, общая схема которого показана на рис. 20.
При проектировании механизмов данного вида может быть задано
относительное перемещение подвижных звеньев друг относительно
друга или скорость их относительного движения.
Пусть движение звена 2 (рис. 248) задано качением центроиды
Z/2n, представляющей собой
представляющей собой
неподвижную прямую, при-
надлежащую звену 7. Пусть,
далее, известна центроида
773н, представляющая собой
прямую, принадлежащую
звену 7. С центроидой 772п
жестко связана прямая хх,
представляющая собой ось
поступательной пары. Так
как движение звена 2 зада-
но центроидами Т/2н и И*™ то
в каждом положении звена 2
известно положение прямой
хх. Следовательно, если,
например, задано положение
этой прямой в начальном
положении, то, проведя че-
рез мгновенный центр вра-
щения Р!, прямую P\D,
перпендикулярную к пря-
мой хх, найдем на пересе-
чении с центроидой 7/3н точ-
ку PJ — мгновенный центр
вращения звена 3. Аналогично определятся мгновенные центры вра-
щения PJ1, Pj11, Pjv, ... Далее, обычными методами строится подвижная
центроида 7/3п. Вследствие того, что звенья 2 и 3 входят в поступа-
тельную пару С, угловые скорости w2 и <и3 будут равны, т. е.
со2 = (1)3.
Относительная скорость т>32 скольжения в поступательной паре С
будет равна:
f зг = v3 — г»2 = (P3D — PiD) — «>! (РзА), (3.156)
т. е. относительная скорость т?32 будет всегда пропорциональна рас-
стоянию между соответственными мгновенными центрами вращения.
На рис. 249 показан график функции передаточного отношения
176 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИД НЫХ МЕХАНИЗМОВ [ГЛ. Ill
^32= ^32 (?«) механизма, построение которого было сделано на рис. 248,
т. е. функции
k° 3 = ^. (3.157)
Если задана функция передаточного отношения = k^(> (<р2), то из
условия (3.157) определится расстояние между мгновенными центрами
вращения звеньев 2 и 3, т. е. может быть построена неподвижная
центроида звена 3. Эта центроида показана на рис. 248 пункти-
ром для условия ^з2 = const. Значение k[2 в масштабе £°2 показано
пунктиром на рис. 249.
6°. Механизмами указанного вида можно осуществлять огибание
со скольжением различных кривых. В самом деле, если задана какая-
либо кривая аа (рис. 250), то образование этой кривой можно пред-
ставить как процесс перемещения касательной хх к кривой аа и
принадлежащей звену 2, т. е. кривая аа может рассматриваться как
огибающая положений прямой хх. Следовательно, если заданы поло-
жения прямой хх в виде положений xlxl, х11хп, xulxlu, ..., то обыч-
ными методами могут быть построены центроиды движения прямой хх,
принадлежащей звену 2. Далее, если рассматривать прямую хх как
ось поступательной пары, принадлежащей звену 2, то, зная скорость
скольжения звеньев 2 и 3 поступательной пары, может быть опреде-
лена функция передаточного отношения из условия, аналогичного
(3.156). После этого легко определятся центроиды звена 3, входящего
в поступательную пару со звеном 2. Нетрудно видеть, что прямая,
принадлежащая звену 3 и совпадающая с прямой хх, будет огибать
кривую аа и одновременно скользить относительно нее и прямой,
принадлежащей звену 2, с любой заданной скоростью скольжения.
7°. Переходим к рассмотрению механизмов перекатывающихся ры-
чагов с одной парой рычагов. Общие схемы таких механизмов раз-
личных видов показаны на рис. 14, 26 и 29. В этих механизмах одна
кинематическая пара будет центроидной, а остальные две будут низ-
шими парами вращения и скольжения. Из рассмотрения механизма,
Показанного на рис. 14, следует, что одна из точек звена 2 (точка Л)
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 177
должна описывать окружность радиуса В А. Из рассмотрения меха-
низма, показанного на рис. 26, следует, что одна из точек звена 2
(точка Д) должна двигаться по прямой, параллельной оси поступа-
тельной пары. Наконец, из рассмотрения механизма, показанного на
рис. 29, следует, что прямая КК будет всегда огибать неподвижную
окружность радиуса AD. Таким образом, задача о проектировании
механизмов с одной парой перекатывающихся рычагов сводится к рас-
смотрению задачи о воспроизведении профилей звеньев центроидной
пары, у которой одна из точек подвижного звена имеет рулеттой
дугу круга или отрезок прямой, или же в плоскости подвижного
звена прямая огибает неподвижную окружность.
Рассмотрим в общем виде задачу о проектировании профилей
звеньев центроидной пары, когда одна из точек подвижного звена
описывает дугу круга или
прямую. Пусть заданы (рис.
251) профиль Z/зн неподвиж-
ной центроиды звена 3 и
положения В\ Вп, ...
точки В на прямой КК, при-
надлежащей неподвижному
звену /. Из точек В\ Вп,
В1и, ... проводим перпенди-
куляры к прямой КК до
пересечения в точках Р\,
Р”, Р”1, ... с центроидой
7/3н. Точки ^р, ^р1, ... по-
движной центроиды Z/3n
найдутся из условия равен-
ства дуг уу р|рр=^ Р|тсй,
РРРР1 = ^Р^Р1, ... и равенства отрезков Р1^р = РпРр, В1^11 =
РИ1РР1, ... Так, например, точка трр найдется на пересечении двух
окружностей: первой окружности радиуса, равного дуге про-
веденной из центра kJ1, и второй окружности радиуса ^П1Р1И,
проведенной из центра В\
Звено 3 в точке В входит во вращательную пару со звеном 2,
которое движется поступательно в направляющих Л, имеющих своей
осью прямую КК- Нетрудно видеть, что данным механизмом может
быть воспроизведено поступательное движение звена 2 с постоянной
скоростью при постоянной угловой скорости качения центроид £/3п
и 7/3н друг по другу. На рис. 252 рассмотрена задача о проектиро-
ваний профиля подвижной центроиды Ц3п звена 3, если заданы не-
подвижная центроида 7/3н и траектория точки В звена 3 в виде
окружности КК, описанной из точки А, как из центра. Соединяем
точки В1, Вп, Вт, ... с центром А. Далее, для построения профиля
центроиды Z/3n из точек Р[, к11, -in, ... проводим последовательно
окружности радиусами, соответственно равными дугам PJk11—
178 СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ [ГЛ. III
= P'P’’, кз1кзП = vj ррр^1, ...» и находим пересечение этих
окружностей с окружностями, радиусы которых равны ВЧсу = ВИР”,
В1^11 = В1ПР’П, ... Звено 3 входит во вращательную пару со зве-
ном 2 в точке В. Звено 2 вращается около неподвижной точки А.
Так же как и в выше рассмотренном примере, данным механизмом
может быть воспроизведено равномерное вращение звена 2 на задан-
ном интервале движения при равномерном качении центроиды Ц$п
по центроиде Цзн.
Переходим к рассмотрению того случая, когда звенья 3 и 2
(рис. 253) входят в поступательную пару В, а звенья 2 и 7 входят
7
Рис. 252.
во вращательную пару А. В этом случае задача сводится к построе-
нию механизма, у которого прямая КХКХ будет огибать дугу К круга,
описанного из точки А. В точках Вх, В11, В111, ... проводим каса-
тельные А”1№, А^А41, А411^111, ... и соединяем точки касания с цен-
тром А. Тогда на заданном профиле центроиды 7/3н найдем точки
pi, рп, рш,
Для нахождения, например, точки ^У11 профиля центроиды 7/3п
проводим из ранее найденной точки окружность радиуса, равного
РУ’РУ11. Далее, из точки В1 откладываем на радиусе
АВ1 отрезок BTC=BvnPyn и проводим через точку С прямую, па-
раллельную прямой ATW1. Точка ^Уп найдется на пересечении прове-
денной окружности радиуса ^У’^У11 и прямой С^УП. Звено 3 будет
входить со звеном 2 в поступательную пару В, у которой осью
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 179
будет прямая При качении центроиды Z/3n по центроиде Ц3н
прямая будет занимать последовательно положения К11#11,
Л™ Л™, ... и т. д„ обкатывая окружность К.
Во всех рассмотренных задачах профиль неподвижного рычага
был нами задан. В некоторых случаях может быть задана функция
передаточного отношения /32 — /32 (<р2) или ^32 — ^32 (?*)• В этом
случае профиль неподвижного рычага будет определяться заданной
функцией передаточного отношения. Так, для механизма, показанного
на рис. 252, будем иметь:
ДР18 = ДВ'(1—4-V (3.158)
На рис. 252 пунктиром показана центроида Ц'гп, если функция
3
передаточного отношения z32 равна /32 = у = const. Это будет окру ж-
ность, описанная из точки А радиусом, равным —§—• Построение про-
филя центроиды не представляет затруднений, так как это будет
2А В1 О1
также окружность радиуса , проведенная из точки В1.
Для механизма, показанного на рис. 251, точки профиля цент-
роиды £/3н при заданной функции Л32 = &32 (<р2) определятся из
условия
BlPl3 = k3i, (3.159)
где k3i равно /га2 = = k3i (<р2).
Наконец, для случая, показанного на рис 253, точки профиля
центроиды Ц3н при заданной функции /32 = /32 (<р2) определятся из
уравнения (3.158).
180
СИНТЕЗ ТРЕХЗВЕННЫХ ЦЕНТРОИДНЫХ МЕХАНИЗМОВ
[ГЛ. П1
8°. Рассмотрим некоторые частные случаи механизмов с одной
парой перекатывающихся рычагов. Если неподвижной центроидой £/зн
(рис. 254) будет прямая линия, а профиль подвижной центроиды будет
логарифмической спиралью,
то асимптотическая точка О
(полюс
прямую
прямой
равным
спирали) описывает
Д7С, наклоненную к
хх под углом б,
б = у — <?, (3.160)
где ср — постоянный угол,
образуемый касательной к
спирали в любой ее точке Р3,
определяемой радиусом-век-
тором г.
На рис. 255 показан ме-
ханизм перекатывающихся
рычагов при неподвижной центроиде Д3н, заданной в форме прямой.
Точка В звена 3 описывает дугу КК окружности радиуса АВ.
На рис. 256 показан механизм, у которого подвижная центроида
Z/3n представляет окружность центра О. Точка В звена 2 описывает
дугу КК окружности радиуса АВ.
Построение профиля неподвижной центроиды может быть сделано
ранее изложенными методами, если будет задана функция передаточ-
ного отношения /32 = /32 (<р2).
Если профили перекатывающихся рычагов являются окружностями,
го мы получаем механизм, показанный на рис. 16. Точка А механизма,
§ 9] ЦЕНТРОИДНЫЕ МЕХАНИЗМЫ ПЕРЕКАТЫВАЮЩИХСЯ РЫЧАГОВ 181
совпадающая с центром окружности 2, движется по дуге КК окруж-
ности, описанной из центра В. Если окружности входят во внутрен-
нее зацепление (рис. 28) и диаметр подвижной окружности 2 равен
половине диаметра неподвижной окружности 3, точка В, лежащая
на окружности 2, двигается по прямой, представляющей собой
диаметр окружности 3, т. е. мы получаем механизм перекатывающихся
рычагов Кардана.
На этом мы заканчиваем рассмотрение задач о проектировании
механизмов перекатывающихся рычагов.
ГЛАВА IV
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ
ПАРОЙ И ПАРОЙ КАЧЕНИЯ И СКОЛЬЖЕНИЯ
§ 10. Механизмы с одной и двумя центроидными парами
1°. Выше (см. § 1, 8° и 9°) нами было показано, что трехзвенные
механизмы могут быть образованы из кинематической цепи, состоящей
из одной пары IV класса и двух пар V класса. Пары IV класса
представляют собой пары качения и скольжения, образованные взаимо-
огибаемыми кривыми, а пары V класса могут быть центроидными.
вращательными и поступательными *).
Первый возможный вид механизма будет содержать две цент-
роидные пары и одну пару, образованную взаимоогибаемыми кривыми.
Пример одного из механизмов этого вида показан на рис. 34.
Рассмотрим вопрос о проектировании сопряженного профиля пары
IV класса. Пусть движение звеньев 2 и 3 (рис. 257) задано каче-
нием подвижных центроид Ц.1п и Ц2п по неподвижным центроидам
7(2н и ^/зн- Далее задан профиль К% элемента пары IV класса, при-
надлежащий звену 2, и задана функция /32 = /32 (ср2) передаточного отно-
шения. Тогда нетрудно по способу, указанному выше (см. § 7), найти
бицентроиду и по пей сопряженные профили Ц20 и £/30 центроид
в относительном движении звеньев 2 и 3.
Отмечаем на кривой /С2 ряд точек А}2, А|1, А”1, ... и проводим
в этих точках нормали А\1Ь Д’72, /Цп73, ... к кривой АГ2 до пересе-
чения их с центроидой Ц.>(} в точках Щ, Щ, Щп, ...
Далее, на центроиде //30 откладываем дуги ЩЩ1 = о ЩЩ1,
П^Щ11 = ГЦГЩ11, ... Через точки Щ, Щ1, ГЦ11, ... проводим нор-
мали Щ/ц, П^п2, ГЦпл3, ... к центроиде Т/20, а через точки ГЦ, П”,
ГЦ11,...— нормали Щ/П1, Пр/п2, ГЦп/п3... к центроиде 7/30. Нормаль
A!/i к кривой ЛГ2 образует с нормалью ГЦ/q в своем первом поло-
жении угол а во втором положении Д“/2 образует с нормалью
ГЦ1/^ Уг<>л ?2 и т- Д- Углы ср2, <р3, ... нам известны. В моменты
соприкосновения центроид Ц.^ и Ц30 направления нормалей ГЦ/^, ГЦ1/^,
*) Сложных траекторных пар V класса мы не рассматриваем, как не
Имеющих большого практического применения <см. § 1, 8°).
§ 10] МЕХАНИЗМЫ С ОДНОЙ И ДВУМЯ ЦЕНТРОИДНЫМИ ПАРАМИ 183
П*11л3, ... будут последовательно совпадать с направлением нормалей
П|/П1, П’п/п3, ... и, следовательно, нормали к кривой Кч будут
образовывать с нормалями П13/пь П”/п2, njn/n3, ... известные нам углы
<pl, ••• Строим при ЭТИХ нормалях углы срь ср2, срз, ...и про-
водим прямые Ц1/?ь П“/72, П“1^3, ...Тогда при соприкосновении цент-
роид Z/20 и Z/3ft направления прямых П^/?2, ... будут
последовательно совпадать с направлениями нормалей к кривой
а именно, прямая совпадет с нормалью А\1Ь прямая сов-
падет с нормалью А“/2 и г. д.
Согласно свойству кривых Кч и /С3 (см. § 5) эти кривые в точках
соприкосновения имеют одну общую нормаль, проходящую через
мгновенный центр вращения. Тогда точки /Ц, A*1, AJ11, ... , образую-
щие кривую К& должны лежать в моменты соприкосновения цент-
роид соответственно на направлениях нормалей А\1Ъ АХХ1Ъ А^73, • • >
или так как с этими нормалями в эти моменты совпадают прямые
П|рь П^2, Щп/?3, ... , то точки A’, AJ1, А’11,... должны лежать также
на. прямых П>1, П^2, Щп^3, ...
Для того чтобы найти на этих прямых точки AJ, А“, А”1, ... ,
надо отложить отрезки ЩА*=1ЦА!2, П”А” = П^А’1, П”,А”1 =
==П*НА111, ... Соединив полученные точки А*, А*1, А*11, ... плавной
184
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гЛ. IV
кривой, получаем сопряженную с кривой кривую /С3. Из построе-
ния следует, что прямые ЩД*,, Щ’А’1, ... будут нормалями к кривой /<2.
Таким способом по точкам строятся профили элементов высшей
Рис. 258.
центроиде Z/30. Перекатываем
положения заданной кривой /С2
пары, воздействием которых друг на
друга и могут быть воспроизведены
требуемые движения звеньев 2 и 3.
2°. Построение сопряженного
профиля Т<2 можно выполнить иным
путем, пользуясь методом обраще-
ния движения. Для этого сообщаем
звеньям в каждый данный момент
общую угловую скорость, около
оси Р\ равную, но обратную по
знаку мгновенной угловой скорости
о)3 звена 3 (рис. 258). Тогда звено 3
будет как бы неподвижным, и от-
носительное движение звена 2
по отношению к звену 3 можно
будет рассматривать как качение
без скольжения центроиды по
эти центроиды друг по другу и строим
для ряда положений. Построение по-
следовательных положений кривой /С2 может быть сделано по точкам.
Для этого на кривой намечаем ряд
точек. Далее на центроидах отклады-
ваем дуги, на которые перекатываются
эти центроиды. Соединив какую-либо
точку кривой с крайними точками
одной из дуг и перекатывая центроиды
друг по другу засечками из крайних
точек выбранной дуги, получим ряд
последовательных положений выбранной
точки кривой К*. Проведя эти по-
строения для целого ряда точек кри-
вой К* получим последовательные по-
ложения К\, • • • этой кривой,
соответствующие мгновенным центрам
IIJ, П”, Щ11, ... Так как кривая /С3
должна касаться кривой во всех этих
положениях, то построение кривой К3
сведется к построению огибающей всех
положений кривой T<2. Таким
образом, кривая /<2 будет огибаемой, а кривая К3 — огибающей. Огибаю-
щая К3 будет принадлежать центроиде Z/30.
В том частном случае, когда вместо кривой в качестве оги-
баемой задана точка или прямая, построение огибающей может быть
сделано тем же приемом. Пусть, например (рис. 259), на звене 2 за-
§ 10] МЕХАНИЗМЫ С ОДНОЙ И ДВУМЯ’ ЦЕНТРОИДНЫМИ ПАРАМИ 185
дана точка Кч и требуется найти ту кривую /С3, которая воздей-
ствием на точку /С2 воспроизвела бы заданные движения звеньев 2 и 3.
Обращаем движение, для чего сообщаем обоим звеньям общую угло-
вую скорость — <о3 около оси Р3. Тогда центроида будет пере-
катываться по центроиде 7/30, и выбранная точка займет последо-
вательно положения КУ, ATJ11, . • • Соединив полученные точки К\,
/С’1, /С|п, ... плавной кривой, получим кривую /С3, представляющую
собой огибающую всех положений точки /С2. Передачу движения
можно практически осуществить, если в точке /С2 поставить палец,
жестко связанный со звеном 2, а кривую /С3 выполнить в виде ку-
лисы, жестко связанной со звеном 3.
3°. Выше мы рассмотрели методы построения сопряженного про-
филя, использующие центроиды в относительном движении. Более
удобным может оказаться метод обращения движения всего меха-
низма. Пусть заданы центроиды движения звеньев 2 и 3 (рис. 260)
в виде пар центроид Т/2н, ЦЧп и 7/3н, Ц3п и профиль Кч элемента
пары, принадлежащей звену 2. Сообщаем всему механизму общую
угловую скорость, равную и обратную угловой скорости <п3. Тогда
центроида £/3п будет неподвижной, а центроида 77зн будет подвижной.
Пусть в следующий рассматриваемый момент времени центроида £/3н
займет в обращенном движении (показано пунктиром) положение Дзн,
т. е. перекатится на дугу Так как центроида //2и
принадлежит звену 7, которому принадлежит и центроида 7/3н, то,
скрепив центроиду жестко с центроидой 7/3н, найдем в обращен-
186
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гЛ. IV
ном движении новое положение //2н центроиды Z/20 (показано пункти-
ром). При этом точка Р\ перейдет в положение (Р*)°. Соответственно
центроида Z/2n и жестко связанная с ней кривая К% займет в обра-
щенном движении положения Ц%п и Кэ (показаны пунктиром). Далее
перекатываем центроиду в направлении заданной угловой ско-
рости ю2 на дугу (р2)°(рй)°= (ТЦ1)0, соответствующую за-
данному повороту звена 2, т. е. в положение Тогда кривая Кч
перейдет из положения К'г в положение Таким образом, мы нахо-
дим второе положение /С2 кривой А”2, но в обращенном ее движении.
Рис. 261.
Очевидно, что аналогичными построениями могут быть найдены и
другие положения кривой /С2, т. е. получено семейство этих кривых.
Профиль Кл сопряженного элемента пары, принадлежащего звену 3,
определится как огибающая полученного семейства кривых.
4°. Построение профилей элементов высшей пары, построенных
в виде взаимоогибаемых кривых, и исследование условий их работы
удобнее всего выполнить, если построить геометрическое место точек
соприкосновения двух сопряженных взаимоогибаемых кривых, при-
надлежащее неподвижной плоскости. Как известно, такое геометриче-
ское место носит название линии зацепления. Покажем, что
если задан закон движения звеньев 2 и 3 и дана линия зацепления С\,
т. е. кривая ... F() (рис. 261), то всегда могут быть опреде-
§ 10] МЕХАНИЗМЫ С ОДНОЙ И ДВУМЯ ЦЕНТРОИДНЫМИ ПАРАМИ
187
лены соответствующие взаимоогибаемые кривые, точки которых после-
довательно приходят в соприкосновение в точках Ло, Со, ... линии
зацепления.
Пусть движение звена 2 задано качением центроид £/2п и Т/2н,
а движение звена 3 — качением центроид Ц3п и Z/3h и пусть кривая Б
будет бицентроидой. Пусть, далее, искомые взаимоогибаемые кривые
/С2 и /<з приходят в соприкосновение в точке BQ линии зацепления
в тот момент, когда центроиды Z/20 и Z/20 соприкасаются в точке PJ11
бицентроиды. Тогда центроида Ц2п переместится в положение Ц™,
а центроида ZZ3n — в положение Ц™. Пользуясь ранее указанным по-
строением, находим точки Щ11 и Щи, принадлежащие центроидам
и Z/30 и приходящие в соприкосновение в точке Р”1 бицентроиды.
Соединяем точку В^ линии зацепления с точкой Р*и и рш полу-
чаем треугольник Находим, далее, точку принадлежа-
щую центроиде Z/2n, для чего откладываем на подвижной центроиде Ц2п
дугу равную дуге Р[Р^Х. Так как при качении подвижной
центроиды Z/2n по неподвижной точка it”1 совпадет с точкой
а точка П[п совпадает с точкой /*11 бицентроиды, то, очевидно,
отрезок будет равен отрезку Тогда для того, чтобы
найти точку В% центроиды Ц2п, совпадающую при качении с точкой Вь
линии зацепления, достаточно на отрезке (^11ЩП) построить треуголь-
ник В2П|пк|п, равный треугольнику ВцР^Р™. Можно видеть, что
вследствие равенства указанных треугольников при качении подвиж-
ной центроиды Ц2п по неподвижной Ц2н точка В% действительно
совпадет с точкой В^. Аналогичным построением всегда может быть
найдена точка В3, принадлежащая подвижной центроиде Z/3n и при-
ходящая в соприкосновение с точкой В% в точке BQ линии зацепле-
ния. То же самое построение может быть проделано и для точек
линии зацепления Ао, Со, Ро, Е$, ... Тогда получим точки Л2, В2,
Съ Е%, ... и Д3, Р3, С3, Е3, ... , соединив которые плавными кри-
выми, найдем взаимоогибаемые кривые и Л"3; эти кривые будут
иметь линией зацепления кривую С3.
5°. В качестве примера рассмотрим проектирование механизма вида,
показанного на рис. 34. Выше, на рис. 205 был спроектирован цен-
троидный механизм, воспроизводивший качение двух окружностей
Ц2п и Ц3п по неподвижным прямым Ц1и и Ц3п с помощью сопря-
женной пары центроид в относительном движении Z/20 и Z/30. Осуще-
ствим тот же закон движения с передаточным отношением /32 = — 1
с помощью взаимоогибаемых кривых (рис. 262)
Если в качестве огибаемой кривой /Q звена 2 выбрать самую
центроиду Z/21I, то огибающей кривой будет кривая Р3. Таким образом,
профилем элемента высшей пары, принадлежащей звену 2, будет
окружность К*, а профиль элемента высшей пары, принадлежащей
звену 3, будет представлять собой некоторую кривую Р3. Построе-
ние кривой К3 на рис. 262 сделано способом обращения движения.
Для этого останавливаем центроиду Z/30 и перекатываем центроиду Д20
188
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
вместе с окружностью //.2п п0 центроиде //30. Огибающая К3 семей-
ства окружностей К% и будет сопряженным профилем. Если в каче-
стве элемента пары звена 2 выбрана точка А центроиды Ц2п, то про-
филь элемента, принадлежащего звену 3, представится в виде кри-
вой Построение кривой также сделано методом обращения
движения. Если, наконец, центроиду Z/2n выбрать в качестве вспомо-
гательной центроиды, а траектории точки А при качении центроиды Z/2n
по центроидам и Ц30 за взаимоогибаемые кривые, то профили
элементов высшей пары представятся
вляют собой взаимоогибаемые кривые.
в виде кривых К* и К3
(см. § 5, 5°). Первая кривая
будет профилем элемента,
принадлежащего звену 2,
а вторая кривая — профилем
элемента, принадлежащего
звену 3. Из рассмотренного
примера видно, что предпи-
санное движение может быть
воспроизведено взаимодей-
ствием профилей элементов
пары IV класса самого раз-
нообразного вида. В зависи-
мости от выбора огибаемых
кривых задача может иметь
бесконечно большое коли-
чество решений.
6°. Перейдем к аналити-
ческому решению задачи
профилирования элементов
высшей пары в том случае,
когда эти элементы предста-
Как было показано выше,
задача сводится к нахождению огибающей кривой по положениям
огибаемой, заданным в относительном движении. Положения огибае-
мой в относительном движении звеньев пары будут вполне определены,
если известны центроиды относительного движения и мгновенная
угловая скорость относительного движения. Совокупность положений
огибаемой будет образовывать семейство линий, к которому и должна
быть найдена огибающая.
Найдем уравнение огибающей кривой. Как было указано выше,
в качестве огибаемой могут быть выбраны точка или линия. Если
в качестве огибаемой выбрана точка, принадлежащая одному из звеньев
пары, то огибающей будет траектория} описанная этой точкой при
качении центроиды данного звена по сопряженной центроиде, при-
надлежащей другому звену и принятой в относительном движении за
неподвижную. Уравнения этой траектории определятся из следующих
соображений.
§ 10] МЕХАНИЗМЫ с одной И ДВУМЯ ЦЕНТРОИДНЫМИ ПАРАМИ 189
Пусть центроида Ц30 (рис. 263), принадлежащая подвижному звену
перекатывается в своем относительном движении по центроиде Z/20,
принадлежащей звену, принятому за неподвижное. Профиль центро-
иды Z/20 задан в параметрической форме уравнениями х— f(t) и
у = <р где х и у— текущие координаты в неподвижной системе
координат Оху. В качестве системы координат, принадлежащей
центроиде Z/30, выберем систему ось П£ которой совпадает в
каждом положении с направлением касательной к центроидам в их
точке соприкосновения, а ось ГЦ совпадает с направлением нормали
в той же точке. Таким образом, начало П системы координат
будет следовать закону перемены мгновенного центра вращения в
относительном движении. Положение системы координат Шт| в каждый
момент времени будет определяться известными значениями координат
х и у и угла а наклона оси Ш к оси Ох. Переменные координаты
$ и т] какой-либо точки А, принадлежа-
щей центроидеZ/30 звена 3, в системе
будут известны для каждого положения
центроиды Z/30. Тогда координаты хд,
у а точки А в системе Оху будут:
Ха = х 1 cos а — т| sin а
у а=у -J- £sin а Н- cos а-
Заменяя sin а и cos а их выраже-
ниями:
dy dx
sin а — и cos а — — ,
ds ds f
где ds есть дифференциал дуги центроиды Ц^, пробегаемой точкой П,
и имея в виду, что
ds==V(dx^Ar(dy)\
перепишем уравнения (4.1) в следующем виде:
5 dx — \dy
ds
^dy + ^dx
ds ’
(4.2)
Это есть параметрические уравнения траектории точки А в системе
координат Оху,
Таким образом, если в качестве огибаемой выбрана точка А, то
уравнения (4.2) вполне определяют огибающую кривую. Если же
в качестве огибаемой будет выбрана какая-либо линия, принадлежа-
щая центроиде Ц^, то координаты любой точки этой линии могут
190 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЁНТРОИДНОЙ ПАРОЙ [ГЛ. IV
быть также определены из уравнений (4.2) для каждого положения
центроиды Ц30.
Если уравнение выбранной линии задано в виде:
F(x, j) = 0,
то совокупность линий для всех положений центроиды представляется
уравнением
Ф (х, у, а) = 0, (4.3)
где а есть переменный параметр, определяющий закон перемены поло-
жений выбранной линии. Уравнение (4.3) есть уравнение семейства
кривых. Для нахождения уравнения огибающей определяем частную
производную от уравнения семейства по параметру а и приравниваем
ее нулю:
= (4.4)
Исключая из уравнений (4.3) и (4.4) параметр а, получаем уравнение
искомой огибаемой в виде:
Т(х, _у) = 0.
(4.5)
Если огибаемая и огибающие строятся с помощью вспомогательной
центроиды (см. § 5) как траектории какой-либо ее точки А (рис. 154),
то уравнения огибаемой и огибающей можно найти, используя урав-
нения (4.2). Для кривой /Ci (рис. 154) эти уравнения будут сле-
дующие:
и
b'dy' 4~ y'dx'
ds'
(4.6)
где х' и у суть координаты начала О' координатной системы OTrf,
принадлежащей вспомогательной центроиде S. Ось OV будет каса-
тельной к центроиде звена 1 и вспомогательной центроиде S, про-
веденной в точке их соприкосновения. Ось О'т/ совпадает с общей
нормалью к тем же центроидам, проведенной через точку касания.
Координаты Е' и у определяют положение точки А в системе ОТ?/.
Для кривой уравнения (4.2) напишутся так:
w _ ,, । t"dx" — Tydy"
хА — х~^ ds„
Уа=уЧ
£"dy” -j- tf'dx"
ds"
(4.7)
где х* и у9 суть координаты начала О" координатной системы О"?*У,
принадлежащей вспомогательной центроиде 5. Ось О"У будет каса-
I 10] МЕХАНИЗМЫ С ОДНОЙ И ДВУМЯ ЦЕНТРОИДНЫМИ ПАРАМИ 191
тельной к центроиде Ц% звена 2 и вспомогательной центроиде
проведенной в точке их соприкосновения. Ось О"т” совпадает с общей
нормалью к тем же центроидам, проведенной через точку касания.
Координаты В* и rf определяют по-
ложение точки А в системе O'X'tf.
Кривые, определяемые уравнениями
(4.6) и (4.7), будут взаимоогибае-
мыми.
7°. Рассмотрим следующий при-
мер. Пусть центроида относи-
тельного движения звена 2 представ-
ляет собой прямую Ох, а центро-
ида Z/30 относительного движения,
принадлежащая звену 3, представ-
ляет собой окружность (рис. 264).
Пусть, далее, в качестве огиба-
емой выбрана точка К* центроиды £(30. Требуется найти уравнение
огибающей К*
Огибающей будет, очевидно, траектория точки /С3 центроиды
в ее движении относительно центроиды Т/20, принадлежащей непо-
движной системе координат Оху. Тогда уравнения этой центроиды
в параметрической форме будут:
x — t, _у = 0.
Следовательно, dx = dt, dy — Q и
ds — У(dx)2 4- (dy)2 = dt.
Ось O"i" подвижной системы координат О"^', принадлежащей
центроиде Z/30, совпадает с осью Ох, а ось О"т" параллельна оси Оу,
Координаты %" и т/' будут:
V = — г sin а и = г — г cos а,
гд^ г есть радиус центроиды £/30.
Подставляя полученные выражения в уравнение (4.2) и принимая
во внимание, что x — t = s — ra. и dt = rd&, получим:
Г3 sin a da z .
xK = ra------— = r(a— sin a)
и
(г — rcosa)rda .
У к ~ ----7фГ-----= г (1 — COS a).
Это и есть параметрические уравнения циклоиды, т. е. огибающей К<л,
принадлежащей звену /, будет циклоида К*
8°. Рассмотрим теперь вопрос об углах передачи для механизмов
рассматриваемого вида.
Пусть движение звеньев 2 и 3 воспроизводится взаимодействием
двух взаимоогибаемых кривых и Кл (рис. 265). Условимся угол
передачи обозначать с двумя индексами, причем первый индекс
192 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
будет указывать номер ведущего звена, а второй индекс — номер
ведомого звена. Тогда, если ведущим будет звено 2, то угол пере-
дачи будет обозначаться у23. При ведущем звене 3 угол передачи
будет равен у32. Определим величину угла передачи у23. Для этого
построим повернутый план скоростей механизма при точке Р2. Повер-
нутый вектор скорости фА2 точки Д2, принадлежащей звену 2, отложен
в виде отрезка (ра2). Тогда ско-
рость фАз точки Д3, принадлежащей
звену 3, будет равна:
®Лз = + ®Л3Д2-
Из точки а2 проводим направ-
ление повернутой относительной
скорости т%д2, совпадающее с
направлением общей нормали NN
в точке соприкосновения кривых
ЛГ2 и К3. Полная повернутая ско-
рость точки Л3, принадлежащей
звену 3, определится, если из
точки р провести направление,
параллельное отрезку Р3Д23 Д°
пересечения в точке а3 с нор-
малью AW. Скорости ^д2 и
будут равны:
иЛа = <02/2 = О), (рсц), |
так как масштаб плана скоро-
стей выбран равным р^ = <о2.
Из точки Д(а2) опустим пер-
пендикуляр AD на направление
Р2а3, а из точки Р2 — перпендикуляр Р2В на направление Р3А. Имеем:
. AD
Так как
AD = P.,B
И
Da3 = Р2а3 — P2D = Р2а3 — ВА= Р2а3 — (Р3В — Р3А),
то
Р2В
tgT2i— р2Дз_р8Й + />8Л •
Из треугольника Р2Р3В следует:
Р2В = I sin р и Р3В = I cos р.
§ 10] механизмы с одной и двумя центроидными Парами 193
Далее, из уравнения (4.8) имеем:
Р 2а3 = ра3 = — /з = ^з^з- (4.9)
Подставляя значения Р2В, РЛВ и Р2ал в равенство (4.9), получим
окончательно:
. I sin ।> г л < / \ \
tg y23 = —~~ г~7' • • (4Л0)
5,3 Ьа/з — / cos +/3 v
Аналогично может быть определен и угол передачи у3.2,
Из условия (4.10) следует, что в случае передачи движения по-
средством взаимоогибаемых кривых угол передачи у23 в отличие о г
случая передачи центроидами всегда зависит от размеров I и Z3 звеньев.
9°. При проектировании профилей элементов высшей пары по
взаимоогибаемым кривым необходимо иметь в виду, что трение сколь-
жения этих кривых друг по другу будет уменьшать коэффициент
полезйого действия механизма. Так как мощность, расходуемая на
трение, пропорциональна относительной скорости движения взаимо-
огибаемых кривых, то очевидно, что чем больше будут эти скорости,
тем больше будут потери на трение и, следовательно, тем меньше
будет коэффициент полезного действия механизма. Пусть передача
движения между звеньями 2 и 3 осуществляется посредством про-
филей, очерченных по взаимоогибаемым кривым и (рис. 265).
Мощность N, расходуемая на трение скольжения этих кривых, будет
равна:
N = FvA.iAs, (4.11)
где F есть сила трения, a яА:}А:,— относительная скорость кривой
относительно кривой или наоборот.
Силу трения примем равной F=fP, где Р есть давление в точке Л,
направленное по нормали NN, a f—коэффициент трения скольжения.
Скорость скольжения г>дяд2 равна:
•»ASAS = 2 (Р«А),
где S2 есть мгновенная угловая скорость относительного движения
звена 3 относительно звена 2, равная
Q
Следовательно, скорость ^азАз будет равна
«АзА^^Н-ШзКРоА).
Подставляя полученные выражения для силы трения F и скорости
^азАз в равенство (4.11), получим:
/V=/P(u)2 + u)3)(P0A). (4.12)
Из уравнения (4.12) следует, что мощность N зависит от рас-
стояния точки соприкосновения А кривых К* и /С3 до мгновенного
центра вращения Ро в относительном движении и будет тем больше,
7 И. И. Артоболевский
194
СИНТЕЗ ГРёХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
чем больше расстояние Р^А. Как было показано выше, точки сопри-
косновения взаимоогибаемых кривых, принадлежащие неподвижной
плоскости, образуют линию зацепления. Следовательно, чем дальше
удалены точки линии зацепления от соответствующих мгновенных
центров вращения в относительном движении, тем больше будут
потери на трение. В связи с этим при проектировании механизмов
необходимо, чтобы линия зацепления для сопряженных профилей не
имела точек, значительно удаленных от мгновенного центра вращения
в относительном движении. Для этого в некоторых случаях передачу
движения удобно воспроизводить не двумя взаимоогибаемыми кривыми,
а целым рядом таких кривых, последовательно входящих в сопри-
косновение.
10°. Задание неподвижной центроиды, бицентроиды и линии заце-
пления является вполне достаточным для исследования динамических
условий (углов передачи), обеспечивающих передачу движения. Пусть
заданы неподвижная цен-
троида звена 2, бицен-
троида Б и линия зацепле-
ния С3 (рис. 266). Пусть для
первого положения звена 2
мгновенный центр вращения
будет в точке Рт2, мгновен-
ный центр вращения в от-
носительном движении бу-
дет в точке PJ и точкой
зацепления будет точка До.
Соответственно для после-
Рис. 266.
довательных положений звена 2 будем иметь точки PJ1, Ро и т. д.
Точку Ло линии зацепления соединяем с точками Р\ и Р\г Точку Z?o
соединяем с точками Р*1 и PJ1 и т. д.
Величина абсолютной скорости той точки взаимоогибаемой кри-
вой, принадлежащей звену 2, которая приходит в соприкосновение
в точке До с точкой Л3 взаимоогибаемой кривой, принадлежащей
звену 3, будет равна:
Va3 = «>‘ (ЯД о)’
где ю* есть мгновенная угловая скорость, соответствующая рассмат-
риваемому положению звена. Направление скорости Яд2 перпендику-
лярно к прямой Р2А0, соединяющей мгновенный центр вращения PJ,
в абсолютном движении с точкой зацепления Ло. Скорость относи-
тельного движения Т)д2д3 точки Д2 относительно точки будет
равна:
^2a3 = ^(W>
где 21 есть мгновенная угловая скорость относительного движения,
равная для данного момента 21 = ф!,-j-Скорость ^а2а8 направлена
§ 10] МЕХАНИЗМЫ С ОДНОЙ И ДВУМЯ ЦЕНТРОИДНЫМИ ПАРАМИ
195
перпендикулярно к прямой Р10Д0, соединяющей мгновенный центр вра-
щения Р10 в относительном движении с точкой зацепления Ло. Угол,
образуемый скоростями и ®д2д3, будет углом передачи y32 (рис. 266).
Вследствие перпендикулярности прямых Р\А0, PljBQi ... к направле-
ниям скоростей ^д2д3, ^в2в3, • •• и прямых Р\А0, P"BQ, ... к напра-
влениям скоростей ®в2, ... углы, образуемые этими прямыми,
между сооои оудут также всегда
равны углам передачи у*2, .
Таким образом, для того чтобы
исследовать вопрос об углах пере-
дачи в высшей паре, достаточно со-
единить соответствующие точки ли-
нии зацепления с соответствующими
мгновенными центрами вращения. В
том случае, когда угол, образуе-
мый этими двумя прямыми, будет
больше 90°, угол передачи ?32 бу-
дет добавочным до угла в 180° (ри
Рис. 267.
. 267). Для правильной работы
передачи полученные углы должны быть больше заданного угла 7min.
Пользуясь этим свойством линии зацепления, можно решить и
обратную задачу о подборе линии зацепления, наиболее удовлетво-
ряющей заданным динамическим условиям передачи движения. Рас-
смотрим, например, задачу о построении профилей по взаимоогибаемым
кривым с углом передачи, равным углу Тз2 = 90°. Как было показано
выше, при указанном угле передачи мы получаем наивыгоднейшие
динамические условия воспроизведения движения. Пусть задана непо-
движная центроида Ц2н (рис. 268), бицентроида Б и последовательные
положения мгновенных центров вращения Pl2, PJ1, Р|п ... и Р*, Р*1,
PJ11 ... Соединяем точку Р12 с точкой Р1о, точку Р[[ с точкой PJ1 и т. д.
На отрезках (Р\Р\), (P^PJ1), ... строим как на диаметрах окружности.
Первая точка До линии зацепления должна быть выбрана на окруж-
ности /; вторая точка Ро линии зацепления должна быть выбрана на
окружности 11 и т. д. В самом деле, если соединить любую точку
7*
196
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
Рис. 269.
окружности / или окружности II с соответствующими мгновенными
центрами вращения, то проведенные прямые будут всегда образовывать
угол передачи у32, равный 90°. Выбор на окружностях /, II, III, ... точек
зацепления Ло, Z?o, Z)o, ... может быть сделан совершенно произ-
вольно, но в большинстве практических расчетов выбор этих
точек обусловливается дополнительными расчетными данными. Так,
может быть задана по величине или направлению сила, которая должна
4^ действовать на профили, или
. задана максимальная потеря
мощности на трение и т. п.
rZ’"'' зависимости от этих допол-
нительных условий и могут
быть окон ча тел ы о выбраны
точки зацепления Ло, Z?o, 7)0,...
(рис. 268). По выбранной ли-
нии зацепления могут быть по-
строены взаимоогибаемые кри-
вые, принадлежащие звеньям
2 и 3.
Если задан некоторый предельный угол Ymin, то всегда можно
определить ту область, в которой может быть выбрана соответ-
ствующая точка зацепления. Для этого строим на отрезках, соеди-
няющих мгновенные центры абсолютного и относительного вращений,
две окружности, которые будут вмещать в себя заданные углы 7min.
Тогда точка зацепления для рассматриваемого положения может быть
выбрана только в пределах области, ограниченной проведенными
окружностями (на рис. 269 эта область заштрихована).
Проектирование механизмов с одной центроидной парой вида,
показанного на рис. 35 и 36, ведется методами, аналогичными рас-
смотренным.
§ 11. Механизмы с двумя низшими парами
1°. К этим механизмам относится очень большая группа механиз-
мов, широко используемых в технике. Это будут кулачковые меха-
низмы (рис. 38, 39, 49, 50, 58), различные виды зубчатых механизмов
(рис. 37, 41, 44, 47, 48), механизмы перекатывающихся со скольже-
нием рычагов (рис. 43, 53, 54, 60) и механизмы криволинейных и
прямолинейных кулис (рис. 40, 42, 45, 46, 51, 52, 55, 56, 57, 59, 61).
Для всех этих механизмов общей задачей будет задача о проек-
тировании профилей сопряженных элементов пары качения и скольже-
ния, обеспечивающих заданный закон ведущего и ведомого звеньев
механизма.
Методы проектирования сопряженных профилей всех указанных
видов механизмов будут общими, но формы движения, которые должны
воспроизводиться этими механизмами, их конструктивное оформление,
§ И] МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ 197
динамические условия их работы являются различными. Так, напри-
мер, кулачковыми механизмами мы в основном воспроизводим воз-
вратно-поступательное или возвратно-качательное движение ведомого
звена; зубчатыми механизмами мы чаще всего воспроизводим непре-
рывное вращательное движение как ведомого, так и ведущего звеньев,
механизмами перекатывающихся со скольжением рычагов воспроизво-
дится движение одной из точек рычага по заданной траектории и т. д.
Поэтому в дальнейшем мы будем с известной условностью поль-
зоваться той терминологией и тем делением механизмов указан-
ных выше видов, которые установились в современной теории
механизмов. Начнем с рассмотрения методов проектирования про-
филей элементов пары качения и скольжения в кулачковых меха-
низмах.
Ведущее звено кулачковых механизмов называется кулачком, а
ведомое — толкателем. Закон движения толкателя задается обычно
в виде функции положения, при этом задается также профиль эле-
мента пары качения и скольжения, принадлежащий толкателю. Толка-
тели кулачковых механизмов, как правило, имеют возвратно-качатель-
ное или возвратно-поступательное движение; поэтому профили эле-
ментов высшей пары, им принадлежащие, являются незамкнуты-
ми. Профили элементов высшей пары, принадлежащие кулачкам,
совершающим полный оборот вокруг своей оси вращения, будут
замкнутыми. У кулачков, имеющих возвратно-поступательное движе-
ние, профили элементов высшей пары, естественно, будут незамкну-
тыми. Таким образом, особенностью кулачковых механизмов с точки
зрения задач проектирования является то, что в этих механизмах
необходимо по заданным перемещению толкателя и профилю элемента
его высшей пары построить сопряженный элемент, принадлежащий
кулачку. Ниже мы рассмотрим только общую теорию проектирования
профилей кулачков с точки зрения осуществления требуемого закона
движения путем отыскания формы элемента высшей пары, принадле-
жащей кулачку без учета влияния конструктивных элементов, вхо-
дящих в состав кулачкового механизма (ролика толкателя, пружины,
направляющих толкателя и т. д.) на работу механизма. Эти задачи
будут рассмотрены ниже в главе VII.
Пусть требуется спроектировать профиль ^2 кулачка 2 (рис. 270),
если заданы профиль толкателя 3 и функция положения
ср3 = <р3 (<р2). Кулачок 2 и толкатель 3 вращаются около центров А
и В. Для построения профиля кулачка 3 воспользуемся методом
обращения движения. Сообщим всему механизму угловую скорость
— о)2 около оси А, равную и обратную по знаку угловой скорости со2
кулачка 2. Тогда точка В вращения толкателя займет последовав
тельно положения £?п, В111, BIV, ... на окружности, описанной из
точки Л, как из центра. Положения точки В на этой окружности
определятся известными нам углами поворота кулачка 2, равными
^2^»
198 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕПТРОИДНОЙ ПАРОЙ [ГЛ. IV
Для определения последовательных положений толкателя 3 отме-
чаем на профиле какую-либо точку D*. Обозначим угол, образо-
ванный прямой BD{ с линией центров АВ, через ср^. Угол ср* бу-
дет фиксировать начальное положение профиля Кл относительно ли-
нии центров АВ. Далее, по заданной функции положения ср3 = ср3 (ср.,)
находим углы ср3 поворота звена 3. Это будут углы ср*1, ср”1, cpjv, ...,
отсчитываемые от направлений ДР”, ДР1”, AB{V, ... в сторону,
Рис. 270.
соответствующую направлению угловой скорости ю3. Строим ряд
положений кривых /С3, соответствующих углам ср”, ср”1, ср*v, ..
и проводим к полученным положениям кривой /С3 огибающую /62.
Кривые 7С3 и /<2 как взаимоогибаемые кривые представляют
собой профили элементов пары IV класса, в которую входят
звенья 2 и 3.
2°. Построение профиля элемента пары, принадлежащего
кулачку, может быть выполнено и иначе, с помощью линии зацепле-
ния. Пусть профиль элемента пары, принадлежащего толкателю,
задан в виде кривой ZC3 (рис. 271) и задана функция передаточного
отношения /3.2 = /32 (ср2). По заданной функции z3.2 =/3.2 (ср2) определяем
положение мгновенных центров вращения Р*, Р”, Р**1, .,, и углы
§ и|
Механизмы с двумя низшими парами 193
поворота ср*, <р**, ср’1*, ... из условия
«Рй
Z32
б/ср2.
(4.13)
По полученным углам строим положения кривой пользуясь
для этого построением лучей BD], BDn, BDm, ... Так как кривая
нам задана, то известны направления нормалей к любым точкам этой
Рис. 271.
кривой. Проведем нормаль №, которая проходила бы через мгновен-
ный центр Р*. Точка пересечения этой нормали с кривой Кл
в первом ее положении определит точку С, которая будет точкой
соприкосновения сопряженных профилей и /С3. Проводим далее
нормаль 7V1*, которая бы проходила во втором положении кривой К&
через мгновенный центр Р**. Нормаль к кривой /С3 во втором ее поло-
жении, проходящая через Р**, проходит через точку в которой
кривая Кл будет касаться своей сопряженной кривой /С2. Аналогичные
построения проводим для последующих положений кривой К3. Точки
С, Fo, О0> • • •» Qo определят линию зацепления С3 профилей /С2 и
Для нахождения точек е, g, f, ..., q профиля соединяем точку А
с точками Ео, Go, ..., Qo и откладываем от этих направлений извест-
ные углы cpj’, ср***, ... Проводя под этими углами соответствующие
200
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
лучи, делаем на них засечки из центра А радиусами АЕ0, АО0, ...
Соединив точки С, е, g, f, ... плавной кривой, получаем профиль
кулачка 2.
Указанное построение позволяет строить сопряженные профили
по точкам, т. е. более точно, чем это можно сделать по способу,
указанному в § 11, 1°.
3°. Рассмотрим вопрос об углах передачи для кулачковых меха-
низмов данного вида (рис. 272). Угол передачи т23, образованный
векторами скорости ® точки С, принадлежащей звену 3, и вектором
относительной скорости ©отн точки С звена 3 в его движении отно-
сительно звена 2, может быть определен, если точку С соприкосно-
вения профилей соединить с точками В и Ро (см. § 10, 9°). Так как
угол ВСР0 на рис. 272 больше 90°, то угол передачи у23 будет
добавочным углом, равным у23 = 180° — Z. ВСРй. Выбор точек линии
зацепления должен удовлетворять условию, чтобы ни в одном из
положений угол передачи 723 не был бы меньше заданного мини-
мального угла ftnin- Для того чтобы удовлетворить этому условию,
достаточно выполнить следующее построение. Из точки В (рис. 272)
восставляем перпендикуляр тВт к направлению ВА. Далее, при
точке Р$ откладываем угол 90° — '[min вверх и вниз от направле-
§ 11]
МЕХАНИЗМЫ .С ДВУМЯ НИЗШИМИ ПАРАМИ
201
ния ВА и проводим направления Р^М и Р0Л41 до пересечения с пер-
пендикуляром тВт в точках М и Mt. Тогда углы ВМРй и £Ш|РП
будут равны ут1п. Через точки В, М, Ро и В, Mit Ро проводим окружно-
сти центров О и О’. Эти окружности будут вмещать в себя углы ymin.
Нетрудно убедиться, что если точка С линии зацепления выбрана
в области, ограниченной двумя окружностями центров О и О', кото-
рая на чертеже для наглядности очерчена двумя линиями, то угол у23
будет всегда больше угла ут,п, т. е.
Таз Ttnin-
Естественно, что существует и симметрично расположенная область
внизу чертежа, но которая не может быть использована, если про-
филь располагается выше линии АВ. Таким образом, если задан
угол Ttnin, то для каждого положения точки Ро на линии АВ может
быть построена своя область возможного расположения точки сопри-
косновения профилей и, следовательно, намечена линия зацепления,
удовлетворяющая условию наличия углов передачи, всегда больших '[min-
4°. Выбор точек линии зацепления может быть также сделан из
соображений, связанных с расчетом профилей на прочность или износ
или, наконец, из условий меньших потерь на трение и т. д. Пусть,
например, задано условие, чтобы нормальное давление Р на профили
было бы постоянным и заданным. Пусть, далее, задано, что отноеи-
тельная скорость цотн также должна быть постоянной, т. е. чтобы
была постоянной мощность NTp, затрачиваемая на трение скольжения
профилей. Мощность N, сила Р и скорость ®отн связаны условием
= (4.14)
где f—коэффициент трения скольжения, принимаемый постоянным.
Сила Р равна (рис. 273):
(4.15)
202 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
где ТИ2 — заданный момент движущих сил на валу ведущего звена 2
и h's — плечо силы Р относительно точки А.
Следовательно, при заданной силе Р плечо должно быть равно:
% = (4.16)
Скорость цотн равна (рис. 273):
г'отв = (“2 + “з) (ЛО = (Р0С) о>2 (1 — z32), (4.17)
где (РйС) — расстояние от соответствующего мгновенного центра
вращения Ро до точки С соприкосновения профилей. Передаточное
отношение i32 должно подставляться в уравнение (4.17) со своим
знаком.
При заданной скорости ®отн из уравнения (4.17) определяем рас-
стояние (РпС). Имеем:
Тогда определение точки С сведется к следующему простому
построению (рис. 273). По заданной функции /32 = z32 (<р) строим
центроиды Ц2П и Цзо. На отрезке (Р^А) строим как на диаметре
полуокружность. Далее, радиусом, равным h!, — AL (уравнение 4.16),
делаем засечку из точки А на проведенной окружности. Через
точки L и Р10 проводим прямую и откладываем на этой прямой
отрезок (Р’С), полученный из уравнения (4.18). Получаем точку С
линии зацепления С3. Далее, проводим аналогичные построения для
следующего положения механизма и находим точку Е линии зацепле-
ния С3. Для нахождения точек е2 и е3, принадлежащих профилям К*
и К3 и приходящих в соприкосновение в точке Е, проводим дуги
радиусами АЕ и BE и на этих дугах делаем засечки из точек irj1
и л’1 центроид Z/20 и Ц36 радиусами, равными л“е2 = Р''Е и
к[1е3= Р\1Е. Аналогичными построениями могут быть найдены и по-
следующие точки линии зацепления С3, удовлетворяющие поставлен-
ным условиям, а по ней и сопряженные профили и К3.
В некоторых случаях может быть задано условие, чтобы коэф-
фициент потерь у в высшей паре был бы заданным и постоянным, т. е.
N
<? = = const, (4.19)
где — мощность на валу А (рис. 273), равная Д/2 = Л42а>2.
Подставляя в уравнение (4.19) значения Атр из уравнения (4.14),
момента М* из уравнения (4.15) и w0TH из уравнения (4.17), получаем:
<Р =f (1 — 'м) = const. (4.20)
Из уравнения (4.20) следует, что условие постоянства коэффи-
циента <р удовлетворяется при различных отношениях соответствую-
§ 111
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
203
щих отрезков (РпС) и /г2. Следовательно, постоянство коэффициента <р
может быть обеспечено при одновременном постоянстве силы Р.
5е. Переходим к рассмотрению кулачковых механизмов с одной
вращательной и одной поступательной парой. Пусть требуется
спроектировать профиль кулачка 2 (рис. 274), если задан профиль /f3
толкателя 3, движущегося в прямолинейных направляющих и задана
функция положения s3 = s3(<p2). На рис. 274 построение профиля
кулачка показано методом обращения движения. Ось движения тол-
кателя 3 занимает последовательно положения В\ Bli, Вт, ... ТочкаD1
в движении с угловой скоростью — описывает окружность
радиуса AD{. Ось движения толкателя поворачивается на углы,
соответственно равные <р”, <p*v, ... Перемещения толкателя вдоль
оси движения определятся по заданной функции положения s3 == s3 (<р2).
Эти перемещения представляют собой отрезки (З11/)11), (<71||£)ш), •..
Обогнув плавной кривой К* построенные положения кривой Кл, нахо-
дим профиль кулачка 2.
204 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
Та же задача может быть решена с помощью построения линии
зацепления (рис. 275). По заданной функции положения s3 = s3(<p2)
находим последовательные положения кривой /С3. Далее, находим
функцию передаточного отношения k32 = k32 (<р2) дифференцированием
функции s3 — s3 (<р2). Имеем:
, ___dss___d [s3 (ys)|
32 dy2
По функции kai = kai (cp2)
находим на перпендикуля-
ре, восставленном в точке А
к направлению оси движе-
ния звена 3, мгновенные
центры вращения PJ, Р”, ...
Проводим нормали к кривой
Ка в соответствующих ее
положениях, проходящие че-
рез точки Р', Р’1, ... Тогда
определятся точки С, Е6,
Go, ... линии зацепления
С3. Для определения точек
е, /, профиля кулач-
ка 2 из точки А проводим
дуги радиусов АЕй, ДО0, ...
до пересечения с соответ-
ствующими лучами, прове-
денными под углами ср’’,
<р*п, • • • к прямым, со-
единяющим точку А с точ-
ками До, Go, ... линии зацеп-
ления.
6е. Выбор точек линии
зацепления, как это было
показано выше (§ 11, 3° и 4°),
зависит от ряда условий, ко-
торые могут быть поставлены для работы механизма. Решение задач о
выборе этих точек и построение сопряженных профилей по линии зацеп-
ления ничем не отличается от кулачкового механизма с двумя вращатель-
ными парами. Несколько иначе обстоит дело с определением той
области, в которой можно выбирать точки линии зацепления для того,
чтобы угол передачи -р23 был бы более угла ТУпТО- На рис. 276 пока-
зано, что угол передачи f23 определится, если точку С соединить
с мгновенным центром вращения Ро и провести прямую Ср, перпен-
дикулярную к оси движения толкателя 3.
Нетрудно видеть, что /. рСР$= /_ СРаА. Откладываем при
направлении АР0 вверх и вниз угол ^пип и проведем прямые пт
§ 11]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
205
и lq. Нетрудно видеть, что если точка С выбрана внутри области, обра-
зованной углом 1Рйп, то угол уаз будет всегда больше угла fmin, т- е-
7‘2'Л Ttnitl •
На рис. 276 границы этой области отмечены двумя линиями.
Естественно, что такая же область существует в пределах угла тР<д
в случае расположения точ-
ки контакта С ниже ли-
нии ДР0.
7°. Переходим к рассмо-
трению кулачковых меха-
низмов с двумя поступатель-
ными парами. Пусть требует-
ся спроектировать профиль Кг
кулачка 2, если заданы про-
филь Кл толкателя 3, дви-
жущегося в прямолинейных
направляющих, и функция
положения s3 = s3 (s2), где
— перемещение кулачка 2.
На рис. 277 показано по-
строение профиля Кч кулач-
ка 2 методом обращения
движения. Ось движения
толкателя занимает после-
довательно положения В1,
В11, В111, ..., перемещаясь
поступательно со скоро-
стью — в обращенном дви-
жении на величины отрез-
ков s*1, s’11, s'v, ... Точка В* профиля Кл занимает при этом положения
dll,dlu,dw,... Перемещения толкателя 3 вдоль оси движения определятся
по заданной функции s3 — s3 (s2). Эти перемещения представляют собой
отрезки (d11/)11), (d111/?111), (dlvBlv), ... Обогнув плавной кривой К.г
построенные положения кривой /<3, находим профиль Кч кулачка 2.
Вопрос об углах передачи в кулачковых механизмах этого вида
решается весьма просто. На рис. 278 показано, что угол передачи у.23
образован нормалью NN и направлением движения кулачка. Следо-
вательно, если задан угол Ymin и профиль К$ толкателя изменяется
в виде плавной кривой, не имеющей точек перегиба, то всегда могут
быть на этом профиле найдены точки а и Ь, в которых нормали Na
и Nb к кривой Кз будут образовывать углы упИп. Очевидно, что
точкой контакта профилей может быть любая точка профиля Кл,
лежащая на участке ab.
8°. В зубчатых механизмах ведущее и ведомое звенья называются
зубчатыми колесами и элементы пары скольжения и вращения выпол-
206 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ IV
няются в виде ряда профилей, последовательно приходящих в зацепле-
ние и называемых зубцами. Очертания профилей зубцов полностью
Рис. 277.
определяются типом инструмента и
Таким образом, геометрия профилей
Рис. 278.
способом нарезания зубцов,
зубцов неразрывно связана
с геометрией инструмента и
кинематикой относительного
движения инструмента по
отношению к нарезаемому
колесу. Поэтому при про-
ектировании профилей зуб-
цов используются обычно
два основных метода проек-
тирования: метод дополни-
тельных центроид и метод
разверток.
Рассмотрим метод до
полнительных центроид. Об-
щая идея этого метода была
изложена в § 5, 5°. Пусть тре-
буется воспроизвести сопря-
женные профили Кч и зуб-
цов (рис. 279), принадлежа-
щих звеньям 2 и 3, если заданной функции передаточного отношения г32
удовлетворяют построенные профили центроид Цго и Цзо. Пусть
в качестве дополнительной центроиды выбрана окружность S'. Пере-
§ И]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
207
катываем окружность S' по центроидам Цы и Ц-м. В качестве сопря-
женных профилей могут быть использованы любая пара рулетт,
описываемых точками окружности S'. На рис. 279 сопряженные кри-
вые Кэ и Кз представляют собой рулетты центра О' окружности S',
а кривые К? и Кз рулетты точки окружности S', совпадающей
в положении, указанном на чертеже, с точкой Рп. С помощью допол-
нительной центроиды в виде окружности S" можно получить также
сопряженные профили, аналогичные профилям, полученным при каче-
нии окружности S'. Это будут кривые К™, и /f’v, К™. Исполь-
зование для передачи движения тех или иных сопряженных кривых
определяется требуемыми условиями работы механизма. Выбранные
нами окружности S' и $" могут быть выбраны за центроиды инстру-
мента, нарезающего профили зубцов. Очевидно, если с этими окруж-
ностями жестко связана режущая кромка инструмента, то нарезание
профиля зубца может быть получено путем воспроизведения на
станке относительного движения окружностей S' и S" и центроид
Цгй и ZZ30, принадлежащих заготовкам колес. При этом режущая
кромка нарежет профиль зубца на заготовке колеса путем ее огиба-
ния. Практически нарезание профилей зубцов некруглых колес про-
изводится несколько иными методами, позволяющими более техноло-
гично выполнять весь процесс нарезания зубцов [36а], но основан-
ными на этом общем кинематическом приеме.
9°. Метод дополнительных центроид получил достаточно широкое
применение в задаче о проектировании зубцов круглых цилиндриче-
ских колес с циклоидальным и цевочным зацеплениями. Пусть
требуется построить сопряженные профили двух зубцов механизма
208
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
зубчатых колес для воспроизведения заданного постоянного переда-
точного отношения (рис. 280). Центроидами Ц.2О и Цзо этих колес
будут окружности центров А и В. Вспомогательной центроидой может
быть выбрана любая окружность. При качении, например, окружно-
сти S' по центроидам Ц20 и Ц-№ рулетты K'-i и К'з точки окружно-
сти S', совпадающей с центром Ро, могут быть выбраны за профили
сопряженных зубцов. Кривая К2 будет эпициклоидой, так как она
образована качением окружности S' по внешнему очертанию
центроиды Ц20. Кривая К'3 будет гипоциклоидой, образованной каче-
нием окружности S' по внутреннему очертанию центроиды Цап. Про-
фили зубцов могут быть также очерчены и по кривым К2 и К'з,
представляющим собой соответственно гипоциклоиду и эпициклоиду,
полученные качением окружности S" по внутреннему очертанию
Рис. 280
центроиды и по внешнему очертанию центроиды Z/30. В некото-
рых случаях удобно профиль каждого из зубцов образовать из двух
кривых, например кривых К'ъ К-г и К’я, К'з- Зубцы с профилями,
очерченными по циклическим кривым, образуют циклоидальное зуб-
чатое зацепление. Линией зацепления циклоидальных профилей будут
дуги окружностей S' и S". Так, точкам а2 и аа будет соответство-
вать точка Лп на линии зацепления (рис. 280), точкам Ьг и Ьл
точка Ва и т. д.
10°. Пусть в качестве профиля зубца, принадлежащего колесу 3
(рис. 281), выбрана точка К'з центроиды Ц90, совпадающая в началь-
ный момент с центром Рп. Рассматривая центроиду как
вспомогательную центроиду, перекатываем ее по центроиде Uw.
Тогда точка К'3, совпадающая с центром Ро, опишет эпициклоиду K'<z-
Очевидно, что передача движения могла бы быть осуществлена воздей-
ствием точки Кя, принадлежащей центроиде Ца1), на кривую /<2-
§ Hl
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
209
Практически вместо точки устанавливается круглый цилиндрический
ролик К3, носящий название цевки. Тогда профиль Кч, сопряженный
с цевкой, может быть получен как огибающая последовательных
положений цевки /fg. Такое зацепление получило название цевочного
зацепления. На рис. 282 показан
зубчатый механизм с цевочным
зацеплением. На рис. 281 в каче-
стве точки, образующей исходный
профиль, А'г. была выбрана точка К'з,
совпадающая с центром Рп, г. е.
Рис. 283.
Рис. 282.
точка, лежащая на самом очертании центроиды ZZ30. Конструктивно
в некоторых случаях удобно в качестве точки, образующей профиль
зуба колес, выбрать точку, лежащую вне очертания центроиды. На
рис. 283 показан случай передачи движения с внутренним зацепле-
210
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
нием колес при относительно малой разнице в размерах колес. Если
в качестве точки, образующей профиль зуба, выбрать на центроиде Цт
Рис. 284.
точку К'з, то мы получим основной профиль K'i и по заданному
радиусу цевки сможем построить кривую Лг". Если теперь в каче-
Рис. 285.
стве образующей точки выбрать
на центроиде Цм точку К'з, ле-
жащую вне центроиды Ц-м, то мы
легко получим основной профиль
К'ч и далее кривую К3. Таким
образом, в зацеплении будут на-
ходиться цевка К3 и зубец К%.
Такое зацепление получило при-
менение в цевочных редукторах
с передаточным отношением, близ-
ким к единице. На рис. 284 по-
казан цевочный редуктор такого
типа, позволяющий получить боль-
шое передаточное отношение.
Если образующую профиль
зубца точку К'з выбрать внутри
области, ограниченной очертания-
ми центроид (рис. 285), то может
быть получен механизм цевочных
колес Рело. При качении цен-
троиды Ц№ по центроиде Ц9(1 точ-
ка К'<2, принадлежащая центроиде
Z/20, опишет удлиненную гипоцик-
лоиду K's, которая будет основным профилем зубца, принадлежащего
центроиде Ц-м. Профиль К3 зубца получится как огибаемая цевки К*
Зубцы колеса 3 имеют чечевицеобразный вид и располагаются на
тыльной стороне колеса 3,
§ 11]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
211
К механизмам с цевочным зацеплением относятся также зубчатые
колеса Гриссона (рис. 286). Малое колесо 3 выполнено в виде двух
зубцов I и II, смещенных друг относительно друга на угол в 180°.
Зубец / входит в зацепление с цевками а, а зубец II с цевками Ь.
Таким образом осуществляется плавность передачи движения. Для
возможности передачи вращения в любом направлении зубцы колеса 3
Рис. 28<>.
очерчены двумя симметричными участками эпициклоид. Проектирова-
ние профиля колеса 3 (рис. 287) может быть осуществлено пере-
катыванием центроиды Цм по центроиде Ц30. В качестве точки,
образующей основной профиль К'3, выбрана точка К'ъ являющаяся
центром цевки. Профиль К3 найдется как огибающая положений
цевки.
Цевочное зацепление используется также для передачи движения
от колеса к рейке. На рис. 288 показан цевочный механизм колеса
и рейки. При качении центроиды Ц20 по прямой Цм точка К’ъ опишет
циклоиду К'3. Огибающая положений цевки /<2 даст профиль К-л
зубца рейки. На рис. 289 цевки расположены на рейке 3. При каче-
нии прямой Ц20 по центроиде ,Ц30 точка К'ч опишет эвольвенту К3.
Профиль Кц зубца колеса 3 определится как огибающая положений
цевки Кч-
212 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ |гЛ. IV
Рис. 289.
Рис. 288.
§ 1 1J МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
213
11°. Зубчатые механизмы с цевочным зацеплением используются
как механизмы с остановками. На рис. 290 показан зубчатый цевоч-
Рис. 291.
Рис. 290.
ный механизм с остановками с внешним
ведущим является звено 2, снабженное
на цевки Ь. При одном обороте зве-
на 2 звено 3, снабженное цевками, по-
ворачивается на угол <р3, равный
2я
где z есть число цевок. Проектирова-
ние зубца а ведется по общим прави-
лам проектирования цевочных колес с
учетом, чтобы в конце и начале зацеп-
ления скорость колеса 3 равнялась
нулю. Колесо 2 снабжено запирающей
дугой пп, входящей в запирающие ду-
ги тт, число которых равно числу
цевок. Дуги пп и тт предназначены
для предупреждения самопроизвольного
движения колеса 3 после выхода зуб-
ца а из зацепления. Длина дуби пп
определяется углом 8.
На рис. 291 показан другой зубча-
тый цевочный механизм с остановками,
у которого зацепление не внешнее, а внутреннее. Для предупрежде-
ния самопроизвольного движения звена 2 и, следовательно, размыка-
ния кинематической цепи звено 2 снабжено запирающей дугой пп,
скользящей по соответствующим дугам тт колеса 2.
На рис. 292 показан сложный зубчатый цевочный механизм
с остановками, являющийся представителем так называемых звезд-
зацеплением, у которого
зубцом а, воздействующим
Рис. 292.
214 СИНТЕЗ 1РЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
чатых механизмов. Звездчатые механизмы позволяют воспроизвести
движение с различными периодами остановки и движения, а также
с различными передаточными отношениями угловых скоростей в раз-
личные периоды движения, но постоянными внутри каждого периода.
Звездчатый механизм, изображенный на рис. 292, имеет четыре рав-
ных периода движения и четыре равных периода покоя с одним и
Рис. 293.
Рис. 294.
тем же передаточным отношением во все периоды движения; на
рис. 293 показан звездчатый механизм, имеющий три равных пе-
риода покоя.
На рис. 294 показан звездчатый механизм с различными перио-
дами покоя и движения, а также с различными передаточными отно-
шениями в периоды движения.
Рассмотрим, как определяются основные параметры звездчатых
механизмов. Обозначим радиусы начальных окружностей через и
(рис. 292), угол поворота звена 3 на участке между двумя со-
седними зубцами — прерывателями С — через ср3, угол поворота ве-
дущего (цевочного) колеса, соответствующего углу <р3, — через <р2,
время движения ведомого звена 3 — через tR и время покоя ведомого
звена 3 — через tn. Тогда будем иметь:
где Т есть время одного полного оборота ведущего звена 2. Далее
§ 11] МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ 215
имеем:
^=l--g. (4.22)
Обозначим через е отношение углов поворота и звеньев 2
и 3, т. е.
е ——. (4.23)
?8
Из уравнения (4.21) имеем:
Ф2 = .
Угол "р3 равен:
где п есть число зубцов прерывателей С. Подставляя полученные
выражения для углов и в уравнение (4.23), получим:
е = Ду,
откуда
6 ________________________________*д
п — Т •
Так как
f д /, го е п,
г. е. отношение углов поворота должно быть всегда меньше числа
зубцов прерывателей.
Величина отношения е, вообще говоря, не равна передаточному
о
отношению /23 — . Связь между этими величинами выражается сле-
дующим уравнением:
8 = - - 1) 4- « arcsin - 27^-Г • <4-24>
\Z / л <Ц1“Н28)
Ниже приводится таблица значений f23 для различных е и чисел я
зубцов прерывателей.
Задаваясь величиной е, находят по таблице величину п, после
чего легко определяют величины и /?3, используя дополнительное
условие
4^ 7?з = /,
где I есть расстояние между точками А и В.
216 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
D
Таблица значений передаточного отношения i2S=--a- для различных
значений е и п
Е п = 1 п = 2 я = 3 п = 4 п = 5 п = 6
5 4,4165
4 — — — — 3,5329 3,4423
3 — — 2,6480 2,5633 2,4800
2 — 1,7642 1,6902 1,6185 1,5489
1 — 0,8814 0,8276 0,7773 0,7307 0,6874
%= 0,8333 0,7777 0,7260 0,6782 0,6342 0,5938 0,5567
>/3 = 0,8000 0,7455 0,6951 0,6487 0,6060 0,5670 —
«', = 0,7500 0,6975 0,6491 0,6047 0,5641 0,5271 —
«', = 0,6667 0,6176 0,5729 0,5322 0,4952 0,4617 —.
*'8 = 0,6250 0,5779 0,5350 0,4962 0,4611 0,4295 —
3/3 = 0,6000 0,5540 0,5124 0,4748 0,4405 0,4104
>/8 = 0,5000 0,4592 0,4226 0,3901 0,3611 0,3353 —
2 5 = 0,4000 0,3650 0,3343 0,3073 0,2836 — —
3/8 = 0,3750 0,3416 0,3124 0,2869 0,2645
>/3 = 0,3333 0,3028 0,2762 0,2532 0,2332 — —
V, = 0,2500 0,2256 0,2048 0,18706 0,17177 —. —
1 '5 = 0,2000 0,17970 0,16264 0,14821 0,13588 — —
Чв = 0,16667 0,14930 0,13483 0,12268 0,11237 — —
>.,= 0,14286 0,12767 0,11512 0,10464 0,09579 — —
>'s = 0,12500 0,11152 0,10043 0,09121 0,08343 — —
Кроме звездчатых механизмов с внешним зацеплением, могут быть по-
строены и звездчатые механизмы с внутренним и реечным зацеплениями.
Рис. 295.
Рис. 296.
На рис. 295 показан звездчатый механизм с внутренним зацепле-
нием с шестью периодами покоя ведомого звена, у которого ф3 =
— 240°, <р3 = 60° и
На рис. 296 показан звездчатый механизм с внутренним зацепле-
нием с одним периодом покоя, у которого ср2 —240°, <р3 = 360° и
— 0,0.
§ Н]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
217
На рис. 297 показан звездчатый механизм с внутренним зацепле-
нием с двумя периодами покоя, у которого <р2 = 60°, ср3=180° и
7
На рис. 298 изображен звездчатый механизм с реечным зацепле-
нием с двумя цевками, у которого <р2 = 180°.
Рис. 297. Рис. 298.
На рис. 299 изображен звездчатый механизм с реечным зацепле-
нием, у которого звено 2 является ведущим. У этого механизма
180°.
На рис. 300 показан звездчатый механизм с реечным зацепле-
нием и одной цевкой, у которого = 120°.
Проектирование всех этих механизмов выполняется теми же ме-
тодами, как и для случая внешнего зацепления.
Рис. 299.
12 . Кроме метода дополнительных центроид при проектировании
профилей зубчатых колес используется метод разверток или эволь-
вент Как это было показано выше (см. § 6, 7°), траектория любой
точки звена механизма является разверткой (эвольвентой) эволюты
этой траектории. Таким образом, процесс образования тех или иных
траекторий (рис. 301) можно представить как качение без скольже-
ния прямой N по эволюте аа. Точки А, В, С, ... этой прямой опи-
шут при этом эвольвенты Эд, Эд, Эс> ... Точки О, О', О11, ... ка-
сания прямой N с эволютой аа. будут центрами кривизны эвольвент
Эд, Эв, Эс, ... Эвольвенты Эд, Эд, Эс> ... будут равноотстоящими
(эквидистантными) кривыми, так как приращения радиусов кривизны
218 СИНТЕЗ ТРЁХЗВЕННЫк МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
при переходе от одной эвольвенты к другой будут равны между
собой, т. е. АВ = А'В' = дп^п ВС — В'С1 = В"Сп, ... Сопря-
женные профили, очерченные по эвольвентам, могут быть получены
следующим образом (рис. 302). Пусть прямая NN касается двух кри-
вых: аа и рр, принадлежащих звеньям 2 и 3. Выберем на прямой NN
какую-либо точку С. При качении прямой A7V по кривой аа точка С
Рис. 302.
опишет эвольвенту Э2. Соответственно при качении прямой NN по
кривой рр точка опишет эвольвенту Э3. Кривые аа и рр будут эво-
лютами кривых Э2 и Э3. Передача движения между звеньями 2 и 3
может быть осуществлена воздействием эвольвент Э2 и Э3 друг на
друга. Нетрудно видеть, что та же передача могла бы быть осуще-
ствлена, если представить себе вместо прямой NN гибкую нить,
охватывающую кривые аа и рр и закрепленную на них. Тогда, вра-
§ 11] МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
219
щая кривую рр с угловой скоростью о)3, нить будет наматываться на
кривую рр и сматываться с кривой аа, вращая эту кривую с угло-
вой скоростью w2, т. е. мы получаем механизм передачи некруглыми
шкивами с гибкой нитью. В качестве точки, образующей эвольвенты,
может быть выбрана любая точка прямой NN; полученные при этом
эвольвенты будут эквидистантными к эвольвентам Э2 и Э3.
Пусть заданы эволюта аа, принадлежащая звену 2 (рис. 303, а),
и функция передаточного отношения i32 = (<р2). Требуется найти
эвольвенту рр, принадлежащую звену 3. По заданной функции i32 =
= /32(<р2) находим положение мгновенного центра вращения Ро звена
2 относительно звена 3. Через точку Рп проводим прямую NN, ка-
сательную к кривой аа. Пользуясь методом дополнительных групп
(см. § 6), присоединяем группу, состоящую из звеньев а и Ь. Сооб-
щаем далее всему механизму около оси В угловую скорость, равную
и обратную угловой скорости ш3, и рассматриваем вопрос о скоро-
стях точек механизма в этом обращенном движении. Скорость Те
точки С прямой NN будет равна:
•пс = а (р„с)=(<и2 4- ш3) (Рос).
Скорость точки 1>е оси шарнира, соединяющего звенья
будет равна:
Ve~ ч>еу +
и
— vEx -г VEEX-
(4.25)
а и Ь,
(4.26)
220
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
В уравнениях (4.26) вектор ч>Еу есть скорость точки прямой NN,
совпадающей в данном положении с точкой Е; вектор фЕх — ско-
рость точки прямой АВ, совпадающей с точкой Е, вектор ФЕЕу—
скорость поступательного движения ползуна b по прямой NN и век-
тор vEEx — скорость поступательного движения ползуна а по пря-
мой АВ.
Скорость <оЕх равна:
т’Ех = шз (ВРй) — <о2 (АР0). (4.27)
Скорость фЕЕх равна скорости <оРй перемещения мгновенного центра
вращения Рй по направлению АВ. Величина скорости фРа может быть
найдена из условия
про — vEEx
_d(AP0) d(AP0)
dt 2 ’
(4.28)
где (AP0) — переменное расстояние точки Ро от точки А.
Так как
; ___ “я _ АР0
38 ~ ВР0 ’
то, следовательно.
АР, = (АВ) 2; (4.29)
1 I ‘32
где АВ — расстояние между точками А и В (рис. 303, а). Таким
образом, скорость vPo будет равна:
( *32 'j dlsa
vP. = ш2 (АВ) -А И"*»* - = W2 (АВ) -7^-^ - (4.30)
otfs и “Г
Скорость vp0 может быть найдена аналитически по формуле (4.30),
если задана в аналитической форме функция передаточного отноше-
ния /32 = *32 (<Рв). Если функция z32 = Z32 (<р2) задана в виде графика,
то скорость Vp0 может быть найдена графически из условия (4.28).
Зная векторы скоростей vEx и фРо, легко найти векторы скоро-
стей фЕу и ФЕЕу построением плана скоростей (рис. 303, б). Откла-
дываем из точки р отрезки (ре*) и (ехе), пропорциональные вычислен-
ным по формулам (4.27) и (4.30) скоростям фЕх и vPo = vEEx.
Замыкающий отрезок (ре) будет пропорционален скорости фе. Из
точки е проводим направление, параллельное прямой NN, а через
точку р — направление, перпендикулярное к NN. В точке пересече-
ния этих направлений получаем точку еу. Отрезок (реу) определит
скорость фЕу. Откладываем вектор ФЕу в точке Е (рис. 303, а), а
вектор в точке С в направлении, перпендикулярном к прямой NN.
Соединив концы векторов и фЕу прямой, найдем на пересечении
этой прямой с нормалью NN точку D, скорость которой равна нулю.
Точка D будет мгновенным центром вращения прямой NN, т. е.
будет принадлежать эволюте рр (см. § 6, 5°). Аналогичным образом
% П]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
221
могут быть построены и остальные точки эволюты ЭД) для последую-
щих положений точки Рп и значений г32. Имея эволюты аа и рр,
можно построить сопряженные профили как эвольвенты способом,
показанным на рис. 302.
В зубчатых механизмах с круглыми цилиндрическими колесами
в качестве эволют аа и рр (рис. 304) выбираются окружности, рас-
положенные внутри очертания центроид ZZ20 и Z/30, описанные ра-
диусами АС и BD из точек А и В. При таком выборе эволют
всегда удовлетворяется условие о передаче вращения с постоянным
передаточным отношением z32. Для доказательства этого можно вос-
пользоваться построением плана скоростей в обращенном движении
(рис. 304, б) механизма, полученного путем присоединения дополни-
тельной группы. Из плана скоростей следует, что векторы скоростей
vEx и ®ev будут постоянны. Точно также будет постоянным вектор
Рис. 304.
Следовательно, точка D, принадлежащая эволюте рр, должна занимать
постоянное положение на прямой NN. Иначе говоря, точка D в обра-
щенном движении опишет окружность рр, концентрическую центрои-
де Z/30. Нетрудно видеть, что для рассматриваемого механизма
(рис. 304, а) линия зацепления будет совпадать с прямой NN.
13°. В общем случае в механизмах круглых зубчатых колес мо-
гут быть профили зубцов, очерченные не по циклическим или эволь-
вентным кривым, а по любым другим. В этом случае построение
сопряженных профилей может быть сделано по одному из методов,
изложенных выше (§ 12, 1°, 2°). Очень удобным для построения
сопряженного профиля по одному из заданных профилей является
применение метода, указанного в § 5, 13° (рис. 162). Пусть известны
центроиды Z/20 и Z/30 круглых цилиндрических колес (рис. 305) и
задан профиль /<3 зубца, принадлежащего колесу 3. Соединим центр
.кривизны Os профиля К3 с точкой В и продолжим направление О3В
222 синтез трехзвенных механизмов с центроидной парой [гл. IV
До пересечения в точке D с перпендикуляром P0D, восставленным
в точке Ро к нормали NN к профилям. Соединив точку D с точкой А,
находим на пересечении линии DA с нормалью NN точку 0.2 — центр
кривизны профиля Кг зубца колеса 2. Таким методом может быть
построена эволюта кривой Кг и, следовательно, и кривая Кг, как
Огибающая окружностей, описанных из центров кривизны радиусами
Кривизны кривой Кг-
Данный метод может быть применен и для некруглых колес, если
известны радиусы кривизны их центроид в относительном движении.
14°. Механизмы перекатывающихся со скольжением рычагов
(рис. 43, 53, 54 и 60) могут быть использованы для воспроизведе-
ния движения одной из точек рычага по заданной кривой.
Рис. ЗО-э.
Пусть, например, требуется спроектировать механизм по схеме,
показанной на рис. 43, у которого звено 3 (рис. 306), перекатываясь
со скольжением по прямой Къ точкой С описывает дугу окружности 77
радиуса ОС. Пусть точка В звена 2 занимает последовательно поло-
жения В', Вп, Вш, ... По известному расстоянию ВС находим поло-
жения С1, С11, С1П, ... точки С. Зная положения точек В и С, можно
определить положение мгновенного центра вращения Ра звена 3.
На рис. 306 показано определение мгновенного центра вращения P8V
для положения BVCV звена 3. Точка dj соприкосновения кривых Ка
и Ki в данном положении найдется, если из точки Р% опустить на
прямую Ki перпендикуляр P^d^. Для нахождения точки da, принад-
лежащей кривой Kit соединяем точку dx с точками Bv и Cv и полу-
ченный треугольник diBx'C'' двигаем вершинами £?v и Cv по траекто-
риям рр и 77 до совпадения отрезка (BVCV) с положением (В'С).
Точка da определит точку профиля Kt, приходящую в соприкосно-
вение с точкой di прямой Ki- Таким образом, задача нахождения
профиля Кз звена 3 решается с помощью линии зацепления, точками
которой будут точки d,, еь flt ... Если профиль, принадлежащий
§ И]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
223
неподвижному звену, будет представлять собой некоторую кривую
(рис. 307), то точка d линии зацепления определится, если провести
к кривой К\ ряд нормалей. Нормаль N, проходящая через центр Р;),
определит положение точки d, принадлежащей линии зацепления
На рис. 308 показано проектирование профиля К3 звена 3, если
механизм имеет кинематическую схему, указанную на рис. 54. Точка С
224
Синтез ТЙЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ парой [гл. IV
для положения, когда отрезок (ВС)
У
У
Рис. 308.
звена 3 должна описывать траекторию уу, представляющую собой
прямую. На рис. 308 показано определение точки dt линии зацепления
анимает положение (BVCV).
Точка d3 профиля /<3, сопря-
женная с точкой dt, най-
дется, если сторону (BVCV)
треугольника diBvC'1 со-
вместить с отрезком (УУ’С1)
и построить треугольник
т/зВ’С1, равный треугольнику
(ЦВ^С1.
Проектирование механиз-
ма с кинематической схемой,
показанной на рис. 53, мо-
жет быть сделано по способу,
указанному выше. Пусть за-
дан (рис. 309) профиль К\
звена 1 в виде неподвижной
прямой. Точка звена 3 дол-
жна двигаться по прямой уу.
Звено 2 занимает последовательно положения АВ1, АВп, АВп', ...
Положения точки С определяются из условия, что кратчайшее рас-
У
Стояние /У1 от точки С до прямой АВ будет постоянным и заданным
Для нахождения, например, точки С11 проводим на расстоянии Н] от
§ 11] МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ 225
прямой АВ" прямую, параллельную этой прямой. Точка пересечения
этой прямой с прямой уу определит положение точки С”. Далее на-
ходим мгновенный центр вращения Р**. Опустив перпендикуляр на
прямую Kt, находим точку gx линии зацепления. Аналогично могут
быть найдены и другие точки hit g\, ft, ... линии зацепления. Далее
находим кратчайшее расстояние Н" точки gt от прямой АВ". Прово-
дим прямую, параллельную прямой АВ', на расстоянии Н" и на этой
прямой из точки С1 делаем засечку радиусом, равным C"gi. Эта за-
сечка определит положение точки g3. Аналогичным построением най-
дем и другие точки профиля Кз-
Профилирование механизма с кинематической схемой, показанной
на рис. 60, может быть сведено к случаю, представленному на рис. 277,
если неподвижным сделать звено, входящее в две поступательные
пары (§ 12, 7°).
15°. Переходим к рассмотрению задач о проектировании механизмов
с криволинейными кулисами, кинематические схемы которых показаны
Рис. 310.
на рисунках 40, 42, 45, 46, 52, 55, 56, 57, 59 и 61. В этих меха-
низмах профиль одного элемента пары качения и скольжения будет
всегда точкой. Сопряженный с точкой элемент будет в общем случае
кривой, а в частном случае может быть прямой. Начнем с рассмотрения
механизма с двумя вращательными парами, кинематическая схема
которого показана на рис. 40. На рис. 310, а и б показаны два ва-
рианта этого механизма. На рис. 310, а показан тот случай, когда
длина кривошипа АС больше расстояния АВ. В этом случае кулиса 3
делает полный оборот на 360°. Если длина кривошипа АС меньше
расстояния АВ, то кулиса поворачивается на угол ф, величина кото-
рого зависит от очертания профиля Кз-
8 И. И. Артоболевский
226
СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гЛ. IV
Углы </ и <р" поворота кривошипа АС, соответствующие вращению
кулисы в двух противоположных направлениях, определяют так назы-
ваемый коэффициент увеличения скорости, равный (рис. 310, б)',
(4 3П
<f" 180 —fl-
Для кулисных механизмов указанного вида линией зацепления
будет окружность, описываемая точкой С, так как профиль, принад-
Рис. 311.
лежащий звену 2, представляет собой точку. Поэтому построение
сопряженного профиля К3 можно воспроизвести, используя для этого
метод построения сопряженных профилей с помощью линии зацепления
(§ 12, 2°, 5°). Пусть требуется построить профиль /<3 кулисы меха-
низма, у которого заданы расстояние АВ (рис. 311), длина кривошипа
АС и функция положения <р3 — ср3 (ср2) (рис. 312). Нетрудно видеть
(рис. 310, а и б), что для механизмов указанного типа функция по-
ложения ср3 = <р3 (<ра) может задаваться в пределах только 180° угла
поворота кривошипа АС, так как если профиль построен для угла
поворота кривошипа от положения АС до положения АС" по часовой
§ 11]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
227
стрелке, то для угла поворота от положения АС" положения АС’
в том же направлении будет использован уже построенный профиль Кз-
Таким образом, если профиль Кл будет одним и тем же за полный
Рис. 313.
оборот кривошипа, то функция положения ср3 = ср3 (ср2) должна зада-
ваться на интервале угла в 180° относительно прямой С С" (рис. 310).
Возможно также задать эту функцию на интервалах, лежащих по
разные стороны от прямой СС", но углы этих интервалов должны в сумме
составлять 180°, так, как это, например, пока-
зано на рис. 313, т. е.
— 180°> или ?'П “Ь ?aV = 180°-
Таким образом, на рис. 312 функция <рз =
= <р3(<р2) задана от положения 1 до положения
7, соответствующих положениям точки С от
Ci до С7 (рис. 311). Окружность, описываемая
точкой Ki, будет линией зацепления. Тогда
точки, образующие кривую Кл, определятся
с помощью следующих простых построений.
Пусть начальное положение кулисы 3 опреде-
ляется прямой BCj. Для того чтобы найти
положение точки К[У кривой Кз, соответствую-
щей повороту кривошипа 2 на угол <р’п, отклады-
ваем от направления ВСг угол <р*п, взятый в
соответствующем масштабе с графика <р3= <р3 (<р2)
(рис. 312). Точка Cj займет тогда положе-
ние С]. Точка Ki совпадает тогда с точкой
угольник BC’iC3 поворачиваем около точки В
роны BC't со стороной ВС\. При этом точка
жение /С*11. Аналогично определятся и другие точки кривой Кз- На
рис. 311 полное очертание оси кулисы дано в положении механизма,
соответствующем точке 3 на гоаФике <р3 = (<р4) (рис. 312). Практи-
8’
Полученный тре-
совпадения сто-
G.
до
С3 (TCj) займет поло-
228 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. IV
ческое очертание кулисы получится после введения ролика 4 и про-
ведения кривых, эквидистантных к кривой /<3 (рис. 311). На рис. 312
пунктиром показан график <р3 = <р3 (<р2) на участке, соответствующем
положениям точки С от С7 до Ct. Этот участок графика <р3 — <р3 (<р2)
получен путем построения углов ср3 поворота кулисы 3 для полу-
ченного очертания профиля кулисы 3. Та же задача может быть
решена и методом обращения движения. Сообщим всему механизму
общую угловую скорость —ы3, равную и обратную угловой ско-
рости ю3 кулисы 3. Тогда точка А переместится в положение А’,
определяемое поворотом прямой ACt на угол —(рис. 311), а
точка С] перейдет в положение Cj'. Далее, поворачиваем кривошип 2
Рис. 314.
из положения А'С" на угол cpj11. Тогда точ-
ка C'i займет положение /С’п. Таким обра-
зом определится точка кривой К3, соот-
ветствующая положению 3 на графике
<Тз = 'Рз(‘Р2) (рис. 312).
В частных случаях механизмов подоб-
ного вида ось кулисы может быть прямо-
линейной (рис. 42, 74, 75). Тогда закон
движения звеньев будет полностью опре-
деляться прямолинейным профилем кулисы
и его расположением относительно оси
вращения. В механизме, показанном на
рис. 311, функция i32 — i32 (<р2) переда-
точного отношения переменна. Если эта
функция будет постоянна, то мы получим
вышерассмотренные случаи цевочного за-
цепления (см. § 12, 10°) (рис. 41). Для по-
лучения непрерывного вращения в одном
направлении кулисы 3 с переменным пе-
редаточным отношением г32 можно спроек-
тировать зацепление по типу цевочного.
Для этого необходимо ведущее звено 2 снабдить несколькими цевками,
а звено 3 будет содержать несколько пазов. При проектировании
таких механизмов необходимо обеспечивать свободный выход цевок
из пазов и устройство запирающих дуг, если движение вдоль звена
происходит с остановками.
Механизм качающей кулисы (рис. 311) может быть спроектирован
с остановками кулисы. На рис. 314 показан кулисный механизм,
у которого на угле <р2 поворота кривошипа 2 кулиса 3 будет непод-
вижной. Совершенно очевидно, что на участке СС° кривая К3 будет
окружностью радиуса, равного АС.
Угол передачи у23 в каждом рассматриваемом положении опреде-
лится, если соединить точку К3(С) (рис. 310, б) с мгновенным центром
вращения Рй и с точкой В. На рис. 310, б этот угол является доба-
вочным до 180°, Если задано минимальное допустимое значение ут)П
§ И]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
229
угла передачи, то точки линии зацепления, удовлетворяющие этому
условию, найдутся путем следующего построения. Пусть заданы
Рис. 315.
(рис. 315) положения центров вращения А и В звеньев 2 и 3 и известна
функция передаточного отношения i32 = z32 (<р.г).
шипа АС, определяемого углом <р2, находим
по функции /34=132(^2) положение мгновен-
ного центра вращения Ро. Далее, обычным
методом строим на отрезке РЬВ окружность
центра О, вмещающую угол ymin, и симметрич-
ную ей окружность центра О'. Из точки А
проводим направление звена АС под углом
к линии ВР6. Тогда точка /С8(С) звена 2 мо-
жет быть выбрана на проведенной прямой в
пределах отрезка (ab). Из чертежа видно, что
выбрав точку Kt{C) в пределах указанного
участка, мы получим угол у33 всегда большим
угла Yniin. Если аналогичные построения вы-
полнить для последующих положений меха-
низма, то может быть выделена область, в кото-
рой должна находиться окружность, описанная
Для положения криво-
Рис. 316.
из центра А радиусом, равным длине АС.
16°. Переходим к рассмотрению задачи о проектировании профиля ку-
лисы механизма с поступательно движущейся кулисой вида, показанного
на рис. 51 и 52. Так же как и в ранее рассмотренном виде механизмов,
закон Движения в форме функции положения 8з = 83(<р.г) может быть
задан только на интервале изменения <р2, равном 180° (рис. 316),
230 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [ГЛ. IV
т. е. функция положения может быть задана на любой сумме
углов:
?! + = ?! + Ч>" = <?1П + ?sv = + <rfv = 180°.
На рис. 317 показано построение профиля кулисы 3 с помощью
линии зацепления, которой будет окружность, описанная радиусом АК*
Профиль Д'з построен для функ-
ции положения s3 = s3(<p8), по-
казанной на рис. 318 на интер-
вале, равном 180°, от положе-
ния 1 до положения 7. Для на-
хождения точки Kll профиля Кз,
приходящей в соприкосновение
в точке С2> проводим через
точку прямую, параллель-
ную оси движения звена 3, и
на этой прямой откладываем
из точки С2 отрезок (С2, К"),
пропорциональный перемеще-
нию звена 3 (рис. 318)
на угле поворота звена 2.
Полный профиль К3 кулисы 3
построен во втором положе-
нии механизма. Функция $3 =
= $s((Pa) на интервале, рав-
ном 180°, от положения 7 до положения 1, показана на рис. 318
пунктиром. Та же задача может быть решена и методом обраще-
ния движения. Для этого сообщаем всему механизму скорость — ®3,
равную и обратную скорости движения звена 3. Тогда для опреде-
ления точки /С*1 профиля К3 перемещаем точку А в положение А'
так, чтобы отрезок (А А') был пропорционален перемещению
(рис. 318). Точка С> при этом переместится в положение Ср Далее
§ И]
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
231
поворачиваем отрезок (A'Cj) около точки Л' на угол ср*1. Тогда точка С'
займет положение Д'11. Действительный профиль кулисы определится,
если провести эквидистантные кривые к кривой Ks.
Угол передачи т23 (рис. 319) в каждом рассматриваемом положении
определится, если соединить точку Кч(с) с мгновенным центром вра-
щения Ро и провести через точку Къ прямую К±Е, перпендикулярную
к оси движения звена 3. Если при точ-
ке Ро отложить углы -[min от прямой AD
и провести направление AF звена 2 под
углом <рз к прямой AD, то область воз-
можных положений точки Kt (с) для
рассматриваемого положения опреде-
лится отрезком (ab). Аналогичным по-
строением можно определить область
возможных положений точки звена 2
за полный его оборот.
Кулисные механизмы с двумя по-
ступательными парами вида, показанного
на рис. 59, проектируются аналогич-
ными методами.
Рис. 320.
Рис. 319.
17°. Переходим к рассмотрению вопроса о проектировании профиля
кулис кулисных механизмов вида, показанного на рис. 45, 46, 55
и 61. Кулисы механизмов указанного вида имеют сложное движение.
Профили Кя этих кулис огибают неподвижную точку Kt- Задачей
этих механизмов является воспроизведение заданного движения кулисы.
Это движение может быть задано различно в зависимости от порядка
сочетания пар, из которых образован механизм.
Рассмотрим механизм (рис. 320) вида, показанного на рис. 45.
У этого механизма точка В звена 3 движется по окружности ра«
232 СИНТЕЗ ТРЕХЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНОЙ ПАРОЙ [гл. !V
диуса АВ, занимая положения Вь Вг, В3, ... Пусть точка D звена 3
описывает произвольную заданную кривую. Зная расстояние BiDi,
находим положение точки D на заданной кривой. Пусть это будут
положения: Dit Dt, D3, ... Задаемся положением огибаемой точки АГ2(С),
принадлежащей неподвижному звену 1. Тогда нахождение точек про-
филя Кз кулисы может быть сделано обычным методом, учитывая,
что точка К % (С) будет точкой зацепления для всех положений кулисы.
Так, например, для положения номер десять имеем треугольник
ВцьОюКь Совмещаем сторону BMDl6 этого треугольника с отрезком
Рис. 321.
(/?iZ?i). Тогда точка /С2(С) этого треугольника займет положение С1в,
которое и будет той точкой профиля К3 кулисы, которая в положении
номер десять совпадает с точкой Kt(C).
Аналогичным построением могут быть построены и другие точки
профиля К3. Полученная кривая К3 будет осью кулисы; действи-
тельные ее очертания могут быть получены как эквидистантные кри-
вые, отстоящие на величину радиуса ролика, который можно устано-
вить в точке Кг(С). На рис. 320 для упрощения чертежа это по-
строение не показано. На рис. 321 показано построение профиля Кз
кулисы, когда одна пара будет вращательной, а другая пара будет
поступательной. В этом случае точка В движется по прямой fijp,
занимая положения Вь В%, В3, ... Пусть требуется, чтобы точка D
звена 3 двигалась по дуге а — а окружности. Находим положения
£>!, D& D3, ... на дуге аа. Для нахождения, например, точки С2
профиля Кз кулисы совмещаем сторону В.^^ треугольника В.2О.2Кч
со стороной BJ)i. Точка К2(С) займет тогда положение С2. Анало-
§ Ш
МЕХАНИЗМЫ С ДВУМЯ НИЗШИМИ ПАРАМИ
233
гичным построением можно найти и последующие точки профиля л3
кулисы 3. Действительные очертания кулисы получатся как экви-
дистантные кривые, отстоящие от профиля А"3 на величину радиуса
ролика 4, который установлен в точке A'sCQ.
В заключение рассмотрим еще тот случай механизма, когда непо-
движной будет криволинейная
Рис. 322.
кулиса, как это имеет место, напри-
мер, для механизма, показанного на
рис. 57.
На рис. 322 показано проекти-
рование механизма с неподвижной
криволинейной кулисой по заданной
функции положения звена 3 отно-
сительно звена 2, т. е. когда задана
функция <р32 = <?з2 (?s) (рис. 323). По-
ложения точек Си С2, С3, ... опре-
делятся, если для каждого поло-
жения звена АВ отложить при
точках Ви В9, Вл, ... углы <р*8, <р’*,
... и на проведенных направ-
лениях отложить длину Bfii = Д2С2 = В^С-ь ... Полученные точ-
ки С|, С2, С3, ... определят профиль кулисы. Эквидистантные кри-
вые определятся обычным методом.
ГЛАВА V
СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ
ПАРАМИ И ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ
§ 12. Четырехзвенные механизмы с центроидными парами
1°. Четырехзвенные механизмы с одной центроидной парой, один
из элементов которой является неподвижным, показаны на рис. 84—89.
Общей кинематической схемой этих механизмов будут схемы, пока-
занные на рис. 84 и 88. Рассмотрим вопрос о проектировании подоб-
ных механизмов. Пусть точка В звена 2 (рис. 324) занимает после-
довательно положения В„ В.,, В3,... Точка С звена ВС должна
двигаться по заданной кривой уу. Элемент центроидной пары, принад-
лежащей звену /, задан в виде неподвижной центроиды Ц^я
звена 4. Требуется построить элемент центроидной пары, принадле-
жащей звену 4, т. е. подвижную центроиду Ц<а. Такая задача мо-
жет быть решена следующим методом.
Находим на заданной кривой уу последовательные положения
точки С. Это будут точки Сь С.2, С3„.. Далее, в точках Сь С2,
С3„.. проводим нормали к кривой уу. Эти нормали пересекут центро-
иду Ц1а в точках P't Pl'lt... Для нахождения сопряженных то-
чек it', л’11, .... принадлежащих центроиде £/4п, проводим из
точки С] дуги радиусами C2P|'f С3Р’п, ... и засекаем па них после-
довательно точки л’1, л”1, ... радиусами, равными дугам
о Р|Р” = л]л|[; = о ’г”w"1. .. - Соединив точки л’(
л*^ л*11, ... плавной кривой, получим центроиду Ц1п, образующую
профиль элемента центроидной пары, принадлежащей звену 4. Под-
вижная центроида Uin можетбытыюстроена более точно, еслибудутопре-
делены центры кривизны и радиусы кривизны этойцентроиды(см. § 5,14°).
Для нахождения центра кривизны О’ центроиды Z/4n в первом поло-
жении механизма (рис. 324) откладываем на направлении С{Р^ радиус
кривизны заданной кривой уу в виде отрезка CiO11. В точке PJ вос-
станавливаем к этому отрезку перпендикуляр. Далее, проводим на-
правление СР\ нормали к заданному профилю центроиды Z/4h и от-
кладываем радиус кривизны этого профиля в виде отрезка ОР|.
§ 12] ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ С ЦЕНТРОИДНЫМИ ПАРАМИ 235
Соединив точки О и О11, продолжаем это направление до пересече-
ния в точке D с перпендикуляром к направлению CjO11, восставлен-
ным в точке Р*. Соединив точку D с точкой Сь находим точку О' —
центр кривизны профиля центроиды Ц1п на пересечении направлений
CtD и ОР]. Радиус кривизны центроиды Ц1и в данной точке
будет равен (7Р*.
Проектирование механизмов с кинематической схемой, показанной
на рис. 88, может быть сделано методом, аналогичным тому, кото-
7
Рис. 324.
рый был нами применен к механизму, показанному па рис. 324. При
этом надо использовать метод обращения движения, сообщив всему
механизму угловую скорость, равную и обратную угловой скорости
звена. 1 (рис. 88). Тогда задача сведется к случаю, показанному на
рис. 84.
2°. Для механизмов с двумя центроидными парами с кинематиче-
ской схемой, показанной на рис. 91, обычно заданы элементы центро-
идных пар рр и ЬЬ, принадлежащие неподвижному звену. Далее за-
даны последовательные положения точки В звена 2 и траектория
точки С звена 4 и длина звена ВС. Проектирование профилей аа й
77 элементов центроидных пар, принадлежащих звеньям 2 и 3, сво-
236 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гЛ. V
дится к задаче о построении подвижной центроиды по заданной ру-
летте и может быть сделано так, как это было бы показано на при-
мере механизма (рис. 324).
Механизм с кинематической схемой, показанной на рис. 93, легко
сводится к механизму с кинематической схемой, показанной на
рис. 91, если в первом обратить движение, остановив звено 2.
Четырехзвенные механизмы с центроидными парами могут иметь
не только вращательные, но и поступательные пары или пары каче-
ния и скольжения. Пример такого механизма показан на рис. 123.
Звенья 1 и 2 входят в центроидную пару, звенья 2 и 3 входят в
пару качения и скольжения. В пару качения и скольжения входят
также звенья 3 и 4. Наконец, звенья 4 и 1 входят в поступатель-
ную пару. Проектирование подобных механизмов может быть сделано
общими, рассмотренными выше приемами.
§ 13. Четырехзвенные механизмы с парами качения
и скольжения
1°. Четырехзвенные механизмы с двумя парами качения и сколь-
жения весьма разнообразны. Кинематические схемы этих механизмов
и некоторые примеры показаны на рис. 97—114. Ряд механизмов,
указанных на этих рисунках, может быть спроектирован методами,
изложенными выше в главе IV, так как в основе их лежат трехзвен-
ные механизмы, к которым присоединено одно звено, входящее в
одну низшую пару V класса и одну пару качения и скольжения.
К таким, например, механизмам относятся механизмы, показанные на
рис. 97 и 98. Для этих механизмов, если ведущими будут звенья
2 или 4, то обычно заданными будут: функция положения <р4 = <р4 (<Ра)
(рис. 97) или s4 = s4(<p2) (рис. 98), или функция передаточного отно-
шения /24 = /24(<р2) (рис. 97). Кроме того, обычно задаются профиль
элемента пары качения и скольжения, принадлежащей звену 3
(центр ролика а на рис. 98), и очертания профилей элементов пары,
в которую входят звенья 3 и 4 (рис. 98).
Если ведущим будет звено 3 (рис. 97), то могут быть заданы
функции положений <р2 = <р2(<р3) и <р4 = <р4(<р3) и по одному из про-
филей элементов высших пар, в которые входят звенья 2 и 4. Для
механизмов вида, показанного на рис. 99 и 100, обычно заданы
функции положения звеньев 2 и 4 в их движении относительно
звена 3, т. е. функции — <р23 (<р3) и <р43 = <р43 (<р3) (рис. 99) и
s23 = s23(<p3) и «4з = ®4з(?з) (рис- 100), и профили элементов высших
пар, принадлежащих звеньям 2 и 4. Механизмы вида, показанного на
рис. 101 и 102, представляют собой механизмы смешанного вида,
т. е. для этих механизмов должны быть заданы функции положения
<Рз = ?з(<Ра) и ?4з = ?4з (?s)- Таким образом, задача проектирования
профилей элементов высших пар для рассмотренных механизмов сво-
дится к ранее изложенным задачам.
§ 13] ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 237
Благодаря наличию в механизмах рис. 97—114 двух пар качения
и скольжения, профили элементов которых могут быть спроектиро-
ваны различного очертания, эти механизмы могут воспроизводить
зависимые движения двух ведомых звеньев. Так, механизм, показан-
ный на рис. 100, воспроизводит поступательное движение двух ве-
домых штоков 2 и 4 относительно ведущего корпуса 3. Механизм,
101, воспроизводит
показанный на рис.
мого звена 2 и сложное дви-
жение ведомого звена 4 и т. д.
Если ведомым будет одно зве-
но, то может быть воспроизве-
дено сложное движение этого
звена. Так, например, меха-
низмы вида, показанного на
рис. 103—114, воспроизводят
сложные движения ведомых
звеньев. Так, у механизма, по-
казанного на рис. 104, точка D
звена 3 движется по дуге
круга. При этом кривая К,
принадлежащая этому звену,
проходит через точку L, имею-
щую сложную траекторию, за-
висящую от профиля кулисы,
принадлежащей неподвижному
звену 1. У механизма, пока-
занного на рис. 100, звено 2
имеет сложное движение. Точ-
ка О звена 2 движется по
дуге круга, а точки L и С дви-
жутся по кривым, которые опре-
деляются профилями кулис, при-
надлежащих неподвижному зве-
ну 7. Сложное движение имеют
звенья 3 механизмов, показан-
ных на рис. 106, 110 и 114.
качательное движение ведо-
а
Рис. 325.
2°. Рассмотрим некоторые типовые задачи, связанные с проекти-
рованием механизмов вида, показанного на рис. 103—114. Пусть
требуется спроектировать механизм по схеме, показанной на рис. 104,
по следующим заданиям. Ведомое звено 4 должно точкой G дви-
гаться по дуге круга аа (рис. 325, а) радиуса CG, а точкой L — по
заданной кривой рр. Движение ведомого звена 3 задано в виде функ-
ции положения <рзв = <р32 (<р2) (рис. 325, б). Размеры звеньев 2 и 4
заданы. По заданным углам ср2 производим разметку траекторий аа
и Yf точек О и D. Это будут точки Оь О2, О3, ... и Db Ог, 7Э3, ...
Далее, по известному размеру GxLi звена 4 находим точки Llt Lit
238 синтез многозвенных механизмов с центроидными парами [гл. V
L3, ... на заданной траектории рр точки L. Так как размеры тре-
угольника GiLiMi, образующего звено 4, известны, то находим поло-
жения точки М. Точки ЛД, ЛД, ЛД, ... определят кривую КК,
являющуюся профилем элемента пары качения и скольжения, принад-
лежащего неподвижному звену 1. Действительные очертания кулисы
получатся как эквидистантные кривые профиля КК, если задан ра-
диус ролика а. Для построения профиля
Рис. 326.
К К' элемента пары, прина-
длежащего звену 3, при
точках Dj, Dit D3, ... от-
кладываем углы
<р.'2, ..., взятые с графика
to = ?з2 (<Ps) (Р'’с. 325, б),
от направлений CDlt CDt,
CD3, ... Тогда, если, напри-
мер, при точке Di построить
угол и на проведенном
направлении отложить от-
резок DiL” = DiL1 и соеди-
нить точки Di и Ц с точ-
кой то мы получим тре-
угольник DiL\Li. Если
теперь на отрезке DXLX по-
строить треугольник DiLyL^,
равный треугольнику O2Z.iZ.a,
то определится точка Z.2,
принадлежащая кривой про-
филя кулисы, принадлежа-
щей звену 3. Аналогичным
построением определятся и
последующие точки L'3, L\,
L'f,, ... профиля К'. Действи-
тельные очертания кулисы 3
получатся как эквидистант-
ные кривые к профилю К'.
3°. Пусть требуется
спроектировать механизм ви-
да, показанного на рис. 110, по следующим заданиям. Движение звена 4
(рис. 326, а) задано в виде функции положения <р4 = <р4(<р2)(рис. 326, б).
Движение звена 3 задано движением точки D по дуге окружности аа и
точки С по прямой рр, представляющей собой профиль кулисы. Тре-
буется спроектировать профиль элемента звена 2, входящего в точ-
ке Е в пару качения и скольжения со звеном 3. По известным углам по-
ворота ср’11, <p|v, ... звена 4 находим положения точек Db D3,
D3, ... Далее, находим положения точек Сь С2, С3, ... на прямой рр.
По заданным размерам звена 3 находим траекторию -рТ точки Е и
§ 13] ЧЕТЫРЕХЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 239
ее положения £1; Ег, Е3, ... на этой траектории. Траектория уу бу-
дет линией зацепления пары качения и скольжения. Для построения
профиля элемента пары, принадлежащей звену 2, находим точки
Ei, Е'ъ Е'з, ... этого звена, приходящие последовательно в по-
ложения Ei, Е%, Е3, ... Последнее может быть сделано если, напри-
мер, для положения звена 2, определяемого углом повернуть
треугольник АН(,Е{, в положение АЕ^Нё (рис. 326, а). Аналогично
найдутся и все другие точки профиля К элемента пары. На рис. 326, а
показаны теоретический профиль К кулачка 2 и теоретический про-
филь рр кулисы. Действительные очертания кулачка и кулисы най-
дутся как эквидистантные кривые к профилям К и рр после уста-
новки роликов в точках С и Е.
4°. Рис. 327 иллюстрирует метод проектирования механизма
двойного кулачка вида, указанного на рис. 112. Звено 3 должно
вращаться равномерно около оси В. Звено 4 должно двигаться поступа-
тельно параллельно направлению АВ. Таким образом, точка С звена 3
движется по дуге а круга, занимая положения Сь С2, С3, ...;
точка D звена 3 движется по дуге р, занимая положения £)ь Dit
D3, ..., а точка Е движется по дуге у, занимая положения Et, Et,
Е3, ... При этом дуги р и "( будут дугами равного радиуса и будут
соответственно равны дугам DiD^ = у_, ЕгЕг, DtD3 = ЕгЕ3, ...
Таким образом, дуги и и у будут линиями зацепления кулачков, при-
надлежащих звену 2. Для построения профилей К и К' элементов
240 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ парами [гл. V
пар, принадлежащих кулачкам, находим точки С[, Сг, С'3, ... и
точки Е\, Е?, Е'3, ..., последовательно приходящие в положения Ci,
С3, С3, ... и Е1г Е2, Е3, ... Последнее может быть сделано, если,
например, для положения звена 2, определяемого углом у™, повер-
нуть четырехугольник ЛС4С4Е4 в положение AC4HJE4. Аналогично
найдутся и все другие точки профилей К и К’ элементов пар, при-
1 г з « 5 е <рг
Рис. 328.
надлежащих кулачкам. Профили К и К' будут теоретическими про-
филями кулачков.
5°. На рис. 117—122 показаны кинематические схемы и примеры
механизмов, которые образованы двумя парами V класса и четырьмя
парами качения и скольжения. Подобные механизмы могут быть
спроектированы методами, разобранными выше. В качестве примера
рассмотрим механизм, представленный на рис. 121 и рис. 122.
Пусть движение точек В и С (рис. 328, а) задано функциями
положения 5в = 5в(<р2) и $с = $с(<ра) (рис. 328, б). При этом точки
В и С движутся по взаимно-перпендикулярным прямым аа и рр, за-
нимая на них положения В2г В3, ... и Cj, С2, С3, ... Тогда по
заданным размерам звеньев 3 и 4 находим траекторию •pf точки D,
14] ПЯГИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 241
траекторию 88 точки Е и траекторию ее точки F и находим поло-
жения Dlt Dit D3, Еь Е2, Е3, ... и Fit Ft, Ел, ... точек D, Е
и F. Траектории 88 и ее точек Е и F будут линиями зацепления
кулис или профилей пазовых кулачков, принадлежащих звену 2. Для
построения профилей К и К' элементов пар, принадлежащих кули-
сам, находим точки Е\, Е'ъ Е'з,... и Fj, F'i, F3, .последовательно
приходящие в положения Е,, Е2, Е3, ... и Fi, F2, F3, ... Последнее
может быть сделано, если, например, для положения звена 2, опре-
деляемого углом (рис. 328, а), повернуть треугольники All,tEt и
на угол соответственно в положения АЕ^Е'ц и AEtFi
Аналогично найдутся и другие точки профилей К и К'. В точках В,
С, Е и F могут быть установлены ролики. Проведя эквидистантные
кривые, получим очертания кулис, в которых будут скользить ро-
лики а. Вопрос об углах передачи подобных механизмов должен
рассматриваться отдельно для каждой конкретной схемы механизма,
так как мы имеем несколько ведомых звеньев и большое количество
параметров, от которых будут зависеть углы передачи. В каждом
конкретном случае всегда варьированием этих параметров можно
обеспечить наилучшие условия работы механизма.
§ 14. Пятизвенные механизмы с парами качения и скольжения
Г. Пятизвенные механизмы с одной парой качения и скольжения
показаны на рис. 124—129. Кулачковый механизм, показанный на
рис. 124, легко может быть спроектирован методами, указанными в
§ И, так как если задана функция положения звена 5, г. е. функ-
ция % = (<р2), то легко может быть построена функция положения звена 3,
т. е. функция (<р2), после чего проектирование механизма сводится
к задаче о проектировании трехзвенного кулачкового механизма. Теория
проектирования механизмов мальтийских крестов с приводом от шарнир-
ного четырехзвенника (рис. 125) подробно изложена в работе [50а]. В дан
ном пара графе’остановимся на методике проектирования кулачкового меха-
низма (рис. 126), профиль кулачка которого воздействует на точку
звена, имеющего сложное движение. Такого вида механизмы исполь-
зуются в ряде машин для воспроизведения качения коромысла по за-
данному закону. Пусть движение коромысла 5 (рис. 329, а) задано
функцией положения <рв = <ps (<р2) (рис. 329, б). Г1о заданной функции
cps = <р5(<р2) находим положения Сц С2, С3, ... точки С на дуге а,
описанной радиусом ВС. Далее, через точки С1Л С2, С3, ... проводим
прямые, проходящие через точку А, и на этих прямых откладываем
отрезки (CjDj) = (С2С2) = (С3Е3) ..., представляющие собой постоян-
ное расстояние центра D ролика от точки С. Точки Dlt Dt, D3, ...
дадут нам линию зацепления рр. Далее, обычными методами находим
точки профиля КК кулачка. Для этого, например, для положения 3
повертываем треугольник ADtD3 на угол <р],и в положение AH3D3.
242 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
Этим самым определяется положение точки D'3 профиля КК кулачка,
которая придет в зацепление с центром ролика D в точке Da линии за-
цепления. Аналогично найдутся и другие точки профиля АТС. В
точке D устанавливается ролик и очертание действительного про-
филя кулачка может быть получено как эквидистантная кривая к
кривой КК.
Рис. 329.
2°. Большую группу пятизвенных механизмов с одной парой ка-
чения и скольжения образуют зубчато-рычажные механизмы вида,
показанного на рис. 127—129. В этих механизмах два звена пред-
ставляют собой круглые цилиндрические зубчатые колеса с внешним
или внутренним зацеплениями. Этими механизмами могут быть вос-
произведены весьма разнообразные формы движения ведущих и ве-
домых звеньев. Данные механизмы можно с точки зрения задач про-
ектирования рассматривать как механизмы, в основе которых лежит
трехзвенная кинематическая цепь, состоящая из двух круглых ци-
линдрических зубчатых колес и звена, входящего в кинематические
пары с этими колесами.
На рис. 127 и 128 это будут колеса 3 и 5 и звено 4. На
рис 129 это будут колеса 1 и 3 и звено 2. К этой трехзвенной
цепи присоединяется двух поводковая группа, состоящая из двух
звеньев I и 2 на рис. 127 и 128 и 4 и 5 на рис. 129. Присоедине-
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 243
ние звеньев двухповодковых групп может быть сделано к различ-
ным звеньям трехзвенной кинематической цепи и в различных точ-
ках этих звеньев, позволяя осуществлять сложные движения звеньев
присоединенной двухповодковой группы.
Как было показано выше (§ 11), относительное движение круг-
лых зубчатых колес, входящих в трехзвенную кинематическую цепь,
сводится к качению двух центроид, принадлежащих этим колесам и
представляющим собой две окружности. Траектории, описываемые
Рис. 330.
точками этих окружностей, будут циклическими кривыми. Рассмот-
рим вопрос о форме и уравнениях этих кривых. На рис. 330 пока-
заны траектории, описываемые точками D, О' и D" окружности 2 ра-
диуса R3, которая перекатывается без скольжения по неподвижной
окружности 1 радиуса Rj. Точка D, лежащая на окружности 2, опи-
сывает траекторию а, являющуюся эпициклоидой. Точка £)', ле-
жащая вне окружности 2, описывает траекторию с, являющуюся уд-
линенной эпициклоидой. Наконец, точка ЕГ, лежащая внутри окруж-
ности 2, описывает траекторию Ь, являющуюся укороченной эпи-
циклоидой. На рис. 330 соотношение п между радиусами равно
п = — = 2. Поэтому эпициклоиды состоят из двух симметрично
расположенных равных ветвей. Количество ветвей на всей окружно-
сти будет целым, если отношение п будет целым числом. При дру-
гих отношениях п могут быть получены эпициклоиды с другим чис-
лом ветвей. При дробных отношениях п могут быть получены и более
сложные формы эпициклоид, имеющие точки самопересечения и точки
244 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
возврата, положения которых будут определяться отношением п и
выбранным положением точки D на подвижной окружности.
На рис. 331 показаны траектории, описываемые точками D, D' и
D” при качении окружности 2 по окружности 1. Точка D описывает
гипоциклоиду а, точка D' описывает удлиненную гипоциклоиду с и
точка D" описывает укороченную гипоциклоиду Ь. Отношение п
равно п—~ = ^.
Кч
Рис. 331.
Если отношение п равно п=1, то эпициклоида (рис. 330) пере-
ходит в кардиоиду а (рис. 332). Кривые b и с будут соответственно
укороченной и удлиненной кардиоидами («улитки Паскаля»), При
отношении п, равном п — 2, гипоциклоиды переходят в эллипсы а
(рис. 333), а точки, лежащие на окружности, описывают прямые Ь,
проходящие через центр окружности радиуса
3°. Рассмотрим, каковы будут уравнения эпициклоид и гипоцик-
лоид, описываемых точками рассмотренных выше механизмов. Пусть
точка D (рис. 334) переместилась в положение £)0, а точка D', рас-
положенная на расстоянии а от точки D, — в положение Do. Тогда
из очевидных соображений получим следующие выражения для коор-
динат точки Z)';
X — (Ri 4- Ri) cos я 4- (Rt fl) sin | <p — — ajj =
= (/?i 4~ Ri) cos я — (/?2 4- a) cos (a 4” <?) (5.1)
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 245
Рис. 332.
246 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ {гЛ. V
И
У = (Rt -|- R-4 sin <Х -j- (R2 4- a) cos [? — 0г — а\| =
= (Rt J- R2) sin а — (R3 -j- a) cos (я ?)> (5.2)
Углы а и <p связаны уравнением
/?> ?’
Поэтому уравнения (5.1) и (5.2) можно представить так:
x = (Rl + ^)cos^? —№4-a)cos (5.3)
Ai Ai
И
J = (Ri + Ri)sin ^<j> — (R2 + a) sin (5.4)
Это будут общие уравнения эпициклоид в параметрической форме.
Если точка, описывающая эпициклоиду, лежит на перекатывающейся
окружности, то величина а будет равна «—О и уравнения (5.3) и
(5.4) примут вид:
x = (/?14-R2)cos^t — tt2cos^-t—(5.5)
Ai Ai
И
У = (/?, + R2) sin ср -R, sin ср. (5.6)
А1 А1
При эпициклоидальном движении радиус Re круга катания (§ 5,
15°) будет равен;
<б-7>
и будет всегда постоянен. Точно так же постоянным будет и диа-
метр d поворотного круга:
d=Re. (5.8)
Радиус кривизны в любой точке эпициклоиды может быть опре-
делен графически так, как это было показано на рис. 185 (§ 6, 8е).
Общие уравнения гипоциклоиды в параметрической форме могут
быть получены из аналогичных соображений.
Имеем:
х = № — Rs) cos ср -f- (R2 4- d) cos Rt^Rs <p (5.9)
At r Al
И
j = (R1-^)sin^<p-(R.24-a)sin^i^?, (5.10)
Для точки, лежащей на окружности 2, будем иметь:
х = (Ri-Rt) cos 4- Rt cos (5.11)
Al Ai
И
У = (Ri — Ra) sin § cp - R, sin ^=^-2 <p. (5.12)
Ai At
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 247
При гипопиклоидальном движении радиус Ro круга катания будет
равен:
«•=т£Х ₽-13)
Радиус кривизны любой точки гипоциклоиды может быть опреде-
лен графически по способу, указанному в § 6, 8°.
Уравнения кардиоид, описываемых точкой D', получатся, если в
уравнениях (5.3) и (5.4) положить Ri = R.2 = R. Имеем тогда:
x = 2Rcoscp— (R a) c°s 2<р (5.14)
и
_у = 27? sin <р — (R -f- й) sin 2<р. (5.15)
4е. Циклические кривые обладают важным свойством, заключаю-
щимся в том, что каждая из них может быть образована двумя раз-
ными парами сопряженных окружностей. Пусть точка D (рис. 335),
Рис. 335.
принадлежащая подвижной окружности 2, описывает при перекаты-
вании по неподвижной окружности 1 эпициклоиду а. Присоединим
в точках D и А двухповодковую группу, состоящую из звеньев 4
и 5, размеры которых соответственно равны DE = BA и AE—BD.
Тогда фигура ABDE будет всегда параллелограммом. Точку D соеди-
няем с мгновенным центром вращения C(P2t) и продолжаем это напра-
вление до пересечения в точке F с направлением ЕА. Из подобия
треугольников ACF и BCD имеем:
AF _BD
~АС~ ВС’
248 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
Рис. 336.
гипоциклоиды. Для гипоциклоиды
или
Ri — AF—= = = const, (5.16)
DG /\2 Лз
где b — расстояние точки D от оси В колеса 2.
Далее имеем:
^ = EF = EA^AF = b-\-b (7?tR2) = const. (5.17)
г\2
Проведем окружности радиусами R[ = AF и R^ — EF из точек А
и Е. Точка F соприкосновения этих окружностей будет мгновенным
центром вращения Pit звена 4 относительно неподвижного звена 1.
Последнее непосредственно
следует, если учесть, что
точки А, В, С, D и Е
суть мгновенные центры
вращения: PS|, Р23, Р21, Р42
и Р48.
Таким образом, если точ-
ку D считать принадлежа-
щей окружности 2', то при
качении окружности 2' по
неподвижной окружности
точка D опишет ту же эпи-
циклоиду а. Следовательно,
любая эпициклоида может
быть получена как траекто-
рия точек, принадлежащих
двум различным перекаты-
вающимся окружностям.
На рис. 336 показано
аналогичное построение для
соответственно радиусы R{ и R%
будут равны:
R’i = b ~ = const (5.18)
Лз
И
R'i = (/?1 — R?) = const, (5.19)
где b — расстояние точки D от оси В колеса 2.
Если точка D, описывающая эпициклоиду а, лежит на окружности 2
(рис. 337), то Ri = b и уравнения (5.16) и (5.17) принимают вид:
и
Ri — R\ -f- R&
§ 14[ ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 249
Следовательно, окружность Г совпадает с окружностью 1, и
эпициклоида а может быть воспроизведена как траектория точки D,
принадлежащей окружностям 2 или 2' при их качении по неподвиж-
ной окружности 1 (Г).
На рис. 338 показана эпициклоида а, полученная как траектория
точки D, принадлежащей окружностям 2 или 2' при их перекатыва-
нии по неподвижной окружности 1(1') с отношением п радиусов Ri
и равным п — = 2.
Рис. 337.
Рис. 338
Если точка D, описывающая гипоциклоиду а, лежит на окружно-
сти 2 (рис. 339), то b—Ri и уравнения (5.18) и (5.19) принимают
вид:
R't = Ri
и
R* = Rt — Rt.
Следовательно, окружность Г совпадает с окружностью 1 и гипо-
циклоида а может быть воспроизведена как траектория точки D,
принадлежащей окружностям 2 или 2' при перекатывании по непо-
движной окружности 1 (Г),
На рис. 340 показана гипоциклоида а, полученная как траектория
точки D, принадлежащей окружности 2 или 2' при их перекатывании
по неподвижной окружности 1 (Г) с отношением п радиусов Ri и R.it
равным
250 синтез многозвенных механизмов с центроидными парами [гл. V
5°. Мы рассмотрели выше (§ 14, 2°, 4°) основные свойства кри-
вых, описываемых точками звеньев трехзвенной кинематической цепи,
Рис. 339.
Рис. 340.
состоящей из двух круглых цилиндрических колес и промежуточного
звена, входящего во вращательные пары с этими колесами.
Если в указанной кинематической цепи присоединить двухповод-
ковую группу, то мы получим пятизвенный механизм одного из видов,
показанных на рис. 127, 128 и 129. Из этих механизмов практический
интерес представляют механизмы для продолжительного выстроя ведо-
мого звена. Один из таких механизмов показан на рис. 341. Окруж-
ность 2 катится без скольжения по окружности 1. При передаточном
§14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 251
отношении i12 для колес радиусов и Rit равном Z12 = ^ = -g-,
точка С окружности 2 описывает гипоциклоиду, состоящую из трех
ветвей. Шатун 4 входит в точке С во вращательную пару с окруж-
ностью 2. Если подобрать длину b шатуна так, чтобы окружность,
описанная из точки D радиусом, равным Ь, проходила через три
точки С, С и С" гипоциклоиды, то ползун 5 будет находиться почти
в покое за время движения точки С по участку СС'С” гипоциклоиды.
Более точное приближение окружности к гипоциклоиде может быть
получено по методу Чебышева Проведенные исследования показы-
вают, что приближение по Чебышеву мало отличается от подбора
дуги окружности, проходящей через три точки гипоциклоиды.
Рассмотрим, как определяется длина b шатуна для гипоциклоид,
описываемых для различных значений ilt точкой С, лежащей на окруж-
ности 2 (рис. 342). Из треугольника ACD имеем:
= RI + + (Ri — 2R2)]3 — 2Rt [ft 4- (Ri — 2R2)] cos a. <5.20)
Имея в виду, что
Rs =
и a —
получаем из уравнения (5.20):
Ra . 1 + (1 — 2<1з)8 — 2 (1 —t12) cos 7tfls 9n
2«i2 cos Tt/12 — (1 — 2/j2) " 1-7
Угол у (рис. 342) поворота шатуна определится из условия
п
sin 7 = sin та12. (5.22)
Полные углы поворота звена 3 около точки А и шатуна 4 около
точки D за время выстоя ползуна 5 будут равны 2a и 27.
252 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
Для механизма, показанного на рис. 341, имеем и а = 60°.
О
Из уравнений (5.20) и (5.21) получаем, что длина b шатуна будет
равна Ь== 7Д2 и угол у равен 7 «а 14°. Выстой ползуна 5 со-
Рис. 343.
ответствует углу поворо-
та а звена 3, равному
а =120°, т. е. при равно-
мерном вращении звена 3
время выстоя будет равно
одной трети полного цикла
движения механизма.
Для механизма, прказан-
ного на рис. 343, имеем =
= А- и а = 45°. Из уравне-
ний (5.20) и (5.21) получаем,
что длина b шатуна 4 будет
равна &^5,247Д2 и угол у
равен т=32°40'. В этом
механизме вместо ползуна
установлено коромысло 5,
которое будет двигаться с
длительной остановкой.
Для г1а = -|- угол а бу-
дет равен а = 30°, дли-
на b шатуна будет равна
b лз 4,696Да и угол у будет равен у=39°40'. Таким образом, при
уменьшении уменьшается длина b шатуна и увеличивается угол 7.
На рис. 344 показан механизм, у которого использованы участки
и 88 удлиненной гипоциклоиды, описываемой точкой D окружности 2.
§14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 253
На этих участках гипоциклоида весьма близко приближается к пря-
мым. Присоединяя к механизму • двухповодковую группу с дву-
мя поступательными парами,
можно осуществить движе-
ние звена 5 с двумя останов-
ками, когда точка D бу-
дет двигаться по участкам
РР и 88.
6°. Пятизвенные меха-
низмы, в состав которых
входит трехзвенная кинема-
тическая цепь с двумя низ-
шими парами и одной парой
качения и скольжения, мо-
гут быть использованы и
для воспроизведения слож-
ных траекторий. На рис. 345
показан пример механизма
данного вида с двумя круг-
Рис. 345.
лыми цилиндрическими ко-
лесами и нанесены траекто-
рии, описываемые отдельными точками звеньев этого механизма.
Уравнения этих траекторий являются весьма сложными, поэтому
их построение обычно ведется
графически. При необходимо-
сти более точного построения
этих траекторий по точкам
можно воспользоваться анали-
тическими выражениями для ко-
ординат точек траекторий. В ка-
честве примера рассмотрим общий
случай пятизвенной цепи, показан-
ной на рис. 346, для которой
требуется найти уравнения, связы-
вающие координаты точки Е, если
функция передаточного отноше-
ния z32 = z3g (<р2) звеньев 2 и 3
является заданной. Из рис. 346 следует:
х = /j cos <ра -ф- Z4 cos ср42
и
У = 4 Sin <р2 -ф- Z4 sin <р42.
Далее, . . ,
Ч----X----COS срз -j- ZB COS <рвз
и
J = Z3sin <р3 4-ZB sin <р83,
где Zi, Z2, Z3, Z4 и Z8 — соответственно длины звеньев цепи.
(5.23)
(5.24)
254 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
Исключая из уравнений (5.23) и (5.24) углы и <рвз, после
несложных преобразований получаем:
х2 _j_ — 24 (х cos <f>2 У sin ?«) = ° (5.25)
и
(Л-2 4-У) 4- II4- II — 4 4- 24 (х cos <р3 — у sin <р3) —
— 2ltx — 21^з cos <р3 = 0. (5.26)
Вычитая из уравнения (5.25) уравнение (5.26), получаем:
Ч — 4 —1\ — 4 — 4 4~ 2'ri-v + 2/iZ3 cos <р3 — 24 (х cos 4-у sin tp4) —
— 2/3 (х cos ср3 —у sin ср3) = 0. (5.27)
Таким образом, мы имеем три уравнения — (5.25), (5.27) и уравне-
ние, связывающее углы и <р3:
<Рз = 4~ Тз’ (5.28)
’2
где и <р3 — углы, определяющие начальные положения звеньев 2 и 3.
Если из уравнений (5.25) и (5.27) исключить углы и <р3; то
мы получим уравнение траектории точки Е. Для частного случая,
когда величина функции передаточного отношения 133 постоянна,
т. е. звенья 2 и 3 представляют собой круглые, цилиндрические
колеса, вопрос о порядке уравнений траекторий точки Е рассмотрен
был В. В. Добровольским [18и].
Практически подсчет координат точки Е удобнее вести последо-
вательно. Задаваясь значениями угла <р2, находим из уравнения (5.28)
значения угла <р3. Подставляя их в уравнение (5.27), находим выра-
жение для х через у. Подставляя его в уравнение (5.25), получим
квадратное уравнение относительно у, из которого определится ко-
ордината у. Два значения для у будут соответствовать двум воз-
можным способам присоединения двухповодковой группы CED и CE'D
(рис. 346).
Рассмотрим вопрос о проектировании подобных механизмов. Пусть
требуется воспроизвести траекторию ее точки Е (рис. 347), пред-
ставляющую собой две дуги окружности, описанные из точек Ot и О2.
Так как задана незамкнутая траектория, то очевидно, что звенья 2
и 3 будут иметь качательное движение.
Выбор размеров звеньев 1, 2, 3, 4 и 5, вообще говоря, может
быть произвольным, но практически эти размеры выбираются из раз-
личных конструктивных соображений. В частности, на рис. 347 пол-
ные углы поворота звеньев 2 и 3 выбраны соответственно равными
120 и 40°, углы поворота звена 2, соответствующие положениям 1,
с
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 255
2, 3, ... , равны между собой. Тогда, описав окружность радиусом
AD и разметив положения точки D, задаемся длиной звена DE и
размечаем заданную траекторию ее. Далее, подбираем размеры звеньев
4 и 3 так, чтобы угол размаха звена ВС равнялся 40°. После этого
находим положения точки С. Таким образом, определится функция
положения <р3 = (<р2). Зная функцию <р3 = <f>3 (<р2), нетрудно ранее
изложенными методами спроектировать трехзвенный механизм, воспро-
изводящий эту функцию. Это можно сделать, спроектировав некруг-
лые секторы или кулачковый механизм, или криволинейную кулису.
На рис. 347 передача движения между звеньями 2 и 3 осуществляет-
ся с помощью кулисы, жестко связанной со звеном 3. воздейст-
вующей на ролик установленный в точке F. Построение ведется
с помощью линии зацепления, которой будет дуга окружности FXFS.
Так, точка кулисы, приходящая в зацепление в точке D^Fi), най-
дется, если сторону BCi треугольника BCiFi совместить со стороной
ВС* Аналогично определятся точки Fi, F'3, ... профиля кулисы.
В некоторых счетно-решающих устройствах, математических машинах и
механизмах приборов, подъемных механизмах сельскохозяйственных
машин ставится задача о синтезе передаточного механизма для точ-
ного воспроизведения зависимости, заданной в форме алгебраического
или трансцендентного уравнений. Задача эта может быть решена с
помощью механизмов с некруглыми колесами (§ 8). Та же задача
может быть решена с помощью пятизвенного кулисного механизма,
что является в некоторых случаях более простым с точки зрения
практического осуществления, так как не требует нарезания
зубьев.
256 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [ГЛ. V
На рис. 348 показано проектирование пятизвенного кулисного
механизма данного вида. Пусть, например, требуется спроектировать
Рис. 348
механизм, который
следующего вида:
воспроизводит зависимость в форме полинома
JL 2
у=ах3 -\-Ьх'л -j-cx,
где а, b и с — заданные постоянные. 4
Величина х вводится в виде угла <р2 поворота звена 2, а вели-
чина у должна быть получена в виде угла поворота.<р3 звена 3.
Таким образом, имеем:
= х и =у.
Следовательно:
-I L
= P<f>2 -J- Q<P2 И- (5.29)
1 а
3 3
где P=a—, Q = b—, /? = с — суть постоянные, в которых [х2"и
рз Из Из
(т3 — масштабы углов поворота ср2 и <s3. Для механизма, показанного
на рис. 348, постоянные Р, Q и R были приняты равными P=Q =
= R=\. Примем начальные углы положений звеньев <р2 и ©3
равными <р0 (рис. 348). Длины звеньев АС и ВЦ примем равными
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 257
AC = BD. Размечаем положения точек С и D так, чтобы удовлет-
ворялось условие (5.29). Получаем точки Cj, С2, С3, ... и им соот-
ветствующие точки Db D-i, D3, ... Далее, в точках С и D присо-
единяем двухповодковую группу CED и строим траекторию ее точки
Е. Звенья 4 и 5 группы CED выбраны равными, т. е. CE = DE.
Для того чтобы воспроизвести заданные (5.29) условия движения,
звено 5 снабжаем кулисой, скользящей по ролику 6, центр F кото-
рого принадлежит неподвижному звену 1. Для того чтобы найти
точки Fb F2, F3, ... профиля кулисы, поступаем следующим образом.
Пусть, например, требуется найти точку F4 кулисы, которая совпа-
дает с точкой F в положении, когда звено ED занимает положение
ErJJr,. Соединив точки F4 и О4 с точкой F, получим треугольник
EiPiF. Строим на стороне EiD\ треугольник EiDiFlt равный тре-
угольнику ElDsF, и тем самым определяем положение точки F4.
Аналогично найдутся и другие точки профиля криволинейной кулисы,
принадлежащей звену 5. Зависимость (5.29) между углами <р2 и <р3
нами была выбрана произвольно. Нетрудно видеть, что механизмом
рассмотренного вида может быть осуществлена любая зависимость,
заданная алгебраическим или трансцендентным уравнением, в котором
одно переменное может быть выражено через другое.
7°. Проектирование пятизвенных механизмов с тремя (рис. 130),
с пятью (рис. 133) или с семью (рис. 135) парами качения и сколь-
жения может быть сделано общими методами, изложенными нами выше.
В качестве примера рассмотрим проектирование механизма с пятью
парами качения и скольжения вида, показанного на рис. 133. Пусть
требуется воспроизвести сложное движение звена 5 (рис. 349) так,
чтобы точки F и G описывали заданные траектории аир. Ведущее
звено 2 имеет равные углы поворота, соответствующие равным путям,
проходимым точкой F. За полный ход в одном направлении точки F
звено 2 должно повернуться на угол, равный 180°. По заданным по-
ложениям Fb Fit F3, ... точки F находим положения Gb G2, G3, ...
точки О и положения Н\, H.L, Н3, ... точки Н. Далее, со звеньями
3 и 4 жестко скрепляем прямолинейные кулисы, в которых скользят
ролики с центрами в точках F и G. На звеньях 3 и 4 выбираем
точки Д и Е] й находим обычным методом точки D\, D?, D3, ... и
Е{, Е'ъ Е'з, , принадлежащие теоретическим профилям 2' и 2"
кулачков, жестко связанных со звеном 2. Зная положения точек
Н\, Нг, На, ... звена 5, легко найти точки Н{, Нъ На, • • • , при-
надлежащие теоретическому профилю 2"', также жестко связанному
со звеном 2. Построение дано для половины оборота звена 2.
Мы не рассматриваем подробно вопросы проектирования шести-
звенных механизмов с большим количеством звеньев, так как их
проектирование в большинстве случаев сводится к ранее рассмот-
ренным задачам.
Так, например, на рис. 350 показано проектирование шестизвен-
ного механизма по следующим заданиям. Точка С ведущего звена 2
9 И. И. Артоболевский
258 СИНТЕЗ МНОГОЗВЕННЫХ МЕХАНИЗМОВ С ЦЕНТРОИДНЫМИ ПАРАМИ [гл. V
на угле поворота в 180° проходит равные пути, занимая положения
Сь С2, С3, ... Ведомое звено 6 за угол поворота звена 2 на 60°
(из положения АС\ в положение АС3) должно переместиться вверх
в направляющих F на величину EiE3. Далее, на следующем угле
поворота звена 2 в 30’ (из положения АС3 в положение ДС4)
звено 6 должно переместиться вниз на величину E3E^ = EiE3. На-
конец, на следующем угле поворота звена 2 на угол в 90° (из по-
Рис. 349.
ложения ACi в положение ДС7) звено 6 должно быть неподвижным.
Спроектируем механизм по следующей схеме. В основу механизма
положим пятизвенный механизм ACEDB, у которого точка Е должна
описывать траекторию, состоящую из отрезков двух взаимно-перпен-
дикулярных прямых Еу и Ех. По заданным положениям Cit С2, С3, ...
точки С находим положения Еь Eit Е3, .’.. точки Е. Далее, задаваясь
длиной звеньев 5 и 3, находим положения Db D3, D3, ... точки D
на окружности, описанной радиусом BD. Таким образом определится
функция положения <s3 = <s3 (ц>2) звеньев 2 и 3. По функции <s3 = <р3 (<s2)
методами, рассмотренными выше, строим профиль кулисы, принадле-
жащей звену 2, воздействующей на ролик, установленный в точке D
§ 14] ПЯТИЗВЕННЫЕ МЕХАНИЗМЫ С ПАРАМИ КАЧЕНИЯ И СКОЛЬЖЕНИЯ 259
звена 3. Со звеном 6 жестко связана прямолинейная кулиса, ось
которой параллельна направлению Ех. Нетрудно видеть, что при
Рис. 350.
прохождении точкой Е пути Е^Е^, звено 6 будет двигаться вверх
вдоль направления Еу. Далее, звено 6 будет опускаться при прохо-
ждении точкой Е пути EsEt. При прохождении точкой Е пути EjEj
звено 6 будет неподвижным.
9*
ГЛАВА VI
НЕКОТОРЫЕ ЗАДАЧИ СИНТЕЗА МЕХАНИЗМОВ С НИЗШИМИ
ПАРАМИ ДЛЯ ТОЧНОГО ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
§ 15. Общие методы решения
1°. Выше было показано, что воспроизведение любой заданной
кривой может быть выполнено с помощью механизмов, в состав ко-
торых входят высшие и низшие кинематические пары. Механизмы
этого вида обладают рядом достоинств, заключающихся в возмож-
ности воспроизведения весьма сложных кривых как траекторий от-
дельных точек звеньев. Это могут быть как алгебраические, так и
трансцендентные кривые. Порядок и вид этих кривых, вообще говоря,
могут быть любыми.
Одновременно с большими достоинствами механизмов, в состав
которых входят высшие пары, они обладают и серьезными недостат-
ками. Высшие пары этих механизмов требуют кинематического или
силового замыкания. Точность воспроизведения заданной кривой
в механизмах, образованных одними только низшими парами, обычно
будет большей, чем у механизмов с высшими парами. Крупнейшим
недостатком механизмов с высшими парами является трудность их
перенастройки по различным параметрам воспроизводимых кривых.
В большинстве случаев перенастройка этих механизмов требует смены
элементов высших пар, в то время как при перенастройке механизмов с
одними низшими парами требуется только изменение длин звеньев
или порядка их соединения. Последнее обстоятельство имеет особое
значение при проектировании приборов и машин-автоматов, в которых
требуется гибкость в изменении форм и режимов движения рабочих
органов.
Поэтому важное место в теории синтеза механизмов в ближай-
шие годы должно занять развитие методов синтеза механизмов с
низшими парами, выполняющих заданные движения в виде траекто-
рий, описываемых отдельными точками звеньев механизмов или ме-
ханизмов с простейшими элементами высших пар (например, круглыми
зубчатыми колесами).
2‘. В своей работе В. В. Добровольский [18е] различает четыре
метода образования кривых и соответственно получения механизмов
§ 15] ОБЩИЕ МЕТОДЫ РЕШЕНИЯ 261
для их воспроизведения: метрико-синтетический, аналитический, про-
ективный методы и метод преобразований.
Если обратиться к многочисленным исследованиям, посвященным
теории алгебраических и трансцендентных кривых, то можно эти ис-
следования разбить на две группы. К первой группе относятся ис-
следования, в которых применяются общие методы дифференциальной
геометрии *). Ко второй группе относятся исследования, в которых
используются общие методы проективной геометрии. С этой точки
зрения нам кажется недостаточно оправданной дробность деления
методов проектирования, установленная В. В. Добровольским. В самом
деле, едва ли есть необходимость с точки зрения синтеза механиз-
мов разделять метрико-синтетический метод и аналитический (в тер-
минологии В. В. Добровольского), так как в том и другом методах
одновременно используются уравнения кривых и геометрические
методы их построения. В этом отношении очень характерна цитиро-
ванная выше работа Г. Дориа, в которой эти методы исследования
кривых не разделяются, а синтезируются. Точно так же любой
из механических преобразователей можно рассматривать как с пози-
ций дифференциальной, так и проективной геометрии. Поэтому мы
считаем более правильным методы построения механизмов для вос-
произведения кривых разбить только на две группы. Первая группа ме-
тодов относится к дифференциально-алгебраическим методам, т. е. ме-
тодам, использующим дифференциальную геометрию, и вторая группа
методов, которая использует кинематическую геометрию, т. е. чисто
синтетические приемы решения задач.
Применение методов проективной геометрии для рассматриваемого
типа механизмов, как правило, приводит к синтезу многозвенных ме-
ханизмов с большим количеством кинематических пар. Поэтому, не-
смотря на очень большую общность этих методов, полученные таким
путем механизмы практически мало пригодны.
Более простые по структуре механизмы могут быть получены,
если широко использовать геометрические свойства, заложенные в
теорию построения отдельных видов кривых, и, объединив их со
свойствами различных кинематических цепей, получать механизмы,
воспроизводящие требуемые кривые. Любопытно, что именно этот
второй путь решения задач синтеза механизмов для воспроиз-
ведения кривых и получил широкое использование в многочисленных
работах, опубликованных в XIX и XX столетиях русскими и зарубеж-
ными учеными.
В дальнейшем будут изложены некоторые задачи теории синтеза
механизмов для воспроизведения кривых, основанные на использовании
геометрических методов построения кривых в сочетании со свойст-
вами кинематических цепей различной структуры.
*) См., например, капитальный труд G. Loria, Spezielle algebraische und
transccndente ebene Kurven, Leipzig, 1902.
262 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
3°. Известно, что любая алгебраическая кривая может быть вос-
произведена соответствующей кинематической цепью, образованной
низшими парами V класса.
Теорема о возможности воспроизведения любой алгебраической
кривой механизмом, образованным парами V класса, принадлежит
А. Кемпе [836]. Пусть уравнение алгебраической кривой в неявной
форме, имеющее общий вид
f(x, у) = 0, (6.1)
представлено в следующем виде:
2 Ax'" уп = 0, (6.2)
где А — некоторые постоянные.
Нетрудно показать, что воспроизведение с помощью кинемати-
ческой цепи кривой, данной уравнением (6.2), сводится к проведе-
нию ряда последовательных математических операций, выполняемых
отдельными механизмами, соединенными в общую, искомую, кинемати-
ческую цепь.
Для этого достаточно иметь следующие механизмы:
а) механизм для перемещения точки по заданной прямой;
б) механизм для проектирования заданной точки на заданную
прямую;
в) механизм, отсекающий на осях Ох и Оу равные отрезки;
г) механизм для проведения через заданную точку прямой, па-
раллельной данной;
д) механизм для получения пропорциональных отрезков на двух
прямых, проходящих через заданную точку (множительный механизм);
е) механизм для сложения заданных отрезков (суммирующий
механизм).
Из указанного выше видно, что эти механизмы должны выполнять
путем геометрических построений все те математические операции,
которые необходимы для получения суммы членов, входящих в урав-
нение (6.2), т. е. операции сложения, вычитания, умножения и возве-
дения в степень или деления и извлечения корня, опускание пер-
пендикуляра, черчение параллельных линий и др.
Механизмы для перемещения точки по прямой могут быть весьма
различны. Это могут быть механизмы только с вращательными парами,
например точные направляющие механизмы. Более простыми будут
механизмы, имеющие в своем составе поступательные пары, например
кривошипно-шатунные механизмы, некоторые виды кулисных механиз-
мов и т. д.
Механизмы для проектирования заданной точки на заданную
кривую могут также состоять или из одних только вращательных
рар, как, например, механизм, показанный на рис. 351, а. Если раз-
меры звеньев удовлетворяют условиям АС=^СЕ и АВ = ВС = CD =
DE ~ ВС— CD и ерли двигать весь механизм так, чтобы точки
§ 15]
ОБЩИЕ МЕТОДЫ РЕШЕНИЯ
263
А и Е перемещались по заданной прямой аа (например, с помощью
механизмов, указанных выше для осуществления движения по прямой),
то точка С будет всегда лежать на прямой аа и будет проекцией
точки С на эту прямую.
Проектирование точки С на прямую аа может быть осуществлено
значительно проще, если мы, например, используем крестообразный
ползун 2 со взаимно-перпендикулярными направляющими, в котором
скользит звено 1 (рис. 351, б).
Механизм, отсекающий на осях Ох и Оу (рис. 351, в) равные от-
резки OM=ON, может быть образован из трех механизмов, воспро-
изводящих движение точки М по оси Оу, точки N по оси Ох и
Рис. 351.
точки Д' по прямой ОК, являющейся биссектрисой угла хОу. Если
точки М, К и N соединить двумя звеньями МК и /\W равной
длины, то мы и получим искомый механизм. Возможны и другие ме-
ханизмы для воспроизведения данного геометрического построения,
например механизм с поступательными парами, показанный на рис. 351, г.
Механизм для проведения через заданную точку М прямой а'с’,
параллельной данной прямой аа, показан на рис. 351, д. Это будет
транслятор, представляющий собой механизм двойного параллело-
грамма, звенья которого удовлетворяют условиям AB=CD=EF', АС==
— BD и CE = DF. Устанавливая звено АВ вдоль заданной прямой аа,
а звено EF так, чтобы его направление проходило через точку Л1,
получаем направление прямой а'а', параллельное аа. Вариант меха-
низма с поступательными парами показан на рис. 351, е. Угол между
направляющими ползуна 2, вообще говоря, может быть выбран про-
извольным.
264 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Механизм для получения пропорциональных отрезков на двух
прямых Оа и ОЬ (рис. 351, ж) может быть создан, используя ранее
рассмотренные кинематические цепи.
Пусть на прямых Оа и ОЬ заданы точки М, N и Д', требуется
найти на прямой ОЬ точку L, удовлетворяющую условию
OL __ON
ОК ~ ОМ •
(6.3)
Для этого с прямой МК связываем механизм вида, показанного
на рис. 351, д таким образом, чтобы прямая NL была бы парал-
лельна прямой МК. Тогда прямая NL отсечет на прямой ОЬ отре-
зок (О£), удовлетворяющий условию (6.3), если точки Л1, N и К пе-
ремещать по прямым Оа и ОЬ.
Для сложения заданных отрезков ОМ и ON (рис. 351, з) так,
чтобы
OM-\-ON—OP, (6.4)
можно дважды применить механизм пантографа. Первый пантограф
MARCNK осуществляет деление отрезка MN пополам так, что от-
резок ОК равен:
ОК= 0M+9N(6.5)
Второй пантограф ODEFPK удваивает отрезок ОК таким образом,
что отрезок ОР равен:
ОР=ЧОК. (6.6)
Таким образом, всегда могут быть построены механизмы, выполняю-
щие указанные выше геометрические построения.
4°. Как показывает А. Кемпе, сочетанием рассмотренных механизмов
может быть осуществлено воспроизведение любой алгебраической
кривой, описываемой уравнением вида (6.2). Пусть точка М есть не-
которая точка плоскости хОу. С помощью механизмов, показанных
на рис. 351, а или б, можно всегда найти проекции Мх и Mv этой
точки на оси Ох и Оу так, что х = ОМХ и у = ОМу. Отметим да-
лее на оси Ох некоторую точку S, для которой
OS = ^. (6.7)
Тогда можно с помощью механизма вида, показанного на рис. 351, з,
на оси Оу построить точку Р, которая бы удовлетворяла бы условию
или
OP _ОМУ
ОМХ ~ OS
(6-8)
OP —А- ОМХ - ОМу = Аху.
Аналогично путем последовательного наслоения можно получить
отрезки, выражающие Ах2у, Аху2, Ах2у2, Ах3у, Аух3, ... , и окон-
§16] ИНВЕРСОРЫ, ПАНТОГРАФЫ И ПРЯМОЛИНЕЙНО-НАПРАВЛЯЮЩ. МЕХАНИЗМЫ 265
чательно на оси Ох или Оу может быть получена некоторая точка Q,
удовлетворяющая условию
OQ = Axmyn. (6.9)
При этом перенос отрезка OQ с одной оси на другую может быть
всегда осуществлен механизмами вида, показанного на рис. 351, в и г.
Аналогичными построениями могут быть построены и слагаемые
уравнения (6.2), имеющие форму Вхт или Суп.
Далее, с помощью механизма вида, показанного на рис. 351, ж,
можно получить сложение отрезков (6.9) в форме
OQi-j-OQs, OQi~\~ OQ^-\-OQ3,
OQ. + OQ2 + OQ3 +.. • + OQn = OR.
Сумма всех этих отрезков должна равняться согласно (6.2)
OQ. OQ>2 OQ3 ... -|- О Qn = 0.
Следовательно, если полученный путем сложения отрезок OR,
равный
OR=£Axmyn = 0,
приравнять нулю, т. е. совместить полученную точку R с началом
координат О, то точка М будет описывать заданную алгебраическую
кривую.
Таким образом, теорема Кемпе в его доказательстве содержит
только указание на возможность построения любой алгебраической
кривой кинематическими цепями с парами V класса, но не дает ука-
заний на наилучшие решения этой задачи. Совершенно очевидно,
что прямое решение такой задачи с помощью тех цепей, которые
рассмотрел Кемпе, в подавляющем числе случаев приведет к настолько
сложным механизмам, что практическое их осуществление явится со-
вершенно нереальным. Вот почему при построении механизмов ис-
пользуются кинематические цепи, обладающие различными геометри-
ческими свойствами, с помощью которых наиболее просто решаются
задачи о воспроизведении отдельных алгебраических кривых или це-
лых классов этих кривых. В последующих параграфах нами будут
рассмотрены различные виды таких цепей и изучены их геометри-
ческие свойства.
§ 16. Инверсоры, пантографы и точные
прямолинейно-направляющие механизмы
1°. Рассмотрим вопрос о проектировании механизмов, в которых
используется метод инверсии или взаимно-обратных кривых.
Пусть имеются три точки: О, Р и Q, лежащие на одной прямой
(рис. 352). Закрепим неподвижно точку О и будем вращать прямую
около точки О так, чтобы точка Р, скользя вдоль прямой, описала
некоторую кривую рр. Тогда на прямой можно найти такую точку Q
которая, скользя вдоль этой прямой, описала бы кривую qq, чтобы при
266 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [ГЛ. VI
этом радиусы-векторы pj = OP и p2 = OQ, определяющие положения
точек Р и Q на кривых рр и qq, удовлетворяли условию
pip2 = А2 = const, (6.10)
где k — некоторая постоянная величина. Любая из кривых рр и qq
является инверсией другой или взаимно-обратной кривой.
Ниже мы рассмотрим некоторые виды кинематических цепей, с
помощью которых может быть осуществлено соотношение (6.10).
Пусть имеется семпзвенная кинематическая цепь (рис. 353). Если
размеры звеньев удовлетворяют условию BD — BE, CD —СЕ, то
направление ВС будет всегда перпендикулярно к направлению DE.
Если, далее, кинематическая цепь удовлетворяет условию, что точки
A, D и Е лежат на общей прямой, то кривая, описываемая точкой Е,
будет инверсией кривой, описываемой точкой D или наоборот. Если
обозначить длины звеньев соответственно через /2, /3, 4 — 4 и 4 —
— 4, то из треугольников АВЕ и BDF имеем:
AD — AF — DF и AE = AF-\-EF.
Далее, имеем:
Л£» = РГ, ЛД = р2; AF = Vll — (BFf
и
DF = EF=Vi} — (BF? .
Следовательно:
Pl =
И
ра=K43-(W + /42-(W.
откуда
piPs = ^ — ^ = const. . (6.11)
Точно так же из рассмотрения треугольников ACF и CDF получим:
PiPs=4—4=const-
§ 16] ИНВЕРСОРЫ, ПАНТОГРАФЫ И ПРЯМОЛИНЕЙНО-НАПРАВЛЯЮЩ. МЕХАНИЗМЫ 267
Следовательно, должно удовлетворяться условие
р_________________________I2 — I1 — Is
Таким образом, данная кинематическая цепь может быть положена
в основу механизма, чертящего взаимно-обратные кривые, т. е. в ос-
нову механизма инверсора.
Обычно размеры этой
цепи выбираются так, чтобы
/4 ;==/( И 1±----------
т. е. выбирается симметрич-
ная относительно направле-
ния АЕ цепь.
На рис. 354 показан ин-
версор для черчения окруж-
ности qq центра Оь когда
точка D описывает окруж-
ность рр центра О.
Для доказательства того, Рис. 354.
что точка Е действительно
описывает окружность, найдем вторую точку D' пересечения прямой АЕ
с окружностью рр. Из известного условия геометрии имеем:
AD-AU = т2,
В
где т — длина касательной, проведенной из точки А к окружности рр.
Далее имеем:
AD-AE=k2.
В
К
г
Рис. 355.
Следовательно:
АГУ та Rt ,
-.— ' тг — const,
АЕ k2 Ra
где Ri и /?2 —радиусы ок-
ружностей рр и qq, т. е.
эти окружности отличаются
на величину масштаба, рав-
та
ного .
Если точка А инверсора
лежит на окружности рр
(рис. 355), то окружность
qq (рис. 354) превращается
в прямую qq, перпендикулярную к прямой АО К- Таким образом, мы
получаем точный прямолинейный направляющий механизм, носящий
название механизма Поселье-Липкина.
В этом механизме всегда будет удовлетворяться условие
AD -АЕ — AG АК—k2 — const.
268
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[ГЛ. VI
Если точка А окажется лежащей внутри окружности рр (рис. 356),
то мы получим также механизм для инверсии окружностей; при
этом окружность рр будет находиться внутри окружности qq.
На рис. 353 точка А лежит вне ромба BDCE. Такой механизм
носит название положительного инверсора Поселье. Если точка А
Рис. 358.
т. е. точки D и Е
лежит внутри ромба BDCE (рис. 357), то мы получим механизм от-
рицательного инверсора Поселье. На рис. 357 показан прямолиней-
но-направляющий механизм инверсора Поселье.
2°. Рассмотрим следующую кинематическую
цепь, являющуюся инверсором. Эта цепь пред-
ставляет собой (рис. 358) шарнирный антипарал-
лелограмм BCQF, стороны которого удовлетво-
ряют условию FG — BC и CG = FB. Нетрудно
видеть, что направление FC будет при любом
положении антипараллелограмма BCGF парал-
лельно направлению GB. Если на стороне ВС
антипараллелограмма выбрать произвольную
точку А и провести прямую АЕ, параллельную
прямой GB, то будет всегда удовлетворяться
условие
X£)-i4E' = A2 = const, (6.12)
описывают взаимно-обратные кривые с центром
инверсии в точке А. Обозначаем АВ = а, AC = b, FB = c, FC — d,
AD = px и ЛЕ = р2. Проводим прямую FH, параллельную прямой СВ,
и обозначим отрезок GH=e.
Из подобия треугольников ADB и CFB имеем;
d
Р1 — а---j ; .
г 1 а + b t
§ 16] инверсоры, пантографы и прямолинейно-направляющ, механизмы 269
Далее, из подобия треугольников АСЕ и ВС С имеем:
• d -р £
а + b
Следовательно:
(<*+*)- (6.13)
Из треугольников GFL и BFL имеем.
{ р \2
Следовательно, отрезок е будет равен:
g=c8 rfa (c + fe)^ (614)
Подставляя полученное значение для е в уравнение (6.13), полу-
чаем окончательно:
Р iP* = CTv -(а + = k*= const’ (6‘15)
Iе -j- и)
т. е. действительно условие (6.12) для данной кинематической цепи
всегда удовлетворяется.
Данный инверсор, предложенный Гартом, может быть использо-
ван для преобразования окружности в прямую, т. е. получения точ-
ного прямолинейно-направляющего механизма. Для этого центр инвер-
сии — точка А (рис. 359, а) должна находиться на окружности рр.
Точка О — центр вращения звена 6—должна- находиться на перпен-
270 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
дикуляре, восставленном из середины отрезка AD. Тогда окруж-
ность рр пройдет через точки А и D. Уравнение прямой qq легко
может быть получено из условия (6.15). Для окружности рр имеем
уравнение
p1 = 2/costp, (6.16)
где 7—длина звена 6и<р=/, DAO.
Подставляя значение pi в уравнение (6.15), получаем уравнение
для прямой qq. Имеем:
№ ks h
Dq — ——- ' ~ -- .
* Pl zZ COS ср COS ср
где h — отрезок, равный
h — = const.
Таким образом, инверсией окружности рр будет прямая qq. На
рис. 359, б показан второй вариант прямолинейно-направленного ме-
Рис. 360.
ханизма Гарта, когда точка А
выбрана за точками В и С.
3°. Рассмотрим еще не-
которые типы инверсоров.
На рис. 360 показан инвер-
сор Перролаца, представ-
ляющий собой семизвенную
кинематическую цепь. Звенья
2 и 3 равны между собой
и вращаются около точки А.
Точка А расположена посредине этих звеньев гак, что АВ — АС =
= AF — AG = a. Звенья 4, 5, 6 и 7 равны между собой, т. е.
FD — GE = CD — BEt=b. Точки A, D и Е расположены на одной
прямой. В механизме всегда выполняется условие
A D АЕ —/г* ~ const.
В самом деле:
AD-AE — (HD — НА) (AL -f- LE).
Из равенства треугольников CFA и GBA следует, что AL = AH,
а из равенства треугольников CFD и QBE следует, что LE = HD.
Следовательно:
AD • AE = (HD — НА) (HD + НА) = (HD)* — (НА)* -
= [(FD)* — (HF)*] — [(/IF)2 — (HF)*] =
= (FD)* — (AF)* = Ьг — а* = const,
т. е. данная кинематическая цепь будет инверсором.
§ 16] ИНВЕРСОРЫ, ПАНТОГРАФЫ И ПРЯМОЛИНЕЙНО-НАПРАВЛЯЮЩ. МЕХАНИЗМЫ 271
На рис. 361 показана семизвенная
щаяся инверсором. Звено 2 выполнено
жестким углом АВЕ, равным 90°.
Оси направляющих крестообраз-
ного ползуна 6 образуют также
угол 90°. Таким образом, при
любом положении звеньев цепи
треугольники АВЕ и ABD будут
прямоугольными. Тогда если по-
стоянное расстояние АВ обозна-
чить через а, то всегда будет
выполняться условие
AD-AE—a2=const. (6.17)
Последнее следует из того, что
циональная между всей гипотенузой
Данный инверсор может
кинематическая цепь,
в виде коленчатого
являю-
рычага с
Ъ
6
7
—А
Рис. 362.
в
R
катет АВ есть средняя пропор-
с прилежащим к нему отрезком,
быть использован для получения точного
прямолинейно - направляюще-
го механизма (рис. 362).
Для этого в точке D ин-
версора присоединяем звено
FD длиной, равной R.
Центр инверсии — точка
А — должен при этом на-
ходиться на окружности
рр. Следовательно, центр
вращения F звена FD дол-
жен быть выбран на пер-
пендикуляре тт к отрезку
AD, проведенному через
точку N—середину этого
отрезка. При движении точ-
ки D по окружности рр
точка Е движется по прямой
qq, перпендикулярной к на-
правлению AF.
Уравнение окружности
рр будет:
AD — 4R cos ©, (6.18)
где © — угол DAF.
Подставляя значение (6.18) в уравнение (6.17), получаем:
АЕ = ——------= —Л—
2R cos<p cos?
где h—отрезок (рис. 362), равный =
272
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[ГЛ. VI
Таким образом, отрезок АК будет равен:
AK — h — const.
4°. Инверсоры могут быть использованы для образования меха-
низмов, чертящих не только окружности и прямые, но и другие
кривые.
Так, например, если одну точку инверсора вести по кривой, яв-
ляющейся улиткой Паскаля, то взаимно-обратной кривой будет ко-
ническое сечение, т. е. другая точка инверсора будет двигаться по
коническому сечению.
В самом деле, уравнение улитки Паскаля будет:
Pi = 2г cos (6.19)
где гий — постоянные коэффициенты.
Пусть коэффициент инверсии (6.10) будет = Тогда, под-
ставляя в уравнение (6.10) значение рь получим уравнение
будет вычерчивать параболу. На рис.
Л2 Ъ*
р._> = - = ——•—।— . (6.20)
r Pi 2r cos f -ф a v ’
Уравнение (6.20) будет урав-
нением конического сече-
ния. Если постоянная 2г
будет больше постоянной а,
то механизм будет вычерчи-
вать гиперболу. Если 2г бу-
дет меньше а, то механизм
будет вычерчивать эллипс
и, наконец, если 2г бу-
дет равно а, то механизм
363 показан механизм кони-
кографа, построенный на использовании инверсора, указанного на
рис. 361. Обозначим длины звеньев механизма через AB = b, АЕ—
= FC==r и СБ = а. Тогда уравнение траектории точки Е относи-
тельно полярной оси Ах будет уравнением улитки Паскаля. Имеем:
АЕ = 2r cos <р -ф- а.
Из уравнения (6.17) имеем:
AD=~ = -к-------------—г-.
АЕ 2r cos у а
(6.21)
Уравнение (6.21) будет уравнением конического сечения. Следо-
вательно, в зависимости от соотношений между параметрами 2г и а
механизм (рис. 363) может описывать точкой D: эллипс, гиперболу
или параболу. Естественно, что для получения конического сечения
путем инверсии улитки Паскаля можно применить любой из ука-
занных выше инверсоров.
§16] ИНВЕРСОРЫ, ПАНТОГРАФЫ И ПРЯМОЛИНЕЙНО-НАПРАВЛЯЮЩ. МЕХАНИЗМЫ 273
Если уравнение одной кривой будет:
Pi = pi (®)>
то уравнение взаимно-обратной кривой, получаемой путем инверсии,
будет:
а2
Ра Pi (?) ’
(6.22)
где а — постоянная, представляющая собой коэффициент инверсии.
Так, например, взаимно-обратными кривыми являются архимедова
спираль и гиперболическая спираль. Уравнение архимедовой спирали
в полярной форме будет:
р, = ц<р, (6.23)
где а — постоянный коэффициент.
Подставляя выражение для pt (6.23) в уравнение (6.22), полу-
чим уравнение гиперболической спирали в полярной форме:
__а2 с
Р2 су у
Взаимно-обратными кривыми являются также кардиоида и па-
рабола.
Уравнение кардиоиды в полярной форме будет:
Pi = a cos2
Подставляя выражение для pj в уравнение (6.22), получаем урав-
нение параболы в полярной форме с фокусом в полюсе и пара-
метром 2а:
а2 а
р2 =--------=--------.
ф ф
a cos2 cos2 -i-
Таким образом, проектирование
механизмов для черчения некото-
рых видов кривых может быть
сделано путем присоединения ин-
версора к механизму, чертящему
одну из взаимно-обратных кривых.
5°. Кинематические цепи, с
помощью которых могут быть вы-
черчены подобные друг другу
траектории, носят название панто-
графов. Рассмотрим два наиболее
распространенных типа пантогра-
фов. На рис. 364 показана схема
Рис. 364.
пантографа Сильвестра. Этот механизм дает возможность
получать
подобные траектории, повернутые друг относительно друга на опре-
деленный угол а. Пантограф представляет собой пятизвенную
274 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
кинематическую цепь, образующую параллелограмм ABCD. Звенья 3
и 4 имеют точки Е и F, образующие вместе с точками В, С и D
два подобных треугольника ВЕС и DCF.
Из подобия треугольников ВЕС и DCF получаем:
BE___CD
ВС ~~ FD ’
так как CD = AB и BC—AD, то
BE_AD
АВ~ FD‘
Углы СВА и ADC равны между собой. Следовательно, будут
равны между собой и углы АВЕ и ADF. Тогда треугольники АВЕ
и ADF будут подобны и, следовательно, будет иметь место соотно-
шение
BE АВ АЕ . п..
АЙ FD AF Const (6.24)
и угол АЕВ равен углу FAD.
Далее, угол EAD равен:
/_ EAD=LEGC=/_ AEB-\-a=LFAD-\-a.=^FAD-\- L EAF,
т. е. угол EAF равен:
/ EAF= а—const.
(6.25)
Из уравнений (6.24) и (6.25) следует, что траектория, описывае-
мая точкой F, будет подобна траектории, описываемой точкой Е, и
подобные друг другу с центром
из подобия треугольников: ОАМ,
эти траектории повернуты друг
р относительно друга на посто-
янный угол а.
Другим пантографом будет
пантограф Шейнера, показанный
на рис. 365. Пантограф пред-
ставляет собой пятизвенную
кинематическую цепь, состоя-
щую из параллелограмма ABCD
с удлиненными сторонами АВ
и CD. Если какую-либо точ-
ку Р звена DC соединить с
точкой О, то точки Р, N и М
будут описывать траектории,
подобия в точке О. Это следует
OBN и ОКР. Имеем:
ОМ: ON: ОР= О А : ОВ : (05 СР).
§ 16] ИНВЕРСОРЫ, ПАНТОГРАФЫ И ПРЯМОЛИНЕЙНО-НАПРАВЛЯЮЩ. МЕХАНИЗМЫ 275
На рис. 366 показан частный случай пантографа, когда точки Р
и N (рис. 365) совпадают с точкой С. На рис. 367 показан панто-
граф, у которого точки М и Р (рис. 365) совпадают с точкой D.
Пантографы могут быть присоединены одной из точек к механизму,
вычерчивающему ту или иную кривую. Тогда соответствующие точки
пантографов будут чертить подобные кривые, расположенные подобно
или повернутые на определен-
ный угол.
Пантографы также могут
быть использованы в механиз-
мах счетно-решающих уст-
ройств, например для умножения
вектора на постоянный скаляр,
как с поворотом, так и без
поворота векторов, и для меха-
нического осуществления дру-
гих математических операций.
6°. Выше было показано,
что точные прямолинейно-на-
правляющие механизмы могут
быть получены путем исполь-
зования инверсоров. Рассмо-
трим получение других точ-
ных прямолинейно-направляю-
Рис. 368.
щих механизмов.
Одним из таких механизмов является механизм Гарта. В основе этого
механизма лежит шарнирный четырехзвенник ABCD (рис. 368), к ко-
торому присоединена двухповодковая группа FQE. При некоторых
соотношениях звеньев механизма точка О будет двигаться по прямой.
Эти соотношения были подробно изучены Дарбу и Брикаром *). Позднее
в работе Н. М. Алексеева [1] были выведены все необходимые и до-
статочные условия для существования механизма типа Гарта. Мы
*) R. В г i с а г d, Lemons de cinemalique, Paris, 1927.
276 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
приводим только окончательные результаты, опуская все промежу-
точные выкладки. Имеем (рис. 368):
. edd Р d2 ’ c = add P — d2'
ads а Р — d2 ’ e = e,l2 P — d2’ (6.26)
atd2 p ds , e,d2 P — d2'
прямой, определяемой уравнением
Точка С будет двигаться по
Z (о2 - — d2-|- Z2)
2 (z2 — d2)
(6.27)
В уравнениях (6.26) и (6.27) произвольными величинами будут
величины eh d и I, т. е. длины звеньев четырехзвенника ABCD.
Если положить, что = d и et = I, то основной четырехзвенник
превратится в ромбоид. Соответственно длины звеньев будут равны:
Pd __________ id2 I
Z2 — ds ’ С Z2 — d2 ’ I
dZ2 Z3
G = Z2 —d2’ e = Z2 — d2 ’ } (6’28)
__ d3 ___________ Zd2 I
g2 Z2 —d2’ e% P — d2' |
Из условий (6.28) и (6.27) следует, что с = еу, а = Ь
и точка G движется по прямой Ау, проходящей через точку А пер-
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 277
пендикулярно к направлению AD (рис. 369). В этом механизме углы
AFG и СЕО равны между собой, и угол ОСВ за время движения
механизма будет постоянным и равным 90°. Это позволяет получить
еще одну модификацию данного механизма. Для этого сделаем непо-
движным звено 3 (рис. 370). Тогда точка О полученного механизма
будет двй?аться по прямой, перпендикулярной к направлению ВС.
Направляющие по прямой механизмы применяются в приборах
для приведения в движение записывающих показания приборов орга-
нов, в некоторых машинах-автоматах как исполнительные механизмы,
в подъемно-транспортном оборудовании и т. п.
§ 17. Механизмы для черчения и огибания конических сечений
1°. Рассмотрим некоторые типы коникографов, т. е. механизмов
которые могут вычерчивать различные конические сечения при соответ-
ствующей настройке их параметров. На рис. 371 показан конико-
граф Каминского [24]. Как видно по чертежу, в основе механизма
лежит шарнирный четырехзвен-
ник ABCD, у которого суммы
квадратов противоположных
сторон равны. Звено 8 будет
всегда совпадать с направле-
нием диагонали DB четырех-
звенника ABCD. Крестообраз-
ный ползун 7 обеспечивает
постоянную перпендикуляр-
ность направления CF к на-
правлению DB. Точка F описы-
вает коническое сечение.
Обозначим длины звеньев со-
ответственно: АВ —а, ВС—Ь,
CD == с, AD = d. У равнение
траектории точки F будет:
р=р(Т), (6.29)
где р — расстояние AF и ср —
угол относительно полярной
оси, совпадающей с направ-
лением AD. Так как в четы-
Рис. 371.
рехугольнике суммы квадратов противоположных сторон равны, то,
следовательно, имеет место условие
(c+p)2 + c2 = fc2 + (£»F)2. (6.30)
Далее, из треугольника ADF имеем:
(Z7F)2 = р2 _[_ (fl -|- 2р d cos ср.
(6.31)
278 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Подставляя полученное выражение (6.31) в (6.30), после неслож-
ных преобразований получаем:
4- d2 — в2 — с2
/Д I- fP _ aS _ С2 ([
Обозначая —'------— -------= р а ~ = е, получаем уравнение ко-
нического сечения в обычном виде:
Р = 7-----, (6.33)
r 1 — е cos ср ’ v '
где р — параметр конического сечения, а е — эксцентриситет.
Таким образом, точка F механизма коникографа описывает кони-
ческое сечение. Черчение различных конических сечений достигается
путем изменения параметра р и эксцентриситета е. Если е^>1, то
точка F чертит гиперболу. Если е<^1, то точка F чертит эллипс.
Если, наконец, е=\, точка F чертит параболу. Настройка механизма
может быть сделана путем регулирования длины звена AD, т. е.
путем перестановки шарнира А по направлению AD.
Другой коникограф показан на рис. 363. В этом коникографе,
как это было показано выше, используется принцип инверсии улитки
Паскаля в коническое сечение. Аналогичные коникографы могут быть
созданы с использованием и других типов инверсоров и других типов
кривых, связанных условием инверсии.
На рис. 372 показан коникофаф Кроуфорда [92]. В этом конико-
графе, так же как и в коникографе, показанном на рис. 363, исполь-
зуется свойство инверсии улитки Паскаля в коническое сечение.
В качестве инверсора используется кинематическая цепь, состоящая
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 279
из звеньев 2, 3, 5, 6 и 7. Нетрудно видеть, что в этой цепи всегда
удовлетворяется условие
AD • АЕ = АВ* = b* = const.
сечение, па рис. а /а
теории этого меха-
Рис. 373.
Обозначим: AF = FC = r, СЕ = а и АВ = Ь. Тогда уравнение для
улитки Паскаля, описываемой точкой Е, будет:
АЕ — 2r cos <р + а = р2. (6.34)
Из уравнения (6.22) имеем:
Ь2 Ь2
Pt=AD = ~ = -.---------—г-. (6.35)
г АЕ 2r cos у Ц- а
Таким образом, точка D чертит коническое
показан коникограф Богуславского. Основы
низма были изложены И. Ньюто-
ном [18е]. Теория этого меха-
низма основана на известном по-
ложении проективной геометрии,
заключающемся в следующем.
Пусть из центров А и В (рис. 373)
проведены пучки, лучи которых
образуют постоянные углы, и пара
лучей всегда пересекается на од-
ной и той же прямой. Если лучи /
первого пучка повернуть на про-
извольный угол, то лучи второго
пучка повернутся на другой угол.
При этом точки пересечения соот-
ветствующих лучей этих пучков
будут образовывать коническое се-
чение. Таким образом, если точку D
(рис. 373) двигать по прямой, то точка С
сечение. При своем движении точка С
точки А и В. Кроме того, в положении Do, когда точка D придет
на прямую АВ, точка С будет находиться в положении Со. Точки А,
В и Со являются главными точками относительно рассматриваемого
преобразования прямой линии в коническое сечение. Если при дви-
жении точки D по прямой направления АС и BD не стремятся стать
параллельными между собой, то коническое сечение, вычерчиваемое
точкой С, будет эллипсом, так как в этом случае вычерчиваемая кривая
не имеет бесконечно удаленных точек. В том случае, если они стре-
мятся сделать это дважды, то вычерчиваемая кривая будет гипер-
болой, т. е. кривой, имеющей две бесконечно удаленные точки. Если,
наконец, эти звенья стремятся один раз к взаимной параллельности,
то вычерчиваемая кривая будет параболой, т. е. кривой, имеющей
одну бесконечно удаленную точку.
будет чертить коническое
обязательно пройдет через
280
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[ГЛ. VI
Механизм может вычерчивать и кривые других порядков, но для
этого одна из точек С или D должна двигаться не по прямой, а по
кривой. Пусть, например, точка D описывает некоторую кривую аа
/г-го порядка, не проходящую через главные точки. Тогда точка С
вычертит какую-то кривую рр. Пересечем кривую рр какой-либо пря-
мой qq, не проходящей через главные точки, и будем двигать точку D
механизма по этой прямой. Тогда точка С опишет некоторую кри-
вую 77 2-го порядка. Общим точкам прямой qq и кривой рр будут
соответствовать общие точки для кривой аа и кривой 77. Так как
кривая 77 может иметь с кривой аа тг-го порядка 2л общих дей-
ствительных или мнимых точек, то, следовательно, и прямая qq имеет
с преобразованной кривой рр такое же число общих точек. Таким
образом, если точка D двигалась бы по кривой л-го порядка, то
точка С вычертила бы кривую 2п-го порядка. Легко показать, что
если кривая аа будет проходить через одну из главных точек, то
порядок вычерчиваемой кривой рр будет понижаться на единицу для
каждого прохождения кривой через ту или иную главную точку.
Следовательно, если кривая аа будет кривой 2-го порядка, то в общем
случае кривая рр будет кривой 4-го порядка. Если кривая аа прохо-
дит через одну главную точку, то кривая рр будет кривой 3-го по-
рядка. Если кривая аа пройдет через две главные точки, то кривая рр
будет кривой 2-го порядка, и наконец, если кривая аа пройдет через
три главные точки, то кривая рр перейдет в прямую.
2°. Выше были рассмотрены коникографы для черчения кониче-
ских сечений. Переходим к рассмотрению коникографов для огибания
конических сечений [Зд].
Механизм для огибания эллипса (рис. 374) представляет собой
кулисный механизм АВС с вращающейся кулисой СЕ. Длина криво-
шипа АВ равна половине длины большой оси эллипса. Расстояние
между осями вращения А и С звеньев 7 и 3 равно половине фокус-
ного расстояния. Ось вращения А совпадает с центром эллипса, а ось
вращения С — с одним из фокусов эллипса (в рассматриваемом слу-
чае с Fi). Звено 4 представляет собой ползун, скользящий по напра-
вляющей СЕ. С ним жестко скреплена прямая tt, образующая с осью
его движения угол 90°. При вращении кривошипа АВ прямая tt будет
всегда касательной к эллипсу, имеющему в качестве фокусов точки
F\ и F2 и большую ось, равную 2АВ.
Таким образом, прямая tt будет огибающей кривой, а эллипс —
огибаемой кривой. Для доказательства того, что огибаемая кривая
положений прямой tt будет действительно эллипсом, отложим от
точки А влево по направлению АС отрезок ДД2, равный
AFi — AC = AF1.
Далее, от точки В в направлении СЕ отложим отрезок ВС,
равный
ВС = ВС,
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 281
Соединим точку С с точкой Fa и найдем точку D пересечения
прямой F2C' с прямой tt. Соединим точку D с точкой C{Fi). Из по-
строения следует, что
DC = DFi.
Далее, из подобия треугольников АВС и F.^C'C получаем:
F iFs FаС* q
— АВ ’
откуда
FiC = ‘2AB.
Так как отрезок
F2C' = FJD + DC’ = F.D 4- OFt,
то, следовательно:
F^D -[- DFt = 2 АВ = const,
т. е. огибаемая кривая есть действительно эллипс с фокусами в точ-
ках Ft и F2 и большой осью, равной 2 АВ.
Нетрудно далее показать, что прямая tt будет всегда касательной
к построенному эллипсу. Обозначим угол, образованный прямой F2C'
с прямой tt через а Тогда вследствие равенства треугольников BDC'
и BDC углы C'DB и BDC будут равны между собой и равны углу а.
Таким образом, радиусы-векторы F2D и FJJ, соединяющие фокусы
эллипса с точкой D, в которой эллипс соприкасается с прямой tt,
образуют равные углы а с этой прямой, т. е. прямая tt есть действительно
282 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
касательная к построенному эллипсу. Положение точки D может быть
всегда определено из чисто кинематических соображений. Мгновенный
центр вращения Р звена 4 найдется на пересечении прямой PC, про-
ходящей через точку С и перпендикулярной к направляющей СЕ,
с осью звена АВ. В свою очередь точка D должна лежать на пер-
пендикуляре, опущенном из точки Р на направление огибающей пря-
мой tt.
Из проведенного построения следует, что из всех точек прямой tt
точка касания D имеет минимальную по модулю скорость, направле-
ние которой будет всегда совпадать с соответствующими направле-
ниями прямой tt. Так как длина звена АС меньше АВ, то рассмотрен-
ный механизм представляет собой кулисный механизм с вращающейся
кулисой СЕ. Огибание эллипса может быть сделано непрерывным
вращением кривошипа АВ на полный оборот. Для получения эллипсов
с различными фокусными расстояниями и большой осью достаточно
изменять длину звена АВ и расстояние АС между осями вращения
звеньев 2 и 3.
Предложенное здесь доказательство и построения могут быть
выведены из свойств подэр. Как известно, подэрами называются кри-
вые, представляющие собой геометрическое место подошв перпенди-
куляров, опущенных из какой-либо точки плоскости на направления
касательных, проведенных к заданной на плоскости кривой. В случае
выбора в качестве точки, из которой опускаются перпендикуляры,
одного из фокусов эллипса подэрой эллипса будет всегда окруж-
ность с радиусом, равным половине большой оси эллипса. На рис. 374
нетрудно видеть, что действительно окружность, описанная радиу-
сом АВ, является подэрой построенного эллипса.
Если длина звена АС будет больше длины звена АВ, то кулисный
механизм с вращающейся кулисой переходит в кулисный механизм
с качающейся кулисой (рис. 375). При этом прямая tt будет огибаю-
щей одной из ветвей гиперболы с фокусом в точке С (F\). Для дока-
зательства последнего отложим от точки А влево по направлению АС
отрезок AF3, равный ДД2 = ДС = ЛД1.
Далее, от точки В в направлении СЕ отложим отрезок ВС = ВС.
Соединим точку С с точкой Д2 и найдем на продолжении прямой Д2С'
точку D пересечения прямой F3C с прямой tt. Соединяем ее с точ-
кой С (Ft). Из построения следует:
DC' = DFi.
Далее, из подобия треугольников АВС и F3C'C получаем:
F.F, _ FtC' _ 2
AFi АВ
откуда
Р3С — 2АВ.
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 283
Так как отрезок FSC' равен:
F/Г = FiD — DC = 1\D — DFb
то, следовательно:
F2Z) — £>Fi = 2 АВ = const,
т. е. огибаемая кривая есть действительно гипербола с двумя ветвями
имеющими в качестве фокусов точки Ft и F2. Ветви гиперболы будут
касательны к окружности радиуса АВ.
Из построения непосредственно следует, что радиусы-векторы F.2D
и FjD, соединяющие фокусы гиперболы с точкой D, в которой имеет
место соприкосновение гиперболы с прямой tt, образуют равные углы а,
т. е. прямая tt есть действительно касательная к построенной гипер-
боле. Положение точки D, так же как и в ранее рассмотренном меха-
низме, может быть определено, если из мгновенного центра враще-
ния Р звена 4 опустить на прямую tt перпендикуляр. Его подошва
и будет искомой точкой D. Из всех точек прямой tt точка D имеет
минимальную по модулю скорость, совпадающую по направлению
с соответствующими направлениями прямой tt.
Так как длина звена АС больше длины звена АВ, то рассмотрен-
ный механизм представляет собой кулисный механизм с качающейся
кулисой. Огибание обеих ветвей гиперболы может быть сделано не-
прерывным вращением кривошипа АВ на полный оборот. Для полу-
чения гипербол с различными фокусными расстояниями и расстояниями
между вершинами ветвей достаточно изменять длину звена АВ и рас-
284 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
стояние ДС между осями вращения звеньев 1 и 3. Нетрудно да-
лее убедиться, что окружность, описанная радиусом АВ, является
Рис. 376.
образом, движение звена
подэрой построенной ги-
перболы.
Представляют интерес
два частных случая рассмо-
тренных механизмов. Пер-
вый, когда длина звена АС
равна нулю, т. е. фокусы
Fi и F2 совпадают с точ-
кой А (рис. 376, а), и вто-
рой, когда длина звена АС
равна длине звена АВ, т. е.
фокусы Fi и F2 лежат на
подэре (рис. 376, б).
В первом случае четырех-
звенный кулисный механизм
вырождается в двухзвенный
механизм АВ (рис. 376, а),
у которого со звеном
2 жестко соединена прямая
11. Прямая 11 будет оги-
бать окружность радиуса
АВ, т. е. подэра и огибае-
мая кривая совпадают.
Во втором случае (рис.
376, б) прямая tt будет
всегда проходить через по-
стоянную точку F2, так как
угол F2FFj всегда прямой.
Таким образом, здесь мы
получаем пучок прямых,
проходящих через точку F2.
Мгновенный центр враще-
ния Р будет лежать на
самой подэре. Неподвижной
центроидой звена 4 явится
сама подэра, а подвижной
центроидой — окружность,
описанная из точки В ра-
диусом, равным 2АВ. Таким
4 сводится к так называемому обращенному
карданов у движению.
Переходим к рассмотрению механизма для огибания параболы. Он
может быть получен как частный случай ранее рассмотренных меха-
низмов. Если центр вращения А звена 2 удалить в. бесконечность
§17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 285
прямую dd, параллельную прямой аа.
параболы с фокусом в
точке С (Ft).
(рис. 377), то окружность, описанная радиусом АВ, превратится
в прямую аа, а звено АВ выродится в ползун, движущийся посту-
пательно вдоль неподвижной прямой аа. При этом фокус Fa также
будет находиться в бесконечности. Таким образом, механизм для оги-
бания параболы (рис. 377) представит собой четырехзвенный меха-
низм с двумя поступательными парами, расположенными между вра-
щательными парами.
Для доказательства того, что огибаемая кривая положений прямой
tt будет действительно параболой, отложим от точки В в направле-
нии СЕ отрезок ВС, равный ВС = ВС.
Через точку С проводим
Прямая dd будет директрисой
Точку С соединяем с беско-
нечно удаленным фокусом F2,
т. е. проводим прямую, пер-
пендикулярную к прямой dd.
Находим далее точку D пере-
сечения проведенной прямой с
прямой tt и соединяем эту
точку с точкой С (Ft). Из по-
строения непосредственно сле-
дует, что DFi = DC', т. е.
точка D равно отстоит от фо-
куса Ft и директрисы dd. Та-
ким образом, огибаемая кривая
есть действительно парабола.
Из построения следует, что
углы CDB и BDC равны
между собой. Следовательно,
углы а, образованные прямы-
ми DC и FiD с прямой tt,
равны между собой, т. е. пря-
мая tt есть действительно ка-
сательная прямая к построенной
параболе. Положение точки D может быть определено, если из
венного центра вращения Р звена 4 опустить на прямую tt
пендикуляр. Его подошва и будет искомой точкой D. Из всех
прямой tt точка D имеет минимальную по модулю скорость, совпа-
дающую по направлению с соответствующими направлениями пря-
мой tt. Для огибания парабол с различными положениями фокуса
относительно вершины достаточно изменить в механизме кратчайшее
расстояние от оси вращения С звена 3 до неподвижной направляю-
/цей аа звена 1.
В основе рассмотренных механизмов лежит механизм четырех-
йвенного коникографа для огибания конических сечений, настройкой
которого можно получить: окружность, гиперболу, эллипс и как част-
МГНО-
пер-
точек
286 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
ный случай огибание точки. Для огибания параболы механизм требует
небольшого структурного изменения, а именно замены одной враща-
тельной пары парой поступательной.
3°. Переходим к рассмотрению коникографа для одновременного
обкатывания двумя прямыми одного конического сечения или двух
софокусных конических сечений [Зз].
Рассмотрим шестизвенный кулисный механизм (рис. 378), у кото-
рого кулиса 3 выполнена в виде жесткого прямого угла, вращающе-
гося около неподвижной точки С, совпадающей с одним из фоку-
сов Ft огибаемого эллипса. Звенья 2 и 5 вращаются около точки А,
совпадающей с центром огибаемого эллипса, и имеют длину, равную
половине большой полуоси эллипса. Восставим в точках В и D пер-
пендикуляры к сторонам звена 3. Точку пересечения этих перпенди-
куляров обозначим через Е. Нетрудно доказать, что при движении
механизма геометрическим местом точек Е будет всегда окружность,
описанная из точки А радиусом I, равным
(6.36)
где а и b — половины малой и большой осей огибаемого эллипса.
В самом деле, опустим из точки А перпендикуляры АН и АР
на направления BE и ВС и продолжим направление CD до пересе-
чения в точке G с перпендикуляром АН.
Из рис. 378 следует
F {ЕНТ 4- (А/7)’ (6.37)
И
с« = (РС)а + (АР)а, (6.38;
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 287
где с = АС есть фокусное расстояние эллипса, как известно, равное
с*=Ь* — а2. (6.39)
Нетрудно видеть (рис. 378), что:
EH=DG = b cos р; 7?C = />sinp, }
AH=PB — b cos a; ^4P = />sina. J
Подставляя величины (6.40) в уравнения (6.37) и (6.38) с учетом
условия (6.39) и складывая их, получим:
/2 = с24-^, (6.41)
откуда
I = ]/я2 -|- b2 = const, (6.42)
т. е., действительно, точка Е описывает окружность постоянного ра-
диуса, равного I.
Прямые ЕВ и ‘ED будут всегда касательными к эллипсу, что сле-
дует из известного условия аналитической геометрии. В самом деле,
соединим точку Е с фокусом и построим на отрезке ЕС, как на
диаметре, окружность с центром в точке О. Так как углы ЕВС и
EDC прямые, то точками пересечения этой окружности с окружно-
стью радиуса, равного Ь, будут точки В и D. Следовательно, пря-
мые ЕВ и ED будут всегда касательными к эллипсу и образуют
между собой прямой угол BED. Если теперь с ползунами 2 и 4
соединить жестко две прямые, перпендикулярные к осям движения
этих ползунов, то эти прямые будут одновременно обкатывать один
и тот же эллипс.
Нетрудно видеть, что полученный механизм представляет собой
как бы два спаренных механизма, рассмотренных нами ранее (§ 17, 2°),
у которых кулисы образуют постоянный жесткий угол, равный 90°.
На основе указанных ранее свойств точки Е может быть спроек-
тирован шестизвенный механизм, показанный на рис. 379. В основе
этого механизма лежит кулисный механизм АВС, у которого длина
кривошипа АВ равна Ь, а длина стойки АС равна с. Прямая tt, при-
надлежащая ползуну 6 и перпендикулярная к оси кулисы 3, будет
касательной к эллипсу.
К механизму АВС присоединим двухповодковую группу, состоя-
щую из звеньев 4 и 5. При этом длина кривошипа АЕ должна быть
равна I = Vс<2 + Ь*. Ползун 4 должен скользить вдоль по прямой tt.
Тогда прямая qq, принадлежащая ползуну 4 и перпендикулярная к
прямой tt, будет также касательной к эллипсу. Таким образом, по-
лучаем механизм с двумя прямыми tt и qq, одновременно касатель-
ными к одному и тому же эллипсу.
Если по условиям использования механизма на практике необхо-
димо иметь жесткий прямой угол, огибающий эллипс, то это может
288 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
быть осуществлено восьмизвенным механизмом, показанным на
рис. 379, б. Здесь два кулисных механизма АВС и АЕС соединены
Рис. 379.
одним звеном 7, входящим во вращательную пару в точке Е со
звеном бив поступательную пару в точке В со звеном 3. Звено 3
Рис. 380.
щее фокусное расстояние с.
выполнено в виде кресто-
образного ползуна с взаимно-
перпендикулярными осями
движения. Звено 7 пред-
ставляет собой жесткий пря-
мой угол tEq, огибающий
эллипс. Последнее непо-
средственно следует из ус-
ловия, что АВ = Ь, АС = с,
АЕ = 1— у а2 б2 и ок-
ружность центра О, пост-
роенная на АЕ, как на
диаметре, всегда пересекает
окружность радиуса АВ в
точке В.
Рассмотрим далее меха-
низм, который осуществляет
одновременное огибание
двух софокусных эллипсов.
Для этого построим механизм
(рис. 380), аналогичный по схеме механизму, показанному на рис. 378,
но с размерами, соответственно равными AD — Ьъ АВ = Ьг и АС с,
где Ьх и bt—половины длин больших осей эллипсов, имеющих об-
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 289
Из рис. 380 следует:
Гг = (ЕЯ)24-(ДЯ)2,
с2 = (РС)2 4 (АР)2,
или так как
ЕН= DG — bx cos Р; PC = b} sin р,
АН — РВ = Ь.2 cos а; АР = b2 sin а,
то, следовательно:
^ = а| + ^ = а|4-й|,
(6.43)
(6.44)
(6.45)
(6.46)
откуда
Z = |/а|Ц-6] = У а;= const. (6.47)
Таким образом, точка Е механизма рис. 380 будет всегда опи-
сывать окружность постоянного радиуса, равного I. Механизм, осу-
ществляющий огибание двух софокусных эллипсов, показан на
Рис. 381.
рис. 381, а. Он аналогичен по схеме механизму, показанному на
рис. 379, а, но имеет соотношения размеров, удовлетворяющие усло-
виям:
АВ = 62 и АЕ = / = ]/а| 4-bl — j/'a|4~ bf. (6.48)
Прямые tt и qq будут огибать софокусные эллипсы с полуосями:
aIt Ьх и а2, Ь2.
Если необходимо иметь огибание двух софокусных эллипсов од-
ним жестким прямым углом, то это может быть сделано механизмом
(рис. 381, б), аналогичным по схеме механизму, показанному на
рис. 379, б, но с размерами, удовлетворяющими условиям (6.48).
10 И. И. Артоболевский
290 СИНТЕЗ МЕХАНИЗМОВ ДЛИ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
В заключение отметим, что из аналогичных соображений могут
быть получены механизмы для огибания двумя взаимно-перпендику-
лярными прямыми гипербол и парабол.
4°. Рассмотрим коникограф, у которого одновременно имеется
точка, чертящая коническое сечение, прямая, огибающая это сечение
[Зи], и прямая, обкатывающая эволюту конического сечения. В основу
этих механизмов можно положить вышерассмотренные четырехзвен-
ные механизмы для огибания конических сечений. В основу меха-
низма для одновременного черчения и огибания эллипса положен
ранее рассмотренный (§ 17, 2°) четырехзвенный механизм (рис. 382),
состоящий из подвижных звеньев 7, 2 и 3. Если точка А совпадает
Рис. 382.
с центром эллипса, а точка С с одним из его фокусов Ft, то прямая tt,
принадлежащая звену 2 будет, как это показано в § 17, 2°, огибать
эллипс. Выполним звено 3 в виде жесткого прямоугольного рычага
ЕСт и присоединим к звеньям 7 и 3 двухповодковую группу, со-
стоящую из звеньев 4 и 5. Тогда точка Р будет всегда совпадать
с мгновенным центром вращения звена 2 и при движении механизма
будет описывать неподвижную центроиду звена 2. Нормаль в точке
соприкосновения огибаемой и огибающей всегда проходит через мгно-
венный центр вращения в относительном движении огибаемой по оги-
бающей: поэтому если из каждого положения точки Р опускать
перпендикуляр на соответствующее положение прямой 11, то геоме-
трическое место подошв D этих перпендикуляров будет представлять
собой эллипс. Для того чтобы получить механизм, который имел бы
точку D, чертящую эллипс, с ползуном 4 жестко связываем прямую п—п.
§ 17]
МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 291
углом 90° к оси движения ползуна 4.
связываем крестообразным ползуном 6. Таким
расположенную под
Далее, прямые пп и tt
образом, прямые пи и tt могут
свободно скользить в ползу-
не 6 вдоль своих собственных
направлений. Центр D ползу-
на будет чертить эллипс. При
этом прямая tt будет всегда
касательной к эллипсу, вычер-
чиваемому точкой D.
Вследствие того, что фи-
гура PDBC будет всегда пря-
моугольником, механизм имеет
пассивную связь. Поэтому в
нем будет вместе с неподвиж-
ным семь звеньев. Прямая пп
будет нормалью к эллипсу, сле-
довательно, она будет всегда
обкатывать эволюту ЭЭ эл-
липса (рис. 382), т. е. прямая
пп, являясь как бы подвиж-
ной центроидой, катится без скольжения по неподвижной центроиде ЭЭ.
В основе механизма для одновременного черчения и огибания ги-
пербол и обкатывания эволют имеем четырехзвенный кулисный механизм
АВС (рис. 383). Прямая tt,
принадлежащая звену 2, бу-
дет огибать гиперболу, если
точка А совпадает с центром
гиперболы, а точка С с одним
из фокусов Fj гиперболы.
Присоединяя к основному
кулисному механизму анало-
гично случаю, рассмотрен-
ному на рис. 382, двухпо-
водковую группу, состоящую,
из звеньев 4 и 5 и крестооб-
разный ползун 6, получим се-
мизвенный механизм. Точка
D звена 6 этого механизма
будет чертить гиперболу.
Одновременно с этим пря-
мая tt будет огибать гипер-
болу и прямая пп будет
обкатывать эволюту ЭЭ.
построен механизм для одно-
Аналогичным приемом может быть
временного черчения и огибания парабол (рис. 384). В основе его
10*
292 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
лежит четырехзвенный кулисный механизм с двумя ползунами 7 и 2.
Прямая tt, принадлежащая звену 2, будет огибать параболу, если
точка С совпадает с фокусом Fx параболы, а ползун 7 будет дви-
Рис. 385.
ка механизмов, показанных на
гаться поступательно вдоль прямой аа,
параллельной директрисе параболы и
касательной к вершине параболы. При-
соединяя к основному кулисному меха-
низму аналогично случаям, рассмотрен-
ным на рис. 382 и 383, двухповодковую
группу, состоящую из звеньев 4 и 5,
и крестообразный ползун 6, получим
семизвенный механизм. Точка D звена 6
этого механизма будет чертить пара-
болу. Одновременно с этим прямая tt
будет огибать эту параболу и прямая
пп будет обкатывать эволюту ЭЭ.
Таким образом, задача об одновре-
менном огибании и черчении кониче-
ских сечений и обкатывании их эволют
может быть разрешена семизвенными ме-
ханизмами с парами V класса. Настрой-
рис. 382 и 383, производится измене-
нием длин звеньев 7 и АС, а механизма,
показанного на рис. 384, —
изменением длины кратчайшего расстояния от
5°. Следующим типом конихографов могут
быть механизмы, в которых использован метод,
изложенный в § 6, 2°. Метод основан на воз-
можности для любого плоского механизма с
парами V класса механически вычертить под-
вижную и неподвижную центроиды путем
присоединения к основному механизму необ-
ходимого количества двухповодковых групп с
одной средней вращательной парой и двумя
крайними поступательными парами.
Применительно к четырехзвенному шар-
нирному механизму ABCD (рис. 385) схема
механизма для черчения подвижной и непод-
вижной центроид звена 4 будет иметь сле-
дующую структуру. К звеньям 2 и 3 присое-
точки С до прямой аа,
Рис. 386.
диняется двухповодковая группа, состоящая из звеньев 5 и 6, входящая
в поступательные пары со звеньями 2 и 3. Звенья 5 и 6 входят во вра-
щательную пару Е. При неподвижном звене 7 точка Е будет чертить
неподвижную центроиду Цк. Для получения подвижной центроиды Цп
необходимо остановить звено 4, т. е. обратить движение механизма.
Рассмотрим механизм антипараллелограмма (рис. 386), у кото-
рого неподвижным будет малое звено AD, Присоединим к ме-
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 293
ханизму ABCD двухповодковую группу, состоящую из звеньев
5 и 6.
Так как АВ —DC и AD = CB, то, следовательно, треугольники
АВС и CDA будут иметь равные стороны и будут расположены
симметрично. Тогда углы АВС и CDA будут равны и, следовательно,
треугольники СВЕ и ADE будут также иметь равные стороны и
будут симметричны. Из равенства сторон указанных треугольников
следует, что EB = ED, откуда получаем:
АЕ + ED = АЕ + ЕВ = АВ = const.
Таким образом, сумма расстояний
низма будет всегда постоянной. Сле-
довательно, кривая, описываемая
точкой Е механизма, будет эллипсом
с фокусами Fi и Р2, совпадающими
с точками А и D и большой осью,
равной длине звена АВ. Настройка
механизма для черчения эллипсов с
различными параметрами сводится к
изменению длин звеньев механизма.
Если неподвижным сделать одно
из больших звеньев антипараллело-
грамма (рис. 387), то, присоединив
двухповодковую группу, состоящую
из звеньев 5 и 6, получим меха-
низм, у которого точка Е будет
чертить гиперболу. В самом деле,
треугольники АВС и CDA будут
иметь равные стороны и будут рас-
положены симметрично. Тогда углы
ЕВС и EDA будут равны и, следо-
вательно, треугольники СВЕ и
ADE будут иметь равные стороны
трично.
Из равенства сторон указанных
EB — ED, откуда получаем:
точки Е от точек А и D меха-
и будут расположены симме-
треугольников следует, что
АЕ — ED = АЕ — ЕВ = АВ — const.
Таким образом, разность расстояний точки Е от точки А и D
будет всегда постоянной. Следовательно, кривая, описываемая точ-
кой Е механизма, будет гиперболой с фокусами Fv и совпадаю-
щими с точками А и D. Расстояние между вершинами ветвей гипер-
болы равно длине звена АВ. Настройка механизма для черчения
гипербол с различными параметрами сводится к изменению длин звеньев.
На рис. 387 показано положение механизма для черчения правой
ветви тп гиперболы. Гипербола вычерчена для поворота звена DC
294 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
на угол, равный 180°. Точка С перемещается в направлении, указан-
ном стрелкой, из положения С' в положение С". При этом звено АВ
поворачивается на угол, равный В'АВ". Для вычерчивания сопряжен-
ной ветви гиперболы необходимо установить механизм в поло-
жение AB^D (на рис. 387 это положение показано пунктиром).
Механизм для черчения парабол показан на рис. 388. Ползун 2
движется по неподвижной прямой hh. С ползуном 2 шарнирно скреплен
рычаг 4. Прямая 11 этого рычага скользит в ползушке 3, вращаю-
щейся около неподвижной оси D. Отрезки АК и LD равны и обра-
зуют прямые углы с прямыми 1I и hh. Присоединив двухповодковую
группу, состоящую из звеньев 5 и 6, получим механизм, у которого
точка Е будет чертить параболу пгт. В самом деле, треуголь-
ники AKD и LDA будут иметь равные стороны и будут расположены
симметрично. Из равенства сто-
рон указанных треугольников
следует, что KD = AL. Тогда
имеем равенство сторон сим-
метрично расположенных тре-
угольников EAL и EDK. От-
сюда следует, что ЕА — ED.
Таким образом, расстояния
точки Е от точки D и от
прямой hh будут всегда равны.
Следовательно, кривая, описы-
ваемая точкой Е механизма,
будет параболой с фокусом F,
совпадающим с точкой D, и ди-
ректрисой, совпадающей с пря-
мой hh. Настройка механизма
для черчения парабол с различ-
ными параметрами сводится к изменению длин АК и DL. Все рассмо-
тренные механизмы являются шестизвенными механизмами с общей
структурой, позволяющей рассматривать их как коникограф, тре-
бующий соответствующей настройки звеньев для черчения различных
конических сечений.
6°. Механизмы, вычерчивающие различные кривые 2-го порядка,
весьма многообразны. В настоящем параграфе мы рассмотрим только
наиболее простые по своей структуре механизмы. На рис. 389 пока-
зан четырехзвенный механизм эллипсографа, представляющий собой
кривошипно-шатунный механизм с кривошипом АВ, длина которого
равна длине шатуна BD. Механизм основан на известном свойстве
отрезка, скользящего своими концами по двум взаимно-перпендику-
лярным прямым Ау и Ах. Как известно, в этом случае средняя точка В
CD
отрезка CD опишет окружность радиуса АВ, равного АВ = -^~.
Любая другая точка звена 3, например точка Е, вычертит эллипс,
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 295
уравнение которого будет
-J—-I_____^-=1
(СЕ)2 । (DE)S
(6.49)
относительно системы координат хАу.
Следовательно, большая полуось эллипса будет равна DE и
малая полуось СЕ. Точка С механизма всегда движется по прямой.
Следовательно, если в этой точке
ввести звено 3 в кинематическую
пару с ползуном 5 (показан на
рис. 389 пунктиром), то кри-
вошип 2 может быть удален
из механизма, и механизм эл-
липсографа будет представлять
собой четырехзвенный меха-
низм с двумя последователь-
но расположенными вращатель-
ными и поступательными па-
рами.
Движение отрезка CD в
прямом угле может быть вос-
произведено качением подвиж-
ной центроиды 7/3п, принадле-
жащей звену 3, по неподвиж-
Рис. 389.
ной центроиде принадлежащей звену 1. Центроида Ц3п будет
окружностью радиуса, равного длине отрезка CD, а центроида будет
Другим механизмом для черчения
сографа (рис. 390), предложенный Н.
окружность радиуса, равного
CD
длине отрезка АВ — -?~. При
качении окружности Ц3п по
окружности /_/3н точки, лежа-
щие на самой окружности, бу-
дут описывать прямые, являю-
щиеся диаметрами окружно-
сти А/зн> а любая другая точка,
принадлежащая плоскости ок-
ружности Z/3n, будет описывать
эллипс.
эллипсов будет механизм эллип-
Б. Делоне [17] и названный им
«проектором», так как он основан на принципе проектирования
окружности на плоскость, образующую некоторый угол с плоскостью,
содержащей проектируемую окружность. Механизм состоит из двух
равных звеньев ВС и BD, точки С и D которых скользят вдоль
оси х. Фигура EBFG представляет собой ромб. Обозначим BC=BD—l\
296 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
абсциссах точек Вии. Тогда точка
Рис. 39С
для черчения как конических
EB = BF = FG = GE = а. Если точка В описывает окружность, то
точка G будет описывать эллипс. Последнее следует из того, что
механизм всегда удовлетворяет условию
l^ = k = const. (6.50)
Следовательно, ординаты всех точек окружности, описываемой
точкой В, уменьшаются в одинаковое число раз при неизменных
G будет описывать эллипс. Из
чертежа (рис. 390) следует:
LG = LB — 2BM =
=Lb{i-2™), (6.51)
но
ВМ _ а
LB — I '
Следовательно:
LG = LB(1 — 2у) =
— k-LB, (6.52)
откуда и следует условие
(6.50).
П. О. Сомов [49] развил
теорию механизма, предло-
женного Н. Б. Делоне, и
показал большое количе-
ство модификаций механизма
сечений, так и кривых более
высоких порядков. Ниже приводится один из механизмов П. О. Сомова,
предназначенный для черчения эллипсов (рис. 391). По оси Ох дви-
гаются ползуны 2 и 3. Фигура LCMD образует параллелограмм.
Точка М ползуна 8 движется по прямой ON, Обозначим: AL = BL = l,
LC = DM = qlli LD = CM = qJ.
При движении точки /И по прямой ON точка L будет описывать
эллипс.
Пусть уравнение прямой ON будет:
ум = ахм- (6.53)
Спроектируем точки С, D и L на ординату г4ц. Имеем:
DD = CC'— LL', (6.54)
Xm — xl-\-LL\ (6.55)
ум =yL 4- L'D' + D'M =yL + C'M 4- MD' =
=yL + /W-(CC/ 4- v (<<V)a-(W. (6.56)
§ 17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 297
Далее, из подобия треугольников имеем:
/
q«J____qii
С С DD' ’
(6.57)
Решая совместно уравнения (6.53) — (6.57), получим окончатель-
ное уравнение кривой, описываемой точкой £, в следующем виде:
a^xi + l(l+^i + 9i)2 + a2(92 — ?i)2]J'l —
- Ча (1 4- 4- <h)xLyL -a4qi-qt)^ = 0. (6.58)
Уравнение (6.58) будет уравнением эллипса, так как его инва-
риант I будет равен:
/ = а4 (91 — <74*.
(6.59)
Нетрудно видеть, что инвариант / будет больше нуля, т. е.
/>0.
7°. Переходим к рассмотрению
вычерчивания гипербол. На
рис. 392 показан механизм
Н. Б. Делоне для черчения
гипербол. Фигура BDCE пред-
ставляет собой ромб, точки В
и С которого двигаются по
оси Оу с помощью ползунов
5 и 6, Равные рычаги АВ и
АС входят в кинематические
пары с ползуном 2, который
двигается по неподвижной пря-
мой qq, образующей с осью х
угол ср. При движении пол-
зуна 2 вдоль прямой qq точки
Е и D чертят две ветви од-
ной гиперболы. Прямая qq при
этом будет одной из асимптот.
Обозначим: BD = DC —СЕ =
ЕВ —а и АВ — АС=^Ь. Тогда
имеем для точки D:
для
некоторых механизмов
Рис. 392.
из треугольников CDG и CAF
(у-У IG)2 а3 — х3
(у 4- KF)3 = b3 — (CF)2 = Ь3 — (ОК)3 = Ь3—
Так как отрезок IG = KF, то, следовательно:
откуда окончательно получаем уравнение гиперболы, описываемой
298 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
точками D и Е. Имеем: '
v2 у2
a2 —«s — tg2<p(a2— 6s)= 1 ’ (6’6°)
Механизм, показанный на рис. 393, является модификацией меха-
низма П. О. Сомова (рис. 391). В отличие от последнего фигура LCMD
образует четырехугольник, у которого противоположные стороны не
равны, а удовлетворяют условию
(W)2 + (С7И)2 = (ТИП)2 + (CL)2. (6.61)
Кроме того, если обозначить отрезки AL и LB через Ц и /,2,
то отрезки LD и LC должны удовлетворять условию LD — qlx и
LC = qL1. Нетрудно видеть, что в этом случае диагональ ML будет
всегда перпендикулярна к оси Ох, а диагональ CD перпендикулярна
к оси Оу. Если уравнение
прямой ON будет
•— ОХд! —- QX£,
то уравнение кривой, очер-
чиваемой точкой L, будет
уравнением гиперболы:
а*хь + (I -}- 2q)yl —
— 2а(1 -j-q) xLyL 4-
+ И2—£0=0, (6.62)
где
Д2 = LC = ql% и = CM.
Инвариант уравнения
(6.62) равен:
/= — a2q\
т. е. инвариант I будет меньше нуля и, следовательно, точка L
чертит гиперболу.
На рис. 394 показан механизм для черчения гипербол Г. П. Вят-
кина *). Звенья 7, 3 и 7 входят в поступательные пары, образуя
трехзвенный механизм четвертого семейства с одними поступатель-
ными парами. Направление CF звена 3 при его движении остается парал-
лельным оси Оу. К этому механизму присоединен инверсор, состоящий из
звеньев 2, 5, 4 и 6. Звено 5 инверсора входит в поступательную
пару со звеном 3, при этом отрезок ED постоянной длины, равной Ь,
образует с отрезком CF прямой угол.
Из чертежа непосредственно следует, что
CD = xtgy—у и DF = xtgy
*) Г. П. Вяткин, Механизмы для вычерчивания плоских кривых и аксо-
нометрических изображений, кандидатская диссертация, Станкин, Москва, 1919,
§17] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КОНИЧЕСКИХ СЕЧЕНИЙ 299
Далее, имеем:
CD- DF = (ED)2 = b2.
Следовательно:
(х tg ср — J) (х tg ср у) = Ь*,
(6.63)
откуда получаем уравнение гиперболы, описываемой точкой D
_ь_
tg?
-2-§=1.(6.64)
Нетрудно видеть, что
звено 5 имеет поступатель-
ное движение. Следователь-
но, все его точки описы-
вают одни и те же кривые,
в данном случае гипер-
болы.
8°. Рассмотрим некото-
рые механизмы для черче-
ния парабол. На рис. 395
показан механизм Антонова
[17а] для черчения парабол.
Механизм основан на теореме
Рис. 394.
о том, что если вращать пря-
мой угол qAm вокруг своей
вершины А, то геометриче-
ским местом точек В пересечения его стороны Ат с перпендикуля-
hh, будет парабола с вершиной в точке А. Осью параболы будет
ось Ах, перпендикулярная к прямой hh.
300
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[гл. VI
Из подобия треугольников ABD и АСЕ следует:
AD — AE
BD~ ЕС
или
откуда получаем уравнение параболы, описываемой точкой В меха-
низма. Имеем:
у2 = 2рх. (6.65)
На рис. 396 показан другой механизм для черчения парабол. Оси
звеньев 2 и 4 образуют прямой угол. Звено 5 выполнено в виде
прямоугольного рычага qCm. Осью параболы, описываемой точкой В,
будет прямая тт. Вершиной параболы будет точка О. Расстояние С А
равняется 2р. Из подобия треугольников ОВС и АСВ имеем:
ОС
ВС
ВС х у
или — = ^~ ,
С А у 2р ’
откуда получаем уравнение параболы, описываемой точкой В
у2 = 2рх.
(6.66)
§ 18. Механизмы для черчения и огибания некоторых кривых
высших порядков
1°. Рассмотрим некоторые механизмы для черчения кривых высших
порядков. Пусть около точки А (рис. 397), находящейся на расстоя-
нии а от начала координат О, вращается прямая Ат. Если от
Механизм для черчения строфоиды
точки Р пересечения прямой
Ат с осью Оу отложить на
ней в обе стороны от точки Р
отрезки PC и РВ, равные
PC — РВ = РО, то геометри-
ческим местом полученных то-
чек В и С будет строфоида,
уравнение которой в прямо-
угольной системе координат
будет
<6-67)
и в полярной системе координат
cos 2ср
р = а---------
г COS ср
(6.68)
Прямая qq является асимп-
тотой строфоиды.
показан на рис. 398. Он пред-
ставляет собой четырехзвенный механизм, у которого звено 3 выпол-
нено в виде прямоугольного рычага со стороной АС, равной АС = а.
£_ У_
У ’
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 301
Точка В лежит на кратчайшем расстоянии от оси Оу, равном также а.
Строфоиду описывает точка С. Из подобия треугольников ADC
и ВЕС имеем:
AD _ВЕ
DC~~ СЕ
или
)а2 — х2 а —х
х у 1
откуда получаем уравнение строфоиды, вычерчиваемой точкой С,
Имеем:
У = (6.69)
а-{-х
В § 17 (рис. 388) было показано, что звено 3 механизма вида,
показанного на рис. 398, имеет в качестве подвижной и неподвиж-
ной центроид равные пара-
болы. Известно [18е], что
при качении друг по другу
таких парабол точки, при-
надлежащие подвижной цен-
троиде, будут описывать
циркулярные уникурсальные
кривые 3-го порядка. Точ-
ки, лежащие вне очертания
подвижной параболы, описы-
вают кривые с двойной точ-
кой. Точки, лежащие на
очертании параболы, опи-
сывают кривые с ючками
возврата, лежащими на очер-
тании неподвижной центро-
иды, а точки, лежащие внутри
очертания подвижной центро-
иды, будут описывать кривые
с изолированными точками. Таким образом, механизм, показанный
на рис. 398 позволит вычерчивать большое разнообразие кривых
фокального типа. Как это будет показано ниже (рис. 400), этим же
механизмом могут быть воспроизведены кривые типа циссоид. Если
расстояния ОВ и АС механизма выбрать неравными, то этим же
механизмом можно воспроизводить кривые 4-го порядка. В. В. Добро-
вольским были предложены механизмы для воспроизведения кривых
Бурместера, кривых круговых точек и кривой центров, которые
являются кривыми 3-го порядка фокального типа *). Если эти меха-
*) В. В. Добровольский, Теория механизмов для образования плоских
кривых, стр. 72—74, Москва, 1953.
302
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[ГЛ. VI
низмы образовать из сочетания только пар V класса, то в общем
случае механизмы должны быть четырнадцатизвенными, что дает
основание предполагать, что практическая ценность таких механизмов
для решения задач метрического синтеза едва ли достаточно велика.
2°. Пусть около точки О (рис. 399) вращается прямая От. кото-
рая пересекает окружность диаметра, равного 2а и касательную qq
к этой
окружности в точках
Рис. 399.
С и Р. Если от точки О на прямой От
откладывать отрезки, заключенные
между окружностью и прямой, т. е.
отрезки ОВ = СР, то геометрическим
Диоклеса,
уравнение ко-
(6.70)
(6-71)
местом полученных точек В будет циссоида
торой в прямоугольной системе координат будет
2 *3
У =2^
и в полярной системе координат
2а sin2 v
г COS
Асимптотой циссоиды Диоклеса будет прямая qq. Механизм для
черчения циссоиды Диоклеса показан на рис. 400. Циссоиду вычер-
чивает точка D прямоугольного рычага 3. длина стороны АС которого
равна 2а. Точка D расположена посредине между точками А и С.
Из подобия треугольников AED и DFG имеем:
АЕ_ DF
ED~ FG
или
/а2 — х2 _ У
---Т--- OG х'
(6.72)
Далее, из подобия треугольников AED и AOG имеем:
AG __ а
OG~"x’
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 303
или так как
A G = АС — GC = АС — 03 = 2а — OG,
то, следовательно:
откуда получаем:
2а — OG __ а
00 ~ х
00 =
2ах
а + х
(6.73)
Подставляя полученное выражение (6.73) в уравнение (6.72)
получаем уравнение циссоиды Диоклеса, вычерчиваемой точкой D,
Имеем:
У = --2-. (6.74)
у а + х v 7
На рис. 401 показан другой ме-
ханизм для черчения циссоиды
Диоклеса [Зк]. Механизм (рис. 401)
состоит из кулисы 8, вращающейся
вокруг точки А. По кулисе 8 сколь-
зит ползун 2, входящий в точке С
во вращательную пару со сдвоен-
ным кривошипом 3, вращающимся
вокруг точки В.
Кривошип 3 входит в точке D
во вращательную пару с кулисой 4.
Кулиса 4 в точке F входит во вра-
щательную пару с кривошипом 5,
вращающимся вокруг точки Л4. По
кулисе 4 скользит ползун 6, вхо-
дящий в точке О во вращательную
пару с ползуном 7, который сколь-
зит по кулисе 8.
Рис. 401.
Размеры звеньев механизма должны
удовлетворять условию
AB = BC=BD = FM = a,
где а — радиус производящей окружности, и
DF = BM,
т. е. фигура BDFM должна быть параллелограммом.
При движении механизма точка О вычерчивает циссоиду тт.
Для доказательства рассмотрим два подобных треугольника
AGE и АСИ. Имеем:
GE _ АЕ
СН “ АН ’
304 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Обозначая GE —у, АЕ = х и имея в виду, что АЕ = НК, полу-
чаем:
У=ХТ^- <6-75)
Далее, из условия
АН __ СН_
СИ ~~ НК
имеем:
АН • НК=(СН)\
можно представить так:
СЕ _ ( СНУ
сн' \АН) ’
откуда
(сну
у АН2 '
(6.76)
Исключая из уравнения (6.75) и (6.76)
величину СН, получаем уравнение цис-
соиды Диоклеса, которую вычерчивает
точка G:
/ = (6-77)
3°. Пусть прямая От (рис. 402) вра-
щается около точки О и пересекает ок-
ружность диаметра, равного 2а, и пря-
мую qq, касательную к этой окружности,
в точках С и Р. Геометрическим местом
точек В, полученных на пересечении пря-
мых, параллельных осям координат, про-
веденных через точки Р и С, будет
версьера (аньезьера). Уравнение этой кривой в прямоугольной системе
координат будет:
2___ 4а2 (2а х)
(6.78)
Асимптотой версьеры будет ось Оу.
На рис. 403 показан механизм для вычерчивания версьеры.
Механизм (рис. 403) состоит из кулисы 8, вращающейся вокруг
точки А. По кулисе 8 скользит ползун 2, входящий в точке С
во вращательную пару с кривошипом 3, вращающимся вокруг точки В.
По кулисе 8 скользит ползун 4, входящий в точке D во вращатель-
ную пару с прямоугольным рычагом 5. Рычаг 5 движется поступа-
тельно в неподвижных направляющих Н в направлении, перпендику-
лярном к диаметру производящей окружности. Сторона Da рычага 5
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИВ ЧНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 305
скользит в крестообразном прямоугольном ползуне 6\ Звено 7, вхо-
дящее в точке С во вращательную пару с ползуном 2, скользит
в ползуне 6. Механизм должен удовлетворять условиям:
АВ = ВС = а,
где а — радиус производящей окружности. Углы dEa ubDa равны 90 •
Прямая QD является касательной к производящей окружности в
точке G. При движении механизма точка Е вычерчивает версьеру
тт (рис. 403).
Для доказательства рассмотрим
два подобных треугольника ADO и
АСЕ.
Имеем:
GI) __ AG
FC ~ AF л
Так как GD — FE=y и AF—
= х, то, следовательно:
FC=g-. (6.79)
Далее, из условия
AF __ FC
FC FG
получаем:
(FC)'2 = х (2а — х). (6.80)
Рис. 403.
Исключая из уравнений (6.79) и (6.80) величину FC, получаем
уравнение версьеры, которую вычерчивает точка Е:
з 4д2 (2а — х)
(6.81)
4®. На рис. 404 показан лист Декарта, уравнение которого в
прямоугольной системе координат будет:
х3 -|-у* = Заху.
(6.82)
Асимптотой этой кривой будет прямая qq, отсекающая на осях Ох
и Оу отрезки, равные а.
Механизм для вычерчивания листа Декарта показан на рис. 405.
Ползун 6 двумя равными по длине шатунами 4 и 5 приводит
во вращение звенья 2 и 3, у которых отрезки ОО и OF равны
между собой. Нетрудно видеть, что углы у, образованные криво-
шипами ОО и OF с осью движения ползуна, будут всегда равны
306
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[гл. VI
Рис. 105.
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 307
между собой. Нетрудно далее видеть, что углы ср и ф, образуемые
звеньями 2 и 3, будут равны:
ср = 45° Т и ф = — Ъ
откуда имеем:
6 = 90° — ср,
или
tg’f = Gtgcp.
Звенья JO и 11 двигаются поступательно вдоль осей Ох и Оу и
входят в кинематические пары с ползунами 7, 8 и 9 и звеном 14.
Точка D двухповодковой группы,
состоящей из звеньев /2 и 13,
вычерчивает лист Декарта.
Из подобия треугольников
ОЕС и KDC имеем:
ОЕ KD _______ у qqx
-ОС^-КС- ОС~х • (6ЛЗ)
Отрезок ОЕ из треугольника
ОЕА равен:
ОЕ = За ctg ср.
Отрезок ОС из треугольника
ОСВ равен:
ос=-^~.
ctg?
Подставив полученные выражения для отрезков ОЕ и ОС в
уравнение (6.83), после несложных преобразований получаем уравне-
ние листа Декарта, вычерчиваемого точкой D. Имеем:
х3 4- _У3 = Заху.
(6.84)
Механизм может вычерчивать только отдельные участки этой
кривой.
5°. На рис. 406 показана улитка Паскаля. Эта кривая получается,
если от точки В пересечения с окружностью прямой От, вращаю-
щейся около точки О, откладывать по обе стороны от точки В два
равных отрезка:
АВ = ВС = Ь.
Уравнение улитки Паскаля в полярной системе координат будет:
р = 2г cos ср ± b, (6.85)
где г—радиус производящей окружности.
308 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
На рис. 407 показан четырехзвенный .механизм, точки Е и D
которого описывают улитку Паскаля. В этом механизме длина
кривошипа АВ должна равняйся расстоянию АС, или
АВ = АС = г.
Нетрудно тогда видеть, что радиус-вектор р кривой, описываемой
точками D и Е, равен:
р = CD = 2r cos ср -\-Ь или p = CE—2r cos ср — Ь.
Если величина b в уравнении (6.85) будет равна 2г, то мы полу-
чаем кардиоиду (рис. 408)
уравнение которой будет:
р = 2г(1 ч-cos ср). (6.86)
Механизм для черчения кар-
диоиды показан на рис. 409.
Он представляет собой прямо-
угольный рычаг 3, скользящий
своими сторонами во вращаю-
щихся ползунах 2 и 4, Кар-
диоиду описывает точка С,
лежащая на расстоянии 2г от
точки D.
Из рис. 409 непосредственно следует:
р — 2г — BD = 2г — 2r cos <р = 2r (1 — cos ср), (6.87)
т. е. точка С действительно описывает кардиоиду.
6°. Если прямая От вращается около точки О (рис. 410) и
пересекает прямую qq в точке В, то, отложив от точки В в обе сто-
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 309
роны равные отрезки ВС=^ ВА=Ь, получим геометрическое место
точек А и С, образующих конхоиду Никомеда. Уравнение конхоиды
в полярной системе координат будет:
р= —— + Ь. (6.88)
‘ COS v
Асимптотой конхоиды будет прямая qq.
На рис. 411 показан механизм для черчения конхоиды. Ветви
конхоиды описывают точки D и С звена 3.
7°, На рис. 412 показана лемниската Бернулли.
Лемниската Бернулли представляет собой кривую, для каждой
точки которой удовлетворяется условие, что произведение расстояний
310 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
этой точки от точек F’ и F", лежащих на расстоянии OF' =
= OF" = —от точки О, есть величина постоянная. Уравне-
ние лемнискаты в прямоугольной системе координат будет:
(х2 +У)2 = а2 (х2 —У), (6.89)
т. е. это будет кривая 4-го порядка.
В полярной системе координат уравнение этой, кривой будет:
р2 = а2 cos 2<р. (6.90)
Механизм для черчения лемнискаты представляет собой механизм
шарнирного антипараллелограмма (рис. 413). Средняя точка Е шатуна
будет описывать лемнискату. Пусть длины звеньев соответственно
равны
с С
AB = DC = a
и В с
и
D. Нетрудно
Рис. 413.
треугольников DBA
Из
ВС = AD = аУ 2. Соединим точки А
видеть, что прямые АС и BD
будут параллельными. Продол-
жим далее направление радиу-
са-вектора р = ОЕ до пересе-
чения в точках О и F с кри-
вошипами DC и АВ. Треуголь-
ники АВС и CD А равны между
собой. Прямая ОЕ, как соеди-
няющая середины равных сто-
рон AD и СВ, будет парал-
лельна прямым АС и BD и
будет средней линией равно-
бочной трапеции ABDC. Сле-
довательно, длина отрезка FG
будет равна:
р0=АС±ВР
Радиус-вектор р будет равен:
р = ОЕ = FG — (FO + EG).
имеем:
и DBC
FO — EG
BD
2 *
Следовательно:
р _ AO±BD_ _ BD>
ИЛИ
AC- BD
Р =--2---
(6.91)
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 311
Опустим из точки А перпендикуляр АН на направление BD.
Нетрудно видеть, что отрезок НВ равен:
(6.92)
Сравнивая выражения (6.9 Г) и (6.92), видим, что отрезок НВ
равен радиусу-вектору р.
Из треугольника AHD имеем:
AH=AD sin <р = а]/2 sin ср.
Далее, из треугольника АНВ имеем:
(ДЯ)2-|-(НВ)2 = (ЛВ)2,
или
(а \/(2 sin ср)2 р2 = а2,
откуда получаем:
р2 = а2 (1 — 2 sin2 ср) = а2 cos 2ср, (6.93)
т. е. точка Е механизма действительно описывает лемнискату Бернулли.
8°. На рис. 414 показана четырехлепестковая роза. Уравнение
этой кривой в полярной системе координат будет
р = a sin 2ср (6.94)
и в прямоугольной системе координат будет
(х2 |>2)3 = 4а2х-_у2, (6.95)
312 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Механизм для черчения четырехлепестковой розы показан на
рис. 415. Эту кривую чертит точка D крестообразного ползуна 6.
Длина звена 5 равна 2a. Оси звеньев 2
механизма взаимно-перпендикулярны. Угол
и 5 во всех
DAC равен
положениях
углу DBA.
Обозначим эти углы через ср. Тогда
радиус-вектор p=AD точки D
будет равен:
р = AD = АВ sin ср,
или
так как
АВ = 2a cos <р,
то, следовательно:
р = 2a sin ср cos ср =
= asin2cp, (6.96)
г. е. точка D механизма описы-
вает четырехлепестковую розу.
9°. На рис. 416 показана
астроида. Астроида представляет
собой гипоциклоиду, описываемую точкой D, лежащей на окружности
радиуса г при качении этой окружности по неподвижной окружности
р
радиуса R. Соотношение п радиусов равно п= — = 4. Уравнение
астроиды в прямоугольной системе координат будет:
где а равно a = R.
2 2 2
х3 -|-у3 = а3 ,
(6.97)
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 313
Механизм для черчения астроиды, разработанный Г. П. Вяткиным,
показан на рис. 417. Крестообразные ползуны 4 и 6 обеспечивают
перпендикулярность направлений АС с ВС и АВ с CD. Длина звена
АВ равна а. Из чертежа непосредственно следует;
х = ED = AD • cos ср
и
y = DF = BD • sin ср.
Далее,
AD = АС • cos ср = АВ cos2 ср = a cos2 ср
и
BD = ВС • sin ср = АВ sin2 ср = a sin2 <р.
Следова гельно: х — а cos3 ср
и у = a sin3 ср,
откуда имеем: J 1 х3 = a3 cos ср
и i i у3 — a3 sin ср,
или 2 2 х3 = a3 cos2ср (6.98)
и 2 2 у* = a3 sin2 ср. (6.99)
314 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Складывая уравнения (6.98) и (6.99), получаем уравнение астроиды,
описываемой точкой D механизма:
2 2 2
х3 -|~_у3 = а'А .
(6.100)
Нетрудно видеть, что вследствие перпендикулярности направле-
ний CD и АВ отрезок АВ будет касательной к астроиде. Таким
образом, астроида может быть получена как огибаемая при движении
Рис. 418.
будет нормалью к траектории
обкатывать эволюту траектории
точки D может быть получена
звена 2 с точками А и В по осям
Оу и Ох.
С помощью метода дополнитель-
но присоединяемой группы, ука-
занного в § 6, 8°, может быть
получена кривая, представляющая
собой аффинное преобразование ас-
троиды (вытянутая астроида). Для
этого берем обычный механизм эл-
липсографа (рис. 418), состоящий
из звеньев 2, 3 и 5. Выбираем на
звене 5 точку D. Эта точка опи-
сывает эллипс с полуосями а и Ь,
равными a = AD и b = BD. Зве-
нья 2 и 3 выполняем в виде рыча-
гов, скользящих в крестообразном
ползуне 4, обеспечивающем пер-
пендикулярность направлений АС и
ВС к осям Оу и Ох. Тогда точка С
будет всегда чертить неподвиж-
ную центроиду звена 5. Присоеди-
ним в точке С к ползуну 4 звено 7,
скользящее в ползуне 6, вращаю-
щемся около точки D. Прямая Ст
точки D. Следовательно, она будет
этой точки, т. е. эволюта траектории
:ак огибающая положений прямой Ст.
Как известно, эволюта эллипса представляет кривую типа астроиды.
На рис. 418 показана одна ветвь этой кривой, расположенная в одном
квадранте. Если текущие координаты этой астроиды обозначить че-
рез £ и т], то уравнение кривой типа удлиненной астроиды будет:
2 2 2
(aS)3 - г (Ьц)3 — (а2 — Ь2)3 .
(6.101)
10е. Аналогичным методом можно получить и другие кривые,
если они являются эволютами тех или иных более простых кривых.
Как известно, эволютой параболы у1 — 2рх будет полукубическая
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 315
парабола Нейля, уравнение которой, если ее текущие координаты
будут £ и т], имеет следующий вид:
27/и]2 = 8($—р)3. (6.102)
На рис. 419 показан механизм для получения полукубической
параболы Нейля как огибающей нормали Dn в точке D механизма
для черчения параболы. Кривая qq, огибающая последовательные по-
ложения нормали пп, будет полукубической параболой, уравнение
которой будет (6.102).
Рис. 419.
11°. Механизмы для черчения циклических кривых, образованных
качением окружностей по прямой или окружности, представляют собой
планетарные механизмы вида, рассмотренного вами в § 14. Различные
формы кривых, которые этими механизмами могут быть получены,
показаны на рис. 330—340.
Более сложные циклические кривые могут быть получены каче-
нием различных кривых друг по другу, так как в общем виде цик-
лические кривые можно всегда представить как рулетты точек под-
вижной центроиды при ее качении по неподвижной центроиде.
Рассмотрим некоторые механизмы для черчения таких рулетт.
Пусть у четырехзвенного механизма, неподвижное звено сделано
подвижным. Тогда получим механизм, показанный на рис. 420. На
звеньях 2 и 3 установим колесики 7 и 8, имеющие острые ребра.
316 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Колесики 7 и 8 установим так, чтобы они могли свободно вращаться
около своих осей, но не могли перемещаться вдоль этих осей. По-
ложим механизм на горизонтальную плоскость так, чтобы он опи-
рался на колесики и на острие, установленное в точке Е. Тогда,
если перемещать острие по какой-либо кривой, принадлежащей пло-
скости (на рис. 420 взята прямая аа), то любая точка плоскости
звена 4 будет описывать соответствующую рулетту центроиды Z/i, при-
надлежащей звену 4, при качении этой центроиды по выбранной кривой.
В самом деле, вследствие наличия у колесиков 7 и 8 острых
ребер звенья 2 и 3 не могут перемещаться вдоль направлений своих
осей. Центры роликов, а следовательно, и все точки звеньев 2 и 3
будут перемещаться только в плоскостях, перпендикулярных к на-
правлениям АЕ и DE, т. е. звено 4 будет вращаться около после-
довательных точек соприкосновения центроиды Ц4 и выбранной кри-
вой. На рис. 420 показана рулетта ff точки F, принадлежащей
центроиде при ее качении по прямой аа.
Устанавливая карандаш в различных точках плоскости, принадле-
жащей звену 4, можно начертить все возможные рулетты точек центрои-
ды Ut. Если устанавливать карандаш в различных точках звена 1, этим же
механизмом могут быть начерчены рулетты центроиды Цх, принадле-
жащей звену 1. Так как выбор кривой, по которой происходит каче-
ние центроид, является произвольным, то данный механизм является
универсальным для черчения рулетт двух сопряженных центроид.
Из этих общих соображений легко получить механизмы для чер-
чения рулетт конических сечений. Для этого можно использовать
механизмы, рассмотренные нами выше для черчения конических сече-
ний (рис. 386, 387, 388).
Так, если у механизма, показанного на рис. 386, сделать под-
вижным звено 1 и установить колесики 7 и 8 (рис. 421), то мы по-
§ 18] МЕХАНИЗМЫ ДЛЯ ЧЕРЧЕНИЯ И ОГИБАНИЯ КРИВЫХ ВЫСШИХ ПОРЯДКОВ 317
лучим механизм для черчения рулетт эллипса. Если у механизма,
показанного на рис. 387, сделать подвижным звено 1, мы получим
механизм для черчения рулетт гиперболы (рис. 422). Если, наконец,
у механизма, показанного на рис. 388, сделать подвижным звено 1
и установить колесики 7 и 8
(рис. 423), мы получим ме-
ханизм для черчения рулетт
параболы.
Может быть также по-
лучен механизм для черче-
ния рулетт окружности, со-
стоящий из одних только
пар V класса. Для этого
можно использовать изве-
стный механизм эллипсо-
графа, у которого надо сде-
лать подвижным звено 4
(рис. 424) и установить на
звеньях 2 и 3 колесики 7
к прямым BE и СЕ. Рулетты
и 8, плоскости вращения
которых были бы перпендикулярны
окружности обычно вычерчиваются
механизмами фрикционных или
зубчатых колес и требуют для своей настройки сменных колес.
Рис. 423.
Настройка механизма (рис. 424) может быть сделана изменением длины
звена ВС.
Циклические кривые типа циклоид, эпициклоид и гипоциклоид
окружностей могут быть также образованы путем обкатывания, если
использовать то свойство, что эволютами этих кривых будут также
циклические кривые. Так, эволютой циклоиды будет также циклоида,
но смещенная по оси Ох на величину т.г, где г —• радиус перекаты-
318 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
вающейся окружности, а по оси Оу смещенную в отрицательную
сторону на величину 2г.
Эволютами эпициклоиды и гипоциклоиды будут также эпициклоида
и гипоциклоида, уменьшенные или увеличенные в отношении X, равном
где I — отношение радиуса г малой окружности к радиусу R боль-
шой окружности, и повернутые на угол, равный + кХ.
Механизм для получения эпициклоиды методом обкатывания по-
казан на ряс. 187. На рис. 425 показан механизм для получения
гипоциклоиды а как эволюты гипоциклоиды г по способу, аналогич-
ному для механизма, показанного на рис. 187. Гипоциклоида а имеет
коэффициент X, равный X —3,
§ 19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 319
§ 19. Механизмы для воспроизведения различных
функциональных зависимостей
1°. Механизмы для черчения кривых имеют своей задачей не
только механическое воспроизведение различных кривых. Гораздо
более важным практическим приложением этих механизмов является
их использование для получения различных функций или систем
функций. Особое значение это имеет
приборов и счетно-решающих ус-
тройств.
Выше (в § 18) были рассмо-
трены механизмы, позволяющие
воспроизводить сложные функции
различных порядков в виде алгеб-
раических и циклических кривых.
Рассмотрим некоторые меха-
низмы, которые позволяют вос-
производить тригонометрические
функции в виде передаточного
отношения между ведущим и ве-
при проектировании механизмов
Рис. 427.
домым звеньями.
На рис. 426 показан кривошипно-шатунный механизм, у кото-
рого длины АВ и ВС звеньев 2 и 3 равны АВ = ВС = а.
Тогда перемещение х ползуна 4 будет всегда равно:
х — 2а cos ср = 2а sin (?
(6.103)
т. е. данный механизм позволяет получать функции синуса и коси-
нуса.
На рис. 427 показан другой механизм для получения функций
синуса и косинуса. Для этого механизма, если длину кривошипа АВ
принять равной а, будем иметь:
х = a cos = a sin ( j <р
(6.104)
320
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[гл. VI
На рис. 428 показан механизм для получения функций тангенса
и котангенса. Для этого механизма имеем:
х = а tg = — a ctg ?
(6.105)
Наконец, на рис. 429 показан механизм для получения функций
секанса и косеканса. Для этого механизма имеем:
(т + ?)'
х = a sec ср = a cosec
(6.106)
2°. Широкие возможности с точки зрения получения различных
функций дают механизмы, чертящие кривые высших порядков [Зт, 99].
На рис. 430 показан механизм для черчения циссоиды, рассмотрен-
ной нами выше (§ 18, 2°). Циссоиду описывает точка D, лежащая
посредине отрезка АН, длина которого пусть будет равна АН= 1.
Тогда отрезки ВО и OF будут равны ВО = OF = у . Отложим еще
отрезок FC также равный FC = Тогда, если текущую координату
точки А ползуна 2 вдоль неподвижной направляющей обозначить через с,
то из подобия треугольников BAF и ODK имеем:
AF _DK
~BF~UR'
или
1=^, (6.Ю7)
где х и у — текущие координаты точки D. Из уравнения циссоиды
(6.70) имеем:
(6.108)
§ 19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 321
Подставляя выражение для у в уравнение (6.107), получим:
(6.109)
И
£3
y = KD=LC = Tj-^. (6.110)
Таким образом, если, например, в точке D присоединить к звену 3
звено 5, которое свободно движется в крестообразном прямоугольном
ползуне 6, то координате £ точки А будет всегда соответствовать
Рис. 430.
ез
координата утрр
поводковую группу, состоящую из звеньев 7 и 8 (на
звенья показаны пунктиром), то мы получим механизм,
Е2
дет давать функцию . Далее имеем: отрезок КС
точки L. Если присоединить аналогичную двух-
рис. 430 эти
который бу-
равен:
кс=ос-ок=х-^=т^.
(6.111)
Следовательно, тот же механизм может давать и функцию ви-
1
да 1 + $а.
Далее, отрезок KF равен:
KF=OF-OK=^ —(6.112)
11 И. И. Артоболевский
322 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
т. е. этим же механизмом мы можем вычислять функцию ви-
1 —V
да 1+^’
Оставив в основе тот же механизм для черчения циссоиды, при-
соединим к нему двухповодковую группу (рис. 431), состоящую из
звеньев 5 и 6.
Отрезок ОМ равен (рис. 430):
0М = 0К — МК—х — МК. (6.113)
Отрезок МК может быть определен из подобия треугольника
AMF и DMK (рис. 430). Имеем:
AF _ MF _ МК + KF
DK~~ МК ~ МК ’
или
1 1 _fS
у ~~ МК
откуда имеем:
(6Л14)
Подставляя в уравнение (6.113) значения МК из уравнения (6.114)
и х из уравнения (6.109), получим после упрощений:
ОМ = ~?. (6.115)
Таким образом, данный механизм (рис. 431) может рассматри-
ваться как механизм для возведения в квадрат или для извлечения
квадратного корня, так как из уравнения (6.115) следует:
£=У2(0М). (6.116)
Соответственно отрезок MF будет равен:
MF = ~- — ОМ= 1(1 — Е2), (6.117)
т. е. этим же механизмом можно вычислять функцию 1 — ?2.
На рис. 432 к основному механизму, чертящему циссоиду, при-
соединена двухповодковая группа, состоящая из звеньев 5 и 6.
Звено 6 отсекает на оси Оу отрезок ОР, величина которого опре-
делится из подобия треугольников OPF и KDF. Имеем:
Подставляя значения отрезков КВ и KF из уравнений (6.110) и
(6.112), получим:
0/»=^. (6.И9)
Следовательно, данным механизмом можно вычислять функ-
Е8
цию Г^г-
§ 19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 323
324
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[гл. VI
На рис. 433 показан механизм, аналогичный механизму, показан-
ному на рис. 432, но у которого ось вращения звена 6 будет нахо-
диться в точке С. Тогда звено 6 отсекает на оси Оу отрезок OG,
величина которого определится из подобия треугольников GOC и
DKC. Имеем:
Подставляя значения отрезков KD и КС из уравнений (6.110) и
(6.111), после сокращений получим:
OG = e. (6.121)
Таким образом, данный механизм может рассматриваться как ме-
ханизм для возведения в куб или для извлечения кубического корня,
так как из уравнения (6.121) следует:
Е = К(ОО). (6.122)
Путем присоединения к основному механизму, чертящему циссо-
иду, других двухповодковых групп можно получить механизмы для '
вычисления и более сложных функций. Нетрудно, например, показать,
что отрезок МК (рис. 430) равен:
МК~ 2 1+? •
Отрезок OD равен:
1+е
Р т. д,
§19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 325
3°. Механизмы для черчения кривых и получения различных функ-
ций могут быть использованы и для решения уравнений различных
степеней. Для решения квадратных уравнений вида
х2 — px-\-q = 0 (6.123)
может быть использован механизм [Зу], показанный на рис. 434.
Неподвижные направляющие 1 и 2 параллельны между собой и
снабжены шкалами, с помощью которых на направляющей 1 может
быть отложено число, равное l/р, а на направляющей 2 — число,
равное q/p. Звено 3 имеет Т-образную форму и одним своим кон-
цом Mt скользит в ползуне 4, вращающемся около неподвижного
центра К, а другим концом Ми скользит в ползуне 5, вращающемся
около неподвижного центра N. Так как угол KMN прямой, то точка 714
будет описывать окружность, имеющую диаметром расстояние KN-
Звено 3 в точке М входит во вращательную пару с ползуном 6.
Стержень 7, скользящий в ползуне 6, в точке С входит во враща-
тельную пару с ползуном 8, имеющим возможность перемещаться
вдоль направляющей 1.
Для решения уравнения (6.123) устанавливаем ползун 8 так, чтобы
расстояние КС — — . Далее, закрепив звено 8 в этом положении,
перемещаем звено 3 до тех пор, пока прямая Cv звена 7 не пересе-
чет направляющую 2 в точке D так, чтобы расстояние ND = -~.
Тогда прямая tt звена 3 отсечет на шкале, принадлежащей направляю-
щей 2, отрезок NA, равный х2— одному из корней уравнения (6.123).
326
СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ
[ГЛ. VI
Нетрудно видеть, что прямая Cv пересекает окружность диаметра KN
в общем случае в двух точках М и М. Тогда для нахождения дру-
гого корня уравнения (6.123) перемещаем звено 3 так, чтобы точка М
заняла положение М. При этом прямая Cv звена 7 должна прохо-
дить через точку D, принадлежащую направляющей 2 и находящуюся
на ранее отложенном по шкале расстояния ND = ~-. Тогда прямая tt
звена 3 займет положение ft' и отсечет на шкале, принадлежащей
направляющей 2, отрезок NB, равный — другому корню уравне-
ния (6.123).
Действительно, примем постоянное расстояние между направляю-
щими 7 и 2 равным единице. Тогда (рис. 434) имеем:
tg а = х, и tg р = х2.
Далее, из треугольника КСМ имеем:
КС__________________________ cos а
КМ sin (а 4- ₽) "
(6.124)
(6.125)
Из уравнения (6.125), учитывая, что 04 = cos р, получаем:
tg “ + tg ₽ ’
(6.126)
Подставляя в уравнение (6.126) вместо tga и tg [3
из уравнений (6.124) и имея в виду, что отрезок КС
чаем:
1 ______1_
Р Xi -р Х2 ’
откуда
xt — р.
Далее, из треугольника NM'D имеем:
ND_____ sin р
NM' sin (a + ₽) ’
их выражения
1
равен — ,полу-
(6.128)
Из уравнения (6.128), учитывая, что 2WH' = sina, получаем:
ND
lg a tg р
tg “ + tg ₽' •
(6.129)
Подставляя в уравнение (6.129) вместо tga и tgр выражения из
уравнений (6.124) и имея в виду, что отрезок ND равен полу-
чаем: 9=_х^_ (6.130) р Xi~\~ Хц
откуда, учитывая уравнение (6.127), имеем: XiXt — q. (6.131)
§ 19j МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 327
Из условий (6.127) и (6.131) следует, что отрезки NA = x<1 и
NB — Х[, отсекаемые на шкале, принадлежащей направляющей 2,
равны корням уравнения (6.123).
На рис. 435 показан другой вариант механизма для решения урав-
нения (6.123). Доказательство будет аналогичным вышеизложенному.
Так как вершина М прямого угла KMN описывает окружность, то,
Рис. 435.
следовательно, предлагаемый механизм автоматически выполняет ре-
шение уравнений второй степени с помощью так называемой «штей-
неровой окружности» *).
4°. Рассмотрим далее механизм, предназначенный для решения
квадратных уравнений вида
QiX2 -|- а2х аа — 0. (6.132)
Механизм (рис. 436) состоит из неподвижной направляющей 1, по
которой может двигаться поступательно звено 2 с траверсой bb,
образующей с направляющей / угол, равный 90°. Звено 3 вращается
вокруг центра А. Вдоль оси Ас этого звена скользит ползун 4
с жестко связанной с ним траверсой dd, образующей с осью Ас угол,
равный 90°. Звено 4 входит во вращательную кинематическую пару
с ползуном 5, который может скользить по направляющей /.
Для решения уравнения (6.132) необходимо на шкале, жестко свя-
занной с направляющей /, отложить вправо или влево от точки £)
отрезок DE, равный DE = ~-. Звено 2 жестко закрепляется на на-
правляющей / так, чтобы траверса bb проходила через точку Е. Пе-
ремещаем, далее, ползун 5 по направляющей 1 до тех пор, пока
*) А. Адлер, Теория геометрических построений, Одесса, 1924.
328 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
траверса dd звена 4 не отсечет на шкале, жестко связанной со зве-
ном 2, отрезок ЕС, равный ЕС=~. Тогда отрезок DB будет чис-
а.1
ленно равен одному из корней уравнения (6. 132), например корню хг.
Для определения другого корня уравнения (6. 132) находим второе
положение механизма, при котором ползун 5 займет положение 5',
а траверса dd — положение d'd’.
На рис. 436 это положение механизма показано пунктиром. Тогда
отрезок DB' будет численно равен корню х.г уравнения (6. 132).
При пользовании данным механизмом необходимо учитывать сле-
дующие условия, относящиеся к знакам коэффициентов alt и а3
уравнения (6.123).
Пусть коэффициент будет всегда положительным числом. Если
коэффициент а3 будет также положительным числом, то отношение ,
равное отрезку ЕС, надо отсчитывать по шкале, принадлежащей
звену 2, от точки Е вверх. Если коэффициент а3 будет отрицатель-
ным числом, то отношение —, равное отрезку ЕС, надо отсчитывать
от точки Е вниз.
Соответственно отрезки DB и DB', расположенные вправо от
точки D, будут иметь знак минус, т. е. корни хх и х2 будут отри-
цательными. Отрезки DB и DB', расположенные влево от точки D,
будут иметь знак плюс, т. е. корни Xj и х2 будут положительными.
Случай совпадения знаков коэффициентов и а3 показан на
рис. 436. Корни Xi и х2 имеют одинаковые знаки. Случай несовпадения
§ 19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 329
знаков этих коэффициентов показан на рис. 437. Корень имеет
знак плюс, а корень х2 имеет знак минус.
Доказательство проведем для случая, показанного на рис. 436. Из
подобия треугольников ABD и ВСЕ имеем:
DB_
AD~ BE'
Из подобия треугольников АВ'Г) и В'СЕ имеем:
DB’ _ЕС
AD ~~ В'Е’
(6.133)
(6.134)
Примем постоянную для механизма величину AD равной единице.
Тогда из отношений (6.133) и (6.134) получим:
ПО ЕС — ЕС
ВВ BE DE — DB (6.135)
и
__ ЕС _____ ЕС fn 1
В,Е DE_ DE, (6.136)
Исключая из уравнений (6.135) и (6.136) величину ЕС и учиты-
вая, что DE — ~, получим:
DB-\-DB' — a~, (6.137)
Обозначая величину DB (рис. 436) согласно принятому правилу
знаков через —хь а величину DB' — через —х2, получаем из усло-
вия (6.137):
+ = . (6-138)
Из условия (6.138) следует, что отрезок B'E—Xi, а отрезок
ВЕ = Хъ- Тогда из отношения (6.133) имеем:
DB =
ЕС
BE'
(6.139)
или так как DB = — хь ЕС — ^- и BE — — х2, то, следовательно:
XlXi = at'
(6.140)
Таким образом, отрезки DB и DB' представляют собой корни xt
и х2 j равнений (6.132).
330 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Из условия (6.138) следует, что для нахождения корней уравне-
ния (6.132) достаточно установить механизм только в одном из пока-
занных на рис. 436 или 437 положений. Так, установив механизм
в положении, указанном на рис. 436 или 437 сплошными линиями,
имеем отрезок DB, представляющий собой корень xlt и отрезок BE,
представляющий собой корень х2.
5°. Решение уравнений 3-й степени вида
х3 ах2 -ф- Ьх 4- с — 0 (6.141)
Уравнение (6.141) разрешается с помощью следующих конических
сечений:
у = х2 (6.142)
и
ху -ф- ау -ф- Ьх -ф- с — 0, (6.143)
так как нетрудно видеть, что, исключив из уравнений (6.142) и
(6.143) у, получим уравнение (6.141). Уравнение у = х2 представ-
ляет собой параболу qq (рис. 438), не зависящую от коэффициентов
уравнения (6.141). Поэтому эта парабола может быть построена как
постоянная. Равносторонняя гипербола рр, представленная уравнением
(6.143), может быть вычерчена одним из механизмов, указанных в § 17
для черчения гипербол. Проекции точек пересечения параболы и ги-
перболы на ось Ох определят корни уравнения (6.141).
§ 19] МЕХАНИЗМЫ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ 331
Если уравнение 3-й степени задано в виде:
ах? Ьх2 ex k = 0, (6.144)
то его решение может быть сделано с помощью следующих кониче-
ских сечений:
ху =— k (6.145)
и
у = ах1 -\-bx-\-c. (6.146)
Уравнение (6.145) представляет собой уравнение равносторонней
Рис. 438.
гиперболы рр (рис. 439), а уравнение (6.146) будет уравнением пара-
болы qq. Следовательно, нахождение корней уравнения (6.144) может
быть сделано с помощью двух механизмов, один из которых чертит
параболу, а другой равностороннюю гиперболу.
6°. Решение уравнений 4-й степени вида
zi_!rpzi^qZJrC==0 (6.147)
может быть сделано с помощью двух конических сечений. Первое
коническое сечение будет параболой с уравнением
у2 = — х. (6.148)
332 СИНТЕЗ МЕХАНИЗМОВ ДЛЯ ВОСПРОИЗВЕДЕНИЯ КРИВЫХ [гл. VI
Второе коническое сечение будет окружностью с уравнением
(х — а)‘2Ц-(_У — ЬУ = Л
(6.149)
В самом деле, исключая из
уравнений (6.148) и (6.149)
координату х, получим:
У + (2а+ 1)У—2/>у +
+(a2-J-fe2 — г2) —О, (6.150)
Р
т. е. получаем уравнение ви-
да (6.147), у которого коэф-
фициенты равны:
p = 2a-j-l; q =— 2b
и
с = а2-|-62 —г2.
Парабола (6.148) не за-
висит от коэффициентов
разрешаемого уравнения.
Поэтому она может быть
440); окружность (6.149) будет
Рис. 439.
построена как постоянная (рис.
иметь в качестве центра точку О' с координатами: а=? ?—
иЬ = —Радиус окружности будет равен: r = ]/a2-j-b2— с2.
Аналогичным методом можно решить и другие уравнения более
высоких порядков, если использовать другие механизмы для чер-
чения кривых, рассмотренные нами выше.
ГЛАВА VII
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
§ 20. Исходные данные для синтеза кулачковых механизмов
1°. Основные типы кулачковых механизмов. В § 1 главы I
были рассмотрены основные типы трехзвенных механизмов, к которым
принадлежат, в частности, и кулачковые механизмы, т. ё. трехзвенные
механизмы с двумя низшими парами и одной высшей парой качения
и скольжения. В этих механизмах при проектировании высшей пары
для одного из звеньев обычно выбирают какую-либо простую форму
элемента кинематической пары (круглый цилиндр, конус, плоскость,
отрезок прямой линии и т. д.). Тогда для другого звена форма
элемента кинематический пары получается из условий воспроизведе-
ния требуемого относительного движения звеньев пары, как было
показано в § 11 главы I. То звено высшей пары, которое имеет простую
форму элемента кинематической пары, называют толкателем (штангой),
если оно совершает прямолинейное движение, и коромыслом, если
оно совершает возвратно-вращательное движение. Другое звено высшей
пары, форма элемента которого выбрана из условий воспроизведения
требуемого относительного движения, называют кулачком.
В большинстве случаев кулачок является ведущим (движущим)
звеном, толкатель или коромысло — ведомым звеном. В дальнейшем
рассматриваются только кулачковые механизмы с ведущим кулачком,
поэтому вместо терминов «толкатель» и «коромысло» будет при-
меняться преимущественно термин «ведомое звено». На рис. 441—444
показаны основные типы плоских кулачковых механизмов. В зависи-
мости от вида движений кулачка и ведомого звена эти механизмы
можно подразделить на четыре группы.
1-я группа — преобразование прямолинейного движения кулачка
в прямолинейное движение ведомого звена. Направления движения
кулачка и ведомого звена могут пересекаться под прямым углом
(рис. 441, а) или же под произвольным углом (441, б).
2-я группа — преобразование прямолинейного движения кулачка
во вращательное движение ведомого звена (рис. 442, а, б).
3-я группа — преобразование вращательного движения кулачка
в прямолинейное движение ведомого звена (рис. 443, а, б, в).
334
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VU
РиС. 443.
§ 20] ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА КУЛАЧКОВЫХ МЕХАНИЗМОВ 335
4-я группа — преобразование вращательного движения кулачка
во вращательное движение ведомого звена (рис. 444, а, б).
Ведомые звенья в плоских кулачковых механизмах могут иметь
различную форму тех частей, которые входят в соприкосно-
вение с кулачком. Форма этих частей может быть заостренной
(рис. 445, а), дуговой (рис. 445, б) и плоской (рис. 445, в). Кроме
того, ведомые звенья могут взаимодействовать с кулачком через
промежуточное звено — ро-
лик (рис. 445, г).
На рис. 441—444 для
каждой схемы кулачкового
механизма показаны только
некоторые из указанных
форм ведомых звеньев. По-
этому число возможных ти-
пов кулачковых механизмов
больше числа схем, пока-
занных на рис. 441—444.
Например, в кулачковом ме-
ханизме, схема которого
показана на рис. 441, а, ве-
домое звено может взаимо-
действовать с кулачком че-
рез ролик, а в механизме
по рис. 441, б ведомое зве-
но может быть заостренной
формы и т. д.
Наибольшее распростра-
Рис. 444.
нение имеют механизмы,
показанные на рис. 443 и 444. Для удобства изложения условимся
применять следующие сокращенные названия этих механизмов:
кулачковый механизм с центральным толкателем (рис. 443, б) *);
кулачковый механизм со смещенным толкателем (рис. 443, а) **);
кулачковый механизм с плоским толкателем (рис. 443, в);
коромысловый кулачковый механизм (рис. 444, а);
кулачковый механизм с плоским коромыслом (рис. 444, б).
Кроме плоских кулачковых механизмов, в рабочих машинах имеют
распространение пространственные кулачковые механизмы, задачи
синтеза которых часто сводят к задачам синтеза плоских кулачковых
механизмов. Схемы этих механизмов показаны на рис. 446—448.
*) Название происходит от того, что направление движения центра ролика
или точки касания заостренного толкателя с кулачком проходит через центр
вращения кулачка.
**) Название происходит от того, что направление движения центра ро-
лика или точки касания заостренного толкателя с кулачком смещено от центра
вращения кулачка.
336
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. VII
Если подразделить пространственные кулачковые механизмы по виду
движений кулачка и ведомого звена на такие же группы, как и
плоские механизмы, то можно заметить, что механизмы первой группы
(преобразование прямолинейного движения кулачка в прямолинейное
движение ведомого звена) всегда
могут быть выполнены в виде
плоских механизмов.
Механизмы второй группы
(преобразование прямолинейного
движения кулачка во вращатель-
ное движение ведомого звена) при-
меняются очень редко (рис. 446).
Механизмы третьей группы
(преобразование вращательного
движения кулачка в прямолиней-
ное движение ведомого звена)
имеют применение главным обра-
зом при параллельности оси вра-
щения кулачка и направления
движения ведомого звена (рис. 447, а). Очень редки случаи, когда
ось вращения кулачка и направление движения ведомого звена
пересекаются или скрещиваются (рис. 447, б).
Механизмы четвертой группы (преобразование вращательного
движения кулачка во вращательное движение ведомого звена) имеют
широкое распространение для передачи вращения между осями,
скрещивающимися под прямым углом, причем ось ролика параллельна
оси вращения ведомого звена (рис. 448, а). Реже встречается случай,
когда ось ролика перпендикулярна оси вращения ведомого звена
§ 20] ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА КУЛАЧКОВЫХ МЕХАНИЗМОВ 337
(рис. 448, б). Редкими являются также случаи передачи вращения
между пересекающимися или скрещивающимися осями.
В зависимости от формы заготовки кулачки подразделяют на
дисковые (рис. 441—444), цилиндрические (рис. 447, а), конические,
гиперболоидные (рис. 447, 6), а также кулачки в виде других тел
вращения, например образованных вращением дуги окружности
(рис. 448, б) или какой-либо другой кривой.
Отметим, что цилиндрическая форма кулачка полностью соответ-
ствует лишь типу кулачкового механизма, показанного на рис. 447, а.
Но и для некоторых других типов кулачковых механизмов
(рис. 447, б, 448, а, б) могут применяться цилиндрические кулачки,
приближенно заменяющие ту форму кулачка, которая соответствует
относительному движению толкателя и кулачка. Например, если
в кулачковом механизме, показанном на рис. 448, а, рассмотреть
относительное движение ведомого звена и кулачка, то центр ролика
опишет поверхность, образованную вращением вокруг оси кулачка
дуги окружности, расположенной в плоскости касательной к по-
верхности цилиндра. Для того чтобы ролик был погружен в паз
кулачка на одну и ту же глубину, следует выполнить наружную
поверхность кулачка в соответствии с указанной поверхностью враще-
ния. Однако при небольших углах размаха ведомого звена или доста-
точной его длине можно заменить эту поверхность цилиндрической,
предусмотрев соответствующее увеличение глубины паза кулачка.
Кроме подразделения кулачков по форме заготовки, кулачки
различаются также по способу замыкания высшей кинематической
пары, т. е. по способу обеспечения постоянного соприкосновения
кулачка и толкателя. Различают открытые кулачки (рис. 449, а, б),
которые требуют силового замыкания, т. е. прижатия ведомого
звена к кулачку под действием пружины, груза или динамической
338
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
нагрузки (сил инерции), и пазовые кулачки (рис. 449, в, г),
обеспечивающие геометрическое замыкание. Открытые цилиндричес-
кие кулачки называют также торцовыми (рис. 449, б). Применяются
также комбинированные кулачки, в которых геометрическое замыка-
ние осуществляется только на некоторой части профиля (рис. 449, д, ё).
Кроме трехзвенных кулачковых механизмов с ведущим кулачком,
рабочих машинах
имеют применение
в
плоские трехзвенные меха-
низмы с неподвижным ку-
лачком. Эти механизмы мо-
гут быть получены из меха-
низмов, показанных на рис.
441—444, если закрепить
кулачок и сообщить дви-
жение двум другим звеньям.
Например, на рис. 450, а по-
казан механизм, полученный
из механизма по рис. 444, а.
С помощью этого механизма
можно осуществлять движе-
ние точки М рабочего орга-
на по заданной траектории,
построив ’ в соответствии с
этим условием профиль не-
подвижного кулачка. В ка-
честве примера можно ука-
зать на механизм закаты-
вающего ролика машины
для закатки консервных
банок [6]. На рис. 450, б
показана схема механизма, по-
лученного преобразованием
механизма на рис. 443, а
(механизм выталкивания
кусков теста в делительной
машине [6]).
2°. Кулачково-рычажные механизмы. В кулачковых механизмах,
состоящих из трех звеньев, рабочий орган машины непосредственно
соединяется с ведомым звеном. Широко применяются также меха-
низмы, в которых рабочий орган присоединяется к ведомому звену
кулачкового механизма посредством дополнительной рычажной пере-
дачи. Механизм, который образован путем присоединения к кулач-
ковому механизму рычажной передачи, называется кулачково-рычаж-
ным механизмом. На рис. 451 показаны некоторые схемы кулачково-
рычажных механизмов, применяемые в рабочих машинах. Наиболее
простой является схема (рис. 451, а), в которой ведомое звено
кулачкового механизма выполнено в виде рычага, непосредственно
§ 20] ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА КУЛАЧКОВЫХ МЕХАНИЗМОВ 339
Рис. 450.
Рис. 451.
340 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
воздействующего на звено, соединенное с рабочим органом (рабочее
звено). В зависимости от соотношения плеч рычага можно получать
в этом механизме увеличение или уменьшение хода рабочего органа
по сравнению с ходом центра ролика В.
В кулачково-рычажном механизме по схеме, показанной на рис. 451, б,
ведомое звено кулачкового механизма, выполненное в виде угло-
вого рычага, воздействует на рабочее звено через промежуточный
поводок.
Более сложной является схема кулачково-рычажного механизма
(рис. 451, в) подачи заготовок в чаеупаковочном автомате [6], в кото-
ром движение точки М по заданной траектории обеспечивается
соответствующим построением профиля двойного кулачка. В основе
этого механизма лежит пятизвенный шарнирный механизм HLKED,
на шатуне LK которого расположена точка М. Звенья LH и ED
этого механизма приводятся в движение ' от двойного кулачка,
причем звено ED непосредственно взаимодействует через ролик
с кулачком, а звено LH — через промежуточные рычаги FQ и FC.
Разумеется, можно указать еще большое количество различных
схем кулачково-рычажных механизмов, применяемых в рабочих маши-
нах. Эти схемы отличаются видом и числом отдельных групп
звеньев, присоединяемых к основному кулачковому механизму.
В дальнейшем рассматриваются в основном только трехзвенные
кулачковые механизмы.
3°. Условия применения кулачковых механизмов. Кулачковые
механизмы применяются в основном для воспроизведения заданного
прямолинейного или возвратно-вращательного движения ведомого
звена (рис. 441—444 и 446—448). Реже встречаются кулачковые
механизмы для воспроизведения заданного сложного движения рабо-
чего звена (рис. 450, 451, в).
Кулачковые механизмы относятся к наиболее распространенным,
что объясняется рядом их положительных свойств по сравнению
с другими механизмами, и в частности с кривошипно-рычажными
механизмами.
Достоинствами кулачковых механизмов являются:
1) возможность воспроизведения почти любого закона движения
ведомого звена путем соответствующего профилирования кулачка;
2) возможность достижения высокой производительности за счет
рационального выбора закона движения ведомого звена;
3) возможность изменения закона движения ведомого звена путем
замены кулачка;
4) возможность получения малых габаритов механизма;
5) простота выполнения согласованной работы нескольких меха-
низмов в машинах-автоматах.
Поэтому кулачковые механизмы получили широкое применение
в механизмах подачи металлообрабатывающих станков-автоматов,
в механизмах перемещения рабочих органов различных машин-авто-
§ 20] ИСХОДНЫЕ ДАННЫЕ ДЛЯ СИНТЕЗА КУЛАЧКОВЫХ МЕХАНИЗМОВ 341
матов и во многих других случаях, когда требуется получить
возвратно-вращательное или прямолинейное движение ведомого звена
по заданному закону.
Недостатками кулачковых механизмов по сравнению с криво-
шипно-рычажными и некоторыми другими механизмами являются зна-
чительные величины удельных давлений на поверхности соприкосно-
вения звеньев и как следствие повышенный износ трущихся поверх-
ностей и уменьшение долговечности механизма. Кроме того, при
большой скорости движения ведомого звена возможно возникновение
ударов, в особенности, если предусмотрено только силовое замыкание.
Указанные недостатки однако в значительной мере могут быть
смягчены путем правильного выбора закона движения ведомого звена
и основных параметров, определяющих схему и конструктивное
оформление кулачкового механизма.
4°. Исходные данные для синтеза кулачковых механизмов.
Для того чтобы построить профиль (или поверхность) кулачка при
заданной форме ведомого звена, необходимо выбрать схему меха-
низма, закон движения ведомого звена, т. е. зависимость пути ведо-
мого звена от времени, закон движения кулачка и основные размеры,
характеризующие данную схему механизма. Например, из основных
размеров схемы механизма по рис. 444, а следует выбрать минималь-
ный радиус кулачка, радиус ролика, радиус дуги, описываемой цент-
ром ролика ведомого звена, и расстояние между центрами вращения
кулачка и ведомого звена.
Закон движения кулачка во всех практически встречающихся
случаях соответствует равномерному движению, и следовательно,
для вращающихся кулачков достаточно знать угловую скорость,
а для прямолинейно движущихся кулачков — линейную скорость то-
чек кулачка, причем величины этих скоростей определяются обычно
из условий проектирования всей машины в целом. Схема механизма
также в значительной мере предопределяется общей компановкой машины,
поэтому в дальнейшем будет рассматриваться в основном только
выбор закона движения ведомого звена и основных размеров, харак-
теризующих схему механизма.
Этот выбор должен производиться так, чтобы были выполнены
следующие условия:
1) соответствие закона движения ведомого звена требованиям
технологического процесса;
2) получение высокой производительности машин;
3) минимальный расход энергии для приведения механизма в дви-
жение;
4) обеспечение прочности и долговечности механизма;
5) простота изготовления кулачка.
Первое условие является основным, так как механизм прежде всего
должен соответствовать своему функциональному назначению, т. е.
перемещения рабочего органа, связанного с ведомым звеном механизма,
342 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. vn
должны обеспечивать выполнение определенной технологической опе-
рации при надлежащем ее качестве. Это условие может быть удов-
летворено выбором закона движения ведомого звена, причем в неко-
торых случаях закон движения на определенном участке движения
задается технологическим процессом. Например, в механизмах подачи
часто требуется равномерное перемещение ведомого звена на опре-
деленную длину в течение заданного промежутка времени, который
определяется величиной скорости движения ведомого звена или же
условиями согласованной работы механизмов. Во многих случаях,
однако, требования технологического процесса определяют только
некоторые отдельные параметры закона движения ведомого звена.
К этим параметрам относятся: величина полного перемещения ведо-
мого звена (в одну сторону), максимальная скорость и максимальное
ускорение, а также величины скорости и ускорения ведомого звена,
соответствующие определенным его положениям.
Задание максимальных величин скорости и ускорения ведомого
звена связано с тем, что увеличение скорости или ускорения рабочего
органа сверх максимальной величины может вызвать нарушение тех-
нологического процесса или снижение его качества. Кроме того,
к задаваемым параметрам могут быть отнесены полное время движения
ведомого звена и времена отдельных этапов его движения (например,
время ускоренного движения, время движения с постоянной скоростью,
время замедленного движения, время остановок и т. д.). Эти времена
иногда определяются только последовательностью выполнения отдель-
ных этапов технологического процесса и условиями согласованной
работы механизмов.
Второе условие — получение высокой производительности ма-
шины—также связано с выбором закона движения ведомого звена,
так как из всех различных законов движения, удовлетворяющих
требованиям технологического процесса, можно выбрать тот, при
котором время выполнения отдельных этапов движения, включая хо-
лостые хода, оказывается минимальным. Уменьшение времени выпол-
нения отдельных этапов движения связано с увеличением динами-
ческих нагрузок, потерь на трение и крутящего момента на валу
кулачка. Поэтому правильный выбор закона движения ведомого звена
из условий получения высокой производительности машин предусмат-
ривает обязательный учет влияния уменьшения времени движения
на изменение различных динамических факторов. Кроме того, следует
иметь в виду, что повышения производительности машины можно
достигнуть путем совмещения отдельных операций, причем, выбирая
форму графика закона движения рабочих органов отдельных механиз-
мов, можно получить более тесное совмещение операций во времени.
Третье условие — получение минимального расхода энергии для
приведения механизма в движение, так же как и предыдущее усло-
вие, связано с оценкой экономичности машины и должно рассматри-
ваться совместно с другими основными требованиями, предъявляемыми
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 343
к правильно спроектированному механизму. Если учитывать трение
в кинематических парах, то это условие оказывается связанным не
только с выбором закона движения, но и с установлением основных
размеров схемы механизма (минимальный радиус кулачка, длина на-
правляющей и т. д.). Однако и путем только рационального выбора
закона движения ведомого звена можно, как будет показано в по-
следующем, значительно уменьшить величину крутящего момента
на валу кулачка и, следовательно, уменьшить расход энергии для
приведения механизма в движение.
Четвертое условие — обеспечение прочности и долговечности ме-
ханизма — достигается не только выбором материала для изготовле-
ния звеньев механизма и определения размеров звеньев путем расчета
на прочность, но и путем максимального снижения действующих
нагрузок на звенья механизма и рационального конструирования
отдельных узлов. Нагрузки на звенья механизма зависят от закона
движения ведомого звена, поэтому при выборе этого закона следует
стремиться к уменьшению сил, действующих на звенья механизма.
§ 21. Выбор закона движения ведомого звена*)
1°. Характеристики кулачковых механизмов, влияющие на
выбор закона движения ведомого звена. Из изложенного в пре-
дыдущем параграфе следует, что при определении профиля кулачка
и основных размеров звеньев механизма надо учитывать различные
и часто противоречивые условия. Поэтому, прежде чем рассматривать
конкретные примеры выбора закона движения ведомого звена, опре-
деляющего профиль кулачка, необходимо изучить влияние отдельных
характеристик механизма на выбор закона движения.
К характеристикам, общим для всех кулачковых механизмов, отно-
сятся следующие:
1) максимальная скорость ведомого звена;
2) максимальное ускорение ведомого звена;
3) коэффициент динамичности нагрузки;
4) постоянная пружины;
5) максимальный вращающий момент на валу кулачка;
6) максимальная величина давления кулачка на ведомое звено.
Указанные характеристики, разумеется, не исчерпывают полностью
все требования, которые могут встретиться при проектировании всего
многообразия кулачковых механизмов. Например, для кулачковых ме-
ханизмов привода к клапанам машин-двигателей при выборе закона
движения ведомого звена учитываются также величина «время-сечение»
и удар при переходе зазора (имеется в виду зазор между кулачком
и толкателем, предусмотренный из-за наличия значительных тепловых
*) При составлении § 21 в основном использованы работы С. И. Арто-
болевского [6], К. В. Тира [52а] и X, Финкельнбурга [71а, б].
344
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
деформаций). Однако в подавляющем большинстве случаев сравнение
различных законов движения по этим характеристикам дает достаточ-
ные основания для такого выбора закона движения, при котором
в наибольшей мере удовлетворяются те пять условий, которые были
сформулированы выше. Рассмотрению этих характеристик предпослан
раздел, содержащий данные о некоторых законах движения, имеющих
распространение в практике конструирования машин-автоматов. В конце
каждого раздела, посвященного рассмотрению отдельной характери-
стики, даны выводы, оценивающие ее влияние на закон движения
ведомого звена.
Только после подробного рассмотрения отдельных характеристик
указываются примеры выбора закона движения ведомого звена для
некоторых наиболее распространенных случаев.
2°. Некоторые законы движения ведомого звена. Для того
чтобы облегчить выбор закона движения ведомого звена, рассмотрим
некоторые распространенные законы движения, которые, однако, не
исчерпывают всего разнообразия практически осуществимых и целесо-
образных законов движения. В данном параграфе будут приведены
сравнительные характеристики рассматриваемых законов движения и
указаны выводы, которые дают основание для выбора других законов
движения.
В рассматриваемых механизмах ведомое звено движется возвратно,
совершая прямолинейное или вращательное движение, причем за один
оборот кулачка оно может совершать несколько двойных ходов оди-
наковой или различной протяженности. Между этими ходами могут
быть участки, соответствующие остановке ведомого звена. Например,
на рис. 452 показан график закона движения ведомого звена с тремя
двойными ходами различной протяженности и несколькими участками
остановок за время Т одного оборота кулачка, причем по оси абсцисс
отложено время t, а по оси ординат — перемещения прямолинейно
движущегося ведомого звена S, отсчитываемые от наинизшего его
положения.
Условимся в дальнейшем при исследовании различных законов
движения ведомого звена рассматривать только участок перемещения
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ. ВЕДОМОГО ЗВЕНА 345
ведомого звена в одном направлении от одного момента остановки
до следующего за ним, так как все выводы, которые могут быть
сделаны при таком рассмотрении, легко распространить на случай
движения ведомого звена с любым числом остановок и двойных ходов
за полный оборот кулачка. Кроме того, условимся все графики,
формулы и зависимости приводить только для прямолинейно движу-
щегося ведомого звена. Очевидно, что для вращающегося ведомого
звена следует заменить соответственно линейные перемещения, ско-
рости и ускорения на угловые.
Обозначим через tH время интервала от одного момента остановки
ведомого звена до следующего за ним и через — величину прой-
денного пути на этом интервале. Тогда путь S, скорость v и уско-
рение а в любом положении ведомого звена могут быть выражены
через величины S„ и tH:
S=CS„; (7.1)
v = 8-^-; (7.2)
*и
с
(7.3)
В этих формулах безразмерные коэффициенты (, 8 и £ зависят
от выбранного закона движения и являются переменными величинами,
которые удобно выражать в функции безразмерной величины k, изме-
няющейся от 0 до 1 и представляющей собой отношение времени t
ко времени всего интервала tH или угла поворота кулачка ср к углу
поворота за весь интервал <ри (при равномерно вращающемся
кулачке), т. е.
k = ^~=
<И 4>и
В таблице 7.1 дана сводка величин С, 8 и £ в функции величины k
для некоторых законов движения. Для иллюстрации в этой таблице
даны также графики ускорений a=^f{k\
Все рассматриваемые законы движения ведомого звена в кулачко-
вых механизмах можно подразделить на три группы:
1) законы движения, которые обеспечивают получение оптимальной
величины какой-либо отдельной характеристики механизма;
2) законы движения, которые определяются видом графика уско-
рений или графика пути;
3) законы движения, которые определяются формой кривых, слу-
жащих в качестве профиля кулачка.
Рассмотрим сперва законы движения первой группы.
Оптимальная величина какой-либо характеристики механизма соот-
ветствует обычно условию ее постоянства, так как при этом она
346
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Некоторые законы двн
№ п/п. Наименование График ускорения Е Пределы для k
от ДО
1 Постоянная скорость а *в 0 1 --
1 1 К
2 Постоянное ускорение 1 q 0 и и 1
и |/ *
3 Равномерно убывающее ускорение (симметричная тахограмма) я 0 1
О 1/ А
4 Равномерно убывающее ускорение (несимметричная тахограмма) D 0 и и 1
7 _ * 17 А
5 Изменение ускорения по тре- угольнику а й \ 075 0 0,25 0,75 0,25 0,75 1,0
Ц25 Ц5\ // А
6 Изменение ускорения по трапеции /\^75 \\Д£Я 7175 0 0,125 0,375 0,625 0,875 0,125 0,375 0,625 0,875 1,0
W5 #\l \/’ *
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
347
Таблица 7.1
жения ведомого звена
Коэффициент пути С Коэффициент скорости S Коэффициент ускорения И
k 1 0
1 2 , 2
— й2 — й
и и и
, a-fe)2 1—и 2 (1—k) 1 — и ' 2 1—и
-се cq |eo 1 ' от -се CO 6й (1 — й) 6(1—2й)
Зй2 /. 1 ,\ Зй f„ 1 \ 3 /, 1 ,\
— 1 S- k ) - И й)
2u \ 3u / 2и \ и / w \ « )
2us — и — 3 (2u — 1) й + Зий2 — й8 3(1 — 2« + 2ий — й2) 3(и — k)
2(1-u)2 2(1 — и)2 (1-U)2
16 Й® 16й2 32й
3
_^_2й + 8й2— ~й3 16й(1 — й) — 2 16(1 — 2й)
l-J^(l-ft)3 О 16 (1 — й)2 — 32(1 —й)
64 64 128 .
-7Г й3 k —^~k
9 3 3
4 (— 1 + 16й) о 16 3
1 (1-10Й + 32Й3—уй3) о \ о о / 2 4(— 5-h 32/г — 32/г2) о -у (1 — 2й)
4-(15— 16Й) о 16 3
64 64 , 128 „ ,
м 1 —- J05 1 -ТТ о-*)2 О
348
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
№ п'п. Наименование График ускорения Предель от ДЛЯ k до
7 Изменение ускорения по коси- нусоиде (симметричная тахо- грамма) а 1 0 1
8 Изменение ускорения по косину- соиде (несимметричная тахо- грамма) * - 1 с4- _J> к 0 и и 1
9 Изменение ускорения по синусо- иде Z? f 0.L\ /1 "к 0 1
10 Изменение ускорения по наклон- ной синусоиде с b=0J5 0 1
11 Постоянная скорость с переход- ными участками по синусоиде | u л 0 и 1—и и 1 — и 1
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
349
Продолжение табл. 7.1
Коэффициент пути С Коэффициент скорости о Коэффициент ускорения £
(1 — cos -/г) sin r.k л2 — cos л/г
U(l-C№ik) , . Л (1 — k) » + (!-«) cos 2 (1- ы) Л Л sin k Z Zu Л . Л (1 k) 2 Sm 2(1—и) л2 л - COS n— k 4и Zu —л(1—й) TTi < COS’-т Г 4(1—и) 2(1 —и)
(2лй — sin 2- k) 1 — cos 2 л/г 2я sin 2лй
z — -J— sin Zit . b • о k = z sin 2лг 2л [ — cos 2л z 1 —b cos 2л? о /1 sin Т" ( \ 1 — b cos 2irz)3
u U и k— - sin — k T. и 1 — cos — k и • 71 и л sin - k и
2(1 — и) k-- 2 1 — и < . и sin — (1—k) 1 1 — k 1 ы 2(1 —и) 1 1— и 1 — cos — (1 k) и 2и (1 — и) 0 л sin ~ (1 —k)
2 (1 — и) 2л (1 — и) 2(1 -и) 2и (1 — и)
350 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
получается минимальной. Поэтому среди законов движения первой
группы получили широкую известность закон постоянной скорости,
закон постоянного ускорения, закон постоянного угла давления и
закон постоянного вращающего момента.
При законе постоянной скорости (табл. 7.1, п. 1) имеет место
равномерное движение ведомого звена с минимальной скоростью (при
заданных 5И и /и), но в начале и в конце движения ускорение равно
бесконечности, т. е. возникают жесткие удары.
Закон постоянного ускорения (табл. 7.1, п. 2) соответствует
равнопеременному движению, причем график ускорения имеет раз-
рывы, т. е. получаются мягкие удары. График пути представляет
собой сочетание квадратных парабол, поэтому этот закон движения
иногда называют также параболическим. Значение величины k в том
положении, когда ускорение меняет знак, т. е. имеет место максимум
скорости, обозначено через и. График скорости (тахограмма) будет
симметричным при п = 0,5.
Закон постоянного угла давления выражается условием
& = &0 = const,
где & — угол давления, т. е. угол между линией действия силы Q,
действующей на ведомое звено со стороны кулачка (без учета сил
трения), и скоростью точки приложения этой силы v.
Угол давления в общем случае является функцией скорости и
положения ведомого звена*). Поэтому из условия & = &0 можно по-
лучить закон движения ведомого звена. Так как зависимость, связы-
вающая угол давления со скоростью и положением ведомого звена,
оказывается различной для различных схем кулачковых механизмов,
то закон движения ведомого звена, а следовательно, и профиль
кулачка также получаются различными. Например, в кулачковом
механизме с прямолинейно движущимися звеньями (см. рис. 441, а)
угол давления пропорционален скорости ведомого звена, и в этом
случае законы постоянной скорости и постоянного угла давления
совпадают. В центральных кулачковых механизмах (см. рис. 443, б)
эти законы уже не совпадают. Уравнения пути, скорости и ускоре-
ния в функции времени в этом случае обычно не строятся, а непо-
средственно определяется профиль кулачка, который представляет
собой логарифмическую спираль. В смещенных механизмах профиль
кулачка будет кривой, эквидистантной к логарифмической спирали,
и т. д. Во всех случаях при законе постоянства угла давления
в начале и конце движения имеют место жесткие удары.
Закон постоянного вращающего момента выражается условием
М = const,
*) См., далее, § 22,
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
351
причем обычно под величиной М понимают значение вращающего
момента на валу кулачка без учета трения. Из условия равенства
мощностей на ведущем и ведомом звеньях имеем:
dS М
dt~~^ Р ’
(7.4)
где ш— угловая скорость кулачка; Р—сила, действующая по оси
ведомого звена.
Интегрируя это дифференциальное уравнение, можно получить
закон движения ведомого звена и, следовательно, профиль кулачка,
причем закон движения и профиль кулачка получаются различными
при различных предположениях о характере изменения сил, действую-
щих на ведомое звено.
Если силу, действующую на ведомое звено, можно считать по-
стоянной, то в соответствии с уравнением (7.4) при М — const
д dS ,
должно быть — const, т. е. в этом случае закон постоянного
вращающего момента совпадает с законом постоянной скорости.
Если сила сопротивления состоит из нагрузки от пружины, то.
P=tfo($4-Sn), (7.5)
где — постоянная пружины; Sn — деформация пружины, соответ-
ствующая предварительному натяжению.
Подставляя значение силы Р в уравнение (7.4) и интегрируя его,
имеем:
'=Я7(т+М + С'
где С — постоянная интегрирования.
Принимая во внимание граничные условия: при S —О t = 0 и
при S = SH £ = ^и, получаем:
t = -----(S2 + 2SnS).
52и+25п8и
Отсюда искомый закон движения выражается уравнением
S = - Sn + + (Sf, + 2SA) ~ •
или в безразмерных величинах
<7-6’
Аналогично можно получить закон движения ведомого звена, соот-
ветствующий постоянству вращающего момента на валу кулачка, при
любом законе изменения силы Р, причем, если уравнение (7.4) не
интегрируется в квадратурах, следует применить численные или
графические методы интегрирования.
352 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Интегрируя уравнение (7.4), можно получить закон движения
ведомого звена не только при 714 = const, но и при любом заданном
законе изменения вращающего момента 714.
Отметим, что при 714 = const имеют место жесткие удары в на-
чале и в конце движения, если не применять переходных участков,
очерченных по другим законам.
Из приведенных примеров законов движения первой группы
видно, что стремление удовлетворить полностью только одной
какой-либо характеристике механизма (минимуму наибольшей скоро-
сти или ускорения или вращающего момента и т. д.) приводит
к тому, что другие характеристики оказываются весьма неблагопри-
ятными. Поэтому широкое распространение получили законы движе-
ния второй группы, которые определяются видом графика ускорений.
Изменяя форму графика ускорений, можно получать различные
значения характеристик механизма и находить оптимальное решение.
Сначала рассмотрим законы движения, у которых графики уско-
рений составлены из отрезков прямой линии. Простейшим примером
служит рассмотренный ранее закон постоянного ускорения. При этом
законе получаются мягкие удары (скачки ускорений) в середине
движения, а также в начале и конце движения, если в эти моменты
есть выстой (остановка конечной продолжительности).
Скачка ускорений в середине движения можно избежать, приме-
няя закон движения с равномерно убывающим ускорением (табл. 7.1,
пп. 3 и 4), который иногда называют законом движения по кубиче-
ской параболе в соответствии с видом графика пути. В таблице 7.1
указаны отдельно случаи симметричной тахограммы (и = 0,5) и
общий случай несимметричной тахограммы (и ^0 ,5).
Условию полного отсутствия скачков ускорения удовлетворяет
закон движения с ускорением, изменяющимся по треугольнику, при
котором график пути состоит из нескольких отрезков кубической
параболы (табл. 7.1, п. 5).
Более общими являются законы движения с ускорением, изменя-
ющимся по трапеции (табл. 7.1, п. 6), из которых могут быть полу-
чены все предыдущие законы с графиками ускорений, составленными
из отрезков прямой линии. В таблице 7.1 указаны уравнения для
коэффициентов С, 8 и $ при частном условии, что график скоростей
является симметричным и участки постоянного ускорения составляют
по 0,25 от рассматриваемого интервала.
Кроме отрезков прямой линии, можно использовать для построе-
ния графиков ускорений степенные многочлены более высоких по-
рядков. Однако эти законы движения имеют сравнительно неболь-
шое распространение. Значительно более распространены законы
движения с графиками ускорений, представляющими собой тригоно-
метрические многочлены. Простейшими случаями будут графики
в виде косинусоиды и синусоиды. Закон движения с ускорением,
изменяющимся по косинусоиде, иногда называют гармоническим
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 353
законом движения (табл. 7.1, п. 7). Закон движения с ускорением,
изменяющимся по синусоиде, иногда называют циклоидальным зако-
ном движения (табл. 7.1, п. 9). Этот закон движения не имеет мяг-
ких ударов (скачков ускорений) в отличие от закона движения
с ускорением по косинусоиде, при котором будут скачки ускорений,
если между интервалами движения (О, £и) есть участки выстоя.
С другой стороны, закон движения с ускорением по косинусоиде,
как будет показано далее, во многих случаях дает более благопри-
ятные значения характеристик механизма вследствие смещения центра
тяжести графика положительных ускорений к началу движения.
Удачное сочетание свойств синусоиды, и косинусоиды можно
получить, применяя закон движения с графиком пути в виде наклон-
ной синусоиды (табл. 7.1, п. 10). Форма наклонной синусоиды харак-
теризуется некоторым постоянным параметром Ь, изменяющимся
в пределах от — 1 до -|- 1. В таблице 7.1 графики ускорений пока-
заны для двух значений этого параметра: # = 0,15 и Ь = — 0,15.
Из этих графиков видно, что, изменяя параметр Ь, можно смещать
центр тяжести графика положительных ускорений, сохраняя отсутст-
вие скачков ускорений, причем при положительном b центр тяжести
графика положительных ускорений смещается к началу координат,
а при отрицательном от начала координат. При # = 0 имеем обыч-
ную синусоиду. Коэффициенты С, В и Е выражаются через z— вспо-
могательный переменный параметр, изменяющийся от 0 до 1. Этот
параметр связан с переменной k следующим соотношением [26г]:
k — z — -jT- sin 2лг.
Z7C
Кроме законов движения с ускорением по косинусоиде, синусоиде
и наклонной синусоиде, предлагались также законы движения, для
которых графики ускорений представляют собой тригонометрические
многочлены в виде суммы гармоник различных порядков [14в, г].
Законы движения, указанные в "пунктах 2-j-10 таблицы 7.1,
имеют двухпериодную тахограмму, т. е. цикл движения состоит
из периода разгона и периода выбега. Если между этими периодами
требуется осуществить движения с постоянной скоростью (трехпе-
риодная тахограмма), то можно воспользоваться для периодов раз-
бега и выбега любым из законов движения, указанных в пунк-
тах 2-i-lO таблицы 7.1. В качестве примера указан случай трехпе-
риодной тахограммы с переходными участками по синусоиде
(табл. 7.1, п. 11).
Законы движения третьей группы определяются формой кривых,
служащих в качестве профиля кулачка. Появление этих законов
движения вызывается стремлением обеспечить наиболее простую
технологию изготовления кулачков. Например, на универсальном
оборудовании можно получать профили кулачков, очерченных
по дугам окружностей. Уравнения для S, © и а в этом случае
12 И. И. Артоболевский
354
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. VII
обычно не составляются, так как профиль кулачка определяется
непосредственно из условия составления его из дуг окружностей,
а экстремальные значения скорости v и ускорения а находятся при
помощи обычных методов кинематического анализа. Отметим только,
что график ускорений содержит точки разрыва, которые неизбежны
при профиле, составляемом из дуг окружностей, так как в местах
их сопряжения касательные совпадают, но радиусы кривизны раз-
личные.
Кроме профилей, составленных из дуг окружностей, предлага-
лись также профили, очерченные по растянутой эвольвенте, которые
также могут быть легко получены на универсальном оборудова-
нии [476].
3°. Максимальная скорость ведомого звена. Рассмотрение
характеристик, влияющих на выбор закона движения ведомого звена,
начнем с выяснения зависимости максимальной скорости ведомого
звена wma!C от закона движения при заданных S„ и
Обозначая максимальное значение коэффициента 8 в формуле (7.2)
через 8тм, имеем:
®тах == ^шах • Р-7)
1и
Связь величины Втах с законом движения можно выяснить, исполь-
зуя следующее свойство графиков пути, скорости и ускорения, ука-
занное Я. Л. Геронимусом [14г].
Приращение пути на некотором интервале равно произведению
площади графика ускорения на расстояние от центра тяжести этой
площади до конца интервала, если скорость есть монотонная функ-
ция, равная нулю в начале интервала.
Обозначая время, соответствующее расстоянию от начала интер-
вала до центра тяжести графика положительных ускорений через ta,
имеем на основании этой теоремы для законов движения с симмет-
ричной тахограммой (рис. 453 и 454)
2
4й = (0,5/и-7ц) J adt. (7.8)
О
Принимая во внимание, что
А
2
I a dt —
О
имеем из уравнения (7.8):
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 355
Обозначим через к расстояние от начала интервала до центра
тяжести площади графика положительных ускорений, выраженное
в долях участка разбега (0, uQ:
Х = -^-
«4
(7.10)
Тогда, сравнивая выражения (7.7) и (7.9), получим для законов дви-
жения с симметричной тахограммой
8~-=т^г- <7П>
При и = 0,5 (симметричная двухпериодная тахограмма)
^тах ==1 (7.12)
12-
356
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Для законов движения с несимметричной двухпериодной тахо-
граммой (рис. 455) на основании указанного выше свойства графи-
ков пути, скорости и ускорения имеем:
Si = (1 — utK vm!a, (7.13)
где Si — путь, пройденный в период разбега.
На основании той же теоремы путь, пройденный в период выбега:
SH-S1 = (l-k)X
Х(1 — к)^иг>тах-(7.14)
Отсюда
t или
‘ Si = uSw (7.16)
т. е. точка сопряжения кри-
вой разбега и выбега на
графике пути лежит на пря-
мой, соединяющей началь-
ную и конечную точки это-
го графика.
Из формул (7.13) и (7.16)
имеем:
1 «и
’’ma* 1 _ X t„ ’
т. е. коэффициент 8тах оп-
ределяется по формуле
(7.12) и не зависит от соот-
ношения между периодами
разбега и выбега.
Значения коэффициента
8шах, подсчитанные по фор-
мулам (7.11) и (7.12), по-
мещены в таблицу 7.2, в которой собраны все рассматриваемые ха-
рактеристики для большинства законов движения, помещенных в
таблице 7.1. На основании формул (7.11) и (7.12) и рассмотрения
таблицы 7.2' можно сделать следующие выводы.
1. Все законы движения с двухпериодной тахограммой (т. е. без
участка постоянной скорости), у которых графики положительных
и отрицательных ускорений каждый в отдельности являются симмет-
ричными (Х = 0,5), имеют коэффициент максимальной скорости Втах=2.
2. Для уменьшения коэффициента 8тах надо смещать центр
тяжести графика положительных ускорений к началу интервала.
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
357
СМ
03
а
S
ч
\О
03
Характеристика некоторых законов движения
Способ обработки CJ а a CJ СХ \О f; ₽ Л fc ® g *> f> £. О о ! id к о s Г~ » t К fc № Dm E
Давление кулачка excAJjeh ВЕМЭЭНИИЕШф oo OO, lD lD OO CM, O) , _ 05, CD <© — —. Tf Ci 00 CO iQ q£
%Ь Е1ГИЭ ВЕЙЮ1ЕЯ1Ч9А ю — О CM О CM — "1 1 — CM —' o' — — —" — — —' — —
*b ЕЕИЭ BEtoOTEXOEdEOg lO — см о о CM — — — — CM — —Г o' —' — -Г — —' — —
Максимальный вра- щающий момент вяеЛдлЕН ВЕЯЭЭЬИНЕИИЙ' Ю CO co ID 05 00 OO iD CD ooco'coco'oooocor^ of
BITИЗ ввШсявшчдд ID — О О CO CM, О CO, —1 о —7 О — —7—7 —7 _7 _7 _7 _7-
В1ГИЗ BBinOIEXOEdEOa <o -l^C^OCOCMOCO — O' —Г — о — —7 — —7 — — —г
х ннижХсТп ВЕННВОХЭОЦ lOiO 00 CM — О CM CD 00 сГ of CD 00 Г-7 <o r-7 co (-Г
ШЙГф ИХЭОННИНЕНИИ хиэийиффбоу] So m § song co TO rog-&,gg- -coo S- - - C-l tt- CM в -- e
ХЕШ^ аинасТоязЛ аОНЧ1ГЕН ИЗМЕНУ r-cor-cc» CO CO OO co о, ем, o, со'о ГсЬ'см' CO 00 ID тГ ccT lb" 1 1
ХЕШ§ чхэойояэ ВЕНЧ1ГЕИИЗНЕОД iQ iD Г^, CMCNCM-^CMCM — CM
Наименование закона движения CD OJ • O) • 0-»* 0’0’ О’ О * О CD * o ' ej ’ 2i • c • «= • e • c • e ч • S =5 • ex • ex • ex • £ • £ • S • £ • £ • £ 8 • q У 3 • g • g -g • S • S -S • 5 - S -Sg> • §.”>•• S -S -S . § . a.a. p. p. .&g . c . o^c . go g o= ,g a . * • • • <-> S о • У s У • E gj • qj • (D о £ ® •₽< 2 ti iQ4 C' a о о о д £ cj л о s У S! 3 2 n5o — я «о я a co g. = s 5 s S s £о£ж^=§е<-г 5 o' s 0 = 0 go. g ° 5 5 gs 5 8 g § ° = 8 ® g II g 11 £ II | § S 0 S £ S 8 5 a S g II £ 8. II “aSa£a S £ s &* & ® S S 55 aS-5 c о 3 о 3 о 3 « л н л н го го ° го 3'-'о с г CCCcuSSSSS С
]’L •IfpEX OU Stf •u u см см см со Ю СО г- О О -^СМСО^ЮСО^ОООЗ о
358
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Например, закон равномерно убывающего ускорения (8шах = 1,5), закон
с изменением ускорения по косинусоиде (8тах = 1,57) и закон
с изменением ускорения по наклонной синусоиде при 6^>0.
3. Несимметричность двухпериодной тахограммы не влияет
на величину 8тах.
4. Минимальная величина коэффициента 8тах получается при за-
коне постоянной скорости (8гаах=1), но так как при этом законе
будут жесткие удары в начале и конце движения, то в таблице 7.2
дан пример трехпериодной тахограммы с переходными участками
по синусоиде при и = 0,1 (8тах = 1,1). Для уменьшения 8тах следует
смещать центр тяжести графика положительных ускорений к началу
интервала, т. е. уменьшать к или уменьшать и, причем уменьшение
величины и ограничивается условием возрастания ускорений.
4°. Максимальное ускорение ведомого звена и коэффициент
динамичности нагрузки. Максимальное ускорение ведомого звена
«max характеризуется коэффициентом Втах, представляющим собой
максимальную величину коэффициента S, т. е. ’
_ Sn
; ^max — 5max •
1 t
И
Обозначим отношение среднего ускорения к максимальному через
(7.17)
' °П1ах
ёто отношение называют коэффициентом заполнения площади гра-
фика однозначных ускорений [52а], Для законов движения, имеющих
симметричные тахограммы, имеем:
или
* О ,
л ___ max °и
«ср=—-------S. (7.19)
*и
Подставляя в формулу: (7.18) значение «тах из выражения (7.17),
ptp из выражения (7.19) и 8тах из выражения (7.11), имеем:
! - ’ Ux=-^, (7.20)
Йлн "
; . ?тах = от (1 — 2иХ) • <7-21>
Для несимметричных шухпериодных тахограмм аналогично получаем
для периода разбега
г . . = <7-22>
- *** }
§ 21 ] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 359
и для периода выбега
^ = -(1^-. (7.23)
Следовательно, отношение модулей максимальных ускорений в период
разбега и выбега обратно пропорционально соответствующим относи-
тельным продолжительностям периодов:
Из формул (7.20), (7.22) и (7.23) следует, что для уменьшения
?тах надо увеличивать коэффициент заполнения v и уменьшать коэф-
фициент Втах, т. е. сдвигать к началу интервала центр тяжести гра-
фика положительных ускорений.
Минимальная величина Smax получается при законе постоянной
скорости с симметричной тахограммой (£тах = 4). Следует иметь
в виду, что обычно нельзя сравнивать законы движения по величине
максимального ускорения, не принимая во внимание наличие или
отсутствие скачков ускорений (мягких ударов). В самом деле, вели-
чина максимального ускорения часто ограничивается величиной дина-
мической нагрузки на звенья механизма. Если учесть упругость
звеньев механизма, то мгновенное изменение величины или величины
и направления силы инерции вызывает упругие колебания и увели-
чение динамических нагрузок. В тех случаях, когда преобладают
динамические нагрузки (нагрузки от сил инерции), это увеличение
можно оценивать коэффициентом динамичности нагрузки Адин, пред-
ставляющим собой максимальную величину отношения силы, дейст-
вующей на ведомое звено, к произведению массы ведомой системы
т на максимальное ускорение ведомого звена. Обозначая через Рдин
величину силы, действующей на ведомое звено (с учетом упругости
звеньев), имеем:
» __ I Т’циИ" \
«дин I—- I - .
\'“umax/max
Теоретическим и экспериментальным путем установлено, что ве-
личина коэффициента динамичности нагрузки Адии зависит от пара-
метров, определяющих величину упругих колебаний звеньев кулач-
кового механизма (масса звеньев, их упругость, характер трения
и т. д.) и от поведения первой производной от ускорения [26в, 93].
В первом приближении можно считать, что после изменения ускоре-
ния по величине Адии 2, а после изменения ускорения по величине
и направлению Адии а» 3. При отсутствии скачков ускорения в боль-
шинстве случаев Адин 1.
Следовательно, при законе постоянного ускорения вследствие из-
менения ускорения и по величине и по направлению коэффициент
динамичности нагрузки оказывается равным 3. Поэтому действительная
360
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
величина максимальной нагрузки на звенья механизма при этом
законе оказывается значительно большей, чем, например, при законе
движения с ускорением по синусоиде 0тах = 6,28), хотя сравнение
только по величине максимальных ускорений дает обратные резуль-
таты.
Если ускорение изменяется только по величине на концах интер-
вала, что имеет место, например, при законе с ускорением по коси-
нусоиде и законе равномерно убывающего ускорения в случае дви-
жения с выстоями (остановками конечной продолжительности), то
коэффициент динамичности нагрузки равен 2. При тех же законах
движения, но в случае движения без выстоев коэффициент динамич-
ности нагрузки равен 1, так как ускорение в этом случае не меняет
величины на концах интервала.
Если сравнить законы движения по величине максимального уско-
рения при условии отсутствия скачков ускорения, то к минималь-
ной величине атах можно близко подойти при помощи закона движения
с ускорением, изменяющимся по трапеции (см. табл. 7.2). Из про-
стейших законов движения в виде тригонометрических многочленов
небольшую величину атах дает закон движения с ускорением по ко-
синусоиде. При наличии выстоев хороший результат можно получить
при помощи закона движения с ускорением по наклонной синусоиде.
5°. Постоянная пружины. Силовое замыкание высшей пары в ку-
лачковом механизме осуществляется обычно пружиной, размеры ко-
торой должны быть подобраны так,
чтобы обеспечить отсутствие отрыва
ведомого звена от кулачка.
Рассмотрим отдельно прямой и обратный ход ведомого звена,
причем будем считать, что нагрузка на ведомое звено складывается
только из силы пружины и силы инерции.
. На рис. 456 показаны графики изменения величин ускорения а,
силы инерции Рп и силы пружины Рв в зависимости от пути ведо-
мого звена S при прямом ходе, причем ускорение и сила считаются
положительными, если их направление совпадает с направлением ско-
рости при прямом ходе. На рис. 457 те же графики даны для обрат- ’
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
361
ного хода. Законы изменения ускорения а для закона движения
с симметричной тахограммой примем одинаковыми для прямого и об-
ратного ходов, а для закона движения с несимметричной тахограм-
мой, кроме того, будем считать, что интервал выбега при прямом ходе
равен интервалу разбега при обратном ходе.
Величина силы пружины
(7.25)
где Кй — постоянная пружины; Sn — деформация пружины, соответ-
ствующая предварительному натяжению.
Для того чтобы не было отрыва ведомого звена от кулачка,
должно быть выполнено условие
(7.26)
на интервале выбега при прямом ходе и на интервале разбега при
обратном ходе.
Этому условию можно удовлетворить путем подбора постоянной
Ко и величины предварительного натяжения. Наиболее просто ре-
шается задача о подборе указанных величин графическим путем. Для
этого надо совместить график Pll==f1(S) и график Pt,=ft(S), по-
местив последний так, как показано на рис. 456 и 457 пунктиром
с точками. Условие (7.26) удовлетворяется, если график Pn—ft(S)
располагается выше графика Ри =ft (S).
В предельном случае (если пружина взята без запаса) кривая
Ри = /1 (S) касается прямой Рп = /2 (S), причем точка касания обычно
близка к точке, где ускорение имеет экстремальное значение.
Сравнивая построения, показанные на рис. 456 и 457, можно ви-
деть, что постоянная пружины получается одной и той же, если за-
коны изменения ускорения прямого и обратного ходов удовлетво-
ряют принятым ранее условиям.
Для определения постоянной пружины следует в каждом случае
найти точку касания графиков Ри=/1(5) и Pn=/2(S). Положение
с
этой точки определяется безразмерным коэффициентом Cw=-^, где
'“’и
— путь ведомого звена, соответствующий указанной точке каса-
ния. Безразмерный коэффициент, характеризующий величину отрица-
тельного ускорения в этой же точке, обозначим через Вт. Тогда
условие (7.26) принимает следующий вид:
где т — масса ведомого звена.
Отсюда
(7.27)
362 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Принимая в дальнейшем для сравнения законов движения Sn = 0,
получаем для их оценки безразмерный коэффициент
х==^. (7.28)
В таблице 7.2 указаны значения коэффициента х, подсчитанные по
формуле (7.28).
- Лучший результат дают те симметричные законы движения, у ко-
торых максимум отрицательного ускорения смещен к концу интер-
вала (при прямом ходе). Поэтому законы движения с ускорением
по косинусоиде, с ускорением по наклонной синусоиде (при Ь^>0)
и с равномерно убывающим ускорением дают значительно меньшую
величину силы пружины по сравнению с законом постоянного уско-
рения.
6°. Максимальный вращающий момент на валу кулачка. Рас-
смотрим теперь соотношения, определяющие величину максимального
вращающего момента на валу кулачка, при условии, что силами тре-
ния можно пренебречь. Будем рассматривать при этом только меха-
низмы с вращающимся кулачком и поступательно движущимся ведо-
мым звеном. Полученные при таксам рассмотрении выводы будут
в первом приближении справедливы и для других типов кулачковых
механизмов. Для того чтобы учесть влияние закона движения на ве-
личину вращающего момента, удобно рассмотреть следующие четыре
случая нагружения ведомого звена.
Первый случай — преобладает статическая нагрузка, т. е.
нагрузка от внешних сил сопротивления, причем сила сопротивле-
ния Р— постоянная по величине.
Этот случай имеет значение для тех тихоходных и тяжелонагру-
женных механизмов, в которых силы инерции малы по сравнению
е внешними силами сопротивления.
Из условия равенства мощностей для ведущего и ведомого
звеньев имеем:
M = Pv~, (7.29)
где <в—т угловая скорость кулачка.
Из формулы (7.29) следует, что при постоянной величине <о и
постоянной силе сопротивления закон изменения вращающего момента
на валу кулачка совпадает с законом изменения скорости ведомого
звена. Поэтому наиболее выгодными в отношении уменьшения враща-
ющего момента будут в этом случае те законы движения, которые
дают наименьшую величину коэффициента Втах.
Второй случай — сила сопротивления возрастает по линей-
РРтах о
— —я----------------О.
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 363
Вращающий момент на валу кулачка в соответствии с формулой
(7.29) имеет следующее значение:
M = vS-^p*- (7.30)
или
Л1 = 8С Рта/—, (7.31)
<<
т. е. при заданных Pmax, Su, w и tK вращающий момент пропорцио-
нален произведению пути ведомого звена на его скорость. Поэтому
при возрастающей силе сопротивления, пренебрегая силами инерции,
можно сравнивать различные законы движения по величине макси-
мума произведения безразмерных коэффициентов 8 и С
Величина максимума произведения 8£ вычисляется для каждого
закона отдельно по обычным правилам нахождения экстремальных
значений функции. Для уменьшения этой величины выгодно смещать
максимум скорости к началу интервала.
Третий случай — сила сопротивления убывает по линейному
закону
р— р fi____
Llmax у 1 S J '
Вращающий момент на валу кулачка в соответствии с формулой
(7.29) имеет следующее значение:
M = v(Sa-S)-^~ (7.32)
или
лт=а (1 — 0 ^s", ' (7.зз)
и законы движения можно сравнивать по величине максимума произ-
ведения 8(1—С). Для уменьшения этой величины выгодно смещать
максимум скорости к концу интервала.
Четвертый случай — преобладает динамическая нагрузка (на-
грузка от сил инерции).
Этот случай имеет значение для тех быстроходных и малонагру-
женных механизмов, в которых силы инерции велики по сравнению
с внешними силами сопротивления. В этом случае Р= та и из усло-
вия равенства мощностей для ведущего и ведомого звеньев имеем:
M=va^- (7.34)
или
= А. ~ (7.35)
364 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Следовательно, максимальная величина вращающего момента про-
порциональна максимальной величине произведения скорости и уско-
рения ведомого звена [6, 52а]. Поэтому при преобладании динами-
ческой нагрузки можно сранивать различные законы движения по
величине максимума произведения безразмерных коэффициентов
8 и £.
На основании рассмотрения формул (7.29) -4- (7.35) и таблицы 7.2,
в которой приведены для конкретных законов движения значения
коэффициентов, входящих- в эти формулы, можно сделать следующие
выводы.
1. Если сила, действующая на ведомое звено, может считаться
постоянной и силы инерции малы, то минимальную величину враща-
ющего момента дают те законы движения, которые имеют наимень-
шую величину 8тах, т. ё. для этого случая справедливы выводы,
относящиеся к уменьшению величины максимальной скорости.
2. Если сила, действующая на ведомое звено, прямо пропорци-
ональна пути ведомого звена (возрастающая сила сопротивления),
то выгодно иметь несимметричные тахограммы при и <^0,5. Из за-
конов движения с симметричными тахограммами наиболее выгодными
оказываются законы движения типа закона движения с ускорением
по косинусоиде вследствие уменьшения коэффициента 8тах.
3. Если сила, действующая на ведомое звено, убывает с возра-
станием пути, то выгодно иметь несимметричные тахограммы при
и >0,5, а для законов движения с симметричными тахограммами
справедлив предыдущий вывод.
4. Если сила сопротивления, действующая на ведомое звено,
мала по сравнению с силой инерции (динамическая нагрузка), то хо-
рошие результаты дают законы движения, в которых центр тяжести
площади графика положительных ускорений смещен к началу коор-
динат (равномерно убывающее ускорение, ускорение по косинусоиде
и по наклонной синусоиде при 5>0). Например, закон движения
с ускорением, изменяющимся по косинусоиде, дает в два раза мень-
шую величину максимального вращающего момента по сравнению
с законом постоянного ускорения.
Для других случаев нагружения ведомого звена, не рассмотрен-
ных здесь, остается справедливым вывод, что следует уменьшать
величину 8тах.
7°. Максимальная величина давления кулачка на ведомое
звено. Если ведомое звено имеет прямолинейное движение, то без
учета сил трения величина давления кулачка на ведомое звено Q
находится из условия
<?=<7'36’
где Р—величина силы, действующей по оси ведомого звена (вклю-
чая величину силы инерции); & — угол давления (рис. 458).
§ 21]
ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА
365
При прямолинейном движении кулачка и ведомого звена профиль
кулачка совпадает с графиком S—f(xk), где xk— перемещение
кулачка, а угол давления 8
филю кулачка и направле-
нием скорости кулачка.
Отсюда
= <7'37>
Принимая во внимание, что
скорость кулачка
равен углу между касательной к про-
имеем:
tg» = ^. (7.38)
Тот же результат можно получить из рассмотрения повернутого
на 90° плана скоростей, показанного на рис. 458, б, или же из
условия равенства мгновенных мощностей на кулачке и ведомом звене.
Обозначая величину перемещения кулачка за время t„ через L
(длина профиля) и считая, что кулачок движется равномерно,
получаем:
и, следовательно,
tg& = 8c, (7.39)
где
Подставляя это значение угла давления в соотношение (7.36),
имеем:
Q = Р/14-8V. (7.40)
При вращающихся кулачках зависимость угла давления и, следо-
вательно, силы Q от закона движения получается более сложной, но
в первом приближении можно оценивать влияние закона движения
на величину максимального давления кулачка на ведомое звено
по формуле (7.40).
Рассмотрим те же четыре случая нагружения ведомого звена,
которые рассматривались в предыдущем пункте.
Первый случай — сила, направленная по оси ведомого звена,
может считаться приближенно постоянной.
366
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
(ГЛ. VII
В этом случае из формулы (7.36) следует, что минимальная ве-
личина давления Q получается при & = const, т. е. при законе движе-
ния с постоянным углом давления. Из законов движения, унизанных
в таблице 7.1, меньшую величину дают законы движения, имеющие
соответственно меньшую величину 8гпах.
Второй случай — возрастающая сила сопротивления: Р =
5
= Лпах о-. В этом случае, подставляя в формулу (7.40) значение
силы Р и учитывая формулу (7.1), получаем:
(7.41)
т. е. различные законы движения можно сравнивать по величине
91 = |СУ14-82са |шах.
(7.42)
В формуле (7.42) коэффициент С непрерывно увеличивается при
изменении S в интервале (0, £и). Коэффициент 8 в том же интервале
изменяется от нуля до максимального значения 8тах при о = отах
и затем опять до нуля. Поэтому коэффициент qx будет тем меньше,
чем ближе к началу интервала положение, соответствующее ®тах,
т. е. чем меньше коэффициент и.
Третий случай — убывающая сила сопротивления: Р=
/ \
= Т*таХ 1-----. В этом случае получается обратный вывод, т. е.
\ /
для уменьшения максимальной величины давления Q коэффициент и
должен быть больше, так как
Qmax — QtPmax>
где
^ = I(1-Q/1+§V |max. (7.43)
Четвертый случай — сила сопротивления и сила пружины
малы или отсутствуют, т. е. можно считать, что сила, направленная
по оси ведомого звена, складывается только из силы инерции Р=та.
В этом случае
Q=В/1 + 8 V , (7.44)
т. е. различные законы движения можно сравнивать по величине
% = |£/14-8V |max
(7-45)
В таблице 7.2 указаны значения величин qu q^ и q3 для различ-
ных законов движения при постоянной величине с = 0,7.
Из формул (7.41)-г-(7.45) и данных таблицы 7.2 следует, что
выводы, относящиеся к влиянию величины максимального давления
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 367
кулачка на ведомое звено, в значительной мере совпадают с выво-
дами, сделанными в предыдущем параграфе при рассмотрении вели-
чины максимального крутящего момента.
8°. Величина «время-сечение» и величина удара при пере-
ходе зазора в кулачковых механизмах машин-двигателей. Для
кулачковых механизмов привода к клапанам машин-двигателей при
выборе закона движения ведомого звена следует учитывать величину
«время-сечение», под которой понимается величина
= J F dt,
где F — площадь проходного сечения между седлом клапана и та-
релкой клапана.
Величину «время-сечение» желательно иметь возможно большей
для того, чтобы уменьшить эффект дросселирования газа при про-
хождении через щель между клапаном и седлом. Площадь F можно
считать величиной, пропорциональной пути ведомого звена S. Поэтому
для увеличения «время-сечение» надо увеличивать площадь графика
зависимости путиведомого звена по времени, т. е. величину
Fs = У S dt.
о
При выводе зависимости величины 8тах от закона движения *)
была использована теорема, устанавливающая связь между графиком
пути и графиком ускорений. Аналогично можно сформулировать тео-
рему, устанавливающую связь между графиком величины Fs и гра-
фиком скоростей в следующем виде: приращение величины Fs на не-
котором интервале равно произведению площади графика скорости
на расстояние от центра тяжести этой площади до конца интервала,
если путь есть монотонная функция, равная нулю в начале интервала.
Обозначая через tv время, соответствующее расстоянию от на-
чала интервала до центра тяжести графика скоростей (см. рис. 455),
имеем на основании этой теоремы:
I"
^ = (^и-и У *dt.
б
Принимая во внимание, что
t
и
I T4# = SB>
*) См. стр. 354.
368 синтез кулачковых механизмов [гл. VII
и обозначая через ХТ)=-^ — расстояние от начала интервала до центра
тяжести площади графика скоростей, выраженное в долях интервала,
получаем:
Fs=(l-K)SHt„- (7.46)
Следовательно, для увеличения площади Fs и величины «время-
сечение» надо уменьшать коэффициент Х^, т. е. сдвигать центр тя-
жести графика скоростей к началу интервала. Так как коэффициент
уменьшается с уменьшением величины и, то в данном случае выгодно
применять несимметричные тахограммы с максимумом скорости, сме-
щенным к началу движения (и<^0,5). Уменьшение величины и ограни-
чивается обычно возрастанием максимального ускорения ведомого
звена.
Для кулачковых механизмов привода к клапанам машин-двигате-
лей законы движения ведомого звена сравнивают иногда также по
величине удара при переходе зазора, который предусмотрен между
кулачком и толкателем в его крайнем положении для возможности
теплового расширения. Это сравнение сводится к сравнению различ-
ных законов движения по величине 8П, т. е. по значению коэффи-
циента скорости ведомого звена 8 при k = где ta — время, необхо-
*и
димое для перехода зазора. Здесь мы не приводим этого сравнения,
так как в. правильно спроектированном кулачковом механизме для
перехода зазора должен быть предусмотрен переходной профиль,
построенный с учетом отсутствия жесткого удара в момент начала
движения ведомого звена.
9°. Способ обработки профиля кулачка. Все предыдущие вы-
воды в отношении получения законов движения с оптимальными ве-
личинами отдельных характеристик будут соответствовать действи-
тельности только в том случае, если способ обработки профиля
кулачка обеспечивает получение такой точности воспроизведения за-
данного профиля, при которой отклонения от принятого закона дви-
жения будут меньше соответствующей разности между сравниваемыми
законами движения.
Все существующие способы обработки серии кулачков можно
подразделить на три группы:
а) Обработка на универсальных станках, с помощью которых
можно достаточно просто получить профили дисковых кулачков,
очерченных по дугам окружностей, По архимедовой спирали и по
растянутой эвольвенте, а также профили цилиндрических кулачков
по винтовой линии. При обработке этих профилей заготовка и инстру-
мент имеют такое же относительное движение, какое, имеют кулачок
и ведомое звено в механизме (кинематический способ обработки).
Обработка других профилей, производящаяся путем последователь-
ных перемещений инструмента и заготовки на определенную вели-
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 369
чину в соответствии с рабочим чертежом профиля, является трудо-
емкой и часто не обеспечивает надлежащей точности.
б) Обработка в приспособлениях, с помощью которых в настоящее
время можно получать профили кулачков, соответствующие законам
движения с ускорением, изменяющимся по косинусоиде и по наклон-
ной синусоиде, а также по их сочетаниям с законом постоянной скорости.
в) Обработка на копировальных станках, с помощью которых
можно получать любые профили кулачков, допускающие изготовление
копиров.
Наиболее перспективным видом обработки является кинематический
способ, так как он обеспечивает значительно большую точность изго-
товления, чем способ копирования. Для того чтобы в этом убедиться,
достаточно вспомнить, что надлежащая точность изготовления про-
филей зубьев в зубчатых колесах была получена только после пере-
хода от способа копирования к способу обкатки (кинематический
способ). Поэтому при сравнении различных законов движения, име-
ющих примерно равные характеристики, следует предпочесть те за-
коны, которые допускают обработку в приспособлениях или на уни-
версальных станках по кинематическому способу (см. последнюю
графу табл. 7.2).
10°. Примеры выбора закона движения ведомого звена. Для
правильного выбора закона движения, при котором выполняются
условия, обеспечивающие полное соответствие требованиям техноло-
гического процесса, а также достигается получение высокой произ-
водительности машины при минимальном расходе энергии и надле-
жащей прочности и долговечности механизма, требуется произвести
сравнение нескольких вариантов законов движения, так как полностью
удовлетворить всем указанным требованиям часто не представляется
возможным. Однако для некоторых типовых случаев все же возможно
дать некоторые рекомендации по применению законов движения из
числа указанных в таблицах 7.1 и 7.2.
1. Требуется получить постоянную скорость ве-
домого звена. Такое условие, например, ставится при проектиро-
вании кулачков подачи в металлообрабатывающих станках.
При выборе закона движения, удовлетворяющего точно или при-
ближенно этому условию, следует учитывать величину сил, действу-
ющих на звенья механизма. Если можно допустить жесткие удары
(тихоходный и малонагруженный механизм), то для профилирования
кулачков следует непосредственно использовать закон постоянной
скорости, проверяя величину динамической нагрузки в момент удара
с учетом упругости звеньев.
Профиль прямолинейно движущегося кулачка получится в виде
отрезка прямой линии при прямолинейном движении ведомого звена
и в виде циклоиды при вращательном движении.
Профиль вращающегося дискового кулачка получится: при цент-
ральном толкателе в виде архимедовой спирали, при смещенном
370 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
толкателе в виде растянутой эвольвенты, при вращающемся ведомом
звене в виде эпициклоиды (или гипоциклоиды).
Профиль цилиндрического кулачка с прямолинейно движущимся
ведомым звеном получится в виде винтовой поверхности.
Все указанные профили допускают обработку по кинематическому
способу.
Если при заданной скорости ведомого звена и и его массе т
жесткие удары оказываются недопустимыми, но мягкие удары (скачки
ускорений) не вызывают еще значительных нагрузок (вследствие
малости сил инерции), то следует применять для образования про-
филя кулачка те же кривые, но с добавлением переходных участков,
очерченных по дугам окружностей, которые обеспечивают плавное
изменение скорости от нуля до постоянной величины и затем опять
до нуля *).
Наконец, если нужно избежать и мягких ударов (что устанавли-
вается путем предварительного определения максимальной величины
силы инерции с учетом коэффициента динамичности нагрузки и срав-
нения этой величины с допускаемой из условий прочности ведомого
звена), то следует применить закон движения с трехпериодной та-
хограммой. Например, можно использовать закон постоянной скорости
с переходными участками по закону движения с изменением ускоре-
ния по синусоиде (табл. 7.1, п. 11), так как этот закон движе-
ния допускает обработку профиля кулачка по кинематическому
методу [19].
2. Требуется получить минимальную скорость
ведомого звена при заданных величинах перемещения
ведомого звена и времени интервала. Этот случай совпа-
дает с предыдущим.
3. Требуется получить минимальную величину
ускорения ведомого звена при заданных величи-
нах и t„, причем скачки ускорений допустимы.
Этот случай имеет место при перемещении изделия, которое
не имеет жесткой связи с ведомым звеном.
Например, в расфасовочных и упаковочных автоматах пищевой
промышленности изделие (пачка кофе, кусок мыла и т. п.), свободно
лежащее на поворотном столе (или транспортере), не должно сдвигаться
относительно стола, который приводится в периодическое движение
с остановками посредством кулачкового механизма. Если изделие
не должно сдвигаться относительно ведомого звена ни при ускорен-
ном, ни при замедленном движении, то следует применить закон
постоянного ускорения с симметричной тахограммой (и = 0,5). Если
же движение изделия при ускоренном или замедленном движении
ограничивается упором, т. е. если изделие может сдвигаться только
*) Расчет переходных участков, очерченных по дугам окружностей, см.
стр. 424.
§ 21] ВЫБОР ЗАКОНА ДВИЖЕНИЯ ВЕДОМОГО ЗВЕНА 371
в одном направлении, то следует применить закон постоянного уско-
рения с несимметричной тахограммой. Например, если недопустимым
является сдвиг изделия в направлении движения ведомого звена,
то надо уменьшить величину отрицательных ускорений, т. е. при-
нимать и <0,5.
4. Требуется получить минимальную величину
ускорения ведомого звена при заданных величи-
нах Хи и t„ и дополнительном условии отсутствия
скачков ускорения. Это требование имеет место в тех же
машинах-автоматах, которые указаны в предыдущем случае, причем
дополнительное условие отсутствия скачков ускорения соответствует
быстроходным автоматам.
Если нет выстоев (остановок конечной продолжительности) в на-
чале и конце интервалов, то можно рекомендовать закон движения
с ускорением по косинусоиде, так как в этом случае отсутствуют
скачки ускорений, максимальное ускорение имеет небольшую вели-
чину ^а1пах = 4,93 > максимальная величина произведения скорости
и ускорения, характеризующая величину вращающего момента, также
является достаточно малой, а профиль кулачка может быть обрабо-
тан по кинематическому способу. Если есть выстой в начале и
конце интервала, то можно рекомендовать закон движения с уско-
рением, изменяющимся по наклонной синусоиде при параметре
(например, при b = 0,15). Несколько лучших результатов можно
достичь при законе движения с ускорением, изменяющимся по тра-
пеции (общий случай несимметричного графика ускорений). Однако
в отличие от закона наклонной синусоиды этот закон приводит
к такому виду профиля кулачков, для которого не имеется доста-
точно простых приспособлений, позволяющих производить обработку
по кинематическому методу.
5. Требуется получить минимальное время интер-
вала t„ при заданной величине 5И, причем силы инер-
ции малы по сравнению с силами сопротивления,
которые считаются постоянными (тихоходные меха-
низмы с постоянной нагрузкой). Например, в металлообра-
батывающих станках это условие имеет место при профилировании
кулачков на участках, соответствующих холостым ходам, так как
с уменьшением времени холостого хода увеличивается производи-
тельность станка.
Уменьшение времени интервала tn при заданной величине S„
ограничивается увеличением величины давления кулачка на ведомое
звено и величины максимального крутящего момента. Условия мини-
мума этих величин в общем случае не совпадают, но в рассматрива-
емом случае обычно ограничиваются сравнением законов движения
только по максимальной величине давления кулачка на ведомое
звено. Тогда при равных величинах основных размеров механизма
372 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ (гл. VII
>
меньшую величину времени интервала tK дадут те законы, которые
имеют соответственно меньшую величину угла давления !>. Мини-
мальная величина угла давления получается при законе постоянного
угла давления, который при прямолинейно движущихся и цилиндри-
ческих кулачках совпадает с законом постоянной скорости (см. п. 1),
если ведомое звено имеет прямолинейное движение. При дисковых
вращающихся кулачках с центральным толкателем профиль кулачка
с постоянным углом давления получается в виде логарифмической
спирали, которая не может быть достаточно просто обработана
по кинематическому способу и, кроме того, дает жесткие удары
в начале и конце движения. Еще более сложные кривые получаются
в механизмах со смещенным толкателем и при вращающемся ведомом
звене, причем сохраняются жесткие удары. Поэтому при дисковых
вращающихся кулачках применение закона постоянного угла давле-
ния (логарифмической спирали) без переходных участков не может
быть рекомендовано. Так как вследствие малости сил инерции до-
пустимы мягкие удары, то следует применять профили, составленные
из дуг окружностей с переходными участками, обеспечивающими
плавное изменение скорости *).
Если обработка производится по кинематическому способу в при-
способлениях, то можно применить также закон движения с ускоре-
нием, изменяющимся по косинусоиде (табл. 7.1, п. 7). Наконец, если
профиль будет обрабатываться по способу копирования, то можно
применить комбинацию закона постоянного угла давления (логарифми-
ческой спирали) с переходными участками по закону постоянного
ускорения.
6. Требуется получить минимальное время интер-
вала t„ при заданной величине SH, причем силы инер-
ции велики по сравнению с силами сопротивления
(быстроходные малонагруженные механизмы). Это тре-
бование имеет место в тех же машинах, которые указаны в преды-
дущем случае.
В данном случае получаются те же рекомендации, что и в
пункте 4, т. е. закон движения с ускорением по косинусоиде при
отсутствии выстоев в начале и конце движения и закон движения
с ускорением по наклонной синусоиде (Ь 0) при движении с
выстоями.
Указанные рекомендации для шести рассмотренных случаев отно-
сятся в основном к кулачковым механизмам машин-автоматов.
Они справедливы лишь при выполнении тех условий, которые
оговорены в задании (соотношение между силами инерции и силами
сопротивления и т. д.). При отступлении от этих условий необхо-
димо произвести более детальное сравнение характеристик различ-
ных законов движения, пользуясь выводами, сформулированными
!) Пример расчета переходных участков см. стр. 426.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 373
при рассмотрении каждой отдельной характеристики. Например, для ..
кулачковых механизмов привода к клапанам машин-двигателей нужно
учесть величину «время-сечение», что, как было показано, приводит
к необходимости иметь несимметричную тахограмму.
§ 22. Определение основных размеров кулачковых
механизмов
1°. Угол давления. Для нахождения профиля кулачка необхо-
димо кроме выбора закона движения ведомого звена выбрать также
основные размеры механизма, от которых зависят величина давления
кулачка на ведомое звено и коэффициент полезного действия меха-
низма. Эти характеристики механизма в значительной мере определя-
ются величиной угла давления. Поэтому рассмотрим более подробно
определение угла давления для различных кулачковых механизмов.
В § 21 *) было показано, что при
прямолинейном движении кулачка и ве-
домого звена угол давления опреде-
ляется по формуле (7.39):
tg& = 8^,
т. е. при заданной величине перемеще-
ния S„ угол давления зависит от вы-
бранного закона движения ведомого
звена и от длины профиля L.
Для кулачковых механизмов с цен-
тральным толкателем (рис. 459) угол
давления & можно определить из усло-
вия равенства мощностей на ведущем
кулачке и ведомом звене при отсут-
ствии сил трения:
P^ = Ptg&(/?04-S)<u,
где — минимальный радиус-вектор кулачка,
наинизшему положению ведомого звена. Отсюда
соответствующий
(7Л7)
Тот же результат можно получить из рассмотрения повернутого
на 90° плана скоростей (рис. 459, б)’.
*) См. стр. 365.
374
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. vn
ИЛИ
tg»
as
da
X+S’
где а — угол поворота кулачка.
Изменение угла давления 8 можно исследовать графически, если
построить график := /(S) и затем на продолжении оси S отложить
величину минимального’ радиуса-вектора кулачка Ro (рис. 460). Для
того чтобы определить угол давления & для положения, соответству-
ющего некоторой точке М построенного графика, достаточно со-
единить точку М с точкой О и измерить величину угла между на-
Рис. 460. Рис. 461.
правлением ОМ и АО, так как тангенс этого угла удовлетворяет
условию (7.47). Для нахождения максимальной величины угла дав-
ления &тах следует провести Касательную из точки О к графику
= /(S). Из построения, показанного на рис. 460, видно, что
в Общем случае максимум скорости ведомого звена и максимум
угла давления не совпадают. Минимальное значение 8тах будет соот-
ветствовать закону движения с постоянным углом давления &0. Гра-
фическое построение, показанное на рис. 460, принимает в этом
случае вид, соответствующий рис. 461. Из рассмотрения рис. 461
следует, что при этом законе движения будут жесткие удары
в начале и конце движения.
Для кулачковых механизмов со смещенным толкателем, в кото-
рых направление движения точки касания ведомого звена с кулач-
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 375
ком отстоит от центра вращения кулачка О на величину смещения е
(рис. 462 и 463), угол давления также можно определить из усло-
Рис. 463.
вия равенства мощностей на ведущем кулачке и ведомом звене при
отсутствии сил трения:
Pn = (Ptg&^-±Pe)w
или
tg»=tgx(X ±1 I.
(7.48)
376
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
где х — угол смещения, определяемый из соотношения
tgy =------ е . —
(7-49)
Отсюда получаем:
tg»
V
— ± е
СО
s+
(7.50)
причем знак плюс соответствует расположению смещения влево от
оси вращения кулачка (рис. 463), а знак минус — расположению сме-
щения вправо от оси вращения кулачка (рис. 462) при условии, что
ведомое звено движется вверх и кулачок вращается против хода
часовой стрелки. Если ведомое звено движется вниз, то при том же
направлении вращения кулачка правило знаков — обратное. Тот же
результат можно получить из рассмотрения планов скоростей, повер-
нутых на 90° (рис. 462, б и 463, б).
Графическое построение для определения угла давления при подъеме
ведомого звена и смещении, расположенном вправо, показано на рис. 464.
Из формулы (7.50) и построения, показанного на рис. 464, сле-
дует, что, применяя смещение вправо, можно при подъеме ведомого
звена уменьшить величину максимального угла давления. Например,
v
при величине эксцентриситета е = — и постоянной скорости угол
давления 8 = 0 на всем интервале подъема ведомого звена, за исклю-
чением моментов начала и конца движения (рис. 465). Однако при
опускании углы давления получаются увеличенными.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 377
Максимальное значение угла давления &тах может в зависимости
от величины и знака смещения достигаться или в положении, близ-
ком к положению, в котором скорость ведомого звена максимальная,
или же в моменты начала и конца движения. В последнем случае
величина &тах зависит только от величин Цо, S„ и е.
Дисковые кулачковые механизмы с вращающимся ведомым звеном
можно рассматривать как кулачковые механизмы с переменной вели-
чиной смещения толкателя е, под которой в этом случае понимается
величина перпендикуляра, опущенного из центра вращения кулачка
на направление скорости ведомого звена
Рис. 466. Рис. 467.
Угол давления можно определить по формуле (7.48), вычисляя
переменную величину смещения е из соотношения
е — Zo cos (ф-ф-ф0) — Z, (7.51)
где Zo — расстояние между центрами вращения кулачка и ведомого
звена (рис. 467); ф— угол поворота ведомого звена, отсчитываемый
от начального положения; ф0 — угол между начальным положением
ведомого звена и линией, соединяющей центры вращения кулачка
и ведомого звена.
Угол смещения х вычисляется из соотношения
£
tg /0 sin (ф + ф0) ‘ (7-52)
Подставляя это значение угла х в формулу (7.48), имеем:
v
— ± е
6 /0 sin (ф + ф0) 4 1
Правило знаков то же, что и» для кулачковых механизмов
со смещенным толкателем.
378 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. V1I
Из сравнения формул (7.53) и (7.50) видно, что влияние пере-
менного эксцентриситета е на величину угла давления & в кулачко-
вых механизмах с качающимся ведомым звеном то же, что и в кулач-
ковых механизмах со смещенным толкателем. Для пространственных
кулачковых механизмов с цилиндрическими кулачками можно в пер-
вом приближении определять углы давления, как и в механизмах
с прямолинейно движущимися кулачками, если развернуть на плос-
кость профиль кулачка по среднему сечению.
Кроме того, в подавляющем большинстве случаев для всех рас-
смотренных схем кулачковых механизмов остается справедливым вы-
вод, сделанный ранее при рассмотрении механизмов с прямолинейно
движущимися кулачками, а именно, что для уменьшения угла давле-
ния и, следовательно, для уменьшения величины давления кулачка
на ведомое звено следует выбирать законы движения, дающие мень-
шую величину коэффициента 6тах.
2°. Коэффициент возрастания усилий. От величины угла дав-
ления в кулачковом механизме зависит величина давления Q кулачка
на ведомое звено. Чтобы полнее оценить влияние угла давления
и размеров механизма на величину давления кулачка Q, следует
учесть трение в кинематических парах и рассмотреть различные
конструкции кулачковых механизмов.
С этой целью удобно ввести в рассмотрение коэффициент возра-
стания усилий е [47а], под которым в кулачковых механизмах с пря-
молинейно движущимся ведомым звеном понимается отношение вели-
чины давления Q к величине силы Р, направленной по оси ведо-
мого звена (включая и силу инерции):
«=£. (7-54)
Коэффициент возрастания усилий, вычисленный без учета трения,
обозначим через е'. Тогда из формул (7.36) и (7.54) имеем:
Если же учесть трение в кинематических парах, то зависимость
коэффициента возрастания усилия от угла давления оказывается
различной для различных конструкций ведомого звена.
В первую очередь рассмотрим кулачковый механизм, в котором
кулачок и ведомое звено движутся прямолинейно, ведомое звено
имеет заостренный профиль, а направляющие располагаются по обе
стороны от точки касания кулачка с ведомым звеном, благодаря
чему отсутствует перекос ведомого звена (рис. 468). В этом
случае давление Q отклонено от нормали AW на угол трения
= arc tg/b где j\— коэффициент трения между ведомым звеном и
кулачком, а давления в направляющих и отклонены от нор-
мали на угол трения <р4 = arctg/s> гДе /а— коэффициент трения
в направляющих.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 379
При подъеме ведомого звена из плана сил (рис. 468, б) имеем:
Q___________cos у3
Р cos (» + + ?«) ’
(7.56)
где & — угол давления, определяемый в данном случае по фор-
муле (7.39).
Подставляя значение угла & из формулы (7.39) в формулу (7.56),
имеем:
е
COSp2
(7-57)
Из формулы (7.57) следует, что при изменении скорости ведо-
мого звена от нуля до максимума й затем опять до нуля, коэф-
фициент возрастания усилий изменяется от значения
COS
е» COS (<р, + ра)
до максимального значения етах и затем опять до значения е0.
В рассматриваемом случае положение, в котором достигается
максимум коэффициента возрастания усилий, совпадает с положением,
соответствующим максимуму скорости ©тах. Принимая во внимание
формулу (7.57), имеем:
COS ра
Етах — 7 g
cos ^arc tg + p, +
т. e. в рассмотренном механизме для уменьшения величины етах надо
уменьшать коэффициент 6шах и, следовательно, применять законы
(7.58)
380
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
движения, соответствующие меньшим значениям <?тах, увеличивать
величину перемещения кулачка L и уменьшать углы трения <pi и <р2.
Теперь рассмотрим тот же механизм, который был рассмотрен
выше (см. рис. 468), но с изменением конструкции ведомого звена.
Направляющая ведомого звена теперь располагается по одну сто-
рону от точки касания, а ведомое звено взаимодействует с кулач-
ком через ролик (рис. 469).
Давление кулачка на ведомое звено Q направлено по касатель-
ной к кругу трения, радиус которого для приработавшейся цапфы
Рис. 469.
равен 1,27/iH, где — коэффициент трения цапфы в подшипнике;
г, — радиус цапфы.
Угол <р1п, на который отклонена реакция Q от нормали NN,
определяется в этом случае из условия *)
sin Т1п^ 1,27/,(7.59)
где г — радиус ролика.
В направляющей вследствие перекоса возникают реакции RY и
Rit которые будем считать приложенными по концам направляю-
щей**). Направления этих реакций отклонены от нормали на угол
*) Указанное условие получено в предположении, что между роликом и
кулачком нет проскальзывания, трение качения ролика мало и инерцией ролика
можно пренебречь [18 ж].
**) Если считать давление в направляющей распределенным по закону тре-
угольника, то реакции Rt и /?3 будут приложены каждая на расстоянии ~ /„
от концов направляющей, т. е. расчетная длина направляющей уменьшится.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИКОВ 381
трения <p2 = arctg/2. Направление суммарной реакции R отклонено
от нормали на угол <р2п. Величина этого угла может быть определена
из условия, что направление суммарной реакции R должно проходить
через точку пересечения направлений реакций /?, и /?2 и через точку
пересечения сил Р и Q, если пренебречь моментом от сил инерции
ролика [476].
При малой величине круга трения из этого условия имеем:
tg%n=A(i4-2^
(7.60)
где h — расстояние от наинизшего положения оси ролика до на-
правляющих; d — ширина направляющих.
Обычно dfi значительно меньше h — S и можно определять при-
веденный угол трения по формуле
tgcp2n=/2(l +2^).
Построив план сил (рис. 469, б), получаем:
Q __ cos <fSn
Р COS (8 -|" <Рхп 4" ?зп) '
(7.61)
т. е. формулы (7.56) и (7.61) для определения коэффициента воз-
растания усилий совпадают, если вместо углов трения <pf и <р2 ввести
в рассмотрение приведенные углы трения <р1п и ср2п. Связь между
углом давления S и законом движения ведомого звена по-прежнему
определяется соотношением (7.39), так как эта связь не зависит от
конструкции ведомого звена.
В некоторых конструкциях направление силы Р смещено от оси
ведомого звена или же составляет с ней некоторый угол. Направле-
ние движения точки касания ведомого звена с кулачком также мо-
жет быть смещено от оси ведомого звена. Для всех этих случаев
справедлива формула (7.61), но приведенный угол трения в направ-
ляющих будет определяться из более общей формулы, выведенной
также из условий равновесия плоской системы сил, но с учетом
указанных смещений и наклонного расположения силы Р [286, 46].
Формула (7.61) применима и для вращающихся кулачков, причем
угол давления нужно определять в соответствии со схемой механизма
по формуле (7.47) или (7.50), а приведенный угол трения в направ-
ляющих находить в зависимости от конструкции ведомого звена.
Для случая плоского толкателя (рис. 470, а) в формуле (7.61)
следует считать угол давления 8=0, а приведенный угол тре-
ния <р2п определять из условия
+ - <7'62)
382
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
где rt — расстояние от точки касания ведомого звена с кулачком
до оси направляющих ведомого звена.
Из чертежа (рис. 470, а) имеем:
n = e + /?cos
где R— радиус-вектор кулачка в месте касания с ведомым звеном;
от оси направляющих ведо-
мого звена; yj — угол
между радиусом-вектором R
и плоскостью толкателя.
С другой стороны, из
плана скоростей (рис. 470, в)
имеем:
v v
cos т, = — = .
Следовательно,
или
р-63»
Рис. 470. Формула (7.62) получена
так же, как и формула
(7.60), из условия равновесия ведомого звена под действием сил
Р, Q и (рис. 470, б). Верхние знаки соответствуют
тому случаю, когда точка пересечения сил Р и Q находится выше
направляющих, а нижние знаки — когда эта точка находится ниже
направляющих. Если точка пересечения сил Р и Q находится в
пределах длины направляющей, то ведомое звено прижимается к
направляющей одной стороной (перекос отсутствует) и ср2п = <р2 [286].
Из этих условий, пренебрегая величиной <//2 по сравнению
с величиной h, получаем, что перекос отсутствует (^2п = <р2) при
выполнении следующих неравенств:
№ - е < 1 -\-fxS <Д (Л + /и) - в.
(7.64)
Если ведомое звено выполнено в виде коромысла (рис. 471, а),
то все внешние задаваемые силы и силы инерции будем приводить
к одной силе (главному вектору) Р, выбирая точку, через которую
проходит ее линия действия, так, чтобы главный момент равнялся
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 383
нулю *). Плечо этой силы относительно оси вращения коромысла
обозначим через /г0. Тогда из уравнения моментов относительно
оси вращения коромысла
имеем:
QI cos (& ?1) =
= Р/г0+ \,21fatR,
где I — длина коромысла;
г2 — радиус цапфы в шарни-
ре, соединяющем коромысло
со стойкой; /2 — коэффици-
ент трения в этом шарнире.
Величину реакции R
определим из плана сил
(рис. 471, б); построенного РИС. 471.
без учета сил трения. Полу-
чаемая при этом ошибка в определении момента сил трения 1,27/2г97?
незначительна п|>и обычных для кулачковых механизмов величинах
коэффициентов трения.
Имеем:
п—р sin (t+ 8)
sin (т-|-»-|-р) ’
где величина угла р определяется из соотношения
Ар
Р / sin 1 — (h0 — I COS t) Ctg (г -f- &) "
Подставляя величину реакции R в написанное выше уравнение
моментов, находим коэффициент возрастания усилий для коромысло-
вого кулачкового механизма:
h I 1 97/ г S*n в)
Q Ло + 1’27/8 8sin(T:+» + p)
(7.65)
е ==
Р
Zcos(&4~<pi)
Если коромысло взаимодействует с кулачком через ролик, то
в формулу (7.65) вместо надо подставить угол <р1п, определяемый
по формуле (7.59). Без учета трения коэффициент возрастания уси-
лий коромыслового кулачкового механизма равен:
е’ =________
l cos & '
Во всех рассмотренных случаях предполагалось, что система сил,
действующих на ведомое звено (включая и силу инерции), сводится
*) Случай, когда главный вектор внешних задаваемых сил и сил инерции
равен нулю, здесь не рассматривается как трудно осуществимый в кулачко-
вых механизмах.
384 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
к плоской системе сил. При пространственном расположении сил
коэффициент возрастания усилий следует определять для каждого
случая по кинетостатическому принципу из уравнений равновесия
пространственной системы сил, задаваясь законом распределения де-
формаций по граням направляющих [18з].
Кроме того, во всех рассмотренных случаях предполагалось, что
кинематическая пара кулачок — ведомое звено имеет силовое замы-
кание (например, под действием пружины). При кинематическом за-
мыкании (пазовый кулачок) в период замедленного движения в соот-
ветствии с изменением направления силы инерции возможно измене-
ние направления силы Р на обратное по сравнению с показанным
на рис. 469. Но при этом одновременно изменяются направления ре-
акций Q, Рх и Рг. Построив для этого случая план сил, получаем, что
формула для определения коэффициента возрастания усилий при
прямолинейном движении ведомого звена принимает вид:
с _ C0S ?8П COS(»—<pin —<р2п) ' (7.66)
При вращающемся ведомом звене аналогично имеем:
h _| 27Лг SiR + l,27/,r8sin(T+a+p) / COS (» — <f>i) (7.67)
При опускании ведомого звена сила Р в случае силового замы-
кания имеет то же направление, что и при подъеме, но силы тре-
ния направлены в обратную сторону, т. е. знаки углов трения из-
меняются на обратные. Поэтому формула для определения коэффициента
возрастания усилий при прямолинейном движении ведомого звена
(толкателя) принимает вид формулы (7.66).
При вращающемся ведомом звене (коромысле) аналогично получаем
формулу (7.67).
В случае кинематического замыкания при опускании сила Р для
толкателя может быть направлена вверх. Тогда все силы, действующие
на толкатель, имеют обратное направление по сравнению с фазой
подъема, и для определения коэффициента возрастания усилий справед-
лива формула (7.61). Если же сила Р для толкателя направлена вниз
(например, замедленное движение), то коэффициент возрастания усилий
определяется как и при силовом замыкании, т. е. по формуле (7.66).
Для коромысла в зависимости от направления силы Р аналогично
получаем или формулу (7.65) или (7.67).
3°. Коэффициент полезного действия. От угла давления зависит
также коэффициент полезного действия кулачкового механизма *).
*) В дальнейшем коэффициент полезного действия обозначается к. п. д.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОвЫх МЕХАНИЗМОВ 386
В механизмах с прямолинейно движущимся кулачком мгновенная
величина к. п. д. при подъеме ведомого звена может быть определена
из отношения
tj<7-68)
где Рк — величина силы, действующей на кулачок с учетом трения,
Рк — величина той же силы, но без учета трения.
Из плана сил для кулачка (рис. 472, б) имеем:
Рк_ sin (a -f- 4~ ук)
Q cos ’
где срк — угол трения направляющих кулачка.
Рис. 472.
Принимая во внимание, что Q = гР и Рк — е.'Р sin 0, из
(7.68) получаем при <р1==ср1П:
_________________________________е' sin Я cos <fK
sin(а + 'рш+ч’к)’
при <рк^о
формулы
(7.69)
е’ sin S
~ sm (»+?!„)’
(7.70)
Подставляя значения е' и е из формул (7.55) и (7.61), получаем
для случая прямолинейно движущегося ведомого звена;
е’ _ cos (fr-f-yin + van)
е COS a COS (fan
и, следовательно,
_ tg a cos <fK cos (a + y,n + y8n)
ЯП(а-|-?1п + ?к) cos<p2„ •
При cpK 0 имеем:
«(»+*,..> -‘г»1**-
13 И. И. Артоболевский
(7.71)
(7-72)
386
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. Vtt
Для дисковых вращающихся кулачков будем считать, что силы,
действующие на кулачок, приводятся к паре сил. Тогда для меха-
низма с центральным толкателем (рис. 473) величина вращающего
момента М определится из условия
М = Q [Я sin (& + «рО 4- 1,27/кгк], (7.73)
где R — радиус-вектор кулачка, соответствующий рассматриваемой
Рис. 473.
точке касания; /к — коэффициент трения для
щарнира, соединяющего кулачок со стойкой;
гк — радиус цапфы этого шарнира.
Мгновенный к. п. д. механизма может быть
определен из соотношения
где 714' — величина вращающего момента на
валу кулачка без учета трения.
Обозначая по-прежнему через е' коэффи-
циент возрастания усилий, вычисленный без
учета трения, и принимая во внимание, что
Q — ьР, получаем:
е| sin(»+?l)+l,27/K^|'
Обычно отношение мало и поэтому можно считать Тогда
формула (7.75) переходит в формулу (7.70) и, следовательно, мгно-
венный к. п. д. кулачковых механизмов с центральным толкателем
можно определять по формуле (7.72). Из этой формулы следует,
что мгновенный к. п. д. зависит’ от угла давления О и от приведен-
ных углов трения <р1п и ср2п. Характер этой зависимости иллюстри-
руется графиками (рис. 474), построенными для комбинаций /1п =
= tgcpin и Лп — tg'Pan, указанных в таблице 7.3 [596].
Таблица 7.3
Графики 1 2 3 4 <5 6 7 8
Ап 0,2 0,1 0,01 0,2 0,01 0 0,1 0,01
/ап 0,4 0,4 0,4 0 0,2 0,2 0 0
Из этих графиков видно, что при малых величинах угла давле-
ния 9 и при /1п 0 может получиться малая величина мгновенного
к. п. д. и, следовательно, возможны случаи, когда уменьшение угла
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 387
давления не будет желательным. Этот результат легко объяснить,
если рассмотреть два предельных случая: /)п = 0 и /2п — 0. В пер-
вом случае формула (7.72) со- ----------------------------г—-----
ответствует к. п. д. ползуна 7
т]п, на который действует сила х
Q под углом 9:
•/in = 1 — tg»tgcp2n.
Во втором случае получается
формула к. п. д. наклонной
плоскости:
______ tg»
^.п— tg(» + ?ln) '
В первом случае к. п. д. с уве-
личением угла давления непре-
рывно уменьшается (рис. 475).
Во втором случае к. п. д. при
9 = 0 равен нулю, затем воз-
растает до максимального зна-
чения при 9 = 45° — и да-
лее уменьшается до нуля при &
О 10 го 30 ЦО 50 00 70 во о
Рис. 474.
90° — с[>|П, как показано на рис. 476.
Рис. 475.
Рис. 476.
Рассматривая кривые мгновенного к. п. д. кулачкового механизма,
можно видеть, что они приближаются по виду к одной из кривых,
показанных на рис. 475 и 476, в зависимости от значений коэффи-
циентов /1П и /2п.
13’
388
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Снижение мгновенного к. п. д. кулачкового механизма при малых
углах давления означает также, что, несмотря на снижение величины
давления кулачка на ведомое звено Q, потери на трение увеличи-
ваются вследствие увеличения относительной скорости кулачка и ве-
домого звена в точке касания при заданной величине v (см. планы
скоростей на рис. 458 и 459).
Обозначим через В„р значение угла В, при котором к. п. д. стано-
вится равным нулю (самоторможение). Из формулы (7.72) получаем:
ffnp = 90°-(^„-На-
(7.76)
значение угла В, которое соответствует максимуму мгновенного
к. п. д. при данных приведенных коэффициентах трения /1п и /2п,
обозначим через Вк. Величина этого
угла может быть определена по фор-
муле
tg&K =
Величина L в прямолинейно движу-
щихся кулачках и величина во вра-
щающихся кулачках выбираются так,
что в любом положении механизма угол
давления 9 меньше предельного зна-
чения Впр *)• Но при этом максималь-
ное значение угла Втах может быть
больше или меньше значения Вк, кото-
рое соответствует максимально возмож-
ному значению мгновенного к. п. д. т]к при
данных коэффициентах трения /1п и /2)Г
В первом случае (Вп1ах 2> Вк) ПРИ Угле давления, изменяющемся
от нуля до максимума и опять до нуля (рис. 477, а) кривая изме-
нения к. п. д. в зависимости от угла поворота кулачка имеет вид,
показанный на рис. 477, б, т. е. мгновенный к. п. д. дважды достигает
максимума при В = ВК и обращается в нуль по концам интервала и,
кроме того, имеет минимум при
ft — ft
и----и щах»
Во втором случае (ftmax <С М ПРИ том же характере изменения
угла давления В (рис. 478, а) кривая к. п. д. в зависимости от угла
поворота кулачка (рис. 478, б) имеет только один максимум при
ft=ftmax, причем величина максимального мгновенного к. п. д. оказы-
вается меньше, чем в первом случае.
*) Более подробно о выборе величин L и сказано далее на стр. 400.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 389
Средняя величина к. п. д. за время интервала может быть найдена
по графику изменения мгновенного к. п. д. путем нахождения среднего
значения *). Максимальное значение среднего к. п. д. получается обычно
при соотношениях между &тах и &к, близких к условию
»п>ах=»к- (7.78)
На рис. 479 показан график зависимости угла давления от при-
веденных коэффициентов трения /in и /2п. На том же графике даны
максимальные значения мгно-
венных к. п. Д. 7]к.
Для кулачковых меха-
низмов со смещенным тол-
кателем величина вращающего момента определится из соотношения
М = Q [Я sin (» ± z + Т1п) ф- 1,27/кгк],
(7.79)
где у — угол смещения, определяемый по формуле (7.49), причем
знак плюс соответствует расположению смещения по рис. 480,
а знак минус — по рис. 481, при условии, что ведомое звено совер-
шает подъем. Остальные обозначения совпадают с обозначениями
в формуле (7.73).
*) Среднее значение мгновенного к. п. д. i)cp не совпадает со значением к. п. д.
I f Ч р'"”
за весь интервал »]„, так как riCD — — I тт~ da, а ци =--------------
v «и и iViK аи
0 С лл л
\ А1к da
Однако в первом приближении можно оценивать величину ц, по величине 'icp-
390
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Подставляя в формулу (7.74) значения М и М для
механизма со смещенным толкателем, имеем:
____________sin (8 ± у)________.
кулачкового
|sinO± -z + 9ln)+l,27/K J | ’
(7.80)
при 1,27/к я» 0 получаем:
е' sin(8±x)
6 Sin(»±x+<?in) ’
В тех случаях, когда система сил, действующих
звено, сводится к силам, расположенным в одной плоскости, в фор-
мулы (7.80) и (7.81) надо подставить е и е',
определяемые по формулам (7.61) и (7.55).
(7.81)
на
ведомое
Рис. 481.
Формула (7.81) после подстановки значений е и г' и преобразо-
ваний имеет вид:
тп —Г tg8 - —tp&fgm I ^tgyinCtg» ,7Я9.
I tg^ + vin) g g,f8n I 1 + tg Ctg (» ± X)
Сравнивая формулы (7.82) и (7.72), можно видеть, что при сме-
щении оси ведомого звена вправо от оси вращения кулачка
(см. рис. 480) мгновенный к. п. д. для подъема ведомого звена полу-
чается больше, чем в механизме с центральным толкателем. При сме-
щении влево (см. рис. 481) к. п. д. получается меньше.
Для кулачковых механизмов с плоским толкателем (см. рис. 470)
величина вращающего момента определится по формуле
Q | cos <pi ф- № + 5) sin + Ь27/кгк]. (7-83)
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 391
Мгновенный к. п. д. этих механизмов определится по формуле (7.74)
после подстановки значений /И согласно формуле (7.83) и М' = Q —-.
Имеем:
е’
v
ей
Подставляя значение е из формулы (7.61) при 0 — 0 и прене-
брегая величиной 1,27/кгк, после преобразований получаем:
,г 1 —ft tg ¥»п
(7.84)
Наконец, для Промысловых кулачковых механизмов (см. рис. 471)
величина вращающего момента на валу кулачка определится по фор-
муле (7.79).
Поэтому мгновенный к. п. д. можно определять по формуле'(7.80).
Подставляя в эту формулу значения е и е' в соответствии с фор-
мулой (7.65), после преобразований имеем:
cos (» + yin) sin (» ± у)
(7.85)
Если учитывается только трение между ведомым звеном и кулач-
ком, то формула (7.85) после преобразований принимает вид:
т) = , -с (7.86)
1+/inctg(&±y.)
Если величина смещения /««0, то формула (7.86) переходит
в формулу к. п. д. наклонной плоскости и, следовательно, максимум
к. п. д. достигается при & = 45° — .
Все приведенные выше формулы для определения к. п. д. относились
к фазе подъема ведомого звена при силовом замыкании кинематической
пары кулачок — ведомое звено. При опускании ведомого звена в слу-
чае силового замыкания сила Р является движущей. Поэтому к. п. д.
определяется по формуле
(7.87)
где Р—величина силы, действующей на ведомое звено, Р’ — вели-
чина той же силы, вычисленной без учета трения.
Для прямолинейно движущихся кулачков из плана сил при опуска-
нии имеем: -
Рк sin (S —<fln —<рк)
Q cos -f к
392
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
Отсюда
р— Q — р .____________________cos Ук . ту_______________ р 1
е к е sin (8 — <р1п — <рк) ’ к е' ® '
Подставляя значения сил Р и Р' в формулу (7.87), получаем:
е sin (8 — у1п —- ук)
‘ е' sin 8 COS<pK
Для прямолинейно движущегося ведомого звена коэффициент
возрастания усилия при-опускании и силовом замыкании определяется
по формуле (7.66). Подставляя это значение е в выражение для
к. п. д. и учитывая, что е' — —Ц-, имеем:
J cos» ’
„ _ cos ?8п sin (в — Уш — Ук) /7 RRA
tg 8 cos ук cos (»— <р1п — <pSn) ' 1 ’
Сравнивая формулы (7.88) и (7.71), можно видеть, что выражение
для к. п. д. при опускании ведомого звена получается из выражения
для к. п. д. при подъеме, если изменить знаки углов трения на
обратные и поменять местами числитель и знаменатель.
При <рй«=гО после преобразований получаем:
>'+».„ • <7-89>
Эта же формула справедлива и для дисковых вращающихся кулач-
ков с центральным толкателем, если можно пренебречь трением в опоре
кулачка. Графики зависимости к. п. д. ц от угла давления & при
различных значениях приведенных коэффициентов трения /ln = tg«>ln
и /2п = tg <р2п напоминают графики, показанные на рис. 474; к. п. д.
обращается в нуль при & = cpJn и & = 90°. Максимум к. п.д. дости-
гается при
tg»K= +/?п)+/1п- (7.90)
Сравнивая формулы (7.90) и (7.77), можно видеть, что при
опускании максимум к. п. д. достигается при больших значениях
угла давления.
В механизмах со смещенным толкателем к. п. д. при опускании
и силовом замыкании найдется по формуле
£ [/? sin (8 ± X - у»„) - 1,27 Агк]
е' R sin (8 ± у)
При 0, считая, что коэффициент возрастания усилий е опре-
к
деляется по формуле (7.66), после преобразований получаем:
„ =________ctg 8__________1 — tg У1П ctg (8 ± у)
ctg(8 — yiu) + tg<pSn 1— tg ?1П ctg 8 ’ 1 ’
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 393
В механизмах с плоским толкателем соответственно имеем:
(/?0 + S)<0
ц =----i-----------• (7.92)
‘ 1— /ltg?2n V ’
Для коромысловых кулачковых механизмов формула для опре-
деления к. п. д. при опускании ведомого звена и силовом замыкании
имеет вид:
cos 8 | [1-1,27/,^- J | Йо sin (т 4- & + р) J [ sin (& ± у — ?1п) — 1.27/К-Ь-1
cos(S — ?1п) sin (» ± х)
(7.93)
Если учитываются только потери в кинематической паре кулачок —
ведомое звено, то формула (7.93) принимает вид:
„ __ 1 —/inctg (»±'Х)
l+/intg&
При //=^0 максимум к. п. д. достигается при &45°-ф-.
Указанные формулы для к. п. д. при опускании толкателя справед-
ливы и для случая кинематического замыкания, если сила Р направ-
лена вниз. Если же сила Р направлена вверх, что может иметь
место при ускоренном движении, то получаются формулы к. п. д.
для подъема ведомого звена, но с изменением знака при угле сме-
щения у, а именно, формула (7.82) для кулачкового механизма со
смещенным толкателем имеет вид:
Н®<rRj-le8le<p’"l
1 + tg <Р1п Ctg &
1-Hg<plnctg'(&±-z) ’
где знак минус при угле у соответствует смещению оси ведомого
звена вправо от оси вращения при вращении кулачка против хода
часовой стрелки.
Аналогично изменяются знаки в формулах (7.85) и (7.86) для
коромысловых кулачковых механизмов.
При кинематическом замыкании на фазе подъема к. п. д. опреде-
ляется по формулам для опускания ведомого звена, если сила Р изме-
няет знак на участке замедленного движения.
4°. Выбор допускаемого угла давления. Из формул (7.39),
(7.47) и (7.50) видно, что угол давления зависит от выбранного
закона движения ведомого звена и от основных размеров кулачкового
механизма, которыми являются длина профиля L в прямолинейно
движущихся кулачках (рис. 482), длина направляющей /н, радиус-
вектор дискового кулачка в начале интервала /?0 и др. Поэтому
при выбранном законе движения ведомого звена можно, изменяя
основные размеры кулачкового механизма, соответственно изменять
величины углов давления, от которых в свою очередь зависят реак-
ции в кинематических парах и к. п. д. механизма. Обычно основные
394
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
ДОП.
допускаемого угла давления можно различать два
получить наименьшие габариты механизма при за-
интервала или наименьшее время интервала при
размеры кулачкового механизма определяют считая, что максимальное
значение угла давления не должно превосходить некоторой допуска-
емой величины
При выборе
основных случая:
1) требуется
данном времени
заданных габаритах механизма;
2) требуется получить наименьшую величину потерь на трение
в кинематических парах.
В первых работах по кулачковым механизмам эти случаи отдельно
не рассматривались и при определении основных размеров принима-
лась величина допускаемого угла давления &доп = 30° при прямоли-
нейно движущемся ведомом звене и &доп =
— 45° при вращающемся ведомом звене.
Значительным шагом вперед явились исследо-
вания Г. А. Шаумяна [59а, б], в которых
была дана номограмма для выбора допускае-
мого угла давления в зависимости от суммы
приведенных коэффициентов трения /1П
И. М. Кучер [32] продолжил исследования
Г. А. Шаумяна, показав, как при построении
графика для выбора допускаемого угла дав-
ления можно учесть не только значения
коэффициентов трения, но и точность обра-
ботки профиля кулачка и возможную величину
изменения коэффициентов трения при работе
Г. А. Шаумяна и И. М. Кучера также не рас-
механизма. В работах
сматриваются отдельно указанные выше два основных случая выбора
допускаемого угла давления. Между тем требования, предъявляемые
к значениям допускаемого угла давления, в этих случаях являются
противоречивыми, так как в первом случае допускаемый угол давле-
ния должен быть наибольшим, а во втором случае соответствовать
минимуму потерь на трение, который имеет место обычно при малых
углах давления [46].
Рассмотрим сначала выбор допускаемого угла давления &доп для
первого случая в предположении, что ведомое звено имеет прямоли-
нейное движение. С увеличением угла давления увеличивается реак-
ция кулачка на ведомое звено и, следовательно, увеличивается коэф-
фициент возрастания усилий. Из формулы (7.61) следует, что коэффи-
циент возрастания усилий есть функция трех переменных &, <р1п и
COS
е =
COS (S 4-¥1п + ?ап) '
Однако, учитывая, что cos <р2п сравнительно мало отличается
о г единицы при обычных значениях угла трения (например,
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 395
при tg<p2n —0,3 имеем cos <р2п == 0,95), можно построить графики
величины -------- в функции угла давления 8 при различных значе-
COS <р2п .
ниях суммы (<р1п -ф- ср2п) и по этому графику судить о характере
изменения коэффициента возрастания усилий и, следовательно, ве-
личин реакции кулачка на ведомое звено. Отметим также, что под
суммой приведенных углов трения <р1п-]-<р2п практически можно
понимать также сумму приведенных коэффициентов трения. Например,
при /1П =/2п = 0,3 имеем/1п 4-/зп — 0,6 и ср1п -ф- <р2п = 0,58.
На рис. 483 показаны графики зависимости ------- от угла дав-
ления & при различных величинах суммы cpjn -ф- <р2п. Из графиков
видно, что по мере приближения угла давления к предельному зна-
чению 81ър = 90° — (ср1п -ф- ф2п), при котором имеет место заклинивание
механизма, коэффициент возрастания усилий увеличивается, причем
это увеличение сначала идет медленно, а затем весьма быстро. Оче-
видно, что допускаемое значение угла давления &доп должно быть
выбрано таким образом, чтобы соответствующая точка графика
—рД =/(&, <рп “Ь ?2п) располагалась на том участке, где неболь-
шие колебания угла давления &, происходящие, например, от ошибок
изготовления профиля, не вызывают значительного изменения ве-
личины ---------.
COS "fan
Кроме того, значение &доп должно быть выбрано
396
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. УП
таким образом, чтобы при изменении суммы коэффициентов трения
<р1п -ф- <р8п, происходящем от изменения состояния трущихся поверх-
е ,
ностей и других причин, величина ------ также не имела бы зна-
COS ?2п
чительных колебаний. Следовательно, для выбора &доп надо задаться
возможными пределами изменения угла давления &, суммы приведен-
ных углов трения cpJn -ф- <р.2п и коэффициента возрастания усилий е,
причем опасным является только увеличение угла давление & и сум-
мы <Р1п + <Р«п-
Обозначим максимальное положительное отклонение угла давления
от расчетного значения через Д&, максимальное относительное уве-
личение суммы углов трения через Д<р и допускаемое относительное
увеличение коэффициента воз-
растания усилий через Де.
Тогда задача об определении
&доп сводится к нахождению
такой точки на графике —-— ,
т COS <р2п
в которой изменение угла дав-
ления на величину Д& и изме-
нение суммы углов трения на
величину Дер (cpin -ф- ср2п) вызы-
вают изменение величины коэф-
фициента возрастания усилий е
на величину не более чем еДе.
На рис. 484 показано, как
можно графически определить
для каждого значения ср1п-[-<Рап значение &доп по заданным Дер, Д& и
Де *). Для этого выбираем на графике ер1п -ф- ср2п некоторую точку В,
проводим вертикаль на расстоянии Д& от точки В до пересечения
A,Bi
с графиком (ср1п4-<р2п)(1Д:р) в точке Въ Если отношение -77.
равно 1 -ф- Де, то выбранная точка В соответствует &доп; если это
отношение меньше, то нужно выбрать точку В правее; если больше, —
то левее.
Графический путь решения является в данном случае наиболее
удобным и простым, причем точность его вполне соответствует точ-
ности задания величин Д<р, Д& и Де.
Пусть, например, допуски на изготовление профиля кулачка будут
указаны такие, что максимальное увеличение угла давления не пре-
взойдет величины Д& = 5°, а углы трения при эксплуатации механизма
не могут увеличиться более, чем на 50%, т. е. Д<р = 0,5. Тогда,
считая допустимым согласно выбранным запасам прочности увеличе-
*) Аналитическое решение аналогичной задачи, основанное на разложении
в ряд, имеется в работе И. М. Кучера «Конструирование специализиро-
ванных станков-автоматов и полуавтоматов», Машгиз, 1952 [32].
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 397
ние давления кулачка на ведомое звено и, следовательно, коэффи-
циента возрастания усилий на 50% (Де = 0,5), можно определить
для каждого значения суммы + величину допускаемого угла
давления 8ДОП. Значения этих углов при Д& = 5°, Дер = 0,5 и Де =
ч=0,5 отмечены кружками на рис. 483. По этим значениям построена
кривая 1 на рис. 485.
Если принять изменение углов трения (или коэффициентов трения)
на 25% (Дер = 0,25), то при тех же значениях ДО и Де получим
на рис. 483 точки, отмеченные крестами, а на рис. 485 кривую 2.
Следовательно, графиками, показанными на рис. 485, можно пользо-
ваться только при тех условиях изменения величин е, & и <pin-|-<p2n,
которым они соответствуют. В других случаях следует непосредст-
е
COS <pSn
венно пользоваться кривыми
выбирая значение 0ДО11, исходя
из анализа возможных отклонений угла давления и коэффициентов
трения в проектируемом механизме.
Кривые, показанные на рис. 483, относятся к фазе подъема ведо-
мого звена при силовом замыкании. Для фазы опускания при силовом
замыкании коэффициент возрастания усилий определяется по фор-
муле (7.66).
Графики
---------=/(&) при различных значениях cpin-|-<p2n для
данного случая показаны на рис. 486. Как видно из графика, коэф-
фициент возрастания усилий при больших значениях угла давления &
является значительным. Поэтому и при опускании, так же как и при
подъеме, можно определять величину Здоп, задаваясь величинами Де,
Д^ и ДО. На рис. 486 кружками отмечены значения 0ДОП, получен-
ные при Де = 0,5; Д<р = 0,5 и Д& = 5°, а на рис. 485 соответственно
построена кривая 3. Очевидно, что при опускании допускаемые углы
398
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. VH
давления больше, чем при подъеме, если применено силовое замыка-
ние кинематической пары кулачок — ведомое звено.
При кинематическом замыкании допускаемые углы давления при
опускании те же, что и при подъеме, если сила Р имеет примерно
одну и ту же величину. Если же сила Р при опускании меньше, то
и допускаемые углы давления можно брать меньше, сохраняя, напри-
мер, одну и ту же величину давления кулачка на ведомое звено.
Допускаемый угол давления определяемый по графикам, показан-
ным на рис. 485, является наибольшим возможным для принятых
условий. Получающаяся при этом величина давления кулачка на ве-
домое звено иногда оказывается настолько значительной, что кон-
ЗВ ЧВ 50 БВ 70 8В
О
Рис. 486.
из графика, показанного на рис. 483,
структивные размеры кулач-
ка и ведомого звена не мо-
гут быть практически вы-
полнены. В этом случае до-
пускаемый угол давления
определяется допускаемой
величиной давления кулачка
на ведомое звено фдоп, ко-
торая находится из условий
прочности той части меха-
низма, которая является
наиболее напряженной. По
величине фдоп определяется
допускаемый коэффициент
возрастания усилий едоп =
0^п и далее по задан-
ным углам трения <р1в и <ра,
находится величина допу-
скаемого угла давления 8Д0П
или же по формуле (7.61).
В таком же порядке производится поверочный расчет выполненной
конструкции механизма с целью установления наименьшей величины
времени интервала ta, исходя из условий прочности механизма.
Изложенный метод выбора допускаемого угла давления по коэф-
фициенту возрастания усилий исходит из получения наименьших габа-
ритов механизма или из получения наименьшей величины времени
интервала. Могут быть случаи, когда не требуется получения наи-
меньших габаритов или наименьшей величины времени интервала.
Тогда основные размеры кулачкового механизма следует выбирать из
условия получения наименьших потерь на трение в кинематических
парах. Если величину этих потерь оценивать величиной к. п. д. меха-
низма, то величину допускаемого угла давления можно определить
из условия (7.78). Для того чтобы выполнить это условие, можно,
задаваясь величинами h, d и /в и зная угол трения ц>2, найти по
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 399
формуле (7.60) приведенный угол трения <р2п. Затем по формуле (7.77)
или из графика, показанного на рис. 479, находим значение угла
давления 8К, при котором мгновенное значение к. п. д. является
максимальным. Это значение угла давления и принимаем в качестве
допускаемого при определении величины L.
Возможен и другой вариант расчета. Зная приведенный угол тре-
ния <р1п, можно по графику, показанному на рис. 479, подобрать та-
кое значение приведенного угла трения <р4п, при котором максималь-
ное значение мгновенного к. it д. имеет заданное значение. Одновре-
менно определяется угол давления 8К, который принимается в качестве
допускаемого при определении величины L. Выбранное значение при-
веденного угла трения <р2п при заданном <р2 должно быть обеспечено
подбором длины направляющей ZH по формуле (7.60).
При вращающемся ведомом звене допускаемый угол давления 9ДО11
также может выбираться или по коэффициенту возрастания усилий
или по величине к. п. д. В первом случае используются формулы (7.65)
и (7.67), по которым можно выбрать 8ДОП для подъема и опускания,
исходя из заданных Де, ДО и Д<р. Если -^- «а 1 и потерями в шар-
нире ведомого звена в первом приближении можно пренебречь, то
для установления 0ДОП пригодны графики, показанные на рис. 483 и 485.
Во втором случае допускаемый угол давления 8ДОП выбирается
так, чтобы к. п. д„ определяемый по формуле (7.85), имел максималь-
ное значение. Если учитываются только потери на трение кулачка
о ведомое звено и угол смещения у^О, то допускаемый угол давле-
ния при подъеме ЯДОП = 45О— -^п-, т. е. близок к 45°. При опуска-
нии в случае силового замыкания &доп = 45° .
5°. Аналитические и графические методы определения основ-
ных размеров кулачкового механизма. Прежде чем графическим
или аналитическим путем определять профиль кулачка, необходимо
найти некоторые размеры механизма, которые называются основными.
К основным размерам кулачка относится длина профильной части
поступательно движущегося кулачка L, средний радиус цилиндриче-
ского кулачка /?ср, радиусы-векторы дискового кулачка /?0 и /?тах.
соответствующие началу и концу рассматриваемого интервала движе-
ния ведомого звена (наименьший и наибольший радиусы-векторы),
угол профиля кулачка, заключенный между этими радиусами-векто-
рами, ри и смещение е в дисковых кулачках.
Кроме того, к основным размерам кулачкового механизма можно
отнести также длину направляющих ведомого звена /н, длину вра-
щающегося ведомого звена I, расстояние между центрами вращающе-
гося кулачка и ведомого звена /0 и начальный угол поворота ведомого
звена ф0 (см. рис. 467). При установлении указанных основных раз-
меров часто стремятся к получению наименьших габаритов механизма^
400 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
поэтому задачу об определении основных размеров кулачкового
механизма называют иногда задачей об определении наименьших га-
баритов механизма.
Сначала рассмотрим наиболее простой кулачковый механизм, в ко-
тором кулачок и ведомое звено движутся прямолинейно (см. рис. 482).
В этом механизме подлежит определению длина профильной части
кулачка L, от которой зависит общая длина кулачка (его габарит) и
длина направляющей /н.
Время интервала при равномерном движении кулачка
= (7.95)
Для уменьшения времени интервала и для уменьшения габари-
тов механизма следует уменьшить длину профильной части кулачка L.
Однако при этом согласно формуле (7.39) увеличивается максимальный
угол давления
с
tg»max =8тах -2” (7.96)
и, следовательно, увеличивается величина давления кулачка на ведо-
мое звено. Поэтому длину L следует определять из условия огра-
ничения максимального угла давления некоторой допускаемой вели-
чиной »доп.
Из формулы (7.96) имеем:
По формуле (7.97) определяется длина Айв тех случаях, когда
нужно получить наименьшие потери на трение в кинематических парах,
но значение допускаемого угла давления, как было показано ранее,
будет иное*).
Длину направляющей /н обычно выбирают наибольшей допустимой
по условиям размещения механизма. Чем больше длина направляющей,
тем меньше согласно формуле (7.60) величина приведенного угла
трения <р2п и, следовательно, длина профильной части кулачка L.
Однако при увеличении длины /н сверх некоторого значения умень-
шение длины L оказывается незначительным, и поэтому можно путем
проб установить некоторое оптимальное значение длины направля-
ющей 1а из условия получения небольших габаритов механизма.
Для других типов кулачковых механизмов (кроме механизмов
с плоским толкателем) методика определения основных размеров та
же, что и для рассмотренного механизма. Отличие состоит только
в формулах или графических построениях для определения искомых
размеров, исходя из заданного &доп или желаемого значения к. р. д,
*) См. стр. 399,
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 401
В цилиндрических кулачках средний радиус кулачка Rcp связан
с длиной профильной части кулачка L при развертке на плоскость
следующим соотношением:
(7.98)
L ^срТи>
где уи — центральный угол, соответствующий перемещению кулачка
за время интервала tH.
Принимая во внимание формулу (7.97), имеем:
*
q ___ °шах о
Кср— T„tg^on и'
По этой формуле можно определять минимальную величину Rcp
при заданной величине центрального угла Чаще, однако, прини-
мают величину Rcp наибольшей возможной по условиям размещения
механизма и определяют минимальную величину центрального угла уи
из соотношения
(7.99)
__ ^гпах
1и tP & /? '
^доп ср
Очевидно, чем меньше угол fH, тем меньше время интервала <и, т. е.
тем выше производительность машины.
В дисковых' вращающихся кулачках с центральным толкателем
во многих случаях можно считать, что максимальное значение угла
давления достигается в положении, соответствующем максимальной
скорости. Тогда из формулы (7.47) и принимая во внимание, что для
этого положения
получаем:
Q
^max = ^max ~~f~ И
ги
S == tiS,
Sh
tn
Отсюда
tg^on — u(7?o_|_kShp
Gm ах
’и»
(7.100)
® max
где аи = ш^и—угол поворота кулачка за время .
Выбор величины &доп производится так же, как и для прямо-
линейно движущихся кулачков, так как формулы для коэффициентов
возрастания усилия и для к. п. д. совпадают.
Если по условиям размещения механизма задана величина началь-
ного радиуса-вектора Ro или величина максимального радиуса Ra -|-SB
и требуется найти минимальную величину угла поворота аи с целью
получения минимального времени интервала <н , то из формулы (7.100)
можно найти значение угла поворота а„• Имеем;
°тах
(7.101)
аи =
tg ^лоп
402 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VH
Для тех случаев, когда максимумы скорости и угла давления не
совпадают, формулы (7.100) и (7.101) будут только приближенными.
При необходимости получить более точное значение Ro или аи можно
использовать графическое построение, которое было показано на
рис. 460.
Для определения величины До строим график — =/(5) или, что
£
то же, 8 ~ = f (S) (рис. 487) и проводим касательную к графику под уг-
£
лом &доп. Расстояние между началом координат графика 8 —— = f(S)
«и
и точкой пересечения касательной с осью пути S дает величину на-
чального радиуса-вектора Пунктиром на том же рис. 487 показа-
но аналогичное построение для фазы опускания ведомого звена. Так
как для фазы опускания допускаемый угол давления &доп обычно
больше (см. кривую 3 на рис. 485), то во многих случаях можно
ограничиться определением начального радиуса-вектора /?0 только
для фазы подъема.
Для определения величины аи по заданной величине /?0 предвари-
тельно определяем приближенное значение угла поворота аи по фор-
муле (7.101) и затем строим график 8—— =/(S) (рис. 488). Да-
аи
лее проводим касательную к графику под углом &доп и определяем
величину До, которая в общем случае не совпадает с заданной ве-
личиной До- Уточненное значение угла поворота аи можно найти
из соотношения
г>'
(7.102)
/Л)
Для кулачковых механизмов со смещенным толкателем начальный
радиус-вектор определяется обычно путем графического по-
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 403
строения (рис. 489), которое вполне аналогично показан-
ному на рис. 487. Только при наличии большого смещения оси
ведомого звена вправо от центра вращения кулачка, кроме проведе-
5
ния касательной к графику 8——=/(S), надо провести также ли-
аи
нию через начало координат под углом &доп, так как максимальный
угол давления может быть до-
стигнут при достаточном смешении
в момент начала движения. На
рис. 489 показан случай, когда центр
вращения кулачка и, следователь-
но, начальный радиус-вектор опреде-
ляются при пересечении касатель-
ной к графику 8 —S-=/(S) с прямой
®М
I—I, проведенной параллельно на-
правлению оси S, на расстоянии,
равном смещению е. На рис. 490
показан случай, когда начальный
радиус-вектор определяется при
пересечении прямой I—I с линией
II—II, проведенной через начало координат графика под углом &доп.
Иногда смещение е и начальный радиус-вектор кулачка /?0 опреде-
ляют путем выбора центра вращения кулачка в точке пересечения
касательных к графикам 8—~ = /(S), построенным для подъема и
“и
опускания ведомого -звена (рис. 491), что обеспечивает минимальную
величину начального радиуса-вектора. Но при этом обязательно сле-
дует принимать во внимание, что при опускании допускаемый угол
давления &'ДО11 обычно больше, чем при подъеме.
404
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. VII
Угол поворота аи при заданных величинах смещения и начального
радиуса-вектора определяется предварительно из формулы (7. 50),
которая при совпадении положений максимумов скорости и угла дав-
ления имеет следующий вид:
Отсюда
(7.103)
(7.104)
Приближенное значение угла поворота а1Р найденное по формуле
(7.104), обозначим через а'и. Это значение может быть уточнено
путем графического определения начального радиуса-вектора Ro п0
заданным величинам а'„ и е. Далее уточненное значение угла поворо-
та находится по формуле
. 1/'(^о)2-^
7 R^-e’
= а
а
И
(7.105)
Выбор допускаемого угла давления &доп для кулачковых меха-
низмов со смещенным толкателем не отличается от выбора этой ве-
личины при центральном толкателе, если принимается во внимание
только коэффициент возрастания усилий. Так как допускаемые углы
давления при опускании больше, чем при подъеме (если замыкание
силовое), то в результате построения, показанного на рис. 491,
обычно получается смещение оси ведомого звена вправо от оси вра-
щения кулачка (при вращении кулачка против хода часовой
стрелки). Если же определение основных размеров кулачкового ме-
ханизма со смещенным толкателем производится из условия получе-
ния максимального к. п. д., то следует принять во внимание, что,
применяя смещение оси ведомого звена вправо от оси вращения
кулачка, можно к. п. д. механизма при силовом замыкании увеличить.
Величину смещения в первом приближении можно определять из ус-
ловия равенства максимальных углов давления в начале подъема
и в среднем положении, т. е. выбирать центр вращения в точке О,
как показано на рис, 490. Допускаемый угол давления &доп опреде-
ляется при .этом, как и в механизмах с центральным толкателем,
т. е. по формуле (7.77).
При кинематическом замыкании применять смещенный толкатель
обычно нецелесообразно, так как, улучшая за счет смещения к. п. д. и
коэффициент возрастания усилия при подьеме, одновременно ухуд-
шаем эти характеристики при опускании.
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 405
В коромысловых кулачковых механизмах при заданной величине
угла поворота аи подлежат определению следующие основные раз-
меры: длина ведомого звена I, расстояние /0 между центрами вра-
щения кулачка и ведомого звена и начальный радиус-вектор ку-
лачка /?0 (рис. 492). Указанные три величины определяют треуголь-
ник ОВС, характеризующий начальное положение кулачка и ведо-
мого звена. Основными размерами можно считать также начальный
угол наклона ведомого звена ф0 и начальный угол профиля кулачка ро.
Независимыми величинами будут любые три размера из указанных
пяти размеров: I, /0, Ro, [i0 и ф0. Кроме того, можно задавать в раз-
личных положениях значения переменного смещения е, т. е. вели-
чину перпендикуляра, опущенного из центра вращения кулачка на
направление скорости точки В ведомого звена (см. рис. 466).
Из сказанного ясно, что для этого типа кулачкового механизма
возможно несколько вариантов определения основных размеров. Рас-
смотрим, например, определение ос-
новных размеров механизма и угла
поворота %• при условии, что
эксцентриситет е равен нулю в по-
ложении, соответствующем макси-
мальной скорости.
Для тех случаев, когда макси-
мальное значение угла давления до-
стигается в положении, соответст-
вующем максимуму скорости, из
формулы (7.53) получаем:
tg 8доп ш/0
^тах
sin (ф -ф- фо)
(7.106)
Обозначая через фи угол поворота ведомого звена за время
интервала tK и принимая во внимание, что максимальная угловая
скорость ведомого звена ютах = Втах имеем:
v max--‘"max .
Подставляя это значение цтах в формулу (7.106) и учитывая, что
<о и в указанном положении ф = г/фи, получаем:
*и
(7.107)
Отсюда можно определить любой из следующих основных разме-
ров: I, фи, яи, ф0, если задаться значениями всех других.
Например, при заданных величинах /, фи, аи и ф0, имеем:
1 __ ®тах^Уи 7 .
0 ~ “И tg &ДОП Sin («ф„ + ф0) - О
406
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. vtl
Если требуется определить угол движения то из формулы
(7.107) имеем:
8 /'L
а —___________™_х . (1 1 псп
" — /otg»aon sin(M% + d0) •
Значения основных размеров для рассматриваемого случая можно
уточнить, если применить графическое построение, показанное на
рис. 493. Это построение отличается от указанного на рис. 487
только тем, что путь точки касания ведомого звена с профилем
откладывается не на прямой, а на дуге протяженностью и
V 1'^
величины — = а" 8 откладываются в каждой точке дуги по на-
правлению ее радиуса от центра вращения ведомого звена, если
при подъеме кулачок и ведомое звено имеют разные направления
вращения, и к центру вращения ведомого звена, если эти направле-
ния вращения кулачка и ве-
домого звена совпадают.
SD ~ Кроме того, вместо проведе-
/\у ния касательных к по-
строенному графику сле-
„ о'Дует в нескольких положе-
&/? '' ниях (обычно близких к по-
\д ' / ложению максимума скоро-
\\ I /'^о сги) провести прямые, на-
\\\| / клоненные к радиусам под
/' углом 90° — &доп. Наиниз-
' шая точка пересечения этих
р прямых с направлением мак-
симальной скорости ведо-
Рис. 493. мого звена определяет по-
ложение центра вращения
кулачка и, следовательно, определяет искомые основные раз-
меры: Zo, ф0 и /?0.
Аналогичным построением уточняется значение угла поворота ап
после предварительного определения его по формуле (7.109).
В качестве другого примера определения основных размеров
кулачкового механизма с вращающимся ведомым звеном рассмотрим
случай, когда при заданных величинах аи, и I требуется найти
основные размеры /0, ф0 и 7?п из условия получения наименьшей
величины начального радиуса-вектора /?0, причем должны быть
приняты во внимание как условия подъема, так и условия опускания
_ v -
ведомого звена. В этом случае величины — должны быть построены
и для подъема и для опускания (рис. 494).
Выбрав центр вращения кулачка О в заштрихованной области,
которая получается после проведения прямых, наклоненных к радиу-
§ 22] ОПРЕДЕЛЕНИЕ ОСНОВНЫХ РАЗМЕРОВ КУЛАЧКОВЫХ МЕХАНИЗМОВ 407
сам под углом 90° — &доп, находим из чертежа искомые основные
размеры: Zo, и %.
Иначе решается задача об определении основных размеров ку-
лачковых механизмов с плоским толкателем или коромыслом. При
проектировании этих меха-
низмов ставится условие,
чтобы профиль кулачка был
только выпуклым. Обозна-
чив радиус кривизны кулач-
ка через р, запишем это
условие в следующем виде:
р>0. (7.110)
Чтобы выразить радиус
кривизны кулачка через ос-
новные размеры механиз-
ма и параметры движения,
построим план ускорений
для кулачкового механизма
Рис. 494,
с плоским коромыслом
(рис. 495). План ускорений будем строить по уравнению
ак— °пер “Г «пер + °О,Н + °пов’
где ак — ускорение точки К — центра кривизны кулачка в месте
касания с ведомым звеном;
°пеР — нормальное ускоре-
ние точки К в переносном
движении вместе с ведомым
звеном; а* — тангенциаль-
ное ускорение точки К в
том же движении; аотн —
ускорение точки К в дви-
жении относительно ведо-
мого звена; а — поворот-
ное (кориолисово) ускоре-
ние.
Рис. 195. Приняв за полюс плана
ускорений точку Д' и вы-
полняя построение в масштабе (ха = [тги>а, где — масштаб схемы
механизма, получаем из чертежа (рис. 495):
и оп
f = /,sin(tTW4-^ + ^sin8i-^cos<V (7.111)
408 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Модули ускорений, входящие в формулу (7.111), определяются
по известным соотношениям:
at
пер cos 8с I Л2 | •
Введем обозначения:
(1'Ъ
V = d^ (7.ИЗ)
Ф =rf-s-, (7-114)
причем условимся считать величину ф' отрицательной, если угловые
скорости кулачка и ведомого звена имеют противоположное на-
правление, а величину ф"—отрицательной при замедленном движе-
нии на фазе подъема и ускоренном на фазе опускания.
Кроме того, из условия, что точка Р есть мгновенный центр
вращения в относительном движении, при ф'<^0 имеем:
d'b
OP ~~dt
/=С/’со8(ф4-ф0) = т^р cos (ф —фо), (7.115)
Т,отн = КР (ю — J) = I [tg (Ф + ф0) — tg 8J (1 - ф') <0. (7.116)
Подставим значения модулей ускорений из соотношений (7.112)
в формулу (7.111). Тогда, учитывая формулы (7.115) и (7.116) и
</ф Й2ф IW 9 х » р
принимая во внимание, что -±=фо>, ,(2=фт2 и = после
преобразований получим [536]:
(1 — 2ф’) 1ё(ф + фо)
Р=-----------(ГГфу------?" Ч cos (Ф + Фо)- (7.11.7)
Если ведомое звено движется прямолинейно, то
ф' = 0, sin (ф + ф0) = Ro + S, ф'70со8(ф + фо)=^,
и формула для определения радиуса кривизны имеет вид:
p = R„ + S + “aa. (7.118)
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
409
величины начального угла поворота
для ряда значений угла поворота
Условие выпуклости профиля (7.110) при вращающемся ведомом
звене получается в виде неравенства
tg (Ф Фо) (1 — ф')(1 — 2Ф') ’ (7.119)
Если ведомое звено движется прямолинейно, то условие (7.110)
получает вид [14д]:
Ro> —SS- (7Л20>
Для нахождения минимальной
ведомого звена ф0 вычисляется
кулачка а на участках движения
с отрицательным ускорением
функция
Ф-(Г.-^(Г 2ФУ <7Л21>
Затем на заданном графике
ф = /(а) откладываем вниз от
соответствующих точек графика
значения углов ф, вычисленные
из условия ф = arc tg Ф, и соеди-
няем полученные точки плавной
кривой (рис. 496). Наибольшая отрицательная ордината этой кривой
и определит искомый угол ф0.
Величина начального радиуса-вектора кулачка определится по фор-
муле
7?0 =/0 sin ф0. (7.122)
Если ведомое звено движется прямолинейно, то на заданном гра-
фике S=/(a) откладываем вниз от соответствующих точек графика
dsS
отрезки, изображающие - на участках с отрицательным ускоре-
нием, и соединяем полученные точки плавной кривой. Наибольшая
отрицательная ордината этой кривой и определит искомую величину 7?0.
§ 23. Определение профиля кулачка по заданному закону
движения ведомого звена
1°. Определение профиля прямолинейно движущегося кулачка.
После выбора закона движения ведомого звена и определения основ-
ных размеров кулачкового механизма можно приступить к определе-
нию профиля кулачка.
При прямолинейно движущемся кулачке с заостренным толкате-
лем профиль кулачка совпадает с графиком зависимости пути ведо-
мого звена от перемещения кулачка, если ведомое звено движется
410
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VI1
прямолинейно. Если же ведомое звено имеет вращательное движение,
то определение профиля кулачка можно произвести или графическим
или аналитическим путем. Для этого должна быть задана зависимость
углов поворота ведомого звена от перемещения кулачка хк:
Ф=А*к)>
а также основные размеры Z и 4 (рис. 497). Графический путь реше-
ния основан на методе обращения движения. Согласно этому методу
профиль кулачка при ведомом звене, имеющем заостренный профиль,
получается как траектория точки касания ведомого звена с профилем
кулачка в относительном движении, т. е. считая кулачок неподвиж-
ным, надо перемещать
направлению движения
кулачка, одновременно
ведомое звено в сторону, противоположную
кулачка на величины, равные перемещению
поворачивая его
на углы поворота ф, соот-
ветствующие принятому за-
кону движения. Соединив
последовательные положе-
ния точки В ведомого зве-
на, получим профиль кулач-
ка. Надо заметить, что гра-
фические методы определе-
ния профиля кулачка могут
быть использованы только
для предварительного выяс-
нения характера профиля и
получения данных для расче-
та механизма (например, для
определения радиусов кри-
Для составления же рабочего чертежа, по
изготовлен кулачок, необходимо даже при
визны профиля кулачка),
которому должен быть
сравнительно грубом способе обработки произвести аналитическое
вычисление координат профиля для достаточного числа точек про-
филя и проставить их на чертеже с указанием предельных отклоне-
ний. В противном случае неизбежные ошибки при вычерчивании про-
филя при перенесении его на заготовку настолько исказят профиль,
что закон движения ведомого звена будет иметь мало общего с при-
пятым при проектировании.
Аналитическое вычисление координат профиля поступательно дви-
жущегося кулачка при вращающемся ведомом звене производится пр
формулам:
у — 4—1 cos (Ф + Фо).
x = xK-[-/sin ф0 — Zsin (ф-ф-фо)»
(7.123)
которые следуют непосредственно из рассмотрения рис. 497.
При ведомом звене, снабженном роликом, построение, указанное
на рис. 497, дает относительную траекторию центра ролика, которая
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
411
называется теоретическим или центровым профилем кулачка. Для по-
строения профиля кулачка, который в этом случае называется кон-
структивным или практическим, надо, выбрав радиус ролика г, пока-
зать его положения при различных значениях у и затем провести
огибающую к построенным окружностям.
Величина радиуса кривизны конструктивного профиля рп связана
с величиной радиуса кривизны центрового профиля р и радиуса
ролика г следующим соотношением:
Р„ = р-г. (7.124)
При р = г радиус кривизны профиля рп = 0 (заострение профиля).
Поэтому радиус ролика г должен быть меньше минимального радиуса
кривизны центрового профиля.
Обычно принимают
’ г<О,7рга)|, (7.125)
и не более г = О,4До.
Для аналитического вычисления координат конструктивного про-
филя хп и уп надо уравнение семейства окружностей, представля-
ющих собою последовательные положения ролика
(хл — х)2 4- (уп — у)2 — г2 = О,
(7.126)
продифференцировать по переменному параметру семейства (при по-
ступательно движущемся кулачке в качестве параметра семейства
можно принять координату хк) и приравнять нулю.
Полученное уравнение
(хп — х) х' 4- (jn — v)у = О
п
следует решить совместно с уравнением семейства (7.126) и найти
координаты огибающей хп и v„. Имеем:
гу' 1
У(л-Т + (уТ ’ I
гл' I
VW + W ' I
(7.127)
Верхние знаки относятся к одной огибающей, нижние — к другой
огибающей.
При ведомом звене, имеющем поступательное движение, получаем
j = S.
К»
Следовательно:
яхк
где с = .
412 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Подставляя указанные значения х' и у' в формулы (7.127), имеем:
сб
П = ± г —г-
п Е ]Л1-|-с2б2 ’
(7.128)
(7.129)
v„ = S г г 1 — —
При ведомом звене, имеющем вращательное движение, получаем:
х' = 1 — /8 - д’ cos (ф ф0), )
У = /8 sin (ф-|-ф0). I
(7.130)
Координаты конструктивного профиля (огибающей) определяются в
этом случае непосредственно
из формул (7.127) после подстановки
в них значений х, у, х' и у', вычи-
сленных по формулам (7.123) и
(7.130).
2°. Определение профиля диско-
вых вращающихся кулачков. Для
дисковых вращающихся кулачков
уравнение профиля удобнее выражать
в полярных координатах, принимая
за начало координат центр враще-
ния кулачка и отсчитывая полярные
углы от начального радиуса-вектора.
Радиусы-векторы кулачка обозначим
через R, полярные углы — через [3.
В дальнейшем полярные углы про-
филя кулачка будем называть углами
профиля.
При отсутствии смещения углы
профиля [3 равны углам поворота а и
разность между двумя соседними радиусами-векторами равна прой-
денному пути ведомого звена. Поэтому полярные координаты центро-
вого профиля кулачка для каждого значения р=а вычисляются по
формуле
tf = /?04-S, (7.131)
причем зависимость S=/(a) предполагается заданной.
Графическое построение центрового профиля и огибающей (кон-
структивного профиля) по методу обращения движения показано на
рис. 498.
Для вычисления координат огибающей можно воспользоваться
формулами (7.127). В рассматриваемом случае, принимая, что ось хх
413
§ 23] ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
направлена по начальному радиусу-вектору, имеем:
x — R cos a, y = R sin а.
Следовательно:
г чл . It Г\ f чу т--, . . ЧГ\
х=-г- =—R sin а. -г- cos а , у = т = R cos а -4- sin а , .
da ' 1 da ’ J da 1 da
Подставляя эти значения в формулу (7.127) и учитывая, что
dR dS s S„
—г- = - —о—- , получаем:
da da аи ’ J
§
cos а -|- 8 sin а
x. = Rcosa±r77==S=r, (7.132)
1 l + l8Rt/
— sin a -J- b cos a
у = R sin a. 4= r ——_ =:_^л х- —. (7.133)
/+(•*)’
После вычисления координат хп и _уп можно определить поляр-
ные координаты конструктивного профиля R„ и рп на основании из-
вестных соотношений:
7?п = /^п + рй,
(7.134)
Л-п
(7.135)
Легко видеть, что при равных интервалах изменения угла а полу-
чаются неравные интервалы изменения угла р„. Если требуется полу-
чить равные интервалы изменения угла (Зп, то при большом числе точек,
для которых вычисляются координаты, можно с достаточной точностью
найти значения Rn, соответствующие равным интервалам изменения
угла рп путем интерполирования.
При наличии смещения построение профиля дискового вращаю-
щегося кулачка также может быть выполнено по методу обращения
движения (рис. 499), причем из построения видно, что углы профиля
кулачка р в этом механизме уже не совпадают с углами поворота
кулачка а. Для установления зависимости между углами аир рас-
смотрим начальное положение звеньев механизма, когда ведомое звено
касается центрового профиля кулачка в точке, радиус-вектор которой
равен Ro, и положение ведомого звена в обращенном движении после
поворота на угол а. Из чертежа рис. 500 следует;
(7.136)
414
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
I ГЛ. VI
где у— переменный угол смещения, определяемый по формуле (7.49);
е
tg 7 = г---------
—е2 ;
у0 —начальный угол смещения, определяемый по условию
е
slnZ-«=^
(7.137)
Величина радиуса-вектора при заданном значении угла а вычис-
ляется по формуле
е
sin у
(7.138)
По формулам (7.136) и (7.138) для равных интервалов измене-
ния угла а вычисляются значения угла р и радиуса-вектора R. Для
Рис. 499.
получения равных интервалов угла р применяется вычисление радиуса-
вектора R путем интерполирования между двумя соседними значе-
ниями, вычисленными по формуле (7.138).
Можно также вычислить радиус-вектор по формуле’
R = j/e* + (S+(7.139)
Угол смещения у в этом случае определяется по формуле
siny=H". (7.140)
Для вычисления координат конструктивного профиля при ведомом
звене, имеющем ролик, принимаем расположение координатных осей,
показанное па рис. 5U0,
§ 23] ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА 415
Тогда
X = RCOS₽' I (7.141)
у = R sin р. )
Следовательно:
л'= = — R (1 -ф- -!-) sin р Ц- ~ cos р,
da \ 1 da / г 1 da г
/ == = R (1 4- cos Р + 4^ sin р.
da \ 1 da / 1 1 da г
Принимая во внимание, что
dy tg у dR dR dS dS s S..
-. = — —, ~r =^ cosy и = 8-5 ,
da R da. da da ' da аи ’
получаем:
x' = — (R — 8 S» Sin f 'j sin p 4- 8 ^5- cos у cos 8 ,
\ an V ’ “и ''
/ S \ S <7- l42>
У = [R — 8 -5- siny I cos 8 -j- 8 cos / sin p.
Координаты конструктивного профиля (огибающей) определяются
в этом случае непосредственно из формул (7.127) после подста-
новки значений х, у, х' и у, вычисленных из формул (7.141) и (7.142).
Рис. 501. Рис. 502.
При вращающемся ведомом звене углы профиля кулачка р также
не совпадают с углами поророта кулачка а, что можно видеть из гра-
фического построения профиля кулачка по методу обращения движе-
ния (рис. 501).
Для вычисления координат профиля рассмотрим начальное поло-
жение звеньев механизма, когда ведомое звено касается теоретиче-
ского профиля кулачка в точке, радиус-вектор которой равен Ro, и
положение ведомого звена в обращенном движении после поворота
на угол а (рис. 502).
(7.145)
— а). I
} (7-146)
— а), I
416 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гЛ. Vtl
Из чертежа следует:
Я = /Zo + ~ 2ZZ0 cos (ф 4- ф0). (7.143)
Угол р определяется из соотношения
sin(p4-p0 —а) —^-8'п(Ф + Фо). (7.144)
Для вычисления координат конструктивного профиля при ведомом
звене, имеющем ролик, принимаем расположение координатных осей,
показанное на рис. 502.
Тогда
х = /0 cos а — I cos (ф 4~ Фо — «),
у = /0 sin а -J- z sin (Ф + Фо — «).
Следовательно,
•^=2 = — /„sin а-ф-/ (-J — 1) sin (ф + фо
У = =4 cos «4-/(2 —1) cos(ф4-ф0
где
2 = 8 .
da а„
Координаты конструктивного профиля лгп и _уп определяются по
формулам (7.127) после подстановки значений х, у, х' и у, вычис-
ленных по формулам (7.145) и (7.146).
Указанный путь вычисления полярных координат профиля кулачка
применим при любом законе движения ведомого звена, но при этом
уравнение профиля кулачка в виде R = /(р) не определяется, а на-
ходятся лишь отдельные значения угла р и радиуса-вектора R, удов-
летворяющие уравнению профиля.
В некоторых случаях возможно непосредственное определение
уравнения профиля кулачка. Например, для дискового вращающегося
кулачка при законе движения с постоянной скоростью имеем:
Принимая во внимание, что а = р, по формуле (7.131) получаем:
/? = /?„4-Р^ , (7.147)
аи
т. е. центровой профиль кулачка представляет собой архимедову
спираль.
При наличии смещения вместо архимедовой спирали получается
уравнение растянутой эвольвенты и при вращающемся ведомом звене
уравнение эпи- или гипоциклоиды.
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
417
Если принять в качестве закона движения ведомого звена закон
постоянного угла давления, то для вращающегося дискового кулачка
без смещения имеем:
L„n v dR
Rda •
Отсюда
=tg&eda.
После интегрирования получаем:
In R = a tg 4- С.
Принимая во внимание, что а = р и постоянная
С=1п/?0, имеем:
Я = (7.148)
т. е. центровой профиль кулач-
ка представляет собой логари-
фмическую спираль.
Для механизмов с плоским
толкателем или коромыслом
вычисление координат профиля
производится
зависимостей,
предыдущем
рассмотрении
мостей из рассмотрения чертежа, показанного на рис. 503, имеем:
на основании
полученных в
параграфе при
условий выпуклости
интегрирования
кулачка. С учетом этих зависи-
, 1 — 2Ф' >
1 — 7i^npjTC0S (Ф + Фо). I
(7.149)
где
₽ = “ ~ arcsin-(1-^^,)7? • cos (ф + %), I
i. s фи
Ф = ~Ь б -— ,
т — ви
Величина <[/ отрицательная при противоположных направлениях
вращения кулачка и коромысла.
При прямолинейно движущемся ведомом
имеем:
звене (см. рис. 470)
и
(7.150)
1
р । . 1 dS
р - а -4- arcsin .
1 R da.
)
Отметим, что в механизмах с плоским коромыслом, чтобы получить
возвратное движение, радиус-вектор кулачка R должен быть всегда
14 И, И. Артоболевский
418
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[ГЛ. VII
меньше межцентрового расстояния /0. Это условие аналогично усло-
вию получения качающейся кулисы (радиус кривошипа должен быть
меньше межцентрового расстояния). Из формулы (7.149) следует,
что это условие выполняется при
ф' 0,5
(7.151)
ИЛИ
(7.152)
Например, для законов движения с 8тах — 2 (см. табл. 7.2) имеем:
ф„ < 0,25аи.
3°. Определение профиля кулачка, очерченного по дугам
окружностей. При прямолинейно движущемся кулачке центровой про-
филь кулачка совпадает с графиком пути. Если для построения гра-
фика пути использовать две дуги окружности, то при симме-
Рис. 504.
тричной тахограмме и отсутствии жестких
ударов этот график полностью определяется
значениями S„, /и и с = -£1 .
При вращающемся дисковом кулачке,
если задать величины S„, /?0 и аи, то при
условии отсутствия жестких ударов можно
варьировать только один параметр, например
радиус одной из дуг окружностей, причем
величина варьируемого параметра может из-
меняться только в определенных пределах.
Пусть, например, требуется, чтобы для
ускоренного и для замедленного движения
были равны углы поворота и пройденные пути.
В соответствии с этими условиями искомые ду-
ги окружности должны пройти через точки Вь
Bt и Вс (рис. 504). Кроме того, из условия
отсутствия жестких ударов в начале и конце движения центр At
должен лежать на прямой, проходящей через точки О и Bt, а центр
Л-2 — на прямой, проходящей через точку О и В.>. Поэтому центр At
найдется на пересечении перпендикуляра, восставленного из середины
отрезка BiBc, с направлением ОВ1г а центр А.г — на пересечении
перпендикуляра, восставленного из середины отрезка ВсВг с напра-
влением ОВ3. Разумеется, в общем случае точки А3 и Вс оказы-
ваются не лежащими на одной прямой, т. е. в точке Вс должен быть
жесткий удар. Удовлетворить условию отсутствия жесткого удара
при переходе от ускоренного движения к замедленному можно, если
точку перехода с одной дуги окружности на другую взять не в
точке Вс, а на линии AtA3, г. е. в точке В'с. При этом углы пово-
рота кулачка и перемещение ведомого звена в периоды ускоренного
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
419
и замедленного движения уже не будут равны. Из приведенного
примера видно, что применение профиля, составленного только из
двух дуг окружностей, сильно ограничивает возможности изменения
характеристик механизма. Поэтому, не останавливаясь более подробно
на рассмотрении этого случая, перейдем к установлению формул,
которые позволяют определить профиль кулачка, составленного из
трех дуг окружностей или из комбинации какой-либо кривой с двумя
дугами окружностей в начале и конце движения.
С этой целью рассмотрим условия сопряжения дуги окружности
с кривой, для которой должны быть известны радиусы-векторы Rt
и Ri (в местах сопряжения), угол между этими радиусами и углы
и т2 между касательными к профилю и перпендикулярами к радиу-
сам в точках Bi и В.> (рис. 505). Эти углы в механизмах с посту-
пательно движущимся ведомым звеном без смещения равны углам
давления О, и &>. Искомые радиусы окружностей обозначим через
Г1 и rit углы профиля, соответствующие этим участкам, через р01
и раз, начальный радиус-вектор — через /?0, радиус-вектор в конце
интервала — через R3. Тогда в треугольнике угол при вер-
шине Bi равен 180° — т2 и сторона OAt равна В треуголь-
нике OB^Ai угол при вершине В.2 равен т2 и сторона ОА3
равна R3 — г2. Из решения треугольников OBiAi и ОВ2А2 можно
найти искомые величины, считая заданными три параметра для каждого
из треугольников. Уравнения, следующие из решения указанных
треугольников, надо решать совместно с уравнениями, определяю-
щими значения Rb R.>, т, и т2 в соответствии с заданным законом
движения или профилем на участке BiBq. Полученная система урав-
нений является нелинейной и обычно ее приходится решать путем
последовательных приближений.
Пусть, например, ведомое звено движется поступательно и смеще-
ние отсутствует. Тогда углы т, и т.2 равны углам давления &, и &2 и
углы профиля р равны углам поворота кулачка. Требуется построить
14’
420 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VH
профиль по закону постоянной скорости (по архимедовой спирали)
с переходными участками, очерченными по дугам окружностей. Задан-
ными величинами считаем Ro, SH и аи = ри,- Уравнение профиля на
участке ВуВ.2 имеет согласно формуле (7.147) следующий вид:
R^Ri + ^p^-1 (Р~М» (7.153)
а углы давления в точках By и вычисляются в соответствии
с формулой (7.47) из соотношений:
tg&i=^^-, (7.154)
Р12О1
• (7.155)
Р12*\2
Вычисления искомых величин можно производить в следующем
порядке:
1) выбираем относительную продолжительность периодов движе-
ния по дугам окружностей пх = щ=и и определяем предварительно
углы профиля на этих участках
Р®1 = Р-2з= нРи> (7-156)
а также путь, проходимый ведомым звеном, считая, что его величина
равна полусумме пути при равномерном движении и при равноуско-
ренном движении:
Soi = S.23 = k(» + O,5)Sh; (7.157)
2) определяем радиусы-векторы:
Ri = Ro 4- S01, (7.158)
R2 = Ro + «„- (7-159)
угол профиля
₽w = ₽H —₽oi —Раз (7.160)
и угол давления fl, по формуле (7.154);
3) по вычисленным Rb и р0] определяем из треугольника ОВуА,
величины Г1 и Ro по формулам:
= sinS-M '
= <7Л62>
4) если вычисленная величина Ro, которую обозначим через /?о,
отличается от заданной величины Ro, то определяем новое значение
пути S0i = S23= Ri — Ro и повторяем вычисления величин R,,
®i, Гу и Ro до совпадения величины Ro с заданной в соответствии
с требуемой точностью расчета;
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
421
5) вычисляем угол давления 02 по формуле (7.155) и определяем
из треугольника ОВгАг величины г2 и /?3 по формулам;
'•-'tsJ&T <7Л“>
% = '?>TSWTw+4 <71М>
6) если величина разности /?3 — /ф не равна заданной величине
S„ с требуемой степенью точности, то находим новую величину пути
S23 из условия
$23 — /?з —
вычисляем новую величину по формуле (7.159) и повторяем
вычисления по пункту 5 до получения величины 5И с требуемой
степенью точности.
В заключение следует проверить значение угла р23 по формуле
sin ₽23' = sin » р Га! -- (7.165)
'<3 г2
и угла давления ф при новом значении /?2. Совпадение обычно
получается достаточное. В противном случае придется повторить
вычисления по пункту 3 и т. д.
Для удобства изготовления кулачка можно принять rl=ri = r.
Тогда в треугольнике ОД2Д2 считаем заданными Ri: 02 и г, а вели-
чины /?3 и р23 находим по формулам;
/?з = V~R^ ~Ь г‘2 — 2rAJ2cos 1>2 ф г, (7.166)
sin р23 = Г - sin &2. (7.167)
/\а — г
Далее уточняются значения /?2 и р12 для получения требуемых
величин и и вновь производятся вычисления по пункту 3 и т. д.
После определения размеров переходных участков можно вычи-
слить значения максимальной скорости п,Лах и максимального ускоре-
ния £?гпах.
Легко видеть, что кинематика кулачков, очерченных по дугам
окружностей, при ведомом звене, движущемся поступательно, совпа-
дает с кинематикой кривошипно-шатунного механизма, у которого
радиус кривошипа равен расстоянию между центром вращения кулачка
и центром дуги окружности профиля, а длина шатуна равна радиусу
этой дуги.
Применяя обычные формулы кинематики кривошипно-шатунного
механизма, имеем в наших обозначениях: для участка B0Bi
т _____ Во + г, sin (»i — 3CI) 8„
Wn’a*— —a" cos», t~>
Во Ч-Г, I 1
amaxj— gB -0-^- [COS (&, — р01) -ф
Ro Ч" г 1 cos2 ро j S,
(7.168)
<7-169)
422
СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ
[гл. VII
и для участка В.гВ^
^глах
^тах2
Въ — r2 а s'n (^s ~k Р23) SH
S„ и cos S2 /и ’
#3 —ra а2 Г P„_ ra COS2|323
SH cos »2 I C0S ( 2 ~H 23) 4“ rs COS2 »2
(7.170)
(7.171)
no
Значения ускорений в начале и конце движения определяются
формулам (7.169) и (7.171), полагая !>, = р(|1 = 0 и 02 = = 0:
_ Ro + ri 2! 1 । Ro + n \ S„
— с “и I 1 ~1 ~ ...
\ Г1 / ’
(Rs — rs)R3
(7.172)
(7.173)
Значения цтах, вычисленные по
должны совпадать, а ускорения йтаХ1
При рассмотрении примеров на
формулам (7.168) и (7.170),
И йтах„ будут различными,
выбор закона движения ведо-
мого звена указывалось на применение переходных участков,
очерченных по дугам окружностей, не только
для закона движения с постоянной скоро-
стью, но и для закона движения с постоян-
ным углом давления.
При законе движения с постоянным углом
давления в рассматриваемом случае профиль
получается в виде логарифмической спирали,
уравнение которой на участке ВхВа_ со-
гласно формуле (7.148) имеет следующий
вид:
^=Rief₽-Mtg»o, (7.174)
Рис. 50b. где —-значение угла давления на этом
участке.
Логарифмическая спираль в отличие от архимедовой не обрабаты-
вается на универсальных станках. Поэтому заменим логарифмическую
спираль на участке В^В^ дугой окружности по способу, указанному
Л. Н. Решетовым *).
В соответствии с обозначениями, принятыми на рис. 506, имеем:
(7.175)
(7.176)
*) Л. Н. Решетов, Кулачковые механизмы, стр. 247—250, Машгиз, 1953.
§ 23] ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА 423
Углы давления О, и 02 вычисляются из соотношения
sin — sin &.2 = — cos , (7.177)
максимальный угол давления определяется по формуле
sin»n.ax=-^ (7.178)
Заданными величинами в этом случае обычно считают /?0, S„ и &0,
причем &0 будет равно среднему значению угла давления на участке
В^В*
Порядок вычисления при этом будет несколько иной.
1. Выбираем относительную продолжительность периодов движе-
ния по дугам окружностей гг1 = гг.2 = /г и определяем пути Sqi и S23,
проходимые на этих участках, по формуле (7.157). Так как при
логарифмической спирали скорость ведомого звена в конце движения
всегда больше, чем в начале, то при округлении величин SOi и S23
берем S23 больше вычисленного,- a Sol—меньше.
2. Вычисляем радиусы R, и по формулам (7.158) и (7.159)
и угол Р12 из уравнения (7.174) по формуле
. Вг
п />
₽»=->?£- <7Л79)
3. Находим радиус и положение центра заменяющей окружности
по формулам (7.175) и (7.176), а также минимальное 8min и макси-
мальное &тах значения угла давления на участке В^В^ по формулам
(7.177) и (7.178).
4. Вычисляем из треугольника ОВ{А\ (см. рис. 505) радиус
переходной окружности г, и угол р0, по формулам:
.. bi-bi (1
1 2(Я0—/?1Cos &,) ’ (7’180)
sin рю = 7 ~ sin (7.181)
5. Вычисляем из треугольника 0/<2Л2 (см. рис. 505) радиус дру-
гой переходной окружности г2 и угол р.23 по формулам:
Г* == 2(/?3 —/?scos М * (7.182)
sin 623 = -5- Га— sin &2. (7.183)
Bs — rs
6. Определяем полный угол профиля
Р — Pul + pi > + Раз- (7.184)
Пример 1. Дано: 5'и — 60 мм; 7^ = 90 мм; ри = 45° =
= 0,785 радиана.
424 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Определить профиль дискового вращающегося кулачка по архи-
медовой спирали с переходными участками по дугам окружностей.
Принимаем и = 0,1. Тогда по формулам (7.156) и (7.157) имеем:
Poi = ₽i3 = 0>1 • 45° = 4° 5 = 0,07854 радиана,
Sol = = 0,1 (0,1 -[- 0,5) S,, = 3,6ло<.
Радиусы-векторы архимедовой спирали находим по формулам
(7.158) и (7.159):
R, = 90 4- 3,6 = 93,6 мм; R2 = 90 4- 60 — 3,6 = 146,4 мм.
Угол профиля по формуле (7.160) имеет величину
р 12 = 45° — 2-4,° 5 = 36° = 0,6283 радиана.
Угол давления в начальной точке архимедовой спирали вычисляем
по формуле (7.154):
»• = WW = °'896'; ’ =41 °52'-
Величину радиуса окружности rt находим по формуле (7.161):
„ sin 4с30' , „ ,
Г*~93,6 sin37°22'= 12’1 ММ-
Начальный радиус-вектор вычисляем по формуле (7.162)
Ro = 93,6 -12,1 = 90,8 мм,
т. е. он отличается от заданного на 0,8 мм.
Принимаем новое значение пути Soi = S23:
S01 = 93,6 — 90,8 = 2,8 мм.
Уточненные значения R, и Ra:
R1== 90-|-2,8 = 92,8 мм; R2 = 90 Ц-60 — 2,8 = 147,2 мм.
Уточненные значения г, и Ro:
‘6*‘=Й&НЙ=°’933О; ».=43’»Г;
„„ „ sin 4с30' , , „
г, _ 92,8 sjn 3g€3I, — 11,7 мм;
R.=92’e4n8r— Ч.7 = 90,0«
Далее вычисляем значение угла давления в крайней точке архи-
медовой спирали по формуле (7.155):
‘S8«=<®few = °-5882- 8«=30р28’-
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
425
Величину радиуса окружности г2 находим по формуле (7.163):
, ._ „ sin 4'30' ,
г.2 = 147,2 sin 34о58,- — 20, мм.
Радиус-вектор /?3 вычисляем по формуле (7.164):
R3 = 147,2 4- 20,1 = 150,3 мм.
’ ’ sin 34 58' 1
Принимаем новое значение пути S.23= 150,3— 147,2 = 3,1 мм
и уточненное значение R.2 = 150 — 3,1 = 146,9 мм.
Уточненные значения г.2 и R3:
‘е^оХи^0'5860' ».=8о°22';
1 1 г* г» sin 4 30 мп 1
г^— 146,9 ————57-= 20,1 мм\
* * sin 34 52
R, = 146,9 Sin S' -4- 20,1 = 150,0 мм.
л ’ sin 34 52 1
Уточненные значения р.23) г и Rn-.
, .. 146,9 — 92,8 nn„. <1 лоо-7'.
tg^i— o,6283 • 92,8 — °-931’ — 42 о7 ,
г, = 92,8 sin.,4X°f7- = И ,7 мм;
1 ’ sin 38 27
Ъ = 92’8 Sin 382j77-- 11 '7 = 9О’°
т. е. значения rt и Ro совпадают с точностью до трех знаков
с вычисленными ранее;
20 I
sin ря = sin 30°22' • -jqn ’‘тп = 0,0786; = 4°3 Г.
1 OU ~~~ 1
Максимальную скорость ведомегэ звена вычисляем по
ле (7.168):
904-11,7
г’тах = pg
форму-
0,7854
sin 38r27' SH
cos 42'57’ /н
= 1,12-^.
Для контроля вычисляем ту же величину по формуле (7.170):
150 — 20,2 sin 34с45' S„ S.,
^=—бб—°-7854^w-e=i’i2-c-
Максимальное ускорение в конце первого переходного участка
находим по формуле '(7.169):
_ 90 4- 11,7 0,78542 / о 90 4-11,7 cos84°30'\ 8И
°тах* — 60 cos 42 57' yC0S 38°27 Н ИД ^os2“42 ФГ ] ~
= 24,0-^-.
t И
426 СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ [гл. VII
Максимальное ускорение в начале второго переходного участка
150 — 20,1
йтах2 = —go
0,7854s 150 — 20,1
cos 30°22' C0S 34053 20?l
cos2 4СЗГ X
cos2 ЗСГ22'
SH_
— 14 1
ж /2
И
Ускорение в начале движения находим по формуле (7.172):
90+Н,7 „ 90+11,7\ S„ S„
»=—я— °'7854’ (1 + - ) ТГ =1 °'° -7Г
Ускорение в конце движения вычисляем по формуле (7.173):
150 — 20,1 „ S„ 5„
= °,78542-150-~—— 10,0
ZJ,l ои г- г-
Пример 2. Дано: S„ = 80 мм; Rv = 7(.) мм; 1)0 = 45°
Определить профиль дискового вращающегося кулачка без смеще-
ния, очерченного по трем дугам окружностей из условия получения
приближенно постоянного угла давления и безударной работы.
Выбираем п== 0,05 и определяем пути SOi и SS3 по форму-
ле (7.157):
S01 = 8И = 0,05 (0,05 ф- 0,5) • 80 = 2,2 мм.
Принимаем: SOi = 2 мм; S.23 = 3 мм. Следовательно:
^ = 70-4-2 = 72 мм; R2=150 — 3= 147 мм.
Вычисляем угол профиля р12 по формуле (7.179):
А 1П 147 --- 1Г172 АТ, Л .„о.п,
₽12 =---— =0,714 радиана=40 48.
Находим радиус и положение центра заменяющей окружности по
формулам (7.175) и (7.176):
/л== 2'Sin~2(r24^=107’5^’ '•-,= 107,0 J/ 1 + = 148,5 ММ.
Значение угла давления в точках S, и Д2 вычисляем по фор-
муле (7.177):
sin &! = sin »2 = cos 20°24' = 0,68, »i = »2 = 42°50'.
Максимальное значение угла давления &тах находим по формуле
(7.178):
sin »тах = = 0,727, &тах = 46°40'.
§ 23]
ОПРЕДЕЛЕНИЕ ПРОФИЛЯ КУЛАЧКА
427
Вычисляем из треугольника ОВ^А^ (см. рис. 505) радиус пере-
ходной окружности г, и poi по формулам (7.180) и (7.181):
Г| = 2(70 — 72 cos 42е 50') = 8,7 ММ’ S‘n = 78,7 ' 0,68 = °’075’
₽01 = 4°18'.
Затем вычисляем радиус переходной окружности г2 и угол |323
по формулам (7.182) и (7.183):
г — (150+ 147)-3
2(150—147 cos42е 50') U,U ММ’
sin р23 = п sin42°50' = 0,0535, ^3 = 3°01'.
Полный угол профиля находим по формуле (7.184)
Р„=4С18' ф 40°48' 4- 3°01' = 48' 07'.
ГЛАВА VIII
Синтез мальтийских механизмов
§ 24. Схемы мальтийских механизмов с круговым
равномерным движением цевки
1°. Осуществление прерывистого движения. В практике про-
ектирования машин-автоматов и различных устройств точной механики
часто возникает задача осуществления прерывистого движения, т. е.
движения постоянного по направлению, но с периодическими оста-
новками. Отношение времени движения к времени остановки обычно
является заданной величиной при проектировании механизма.
В тех случаях, когда величина перемещения ведомого звена
между его остановками должна быть точно фиксированной, при-
меняются звездчатые (см. 10° § 1) и мальтийские механизмы.
Звездчатые механизмы позволяют в широких пределах изменять
отношение времени движения к времени остановки. Однако изготов-
ление деталей этих механизмов с той точностью, которая обеспе-
чила бы их надежную и длительную работу, является делом весьма
трудным. Поэтому звездчатые механизмы в современном машино-
строении и особенно в приборостроении применяются очень редко.
Простейшие мальтийские механизмы (крест с радиальными пазами,
цевка с круговым равномерным движением) не позволяют произвольно
выбирать отношение времени движения к времени остановки. Но
зато конструктивно эти механизмы очень просты, не вызывают ника-
ких затруднений в изготовлении; их наиболее изнашиваемые части
(щеки пазов) легко сделать сменными, чем упрощаются ремонт и
эксплуатация. Эти конструктивные и эксплуатационные достоинства
обеспечили мальтийским механизмам широкое применение в машино-
строении и в отдельных областях точной механики.
Мальтийские механизмы применяются в поворотных устройствах
блока шпинделей в многошпиндельных токарных автоматах, для пово-
рота столов агрегатных станков, в устройствах автоматической
подачи материала в прессах, в поворотно-фиксирующих устройствах
различных упаковочных автоматов и др.
В настоящем параграфе рассматриваются трехзвенные маль-
тийские механизмы с круговым равномерным движением цевки,
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 429
усложнен-
в отдель-
выясняются их основные характеристики и приводятся справочные
данные, которые могут облегчить проектирование этих механизмов.
В следующих параграфах (§§ 25 и 26) рассматриваются
ные схемы мальтийских механизмов, которые позволяют
ных случаях в большей степени
удовлетворить поставленным ус-
ловиям, чем механизмы, указан-
ные в настоящем параграфе.
2°. Мальтийские механизмы
с внешним зацеплением. На
рис. 507 изображена наиболее рас-
пространенная схема трехзвенного
мальтийского механизма. Подвиж-
ными звеньями этого механизма
являются кривошип а, который
несет на конце цевку А, и маль-
тийский крест Ь, снабженный ра-
диальными пазами, расположен-
ными равномерно по его окруж-.
пости.
При равномерном вращении
кривошипа а в направлении, ука-
занном стрелкой, цевка А (выпол-
няемая в виде ролика или цилинд-
рического пальца) входит в ради-
альный паз креста и заставляет
последний вращаться неравно-
мерно в обратном направлении.
Когда цевка А кривошипа вы-
ходит из паза креста, цилиндриче-
ский выступ alt жестко связанный
с кривошипом, начинает сколь-
зить по цилиндрической поверхно-
сти, имеющейся на кресте, фикси-
руя последний в этом положении до момента входа цевки А криво-
шипа в следующий паз; в этот момент фиксирующее воздействие
цилиндрического выступа а, на крест прекращается и крест начинает
вращаться.
Основные параметры рассматриваемого механизма выбираются так,
чтобы в момент входа цевки в паз креста и в момент ее выхода
вектор скорости центра цевки совпадал по направлению с осью
радиального паза. При этих условиях в указанные моменты ско-
рость креста оказывается ’ равной нулю. Тем самым в момент входа
цевки в паз исключается жесткий удар, а в момент выхода
цевки из паза креста облегчается фиксация креста в требуе-
мом положении.
430
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
Углы поворота ведущего кривошипа и креста обозначим соответ-
ственно я и ф. График функции положения механизма на отрезке,
равном одному обороту ведущего кривошипа, имеет вид, показанный
на рис. 508. Поворот креста на угол 2<р(, равный углу между смеж-
ными пазами, происходит за время поворота кривошипа на угол 2яь
В течение остальной части оборота кривошипа на угол 2я0 крест
остается неподвижным. Сумма углов 2л, и 2яп:
2 (я, Ц-я0) = 2тс. (8.1)
Угол поворота 2у{ креста, называемый углом деления, опреде-
ляется числом z пазов креста:
2?-=Г‘ (8.2)
Из условия безударного зацепления цевки ,4 кривошипа с пазами
креста вытекает очевидная зависимость между углами поворота 2aj
и 2<f>t ведущего кривошипа и креста (см. рис. 507):
2 (я1<pi) = т, (8.3)
откуда
2я.! = тс — 2^ = тс — (8.4)
и
2я0=2(тс —а,) = тс-ф-у-. (8.5)
Примем, что кривошип вращается с постоянной угловой ско-
ростью п об[мин или wK= ™ 'Тёк'' ^гловые ег0 перемещения будут:
я — OJKC
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 431
Время поворота креста на угол 2?! будет:
ч 2а 1 __ сок г — 2 30
п сек,
Z
а время /0 остановки креста
2а0 г + 2 30
А) “к Z п сек.
(8-6)
(8.7)
Время tn остановки креста в большинстве случаев задается тем
технологическим процессом, который выполняется соответствующей
машиной. Оно определяется наибольшей длительностью операции, при
которой ведомое звено или узел машины должны оставаться непо-
движными. При выбранном числе z пазов креста время определяет
требуемую угловую скорость ведущего кривошипа:
«4-2 30 ,,
п —-------• -т- o6i мин,
z t0 1
или - (8.8)
z 4- 2 я , ,
~ т х!сек'
где t0 выражается в секундах. «
В машинах-автоматах пределы для выбора времени поворота
креста обусловливаются циклограммой, которая устанавливает необ-
ходимую согласованность в перемещениях ведомых звеньев всех
механизмов автомата. В этих пределах время обычно стремятся
иметь возможно меньшим, чтобы избежать потерь производительности,
связанных с периодическими поворотами креста. Учитывая это, в
качестве одной из характеристик мальтийского механизма принимается
отношение времени поворота креста к времени его остановки
которое принято называть коэффициентом времени работы мальтийского
механизма. Это отношение зависит от числа пазов z, и оно тем
меньше, чем меньше г. В мальтийских механизмах с внешним
зацеплением коэффициент k всегда меньше единицы; значения
его приведены в таблице 8.1, в которой указаны также углы 2а0,
2оц и 2<р(.
Число остановок, которое должно иметь в течение полного обо-
рота ведомое звено мальтийского механизма (например, поворотный
стол агрегатного станка), назовем числом позиций этого звена и
обозначим через Z. Если это ведомое звено укреплено на одном
валу с крестом мальтийского механизма, то, очевидно, число z пазов
креста должно быть равно числу Z заданных позиций (z = Z).
432
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. VIII
Таблица 8.1
Параметры, характеризующие продолжительность остановки и
поворота креста мальтийского механизма с внешним зацеплением
Число пазов креста г Угол поворота кривошипа, соответствующий Угол поворота креста 2?1 = п — 2сц Коэффициент времени работы *0
остановке креста: 2''о = я + -у повороту креста: 2«1 = 2 (п — а0)
3 300° 60° 120° 0,20
4 270° 90° 90° 0,33
5 252° 108° 72° 0,43
6 240° 120’ 60° 0,50
7 231’26' 128'34’ 51’26’ 0,56
8 225° 135° 45° 0,60
9 220° 140е 40° 0,64
10 216° 144е 36° 0,67
11 212’44' 147’16' 32’44’ 0,69
12 210' 150° 30' 0,71
13 207'42’ 152е 18’ 27’42’ 0,73
14 205’42’ 154’18’ 25'42’ 0,75
15 204° 156° 24° 0,76
Если вал ведомого звена соединен с валом креста промежуточ-
ной передачей, то число z пазов креста может быть отличным от
заданного числа позиций Z. В этом случае может быть как z Z,
так и z^>Z.
Для осуществления такой передачи обычно применяют зубчатую
передачу (см. § 25).
Наименьшее число радиальных пазов креста, которое допускает
приведенная схема мальтийского механизма, г = 3. Этому числу
соответствует наименьший коэффициент времени работы креста
k = 4 - 0,20.
*0
С увеличением числа z пазов отношение k = tt/t0 возрастает, доходя
при г =15 до величины k = 0,76.
Следует отметить, что число z радиальных пазов на кресте теоре-
тически не имеет верхнего предела, однако на практике мальтий-
ские механизмы с числом пазов z^>12-j-15 редко находят приме-
нение.
Установим соотношения между основными конструктивными раз-
мерами звеньев мальтийского механизма. Введем для этого обозна-
чения (рис. 509): L — расстояние между осями вращения кривошипа
и креста: R — длина ведущего кривошипа; S — расстояние от оси
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
433
вращения креста до торцов его пазов; г — радиус цевки кривошипа.
Тогда по рис. 509 получим (см.
R - L sin ср! = Z. sin у,
Длина h паза креста должна
быть
h^> R -|-S — L -|- г =
= L ( sin-- 4- cos —— H -4- r.
(8.11)
Диаметр d вала, на который
насаживается крест, ограничи-
вается условием:
d<2(£ — R — г) =
= 2£^1 — sin y--£).(8.12)
Диаметр dK вала, на кото-
ром крепится ведущий криво-
шип, ограничивается условием:
dK<2(£—S) =
= 2£ (1 — cos у). (8.13)
Рис. 509.
Таблица 8.2
Соотношения между конструктивными размерами звеньев мальтийского
механизма с внешним зацеплением
Z L 3 L h - г L а + “2г L L
3 0,86603 0,50000 0,366 0,268 1,000
4 0,70711 0,70711 0,414 0,585 0,586
5 0,58779 0,80902 0,397 0,824 0,382
6 0,50000 0,86603 0,366 1,000 0,268
7 0,43388 0,90097 0,335 1,132 0,198
8 0,38268 0,92388 0,307 1,235 0,152
9 0,34202 0,93969 0,282 1,316 0,120
10 0,30902 0,95106 0.260 1,382 0,098
11 0.28173 0,95949 0,241 1,437 0,082
12 0,25882 0,96593 0,225 1,482 0,068
13 0,23931 0,97094 0,210 1,521 0,058
14 0,22252 0,97493 0,197 1,555 0,050
15 0,20791 0,97815 0,186 1,584 0,044
434
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
При невыполнении условий (8.12) и (8.13) возникает необходи-
мость в консольном креплении креста или ведущего кривошипа.
В ряде случаев это является нежелательным, так как усложняет
получение достаточно жесткой конструкции отдельных узлов меха-
низма.
3°. Кинематика механизма мальтийского креста с внешним
зацеплением. Для произвольного положения мальтийского механизма,
изображенного на рис. 510, имеем:
R____ sin у
' L sin (ct Ц- у) ’
где углы a и ср отсчитываются от линии, соединяющей оси вращения
углы считать положительными,
если направление их отсчета
совпадает с направлением уг-
ловой скорости.
Обозначив
найдем:
, X Sin Ct /о 1
tg Ф — ------5------. (8.14)
6 т 1 — X COS a ' ’
Полагая угловую скорость
da.
ведущего кривошипа ==t0
постоянной, получим угловую
скорость о? и угловое ускоре-
ние креста е равными:
dtp
где переменное передаточное отношение i и коэффициент ks равны:
- X (cos ct — X) , X (1 — X2) sin a _
l— 1— 2Xcosa-p.8 ’ e— (1—2X cos ctX2)2 ‘ v 7
Началу и концу поворота креста соответствует угол поворота
кривошипа ±04, где
<817>
Подставив эти значения в формулу (8.15), получим <о = 0 в соот-
ветствии с поставленным ранее условием, чтобы в начале и в конце
поворота отсутствовали жесткие удары.
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 435
Из условия е = -^- —О получим, что экстремум угловой ско-
рости креста должен быть при а = 0, т. е. при совпадении оси паза
креста с линией, соединяющей оси вращения креста и кривошипа.
Это экстремальное значение угловой скорости креста будет:
0Jmax == ^'niaxwK == ) ***«- ' $)
Передаточное отношение imax в зависимости от числа z пазов кре-
ста приведено в таблице 8.3.
Таблица 8.3
Параметры, определяющие кинематику креста мальтийского механизма
с внешним зацеплением (время tn— в сек)
'г + — ~ “к + — ~ “к Углы поворота, при которых возникают экстремальные уско- рения креста “тах^о радиан i - — СН £0 радиан радийн
‘”К
± «Э 1 Ts
3 6,46 1,73 31,4 4Г45' 27’4 Г 33,8 47,5 860
4 2,41 1,00 5,41 11 28' 24'36’ 11.4 22,2 120
5 1,43 0,727 2,30 17=34' 2159' 6,27 14,0 44,5
6 1,00 0,577 1,35 22'54' 19 50' _ 4,19 10,1 23,7
7 0,766 0,482 0,928 *27'33’ 18'04’ 3.09 7,86 15,1
8 0,620 0,414 0,700 31=39’ 16'35’ 2.44 6,38 10,8
9 0,520 0,364 0,559 35'16’ 15'19' 2,00 5,37 8,24
10 0,447 0,325 0,465 *38=29' 14'14’ 1,68 4,62 6,61
11 0,392 0,294 0.398 41'23' 13'17’ 1.46 4,05 5,49
12 0,349 0,268 0,348 44°00’ 12 28' 1.28 3.60 4,68
13 0,315 0,246 0,309 46 23’ 11 43’ 1.14 3,23 4,06
14 0,286 0,228 0,278 48'32’ 11 04' 1.03 2,94 3,58
15 0,262 0,212 0,253 50'30’ 10'29' 0,933 2,69 3,21
Угловые ускорения еи креста в моменты начала и конца поворота,
т. е. при а = ± ---, будут:
eH = ±<tg-J. (8.19)
Так как величина — ^>0, то всегда еи 0, т. е. начало и конец
поворота креста всегда сопровождаются мягким ударом (скачком
ускорений).
В середине поворота креста, т. е. при а = 0, угловое ускорение
в = 0. Условие — 0 приводит к уравнению
2k cos2 а -]- (1 k2) cos а — 4к = 0,
436
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
которое имеет следующий действительный корень, определяющий те
значения zt аэ угла а, при которых угловое ускорение е креста при-
нимает экстремальные значения еэ:
cos аэ
4Х
+ >8)8
16Ла
(8.20)
так как при этом
аэ и срэ, которым
величины отношений
гэ/а>к в зависимости
(Знак «—» перед корнем не дает решения,
| cos ae |> 1.)
В таблице 8.3 приведены значения углов
соответствуют экстремумы ускорений, и
ен/*»к и
от числа пазов креста г.
На рис. 511 показаны
графики ш/шк и e/coj; Для
четырехпазового креста.
В последних трех столб-
цах таблицы 8.3 максималь-
ная угловая СКОРОСТЬ Wmax
креста, угловое ускорение еи
креста в момент начала его
движения и экстремальное
угловое ускорение еэ кре-
ста даны в функции от вы-
бранного времени /0 оста-
новки креста.
Угловые ускорения, воз-
никающие
креста,
тельные
грузки в
рах мальтийского механизма.
Ниже будет рассмотрен
ряд других схем мальтий-
ских механизмов; одни схемы
позволят уменьшить вели-
чины экстремальных угловых
ускорений креста; другие
схемы, выбираемые с целью
к увеличению модуля уско-
Рис. 511.
при вращении
создают дополни-
динамические на-
кинематических па-
сокращения времени деления, приводят
рений креста.
Здесь важно подчеркнуть, что целесообразность выбора той или
иной схемы в каждом конкретном случае может быть выявлена
только в результате всестороннего сравнительного анализа различ-
ных схем механизма. Данные кинематического анализа дают лишь ука-
зания относительно того направления, в каком следует искать варианты,
удовлетворяющие заданным условиям.
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 437
Из таблицы 8.3 следует, что при уменьшении числа z пазов
креста его экстремальные ускорения и угловые ускорения в
начале и в конце поворота возрастают по абсолютной величине.
Особенно резко возрастают при этом по абсолютной величине экстре-
мальные угловые ускорения креста. При одинаковом времени 70
остановки креста максимальное ускорение креста с числом пазов
г, = 5, 4 и 3 соответственно в 4,1; 11,1 и 79,6 раза выше, чем у
креста с числом пазов z = 8.
Это резкое возрастание ускорений, а с ними и динамических
нагрузок является существенным недостатком мальтийских механиз-
мов с малым числом пазов креста.
4°. Силовой расчет мальтийского механизма с внешним за-
цеплением. При силовом расчете мальтийских механизмов возникают •
следующие основные задачи:
а) определение величины максимального давления ведущей цевки
на паз креста *), по которому ведется расчет на прочность деталей
механизма;
б) определение средней мощности, потребной на поворот веду-
щего кривошипа;
в) определение отношения максимальной мгновенной мощности
на ведущем кривошипе механизма к средней потребной мощности,
по которому ведется проверка мотора на перегрузку в случае инди-
видуального привода механизма.
Рассмотрим последовательно эти задачи. х
Напишем дифференциальное уравнение вращения креста вокруг
его оси
Л = М — А1С, (8.21)
здесь J—момент инерции креста и вращающихся вместе с ним
масс, приведенных к валу креста;
е — угловое ускорение креста;
М и Л4С соответственно — движущий момент на валу креста
и постоянный момент сопротивления.
Введя обозначение **)
J^K
~Ж = А> (8.22)
получим из уравнения (8.21) выражение для момента на валу креста:
/И = Л7С(1 +М)- (8.23)
*) Здесь и в дальнейшем изложении под давлением ведущей цевки на
паз креста подразумевается давление между цевкой и пазом креста, опреде-
ляемое без учета сил трения. Ниже при определении средней мощности, пот-
ребной на поворот креста, силы трения учитываются введением к. п, д. мальтий-
ского механизма.
**) См. [596].
438
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ, V1H
Давление Р ведущего ролика на паз креста будет:
Р= М = М
(£+£4
(8.24)
где гх— расстояние от центра вращения креста до центра ролика.
Из рис. 510 видно, что
гх = |/R2 sin2 а -}- (L — R cos а)2 = L ]/1 4" cos а > (8.25)
где по-прежнему положено
R . я ,
-г = sin — = Х,
L z
Для проверки на прочность боковых поверхностей пазов креста
и деталей кривошипа необходимо отыскать максимальную величину
dP
давления РГТ1ах ролика на паз креста. Условие = 0 при задан-
ном А дает
.___ sin а (1 -|- X2 — 2Х cos я)2
(1 — X2) [ cos я (1 -|- Xs — 2Х cos а) — 5Х sin2a| ‘
Решить это уравнение можно лишь графическим путем. Для упро-
щения расчетов обычно ограничиваются приближенным подсчетом
величины Ртах > ПОЛЬЗуяСЬ формулой
Ртах
(8.26)
При Л — 0 соотношение (8.26) определяет точное значение Ртах >
при других значениях А оно будет давать несколько завышенные
значения величины Р тах, так как сумма максимумов функций — и
гх
k
-у А больше максимума суммы этих функций. Подсчеты показали,
что при любом числе пазов z ошибка в величине давления Ртях
при вычислении его по формуле (8.26) не превышает 7%. Такая
погрешность в определении вполне допустима для целей последую-
щей проверки на прочность соответствующих деталей механизма.
Из рис. 510 очевидно, что максимум функции —
г х
а = 0; при этом
1 1 1
Гх/тах L — R L 1—X’
Используя выражения (8.16) и (8.25), получим:
1 —X (1 — X2) sin я
гх “ т Т’
(1 + Xs —2Х cos я) 2
будет при
(8.27)
(8.28)
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
439
Условие ^-^^ = 0 приводит к уравнению
ЗХ cos2 а (1 X2) cos а — 5Х = 0,
которое дает угол
eosa,= У(1. (8 29)
Соотношение (8.26) удобно представить в форме:
Ртах =^(а + М), (8.30)
где принято
a = L(—) , b = d--} = -х<1~ха) (8.31)
\ Гх/max \Гх/гмах 5 v '
(1 _|_ X»_ 2Х COS ат)2
В последнюю формулу следует подставлять отрицательный угол ат,
определенный по соотношению (8.29).
Безразмерные коэффициенты- а и Ь, подсчитанные для механиз-
мов с различным числом z пазов креста, приведены в таблице 8.4.
Таблица 8.4
Коэффициенты а и b формулы (8.30)
Z 3 4 5 6 7 8 9 10 11 12 13 14 15
а 7,464 3,414 2,426 2,000 1,766 1^20 1,520 1,447 1,392 1.349 1,315 1,286 1,262
b 206,7 16,28 4,928 2,392 1,456 1,009 0,7584 0,6021 0,4967 0,4219 0,3662 0.3234 0,2896
Переходим к определению средней мощности Ncp потребной на
поворот ведущего кривошипа механизма. Она выразится формулой
(Vcp = Mcp«>K> (8.32)
где wK — угловая скорость ведущего кривошипа, которая принимается
постоянной; Л!ср—-средний крутящий момент на валу ведущего кри-
вошипа.
Для определения крутящего момента Л4К на ведущем валу напи-
шем дифференциальное уравнение вращения вала
j —дл
JK 7nnp > I /
здесь 7Ипр — приведенный к валу момент на оси мальтийского креста,
т. е.
где Т| — к.п. д. мальтийского механизма.
440 СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ [гл. VHt
Так как мы приняли wK = const, то, использовав выражение (8.23),
получим из (*):
МК = ^/И^ = ^М(1+М). (8-33)
Н. С. Ачеркан [7] рекомендует для к. п. д. мальтийского механиз-
ма принимать следующие средние значения (за один поворот веду-
щего кривошипа): если вал креста лежит на опорах скольжения, то
ц = 0,8-ь 0,9, если на опорах качения, то т; = 0,95; если крест со-
ставляет одно целое со шпиндельным блоком, барабаном и диаметр
опорной поверхности креста больше его наружного диаметра, то т; =
= 0,75.
При определении величины среднего момента /Иср на ведущем
кривошипе принято рассматривать только первую половину времени
деления, когда момент полезных сопротивлений и инерционный мо-
мент совпадают по направлению.
Ранее было условлено отсчитывать угол поворота кривошипа а и
угол поворота креста <р от линии, соединяющей центры вращения
этих звеньев. Причем эти углы в первой половине времени деления
будут отрицательными; угол а будет при этом изменяться от —а,
до 0, где величина at определяется соотношением (8.17).
Среднее значение момента Д4ср на ведущем кривошипе в течение
указанного времени интервала выразится:
о
+ е/) ю da- <8-34)
—“1
Так как при а = — at будет ?=* и со = О, а при а = 0 соот-
ветственно <р = 0 и а> = и)тах получим после интегрирования:
7ИСР = -!—(- 7ИС + (8.35)
Ср Тр, \ Z С 1 2 / '
Обозначим:
• ГС 2 _ *rrlax X®Z
I = — =--------к. т — "о------= —71----TVF7-----• (8.36)
aLz г — 2’ 2at гг (1 — X)2 (г-—2)
Тогда средний момент на ведущем кривошипе можно представить
в виде:
Жср=-^(/+»гА). (8.37)
Безразмерные коэффициенты I и т, подсчитанные в функции
от числа z пазов креста, приведены в таблице 8.5.
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
441
Коэффициенты / и т формулы (8.37)
Таблица 8.5
г 3 4 5 6 1 8 9 10 11 12 13 14 15
1 2,000 1,000 0,667 0,500 0,400 0,333 0,286 0,250 0.222 0,200 0,182 0.167 0,154
т 39.90 3,710 1,079 0,477 0.261 0.163 0,111 0,0795 0,0598 0,0485 0,0373 0,0304 0,0252
После отыскания среднего момента Л4ср на ведущем кривошипе
средняя мощность 7Vcp на его валу, потребная на поворот креста,
найдется по соотношению (8.32).
Если мальтийский механизм приводится в движение от инди-
видуального электромотора, возникает вопрос о перегрузке послед-
него, которая определяется как отношение максимального момента
Мктах к его среднему значению /Иср:
^кшах . I* "Ь ^e-^lmax
И =------П--- — а1 ----------------
Мер те -^'тах
г 1 2
(8.38)
Отыскание точного значения Л7кП1ах сложно; поэтому для оценки
величины перегрузки и при. заданном А применяют приближенное
выражение, в котором максимум числителя заменен суммой максиму-
мов слагаемых этого числителя:
и
«1
*'тах “Ь О'^е)тах
те । Ai max
1 1 2
(8.39)
Это выражение При А — 0 и при А = оо определяет точные зна-
чения перегрузки и; при промежуточных величинах А подсчет по
соотношению (8.39) должен давать в общем случае несколько завы-
шенные значения перегрузки и, так как сумма максимумов двух
функций больше максимума суммы этих функций или равна ему.
Дифференцируя выражение (8.39) по А, получим:
л (ib 1 ____ 1 ;з
dll _ г ЧМтах 2 *тах
/те ^'niaxV
2 /
откуда видно, что знак не зависит от величины А. Это дока-
G/t
зывает, что перегрузка и, вычисляемая по соотношению (8.39), ме-
няется монотонно в функции от величины А. Поэтому представляет
442
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
интерес определение предельных значений перегрузки
и А = оо, которые обозначим соответственно:
.. _ a>z; _ (z —2)Х
1‘0-- _ 4тах ------------
при А = О
— 2(1 — X) ’
и — (Ik ) — 71 (г 2)(1 А)а .
“со--- ;s v«eltnax — (/«Jmax.
max
(8.40)
Привлекая выражения (8.16), уравнение
i(«.) = 0.
с помощью которого должно определиться значение (гТгДпах > можно
представить в виде:
cos3 а ~ Х cos2 a— cos а -|- - * ~ 1 = 0. (8.41)
Величина I достигает максимума при а = 0, а величина ke при
а = аэ, который определяется соотношением (8.20). Искомый ко-
рень cos а* уравнения (8.41) будет лежать в пределах
cos аэ -=7 cos а* < 1.
Величины перегрузок и0 и ит при крестах с различным числом z
пазов сведены в таблицу 8.6.
Величины перегрузок «0 и «со
Таблица 8.6
Z 3 4 5 6 7 8 9 10 11 12 13 14 15
ив 3,23 2,41 2,14 2,00 1,92 1,86 1,82 1,79 1,76 1,73 1,73 1,72 1,70
Исо 4,00 2,70 2,28 2,07 1,96 1,88 1,82 1,79 1,76 1,73 1,71 1,70 1,69
Все эти кинематические и силовые соотношения установлены в
предположении, что звенья, механизма являются абсолютно жесткими,
зазоры в их парах отсутствуют, и двигатель, а с ним и вал веду-
щего кривошипа, не меняет своей скорости с изменением нагрузки
на него. Понятно, что в реальном механизме ни одно из этих пред-
положений в точности не выполняется, поэтому все величины, оты-
скиваемые по указанным расчетным соотношениям, должны рассмат-
риваться как первые приближения.
Наблюдения над износом направляющих креста выявили резкие
его возрастания в местах внезапного приложения усилия, когда
контакт цевки переходит с одной стороны паза на другую. Это
внезапное приложение нагрузки имеет характер удара вследствие
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
443
наличия зазора между пазом креста и цевкой и вследствие упруго-
сти отдельных звеньев механизма.
Учитывая это, в качестве одной из сравнительных характеристик
мальтийских механизмов Е. Г. Нахапетян *) предложил учитывать
число переходов цевки с одной стороны паза на другую на участке
движения креста. Для определения этого числа воспользуемся форму-
лой (8. 24), которая дает величину давления ведущей цевки на паз:
Р = М(.
Гх
Моменты перехода цевки с одной стороны паза креста на другую
определяются условием Р = 0, которое приводит к равенству
>4-ЛеЛ = () (8,42)
или ksA = — 1.
Исследуем уравнение (8.42) на интервале —з.|<агСа1. Так
как А всегда положительно, график функции ЛА. (а) будет отли-
чаться от графика ks (а) только масштабами. Из формы графика Ak. (а)
следует (рис. 512), что он может пересекаться с прямой Ake — — 1
в зависимости от величины А либо в одной точке, либо в двух
или, наконец, может совсем не пересекаться. Указанным случаям
соответствуют на рис. 512 прямые ЛА. =—1 с номерами III, II и /.
В мальтийском механизме этим трем случаям соответствуют сле-
дующие условия работы за время одного оборота ведущего криво-
шипа: а) ведущий ролик один раз переходит с одной стороны паза
на другую; б) ведущий ролик дважды переходит с одной стороны
*) См. [596].
444
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
(гл. VIII
паза на другую; в) ролик за весь период деления находится в со-
прикосновении только с одной стороной паза креста.
Если обозначить значения величины А, соответствующие переходу
из области / в область II и из последней в область III соответственно
через Л] и Дц, то, как видно из рис. 512, будет:
^=ГГТ. Л» = Т7Г1- (8-43)
I кеЭ । I КЕН i
Значения Д] и Дп приведены в таблице 8. 7.
Таблица 8.7
Граничные значения и Дц
2 3 4 5 6 8 9 10 12
А 0,03 0,18 0,43 0,74 1,4 1,8 2,1 2,9
^11 0,6 1,0 1Д 1,7 2,4 2,7 3,1 3,7
Можно предполагать, что наиболее неспокойная
будет при двух переходах цевки с одной стороны
т. е. при наличии двух ударов за время поворота
чай возникает при Д1<^Д<^Дц.
Напомним, что коэффициент
работа механизма
паза па другую,
креста. Этот слу-
где о)к — угловая скорость ведущего кривошипа; J—приведенный
к кресту момент инерции вращающихся с крестом деталей; Л4С —
приведенный к кресту момент сопротивления вращающихся с кре-
стом деталей.
Из выражения, определяющего величину Д, видно, что механизм
из области Д1<^Д<^Дц с двумя ударами за время поворота креста
(и даже из области Д^Дц с одним ударом) можно перевести в
безударную область 0<^Д<^Д1, увеличивая Л4С путем торможения
вращающихся деталей.
5°. Кинематика мальтийского механизма с внутренним зацеп-
лением. На рис. 513 сплошными линиями показана схема мальтий-
ского механизма с внутренним зацеплением. Для простоты изобра-
жен только один из пазов. В этом механизме, в отличие от меха-
низма с внешним зацеплением, скорость центра цевки при входе ее
в наз креста оказывается направленной не к центру креста, а от
центра его. Крест в этом случае вращается в том же направлении,
как и ведущий кривошип.
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 445
Пунктиром на рис. 513 показана схема мальтийского механизма
с внешним зацеплением. Пазы крестов в этих механизмах являются
продолжением друг друга, откуда ясно, что мальтийские механизмы
с внешним и внутренним зацеплением кинематически эквивалентны
одному и тому же кулисному механизму, отличаясь друг от друга
лишь пределами изменения угла поворота ведущего кривошипа, на
которых происходит поворот ведомого звена.
Рис. 513.
Мальтийский механизм с внешним безударным зацеплением можно
рассматривать как указанный кулисный механизм на угле поворота
кривошипа в пределах от —до -аь где
Мальтийский механизм с внутренним безударным зацеплением
можно рассматривать как тот же кулисный механизм на угле пово-
рота ведущего кривошипа от —а, до где
= к — СЦ = . (8.44)
Здесь z по-прежнему обозначает число пазов креста; углы а* и <р
отсчитываются от прямой OOh причем углу а* = 0 соответствует
по рис. 513 нижнее вертикальное положение кривошипа О А.
Угол поворота ведущего кривошипа, на котором происходит
вращение креста при внутреннем безударном зацеплении, будет:
ч=^4-5=л(,+:)» <8-45)
446
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
а угол поворота кривошипа, на котором крест остается непод-
вижным, вырази гея:
2а* = 2- — 2< = ~ fl — - к
\ z )
Время tt поворота креста (время деления) и время /0 остановки кре-
ста будут в этом случае:
При выбранном времени t0 остановки мальтийского креста и задан-
ном числе пазов креста требуемая угловая скорость ведущего кри-
вошипа определится соотношением
п = —g - • у об)мин. (8.46)
Коэффициент времени работы механизма с внутренним зацеплением
будет:
<««>
где k — тот же коэффициент для механизма с внешним зацеплением,
определяемый зависимостью (8. 9).
Значения коэффициента k* в мальтийских механизмах с внутрен-
ним зацеплением разобранного Типа больше единицы, т. е. в этих
механизмах время деления всегда больше времени остановки креста.
Табл и ц а 8.8
Параметры, характеризующие продолжительность остановки и поворота креста
мальтийского механизма с внутренним зацеплением.
Число пазов креста г Угол поворота кривошипа, соот- ветствующий Угол поворота креста 2^’ Коэффициент времени работы /г* == — *0
остановке креста ч повороту креста 2а*
3 60° 300° 120° 5,00
4 90° 270° 90° 3,00
5 108° 252° 72° 2,33
6 12(Г 240° 60° 2,00
7 128°34' 231°26’ 5126’ 1,80
8 135° 225° 45° 1,67
9 140° 220° 40° 1,57
10 144° 216° 36° 1,50
11 147° 16' 212°44’ 32’44' 1,44
12 150 210° 30' 1,40
13 152°18' 207с42' 27°42' 1,36
14 154°18' 205с42' 25°42' 1,33
15 156° 204° 24° 1,31
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 447
Значения коэффициента k* приведены в таблице 8.8; в этой
таблице указаны также углы 2а* и 2а‘, а также углы 2<р* делитель-
ного поворота креста.
Длина R — О А кривошипа и расстояние S от оси вращения
креста до торцов его пазов связаны с расстоянием L = ()О\ между
осями вращения кривошипа и креста прежними соотношениями (8.10),
подсчет которых приведен в таблице 8. 2.
Длина h паза креста здесь должна быть
h R L — S г = L \Л 4- sin — cos + г >
где z — число пазов креста; г — радиус цевки креста.
Для возможности осуществления неконсольного крепления креста
па его валу диаметр d последнего должен удовлетворять прежнему
условию (8.12).
Кривошип здесь может крепиться на своем валу только консоль-
но; эго является одним из конструктивных недостатков механизма с
внутренним зацеплением.
Углы а* и ср поворота кривошипа и креста условимся по-преж-
нему считать положительными влево от линии центров ООЪ а за
положение а* = 0 примем то, в котором цевка кривошипа» распола-
гается вне центров ООр
Подставляя в формулы *(8.14)—(8.16) значение = — а,
получим следующие зависимости, определяющие кинематику креста
при внутреннем зацеплении:
X sin я*
I -р X cos я* ’
u> = z*o>K, е =
(8.48)
(8.49)
где сок — постоянная угловая скорость ведущего кривошипа, а г* и
kf — переменные коэффициенты, которые выражаются соотношениями:
X(cosa* + X) X(l— Xs) sin я* /еклч
— l+2Xcosa*+X»’ (I -р 2 X cos a:i:-р X2)2 ‘ v '
Экстремальное значение угловой скорости креста будет при а* = 0
штах — ^'тах и)к — । । у шк. (8.51)
При внутреннем зацеплении наибольшие по абсолютной величине
ускорения получаются в начале и в конце движения, т. е.
— X (1 — л2; sin я*
— (1 -Р 2Х cos я* 4- X2)2
(8.52)
где угол а* определяется формулой (8.45).
448
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
На рис. 514 показаны графики 1 = ~и-^ для четырехпазового
креста с внутренним зацеплением.
Таблица 8.9
Параметры, определяющие кинематику креста мальтийского механизма с внут-
ренним зацеплением (время t0 — в сек)
Z “max шк — &S Э — — k S н “max радиан радиан
3 0,464 1,729 0,486 1,89
4 0,414 1,000 0,650 2.47
5 0,370 0,727 0,697 2,58
6 0,333 0,577 0,698 2,53
7 0,303 0,481 0.680 2.42
8 0,277 0,414 0,653 2,30
9 0.255 0,364 0,623 2,17
10 0,236 0,325 0,593 2,05
И 0.220 0,294 0,566 1,94
12 0,206 0,268 0,539 1,84
13 0,193 0,246 0,513 1,74
14 0,182 0,228 0,490 1,65
- 15 0,172 0,213 0,468 1,58
I
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ
ДВИЖЕНИЕМ ЦЕВКИ 449
внутреннем зацеплении
скорости креста при
Г рафик угловой
мало отличается по своему характеру от такого же графика при
внешнем зацеплении.
В обоих случаях угловая скорость креста возрастает монотонно
от нуля в начале поворота до максимума в среднем положении кре-
ста и затем опять монотонно убывает до нуля в конце поворота.
Графики углового ускорения креста при внешнем и внутреннем
зацеплении резко отличаются друг от друга. При внутреннем
зацеплении в начале поворота креста его ускорение мгновенно
достигает максимального значения, а затем изменяется монотонно,
переходя через нуль в среднем положении креста; в конце поворота
креста ускорение принимает значение, равное по модулю первоначаль-
ному, но противоположное ему по знаку.
При заданном времени 20 остановки максимальная величина угло-
вого ускорения при внутреннем зацеплении, в отличие от внешнего,
меняется в узких пределах от е920=1,58 до е920 = 2,58 при изме-
нении числа пазов от z=3 до z=15.
6°. Силовой расчет мальтийского механизма с внутренним
зацеплением. Давление ведущей цевки па паз креста определится
прежним соотношением (8.24):
/1 \
Р=М. —+~ А .
4>\гх гх /
Максимальная
его величина будет:
(8.53)
А .
/max
приближенного равенства (8.26) приведенной выраже-
точным, так как в рассматриваемом случае максимумы
А*
функции — и /гЕ, а следовательно и —, наступают в одном и том же
ГХ Г х
начальном положении механизма при а* = а*.
Из рис. 513 очевидно, что
m =1=_________________
\Гл-/тах 8 L )/ 1 — X2
Учитывая соотношения (8.50) и (8.54), получим:
\ Гх
В отличие от
ние является
1
шах
X рг1 — Xs sin а*
2.(1 +2Х cos а* + X2)» •
(8.54)
Рmax Л41
1
В эту формулу следует подставлять угол а? со знаком минус,
соответствующий началу поворота креста.
Соотношение (8.53) удобно представить в форме:
м
Ртах = (a* -L ft* А), (8.55)
15 И. II. Артоболевский
450
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. VIII
обозначив по-прежнему
\Г х/гпах
Безразмерные коэффициенты а* и Ь*, подсчитанные для механиз-
мов с внутренним зацеплением в функции от числа z пазов креста,
приведены в таблице 8.10.
Таблица 8.10
Коэффициенты а* и Ъ* формулы (8.55)
2 3 4 б 6 7 8 9 10 11 12 13 14 15
а* 2,000 1,414 1,236 1,155 1,110 1,082 1,064 1,051 1,042 1,035 1,030 1,026 1.022
Ь* 3,458 1,414 0,899 0,666 0,534 0,448 0,387 0,342 0,306 0,277 0,253 0,234 0,218
Средний крутящий момент 7Иср на ведущем кривошипе опреде-
лится прежним соотношением (8.35), которое представим в виде
Мср = ^(/*-1~т*А), (8.56)
где
•*2
.... 2 'max A2z .л
/* = - ~ • т = =---/1 i Т о, . (8.57)
a* z Z-|-2’ 2а* л (1-|-X)2 (z2)
Безразмерные коэффициенты I* и т*, подсчитанные в функции
от числа z пазов креста, приведены в таблице 8.11.
Таблица 8.11
Коэффициенты I* и т* формулы (8.56)
Z 3 4 5 6 7 8 9 ю 11 1 12 13 14. 15
7* 0,400 0,333 0,286 0,250 0,222 0,200 0,182 0,167 0,154 0,143 0,133 0,125 0,118
т* 0,0411 0,0364 0,0311 0,0265 0,0227 0,0195 0,0169 0,0148 0,0130 0,0116 0,0103 0.00923 0.00831
Средняя мощность Л/ср на валу ведущего кривошипа, потребная
на поворот креста, определится очевидным соотношением:
^ср ^cp0JK-
Для оценки перегрузки и двигателя при выборе его по средней
мощности /Vcp будет справедливо выражение (8.38), которое принимает
здесь вид:
$___Л1ктах * [t* -ф I*fee:M]max
~ <р 1
(8.58)
л *
я . /Птах
Z ‘
2
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 451
Если, как прежде, воспользоваться приближенным выражением
U* а* +(^)таХ А , (8.59)
я , Д/niax
7 4 2~
то предельные значения перегрузки z/о и «£> при А = 0 и А = оо
определятся формулами:
____“** _ (z + 2) X
«о— я ‘max-- 1+х ,
„*_2а* _2(z + 2)(l+X)» * . <8‘60)
«оо V ке7тах ——«'sjmax
Imax
Условие
д (<•«) = О
приводит к уравнению
cos3a — —cos2a —' (5 -]- ^2) cos a — ~ * = 0. (8.61)
Искомый корень cos а* этого уравнения должен лежать в пределах
cos a* -С cos я* 1.
Величины перегрузок а* и ti$g при крестах с различным числом z
пазов сведены в таблицу 8.12.
Таблица 8.12
Величины перегрузок и* и «*>
Z 3 4 5 6 7 8 9 10 11 12 13 14 15
«0 1,16 1,24 1,30 1,33 1,36 1,38 1,40 1,42 1,43 1,44 1,45 1,46 1,46
* «СО 3,88 2,48 2,04 1,85 1,74 1,68 1,62 1,60 1,58 1,58 1,58 1,57 1,57
При малом числе пазов величины и* и и*,-. достаточно резко отли-
чаются друг от друга. В этих случаях может потребоваться уточ-
ненный подсчет перегрузки и. Для этого следует построить график
функции
F (a)=u* (1 -|-^Л),
стоящей в числителе формулы (8,58), и по нему установить макси-
мум этой функции.
16’ - *
452
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
7°. Другие схемы трехзвенных радиальных мальтийских
механизмов. Рассмотрим еще некоторые схемы трехзвенных ра-
диальных мальтийских механизмов, находящие практические прило-
жения.
а) Механизм, у которого цевка не входит последо-
вательно в каждый соседний паз креста. На рис. 515
показан радиальный мальтийский механизм с семипазовым крестом, у
которого пазы размещены равномерно по окружности. Цевка в этом
механизме входит не в каждый со-
Рис. 515.
седний паз, а через паз.
В подобных механизмах крест
имеет нечетное число z пазов, при-
чем очевидно, что должно быть
г^>3. Применимы эти механизмы
только в тех случаях, когда ведо-
мый узел машины не крепится не-
посредственно на валу мальтийского
креста, а связан с последним через
зубчатую передачу.
Угол 2ср] поворота креста в этих
механизмах определяется соотно-
шением
2<Р1=у- (8-62)
Соответствующий угол поворота
ведущего кривошипа будет:
2a, = it —2<р! = к—(8.63)
Время t, поворота креста на угол
2<pt и время /(1 остановки
опре-
делятся зависимостями:
2а,z — 4
"к г
30
п
сек,
30
п
сек;
(8.64)
. 2а0___г + 4
0 — “к — г
отношение этих времен будет:
ь — *1 —
4 г + 4-
(8.65)
Значения коэффициента k времени работы механизма, а также
соответствующих углов поворота креста и ведущего кривошипа в
функции от числа z пазов креста приведены в таблице 8.13.
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРЛ'ГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
453
Таблица 8.13
Параметры, характеризующие продолжительность остановки и
поворота креста
Число пазов креста Z Угол поворота кривошипа, соответствующий Угол поворота креста 2<pi Коэффициент времени работы k
остановке креста 2а0 повороту креста 2«i
5 324°00' 36°00’ 144°00' 0,111
7 282°52' 77°08' 102o52' 0,273
9 260°00' 100°00' 80°00’ 0,385
11 245°28' 114э32' 65°28’ 0,467
13 235°24' 124°36' 55"24' 0,529
15 228е 00' 132°00' 48г00' 0,578
Если обозначить по-прежнему через L расстояние между осями
вращения кривошипа и креста, а через R—длину ведущего криво-
шипа и ввести коэффициент
X = siny = ^, (8,66)
то формулы, установленные в пунктах 3° и 4° настоящего параграфа, бу-
дут полностью справедливы ^ля исследования кинематических и сило-
вых соотношений в рассматриваемых механизмах *).
В таблице 8.14 приведены параметры, определяющие кинематику
креста рассматриваемых мальтийских механизмов.
Таблица 8.14
Параметры, определяющие кинематику креста
Z “max £н — 2 “к 1+ Углы поворота, соот- ветствующие экстре- мальным ускорениям креста “тах^о । радиан 4- ен^ — Но радиан 4-Е /2 “ Э О радиан
со к
5 19,43 3,078 258,0 1°40' 29-11' 109,9 98,43 8251
7 3,585 1,254 10,7 8с08' 26'05’ 17,69 30,53 260,5
9 1,799 0,839 3,32 14'37' 23° 13” 8,160 17,27 68,32
11 1,177 0,643 1,72 20°20’ 5,043 11,80 31,58
13 0,869 0,525 1,10 25е 18' 18с55' 3,571 8,862 18,57
15 0,686 0,445 0,799 29е 40' 17“18' 2,730 7,049 12,66
В таблицу 8.15 сведены вспомогательные коэффициенты, упро-
щающие подсчет силовых соотношений. Коэффициенты а и b слу-
жат для подсчета по формуле (8.30) максимального давления Ртах
*) Исключение составляют формулы (8.17) и (8.19), в которых вели-
л 2я
чина — должна быть заменена на - -. А
z г *»
454
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
ведущего ролика на паз креста, коэффициенты I и т — для под-
счета по формуле (8.37) среднего момента на ведущем кривошипе,
величины и9 и Поз выражают собой предельные величины перегрузок
мотора при индивидуальном приводе мальтийского креста, и величины
А1 и У1ц представляют собой те граничные значения коэффициента Л,
отыскиваемые по формуле (8.43), при которых меняется число пере-
ходов цевки с одной стороны паза креста на другую при движении
креста.
Таблица 8.15
Вспомогательные коэффициенты для силового расчета
2 5 7 9 11 1 13 15
а 20,43 4,585 2,799 2,177 1,869 1,686
ь 46,44 43,34 8,214 3,306 1,830 1,197
1 40,00 1,333 0,800 0,571 0,444 0,364
т 60,09 9,547 1,854 0,693 0,347 0,204
«0 4,86 2,69 2,25 2,06 1,96 1,89
«со 6,61 3,12 2,45 2,16 2,01 1,91
А 0,0039 0,093 0,301 0,581 0,909 1,25
0,325 0,797 1,19 1,56 1,90 2,25
Из сравнения коэффициентов, приведенных в таблицах 8.13, 8.14
и 8.15, с коэффициентами, имеющимися в таблицах 8.1, 8.3 — 8.7,
легко усмотреть, что рассматриваемая схема мальтийского механизма
с числом пазов, например, z=15 по своим параметрам занимает
среднее положение между обычными мальтийскими механизмами с внеш-
ним зацеплением, имеющими числа пазов г = 7 и z =8; рассматри-
ваемая схема с числом пазов z =13 — среднее положение между
обычными механизмами с внешним зацеплением, имеющими числа па-
зов г =6 и z~l, и т. д.
Рассматриваемый механизм с числом пазов z = 5 имеет отноше-
ние А =<1/4=0,11, т. е. вдвое меньшее, чем в обычном мальтий-
ском механизме с* числом пазов z = 3; однако его максимальное
угловое ускорение оказывается в восемь раз больше, чем у послед-
него механизма.
б) Механизмы с несколькими цевками. Имеются слу-
чаи, когда целесообразно применение мальтийских механизмов с не-
сколькими цевками.
Сюда прежде всего относятся случаи, когда число требуемых
позиций периодически проворачиваемого звена машины при ее пе-
реналадке на новый процесс может изменяться. Например, при обра-
ботке на металлорежущем автомате сравнительно простых по техно-
логии изделий из четырех позиций револьверной головки может по-
требоваться только две. В этом случае с целью сокращения общего
времени цикла обработки часто целесообразно поставить вторую
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ _ 455
цевку В, которая будет входить в паз креста в момент выхода пер-
вой цевки А из соседнего паза, как показано на рис. 516.
При малом числе г позиций проворачиваемого звена и при инди-
видуальном приводе мальтийского креста, когда время tx его пово-
рота не зависит от времени Zo остановки, может оказаться выгодным
с точки зрения уменьшения максимального углового ускорения периоди-
чески проворачиваемого узла применение креста с числом пазов z = 2Z
и ведущего кривошипа с двумя цевками. Так, из приведенной выше таб-
лицы 8.14 видно, что при одном
и том же времени Н поворота кре-
ста максимальное ускорение трехпа-
зового креста с внешним зацепле-
нием примерно в 5,8 раза больше,
чем у шестипазового креста с тем же
зацеплением. Отсюда следует, что
при числе позиций Z = 3 примене-
ние шестипазового креста и двух
цевок на ведущем звене может сни-
зить угловое ускорение креста в
1,45 раза.
Выше нами подчеркивалось, что
во многих случаях стремятся к
максимальному сокращению отно-
шения времени движения креста
ко времени /(| остановки для тогц,
чтобы уменьшить потери произво-
дительности машины, связанные с
периодическими поворотами кресту.
Однако имеются случаи, когда цик-
лограмма автомата требует наобо-
рот повышения этого отношения по
сравнению с тем его значением, ко- Рис. 516.
торсе дает одноцевочный механизм
с числом z пазов креста, равным числу Z позиций проворачиваемого
узла. В этом случае приходится либо переходить к кресту с другим
числом пазов, принимая z^-l и включая между проворачиваемым
узлом и крестом зубчатую передачу, либо применять мальтийский
механизм с несколькими цевками.
Исходя из предположения, что цевки расположены симметрично
по окружности, установим, во-первых, их возможное число j при
данном числе z пазов; во-вторых, отношение времени tx/t0 в функции
от г и j при внешнем зацеплении.
Угол 2а] поворота ведущего кривошипа, на котором происходит
перемещение креста, по соотношению (8.4) равен:
456
СИНТЁЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. vni
При j цевках центральный угол между ними будет 2^. Для воз-
можности работы мальтийского механизма как механизма прерыви-
стого движения должно существовать неравенство
2я-^о /1 2\
—-~~г 2а< = те ( 1-,
J \ г)'
откуда для числа цевок получаем условие
(8.67)
Z
По неравенству (8.67) получим: при
z==3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
должно быть
j SS 6, 4, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2.
На рис. 516 показан мальтийский механизм с z = 4 и / = 3. При j
цевках угол поворота кривошипа, на котором крест остается непо-
движным, будет:
2ао=2^ —2а1=те(|+|-1). (8.68)
Отношение времени поворота креста ’к времени t0
выразится: 9
1—--
k— А = ?__
R— t0 а0 _2 + 2_1 ‘
j 2
его остановки
(8.69)
Таблица 8.16
Параметры, характеризующие продолжительность остановки и поворота’ креста
Я 2«1 2а0 *0
7=1 7=2 7 = з 7 = 4 7=5 /=| 7 = 2 7=3 7=4 7=5
3 60° 300° 120° 60° 30° 12° 0,20 0,50 1,00 2,00 5,00
4 90° 270° 90° 30° 0,33 1,00 3,00
5 108° 252° 72° 12° 0,43 1,50 9,00
6 120° 240° 60° 0,50 2,00
7 128’34' 231°26’ 51’26' 0,56 2,50
8 135° 225’ 45° 0,60 3,00
9 140° 220° 40° 0,64 3,50
10 144° 216° 36° 0,67 4,00
11 147’16' 212°44' 32’44' 0,69 4,50
12 150° 210° 30° 0,71 5,00
13 152’18' 207’42' 27’42' 0,73 5,50
14 154°18' 205°42' 25°42' 0,75 6,00
15 156° 204° 24° 0,76 6,50
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 457
В таблице 8.16 приведены значения углов 2«j и 2а0 и коэффици-
ента й = в функции от числа z пазов креста и числа j цевок
для случая внешнего зацепления.
Понятно, что при необходимости цевки могут быть расположены
по окружности ведущего кривошипа несимметрично. Тогда периоды
остановки креста не будут
равными между собой.
Если соотношение (8.67)
использовать только как ра-
венство, то в пределах
г =3-4- 15 получим три ре-
шения:
при z = 3, 4, 6
соответственно j = 6, 4, 3.
Этим случаям соответ-
ствуют мальтийские меха-
низмы, у которых крест
имеет только мгновенные
остановки.
Фиксирующих устройств
этот механизм не требует,
так как при выходе из паза *
одной цевки в следующий
паз входит другая цевка.
Очевидно, что кинемати-
ческие и силовые соотноше-
ния на участке поворота
креста, а также соотноше-
ния между размерами кре-
ста и кривошипа во всех
этих механизмах с числом цевок 1 будут такими же, как в рас-
смотренных выше одноцевочных механизмах.
в) Механизмы с неравномерно расположенными
пазами. Рассмотрим еще мальтийские механизмы, кресты которых
имеют радиальные пазы, расположенные неравномерно по окружно-
сти, как показано на рис. 517. В этом случае углы поворота креста
не будут равны между собой.
Предположим, что в зацепление пазы креста входят последова-
тельно. Из-за неравномерного расположения пазов по окружности кре-
ста число j цевок должно быть кратно числу z пазов, чтобы обеспечить
нормальное действие механизма. В вытекающем отсюда соотношении
z = aj
(8.70)
а — некоторое целое число, равное числу оборотов ведущее криво-
шипа за один полный оборот креста.
[гл. VIII
458
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
Обозначим углы поворота креста с одной позиции на другую
при одном повороте кривошипа через 2<р,-, где индекс i принимает
значения i—1, 2,..., j. Сумма этих углов равна:
(8.71)
или, учитывая предыдущее равенство,
2п/
z
(8.72)
Угол поворота ведущего звена, соответствующий повороту креста
на угол 2<рг, обозначим через 2аг. Он равен:
. 2а,= тс—2<р,- (8.73)
Сумма этих углов должна быть:
j
У <Х; ’ “ 2ir.
i=l
Учитывая соотношения (8.73) и (8.72), получим:
)' i i
У ai= £ (« — 2<р,-) 2tPi —
;=i i=i i=i
откуда для числа цевок получим второе условие:
(8.74)
совпадающее с ранее установленным условием для числа цевок в
мальтийских механизмах с равномерным расположением пазов по
окружности креста. Очевидно, что здесь нас не может интересовать
решение /= 1, так как при одной цевке нельзя построить маль-
тийского механизма, у которого крест имеет неравномерное располо-
жение радиальных пазов по окружности креста.
Ограничимся знаком неравенства в соотношении (8.74) для полу-
чения механизмов с конечными по длительности остановками креста.
При z=3 из соотношения (8.74) получим /<^5; в силу усло-
вия кратности чисел z и j получаем, кроме j—1, решение /=3.
При z = 5 по соотношению (8.74) получим /<^4; здесь условие
кратности (8.70) выполнимо только при /= 1. То же имеет место
при любом нечетном z 5.
Отсюда следует, что при нечетном числе пазов и неравномерном
их расположении по окружности возможен единственный мальтийский
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ
459
механизм с числом пазов z = 3 и числом цевок также j — 3. Такой
механизм изображен на рис. 517. Углы поворота его креста приняты
соответственно ср, = 52°30', ф2 = 60°00' и <ря = 67С’ЗО'.
При любом четном числе пазов z 4 получаем по соотношению
(8.74) число цевок 2<^у<^3. В этом случае условие кратности (8.70)
выполнимо, кроме у = 1, еще при у = 2. Следовательно, при любом
четном числе пазов и неравномерном их расположении по
окружности число цевок может быть принято только у = 2.
На рис. 518 изображен мальтийский механизм с числом пазов
г=4 и числом цевок у = 2, у которого углы поворота креста соот-
ветственно равны cpi = 52°30' и
<р2 = 37°30'.
Отметим, что при неравномер-
ном расположении пазов по ок-
ружности креста величины углов
поворота 2срг (где I принимает
значения z = 1, 2,..., у) подчи-
няются единственному условию
При заданном расстоянии L
между центрами креста и кри-
вошипа радиус Rt окружности,
на которой должен находиться
центр соответствующей цевки и
отрезок между центром вра-
щения креста и торцом его паза,
определяется прежними форму-
лами (8.10):
Ri = L sin <р;, ]
Si = LcosU (8'75)
Рис. 518.
В зависимости от относительного расположения цевок по окруж-
ности кривошипа меняется время остановки креста на той или
иной позиции.
Если выбранный угол 2<рг поворота креста отличается от тех,
которые возможны при равномерном расположении пазов по окруж-
, л
ности креста, т. е. если где z—целое число, то кинемати-
ческие и кинетостатические характеристики механизма на этом угле
2ср{ можно приближенно отыскать посредством интерполирования со-
ответствующих величин, приведенных ранее в таблицах для ме-
ханизмов с равномерным расположением пазов по окружности
кривошипа.
460
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. VIII
8°. Фиксаторы. На рис. 507 указано дисковое устройство, при-
меняемое для фиксирования креста в мальтийских механизмах. В метал-
лорежущих станках (револьверных и многошпиндельных автоматах,
многопозиционных агрегатных станках и т. п.) предъявляются очень
высокие требования к точности фиксирования поворачиваемых узлов,
так как точность фиксирования непосредственно отражается на точно-
сти обработки деталей. Дисковые фиксирующие устройства часто не
удовлетворяют этим требованиям.
Более высокую точность фиксирования обеспечивают фиксато-
ры, приводимые в движение от кулачкового механизма (см. рис. 519).
Фиксатор а представляет собой цилиндрический или призматический
стержень, конусообразный конец которого входит в соответ-
ствующий паз фиксируемой детали Ь. Особенно точное фиксирова-
ние обеспечивается устройствами двойной фиксации. Схема одного
Рис. 519.
из этих устройств приведена на рис. 520. Фиксатор а, приво-
димый в движение от кулачка, доводит фиксируемую деталь Ь
до упора, создаваемого собачкой с, которая перемещается де-
талью Ь. Замыкание между собачкой с и деталью Ь создается
пружиной.
В тех случаях, когда поворачиваемая деталь (поворотный стол,
шпиндель, узел машины и т. д.) не жестко скреплена с мальтийским
крестом, а связана с ним через ту или иную кинематическую цепь,
элементы которой обладают упругостью, а кинематические пары имеют
зазоры, часто фиксируется не крест, а сама поворачиваемая деталь или
одновременно поворачиваемая деталь и крест. В последнем случае
§ 24] МАЛЬТИЙСКИЕ МЕХАНИЗМЫ С КРУГОВЫМ ДВИЖЕНИЕМ ЦЕВКИ 461
для фиксирования креста применяется дисковое фиксирующее устрой-
ство, а для фиксирования детали — фиксирующие устройства типа
указанных на рис. 519 и 520.
Рассмотренные в настоящем параграфе трехзвенные радиальные
мальтийские механизмы отличаются простотой конструкции, но вместе
с тем обладают рядом отрицательных качеств. Отметим два из них,
являющихся наиболее существенными:
1) при малом числе пазов креста эти механизмы имеют относительно
большие угловые ускорения креста и связанных с ним деталей; это
приводит к возникновению значительных динамических нагрузок в
кинематических парах механизма и требует (при индивидуальном при-
Рис. 520.
воде) выбора мотора с завышенной мощностью из-за высокого отно-
шения максимального момента к среднему моменту на ведущем валу;
2) в схемах с непрерывным вращением ведущего вала с увеличе-
нием числа• пазов креста ускорения последнего и связанных с ним
деталей резко уменьшаются, но вместе с тем заметно возрастает
отношение времени поворота креста tx к времени его оста-
новки это приводит к повышению потерь производительности
машины.
В связи с этим в последующих двух параграфах будут разобраны:
1) схемы мальтийских механизмов, обеспечивающие уменьшение аб-
солютной величины экстремальных угловых ускорений креста; 2) схе-
мы, позволяющие сократить время деления креста. .
462
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
§ 25. Схемы мальтийских механизмов, позволяющие уменьшить
экстремальные значения угловых ускорений креста
1°. Промежуточная зубчатая передача между мальтийским
крестом и периодически проворачиваемым звеном машины. Пусть
периодически проворачиваемое звено машины (например, многопозици-
онный стол агрегатного станка, шпиндельный блок многошпиндельного
автомата и т. д.) должно иметь Z позиций. Будем предполагать, что
на каждой позиции время tu остановки этого звена одно и то же и,
следовательно, делительные
перемещения этого звена
могут быть осуществлены
мальтийским механизмом, у
которого пазы на кресте
равномерно расположены по
окружности. Крест при этом
может иметь любое число
пазов z^3, отличное от
числа Z позиций периоди-
чески проворачиваемого зве-
на, если между этим зве-
ном, обозначенным буквой с
на рис. 521, и крестом b
мальтийского механизма
включить промежуточную
зубчатую передачу с
передаточным отношением
Рис. 521. __ г
'ьс — Т-
Тогда при мы получим механизм, у которого угловые уско-
рения периодически проворачиваемого узла будут меньше по абсо-
лютной величине, чем при использовании мальтийского креста с
числом пазов, равным числу требуемых позиций z = Z. Это обуслов-
ливается возрастанием времени деления. В результате вместе с
понижением угловых ускорений проворачиваемого звена могут од-
новременно возрастать потери производительности машины или станка,
связанные с периодическими поворотами этого звена.
/ Отметим, что к схеме z^>Z приходится обращаться при числе
/ позиций проворачиваемого звена Z = 2. Иногда в промежуточную
передачу включают сменные колеса для того, чтобы с помощью
одного мальтийского механизма можно было производить пово-
/ рот ведомого,—звена на различные углы. Подобные условия воз-
/ никают при проектировании делительного устройства зубообра-
батывающих станков и механизмов автоматических делительных
головок.
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 463
Полагая время остановки t0 на каждой позиции заданным, оценим
изменения времени деления и экстремальных ускорений периоди-
чески проворачиваемого звена в случае z 7-7 но сравнению со
случаем z = Z, где Z—заданное число позиций, a z — число пазов
креста того мальтийского механизма, который предназначается для
осуществления делительных перемещений этого звена.
Обозначим: (^)z — время деления в случае г #= Z, (t^z—время
деления при z = Z и и?—их отношение; тогда получим:
„ (/,)г _(2-2)(Z + 2)
UT~^)z~ (^-2)(z + 2)‘
(8.76)
Аналогично обозначим: (е,)2 — экстремальное угловое ускорение
креста в случае z A Z, (&3)z — экстремальное угловое ускорение при
г = Z и и, —ютношение их абсолютных величин:
и' =
(ч)г
(Ч)г
Значения (еэ)2 и (e,)z могут быть взяты из соответствующего
столбца таблицы 8.3, если положить число пазов креста равным
соответственно z и Z.
При отыскании абсолютней величины «е — отношения экстремаль-
ного углового ускорения периодически проворачиваемого звена в слу-
чае z Z к максимальному угловому ускорению этого звена в
Таблица 8. 17
Коэффициенты ит.и ие в случае z > Z
z Z Uj и Е
3 5 2,1 0,086
3 6 2,5 0,055
3 8 3,0 0,033
3 10 з,з 0,026
- 3 12 3,6 0,022
3 15 3,8 0,019
4 5 1,3 0,46
4 6 1,5 0,29
4 8 1,8 0,18
4 10 2,0 0,14
4 12 2,1 0,12
4 15 2,3 0,10
5 6 1,2 0,62
5 8 1,4 0,38
5 10 1,6 0,29
5 12 1,7 0,25
5 15 1,8 0,22
464 СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
случае z = Z — следует учесть передаточное отношение
ной зубчатой передачи ibc — ^-^ тогда получим:
[гл. VIII
промежуточ-
(8.77)
Подсчитанные величины ит и и, для ряда сочетаний z и Z при-
ведены в таблице 8.17.
Таблица показывает, во сколько раз уменьшаются по абсолютной
величине экстремальные угловые ускорения периодически провора-
чиваемого звена при выборе z^>Z и во сколько раз одновременно
возрастает при этом время деления (при неизменном времени оста-
новки 70).
В практике станкостроения при малом числе позиций (Z=3 ч- 4) с
целью снижения угловых ускорений ведомого звена обычно приме-
няют крест с числом пазов г = 6ч-8. Из таблицы 8.17 видно, что
при дальнейшем увеличении числа z пазов креста снижение наи-
больших угловых ускорений проворачиваемого звена оказывается отно-
сительно незначительным. Например, при заданном числе позиций
Z=3 и при выборе на кресте г = 8 пазов достигается уменьшение
V экстремальных угловых ускорений периодически проворачиваемого
звена в 30 раз (при заданном времени 70 остановки); при дальней-
шем увеличении числа пазов креста до 10 и 12 экстремальные уг-
ловые ускорения проворачиваемого звена уменьшаются еще соот-
ветственно в 1,3 или 1,5 раза.
2°. Планетарная передача в схеме мальтийского механизма.
Представим себе ведущий кривошип мальтийского механизма составлен-
ным из двух звеньев: звена ОВ = R, вращающегося вокруг непо- 1
движной оси О, и звена В А —г с цевкой А, которое вращается
вокруг шарнира В (рис. 522). ‘Угловую скорость звена ОВ обозна-
чим о)к и направим против часовой стрелки; абсолютную угловую
скорость звена ВА обозначим и зададим ей направление по вра-
щению часовой стрелки.
Соотношение между скоростями шк и выберем из следующих
условий. Потребуем, чтобы при входе и при выходе цевки А из паза
креста звено ВА составляло продолжение звена ОВ. При переходе
из одного упомянутого положения в другое звено ОВ повернется на
угол
2Я1 = к — = ~(г~ 2), (8.78)
где z—число пазов креста.
Звено ВА за это же время должно совершить один оборот в
относительном движении по отношению к звену ОВ’, в абсолютном
движении звено ВА за это время повернется на угол
2₽х = 2=4 — 2к = — (8.79)
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 465
Передаточное отношение j между звеньями ВА и ОВ в абсолют-
ном движении будет:
____Pi __________ 2 Ч~ 2
<"к ai 2 — 2
(8.80)
Это передаточное отношение между звеньями ОВ и ВА не пред-
ставляет труда осуществить посредством планетарного зубчатого
механизма, приведенного на рис. 522.
Здесь центральное колесо с является неподвижным, а движение
на сателлит Ь, жестко связанный со звеном ВА, передается через
сателлит d, ось которого закреплена на кривошипе ОВ.
По известной формуле для планетарных механизмов, учитывая,
что центральное колесо с, является неподвижным, получим:
(8.81)
zc ____ wb ык __ l ।
*b '-“к wk '
где zb и zr-—числа зубцов колес b и с. Привлекая соотношение
(8.80), получим окончательно:
2с _ 2г
zb z— 2 ’
Для воспроизведения требуемого передаточного отношения / мо-
жет быть также использован планетарный механизм с внутренним
зацеплением зубчатых колес, изображенный на рис. 523,
466
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
В этом механизме неподвижное колесо с входит в зацепление
непосредственно с сателлитом Ь. Соотношение между числами зуб-
цов zc и zb колес с и b определяется при этом той же формулой,
как и в первой схеме.
На рис. 524 первая из рассмотренных схем представлена в полу-
конструктивном виде*). На схеме предусмотрев регулировочный рычаг 5,
имеющий целью закрепление неподвижного зубчатого колеса 4 в таком
Рис. 523.
Рис. 524.
положении, при котором обеспечивается правильное вхождение цевки 2
в паз креста 1. Этот рычаг жестко связан с неподвижным колесом 4,
и положение его регулируется с помощью стопорного устройства
в виде двух болтов, упирающихся концами в неподвижный стер-
жень 7.
На рис. 525 представлена фотография выполненной конструкции
по указанной схеме. Слева показан блок зубчатых колес; справа —
обратная сторона того же блока. Цевки выполнены в виде роликов,
вращающихся на пальцах, эксцентрично посаженных в торцах соот-
ветствующих валиков.
Возвращаясь к рис. 522, отметим, что при движении механизма
центр цевки А звена ВА будет описывать некоторую сложную кри-
вую а. Эта кривая по мере приближения к прямой OOt, соединяю-
щей оси вращения кривошипа ОВ и креста, удаляется от окруж-
ности аь описанной около центра О радиусом — R Ц- г. В резуль-
*) Описание этой конструкции см. в Mashine Design, 1951, № 4.
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 467
тате максимальная угловая скорость и максимальное угловое ускоре-
ние креста снижаются по сравнению с теми, которые получаются,
когда цевка А закреплена на кривошипе, вращающемся вокруг не-
подвижной оси О.
Для выяснения ограничений, накладываемых на выбор размеров
звеньев OB = R и ВА—г, найдем уравнение кривой а. Условимся
углы поворота а, р и ср звеньев ОВ, ВА и креста отсчитывать от пря-
мой ОО\ (рис. 523). Отметим, что при совпадении направления звена ОВ с
прямой ОО\, когда угол а = 0, звено В А наложится на звено ОВ,
т. е. будет р = к.
Рассмотрим положение механизма, определяемое текущим углом а
поворота звена ОВ, которому соответствует угол р поворота вто-
рого звена
Р = it уа, (8.82)
Уравнение траектории центра цевки А в параметрическом виде
будет:
х — R sin а — r-sin (уа), у = R cos а — г cos (уа). (8.83)
Примем расстояние между осями вращения звена ОВ и креста
OOi — 1 и обозначим S расстояние от центра Ot вращения креста
до торцов его пазов. Рассматривая момент входа цевки А в паз
креста (см. рис. 522), получим:
S=cosy, (8.84)
R4“r=sin Y' (8.85)
468 Синтез мальтийских механизмов [гл. vin
Последнее соотношение является основным, которому должны
удовлетворять размеры R и г звеньев ОВ и ВА.
Для отыскания радиуса кривизны р кривой а воспользуемся из-
вестным выражением дифференциальной геометрии:
dx2
Нас интересует положение входа цевки в паз и выхода из паза,
когда звено ВА является продолжением звена ОВ и, следовательно,
и
sin а, = — sin (/Я])
cos 04 = — cos (jO-i).
(8.86)
Учитывая, что по соотношению (8.85)
гл • я
R = sin----------г,
г
получим следующее выражение для радиуса кривизны рн кривой в
упомянутых положениях механизма через его параметры:
(8.87)
Разрешая это выражение относительно г, найдем квадратное урав-
нение:
Г2 (1 -j)2 - Г [2 sin (1 —у) + Рн (f - 1) ] +
+ siny (sin у— pJ = O. (8.88)
Оба корня (fi и о2) этого уравнения остаются положительными,
когда радиус кривизны рн принимает значения от 0 до X = /?-)- г, и
изменяются соответственно Г1—от X до о и г2 — от X . до X.
Более подробное исследование показывает, что больший корень г.2
уравнения (8.88) соответствует такой траектории а центра цевки /4,
которая имеет замкнутую петлю, как показано на рис. 526, и может
быть использована в схеме мальтийского механизма с внутренним
зацеплением цевки с крестом, которая рассматривается ниже.
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 469
обозначать через г без
внешнее зацепление цевки
Рассмотрим меньший корень rt (в дальнейшем
индекса), при котором
с крестом *).
мы его будем
обеспечивается
3°. Схема с внешним зацеплением цевки с
пазом креста
(рис. 522—523). Выбирая радиус кривизны рн и пользуясь уравне-
ниями (8.88) и (8,85), можно установить соответствующие значения
длин звеньев OB = R и ВА=г. Результаты подсчетов приведены
I в таблице 8.18, в которой все размеры даны в относительных вели-
| чинах по отношению к принятому ранее расстоянию между центрами
J вращения звена ОВ и креста OOt = 1.
Таблица 8.18
Длины звеньев О В = В и В А = г
z = 3 z = 4
Рв 0,04 0,08 0,12 0,04 0,08 0,12
г 0,0870 0,0693 0,0577 0,1133 0 0919 0,0771
в 0,7790 0,7967 - 0,8083 0,5938 0,’6152 0,6300
Для возможности входа цевки в паз креста радиус цевки ги
должен приниматься меньше радиуса кривизны рн траектории цен-
тра цевки в точке, соответствующей входу цевки в паз креста.
*) Внешним зацеплением цевки с пазом креста нами названо такое, когда
скорость центра цевки при входе в паз креста направлена к центру креста
(см. рис. 522), а внутренним, когда упомянутая скорость направлена от центра
креста (рис. 526).
470
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. Vtl|
Как видно из таблицы, при меньших длинах звена ВА=г допус-
тимы большие радиусы гц цевки, и наоборот.
Возвращаясь
(8.83), угол <р
откуда угловая
к рис. 523, устанавливаем, что, привлекая формулы
поворота креста можно определить по соотношению
, __ R sin « — г sin ja
° У 1 — R COS а -|- Г COS ja *
скорость креста
dv kt
(8.89)
(8.90)
где
ki =— jr2—R2--[-rR(l /) cos(l —y)a-[-Rcosa—jr cos /а,
1 I r2 I OS
— —- 2 —--------rR cos (I — j) a — R cos a -j- r cos /а,
da
a u>K = — угловая скорость ведущего кривошипа, которую счи-
таем постоянной.
Угловое ускорение креста будет:
dw ~|- kik$ g
е = ~dt~ W (°к'
2
(8.91)
(8.92)
где обозначено дополнительно:
(8.93)
k3 = rR (1 — j) sin (1 — /)а R sin a. — jr sin /а,
*4 = rR (1 — j'2) sin '1 — j)a~\~ R sin а— /2Г sin ja.
По формулам (8.90) и (8.92) легко установить, что <и(—а) = ш(а)
и е(—а) =— е(а). Таким образом, скорости и ускорения креста
достаточно рассчитать для первой половины времени деления (— at
=С а 0).
При а = 0 имеем е = 0 и, следовательно, максимальная скорость
креста о>тах определится подстановкой а = С) в соотношения (8.91)
и (8.90):
<8-94>
Аналитическое определение экстремальных значений ускорения
креста приводит к очень громоздким расчетам и поэтому представ-
ляется более целесообразным подсчет ускорения по формуле (8.92)
для ряда значений а с последующим графическим определением
экстремума.
Для определения ускорения ен в начальный момент движения
креста может быть получена более простая формула; подставляя в
выражение (8.92) а = 04 и учитывая соотношения (8.86), получим:
_ R + A (8.95)
7С
COS --
2
§ 25] уменьшение экстремальных значений угловых ускорений 471
На рис. 527 и 528 сплошными линиями показаны графики отноше-
ний и Для трехпазового креста, а на рис. 529 и 530 —
для четырехпазового креста, подсчитанные по указанным ранее со-
отношениям (8.90) — (8.92). Для сравнения там же нанесены
штрих-пунктиром графики отношений
четырехпазовых мальтийских меха-
низмов.
Графики свидетельствуют, что
рассматриваемая схема приводит
к значительному снижению макси-
мальных угловых скоростей креста
(это снижение для трехпазового
креста колеблется в пределах от 32
креста в пределах от 21 до 25%) и к еще более значительному
снижению по абсолютной величине экстремальных угловых ускорений
креста (это снижение на указанных графиках для трехпазового
креста колеблется в пределах от 58 до 67 %, а для четырехпазового
креста от 41 до 47%).
Силовой расчет этого механизма проводится аналогично уже разо-
бранному нами в § 24, 4°. Крутящий момент 7ИК на валу водила под-
считывается по формуле (8.33), где
11='Чк'Чпл-
(8.96)
О выборе величины к. п. д. мальтийского механизма т)к говорилось
выше, а к. п. д. планетарного механизма ijnjl следующим образом
472
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. VIII
выражается через передаточное отношение j от колеса b к водилу ОВ и
к. п. д. зубчатой передачи: для схемы на рис. 522
для схемы на рис. 523
Л
’ll+ 7-1
7]пл~->1з + j—Г
Если учесть, что, например, при четырехпазовом кресте по фор-
муле (8.80) имеем J = —3, то, принимая т]3 = 0,97, по приведенным
соотношениям найдем для обеих
схем
*1™ = °>96-
Величина среднего крутящего
момента на валу водила и значе-
ния перегрузки для предельных
значений коэффициента А определяются по формулам (8.35) и (8.40)
§ 24, 4°, причем для рассматриваемой схемы в этих формулах нужно
принять
и
; _ В — rj
«max —+ /
(см. формулу (8.94)).
Аналитическое определение максимального значения произведения
ike затруднительно и поэтому для отыскания его приходится под-
считывать i и kc в последовательных положениях механизма. Полу-
ченные таким путем предельные значения и0 и для трех- и
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 473
четырехпазового крестов и для рассмотренных выше радиусов кри-
визны рн сведены в таблицу 8.19.
Таблица 8.19
Величины перегрузок и0 и «со
Рн «0 Uoo 2 = 3 г = 4
0,04 1,97 2,07 0,08 2,10 2,26 0,12 2,20 2,42 0,04 1,80 1,80 0,08 1,87 1,88 0,12 1,93 1,96
Напомним, что « при обычных мальтийских механизмах с тремя
и четырьмя значениями: пазами коэффициенты и0 и ит выражаются следующими
трехпазовый крест иа = 3,23, иа = 4,11;
четырехпазовый крест = 2,41, ит =2,70.
Необходимо отметить, что величина средней мощности, потреб-
ной на поворот креста, также снижаемся при переходе от обычной
схемы к рассматриваемой вследствие более благоприятного хода
изменения угловой скорости креста.
Если принять, что к. п. д. мальтийского механизма рассматривае-
мой схемы мало отличается от к. п. д. механизма обычной схемы
и обозначить через
А?ср = ^ср^к . <8-97)
среднюю мощность, необходимую на поворот креста, то отношение
___________________________ ^ср обычной схемы
N
ср рассм. схемы
выразится значениями, приведенными в таблице 8.20.
Таблица 8.20
Значения отношения х
z = 3 2 = 4
Рн 0,04 0,08 0,12 0,04 0,08 0,12
А = 0 1,0 1,00 1,00 1,00 1,00 1,00
А = 0,1 1,72 1,63 1,55 1,14 1,12 1,11
А = 1,0 2,49 2,23 2,04 1,53 1,46 1,39
4 = 10 2,66 2,36 2,14 1,76 1,63 1,54
А = со 2,69 2,38 2,15 1,79 1,66 1,56
474
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. vut
Таким образом, при индивидуальном приводе мальтийского меха-
низма с трех- или четырехпазовым крестом переход от обычной схе-
мы этого механизма к рассматриваемой схеме может существенно
снизить требуемую мощность двигателя.
Составляющая Р силы, с которой цевка действует на паз креста,
направленная перпендикулярно к пазу, определится по формуле
(8.24), где следует положить гх = у ,
р
При отыскании максимума отношения выяснилось, что уже
для А 2^0,1 оно достигает наибольшей величины при угле а, близ-
ком к тому значению, которое соответствует экстремуму функции
. В результате просчета графиков этой функции и отыскания
У
на них экстремумов установлена следующая приближенная формула
! Р \
для определения значений при заданных z и р„:
\ /max ‘
(-^-)тах=ОТ + ЛА <8-98)
Величины коэффициентов т и п при выбранных рв для механиз-
мов с трех- и четырехпазовыми крестами сведены в таблицу 8.21.
Здесь же для сравнения приведены значения этих коэффициентов
для механизмов обычной схемы [столбцы (*)].
Таблица 8.21
Величины коэффициентов т и п формулы (8.98)
£ = 3 £ = 4
Рв 0.04 0,08 0,12 (•) 0,04 0,08 0,12 (*)
т п Ошибка при А == 0 > > Д^0,1 2,898 28,83 11% 1% 3,263 37,75 11% 1% 3,596 46,31 11% 0,3% 6,72 206,5 1,732 4,846 10% 2% 1,888 5,675 Ю»/о 2% 2,015 6,437 10% 2% 3,05 16,3
В двух последних строках этой таблицы показаны ошибки, полу-
чающиеся при использовании приближенной формулы (8.98). Наиболь-
шая ошибка получается при А — 0; при возрастании А погрешность
вычисления по формуле (8.98) быстро уменьшается. Для сравнения в
последней строке таблицы 8.21 дана величина погрешности при А 0,1.
Таблица 8.21 свидетельствует, что при прочих равных условиях
переход от обычной схемы мальтийского механизма к рассматривае-
мой приводит к резкому снижению величины Pmax максимального
давления на паз креста. Значения отношения
р
г max обычн. схемы
У=~Р----------------
л max рассм. схемы
25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 475
фиведены в таблице 8.22. Снижение Ртах в рассматриваемой схеме
обусловливается двумя причинами: увеличением плеча, на котором
[риложено это усилие, вследствие отклонения траектории центра
[евки от окружности и уменьшением динамических нагрузок вслед-
:твие снижения ускорения креста.
Таблица 8.22
Значения отношения у
г=3 | г=4
Рн 0.04 | 0,08 | 0.12 0.04 0,08 z 0.12
II II II II II 8з-“е° 2,3 4,7 6,7 7,1 7,2 2,0 3,9 5,2 5,4 5,5 1,9 3,3 4,3 4,4 4,4 1,8 2,1 2,9 3,3 3,4 1,6 1,9 2,6 2,8 2,9 1,5 1,9 2,3 2,5’ 2,5
Снижение величины Ртах должно благоприятно Сказаться в отно-
шении абразивного износа планок креста и может облегчить кон-
струкцию креста.
Существенное упрощение конструкции креста в рассматриваемой
схеме получается за счет резкого ссТкращения длины паза.
Если принять по-прежнему расстояние между центрами вращения
О и О{ ведущего кривошипа и креста за единицу, то длина h паза
при обычной схеме мальтийского механизма до/Гжна быть:
при числе пазов z— 3
при числе пазов г = 4
/г > 0,366гц,
h > 0,414 + гц,
при рассматриваемой схеме мальтийского механизма длина h паза
креста определится неравенством, которое легко получить по
522 *):
h>|cos J |+гц, (8.99)
где z—число пазов креста; R = OB— радиус ведущего кривошипа,
= В А — радиус вспомогательного кривошипа, гц — радиус цевки
как в приведенных выше соотношениях, так и в последнем со-
таошении).
Привлекая величины R и г из таблицы 8.18, получим для длины
паза креста значения, приведенные в таблице 8.23.
*) В формуле (8.99) знаки абсолютной величины в правой части поставлены
целью обобщения ее на схему с внутренним зацеплением цевки с крестом
«. подробнее ниже).
476
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ [гл. VIII
Таблица 8.23
Длина паза креста
2 = 4
Рн = 0,04 0,08 0,12 0,04 0,08 0,12
л> 0,192 0,227 0,251 0,188 0,231 0,260
Сокращение длины паза креста, уменьшая скольжение по нему
цевки, также должно благоприятно сказаться на абразивном износе
планок креста.
4°. Внутреннее зацепление цевки с пазом креста. Вернемся
к уравнению (8.88). Больший его корень г2 (ниже он обозна-
чается г) позволяет осуществить требуемое движение креста, ис-
пользуя внутреннее зацепление. Схема такого механизма показана
на рис. 526. Размеры звеньев г=ВА и R = OB, подсчитанные
по соотношениям (8.88) и (8.85) для трех значений ри, сведены в
таблицу 8.24.
Таблица 8.21
Длины звеньев г и R
2 = 3 2 = 4
Рн = 0,04 0,08 0,12 0,04 0,08 0,12
Г = 0,2283 0,2727 0,3110 0,2603 0,3017 0,3364
0,6377 0,5934 0,5551 0,4468 0,4054 0,3707
На рис. 527 и 528 пунктиром показаны графики угловых скоро-
стей и ускорений трехпазового креста, а на рис. 529 и 530 четырех-
пазового креста, подсчитанные по формулам (8.90) и (8.92). Макси-
мальная узловая скорость креста по-прежнему получается при а = 0
и подсчитывается по формуле (8.94).
Эта схема приводит к дальнейшему снижению максимальной
угловой скорости креста, а, следовательно, и среднего момента Д1ср
и средней мощности Ncp, необходимых на поворот креста. Значения
отношения
__ ^ср обычн. схемы
N
рассм. схемы
приведены в таблице 8.25.
Наибольшее угловое ускорение креста при этой схеме полу-
чается в начале движения и поэтому может быть определено по
формуле (8.95). Оно получается несколько выше, чем в схеме с
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 477
Значения отношения х
Таблица 8.25
2 = 3 2 = 4
Рн 0,04 0,08 0,12 0,04 0,08 0,12
л= о 1,00 1,00 1,00 . 1,00 1,00 1,00
А — 0,1 2,09 2,14 2,18 1,20 1,21 1,21
Д= 1 3,93 4,22 4,22 1,92 1,99 2,04
4 = 10 4,52 4,93 5,25 2,45 2,61 2,71
А =оо 4,60 5,03 5,36 2,55 2,72 2,84
внешним зацеплением. Однако иной характер изменения ускорен^
значительно снижает перегрузку
как показывает таблица 8.26.
Таблица 8.26
Величины перегрузок и0 и «со t
2 = 3 2 = 4
Рн 0,04 0,08 0,12 0,04 0,08 0,12
«0 1,55 1,44 1,40 1,51 1,46 1,43
«со 1,41 1,46 1,88 1,48 1,49 1,57
Максимальное давление цевки на паз креста Pwax имеет место
в начале движения креста и может быть подсчитано по формуле
(8.24) при подстановке в нее а = а1*). Полученные таким образом
значения коэффициентов т и и формулы (8.98), выражающей вели-
чину Ртах как функцию от А, сведены в таблицу 8.27.
В таблице 8.27 для сравнения приведены значения этих коэф-
фициентов для механизмов обычной схемы [столбцы (»)].
Таблица 8.27
Коэффициенты т и п формулы (8. 98)
2 = 3 2 = 4
Рн 0,04 0,08 0,12 (*) 0,04 0,08 0,12 (*)
tn 2,00 2,00 2,00 6,72 1,41 1,41 1,41 3,05
п 25,4 29,6 33,3 206,5 5,58 6,24 6,80 16,3
*) Это следует из монотонного вида функций ks и гх, входящих в фор-
мулу (8.24), на отрезке (0, а,).
478 СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ [гл. VIII
Значения отношения
р
г шах обычн. схемы
У ~р '
* max рассм. схемы
приведены в таблице 8.28.
Таблица 8.28
Значения отношения у
г = 3 <? = 4
рн 0,04 0,08 0,12 0,04 0,08 0,12
А = 0 3,4 3,4 3,4 2,2 2,2 2,2
А= 0,1 6,0 5,5 5,1 2,4 2,3 2,2
А = 1,0 7,8 6,7 6,0 2,8 2,5 2,4
А =10 8,1 7,0 6,2 2,9 2,6 2,4
А = со 8,1 7,0 6,2 2,9 2,6 2,4
Таблица 8.28 показывает, что рассматриваемая схема приводит
к еще большему снижению величины Ртах максимального давления
на паз креста, чем схема с внешним зацеплением. Снижение Ртак в
рассматриваемой схеме обусловливается увеличением плеча, на кото-
рое приложено усилие, и уменьшением динамических нагрузок в
результате снижения ускорений.
Длина паза креста в рассматриваемой схеме определится по фор-
муле (8.99), если принять по-прежнему расстояние между центрами
вращения ведущего кривошипа и креста 001=1,0. Привлекая вели-
чины R и г из таблицы 8.24, получим для длины паза h креста
значения, приведенные в таблице 8.29.
Таблица 8.29
Длина паза креста
z = 3 z — 4
Рн 0,04 0,08 0,12 0,04 0,08 0,12
0,091 0,179 0,256 0,106 0,189 0,259
В схеме с внутренним зацеплением цевки с пазом креста (см.
рис. 526) планетарный механизм для привода в движение вспомога-
тельного кривошипа ВА может быть конструктивно оформлен или
как изображено на рис. 522 (схема планетарного механизма с сател-
литом и с внешним зацеплением зубчатых колес) или как показано
на рис. 523 (схема планетарного механизма без сателлитов с внут-
ренним зацеплением зубчатых колес).
Таким образом, рассматриваемый мальтийский механизм с услож-
ненной схемой, включающей в себя планетарную передачу, обладает
рядом серьезных достоинств. Ему свойственны: 1) значительно мень-
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 479
шие по абсолютной величине экстремальные угловые ускорения креста,
что обеспечивает существенное снижение динамических нагрузок на
звенья механизма; 2) более благоприятный ход кривой угловых скоро-
стей креста, что обеспечивает заметное снижение средней мощности,
потребной на поворот креста; 3) снижение максимальных давлений
на планки креста, что должно оказывать заметное положительное влия-
ние на долговечность работы планок креста; 4) значительное сокраще-
ние необходимой длины паза, что упрощает и облегчает конструкцию
креста.
Все эти положительные стороны мальтийского механизма рас-
сматриваемой схемы выявляются тем резче, чем меньшее число иазов
Рис. 531.
имеет крест, т. е. чем меньше требуемое число делений. Практически
эту схему целесообразно применять при числе пазов креста 6.
Механизм с внутренним зацеплением цевки с крестом при прочих
равных условиях характеризуется лучшими параметрами, чем механизм
с внешним зацеплением.
В мальтийских механизмах рассматриваемой схемы как при внеш-
нем, так и при внутреннем зацеплении цевки с пазом креста веду-
щий кривошип и крест вращаются в противоположных направлениях
(см. рис. 522 и 526). Вследствие этого при заданном расстоянии
между центрами вращения ведущего кривошипа и креста габариты
механизмов рассматриваемой схемы с внешним и внутренним зацеп-
лениями отличаются весьма незначительно.
5°. Мальтийский механизм с кулачковым приводом ведущей
Цевки. Рассмотрим схему мальтийского механизма, изображенную на
рис. 531. Здесь цевка А может перемещаться вдоль ведущего кри-
480
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIH
вошипа, что позволяет с помощью кулачка с заставить двигаться
цевку по некоторой криволинейной траектории а. От вида этой
траектории зависит закон движения мальтийского креста. Поставим
следующую задачу: зная закон изменения ускорения креста, найти
Рис. 532.
уравнение траектории а, по кото-
рой должна двигаться цевка А,
при постоянной угловой скорости
ведущего кривошипа.
Обозначим по-прежнему углы
поворота кривошипа и креста со-
ответственно через а и <р (см.
рис. 532). Их абсолютные вели-
чины в момент начала зацепления
будут:
К К 7С
а1 = У-----z И <F1 = T’
Пусть заданный закон изменения
ускорения креста есть
Б
= *.=/(«)•
(8. 100)
Интегрируя дважды это выражение, найдем закон движения креста:
<p = F(a, С1; С2). (8.101)
Произвольные постоянные интегрирования и параметры функции/(а.)
найдутся по условиям
при a = — «1 <f —-----— и I == 0
и л
при a = a.j <р = —- и i — 0
(где, как и прежде, z= — L
Примем межцентровое расстояние OOj равным единице
значим через г переменное расстояние ведущей цевки от
вала кривошипа. Тогда
sin?
sin (a + <f) ’
Если в это выражение для г подставить у из уравнения
мы получим уравнение искомой траектории в полярных координатах
(а, г) с полюсом в О и полярной осью OOt.
Пример 1. Пусть задан следующий закон изменения ускоре-
ния креста
~ = k (a) = — A sin (8. 104)
(8. 102)
и обо-
центра
(8. 103)
(8.101),
§ 25] УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ УГЛОВЫХ УСКОРЕНИЙ 481
Интегрируя уравнение (8.104), получим:
ю ., ч . 2aj яа
— = I (а) = А - cos я I- С|.
ык ' ’ я 2аi 1
Из условия I (— а.]) = 0 следует, что С) = 0, и
i (Д- а,) = 0 также удовлетворяется. Интегрируя
получим:
. ./2аД“ . яз .
?(а) — + 'ДтГ) Sln 2ai“f~^s’
(8.105]
тогда условие
далее (8.105),
или после определения С2 из условия <у(—а,) =— •- :
<?(«)=/(-:*) |1 + sin ™
(8.106)
Наконец, используя последнее условие <р (Д-уД — Д- у, опреде-
ляем из (8.106) величину А:
А = ^- * (8.107)
или
(S.108)
Подставляя это значение А в уравнения (8.106), (8.105) и (8.104),
получим соответственно:
, , , я яа
'Р(а) = + ~ sin -g—,
тс ка
----—5 COS -г,---
z — 2 2а t
е , — 7CZ . тса
Д> ----- 7 Q\O SIH Q •
Ы2К (z — 2)2 2а!
* (8.109)
(8.110)
(8.111)
Из этих выражений определим экстремальные значения угловой
скорости и углового ускорения креста;
u>ma?1- - -— при а — 0 (8.112)
“к г —2
и
£ £ TtZ
-^-=^- = ±(7^77 при « = (8.ИЗ)
Графики функций <р, z и ks приведены на рис. 533.
По уравнениям (8.109) и (8.103) можно построить по точкам
траекторию ведущего пальца. Давая ряд значений а в интервале
16 И. И. Артоболевский
482
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
(—а, 0) *), найдем соответствующие значения <?, а затем и г. Необ-
ходимо отметить, что из формулы (8.103) нельзя получить значение г
в среднем положении г0, где
п 0
а = ср = 0 и г = -, поэтому в
указанном положении г опреде-
ляется по следующей формуле:
.. cos <р • i
0 я_0 c°s(a + <f)(! +0
Р-.0
= lim . (8.114;
a -.0 1 T 1
Для примера 1 получаем:
В разобранном примере
угловое ускорение креста в на-
чале и конце промежутка
деления изменяется скачками
и, следовательно, в механизме
имеют место мягкие удары,
как, впрочем, и во всех опи-
санных выше механизмах. В сле-
дующем примере рассматри-
вается механизм, осуществляю-
щий безударное зацепление
цевки с крестом.
Пример 2. Пусть угловое ускорение креста изменяется по еле
дующему закону:
kc (a) = — A sin a,
(8.116)
т. е. трижды обращается в нуль на угле деления: при a = — аь а = 0
и а = -ф- аь
График этого закона показан на рис. 534, в. По своему виду
он напоминает график изменения углового ускорения креста при
внешнем зацеплении, но существенно отличается от последнего
тем, что имеет нулевые ускорения в начале и конце периода деления.
*) В силу симметрии кривой г (а) относительно прямой а — и достаточно
исследовать изменение г на половине всего интервала изменения а.
§ 25]
УМЕНЬШЕНИЕ ЭКСТРЕМАЛЬНЫХ
ЗНАЧЕНИЙ .УГЛОВЫХ УСКОРЕНИЙ
483
Дважды интегрируя уравнение
7(—«1) = 0 и (—а, - ------1
(условие z(-j~a1) = O удов-
летворяется при этом),
лучим соответственно:
по-
= Z(a) =
“к
Cti « тс I
* Л л'/.с ___ П - I
(8. 117)
<Р (а) =
ai
Zs
A sin —
«1
“1
а:
А — - .
Z
(8.118)
Используя
условие
оставшееся
найдем:
(8.119)
или
4z
(г —2)2 • <SJ2°)
Заменяя в уравнениях (8.118),
нием по формуле (8.120), получим:
(8 I 16)
и используя условия
(8.117)
и (8.116) А его значе-
г ’
А
га1
А —
Т = у sin а 4- ~ , (8.121)
<Сг С, CZj
--=/ =—-T7V- (1 + cos — а), (8.122)
а>к z — 2 \ 1 ai ) 4
~ = k= 4* - sin — а. (8.123)
“к ‘ (г —2) «1 v '
Графики этих функций приведены на рис. 534. Экстремальные
значения угловой скорости и ускорения будут:
со 4
тах гх /с\
~ = ПР“ а = 0’ <8J24>
е 4z а,
-^-=±(737^- "Ри а=й=^-- <8-125)
16
484
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VH1
Траектория ведущей цевки определяется по уравнениям (8.121)
и (8.103). Радиус-вектор траектории цевки в среднем положении
(а ф 0) получим по формуле (8. 114):
4
Го— z4-2 ‘
(8.126)
Числовые значения радиуса-вектора траектории, подсчитанные по
формулам (8.103), (8.109) и (8.103), (8.121), даются в таблице 8.30.
Г а б л и ц а 8.30
Радиус-векторы траектории цевки
а 45" 40е 35° 30° 25° 20° 15° 10° 5° 0°
Пример 1 0,707 0,702 0,690 0,674 0,657 0,642 0,629 0,619 0,613 0,611
Пример 2 0,707 0,709 0,710 0,707 0,701 0,692 0,682 0,674 0,669 0,667
Приведем еще таблицу экстремальных значений угловой скорости
<°тах и углового ускорения ев креста, подсчитанную по формулам
(8.112), (8.113) и (8.124), (8.125) для трех-, четырех-, пяти- и
шестипазовых крестов.
Таблица 8.31
Экстремальные значения углового ускорения и угловой скорости креста
Z ен 2 =о Шшах о “max 2 “max 1
Еэо =э 2 — °н. SH О
3 31,4 12,0 9,42 1,73 6,47 4,00 3,14
4 5,40 4,00 3,14 1,00 2,41 2,00 1,57
5 2,30 2,22 1,74 0,73 1,43 1,33 1,05
6 1,35 1,50 1,18 0,58 1,00 1,00 0,785
В этой таблице значения <umax и еэ снабжены индексами 1 и 2,
указывающими, к какому примеру они относятся. Для сравнения здесь-
же приведены с индексом «о» значения <umax, ен и еэ для обычного
креста.
Как видим из таблицы, применение кулачкового привода веду-
щей цевки может оказаться целесообразным в случае малого
числа пазов креста. Рассмотренная схема может быть конструк-
тивно оформлена как изображено на рис. 531 или как изображено
на рис. 535. Ведущее звено а свободно радиально перемещается
в направляющих ступицы Ь, жестко скрепленной с ведущим валом
механизма. Эти радиальные перемещения звена а обеспечиваются
§ 26]
СОКРАЩЕНИЕ ВРЕМ!НИ ДЕЛЕНИЯ КРЕСТА
485
роликом с, который постоянно скользит в пазу дискового кулачка d.
Цевка е, которая приводит в движение крест g, закреплена на звене а.
На этом мы закончим рассмотрение схем мальтийских механизмов,
дающих возможность понизить угловые ускорения креста. Однако
в следующей главе при рассмотрении механизмов, сокращающих
время деления креста, выявляются также и экстремальные значения
угловых ускорений.
§ 26. Схемы мальтийских механизмов, позволяющие сократить
время деления креста
1°. Механизмы с промежуточной зубчатой передачей между
мальтийским крестом и периодически проворачиваемым звеном
машины. Схема такого механизма уже была рассмотрена в § 25, 1°
и показана на рис. 521. Эта же схема может быть применена, когда
при заданном числе Z позиций периодически проворачиваемого звена
и заданном времени остановки на каждой позиции требуется полу-
чить меньшее время tt деления по сравнению с тем, которое обеспе-
чивается мальтийским механизмом, у которого крест имеет число z
пазов, равное заданному числу позиций (z = Z). Если, например,
заданное число Z позиций проворачиваемого звена Z —9, то, исполь-
зуя для его периодического движения мальтийский механизм, у кото-
рого крест имеет то же число пазов z — Z = 9, получим время
деления tx = ktn = 0,64 tQ (см. табл. 8.1).
Если для делительных перемещений упомянутого звена применить
мальтийский механизм, у которого крест имеет число пазов z=4,
включив между этим звеном и крестом зубчатую передачу с пере-
486
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VIII
z 4
даточным отношением i = — -д-, то время деления уменьшится до
tf = 0,33 /0, т. е. почти наполовину.
Таким образом, для сокращения времени деления нужно применять
крест с числом пазов z, меньшим числа заданных позиций (z%Z).
Однако сокращение времени деления влечет за собой возраста-
ние угловых ускорений проворачиваемого звена.
Для количественной оценки снижения времени деления и воз-
растания угловых ускорений обратимся к формулам (8.76) и (8.77)
из § 25, 1°. Подсчитанные по этим формулам значения ит и и,
для ряда значений z и Z сведены в таблицу 8. 32.
Таблица 8.32
Коэффициенты ит и ие в случае z <7
Z Z ,7Г ие
15 3 0,26 54
15 4 0,44 10
15 5 0,56 4,6
15 6 0,65 3,0
12 3 0,28 46
12 4 0,47 8,6
12 5 0,60 4,0
12 6 0,70 2,t>
10 3 0,30 39
10 4 0,50 7,3
10 5 0,64 3,4
10 6 0,75 2,2
8 3 0,33 30
8 4 0,56 5,6
8 5 0,71 2,6
8 6 0,83 1.6
6 3 0,40 18
6 4 0,67 3,4
6 5 0,86 1,6
Из таблицы 8.32 следует, что при числе заданных позиций Z — 8,
12 или 15 периодически проворачиваемого звена использование маль-
тийского механизма с числом пазов на кресте z= 3 позволяет умень-
шить время t) деления (при неизменном времени остановки) соот-
ветственно на 67, Is! или 74%, но при этом экстремальное угловое
ускорение проворачиваемого звена возрастает по абсолютной вели-
чине соответственно в 30,46 или 54 раза.
Если при том же числе Z заданных позиций проворачиваемого
звена использовать мальтийский механизм с числом пазов на кресте
z = 4, то время tx деления (при неизменном времени /0 остановки)
уменьшится соответственно на 45,53 или 56%, но при этом экстре-
мальные угловые ускорения проворачиваемого звена возрастут всего
лишь СООТ1 етственно в 5,6; 8,6 или 10 раз,
§ 26] СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА 487
Отсюда понятно, что, стремясь к уменьшению времени деления и
выбирая с этой целью мальтийский механизм с числом z пазов, мень-
шим числа Z заданных позиций проворачиваемого звена, нельзя не
учитывать связанное с этим возрастание угловых ускорений звена.
2°. Мальтийский механизм с приводом от эллиптических зубча-
тых колес. Сократить время деления мальтийского механизма при ука-
занном времени остановки на каждой позиции можно путем задания кри-
вошипу с цевкой неравномерного вращения. Для этого между распре-
делительным валом соответствующей машины, вращающимся с постоян-
ной угловой скоростью, и ведущим кривошипом мальтийского механизма
следует включить соответствующую передачу с переменным переда-
точным отношением.
В качестве такой передачи используются, например, некруглые
зубчатые колеса, центроиды которых имеют форму равных эллипсов.
Каждое из колес пары вращается вокруг одного из фокусов своей
центроиды.
До сих пор известны только единичные примеры применения эл-
липтических зубчатых колес в схемах мальтийских механизмов, пред-
назначенных для осуществления делительных перемещений в металло-
режущих автоматах. Объяснялось это полной неразработанностью во-
просов теории и практики технологии некруглых зубчатых колес.
В настоящее время теория этих вопросов существенно продвинута
вперед [36] и разработаны простые приспособления для нарезания этих
колес методом обката на серийных зубофрезерных станках. Таким
образом созданы предпосылки для широкого внедрения некруглых
зубчатых колес в практику конструирования машин.
Займемся установлением того, насколько можно изменить условия
работы мальтийского механизма посредством включения в схему эл-
липтических зубчатых колес.
В главе III уже указывались основные соотношения между пара-
метрами эллиптических колес и приводилось уравнение их профиля
в полярных координатах (см. уравнения (3.67)).
Углы поворота ведущего 1 и ведомого 2 эллиптических колес
(рис. 536) обозначим соответственно через а и at и условимся отсчи-
тывать их от прямой OOi, соединяющей их оси вращения. В этих
обозначениях формула (3.85), связывающая указанные углы поворота
эллиптических колес, принимает следующий вид:
tgT = (T=f)tgT: (8Л27)
обозначив постоянный коэффициент
= (8.128)
получим:
х “1 . а
tg-g- —rttg^- ..
(8.129)
488
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[ГЛ. VIII
Эллиптическое колесо 1 жестко посажено на распределительный
вал машины; на одном валу с эллиптическим колесом 2 жестко наса-
жен кривошип А мальтийского механизма. Угол поворота кривошипа
будет равен углу 04 поворота колеса 2.
Угол поворота креста условимся отсчитывать от прямой О|ОК,
соединяющей оси вращения колеса 2 и мальтийского креста. Тогда
угол в функции от угла поворота кривошипа а, определится по
формуле (8.14):
где по-прежнему обозначено
sin — = А.
г
Выражая функции sin а, и cos 04 через tg а,, получим:
tg<p = —------------ (8.131)
4Л1—tg2<4 —X. v
Используя соотношение (8.129), установим следующую зависи-
мость между углом поворота креста мальтийского механизма и
углом а поворота распределительного вала машины:
2лХ tg-?
tg ? = ------------------ , (8 132
l-X + n41 + X)tg2|
откуда получаем квадратное уравнение относительно tg^-:
/г2(1 + х)fg¥ 1ё’ 2/zXtg * +(1 —^)tg<? —0. (8.133)
§ 26]
СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА
489
Началу и концу движения креста соответствует угол <р ==•+ " и,
следовательно,
„ Х
tg <PH = tg-= pqTTxs. (8.134)
При подстановке этого значения в последнее уравнение должен
отыскаться угол а = ан поворота распределительного вала машины,
соответствующий началу вращения креста. Так как дискриминант урав-
нения (8.133) при подстановке ф = <рн = — дает *
4/i2X2 — 4/z2 (1 — X2) tg2 <р„ = О,
ю получаем один корень:
>8135>
Угловая скорость = ш креста в функции от угла а поворота
da *
распределительного вала и его угловой скорости — = шк, которую
будем считать постоянной, выразится:
dtp
(1 — X)[ (1 — X) — л2 (1 + X) ] tg2-S-— и2 (1 -|-X) tg4 “
=-----------------------------:— ------------------- иХсок. (8.136)
(1 - W + 2л! (1 + X2) tg2 у + (I + X)2 tg’ у
Легко убедиться, что при а = ан получим и> = 0, что соответствует
условию безударного зацепления цевки кривошипа с крестом.
Угловое ускорение креста будет:
nh ^D+Etg2-|--4-Ftg4 y + Gtgey) tgy
^ + Btg2-“- + Ctg44y
। де введены обозначения:
A = (l-X)2,
В —2п2(1 4-Х2),
С=п4(1 +^>
G = (l-X)[(l -X)2-и2(3 4-Х2)],
£ = (1 —X) [Д — 4ЧХ2— 5д2(1 — X2) —2С],
F = [С — 5 п1 (I — X2) — 2А — 4«2Х2] л2 (1 4- X),
G = [С—- 4/z2X2 — Зл2 (1 — X2) ] №(1 4- X).
(8.137)
(8. 138)
1
490
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VHI
Из условия е = 0 получаем, что экстремальное значение угловой ско-
рости и креста будет при а = 0; более подробный анализ показы-
вает, что при а = 0 угловая скорость w креста достигает максималь-
ного значения, которое определяется по формуле
U>max = f^. (8.139)
Подставляя в формулу (8.137) значения а = ан, определенное из со-
отношения (8.135), можно подсчитать угловые ускорения ен маль-
тийского креста в начале и в конце его перемещения.
Условие — 0 приводит к следующему уравнению для отыскания
тех значений угла аэ, которым соответствуют экстремальные значе-
ния угловых ускорений еэ мальтийского креста:
«о + «I у У as tg4 у + ал tg6 -| + fg8 у + «в tg10 у = 0 > (8.140)
где обозначено:
atl = AD,
а, = 3 (АЕ — BD),
с, = 5AF — BE — 1CD,
а-л = 7AGBF -—5CE,
ai — ‘i(F>O — CF},
а5 — — СО.
(8.141)
Уравнение имеет только четные степени аргумента tg | , поэтому
может быть понижено до пятой степени. В исследуемых нами интер-
валах 3=СгУ 15 и 0geg0,6 уравнение (8.140) на отрезке —
eg a sg ан имело два действительных корня +- tg , которые при под-
становке в формулу (8.137) дают экстремальные значения углового
ускорения ±еэ мальтийского креста.
В таблицах 8.33, 8.34 и 8.35 приведены параметры, определяю-
щие кинематику креста мальтийского механизма при включении в схему
последнего эллиптических колес, эксцентриситеты которых соответ-
ственно е = 0,2; е = 0,4 и е = 0,6. Подсчет этих параметров прове-
ден по указанным выше формулам.
Анализ данных, содержащихся в таблицах, позволяет сделать ряд
заключений.
Таблицы прежде всего свидетельствуют, что эллиптические ко-
леса позволяет существенно снижать отношение k — т. е. позво-
*0
ляют существенно сокращать время деления tt при заданном вре-
мени t0 остановки. Например, при переходе от обычной схемы маль-
§ 26]
СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА
491
Таблица 8.33
Параметры, определяющие кинематику креста мальтийского механизма при
включении в схему последнего эллиптических колес с эксцентриситетом е = 0,2
Z “max £н еэ “к “э 2Щ 2а0 шгпах радиан Ен«В радиан радиан к=г Ч)
“к
3 9,69 + 3,61 4- 73.50 3'10' 40°32» 319°28' 54,03 + 112,2 + 228,5 0,127
4 3,62 + 1,90 + 12,24 7’42’ 61'44' 298'16' 18,8-1 + 51.49 + 331,7 0,207
5 2,14 + 1,28 + 5,22 11’26' 75W 284'56' 10,64 + 31,65 -1-129,1 0,263
6 1.50 + 0,964 + 3,06 14°38* 84'12' 275г48' 7,22 + 22,34 + 70,90 0,305
8 0,930 I- 0,640 -1- 1,53 19’36' 96W 263'56' 4,28 + 13,58 + 32,47 0,364
9 0,780 + 0,547 1.25 21W 100°04' 259'56' 3,54 + 11,26 + 25,72 0,381
10 0,671 + 0,478 + 1,03 22’34' 103°24' 256'31’ 3,00 + 9,58 + 20,65 0.403
12 0,524 -4- 0,380 +- 0,758 24'54' 108°24' 251'36' 2,30 4 7,33 + 14,61 0,431
14 0,429 + 0,316 + 0,597 26°38’ П2°00* 248W 1,86 + 5,92 + 11,18 0,452
15 0,394 +- 0,291 + 533 270’20' 113'28' 246 32' 1,70 ± 5.39 + 9.87 0,460
Т а б л и ц а 8.34
Параметры, определяющие кинематику креста мальтийского механизма при
включении в схему последнего эллиптических колес с эксцентриситетом е = 0,4
Z штах ен “к £Э “к 2«! 2а0 штах/о радиан ен <5 радиан радиан *4- чг
“к
3 15,08 + 8,43 + 171,3 2'02' 26е12' 333°48’ 87,86 + 286,1 + 581,4 0,078
4 5,63 + 4,23 + 29,74 4 51' 4О°16’ 319-44' 31,41 + 131,7 4 926,1 0,126
5 3,33 + 2,93 +~ 13.81 7е 16' 49° 16' 310-44» 18,06 + 86,17 -1 406,2 0.155
6 2,33 + 1,99 + 7.45 9е 14' 55'36' 304°24» 12,38 + 56,18 + 210,3 0.183
8 1,45 + 1,26 + 3,82 124)2' 63°56’ 296°04' 7.4) + 33,64 + 102,0 0,216
9 1,21 + 1,04 + 2,96 13с02' 66°48’ 293°12' 6,1!) + 27,23 +- 77,5 0,228
10 1,04 + 0,913 + 2,50 13'52' 69° 12' 29048' 5.2S + 23,52 + 64,4 0,238
12 0,815 + 0,711 + 1.79 15°08' 72'48' 287°12’ 4,08 + 17,86 + 45,0 0,253
14 0,668 + 0,579 + 1.44 16°04’ 75'28' 284-32' 3,32 + 14,28 + 35,5 0,265
15 0,613 + 0,530 ± 1,28 16°28» 76с32' 283°28' з,оз + 12,97 + 31,3 0,270
Таблица 8.35
Параметры, определяющие кинематику креста мальтийского механизма при
включении в схему последнего эллиптических колес с эксцентриситетом е = 0,6
Z “max ен <4 £э «4 “э 2й! 2«0 “rnax^i радиа I гн/о радиан э 0 радиан * = 7*- *0
“к
3 25,85 + 24,42 + 499,5 1°|2» 15'20' 344е40' 155,5 + 883.8 + 180,77 0,044
4 9,65 + 11,93 + 87,76 2г50' 23’40' 336'20' 56,68 + 411,1 + 302,4 0,070
5 5,70 + 7,56 + 37,37 4° 14' 29W ЗЗО°56' 32,95 4 252,2 + 124,7 0,088
6 4,00 + 5.41 + 21,94 5'20' 32°52' 327’08' 22,84 + 176,5 + 715,2 0,100
8 2,48 + 3,34 + 11,34 6'58' 37'56' 322°04' 13,95 + 105,6 + 358,3 0.118
9 2,08 + 2.78 + 8,92 7°30' 39'44' 320" 16' 11.62 + 87,00 + 278,7 0,124
10 1,79 1 2,38 + 7,41 7'55' 41'12' 318'48' 9,93 + 73,59 + 229,5 0,129
12 1,40 + 1,82 + 5.39 8С38' 43°24' 316’36' 7,72 + 55,72 + 164,5 0,137
14 1,14 + 1,48 + 4.23 9°08' 45°08' 314’52' 6,29 + 44,54 + 127,7 0,143
15 1,05 + 1.34 ± 3,81 9с20' 45’48' 314’12' 5,76 + 40,41 ±114.7 0,146
тийского механизма к схеме с эллиптическими колесами, эксцентри-
ситет которых е = 0,6, время деления при неизменном времени /(|
остановки сокращается в четыре-пять раз.
492
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
(гл. VIII
Абсолютные величины угловых ускорений креста при том же
времени t9 остановки и том же отношении k — при схеме С эллип-
Ч)
тическими колесами оказываются значительно меньшими, чем в обыч-
ном мальтийском механизме или в
Рис. 537.
схеме мальтийского механизма
с промежуточной зубчатой пе-
редачей (см. § 26).
Например, если при k —
= ф- = 0,2 в обычном маль-
'0
тийском механизме с числом
пазов креста z = 3 экстремаль-
ное угловое ускорение опре-
деляется величиной =
— ± 860 радиан (см. таблицы
8.1 и 8.3), то при схеме с эл-
липтическими колесами, когда
е = 0,2, г = 4 и k = ~=-
= 0,207 (см. таблицу 8.33),
то же ускорение определяется
величиной е9£* * = 331,7 радиа-
на, а когда е = 0,4, г=1
и k= ~ = 0,201 (см. табли-
*о
цу 8.34), то же ускорение
определяется величиной est20 =
= 139,5 радиана.
3°. Планетарная передача.
В § 25, 2° были рассмотрены
схемы планетарных механиз-
мов для привода мальтийского креста с числом пазов 3 или 4.
Эти же планетарные механизмы могут быть использованы для привода
креста с большим числом пазов, если отказаться от условия, чтобы в
начальный момент водило ОВ и кривошип АВ (рис. 537) составляли
одну прямую линию. Тогда в качестве начального значения угла а
может быть взято какое-то значение а*, отличающееся от прежнего
04. Соответственно, и скорость точки А в этот момент будет направ-
лена не к центру О1г а к некоторой точке О,, в которой и следует
расположить центр нового креста. Найдем соотношение, связывающее
новое число г* пазов креста и соответствующий ему угол деления 2а*.
Из уравнения (8.83) траектории цевки А, ведущей мальтийский
крест, нетрудно' получить следующее выражение для тангенса угла у
наклона касательной к траектории:
tg — /? sin а + jr sin /а
° * R COS a — jr COS ja
(8.142)
§ 26]
СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА
493
Для того чтобы скорость ведущей цевки А была направлена
в момент начала деления вдоль паза креста и тем самым исключа-
лись жесткие удары при входе цевки в паз, должно быть
—V- <8-143>
tg
z
Сравнивая соотношения (8.142) и (8.143), получим следующее
уравнение для отыскания угла а* (в котором обозначено tg - —т):
Z
niR sin а* — tnjr sin /а* jr cos /а’ — R cos a* = 0. (8.144)
Все вышеизложенное в этом параграфе можно отнести и к механизму
с внутренним зацеплением (см. § 25, 4°). Значение угла а* по урав-
нению (8.144) находится методом последовательных приближений;
однако это вычисление значительно упрощается в силу того, что
около положения водила а. = а, малым изменением угла а соответ-
ствуют значительные изменения угла -у.
Обратимся в качестве примера к планетарному механизму четы-
рехпазового (а] = 45°) мальтийского креста, рассмотренного в § 25, 2°.
Для значения радиуса кривизны рн = 0,08 траектории ведущей
цевки в момент начала движения мы получили следующие размеры
водила R и кривошипа г планетарного механизма:
Механизм с внешним
зацеплением
/? = 0,615 24
г = 0,091 87
Механизм с внутренним
зацеплением
R = 0,405 42
г = 0,301 69
(8.145)
Для этих планетарных механизмов были определены значения
угла поворота водила а, в момент начала зацепления ведущей цевки
с крестом в случае использования их для привода в движение кре-
ста с числом пазов z^=6, 8, 10, 12.
Результаты подсчета по уравнению (8.144) для случаев внешнего
и внутреннего зацепления сведены в таблицу 8.36. Здесь же для
сравнения приведены значения угла а( в случае простого мальтий-
ского механизма с внешним зацеплением.
Т а б л и ц а 8.36
Значения угла а, для трех типов мальтийских механизмов
Z 4 6 8 10 12
Г внешнее зацепление 45 48'40' 50 48' 52е 17' 53 25'
“1 внутреннее зацепление 45 42с34' 41'18' 40'8 Г 39'58'
( простая схема 45 60600’ 67 30' 72 00' 75'00'
494
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
|гл. VIII
Как видно из таблицы, значения половины угла деления в обеих
схемах значительно ниже, чем при обычной схеме. Это приводит
в свою очередь к еще большему снижению коэффициента k времени
работы мальтийского механизма. Значения этого коэффициента для
случаев внешнего и внутреннего зацепления, а также для обычной
схемы приводятся в таблице 8.37.
Табл и ц а 8.37
Значения коэффициента времени работы t для трех типов
мальтийских механизмов
г 4 6 8 10 12
Г внешнее зацепление 0,33 0,37 0,39 0,41 0,42
k < внутреннее зацепление 0,33 0,31 0.30 0,29 0,28
1 простая схема 0,33 0,50 0,60 0,67 0,71
Подсчет угловых скоростей и ускорений креста может и в этом
случае проводиться по формулам (8.90) и (8.92) § 25, 2°, в которых
нужно г и R привести к новому межцентровому расстоянию L,
так как при выводе формул (8.90) и (8.92) было принято, что меж-
центровое расстояние ОО| = 1.
Найдем координаты (х1; ведущей цевки в момент начала
зацепления (см. рис. 537):
Xi = R sin а* — г sin /а*, _y1 = Rcosa®— г cos уа*; (8.146)
отсюда новое межцентровое расстояние L будет
Z. =>, 4- xt ctg у.
(8.147)
Подставляя в формулы (8.146) и (8.147) значения R и г из (8.145),
а из таблицы 8.36 значения а* для соответствующих г, получим таб-
лицу 8.38 межцентровых расстояний.
Таблица 8.38
Межцентровые расстояния L для трех типов мальтийских механизмов
г 4 6 8 10 12
L внешнее зацепление внутреннее зацепление 1 1 1.371 62 1.371 54 1,724 07 1.723 37 2.069 86 2,067 93 2,412 76 2,409 05
Если считать по-прежнему'£= 1, в формулы (8.90) и (8.92) сле-
дует подставить новые значения длины водила OB—R' и кривошипа
§ 26] СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА 495
ДВ=г’, связанные с указанными в (8.145) значениями R и г фор-
мулами:
и г'=£. (8.148)
В этих формулах следует брать значения L из таблицы 8.38 для
соответствующего вида зацепления и требуемого числа пазов креста.
Указанные значения R' и г' приведены в таблице 8.39.
Таблица 8.39
Пересчитанные размеры звеньев /?' и г'
г 4 6 8 Ю 12
Внешнее зацепление г = 0,081 87 0,066 98 0,053 29 0,044 38 0,038 08
/? = 0,61424 0,448 55 0,356 85 0,297 24 0,254 99
Внутреннее зацепление г = 0,301 69 0,219 96 0,175 06 0,145 89 0,125 23
R = 0,405 42 0,295 59 0,235 25 | 0,196 05 0,168 29
Подставляя эти значения г и R в формулы (8.94) и (8.95)' най-
дем максимальную угловую скорость креста и начальное угловое
ускорение. Экстремальные угловые ускорения по-прежнему находятся
просчетом ряда точек кривой ускорений с последующим графическим
отысканием экстремума.
Результаты этих подсчетов приведены в таблице 8.40.
Таблица 8.40
Кинематические параметры
Z 6 8 10 12 \
“>т “к (внешн.) (внутр.) 1,050 1,034 0,742 0,809 0,576 0,667 0,472 0,568
ен (внешн.) 1,31 0,902 0,664 0,514
2 (внутр.) 3,00 2,24 1,77 1,47
Еэ (внешн.) 1,63 1,15 0,880 0,710
2 (внутр.) 3,00 2,24 1,77 1,47
496
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
[гл. VH1
- Необходимо отметить также, что для механизмов настоящего
параграфа еще более сокращается длина h паза креста, которая,
как нетрудно установить, равна:
h — \S~ (L — (8.149)
где
S=-^i— (8.150)
sin —
2
— расстояние от центра креста до торцов его пазов.
В формуле (8.149) берется абсолютная величина правой части,
так как имеем для внешнего зацепления
S>L — R + r,
а для внутреннего
S<L — R-\-r.
Результаты просчетов длины паза сведены в таблицу.
Таблица 8.41
Длина паза креста
г 6 8 ю 12
* 1 внешн. | внутр. 0,130 0,176 0,091 0,154 0,070 0,135 0,058 0,120
4°. Кулачковый привод ведущей цевки. В § 25, 5е было показано,
как выбрать профиль кулачка (т. е. траекторию ведущей цевки), чтобы по-
лучить наперед заданный закон изменения угловых ускорений мальтий-
ского креста. В рассмотренных примерах 1 и 2 было дано решение задачи
о воспроизведении косинусоидального и синусоидального закона уско-
рений в предположении, что время деления такое же, как и у обыч-
но! о мальтийского механизма, т. е. когда угол поворота кривоши-
па 2сХ1, соответствующий делительному перемещению креста, равен:
1 2
Считая в формулах (8.107) и (8.119) для максимальной амплитуды А
углового ускорения угол aj произвольным параметром, получим
для креста с заданным числом пазов целую гамму механизмов, вос-
производящих одинаковый по характеру закон изменения ускорений
и отличающихся коэффициентом времени работы k — -, а следова-
«О
тельно и максимальными ускорениями А.
§ 261
СОКРАЩЕНИЕ ВРЕМЕНИ ДЕЛЕНИЯ КРЕСТА
497
Подставляя из формул
ственно в (8.106), (8.105),
получим следующие законы
рости и углового ускорения
а) для первого примера
(8.107) и (8.119) значения А соответ-
(8.104) и в (8.118), (8.117), (8.116),
изменения угла поворота,
мальтийского креста:
угловой ско-
откуда
6>max
2га,
-- sin
z
Tt®
2га,
ла
2а,
ла
C0S 2а, ’
ла
, SIH к~
4га; 2а,,
(при а = 0),
(8.151)
(8.152)
«Г — 4га?
К к
б) для -второго примера
(при
(8.153)
откуда
sin — а
«1
co Л / I r.
— = — 1 - - COS -
га, \ 1 a,
e л2
co2 га2
sin — а,
®тах
2г.
га.
(при а = 0),
2/’
(8.154)
(8.155)
(8.156)
здесь ен = 0 (при а - а-i).
Уравнение траектории ведущей
теоретического профиля кулачка) находится так же, как в § 25, 4°.
Необходимо отметить, что по формуле (8.103) мы получаем вели-
чину г относительно межцентрового расстояния L, которое в> настоя-
щем случае определяется по формуле
£ —g sin(ai + ?i)
sin а, ’
цевки (или,
ЧТО то
же, линии
W
%
%
~ га?
а
а
при а — +-
где S определяется по (8.10). Радиус-вектор траектории в среднем
положении (а = 0) найдем по формуле (8.114). Получим для первого
примера
г° Г.® ф- 2za,
(8.157)
11
500
СИНТЕЗ МАЛЬТИЙСКИХ МЕХАНИЗМОВ
(ГЛ. VIII
и для второго примера
2 г.
Г° 2г. ф- га, ’
(8.158)
Таким образом, для любого из рассматриваемых механизмов r0<^ 1,
и следовательно, для креста с любым числом пазов (г ^>2) теорети-
чески возможно осуществить заданные законы изменения угловых
ускорений креста с наперед выбранным коэффициентом времени его
работы.
Возникающие при этом максимальные угловые скорости и ускоре-
ния легко подсчитываются по формулам (8.152), (8.153) и (8.155),
(8.156). На рис. 538, 539 приводятся графики величин
Ютах j /
для первого примера в функции от коэффициента k времени деления
креста, который связан с половиной угла деления следующей
зависимостью: ,
(8.159}
На рис. 540, 541 эти графики приводятся для второго примера
(на рис. 538 и 540 величина wmax обозначена через wm).
Графики даны для мальтийских крестов с числом пазов 3, 4,
6 и 8. Для сравнения точками отмечены значения и Е’ в схемах
“к “к
с круговым движением ведущей цевки для значений коэффициента k,
соответствующих данному числу пазов.
ЧАСТЬ ТРЕТЬЯ
ТЕОРИЯ ПРИБЛИЖЕННЫХ МЕТОДОВ СИНТЕЗА
МЕХАНИЗМОВ
А. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ
ГЛАВА IX
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
§ 27. Теория приближения функций и связь ее с .задачами
приближенного синтеза механизмов
1 . Задача о приближении функций как основа аналитических
методов синтеза механизмов ,с низшими парами. При помощи
механизмов с низшими парами выполняются весьма разнообразные
законы движения ведомых звеньев. Однако из обширного круга
задач, связанных с их синтезом, можно выделить две наиболее рас-
пространенные задачи: воспроизведение заданных перемещений ведо-
мого звена (синтез передаточных механизмов) и воспроизведение
заданной траектории (синтез направляющих механизмов). Примерами
синтеза передаточных механизмов могут служить задачи о синтезе
механизмов с равномерным движением ведомого звена, которые при-
меняются в указательных приборах, строгальных станках и вытяжных
прессах. Кроме равномерного движения, для ведомого звена могут
быть заданы и более сложные законы движения. Таковы, например,
задачи о синтезе механизмов двигателей, грохотов, конвейеров, сор-
тировок, самонакладов, исполнительных механизмов машин-автоматов,
механизмов подачи и многих других. Наконец, к задачам о синтезе
передаточных механизмов сводятся задачи синтеза механизмов для
выполнения математических операций, применяемых в счетно-решаю-
щих устройствах и в приборах для управления артиллерийским огнем,
а также задачи синтеза механизмов для получения равномерных шкал,
применяемых в приборах с упругими чувствительными элементами.
Примерами синтеза направляющих механизмов могут служить
задачи о синтезе прямолинейно-направляющих механизмов, применяе-
мых в приборах, механизмов с остановками, применяемых в маши-
нах-автоматах, грейферных лентопротяжных механизмов, некоторых
механизмов подъемных кранов, механизмов перемешивающих устройств,
механизмов для обработки фасонных изделий и других механизмов.
502
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Теоретически точное воспроизведение заданных перемещений
ведомого звена или заданной траектории при помощи плоских меха-
низмов с низшими парами удается только в отдельных частных случаях.
В главе VI собраны наиболее важные механизмы, которые теоре-
тически точно воспроизводят некоторые заданные функциональные
зависимости между углами поворота звеньев и некоторые простей-
шие кривые.
Однако в большинстве случаев синтез механизмов с низшими
парами сводится к нахождению таких механизмов, которые обеспе-
чивают только приближенное воспроизведение заданной функции.
Заметим, что вследствие неизбежных погрешностей в изготовле-
нии механизма, упругости его звеньев, зазоров в кинематических
парах и других причин действительная функция, воспроизводимая
механизмом, всегда отличается от теоретиче-
о. ски предполагаемой; поэтому при синтезе
/ механизмов нет смысла добиваться воспроиз-
/ ведения заданной функции с точностью, из-
•" I лишней по сравнению с допускаемой.
/ I Можно показать, что аналитическое ре-
/ I шение задачи синтеза механизмов в такой
/ I постановке представляет собой известную в
Д, /у математике задачу о приближении функций,
которая заключается в том, что заданная
Рис. 542. функция приближенно заменяется другой
функцией, мало от нее отличающейся.
Обозначим заданную функцию, которая должна быть воспроизве-
дена механизмом, через
y = F(x).
В задачах синтеза передаточных механизмов функция у есть тре-
буемое перемещение ведомого звена (или величина ему пропорцио-
нальная), а х — перемещение ведущего звена (или величина ему
пропорциональная). Например, в шарнирном четырехзвеннике ABCD
переменные х и у должны быть соответственно пропорциональны
углам поворота звеньев АВ и CD (рис. 542). В задачах о воспро-
изведении заданной траектории х и у суть координаты точек кривой,
которая должна точно или приближенно совпадать с траекторией ка-
кой-либо точки на шатуне (например, точки М на шатуне шарнир-
ного четырехзвенника).
Как уже указывалось, в общем случае проектируемый механизм
воспроизводит заданную функцию лишь приближенно. Обозначим
функцию, воспроизводимую механизмом, через
y — FM(x).
Вид этой функции зависит от параметров кинематической схемы.
К параметрам кинематической схемы будем относить те геометриче-
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
503
ские параметры механизма, которые определяют его кинематические
свойства. Например, в шарнирном четырехзвеннике, показанном на
рис. 542, к параметрам кинематической схемы относятся расстояния
между осями шарниров, углы, определяющие начало отсчета углов
поворота звеньев АВ и ВС, и размеры, координирующие положение
точки М на шатуне.
В задачах синтеза механизмов параметры кинематической схемы
(все или часть их) являются искомыми величинами. Очевидно, они
должны быть выбраны таким образом, чтобы функция у = Рм(х)
возможно мало отличалась от функции у — F (х) на заданном отрезке
изменения аргумента х. Для этого нужно решить задачу о прибли-
женной замене заданной функции y=F(x) при помощи функции
вида у = Р[(х). Другими словами, нужно решить задачу о при-
ближении функции у — F (х) при помощи функции j = (х).
Успех решения поставленной задачи при проектировании мехашз-
мов во многом зависит от удачного выбора аналитического выражения
отклонения от заданной функции. Условимся называть отклонением
от заданной функции Д измеренное по определенному направлению
расстояние между графиком заданной функции _y=F(x) (показан
пунктиром на рис. 543) и графиком функции у = Рм (х).
Следовательно, под отклонением Д мы можем понимать не только
разность ординат Д>г = ДЛ1(х) — F (х) (см. рис. 543), но также и раз-
ность абсцисс Д*. или вообще расстояние Д между графиками функ-
ций, измеренное по определенному направлению, в частности по
нормали к графику заданной функции. Например, в задачах о вос-
произведении заданной траектории разность Д„, измеренная по нор-
мали к графику заданной функции, наиболее правильно выражает
близость графиков функций y = F (х) и у = Fm (х). Кроме того,
выбор направления, по которому должно измеряться отклонение Д,
в некоторых случаях определяется условиями работы механизма.
Аналитическое выражение отклонения Д при решении задачи о
воспроизведении заданных перемещений ведомого звена или задан-
504 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
ной траектории оказывается весьма сложным даже для простейшего
четырехзвенного механизма. Поэтому оно используется для решения
этих задач только в некоторых частных случаях, например при реше-
нии задачи о приближении шатунной кривой симметричного механизма
к прямой линии. В большинстве же случаев используются или при-
ближенные выражения разности Д, или же взвешенная разность
(взвешенное отклонение), т. е. выражение вида
где вес q — произвольная непрерывная функция аргумента х, не
обращающаяся в нуль на рассматриваемом отрезке изменения аргумен-
та х. Значения функции q удовлетворяют неравенству
0 т q -/ М или 0 т q
Если пределы т и М достаточно близки между собою, т. е.
вес q незначительно отличается от постоянной величины, то взве-
шенная разность Д? может характеризовать собою изменение откло-
нения от заданной функции.
Произвольность выбора веса q (с указанным ограничением) дает
возможность изменять вид функции Д9, поэтому соответствующим
выбором веса q можно значительно упростить аналитическое выраже-
ние функции, характеризующей отклонение Д.
Еще большего упрощения можно достигнуть, если условиться
считать вес не только функцией аргумента х, но и неизвестных
параметров, подлежащих определению при решении задачи о при-
ближении функций. Этот вес будем называть параметрическим,
гак как его числовые значения можно определить после определе-
ния искомых параметров, т. е. после решения задачи о приближении
функции. Параметрический вес обозначим через qp. Его значения
также должны удовлетворять неравенству
0 т -у qp -g М или 0 т qp у- М.
Использование параметрического веса может во многих случаях
настолько упростить аналитическое выражение взвешенной разности,
что решение задачи о приближении к заданной функции становится
возможным при помощи простейших методов.
Например, пусть заданная функция представлена уравнением
прямой линии, параллельной оси хх\
У = Ь,
а функция, воспроизводимая механизмом, имеет следующий вид:
у = VРох3 4- ptx2 -ф- р^х р3,
где рй, р\, Pt и р3— коэффициенты, зависящие от параметров кине-
матической схемы механизма.
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
505
Отклонение от заданной функции, измеряемое как разность
ординат, является иррациональной функцией
Д = + PiX2 4- PiX Ц- р3 — Ь.
Эта функция мало удобна для вычисления неизвестных коэффи-
циентов /?0, рь pi и р3. Чтобы упростить решение задачи, постараемся
подобрать такой параметрический вес, чтобы взвешенная разность
имела простое аналитическое выражение и чтобы на рассматриваемом
отрезке изменения аргумента х параметрический вес был прибли-
женно постоянен. Этим условиям удовлетворяет параметрический вес
Яр = I' Р^ + Р^ + Pix + Pi + b-
Взвешенная разность при этом весе имеет вид:
= Д<7/> = Р"Х' + PlX* + Pix + Pi — b2,
г. e. представляет собой многочлен третьей степени. Определить
значения коэффициентов рп, рь р% и р3, при которых Д будет мало
отличаться от нуля на рассматриваемом отрезке, не представляет
особых затруднений *). При этих значениях коэффициентов разность Д
также будет мало отличаться от нуля, так как вес qp приближенно
постоянен, а именно, полагая
у = +pix2 + р^х A-p-i^b,
получаем, что вес qp 2Р. Полученное приближение будем называть
взвешенным приближением с параметрическим весом.
В задачах синтеза направляющих механизмов взвешенное прибли-
жение с параметрическим весом было применено в 1884 г. П. Л. Че-
бышевым при решении задачи о приближении симметричной шатун-
ной кривой шарнирного четырехзвенника к дуге окружности [55п].
В этой задаче Чебышев характеризует отклонение от заданной функ-
ции величиной
Д9==^ — R*.
где R — радиус окружности, к которой должна быть приближена
шатунная кривая; RM — переменное расстояние от центра этой окруж-
ности до точек шатунной кривой.
Вес q — очень близок к постоянному, так как расстоя-
ния отличаются от радиуса R на величину Д, которая мало
отличается от нуля.
Последующие применения взвешенного приближения при решении
задач синтеза механизмов привели к случаям, когда параметрический
вес заметно отличается от постоянной величины. В этих случаях
взвешенное приближение может быть полезно для получения первого
*) Они должны быть коэффициентами многочлена Чебышева третьей степени
(см. далее, стр. 532).
506 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. IX
приближения, которое затем уточняется путем введения малых
поправок.
При решении задач синтеза передаточных механизмов приборов
могут быть случаи, когда точность приближения к заданной функции
на некотором участке изменения аргумента должна быть больше,
чем на других участках. В этих случаях вес применяется не для
упрощения вычислений, а для выполнения заданных условий прибли-
жения, а именно на участках, где требуется большая точность при-
ближения, соответственно и вес выбирается большим.
Приближенные выражения отклонения от заданной функции могут
быть получены также путем разложения в ряд аналитического выра-
жения отклонения А или взвешенной разности Д,; с удержанием в
этом ряду только нескольких первых членов. Для получения этих
выражений применяются степенные ряды, тригонометрические ряды
и, наконец, ряды, получаемые из разложения по теореме Тейлора
для функции многих переменных. Используя эти приближенные выра-
жения, необходимо иметь в виду, что качество получаемого прибли-
жения в значительной мере определяется точностью, с которой они
заменяют отклонение А.
Итак, аналитические методы синтеза механизмов связаны с реше-
нием задачи о приближении заданной функции y — F(x) при помощи
функции вида у = рм(х), которая содержит искомые параметры
кинематической схемы.
Задача о приближении функций может быть решаема различными
методами в зависимости от того, что понимать под приближенной
заменой заданной функции. Основными методами приближения функ-
ций, применяемыми при синтезе механизмов, являются: метод интер-
полирования, метод квадратического приближения (способ наимень-
ших квадратов) и метод наилучшего (равномерного) приближения.
Рассмотрению этих видов приближения посвящена обширная мате-
матическая литература. В дальнейшем изложении будут даны только
те краткие сведения, которые необходимы для решения задач, свя-
занных с синтезом механизмов.
2°. Интерполирование функций. Простейшим видом приближе-
ния функций является интерполирование, которое применяется при
синтезе механизмов для приближенной замены заданной непрерывной
функции
y = F(x)
некоторой другой непрерывной функцией
у=Р(х),
содержащей ряд неизвестных параметров. Функцию Р(х) в дальней-
шем будем называть приближающей функцией. Разность между при-
ближающей функцией и заданной обозначим через
^ — Р(х) — F(x). (9.1)
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
507
При интерполировании под приближенной заменой заданной функ-
ции понимается совпадение значений функций y = F(x) и у—Р(х)
в k точках рассматриваемого интервала изменения аргумента (х0, хт).
Аналитическое решение задачи о нахождении неизвестных параметров
приближающей функции у = Р(х) сводится в этом случае к реше-
нию k уравнений, которые получаются, если приравнять нулю зна-
чения разности А в k выбранных точках.
Имеем:
А(х;) = Р(хг) — F(х£) = 0, 1=\, 2 ..., k. (9.2)
Геометрические методы решения этой задачи основаны на том,
что графики заданной функции y = F(x} и приближающей функции
у—Р(х) пересекаются в k точках (рис. 544), называемых узлами
интерполирования.
Мы будем рассматривать лишь аналитические методы интерполи-
рования, применяемые при проектировании механизмов. Наиболее
просто решается задача, если приближающая функция линейна отно-
сительно определяемых коэффициентов, т. е. имеет вид обобщенного
полинома
р (X) = Ро/о (X) + Pl /, (х) +... + Pnfn (х), (9.3)
где /’«, /л,..., рп — неизвестные коэффициенты, подлежащие опреде-
лению; /„И, /i (х),..., fn(x) — линейно независимые*) непрерывные
функции переменного аргумента х, не содержащие неизвестных ве-
личин. t
Число узлов интерполирования k не может быть в этом случае
больше числа неизвестных коэффициентов. Отсюда следует условие
п -|- 1.
*) Функции называются линейно независимыми, если ни одна из них не
является линейной комбинацией других.
508
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Обычно число узлов интерполирования принимается равным числу
искомых коэффициентов. Обозначим значения аргумента, соответ-
ствующие узлам интерполирования, через хь х2,..., xk. Тогда си-
стема уравнений (9.2) для определения неизвестных коэффициен-
тов р0, рь ..., рп принимает следующий вид:
«00 То “И «01 Pt 4" • • • 4~ «оге Рп = Ьъ, I
«10/'(I 4“ «11 Pt + • • Ч~ а\пРп — I (д
«поАо4 ««1А1 + - •+«„„Pn = bn, I
где
«<-i, j == /j (х;) (z ==l, 2,..., 7г ф-1;у=0, 1,..., п), (9.5)
6U1 = F(jc;) (г=1, 2,..., п -[-I). (9.6)
Система уравнений (9.4) имеет единственное решение, если опре-
делитель, составленный из коэффициентов при неизвестных, не равен
нулю:
«00, «01, • • > «0„
«10> «11> • • •> а\п
#0.
«гаг «nt, • • •> «пл
Следовательно, определение приближающей функции у = Р(х)
по методу интерполирования сводится в рассматриваемом случае к
вычислению коэффициентов а,.!, и Ь1Л в k выбранных точках по
формулам (9.5) и (9.6) и решению системы линейных уравнений (9.4),
которое может быть выполнено по любой из известных схем.
При решении линейных уравнений в последующих числовых при-
мерах мы будем пользоваться схемой, основанной на методе последо-
вательного исключения неизвестных, так как при вычислении по этой
схеме надежно и четко производится контроль всех промежуточных
операций. Для решения системы трех линейных уравнений эта схема
при обозначениях, принятых в уравнениях (9.4), имеет вид, указан-
ный в таблице 9.1. Звездочками в этой таблице обозначены уравне-
ния, из которых определяются неизвестные. Аналогичный вид име-
ют схемы для решения линейных систем с большим числом неизве-
стных.
При решении по этим схемам рекомендуется так располагать
уравнения, чтобы коэффициенты о()П, г/в и т. д. были наибольшими
по модулю. Кроме того, умножением или делением неизвестных на
числа, кратные десяти, следует так выравнять значения коэффици-
ентов й[_л, h чтобы они имели по возможности одинаковый порядок
их абсолютных величин. Промежуточные вычисления должны произ-
водиться с повышенной точностью по сравнению с точностью задания
коэффициентов, чтобы избежать накопления ошибок ог самих вычис-
лений.
§ 271
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
509
!хема решения системы линейных уравнений Таблица Э.
Проверка S1 _ „ оо V) II 31 со о е со II СО СФ СО н 01 со © ОТ е co II CO Ф co co II co 6^21 Sa — Siu co II co .co 2 1 J1.. ’ w
Сумма *!<> + + © Cl 1 о « 0=1 а + + + + О г—< i « от и и ° । ® °1о a ’ с о ет е 1 е е 2 t + е - 2 4- 2 <з е II t с? е II со + О) •е 4- •8 и со ©1 S *Ие о С1 е от ? + -г ©1 о « a 1 а" Cl а S t 4- Cl = S § 4- %* 5 a 3 4- II t «« a II CO ci Ckj 4- Cl Cl *e “b Cl *e II co ;"e 4- 31 <S «”« 4" T о CO -4? •e’ + Cl r4 “ -a у a' 4~ Cl •e 11 © <s 4- Cl II co 4- 01 co
Свободный член О ©1 О -е -е 1 ?3 <• 1 е е -el ° О е 1 ci >e 1 p? о 1 e e -el § I q о Cl e ’ll ci l*<3 J *l’a Cl ’e -e •e €> II от CvO от I от ^l<
ОТ С> | О О О С а <з 1 е GI I о о С ет е 1 е е С1 © О I о е 1 е о е 1 О1 е II ©1 “е ?! e: e e © e e e e e II •e « 2 T3 ’e I’e ©I *e'*e Cl *e -e !*e CT •e •e II ,^C1 •»
-ч . о О 0'0 <3 ее ♦м © о о -ее е о е -< © О О е е о ч—1 е Л е II е -4 © © Ф S 5S e <3 © Cl e о о e e e e II *e *e Cl ОТ *e *e о
° <3 « •» о о е е о © © fft Cl e e о
510
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Если приближающая функция Р(х) не является обобщенным
полиномом, т. е. если все искомые коэффициенты или часть их вхо-
дят в выражение приближающей функции нелинейно, то система
уравнений для вычисления неизвестных коэффициентов приближающей
функции будет уже нелинейной. Например, при решении задач про-
ектирования механизмов встречается приближающая функция следую-
щего вида:
Р U) = Ро Л (*) + Pt /1(*) 4~ • • • + Рп fn (*) + Ptft fn+t (-V)- (9.7)
После вычислений коэффициентов а^, ; и bt_x по формулам (9.5)
и (9.6) получаем систему уравнений:
4~ ^OlA + • • • + а(}пРп 4~ °0> n+1 Pt>Pt -^0> 1
ОюРо 4“ «hPi 4-. • • 4- а\пРп 4- at> п+1 РйР1 ~ ^1>
(9.8)
«пО/’о 4- ап1Р1 4- • • • 4- аппРп 4- П+1 PtlPl — bn-
Для решения системы (9.8) пользуемся схемой, указанной в таб-
лице 9.2 для случая д = 2. После исключения неизвестных и
рйрх получаем в последней строке таблицы 9.2 уравнение, связыва-
ющее неизвестные рй и рр
Pt 4- АРо — В-
(9.9)
Кроме того, в строке, отмеченной двумя звездочками, содер-
жится уравнение следующего вида:
PvPt 4- AtP\ 4- А^ро — В{.
(9.10)
Подставляя в уравнение (9.10) значение неизвестного pt из
уравнения (9.9), получаем квадратное уравнение для определения
неизвестного р():
Ар^ 4~ (AAt — В — Ая)р0 4-51 — А\В — 0.
(9.И)
Определив из уравнения (9.11) значение неизвестного р0, соот-
ветствующее условиям задачи, из уравнений, отмеченных звездоч-
ками в таблице 9.2, находим значения неизвестных р^ и /л2. Анало-
гично составляются таблицы при других значениях п.
При решении задач проектирования механизмов встречается также
приближающая функция следующего вида:
5(х) = р0/0(х) 4-р1/1(х)4-. ..4-р6/в(х),
(9.12)
причем коэффициенты р5 и pG связаны с другими коэффициентами
соотношениями:
—(№4-Р1Рз).
P6=PiPt — PoP*
(9.13)
(9.14)
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
511
Схема решения системы уравнений (9.8) Таблица 9.2
ге х сх ей О С от 1 *|ё II, от с II "ф 1 II от от е 00 <о 0. СО 1 с? II |[ «о‘ от 1 7 с? ст 1_
сз я Я О 4- -°1е g + ° о| S 4- cic г + ° 31 2 4- els S + в g| “ elе S + <3 — II II -ч CI «О СО ©1 с •®1<з -5“ <з +- + 2 ei ci ? ё1ё 3 т е я 2 4- 4- ° 2 1 <3 со от + ё ё + II ё1ё " 2 (3 + CU +- о та + та 4- м •Q й_ Ч> _t от ® © " S t + С-1 О С) X «Г1£ t+ от от Т С е от 4- + с « II °| = * t <з1е '3 Со от 1 от т- О от 1 от -к <3 II £| 8 'L elo 4 S с + от си + о от чз + + II со Со 4- 2 + 21 2 4~ :А= ё i ”, « < -S £. ^!ё t f Ъ . Г~ 4-+ SI 2 Т STsIb Cl >5 ” + “ I t s + ii *b=. co «1 +- to + с от 4- от т «0 ст] ««к + Л1-5 + "ii ст
Свободный член « о| g О в|<? ®| = w ^le •а от <3 '-II 43 ОТ II ё J 1 . -If от С5 от -с> ОТ II ё £ 1 “ ё|ё -1 2 от *|ъ * от "tt вИё «< и II -ё 5 1 «к
5 О SI S с <з|<з ©1 © © сс © от С 1 gi g S в!е е •» II « S 1 •в ©1 от © £ 1 <3 « g S3 1 OJ от от с 1 <3 <3 ci .. от II е ° 1 от 1 тз тз Ъ 1ъ Ol се s ё1ё в S е 1 ©1 Св ’сИтТ ТЗ «1 II ®' II -е ° 1 от ' от| ст
£ — -U от О о| с <3 QIC Я s W С' С С От <3 L ?|s <3 1 <3 (3 от и ё 3 1 В — 1 от 3 «°|ё « от Q от <з1сГ (3 от II с 3 1 в тз Чз1’« 3 2 - -еЬ 13 S •в Зё1ё ? S II ъ ё 1 *
ев Г5| ОТ С © © <3 СЗ 1 <3 «| от 2 <з1<з 3 От е 1 Si S 2 <з|е <3 от и ё 2 1 в СФ| от 2 <31<зс 3 от ОТ е 1 ге,=> « с с ®’ clc С от II ё W 1 ё 1 ё : « «е от от о
=х 2 * <3 <3 t- ОТ от от от <3 (3 с
512
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
После вычисления коэффициентов а(_цу и по формулам (9.5) и
(9.6) получаем систему уравнений для определения неизвестных pw
Pi, Pi, Рл и p4:
aoo/’o 4~ aoiPi 4~ — 4“ °об/’в= Ьо,
aioPo + аиР1 4“ ••• 4" а1бРв — bi,
(9-15)
ai»Po 4“ а41Р1 4~ • •• 4~ а1чРб-- bi-
Система уравнений (9.15) с учетом соотношений (9.13) и (9.14) в
результате последовательного исключения неизвестных сводится к
одному уравнению третьей степени, если заданная функция F(x) — 0,
т. е. если все коэффициенты _j = 0 [40]. В этом случае путем
последовательного исключения pit ps, р6, р.г и р3 по схеме решения
линейных уравнений, аналогичной схеме таблицы 9.1, получаем:
Pt = kiPi -}-/г^0,
Pi — k'iPl Ь^рй,
p6=^Pi4-AePo>
p^=knpi 4-fe8jt>0,
Pt—b<jPi 4- a10/70.
(9.16)
Разделив
Из этого
первое уравнение системы (9.16) на второе, получаем:
рз ktpt -|- fe8p0
Ра k»Pi ф- kt р0
соотношения, обозначая — =5, имеем:
Р»
Рз __ fe»; +
• ра ksi +
(9.17)
Разделив четвертое уравнение системы (9.16) на третье и принимая
во внимание соотношения (9.13) и (9.14), получаем:
Pops 4~ PiPs __ bjp, 4~ fe»Po .g
PoPs—PiPs fespi+Mip»
Разделив числитель и знаменатель левой части уравнения (9.18) на
рор.,, а правой части на р0, получаем после подстановки отношения
р‘ из уравнения (9.17):
Р 1 । > k'-- + fes
~г' fe3$ + __ fe7'; + fe»
4“ ks r Po? 4“ ^o
k3--Ykt~^
Отсюда получаем относительно E кубическое уравнение
/1.41 4-4" = °- <9-19>
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 513
где
Л| = A5Ai k3k-~,
At = (А2 -ф- А3) Aj “р (А4-Aj) А7~]-AjAj 4“^8^3,
Л3 = (А2 -|— kA kf, -ф- (Ав -ф- А8) А4 — A8Aj — А7А2,
Л4 = А4А6 — А2А8.
После определения величины $ определяем неизвестные коэффици-
енты р2 и р3 из системы уравнений, которые получаются из третьего
и четвертого уравнений системы (9.16) после подстановки значений
/?в и Рв из соотношений (9.13) и (9.14) и деления всех членов урав-
нений на величину коэффициента р0:
^Р-2 — Рз — 4~ ^в> (9.21)
Рч — ^Рз = А7£ -ф- А8. (9.22)
Далее из первых двух уравнений системы (9.16) находятся неизвест-
ные коэффициенты р{ и р() и, наконец, из последнего уравнения
системы (9.16) определяется коэффициент рл.
Решение задачи о приближении функций по методу интерполи-
рования дает такую систему параметров приближающей функции,
которая обеспечивает совпадение значений заданной и приближающей
функций в нескольких точках. Между этими точками (узлами интер-
полирования) отклонение от заданной функции может достигать зна-
чительной величины. Изменяя расположение узлов интерполирования,
можно уменьшить величину максимального отклонения от заданной
функции. В дальнейшем после рассмотрения методов наилучшего
приближения функций будут даны рекомендации по выбору узлов
интерполирования из условий получения минимального отклонения от
заданной функции *). Отклонение от заданной функции между узлами
интерполирования можно уменьшить также путем увеличения числа
узлов интерполирования, но это увеличение ограничено во многих
задачах числом вычисляемых параметров или же максимальным числом
точек пересечения приближающей функции с заданной **).
Кроме указанного вида интерполирования, применяется интерпо-
лирование с кратными узлами. При этом виде приближения функций
требуется, чтобы во всех или некоторых узлах интерполирования
совпадали не только значения функций y = F(x) и у = Р(х), но и
значения их производных до А-го порядка включительно. Соответст-
вующие узлы интерполирования называются узлами кратности А-|-1.
*) См. далее, стр. 544.
**) Увеличение числа узлов интерполирования не всегда обеспечивает малое
отклонение от заданной функции между ними. Однако эти случаи следует рас-
сматривать как особые [16].
17 И. И. Артоболевский
814 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. IX
При кратном интерполировании, кроме системы уравнений (9.2),
должны удовлетворяться уравнения следующего вида:
Д(й) (х,) = 0, (9.23)
где A(ft) (хг) — значение производной Л-го порядка от разности Д =
= F(x)— Р(х) по аргументу х при х = х,. Частным случаем этого
вида приближения функций является то приближение, которое полу-
чается, если приравнять нулю первые члены разложения в степенной
ряд разности Д.
Каждый кратный узел интерполирования с кратностью k -f-1
можно рассматривать как совпадение k -j-1 простых узлов при
стремлении к нулю расстояния между этими узлами. Поэтому при
подсчете максимального числа узлов интерполирования, которое не
должно превышать числа неизвестных коэффициентов, каждый узел
кратности k 1 считается соответственно за простых узлов.
3°. Квадратическое приближение функций. При квадратическом
приближении функций параметры приближающей функции вычис-
ляются из условия обращения в минимум среднего квадратического
отклонения от заданной функции y = F(x).
Средним квадратическим отклонением от заданной функции на
отрезке (х0, хт) называется величина
Дкв = 1/ ' , (9.24)
г ло
где I—интеграл, вычисляемый по формуле
хт
(х)]2 dx. (9.25)
х0
Если функция задана рядом ее числовых значений, то средним
квадратическим отклонением называется величина
<м»
где S-—сумма, вычисляемая по формуле
/ = т
S= 2 [^(^-^(х,)]2. (9.27)
/=о
С увеличением числа точек т-]-1 величина Дкв , вычисляемая по
формуле (9.26), стремится к своему предельному значению, опреде-
ляемому по формуле (9.24), если расстояния между любыми двумя
соседними точками стремятся к нулю.
С другой стороны, если число точек т -{- 1 взято равным числу
вычисляемых коэффициентов приближающей функции, то квадрати-
ческое приближение переходит в интерполирование и Дкв = 0 (если
решение задачи существует).
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
515
На рис, 545 показана геометрическая интерпретация среднего
квадратического отклонения как корня квадратного из числового
значения ординаты прямо-
угольника, равновеликого по
площади интегралу /. Очевид-
но, среднее квадратическое от-
клонение, определяемое по фор-
муле (9.24), будет минималь-
ным при обращении в ми- рис 545.
нимум величины интеграла /.
Если приближающая функция есть обобщенный полином (9.3),
то интеграл I принимает следующий вид:
хт
1 = j [/Vo (*) +Р1/1 (х) 4- • • • +Pnfn (*) — F (x)}9dx.
х»
Для определения тех значений коэффициентов р0, р1г..., рп, при
которых интеграл I обращается в минимум, нужно приравнять нулю
частные производные от I по всем коэффициентам. Тогда мы по-
лучим систему линейных уравнений:
Т Д = J [До/о (*) + /V1 (*)+-- -\-Pnfn (X) —
— F (х)]/0 (x)dx = 0,
Т = J IPo/o (*) + Pi fi (х) +... 4- pnfn (х) —
•г0
— F (х)] fi (х) dx = О,
(9.28)
2 дрп~ fP«f»(x)~bPifi(x)~l~--.~kPnfn('x) —
— F(x)]fn(x)dx = 0.
Введем обозначения
хт
Тй=У F{x)fk{x)dx, k = G,\,...,n, (9.29)
*0
хт
см = с Ik = j fk (x)fi {X)dx, Л = 0, 1,..., w; Z=0,1,..., n. (9.30)
X»
17
516
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
С помощью этих обозначений системе (9.28) можно придать вид:
СмРо “Ь QiPi 4“ • 4" сьпРп — То, '
cwPo 4~ спР14~ • • • 4- cinPn — Ть
(9.31)
СпЧРй 4~Cnl/’l + • • ~1ГСппРп-Тл-
Определитель системы
ЙО» с01> • • •> С0л
Ио> си> • •> с1п
сп0> cnb • •> спп
не равен нулю *). Следовательно, существует лишь одна система
значений pk, удовлетворяющая необходимым условиям экстремума. Эта
система значений соответствует минимуму интеграла I, так как подын-
тегральная функция есть многочлен второй степени относительно
коэффициентов pk и не может принимать отрицательных значений.
Решая систему уравнений (9.31), получаем формулу для опреде-
ления коэффициентов pk:
1
Pk G
соо, coi> • • • > со,л-1> То» со.*+1.................^ол
Сю» Сц, . . ., fj, Cj ft+i, . . ., cin
(9.32)
cn»> cnl’ • • •> Cn,k-1’ Tn’ Cn,k+1> • • •> cnn
где
c00> c0b • • > с0л
z-. <40, Cll> • • • , Cln
cn0> <7il> • • • > Gin
Практически удобнее, однако, решать систему уравнений (9.31)
не с помощью определителей, а по методу последовательного исклю-
чения, так как при этом методе четко и надежно производится конт-
роль вычислений. Схема, по которой следует располагать вычисления,
указана в таблице 9.1.
Минимум интеграла I, соответствующий найденным значениям
коэффициентов р0, рг, , рп, может быть определен по формуле
min----
*) Доказательство см. [16].
g, То, Ть • Т„
To, coo> Qll..........C0n
Ть Ho, cii> • • •, cin ’
Tn, cn0, <nb • • • > <-nn |
(9.33)
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
617
§ 27]
хт
где g= j [Р (х)]2 dx, а О имеет то же значение, что и в фор-
*0
муле (9.32).
Из формул (9.32) и (9.33) после преобразований можно получить
формулу для определения /min также в следующем виде:
= £ —Торо —Т1Р1 — • - —InPn- (9-34)
Среднее квадратическое отклонение в этом случае равно:
Дкв = |/'g—W —W —• -.. — InPn, (9.35)
г хт хч
Если функция F (х) задана в графическом виде или рядом ее
числовых значений, то для вычисления коэффициентов и ск1 можно
воспользоваться любой формулой приближенных квадратур (формулой
трапеции, формулой Симпсона и т. п.) или же находить коэффици-
енты р0, plt..., рп из условий минимума среднего квадратического
отклонения в т выбранных точках. Эти условия соответствуют обраще-
нию в минимум суммы (9.27), которая в рассматриваемом случае имеет
следующий вид:
i=m
$ = J, We(^)+A/i(-Vi)+---4-Pn/n(^) — ^’(-V;)]2. (9.36)
r=0
Приравнивая нулю частные производные от суммы по всем коэф-
фициентам pk, получаем для определения их опять систему уравнений
(9.31), в которых коэффициенты у/г и сы имеют следующие значения:
i=m
Ъ = 2 k = 0, 1,..., я; (9.37)
1=0
i—m
= 2 fk(.xi}fdXi\ k = Q, 1,..., и; I—0, (9.38)
i=0
Схема расположения вычислений при п = 1 приведейа в таблице 9.3.
Аналогичный вид имеют схемы при других значениях п. Контроль
вычислений производится по формулам:
i=m
То 4" йю 4" coi 4" • • • 4~ соп — (xt) si>
i=0
i=m
Ti + c io + £ц + •. • + c\n = sb (9.39)
i=0
i=m.
In = cn0 + c ni + • • • + cnn = C*7*) Sb
i=0
618
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Таблица 9.3
Вычисление коэффициентов и ckl
i Мх( )Р(х;) |/о(*/))2 fotx^fiiXj)
1 2 3 4
0 1 2 т •
7» соо С01
1]
i /of*/) flixpFtxfl 1/1(*/)P fl (Xi) S{
5 6 7 8
0 1 2 in
т« cli
2
где
Si = F (xf) + /0 (х{) + Л (*«) + ••• + fn {Xi}.
Для простейших видов обобщенных полиномов, например для
степенных полиномов (многочленов) и для тригонометрических поли-
номов, можно указать формулы для нахождения коэффициентов р0,
рь..рп, которые не требуют вычисления определителей или реше-
ния системы линейных уравнений, а именно, если приближающая
функция есть многочлен степени п:
РЩ =(Ч л" ±Pi хп 1 -f...
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 519
то для вычисления коэффициентов р9, pit..рп, при которых при-
ближающая функция Р(х) мало отличается от заданной функции F (х),
следует преобразовать заданный отрезок (х0, хт) в отрезок (— 1,1)
путем подстановки
х = Xo + Xg, xm — х° t (9 40)
Тогда на основании свойств полиномов Лежандра *) имеем:
\F(t)Pk(t)dt, А = 0, 1,..., и, (9.41)
где Pk (t) — полиномы Лежандра, которые даются формулой
Р (fl— ' [(О l)fe] /'9 42')
' ИО — 2fe ft| -. (9.42)
Для значений k от 0 до 6 получаем следующие полиномы:
Р«(О = Ь ]
Р.(0 = 0
р2 (0 = 1 (3^—1),
р3(о=4-<5^—30.
1 ' (9.43)
Р4 (0 = ± (350 — 300 4- 3),
ps (t) = ± (630 — 700 4-150,
Р6 (0 = ± (231F — 3150 4-1050 — 5).
Вычислив значение коэффициентов pk по формуле (9.41), следует
составить выражение приближающей функции в виде
Р(О=р0Рп(О+р1Рп-1(О + -.-4-рпР«(О » (9-44)
и затем, используя подстановку (9.40), вернуться вновь к аргументу х.
Пусть, например, из всех многочленов степени я с коэффициен-
том при старшем члене, равном единице:
Рп(х) = хл4-р1Хл-’4-...4-/?п, (9.45)
требуется найти такой, который на участке от х0 =—1 до хт=1
имеет минимальную величину:
1
\в= J[F„(x)]2dx. (9.46)
-1
*) В. И. Смирнов, Курс высшей математики, т. III, ч. 2, стр. 378, 1951.
520
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
При выполнении этого условия многочлен Fn(x) будет в среднем
отличаться от нуля на отрезке (— 1, 1) менее всех других многочле-
нов той же степени.
Поставленная задача равносильна задаче о приближении функ-
ции у = — хп при помощи полинома
р (х)=/?1 л-"-’ 4- />2 х"-« 4-... 4- Рп.
Используя формулы (9.41) и (9.43), получаем для п от 0 до 6
следующие выражения полиномов (9.45):
Fo(x) = O,
F| (x) = x,
F2(x) = x2 —y,
F3 (x) = x3 — x, «J (9-47)
F4(x) = X4—yX24-^,
Fe(x) = xe —yX34-y|X,
F6(x) = x — jjx +jj*— 23i -
На рис. 546 показаны графики многочленов F2(x), F;t(x), F4(x)
и FB(x).
Если приближающая функция есть тригонометрический полином
S (х) = у 4^ ai cos юх cos %шХ + • • • Ч~ ап cos 4"
4- bi sin wx 4- bi sin 2wx -j-... -j- bn sin /гшх, -(9.48)
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
521
где ю = у и Т — период функции, то коэффициенты ah и bh, при
которых тригонометрический полином (9.48) дает квадратическое
приближение заданной функции F (х), являются, как известно, коэф-
фициентами Фурье. Эти коэффициенты могут быть найдены по фор-
мулам
.-*<i4 Г
= у- J F (х) cos kwx dx,
^0+^
— у У F (х) sin ki»x dx
*0
>
(9.49)
или же получены при помощи гармонических анализаторов.
Итак, если приближающая функция Р(х) может быть представ-
лена в виде обобщенного полинома, то вычисление квадратического
приближения сводится к решению системы линейных уравнений (9.31)
или же (в частных случаях) к вычислению по формулам типа фор-
мул (9.41) и (9.49). Если же приближающая функция не является
обобщенным полиномом, то система уравнений для вычисления неиз-
вестных коэффициентов приближающей функции будет уже нели-
нейной.
В качестве примера решения нелинейных систем рассмотрим те
же два вида приближающих функций, которые были рассмотрены при
изложении метода интерполирования. Сначала рассмотрим приближе-
ние с помощью функции вида (9.7):
р W = Ро /о (*) 4- Ft /1 (*) + А А (*) + А /з (•*) + А А Ш-
Введем обозначение:
PoPi=Pt- (9-50)
Тогда вычисление неизвестных коэффициентов р6, рь р$ и р3 сво-
дится к нахождению минимума интеграла f
xm
1 = 1р0 Pl fdx)Pi fi(x) — F(x)]2dx (9.51)
xo
при дополнительном условии (9.50).
Для вычисления коэффициентов ръ р3 и р3 можно взять част-
ные производные от интеграла I по указанным коэффициентам и
приравнять их нулю. Однако более простая система уравнений полу-
чается, если воспользоваться правилами нахождения условного мини-
мума *).
*) См., например, «Машиностроение», Энциклопедический справочник, т. I,
КН. I, стр. 158, Мащгиз, 1947.
522
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX"
Согласно этим правилам коэффициенты рй, рь р2, р3 и множитель
Лагранжа X должны быть определены из уравнений *):
ЭФ „ дФ „ дФ п <)Ф „ дФ „
з-=0, 5-— 0, 3-=0, з-= 0, л-— 0, no.=p4, (9.52)
др0 ’ dpt ' др2 ’ dps ’ др, ’ л 1 v -*
где
ф = / Н-(РоР1 — Р4)-
Для рассматриваемого случая система уравнений (9.52) приво-
дится к следующей:
cwPo 4“ ^oi/7! 4~ 4- c«ip?, 4- с<яРпр14- ^Pi= То1 (
с\оРо 4- смР1 4- спРч 4“ с1зРз 4- сиРоР14- ^'Рч = Tt, |
Qo/’o 4- C2lPl 4- С22/?2 4" С2лРз 4“ С2iP«Pl — Т«> ’
СЗв?0 4" C3\Pl 4- С32/?2 4~ с‘л:\Рл 4- c3iP«Pi = Тз>
сиРо 4- cuPi 4- с42/'а 4" с4зРз 4- саРпР1 — = Т1,
(9.53)
где коэффициенты ckl и -[k определяются по формулам (9.29) и (9.30)
или по формулам (9.37) и (9.38), если функция F (х) задана
в т 4~ 1 точках.
Неизвестные р% и р3 исключаются из уравнений (9.53) по схеме,
аналогичной схеме, указанной в таблице 9.1. Перед исключением
располагаем уравнения (9.53) в следующем порядке:
сззРз 4- слчРз 4- cnPi4“ сзоРо 4" с3iPnPi — Тз>
СЧЗРЗ 4" С22р2 4“ CtlPl 4- С2»Ро 4 ' C2iPbPl = Т«>
t С 1зРз 4- СчР2 4- СпР1 4" СмРо 4- СllPoPl 4- 1Ро — Т1,
С0зРз 4- С«2р2 4- ^OlT7! 4” СЫ)Ро 4 ‘ Ct)tPoPl 4“ ^Pl = То,
с1зРз 4~ ci.2Pl 4- cilPl 4- ci»Po 4“ сиРйР\-— Т4-
Из формул (9.29) и (9.37) следует, что cfcz = c№, поэтому коэф-
фициенты при неизвестных р3, pit plt р0 и рор, симметричны относи-
тельно диагонали. После исключения получаем систему трех уравне-
ний, в которых коэффициенты при неизвестных рь рй и рйр, также
симметричны относительно диагонали.
Имеем:
a\Pi 4- ^tpo 4~ ciP^p\ 4- ^Ло—^i>
I’lPt 4“ ^Ро 4“ CvPoPi 4- ^Pl --
ClPl 4- С2Рч 4' СзРйР\
(9.54)
Для решения полученной системы трех нелинейных уравне-
ний (9.54) можно применить метод последовательного исключения
*) Уравнения (9.52) дают необходимые условия экстремума. О доста-
точных условиях см. Немыцкий В. В., СлудскаяМ., Черкасов А.,
Курс математического анализа, т. 2, стр. 259, ГТТИ, 1944.
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
523
неизвестных, метод итерации (последовательных приближений) и ме-
тод линейных поправок.
При решении по методу последовательного исключения неизве-
стных исключаем сперва множитель X. После исключения коэффи-
циента ре (или />1) получаем для определения коэффициента pt (или
р0) уравнение пятой степени.
В задачах проектирования механизмов проще, однако, применить
метод итерации или метод линейных поправок, так как обычно при
решении этих задач множитель Лагранжа Х₽«0. При решении по
методу итерации уравнения (9.54) записываются в следующем виде:
, _ ^1 —(^1 + Х)Ро 1
1 «1 + С1Ро ’
7 __dj — (^1 ~Ь X) pi
° b% + Cspi ’
X = CiPi -ф- с2р0 -|- ctf^pi — d3.
(9.55)
Полагая X?%=jO из первого и второго уравнений системы (9.55),
получаем квадратное уравнение для определения приближенного зна-
чения коэффициента рр
— byCijp^ (Ь^а1 — 4- ' c%di)Pi bidi — b^di = 0. (9.56)
Приближенное значение коэффициента р0 определяется из вто-
рого уравнения системы (9.55) при Х = 0. Подставляя найденные
значения /~(1 и рг в третье уравнение системы, находим величину X.
Если она оказывается в пределах требуемой точности вычислений
не равной нулю, то следует вычислить новое значение коэффици-
ента pi по первому уравнению системы (9.55), принимая X = X и
р0 = р0. Далее находится из второго уравнения системы (9.55) уточ-
ненное значение коэффициента д0 и т. д. Последовательная подста-
новка приближенных значений неизвестных рй, р{ и X в уравнения
(9.55) продолжается до совпадения этих значений в пределах тре-
буемой точности. Метод итерации в большинстве случаев дает хоро-
шие результаты. Однако иногда сходимость процесса оказывается
очень медленной или же вовсе отсутствует *).
Если из условия Х = 0 или из условий грубого приближения к
заданной зависимости получены значения неизвестных величин, доста-
точно близкие к их точным значениям, то можно применить также
метод линейных поправок **).
Обозначим приближенные значения неизвестных через д0, рх и
искомые поправки к ним — через 8/?0 = рй — р0, <jp1 = Pi — pt и
8Х = Х —X.
*) О сходимости метода итерации см., например, Скарборо Д., Числен-
ные методы математического анализа, ГТТИ, 1934.
**) О применении метода линейных поправок к решению системы нелиней-
ных уравнений см. там же, стр. 187.
524 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
Тогда, разлагая функции, стоящие в левых частях уравнений
(9.54), в ряды по теореме Тейлора для функции многих переменных
и ограничиваясь первыми двумя членами рядов, получим следующую
систему для определения искомых поправок:
(ai 4~ ciTo) fyi 4~ (А Ч- Г1Р14~М®то — *4 — j
(&! -ф- -ф- X) bpt (&2 -ф- c^Pi) 8ц0 -ф- pfik — d3 — d2, } (9.57)
(ci -j- c3p3) ZPl 4- (c2 4- c3pt) 8^0 — 8X = d3 — d3, j
где
4 — arpi bipv 4- cipopi 4- X p3,
~d^ — ь1р14~ ь2р0 4- c^p^pi 4~ x^i,
— ciPi 4- c2?o 4- czP«p\ — x.
После решения системы трех линейных уравнений (9.57) нахо-
дим уточненные значения неизвестных р0, рх и X и затем вновь вы-
числяем значения dlt d^ и d3. Если эти значения не совпадают в
пределах требуемой точности вычислений со значениями dlt d2 и d3,
то вычисляются следующие поправки из уравнений (9.57) и т. д.
При решении системы уравнений (9.57) точность вычислений следует
согласовывать с ожидаемым порядком поправок, т. е. увеличивать
точность вычислений по мере уменьшения абсолютных величин поправок.
Теперь рассмотрим вычисление коэффициентов приближающей
функции (9.12):
Р(х) —рй/0 (х) -ф- pxfi (х) -ф- • • 4-Тб/б (х),
в которой коэффициенты ps и р6 связаны соотношениями:
Ро = (PoPi 4" /?1Тз)> Рб ^^PlP‘2 РоРз-
Как и при решении задачи интерполирования, будем рассматривать
только случай F(x) = 0. Тогда неизвестные коэффициенты должны
быть определены из условий минимума интеграла
1= § [Pofo(x) + Pifi(x)-[~...-i-p6f6(x)]2dx.
Применяя опять правила нахождения условною минимума, полу-
чаем для нахождения коэффициентов рц, pi,..., рц и неопределен-
ных множителей X и Xj следующую систему уравнений:
дф___„ дФ____„ дФ____„ дФ
Фо ’ дрп ’ др2 ’ др3
. ^ф=0, ** = 0, ^’-0,
dpt др-„ дре
(9.58)
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
525
где
Ф ---/--- X (PnPt -|- PlPi Ч- Ps) 4“ \ (рхРъ РпГ>3 Ре)-
Система уравнений ,(9.58) после преобразований приводится к
следующей:
сккРк Ч~ cV.\P'i “И ckf,Pf> 4~ скзРз Ч- с&зРз 4~ cuPi Ч- сшРо — 0>
СмРк Ч- С’.КРи “Г съъРч Ч~ съчРг Ч- свзРзЧ“ СЧ\р1 Ч- сзпРо X =0,
СмРк Ч- C6tPs “Ч С6б/76 Ч- C4iPi Ч~ С6зРз Ч- C6lPl 4“ СмРо Xj = 0,
CuPl Ч- C2»/7S Ч- С2б/Ч Ч- CaPi Ч~ С2зРз “Ч С21Р1 4“ С2йРо
— Х/?о + Mi = О,
сзкРк Ч- сзъРз Ч- сзеРъ Ч- сзаРа Ч- сззРзЧ~ c3iPi Ч- сзоРо
(9.59)
— Хр, — Xi/>0 = 0,
СиРк 4“ СКРъ Ч- С1бРб 4“ CiiPi Ч- С1зРз Ч~ CllPl Ч- С1чР« ------------------------
— Хрз -|- X. ,/?.2 = о,
Ct)lPk “Ч С0вРб Ч~ СЫ,Рй Ч- <?о2/Л2 Ч~ с»зРз Ч~ Ч~ СЫ>Р»--------------------------
— *Ръ — Х1/7з = О,
где коэффициенты сы определяются по формуле (9.30) или по фор-
муле (9.38), если функции приближающего полинома заданы в т 1
точках.
Для решения полученной системы принимаем в первом приближе-
нии X —Х( = 0 и исключаем последовательно из первых пяти урав-
нений по схеме решения линейных уравнений неизвестные р^, ръ =
= — (№+Р1/7з)> Р(,=Р1Рг — РзРз, Р2 и Л- В результате исключе-
ния получаем систему уравнений (9.16), решение которой было ука-
зано при рассмотрении задач интерполирования. После вычисления
коэффициентов /?0, plt pit рл и pi находим коэффициенты X и Xj из
последних двух уравнений системы (9.59). Если эти крэффициенгы
в пределах точности вычислений оказываются не равными нулю, то
следует вновь произвести определение коэффициентов рй, рь..., pt
из системы уравнений (9.59). Однако в задачах проектирования меха-
низмов коэффициенты X и Xj в пределах точности вычислений обычно
равны нулю*).
4°. Наилучшее (равномерное) приближение функций. Наилуч-
шее (равномерное) приближение функций применяется в тех случаях,
когда нужно получить минимально возможную величину максималь-
ного отклонения от заданной функции на всем рассматриваемом ин-
тервале изменения аргумента. В каждой отдельной точке этого ин-
тервала отклонение от заданной функции оценивается величиной
*) Числовой пример см. стр. 564.
526 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. IX
разности между приближающей функцией Р(х) и заданной функ-
цией F(x):
& = P(x) — F(x). (9.60)
Для каждой системы параметров рп, ръ.-..рп, определяющих при-
ближающую функцию Р(х), можно найти на рассматриваемом отрезке
(х0, хт) максимальную по модулю величину разности А. Обозначим
эту величину через
Дтах = max |P(x) — F(x)|. (9.61)
Очевидно, варьируя величины параметров рй, plt.рп, будем
получать различные Дтах , т. е. максимальное отклонение от заданной
функции Атах есть функция параметров приближающей функции:
Атах =/(/’о> Р1’ • • > Рп)-
Тогда возникает вопрос, существует ли такая система значений
коэффициентов рй, рь р2,..., рп, при которой выражение Дтах обра-
щается в минимум. В теории приближения функций доказывается,
что если приближающая функция может быть представлена в виде
обобщенного полинома (9.3):
Р U) = Pja (*) + Pi fi (х) -f-... -j- pnfn (x),
то значения коэффициентов рй, рь..., рп, соответствующие иско-
мому минимуму, существуют [16]. Величину минимума Дтах обозна-
чим через L.
Если подберем коэффициенты рп, Pi,..., рл таким образом, чтобы
Дтах было наименьшим, т. е. равно L, то всякое другое приближе-
ние даст или большее отклонение от заданной функции, или, по
крайней мере, равное L. Вот почему такого рода приближение полу-
чило название наилучшего*).
Итак, наилучшим приближением называется тот вид
приближения, который получается, если на рассматриваемом отрезке
(х0, хт) обращается в минимум выражение
Дтах = max I Р(х) — F (х)|.
Геометрически это приближение характеризуется тем, что график
приближающей функции Р(х) оказывается заключенным между двумя
кривыми, отстоящими от графика заданной функции F (х) на вели-
чину ± L (рис. 547). Равномерным это приближение называется по-
тому, что отклонение А (х) равномерно достигает своих предельных
значений ztzL на рассматриваемом отрезке.
•) Наилучшим называют иногда и квадратическое приближение, т. е. раз-
личают наилучшее среднее приближение и наилучшее равномерное. В даль-
нейшем термин снаилучшее» будет относиться только к равномерным прибли-
жениям.
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 527
Если приближающая функция есть обобщенный полином (9.3),
содержащий и 1 неизвестных коэффициентов, то непосредствен-
ное вычисление значений этих коэффициентов, соответствующих
наилучшему приближению непрерывной функции y = F(x), основы-
вается на том, что разность
Д = Р(х) —F(x)
должна достигать на рассматриваемом отрезке (х0, хт) своих пре-
дельных значений ± L не менее чем п -|- 2 раз, последовательно
меняя знак (рис. 548).
Это условие, известное под названием теоремы Чебышева, яв-
ляется необходимым и достаточным для тех обобщенных полиномов,
которые имеют на отрезке (х0, хт) не более п корней, т. е. для
полиномов системы функций Чебышева.
Системой Чебышева порядка п называется совокупность п -|-1
линейно независимых и непрерывных функций /0 (х), f\ (х),..., fn (х),
если всякий полином, составленный из этих функций, имеет на дан-
ном отрезке не более п корней. Например, совокупность трех
функций
Их (1 — х); х; 1
528
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
рассмотренная Чебышевым при решении задачи о приближении шатун-
ной кривой к дуге окружности, образует на любом отрезке (х0, хт)
систему Чебышева второго порядка, так как полином, составленный
из этих функций:
Р (*) = PeK-v(l —-V) + Pix 4- Pi,
имеет не более двух корней на любом отрезке.
Теорема Чебышева дает возможность вычислить неизвестные ко-
эффициенты plt, Pi,..., р„ приближающей функции Р(х), предельное
отклонение £ и те значения аргумента х, при которых оно дости-
гается.
Обозначим через xlt х$,..., х„+2 те значения х, при которых
разность
Д=:Р(х) — F(x)
достигает предельных значений -+- £. Тогда на основании теоремы
Чебышева имеем следующие п -J- 2 уравнений:
Д (Xj) = е£, Д (х2) = — е£, (9.62)
Д(х„+2) = (-1)п+1е£,
где е = -)-1 или —1.
Кроме того, так как значения х}, х2,..., хл+2 соответствуют мак-
симуму или минимуму разности Д (х), то производная Д' (х) в этих
точках должна равняться нулю*).
Это условие также даст п -[- 2 уравнений:
Д' (xi) = 0, Д' (х2) = 0, (9.63)
Д' (*п+8) = о,
Общее число уравнений, которые мы можем составить на основа-
нии теоремы Чебышева, равно 2/г 4.
Эти уравнения содержат 2/г -|- 4 неизвестных:
Ро’ Ръ • • > Рпу > -^n+2> Р-
Следовательно, число неизвестных равно числу уравнений. Если
одна или две из точек предельного отклонения лежат на концах
рассматриваемого отрезка, то число неизвестных в уравнениях (9.62)
уменьшается на одно или два. Но тогда и число уравнений умень-
шается на одно или два, так как на концах отрезка производная
Д' (х) может быть не равна нулю.
*) Предполагается, что функция Д (х) имеет производную Д’ (х) на от-
резке (х0, хт).
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 529
В дальнейшем будем считать, что концы рассматриваемого отрезка
совпадают с точками предельных отклонений *). Тогда система урав-
нений (9.62) и (9.63) может быть записана в следующем виде:
Д(х0) = е£, Д,(х1) = 0, j
Д(Х|)=—е£, Д'(х.2) = 0, (9.64)
д (х„+1) = (- 1)”+,е£. Д' (х„)= О, |
где е = —]— 1 или — 1; хп + । = xm; п — порядок приближающего по-
линома.
Согласно теореме о существовании полинома, дающего наилучшее
приближение к данной функции F (х), система (9.64) непременно имеет
действительное решение, если на выбор коэффициентов р0, рь...,рп
не наложено никаких ограничений **). Решив систему (9.64), найдем
значения коэффициентов р0, ръ..., рп, которые определяют полином,
дающий наилучшее приближение функции F (х). Для данной системы
функций Чебышева /0(х), /1 (х), (х) этот полином является
единственным ***), т. е. всякий другой полином, составленный из тех
же функций, имеет большее максимальное отклонение от заданной
функции.
Уравнениями (9.64) можно воспользоваться и для вычисления ко-
эффициентов приближающих функций, не являющихся обобщенными
полиномами системы функций Чебышева. В данном случае при опре-
делении числа точек предельного отклонения следует иметь в виду
достаточные условия, сформулированные в теореме Я. Л. Геронимуса.
Если разность
Д = £>*(х) — F (х) (9.65)
достигает своего наибольшего модуля L, по крайней мере, в лф2
различных точках отрезка (хй, хт), последовательно меняя знак, то
для всякой функции Р(х), непрерывной на (х0, хт),'справедливо не-
равенство
Мах | Р(х) —• F (х) | Мах | Р* (х) — F (х) | (9.66)
при условии, что разность Р(х) — Р* (х) имеет на отрезке (х0, хт)
не более п нулей (корней).
Из этой теоремы следует, что для семейства приближающих
функций Р(х) равномерное приближение с числом точек предельного
*) Если точки предельных отклонений не совпадают с концами рассмат-
риваемого отрезка, то всегда можно увеличить длину отрезка, на котором
отклонение Д не выходит за пределы ± L.
**) См. С. Н. Бернштейн, Экстремальные свойства полиномов, стр. 15,
ОНТИ, 1937.
Доказательство единственности полинома наилучшего приближения для
систем функций Чебышева см. С. Н. Бернштейн, Экстремальные свойства
полиномов, ОНТИ, 1937,
530
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
отклонения п -[-2 будет наилучшим, если любые две приближающие
функции этого семейства имеют не более п общих точек на отрезке
приближения.
Непосредственное вычисление коэффициентов приближающей функ-
ции из уравнений (9.64) возможно только в некоторых частных слу-
чаях, так как система этих уравнений в общем случае .нелинейная.
Пусть, например, из всех многочленов третьей степени с коэф-
фициентом при старшем члене, равном единице:
?з (х) = х3 -ф piX2 -ф рз х -ф р3,
требуется найти такой, который на отрезке (—1, 1) наименее укло-
няется от нуля, т. е. имеет на этом отрезке наименьшую величину
(по модулю). Поставленная задача равносильна задаче о наилучшем
Рис. 549.
приближении функции F(x} =
= — х3 при помощи много-
члена
р (х) = Pi*2 + Рг* + Рз,
который составлен из системы
функций Чебышева второго
порядка (л = 2). Следовательно,
по теореме Чебышева разность
между заданной функцией и
приближающей должна дости-
гать своего предельного значения ± L четыре раза, последовательно
меняя знак.
В данном примере эта разность равна многочлену 7'3(х). Обо-
значим значения аргумента х, при которых достигается предельное
отклонение L, через
х0, хь х2 и х3
и будем считать, что крайние точки предельного отклонения х0 и х3
соответствуют концам рассматриваемого отрезка, т. е. х0 =— 1, х3 =
= I. Полагая е = —1, т. е. считая, что при значениях х = х0 и
х = х2 многочлен Ф(х) достигает предельного отклонения —L, а
при x — xt и х = х3 предельного отклонения L (рис. 549), имеем
систему уравнений (9.64) в следующем виде:
— 1 -Ь Р>1 —Рг -гС.з = — L,
х’-ф PiXf -фp2xt -ф р3 = L,
xj ф- PtX'2 -j- р2х2 -ф- = — L,
1 + Pi 4~ Рз — Ф
Зх; -ф 2 рхХ -ф р^ = 0,
?х| -ф 2pjXa -ф- р^ = 0.
(9.67)
§ 271
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
531
Полученная система (9.67) шести уравнений с шестью неизвестными
Ръ Pi, Рз, L, Xi и х2 может быть решена. Но значительно проще
воспользоваться другой эквивалентной ей системой уравнений, кото-
рая получается при помощи метода неопределенных коэффициентов *).
Согласно этому методу пишем систему двух уравнений, которые
получаются, если многочлен Г3(х) приравнять его предельным зна-
чениям ± L (см. рис. 549):
x3-]-/?iX2+p2x + ^ — L = 0, )
Далее замечаем, что первому уравнению соответствуют корни xt и
х3=1, а второму — корни х0 =—1 и х2. Так как при значениях
x = xt и х = х2 многочлен Тл(х), достигнув предельных значений,
не должен переходить за них, то корни х{ и х2 должны быть двой-
ными. Тогда на основании известной теоремы алгебры имеем:
х3 - piX2 -|- рчх -ф- р3 — L = (х — 1) (х — xj2,
х3 -J- piX2 4- р2х 4- рз 4- L = (х 4- 1) (х — х2)2.
(9.69)
Приравнивая коэффициенты при одинаковых степенях х, получаем
систему шести уравнений для определения шести неизвестных ве-
личин рь р.2, рз, хь х2 и L:
Pi = — 1 — 2х,,
Рг == 2Х( 4~ х^>
Рз — L — — xj,
/4 = 1 — 2х2,
Pi — — 2x2-j-x|,
Ps + L = xi.
(9.70)
Очевидно, что система уравнений (9.70) проще системы (9.67). Ре-
шая систему (9.70), получаем: . f
„ 3 1 1 г 1
Р1 = Рз=0, р2 = -—Xi — — у, х2=у, L = —,
т. е. искомый многочлен имеет вид:
7'3(х) = х3 —^-х.
Вычисление коэффициентов этого многочлена приведено лишь для
пояснения метода составления и решения уравнений, вытекающих
из условий наилучшего приближения, так как для многочленов любой
степени п:
тп (х)=х" 4- piX"-14- Pixn -2 4-... 4- Рп,
известны готовые формулы для нахождения значений коэффициентов
Pi, Рч,---,Рп> ПРИ которых максимальная величина многочлена 7'п(х)
*) Пример использования этого метода имеется в работе П. Л. Чебышева [55п].
532
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
является минимальной (по модулю) на заданном отрезке (х0, хт).
Эти многочлены называются наименее уклоняющимися от нуля и но-
сят имя Чебышева. Многочлен Чебышева, наименее уклоняющийся
от нуля в пределах от х = х0 до х — хт, имеет следующий вид:
Тп (X)=(х — ]/х2 — (х0 хт) х хохт^ +
+ i (х — А° ~2 Хт ~ VX*~ <хо + *т) Х + Хйхт)П • (9-71)
Легко убедиться, что при возведении в степень п по формуле
бинома радикалы исчезают и представленное выражение есть действи-
тельно многочлен степени п с коэффициентом при старшем члене
Xя, равным р0=1.
Максимальное абсолютное значение этого многочлена (предель-
ное отклонение) на отрезке (х0, хт) равно:
L= (9-72)
Предельное отклонение достигается при значениях аргумента х,
равных
где k — 0, 1, 2, ..., п.
Все нули (корни) многочлена Чебышева действительные, простые
и заключены в промежутке (х0, хт). Значения хг, соответствующие
нулям, определяются из условия
X. = хт. + х°-Х!П cos , i=l, 2, .... л. (9.74)
В таблице 9.4 даны вычисленные по формулам (9.71), (9.72) и (9.73)
для /г=1, 2, ..., 5 коэффициенты многочлена 7'„(х), предельные
отклонения L и значения аргумента xk, при которых это отклонение
достигается.
Если принять х0 = — h и xm = h, то формулы (9.71), (9.72) и
(9.73) упрощаются.
В этом случае имеем:
(*+ /х8 — /г8 )" + (* — ]Аг8 — A8)" (Q.75)
* п — 2п 1
L = (9.76)
хй = — h cos k = 0, 1, 2, ..., п. (9.77)
§ 27)
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
533
'Г а б л и ц а 9.4
ч? н + О £ 1П ОТ 1 + •я GO 4~ 'V + л сю ОТ -L яю ш 1* ”ц in + *'А* о ОТ 4- 4- -F in ,оэ 4-Т 1 in сю . л+ ОТ /=> + S 4- 4“ со LQ |£2 1 4" и =н’ н S + ”«“= ’° in оэо тг О + ОТ 4- 1 5 от «п о GO о о ст СЮ О § СЮ О 1 © - + © Т от от W Ч
ч 1 - + ч от от 1 - 4- © и от - От л 1 © И - + © и от от
ч- н 4- от 1 in £ + •П сто н + сю 1 ”ч + С1£- о 4~ 00 от со 'со — от + 2 Cl-Ф "Г ++ 1 "о 1 оо от о И О от X + от _|_ от X 1 от ч- jT от © и 1от 1 от + + от г с * 1
СО £ го ]от 1 СО 4- ее о -J- сю X* СО 4" к I + ГЭ© ^4 ”fT + © + । 1 н 1 £ S3 о L. Яф 4- ег н 1
СО 1 *
СТ 4- ч 1 С1И J. н и + *5? оо 1 1 1 о н с» 00 о И ст И 4- от И 1
- "с >« 4- — |от 1 1 1 1 и 1 и от о И н 1
£ 5 С *ф S о И и м * ш
(•*) и1 ЕИ0НН1Г0П ЯОХНЭИЯпффбОЛ BHH9IiBH£ о о с ф к с =; £ О аинанОЕяхо зон -qvaradu вэхарлихэоЯ хнёохоя Hdu *х EXHawZxdu винаьия£
534
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Значения рь ръ ..., рп, L и хк, вычисленные по этим формулам,
даны в таблице 9.5. На рис. 550 показаны графики этих многочле-
нов при h = 2.
Отметим, что при h = 1 многочлены Чебышева могут быть пред-
ставлены в тригонометрической форме
Тп(х) = cos [п arc cos х]. (9.78)
Применяя подстановку х — cos 0 и формулу
cos дО = у [(cos 0 —[— z sin 6)"-J-(cos 0—r sin 0)"],
можно убедиться, что Тп(х), определяемый по формуле (9.78),
Рис. 550.
действительно есть многочлен степени п, тождественный многочлену
Чебышева при h=\.
Для различных п эти многочлены имеют следующий вид:
Tt (х) = cos [arc cos х] = х,
Т3 (х) - [2 arc cos х] = х2--~,
73(х) = -^ [3 arc cos х] = х3—-|-х,
7'i(x) = -g- [4 arc cos х] = xi — х2-[-у,
(х) = [5 arc cos х] = х8 — х3 -ф- х.
(9.79)
Итак, если разность Д (х) между приближающим полиномом
и заданной функцией может быть представлена в виде многочлена,
то коэффициенты приближающего полинома находятся по готовым
формулам. Но при решении задач проектирования механизмов ветре-
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
535
Таблица 9.5
п
1 2 3 4 5
Значения коэффициентов поли- нома Тп (х) /’1 0 0 0 0 0
Ps — 1 ftS 2 1 *7© — A2
Рз — — 0 0 0
Р4 — — — ih' 5 ,, 16й
Рз — — — — 0
Предельное отклонение L h A2 2 h3 4 h* 8 A5 16
Значения аргумента х, при которых ' достигается предельное отклонение х0 — h — h — h — h — h
Х1 h 0 h i - Г2 h 2 h — A cos 36c
х2 — h to| a- 0 — h cos 72°
х3 — — h /2 2 h — h cos 108°
х4 — — — h — h cos 144°
Х6 — — — — h
чаются аналитические выражения разности Д (х) и в виде более
сложных степенных полиномов, которые могут иметь члены с отри-
цательными степенями аргумента х. В этом случае можно использо-
вать непосредственно уравнения (9.64) или же, как было показано
на примере вычисления коэффициентов многочлена Т3 (х), применить
метод неопределенных коэффициентов, который дает обычно более
простую систему уравнений. Пусть, например, требуется найти из
условий наименьшего отклонения от нуля коэффициенты полинома
Д (х) = х"+г -J- p!x”+r-1 -J- • • + рпхг, .
536
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
где п и г — целые числа, которые могут быть положительные и
отрицательные. Поставленная задача равносильна приближению функ-
ции — хл+г при помощи полинома
Р (х) = Р1ХП^Г~1 + ргХП+г~2 + • • • + РпхТ-
Этот полином составлен из системы функций Чебышева порядка
п — 1, т. е. он имеет не более п—1 корней, если не считать
обязательного для всех функций корня х = 0, который может быть
при г^>0 *). Следовательно, число предельных отклонений должно
быть равно п —j- 1. Обозначим их через х(1, xt, .... хп.
Заметим, что во всех рассматриваемых нами случаях число пре-
дельных отклонений на единицу больше числа вычисляемых пара-
метров.
Если приближающий полином имеет нулевую точку (г^>0), то
определение неизвестных коэффициентов производится обычно из
системы уравнений (9.64). В других случаях (г 0) удобнее вос-
пользоваться системой уравнений, получаемых по- методу неопреде-
ленных коэффициентов, а именно, написав систему двух уравнений:
х”+г -|- -ф- рпхг — tL = 0,
xn+r + p1xn+r-1^...^pnxr-^sL = 0, (9’80)
е = -]— 1 или — 1,
будем считать, что при п нечетном первому уравнению соответст-
вуют корни хъ х3,..., хп, а второму уравнению — корни х0, хъ..., xn_i,
причем все корни, кроме х0 и хп, — двойные. При п четном перво-
му уравнению соответствуют корни х0, х.2, ..., xn_i, вто{
Xi, х;|,..., xn_i. Каждое из уравнений (9.80) после умножения
дает многочлен степени п:
хп ^--Atxn-1-'rA.ixn-‘2-\-...~\-Лп = 0, 1
где
Ak - В^ ==Pk> === 1 , 2,..., п —|— г — 1, н —J— г -j- 1,..., л,
Ап+г== Рпаг
Вп+г == Рп+r Ч- е^”
На основании свойства корней многочлена при п нечетном
на х г
(9.81)
(9.82)
имеем:
ХП + AtXn-t АзХп-2 + . . . + Ап =
= (X — X,)2 (X — Х3)2 . .. (X — хп_ о)2 '(X — Хп),
хР -]- BiXn * В2хп 2 -j-... -|- Вп =
— (.х х0) (х х2) (х Xj) ... (х х„_3)2 (х Хп_1)2.
(9.83)
*) Системы функции Чебышева с обязательным для всех функций корнем
х = 0 называются системами с нулевой точкой. Заданная функция также
должна иметь нулевую точку.
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
537
Приравнивая коэффициенты при одинаковых степенях х, получаем си-
стему 2п уравнений для определения коэффициентов ръ р2,.. ,,рп пре-
дельного отклонения L и значений аргумента, при котором оно дости-
гается: хь х.2,..Xn_i-
При п четном следует поменять местами правые части уравне-
ний (9.83).
В таблице 9.6 даны для л=1, 2, 3, 4 значения коэффициентов
Ai, А2,..Ап, В1,В2,...,Вп и геометрическая картина приближения
(график отклонений). Сплошной линией указан график отклонений
при е=1, пунктиром при е = —1.
Пусть, например, требуется определить коэффициенты полинома
Р(х) = х2 + piX -|-р2
из условий наименьшего отклонения от нуля на отрезке (х0, хт),
не содержащем х = 0[9е]. В данном случае имеем г = —1, п — 3.
Предельное отклонение достигается при значениях аргумента: х0,
xt, х2, х3 = хт. Принимая е=1, получаем по формулам (9.82) сле-
дующие значения коэффициентов, входящих в уравнения (9.81): ’
А> =Pi, ^i—Pi,
А2 — p_i ~— Z., В2 — р2 4~ т.,
A s = р-л, В3 = ря.
Подставляя из таблицы 9.6 значения коэффициентов Ait Л2, А3, Bt,
В2 и В3, выраженные через значения аргумента xe, xt, х2 и х3,
получаем следующую систему уравнений:
Pt = — (2*1 4“ *з) = ~ (*о + 2*а), 1
р2 — L = х, Д- 2xiX3, I
" । , о - „ ( (9.84)
Рч + L — 2х„х2 + х-, (
/?3 — --- АГцАГд. |
Решив эту систему уравнений, имеем:
*1 = 4 (*о 4- V *о*з)>
*2 = “2“ (*3 4“ *о*з)>
Pl = — (*0 + *3 4- 1^*л)>
Т’з = 4 + Х1 + 1 °*0*з + 6 (*0 + *з) V *0*з]>
Р» = — 4 (х«Хз + + 2*0*3 V*0*з)>
7- = (х3 х0) (Р^Хз |/ Xq)2.
(9.85)
538
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Таблица 9.6 CQ 2 2 1 3
S
СФ «3 ст Ч ч 1 i + i 1 X
СФ С15 м £ 4 ч О V 1 э- ст
CQ СТ ч ст^о» + о ч см "от £ ст^еэ + +
ст ст о * 5 + + + 1? 5 Н > 0,1 4 +
CQ еэ Ч СМ 1 "ст * О1 + о £ 1 н + см 1
Ч — (х0 1) н 4* ч см т с ст Ч н ? 1
График отклонений Ц" г
i\ Л । \ । \ । \ । \ । \ । \ । \ 1 \/ /1 /1 / 1 ,/i t 1 V 1 \ 1 \ 1 \ 1 \ 1 \1 1'ч 1 X । > 1/ к 1 2 1 / ”71 \ 1 \ 1 \ 1 \ f /1 / 1 / J < 1 1 S 1 /Г 1 X. 1 г" - i J.1 X. 1
1? t?
Число пре- дельных от- клонений п 1 с* то -г 1П
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
639
Методом неопределенных коэффициентов можно решать также
задачу о приближении к постоянной величине функции, заданной
в неявном виде f(x, _у) = 0, если выражение f(x, _у) может быть
представлено в виде степенного полинома от аргумента х с коэффи-
циентами, зависящими от функции у [56м]:
/(х, у) = Хп + А (у) х"1 +... + Ап (у) = 0. (9.86)
Постоянную величину, к которой надо приблизить функцию у,
обозначим через k. Число предельных отклонений примем на единицу
больше числа неизвестных коэффициентов *). Тогда после подста-
новки в уравнение (9.86) вместо у его предельных значений k-\- L
и k — L, получим два многочлена:
/(х, /Н-£) = х'1 + А(/г + £)х'1-1+... + А1(^ + 1),
/(х, /г—£) = х'1-]-Л1(/г —£)х'1-1+... + Л,г(/г —L).
Пусть первый многочлен имеет корни хь х3,..., х„, второй много-
член— корни х0, х2,...,xn_v Тогда для определения параметров,
входящих в неизвестные коэффициенты Аь А3,..Ап, можно соста-
вить систему уравнений, если приравнять значения At (k -|- L) зна-
чениям А} из таблицы 9.6, а значения At (k — L) значениям В{ из
той же таблицы.
Пусть, например, имеем функцию
/(х, у) = х3 4- At (у) х2 Аг (у) х 4- А3 (у) = 0,
которую надо приблизить к постоянной величине у=/г. Принимаем
число предельных отклонений п -|-1 = 4. Тогда в соответствии с
данными таблицы 9.6 получаем следующую систему уравнений:
А 4" — — (2Хх 4- -v3),
А (А 4~ ^")И- 2x3Xi,
А (^ 4“ =-----ЧХ3>
Al (k — L) - — (х0 4- 2х2),
Аг (k — L) — 2х0ха х®, (9.87)
А3 [k — L) = —x^.
Эта система уравнений устанавливает соотношения между парамет-
рами, входящими в коэффициенты At А? и А3, постоянной величи-
ной k, предельным отклонением L и значениями аргумента х, при
которых это отклонение достигается **).
Возможно также непосредственное определение из уравнений (9.64)
коэффициентов приближающей функции, представленной в виде три-
гонометрического полинома. Но при решении задач проектирования
механизмов только в некоторых частных случаях удается получить
отклонение от заданной функции в форме, допускающей непо-
средственное решение уравнений (9.64). Основное значение имеют
*) Полученное приближение будет наилучшим, если при этом удовлетво-
ряется условие Геронимуса (см. стр. 529).
**) Пример использования уравнений (9.87) см. стр. 630,
540 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. (X
поэтому те методы вычисления наилучшего приближения, которые
можно применить для любой заданной функции _y = F(x), представ-
ленной в аналитической форме или в виде таблицы ее значений.
Из этих методов рассмотрим метод уравнивания отклонений *).
Пусть, например, заданная функция y = F(x) представлена таб-
лицей ее значений в т -|- 1 точках на отрезке (х0, х,„). Требуется
подобрать такую систему коэффициентов рй, ръ...,рп приближающей
функции
Р (х) = р0/0 (х) -|-pJi (х) 4-... А (х),
при которой разность
Д (х) =ро/о (х) 4- ptfi (х) 4-... 4- pn jn (х) — F (х)
достигает своих предельных значений чн L в п 2 различных точ-
ках отрезка (х0, хт), последовательно меняя знак**).
Так как значения функции y = F(x) даны в табличной форме,
то для решения системы (9.64) необходимо заранее знать значения
аргумента xh, соответствующие точкам предельного отклонения. Число
неизвестных, определяемых из уравнений (9.64), сокращается при
этом до п -|- 2 (коэффициенты р0, ръ...,рп и величина предельного
отклонения L). Эти неизвестные вычисляются из уравнений (9.62),
которые могут быть в рассматриваемом случае представлены в виде
системы п -|- 2 линейных уравнений:
Ро/о (xft) + Pl fl (х.) 4-... 4-Pnfn (xj 4- (-1 )ft+1eL = F (xft), (9.88)
где
k = 0, 1, 2,...,«+ 1,
e = -j-1 или —1;
xk — значения аргумента x в предполагаемых точках предельного
отклонения.
После определения коэффициентов ре, pt,..рп подсчитываются
отклонения Д для всех заданных точек функции y = F(x). Если
выбранные значения xft действительно соответствуют точкам предельного
отклонения, то при всех других значениях х отклонения Д будут
по абсолютной величине меньше L.
Если же существуют точки на рассматриваемом интервале, в кото-
рых отклонение Д больше L, то следует выбрать новую систему то-
чек xft. Выбор этих точек производится так, чтобы в одной из них
достигалось наибольшее по абсолютной величине значение, а во всех
остальных -— значения, возможно большие по абсолютной величине.
*) Валле-Пуссен, Лекции по теории апроксимации; Ремез Я. Я.,
Про методи найкращого врозумшш Чебишова наближеного представления функ-
ц!й, Кшв, АН УССР, 1935.
**) Полученное приближение будет наилучшим на заданных точках, если
функции /о (х), fi (х).fn(x) образуют систему функций Чебышева порядка
и или если удовлетворяется условие Геронпмуса (см. стр. 529).
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 541
Кроме того, знаки Д в выбранных точках должны чередоваться. Для
новых значений xk вычисляются величины коэффициентов р0, plt.. .,рп
и отклонения Д. Процесс последовательных приближений повторяется
до тех пор, пока во всех точках отрезка (х0, хт) отклонения Д
будут по абсолютной величине меньше L.
Аналогично решается задача о вычислении наилучшего приближе-
ния по методу уравнивания отклонений, если приближающая функция
имеет более сложный вид. Например, для приближающей функции
р (•*)—/'о/о (-*) 4“ Ai/1 (х) 4“ • • • И- Pnfn (х) И- PoPt fn+i (х)
коэффициенты рп, Pi,..-,pn вычисляются из уравнений
Ро/о (хк) 4“ Pifi (xk) 4" • 4 Pnfn (xk) 4“ PoPifn+i (xk) +
+ (-l)fc+1eL=F(xft), (9.89)
где
k = 0, 1,..., n 1,
e = —|— 1 или —1.
Сравнивая уравнения (9.89) с уравнениями (9.8), которые приме-
няются при интерполировании, можно заметить, что они отличаются
только дополнительным линейным членом (—l)fc+1eZ. и, следовательно,
схема решения уравнений (9.89) совпадает со схемой, указанной для
уравнений (9.8). Во всех других случаях также система уравнений,
применяемых при вычислении наилучшего приближения по методу
уравнивания отклонений, отличается от системы уравнений, получа-
емых при интерполировании, линейным членом (—1)*+1е/_. Поэтому
все схемы решения, разработанные для интерполирования, применимы
и для вычисления наилучшего приближения. В частности, можно
вычислять коэффициенты функции (9.12): *
Р(х) — P»fo (х) 4" Pi fi (х) 4“ • • + As/б (х),
где
Ръ — ~ (/ о.'Аг 4~/?1/7з)> P6=PiPi— РоРз,
из условий наименьшего отклонения от нуля, применяя схему реше-
ния, указанную при рассмотрении задач интерполирования.
Быстрота сходимости процесса уравнивания отклонений опреде-
ляется удачным выбором системы точек xk в первом приближении.
Рекомендуется располагать точки xfl так же, как располагаются точки
предельных отклонений многочленов Чебышева. Предварительно надо
установить число этих точек, руководствуясь теоремой Геронимуса *)
и анализируя свойства приближающей функции Р(х). Пусть число
точек предельного отклонения равно где т — число нулей
отклонения Д (х). Если отклонение Д (л:) заменить многочленом Чебы-
шева Тт (х) = хт 4-/'i-Vm l -J-.., -\-рт> то приближенные .значения
*) См. стр. 529,
542
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
абсцисс точек предельного отклонения х[ найдутся по формуле (9.73),
которая после замены обозначений имеет вид:
4 = ^Ц^ + ^=2^СО8~, А = 0, 1, 2,...,т. (9.90)
Но отклонение А (х) можно также заменить многочленом Чебышева
Рис. 551.
тт(у)=ут+Р1ут-1 + ...+Рт,
где у = F (х) — заданная функ-
ция. Тогда, вводя обозначение
x — Fi(y), получаем, что прибли-
женные значения абсцисс xk най-
дутся по формуле
4'=F1(X')- (9.91)
где
„И Уо Н~ Ут | У о Ут
i-k— 2 "Г 2 C°S «I *
k = 0, 1, 2,..., т.
Значения xlk и х" не совпадают,
за исключением случая линейной
зависимости между х и у.
При одной и той же прибли-
жающей функции Р(х) в зависи-
мости от вида заданной функции
y = F(x) действительные точки
предельных отклонений распола-
гаются ближе или к точкам xlk или
к точкам х(п. На рис. 551 для ил-
люстрации этого положения пока-
зано наилучшее приближение
функций у = х3 и у = х на от-
резке (0, 1) при помощи линейной
функции Р (х) = рпх -|- pi. Точки
Xfe отмечены квадратами, а х” — треугольниками. Как видно из графика,
действительные точки предельных отклонений (обозначены кружками)
располагаются ближе к точкам х’ для функции _у=х3 и ближе к
точкам х*1 для функции у = |/х. Отметим, что в данном примере
точки предельных отклонений точно совпадают с x’fc при _у = х2 и
с точками х” при _у = |/Лх.
При решении задач синтеза механизмов во многих случаях трудно
установить, будут ли абсциссы точек предельных отклонений ближе
к значениям х£ или х1*
§ 27]
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
543
Поэтому в общем случае мы не можем отдать предпочтение
системе точек предельных отклонений с абсциссами xk по отношению
к системе с абсциссами xlk. Считая, что вероятности приближения
систем х\ и х” к действительной системе точек предельных откло-
нений равны, получаем для выбора абсцисс точек предельного
отклонения приближенную формулу
х’ + х"
^=-^2— (9'92>
Для рассмотренных функций у — j/x, _у = х3, а также для многих
других заданных функций выбор точек предельных отклонений по
этой формуле дает лучшее приближение к заданной функции, чем
выбор по формуле (9.90). Хороший результат получается также,
если воспользоваться приближенным выражением отклонения от
заданной функции в виде многочлена степени т от переменной
длины дуги графика заданной функции, измеряемой от начала участка
приближения.
Обозначим длину этой дуги через s. Тогда положение точек
предельного отклонения может быть выбрано по формуле
sk = 0,5^1—cos^p-^S, k = 0, 1, 2,..., in, (9.93)
где sk — длина дуги графика заданной функции, измеряемая от
начала участка приближения до /г-й точки предельного откло-
нения; S — длина дуги графика заданной функции на участке при-
ближения.
Лучший результат, который во многих случаях достигается при-
менением формул (9.92) и (9. 93) по сравнению с формулой (9.90),
может быть объяснен тем, что формулы (9.92) и (9.93) учитывают
в некоторой мере форму графика заданной функции, в то время
как по формуле (9.90) расположение точек предельного отклонения
зависит лишь от их числа и длины участка приближения.
Положение точек предельного отклонения при вычислении
по формулам (9.92) и (9.93) достаточно определить с точностью
до трех значащих цифр, так как любая формула для выбора этих
точек дает лишь приближенное их расположение. Поэтому опреде-
ление длины дуги S может быть произведено простейшими приемами,
например путем замены дуги S ломаной, состоящей из хорд, мало
отличающихся от стягиваемых ими дуг. На основании формулы
(9.93) составлена таблица 9.7, в которой указаны значения sk
для т 6.
Для выбора точек предельного отклонения можно также исполь-
зовать первое приближение, полученное путем простого или крат-
ного интерполирования. При простом интерполировании рекомендуется
544 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
Таблица 9.7
т ‘*0 Я $2 53 Л-4
1 0 8
2 0 0,5 8 S — — — .
3 0 0,25 8 0,75 S 8 — — —
4 0 0,146S 0,5 8 0,8548 S —
5 0 0,0958 0,3458 0,6558 0,9058 8 ,—
6 0 0,0078 0,25 8 0,5 8 0,75 S 0,933S S
располагать узлы интерполирования в соответствии с расположением
нулей многочлена Чебышева Tm(s), т. е. по формуле (9.74), которая
для рассматриваемого случая принимает вид:
8; = 0,5 f 1 — cos 2<2n 1 it j S,
i=l, 2,...,n, (9.94)
где n — число узлов интерполирования; st — длина дуги графика
заданной функции, измеряемая от начала участка приближения до
г-го узла интерполирования; S—длина дуги графика заданной функ-
ции на участке приближения.
На основании формулы (9.94) составлена таблица 9.8, в которой
указаны значения я,- для п 6.
Таблица 9.8
п •ч «2 $3 •Ч Se
1 0,5 8
2 0,146S 0,8548 — — —- —
3 0,0678 0,5 8 0,9338 — — —-
4 0,0388 0,3088 0.692S 0,9628 — —
5 0,0218 0,2068 0,5 8 0,7948 0,9798
6 0,0168 0,146S 0.370S 0,6308 0,8548 0,984S
Можно также выбирать расположение узлов интерполирования
по формуле
(9.95)
где х! = х0 4- 0,5 ( 1—cos — я — д j (хт—х0), 1=1,
(у1!); у]1 =у0+0,5 (1 — cos (Ут — j0).
5°. Выбор метода приближения функций при решении задач
приближенного синтеза механизмов. Аналитические методы решения
задач приближенного синтеза механизмов к настоящему времени
§ 27] ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ 545
настолько разработаны, что в каждой из решенных задач можно
применить любой из трех рассмотренных методов приближения фун-
кций *). Поэтому отметим основные положения, которыми можно руко-
водствоваться при выборе метода приближения функций.
Интерполирование функций обеспечивает выполнение задан-
ных кинематических условий в нескольких положениях механизма.
Могут быть заданы положения звеньев, скорости и ускорения отдель-
ных точек, углы передачи. Число задаваемых условий не может
быть больше числа вычисляемых параметров кинематической схемы
механизма.
В соответствии с осуществляемым видом приближения интерполи-
рование рекомендуется применять в тех случаях, когда условия
работы механизма приводят к заданию кинематических величин в
отдельных положениях механизма. Например, при проектировании
исполнительных механизмов машин-автоматов и других рабочих машин
заданными величинами, как было показано в главе VII**), могут быть
максимальная скорость и максимальное ускорение ведомого звена,
величина перемещения его из одного крайнего положения в дру-
гое и т. п.
Кроме того, интерполирование может быть использовано для
получения первого приближения при вычислении искомых параметров по
методу наилучшего или квадратического приближений. Это свойство ин-
терполирования основано на том, что, выбирая узлы интерполирования
совпадающими с расположением нулей (корней) полиномов Чебышева
или полиномов Лежандра, мы получаем соответственно приближение,
близкое к наилучшему или квадратическому ***). Иногда это первое
приближение оказывается вполне приемлемым в отношении точности,
и дальнейших уточнений не требуется.
Наилучшее приближение обеспечивает получение мини-
мального по модулю отклонения от заданной функции. Этот метод
приближения рекомендуется применять в тех случаях, когда нужно
получить воспроизведение заданной зависимости с максимальной точ-
ностью, причем ни в одной из точек рассматриваемого отрезка при-
ближения отклонение от заданной зависимости не должно превосхо-
дить допускаемое.
Квадратическое приближение обеспечивает получение
минимального среднего квадратического отклонения от заданной
функции. Этот метод рекомендуется применять в тех случаях, когда
должно быть мало среднее значение отклонения от заданной
функции.
*) При этом имеется в виду, что вычисление наилучшего приближения
производится по методу уравнивания отклонений, который, строго говоря, не
обеспечивает получение наилучшего приближения, но практически дает прибли-
жение, близкое к нему.
**) См. стр. 342.
♦*f) О выборе узлов интерполирования см. стр. 544.
18 И. И. Артоболевский
546
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
|гл. IX
Например, если точность показаний прибора зависит от суммы
значений модуля отклонений от заданной функции на некотором
отрезке перемещений, то должно быть мало среднее значение
отклонения.
Для того чтобы показать отличие квадратического приближения
(приближение в <Я£еднем») и наилучшего приближения (равномерного),
на рис. 552 приведены графики двух многочленов второй степени,
наименее уклоняющихся от нуля на отрезке (—1, I) и имеющих
й 1: многочлена Чебышева
(х) = ха — i и много-
члена Лежандра Р.г (х) =
при старшем члене,
Из сравнения этих гра-
фиков видно, что максималь-
ное по модулю отклонение
от нуля у многочлена Че-
бышева меньше, но в сред-
нем, если рассматривать зна-
чение всех ординат, много-
член Лежандра ближе под-
ходит к оси абсцисс. (Сред-
нее квадратическое значе-
ние отклонения для много-
члена Чебышева—0,2333, а
для многочлена Лежандра—0,1778.) Максимальное отклонение при
квадратическом приближении в некоторых случаях может значительно
отличаться от максимального отклонения при наилучшем приближении.
Но для многочленов и других функций, которые встречаются при реше-
нии задач проектирования механизмов, не наблюдается очень большой
разницы между этими отклонениями. Нередко эти два вида прибли-
жения практически совпадают.
Кроме тех случаев, когда требуется минимальное значение сред-
него отклонения, квадратическое приближение рекомендуется при-
менять при вычислении небольшого числа параметров, если остальные
параметры выбраны из конструктивных соображений, так как в этом
случае равномерное приближение не будет наилучшим *), а интер-
полирование дает малую точность вследствие небольшого числа узлов
интерполирования.
*) Для того чтобы равномерное приближение было наилучшим, в задачах
синтеза механизмов обычно надо иметь максимально возможное число точек
предельного отклонения. Если вычисляется только часть параметров, то нстьзя
получить максимальное число точек предельного отклонения и получаемое
приближение не будет наилучшим.
§ ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ 547
§ 28. Постановка задачи о приближенном синтезе передаточных
механизмов и аналитические выражения отклонения от заданной
функции для некоторых механизмов
1°. Шарнирный четырехзвенник. В соответствии с рис. 553
введем следующие обозначения; й, Ь, с — относительные длины
звеньев АВ, ВС, CD при длине стойки, принятой за единицу, т. е.
, ЯС . — О®.
а~ AD' b~AD' C~~AD’
cp—входная координата, г. e. угол поворота ведущего звена АВ,
отсчитываемый против хода часовой стрелки от линии начала отсче-
тов AI; ф— выходная координата, т. е. угол поворота рабочего
(ведомого) звена CD, отсчитываемый против хода часовой стрелки
от линии начала отсчетов DII; а — начальный угол, отсчитываемый
против хода часовой стрелки от ли-
нии, соединяющей центры А и D,
до линии начала отсчетов углов ср;
р — начальный угол, отсчитывае-
мый против хода часовой стрел-
ки от линии, соединяющей центры
А и D, до линии начала отсчетов
углов ф; срт — входной угол, т. е.
значение угла ср в конце рассма-
триваемого отрезка изменения этого
Рис. 553.
угла; фга — выходной угол, т. е.
значение угла ф в конце рассматри-
ваемого отрезка изменения этого угла; й — угол
ВС к рабочему, (ведомому) звену CD, т. е. угол
шатуна ВС и направлением скорости точки С*).
давления отЛцатуна
между направлением
(9.96)
Передаточные механизмы служат для воспроизведения заданной
функции
Эту функцию будем в дальнейшем называть функцией положения.
При проектировании . передаточных механизмов счетно-решающих
устройств, указывающих механизмов приборов и других механизмов
задается не функция положения, а функциональная зависимость
между некоторыми физическими или иными величинами w и г:
w=f(z\
(9. 97)
которая должна быть воспроизведена механизмом так, чтобы
перемещения ведущего звена были пропорциональны изменению
«О 12ST-O
*) Направление шатуна ВС совпадает с направлением реакции в шарнире
С, если шатун не нагружен внешними силами и силами инерции можно пре-
небречь.
18’
548 синтез передаточных механизмов [гл. IX
аргумента z, а перемещения рабочего звена пропорциональны из-
менению функции w.
Коэффициенты пропорциональности обозначим через и и
назовем масштабами шкал. Кроме того, будем считать, что при z — z^
заданные углы ср и ф равны нулю.
Тогда
*0 = 1М>. w — да0 = М>- (9.98)
Из соотношения (9.98) следует, что масштабы рг и p.w можно
определить по заданным значениям углов <рт и и по значениям
переменных z и да в начале и конце рассматриваемого участка *).
Имеем:
b = (9.99)
тот чт
Подставляя значения z и w из соотношений (9.98) в уравнение
(9.97), получаем:
+ М» =/(го 4- Рг?)-
Следовательно, заданная функция положения имеет вид:
Ф = — «М- (9.100)
Если зависимость между величинами гида представлена в виде:
г=/1(да),
то заданная функция положения принимает вид:
? = ^ЕЛ(®о+М)-гв]. (9.101)
Иг
Например, если требуется воспроизвести логарифмическую зави-
симость
да — lg z или z =10®
на отрезке от г0=1 до zm—10, то
да0 = 0 и дат=1.
Отсюда
9 1
¥т и Р«-—
Заданная функция положения (9.100) или (9.101) при углах размаха
?т и '?т принимает следующий вид:
*) Функция w —f(z) предполагается непрерывной и монотонной.
§ 28] ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ 549
или
г — 1
<Р = ^ .10 — 1 .
К воспроизведению заданной функции положения сводится также за-
дача о воспроизведении заданного закона движения звена АВ при
заданном законе движения звена CD.
Пусть закон движения звена АВ выражается уравнением
<Р=А(0. (9-102)
а требуемый закон движения звена CD — уравнением
Ф=Л(0- (9.103)
Исключая аналитически или графически время t из уравнений (9.102)
и (9.103), получаем непосредственно заданную функцию положе-
ния (9.100):
ф = Д(<р),
причем в этом случае значения заданных углов и в начале от-
резка приближения могут отличаться от нуля.
Шарнирный четырехзвенник может обеспечить точное воспроизве-
дение заданной функции (9.100) только в некоторых частных слу-
чаях. В обшем же случае он воспроизводит некоторую другую функ-
цию:
<p=FM(o, b, с, а, р, <р), (9.104)
в которую кроме переменной <р входят параметры а, b и с, опреде-
ляющие относительные длины звеньев, и параметры а и (3, определяю-
щие начало отсчетов углов о и ф.
Для того чтобы механизм воспроизводил заданную функцию до-
статочно точно, следует выбрать такую комбинацию этих параметров,
при которой функция (9.104) возможно мало отличается от заданной
функции (9.100) на рассматриваемом отрезке.
Условимся при этом измерять отклонение от заданной функции
величиной разности
Дф = Фм~Ф. (9-105)
где ф — заданная величина угла при некотором значении угла
фм — величина угла ф, получающегося в механизме при том же зна-
чении угла <р.
Учитывая зависимости (9.100) и (9.104), можно отклонение Д
представить также в следующем виде:
ДФ = /:'м(«. Ь, с, а, р, ?)-“ [/(*o + lM>) —®’о] . (9.106)
В выражение отклонения Д. входят семь независимых парамет-
ров: а, Ь, с, а, р, p,w или а, Ь, с, а, р, <рт,
550
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Параметры а, b и с определяют график функции ф -|~р = /7м (<?-[-а)
(на рис. 554 график этой функции показан пунктирными линиями).
Параметры цг и jj.w (или <рт и фт) определяют совместно с функцией
w — f(z) график заданной функции положения (показан на рис. 554
сплошной линией при условии, что wo = zo = O). Наконец, параметры
аир определяют положение графика заданной функции положения
по отношению к графику функции -J- р = FM (<р-|-а).
Кроме того, в выражение разности Д^ могут входить также коэф-
фициенты, входящие в функцию ®'=/(z) или в заданную функцию
положения.
Аналитическое выражение разности Д^ можно получить, если вос-
пользоваться формулами, устанавливающими зависимость между уг-
лами <р и ф в шарнирном четырехзвеннике.
Например, зависимость между этими углами может быть пред-
ставлена в следующем виде:
. । о l sin (ф 4- a) cos 8
ф 4~ р = a rc tg-----IXZT-A-p -+- arc tg------------
cos Cf + а; — — у — sin »
(9.107)
где & — угол давления от шатуна к ведомому звену, определяемый
из соотношения
sin В = + с\Ьс -------- -j- ~ cos (<? 4- a). (9.108)
Знак плюс или минус в формуле (9.107) соответствует двум возмож-
ным положениям звеньев ВС и CD при одном и том же положении
звена АВ. На рис. 553 второе возможное положение звеньев ВС и CD
показано пунктиром. Выбор того или иного расположения этих звеньев
при вычислении углов ф по заданным углам ср производится из усло-
вия непрерывного перехода звена CD из одного положения в следую-
щее за ним, начиная с начального положения. Для правильного выбора
§ 28] ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ 551
значений углов ио их тригонометрическим функциям проще всего вы-
чертить механизм в начальном или рассматриваемом положении.
Однако для вычисления искомых параметров кинематической схемы
формула (9.107) оказывается неудобной, так как вследствие наличия
в этой формуле обратных круговых функций не удается получить
достаточно простых уравнений для нахождения искомых параметров.
Поэтому для аналитического решения задач синтеза передаточных
механизмов используем другую функцию, которая имеет более
простой вид и в то же время при некоторых ограничениях достаточно
точно следует за изменениями отклонения Дф.
В § 27 было указано, что этими свойствами обладает взвешенная
разность с параметрическим весом, т. е. функция
\ = (9.109)
при условии, что параметрический вес qp мало отличается or пос тоян-
ной величины.
Для получения достаточно простого выражения взвешенной раз-
ности Дч воспользуемся приемом, использованным впервые при реше-
нии задачи о воспроизведении заданной траектории точки шатуна [33 г].
Представим себе, что в шарнирный четырехзвенник, показанный
на рис. 553, введено дополнительное звено в виде ползуна, переме-
щающегося по оси шатуна (рис. 555, а). Полученный пятизвенный
механизм обладает двумя степенями свободы, т. е. двум звеньям этого
механизма могут быть заданы независимые законы движения. По-
этому в отличие от шарнирного четырехзвенника в рассматри-
ваемом механизме звенья АВ и CD могут в каждый момент времени
занимать предписанные положения под заданными углами ф и ф. Но
при этом длина шатуна, т. е. расстояние между центрами шарниров
В и С, будет переменной. Обозначим эту переменную длину шатуна
в указанном пятизвенном механизме через Ь^. Чем меньше отклонение
переменной длины от постоянной величины Ь, тем соответственно
меньше отклонение угла поворота звена CD в шарнирном четырех-
звеннике от заданной величины ф. Следовательно, отклонение от за-
данной функции Дф связано с величиной
Д„ = ^-^ф, . (9.110)
552 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
аналитическое выражение которой имеет более простой вид, чем
функция Д^.
Еще более простой вид имеет функция
bq = b2 — b& (9.111)
которая получается умножением функции Дй на коэффициент b-\-b$,
мало отличающийся от постоянной величины, равной 2Ь.
Для получения аналитического выражения функции Д? спроекти-
руем контур ABCD на направление отрезка AD и на направление,
перпендикулярное к нему:
b^ cos 8 — с cos (ф -ф- р) 4* 1 — о cos (ср -ф- а), (9.112)
/?Ф sin 8 = с sin (6 -j- р) — a sin (ср -ф- а). (9.113)
Возводя в квадрат правые и левые части уравнений (9.112) и
(9.113) и складывая их, получаем:
Ь$ — а2 -ф- с2 -ф- 1 — 2ас cos (6 — <р -ф- р — а) —
— 2а cos (ср -ф- а) ф- 2с cos (ф -ф- р). (9.114)
Подставляя найденное выражение Ьф в формулу (9.111), полу-
чаем искомое выражение функции Д? в следующем виде:
Д? = 2ас cos (ф — tp -ф- р — а) 2а cos (ср -ф~ а) —
— 2 с cos (ф -ф- р) -ф- Ь2— а2 —с2—1. (9.115)
Выражение Д? есть взвешенная разность, т. е. произведение
действительной разности Д^ на вес q, который в данном случае
является параметрическим, так как зависит от искомых параметров.
Величины функции Д^ и Дй малы, поэтому для выяснения связи
между ними можно воспользоваться планом малых перемещений
[12в], построение которого основано на том, что малые перемеще-
ния точек механизма можно считать величинами, пропорциональными
их скоростям. Полагая ведущее звено закрепленным под заданным
углом ср —а, строим план скоростей (рис. 555, б), в котором вектор
рс изображает скорость центра шарнира С, а вектор ссх — относи-
тельную скорость точки Сх на шатуне по отношению к центру
шарнира С. Угол между векторами ссх и рсх равен 90°, угол между
векторами рс и ссх равен углу давления &. Вследствие почти точной
пропорциональности скоростей и малых перемещений отрезок рс
представит в некотором масштабе перемещение центра шарнира С
по отношению к стойке, равное величине сДф, а отрезок ссх — пе-
ремещение точки С по отношению к шатуну, равное величине Дь.
Из треугольника рсхс имеем:
Дь = сДф cos &. (9.116)
С другой стороны, из формулы (9.111) следует:
<9Л17>
§ 28] ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ 553
Подставляя значение Д& из соотношения (9.117) в формулу (9.116),
получаем:
Д9 = 2&с cosS-Д (9.118)
или
Д ————S
Ф 2bc cos & ’
(9.119)
Следовательно, для взвешенной разности Д?, определяемой по
формуле (9.115), параметрический вес qp при малых величинах откло-
нения Дф имеет следующее значение:
qp = 2b с cos &. (9.120)
Величина угла & при вычислении отклонения Д^ по формуле (9.119)
находится по формуле (9.108). Кроме того, можно воспользовать-
ся соотношением
sin (<р Р) = a sin (<р — ф + Р — a) -ф- b cos &, (9.121)
которое получается, если спроектировать контур ABCD на направле-
ние, перпендикулярное к отрезку CD.
Из соотношения (9.121) имеем:
cos 8 = -^ sin (6 Р) — у sin (ф — р — а). (9.122)
Приближенная формула (9.119) для вычисления отклонений Д^
имеет в этом случае вид:
Аф 2с { sin (•!> —|- р) — a sin (<р — Ч- Р — а] ’ (9.123)
Так как взвешенное приближение дает хорошие результаты
только при весе, мало отличающемся от постоянной величины, то
из формулы (9.119) следует, что пользоваться величиной Д?, опре-
деляемой из соотношения (9.115), недопустимо при значениях угла 9,
близких к 90°, т. е. в положениях механизма, близких к предель-
ным. Это условие, однако, не накладывает серьезных ограничений
на применение взвешенной разности для вычисления искомых пара-
метров, так как при проектировании шарнирного четырехзвенника
ставится обязательное условие, чтобы угол давления & был не
больше &доп, например не больше 60°. Поэтому если в результате
вычисления искомых параметров обнаруживается, что значения угла дав-
ления превышают допустимые, то механизм считается неудовлетвори-
тельным и требуется изменение начальных данных (углов <рт и фт, пре-
делов изменения аргумента и т. п.).
Итак, при решении задач синтеза передаточных механизмов будем
вычислять искомые параметры шарнирного четырехзвенника из усло-
вий малого отклонения от нуля функции (9.119) или (9.123), в которую
входит взвешенная разность Д?, определяемая по формуле (9.115).
554
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
2°. Плоские механизмы с поступательными парами. Для всех
передаточных механизмов (как плоских, так и пространственных)
сохраняется постановка задачи приближенного синтеза, указанная
при рассмотрении шарнирного четырехзвенника, изменяются лишь
формулы для вычисления взвешенной разности Д? и отклонения Д<р
Укажем, например, какой вид имеют эти формулы для плоских
четырехзвенных механизмов с поступательными парами. Для криво-
шипно-шатунного механизма (рис. 556, о) при Д,, = /г— Ь°ф имеем:
Д^ — 2а ($ It) sin (<р -[* «) 4“ %ае cos (о 4- а) —
— (s /г)2 4- /А — а2 — е2, (9.124)
где ср — угол поворота звена АВ, отсчитываемый от начала отсчета
AI, а — начальный угол, т. е. угол между линией начала отсчета AI
и линией, перпендикулярной к направлению движения ползуна; $—-
расстояние точки С ползуна от начала отсчета //-//; h — расстояние
от точки А до начала отсчета расстояний s, измеренное параллельно
направлению движения ползуна; а — длина кривошипа АВ (расстоя-
ние между центрами шарниров А и В); Ь — длина шатуна ВС (рас-
стояние между центрами шарниров В и С); е — эксцентриситет, т. е.
величина перпендикуляра, опущенного из центра А на направление
движения ползуна.
Приближенная формула для определения разности Д-, т. е. раз-
ности между значением угла ср в механизме и заданным значением
того же угла при одном и том же положении ползуна, имеет вид
(см. рис. 556, б)-.
Д.„=—(9.125)
f 2ab cos z
§ 28]
ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ
555
где — угол давления
условия
от шатуна к кривошипу, определяемый из
„2 _ „2 _ _|_ (S _|_
Приближенная формула для определения разности Д„ т. е. раз-
ности между значением расстояния s в механизме и заданным значе-
нием того же расстояния при одном и том же угле ср, имеет вид
(см. рис. 556, s):
Д, = -^Ц-, (9-127)
4 2b cos 8 ’
где ft — уГол давления от шатуна к ползуну, определяемый по фор-
муле
Sin&=g~a7(;F-M(9.128)
Точная формула для вычи-
сления расстояния s по за-
данному углу ср:
s = a sin (ср а) — h ±
± VЬ* — [е — a cos (<р а)]2.
(9.129)
Точная формула для вычисления угла ср по заданному расстоя-
нию s:
sin + .)=£<» + '> g + . (9.130)
где
Z =
(s + ft)2 + <z2 + е2 — ft2
2a
Для кулисного механизма взвешенная разность Д^ = Де — е — в соот-
ветствии с обозначениями, показанными на рис. 557, имеет вид:
Д9 = а — a cos (<р — <р -|- р — а) 4~ cos (<р -]-§). (9.131)
Приближенная формула для определения разности Дф имеет вид
(рис. 558):
Дф=^, (9.132)
*2
где
ti — |/ а2 -|-1 — е2 — 2а cos (ср 4- а).
556
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Приближенная формула для определения разности Д? имеет вид
Рис. 558.
Точная формула для вычисления угла по заданному значению
угла <р имеет вид:
ф -|~ р == arc tg —gin(? + a> .42 arc cos (9.134)
cos (<f + «)— —
где
G = + 1 — 2a cos (<p —f- a) •
0)
Точная формула для вычисления угла <р по заданному значению
угла имеет вид:
<р4-а = ф4-Р±(90° —»), (9.135)
причем угол давления & определяется из соотношения
. „ е-|- cos (<!/-]- р)
sin V — —----— .
а
§ 28] ПОСТАНОВКА ЗАДАЧИ О ПРИБЛИЖЕННОМ СИНТЕЗЕ
557
Для механизма эллипсографа взвешенная разность в соответствии
с обозначениями, показанными на рис. 560, а, имеет вид:
Ьд = Ь2 — (s-l-Zz)2 — (x-j-/?1)a4-2(s4-/z) (х 4- hi) cos tj. (9.136)
Приближенная формула для
(рис. 560, б):
(9.137)
4 2b cos & ’ '
где
cos & =
ft2 -J- (s + Zi)a — (x-f- fh)2
2b (s -I- h)
определения
разности
Д5 имеет вид
заданному расстоянию х имеет вид:
Точная формула для вы-
числения расстояния s по
S = (х hi) cos щ — (х/Zj)2 sin2i] —h. (9.138)
Формулы для вычисления разности Дх и величины расстояния х
по заданному расстоянию s получаются из
заменой х на s и обратно.
формул (9.137) и (9.138)
Для синусного механизма *) (рис. 561) при вычислении искомых
параметров можно использовать непосредственно разность между
значением расстояния s в механизме и заданным значением того
же расстояния при одной и той же величине угла <р.
Имеем:
As = s4^/Z — asin(<p4~a)- (9.139)
Приближенная формула для определения разности Д? имеет вид:
*) Свое название механизм получил в соответствии с видом зависимости
s + h — a sin (<р + а).
558
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Для тангенсного механизма *) (рис. 562) имеем:
bQ = e (tg ? + tg «) — А 4~ Л) (1 — tg ? tg a), дл = е tg ('р - | - a) — х — Л, Д? = аге tg у ср а. (9.141) (9.142) (9.143)
§ 29. Синтез передаточных механизмов по условию минимального
отклонения от заданной функции
1°. Шарнирный четырехзвенник. Если при синтезе пере-
даточных механизмов поставить только условие получения минималь-
ного отклонения от заданной функции, то оно может быть выпол-
нено путем вычисления максимально возможного числа параметров
кинематической схемы. Для шарнирного четырехзвенника при задан-
ных углах срт и максимальное число параметров равно пяти
(а, Ь, с, а и р). Чтобы вычислить эти параметры, представим выра-
жение взвешенной разности (9.115) в виде обобщенного полинома,
полагая, что cp = F(cp). Имеем:
\ = 2 [р0ЛШ-РЛ(<?) + . ..4~РсА (<?)]> (9-144)
где
A(?) = cos©,
А (ср) = sin А(<?) = 1, (9.145)
А (?) = cos ср = cos [F (<р)], /B(?)=cos(<p — rp) = cos [F(<p)—ср],
A(?)=sin cp = sinF(c?)l, /6(<p) = sin(<p —cp)=sin |F(cp) — <p|;.
pa = a cos a,
Pi = — a sin a,
Pi = — c cos f>,
p3 =c sin 3,
b'2 —
Pi = —-------2-------’
Ps = — (P0P2 + P\Рз).
Pe=PiP-2 —РоРз-
(9.146)
Выражение (9.144) совпадает с функцией (9.12), для которой, как было
показано в § 27, можно вычислить коэффициенты /»„, plt ..., р4, при-
меняя любой из трех рассмотренных видов приближения функций.
Если требуется получить квадратическое приближение, то состав-
ляется система уравнений (9.59), которая решается в предположении,
что 1 = Л1 = 0.
Если требуется получить наилучшее приближение, то сначала вы-
бирается число точек предельного отклонения, которое на основании
*) Свое название механизм получил в соответствии с видом зависимости
s h = е tg (у ф- а).
§ 29] СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 559
необходимого условия Чебышева должно быть не менее чем на еди-
ницу больше числа искомых параметров, т. е. для шарнирного четы-
рехзвенника при заданных углах и ф„ число точек предельного
отклонения должно быть не менее шести. Полученное приближение
будет наилучшим, если выполняются достаточные условия, следующие
из теоремы Геронимуса, т. е. если любые две функции <p = F(<p) шар-
нирного четырехзвенника имеют на отрезке приближения не более
четырех нулей. Это условие в общем случае не выполняется, так как
при решении задачи о приближении к заданной функции ф = /7(<р) по
методу интерполирования можно получить три шарнирных четырех-
звенника с общими узлами интерполирования, число которых равно
пяти. Однако в дальнейшем мы будем всегда принимать число точек
предельного отклонения равным шести, если отклонение от заданной
функции выражается обобщенным полиномом (9.12).
Если в результате решения задачи получается три различных
механизма, то путем непосредственного подсчета отклонения Д можно
выбрать тот из них, который дает меньшую величину предельного
отклонения.
Вычисление наилучшего приближения производится в данном слу-
чае путем последовательных приближений. Сначала находятся значе-
ния углов ср/;, близкие к тем значениям углов при которых дости-
гаются предельные отклонения функции Д.
Для .первого приближения рекомендуется принимать значения уг-
лов по формуле (9.92) или (9.93).
Коэффициенты ръ ..., и Lq — предельное отклонение взве-
шенной разности Д? в первом приближении находятся из системы
шести уравнений:
Ро/о Ы + PJi Ы +... +Рб А (?*) - (-1 )fc у = о, (9.147)
k = 0, 1,2,3,4,5.
После последовательного исключения по схеме решений линейных
уравнений неизвестных Lq, рь ръ, р6, р.2 и р3 получаем систему урав-
нений (9.16), решая которую находим неизвестные коэффициенты рп,
Ръ Pi, Рл и plt а затем и величину предельного отклонения взвешен-
ной разности Lq.
После вычисления коэффициентов рв, pit ..., pi находим искомые
параметры механизма из соотношений (9.146).
Имеем:
tg а = — £1 а — — ,
° /'о sin а
‘ р21 sin .J
b = ]/а2 -ф с2 ф 1 -ф 2pi-
(9.148)
560 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. IX
Если полученные параметры дают удовлетворительный в конструк-
тивном отношении механизм и величины углов давления не превосхо-
дят допускаемых, то вычисляем значения отклонений Д^ по формуле
(9.119), причем следует найти экстремумы взвешенной разности Д?,
которые практически совпадают с экстремумами отклонения Дф, вы-
числяя в точках <рь и в точках, близких к <fk, значения производной
dbq
Дифференцируя выражение (9.144), имеем:
Y =— A, sin ? + Pi cos <р — ipt sin ф -f- ip3 cos ф — (i — 1)ps sin (ф — <p) Ц-
4 G—1)^6 c°s (Ф—?), (9.149)
где
.__d'b__dw у.г
d<f dz p.w‘
Вычислив значения 0,5Д^ в двух или трех точках вблизи каж-
дого значения tpk, нетрудно путем линейной интерполяции найти те
значения <р, при которых Д^_ 0, т. е. точки предельных отклонений
во втором приближении.
Если полученные величины отклонений Дф желательно уменьшить,
то следует вычислить искомые параметры во втором приближении из
системы шести уравнений:
Pofo fe) 4" Р> fi (?fc) + • • • + Pe/e (?fc) — (— !)ft be cos = 0,
k = 0,1,2, 3,4,5, (9.150)
где L — величина предельного отклонения разности Дф; <pfe и —
значения углов <у и Я в тех положениях, где Д^ = 0, и по концам
рассматриваемого отрезка.
Решение системы уравнений (9.150) не отличается от решения си-
стемы (9.147). Но так как значения параметров механизма в первом и
втором приближениях обычно мало различаются между собой, то
можно для решения системы уравнений (9.150) воспользоваться мето-
дом линейных поправок.
Обозначим значения коэффициентов />0, plt..., pt в первом приближе-
нии через р0, pi,pt, а искомые поправки через = рп — р0,
Ърх=р1—Pi,..., ^Pt^Pt — Pi- Тогда, пренебрегая малыми величи-
нами произведений поправок, можно представить систему уравне-
ний (9.150) в следующем виде:
(Ро 4" W» (?л) + (Pi + 8Pi)/i (?*) — + (Pt 4" (?*) 4*
+ <Pt —P^Pt — Р-^Ро ~ Р^Рз — P^Pl)flS (Tt) 4-
4- (Ре — Ро8Рз — Л8Ро4-Р18^4-рЛМЛ(%) —cos 'dkL = о,
£ = 0, 1, 2, 3, 4, 5.
29] СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 561
Кроме того, примем во внимание, что
Poft> (?*) ~}~Pifi (?*) — 4“ A A (Vk)==(—i)fc be cos
где Lk — значения отклонений при <р = <fk, полученные при
первом приближении. Тогда система шести уравнений для вычисле-
ния поправок 8pn, 8рь8/?4 и величины предельного отклонения L
принимает вид:
Г/о (?*) - Pift (?*)— Pi ft, (?*)] S/’o + (Л (?*) — РзА (?*) + Ptft (?*)] 8Pi +
+[А(?*)~ А)А(?*)+АА (?*)] +[/з (?*)— Pifs Ср*) —й>А(?*)] 8/>з +
4" А Ср*) fyi — (—1)" be cos »ftL = — (— l)Kbc cos ttkLk, (9.151)
k = 0, 1, 2, 3, 4, 5.
Второе приближение дает обычно приближение, очень близкое к наи-
лучшему. Во многих случаях можно ограничиться даже первым при-
ближением, так как точки предельных отклонений выбираются с уче-
том получения наилучшего приближения, а параметрический вес изме-
няется сравнительно незначительно, если механизмы с большими зна-
чениями углов давления отбраковываются. Для первого приближения
можно использовать также интерполирование, выбирая узлы интерполи-
рования по формуле (9.95). Указанный порядок вычислений коэффициен-
тов /?0, pi, ...,pt имеет место во всех случаях, когда отклонение от заданной
функции или взвешенная разность приводятся к функции (9.12). На осно-
вании рассмотрения методов вычисления коэффициентов этой функции,
а также некоторых других функций, рассмотренных в § 27, можно
сделать заключение, что если удается получить аналитическое
выражение отклонения от заданной функции или взвешенной раз-
ности в форме, допускающей вычисление параметров из условий
интерполирования, то можно применить также квадратическое или
наилучшее приближение (путем выравнивания отклонений). Поэтому
в дальнейшем для различных механизмов будут указываться только
выражения, допускающие вычисление параметров из условий трех
указанных видов приближения функций, имея в виду, что выбор
вида приближения производится на основании требований, сформули-
рованных в § 27 *).
Кроме того, будут указываться формулы для определения
искомых параметров кинематической схемы по вычисленным коэффи-
циентам
2°. Плоские механизмы с поступательными парами. Для
кривошипно-шатунного механизма выражение взвешенной разности
(9.124) при s = f1(<p) может быть приведено к виду:
А, =Л/о (?) 4~Л А (?) 4- - 4- Ръ А (?) - F(?). (9.152)
*)’См. стр. 544,
562
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
где
F(?) = s2=[F1(¥)]2, /3(?)=1
/о (ср) = s = Fi (<р), fi (?) = cos ?,
/1 (?)=scos <p = Ft(?) cos ср, /в (<р) = sin <р;
Л(?) = « sin <р = F, (ср) sin ?,
(9.153)
Рп — — 2/г,
Pt = 2а sin а,
Pi = 2а cos а,
р3 = Ь'1 — а2 — е2 — /?2,
РоР1 .
Pl = — ч—^р^'
PoPs
Pn = ~L2------Pie.
(9.154)
Для вычисления коэффициентов р(}, pt, рг, р3 и параметра е
по методу интерполирования составляем систему уравнений:
Ptifu (?D ~\~Pifi (?/) ~F — +Fs/b (?<)— F (?<)> 1—1, 2, 3, 4, 5.
Исключая последовательно из этих уравнений р^,р^р^,р.2 и рх, получаем:
Р0Р2
2 «1 “Г гз—«8_г/гсГо’
Р<1>1 2 Ч~ Pie — k3 ^рй, Р2—ksp0, 1 (9.155)
7’1 = ^зЧ-^1о/’о- j
Исключая из первого и второго уравнений системы (9.155)
параметр е и подставляя значения коэффициентов р.2 и р{ из четвер-
того и пятого уравнений, получаем кубическое уравнение для опре-
деления коэффициента р^. После вычисления коэффициента pi} нахо-
дятся из уравнений (9.155) коэффициенты рх, р2 и р3 и параметр е.
Другие искомые параметры вычисляются по формулам:
= ^К^з + «а + ^ + /г2.
г 2
(9.156)
Аналогично вычисляются квадратическое приближение или наи-
лучшее приближение.
Для кулисного механизма из формулы (9.131) при = F, (?)
имеем:
^ = А [Ао/о(?)+А1/1(?)+^/2(?)+Аз/3(?)-/7(?)], (9-157)
§ 29]
синтез по условию минимального Отклонения
563
где
F (<р) = cos ф = cos F) (ср),
/о (?) — sin Ф = sin F1 (ср),
/1(<Р)= sin (Ф — »)=sin [Fi (ср) — <р],
А (?) = cos (ф — <р) =
= cos [Fi (ср) — <р],
А (<?) = !;
(9.158)
А — — cos 3,
Ро = tg з,
Pi = a (sin а'— tg (3 cos а),
Ръ = а (tg 3 sin а 4- cos а), I
р
Н9-159)
Формулы для вычисления искомых параметров:
tg ₽ +—
tgp=7’n> tga =------------ Pi ,
e =Pi cos 8, a — . . .
rA ‘ tg p Sin a + COS a
(9.160)
Для механизма эллипсографа при s — f\(x) из формулы (9.136)
имеем:
А = Р« А (*) + Р1 /1 (х) + Pifi (*) + Рз/з (*) — F (*)> (9.161)
где
F (х) =.х2 s'2 = х2 + [Fi (х)|2, fs(x) = sx = xFi (x),
./o(x) = 2x, /3(x)=l;
/i(x) = s = Ft(x),
pn = — 2 (/h — h cos 7]), p., = 2 cos t;,
Pi = — 2(h — ht cos 7]), p^ — b2 — h'2 — h2lA-2hhl cost;.
Формулы для вычисления искомых параметров:
Ра
COS 7] = -9 •
b = J/jp8 h h2 — 2hhi cos tj ,
po COS 7)J-fi
2 sin2 •»)
Pc + Pl COS 7)
2 sin2 7]
(9.162)
(9.163)
. Для синусного механизма при s==Fi(<p) из формулы (9.139)
д5 =Ро А (?) + Pi А (?) + Pi А (?) — F (ср), (9.164)
564
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
(ГЛ. IX
где
= —s = —Fi(cp), /1(<p) = cos<p,
/o(?) = sin ср, /2(<р)=1;
p0= — a cos а, рг = h.
Pi = — a sin a,
(9.165)
(9.166)
Формулы для вычисления искомых параметров:
h=Pi,
P>
sin a
tg a = £L
(9.167)
Для тангенсного механизма про s = Ft(<p) из формулы (9.141)
имеем:
д9 = /'о А (?) + Pi /1 (?) + Pt h (?) — F (ср), (9.168)
где
F (?) - - s = Ft (ср), fi (<р) = s tg ср = Ft (ср) tg ср,
A(?)=tg?> /«(?)= 1;
Po — e~b,ltga> Pi — etga—h.l
Pi = tga, J
Формулы для вычисления искомых параметров:
tga=Pi,
Г. PoPl — Ps
F+рГ
е Рг-F h
Pi
(9.169)
(9.170)
(9.171)
3°. Пример вычисления квадратического приближения. Число-
вые примеры, которые приводятся в данном параграфе и в после-
дующих, имеют своей главной целью показать не только достоин-
ства предлагаемых методов, но и ограничения, им присущие, а также
некоторые особенности решения задач синтеза механизмов, не под-
дающиеся рассмотрению в общем виде.
В качестве первого примера решим задачу о проектировании
шарнирного четырехзвенника для воспроизведения логарифмической
функции
w = lgz, IsgZsglO,
причем требуется получить минимальную величину среднего (по
модулю) отклонения от заданной функции *). В этом случае параметры
* О выборе метода приближения см. стр. 544.
§ 291 СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 565
кинематической схемы механизма вычисляются сначала из условия мини-
мума среднего квадратического значения взвешенной разности Д?
в т -|- 1 точках графика заданной зависимости, т. е. из условия мини-
мума суммы
i=m
^=2(MS- (9172)
i=0
После вычисления искомых параметров из условия минимума суммы Sq
в случае надобности производится их уточнение из условий минимума
среднего квадратического значения отклонения от заданной функции,
т. е. из условий минимума суммы
i=m
s= 2
i=»0
которая для шарнирного четырехзвенника имеет вид:
i—m
<9173>
i = 0
причем значения параметров Ь и с, а также значения углов давле-
ния Я,- принимаются равными их значениям, полученным при первом
приближении.
Однако обычно нет надобности производить уточнение параметров,
так как функции Д(/ и Дф близки между собой, если угол & на от-
резке приближения не более допускаемого значения &доп *). Например,
при &доп = 60° величина cos меняется не более чем в два раза.
Если же максимальный угол Я после вычисления параметров из усло-
вия минимума взвешенной разности Д? оказывается более допускае-
мого, то механизм является неудовлетворительным и уточнять значе-
ния полученных параметров обычно нет смысла.
Для решения поставленной задачи задаемся величинами входного
угла срт и выходного угла фт:
?т = 55°, фт = —90°.
Тогда масштабы р.д и вычисляемые по формулам (9.99), получают
следующие значения:
—_ 9 | 1 I
г Чт 55 | град]’
_ wm—w0 ________1 Г 1 1
1w~ i>m — 90 I град Г
Заданная функция положения (9.100) при этих масштабах имеет вид:
*) При выборе допускаемого угла давления можно руководствоваться ука-
заниями, сделанными в главе VI (см. стр. 393).
566
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
или
f ф \
55° . - 90 . [
-1/-
График заданной функции w = lgz в рассматриваемом интервале
показан на рис. 563. В соответствии с характером этого графика
выбираем на нем 11 точек через равные промежутки по оси w вели-
чиной 0,1. Координаты этих точек указаны в таблице 9.9 *).
Таблица 9.9
Вычисление углов у и 4
wo = O, z0 = l, —=—90° = —1,57079 радиана,
1Л®
1 45°
— = = 0,10666 радиана
9
i 1£) Z =10® £ — 1 с —12)—- {1 14) <р=(г-гс) —
радианы гра- дусы радианы градусы
0 0 1 0 0 0 0 0
1 0,1 1,2589 0,2589 —0,15708 — 9 0,02761 1’34'55"
2 0,2 1,5849 0,5849 —0,34416 —18 0,06238 3’34'26"
3 0,3 1,9953 0,9953 —0,47124 —27 0,10616 6’04'55"
4 0,4 2,5119 1,5119 —0,62832 —36 0,16126 9°14'20"
5 0,5 3,1623 2,1623 —0,78540 —45 0,23063 13’12'50"
6 0,6 3,9811 2,9811 —0,94247 —54 0,31796 18’13'05"
7 0,7 5,0119 4,0119 —1,09955 —63 0,42791 24’31'01"
8 0,8 6,3096 5,3096 —1,25663 —72 0,56632 32’26'53"
9 0,9 7,9433 6,9433 — 1,41371 —81 0,74057 42’25'55"
10 1 10 9 — 1,57079 —90 0,95993 55’00'00"
*) Вычислять углы у и 4 одновременно и в радианах и в градусной мере
необязательно.
§ 29] СИНТЕЗ ПО 5'СЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 567
Решение задачи начинаем с вычисления функций (?)> •
по формулам (9.145). Далее вычисляются коэффициенты ск[ по фор-
муле (9.38). Вычисления производятся по схеме, аналогичной указан-
ной в таблице 9.3. Проверка вычислений коэффициентов ск1 произ-
водится по формулам (9.39), полагая у/г и F (х,) равными нулю.
В соответствии с полученными значениями коэффициентов ckl
система уравнений (9.59) может быть записана в следующем виде:
11р4 3,71084ps — 6,98502р6 4- 6,85312р9 —6,85312р3 4- 3,34302р. 4-
-ф- 9,96784р(| — 0;
3,71084р4 — 5,438359р5 — 1,090 38р6 + 4,57992ра —
— 0,292962р3 — 0,655802р. -{- 4,194198pft — X — 0;
— 6,98502р4 — 1,09038ръ -ф- 5,561608ре — 3,635997ра -ф-
-ф- 5,38794р3 — 2,658872р. — 6,197281р0 — Л. = 0;
6,85312р4+ 4,57992р5 — 3,635997р6 -ф- 5,500031ра —
— 3,156895р3 -ф- 1,115981р. 4- 6,657043р„ — Хр0 -ф- Х.р. = 0;
— 6,85312р4 — 0,292962ps5,38794pe — 3,156895ра -ф- 5,500031р3 —
— 2,946175р. — 5,86907рп — Хр. — Х.р0 = 0;
3,34302р4 — 0,655802р5 — 2,658872р6 4- 1,115981ра —
— 2,946175р3 4- 1,777937р. 4~ 2,671286р0 — Хр3 4-Х|Ра=.0;
9,96784р4 4-4,194198ps — 6,197281р6 -ф- 6,657043ра —
— 5,86907р3 4- 2,671286р. -ф- 9,222036р„ — Хр4 — Х.р3 = 0-
Полагая Х = Х. = О, исключаем из первых пяти уравнений по
схеме решения линейных уравнений (табл. 9.1) последовательно неиз-
вестные: р4, р8 = — р0р2 — Р1Рл, Pt,=P\P~i— РоРг, Pt и p3.
В результате исключения получаем систему уравнений (9.16)
в следующем виде:
р3 = 0,430330р. —0,572316р0;
р2 = —0,226381р. — 0,415220р0;
р6 = —0,241794р. 4- О,5О4768ро;
ps = —0,414262р. — 0,149671рс;
р4 = 0,091438р. —0,633143р0.
В соответствии с полученными значениями коэффициентов Л.,
Ла, ..., й.о подсчитываем далее по формулам (9.20) коэффициенты
А., А.г, А3 и Д4, входящие в уравнение (9.19).
После деления их на А. получаем следующее кубическое урав-
нение;
е — 0,13233*2 4- 0,9716512$ 0,6264427 = 0.
I
568 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гЛ. IX
Решая данное кубическое уравнение, имеем один действительный
корень:
5 = -£!- = —0,49051.
Ро
Система уравнений (9.21) и (9.22) для определения неизвестных ръ
и р3 принимает вид:
— 0,4905 — р3 — 0,6233706;
— р.2 4- 0,49051^3 = — 0,0535280.
Отсюда
р 2 = —0,203321;
р3 = —0,523639.
Подставляя полученные значения в первое и второе уравнения
системы (9.16) и решая их, найдем:
р0 = 0,668425;
/?! = —0,327863.
Значения ръ и р6 определяются из третьего и четвертого урав-
нений системы (9.16), а также для контроля из соотношений:
Ръ = — Р№ — Р1Рз, P6=PiPi—Pops-
§ 29] СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ
Имеем:
569
рв = 0,0357766;
рй = —0,41667-53.
Из последнего уравнения системы (9.16) находим:
А = —0,428967.
После подстановки найденных значений р0, рь ... , р6 в послед-
ние два уравнения системы (9.59) получаем X = Х(^0. Следовательно,
уточнения полученных значений р0, р1г ..., pt не требуется.
Далее по формулам (9.148) находим искомые параметры механизма:
а = 0,744498;
Ь= 1,005925,
<7 = 0,561730.
а=26°07'38",
Р = — 68°46'45"
Полученный механизм показан на рис. 564.
Для определения максимального отклонения от заданной функции
подсчитываем по формуле (9.144) значения взвешенной разности Д9
во всех выбранных точках.
Затем вычисляем отклонения от заданной функции Д по фор-
муле (9.119).
Таблица 9.10
Вычисление отклонений
фт=1,57; 2Ьс= 1,1301
i COS & д Q д. ф д Д =—Д-.100% Отн Pml
0 0,18 0,00070 0,00346 0,22
1 0,25 —0,00088 —0,00330 —0,21
2 0,33 —0,00064 —0,00170 —0,11
3 0,40 0,00020 0,00044 0,03
4 0,48 0,00078 0,00144 0,09
5 0,57 0,00056 0,00086 0,06
6 0,67 —0,00022 —0,00028 —0,02
7 0,77 —0,00084 —0,00096 —0,06
8 0,87 —0,00038 —0,00038 —0,02
9 0,95 0,00102 0,00094 0,06
10 1,00 —0,00038 —0,00034 —0,02
Все вычисления указаны в таблице 9.10, где приведены также
относительные значения отклонений
А,
Л°ТН==|Фт-^|,1000/о'
570
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
График изменения взвешенной разности Д показан на рис. 565
и график изменения отклонений Дотн— на рис. 566. Из таблицы 9.10
и рис. 565 следует, что для функции Д? квадратическое приближе-
ние очень близко к наилучшему, так как максимальное отклонение
шесть р.аз принимает свои предельные значения с последовательно
чередующимися знаками.
Предельные значения функции Д указанные в таблице 9.10, не
совпадают по величине вследствие значительного изменения cos &
на интервале приближения. Максимальный угол давления равен почти
80’, что нельзя считать удовлетворительным. Поэтому уточнения
параметров механизма производить не будем, а попытаемся получить
воспроизведение той же функции при других значениях входных и
выходных углов (<рт=100°, фт = —50°). Но для иллюстрации раз-
личных методов решения применим не квадратическое, а наилучшее
приближение.
4°. Пример вычисления наилучшего приближения. В качестве
примера возьмем ту же задачу о воспроизведении функции w— lg z
на участке от г0=1 до £„, = 10, которая была решена при помощи
квадратического приближения, но значения углов и фт примем:
<рт=100° и фт = —50е.
Тогда масштабы рг и вычисляемые по формулам (9.99), по-
лучают следующие значения:
§ 29] СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 571
Заданная функция положения (9.100) при этих значениях мас-
штабов имеет вид:
ф = — 50 lg (1 + 0,09?).
Число точек предельных отклонений принимаем равным шести.
Считая, что концы отрезка приближения совпадают с точками пре-
дельных отклонений, вычисляем значения углов ? для точек пре-
дельного отклонения по формуле (9.90):
?J = 0°, ?1a = 0,65451?m = 65°27'03’,
?]= 0,09549?,,,= 9°32'57", ? = 0,9045 1?ш = 90°27'03",
?‘ = 0,34549?т = 34°32'57", ?' = 100°.
Эти значения углов ? соответствуют расположению точек пре-
дельного отклонения многочлена Чебышева пятой степени при аргу-
менте ?. Если принять за аргумент угол ф, то значения углов ?,
соответствующие расположению точек предельного отклонения мно-
гочлена Чебышева пятой степени, найдутся по формулам (9.91).
Имеем:
= 0°, = (100'6545’ — 1) =39°02' 17’,
?п=(10о,09549_ 1) 2°43'57", ?" — ( 1 о0-90451 — 1) ~ =78°04'07',
?«=( 109.34549_!) 13°29'23", ?!‘ = 100°.
Таблица 9.11
k Ф Ф — V
0 0 0 0
1 6'08'27" — 9'33'14" — 15'41'41"
2 24'01'40" —25'00'06" — 49'01'46'
3 52=14'40" —37=48'05" — 90=02'45"
4 84=15’35" —46=40'58" —130'56’33"
5 100= —50° —150°
Принимаем в качестве первого приближения значения абсцисс
точек предельного отклонения равными полусумме значений ?^ и ?”:
?0= 0°, ?3 = 52° 14'40’,
?,= 6с08'27", ?4 = 84°15'35",
?s = 24°01'40", ?в=100°.
В таблице 9.11 указаны значения углов ? и ф, а также разно-
сти ф — ? для выбранных точек предельного отклонения.
572 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
Далее вычисляем функции /0(<р), />(?).........ft, (ф) по формулам
(9.145). В соответствии с полученными значениями функций система
уравнений (9.147) имеет следующий вид:
Pt> — 0,57,0 — 0,
0,9942619/?0 -|- 0,1069728^1 + 0,9861299/?2 — 0,1659751/?3 -ф-
+ Pl -|- 0,9627161ръ — 0,2705117/?6 -ф- 0,57,, = 0,
0,9133482р0 4- 0,4071735/?j + 0,9062995^ — 0,4226359/?3 ф-
4-Pl 4- 0,6556785/?в — 0,7550402/?6 — 0,57,, = 0,
О,612292О/?о 4- 0,7906315/?i + 0,730140 \Pi — 0,6129263/?3 4-
4- Pi — 0,0008032/?в — 0,9999997/?6 -j- 0,5L,=0,
O,lOOO192/?o 4- 0,9949855/?! 4- 0,6860371/?a — 0,727566 Рз 4-
4- — 0,6553012/?B — 0,7553676/?6 — 0,5L,=0,
— 0,1736482/?0 4- 0,9848078/?! 4- 0,6427876/?2 — 0,7660444/?3 4-
4~/?4 — 0,8660254/?s — 0,5000000/?6 -j- 0,57.,=0.
Для решения этой системы уравнений сначала исключаем неиз-
вестное L, непосредственным сложением каждой пары уравнений.
Затем по схеме решения линейных уравнений (табл. 9.1) исключаем
неизвестные /?в, Рб> Pi и Рз и получаем систему уравнений (9.16):
Рз = — 0,06629534/?! — 0,86007159/?0,
/?8 = — 0,56005615/?! — 0,43607825/?0,
Рб== 0,39152408/?! 4-0,57912560/?0,
р.. = —P{)Pi — Р1Рз — 0,55779094/?! — 0,34722495/?п,
/?4 = 0,00274716/?! —0,21636993/?0.
В соответствии с полученными значениями коэффициентов kt, k.2,...
..., Am подсчитываем по формулам (9.20) коэффициенты Аи Аг, А3 и
Д4, входящие в уравнение (9.19). Тогда уравнение (9.19) имеет вид:
0,33835047е3 4- 0.60620363I2 4- 0,38502947^ 4~ 0,5511839 = 0.
Решая данное кубическое уравнение, имеем один действительный
корень:
1,6889528.
Система уравнений (9.21) и (9.22) для определения неизвест-
ных /?з и Рз принимает вид:
— 1,6889528/?а — /?3 = —0,08214007.
—/?24- 1,6889528/?3 = — 1,28930750.
Отсюда
/?8 = 0,3706724; /?3 = —0,5439081.
§ 29] СИНТЕЗ ПО УСЛОВИЮ МИНИМАЛЬНОГО ОТКЛОНЕНИЯ 573
Далее из первых двух уравнений системы (9.16) находим неиз-
вестные рй и рг:
Ро — 0,7270507, />, = — 1,2279544.
Значения ръ и />6 определяются из третьего и четвертого уравне-
ний системы (9.16), а также для контроля из соотношений
Ръ = — РоРч — Р1Рз, P6=PiPi— РоРз-
Имеем:
/>в = —0,9373920; р6 = — 0,0597200.
Из последнего уравнения системы (9.16) находим:
Pi = — 0,1606853.
Далее подставляем найденные значения коэффициентов рп,
Pi, ..., Рй и значения функций /0(<р), /1 (<р), ...,/«(<р), вычисленные
для предполагаемых точек предельного отклонения, в формулу (9.144)
и убеждаемся в том, что с точностью до четырех знаков значения
взвешенной разности в этих точках равны величине 7.^ = 0,0007084.
Искомые параметры находятся по формулам (9.148):
а = 59°22'16", а = 1,42705,
р = 235°43'58”, с = 0,65832,
b =1,77440.
Схема полученного механизма показана на рис. 567. Максималь-
ный угол давления в этом механизме составляет 65°, т. е.
по сравнению с предыдущим примером получены более благоприят-
ные соотношения между размерами звеньев.
574
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Для выявления величины максимального отклонения от заданной
функции устанавливаем сначала точки экстремумов взвешенной раз-
ности Д9, подсчитывая величины 0,5 Д^ по формуле (9.149).
В таблице 9.12 приведены экстремальные значения взвешенной
Таблица 9.12
<₽ Ф W л<7 АФ дотн
0 0 0 —0,000708 58°5Г —2'01" 0.067
6°42' —10° 15’ 0,2049 0,000792 46°48' 1'42" —0,057
24’45' —274 Г 0,5487 —0,000771 17’09' —1'11" 0,039
58°54' —39°58' 0,7994 0,000866 20° IV 1'21" —0,045
88’00' —47°31’ 0,9504 —0,000810 52°42’ —1'58" 0.065
100° —50° 1 . 0,000708 65°29' 2'31" —0,084
разности Д§ на рассматриваемом отрезке и величины угла <р, при кото-
рых достигаются эти значения. В этой же таблице указаны значения
*0,001
0
. A i
]ог хшojn о,8 \ \i,o w
'0,001
Рис. 568.
углов давления, подсчитанные по формуле (9.108), и отклонения
от заданной функции Д^, вычисленные по формуле (9.119) в минутах
и в процентах к величине <рт. На рис. 568 показан график измене-
ния взвешенной разност До, а на рис. 569 — график изменения стало-
§ 30]
СИНТЕЗ С-УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
575
нений Доти. Из таблицы 9.12 и рис. 569 видно, что максимальное
отклонение от заданной функции не превышает 2'31", т. е. 0,084%
от заданной величины изменения уела ф.
Так как максимальное значение модуля отклонения Д, (2'31")
не равно минимальному значению (2'01"), то максимум модуля этого
отклонения можно уменьшить до величины 0,5 (2'31" + 2'01") = 2'16",
что составляет 0,076% от задан-
ной величины изменения угла ф.
Для этого надо только изменить
значение начального угла р на ве-
личину 8? = 0,5 (2'31" — 2'01 ")=
= 15". Новое значение этого угла
в соответствии с рис. 554 и по-
строением, показанным на рис. 570,
найдется из условия
р=3-г 8? = 235-43'58"+ 15" =
= 235°44'13".
Определив указанным образом
угол р, мы достигнем равенства
отклонений Д^ на концах интерва-
ла. Экстремальные значения откло-
нения Д^ внутри отрезка прибли-
жения меньше величины L = 2'16".
Минимальная величина модуля эк-
стремальных значений отклонения
Дф равна Г06". Поэтому возможно дальнейшее уменьшение предельного
отклонения L до величины, заключенной в пределах от 1'06" до 2'16"
(обычно ближе к нижнему пределу), т. е. приблизительно до вели-
чины 1'35". Для этого следует выравнять экстремальные значе-
ния разности Д,, решив систему линейных уравнений(9.151). Однако уже
в первом приближении достигнута высокая точность приближения к за-
данной функции (L = 2'16"), и дальнейшее уменьшение величины L
на 40" не имеет существенного значения, так как ошибка положения
ведомого звена, получающаяся от погрешностей изготовления и
сборки механизма, больше этой величины даже при очень тщательном
изготовлении всех звеньев механизма.
§ 30. Синтез передаточных механизмов с учетом
дополнительных требований
1°. Графический метод определения параметров передаточных
Механизмов. Методы, изложенные в предыдущем параграфе, обеспе-
чивают получение максимально возможного приближения к заданной
функции, но часто дают механизмы, не удовлетворяющие дополни-
тельным требованиям, к которым относятся: значения углов давления,
576 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
проворачиваемость звеньев, конструктивно приемлемые размеры
звеньев, габариты механизма и т. д. Поэтому необходимо иметь
методы, которые позволяют получать приемлемую величину отклоне-
ния от заданной функции (хотя и не минимально возможную) и
в то же время дают возможность удовлетворить указанным дополни-
тельным требованиям.
В данном параграфе излагается метод, при котором решение
задачи синтеза передаточных механизмов разделяется на два этапа.
Первый этап состоит в систематическом обозрении всех возможных
вариантов механизмов, удовлетворяющих условию приближенного
воспроизведения заданной функции при помощи наиболее простых
способов с целью предварительного выявления тех вариантов, кото-
рые удовлетворяют дополнительным требованиям. Второй этап состоит
в уточнении полученных приближенных значений параметров меха-
низма. Для первого этапа можно использовать или атласы функций,
воспроизводимых различными механизмами, или же применить
графический метод варьирования параметров механизма.
Исходными данными для определения искомых параметров гра-
фическим методом являются заданная функция w=/(z), представ-
ленная в виде графика (рис. 571), и значение максимального угла
давления &ДОп от шатуна ВС к ведомому звену CD (рис. 572).
Для решения задачи выбираем на графике заданной функции т -|~ 1
точек так, чтобы они соответствовали равным перемещениям ведущего
звена. (В рассматриваемом примере принято т — 9.) Число точек
зависит от вида заданной функции. Рекомендуется выбирать такое
число точек, чтобы максимальное расстояние от хорды, соединяющей
две соседние точки, до линии, изображающей заданную функцию
между этими точками, не превосходило допускаемого отклонения.
Затем задаемся величиной фт, определяем по формуле (9.99) мас-
штаб шкалы ведомого звена и вычисляем для выбранных точек
из соотношений (9.98) углы поворота ведомого звена CD, отсчитыва-
емые от начального положения: фь ..., фт.
Определив углы поворота звена CD, приступаем к графическому
определению искомых параметров кинематической схемы.
Построение начинаем с вычерчивания положений ведомого звена CD,
соответствующих равным интервалам изменения углов поворота веду-
щего звена, причем длина звена CD может быть выбрана произ-
вольно, так как зависимость между углами поворота звеньев АВ
и CD зависит лишь от относительных размеров звеньев. На рис. 572
построенные положения звена CD обозначены через Со£>, C^D,.CmD,
причем Z, C$DCr — (рь Z Со£>С2 — фг и т. д. Далее, выбрав опреде-
ленную длину шатуна ВС, описываем из точек Со, С), ..., Ст, как
из центров, окружности радиусом, равным выбранной длине шатуна,
и проводим к направлениям C0D, CVD, ..., CmD прямые под углом,
равным 90° — &доп- -Участки окружностей с центрами в Со, Сь ..., Ст,
которые оказываются заключенными между этими прямыми, обозначены
§30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
677
19 И. И. Артоболевский
578 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
на рис. 572 жирными линиями. Очевидно, что положения шарни-
ра В не должны располагаться на этих участках, так как при
этом угол давления будет больше допустимого. Выбрав положение
точки В при некотором допустимом значении угла давления О, най-
дем положение точки А и длину звена АВ из условия получения
равных изменений углов поворота ведущего звена АВ или, что то
же самое, равных расстояний между точками Вй, Bt, ..., Вт, пред-
ставляющих собой положения шарнира В, соответствующие данным
положениям Со, Сь ..., Ст шарнира С. С этой целью задаемся
величиной хорды B^Bi и, взяв ее в раствор циркуля, отложим после-
довательно от точки Во на окружностях, проведенных из цент-
ров Со, Ci,..., Ст. Полученные точки, которые обозначены на чер-
теже через Вй, Bi, ..., Вт, образует ломаную линию, которая
с некоторой погрешностью может быть заменена дугой окружности.
Центр этой окружности определяет искомое положение точки А,
а радиус этой окружности — длину звена АВ. Одновременно опре-
деляется также входной угол <рт и начальные углы аир.
Для получения допустимых углов давления достаточно только,
чтобы точки Ве, Въ ..Вт не располагались на участках, обозна-
ченных жирной линией. Кроме того, полученный механизм можно
проверить в отношении других дополнительных условий (габаритов,
соотношений между размерами звеньев и т. д.).
Однако при произвольно выбранном положении начальной точки Во
ломаная Вп Вг... Вт может значительно отличаться от дуги окруж-
ности, поэтому следует построить несколько ломаных В(! Bi... Вт
и выбрать из них ту, которая ближе всего подходит к дуге окруж-
ности. Вид этих ломаных изменяется закономерно, поэтому область
положений точки Во, в которой ломаные Во Вх... Вт близки к дугам
окружностей, определяется очень быстро. Например, при длине
хорды B^Bi, принятой на рис. 572, достаточно исследовать лишь
участки В'йВ" и В"'В™.
Далее можно использовать варьирование величины хорды В{}ВХ,
которая, однако, может меняться в сравнительно небольших пределах,
так как нижняя граница этой величины зависит от максимальной
величины расстояния между двумя соседними окружностями, прове-
денными из центров Со, Сь ..., Ст, а верхняя граница определяется
из условия расположения точек Во, Bit Вт на участках, соот-
ветствующих допустимым углам давления на всем интервале измене-
ния углов поворота ведущего звена. Во избежание затемнения чер-
тежа рекомендуется для каждой величины хорды ВйВ\ оставлять
лишь одну ломаную В^Вх ... Вт, наиболее близко подходящую к дуге
окружности.
Предложенный прием позволяет на одном чертеже непосред-
ственно определять пять параметров кинематической схемы (длины
звеньев АВ и AD, начальные углы а и f и входной угол <рт). Выбор
указанных пяти параметров обеспечивает обычно в первом приближе-
§301
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
579
нии достаточную точность воспроизведения заданной функции при
соблюдении дополнительных условий. В случае необходимости можно,
однако, использовать также варьирование длины шатуна ВС и угла
размаха ведомого звена <рт-
В рассмотренном способе графического варьирования параметров
кинематической схемы угол размаха ведущего звена, соответству-
ющий условию достаточно точного приближения к заданной функции,
получался в процессе варьирования параметров. Однако в некоторых
случаях углы размаха ведущего и ведомого звеньев могут быть
Рис. 573.
заданными. Тогда процесс графического варьирования параметров
кинематической схемы несколько видоизменяется, а именно, для
отыскания длины ведущего звена АВ и положения центра А при-
меняется в этом случае шаблон, выполненный на кальке. Этот шаб-
лон (рис. 573) представляет собой сектор с центральным углом, рав-
ным углу размаха ведущего звена срт. Этот сектор разделен на рав-
ные части, число которых равно числу рассматриваемых положений
щ-|- 1. Кроме того, на секторе проведены концентрические окруж-
ности, соответствующие различным значениям длины ведущего
звена АВ.
Так же как и в предыдущем случае, построение начинают с вы-
черчивания требуемых положений ведомого звена CD, соответству-
19*
580
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
ющих равным интервалам изменения углов поворота ведущего звена АВ.
Затем из центров Со, Сь ..., Ст (рис. 574) описывают окружности
радиусом, равным выбранной длине шатуна. Эти окружности обозна-
чены цифрами 0, 1,..., тп. Далее проводятся к направлениям Со£),
C\D, ..., CmD прямые под углом, равным 90° — &доп. Участки окруж-
ностей 0, 1, ..., т, которые оказываются заключенными между этими
прямыми, обозначены жирными линиями. На этих участках нельзя
выбирать положения шарнира В, так как при этом угол давления
будет больше допустимого.
Все указанные выше построения выполняются на листе бумаги и
полностью совпадают с соответствующими построениями для преды-
дущего случая. Далее для нахождения искомых параметров кинема-
тической схемы (АВ, AD, а и f) накладывают на лист бумаги с по-
строениями, показанными на рис. 574, шаблон, выполненный на кальке
в соответствии с рис. 573, и перемещают его в плоскости чертежа,
стремясь найти такое положение шаблона, при котором точки пере-
сечения радиальных лучей шаблона,обозначенных цифрами 0, 1,..., т,
с окружностями 0, 1, ..., т, имеющими тот же номер, располо-
жились на одной из концентрических окружностей шаблона. Переме-
щение шаблона можно выполнять, например, в следующем порядке.
§ 30] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 581
Задавшись длиной звена АВ, т. е. выбрав одну из концентрических
окружностей, нанесенных на шаблоне, за траекторию точки В, уста-
навливают шаблон так, чтобы точка пересечения радиального луча «0»
с этой концентрической окружностью расположилась на окружности «0»
в конце участка, обозначенного жирной линией, а точка пересечения
луча «ш» с той же концентрической окружностью расположилась
на окружности «т» (см. рис. 574). Обозначим указанные точки пе-
ресечения через B'q и В'т. Тогда точки пересечения окружностей
1, 2,..., т—1 с выбранной концентрической окружностью в общем
случае не совпадут с точками пересечения радиальных лучей с кон-
центрической окружностью. Обозначим точки пересечения концентри-
ческой окружности с окружностями 1, 2, ...,т—1 через В\, В'?,...
..., В'т- |. Расстояния между этими точками и точками пересече-
ния радиальных лучей, измеренные по концентрической окружности,
представят в некотором масштабе величины отклонения от заданной
функции Д^. Далее перемещаем шаблон так, что точка пересечения
радиального луча «0» с выбранной концентрической окружностью
остается на окружности «0», а точка пересечения радиального
луча «т» с той же концентрической окружностью остается на окруж-
ности «т». Пусть, например, указанные точки пересечения после
перемещения шаблона займут положения В’о и Вт- При этом можно
видеть, что отклонения Д, для положений 1, 2,..., т—1 будут
отличаться от тех значений, которые они имели при первом положе-
нии шаблона. Следовательно, перемещая шаблон указанным образом,
можно непосредственно видеть изменение величин отклонения Д^ и
выбрать то положение шаблона, при котором максимальная величина
отклонения Д или его средняя величина будет наименьшая. При
перемещении шаблона необходимо следить за тем, чтобы точки Ва
и Вт не заходили на участки, отмеченные жирной линией, так как
при этом углы давления будут больше допустимых. В силу этого
ограничения шаблон приходится перемешать в сравнительно неболь-
ших пределах. Установив наилучшее положение шаблона при выбран-
ной длине звена АВ, следует далее повторить все операции пере-
мещения шаблона при другой величине длины звена АВ, т. е. поль-
зуясь другой концентрической окружностью шаблона. Следует
заметить, что длина звена АВ также может варьироваться только
в сравнительно небольших пределах, так как наибольшая величина
этой длины определяется из условия расположения точек В() и Вт
на участках, соответствующих допускаемым углам давления, а наи-
меньшая величина — из условия расположения точек Во и Вт на
окружностях «0» и «т». Если варьирование длины звена АВ и пере-
мещение шаблона не дают приемлемой величины отклонения Д^, то
следует изменить длину шатуна, что связано с изготовлением нового
чертежа окружностей 0, 1,..., т. После установления надлежащего
положения шаблона непосредственно по чертежу определяется длина
стойки AD и начальные углы аир.
582
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
2°. Аналитическое уточнение параметров шарнирного четырех-
звенника. После нахождения графическим методом параметров
механизма, удовлетворяющего воспроизведению заданной функции
с учетом дополнительных требований, следует выполнить второй этап
синтеза — аналитически уточнить значения полученных параметров
с целью повышения точности приближения к заданной функции.
При этом вычисляется только часть параметров, а остальные пара-
метры сохраняют значения, которые были получены графическим
путем. Уменьшение числа вычисляемых параметров уменьшает (иногда
очень значительно) трудоемкость вычислений и в то же время умень-
шает опасность того, что вычисленные параметры будут сильно отли-
чаться от первоначальных и будут нарушены вследствие этого при-
нятые дополнительные требования.
Для шарнирного четырехзвенника при аналитическом уточнении
можно вычислять три или четыре параметра. При вычислении трех
параметров группируем члены в выражении взвешенной разности (9.115)
так, чтобы оно имело вид обобщенного полинома
Д<7 = A [pofo (<р) + pj\ (ср) 4- АЛ (?) — Р (?)]• (9.174)
Значения коэффициентов рй, рх и р% и функций F (<р), /0 (<р), /у (<р),
/8(<р) будут различными для различных комбинаций искомых парамет-
ров. Пусть, например, требуется вычислить относительные размеры
звеньев а, b и с. Тогда в соответствии с обозначениями, принятыми
в формуле (9.174), при ф — (<р) *) имеем:
F (<р) = cos (<р 4- a), fi (<р) = cos (ф — <р 4- р — а),
Zo (?) = cos (ф 4-р), /8(<р)=1;
А = — 2а,
С
=
— с,
1 4-a24-cs — bs
Р* =-------Та-------
(9.175)
(9.176)
Для определения коэффициентов рп, рг и р% рекомендуется применять
квадратическое приближение, т. е. вычислять их из системы уравне-
ний (9.31). После вычисления коэффициентов p(i, рх и р.2 находятся
искомые параметры а, b и с по уравнениям (9.176). Для повышения
точности приближения можно вычислять искомые параметры из усло-
вий минимума не взвешенной разности Д?, а отклонения Д^, которое
имеет вид:
\ = A [Pofo (?) 4- Ptfi (?) + F2/2 (?) — Р (?)] > (9-177)
*) В дальнейшем для краткости в формулах для F (f) и /у (у) не указы-
вается, что ф = Р\ (<f).
§ 30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
583
где
F(?)
COS (y + g)
cos ft
Л(?)
/о(?)
cos ft
А(?) =
COS (ф — У + P — a)
cos ft
1___.
cos ft ’
(9.178)
A
be
1 + a2 4- c2 — *2
Pt = —1----------------
(9.179)
2a
Pi = — G
c
В формулах (9.178) значения cos D для каждого значения угла <р
определяются графически, используя построения, которые выполня-
лись при графическом определении искомых параметров или же путем
вычисления угла & из соотношения
о й2 + с2 — а2—1 , а , . .
sin Э = 2Ьс-------------Н ЗГ cos (? + а)- (9.180)
Следующая возможная комбинация искомых параметров состоит из
относительных размеров звеньев механизма а, b и начального угла а.
Тогда в выражении отклонения Д^ по формуле (9.177) изменяются
значения функций F (у), /о (?), /1 (?) и коэффициентов р0, рх и pt.
Имеем:
F (Т) = _£2^Щ)
VT/ COS й
COS (ф — ¥ -J) _|_ cos у
=---------------cosft-------------
sin (ф — у Р)---------- sin J
fo (?) cos у I ft (?) cos у >
. 1
A — , Pi — a cos a,
b r
b2 — a2 — c2 — 1
Po = a sin a, pv = --------------------------
(9.181)
(9.182)
При определении параметров b, с и р имеем:
Р (?) =
COS (у + а)
cos 8
--- COS (ф — у — а) -|---— COS ф
COS ft
sin (ф — у — а) —• — sin ф .
Л W ToUT '
p0 — c sin p ,
Pl = C COS p,
e2 -L £S I ]
--------2a-------
(9.183)
(9.184)
584
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[Тл. IX
Не останавливаясь на других комбинациях трех искомых параметров,
отметим, что более высокую точность дает вычисление четырех пара-
метров. Пусть, например, требуется вычислить параметры а, Ь, си р.
Тогда функция Дф может быть представлена в следующем виде:
ДФ = А Wo (?) + Pifi (?) ~Т Pifi (?) "h Psf-л (?) +
+W1A(?)-F(?)], (9.185)
где
(9.186)
(9.187)
методу
F(y) = coS(?-y-jO /() = ^(ф) 1
V ‘7 cos ft * J ' cos &
r f X __ COS Ф Г r x ___ 1
/о (?) cos ft » /3 (?) cos ft >
r z x sin (0 — — a) x / \ sin ?
/1 (?) cos $ > fl (?) cos g ’
. a n 1
A =------7- cos 0, p2 =---------7-,
b r’ c cos
__ 1 _ a2 4- c2 + 1 — t>2 .
a ’ 2ac cos ₽
Pi = tg ₽,
Значения коэффициентов p0, plt р.г и р3 вычисляются no
квадратического приближения из системы уравнений (9.53).
После определения коэффициентов ра, ръ и р3 находим из
соотношений (9.187) параметры кинематической схемы механизма.
Аналогично производятся вычисления при других комбинациях
четырех искомых параметров. Например, для вычисления параметров
а, Ь, с и а отклонение Д^ представляется также в виде функции (9.185):
дф = А Wo (?) + Pifi (?) + РчЛ (?) + Рз/з (?) + PuPifi (?) — F (?)]>
где
р (ал _ cos (? — ? + ₽) f (а>) _ cos (?4
cos» • A(?)— coU
f e x COS <p z z \ 1
/о (?) cos $ > /з (?) cos у >
f _ sin (? — ч + ₽) f _ sin ¥ .
fiW— cos& ’ fiW —
. a 1
A —----г cos a, =----------,
b a COS a ’
______I ___ 1 -у д2 4- c2 — b2
P® c ' Fa 2ac cos a
Pi = — tg a,
(9.188)
(9.189)
Четыре параметра шарнирного четырехзвенника можно вычислять
и не прибегая к предварительному графическому определению пара-
§ 30] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 585
метров механизма, а именно, можно путем варьирования значения
пятого параметра получить множество различных механизмов,
осуществляющих приближение к одной и той же функции, и затем
выбрать из них тот механизм, который удовлетворяет дополнитель-
ным требованиям. Обычно для этой цели используется метод интер-
полирования. Решая систему уравнений Д/?; = 0 для z= 1, 2, 3, 4,
можно получить функцию а = /(а) или c=j\ (Р). Г рафические
изображения этих функций известны в синтезе механизмов под
названием кривой круговых точек и кривой центров. Вывод анали-
тических выражений этих функций и их анализ здесь не проводятся,
так как они подробно будут изучаться в той части книги, которая
посвящена методам синтеза механизмов с применением кинематической
геометрии.
3°. Аналитическое уточнение параметров механизмов с по-
ступательными парами. Для кривошипно-шатунного механизма
(см. рис. 556) укажем в качестве примера вычисления трех парамет-
ров комбинацию а, b и е. Тогда
д<7 = Го/о (?) +/’1/1 (?) + /’« А (?) — ? (?), (9.190)
где
F(?) = (« +/г)2, /г (?) = cos (<р -|-а),
А (?) = (s +,г) sin (? + а)> А (?) = 1 >’
/70 = 2а, pi==b- — а2 — а2.
Pi = Чае,
Можно вычислять эти же параметры также из условия минимума
отклонения Д? или Д5. В первом случае функции F (<р), /0(?), Ут (?)
и А(?) следует делить на величину cos &ь а во втором случае —
на величину cos 0, где 9| — угол давления от звена ВС к звену АВ,
0—угол давления от звена ВС к ползуну (см. рис. 556).
Другая возможная комбинация вычисляемых параметров: Ь, е и h.
В этом случае функции F (р), /0(?), Л(?) и /2(?), а также коэффи-
циенты рй, Pi и ря в формуле (9.190) имеют вид:
F (<р) = s2 — 2as sin (<р a), (<p) = a sin (y —[— a) — s,
A (?) = cos (<P + a), A (?) = 1;
pa = Чае, p.2 = F2 — a2 — <?2 — /г2. ]
о/ (9-194)
Pi = 4h, J
He останавливаясь на других комбинациях трех параметров, укажем
формулы для вычисления четырех параметров а, Ь, е и /г:
Д ч = Ро А (?) + Pi fi (?) + Pi А (?) + Ро А (?) + /’o/’i А (?) — F (?),
(9.195)
(9.191)
(9.192)
(9.193)
586
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
где
F('f) = s2, Л (<р) = cos (<р -ф- а),
/о(<р) —ssin(<f>4-a), /з(<р)=1,
f _________ йп (у + °).
/1 (?) = •», 2 ’
рй — 2а, р% = 2ае, 1
Pi = — 2ft, р3 - - ft2 — а2 — а2 — ft2. J
(9.196)
(9.197)
Формулы для аналитического уточнения параметров других меха-
низмов с поступательными парами (кулисного, синусного, тангенс-
ного и эллипсографа) не приводим, так как они с очевидностью
следуют из формул (9.131), (9.139), (9.141) и (9.136).
4°. Пример вычисления трех параметров механизма. В ка-
честве примера вычисления трех параметров механизма рассмотрим
решение задачи о проектировании механизма, у которого ведомое
звено должно на некотором участке рабочего хода двигаться при-
ближенно равномерно. Кроме того, время движения, соответствующее
обратному ходу ведомого звена, должно быть меньше времени ра-
бочего хода. Подобного рода механизмы распространены в общем
машиностроении, например в прессах и в станках для обработки
плоскостей. Схема одного из этих механизмов показана на рис. 575.
В соответствии с условиями работы механизма задано, что при
равномерном движении ведущего звена АВ ведомый ползун должен
в течение рабочего хода двигаться приближенно равномерно на про-
тяжении участка, составляющего 60% от всего хода ползуна. Кроме
того, время обратного хода ползуна должно быть меньше времени
рабочего хода.
Длина шатуна СЕ в этом механизме мало влияет на равномер-
ность движения ползуна и может быть выбрана поэтому из конст-
руктивных условий. В рассматриваемом примере выберем / = 2,5с,
где с — длина звена CD при длине AD, принятой за единицу.
§30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
587
Начало отсчета углов <р примем совпадающим с линией стойки AD,
т. е. примем а = 0. Начало отсчета углов ф примем совпадающим
с направлением движения точки Е ползуна. Тогда подлежат опре-
делению относительные размеры звеньев шарнирного четырехзвен-
ника а, Ь, с, начальный угол р и значение угла <р в начале и
конце отрезка приближения <р0 и <рт*). Из шести искомых парамет-
ров будем вычислять в данном примере только три параметра а, b
и с. Значения остальных трех параметров выберем, применяя графи-
ческий метод так, чтобы удовлетворить грубо приближенно задан-
ным условиям.
Имеем: <pfl = 185°30', <?т = 287°30', р=117°30'.
Решение задачи начинается с вычисления требуемых углов пово-
рота ф звена CD. Обозначим через s перемещения точки Е, отсчи-
тываемые от ее крайнего правого положения. Перемещение s и угол
ф связаны соотношением, которое получается из формулы (9.130)
при е — 0, а = с, Ь = 1, <р = ф, а = 90° и h = c-\-l:
cos ф - 1
2/ — s s
с1 — s 2c
Обозначая относительное перемещение точки Е через
(9.198)
получаем:
(9.199)
Согласно заданным условиям перемещение точки Е должно быть
пропорционально углу поворота ведущего звена <р на участке от
хо = 0,2 до хт = 0,8. Выбирая на этом участке семь точек через
равные промежутки, вычисляем по формуле (9.199) значения углов ф.
Значения углов ф приведены в таблице 9.13.
Найденным значениям углов ф должны соответствовать равные
углы поворота ведущего звена от <рв = 185°30' до <рт = 287°30'. Значе-
ния этих углов, а также углов ф р и ф р — <р указаны в таб-
лице 9.13. Затем производим вычисление функций F (ср), f\ (<р) и /2(<р)
по формулам (9.175) **) и вычисление коэффициентов и ckl по
*) Углы ф„ и определяются заданием отношения—и участка, на ко-
тором движение ползуна приближено к равномерному.
*♦) В данном случае нет необходимости применять формулы (9.178), так
как из графического построения следует, что углы давления & меняются
в сравнительно небольших пределах.
588
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Таблица 9.13
Углы ср и
1 X Ф <₽ Ф + ₽ Ф + ₽ — <е
0 0,2 45е 18'48" 185с30’ 162°48’48" —2741'12"
1 о,з 56 59 13 202 30 174 29 13 —28 00 47
2 0,4 67 48 14 219 30 185 18 14 —34 11 46
3 0,5 78 27 47 236 30 195 57 47 —40 32 13
4 0,6 89 30 06 253 30 207 00 06 —46 29 54
5 0,7 101 32 13 270 30 219 04 13 —57 25 47
6 0,8 115 34 04 287 30 233 04 04 —54 25 56
формулам (9.37) и (9.38). Для проверки вычислений служат следу-
ющие равенства:
i=m
То + соо + с01 + fo2 = 2A (?<) s«> (9.200)
/ = 0
Ti Н- coi 4~ си Ч- си — ^,/i (*Pi) si- (9.201)
i = 0
В результате вычислений система уравнений (9.31) принимает
следующий вид:
5,576944/?0— 4,761337/?! — 6,176114ра = 3,235123,
— 4,761337/?04- 4,093272/?! 5,286091/?2 = — 2,806867,
— 6,176114/?0-j~ 5,286091/?! -ф- 7/?2 = — 3,217419.
Решая эту систему по схеме последовательного исключения не-
известных, имеем:
^2=2,505361, /?! = —2,758609, /?0 = 0,999445.
Искомые параметры механизма определяются в соответствии
с формулами (9.176):
с= 2,75861, с = 2,76014, b = 2,19632.
Для определения максимального отклонения от заданной функции
установим связь, которая существует в этом механизме между вели-
чиной — Ьф и величиной
= sM — 8,
(9.202)
где 8 — требуемое перемещение точки Е', sa — действительное пере-
мещение точки Е в механизме.
§ 30] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 589
Эта связь проще всего определяется путем построения плана
малых перемещений, т. е. плана скоростей преобразованного меха-
низма, который получается из исходного, если закрепить в данном
положении ведущее звено АВ, а длину шатуна ВС сделать пере-
менной посредством введения дополнительного ползуна. На рис. 576
показаны преобразованный механизм и его план скоростей. При ма-
лых величинах отклонений перемещения можно считать пропорцио-
нальными скоростям. На основании этого свойства получаем:
4^ = -^-. (9.203)
Д6 ссх '
рс
Планы скоростей для определения отношения —— практически
се*
удобно строить из одного полюса повернутыми на 90° и совмещен-
ными с планами положений (рис. 577).
Величина Дь может быть вычислена по формуле
которая при вычислении параметров а, b и с имеет следующий вид!
дь = — у [/Vo (?) +Р*Л (?) +A. -F (?)]• (9.204)
590
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Кроме того, условимся оценивать точность заданных перемеще-
ний по величине
Дл = *м — х, (9.205)
где х= s —требуемое относительное перемещение точки хн=
= 8"----действительное относительное перемещение точки Е в ме-
ханизме.
Величины Д5 и Дх связаны очевидным соотношением:
Подставляя в эту формулу соотношения (9.203) и (9.204), полу-
чаем:
Д- = --^[/’оЛ(<Р) + /’1Л(?)+р2-/7(?)] (9-206)
В этой формуле условимся приписывать отношению отрица-
тельный знак, если отклонения Д6 и Дх имеют различные знаки.
Вычисление отклонений
Таблица 9.14
i F (tp) Pofo <v) Pifi <¥) [1] -12|- -13)-Pa ccx дх-103 = = 15116)
1 2 3 4 5 6 7 8
0 —0,995396 —0,954817 —2,545170 —0,000770 —0,175 —1,07 0,187 —0,449
1 —0,923879 —0,994821 -2,435413 0,000994 0,226 —1,16 —0,262 0,294
2 —0,771625 —0,995165 —2,281698 —0,000123 —0,028 —1,16 0,032 —0,059
3 —0,551937 —0,960905 —2,096507 0,000114 0,025 — 1,08 —0,027 0,008
4 —0,284015 —0,890498 —1,898960 0,000082 0,019 — 1,01 —0,019 0,176
5 0,008727 —0,775942 —1,719921 —0,000771 —0,175 —0,90 0,157 —0,240
6 0,300706 —0,600536 —1,604589 0,000470 0,107 —0,78 —0,083
Относительное отклонение скорости движения точки Е от посто-
янной величины можно приближенно измерять величиной отношения
д ____ Р"СР
v vcp
(9.207)
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 591
г
§30]
где
(9.208)
(9.209)
Принимая во внимание формулы (9.205), (9.208) и (9.209), можно
представить отклонение Дв в следующем виде:
Д„.— Д„. ,
(9-2Ю)
В таблице 9.14 приведены вычисления отклонений Дл и До по
формулам (9.206) и (9.210).
Из этой таблицы следует, что максимальное отклонение от задан-
ных перемещений точки Е составляет от всей длины рабочего хода
приблизительно 0,026°/в. или приблизительно О,О43о/о от длины участка,
на котором движение точки Е приближено к равномерному. Макси-
мальное отклонение скорости от среднего значения на этом участке
составляет приблизительно О,45°/о.
На рис. 578 и 579 показаны графики изменений величин Дх и Д„.
592
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
5°. Вычисление семи параметров шестизвенного шарнирного
механизма. С помощью шестизвенных механизмов можно получить
более точное приближение к заданной зависимости. Однако вычисле-
ние всех параметров' этих механизмов удается выполнить только для
наиболее простых схем *). В большинстве же случаев удается вычи-
слить только часть параметров.
Рассмотрим, например, вычисление семи параметров шестизвенного
шарнирного механизма, показанного на рис. 580. Схема решения этой
задачи рассматривалась 3. Ш. Блохом с применением комплексных
чисел. Здесь приводится другой метод решения, аналогичный методу,
использованному при синтезе шарнирного четырехзвенника.
Проектируя замкнутый контур ABMEFA на направление от-
резка AD и на направление, к нему перпендикулярное, получаем:
cos (<р —[— —[— т cos (/ 4-8) — I cos р. — г cos (ф 4~ Р) — cos 1 — 0,
sin (<р а) + т sin (X 4" &) — I sin 1Л — r s*n (Ф 4~ Р) — d sin 7 = 0.
Исключая из этих уравнений угол р., имеем:
/2= [cos (<р 4- а) 4- т cos (у — r cos (Ф + Р) — d cos у]2 -|~
[sin (<р 4~ а) 4~771 sin (X 8) — r sin (Ф Р) — d sin f]2.
Раскрывая скобки и выполняя преобразования, получаем:
Z'2= 1 -[—zzz2-[—2mc°s —<f>4~^—а)—2r cos (ф—<р 4- Р — а) —
— 2d cos (<р 4- а — у) — 2г/и cos (ф — X 4~ ₽ — —
— 2dm cos (х 4~ —'() 4"2rd cos (Ф 4~ Р — l)-
*) Например, для шестизвенного кулисного механизма, показанного на
рис. 598 (см. следующий параграф, стр. 632).
§ 30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
593
Следовательно, по аналогии с решением для шарнирного четырех-
звенника взвешенная разность может быть представлена в виде:
Д9 = 2r cos (ф — ? 4~ ₽ — а) — 2/п cos (х — ? -]- 8 — а) Ц-
-]- 2d cos (<р -|- а — -j) 2r т cos (ф — у ₽ — &) 4"
-]-2dm cos (х4-8 — ?) —2rd cos (ф4~р —y)4-/2 —zn2 —г2 —d2 — 1.
(9.211)
Угол наклона шатуна ВС, который входит в выражение взвешенной
разности, вычисляется по формуле *)
. , Sin fa 4- а) „„ . COS 4 /А о 1 ох
X = ? + а — arc tg ~[-----—— -------± arc tg , (9.212)
—----COS (f + а) ---sin ®1
ui С
где
с2 + б2 — а2,— 1 и,
sin =----------кт----------к -г“ cos (<р 4- а).
2bc 1 ос ‘ 1 ’
В выражение взвешенной разности (9.211) входят 11 параметров,
из которых семь параметров (г, т, d, I, р, 8, у) входят явно, а осталь-
ные четыре параметра (b, с, db а) входят в выражение для угла на-
клона шатуна х-
Для вычисления этих семи параметров представим выражение
взвешенной разности Д? в следующем виде:
= 2 [р0/0 (<р) 4-pJi (<р) 4- • • • + PJi (?) — (/’оГз 4- PiP^fi (?) 4-
4- (PiPt — РоРзУЛ (?) — (PoPt + PiPslfs (?) 4- (PtPi~PoPsYfto (?) —
— (№ 4- РзРв)/и (?) 4- (РзРз — PiPs) fn (?)], (9-213)
где
/»(?)= COS <p,
41 (?) — sin ®,
7a(?)=sin (ф —<p),
A(?)=cos (ф — <p),
/4(?)=sin(x~ ?)»
Рь-d cos (a —7),
Pi = — d sin (a — 7),
Pt = — r sin (P — a),
A(?)==cos (x — ?),
/.(?)=!,
/7(?)=sin ф,
/»(?)= cos Ф»
A(?) = sinx,
p3 = z-cos (P—a),
jdj = m sin (8 — a),
p9 = -r- tn cos (8 — a),
/in (?) = cos x,
Zu (?)= cos (ф — у),
fn (?) = sin (ф — x);
(9.214)
Is— ms—rs—d2— 1
(9.215)
*) 11ри вычислении угла у правильный выбор значений углов по их триго-
нометрическим функциям может быть сделан путем графического построения
Контура ABCD.
594 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX ‘
При решении задачи по методу интерполирования следует определить
по формуле (9.95) значения углов <р в семи точках, вычислить углы у
по формуле (9.212) и решить систему семи уравнений:
Pofo (Т.) + Pi fi (А А • • А Ро — (РоРа + PiPs)fi (<?i) А
A (PiPt ~РоРз) fs (Т.) — (PoPi ~\~Р1Рз)Л ('?,) + (PiPi — PoPo)fto (?,) —
— (РаР4 АРзРвЭ/пСрО А(РзР4 — = 2,..., 7.
(9.216)
Исключая по схеме решения линейных уравнений (табл. 9.1) пара-
метр р6 и группы Параметров: /?7 = рпр.2 Apip3, р^=рур2—рпр.л,
Рэ=РоР4 АР1Рв> Pio=PiPi~PoPi>, Pit=PiPi^-p3Ps> Pn=P3Pi~
— РъРъ, получаем систему шести уравнений:
Р0Р2 А Р1Рз — АпРо А АцР1 А АзРа А АцРз 4" AsPi А 1ер$,
PiPi — РоРз — АцРо 4- Aw.Pi 4- AvaPi 4- Ацр3 А ^-2вРг A АвРв,
PoPi 4- Р1Ръ — AiPo A A3ipi А А-ззРя 4- A4P3 4- AibP4 А ^зеРв. (9 217)
PlPl--РоРъ — ^41Ро _|~ АаР1 4- АзР« 4- ^44Рз 4" АоР4 4" АбРв»
P-iPi 4- РзРп — AiPo 4“ Asipi 4" АзРа “к АиРз 4“ A^pi А АвРв>
Рз!?1 РчРз — AolPo 4* АаР1 4- АзРа 4- А4Р3 4- AliPl 4- A6oPs-
Далее по схеме решения линейрых уравнений определим из первых
двух уравнений системы (9.217) параметры pt и ps. Имеем:
Pi = ВиРо 4- AaPi А В13ръ -|- Вцр9 -[- BKPoPi -[- Д167'17'3 -|-
А Bv.PiPi А В19р0р3, (9 218)
р9 — в^1р9 4- Bv>pi в.23р9 -ф- B9ip9 -ф- ВжРъРъ 4- B~29pip3 4“
4 - в^р^ч 4- вг9р9р9.
Подставляя значения параметров pt и р3 по формулам (9.218) в третье
и четвертое уравнения системы (9.217), получаем:
СцР9 4- С^Рз — B)lt 1 1
C9ip9-\-C92p9 = D.2, j (9.219)
где 1
Сц = Аз А (Ав — Ро) (Аз А Вкр0 BwPi) -ф-
+ (As Pi) (Bi3 -ф- в№Ро A B^Pi),
Ci2=А4 А (Ав —Ро) А ВюРо А В10Р1) А
А (Ав—Pi) (вси A Bwp0 А в2оР1), ,
c2i = Аз А (Ав —pi) (Аз А &кРо А В11Р1) А
А (^4в А Ро) (в23 А в2-АРо A b^pi),
С22 = Ац А (^4в —Pi) (Вц А В10Р0 А В10Р1) А
А (-^46 А Ро) (А4 А ВыРо A BibPl)>
А — (А1Л) А В12Р1) {Ро — Ав) А {Впрй А А2Г1) (Pi — Ав)—АгРо—АаРь
D9—{В A Bl2pi) (pi — А№)—(Вцр0 А АзР1)(РоА Аз)—А11Р0—-^aPi-
I
§ 30] СИНТЕЗ' С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 595
Отсюда
п ___ DiCss — DsCiS ____________ DsClt — DiCsl го 99m
р*~ CnC!S — C12C21 ’ /я CnC.2— C12C21- 4
Подставляя значение параметров pt и p6 по формулам (9.218)
в пятое и шестое уравнения системы (9.217), получаем:
£hA> + £i^i = F1’ 1 (9.221)
Ецр0 4~ ЕюРг — Fit J
где
fin = An 4~ (Ав — Pi) (fin 4~ fiiB/'a 4~ fits/7») 4~
4~ (Ae. — Pi) (fi^i “G fiasfia 4~ B.№p^),
fiia — ASi Ч- (As — Pi) (fiia А Епр^ 4~ fiie/’з) 4"
4- (^bb — Pi) {Ba 4~ fiiw/’a 4~ fiaeA’s) >
fi2i = A6i 4~ (Ab —Pi) (fin 4- fiie/’a 4- fiis^a) 4“
4- (-^66 4~fia) (fiai 4- fias/’a A В№рл),
fi22 = Д62 -]- (AeB —/23) (fi2i 4~ fin/’a 4- fiie/’з) A
4- (As 4- Pi) (fiaa 4- B^Pi 4~ fi-26/':<)>
fii=(ByjPi 4- виРз) (р^—ABB) 4~
“Hfiaa/’a 4“ Bup3) (p3 — AB6) — Аъзр%— Аъ1р3,
F2=(Bi3pi-[-Biip3)(p3 — Ав)—(B^Pi 4~ B2ip3) (p2 4~ A66)—Afi3/72—A eip3.
Отсюда
___ Ei^ss — F2^12 ___ ЕцЕ2 — F^iFi
EiiE-si — Esi^is * pi fiifss — EsiEis
(9.222)
Систему уравнений (9.220) и (9.222) удобно решать по методу
итераций. После вычисления параметров рй, plt р% и р3 находятся
параметры /?4 и р3 из формул (9.218) и затем параметр р* из какого-либо
уравнения (9.216). Затем из формул (9.215) находим искомые вели-
чины d, у, г, р, т, 8, I.
6°. Синтез механизмов по заданным значениям скоростей и
ускорений (кратное интерполирование). Под заданием значений
скоростей и ускорений при синтезе передаточных механизмов по-
нимается задание производных от функции положения по углу пово-
рота <р. Например, для шарнирного четырехзвенника могут быть
заданы величины
л ds'b IV
ф =W' ф и ф
596
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Обозначим через угловую скорость звена АВ. Тогда угловая
d'b
скорость звена CD будет равна = При w = const угловое ус-
^2ф
корение 1-го порядка равно —^- = ф"<и2, угловое ускорение 2-го по-
... о сРф >«, ,
рядка — от и угловое ускорение 3-го порядка
Если задана непрерывная и дифференцируемая функция положе-
ния ф —f (ср), то тем самым заданы и значения ее производных.
Поэтому методы приближения к заданной функции положений, изложен-
ные выше, обеспечивают не только приближение к заданным по-
ложениям, но и к заданным значениям скоростей и ускорений раз-
личных порядков. Однако при решении задач синтеза передаточных
механизмов по методу интерполирования иногда выбирают в качестве
заданных величин значения функции положения в узлах интерполи-
рования и значения ее производных, т. е. используют кратное интер-
полирование *).
В этом случае искомые параметры механизма определяются
из системы уравнений:
Д(<рг) = О;
Д'(<Р/)=О;
Д" (?/) = О,
(9.223)
где Д'(ср) — первая производная отклонения Д по аргументу ср, Д"(ср) —
вторая производная и т. д. Кратность узлов интерполирования может
быть различной, т. е. некоторые узлы могут быть простыми (Д (ср;) = 0),
другие — двукратными узлами (Д (<pf) = О, Д'(<pf) = 0), трехкратными
(Д (ср;) = О, Д' (срг) — 0, Д"(с₽/) = О) и т. д. Двукратный узел соот-
ветствует заданию положения ведомого звена и значения производ-
ной ф' в том же положении или, что то же, заданию ординаты некото-
рой точки графика функции положения и направления касательной
в этой точке. Трехкратный узел соответствует заданию положения
ведомого звена и значений производных ф' и ф" в этом положении
или заданию ординаты некоторой точки графика функций положения,
направления касательной в этой точке и радиуса кривизны и т. д.
Число уравнений (9.223) должно быть равно числу вычисляемых
параметров. Кроме того, следует иметь в виду, что при задании
в каком-либо узле производной некоторого порядка должны быть
также заданы производные всех более низких порядков. Отсюда
следует, например, что для шарнирного четырехзвенника при вычисле-
нии пяти параметров (максимально возможное число вычисляемых
*) О кратном интерполировании см. стр. 513.
§ 30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 597
параметров) возможны следующие варианты задания при кратном
интерполировании:
Для вычисления искомых параметров во всех случаях можно
воспользоваться выражением взвешенной разности Д?. Отклонение
от заданной функции Д и взвешенная разность Д обращаются
одновременно *). Поэтому вместо системы уравнений (9.223)
рассматривать эквивалентную ей систему следующего вида:
д9(?,) = 0;
ДЖ) = 0;
д? (?/) = 0,
в нуль
можно
(9.224)
где Д^ (<р), Д^'(<р),... — производные от Дв по аргументу ср.
Для шарнирного четырехзвенника при пяти вычисляемых пара-
метрах выражение взвешенной разности согласно формуле (9.144)
д<7 = 2 [До А (?) Pt ft (?) + Pi fi (?) + Pi A (?) Pi —
— (PnPi + PtPi) fs (?) + (PlPi — P0P3)f3 (?)],
где
A (?) = cos ?> A (?) = cos ф; A (©) = cos (ф — <p);
ft (?) = sin <?; f3 (?) = sin ф; /6 (у) = sin (ф — ?);
рй = а cos «; Рг = — c cos [i;
Pi — — n sin a; p3 — c sin p;
b2 — a2 — ca — 1
/’4 =----------§---------
*) См. стр. 504.
598
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гЛ. IX
Производные взвешенной разности До по аргументу ср получаем
путем дифференцирования функций Д (<р), Д (<р), ..., /в (<р).
Имеем:
Д7 — 2 [pofo (ср) (?) (?) -\-P3f3 (?) —
— (AA + PiP-л) f 5 (?) + (AA — аа)Л (?)];
Д9 = 2 [/7o/o (?) -J- PJ f" (?) Pif'i (?) Рз/з (?) —
— (AA +Р1Рз)/б (?) + (PiPi —PoPslfe (?)];
Как видно, выражения для производных взвешенной разности (9.225)
могут быть получены из выражения взвешенной разности заменой
функций /ц (ср), Д (ср), ..., /6(?) на их производные соответствующего
порядка. Приведем значения этих производных до 4-го порядка вклю-
чительно:
/о (?) = — sin ср; /з (ср) = ф' cos ф;
/'1 (?) = cos ср; /5' (ср) = — (ф' — 1) sin (ф — ?);
Л (?) = — ф' sin ф; /е (?) = (ф' — О cos (ф — ср);
(9.226)
Л (?) = — C0S ср; Д' (ср) = — sin ср;
Л (?) = — (ф')2 cos ф — ф" sin ф; /3 (ср) = — (ф')2 siп ф -{— ф" cos ф;
/б(?)=—(ф'— I)2 cos (ф—ср)—Ф"5Ш (Ф—ср);
/б (?) = — (ф' — I)2 sin (ф — <?) + ф" cos (ф — ср);
(9.227)
/о"(?) = sin ср; Д” (ср) =—cos ср;
Д" (ср) = [(ф')3 — ф'"] sin ф — Зф'ф" cos ф;
/з"(?) = — КФ')3 — Ф"'] cos ф — Зф'ф" sin ф;
Л"(?) = [(Ф'~ I)3 —Ф'"1 sin (ф — <р) — 3(ф'— 1)ф" cos (ф—ср);
Л" (?)=—[(ф' — 1 )3—ф'"] cos (ф—<р)—3 (ф' — 1) ф" sin (ф—?);
(9.228)
/o1V (?) = cos ?; /}v (ср) = sin ср; 1
fv (?) = [(ф')4 _ 4ф'ф"' — 3 (ф")2] cos ф + [6 (ф')2ф" — ф’У] sin ф;
/Г (?) = КФ')4 - 4ф'ф'" - 3 (ф")2J sin ф - [6 (ф')2ф" - фПГ] cos ф;
flv (?) = КФ' - 1 )4 - 4 (ф' - 1) ф'" - 3 (ф")2] cos (ф - ср) +
+ [6 (ф' - W - Ф'Ч sin (ф - ср);
//(?)=[(ф" -1)4-4 (ф' - I) ф'" - 3 (ф")2 ]sin (ф-?)-
- [6 (ф' - I)2 Ф" - Ф'Д cos (ф - ср).
(9.229)
§ 30]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 599
Схема решения системы урзвнений (9.224) при вычислении пяти
параметров шарнирного четырехзвенника для любого варианта, ука-
занного в таблице 9.15, совпадает со схемой решения уравнений (9.12).
Следует только в кратных узлах интерполирования при составлении
выражений &'9 (<?), М?)’ ••• вмест0 ФУн'<ций /о (р)> Л (р), ••• соот-
ветственно подставлять функции Л(р), /1 (р), ••• или функ-
ции /о (ср), /\ (р)> • • и т- Д- Следовательно, во всех случаях, ука-
занных в таблице 9.15 для вычисления пяти параметров, решение
системы уравнений (9.224) приводится к решению одного уравнения
не выше третьей степени.
Например, пусть имеем вариант № 4 по таблице 9.15, т. е. для
двух положений ведущего звена (<pt и <р2) заданы два положения
ведомого звена (ф( и ф2), значения производной ф' в этих положе-
ниях и значение производной ф" в одном из этих положений. Тогда
система уравнений (9.224) для вычисления пяти параметров шарнир-
ного четырехзвенника имеет следующий вид:
/’о/о (Pi) -b/’i/i (Pi) -\-Ръ/з (pi) “h/’з/з (рi) “h Pt — (РаРч “b/’i/’s)/в (Р1) +
+ (PiPi — Р0Рз)/б (Pi) = 0;
P»fо (фа) “b^i/i (фа) —1~ Л^в/а (Ра) “Ь/’з/з (ра) “Ь/Ч — (/’о/’а _Ь/’1/’з)/в (Ра) ~Ь
+ (PiPv — PdP^ U (Ра) = 0;
Pdf О (Pl) ~\~Plf \ (Pl) -}~Pif 2 (Pl) Рз/з (pi) — (PdPi ~}~Р1Рз)/ъ (pi) “h
+ (PiPt — РоРз) /в (Pi) = 0;
/’о/о (Pa) “b Ptf\ (Pa) “Ь/’а/г (Pa) + Рз/з (Pa) — (/’o/’a + Р\Рз)Гь (pa) ~b
+ (/’i/’a — РйРз) ft, (Pa) = 0;
Pdf о (Pi) P\f" (Pi) ~bPif 'i (Pi) -f-Рз/з (Pi) — (/’o/’a “Ь Р1Рз) fb (Pi) ~b
+ (/’i/’a — /’о/’з)/б (Pi) = 0.
В этих уравнениях функции /0 (ср), fx (ср), ..., fe (ср) вычислятся
по формулам (9.145), функции /о(р), ft (ср), .... /б(р) — по форму-
лам (9.226) и функции /о (р), ft (р)> .... /о' (р) — по формулам (9.227).
Решение указанной системы уравнений не отличается от решения
системы уравнений (9.12) и в общем случае приводится к решению
одного кубического уравнения.
Аналогично решаются и все другие варианты задач, указанных
в таблице 9.15.
При вычислении четырех параметров шарнирного четырехзвенника
функции /о (р)> /5 (р)...... а также функции /о (р), ft (р), ... на-
ходятся путем дифференцирования функций /0 (<р), (<р), ..., которые
имеют различный вид при различных комбинациях вычисляемых пара-
метров *). Решение получаемой системы уравнений производится
по схеме решений уравнений (9.8) и приводится в общем случае
к решению квадратного уравнения.
*) См. с гр. 584,
600 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [ГЛ. IX
Для механизмов с поступательными парами решение задач син-
теза механизмов с применением кратного интерполирования также
производится но схемам, применяемым при простом интерполировании.
Из рассмотренных случаев задания производных <[/, ф", ...
в отдельных точках графика функции положений наибольший интерес
представляют частные случаи задания ф' = 0 (задание крайних
положений)*) и ф" = 0 (задание экстремальных значений скоростей). Эти
случаи характерны для проектирования механизмов машин-автоматов.
§ 31. Синтез механизмов с равномерным движением
ведомого звена
1°. Шарнирный четырехзвенник. В предыдущих параграфах
решение задач синтеза передаточных механизмов было дано для
общего случая произвольно заданной функции ®i=/(z). Вычисление
приближения к заданной функции при этом основывалось на числен-
ных методах. В частном случае, а именно, когда требуется полу-
чить постоянство передаточного отношения между ведущим и ведо-
мым звеньями, возможно представить искомое решение в виде фор-
мул, связывающих параметры заданной функции и параметры
кинематической схемы механизма. Если исключить тривиальный слу-
чай шарнирного параллелограмма, то при помощи шарнирных меха-
низмов можно получить постоянство передаточного отношения
только приближенно на некотором участке изменения угла поворота
ведомого звена. Эти механизмы применяются в приборо- и машино-
строении и называются обычно механизмами с равномерным движе-
нием ведомого звена.
Для шарнирного четырехзвенника задачу о воспроизведении
равномерного движения можно свести к задаче о' приближении
шатунной кривой кулисного механизма к дуге окружности.
На рис. 581 представлен кулисный четырехзвенник АВТ. Допус-
тим, что траектория точки С, лежащей на линии шатуна ВТ,
*) Графическое решение этой задачи указано далее на стр. 825.
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 601
на конечном участке совпадает с дугой окружности, описанной
из центра D на линии стойки АТ. Соединим точку С с центром D
жестким коромыслом CD и отбросим звено $. Тогда в получившемся
шарнирном четырехзвеннике ABCD точка Т будет представлять
собой мгновенный центр вращения кривошипа АВ относительно
коромысла CD. Следовательно, угловая скорость коромысла будет равна:
АТ
%,
где %—угловая скорость кривошипа.
На том участке, где шатунная кривая *) точки С исходного
кулисного механизма АВТ будет совпадать с дугой Окружности 7,
шатун ВС шарнирного четырехзвенника должен постоянно проходить
через неизменную точку Т на линии стойки. Это означает, что
на рассматриваемом участке должны быть постоянными как угловая
скорость коромысла CD, так и линейная скорость точки С,
независимо от того, принадлежит ли эта точка кулисному механизму
или шарнирному четырехзвеннику. В действительности, однако,
нельзя на конечном участке осуществить совпадение шатунной кри-.
вой кулисного механизма с дугой окружности. Можно лишь до-
биться приближения с той или иной точностью шатунной кривой
к дуге окружности. Следовательно, нельзя осуществить на конеч-
ном участке и постоянство скорости шатунной точки кулисного
механизма, а можно лишь добиться с той или иной точностью при-
ближения скорости этой точки к постоянной. Важно здесь отметить
одно свойство кулисного механизма, непосредственно вытекающее
из приведенного рассмотрения: если шатунная точка лежит на на-
правлении кулисы несмещенного механизма, то при приближении
траектории этой точки к дуге окружности с центром на направле-
нии стойки линейная скорость рассматриваемой точки будет прибли-
жаться к постоянной. В частном случае при радиусе, равном беско-
нечности, соответствующая окружность превращается в прямую,
перпендикулярную к стойке.
Отсюда следует второе аналогичное свойство кулисного механизма:
если шатунная точка лежит на направлении кулисы несмещенного
кулисного механизма, то при приближении траектории этой точки
к прямой, перпендикулярной к направлению стойки, линейная ско-
рость рассматриваемой точки будет приближаться к постоянной.
При использовании этих свойств некоторые задачи об осущест-
влении приближенно равномерного движения в четырехзвенных и
шестизвенных механизмах могут быть сведены к задаче о наилуч-
шем приближении шатунных кривых кулисного механизма к дуге
окружности или к прямой**).
*) О шатунных кривых см. § 33.
** ) Задача о приближении шатунной кривой кулисного механизма к дуге
окружности или к прямой рассмотрена впервые 3. Ш. Блохом [9ej.
602 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
Примем за единицу расстояние AD (см. рис. 581, а) и введем
следующие обозначения: а — относительная длина звена АВ\ d—отно-
сительная длина стойки в кулисном механизме или расстояние
от центра А до мгновенного центра вращения звена АВ относи-
тельно звена CD в шарнирном четырехзвеннике; b — координата,
определяющая положение шатунной точки С на направлении кулисы,
или относительная длина шатуна в шарнирном четырехзвеннике;
с — радиус окружности у, к которой приближается шатунная кри-
вая точки С или длина звена CD в шарнирном четырехзвеннике;
t — вспомогательный Переменный параметр, равный расстоянию между
точками Ви Г; его значения t0, tlt и t.t отвечают тем положе-
ниям механизма в пределах 0 sg ср 180°, где уклонения шатунной
кривой точки С от дуги окружности достигают предельных значе-
ний; 1=^ —передаточное отношение между звеньями CD и АВ,
постоянство которого надлежит осуществить.
На рис. 581, б показаны ход шатунной кривой 8 и соответствую-
щие точки предельных отклонений этой кривой от дуги окружности
7, обозначенные через Со, С2 и С3.
Величины а, b и с существенно положительны, величины t и d
имеют знак. За начало отсчета для t принята точка В, и положи-
тельная ось направлена вдоль линии шатуна от В к Т. За нача-
ло отсчета для d принята точка А, и положительная ось направле-
на вдоль линии стойки от А к D. Рассмотрим сначала случай г<^0.
В этом случае направления вращения звеньев АВ и CD противопо-
ложны и точка Т располагается между центрами А и D (см. рис. 581, а),
т. е. с?^>0.
Для получения условий наилучшего приближения шатунной кри-
вой точки С к дуге окружности f составляем выражение взвешен-
ной разности:
где сф — расстояние от точки D до точек, лежащих на шатунной
кривой. Из треугольников CTD и АТВ имеем:
4 = (1— — 2(6 — 0(1 — <0cosZ;
с2 = г/2 В — 2dt cos /.
Отсюда
= г - b +1 + - d - * - »№-%<-«>.
Следовательно:
^q-----A [t* + Pll + Pi 4“ Pi
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 603
где А =
pt = — b(l 4-d); (9.230)
^ = d^4-14-O«_ С1 — d — ~у, (9.231)
ps = — b(d2 — c*)(l — d). (9.232)
Обозначим через Lq — предельное отклонение взвешенной раз-
ности Д,. Тогда предельное отклонение функции равно dLg и на
основании формул (9.84) функция -1 будет наименее уклоняться от
нуля при выполнении условий:
А = —(2f14-f3)=-a0 + 2(2); (9.233)
А — dLIJ = tl-\-2tit3, (9.234)
p^dL^Zt^tfr (9.235)
p3 = -tU3 = -t^2. (9.236)
Складывая уравнения (9.234) и (9.235) и подставляя значение р2
из соотношения (9.231), получаем радиус окружности 7:
с = уГ Ь2 4- 1 4- а2 — d — £ — g +—1<8 + 2ZoZa . (9.237)
Предельное отклонение точек шатунной кривой от точек окружности
7 равно:
(9.238)
где
L4 = Td & + % ~ fi~ 2^з)- (9-239)
Углы поворота кривошипа <р0 и <р3, соответствующие началу и
концу участка наилучшего приближения шатунной кривой к дуге ок-
ружности, равны:
CS-|_dS —fS a2_|_6fS_ZS
C0S^=-------2dd~^ И COS'P3 = -12^—'• (9-240>
Из уравнений (9.233) и (9.236) имеем:
= —(0(^ + ^0)2. (9.241)
Передаточное отношение но абсолютной величине будет равно:
1г‘1 = Ь=^’ (9-242)
откуда
‘' = |7RT (9.243)
604
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Подставляя в (9.241) значения рг и /»3 из (9.230) и (9.232), на-
ходим следующую зависимость между размерами исходного кулис-
ного механизма АВТ'.
4Z? (tf — а2) (1 — О = /0 \Ь (1 d) — ^]4. (9.244)
Предположим, что £0^>0. Тогда, учитывая, что d<^l, получаем
из соотношения (9.244):
a<rf. (9.245)
Решая (9.244) относительно Ь,. получаем:
/Д1 +<Z) + 2(d2— fls)(l — d)±21TtT(d2 — а2)(1 — d^4-(d2 —
(9.246)
где возможными пределами для /(), как это непосредственно следует
из рис. 581, будут:
d — a-<:_tn^d-[-a. (9.247)
Для нас интересны будут лишь те решения, которые удовлет-
воряют условию
Из уравнений (9.230) и (9.233) получаем:
, _ t(l + d)-t0 2 (9.248)
Из уравнений (9.233) и (9.236) найдем: 4 = — V to ~Ь • (9.249)
ti = 2 (^о + /^з) • (9.250)
Решения будут давать лишь те значения tb С и /3, которые
удовлетворяют пределам (9.247), указанным для /0. Если задано I,
постоянство которого требуется осуществить, то одна из возмож-
ных схем нахождения соответствующего четырехзвенника будет сле-
дующей. Подсчитываем по формуле (9.243) величину d. Далее за-
даемся значениями а и t0, удовлетворяющими наравенствам (9.245)
и (9.247), и находим по формуле (9.246) длину шатуна b искомого
четырехзвенника. По формулам (9.248), (9.249) и (9.250) подсчиты-
ваем значения £g, £3 и tb а по формулам (9.240) — углы <р0 и <р3,
разность которых <рт = | <р0 — уа | определяет угол поворота звена
АВ, соответствующий участку приближенно равномерного движения.
Длиной звена CD искомого четырехзвенника будет радиус с, оп-
ределяемый по формуле (9.237).
Передаточное отношение i в полученном четырехзвеннике будет
равно заданному только в тех положениях, где центр шарнира С
совпадает с точками С, С" и С" (рис. 581, б), в которых окруж-
т
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 605
ность 7 пересекается с шатунной кривой 8 исходного кулисного ме-
ханизма. Для нахождения предельного отклонения передаточного
отношения от заданного на участке наилучшего приближения между
и 'Рз можно поступить следующим образом.
Подсчитываем по формуле (9.239) значение Lq и по формуле
(9.238) предельное отклонение L точек шатунной кривой исходного
кулисного механизма от точек окружности у, которое имеет место
в точках Со, С1; С2 и С3. Чтобы в положениях четырехзвенника, отвеча-
ющих предельным уклонениям шатунной кривой от окружности у,
передаточное отношение было равно заданному, длина коромысла
должна быть соответственно не с, а с’= с-\-L или = с— L.
Следовательно, можно условно считать, что в этих положениях на-
рушение передаточного отношения вызывается ошибкой в длине ко-
ромысла, равной ±L.
Присоединим к найденному четырехзвеннику ABCD (рис. 582, а)
диаду в виде двух шарнирно соединенных ползушек S и q. Через
одну из них пропустим шатун найденного механизма, вторую заста-
вим двигаться вдоль линии стойки. Примем, далее, L за ошибку в
размере коромысла CD и, пользуясь методом Н. Г. Бруевича [12в],
определим графически из картины малых перемещений (рис. 582, б)
ошибку (Д</) в положениях шарнира Т на линии стойки при tn, tx, С
и t3. Тогда соответствующие отклонения в передаточном отношении
(9.242) будут выражаться приближенной формулой
1Д/1 = {Т=^(Д^) • (9-251)
Если наибольшее значение (Дй) при /0, tlf или t3 будет равно
(Дс()Пред, то соответствующее предельное отклонение в передаточ-
ном отношении |z| на участке наилучшего приближения составит:
I |пред = (Д^)пред • (9.252)
Пример. Допустим, что требуется спроектировать четырехзвен-
ник, у которого на угле поворота кривошипа <р — 60° передаточное
606
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
отношение должно быть приближенно равно I ——1. По формуле
(9.243) определяем d = 0,5. Задаемся а—0,2 и для последователь-
ных t0 в пределах (9.247) находим по указанным выше формулам
соответствующие углы поворота кривошипа <рт = | <р0 — ср3|. Получен-
ная зависимость между 70 и представлена на диаграмме рис. 583.
Если провести на ней прямую, соответствующую <рт = 60°, то она
пересечет кривую в точках k' и А", которые будут определять со-
бой не два механизма, а два параметра одного и того же механизма.
Если обозначить значения 70, соответствующие k' и k", через t'
и t", то, принимая /0 = /', мы получим после подсчетов по приведен-
ным формулам /3 = f'; наоборот, если принять f0 = (", то подсчеты
дадут 4 = f. Это есть непосредственное следствие того, что исход-
ные зависимости (9.233) и (9.236) симметричны относительно 70 и <3,
и t2.
Из рис. 583 следует, что f 0,575; если принять /0 = 0,575, то
подсчет по этому значению дает механизм со следующими парамет-
рами: b = 0,934, с = 0,2003, (р0 = 102°, ср3 == 39°, = 63°, L 0,003,
Д(/ = 0,0105, | Дг|пред = 0,042, максимальный угол давления на
участке приближения 8тах = 30°. Полученный механизм показан па
рис. 584, где на окружностях шарниров В и С указаны участки наи-
лучшего приближения. Следует отметить, что наложения направле-
ний шатуна ВоСо и В3С$ в положениях механизма, отвечающих на-
чалу и концу участка наилучшего приближения, имеющие место на
рис. 584, являются случайными и не представляют общего правила.
При решении поставленной задачи длина звена АВ выбиралась
произвольно. Меняя ее, можно еще далее снизить | Д/ |„ред или по-
низить &тах.
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 607
быть: либо /^>0, как на рис. 585,
Отметим, что выше нами был рассмотрен случай /(|^>0. Если
Z0<^0, то по формуле (9.248) должно быть 42>О и, следовательно,
в интервале между t0 и параметр t должен обратиться в нуль, что
возможно лишь при d — a.
Но в этом случае й = 0 и
по формуле (9.236) /2 = 0,
что противоречит формуле
(9.248). Иначе говоря, рас-
смотренный при /<0 слу-
чай Z0^>0 является един-
ственно возможным.
При /^>0 направления
вращений звеньев АВ и CD
совпадают. Величина t может
либо t<^0, как на рис. 586.
Выражение взвешенной разности Д9 совпадает с выражением для
случая /<^0, если считать величину d отрицательной.
Передаточное
ввеннике равно:
отношение между звеньями АВ и CD в четырех-
ык ____ I d.|
“о ~ l + |d| ’
(9.253)
откуда длина стойки исходного кулисного механизма
i
1— i
(9.254)
Из уравнения (9.244), поскольку d<^0, при Z0^>0 (рис. 585)
должно быть:
(9.255)
a<|d|.
608
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Второе ограничение
И<1
(9.256)
при t0^>0 получается из условия ^^>0 в соотношении (9.248).
Аналогичным путем получаем, что при /0<^0 должно быть:
а>|с?|; (9.257)
|d|>l. (9.258)
В остальном ход' решения задачи при z’^>0 ничем не будет
отличаться от решения при z<^0.
Поскольку при существует ограничение |с?|^> 1, в этом
случае согласно (9.253) может быть лишь i<^z<^l. Если спроек-
тировать механизм с передаточным отношением, лежащим в указан-
ных пределах, а затем принять в нем первоначально ведомое звено
за ведущее, то передаточное отношение окажется лежащим в пре-
делах l<^z<^2.
Следовательно, возможными пределами для z^>0 в механизмах,
удовлетворяющих ограничению (9.258), будут:
y<z<2. (9.259)
Обозначим через zM переменное значение передаточного отноше-
ния между звеньями АВ и CD, которое получается в механизме.
Так как на участке 0 «S 180° шатунная кривая исходного кулис-
ного механизма четыре раза достигает предельных отклонений от
окружности (точки Со, Ci, С2 и С3 на рис. 581), то по условию
31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 609
чередования знаков этих отклонений шатунная кривая на том же
участке может пересекать окружность 7 только в трех точках: С,
С" и С". Следовательно, передаточное отношение /м будет равно
заданному i именно в тех положениях, когда центр шарнира С будет
совпадать с С, С и С"'. Отсюда следует, что кривая /м=/(<р)
в пределах 0=g<?=gl80° будет пересекать прямую iM — i, отвеча-
ющую заданному i также в трех точках С, С, С" (рис. 587).
Напомним, что участок наилучшего приближения лежит между
углами <р0 и <р3. Точки С, С" и С"’ будут располагаться внутри
этого участка. Непосредственно из хода кривой гм =/(<?) на участке
<Ро 180° вытекает следующее общее свойство механизмов
с наилучшим приближением к заданному i = const: в пределах
0 гС «С <?0 их передаточное отн<
(или меньше) заданного I, а на
меньше (или соответственно боль-
ше) заданного I.
Чтобы механизм был прово-
рачивающимся, он должен прохо-
дить через положения </ = 0 и
7/'= 180°. Согласно рис. 587 в
одном из этих положений пере-
даточное отношение должно быть
больше заданного Z, а в другом
меньше заданного I. Геометриче-
иение 1М будет неизменно больше
участке <р3 ==g <р sg 180° неизменно
ски это означает, что в провора-
чивающемся механизме с наилучшим приближением к i = const отно-
сительный мгновенный центр Т, отвечающий заданному I, должен
лежать между относительными мгновенными центрами V и Т" при
</ - - 0 и ср" = 180°.
Относительные мгновенные центры Т и Т" (см. рис. 581) при ср' = О
и </' = 180° будут определяться в пересечении окружности
центра шарнира В с линией стойки. Следовательно, АТ'—АТ" = а.
Так как по предыдущему У17~ = 1г£], то, чтобы Т располагалось
между Т и /", должно быть:
а.
Это неравенство является необходимым .условием проворачивае-
мое™ шарнирных четырехзвенников с наилучшим приближением
к I — const. При г<^0 оно не выполняется, а при z^>0 выполняется
только в случае где имеет место ограничение (9.257). Сле-
довательно, проворачивающиеся механизмы с наилучшим приближе-
нием к равномерному движению могут быть только двухкривошип-
ными. Пределы для 1 = const в этих механизмах определяются
неравенством (9.259).
Если постепенно сближать точки Со, Сь С2 и С3 (см. рис. 581, б),
отвечающие наибольшим отклонениям шатунной кривой исходного
20 И. И. Артоболевский
610
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
кулисного механизма от окружности 7, то одновременно будут
сближаться и точки С, С" и С'", в которых шатунная кривая сов-
падает с окружностью 7. При постепенном сближении этих точек
в пределе шатунная кривая будет совпадать с окружностью в трех
бесконечно близких точках. На кривой гм=/(т>) этому будет соот-
ветствовать расположение трех
прямой I — const (рис. 588) или,
мерным движением. Практически же приближенно
ее бесконечно близких точек на
иначе говоря, точка перегиба С.
Звено CD шарнирного четырех-
звенника в положении, соответст-
вующем этой точке перегиба, бу-
дет иметь угловые ускорения 1-го
и 2-го порядка, равные нулю
(е = 0 и е' = 0). Следовательно,
в трех бесконечно близких поло-
жениях механизма передаточное
отношение будет постоянным.
Такие механизмы будем называть
механизмами с мгновенно равно-
постоянным будет
на известном конечном участке; именно поэтому подобные механизмы
могут представить прикладной интерес.
Рассматриваемый случай аналитически соответствует равенству
tu = tl = ti = ts. Тогда получается из уравнений (9.230) — (9.237):
(9.260)
° у 1 + d ’ '
b = -^d^ (9.261)
с = '|А24-аг+ 1 — d — ~ (й2 — 3/2). (9.262)
Здесь при г<^0 следует принимать d^>0, а при г^>0, наоборот,
с?<0.
Угол поворота кривошипа, соответствующий точке перегиба на
кривой гм =/(?), равен:
/?а _1_ /72___________________________/2
cosyi) = —°. (9.263)
Механизмы с мгновенно равномерным движением представляют собой
частный случай механизмов с наилучшим приближением к I = const.
Для них будут справедливы все ограничения, установленные выше,
в частности условия проворачиваемое™.
Допустим, что задано I и по нему определено соответствующее d.
Задаваясь последовательными значениями а, можно найти по фор-
мулам (9.260)—(9.262) соответствующие /0, b и с и построить на
стойке AD семейство механизмов, обеспечивающих мгновенно рав-
г т* -
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 611
номерное движение с заданным I (рис. 589). Шарниры В этих
механизмов будут располагаться на геометрическом месте а, а шар-
ниры С—на геометрическом месте р. Установим эти геометрические
места.
Возьмем прямоугольные оси координат (см. рис. 589) с началом
в точке Т и осью х, направленной влево.
Квадрат расстояния между точками А и В равен:
а*=(х — б/)2+У2.
Квадрат расстояния между В и Т равен:
Подставляя эти выражения для а
2 . „ 3d(l—d) „
*2+У--------2-d~x==0>
откуда следует, что геометри-
ческим местом а будет окруж-
ность, проходящая через полюс
Т и имеющая центром точку
М с координатами
3d(l— d)
Хм — 2 (2 — d) ’ Ум — •
(9.264)
Из пропорциональности /()
и b по формуле (9.261) непо-
и tu в формулу (9.260), получаем:
окружность, проходящая через Т
средственно следует, что гео-
метрическим местом р будет также
и имеющая центром точку К с координатами
К 2(1+d) '
№ = 0.
На рис. 585 и 586 показаны пунктиром соответствующие геомет-
рические места аир шарниров В и С для механизмов с мгновенно
равномерным движением при /^>0 (на рис. 585 для / = 0,333, на
рис. 586 для ( = 0,70).
Для проверки построения может служить геометрическое условие
равенства ^- = 0: прямая РТ, соединяющая мгновенный центр Р
абсолютного движения шатуна с мгновенным центром относительного
движения Т кривошипа и коромысла, должна пересекать линию ша-
туна АВ под прямым углом (см. рис. 585, 586, 589).
В заключение установим области существования механизма.
Отметим прежде всего, что ранее был установлен только один
предел выбора длины звена АВ, а именно: при и при /^>0,
20*
612
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
когда tn 0, должно быть а <f | d |, а при I 0, к'огда t0 0, должно
быть а^>| d\. Установим вторую границу выбора а.
В пределе при = — участок наилучшего приближения
получается бесконечно малым. Обозначим вторую точку пересечения
окружности а (см. рис. 589) с линией стойки через £; тогда получим,
что при а<^АЕ не может быть механизмов даже с бесконечно малым
участком наилучшего приближения. Следовательно, отрезок АЕ будет
определять собой предельную величину а — ай, при которой возможно
еще наилучшее приближение; хотя и на бесконечно малом участке.
Так как а^ — Чхм — d, то, подставляя сюда значение Хм из (9.264),
получим:
d (l—2d)
а»~ 2-d
(9.265)
Таким образом, при z<^0 и при г^>0, когда Z0^>0, пределами
для выбора а будут:
• (9.266)
При z 0, но при t0 0 пределами для выбора а будут:
l^l<Q<-ri(21-Sjd) • (9.267)
Напомним, что кривая =/(<рт) (см. рис. 583), состоящая из двух
ветвей, пересекается с прямой, отвечающей заданному ср в двух точ-
ках k' и k", которые определяют один и тот же механизм. Точка /г0,
отделяющая друг от друга две ветви кривой £0=/(<рт), лежит
на оси абсцисс (/0 = f3); следовательно, она будет определяться зна-
чением t0, выражаемым формулой (9.260). Чтобы найти механизм,
у которого участок приближения будет лежать на заданном угле
поворота звена АВ, достаточно исследовать кривую ^n = /(<pm) либо
на первой ветви, либо на второй. Из соображений повышения точно-
сти подсчетов целесообразно исследовать кривую на первой ветви,
т. е. между
d + ° > t0 > У ^(d^-a^l-d) _ (9.268)
Неравенства (9.266) — (9.268) определяют собой всю область
механизмов, которые при заданном I могут давать наилучшее при-
ближение (по Чебышеву) к равномерному движению.
2°. Кривошипно-шатунный механизм. Для синтеза кривошипно-
шатунного механизма с приближенно равномерным движением ведо-
мого звена можно воспользоваться свойством кулисного механизма,
установленного при рассмотрении синтеза шарнирного четырехзвен-
ника с приближенно равномерным движением ведомого звена, а именно,
если шатунная точка С лежит на направлении кулисы несмещенного
кулисного механизма АВТ (рис. 590), то при приближении траекто-
рии этой точки к некоторой прямой -jy, перпендикулярной к направ-
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 613
лению стойки АТ, линейная скорость рассматриваемой точки будет
приближаться к постоянной. Указанное свойство позволяет свести
задачу об осуществлении кривошипно-шатунным механизмом прибли-
женно равномерного движе-
ния к задаче о наилучшем
приближении шатунных кри-
вых некоторого кулисного
механизма к прямой линии.
Рассмотрим предвари-
тельно задачу о наилучшем
приближении шатунной кри-
вой 8 точки С кулисного
механизма АВТ (рис. 590) к
некоторой прямой -yj, перпен-
дикулярной к стойке А Т *).
На рис. 590 обозначим:
АВ —a, AT = d vt BC—b.
В качестве переменного па-
раметра примем величину
t — BT. Как и в шарнирном
четырехзвеннике, будем счи-
тать, что £^>0, если точка
Т расположена между В и С,
и t<^0, если точка Т расположена вне отрезка ВС. Исключая угол
поворота кривошипа <р, из очевидных соотношений
х — d __ d -f- a cos <f
b — t t
и
В — d2-j- a2-j- 2ad cos <p (9.269)
получим следующее выражение для абсциссы х точки С:
Отклонение Дл шатунной кривой 8 точки ,С от прямой х = е
(прямая ут) выразится соотношением
&х = х~ (9.271)
где
Pt —— b; pt = 2de — d2— а2-, р2 = — Ь(<В— а2). (9.272)
*) Задача о приближении шатунной кривой кулисного механизма к пря-
мой линии впервые решена 3. Ш. Блохом [9ej.
614
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Обозначим через L предельное отклонение разности ДЛ. Тогда
предельное отклонение функции — равно — 2с?£, и на основании
/Я
формул (9.84) функция -- будет наименее уклоняться от нуля
при выполнении условий:
/? = 2(1+/3 = г0-]-2Л2; (9.273)
2de 2dL = t\2f,/3; (9.274)
2de — d2 — а2 — 2dL = 2t^ -)- (9.275)
Z?(rf2 —а2) = ^3 = Ш (9.276)
В силу симметрии шатунной кривой 8 точки С относительно оси х,
участку приближения С0С3 при >^>0 будет соответствовать симмет-
ричный участок приближения при _у<^0. Если точка Со, отвечающая
началу участка приближения, совпадает с осью х, то оба симметрич-
ных участка приближения сольются в общий участок приближения.
3. Ш. БлохОм система уравнений (9.273) — (9.276) была использована
для исследования именно последнего случая. Нас интересует, наобо-
рот, тот случай, когда симметричные участки приближения остаются
раздельными. Рассмотрим этот случай.
Примем в качестве искомых в системе уравнений (9.273) — (9.276)
величины tlr t2, ts, е, L и b, полагая /0, а и d заданными как началь-
ные условия задачи.
Исключая из уравнений (9.273) и (9.276) величину tit получим:
ь = + 2 (tf* - as) ± 21/(d* - д») (d* - а* + tfr
to
Уравнение (9.273) дает;
= (9.278)
Отсюда, если i0<^0, то /2^>0 и параметр t обращается в одном
из положений механизма в нуль, что возможно лишь при d = a.
Но в этом случае из формулы (9.276) /2 = 0, что противоречит
формуле (9.278).
Следовательно, возможно лишь ^>0.
Из соотношения (9.276) следует, что рассматриваемое приближе-
ние возможно лишь при
d^a. (9.279)
Возможными пределами для i0 согласно рис.’ 590 являются
\d — a\^t0^d-{- а.
(9.280)
Далее из уравнений (9.273) и (9.276) найдем:
i3 — (io 1 4i2zt| Zj)-|-84^2)»
(9.281)
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 615
Для определения знака перед корнем имеем условия:
или (9.282)
Уравнение (9.273) дает еще:
(9.233)
Наконец, уравнения (9.274) и (9.275) приводят к выражениям:
е = 1Л (^ + 2f3) + <8 (^ + 2(0) + 2 (d8 + с8)]; (9.284)
£ = ~ ^(^ + 2/3)-^(Лг + 2ад]. (9.285)
Текущий угол поворота <р звена АВ определяется из соотноше-
ния (9.269);
Подставляя в это соотношение значения /=(о и ^ = г‘з> получим
значения углов <р = <р0 и = <р3, отвечающих начал) и концу участка
приближения С0С3. Угол
Чт = I <Рз — ?ol (9.287)
представит собой угол поворота кривошипа, соответствующий пере-
мещению шатунной точки С по участку приближения С0С3.
Допустим, что, используя установленные выше соотношения, мы
нашли на шатуне несмещенного кулисного механизма АВТ (см.
рис. 590) такую точку С, траектория которой В наименее откло-
няется от прямой YT, перпендикулярной к линии стойки АТ. Тогда
скорость точки С на соответствующем угле поворота кривошипа
будет приближенно постоянной согласно свойству, указанному в начале
параграфа.
Присоединим теперь к шатуну ВТ кулисного механизма (рис. 591)
в найденной шатунной точке С шарнирно ползушку q и примем за
ее направляющую прямую у у. Если теперь отбросить ползушку р
в кулисном механизме, то получится кривошипно-шатунный меха-
низм АВС с приближенно равномерным движением ползушки q на
том же угле поворота кривошипа.
Наметим конкретный путь проектирования таких кривошипно-ша-
тунных механизмов и установим области существования решений.
Точка пересечения Т шатуна ВС кривошипно-шатунного меха-
низма АВС с линией АТ представит собой мгновенный центр в отно-
сительном движении звена АВ и ползушки q. Если обозначить угло-
вую скорость звена АВ через ы, то линейная скорость ползушки q
будет:
V — о) АТ.
(9.288)
616
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
В тех положениях кривошипно-шатунного механизма, где центр шар-
нира С совпадает с точками С, С и С"', в которых прямая у -у пере-
секается с шатунной кривой 8 исходного кулисного механизма (см.
рис. 590), величина А Т — d. Следовательно, скорость ползушки q
в этих положениях равна:
= со d - const.
(9.289)
Переменная скорость ползушки q на участке о г до <ра будет
приближаться к этому постоянному значению vG.
Закон перемещений ползушки q, если
стоянной скоростью v0, выразился бы:
бы она двигалась с по-
S = S0 + ^ *)•
Так как wt = <f, то, принимая, что при <р = <р0 соответствующее ^ = 0,
можно этот закон перемещений записать так:
S = d|<p — <ро|. (9.290)
Полное перемещение ползушки q при изменении <р от ср0 до <ра
в предположении постоянной скорости ползушки г>0 будет равно
Sm = d|<P3-?o| = rf?m. (9.291)
Действительное значение этого перемещения или, иначе, действитель-
ная длина участка приближенно равномерного движения получается
из следующих соображений. Проведем прямоугольные оси коорди-
*) В этом уравнении через t обозначено время.
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 617
нат хАу (см. рис. 591). Если обозначим ординату центра шарнира С
через у, то найдем:
(a cos <р е)® 4" (о sin ср _у)® = &®,
откуда, учитывая схему механизма, получим:
у = — a sin ср — е® — a cos <р (2е -1- a cos ср). (9.292)
Подставляя в эту формулу значения углов ср = срв и ср=ср3, полу-
чим ординаты уо и у3 конечных точек участка приближенно равно-
мерного движения ползушки и точную длину sm этого участка:
5т=1>з->0|- . (9-293)
Если то максимальный угол давления на участке приближенно
равномерного движения при ведущем кривошипе будет:
rf2 -1- /2 _
sin »max = т^ ---, (9.294)
а при ведущей ползушке
/72 -U /2 _ ft2
sin &lmax = - • (9-295)
Если окажется то в выражениях (9.294) и (9.295) значение
следует заменить значением t3.
Вероятными исходными данными в прикладной задаче синтеза кри-
вошипно-шатунного механизма с приближенно равномерным движе-
нием ползушки могут быть: длина участка приближенно равномерного
движения sm и соответствующий угол поворота кривошипа <рт.
Наметим одну из возможных схем решения задачи синтеза криво-
шипно-шатунных механизмов приближенно равномерного движения
по указанным условиям.
Для того чтобы упростить соответствующие подсчеты, на
рис. 592 приведена диаграмма зависимости угла <рт от отношений a[d
и t0/d и показаны границы областей тех механизмов, у которых
наибольшие углы давления &п1ах и &1тах на участке приближенно
равномерного движения соответственно равны 30, 45, 60, 30, 50 и 70°.
Допустим, что нам заданы: 1) длина участка приближенно рав-
номерного движения sm и 2) соответствующий угол поворота кри-
вошипа <рт.
Примем d=\ и зададимся некоторым значением а с учетом угла
давления 9п;ах или Э1П1ах по рис. 592 в зависимости от того, какое
из звеньев в проектируемом механизме — звено АВ или пол-
зушка q — является ведущим. По заданному tpm и принятому а можно
найти из диаграммы на рис. 592 соответствующее значение f0. После
этого по формуле (9.277) определяем длину шатуна b искомого кри-
вошипно-шатунного механизма, а по формулам (9.278) и (9.281) —
618
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
значения и t2. Подставляя величины tn и t3 в формулу (9.286),
находим углы <р0 и <р;, и проверяем общий угол поворота кривошипа
Рис. 592.
Если это условие не выполняется, то пои гом же значении а,
используя диаграмму на рис. 592, несколько увеличиваем значение
и делаем новый подсчет углов <р<„ ср3 и <рт. Если это условие
оказывается выполненным, то находим далее по соотношению (9.284)
координату е направляющей у у. Примем положение кривошипа,
определяемое значением ср = ср0, за начало отсчета угла поворота
кривошипа.
Тогда угол
(9.296)
?з' = <Po + (Pra
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 619
отметит конец требуемого участка приближенно равномерного дви-
жения. Подставляя в (9.292) углы <р = <р0 и найдем коорди-
наты у0 и у3', которые определят длину участка приближенно рав-
номерного движения:
V = iy3-J’«l> (9.297)
соответствующую <рт при d = 1.
Если теперь умножить а, b и е на коэффициент
Х = (9.298)
s т
то найдутся размеры
АВ = \а, ВС = М> и AD = ~ke (9.299)
такого кривошипно-шатунного механизма, который 'будет иметь
длину участка приближенно равномерного движения, равную sm,
при угле поворота кривошипа, ранном <от.
Решение задачи об оценке отклонения скорости от постоянной
в запроектированном кривошипно-шатунном механизме можно рас- \
членить на два отдельных вопроса. Первый вопрос —-установление
того положения механизма, при котором получается наибольшее
отклонение скорости от постоянной на участке приближения; вто-
рой вопрос — нахождение величины этого наибольшего отклонения.
Обратимся ранее к рассмотрению первого из указанных выше
вопросов.
Допустим, что нами подсчитана по формуле (9.285) величина
наибольшего отклонения L траектории точки С исходного кулисного
механизма АВТС (см. рис. 590) от прямой уу, которое имеется
в точках С(Р Ct, С> и С3.
Покажем исходный кулисный механизм АВТС на рис. 593, а,
поставив его в положение АВйТСй, определяемое углом <р0, когда
620 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
шатунная точка С совпадает на своей траектории с точкой Со.
Напомним, что по условию в исходном кулисном механизме AT — d.
Отбросим затем ползушку р и присоединим к шатуну В0С0 в шар-
нире Со ползушку q, т. е. перейдем от рассмотрения исходного
кулисного механизма АВйТ к рассмотрению интересующего нас
кривошипно-шатунного механизма АВпСй. Если в последнем за на-
правляющую ползушки q принять прямую 77, проходящую через Со,
то скорость этой ползушки в данном положении механизма будет
равна:
v0 —«оДТ = <ud.
Однако в запроектированном кривошипно-шатунном механизме за
направляющую ползушки q нами принимается прямая 7'7', отстоящая
от 77 на расстоянии L. Вследствие этого запроектированный кри-
вошипно-шатунный механизм при угле <р0 будет в действительности
занимать некоторое положение ABdC'o- Соответствующий мгновенный
центр Т' в относительном движении кривошипа АВ$ и ползушки q
будет отстоять от А не на расстоянии d, а на расстоянии </ф-(Дг/)0.
Действительная скорость ползушки q в этом положении механизма
будет равна:
J?l = U) [d -ф- (Д</)о|.
Относительное отклонение этой скорости от значения т>0 выразится:
А __»1—______ (Д^)о
0— — d
или при d — 1
Д0 = (Дй)о- (9.300)
Величину (Д(/)в можно определить таким образом. Пусть пол-
зушка р не связана со стойкой и свободно перемещается вдоль
шатуна Д0С0 (см. рис. 593, а). Присоединим к ней шарниром Т вторую
ползушку и, которую заставим перемещаться вдоль стойки АТ.
Тогда величину (Д</)п можно определить, пользуясь методом
Н. Г. Бруевича [12в], как ошибку в положении шарнира Т шести-
звенного механизма АВ^ТСй, вызванную первичной ошибкой сме-
щения, равной L. Ход графического нахождения (Д</)о будет
следующим (рис. 593, б).
Откладываем в произвольном масштабе ошибку смещения L
в виде отрезка на прямой I-J, перпендикулярной к 77. Через р(,
проводим прямую 11-11, перпендикулярную к шатуну Д0С0, а через с0
прямую III-III, параллельную направляющей 77, которые пересе-
каются в точке сХо. На отрезке рпсХо находим точку tX(i из условия
Рбхп росХв ~
Затем проводим через tXo прямую IV-JV, параллельную ша-
туну В0С0. Точку пересечения прямых 1V-IV и 1-1 обозначим Zu.
Тогда отрезок р^в в том же масштабе выразит величину (Д^)о.
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 621
Указанное на рис. 593, б построение можно повторить для
остальных трех углов ср2 и <р3, соответствующих tb t* и
(когда траектория 8 шатунной точки С исходного кулисного меха-
низма АВТ на рис. 590 имеет наибольшие отклонения от прямой -р(,
равные ± L), и найти смещения (A<7)ls (Ad)s и (Ad)3.
Если
(9.301)
то по рис. 593
&о 61 83.
С уменьшением угла бис одновременным уменьшением отно-
шения (В^Т: Д0С0) при неизменном L величина (Ad) на рис. 593, б
должна уменьшаться. Отсюда следует, что при выполнении условия
(9.301) заведомо будет:
| До|>| Д, |>| Л«1> I д3|.
(9.302)
Учитывая пропорциональность А и Ad согласно выражению (9.300),
заключаем из последнего неравенства, что при выполнении условия
(9.301) отклонение скорости ползушки q в кривошипно-шатунном
механизме от значения т0 будет иметь наибольшую величину в по-
ложении механизма, определяемом углом <р0.
Наоборот, при условии
'о<^1
з
(9.303)
наибольшее отклонение скорости ползушки q от значения будет
в положении механизма, определяемом углом <р3.
Установив то положение механизма, которое отвечает наиболь-
шему отклонению скорости от постоянной на участке приближения,
можно дать формулу для прямого подсчета этого отклонения.
Дифференцируя по времени соотношение (9.292), получим действи-
тельную скорость ползушки q кривошипно-шатунного механизма:
v = си — a cos <р
a sin ср (a cos ср ё) I
— е! — a cos ср (2е -ф a cos ср) J ’
(9.304)
где ю — угловая скорость кривошипа.
Относительное отклонение этой скорости от значения т0 = wd
будет:
л 1 Г j । a sin ср (a cos ср 4- е)
А = d -ф- a cos <р — —r—- - - -......- - .
“ [ 1^6“ — е‘ — a cos ср (2е -ф a cos ср) J
(9.305)
Для определения наибольшего относительного отклонения ско-
рости от постоянной на участке приближения следует подставлять
в это выражение значение = при наличии неравенства (9.301)
или значение = <р3 при наличии неравенства (9.303). Напомним при
этом, что углы ср0 и ср3 получаются из соотношения (9.286) при
подстановке в него t=tn или t — t3.
622
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
На рис. 594,а представлен общий ход диаграммы т=/(ср) кри-
вошипно-шатунного механизма на участке приближенно равномерного
движения при наличии условия (9.301). При <р = ср0 в точке Со
Рис. 594.
отклонение Дт0 скорости ползушки от значения т>0 будет наиболь-
шим по абсолютной величине. При ср = ср1( ср — ср2 и ср = <р3 в точ-
ках Сь С2 и С3 абсолютные отклонения скорости от значения р0 будут:
| Дт»01 > | Дщ | > | Ди21 > | Дт?31
в соответствии с неравенством (9.302), определяющим относитель-
ные отклонения скорости от значения 170.
Поскольку на участке
О <р^ тс
шатунная кривая 8 исходного кулисного механизма АВТ (см. рис. 590)
четыре раза достигает предельных отклонений от прямой (точки Со,
С], С2, С3), то по условию чередования знаков этих отклонений
шатунная кривая на том же участке может пересечь прямую рр только
в трех точках С', С" и С". Скорость ползушки кривошипно-шатун-
ного механизма АВС (см. рис. 591) будет равна = именно
в тех его положениях, где центр шарнира С ползушки q будет
совпадать на прямой рр с точками С', С" и С"', так как только
в этих положениях абсцисса мгновенного центра Т в относительном
движении равна AT — d. Отсюда следует, что кривая ц=/(<р)
(рис. 594, а) в пределах О --С ср тс может пересечь прямую
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 623
также только в трех точках С, С" и С". Таким образом, в пре-
делах
О ? -С?()
скорость ползушки q должна быть а в пределах
неизменно
®Оо-
Для того чтобы кривошипно-шатунный механизм был проворачива-
ющимся, он должен проходить через положения <р = 0 и <p = it. Как
было только что установлено, в одном из этих положений скорость
ползушки q будет а в другом Геометрически последнее
означает, что в проворачивающемся кривошипно-шатунном механизме
мгновенный центр Т относительного движения звена АВ и ползушки q
(см. рис. 591), отвечающий значению vn = iad, должен лежать между
мгновенными центрами и Т_относительного движения приф=Ои<р=гс.
Мгновенные центры Го и Т. относительного движения при <р == О
и <р = л будут определяться в пересечении окружности, описываемой
точкой В, с линией Следовательно, будет АГ0 = ЛГх = а.
Так как, далее, AT = d, то чтобы мгновенный центр Т располагался
между То и Тт, должно быть:
d<^a.
Однако это неравенство противоречит условию (9.279) существова-
ния исходных кулисных механизмов. Это доказывает, что кривошипно-
шатунные механизмы приближенно равномерного движения являются
непроворачивающимися механизмами. Вследствие этого их основной
областью применения может быть, по-видимому, не машиностроение,
а приборостроение. В таком случае больший практический интерес
должна представлять не оценка отклонений скорости от постоянной,
а оценка отклонений кривой перемещений от прямолинейного закона
или, иначе, оценка отклонения перемещений от равномерной шкалы.
В связи с этим возникаег вопрос об оценке отклонения пере-
мещений от равномерной шкалы. Покажем нахождение этого откло-
нения в кривошипно-шатунных механизмах, синтез которых был
изложен выше.
Кроме значений Ze, tu t.2 и t3 параметра t, введем еще его значе-
ния Г, I" и t'", при которых траектория 8 шатунной точки С (см.
рис. 590) исходного кулисного механизма АВТ пересекает в точ-
ках С, С" и С" прямую ту. Эти значения Г, t" и t'" будут кор-
нями кубического уравнения
В — ЬВ — (<Г- 4- а2 — 2de) t — b(cB~ а*) =0, (9.306)
которое получается из уравнения (9-270) при подстановке х — е.
624 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. IX
Подставляя t = t', t = t" и f = в соотношение (9.286), полу-
чим значения
? = ?', 7 = 7" и ? = ?"'• (9.307)
при которых кривая v=f(y) пересекает на рис. 594, а прямую v = vn.
На рис. 594, б изображен общий ход кривой перемещений пол-
зушки q кривошипно-шатунного механизма на участке приближенно
равномерного движения. Прямая КК отвечает прямолинейному за-
кону движения, который осуществляла бы ползушка q, если бы она
имела постоянную скорость, равную г>0.
Так как на отрезке <рв р <^р' постоянно а на отрезке
7'-<17^7, постоянно х><^г0, то наибольшее отклонение (Д.х)' кри-
вой перемещений ползушки q от прямолинейного закона КК на отрезке
?о р
будет при <р = ср'.
Аналогично на отрезках
7 И 7 =СС?3
наибольшие отклонения (Д»)" и (Дх)"' должны быть соответственно
при <Р = ср" И ср : ср'".
Если по значениям ср( и ср', используя (9.292), найти соответству-
ющие координаты j/j и у', то их разность
s' = |j’i—У! (9.308)
определит действительное перемещение ползушки q кривошипно-ша-
тунного механизма при повороте кривошипа от cpj до ср'.
Подставляя 7=7' в соотношение (9.290), получим перемещение
ползушки
S' — djcp'—cpt| (9.309)
на том же угле поворота кривошипа при условии, если бы она
двигалась по прямолинейному закону.
Величина
(Дх)'=|х' — S'i (9.310)
представит собой отклонение кривой перемещений от прямолиней-
ного закона КК при ср = ср'.
Если величина перемещений s' и S' подсчитывалась по значениям
параметров механизма, соответствующих d—1, то истинное значе-
ние искомого отклонения будет:
(As)' = X(s' —S'), (9.311)
где X — ранее указанный множитель (9.298).
Используя вместо 7' соответственно углы 7" и 7"', по тем же
соотношениям можно найти отклонения (Дх)" и (Дх)"' при 7 = 7"
и 7 —- 7'".
§ 31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 625
АВ, то прихо-
измеряемые на
Рис. 595.
Наибольшее из отклонений (As)', (As)" и (As)"' представит собой
предельное отклонение перемещений от равномерной шкалы при
условии начала отсчета ее от положения механизма, определяемого
углом <ро-
Если ведущим звеном в проектируемом кривошипно-шатунном
механизме является ползушка q, а ведомым — звено
дится определять отклонения от равномерной шкалы,
рис. 594, б по оси абсцисс, т. е. значе-
ния (Дер)', (Д<р)" и (А®)"'.
Из уравнения (9.290) следует, что
при d = 1 угол наклона прямой КК к
оси абсцисс будет равен 45°. Это приво-
дит к равенствам:
(Д<р)' = (As)', (Дф)" = (As)" и (Д<р)'"=(Дs)"',
(9.312)
если (As)' и (As)" и (As)"' подсчитаны
при значении d=l.
В качестве примера спроектируем кри-
вошипно-шатунный механизм АВС для
указательного прибора (рис. 595), в кото-
ром равномерное поступательное движе-
ние стержня q, равное sm
равномерное вращательное движение стрелки р
стрелки <рт = 60г.
Принимаем d=\ и задаемся а = 0,70. Тогда
рис. 592 получим соответствующее значение
^0=1,54.
= 10 мм, должно преобразоваться в
прибора; размах
по диаграмме на
По формуле (9.277) определяем длину шатуна
Ь = 3,7767,
а по формулам (9.278) и (9.281) значения.
^= 1,1184 и ^3 = 0,9974.
Подставляя значения С и t3 в (9.286), находим углы:
= 50и58' и <рз = 110° 43'.
Проверяем угол поворота кривошипа, соответствующий участку
приближенно равномерного движения:
Тт = !Тз — То1 — 59°45' < 60°.
Следовательно, условие <рт2&60° здесь не выполняется, и при
полном размахе стрелки на угол срт = 60° некоторые положения
механизма будут вне пределов области приближенно равномерного
Движения. Это, естественно, должно несколько повысить предельное
626 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. t\
отклонение перемещении механизма от равномерной шкалы. Однако,
учитывая малую разницу между полученным и заданным углами ср
будем продолжать решение без пересчета для выполнения условия
«т = 60°.
Находим по соотношению (9.283) значение t, = 1,3897 и по соот-
ношению (9.284) — координату
е = 3,0946.
Если положение кривошипа, определяемое углом ср(| = 50°58'.
принять за начало отсчета углов поворота кривошипа, то угол
?'з = = 110°58'
отметит конец требуемого участка приближенно равномерного дви-
жения.
Подставляя углы ср = ср0 и <р = ср'3 в уравнение (9.292), найдем
координаты начала и конца участка приближенно равномерного дви-
жения ползушки:
j’o = 0,784 и Уз—1,831.
Длина этого участка выразится по соотношению (9.297)
s'm = у'з — J’ni = 1,047,
коэффициент X по выражению (9.298) будет равен:
, Sm 10 АГАТ
А = ~ = 9,551 мм.
s т 1,047
Тогда искомые размеры механизма АВС (см. рис. 595) опреде-
лятся по соотношениям (9.299):
Д£? = Ха = 6,69 ям: ВС = М> = 36,07 мм и ДО = Хе = 29,56 мм.
Относительное отклонение скорости от постоянного значения по
формуле (9.305) при ср = <р0 равно:
А = — 0,00647.
Для определения отклонений перемещений от равномерной шкалы
составляем кубическое уравнение (9.306):
f _ з j;; tt 4,5991 — 1,926 = 0.
Решение его дает:
f =1,499; t" =1,251; Г" = 1,029.
Находя по (9.286) соответствующие углы ©', ср" и ср'", а за-
тем используя (9.292), (9.308), (9.309), (9.310) и (9.312), найдем
31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 627
отклонения:
(Д<р)' = 0,00025 радиана; (Д-s)" = 0,00080 радиана
и (ДерУ" — 0,00047 радиана.
Предельное отклонение с округлением в большую сторону будет:
(Д<р)пред =(Д<р)"^0°03'.
Максимальный угол давления по формуле (9.295) оказывается
равным
бщшх =60°.
Понятно, что полученное предельное отклонение не является
наименее возможным при заданных значениях sm и -fm. При неизмен-
ном а = 0,70 это отклонение можно несколько уменьшить за счет
выполнения условия срт5э 60е путем увеличения значения /0. Но, кроме
того, следует иметь в виду, что длина звена АВ а = 0,70
была принята нами произвольно. Задаваясь другими значениями а
и повторяя расчет, можно ожидать нахождение механизмов со значи-
тельно меньшими величинами (Д<р)пред-
Если постепенно сближать по оси ординат точки Со, Cj, Са и С3
(см. рис. 590), отвечающие наибольшим отклонением ша-
тунной кривой исходного кулисного механизма от прямой -р-р, то
одновременно будут сближаться и три точки С', С", С", в которых
шатунная кривая 8 совпадает с прямой -ру. В пределе шатунная кри-
вая 8 будет совпадать с прямой уу в трех бесконечно близких точках.
На кривой w=/(<p) соответствующего кривошипно-шатунного
механизма в указанном предельном случае будет получаться точка
перегиба С.
Ползушка q такого кривошипно-шатунного механизма в поло-
жении, соответствующем этой точке перегиба С, будет иметь уско-
рения 1-го и 2-го порядков, равные нулю. Следовательно, в трех
бесконечно близких положениях такого кривошипно-шагунного меха-
низма скорость ползушки q будет постоянной. Практически скорость
ползушки будет приближенно постоянной на известном конечном
участке. Именно поэтому подобные механизмы могут представить
прикладной интерес. Кроме того, исследование данного семейства
механизмов приводит к некоторым общим выводам.
Рассматриваемый случай аналитически соответствует в системе
исходных уравнений (9.273)—(9.276) равенству
При этом условии из уравнений (9.273) — (9.276) получаем:
fe = V3(d2 —а2); (9.313)
й = 34; (9.314)
е= (5гГ—4а2). (9.315)
628 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ [гл. и
Угол поворота, соответствующий точке перегиба С на кривой
-и=/(<р), будет определяться соотношением
coscp0==^-2Qrf—. (9.316)
При выбранном d, задаваясь последовательными а, можно найи
по формулам (9.313)—(9.315) соответствующие ta, bnen построит i
на стойке AD (рис. 596) семейство механизмов с мгновенно равно
мерным движением. Шарниры В механизмов этого семейства буду
располагаться на некотором геометрическом месте а, а шарниры С-
на некотором геометрическом месте р. Установим эти геометрически!
места.
Проведем прямоугольные оси координат с началом в точке Т {AT—d).
Тогда расстояние между шарниром А (—d, 0) и произвольным шар-
ниром В{х, у) на а будет
а ==/(х+
Расстояние между точкой
Т (0, 0) и шарниром В равно:
Подставляя эти выражения для
а й в соотношение (9.313),
получим:
-с2- J'21,5 dx = 0.
Отсюда следует, что геометрическим местом а является окруж-
ность, проходящая через мгновенный центр Т и имеющая центром
точку М с координатами:
хм —— 0,75 cZ; у,и = 0. (9.317)
Из пропорциональности и b по выражению (9.314) непосред-
ственно следует, что геометрическим местом р будет также окруж-
ность, проходящая через мгновенный центр Т и имеющая центром
точку К с координатами
x^ — l,5d; ук=0. (9.318)
Напомним, что ранее был установлен только один предел для
выбора длины звена АВ, именно a<^d. Установим вторую границу
для выбора а.
В пределе при = t.2 = участок приближенно равномерного
движения получается бесконечно малым. Обозначим вторую точку
пересечения окружности а с осью абсцисс через Е.
Тогда получим, что при
а <2 АЕ
§31]
СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 629
ие может быть кривошипно-шатунных механизмов даже с мгновенно
равномерным движением ползушки q. Следовательно, АЕ представит
собой наименьшую длину звена АВ, при которой в кривошипно-ша-
тунном механизме осуществимо приближенно равномерное движение
при данном методе решения.
Так как АЕ = 2 | хм | — d, то, подставляя сюда значение хм по
формуле (9.317), получим:
AE = 0,5d.
Таким образом, пределами для выбора a/d при синтезе кривошипно-
шатунных механизмов с приближенно равномерным движением ползушки
будут:
0,5 (9.319)
£)ти пределы и отражает диаграмма на рис. 592.
Соответствующими пределами для ~ будут по рис. 596
O==S-^==S1,5. (9.320).
Неравенства (9.319) и (9.320) определяют собой всю область
кривошипно-шатунных механизмов, которые могут осуществлять ука-
занный вид приближенно равномерного движения.
Рассмотренное решение позволяет получить сравнительно простые
соотношения, определяющие область существования механизма, и фор-
мулы для вычисления искомых параметров. Однако получаемое при
этом приближение основано на использовании взвешенной разности и,
следовательно, получаемое приближение не будет равномерным. Можно
указать другой путь решения той же задачи, который приводи!
к равномерному приближению.
Скорость ползушки в заданном положении механизма
v = du>, (9.321)
где ш — постоянная угловая скорость звена АВ.
Из уравнения (9.271), полагая ДЛ.= 0, получаем:
/(«/, 0 == В — ЬВ (2<Ze — d2 — a2) t — b(d2 — а2) = 0. (9.322)
Кривая, выражаемая этим уравнением, в определенном масштабе пред-
ставит собой кривую изменения скорости ползушки v в функции от
аргумента t. Равномерное приближение этой кривой на известном
отрезке к прямой d — k будет означать одновременно равномерное
приближение скорости ползушки v на том же отрезке к значению
т>0 == wk = const. (9.323)
Так как наивысший показатель степени у аргумента t в уравне-
нии (9.322) и = 3, то геометрически картина наилучшего равномер-
630 СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ |гл. ц
ного приближения этой кривой к прямой d-=k изобразится так, как
показано в таблице 9.6 при четырех предельных отклонениях ца
отрезке приближения: tn, 7,, t2 и t3.
Тогда уравнения (9.87), если обозначить k 4- L через kt и k — /.
через /г.2) в соответствии с уравнением (9.322) будут иметь вид:
= 2714~ 73 = 70 4~ 272; (9.32 4)
2&je — k\— c? = t\ -|- 27,73; 2/г2е—k%— dl =. -f- 27072; (9.325)
b (k{ — o2) = 7;73; b (A| — a2) = 7|7O. (9.326 (
В данной системе шести уравнений содержится девять параметрон;
a, b, е, kit k.,, t6, tt, 72 и 73. Будем считать за неизвестные е, klt А
71( 72 и 73, полагая а, b и 70 заданными в качестве начальных усло-
вий. Тогда из правых уравнений системы (9.324) — (9.326) находим:
р___bl -|- а- + -f" 2Гобг
е~ 2Л2
Из левых уравнений (9.324) — (9.326) находим:
Aj = е ± Уе- — аг 4~ 37; — 27J&.
(9.327)
(9.328)
(9.329)
(9.330)
Приравнивая правые части последних соотношений и возводя в квад-
рат, получим следующее уравнение для нахождения t\:
4-7; — bti — a2 -4 е a2-|-7J —^ = 0. (9.331)
Искомый корень должен лежать в пределах:
7о 7i 7.2,
если
если
(9.332)
При равномерном приближении точки предельных отклонений
обычно сгущаются к концам интервала. Поэтому 7] всегда распола-
гается ближе к 70, чем к 72. Это позволяет в качестве первых зна-
чений 7] при последовательном приближении по способу ложных поло-
жений принимать, например:
7;=7О и 7'; = ^.
(9.333)
§ 31 ] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 631
После определения значение определяется по формуле (9.330),
а значение t3 найдется из уравнений (9.324):
t3 = b — 27,. (9.334)
Предельное относительное отклонение скорости ползушки ъ от
значения
Т'о = со/г = со — (9.335)
на отрезке приближения tn<^t<^t3 (или найдется по
формуле
Л = | ,fel7^-|. (9.336)
| *1 + *S I
Углы поворота звена АВ, соответствующие значениям t0 и t3, най-
дутся по формуле (9.286):
tf — k?, — а*
cos?0= 2afeg—; (9.337)
/2__ Ь2_Л2
cosTa = fr 2^г~. (9.338)
Угол поворота кривошипа, соответствующий участку приближенно
равномерного движения, получится как разность:
?т=1?з —<Ро1- (9.339)
Длина участка приближенно равномерного движения ползушки
найдется по формуле
Sm = ij3~ Jel. (9.340)
где у3 и _у„ — значения ординат центра шарнира С, определяемые по
формулам (9.292):
_у;! = — а sin <р3 —|f Ь* — е1 — а cos <р3 (2е ° cos <р3):
j'o = — а sin ю(1 |/ № — е'2 — а cos <рп (2е а cos <р0).
Пример. Задано: а = 7> = 70=1; найти е, Д, <рт и sm. Формулы
(9.327) —(9.329) дают:
f.2 — 0; = е = 1.
Уравнение (9.331) принимает здесь вид:
+t\ -h - 1 - =0.
Интересующий нас корень его лежит по соотношениям (9.332) в пре-
делах 1 7» 7, 7" 9- Решение дает:
tl== 0,700.
После этого по формулам (9.330), (9.334) и (9.336) получаем:
** = 0,921; Л, = — 0,400; Д = 0,041.
632
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. 1Х
По соотношениям (9.337), (9.338) и (9.339) находим:
% = 240с00'; <р3 = 156°25'; = 83с35'.
Наконец, используя формулу (9.340), получаем:
sm= 1,40.
Полученный механизм показан на рис. 597 в крайних положениях
участка приближенно равномерного движения.
В качестве второго примера рассмотрим задачу, решенную рано
по методу взвешенного приближения.
Заданы: а = 0,7; Ь = 3,777; tn =
= 1,54. Формулы (9.327)4- (9.329)
дают:
t2=l,1185; kt —1,000; е = 3,093.
Уравнение (9.331) принимает вид:
0,265/,’ — 3,377/, — 0,490
Ц- 3,093 Иб.490 -Hi —0,530/1 = 0.
Интересующий нас корень лежи,
по соотношениям (9.332) в пределах
1,54>/,> 1,1185.
Решение дает:
/,= 1,4446.
После этого по формулам (9.330),
(9.334) и (9.336) получаем:
Л, = 0,9895; /3 = 0,8878;
Рис. 597.
Д = 0,00530,
т. е. отклонение от постоянного значения скорости уменьшилось
(в первом приближении величина Д = 0,00647).
По соотношениям (9.337), (9.338) и (9.339) находим:
То = 5О°59г; <р3 = 119°26' и <рт = 68°27'.
Наконец, используя формулу (9.340), получаем:
Sm = 1,190.
3°. Шестизвенный кулисный механизм. Из механизмов с посту-
пательными парами кроме кривошипно-шатунного механизма приме-
няются для воспроизведения приближенно равномерного движения
шестизвенные кулисные механизмы. Одна из возможных схем этих
механизмов показана на рис. 598,
31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА
633
Структурно этот механизм можно представить себе образованным
путем присоединения в шарнире С к исходному кулисному четырех-
звеннику ABD диады, состоящей из ползушки р и поступательно
движущегося звена s. Направляющие звена s приняты перпендику-
лярными к стойке AD. Ведущим звеном механизма является кулиса BD.
Рис. 598.
Пусть АВ —а, АС — b и длина стойки AD=\. В качестве неза-
висимого переменного параметра примем длин)' отрезка BD = u. Пре-
делами его изменения будут:
а — 1 •< it s- a -f- 1.
Проведем ось у перпендикулярно к AD. Тогда ордината у шарнира С
определится формулой
у = Ь sin ф.
Так как из треугольника ABD
sin ф_ и
sin ф а ’
где ср — угол поворота ведущего звена BD, то
_y = --«sincp. (9.341)
Если ш—постоянная угловая скорость ведущей кулисы BD, то
линейная скорость звена s будет:
dy ubidti . . \
x’ = U)^ = Tfesin'?+"cos ?)
634
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1*л. IX
Из треугольника ABD имеем:
а2 — 1 -ф- и2 -f- 2zz cos ср,
откуда
du_____ и sin tf
d? и + cos s
и
COS <p
a2 — 1 — u2
2u
(9.342)
Подставляя эти соотношения в выражение для v, получаем:
____ шЬи2 (а2 -|- 1 — и2)
v— о (о2 — 1 + и2)
(9.343)
Поставим задачу найти механизмы с наилучшим равномерным прибли-
жением скорости v звена s к постоянному значению k = const. Для
этого в формулу (9.342) вводим новую переменную:
z = zz2. (9.344)
Развертывая указанную формулу по степеням z, получаем:
f[v, z)~z2A- - - Д Т Л z 4- _ ' = 0. (9.345)
Так как наивысший показатель степени у аргумента z равен п = 2,
то в соответствии с таблицей 9.6 и соотношением (9.345) при kx =
— k — L и к? — k-\- L имеем:
?^—y+_L)==_2Zb ^-J^±l) = _(Zo + z2); (9.346)
— Zl'
ak2(a2—\}_
wb ~ °2’
(9.347)
В четырех уравнениях этой системы содержится восемь парамет-
ров: со, a, b, kx, k.2, zn, zx и z2.
Будем считать за неизвестные kx, kit zx и z.2, полагая w, а, b и z„
заданными в качестве начальных условий.
Тогда из левых уравнений системы (9.346) и (9.347) находим:
Л,=оТ;|за— -А-±2/2(аа— 1) |, (9.348)
zx = 1 — а2 ± а ]/2 (а2 — 1). (9.349)
Из соотношения (9.349) следует, что интересующее нас прибли-
жение осуществимо лишь при условии
а>1. (9.350)
Так как согласно выражению (9.344) должно быть zx 0, то
в формуле (9.349) следует учитывать только верхний знак. Подсчеты
§31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 635
показали, что в формуле (9.348) нужно учитывать только нижний
знак.
Для того чтобы получить приближение диаграммы скоростей
к прямой •u = k с пятью точками предельных отклонений,
принимаем :рп=0. Тогда соответствующие значения ий и z0 по рис. 598
будут равны:
itn — a—1, (9.351)
^о = «о = («- 1)2- (9.352)
Подставляя данное значение zn в правые уравнения системы (9.346)
и (9.347) и решая их относительно и г9, получаем:
= 1)>
zz2 = ]/^ = ]/а 4- 1.
(9.353)
(9.354)
Внося это выражение п2 в соотношение (9.342), находим:
COS <р2 =
а(а — 1) —2
2 /а+ 1
(9.355)
Общий угол поворота <рт ведущей кулисы BD, соответствующий
участку приближения — ср2 <р -С <р4:
(9.356)
Для нахождения значения а, отвечающего заданному углу <рт,
из формулы (9.355) получаем следующее уравнение 4-го порядка:
с4 — 2а3 — За2 -j- 2 (1 — cos <рт) а -ф- 2 (1 — cos <рт) = 0. (9.357)
При решении уравнения (9.357) по способу последовательных при-
ближений первоначальное значение а следует выбирать по приводи-
мой ниже таблице 9.16*).
Значение k, к которому приближается скорость звена s на соответ-
ствующем отрезке — <ps, равно:
k = = g [За2 -ф- а — 2 — 2а )/2(а2 — 1)]. (9.358)
Относительное отклонение скорости v от значения k на отрезке
приближения определяется по формуле
д __ I kt — kj I _ За2 — о — 2а )Л2 (о2 — I) ,д 35д
3os_|_a_ 2— 2а 2 (а2— 1) * ’
Таким образом, относительное отклонение А оказывается завися-
щим только от величины а.
*) См. стр. 637.
636
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
|ГЛ. 1Х
Подставляя в выражение (9.341) значения и = и2 и <р = <р2, опре-
деляемые соотношениями (9.354) и (9.355), можно найти ординату v.,
шарнира С в конце участка приближения. По симметрии положении
механизма общая длина участка приближения
S = 2у2 = b р/3 -ф- 2а— a*. (9.36Н)
Ход Н звена $ при полном обороте ведущей кулисы:
Н=2Ь.
Отношение длины участка приближения S к общему ходу Н звена <
3 —2о —(9.361)
На рис. 598 представлена диаграмма скорости v звена $ в зависи-
мости от его перемещений у. При прямом ходе максимальная ско-
рость v звена s равна kt и определяется соотношением (9.348), при
обратном ходе максимальная по абсолютной величине скорость ц1П
найдется по формуле (9.343), если подставить в последнюю и = а -ф- i:
|7.
I vmax | ~ -
Отношение максимальной скорости г>тах обратного хода к макси
мальной скорости kx прямого хода будет:
kt За2—1—2с /2 (а2 — ])’
При ведущей кулисе BD угол давления со стороны звена у на
звено s всегда будет равен 0°, т. е. будет наилучшим. В исходном
кулисном четырехзвеннике ABD углом давления явится угол между
направлениями кулисы BD и ведомого звена ВА. Если из точки /1
опустить перпендикуляр (см. рис. 598) на направление ведущей
АЕ
кулисы BD, то получим sinft = ^-g. Поскольку длина АВ постоян-
ная, то Йтах будет соответствовать максимальное значение длины
перпендикуляра АЕ. Так как угол AED прямой, то при вращении
механизма основания Е всех перпендикуляров, опущенных из точки .4
на соответствующие направления ведущей кулисы, будут распола
гаться на окружности с диаметром AD. Отсюда следует, что
sin»max=^. (9.363)
Для того чтобы показать прикладные возможности данного механизма
как механизма для осуществления приближенно равномерного движе-
ния, приводим таблицу 9.16, в которой даны значения основных харак-
теристик этого механизма.
31] СИНТЕЗ МЕХАНИЗМОВ С РАВНОМЕРНЫМ ДВИЖЕНИЕМ ВЕДОМОГО ЗВЕНА 637
Таблица 9.1 б
а 3,0 2,9 2,8 2,7 2,6 2,4 2,2
д 0 0,06% 0,3% 0,6% 1,0% 2,5о/0 5,0%
0° 55° 77° 95° 111° 137' 166°
S/H 0 0,31 0,44 0,53 0,60 0,72 0,80
^тах^1 2,0 2,07 2,И 2,15 2,20 2,34 2,66
О vmax 19° 20° 21° 22° 23° 25° 27°
П р и м е р. Спроектировать механизм (см. рис. 598), в котором на
участке перемещения ведомого звена S = 200 мм, соответствующем
углу поворота ведущего звена <рт = 120°, скорость ведомого звена s
наилучшим образом приближалась к постоянной. Длина стойки меха-
низма AD = 40 мм. Ведущий вал делает п = 150 об'мин, или, сле-
довательно, 15,71/сек.
Уравнение (9.357) при заданных условиях принимает вид;
а4 — 2а» —" За2 —За3 = 0.
Согласно таблице 9.16 при <?т=120° искомый корень будет
лежать в пределах 2,6 % а % 2,4. Решая это уравнение по спо-
собу последовательных приближений, получаем:
а = 2,532.
Следовательно, АВ = 40 2,532 = 101,3 мм.
Из формулы (9.360) имеем:
Ь = 3,887; ЛС = 40-3,887 = 155,5 мм.
Величина k, к которой приближается скорость звена s механизма
на отрезке приближенно равномерного движения, найдется по фор-
муле (9.358):
k =1498 мм/сек.
Относительное отклонение скорости от этого значения на отрезке
приближения по выражению (9.359):
А 0,014= 1,4%.
Наконец, по формулам (9.361), (9.362) и (9.363) получаем:
С
| = 0,64;
Механизм с найденными
ставлен на рис. 598, а.
г>=/(у) для звена s.
-"— = 2,25; »так = 24°.
соотношениями между размерами и пред-
На рис. 598, б показана также диа> рамма
638
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
В приборостроении нашла применение упрощенная модификация
рассматриваемого механизма, характеризующаяся равенством а = 1>.
Схема этой модификации показана на рис. 599, а конструктивное
оформление — на рис. 600.
ч
§ 32. Применение метода комплексных чисел к синтезу
передаточных механизмов
1°. Основные сведения из теории комплексных чисел. В преды-
дущих параграфах данной главы все изложение велось только на
основе теории функций действительного переменного. Можно, однако,
во всех рассмотренных задачах применить теорию функций комплекс-
ного переменного, используя то положение, что конфигурацию
кинематической схемы механизма можно представить в виде замкну-
того векторного контура, причем векторы, входящие в этот контур,
можно характеризовать комплексными числами. Метод комплексных
чисел в применении к теории механизмов неоднократно использо-
вался различными авторами. Поэтому в настоящем параграфе мы даем
краткое изложение его применения к синтезу передаточных меха-
низмов с целью облегчить читателю чтение тех отдельных работ
по синтезу механизмов, в которых изложение ведется с применением
комплексных чисел, хотя в настоящее время все основные задачи,
решенные с применением комплексных чисел, решены соответственно
алгебраическими методами, использующими только функции действи-
тельного переменного. Предварительно напомним основные сведения
из теории комплексных чисел *) в применении к некоторым опера-
циям над векторами.
Вектор всегда может быть представлен в виде комплексного числа.
С этой целью рассмотрим прямоугольную систему координат, по оси абсцисс
которой отложены действительные числа, а по оси ординат — мнимые (рис. 60Г>.
Тогда некоторому вектору а соответствует комплексное число но условию
a = cx-piav. (9.364)
*) Эти сведения изложены по статье К. 3 и кер а (111г|.
§ 32]
ПРИМЕНЕНИЕ МЕ10ДА КОМПЛЕКСНЫХ ЧИСЕЛ
639
где ах — действительная часть комплексного числа (вектора); iay— мнимая
часть.
Обозначив через а угол наклона вектора к оси абсцисс и через а — модуль
вектора а, имеем:
ах — a cos а, (9.365)
av~ a sin а. (9.366)
Из уравнений (9.365) и (9.366) имеем:
в = ]/ а2х + (9.367)
tga = ®>. (9.368)
Подставляя (9.365) и (9.366) в (9.364), получаем:
а — а (cos a + i sin a). (9.369)
Применяя формулу Эйлера
cos а i sin a = e'“, (9.370)
имеем:
a = ae‘a. (9.371)
Уравнения (9.364), (9.369) и (9.371) дают три возможных выражения одного
и того же вектора через комплексные
числа.
Сложение двух векторов а и Ь, показанное на рис. 602, дает вектор
г = а -|- b (9.372)
или
г (cos р + i sin р) = а (cos а i sin а) b (cos ? + i sin js). (9.373)
Отсюда
r cos р = a cos а b cos {1, (9.374)
г sin р = a sin а b sin ?. (9.375)
Аналогичные соотношения имеют место при вычитании. Умножение двух векто-
ров а и Ь, представленных комплексными числами, дает вектор (рис. 603, о):
с — ab. (9.376)
<>40
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
Применяя формулу (9.371), имеем:
ce't — ае‘“Ье'Р. (9.377,
Отсюда
с — ab, (9.37 s,
7 = “ + ?- (9.379,
Так же производится и деление двух комплексных чисел.
Если обозначить через е = е‘? единичный вектор, т. е. вектор, модель
которого равен единице, то умножение вектора а на единичный вектор при
представлении их в комплексных числах дает следующее условие:
ае — ае'ае‘т.
Отсюда
ае — а <•«+?', (9.38о,
т. е. вектор и поворачивается на угол <f (рис. 603, б). Вектор, сопряженный
с вектором а, обозначим через а (см. рис. 601). У сопряженных комплексных
чисел действительные части равны, а мнимые отличаются знаком. Отсюда для
сопряженного вектора получаем следующие выражения:
а — ах — iav,
а = а (cos а — i sin а),
а — ае~'а.
(9.381 >
Сумма или произведение двух сопряженных комплексных чисел (векторов)
дает действительные числа:
а + а = 2аж, (9.382)
ай = а2. (9.3831
Вычитание двух сопряженных комплексных чисел (векторов) дает мнимое
число:
а — а = 12ау. (9.384)
Деление двух сопряженных комплексных чисел дает условие
~ = е'-а, (9.315)
т. е. частное этого деления может быть представлено в виде единичного
вектора, имеющего удвоенный аргумент вектора, стоящего в числителе.
§ 32] ПРИМЕНЕНИЕ МЕТОДА КОМПЛЕКСНЫХ ЧИСЕЛ 641
2°. Метод 3. LU. Блоха. Одними из первых работ по синтезу
механизмов с применением комплексных чисел были работы
3. Ш. Блоха *). Им были решены в аналитической форме задачи син-
теза шарнирного четырехзвенника по трем, четырем и пяти условиям,
включая и задание скоростей и ускорений, а также соответствующие
задачи для четырехзвенных механизмов с поступательными парами.
Кроме того, для шестизвенного шарнирного механизма указана схема
вычисления семи параметров. Все задачи решались путем интерполи-
рования. К настоящему времени эти задачи решены другими алге-
браическими методами и изложение их дано в предыдущих парагра-
фах. Поэтому здесь ограничимся лишь кратким рассмотрением схемы
решения задач синтеза шарнирного четырехзвенника по заданным
положениям его звеньев.
Пусть, например, требуется построить шарнирный четырехзвенник
по трем заданным положениям его звеньев АВ и CD (рис. 604).
Принимая первые положения этих звеньев за начальные, определим
остальные их положения углами
и **), Начальный угол наклона
шатуна обозначим через х, а углы
поворота по отношению к началь-
ному углу через Рассматривая
контур ABCD как замкнутый кон-
тур, состоящий из векторов а, Ь, с
и 1, получаем уравнение
G-L& — с — 1=0. (9.386)
Рис. 604.
Применяя это уравнение к трем
рассматриваемым положениям и используя формулу (9.371), получим:
ае1" be1' — се'13 = 1,
ае ' ,ei_hPi) be1 + -0 — се1’ (3 + 4i) == i ,
ае^ "г тз) —I fygi (х +Ев) — се^ (РТФз) — 1,
(9.387)
В дальнейшем под комплексными числами (векторами) а, b и с будем
понимать их значения в начальном положении, т. е.
а = ае,а, b=beL\ с = се‘^.
Тогда система уравнений (9.387) принимает вид;
а --б — с= 1,
ое'я -J- Ье''^ — ce‘^i = 1,
ае1<ег _|_ 6е';2 — — 1,
*) Изложение схемы решения задач синтеза механизмов по методу
3. Ш. Блоха приводится здесь по книге И. И. Артоболевского,
В. В. Добровольского и 3. Ш. Блоха «Синтез механизмов», ГТТИ,
1944, стр. 2оЗ—374.
**) Обозначения изменены по сравнению с принятыми в работах 3. Ш. Блоха
для единообразия с обозначениями, принятыми в данной книге, а также с обо-
значениями К. Зикера [111г].
21 И. И. Артоболевский
(9.388)
(9.389)
642
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
Для решения этой системы уравнений, линейной относительно неиз-
вестных а, b и с, составляем определитель системы из коэффициен-
тов при неизвестных в левой части
(9.390)
и, заменяя последовательно его столбцы на столбец, состоящий
из свободных членов, получим:
<h =
dt =
Тогда неизвестные а, b и с определятся по формулам:
о = 6 = ^, с=%. (9.392)
Со Со Со
Следовательно, при вычислении трех параметров шарнирного
четырехзвенника по заданным положениям его звеньев как по методу
3. Ш. Блоха, так и по методу, указанному в § 30 *), мы получаем
систему линейных уравнений. Отличие состоит лишь в том, что по
методу 3. Ш. Блоха надо для определения параметров а, Ь, с, а и р
выбрать дополнительно к заданным углам <?, и еще два угла пово-
рота шатуна и ;2, а по методу, указанному в § 30, углы наклона
шатуна не входят в расчетные уравнения и для определения трех
параметров можно непосредственно задать два других параметра.
Например, можно задать а и р и вычислить а, Ь, с или же задать
с и а и вычислить Ь, с и р и т. д.
При вычислении четырех параметров шарнирного четырехзвенника
по заданным положениям его звеньев, следуя методу 3. Ш. Блоха, выпи-
сываем систему четырех уравнений, аналогичных уравнениям (9.389):
_!_ бе'-1 — ce'4i= 1,
ae'TsJ- — се'+»__ ],
ее*?» -j- — се'43— j _
(9.393)
*) См. стр. 582.
§ 32]
ПРИМЕНЕНИЕ МЕТОДА КОМПЛЕКСНЫХ ЧИСЕЛ
643
Очевидно, что неизвестные а, Ь и с определяются из любых трех
уравнений написанной системы, например первых трех, и их значения
вычисляются по формулам (9.392). Остается выяснить, при каком
условии найденное решение (9.392) первых трех линейных уравнений
будет удовлетворять четвертому уравнению системы (9.393). Это
условие получим, подставляя значения а, Ь и с из формул (9.392)
в четвертое уравнение системы (9.393).
Имеем:
dje'Va-j- </.,^3 — d3e'4s— d6 = 0. (9.394)
Уравнение (9.394), которое в дальнейшем будем называть уравне-
нием совместности, можно, учитывая формулы (9.391), представить
также в форме определителя 4-го порядка:
11 1—1
1 е1’* —
1 е’? - е‘~- ' - -
1 6‘тРз е'-з —
(9.395)
Комплексное уравнение (9.395) эквивалентно системе двух обыч-
ных уравнений с двумя неизвестными. Поэтому, выбрав дополнительно
к заданным значениям углов и угол поворота шатуна Е3, можно
из уравнения (9.395) найти значения углов поворота шатуна и
и затем вычислить искомые величины а, b и с по уравнениям (9.392).
Решение уравнения (9.395) приводится к решению одного квад-
ратного уравнения и, следовательно, сложность вычислений по методу
3. Ш. Блоха и по методу, указанному в § 30 *), оказывается одной и той же.
Отличие состоит лишь в том, что по методу 3. Ш. Блоха надо
для определения параметров а, Ь, с, а. и р выбрать дополнительно
к заданным углам и фг еще один угол поворота шатуна (напри-
мер, £3), а по методу, указанному в § 30, углы наклона шатуна не
входят в расчетные уравнения и для определения четырех парамет-
ров можно непосредственно задать один параметр (например, а) и
вычислить остальные четыре **).
При вычислении пяти параметров шарнирного четырехзвенника по
заданным положениям его звеньев, следуя методу 3. Ш. Блоха,
выписываем систему пяти уравнений:
a -j- b — с 1, 1
ae'fi Ье^л — се^1= 1,
aeif? -|- — се''^= 1, у
(9.396)
-ф- бе'-» — се''^ = 1,
Ъе1'-'1 — се‘^'1— 1.
*) См. сгр. 584.
** ) Квадратное уравнение, не содержащее углов поворота шатуна, для слу-
чая вычисления по методу интерполирования четырех параметров шарнирного
четырехзвенника получено в работе В. А. Зиновьева 122а].
21*
644
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[гл. IX
Любые три уравнения этой системы могут служить для определения
неизвестных а, b и с. Остальные два уравнения будут уравнениями
совместности, если подставить в них значения а, b и с из фор-
мул (9.392). Уравнения совместности имеют вид:
— </ае'4з—tZo = O, |
dje'Ti -J- dieiii — d3^* — du = 0. f
После подстановки определителей dn, dh d, и rf3 эти уравнения
можно представить в форме определителей 4-го порядка:
1 1 — 1
eui — e'+i
ei'ti ei:-> — е‘42
— е«Фз
1 1 — 1
e'Ti е'и — e'4i
е'тз <?‘4з
e'-i — е'Ъ
(9.398)
Система двух комплексных уравнений (9.398) эквивалентна системе
четырех обычных уравнений с четырьмя неизвестными, которыми
в данном случае являются углы поворота шатуна 64, В3 и Е4. Для
определения неизвестных а, Ь и с по формулам (9.392) достаточно
вычислить углы Ej и е.,. Решение уравнений (9.398) в работах
3. Ш. Блоха предлагается выполнять путем последовательных при-
ближений. Поэтому в отличие от случаев вычисления трех и четырех
параметров имеется существенная разница в вычислительных опера-
циях по методу 3. Ш. Блоха и по методу, указанному в § 29 *), а
именно, применение метода, указанного в § 29, сводит решение
задачи к решению системы линейных уравнений и одного алгебраи-
ческого уравнения третьей степени **).
Аналогично решаются по методу 3. Ш. Блоха задачи синтеза
шарнирного четырехзвенника при задании производных от функции
положений, а также задачи синтеза других четырехзвенных механизмов.
3е. Метод К. Зикера. После краткого изложения работ 3. Ш. Блоха,
которые были одними из первых работ по синтезу механизмов с при-
менением комплексных чисел, рассмотрим одну из последних по
времени работ, использующих в синтезе механизмов метод комплекс-
ных чисел, а именно, дадим краткое изложение метода, который
используется в работе К. Зикера (И 1г].
*) См. стр. 558.
**) Уравнение третьей степени, не содержащее углов наклона шатуна, для
случая вычисления по методу простого интерполирования пяти параметров
шарнирного четырехзвенника получено в работе Е. П. Новодворского ]40].
§ 32] ПРИМЕНЕНИЕ МЕТОДА КОМПЛЕКСНЫХ ЧИСЕЛ 645
В отличие от работ 3. Ш. Блоха в работах К. Зикера углы пово-
рота шатуна исключаются при выводе уравнения, связывающего иско-
мые параметры, и потому получаемые схемы решения задач синтеза
передаточных механизмов по методу интерполирования не отличаются
по существу от изложенных выше в §§ 29 и 30.
Покажем, например, вычисление пяти параметров шарнирного
четырехзвенника по заданным положениям его звеньев.
Как и в методе 3. Ш. Блоха, сначала выписывается условие
замкнутости векторного контура ABCD (см. рис. 604) в форме
уравнения (9.386) и уравнения ему сопряженного:
Вращение векторов а, b и с на углы <р(-, и ф, дает соответствнно
уравнения:
ae9i be'i—- Ce^i — 1=0,
be~''i — ce'^t— 1 =0.
Из уравнений (9.399) имеем:
bb = (\ Ц-с — а)(1 -|~с — а).
Соответственно из уравнений (9.400) получаем:
bb — (1 ce‘4i— ae‘Vi) (1 -| - Ce~‘^i — ae~‘vi).
Из уравнений (9.401) и (9.402) после раскрытия скобок и
ния подобных членов имеем:
a (elvi — 1) + «(с*¥‘ — 1) — с (е*’*'» — 1) — с (е-"*'»— 1)4-
4-flC(e't'f<-"':'il— 1)_|_ос(е-г'^-4р_ 1) = о.
Обозначая через ft комплексные числа (векторы), стоящие в скобках,
имеем:
aft (?) 4- af, (?) — cfi W—cfi (Ф) + acfi (?Ф) + acft (?Ф)=0. (9.404)
Для вычисления пяти параметров записываем уравнение (9.404)
в следующем виде:
cfi (ф) 4- cfi (ф) — acft (?ф) — ас/, (фф) = aft (<р) 4- af (?). (9.405)
Полагая г=1, 2, 3, 4, получаем четыре уравнения, которые можно
решить относительно неизвестных с, с, ас и ас.
Имеем:
(9.400)
(9.401)
(9.402)
приведе-
(9.403)
cd = adt -|- ad.,; (9.406)
cd=ad^adf, (9.407)
aid = od:,4 od4; (9.408)
acd ^=adri\-ad-f. (9.409)
646
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
[ГЛ. IX
В этих четырех уравнениях комплексные числа dt, dit dt, d,t и сопря-
женные им комплексные числа представляют собой определители
4-го порядка, составленные из коэффициентов ft и
<*=1Л(Ф) Л(Ф) fi№ /(тф) 1, (9.410)
di = !/,(<?) Л(Ф) fi (?ф) /(<?ф)|, (9.411)
Л='Л(Ф) Л(?) Л(?ф) fi (?ф) 1, (9.412)
^ = 1Л(Ф) Я(Ф) Л(?) —Л(тФ)Ь (9.413)
<*4=1Л(ф) Л(Ф) —Л (?ф) f (?) I- (9.414)
Разделим теперь почленно уравнение (9.408) на уравнение (9.407) и
уравнение (9.409) на (9.406).
Имеем:
__ cd3 + adt ctcl^ —р adi (9.415)
~ adsi —{— (id-'t, adi + ad2 (9.416)
Разделив выражение (9.415) на (9.416), получим:
еа. = + (e^di + d2)
(e^ + dO^di + t/s) '
После преобразований это уравнение можно представить в следую-
щем виде:
e‘3ad.2d4 — e“‘3ad2d4 е,а {d,dA -ф- d,d4 — d,d3) —
— е (d2d:t Ц- d1d4 — d,d3) = 0. (9.418)
Полагая для сокращения
d2d4 = d„, (9.419)
d.,d;i -|- d|d4 — dld,t — db, (9.420)
получаем уравнение (9.418) в следующем виде:
dae'2tt — dae~‘3* -| - dbeia — dbe~™ — 0. (9.421)
Для дальнейших вычислений переходим от уравнения в комплексных
числах к уравнению в действительных числах, применяя на основании
формул (9.364), (9.381) и (9.370) следующие соотношения:
= Dxa —|— iUya, db Dxb -f- iDyb,
da Dxa il)ya, db — Dxb iDyi,,
et3a = cos 3a. ф- i sin 3a, e = cos 3a — z sin 3a.
Имеем:
Dyn sin 3a 4- Dya cos 3a -j- Dxb sin a -ф- Dyb cos a = 0. (9.422)
§ 32] ПРИМЕНЕНИЕ МЕТОДА КОМПЛЕКСНЫХ ЧИСЕЛ 647
Принимая во внимание соотношения:
sin За = 3 sin а — 4 sin3 а,
cos За = — 3 cos а -]- 4 cos3 а,
получаем после преобразований:
(Dxb - Dxa) tg3 а + (Dv6 - 3Dya) tg2 а +
4 - {Dxb -I- 3Dxa) tg a J- Dyb + Dyn = 0. (9.423)
Из этого кубического уравнения определяется угол а. Далее из
уравнения (9.416) находим модуль а:
Из уравнения (9.406) определяем комплексное число (вектор) с:
с = Сх -ф- icy = ——г . (9.42а)
После определения сх и cv модуль с и угол наклона р находятся
в соответствии с формулами' (9.367) и (9.368).
Определив параметры а, а, с и р, можно найти и параметр b из
уравнения (9.401).
Аналогично решаются задачи синтеза шарнирного четырехзвенника
при задании производных от функции положения, а также задачи
синтеза кривошипно-шатунного механизма. Решение всех этих задач
охватывается методами, изложенными в предыдущих параграфах, и
поэтому дальнейших примеров па использование метода комплексных
чисел в синтезе механизмов не приводим. Заметим, что и в синтезе
направляющих механизмов, которые рассматриваются в следующей
главе, также все основные задачи могут быть решены как с исполь-
зованием комплексных чисел, так и без них *).
При использовании тех или иных алгебраических методов для
решения задач синтеза механизмов решающими являются количество
вычислительных операций и их трудоемкость. Рассмотренные методы
синтеза механизмов с использованием комплексных чисел не имеют
в этом отношении преимуществ по сравнению с изложенными в пре-
дыдущих параграфах. Поэтому мы не приводим числовых примеров
синтеза механизмов с использованием комплексных чисел.
*) В упомянутой выше работе К. Зикера [111г] рассматривается задача
синтеза шарнирного четырехзвенника по девяти точкам шатунной кривой, кото-
рая еще нс решена без использования комплексных чисел. Но приводимое
К. Зикером решение является ошибочным.
ГЛАВА X
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
§ 33. Шатунные кривые
1°. Несимметричные шатунные кривые шарнирного четырех-
звенника. В главе VI были описаны многие теоретически точные
направляющие механизмы, г. е. механизмы, которые служат для вос-
произведения (черчения) кривых. Однако во многих случаях при
проектировании механизмов, в которых используется движение по
заданной кривой (например, механизмы для перемешивания, для обра-
зования петель, механизмы захватов, механизмы с периодическими
остановками ведомого звена и т. д.), среди теоретически точных
направляющих механизмов или вовсе не оказывается механизмов,
Рис. 605.
воспроизводящих заданную кривую,
или же имеющийся механизм не удов-
летворяет условиям проектирования
с точки зрения уменьшения числа
звеньев, получения благоприятных
углов давления и т. д. Поэтому возни-
кает задача о приближенном воспро-
изведении заданной кривой при помо-
щи простейших механизмов. С этой
целью чаще всего используются свой-
ства шатунных кривых шарнирного
четырехзвенника, т. е. тех кривых, которые являются траекториями то-
чек, принадлежащих шатуну шарнирного четырехзвенника. Вид и раз-
меры шатунной кривой, описываемой, например, точкой Л4 шарнирного
четырехзвенника (рис. 605), зависят от шести параметров, в которые
входят длины звеньев: a, b, с, d, а также расстояние от центра
шарнира С до чертящей точки М, обозначенное через k и угол ш.
Благодаря тому, что в уравнение шатунной кривой входят шесть
независимых параметров, которые при проектировании можно выби-
рать, можно во многих случаях найти шатунную кривую, мало отли-
чающуюся от заданной кривой на отдельном участке или на всем
своем протяжении. Используя шатунные кривые шарнирного четырех-
звенника. можно иногда получить механизм, более благоприятный
§ 33]
ШАТУННЫЕ КРИВЫЕ
649
в отношении учета дополнительных требований по сравнению с меха-
низмом, воспроизводящим заданную кривую теоретически точно.
Например, воспроизведение движения по прямой линии теоретически
точно может быть выполнено с помощью шестизвенных прямолинейно-
направляющих механизмов *). Однако при синтезе механизмов, исполь-
зующих свойства прямолинейно-направляющих шарнирных механизмов
(механизмы индикаторов, некоторых кранов и т. п.), предпочитают
четырехзвенные механизмы, которые вследствие меньшего числа
звеньев оказываются более удобными, хотя среди шатунных кривых
шарнирного четырехзвенника можно найти кривые, лишь приближенно
совпадающие с отрезком прямой линии на некотором участке или на
всем своем протяжении.
Итак, синтез приближенных направляющих механизмов сводится
к отысканию среди семейства шатунных кривых шарнирного четырех-
звенника (или других простейших механизмов) такой кривой, которая
мало отличается от заданной. Поэтому, прежде чем излагать методы
синтеза этих механизмов, следует по-
лучить уравнения шатунных кривых.
С этой целью можно использо-
вать соотношения между координа-
тами точек, принадлежащих звеньям
двухповодковых групп. Эти со-
отношения известны под назва-
нием рекуррентных. Рекуррентными
соотношениями или рекуррентными
формулами в математической лите-
Рис. 606.
ратуре называются те соотношения, при помощи которых можно для
последовательности функций
/о. /ь /«• • • >
зная функцию fk, вычислить функцию fk+i. Если известна функция /п,
то последовательное применение рекуррентной формулы дает возмож-
ность вычислить все функции данной последовательности.
Аналогично уравнение шатунной кривой любого /z-звенного меха-
низма может быть получено путем последовательного применения
некоторых рекуррентных соотношений, зависящих от типа структур-
ных групп, в него входящих.
Пусть, например, требуется написать уравнение шатунной кривой
точки шестизвенного механизма, схема которого изображена на
рис. 606. Механизм этот образован следующим образом. К звену АВ,
которое будем называть начальным, присоединена двухповодковая
группа BCD. Затем к шатуну четырехзвенного механизма ABCD и
стойке присоединена вторая двухповодковая группа BiCxD\, на шатуне
которой и расположена точка Mt. Для каждой двухповодковой группы
*) См. с гр. 275.
650
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
|ГЛ. X
первого вида, г. е. двухповодковой группы с одними вращательными
парами (рис. 607), существует определенная зависимость между коор-
динатами точек В (хц, у в) и М (х, _у), если один из крайних шарни-
ров присоединен к стойке.
Эти зависимости
Хв = f\ (*. Д’) > |
У в —ft (*, J') J
(Ю.1)
и называются рекуррентными соотношениями двухповодковой группы
первого вида. Подставляя значения Хд и ув из соотношений (10.В
в уравнение окружности, описываемой точкой В (см. рис. 606), полу-
чим уравнение шатунной кривой четырехзвенного механизма. Так как
рекуррентные соотношения для двухповодковой группы B\CxDi выра-
жаются также формулами (10.1), то, полагая начало координат
в точке 7ф и подставляя в уравнение шатунной кривой четырехзвен-
ного механизма рекуррентные соот-
ношения (10.1), получим уравнение
шатунной кривой шестизвенного
Рис. 608.
механизма. Таким же путем можно получить уравнения шатунных кривых
восьмизвенных механизмов или механизмов с поступательными парами.
Следовательно, вывод уравнения шатунной кривой п-звенного
механизма сводится к последовательной подстановке некоторых ре-
куррентных соотношений в уравнение окружности или прямой линии,
так как любой плоский механизм может быть образован путем при-
соединения структурных групп к начальному звену. Необходимо лишь
иметь для каждой структурной группы и ее различных видов соот-
ветствующие рекуррентные соотношения.
Рассмотрим сперва двухповодковую группу первого вида, присо-
единенную к стойке одним из крайних шарниров (рис. 608). Длины
звеньев этой группы и положение произвольной точки М на звене ВС
определяются следующими величинами:
CD —с, BC — b, BM = k, /,ВСМ = ы.
Рекуррентными соотношениями будут соотношения (10.1) между ко-
ординатами точек М (х, _у) и В (хд, _уд):
А'в=/1(х, >), у в — /?(-С у).
§ 33]
ШАТУННЫЕ КРИВЫЕ
651
Для вывода их поместим начало координат в точке D. Тогда,
обозначая через а переменный угол, образованный направлением
отрезка ВС с осью Ох, получаем:
Хн = х — k cos (to -U a) b cos a, )
г (Ю.2)
yi> =y — k sin (to a.) -f- b sin a. )
Кроме того, имеем:
a = y-|-p— w, (10.3)
где р = /, ОМС, у — угол, образованный направлением радиуса-век-
тора точки М с осью Ох.
Тригонометрические функции угла р определяются из треуголь-
ника CDM:
D р2 + /г3 — с2
cos 8 — -—- v,,----,
г 2/ер
'__________________ (10.4)
sin о _ . V w - (р2 + й2 - с2)2
мпр— ± 2fep ,
где р "= ] Ла'2-р J'2 есть величина радиуса-вектора точки Л-1.
Тригонометрические функции угла у имеют следующие значения:
cos х= (10.5)
sin у = у . (10.6)
Подставляя в соотношения (10.2) значение угла а из уравне-
ния (10.3) и значения тригонометрических функций углов р и / из
формул (10.4), (10.5) и (10.6), получаем после преобразований иско-
мые рекуррентные соотношения:
. VQ 4- W T Х/з — x , VT — w 2k ’ (Ю.7)
где ±1/4й2р2-(р2 + Л2- c2)2. (10.8)
f2 »
IT (10.9)
Q = xb sin to — у (b cos to — -/г); (10.10)
T —yb sin co x (b cos to — -/г). (10.11)
Отметим также, что квадрат радиуса-вектора точки В может
быть определен по следующей формуле:
?Ъ = хв-\-ув =——(р — с1— /г)± -k— U-\-b- -J-с-, (10.12)
652
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
где
U =± /Щ? — (р2 + — с2)2.
(10.13)
Двойному знаку квадратного радикала в формулах (10.8) и (10.13)
соответствуют два различных положения точки В (хд, уд) при одном
и том же положении точки М (х, _у). На рис. 609 такими положе-
ниями являются точки В и В'. Аналогично одному и тому же поло-
жению точки В соответствуют два различных положения точки Л1.
Формулы (10.8), (10.9) и (10.12) значительно упрощаются для частного
случая, соответствующего условию
k = c. (10.14)
В этом случае имеем:
(1015)
IF=1, (10.16)
p’b=t^(p2—2&8)±^^ р у 4/;2 _ р2 Ц0.17)
Двухповодковая группа, удовлетворяющая условию
k = b — c, (10.18)
называется диадой Чебышева.
Для нее формулы (10.7) имеют весьма простой вид после поворота
координатных осей Ох и Оу на угол ~ по отношению к осям Охд
и Оуд (рис. 610). В этом случае после преобразования координат
имеем:
/ о) l/~ 4Л2 — р2 \ 1
Хд = Xi COS у zt Sin у --------— I ,
v “ ,-..Р __' (10.19)
/ со . со I/ 4&2— р«\
№=j’^cos 2±sm 2
ШАТУННЫЕ КРИВЫЕ
653
§ 33]
С помощью рекуррентных соотношений можно вычислить значения
координат точек шатунных кривых. Эти вычисления сводятся к под-
становке числовых значений координат точки В (см. рис. 605), т. е.
координат окружности
(л-в-</)2+_уЬ = а2, (10.20)
в уравнения, связывающие искомые координаты точки М (х, у) с коор-
динатами точки />(хд, у в). Эти уравнения получаются из соотноше-
ний (Ю.7) заменой обозначений k на b, b на k и to на
— со.
Имеем:
где
I WB-(pb+fta-r8)2
+ ь~ —с2
Qb= — Хрk sin со —ye(k cos со — b).
(10.21)
(10.22)
(10.23)
(10.24)
Tg — —з'д Л sin cu j-Л'/; (/? cos n> — b). (10.25)
Следовательно, давая различные значения абсциссе Хв (ординате у в),
можно вычислить из уравнения (10.20) соответственно значения ор-
динат у в (абсцисс хв) и затем значения координат х и у шатунной
кривой по формулам (10.21).
Указанный способ вычисления координат шатунной кривой удобно
применять не только при решении задач анализа, но и синтеза меха-
низмов в тех случаях, когда требуется вычисление величин отклоне-
ния шатунной кривой от заданной.
Отметим, наконец, что для решения задач синтеза направляющих
механизмов требуется знать вид рекуррентных соотношений при про-
извольном расположении координатных осей Ох и Оу. Обозначая
координаты точки D через х^ и уо, получаем после преобразования
координат соотношения (10.7) в следующем виде:
. VQ + WT
“Г 2/г
Ув=У
. VT — WQ
+ 2/г
(10.26)
654
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. \
где
V = ± ~ V 4А2А/2 — (№ 4- А2 — с2)2 (10.27)
/V2 = р2 — 2xDx — 2yDy 4- хЪ 4-У'Ь, (10.28)
w=-2^ -~с° N- (10.29)
1' = (у yD) Ь sin го 4~ {х л'о) (b COS U) — А), (10.30)
Q = (х — Хп) b sin го — (у — yD) (b cos го — А). (10.31)
Соотношение (10.12) для определения квадрата радиуса-векгора
p/j принимает в этом случае следующий вид:
Рв = —-k— (М — с2 — А2) 4----— U-\- Ь2 + с2 — x-D ~УЪ 4-
4~ 2хохй 4~ 2уо_ув, (10.32)
где
С/ = ± } 4/AV2 — (А/2 - L А’2 — с2)2 • (10.33)
Наконец, можно получить уравнение шатунной кривой шарнир-
ного четырехзвенника, если в уравнение (10.20) подставить соотно-
шения (10.7).
Имеем:
/ . VQ-\-\VT ,\2 / W—W\2 2 /inQ..
И4--^-----------d) + '/+—~2k~~= а (10-34)
Подставляя в это уравнение величины V, W, Q и Т из соотно-
шений (10.8), (10.9). (10.10) и (10.11) и производя преобразования,
можно получить уравнение шатунной кривой, описываемой точкой М
в виде алгебраического уравнения 6-го порядка.
Например, при k — c уравнение (10.34) принимает вид:
9 Г Ь COS СО о d , . .
Р [—~— Р — ~ (с 4- b cos ю) х —
— db sin о> _j_ ^2 _ р сч ^2 — а2 — 2cZ> cos го | —
4С2_ р2 Г 12
----------- ixM sin со—j/rf(Acosro—• с) 4- p-b sin го =0, (10.35)
где
Р —х •
Аналогично можно получить уравнение шатунной кривой шести-
звенного механизма, схема которого показана на рис. 606, в виде
алгебраического уравнения 18-го порядка [ЗЗд, е].
2°. Симметричные шатунные кривые шарнирного четырех-
звенника. При решении задачи синтеза приближенных направляющих
механизмов нередко заданная кривая является симметричной кривой
§ 33]
ШАТУННЫЕ КРИВЫЕ
655
(прямая, дуга окружности, дуги конических сечений и т. д.). В этом
случае естественно воспользоваться механизмом, дающим симметрич-
ные шатунные кривые,
ного четырехзвенника
условии (рис. 611)
b — c = k
или при условии (рис.
ь
Таким
при
612)
а = с, k
2 cos и
В дальнейшем будет пока-
зано, что схема механизма,
показанная на рис. 612, мо-
жет быть получена из схе-
мы, показанной на рис. 611,
путем преобразования, из-
вестного под названием тео-
ремы Робертса *). Поэтому
в дальнейшем будет рассма-
триваться только схема, по-
казанная на рис. 611, так
как в практических прило-
жениях механизмы, выпол-
ненные по этой схеме, ока-
зываются более удобными.
Точка М этого механизма
описывает кривую, симме-
тричную относительно осп,
составляющей с линией DA
<0 гг
угол . Для доказатель-
ства этого свойства заметим,
что точки Al, D и В
жат на окружности с
Поэтому угол BDM,
ВМ — ы, есть величина
является, например, механизм шарнир-
ле-
центром в точке С,
как вписанный угол,
постоянная и равная
так как b = c = k.
опирающийся па дугу
~. Отсюда следует:
Z. 8 = / BDA.
с центром в точке А
При движении точки В по окружности
симметричным положениям точки В относительно оси DA соответст-
вуют равные углы BDA и, следовательно, равные углы 8, т. е. сим-
метричным положениям точки В относительно оси DA будут соот-
*) См. далее стр. 669.
656 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ |ГЛ. X
ветствовать симметричные положения точки М относительно оси, со-
ставляющей угол с осью DA.
Те положения механизма, при которых точка А1 находится на
оси симметрии, будем называть средними положениями механизма.
Центр шарнира В в этих положениях располагается на линии цент-
ров DA (внутреннее среднее положение) или на продолжении ее
(внешнее среднее положение).
Если выбрать начало координат в точке D и ось у направить по
оси симметрии, то можно получить уравнение симметричной шатун-
ной кривой шарнирного четырехзвенника в параметрической форме,
приняв за переменный параметр угол передачи р, который равен
90°—8, где 0— угол давления от шатуна ВС к звену CD. Сначала
получим это уравнение в полярных координатах, за которые при-
мем радиус-вектор р = £)7И и угол 8.
Представим эти координаты, как функции переменного параметра р.
Из A ABD имеем:
cos / BDA = cos 8 — (ВРУ + (АРУ-(АВУ
COS z. DUA _ COS 6 — 2
Величина BD из равнобедренного треугольника равна:
BD=2b sin
Следовательно,
4й3 sin2 d- — a2
cos 8 == —----------------. (10.36)
4b d sin t
Радиус-вектор p = DM определяется из равнобедренного тре-
угольника MCD'.
p = 2frsin м + . (10.37)
Соотношения (10.36) и (10.37) дают уравнение симметричной
шатунной кривой в полярных координатах, выраженное через пере-
менный параметр р.
Для перехода к декартовым координатам имеем соотношения:
j>=:pcos8; x = A=l'rps—y3.
Подставляя значения р и cos 8 из соотношений (10.36) и (10.37),
получим уравнение симметричной шатунной кривой в декартовых ко-
ординатах, выраженное через параметр р:
у = |_4//2 sin ~ sin у cos у -ф- 4Ь2 cos у sin2~ -ф-
-ф- (d2 — a2) sin ~ ctg у -ф- (d2 — а2) cos ~ j;
х = ± "j/"4/У2 sin2 —+ - —j’2.
§ 331
ШАТУННЫЕ КРИВЫЕ
657
Обозначив sin2 [~ = z, получим уравнение траектории точки Л1 в
следующем виде:
У— .^[4ft2 sin | z(l — z) Ц 4ft2z cos ~ Ц-
(Д2 — «2) j/ —sin ~ (^2 — °2) c°s ’ (10.38)
x = ± ^*^4ft3 ^sin У 1 —z 4’ И2 cos — y2, (10.39)
Для частного случая o> — г имеем:
> = -Ь [4z?2 ~~z} +{d'2 ~ g2) V I ’ (1 °-4G)
X = ± J a'4F(1 — z) —У*. (10.41)
Уравнение симметричной шатунной кривой в виде алгебраиче-
ского уравнения 6-го порядка можно получить путем исключения па-
раметра z из уравнений (10.38) и (10.39) или же из уравнения-
(10.35), полагая с =Ь.
Имеем:
р2 [р2 cos ш — d (1 4* cos w)x — dy sin <0 4- 2ft2 4“ d2— a2—-2b2 cos w]2-—
---46 у I xdb sin <0—ydb (cos w— 1) P2ft sin 10 | =0. (10.42)
Для частного случая <и = т: получаем уравнение симметричной
шатунной кривой в следующем виде:
Уе 4 Xе 4- 3_у4х2 4- 3_у2х4 4- 2 (d2 4- а2 — 4ft2)j4 —
— 2 (d2 — а2 4- 4ft2) х4 — 4 (4ft2 — а'2) х2у2-'г
4- |((/2 — а2 4- 4ft2)2 — 16ft2cP] У 4- (d2 — а2 4- 4ft2) х2 = 0. (10.43)
Полагая в уравнении (10.43) _y2 — s, получаем уравнение третьей
степени. Следовательно, для данного частного случая можно полу-
чить ординату шатунной кривой у в виде явной функции абсциссы х.
Решая задачи синтеза приближенных направляющих механизмов
с помощью теории наилучшего приближения функций, мы встреча-
емся с необходимостью выяснять области существования механизма,
т. е. определять те значения переменных параметров, при которых воз-
можны действительные решения. Для симметричных механизмов этот
анализ получает весьма простую геометрическую интерпретацию,
если предварительно рассмотреть различные виды симметричных
шатунных кривых и определить области их существования.
Вид шатунной кривой определяется относительными размерами
звеньев механизма. Для симметричного механизма достаточно задать
658 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [ГЛ. X
три параметра, например a, d и ю. Варьируя значения этих пара-
метров, мы будем получать различные по своему характеру шатунные
кривые. Особенно наглядно получается изменение характера шатун-
ных кривых, если при постоянных а и d изменять величину угла <о.
На рис. 613 показаны различные виды симметричных шатунных
кривых при условии, что
а d и а d 2/т
Основным признаком, по которому произведено разделение ша-
тунных кривых на виды, являются наличие особых точек, их число,
характер и расположение.
Рис. 613.
При значениях угла <о, близких к 2л, кривая, описываемая некото-
рой точкой шатуна Afb особых точек не имеет (вид /). Уменьшая
угол <о, мы найдем такую точку М2, которая во внутреннем среднем
положении механизма совпадает с центром D, т. е. с мгновенным
центром вращения для этого положения. Кривая, описываемая точ-
кою ТИ2, будет вследствие этого иметь точку возврата (вид II) *). При
дальнейшем уменьшении угла ю симметричные кривые, описываемые
точками шатуна, будут иметь вид восьмерки, причем ее двойная
точка всегда совпадает с центром D (вид III). Как предельный слу-
чай восьмерки мы опять получим кривую с точкой возврата (вид IV).
Точка ТИ4, описывающая эту кривую, совпадает с центром D во
внешнем среднем положении механизма. Далее в некоторой области
значений угла <о симметричная шатунная кривая вновь особых точек
*) Для большей ясности чертежа кривые, описываемые точками /И2, АД,
Мц и А18 вынесены в сторону.
§ 33]
ШАТУННЫЕ КРИВЫЕ
659
не имеет (вид V). Однако характер кривых этого вида существенно
отличен от кривых вида I, а именно, кривые вида V вследствие на-
личия характерных для них изгибов могут иметь с прямой, окруж-
ностью и некоторыми другими кривыми максимально возможное число
точек пересечения. Границей этой области является то значение
угла о), при котором точка шатуна 7И6 совпадает в одном из поло-
жений с мгновенным центром вращения для шатуна. Так как это по-
ложение не является средним, то кривая, описываемая точкой Л1в,
имеет уже две симметрично расположенные точки возврата (вид VI).
Затем в небольшом интервале изменения угла <о существует область
симметричных шатунных кривых в виде двойной восьмерки, т. е.
кривой, имеющей две двойные точки (вид VII). К этому виду при-
надлежат те симметричные шатунные кривые, которые могут быть
приближены на всем своем протяжении к прямой или дуге окруж-
ности. С уменьшением угла <о обе двойные точки кривой вида VII
сближаются и, наконец, при некотором значении угла <и они совпа-
дают. Точка М), соответствующая этому значению угла <о, описы-
вает кривую, имеющую точку самоприкосновения (вид VIII). При
дальнейшем уменьшении угла <о симметричные кривые, описываемые-
точками шатуна, особых точек не имеют (вид IX).
Аналогично могут быть подразделены на виды симметричные кри-
вые, получающиеся при соотношениях
а d и а d j> ‘2Ь.
При этих условиях для симметричного механизма достаточно рас-
смотреть изменение вида шатунных кривых для значений угла <о от
360 до 180°, так как кривые, описываемые точками шатуна при
значениях угла <о и 360 — <о, совпадают.
На рис. 614 показаны различные виды этих кривых.
Вид X характеризуется наличием двух двойных точек. Границей су-
ществования этого вида будет то значение угла ш, когда некоторая
точка шатуна 7ИП совпадает в одном из положений с мгновенным
центром вращения. Кривая, описываемая точкой 7Ии, имеет две сим-
метрично расположенные точки возврата (вид XI). Далее в неко-
торой области значений угла <о симметричные шатунные кривые осо-
бых точек не имеют (вид XII). Уменьшая угол ы, мы получим точку
Л113, которая в среднем положении механизма совпадает с центром
D. Кривая, описываемая точкой М13, имеет одну точку возврата
(вид XIII). Наконец, при дальнейшем уменьшении угла <ч симмет-
ричные кривые, описываемые точками шатуна, имеют вид восьмерки,
двойная точка которой совпадает с центром D (вид XIV). Для зна-
чения <о=180° эта кривая является симметричной относительно двух
взаимно-перпендикулярных осей и может быть приближена к двум
пересекающимся в центре D прямым, в то время как кривые видов
XI и XII могут быть приближены к прямым, перпендикулярным к оси
симметрии.
660 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Рассмотренные случаи охватывают наиболее важные для пракщ-
ческого использования виды симметричных шатунных кривых, поэтому
анализ симметричных кривых, получающихся при иных соотношениях
между размерами звеньев, здесь не приводится.
Из рассмотрения различных видов симметричных шатунных кри-
вых, представленных на рис. 613 и 614, следует, что границами,
определяющими переход одного вида в другой, служат кривые, име-
ющие какую-либо особенность (виды //, IV, VI и VIII на рис. 613
и виды XI и XIII на рис. 614). Поэтому, для того чтобы опреде-
лить области существования различных видов симметричных шатунных
кривых, необходимо получить соотношения между размерами звеньев
механизма, при которых имеют место кривые с особыми точками.
Рис. 614.
Вид II получается в том случае, если некоторая точка шатуна
ТИ2 совпадает с центром D во внутреннем среднем положении меха-
низма. Следовательно, размеры механизма должны удовлетворять со-
отношению
где через <оа обозначено значение угла oj, при котором имеет место траек-
тория вида II.
Аналогично вид IV получается при совпадении точки ТИ4 с цен-
тром D во внешнем среднем положении механизма. Размеры меха-
низма при этом связаны зависимостью
ы. d 4- и
Sln 2~ ~2Ь~ •
ШАТУННЫЕ КРИВЫЕ
661
Для получения траектории вида VI нужно выбрать размеры ме-
ханизма таким образом, чтобы точка шатуна Л46 совпала в некото-
ром положении с мгновенным центром вращения шатуна. На рис. 615
изображено это положение механизма.
Из Л ADMtl имеем:
(Z2 = 4/г -j- [а -|- c2b sin -у j2 — 4b f а - 2b sin j cos —.
Производя упрощения, получим зависимость, которой должны
удовлетворять размеры звеньев механизма, чтобы имела место тра-
ектория вида VI:
Вид VIII, т. е. симметричная шатунная кривая с точкой самопри-
косновения, получается, если в обоих средних положениях механизма
некоторая точка шатуна Л18 занимает одно и то же положение на
оси симметрии.
На рис. 616 показан механизм, удовлетворяющий этому условию
в средних своих положениях (во внутреннем среднем положении
звенья механизма показаны пунктиром). Так как д М8ВВ' равнобед-
ренный, то искомая точка /И8 лежит на перпендикуляре к линии
центров AD, восставленном из центра А.
Из д ЛДЛ18 имеем:
(ДЛ1?)2=4йг sin2-^ — а2.
Кроме того, имеем из д ДД)ТИ8:
(AM8) = dtgZ AD М8.
Подставляя это значение АЛ18 в предыдущее уравнение и при-
нимая во внимание, что угол, образованный осью симметрии с линией
662 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. х
центров AD, т. е. угол АОА18, всегда равен получаем соотно-
шение, которому должны удовлетворять размеры звеньев механизма,
чтобы имела место траектория вида VIII:
г/2 tg2 ™-= 4//2 sin2 й2.
Полученные зависимости определяют области существования раз-
личных видов симметричных шатунных кривых при условии a<^d и
а d<^2b.
Аналогично исследуются области существования симметричных
шатунных кривых при условии
а d: а d^>2b.
Вид XI (рис. 614 и 617) имеет место при условии, что
торая точка шатуна М-
неко-
совпадает в одном из положений ша-
туна с его мгновенным центром вра-
щения.
Из равнобедренного треугольника
BCD имеем:
/_ CBD =
2 •
Из равнобедренного треугольника
ВСМц имеем:
L СВМи
2
Следовательно DBMU =
Из прямоугольного треугольника BAD получаем:
4^ sin2-^ii^ = d2- й2.
Отсюда следует:
cos-i
)/rfs — а5
2b
Вид XIII (см. рис. 614) получается при совпадении точки Л1|:1 с
центром D в среднем положении механизма. Отсюда следует, что
размеры механизма должны в этом случае удовлетворять условию
“13
2
sin
d — а
~~2Ь~
3°. Механизмы с поступательными парами. Уравнение шатун-
ной кривой точки М кривошипно-шатунного механизма (рис. 618)
можно получить, если подставить в уравнение прямой, описываемой
§ 33] ШАТУННЫЕ КРИВЫЕ 663
точкой С, соотношения (10.21). Можно использовать также другой
путь, а именно, получить рекуррентные соотношения для двухповод-
ковой группы второго вида (рис. 619) и подставить их в уравнение
окружности, описываемой точкой В. Эти соотношения можно
получить, если совместить ось х с направлением движения ползуна
и воспользоваться очевидными уравнениями:
Хв = х^/г cos В — b cos (а>-]-8), 1 (Ю44)
У в — b sin (<» В), )
где В — переменный угол ЛКО.
Тригонометрические функции этого угла имеют следующие значения:
sin 6 = ^-
R
R , К k-—y"'
cos В == ± ' —т—- .
k
Подставляя эти значения в уравнения (10.44), получаем искомые
соотношения:
b sin ы , k — b cos ы п -7з-----у ।
= -------—у ±--------т----4 /г'—,1
АЛ- I (10'45>
Кроме того, отметим значение квадрата радиуса-вектора точки В:
Рв = р2 -]--|-[(b cos о> — k)y -\-xb sin (о]_у±
± sin <о — (b cos" сю — k)x] ]^/г2 —у2 -}-
— 2А& cos w-J-А2. (10.46)
Двойному знаку перед квадратным радикалом в формулах (10.45)
и (10.46) соответствуют два различных положения точки В при од-
ном и том же положении точки 7И. На рис. 619 эти положения
664 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [ Гл. \-
обозначены через В и В'. Аналогично одному и тому же поло-
жению точки В соответствуют два различных положения точки М.
При значении угла <о = 0 соотношения (10.45) и (10.46) прини-
мают следующий вид:
xB=x±b~kk /л2—у, jb = Aj,
р2в = Р2 4- у ± х + (b — /г)2.
При значении угла <0=180° получаем:
хв = х ± -6 + fe- \k‘2 — у ,
b
о о 2 (Ь -р &) % ! 2(^ + fe) । /ТБ Т I /# 1 г\9
рв = р-------у У - ‘ - fe х V k — У -Ь (ft ft)2-
С помощью этих соотношений можно вычислять координаты то-
чек шатунных кривых. Например, для вычисления координат точек
шатунной кривой кривошипно-шатунного механизма Совмещаем ось
х с линией движения точки С, подсчитываем координаты точек В
из уравнения окружности радиуса АВ = а с центром в точке А и
затем подставляем найденные значения координат хв и ув в со-
отношения:
k COSo) k sin w , r-Ta-J-
У =----fe—J——Jb, (10.48)
которые получаются из соотношений (10.45) путем замены обозна-
чений k на b и <о на — ш.
Для вывода уравнения шатунной кривой, описываемой точкой М
дезаксиального кривошипно-шатунного механизма, запишем уравнение
окружности, описываемой точкой В:
х2в-[-(Ув~еУ = а* (10.40)
или
pb— 2ej/B4-e2 — а2 = 0. (10.50)
Уравнение шатунной кривой, описываемой точкой /14, получается
после подстановки в уравнение (10.50) рекуррентных соотношений
(10.45) и (10.46):
2
р'2 h y [(ft cos <о — ft)/-)- xb sin <o]у ±
±~[(ft— ft cos o>)x-!-j/ft sin <o]| k-—yi—
----- —-y (---------[ k1 —у 4- b- k- — e- — a- — 2 kbcos w= 0.
§ 33]
ШАТУННЫЕ КРИВЫЕ
665
Освобождаясь от радикала, получаем уравнение шатунной кривой,
описываемой точкой Л1 в виде алгебраического уравнения 4-го по-
рядка:
Рр2 -]- 2 (b cos <о — k) у -|- 2xyb sin со —у 2eb cos ш -| -
' - /г (// -[- A2 -j- с2 — а2 — 2kb cos со)]2 =
= 4 (Л2 —у2) [eb sin со (b cos со — k)x —yb sin со]2. (10.51)
При со — 0° или ш= 180° шатунная кривая кривошипно-шатунного
механизма является симметричной относительно оси х. Уравнение этой
кривой при со = 0 имеет вид:
[Ар2 -4- 2 (b — k — eb)у -]- k (b — А)2 k (е2 — a2)]2 =
= 4(b — b)2(b2—y2)x2. (10.52)
Если к шатуну кривошипно-шатунного механизма присоединить
двухповодковую группу второго вида, то получится кривошипно-
шатунный механизм с прицепным шатуном. Уравнение шатунной
кривой прицепного шатуна получается уже в виде алгебраического
уравнения восьмого порядка [ЗЗе].
В механизме эллипсографа (рис. 620) точки шатуна описывают
эллипсы. Уравнение этих эллипсов получается путем подстановки
рекуррентных соотношений (10.45) в уравнение прямой линии, по
которой движется точка В:
ув = хц^г{.
Имеем:
b cos ы , b sin о) , -т
—k~~y =
/ • , b sin <o , k — b cos <o , 773---,
= (*+ ---~k-----И A2 — yJtgTj.
Отсюда
{yb cos co — xk tg 7] — yb sin <0 tg -г;)2 =
= [(A — b cos co) tg 7] — b sin co]2 (A2 —y2). (10.53)
Для вывода рекуррентных соотношений двухповодковой группы
третьего вида (рис. 621) выбираем начало координат в центре
666
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
выразить
(10.55)
функции
(10.56)
(10.57)
шарнира D и вводим обозначения: BN — e, BM = k и /_ BTN = u.
Тогда искомые соотношения между координатами точек В{хц, у в) и
М (х, _у) могут быть представлены в следующем виде:
хв = х -|- k cos а, у в = у -|- k sin л, (10.54)
где а — переменный угол, образованный направлением отрезка ВЛ1
с осью х.
Для получения рекуррентных соотношений следует
функции sin а и cos а через координаты (х, _у) точки 7И.
Имеем:
a = co-|-z— 8,
где 8 = /_ MDN и -у = /_ MDK.
Из треугольника DNiM определяем тригонометрические
угла 8:
. л е — k sin «
Sin о - =--------,
Р
s । J^p2 — (е — k sin ы)2
cos 8 — zt -х—---v - -—----,
Р
где
Тригонометрические функции угла у определяются из треуголь-
ника DKM:
sinZ=^, (10.58)
cosZ = y. (10.59)
На основании соотношения (10.55) имеем:
sin а = (sin со cos у -j- cos со sin /) cos 8 —
— (cos w cos у — sin co sin y) sin 8, (10.60)
cos a. = (cos co cos у — sin co sin /) cos 8 -j-
(sin co cos cos u> sin /) sin 8. (10.61)
Подставляя в соотношения (10.60) и (10.61) значения тригоно-
метрических функций углов 8 и у из формул (10.56), (10.57),
(10.58) и (10.59), получаем:
. V р2 — (е — k sin со)8 z . I x
Sin a = zt -X-!--X— -------— (x sin co -f- у cos co) —
e — fe sin co . .
-------—-----(x cos co —j sin co), (10.62)
, lzp2— (e— k sin <o)2 . -xi
COS ОС = _±: -С-Д- —— -----( X COS CO — у sin co) “f-
। e — k sin co . , 4
4------J------(x sin co -j-у COS co). (10.63)
§ 33]
ШАТУННЫЕ КРИВЫЕ
667
Искомые соотношения между координатами точек В и М полу-
чим после подстановки значений sin а и cos а по формулам (10.62)
и (10.63) в соотношения (10.54).
Имеем:
, , . ч pV — (е — k sin ш)2 .
хв = х ± k (х cos w —у sin а>) —----------------------р
, , , . . х sin ы 4- у cos ы ,, _ „ ..
-]• - k (е — /г sin <•>)-—-------; (10.64)
, , , , . J/V—(в—k sinw)2
ув =у ± k (X Sin u> -f~ J' C0S u>) ~---*S-------------
, , , . 4 x cos ы — _y sin ш
— k (e — k sin <o)-------------—; (10.65)
рв = xB ув = p2 ± 2Л cos <o ]/p2 — (e — k sin <o)2 -|-
2ek sin o) -|- k2 (1—2 sin2 to). (10.66)
Двойному знаку в формулах (10.64), (10.65) и (10.66) соответст-
вуют два различных положения точки В(хв, у в) при одном и том
же положении точки М (х, у).
Формулы (10.64), (10.65) и (10.66) значительно упрощаются при
значении величины AlAj — 0, т. е. при условии
е — k sin ш.
Имеем:
, . х cos <o — v sin u>
Xb — x ± k----------
p
, , x sin ы 4- v cos ш
yB=y±k--------------
рй — p2 ± 2£p cos w Ц- k2.
(10.67)
(10.68)
(10.69)
(10.70)
В тех случаях, когда точки В и М располагаются на прямой,
проходящей через центр D, т. е. при значениях угла <i) = 0 или
<о=180°, формулы (10.68), (10.69) и (10.70) принимают следующий
вид: X/j = X-L=A, (10.71) (Ю.72)
Р73-=(р»= /г)2.
(10.73)
Из уравнений (10.71) и (10.72) следует, что если точка В описывает
кривую, симметричную относительно оси х или у, то точка 714 также
описывает кривую, симметричную относительно этой оси.
668 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Пусть, например, точка В (рис. 622) движется по окружности,
уравнение которой относительно координатных осей Ох и Оу буде,
рв — 2т/л'й</г — о® = 0, (10.74)
где а —длина звена АВ', d — расстояние между неподвижным,
центрами D и А.
Тогда точка М, расположенная на линии BD, описывает симме-
тричную шатунную кривую, уравнение которой получается после
подстановки рекуррентных соотношений (10.71) и (10.73) в уравне-
ние (10.74).
Имеем:
р24- 2р£ + Д2 — 2dx л_с12 — а2^0
ИЛИ
х2 +У - J- 2А I _|_у — 2с/х — 2dkxl'*~+^ -j-k2-f-d2 — a2 = и.
Освобождаясь or знаменателя и радикала, получаем уравнение сим-
метричной шатунной кривой кулисного механизма в виде алгебраи-
ческого уравнения 6-го порядка:
р2 (р2 — 2dx d2 — а2)2=
= 4k2(dx — р2)2. (10.75)
В общем случае шатунная кривая
кулисного механизма является не-
симметричной. Ее уравнение в ви-
де алгебраического уравнения 6-го
порядка получается после подста-
новки в уравнение (10.74) рекур-
рентных соотношений (10.64) и
(10.66).
Если точка В (рис. 623) движется по прямой, уравнение кото-
рой относительно координатных осей х и у будет:
Хц — е = 0,
(10.76)
§ 331
ШАТУННЫЕ КРИВЫЕ
669
то точка Af, расположенная на линии BD, описывает симметричную
шатунную кривую, уравнение которой получается после подстановки
рекуррентного соотношения (10.71) в уравнение (10.76);
л--{-Л
№ + у-
Освобождаясь от знаменателя и радикала, получаем уравнение сим-
метричной шатунной кривой, описываемой точкой Af в виде алгебраи-
ческого уравнения 4-го порядка:
р2(х--‘е)‘2 = /г2. (10.77)
Аналогично получается уравнение несимметричной шатунной кри-
вой в виде алгебраического уравнения 4-го порядка, если в уравне-
ние прямой, по которой движется
точка В, подставить рекуррент-
ное соотношение (10.64).
4°. Преобразование направляю-
щих механизмов. Если имеется
плоский механизм с низшими пара-
ми, в котором одна из точек ка-
кого-либо звена описывает заданную
кривую, то можно путем преобразо-
ваний найти другие механизмы, вос-
производящие ту же самую кривую.
Значение этого преобразования
для практики заключается в том,
что, получив каким-либо путем
один из механизмов, воспроизводя-
щих данную кривую, мы можем
найти ряд других механизмов, осу-
ществляющих ту же самую кривую,
в условиях данной задачи представ.
Простейшим частным случаем этих преобразований является из-
вестное построение Робертса [103].
Пусть точка 714 шарнирного четырехзвенника 01.415102 (рис. 624)
описывает некоторую шатунную кривую. Присоединим в точках 714
и О., двухповодковую группу 714А>СС так, чтобы образовался пан-
тограф Сильвестра*). Тогда траектория точки В.г будет подобна
траектории точки .4, и, следовательно, точка В.2 будет описывать
Дугу окружности, радиус которой равен радиусу OjAi, умноженному
на отношение подобия k. Центр О, этой окружности на основании
свойств пантографа найдется из условия, что Д OiO.2Oi -V Л A1B1M.
Соединив точки Вэ и О. при помощи звена, входящего в
Рис. 624.
и из них выбрать тот, который
яется наиболее удобным.
две вращательные пары, мы подвижности механизма не нарушим.
*) См. стр. 273,
670
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
(гл. X
Отсоединив же исходный четырехзвенник С^А^О» получим пре-
образованный механизм 0.2<427?.20з, точка М которого описывает ту же
кривую, что в исходном механизме. Производя аналогичное построе-
ние у центра Оь получим третий четырехзвенный механизм О\А^ВЛО.К,
описывающий ту же шатунную кривую.
Если точка М лежит на линии, соединяющей центры шарниров
шатуна, то пантограф Сильвестра превращается в пантограф Шей-
Рис. 625.
нера, и соответственно подобие
треугольников переходит в
пропорциональность отрезков
(рис. 625):
1,41 _ МВ., __
. 41.4 s
__ __ OLOX 7„
-дГлГ-7Ш- (10-78)
Шатунная кривая четырех-
звенника может быть также
воспроизведена при помощи некоторых многозвенных механизмов,
причем преобразование четырехзвенного механизма в многозвенный
можно осуществлять несколькими способами.
Всякое преобразование с увеличением числа звеньев повышает
сложность механизма, что, однако, может быть оправдано, если пре-
образование дает возможность в широких пределах изменять неко-
торые характеристики меха-
низма. Рассмотрим, напри-
мер, способ преобразования
четырехзвенного механизма
в шестизвенный, при помо-
щи которого можно легко
изменять габариты механиз-
ма и расположение задан-
ной кривой относительно
стойки.
Пусть в четырехзвенном
механизме OiABO., (рис. 626)
точка М описывает заданную
кривую. Присоединим двухповодковую
группу MDO^ так, чтобы образовался параллелограмм O.,BMD. Тогда
на основании свойств пантографа Сильвестра траектория произвольно
выбранной точки звена 2' подобна траектории некоторой точки Е
звена 2, положение которой определяется из условий*):
, ..nr- ч • г- г. MB DE, ,
— МВЕ _ MDEt —- fl; — /г.
*) См. стр. 274.
§ 33]
ШАТУННЫЕ КРИВЫЕ
671
Следовательно, траектория точки Е} есть шатунная кривая че-
тырехзвенника, который по отношению к четырехзвеннику OiABO2
повернут на угол р и уменьшен (пли увеличен) в отношении подо-
бия k. Построив при точке Ех четырехзвенник, удовлетворяющий
этим условиям, и отсоединив исходный механизм, получим преобра-
зованный шестизвенный механизм, показанный на чертеже сплошными
линиями. Точка 714 преобразованного механизма описывает ту же
кривую, что и в исходном механизме. Так как точка Ех может быть
выбрана произвольно в плоскости звена 2', то число преобразован-
ных механизмов, получаемых по этому способу, равно числу произ-
вольных точек на плоскости, т. е. оо2. Выбирая различные значения
отношения подобия k, можно в широких пределах изменять габариты
механизма. Например, для построения, указанного на рис. 626,
Рис. 627.
принято /е = 0,5 и преобразованный механизм получился более ком-
пактным, чем исходный, хотя абсолютные размеры траектории точки М
в обоих механизмах одинаковые. Выбирая различные значения
угла р, можно изменять расположение заданной кривой относительно
стойки.
Используя свойства пантографа, можно преобразовать механизмы
с большим числом звеньев, чем четыре.
Например, пусть точка М (рис. 627), осуществляющая движение
по заданной кривой, расположена на звене 2 исходного шестизвен-
ного механизма, образованного путем присоединения двухповодковой
группы к стойке и к шатуну четырехзвенного механизма. Звенья
исходного механизма показаны на чертеже пунктирными линиями. Пре-
образованный механизм может быть получен следующим построе-
нием.
Присоединим в точках /14 и О4 двухповодковую группу MDiOn
так, чтобы образовался параллелограмм MDfiiD. На стороне MDY
построим Д C\MDlt подобный Л CMD, принимая за сходственные
672 СИНТЕЗ ПРИБЛИЖЕННЫХ направляющих МЕХАНИЗМОВ [гл.
стороны DC и MD\ и сохраняя направление обхода углов a, fi,
Тогда мы получим пантограф Сильвестра, состоящий из звеньев /,
2', который осуществляет преобразование подобия с поворотом
на угол рис отношением подобия
О.С,
О4С
sin 1
sin 7
(10.79)
Следовательно, траектория точки С, будет подобна траектории
точки С и может быть осуществлена при помощи четырехзвенника
который по отношению к четырехзвепнику ОуАВО.} повернут на угол 3
и уменьшен (или увеличен) в отношении подобия k. Построив че-
тырехзвенник, удовлетворяющий этим условиям, и соединив его шар
ниром с точкой Съ мы, очевидно, подвижности механизма не нарт
шим. Отсоединив же звенья исходного механизма, получим преобра
зованный шестизвенный механизм, показанный на рис. 627 сплошными
линиями. Точка Л1 в iipt
образованном механизме
описывает ту же самую
траекторию (шатунную кри-
вую), что и в исходном ме-
ханизме. Так как каждый
из четырехзвенных механиз-
мов O^ABOt и O6AiBiO.,
может быть преобразован
по теореме Робертса в два
других четырехзвенных ме-
ханизма, то общее количе-
ство шестизвенных механизмов данного типа, описывающих одну и
ту же шатунную кривую, будет шесть.
При наличии в механизме как вращательных, так и поступатель-
ных пар преобразование его также может быть осуществлено при
помощи указанного метода, но свойства пантографа могут быть ис-
пользованы только, если взаимное расположение шарниров и посту-
пательных пар допускает его образование. В зависимости от типа
механизма можно получать преобразованные механизмы как с боль-
шим числом звеньев, так и с тем же числом звеньев, что и у исход-
ного механизма. В последнем случае на звене, содержащем точку,
описывающую заданную кривую, должны быть точки, траектории
которых могут быть получены при помощи механизма с меньшим
числом звеньев, чем у исходного механизма.
Например, в кривошипно-шатунном механизме ОАВ (рис. 62S),
образовав пантограф у точки О, мы получим ца звене 2' точку В\,
описывающую траекторию, подобную траектории точки В, т. е. пря-
мую линию, повернутую по отношению к линии движения точки /?
на угол р. Поставив в точке В{ ползун, получим второй кривошип-
но-шатунный механизм ОА^, в котором точка Л1 описывает ту же
§331
ШАТУННЫЕ КРИВЫЕ
673
щатунную кривую, что и в' исходном механизме. Третьего криво-
(пипно-шатунного механизма, осуществляющего движение по той же
кривой, получить этим методом нельзя, так как пантограф можно
образовать лишь у точки О. Шестизвенных же Механизмов, воспро-
изводящих шатунную кривую кривошипно-шатунного механизма,
можно получить бесконечное множество, выполняя преобразования
так же, как и в общем случае четырехзвенного механизма.
Если точка М, описывающая заданную кривую, расположена на
Рис. 629.
ползуне кулисного механизма, то второго четырехзвенного кулисного
механизма, воспроизводящего ту же
самую кривую, получить указанным
методом нельзя.
Во многих случаях удобнее пре-
образованные механизмы получать
не путем геометрического построе-
ния, а н$1 основании весьма простых
соотношений между размерами
звеньев механизмов, описывающих
одну и ту же кривую.
Определим сначала соотношения
между размерами звеньев шарнир-
ных четырехзвенных механизмов,
получаемых по теореме Робертса.
Предположим известными длины
звеньев исходного механизма
О.А.В.О^ (см. рис. 624). Тогда на
основании свойств пантографа для
определения размеров преобразован-
ного механизма О.2Л.2/?.2О;( имеем
следующие соотношения:
О.2Д.2 == MBf,
АгВ^О.гВ{^~--
л. л МВ.
O3Bt — OMi .
ОЛ = О1О^.
(10.80)
Как видно, каждая сторона преобразованного механизма полу-
чается умножением длины некоторой другой стороны исходного четы-
рехзвенного механизма на отношение подобия, так как отношение
МВ.
равно отношению подобия. Аналогичные соотношения суще-
ствуют и для второго механизма. Особенно просто эти соотно-
шения выглядят, если определять лишь относительные размеры
звеньев.
22 И. II. Артоболевский
674 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл.
гласно написанным условиям
будет Ь, относительная длина
сительная длина стойки будет
Если в исходном механизме за единицу принять длину шатуна
(рис. 629), а размеры других звеньев обозначить а, b и с, в преоб
разованном же механизме за единицу принять длину О2Д2, то со-
(10.80) относительная длина шатуна
звена В2ОЛ будет а и, наконец, отно-
с, т. е. совпадает с исходной. Ана-
логично поступаем со вторым пре-
образованным механизмом и оконча-
тельно устанавливаем, что относи-
тельная длина стойки у всех трех
механизмов одинаковая, а длины
других трех звеньев получаются
путем перестановки. Три возмож-
ных варианта перестановки и дают
три возможных механизма. Что же
касается расположения углов а.,
Р, 7, то заметим в первую оче-
редь, что направление обхода этих
углов совпадает во всех трех
механизмах. Далее, если механизм,
у которого за единицу принята
длина шатуна, назвать исходным
механизмом, механизм, у которого
длина шатуна равна а, — механиз-
мом А и механизм, у которого дли-
на шатуна равна Ь, — механизмом В,
то в исходном механизме углы а.
и р располагаются соответственно
у точек А и В; в механизме А
у единицы располагается угол а;
полагается угол Р; у точки В в обоих
преобразованных механизмах располагается угол у.
Если точка Л1 лежит на оси шатуна, то на основании соотноше-
ний (10.78) положение ее в преобразованных механизмах определится
по относительным размерам, указанным на рис. 630. Зная относи-
тельные размеры звеньев механизмов, можно легко определить и их
абсолютные размеры. Для этого достаточно умножить относительные
размеры на величину МВ\ для механизма В и на величину Л1А, для
механизма А.
По относительным значениям длин звеньев преобразованных меха-
низмов легко проследить, как выражаются условия Грасгофа для
этих механизмов, а именно: если сумма длин наибольшего и наимень-
шего звеньев меньше суммы двух других звеньев, причем наимень-
шим звеном будет а, то исходный механизм будет кривошипно-ко-
ромысловым, механизм А — двухкоромысловым, так как наименьшее
ввено у него противоположно стойке, а механизм В — опять криво-
Рис. 630.
в механизме В у единицы
§ 34]
СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 675
шипно-коромысловым. Если механизм будет двухкривошипным, т. е.
если при том же соотношении сумм длин звеньев стойкой сделано
наименьшее звено, то другие два механизма также будут двух-
кривошипными, так как относительная длина стойки не меняется. На-
конец, если сумма длин наибольшего и наименьшего звеньев больше
суммы двух других звеньев, то механизм всегда двухкоромысловый
вне зависимости от того, какое звено будет стойкой, и потому все
три механизма будут двухкоромысловыми.
Для кривошипно-шатунного механизма соотношение между отно-
сительными размерами также чрезвычайно простое, а именно для
получения второго механизма достаточно, сохраняя относительный
дезаксиал, поменять местами относительные длины шатуна и криво-
шипа, а также углы р и 7 при постоянном направлении обхода
(рис. 631). Отсюда ясно, что если в одном из кривошипно-шатунных
механизмов звено О А может совершать полный оборот, то во вто-
ром механизме оно уже будет коромыслом.
§ 34. Синтез направляющих механизмов по условию
минимального отклонения от заданной функции
1°. Прямолинейно-направляющие механизмы Чебышева. В пре-
дыдущей главе было показано, что четырехзвенные передаточные
механизмы допускают непосредственное вычисление всех параметров
кинематической схемы из условия минимального отклонения от про-
извольно заданной функции. Четырехзвенные направляющее меха-
низмы имеют большое число параметров кинематической схемы, и
в настоящее время мы не располагаем еще эффективными методами
Для непосредственного вычисления всех параметров из условия мини-
22»
676
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
мального отклонения от произвольно заданной кривой *). Известны
лишь решения этой задачи для некоторых простейших кривых, напри-
мер решение задачи о воспроизведении движения по прямой линии
и кривым 2-го порядка. Указанные кривые являются симметричными
и поэтому, следуя Чебышеву, для их воспроизведения используют
механизмы, даюшие симметричные шатунные кривые.
В первую очередь рассмотрим решение задачи о приближении
симметричной шатунной кривой шарнирного четырехзвенника к пря-
мой линии, т. е. решение задачи о синтезе прямолинейно-направляю-
щих механизмов, данное П. Л. Чебышевым [55п].
Для шарнирного четырехзвенника, показанного на рис. 611, воз-
можно приближение симметричной шатунной кривой точки /И к пря-
мой линии, перпендикулярной к оси симметрии.
Уравнение этой прямой имеет вид:
У=Уг
Составляя разность между ординатой шатунной кривой, выражаемой
уравнением (10.38), и заданной ординатой _у0, получаем аналитическое
выражение отклонения от заданной зависимости:
А = А [Ро/о (-г) 4- Pi/i (*) + РгА (г) — F (г)], (10.81)
где
/0(-г)=/-г(! — г), /2(г)=1;
d2 — а2
2d
462
Рй ~~ da — а2 *
46s ctg
ds_cs >
Рг = ctg|—
2d
(da — a2) sin
(10.82)
(10.83)
Функции /0 (г), /1 (г) и /2 (г) образуют систему Чебышева 2-го
порядка, так как любой полином, составленный из этих функций,
имеет не более двух корней. Поэтому на основании теоремы Чебы-
шева **) отклонение Д должно достигать своих предельных значе-
*) Вычисление всех параметров по методу линейных поправок предполагает,
что предварительно каким-либо другим путем получены значения искомых па-
раметров, и требуется лишь уточнение их величин.
**) См. стр. 527.
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИН. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 677
ний на отрезке между z = z0 и z = zm не менее четырех раз, что
соответствует трем точкам пересечения шатунной кривой с прямой
линией на рассматриваемом отрезке. Вследствие симметрии шатунной
кривой отрезку изменения параметра (z0, zm) соответствуют два
симметрично расположенных участка шатунной кривой. Поэтому об-
щее число точек пересечения шатунной кривой с прямой линией
при выполнении условий теоремы Чебышева равно шести, т. е.
максимально возможному их числу.
Обозначим через z0, zit z2 и z3 значения переменного параметра г,
при которых достигается предельное отклонение L. Тогда на осно-
вании условий теоремы Чебышева получаем, что уравнения
+ /г(1 — z)+ (10.84)
+ КгО-г)-]-^+р2-4 = 0 (Ю.85)
должны иметь по одному простому и одному двойному корню *).
Полагая, что уравнению (10.84) соответствует простой корень z = z0
и двойной корень z=z2, а уравнению (10.85) простой корень z = z3
и двойной корень z = zlt получаем, что система уравнений (10.84)
и (10.85) имеет те же корни, что и уравнения следующего вида:
(10.86)
(г’ — V (F '-"v212 - ’ = 0. (10.87)
Приравнивая коэффициенты при одинаковых функциях в уравне-
ниях (10.84) и (10.86) и соответственно в уравнениях (10.85) и (10.87)
* Ч Р'
и принимая во внимание, что z=sinzy, получаем:
Pi + ~A = — ctg-g9 — 2ctg^>
А — А'- = — ctg-2- — 2 ctg
(10.88)
(10.89)
(10.90)
(10.91)
*) Решение уравнений (10.84) и (10.85) приводится с некоторым изменением
обозначений по работе П. Л. Чебышева [55и].
678 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Из этой системы шести уравнений выражаем параметры р0, plt р
4". Pi и Н через р.о и |х3. Сначала определяем углы (xt и |ха. Разде-
лив уравнение (10.91) на уравнение (10.90), получаем:
(ра + тг) = tg (р> + у) •
Так как углы [х0, [хь [х2 и р.3 заключаются между 0 и it (см. рис. 611),
то это уравнение возможно или при
На у = Hi 4~ (10.92)
или при
Ра т у — 1А1 "г ~2 ~ к'
Замечая же, что в последнем случае из уравнений (10.90) и (10.91)
следует равенство
sin sin2 Ц = — sin sin2,
которое невозможно при |х0, р.ь [х2 и ;х3 положительных, не превос-
ходящих ~, мы заключаем, что должно быть только равенство (10.92),
вследствие чего из уравнений (10.90) и (10.91) получаем:
sin!Jsin2^=sin^sin2^.
(10.93)
Исключая из уравнений (10.92) и (10.93) угол [хь получаем урав-
нение для определения |х2:
sin ~
sin2 yii ctg* sin ctg ---------------------- 4- cos2 = 0.
sinT
Решая это уравнение относительно ctg у и ограничиваясь одним
положительным корнем, находим:
(10.94)
Теперь угол р-! определяется из уравнения (10.92), коэффициенты
ри и pt находятся непосредственно по уравнениям (10.90) и (10.91),
а для определения коэффициента /?2 и величины 4- складываем и вы-
читаем уравнения (10.88) и (10.89).
$341
СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 679
Имеем:
Pi = — 4 ctS у ~ ctg У ~ ctg “2" ~ 4 ctg Ч ’ (10-95)
4=-|ctg^4-ctg^-ctg^+ ’ ctg§. (10.96)
Приравнивая значения коэффициентов /?0, /?ь р.г и р-л, выраженные
через углы р.о, п2 и р3, их значениям из уравнений (10.83), полу-
чаем систему уравнений, которая определяет искомые соотношения
между параметрами механизма:
sin (м2 + 2 ) 4^2 —, (1 °-97) . . р.2 ds — а* ’ sin у sin® ~ cos (— + 4Z>2 cig у — = -й. , (10.98) . fi0 . [Л2 d2 — а- . sin у sm 2 у
|ctg § 4- ctg!J + ctg +1 ctg - ctg | + j'o ———------------------------- • (10.99)
(d- — a-) sin
Шесть уравнений (10.92), (10.94), (10.96), (10.97), (10.98) и (10.99)
связывают десять параметров: a, b, d, ш, ;т0, р.,, |х2, |х3, _у0 и L. Сле-
довательно, можно задать четыре параметра и найти из указанных
уравнений остальные шесть.
Пусть, например, заданы параметры р.о, р3, dub. Тогда по фор-
мулам (10.94) и (10.92) находим углы jx2 и [хР Затем из уравнений
(10.97) и (10.98) получим:
о)=2л—2р.2 — ро- (10.100)
Из уравнения (10.97) находим величину а:
4bs sin sin2 '-4
d1------------F-------
sin + уJ
а =
(10.101)
Максимальное отклонение от прямолинейности найдется по фор-
муле
'=т(-4«е¥+с‘ет-ает+|с1е!¥)’‘"т- <10-102>
Ординату _у0 находим из уравнения (10.99). Угол поворота звена АВ
при прохождении точки М по приближенно прямолинейному участку
траектории <рп определяется по формуле
<Р» =
680 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
где срз и ср0 — углы ср, соответствующие значениям р(| и р.3) — опре-
деляются из Д BDA (см. рис. 611):
4*2sins^’- — ds — as
cos ?3 = —----2ad~^-----, (10.103)
45s sin8 — d2 — a-
cos cp0 =----------------. (10.104)
При использовании указанных уравнений мы получаем механизм,
в котором шатунная кривая приближена к прямой линии на двух
отдельных симметрично расположенных участках. Если требуется
получить один участок, но значительной длины, то угол р.о должен
соответствовать положению точки М на оси симметрии во внешнем
среднем положении механизма. Это дает дополнительно к уравнениям
(10.92), (10.94), (10.96)-ь( 10.99) условие
а-|-с? = 2& sin у. (10.105)
Следовательно, в этом случае можно задавать только три пара-
метра, например р0, р3 и cl.
Все формулы значительно упрощаются для частного случая ш = л.
В то же время именно этот частный вид прямолинейно-направляющих
механизмов Чебышева имеет наибольшую известность. Поэтому для
этого частного случая укажем не только формулы для определения
параметров кинематической схемы механизма, но и пределы, в кото-,
рых можно выбирать эти параметры.
Из уравнения (10.100) при ш = получаем:
Р-2 = у —'у. (10.106)
Уравнение (10.92) при этом принимает вид:
И = (10.107)
Подставляя значения углов р, и в формулу (10.93), получаем:
sin^=l — sin у. (10.108)
Следовательно, в данном случае можно выбирать произвольно только
один из углов р., например угол р.о. Остальные углы (рц, р.2 и р3)
определяются по формулам (10.106), (10.107) и (10.108).
Уравнение (10.97) после подстановки значения из форму-
лы (10.106) принимает вид:
d2 — а'= 2b1 sin1 — sin у^. (10.109)
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 681
В дальнейшем считаем, что угол [±0 соответствует положению точки М
на оси симметрии, т. е. симметрично расположенные прямолинейные
участки траектории точки М образуют один общий участок. Поэтому
одновременно с уравнением (10.109) должно удовлетворяться уравне-
ние (10.105). Решая совместно эти уравнения, получаем связь между
длинами звеньев механизма:
3d — а = ЧЬ. (10.110)
Формула для определения максимального отклонения от прямо-
линейности (10.102) после йодстановки значений и щ из формул
(10.106) и (10.107) принимает вид:
I = ^sin'^^(cos^—coS^y. (10.111)
Дл1 на приближенно прямолинейного участка находится по формуле
7=2х3, (10.112)
где х3—значение абсциссы х, определяемой по формуле (10.41)
• 2 P'S
при Z= Sin у •
Из формул (10.105), (10.108) и (10.110) следует, что
z = sin2§ = (l-^±4)’. (10.113)
Подставляя это значение z в формулы (10.40) и (10.41), полу-
чаем координаты точки 7И при [л = [л3, т. е. в конце приближенно
прямолинейного участка
Уз = 5rf-^ /(а d) (5d - За), (10.114)
х3= ]/3 (3d — а) (За — d) (5d — За) (d а). (10.115)
Следовательно, формула (10.112) для определения длины прибли-
женно прямолинейного участка примет вид:
7 = 1 ]/3(5d — За) (d а) (3d — а) (За — d). (10.116)
Ha рис. 632, а показан один из прямолинейно-направляющих меха-
низмов Чебышева при d — 1 и а = 0,5. В этом случае по формулам
(10.110), (10.105), (10.108), (10.111) и (10.116) имеем:
6=1,25; [хо = 73°5О'; р.3 = 47°10'; /.= 0,00518; 7=2,22.
Шатунная кривая точки М этого механизма на участке длиною
7 = 2,22d располагается между двумя параллельными прямыми, рас-
стояние между которыми равно 2/ = 0,01036d, как показано в утри-»
рованном виде на рис. 632, б.
682 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Прямолинейно-направляющие механизмы Чебышева при ш==к
в среднем положении напоминают греческую букву X (см. рис. 632)
и называются поэтому лямбдообразными. Преобразование по теореме
Робертса дает другую модификацию того же механизма, известную
под названием перекрестной (показана на рис. 632, а пунктирными
линиями).
Установим теперь пределы изменения параметров кинематической
схемы механизма. При р3 = р.о все шесть точек пересечения прямой
линии с шатунной кривой сливаются в одну (касание 5-го порядка).
Отклонение L и длина I по формулам (10.111) и (10.112) равны нулю,
но практически шатунная кривая мало отличается от прямой линии
на некотором участке вследствие того, что имеет место касание вы-
сокого порядка. Для этого предельного случая из формулы (10.108)
и (10.105) имеем:
|т0 = 60°, a -j- d - b,
т. е. во внешнем среднем положении A BCD является равносторон-
ним. Из формулы (10.110) в этом случае получаем:
1 .
а = -5- а.
О
Приа^>^-</ из формул (10.110), (10.105) и (10.108) получаем
[а3<Д1о, т. е. при а <7-5- d условия наилучшего приближения не удо-
влетворяются. С увеличением параметра а увеличивается длина при-
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ от заданной функции 683
ближенно прямолинейного участка, но одновременно увеличивается
величина отклонения от прямолинейности. Для установления макси-
мальной величины параметра а и для выбора его по заданным вели-
чинам длины прямолинейного участка и отклонения от прямолиней-
ности удобно пользоваться графиком (рис. 633), который построен
Г, Г. Барановым [8в]. На этом графике показана зависимость вели-
2L I а
чин -г- и -г от отношения -у.
4 id d
Пусть, например, требуется получить прямолинейный участок
длиною 100 мм с отклонением от прямолинейности не более 0,1 мм.
Тогда у = 2- 10~3. Из графика находим -^ = 0,495 и -^ = 2,2 (на- ’
хождение этих величин показано на графике пунктирными линиями).
Рис. 633.
Отсюда d = 45,4 мм', а = 22,5 мм. Размер b находится по фор-
муле (10.110):
b= 113,7 мм.
Механизм по своим размерам близок к показанному на рис. 632.
Аналогично могут быть решены задачи синтеза приближенных
прямолинейно-направляющих механизмов с поступательными парами.
Здесь они не рассматриваются, так как по сравнению с шарнирным
четырехзвенником они являются практически менее удобными вслед-
ствие значительного трения в поступательной паре и меньшей точ-
ности.
2°. Симметричные механизмы, направляющие по дугам окруж-
ностей. При построении механизмов с периодическими остановками
ведомого звена кроме кулачковых механизмов могут быть использо-
ваны шарнирные механизмы, в которых шатунная кривая некоторой
точки приближена к дуге окружности на участке, соответствующем
684 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. х
периоду остановки ведомого звена. На рис. 634 показан один из
шарнирных механизмов с остановками, предложенный П. Л. Чебыше-
вым. Длина звена ME равна радиусу окружности, к которой прибли-
жена траектория точки М на участке, соответствующем приблизи-
тельно половине оборота кривошипа (этот участок показан жирной
линией). Положение центра F выбрано таким образом, что в одном
из крайних положений звена FE точка Е совпадает с центром этой
окружности. Вследствие этого ведомое звено FE имеет в одном из
крайних положений остановку, продолжительность которой равна вре-
мени прохождения точкой Л1 участка траектории, приближенного к
окружности.
При решении задачи о приближении симметричной шатунной кри-
вой к дуге окружности представляется удобным измерять величину
Рис. 634.
разности между заданной кривой и шатунной кривой по нормали к
заданной кривой.
Пусть центр заданной окружности находится на оси симметрии
в точке Оу (см. рис. 611). Тогда разность между шатунной кривой
и заданной функцией, измеренная по нормали, имеет вид:
Д = (7400 — R,
где R — радиус заданной дуги окружности.
Величина МОЪ а следовательно, и разность А могут быть выра-
жены в виде функции размеров механизма и переменного параметра
z, но применить теорему Чебышева к этой функции не представляется
возможным. Поэтому Чебышев [55п] для решения задачи о прибли-
жении шатунной кривой к дуге окружности определяет условия, при
которых наименее уклоняется от нуля не разность А, а выражение
вида:
A, = (W- Я2,
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 685
что соответствует наилучшему взвешенному приближению при пара-
метрическом весе
9 = (MOt) + /?.
Если рассматривать участок, на котором шатунная кривая мало
отличается от дуги окружности, то величина /ИО, приближенно равна
R и, следовательно, вес остается также приближенно постоянным.
Из Д М0{О имеем:
(ТИО,)2 — р2 + /г2 — 2р/г cos 8,
где р = DM uh — OtD.
Принимая во внимание соотношения (10.36) и (10.37), получим:
4й2 sin2 £ + d2 —а2
MOI = W* sin2 —+ h2~ 4Wi sin ------------------------------------•
Abd sin ~
Следовательно, взвешенная разность равна:
Д9 = (ТИО,)2 — Я2 = 4й2 sin2 4 /г2 —
4b2 sin2 t d2—
— 4bh sin —tt-------------------------— R\
4bd sin t
Вводя обозначение z — sin2t после преобразований получим;
д9 = А [р0 ]/z (1 - г) +/М , (10.117)
где
tn 1
sin g- (^2 — о2) h
d sin ш h sin
-------------------—,
sin — (d2 — a ) h
a cos co — h cos jy
Pi = - 4*2--------------------,
h (d2 — a2) sin
(R2 — 2Z-2 + lb2cos » — h2) d + h (d2 -a2) cos у
.
h(d2 —a2) sin T
Z )
686
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
Функция (10.117) совпадает по виду с функцией (10.81), рас-
смотренной ранее при решении задачи синтеза прямолинейно-напра-
вляющих механизмов. Поэтому для определения углов р.2 и по
заданным углам р.() и g3 остаются в силе формулы (10.94) и (10.92):
Ctg%
4
.. ________,, I Po Р»
[i] — -f- y — y
Приравнивая значения коэффициентов plt, pt, p2 и p3, выраженные
через углы p0, [ij, [i2 и p.3, их значениям из уравнений (10.118), по-
лучаем систему уравнений, которая определяет искомые соотношения
между параметрами механизма:
sin(ps-)-^) —d sin ш 4- h sin y
---=4b2----------------------- , (10.119)
sin ''y sin2h(d2 — a2) sin -~
cos (+ p2) d cos u> — h cos y
---------L — 4/4------------£. t (10.120)
sin sin2 h (d2 — a2) sin A.
1 ctg 'J + ctg + ctg +1 Ctg 'J =
— (№ — 2b2 — 2i2cos ш —h2)d—h(d2—fl2) cos —
=------------------------------——(10.121)
h (d2 — a2) sin ~
Пять уравнений (10.92), (10.94), (10.119), (10.120), (10.121) свя-
зывают десять параметров: a, b, d, ш, [х0, р.ь (i3, р.3, h и R. Следо-
вательно, можно задать пять параметров, например р0, р3, d, b и о>,
и найти из указанных уравнений остальные пять параметров.
Если считать, что при |х = |х0 точка /И находится на оси сим-
метрии во внешнем среднем положении механизма, то имеет место
условие (10.105):
a-}-d = 2b sin —.
В этом случае число независимых параметров сокращается до
четырех. Пусть, например, заданы параметры [ie, g3, о> и b = 1.
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 687
Тогда, определив по формулам (10.94) и (10.92) углы
ходим из уравнений (10.119), (10.120) и (10.105) параметры
и р.ь на-
fl, d и h.
а = sin --------------г
sin (и
sin2
(10.122)
d — sin -------------
sin
ein2
(10.123)
sin
/? =—
sin
sin
sin2';-2
.(10.124)
Радиус окружности, к которой приближена шатунная кривая, на-
ходится из уравнения (10.121) и, наконец, максимальное откло-
нение шатунной кривой от окружности можно определить по формуле
(10.96), в которой величине L в данном
случае соответствует максимальное зна-
чение взвешенной разности
Применяя приближенную формулу для
отклонения шатунной кривой от дуги ок-
ружности
получаем, что максимальная величина этого отклонения
h(<P—a2) sin ~ .
L = ~ 2^—- (“ictg? + ctg¥-ctg? + ictg?)• (1CU25)
Особенностью всех решений задач синтеза механизмов с исполь-
зованием условий наилучшего приближения является необходимость
выяснения областей существования механизма, так как не все воз-
можные комбинации заданных параметров дают действительные зна-
чения для остальных параметров. Например, выясняя области суще-
ствования симметричных механизмов Чебышева, направляющих по
дугам окружностей, мы убеждаемся, что для симметричной шатунной
кривой вида V (см. рис. 613) возможно приближение к дуге окруж-
ности только в нижней ее части аа (рис. 635). Геометрически это
объясняется тем, что в нижней части симметричная шатунная кривая
688 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
имеет точки перегиба, вследствие чего взвешенная разность между
шатунной кривой и дугой окружности может достигнуть своих пре-
дельных значений такое количество раз, какое требуется по теореме
Чебышева, т. е. семь раз. В верхней же части bb точки перегиба
отсутствуют, и поэтому количество точек, в которых взвешенная
разность может достигнуть своих предельных значений, получается
меньше, чем требуется по теореме Чебышева. Если уменьшить число
точек предельного отклонения до пяти, то получаются действитель-
ные решения и для приближения к дуге окружности на участке bb
симметричной шатунной кривой [33а].
Для выяснения областей изменения параметров механизма, кото-
рые соответствуют максимально возможному числу точек предель-
ного отклонения, следует рассмотреть в первую очередь предельные
случаи. Для механизмов, направляющих по дугам окружностей, та-
кими предельными случаями являются случай касания пятого порядка
шатунной кривой с дугой окружности (р.о — р:() и случай приближе-
ния всей шатунной кривой к окружности, который имеет место при
условии
Методику выявления областей существования симметричных напра- »
вляющих механизмов покажем на примере решения задачи синтеза
механизмов, направляющих по гиперболе.
3 . Симметричные механизмы, направляющие по гиперболе.
В главе VI были указаны механизмы, которые дают теоретически
точное воспроизведение движения по гиперболе. Однако эти меха- t
низмы имеют в своем составе поступательные пары, обладающие по-
вышенным трением по сравнению с шарнирами, и практическая точ-
ность их в большинстве случаев невысокая вследствие большого
числа звеньев. Поэтому представляет интерес получить приближен-
ное воспроизведение движения по гиперболе с помощью шарнирного
четырехзвенника.
Пусть уравнение гиперболы дано в виде:
у = ±У&х2 + Ь*.
Так как гипербола есть кривая, симметричная относительно двух
взаимно-перпендикулярных осей, то для ее воспроизведения выберем
симметричный механизм при значении угла и> = тг, который дает ша-
тунные кривые, симметричные относительно осей х и у.
Разность ординат шатунной кривой и гиперболы имеет вид:
А —Ум — У = Ум — УkaxsM 4- bl,
*
где _ум и хм — координаты симметричной шатунной кривой, опреде-
ляемые по уравнениям (10.40) и (10.41).
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 689
Теорема Чебышева к функции А в данном случае неприменима,
поэтому обращаемся к взвешенному приближению, принимая в ка-
честве параметрического веса функцию
(10.126)
Тогда взвешенная разность будет представлена в виде функции
Д? = Д • q =yQ-У2 =Ум - &х*м - bl (10.127)
Подставляя в уравнение (10.127) значения уЛ1 и хм из уравне-
ний (10.40) и (10.41) и полагая Ь—\, получим:
д,=Чг14 - «2) Ч^]8~ F’4 о =
= А + (10-128)
где
4(1+й=)
А~ ’
, , d2 — a2 k2d2
А*1 1 “Г 9 1 -L k2 ’
(10.129)
rf2_aS (4k2 + Wd2
Р*~-------1б“ (8 “ d + а > + 4(1 +Н ' ’
_ (d2 — а2)2
Р\— 16
Значения ’коэффициентов рх, р.2, р3, при которых функция (10.128)
наименее уклоняется от нуля на отрезке (г0, г3), известны *), поэтому
дальнейшее решение задачи не представляет особых трудностей.
Отметим, что такое же выражение взвешенной разности дает
прием, указанный 3. Ш. Блохом [9о], а именно, представив уравнение
гиперболы в виде
и подставляя в это уравнение вместо текущих координат гиперболы
хну значения координат шатунной кривой хм и ум, получим
взвешенную разность (10.127), которая соответствует параметриче-
скому весу q=yM-\-y. Этот вес, однако, не является единственным.
Можно, например, выбрать другой параметрический вес, при котором
аналитическое выражение взвешенной разности получается более про-
стым. Действительно, выбирая в качестве параметрического веса
функцию
71 = Я2 = (Ум + У sin2 j. (10.130)
*) См. стр. 537.
690 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гЛ. X
получим взвешенную разность в виде многочлена Чебышева
^51 — A (г3 PiZ^ p^z -f- Рй), (10.131)
где A, pit рч, ря имеют прежние значения (10.129).
Возможны и другие значения параметрических весов. Следова-
тельно, возникает задача выбора оптимального веса. Имея в виду,
что обычно практика требует равномерного приближения, будем счи-
тать оптимальным тот параметрический вес, который дает наимень-
шую величину максимального отклонения от заданной функции. Как
уже указывалось, таким весом является постоянный вес. Если же по
условиям задачи нельзя применить постоянный вес, то следует выбрать
тот вес, который наиболее близок к постоянному.
Сравнивая значения параметрических весов q (10.126) и qx (10.130),
мы видим, что первый вес является монотонно возрастающей функ-
цией. Этот вес обеспечивает лучшее приближение к тому концу
рассматриваемого промежутка, который имеет ббльшую по модулю
ординату. Чем меньше коэффициент А:2 в уравнении гиперболы, тем
ближе вес q к постоянному. Вес q^ при небольших значениях коэф-
фициента ft2 является монотонно убывающей функцией, так как зна-
чения переменного параметра z убывают скорее, чем значения орди-
наты у. Чем больше коэффициент £2 в уравнении гиперболы, тем
ближе вес qx к постоянному. Отсюда следует, что выбор оптималь-
ного веса определяется не только видом заданной функции, но и
значениями коэффициентов, входящих в уравнение заданной функции.
Для более отчетливого сравнения параметрических весов q и qx
рассмотрим решение задачи при обоих весах.
Если принять в качестве параметрического веса функцию
9' = (jAi+j')sin2-^,
то взвешенная разность (10.131) будет многочленом Чебышева тре-
тьей степени. Приравняв значения коэффициентов ръ рг, р3 из ура-
внений (10.129) и из таблицы 9.4, получим систему уравнений:
-4^+^)=-! + ^-^;
/6 (34 + 10^3 + 34) = - (8 - + 4) + ;
(10.132)
— 39 (4 к 1 54*з i 5zo4 4-4) = jg—— >
где
z0=sin2^, z3 = sin2^; (10.133)
u0 и р3—значения переменного угла BCD (см. рис. 611), соответ-
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 691
ствующие началу и концу участка траектории точки М, прибли-
женной к гиперболе.
Так как три уравнения (10.132) связывают шесть переменных
величин: a, d, z(1, z3, Ьо и k, то независимых параметров, определяю-
щих механизм, будет три (при £=1).
Можно потребовать,' чтобы значение z0 переменного параметра z
соответствовало бы положению точки Л1 на оси симметрии. Тогда
оба участка, приближенных к гиперболе, соединяются, образуя один
участок, расположенный симметрично относительно оси j. Это усло-
вие дает дополнительно к уравнениям (10.132) следующее соотно-
шение:
а -]- d = 2 у г0.
(10.134)
Число независимых параметров, определяющих механизм, теперь
сокращается до двух.
Пусть, например, заданы величины zfl и z3.
Тогда из уравнений (10.132) и (10.134) определяем относительные
размеры механизма (при Z>=1):
d^Vz.+ У^-, (10.135)
F zo
Q==VTO-1/'^, (10.136)
F
где
p3 — — 32 '5го2з + 1-|- z3).
Коэффициент внения (10.132); k2 в уравнении гиперболы находим из первого ура- = (10.137) 2(1 +pi) + d24-e2’ ' ’
где Р\ = — у (го 4~ гз)-
Коэффициент определяется по второму уравнению (10.132):
bl = - 4A2 + (8 - di + a2) (1 + A2), (10.138)
где
я
Pi — 16 + 10z0z3 + 3z|).
Максимальная величина взвешенной разности равна:
Lg = AL,
где L — величина предельного отклонения многочлена Чебышева,
определяемая по таблице 9.4.
692 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ |ГЛ. X
Подставляя значения А из уравнений (10.129) и L из таблицы 9.4,
получим:
^=-(1-jr--a-(z°y)8. (Ю.139)
Это отклонение достигается при значениях аргумента г0 и z3, а
также при значениях г, и г.2, определяемых по таблице 9.4:
_ _ 3z0 -J- za ___ 3zs -|- z0
г1 — ‘ J" — > —-----J-— •
Действительное отклонение шатунной кривой от гиперболы при
этих значениях аргумента будет:
(10.140)
где qt — параметрический вес при значениях аргумента г0, zlt z,2 и z3.
Значения веса q у вершины гиперболы и в конце участка, при-
ближенного к гиперболе, определяются по формулам:
g0^2j0z0, q3^2y3z3, (10.141)
где j’o и у3— ординаты шатунной кривой у вершины гиперболы и в
конце участка, приближенного к гиперболе, определяемые по фор-
муле (10.40).
Так могут быть найдены все параметры механизма, если заданы
величины z0 и г3. Однако обычно задаются не эти величины, а коэф-
фициенты k2 и Ь',, в уравнении гиперболы. В этом случае задача мо-
жет быть решена путем последовательных приближений.
Пренебрегая в первом приближении величиной отклонения L,
принимаем:
^Л^2/1 ~~ 2о-
Отсюда определяется величина г0:
h2
г0=1-^. (10.142)
Подставляя в уравнение (10.137) значения d и а по формулам
(10.135) и (10.136), получаем уравнение для определения z3.
После нахождения величины z3 задача решается, как было ука-
зано выше. Коэффициент k2 при этом точно соответствует заданному,
а коэффициент = (j'o -f- L(l)2 и при малой величине L мало отли-
чается от заданного. Если требуется уточнение, то принимаем во
втором приближении
„ t ib'-Ltf
*e — 1 4 >
и далее расчет повторяется в том же порядке.
Пример. Дано уравнение гиперболы:
у = ± /10х®+ 1.
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 693
Определить параметры механизма для воспроизведения данной
гиперболы.
По формуле (10.142) имеем:
гп = 0,75.
Подставляя в уравнение (10.137) значения коэффициентов d на
по формулам (10.135) и (10.136), а также данное значение А'2 и най-
денную величину гп, получим после преобразований уравнение для
определения г3:
177,8г] 4000г’ 4- 11420г] — 119402г;] -J-
-ф-221687г] — 167268г3 4- 40780 = 0.
Действительный корень этого уравнения, удовлетворяющий усло-
виям задачи, будет:
г3 = 0,507.
Относительные длины звеньев а и d (при &=1) определяются
по формулам (10.135) и (10.136):
d= 1,432; а = 0,302.
Максимальная величина взвешенной разности по формуле (10.139)
равна:
Lq = 0,0099.
Ординаты шатунной кривой у вершины гиперболы и в конце
участка, приближенного к гиперболе, находятся по формуле *)
(10.40):
_Уп=1; у3 = 1,31.
Значение веса у вершины гиперболы и в копие участка, прибли-
женного к гиперболе, определяется по формулам (10.141):
^0=1,5; ^3=1,33.
Отклонения шатунной кривой от гиперболы, измеренные как раз-
ность ординат, найдутся по формуле (10.140):
£0 = 0,0066; Д3 = 0,0074.
Так как величина отклонения шатунной кривой от заданной гипер-
болы Lo мала по сравнению с величиной j’o, то значение коэффи-
циента b в полученном механизме
b = _у’(1 = 1,0066
близко к заданному Ь=1, и дальнейшего перерасчета с целью полу-
чения лучшего приближения не требуется.
*) Величины ординат у, веса q и отклонений L можно вычислять с двумя
или тремя значащими цифрами.
694
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[ГЛ. X
Полученный механизм изображен на рис. 636.
Если принять в качестве параметрического веса функцию
Ч-У1Л~\-У>
то взвешенная разность представится в виде функции (10.128). Зна-
чения коэффициентов pt, pit ря, при которых функция (10.128) наи-
менее уклоняется от нуля на отрезке (г0, z3), даны уравнениями (9.85),
если заменить обозначения х на z. Приравняв значения этих коэф-
фициентов их выражениям из уравнений (10.129), получим систему
уравнений:
— (го 4“ 2з + V гогз)— — I 4-----2-----] _|5 fcs > (10.143)
-g (2з + zi 4~ 6z3 V2о2з 4" z0z3 1 Ozoz3) —
(4/г2 + bs) d3
4(1 +ks)~
1
4
(Фз ~Ь 2o23 4- 2<>гз V ^з) —----------------------—rs---------
Максимальная величина
взвешенной разности
(10.144)
(10.145)
Lg=AL.
Подставляя значение А из уравнений (10.129) и L из уравнений
Рис. 636.
при этих значениях аргумента будет:
(9.85), получим:
= г«—^з)2.
(10.146)
Это отклонение достигается
при значениях аргумента г0 и z3
и значениях zt и z2, определяемых
по уравнениям (9.85):
2i = ~2 (2о 4- V2«2зУ
2ъ = 2 (2з 4* V2о2з)-
Действительное отклонение
шатунной кривой от гиперболы
где qt — параметрический вес при значениях аргумента z0, zlt z2, г3.
Если значение z0 переменного параметра z соответствует положе-
нию точки М на оси симметрии, то размеры механизма d и а опре-
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 695
деляются по уравнениям (10.135) и (10.136), а коэффициенты А2 и
Ьо — по уравнениям (10.137) и (10.138). Значения коэффициентов рь
Рг, Рз в этих формулах должны быть определены по формулам (9.85).
Пример. Дано уравнение гиперболы:
у = ±У 10х24-1.
Сравнить величины отклонений шатунной кривой от данной функции
для механизмов, полученных при различных параметрических весах.
При параметрическом весе q = (yM -J-y)z отклонение у вершины
гиперболы согласно предыдущему примеру равно *):
Lo = 0,0066.
Отклонение в конце участка, приближенного к гиперболе:
/.., = 0,0074.
При параметрическом весе q=yM^-y, решая задачу аналогично
предыдущему примеру, получаем:
zo = O,75; z3 = 0,51; а = 0,302; d= 1,432; je=l,0; _у3=1,31.
Максимальная величина взвешенной разности по формуле (10.146):
Lq = 0,0147.
Значения параметрического веса q в середине и по концам уча-
стка, приближенного к гиперболе:
<7 0 ?=« 2у0 = 2,0; <73 аи 2_у3 = 2,62.
Действительные отклонения шатунной кривой от заданной функции
при этих значениях веса:
/,0 = -9 = 0,0074; 1-3 = ^ = 0,0056.
Ял
При данном значении коэффициента А2 максимальное отклонение
получилось одинаковое для обоих весов, но при весе ^ = (уЛ1-|-_у)
оно достигается при вершине гиперболы, а при весе q=(yM —J’)^ — п0
концам участка, приближенного к гиперболе. Отметим, что значения
относительных размеров звеньев совпадают при обоих весах прибли-
зительно с точностью до третьего знака после запятой. Следовательно,
разница между механизмами, полученными при рассмотренных пара-
метрических весах, будет практически ощущаться только, если отно-
сительные размеры звеньев механизма будут выполнены с точностью
до ~ 0,0001. Выполнение этого требования весьма затруднительно
даже для наиболее точного приборостроения, поэтому практически
следует считать оба рассмотренных веса равноценными. Если путем
последовательных приближений вычислить наилучшее равномерное
*) См. стр. 693,
696
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
приближение, то величина максимального отклонения несколько сни-
зится, но при этом размеры звеньев механизма также будут отли-
чаться на столь малые величины, что практическая реализация этого
уменьшения отклонения становится сомнительной.
Симметричный механизм, направляющий по гиперболе, в случае
приближения на одном участке, симметричном относительно вершины,
определяется двумя независимыми параметрами (при b— 1). Это не
значит, однако, что можно задавать любые значения двух независимых
' параметров. Механизм возможен лишь в определенной области изме-
нения выбранных параметров. Верхнюю границу этой области дает
предельный случай механизма при z3 = zn. Для общего случая это
условие соответствует соприкосновению второго порядка гиперболы
с шатунной кривой в двух симметрично расположенных точках.
Коэффициенты р{, р.2 и р3 определяются в этом случае по фор-
мулам:
Р1 = — Зг0; />2 = 3zjj; р3 = — г". (10.147)
Если дополнительно к условию z3 = z0 выбирать значение z0,
соответствующее положению точки М на оси симметрии, то шатунная
кривая будет иметь соприкосновение 5-го порядка с гиперболой.
Для этого случая при z0 = z3 имеем:
с?==]лго+^о;
а = ] /z0 — z0;
,2__3*o + 2*o|/z^— j .
-- 2z0 + 1 + zo
fei = 4(l — z0).
(10.148)
(10.149)
(10.150)
(10.151)
Полученные зависимости для предельного случая z3=zn позво-
ляют установить одну из границ области существования механизма,
направляющего по гиперболе.
Рассмотрим, например, область изменения коэффициентов k- и Ь°и
в уравнении гиперболы у = ± У/е2л'2 -ф- b'i в случае, если приближе-
ние к гиперболе производится на одном участке, симметричном отно-
сительно вершины.
Для предельного случая z3 = г0 максимальное отклонение L — О,
а коэффициенты k'2 и Ьо связаны зависимостью, получающейся из
уравнений (10.150) и (16.151):
|(4-^) + 4 (4-й-О j/4-^-l
(10.152)
На рис. 637 сплошной линией показана кривая изменения k2 в за-
рисимости от Ь'о при £ = 0, полученная по уравнению (10.152). Так
§ 34] СИНТЕЗ ПО УСЛОВИЮ МИНИМ. ОТКЛОНЕНИЯ ОТ ЗАДАННОЙ ФУНКЦИИ 697
как в рассматриваемом механизме z3 г0! то при данном z0 вели-
чина k2 из формулы (10.137) будет всегда меньше, чем значение k2
из формулы (10.152). Отсюда следует, что область изменения коэф-
фициентов k2 и b'l лежит влево от кривой L — 0 (см. рис. 637). По
мере удаления от этой кривой влево величина максимального откло-
нения L будет увеличиваться. При больших значениях величины L
шатунная кривая уже не может быть практически использована для
воспроизведения гиперболы, поэтому линией, ограничивающей область
изменения коэффициентов k2 и b,t слева, должна быть кривая, соот-
ветствующая наибольшему практически допустимому значению L.
Эта кривая может быть построена, если воспользоваться уравнениями
(10.134)-£- (10.140), что, однако, приводит к достаточно громоздким
вычислениям. Поэтому представляется целесообразным получить кри-
вую, ограничивающую слева область изменений k2 и Ь%, из некоторых
других геометрических соображений.
Заметим, что по мере удаления влево от кривой L = 0 длина
участка, на котором шатунная кривая приближена к гиперболе, уве-
личивается, и точка Mi (см. рис. 636), соответствующая концу этого
участка, все более и более удаляется от оси симметрии. Так как
шатунная кривая есть кривая замкнутая, то наступит момент, когда
расстояние от точки Mt до оси симметрии, достигнув своего макси-
мального значения, начнет вновь уменьшаться. Значение параметра k2,
при котором для данного b'l достигается наибольшее расстояние точки М\
от оси симметрии, и будем считать предельным, ограничивающим
слева область изменений k2 и Ь%. Это положение близко совпадает
с тем положением, когда угол 8 (см. рис. 611) является наибольшим.
Так как угол 8 равен углу BDA, то максимум угла 8 будет тогда,
698 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
когда линия BD станет касательной к траектории точки В. Принимая
во внимание, что
2 sin у = 2 УТ,
из &BDA получим следующее равенство для нахождения предельного
значения величины *3:
4*3 = rf2 —а2.
Подставляя это значение в уравнение (10.132), получим:
4 = — Рл
или
*1 = §2 (го + 1+ 15*0*1 + zl)- (10.153)
Для данного значения мы можем, пользуясь приближенным
равенством
(’о = 4(1 — *0),
найти величину *0, затем по уравнению (10.153) — величину z3 и,
наконец, из уравнения (10.137) — значение коэффициента А2, которое
и будем считать предельным.
Таким путем была построена кривая, указанная пунктирной линией
на рис. 637.
В силу принятых упрощений влево от этой кривой имеется еще
некоторая область возможных значений Ь* и А2, но практически она
не может быть использована из-за больших величин отклонения шатун-
ной кривой от гиперболы. Следовательно, значения коэффициентов А2
и А2 в уравнении гиперболы при воспроизведении ее при помощи
шарнирного четырехзвенника должны находиться в области, указанной
на рис. 637 штриховкой. Чем ближе располагаются выбранные зна-
чения А2 и Ь* к кривой, указанной пунктирной линией, тем больше
длина участка, приближенного к гиперболе, но соответственно больше
и величина отклонения L. Для значений А2 и Ь* лежащих на этой
кривой, величина L возрастает с увеличением А2 от L — 0,006 при
А2 = 0 до Z. = 0,012 при А2 = 20.
Сравнительно небольшая область возможных значений А2 и А®
в уравнении гиперболы и является основным недостатком воспроиз-
ведения гиперболы при помощи шарнирного четырехзвенника.
Аналогично построены графики для определения области изменений
размеров механизма а и d (рис. 638) и- параметров *0 и *3 (рис. 639).
В заключение отметим, что при А = 0 гипербола вырождается
в систему двух прямых, параллельных оси х, и рассмотренные меха-
низмы переходят в прямолинейно-направляющие механизмы Чебышева.
При А = 0 гипербола вырождается в систему двух прямых, пересе-
кающихся в начале координат.
§35]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
699
Кроме того, известны решения задач синтеза приближенно напра-
вляющих механизмов, воспроизводящих движение по параболе и
эллипсу (без подробного выяснения областей существования), а также
известны решения задач синтеза несимметричных направляющих меха-
низмов [9о, 23а, б, 33а]. Однако в общем случае произвольно задан-
ной кривой определить все парамет-
ры из условий минимального откло-
нения от заданной зависимости не
представляется пока возможным.
§ 35. Синтез приближенных
направляющих механизмов
с учетом дополнительных
требований
1°. Шарнирный четырехзвенник.
В общем случае задача синтеза
шарнирного четырехзвенника, на-
правляющего по заданной траектории,
формулируется следующим образом.
Дана некоторая плоская кривая
Рис. 640.
j/=/i(x), которая может быть
задана своим уравнением или таблицей значений координат х и у.
Определить размеры и положение шарнирного четырехзвенника, на
шатуне которого имеется точка М, описывающая шатунную кривую
У=/г(х), мало отличающуюся от заданной кривой на некотором
участке или на всем своем протяжении рис. 640.
Подлежат определению следующие величины: АВ = а, ВС=Ь,
CD —с, AD — d, CM — k, /_ ВСМ = ш, координаты центра D(xu, у и)
700 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
и угол наклона стойки т(. Кроме того, в некоторых случаях прихо-
дится определять также параметры, входящие в уравнение заданной
кривой, например радиус и положение центра окружности, к которой
должна быть приближена шатунная кривая.
Если уравнение заданной кривой не содержит неизвестных пара-
метров, то задача сводится к вычислению девяти неизвестных вели-
чин из условий малого отклонения заданной траектории от шатунной
кривой, описываемой точкой М механизма. При этом необходимо усло-
виться о выборе величины, характеризующей отклонение от заданной
траектории. В рассматриваемой задаче наиболее естественно выбрать
в качестве этой величины расстояние между заданной траекторией и
шатунной кривой Д, измеренное по
Рис. 641.
определенному направлению, на-
пример по нормали к заданной
траектории.
Но аналитическое выражение
расстояния Д оказывается в об-
щем случае достаточно сложной
функцией. Поэтому для упроще-
ния поставленной задачи будем
рассматривать эквивалентную ей
задачу о приближении к окруж-
ности траектории точки В, кото-
рую она будет описывать при дви-
жении точки М по заданной кривой,
если между звеном АВ и шатуном
ВС ввести дополнительное звено
в виде ползуна, перемещающе-
гося по направлению АВ (рис. 641).
Тогда в качестве величины, характеризующей отклонение траекто-
рии точки В от окружности, можно принять расстояние между ними,
измеренное по нормали к окружности:
Дд = а —аф, (10.154)
где Пф — переменное расстояние от точки В до неподвижного центра
при движении точки РЛ по заданной траектории.
Нетрудно видеть, что при обращении в нуль величины Дд обращается
в нуль также и величина Д, т. е. число точек пересечения шатунной кри-
вой с заданной траекторией равно числу точек пересечения траектории
точки В с окружностью в указанном движении. Кроме того, малым
величинам расстояния Дд соответствуют, за исключением особых слу-
чаев, малые величины расстояния Д.
Отсюда следует, что расстояние Дд можно принять в качестве
величины, характеризующей отклонение шатунной кривой от задан-
ной траектории.
Задача еще более упрощается, если принять в качестве функции,
характеризующей отклонение шатунной кривой от заданной траекго-
§ 35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЯ 701
рии, величину
Д9 = а2—4, (10.155)
что соответствует взвешенному приближению с параметрическим весом
^ = а + аф. (10.156)
Подставляя в формулу (10.156) значение аф из соотношения (10.154),
получаем:
9р = 2а—Дв. (10.157)
В рассматриваемых случаях величина отклонения Дв мала по
сравнению с величиной а, поэтому выбранный вес близок к постоян-
ной величине:
qp = 4a. (10.158)
При обращении в нуль взвешенной разности Д? обращается в нуль
и величина Дд, а следовательно и величина Д действительного откло-
нения шатунной кривой от заданной траектории. В предыдущих пара-
графах было показано, что взвешенное приближение при параметри-
ческом весе, мало отличающемся от постоянной величины, дает
достаточно хорошее приближение к заданной зависимости. Поэтому,
определяя искомые параметры механизма из условия малого отклоне-
ния от нуля взвешенной разности Дч, можно, не ухудшая заметно
получаемого приближения, значительно упростить задачу, так как
функция Д?, определяемая по формуле (10.155), сравнительно просто
выражается через искомые параметры механизма.
Итак, задача о воспроизведении заданной траектории при помощи
шарнирного четырехзвенника может быть сведена к задаче о нахо-
ждении искомых параметров из условия малого отклонения от нуля
взвешенной разности Д^, определяемой по формуле (10.155).
В механизме, схема которого изображена на рис. 640, точка В
движется по окружности, если точка Л4 перемещается по шатунной
кривой. Если же точка М перемещается по заданной траектории,
отличающейся от шатунной кривой, то точка В движется по некото-
рой кривой, не совпадающей с окружностью. Обозначая через хв и
и _уд координаты точек этой кривой, получим следующее выражение
для переменного расстояния точки В от неподвижного центра А:
аф = Y (хв—xD—d cos iq)a -|~ (у в—yD—d sin т;)2. (10.159)
Следовательно, взвешенная разность Д7, определяемая по фор-
муле (10.155), имеет такой вид: •
Д9 = «2— (хв — xD—d cos т()2—(ув—yD—rfsinv])3. (10.160)
В § 33 было показано, что координаты точек В и Л1 всегда
связаны соотношениями (10.26). Подставляя значения координат хв и
702 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
ув из этих соотношений в формулу (10.160) и производя преобразо-
вания, получаем для функции Д9, характеризующей отклонение шатун-
ной кривой от заданной траектории, следующее выражение:
. b cos w . _о , о. b sin to -, ।
\ =------— (№ —с2 —A2)---------k~u +
4~-J- V {\b sin (u> -j- Tj) — k sin Ч]] (x — xD) —
— [b cos (o> + Tj) — k cos rj (y —yD)} 4~
4~ | IT {[Д cos (w -f- 7j) — k cos rj (x — xd) 4- (Д sin (to -f- 4) —
— k sin tJ (y —yo)} + 2d [(x — xo) cos tj 4-
—Уо) sin 4— c2— b2— d2-\-a2, (10.161)
где
№ = p2 — 2xd x — 2yDy 4- xb -f- jb;
U= ± j/IW2 — (N* 4- Л2 — c2)2;
V—U- U7 — № + k*-c‘
№ ’ №
Вычислить из условия минимума отклонения Дд все девять вели-
чии, входящих в формулу (10.161), достаточно простым путем пока
не представляется возможным. Поэтому будем вычислять лишь часть
параметров, выбирая остальные графическим путем или на основании
дополнительных аналитических условий. Такой путь представляется
целесообразным не только в отношении упрощения вычислений, но
и в отношении возможности удовлетворить дополнительным условиям
(конструктивно приемлемые размеры звеньев, допускаемые углы
давления, заданные углы поворота ведущего звена и т. п.).
Для выбора независимых параметров можно воспользоваться атла-
сами шатунных кривых или же определить параметры механизма гра-
фическим путем. С этой целью задаемся положением точки D отно-
сительно заданной траектории, а также размерами CD и СМ. Пере-
мещая точку М по заданной траектории и точку С — по окружности
радиуса CD, описанной из центра D, вычерчиваем траектории раз-
личных точек, связанных с отрезком СМ.
Из всех построенных траекторий выбираем ту траекторию, которая
на всем своем протяжении наиболее подходит к дуге окружности
или к полной окружности. Радиус этой окружности определяет раз-
мер АВ —а, а положение центра окружности — длину стойки AD = d.
Положение же выбранной точки В дает длину шатуна ВС=Ь и угол
наклона отрезка СМ к отрезку ВС, т. е. угол tu. Если полученное
приближение к заданной траектории является слишком грубым или же не
удовлетворяет дополнительным условиям, то можно, изменив располо-
жение центра D относительно заданной траектории или выбрав другие
значения размеров DC и СМ, вновь произвести указанные построения.
§ 351
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
703
Получив указанным путем приближенные значения всех парамет-
ров искомого механизма, будем в дальнейшем для уменьшения откло-
нений от заданной траектории вычислять три, четыре или пять пара-
метров механизма.
Координаты Хр и уо неподвижного центра D будем считать
известными. Тогда аналитическое выражение функции Д,; упрощается,
так как начало координат можно перенести в точку D. Принимая во
внимание, что в новых координатах хг> = 0 и yD — 0 и производя груп-
пировку членов, получаем выражение для функции Д? в гаком виде *):
L£2S “ (р8 _ — с2) — ^/^_dZ,sin(m + 7i)
К К К
db cos/o+j)_dsin U2’V_2JZ)_
— d cos tj (Wx — Vy — 2x) — с2 — b2 — d2 -ф- a2, (10.162)
где
(10.163)
U = ± j/4Ay — (p2 4- k* — c2)2;
V = 4; W=^ + ki~c\
P2 P2
воспроизведении симметричной траектории целесообразно
При
воспользоваться симметричным механизмом, в котором выполняются
соотношения:
k = c = b; т] = 90°— “.
(10.164)
После подстановки соотношений (10.164) в формулу (10.162)
получаем:
Д9 — — р2 cos ш + р | 4Ь2 — р2 sin w -ф- 2dy cos у- —
zt 2d sin -j- • — р4 4ft2 — p2 — 4ft2 sin2 -d2 -ф- a2. (10.165)
Наконец, для симметричного механизма при значении а>=180°
имеем:
Д9 = р2 ± 2d У 4b2—p2 — 4ft2 — d2 -ф- a2. (10.166)
Для определения пределов применимости полученных выражений
взвешенной разности при нахождении искомых параметров механизма
выясним связь между взвешенной разностью Дф и действительным
отклонением шатунной кривой от заданной траектории.
Условимся измерять отклонение Д по нормали к шатунной кривой,
так как при малых величинах отклонения это направление весьма
мало отличается от направления нормали к заданной траектории.
*) Знак перед радикалом U выбирается в зависимости от того, какая из
двух ветвей шатунной кривой должна быть приближена к заданной траектории.
704 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ | гл. X
Кроме того, при малых величинах отклонения Д можно исполь-
зовать для установления зависимости между перемещениями точек в
и М графический метод, основанный на построении планов малых
перемещений.
Согласно этому методу следует построить преобразованный меха-
низм, который получается из показанного на рис. 641, если закре-
пить в данном положении звено АВХ (рис. 642, а). Переместив точку В
в этом механизме на величину
(10.167)
получим искомое отклонение шатунной кривой от заданной траекто
рии, если спроектировать перемещение точки М на направление нор-
мали к шатунной кривой в исходном механизме. Так как величина Aj
мала, то рассматриваемые перемещения с достаточно высокой сте-
пенью точности можно считать пропорциональными скоростям соответ-
ствующих точек. Отсюда следует, что отклонение шатунной кривой
от заданной траектории Дп, измеренное по нормали к шатунной кри-
вой, найдется из соотношения
VM
Д„ = ДВ—cost, (10.168)
VB
где vm и vB — скорости точек М и В в преобразованном меха-
низме;
•у — угол между скоростью точки М и направлением нормали
к шатунной кривой точки 714 в исходном механизме.
Это направление определится, если соединить точку М с полюсом
мгновенного вращения Р шатуна ВС исходного механизма.
§35]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
705
На рис. 642, б показан план скоростей преобразованного меха-
низма, из которого находим:
VM
VB
(pm)
COS 7 = . - , ' COS т
1 (pb) . 1
_ (pm')
(Pb) •
(10.169)
Подставляя в формулу (10.168) соотношения (10.167) и (10.169),
получаем для определения действительных отклонений шатунной кри-
вой от заданной траектории следующую формулу:
Д„ = (Ю. 170))
" 2а (pb) v '
или
д (10.171)
п 2а pb ’
Для вычисления трех параметров группируем члены в выражении
взвешенной разности Д^ (10.162) так, чтобы оно имело следующий вид:.
\ = A [pofo(x) + Pifi(x)+PiA(x) — Д(х)], (10.172)
где А — постоянный коэффициент;
F (х), /0 (х), fi (х), /2 (х) — функции переменного аргумента х,
не содержащие неизвестных параметров;
Ра, р\ и р2 — коэффициенты, зависящие от искомых параметров.
Пусть, например, требуется вычислить параметры a, d и щ при
заданных Хд, у и, k, Ь, с и <о. Тогда, принимая начало координат
в точке D, получаем, что взвешенная разность (10.162) может быть
представлена в следующем виде:
д9 = А [Рй/й (х) 4- Plfl (х) p2f2 (х) — F (х)],
где
F(x) = p2-|-t/tgu>; 1
fa (х) = VI х tg <o 4- v -1)1+ тг~— x -4-
+ r|jtgU>-x(TT+;r-l)];
/l(x)=l/|jtgco-x(T^-l)]-
— ITI x tg w -I- у ----1’ I -4- ». 2fe~~ v;
ft (x) = 1;
, _ b COS co
A~ k :
Pa=d cos r(; ,
Pi = d sin r(;
Pi = 4- k2 — [Ьг 4 cz -4- — n2).
1 b COS co ' 1 1 7
23 II. Il, Артоболевский
(10.173)
(10.174)
(10.175)
(10.176)
706 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гЛ. х
Напомним, что величины U, V и W в формулах (10.174) имеют вид-
U - др )/4Аг2р2 — (р2 ~г А:5 — г2)2,
v=^,
р2
rc.= p4-fes-c*
Р2
Функции F(x), /о(х), j\(x) и /2(х) известны, так как предпо-
лагаются известными координаты точек заданной траектории х и у,
а также параметры k, с, b и ю. Коэффициенты А, ре, р} и р2 завися!
от неизвестных параметров механизма. Для определения их можно
использовать любой из трех рассмотренных в § 27 методов прибли-
жения функций. Но, как будет показано в числовом примере *),
при уточнении малого числа параметров целесообразно применить
квадратическое приближение, т. е. вычислять искомые параметры из
условия минимума суммы
i = m
s9= 2 [д9(хг)г
i=0
или интеграла
хт
А'О
Значения коэффициентов р(), pt и р.2, при которых достигается мини-
мум суммы или интеграла Iq, определяются из системы уравне-
ний (9.31):
сы)Рй 4" со17’1 4“ смР2 = То»
сюРо 4" cnPt 4" = 71»
С2ПР<> 4г C2lPl 4” CtiPi — Тг>
где коэффициенты и ckl вычисляются по формулам (9.29) и (9.30)
или (9.37) и (9.38).
В числовых примерах мы будем пользоваться формулами (9.37)
и (9.38):
i=m i=m
I* = У р (xt) fk (*<); СЫ = cik — 2 A fl ^xif
i=0 i=0
Получив числовые значения коэффициентов р0, pt и pit находим
размеры механизма:
d — }fp‘o -|- pl; (10.177)
4j=arctg^-; (10.178)
______________Ро______________
а= j/S24-C24-d2-^^(c24-A2-№)- (Ю.179)
*) См. стр. 718.
§ 35]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
707
Максимальное отклонение шатунной кривой от заданной траек-
тории можно определить, вычисляя последовательно координаты ша-
тунной кривой по методу рекуррентных соотношений. Но при малых
отклонениях проще применить графический метод, основанный на
построении планов малых перемещений.
Для определения максимального отклонения шатунной кривой от
заданной траектории по этому методу следует подсчитать значения
взвешенной разности Д? по формуле (10.173). Построив затем планы
скоростей преобразованного механизма, можно найти отношения
и величины отклонения Дп по формуле (10.171) для каждой
(рЬ)
точки заданной траектории. При мало изменяющейся величине отно-
(рт')
(Рь)
шения
достаточно определить отклонение Дп в тех точках,
где взвешенная разность имеет максимальные по модулю значения
или значения, близкие к максимальным.
Аналогично решается задача при других комбинациях трех иско-
мых параметров. Группируя члены в выражении взвешенной раз-
ности Д? так, чтобы оно имело вид функции (10.172), будем полу-
чать для различных комбинаций искомых параметров различные фор-
мулы для функций F (х), /0(х), /1(х) и коэффициентов р0, pt и р2.
Приведем некоторые из них. Пусть, например, требуется опре-
делить параметры a, d и Ь. Тогда выражение взвешенной разности
(10.162) представляется в следующем виде:
Дq = А [ро/о (х) pifi (х) (х) — F (х)],
где
F(x) = p24-Z7tg<o; 1
к = ~ЕоГ<7 ^Wx — cos (o) + +
-| (Vx Ц- Wy) sin (w ij)];
J\== "cUs — Vx ~ sin 73 +
4~ (2x Ц- Vy — Wx) cos i)];
/8(x)=l;
. __ b cos co
A—
Pq = d‘,
d
P' = T'
p2==c*^kv_ (b* 4- с2 -I - <P — a2).
1 b COS co k 1 < '
(10.180)
(10.181)
(10.182)
23*
708
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[ГЛ. X
Формулы для вычисления функций /о (х) и (х) могут быть
представлены в более простом виде, если повернуть координатные
оси на угол т] так, чтобы ось х совпала с направлением отрезка AD.
В этом случае имеем:
/0 (х) = Wx — Vy 4- (Vx Ц- Wy) tg o>,
Л = “cosT <2x +
(10.183)
Искомые размеры механизма вычисляются по формулам:
d=p0; (10.184)
ь = (10.185)
а=]А24-с2-Н2 — -^^(с24-А2 — р.2). (10.186)
Следующая возможная комбинация трех вычисляемых параметров
состоит из параметров а, b и о>. Взвешенная разность Д? может
быть представлена для этого случая в следующем виде:
д9 = A [Pofo (л‘) 4- pifi (х) 4- pzft (х) — F (x)],
тде
F (x) = p2 — d [(Wx — Vy) cos i] 4~ (Vx 4~ Wy) sin tj];
/о (x) = d [(Vx 4~ Wy) cos t] — (Wx — Vy) sin rj — C7;
/i (x) = d [(2x 4- Vy — Wx) cos tj 4- (2y — Vx — Wy) sin vj];
Л(*)=1;
,___ b COS ш
Po = tgo>;
__ k
P* b cos <o ’
A = c2 4- k* — ----(b* 4- c2 4- d2 — a2).
r 1 b cos 1 ' )
(10.187)
(10.188)
(10.189)
Если направить ось хх по направлению отрезка AD, то фор-
мулы (10.187) принимают следующий вид:
F (х) = р2 — d (Wx — Vy);
Mx) = d(Vx+Wy)-U-,
ft (x) = d (2x 4- Vy — Wx)-,
ft(x)^= 1.
He останавливаясь далее на исследовании всех возможных ком-
бинаций трех вычисляемых параметров, укажем только, что вычисле-
§ 35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 709
ние трех параметров механизма может служить лишь для уточнения
предварительно выбранных параметров.
Отметим также, что, применяя теорему Робертса *), можно полу-
чить несколько различных механизмов для воспроизведения одной
и той же заданной траектории.
Для вычисления четырех параметров механизма группируем члены
в выражении взвешенной разности Д? (10.162) так, чтобы оно имело
вид следующей функции:
Д? — A [Pofo (х) -|- pi ft (х) -j- р^ (х) -|- р3/з (x) 4- po/’i/t (x) — F (x)J,
(10.191)
где F(x), /o(x), f\ (x), ... ,/4(x)— линейно независимые функции
аргумента х, не содержащие неизвестных величин;
А, Ро, Pt, Pi и рз — коэффициенты, зависящие от искомых пара-
метров.
Пусть, например, подлежат определению параметры a, d, b и ш.
Тогда взвешенная разность может быть представлена в таком виде:
Aq = A [pofo (х) 4- ptfi (х) 4- р2/2 (х) 4- рз/з (х) 4-poPift (х) — F (х)],
где
F(x) = p2;
/о(х) = -С7;
fi (х) = (Vx 4~ Wj) sin т] — (Vy — Wx) cos т;;
/2 (x) = k |(2y — Vx — Wy) sin r( 4- (2x f-Vy — Wx) cos ij];
/з(х)=1;
/4(x) = (Vx 4- Wy) cos 4* ( Иу — ^x)sin V,
, b cos о
A =--------------------------------k~>
Po = tgw; 1
Pi = d-,
d
P'2 b cos <» ’
P,=c> + + C‘+d‘ - a’).
(10.192)
(10.193)
Формулы для fi (x), fq (x) и /з (x) упрощаются, если повернуть
координатные оси на угол т; так, чтобы ось х совпала с направле-
нием отрезка AD.
*) См. стр. 669,
710
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
В этом случае имеем:
/, (х) = Wx — Vy;
fi (х) = k (2х — Wx V»;
/Дх^Ух-^у
(10.194)
Если неизвестные коэффициенты рп, ръ р2 и р3 вычислять из
условий обращения в минимум среднего квадратического значения
взвешенной разности, то получаем систему уравнений (9.53), решив
которую по способу, указанному в § 27, находим числовые значения
коэффициентов р,„ ръ pt и ря.
Искомые размеры механизма определятся тогда по следующим
формулам:
ш =агс tgp0;
b =--------;
Р2 COS О)
а = 1/^4- + d'2 — (с2 + Л2 — р3).
V
(10.195)
Для определения максимального отклонения шатунной кривой от
заданной траектории поступаем так же, как и при вычислении трех
параметров, т. е. подсчитываем величины взвешенной разности Д?
по формуле (10.191) и затем, строя план скоростей преобразован-
(рт’)
ного механизма, находим отношения в тех положениях, где
взвешенная разность имеет значения, близкие к максимальным.
Величины отклонений подсчитываем при этом по формуле (10.171).
Аналогично решается задача при вычислении параметров a, d, b и vj.
В этом случае взвешенная разность представляется в следующем
виде:
д? — А Wo (х) + Ptf (х) Pift (х) 4- p3f3 (х) 4- pupifi (х) — F (х)],
где
F(x)=Vy—Wx— tg(i>(V'xW4);
/• = "<sL (2x + yy -
ft (X) = Vx 4- Wy 4- tg O) ( Vy — Wx);
, . . 2 1 rrc (10.196)
/2(x) = p24-f7tgo>;
Л(х)= 1;
f^ = -^{'2y-Vx-Wyy,
.___________ db cos tj cos ш
§ 35]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
711
1
A=tg4;
1
р2 - — —----•
г a cost] ’
-Г^— 1 с2
d cos i) |
(10.197)
Рз
---(с2 + fc’-l-rf'-e8
Ь COS ш ' 1 1
Для вычисления других комбинаций параметров механизма, вклю-
чающих в свой состав размеры k и с, можно воспользоваться выра-
жением взвешенной разности Д?с, получаемой из условия прибли-
жения к окружности траектории, которую описывает точка С при
движении тбчки М по заданной траектории. Аналитическое выраже-
ние для взвешенной разности Д9(? может быть получено из формулы
(10.171) путем соответствующей замены обозначений.
Для вычисления пяти параметров (a, b, d, ш, rt) группируем
члены в выражении взвешенной разности (10.162) так, чтобы оно
имело вид следующей функции:
\ = Ро/о(*) I Pift (*) Д-Pifi (*) + • • • + Psfs (*)> (Ю.198)
где
I? 5? 5? £ II II II II II II II •5 1 “ 1 % If I 1 -’t JI -5 ? Г II h - (10.199)
b cos <o
P" k ’
b sin ы
ts -5S ts "T3 t «i ce W “ II II II II II 1 'з I а a. a. "4 J. . О и кГ “ts OS'S- 1 i s < Тз I 1 “ 1 а. ю (10.200)
Коэффициенты Pc, Pi ,... , p6, при которых достигается минимум
взвешенной разности Д9, вычисляются как указано в § 27*).
*) См. стр. 524,
712 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
2°. Кривошипно-шатунный механизм. Если уравнение заданной
кривой не содержит неизвестных параметров, то задача синтеза
кривошипно-шатунного механизма, направляющего по заданной траек-
восьми параметров из условий малого
тории, сводится к определению
Аналитическое выражение этого
отклонения заданной траектории
от шатунной кривой точки Л1
(рис. 643). В состав этих пара-
метров входит пять параметров,
определяющих размеры механизма
(АВ=а, BC=b-, AD = e; СМ~
= k, /_ ВСМ — ш), и три пара-
метра, определяющих расположе-
ние механизма (хА, уА и т]).
Отклонение шатунной кривой
от заданной траектории Д будем
оценивать по величине расстоя-
ния между ними Д„, измеренного
по нормали к шатунной кривой *).
отклонения оказывается в общем
случае весьма сложной функцией. Поэтому для упрощения вычисле-
ний будем определять искомые параметры из рассмотрения эквива-
лентной задачи о приближении к окружности траектории точки В,
которую она описывает, если в состав механизма вводится допол-
нительное звено в виде ползуна, перемещающегося по направлению
радиуса АВ, и точка 7И перемещается по заданной траектории
(рис. 644, а).
*) Это направление при малых величинах отклонений практически совпа-
дает с направлением нормали к заданной траектории.
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
713
§ 351
Так как заданная траектория в общем случае отличается от
шатунной кривой, описываемой точкой Л1, то расстояние АВ в полу-
ченном пятизвенном механизме будет иметь переменную величину.
Обозначим эту величину через аф. Тогда отклонение шатунной кри-
вой от заданной траектории можно характеризовать величиной
Дв = а —йф, (10.201)
так как, за исключением особых случаев, малым величинам Дд соот-
ветствуют малые величины Д„.
Кроме того, при обращении в нуль величины Дд обращается
в нуль и величина отклонения Д„, т. е. число точек пересечения
шатунной кривой с заданной траекторией равно числу точек пере-
сечения траектории точки В в пятизвенном механизме с окружно-
стью радиуса АВ.
Для установления зависимости между отклонением Д„ и величи-
ной Дд воспользуемся построением плана малых перемещений.
Согласно этому методу следует построить плав скоростей для меха-
низма, изображенного на рис. 644, полагая звено АВ закрепленным
под углом, соответствующим рассматриваемому положению точки Л-1.
Из построенного плана скоростей (см. рис. 644, б) следует, что
малые перемещения точек В и Л1 связаны зависимостью
Отклонение Д„, измеренное по нормали к шатунной кривой точки М
в исходном механизме, при малых величинах Д.ц может быть полу-
чено из соотношения
Дя = Д.цСО8у, (10.203)
где 7 — угол между перемещением Д^, т. е. скоростью точки М
в преобразованном механизме, и направлением нормали NN к шатун-
ной кривой точки М в исходном механизме. Это направление опре-
делится, если соединить точку М с центром мгновенного вращения Р,
который найдется на пересечении продолжения отрезка АВ с линией,
проведенной через точку С перпендикулярно к направлению движе-
ния ползуна (рис. 644, а). Из формул (10.202) и (10.203) получаем
зависимость между величинами Дд и Д„:
Д„ = Дд-^-с08Т (10.204)
или
Дя = Дв-(^1, (10.205)
где (pnf) — проекция скорости точки М в преобразованном меха-
низме на направление нормали NN.
714 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Аналитическое выражение величины Дв значительно проще, чем
выражение отклонения Дл. Еще более простой вид имеет взвешен-
ная разность
Д? —я2 *— яф, (10.206)
которая получается путем умножения величин Дв на параметриче-
ский вес
9' = я-фяф. (10.207)
При малых отклонениях Дл и Дв этот вес близок к постоянной
величине, равной Ча.
Из формул (10.206), (10.207) и (10.201) получаем:
(10-208)
Отклонение шатунной кривой от заданной траектории, измерен-
ное по нормали, связано с величиной взвешенной разности соотно-
шением
Д„ = 4«--^1, (10.209)
" Ча (pb) ’ 4 * ’
которое следует из формул (10.205) и (10.208).
Для вывода аналитического выражения взвешенной разности Д.
рассмотрим сначала случай, соответствующий значению угла т] = 0
и У а = е-
Переменное расстояние яф в этом случае связано с координатами
точки В соотношением
«Ф = (хв — хд)2 -ф- (у в — я)2.
Отсюда взвешенная разность Д? = я2 — яф может быть пред-
ставлена в следующем виде:
Д9 — — Рд + 2хдхв ф Чеув — х2а — е2 -ф- я2, (10.210)
где
рв = -фув.
Подставляя в формулу (10.210) рекуррентные соотношения
(10.45) и (10.46), получаем после преобразований:
2
Д(? =— р2 ф- ЧхдХ----[(/?cos<o — Л)_у-ф(х— Хд)#81п<1) — ebcosco]_y±
± Т [(Д' — e)&sin со— (b cosco — k)(x—хл)] флЛ2 —j2 —х\— е2— £2-ф
-ф 4kb cos о — k2 -ф a2. (10.211)
§ 35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 715
Для общего случая выражение взвешенной разности можно полу-
чить из формулы (10.211) преобразованием координат. Имеем:
Д? = — р2 — (уа — е) (х sin т( — у cos -q) -ф- 2хл (у sin tq х cos tq) —
2
---£ [ (b cos w — k) (y cos T( — x sin q —уд -]~ e) —
— (y sin т(-ф xcos к;—Хд)/щпш—eb cos w](y cost( — xsin q—Уд-[-^)±
9
— фф 1(У cos Д — x sin iq —ул) b sin <u — (b cos <» — k) X
X (y sin -q -ф- X COS Д — Хд)] ]/A2 — (y COS TQ — x sin -q — уд-]-е)2 —
— х2д _ — /г2-ф 2M cos шX. (10.212)
Формула (10.211) значительно упрощается при значении угла ш — 0.
В этом случае мы имеем:
„ . _ 2(b — k) <> , 2еЬ , 2(Ь — k) . . /75-—~з
д9=—р2 + 2хдх ——^-у + У—~ ~Г~ ~Хл) k ~У ~
— Хд — ei~ (b— /г)2 фо2. (10.213)
При значении угла а>=180° получаем:
Д, = - Р2 + 2ХДХ-1- ^Щу2 -^у ± ^(х-хд) /F=72 -
— хд —е2 —(fe+^)24-a2. (10.214)
В формулах (10.211)ч-(10.214) двойному знаку перед квадрат-
ным радикалом соответствуют две ветви шатунной кривой. Переход
точки М с одной ветви на другую возможен только в предельных
положениях механизма.
Для вычисления трех параметров механизма группируем члены
в выражении взвешенной разности так, чтобы оно имело вид следую-
щей функции:
А, = Го/о (-v) + PifM + Р*А (*) - F (-*)> (10-215)
где рп, Pi и р.2 — коэффициенты, зависящие от искомых параметров;
Р /«(х), AW> — функции аргумента х, не содержащие
неизвестных величин.
Пусть, например, требуется определить параметры а, b и е. Зна-
чения остальных параметров выберем эмпирически из условия гру-
бого приближения к заданной зависимости *). В соответствии с вы-
бранными значениями располагаем координатные оси так, что ось х3
совмещается с линией движения точки С ползуна, а осьу3 проходит
*) Для эмпирического подбора значений невычисляемых параметров может
быть полезен метод, указанный для шарнирного четырехзвенника (см. стр. 702).
716 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
через неподвижный центр А. В этом случае из формулы (10.211)
при хд = 0, х=х} и у—уу имеем:
F (х) = р2 — 2у* ± 2xt //г8—У;
/0 (х) =ji cos (о Ц-Xj j/j sin ei ±(>4 sin ш— xt cos ш) у/k2—у!;
ft (x) = —ji cos io -f- pp'2—yi sin <o;
AW=i.
2i 2’p
po~~T'’ p' — — k :
Pi — a1 — ei — b* ‘Ikb cos w — k'2.
(10.216)
(10.217)
Искомые параметры могут быть вычислены, например, из условия
минимума среднего квадратического значения взвешенной разности Д?,
т. е. из системы уравнений (9.31).
После вычисления коэффициентов р0, pt и р3 из этой системы
уравнений определяются искомые размеры механизма из формул (10.217)
и затем — отклонения от заданной траектории по формуле (10.209).
Возможна также следующая комбинация трех вычисляемых па-
раметров: а, b и io. В этом случае, полагая Хд = 0, ц = 0, уд = е,
x — Xt и у=уь из формулы (10.211) получаем:
F (х) = pf — 2у? ± 2xj yf;
/о (х) = х,у( ± (ji — е) /^2—уу;
/, (х) = — ji -ф- eji ± х
/2(х)=1.
2Л> sin щ 2f>cos<o
Р» =------k ' k '
Pi = а2 — ег — b2 ~|- 2kb cos ш — k2.
(10.218)
(10.219)
Порядок решения задачи о нахождении искомых параметров оче-
видно тот же, что и в ранее рассмотренном случае.
Для вычисления четырех параметров механизма группируем
члены в выражении взвешенной разности так, чтобы оно имело
вид следующей функции:
\ = А [РьЪ (х) 4- Pt ft (х) 4- Pifi (х) 4- р3/3 (X) 4- poPi/i (х) — F (х)].
(10.220)
Пусть, например, подлежат определению параметры а, Ь, е
и и. Тогда при Хд = 0, ц = 0, уд = е, х — хь у =У1 в
35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 717
соответствии с обозначениями, принятыми в формуле (10.220),
имеем: ____
F (х) = zb Xi У k* —у] —jf;
Л
/1 (*) = *1 Ji ± Ji флА2 —у,
. pf v-тг—2. } (10.221)
ft (x) = у —Ji zb JCi I y\,
fAx)=F,
/4(х) = ±флА2 — уГ,
26 cos <o
A =-----1—J (10.222)
p0 = — e‘, pl = tgw;
k k . 2 . ,2 , ,2 2. ,2 (10.223)
Pi = z---; Ps = OS-----(e + b + k — a2) — A2. v
bcosa ’ 2b cos <o 1 1 '
Определив одним из методов, указанных в § 27, числовые значения
коэффициентов /?0, рь р2 и р3, находим затем из формул (10.223)
искомые параметры а, е, b и со. Для определения отклонений ша-
тунной кривой от заданной траектории подсчитываем значения взве-
шенной разности A,z по формуле (10.220) и затем—отклонения Д'ге
по формуле (10.209), причем отношения определяются из пла-
нов скоростей преобразованных механизмов. ;
Аналогично решается задача при комбинации вычисляемых пара-
метров: а, Ь, е, хА. В этом случае в соответствии с обозначениями,
принятыми в формуле (10.220) при т( = 0 и уА = е, имеем:
F (х) = р2 — 2у2 : b 2х Vk* — j2;
А (х) = х;
fi (х) = j2 cos ш -ф- ху sin ш zb (у sin и> — х cos <о) рлА2 —у2',
f2 (х) = у cos <л zfz ф А2 —у2 sin со’,
/з (-*0 = 1;
/4 (х) = — (—у sin ш ± А2 •—_у2 cos о>);
(10.224)
’ (10.225)
А = 1;
2
А=2хд; pt = — -^b;
2
eb\ р3 = а2 — хд — е2 — А2 -ф- 2АА cos со — А2.
718
СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
[гл. X
Для вычисления пяти параметров (хд, Ь, и>, е, а) группируем
члены в выражении взвешенной разности (10.211) так, чтобы оно
имело вид следующей функции:
д9 =P«ft> (х) +Р1/1 О) (У 4- p3f3 (х) 4- (popi 4- р2р^^ (х) 4-
4- <Р№ — PiPdfi (У — F (У> (Ю.226)
где
F (x) = p2 —- 2_y2 чЗ 2x ]Лk2 —У,
/0 (x) = 2 (x+У kl —у), /3(x) = l,
/1 (У = (—• xy ±у ]fk2 —У), A (x) = y,
ft (У=—4 O'2 ± x Vk2 —у2}, fs (x)=± 4 V k* —y;
Po = Xa', Рз = а2 — e2— b2— хд— k2 - [- 2kb cos ю,
Pi — b sin u>, Pi = e.
Pz — b cos u>,
(10.227)
(10.228)
Вычисление параметров рй, рь Pi производится так же, как
и для функции (9.152)*).
3°. Примеры. Сначала решим задачу синтеза шарнирного четы-
рехзвенника, в котором заданная траектория (рис. 645) представляет
'0 i~
Рис. 645.
собой криволинейную шкалу счетно-решающего механизма для ре-
шения баллистического уравнения **). Из условий минимального от-
клонения от заданной зависимости будем вычислять параметры a, d и тр
Значения остальных параметров выберем из условия грубого при-
*) См. стр. 561.
**) Заданная траектория взята из книги А. Свободы [112].
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
719
г
§ 35]
ближения шатунной кривой к заданной траектории при равномерной
шкале на ведомом звене.
В соответствии с эмпирически найденным механизмом имеем:
k = 66 мм; с = 45 мм; Ь — 58 мм; <о = 354сЗО'.
Далее на заданной траектории выбираем семь точек, коорди-
наты которых х и у при выбранном начале координат имеют значения,
указанные в таблице 10.1. В этой же таблице указаны значения
Таблица 10.1
Исходные данные
i 0 I 2 3 4 5 6
X — 89 — 83,5 — 76 — 67,5 — 59 — 50 — 39,5
У 56,5 51 47,5 47 48 52,5 61
Р* 11 113 9573,25 8032,25 6765,25 5785 5256,25 5281,25
Определение искомых параметров начинается с вычисления функ-
ций F(x), f0(x) и fi (х) по формулам (10.174).
Подсчитав затем коэффициенты ckl и по формулам (9.37) и
(9.38), получаем, что система уравнений (9.31) для определения не-
известных коэффициентов /?0, р{ и р% имеет такой вид *):
137839,2р0 10~2 —96973,Ipj • 10-2 —94588,4/>2 104 = — 70557,11;
— 96973,lp0. IO"2 4-75357,5/?, • 102 -f- 72 341/?2 10-4 = 49763,08;
— 94588,4/>0 • 10-3 4- 72 341р, 10-2 4- 70 000рг 10-4 = 48165,20.
Решив эти уравнения по схеме, указанной в таблице 9.1, полу-
чаем:
Рг — — 9239 мм*;
/?!= 76,79 ММ',
Рн — — 60,56 мм.
Искомые параметры механизма вычисляются по формулам (10.177),
(10.178) и (10.179):
d = 97,79 мм;
т(= 128° 15';
а — 35,89 мм.
*) При составлении этих уравнений свободные члены и коэффициенты
при неизвестных выравнены умножением и делением их на числа, кратные
десяти.
720 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
Схема полученного механизма изображена на рис. 646.
Для определения максимального отклонения шатунной кривой от
заданной траектории вычисляем предварительно значения взвешенной
разности по формуле (10.173).
из планов ско-
Дя, вычислен-
Далее находим величины = отношения
ростей преобразованных механизмов и отклонения
ные по формуле (10.171). (На рис. 647 показано построение преоб-
разованного механизма и его плана скоростей для одного положе-
ния.) В таблице 10.2 указаны значения этих величин, а на рис. 648
показан график изменения величины Дп, из которого следует, что
в полученном механизме шатунная кривая имеет с заданной траек-
торией пять точек пересечения, отклоняясь от нее не более чем
на 0,33 мм.
Таблица 10.2
Отклонения шатунной кривой от заданной траектории
i 0 1 2 3 4 5 6
8 — 11 - 12 21 — 11 6 — 4
Дв, мм 0,111 — 0,153 — 0,167 0,292 — 0,153 0,084 — 0,056
(рт') (pb) 1,04 1,12 1,13 1,13 1,08 1,03 0,99
Дп, мм 0,12 — 0,17 — 0,19 0,33 — 0,17 0,09 — 0,05
§ 35]
СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ
721
Величину максимального отклонения можно уменьшить до вели-
чины, равной приблизительно полусумме модулей максимального по-
ложительного и максимального отрицательного отклонения, если из-
менить величину радиуса а так, чтобы максимальное положительное
значение отклонения Дд равнялось максимальному отрицательному
значению. Обозначая через Дд модуль максимального положительного
отклонения Дд и через Д«—
модуль максимального отри-
цательного отклонения, по-
лучаем, что новая величина
радиуса а может быть опре-
делена из соотношения
В рассмотренном при-
мере
„„ 0,29 — 0,17
й1 = Зо,89------——~ —
= 35,83 мм.
При этой величине параметра а максимальное отклонение шатун-
ной кривой от заданной траектории будет приблизительно 0,26 мм,
но при этом увеличится средняя величина отклонения.
Если есть необходимость в дальнейшем уменьшении максималь-
ного отклонения, то следует вычислить из условия минимума сред-
Рис. 648.
него квадратического отклонения че-
тыре или пять параметров механизма.
Покажем теперь, что в данном
случае среди шатунных кривых
кривошипно-шатунного механизма
можно найти такую кривую, кото-
рая будет приближена к заданной
траектории, с той же степенью
точности, что и в шарнирном четы-
рехзвеннике.
Будем определять аналитически три параметра механизма: а, b
и е. Значения остальных параметров выберем из условия грубого
приближения к заданной траектории *).
Координатные оси в соответствии с найденными величинами х&,
Уа и к] располагаем так, чтобы ось xt совместилась с линией дви-
жения точки С ползуна, а ось проходила через неподвижный
*) В данном примере выбор вычисляемых параметров производился по
атласу шатунных кривых кривошипно-шатунного механизма, который имеется
в книге И. И. Артоболевского [36].
(10.229)
722 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
центр А (см. рис. 644). Тогда значения координат заданной траек-
тории в новой системе определятся по формулам:
Xj = (у —Jo) Sin Tj -|- (х — х0) cos If],
Vi = (j — Jo) cos — (x — x0) sin tq,
где x и j — координаты точек заданной траектории, указанные в
таблице 10.1; х0 и j0 — координаты выбранного начала координат в
системе х, у.
Из эмпирически найденного механизма имеем:
xfl =— 81 мм\ Уо — 81 мм~, т;=126о; ш = 0; Л = 52,5 мм.
Таблица 10.3
Преобразование координат
i 0 1 2 3 4 5 6
Х1 — 15,12 — 22,80 — 30,04 — 35,44 — 39,63 — 41,28 — 40,57
У1 20,87 19,66 15,65 9,06 1,60 — 8,33 — 21,82
В таблице 10.3 приведены координаты заданной траектории в при-
нятой системе координат, вычисленные по формулам (10.229). По
этим значениям координат вычисляем в соответствии с формулами
(10. 216) функции F (х), /0(х) и /1(х) для семи выбранных точек.
Искомые параметры будем определять из условий минимума сред-
него квадратического отклонения, т. е. из системы уравнений (9.31).
Вычислив коэффициенты и сы по формулам (9.37) и (9.38), по-
лучаем следующую систему уравнений:
25363986j0 — 30721,28/?! ф- 13030,1 lj2 = — 31713930;
— 30721,28/>0 ф- 1697,140/?! — 36,65р8 = 58242,3;
13030,11/?0— 36,65/?! ф- 7р8 = — 16535,74.
Отсюда получаем: р$ =—1,3017; Pi —13,607 мм", />2=132,11 мм2.
По найденным значениям коэффициентов рй, pt и р8 определяем
из формул (10.217) искомые параметры механизма:
Ь = 34,17 мм\ е = — 10,45 мм\ с = 24,03 мм.
Схема полученного механизма изображена на рис. 649.
Для определения отклонения шатунной кривой от заданной тра-
ектории подсчитываем значения взвешенной разности Д? по фор-
муле (10.215) и затем отклонения Дп по формуле (10.217), причем
отношения
(рт')
(pb)
определяются
графически из построенных планов
§ 35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 723
скоростей преобразованного механизма. Преобразованный механизм
и его план скоростей показан только для положения 7 = 5, соот-
Полученные величины указаны в таблице 10.4.
Таблица 10.4
Вычисление отклонений
i Д<7 Д — (/’«') (pb) В (рь)
0 — 3,26 — 0,068 1,51 — 0,10
1 3,19 0,066 1,42 0,09
2 — 5,91 — 0,123 1,22 — 0,15
3 7,84 0,163 1,14 0,19
4 — 8,78 — 0,183 1,09 — 0,20
5 14,68 0,305 1,03 0,31
6 — 7,77 — 0,162 1,07 — 0,17
На рис. 651 показан график изменения величины Дл.
Из построенного графика и таблицы 10.4 следует, что в полученном
механизме шатунная кривая точки М имеет с заданной траекторией
шесть точек пересечения, откло-
няясь от нее не более чем на 0,31 мм,
т. е. точность приближения оказы-
вается примерно такой же, как и в
случае шарнирного четырехзвенни-
ка. Отметим также, что если для
решения данной задачи применить
метод интерполирования, то при
произвольном выборе узлов интер-
полирования мы могли бы получить
Рис. 651.
только три точки пересечения
шатунной кривой с заданной траекторией и точность приближения
была бы соответственно меньше, чем при квадратическом приближении.
724 СИНТЕЗ ПРИБЛИЖЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ [гл. X
4°. Синтез направляющих механизмов с заданным движением
чертящей точки. Во всех предыдущих параграфах этой главы пред-
полагалось, что при синтезе направляющих механизмов требуется
только воспроизведение заданной траектории некоторой точки меха-
низма. Однако в некоторых случаях (например, при проектировании
счетно-решающих устройств) требуется, чтобы точка, чертящая за-
данную траекторию, двигалась по заданному закону движения. Вы-
полнения этого условия можно достичь, если, кроме задания коорди-
нат чертящей точки, задать дополнительно зависимость между этими
координатами и углом поворота одного из звеньев. Например, для
шарнирного четырехзвенни-
ка, показанного на рис. 652,
можно задать для точки М
уравнение ее траектории
y=ft(x) (10.230)
и угол поворота звена CD
как функцию от коорди-
наты х:
ф=/2(х). (10.231)
Тогда искомые параметры
механизма должны выби-
раться из условий миниму-
ма двух функций: отклоне-
ния шатунной кривой точ-
ки Ж от заданной траекто-
рии Д, (х) и отклонения значений угла ф в механизме от значений
заданной функции (10.231) Д.2(х).
Условия минимума отклонения А! (х) могут быть заменены, как
было показано ранее *), условиями минимума взвешенной разности
(10.161), которую будем здесь обозначать через Д91- Условия ми-
нимума отклонения Д.2(х) также заменим условиями минимума взве-
шенной разности А9о, аналитическое выражение которой можно полу-
чить следующим образом.
Спроектируем контур 0MCDN0 (см. рис. 652) на координатные
оси. Тогда при обозначениях, принятых на рис. 652, получаем:
(10.232)
/гф cos £ = р cos у — с cos (ф -ф- р т]) — хо;
Лф sin £.= р sin у — с sin (ф + ₽ + т() —yD.
Здесь под Лф понимается то переменное значение расстояния СМ,
которое устанавливается, если точка М располагается на заданной
траектории и угол ф соответствует заданной функции (10.231). В ка-
*) См. стр. 702.
§ 35] СИНТЕЗ С УЧЕТОМ ДОПОЛНИТЕЛЬНЫХ ТРЕБОВАНИЙ 725
честве взвешенной разности с параметрическим весом выберем
величину
Д?о = А2 — k^. (10.233)
Определяя из уравнений (10.232) величину k$ и подставляя ее зна-
чение в уравнение (10.243), получаем:
Д?2 = — р2 2р С COS (ф — / + Р + Ч) — ^CXD COS (ф Р Tj) —
— 2cyD sin (ф 4- р 4- Ч) 4- 2Р xd cos х 4~
4- 2руо sin у 4" k1 — сг — x2d —у~в. (10.234)
В выражение взвешенной разности Д91, как следует из формулы
(10.161), входят девять параметров (а, Ъ, с, d, k, ш, т], хв, Уо)-
В выражение взвешенной разности Д?2 входят шесть параметров
(Л, с, •»], xq, уо, Р), из которых пять параметров входят и в выражение
для Д9]. Таким образом, к девяти параметрам, характеризующим на-
правляющий механизм, прибавляется только один параметр р — угол
между линией AD и линией начала отсчета углов ф. Для вычисления
этих десяти параметров можно поступить следующим образом. Из усло-
вия минимума отклонения Д2 вычислить параметры k, с, хв, Уо и
Р 4~ "«J- Затем, как было показано ранее *), можно вычислить парамет-
ры a, b, d, и, т( и, таким образом, определить все искомые параметры.
Для вычисления параметров k, с, Хв, у в и р -|~т] представим
выражение взвешенной разности Д?2 в следующем виде:
Д?2 = 2 Wo (*) + Pi ft (•*) + Pifi W + Pa fa (x) + Pifi (•*) +
4- Wi! + PiPf) fa (•*) + (PiPz — РеРз) fa (•*) — F (*)L
где
F (•*) = у , f3 (X) = p sln
(x) = p cos (ф —/); /4(x)=l;
fi (x) = — p sin (ф — у); /B (x) = — cos ф;
/2(х) = р cos/; /6(х)=5шф.
P<> = c cos (P 4-T]); p-i=yD\
Pl = c sin (P 4- tq); /г2 — c2 — x°b — y°B
Pi ---------n-------->
Pl = xD’, Z
При решении задачи по методу интерполирования для
ния параметров рй, plt ..., pt выбираем на графике заданной функции
(10.231) пять точек, вычисляем для этих точек значения р, ф и у и
затем значения функций F (х), /0 (х), fx (х), ..., /к (х) по формулам
(10.236). Полагая значения Д?2 в выбранных точках равными нулю.
(10.235)
(10.236)
(10.237)
вычисле-
’) См. стр. 711.
726
СИНТЕЗ ПРИБЛИЖЕННЫХ направляющих механизмов
[гл. X
получаем следующую систему пяти уравнений *):
Pt ft (•*)) 4" P'ifs (-*7) 4~ Pi ft (Хг) 4~ (P»Pi 4“ PlP'i) fs (X i) 4"
4- (PiPt — РоРз) ft, (Xt) =F (xi)— Pofo (Xi) — Pl fl (x,),
z= 1, 2, 3, 4, 5. (10.238)
Исключая по схеме решения линейных уравнений неизвестные р4,
Рз, Ръ (РоР°.-\~Р1Рз) и (piPi — РоРя), получаем:
^4 — 4* BiPii 4 CiPi, Рор-j 4-PiPs — At I BtPt> 4" ^tPi,
Рз=Ai 4- B-iPv 4- CiPi, PiPi—рйрз—xs 4 - върй 4- c8pi.
Pi — A 4- B3P0 4~ C3pi;
(10.239)
Подставляя значения параметров p3 и ps из второго и третьего
уравнений системы (10.239) в четвертое и пятое уравнения этой же
системы, получаем систему двух квадратных уравнений, по которой
получаем для определения параметра р0 (или р,) уравнение четвер-
той степени. Применение наилучшего приближения (путем уравнива-
ния отклонений) или квадратического приближения (при неопределен-
ных множителях Лагранжа Х1 = Х(! = 0) приводит также к решению
уравнения четвертой степени. В тех случаях, когда все корни этого
уравнения оказываются мнимыми, можно рекомендовать вычислять лишь
четыре параметра, например с, хр, у о, k.
Тогда взвешенная разность представляется в виде:
^q 2 [ро/о С*7) 4’ Pl /1 (Х) ^rPifi С*7) 4~Лз/з (х) PoPlfl (х) 4~
4- PoPifs (х) — F (-*)]> (10.240)
где
F(x)=%-,
/o(A;) = pcos (ф — х + ₽ 4- Т]);
/i (-*) = р cos у;
fi (х) = р sin у;
A(-v) = i;
ft С*7) = — cos (ф -Н -f- tj);
h(x)= — sin (ф + Р + ч).
p0 = c; Pi=yD\
Pi=xD-, D _к2-с2~хЪ-уЪ
Рз— 2
(10.241)
(10.242)
Поступая так же, как и при решении предыдущих случаев, при"
ходим для определения параметра р0 к уравнению третьей степени-
*) Решение этой системы уравнений дано в работе Е. П. Новодвор-
ского и И. Ш. Пинскера [41].
Б. МЕТОДЫ, ОСНОВАННЫЕ НА КИНЕМАТИЧЕСКОЙ
ГЕОМЕТРИИ
ГЛАВА XI
КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ
КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ
§ 36. Два и три положения плоской фигуры
Рис. 653.
£
S'-fKp)
\
1°. Две группы задач синтеза механизмов с низшими парами.
В исследованиях немецкого ученого Л. Бурместера [67 а, б], кото-
рые появились в последней четверти прошлого столетия, была раз-
работана кинематическая геометрия конечно удаленных положений
плоской фигуры, движущей-
ся в своей плоскости. Ме-
тоды кинематической гео-
метрии привели Бурместера
к сравнительно простым
графическим решениям за-
дач синтеза направляющих
механизмов с низшими па-
рами. Дальнейшая разра-
ботка методов кинематиче-
ской геометрии позволила
решить широкий круг прак-
тически важных задач син-
теза четырехзвенных и мно-
гозвенных механизмов с низ-
шими парами. Задачи син-
теза механизмов с низшими
парами, решаемые методами
лить на две группы, отличающиеся по характеру задания функции
положения механизма.
1) Задачи синтеза по положениям. В задачах этой
группы параметры кинематической схемы механизма определяются по
следующим условиям: задан ряд точек Qi(<p1( ф1), Q2(cp2, Фа), ...
(рис. 653); требуется, чтобы график <р=/(ср) функции положения меха-
низма проходил через все указанные точки. Ход графика /(?) между
точками ... иногда уточняется заданием передаточного от-
. <Н> „ di
ношения механизма i — или его производной — — - , а.
a? drf
кинематической геометрии, можно разде-
728 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
Каждая из заданных точек Qlt . определяет соответствен-
ные положения ведущего и ведомого звеньев механизма. Отсюда
наименование указанных задач как задач синтеза по положениям.
С математической точки зрения задачи синтеза по положениям
представляют собой интерполяционные задачи с наперед задан-
ными узлами интерполяции. Эти задачи возникают в практике проек-
тирования исполнительных механизмов различных машин-автоматов
легкой, пищевой и других отраслей промышленности.
2) Задачи по воспроизведению непрерывной функ-
ции на заданном отрезке. Задачи синтеза, принадлежащие
к этой группе, характеризуются следующими условиями: зада-
на функция (рис. 654) = F (?), непрерывная на отрезке |?0, ?т|;
требуется эту функцию на указанном отрезке воспроизвести меха-
низмом. В этом случае функцию положения шарнирного механизма
ф=У?(<р) приближают на заданном отрезке [?0, ?т] к предписанной
функции = F (?) с необходимой точностью. Это приближение можно
осуществить как при помощи интерполирования, так и другими
методами приближения функций. Следовательно, задача синтеза по
приближенному воспроизведению непрерывной функции на заданном
отрезке с точки зрения возможных методов решения является более
общей, чем задача синтеза по положениям.
Задачи синтеза этой группы чаще всего возникают при-проекти-
ровании механизмов различных областей приборостроения. Сюда же
относятся задачи синтеза шарнирных механизмов с остановками и
шарнирных механизмов приближенно равномерного движения, которые
применяются в обрабатывающих машинах-автоматах.
При решении задач синтеза обоих указанных групп методы кине-
матической геометрии до последнего времени позволяли опреде-
лить параметры схемы механизма по заданным условиям только
графически. Но: графическое решение не обеспечивает необходимой
§ 36]
ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
729
точности определения параметров схемы механизма и нередко за-
трудняет само отыскание этих параметров из-за ухода соответст-
вующих построений за пределы чертежа.
Ниже дано такое изложение основ кинематической геометрии ко-
нечно удаленных положений плоской фигуры, движущейся в своей плос-
кости, которое позволяет ана-
литическое решение упомяну-
тых задач синтеза механизмов.
2°. Плоская фигура. Чтобы
изучить плоское движение твер-
дого тела U (рис. 655), доста-
точно изучить движение плос-
кой фигуры S, выделенной из
этого тела посредством сече-
ния его произвольной плоско-
стью VJ, параллельной плоскости
движения. Поэтому в качестве
Рис. 655.
объекта ближайшего рассмотре-
ния выберем неизменяемую плоскую фигуру S, которая перемещается
в своей плоскости. Безграничную неподвижную плоскость У усло-
вимся в последующем считать совпадающей с плоскостью чертежа.
Плоская фигура S, представляющая
собой сечение плоскостью У, твердого
тела (звена), движение которого нас
интересует, должна иметь, как и само
твердое тело (звено), конечные разме-
ры. Однако в дальнейшем для получе-
ния определенных обобщений условимся
предполагать размеры плоской фигуры
S безграничными, т. е. будем в
число принадлежащих ей точек вклю-
чать и бесконечно удаленные точки.
Это согласуется с принятым в теории
механизмов приемом приписывать в не-
которых схемах механизмов отдельным
звеньям бесконечную длину. Например,
кулисный механизм ABD (рис. 656)
иногда удобно рассматривать как предельный шарнирный четырех-
звенник ABCD, у которого шарнир С удален в бесконечность в
направлении, перпендикулярном к оси кулисы, а звенья ВС и DC
имеют бесконечную длину.
Ниже нас интересуют геометрические соответствия, возникающие
между точками и линиями неподвижной плоскости У и точками и
линиями перемещающейся в этой плоскости фигуры S. Исследование
этих соответствий составляет предмет кинематической гео-
метрии плоского движения. В отличие от кинематики,
730 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
в которой движение рассматривается во времени* в кинематической
геометрии движение изучается отвлеченно от времени.
3°. Задача Бурместера. Поясним ту основную задачу, которая
была поставлена и разработана Л. Бурместером в кинематической
геометрии плоского движения.
Рис. 657.
Положения плоской фигуры S, совершающей движение в своей
плоскости, вполне определяются положениями двух ее точек Е и F.
Пусть на рис. 657 точками Еъ Ft; Е2, F3; Е3, F3; ... заданы после-
довательные положения Sj, S2, S3,... плоской фигуры.
Выберем в произвольную точку при перемещении плоской
фигуры S в положения S2, S3, ..., точка Bt будет занимать положе-
ния В2, В3, ..., которые найдем построением треугольников В2Е2Р2,
B3E3F9, ..., равных треугольнику BiEiFt.
Бурместер поставил следующую задачу: отыскать такие точки В,
в 5,, которые со своими положениями В.2, В3, ... располагаются на
одной окружности, и определить центры М этих окружностей.
При задании трех положений Sb S2 и S3 плоской фигуры произ-
вольная точка В| в S, всегда располагается на одной окружности
со своими положениями В.г и В3, так как через три точки всегда
можно провести окружность.
Если задано четыре положения S1; S2, S3 и S4 плоской фигуры,
то окружность Ь, которая проходит через произвольно выбранную
точку Bi в S, и ее положения В.2 и Вл, как правило, не пройдет
через ее четвертое положение В4.
Бурместер, однако, доказал, что в положении S, всегда можно
установить геометрическое место таких точек Вь которые со своими
положениями В2, В3 и В4 располагаются на одной окружности. Этим
геометрическим местом является кривая 3-го порядка, названная Бур-
местером кривой круговых точек; геометрическим местом центров
соответствующих окружностей оказывается также кривая 3-го порядка,
которую Бурместер назвал кривой центров.
§ 36]
ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
731
При рассмотрении пяти положений St, S2, S3, S4, Ss плоской фи-
гуры Бурместер установил, что может быть или четыре или две, или
ни одной такой точки Bi в Si, которые со своими положениями В.г,
B-i, Bi и Bf располагаются на одной окружности. Эти точки полу-
чили наименование точек Бурместера, а центры соответствующих ок-
ружностей — центров Бурместера.
Рассматривая более пяти положений плоской фигуры в общем слу-
чае нельзя найти такой точки Bi в Sb которая со своими осталь-
ными положениями располагается на одной окружности.
Рассмотрим те соответствия, которые возникают между точками
движущейся плоской фигуры S и точками неподвижной плоскости 2}
в случаях, когда задано два и три положения фигуры S.
4°. Полюс и угол поворота. Пусть неизменяемая плоская фигура S
движется в своей плоскости. На рис. 658 точками Elt Ft и Е.г,
Е2 заданы два ее положения S! и S2. Восставим перпендикуляры
kg и kf из середин отрезков EtE2 и Р2Е2. Точку пересечения этих
перпендикуляров обозначим Р12.
Вследствие неизменяемости фигуры S имеем Е}1\ — E2F2 и по
построению Е2РХ2 = E2Pi2 и FiPi2=F2Pi2. Отсюда следует, что
заштрихованные треугольники EiFtPn и E2FtPl2 равны. Это доказы-
вает, что всякое конечное перемещение плоской фигуры в ее плоскости
может быть осуществлено одним поворотом вокруг точки Р12, которую
условимся называть полюсом конечного поворота*).
•) Шаль назвал эту точку центром поворота, и этот термин в на-
стоящее время широко применяется как в теоретической механике, так и в
теории механизмов. Бурместер ввел для указанной точки наименование полюс,
которое прочно вошло во все работы, касающиеся кинематической геометрии
конечно удаленных положений плоской фигуры. В таких работах применять
термин Шаля «центр» неудобно, так как в них столь же часто его прихо-
дится употреблять в смысле понятия о центре окружности, проходящей через
последовательные положения точки движущейся фигуры S, координаты которого
являются искомыми в задаче Бурместера.
732 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
Отметим угол
Z-ElP 12Z?2 —- /_FiPizF2 — 0i2.
(И-l)
Назовем 612 углом поворота положений Sj и S2. За поло-
жительное направление отсчета угла 613 выберем направление против
движения часовой стрелки, считая 612 = —
Два положения и S.2 плоской фигуры, заданные двумя парами
точек Ei, Fi и Eit Fit всегда однозначно определяют полюс Рк2 и угол
поворота 6j2 *).
Рис. 659.
Если, как показано на рис. 659, перпендикуляры, восставленные
из середин отрезков ЕуЕъ и FjFj, совпадают друг с другом, то по-
люс Р12 определится как точка пересечения направлений F,Fi и E^F*.
Для угла поворота 6|2 останутся справедливыми прежние равен-
ства (11.1).Если заданные отрезки ДД’] и параллельны (рис. 660),
то полюс Р13 совпадет с бесконечно удаленной точкой, направление
которой укажут перпендикуляры к отрезкам ДДД и FtF2. Переме-
щение вокруг этого бесконечно удаленного полюса представит собой
поступательное перемещение плоской фигуры из положения S( в по-
ложение S.j. Вектор указанного поступательного перемещения усло-
вимся обозначать
Возвратимся к общему случаю двух положений Si и S2 плоской
фигуры S (рис. 658). Выберем произвольную точку в Sp Ее поло-
жение в S4 найдем как вершину треугольника В*ЕгРъ рав-
ного треугольнику B^Ft. Положение В$ можно установить также
посредством перемещения точки Bi вокруг полюса Рц на угол 0|2.
Особыми точками в положениях St и S2 являются точки, совпа-
дающие с полюсом Р12: при выборе точки Bt в St> совпадаю-
*) Индекс у полюса Р12 и у угла 612 следует читать «один-два», а не
«двенадцать».
г
§ 36]
Два и три ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
733
шей с полюсом Р12, ее положение В.г совпадет с гем же по*
люсом Р12 как вершина треугольника P^EiFi, равного треуголь-
нику P12£2F2.
Полюс Р12 й угол поворота 612 вполне определяют два поло-
жения S1 и S2 плоской фигуры: имея полюс Р12 и величину
угла б12, можно для любой точки Вх в Si установить ее поло-
жение Р2. Поэтому два положения S,
задать не только положениями то-
чек Ei, Fi и Е2, Ft, но и не-
посредственно полюсом Р12 и углом
поворота 612.
5е. Центры в неподвижной
плоскости. Пусть на рис. 661 два
положения Sj и Sj плоской фигу-
ры заданы полюсом Р12 и углом
поворота 6|2. Переместив выбран-
ную точку Bt в Si вокруг полюса Р12
на угол 612, определим ее положе-
ние В.2. Центр 7И любой окруж-
ности, которую можно провести
через выбранную точку и ее
положение Вг, условимся считать
принадлежащим неподвижной пло-
скости У]. Геометрическим местом
центров Af этих окружностей будет
биссектриса /л12 угла BiP^Bi.
и S2 плоской фигуры можно
Рис. 661.
Для упрощения дальнейшего изложения удобно ввести понятие
об угле пересечения прямых линий.
Под углом пересечения прямых линий В2Рц и Л'1Р12
(рис. 661) условимся понимать угол, на который следует повернуть
вокруг вершины Р12 в выбранном направлении безграничную прямую
BiPti до совмещения ее с безграничной прямой А1Р12. Этот угол
будем обозначать с чертой наверху: /. в^цМ.
За положительное направление поворота прямой В2Рц вокруг
полюса Р12 будем считать направление против движения часовой
стрелки. Очевидно, что /, BiPnM, отсчитываемый против движения
часовой стрелки, и тот же угол, отсчитываемый по движению
часовой стрелки, по абсолютной величине дополняют друг друга
ДО я.
Под углом б12 или ~ (с чертой наверху) условимся понимать не
только угол, равный по величине 612 или соответственно и опре-
деляемый по направлению знаком, но и угол, равный по величине л — 0i2
012
или соответственно к----и обратный по направлению.
734 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. X!
Из рис. 661 непосредственно следует равенство
(11.2)
Это равенство справедливо независимо от того, располагаются
центр М и точка Bj по одну или по разные стороны от по-
люса Р12.
Если выбрана точка Bi в
поворот прямой Р12В вокруг
Рис. 662.
Si, то на основании равенства (11.2)
_ 612
полюса Р12 на угол ~ определит пря-
мую Pt2M ~ tnXi. Наоборот, если вы-
бран центр М, то на основании того же
равенства (11.2) поворот прямой Р12Л1
/ е1а\
вокруг полюса на угол (--~ } опреде-
лит прямую PuBi = Ьы. Любая ее
точка Bi со своим положением В2 бу-
дет лежать на окружности, описанной
вокруг выбранного центра М.
6°. Бесконечно близкие положе-
ния плоской фигуры. Мгновенный
полюс. Предположим, что на рис. 658
положение S2 плоской фигуры, задан-
ное точками В2 и Р2, непрерывно при-
ближается к положению Sb заданному
точками Et и Когда положение S2
переходит в положение S], бесконечно
близкое к положению S(, полюс конечного поворота Р12 обращается
в мгновенный полюс Рп (рис. 662), определяющий эти беско-
нечно близкие положения Si и S] плоской фигуры *).
Перемещение плоской фигуры из положения Si в бесконечно
близкое положение SJ можно представить себе как поворот этой
фигуры на бесконечно малый угол вокруг указанного полюса Рп.
Поэтому для произвольной точки Bt в Si соответственное беско-
нечно близкое положение В\ определится направлением Bit J_BiPn,
которое совпадет с направлением вектора скорости точки Bt.
Если в положении St известны направления скоростей ve и tjf
двух ее точек Ei и Е\, то мгновенный полюс Рл найдем как точку
пересечения перпендикуляров, восставленных из указанных точек Et
и Ft к направлениям этих скоростей.
*) В дальнейшем положение плоской фигуры, бесконечно близкое к поло-
жению St или Ss, условимся обозначать соответственно Sj или S'2, Мгновенные
полюса, определяющие положения S( и SJ или S2 и Sj, ниже обозначаются
соответственно Plt или Pi2. Индексы у этих полюсов следует читать соответ-
ственно «один-один» и «два-два».
§ 36]
ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
735
Так как для произвольной точки в S, ее бесконечно близкое
положение В\ определяется направлением Bit, то окружность, про-
ходящая через бесконечно близкие точки Bi и В\, будет касаться
прямой Bit в точке Bt *). Геометрическим местом центров М окруж-
ностей, которые можно провести через соответственные бесконечно
близкие точки Bi и B'i, явится прямая BiP\i. Это можно записать
в виде равенства
Z BiPnM = 0, (11.3)
фигуры. Полюсный треугольник.
Ei, Fi, Et, F\ и E3, F3 заданы три
в которое преобразуется здесь соотношение (11.2).
7°. Три положения плоской
На рис. 663 тремя парами точек
конечно удаленных друг от
друга положения S2, S3
плоской фигуры. В пересе-
чении перпендикуляров к
серединам отрезков ЕХЕ^ и
FiF2, E}E3 и F\F3, Е^Е;\ и
Р2Р3 найдем три полюса 'по-
ворота Рц, PJ3 и Рп соот-
ветственно положений S,, Х2;
Sp S3 и <S2, S3.
Эти три полюса обра-
зуют так называемый п о- '
люсный треугольник. '
Углы поворота, относя-
щиеся к полюсам Р12, Р13 Рис. 663.
и Р23, обозначим соответст-
венно 612, 013 и 623. Величина каждого из этих углов поворота опреде-
ляется полюсным треугольником. Для доказательства выберем точку В2
в Х2 (рис. 663) в полюсе Р23. Ее положение В-л совпадет с тем же полюсом
Р23, а положение Вх должно лежать на дуге, описанной вокруг полю-
са Р12 радиусом Р|2Д2 = РпРчз- Точку В, можно также рассматри-
вать как соответствующее положение точки В3; следовательно,
точка Bt должна также лежать на дуге, описанной вокруг полюса Р13
радиусом Р13£?3 = Р13Р23. Таким образом, для точки /Д в S2, сов-
падающей с полюсом Р23, ее положение Вг определим как вторую
точку пересечения указанных дуг.
Точка Bi расположится симметрично полюсу Р23 (и совпадающим
с ним точкам Въ и В3) относительно стороны P12Pt3 полюсного тре-
угольника. Угол, на который перемещается точка Вх вокруг полюса Р12
до совмещения с точкой Д2, есть соответствующий угол поворота 612,
*) Из двух соответственных бесконечно близких точек В, и В{ на чертеже
ниже указывается всегда только одна, а именно точка В,, а для второй
точки B'i указывается прямая Bit, на которой она лежит.
736 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. Xt
а угол, на который перемещается точка В{ вокруг полюса Р13 до
совмещения с точкой В3, есть соответствующий угол поворота 013.
Пользуясь понятием об угле пересечения прямых линий, получим:
ZW^ = y, (11.4)
Z (11-5)
Аналогичным образом, выбрав точку В\ в Sb совпадающей
с полюсом Р13, и отыскав ее положения 5.2 и В3, можно устано-
вить, что угол поворота 6аз, который
относится к полюсу Р.23, удовлетворяет
равенству
Z = (И.6)
Равенства (11.4) — (И-6) доказы-
вают основное свойство полюсного тре-
угольника: его стороны пересекаются
в соответствующем полюсе под углом,
равным половине угла поворота тех по-
ложений плоской фигуры, которые оп-
ределяются этим полюсом.
Отметим следующее простое пра-
вило: если в левой части любого из
равенств (И-4) — (11.6) вычеркнуть
общие цифры в индексах крайних по-
люсов, то цифры, оставшиеся в индек-
Рис. 664. сах этих полюсов, будут теми же и
расположенными в той же последова-
тельности, что и цифры индекса угла поворота, стоящего в правой
части равенства. Это правило назовем правилом последова-
тельных индексов. Все равенства, подобные равенствам
(11.4) — (11.6), которые приводятся ниже, подчиняются этому
правилу.
8°. Центры, относящиеся к трем положениям плоской фигуры.
Если задан полюсный треугольник РцР^Р^ (рис. 664), то по выбран-
ной точке Bi в Sj легко установить ее положения В.г и В3. Для
этого достаточно точку В} переместить вокруг полюсов Р12
и Р13 соответственно на углы 6)2 и 613, определяемые равенствами
(11.4) —(11.6).
Центр М окружности, которую можно провести через точку В{
и ее положения и В3, условимся по-прежнему считать принадле-
жащим неподвижной плоскости Этот центр геометрически найдем
как точку пересечения прямых и //г13, полученных в результате
поворота прямых Р^Ву и Pl3Bt вокруг полюсов Р14 и Р13 соответ-
§ 36] ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 737
ственно на углы и Прямая т12 представит собой геометри-
ческое место центров М окружностей, которые проходят через
точки Bi и В-2, а прямая от13 — геометрическое место центров М
окружностей, которые проходят через точки В\ и В3.
Таким образом, каждой точке В{ в Si приводится в соответ-
ствие центр Л1 в плоскости Е. Это будет центр окружности, которая
проходит через точку Bi и ее положения В2 и В3.
Согласно изложенному точка Bi в S( и соответственный ей
центр М в Е подчиняются двум равенствам:
LBiPi2m^ ,
Z BiP13ai = ®
(11.7)
(П.8)
Равенства (11.7) и (11.8) дают также решение обратной задачи:
по заданному центру М в У, отыскать соответственную ему точку
Bi в Si, которая со своими положениями В2 и В3 лежит на ок-
ружности, описанной вокруг упомянутого центра. Эту точку Вх
в Si можно найти как точку пересечения прямых P^Bi и Pi3Bi,
которые получим, повернув прямые МРц и МР13 вокруг полюсов
Р12 и Р13 соответственно на углы (—и (—
Из изложенного следует, что при задании трех положений Sb
Ss и S3 плоской фигуры имеется взаимно-однозначное соот-
ветствие между точками В] в Si и центрами М в У}. Однако это одно-
значное соответствие нарушается при выборе центра М в любом из
полюсов Pl2, Pi3 или Р23. Обратимся к рис.665, на котором кроме полюс-
ного треугольника Pi2 Pi3 Р23 нанесена точка Р?3, представляющая собой
зеркальное отображение полюса Р23 относительно противолежащей
стороны РцРгз полюсного треугольника. Назовем точку Р^з отобра-
женным полюсом, а треугольник Р12Р13Р23 — отображенным
полюсным треугольником.
Выберем точку Bt в St на прямой Р^Рзз- Переместив эту точку
вокруг полюсов Р12 и Р)3 соответственно на углы 6|2 и б13, найдем
ее положения В2 и В3. Очевидно, что точка В3 расположится на
прямой Р13Р23 симметрично точке В{ относительно стороны РцРц
полюсного треугольника. Окружность Ь, описанная вокруг полюса Р!2
через точки и В2, одновременно пройдет через третью точку В3.
Отсюда следует, что центру М, совпадающему с полюсом Р12, соот-
ветствует в Si любая точка прямой Р^Ргз-
Аналогичным путем легко доказать, что центру М, совпадающему
с полюсом Р13, соответствует в St любая точка прямой Р^Ргз, а
центру Л1, совпадающему с полюсом Р23, — любая точка прямой РцРа.
24 И. И. Артоболевский
738 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
При задании трех положений Si, S2 и S3 плоской фигуры однозначное
соответствие между точками в Si и центрами М в У нарушается также
Рис. 665.
Аналогичным путем легко
при выборе точки В{ в Si в одном
нз полюсов Р12 или Р13, или в отоб-
раженном полюсе Р23. Выберем
точку В* в Si совпадающей, нап-
ример, с отображенным полюсом
Р%3 (рис. 665). Тогда ее положе-
ния В? и В* совпадут с полюсом
Р23. Окружность, описанная че-
рез отображенный полюс Р23 вок-
руг любого центра Л1, лежащего
на прямой Р12Р13, пройдет через
полюс Р23. Отсюда следует, что
точке В* в Si, которая совпадает
с отображенным полюсом Р'23,
в неподвижной плоскости У,
соответствует любой центр
М, лежащий на прямой РцРц.
доказать, что точке В\ в Si, которая
совпадет с полюсом Р№ в неподвижной плоскости У соответствует
любой центр Af, лежащий
на прямой Р13Р23, а точ-
ке Bt в Si, которая совпа-
дет с полюсом Р13, — лю-
бой центр 7И, лежащий на
прямой Pi2P23.
9°. Вспомогательное
геометрическое место.
Пусть три положения Sb S2
и S3 плоской фигуры заданы
на рис. 666 полюсным тре-
угольником РцРц^з- Вы-
берем произвольный центр
М в У и установим со-
ответственную ему точку В,
в Si и ее положения В2 и В3.
Через точки В}, В2 и В3
пройдет окружность, опи-
санная вокруг центра М.
Углы между радиусами МВЪ МВг и MBS обозначим соответственно:
712 — Z. BiMB^,
723 — Z. В,МВ„ у13 — BVMB3.
На рис. 666 угол 723 отсчитывается по направлению движения
часовой стрелки, а углы 7i2 и 713 — в противоположном направлении.
§ 36]
ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
739
Проведем биссектрису mti угла у12, которая пройдет через
полюс Р12. Угол пересечения этой биссектрисы с направлением
радиуса МВ^ будет:
(11.9)
Проведем далее биссектрисы /я23 и /я13 углов -|-23 и -|-13, которые
пройдут соответственно через полюса Р23 и Р13. Углы пересечения
этих биссектрис с направлением радиуса МВ{ будут:
Z. 5^3=^ + ^,
Вычитая почленно второе равенство из первого и учитывая равенство
(11.9), получим:
L Р13/ИР28 = = Z 5Й1Р^. (11.10)
Равенство (11.10) доказывает, что пря-
мые, соединяющие центр М с полюса-
ми Р13 и Р23 (в индексах которых после
вычеркивания общей цифры 3 остаются
цифры 1 и 2), пересекаются под углом,
равным половине угла у12 = /,В1А152
(рис. 666).
Проведем окружность через вы-
бранный центр М и полюса Р13 и Р23
(рис. 667). Эта окружность представит
собой геометрическое место центров
М, которые удовлетворяют условию
Ti2 = const.
Л
Рис. 667.
Обозначим указанную окружность через Л1123— у, где верхние
индексы отмечают те положения S2 и S3 плоской фигуры, с рас-
смотрением которых связано это геометрическое место *).
Если центр 711 принадлежит геометрическому месту 7И123— у, то
для отыскания соответственной ему точки Bi в кроме равенств
(11.7) и (11.8), можно использовать также равенство (11.9) или
любые два из этих трех равенств.
10°. Необходимые аналитические зависимости. Проведем декар-
товы оси х, у (рис. 667) с началом в полюсе Р12 и установим ана-
литическую зависимость между координатами центра М (хм, Ум) и
соответственной ему точки Вл (хв, ув) в St. Обозначим через
*) Индекс в обозначении A11S8 — у следует читать «один-два-три».
24’
740 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
и 8В углы наклона к оси х прямых МРЫ и В{Рц, которые соеди-
няют соответственные центр М и точку Bi с началом координат Pt2.
Имеем:
tg§
Ум
м = —
хм
tg8B = tg (Sm-42-)
61»
З’м - хм 2
6 *
ХЛ1+-Vai tg 2^
(П.П)
Обозначим далее через 8В i3 угол наклона к оси х прямой BtPi3
и через 8 угол наклона к той же оси прямой МРК.
Тогда получим:
8В113=8-^;
i Л13 л
и, окончательно
613
Д’1з — Удо — (-vis — ХМ> tg "o'
tg 8Л !3=-----------------------, (11.12)
*43 — + (У13 —Уtg
где х13, _У1з — координаты полюса Р13.
Координаты точки В} (хв, ув) найдем как координаты точки
пересечения прямых BiPl2 и BiPK:
У1з — А1з tg 8В 13
о D О 15, 10
(11.13)
Воспользовавшись равенством (11.4):
Z. РцР 12^23 — “2* >
получим следующую зависимость между координатами (xi3, _у13) и
(Л'23> _у23) полюсов Р13 и Р23 и углом поворота 012 положений Si и S2
плоской фигуры при условии, что начало осей координат выбрано
в полюсе Р]2:
Jhs JCiaysa УазУ1з / j j j
2 АчзУга +У1зУаз
Уравнение прямой MPi3 будет:
У— Ук = (х — *i3)tg8.
На основании равенства (11.10)
Z Р13МРй = ^
уравнение прямой ТИР23 можно записать:
(У —J23) — (х — х2з) tg ^8 -ф- j.
§ 36]
ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
741
При постоянном угле , независимо от величины угла 8, точка пере-
сечения М прямых 2ИР1з и Л1Р23 определяемых указанными уравнениями,
принадлежит окружности А1ш — у. Исключим из этих уравнений
угол 8. Тогда, учитывая равенство (11.14), получим уравнение окруж-
ности Af123— у:
[х* 4~у2 — X (луз х23) —у (_У13 -J-Таз)] 18 — х (У13 Таз) 4~
4- Т (-^ы — -V23) 4- (х 13х2з 4~Т1зТаз) 18 2 ) — (11 • 1
Пусть на рис. 668 вместо трех положений Slt S2 и S3 плоской
фигуры заданы полюсным треугольником РпРцР» ее три другие
положения: Sj, S2 и S4. Углы
поворота 0)2, 014 и 024 этих
положений определятся следу-
ющими равенствами, аналогич-
ными равенствам (11.4) —(11.6):
L P^P^=bf,
L Р1гРЛ=-%,
- = •
(11.16)
Выберем произвольный
центр М в неподвижной плос-
кости Точку Bt в S], ко-
торая со своими положени-
ями Bi и В4 лежит на окруж-
ности, описанной вокруг выб-
ранного центра М, найдем
(11.8):
при помощи
равенств, аналогичных равенствам (11.7) и
/.BiPnM = ^ ,
(11.17)
Переместив точку В, вокруг полюсов Р12 и Р14 на углы 012 и 0ц,
получим ее положения В2 и В4. Отметим угол у12 = /. Sj/UBj. Про-
ведем окружность через выбранный центр М и полюса Рц и Р№.
Точки ее будут удовлетворять равенству
Z РцМР21 =^= L BiMP№
(11.18)
аналогичному равенству (11.10).
742 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
Эта окружность представит собой геометрическое место центров М,
удовлетворяющих условию '(12 = const. Аналогично прежнему обозна-
чим ее 7И124— у.
Если центр М принадлежит геометрическому месту 7И124 — у, то
-для построения соответственной ему точкив Si, кроме равенств (11.17),
можно использовать также равенство (11.18).
В декартовых осях координат х, у с началом в полюсе Р12 урав-
нение окружности /И124— 7 будет:
---А'(х14 4“ х21)—У (_У14 4~ .У24)] tg — х (_Vi*—J'24)
----X2i) 4~ (-^14-^24 ~4~_1'|4_У24) tg y-j ------- 0. (11.19)
Это уравнение получено из уравнения (11.15) посредством замены
в индексах координат цифры 3 на цифру 4.
11°. Три положения плоской фигуры, два из которых бес-
конечно близкие. Пусть на рис. 669 полюсом Р12 и углом 012
заданы два конечно удаленные положения Si и S2 плоской фигуры,
Рис. 669.
не изображена). Центр М упомянутой
пересечении прямой В^ц
а мгновенным полюсом
Рп — ее третье положение
Si, бесконечно близкое
положению Sp
Выберем в Si произ-
вольную точку Bi, ее
бесконечно близкое положе-
ние В'\ определим направ-
лением Bit I ВхРц, а пе-
реместив точку В\ вокруг
полюса Рп на угол 0t2,
найдем ее положение Z?2.
Окружность, которая
проходит не только через
точки Bi и В2, но и третью
бесконечно близкую точку
В\, должна в точке В,
касаться прямой BJ (на
рис. 669 эта окружность
окружности определится в
с прямой /ии, которую получим, повер-
P6i s
i2 на угол
нув прямую P^Bi вокруг
Следовательно, если заданы три положения Sb Si и S2 плоской
фигуры, то произвольная точка Bi в Si и соответственный ей центр М
в У удовлетворяют равенствам:
Z , Z BiPnM= 0.
(11.20)
§ 36] ДВА И ТРИ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 743
Можно поставить обратную задачу: по заданному центру М,
в У определить такую точку Bi в S,, которая со своими положе-
ниями В\ и лежит на окружности, описанной вокруг центра М.
Равенства (11.20) показывают, что эта точка Вх в Si будет точкой
пересечения прямой МРц с прямой Pi2Bi, которую получим, повернув
прямую РцМ вокруг полюса Р13 на угол (—-J-j.
Проведем декартовы оси с началом в полюсе Pi3. В этом случае,
формулы (11.11)—(11.13) для подсчета координат точки В\ (хв, j»B)
в Si по известным координатам центра М (хм, Ум )> перейдут в сле-
дующие:
, ®12
Ум — хм "2"
В~ (хн-хм)&в-(уи-уи) ’ в,
где —угол наклона к оси х прямой BiPXi.
Отметим, что прямая тм = Р12М будет биссектрисой угла
у12 = Z. BtMB2 между направлениями радиусов MBt и МВ.2. Отсюда
получим прежнее равенство (11.9):
£BiMPl2 = ^.
Прямая BiM здесь совпадает с прямой РцМ. Поэтому можно
записать:
Z РцМРк = В^РЫ. (11.22)
Равенства (11.22) доказывают, что прямые, которые соединяют центр М
с полюсами Рц и Ру2, пересекаются под углом, равным половине угла
Т12 = Z BiMB2.
Проведем окружность через центр М и полюса Рц и Р12. Она пред-
ставит собой геометрическое место центров, которые удовлетворяют
условию
у12 = const.
Обозначим эту окружность через Af112— у; верхние индексы указы-
вают те положения Si, Sj и S2 плоской фигуры, с рассмотрением
которых связано это геометрическое место *).
Уравнение окружности 7Й112— f в декартовых осях х, у с началом
в полюсе Р12 будет:
(х2 |-У2 — ххп— yyu)tg^ — хуп -]-jxii=.O. (11.23)
*) Индекс в обозначении Л1118 — к следует читать «один-один-два».
744 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
Рис. 670.
Вывод его не отличается от вывода уравнения (11.15) окружности
/И123 — у.
Если центр М принадлежит геометрическому месту Л4112 — у, то
для определения соответственной ему точки Bi в Sb кроме равенств
(11.20), можно использовать равенство (11.9) или любые два из этих
трех равенств.
Рассмотрим еще три положения St, S2 и S2 плоской фигуры, из
которых S2 и S2 являются бесконечно близкими друг другу. Пусть
конечно удаленные положения Si и S2 заданы полюсом Р1Ъ и углом
поворота 612 (рис. 670), а беско-
нечно близкие положения S2 и
S-2 — мгновенным полюсом Р22.
Выберем произвольную
точку в S,. Переместив
ее вокруг полюса Р|2 на
угол 612, найдем ее положе-
ние В2, а положение В2, беско-
нечно близкое положению Вг,
определим направлением B2t
_LB2P2i. Окружность, которая
проходит не только через точ-
ки Bi и В2, но и через третью
бесконечно близкую точку В2,
должна в точке В2 касаться
прямой B2t. (На рис. 670 эта
окружность не изображена).
Центр М упомянутой окруж-
ности будет точкой пересечения прямой В2Р22 с прямой /я)2, получен-
ной в результате поворота прямой BtPi3 вокруг полюса Р12 на
6ц
угол
Обозначим по-прежнему угол ?i2 = Z BiMB2. Прямая MPi2 будет
его биссектрисой. Поэтому сохранится равенство (11.9):
Так как прямая В2М здесь совпадает с прямой Р22М, то можно
записать:
Z РпМРп = ^- = Z. B^I\2. (11.24)
Окружность, которая проходит через указанный центр М и по-
люса Р12 и Р22, представляет собой геометрическое место центров,
удовлетворяющих условию
f12 = const.
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 745
Обозначим ее через /И122 — у. Уравнение этой окружности в декар-
товых осях х, у с началом в полюсе Pj2 будет:
(х2 4- уг — хх22 —yy2i) tg 4- ху& — yx2i = 0. (11.25)
Если центр М выбран на этой окружности, то для отыскания
соответственной ему точки Bi в Sj, кроме равенства (11.9), можно
использовать равенство (11.7) и равенство
^ВХМР22 = ^, (11.26)
непосредственно очевидное из рис. 670, или любые два из этих трех
равенств.
§ 37. Четыре положения плоской фигуры
1°. Однородные координаты. Циклические точки плоскости.
Циркулярные кривые и их фокус. Прежде чем непосредственно
перейти к рассмотрению четырех положений плоской фигуры, сообщим
кратко некоторые сведения из высшей геометрии, необходимые для
дальнейшего изложения.
Положение точки М (рис. 671) на плоскости вполне опреде-
ляется ее декартовыми координатами х, у. Однако это справедливо
только для конечных точек плоскости.
Все бесконечно удаленные точки плос- у
кости имеют в декартовых координатах
одно и то же условное выражение:
х — оо; у = оо.
Чтобы устранить этот разрыв между
конечными и бесконечно удаленными эле- &
ментами плоскости, в высшей геометрии &
используются так называемые однород- Рис. 671.
ные координаты. В однородных коор-
динатах положение точки на плоскости характеризуется тремя числами
х,у и t, которые подчинены условиям:
гМ,@ьУ1,Ц
Mfx.yt)
х = y = f, (11.27)
Если заданы три числа х, у и t, то точка на плоскости вполне опре-
делена, так как приведенные равенства позволяют отыскать ее де-
картовы координаты.
Обратимся теперь к точке М. (х, у) или в однородных
координатах к точке Л1 (х, у, t) на рис. 671. Соединим ее с
746 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
началом координат О. Тогда угловой коэффициент прямой ОМ будет:
Предположим, что при неизменных координатах х и у коорди-
ната t стремится к нулю (й —0). Тогда декартовы координаты точки М
будут стремиться к бесконечности, но отношение ~ будет оста-
ваться постоянным. Следовательно, точка М будет удаляться по пря-
мой ОМ в бесконечность и в пределе при t = 0 однородные коор-
динаты (х, у, 0) определят бесконечно удаленную или
несобственную точку этой прямой.
Если взять другую прямую OMt с угловым коэффициентом
tgSj = —= =А то однородные координаты бесконечно удаленной
Xi Xi
(несобственной) точки этой прямой будут (xlt j^, 0).
Следовательно, бесконечно удаленных (несобственных) точек на
плоскости бесконечное множество. Совокупность их называется бес-
конечно удаленной (несобственной) прямой. Поскольку
в однородных координатах все бесконечно удаленные точки плоскости
имеют общую координату t = 0, условие
t = 0
принимают за уравнение бесконечно удаленной прямой. С этим урав-
нением можно свободно оперировать и находить пересечение беско-
нечно удаленной прямой с любой прямой и любой кривой плоскости.
Рассмотрим уравнение
а2 й2 ~ ’
которое в осях Оху изображает гиперболу. Введя однородные коор-
динаты по соотношениям (11.27), получим уравнение
Т-2 713
-2 __У ___л
аа Ь* '
Найдем точки пересечения этой гиперболы с бесконечно удаленной
прямой плоскости. Для этого решим последнее уравнение совместно
с уравнением бесконечно удаленной прямой й = 0. Тогда для опре-
деления координат бесконечно удаленных точек гиперболы получим:
= ,=0.
Отсюда координаты двух бесконечно удаленных (несобственных)
точек гиперболы (xb 0) и (х2, у2, 0):
1) = * = 0; 2) f = o.
' Xi 1 а ’ . ’ ' xt а ’
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
7.47
Направления, в которых удалены несобственные точки данной
кривой, называются асимптотическими. Угловые коэффициенты
асимптотических направлений совпадают с угловыми коэффициентами
асимптот кривой.
Использовав координаты бесконечно удаленных точек гиперболы,
получим, что ее асимптотические направления определяются угловыми
коэффициентами:
Х1
6 .J’S
— и кз - ~
а
b
а '
В зависимости от того, являются ли однородные координаты
бесконечно удаленной точки действительными или мнимыми, кривая
имеет действительные или мнимые асимптоты.
В качестве второго примера рассмотрим пересечение бесконечно
удаленной прямой с окружностью
(х — а)2 + (у — b)* — R2 = 0.
Подставим в это уравнение вместо декартовых координат однородные,
используя равенства (11.27):
(х — аОа + (7 — btf — tf2f2 = 0. (11.28)
Решив последнее уравнение совместно с уравнением бесконечно
удаленной прямой t = 0, получим:
= t = Q
или
(х -ф- (у) — iy) = 0; t = 0,
где
i=V— 1.
Это дает две точки пересечения:
2=4-/; / = 0 и 2 = — /; f = 0. (11.29)
Следовательно, окружность пересекает бесконечно удаленную-
прямую в двух точках, которые принадлежат прямым с мнимыми
угловыми коэффициентами 1.
Так как координаты найденных точек пересечения не зависят от
параметров окружности (a, b, R), то можно утверждать, что через
них должны проходить все окружности плоскости. Эти сопряженные
мнимые бесконечно удаленные точки с координатами (11.29) носят
особое наименование — циклических точек плоскости. Все
кривые, которые проходят через циклические точки, называются цир-
кулярными кривыми.
Две окружности, как кривые 2-го порядка, должны пересекаться
в четырех точках. Две из этих четырех точек пересечения всегда совпа-
дают с мнимыми циклическими точками плоскости. Поэтому число
748 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
действительных точек пересечения двух окружностей не превышает
двух. Таким образом, понятие о циклических точках плоскости
позволяет устанавливать наибольшее число действительных точек
пересечения циркулярных кривых.
В теории циркулярных кривых доказывается, что мнимые каса-
тельные к этим кривым в их мнимых циклических точках всегда
пересекаются в действительной точке — особом фокусе цирку-
лярной кривой, называемом ниже просто фокусом.
Уравнение касательной к кривой
F(x, у, 0 = 0
в точке с координатами (xit yit tt) имеет вид:
- . dFMi, tt) d_F Mh ti) t dFM, ti)
ox 1 л dy 1 dt v ’
На основании этого, уравнение касательной к окружности (11.28)
в точке с координатами (хг, yit tt) будет:
х (х, — ati) 4-у (yt — bti) — ti [(х,- — att) а Ц- (J,- — btt) b -ф- /?%] = 0.
Касательные к этой окружности в ее циклических точках с коорди-
натами (11.29) определятся уравнениями:
х iy — t (а -ф- ib) = 0;
х — iy — t(a — ib) = 0.
Координаты точки пересечения этих мнимых прямых будут:
х = at‘, у =bt
или, если перейти от однородных координат к декартовым:
х=а\ у = Ь.
Это значит, что мнимые касательные к окружности в ее мнимых
циклических точках пересекаются в действительной точке, совпадаю-
щей с центром окружности, который является вместе с тем фокусом
окружности.
2°. Кривая центров Л11234. Пусть на рис. 672 двумя полюсными
треугольниками PltPi3Pi3 и РпРцРи с общей вершиной Pi2 заданы
четыре положения Si, S2, S3 и S4 плоской фигуры. Углы поворота
61а, 613 и 614 этих положений определим на основании равенств:
Z. Р\3РцРц = Z. РцРчРц — , (11.31)
Z P»Pl3Pi3 = ; L Р4Р4Р11 = ®f. ' (11 -32)
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
749
Рассмотрим сначала три положения Si, S2 и S3 плоской фигуры,
определяемые полюсным треугольником РцРцРц. Выберем произволь-
ный центр М, не совпадающий с полюсами. Пользуясь равенствами
и Z = ,
найдем соответственную ему точку Bi в Sj. Переместив ее вокруг
полюсов Pi2 и Р1Л на углы 012 и 0J3, получим положения В.2 и Ва.
Через точки В1г Вг и В3 пройдет окружность Ь, описанная вокруг
выбранного центра М. Переместив точку Вх вокруг центра Рп на
угол 014, установим ее положение fi4. Точка В^ при произвольном
Рис. 672.
выборе центра Л1 в общем случае не будет лежать на одной окруж-
ности b с точками Blt В2 и В3.
Рассмотрим теперь другие три положения плоской фигуры, а
именно Si, S2 и Si, определяемые полюсным треугольником РцРцРц-
Пользуясь равенствами
= и
найдем точку В* в соответственную ранее выбранному центру М.
(При произвольном выборе центра Л1 точка В* в общем случае не
совпадет с ранее установленной точкой 5р) Переместив точку В*
вокруг полюсов Р12 и Рц на углы 012 и 014, установим ее положе-
ния В2 и В*. Через точки В*, В2 и Bf пройдет окружность Ь*,
описанная вокруг центра М. Переместив точку В* вокруг центра Р13
750 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
на угол 613, получим ее положение В*, которое в общем случае не
будет лежать на окружности Ь*. Таким образом, окружность Ь,
описанная вокруг центра Af, проходит через найденную точку В, и
два ее положения Д2 и В3, а окружность Ь*, описанная вокруг того же
центра, проходит через вторую найденную точку й* и два ее поло-
жения В* и В%.
Поставим задачу найти такой центр М, которому в Si соответ-
ствует точка Въ лежащая со своими тремя положениями Bit В3 и Bt
на одной окружности, описанной вокруг упомянутого центра М.
Для этого выберем произвольный угол у|2 = /_ BtMB.2. На отрезке
Р13Р23 (рис. 673) как на хорде построим окружность Al123 — у, точки М
которой удовлетворяют равенству
(11.10):
На отрезке PtiPu как на хорде
построим окружность Af124 — 7,
точки М которой удовлетворяют
равенству (11.18):
ZP^W^4 = S.
Выберем за центр А1 точку
пересечения этих окружностей и
рассмотрим сначала три положе-
ния Si, S2 и S3 плоской фигуры,
определяемые полюсным тре-
угольником РцР13Р23. В этом слу-
чае для построения по выбранному
центру Af, лежащему на окружности Af123 — 7, соответственной точки
В{ в Si достаточно использовать два равенства (см. § 36, 9°):
/.BiP^M^-, LBiMPi^1-^.
(11.33)
Рассмотрим далее три положения S|, S2 и S4 плоской фигуры, опре-
деляемые полюсным треугольником Pi2P14P24. В этом случае для
построения по выбранному центру Л1, лежащему на окружности
Af124 — 7, соответственной точки Вх в St достаточно использовать
те же два равенства (11.33) (см. § 36, 10°).
Следовательно, центру Af, совпадающему с точкой пересечения
окружностей А1123 — 7 и AJ124 — 7, в обоих указанных случаях соот-
ветствует в St одна и та же точка Переместив ее вокруг полюсов
Р12, Аз и Рм. на углы 012, 613 и 614, получим ее положения Bt, В3
и Blt которые будут лежать на окружности Ь, описанной вокруг
центра М радиусом MBt.
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 751
Точка Bi в St, которая со своими положениями Въ Вл и Т?4 лежит
на одной окружности, называется круговой точкой. Геометри-
ческое место круговых точек Bt в St называется кривой круговых
точек, а геометрическое место центров Af тех окружностей, которые
проходят через четыре положения круговой точки, называется к р и-
вой центров.
Кривая круговых точек и кривая центров установлены и исследо-
ваны Бурместером [67а, б] и поэтому называются также к р и в ы м и
Бурместера.
Между точками кривой центров и кривой круговых точек имеется
однозначное соответствие и с точки зрения практических приложений
в синтезе механизмов достаточно знать свойства и способы построения
одной из этих кривых. Ниже при решении задач синтеза механизмов
используется только кривая центров. Поэтому изложение теории
кривых Бурместера начнем с изложения свойств кривой центров.
Центр М на рис. 673, совпадающий с точкой пересечения окруж-
ностей /И123 — у и /И124 — у, принадлежит кривой центров, так как
соответственная ему точка Bi в St есть круговая точка. Напомним,
что окружности А!123 — у и А1124 — у были построены при произвольно
выбранной величине угла у12. Точка их пересечения М должна удовле-
творять равенствам (11.10) и (11.18) и вытекающему из них равенству
(рис. 674):
= (И-34)
Если последовательно изменять величину вписанного угла и опре-
делять точки пересечения М соответственных пар окружностей
А1123— у и Д7124 — у, т0 по тОЧ1<ам можно построить всю кривую
центров, которую условимся обозначать /И1234. По самому построению
она должна пройти через полюса Р13, Р23, Р14, Р24, а на основании
равенства (11.31) на ней будет лежать также полюс Р12. Кривая /И1234
изображена на рис. 674. Одна ее ветвь является замкнутой; она про-
ходит через полюсы Р13 и Р23. Вторая ветвь проходит через полюсы
Р12 и Р24 и уходит в бесконечность *).
Так как равенства (11.34) при любом угле определяют точки М,
принадлежащие кривой центров Af1234, то для отыскания точек этой
кривой можно пользоваться одним равенством:
Z Л3Л1Р23= L РпМР^. (11.35)
Это равенство подчиняется правилу последовательных индексов. Если
в левой части равенства в индексах полюсов вычеркнуть общую
*) В зависимости от взаимного расположения полюсов кривая центров №3‘
состоит или из двух обособленных ветвей, как на рис. 674, из которых одна
является замкнутой, а другая уходит в бесконечность, или только из одной
ветви, уходящей в бесконечность.
752 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
цифру 3, а в правой части равенства — общую цифру 4, то останутся
цифры 12, расположенные в одинаковой последовательности. Это
правило облегчает запись указанного равенства.
3°. Уравнение кривой центров Л11234. Серединная прямая. Вы-
берем декартовы оси х, у (рис. 674), начало которых совместим
с полюсом Р12. В этих осях окружности /И123 — у и /И’24— у выра-
жаются уравнениями (11.15) и (11.19). Если при исключении из по-
Рис. 675.
следних уравнений общего параметра tg^y учтем формулу (11.14),
то получим следующее уравнение кривой центров:
С^8 4~>2) (fax —j\y) 4* (71^2 ——7а) X* (71^2 —7г^1 4~7з) >8 4~
4“ 2/4ху Ц- (—j\k3 4-7г^4 4*7з^1 —71^г) X -|-
где обозначено:
== xJ3 х24,
^2 = >13 4~ Уы>
71 = х2з4-л-14 —
fa =>23 4* >14 ^2,
4* (71^4 4~72^з —7з^2 —j^iiy — о,
А) == Л'13>24 4~>13Л'24> 1
^4 = х 1з-£24 — у 13_у24; J
7з = -^23>14 4" *'14>23 ^3,
74 = х^3Хц >23>14 ^4-
(11.36)
(11.37)
(11.38)
Обозначим через 8 (рис. 675) угол наклона к оси х произволь-
ной прямой z, проходящей через начало координат Рц. Отметим точки
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
753
§ 37]
пересечения Л1 и М' прямой z с кривой центров. Координаты этих
точек найдем, решив совместно уравнение (11.36) с уравнением
прямой Z'.
j = xtg 8.
Тогда для определения координат точек М. и М' кривой центров
/И1834 получим формулы:
(„.Зв)
где обозначено:
Wi ——/1^3 4~ /2^4 4~/'з^1 —iJh 4-
4* (/1^4 + 7^3 /з^2 /4^1) tg 8,
=/'1^2 —/2^1 —7з + (71^2 — (11.40)
— Mi4-7з) tg2 8 4- 274 fg й>
®’з = (Л —71 tg 8) (1 4- tg28)-
Введем в уравнение (11.36) кривой центров 7И*234 однородные коор-
динаты, пользуясь соотношениями (11.27):
(х2 _у2) (/gx —j\y) C/'i^g —j\k\ —j3) x2f
4~ (71^2 —4~ hYy* ^j\xyt 4- (—j'i^3 4~/2^4 4~/з^1 —j\kt) xt? 4-
4“ (71^4 4_7a^3 —/3^2 —/4fei)_y/2= 0. (11.41)
Решив последнее уравнение совместно с уравнением бесконечно уда-
ленной прямой t = 0, будем иметь:
(x24-j2)(y2x— y,J7) = O; t = 0.
Это показывает, что кривая центров 7И1234 имеет три точки пересе-
чения с бесконечно удаленной прямой, которые определяются угло-
выми коэффициентами:
где i = ] — 1.
Первые две точки пересечения суть мнимые циклические точки
плоскости. Отсюда следует, что кривая центров 7И1234 принадлежит
к циркулярным кривым. Третья точка пересечения — действительная.
Наличие ее свидетельствует, что кривая центров /И1234 имеет беско-
нечно удаленную ветвь с асимптотическим направлением, определя-
емым угловым коэффициентом:
tg800 =^. (11.43)
754 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
Отметим середины К и N отрезков Р^Рц и РцР^ (рис. 675).
Прямую AW. обозначим Ш|234. Ее угловой коэффициент будет:
g__ -У Zf Ум __У1а 4~3’2л —У аз ~~ Уи
X — XXta ф- Л'24 — А?йз — Хц
Выразив в уравнении (11.43) величины ]\ и /я через координаты по-
люсов Р13, Р24, Р14 и Р23 по формулам (11.37) и (11.38), убедимся,
что угловой коэффициент прямой tnKii = KN равен угловому коэф-
фициенту асимптотического направления кривой центров /И1234. Пря-
мая /zz1234 играет большую роль в теории кривых центров и называется
серединной прямой.
4°. Свойства фокуса и бесконечно удаленной точки кривой
центров. Отыщем координаты фокуса кривой центров Л4*234. Исполь-
зовав формулы (11.30) и (11.36), напишем уравнения касательных
к кривой 7Й1234 в ее мнимых циклических точках:
х (Ji — у\) +7 (Ji -ф- iji) — t (/3 — Z/4) = 0,
x (ji (Ji) ~г У (Ji — iji} — ^(/з + (A) = 0-
Точка пересечения этих мнимых прямых определит фокус кри-
вой /И1234. Перейдя к декартовым координатам и решив эти урав-
нения, получим для координат фокуса следующие формулы:
о1-44)
JI J2
Возвратимся к равенству (11.35):
L P^MP^= LPuMPtl,
которым определяются центры М, принадлежащие кривой центров
А11234. Два полюса Р13 и Р24 или Р23 и Р14, занимающие в последнем
равенстве крайние или средние места, назовем противопол юсами.
В декартовых осях с началом в полюсе Р12 (рис. 675) кривая д[12м
определяется уравнением (11.36), коэффициенты которого klt k2, k3,
fe4, Ji, Ji, j3 и j\ выражаются через координаты полюсов Р13, Р23,
Рм и Рц- Отметим, что координаты противополюсов Р13 и Р24 входят
во все указанные коэффициенты уравнения (11.36), а координаты
противополюсов Р23 и Р14 входят только в коэффициенты у8,
/3 и Jt- Отметим далее, что уравнение (11.36) является однородным
относительно коэффициентов j\, jt, j3 и /4. Следовательно, эту кри-
вую определяют не абсолютные величины указанных коэффициентов,
а их отношения:
Уз Ум ф-Д’и — У 1з — 5'24
У1 Х23 Ф" ------ -*13 - А24
/в___ хмУн Ф- Ац5'гЗ ---- А'!3_У24-Х~24_У13
Jt А'зз-рХл — A'ia— A'S1
jt___х2зХц —УмУн — xiaXsi -f-УмУм
Ji A'sa ф- А и — Aia — Xai
(11.45)
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 755
Если выбрать на кривой центров /И1234 (рис. 675) две произволь-
ные точки F(xp, ур) и G{xq, у о) и заменить ими противополюсы
Pi3 и P\i в равенстве (11.35), то оно примет вид:
L PisMF= L GMPVi. (11.46)
Это равенство определит такое геометрическое место точек /И, урав-
нение которого по форме совпадет с уравнением (11.36) кривой
центров 7И'234. Однако коэффициенты j\, jt, j3 и j\ этого уравнения,
обозначаемые ниже /*, у*, /* и определятся формулами:
Л — хР Xq — xt3 — xti,
Л —Ур +J'g —_У1з —Уа>
Л = ХгУо хоУг — х\зУи. —У1зхы>
Л = XFXQ ~ урУа — *13*24 +№№•
(П-47)
Эти формулы получены из формул (11.38) посредством замены в них
координат противополюсов Р23 и ри координатами точек F и G.
Геометрическое место точек М, удовлетворяющих условию (11.46),
может быть построено подобно кривой центров Л41234 как геометри-
ческое место точек пересечения двух таких семейств окружностей,
которые опираются на отрезки Pt3F и GPU равными вписанными уг-
лами. Это геометрическое место пройдет через полюса Р\3 и Рп и
точки F и О, выбранные на кривой /И1234.
Выберем теперь за точку G, которая входит в равенство (11.46),
не произвольную точку кривой центров /И1234, а ее бесконечно уда-
ленную точку. Выбор координат точки F подчиним следующему
требованию: геометрическое место точек М, определяемое условием
(11.46), должно быть тождественно кривой центров /И1234. Для этого,
очевидно, достаточно, чтобы были соблюдены следующие три ра-
венства:
— = — 7з__Л. Р=Р (1148)
/1 Л /1 /Г л i'F ’ ’
Левые части этих равенств подсчитаем по заданным координатам
полюсов Р13, Р23, Р)4 и P2i [см. формулы (11.38)]; в правые части
этих равенств, кроме заданных координат полюсов Р13 и Р24 и вы-
бранных координат точки G, входят искомые координаты точки F
[см. формулы (11.47)]. Так как точка G совпадает с бесконечно уда-
ленной точкой кривой центров, то ее декартовы координаты будут
хо = оо и _уо = оо, а их отношение равно угловому коэффициенту
асимптотического направления кривой центров, т. е.
Ус___Js
Xq Ji
756 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. \|
Тогда на основании равенств (11.48), учитывая формулы (11.47),
получим: . .
h=yF-\-xFJ4‘, j4 = xF—yFJ*.
Ji ' A A Л A
Отсюда координаты точки F:
Jih H~ ДА .
Л+Л ’
A/'s — jtjt
П + Л ’
Сравнив эти формулы с формулами (11.44) убедимся, что найденная
точка F совпадает с фокусом кривой центров 7И1234. Следовательно,
если в условии (11.46) точка G есть бесконечно удаленная точка кри-
вой центров Л41234 (в дальнейшем бесконечно удаленную точку
кривой центров будем обозначать А!ю), а точка F— фокус этой
кривой, то геометрическое место точек М, определяемое равенством
L PKMF= £ М^МРи, (11.49)
будет тождественно кривой центров /И1234. В этом равенстве сторона
ММт угла МтМР21 параллельна асимптотическому направлению кри-
вой центров, т. е. параллельна серединной прямой от1234.
Так как уравнения (11.47) симметричны относительно координат
точек F и G, то кривую центров определит также равенство
£ ЛзТИТИоо = Z FMP^, (11.50)
получаемое из предыдущего путем перестановки местами фокуса
F и бесконечно удаленной точки кривой центров Af1234.
Если для произвольной точки Af кривой центров /И1234 справед-
ливы порознь каждое из трех равенств (11.35), (11.49) и (11.50),
то будут справедливы и производные от них равенства:
£FA1P23 = £ РиММт (11.51)
и
£ М^МР^ = £ PltMF. (11.52)
Каждое из четырех равенств (11,49) — (11.52) позволяет указать
прямую, которая проходит через фокус F кривой центров А11234. Это
дает простой способ графического нахождения фокуса F. Обратимся
к рис. 676, на котором нанесены полюсы Р12, Р)3, Р23, Р14, Р24 и
серединная прямая /П|2:14, направление которой совпадает с асимптоти-
ческим направлением кривой центров AI1234. Так как полюсы Р23 и
Р14 лежат на этой кривой центров, то, подставив в равенство (11.49)
вместо центра М сначала полюс Р23, а затем полюс Р44, получим:
£ PiaP^F — £ 7ИооР23Р24, (11.53)
£ РцРцР= £ Л^соРцРщ- (11.54)
Стороны М^Р23 = т23 и М^Рц == ти углов M^P2iP2l и МтР^Р21,
входящих в последние равенства, параллельны прямой т1234. Учитывая
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
757
ЭТО, на основании указанных равенств получим две прямые FP23=/23
и FPU = /и, в пересечении которых получим фокус F.
Заменив в равенстве (11.51) точку М сначала полюсом Pi3, а за-
тем полюсом Р24, получим равенства:
ЭТО-
ПО-
Z.FPi3Pi3—Z, РиАз^оо» (11.55)
Z, FP^P^ = РцРцМсо- (11-56)
Эти равенства позволяют установить еще две аналогичные прямые /13
и /2i, которые проходят через фокус F.
Если один из полюсов оказывается в бесконечности, т. е. совпа-
дает с бесконечно удаленной точкой
совпадает с противополюсом
го бесконечно удаленного
люса.
5°. Способы построения
вой центров Л11234.
Первый способ (способ
Альта). Этот способ основан
на использовании равенства (11.35):
ЛТоо кривой
УН1234, то фокус F
кри-
Z. РцМР%3- L- РцМР^,
которому должна удовлетворять
каждая точка М кривой центров
/И1234. Разделим хорды P13Pi3 и
РхцРц (рис. 677) пополам. Точки
этого деления обозначим соответ-
ственно D и Е и восставим из них
перпендикуляры d и е к соответ-
ствующим хордам. На произволь-
ной оси Ох отложим отрезки OD3 = Pi3D и ОЕ0 = РцЕ и из точек Do и
Ев восставим перпендикуляры d0 и е0 к оси х. Проведем через
точку О произвольный луч Oz', который пересечет прямые </0 и е0
в точках Ь'„ и Е'п. Тогда отрезки OD3 и ОЕ3 определят радиусы
таких окружностей т‘г! и т'е, опирающихся соответственно на хорды
Pi3Pi3 и РцРц> точки пересечения которых М и М' принадлежат
кривой центров Af1234. Центры этих окружностей D' и Е будут ле-
жать соответственно на прямых d и е. Центр £)' может быть выб-
ран на прямой d по любую сторону от хорды Pi3Pi3.
центр Е должен быть выбран на прямой е по ту
хорды РцРц, где удовлетворится равенство
После этого
сторону ОС
Z Pi3D’Pi3^ Z PuEP^.
Проводя последовательно другие лучи Oz", Oz'", ... и описывая
соответственные окружности, опирающиеся на хорды Pl3Pi3 и РцРц,
построим по точкам всю кривую AI1234.
758 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
Этот способ не дает возможности получить достаточно точное
построение тех участков кривой /И1234, на которых соответственные
окружности пересекаются под малыми углами*).
Второй способ основан на использовании установленного
выше равенства (11.49):
Z P^MF = Z /ИооЖР24,
которому должна удовлетворять каждая точка М кривой центров /И1234.
Проведем прямую k (рис. 678), параллельную серединной пря-
мой w1234, на расстоянии РцК=-^ PkF от полюса Р24, где F — фо-
кус искомой кривой. Из середины D отрезка PViF восставим перпен-
дикуляр d. Далее через полюс Р24 проведем произвольную прямую г',
которая пересечет прямую К в точке К'. Через полюс Р13 и фокус F
проведем окружность гп’ радиусом D'Р13 = РцК'. Центр D' должен
при этом лежать на прямой d по ту сторону отрезка Pi3F, где
соблюдается равенство углов
Z. P\?,D'd = /_ kK'Рц.
Легко сообразить, что в этом случае точки пересечения М и М'
прямой г' и окружности т' будут удовлетворять упомянутому выше
*) Угол пересечения двух окружностей — это угол, образованный касатель-
ными к окружностям в точке их пересечения.
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 759
равенству (11.49) и, следовательно, будут принадлежать кривой
центров ЛР234.
Если через полюс Р24 проведем новую прямую и опишем на
хорде P13F новую соответственную окружность, то в пересечении
их получим новые точки кривой центров /И*234.
При необходимости уточнить тот или иной участок кривой /И1234
можно вместо равенства (11.49) воспользоваться любым из трех дру-
гих равенств (11.50) — (11.52), которые дадут три аналогичных спо-
соба построения искомой кривой центров. В этих случаях узлом пучка
прямых z и неизменной хордой соответствующего пучка окружностей,
Рис. 679.
вместо полюса Р24 и хорды FP13 соответственно будут: полюс Р13 и
хорда FPU, полюс Р14 и хорда FP23 или полюс Р23 и хорда FPU.
Третий способ (способ Бурместера). Напомним, что
первые два способа построения кривой центров ЛР234 основаны непо-
средственно на использовании равенств (11.35) и (11.49) — (11.52).
Излагаемый ниже способ построения предложен Бурместером [67а, б].
Не останавливаясь на обосновании этого способа, которое требует
знания ряда теорем проективной геометрии, покажем последователь-
ность его построений.
Соединим фокус F (рис. 679) с двумя произвольными полюсами,
например Р13 и Р24. Вокруг точек пересечения К\ и Кч прямых FPI3
и FP24 с серединной прямой /«1234 опишем окружности kx и про-
ходящие соответственно через 'полюсы Р13 и Р24. Обозначим точки
пересечения этих окружностей буквами Нх и /72. Эти точки распо-
лагаются симметрично серединной прямой w1234.
760 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. Х|
Проведем через фокус F произвольную прямую г', которая пересече;
серединную прямую /и1234 в точке D'. Опишем вокруг точки ГУ окру-д-,
ность т' через точки и Нг. Тогда точки пересечения М и М' прямой
г' с окружностью т' будут принадлежать кривой центров /И1234.
Способ построения Бурместера выгодно отличается от предыду.
щих двух способов тем, что соответствующая прямая z' и окруж-
ность т' всегда пересекаются под прямым углом, что позволяет более
точно устанавливать положение точек их пересечения. Но ему при-
сущи и свои недостатки. Нередко вспомогательные окружности в
kt пересекаются под острым углом (как получилось на рис. 679).
В этом случае определить точное положение их точек пересечения Н1
и Hi затруднительно. Ошибки в определении положения упомянутых
точек непосредственно отражаются на точности нахождения точек
Рис. 680.
окружности, соответствующей
кривой центров /И1234. Далее из самого
способа построения очевидно, что
нельзя обеспечить достаточной точно-
сти построения кривой /И1234, если фо-
кус F располагается очень близко к
серединной прямой т]234. Наконец, са-
мым существенным недостатком ука-
занного способа Бурместера является
то, что он применим только для таких
кривых центров, которые состоят из
двух обособленных ветвей. Если кри-
вая центров состоит из одной ветви,
то, как показал Бурместер, вспомога-
тельные окружности kt и k2 не пересе-
каются друг с другом. Для этого слу-
чая Бурместер [67 а, б] дал другой
способ построения кривой центров
/И1234, при котором для определения
произвольной прямой г', проведенной
через фокус F, требуется ряд вспомогательных построений, суще-
ственно снижающих точность нахождения точек кривой центров. Этот
способ Бурместера мы не излагаем и для построения кривых центров,
состоящих из одной ветви, рекомендуем пользоваться вторым спосо-
бом, указанным выше.
6е. Четыре полюсных треугольника. Из четырех заданных поло-
жений Si, S2, S3 и S4 плоской фигуры можно составить четыре соче-
тания по три: Sj, S2, <S3; <S„ S2, <S4; Sn S3, S4 и S2, S3, S4. Каждому
из этих сочетаний по три соответствует свой полюсный треугольник:
РцРцР^ РцРцРц> РазРцРц и Ря»РцРз1-
Любые два полюсных треугольника, из указанных четырех, опре-
деляют четыре заданных положения S,, S2, S3 и S4 плоской фигуры,
а следовательно, и два других полюсных треугольника. Пусть на
рис. 680 заданы два полюсных треугольника РцР^Р^ и РцРцРц
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
761
с общей вершиной Рп. Требуется найти полюсные треугольники Р^РцРц
и Р^Р^Ры.- Практически это сводится к отысканию неизвестного
шестого полюса Рм. На основании свойств полюсного треугольника
можно написать четыре следующих равенства:
Z Р^Р^Ры = Z у,'
Z РпР^Ри = Z Р1зА4РМ = %*,
Д .
z Wi»= z адДД=<2з>
Z РцРцРц — £- РцРцР-м — "2" •
(11.57)
Чтобы безошибочно написать эти равенства, достаточно вспомнить
правило последовательных индексов (§ 36, 6°): вычеркнем в левых
частях этих равенств общую цифру в индексах полюсов, зани-
мающих крайние положения; затем ту же операцию повторим со сред-
ними частями этих равенств; тогда оставшиеся цифры в индексах
соответствующих полюсов совпадут с цифрами в индексах соответ-
6
ствующих углов 2" и с цифрами в индексах полюсов, определяющих
вершины соответствующих углов. Например, проделав эти операции
для верхней строки, получим:
Z W, = L W = Д.
k J У
Каждая строка равенств (11.57) определит прямую, которая проходит
через полюс Р34. Таким образом, найдем полюсные треугольники РцР^Рц
и РълРцРц-
Из четырех полюсных треугольников Р^Р^Р^, РцРцРц, РцРцРщ
и Р23Р24Р34 можно составить шесть сочетаний по два, причем тре-
угольники, входящие в каждое из этих сочетаний, будут иметь общую
вершину. Ниже дан перечень этих сочетаний; в верхней строке ука-
зана упомянутая общая вершина соответствующих полюсных тре-
угольников:
pia Pi> Рн Раз Pst P»4
28 РцРцРаз РиРцРц р 18р18р!8 РцР11Р«4 PisPkPsi
PisPuPsi РцРцРц Р18РцР»< Ра8Р81Р81 РSsP84P84 PS8PS4P84
Ранее (на рис. 672—675 и 680) четыре положения Sb S2, S3 и S4 пло-
ской фигуры мы постоянно задавали двумя полюсными треугольни-
ками Pi2Pi3P23 и РцРцРц с общей вершиной Р12. Использовав
762 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. Xt
окружности /И123 — у и /И’24 — -у, определяемые углом -fl2 = /_
(см. § 36, 9г), мы установили, что все точки М кривой центров
УИ1234 удовлетворяют равенству (11.35):
Z РцМРц.
Выбрав другие сочетания полюсных треугольников по два для
определения четырех положений S1; S2, S3 и S4 плоской фигуры,
можно аналогичным путем установить, что все точки кривой цент-
ров 7И1234 должны также удовлетворять каждому из пяти следующих
равенств:
Р13: L PnMPVi= L РцМР31, (11.58)
Ри- Z РКМР^= £ Р13МРЛ1, (11.59)
Pt3- L PnMPl3= L PtiMP3i, (11.60)
Ры Z PttMPtl= A PtsMPilt (11.61)
P3i: L Pl3MPtl = /_ P^MP^. (11.62)
Слева стоит общая вершина тех двух полюсных треугольников, из
рассмотрения которых получено соответствующее равенство. Легко
заметить, что из шести аналогичных равенств (11.35) и (11.58)—
(11.62) только три являются независимыми. Равенства (11.62) и (11.61)
можно получить соответственно из равенств (11.35) и (11.58), поменяв
местами полюса Pi3 и Р14. Равенство (11.60) получим из равенства
(11.59), поменяв местами полюса Р13 и Р24.
Каждое из этих равенств может быть непосредственно использо-
вано для построения кривой центров Л41234 по первому из указанных
способов. Заменив в каждом из этих равенств полюсы, занимающие
средние положения, или полюсы, занимающие крайние положения,
фокусом F и бесконечно удаленной точкой Мт, получим равенства,
аналогичные равенствам (11.49)—(11.52). Ими можно воспользоваться
для построения кривой центров /И1234 вторым способом.
7°. Отдельные случаи задания четырех положений плоской
фигуры.’ Выше рассмотрен случай, когда четыре заданных положе-
ния Sj, S2, S3 и S4 плоской фигуры являются конечно удаленными
друг от друга. Относящаяся к этому случаю кривая центров была
обозначена /И1234. Ио могут быть случаи, когда некоторые из четы-
рех заданных положений плоской фигуры или даже все эти положе-
ния являются бесконечно близкими. Перечислим отдельные возможные
случаи задания четырех положений плоскости и укажем соответствую-
щие кривые центров.
1) Из четырех положений плоской фигуры два положения являются
бесконечно близкими. Например, может быть задано четыре положе-
ния Si, Sj, S2 и S3 плоской фигуры, из которых положения St и SJ
бесконечно близкие, или задано четыре положения Si, S2, S2 и S3,
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 763
-из которых положения S2 и S2 бесконечно близкие. Соответствующие
этим случаям кривые центров обозначим Л4П23 и /И1223.
2) Четыре положения плоскости попарно являются бесконечно
-близкими. Например, может быть задано четыре положения Sb Sb
,S2 и S2, из которых положения и Sb S2 и S2 являются бесконечно
близкими. Кривую центров, соответствующую этому случаю задания
четырех положений плоской фигуры обозначим /И1122.
-- 3) Из четырех положений плоской фигуры три являются беско-
нечно близкими. Например, может быть задано четыре положения Sb
S], S* и S2 плоской фигуры, из которых три положения Sb S'] и Sj
являются бесконечно близкими. Соответствующую кривую центров
обозначим 7И1112.
Рис. 681.
4) Все четыре положения Sb S’b Sj' и S]" плоской фигуры являются
•бесконечно близкими. Соответствующая кривая центров будет Л1|Ш.
Кривые центров, в индексах которых содержится не более двух
одинаковых цифр (кривые центров А/1123, /И1223 и Ж1122), легко полу-
чить как частные случаи кривой центров /И1434 путем предельного
перехода от конечно удаленных положений плоской фигуры к ее
бесконечно удаленным положениям. Кривые центров, в индексах которых
содержится более двух одинаковых цифр (кривые центров /И1112 и 7И1111),
не удается получить путем предельного перехода от конечно удаленных
положений плоской фигуры к ее бесконечно удаленным положениям. Для
установления этих кривых требуется особые методы (см. главу XVI).
8°. Случай четырех положений плоской фигуры, из которых
два являются бесконечно близкими. Рассмотрим случай, когда из
четырех заданных положений Sb Sb S2 и S3 плоской фигуры два
положения S и Sj являются бесконечно близкими. Па рис. 681 эти
764 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. м
четыре положения плоской фигуры заданы полюсным треугольни-
ком Pt2P13Pw и мгновенным полюсом Рп. Кривая центров, соответ-
ствующая указанным положениям плоской фигуры, будет Ж1123. Эта
кривая но-прежнему представит собой геометрическое место таких цент-
ров М, которым соответствуют в St круговые точки Вх, т. е. точки,
лежащие на одной окружности со своими положениями Bj, В2 и В3.
Выберем произвольную величину угла у12 = ВХМВ2 (см. § 36, 9°)
и построим на хорде Pj3P23 окружность Ж123 — 7, а на хорде РмРц —
окружность Ж112— у (см. § 36, 11°). Точки их пересечения Ж буду!
принадлежать кривой центров Ж1123 *). Отсюда получим, что для
каждой точки Ж кривой центров Ж1123 справедливо равенство
Z. Pi3-44P23= Z, РПЖР12, (11.63)
удовлетворяющее правилу последовательных индексов.
По выбранному центру Ж на кривой Ж1234 соответственная точка В,
в Sj может быть построена на основании равенств:
Z ВхРмМ = L ВДА = ~,
L ~В^М = Z Р.аР13Раз = v, [ (lk64)
Z5iPuAl = 0. '
В декартовых осях х, у, начало которых совмещено с полюсом Р12,
зависимость между координатами центра Ж (хм, АлО и соответствен-
ной точкой Вх(хв, У в) определяется формулами (11.21).
Исключив из уравнений (11.15) и (11.23) окружностей Ж123 — 7
и Ж112 — 7 общий параметр tg 4^ , получим следующее уравнение кри-
вой центров Ж1123:
(jc2 “Fa2) (jtx —ВУ) 4~ (ЛА1з —jixK —/з)x<i 4“ С/1А13 —jixi3 ~\~.Ь)у9 4“
4“ 2jtxy -j- (Jsxi3 —Jtyis)x — Usyw “F Jtxii)У — 0, (11.65)
где обозначено:
Ji —xxl — xI3 -F x23, J3 = ХцА«3 4“ х2зА11>
/2 —Au —A13 4“ А23» J i — xiXxi3 —АнАзз-
При выбранном на рис. 681 расположении полюсов кривая центров Ж1123
состоит из одной ветви. По своим свойствам эта кривая не отли-
чается от кривой центров Ж1234. Она является циркулярной кривой
3-го порядка, которая проходит через все четыре полюса Р12, Pi3,
Pi3 и Ри и имеет ветвь, уходящую в бесконечность.
*) Доказательство последнего не будет отличаться от приведенного выше
доказательства того, что точки пересечения соответственных окружностей Л41гз—7
и Л1124 — 7 принадлежат кривой центров Ж1231 (см. § 37, 2°).
(11.66)
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 765
Отметим середину К (рис. 682) отрезка, стягивающего противо-
полюсы Р13 и Р12, и середину N отрезка, стягивающего противо-
полюсы Pi3 и Рц*). Прямая будет серединной прямой
для кривой центров Af1123. Угловой коэффициент прямой /иП2з анали-
тически подсчитаем по формуле (11.43):
где ji и у2 определяются формулами (11.66). Координаты фокуса F
кривой /И1123 найдем по прежним формулам (11.44):
„ __JiJt-Fjah . ___jih — hjt
F~~ jl + Л ’ JI+jI •
Кроме равенства (11.63), точки кривой центров А!1’23 удовлетво-
ряют каждому из четырех следующих равенств:
Z FMPi3 = Z МК, L ~P^MF = Z Жсо/ИРм,
Z М^МР^ = Z Pu^F, Z /<алшт= Z РМР^.
(11.67)
Эти равенства получим, заменив в исходном равенстве (11.63)
противополюса Р13 и Р12 или Р23 и Рп фокусом F и бесконечно
удаленной точкой /Исо кривой ^А11123. Каждое из указанных ра-
венств можно использовать для построения по точкам кривой /И1123
вторым способом, изложенным- в пункте 5° настоящего параграфа.
*) Противополюсами здесь по-прежнему названы полюсы Р13 и Р12, Р23 и
Рн, которые занимают в равенстве (11.63), определяющем точки кривой цент-
ров Л411аз, крайние и средние места.
766 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
Графически фокус F найдем как точку пересечения любой пары
из четырех прямых Pi2F, Pl3F, P^F или РПР, которые удовлетво-
ряют равенствам, аналогичным равенствам (11.53)—(11.56):
Z РliFfiF Z МсаР23Рj4,
Z FPriPi3=/_ РпРпМ",,
Z FP^Pi3— РцРцМоо,
Z Г*1зРцР= Z МооРцР^,
(11.68)
где /Иоо — бесконечно удаленнная точка кривой центров Л!1123, на-
правление которой определяется серединной прямой /д1123. Сто-
роны Л4ооР8з> Р^Мсо, РцМоо и Л1соРц соответствующих углов, вхо-
дящих в равенства (11.67), параллельны серединной прямой /ггИ23.
(На рис. 682 нанесены толь-
ко прямые /13 = Р13Р и
/^ = Р^Р, проходящие че-
рез фокус F, и вспомогатель-
ные прямые т13 = РпМт и
т13 = MmPi3.) Когда один
из полюсов Р12, Р13, Р23 или
Рп оказывается в бесконеч-
ности, фокус кривой /И’123
совпадает с его противопо-
люсом.
Рассмотрим еще случай,
когда при задании четырех
положений плоской 'фигуры
бесконечно близкими яв-
ляются положения S2 и S2,
а не положения S, и SJ, как
в предыдущем случае. Пусть
четыре положения Sb S2, S2
и S3 заданы полюсами ко-
нечного поворота Р12, Р13, Р23 и мгновенным полюсом Р22 (рис. 683).
Выберем опять произвольную величину угла -[12 = ВХМВ2 (см. § 36, 9°)
й построим на хорде РхзРгз окружность /И123 — а на хорде Р12Р22 —
окружность /И122— 7 (см. § 36, 11°). Точки их пересечения М и М'
будут принадлежать кривой центров /И1223 и удовлетворять равенству
Z PViMPi3 = z Р12ЖР22.
(11.69)
Это равенство подчиняется правилу последовательных индексов.
Уравнение кривой центров 7И1223 получим, исключив из уравнений
(11.15) и (11.25) окружностей /И123 — у и /И122 — -у параметр tg^:
(х2 -ф- J2) (j2x —Ду) + ОУм —/2х23—/а) х2 4-
+ (/1У2з—jixa 4-/з)У ~г 2/4х_у -j-
4~ —h Уи) х — {кУю У Йх-1а)У = О, (11 -70)
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 767
где обозначено:
д = х22-ф-Xi3— лг23, /3 = -v22_v,3-|-x13j22, | (1171)
/2 = Уи2 “J- .Via—_У23> У4==-^22-'-1з ’-УаОЧз- I
Это будет опять циркулярная кривая 3-го порядка, которая проходит
через все четыре полюса Р)2, P(3, Р23 и Р22. При выбранном на
рис. 683 расположении полюсов она состоит из двух обособленных
ветвей. Одна из них уходит в бесконечность.
Отметим середину К отрезка, стягивающего противополюсы Р12 и Р23,
и середину N отрезка, стягивающего противополюсы PJ3 и Р22. Пря-
мая К?/=/«1523 будет серединной прямой для кривой центров /И1223.
Угловой коэффициент этой прямой подсчитаем по-прежнему по фор-
муле (11.43), а координаты фокуса F кривой /И1223 найдем по фор-
мулам (11.44), в которых коэффициенты jb js и /4 определяются
формулами (11.71).
Для построения этой кривой можно использовать любое из четы-
рех равенств, аналогичных равенствам (11.49)—(11.52):
Z Pi3MF = L МеьМРы LFMPi3 = Z РпММт,
________ _______________________ (11.72)
Z Pia/WWoo = Z FMP№, Z MmMPi3 = z PnMF.
Они получаются путем замены в исходном равенстве (11.69), опре-
деляющем кривую центров 7И1223, противополюсов Р13 и Р22 или про-
тивополюсов Р23 и Р12 соответственно фокусом F и бесконечно уда-
ленной точкой Ma, исследуемой кривой.
Графически фокус F можно найти при помощи любых двух
равенств из следующих четырех, аналогичных равенствам (11.53)—
(11.56):
Z РцРучР = Z Л1ооР12Р22, Z FPl3Pi3 = РцР^Мсо, (и
Z PtsP^F = Z /^ооГ’гз^гг» Z FP^Pi3 = Z РцРгъМоо.
Воспользуемся для построения кривой Л1'223 вторым способом,
изложенным в пункте 5° настоящего параграфа. Будем исходить из
равенства
Z Р13ЛЖо = Z FMPti. (11.74)
Проведем прямую k (рис. 684) на расстоянии Pl3K = P¥iF от по-
люса Р13. Из середины D отрезка Р22Р восставим перпендикуляр d.
Далее через полюс Р13 проведем произвольную прямую г', которая
пересечет прямую k в точке К'. Проведем через полюс Р22 и фо-
кус F окружность Ь' с радиусом, равным отрезку Pi3K'. Центр D'
этой окружности должен лежать на прямой d по ту сторону отрезка
P22F, где соблюдается равенство углов
Z Pi3K'k= £ dD'Pi3.
768 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. Х|
Точки пересечения М окружности Ь' с прямой г' принадлежат кри-
вой центров Ж1223. Для доказательства этого проведем через любую
из точек М прямую т=ММа || zzzi223. Тогда получим очевидные
равенства:
Z PKK'k= Z Р13ЖЖЛ; z diyp^= L'FMP^,
которые при учете предыдущего равенства приводят к исходному
равенству (11.74), определяющему точки кривой центров /И1223.
9°. Кривая центров Ж”22. Рассмотрим еще случай, когда четыре
заданные положения Sb Sj, S2, S2 плоской фигуры попарно являются
бесконечно близкими. Эти положения заданы на рис. 685 полюсом
конечного поворота Р12, углом поворота
Рис. 684.
612 и мгновенными полюсами
Р„ и Р22. Соответствующую
кривую центров обозначим
/И1122. К этому случаю можно
перейти от ранее рассмо-
тренного случая, в котором
из четырех положений Sb
S2, S2 и S3 плоской фигуры
два S2 и S2 заданы беско-
нечно близкими (рис. 684).
Пусть полржение S3 стре-
мится к положению Si и в
пределе переходит в поло-
жение SJ, бесконечно близ-
кое положению Si. Тогда
полюс Р23 совпадет с полю-
сом Р12, а полюс Р13 перей-
дет в мгновенный полюс
Рн (рис. 685). Заменив в
равенстве (11.69) полюсы Р13
и Р23 соответственно полю-
сами Рц и Р12, получим следующее равенство, которому должны
удовлетворять точки упомянутой кривой Ж1122:
L Р»МРЫ= LP^MP^.
(11.75)
Заменив в уравнении (11.70) кривой центров /И1223 координаты по-
люса Р13 (х13, _у13) координатами полюса Рц (xlb j'n), а координаты
полюса Р23(х23, _у23) координатами полюса Pi2(0, 0), получим уравне-
ние кривой центров Ж1222 в осях х, у с началом в полюсе PJ2:
(х2 -|-j2) (j2x—jty) —j\ (х2 —j2) 2j\xy — 0, (11.76)
где обозначено:
j\ ==-*ll + X22>
ji =Уи 4“
73----*ll У-22 4- X2i_У11>
A — Xll Х22 ---УпУ22-
(11.77)
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 769
Кривая центров /И1144 является по-прежнему кривой 3-го порядка
и проходит через все три полюса Рц, Р12 и P2i. В полюсе Р12 эта
кривая имеет двойную точку. Если введем в уравнение (11.76) одно-
родные координаты, то убедимся, что кривая 7И1122 есть циркулярная
кривая с бесконечно удаленной ветвью. Угловой коэффициент ее
асимптотического направления равен:
tg8oo=£=£“±^>. (1L78)
J1 Х11 “Г
Серединная прямая параллельная асимптоте, определится
здесь как прямая P^N, где /V —середина отрезка РцР22.
Для координат
мулы (11.44):
фокуса F (хг, у г) остаются справедливыми фор-
v ДД+Д/з . ДЛ— hjt
в которых коэффициенты jit /3 и /4 определяются формулами (11.77).
Обозначим по-прежнему через бесконечно удаленную точку
кривой М'ш. Заменим в равенству (11.75) точками Л-1^ и F сна-
чала полюсы, занимающие в нем средние положения, а затем полюсы,
занимающие в нем крайние положения. Тогда получим три равенства,
которым удовлетворяют точки кривой центров /И1124:
LFMP^, . (11-79)
Z P^MF = Z (И .80)
Z FMPlt= Z P^MMm. (11.81)
25 И. И. Артоболевский
770 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
Воспользуемся этими условиями для графического нахождения
фокуса F кривой 7И1122. Так как последняя проходит через полюсы
Рп и то, подставив в равенство (11.81) сначала полюс Ри, а
затем полюс Р22, получим (рис. 685):
£FPitPti = £ Р^М», (11.82)
Z. РРцРц — Z. РцРцМсо . (11.83)
Проведем прямые /лп = РцЛ4от и тгг = /А22Л1ОТ параллельно се-
рединной прямой /Йим. Использовав их, на основании последних
равенств получим две прямые PnF=fn и Р^Р=/^г, которые в
пересечении определят искомый фокус F. Если в условие (11.79) вме-
сто центра М подставим полюс Р12, то получим;
L РпРкМт= L FPnPn. (11.84)
При помощи этого равенства можно установить еще одну пря-
мую /12, которая проходит через фокус F.
Если один из полюсов Ри или Р22 оказывается в бесконечности,
т. е. совпадает с бесконечно удаленной точкой Л4те кривой /И1122, то
фокус F совпадет со вторым из указанных полюсов. Если полюс Р12
совпадает с бесконечно удаленной точкой Мж кривой /И1122, то фокус F
совпадет с той же точкой, так как в равенстве (11.75) полюс Pti
занимает оба средних положения, являясь сам себе противополюсом.
Кривую центров /И1122 можно построить любым из трех способов,
указанных в пункте 5° настоящего параграфа. Особенно простое
построение этой кривой получается по третьему способу (способу
Бурместера), который получает здесь простое обоснование. Это по-
строение заключается в следующем. Проведем через фокус F
(рис. 686) произвольную прямую г', которая пересечет серединную
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
771
прямую /«им в точке 1У. Вокруг этой точки опишем окружность Ь',
проходящую через полюс Р12. Точки пересечения М окружности Ь'
с прямой У принадлежат кривой /И1122. Чтобы доказать это, соеди-
ним полученную точку М с полюсом Р12 и проведем через ту же
точку прямую т || /яи22. Отметим равные углы, образуемые прямой
ЖР12 с прямыми т и z«n22- Отметим далее равные углы, прилегаю-
щие к вершинам Р12 и М равнобедренного треугольника PuLfM.
Тогда получим ранее установленное равенство (11.79)
РМР^=РкММт,
определяющее точки
кривой /И1122. Это построение не обеспечит до-
статочной точности, когда фокус F располагается
прямой. В этом случае сле-
дует использовать второй
способ построения, изложен-
ный в пункте 5° настояще-
го параграфа. Выполним
это построение на основа-
нии равенства (11.79):
Z = / FMP2i.
Проведем прямую k || пгШ2
(рис. 687) на расстоянии
РцК = у FP2i от полюса
Рп. Из середины D отрезка
FP.2i восставим перпендику-
ляр d. Проведем через по-
люс Рц произвольную пря-
мую z', которая пересечет
прямую k в точке К', и от-
вблизи серединной
ложим на прямой d отрезок DD = KK'. Точка D должна быть рас-
положена по ту сторону отрезка FP22, где соблюдается равенство
Z PuK’k = z dD'p^.
Через полюс Р.22 и фокус F проведем окружность Ь' с центром D'.
Точки пересечения М окружности Ь' с прямой г' принадлежат кри-
вой центров Л11122. >
Если вместо равенства (11.79) воспользуемся равенством (11.80)
или (11.81), то получим два других способа построения кривой Ж1122.
Они отличаются от указанного выше способа построения тем, что
узлом пучка прямых z и неизменной хордой семейства окружностей
b вместо полюса Рц и хорды РР22 будут соответственно полюс Р22
и хорда FPn или полюс Р12 и хорда FPl2.
Для подсчета координат точек кривой центров Л!1122 удобно
использовать ее параметрическое уравнение. Выберем по-прежнему
25’
772 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. Х4
за начало декартовых осей координат х, у полюс Рц (рис. 688).
Проведем через него прямую z под углом 8 к оси х. Уравнение
прямой z будет:
j = xtg8.
Решив его совместно с уравнением (11.76), получим координаты
точки М, в которой прямая z пересекает кривую /И1122:
Хм~ G 4-tgsB)(X —Л tgB) ’ №=-WgS- (11.85)
Эти уравнения можно рассматривать
Рис. 688.
тате поворота прямой Р12/И вокруг
как параметрические уравнения
кривой /И1122, в которых пара-
метром является угол 8 накло-
на прямой z к оси абсцисс.
Для каждого центра М,
принадлежащего кривой цен-
тров /И1122, можно установить
круговую точку Bi в Si, ко-
торая со своими положениями
B’i, В% и П';, лежит на окруж-
ности с центром М. Графиче-
ски эту точку Bt в Si можно
определить при помощи ра-
венств:
L BiPnM^=0.
Это будет точка пересечения
прямой МРц с прямой РцВц
которую получим в резуль-
полюса Рц на угол I------
По известным координатам центра М(хм, Ум), принадлежащего
кривой Л11122, координаты соответственной ему круговой точки
В(хв, у в) в St можно подсчитать по формулам (11.21).
10°. Некоторые случаи распадения кривой центров /И1122. Каж-
дая из кривых центров Ж1234,/И1123, /И1223 и Л11122, которые были рас-
смотрены выше, является кривой 3-го порядка, проходящей через
бесконечно удаленные мнимые точки плоскости. При особых случаях
расположения полюсов, определяющих эти кривые, они могут распа-
даться. Один из элементов, на которые распадаются эти кривые,
должен проходить через указанные мнимые бесконечно удаленные
точки плоскости. Это может быть или окружность или бесконечно
удаленная прямая плоскости. В результате каждая из указанных
кривых может распадаться или на окружность и конечную прямую,
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
773
или на кривую 2-го порядка и бесконечно удаленную прямую, или
на три прямые, из которых одна бесконечно удаленная. Случаи рас-
падения кривой центров 7И1234 были исследованы Бурместером [67а, б]
и Альтом [61з, и, к, м].
Для прикладных задач синтеза особый интерес представляют слу-
чаи распадения кривой центров /И1122. Некоторые из них будут рас-
смотрены ниже.
Предположим, что мгновенные полюсы Р(1 и Р22 (рис. 689) рас-
полагаются на равных расстояниях от полюса конечного поворота Р1г.
Опишем на равных отрезках РцРм и Pi2P22 равные окружности
Л4112— -у и /и122— у (см. § 36, 11°). Точка их пересечения М удо-
влетворяет равенству (11.75) и, следовательно, принадлежит кривой
центров Л41122. Изменяя последовательно вписанный угол, которым
окружности 7И*12 — [ и Л4122— у
Р|2Р22, можно по точкам найти
всю кривую 2И1122. В данном слу-
чае она распадается на прямую
лн1122, совпадающую с биссектри-
сой угла РцРцР^ и окружность
т, которая проходит через все
три полюса Рц, Р22 и Р12. В де-
картовых координатах с началом
в полюсе Р12, уравнение прямой
'«1122 будет:
У = ^х, (11.86)
а уравнение окружности т вы-
разится:
— ^_у = 0, (11.87)
h
Рис. 689.
где коэффициенты j.2, j3, j\ подсчитываются по формулам
(11.77). Уравнение (11.87) получим, деля уравнение (11.76) на урав-
нение прямой (11.86).
Проведем через начало координат Р12 под углом 8 к оси абсцисс
прямую z. Координаты точки пересечения 7И этой прямой с окруж-
ностью т определятся формулами:
“LS8>
Эти формулы получены в результате совместного решения урав-
нения прямой z с уравнением (11.87) окружности пг.
По известным координатам центра Л1(хл1, ум), выбранного на
окружности т или на прямой тп22, координаты соответственной ему
круговой точки Bi (х0, уц) в 51 определим по формулам (11.21).
774 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
Если мгновенные полюсы Рп и P2i совпадают друг с другом
(рис. 690), то кривая центров распадается на прямую /и1|22 = РцРц —
= PtiPw и окружность т, построенную на отрезке РпР12 = P22Pt2,
как на диаметре.
Когда один из полюсов Рп или Р22 оказывается в бесконечно-
сти, то фокус кривой /И1122 совпадает с другим полюсом. В этих
случаях построение кривой М1Ш не отличается от построения, опи-
санного выше.
Особый случай дает уход полюса Р12 в бесконечность (рис. 691).
В этом случае окружность /И112 — у; точки которой удовлетворяют
равенству РпМР12 = , распадается на бесконечно удаленную
Рис. 691.
прямую и прямую Рц^ъ образующую с направлением, в котором
удален полюс Р12 в бесконечность, угол —Аналогично окруж-
ность Мш— у, точки которой удовлетворяют равенству £ Р12МР22 =
= ~ , распадается на бесконечно удаленную прямую и прямую P22z2,
образующую с направлением, в котором удален полюс Р12 в беско-
нечность, угол Точка М, в которой пересекаются прямые z,
и z2, удовлетворяет равенству (11.75) и, следовательно, принад-
лежит кривой центров ТИ1122. Последовательно изменяя угол ,
можно по точкам построить всю кривую центров Л4П22.
Выберем за начало осей х, у полюс Рп. Напишем уравнения
прямых г, и z9:
У — J22 = (х — х22) tg (8«,4- ^2
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
775
уравнений угол иобо-
гиперболу, прохо-
где За, — угол, определяющий направление, в котором полюс
ушел в бесконечность. Исключив из этих
значив для сокращения (2800= Л, получим:
2 (/ — х2) k -|- Чху (1 — А2) —
— № (1 — £2) — 2х22Л] —
—У [Xi2 (1 ^2) 2умЛ] = 0.
Это — уравнение равносторонней гипер-
болы, у которой одно асимптотическое
направление совпадает с направлением, в
котором полюс Р12 удален в бесконеч-
ность. Следовательно, в рассматриваемом
случае кривая центров распадается на
бесконечно удаленную прямую и равностороннюю
дящую через полюсы Рц и и бесконечно удаленный полюс.
В частном случае, когда сама прямая РцР& (рис. 692) опреде-
ляет направление, в котором полюс Р12 ушел в бесконечность, ги-
пербола распадается на две взаимно-перпендикулярные прямые: пря-
мую РцРц и прямую z, проходящую через середину О отрезка РцРм.
11°. Вспомогательные геометрические места. На рис. 693 по-
люсным треугольником РцР^Рц заданы три положения Sj, S2 и S;,
плоской фигуры. Выберем произвольный угол у12 = /. *)
*) Положение Ва точки В, не изображено на рис. 693 (см. рис. 666).
776 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
и построим окружность /И123 — 7 (см. § 36, 5°), точки которой удо-
влетворяют равенству (11.10):
Z р13жр23=^= / я,жр12.
Для центра Ж, выбранного на окружности
ную точку Bt в St можно определить при
трех следующих равенств:
Ж123 — у, соответствен-
помощи любых двух из
/ BiP^M — Z ,
L ВхРпМ= /_ Р^РКР^=Ц,
(11.89)
/ В{МР^ =
На рис. 693 для определения по выбранному центру М на окруж-
ности Ж1’23— 7 соответственной точки Bi в использованы первая
и последняя строчки равенств (11.89). В треугольнике PKMBt, ко-
торым определяется это преобразование, угол при вершине Рк равен
а внешний угол при вершине/И равен ~ . Эти углы не зави-
сят от координат центра /И. Отсюда следует, что упомянутое пре-
образование координат центра Ж на окружности /И123 — 7 в коор-
динаты соответственной точки Вх в St есть преобразование подобия
с центром подобия в полюсе Р12.
Геометрическое место точек Bt в S„ соответственных центрам М
на окружности Ж123 — 7, обозначим Pj23 — 7. Из установленного
преобразования подобия следует, что геометрическим местом В)23 — 7
будет также окружность. Использовав первые две строки равенств
(11.89), легко убедиться, что для центра М*, выбранного в точке
пересечения окружности Ж123 — 7 с прямой РцР%я, соответственная
точка В\ в St совпадет с полюсом Pi3, а для центра Ж**, выбранного
в точке пересечения окружности Ж123 — 7 с прямой Р12Р13, соответ-
ственная точка В{ в St совпадет с отображенным полюсом
Р23, расположенным симметрично полюсу Р23, относительно противо-
лежащей стороны полюсного треугольника. Отсюда следует, что
окружность В[23 — 7 проходит через полюс Р13 и отображенный по-
люс Р23.
Чтобы выяснить тот вписанный угол, которым окружность BJ23 — 7
опирается на хорду Р13Р23, выберем центр Ж на окружности Ж123 — 7
совпадающим с полюсом Р13. На основании первой и последней строк
равенства (11.89) соответственную точку В* в St определим в пере-
сечении прямой Р(2Р23 с прямой Р^В*, которую получим в результате
поворота прямой Р13Р12 вокруг точки Pt3 на угол — . В треуголь-
§ 37|
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
777
нике РцРцВ* угол при вершине Р12 равен , внешний угол при
вершине Pj3 равен , а угол при вершине в* равен:
(11.90)
Каждая точка Bt в St, лежащая на окружности Z?[23— у, удовлетво-
ряет равенству (11.90).
Точка Р2з является зеркальным отображением полюса Р23 отно-
сительно прямой Р12Р13. Из очевидного равенства
L Wa=8li
следует, что полюс Р2з можно также найти, переместив полюс Р23
вокруг полюса Р12 на угол — 6]2.
Если положение Sa будет приближаться к положению S2 и в
пределе перейдет в положение S2, бесконечно близкое положе-
нию S2, то полюс Рп сов-
падет с полюсом Рц, полюс
Р23 перейдет в мгновенный
полюс Р2.2 (рис. 694), а полюс-
ный треугольник РцРцР-2я
выродится в прямую РцР-22.
Переместив полюс Рц во-
круг полюса Рц на угол
— 612, где 612 есть заданный
угол поворота положений
S, и S2 плоской фигуры, най-
дем точку Р|2, которую по-
прежнему назовем отобра-
женным полюсом.
Выберем опять произ-
вольный по величине и на-
точки М которой удовлетворяют ра-
правлению угол у12 и пост-
роим окружность 7И122 — у,
венству (11.8):
Z Р12Л1Р22 = ^.
Для центра /И, выбранного на окружности /И122 — у, соответствен-
ную точку Bt в Sj можно определить при помощи следующих ра-
венств (см. § 36, 11°):
Z. BtPiaM , Z 5^2= (11.91)
Использовав эти равенства, легко доказать, что геометрическим ме-
стом В[22— ) таких точек В2 в Sj, которые соответствуют центрам М
118 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
на окружности Л!122 — у, будет также окружность, опирающаяся
на хорду Pl2P'it. Точки В\ окружности В™ — у будут удовлетворять
следующему равенству, аналогичному равенству (11.90):
Z РМ = - ®f. (11.92)
Доказательство этого не будет отличаться от приведенного выше
доказательства, что каждая точка Bi геометрического места Д|23— у
удовлетворяет равенству (11.90).
12°. Кривые круговых точек. На рис. 695 полюсными треуголь-
никами РцРкР-2з и РцРцРц заданы четыре положения S1( S3 и
S4 плоской фигуры. Переместив полюсы Р.23 и Р.24 вокруг полюса
на угол —612, найдем отображенные полюсы Р23 и Р24. Выберем про-
извольный угол у12 и построим окружность /З}23— у, точки которой
удовлетворяют равенству (11.90). Построим далее окружность В{№—у,
точки которой по аналогии удовлетворяют равенству
ZW^y-y. (11.93)
Точки пересечения Bt этих двух окружностей явятся круговыми
точками, т. е. будут такими точками В{ в которые со своими
положениями Вг, В3 и В4 лежат на одной окружности. Центр М
этой окружности будет лежать на кривой центров Л11234. (Доказа-
тельство этого свойства точек пересечения окружностей £?J23— у и
$J24 — у не отличается от доказательства того, что точки пересече-
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
779
нпя окружностей /И123 — -у и 7И124— у есть центры, принадлежащие
кривой центров /И1234.)
Изменяя последовательно угол у12, можно по точкам построить
геометрическое место указанных круговых точек Вх в которое
называется кривой круговых точек. Условимся обозначать
эту кривую Z?]234. Из указанного построения следует, что круговая
точка В\ удовлетворяет равенству
z z р^р1*. (11.94)
На рис. 696 кривая центров УН1234 нанесена сплошной линией, а
соответственная кривая круговых точек В'™ — пунктирной линией.
Рис. 696.
Сравнив равенство (11.92) с равенством (11.35), которому удовле-
творяют точки М кривой центров /И1234, можно утверждать:
а) Кривая круговых точек Р]234 по своим свойствам не будет
отличаться от кривой центров /И1234: она так же будет циркулярной
кривой 3-го порядка. Одна ее бесконечно удаленная точка будет
действительной, а две другие — сопряженными мнимыми.
б) Кривую круговых точек fi]284 можно построить на полюсах
Рк, Р?з, Рц и Ры теми же способами, какими кривая центров /И1234
строится на полюсах Р13, Р23, Р14 и Р24. Кривая круговых точек P]£3i
пройдет через полюсы Р12, Р13, Р23, Р14 и Р24 и через отображенный
полюс Р34, который получим, переместив полюс Р34 вокруг полюса
Р|2 на угол — 012. (Полюсы Р34 и Р34 на рис. 696 не изображены.)
780 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
в) Уравнение (11.36) будет уравнением кривой круговых точек
2?i231, если при подсчете его коэффициентов kb k.2, k3, kt, Jb j2, J3
и /4 координаты полюсов P23 (x23, _y23) и P.2l (x.2i, y.2i) заменить коор-
динатами отображенных полюсов Р)з и Р^.
г) Серединная прямая кривой круговых точек 23[234 пройдет через
середины отрезков Р13Рг4 и РцР?з- Координаты фокуса F (уу, yF)
этой кривой определим по формулам (11.44), подсчитав коэффи-
циенты У1, j.2, /3 и /4 как указано в пункте в).
д) Точки кривой круговых точек B\2S\ кроме равенства (11.94),
будут удовлетворять пяти другим равенствам, которые получим из
равенств (11.58) — (11.62), заменив в них центр М на точку Blt
а полюсы Р23, Р21 и Р34 на отображенные полюсы P-я, и Р34.
Для кривой центров 7И1123, точки которой удовлетворяют равен-
ству (11.63), соответственная кривая круговых точек 23J128 в S,
определится равенством
Z Р^В^з = (11.95)
Для кривой центров /И1122, точки которой удовлетворяют равенству
(11.75), соответственная кривая круговых точек В\122 в Sj опреде-
лится равенством
Z Р11Д1Р12 = ЛР^Р^. (11.96)
Как определяется положение отображенного полюса Р' показано на рис.
694. Кривая круговых точек 2?!122, так же как кривая центров 2И1122, бу-
дет дважды проходить через полюс Р1И.
13°. Соответствие между точками кривой центров и кривой
круговых точек. Если кривая центров /И1234 и соответственная кри-
вая круговых точек BllSSi не распадаются, то каждой точке кривой
центров соответствует единственная точка кривой круговых точек,
и, обратно, каждой точке кривой круговых точек соответствует
единственная точка кривой центров. На рис. 696 изображены кривая
центров Ж1234 (сплошная линия) и соответственная кривая круговых
точек 23J234 (пунктирная линия). Если на кривой /И1234 выберем про-
извольный центр /И, то соответственную ему точку В2 на кривой B^2Si
графически можно определить, используя равенства:
Z В2Р12М = = Z Р^РпРы
Z В2Р13М = ~= L P^P13Pi3,
(11.97)
Z BiP^M = ~= Z PuPuPtt.
По выбранным координатам центра М (хм, ум) координаты соот-
ветственной круговой точки В^хв.ув) можно подсчитать по формулам
(11.11) —(11.13).
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ 781
Взаимно однозначное соответствие между точками кривых
/И1234 и В[231 сохраняется и при совпадении этих точек с полюсами. Вы-
берем, например, центр М на кривой /И1234 совпадающим с полюсом Р1а
(рис. 697). Тогда, привлекая вторую и третью строку равенств
(11.97), получим, что соответственная точка В( кривой В}234 должна
лежать с одной стороны на прямой РкР?з, а с другой стороны —
на прямой Р14Р24, т. е. эта точка Bj определится в пересечении
упомянутых прямых. (На рис. 697 эти прямые пересекаются в ко-
нечной точке Bt, лежащей вне пределов чертежа.)
Рис. 697.
Если центр М выберем на кривой 7И1234 не совпадающим с по-
люсом Р12, а расположенным вблизи этого полюса и проведем секу-
щую Pi2M, а затем центр Л1 будем приближать по кривой 7И1234
к полюсу Р12, то в пределе упомянутая секущая Р13Л1 перейдет в
касательную t к кривой /И1234 в полюсе Р12. Тогда согласно первой
строке равенств (11.97) поворот касательной t на угол —
определит еще одну прямую (прямую РцВ^, которая проходит че-
рез соответственную точку В, кривой В]281.
Первую строку равенств (11.97) можно использовать также для
графического построения касательной t к кривой /И1234 в полюсе Р12.
Для этого точку Bi кривой В|234, которую найдем в пересечении
прямых Р13Р23 и РиРы, следует соединить с полюсом Р,2. Поворот
прямой PuBi вокруг полюса Р1а на угол -|- определит искомую ка-
сательную t к кривой 2И1234 в полюсе Р12.
782 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
Взаимно однозначное соответствие между точками кривой цент-
ров и кривой круговых точек не нарушается и при распадении этих
кривых. Пусть на рис. 698 полюсами Pti, Рц, Р22 и углом поворота 612
заданы четыре положения St, SJ, S3, S'2 плоской фигуры, попарно беско-
нечно близкие. Пусть, далее, полюсы расположены так, что выполняется
равенство Р12РП = Р^Рц. В этом случае кривая центров Л4112? распа-
дается на прямую и)122, совпадающую с биссектрисой угла РцРцР^,
и окружность in, которая проходит через все три полюса Рц, Р22 и Р12
(см. § 37, 9е). Центр Е окружности
найдем в пересечении пря-
мой /пП22 с перпендикуля-
ром, восставленным из се-
редины D отрезка РпРц.
Переместив полюс Р22
на угол —612 вокруг полю-
са Р12, найдем отображен-
ный полюс Р'22. Соответст-
венная кривая круговых
точек S|,1!2 представит со-
бой геометрическое место
точек В,, удовлетворяющих
равенству (11.96):
^РцЯ1Л2= LPnB^P'22.
Вследствие очевидного ра-
венства Р12РП = PxiP'22 эта
кривая здесь также распа-
дается на прямую ГИ‘|22>
совпадающую с биссектри-
сой утла РцРцР'22, и окруж-
через полюсы Рп, Р12 и Р^. Центр Et
пересечении прямой /«{122 с прямой DE.
т
ность Ь, которая проходит
этой окружности найдем в
Легко сообразить, что будет /_ т\1ЮРптц№=^-.
Если центр М выберем на окружности т, то соответственную круго-
вую точку Bi найдем в пересечении окружности b с прямой Рц /И.Если
центр М * выберем на прямой /я1122, то соответственную круговую точку
В*найдем в пересечении прямой /«{122 с прямой РцМ*. Если центр М вы-
берем совпадающим с полюсом Р12, то соответственная круговая точка Bt
совпадет с тем же полюсом Р12, так как в нем прямая Р12РП пересе-
чет окружность Ь. Если, наконец, центр 7И выберем совпадающим с
полюсом Рц, то соответственную круговую точку /?** найдем в пересе-
чении окружности b с касательной t к окружности т в полюсе Рц.
14°. Точки, соответственные бесконечно удаленным точкам
кривой центров и кривой круговых точек. Бесконечно удаленному
центру М на кривой центров Л!1234 в общем случае соответствует конеч-
ная точка В\ на кривой круговых точек а бесконечно удаленной
§ 37]
ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
783
точке кривой Р{234— конечный центр Л1 на кривой центров /И1234.
Покажем нахождение этих конечных точек кривых B‘ssi и Л11234.
Пусть на рис. 699 полюсными треугольниками Р\2Р\3Р23 и
Р^РмРц заданы четыре положения S2, S3 и S4 плоской фигуры.
Проведем серединную прямую /п1234; она пройдет через середины
отрезков Р13Р24 и Р23Р14; (см. § 37, 3°). Эта серединная прямая
определит направление бесконечно удаленного центра Л1ет, принадлежа-
щего кривой центров /И1234 (не изображенной на рис. 699). Проведем
через полюсы Р12 и Р1Я прямые гп12 = Р^Л!^ и w?13 = P13AfOT, парал-
лельные серединной прямой дг1234. Повернув прямые wz12 и zzz13
х 012 Oja
вокруг упомянутых полюсов соответственно на углы--------и--------,
получим прямые, которые пересекутся в точке Вь которая соответ-
ствует бесконечно удаленному центру кривой центров /И1®4.
Переместив точку Bt вокруг полюсов Р12, Р13 и Р14 соответственно
на углы 612, 6|3 и 6|4, получим ее положения В2, В3 и Вц. Точка В}
со своими положениями Вг, В3 и Р4 расположится на окружности
бесконечно большого радиуса, т. е. на прямой линии. Эта прямая
BiB2B3Bi будет перпендикулярна к серединной прямой wz1234.
Угловой коэффициент tgSco серединной прямой /zz4234 и параллель-
ных ей прямых wz12 и zzz13 найдем по формуле (11.43). Уравнения
прямых P12Pt и P13Z?i будут:
У ~~ tg (йсо — ) х, у —у)3 = tg ^оо — (х — х13),
784 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
где 612 и GI3 — соответствующие углы поворота положений Si и S3,
Si и S3 плоской фигуры, а х13, ji3 — координаты полюса Pi3 в
осях х, у, начало которых совпадает с полюсом Pi3.
Координаты точки В, (хв, Ув) найдем как координаты точки пе-
ресечения указанных прямых:
У1з — *13 tg (вет-
хв=—,------------7------------yB = xBtg 8оо-^ . (11.98)
& оо 2 j - \ 00 2 /
Рассмотрим еще случай, когда полюсами Р12, Рп и Р22 и углом
поворота 612 (рис. 700) заданы четыре положения Sb Sj, S2 и Si
конечно близкие соответственно
плоской фигуры, попарно беско-
нечно близкие. Серединная пря-
мая т1Ш кривой центров 7И1122
пройдет через полюс Р12 и сере-
дину отрезка РцР22. Эта прямая
определит направление бесконечно
удаленного центра кривой цен-
тров 7И1122. Повернем серединную
прямую гиц22 вокруг полюса Р12 на
угол —На пересечении по-
лученной прямой с прямой Pltmlt ||
|! wz1122 найдем точку Bt, принад-
лежащую кривой круговых точек
соответственную центру Мт.
Переместив точку Bt вокруг по-
люса Р12 на угол 012, получим ее
положение В.2. На прямой ВХВ2,
перпендикулярной к прямой т1122,
будут лежать точки В\ и Bi, бес-
точкам Вх и В2. Это означает, что
с прямой ВхВг совпадут направления BJ I ВхРп и B3t | B3P3i.
Координаты указанной точки Вх (хв, Ув) подсчитаем по формулам:
Уи—*и tg8Ю
2 у '
хв =
Ув= Xfitg (Sco --
(11.99)
где tg&oo — угловой коэффициент серединной прямой /п1122, опреде-
ляемый по формуле (11.43), в которой коэффициенты и /2 выра-
жаются через координаты полюсов Рп (хп, _уп) и Р22 (*22, _у22) фор-
мулами (11.77).
Пусть на рис. 701 полюсными треугольниками Р^Р^Р^ и
Р\гРцРц заданы четыре положения Sj, S2, S3 и S4 плоской фигуры.
Построим полюс Р23 как зеркальное отображение полюса Р23 отно-
§ 37] ЧЕТЫРЕ ПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
785
сительно прямой РцРц и полюс Рг\ как зеркальное отображе-
ние полюса Р24 относительно прямой РцРц- Напомним, что кривая кру-
говых точек Р]234 (не изображенная на рис. 701) может быть
построена как геометрическое место точек Bt, удовлетворяющих
равенству (11.94):
ZP13B1P23 =
Проведем прямую wzj234 через середины отрезков Р13Р24 и РъзРц,
соединяющих противополюсы в этом равенстве. Прямая w|2,m
явится серединной прямой для кривой круговых точек Р]’34, и
Рис. 70].
она определит собой направление бесконечно удаленной точки
этой кривой.
Проведем через полюсы Р12, Р13 и Р14 прямые miit tnt3 и mlit
параллельные прямой Это будут прямые, соединяющие указан-
ные полюсы с бесконечно удаленной точкой кривой центров Р|234.
Повернем прямые z/z12, wla и ти вокруг полюсов Р13, Р13 и Р14
012 013 0ц т
соответственно на углы и . Тогда полученные прямые
согласно равенствам (11.97) пройдут через центр /И, принадлежа-
щий кривой центров Af1234, соответственный бесконечно удаленной
точке кривой круговых точек Р]234.
Так как кривая круговых точек Р]234 в общем случае имеет
единственную реальную бесконечно удаленную точку, то на кривой
центров /И1214 в общем случае имеется единственный центр Л4, ко-
торому соответствует бесконечная удаленная точка Bt в Sj.
786 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [ГЛ. XI
15°. Второй способ отыскания центра, соответственного бес-
конечно удаленной круговой точке. Изложенный выше способ
нахождения центра М, соответственного бесконечно удаленной
точке кривой В|28*, требует при графическом решении предваритель-
ного отыскания отображенных полюсов Р23 и Р^. Часто более удоб-
ным оказывается способ нахождения центра М, соответственного
бесконечно удаленной точке кривой В{234, который не требует предвари-
тельного определения координат отображенных полюсов. Чтобы по-
дойти к изложению этого способа, установим некоторые вспомога-
тельные соответствия.
Пусть на рис. 702 полюсным треугольником Р^РпАз заданы три
положения S,, В2 и В3 плоской фигуры. Выберем угол 7,2 = 6,2,
где угол 7,2= /. В,Л1В2 (см.'§ 36, 9°), а 6,2 — угол поворота положений
S, и S2. Построим окруж-
ность ТИ123 -— 7, точки ко-
торой удовлетворяют равен-
ству (11.10):
ZP13A1P.23^^.
При условии 7,2 — 6,2 ок-
ружность Л1,и — y пройдет
через полюс Piit так как
Z Аз Аз Аз-
Выберем на указанной
окружности 7И123— 7 произ-
вольный центр М. Для отыскания соответственной точки Р, в S,
воспользуемся первой и третьей строками равенств (11.89). Соглас-
но первой строке этих равенств получим прямую PKBit по-
вернув прямую PtiM вокруг полюса Р12 на угол —соглас-
но третьей строке упомянутых равенств получим прямую ТИР,, по-
вернув прямую МРц вокруг центра 7И на угол — Так как по
условию ~, то прямые P^Bi и MBt будут параллельны и
точка их пересечения В, будет бесконечно удаленной точкой. Это
доказывает, что каждому центру /И, выбранному на окружности
ТИ123— построенной при условии 712 = 6,2, соответствует беско-
нечно удаленная точка В, в В,.
Пусть на рис. 703 полюсными треугольниками Р12Р13А3 и
Р^РцРц заданы четыре положения В,, В2, В3 и В4 плоской фигуры.
четыре положения ПЛОСКОЙ ФИГУРЫ
787
§ 37]
Выберем опять у12 = 612 и построим окружности Л1123 — у и Mlii — у.
Первая из них пройдет через все вершины полюсного треуголь-
ника РцР^Рц, а вторая — через все вершины полюсного треуголь-
ника РцРцРц- Центр М, совпадающий с точкой пересечения ука-
занных окружностей, будет принадлежать кривой центров ТИ1234.
Этому центру соответствует бесконечно удаленная круговая точка,
т. е. бесконечно удаленная точка кривой Проведем декартовы
оси х, у с началом в полюсе Р12. В этих осях уравнения окруж-
ностей ТИ123 — у и ЛТ2— у
будут:
О2 -|~_у2 — х (х13 4- х23) —
~У О1»+№)] tg —
— х СУ 1з —.Угз) +
+J(X13—х23) = 0,(11.100)
О2 4- у2 — X (х14 4- х24) —
— -У 014 +-V24)] tg —
—х 0'14 —Уы) 4"
4- у (х и — x-2i) == о. (и. id)
Они получены из уравнений
(11.15) и (11.19) путем под-
Рис. 703.
Pia с
становии 1^=^. Вычтем
из уравнения (11.101) урав-
нение (11.100). Тогда полу-
чим уравнение прямой Р12Л1, соединяющей начало координат
найденным центром /И:
[х (х13 -|- х2з х|4 —- х24) 4~_У О1з 4"-У2з —.Ун —-V24)] tg 4"
4~ x(j’13 —_у23——У О1з — х2з — Х24)=0. (11.102)
Угловой коэффициент указанной прямой Pi2M будет:
У13 —Уаз —Ун + У»| -Т 013 + A'ss — Хи — Х24) tg —
tg8M = ----------------------------------4-. (П.ЮЗ)
Л'13 — х23 — Х14 -|" Л'2) — (Ухз -[- ysa J'l4 J24) tg 4-
Уравнение прямой Pi2M через угловой коэффициент tg 8Л1 можно
записать кратко:
у = xtg 8Л1.
788 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДЭЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
Решив это уравнение совместно с уравнением (11.100) окружности
/И123 — у, получим координаты центра М (хм, -УлО-'
Л'1з Уаз —(л"1з — XS3) tg 6д| -|"
ХЛ1= ---------------------Е--------
(1 Ч-tg« вд1) tg^
+ f-vi3 + A‘S3 + (.У13 + >'sa) tg 8Л1] tg
(l + tg35M)tg^
= tg 8Л1.
(11.104)
Чтобы определить направление, в котором соответственная точка Вх
в Si удалена в бесконечность, достаточно прямую Р^М повернуть
вокруг полюса на угол---------Угловой коэффициент этого на-
правления определим из очевидного равенства:
tgSa = tg^BM — (11.105)
Рассмотрим еще случай, когда полюсным треугольником РцРцРъз
и мгновенным полюсом Рп (рис. 704) заданы четыре положения Sb
<Sp S2 и Ss плоской фигуры, из которых два S) и S, являются бес-
конечно близкими. Выберем угол уп = 012 и построим окружности
§ 38] пять положений плоской фигуры 789
/И123— .у и др 12— Первая из них будет описана вокруг полюсного
треугольника РцРцР^. Точки второй окружности должны удовле-
творять равенству (11,22), которое, учитывая условие у12 = 61г, при-
мет вид:
= (11.106)
Центр М, совпадающий с точкой пересечения указанных окружностей,
будет принадлежать кривой центров Ж1123. Этому центру соответ-
ствует бесконечно удаленная точка кривой
Выберем начало координат х, у по-прежнему в полюсе Р№
В этих осях угловой коэффициент прямой Р^М будет:
5’11 —5’13 4-5’23 4" (-У11 — Л'1з — -Уаз) tg-g-
tg^ =------------------------------------(П.107)
л'ц — Л1з -|- Xss — (5’11 —5’13 —5'аз) tg -g-
где (Хц, Ju), (х13, _У13) и (х83, yia) — координаты полюсов Рп, Р13
и Р83. Поворот прямой Р1гЛ1 вокруг полюса Р18 на угол — опре-
делит направление соответственной бесконечно удаленной точки В\
в Угловой коэффициент этого направления подсчитаем по фор-
муле (11.105). Прямая, которая соединяет центр М с соответствен-
ной ему бесконечно удаленной точкой Р, в Sj, должна пройти через
мгновенный полюс Рц. Поэтому угловой коэффициент прямой РцТИ
определим по той же формуле (11.105). Координаты центра Л1(хл1, ум)
в осях х, у с началом в полюсе Р12 можно подсчитать по формулам:
5’и — A'1(tgbB
----ы"’ Ум = хм*ё*м- (11.108)
tg °Л1 — tg ° в
Эти формулы получим, решив совместно уравнение прямой Р^М
с уравнением прямой РП7И. В этих формулах (хп, _уц) — коорди-
наты мгновенного полюса Рп.
§ 38. Пять положений плоской фигуры
1°. Пять положений плоской фигуры. На рис. 705 тремя по-
люсными треугольниками Р)2Р13Р8з, РцРцРц и P)8Pi5P8s заданы пять
положений 5ц S8, 53, S4 и плоской фигуры. Использовав полюс-
ные треугольники Р^РКР^ и РцРцРц, определяющие четыре поло-
жения 58, S.( и Si плоской фигуры, построим кривую центров /И1234
(она изображена на рис. 705 сплошной кривой; на рис. 706 отдельно
изображен небольшой участок этой кривой). Для каждого центра М
790 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
на этой кривой соответственную точку В, в В, можно найти при
помощи любых двух из следующих трех равенств:
L = L РпРпР^,
L BiPi3M РпР^Р^
L В,Р^М=^ = L PttPA
(11.109)
Использовав полюсные треугольники Р^Р^Р^ и РцРцР^, опре-
деляющие четыре положения Sb S2, S3 и S3 плоской фигуры, построим
кривую центров Д41233 (она изображена на рис. 705 пунктиром; на
рис. 706 отдельно изображен небольшой участок этой кривой). Для
каждого центра /И на этой кривой соответственную точку В( в 5|
можно найти при помощи любых двух из следующих трех равенств:
Z BtPt2M = L Р13Р^,
L ВхР^М = ^- = L РцРЛ,
(11.110)
Z. BiPi3714 — -у- — Z Р\гР\3Рза-
Отметим точки пересечения М и М' кривых центров Л!1234 и Л41238,
не совпадающие с полюсами. Эти точки отдельно изображены на
§ 38] пять положений плоской фигуры 791
рис. 706. Считая центр М принадлежащим кривой центров 7И1234 и
привлекая первые две строки равенств (11.109), построим соответ-
ственную указанному центру точку Bi в Прямую P\2Bi получим,
повернув прямую Р12М вокруг полюса Р12 на угол — , а прямую
Pi3Bi — повернув прямую Р13/И вокруг полюса Р13 на угол —
Переместив полученную точку В\ вокруг полюсов Р|2, Р13 и Р14
соответственно на углы 612, 613 и 614, найдем ее положения В2, В3
и Р4. Окружность Ь, описанная вокруг центра М через точку
пройдет через ее положения Вг, Вл и /34.
Считая теперь центр М принадлежащим другой кривой центров
/И1238 и привлекая первые две строки равенств (11.110), построим
второй раз соответственную этому центру точку В{ в Так как
первые две строки равенств (11.109) и (11.110) одинаковы, то вто-
рое построение совпадет с первым и приведет к ранее найденной
точке Bi. Переместив ее вокруг полюса Р18 на угол 618, найдем ее
положение В3. Окружность Ь, описанная вокруг центра М через точ-
ку Bi, пройдет не только через ее положения В.2, Вл и Bit но и через
ее положение Вл. Такая точка В2 в S1( которая со своими четырьмя
положениями В.2, В3, ВГк и В3 лежит на одной окружности Ь, называется
точкой Бурместера, а соответственный ей центр М — центром
Бурместера. Условимся их обозначать соответственно Z?[s345 и 7И12348.
2°. Число точек и центров Бурместера. Каждая точка пересе-
чения кривых центров /И1234 и 7И1238, не совпадающая с полюсами,
будет центром Бурместера /И12348. Соответственную ему точку Бур-
местера В]2315 графически можно построить, использовав любые две
строки равенств (11.109) или (11.110). По известным координатам
Хм, Ум центра Бурместера координаты хц, ув соответственной точки
Бурместера можно подсчитать по формулам (11.11) — (11.13).
Точки пересечения кривых центров /И1234 и /И1238, совпадающие
с полюсами Р12, Р13 и Р23, через которые проходят обе указанные
кривые, в общем случае не будут центрами Бурместера. Чтобы по-
казать это, выберем центр М совпадающим с полюсом Р12. Тогда для
центра М, принадлежащего кривой 7И1234, направление /ИР12 совпадет
с направлением касательной tt (рис. 705) к этой кривой в полюсе Р12.
Для центра М, принадлежащего кривой 7И1238, направление MPi2 сов-
падет с направлением касательной t2 к последней кривой. Перенесем
с рис. 705 на рис. 707 центр М, совпадающий с полюсом Р14, и
касательные tt и t2. Пользуясь двумя первыми строками равенств
(11.109), построим точку В* в (рис. 707), соответственную центру
М, принадлежащему кривой 7И1234. Эту точку найдем на пересечении
прямой Pi3P^ с прямой blt полученной в результате поворота каса-
тельной вокруг полюса Р12 на угол — ~~ (на рис. 707 упомянутая
точка В* оказалась вне чертежа). Пользуясь двумя первыми
792 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
строками равенств (11.110), построим точку В** в Sb соответственную
центру Л1, принадлежащему кривой /И|23в. Эту точку найдем на пере-
сечении прямой с прямой Z>8, полученной в результате пово-
рота касательной вокруг полюса Р12 на тот же угол-------(точка
В** на рис. 707 также оказалась вне чертежа).
Если для точки В* построим ее положения В*, В*, В* и В* (не
изображенные на рис. 707), го окружность, описанная вокруг полюса
Р12 пройдет через положения В*, В*, В* и В*, но не пройдет через
положение В*. Если для точки В** построим ее положения В**, В**,
В** и В** (также не изображенные на рис. 707), то окружность,
Рис. 707.
описанная вокруг полюса Р12, пройдет через ее положения В™, В**,
В** и В**, но не пройдет через положение £**.
Только в частном случае, когда кривые центров Л1’234 и Д1123В
не пересекаются в полюсе Р1г, а касаются, указанные две точки б*
и В** совмещаются в точку В2. В этом случае (он не изображен
на рис. 707) окружность, описанная вокруг полюса Р12 через-точку Въ
пройдет через ее положения В.г, Вл, В^ и Вв. Следовательно, только
в этом частном случае центр М, совпадающий с полюсом Рм, явится
центром Бурместера /И12343, а соответственная ему точка В, в St —
точкой Бурместера В}2348.
Подсчитаем число центров Бурместера. Кривые центров ТИ'234 и
дразв ЯВЛЯЮтся алгебраическими кривыми 3-го порядка, поэтому эти
кривые не могут иметь более девяти общих точек. Две из них
всегда совпадают с мнимыми бесконечно удаленными точками плос-
кости (циклическими точками), которые принадлежат обеим кривым.
Три точки совпадают с полюсами Plit Р13 и P.i3, через которые про-
§ 38] пять положений плоской фигуры 793
ходят обе упомянутые кривые. Таким образом, центров Бурместера
может быть или четыре, или два, или ни одного.
Если кривые центров /И1234 и Ж1238 касаются в одном из полюсов
Р12, Р|3 или Р23, то в геометрическом представлении с этим полюсом
совпадут две бесконечно близкие общие точки указанных кривых.
Одна из них явится центром Бурместера и предыдущий подсчет
числа этих центров остается справедливым и для данного случая.
Так как центру Бурместера соответствует единственная точка
Бурместера, то можно утверждать, что точек Бурместера В]2349 мо-
жет быть также или четыре, или две, или ни одной. Точки Бурме-
стера 73J234S можно найти как точки пересечения кривых круговых
точек в]234 и в}238, не совпадающие с полюсами Р12, Р13 и Р'3,
через которые проходят обе указанные кривые. Точка Бурместера
В]2315 совпадает с полюсом Р12, Р13 или Р',А только в том случае,
если в этом полюсе кривые S]"28’ и Z?[s36 не пересекаются, а касаются.
3°. Другой способ отыскания центров Бурместера. Из пяти
положений Sj, S2, S3, и Ss плоской фигуры можно образовать
пять сочетаний по четыре. Эти сочетания приведены в верхней строке
указанной ниже таблицы. Во второй строке этой таблицы даны кри-
вые центров, относящиеся к соответствующим четырем положениям
плоской фигуры.
Si, Sg, S3, S4 Si, Sg, S3, S5 Si, S2, S4, Sg 81, S3, Sf, S;, S2, S3, S4, Sg
Л4133‘ Ж1286 Др 245 Др 345 /И2316
Через центр Бурместера Л/12348 пройдет каждая из пяти кривых
центров Ж1234, Ж1238, Ж'248, Ж1348 и Ж2348. Поэтому этот центр можно
определить как общую точку не только кривых центров Ж1234 и
Ж’238, но любых двух кривых центров из пяти, указанных в приве-
денной таблице.
Можно указать еще один способ нахождения центра Бурместера
Ж12348. Выберем произвольный по величине и направлению угол
= Z B^MBi (см. § 36, 9°). Построим на отрезках PV3Pi3 и РцРц,
(рис. 708) окружности Ж123 — у и Ж124— у, точки Ж которых удо-
влетворяют равенствам (11.10) и (11.18), которые, сократив, запишем:
LP^MPi3 = ^,
/.РпМРи = 1±.
(11.111)
(11.112)
Точка пересечения Ж этих окружностей принадлежит кривой цен-
тров Ж'234.
794 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
кривых центров
Рис. 708.
Построим на отрезке Р13Р2В третью аналогичную окружность
At128— -у, точки М которой удовлетворяют равенству
ZP1sA4P28 = ^. (11.113)
При произвольном угле окружность А!128 — -у не пройдет через
ранее найденный центр М.
Точка пересечения окружности Af128 — у с окружностью А1123— у
будет принадлежать кривой центров А11238. Допустим, что нами найден
такой угол ~~, что определяемые им три окружности А/123 — у,
А!124 — у и А1128 — у пересекаются в одном центре А1 (как изобра-
жено на рис. 708). Этот центр Л4, удовлетворяющий равенствам
Z. Р13^Р2з = Z. РцМР21 = Z. Р1дТИР25, (11.114)
AI'234 и А/1238 и представит
собой центр Бурместера
А112348. Таким образом, задача
отыскания центра Бурмес-
тера М12348 может быть све-
дена к отысканию угла у12,
при котором три указанные
окружности пересекаются в
одной точке. Легко дать
аналитическое решение этой
задачи и установить фор-
мулы для подсчета координат
центра Бурместера А112348 по
известным координатам шес-
ти полюсов Р13, Р23, Р14, Р24,
р1з и Р28.
4°. Формулы для под-
счета координат центра
Бурместера. Выберем де-
картовы оси х, у (рис. 708)
с началом, совмещенным с по-
люсом Р12. В этих осях окружность Af123 —у выразится уравнением (11.15):
Iх2 4~ — х (х1з х-2з) —У (_У1з 4~Э'аз)] tg — х (_У1з —.Угз) 4~
'‘гУ (х13 х2з) 4- (х13х23 4“ J13J23) (tg 2” — tg = tt-
Окружность TH124 — у выразится уравнением (11.19):
[№ 4- у—х (х14 4- х24)—у (j, 14 4- _у24)] tg — х (уи —_у24) 4-
4-j’ (*14 — x2i) 4- (х14х24 4- ji4j24) (tg — tg= о.
§ 38] пять положений плоской фигуры 795
Уравнение окружности 7WI2S — 7 напишем по аналогии:
[л:2 Ч~-У2 — х (xis 4~ х8в) —У (.Vis 4~-У2з)1 tg *2 х (-Via —-Уаз) 4~
4“У (xis — xts) 4~ (xi3x2g 4'_У1з-Уав) (tg *2 tg — 0. (11.115)
В этих уравнениях (x13, j>l3), (x23, yi3), (x28, _у2з) координаты
полюсов PI3, P23, .... Р2з. Угол -%— вписанный угол окружностей
/И12'* — Д4>24 — у и /и’29.— опирающийся на хорды Р13Р23,
РНР24 и PlsP23 в соответствии с равенствами (11.111) — (11.113).
Угол -Р представляет собой половину угла поворота положений S(
и S2 плоской фигуры. Он удовлетворяет равенствам:
% = L Р1зР12Раз= L РиР^Рц= L (11.116)
На основании этих равенств в указанных осях получим:
612 -У|зУаз — -УазУи хмУм — ХцУц Х^Уг;, — Xas.Vis
2 XjgXss + УхзУаз У 11^'24 Ч-УиУн -Ухз-Узз Ч-УхзУз»
.(11.117)
Чтобы найти значение угла , при котором все три окружности
/И123— дрм — 7 и д{12о — пересекутся в одной точке — центре
Бурместера /И12343, достаточно исключить из уравнений указанных
трех окружностей переменные х и у. Введем обозначения:
di = х,5 4- х2з;
d2 = Х1Я - х2з;
<4 — J15 4’-Уаз>
—у is —№!
С\ = di — х13 — х23;
с2 = d-2 — х13 4- х23;
ез = d3 —_у13 —_у23;
ei = d-i —_У13 4“ >231
— di — Xj4 — х24; 1
k2 — d2 Х14 4“ х24> !
k3 — d3—J14—_у24; ।
А4 = сГ4—Уц-\~Уи', J
(11.118)
4 =-У13Х2.з4~-У13-У23--
z2 == хi4x24 4~.у 14.У21—4>
4 — х1зх2в 4- Jis Угз-
(11.119)
Вычтем почленно уравнение (11.115) окружности Л4123 — у сначала
из уравнения (11.15) окружности Л11’23 — у, а затем из уравнения
(11.19) окружности/И124 — Тогда получим уравнения двух прямых:
tg +^) х 4- (^3 tg -е2) у 4- 4 (tg - tg = О, (11.120)
(fejtg4~^i)x4~(^3tg —kzjу 4~4 (tg ^2 —2*)“^’ (ii’i^i)
796 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
Геометрический смысл этих прямых следующий: прямая тх (рис. 709),
определяемая уравнением (11.120), соединяет точки пересечения М
и М* окружностей /И123 — и /И123 — f, а прямая т2, определяемая
уравнением (11.121), соединяет точки пересечения М и М** окруж-
ностей Л1124 и /И123.
У
Рис. 709.
Для дальнейшего сокращения записей обозначим переменный па-
раметр
= « (11.122)
и введем постоянные:
Р1 = А36>1 —/?ie3, 1
р2 = Л3₽44-Л1ег — —kte3, > (11.123)
Рз z= ^4е2 — k3e^. j
Координаты точки Л4 пересечения прямых тх и дг2 определятся фор-
мулами:
— tg [4 (^2 — *3 • «) — /2 (е2 — е3 • и)]
Х1Л= Pi^+^+p. ’ (11124)
— tg [/* (k, 4- ktu) — /s (ei + ехи)1
Ул1 “ Р1«2+р2ы + Рз '
Подставим переменные х и у, определяемые последними формулами,
ПЯТЬ ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ
797
§ 381
в уравнение (11.115) окружности Л!12'* — 7. Тогда получим следующее
уравнение 4-го порядка относительно параметра tgt—- = п:
/д4и4 -ф- т3и3 -ф- -ф- mpi -ф- /«о = 0.
(11.125)
Коэффициенты этого уравнения выражаются через ранее указанные
величины dlt d2, d3, dt, e2, eit e3, e4, kb k2, k3, lb 4, 4, plf p2,
p3 и величины:
hi — kil\ —
= k2l\ —
h3 = k3li e3l2,
h^ :— kiji Cf/i,
q« = dih3 — d3hi,
Q\ — ddh, djit,
Qi = — d2h2 -j- d.2ht — d3h^ -ф- dji3,
Q3 = hl + hl-,
Qi — In -I- h3,
q3 = 2(hihi — hih3).
При этих обозначениях будет:
w4 = (<7о -ф- l3pi) pi -ф- Qt,
т3 = Qtf>2 -ф- (_Q‘2 -ф- 273/?а) р2 — qt tg -ф- qs;
т2 = Q0p3 -ф- QiPi Qipi -ф- (р? -ф- 2Р1Р3) h — <7i4g ф- <?з',
t^i = (Qi 4~ 24/4) р2 -ф- q2p3 — q3 tg -у ;
wr0 == (qi 4Гз) /73.
(11.126)
(11.127)
Если корень уравнения (11.125) подставим в формулы (11.124), то
получим координаты хЛ1,уЛ1 соответственного центра Бурместера /И12348.
Кроме рассмотренного здесь случая пяти конечно удаленных по-
ложений S1( S2, S3, S4 и S6 плоской фигуры, возможны случаи зада-
ния таких пяти положений плоской фигуры," из которых некоторые
являются бесконечно близкими. В настоящем параграфе будет рас-
смотрен случай пяти положений St, Si, S2, S3 и S4 плоской фигуры,
из которых два St и S' являются бесконечно близкими, и случай пяти
положений St, S', S2, S' и S3 плоской фигуры, из которых четыре
St и S', S2 и S3 являются попарно бесконечно близкими.
Наиболее интересные приложения в задачах синтеза механизмов
имеет второй из указанных частных случаев. С него и начнем рас-
смотрение.
б°. Случай пяти положений плоской фигуры, из которых че-
тыре являются попарно бесконечно близкими. На рис. 705 пять
конечно удаленных друг от друга положений St, S2, S3, S4 и Se
плоской фигуры были заданы семью полюсами Р12, Р13, Р33, Р14, Р24,
Pis и Pts- Предположим теперь, что положение S6 непрерывно при-
ближается к положению S\ и в пределе переходит в положение S',
798 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
бесконечно близкое положению Sb а положение S4 непрерывно при-
ближается к положению S2 и в пределе переходит в положение S',
бесконечно близкое положению S2. В результате полюс Рк перейдет
в мгновенный полюс Plt (рис. 710), полюсы Р28 и Р]4 совпадут с по-
люсом Р12, а полюс Р24 перейдет в мгновенный полюс Р32. Пять по-
ложений Sb S', S2, S' и S3 плоской фигуры, из которых четыре S(
и S’, S2 и S’ являются попарно бесконечно близкими, определятся
пятью полюсами Р12, Р13, Р23, Рп и Р22. Относящиеся к этому случаю
центр Бурместера и точку Бурместера условимся обозначать
/И11223 и В)1223. Центр Бурместера Л11’223 будет общей точкой Л1
пересечения трех окружностей А!123— у, /И"2 — у и /И122 — у, опре-
деляемых одним и тем же углом *[12, величина которого подлежит
отысканию. Точки этих окружностей удовлетворяют соответственно
равенствам (11.10), (11.22) и (11.24):
APiaMPi3 LP"MPK=^, LP^MPn =
Следовательно, центр Бурместера А11’223 будет удовлетворять равен-
ству
Z P~X= L~PuMPn = L РпМР^, (11.128)
в которое переходит в рассматриваемом случае равенство (11.114).
В декартовых осях, начало которых совмещено с полюсом Р12, окруж-
ности /И123 — 7, А1112— у и А1122—7 определяются соответственно уравне-
ниями^ 1.15),(1 1.23)и (11.25). Чтобы найти значения угла 71а,при которых
§ 38|
ПЯТЬ ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ
799
все три окружности Л41'23 — у, ТИ112 — у и /И1’22 — у пересекутся в одной
точке—-центре Бурместера Л111223, по-прежнему достаточно исключить
из уравнений этих трех окружностей переменные х и у. Это исклю-
чение приводит к уравнению четвертой степени относительно пара-
метра tg^j, совпадающему по форме с уравнением (11.125). Подсчет
его коэффициентов rnt, т3, т.2, т2 и /и0 можно выполнить по прежним
формулам (11.118), (11.119), (11.123), (11.126) и (11.127), заменив
в них предварительно координаты полюса Рк (х1в, _у15) на координаты
полюса Рп(Хц, _Уп), координаты полюсов Pi5 (х28, _у25) и PI4 (xl4, j14)
на координаты полюса Рк(0, 0) и, наконец, координаты полюса Ри (x24,j/24)
на координаты полюса Р22 (хи, jM). Порядок этой замены установлен
путем сравнения равенства (11.114), определяющего центр Бурмес-
тера /И’2348, с равенством (11.128), определяющим искомый центр
Бурместера Л111223. После этой замены формулы (11.118) и (11.119)
примут вид:
= — -’Эз— -^2з> kl^=Xn — x22; ।
ег = el “Н 2^23» k-1 = xll Г -V82>
ез — _V it — V13 —_Уаз» k3 =уц —Уа',
et = 2у2з1 ^4 =_У11 "Ь J22-
Л — хгзхгз УмУгз, 1% — 1з = 0.
(11.129)
(11.130)
Формулы (11.123) остаются неизменными. В формулах (11.126) отпа-
дает необходимость предварительного подсчета коэффициентов /гь
ht, h3, ft4 и q%. Коэффициенты q{„ qit q2, q3 и qk подсчитаем по со-
отношениям:
71 — — 7o — xii J'a-z — х22^и>
7г — 2 (ХцХг2 4-Jii Ун),
7з — I (A!~|- hi),
(11.131)
Формулы (11.127) для подсчета коэффициентов уравнения (11.125)
также несколько упрощаются:
^4 = —71Р1 -|- 74,
т3 = — qt (4/ — р2) — q2px — </4 tg ,
,/г2 — — 7il^4/tg — Pi 4- p3j — Ч2Рч~\~Чз,
, 012
rni — <РРъ — QiPi — <рз ig ~2 »
/тг0==71Р3.
(11.132)
Определив корень уравнения (11.125), можно по формуле u = tg^
установить значение угла при котором три окружности — 7,
800 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гЛ. XI
7И112— f и 7И122— у (рис. 710) пересекаются в одной точке Л4, предста-
вляющей собой центр Бурместера 7И11223. Чтобы подойти к подсчету
его координат, вычтем из уравнения (11.23) окружности Л1112 — 7
сначала уравнение (11.15) окружности Л1123— 7, а затем уравнение
(11.25) окружности Ж’22— 7. Тогда получим уравнения двух прямых,
аналогичные уравнениям (11.120) и (11.121):
(eitg-y+ х + tg tg^ = O, (11.133)
+ (11.134)
Прямая, определяемая уравнением (11.133), соединяет точки пересе-
чения Л1 и 7И* (рис. 711) окружностей 7И123— 7 и Л1112 — 7, а прямая,
определяемая уравнением (11.134), соединяет точки пересечения
Л4 и Р)2 окружностей Л1112 — 7 и Л1122 — 7. Решив уравнения (11.133)
и (11.134) относительно переменных х и у и подставив в полу-
ченные формулы корень tg у уравнения (11.125), найдем
координаты соответствующего центра Бурместера 7И11223. Но можно
для подсчета этих координат указать более простые формулы. Из
уравнения (11.134) следует, что угловой коэффициент tgSAI пря-
мой РцМ, соединяющей искомый центр Бурместера М с началом коор-
динат Р12, равен:
tg =
kill
k% k-^ll
(П.135)
§ 38]
ПЯТЬ ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ
801
Тогда координаты центра Бурместера Л1 (хм, _ум) как точки пересе-
чения прямой М1\.2 с окружностью Л1112— у определим по формулам:
А'и (н— tg + У11 (« tg 8Л1 + 1) , й ...
Хм =-------------/I _.| _т„-в к ~Г7,---’ Тлг = Хм tg ЬЛ1. (1L.136)
(! 8Л1)«
В этих формулах u = tg^ есть корень уравнения (11.125).
После отыскания центра Бурместера Л111223 соответственную ему
точку Бурместера Л"'223 можно найти графическим построением на
основании следующих равенств:
^ад.2л1= = Z р13р12р33)
/_ВхРиМ=&- = L адЛз ,
Z’51Pi144 = 0.
(11.137)
На рис. 710 соответственная точка Бурместера В}1223 обозначена В\
и показано ее построение на основании первой и третьей строк по-
следних равенств. Ио известным координатам хм, Ум центра Бурме-
стера 7И11223 координаты Хд, у в соответственной точки Бурместера
подсчитаем по формулам (11.21).
6°. Графоаналитический способ определения координат центра
Бурместера. Продолжим рассмотрение таких пяти положений Sb Sj,
S2, S2 и S3 плоской фигуры, из которых положения S] и SJ и поло-
жения S2 и S.2 являются бесконечно близкими. Пусть эти пять положений
плоской фигуры заданы на рис. 712 пятью полюсами Р12, Рта, Рц>
Рп и Р.2.2. Соответствующий центр Бурместера Л111223 будет принад-
лежать каждой из трех кривых центров Л11123, /И1122 и Л11223 и, сле-
довательно, может быть найден как точка пересечения любых двух
из трех перечисленных кривых. '
На рис. 712 построены кривые центров /И1122 и 7И1223. Эти кри-
вые, кроме полюсов Р12 и Р22, пересекаются в двух точках М и ЛГ,
представляющих собой центры Бурместера 7И11223. Как и в общем
случае, здесь легко доказать, что центр Бурместера 7И11223 только
в том случае совпадет с полюсом или Р22, если в этом полюсе
кривые Ж1122 и 7И1223 будут не пересекаться, а касаться; точек
Бурместера 7И11223 может быть или четыре, или две, или ни
одной.
Очевидно, что графическое отыскание центра Бурместера 7И11223
как точки пересечения кривых центров 7И1122 и 7И1223 (или других
двух кривых центров из трех указанных выше) часто не может обеспечить
необходимой точности в определении его координат. Покажем способ
последовательного уточнения этих координат.
Обозначим значения координат центра Бурместера, снятые непо-
средственно с чертежа хм, Ум- Подсчитаем угловой коэффициент tg 8д1
26 И. И. Артоиодевский
802 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
прямой ТИР12 (рис. 712), которая соединяет центр Бурместера М с на-
чалом координат:
tg8Ai= = .
хм
Решив уравнение (11.135) относительно величины и, получим:
^2 tg — ki
Ъ tg 8ai -j- k\•
(11.138)
Подсчитав эту величину и подставив ее в формулы (11.136), найдем
новые приближенные значения Хм, Ум координат центра Бурместера.
Эти формулы определяют
Бурместера как точку пересече-
ния окружностей Л1112 — у
и /И122— у (рис. 711), у
которых вписанный угол
712
удовлетворяет равенству
tg~ = u. Но через центр
Бурместера /И11228 должна
пройти третья окружность
Л1|2;|.— точки которой
удовлетворяют равенству
(11.10):
центр
^_Р13Л1Р2:, =^,
и, следовательно, равенству
tg(Z/?13^23) —
— tg^ = O. (11.139)
Предположим, что второй член этого равенства подсчитан по форму-
ле (11.138), в которой для сокращения обозначено tg—^ = и. Пер-
вый член равенства (11.139) обозначим
© = 1ё(^Р18Л1Рм) (11.140)
и подсчитаем его через координаты полюсов Р13 (х13, у1;|), Р23 (х23, j'23)
и координаты хм, Ум центра Бурместера по очевидной формуле:
__(хм~ (Ли —ЛЭ — (Ли -х'вз) (Ум ~Ут) 14
(Ли — х^) <хм — х^ 4" (Ли — -У18) (Ли — Ла)
§ 38] пять положений плоской фигуры 803
После подсчета величин и и и возможны два случая:
1) в пределах точности подсчета разность
Ди = и — V — 0;
это будет означать, что в пределах точности расчета найденные по
формулам (11.136) координаты Хм, .Vai совпадают с истинными зна-
чениями координат центра Бурместера Л111223 и не подлежат уточне-
нию;
2) в пределах точности подсчета разность
ки = и — и 0;
это будет означать, что найденные координаты хм, J-'ai центра Бур-
местера подлежат уточнению. Процесс уточнения может быть выпол-
нен способом последовательного приближения.
Подставим в формулы (11.135) и (11.136) произвольную вели-
чину и', близкую к величине и, найденной по формуле (11.138). Под-
считаем соответственные значения хм, у’м и затем по формуле (11.141)
найдем новое значение величины т/ и разность
Ди' = и' — ъ'.
По формуле линейной интерполяции вычислим уточненное значение и"
» 712
величины и — tg —:
Подставив и" в формулы (11.135) и (11.136), найдем уточненные
координаты Хм, ум центра Бурместера. По формуле (11.141) под-
считаем соответственную величину в" и найдем разность
Дп" = н" — и",
которая покажет, подлежат ли найденные координаты хм, ум даль-
нейшему уточнению. Если они подлежат дальнейшему уточнению, то,
использовав значения и", Ди" и Ди', и’ (или Ди и и), по формуле
линейной интерполяции найдем новое значение и'" величины и, по
формулам (11.135) и (11.136) — новые координаты х'м, у’м центра
Бурместера, которые подлежат новой проверке и в случае необходи-
мости новому уточнению.
Таким путем можно определить координаты центра Бурместера
с любой необходимой точностью.
7°. Случай пяти положений плоской фигуры, из которых два
бесконечно близкие. Рассмотрим другой частный случай задания пяти
положений 8Ь 8J, S2, S3 и Si плоской фигуры, когда два из этих
положений Si и являются бесконечно близкими. На рис. 713 эти
пять положений заданы мгновенным полюсом Рп и двумя полюсными
26*
804 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ КОНЕЧНО УДАЛЕННЫХ ПОЛОЖЕНИЙ [гл. XI
треугольниками Р12Р13А3 и РцРцРц- В этом случае соответствую-
щий центр Бурместера Ж11'234 определяется равенством
ZPisMPg, = АРцМРи= £PtlMPl2. (11.143)
Он будет общей точкой пересечения трех окружностей ТИ123— 7,
ТИ124 — 7 и Л1112— 7, определяемых одним и тем же углом 7,2,
величина которого, как и в предыдущих случаях, может быть
У1
Рис. 713.
определена в результате решения уравнения (11.125). Корень этого
уравнения
Формулы (11.118) и (11.119) переходят в этом случае в следующие:
(/] — хи;
-^н:
<4—Уц;
<4=3'и;
О = Хи — х|3 — х.23;
с а = Хц — х13 х.>3;
ез=3'п —3'1з —Уъ'л\
ei~yil --3'13 “Г J23;
^1 — -^11 ------*44------*-24:
k2 — Xlt — Х14 -|- X.2i,
^3 — 3'11 3'14 —3'241
^4 —3'11 3’14 4-3'24-
(11.144)
4 — х|3х23 4~3'1з3'2з>
4 = -v14-v24 4-3'143,24>
4 = о.
(11.145)
Они получены путем замены в формулах (11.118) и (11.119)
координат полюса PiS(xls, j>IB) на координаты полюса РцСЧь J^n),
а координат полюса P2S (х2в, у2В) на координаты полюса Р12 (0, 0).
§ 38]
ПЯТЬ ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ
805
Порядок этой замены установлен путем сравнения равенства (11.114),
определяющего центр Бурместера Л112348, с равенством (11.143),
определяющим центр Бурместера /И11234. Формулы 11.120—(11.126)
остаются в этом случае без изменения, а для коэффициентов урав-
нения (11.125) получим формулы:
/«4=wi+«’4;
т-А = q^Pi + ЧгР1 — ?4 tg + Чъ,
=ЯъРъ “И q^Pi ~Ь qiPi—tg -у + %;
т\—qq}4 q^Pi — <7з tg ;
(11.146)
m<s = qiP3-
По известному корню и уравнения (11.125) координаты (хм, ум)
центра Бурместера подсчитаем по формулам (11.124). Число центров
Бурместера Л111234 определяется числом действительных корней урав-
нения (11.125), т. е. их может быть или четыре, или два, или ни. од-
ного.
Графически центр Бурместера /И11234 можно найти как точку пере-
сечения любых двух из следующих четырех кривых центров: Л11123,
ТИ1124, Л11134 и ТИ1234.
По известным координатам Хм, Ум центра Бурместера ТИ11234 ко-
ординаты Хв, у в соответственной точки Бурместера Z?]1234 можно
подсчитать по формулам (11.11) — (11.13). Графически точку Бурме-
стера можно построить при помощи следующих равенств:
Z В^М =^-= LPM,
LB.PKM = = L Р^РА,
/_ВхРиМ = ^= /.РпРцРы,
(11.147)
£BlPnM=Q.
В этих равенствах /И — это центр Бурместера Л111234, а В( — иско-
мая соответственная точка Бурместера fi]1234.
ГЛАВА XII
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
§ 39. Синтез шарнирного четырехзвенника по двум и трем
положениям
1°. Задача синтеза шарнирного четырехзвенника по двум
положениям. Пусть требуется определить шарнирный четырехзвен-
ник, у которого при переходе из первого положения AB^C^D
(рис. 714) во второе AB^D заданному углу поворота <р13 ведущего
звена АВХ соответствует заданный угол поворота ф12 ведомого
звена CxD. Углы <pi2 и ф12 заданы не только по величине, но и по
направлению: их направления указаны на рис. 714 стрелками. Изло-
жим геометрическое решение этой задачи синтеза шарнирного четы-
рехзвенника по двум положениям, данное Альтом [61а].
§ 39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ 807
Выберем произвольно стойку AD искомого четырехзвенника. Вдоль
нее направим ось координат X. Проведем через точки А и D прямые
соответственно под углами —и —к оси X. Точку пересе-
чения этих прямых обозначим Pt3.
Предположим, что Р12 — это полюс положений St и $.2 некоторой
плоской фигуры, совершающей движение в плоскости чертежа. Угол
поворота 012 положений St и S2 определим через заданные углы
<Р12 и ф12 равенством
®12 = СР12-Ф12- (12.1)
Графически в соответствии с последним равенством получим, что
в A APtiD внутренний угол при вершине Р12:
= (12.2)
Выберем в плоскости чертежа произвольную точку за центр Л1 и- по
общему правилу (см. § 36, 5°), повернув прямую Р12ТИ вокруг
полюса Р12 на угол----, установим прямую о12 —- геометрическое
место точек Вх в 8^ которые со своими положениями Д2 лежат на
окружностях, описанных вокруг этого центра /И. Произвольную
точку Bi на прямой й12 выберем за подвижный шарнир ведущего
звена механизма; подвижный шарнир С) его ведомого звена сов-
местим с центром М. Тогда фигура ABXC\D определит первое по-
ложение искомого шарнирного четырехзвенника. Докажем это.
Переместим отрезок ABt вокруг полюса Р12 на угол 012 в поло-
жение Д2Д°™ (смысл обозначения Д“тн выяснен ниже). Точки Bt
и расположатся при этом симметрично относительно прямой
CiPi2 Л1Р12, а точки А и Д2 — симметрично прямой DPl2. Отсюда
следует, что кроме очевидного равенства Д/?1?=Д2£?°™ будут спра-
ведливы равенства
Ci В! = ед™; DA = DA2; Z ADA = ф^.
Повернем A2D°™CiD как жесткую фигуру вокруг точки D на угол ф12.
Тогда точка Л2 совпадет с точкой А, а сама указанная жесткая
фигура переместится в положение AB2C2D. Это будет второе поло-
жение указанного шарнирного четырехзвенника ABiCxD, соответ-
ствующее повороту его ведомого звена CtD на заданный угол ф12.
Найдем величину угла В^В^, на который повернется при этом
ведущее звено АВг.
Отрезок АВ2 получен в результате двух последовательных вра-
щений отрезка АВХ: одного вращения вокруг полюса Р12 на угол 012
в положение А2Р°™ и второго — из положения А2В°™ в положение АВЛ
808 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ звеньев |гл. XII
вокруг шарнира D на угол <р12. Из равенства (12.1) получим, что
сумма углов
®ia Ф12 =?12-
Следовательно, / ВхАВг = <р12. Этим доказано, что шарнирный четырех-
звенник AB^CiD удовлетворяет соответствию заданных углов <р12 и ф12.
2°. Полюс и угол поворота относительных положений. Гео-
метрическое и кинематическое выполнение заданных условий.
Выясним геометрический смысл полюса Р12 и угла поворота 012, кото-
рые использованы в приведенном выше решении задачи синтеза шар-
нирного четырехзвенника по двум положениям (рис. 714). Для этого
переместим второе положение найденного четырехзвенника AB2C2D
как жесткую фигуру вокруг шарнира D на угол —<р12 обратно
в положение Д2Д°ТНС1Д. Тогда фигуры AB^D и A2fi°THCiD опре-
делят собой два относительных положения найденного шарнирного
четырехзвенника по отношению к первому положению C\D его ведо-
мого звена; отрезки А1В1 (точка Д! = Д) и Д2Д°ТН отметят первое
и второе относительные положения ведущего звена четырех-
звенника по отношению к первому положению CtD ведомого звена.
Указанные полюс Р12 и угол поворота 612 определяют эти отно-
сительные положения ведущего звена.
На основании приведенных построений получим следующее
равенство:
L B^Cr = L BtP^M = , (12.3)
где Bt и Ct — подвижные шарниры четырехзвенника (в первом его
положении), удовлетворяющего соответствию заданных углов ср12
и Ф12, а угол 612 вычисляется по формуле (12.1).
Напомним постановку задачи синтеза шарнирного четырехзвенника
по двум положениям, сформулированную в предыдущем параграфе:
требуется определить шарнирный четырехзвенник, у которого при
переходе из первого положения AZJjCjD во второе AB2C2D заданному
углу поворота <р12 ведущего звена АВ{ соответствует заданный угол
поворота ф12 ведомого звена СгВ.
Повторим еще раз решение этой задачи (рис. 715) при тех же по
величине и направлению углах <р12 и ф12, что и на рис. 714, но за
центр Л4, с которым совпадает шарнир С1г выберем точку плоскости
чертежа, отличную от выбранной на рис. 714. Найдем соответствен-
ную этому центру прямую й12, и произвольную точку этой прямой
выберем за шарнир В}. Тогда по-прежнему фигура AB^D опре-
делит первое положение искомого механизма. Отметим второе его
положение AB2C2D, при котором удовлетворяется соответствие за-
данных углов:
«_ В\АВ% — <pi2; _ C\DC2 —<pj2.
§ 39] СИНТЕЗ четырехзвенника по двум и трем положениям 809
Однако два решения одной и той же задачи синтеза четырехзвен-
ника, полученные на рис. 714 и 715, существенно отличаются друг
от друга. Четырехзвенник, установленный на рис. 715, нельзя пере-
вести из первого положения во второе путем поворота ведущего
звена АВ\ на заданный угол <р12. Связано это с тем, что при враще-
нии ведущего звена АВХ в заданном направлении механизм при-
ходит в положение AB'C'D, в котором звенья В'С и CD вытя-
гиваются в одну прямую, и дальнейшее движение механизма
становится невозможным без нарушения его целостности.
Таким образом, четырехзвенник ABfi^D, полученный на рис. 715,
Рис. 715.
удовлетворяет соответствию заданных углов ф|2 и ф12 только геомет-
рически, а не кинематически.
В отличие от этого четырехзвенник AB^C^D, найденный на
рис. 714, удовлетворяет соответствию углов <р12 и ф12 не только
геометрически, но и кинематически: его можно переместить из
указанного первого положения во второе положение путем поворота
ведущего звена ABi на заданный угол <р12.
Следовательно, при решении задачи синтеза четырехзвенника по
двум положениям мы можем получить наряду с четырехзвенниками,
которые удовлетворяют заданному соответствию между углами <р12
и ф12 к и н е м а т и ч е с к и, также четырехзвенники, удовлетворяющие
этому соответствию только геометрически.
Для практических приложений представляют интерес только те
четырехзвенники, которые удовлетворяют заданным условиям кине-
матически.
Требование, чтобы полученный четырехзвенник удовлетворял
заданным условиям кинематически, т. е. чтобы его ведущее и ведо-
мое звенья проворачивались на заданные углы <р12 и ф12, накладывает
определенные ограничения на выбор центра М в плоскости чертежа
и на выбор шарнира Вг на соответственной прямой й12. Но указанное
810
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
[ГЛ. XII
требование проворачиваемое™ является частным случаем более общего
требования, которое всегда учитывается в практике проектирования,
а именно требования, чтобы угол передачи во всех положениях меха-
низма, которые он должен занимать в процессе работы, не выходил
из заданных пределов.
3°. Угол передачи. Углом передачи рв шарнирном четырех-
звеннике ABCD (рис. 716) называется угол между направлениями абсо-
лютной скорости шарнира С ведомого звена ВС и относительной скоро-
сти этого шарнира по отношению к шарниру В ведущего звена АВ.
Так как первая упомянутая
скорость перпендикулярна к
направлению CD, а вто-
рая — перпендикулярна к
направлению ВС, то угол
передачи р можно замерить
как угол между направлени-
ем шатуна ВС и направле-
нием ведомого звена CD.
Условимся за угол передачи
считать угол р 180°.
Отметим два положения
fi(+) и шарнира В ве-
дущего звена, когда направ-
ление этого звена совпа-
дает с направлением стойки AD. В положениях механизма АВ(+)С(+)£)
и AB.yC^D угол передачи р имеет экстремальные значе-
ния. Обозначим длину стойки AD = 1, а относительные длины звеньев
четырехзвенника соответственно a, b и с. Тогда по рис. 716 получим:
62 + с2 —(1—л)2
COS Р(_, =-----2b'c ; cos р(+)
Ь±+С^(1+аГ^ (124)
2Ь с
Между экстремальными значениями р^ и р^+) угол передачи изме-
няется монотонно в функции от угла поворота ведущего звена АВ.
Угол передачи характеризует условия статической передачи
усилий в механизме. Чтобы пояснить смысл этого утверждения, пред-
положим, что к ведомому звену CD четырехзвенника приложен внеш-
ний момент сопротивления Ме. Найдем в первом приближении (прене-
брегая силами трения) нормальные реакции в шарнирах В, С и D меха-
низма, вызываемые приложенным моментом /Ис. С этой целью отделим
от механизма двухповодковую группу Ассура BCD (рис. 717, а) и рас-
смотрим условия ее равновесия. Нормальную реакцию в шарнире D
разложим на составляющие Rd и Rd, направленные вдоль звена CD
и перпендикулярно к нему. Из условия равновесия звена CD
получим:
§ 39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ
811
Так как на звено ВС не действуют внешние нагрузки, то нормаль-
ные реакции RB и Rc в шарнирах В и С будут направлены вдоль
указанного звена и будут равны по абсолютной величине. Построим
план сил (рис. 717, б) на основании следующего уравнения равно-
весия группы BCD:
Rd+RdA-Rb^O.
Из плана сил получим, что по абсолютной величине:
Отсюда следует, что при том же внешнем моменте Мс и при той же
длине с ведомого звена CD нормальные реакции в шарнирах В, С
и D должны непрерывно возрастать при приближении угла передачи р.
Рис. 717.
к 0° или к 180°. Вместе с ними будут возрастать и силы трения
в указанных шарнирах. Чтобы избежать появления больших реакций
в шарнирах механизма и больших нагрузок на звенья механизма, при
проектировании последнего учитывается следующее требование: угол
передачи р. ни в одном из тех положений механизма, которые послед-
ний занимает в процессе работы, не должен выходить -из определен-
ных пределов *). В механизмах приборов внешние нагрузки, прило-
женные к механизму, часто оказываются очень малыми. Тем не менее
при. практическом проектировании этих механизмов также учиты-
вается указанное требование. Здесь это требование связано с необ-
ходимостью избежать больших ошибок положения или ошибок пе-
ремещения ведомого звена. В теории точности механизмов **)
*) Угол, дополняющий угол передачи р до 90°, если р < 90°, или равный
р — 90°, если р > 90°, называется углом давления. Угол давления, так же как
и угол передачи, характеризует условия передачи усилий в механизме. В кулач-
ковых механизмах для исследования этих условий часто пользуются углом
давления (см. главу VII), в шарнирно-рычажных механизмах для той же цели,
как правило, используется угол передачи.
**) См., например, |12в|.
812 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [ГЛ. XII
доказывается, что при тех же первичных ошибках в длинах звеньев
и при тех же зазорах в шарнирах ошибки положения и ошибки пере-
мещения ведомого звена непрерывно возрастают с приближением
угла передачи к 0° или к 180°.
Как показано на рис. 715, вращение ведущего звена АВ' становится
невозможным без нарушения целостности механизма, когда звенья В'С
и CD вытягиваются в одну линию. Положение механизма AB'CD,
называемое положением разрыва, характеризуется углом передачи
(1 = 0° или (1=180° (в зависимости от выбранного направления от-
счета этого угла).
Пусть шарнирный четырехзвенник спроектирован так, что на
заданном угле поворота ср12 ведущего звена угол передачи р. удовле-
творяет неравенству
180°— (in, (12.6)
где (10 — допускаемый угол передачи. Если условие (12.6) выполнено,
то при повороте на угол <р12 механизм не будет приходить в по-
ложение разрыва. Таким образом, условие (12.6) является до-
статочным для получения механизма, проворачивающегося на задан-
ном угле
4°. Учет угла передачи при решении задачи синтеза
механизма. Вернемся еще раз к задаче синтеза четырехзвенника
по двум заданным углам <р12 и ф12, усложнив ее требованием, что-
бы угол передачи fi при переходе механизма из первого поло-
жения во второе не выходил из пределов, определяемых неравен-
ствами (12.6).
Выберем стойку механизма AD (рис. 718) и, использовав задан-
ные углы ср12 и ф12, найдем полюс РХ1. Выберем произвольный
центр 7И, с которым совместим подвижный шарнир ведомого
звена CtD. Построим соответственную прямую Ьп и выберем на ней
произвольную точку Bt за подвижный шарнир ведущего звена АВг.
Тогда ABiCiD определит собой первое положение шарнирного четы-
рехзвенника, удовлетворяющего соответствию углов <р12 и ф12. Отме-
тим угол передачи щ в первом положении механизма как угол между
направлениями звеньев DC\ и BiC. Условимся его отсчитывать от
направления ведомого звена DCi по движению часовой стрелки.
Отметим точку В°™, симметричную точке Ву относительно пря-
мой PKCt. Тогда угол между направлениями 1)С\ и С\В°™ будет
равен углу передачи р2 механизма во втором его положении. (Чтобы
убедиться в справедливости этого утверждения, следует вновь
обратиться к рис. 714, где показано, что жесткая фигура Л2В°ТНС1О
после поворота ее вокруг шарнира D на угол ф12 определяет второе
положение AB^C^D найденного механизма AZ?1C1D.) Обозначим на
рис. 718 угол B1Ci^TH=fi2. Тогда получим:
[i2 = [ii-|-Yta- (12.7)
§ 39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ 813
При выбранном отсчете угла передачи необходимым условием для
проворачивания механизма на заданный угол <р12 будет неравенство
р2<^180°. Если окажется р2^>180°, то при переходе механизма из
первого положения АВ^С^Ё во второе, определяемое заданным углом
поворота <р1-2 ведущего звена, угол передачи должен пройти через
значение р=180°, т. е. механизм должен стать в положение раз-
рыва. Следовательно, величина р2^>180° будет свидетельствовать
о непроворачиваемости механизма на заданный угол <р12.
Предположим, что шарнир В{ выбран на соответственной пря-
мой Ьп таким образом, что при повороте ведущего звена ABt на
угол <р12 это звено не будет проходить ни через положение АВ^,
ни через положение АВ,_} (рис. 716), которым соответствует экстре-
мум угла передачи. Тогда на указанном угле поворота ведущего
звена угол передачи р будет изменяться монотонно щ пределах
рх^р^р2 (рис. 718). Тогда условие р.2<^ 180° (при pt^>0) будет
достаточным условием проворачиваемое™ четырехзвенника на задан-
ном угле «рта- Если, наконец, при всех тех же условиях будет
Pj^Po, a p2sC180° — р0, где р0— допускаемый угол передачи, то
на- всем заданном угле поворота <р12 ведущего звена угол передачи р
будет удовлетворять неравенству (12.6):
posgpsg 180° — р0.
Если шарнир Bt па прямой btl выбран так, что при повороте
ведущего звена ABt на угол <р12 это звено проходит через положе-
814
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
[гл. хн
ние АВ(+) или АВ(_}, то необходимо отдельно проверить экстре-
мальное значение угла передачи р.(+) или соответственно
Если по условиям работы механизма ведущее звено должно совер-
шать полный оборот, то для выполнения неравенства (12.6) в тече-
ние всего оборота ведущего звена достаточно обеспечить неравен-
ства и [1(+)2э 180° — p.n*).
5°. Задача синтеза шарнирного четырехзвенника по трем
положениям. Обратимся к задаче синтеза шарнирного четырехзвен-
ника по трем положениям. Пусть требуется отыскать первое поло-
жение такого четырехзвенника, у которого при переходе из первого
во второе и третье положения заданным углам поворота <р)2 и <р13
ведущего звена ABi соответствуют заданные углы поворота ф12 и ф13
ведомого звена Cj£) (рис. 719). Для решения этой задачи выберем
опять стойку AD механизма. По заданным соответственным углам <р12
и <р12 найдем полюс Р12 и величину угла 6)2 и тем же путем по за-
данным соответственным углам <р13 и ^|3 установим полюс Рц и угол
поворота
®1з — Т1з — фгз-
(12.8)
Величина последнего удовлетворяет также равенству
(12.9)
Полюсы Р12, Р13 и углы поворота б12, 013 определят три относи-
*) О проектировании шарнирного четырехзвенника с ведущим звеном,
совершающим полный оборот, с учетом угла передачи см. [56з].
§ 39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ
815
тельных положения Si, S2, S3 ведущего звена АВ по отношению
к первому положению ведомого звена CrD.
Выберем произвольный центр /И в плоскости чертежа. Повернув
прямую РцМ вокруг полюса Рк на угол--------*-, получим прямую
Ь13 — геометрическое место таких точек В\ в Si, которые со своими
положениями В.2 лежат на окружностях, описанных вокруг выбранного
центра М (см. § 36, 5°). Затем, повернув прямую Р13Л1 вокруг полюса Pn
013 ' г.
на угол---, получим прямую »i3 — геометрическое место таких
точек Bt в Si, которые со своими положениями Вя лежат на окруж-
ностях, описанных вокруг того же центра М. Точка пересечения
прямых Ьк и &1з представит собой такую точку В\ в Sb которая со
своими положениями В2 и Вя (они не показаны на рис. 719) лежит на
окружности, описанной вокруг центра М. Выберем установленную
точку Bi в Si за подвижный шарнир ведущего звена, а подвиж-
ный шарнир Ci ведомого звена совместим с центром М. Тогда
фигура ABiCiD определит первое положение шарнирного четырех-
звенника, который удовлетворяет как соответствию углов <р!2 и <pi2,
так и соответствию углов <pi3 и ф13.
Отметим угол передачи jaj = Z. BiCiD в первом положении меха-
низма. Выполнив построение, аналогичное проведенному на рис. 718,
легко установить углы передачи р.2 и р.3 во втором и третьем поло-
жениях механизма, определяемых углами <р12 и ср1Я.
6е. Координаты полюсов относительных положений. Условимся
в последующем предполагать, что длина стойки четырехзвенника
AD=\ (рис. 720). Проведем декартовы оси X, Y, с началом, совме-
щенным с шарниром D, и осью X, совпадающей по направлению
с вектором AD. Координаты полюса Р12, как точки пересечения
прямых .4Р(2 и DPu, которые проведены под углами — -ч>1- и —
к оси X, подсчитаем по формулам:
tg Г I
АЪ=—у— ।
’} (12.10)
По аналогии координаты полюса Р13 в тех же осях будут:
13
(12.11)
Fl3=-AI3tg'^.
816 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [гЛ. XII
Если известны координаты двух полюсов Р12 и Pi3 и относящиеся
к этим полюсам углы поворота
----?12------^1-2 И ®13 — ?13-----------------ф13>
то третий полюс Р23 полюсного треугольника РнР^Ргз будет точкой
пересечения прямых РцР23 и Pi3P23, которые удовлетворяют равен-
ствам (11.4) и (11.5):
Z Р13Р|2^3 = , L РПРаРт = .
\г ®18 —
Углы -g- и -у, входящие в последние равенства, могут быть
определены непосредственно по чертежу на основании равенств
(12.2) и (12.9).
Рис. 720.
Установим еще третью прямую, которая проходит через полюс Р23,
и используем ее для нахождения координат этого полюса (рис. 720).
Считая точку (которая совпадает с шарниром А), принадле-
жащей положению Si ведущего звена, переместим ее вокруг полю-
сов Р12 и Р13 соответственно на углы 012 и 6(3 в положения Л2
и -4;1. Точки А2 и A3 расположатся симметрично точке At относи-
тельно прямых DPK и DPK. Отсюда
Z. AXDA2 =<pi2; A\DA3 = <р13
и центр окружности, проходящей через три указанные точки Ait А2
и Д3, совпадет с неподвижным шарниром D. Так как точки Д2 и
должны одновременно лежать на окружности, описанной вокруг
полюса Р23, то прямая ОРгз будет биссектрисой угла Д2£Х4а>
§ 39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ 817
Обозначим через 8)3 и 823 углы наклона прямых РкРп и РцРц
к оси X, а через 8О1 23 — угол наклона к той же оси биссектрисы DP^
(углы 813 и 823 на рис. 720 не показаны). Эти углы наклона опреде-
лим из соотношений:
tg8ia = ^^, 828=8lj+^, 8D, 23=^+111. (12.12)
-Л 12--А 13 Z 4
Координаты полюса Р23 как точки пересечения прямых Pi2P23
и DPm подсчитаем по формулам:
А93=^^=^, r83=^3tg8D,23. (12.13)
Непосредственно по рис. 720 получим равенство
_ р13др23= —, (12.14)
необходимое для дальнейшего изложения.
7°. Мгновенный полюс относительного вращения. Допустим,
что при неизменном первом положении AiBx(\D шарнирного четырех-
звенника рис. 721 угол поворота ср12 его ведущего звена АВ\ непре-
рывно уменьшается; вместе с ним непрерывно уменьшается и соот-
ветственный угол поворота <pt2 ведомого звена CXD. В пределе
бесконечно малому углу поворота ведущего звена будет соответ-
ствовать бесконечно малый угол поворота dty ведомого звена, выра-
жаемый соотношением:
dtp = z1d<p, (12.15)
где li — передаточное отношение между ведущим и ведомым звеньями
механизма в первом его положении ДЯ1С1£). В этом случае относи-
тельное положение S2 ведущего звена, конечно удаленное от его
положения Sj, перейдет в относительное положение Si, бесконечно
близкое к положению Si. Полюс конечного поворота Р]2 относитель-
ных положений St и S2 перейдет в мгновенный полюс относительного
вращения Рп, определяющий эти бесконечно близкие относительные
положения ведущего звена по отношению к первому положению C\D
ведомого звена.
Угол поворота этих бесконечно близких положений стремится
в пределе к нулю:
• df) = rfcp — dty —> 0.
Поэтому равенства (12.2) и (12.3) в пределе перейдут в сле-
дующие:
Д ДРиО = 0, (12.16)
BiPiXCi = 0, (12.17)
818 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [ГЛ. XII
Первое равенство показывает, что полюс Ри должен лежать на
направлении стойки AD механизма (рис. 721), а второе, — что этот
полюс должен лежать на направлении шатуна ВХС\ механизма в пер-
вом его положении. Следовательно, полюс Рп совпадет с точкой
пересечения указанных направлений.
Рис. 721.
Для установления координат полюса Рп подставим в фор-
мулы (12.10) вместо конечных углов поворота <р12 и ф12 бесконечно
малые углы Фер и dty. Тогда с учетом соотношения (12.15) в пределе
получим:
-^11= 'Ц— 1 ’ — (12.18)
Напомним, что длина стойки четырехзвенника предполагается при
этом AD= 1.
Укажем области расположения полюса Рц в зависимости от вели-
чины передаточного отношения
При изменении 1г в пределах
— оо •' ij 0
координата Хп меняется в пределах
-l^Xlt^0,
т. е. полюс Рп в этом случае располагается постоянно на отрица-
тельной стороне оси X в пределах стойки AD.
При изменении в пределах
0 ==g/x =s=S-|- I
§39] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ДВУМ И ТРЕМ ПОЛОЖЕНИЯМ 819
пределы для координаты Ап будут:
— со - Ац — 1,
т. е. в этом случае полюс Рп располагается постоянно на отрица-
тельной стороне оси А' вне пределов стойки AD.
Наконец, при изменении 1Х в пределах
+ 1 - it' ' + оо
координата А’п лежит в пределах
О А’ц «Соо,
т. е. в этом случае полюс Рц располагается постоянно на положи-
тельной оси А'.
Отметим, что крайнее положение ведомого звена, в котором
направление его скорости изменяет знак, характеризуется передаточ-
ным отношением
Если крайнее положение ведомого звена помечено как первое поло-
жение, то полюс Рц совпадет в этом случае с неподвижным шар-
ниром А ведущего звена.
8°. Учет передаточных отношений при решении задач синтеза
шарнирного четырехзвенника по положениям. Допустим, что в за-
даче синтеза шарнирного четырехзвенника, наряду с соответственными
положениями ведущего и ведомого звеньев, которые заданы углами <р12
и <р12, задано еще передаточное отношение i, в первом положении
механизма. Из изложенного в п. 7° следует, что задание передаточ-
ного отношения эквивалентно заданию двух бесконечно
близких положений механизма. Г еометрически задание
величины it выражает следующее требование: направление шатуна BjCj
(рис. 721) в первом положении механизму должно проходить через
мгновенный полюс Рц с координатами (12.18). Чтобы при решении
поставленной задачи синтеза учесть это передаточное отношение it,
достаточно добавить к относительным положениям Sj и S2 ведущего
звена, которые определяются полюсом Р12 и углом 612, его относитель-
ное положение SJ, бесконечно близкое к положению Si и определяе-
мое указанным мгновенным полюсом Рц.
Предположим теперь, что, кроме (или вместо) передаточного отно-
шения 1Ъ в первом положении механизма задано передаточное отно-
шение Z2 во втором положении механизма. Задание величины /2 геоме-
трически эквивалентно требованию, чтобы шатун во втором
положении механизма ABfi^D проходил через полюс Р22 с коорди-
натами
= и ^' = 0, (12.19)
Z2 - 1
820 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ звеньев [гл. XII
которые определяются по формулам, аналогичным формулам (12.18)
для координат полюса Рц. Полюс Р$, расположенный, как и полюс Рц,
на направлении стойки AD, определит собой относительное положение
ведущего звена, бесконечно близкое к его второму положению АВ.},
по отношению ко второму положению С2£> ведомого звена. Верхний
индекс у полюса Р£ показывает, что речь идет о мгновенном полюсе
относительных положений ведущего звена по отношению ко второму
положению ведомого звена (а не к его первому положению, как было
во всех полюсах, встречавшихся до сих пор в данной главе).
Переместим P'.^AB^C^D как жесткую фигуру (рис. 721) вокруг
шарнира D на угол — ф,2 в положение Р^АгВ°™СхЪ. Тогда фигура
A2B°IHCtD определит собой относительное положение шарнирного
четырехзвенника по отношению к первому положению CVD ведомого
звена. Отрезок Д2В"ТН отметит второе относительное положение S2
ведущего звена по отношению к тому же первому положению ведо-
мого звена. Наконец, мгновенный полюс Р22 определит относительные
бесконечно близкие положения S2 и S2 ведущего звена по отношению
к первому положению ведомого звена. Координаты полюса Р22 в осях
A, Y с началом в шарнире D найдем по формулам:
А12 = -С°^Ц2, П22 = — 4^. (12.20)
Из рис. 721 очевидно, что при переходе к относительным поло-
жениям ведущего звена по отношению к первому положению ведомого
звена задание передаточного отношения г2 геометрически эквивалентно
требованию, чтобы направление шатуна В°™С\ во втором относитель-
ном положении механизма проходило через полюс мгновенного вра-
щения Р22 с координатами (12.20). Чтобы при решении задачи синтеза
учесть передаточное отношение z2, достаточно к заданным относи-
тельным положениям St и S2 ведущего звена добавить его относи-
тельное положение S2, бесконечно близкое к относительному поло-
жению <$2 и определяемое указанным мгновенным полюсом Р22.
В качестве примера рассмотрим задачу проектирования шарнирного
четырехзвенника по двум положениям, заданным соответственными
углами ср|2 и <р12, и передаточному отношению 1Г в первом положении
механизма. Пусть задано Zj = O, кинематически это означает, что
в первом положении механизма ведомое звено должно занимать крайнее
положение.
Выберем стойку механизма AD — 1 (рис. 722) и по заданным
углам <р12 и ф12 найдем полюс PJ2. В декартовых осях A’, Y с началом
в шарнире D и направлением положительной оси X, совпадающим
с направлением вектора AD, координаты полюса Рц по формуле (12.18)
будут:
аи=7-!-т = -1; Ги = о.
«1 — 1
Следовательно, в этом случае полюс Рц совпадет с шарниром А.
40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ
821
Выберем произвольно центр /И, с которым совместим шарнир Ci
ведомого звена в первом положении механизма. Повернув прямую Р12Л1
вокруг полюса Р12 на угол---у где
= L AP^D,
найдем прямую b{i. Точку fij, в которой прямая />12 пересекается
с прямой Р\\С\, выберем за подвижный шарнир ведущего звена четы-
рехзвенника в первом его положении. Тогда получим четырехзвен-
ник ABiC\D, удовлетворяющий соответствию заданных углов <р12 и ф12,
у которого в первом положении передаточное отношение ix = 0.
Рис. 722.
Отметим угол передачи в первом положении механизма. При
помощи отрезка МВ°™, симметричного отрезку МВХ относительно
прямой Р12/И, установим угол передачи (т2 во втором положении
механизма.
§ 40. Синтез шарнирного четырехзвенника по четырем
ч и пяти положениям
Iе. Графическое решение задачи синтеза шарнирного четырех-
звенника по четырем положениям. Пусть требуется отыскать
четырехзвенник, у которого при переходе из первого положения во
второе, третье и четвертое заданным углам поворота <р12, <р13 и <р14
ведущего звена соответствуют заданные углы поворота <р12, <р13 и ф14
822 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [гл. X1I
ведомого звена. Начнем решение этой задачи с нахождения полюсов
относительных положений.
Выберем стойку механизма AD (рис. 723) и, использовав заданные
соответственные углы <р)2, <р13, ф12 и ф13, найдем полюсы Р)2 и Рг,
при помощи построений, указанных на рис. 719. Положение полю-
са P.i3 определится двумя равенствами (см. рис. 720):
Z PiSPnPi3 = Z AP^D = , / Лз£»Р2з = —(12.21)
Нахождение полюса' Р14 (рис. 723) по заданным углам <р14 и ф14 щ-
отличается от нахождения по заданным углам <р(2 и ф|2 полюса Рх,.
После этого полюс Р24 определится на основании двух равенств,
которые получим из равенств (12.21), заменив в индексах полюсов
цифру 3 на цифру 4 *):
L Р^РКР^= L APnD = ^ , Z PuOP84 = —4’- (12.22)
Таким образом получим два полюсных треугольника РцР^Рзз 11
Р12Р14Р24 с общей вершиной Р]2, определяющих четыре относительных
*) Забегая вперед, укажем, что если углами <р16 и ф45 задано пятое поло-
жение четырехзвенника, то после отыскания полюса полюс Р25 определится
на основании равенств
L Р15Р18Р2Г, = Z AP^D = °” ; Z Р,6СР25 = — , (12.23)
которые получим из равенств (12.21), заменив в индексах полюсов цифру 3 на
цифру 5. (На рис. 723 полюсы Pti и Рг-„ не показаны.)
§ 40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ 823
положения ведущего звена по отношению к первому положению ведо-
мого звена.
Использовав найденные полюсные треугольники, построим кривую
центров (рис. 724). Она проходит через все пять полюсов Р1а,
р1а, Аз, Рц и Рц- Точки ее удовлетворяют равенству (11.35):
Z. РкМР^— РцМРщ.
Из равенств (12.21) и (12.22) имеем:
Z Р^ОР^ = L Р^РР*=—-%? • (12-24)
Последнее свидетельствует, что точка D удовлетворяет предыдущему
равенству (11.35). Следовательно, кривая центров /И1234 проходит
также через шарнир D.
При расположении полюсов PI2, Ра, Р23, Р]4 и Р24, указанном
на рис. 724, кривая центров ТИ'234 состоит из двух обособленных
ветвей: замкнутой ветви, которая проходит через полюсы Pi3 и Р24,
и ветви, которая проходит через полюсы Р12, Р13, Р14, шарнир D
и уходит в бесконечность.
Выберем на кривой центров Л1’2М произвольный центр М (на
рис. 724 он выбран на замкнутой ветви этой кривой) и на основании
равенств
/ В[Р^М=РАРйЬ^ (12.25)
824 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [гл, XII
построим соответственную ему круговую точку Bt. Выберем ее за
подвижный шарнир ведущего звена ABt. Подвижный шарнир С,
ведомого звена DCi совместим с центром М. Тогда получим первое
положение механизма ABtCiD, который удовлетворяет соответствию
заданных углов <р12, tp13, ср14 и <р12, <р13, ф14.
Выбирая за центр М, с которым совмещается шарнир Ct искомого
механизма, последовательные точки кривой центров 7И1234, можно
получить бесконечное множество механизмов, удовлетворяющих по-
ставленным условиям. Часть из этих механизмов может удовлетворять
этим условиям кинематически, а часть будет удовлетворять только
геометрически. Остановимся, в частности, на следующем случае: вы-
берем центр М на кривой центров /И1234 совпадающим с неподвиж-
ным шарниром D ведомого звена. Тогда на основании равенств (12.25)
получим, что соответственная ему круговая точка В'234 совпадет
с неподвижным шарниром А ведущего звена. Следовательно, в этом
случае получим шарнирный четырехзвенник с длинами ведущего и
ведомого звеньев ABl — C]D— 0, который не дает решения.
Предположим, что в рассмотренной задаче поставлено следующее
дополнительное требование: ведущее звено АВ] должно совершать
полный оборот, а ведомое звено CtD — возвратно-колебательное
движение. При этом условии ведомое звено С]Г) в процессе движения
механизма не может проходить через линию стойки. Это ограничивает
выбор центра М, с которым совмещается шарнир Cj ведомого звена
в первом положении механизма.
В нашем случае (рис. 724) наибольшим по абсолютной величине
из заданных углов поворота ф12, 613 и ф14 ведомого звена является
угол ф13. (Прямая P^D образует с осью X на рис. 724 больший по
абсолютной величине угол, чем прямые РцО и РцО.) Проведем через
шарнир D прямую d под углом — ф13 к оси X. Чтобы ведомое звено C]D
при повороте на заданный угол <р13 не проходило через линию стойки AD,
центр М должен лежать на участке кривой центров А11234, рас-
положенной правее прямой линии d. На рис. 724 это будет участок М'ММ"
замкнутой ветви кривой центров 7И’234, где М и М" — точки пере-
сечения этой ветви с прямой d. Отсюда видно, что при заданных
соответственных углах <р12, <р13, ср14, ф12, ф13 и <р14, поиски прово-
рачивающихся механизмов можно вести только в узкой области
углов 8, где 8 = /_ СхРХ2х.
2°. Аналитическое решение задачи синтеза четырехзвенника
по четырем положениям. Точность графического решения иногда
может оказаться недостаточной для практических целей. Использовав
уравнение кривой центров /И1234, легко дать аналитический подсчет
координат шарниров В] и С4 в первом положении механизма. Для
этого проведем декартовы оси X, Y с началом в шарнире D и
направлением положительной оси X, совпадающим с направлением
вектора AD. По формулам (12.10)—(12.13) подсчитаем координаты
Т|2), (АТз, Г13) и (Az23, ^зз) полюсов Р12, Р13 и Р23, имея в виду,
§ 40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ 825
что 62 = ©12 — ф12- Координаты полюсов Р14 и P.2i подсчитаем по
формулам:
Ki4 = -A-14tg^;
_Г12— 1’11. f g tg 614 + tg _ Фи + Ф14 .
°14 Х»-Хц' tgG* } ^£>,24 1—tg8Htg-^ 2
А 24 = _ xYia tg Kia . tg6ai — tg 24’ 124 = A 24 tg 24.
(12.26)
Они получены из формул (12.11)—(12.13) путем замены в индексах
цифры 3 на цифру 4.
Введем новые декартовы оси х, у, параллельные прежним,
но с началом в полюсе Pi2. В этих осях координаты указанных
полюсов Ргл, Р2Л, Рц и определим по формулам преобразования
координат:
xik — — А12; y2k—Уjk—Па- (12.27)
Координаты неподвижных шарниров А и D будут соответственно
ха— — (I'FA'jg); у а——К12-,
X[J - —Аи! Уо ——У12-
(12.28)
По формулам (11.37) и (11.38) подсчитаем вспомогательные коэффи-
циенты kb kit k3, kt, jb j2, j3 и jt. Замерим непосредственно с чер-
тежа (рис. 724) угол 8 наклона прямой Р13Л1 (где М — выбранный
центр на кривой 7И,2М) к оси х. Подсчитаем по формулам (11.40)
коэффициенты -wlt wt и w3, а по формулам (11.39) — коорди-
наты выбранного центра М(хм, Ум)- Координаты соответственной
круговой точки Bi(xb, ув) подсчитаем по формулам (11.11)—
(11.13).
3°. Син1ез шарнирного четырехзвенника по крайним положе-
ниям. Рассмотрим частный случай задачи синтеза шарнирного четырех-
звенника по четырем положениям, представляющий значительный
интерес для практических приложений. Обозначим AB2C\D и AB2C2D
(рис. 725) два положения шарнирного четырехзвенника, в которых
ведомое звено CD занимает крайние положения. Требуется,
чтобы при переходе шарнирного четырехзвенника из первого поло-
жения во второе углу поворота <р12 ведущего звена АВ соответствовал
угол поворота ведомого звена CD.
826
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
[ГЛ. ХЦ
Рис. 725.
В крайнем положении механизма передаточное отношение i =
d'b
Поэтому указанную задачу кинематически можно сфор-
мулировать так: требуется спро-
ектировать шарнирный четы-
рехзвенник по двум поло-
жениям, заданным углами
и ф12, и по передаточным отно-
шениям в этих положениях
4 = /2 = 0. Альт [616] дал
следующее решение этой зада-
чи, основанное на использова-
нии соответствующей кривой
центров и кривой круговых
точек.
Выберем стойку механизма
AD=l (рис. 726) и по за-
данным углам <р12 и ф12 найдем
полюс Р12. Соответствующий угол поворота 612 можно определить по
формуле (12.2):
Z .
Мгновенный полюс Рц при ij —0 совпадет с шарниром А ведущего
звена (см. § 39, 7°). Мгновенный полюс Р22 при г2 = 0 совпадет
Рис. 726.
с тем же шарниром А. Переместим полюс Р22 вокруг шарнира D
на угол —<р12 в Положение Р22. Из симметрии полюсов Р$ и Р22
относительно прямой P^D получим:
/Р^Р^Ри = ёГ2) (12.29)
Pd\p= (12.30)
40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ
827
- Прямая Pl2D явится биссектрисой угла РцРцРц. Вследствие ра-
венства (.12.30) кривая центров 7И1122 распадается здесь на прямую Рп[)
и окружность которая проходит через полюсы Р12, Рп и Р22 (см.
§ 37,9е). Центр с окружности Cj определим как точку пересечения
прямой PhD с перпендикуляром, восставленным из середины b
отрезка Р12РП.
Чтобы найти соответственную кривую круговых точек по
общему правилу (см. рис. 698) переместим полюс Р22 вокруг полюса Р12
на угол — 612 в положение Р22, которое совпадет с полюсом РП.
(Полюс Р22 на рис. 726 не помечен, чтобы не перегружать чертеж
обозначениями.) Кривая круговых точек В\1-~ строится на полюсах Р12,
Рп и Р.‘2 так же, как кривая центров /И1122 строится на полюсах Ри,
Рп и Рчч- Вследствие совпадения друг с другом полюсов Рп и Р32
кривая круговых точек P]12S распадется *) здесь на прямую Р12РП
и окружность bi с центром Ь, построенную на отрезке АгРц, как
на диаметре.
Проведем через полюс Рц, совпадающий с шарниром А, прямую z
под произвольным углом к оси х. Точки пересечения прямой z
с окружностями су и bi определят центр М и соответственную ему
круговую точку Bt. Выберем точку Bi за подвижный шарнир веду-
щего звена ABt механизма, а подвижный шарнир Ct ведомого звена
CiD механизма совместим с центром М. Тогда получим первое поло-
жение ABiCtD искомого шарнирного четырехзвенника, удовлетворяю-
щего соответствию углов ср12 и ф12, у которого в первом и втором
положениях ведомое звено занимает крайние положения.
Изменяя угол <р, наклона к оси х прямой z, будем получать новые
механизмы, удовлетворяющие тем же условиям. На рис. 726 жирно
выделен участок окружности съ отсеченный от нее прямой DP22.
Проворачивающиеся механизмы дадут только такие прямые z, которые
пересекают окружность С] на указанном участке, так как только при
этом условии ведомое звено DCi механизма при повороте на заданный
угол ф12 не пройдет через стойку AD.
Предположим, что, поставив найденный проворачивающийся меха-
низм в соответствующие положения AB^C^D и AB^C^D
(рис. 716), мы нашли экстремальные значения |л(+) и угла передачи.
Обозначим:
Н(+) =: t^niin > еСЛИ 180 Р'(-) P’mitl >
или
180 Р'(-) == P'min> если " Hmin •
Среди проворачивающихся механизмов, определяемых построением
на рис. 726, можно найти такой, у которого величина |imin будет
наибольшей из возможных, которую обозначим ([J.min)max. На рис. 727
изображена диаграмма Альта [61н], на которой в осях <р12 и ф12
Так же как распалась кривая центров 7И1122 на рис. 690 при совпадении
друг с другом полюсов Рп и Pss.
828
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
1гл. хи
нанесены кривые (pmitl)max и кривые угла при котором отыскп
вается механизм с углом передачи (p.min)max. Рассмотрим пример. Нус и,
заданы <р12= 165° и ф12 = 60°. Точка с этими координатами располп
жена очень близко от кривой = 40°. Это означает, что, построив
Рис. 727.
по заданным ’ углам <р|2 = 165° и (р12 = 60° соответствующие окруж-
ности Cj и bi (рис. 726) и проведя прямую z под углом ср1 = 40°
к оси х, найдем шарнирный четырехзвенник с углом передачи (p-min)max-
По диаграмме он будет 30°. Удаляясь от угла ср, = 40°, мы будем по-
лучать механизмы с углом передачи р.П1|П 30°.
Диаграмма на рис. 727 свидетельствует, что в рассматриваемой
задаче по крайним положениям ведомого звена после задания угла
§ 40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ 829
размаха <р)2 этого звена и выбора допускаемого угла pmin угол
можно задавать только в определенных пределах, которые быстро
сужаются с возрастанием угла размаха ф12. Соответствующие числен-
ные значения приведены в таблице 12.1.
Таблица 12.1
Пределы для выборка угла поворота 'у|2 ведущего звена при
заданном угле размаха <р12 ведомого звена шарнирного четырех-
звенника и выбранном минимальном угле передачи pnljn
;xniin <pj2 3(Г 35" 10е
15° 153е 222° 157 е 214 е 161' 208°
30 156 225 160 212 164 205
45 161 219 165 210 169 202
60 166 216 169 204 172 195
75 170 209 172 197 174 189
90 105 173 196 180 176 188 178 182
Отметим, что при возрастании угла размаха ip12 пределы для вы-
бора о)2 стремятся к 180°. При любом угле размаха ф12 выбор
180° обеспечивает наиболее благоприятные решения в отношении
величины pniin-
4°. Синтез шарнирного четырехзвенника по заданному коэф-
фициенту изменения скорости хода. Рассмотрим шарнирный четырех-
звенник, у которого ведущее звено совершает непрерывное враща-
тельное движение, а ведомое звено возвратно-колебательное движение.
В практике применения этого механизма в машинах-автоматах движение
ведомого звена в одном направлении является обычно рабочим ходом,
а движение в другом направлении — холостым ходом. Имеются случаи,
когда требуется, чтобы движение ведомого звена происходило с раз-
личными скоростями во время рабочего и холостого хода. В частности,
часто требуется, чтобы средняя угловая скорость рабочего хода о)ра6
ведомого звена была меньше средней угловой скорости холостого
хода ыХШ1 этого звена.
При постоянной угловой скорости ведущего звена средние ско-
рости ведомого звена wpa6 и юхол обратно пропорциональны углам
поворота ведущего звена, соответствующим рабочему и холостым
ходам. Если для определенности принять, что угол поворота веду-
щего звена, соответствующий рабочему ходу ведомого звена, есть <р12,
то получим:
“ ХОЛ _ __________ А
“раб 360° — ?13
830 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [ГЛ. XII
Величина k называется коэффициентом изменения скорости хода. При
заданной величине этого коэффициента найдем угол:
ь
'Р1-2=ТТ^,36О°- (12.31)
Пусть поставлена задача: спроектировать шарнирный четырехзвенник
по заданному углу размаха ф12 ведомого звена и заданной величине
коэффициента изменения скорости хода k. Подсчитав по формуле (12.31)
соответствующий угол поворота ведущего звена <pt2, сведем поста-
вленную задачу к рассмотренной выше задаче синтеза по крайним
положениям ведомого звена.
При помощи диаграммы на рис. 727 среди решений поставленной
задачи легко выделить такой шарнирный четырехзвенник, у которого
минимальный угол передачи fxmin имеет наибольшую величину (pmin)max-
Та же диаграмма при выбранном допускаемом угле передачи p.mjn
позволяет установить наибольшие значения коэффициента изменения
скорости хода k, осуществимые шарнирным четырехзвенником
(табл. 12.2):
Таблица 12.2
Наибольшие значения коэффициента k изменения скорости хода,
осуществляемые шарнирным четырехзвенником при заданном
угле размаха ведомого звена 4>ls и выбранном допускаемом угле
передачи pmin
Hnin Ф13 30° 35° 40°
15’ 1,61 1,47 1,37
30 1,59 1,43 1,32
45 1,55 1,40 1,28
60 1,50 1,31 1,18
75 1,38 1,21 1,Н
90 1,20 1,09 1,02
105 1,00 1
5°. Задача синтеза шарнирного четырехзвенника по пяти
положениям (графическое решение). Поставим задачу отыскать
четырехзвенник, у которого при переходе из первого положения во
второе, третье,’четвертое и пятое заданным углам поворота <р12, <р13,
<р14 и <р1в ведущего звена соответствуют заданные углы поворота ф12>
Фи, фи и Ф1в ведомого звена. В этом случае к полюсным треуголь-
никам Р)4Р)3Р2з и РцРцРц (Рис- 728), построение которых указано
на рис. 720 и 723, присоединится еше полюсный треугольник Р\гР\ъР-№-
Полюс Р1В определится по заданным углам ф1в и ф1в так же, как
определялся полюс Р12 по заданным углам <р,2 и ф12 (см. рис. 714),
а полюс PiB построим на основании равенств (12.23).
§ 40J СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ 831
Чтобы установить первое положение ABfiiD механизма, удовле-
творяющего поставленным условиям, необходимо шарнир Ci ведомого
звена выбрать совпадающим с центром Бурместера 7Й12348, который
определяется указанными тремя полюсными треугольниками, а шар-
нир В\ ведущего звена —- совпадающим с соответственной точкой
Бурместера #}S3,\
Центр Бурместера Af12348 удовлетворяет равенству (11.114):
/, Р1зТИ/->2з= А_ PiKMP.^.
Графически этот центр можно найти как точку пересечения двух
кривых центров 7И1234 и /И1238 (на рис. 728 эти кривые не изобра-
жены).
Рис. 728.
Ранее было установлено равенство (12.24):
/ = Z Р^ОР№ = - ,
доказывающее, что кривая центров /И1234 проходит через неподвиж-
ный шарнир D ведомого звена. Аналогичным путем можно установить
равенство *)
/ (12.32)
которое докажет, что кривая центров А11238 также проходит через
шарнир D. Точка пересечения кривых центров Af1234 и А41238, совпа-
дающая с шарниром D, явится центром Бурместера Af’2348. Она будет
удовлетворять равенствам (11.114), так как на основании равенств
*) На рис. 728 не проведены прямые, соединяющие шарнир D с полюсами
Pia, Раз, Pnt Рза, и /А&.
832 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [гл. XU
(12.24) и (12.32) получим:
/ Р13ОР23 = L PuDP^ = L PKDPW = — . (12.33)
Для отыскания точки Бурместера BJ2845, соответственной упомянутому
центру, достаточно воспользоваться равенствами (см. § 38):
_в,рпм=^ и
Так как
^ = APnD и Ц = АР^О,
то, очевидно, что для центра Бурместера, совпадающего с неподвиж-
ным шарниром D ведомого звена, соответственная точка Бурместера
совпадет с неподвижным шарниром А ведущего звена. (Подобно тому,
как это было в задаче синтеза по четырем положениям в пункте 1°
настоящего параграфа.) Центр и точка Бурместера, совпадающие
с неподвижными шарнирами А и D, определят шарнирный четырех-
звенник с длинами ведущего и ведомого звеньев, равными нулю,
который должен быть исключен из дальнейшего рассмотрения.
Так как в общем случае центров Бурместера может быть или
четыре, или два, или ни одного, то в рассматриваемом случае центров
Бурместера, не совпадающих с шарниром D, может быть или три или
один. Каждый из этих центров Бурместера, не совпадающих с шар-
ниром D, определит шарнирный четырехзвенник, у которого заданным
углам поворота <ри, <р13, <р14 и <р1в ведущего звена соответствуют
заданные углы поворота ty12, <р13, ty14 и ф15 ведомого звена. Но может
оказаться, что некоторые из этих четырехзвенников или даже все
они удовлетворяют заданным условиям только геометрически, а не
кинематически, т. е. не дают решения поставленной кинематической
задачи.
6°. Задача синтеза шарнирного четырехзвенника по пяти
положениям (аналитическое решение). Можно аналитически под-
считать координаты центра и точки Бурместера, которые одновре-
менно явятся координатами подвижных шарниров Cj и Bt ведомого и
ведущего звеньев искомого четырехзвенника в его первом положении.
Для этого проведем на рис. 728 декартовы оси X, Y с началом
в шарнире D и направлением положительной оси X, совпадающим
с направлением вектора AD. По формулам (12.10)—(12.13) и (12.26)
подсчитаем координаты (А)2, К12), (А13, У13), (А23, /23), (Az14, Ku) и
(А24, К24) полюсов Pl2, Pt3, Pi3, Рп и Р24, имея в виду, что здесь
6|2=:<р12 — ф12. Координаты полюсов Р1а и Р.25 подсчитаем по тем же
формулам (12.26), заменив предварительно в индексах всех величин
цифру 4 на цифру 5.
§ 40] СИНТЕЗ ЧЕТЫРЕХЗВЕННИКА ПО ЧЕТЫРЕМ И ПЯТИ ПОЛОЖЕНИЯМ 833
Введем новые декартовы оси х, у, параллельные прежним, но
с началом в полюсе Р12. В этих осях координаты любого из полюсов
Рк, Р?з, Pit, Pit, Pie и As определим по формулам (12.27):
xjk = jk — i«5 yjk — jk — ^12-
Координаты неподвижных шарниров А и D подсчитаем по форму-
лам (12.28). Далее по формулам (11.117)—(11.119), (11.123), (11.126)
и (11.127) подсчитаем коэффициенты mit т%, т.г, тл и тй уравнения
(11.125):
/я4и4 -ф- »г3н3 -ф- »г2н2 -ф- тхи -ф- тй = 0.
Корень этого уравнения
где — то значение вписанного угла, при котором три окружности
/И143— у, ЛД24— y и Л1,и— у (рис. 728) пересекаются в соответ-
ственном центре Бурместера (см. § 38,3°).
Корень указанного уравнения четвертой степени, соответствующий
центру Бурместера, который совпадает с шарниром D, согласно равен-
ствам (12.33) будет:
K==tg(-^),
где ф12 — заданный угол поворота ведомого звена при переходе четы-
рехзвенника из первого положения во второе.
Исключив этот корень из уравнения четвертой степени (11.125),
получим кубическое уравнение относительно переменной и:
w3 —|— т[ит'0 = 0. (12.34)
Его коэффициенты лч2, т\ и т'п выражаются через коэффициенты mit
ni't, nii и /«0 уравнения (11.125) и известный его корень:
* , ’-'la ’ W/g ' , 'is * /, с о
/я2 =------tg ’ , т,—~ — тД&~, т,.=---------------:—. (12.35)
а й 2 1 и, 2 к 2 0 v •
'ni tg ~2
Если уравнение (12.34) имеет один действительный корень и, то, под-
ставив его в формулы (11.124), получим координаты центра Бурме-
стера Л412348, а затем по формулам (11.11)—(11.13) найдем координаты
соответственной точки Бурместера Д]2343. Они явятся координатами
подвижных шарниров С\ и Вх ведомого и ведущего звеньев искомого
четырехзвенника в первом его положении.
Если уравнение (12.34) имеет три действительных корня иь иг и
и3, то, подставляя их последовательно в указанные формулы, найдем
27 И. И. Артоболевский
834
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
[гл. XII
координаты трех центров Бурместера и трех соответственных им
точек Бурместера. Эти три центра и три точки Бурместера определят
три шарнирных четырехзвенника, удовлетворяющих заданным условиям
или кинематически или только геометрически.
§ 41. Синтез кривошипно-шатунного механизма и кулисного
механизма по положениям
1°. Кривошипно-шатунный механизм как шарнирный четырех-
звенник с бесконечно большой длиной стойки. Выберем на схеме
шарнирного четырехзвенника ABCD (рис. 729) декартовы оси X, Y
с началом в шарнире А и с осью X, направленной вдоль стойки AD.
Будем неподвижный шарнир D четырехзвенника удалять вдоль оси X
в бесконечность, тогда в
пределе четырехзвенник
перейдет в кривошипно-
шатунный механизм АВС,
а его ведомое звено CD
изобразится ползушкой и.
Движение ползушки и
вместе с шарниром С как
вращение вокруг беско-
нечно удаленной точки D
будет поступательным
движением в направлении,
параллельном оси Y.
Так как кривошипно-
шатунный механизм мож-
но рассматривать как шар-
нирный четырехзвенник с бесконечно удаленным неподвижным шар-
ниром D ведомого звена, то изложенные ранее способы решения
задачи синтеза шарнирного четырехзвенника по положениям применимы
к решению той же задачи синтеза кривошипно-шатунного механизма.
Необходимо лишь учесть те изменения, которые вносит в соответ-
ствующие построения и расчетные формулы уход неподвижного шар-
нира D в бесконечность. Эти изменения касаются прежде всего опре-
деления координат полюсов относительных положений ведущего
звена АВ по отношению к первому положению ползушки и.
Изложим решение задачи синтеза кривошипно-шатунного меха-
низма по двум положениям, в которой заданы угол поворота <р12 ведущего
звена АВ и соответственное перемещение s12 ползушки. Выберем положе-
ние неподвижного шарнира А (рис. 730). Проведем декартовы оси X, Y,
начало которых совместим с этим шарниром. Положим, что направление
движения ползушки совпадает с направлением оси ординат Y. По-
люс Р12 относительных положений ведущего звена по отношению
к первому положению ползушки найдем в пересечении двух прямых:
§ 41] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 835
прямой, проведенной через точку А под углом — у к оси X, и пря-
мой, которую получим, переместив прямую АХ поступательно на ве-
личину — ~ . Соответствующий угол поворота 0,.2 найдем при помощи
формулы (12.2), заменив в ней букву О на букву
£ АР^Х=6^ .
Отсюда следует, что
— ?12-
После установления полюса Р12 относительных
ветственного угла поворота 612 отыскание первого
шипно-шатунного механизма, удов-
летворяющего заданным условиям,
не будет отличаться от отыска-
ния первого положения шарнир-
ного четырехзвенника по задан-
ным углам <р12 и <]>12 (см. § 39,
1° и 2°). Выберем произвольную
точку за центр М. Повернув
прямую Р)2/И вокруг полюса Р13
612
на угол----установим геоме-
трическое место точек Вь кото-
рые со своими положениями В3
лежат на окружности, описанной
вокруг центра /И. Выберем далее
произвольную точку Bt на пря-
мой />|2 за подвижный шарнир ве-
дущего звена (кривошипа) ABt.
Шарнир С, ползушки совместим
с центром /И. Тогда фигура ABtCt
определит первое положение иско-
мого кривошипно-шатунного меха-
низма, у которого при повороте кривошипа ABt на заданный угол <р12
ползушка и получит заданное перемещение $|2.
Решение задачи синтеза кривошипно-шатунного механизма по
трем, четырем или пяти положениям будет отличаться от решения
соответствующей задачи синтеза шарнирного четырехзвенника по трем,
четырем или пяти положениям также только способом определения
координат полюсов относительных положений.
Л*):
(12.36)
(12.37)
положений и соот-
*) В равенстве (12.36) под стороной Pi2X угла АР12Х следует понимать
прямую, которая проходит через полюс Pi2 параллельно оси X.
27’
836 СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ [гл. ХЦ
2°. Координаты полюсов относительных положений. Пусть
в задаче синтеза кривошипно-шатунного механизма заданы два угла
поворота <р12 и <р13 кривошипа и соответственные перемещения $12
и s13 ползушки. В этом случае можно установить полюсный треуголь-
ник РцР^зРгз (рис. 731), определяющий три относительных положения
кривошипа по отношению к первому положению ползушки. Нахожде-
ние полюса Р12 по заданным углу <р12 и соответственному перемеще-
нию s12 указано на рис. 730. Аналогичным путем на рис. 731
Y
Рис. 731.
установим полюс Р1Л по заданным углу <р13 и соответственному
перемещению s13. Здесь будут справедливы формулы, аналогичные
формулам (12.36) и (12,37):
£АР13Х=Ц; 613 = ?13. (12.38)
Для подсчета координат полюсов Р12 и Pls в декартовых осях X, Y
с началом в неподвижном шарнире А кривошипа получим формулы:
*13=+-^-; Г13 = -^. (12.40)
2tg^3 2
Полюс Р23 найдем в пересечении двух прямых: прямой, проведен-
ной через полюс Р12 под углом = к прямой Pi2P13, и прямой,
которую получим, переместив прямую АХ поступательно на вели-
Sig + Si3
чину---
§41] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 837
Координаты полюса Р23 как точки пересечения указанных прямых
подсчитаем по формулам:
tgS-23 =
Az23 —
(Kls-K1£) + (^ls-Xls)tg^
(А,в - Xlg) - (Pl3 - y12) tg ’
Sis I v V Sib + s18
"~2tP^ “Г ,2’ a3— 2
(12.41)
(12.42)
Здесь 823— угол наклона прямой РцР^з к оси А.
Если в задаче синтеза кривошипно-шатунного механизма кроме
соответственных величин ср12, ср13
поворота кривошипа и соответ-
ственное перемещение ползуш-
ки $14, то, заменив цифру 3 на
цифру 4 в формулах (12.40)—
(12.42), получим формулы для
подсчета координат полюсов
Р14 и Р24 (рис. 732), которые
вместе с полюсом Р)2 обра-
зуют полюсный треугольник
Pi2Pi4P24. Если, наконец, за-
даны еще один угол поворота
<р13 кривошипа и соответст-
венное перемещение ползушки
s1B, то аналогичным путем най-
дем координаты полюсов Р1В и
Р2В, образующих полюсный тре-
угольник РцР^Ргз- (Полюсы
Р18 и Р28 не изображены на
рис. 732.)
Если в первом положении
механизма задана величина про-
„ ds
изводной , то для отыскания
ау ’
координат мгновенного полюса
Рп (рис. 731) относительного
вращения следует в формулы
(12.39) вместо конечных пере-
мещений <pi2 и $12 подставить
и Дх, перейти к пределу Дер—►
тате получим:
и s12, s13 заданы еще один угол <р14
Рис. 732.
бесконечные малые перемещения Д<р
0, а затем положить <р = <р4. В резуль-
Уп = 0.
и
(12.43)
838 синтез механизмов по положениям звеньев [гл. XII
Если во втором положении механизма задана величина производ-
ной , то для координат вспомогательного мгновенного полюса Р$
по аналогии получим:
к»-°- <12Л4>
Переместив полюс Р'.^ на величину —s12, установим полюс Р22;
его координаты будут:
= (12.45)
При решении задачи синтеза кривошипно-шатунного механизма мгно-
венные полюсы Рп, Р'^ и Р22 имеют такой же геометрический смысл,
как при решении задачи синтеза шарнирного четырехзвенника
(см. § 39, 7° и 8°).
3°. Решение задачи синтеза кривошипно-шатунного меха-
низма по четырем и пяти положениям. При аналитическом решении
задачи синтеза кривошипно-шатунного механизма по четырем или пяти
положениям соответственные расчетные формулы несколько упро-
щаются по сравнению с решением той же задачи синтеза шарнирного
четырехзвенника.
Рассмотрим сначала задачу синтеза кривошипно-шатунного меха-
низма по четырем положениям. Пусть заданы углы поворота <р12, <р13
и <р14 кривошипа и соответственные перемещения s12, $13 и $14 пол-
зушки. Требуется определить кривошипно-шатунный механизм, удо-
влетворяющий этим условиям. По заданным величинам ср12, ср13, ср14,
sI2, s13 и Sj4 построим полюсные треугольники Pi2P13P23 и Р42Р14Р24
(рис. 732) с общей вершиной Р12, определяющие четыре относитель-
ных положения кривошипа по отношению к первому положению пол-
зушки. Построим кривую центров Л41234. Она проходит через все пять
полюсов и шарнир D, удаленный в бесконечность в направлении
оси X. Отсюда следует, что в рассматриваемой задаче ось X будет
определять асимптотическое направление кривой ЛР234.
Выберем на этой кривой произвольный центр М и построим соот-
ветственную ему круговую точку б4. Выберем ее за подвижный
шарнир кривошипа Подвижный шарнир С| ползушки совместим
с центром М, Таким образом получим первое положение кривошипно-
шатунного механизма, удовлетворяющего заданным условиям.
Чтобы аналитически определить координаты шарниров Bt и С),
подсчитаем по указанным выше формулам координаты полюсов Piit
Р13, Рц> Рж> Рц в декартовых осях X, Y, начало которых совмещено
с неподвижным шарниром А кривошипа. Введем новые декартовы
оси х, у, параллельные прежним, но начало которых совмещено с по-
люсом Р12, и подсчитаем в них координаты полюсов Р13, Р14, Р23
и Р24 по формулам (12.27).
По формулам (11.37) и (11.38) подсчитаем вспомогательные коэф-
фициенты ki, kit k3, klt Ji, jit j3 и j4. Замерим непосредственно на
§ 41] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 839
выполненном чертеже (рис. 732) угол 8 наклона прямой Р12Л1 к оси х,
где М — выбранный центр на кривой /И1234. Подсчитаем по фор-
мулам (11.40) коэффициенты wt, w2 и w3, а по формулам (11.39)
координаты центра М (хл1, ум). Координаты соответственной круговой
точки Ву (хв, ув) подсчитаем по формулам (11.11)—(11.13).
Так как асимптотическое направление кривой центров М1234 сов-
падает с осью X, то должно быть /2=0. Чтобы убедиться в этом,
установим по формулам (12.40), (12.42) и (12.27) ординаты _у|3, j'14,
У-гз и J'm полюсов Р13, Р14, Р23 и Р24. (Напомним, что ординату у/14
полюса Рн найдем по формуле (12.40), заменив в индексах цифру 3
на цифру 4.)
„ S13 j 812 814 I S12
— *2 ~Г~2 ’ -Уи — ~ “2 -Г "2,
S12 + S13 I S12 _ S]3 Sis “Ь SJ4 | Sig _ S14
Ун— 2 ' 2~ ~2’ -У24~ 2 Г 2~— 2’
По формулам (11.38) убедимся, что
J-2 — >23 “Ь>14->13-->24 = 0-
В результате упрощается подсчет коэффициентов w2 и w3 по
формулам (11.40).
В задаче синтеза кривошипно-шатунного механизма по пяти поло-
жениям, когда заданными являются углы <?12, <?13, <р14, а>18 и ф12, ф13,
фи, Ф1в, к указанным на рис. 732 полюсным треугольникам Р12Р13Р2з
и РцРцРц прибавится третий полюсный треугольник Р13РКР№ (не
изображенный на рис. 732). Использовав полюсные треугольники
P12Pi3p23 и Р12Р18Р2В, можно построить вторую кривую центров /И1238
(не изображенную на рис. 732). Кривые центров Л41234 и Л11238 будут
иметь общую бесконечно удаленную точку, направление которой сов-
падает с направлением оси X, общие точки, совпадающие с полю-
сами Р12, Р13 и Р23, а также еще или одну, или три общие точки,
определяющие центры Бурместера /И12’48. Если шарнир Ct ползушки
совместить с центром Бурместера, а шарнир Bt кривошипа — с точкой
Бурместера, соответственной упомянутому центру, то получим первое
положение AByCt кривошипно-шатунного механизма, удовлетворяющего
соответствию всех заданных углов: <р12, <р13, <?14, ср1в и ф12, ф13, <pi4, <pJB.
Так же как задача синтеза шарнирного четырехзвенника по пяти
положениям, задача синтеза кривошипно-шатунного механизма по пяти
положениям имеет или одно, или три решения.
При аналитическом решении этой задачи формулы (11.123)—
(11.127) несколько упрощаются, так как коэффициенты е4 и Л4 по
формулам (11.118) получаются:
е4 = #4 = 0,
подобно тому как в задаче синтеза кривошипно-шатунного механизма
по четырем положениям получился коэффициент у2 = 0.
840
СИНТЕЗ МЕХАНИЗМОВ ПО ПОЛОЖЕНИЯМ ЗВЕНЬЕВ
[гл. XII
В результате оказывается в формулах (11.123)
Рз = 0.
В формулах (11.126):
/?4=0
и, наконец, в формулах (11.127)
тй= 0.
Из уравнения четвертой степени (11.125) непосредственно отде-
ляется корень и = 0, определяющий бесконечно-удаленную общую
точку кривых УН1234 и 7И123В, и указанное уравнение переходит в урав-
нение 3-го порядка:
/и4м3 -ф- т-^и1 -ф- т^и 4- = 0. (12.46)
Корни этого уравнения определят или один, или три центра Бурме-
стера, дающие одно или три
/ решения поставленной зада-
/}// чи синтеза кривошипно-ша-
'/ тунного механизма, по пяти
\ положениям.
'к д 4°. Синтез кулисного
/ механизма по положениям.
/ На рис. 733 нанесена схема
шарнирного четырехзвенни-
X. ка ABCD. Если звено АВ
У будет непрерывно возра-
/ стать, а шарнир В — уда-
ляться в бесконечность по
линии АВ, то в пределе,
Рис. 733. когда шарнир В уйдет в
бесконечность, шарнирный
четырехзвенник преобразуется в кулисный механизм ACD, у которого
ось кулисы перпендикулярна к направлению, в каком шарнир В уда-
лен в бесконечность. Такое понимание кулисного механизма как осо-
бого случая шарнирного четырехзвенника, у которого шарнир В уда-
лен в бесконечность, позволяет рассматривать задачу синтеза кулис-
ного механизма по положениям как частную задачу синтеза шарнирного
четырехзвенника по положениям.
Рассмотрим следующую задачу синтеза кулисного механизма по
положениям: заданы углы поворота <р12, <р13 кулисы и соответственные
углы поворота <р1а, <р13 ведомого звена CD и задано передаточное
отношение механизма it в первом положении. Требуется установить
первое положение кулисного механизма, удовлетворяющего заданным
условиям. Укажем кратко ход решения этой задачи.
§41] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 841
Выберем стойку механизма AD (рис. 734). По заданным условиям
установим полюсы относительных положений Р12, Р13, Р23 и Рц,
как изложено в § 39, 6° и 7°. Эти полюсы определят четыре отно-
сительных положения Sj, S,, S2 и S3 ведущего звена по отноше-
нию к первому положению ведомого звена. Опишем вокруг полюс-
ного треугольника РцР^Р^з окружность Af123 — у для угла уп=612
(см. § 37, 14°) и построим на хорде РцРц окружность Л4Ш —"(12 для
угла у12 = 012, точки ко-
торой удовлетворяют ра-
венству
£РпМРк=Ц,
где 6jg = yi2 — — угол
поворота относительных
положений. Графически
этот угол определим по
формуле (12.2);
= £AP^D.
Точка пересечения указанных окружностей представит собой центр М,
которому соответствует бесконечно удаленная круговая точка Вц
Прямая РцМ определит направление, в котором эта круговая точка
удалена в бесконечность. Совместим шарнир Q звена C\D механизма
в первом его положении с указанным центром /И. Кулису направим
перпендикулярно к прямой РцМ. Тогда получим первое положение
кулисного механизма ACiD, удовлетворяющего заданным условиям.
Так как при указанных условиях имеется только один центр М,
которому соответствует бесконечно удаленная круговая точка, то рас-
сматриваемая задача синтеза кулисного механизма по положениям
имеет в общем случае одно решение.
ГЛАВА XIII
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ ПО МЕТОДУ
ИНТЕРПОЛИРОВАНИЯ
§ 42. Интерполяционное приближение с двукратными узлами
1°. График отклонений и его усреднение. Настоящая глава
посвящена второй группе задач синтеза механизмов перечисленных
в § 36, 1°, а именно задачам по воспроизведению непрерывной функ-
ции на заданном отрезке. При этом рассматриваются такие задачи
синтеза четырехзвенных механизмов, в которых используются все
параметры схемы этих механизмов, чтобы получить решения с доста-
точно высокой точностью
приближения.
На схеме шарнирного
четырехзвенника (рис. 735)
координату ср звена АВ ус-
ловимся отсчитывать от не-
которой вспомогательной
оси А1, а координату ф зве-
на CD — от вспомогатель-
ной оси DII. Положения
этих осей относительно на-
правления стойки AD опре-
Рис. 735.
делим углами аир. Условимся приписывать углам ср, ф, сх и р знак
плюс, когда они отсчитываются против движения часовой стрелки, и
знак минус, когда они отсчитываются в противоположном направлении.
Напомним, чдо координата ф ведомого звена CD как функция
от координаты ср ведущего звена АВ
Ф=/(?)
называется функцией положения механизма. Эту функцию
в задачах синтеза будем подсчитывать для идеального механизма,
у которого отсутствуют зазоры в кинематических парах, а звенья
являются абсолютно жесткими и выполненными абсолютно точно.
§ 42] ИНТЕРПОЛЯЦИОННОЕ ПРИБЛИЖЕНИЕ С ДВУКРАТНЫМИ УЗЛАМИ 843
Выберем длину стойки четырехзвенника равной единице (AD = 1).
Относительные длины остальных звеньев четырехзвенника обозначим:
длину ведущего звена АВ = а,
длину шатуна ВС = Ь,
длину ведомого звена CD = c.
В задачах синтеза четырехзвенника длины звеньев а, Ь, с и
углы а, р являются искомыми. Следовательно, координату ф ведо-
мого звена четырехзвенника можно рассматривать как функцию от
координаты ведущего звена ср и от пяти независимых параметров а,
Ь, с, а и р:
ф=/(ср; а, Ь, с, а, р). (13.1)
Уравнение (13.1) представит собой уравнение семейства кри-
вых, определяемых пятью указанными параметрами, называемыми
параметрами кинематической схемы четырехзвен-
ника.
Длина четвертого звена этого механизма не входит в число пара-
метров его кинематической схемы*), так как кривые указанного
семейства определяются не абсолютными длинами звеньев, а их отно-
сительными длинами.
Пусть при выбранных параметрах а, Ь, с, а и р схемы четырех-
звенника ABCD (рис. 735) функция положения
ф=/(ср)
приближена на отрезке [<р0, <pm] к заданной функции
ф = Д(сР),
непрерывной на указанном отрезке. Графики этих функций обозна-
чены на рис. 736 (вверху) соответственно /(ср) и О (ср).
Разность
Дф=/(?)-О(?) (13.2)
называется отклонением функции положения механизма от задан-
ной функции.
Геометрически отклонение изобразится вектором
Д<р — QQ*,
*) Ради краткости условимся в дальнейшем вместо «кинематическая
схема механизма» говорить просто «схема механизма», а вместо
«параметры кинематической схемы механизма»—«параметры схемы ме-
ханизма».
844 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[гл. xin
равным расстоянию между графиками /(ср) и F (ср) по оси ф и
направленным от графика заданной функции F(cp) к графику функции
положения механизма /(ср).
Из уравнения (13.2) следует, что отклонение есть функция от
координаты ведущего звена, т. е. что
Дф = Д(ср). (13.3)
График Д(ср) функции (13.2) нанесен на рис. 736 (внизу) в осях ср,Дф
и называется графиком отклонений.
Укажем на следующие очевидные соответствия:
а) точке пересечения Q; графиков /(ср) и F (ср) соответствует
точка пересечения gt графика отклонений Д (ср) с осью абсцисс;
б) точке касания Qj графиков /(ср) и /7(<р) соответствует точка
касания gj графика отклонений Д (ср) с осью абсцисс.
Отметим на графике Д (ср) точки ft' и h", в которых отклонения
на рассматриваемом отрезке [ср0, срт] достигают значения Дфтах и
Дфпнп- Найдем среднее из этих отклонений:
Дф^?Фта* + Аф™п . (13.4)
Переместим ось DII (рис. 735) для отсчета координаты ф ведо-
мого звена CD вокруг шарнира D на угол Дф^, т. е. перейдем к от-
§ 42] ИНТЕРПОЛЯЦИОННОЕ ПРИБЛИЖЕНИЕ С ДВУКРАТНЫМИ УЗЛАМИ 845
счету указанной координаты от новой оси DIIy, определяемой отно-
сительно направления стойки AD углом
= Р + (13.5)
При отсчете координаты ф ведомого звена от оси DIfy график
У(<р) функции положения механизма сместится вдоль оси ординат
(рис. 736, вверху) на величину—Д<|у График заданной функции F(tp),
не связанной с параметрами Схемы механизма, не изменит при этом
своего положения. В результате, на ту же величину — Дф5, вдоль
оси ординат сместится график отклонений Д (<р). Новое его положе-
ние Дд, (ip) нанесено на рис. 736 (внизу) пунктиром. Точки h' и h",
в которых отклонения достигали значений Дфтах и Дфт1П, пере-
местятся в положения hy и hy и отметят новые наибольшее и наи-
меньшее отклонения:
(Дф^)тах — Дфтах Дф-у — 'ф
ДФтах ДФтт
~2
,. , \ __ * . л > ______ ДФтах ДФ1
(Дфу)тт — Дфтт Д Ф>’ — 2
которые равны между собой по модулю, но противоположны по
знаку.
Величину Дфл„ определяемую по формуле (13.14), назовем усред-
няющим смещением, а график Дv(ср) — графиком усред-
ненных отклонений. Наибольший модуль усреднен-
ных отклонений L будет:
т I ДФтах — ДФтт I „ 0
Во всех случаях, когда в результате решения задачи синтеза
механизма отклонения Дфтах и Дфтт на заданном отрезке [<ро,
оказываются не равными друг другу по модулю, точность приближе-
ния функции положений механизма /(ср) к заданной функции F (ср)
условимся оценивать не по значениям Дфтах и Дфтт, а по наиболь-
шему модулю усредненных отклонений L.
2°. Интерполяционное приближение с двукратными узлами.
Пусть задана непрерывная на отрезке [ср0, срт] функция
Ф=г(т); (13.7)
требуется эту функцию на указанном отрезке приближенно воспро- '
извести шарнирным четырехзвенником. Это будет задача о приближе-
нии функции положения механизма к заданной функции на заданном от-
резке. В соответствии с этим отрезок [ср0, <рт], на котором требуется
приближенно воспроизвести заданную функцию (13.7), называется
отрезком приближения.
846
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XHI
Методы приближения функции различаются между собой усло-
виями, по которым определяются параметры функции, приближаю-
щейся к заданной.
Наиболее распространенными в инженерной практике методами
приближения функций являются методы интерполирования, а среди
последних — интерполирование с простыми узлами. При интерполиро-
вании с простыми узлами
параметры функции, кото-
рая приближается к задан-
ной, определяются по усло-
виям совпадения этих функ-
ций в предписанных точках.
В геометрическом пред-
ставлении упомянутые усло-
вия и сама картина этого
интерполяционного прибли-
жения выглядят следующим
образом (рис. 737). На гра-
фике заданной функции F (ср)
в пределах отрезка прибли-
жения [<р0, срт] выбирают ряд
точек Qi, Qz, ... Параметры
приближающей функции ср =
=f (?) отыскиваются из ус-
ловия, что ее график f (ср) в
выбранных точках Q2, ...
должен пересекать график
заданной функции (13.7).
Указанные точки (Q2, ...
называются простыми
узлами интерполирования.
В задаче синтеза четырехзвенника приближающей функцией ср=/(ср)
является функция (13.1).
Для определения пяти параметров а, Ь, с, а. и р схемы четырех-
звенника выбирают на графике F (ср) заданной функции (13.7) пять
простых узлов интерполирования Q1( Q2, Q3, Qt, Qs *).
В синтезе механизмов, кроме интерполирования с простыми узлами,
применяется интерполирование с кратными узлами, в которых гра-
фики /(<р) и F (ср) по условию имеют точки касания того или иного
(заранее предписанного) порядка**). Точка касания 1-го порядка назы-
вается двукратным узлом, точка касания 2-го порядка — трех-
кратным узлом и т. д.
*) Алгебраический метод определения параметров схемы четырехзвенника
по этим условиям изложен в главе IX.
**) См. предыдущую сноску.
§ 42] ИНТЕРПОЛЯЦИОННОЕ ПРИБЛИЖЕНИЕ С ДВУКРАТНЫМИ -УЗЛЗМИ 847
С точки зрения инженерных расчетов особый интерес предста-
вляет интерполирование с двукратными узлами, подчиненное следую-
щим требованиям: 1) внутри отрезка приближения [<р0, <рт] узлы вы-
бираются двукратными; 2) на границах отрезка приближения рас-
полагаются только простые узлы; 3) общее число узлов интерполяции
на отрезке приближения выбирается равным числу независимых пара-
метров схемы механизма; при
этом двукратный узел счи-
тается за два простых
узла.
Это приближение в за-
даче синтеза четырехзвен-
ника зададим следующим
образом (рис. 738) *). На гра-
фике F (у) функции (13.7),
подлежащей воспроизведе-
нию четырехзвенником на от-
резке [?о, фт], где
выберем два узла и Qt с
абсциссами
и третий узел ф3 с абсцис-
сой <ра = >рт(т. е. расположим
узел Qz на границе отрезка
приближения). Пять параме-
тров а, Ь, с, а. ир схемы
четырехзвенника определим
так, чтобы график/(<р) функ-
ции положения четырехзвен-
ника в узлах Qj и Q2 касался
графика F (<р), а в узле Q3 пе-
Qi и Q2 были двукратными, а узел
ресекал его, т. е. чтобы узлы
Qs — простым **).
Абсциссы ср, и ср2 двукратных узлов могут выбираться внутри
отрезка приближения произвольно или с учетом рекомендаций, кото-
рые даны ниже, в § 44, 6°.
Укажем некоторые свойства графика отклонений А (ср) (рис. 738,
внизу), получаемого при таком интерполяционном приближении. В точ-
ках gi и giy абсциссы которых равны абсциссам двукратных узлов Qx
и Q.2, график Д (ср) будет касаться оси абсцисс, а в точке g3, абсцисса кото-
рой равна абсциссе ср3 простого узла Q3, — пересекать ось
*) См. [56 р].
**) В каждом двукратном узле как точке касания следует считать совпа-
дающими по две бесконечно близкие точки графиков f (<j>) и F (у). Поэтому
на рис. 738 двукратный узел изображен в виде двух соприкасающихся точек
в отличие от простого узла, изображенного одной точкой.
848 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
абсцисс*). Если графики и F (у) не имеют на отрезке
[<р0, ¥ml иных общих точек, кроме тех пяти, которые по условиям
приближения совпадают с узлами Qlt (Q2 и Q3, то график отклоне-
ний Д (ср) на этом отрезке расположится по одну сторону от оси
абсцисс. В этом случае отклонения на отрезке [<р0, cpffl] будут одного
знака.
Напомним, что точность приближения одной функции к другой
мы условились оценивать по усредненному графику отклонений. При
этом условии интерполирование по пяти простым узлам (рис. 737) и
интерполирование по двум двукратным узлам и одному простому
(рис. 738) обеспечивают точность приближения на заданном отрезке
[ср0, <?т] одного и того же порядка. Но при интерполировании с двукрат-
ными узлами расчетные формулы для вычисления пяти параметров
четырехзвенника значительно упрощаются по сравнению с теми же
формулами при интерполировании с простыми узлами, снижая трудо-
емкость подсчетов. Поэтому ниже мы пользуемся интерполированием
с двукратными узлами.
3°. Кинематические условия интерполяционного приближения
с двукратными узлами. Пусть по-прежнему
— заданная функция, к которой на отрезке [ср0, срт[, где <ро<^<рт**), тре-
буется приблизить функцию положения ф=/(ср) шарнирного четырех-
звенника. Будем искать указанное выше интерполяционное приближение,
определяемое двумя двукратными узлами и ф2 (рис. 738) и одним
простым узлом Q3. Абсциссы и ср2 двукратных узлов Qx и Q2 выберем
'Ро 'Pi 'Ра Рт> а абсциссу простого узла Q3 выберем <р3 = <рт.
Ординаты этих узлов подсчитаем как ординаты точек графика F (ср)
заданной функции (13.7) по формулам:
Ф1=^(®1); ф2=^(Р2); фз=^(?з)-
Найдем разность между абсциссами и ординатами узлов Q2 и Qt
и узлов Q3 и Qp-
<Pis —«Ра —?15 Ф12=/7 (Ta) — ^‘('Pi); (13.8)
<Р1з = <Рз —Pf. Ф1з = ^ (<Рз)—F('Pi)- О 3.9)
Предположим, что тем или иным путем нами найдены те значения
пяти параметров а, Ь, с, а и [i схемы четырехзвенника, при которых
функция положений механизма удовлетворяет условиям искомого
приближения, т. е. график этой функции /(<р) в узлах и ф2
касается графика заданной функции F (ср), а в узле Q3 — пересекает
его. Пусть сам четырехзвенник, определяемый совокупностью упомя-
*) Точки касания gt и g2 на рис. 738 изображены в виде двух соприкасаю-
щихся точек в отличие от точки пересечения g3, изображенного одной точкой.
**) В последующем задавая отрезок приближения [ср0, <ьт|, постоянно
будем предполагать <р0 < <рт, не повторяя это каждый раз.
§ 42] ИНТЕРПОЛЯЦИОННОЕ ПРИБЛИЖЕНИЕ С ДВУКРАТНЫМИ УЗЛАМИ 849
нутых значений пяти параметров схемы, изображен на рис. 739 в поло-
жениях ABiCfD, AB^C^D и ABiC^D, в которых координаты ведущего
звена АВх равны выбранным абсциссам <рь <р2, ср3 узлов Qit Qt
на рис. 738.
В этом случае величины <р12, и <pi3, <]>i3, подсчитанные по фор-
мулам (13.8) и (13.9), определят соответственные углы поворота ве-
дущего и ведомого звеньев ABt и CiD механизма при переходе его
из первого положения ABtCiD во второе АВгСгО и в третье AB^C^D.
Рис. 739.
Так как график /(ср) функции положения механизма в двукратных
узлах Qi и (рис. 738) должен касаться графика F (<р) заданной
функции, то передаточные отношения
z = ^ = F(<p)
a<f ‘
между ведомым и ведущим звеньями механизма в первом и во вто-
ром положениях механизма должны быть равны соответственно:
= 1г = Р’(<?*). (13.10)
Таким образом, чтобы найти на отрезке [ср0, срт] указанное интер-
поляционное приближение функции положения четырехзвенника к задан-
ной функции (13.7), достаточно найти четырехзвенник, который удо-
влетворяет следующим кинематическим условиям: при переходе
четырехзвенника из первого положения во второе и третье положе-
ния углам поворота ведущего звена <р12 и <р13, вычисленным по фор-
мулам (13.8) и (13.9), соответствуют углы поворота ведомого звена
и ф»13, вычисленные по тем же формулам, а передаточные отношения
между этими звеньями в первом и во втором положениях механизма
и равны вычисленным по формулам (13.10).
Эти кинематические условия приводят нас к задаче синтеза
четырехзвенника по трем положениям механизма и двум переда-
точным отношениям, которая практически представит собой задачу
по пяти положениям, так как задание передаточного отношения эк-
вивалентно заданию двух бесконечно близких положений механизма.
850 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
Аналитическое решение этой задачи будет отличаться от изложенного
в § 42,6° только отдельными расчетными формулами. Ход этого
решения приведен ниже в 43,1°.
§ 43. Синтез шарнирного четырехзвенника по полному числу
параметров схемы
1°. Последовательность аналитического подсчета пяти пара-
метров шарнирного четырехзвенника. Задача синтеза четырехзвен-
ника, решение которой нас интересует, следующая: дана непрерывная
на отрезке [<р0, срт] функция
ф=^ (9);
требуется приближенно воспроизвести ее на этом отрезке при помощи
шарнирного четырехзвенника. С этой целью отыщем пять параметров
схемы четырехзвенника по условиям интерполяционного приближения
его функции положения к заданной функции, которое определим двумя
двукратными узлами Q, и Q2 и одним простым узлом (Q3.
Наметим последовательность решения этой задачи и приведем все
необходимые расчетные формулы.
1) Установление кинематических условий интер-
поляционного приближения. По соображениям, приведенным
в § 43,2°, для простого узла Q3 выберем абсциссу <р3 = <рт. Выберем,
далее, абсциссы и <р2 двукратных узлов Qt и произвольно
в пределах 9о 91 9г 9m или с учетом рекомендаций, которые
даны для их выбора ниже (см. пункт 6° настоящего параграфа).
Подсчитаем соответственные углы поворота ведущего и ведомого
звеньев:
Ты = 9г — 91» Ф12= (9г) — F (9i)J
91з = 9з —9ь Ф1з = ^(9з)—f (9i)
и передаточные отношения
'ii = f'(9i); /2 = /?,(92)
в первом и втором положениях механизма.
2) Подсчет координат полюсов относительных
положений ведущего звена. Подсчитаем вспомогательные
углы (см. § 39,6°):
612 912 'Pis. 2 __ | Ф»В ~4~ *)
~2 =----2 ’ 23 —-[ 2----- ’
*) Прежде чем обратиться к дальнейшим подсчетам, целесообразно выпи-
сать из таблиц тригонометрических функций значения восьми величин tg ,
tgXp tg^y. 2з> sinipi2 и cos<b13. После этого вплоть до
определения длин звеньев механизма к таблицам тригонометрических функций
обращаться не нужно. Это дает возможность при выполнении подсчета произ-
водительно использовать счетные машины.
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
851
Выберем длину стойки искомого четырехзвенника А£)=1 (рис. 740).
Проведем декартовые оси X, Y с началом в неподвижном шарнире D;
ось X совпадает с направлением вектора AD. Подсчитаем в этих
осях координаты полюса Р12 по формулам (12.10):
Х12 =-----,---±-----
^12---------^12 tg .
Нанесем на рис. 740 полюс Р12 и совместим с ним начало новых де-
картовых осей х, у, параллельных осям X, Y. Подсчитаем в осях х, у
координаты остальных полюсов Pt3, Р23, Рц и Р22 и шарнира D по формулам:
tg^
-Via —----т - Х12',
tgf-tg^
>1з =— (-Чз 4~ ^12) —Yl3; tg813=^-;
Z Л13
(*is tg Вд, 2з 4“ Yis) 1 — tg Sis tg -g-j
X23 = - tg 8la + tg ( 1 - tg 81, tg tg 6D> 23 ’ ’ tl3.11)
J'23 = — (Л'2з A i2) tg 23 — Y|2; '
-^n=7-----т----Xfi, Уи = —Yu}
ii — i
__ COS Ф18 v . .. _ V
хы — j2[-------ли> № — j3 i— 1 !«•
— Xi<2, yo=—Y
852 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
Эти формулы получены из формул (12.11) — (12.13), (12.18) и (12.20)
путем перехода от осей X, Y к осям х, у.
Полюсы Р12, Р13, Р23, Ptl и определят пять положений веду-
щего звена по отношению к первому положению ведомого звена.
Относящиеся к ним точки и центры Бурместера будут /И11223 и В[1223
(см. § 38,5° и 6°).
3) Вычисление коэффициентов кубического урав-
нения. Подсчитаем последовательно по формулам (11.129)— (11.132)
коэффициенты уравнения (11.125):
— Х13 ^’1 -^11 —~ -^22>
е2 = Хц— -Vi3-J-х23; А2 = Хц -j- х22;
ез=Уп —Из —1'2з1 ^з — Ун —Узз'г
е1=Ун —1'13 “Ь-Узз! ^4=1'11 4-1'221
/=Xi3x23 Ч-ЦхУзз!
Pi= ^зО — ^1ез>
Рг = — k^,
(1312)
91 --X111'22--Л'221'И> 9з-----I (^2 4“ ^I)>
9г = 2 (-^н-^гг 4-1'111'22)1 94 = 9з — 2/iy2;
//z4 —--91/1 4- 941
'«з = 9i(4Z — p$ — q^ — q^ tg ;
'"2 = — 9i (4/ tg — Pi 4- p3 j — qiPi 4- f3;
'«(1 = 91Рз1
Подсчитаем по формулам (12.35) '
коэффициенты кубического уравнения
и3 4- tn'i^ 4~ т\и 4~ ,ло = °>
которое получим из уравнения (11.125) путем исключения из него
известного корня « = tg^ — соответствующего центру Бурме-
стера, совпадающему с неподвижным шарниром D.
4) Решение кубического уравнения и подсчет
координат центров Бурместера. Решим полученное куби-
ческое уравнение, которое имеет или один действительный корень Hj или
три: иь ц2 и и3.
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
853
Воспользуемся сначала
ветствующего ему центра
(11.135) и (11.136)*):
корнем Н| и подсчитаем координаты соот-
Бурместера Л111223 (хм, ум) по формулам
tg Sai
kt + kiU .
ka — kzu '
*11 (и — tg оЛ1)+ Уи(и tg ВЛ1 + 1)
*Л1 =-----------/1 _Lt„aR л „--------> Ум = ХМ tg Оль
(13.13)
(1 + tg3 ВЛ1) "
5) Проверка точности подсчета координат цент-
ров и их уточнение. Для проверки точности подсчета этих
координат подсчитаем по формуле (11.141) величину
_ (ХЛ1 — х1з) (.Ум —У*») — (хм — х»8) (Ум —-У1»)
(ХЛ1 — х*з) — *2з) + ( Ум ~Уи) (Д'Л1 —У**)
Если разность
Ди = и — v
окажется в пределах точности расчета, то обратимся к вычислению
координат соответственной точки Бурместера Д}1223; в противном
случае прежде уточним координаты центра Бурместера Л111223. С этой
целью подставим в формулы (13.13) вместо выбранного корня и ку-
бического уравнения произвольную величину и’, близкую к этому
корню. Подсчитаем соответственные значения х'м, ум, новое значе-
ние v' величины v и разность
Дг/ = и' — ъ'.
Затем по формуле линейной интерполяции (11.142):
Дм' — Ди
подсчитаем уточненное значение и" корня и и, подставив его снова
в формулы (13.13), найдем уточненные координаты х'м, у'м центра
Бурместера /И112'23. Эти координаты подлежат новой проверке и в слу-
чае необходимости дальнейшему уточнению.
6) Подсчет координат соответственной точки
Бурместера. Для подсчета координат соответственной точки Бур-
местера Д}1223 (_гд, ув) воспользуемся формулами (11.21):
Ум~хмх&-т
tg ё,
<м+.Ул11£~^’
хпУм — хмУ11 \ s
Хв = (х -х Пай -v' -k'v-------’ Ув = хВ tg 8д,
Ии — хм > 6 в — Уч "гУм
где хм, Ум — уточненные координаты центра Бурместера 7И11223.
*) В последующих формулах корень Uj будем обозначать просто и (без
индекса), чтобы не усложнять чтение этих формул.
854
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гЛ. ХП1
По подсчитанным координатам нанесем на рис. 740 центр и
точку Бурместера, обозначив их соответственно М и В{. Выберем
точку Бурместера Bt за подвижный шарнир ведущего звена механизма,
а с центром Бурместера М совместим подвижный шарнир С( ведо-
мого звена механизма. Тогда получим первое положение AB^CtD иско-
мого шарнирного четырехзвенника.
7) Подсчет параметров схемы механизма. Подсчи-
таем длины звеньев механизма через координаты его шарниров по
очевидным формулам (учитывая, что длина стойки по условию AD = 1):
О = ЛВ] =|/Л(1|-хл—хо)44-(з'Д —yD)'2,
b = BiC1 = У(хв — хм )2 + (у в —ум )2,
с = CXD = У(хм — XD )2 4- (ум —yDy.
(13.14)
Обозначим через и (рис. 740) координаты ведущего и ве-
домого звеньев четырехзвенника в первом его положении, отсчитан-
ные от вспомогательных осей AI и DII. По численной величине
угол ср, равен выбранной абсциссе узла интерполяции (см. § 42):
а угол <pi — ординате этого узла, которую подсчитаем по уравнению
заданной функции
Ф1 = /=,(Т1)-
Обозначим, далее, через аир углы наклона к оси X вспомога-
тельных осей отсчета А! и DII. Углы поворота ведущего и ведомого
звеньев четырехзвенника в первом его положении, отсчитанные от
оси X, будут (а -|- <fi) и (Р4~Ф1)- По рис. 740 имеем:
tg(« + ?i)=-i ; ^<Р + Ф1)= (13.15)
1-ГАВ XD АЛ1— XD
Следует при этом учесть, что
(а + ?1) <">
если Ув—_Ур^>0,
и, наоборот, (а -|- cpj) 4> к,
если у в—yo<Z^
(P + ’PiX17-
если ум—J’o>0,
и, наоборот, (Р -J- <р!) 4> тс,
если ум—Уо<0.
При помощи формул (13.15) найдем неизвестные углы а и р. Та-
ким образом, отыщем все пять параметров схемы четырехзвенника
а, Ь, с, а и р, определяемого корнем izj кубического уравнения
и3 4~ -j- /«о = 0.
Если это уравнение имеет еще два действительных корня п2
и «з, то. использовав их, получим параметры схемы еще двух четы-
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
855
рехзвенников, удовлетворяющих кинематически или только геометри-
чески условиям задачи, сформулированной в начале настоящего па-
раграфа.
2°. Подсчет отклонений функции положения механизма от
заданной функции на отрезке приближения. В произвольном по-
ложении шарнирного четырехзвенника ABCD (рис. 741), которое
определяется координатой <р;, угол между ведущим звеном АВ и
направлением стойки AD будет (а <р;).
Из Л ABD, учитывая, что длина стойки AD=\, получим:
sin (;; + « + ?>) ___ 1
sin Ег а
Отсюда
— — COS (а + у,)
Ctg , X \---* • (13.16)
ь ' Sin (а г) ' 1
Исключив отрезок BD из очевидных равенств:
= 1 —|— BD2 — 2BD cos Ег, Ь2 — с2 BD2— 2сBD cos
BD2 — 1 -]- а2 — 2а cos (а <рг),
найдем:
COS^- [COSja+ya.-^eosE,.^ (1317)
с cos + I
где обозначено:
Ц3.18)
856 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гЛ. XIII
Угол поворота ведомого звена отсчитываемый от направления
стойки AD, определим из равенства
₽ + = (13.19)
При тех же длинах звеньев а, Ь, с (AD=l), при данной вели-
чине угла (а -|- <рг) и тех же значениях вспомогательных углов и
т;г четырехзвенник может занимать положение ABC*D. В этом поло-
жении угол будет равен:
Р + = +
Обратим внимание, что на рис. 741 угол поворота ведущего звена,
отсчитываемый от направления стойки, а тс. При угле а cpf к
также возможны два отдельных случая, показанные на рис. 742; для
Рис. 742.
механизма ABCD угол опреде-
лим из равенства *)
Р + Ф/ = * + — -гц,
для механизма ABC*D
Р + фГ^ЧЧ-4-^
Угол Р4-фг в этих равенствах
изменяется в пределах 0 =g ф =g 2тс,
а вспомогательные углы и
определяемые по формулам (13.16)
— (13.17) в пределах
О =g =g тс; 0 =g т]г s'' тс.
Отклонение функции положения механизма от заданной функции
<p = F(cp) найдем по формуле
ДФ/ = Ф< — F (?«)>
где <р; — угол поворота ведомого звена, подсчитанный по только что
указанным формулам, a F(<f,)— угол поворота, определяемый задан-
ной функцией.
3°. Пример аналитического подсчета пяти параметров схемы
четырехзвенника. Требуется воспроизвести шарнирным четырехзвен-
ником функцию **)
q
<13-20)
*) Чтобы верно выбрать величину углов и 1;г по их тригонометриче-
ским функциям и составить правильную формулу для подсчета угла р + ф,,
целесообразно предварительно вычертить схему механизма по найденным па-
раметрам.
**) Настоящий пример, как и ряд последующих, имеет прежде всего слу-
жебную цель: исследовать некоторые вопросы, возникающие при использовании
§ 43] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 857
на отрезке 0 ср ^100°. Углы <р и ф в этой формуле выражены в
градусах и направлены против движения часовой стрелки.
Отыщем пять параметров схемы четырехзвенника по условиям ин-
терполяционного приближения, определяемого двумя двукратными
узлами и одним простым. Используем при этом последовательность
решения, указанную в пункте 1° настоящего параграфа.
1) Выберем абсциссы и двукратных узлов интерполяции * *)
ср1 = 9°33', Та = 65°27,
а абсциссу <р3 простого узла интерполяции
<р3= 100°00'
— равной абсциссе второй границе отрезка приближения.
Вычислим ординаты узлов интерполяции по формуле (13.20):
ф1 = 0°49'15"; ф2 = 38°33'12"; ф3 == 90°00'00".
Соответственные углы поворота ведущего и ведомого звеньев
будут:
= 55°54'00", фн = 37°43'57",
cpi3 = 90°27'00", ф13 = 89°10'45".
Функция передаточного отношения:
г=^=°'018^
где ср следует подставлять в градусах.
Передаточные отношения в первом и втором положениях механизма
при cf>i = 9°33' и ср2 = 65°27' будут:
= 0,1719000,
/г= 1,1781000.
2) Подсчитаем вспомогательные углы:
= 9°05'01",5, BD, 23 = 4- 63с27'21".
в синтезе механизмов интерполирования, которые в общем виде анализу не
поддаются. К этим вопросам относятся: появление нулевых точек, влияние по-
следних на точность приближения и др. Воспроизводимые функции, фигури-
рующие в примерах, выбирались учитывая указанную цель. Но понятно, что
каждый пример, взятый в отдельности, выполняет еще свое обычное назначе-
ние — наглядного численного расчета.
*) Как подчеркивалось выше, эти абсциссы могут быть выбраны произ-
вольно в пределах отрезка приближения. Здесь они выбраны, сообразуясь
с теми рекомендациями, которые даны ниже, в пункте 6° настоящего пара-
графа.
858 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. хш
Выпишем из таблиц тригонометрических функций значения восьми
величин:
tg^ = -40,5305906; tgfe = 4-0,9857755;
tg^- = 4-0,3417186; tg4 = -40,1598832;
tg?f =-4 1,0078850; tg &D, 23 = 4-2,0018239;
Sin<pi2 = -40,6119758; COS <J)12 = -40,7908765.
Выберем длину стойки AD=1. Подсчитаем координаты полюсов
К12), Pri _у23), Рц(Х11, Уп)> Рц(Хц> yti) и
неподвижного шарнира D(xd, уо) по формулам (13.11):
^ = — 2,809260; У12 = -[- 0,9599765;
х13 = —42,77680; у13 = 4- 43,97764;
tg813 = — 1,028072;
= 4-3,712557; у23 = — 2,768189;
х„ =-41,601677; = — 0,9599765;
х23 = 4-7,249894; ум = —4,396114;
xD = -j- 2,809260; yD = — 0,9599765.
3) Подсчитаем коэффициенты кубического уравнения по форму-
лам (13.12) и (12.35):
е, = 4-40,66592; /4 = —5,648213;
= -[-48,09103; Л2 = 4- 8,851571;
£?3 = —42,16943; /г3 =|-3,436138;
е4 = —47,70581; Л4 = —5,356091;
/= — 280,5497;
р, = —98,44840; g, = —0,0814268;
А = — 1021,373; g2 = 4-31 >66431;
р3 = -4 164,6914; g3 = —30029,484;
g4 = — 12262,66;
пц — — 12270,68; т\ = — 0,7562110;
zzz3 = 4-5086,104; //?[ =-4 0,0694737;
2/22 = 4-2318,394; /«; = 4-0,0031981;
mh = — 13,41009;
отсюда получим следующее кубическое уравнение:
и3 —0,7562110и® 4- 0,0694737м 4* 0,0031981=0. (13.21)
§ 43] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 859
4) Решение указанного кубического уравнения дает три дейст-
вительных корня:
и, = — 0,0333739, щ = -(-0,1497703, и3 = -|- 0,6398145.
Воспользуемся пока первым корнем ut = — 0,0333739 и, обозна-
чая его в последующих формулах просто и (без индекса), подсчи-
таем координаты хм, ум соответственного центра Бурместера по
формулам (13.13):
tg 8Л1 = — 0,5763376, хл] = + 2,446917, ум — — 1,410250.
5) Для проверки координат хм, ум подсчитаем вспомогательную
величину по формуле (11.141):
v = — 0,0333657.
Разность bii = a-— т» =— 8,2 • ИГ6. Предположим, что отно-
сительные длины звеньев должны быть определены с точностью до
пятой цифры после запятой. В этом случае, как показывает полученная
разность Д/г, подсчитанные координаты хм. Ум центра Бурместера
требуют уточнения.
С целью их уточнения выберем новое значение корня
и'= v = — 0,0333657.
По формулам (13.13), использовав значение и', найдем новые зна-
чения:
tg Sin = —0,5763448;
j^ = + 2,446855; х^ = — 1,410232; т»' = —0,0333483.
Новая разность Дг/ = it — к' = — 17,4 • 1(Г6. Подсчитаем по фор-
муле линейной интерполяции (11.142) уточненное значение корня и:
и" = — 0,0333812
и по формулам (13.13), использовав значение и", найдем еще раз
соответствующие значения:
tg 8 л] =—0,5763316;
х’м = + 2,446963; у’м = — 1,410262; ъ” = — 0,0333807.
Разность Ди" = и"— v” = —0,5- 10 6 позволяет принять подсчи-
танные значения и”, хм и у"м за расчетные значения корня и, и ко-
ординат Хм и ум центра Бурместера.
6) Подсчитаем координаты соответственной точки Бурместера В]1223
по формулам (11.21):
tg8B = —0,810939; хв = -]- 0,383702; ув = — 0,311160.
7) Определим? параметры схемы четырехзвенника:
а — 1,5663; 6 = 2,3378; с = 0,57794;
а = + 145°58',7; Р = -ф- 230°21',6.
860
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[ГЛ. ХП!
На рис. 743 найденный механизм изображен в положениях, соот-
ветствующих концу и началу отрезка приближения 0 <р + -|- 100°.
Таблица 13.1
Отклонения функции положения трех шарнирных четырехзвенников
от функции (13.20)
Углы поворота Отклонения Дф
ведущего звена £ 1-й механизм 2-й механизм 3-й механизм
—04°00' 0 —10',3 —04,8 -*) + 7',9 -*) + 117', 6
¥1 - -|- 09 33 0 0 0
+ 20 00 —03,3 + 2,4 н 016,5
+ 30 00 —07,6 4-4,0 Н 0 29,9
+ 35 00 —08,7 + 3,8 Н 0 31,5
+ 37 30 —08,7 + 3,5 - 0 29,4
+ 40 00 —08,4 + 3,1 - 0 27,6
+ 50 00 —05,0 4-1,2 -0 14,7
+ 60 00 —00,8 + 0,2 - 0 02,3
<р2 = + 65 27 0 0 0
+ 70 00 —00,6 + 0.1 - 1-001,7
+ 80 00 —06,3 — 0,1 - -0 15,6
+ 90 00 — 12,4 — 1,0 -0 28,0
+ 91 00 — 12,5 — 1,1 - -0 27,8
+ 92 30 —12,2 — 1,2 - - 0 26,7
+ 95 00 —10,5 — 1,2 -0 22,2
<р3 = + 100 00 0 0 0
В таблице 13.1 (графа «1-й механизм») приведены отклонения функ-
ции положения этого механизма от заданной функции (13.20), а на
рис. 744 (сплошной кривой) изображен график отклонений Дь(ср) этого
механизма. В соответствии с условиями интерполяционного прибли-
жения этот график в точках gt и gt с абсциссами ср, = 9,33' и
<р2 —65°27' касается оси абсцисс, а в точке g9 с абсциссой ср3 = 100°
пересекает упомянутую ось. Иных общих точек с осью абсцисс график
Д’(ср) на отрезке приближения Osg ср ^-[-100° не имеет и показывает
на этом отрезке постоянные по знаку отклонения **). Три верхние
предельные отклонения ***) этого графика (в узловых точках gb g3
и g3) равны нулю. Нижние предельные отклонения графика Д’ (ср) в
точках h\, h\ и h\ равны соответственно:
Дф0 == — 4',8; Дф, = — 8',7; Дф2 == — 12',5.
*) Отклонения для этого механизма при данной абсциссе <р не подсчиты-
вались.
**) На рис. 744 и последующих отклонения Дф нанесены в функции от
координат ведущего звена <р. Для практических целей иногда удобней иметь
кривую отклонений в функции от координаты ведомого звена ф. Очевидно, что
первый график легко может быть перестроен во второй.
***) Предельными отклонениями называются отклонения в точках экстремума
графика Д (<р) и отклонения на границах отрезка приближения.
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
861
Рис. 744.
862 синтез механизмов по методу интерполирования [гл. хт
Максимальное по модулю отклонение max [ Дф | = | Дф21. После
усреднения графика отклонений, т. е. после перехода к новому зна-
чению параметра [3:
= р 4- Д2^ = —|—230°2 V.6 — = 4- 230°15',4,
наибольший модуль усредненных отклонений, характеризующий точ-
ность полученного приближения, будет L — | ДД | = 06',2. Его отно-
сительная величина
I £ |_ 0’06’,2 _0120/
| Д'>„, | 90’00',0 — и>12 /о-
Если привлечь два другие корня кубического уравнения (13.21):
иа = 4- 0,1497703 и и3 = -|-0,6398145,
то таким же путем после уточнения координат Хм, ум соответствую-
щих центров Бурместера найдем параметры схемы двух других
a=Z59°3Z,'5
механизмов, приведенные в таблице 13.2. В той же таблице указаны
предельные отклонения функции положений этих механизмов от задан-
ной функции (13.20), наибольшие модули L усредненных отклонений
и их относительные величины I Д I.
I '\т I
Схема второго механизма в положении, соответствующем концу
отрезка приближения, показана на рис. 745, а схема третьего меха-
низма в положениях, соответствующих началу и концу отрезка при-
ближения,— на рис. 746. В таблице 13.1 приведены для этих меха-
низмов значения отклонений в последовательных точках приближения.
Графики отклонений Д11 (<р), ДП1(<р) второго и третьего меха-
низмов изображены на рис. 744 пунктиром. График ДП| (?) (не уместив-
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
863
шийся целиком на рис. 744 из-за больших предельных отклонений)
подобно графику отклонений первого механизма Д1 (ср) не имеет
с осью абсцисс на отрезке приближения иных общих точек, кроме
тех, которые совпадают с точками g\, giy g%. Поэтому график Д,п (ср)
показывает постоянные по знаку отклонения на отрезке приближения.
Особый вид имеет график отклонений второго механизма А11 (ср).
Этот график отклонений, как и графики отклонений остальных двух ме-
ханизмов, в точках gx и касается оси абсцисс, а в точке пересекает
ее; но кроме этих точек, он имеет с осью абсцисс еще одну общую
точку g. В результате график Дп (ср) показывает на отрезке приближе-
ния переменные по знаку отклонения; число предельных отклонений на
том же отрезке увеличивается до семи (точки git git g-iy h'J, Л}1, Л11, h").
Сравнив между собой три полученных четырехзвенника, можно
отметить следующее. Наименьшими отклонениями обладает второй
i L
механизм L—
I
механизм неудобен (см. рис. 745, из-за резких различий в длинах
звеньев; первый механизм (см. рис. 743) показывает несколько боль-
шие
шениями между длинами звеньев и хорошими углами передачи (на
отрезке приближения [Tmin = 69°). Третий механизм дает предельные
отклонения в несколько раз большие, чем два других механизма.
Таким образом, учитывая требования конструктивного оформления
и получаемую точность приближения функции положений механизма
к заданной функции, наиболее удачным решением в этой задаче сле-
дует признать, по-видимому, первый механизм.
= 0,073% |. Но с конструктивной точки зрения этот
отклонения |~ = 0,12% |, но обладает благоприятными соотно-
Таблица 13.2
Параметры схемы трех шарнирных четырехзвенников, функция положения
которых приближена к функции (13.20). (Длина стойки у всех
механизмов AD = 1.)
Механизмы Величины Первый механизм Второй механизм Третий механизм
а 1,5663 48,301 2,4443
ь 2,3378 49,409 1,1239
с 0,57794 0,94630 1,7307
а 145°58’7" 125°27'8" 259'32'5"
₽ 230^21’6" 249'12'5" 229СОГ1"
| Дф 1 1 т шах 12',5 7',9 1 17'6"
L 6'2 4',0 38',8
1^т 0,12% 0,073% 0,72%
Опт in *) 69‘ 65° 25°
*) (xmin —минимальный угол передачи на отрезке приближения.
864 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гЛ. XIII
Ниже показано (см. главу XIV), что путем уравнивания на гра-
фике Д' (ср) нижних предельных отклонений точность приближения
функции положений первого механизма к заданной функции может
быть заметно повышена.
4°. Масштабы шкал ведущего и ведомого звеньев *). Углы
входа и выхода. В практике проектирования механизмов встречается
следующая задача: имеется непрерывная на отрезке [z0, zm] функция
w—Ф(г) (13.22)
от аргумента z, причем как сама функция w, так и ее аргумент z
представляют собой определенные физические величины; требуется
эту функцию на указанном отрезке воспроизвести механизмом в за-
данных масштабах. В этом случае, прежде чем обратиться к ре-
шению задачи синтеза механизма, необходимо функцию (13.22) пре-
образовать в функцию
ф=Г(<р), (13.23)
которая представит собой переменную координату ведомого звена
механизма, а ее аргумент ср — координату ведущего звена механизма.
Обозначим масштабы, в которых должны быть воспроизведены
механизмом переменные w и z, через и и свяжем их с коорди-
натами ср и ф линейными выражениями:
z — г0 = (лгср; w — w0 = [i№<}». (13.24)
(13.25)
Здесь г0 — граница заданного отрезка [z0, zm], а ®0 = Ф (z0).
Исключив из уравнения (13.22) переменные z и w посредством
выражений (13.24), получим функцию (13.23), к которой должна быть
приближена функция положений механизма.
При г = г0 и w = w0 по уравнениям (13.24) имеем:
сро = О; сро = О.
При z = zm и w = = Ф (zm) по тем же уравнениям найдем:
__zm — z0 . . _wm —ш0_Ф(гт) —Ф(г0)
™ Рг ’ ™ Pw P-w
Следовательно, при преобразовании, определяемом выражениями
(13.24), изменению аргумента z от z0 до zm соответствует изменение
аргумента ср от 0 до срт, функции ср от 0 до срт.
Если функция (13.22) монотонна на отрезке [г0, zm], то углы
и Фт определят полные перемещения ведущего и ведомого звеньев
при воспроизведении механизмов этой функции на указанном отрезке.
В этом случае вместо масштабов р.г и задают непосредственно
*) Подсчет масштабов шкал был уже дан выше (см. § 23). Здесь мы созна-
тельно допускаем известное повторение, чтобы дать возможность читателю
знакомиться с синтезом механизмов методами кинематической геометрии, которые
имеют самостоятельное значение, не обращаясь к предыдущим разделам книги.
I
§ 43] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 865
величины углов срт и срт, называемых соответственно углом входа
и углом выхода. Угол срт (угол срт) условимся считать положитель-
ным, если при изменении аргумента ср от 0 до срт (функции <р от О
до фт) ведущее звено (ведомое звено) механизма должно вращаться
против движения часовой стрелки.
Из формул (13.25) найдем величины масштабов и |ia, по задан-
ным срт и фт:
.. _zm — z0_ .. _wm — w0
! г~ Чт ’ "
Исключив масштабы из равенств (13.24), получим:
•* = ^4+^; (13.26)
тт .т
В этом случае для отыскания функции (13.23) исключают переменные
г и w из уравнения (13.22) при помощи выражений (13.26).
Если функция (13.22) преобразуется в функцию (13.23) посред-
ством линейных выражений (13.24) или (13.26), то при z = z^ получим
ср = 0. Положение механизма, определяемое этими значениями аргу-
ментов z и ср, назовем начальным положением. В этом положении
направление ведущего звена механизма АВ0 (рис. 747) совпадает с
осью А1 для отсчета координаты ср этого звена. Так как механизм
воспроизводит функцию (13.23) приближенно, то начальное положение
ведомого звена DC6 может не совпасть с осью DII отсчета коор-
динаты ср этого звена. Угол Д<р0 между направлениями DCc и D1I
определит отклонение функции положения механизма от функции
(13.23) в начальном положении последнего.
Постоянные масштабы рг и позволяют нанести последователь-
ные деления равномерной шкалы или равноотстоящие значения коор-
динаты ср, или пропорциональные им равноотстоящие значения аргу-
мента z. Аналогично на последовательные деления равномерной шкалы
ведомого звена можно нанести равноотстоящие значения координаты ср
или пропорциональные им равноотстоящие значения функции w.
28 И. И. Артоболевский
866 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гЛ. ХЧ1
Рассмотрим пример на указанное преобразование функции. Пусть
задана функция
ii) = z\ (13.27)
которую нужно воспроизвести шарнирным четырехзвенником на отрезке
отг0 = 0 до zm = 100. (Функция (13.23) на указанном отрезке мо-
нотонна.) Заданы входной и выходной углы:
<рт=-|-100°; ^ = 4-90°.
Так как при го = О имеем wo = O, а при гт=100 получим
wm = 10 000, то формулы преобразования (13.26) примут вид:
1000 ,
Z = r, = — ф.
В них ср и ф выражены в градусах. Подставив эти значения z и w
в заданную функцию (13.27), получим функцию
, 9 2
1000° •
Отрезок, на котором должна быть воспроизведена эта функция
четырехзвенником, 0-Сгу 100\ Именно по этим условиям и решена
задача синтеза в предыдущем примере.
5°. Действия над функциями, заданными таблицей. Пусть
функция, которая должна быть воспроизведена механизмом в задан-
ных масштабах (или на заданных углах входа и выхода), определена
не уравнением, а таблицей последовательных значений аргумента z и
соответственных значений самой функции w.
1
wo, ®1, w2,..., wm.
Пусть [z0, zm] — отрезок, на котором эта функция должна быть
воспроизведена механизмом.
По формулам преобразования (13.24) или (13.26) подсчитаем таб-
лицу последовательных значений аргумента ср и соответственных зна-
чений функции ф:
4 4 4.........4' I (13.28)
Фо. Ф1> Ф2> • • • > Фт- J
В общем случае последовательные значения аргумента z (z0, zt, ...
... , zm) и пропорциональные им последовательные значения аргумента
ср (<Ро. Ть ?2. • • • > 'pm) могут быть не равноотстоящими.
При решении задачи интерполяционного приближения функции
положений шарнирного четырехзвенника к функции (13.28) абсциссы
двукратных узлов могут быть выбраны не совпадающими ни с одним
из значений аргумента ср, имеющихся в таблице (13.28). Тогда воз-
никает задача: найти для выбранной ср*, не совпадающей численно ни
v
Г § 43] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 867
с одним из значений аргумента ср, соответствующее значение функ-
ции В этом случае можно воспользоваться той или иной интер-
поляционной формулой, известной из теории приближенных вычислений,
например формулой Ньютона *):
Фл= Фо + (?Л — <Ро)/('Ро» <Р1)+ (<?.« — ?о)(^ — ?1)/(?0> <Р1> ?«) +
+ (?х — ?е) ('f’x — ?i) (?Л — ТаШуо. <Р1> <Рз» ?з) + ---
• •• + (?* — То)(Тх — ®1.........?«). (13.29)
где /(<р0, cpi), /(?о> ?i, У-г), • • • — разделенные разности, которые под-
считываются по формулам:
/(<Ро, '₽1) = ——-------1-------——;
j vro> ты у0 — yi ?1 — Уо
/(?о> Уь Уз) __ 4
(Уэ — Уо) (Уг —У1)’
.......................................................
'Р*..(Уо —У1)(у0 —У2)...(Уо —Ут)
_|______________.с!_______________ 4-
1 (У1 —Уо)(У1 —ys) ...(У1 —Ут)
।______________, _
’ ’ ‘ ' (Ут — Уо) (Ут ~ У») • • • (Ут — Ут-0
(13.30)
В этих формулах е0, ср,, ..., срт и ф0, <]ч, — значения
аргумента и функции, заданные таблицей (13.28).
При подсчете приходится использовать не все члены ряда
(13.29), так как, начиная с некоторого члена, остальные члены ряда
обычно оказываются настолько малыми, что их нет смысла учитывать
при выбранной точности расчета.
При интерполировании с двукратными узлами необходимо иметь
не только значение функции tyx, соответствующее выбранной абсциссе <рх
/ d'l> \ ,
узла, нои значение= 1-7—1 . Оно может быть подсчитано по фор-
муле
=/(?«—?1) + (%4- Уз)4-
ЧЧа0а1 + а1)а2 + а1а2)/('?0, У1> Уз> Уз) + --.. (13.31)
где обозначено для сокращения
_________ао=(Ух—у0); «1 = (ух—?1); а2=(?х—уз);
*) См. курсы приближенных вычислений акад. Н. М. Крылова, Уиттекера
и Робинсона и др.
28*
868 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [ГЛ. XIII
В том случае, когда таблица (13.28) содержит равноотстоящие
значения аргумента ср, формулы (13.29) — (13.31) для подсчета по
выбранному значению аргумента срл соответственных значений фх и
I d-'j \
("dy"/ существенно упрощаются.
6°. Выбор абсцисс двукратных узлов интерполяции. На рис.
748 еще раз изображена геометрическая картина такого интерполя-
ционного приближения функции положений шарнирного четырехзвен-
ника ф=/(ср) к заданной функции ф = F(ср) на отрезке [ср0, срт],
которое определено двумя двукратными узлами Qt и Qi и одним
простым узлом Qa. Абсцисса ср3 простого узла Q:t выбрана ср3 = срт>
а абсциссы ср, и ср2 двукратных узлов Qt и Qa выбраны в преде-
лах ср0 < ср, < ср2 <срт.
На рис. 748 изображен случай, когда графики /(ср) и F(ср)
на отрезке приближения не имеют иных общих точек, кроме тех пяти,
которые совпадают с узлами Qt, ф2, Qa. В этом случае график откло-
нений А (ср) располагается по одну сторону от оси абсцисс, касаясь
ее в точках и с абсциссами ср, и ср2 и пересекая ее в точке ga
с абсциссой ср3. Если отклонения оказываются положительными (как
показано на рис. 748), то точки glt g^ и ga отметят на графике А (ср)
нижние предельные отклонения, равные нулю. Точки верхних пре-
дельных отклонений обозначены буквами /гп, /г, и /г2. При произволь-
ном выборе абсцисс ср, и ср2 двукратных узлов Q, и Q2 предельные
§431
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
869
отклонения Д%, Дф, и Д-{/2 в точках Ло, ht и /г2 получаются, как
правило, не равными друг другу.
Если изменять абсциссы ср, и ср2 (сохранив неизменной абсциссу
<р3 = срт), то будут изменяться как абсолютные, так и относительные
значения всех трех предельных отклонений Д%, Дф, и Дф2 на отрезке
[<р0, срт(. При таком подборе абсцисс ср, и <р2 двукратных узлов Q,
и Q2, при котором выполняется условие
Дф0 = Дф, = Д<р2, (13.32)
эти отклонения будут меньше по абсолютной величине, чем наиболь-
шее предельное отклонение на отрезке [ср0, срт], получаемое при лю-
бом другом выборе указанных абсцисс *).
На рис. 748 изображен именно тот случай, когда предельные
отклонения Дф0, Дф, и Дф2 графика Д (<р) удовлетворяют условию (13.32).
Тогда после усреднения этого графика получим на отрезке [ср0, срт]
график Д, (ср) с ш е с т ью предельными отклонениями, равными между
собой по абсолютной величине, но чередующимися по знаку (точки этих
предельных отклонений обозначены hOy, gly, hiy, giy, h2y, giv). Прибли-
жение функции /(ср) к функции F(ср)', определяемое таким графиком
Ду (ср), называется равномерным приближением. Наибольший
модуль усредненного отклонения L при этом приближении будет
наименьшим по сравнению с наибольшими модулями усредненных
отклонений тех приближений, которые определятся другими абсцис-
сами ср, и ср2 двукратных узлов.
К сожалению, в задачах синтеза четырехзвенника нельзя заранее
указать те значения абсцисс ср, и ср2, при которых выполняется усло-
вие (13.32). Практика подсчетов показала (см. главу XIV), что эти
значения зависят от вида заданной функции, подлежащей воспроиз-
ведению, от отрезка приближения и величины углов входа и выхода.
Кроме того, если задача синтеза четырехзвенника (при заданной
функции, подлежащей воспроизведению, заданном отрезке приближе-
ния и заданных углах входа и выхода) имеет не одно, а два или
три решения (как получилось в приведенном выше примере), то каж-
дая кривая отклонений требует для выполнения условия (13.32) под-
бора своих значений абсцисс ср, и ср2 двукратных узлов Q, и Q2.
Поэтому можно поставить вопрос лишь о таких рекомендациях для
выбора абсцисс ср, и ср2, на основании которых во многих случаях
удастся получить отклонения Дф0, Дф, и Дф2, мало отличающиеся
друг от друга по величине. Имеющиеся в литературе рекомендации
исходят из некоторых результатов, установленных Чебышевым. По-
следние кратко заключаются в следующем**).
Пусть разность
*) См. главу XIV.
♦*) Подробнее об этом см. главу IX.
870 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
которая выражает отклонения приближающей функции /(ср) от задан-
ной F (ср) на отрезке [ср0, срт], есть полином степени п от аргумента ср:
А (ср) = ср" ф-ап_! ср"-1 -J— а,ср —гг(),
где ..., аь а0 — параметры, определяемые из условий интер-
поляционного приближения. Тогда график А (ср) в случае равномерного
приближения может иметь п —[— 1 точек предельных отклонений на отрез-
ке [?о- 'Pm! и эти точки, как и точки нулей, располагаются вдоль оси
абсцисс строго закономерно *). Абсциссы этих точек определяются на ос-
новании следующего геометрического построения, выполненного на
Следовательно, при указанном
рис. 749 для случая п = 5.
Опишем на отрезке приближения
[0, ?т! (на Рис- ^49 для упро-
щения отрезок приближения выб-
Рзн [0, срт], а не [ср0, срт]), как
на диаметре, полуокружность и
разделим ее на пять равных
частей, обозначив точки деле-
ния цифрами: 0, 1, 2, 3, 4, 5.
Тогда абсциссы точек 1, 3, 5
будут равны абсциссам точек пре-
дельных отклонений gb g2, g3, а
абсциссы точек 0, 2, 4 — абсцис-
сам точек предельных отклонений
/?0, Л], /г4. Если точками /, II,
III, IV, V отметим середины дуг,
заключенных между предыдущи-
ми соседними отметками, то абс-
циссы этих точек определят абс-
циссы нулей графика А (ср).
равномерном приближении как точки
предельных отклонений, так и точки нулей располагаются вдоль
оси абсцисс, резко сгущаясь к концам отрезка приближения.
По указанному на рис. 749 построению из элементарных сообра-
жений найдем следующие формулы для абсцисс точек gb g3 и g3:
= — cos у) cpm = 0,0955 <fm, |
= —cos ?т = 0,6545 <f>m, |
¥.3 = <?m- I
(13.33)
*) На графике (рис. 748) число точек предельных отклонений
п -ф 1 = 6. В задаче Чеоышева подобный график получим, если разность А (у)
есть полипом степени и = 5, т. е.
A (<f) = -ф 1 -ф «зу3 -ф -ф at<f -ф
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
871
Эти формулы получены в предположении, что отрезок приближе-
ния [О, <рт]. Если отрезок приближения (ср0, <рт], то формулы (13.33)
перейдут в следующие:
Ti = То + 0,0955 — <р0),
= То + 0,6545 (срт — <р0),
?з = ?га-
(13.34)
В интерполяционных задачах синтеза шарнирного четырехзвенника
разность Д (ср) — f (ср)—(ср) не может быть выражена в виде поли-
нома от аргумента ср. Но опыт подсчетов показал, что в тех слу-
чаях, когда отсутствуют данные о целесообразном выборе абсцисс ср,,
ср2 и ср3 узлов QI( Q2 и (рис. 748), основанные на предыдущих
расчетах, можно рекомендовать определять эти абсциссы но форму-
лам (13.33) и (13.34). Во многих случаях такой выбор абсцисс
узлов приводит к графику отклонений Д(ср) с тремя предельными
отклонениями Д<р0, Дф> и Д<р.2 мало отличающимися друг от друга по
величине.
Отметим еще абсциссы точек предельных отклонений /г, и /г2
(рис. 749) на отрезке |0, срт]:
Ср’| =
СР2
4(1 — cos у-) = 0,3455 срт,
4 (1 — cos "Т ) <fm ~ 0,9045 •
(13.35)
В общем случае, если отрезок приближения [ср0, срт], то абсциссы
этих точек будут:
?1 = + 0,3455 (срт — ср0),
?2 = То + 0,9045 (срт — ср0\
(13.36)
Если при выборе абсцисс двукратных узлов по формулам (13.33)
и (13.34) предельные отклонения Д40, Д-р, и Д<р.2 получаются мало
отличающимися друг от друга, то точки предельных отклонений Д'Р,
и Дср.2 обычно имеют абсциссы, близкие к тем, которые опреде-
ляются формулами (13.35) и (13.36). Это целесообразно иметь ввиду
при подсчете отклонений и отыскании предельных отклонений Дер,
и Д<р.2 (рис. 748).
Расположение узлов интерполяции Qit Q3 вдоль оси абсцисс,
определяемое формулами (13.33) и (13.34), условимся называть рас-
положением их по Чебышеву.
7°. Графоаналитический подсчет пяти параметров шарнир-
ного четырехзвенника. Пусть в задаче синтеза четырехзвенника
поставлены те же условия, какие были сформулированы в пункте 1°
настоящего параграфа. Кроме аналитического решения этой задачи,
872 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
приведенного выше, можно указать для нее графоаналитическое ре-
шение. В отношении точности графоаналитическое решение не отли-
чается от аналитического, так как соответствующие графические
построения служат
лишь для предвари-
тельного определения
координат центра Бур-
местера, которые за-
тем аналитически уточ-
няются до требуемого
числа знаков.
Наметим последо-
вательность графоана-
литического решения
поставленной задачи,
подобно тому как это
было сделано при ана-
литическом решении в
пункте 1° настоящего
параграфа.
1) Установим кине-
матические условия ин-
терполяционного при-
ближения (по форму-
лам пункта 1° настоя-
щего параграфа).
2)Подсчитаем коор-
динаты полюсов отно-
сительных положений
ведущего звена и координаты неподвижных шарниров четырехзвенника
(по формулам того же пункта 1° настоящего параграфа).
3) Подсчитаем координаты фокуса F(xpt ур) кривой центров 7ИН23
по формулам (11.71) и (11.44):
Ji — ха -Хдз ~* -ХЪ!
Ji —У а Ч" J13 —Угз,
h — хаУк Ч~ х1зУа,
Ji = xi2xl3 —УиУ1з',
Хр =
Уг
J ijs — Js J I
J1+J2
4) Подсчитаем по формулам
(11.77) коэффициенты:
Jl----xll ~|~ xiii
J2 — 3'11 4" Уа,
j3 — xu _y22 -j- X22J'n,
J1== xiixa —3'11 Уа-
Подставив их в только что указанные формулы (11.44), найдем ко-
ординаты фокуса кривой центров 7И11Й.
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
873
5) Нанесем на рис. 750 стойку механизма AD—\, полюсы Р12,
Р13, Pvm Рп> Рц и фокусы F обеих кривых центров Ж1223 и Ж1122.
Построим эти кривые (на рис. 750 кривая Л11223 нанесена сплошной
жирной линией, а кривая УН1122 — пунктиром). В пересечении их
найдем центры Бурместера Ж11223. Один из них всегда совпадает
с неподвижным шарниром механизма D и поэтому через последний
должны пройти обе кривые Ж1223 и /И”22. Это служит контролем
правильности построения кривых центров. Центр Бурместера, совпа-
дающий с шарниром D, не дает решения поставленной задачи. Цент-
ров Бурместера /И11223, которые не совпадают с шарниром D, может
быть или один, или три (на рис. 750 получен один центр Бурместера,
отмеченный точкой М). Координаты центра Бурместера Ж1'223 в осях х, у
с началом в полюсе Рк, снятые непосредственно с чертежа, обозна-
чим через хм, ум. Угловой коэффициент прямой, которая соединяет
этот центр с началом координат Pt2, будет tg 8Л1 =-^-.
АЛ1
6) Подсчитаем по формулам (11.129) коэффициенты:
^1 = Хц—-х.22; k3=yu У22',
— xti -|- х2а; кц—уц
по формуле (11.138)—величину
кг tg ^м —
',== Mg Ъм + к*
и, наконец, по формулам (11.136)—-приближенные значения коорди-
нат ХМ, Ум-
Хц (U — tg 8Л1) +.У11 (W tg 8Л1 + I)
— ----------- ------------- ---------
.УМ = ХМ tg 8л1.
(1 + 1Яа8Л1)«
Подсчитаем далее по формуле (11.141) величину
__(хм ~ Ц’Л1 Ум) (Хд1 х23) (уЛ1 У1з)
(Хуц — х13) (хм — Х23) 4- (уЛ1 —у23) (УД[ —У1з)
и определим разность Дн = и — v. Если последняя не равна нулю
в пределах точности расчета, то координаты центра Бурместера
уточним тем способом, который изложен в пункте 1° настоящего па-
раграфа.
7) Подсчитаем координаты соответственной точки Бурместера
В*1223 (хв. у/д) по формулам (11.21). Координаты этой точки графиче-
ски (для проверки их подсчета) можно определить при помощи ра-
венств (11.20). (На рис. 750 точка Бурместера обозначена £?(.)
8) Определим параметры схемы механизма по формулам (13.14) и
(13.15), выбрав подвижный шарнир ведомого звена Ct в центре Бур-
местера М, а подвижный шарнир ведущего звена — в точке Бурме-
стера Bi-
874
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[гл. XIII
Если в пределах чертежа оказываются два или три центра Бур-
местера УИ11223, не совпадающие с шарниром D, то, уточнив коорди-
наты каждого из них и подсчитав координаты соответственных точек
Бурместера В]1223, получим два или три шарнирных четырехзвенника,
удовлетворяющих заданным условиям приближения.
В тех случаях, когда кривые М1223 и Л1*122 пересекаются в
соответствующем центре Бурместера Л111223 под острым углом и по-
ложение искомого центра точно определить трудно, целесообразно
в его окрестности построить участок третьей кривой центров 7И”23
(см. § 37, 8°), которая также должна пройти через этот центр Бур-
местера.
8°. Пример графоаналитического определения пяти параметров
схемы шарнирного четырехзвенника. Требуется воспроизвести
шарнирным четырехзвенником логарифмическую функцию
на отрезке от z0 = -|-l до zm = -\1- 10. Заданы входной и выходной
углы механизма;
Тт = +100°; фт=-50°.
По этим условиям на основании формул (13.26) получим следующую
функцию, к которой должна быть приближена функция положений
четырехзвенника;
ф = — 50 lg (1 -ф- 0,09<р)
(13.37)
(здесь ср и ф выражены в градусах). Отрезок приближения
от <р„ = 0 до = + Ю0°.
Отыщем пять параметров схемы четырехзвенника по условиям
интерполяционного приближения, определяемого двумя двукрат-
ными узлами и одним простым. Используем для решения этой
задачи графоаналитический способ, придерживаясь той последо-
вательности расчета, которая намечена в пункте 7° настоящего
параграфа.
1) Выберем абсциссы узлов по формулам (13.33):
<р1 = 0,0955-100° = 9°33',
<р2 = 0,6545 -100° = 65°27',
<р3 = Тт = Ю0°00'.
Вычислим ординаты узлов интерполяции:
ф1 = — 50 1g (1 4- 0,09-9,55) = — 13°28'11 ",3,
ф., = — 50 lg (1 4- 0,09 65,45) = — 41 '-54'45". 1
фз = — 50 lg (1 0,09 • 100,00) = — 50' 00'00'.
| 43] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 875
Соответственные углы поворота ведущего и ведомого звеньев
будут:
<р12 = 4- 55с54'00",0: <р12 = — 28°26'33" ,8;
?13 = -|- 90°27'00",0; фи = — 36°31'48",7.
Учитывая, что lg^ = /nln^, где т = 0,4342945 — модуль пере-
хода от натуральных логарифмов к десятичным, получим:
ф = —50-0,4342945 In (1 -|-0,09ср);
отсюда передаточное отношение равно:
.________________________ dp ___ 1,954325
1 d<f 1 -I- 0,09 <f ’
куда с? по-прежнему следует подставлять в градусах.
Передаточные отношения в первом и втором положениях меха-
низма:
/1==—1,050995; 13 = — 0,283626.
2) Определим вспомогательные углы:
~12 = -р 42°10'16", 9; 5D.23 = + 32O29'11", 25.
Выпишем значения тригонометрических функций, которые исполь-
зуются в последующем подсчете:
tg^H-= 4- 0,5305906; tg -^- = 4-1,007885;
z z
tg Jb- = _ 0,2534356; tg -^- = — 0,3300427;
tg = 4- 0,9058343; tg SD.23 =4- 0,6367381;
sin <pi2 = — 0,4762799; cos ф12 = |- 0,8792936.
Подсчитаем координаты полюсов P,.> (Х1г, У|2), Pi3 (xi3, _у13),
Р33 (-^2з> _Угз)> Ри (Хц. _Уи)» 7 и (х33, у33) и неподвижного шарнира
£)(хс, у о), полагая длину стойки механизма AD= 1:
Х12 = —0,6767511;. У12 = —0,1715128;
х13 = — 0,0765669; _у13 = — 0,0771143;
tg813 = 4- 1,007148;
х23 = —0,0122484; >23 = — 0,2671994;
Хц =4- 0,1891829; _уп = -]- 0,1715128;
х22 = —0,0082566; _у22 = —0,1995298;
xD = -f- 0,6767511; yD = 4- 0,1715128.
876
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[гл. хш
3) По формулам (11.71) и (11.44) подсчитаем коэффициенты
7а» 7з, Л и координа ты фокуса F (ху, ур) кривой центров ТИ1223 *);
Л = — 0,0726; Л = + 0,0153;
Л = — 0,0094; у; = — 0,0147;
xf=4-0,173; jf= —0,233.
4) По формулам (11.77) и (11.44) подсчитаем соответствующие
коэффициенты j\, J2, ja, /4 и координаты фокуса F кривой центров
Л11122 *):
71 = + 0,1809,
/2 = — 0,0280,
Х/г = + 0,2090,
7з = — 0,0392,
Л =+0,0327,
yf = — 0,1840.
5) Нанесем на чертеж стойку механизма AD, полюсы Р12, Рк,
Рц, Рц> Рц и фокусы F обеих кривых Л11223 и Л41’22 (расположе-
ние всех этих точек, соответствующее подсчитанным координатам,
показано на рис. 750). Построим кривые центров ТИ1223 и Л11122.
Эти кривые, кроме полюсов Р12, Р22 и шарнира D, пересекаются
еще в одной точке М— искомом центре Бурместера Л1"223, коорди-
наты этого центра хм, ум, снятые с чертежа, дают:
tg8M = ^L^_i,5.
6) Подсчитаем по формулам (11.129), (11.138) и (11.136) коэф-
фициенты kb ka, k3, kt, параметр и и приближенные значения коор-
динат хм, Ум центра Бурместера:
kx = + 0,1974396; Л3 = 4-0,3710426;
Л2 =-|-0,1809262; Л4 = —0,0290170;
и = -[- 0,6776826;
хл! = +0,1857671; ум = — 0,2786506.
Подсчитаем по формуле (11.141) величину v и разность Дп:
и = + 0,6801948; Дп = и — v = — 2512,2-10 6.
Полученная разность Ди свидетельствует о необходимости уточне-
ния координат центра Бурместера. С этой целью выберем:
«' = « = -[-0,6801948.
*) Координаты фокусов кривых Л41223 и Л41122 как исходные данные для
графического построения достаточно иметь с тремя знаками после запятой,
если длина стойки механизма считается AD = 1.
§431 СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 877
По формулам (13.13), использовав значение и’, подсчитаем:
tg8^ = —1,487375;
х'м = 4-0,1867567; у'м = — 0,2777773;
г>' = ф- 0,6812904.
Новая разность &и' = и'— v'= — 1095,6-10-6. По формуле
линейной интерполяции (11.142) подсчитаем уточненное значение
параметра и:
tf = -|-0,6821377
и по формулам (13.13), использовав значение if, подсчитаем снова
tg 8^ = —1,477834;
хм = 4-0,1875034; ум = — 0,2770989;
v" = 4- 0,6821549.
Разность Дп" = п"— v" =—17,2-10“6. По формуле линейной интер-
поляции (11.142), использовав значения и', hit’, и" и Ди", найдем
новую уточненную величину параметра и:
и'" = 4-0,6821687.
По формулам (13.13), использовав значение и"', подсчитаем еще раз:
tg8M = — 1,477683;
Хм = + 0,1875152; jm = —0,2770880;
if’= 4- 0,6821689.
Разность Ди"' = а"'— if' = 0,2 • 10“6. Она позволяет принять
подсчитанные значения х'м и у'м за расчетные значения координат
Хм и ум центра Бурместера Л111223.
7) Подсчитаем по формулам (11.21) координаты хв, ув соответ-
ственной точки Бурместера В[1223:
tg 8В = 4- 7,040637;
хв =-]-0,193613; ув =-|- 1,363159.
8) По формулам (13.14) и (13.15) найдем параметры схемы
четырехзвенника:
а =1,2989; £>=1,6403; с = 0,66377;
а — -|- 57°00', 1; р = -|-235°59',3.
878 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
В таблице 13.3 приведены отклонения функции положения этого
механизма от заданной логарифмической функции (13.37), а на рис. 751
изображен график этих отклонений. Три верхних отклонения (в узло-
вых точках gt, g2 и g3) в соответствии с условиями интерполяцион-
ного приближения равны нулю. Три нижних отклонения (в точках h0,
hi и h2) оцениваются соответственно:
Д% = — 12',2; Дф1 = —3',1; Дф2 = —2',3.
Наибольший модуль усредненных отклонений, характеризующий
точность полученного приближения, будет L = | 4^-j = 06',1. Его
относительная величина I | = 0,20%. Минимальный угол передачи
на отрезке приближения pmin = 26°.
Графоаналитический способ позволяет со сравнительно неболь-
шими затратами труда отыскивать приближенные решения. При обна-
ружении среди этих решений заведомо неприемлемых механизмов
можно избежать напрасных потерь труда и времени на подсчет
точных параметров схемы этих механизмов. К таким механизмам
относятся механизмы, не проворачивающиеся на заданном отрезке
(т. е. удовлетворяющие условиям интерполяционного приближения
только геометрически, а не кинематически), обладающие недопустимо
малыми углами передачи на том же отрезке или имеющие некон-
структивные длины звеньев.
§43]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
879
Таблица 13.3
Отклонения функции положений шарнирного
четырехзвенника от заданной функции (13.37)
Угол поворота ведущего звена V Отклонения Дф Точки на графике Д (?) (рис. 751)
0 — 12',2 Ло
03с55' — 02,7 С
<f j = 09 33 0 gt
20 00 — 02,1
27 30 — 03,0
30 00 — 03,1 ht
32 30 — 03,1
40 00 — 02,5
50 00 — 01 ,0
60 00 — 00,2
= 65 27 0 gs
70 00 — 00,1
80 00 — 01 ,1
90 00 — 02,3
91 30 — 02 ,3 hs
92 30 — 02,3
<рз = 100 00 0 g*
Применение графоаналитического способа особенно целесообразно
при отыскании решений, порождаемых изменением абсцисс узлов
интерполяции или входного, или выходного углов (fm или <|>т (см.
главу XIV). В этих случаях легко прослеживается общая закономер-
ность в изменении положения центров Бурместера в функции от
изменяемой величины. В результате для нахождения положения
центра Бурместера, соответствующего новому значению переменной,
достаточно, как правило, построить только небольшие участки кри-
вых Мш* и 7И1223 или 7И1123.
Изложенные аналитическое и графоаналитическое решения интерпо-
ляционной задачи синтеза четырехзвенника получены в предположении,
что углы <р12 -£ <р12 и координаты полюса Р12 конечны. Это условие
всегда может быть обеспечено посредством соответствующего выбора
абсцисс <f>i и <р2 узлов Qj и Q2. Для случая, когда указанное усло-
вие не выполняется, т. е. когда углы <pi2 = 4>12 и полюс Рп уходит
в бесконечность, решение задачи синтеза четырехзвенника также не
представит никаких затруднений. Центр Бурместера 7И11223 найдем
в этом случае как точку пересечения гиперболы, на которую рас-
падается кривая центров Л11122 (см. § 37, 9°), с кривой центров Af1223 или
7И1123. Для построения этих кривых в рассматриваемом случае не нужно
предварительно находить координаты их фокусов. Фокус кривой 7И1223
совпадает с полюсом /J23, а фокус кривой 7И1123 — с полюсом Р^.
Упомянутая гипербола строится на полюсах Рп и Pit.
880 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
Для нахождения по известному центру Бурместера Л4 соответ-
ственной точки Бурместера следует использовать равенства
/_В^М=Ц
вместо равенства (11.20).
§ 44. Синтез кривошипно-шатунного и кулисного
механизмов по полному числу параметров схемы
1°. Параметры схемы кривошипно-шатунного механизма. Выбе-
рем на схеме кривошипно-шатунного механизма АВС (рис. 752) декар-
товы оси X,
У с началом
в
ДМ
Рис. 752.
неподвижном шарнире А и осью У, на-
правленной по движению ползушки.
Звено АВ в кривошипно-шатунном
механизме условимся называть коромыс-
лом, так как в исследуемых здесь
механизмах для воспроизведения задан-
ной функции на ограниченном отрезке
оно не совершает полного оборота. Ко-
ординату <р коромысла будем отсчиты-
вать от вспомогательной оси А/. Угол,
который образует ось AI с осью X,
обозначим буквой а.
Координату s шарнира С ползушки
условимся отсчитывать от некоторого
его положения Со, определяемого ор-
динатой Н. Положительное направле-
совпадающим с положительным направлением
ние отсчета s выберем
оси У.
Параметры а и Н относятся к параметрам схемы кривошипно-ша-
тунного механизма наряду с длинами звеньев АВ = а, ВС = Ь и
координатой Хс, определяющей смещение линии движения шарнира С
от оси У.
Для определенности условимся, что аргумент <р подается на коро-
мысло АВ, а функция s снимается с ползушки, т. е. коромысло
является ведущим звеном, а ползушка — ведомым.
Пусть функция, которую должен воспроизвести на отрезке [<р0, <рт]
кривошипно-шатунный механизм, есть
s = F (<?).
(13.38)
Интерполяционное приближение функции s=/(<p) положения кри-
вошипно-шатунного механизма к заданной функции (13.38) опреде-
лим по-прежнему тремя узлами Qj, (?.2 и Q3 (рис. 753). Два из них
(?! и с абсциссами <р, и <рг (<р0 <Z <С ®т) выберем двукрат-
ными, а третий узел Q3 с абсциссой — простым.
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 881
Кинематические условия этого приближения выразятся соответ-
ственными перемещениями <р12 и sl2, <р)3 и s13 ведущего и ведомого звеньев,
которые подсчитаем по формулам:
= —Si2 = ^(<Ps) —
?1з = ¥з — <Р1= «1з = ^(?з) —
(13.39)
и значениями производной в первом и втором положениях механизма:
($),-, (,зло>
В § 41 было показано, что кривошипно-шатунный механизм АВС
(рис. 752) можно рассматривать как шарнирный четырехзвенник ABCD
с бесконечно удаленным шарниром D. В результате решение задачи
синтеза кривошипно-шатунного механизма отличается от решения
соответственной задачи шарнирного четырехзвенника в основном
лишь расчетными формулами для определения полюсов относитель-
ных положений ведущего звена (коромысла) по отношению к первому
положению ведомого звена (ползушки).
2°. Последовательность аналитического подсчета пяти парамет-
ров схемы кривошипно-шатунного механизма. Наметим последова-
тельность подсчета пяти параметров схемы кривошипно-шатунного
882
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[гл. XIII
механизма по условиям интерполяционного приближения, описанного
в 1°, и дадим сводку необходимых расчетных формул.
1) Вычисление кинематических условий интерпо-
ляционного приближен
Рис. 754.
рые получены из формул (12.
X, Y к осям х, у:
2tg
и я. Но соображениям, указанным
в § 44, 6°, выберем абсциссы <рь
<р2 и <р3 узлов интерполяции по
формулам (13.33) или (13.34). За? ем
по формулам (13.39) и (13.40) под-
считаем соответственные перемеще-
ния <р12, <р13, s12 и s13 коромысла и
ползушки и найдем значения произ-
водной в первом и втором положениях
механизма.
2) Подсчет координат
полюсов относительных по-
ложений коромысла. Прове-
дем декартовы оси X, Y (рис. 754)
с началом в неподвижном шарнире
А. Подсчитаем в этих осях
по формулам (12.39) координаты
полюса Pl2 (А’12, К12). Нанесем
полюс Р|2 на чертеж и выберем его
за начало новых декартовых осей х,у,
параллельных осям X, Y. Под-
считаем в этих осях координаты
остальных полюсов Р13, Ра9, Рп и
P.2i по следующим формулам, кото-
0) — (12.45) путем перехода от осей
• . ,, ____ S12---- S13
12, У 13-------- -----------
2
У13 + Х13 tg
tg 8 23 =----------~’
Х1з — .У1» tg
1 (13.41)
Хм== — w № = —
х" У" = + Т :
Хи=(5)^ “ *м; №=— т •
Отметим в осях х, у координаты неподвижного шарнира А (хд, _уд):
Хд= А)2; _уд =—К12. (13.42)
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 883
3) Вычисление коэффициентов кубического урав-
нения. Подсчитаем последовательно (см. формулы (11.129)—(11.132)):
С1 = Хц — х13— х2:|, е2==-^и —АГ]з(13.43)
*1 = -Гц — х22, = хи 4“ (13.44)
I = -^13-^23 +_У1з_Угз- (13.45)
Коэффициенты е3, е4, /г3 и /г4 здесь подсчитывать не нужно,
так как
₽3=Jn —Ji3— № = №> e4=j’n— №+>'23 = 0,
^3=J11---№ = SU> ^4 = Уи +№= 0-
В связи с этим оказывается, что /?3 = 0, а для коэффициен-
тов рх и получим выражения:
Г1 = 512е1—*isis> P2 = ktei — £2₽,. (13.46)
Формулы (11.131) перейдут в следующие:
91 = хп№ — ЗДь ^ = ^1 1 (13 47)
?2=2(Xi1x22+№№). ^4 = ?з —2Z92. J
Наконец, формулы (11.132), если в них подставить ^ = 47^, при-
мут вид:
«4 = — fllPl + ?4> «з = Vi (4Z — Pi) — q*Pi — qi tg Щ = — qi (4Z tg — Pi j — q-iPi + ?з, (13.48)
Wi=<7iP2 —f/atg’^2,
z«0 = 0.
Так как /ип = 0, то из уравнения (11.125) выделяется ко-
рень и = 0, и мы получим уравнение третьей степени:
/л4п3 + щ3п2 /и8и + = 0 (13.49)
относительно переменной
*Y 12
где ------величина вписанного угла, при которой три окруж-
ности Ж123‘— у, Ж112 — у и Ж122 — у пересекаются в одной точке —
центре Бурместера Ж11223 (см. § 38, 5°)-
884 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XII1
Корень н = 0, выделившийся из уравнения (11.125), определяет
центр Бурместера, совпадающий с бесконечно удаленным шар-
ниром D.
4) Решение кубического уравнения (13.49) и под-
счет координат центров Бурместера. Решаем кубическое
уравнение (13.49), которое имеет либо один действительный корень и,
либо три действительных корня иь п2, и3.
Подсчитаем координаты соответствующих центров Бурме-
стера М11223 (хуи, Jai), подставив последовательно корни иь п.2, п3
в формулы (11.135) и (11.136), которые с учетом того, что
здесь ft3 = s12 и kl = 0, перепишем таким образом:
tg8jM =
ktU
— SisU
Хц (и — tg 8Д() 4- Ун (w tg 8Д1 4- 1)
Хм = —— -----------------—-------------
Ум = хм tg 8Л1.
(13.50)
5) Проверка координат центров Бурместера и их
уточ нение. Для проверки точности этих координат вычислим
величину
___(Л-Л1 Х|»)(Ул1 У^) (* * * * * * * * * хм х^)(Ум У1з)
(ХМ х1») (ХМ — *2з) + (Уд! — >1з) (Л’л1 — №) ’
Если разность Дп = п—v выходит за пределы точности рас-
чета, то координаты центра Бурместера Хм, Ум подлежат уточнению
тем способом, который изложен при решении задачи синтеза шар-
нирного четырехзвенника (см. § 43, 1°).
6) Подсчет координат соответственной точки
Бурместера В\1223 (хв, у в)- Для подсчета этих координат
используем формулы (11.21), которые после подстановки tg — tg
будут иметь вид:
(13.51)
tg 8д = —-------—,
хм + Ум у-
хмУп
хв — (~~ ~ ---г, Тц > Ув — ХвщЬв,
(Хи — хд1) tg у И +УД1
где Хм, Ум — уточненные координаты центра Бурместера /И”223.
Нанесем на рис. 754 по подсчитанным координатам один из
центров Бурместера и соответственную ему точку Бурместера" (на
рис. 754 они обозначены соответственно М и Вх). Точку Бурместера
выберем за подвижный шарнир коромысла Въ а с центром Бур-
местера совместим шарнир ползушки Ср Тогда, как уже указывалось,
фигура АВ1С1 определит первое положение искомого кривошипно-
44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ
885
шатунного механизма, у которого направление движения ползушки и
параллельно оси Y.
7) Подсчет параметров сх е мы механизма. Длины
звеньев механизма через координаты его шарниров подсчитаем по
формулам:
a = ABi = y^XB_ Хд)2-|-(ув — уАу । мок™
b — BiCi = У(хе — Хм)1 (Ув —УмУ*’ J
Смещение линии движения шарнира С от оси Y будет:
А"с = A"i2 4"-^ль (13.53)
Остается найти еще два параметра схемы кривошипно-шатунного
механизма, а именно, угол а, определяющий положение оси А/, от
которой отсчитывается координата коромысла и ординату
Н точки Со, от которой отсчитывается координата s шарнира
С ползушки. Их можно установить на основании тех же сообра-
жений, какие были изложены в § 43, 1° при отыскании параметров у.
и £1 схемы четырехзвенника.
В первом положении механизма, изображенном на рис. 754,
координата коромысла, отсчитанная по оси AI, по численной вели-
чине должна быть равна выбранной абсциссе ср, двукратного узла
интерполяции. В том же положении механизма угол, образованный
коромыслом с осью X, равен а —| - <р,. Для определения угла а
получим:
tg(4-= (13.54)
где (хд, у а) и (хв, у в) — координаты неподвижного шарнира А
и точки Бурместера Bt в осях х, у. Следует учесть при этом,
что если ул—_ув^>0, и, наоборот,
если уд— ув>0.
Координату Xj шарнира С) в первом положении механизма, от-
считанную от точки Со, найдем по уравнению заданной функции (13.38):
S1=F(?1)- (13.55)
Шарнир Ct в первом положении механизма совпадает с центром
Бурместера М. Ордината этого шарнира в осях X, Y будет Ym.
Из рис. 754 имеем очевидные равенства:
Км = Yi2 ум =
Отсюда
H=Y+yM-sl. (13.56)
Таким образом найдем все пять независимых параметров схемы
кривошипно-шатунного механизма: а, Ь, Хс, « и И.
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 887
886 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
До сих пор предполагалось, что ведущим звеном в кривошипно-
шатунном механизме является коромысло. В соответствии с этим
функция, подлежащая воспроизведению механизмом, была задана:
s = F(cp).
Предположим теперь, что ведущим звеном будет ползушка, и
функция, подлежащая воспроизведению на отрезке [s0, sm], задана:
cp = F(.s). (13.57)
В этом случае нахождение пяти параметров схемы кривошипно-
шатунного механизма по условиям интерполяционного приближения,
которое определено двумя двукратными узлами и одним простым, не
будет отличаться от изложенного. Следует только учесть, что абсцис-
сами узлов интерполяции здесь будут координаты ползушки $1( s2,
$3. Их можно выбирать по формулам, аналогичным формулам (13.33):
Sj = 0,0955 sm;
s2 = 0,6545 sm;
s3 — sm<
когда отрезок приближения [0, sm], или по формулам, аналогичным
формулам (13.34):
(13.58)
Si = So + 0,0955 (sm — s0),
s2 = So + 0,6545 (sm — So),
s3 = Sm,
(13.59)
когда отрезок приближения [s0, sm]. Здесь s1 и s.2 — абсциссы дву-
кратных узлов, a s3— абсцисса простого узла.
3°. Подсчет отклонений. При подсчете отклонений функции по-
ложений кривошипно-шатунного механизма от заданной функции при-
‘ ходится различать случаи ведущего коромысла и ведущей ползушки.
1) Случай ведущего коромысла. Выберем декартовы
оси X, Y (рис. 755) с началом в неподвижном шарнире А. В произ-
вольном положении механизма, определяемом координатой <ро угол,
образованный коромыслом АВ с осью X, равен (а Ц- <р,). Для коорди-
нат шарнира В имеем:
Хв = a cos (a -J- ср,); Ув ~ a sin (а —J—<р,-). (13.60)
Абсцисса Хс шарнира С не зависит от положения механизма.
Она подсчитана по формуле (13.53). Для подсчета ординаты Ус шар-
нира С воспользуемся очевидным равенством:
Учитывая выражения (13.60), получим окончательно:
У с = a sin (а -ф- <р) ± У Ь'2 — [а cos (а -[- <рг) — zYc]a. (13.61)
Знак в этой формуле выбираем из условия, чтобы при =
было
Ус = Н + s’>
где st и Н подсчитаны по форм
Положение шарнира С, опреде-
ляемое заданной функцией s —
= F(<p), будет:
rc^/74-F(T,.).
Отклонение функций положе-
ния механизма от заданной функ-
ции подсчитаем по формуле As, =
= Ус — У'с, т. е.
= Ус-Н— F(Ti). (13.62)
При значениях <р, равных вы-
бранным абсциссам срь <р3 и <р3 узлов
интерполяции, отклонения должны
быть As=0. Это служит провер-
кой правильности подсчетов.
2) Случай ведущей
ползушки. Рассмотрим произ-
вольное положение механизма,
определяемое координатой sf
(рис. 755). Соединим шарнир С с
неподвижным шарниром А и обо
£САХ = ^ и £САВ = 1Ц
Получим:
tg£/ = ^±lL. (13.63)
лс
Исключив отрезок АС из очевидных равенств:
b* = ar -j- АС2 — ‘2 AC a cos т);,
Хс = AC cos АС2 = XI4- (Н 4- 5г)8,
найдем:
[d -f- S; (s; + 277) ] cos Ь
COS = 2Xca ---------------<13-64>
где
d = a2 _^4-A^4-/F.
Отсюда
b = V (A'B - XCY 4- ( Yb - Yc)'2.
Из очевидного равенства
a 4"
Yc =YB±Vb2- (A B - Xc)2.
888 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. хш
получим:
= — Tjj — а. (13.65)
Так же как в случае шарнирного четырехзвенника (см. § 43,1°),
здесь в правой части последней формулы знаки перед Ег и ц могут
меняться.
Для того чтобы не ошибиться в выборе значения углов S£ и
по их тригонометрическим величинам и составить правильную фор-
мулу для подсчета угла а, целесообразно вычертить схему механизма
по найденным ее параметрам.
Отклонения функции положения механизма от заданной функции
(13.57) найдем по формуле
Д <р,- — <р,- — F (s,), (13.66)
где <рг— действительный угол поворота коромысла, подсчитанный по
формуле (13.65). При значениях аргумента s, равных выбранным аб-
сциссам st, s2 и $3 узлов интерполяции, отклонения должны быть
Д<р = 0. Это служит проверкой правильности подсчетов.
4°. Пример синтеза кривошипно-шатунного механизма. Тре-
буется воспроизвести кривошипно-шатунным механизмом функцию
тангенса
w=tgz (13.67)
на отрезке от z — 0° до zm — -]-50o.
Аргумент z подается на ползушку, а функция w должна сни-
маться с коромысла. Заданы входное перемещение ползушки sm и
выходной угол коромысла срт:
sm“~b',0; <?т = -J- 80J.
По этим данным на основании формулы § 43, 4° получим следу-
ющую функцию, к которой должна быть приближена функция поло-
жений кривошипно-шатунного механизма:
<р= 1,1716041 tg (0,8726646 s) (13.68)
(здесь <р выражено в радианах). Отрезок приближения от s0 — 0
ДО sm = -ф-1.
Отыщем пять параметров схемы кривошипно-шатунного механизма
из условий интерполяционного приближения, определяемого двумя
двукратными узлами и одним простым. Используем для решения
этой задачи аналитический путь расчета, учитывая, что ведущим
звеном (на которое подается аргумент) является ползушка.
1) Выберем абсциссы узлов итерполяции по формулам (13.58)
St = 0,0955; s2 = -ф- 0,6545; s3 — -ф- 1,000.
Соответственные перемещения ползушки и коромысла будут:
st2 = 4- 0,5590; <ри = + 37°31'45",7;
Si3 = 4- 0,9045; = -ф- 74с23'33",4.
44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 889
Находим функцию:
=0,9780741 cos2 (0,8726646s).
Ее значения в первом и втором положениях механизма будут:
= 4-0,9712967; =4-0,6922257.
\d<fjs=st 1 \O'P/S-=S'2
2) Выпишем значения величин:
tg = 4- 0,3397346; tg^ = Ц- 0,7589395.
Подсчитаем по формулам (12.39), (13.41) и (13.42) координаты
полюсов Р12, Р13, Р23, Рп, Pi2 и неподвижного шарнира А:
Л12 = 4-0,8226879; Г12 = —0,2795000;
х13 = — 0,2267906; у„ = — 0,1727500;
tg 823 =-|- 1,4860147;
х23 = — 0,3043375; _у23 = — 0,4522500;
А-и = 4-0,1486088; y,t = 4~ 0,2795000;
х22 = —0,1304622; _у22 = — 0,2795000;
Хд = —0,8226879; уА = 4- 0,2795000.
3) Подсчитаем по формулам (13.43) — (13.48) коэффициенты ку-
бического уравнения (13.49):
е, = 4- 0,6797369; ^ = 4-0,279071;
е2 = 4-0,0710619; ^ = 4-0,0181466;
/ = 4-0,1471471;
р, = 4-0,1275532; р2 = -[-0,0074964;
qt =—0,005072; /и4 = 4-0,058087;
?2 = 0,1950162; м3 =-]-0,002413;
с/з = 4- 0,00004846; /и2 = 4- 0,001878;
^=4-0,0574406; и, = —0,000054.
Получим следующее кубическое уравнение:
0,058087и3 4- 0,00241 За2 4- 0,001878м — 0,000054 = 0.
4) Решение этого уравнения дает один действительный корень:
и = 4-0,027413.
Подсчитаем координаты соответствующего центра Бурместера
Д4*|223(Хл1, ум) по формулам (13.50):
хЛ1 = —0,4302408; ум = 1,166065.
890 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
5) Для проверки их вычислим вспомогательную величину
к =-[” 0,027447.
Разность
Ди = и — т> = —34,0-10+
После уточнения получим следующие значения координат центра
Бурместера:
хм = ~ 0,4303911; ^ = —1,166684.
6) Подсчитаем по формулам (13.51) координаты соответственной
точки Бурместера Bt:
4-0,0725672; ув= 4~ 0,089569.
7) По формулам (13.52)—-(13.56) подсчитаем параметры схемы
кривошипно-шатунного механизма:
а = 0,915181; (>= 1,353196; Л'с = 0,392297;
И— — 1,541684; а = — 1+35'07".
На рис. 756 этот механизм изображен в положениях, соответ-
ствующих концу и началу отрезка приближения Osgssgl.O.
Таблица 13.4
Отклонения функции положения кривошипно-
шатунного механизма от функции (13.68)
Д<р Точки на графике отклонений (рис. 757)
0 —06" *)
S] = +0,0955 0 gl
+0,2 —01
+°,з 0 g
+0,35 +01
+0,4 +02
+0,5 +03
ss = +0.6545 0 g*
+0,7 +01
+0,8 +10
+0,85 +20
+0,9 +28
4-0.95 +27
$з = 1,0 0 gs
') В настоящем примере, чтобы установить
ход изменения отклонений, оказался необходимым
подсчет их с точностью до секунды.
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 891
В таблице 13.4 приведены отклонения функции положений этого
механизма от функции (13.68), а на рис. 757
нений Д (у) этого механизма. Г рафик
д/А в точках gi и g2 с абсциссами
Sj ==-]- 0,0955 и у2 = -ф- 0,6545, рав-
ными абсциссам двукратных узлов ин-
терполяции, касается оси у, а в точке g3
С абсциссой у3 = -(-1, равной абсциссе
простого узла интерполяции, пересекает
упомянутую ось. Но кроме тех пяти
общих точек графика Д (у) с осью $,
которые совпадают с указанными точ-
ками gi, gt, gs*)> имеется еще ше-
стая дополнительная точка g с абсцис-
сой у=-]-0,3. Именно наличием шести
общих точек между графиком Д (у) и
осью у на отрезке приближения сле-
дует объяснить высокую степень полу-
ченного приближения. После усредне-
ния графика Д (у) получим наибольший
модуль усредненного отклонения L —
= 15". Относительная величина этого
0,005%. Ми-
показан график откло-
« I L I
отклонения будет — =
I Vm I
нимальный угол передачи на отрезке
приближения [imin = 27°.
Решения той же задачи ранее дали А. Свобода [112] и Н. И. Ле-
витский [ЗЗз]. В этих решениях график A (у) имеет с осью $ толь-
ко четыре общие точки на отрезке приближения. В результате
*) В каждой точке касания g, и g2 графика Д (s) с осью s в геометри-
ческом представлении совпадают по две общие точки графика и оси.
I
892 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. хш
величина 1^-1 оказывается примерно в 100 раз больше, чем в при-
I rm I
веденном решении.
5°. Графоаналитическое определение пяти параметров схемы
кривошипно-шатунного механизма. Задача синтеза кривошипно-
шатунного механизма по указанным выше условиям может быть
также решена графоаналитическим способом, который изложен в § 43
в качестве способа решения задач синтеза четырехзвенника. При
этом способе сначала отыскиваются приближенные координаты
центра Бурместера Л4"223 как точки пересечения любых двух из
трех кривых центров Бурместера Л11123, /И1223 или /И1122. Затем эти
координаты уточняются до необходимого числа знаков.
При графоаналитическом определении пяти параметров схемы
кривошипно-шатунного механизма можно использовать последователь-
ность расчетов и вспомогательных построений, которая приведена
в § 43, 7° для решения аналогичной задачи синтеза четырехзвенника.
Отличия будут заключаться только в подсчете координат полю-
сов Pti, Р13, Рп, Plt, Р.м и в определении параметров схемы меха-
низма по известным координатам центра Бурместера и точки Бурме-
стера.
Построение кривых центров ТИ1223, Л11123 и М1122, последующее
уточнение координат центров Бурместера /И"223 и нахождение коор-
динат соответственных точек Бурместера /?'1223 в задаче синтеза
кривошипно-шатунного механизма практически не будут отличаться
от изложенных в задаче синтеза шарнирного четырехзвенника. Отме-
тим только некоторые упрощения в подсчете координат фокусов
упомянутых кривых центров, связанные с тем, что неподвижный
шарнир D четырехзвенника, через который проходят все три кри-
вые центров, в случае кривошипно-шатунного механизма оказывается
удаленным в бесконечность.
Пусть направление движения ползушки и параллельно оси орди-
нат Y, как показано на рис. 754. Напомним, что в осях х, у, па-
раллельных осям X, Y, но с началом в полюсе Рп, координаты
фокусов кривых центров выражаются формулами (11.44):
„ JtJt-Yjijs . ,, jt h—JsJt
ур-~л+я •
а угловой коэффициент серединной прямой — формулой (11.43):
где для кривой центров ТИ1223 коэффициенты /(, /2, /3 и /4 вычисляются
через координаты полюсов по формулам (11.71):
jt = л*22 -^13 — хгз\ /з == хгг J'i3 4“ х1зУгг1
Ji —Угг 4~ J13 —Угз< jt — хггх13 —УггУи-
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 893
Использовав формулы (13.41), определяющие координаты полю-
сов Р№ Pi3 и Р23, легко установить, что в случае кривошипно-ша-
тунного механизма будет:
/а = 0.
В результате формулы для подсчета координат фокусов перейдут
в следующие:
yF=k, (13.69)
Ji h
а угловой коэффициент серединной прямой окажется 15800 = 0.
Для кривых центров Af1123 и /И1122 коэффициенты jj, /2, /3, /4 под-
считываются по формулам (11.66) и (11.77). Тем же путем легко
убедиться, что и для этих кривых в случае кривошипно-шатунного
механизма коэффициент у2 = 0, и поэтому для координат их фокусов
будут справедливы формулы (13.69), а угловой коэффициент серединных
прямых останется 15800 = 0. Последнее означает, что серединные
прямые всех трех кривых центров параллельны оси абсцисс, так как
бесконечно удаленные точки этих кривых совпадают с бесконечно
удаленным шарниром D.
Основные особенности графоаналитического определения пяти
параметров схемы четырехзвенника, отмеченные в конце § 43,
остаются справедливыми для графоаналитического нахождения пяти
параметров схемы кривошипно-шатунного механизма.
6°. Условия интерполяционного приближения в синтезе кулис-
ного механизма по полному числу параметров. В кулисном
механизме число независимых параметров схемы равно четырем.
К ним принадлежат (рис. 758)’ внецентренность кулисы а *), длина
звена CD —с (длина стойки по-прежнему предполагается Д/У=1) и
углы аир, которыми определяются относительно стойки AD поло-
жения осей AI и DIJ Для отсчета координат ср и ф кулисы и
*) Ниже речь идет о кулисных механизмах с прямолинейной кулисой.
В них внецентренность кулисы а — это расстояние от шарнира А до оси
кулисы, проходящей через шарнир С,
894 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
звена CD. Отыскивая четыре параметра схемы механизма, можно
потребовать, чтобы функция положения механизма в четырех точках
совпадала с заданной функцией. Учитывая это, зададим интерполя-
ционное приближение, по условиям которого будем определять
четыре параметра схемы кулисного механизма, следующим образом:
на графике F (ср) заданной функции (рис. 759)
= F (?),
которая должна быть воспроизведена на отрезке [<р0, срт] кулисным
механизмом, выберем двукратный узел с абсциссой 9о 9m
и два простых узла Q* и ф3, расположенных на границах упомяну-
того отрезка, т. е. имеющих абсциссами ср2 = <р0 и ср3 = <рт*).
На рис. 759 изображен случай, когда графики /(ср) и F (ср) на
отрезке [<р0, <рт] не имеют иных общих точек, кроме тех четырех,
которые совпадают с узлами Q2 и Q3 **). В этом случае график
*) Нумерация узлов выбрана умышленно не в порядке их расположения
вдоль оси абсцисс. Это позволяет непосредственно использовать ряд установ-
ленных выше формул для подсчета параметров схемы кулисного механизма.
**) В двукратном узле Qi как точке касания совпадают две бесконечно
близкие точки графиков F (а) и /(у). Поэтому задание трех узлов Qb Q2 и QSt
из которых один двукратный и два простых, эквивалентно заданию для этих
графиков четырех общих точек.
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 895
отклонений Д(?) располагается по одну сторону от оси абсцисс, ка-
саясь ее в точке gi с абсциссой ?, и пересекая ее в точках и
g3 с абсциссами ?2 и ?3.
Если отклонения оказываются положительными (как показано на
рис. 759), то точки gt, g2 и g3 отметят на графике Д (?) нижние
предельные отклонения, равные нулю. Точки верхних предельных
отклонений обозначены ht и /г2.
При произвольном выборе абсциссы ?, двукратного узла пре-
дельные отклонения Дф, и Дф2 в точках hi и /г2 получаются, как
правило, не равными друг другу. Если изменять абсциссу ?i (со-
хранив неизменными абсциссы ?2 = ?0 и ?3 = ?т), то будут изме-
няться как абсолютные, так и относительные значения отклонений
Дф1 и Дф2. При таком подборе абсциссы двукратного узла, при
котором выполняется равенство
Дф1 = Дф2, (13.70)
эти отклонения будут меньше по абсолютной величине, чем наиболь-
шее предельное отклонение на отрезке |?0, ?т], получаемое при лю-
бом другом выборе указанной абсциссы ?t (см. об этом подробнее
в главе XIV).
На рис. 759 изображен именно тот случай, когда предельные
отклонения Дф] и Дф2 графика Д (?) удовлетворяют условию (13.70).
После усреднения этого графика получим на отрезке [?0, ?т] гра-
фик Ду (?) с пятью предельными отклонениями, равными по абсолют-
ной величине, но чередующимися по знаку (точки этих предельных
отклонений обозначены gty, hiy, giy, hiy и g3y). Приближение функции
/(?) к функции F (?), определяемое таким графиком Ду (?), назы-
вается равномерным приближением. Наибольший модуль усредненного
отклонения L при этом приближении будет наименьшим по сравне-
нию с наибольшими модулями усредненных предельных отклонений
тех приближений, которые определятся другими абсциссами узлов
интерполяции.
В задаче синтеза кулисного четырехзвенника нельзя заранее ука-
зать величину абсциссы ?ь при которой выполняется условие (13.70).
Эта величина зависит от ряда факторов (от вида заданной функции,
подлежащей воспроизведению, от отрезка приближения, от величины
углов входа и выхода).
Воспользуемся построением, которым определяется по Чебышеву
расположение вдоль оси ? точек предельных отклонений на графике
наилучшего равномерного приближения, когда разность
Д (?)=/(<?) — f (?)
выражается в виде полинома от аргумента ? (см. § 43, 6°). Так как в рас-
сматриваемом случае число предельных отклонений на отрезке прибли-
жения п-1-1 =5, полуокружность (рис. 760), описанную на этом
896
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[ГЛ. XIII
отрезке, как па диаметре, делим на четыре равные части. (Па рис. 760
отрезок приближения выбран [0, <рт], а не [<р0, <?mL) Абсциссы точек
крайних и среднего делений определят абсциссы <р2 и <р3 точек
gi, gi. и g-i *) предельных отклонений на графике отклонений Д (<р)
г
Рис. 760.
равенства (13.70), но часто дает
Д<р2, мало отличающиеся друг от
Отметим еще абсциссы точек
наилучшего равномерного прибли-
жения. Из построения очевидно,
что абсцисса точки gx будет:
<р1 = 0,5<рт. (13.71)
В общем случае, когда отрезок
приближения [<р0, <рт] получим для
абсциссы точки g{.
= (13.72)
В интерполяционных задачах
синтеза кулисного механизма раз-
ность Д (<р) =f (<р) — F (<р) обыч-
но не может быть выражена в
виде полинома от аргумента <р.
Поэтому выбор абсциссы дву-
кратного узла Qi по формулам
(13.71) и (13.72) не обеспечивает
предельные отклонения Дф, и
друга.
предельных отклонений и /?2,
получаемые
[0, <PJ:
на основании указанного построения на отрезке
<?> = i (1 — cos = 0,1465<pm, '
= у (1 — cos = 0,8535<pm.
(13.73)
В общем случае, когда отрезок приближения [<р0, <рот], абсциссы
этих точек будут:
?'i = ?o + °>1465(<pm —?0), 1
?» = <?о4-°>8535((рт — <Ро)- I
Выбрав абсциссы <pi, <р2 и <р3 узлов интерполяции Qb Q2 и Q3.
можно установить соответственные углы поворота ведущего и ведо-
мого звеньев кулисного механизма:
У12 = Ъ — Фн = F (?а) — F (<f>i);
?1з = ?з —?i", <Ь = ^(<Рз) — F(?i)
(13.75)
*) Последовательность нумерации точек нижних предельных отклонений на
рис. 760 сохранена такой же, как на рис. 759.
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ
897
и передаточное отношение в первом положении:
= (13-76)
Подсчитав углы <pI4, <pJ3, ф14 и ф13 и переДаточное отношение
по указанным формулам, мы приходим к задзче синтеза кулисного
механизма по положениям. Изложим кратко реиДение этой задачи.
7°. Синтез механизма с ведущей кулисой. Условимся предпола-
гать, что аргумент <р подается на кулису AkiCt (Рис- 761), а заданная
функция ф = F (<р) должна сниматься с коромысла CtD. Следовательно,
кулиса будет ведущим звеном. Выберем длину стойки механизма AD = 1.
Проведем декартовы оси X, Y с началом в неПодвижном шарнире D
ведомого звена и осью X, направленной вдо/1Ь стойки. По форму-
лам (12.10) подсчитаем в этих осях координать? полюса Pi2(A'14, У12).
Затем нанесем вторые декартовы оси х, у, параллельные первым,
с началом в полюсе Ры. По формулам (13.11) подсчитаем коор-
динаты полюсов Р13 (х13, _у13), Р23 (х23, _у23), Plt (-Vi,, j'n) и шарнира
O(xD,yD).
Полюсы Р12, р13, р23 и Рп определят четь*Ре относительных по-
ложения St, S], S4 и S3 ведущего звена (кУл1,сы) по отношению
к первому положению ведомого звена (коромысла). Шарнир С, в пер-
вом положении механизма выберем совпадающий с таким центром М,
которому соответствует бесконечно удаленная' круговая точка
Кулиса CiKi в первом положении механизма будет перпендику-
лярна к направлению, в котором удалена в бесконечность точка Вк.
Графическое определение координат этого цеИтРа М и направления,
в котором удалена в бесконечность соответств енная точка Вь дано
29 II. И. Артоболевский
898 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
на рис. 734. Аналитически координаты хм, ум этого центра М и угло-
вой коэффициент tg направления, в котором удалена в бесконеч-
ность точка Bt, подсчитаем по формулам (11.107), (11.108) и (11.105).
Так как в общем случае имеется только один центр М, удовлет-
воряющий указанным выше условиям, то рассматриваемая задача син-
теза кулисного механизма может иметь в общем случае одно реше-
ние. Следовательно, три узла интерполяции, из которых один дву-
кратный и два простых, в общем случае однозначно определяют
функцию положения кулисного механизма.
Установим параметры схемы кулисного механизма по известным
координатам центра (хм, Ум), с которым совпадает шарнир Ci в
первом положении механизма, координатам неподвижного шар-
нира D(xD,yo) и угловому коэффициенту tgSB, определяющему на-
правление точки В\.
Длина ведомого звена (\D (рис. 761):
с = V (Хм — xD)a 4- (Ум — Jd)2. (13-77)
Буквой ki обозначим основание перпендикуляра, опущенного из
шарнира А на ссь кулисы, проведенную через шарнир в первом
положении механизма. Прямая Akiy перпендикулярная к оси кулисы,
укажет направление, в котором шарнир Bi удален в бесконечность.
Следовательно,
tg(a + ?i) = tgSB. (13.78)
где — выбранная абсцисса узла интерполяции Отсюда опреде-
лим угол а.
Подсчитаем ординату узла Qt:
ф1=Д(?)). (13.79)
Угол наклона звена C\D к оси А’ в первом положении механизма
будет:
tg(? + 4-i)= (13.80)
Отсюда определим угол р.
Спроектируем замкнутый векторный контур
Aki —|— —[- C\D —DA = 0
сначала на ось А’, а затем на ось Y. Тогда, обозначив Akx = а,
и вспомнив, что А£>=1, получим:
a cos (а -|- <р,) — kiCi sin (а -J- <pt) — с cos (₽ —[— фО — 1 — 0,
a sin (а -|- ср,) -|- kiCi cos (а -[- <р,) — с sin (р -|- фО = 0.
Исключив из этих уравнений переменный отрезок kfii, найдем:
а — cos (а -|- cpj) -[ с cos (Р — а — Ti ~F Ф0- (13.81)
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 899
Таким образом получим все четыре параметра схемы кулисного
механизма.
Пусть угол определяет произвольное положение механизма (не
изображенное на рис. 761). Отклонение Дф от заданной функции
ф = F (<р) в указанном положении будет:
Дф = ф1.-Г(?,-), (13.82)
где фг— угол поворота ведомого звена CD, подсчитываемый по урав-
нению
а — cos (а <рг) с cos (р — а — <рг -(- ф(). (13.83)
Последнее получим из уравнения (13.81), заменив углы и ф1 на
углы и ф;.
8°. Случаи бесконечно удаленных полюсов. Синтез механизма
с ведомой кулисой. В тех случаях, когда отдельные полюсы ухо-
дят в бесконечность, решение задачи синтеза механизма с ведомой кули-
сой упрощается. Например, при ср13 = ф13 полюс Pt3 уходит в бесконеч-
ность (х13 =>1з = со) в направлении, которое определится угловым коэф-
У1 О . ф i О 1 1 ) ТА
фициентом <*£• = tg~ - = tg~. Разделив на х13 числитель и знаме-
Х13 Z Z
натель в правой части формулы (11.107) и перейдя к пределам
х13—-со и >13—--со, получим:
(13.84)
При этом остальные формулы, приведенные выше, не изменяются.
Подобные же упрощения получим при уходе полюсов Р23 и Ри
в бесконечность. Особого рассмотрения требует лишь случай, когда
ср12 = ф12 и полюс Р12 уходит в бесконечность.
Выберем стойку механизма AD = 1 (рис. 762) и проведем декар-
товы оси X, Y с началом в шарнире D и осью X, совпадающей
с направлением стойки. Прямые, проведенные через шарниры А и D
под углом — — = — к оси УкажУт направление, в котором
полюс Р12 удален в бесконечность. По заданным углам <р13 и ф13 по-
строим полюс Р13. Полюс Р23 найдем в пересечении прямой DPi3,
которая наклонена к оси А’под углом—У12 + Y18t и прямой Р13Р23.
которую получим, повернув прямую Pi3PM вокруг полюса Pti
на угол У*» ~ V», Нанесем полюс Рц, абсцисса которого
определяется через передаточное число z’i формулой (12.18). Центр М
на кривой 7Ц1123, которому соответствует бесконечно удаленная
точка Bi, по-прежнему будем искать как точку пересе-
чения окружностей 7И123— у и /И112— у при-у =. Так как в дан-
ном случае 6la = — ф1а = 0, то первая окружность распадется
29*
900 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [ГЛ. XIII
на бесконечно удаленную прямую и прямую Р^Р^з, а вто-
рая— на бесконечно удаленную прямую и прямую PitPn, проходя-
щую через полюс Рп параллельно направлению, в котором полюс
.Р12 удален в бесконечность. Следовательно, упомянутый центр Л1,
с которым совпадает шарнир Сь графически найдем как точку пе-
ресечения двух прямых: прямой, проведенной через полюс Р13 под
углом — Н- "5 к оси и прямой, проведенной через полюс Рп
под углом — к оси X. Бесконечно удаленная точка В1( со-
ответственная найденному центру М, совпадет здесь с полюсом Рк.
Ось кулисы пройдет через центр М перпендикулярно к направле-
нию ЛР12.
Для координат центра М (А'м, Ум) как точки пересечения ука-
занных выше прямых имеем:
А18 tg 2 ^‘2) + 1g у — ^,3
tg(5^) + tg’-a ‘
nt=(Au-*Ai)tg^.
(13.85)
Здесь (Л13, У13) и (Ац, Гц) — координаты полюсов Р13 и Pit в осях
Л, У, подсчитанные по формулам (12.11) и (12.18).
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 901
Параметры схемы механизма найдем по формулам:
с — DCi — }/ Ад} 4- Км;
tg(“4-Ti) = —tg-б2: tg(₽ + <?i) = ^; z лм (13.86)
a = cos (a (p,) 4- c cos(P — a — 4~ Ф1)-
Здесь и ф1 — координаты узла интерполяции Qit а а и
Р — углы, определяющие положения осей для отсчета координат <р
и ф (на рис. 762 эти оси не показаны, чтобы не затемнять чертеж).
Все установленные выше расчетные формулы относятся к слу-
чаю, когда аргумент <р заданной функции ф = F (<р) подается на
кулису, которая является ведущим звеном. Можно поставить
задачу об отыскании такого кулисного механизма, у которого
аргумент <р заданной функции подается не на кулису, а на коро-
мысло, т. е. у которого коромысло является ведомым звеном. В этом
случае для определения параметров схемы кулисного механизма ос-
танутся справедливыми те же расчетные формулы, но в них везде
предварительно следует поменять местами углы <р и ф. Исключение
представит лишь формула (13.82) для подсчета отклонения Дф, ко-
торая останется неизменной.
Задача синтеза механизма с ведомой кулисой по указанным усло-
виям интерполяционного приближения также может иметь в общем
случае только одно решение. Следовательно, и в этой задаче три
узла интерполяции, из которых один двукратный и два простых,
в общем случае однозначно определяют функцию положения кулис-
ного механизма.
9°. Примеры синтеза кулисного механизма.
Первый пример. Требуется воспроизвести механизмом с ве-
дущей кулисой функцию
на отрезке от z = 0 дог = 4~1- Заданы входной и выходной углы:
<рт = Ч-50°; фт = 4-100°.
Переходя на основании формул (13.24) к координатам <р и ф ве-
дущего и ведомого звеньев, получим:
Ф = 2^<?а, (13.87)
где <р и ф выражены в градусах. Отрезок приближения будет от <р = 0°
до <р = 4~ 50°. Абсциссу cpi двукратного узла выберем по формуле
(13.71), абсциссы <р.2 и ©3 простых узлов — на границах отрезка при-
ближения, т. е.
<Р1 = 4-25°00'; <f=i = 0o; <р3 = 50°00'.
902 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XIII
Соответственные углы поворота ведущего и ведомого звеньев будут:
<р13 = — 25°00'; ф12 = — 25°00';
ср13 = —|—25°00'; ф13 = -[-75°00'.
Передаточное отношение в первом положении механизма = 2. При
этих условиях полюс уходит в бесконечность. Угол 612 = 0,
а угол 613 = <р13 •—ф13 =—50°. Координаты полюсов Pt3 и Рц
в осях X, Y с началом в неподвижном шарнире D кулисы и осью X,
направленной вдоль.стойки, подсчитаем по формулам (12.11) и (12.18):
А’13 = |-0,406308; Г13 == — 0,311771;
*„ = 4-1; Уп = 0.
которому соответствует бесконечно
Найдем координаты центра М,
удаленная точка Blt по форму-
лам (13.85):
Хм=0-, Удо = —0,221695.
Параметры схемы механизма
по формулам (13.86) равны:
<z = 0,92831;
с = 0,22169;
а = — 12°30', 0;
р = — 115°00'0.
На рис. 763 найденный ку-
лис ный механизм изображен в по-
ложениях, соответствующих на-
чалу (жирные линии) и концу от-
резка приближения 0 <р sg 50°.
В таблице 13.5 приведены отклонения функции положения этого меха-
низма от функции (13.87), а на рис. 764 показан график отклонений
Д (<р). Этот график на отрезке 0 sg ср 50° не имеет с осью <р иных
общих точек, кроме точек g,, g2 и g3, абсциссы которых равны
выбранным абсциссам <рь <р2 и <р3 узлов интерполяции. В точке g,
с абсциссой, равной абсциссе <р[ двукратного узла, график Д (<р)
касается оси ср. В результате график Д (<р) на отрезке 0 eg ср 50°
располагается целиком на отрицательной стороне оси Дф.
Предельные отклонения в точках hi и Л2 равны соответственно:
Дф1== — 07', 0; Дф2 = — 59', 0.
Наибольший модуль усредненных отклонений, характеризующий
точность полученного приближения, будет; L — I —— | = 29',5. Отно-
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 903
Таблица 13.5
Отклонения функции положений кулисного
механизма от функции (13.87)
Угол поворота ве- дущего звена ср Отклонения Дф Точки на графике отклонений Дер (рис. 764)
<?s = 0 +05°00 4-10 00 0 —02',7 - -06',4
-1-12 30 --1500 +20 00 —07',0 —06',4 —02',7 Л,
у, =+25 00 +30 00 --4000 +44 00 0 —04',8 —45’,8 —58',9 gi
+44 30 +45 00 —59’,0 —58',6 h2
=+50 00 0 g*
сительная величина этого отклонения Н— = 0,49%. Минимальный
коо
угол передачи механизма на отрезке приближения .
Второй пример. Пусть, как и в первом примере, механизмом
с ведущей кулисой требуется воспроизвести функцию
w — z2
на отрезке от г = 0 до г = -|г 1. Заданы входной и выходной углы
?т=+70°; Фт=4-юо°
904 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. ХП1
(в первом примере угол срт = 50°). В этом случае на основании
формул (13.24) получим:
(13.88)
где ф и ср выражены в градусах. Отрезок приближения от <р = 0° до
ср = 4-70°.
Абсциссу <р! двукратного узла выберем по формуле (13.71), а абсцис-
сы <р2 и ср3 простых узлов — на границах отрезка приближения, т. е.
?1==4-35°00'; <р2 = 0; <р3 — 70°00'.
Соответственные углы поворота ведущего и ведомого звеньев будут:
<pia = — 35°00'; ф12 = —25°00';
<р13 = 35°00'; <р13 = 4-75°00'.
„ • 70
Передаточное отношение в первом положении механизма ii = ,
Угол 012 = <р12— cpi2 = —10°00'. По формулам (12.10), (13.11)
подсчитаем координаты полюсов У12), АпРчз, У1з)>
Ряз(.х2з> З'м) и ^и) и неподвижного шарнира D(xp, yD)
ведомого звена, а по формулам (11.105), (11.107) и (11.108) — угловые
коэффициенты tg8B, IgB^ и координаты центра ЛЦхм, ум). После
этого по формулам (13.77) — (13.81) найдем следующие параметры
схемы механизма:
а = 0,94003; с = 0,42467;
а = — 24°34', 2; р = —110°26', 5.
Схема механизма изображена на рис. 765. В таблице 13.6
(в графе «1-й механизм») приведены отклонения функции положений
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 905
Таблица 13.6
Отклонения функции положений кулисного
механизма от функции (13.88)
Угол поворота ве- дущего звена 9 Отклонения Дф
1-й механизм 1 2-й механизм
ср2= 0 4-05°00' 4-ю оо <р<21> = 4-14 00 4-20 00 4-25 00 --30 00 ИЧ = —35 00 4-40 00 --50 00 --60 00 --65 00 ср3 = 4-70 00 + 0 --ОЗ',9 - -04 ,5 --03,6 --01 ,4 —00,2 —00,1 0 —00,6 —09,6 —27,0 —27,5 0 —09', 1 —03,2 —00,5 0 —00,4 —00,7 —00 ,3 0 —00 ,8 —10,7 —28,8 —28 ,3 0
этого механизма от функции (13.88). Наибольший модуль усред-
Относительная величина этого отклонения — = 0,27%. Минималь-
ный угол передачи на отрезке приближения p.min = 58°.
На рис. 766 сплошной кривой изображен график отклонений Д (ср).
В противоположность первому примеру здесь отклонения изменяют
906 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [ГЛ. ХП1
сам <рь
и
свой знак на отрезке приближения. Вызвано это тем, что кроме
точек glt и g3, определяемых условиями интерполирования, гра-
фик Д (ср) имеет с осью абсцисс еще одну общую точку g, располо-
женную между точками g% и gt. Подобные дополнительные общие
точки графика Д (ср) с осью абсцисс играют большую роль в про-
цессе отыскания наилучшего приближения (см. главу XIV). Остано-
вимся поэтому на выяснении некоторых свойств этих точек.
10°. Узловые и нулевые точки. Общие точки gt, git g3 (рис. 767)
графика отклонений Д (ср) с осью ср, абсциссы которых равны абсцис-
са узлов интерполяции Q,, Q2 и Q3, назовем узловыми
точками. Точку glt соот-
ветствующую двукратному
углу Q] назовем двукрат-
ной узловой точкой, а
точки g2 и g3, соответствую-
щие простым узлам ф>2 и Q3,—
простыми узловыми
точками. В двукратной
узловой точке^1 график Д(ср)
касается оси абсцисс, а в
простых узловых точках gt
и g3 пересекает эту ось.
Три узла интерполяции,
из которых один двукрат-
ный и два простых, в общем
случае однозначно опреде-
ляют функцию положения
кулисного механизма (см.
пункт 7° настоящего пара-
графа), а следовательно, и
график отклонений этого
механизма. Так как число,
кратность и абсциссы узлов
интерполяции и узловых точек совпадают, то можно утверждать
также, что три узловые точки, из которых одна двукратная и две
простые, в общем случае однозначно определяют график отклонений
Д (<р) кулисного механизма.
Задание трех узлов интерполяции Qit Q2 и Q3, из которых один
двукратный и два простых, геометрически эквивалентно заданию
четырех точек, через которые должен пройти график функции поло-
жения механизма. Поэтому можно утверждать, что функции по-
общем случае не могут
наличии четырех общих
остальных точках. Этот
и на графики отклонений
что заданная функция, от
ложения двух кулисных механизмов в
иметь более трех общих точек. При
точек эти функции совпадут во всех
вывод непосредственно распространяется
двух кулисных механизмов при условии,
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 907
которой отсчитываются отклонения, для обоих механизмов одна
и та же.
Дополнительную общую точку g (рис. 767) графика Д (ср) с осью
абсцисс, не совпадающую с узловыми точками, условимся называть
нулевой точкой, так как отклонение в этой точке равно нулю. Нуле-
вой точке g графика Д (ср) соответствует дополнительная общая точ-
ка Q графиков /(<р) и F(<p) функции положения механизма и заданной
функции.
Рассмотрим отдельно график отклонений Д (<р) (рис. 768) кулисного
механизма, определяемый одной двукратной узловой точкой g3 и
двумя простыми узловыми точками g^ и g3 и имеющий дополнитель-
ную нулевую точку g между узловыми точками gt и gt.
Оставив неизменными абсциссы и <р3 узловых точек gt и g3,
зададим абсциссе простой узловой точки gt положительное при-
ращение Д©г. Новое положение этой узловой точки, определяемое
абсциссой
Та’=:<¥>2 +
обозначим gj11. Три узловые точки gt, g%' и g3, из которых gt дву-
кратная, а остальные две простые, определят график отклонений
Д‘» (ср), показанный на рис. 768 пунктиром*). Графики Д (ср) и Д11) (<р),
которые касаются в узловой точке gt оси абсцисс, должны в этой
точке касаться друг друга. Геометрически это означает, что в точ-
ке gj совпадут две бесконечно близкие точки графиков Д (ср) и Д(1) (<р).
Третья точка этих графиков совпадает с узловой точкой g3. Более
грех общих точек графики Д (у) и Д(1) (ср) иметь не могут. Отсюда
следует, что при смещении узловой точки g% по оси абсцисс (при
неизменных положениях остальных двух узловых точек gt и g3)
нулевая точка также должна сместиться вдоль оси абсцисс.
*) Для нахождения графика отклонений Д'1’ (у) практически необходимо снова
решить задачу синтеза кулисного механизма, выбрав за абсциссы узлов интер-
поляции абсциссы узловых точек и g3.
908 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гл. XU1
На рис. 768 заштрихована замкнутая область, границами которой
являются участок g2g кривой Д (<р) и участок g2g оси абсцисс. Узло-
вая точка g^1’, выбранная на прямолинейном участке g2g, может быть
или точкой входа кривой Д(1) (ср) в упомянутую замкнутую область,
или точкой касания кривой Д(1) (ср) с осью абсцисс. Рассмотрим оба
возможных случая.
Пусть узловая точка g2 — это точка входа кривой Д(1> (ср) в заштри-
хованную область (как показано на рис. 768). Тогда точка выхода
кривой Д<‘> (ср) из указанной замкнутой области должна лежать на
том же участке g2g оси абсцисс, ограничивающем эту область. Чтобы
точка g(,) оказалась вне участка g2g оси абсцисс, кривые Д (ср) и Д(,) (<р)
должны иметь четвертую общую точку, что по условию невоз-
можно.
Допустим теперь, что узловая точка g2' оказывается точкой каса-
ния графика отклонений Д(2) (ср) с осью абсцисс (как изображено на
рис. 769). Это явится свидетельством, что с ней совпала нулевая
точка, переместившаяся из положения g.
Оба рассмотренных случая приводят к одному и тому же выво-
ду: положительному смещению узловой точки g.2 по оси абсцисс
соответствует отрицательное смещение нулевой точки g по той
же оси.
Если узловой точке g2 задать отрицательное смещение по оси ср,
то подобным же путем можно доказать, что нулевая точка g должна
получить положительное смещение по той же оси. Аналогичные резуль-
таты мы получим, смещая по оси <р узловую точку g} (или g3) при
неизменных положениях остальных двух узловых точек. Таким обра-
зом можно доказать справедливость следующего свойства нулевой
точки: при смещении узловой точки по оси абсцисс ближайшая к ней
нулевая точка получает смещение, обратное по знаку.
На основании указанного свойства можно найти такое положе-
ние g2‘ (рис. 769) простой узловой точки g2, в котором с ней сов-
падет нулевая точка. Тогда простая узловая точка g2’ перейдет
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 909
в двукратную и график Д(2) (ср), несмотря на наличие нулевой точки
на отрезке приближения, покажет отклонения, постоянные по знаку
на этом отрезке.
11°. Совмещение нулевой точки с узловой точкой (общий
случай). Напомним, что в синтезе механизма с ведущей кулисой
решение задачи интерполяционного приближения, которое задано одной
двукратной узловой точкой gt и двумя простыми узловыми точками
g2 и £з> сводится к рассмотрению четырех относительных положе-
ний Sj, S', S2 и S3 ведущего звена по отношению к первому поло-
жению ведомого звена. Эти относительные положения определяются
полюсами Р12, Р13, Р23 и Рп (см. § 44,7°). Подвижный шарнир
ведомого звена в первом положении механизма выбирается совпадаю-
щим с таким центром ТИ1123, которому соответствует бесконечно уда-
ленная точка Bt. Этот центр графически можно найти как точку
пересечения М окружностей /И123 — 7 и /И112— 7 (см. рис. 734 и 704)
7 « О
с вписанным углом
При переходе простой узловой точки g2 в двукратную g1/’ (рис. 769)
к упомянутым четырем относительным положениям ведущего звена
прибавится еще пятое относительное положение S2, определяемое
полюсом Р22. Координаты этого полюса, как и координаты ранее упо-
мянутых полюсов Р13, Р23 и Ри, найдем по формулам (13.11).
В этом случае при решении задачи синтеза механизма с ведущей
кулисой подвижный шарнир ведомого звена С\ должен совпасть с цент-
ром Бурместера ТИ11223, которому соответствует бесконечно удаленная
точка Бурместера Z?]1823.
Чтобы центр /И1123, найденный в пересечении окружностей А/123 — 7
7 О
и /И112— 7 с вписанным углом был одновременно центром
Бурместера Л111223, через этот центр должна пройти третья окруж-
ность ТИ122—7 (рис. 770) с тем же вписанным углом Р- = -^ . Точки Л1
этой окружности будут удовлетворять равенству (11.24), которое при
учете предыдущего равенства переходит в следующее:
L Р12МР22 = °^. (13.89)
Проведем декартовы оси х, у с началом в полюсе Р12. Подсчи-
таем в них по формулам (11.107), (11.105) и (11.108) координаты
хм, Ум центра /И1123, которому соответствует бесконечно удаленная
точка Bi в Sj. Если этот центр М есть одновременно центр Бурме-
стера А111223, то он должен удовлетворять равенству (13.89) и, следо-
вательно, равенству
tg(ZPn^PM) = tg^.
910 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ [гЛ. XIII
Первый член этого равенства обозначим ® = Р^МР^ и вели-
чину его выразим через координаты полюсов Р12 (0, 0) и Р2.2 (х22, _у22):
У 22 — УМ~~ — ХЛ1) *8 Б,М
(13-90)
где tg8,M — угловой коэффициент прямой МР^, подсчитанный по фор-
муле (11.107). Тогда равенство
—tgy = 0 (13.91)
явится достаточным условием того, что центр М(хм, ум), подсчи-
танный по формулам (11.107), (11.105) и (11.108), будет центром
Рис. 770.
Бурместера 714 "22а, которому соответствует бесконечно удаленная
точка Бурместера
После этих предварительных замечаний, обратимся к задаче, по-
ставленной в конце предыдущего параграфа. Эта задача сводится
к следующему: пусть график отклонений Д (ср) (рис.-768) кулисного
механизма, определяемый узловыми точками glt g2, g3 (где узловая
точка gi — двукратная, а узловые точки gt и g3 — простые), имеет
нулевую точку g, расположенную между узловыми точками £2и ^.Тре-
буется найти такое новое положение узловой точки git в котором с лей
совпадет нулевая точка g. Для определения абсциссы этого положе-
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИС1'1ОГО МЕХАНИЗМОВ
911
ния узловой точки g.2 можно указать следукРщий способ последова-
тельного приближения.
Вычислим по формуле (13.91) величину v и разность
Дт, —т, —tg^,
которая не будет равна нулю, так как нулевая точка ё не совпадает
с нулевой точкой g2. Сохранив неизменными абсциссы и <р3 узло-
вых точек g\ и g3, сместим узловую точку ёъ в направлении сбли-
жения ее с нулевой точкой g в произвольное ^сложение g£ (рис. 768)
с абсциссой <р2’. Подсчитаем новые коорди<наты полюсов Р12, Р|3,
Рчя и Рц по формулам (12.10) и (13.11), новые абсциссы центра
A1*123(xai, ум) — по формулам (11.107), (11-И 05) и (11.108), новую
величину —по формуле (13.90) и новую разность
в'1'
Дт/О = 77*0 — fg Д2 .
По формуле линейной интерполяции
‘ 2 Т2 ДГ<1> _ Др
(13.92)
найдем абсциссу нового положения g2' (рис. 769) узловой точки g2.
Прежние узловые точки gt и g2 и узловая т<очка ёч определят гра-
фик отклонений, у которого нулевая точка* будет расположена к
узловой точке g'2‘ ближе, чем расположена нулевая точка g к уз-
ловой точке g2 на графике Д (<р) (рис. 768), или совпадет с узловой
точкой go\
в'2’
Для проверки подсчитываем новую разнсРсть Дт»(2)='О2 —
Если эта разность не будет равна нулю (в пр’,еДелах точности расчета),
то абсцисса <р22’ подлежит дальнейшему уточнению.
12°. Совмещение нулевой точки с уз^ловой точкой. Случай,
когда полюс Р12 удален в бесконечнос'^ть- Пусть при решении
задачи синтеза кулисного механизма (с веРдУщей кулисой) абсциссы
<Pi, <р2 и ср3 узловых точек gx, g.2 и g3 (гдее ё\ — двукратная точка,
a g.2 и g3—-простые точки) выбраны так, ч*10 выполняется равенство
?12--------4*1-2
(13.93)
и полюс Р12 уходит в бесконечность (рис. '*771). В этом случае будет
6)2 — ?12 — Фы = 0- Окружность 7И123 — 7 при = — - 0 распа-
дется на бесконечно удаленную прямую и прямую Р13Р^, а окруж-
ность Л4112 — 7 — на бесконечно удаленную прямую и прямую РцРы,
проходящую через полюс Р1Ь параллельно направлению, в котором
912 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ интерполирования [гл. ХП1
полюс Р)2 удален в бесконечность. Центр Л1, в котором пересе-
каются прямые Р13Р23 и РцР12, принадлежит кривой центров
УИ1123. Этому центру М соответствует бесконечно удаленная точ-
ка Bi, совпадающая с полюсом Р12. Третья окружность А1122— 7
при ^ = -^- = 0 распадется на бесконечно удаленную прямую и
прямую Р22Р12, проходящую через полюс Р22 параллельно направле-
нию, в котором полюс Р12 удален в бесконечность. Если найденный
центр М, принадлежащий кривой центров /И1123, есть одновременно
центр Бурместера Ж11223, то через него пройдет прямая Р22Р12, на
Y 6
которую распалась окружность Л1122— 7 при Р2= -^- = 0. Так как
прямые РцР]2 и P22Pi2 параллельны, то они могут пройти одновре-
менно через конечный центр 7И, только совпадая друг с другом.
Отсюда вытекает следующее геометрическое условие совпадения
нулевой точки с простой узловой точкой g2 в задаче синтеза меха-
низма с ведущей кулисой: если полюс Рц оказывается в бесконеч-
ности, то прямая РцР22 должна быть параллельна направлению, в ко-
тором полюс Р]2 удален в бесконечность.
Прямая РПР22, параллельная направлению, в котором полюс Р12
удален в бесконечность, образует со стойкой AD угол —
Прямая PWD образует со стойкой угол —ф12 (см. § 39, 8°). Учитывая
равенство (13.93), получим, что треугольник РцР22О является равно-
бедренным, в котором P]|D = DP22.
Перенесем полюс Р22 по дуге окружности, описанной вокруг
шарнира D, на линию стойки AD в положение Р22. Тогда будет
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 913
pxxD=DP^ или, если обозначить через А'п и Х'^ абсциссы по-
люсов Рп и Pgj в осях XY с началом в шарнире D,
А'и + А'й’^О. (13.94)
Эти абсциссы подсчитаем по формулам (12.18) и (12.19):
Лп — ГП’ —(7=Т-
Отсюда на основании равенства (13.94) получим следующее усло-
вие совпадения направления прямой РПРИ с направлением, в кото-
ром полюс Р1а удален в бесконечность:
/1-}-4=2. (13.95)
Передаточные отношения Zj и z'2 подсчитываются через заданную
функцию ф = F (<р), подлежащую воспроизведению кулисным меха-
низмом, причем будет
/i==F(Tl); z.2 = F'(<p2), (13.96)
где <р, и <р2 — выбранные абсциссы двукратной и простой узловых,
точек gx и gt.
При наличии равенства <р|2 = ф12, т. е. при уходе полюса Р12
в бесконечность, равенство (13.95) выражает достаточное условие
совпадения нулевой точки g с простой узловой точкой g'£' (см. рис. 769).
Напомним, что речь идет здесь по-прежнему об интерполяционной
задаче синтеза кулисного механизма (с ведущей кулисой), определяе-
мой тремя узловыми точками gx, git g3, из которых точка gx — дву-
кратная, a g% и g3 — простые.
Если воспользоваться уравнением заданной функции ф = F (?), то
равенства (13.93) и (13.95) можно записать в следующем виде:
?i-?1 = F(?i)-F(<pi), ^(?1) + ^(^) = 2. (13.97)
Решив эти два уравнения, можно определить абсциссы и узло-
вых точек gx и g2, обеспечивающие совпадение нулевой точки g
с простой узловой точкой g3.
13°. Пример совмещения нулевой точки с узловой точкой.
Пусть механизмом с ведущей кулисой требуется воспроизвести на
отрезке [<р0, <рт] функцию
ф = Л<Д (13.98)
где k — постоянная. Напишем для этого случая систему уравнений
(13.97):
<у2 — — k<pl, 2k<?x -ф- 2Acf>s = 2.
Эта система удовлетворяется при условии:
+ (13.99)
914
СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ ИНТЕРПОЛИРОВАНИЯ
[гл. XIII
Следовательно, если абсциссы и <р2 двукратной узловой точки gt
и простой узловой точки g2 удовлетворяют условию (13.99), полюс Р,2
уходит в бесконечность и оказывается справедливым равенство (13.95),
которое выражает достаточное условие совпадения нулевой точки g
с простой узловой точкой g%.
Возвратимся ко второму примеру пункта 9е настоящего параграфа.
В этом примере решена задача воспроизведения на отрезке от <р = О
до ср = —]—70° функции (13.88):
, 1 -2
'^49^’
механизмом с ведущей кулисой. При выборе абсцисс узловых точек
gi, gi> gs (где gi — двукратная точка, а & и ga—простые):
ср, — —35°; <р2 ~~ 0 и фз==4—"70°,
был получен график отклонений Д (ср) с нулевой точкой g, изобра-
женный сплошной кривой на рис. 766.
С целью совмещения нулевой точки g с простой узловой точкой
сохраним неизменными абсциссы = —[—35с00' и <р3 =-|-70°00'узло-
вых точек gi и g3, а абсциссу <р2 узловой точки g2 выберем по фор-
муле (13.99):
= ------<Р1 = 49°-<?!=+ 14°.
При этих условиях получим:
<р,а = —21°00'; ф,2 = —21W;
<Р,з = 4- 35W; -}13 = 75°00';
. _ 70 _ I 28
г 49 ; 4 — ~Г 49 •
Полюс Рм уходит в бесконечность. Сумма /,4-4 = 2. По формулам
пункта 8° настоящего параграфа найдем следующие параметры меха-
низма с ведущей кулисой:
а = 0,94469; с = 0,42696;
х = — 24°30',0; р = — 119°40',9.
Параметры схемы этого механизма мало отличаются от параметров
схемы механизма, полученного во втором примере пункта 9° настоя-
щего параграфа и изображенного на рис. 765. В таблице 13.6 (графа
«2-й механизм») приведены отклонения функции положений найден-
ного механизма от функции (13.88), а на рис. 766 пунктиром пока-
зан график Д(1'(<р) этих отклонений. В узловой точке g'£ с абсцис-
сой <р2 = 4- 14° этот график касается оси абсцисс, так как с этой
узловой точкой совпала нулевая точка g. График Д*11 (<р) в отличие
от графика А (<р) показывает постоянные по знаку отклонения на
отрезке приближения 0 ср -С 4- 70°,
§ 44] СИНТЕЗ КРИВОШИПНО-ШАТУННОГО И КУЛИСНОГО МЕХАНИЗМОВ 915
В рассмотренном примере мы настолько сместили узловую точку g2
графика Д (ср) (рис. 766) навстречу нулевой точке g, что обе эти
точки совпали друг с другом. Но нулевую точку g можно совме-
стить с узловой точкой g2, не изменяя положения последней, путем
смещения в положительном направлении оси ср узловой точки gt.
Наконец, можно произвольно выбрать смещение узловой точки gt и
подобрать соответствующее смешение узловой точки g2, чтобы
с последней совпала нулевая точка. В этих случаях по-прежнему
достаточно, чтобы абсциссы cpj и <р2 узловых точек удовлетворяли
равенству (13.99). Соответствующие примеры, иллюстрирующие ука-
занные случаи, приведены в следующей главе.
ГЛАВА XIV
СИНТЕЗ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ ПО МЕТОДУ
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ
§ 45. Отыскание наилучшего приближения в задаче синтеза
кулисного механизма
1°. Теорема Геронимуса и ее следствия. С точки зрения практи-
ческих приложений большой интерес представляет отыскание наи-
лучшего приближения функции положения механизма к предписан-
ной непрерывной функции на заданном отрезке, т. е. приближения,
у которого наибольший модуль усредненных отклонений является
наименее возможным. Чебышев, впервые поставивший задачу нахож-
дения наилучшего приближения, указал необходимые и достаточ-
ные условия такого приближения, но лишь для функций особого
вида, а именно для функций, образующих так называемую систему
Чебышева *).
К сожалению, только в единичных случаях задачу синтеза шар-
нирного рычажного механизма по воспроизведению предписанной
непрерывной функции на заданном отрезке удается свести к рас-
смотрению функций, образующих систему Чебышева.
Для функций общего вида Чебышев указал только необходимые
условия наилучшего приближения.
Я. Л. Геронимус [14а] установил теорему, определяющую доста-
точные условия наилучшего приближения для функций /(<р) и F(<р)
общего вида, удовлетворяющих единственному требованию — быть
непрерывными на заданном отрезке. Теорема Геронимуса гласит:
если разность
(14.1)
достигает своего наибольшего модуля L, по крайней мере, в п-ф2
различных точках отрезка [ср0, срт], последовательно изменяя знак,
то для всякой функции f* (ср), непрерывной на [<рй, <рт], справед-
ливо неравенство
шах |/*(?)—/(?) |^ max |/(ср) — /7 (<р)|= L, срй^<р<<рт,
*) См. § 27.
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 917
если только разность
/(?)-/*(?)
имеет на отрезке ]ср(), ут] не более п нулей.
Поясним геометрический смысл теоремы Геронимуса. Для этого
обратимся к рис. 772, где Д (<р) и Д* (<р) обозначают графики раз-
ности (14.1) и разности
Д* (ср)=/* (©) —F(<p).
Отметим, что
д (?) _ д* (ср) =/(ср) —/* (ср).
Отсюда следует, что каждому нулю разности /(<р)—f* (ср) должна
соответствовать общая точка (hi, h.2, ...) графиков Д (ср) и Д* (<р).
Отрезок приближения-
Рис. 772.
Пусть разность Д (ср) на отрезке [ср0, срт] достигает наибольшего
модуля L, последовательно изменяя свой знак в п —2 точках ait
а2......an+i, an+i с абсциссами
<• • • • <?п+1 <<?п+1 (<P1S=?O*
Эти абсциссы делят отрезок [ср0, срт] на такие w —1 интервалы:
(<?1, <Рз)> > (<РП+1. ?П+«)>
в каждом из которых разность Д (<р) непрерывно изменяется в пре-
делах
-£=СД(ср)^+£.
018 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
Если разность /(?)—/*(?) имеет на отрезке [?ft, ?т] не более
п нулей, то, по крайней мере, на одном из указанных п 1 интер-
валов графики Д (?) и Д*(?) не будут иметь общей точки. Вслед-
ствие непрерывности графиков Д (?) и Д* (?) это возможно только
в том случае, если хотя бы в одной точке упомянутого отрезка
график Д*(?) будет выходить из полосы, ограниченной прямыми
Д(ф) = ± L, т. е. если хотя бы в одной точке этого отрезка мо-
дуль разности Д*(?) будет:
i Д*(<р)!==|/*(ч>)-—/=•(?)!>£-
Это и утверждает теорема Геронимуса.
Укажем на некоторые следствия, вытекающие из теоремы Геро-
нимуса. Пусть имеется семейство непрерывных функций /((?), /2 (?),
/з(?), > характеризующееся тем, что любые две его функции
могут иметь не более яф2 общих точек на отрезке [?0, ?т].
Пусть, далее, в этом семействе можно отыскать такую функцию /(?),
для которой наибольший модуль усредненных отклонений от задан-
ной функции ty = F(?) на отрезке [?0, ?mj будет наименьшим из
возможных. Приближение этой функции указанного семейства к за-
данной функции /?(?) на отрезке [?0, ?т] называется наилучшим
приближением (среди тех приближений, которые можно получить при
помощи функций этого семейства).
На основании теоремы Геронимуса можно утверждать: чтобы
найти в упомянутом семействе такую функцию, которая определит
наилучшее приближение к заданной функции F (?) на отрезке
[?0, ?т], достаточно найти в этом семействе функцию /(?), для ко-
торой разность /(?) — F(?), изображаемая графиком Д(?), дости-
гает своего наибольшего модуля L, по крайней мере, в п 2 раз-
личных точках отрезка [?0, ?от], последовательно изменяя свой
знак.
На рис. 772 разность /(?) — /'(?) достигает своего наибольшего
модуля L в точках экстремумов at, а.2, ... , ап+1 графика Д (?) и
в точке ая+2 этого графика, лежащей на границе отрезка прибли-
жения. Напомним, что отклонения в точках экстремумов графика Д (?)
и отклонения на границах отрезка приближения называются предель-
ными отклонениями. Использовав понятие предельных отклонений,
следствию из теоремы Геронимуса можно дать иную формулировку:
чтобы найти в указанном выше семействе непрерывных функций
/1 (?), fi (?), • • • такую функцию, которая дает наилучшее приближение
к заданной функции /'(?) на отрезке [?0, ?от], достаточно найти в
этом семействе функцию /(?), для которой график отклонений
Д(?)=/(?) — F(?) имеет на отрезке [?п, ?,„], по крайней мере,
n-j-2 предельных отклонений, равных по модулю и чередующихся
по знаку; если при этом на отрезке |?(1, ?т] имеются другие пре-
дельные отклонения, то они должны быть по модулю меньше ранее
упомянутых.
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 919
На графике А (?) (рис. 772), кроме п-ф-2 предельных отклоне-
ний, чередующихся по знаку и равных по модулю L, имеется еще
предельное отклонение в точке а0 (при ?=?„), меньшее по модулю L.
2°. Достаточные условия наилучшего приближения в задаче
синтеза кулисного механизма. Функцию положений кулисного ме-
ханизма (с ведущей или ведомой кулисой) можно в обобщенном виде
записать так:
ф= /(?; а, с, а., р), (14.2)
где а, с, а и р — независимые параметры кинематической схемы этого
механизма.
Уравнение (14.2) определит семейство функций, зависящее от
указанных четырех параметров схемы механизма. В § 45 установлено,
что в общем случае четыре точки однозначно определяют кривую
этого семейства. Поэтому две кривые этого семейства не могут
иметь более п = 3 общих точек.
На основании теоремы Геронимуса можно утверждать: чтобы найти
в семействе (14.2) такую функцию, которая определит наилуч-
шее приближение к заданной функции на отрезке [?0, ?т], доста-
точно найти в указанном семействе функцию, для которой график
отклонений имеет на отрезке [?0, ?т], но крайней мере, п -ф- 2 = 5
предельных отклонений, равных по абсолютной величине и череду-
ющихся по знаку; если при этом на отрезке [?0, ?т] имеются дру-
гие предельные отклонения, то они должны быть по абсолютной
величине меньше ранее упомянутых.
Наметим практический путь нахождения этого наилучшего при-
ближения в задачах синтеза кулисного механизма.
Пусть интерполяционное приближение функции положений кулис-
ного механизма ф=/(?) к заданной функции <p = F(?) на отрезке
[?0, ?от], где <р0 <ф ?т определено тремя узловыми точками glt g% и
g3 (рис. 759): одной двукратной gt с абсциссой ?n<^?i<C?m и двумя
простыми g,2 и g3 с абсциссами ?2 = ?0 и ?3 = ?т. Если график
отклонений Д (?) не имеет нулевых точек, то он расположится на
отрезке [?0, ?,„] по одну сторону от оси абсцисс. Три предельных
отклонения в узловых точках g2 и g3 будут равны между собой
и равны нулю. С ними чередуются предельные отклонения Дф1 и Дф2
в точках экстремумов и й2, одинаковые по знаку, но в общем
случае не равные по величине.
Предположим, что нам так удалось подобрать абсциссу ?t дву-
кратной узловой точки gt, что предельные отклонения Дф>1 и Дф2
оказались равными:
Дф1 = Дф2
(как показано на рис. 759). Тогда, усреднив график отклонений
Д (?), получим график отклонений Д(, (?) с пятью предельными отклоне-
ниями, равными по абсолютной величине L и чередующимися по
920 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
знаку. По теореме Геронимуса этот график отклонений к (ср) будет
характеризовать наилучшее приближение функции положений кулис-
ного механизма к заданной функции на заданном отрезке [ср0. <рт].
Так как при интерполировании по указанным условиям отклоне-
ния Atpj и ДФ2 в общем случае оказываются не равными друг другу,
то основной операцией в процессе перехода от этого интерполяцион-
ного приближения к наилучшему будет уравнивание упомянутых пре-
дельных отклонений ДФ, и Дф2.
3°. Уравнивание предельных отклонений способом последова-
тельного приближения. Пусть на рис. 773 сплошная кривая — гра-
фик отклонений Д (ср) функции положений кулисного механизма от
заданной функции на отрезке |ср0, срт], где <р0 <^<рт*). Пусть, далее,
этот график получен в результате интерполирования, которое опре-
делено тремя узловыми точками: одной двукратной g, с абсцис-
сой <р0 ср, <рт и двумя простыми g2 и g3 с абсциссами ср2 = ср0
и ср3 = срт. График Д (<р) не имеет нулевых точек. Предельные откло-
нения Дф, и Д% в точках экстремумов /г, и /z2 не равны друг другу.
Исследуем, как будут изменяться эти отклонения с изменением
абсциссы ср, двукратной узловой точки g, при сохранении неизмен-
ными абсцисс <р2 и <р3 простых узловых точек g2 и g3. Условимся
при этом предполагать, что графики отклонений, получаемые при дру-
гих значениях абсциссы ср, двукратной узловой точки g„ подобно гра-
фику Д (<р) не будут иметь на отрезке [<рв, <рт] нулевых точек (гра-
фики отклонений с нулевой точкой рассматриваются ниже). Ограни-
чимся такой областью изменения абсциссы ср, двукратной узловой
точки g,, в которой получаемые при интерполировании кулисные ме-
*) Условимся в дальнейшем постоянно полагать ср0 с срт, не повторяя этого
каждый раз. При этом условии выбор абсцисс ср2 = <р0 и <р3 = срт означает, что
узловая точка g2 в осях ср — ДФ (рис. 759) располагается на левой границе от-
резка приближения [<р0, ет], а узловая точка g3 — на правой границе этого
отрезка.
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
921
§ 45]
ханизмы не имеют углов передачи, равных нулю или близких к нулю
на отрезке [?0, ?т]. При этом условии графики отклонений Д (ср) бу-
дут непрерывны на отрезке [<р0, ?т] и непрерывно деформирующи-
мися при изменении указанной абсциссы ?Р
Вернемся к графику Д (?) на рис. 773. Зададим абсциссе ?, дву-
кратной узловой точки gt положительное приращение Д?Р Новое
положение этой точки, определяемое абсциссой
обозначим gj”. Тогда график Д (?) преобразуется в график Д(1’(?)
(показанный на рис. 773 пунктиром) с новыми предельными откло-
нениями Д^1' и Д%” в соответствующих точках ft',1’ и h'/’.
В силу непрерывности деформации графика Д (?) при непрерыв-
ном изменении абсциссы ?„ мы всегда можем подобрать такое
приращение Д?,, при котором новый график д'1’ (?) покажет на
отрезке [?0, ?т] отклонения одинакового знака с отклонениями гра-
фика Д (?).
Графики Д (?) и Д'1’ (?) не могут иметь более трех общих точек
(см. § 44, 10°). Две общие точки этих графиков совпадают с их общими
узловыми точками g% и g3. Докажем, что третья точка указанных
графиков должна лежать в интервале [?ъ ?',“]. Для этого условимся
понимать под Д(?) и Д(1’(?)не только обозначения соответствующих
графиков отклонений, но и текущие значения отклонений, опреде-
ляемых этими графиками. Рассмотрим разность
Д(?)-Д‘1’ (?).
При ? — ?] (где Д (?() = 0) эта разность отрицательна, а при ф — ?,”
(где Д(1’(?i”) = 0) положительна. Так как графики Д(?) и Д(1’(?) на
отрезке приближения по условию непрерывны, то перемена знака ука-
занной разности на интервале [?ь ?'/'] свидетельствует о наличии на
этом интервале третьей общей точки d рассматриваемых графиков.
Поскольку графики Д(?) и Д(”(?) не могут иметь других общих
точек, кроме git g9 и d, неравенство
Д (?)<Д(1> (?),
справедливое при ? = ?(, должно сохраняться при всех значениях ?
в пределах ?0 ^ ? ?ь а неравенство
Д(?)>Д11’(?),
справедливое при ? = ?'1), должно сохраняться при всех значениях ?
в пределах ?/’s^?^?m. Это доказывает следующее свойство гра-
фика отклонений кулисного механизма, определяемого указанными
условиями интерполяционного приближения: при смещении узловой
точки gi по оси абсцисс график отклонений преобразуется так, что
отклонения, расположенные по этой оси в направлении упомянутого
922 СИНТЕЗ механизмов по методу наилучшего приближения [гл. XIV
смещения, уменьшаются по абсолютной величине, а отклонения, рас-
положенные по оси абсцисс в направлении, противоположном смеще-
нию, увеличиваются по абсолютной величине *).
Легко показать, что это свойство остается справедливым и в слу-
чае смещения простых узловых точек по оси абсцисс **).
На рис. 773 узловая точка gt смещена в положение g‘i’ в напра-
влении к точке экстремума А2, в которой предельное отклонение Дф2
больше по абсолютной величине отклонения Дф,. Поэтому на графике
отклонений Д(1) (<р) получены отклонения Дф/’^>Дф, и Дф2п<^Дф2.
Для отыскания того положения узловой точки gt, при котором
предельные отклонения в точках экстремумов уравняются, можно
воспользоваться способом последовательного приближения, основан-
ного на линейной интерполяции. Для этого восставим перпендикуляры
к оси абсцисс (рис. 774) в точках <р,
ляре отложим предельные отклонения
Рис. 774.
и ср'/’. На первом перпендику-
Дф, и Дф-2, которые определят
точки и Л2, а на вто-
ром — предельные отклоне-
ния Дф,п и Дф2”, которые
определят точки й,” и й2'.
Прямые hth‘i' и /г2/?2’ можно
считать за приближенные
графики изменения предель-
ных отклонений Дф| и Дф2
при изменении абсциссы дву-
кратной узловой точки gi
от cpt до ср1!*'. Абсцисса <р*
точки пересечения /г* ука-
занных прямых укажет по-
ложение узловой точки gu
при котором на соответст-
вующем графике отклонений модуль разности предельных отклоне-
ний в точках
отклонений на
по формуле
экстремумов будет меньше модулей разности тех же
графиках Д (ср) и Д(1)(<р). Эту абсциссу подсчитаем
_ (?* — У?) (Дфз —ДфО
Т' Т1 (Дф2 — Дф,) — (Дф^‘ — Дер',11) '
(14.3)
*) Подобное свойство графика отклонений установлено Е. П. Новодвор-
ским [40] для случая интерполяционного приближения с простыми узлами.
**) При наличии нулевой точки это свойство графика отклонений сохра-
няется только на одном из двух участков, на которые делит эта точка отре-
зок приближения, а именно на участке, где расположена сама смещаемая узло-
вая точка. На другом участке отклонения, расположенные по оси абсцисс
в направлении смещения узловой точки, наоборот, возрастают по абсолютной
величине (см. на рис. 768 участок между точками g и g3), а отклонения, рас-
положенные по оси абсцисс в направлении, противоположном смещению, умень-
шаются по абсолютной величине.
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 923
Ордината Дф* точки h будет равна:
ДФ* = Дф, - . (14.4)
Эта ордината определит приближенное значение предельных откло-
нений на графике отклонений, который получим, выбрав абсциссу ср*
узловой точки gt по формуле (14.3). Если на этом графике модуль
разности предельных отклонений окажется еще достаточно большим,
то, воспользовавшись еще раз формулой (14.3), подсчитаем новую
абсциссу <р*‘* двукратной узловой точки gt. Эта абсцисса определит
график отклонений с еще меньшим модулем разности между предель-
ными отклонениями в точках экстремумов. Пользуясь этим способом
последовательного уравнивания, можно найти график отклонений,
у которого предельные отклонения в точках экстремумов будут равны
между собой (в пределах принятой точности расчета). Усреднив этот
график отклонений, найдем наилучшее приближение функции положе-
ний кулисного механизма к заданной функции на указанном отрезке
1?о> ?т]-
4°. Примеры уравнивания предельных отклонений. Рассмотрим
задачу о приближении функции положений кулисного механизма
с ведущей кулисой к функции (13.87):
25° т ’
на отрезке от а = 0 до = -]— 50°. В этой задаче интерполяционное
приближение, определяемое одной двукратной узловой точкой и
двумя простыми узловыми точками g.2 и g3 с абсциссами
— -ф- 25J, — 0» ®3 — ~£>0 >
найдено нами ранее (см. § 44, 9°); параметры схемы соответствую-
щего кулисного механизма:
с=0,22169; а =0,92831;
а = —12°30'; р = — 115с00'.
Схема этого механизма изображена на рис. 763. В таблице 13.5
приведены отклонения, характеризующие найденное интерполяционное
приближение; • на рис. 764 и 775 (сплошная кривая) показан их гра-
фик Д (<р). Предельные отклонения в экстремальных точках и /г2
этого графика равны:
Дф1 = — 7'0; Дф2 = — 59',0.
Модуль разности | Дф2 — Д^ | = 52'. Для уравнивания этих откло-
нений сместим двукратную узловую точку gi на -ф 5° по оси абсцисс
в направлении к точке экстремума ft2 с большим по модулю экстре-
мальным отклонением Дф2. Новое положение g\u узловой точки gt
определим абсциссой 30°. (Абсциссы узловых точек и g3
924 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
сохраним неизменными: <р2 = 0 и ср3 — -ф- 50°.) Тогда получим меха-
низм со следующими параметрами схемы:
с(,) = 0,218 00 а<’> = 0,91374;
12°32',7; ₽(1) = — 119°10',5.
В таблице 14.1 (графа «вспомогательный механизм») приведены
отклонения этого механизма, а на рис. 775 жирным пунктиром изо-
бражен его график отклонений Д(1) (ср). Предельные отклонения в точ-
ках h'^ и Ла' равны:
Дф"^ — 25',8; Дф"’ = — 39',6.
Подсчитаем по формуле (14.3) абсциссу:
„*_25опп, (25W-30W)(-59' + 7') о s,
ср, — 20 00 - T-5g7^-_ 39Гб ^25-,8) — 31 48 •
Сохранив по-прежнему неизменными абсциссы <р2 и сра простых
узловых точек gt и g3, переместим двукратную узловую точку gY
в положение gf с абсциссой ср* = 31°48'. Тогда получим кулисный
механизм с такими параметрами схемы:
с* = 0,21628; о* = 0,90733;
а* = — 12°35',5; [5* = — 121°05',3.
В таблице 14.1 (графа «уравненный механизм») даны результаты
подсчета отклонения, а на рис. 775 тонким пунктиром нанесен их
график Д* (<р). Предельные отклонения в точках экстремумов Л, и
этого графика будут:
Д^ = —37',5 и Д<р.| = — 32',6.
45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
925
Таблица 14,1
Отклонения функции положений кулисного механизма
от функции (13.87)
<₽ Дф Точки на графиках Д,п (<р) и Д‘(<р) (рис. 775)
вспомогатель- ный механизм уравненный механизм
Vs = 0 0 0
- 10 00 —23’,8 —34’,4
г 12 00 —25,6 —37,0
г- 13 00 —25,8 —37,5 л;11, л*
Н 1400 —25,6 —37,4
Г 20 00 —16,7 —26,9
И зо оо 0 —00,9 g'i1'
h 31 48 —01,0 0 g*
- 40 00 —25,4 —18,3
И 44 30 —39.4 —32,3
И 45 00 —39,6 —32,5 h’2u
1-45 30 —39,4 —32,6 /г*
1-46 00 —38,7 —32,2
<ts =- Н 50 00 0 0 gt
Модуль разности | Дф*— Дф*| = 4',9. Таким образом, после первой
ступени уравнивания модуль разности между предельными отклоне-
ниями уменьшен более чем в 10 раз, а модуль наибольшего предель-
ного отклонения примерно на одну треть (с | Дф21 = 59' до | Дф* | =
= 37',5).
Усредним график Д* (<р), перейдя к новому значению параметра
схемы механизма*) р* = р*=—121°05',3——121°24'.
Тогда получим приближение, близкое к наилучшему, у которого пять
чередующихся по знаку предельных отклонений будут приближенно
равны по модулю. Наибольший модуль усредненных отклонений будет
I Д-i*I L*
L* = -у1- = 18',8. Относительная точность приближения — = 0,31 %.
I I Vm
Оценим, насколько может снизить модуль наибольшего усреднен-
ного отклонения вторая ступень уравнивания. Для этого, заменив
в формулах (14.3) и (14.4) <рь Дфь Дф.2 на <р*, Дф*, Дф*, подсчитаем
новую уточненную абсциссу <р** двукратной узловой точки и соответ-
ственную ординату Д<р **, на которой должны уравняться экстре-
мальные отклонения:
__ 0,0,0, _ (ЗГ48'-30°)(-32',6 + 37',5) _
ср, 31 (—З2’,6 + 37’,5) — (—З9’,6 + 25',8)
А ,« OQ,C (31’48’ —31°20’)(—З2’,6 + З9’,6) „ .
Д ф** = - 32 ,6 - А-- 31°48>~-ЗУ = ~ 34 Л
*) См, § 42, 1°.
926 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. xlv
Следовательно, после второй ступени уравнивания мы получим
I ДН/*1'** I
наибольший модуль усредненных отклонений /,**«»—«»17',2.
который отличается от модуля, найденного в результате первом
ступени уравнивания, на L*— L** Г,6.
5°. Уравнивание предельных отклонений при наличии нулевой
точки. При наличии на отрезке приближения [<р0, <рт] нулевой точки
знак отклонений на этом отрезке изменяется. Поэтому, прежде чем
обратиться к уравниванию предельных отклонений, следует прежде
всего попытаться получить их постоянными по знаку на отрезкг
приближения. Для этого в одних случаях целесообразно удалит!
эту нулевую точку из пределов отрезка приближения, а в других
случаях — совместить ее с простой узловой точкой. Рассмотрим
отдельно эти случаи.
Первый случай. Пусть на рис. 776 сплошной кривой изо-
бражен на отрезке приближения [<р0, <рт] график отклонений Д (о),
определяемый тремя узловыми точками gt, g.2 и g3 (из которых gt —
двукратная, a gt и g3 — простые), с абсциссами —
и <р3=<рт. В нулевой точке g, расположенной между узловыми точ-
ками gt и g2, отклонения изменяют знак.
Учитывая, что отклонения между узловыми точками gt и ga больше
по абсолютной величине, чем отклонения между узловыми точками gt
и git переместим узловую точку gt по направлению к узловой
точке g3 в положение Нулевая точка переместится при этом
в противоположном направлении. Предположим, что выбранное сме-
щение узловой точки gx таково, что на новом графике отклоне-
ний Д(,)(<р) (показанном на рис. 776 пунктиром) нулевая точка
оказалась вне отрезка приближения. В результате на всем отрезке
приближения [<р0, <pmj отклонения стали одного знака. Пусть пре-
§ 45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
927
дельные отклонения Дф']’ и Дф’г’ в точках экстремумов й‘|' и h'?
графика Л<])(<р) удовлетворяют неравенству
|ДфТ|<|Дф7|.
(14.5)
Это значит, что для уравнивания этих предельных отклонений тре-
буется дальнейшее смещение узловой точки g-']’ в положительном
направлении оси абсцисс, к точке g3. Нулевая точка продвинется
при этом еще дальше в отрицательном направлении оси абсцисс,
предельное отклонение Дф']’ возрастет по модулю, а предельное
отклонение Дфг’ снизится по модулю. Отыскание абсциссы <р* того
положения g* узловой точки git при котором уравняются предель-
ные отклонения в точках экстремумов, не будет отличаться от
изложенного в пунктах 3° и 4° настоящего параграфа.
Второй случай. На рис. 777 изображен еще раз график
отклонений Д (е>), определяемый тремя узловыми точками glt g2 и g9
(из которых gi — двукратная, a g2 и g3 — простые), с абсциссами
<Ря = фо и <Рз = ?т. ' Де ]?о. <?«] — отрезок приближе-
ния. На этом графике по-прежнему имеется нулевая точка g, распо-
ложенная между узловыми точками gt и g2, а отклонения между
узловыми точками gt и g3 больше по абсолютной величине, чем
отклонения между узловыми точками gi и g3. Сместим узловую
точку gi по направлению к узловой точке g3 в положение £']'.
Нулевая точка переместится при этом в противоположном направле-
нии. Предположим, что выбранное смещение узловой точки gt таково,
что на новом графике отклонений Д(1)(<р) нулевая точка совпадает
с узловой точкой g2. В результате на всем отрезке приближения
1?о> отклонения стали одного знака. Но в отличие от первого
случая предельные отклонения Дф']1 и Дф'г в точках экстремумов ft']’
928 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ |гл. \IV
и /г'г графика Д11,(<р) удовлетворяют не ранее указанному неравен,
ству (14.5), а неравенству
| ДфЧ’1>1 ДфТ
Для уравнивания этих предельных отклонений узловую точку g|-
следует смещать в направлении к узловой точке git но при эюм
нулевая точка переместится в противоположном направлении, войдс|
на отрезок приближения и отклонения на этом отрезке окажутся
опять переменными по знаку. Чтобы избежать последнего, вмеси-
со смещением узловой точки g')’ в направлении к узловой точке g,
следует одновременно смещать в противоположном направлении узло-
вую точку g2. Смещение последней следует выбирать таким, чтобы
с ней совпала нулевая точка и отклонения оставались постоянными
по знаку на отрезке приближения. Процесс уравнивания отклонении
в этом случае покажем непосредственно на примере.
6°. Пример на уравнивание предельных отклонений при нал»
чии нулевой точки. Пусть механизмом с ведущей кулисой требуется
воспроизвести на отрезке от <р —О до ср =-|-70° функцию (13.88)
, 1 2
Ф = '49 V-
Первое решение этой задачи дано в § 44, 9° (второй пример)
При этом решении двукратная узловая точка g} была выбрана по
середине отрезка приближения (<pj = —[—35°), а простые узловые
точки g2 и g3 на границах отрезка приближения (<р2 = 0 и <р3 = -]- 75е)
Соответствующий график отклонений Д (<р) показан сплошной кривой
на рис. 766. Он имеет нулевую точку g, расположенную междх
точками g] и g2.
Сохраним неизменными абсциссы простых узловых точек g2 и g3
(ср2 = 0 и <р3 = —70°), а двукратную узловую точку gx сместим
в такое положение, чтобы нулевая точка совпала с узловой точкой g2.
Для этого новую абсциссу tpj двукратной узловой точки gx опре-
делим по уравнению (13.99):
= y —<р2 = 49° —° = + 49°.
При указанных абсциссах узловых точек получим:
ср12 = —49°; ф12 = -49е;
?1з —Н~21с; ф1з = -]-51°;
6 —- 2; г2 0.
Полюс Р12 уходит в бесконечность. Подсчет по формулам § 48, 8°
дает следующие параметры механизма с ведущей кулисой:
« = 0,41489; о = 0,89723;
а = —24°30'; ₽ = — И 6° 15',5.
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
929
§ 45]
В таблице 14.2
функции положения
(графа «1-й механизм») приведены отклонения
найденного механизма от функции (13.88),
Таблица 14.2
Отклонения функции положения кулисного механизма от функции (13.88)
Углы поворота ведущего звена <р Дф Точки на графиках отклонений A(f), A*(f>) на рис. 778
1-механнзм вспомогатель- ный механизм уравненный механизм
Ср 9 0 0 — 01',9 — 00',6 gz, h'}>, h*
<[>?=- -01’58’ — 00',4 — 00,6 0 g?
?Т= - -05 00 — 02,1 0 — 00,6 g'V
- 10 00 — 07 ,5 — 04,1 — 03 ,7
И 20 00 — 18,4 — 07 ,0 — 12,5
1-23 00 — 19,8 — 07,7 — 13,6
|- 24 00 — 20 ,0 — 07,9 — 13,7
1-25 00 — 19 ,9 — 07 ,9 — 13,7
)- 26 00 — 19 ,7 — 07,7 — 13 ,6
1-30 00 — 17 ,7 — 06,6 — 12 ,0
1-40 00 — 06 ,2 — 01 ,0 — 03 ,2 gl
и- =- Р 44 00 — 02,1 0 — 00,6 gt
¥1 = - 47 02 — 00 ,4 — 00 ,6 0 gl
-49 00 0 — 01 ,8 — 00,4
и 50 00 — 00,1 — 02 ,7 — 00,7
60 00 — 09 ,3 — 16,6 — 12,3
- 63 00 — 12,2 — 19,3 — 15 ,3
)- 64 00 — 12,6 — 19,4 — 15 ,4 h'J>, h*
-65 00 — 12,6 — 18,7 — 15,2 h.
<f8 = - |-70 00 0 0 0 g«
а на рис. 778 сплошной кривой
точка совпала на этом графике
дельные отклонения Дф, и Дф2 в
чились соответственно
показан их график Д (<р). Нулевая
с простой узловой точкой g2. Пре-
точках экстремумов /г, и /г4 нолу-
Дф, = — 20'; Дф.2 = — 12',6.
Для их уравнивания узловую точку g} следует сместить в напра-
влении к узловой точке Но в этом случае нулевая точка, совпа-
дающая с узловой точкой g.b опять войдет на отрезок приближения
и отклонения изменяться по знаку. Поэтому необходимо одновременно
сместить в противоположном направлении простую узловую точку g.2,
притом настолько, чтобы с ней совпала нулевая точка.
Оставим простую узловую точку g3 на границе отрезка при-
ближения (<р3 = -ф-70°). Сместим двукратную узловую точку gA по
оси абсцисс на — 5°, определив новое ее положение £']’ абс-
циссой <р’|‘ = -|—44°. Простую узловую точку g., также сместим, но
в противоположном направлении. Чтобы нулевая точка совпала
30 И. И. Арюболевский
930 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIX
с новым положением g1*' этой узловой точки, определим ее абсциссу ср
по формуле (13.99):
- ср"’ = 49° - 44° = + 5°
При выборе абсцисс узловых точек
<?Т = + 44;; ?’*' = +5° и cp3=-j-70o
решение задачи синтеза дает следующие параметры схемы кулис-
ного механизма:
с = 0,42009; а = 0,91850;
а = —24°30'; ₽ = —113°18',3.
В таблице 14.2 (графа «вспомогательный механизм») приведены
отклонения функции положения этого механизма от заданной функ-
ции (13.88) на отрезке 0 у -j- 70°, а на рис. 778 тонким пунк-
тиром изображен их график Д(|,(ср). Нулевая точка совпала с узло-
вой точкой g'z, и отклонения на указанном отрезке остались посто-
янными по знаку. Вследствие сближения узловых точек g\l> и g1' ’
расположенное между ними предельное отклонение уменьшилось,
а предельное отклонение между точками g\" и g3 увеличилось по мо-
дулю. Обозначим новые предельные отклонения в точках экстре-
мумов /г'{’ и /г" через Дф"’ и Дф*'. Они будут:
Дф;* = —7',9; Дф"’ = — 19',4.
Для отыскания абсцисс ср* и ср* тех положений g* и g* узловых
точек g( и g2, при которых экстремальные отклонения должны урав-
§ 45]
СИНТЕЗ К5'ЛИСН0Г0 МЕХАНИЗМА
931
няться, воспользуемся линейной интерполяцией. Для этого сначала
по формуле, аналогичной формуле (14.3), подсчитаем соответст-
вующую абсциссу узловой точки g*:
• (fi— — Дф1)
•1 — г1 (Д фв — Д 11) — (А 4'4 — д Ф)1’)
_4оо_ (49? - 44с)(— 12',6 + 20')
~ (— 12',64-20')—(—19',4Ц-7’,9)
На основании условия (13.99) соответственная абсцисса узловой
точки g*„ будет »* = -]- 1°58'. Выберем новые абсциссы узловых
точек:
в* =-|-47°02'; = 1°58'; <р3 = —[-70°.
При этих условиях решение задачи синтеза дает следующие
параметры схемы кулисного механизма:
с= 0,41721;
а = — 24°30';
а = 0,90689;
р = — 114°54',9.
В таблице 14.2 (в графе «уравненный механизм») приведен под-
счет отклонений, а па рис. 778 жирным пунктиром изображен их
график Д* (<р). Предельное отклонение Д ф* на границе отрезка при-
ближения (в точке /г*) и предельные отклонения Д <]>* и Д ф* в точках
экстремумов /г* и h* равны соответственно:
Д4* = — О',4; Дф; = — 13',8; Дф‘ = — 15',5.
Усредним этот график, перейдя к новому значению параметра
схемы механизма р*=р*-]~ -=? = — 114°54',9— -=—115°02',6.
Получим приближение, близкое к наилучшему на отрезке 0«^<р^ 70°.
Его пять предельных отклонений, чередующихся по знаку, будут
приближенно равны по модулю. Шестое предельное отклонение на
границе отрезка приближения (при —0) будет меньше по модулю
остальных пяти. Абсолютную точность этого приближения опреде-
IД Ф* I
лит величина L — —— 7$, а относительную точность — вели-
чина -/'-= 0,13°/п. Следовательно, переход к наилучшему прибли-
т L
жению уменьшил величины L и — почти вдвое по сравнению с пер-
Чт
вым интерполяционным приближением (см. второй пример в § 44, 9°).
Продолжив этот сходящийся процесс, можно полностью урав-
нять (в пределах точности расчета) отклонения в точках экстремумов
30*
932 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
и после усреднения установить наилучшее приближение функции
положения кулисного механизма к заданной функции на указанном
отрезке.
График Д* (ср) (рис. 779) с уравненными предельными отклоне-
ниями Д <р* — Д <р* в точках экстремумов, получаемый в результате
указанного преобразования графика отклонений Д (ср) с нулевой
точкой g, не всегда после усреднения определит наилучшее при-
ближение на заданном отрезке [ср0, срт]. Пусть на графике Д* (<р)
с уравненными предельными отклонениями Дф* = Дф* последние
будут больше по абсолютной величине дополнительного предель-
ного отклонения Дф* на границе отрезка приближения (при ср = <р0),
как показано на рис. 779. В этом случае график отклонений, кото-
рый получим в результате усреднения графика Д* (ср), будет удов-
летворять достаточным условиям наилучшего приближения
(см, § 45, 2е): он будет иметь на заданном отрезке приближения
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 933
пять предельных отклонений, равных по абсолютной величине и че-
редующихся по знаку (в точках, в которые переместятся после
усреднения графика Д* (?) точки g*, h’, g*, h* и g-3). Шестое пре-
дельное отклонение (в точке, в которую переместится точка /?’)
будет меньше упомянутых.
Возможен однако другой случай, когда на графике отклонений
Д* (?) (рис. 780) дополнительное предельное отклонение Д 6* на
границе отрезка приближения (при ? = ?0) будет больше по абсо-
лютной величине уравненных предельных отклонений Дф* = Дф*
в точках экстремумов. В этом случае график отклонений, который
получим после усреднения графика Д* (?), не будет удовлетворять
достаточным условиям наилучшего приближения: он будет иметь
на отрезке приближения всего четыре предельных отклонения,
равных по абсолютной величине (в точках, в которые пере-
местятся точки Л‘, g-* и g3). Два других предельных отклоне-
ния (в точках, в которые переместятся точки h* и /г*) будут меньше
упомянутых.
В этом случае, чтобы найти такой график с уравненными пре-
дельными отклонениями, который после усреднения определит наи-
лучшее приближение на заданном отрезке, следует повторить про-
цесс уравнивания графика отклонений Д (?) первого приближения,
внеся в этот процесс следующее изменение: за узловую точку, по-
ложение которой сохраняется неизменным, нужно выбрать точку git
расположенную на левой границе отрезка приближения (вместо
точки g3, расположенной на правой границе4 отрезка приближения),
и смещать одновременно узловые точки gt и g3.
Указанный измененный процесс уравнивания экстремальных от-
клонений практически не будет отличаться от указанного в послед-
нем примере, если предварительно обозначение узловой точки, рас-
положенной на левой границе отрезка приближения, изменить с g2
на g3, а обозначение узловой точки, расположенной на правой гра-
нице отрезка приближения, изменить с g3 на
7°. Влияние нулевых точек на точность приближения и на
угол передачи механизма. Пусть требуется кулисным механизмом
воспроизвести заданную функцию
w — Ф (г)
на отрезке [г0, zm}. Пусть заданы такие входной и выходной углы
fm 11 Фт. что график отклонений первого интерполяционного при-
ближения имеет нулевую точку на отрезке приближения. Если те-
перь при постоянном угле входа ?от (или угле выхода ф,„) изменять
угол выхода (или соответственно угол входа ?т), то нуле-
вая точка будет перемещаться по оси абсцисс. С перемещением
нулевой точки по отрезку приближения должна изменяться
точность приближения. К сожалению, в общем виде исследовать
этот вопрос пока не представляется возможным, Поэтому для
934 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
установления соответствующих закономерностей обратимся к
числовым примерам.
Пусть задана функция
w — z2, (14.6)
которая должна быть воспроизведена механизмом с ведущей кулисой
на отрезке от z = 0 до z = -|-l. Пусть далее задан угол выхода
фт=+ юо°,
а для угла входа заданы значения: ют = 30°; -j- 50°; 4" 70°;
4-90°; -|-110о, 4-130°; +150° и 4-170°.
В этом случае формулы (13.26) имеют вид:
1 1 ,
T77Z .т
Исключив при помощи этих формул из уравнения (14.6) перемен-
ные z и w, найдем функцию
ф = А<р2, (14.7)
к которой должна быть приближена на отрезке 0 «с =£7 <рт функ-
ция положения кулисного механизма. Здесь постоянная k = Если
координаты <р и 4 отсчитывать в градусах, то для k получим следу-
ющие значения в функции от угла входа ©т:
®т = 4-ЗО°; 4-50°; 4- 70°; 4-90°; 4- 110°; -j- 130°; 4- 150°; 4 170°;
k — 4---; + l- ; 4- ' • 4- -1- • 4-—— • 4_____— ’4___— • -I____--
' 9°’ ' 25°’ “ 49 I 81е’ 12Г ’ 1 169°’ 1 225 ’ 289G’
В таблице 14.3 приведены параметры схемы девяти механизмов,
полученные по условиям интерполяционного приближения, которое
задано тремя узловыми точками gx, git и git из которых точка gx —
двукратная, а точки g<> и gA — простые. Координаты этих точек выб-
раны в соответствии с рекомендациями § 44, 6°:
?i = 0,5cpm; ?2 = 0; % —
В таблице 14.4 приведены отклонения функции положения этих
механизмов от функции (14.7) на отрезке 0 т. Рассмот-
рим последовательные столбцы таблицы 14.4. При <рт = [' 30° откло-
нения на отрезке приближения не изменяют знака. Эго означает, что
на отрезке приближения нулевой точки нет. При <рт=4_60° откло-
нения на отрезке приближения также постоянны по знаку. Заметим
§ 45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
935
936 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
однако, что при tpm =50° величина Л = 2^6,а абсциссы узловых то-
чек соответственно <р1 = —25° и —0. Поэтому удовлетворяется
уравнение (13.99): ip, -f-<p2= Следовательно, при pm = -f-50'
нулевая точка совпадает с простой узловой точкой g.> (у._> = 0).
При <рт = -|-70'‘ нулевая точка переместилась внутрь отрезка
приближения, о чем свидетельствует перемена знака отклонений на уча-
стке 0,3pm гС р йС 0,4<рт*). При увеличении угла входа до рст=:-[-90о
абсцисса р нулевой точки оказывается в интервале 0,7рт<^р <^0,8рт.
При рт = —J— 110° нулевая точка переместилась за границу отрезка
приближения, в область р^> рт, но на упомянутом отрезке появилась
вторая нулевая точка, расположенная в интервале 0,2pm <^p<^0,3pm,
вступившая на этот отрезок из области р<^0. При увеличе-
нии угла входа до рт = -{- 130° абсцисса второй узловой точки
оказывается в интервале 0,6pm <^р<^ 0,7рт. При pm =-f- 150° вторая
нулевая точка совпала с простой узловой точкой gv, абсцисса кото-
рой р3 = <рт. Чтобы доказать это, напомним, что при срт = —150°
величина Л = -J-2^5-, а абсциссы узловых точек р, = 0,5рт = -ф- 75°
и р3 = рт — 150°. Следовательно, в этом случае р14-рз = -^-.
При pm =нулевые точки на отрезке приближения отсут-
ствуют. Подсчеты показали, что при pm}>—f—175° непрерывность
отклонений на отрезке приближения нарушается, т. е. соответствую-
щие механизмы на этом отрезке получаются непроворачивающимися.
Таблица 14.4 свидетельствует, что при непрерывном изменении
угла входа рт (при постоянном угле выхода фт) нулевая точка
непрерывно перемещается вдоль оси абсцисс. Это дает возможность
удалять нулевую точку от границ отрезка приближения или, наобо-
рот, вводить эту точку внутрь упомянутого отрезка. Таблица 14.4
показывает далее, что нулевая точка, перемещаясь по отрезку при-
ближения, резко изменяет картину распределения отклонений на этом
отрезке, уменьшая по абсолютной величине отклонения впереди
себя. Одновременно изменяются наибольший модуль L усредненных
отклонений, его относительная величина ~ и минимальный угол пе-
редачи механизма на отрезке приближения. В таблице 14.5 при-
ведены эти величины в функции от угла входа <рт (при постоянном
угле выхода фт — -J-100°). На рис. 781 по даннным таблицы 14.5
построены графики величин L и рт;п в функции от угла у,„.
Анализ таблиц 14.4 и 14.5 и рис. 781 приводит к следующему
выводу: вводя нулевые точки на отрезок приближения, можно на
этом отрезке существенно понизить наибольший модуль L усредненных
*) Подсчет параметров схемы механизма для = -|- 50° и <fm = 70° при-
веден в § 44,9°.
^7niax ^^niin
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 937
Таблица 14.5
Наибольший модуль /. усредненных отклонений IL —
где A'L.. и Д*1> взяты из таблицы 14.4), его относительная величина , —
• max пип " th
Г /7?
и минимальный угол передачи pmin механизма на отрезке приближения
4-зо° +50" 4-70° 4-90° + 110” + 130’ 4-150° + 170°
49’,0 29',3 16’,7 6’,4 6',7 20’, 1 46’,1 1С5Г,2
S 0,8'2"/,, 0,49". о 0,28" „ 0,Н "о 0,11 "'о О,34°/о 0,77ч 1,87»’О
^min 49 52° 57° 60° 53° 38° 24= 6=
Примечание. После L и у- в таблице 14.5 стоит знак приближенного
равенства потому, что эти величины подсчитаны по данным таблицы 14.4, где
отклонения указаны для равноотстоящих значений аргумента.
отклонений, характеризующий точность интерполяционного приближения,
и одновременно повысить минимальный угол передачи p.min механизма.
Поясним кратко причины указанного явления. При интерполировании
одним из наиболее часто используемых средств повышения точности
приближения является увеличение числа узлов интерполяции на от-
резке приближения. Появление нулевой точки на отрезке приближения
938 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
эквивалентно прибавлению одного узла интерполяции. Поэтому
снижение модуля L с появлением нулевой точки на отрезке прибли-
жения является закономерным. Менее очевидным является влияние
нулевых точек на минимальный угол передачи [j.inin на отрезке при-
ближения, но и оно легко поддается объяснению. Дело в том, что
по мере удаления нулевых точек от границ отрезка приближения
отклонения на этом отрезке возрастают по абсолютной величине.
В рассмотренной задаче, как показали подсчеты, уже при <рт = -|- 175°
отклонения становятся настолько большими по модулю, что непрерыв-
ность их нарушается. Последнее практически означает, что при
<рт = -|- 175° в некоторой точке отрезка приближения угол передачи
становится равным 0° или 180° и механизм перестает проворачи-
ваться. И в общем случае, если с изменением угла <рт или
угла отклонения на отрезке приближения непрерывно воз-
растают по модулю, то в известный момент должен наступить раз-
рыв функции отклонений на этом отрезке. Эго будет свидетельство-
вать, что угол передачи механизма в некоторой точке отрезка
приближения становится равным 0° или 180°. Так как с появлением
нулевых точек на отрезке приближения отклонения уменьшаются по
модулю, то опасность разрыва функции отклонений на этом отрезке
уменьшается. Практически это должно выражаться в том, что углы
передачи на указанном отрезке должны удаляться от значений 0°
или 180°.
При <рт = Ц-150° и <р,п = -|-100с нулевая точка располагается на
границе отрезке приближения в точке ср = —150° (см. табл. 14.4).
При постоянном угле выхода фт = -|-100о для перемещения нулевой
точки на отрезок приближения с целью снижения отклонений тре-
буется уменьшать угол входа <рт. Можно, однако, возвратить нуле-
вую точку на отрезок приближения, сохранив угол входа постоян-
ным, а изменяя угол выхода <рт.
В таблице 14.6 приведены результаты интерполяционного прибли-
жения функции положения механизма с ведущей кулисой к функции
(14.7). В отличие от предыдущего случая, здесь угол входа был выбран
постоянным: а?т = —150°, а угол выхода выбирался последовательно:
фт==_|_100°; 4-120°; +140°; +160°; +180° и +200°.
Интерполяционное приближение определялось тремя узловыми
точками той же кратности и с теми же абсциссами, как при под-
счете таблиц 14.3, 14.4 и 14.5.
Таблица 14.6 свидетельствует, что с возрастанием угла <рт (при
постоянном угле входа <рт) нулевые точки непрерывно перемещаются
вдоль отрезка приближения, но в направлении, обратном тому, какое
наблюдалось в случае возрастания угла входа (при постоянном
угле выхода-(рт). При изменении угла выхода от фт=+100° до
фт=—[—160° одна нулевая точка проходит через весь отрезок при-
ближения и появляется на этом отрезке вторая нулевая точка. При
§ 45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
УЗ 9
Таблица 14.6
Отклонения функции положения кулисного механизма (с ведущей кулисой)
от функции (14.7). Угол выхода переменный, угол входа постоянный:
= Рамки, обведенные жирными линиями, указывают положения
нулевых точек
Угол поворота ведущего звена z) Отклонения Дф
d =-j-l()0c m 1 ф = + 120° ф = 4 1 Ym ‘ ф = 4-18)° Yzn 1 4m = +2oo-
0 0 0 0 0 0 0
0,1 rm —Г32’,2 —50',4 —17',3 +08', 1 +28',4 +4Г.З
0,2ут —1 01 ,7 —31 ,0 —03,7 +17 ,6 +33 ,3 +40 ,0
0,3<fm —0 26 ,7 — 10,7 +03 ,3 + 13 ,7 +19 ,5 + 18 ,5
0,4<fm —0 05 ,7 —01 ,5 +02,0 +04 ,4 +04 ,8 +02 ,6
<f i = 0,5<fm 0 0 0 0 0 0
0,6?„, —0 03,0 -|-00,6 +02,9 +02 ,7 +00 ,3 —06 ,3
0,7tfm —0 06 ,9 +04 ,2 +09,6 +01 ,8 —11 ,0 —43 ,9
0,8?m —0 06 ,9 +09 ,3 + 13,1 —04 ,7 —47 ,2 —205',6
0,9?m —0 03 ,0 +09 ,9 +07,1 —23 ,6 —Г 30',4 —3°32',6
'fa = rm 1 o 1 0 0 0 0 0
дальнейшем возрастании угла вторая нулевая точка продвигается
вдоль отрезка приближения. При угле <]>т = 4'200° эта точка нахо-
дится примерно посредине отрезка приближения. Таблица 14.7
Таблица 14.7
Наибольший модуль усредненных отклонений L, его относительная величина ,—
Vm
и минимальный угол передачи pmin на отрезке приближения
Ф Ym = 4-loo 4-120° J-140е 4-160” 4-180” 4-200°
/.Я a46',l 30’,2 15',2 20’,6 1 01',8 2°07',0
L 4m ' «0,77% 0,42% 0,18" „ 0,22% 0,56% 1,06%
Hmin = 24° 32” 42’ 42° 33е 24°
Примечание. После L и -,— стоит знак приближенного равенства
У/П
потому, что эти величины подсчитаны по данным таблицы 14.6, где отклонения
указаны для равноотстоящих значений аргумента.
940 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
содержит величины L, — и Анализ таблиц 14.6 и 14.7 при-
водит к тем же выводам, какие получены при анализе таб-
лиц 14.4 и 14.5: вводя нулевые точки на отрезок приближения, можно
существенно снизить наибольший модуль L усредненных отклоне-
„ L
ний и его относительную величину 4, одновременно повысив на том
же отрезке минимальный угол передачи p.niill механизма.
8°. О выборе углов входа и выхода. На основании результатов,
полученных в предыдущем пункте, можно дать следующую практи-
ческую рекомендацию,- если в задаче синтеза механизма для воспро-
изведения предписанной функции на заданном отрезке не заданы
либо угол входа <рт, либо угол выхода фт, либо оба эти угла, то
целесообразно их выбирать в той области, где на отрезке приближе-
ния имеются нулевые точки, если, понятно, эта область существует.
Существование этой области зависит от характера воспроизводимой
функции и заданного отрезка, на котором она должна быть воспро-
изведена. К сожалению, пока не представляется возможным устано-
вить условия существования упомянутой области. Можно лишь реко-
мендовать следующий способ для непосредственного отыскания ее
границ. Выберем постоянный выходной угол <рт (или входной угол <рт)
и два значения входного угла <рт (или соответственно выходного
угла <рт), отстоящих друг от друга на 20°-е-30о. Найдем параметры
схем двух кулисных механизмов по условиям первого интерполяцион-
ного приближения, т. е. выбрав абсциссы и кратность узлов интер-
поляции согласно рекомендаций § 44, 6°. В двух точках отрезка
приближения, одинаково расположенных относительно его концов,
например в точках 0,1 <?т и 0,9<рт, подсчитаем отклонения. Пусть
все четыре подсчитанные отклонения одного знака. Отметим наи-
меньшее по модулю отклонение и установим то направление в изме-
нении угла tpm (или угла фт), при котором это отклонение должно
далее уменьшаться по модулю. Затем будем последовательно изменять
угол (или угол <рт) в упомянутом направлении до тех пор, пока
отклонение не изменит знак. Это будет означать, что нулевая точка
прошла через границу упомянутой области.
Если отклонение во второй исследуемой точке отрезка приближе-
ния одновременно также уменьшается по модулю, то следует далее
изменять угол <от (или угол tpm) в том же направлении для обнару-
жения второй границы искомой области. Если при уменьшении по
модулю отклонения в первой точке, отклонение во второй точке воз-
растает по модулю, то для установления второй границы искомой
области угол <рт (или угол <рт) следует изменять в противоположном
направлении.
Рассмотрим пример. Предположим, что механизмом с ведущей
кулисой требуется воспроизвести функцию (14.6) на отрезке
Выберем постоянный угол выхода фт = -}-100о и
§ 45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
941
два значения угла входа = —|- 170° и <рт = -1-150°. Решив
задачу синтеза этого механизма по условиям первого интерполяцион-
ного приближения, получим в точках 0,1 <?т и 0,9^т следующие
отклонения и Дф2 (см. табл. 14.4):
при <?т = -|-170о Дф1 = —3°44',3 и Дф2 = —21',2
при <рт = 4-150° Дф, = —1°32',2 и Дф2 = —3',0.
Все отклонения одного знака. Наименьшим по модулю отклоне-
нием является отклонение Дф2 = -—3',0. Для уменьшения его по
модулю угол входа <рт следует уменьшать. В тех же точках найдем,
что (см. далее табл. 14.4):
при 130° Дф1 = — 35',2 и Дф2 = 4“ 5',0.
при ym = 4_iio° Дфт = —8',5 и Дтр2 = _Ь 3',0.
Перемена знака отклонений Дф2 в точке 0,9 и одновременное
уменьшение по модулю отклонений Д(р! в точке 0,1 <fm свидетельствуют,
что нулевая точка движется по оси абсцисс от точки 0,9 <рт к точке
0,1 <рт и входит на отрезок приближения при угле <pm 2> 4~ 130°.
Уменьшая далее угол фш, получим в точках 0,1 и 0,9 <рт:
при <рт = 4- 90° Дф! = - j- 2',9 и Дф2 = — 8',2
при <^т=-(-70° Дф1 = 4_4',5 и Дф2 =— 28'8.
Перемена знака отклонений Дф( в точке 0,1 означает, что
нулевая точка, двигаясь в указанном направлении, прошла через
точку 0,1 <рт при 4 11С >7т> 4~ 90'- Одновременная перемена знака
отклонений Дф2 в точке 0,9 свидетельствует, что на отрезок
приближения вошла вторая нулевая точка, движущаяся в том же
направлении. Продолжим далее уменьшать угол <рт. Тогда найдем, что
при ф/п = 4_50° Дф1 = — 02',7 и Дф2 = —58',6.
при <рт = 4-30° Дф!= —2О',9 и Дф2 = —1°38'.
Вторая перемена знака отклонений Дф»! показывает, что
вторая нулевая точка проходит через точку 0,1 при
4- 70°4> Фт >>4“ 50°. При угле а>т = 4-ЗО° оба отклонения
Д<р! и Д ф2 резко возросли по модулю, что указывает на удаление
нулевой точки от границ отрезка приближения. Следовательно,
в рассмотренной задаче при постоянном угле фт= -(-100° нулевая
точка будет находиться на отрезке приближения при углах входа
<рт, лежащих в пределах -4 130° 2> Напомним, что
более точное исследование, проведенное в пункте 7° настоящего
параграфа, дало следующее неравенство: 150°^ 4~ 50°.
Если в задаче синтеза задан угол входа <рт, то указанным
путем можно установить пределы для угла выхода фт, в которых
следует искать кулисный механизм с наибольшим углом передачи
на отрезке приближения и наименьшим модулем усредненных откло-
нений интерполяционного приближения.
942 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ.Х1У
Если для последовательных значений угла <рт установить
соответствующие пределы угла <рт, то получим область значений <?т
и фт> в которой следует искать механизм, удовлетворяющий упомя-
нутым условиям.
9°. Наилучшее приближение по пяти и шести параметрам.
Если на отрезке приближения имеется нулевая точка, то с измене-
нием угла входа <рт или угла выхода эта точка перемещается
по оси абсцисс. В результате существенно изменяются отклонения
в отдельных точках отрезка приближения (см. пункт 7° настоящего
параграфа). Одновременно должны изменяться предельные отклонения,
которые получим посредством уравнивания предельных отклонений
первого интерполяционного приближения.
Чтобы выяснить характер изменения графиков уравненных откло-
нений с изменением угла <рт, эти графики были подсчитаны для
шести случаев интерполяционного приближения, исследованных выше
(см. табл. 14.3 и 14.4), а именно для углов входа:
<?т = Ц-50°; 4-70°; 4-90°; 4-110°; 4-130° и 4-150°,
при постоянном угле выхода фт = 100°. Во всех этих случаях
на отрезке приближения имелась нулевая точка.
Параметры схемы механизмов, полученные после уравнивания
предельных отклонений, приведены в таблице 14.3. Графики уравнен-
ных отклонений изображены на рис. 782 (для ът~-\-Ъ0Р, -|~70° и
4-90°) и на рис. 783 (для от = 4-110°, -j- 130° и 150е). На этих
графиках верхние предельные отклонения в трех узловых точках,
равные нулю, чередуются с равными нижними предельными отклоне-
ниями в точках экстремумов. Абсциссы узловых точек, определяющих
эти графики, и абсциссы точек предельных отклонений на этих
графиках указаны в таблице 14.8. Там же для сравнения указаны
Таблица 14.8
Абсциссы <plt и уз узловых точек, определяющие графики уравненных
отклонений на рис. 782 и 783, и абсциссы у, и у2 точек экстремумов (не
лежащих на оси абсцисс) упомянутых графиков. В скобках*1тоят абсциссы
тех же точек по построению Чебышева (§ 44, (?)
’т=+50’ <₽то=+?0° ф =4-ЦТ гт ‘ 9 =4-110° гт ‘ 9 =4-130° Тт 1 ?т=+|50°
91= 4-3!с20* (25°) +47°15'(35°) +65°15'(45 ) +30° 10455°) + 41 "(65°) 4-62° (75°)
93= 0(0| -t-le95'(0) + 15°45'(0> 4-90*454110°) 4 128°(130°) 0(0)
Фа== +50°(50”) +7О°(7О’) - 90е» 90°) 0(0) 0(0| +1504150°)
"’Г + 14°(7°2ОЧ 24410°) +41 <13=1 +8416°) + 10419°) 4->2°<22’i
+45°(42'40', +64с(60°) +81 (77°) 4-fiO (.94е) +854111°) + 1074128°)
944 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НЛИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
абсциссы тех же точек, получаемые по построению Чебышева
(см. § 44,6е). Предельные отклонения на графиках рис. 782 и 783
сведены в таблицу 14.9, в которой одновременно дана величина
Таблица 14.9
Предельные отклонения Д% или ДДт на границе отрезка приближения
(в точках Л„2’ или и предельные отклонения Д'^ и ДД8 в точках
экстремумов (в точках hi, Л’,11, ftj8' и й2, Л!,1’, h's-') графиков рис. 782 и 783;
наибольший модуль усредненных отклонений ZH и его относительная
Z.H
величина ,—, характеризующие точность наилучшего приближения
2m
4-50° 4 70° +90° 4-110° 4-130* 150°
д% или 0 — О',3 —5'.2 —5',4 — о,1 0
Д'!/! —33',8 -14’,8 —5’,4 —5’,9 — 17',2 —44’,7
Дф3 —34',5 —15',0 —5’.6 —5’,6 —17’,2 —45’,2
£н 17',2 7\5 2',8 З'.О 8',6 22',6
£н 'Pm 0,29% 0,13% 0,05% 0.05% 0,14% 0,38%
наибольшего модуля LH усредненных отклонений и его относитель-
пая величина -у—. Так как речь идет об усреднении уравненных
2 m
отклонений, то модуль £н характеризует точность наилучшего при-
ближения при выбранных углах <рт и <рт. Проанализируем получен-
ные результаты.
При <рт = —50° график уравненных отклонений (рис. 782)
не имеет иных предельных отклонений, отличных от нуля, кроме
отклонений в точках экстремумов ht и Л2.
При <рт = -ф-70° на графике уравненных отклонений появилось
дополнительное предельное отклонение в точке на границе от-
резка приближения. Оно возникло в процессе уравнивания из-за
смещения узловой точки g2 в положительном направлении оси
абсцисс (см. пункты 5° и 6° настоящего параграфа). Предельные
отклонения в точках экстремумов Л'Ч и резко уменьшились
по абсолютной величине по сравнению со случаем 50° *).
*) Для случаев 50° и срт = -р 70° одна ступень уравнивания откло-
нений выполнена в пунктах 4 и 6е настоящего параграфа. На рис. 782 приве-
дены графики отклонений, полученные после второй ступени уравнивания.
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 945
При <р,„ — 90° дополнительное предельное отклонение в точке h®
возросло по абсолютной величине вследствие дальнейшего смещения
узловой точки gi в положительном направлении оси абсцисс. Пре-
дельные отклонения в точках экстремумов /г*21 и /г*2) далее резко
уменьшились по абсолютной величине *)
При <рт = -|- 110° и <рт = 130° уравнивание графиков первого
интерполяционного приближения способом, изложенным в пункте 5°
и 6° настоящего параграфа, приводит к графику уравненных откло-
нений типа графика Д*(ю) на рис. 780 с дополнительным предель-
ным отклонением Дф*, большим по модулю уравненных предельных от-
клонений Дф] = Дф]. После усреднения такого графика он не определит
наилучшего приближения, так как не будет удовлетворять теореме
Геронимуса. При <рт = 4-110° и <рт = -ф-130о графики уравненных
отклонений, изображенные на рис. 783, получены в результате
одновременного смещения двукратной узловой точки и простой узло-
вой точки, расположенной на правой границе отрезка приближения.
Чтобы в процессе этого уравнивания можно было непосредственно
использовать условие (13.99), простая узловая точка, расположенная на
правой границе отрезка приближения (<р = <рт) и смещаемая в процессе
уравнивания, была обозначена^, а простая узловая точка, расположенная
на левой границе отрезка приближения (<р = <р0) и сохранявшая неизмен-
ное положение в процессе уравнивания,—обозначена g3. Дополни-
тельное предельное отклонение на этих графиках (точки к'т
и h'm) получилось на правой границе отрезка приближения (при
? = ¥т)-
При тт = "|- 1Ю° дополнительное предельное отклонение
(в точке h'm, см. рис. 783) практически совпало по величине с урав-
ненными предельными отклонениями в точках экстремумов h\-' и И'/'.
При переходе к фт = -[- 130° дополнительное предельное отклонение
(в точке h'm) резко снизилось по абсолютной величине по сравнению
с дополнительным предельным отклонением при <рт = -|- 110°, а от-
клонения в точках экстремумов h\l> и h'^', наоборот, резко возросли
по абсолютной величине.
При <рт = —|— 150° дополнительное предельное отклонение отсут-
ствует. Предельные отклонения в точках экстремумов и /?2 далее
резко возросли по абсолютной величине.
Таким образом, графики рис. 782 и 783 наглядно показывают,
что при появлении и возрастании по абсолютной величине дополни-
тельного предельного отклонения соответствующие уравненные пре-
дельные отклонения в точках экстремумов снижаются по абсолютной
*) На рис. 782 и 783 графики отклонений пересекаются более чем в трех
точках. Это связано с тем, что на указанных рисунках длина отрезка прибли-
жения для графиков с различными по величине углами <fm вы-
брана одинаковой и, следовательно, графики изображены в различных масшта-
бах по реи абсцисс.
946 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НЛИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
величине, а модуль LH, характеризующий точность приближения после
уравнивания, стремится к минимуму.
На рис. 781 по данным таблицы 14.9 нанесен (пунктиром) график
модуля £н в функции от утла входа <рт. Он показывает минимум £н
при угле входа ©m««-j-100°. Следовательно, график наилучшего
Рис. 784.
приближения, который мы найдем при угле входа <рт=Ю0° и неиз-
менном угле выхода <Ьт = -)- 100°, определит наилучшее приближение
функции положения механизма с ведущей кулисой к функции (14.7)
по пяти параметрам: по четырем параметрам схемы кулисного меха-
низма и углу входа ?т.
При Тт = Ю0° и бт = -ф 100° функция (14.7) имеет вид:
, _ 1 2
100° ? ’
(14.8)
График уравненных отклонений определился следующими абсцис-
сами узловых точек git g2, g-A:
<Pi = —1-25 ; <p2 = —|—75'; <рз=100°.
(точка gx — двукратная, а точки g2 и g3—простые). Параметры
схемы соответствующего кулисного механизма (с ведущей кулисой):
с = 0,85915; а =1,0603;
а = — 50е 00',0; 0 = — 190°55',5.
Этот механизм изображен на рис. 784 в положении, соответст-
вующем началу отрезка приближения. Он оформлен в виде кулачко-
вого механизма с прямолинейным профилем кулачка, [рафик уравнен-
§ 45]
СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА
947
них отклонений этого механизма представлен на рис. 785. Особен-
ностью этого графика является наличие на отрезке приближения двух
нулевых точек. Одна из них совпала с узловой точкой g.2, а вторая —
с началом координат. Следовательно, здесь оказались использован-
ными обе нулевые точки, которые при первом интерполяционном при-
ближении (см. табл. 14.4) в случае <рт = -|- 100° располагаются вблизи
границ отрезка приближения. Следует подчеркнуть, что указанный
график получен общим способом уравнивания предельных отклонений
Рис. 785.
в точках экстремумов и /?2, который изложен в пунктах 5° и 6°
настоящего параграфа. Отклонение в точке h дополнительного экстре-
мума оказалось равным отклонениям в точках hx и /?2:
Дф = —3',2.
После усреднения этого графика получим наилучшее приближение
с семью равными по модулю и чередующимися по знаку отклоне-
ниями на отрезке 0 <р -j- 100°. Наибольший модуль усредненного
1 I
отклонения L„= = Г,6 определит минимум кривой L„ на рис. 781.
Относительная величина =0,03%.
При отыскании наилучшего приближения по пяти параметрам
в качестве пятого параметра вместо угла входа <рт может быть исполь-
зован угол выхода <рт. Можно, наконец, поставить задачу отыскания
наилучшего приближения функции положения кулисного механизма
к заданной функции по шести параметрам: четырем параметрам схемы
кулисного механизма, углу входа а>т и углу выхода tym. Возможный
ход решения этой задачи следующий: найдем для последовательных
значений угла кривые подобные показанной на рис. 781.
Установим на этих кривых минимальные значения наибольшего мо-
дуля £н усредненных отклонений, которые обозначим £„цП- Затем
построим кривую
^-min =
Если указанная кривая имеет точку минимума в тех пределах угла
где существуют механизмы, то абсцисса этой точки определит угол фт,
948 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
при котором получим наилучшее приближение функции положения
кулисного механизма к предписанной функции на заданном отрезке
по шести параметрам.
10°. Заключительные замечания.
а) Выше большое внимание было уделено отдельным вопросам
наилучшего приближения в синтезе кулисных механизмов, и особенно
тем вопросам, которые возникают в процессе уравнивания предель-
ных отклонений при наличии нулевой точки на отрезке приближения.
Основная цель этого подробного изложения —облегчить рассмотрение
тех же вопросов в синтезе шарнирного четырехзвенника и криво-
шипно-шатунного механизма, так как для этих механизмов должны
остаться справедливыми основные выводы относительно влияния нуле-
вой точки на точность приближения и минимальный угол передачи,
установленные в синтезе кулисного механизма.
б) Число параметров схемы кулисного механизма меньше числа
параметров схемы шарнирного четырехзвенника и кривошипно-шатун-
ного механизма. Поэтому в общем случае от кулисного механизма
можно ожидать меньшей точности приближения к заданной функции,
чем от шарнирного четырехзвенника или кривошипно-шатунного меха-
низма при тех же углах входа и выхода. Однако простота подсчета
параметров схемы кулисных механизмов является существенным пре-
имуществом этих механизмов, облегчая нахождение конструктивно
приемлемых решений в тех случаях, когда не требуется высокой
точности воспроизведения функции.
в) Повысить точность первого интерполяционного приближения
можно или путем перехода к наилучшему приближению при неизмен-
ных углах <рт и <1»т, или путем изменения самих углов <рт и фт.
Второй путь может быть во много раз более эффективным, чем первый.
Используя второй путь, можно найти кулисные механизмы, не усту-
пающие по точности приближения шарнирному четырехзвеннику.
г) Примеры синтеза кулисного механизма, рассмотренные выше,
относились к случаю ведущей кулисы и одинакового направления
ведущего и ведомого звеньев. Следует, однако, иметь в виду, что
в синтезе кулисных механизмов может быть получено четыре отдель-
ных решения при заданных:
1) функции, подлежащей воспроизведению;
2) отрезке, на котором она должна быть воспроизведена;
3) абсолютных величинах углов входа и выхода срт и <рт.
Два решения можно получить при ведущей кулисе, выбрав
в первый раз углы <рт и <рт одного знака, а второй раз — разных знаков.
Таким же путем получим еще два решения при ведомой кулисе.
Эти решения будут отличаться по точности приближения, по вели-
чине минимального угла передачи и по относительным размерам
звеньев, которыми определяется конструктивная приемлемость полу-
ченного механизма. Одни из этих решений могут быть удачными,
а другие, наоборот, совершенно непригодными. Не имея опыта,
§ 45] СИНТЕЗ КУЛИСНОГО МЕХАНИЗМА 949
основанного на предыдущих аналогичных подсчетах, при первой
попытке часто наталкиваются именно на неудачные решения. Необ-
ходимо подчеркнуть, что в сии гезе шарнирно-рычажных механизмов
удачное решение, как правило, требует планомерных поисков.
д) Поиски приемлемого решения можно вести в следующем по-
рядке. Если направления вращения ведущего и ведомого звеньев
по конструктивным условиям могут быть как одинаковыми, так и
различными, то, выбрав желательные по абсолютной величине углы
входа и выхода <рт и фт, отыскивают четыре указанных решения.
Из полученных решений наиболее удачное по конструктивным соот-
ношениям следует попытаться улучшить в направлении повышения
минимального угла передачи или повышения точности приближения в
зависимости от заданных требований, изменяя угол <рт (или угол фт)
при постоянном угле фт (или угле <рт).
Если первое исследованное решение не дает приемлемых резуль-
татов, то следует перейти к улучшению второго из первоначальных
решений и т. д. Подлежат исследованию и те первоначальные ре-
шения, которые дали непроворачивающиеся механизмы. Чтобы в
этом случае войти в область проворачивающихся механизмов (для
поисков в ней приемлемых результатов), следует изменять угол <рт
(или фт) при постоянном угле фт (или <рт) в направлении умень-
шения угла, на котором механизм не проворачивается на отрезке
приближения.
е) Кулисный механизм для воспроизведения предписанной функ-
ции на заданном ограниченном отрезке удобно конструктивно выпол-
нять в виде кулачкового механизма с прямолинейным профилем
кулачка и пружинным замыканием ведомого звена (см. рис. 784).
В этом случае отклонения от заданной функции, обусловленные
ошибками изготовления и зазорами в кинематических парах, могут
быть значительно ниже, чем в шарнирном четырехзвеннике и криво-
шипно-шатунном механизме.
ж) В качестве одного из преимуществ интерполирования с дву-
кратными узлами перед интерполированием с простыми узлами было
указано упрощение расчетных формул. Укажем на второе серьез-
ное преимущество интерполирования с двукратными узлами перед
интерполированием с простыми узлами. При указанном выше выборе
узлов интерполяции (см. § 44, 6е) три предельных отклонения (в трех
узловых точках) непосредственно по условиям интерполяции полу-
чаются равными друг другу. Если на отрезке приближения отсутст-
вует нулевая точка, то для отыскания наилучшего приближения до-
статочно уравнять между собой два предельных отклонения в точках
экстремумов. Уравнивание этих отклонений достигается смещением
одного (среднего) узла интерполяции.
Если бы интерполяционное приближение функции положения
кулисного механизма мы определили четырьмя простыми узлами, то
в общем случае получили бы пять предельных отклонений, различных
950 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
по абсолютной величине. Для уравнивания их потребовалось бы
смещать четыре узла интерполяции. Очевидно, что сходимость про-
цесса уравнивания отклонений при прочих равных условиях будет
во много раз выше в случае уравнивания двух предельных отклоне-
ний по сравнению со случаем уравнивания пяти предельных откло-
нений.
§ 46. Отыскание наилучшего приближения в задаче синтеза
шарнирного четырехзвенника и кривошипно-шатунного
механизма
1°. Достаточные условия наилучшего приближения в задаче
синтеза шарнирного четырехзвенника и кривошипно-шатунного
механизма. Ради упрощения изложения условимся говорить только
о шарнирном четырехзвеннике, постоянно имея в виду, что все ска-
занное целиком относится и к кривошипно-шатунному механизму,
если не оговорено противное. С той же целью отрезок приближения
будем считать в общем случае [0, <рт] (а не [<р(|, <рт] как ранее),
где 0 срт. Следовательно, в декартовых осях левая граница отрезка
приближения в общем случае будет совпадать с началом координат.
Пусть интерполяционное приближение функции положения <р=/(ср)
шарнирного четырехзвенника к заданной функции ф> = Z7 (<р) на от-
резке [0, <рт] определено гремя узловыми точками g,, g2, g3 (рис. 786):
двумя двукратными g, и gt и одной простой g:i. Если абсциссы ср,,
<р2, фз этих точек выбраны согласно рекомендациям, данным в § 44, 6°,
равными
ср, — 0,0955срт; Ф.2 = 0,6545срт; <р3 = <рт, (14.9)
то получаемое приближение назовем первым интерполяцион-
ным приближением. Оно будет вспомогательным для последую-
щего перехода к наилучшему приближению. При выборе абсцисс уз-
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 951
ловых точек по соотношениям (14.9) узловая точка g3 будет указывать
правую границу отрезка приближения.
Задача синтеза шарнирного четырехзвенника по условиям первого
интерполяционного приближения имеет или одно или три решения.
Рассмотрим сначала случай, когда эта задача имеет одно решение.
Пусть соответствующий график отклонений Д (у) изображен на рис. 786
сплошной кривой. Так как этот график не имеет с осью абсцисс
иных общих точек, кроме тех, которые совпадают с узловыми точ-
ками, то он располагается на отрезке приближения [0, ут] по одну
сторону оси абсцисс. Три предельные отклонения в узловых точках
£"i> Si 11 ёз равны нулю. С ними чередуются предельное откло-
нение Д% на границе отрезка приближения в точке /г0 и предель-
ные отклонения Дф] и Д6.> в точках экстремумов /г1 и /г4, одинако-
вые по знаку, но в общем случае не равные по величине.
Рассмотрим сначала случай, когда при любом выборе абсцисс
узловых точек в пределах отрезка приближения, в том числе и при
выборе их по соотношениям (14.9), задача синтеза четырехзвенника
имеет единственное решение. Задание двух двукратных узловых
точек и одной простой узловой точки геометрически эквивалентно
заданию пяти точек, через которые должен пройти график отклоне-
ний шарнирного четырехзвенника. При единственности решения любой
другой график отклонений, отличающийся от первого абсциссами
узловых точек, не может иметь с первым более п = 4 общих точек.
В этом случае согласно теореме Геронимуса наилучшее приближение
определит график отклонений, который имеет на заданном отрезке
[О, ут], по крайней мере, п -1- 2 = 6 предельных отклонений, равных
по абсолютной величине, но чередующихся по знаку. Если при этом
на отрезке приближения [0, ут] имеются другие предельные откло-
нения, то они должны быть меньше по абсолютной величине ранее
упомянутых.
Практический путь нахождения этого наилучшего приближения
очевиден: следует на графике отклонений Д (у) первого интерполя-
ционного приближения уравнять между собой предельные отклоне-
ния Д<ри, Дф! и Дф2 и затем этот график усреднить. Следовательно,
здесь, как и в синтезе кулисного механизма, основной операцией
в процессе перехода от первого интерполяционного приближения к
наилучшему будет уравнивание упомянутых предельных отклонений.
2°. Общий способ уравнивания графика отклонений. Здесь
сохраняется свойство, доказанное в § 44, 10° для графика отклоне-
ний кулисного механизма: при смещении узловой точки по оси абсцисс
график отклонений Д (у) преобразуется так, что отклонения, распо-
ложенные по оси абсцисс в направлении смещения этой узловой
точки, уменьшаются по абсолютной величине, а отклонения, располо-
ложенные по оси абсцисс в направлении, противоположном смещению
узловой точки, возрастают по абсолютной величине. Например, сме-
стив узловую точку gi (рис. 786) в положительном направлении
952 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
оси абсцисс в положение £*, мы получим график отклонений А * (ср),
у которого в соответствующих точках A®, h\ и предельные откло-
нения Дф* Дф* и Дф* будут:
1М1>|Д'?о1; |дф:|>|д-ы |дф:к|дф2|.
Для уравнивания между собой трех указанных предельных откло-
нений Дф0, Дф) и Дф.2 удобно сначала уравнять между собой предель-
ные отклонения Дф! и Дф2 (в точках экстремумов hi и А2), а затем
с ними уравнять предельное отклонение Дфп в точке Ао на границе
отрезка приближения (при ? = 0).
Процесс уравнивания отклонений в точках экстремумов будем
выполнять так, как изложено в задаче синтеза кулисного механизма
(см. § 45, 3°). Чтобы осуществить это уравнивание, следует сместить
двукратную узловую точку g.t по оси абсцисс в направлении боль-
шего по абсолютной величине отклонения Дф! или Дф2. Допустим,
что этот этап уравнивания нами выполнен и получен график откло-
нений Д* (?) с равными между собой предельными отклонениями Дф* =
= Дф* в точках экстремумов А* и А2 (рис. 786). Узловые точки gx и
gz этого графика Д* (?) совпадают с узловыми точками графика
отклонений Д (?) первого приближения, а средняя узловая точка
занимает на оси абсцисс новое положение §*.
Из самого процесса уравнивания предельных отклонений в точках
экстремумов следует, что относительные величины этих отклонений
определяются относительным расположением по оси абсцисс трех
узловых точек: gx, g* и g3. Если при неизменном положении узловой
точки g-i задать узловым точкам gt и gZ такие смешения Д?, и Д?2,
при которых относительное расположение этих трех точек не нару-
шится, то относительные изменения предельных отклонений Дф* =
= Дф* в точках А® и А* должны быть величинами высшего порядка
малости по сравнению с приращением абсолютных величин этих от-
клонений. Чтобы не нарушилось относительное расположение трех
узловых точек, смещения Д?( и Д?2 узловых точек gi и g* должны
быть пропорциональны расстояниям этих точек до постоянной узло-
вой точки git т. е. эти смещения должны удовлетворять пропорции
Ayl ________ Alfa
fa — ?1 <fa — ? * ’
(14.10)
где <pi, ?* и ®3 — абсциссы узловых точек gt, g, и g3.
На графике Д* (?) предельное отклонение Дф® на границе отрезка
приближения больше по абсолютной величине предельных отклоне-
ний Дф* = Дф* в точках экстремумов. Чтобы уравнять предельные
отклонения Дф* и Дф* = Дф*, зададим узловым точкам gt и g* про-
извольные отрицательные смещения, удовлетворяющие пропорции
(14.10). Тогда на новом графике отклонений Д(2) (?) (он изображен
сплошной кривой на рис. 787; там же пунктиром повторен гра-
§ 46]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКЭ
953
фик Д* (<р) с рис. 786) предельные отклонения в точках экстрему-
мов /г'21 и /г’2', как расположенные в направлении, противоположном
смешению узловых точек gt и g'2, возрастут по абсолютной вели-
чине, ошаваясь приближенно равными друг другу, а предельное откло-
нение Дф*,2' (не помеченное на рис. 787) в точке й*2> на границе отрезка
приближения, наоборот, уменьшится по абсолютной величине. Подсчитав
упомянутые предельные отклонения графиков Д* (®) и Д'2) (<р), можно
установить при помощи линейной интерполяции (на основании графи-
ческого построения, подобного изображенному на рис. 774) такие
пропорциональные смешения узловых точек gx и g*, которые опре-
----Отрезок приблио/оения------
Рис. 787.
делят график отклонений с меньшей абсолютной величиной разности
между предельными отклонениями, чем эта разность на графи-
ках Д* (<р) и Д<2) (<р). Продолжив этот процесс, можно упомянутую
разность сделать сколь угодно малой.
Укажем ряд возможных упрощений в этом процессе уравнивания
предельных отклонений, чтобы облегчить его практическое применение.
3°. Упрощенное определение необходимых смещений узловых
точек. Участки графиков Д* (ср) и Д<2) (?) (рис. 787), расположенные
левее узловых точек gx и g*2’, назовем свободными участками.
Предположим, что ни график отклонений Дв (ср), ни графики отклоне-
ций, получаемые посредством смещения узловых точек gY и g*, не будут
иметь с осью абсцисс иных общих точек на отрезке приближения,
кроме тех, которые по условиям приближения совпадают с узловыми
точками*). При этом условии оба графика Д* (ср) и Д(2) (®) покажут
на отрезке приближения отклонения одного знака. Для дальнейшего
*) Напомним, что те дополнительные общие точки графика отклонений
с осью абсцисс, которые не определяются 'С.товиямн интерполяционного при-
ближения, названы ранее нулевыми точками, ['рафики отклонений с нулевыми
точками будут рассмотрены ниже.
954 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
изложения удобно под Д': (ср) и Д<2) (<р) понимать не только обозна-
чения соответствующих графиков отклонений, но и текущие значе-
ния отклонений, определяемых этими графиками.
В интервале [ср'Д epj, где ср’2’ и epi — абсциссы узловых точек g&>
и gb разность
Д*(ер)-Д<2>(т)
изменяет свой знак. При <р = ср<2> она положительна, а при <р =<рг
-отрицательна. Это свидетельствует о наличии на указанном интер-
вале общей точки графиков Д* (ср) и Д,2) (ср). Таким же
путем можно показать, что указанные графики имеют общие точки
в интервалах [ср|( ср*2'] и [ср*2), <р*] (где индексы абсциссы ср совпадают
с индексами точек g на рис. 787). Четвертой обшей точкой графиков
Д* (ср) н Д(2) (ср) будет постоянная узловая точка g3. Так как эти
графики не могут иметь более четырех общих точек, то свободные
участки рассматриваемых графиков пересекаться не могут. Следо-
вательно, при смещении узловых точек gt и g* графика Д* (ср) по
оси абсцисс в выбранном направлении в том же направлении сме-
стятся все точки свободного участка этого графика.
Можно допустить, что при малых смещениях Дср1 и Дср2 упомя-
нутых узловых точек каждая точка свободного участка графика Д* (ср),
расположенная на малом расстоянии от узловой точки git получит
смещение по оси абсцисс, приближенно равное смещению
по той же оси узловой точки gi. На основании этого допущения легко
определить те смещения Дср1 и Дср2 узловых точек gt и gZ, которые
дадут график отклонений Д(2) (ср) с меньшей абсолютной величиной
разности между предельными отклонениями, чем график Д* (ср).
Проведем на рис. 787 через точки экстремумов и А* гра-
фика Д* (ср) прямую, параллельную оси абсцисс. Отметим точку с*,
в которой указанная прямая пересекает свободный участок графика Д*(<р).
Абсциссу точки с* обозначим Дер* и выберем смешение Дер, узловой
точки gt равным Дср>1 = — Дер*. Смешение Дср2 узловой точки g* опре-
делим по пропорции (14.10). Тогда получим график отклонений Д(2) (ер)
(показанный на рис. 787), у которого свободный участок должен пе-
ресечь ось ординат в точке А)2), лежащей на прямой с*А*А!, парал-
лельной оси абсцисс *). Разность между предельными отклонениями
на графике Д<2) (ср) будет равна приращению предельных отклонений
в точках экстремумов If, и А*. Возникает вопрос, при каких усло-
виях это приращение по абсолютной величине будет меньше разности
между предельными отклонениями на графике Д* (ср) или, иначе, при
каких условиях указанный способ подсчета смешений Дер, и Дер2
узловых точек gt и g* определит сходящийся процесс уравнивания
предельных отклонений.
*) На рис. 787 ради отчетливости чертежа равенство ~ — Д-р* (где Др1=
— gig’2') не выдержано.
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 955
Предположим, что узловые точки gx и g*3 непрерывно смешаются
в направлении к постоянной узловой точке gA и соотношения между
смещениями упомянутых точек выбираются постоянно такими, что
предельные отклонения в точках экстремумов остаются равными друг
другу, убывая при этом по абсолютной величине и стремясь в пре-
деле к нулю. Пусть кривая k на рис. 787 есть график изменения
указанных отклонений в функции от абсциссы узловой точки gr.
Кривая k пересекает прямую в точке k* с абсциссой, равной
абсциссе узловой точки gt. Абсолютная величина приращения экстре-
мальных отклонений при переходе от графика Д:= (?) к графику Д(2) (?)
будет приближенно равна ] Д?* tg 7 ], где Д?*—выбранное смещение
точки gt (| А?* | = gig^), a tg 7 — угловой коэффициент касательной
к кривой k в точке k \ Соответствующее изменение предельного откло-
нения на границе отрезка приближения при переходе от графика А * (?)
к графику Д(2) (?), выражаемое по абсолютной величине отрез-
ком h*h^\ будет приближенно равно |A?ctgyc где tg— угловой
коэффициент касательной к графику А* (?) в точке с* его свободного
участка.
Чтобы указанный процесс уравнивания предельных отклонений
на графике А* (?) был сходящимся, необходимо выполнение неравенства
Kl^ctglel
или, сокращая на А?*,
I tgy 1 < I tg7с |.
Таким образом, рассмотренный процесс уравнивания отклонений
на графике Д*(?) будет сходящимся, если угловой коэффициент tg
касательной к графику А (?) в точке c"f его свободного участка
будет достаточно большим. Практически этот процесс оказывается
несходящимся только при появлении вблизи начала координат нулевой
точки, нарушающей монотонный ход свободного участка графика А* (?).
Как уже отмечалось, вопрос уравнивания отклонений при наличии
нулевой точки будет рассмотрен ниже отдельно.
Если на графике Д*(?) (рис. 787) предельное отклонение в
точке А* больше по абсолютной величине равных предельных откло-
нений в точках И{ и А*, то на графике Д12) (?) должно получиться
предельное отклонение в точке А<2) меньше по абсолютной величине
равных предельных отклонений в точках А’2' и А®. Это значит, .что
смещения А?, и Д?2 узловых точек, выбранные по указанным выше
соотношениям: Д?( =— А?*, а Д?.2 удовлетворяющим пропорции (14.10),
оказываются по абсолютной величине несколько больше тех смеще-
ний, которые необходимы для полного уравнивания предельных от-
клонений графика Д*(?). Поэтому малые поправки к этим смещениям A?j
и Д?.2 в сторону их уменьшения по абсолютной величине могут улуч-
шить сходимость указанного процесса уравнивания предельных
S56 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ- [ГЛ. XIV
§ 46]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
957
отклонений графика А* (<?). Ниже мы рекомендуем выбирать смещения
Д<Р1 и Д?2 узловых точек g, и g* по формулам:
Д?1 = -Дф*-*^ ; = (14 и)
бой предельными отклонениями в точках экстремумов. Не
самого графика А* (?), подсчитаем по формуле
(^-^(А^-Д’Ч4)
Дф* = Дф2-------’
отыскивая
(14.13)
В первой формуле поправочный множитель ——(где ф« ф и
<р8 — A?* f 3’ Y1
Д<рс абсциссы точек g3, gt и с*) учитывает расстояние по оси
абсцисс от точки gl до точки с*. Чем больше это расстояние по
абсолютной величине, тем меньше (при прочих равных условиях)
будет угловой коэффициент tgIc, но тем больше — поправочный
множитель. Вторая формула (14.11) получена из пропорции (14.10).
„ ' “®следовательные этапы процесса уравнивания отклонений.
а рис. 788 сплошной кривой изображен график отклонений А (-р)
первого интерполяционного приближения. Три предельных отклоне-
ния Дф0, Дф} и ДФ2 в точках /?0, /г, и /г2 этого графика не равны
друг другу. Изложим последовательные этапы процесса уравнивания
этих отклонений упрощенным способом.
1) Выберем произвольно новую абсциссу <р<>) средней узловой
точки g2, с тем чтобы последняя сместилась в " направлении к той
точке экстремума 1ц или h2, в которой предельное отклонение больше
по абсолютной величине. Новое положение этой узловой точки обо-
значим gW. Сохранив неизменными абсциссы и <р3* узловых точек р. и
g3, найдем новый график отклонений Д(1) (?), показанный на рис 788
пунктиром. Обозначим через Дф(') и Дф(О предельные отклонения
в точках экстремумов /?</> и /г!,').
2) Подсчитаем по формуле линейной интерполяции
(та— <?£')) (Дф2—A-L,)
f2 “ ~'Та- > (14.12)
(аналогичной формуле (14.3)) ту абсциссу средней узловой точки g2 ко-
торая определит график отклонений Д* (?) с уравненными между’ со-
(аналогичной формуле (14.4)) значение ординаты, на которой должны
уравняться экстремальные отклонения этого графика.
3) Проведем на рис. 788 прямую, параллельную оси абсцисс и
определяемую уравнением
Дф = Дф*,
где ДФ*—ордината, подсчитанная по формуле (14.13).
Найдем абсциссы А<рс и Д?(‘> точек си с(1), в которых прове-
денная прямая пересекает свободные участки графиков отклонений Д (?)
и Д(1) (<₽). Определим далее абсциссу Д?* той точки с*, в кото-
рой указанная прямая должна пересечь свободный участок гра-
фика Д*(ф) с уравненными экстремальными отклонениями. Для эюго
заметим, что графики отклонений Д (<р), Д ° (?) и д" (?) в свои*
исходных условиях отличаются только значениями абсциссы средней
узловой точки g2. Эти значения соответственно равны ?2, ?’ и ?2. 1 ак
как значению ?2 соответствует абсцисса Д?с, а значению ?2 а с-
цисса Д?*?, то, имея величину ?*, можно определить абсциссу Д?с
по формуле линейной интерполяции:
(А?с — А ср*1') (<р2 — <f?)
Дф*=Д?с- (y2-<f(i))
(14.14)
4) По формулам (14.11) подсчитаем необходимые смещения Д?1
и Д?2 двукратных узловых точек g\ и g^. Новые абсциссы этих
точек будут:
_j_ Дф1-> <р(2) — <р* Дф2.
Подставив в последние соотношения значения Д?1 и Д?2, опреде-
ляемые формулами (14.11), получим следующие окончательные фор-
мулы для вычисления абсцисс ?(2) и ?!?:
«РзСр.-Д?*). |9, ъ (<?? - А?:)
?1 ------- ц,------Дер* > ?2 ср3 — Дер*
(14.15)
—--------• о'2
¥з-Др* ’
Здесь <pi и <р3 — абсциссы точек gt и g3 графика отклонений А (?)
первого интерполяционного приближения, а ?2 и Д?с абсциссы, под-
считанные по формулам (14.12) и (14.13). Выбрав абсциссы двукрат-
ных узловых точек по формулам (14.15) и сохранив неизменной
абсциссу ?з==?т постоянной узловой точки, мы должны получить
график отклонений с тремя приближенно уравненными предельными
отклонениями.
958 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
5°. Пример уравнивания предельных отклонений. Обратимся
к графику 'отклонений Д (ср) на рис. 751. Этот график получен
в результате интерполяционного приближения функции положения
шарнирного четырехзвенника к функции (13.37):
ф = — 50 lg(l 4-0,09 <р)
на отрезке -ф-100°. Абсциссы узловых точек gu g2 и g3,
определяющих интерполяционное приближение, были:
= 4- 9°33'; <р8 = 4- 65°2 7'; <р3 = 4- 100°-
Задача интерполяционного приближения имела единственное ре-
шение. Подсчет дал следующие параметры схемы механизма:
а— 1,2989; Ь= 1,6403; с = 0,66377;
а = 4-57о00',1; ₽ = 4- 235с59',3.
Значения отклонений в последовательных точках отрезка прибли-
жения приведены в таблице 13.3 (стр. 879). Предельные отклонения
в точках /z0, ht и /г.2 графика Д(р) на рис. 751 равны соответственно:
Д% = —12',2; Дф, = —3',1; Дф2 = —2',3.
Наибольший модуль усредненных отклонений, характеризующий
точность этого первого интерполяционного приближения, был
L — р=| = 6',1. Его относительная величина =0,20%. Чтобы
I - I Vm
I L
уменьшить величины Ди —, уравняем предельные отклоне-
• 771
ния Д%, Д'4 и Дф2 графика Д (ср) на рис. 751 тем упрощенным
способом, который изложен в пункте 4° настоящего параграфа.
1) Выберем новую абсциссу средней узловой точки g2
= 60°,
с тем чтобы эта точка сместилась по оси абсцисс в направлении к
точке экстремума ht с большим по модулю предельным отклонением.
Оставив неизменными абсциссы <р, = 4~ 9С33' и <р3 = 4“Ю0о узловых
точек gt и g3, получим следующие новые параметры схемы механизма:
а = 1,3713; 6=1,7170; с=0,65971;
а = 4-58с32’,4; ₽ = 235°51',2.
В таблице 14.10 (графа „вспомогательный механизм*1) указаны
отклонения этого механизма от заданной функции (13.37). Их гра-
фик Д(1) (ср) изображен пунктиром на рис. 789. Предельные откло-
нения в точках h'i1' и h'2" равны соответственно:
Дф? =— 2',2; Д<$ = — 3',4.
§ 46J
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
959
Таблица 14.10
Отклонения функции положения шарнирного четырехзвенника
от функции (13.37)
Углы поворота ведущего звена Отклонения ДО Точки на гра- фиках Д<1> (гр) и Д'21 (<f) (рис. 789)
вспомогательный механизм уравненный “ механизм
- 00’14’ — 3',3 с'2>
0 — 9',1 — 3,0 /г'1’, h™
4 03'15’ — 2,7 — с'1'
?;г,= 4 г 06 01 — 0 gl2'
= Н - 09 33 0 — g'i"
- 10 00 — — 0,5
- 20 00 — 1,5 — 2,8
- - 25 00 -2,1 — 3,3
г 26 00 — 3,3 h'*'
- 27 30 9 9 — 3,3
г 28 00 — ,? — Л'11
- 30 00 9 9 — 3,2
- 32 30 — 24 —
4 40 00 — 1,5 -2,2
г 50 00 — 0,5 — 0,8
^х,=4 г 60 00 0 — g"’
1 Ч) 1 г 61 50 — 0 gs21
г 70 00 — 0,6 — 0,1
4 80 00 -2,1 — 1,9
4 87 30 — 3,3 — 3,1
4 90 00 — 3,4 — 3,3 ft!,1’, ft</’
4 92 00 — 3,3 — 3,2
?з =- 4 100 00 0 0 gs
2) Подсчитаем по формуле (14.12) абсциссу средней узловой
точки, которая определит график отклонений Д* (ср) с приближенно
уравненными предельными отклонениями в точках экстремумов:
ср2 = 65°27' —
(65°27' — 60°) (— 2',3 4- 3’,1)
(— 2',3 + 3',1) — (— 3’,4 + 2',2)
63°16',2.
По формуле (14.13) подсчитаем ординату, на которой должны
уравняться экстремальные отклонения графика Д* (ср):
(65°27' — 63° 16',2) (— 2',3 + 3',4) ,
65°27’ —60° — 2’7,
3) Проведем на рис. 751 прямую, параллельную оси абсцисс,
определяемую уравнением
Дф* = — 2',3
Дф = —2',7.
960 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
Отметим точку с, в которой эта прямая пересекает свободный участок
графика Д (ср). Из таблицы 13.3 (стр. 879) имеем, что абсцисса точки с:
Д?с = + 3°55'.
Проведем ту же прямую на рис. 789 и отметим ее точку пересе-
чения с(1) со свободным участком графика Д(1) (ср). Из таблицы 14.10
получим абсциссу этой точки:
Д<р^’ = 4-3°15'.
Подсчитаем по формуле (14.14) абсциссу Дер* той точки, в которой
прямая Дф = — 2',7 должна пересечь график отклонений Д* (ср) с урав-
ненными экстремальными отклонениями:
. . — до (3’55' - 345’) (65=27' - 634 6',2) _ , о ,
Д-Ре — 4 65=27' _ — -j 3 39 .
4) По формулам (14.15) подсчитаем абсциссы двукратных узлов
интерполяции, обеспечивающие приближенное уравнивание между
собой всех трех предельных отклонений графика Д (ср) первого ин-
терполяционного приближения:
,8, _ 100° (9=33' - 3=39') _ , о
100° —3°39' —-ф-ои/,
„ 100= (63=16’,2 — 3=39') _ , filoe2,7
?2 ---- 1ОПР —3=39' --- 1 bl
100= — 3=39'
Выберем за расчетные значения этих абсцисс с округлением:
ср';’ = -J- 6°07'; ср^2’ = 4- 61 с53'.
§ 461 СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 961
Оставив неизменной абсциссу <р3 = —J—100° постоянной узловой точки
gz, получим следующие новые параметры схемы механизма:
а =1,4094; 6=1,7547; с = 0,6599;
а=4-58°53',4; £ =-|-235о45'.
На рис. 790 полученный механизм показан в двух положениях,
соответствующих началу и концу участка приближения. Минималь-
ный угол передачи на отрезке приближения p.min = 28°. Отклонения
его функции положения от функции (13.37) указаны в таблице 14.10
(графа „уравненный механизм"). Их график Д<2) (<р) изображен сплошной
линией на рис. 789. Предельные отклонения в точках ho', h\*’, h'>J‘
графика Д(2) (<р) равны соответственно:
Д<]$” = — 3',0; Дф'|а, = —3',3; Д<$“ = — 3’,3.
Наибольший модуль усредненных отклонений, характеризующий
точность найденного приближения после усреднения, будет
А'8' _ _О_ — х'д Его относительная величина — = 0,055%.
Напомним, что при первом интерполяционном приближении были
получены величины А = 6',1 и | у-1 = 0,20%. Таким образом, одна
ступень уравнивания повысила точность приближения примерно в
четыре раза. Столь резкое повышение точности приближения за счет
уравнивания предельных отклонений объясняется большими разли-
чиями в величинах предельных отклонений на графике Д (<р) первого
интерполяционного приближения.
На графике отклонений Д(2) (<р) разность между предельными от-
клонениями по абсолютной величине равна всего | Дфо ’ — Дф|211 = 0',3.
Подсчеты показали, что последующие ступени уравнивания предель-
ных отклонений снижают модуль А(2) менее чем на 0',1.
31 И. И, Артоболевский
962 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
6°. Упрощенный подсчет параметров схемы вспомогательного
и уравненного механизмов. Изложенный выше процесс уравни-
вания отклонений требует подсчета параметров схемы по крайней
мере двух механизмов: вспомогательного механизма и механизма
с уравненными отклонениями. Покажем, что подсчет параметров
схемы обоих механизмов может быть выполнен таким путем, что
по трудоемкости не будет превышать подсчета параметров схемы
первого механизма.
Если график отклонений первого интерполяционного приближения
не имеет нулевых точек и если абсциссы узловых точек при оты-
скании этого приближения выбраны по построению Чебышева
(см. § 43, 6°), то для уравнивания предельных отклонений на упо-
мянутом графике обычно достаточны относительно малые смещения
двукратных узловых точек по оси абсцисс. При малых смещениях узловых
точек координаты Хм, Ум соответствующего центра Бурместера и
вспомогательный параметр и, отыскиваемые по ходу решения задачи
синтеза вспомогательного и уравненного механизмов, мало отли-
чаются от тех же координат Хм, Ум и параметра и, полученных
при решении задачи синтеза первого механизма. В результате при
подсчете параметров схемы вспомогательного и уравненного меха-
низмов можно выбирать за приближенные координаты хм и ум
центра Бурместера и параметра и те их значения, которые найдены
в задаче синтеза первого механизма. Последующее их уточнение
выполняется способом, изложенным в § 43, 1°. В этом случае при
аналитическом решении отпадают подсчет коэффициентов т'^, т\ и
/«о кубического уравнения (см. стр. 852)
и3 -ф- т’иг т{и -ф- т'о — О
и решение самого уравнения, а при графическом решении отпадает
построение кривых центров. Последовательность выполнения этого
упрощенного расчета покажем непосредственно на примере.
Возвратимся к задаче приближения функции положения шарнир-
ного четырехзвенника к функции (13.37):
ф = — 50°lg(l + 0,09^)
(где углы и ф выражены в градусах) на отрезке от <р = 0 до
<р = 4- 100°.
При отыскании первого интерполяционного приближения абсциссы
узлов были выбраны:
<{>! = + 9°33'; == -ф- 65°27'; <?3 = +100°.
Задача имела единственное решение. На соответствующем гра-
фике отклонений Д(<р) (см. рис. 751) предельные отклонения в точ-
ках Ло, hi, hi были равны соответственно:
Дф0 = —12',2; Дф,=—3',1; Дф2 = —2',3.
При уравнивании этих отклонений абсцисса средней узловой точки
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 963
была выбрана (см. 5° настоящего параграфа)
тУ> = Ц60о
и подсчитаны параметры схемы вспомогательного механизма. Этот
подсчет выполнялся упрощенным способом. Ниже приведена его по-
следовательность.
1) Установим кинематические условия искомого приближения по
формулам § 43, 1°:
?12 = 4-50°27'; <pia=: —26°50'27",1
?13 = 4-90°27'; фв = —36°31'48",7
/, = — 1,050995; z2 = — 0,3053633.
0
2) Подсчитаем вспомогательные углы -у- и йО2з и координаты
полюсов относительных положений ведущего звена по формулам,
указанным в § 43, 1°:
Др- = 38°38'43",6;
8d>23 = —31°41'07",9.
Л12 = — 0,66395; У12 = —0,1583806;
х13 = —0,089513; J13 = — 0,0902465;
tgg13 = 4~ 1,008194;
х23 — — 0,0283685; _у23 = — 0,2691675;
х„ = 4-0,1762368; jn = +0,1583806;
= — 0,0197421; = — 0,1874909.
3) Подсчитаем коэффициенты klt k2, k-t и /г4 по формулам § 43, Iе!
Л, = + 0,1959789; /г3 = 4- 0,3458713;
k2 = 4- 0,1564947; /г4 = — 0,0291103.
4) Подсчитаем координаты центра Бурместера по формулам (13.13),
подставив в них только что подсчитанные значения величин Хц,
фи, klt kit k3 и kit и значение и"' — 4- 0,6821687 параметра «, уста-
новленное в результате уточнения при отыскании первого интерполя-
ционного приближения (см. § 43, 8°)- Тогда получим:
хм =4- 0,1976034; _уЛ = —0,2601128.
Для их проверки подсчитаем по формуле (11.141) величину v:
v = 4-0,6469125.
Разность Ьи = и— v = 4“ 35256,2 • 10-6 свидетельствует о не-
обходимости уточнения найденных координат центра Бурместера.
31»
964 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НЛИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
Так как исходные данные при подсчете схемы первого и вспомога-
тельного механизмов мало отличаются друг от друга, то общие за-
кономерности процесса уточнения параметра и и координат центра
Бурместера Хм. Ум должны в обоих случаях также мало отличаться
друг от друга. Используем это обстоятельство для отыскания по-
правки к параметру и. Напомним, что при подсчете схемы первого
механизма (см. стр. 877) приближенное значение и = -ф- 0,6776826 (полу-
ченное на основании координат Хм и ум центра Бурместера, снятых
непосредственно с чертежа) дало разность Ди = — 2512,2 • 106.
После уточнения расчетное значение этого параметра оказалось
и"'= 4-0,6821687. Следовательно, разности Ди =— 0,0025122
соответствовала поправка к приближенному значению параметра и, равная
и"'— и=0,6821687— 0,6776826 =-)-0>0045861. Отношение равно:
_ и’" — и___+ 0,0044861
" Ди —0,0025122
1,785726.
В нашем примере получена разность Д п = 4~ 0,0352562. Поправку
к выбранному значению параметра и = 4- 0,6821687 подсчитаем как
произведение:
п Ди = —1,785726 • 0,0352562 = —0,0629579.
Новое значение параметра и будет:
и' = и -|- и Ди = 0,6821687 — 0,0629579 = 4- 0,6192108.
По формулам (13.13) и (11.141) найдем вновь:
х'м = 0,1781373; j4 = —0,2849134; v' = 0,6171123.
Разность = — v’= 4~ 2098,5 • 10~®. По формуле линейной
интерполяции (11.142) получим уточненное значение и" параметра и:
и" = 4-0,6152263.
Новый подсчет по формулам (13.13) и (11.141) дает:
х'м = 4- 0,1763259; = —0,2864747; v" = 4- 0,6154822.
Разность Ди" =— 225,9-10“®. По формуле линейной интерпо-
ляции следующее уточненное значение и"' параметра и будет:
и"'= 4-0,6156594.
Повторив еще раз подсчет по формулам (13.13) и (11.141), найдем:
Хм = 4-°,! 765297; у'м =— 0,2863102; т/" = 4-0,6156362.
Разность Д и"' = и'" — v'" = 4“ 3,2 10_®. Малая величина этой
разности показывает,- что если еще раз подсчитать по формуле . ли-
нейной интерполяции значение параметра и:
n*v = 4-0,6156234,
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 965
то его можно принять за расчетное. Соответствующие расчетные
координаты центра Бурместера будут:
Хм — + 0,1765129; ^ = — 0,2863239.
По этим значениям Хм иул, используя формулы (11,21), (13,14)
и (13,15), подсчитаны параметры схемы* вспомогательного механизма,
указанные в пункте 5° настоящего параграфа. Этот же упрощенный
путь подсчета параметров схемы механизма был применен и для под-
счета параметров схемы механизма с уравненными отклонениями.
В тех случаях, когда в процессе уравнивания отклонений тре-
буются большие смещения узловых точек (это часто случается при
наличии дополнительной нулевой точки на отрезке приближения),
процесс уточнения координат центра Бурместера можно существенно
сократить, привлекая для контроля графоаналитическое решение. При
этом нет необходимости полностью вычерчивать соответствующие
кривые центров. Достаточно дать построение малых участков этих
кривых в той области, в которой располагается центр Бурместера
при отыскании первого механизма.
7°. Уравнивание предельных отклонений при наличии на гра-
фике отклонений дополнительной нулевой точки. На рис. 791
сверху изображен график отклонений Д (ср), определяемый двумя
двукратными узловыми точками gj и g.> и одной простой — g3, имеющий
нулевую точку g, в которой отклонения изменяют свой знак. Здесь
остается справедливой теорема, установленная в синтезе кулисного
механизма (см. § 44, 10°): при смещении узловой точки по оси аб-
сцисс ближайшая к ней дополнительная нулевая точка получит сме-
щение, обратное по знаку.
Наметим общую последовательность уравнивания отклонений при
наличии на графике Д (ср) дополнительной нулевой точки.
1) Оставив неизменной абсциссу <р3 простой узловой точ-
ки g3, зададим двукратным узловым точкам g\ и такие поло-
жительные смещения, чтобы дополнительная нулевая точка g, сме-
стившись в отрицательном направлении оси абсцисс, оказалась вне
отрезка, определяемого узловыми точками; соответствующий график
отклонений показан на рис. 791 посредине; новые положения дву-
кратных точек, определяющих график Д(1) (ср), обозначены g/’ и g'i'-
Обозначим их абсциссы ср/' и ср!/1.
2) Оставив неизменными абсциссы ср)1’ и ср3 узловых точек gt1* и
g3, отыщем при помощи линейной интерполяции такую абсциссу gz'
двукратной узловой точки g2, при которой уравняются предель-
ные отклонения в точках экстремумов h\1' и hty', расположенных
между узловыми точками g'/’, g%' и g3 графика Д(1) (ср). Тогда полу-
чим график отклонений Д(2) (ср) (нижний график на рис. 791), у ко-
торого предельные отклонения в точках экстремумов ft)®’ и 1 будут
равны, а третье предельное отклонение, в дополнительной точке
экстремума /г(2) с абсциссой <р<^ср/', не равно двум первым.
966 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
3) Если на графике Д(а) (<р), как изображено на рис. 791, пре-
дельное отклонение в дополнительной точке экстремума /г(а) меньше
по модулю предельных отклонений в точках экстремумов h\s> и h™,
расположенных между узловыми точками, то следует задать дву-
кратным узловым точкам g\" и g%‘ положительные смещения по оси
абсцисс, пропорциональные расстояниям этих точек до простой уз-
ловой точки g9. Тогда предельные отклонения в точках экстрему-
мов h\s> и h?1 уменьшатся по абсолютной величине, оставаясь при-
ближенно равными друг другу, а предельное отклонение в допол-
нительной точке экстремума hw возрастет по абсолютной вели-
чине. Используя линейную интерполяцию, легко установить положи-
тельные смещения узловых точек g\1' и g^' графика отклонений
Д (<р), при которых последний преобразуется в график Д (<р) с
тремя приближенно равными предельными отклонениями в трех точ-
ках экстремумов h, h{ и Л2 (см. графики отклонений, изображенные
сплошными кривыми на рис. 792).
График Д (<р) с уравненными предельными отклонениями в трех
точках экстремумов (называемый ниже кратко уравненным гра-
фиком отклонений), который получаем указанным способом, не
всегда после усреднения определит наилучшее приближение. Существен-
§ 46]
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
967
ным является вопрос, где на графике Д (ср) располагаются нулевая точка g
и точка h дополнительного экстремума. Рассмотрим характерные случаи.
а) На уравненном графике отклонений Д (ср) (верхний график на
рис. 792, изображенный сплошной кривой) точка h дополнительного
экстремума располагается вне отрезка приближения. После усред-
нения этого графика отклонений мы не . получим наилучшего
приближения, так как на заданном отрезке будет только пять предель-
ных отклонений, равных по абсолютной величине и чередующихся
по знаку (в точках, в которые переместятся при усреднении точки gx,
hi, gn, ht и g'g). Для отыскания графика отклонений, который после
усреднения определит наилучшее приближение, необходимо дальней-
шее смещение узловых точек gt и ръ в положительном направлении
оси абсцисс, чтобы получить график Д'1' (ср) (изображенный на рис. 792,
вверху, пунктиром), у которого предельное отклонение на границе
отрезка приближения (в точке ho') будет равно предельным откло-
нениям в точках экстремумов Л]11 и Лг1’.
968 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
б) На уравненном графике отклонений Д(у) (средний график
рис. 792) точка дополнительного экстремума располагается на от-
резке приближения, а нулевая точкам—вне этого отрезка или на гра-
нице его. После усреднения этого графика отклонений получим график,
определяющий наилучшее приближение функции положения шарнир-
ного четырехзвенника к заданной функции на указанном отрезке.
в) На уравненном графике отклонений Д (<р) (рис. 792 внизу)
точки g и h располагаются на отрезке приближения. В этом случае
отклонения на отрезке приближения оказываются переменными по
знаку. После усреднения этого графика мы не получим наилучшего
приближения, так как на заданном отрезке будет только четыре
предельных отклонения, равных по абсолютной величине (в точках,
в которые переместятся точки hn, h, hx и /г2 графика Д (<р)). В этом
случае, чтобы отыскать график отклонений, который после усредне-
ния определит наилучшее приближение, следует переместить про-
стую узловую точку g-A с правой границы отрезка приближения на
левую границу в положение g'-2’ и снова выполнить уравнивание
предельных отклонений посредством смещения двукратных узловых
точек gx и g%. Нулевая точка g'1' окажется при этом вне отрезка
приближения, и отклонения на отрезке приближения будут постоян-
ными по знаку.
Прежде чем перейти к численным примерам, которые должны на-
глядно пояснить изложенный процесс уравнивания предельных откло-
нений при наличии на графике отклонений нулевой точки, остановимся
на первом этапе этого уравнивания. Он заключается в перемещении
нулевой точки g в отрицательном направлении оси абсцисс в положе-
ние вне отрезка, определяемого узловыми точками gb g.t и g3 (см. верх-
ний и средний графики отклонений на рис. 791). Чтобы осуществить
указанное перемещение нулевой точки, следует задать двукратным
узловым точкам gt и g, положительные смещения по оси абсцисс.
В тех случаях, когда неизвестно, как выбрать зависимость между
этими смещениями, чтобы упростить последующий процесс уравни-
вания предельных отклонений в точках экстремумов, можно реко-
мендовать после выбора новой абсциссы <р*|‘ узловой точки gx под-
считывать новую абсциссу 92“ второй узловой точки g2 по формуле
<&" = 0,5955^4-0,61809'1“, (14.16)
где 9т — граница отрезка приближения [0, 9т]. Эта формула полу-
чена на основании следующих соображений. При отыскании первого
приближения мы условились выбирать абсциссы узловых точек gt,
g3, g3 по формулам (14.9):
?i = 0,09559m; <f2==0,65459m; 93 = <pm.
Они определяют собой абсциссы нижних (или верхних) предель-
ных отклонений при наилучшем приближении по Чебышеву с шестью
предельными отклонениями на отрезке [0, <рт].
§ 461
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
969
Если график отклонений первого приближения не имеет допол-
нительных нулевых точек на отрезке приближения [0, срт], то во
многих случаях путем малых поправок к указанным абсциссам можно
получить график с уравненными предельными отклонениями, который
после усреднения покажет наилучшее равномерное приближение с
шестью предельными отклонениями на указанном отрезке.
При наличии дополнительной нулевой течки график отклонений
после его уравнивания и усреднения часто будет близок по виду
к графику отклонений при на-
илучшем приближении по Че-
бышеву с семью предельными
отклонениями. Последний изоб-
ражен на рис. 793, вверху. На
этом графике точки нижних
предельных отклонений (точ-
ки gi> gi и g‘.\) имеют на от-
резке приближения [0, срт] аб-
сциссы *):
<Pi = 0,25cpm; <р2 = 0,75<рт;
= ?т-
Линейная зависимость
(14.16) такова, что при равно-
мерном перемещении узловой
точки gx из положения =
= 0,0955<pm в положение <pi = 0,25<pm узловая точка g2 будет рав-
номерно перемещаться из положения <р2 — 0,6545<pm в положение <р2 =
= 0,75<рт.
8°. Примеры уравнивания предельных отклонений при на-
личии дополнительной нулевой точки.
Первый пример. Пусть требуется воспроизвести шарнирным
четырехзвенником функцию
в пределах от г = 0 до г = -|-100. Угол входа = —}—175°
и угол выхода — -|~90°. Выполнив замену переменных, получим
следующую функцию, к которой на отрезке от <р = 0 до ср = 4-175°
должна быть приближена функция положения четырехзвенника:
, I 18 о
"Ь бТгу'? ’
(14.17)
где углы выражены в градусах.
*) Они определяются при помощи построения, указанного на рис. 793,
внизу, аналогичного построению на рис. 749.
970 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
Для отыскания первого интерполяционного приближения выберем
координаты узловых точек по формулам (14.9):
?1 = 4-16°43'; <р8 = +114°32'; <р3 = + 175°.
При этих условиях задача синтеза четырехзвенника имеет одно решс
ние и дает следующие параметры схемы:
а = 0,98129; Ь— 1,76288; с = 1,17899;
а = 95°4(У,9; ₽ = 220°55',2.
В таблице 14.11 (графа «1-й механизм») приведены отклонения функ-
ции положения этого механизма от заданной функции (14.17), а на
Таблица 14.11
Отклонения функции положения шарнирного четырехзвенника от функции (14.17)
У гол поворота звена ср Дф Точки на гра- фиках откло- нений (рис. 794 и 795)
1-й механизм вспомогательный механизм уравненный механизм
0 + 7',2 — 2',4 — З',6 h h<l) h('2
- 05°00' --2,9 — 4,2 — 5,1
- 07 00 -- 1,8 — 4,4 — 5,2 h™
- 09 00 -- 1,0 — 4,5 — 5,1 h">
- 11 00 --0,5 — 4,4 — 4,5
- 15 00 --0,1 — 3,9 — 4,1
~ - 16 43 0 — 3,4 — 3,9 gi
- 30 00 -'1,1 — 0,6 — 0,8 g{", gi2‘
- 40 00 --1,8 0 0
Н 45 00 -- 1,9 — 0,2 — 0,1
н 60 00 -1,0 — 2,2 — 2,4
- 75 00 — 0,5 — 4,6 — 4,8
- 83 00 — 0,8 — 5,0 — 5,4
- 85 00 — 0,9 — 5,1 — 5,4 h'i", h'2
- 87 00 — 0,9 — 5,0 — 5,4
Г 90 00 — 0,9 — 5,0 — 5,2
Г 105 00 — 0,3 — 3,1 — 3,3
?s = - г 114 32 0 — 1,2 — 1,4 ga
- 120 00 — 0,1 — 0,5 — 0,7
^l,=- - 128 56 — 0,9 0 — 0,1 Й1’
<Раа’ = - - 130 00 — 1,3 0 0 g?
- 135 00 — 2,4 — 0,1 — 0,2
- 150 00 — 7,1 -3,2 — 3,0
- 161 00 — 9,1 — 5,6 — 5,3
- 163 00 — 9,0 — 5,7 — 5,4 h',1', h'f
- 165 00 - 8,6 — 5,5 — 5,3
?«=н - 175 00 0 0 0 ft
рис. 794 сплошной кривой изображен их график А (<р). Этот график
отклонений имеет нулевую точку g, расположенную между узловыми
сочками gi и ga. Чтобы нулевая точка оказалась вне отрезка, на
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
971
котором расположены узловые точки, выберем новую абсциссу узло-
вой точки gt:
<р<*’=4-40°,
а новую абсциссу узловой точки g2 подсчитаем по формуле (14.16):
<pj‘’ = + 128°56'.
Если оставить неизменной абсциссу <р3 = —]—175° простой узло-
вой точки g3, то решение задачи интерполяционного приближения
функции положения четырехзвенника к функции (14.17) дает следую-
щие параметры схемы механизма:
а = 0,99614; Ь = 1,72459; 1,16964;
a = -f-95°06',l; ₽ = + 228°16',8.
В таблице 14.11 (графа «вспомогательный механизм») приведены от-
клонения функции положения этого механизма от функции (14.17);
график их Д(1) (ср) изображен на рис. 795. Этот график показывает
постоянные по знаку отклонения на отрезке приближения. Предель-
ные отклонения в точках экстремумов Л'1’, Л'/’ и h%' равны соответ-
ственно:
Дф = —4',5; Дф, = —5',1; Д<]>2 = —5',7.
972 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гл. XIV
Нулевая точка оказалась в области <р<^0. Практически последующее
уравнивание предельных отклонений вряд ли может иметь смысл, так
как дальнейшее снижение наибольшего модуля предельных отклоне-
ний не будет превышать нескольких десятых минуты. Тем не менее
выполним еще одну ступень уравнивания, чтобы получить резуль-
таты, которые облегчат отыскание наилучшего приближения по боль-
шему числу параметров.
Для уравнивания предельных отклонений Д^ и Дф2 в точках
экстремумов И.'" и Л2” графика Д'1’ (<р) следует сместить узловую
точку g2n в отрицательном направлении оси абсцисс. Тогда одно-
временно возрастет предельное отклонение в дополнительной точке
экстремума Л'1’. Выберем новую абсциссу узловой точки g!'1 равной
cp2s’ = + 130°.
Абсциссы 9J” == 40° и ср3 = 4- 175° двух других узловых точек gj1’
и gs оставим неизменными. Решив задачу синтеза четырехзвенника
по этим условиям, получим следующие параметры схемы механизма:
а — 0,99956; Ь — 1,72214; с= 1,16995;
а = 4- 94°57',0; 0 = 4- 227°56',2.
Подсчет отклонений приведен в таблице 14.11 (графа «уравненный
механизм»), график их Д'2’ (<р) изображен пунктиром на рис. 794.
Предельные отклонения в точках экстремумов й'2', й[2’ и Л22’ равны
соответственно:
Дф = — 5',2; Дф»! = — 5',4; Дф2 = — 5',4.
После усреднения этого графика отклонений получим приближение,
близкое к наилучшему с шестью предельными отклонениями на задан-
ном отрезке, приближенно равными по абсолютной величине и чере-
дующимися по знаку. Дополнительное седьмое предельное отклоне-
§ 46J
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
973
ние на границе отрезка приближения (при ср = 0), будет меньше
по абсолютной величине упомянутых шести. Наибольший модуль
усредненных отклонений будет £ = 2',7, относительная точность
приближения
/ 917
s=-fe-=o«.
На рис. 796 полученный механизм показан в положениях, соответ-
ствующих началу и концу отрезка приближения. Минимальный угол
передачи на отрезке приближения pmjn = 55°.
Второй пример. Рассмотрим еще раз задачу воспроизведения
шарнирным четырехзвенником функции
W = Z2
в пределах от г = 0 до г = -{-100. Угол выхода остается как
в предыдущем примере <{т = -{-90о. Угол входа выберем <рт =
= -{-185° (вместо <рт = -|~175° в предыдущем примере). Заменив
переменные, получим:
где углы выражены в градусах. Для отыскания первого интерполя-
ционного приближения выберем координаты узловых точек по фор-
мулам (14.9):
<Р1 = 4-17°40'; <ps = 4-121°05'; ср3 = -{-185°
974 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [гЛ. XIV
При этих условиях задача синтеза четырехзвенника имеет одно реше-
ние и дает следующие параметры схемы:
а= 1,0169; 1,8013; с = 1,2952;
а = + 83°51',6; ₽ = + 217°05',1.
Подсчет отклонений для этого механизма приведен в таблице 14.12
(графа «1-й механизм»), их график Д (ср) изображен сплошной кривой
на рис. 797. Этот график имеет нулевую точку g, расположенную
вблизи узловой точки g^. Переместив нулевую точку g в отрица-
тельном направлении оси абсцисс и уравняв предельные отклонения
в трех точках экстремумов, получим четырехзвенник со следующими
параметрами схемы:
а = 0,99964; Ь— 1,7227; с = 2,7006;
а = -]- 84°56',9; ₽ = + 216°26',3.
Он определен узловыми точками со следующими абсциссами:
<Р1П = 4-5О°; = -|-140о; <р3=4-185°.
График отклонений Д^ (<р) показан пунктиром на рис. 797,
а подсчет отклонений приведен в таблице 14.12 (графа «уравненный
механизм»). На этом графике точка дополнительного экстремума Л(1)
и нулевая точка лежат на отрезке приближения. Поэтому на
указанном отрезке отклонения оказываются переменными. В резуль-
§ 46|
СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
975
Таблица 14.12
Отклонения функции положения шарнирного четырехзвенника
от функции (14.18) (случай выбора абсциссы <ра = 185°)
Отклонения Дф Точки на графиках отклонений Д (р) и ДН»(ф) (рис. 797 и 798)
1-й механизм уравненный механизм
0 + 5°00' -- 10 00 -- 15 00 ¥1= + 17 40 + 20 00 -- 40 00 <fl1’= + 50 00 4- 60 00 - - 80 00 - - 100 00 - - 120 00 Та = 4- 121 05 ?'/’= + 140 00 4- 160 00 - - 165 00 - - 170 00 - - 175 00 - - 180 00 <р, = + 185 00 + 12',7 4-08,9 4-01,7 + 00,1 0 + 00,1 — 04,2 + 05,4 --05,3 + 02,7 + 00,4 — 00,1 0 — 00,9 — 04,6 — 05,6 — 06,7 — 06,4 — 04,0 0 + 06',5 4-оо,з — 02,9 — 04,0 — 04,1 — 04,0 — 00,6 0 — 00,5 — 02,7 — 04,1 — 01,8 — 00,9 0 — 02,3 — 03,9 — 04,0 — 04,2 — 03,0 0 Ло, Ло1’ . gi g'l1' h[l> g» е» W g-г
тате после усреднения график Д(,) (<р) не определит наилучшего при-
ближения.
Если в рассматриваемой задаче синтеза изменять абсциссы дву-
кратных узловых точек <р1 и <р2, сохранив неизменной абсциссу <р3 = срт
простой узловой точки, то нельзя получить графика с уравненными
отклонениями, который после усреднения определит наилучшее при-
ближение на заданном отрезке 0 <р 185°. Для отыскания такого
графика следует узловую точку ga перенести на другую границу
отрезка приближения, т. е. следует выбрать ее абсциссу:
?а = 0.
Первое решение приср3 = 0 можно рекомендовать провести, исполь-
зуя те абсписсы двукратных узловых точек gt и gt, которые соответ-
ствуют приближенному уравниванию трех экстремальных отклонений
при <р3 = 4~185°. Тогда процесс уравнивания обычно выполняется
с малыми поправками к этим абсциссам. (Ход самого процесса уравни-
вания в случае <р3 = 0 не будет отличаться от изложенного выше
для случая <р3 = —]— 185°.) Так, в приведенной задаче, выбрав абсциссы
узловых точек равными
'pl =47°30,j ^>2 =-j-142с30'; 'р3==0,
976 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
получим единственный механизм со следующими параметрами схемы:
а =0,99961; Ь = 1,7227; с =1,2590;
а = 4- 84°57',0; ₽ = + 215°02',4.
График отклонений А (ср) изображен на рис. 798, а подсчет отклоне-
ний дан в таблице 14.13. Нулевая точка графика отклонений лежит
в области <р^>фт. Предельные отклонения
/г2, h равны соответственно:
в точках экстремумов
Д<р1 = —6',0; Дф2 = — 5',9; Дф = —6',1.
Таблица 14.13
Отклонения функции положения шарнирного четырехзвенника
от функции (14.18) (случай, когда абсцисса <р3 = 0)
Отклонения Дф Точки на кривой отклонений Д (?) (рис. 798).
<?« = 0 0
- 10°00' — 05',8
- 12 00 — 05,0
- 14 00 — 05,9 Л,
1- 20 00 — 05,0
- 40 00 — 00,5
<fl = - |- 47 30 0 gl
- 60 00 — 01,1
Н 80 00 — 04,6
Н 92 00 — 05,9
И 95 00 — 05,9 hs
И 97 00 — 05,9
-100 00 — 05,8
- 120 00 — 02,8
<F«=H -142 30 0 gs
- 160 00 — 02,4
Н 175 00 — 05,0
- 177 00 — 06,1 h
- 180 00 — 06,0
+ 185 00 — 04,5 hm
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 977
После усреднения этого графика получим приближение, близкое к наи-
лучшему, с шестью предельными отклонениями на заданном отрезке,
приближенно ранными по абсолютной величине и чередующимися по
знаку. При <р==<рт предельное отклонение будет меньше по абсо-
лютной величине упомянутых шести. Наибольший модуль усредненных
отклонений будет £ = 3',05. Относительная точность приближе-
ния = 0,06%.
9°. Отыскание наилучшего приближения по семи парамет-
рам. В предыдущем параграфе рассмотрены задачи приближения
функции положения шарнирного четырехзвенника к функции w = zi
на отрезке 0 sC z -ф-100. В первой задаче входной и выходной
углы были соответственно — ~j-175° и фт —-]-90°. На рис. 794
пунктиром изображен график уравненных отклонений Д(2) (<р), а под-
счет его дан в таблице 14.11 (графа «уравненный механизм»). Этот
график имеет нулевую точку, которая лежит вне отрезка приближе-
ния 0 Ц-175°. На графике Д(2) (<р) нулевая точка не изоб-
ражена. Подсчеты показали, что абсцисса этой точки лежит в ин-
тервале — 3° <р — 4°.
Во второй задаче входной угол был <рт =185°, а выходной
по-прежнему фт = -ф- 90°. При выборе абсциссы <р3 простой узловой
точки g3, как и в первой задаче на правой границе отрезка прибли-
жения (<р3 = -ф-185°), был получен график Д(,,(?) с уравненными
предельными отклонениями в трех точках экстремумов h'l‘, h'/1 и h‘£,
изображенный пунктиром на рис. 797. Он также имеет нулевую
точку которая располагается на отрезке приближения. Она лежит
в интервале -ф- 6° <р -ф" 7°.
Очевидно, что сохранив выходной угол фт = 90°, но меняя вход-
ной угол в пределах 175°<^срт<^ 185°, можно отыскать такой гра-
фик уравненных отклонений, у которого нулевая точка совпадет
с началом координат. После усреднения этот график определит собой
наилучшее приближение с семью предельными отклонениями, равными
по абсолютной величине и чередующимися по знаку. Это приближение
можно назвать наилучшим приближением по шести параметрам (по пяти
параметрам схемы шарнирного четырехзвенника и углу входа tpm).
Напомним, что в первой из упомянутых выше задач (при <?т —
= -}-175° и = -ф- 90°) координаты узловых точек, определяющие
график с уравненными экстремальными отклонениями, были:
^’ = 4-40°; <р3г’= -ф-130°; = 4-175°.
Во второй задаче (при срт = -ф~ ^5° и фт = 4-90°) координаты
тех же узловых точек были:
<р/’ = 4-50°; <pV’ = 4-140°; <f>3 = 4-185°.
Решим еще раз задачу о воспроизведении шарнирным четырех-
звенником функции ®) = г2 на отрезке 0 sgJzsC 100. Выберем угол
978 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
выхода прежним фот = -1- 90°, а угол входа
В этом случае, заменив переменные, получим:
, _ । 1 2
360° ’
(14.19)
где углы <р и ф выражаются в градусах. Использовав данные преды-
дущих двух задач, найдем посредством линейной интерполяции абсциссы
Рис. 799.
узлов интерполяции, которые должны дать график с уравненными
предельными отклонениями в трех точках экстремумов:
= -(- 45°; = -|- 135°; <рз = 180°.
При этих условиях задача имеет по-прежнему единственное реше-
ние и дает следующие параметры схемы механизма:
а—1,0000; Ь= 1,7373; с = 1,2200;
а = 4-90°00'; р = 217°10',4.
Этот механизм изображен на рис. 799 в положениях, соответ-
ствующих началу и концу отрезка приближения. В таблице 14.14
приведены отклонения его функции положения от функции (14.19),
979
§ 46]
Синтез шарнирного четырехзвенника
Таблица 14.14
Отклонения функции положения шарнирного четырехзвенника
от функции (14.19)
ф Отклонения Дф Точки на графике отклонений Д (ф) (рис. 800)
0 0 £
- НТО’ — 04', 1
- 12 00 — 04,8 h
- 13 00 — 04,7
- 20 00 — 03,8
- 30 00 — 01,6
— н h 45 00 0 gi
- 60 00 — 01,3
г 70 00 — 02,9
- 80 00 — 04,2
- 88 00 — 04,7
- 90 00 — 04,8 Л,
р. 92 00 — 04,7
г 100 00 — 04,2
н 110 00 — 02,9
и 120 00 — 01,3
'fs = Н Н 135 00 0 g»
Н 150 00 — 01,6
1- 160 00 — 03,8
h 167 00 — 04,7
р 168 00 — 04,8 hs
1- 169 00 — 04,7
<р» = - Н 180 00 0 g»
а график отклонений Д (<р) изображен на рис. 800. Отклонения в трех
точках экстремумов Л, и /г2 равны между собой. Нулевая точка
Рис. 800.
совпала с началом координат. После усреднения этот график опре-
делит на заданном отрезке ()==£ 180е наилучшее приближение
по шести параметрам. Наибольший модуль усредненных отклонений
980 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
шпри этом приближении будет L ~ 2',4. Относительная точность полу-
ченного приближения
- = 0,03% *).
В общем случае наилучшее приближение по шести параметрам нужно
искать в той области значений угла входа <рт (или угла выхода фт),
где на графике первого приближения имеется дополнительная нуле-
вая точка. Для установления этой области следует угол входа
(или угол выхода tpm) изменять в том направлении, в котором на
графике первого приближения предельное отклонение при <? — 0 умень-
шается по модулю, так как при пересечении дополнительной нулевой
точкой этой границы отрез-
ка приближения [0, <рш] от-
клонение на ней должно пе-
ременить знак.
Чем ближе значение ше-
стого параметра ут или <рт
к тому, которым опреде-
ляется наилучшее приближе-
ние по шести параметрам, тем
выше точность наилучшего
приближения по пяти пара-
метрам. На рис. 801 изобра-
жена кривая зависимости пре-
дельного отклонения L при
наилучшем приближении по
пяти параметрам в функции
от угла входа срт при воспро-
изведении шарнирным четы-
рехзвенником функции w — z4, на отрезке При неизмен-
ном угле выхода <рш = -|-90° кривая показывает резко выраженный
минимум при значении = 180°, соответствующем наилучшему
приближению по шести параметрам.
10°. Пример повышения точности приближения путем оты-
скания наилучшего приближения по шести параметрам. В § 43,
8° дано решение задачи о воспроизведении шарнирным четырехзвен-
ником функции
® = lgz
(14.20)
на отрезке -pl ^zsC-plO. Углы входа и выхода были гут —
— % 100° и фот =— 50°. Наибольший модуль усредненных отклоне-
ний, характеризовавший точность полученного приближения был
♦) Отметим, что при этом приближении абсциссы узлов интерполяции
(<р, = -ф 45°; tp, = -ф 135°; tp8 = -ф 180°) равны абсциссам предельных отклонений
при наилучшем приближении по Чебышеву с семью предельными отклонения-
ми на заданном отрезке.
§ 46] СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА 981
Е = 06',1. Его относительная величина |^-1 = 0,20%. В пункте 5°
I хт I
настоящего параграфа после уравнивания предельных откло-
нений получено приближение с наибольшим модулем усредненных
отклонений £(2)=Г,6. Его относительная величина +— =0,055%.
I rm I
Попробуем дальше повысить точность приближения, увеличивая угол
выхода фт.
Выбрав по-прежнему угол входа <рт = + 90°, зададим угол вы-
хода фт =— 75°. Заменив переменные в функции (14.20), получим:
ф= — 75°lg(l +0,09?). (14.21)
Координаты узлов интерполяции выберем равными кооординатам
тех же узлов в примере § 43, 8°;
<?1 = + 9°33'; <p2 = + 65°27'; <р3 = -|-100о.
Решение задачи синтеза по этим условиям дает один шарнирный
четырехзвенник со следующими параметрами схемы:
а = 0,84352; 5 = 1,3079; с = 0,54274;
а = + 54°15'; £ = + 224°22'.
Если подсчитать отклонение на границе отрезка приближения при
ср —0, то получим:
Афо = + 2’,1.
Напомним, что при угле входа <рт = +100° и угле выхода
фт = — 50° (см. § 43, 8°) на графике отклонений первого интерпо-
ляционного приближения (см. рис. 751 и табл. 13.3) предельное
отклонение при ср = О было
Дф0 = — 12',2.
Изменение знака отклонений на указанной границе отрезка при-
ближения при переходе от угла выхода фт = — 50° к углу выхода
фст = -—75° свидетельствует о появлении при фт =— 75° на отрезке
приближения дополнительной нулевой точки.
В таблице 14.15 (графа «1-й механизм») приведен подсчет откло-
нений на всем отрезке приближения 0 <р -f- 100°, а их график
Д (<р) изображен пунктиром на рис. 802. Этот график имеет ну-
левую точку g с абсциссой ср + 1°.
Уравнивание предельных отклонений приводит к следующим коор-
динатам узловых точек:
<р'11' = +11о; ^’ = + 64°48'; <р3 = +100°.
Й82
синтез механизмов по методу наилучшёго приближения (гл. xiy
При этих координатах получаем следующие параметры схемы
четырехзвенника:
а = 0,84089; b = 1,3055; с = 0,54260;
«==4-54°11',3; р =219с59',0.
Рис. 802.
Таблица 14.15
Отклонения функции положения шарнирного четырехзвенника
от функции (14.21)
9 Отклонения Дф Точки на графиках откло- нений Д (ср) и Да) (ср) (рис. 802)
1-й механизм уравненный механизм
0 + 2',3 — Г,0 ho, К"
г- 01°00' 0 — 2,3 g
- 02 00 — 0,7 — 4,6
k- 03 00 — 0,8 — 2,4
¥Т=- - 09 33 0 — 0,3 gi
г 1100 — 0,1 0 g'/
- 20 00 — 1 ,6 — 1 Л
г 30 00 — 3,1 — 2,7
- 32 00 — 3,1 — 2,8 Лъ Л'*’
- 34 00 — 3,1 — 2,7
- 40 00 — 2,7 — 1 Л
- 50 00 — 1,3 — 1 ,0
?s”=- - 64 48 — 0,1 0 go
?8=- - 6527 0 — °.2 gs
- 8000 — 0,2 — 1 ,4
- 90 00 — 2,6 — 2,7
- 92 00 — 2,7 — 2,8 hit h'i1
- 94 00 — 2,3 — 2,4
h 100 00 0 0 gt
§ 46]
СИНТЕЗ ШАРНИРНОГО' ЧЕТЫРЕХЗВЕННИКА
983
Полученный механизм изображен на рис. 803 в положениях,
соответствующих началу и концу отрезка приближения. Минималь-
ный угол на отрезке приближения 27°. График отклоне-
ний Д'11 (ср) изображен сплошной кривой на рис. 802. Подсчет откло-
нений приведен в таблице 14.15 (графа «уравненный механизм»). Пре-
дельные отклонения в точках экстремумов h"', h\l>, h?" равны соот-
ветственно:
Дф'1, = —2',6; Дф'11, = —2'8; = —2',7.
Таким образом, при изменении угла выхода от срт =— 50и до
фт = — 75° наибольший модуль усредненных отклонений снизился от
L == Г,6 до L = 1',4, а его
относительная величина — от
0,055 до 0,031%.
11°. Случай, когда интер-
поляционная задача имеет
три решения. До сих пор на-
ми предполагалось, что интер-
поляционная задача синтеза
шарнирного четырехзвенника
по пяти параметрам имеет един-
ственное решение при любых
абсциссах узлов интерполяции.
В этом случае на основании
теоремы Геронимуса можно ут-
верждать, что для отыскания
наилучшего приближения функции
положения шарнирного четырехзвенника к заданной функции на
предписанном отрезке достаточно найти на этом отрезке приближе-
ние, по крайней мере, с шестью предельными отклонениями, равными
по абсолютной величине и чередующимися по знаку.
Однако в общем случае интерполяционная задача синтеза шарнир-
ного четырехзвенника по пяти параметрам имеет не одно, а три
решения. В этом случае пока не представляется возможным строго
сформулировать условия наилучшего приближения. Но можно наме-
тить следующий практический путь отыскания этого приближения *):
обозначим графики отклонений трех механизмов, найденных в резуль-
тате решения задачи первого интерполяционного приближения, через
Д’ (ср), Д» (ср) и Д111 (ср). При изменении абсцисс узлов интерполяции
каждый из этих графиков породит свое семейство графиков отклоне-
ний; посредством уравнивания и усреднения графиков Д1 (<р), Ди(ср)
и ДП1 (ср) отыщем в каждом из упомянутых семейств график, который
имеет на заданном отрезке, по крайней мере, шесть предельных от-
клонений, равных по модулю, но чередующихся по знаку. Каждый
из этих графиков представит собой график отклонений, определяющий
*) Он указан ранее Е. Г. Новодворским [40|.
984 СИНТЕЗ МЕХАНИЗМОВ ПО МЕТОДУ НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ [ГЛ. XIV
наилучшее приближение в том семействе, которому он принадлежит.
Тот из трех упомянутых графиков отклонений, который покажет
наименьшие по абсолютной величине предельные отклонения, опре-
делит наилучшее приближение в задаче синтеза по пяти параметрам
схемы шарнирного четырехзвенника.
В § 43, 3° решена задача интерполяционного приближения функ-
ции положения шарнирного четырехзвенника к функции
, 9 2
v 1000° ?
на отрезке OsgcpsC 100°. Узлы интерполяции
интерполяционного приближения были выбраны
при отыскании этого
по формулам (13.33):
cpi = -|- 9°33'; ср2 = -ф- 65°27'; <р3 = —|— 100°.
В результате решения получено три шарнирных четырехзвенника.
Их графики отклонений Д1 (ср), Д11 (<р), Д111 (ср), изображенные на
рис. 744, оказались существенно отличными друг от друга. Графики
Д1 (ср) и Дш (ср) не имеют дополнительных нулевых точек на отрезке
приближения и показывают на этом отрезке постоянные по знаку от-
клонения, а график Ди(<р) имеет на отрезке приближения дополни-
тельную нулевую точку g, в которой отклонения изменяют свой
знак.
Для уравнивания предельных отклонений на графиках Д1 (ф) и
А" (ср) потребовались различные смещения узловых точек <pt и <р2.
Так, в результате одной ступени уравнивания графика Д1 (ср) по-
лучены следующие абсциссы узловых точек:
<Р! == 12°16'; <р2 = 68°46'; ср3 = 100°.
Соответствующий график Д'^Чср) с приближенно уравненными
предельными отклонениями изображен сплошной кривой на рис. 804.
§ 46)
'СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
985
После его усреднения получен наибольший модуль усредненных
отклонений L Аа 4',5.
В результате одной ступени уравнивания предельных отклонений
графика Д11 (<р) получены такие абсциссы узловых точек:
ср1 = 27°36',7; ср2 = 83°30',7; <р3 = 0.
Соответствующий график Д21’ (ср) с приближенно уравненными пре-
дельными отклонениями показан пунктиром на рис. 804. После его
усреднения получен наибольший модуль усредненных отклонений
L 2',2.
График Д,п (ср) рис. 744 нами не уравнивался, так как заведомо
его наибольший модуль усредненных отклонений не может быть
28'
меньше -у = 14', где 28' — наименьшее по модулю предельное откло-
нение графика Д’11 (ср) (см. таблицу 13.1, графу «третий механизм»).
Во всех примерах настоящего параграфа выполнялось уравнивание
графиков отклонений шарнирного четырехзвенника. Однако все изло-
женное в настоящем параграфе целикрм относится и к уравниванию
графиков отклонений кривошипно-шатунного механизма, схема кото-
рого, так же как и схема шарнирного четырехзвенника, определяется
пятью параметрами.
ГЛАВА XV
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
§ 47. Механизмы с остановкой, у которых ведомая диада
присоединена к шатуну основного механизма
1°. Схемы шарнирно-рычажных механизмов с остановками.
При проектировании машин автоматов большую роль играют меха-
низмы, у которых при непрерывном вращении ведущего звена на
заданном угле его поворота ведомое звено остается неподвиж-
ным. Такие механизмы называются механизмами с остановкой.
В практике машиностроения в качестве механизмов с остановками
чаще всего используются кулачковые механизмы, которые универ-
сальны по своим кинематическим возможностям и просты с точки
зрения расчета. Однако они обладают рядом существенных недо-
статков, из которых главными являются малая износоустойчивость
кулачков, особенно в механизмах с большими нагрузками, и неспо-
койная работа вследствие вибраций в машинах с большим числом
оборотов ведущего вала. В результате кулачковые механизмы в ряде
случаев ограничивают повышение производительности и мощности
отдельных машин. Эти пределы удается переходить, применяя шар-
нирно-рычажные механизмы с остановкой. Но расчет и проектирова-
ние их значительно сложнее, чем кулачковых. Тем не менее шар-
нирно-рычажные механизмы с остановками находят в быстроходных
машинах-автоматах все более широкое распространение.
На рис. 805—808 изображены четыре типовые схемы шарнирно-
рычажных механизмов с остановками. В основе каждой из них лежит
шарнирный четырехзвенник ABCD, к шатуну и стойке которого
соответствующим образом присоединена диада.
На рис. 805 изображены шарнирный четырехзвенник ABCD и
траектория е точки Е его шатуна. Точку Е, принадлежащую шатуну
четырехзвенника, условимся кратко называть шатунной точкой,
а ее траекторию шатунной кривой.
Шатунная кривая е на участке EiEt, соответствующем углу
поворота ср13 ведущего звена АВ, приближена к дуге окружности q
с центром М. Присоединим к указанному четырехзвеннику диаду EFG.
Длину звена EF выберем равной радиусу окружности q. Звено EF
§ 47]
ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ
987
расположим так, чтобы во время движения шатунной точки Е по
отрезку шатунной кривой е, на котором последняя приближена
к дуге окружности q, шарнир F совпал с центром М. Тогда на
соответствующем угле поворота <р12 ведущего звена АВ ведомое
звено FG механизма будет стоять на месте.
На схеме рис. 806 звено EF заменено ползушкой р, которая движется
по круговой кулисе, жестко скрепленной с шатуном ВС и описанной
Рис. 805. Рис. 806.
из точки Е радиусом, равным радиусу окружности q. На угле пово-
рота <Р1я ведущего кривошипа АВ, на котором траектория шатунной
точки Е приближена к окружности q, ведомое звено механизма FG
будет стоять на месте. В тех случаях, когда шатунная точка Е ока-
зывается далеко удаленной от шарниров В и С, эта схема меха-
низма с остановкой может дать более конструктивное решение, чем
предыдущая схема.
В предельном случае при увеличении радиуса окружности до
бесконечности схема на рис. 805 переходит в схему на рис. 807,
где ползушка р диады присоединена шарнирно к такой точке Е
шатуна ВС, траектория которой е на известном участке приближена
к прямой линии g. Тогда на угле поворота ср12 ведущего криво-
шипа АВ, соответствующем участку приближения, ведомая кулиса EG,
ось которой совпадает с направлением прямой g, будет оставаться
неподвижной.
Схема на рис. 806 при увеличении радиуса окружности q до
бесконечности переходит в схему на рис. 808, где ползушка р дви-
жется по такой прямолинейной кулисе q, закрепленной на шатуне ВС,
ось которой на угле поворота ср12 кривошипа АВ огибает неподвиж-
ную точку М. Тогда на указанном угле поворота ведущего криво-
шипа ведомое звено FG, шарнир которого F совпадает с точкой
огибания М, будет иметь остановку.
В каждой из этих типовых схем исходный шарнирный четырех-
звенник может быть заменен кривошипно-шатунным или кулисным
988
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
(ГЛ. XV
механизмом. Вращательная пара G, которой диада присоединяется
к стойке, может быть заменена поступательной, и таким образом ведо-
мое звено в шарнирно-рычажном механизме с остановкой будет иметь не
возвратно-колебательное движение, а возвратно-поступательное.
Задача синтеза шарнирно-рычажного механизма с остановкой по
одной из указанных схем сводится к задаче приближения траекто-
рии шатунной точки исходного четырехзвенного механизма к дуге
окружности или к прямой линии *). Это относится и к схеме на
рис. 808, которая, как будет показано ниже, может быть получена
из схемы рис. 807 путем обращения движения.
2°. Приближение шатунной кривой к дуге окружности (гра-
фическое решение). Пусть исходный четырехзвенник ABtCiD
(рис. 809) нам задан и требуется найти на подвижной плоской фигуре,
жестко связанной с его шатуном BiC\, такую точку Et, траектория
которой будет приближена к дуге окружности на заданном угле
поворота <pi2 кривошипа. Плоскую фигуру, жестко связанную
с шатуном, обозначим через S. Ее положения Si и S2 опреде-
лятся точками BtCi и В%Сг. В пересечении биссектрис углов BxABt
и CtDCv найдем полюс поворота Р12 плоской фигуры S шатуна при
переходе ее из положения St в положение S2. Соответствующий
угол поворота будет:
012 = /, BiP^B^— СгР^С,.
(На рис. 809 угол не изображен.) В пересечении направлений
и CtD найдем полюс Pti (на рис. 809 он располагается вне чертежа),
*) Эта задача рассматривалась П. Л. Чебышевым, Бурместером [67а, б],
Альтом [61е, ж, з, о], Лихтенгельдтом [88в, и] и др. Не повторяя их результа-
тов, укажем в следующем пункте решение, которое является достаточно
простым для инженерных приложений и в то же время обеспечивает необхо-
димую точность приближений. Оно впервые изложено в работе [57а].
§ 47]
ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ
989
определяющий положение S] плоской фигуры, бесконечно близкое
положению В пересечении направлений АВ2 и C2D найдем полюс
Р23, определяющий положение S2 плоской фигуры, бесконечно близкое
положению S2. Построим на полюсах Р12, Ри и Р22 кривую цент-
ров Ж1129 (см. § 37,8°). Она изображена на рис. 809 жирным пунктиром.
Рис. 809.
Так как последовательные положения точки В\ шатуна лежат на
окружности с центром А, а все последовательные положения точки С]
шатуна — на окружности с центром D, то кривая центров Ж1122 должна
пройти через неподвижные шарниры А и D четырехзвенника. Это
может служить контролем правильности ее построения.
Выберем на кривой центров Ж1122 произвольный центр Ж. Соответ-
ственную ему круговую точку можно найти графически, исполь-
зовав любые два из следующих трех равенств:
Z Е,Р12Ж = °‘а-, Z = 0, Z £iAfP12 = Z Р^МРы
(Соответствующие графические построения на рис. 809 не показаны).
Повернув точку Et вокруг полюса Р12 на угол 612, найдем ее поло-
жение Et. Построим шатунную кривую е шатунной точки Е\. Окруж-
990
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[ГЛ. XV
ность q, описанная вокруг центра М через точку Е1г пройдет через
ее положение £2 и в точках Ei и £2 будет касаться шатунной кри-
вой е. Таким образом, на участке ЕХЕ^ шатунная кривая е будет
приближена к дуге окружности q. На рис. 810, чтобы наглядно
показать характер получаемого приближения, отдельно изображены
шатунная точка Е\ и ее положение Еъ шатунная кривая е и дуга
окружности q, описанной вокруг центра М. Это будет интерполя-
ционное приближение, определяемое двумя двукратными узлами Et и Е3.
С точки зрения проектирования механизма с остановкой особый
интерес представляет участок кривой центров 7И1122, расположенный
между шарнирами А и D. Центру на кривой центров Л!1122, совпа-
дающему с шарниром А, соответствует на плоской фигуре шатуна
круговая точка шатунная кривая которой точно совпадает
Построим
их
шатунные кривые
с окружностью. Центру на кри-
вой центров Л41122, совпадающему
с шарниром D, соответствует на
плоской фигуре шатуна круговая
точка Ci, шатунная кривая которой
также совпадает точно с дугой
окружности. На упомянутом участке
кривой центров 7И1122 выберем ряд
центров М, М*, М**, ..., после-
довательно перемещаясь от точки D
к точке А, и найдем соогветствен-
ные им круговые точки Elt £*, Ef*,...
е, е*, е**, ... Найдем наибольшие
по абсолютной величине
отклонения каждой из этих шатунных кривых
от дуги окружности, описанной вокруг соответствующего центра.
При перемещении центра АЛ от точки D к точке А указанные от-
клонения будут сначала возрастать от нуля (нуль получим, когда
центр М совпадет с шарниром £)), а затем снова убывать до нуля
(когда центр совпадет с шарниром А). Следовательно, если задано
допускаемое отклонение шатунной кривой от дуги окружности на
соответствующем угле поворота ср12 ведущего звена четырехзвенника,
то на участке AD кривой центров Л!1122 всегда можно найти область
таких центров Л4 и соответствующих им круговых точек Elt ша-
тунные кривые которых на угле ср12 приближены к дуге окружности
с отклонениями, меньшими допускаемых.
Понятно, что указанное графическое решение задачи о приближе-
нии шатунной кривой к дуге окружности не всегда позволяет полу-
чить ответ с достаточной точностью. Поэтому укажем еше аналити-
ческое решение этой же задачи.
3°. Приближение шатунной кривой к дуге окружности (анали-
тическое решение). По заданным углам и а2 (рис. 809), которые
определяют первое и второе положения АВ{ и АВц ведущего криво-
шипа относительно стойки AD, подсчитаем соответственные углы р.
§ 47]
ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ
991
и (см. § 43, 2°), определяющие первое и второе положения QZ)
и C2D коромысла четырехзвенника относительно той же стойки.
Выберем декартовы оси X, Y с началом в шарнире А и с осью А,
направленной вдоль стойки. Найдем в них координаты полюсов Р12,
Рп и Р22. Для прямых APi2 и DPi2, в пересечении которых опре-
деляется полюс Р12, имеем уравнения:
r=(A'_l)tg
(15.1)
Координаты полюса Р12 как точки пересечения этих прямых:
полюсов Ри
Аналогичным путем найдем координаты мгновенных
и Р22:
Ап = —,--Ц-------; Yn — Xlt tg а,;
tgfil — tgni’ . 11 6
A 22 ~ to 8 ^tP а ’ ^22 == ^22 tg а2-
Ig P2 — tg “2
(15.3)
Для координат шарнира Bt имеем:
XB = a cos at; YB = a sin a1(
(15.4)
где a — длина звена ABt.
Углы наклона прямых ДР12 и ВуРщ к оси X обозначим соответ-
ственно через 8Д и 8В (прямая BtPK и угол 8В на рис. 809 не пока
заны). Тогда получим:
ув-уы
Хв-Хл'
(15.5)
Угол конечного поворота:
т = Z BtPnA = 8д—8В. (15.6)
Перейдем к новым осям координат х, у, параллельным осям X, У,
но с началом в полюсе Р12. В этих осях координаты полюсов P1t
и Р22 найдем по очевидным соотношениям:
ха — Хи — А’12;
х22 = А"22 — А i2;
J11 = ^11-------- I’lsl
Уа = У а — К12;
(15.7)
992 СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ [гл. XV
В осях х, у для кривой центров Л11122 имеем параметрические
уравнения (11.85):
г — Л(1—tg88) —2/itg5 __ , ?
М — (1 + tg2 6) (js - h tg 8) ’ УМ ~ M tg 8’
где Ji, js, Jt — коэффициенты, выражаемые через координаты по-
люсов Рц(хц, jn) и Р22(х22, у22) в тех же осях:
У1 = ХИ 4“ Х?й> J.I = ХнУи Х&УИг
Ji—Ун “bjaal /4 = -*и-*:22—УнУа,
а параметром tg 8 является угловой коэффициент прямой, соединяющий
выбранный центр М(хм, ум) на этой кривой с полюсом Р12, с кото-
рым совпадает начало координат.
Границы интересующего нас участка AD кривой центров опреде-
ляются следующими значениями углового коэффициента:
tg8A = ^; tgSD = ^±l. (15.8)
1 12 '12
По известным координатам центра ЛЦхм, ум) на кривой цент-
ров Mnw координаты соответственной точки Et(XE, уе) в S) найдем
по формулам (11.21), которые перепишем в принятых здесь обозна-
чениях:
, 612
Ум хм tg ~п
tg 8Е = - -------fj— ,
хм+УмЪ^ (15.9)
v _ -Уж*!!" *ж-Уц . s
Е (xn — x^)tg8£ —уп+ум ’ Уе хе S е-
Радиус окружности, к дуге которой приближена на требуемом
участке шатунная кривая точки Еъ найдем по очевидной формуле:
EiM — (xg— Хж)2 -[-( Уе—Ум)2- (15.10)
4°. Пример синтеза шарнирно-рычажного механизма с оста-
новкой. На рис. 811 изображена требуемая функция положения меха-
низма. По оси абсцисс отложены углы поворота а ведущего звена
механизма, по оси ординат — углы поворота у ведомого звена. Ведо-
мое звено должно иметь остановку в крайнем положении на угле
поворота ведущего звена
«т^75°.
Затем ведомое звено должно переместиться в другое крайнее поло-
жение и при повороте ведущего звена на угол a0«gl20o возвра-
титься в первое крайнее положение. Угол размаха ведомого звена
7т = 60°.
§ 47] ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ 993
Спроектируем шарнирно-рычажный механизм с остановкой по схеме
рис. 805. Предположим, что размеры основного шарнирного четырех-
звенника ABiCtD (рис. 809) заданы:
AD=\; a = ABt = 0,4- b = BlCi=\,2- c = C1D = 0,75.
Выберем угол аь определяющий первое положение четырехзвенника
99=4-90°*). Угол поворота четырехзвенника, соответствующий пере-
ходу четырехзвенника из первого положения во второе, выберем
равным а|2 = ага = 75°. Тогда получим а2 = 4~ 165°. Соответственные
углы и р2, определяющие первое и второе положения CtD и С2О
коромысла четырехзвенника, получаются по подсчету:
р1 = 4-78°16',1; р2 = 4-116°07',7.
По формулам (15.2) — (15.4) подсчитаем координаты полюсов Р1г,
Рп, Рц 11 шарнира Bt в осях A, Y с началом в шарнире А:
Д'13 = 4- 1,197046; У12 = — 1,560020;
А'11==0; Уи=—4,815765;
Х2.2 = 4- 1,151324; У 22 = —0,308496;
Аф = 0; YB = 4- 0,400000.
Перейдем к осям координат х, у, параллельным прежним, но
с началом в полюсе Р12. Найдем в них координаты полюсов Рп и Р.,.,-_
хи = Х11 — А’12 = — 1,197046; _уп= У„ — У12 = — 3,255745;
х22 = Х22 — АГ12 = — 0,045722; _у22 = Y22 — У12 = 1,251524.
Подсчитаем коэффициенты параметрического уравнения кривой
центров М1122:
/! = -]-1,242768; /3 = — 1,349273;
/8 = — 2,004221; /4 = 4-4,129374.
*) Для выбора длин звеньев и угла «, известную помощь может оказать
атлас шатунных кривых Хронса и Нельсона (81].
32 И. II. Артоболевский
994 СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ |гл. Х\
(На рис. 809 кривая центров Л4”22 соответствует этим значениям
коэффициентов). Найдем по формулам (15.8) углы 8Л и 8О наклона
прямых Р12Л и РцО к оси X:
8л = 4-127е30'; 8D=4-97°12'.
Точки кривой центров /И1122 на участке AD определяются значе-
ниями параметра 8:
4- 97° 12' sgo^S-i- 127°30'.
Выберем в этих пределах значения
8 = 4-105е; 8* = -4110е; 8** = — 115°.
Координаты соответствующих центров М, /И* и Л4** на уча-
стке AD подсчитаем по уравнениям (11.85):
хм =—0,486758; ум =4~ 1,816607;
х^ = — 0,680590; _у*и = 4- 1,869907;
х^ = —0,863200; _Уд? = 4- 1,851139.
По формулам (15.5) и (15.6) угол оя и угол поворота 6Н будут:
8В= 121°24',8; ^ = 8Л —8в = 6°05',2.
После этого координаты соответственных шатунных точек Elt Е* и Е**
подсчитаем по уравнениям (15.9):
хЕ = — 0,391551; уЕ =4-2,496510
х> =—0,617743; j/J = 4-2,493644
х^ = —0,826522; _у>* = 4~ 2,4! 2205.
На рис. 809 нанесены шатунные кривые е, е* и е** этих точек
и их положения Eit Е* и E.J*.
Радиусы окружностей, к которым приближены эти кривые, найдем
по формуле (15.10):
MEi = 0,68654; М*Е% = 0,62690; Л4**£** = 0,56226.
Отклонения Дг шатунных кривых е, е* и е** от дуг соответствую-
щих окружностей, измеряемые по направлениям радиусов этих окруж-
ностей (от шатунной кривой к дуге окружноеги) в функции от угла
поворота а ведущего кривошипа, приведены в таблице 15.1.
Усредним отклонения путем выбора за окружность, к дуге кото-
рой приближена шатунная кривая, окружность с тем же центром М,
но с радиусом
§ 47]
ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ
995
Таблица 15.1
Отклонения шатунной кривой от дуги окружности
'J. — 75” 901' 150е 120° 127с30 135" 150° 165° 180'
Дг = 0,00066 0,0 0,00030 0,00068 0,00075 0,00070 0,00032 0,0 0,00072
Дг* э» 0,00088 0,0 0,00040 0,00090 0,00099 0,00092 0,00042 0,0 0,00095
Дг** — 0,00091 0,0 0,00011 0,00091 0,00104 0,00096 0,00044 0,0 0,00099
Тогда получим следующие значения радиусов соответствующих ок-
ружностей:
г = 0,68616; г* = 0,62640; г** = 0,56174.
Длина EF присоединяемой диады должна выбираться равной указан
ному радиусу. Длина звена FG (рис.
ного шарнира G определяются на
основании заданной функции поло-
жения механизма (рис. 811). По-
кажем, как практически это выполня-
ется. Выберем шатунную кривую е**
(рис. 809) для использования в проек-
тируемом механизме с остановкой. Она
отдельно изображена на рис. 812 *);
гам же отмечены центр М соответ-
ствующей окружности <7 и первое
положение Et шатунной точки.
Поставим шарнирный четырех-
звенник в положение ABCD, соот-
ветствующее второму крайнему по-
ложению ведомого звена FG. Это
положение определим заданным углом.
_ вАД,=а0= 120'.
805) и координаты неподвиж-
Рис. 812.
Найдем мгновенный полюс Р вращения шатуна в пересечении напра-
влений АВ и CD. В положении механизма ABCD шатунная точка
займет положение Е. Прямая РЕ определит нормаль к шатунной кри-
вой в точке Е. Отложим на этой нормали от точки Е отрезок EF,
равный радиусу r — ExI'x. Точка F укажет второе крайнее положение
подвижного шарнира ведомого звена FG. Первое крайнее положе-
*) При переносе шатунной кривой е** и точек Л4** и Е^-на рис. 812 был снят
индекс ** в их обозначениях.
32-
996 синтез механизмов с остановками [гл. XV
ние Fi этого шарнира совпадает с центром М. Из середины отрезка
FjF восставим перпендикуляр Л и выберем на нем шарнир G из
условия, чтобы угол размаха звена FG был равен заданному углу:
7m — 60°.
Таким образом определится длина звена FG и координата его непо-
движного шарнира G.
Так как шатунная кривая е имеет известные отклонения от дуги
окружности, то ведомое звено FG при повороте ведущего звена АВ
на заданный угол ат будет иметь малые отклонения от некоторого
среднего положения. Ио известным отклонениям шатунной кривой от
дуги окружности легко определить отклонения от среднего положе-
ния ведомого звена на участке остановки, пользуясь методами теории
точности.
Таблица 15.1 свидетельствует, что наибольшие отклонения шатун-
ной кривой от дуги окружности получаются в положении механизма,
определяемом углом
а = = 9.0°-К_165°, = 127°30'.
Подсчет отклонений, приведенный в таблице 15.1, показывает, что
отклонения при
а = 75° и а = Ц- 180е
оказываются еще равными или меньшими, чем отклонение при я =
= -|~127°30'. Это значит, что практически в полученном механизме
приближенный выстой ведомого звена FG будет на угле
у.т^ 180° — 75° = 105°.
Угол а0 сократится соответственно до ап^105°.
5е. О наилучшем приближении шатунной кривой к дуге
окружности. Шатунная кривая четырехзвенника является трицирку-
лярной кривой 6-го порядка *). Это значит, что она трижды проходит
через те мнимые бесконечно удаленные точки плоскости, называемые
циркулярными точками, через которые проходит каждая окружность.
Следовательно, шесть из двенадцати возможных общих точек шатун-
ной кривой и окружности всегда совпадают с упомянутыми цирку-
лярными точками плоскости. Действительных общих точек у шатунной
кривой с окружностью может быть шесть, четыре или две. Наилуч-
шее приближение шатунной кривой к окружности в общем случае
определяется как равномерное приближение с семью предельными
отклонениями на заданном отрезке.
*) См. (63а].
§ 47]
ПРИСОЕДИНЕНИЕ ДИАДЫ К ШАТУНУ
997
До сих пор известны решения о наилучшем приближении шатун-
ной кривой к дуге окружности только для случаев, когда эта кривая
является симметричной. Эти решения для четырехзвенника получены
Чебышевым, а для кривошипно-шатунных и кулисных механизмов —
Блохом [9е, ж, о]. Изложенные выше методы уравнивания кривой
отклонений позволяют дать решение для отыскания наилучшего при-
ближения несимметричной шатунной кривой к дуге окружности.
В качестве первого приближения шатунной кривой е к дуге
окружности q будем искать интерполяционное приближение с двумя
двукратными узлами Е\ и Д2 и одним простым Е3 (рис. 813). Первые
выберем на отрезке приближения, а последний — на границе этого
отрезка. Для отыскания указанного приближения нужно рассмотреть
пять положений плоской фигуры шатуна четырехзвенника: три конечно
удаленные положения St, <S2,и два положения S] и Sj, бесконечно близ-
кие соответственно положениям <Si и &. Эти положения определятся
полюсным треугольником РцР\3Р23
и мгновенными полюсами Рц и
Рад.
Если на полюсах Pi2, Рц, Р22 по-
строить кривую центров ЛД122, а на
полюсах Р12, Р1з, Раз, Рц— кривую цен-
тров ЛД123, то точки их пересече-
ния М, не совпадающие с полю-
сами Р12, Рц, будут центрами Бур- Рис. 813.
местера /И11223. Соответствующие
этим центрам точки Бурместера Д]1223 будут иметь шатунные кривые
с искомым интерполяционным приближением к дуге окружности,
описанной из соответствующего центра Бурместера.
Обе кривые центров ЛД122 и ЛД123 должны пройти через непо-
движные шарниры четырехзвенника А и D. Поэтому центров Бурме-
стера, которые дают интересующее нас решение, может быть два или
ни одного.
Допустим, что в положении S) плоской фигуры шатуна нами уста-
новлена точка Бурместера Ех, шатунная кривая которой в узлах ин-
терполяции Ei и Е2 касается окружности q, а в узле Д3— пересекает
эту окружность, как изображено на рис. 813. В геометрическом пред-
ставлении в узлах Ei, Е2, Е3 мы имеем пять общих точек шатунной
кривой с окружностью. Так как алгебраические кривые могут иметь
только четное число общих точек, то между шатунной кривой и ок-
ружностью будет существовать дополнительная общая точка Е.
Использовав изложенные выше способы уравнивания кривой отклоне-
ний (см. главу XIV), не представляет труда, перемещая двукратные
узлы интерполяции Ех и Е2, уравнять между собой предельные откло-
нения в трех точках экстремумов Н, и Нг. После этого, усреднив
отклонения, получим наилучшее приближение шатунной кривой к дуге
окружности.
998 СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ [гл. XV
6°. О проектировании схем механизмов с остановкой, изобра-
женных на рис. 807 и 808. В задаче проектирования механизма
с остановкой, схема которого изображена на рис. 807, требуется ша-
тунную кривую е основного шарнирного четырехзвенника ABCD
приблизить к отрезку прямой g. Предположим, что размеры основного
четырехзвенника ABCD даны и задан угол поворота <р12 ведущего
звена, на котором ведомое звено должно иметь остановку. Выберем
первое положение четырехзвенника ABXC\D и, повернув ведущее
звено на угол ср|2, найдем второе положение четырехзвенника AB^C^D.
Установим полюсы Р12,- Ри и Р22, определяющие четыре положения
Sj, S2 и 52 плоской фигуры шатуна, как указано на рис. 809. Для
центра 7И совпадающего с бесконечно удаленной точкой кривой цент-
ров /И”22 отыщем соответственную круговую точку fj и ее по-
ложение Е%. (На рис. 809 точки £, и не изображены.)
Шатунная кривая е этой точки будет приближена к отрезку
прямой q так, как показано на рис. 814: в точках Ег и /?2 шатунная
кривая е будет касаться прямой q.
Е Е у По известным полюсам Р12, Рн
---/ и Р22 отыскание круговой точки £),
соответствующей бесконечно уда-
ленному центру на кривой /И1122,
Рис. 814. изложено в § 37, 13°. Схема ме-
ханизма с остановкой на рис. 808
есть предельный случай схемы на рис. 806, когда шатунная точка Е
уходит в бесконечность. Поэтому задача проектирования механизма
с остановкой, изображенного на рис. 808, сводится к отысканию на
той же кривой /И"22 центра /И, которому соответствует бесконечно
удаленная точка Ех плоской фигуры шатуна. Нахождение этого
центра М и установление направления MEt подробно изложены
в § 37, 13° и 14°. После нахождения упомянутого центра М с ним
совмещается шарнир Е ползушки р. Через центр М проводится
прямая q, перпендикулярная к направлению МЕ{. Эта прямая
определит направление оси направляющей для ползушки в первом
положении основного четырехзвенника ABCD, Направляющая
для ползушки жестко соединяется с шатуном основного четы-
рехзвенника, как показано на рис. 808. Остановка ведомого звена
FQ в этом механизме осуществляется за счет огибания направляющей
ползушки центра 7И.
§ 48. Преобразование шатунных кривых
1°. Вспомогательные соотношения. Перейдем к изложению пре-
образования *), которое позволяет по данной шатунной кривой, при-
ближенной к дуге окружности, найти две или три новые шатунные
кривые, приближенные к дуге того же радиуса и с тем же предель-
*) См. [56п].
§ 481
ПРЕОБРАЗОВАНИЕ ШАТУННЫХ КРИВЫХ
999
ным отклонением от этой дуги. Упомянутое преобразование позволяет
по спроектированному шарнирно-рычажному механизму с остановкой
найти ряд новых механизмов с остановками, которые отличаются как
параметрами схемы, так и длительностью остановки, но обеспечивают
одну и ту же точность последней.
Известно, что шатунная кривая точки Е шарнирного четырехзвен-
ника АцАВВь (рис. 815) может быть вычерчена еще двумя чегырех-
звенниками В^ВуС\Сй и Д0Л4С^С0, которые получаются при помощи
построения Робертса. Поскольку этим построением придется ниже
многократно пользоваться, то напомним его.
Построим на стойке Д|ВП исходного механизма треуголь-
ник X(1Z3nCn, подобный шатунному треугольнику АВЕ, причем так,
чтобы углы аир, прилежа-
щие к линии шатуна АВ
исходного четырехзвенника,
оказались одновременно при-
лежащими к линии стойки
АпВ$ этого четырехзвенни-
ка. Чтобы получить второй
четырехзвенный механизм
B^BiCiCf,, находим в пере-
сечении прямых BnBi || BE
и EBt || ВНВ точку Bt и на
отрезке ЕВ{ строим тре-
угольник B^ECi, подобный
шатунному треугольнику
исходного четырехзвенника
с расположением углов, ука-
занным на рис. 815. Найден-
ную вершину Ci соединяем
с неподвижной точкой Со.
Рис. 815.
Для получения третьего четырехзвенника Л0Л2С2С0 поступаем ана-
логичным образом. В пересечении прямых АиА21| АЕ и ЕА.21| АиА нахо-
дим точку А3 и на отрезке ЕА2 строим треугольник АгЕСг, подобный
шатунному треугольнику исходного четырехзвенника с расположением
углов, указанным на рис. 815. Найденную вершину С2 соединяем с
неподвижной точкой Со. Очевидно, что отрезки CnCi || С2Е и С0С21| СгЕ.
Если длины стоек у рассматриваемых трех механизмов обозначить
соответственно через d, dt и d2t а длины остальных звеньев — через
а, Ь, с\ аь Ьъ <?! и а2, Ь2, с2 в последовательности, показанной на
рис. 815, то они удовлетворяют следующим пропорциям:
щ bi Ct di 7
а b с d 1
fig b2 с2 d2 \
а b с d 2‘
(15.11)
(15.12)
1000
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[гл. XV
Из рассмотрения неподвижного треугольника AnBt)Ch получаем, что
постоянные sin а , sin ?
л 1 == —; « ^9 === ~.
С1П V » Sin 7
sin 7 ’
Из равенств (15.11) и (15.12)
индексы у размеров bx, cb dx
ша-
длины звеньев
чегырехзвенных
Тогда можно
Рис. 816.
(15.13)
и
следует, что соответствующие
а2, Ь.г, с.г, (1^ можно опустить,
если под а, Ь, с и d пони-
мать не абсолютные, а отно-
сительные
отдельных
механизмов.
сказать, что при одной и
гой же стойке d шатунами
трех четырехзвенных меха-
низмов на рис. 805, полу-
чаемых по преобразованию
Робертса, оказываются по-
следовательно звенья Ь, с
и а.
Допустим, что тем или
иным путем найден четырех-
звенный механизм А0АВВ,
(рис. 816), у которого
тунная кривая е точки Е
окружности q с центром в
Углы ср' и ср" определяют положения АВА' и А0А‘
соответствующие началу и концу отрезка приближения. Указанный
четырехзвенник будем считать исходным механизмом для дальнейшего
исследования.
На рис. 817 и 818 показаны два других четырехзвенника B„BiCiCn
и A0AiCiCv, которые описывают ту же шатунную кривую е и полу-
чаются из исходного механизма по построению Робертса.
па
точке /И и с радиусом, равным R.
ведущего звена,
участке ЕЕ" приближена к
дуге
§ 48]
ПРЕОБРАЗОВАНИЕ ШАТУННЫХ КРИВЫХ
1001
Будем ниже пользоваться условным обозначением четырехзвенных
механизмов в виде дроби, в которой в числителе должна стоять относи-
тельная длина шатуна, а в знаменателе — относительная длина стойки.
Пусть в исходном механизме (рис. 816) длина стойки по-преж-
нему A0Ba = d, длина шатуна АВ — b, а длины кривошипа и коро-
мысла— соответственно А0А = а и В$В = с. В этом случае рас-
b
сматриваемый исходный механизм запишется дробью .
Если под а, Ь, с и d понимать относительные длины звеньев ме-
ханизма, то два четырехзвенника (рис. 817 и 818), получаемых из
b я
исходного четырехзвенника по построению Робертса, будут иметь,
как указано выше, ту же стойку d, а шатунами их явятся последо-
вательно сна. Таким образом, эти четырехзвенные механизмы дол-
, с а
жны быть обозначены соответственно через и ,
1 d d
значения получаются из обо-
значения исходного механизма
ft н
путем последовательной за-
мены в числителе относитель-
ного размера b двумя другими
размерами с и а.
2°. Преобразование, осно-
ванное на обращении дви-
жения. В любом положении
четырехзвенника A^ABBq (рис.
816) расстояние между шатун-
ной точкой Е на звене b и
центром Л1 на неподвижном
звене d не будет зависеть от
того, какое из звеньев b или d
т. е. их обо-
Рис. 819.
является подвижным и какое — не-
подвижным. Следовательно, если этот четырехзвенный механизм по-
ставить на шатун, как это показано на рис. 819, то шатунная кри-
вая т точки 7И, принадлежащей шатуну d обращенного механизма
АА^В^В, будет приближена на некотором участке ММ" к дуге окруж-
ности qu с центром в точке Е и с радиусом, равным R.
На рис. 820 и 821 отдельно изображена часть участка прибли-
жения шатунной кривой т обращенного механизма к дуге окруж-
ности <у(1 и часть участка приближения шатунной кривой е исходного
механизма к дуге окружности q.
Шатунная кривая т обращенного механизма отличается по виду
от шатунной кривой е исходного механизма. Однако, поскольку при
обращении движения относительное расположение точек Е и М не
меняется, то переменный отрезок р0 = Е7И (рис. 820), определяющий
расстояние между точкой Л1 и центром Е окружности q^ при
1002 синтез механизмов с остановками [гл. XV
обращенном движении, должен последовательно принимать те же зна-
чения, что и отрезок [j = EM (рис, 821), определяющий расстояние
между шатунной точкой Е и центром Л4 окружности q в исходном
четырехзвенном механизме. Отсюда следует, что каждой точке пере-
сечения Е’, Е",... кривой е с окружностью q (рис. 821) в исходном
четырехзвепнике будет соответствовать точка пересечения /И', М",...
кривой т с окружностью q„ (рис. 820) при обращенном движении;
аналогично этому точке Е" предельного отклонения кривой в от ок-
ружности q (рис. 821) при обращенном движении будет соответ-
ствовать точка М” предельного отклонения кривой т от окружности
(рис. 820). Величина предельного отклонения будет в обоих
случаях одна и та же L.
Таким образом, если шатунная кривая е исходного четырехзвен-
но! о механизма (рис. 816) на участке приближения имеет Л точек пересе-
чения с окружностью q, то в обращенном движении шатунная кривая т
на участке приближения будет иметь также k точек пересечения с
окружностью <?0; если шатунная кривая исходного четырехзвенника
имеет п предельных отклонений от дуги окружности q, равных по
абсолютной величине, но чередующихся по знаку, то в обращенном
движении шатунная кривая т будет иметь п предельных отклонений
от дуги окружности ^0, равных по абсолютной величине, но чере-
дующихся по знаку. Отсюда непосредственно следует, что если
приближение шатунной кривой е исходного четырехзвенного меха-
низма к дуге окружности q является наилучшим, то приближение
шатунной кривой т к дуге окружности <;(| в обращенном движении
также будет наилучшим. Иначе говоря, при указанном преобразо-
вании четырехзвенника получается такая новая шатунная кривая,
у которой характер и точность ее приближения к окружности
данного радиуса R остаются теми же самыми, какие получены дл»? соот-
ветствующей шатунной кривой исходного четырехзвенного механизма.
Четырехзвенник (рис. 819), получаемый постановкой на шатун
b , , d
исходного четырехзвенника rf-, будет иметь обозначение -у.
§ 48]
ПРЕОБРАЗОВАНИЕ ШАТУННЫХ КРИВЫХ
1003
_ с а
Если поставить на шатун четырехзвенники — и —, показанные
соответственно на рис. 817 и 818, то получим два новых четырех-
звенника у и (четырехзвенник BiB^C^Ci на рис. 822 и четырех-
звенник АгА„С6С^ на рис. 823), у которых шатунные кривые /д, и
/я2, описываемые точкой /И, будут приближены к окружности qn с
той же точностью, с какой приближена шатунная кривая е исход-
ного механизма к окружности q.
Рис. 822. Рис. 823.
Продолжая далее последовательное применение построения Ро-
бертса и обращения движения, можно получить известную совокуп-
ность четырехзвенных механизмов, вычерчивающих такие шатунные
кривые, которые будут приближены к дуге окружности данного ра-
диуса с той же точностью, с какой приближена к окружности того
же радиуса шатунная кривая е исходного четырехзвенного механизма.
Чтобы выяснить эту совокупность четырехзвенных механизмов, пред-
варительно отметим одну особенность предлагаемого преобразо-
вания.
Как было указано ранее, при построении Робертса относительные
размеры четырехзвенника а, Ь, с и d не изменяются. Непосред-
ственно очевидно, что при обращении движения эти размеры также
не изменяются. Следовательно, они не будут изменяться и при пре-
образовании, состоящем из последовательного применения построения
Робертса и обращения движения.
3°. Совокупность шарнирных четырехзвенников, определя-
емых рассмотренным преобразованием. Поскольку при рассмот-
ренном преобразовании относительные длины звеньев шарнирного че-
тырехзвенника не изменяются, совокупность механизмов, опреде-
ляемых этим преобразованием, будет соответствовать совокупности
возможных размещений по два из четырех заданных относительных
длин звеньев а, Ь, с и d.
1004 СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ [гл. XV
Отсюда следует, что указанное преобразование надцать четырехзвенников: определяет две-
а Ь с . . -j-; (кривая е), а ' а ' а ' ” (15.14)
d с а , . у; у! -у (кривая от), (15.15)
d а b , . -у! (кривая от,), (15.16)
d b с , . 'а' Т’ V (кРивая т^- (15.17)
Три четырехзвенника, принадлежащих одному и тому же гори-
зонтальному ряду, получаются друг из друга по построению Ро-
бертса, как имеющие общую относительную длину стойки, и поэтому
должны описывать одну и ту же шатунную кривую. Эта шатунная
кривая будет приближена к дуге окружности данного радиуса с той
же точностью, как и шатунная кривая в исходном четырехзвенном
механизме.
Отсюда следует, что разобранное выше преобразование позво-
ляет получить по известной шатунной кривой еще три шатунных
кривых, приближенных к дуге окружности одного и того же радиу-
са с одинаковой точностью.
Напомним, что четырехзвенные механизмы и ~ (см. рис. 817
и 818) ряда (15.14) получаются из исходного механизма (рис. 816)
по построению Робертса. Четырехзвенники -у, у и -у (рис. 819,
822 и 823) рядов (15.15), (15.16) и (15.17) получаются путем поста-
новки на шатун соответствующих механизмов ряда (15.14). Осталь-
ные четырехзвенники рядов (15.15), (15.16) и (15.17) можно полу-
чить из найденных механизмов -у, — и — по построению Робертса.
Таким образом, каждый четырехзвенный механизм установленной со-
вокупности может быть получен из исходного механизма путем та-
кого преобразования, в котором будет только одно обращение дви-
жения.
Допустим, что длины звеньев а, Ь, с и d исходного четырех-
звенника удовлетворяют теореме Грасгофа и а является наимень-
шим звеном. Тогда три четырехзвенника ряда (15.17), у которых
стойкой является наименьшее звено а, будут проворачивающимися
а а а
двухкривошипными механизмами, три четырехзвенника у, у- и у
(по одному из остальных трех рядов), у которых наименьшее звено
а служит шатуном, будут непроворачивающимися механизмами, а
остальные шесть четырехзвенников (включая исходный) явятся про-
ворачивающимися однокривошипными механизмами.
5} 49] последовательное соединение четырехзвенных механизмов 1005
Если длины звеньев а, Ь, с и d исходного четырехзвенника не
удовлетворяют теореме Грасгофа, то все двенадцать четырехзвен-
ников (включая исходный), определяемых рассмотренным преобразо-
ванием, будут непроворачивающимися механизмами.
Точность, которую дают геометрические построения, может быть не-
достаточна. Однако на основании равенств (15.11) — (15.13) можно
аналитически подсчитать размеры любого четырехзвенника указанной
совокупности по размерам исходного четырехзвенника.
Допустим теперь, что нами спроектирован механизм по схеме
рис. 805 или 806 с требуемой точностью остановки. Предположим,
что основной четырехзвенник ABCD
является однокривошиппым. Приме-
няя к нему указанное преобразование,
получим еще шесть четырехзвенных
однокривошипных механизмов, вклю-
чая которые в схему рис. 805 или 806,
получим шесть других механизмов
с остановкой, обеспечивающих одну
и ту же точность последней, но отли-
чающихся длительностью остановки.
§ 49. Механизмы с остановкой,
получаемые последовательным
соединением четырехзвенных
механизмов
1°. Последовательное соедине-
ние четырехзвенных механизмов в
предельных положениях. На рис. 824
изображен механизм прижимного пол-
зуна мощного кривошипного пресса
глубокой вытяжки*). В этом механизме
АВ ведущее звено. К шарнирному четырехзвеннику ABCD последо-
вательно присоединен второй шарнирный четырехзвенник DEFA (для
упрощения конструкции неподвижные оси ведущего звена АВ пер-
вого четырехзвенника и ведомого звена FA второго четырехзвенника
совмещены). Ко второму четырехзвеннику последовательно присое-
динен кривошипно-шатунный механизм AFG (по тем же соображениям
совмещены оси подвижных шарниров ведомого звена второго четы-
рехзвенника и ведущего звена кривошипно-шатунного механизма).
Когда четырехзвенник ABCD занимает предельное положение
ABdC^D, соединенные с ним последовательно четырехзвенпые меха-
низмы DEnFnA и AFnGu занимают положения, близкие к предельным.
При этом условии на основании соответствующего расчета можно
*) Пресс К-460Б отечественного производства.
1006
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[гл. XV
получить остановку ползуна т большой точности и большой дли-
тельности.
Расчет подобных шарнирно-рычажных механизмов с остановкой
гораздо проще, чем расчет шарнирно-рычажных механизмов, у кото-
рых ведомая диада присоединяется
к шатуну основного четырехзвен-
ника. Указанная на рис. 824 схема
является типовой для механизмов с
остановкой, получаемых последова-
тельным соединением четырехзвен-
ных
этой
ним
вида.
Из схемы механизма, изображен-
ной на рис. 824, выделим для бли-
жайшего рассмотрения шестизвенный
механизм ABCDEFA (рис. 825), ко-
торый оказывает решающее влияние
на длительность выстоя ползуна т.
Как уже отмечено, этот механизм
представляет собой два последова-
четырехзвенника
общая.
механизмов. Покажем расчет
схемы, который будет приме-
для других схем подобного
гельно
Стойка
низмов
н и в а н и я.
соединенных
AD у обоих
заклинены
шарнирных
механизмов
на общем валу под
ABCD и DEFA.
Звенья CD и DE этих меха-
углом 8 — углом з а к л и-
Разъединим временно звенья CD и DE и поставим первый четы-
рехзвенник в предельное положение AB'C'D, в котором звено СВ'
накладывается на звено АВ', а второй четырехзвенник в предельное
положение DE'F’A, в котором звенья DE' и E’F' вытягиваются в
одну прямую (эти предельные положения показаны на рис. 825 пунк-
тиром). Замерим угол между звеньями CD и DE' в указанных пре-
§ 49] ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХЗВЕННЫХ МЕХАНИЗМОВ 1007
дельных положениях и обозначим его 8пр. Действительный угол за-
клинивания о зададим
8 = 8,1Р + Д8,
(15.18)
где Дб — некоторый малый угол, который пока выберем произвольно.
Произведем разметку траекторий шарниров указанного шести-
звенника и построим график функции положения (рис. 826)
ф = Д(<р), (15.19)
где ч> и — координаты ведущего и ведомого звеньев АВ
и АВ, отсчитываемые от на-
правления стойки AD (рис. 825)
против движения часовой
стрелки.
Точки экстремумов 2 и 4 этого
графика лежат на прямой k'k',
параллельной оси абсцисс. Прове-
дем через точку экстремума 3
прямую k"k”, параллельную той
же оси, и отметим точки 1 и
о, в которых она пересекается
с графиком. На отрезке [сщ %]
график функции положения (15.19)
будет заключен между прямыми
k'k' и k"k". Расстояние между
ними обозначим Д и назовем
углом малого размаха ве-
домого звена ВА в отличие от
угла полного размаха <р0
этого звена. Длину отрезка
Рис. 827.
?18 --?5-----?1
назовем углом выстоя. Прямая kk, проведенная посредине между
прямыми k'k' и k"k", определит среднее положение ведомого
звена на угле выстоя.
2°. Определение углов выстоя и малого размаха. Угол выстоя
'Pis и угол малого размаха Д звена В А легко определить без
построения графика функции положения <р = Д(<р). Поставим первый
четырехзвенник в предельное положение AB^C^D (рис. 827). Второй
четырехзвенник займет положение DE3F-tA, отличное от предельного.
Отметим второе возможное положение ExDC\ звена CDE, которому
соответствует положение ЛД, ведомого звена AF. Отметим, далее,
два возможных положения ABt и ABS ведущего звена, соответству-
ющих одному и тому же положению CiDE\ звена CDE. Очевидно,
что положения AF\ и ,1FB ведомого звена совпадут с ранее ука-
занным его положением AFX.
1008
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[гл. XV
Поставим теперь второй четырехзвенник в предельное положе-
ние DE^FaA и для положения E2DC2 звена EDC найдем два соот-
ветственных положения АВ2 и AB,t ведущего звена. Положение AFl
ведомого звена совпадет с его предельным положением AFit а поло-
жение C'JJEi звена CDE — с его положением С2ВЕ2.
При вращении ведущего звена против движения часовой стрелки,
когда оно последовательно проходит положения Bb В.2, Bit Bit Bs,
ведомое звено последователь-
но занимает положения
F2, F3, Fit Fs. Этим положе-
ниям ведомого звена соответ-
I ствуют на графике функции
‘ <p = F(<p) точки 1, 2, 3, 4, 5
(рис. 826). Искомый угол
малого размаха (рис. 827)
Д<р=£Д1ДД2.
Угол поворота кривошипа
из положения АВХ в поло-
жение ABS явится искомым
углом выстоя <р18.
Указанные графические по-
строения не всегда могут
обеспечить необходимую точ-
определении углов Дф и <р18. Покажем аналитический подсчет
обозначения, указанные на рис. 825:
Рис. 828.
ность в
этих величин. Для этого введем
АВ = а\
DE = e-,
BC = tr, CD —с, AD = d;
EF =f\ FA = g.
Кроме координат <p и ф, определяющих положение ведущего и ве-
домого звеньев АВ и AF, введем еще угол у, определяющий поло-
жение звена DE относительно стойки. Тогда положение звена DC
относительно стойки определится углом (у -ф- 8).
Рассмотрим предельное положение первого четырехзвенника АВ^С^Э
(рис. 828). Угол у3, определяющий положение звена C-zDE-s, найдем
по формуле
cos (у3 -ф- 8 — к) =
с2 + rf3 — (6 —- dy
2с d
(15.20)
Из LDE^A определим переменный отрезок
Е-лА = ф7 с/'2 -j- е* — 2de cos (гс — y3).
(15.21)
Из тою же треугольника имеем:
cos £
_(Е3Л)2-М2 — е2
2 (Е,Д) d
(15.22)
§ 491 ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХЗВЕННЫХ МЕХАНИЗМОВ 1009
Угол <р3, определяющий положение АЕ-Л ведомого звена, найдем
из &Е3АЕЛ:
(15?23)
Поставим теперь второй четырехзвенник в предельное положе-
ние DE-.,F.,A. Тогда получим:
^Я=*±£^±К. (,3.24)
Угол малого размаха будет:
Д<р = <^2 — <р3. (15.25)
Для определения угла выстоя срщ поставим первый четырехзвенник
Рис. 829.
еше раз в предельное положение AB3C3D (рис. 829) и подсчи-
таем переменный отрезок:
ОЕЛ = ]/cf2 -j~ £2 — cos фз- (15.26)
Определим угол /_ADF3 из соотношения
sin т1 = ^Д-sin ф3. (15.27)
Угол [!, который образует со стойкой положение DE\, симмет-
ричное положению DE3 относительно прямой DFit будет:
11 = Т* + 2 [(т: — 4«) — т(| = 2т: — — 2д.
(15.28)
1010
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[гл. xv
Нанесем положения ABt и АВ^ ведущего звена, соответствую-
щие положению EtDCt звена EDC. Угол поворота ведущего звена
из положения АВ\ в положение АВ* есть искомый угол выстоя <pt5.
Подсчитаем из треугольника DCXA отрезок
С| А = ]/с2 -ф- d'1 — 2cd cos (71 —|— 8 — т).
(15.29)
Тогда из
выстоя ср1в:
ACjflgA, симметричного ДСф/фА, можно
подсчитать угол
cos
_(С1АН4-а3-&2
2а (С1-4)
(15.30)
Вычислим еще угол у = LC\AD\
cos у =
(С,А)а + d2 — с2
2d (С, А)
(15.31)
Тогда определятся координаты и ср3 ведущего кривошипа, соот-
ветствующие началу и концу угла выстоя:
ср! —т —Z—Ts = ^ —z+^. (15.32)
Из изложенных построений очевидно, что при уменьшении угла
заклинивания В (рис. 825 и 827) уменьшаются как угол размаха Дф,
так и угол выстоя <р1в. Точки 1, 2, 3, 4, 5 на графике функции
ф = Е (<f>) при этом сближаются. При угле заклинивания 8 = 8пр, при
котором предельное положение первого механизма совпадет с пре-
дельным положением второго механизма, будет <р1В = 0 и Дф = О.
После того как получена функция положения ведомого звена AF
шестизвенника ABCDEFGA
ty = F (ср),
соответствующий угол выстоя <р1В и угол малого размаха Дф, легко
установить функцию положения
8 = /(¥),
угол выстоя и величину малого размаха ползуна интересующего нас
механизма, изображенного на рис. 824.
Выделим из схемы на рис. 824 кривошипно-шатунный механизм AFG,
у которого ведущее звено AF является одновременно ведомым зве-
ном рассмотренного выше шестизвенника.
Пусть этот кривошипно-шатунный механизм изображен на рис. 830.
Точки F3, Ft, Fjj отмечают три совпадающих друг с другом положе-
ния звена AF, которым на рис. 826 соответствуют точки 3, 7, 5 с
абсциссами ср3, <р1( ®в, а точки F.2, Ft отмечают два совпадающих по-
ложения звена AF, которым на рис. 826 соответствуют точки 2, 4
с абсциссами ср.2 и <р4. На угле выстоя <р15 звено AF совершает воз-
§ 49] ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХЗВЕННЫХ МЕХАНИЗМОВ 1 01 1
вратно-колебательные движения между положениями / 3(Fi, FB) и F2(F4)
на малом угле размаха Дф *)•
На рис. 830 нанесена стойка AD шестизвенника и от нее отсчи-
таны углы ф3 и ф2, определяющие положения Арл и AF.2 звена AF.
Пусть направление движения шарнира О ползушки /п проходит через
шарнир А. Относительно стойки AD это направление определим углом
Перемещения ползуна т условимся отсчитывать от некоторой точки О,
выбранной на направлении движения его шарнира G.
Вид графика функции положения ползуна на отрезке приближен-
ного выстоя зависит от того, как располагается прямолинейная траек-
тория шарнира О относительно край-
них положений звена AF на малом
угле размаха Дф. С точки зрения
точности выстоя ползуна наиболее
благоприятный случай изображен на
рис. 830. Он характеризуется тем,
что прямолинейная траектория шар-
нира О совпадает с биссектрисой
указанного угла Дф= _F3AF2 и
следовательно,
(15.33)
В этом случае пяти положениям
звена AF. отмеченных точками
Fj, F2, F3, F4, Fs, соответствуют
пять совпадающих друг с другом
положений G1, 0.2, G3, О4, Gs ползу-
на. При движении звена AF между
указанными пятью положениями кри-
вошипно-шатунный механизм четы-
режды проходит через свое пре-
дельное положение AFiG], в котором
звенья AF и FG вытягиваются
в одну прямую линию. Четыре ниж-
ние предельные положения ползуна, совпадающие друг с другом,
обозначены на рис. 830 соответственно через G], О3, О4.
В этом случае график функции положения ползуна
«=/(<?)
на отрезке приближенного выстоя имеет вид, изображенный на рис. 831.
Точки верхних предельных отклонений 1, 2, 3, 4, 5 соответствуют
положениям ползуна Ot, G2, G3, О4, О8 на рис. 830. Абсциссы <рь <р2,
С53> ®4 и <р8 точек 7, 2, 3, 4, 5 на рис. 831 совпадают с абсциссами
*) Ради наглядности угол малого размаха Дф изображен на рис. 830 в не-
сколько раз большим, чем на рис. 827.
1012
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
(1Л. XV
тех же точек на графике функции положения звена AF, изображен-
ном на рис. 826. Угол выстоя cpiB ползуна совпадает с углом выстоя
звена FA исходного шестизвенника.
Точки нижних предельных отклонений Г, 2', 3', 4' на рис. 831
соответствуют нижним предельным положениям ползуна Gi, Q%, О3, G\
Рис. 831.
на рис. 830. Абсциссы точек Г, 2', 4' могут быть определены
с помощью следующего построения на схеме исходного шестизвен-
ника ABCDEFA (рис. 832). Отметим положение AF' звена AF, сов-
падающее с биссектрисой малого угла размаха Дф. Установим для
Рис. 832.
этого положения соответственные поло-
жения EiDC'i и E'zDC'z звена EDC. Для
каждого из этих положений звена EDC
найдем по два соответственных поло-
жения ведущего звена АВ, которые
отмечены буквами В{, B'z, В3, В\. Зна-
чения угла ср, определяющие эти поло-
жения ведущего звена относительно
оси отсчета AD, будут абсциссами то-
чек Г, 2', 3' и 4' на рис. 831.
Прямая kk, расположенная посреди-
не между прямыми, на которых лежат
точки 1, 2, 3, 4, 5 и Г, 2', 3', 4', опре-
делит среднее положение ползуна на
угле выстоя. На этом угле функция по-
ложения ползуна имеет девять предель-
ных отклонений (равных по модулю, но
чередующихся по знаку) от постоянной
ординаты, определяющей среднее положение выстоя ползуна. Абсолют-
ную величину этих предельных отклонений подсчитаем по приближенной
формуле для кривошипно-шатунного механизма
As___g
2 2
Дф । 1 £ . о A'i'
C0S t + 2 ЛЬ1П 2
(15.34)
§ 49] ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХЗВЕННЫХ МЕХАНИЗМОВ 1013
где Дф — угол малого размаха звена AF, подсчитанный по формулам
(15.20) —(15.25), g = AF и h = FG.
Если направление движения шарнира О ползуна не совпадает с
биссектрисой малого угла размаха F3/1F2 ведущего звена кривошипно-
шатунного механизма, то на угле выстоя tpl8 предельные отклонения
ползуна от среднего положения получаются не равными по абсолют-
ной величине или число их уменьшается. В результате возрастает
абсолютная величина этих отклонений.
Случай, когда ползун на углё выстоя ср1в имеет девять равных
предельных отклонений
знаку
Рис. 833.
по модулю, но противоположных по
от среднего положения выстоя, соот-
ветствует наименьшей величине этих
предельных отклонений.
3°. Проектирование механизма
на заданную длительность выстоя.
Рассмотрим теперь следующую задачу:
1) При выбранных длинах звень-
ев а, Ь, с, d, е, f, g и ft (рис. 833)
найти такой угол заклинивания 8 звень-
ев CD и DE, при котором угол выстоя
<р(в звена AF будет равен заданному.
2) После этого найти значения
параметров Zt и Z2, при которых
ползун на угле выстоя <р1в будет
иметь девять равных по модулю, но
противоположных по знаку предельных
отклонений от среднего положения
выстоя.
Для решения этой задачи по-
ставим звено DC (рис. 829) в такое
положение DCX, которому соответ-
ствуют положения ABi и АВЪ ве-
дущего кривошипа, определяющие заданный угол cpiB. Тогда из LABSCX,
в котором ZCp4Z?b = e: — имеем:
й2 (ЛС))2 _ 2а cos к ,
откуда переменный отрезок *)
ДС, = асов (ir— j/ft2-]_as| 1 — cos2^— (15.35)
*) Знак перед корнем проще всего определить путем графической про-
верки указанного решения.
1014
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[гл. XV
Далее,
cos (A DC У) = £i±A2
2cd
(15.36)
Поставим первый четырехзвенник в предельное положение AB3C3D;
тогда из ДДС3Л найдем:
cos (ADC3) =
с» 4- ds — (b — ay
2cd
(15.37)
Найдем угол е колебания ведомого звена CD при повороте ведущего
звена из положения АВ, в положение ABS на заданный угол вы-
стоя <р1в:
е = /_ADCX— £ADC3. (15.38)
Двум положениям C^DEx и C3DE3 должно соответствовать Одно и
то же положение AF3 звена AF (рис. 829). Это условие позво-
ляет определить требуемый угол заклинивания 8= LC^DEx — £.C3DE3.
Из &DE3F3, в котором /_E3DF3—~, получим*):
DF-, = е cos
(15.39)
Угол A_ADF3 определим из равенства
COS 7] =
2d (DFA
(15.40)
Тогда искомый угол заклинивания
8— Z_ADCi —]— — 9-.
(15.41)
Для определения координаты ф3 положения AF3 имеем:
DFS .
sm ф3 = —— sin т,.
(15.42)
Координату ф.2 и малый угол размаха Дф, характеризующий точ-
ность получаемого выстоя звена AF, найдем по формулам (15.24) и
(15.25). Координаты и <ps, отмечающие начало и конец отрезка
приближения, можно подсчитать по формулам (15.32).
Для выполнения требования, поставленного во второй части за-
дачи, выберем угол р, определяющий направление стойки AD
(рис. 833 и 830) относительно направления движения ползуна т по
формуле (15.33):
*) См. предыдущую сноску.
§ 49] ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЧЕТЫРЕХЗВЕННЫХ МЕХАНИЗМОВ 1015
Пусть направление движения ползуна совпадает с вертикальной
осью, как изображено на рис. 833. Тогда угол а, определяющий по-
ложение стойки AD по отношению к горизонтальной оси, будет:
о ~
а = Р~ 2 '
При заданной длине стойки d координаты шарнира D найдем из
очевидных равенств:
1Л = d sin — yj; 4 = rfcosiB—(15.43)
,, „ Ils
Наибольшую абсолютную величину отклонения у ползуна от сред-
него положения на угле выстоя подсчитаем по формуле (15.34).
4е. Пример расчета механизма на заданную длительность вы-
стоя. Пусть параметры схемы механизма на рис. 833 следующие:
а = 210 мм; Ь = 495 мм; с = 400 мм; d — 516,56 мм:
е = 340 мм; f='245 мм; g = 230 мм; h = 560 мм.
Требуется обеспечить угол выстоя <р1в=160° и получить наимень-
шие предельные отклонения ползуна от среднего положения выстоя
на этом угле.
По формулам (15.35) — (15.38) найдем:
ДС, = 413,25 мм; L AD2X = 51°43'; / ADS3 = 33°15';
= = £ADC{ — /Д£>С3= 18=28'.
Далее, по формулам (15.39) — (15.41) получим:
DFs = 574,44 мм; ?] = 23=35'.
Искомый угол заклинивания звеньев CD и DE будет:
8 = £ ADCi 4- 71 — у = 66°04'.
По формулам (15.42) и (15.24) имеем:
<р3 = 92=29'; <р2 = 95=26'.
Угол малого размаха в этом случае
Дф = ф2 —ф3 = 2°57'.
По формуле (15.33) подсчитаем вспомогательный угол |3, а по фор-
мулам (15.43) координаты 7, и 72 шарнира D (рис. 833):
3 = 93°57’5;
1\ — 35,66 мм; 4 = 515,32 мм.
1016
СИНТЕЗ МЕХАНИЗМОВ С ОСТАНОВКАМИ
[ГЛ. XV
Наибольшая абсолютная величина отклонения ползуна от среднего
положения на заданном угле выстоя ср18=160° будет:
— = 0,Обо мм.
Эта величина будет соизмерима с холостыми ходами механизма,
вызываемыми зазорами в его шарнирах. Поэтому практически на за-
данном угле ср13 ползун будет стоять на месте.
Приведенный пример свидетельствует, что указанные шарнирно-
рычажные механизмы могут обеспечивать остановку высокой точности
на большом угле поворота ведущего звена.
ГЛАВА XVI
КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ
ПОЛОЖЕНИЙ ПЛОСКОЙ ФИГУРЫ И ЕЕ ИСПОЛЬЗОВАНИЕ
В СИНТЕЗЕ МЕХАНИЗМОВ
§ 50- Основы кинематической геометрии бесконечно близких
положений плоской фигуры, движущейся в своей плоскости
1°. Введение. Напомним задачу, которая была поставлена и ре-
шена Бурместером в кинематической геометрии (см. § 36): заданы
пять произвольных положений плоской фигуры S, движущейся в
своей плоскости; требуется найти на фигуре такую точку В, чтобы
ее пять соответственных положений б,, б2, Bit Bs находились
на одной окружности. Выше в главе XI эта задача была исследо-
вана для случая, когда положения плоской фигуры являются конечно
удаленными, и для случая, когда некоторые из этих положений
являются попарно бесконечно близкими.
Рассмотрим теперь задачу Бурместера для случая, когда все
заданные положения плоской фигуры являются бесконечно близкими,
и покажем ее приложения в синтезе механизмов с низшими нарами.
Но прежде отметим, что пока не представляется возможным дать
решение задачи Бурместера для случая, когда все заданные поло-
жения плоской фигуры являются бесконечно близкими путем пре-
дельного перехода от случаев, рассмотренных в главе XI. В случае
бесконечно близких положений плоской фигуры приходится привлекать
свои методы исследования. Один из них указан в работах Р. Мюл-
лера |95а, б] и является по своему характеру геометрическим. Метод
Мюллера допускает лишь графическое решение соответствующих
задач синтеза. Очень глубокое по содержанию и изящное по методам
исследование упомянутого случая задачи Бурместера принадлежит
А. П. Котельникову [31]. Ниже нами используется метод Котельни-
кова, но с теми обобщениями, которые оказались необходимыми для
использования теории Бурместера в задачах синтеза передаточных
механизмов*).
*> См. [57 в, г].
1018 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
В задачах синтеза передаточных механизмов теория Бурместера
для бесконечно близких положений плоской фигуры ранее была ис-
пользована в работе Р. Крауса [85д], в которой получено приближе-
ние функции положения шарнирного четырехзвенника к заданной
функции с четырехкратным узлом интерполяции. Ниже дано
решение задачи о приближении функции положения шарнирных
четырехзвенных механизмов к заданной функции с пятикратным
узлом интерполяции и показана возможность получения приближения
с шестикратным узлом интерполяции.
2°. Общие условия касания траектории движущейся точки
с кругом кривизны. Пусть движение точки в неподвижной системе
кривизны траектории точки (16.1),
координат х, у (рис. 834) задано
уравнениями:
x = x(t), y—y(t). (16.1)
Напишем уравнение круга радиу-
са R с центром в точке Л1
(х — хм? (_v — Ум? = R2-
(16.2)
Условие касания этого круга с
кривой (16.1) будет:
х’ (х — хм) +У (у — ум) = 0.
(16.3)
Чтобы круг (16.2) был кругом
должно выполняться еще условие
х" (х — Хм) +У' (у —Ум) + х’* 4-У2 = 0.
(16.4)
Из уравнений (16.3) и (16.4) определим соотношения, связывающие
координаты точки х, у и координаты соответствующего ей центра
кривизны траектории Хм, ум-
х — Хм
__У(х'8+У8)
х'у" — х"у’ ’
У—Ум
_—х'(х'2-ру2)
х'у"— х"у' ‘
(16.5)
Дифференцируя трижды выражение (16.4), получим:
х"' (х — хм) +У” (> —Ум) 4-3 (х'х" +УУ') = 0, (16.6)
xlv(x — хм) +yv(y —Ум) -j- 4 (х'х" УУУ") 4”
4- 3(х"-4-У'-2) = 0, (16.7)
xv (х — хм) + yv (у —Ум) + 5 (x'xIV 4-УУv) 4-
4- 10 (х"х"' 4-У>'") = 0. (16.8)
§ 50]
ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
1019
Заменим в выражениях (16.6), (16.7) и (16.8) разности х — х,и
и у—ум их значениями по фюрмулам (16.5). Имеем:
(У2 -Lyi) (х"у — х’у'") -у 3 (У У' у у'у") (х’у" — х"у') = 0, (16.9)
(У2 у-у2) (x'vy __ yyv) [4 (Х'У" -ууу") -у 3 (У'2 4~У'2)] X
X (х'у" — х"у') = 0, (16.10)
(У2 -уу"2) (xvy — a->v) -у [5 (УУ v+yyv) + 10 (х”х’" +у"у'")] X
х (х'у" — уу) = 0. (16.11)
Точки траектории, удовлетворяющие уравнению (16.9), имеют со
своим кругом кривизны касание
совпадают четыре бесконечно
близкие точки траектории и
круга кривизны.
Точки траектории, удов-
летворяющие, кроме уравнения
(16.9), еще уравнению (16.10)
или уравнениям (16.10) и
(16.11) определяют точки, имею-
щие касание соответственно
4-го и 5-го порядков.
3°. Определение производ-
ных от координат точки пло-
ской фигуры, движущейся в
своей плоскости. Рассмотрим
движение плоской фигуры S
в содержащей ее неподвиж-
ной плоскости V- для этого
свяжем с плоскостью У,
неподвижную систему ко-
ординат хОу (рис. 835), а с
фигурой S — подвижную £014
3-го порядка, т. е. в точке касания
Рис. 835.
Тогда движение любой точки В (В, тф), принадлежащей S, относи-
тельно неподвижной плоскости определится уравнениями:
х = х0 — £ cos ср — 7j sin ср, |
У = У« + с sin ср -у т( cos ср. f
(16.12)
Здесь х0 и _у(1 — координаты подвижного начала координат Oj
в осях х, у, представляющие собой заданные функции угла ср между
осями Ох и ОД:
*о = л'о(<р), То =То (?)>
(16.13)
а угол ср — заданная функция времени.
Определим первые пять производных от координат точки В по
времени х’, х”, ..xv и у', у", ..., _yv. Перенесем величины х„
1020 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
и ф0 в уравнениях (16.12) в левую часть и продифференцируем по-
лученные равенства. Тогда получим:
(х —х0)' = —ю(ф—ф0), (ф — Л)' = + ‘»(х — х0), (16.14)
где ы = угловая скорость плоской фигуры S.
Остальные производные получим, последовательно дифференцируя*)
выражения (16.14):
(х — х0)" = — <Ь(ф — _у0) — ш2(х — х0), | 15)
(У —фо)" = + w (х — х0) — io® (ф —фй). (
(х — х0)"' = — (й — <о3)(ф — ф0) — 3 охо(х — х0), 1 (16 16)
(ф—Фо)'" = + (<5 — “3)(х —Хо) —310<0(ф—фо). I
(х — x0)IV= — (S — бЛ)(ф— фо)]
4_(1О4_4О)й_Зо)«)(х —х0), I П617)
(ф — фо)1У= + (<« — 6«Ао)(х — х0)~4 I
-j- (0>4 — 4их6 — Зй2) (ф —фо). |
(х — xp)v= — ( w — 15ux62 — 10u>2i6 uj!;) (ф —фо) —
— (5<и о> — 10<о3й 4-10 йсб) (х — х0),
(ф —ф0)у = 4- ( й’ — 15«х62 — 10и>2& 4~ ojS)(x — Хо) — (16.18)
— (5wii>-— 10ы3(о4- 10йй)(ф —фо).
Пусть начало подвижной системы координат совпадает в данный
момент с полюсом мгновенного вращения фигуры S. Тогда х'„ и у'п
будут равны нулю. Если, кроме того, выбрать систему координат хОу сов-
падающей с £Oiij, то для рассматриваемого момента времени будем иметь,-
х« = 0; £ = х; х’—О, 1
® (16.19)
ф« = 0; rt=y, фо = 0. )
Использовав условия (16.19), выражения (16.14)—(16.18) можно
представить окончательно в следующей форме;
Х' = — Оф, 1
у=4~ wx. I
х" - хй — шу — ш2х, |
ф" = То 4~ —ш*у- I
х"’ = х'У — (й — <и3)ф — Зюйх, 1
у'" =ф„"4-(й — я>3)х — Зикоф. )
хп= x’v— (io — 6<о2й)ф 4- (и4 — 4юй — 3(62) х, 1
ф1У =ф^ 4~ (й — 6(o2oi) х -|- (w4 — 4(1>й — 3(62)ф. J
(16.20)
(16.21)
(16.22)
(16.23)
*) Для удобства записи производные по времени от координат будем обо-
значать штрихами, а производные от угловой скорости — точками.
§ 50] ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ 1021
х^—х^ — ('io'— 15(оо>2 — 10о)2о') -ф- ю8)У —
—(5w io — 10(о3(о -j- 1 Ой io) х,
_у(У('('и'—loowo2—10(о2<о <os) х — )
— (5(о io— 10(о3(о Ц- 10(6 io) у.
Поставим теперь задачу определить те точки фигуры S, кото-
рые лежат на одной окружности в трех, четырех и пяти бесконечно
близких положениях этой фигуры и определить центры этих окруж-
ностей. Траектории таких точек будут иметь со своим кругом кри-
визны касание соответственно от 2-го до 4-го порядка.
4°. Три бесконечно близкие положения плоской фигуры. При
трех бесконечно близких положениях плоской фигуры отыскание
центра окружности, которая проходит через последовательные бес-
конечно близкие положения любой точки этой фигуры, сводится
к нахождению центра кривизны траектории этой точки. Зависимость
между координатами точки В (х, у) фигуры S и координатами центра
Ж (хм, Tai) в неподвижной плоскости получим при помощи соотно-
шений (16.5), учитывая выражения (16.20) и (16.21):
— х(х"х+у".у) _ —
М — «2 (х2 + У2) - (х"х + у"у) ’ ум — (х2 + у2) - (х''х + К'у) • °-2
Формулы (16.25) можно представить в более простой форме.
Определим геометрическое место точек фигуры S, для которых
радиус кривизны траектории равен бесконечности. Для этого прирав-
няем нулю общий знаменатель в формулах (16.25). Тогда получим,
что искомым геометрическим местом является окружность
(х2у2) — «’x+X'j') = 0. (16.26)
Эта окружность называется кругом перегибов, так как все ее
точки находятся в точках перегиба своих траекторий.
Координаты хк, ук центра круга перегибов k и его диаметр d
определяются по формулам:
. } (16.27)
Из этих формул следует, что ускорение точки, совпадающей с
полюсом, направлено к центру круга перегибов и в частном случае,
при (о=1, равно диаметру этого круга.
Уравнение касательной к кругу перегибов в мгновенном полюсе
Р(0, 0) будет
*>+Х'.У = 0, (16.28)
и, следовательно, угол наклона ее к оси Ох получим по формуле
tgs;=-4- <16-29)
Уо
1022 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
На рис. 836 построены полюсная касательная tt, полюсная нор-
маль п и круг перегибов k.
Выберем полярные координаты с началом в полюсе Р и полярной
осью Рх. При этом очевидно, что направления радиусов векторов
г в и Гм какой-либо точки В (рис. 836) и соответствующего ей центра
М будут совпадать и определяться одним и тем же углом В.
Обозначим радиус-вектор круга перегибов, определяемый углом о,
через р (рис. 836). Тогда уравнения (16.25) и (16.26) в полярных
координатах запишутся в следующем виде:
— (х(’’ cos 6 -ф у" sin 8) гв
гм и?гв — (х" cos 8 -Ту" sin 8)
и
i !r. - (x'J cos В X' sin g) = 0
(16.30)
(16.31)
Решив совместно уравнения (16.30) и (16.31), получим следу-
ющее соотношение, связывающее радиусы-векторы Гв, Гм и р какой-
либо точки В фигуры S, соответствующего ей центра Л1 в непод-
вижной плоскости У и точки
круга перегибов р:
^ = J--1.(16.32)
гм гв Р
Полюсная касательная делит
всю плоскость х, у на две
полуплоскости.
Одна из них содержит
целиком круг перегибов.
Условимся векторы Гц и< \/в
соотношении (16.32) считать
положительными, если они
расположены в полуплоско-
сти, содержащей круг пере-
гибов, и отрицательными —
в противном случае.
Условие (16.32) дает возможность графически определить центр А1,
соответствующий заданной точке В. Перепишем для этого соотно-
шение (16.32):
__ 'в
Р ~Р — гв
(16.33)
Тогда построение может быть проведено следующим образом.
Наносим на чертеж полюсную касательную tt и круг перегибов k
(рис. 837). Проведем прямую РВ и произвольную прямую Рп. Отложим
на последней от полюса отрезки PL = p и PN=p -^~Гв, учитывая
при этом указанное выше правило знаков. Соединим точки В и N
§ г'<’|
ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
1023
удовлетворять пропор-
и через точку L проведем прямую, параллельную прямой BN,
до пересечения с прямой ВР в точке М. Эта точка и будет
искомым центром, соответствующим точке В, так как по построению
отрезок гм = РМ (с учетом знака) будет
ции (16.33).
Очевидно, что, используя пропорцию
гв __ гм
Р Р + гм ’
(16.34)
можно аналогичным построением определить
соответственному ей центру М.
точку В по заданному
Установим еще некоторые геометрические места для выявления
соответствия областей расположения точек В и М.
По соотношению (16.32) установим, что бесконечно удаленным
точкам В (гв = со) будут соответствовать центры М, для которых
Гм = — р, и следовательно, геометрическим местом таких точек М
явится окружность /г', симметричная кругу перегибов относительно
полюсной касательной tt (рис. 838).
Ее уравнение имеет следующий вид:
^(х^+У) — (у/> — <j) = 0. (16.35)
• Из соотношения (16.32) следует также, что, если центр 714 вы-
брать на круге перегибов гм — р, то соответственная точка В рас-
положится на окружности I, вдвое меньшей круга перегибов, так
как Г/) = -р. Наконец, точке В, расположенной на круге Л'(гв = — р),
соответствует центр Л1, лежащий на окружности Z', вдвое меньшей
круга k', так как Гм~— *, р.
1024 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
Точке В, расположенной в полюсе (гв = 0), будет соответство-
вать при р 0 центр, расположенный также в полюсе (гм = 0), и
обратно.
Таким образом, на любой прямой, проведенной через полюс и
не совпадающей с полюсной касательной, т. е. при р 0, устана-
вливается взаимно-однозначное соответствие точек В и центров М.
Тик, при движении точки В в положительной полуплоскости из
бесконечности (В,) до круга перегибов k (В.2), центр перемещается в
отрицательной полуплоскости от круга В (Л4,) до бесконечности (М2).
При перемещении точки В от круга перегибов k (В.2) до круга
/ (fi3) центр 7И движется в положительной полуплоскости из беско-
нечности (М2) до круга перегибов k (Af3). При движении точки В от
круга /(В3) к полюсу Р центр М движется от окружности Л(/Ия)
к полюсу Р. В полюсе Р точка В4 и соответственный центр Д!4
совпадают и потом переходят в отрицательную полуплоскость.
Когда точка В приходит на круг /г'(Вй), центр располагается на
круге В (А1в). Наконец, при перемещении точки В от круга
В (Вп) до бесконечности (Z^) центр М перемещается от круга
В(Д4в) до круга В (/И,).
Указанное соответствие нарушается в точках, принадлежащих
полюсной касательной, для которой р = 0. По формуле (16.32) по-
лучим, что в этом случае любой точке В (гв ф 0) будет соответ-
ствовать центр 7И, совпадающий с полюсом (гл1 = 0). Обратно, лю-
бому центру Л1, принадлежащему полюсной касательной (тдг 0),
будет соответствовать точка В, лежащая в полюсе (г^ = 0). Урав-
§ S0]
ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
1025
нение круга перегибов (16.26) иногда бывает удобнее использовать
в параметрической форме:
л-," -4- у" tg 6 . s
x=J(r+\^Ty У=х^ (16.36)
здесь 8 — угол наклона к осп абсцисс радиуса-вектора, проведенного
из начала координат в точку круга перегибов (рис. 836).
5°. Четыре бесконечно близкие положения плоской фигуры.
Круговые точки подвижной плоскости S, т. е. точки, лежащие в че-
тырех бесконечно близких положениях на круге кривизны их траек-
тории, должны удовлетворять уравнению (16.9), выведенному в пункте
1° настоящего параграфа. Для составления этого уравнения опреде-
лим, пользуясь формулами (16.20) — (16.22), выражения:
х,2+у2 = а)2(х2+У), (16.37)
х'у” — х"у' = си3 (х2 - |-у2) — W (х"х 4~Х.У)> (16.38)
х'х” -\-у'у" = (х~ -|- у2) 10 (Xх — X'Х> (16.39)
х'"у' —у"'х' — — Зы2<о (х2 4-ф2) 4- “ {х”х 4~ Х"Х- (16.40)
Подставив выражения (16.37) — (16.40) в уравнение (16.9), найдем
следующее уравнение геометрического места круговых точек, удов-
летворяющих условию касания 3-го порядка:
(х2 4~Х) (,l\X 4~ 7аф) — 73_у2 — 1±ху — 1йх* = 0, (16.41)
где
£ © г © •3 -з со со X V 3 *3 - И .. СО СО j "Х® + 1 Ц ? с г © = э со X. со з s' 1 m + II II II II II (16.42)
Уравнение (16.41) представляет собой алгебраическую кривую
3-го порядка с двойной точкой в начале координат, т. е. в полюсе.
В приведенных выше обозначениях (§ 37, 7°) это будет кривая
круговых точек В]111.
Обозначив уравнение кривой (16.41) через Ф(х, _у) = 0, найдем
касательные к ней в полюсе Р(0, 0), который является ее двойной
точкой. Угловые коэффициенты этих касательных tg В] и tg В1/, как
известно, являются корнями квадратного уравнения:
Фи + 2 tg 8 Ф12 у ф22 tg2 8 = 0,
где
Ф11==4^ • Ф12 = -^- • Фм = ^-
11 дхе 1=о’ 12 дхду х=о’ 22 ду2
у=о (у=0 у=0
1/<32 И. И. Артоболевский
1026 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
В нашем случае имеем:
Фи— 2/в; Ф|2 — — 4; Ф22 3= — 2/3.
Заменяя /3, /4, I- их значениями по формулам (16.42) и решая
квадратное уравнение, найдем следующие выражения для угловых
коэффициентов касательных в полюсе к кривой круговых точек:
tg&! = -4-; = + (16.43)
.Уо ло
Как было выяснено выше первый угловой коэффициент определяет
полюсную касательную. Следовательно, второй определит полюсную
нормаль.
Определим, далее, асимптоту кривой (16.41), для чего перепишем
ее уравнение в однородных координатах (х, у, t):
(х2 + J2) (^ + 4J) — t (4J2 — кхУ — 4*2) = 0. (16.44)
Тогда угловой коэффициент tg асимптоты определится по со-
отношению
tg8co = —у-. (16.45)
*2
Из уравнения (16.44) следует также, что кривая круговых точек
(16.41) является циркулярной кривой, т. е. проходит через цикличе-
ские точки плоскости (см. § 37, 1°).
Покажем геометрическое построение кривой (16.41), для чего
определим предварительно положение ее фокуса F(xf, yF). Следуя
выводу, приведенному в § 37, 1° и 4° получим:
г __ 1 44— 44 ,, _ 1 44 + 44
f~~2 II + II > ,
Z6 = /3 /5.
(16.46)
Можно, далее, установить, что любая точка В(х, у) кривой кру-
говых точек (16.41) удовлетворяет угловому равенству
(16.47)
где Вт — бесконечно удаленная точка кривой (16.41), определяемая
угловым коэффициентом tg 8ОТ (16.45).
Для доказательства этого запишем выражение (16.47) в аналити-
ческой форме:
yF-У У у.1^
xF — x X ~x'li
xF — х х А 4
(16.48)
Подставив в уравнение (16.48) координаты фокуса xF и yF из
выражений (16.46), получим уравнение кривой круговых точек (16.41).
§ 50]
ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
1027
С помощью равенства (16.47) кривая (16.41) может быть построена
следующим образом.
Нанесем на чертеж полюс Р и фокус F. В середине D отрезка PF
проведем (рис. 839) перпендикулярную к нему прямую dd и на рас-
стоянии PK = PD = ~<2 PF от полюса Р — прямую kk с угловым коэф-
фициентом tgBoo. Проведем, далее, через полюс Р произвольную пря-
мую г', которая пересечет прямую kk в точке К'. Из точки Р делаем
Рис. 839.
засечку на прямой dd радиусом РЛ", отмечающую точку Z7; ее поло-
жение относительно прямой PF определяется из условия
£ КК’Р= Z PD'D.
Из точки U, как из центра, опишем окружность Ь' радиусом D'P.
Точка пересечения В окружности Ь’ с прямой г' будет принадлежать
кривой круговых точек (16.41), так как по построению следует, что
она удовлетворяет угловому равенству (16.47).
Таким образом, кривая круговых точек всегда может быть по-
строена, если заданы ее фокус и направление асимптоты.
Уравнение (16.41) можно переписать еще в следующей с|)орме:
(х2 +У) (4х 1.2у) — 3 (х'оХ !-у"у) (у"х — Хо'у) = 0. (16.49)
Из этого уравнения следует, что кривая круговых точек В\1" может
распадаться на прямую и окружность, если выполняются условия:
Г = 5 (16.50)
*2 Ли
или
7132’
Л _ __к
4
(16.51)
1028 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ ] ГЛ. XV!
Соотношения (16.50) и (16.51) выполняются, если асимптота кри-
вой круговых точек совпадает по направлению с полюсной касатель-
ной (условие (16.50)) или с полюсной нормалью (условие (16.51)).
Из уравнения (16.49) следует, что кривая BJ111 может распадаться
па три прямые — полюсную касательную, полюсную нормаль и беско-
нечно удаленную прямую. Этот случай имеет место, если
Zi = Z2=0. (16.52)
Выше было показано, что каждой точке В фигуры S соответ-
ствует центр М в неподвижной плоскости V, и дано геометрическое
построение этого центра.
Определив для каждой круговой точки кривой В''" соответ-
ствующий центр, получим кривую центров /И1111. Ее уравнение может
быть получено, если уравнение кривой (16.41) переписать в полярных
координатах и исключить из него радиус-вектор круговых точек
с помощью формулы (16.30).
Если полученное уравнение снова переписать в декартовых коор-
динатах, то получим уравнение кривой центров /И1111:
(х2 4“У2) (Z*x 4" zLv) — Z3J2 — Z4x_y — ZBx® = 0, (16.53)
где
Z* = шх'и — 3oSx", I* = шуо" — 3i»_po, (16.54)
а коэффициенты Z3, Z4, Z5 определяются прежними формулами (16.42).
Таким образом, уравнение кривой центров (16.53) отличается от
уравнения кривой круговых точек (16.41) только величиной коэффи-
циентов Z, и Z2 и, следовательно, кривая (16.53) обладает всеми свой-
ствами кривой (16.41). Угловой коэффициент асимптоты кривой цент-
ров tg 8*о п координаты ее фокуса F* (хд, уф) определятся по фор-
мулам, аналогичным формулам (16.45) и (16.46):
tg8£ = -|,
1 /?/,-/?/<, s_ 1 ф/, + l$le
F 2 Г}2 + К2 ’ УГ 2 /*2 + /*2
(16.55)
(16.56)
Наконец, переписав уравнение (16.53) в виде, аналогичном урав-
нению (16.49):
(х8 -ф- j/2) (Zfx -ф- /фу) — 3 (ХоХ 4-уоУ) (У«х —- х"у) = 0,(16.57)
убедимся, что распадение кривой центров имеет место, если
(16'58)
или
(16.59)
т. е. по-прежнему кривая (16.53) распадается на прямую и окруж-
ность, если ее асимптота совпадает по направлению с полюсной каса-
§ 50]
ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ
1029
тельной или с полюсной нормалью, и, наконец, распадается на полюсную
касательную, полюсную нормаль и бесконечно удаленную прямую, если
Z*=/* = 0. (16.60)
Построение кривой центров (16.53) проводится аналогично построе-
нию, указанному для кривой круговых точек, так как любая точка Л4
кривой центров удовлетворяет угловому равенству
Z. F*MP = L (16.61)
где Ala,— бесконечно удаленная точка кривой центров, определяемая
угловым коэффициентом (16.55), a F*—фокус.
X
Рис. 840.
На рис. 840 построены кривая круговых точек и кривая цент-
ров Л/”11, обозначенные, соответственно, b и tn. Проведем через
полюс Р произвольную прямую z под углом 8 к оси абсцисс. Она пере-
сечет кривую Ъ в некоторой точке В, а кривую т~ в соответствен-
ном этой точке центре М.
Решив уравнения (16.41) и (16.53) совместно с уравнением пря-
мой z, получим следующие параметрические выражения для координат
точек В и М:
В tg2 8 “р ^4 tg 8 Н- Л _____ х 3;
Xe-"(tg!8+l)(/1 + /stgB) > у,{~ в g ’
„ ____ tgs 8 + tg 8 + 4 ___. g
— (tg28 + 1)(/? + /?tg8)’ Ум Хл tg ’
x/233 II. И. Артоболевский
(16.62)
(16.63)
1030 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. Х\1
Заметим, что абсцисса центра М с помощью уравнений (16.62) и
(16.63) связывается следующим выражением с абсциссой соответствен-
ной круговой точки Ву.
хв___+ /У tg &
Аж 6 + A tg о
(16.64)
Определим еще круговую точку подвижной плоской фигуры,
которой соответствует бесконечно удаленный центр, т. е. точку, четы-
ре бесконечно близких положения которой лежат на одной прямой. Эта
точка называется точкой Болла. Очевидно, она определится как точка
пересечения кривой (16.41) и круга перегибов (16.26).
Решив совместно уравнения (16.36) и уравнение кривой круговых
точек в форме (16.62), получим следующий угловой коэффициент
прямой, определяющей точку Болла:
|,М5)
которая является единственной. Нетрудно проверить, что выражение
(16.65) совпадает с угловым коэффициентом асимптоты кривой центров.
Отметим, что при совместном решении уравнений (16.36) и (16.62)
производится сокращение на двучлен х",х -|у "у. Однако потери кор-
ней при этом не происходит, так как уравнение
Х$Х -j—УоУ == 0
определяет, как уже указывалось, полюсную касательную, которая
не имеет с кривой круговых точек других общих точек, кроме
полюса. (Последнее утверждение можно проверить, подставив в урав-
нения (16.62) тангенс угла наклона полюсной касательной, т. е.
v"
tg 8 =— Ц; тогда получим —О, д/в = 0.) Но точке плоской фи-
Уо
гуры, совпадающей с полюсом, соответствует центр, совпадающий
с ним же (см. 3°), и следовательно, полюс не является точкой Болла.
Координаты точки Болла можно определить, подставив значе-
ние углового коэффициента (16.65) в параметрическое уравнение круга
перегиба (16.36) или кривой круговых точек (16.65).
Аналогичным путем можно найти центр Болла, т. е. центр, кото-
рому соответствует бесконечно удаленная круговая точка. Для опре-
деления его координат следует подставить угловой коэффициент
асимптоты кривой круговых точек
tg8oo=-^
«а
в параметрическое уравнение (16.35) круга k' или в параметрическое
уравнение (16.63) кривой центров.
§ 50] ОСНОВЫ КИНЕМАТИЧЕСКОЙ ГЕОМЕТРИИ 1031
6°. Пять бесконечно близких положений плоской фигуры. Для
определения круговых точек, отвечающих требованию касания 4-го по-
рядка их траектории с кругом кривизны, подставим в уравнение (16.10)
значения х',..., xlv и y,...,_yIV из формул (16.20) — (16.23).
Получим:
юа (х1 + У) (т;14- intx msy) — (х”,х Ц-_у« у) ('«!•* ф- тгу -ф- тя) = 0>
(16.66)
где
пгх = 4(и_Уо" — бы2 х3 -ф- бы у!,, |
тг — — 4ы х'о" — 6о)2_уп — бы хЦ,
тл = 3 (х02 -J-J'o2),
Wi=x’v + Sx;’4-wb } (16-67)
Wr.=XV +GX' T-W-2-
Q = X (ы4 — 4ыы -— Зад2),
to- v )
Исключим из этого уравнения и уравнения (16.41) член х2 -\--у‘г.
После сокращения на общий множитель х'('х -|-у'^у *) получим урав-
нение некоторого конического сечения:
AjX2 ф- k2y2 ф- ksxy — А\х — k$y = 0, (16.68)
где
= Зю2 у"} — Цтъ '
-— —- Зю2 /AZg Zg/72-2,
-— Зсо^д^) //Zg'— Зю2 jcq IZ2W], (16.69)
^4=^3 (6 ~ Зы2_у"),
A3 = w3 (Za -ф- Зы2х0).
В пересечении этого конического сечения с кривой круговых то-
чек (16.41) определятся точки, траектория которых имеет касание
4-го порядка со своим кругом кривизны. Они будут точками
Бурместера Z?ln11, а соответствующие им центры—-центрами Бурме-
стера /И]1111.
Для определения точек пересечения кривых, выраженных уравне-
ниями (16.41) и (16.68), подставим в уравнение (16.68):
у = xtgB,
где 8 — по-прежнему угол наклона прямой z, соединяющей точку (х, у)
с началом координат, которое совпадает с мгновенным полюсом Р.
*) При этом сокращении потери корней не происходит, так как уравнение
+ J'oJ’ — 0 определяет, как уже указывалось выше, полюсную, касательную.
‘/,33’
1032 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ |гл. XVI
Тогда получим:
kt + tg 8 is
tg 8 + fea tg8 8 1 y — Xtg •
(16.70)
Приравняв правые части выражений (16.62) и (16.70), получим
уравнение для определения угловых коэффициентов радиусов-векторов
точек пересечения кривых (16.41) и (16.66):
«4 tg48 + «з tg'* 8 + «а tg28 + «i tg 8 + no = O, (16.71)
где
«4 == ~— ^o^‘2> '
«з —
A’3Z4 —
П\ = кх1,^ - /г./в—-
«о == *14 — kJx.
(16.72)
Определив корень tg Вд уравнения (16.71) и подставив его в
любое из уравнений (16.62) или (16.70), найдем координаты точки
Бурместера BJ1111 (Хд, уд). Отметим, что для проверки полезно опре-
делить Хв из обоих указанных соотношений.
Для определения центра Бурместера Ж1’11’, соответствующего
точке Бурместера Д"111, используем соотношение (16.64).
Центры Бурместера Ж,пп можно определить и непосредственно,
использовав кривую центров четвертого порядка, подобную кривой
круговых точек (16.66). Уравнение этой кривой центров выведем,
перейдя в уравнении кривой круговых точек (16.66) к полярным ко-
ординатам и произведя замену радиуса-вектора круговой точки г в
его выражением (16.32) через радиусы-векторы соответствующего
центра гм и круга перегиба р.
Возвратившись после несложного преобразования к декартовым
координатам, получим:
(и2 (х2 4-ф2) (т^х -ф- т$у — т9) — (х"х Д-yjy) (пг2х -j- т.2у wz3) = 0,
(16.73)
где
т * ==mi — т1г = т.2, (16.74)
а тъ тг, ..., ms определяются соотношениями (16.67).
Исключив из уравнений кривых центров (16.53) и (16.73) член
х2-|~у2, получим, как и в случае круговых точек, уравнение кони-
ческого сечения:
kfх2 k^y'2 -J- k^xy — kfx — kiy — 0,
(16.75)
§ 51]
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1033
где
Л* = Зю2 у^'т* — ZJ/n1,
k$ = — 3w2 x'^rn? —
k* = Зи>гуцт£ — Зы2 Xntn* — 1*тг — l*mb
kl=m^ — ЗоАт").
(16.76)
Запишем уравнение (16.75) в параметрическом виде:
ft? + kf tg 8 , s
K? + kf tg6 + /!f tg28 1 y~~ Xtg8-
(16.77)
Приравнивая выражения для абсцисс точек конического сечения
(16.77) и кривой центров (16.63), получим следующее уравнение четвер-
той степени для параметра tg В, определяющего центр Бурместера Л111111:
где
«I tg4 8 -] nJ tg3 8 nJ tg2 8 -ф- nJ tg 8 -|- n0 = 0, (16.78)
-ftJ/J -
л.Г=*Г4 + *2*4 + *3% -ktf - Wi (16.79)
-г^4 -k^i
Координаты центра TW11111 найдутся подстановкой tg 8 в уравнения
(16.63) или (16.77).
Точек Бурместера В*11' и соответствующих им центров Бурме-
стера /И11111 может быть или четыре или две или ни одной, т. к. угло-
вые коэффициенты их радиусов-векторов должны удовлетворять соот-
ветственно уравнению (16.71) или (16.78). Чтобы траектория какой-
либо из точек Бурместера имела касание 5-го порядка с кругом
кривизны, необходимо, чтобы эта точка лежала на кривой, уравнение
которой получим из уравнения (16.11) при подстановке в пего значе-
ний х',..., xv и у', yv из соотношений (16.20) — (16.24).
§ 51. Синтез четырехзвенных передаточных механизмов
Iе. Интерполяционное приближение функции положения шар-
нирного четырехзвенника к заданной функции с одним узлом
высокой кратности. Пусть требуется определить шарнирный четы-
рехзвенник ABCD (рис. 841), воспроизводящий приближенно заданную
33 И. И. Артоболевский
1034 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гЛ. XVI
функцию
<P = F (?)
(16.80)
между углами поворота его ведомого ф и ведущего звеньев.
Потребуем, чтобы заданная функция (16.80) и функция положения
механизма
Ф =/(?)>
(16.81)
удовлетворяли в узле интерполяции следующим условиям:
/"'(?.)=F"'(?1),
Г (<Pi) = F' (?1), /*v (?I) = FIV («?,).
(16.82)*)
Одновременное выполнение условий (16.82) означает, что заданная
функция (16.80) и функция положения механизма (16.81) будут в точке
иметь касание 4-го порядка. Эта точка представит собой узел интерполя-
ших порядков ведомого звена определятся
ции кратности пять. Можно
предполагать, что при этом
функция положения меха-
низма /(<?) будет мало откло-
няться от заданной функции
F (<?) в достаточно большой
окрестности точки <рь
Положим, что угловая
скорость ведущего кривоши-
па постоянна и равна единице:
-У = const =1. (16.83)
dt v
Тогда угловая скорость,
ускорение и ускорения вые-
ло заданной функции (16.80):
<р = 91
= F' (ч>1),
f = F"(<Pi). .... i,v=FV(?1).
(16.84)
Рассмотрим движение ведущего звена АВ относительно ведо-
мого CD. Для этого остановим ведомое звено, сообщив всему ме-
*) В уравнениях (16.82) штрихом обозначена производная по углу по-
ворота <f, которая будет пропорциональна производной по времени, если
= const.
dt
звено АВ
с угловой
(16.85)
(16.86)
§ 51 | СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ передаточных механизмов 1035
ханизму постоянную угловую скорость, равную—L и угловые ускоре-
ния — —iIv.
Тогда в механизме ABCD звено CD будет стойкой, а
будет совершать сложное плоско-параллельное движение
скоростью
w = 1 — I
и угловыми ускорениями первого и высших порядков:
то = — I’, ТО = — I"', 1
ш — — ’тб'= — 11 v. I
Положение мгновенного полюса Р звена АВ в движении его отно-
сительно звена CD определится из равенства
AP==r^-i- (16.87)
(длину звена CD принимаем равной единице).
Совместим начало О подвижной системы координат ;, т(, связанной
со звеном АВ, с полюсом Р; ось О; направим по CD, а ось Оц —
вертикально вверх.
Неподвижные оси х, у примем совпадающими в данный момент
с подвижными. Тогда определение требуемого четырехзвенника све-
дется к задаче, рассмотренной в предыдущем параграфе.
В самом деле, движение звена АВ можно рассматривать как по-
ступательное вместе с точкой, совпадающей с полюсом Р, и враща-
тельное около этой точки.
Первое движение определено, если известны скорость и ускоре-
ния точки, совпадающей с полюсом Р (т. е. х',_у',.... Х>Х)> во вто-
ром — должны быть заданы угловые скорость и ускорения плоскости
звена АВ, т. е. величины то, то... ш’. При этом шарниры В и А
будут располагаться в точках Бурместера плоскости звена АВ, а шар-
ниры D и С в соответствующих им центрах Бурместера.
Величины то, то,..., ’то были определены выше формулами’(16.85)
и (16.86). Покажем определение величин (х'>у'и,..., х^,у^.
2°. Определение производных от координат точки, совпадаю-
щей с полюсом. Обозначим векторы скорости и ускорений первого
и высших порядков точки О, принадлежащей ведущему звену АВ и
совпадающей с полюсом Р, соответственно через ®(Х>Х)» е(Х>Х)>
•' (Х”> X"). • • • > е"'(ху, X)- Имеем:
v = vA-j-vPA, . (16.88)
где 1>А — скорость точки А, а ®Рд— скорость точки О относительно
А. Иначе:
® = (шддХОЛ) + (о>Х^)- (16.89)
33
1036 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
Обозначив единичные векторы правой системы координат х, у, г
через I, J, k (ось z при этом направлена перпендикулярно к плоско-
сти чертежа на нас), получим:
® = WzM(ft X-OA)4-w(ft X АР). (16.90)
Для дальнейшего дифференцирования заметим, что
а(»хол)=(^хол) + (»х^),
t/A? dD А х х л
но — = 0, а -^-=^г)аУ\ОА3 следовательно,
~ (ft X DA) = k X («>ол X DA) = мод (ft • DA) — DA(k- шОА),
но k • DA — 0, так как k | DA и k шдд — ioDA. Окончательно, по-
лучаем:
dt(kXDA) = — <оод DA
и аналогично
^(ЛХАР) = -шАР.
Дифференцируя последовательно выражение (16.90) и собирая
каждый раз члены, содержащие векторы DA, АР, (k X DA) и (ft X АР),
получим:
s = &DA(kXDA)-{-ii>(kXAP) — шЪаОА — ы‘АР, (16.91)
е' = (Лдд — шЬд)(ft х DA) 4- (w — О)3)(ft X АР) —
— ‘Аы[)Аш13аОА — ЗышАР, (16.92)
в" = ( О) од — бшЬл^ da) (kXDA) + C<S — 64)%) (ft X А Р) +
-И (шЬл — 4и>одйод — ЗйЬл)DA 4- (0j4 — 4u>w — 3<я2) АР, (16.93)
е'" = (10ю3ш — Юйш — 5ш ш) АР4-
4-(‘ш— 10ш2й — 15шйа4-<о»)(Л X АР). (16.94)
Проектируем уравнения (16.91) — (16.93) на оси координат х, у, учиты-
вая следующие выражения для проекции отдельных векторов
(DA)X = — 1; (ОА)> = (ОА)г = 0,
(А/\) = ~-, (А Р)у = (А Р)г = 0,
Ц)дд == — I, и> = 1 — i,
V>DA — «« = — I, U>DA—i*> = — !" > —
(16.95)
§ 51] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 1037
Получим:
(16.96)
Л-IV = - -/(1 з/А З/'О - уап
X' = -- — 6/г.
Покажем еще, что отыскание точек Бурместера в случае четырех-
. звенника несколько упрощается, так как одной из четырех таких
точек всегда будет точка А. Для этой точки имеем:
i 1
ХД=-Г=7- I
уд=0, tg8A = 0. j
(16.97)
Подставляя
лучим:
это значение tg В = 0 в формулы (16.62) и (16.70), ио-
д-д
/а ___kt
h ~ kx‘
Следовательно, — и свободный член уравнения (16.71) оказы-
вается пп = 0. v
Таким образом, для определения оставшихся трех круговых точек
получаем кубическое уравнение
tg38 4-p2 tg^B-f-p, tgB-4-/7o = O,
(16.98)
где
Р* = 'Ъ Р'=Ъ Р° = %-
Уравнение (16.78) для определения центров Бурместера также
упрощается, так как для шарнирного четырехзвенника корень tg В =
= 0 определяет центр, совпадающий с шарниром D. Из уравнений
(16.63) и (16.77) получим:
е5 k*
е*—fe*’
откуда л* = 0, и мы получаем вместо уравнения (16.78) уравнение
3-го порядка:
tg3 8 -j- у* tg2 В 4- р* tg 8 ч- у* = 0,
(16.100)
1038 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
где
р*
/77.
«Г
/Ц
«Г
(16.101)
Укажем последовательное гь подсчета параметров схемы шарнирного
четырехзвенника из условия касания 4-го порядка его функции по-
ложения и заданной функции.
I. Выбираем узел и по заданной функции (16.80) определяем
величины I, I',..., zlv по формулам (16.84) и величины о>, ы,.... i» по
формулам (16.85) и (16.86).
2. Определяем х”, у”, х'", у'”, x[,v, _y*v по формулам (16.96).
3. Находим коэффициенты т...., »zs по (16.67) и т*, т* по
формулам (16.74) и /*, /*, /;1, 11г I*— по формулам (16.42) и (16.54).
4. Определяем коэффициенты кубического уравнения р*, р*, р* по
формулам (16.101).
5. Решая уравнение (16.100), находим один или три корня tg 8^,
tg о”., tg определяющие по формуле (16.63) или (16.77) центры
Бурместера Л4Ь Ми, /Ищ.
Любой из центров М может быть выбран в качестве подвижного
шарнира С ведомого звена CD искомого четырехзвенника. Таким об-
разом, мы получим один или три четырехзвенника, удовлетворяющие
поставленным требованиям. Дальнейший расчет проводится отдельно
для каждого четырехзвенника.
6. По известным координатам шарнира М (х..ц, _ущ) определяем
положение шарнира 5(хд, _ув) по формулам (16.64).
7. Рассчитываем координаты неподвижных шарниров А и D по
формулам:
У а = 0, у в — 0,
после чего определяем размеры механизма и подсчитываем таблицу
отклонений его функции положения от заданной функции (см. § 43, 2°).
Первый пример. Пусть требуется воспроизвести шарнирным
четырехзвенником функцию w = z*. Заданы угол выхода и угол
входа <?т:
= 50е, = 60°.
Перейдя к углам ф и ф поворота ведущего и ведомого звеньев, получим:
, 5 I .2
Т 6 60- у ’
где ср и ф выражены в градусах.
Интерполяционный узел выбираем в середине угла входа
ф, = 30е.
§ 51]
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1039
Следуя указанному порядку расчета, определяем далее:
1. I = 0,833333 ш = 4-0,166667,
I' = 1,59155 = —w,
/" = w = i"' = io =... = 0.
ч- х"й— н Р 0,833333, < = 0, x>v = 4-45,1084,
л =Н [- 9,54930, № = 0,555555, j>],v = — 7.95775.
3. /я, =- -91,6983, /* = 4-3,97887,
тг = - Р 6,36620, /* = 4-45,5019,
т-, = [-275,651, /3 = —23,8732,
«:=- -274,539, Д = -|- 271,484,
ОТ? = - - 2613,70, /5 = -|-23,8732.
4. />* = 0,332283, />* = -[-0,0345582,
/>* = 4-0,0011131.
5. Полученное кубическое уравнение имеет три корня:
tg = —0,0640741, tg = — 0,158822, tg 8Ш = — 0,109387.
Этим корням соответствуют три центра Бурместера, с которыми может
быть совмещен шарнир С четырехзвенника. Координаты этих шарниров:
хс, = 4-5,97536, хСп = 4-5,96036, №„, = 4-6,04637,
Уа = — 0,382866, _уС|| = —0,946636, Ус1П = ~ 0,661396.
6. Соответствующие положения шарнира В будут:
хВ[ = 4-3,40956, №„ = 7,93037, №„, =4- 30,9451,
_УВ, = — 0,218465, №„ = — 1,25952, №,„ = — 3,38500.
7. Находим координаты неподвижных шарниров А и D:
№ = 4-5,OOOQO,
№=0,
xD = 4- 6,00000,
№ = °-
Вычисляем далее отдельно для каждого из трех механизмов его
параметры: длину кривошипа АВ = а, шатуна ВС = Ь и коромысла
CD —с и углы а, и рь определяющие положение кривошипа АВ и
коромысла CD в положении, соответствующем узлу интерполяции:
Первый механизм
б/=1,60537.
/> = 2,57106,
с = 0,383658,
Второй механизм
О = 3,18958,
Ь= 1,99470,
с = 0,947465,
Третий механизм
а = 26,1643,
/> = 25,0476,
с = 0,66302,
aj=187o49'17",
р1 = 266°19,04".
. а1 = 336°44'28",
Pj = 267°36'08".
а, = 352°34',
Р, = 274'00'38".
1040 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИИ [гл. XVI
Схемы этих трех механизмов показаны на рис. 842—844. Положе-
ния ABCD соответствуют = 30°. Пунктиром показаны (на рис. 842
и 843) положения механизмов в начале и конце отрезка приближения,
определяемого углом входа <рт — 60°. Приведем таблицу 16.1 отклоне-
ний Дф функции положения трех найденных механизмов от заданной
функции.
§ 511
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1041
Таблица 16.1
<р д-ь
первый второй третий
механизм механизм механизм
0 — 3'40" 4- 45'30" 4 16’45"
10° — 0'45" 4 4'50" 4 1'48"
20 — 0'02" 4 0'08" 4 0'03"
30 0 0 0
40 + 0'04" — 0'07" — 0’02"
.50' 4 1'49" — 3’16" — 0'38"
4 15’55" — 22'02" — 2'53"
Графики отклонений этих трех механизмов показаны на рис. 845.
Обратим внимание, что отклонения изменяют знак при переходе
через узел интерполя-
ции, что и должно быть
при касании 4-го по-
рядка.
Второй при-
мер. Возьмем опять
функцию w = Z*, но
увеличим угол входа
ведущего звена. Пусть
<рт=100° ифт = 50с.
Тогда будет:
, 1 1 2
Л —-_________о -
• 2 100 ‘ ’
Узел интерполяции
выбираем опять в се-
редине угла входа
= 50°. Как и в первом примере определяем следующие величины:
1. / = 4-0,500000.
/' — 0,572958 = — и»,
= ш = ш =. .. = 0.
2. х" = 4-0,500000, х"’ = 0,
X = -1,14592, Х” = °>
(О = -|- 0,500000.
x’v = 4- 1,84468,
Xv = — 1,71887.
1042 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ {ГЛ. XVI
3. гщ = —4,68937, /* = 4-0,859437,
т., =0, /* = -(- 1,96968,
т3 = 4- 4,68937 /3 =— 1,71887,
гл* = 0, 4 =4-3,18937,
Щ* = —5,94658, 4 = 4- 1,71887.
4. />*=1,20044, р* = 0,624505, />* = 0,127017
Кубическое уравнение (16.100) с этими коэффициентами имее!
один корень
tgSA1 = — 0,436332.
Для определения координат центра Бурместера этот корень сле-
дует подставить в уравнение (16.77) либо в уравнение (16.63). Пер-
вая подстановка дает результат
хм = 4-1,80730, № = — 0,788583.
Из второго уравнения хм определить не удается, так как по подста-
новке получим:
О
№1 — "o'-
Этот результат указывает на распадение кривой центров (16.53). Дей-
ствительно, легко убедиться, что значения /*, /*, Хо, Уо удов-
летворяют пропорции (16.58) и, следовательно, кривая центров (16.53)
распадается на окружность с и прямую Pt (рис. 846), являющуюся
полюсной касательной. Коническое сечение (16.75) изображено на
рис. 846 пунктиром. Полученный корень tg уравнения (16.100) также
§ 51|
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1043
определяет направление полюсной касательной, и поэтому на послед-
ней расположен искомый центр Бурместера. Круговая точка В
в этом случае совпадает с полюсом и, следовательно,
хд = 0, У в — 0-
Определив далее координаты шарниров А и D:
хА=1, хо — 2,
у а - о. Уи = 0,
находим параметры механизма:
а=1, £= 1,97185, с = 0,811786,
а, = 180°, ^ = 256° 16'05".
Подсчитываем таблицу отклонений от заданной функции:
т 0' 10° 20° 30° 40° 50° 60е 70е 8(6 90° 10Ц
A-L + 8'03" + 2'06" + 0'22" + 0'02" 0 0 0 + 0'02" + 0'22" + 2'06" + 8'03"
График отклонений приведен на фиг. 847.
Из графика видно, что отклонения по обе стороны интерполяцион-
ного узла получаются одинакового знака. Обусловлено это тем, что
в данном примере удовле-
творяются условия касания
пятого порядка, что нетруд-
но проверить численно.
3°. Интерполяционное
приближение функции по-
ложения шарнирного че-
тырехзвенника к заданной
функции с одним четырех-
кратным узлом с учетом
заданного угла передачи.
При проектировании меха-
низма иногда оказывается целесообразным ограничиться условием ка-
сания 3-го порядка (что соответствует четырехкратному узлу интер-
поляции), чтобы иметь возможность выбора механизма, отвечающего
тем или иным дополнительным требованиям. Например, можно потре-
бовать, чтобы угол передачи р. механизма в данном положении
последнего или на всем отрезке приближения был не меньше неко-
торого выбранного значения р.п.
В случае касания 3-го порядка в качестве шарнира С механизма
может быть выбрана любая точка кривой центров (16.53).
1044 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
На рис. 848 построена кривая центров т в осях хОу, начало кото-
рых совпадает с мгновенным полюсом Р, и неподвижные шарниры А
и D, определяемые абсциссами хА и xL) по формулам (16.102).
На отрезке PD построим окружности а и а', вмещающие задан-
ные углы р0 и 180° — р.о. Кривая центров с каждой из этих окруж-
ностей пересекается только в одной точке, так как из шести возмож-
ных точек пересечения две совпадают с полюсом Р, одна — с шарни-
ром D и, наконец, две — с циклическими точками.
Участок кривой центров, заключенный между указанными окружно-
стями (на рис. 848 он выделен жирной линией), определяет меха-
низмы, у которых угол передачи jj. в том их положении, которое
определяется абсциссой узла интерполяции, удовлетворяет неравен-
ству р.о sg р. 180° — р.й. Один из таких механизмов показан на
рис. 848.
В частном случае можно потребовать, чтобы угол передачи в дан-
ном положении механизма был прямым. При этом окружности а и а’
сливаются в одну окружность а, построенную на отрезке PD, как на
диаметре (рис. 849).
Эта окружность в пересечении с кривой центров определит
единственный центр С и, следовательно, единственный меха-
низм ABCD, осуществляющий касание 3-го порядка и имеющий в пер-
вом положении угол передачи 90е.
Указанное решение можно провести в аналитической форме.
§ 51] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 1045
Уравнения окружностей а и а' (рис. 848) получаются из уравнения
х8 У* — ххо —yxD ctg р = 0
(16.103)
при подстановке в него значений соответственно
!А==|Ап, р=180° — р.о.
(16.104)
Запишем уравнение (16.103) в параметрическом виде:
Ар + Ар Ctg [1 tg 6
l+tg*&
y = xtg8.
(16.105)
Приравнивая выражения для абсцисс окружностей а и а'(16. 105)
и кривой центров (16.63), получим квадратное уравнение для
Рис. 849.
определения параметра 8, соответствующего точке их пересечения:
tg2 S + ?i tg 8 ?0 = 0,
(16.106)
где
?2 = /3 —Z*xcctg[i,
?i = li — xcZ* — l*xc ctg [i,
?0 == 4 — Xcl\.
(16.107)
Заменив в коэффициенте q0 величины l*, 1Ъ, их выражениями
через i и I, убедимся, что ?0 = 0.
1046 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ |ГЛ. XVI
Следовательно, уравнение (16.106), кроме корня tg 8 = 0, соответ-
ствующего точке D, имеет единственный корень
te а = —91 = li~xclt-l*xcc4>v-
k ?s XcCtg[J. /* —/3
(16.108)
Подставив в выражение (16.108) значения ы из (16.104), найдем
предельные значения параметра tg 8, определяющего точки пересече-
ния кривой центров т (рис. 848) с окружностями а и а'. Подста-
вив в равенство (16.108) р. = 90е, определим значение параметра tg о,
определяющего механизм с углом передачи 90°:
tg8 =
хсК —
(16.109)
При проектировании механизма желательно получить удовлетво-
рительный угол передачи не только в положении, определяемом абс-
циссой узла интерполяции, но и на всем отрезке приближения.
Понятно, что эти механизмы нужно искать только среди тех, которые
Рис. 8э0.
в положении, определяемом абсцис-
сой угла интерполяции, удовлетво-
ряют условию p.f,<p<: 180°—р.ц.
Удобно разыскание механизмов, ко-
торые на всем отрезке приближения
удовлетворяют упомянутому усло-
вию начать с механизма, у которого
в указанном ранее положении угол
передачи р=90°, т. е. с меха-
низма, определяемого парамет-
ром tg В по формуле (16.109).
4 . Интерполяционное прибли-
жение функции положения кри-
вошипно-шатунного механизма
к заданной функции с одним
узлом высокой кратности. Пусть
требуется воспроизвести криво-
шипно-шатунным механизмом АВМ
(рис. 850) заданную функцию
s =F(<p). (16.110)
По-прежнему поставим условие, чтобы функция (16.110) и функция
положения механизма
5 = /(<р)
(16.111)
в некоторой выбранной точке <р, имели касание 4-го порядка.
§ 51] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 104/
Это требование выполняется, если в точке <р( удовлетворяются
одновременно следующие условия:
= = *),
f (?i) = F Ы = sb
......................} (16.112)
/v((pi)=Fiv(!?i)=siv.
В этих формулах производные берутся по времени или по углу ср,
так как, не нарушая общности, можно положить угловую скорость
ведущего звена АВ постоянной и равной единице.
Остановим ведомое звено — ползун, сообщив всему механизму
добавочно поступательное движение со скоростями и ускорениями,
определяемыми соотношениями (16.112), но противоположными им по
знаку. При этом ползун остановится, а точка А будет двигаться
прямолинейно со скоростью —s[ и ускорениями —s", —s'", —s]v.
Таким образом, в относительном движении плоская фигура, связан-
ная со звеном АВ, будет участвовать в двух движениях: в посту-
пательном движении вместе с точкой А и во вращении вокруг этой
точки с постоянной угловой скоростью ю, равной единице.
Проведем на рис. 850 координатные оси АТ с началом в точке А,
направив ось X перпендикулярно направлению движения ползуна,
а ось Y—параллельно последнему.
Мгновенный полюс Р относительного движения звена АВ распо-
ложится в точке пересечения прямой ВМ с осью АХ и опреде-
лится координатами:
хР=~, у/р = 0. (16.113)
Свяжем со звеном АВ подвижные оси координат ху с началом
в полюсе Р, параллельные осям X, Y.
Тогда координаты шарнира А определятся по формуле
—J, (16.114)
Задача определения кривбшипно-шатунного механизма по указан-
ным выше условиям сводится к уже рассмотренной задаче нахождения
в подвижной плоскости точек Бурместера, а в неподвижной плоско-
сти — соответственных им центров Бурместера.
Поместив в найденной точке Бурместера шарнир В и определив
соответственный ему центр М, найдем искомый кривошипно-шатунный
механизм АВМ.
*) В формулах (16.112) значения функции s и ее производных в точке
обозначены для сокращения письма индексом «один».
1048 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
Для того чтобы воспользоваться выведенными ранее формулами
для определения координат точек и центров Бурместера, требуется
отыскать ускорения первого и высших порядков для той точки пло-
ской фигуры звена АВ, которая совпадает с полюсом, т. е. х",у", ...
..., xjv, _yjv, а также угловую скорость <а шатунной плоскости и ее
производные <о, ..., ш.
5°. Отыскание ускорений первого и высших порядков для
точки, совпадающей с полюсом. В относительном движении звена АВ
скорость и ускорения его точки, совпадающей с мгновенным полюсом Р.
и их составляющие по осям х, у обозначим соответственно через
Vp(x0', _у0'), гР(х",у"), ър(х'о", у!,") &р (x'v,^'v). Скорость vP получим,
суммируя скорость ©пер переносного движения звена АВ вместе с шар-
ниром А (рис. 850) и скорость ©отн относительного движения точки
этого звена, совпадающей с полюсом Р, относительно точки А:
®Р=®'пер + ®отН (16.115)
или
5р=®д-|-(<йХ АР). (16.116)
Проекции скорости фл на оси координат:
|ФЛ1Д. = О, = —(16.117)
Угловая скорость w шатунной плоскости была нами принята по-
стоянной и равной единице по модулю. Обозначив единичный век гор
оси z (направленной перпендикулярно к плоскости чертежа) через k.
получим:
<о=Л; о’> = о)= Ф =0. (16.1181
Вектор АР направлен по оси абсцисс, и его проекция на эту
ось, согласно формуле (16.113), равна:
(ДР)д. = х1. (16.119)
Перепишем выражение (16.116) для скорости точки, совпадающей
с полюсом:
<oP=vA-{-(k'X АР) (16.120)
и спроектируем его на оси координат.
Учитывая соотношения (16.117), (16.118) и (16.119), получим:
(Vp)x = xo— 0, (Фр)у—уо — — S|-j-si = O. (16.121)
Дифференцируем трижды уравнение (16.120), замечая, что
~(kyt АР) = — АР, ±AP = ky АР.
dty at
Имеем:
бр=фл— АР, e'P = vA—(k)(.AP), z‘p — v'a'-\-AP. (16.122)
§ 51] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 1049
Проектируем равенства (16.122) на оси координат, учитывая соот-
ношения (16.112)—(16.119). Получим:
< = — X"
X"
О,
— s'i" — \>
XV=+^- I
Xv = -*lv- J
(16.123)
Переходим непосредственно к задаче определения круговых точек
и соответственных центров для нескольких бесконечно близких по-
ложений плоскости ведущего звена.
6°. Три и четыре бесконечно близкие положения ведущего
звена. Формулы (16.25) для определения координат Хм, Ум центра
кривизны траектории какой-либо точки Bt (х, у) принимают для случая
кривошипно-шатунного механизма следующий вид:
xM=xQ, yM=yQ, (16.124)
где
п =, , + --- (16.125)
х + у0 у — Л-3 — у2
Уравнение круга перегибов, как геометрического места точек, соот-
ветственные центры которых располагаются в бесконечности, получим
из условия Q = co:
х2 -ф-у2 — х'о х —у'о'у = 0. (16.126)
По этому уравнению находим координаты центра xk, yk круга
перегибов и его диаметр d:
хА = 0,5x6', yft = O,5y6' (16.127)
и
(16.128)
Таким образом, в рассматриваемом случае полное ускорение
точки, совпадающей с полюсом,-равно (по модулю) диаметру круга
перегиба.
В уравнении кривой круговых точек В1"':
(х2 +/) (4х 4- /2 у) — l9y2 — 1,ху — /8х2 = 0, (16.129)
коэффициенты будут:
Zi = -—3s]', /4 = 3 (s]’2 — si2),
Za = 2sl — si", /jj = 3sisi'.
4 =— 3sisi',
(16.130)
Они получаются из коэффициентов (16.42) уравнения (16.41) под-
становкой значений ш, w, хб', ..., уо", определяемых формулами
(16.118) и (16.123).
Производя эту замену в соотношениях (16.50) и (16.51), опреде-
ляющих распадение кривой круговых точек, найдем два условия
1050 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
распадения кривой (16.129) на прямую и окружность:
__ S1
s[” — 2s[ s'' ’
3sJ ’ __s”
2s; —s; •
(16.131)
(16.132)
В практических приложениях представляет интерес случай, когда
при si ф 0 имеем s[’=0 и sj" =0; при этом условие (16.132) удов-
летворяется и кривая (16.129) распадается. Отметим еще случай
распадения кривой центров при 1Х = = 0, что приводит к условию
$1" =0; si" = 2sj ф 0.
Кривая круговых точек распадается при этом на координатные
оси и бесконечно удаленную прямую.
Построение кривой круговых точек было рассмотрено в 4е
настоящего параграфа; необходимые для построения координаты фо-
куса и угловой коэффициент асимптоты определяются по-прежнему
формулами (16.46) и (16.45) при подстановке в них значений Z,, 1г, ...
..., Z8 из формул (16.130).
Уравнение кривой центров Л41111 для рассматриваемого случая при-
нимает следующий вид:
(х2 НJ’2) /а’з’—Z3y2 — Z4xj’ —Zex2 = 0. (16.133)
где
Й = — s\—sC, (16.134)
а коэффициенты Z3, Z4, Z8 определяются по формулам (16.130).
Кривая центров распадается на прямую у = 0 и окружность в
двух случаях:
1) при sj =0 «Г # 0;
2) при si’ =0 sj 0.
Распадение кривой центров на две конечные прямые и бесконечно
удаленную прямую имеет место при si” = si0. Конечными прямыми
будут:
1) при si'=0 оси координат;
2) при sj’ =4 0 полюсные касательная и нормаль.
Формулы для определения углового коэффициента асимптоты 8^
и фокуса кривой центров принимают вид:
tg6co = 0,
1 Л
Xf = , УЕ----
X/в
2 /*
(16.135)
По известным фокусу и направлению асимптоты кривая центров
может быть построена указанным выше способом.
7°. Пять бесконечно близких положений ведущего звена. Оп-
ределение точек и центров Бурместера для случая кривошипно-ша-
тунного механизма выполняется, как указано в пункте 5° настоящего
параграфа.
§51] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ
1051
В уравнении кривой
(х2 -у2) (т3 4- от4х 4~ т3у) — (хох 4-уо'у) (пцх т2у 4- »г3) = о,
(16.136)
которая проходит через точки Бурместера, коэффициенты будут:
т1 = 2s] — 4s I",
/«2 = 6s]',
/7Z3 = 3 (s]2 4-s]'2), (16.137)
/>z4= 2s] — 4s'\" =тъ
nt3 = 5sj' — s]v.
Они получены из коэффициентов (16.67) на основании формул
(16.118) и (16.123).
Уравнение кривой, проходящей вместе с кривой центров через
центры Бурместера, принимает следующий вид:
(х2 у2) (т%у — та) — (хо'х 4~уо'у) (тхх тгу 4- w3) = 0, (16.138)
где дополнительно к формулам (16.137) обозначено:
mt = — Г — s'v. (16.139)
Решая последнее уравнение (16.138) совместно с уравнением кри-
вой центров (16.133), найдем координаты центра Бурместера.
Приведем окончательные формулы для подсчета угла наклона о
прямой, определяющей в пересечении с кривой центров центры Бур-
местера 7И11111. Тангенс этого угла удовлетворяет уравнению
и* tg3S4~«2 tg2&4-«Гtg84~«о =0, (16.140)
где
«? = *?z3 — z2*^, = + Ж —W, 1
nl = kV^ki^ — ^kt,n$=k^—llkt J (16.141)
a
Л* = 3 (s's" 4- 4s" s'" — s'sIV),
k% = 2s'2 4- 3s"2 — 4s'"2 — 2s's'" 4- 3s"slv,
kt = 3 (s'2 4- s"2) (2s' — s'"), (16.142)
k% = ~ 9s" (s'2 — s"2),
Коэффициенты It, Z3, Z4, ZB определяются по формулам (16.134) и
(16.130).
После определения корней tgSAf уравнения (16.140) координаты
центра Бурместера Л411Ш (х^, ум) определятся по параметрическому
уравнению кривой центров:
к -j- Л tg 4“ h tg2 ВЛ1
^ = 41 + tgSWtg^ , ум = хЛ11ёЙЛ1. (16.143;
1052 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
Координаты соответственной точки Бурместера А?[П||(хв, ув)
определятся по соотношениям, аналогичным формуле (16.64)
I* tg Вм
Хв ~ I tg ь 4- / ’ Ув =хв*^м- (16.144)
'2 1g “М “Г ‘1
Координаты шарнира А в осях ху определим по соотношению
(16.114):
Хд= —si, _уд=0. (16.145)
8е. Пример приближения функции положения кривошипно-ша-
тунного механизма к линейной зависимости. Пусть функция
(16.110), которую нужно воспроизвести кривошипно-шатунным меха-
низмом, есть линейная функция
s = A<p. (16.146)
Для определенности будем полагать k^>0. Дифференцируя (16.146),
получим:
sf = k; s” = s'" = slv = 0. (16.147)
Подставив эти значения производных в формулы (16.130) и
(16.134) для коэффициентов кривой круговых точек и кривой цент-
ров, получим:
/1==/3 = /8=0; 4 = 2А; Z4 = — ЗА2; /*= —А.
При таких значениях коэффициентов кривая круговых точек (16.129)
распадается на окружность
х2-|-_у24-1,5Ах = 0 (16.148)
и прямую
_у = 0. (16.149)
Кривая центров также распадается на окружность
х^у2 — ЗАх —0 (16.150)
и прямую
_у = 0. (16.151)
Окружности (16.148) и (16.150) показаны на рис. 851 сплош-
ными линиями.
Нанесем на чертеже точку А, координаты которой определятся
по г|юрмуле (16.145):
хА— — k, ул—®-
Проведем через начало координат, т. е. через полюс Р, произ-
вольную прямую; она пересечет окружность (16.148) в точке В, а
окружность (16.150)—в соответственном центре ЛД Поместив в точ-
ках А и В шарниры и в точке М — шарнир и ползун, получим
§ 511 СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ ПЕРЕДАТОЧНЫХ МЕХАНИЗМОВ 1053
искомый кривошипно-шатунный механизм АВМ-, воспроизводимая им
зависимость будет иметь в данном положении касание 3-го порядка
с прямой (16.146).
Рассмотрим, далее, вторую кривую круговых точек (16.136) и
вторую кривую центров (16.138). Их коэффициенты с учетом выра-
жений (16.147) запишутся:
m1 = 2s'==mi; т3 = 3/'; т2 = тъ — tn* = 0.
При этих значениях коэффициентов кривая круговых точек (16.136)
распадается на окружность
х2+УЦ-/гх = 0 (16.152)
и прямую
х = — 1.5Л. (16.153)
Заметим, что уравнение (16.152) представляет собой, как это сле-
дует из уравнения (16.126), круг перегибов.
Вторая кривая центров (16.138) распадается на бесконечно уда- )
ленную прямую и эллипс:
х24-ЗУ — 3/гх = 0. (16.154) °
Окружность (16.152), прямая (16.153) и эллипс (16.154) показаны
пунктиром на рис. 851.
Таким образом, в качестве точек Бурместера могут быть выбраны
точки А, Р и В'. Но для точек А и Р механизмы получаются вы- 4)
рождающимися, так как в первом случае получаем кривошип нулевой
34 И. И. Артоболевский
1054 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гЛ. XVI
длины, а во втором — шатун. Точке Д' соответствует центр М', и
механизм получается с углом передачи, равным нулю. Следовательно,
в случае заданной линейной функции не удается получить криво-
шипно-шатунный механизм, осуществляющий касание 4-го порядка.
§ 52. Синтез четырехзвенных направляющих механизмов
1°. Общие соотношения. Рассмотрим движение плоской фигуры S
в содержащей ее неподвижной плоскости У (рис. 852).
Свяжем с неподвижной плоскостью У оси координат хО'у, а с
подвижной фигурой S — оси координат Положение какой-либо
Рис. 852.
точки Е фигуры S в неподвижной
плоскости определится векто-
ром ге-
гЕ — гй + ге. (16.155)
Здесь г0 — вектор, определяю-
щий положение подвижного нача-
ла координат О относительно не-
подвижного О', а ге — вектор,
определяющий положение точки
Е в подвижной системе EOtq.
Для определения скорости
точки Е продифференцируем вы-
ражение (16.155):
®£ = ®с + (‘»Хге). (16.156)
Здесь ш — угловая скорость фи-
гуры S.
Если точку Е принять совпа-
дающей с мгновенным полюсом Р вращения плоской фигуры S, обо-
значив ее Ps, то соотношение (16.156) примет следующий вид:
®0 -|- (о> X гр) — (16.157)
так как ©Ps — 0.
Умножив уравнение (16.157) векторно слева на ш и учитывая,
что ц)гр = 0 и wa> = to2, получим:
_ со хд» (16.158)
Р €02
Отсюда радиус-вектор полюса гр равен:
Гр = Го + ^(<»Х®о)-
(16.159)
Дифференцируя это выражение, найдем скорость изменения поло-
жения полюса и:
и = ®0 — (tu X ®о) + 'а X ®о) + X Go). (16.160)
§ 52]
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
1055
где
Но векторы oj и со коллинеарны и, следовательно,
^(а>Х®о) = ^(«>Х®о)-
Учитывая это равенство в соотношении (16.160), получим:
U = ©о + (w X «о) — (<*> X ®о)-
(16.161)
Так как полюс Р перемещается по неподвижной центроиде Цг, ско-
рость и направлена по касательной к этой центроиде (рис. 853),
т. е. по полюсной касательной Pt.
Пусть подвижное начало координат О совпадает с полюсом;
тогда
vn = vps = Q, a^ — aps. - (16.162)
Подставив эти значения ©0 и а0 в (16.161), получим:
« = ^(wX«ps). (16.163)
Из этого следует, что aps_i_u и, следовательно, ускорение точки
фигуры S, совпадающей в данный момент с полюсом, направлено по
прямой, перпендикулярной к полюсной касательной, т. е. по полюс-
ной нормали.
Из формулы (16.163) получим:
(ipg — — (о>Х«)- (16.164)
34
1056 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
Модуль ускорения aps будет равен:
a.ps — ши,
(16.165)
так как <м | и, а его направление определится по векторному ра-
венству (16.164).
В частном случае, при <о = 1, имеем:
aps = u.
(16.166)
Ранее показано, что в этом случае ускорение точки, совпадающей
с полюсом, обозначенное нами cips, равно диаметру круга перегиба d
и направлено по этому диаметру. Следовательно, построив в точке
Р (рис. 853) вектор aPs и описав на нем, как на диаметре, окруж-
ность, мы получим круг перегиба К.
Рис. 855.
2°. Графическое определение центра кривизны шатунной
кривой. Возьмем шарнирный четырехзвенник ABCD (рис. 854), раз-
меры которого заданы. Его положение определяется углом ср, кото-
рый ведущее звено АВ образует со стойкой CD. Покажем, как
отыскать центр кривизны траектории какой-либо точки шатунной
плоскости в заданном положении четырехзвенника.
Определим полюсную касательную. Для этого представим себе
звенья АВ и CD продолженными и снабженными ползушками, ко-
торые соединены шарниром в полюсе Р. Найдем скорость и шар-
нира Р. Для этого построим план скоростей механизма (рис. 855).
Векторы и ®Р(сД), представляющие собой скорости точек,
принадлежащих соответственно звеньям АВ и CD и совпадающих с
точкой Р, известны по величине и направлены перпендикулярно к
звеньям АВ и CD. Через концы этих векторов проведем направления
Скоростей относительного движения ползушек по направляющим
§ 52] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ 1057
АР и DP. Соединив точку пересечения этих прямых с полюсом плана
скоростей, получим скорость и шарнира Р.
Проведем через Р (рис. 854) прямую Pt, параллельную вектору
и, которая представит собой полюсную касательную. Построим, далее,
круг перегибов k. Центр его будет на полюсной нормали. Величина
диаметра d равна:
и V
d = (16.167) а/
Имея полюс Р, полюс- -----
ную касательную Pt и круг
перегиба k, легко опреде- рис 856
лить центр кривизны траек-
тории какой-либо точки плоскости, воспользовавшись построением,
указанным на стр. 1023.
3°. Аналитическое определение центра кривизны траектории
шатунной точки. Рассмотрим шарнирный четырехзвенник ABCD
(рис. 856).
Примем длину стойки CD — 1 и обозначим длины остальных
звеньев:
АВ = а, BC = b, CD = c. (16.168)
Положение ведущего звена АВ определим углом <р, образуемым
этим звеном со стойкой CD\ тогда положение ведомого звена CD
определится углом ф, зависящим от <р (см. § 43,2°).
Рис. 857.
Построим для заданного четырехзвенника (рис. 857) мгновенный
полюс Р движения плоскости шатуна ВС . и мгновенный полюс Q
относительного движения звеньев АВ и CD.
Соединим точки Р и Q прямой и обозначим через а угол, кото-
рый она образует с прямой РА. Дадим ведущему звену малое сме-
1058 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XV!
щение Дер; при этом ведомое звено CD повернется на угол Дф, а
полюс Р перейдет в положение Р', сместившись на отрезок &р=РР’.
Определим угол а', который образует направление Pt переме-
щения полюса Д/7 с ведомым звеном CD. Если бы полюс Р переме-
щался только вместе со звеном АВ или со звеном CD, он занял бы
соответственно положения п или т; тогда ио рис. 857 получим:
Др
___ДР sin (A<f)________OPsin (Дф)
" sin (7 + a') sin а'
откуда
sin а' ______DP sin (Дф).
sin (7 -f- а1) АР sin (Д-р)
(16.169)
Но по малости углов Дер и Дф имеем:
sin (Дф)___дф
sin (Дер) Др '
Далее,
Дф____AQ_____ ДР sin а
Др DQ DP sin (7 + а)'
Сравнив равенства (16.169) и (16.170), получим:
sin а' ____ sin а
sin (7 + а') sin (7 + а) ’
откуда
а' = а.
(16.170)
(16.171)
Следовательно, полюсная касательная Pt образует с ведомым
звеном CD тот же угол а, что и полюсная прямая PQ с ведущим
звеном АВ.
Определим аналитически направление полюсной касательной Pt
и положение полюса Р, шарнира В и шарнира С для заданного угла <р. .
Выберем начало координат в точке А и направим ось X по стойке AD,
а ось Y—вертикально вверх (рис. 858),
§ 52]
СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
1059
Координаты шарниров В и С определятся по формулам:
Хд = a cos ср, А'с = 1 4“ с cos
Yg:=a sin у, Гс —с sin
Полюс Р определим как точку пересечения прямых АВ и CD:
(16.172)
X — tg*
₽~tg'P-tgv’
¥Р = ХР^Ч-
(16.173)
Полюс Q находится в точке пересечения прямых ВС и AD, от-
куда его координаты будут:
— Xci в
х9= Гс-Ув ’
уд=°-
(16.174)
Определим еще угловой коэффициент прямой PQ, образующей
угол |3 с осью Ох:
^=Х^Х~д- (16.175)
Обозначив угол, образованный полюсной касательной Pt и осью
х, через a.t, найдем из треугольников и DLfP и APQ:
я^ = ф 4~ я и я = <р — р,
откуда
= <р 4- ф— р. (16.176)
Найдем скорость и перемены полюса.
Построим план скоростей точки Р.
Из полюса плана проведем вектор ®p(abi
(рис. 859) скорости точки звена АВ, совпа-
дающей с полюсом. Далее, проводим через
полюс Р прямую pt, параллельную полюсной
касательной, а через конец вектора vp(AB}
прямую, параллельную звену АВ (т. е. в
направлении скорости f0T„ смещения полюса относительно звена АВ).
Соединив точку пересечения указанных прямых с полюсом плана
скоростей, получим вектор и скорости перемены полюса.
По рис. 859 замечаем, что угол между векторами и и ®отВ ра-
вен ф — ср я, откуда
Скорость Vp{AB} равна:
и== _______________
sin (ф — ср + “1
(16.177)
VP(AB}---и’1ГР'
(16.178)
где w, — угловая скорость ведущего звена АВ, a Гр — АР. Положение
1060 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
центра кривизны не зависит от угловой скорости ш1( но в дальнейшем
изложении целесообразно полагать угловую скорость о> шатунной
плоскости постоянной и равной единице. Это выполняется, если
“1
_/?Р
~~ АВ
— гр~г
г
(16.179)
Окончательно получаем:
Гр(Гр—г)
Г sin (!> — <р + а) ’
где
г =АР—-^~
р COS <f>
(16.180)
(16.181)
Перенесем начало координат в полюс Р и повернем координат-
ные оси на угол at, чтобы ось х была направлена по полюсной
касательной Pt. В новых осях ху (рис. 858) координаты шарни-
ров В и С определятся по формулам:
х = (Г—Гр) sin ^ — (Х—Хр cos а^, 1
У = — (АГ— Ар) sin az — (Г — Yp) cos а,. j
(16.182)
В этих формулах для определения координат шарнира В (хв< Ун)
следует положить ,Y=Azb и У=Ув, а для определения координат
шарнира С (хс, Jc) — А’= А'с, У= Ус-
Ранее (на стр. 1030) нами были выведены формулы, связывающие
координаты х, у точки шатунной плоскости с координатами хм, ум
соответственного центра. Для выбранных нами осей координат в этих
формулах следует положить х'о = 0, так как ускорение точки, сов-
падающей с полюсом, направлено по нормали к полюсной касатель-
ной, т. е. по оси у. Учитывая еще условие w=l, получим:
Хм — У“ХУ VM — Ао-У8 П6 1831
м уёу — (А-2+уа)’ Ум у?у-(х2+у2)- ')
Входящая в эти формулы величина уо определяется с помощью
соотношений (16.166) и (16.177), так как
(16.184)
Знак у'о выбирается, исходя из направления оси у.
Уравнение круга перегибов (16.126) принимает следующий вид:
—УоА = О, (16.185)
откуда координаты его центра и диаметр d определятся по формулам:
х* = 0, yk=\yu, d=|jo|. (16.186)
§ 52] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ 1061
4°. Кривая круговых точек. Как уже было установлено, геомет-
рическим местом точек шатунной плоскости, траектории которых
имеют со своим кругом кривизны касание 3-го порядка, является
кривая круговых точек S/111. В рассматриваемом случае уравнение
этой кривой имеет вид:
(X- 4“ У) 4“ — кхУ — о, (16.187)
где
Л = хо'4-3>8, 4=Jo", 4 = 3уо2. (16.188)
Эта кривая должна проходить через шарниры В и С четырех-
звенника.
Следовательно, неизвестные коэффициенты 4 и /2 кривой (16.187)
определятся из системы уравнений, полученных подстановкой в
уравнение (16.187) поочередно значений хв, ув и хс, Ус, определен-
ных выше формулами (16.182).
Из этой системы найдем:
4 = 4 = X“~~tlfer •» (16.189)
Йц/?22-^12^21 &11&22--^12^21
где
= хв (Хв 4-Уя); ^12 =Ув (xsB 4- у в)-, К = ^Хвув, 1
kn = хс (-4 4~Ус); ^2=>с(^ас+Ус); к2==^хсус. J
Пользуясь выражениями (16.188), по известным 1Х и /2 найдем
величину производных х'о" и jo '..
После определения величин 1Х и /2 кривая круговых точек 5J111
может быть построена при помощи равенства (16.47), причем угловой
коэффициент tg^ асимптоты и координаты фокуса F определяется
по формулам:
tg8co = —xf= VУр=2 ll-Flf (16Л91>
Асимптоту и фокус можно определить также графически. Отме-
тим какую-либо круговую точку (например, шарнир В четырехзвен-
ника) в системе координат ху, имеющей начало в полюсе Р и
ось х, совпадающей с полюсной касательной (рис. 860).
Проведем радиус-вектор г точки В и перпендикулярную к нему
прямую тп. Восставив в точках тип перпендикуляры к осям ко-
ординат, получим в их пересечении некоторую точку В’. Покажем,
что если точка В принадлежит кривой круговых точек (16.187),
точка В' расположится на некоторой прямой, которую, следуя
В. В. Добровольскому [4], мы будем называть направляющей прямой.
Запишем уравнение кривой (16.187) в полярных координатах (г, S):
sin 6 cos в
cos 6 /s sin 6 ’
(16.192)
1062 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
Радиус-вектор г' точки В' определится по формуле
sin в' cos 8''
(16.193)
Подставив в последнее равенство значение г из (16.192) и заменив
угол 8 на 90 — 8', получим:
/3
It sin 8' 4- /s cos 8' ’
(16.194)
или в декартовых координатах
1уХ “р 1\У — — 6.
(16.195)
Это уравнение направляющей прямой. Для шарнирного четырех-
звенника направляющая прямая
Рис. 860.
может быть построена по двум
точкам В’ и С', соответст-
вующим шарнирам В и С (см.
рис. 860).
Сравнивая угловые коэффи-
циенты асимптоты кривой цент-
ров (16.191) и прямой (16.195),
убеждаемся, что угол, образо-
ванный асимптотой с осью Ох,
равен углу, образованному пря-
мой (16.195) и осью Оу.
Таким образом, построив
направляющую прямую, мы мо-
жем построить асимптоту кри-
вой круговых точек. Для по-
строения фокуса воспользуемся
” угловым равенством (16.47),
которому должны удовлетво-
рять подвижные шарниры В и С.
Получим два угловых соотношения для определения фокуса F:
£FBP= L РВЕт, /_FCP= РСЕт, (16.196)
где Eat — бесконечно удаленная точка асимптоты. На рис. 861 при-
ведено это построение.
Уравнение кривой круговых точек (16.187) можно также напи-
сать в параметрическом виде:
Х== (1 + tg2 &) (А + 4 tg 8)’ y = (16.197)
здесь 8 — угол наклона к оси Ох прямой, соединяющей точку кри-
вой (16.187) с полюсом.
Определим точку Болла, т. е. круговую точку, соответственный
центр которой находится в бесконечности,
§ 52] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ 106$
Перепишем уравнение круга перегибов (16.185) в параметриче-
ском виде:
. J = *tg8. (16.198)
Приравнивая выражения для абсцисс кривой круговых точек и круга
Рис. 861.
перегибов, найдем значение параметра tg ВБ, соответствующего точке
Болла Еб:
tg8B=^T=^ = — С. (16.199)
*2 _Уо
Подставив это значение ВБ в уравнение (16.198), определим ко-
ординаты хб, Уб точки Болла Еб:
Xb — — Ry'o", Уб = Ихо", (16.200)
где
' (16.201)
I Jo
5°. Определение точек Бурместера. Выведенное в п. 6° § 50
уравнение (16.66), которое при совместном решении с кривой кру-
говых точек (16.187) определяет точки Бурместера, для рассматри-
ваемого в настоящей главе случая принимает следующий вид:
(х2 -ф->2) (щ3 + /и4х }- тву) —Уо'у (mix тгу + от3) = 0, (16.202)
где
= 4уо''. mt= x*)V nil
т^ = —4хо —6>о. =^v-|-_Уо Ц-иго. (16.203)
tn3 — 3jo2>
Таким образом, в уравнение этой кривой входят два неизвест-
ных коэффициента т4 и т6, так как они зависят от неизвестных
1064 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
производных и у™. Эти коэффициенты можно определить из ус-
ловия прохождения кривой (16.202) через точки В и С. Однако це-
лесообразнее воспользоваться этим условием для определения коэф-
фициентов конического сечения, получающегося при совместном
решении уравнений (16.187) и (16.202). Уравнение этого сечения будет:
где
kiX2 -ф- k3y2 -ф- k3xy — k^x — ksy — 0,
(16.204)
kt = 3>o'm4 — /iWi, /г4 = m3xo
k3 — m3yo >
k3 = Зу'от3 — — /2Wi.
(16.205)
Неизвестные коэффициенты kx и k3 определим, решив систему
уравнений:
k^R + k3xByB = к&хв -ф- k3yB — k^yl, 1
Кх2с + k3xcyc — Kxc + к3Ус — КУс, J
(16.206)
Здесь хв, ув и xc, yc координаты шарниров В и С, подсчитан-
ные по формулам (16.182). Определив и k3, подсчитываем zn4 и
ms по соотношениям (16.205) и, наконец, по (12.203) находим про-
изводные х™ и _y’v.
Запишем уравнение конического сечения (16.204) в параметриче-
ском виде:
г _______^4 + As tg 8
Ai 4- Аз tg 8 tg2 6 ’
> = xtg8.
(16.207)
Приравнивая выражения для абсцисс из уравнений (16.197) и
(16.207), получим уравнение четвертой степени для определения
параметра 8, соответствующего точке Бурместера:
«4 tg4 8 + «з tg3 8 + «2 tg2 8 + tg 8 + «о = 0, (16.208)
где
и4 — — /2А3, Пз = k^l3 Л/г:; — Z2A4, (16.209)
til = ^0 =
Порядок этого уравнения может быть понижен до второго, так
как нам известны два его корня tg 8В и tgoc, соответствующие
шарнирам В и С. Квадратное уравнение для определения двух
оставшихся корней уравнения (16.208) имеет вид:
tg2 8 + Р tg 8 + Ц = 0, (16.210)
§ 52] СИНТЕЗ'четырехзвенных направляющих механизмов
1065
где
/? = 'S'+tg8B + tg8c’ 9== m;t7»7tg»c ’ (16.211)
а Вв и 8С определяются через углы а, <р и ф (см. рис. 858) по фор-
мулам:
гв=ч> — ф — а, Вс = — а. (16.212)
размеры которого заданы: а = 0,4; b = c = №\ d — AD=1. Меха-
низм находится в положении, определяемом углом поворота веду-
щего звена <р = 0. При этом угол поворота ведомого звена CD
1066 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [гл. XVI
будет равен:
ф = 112°01'.
Мгновенный полюс Р вращения шатунной плоскости и мгновенный
полюс Q относительного движения совпадают соответственно с
положениями шарниров D и В. По рис. 862 видно, что в этом слу-
чае QPA — а. = 0 и, следовательно, полюсная касательная
направлена по звену CD, откуда at = <p= 112°01'. Проведем коорди-
натные оси ху, совместив их начало с шарниром D и направив ось х
по полюсной касательной. В этих осях координаты шарниров fi и С
будут:
хв - 0,22500, хс = — 0,80000,
ув= — 0,55624, ус=0.
Определяем, далее, по формулам (16.179), (16.178) и (16.177) вели-
чины о>1=1,5, vPIAB) = 1,5 и уо — — 1,61800. Тогда уравнение
(16.185) круга перегибов к будет:
Х‘2 + У+ 1,618у = 0.
Для построения кривой круговых точек определяем направляющую
прямую; в данном положении механизма она будет параллельна оси у
и, следовательно, асимптота кривой круговых точек параллельна
оси х, откуда
/1 = 0
и
Хо” = — Зуо = + 4,85400.
Кривая круговых точек (16.187) распадается на прямую
j = 0
и окружность
х2-|-У —Ах=0.
Из условия прохождения этой окружности через точку В получим:
откуда
Уо" = — 4,90860.
Итак, кривая круговых точек распадается на окружность
х«1,6х = 0 (16.213)
и прямую
у = 0.
Шатунные кривые для точек окружности (16.213) будут сим-
метричными, т. е. радиус ее равен длине шатуна. Одна из таких
§ 52] СИНТЕЗ ЧЕТЫРЕХЗВЕННЫХ НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ 1067
шатунных кривых показана на рис. 862. Здесь же показана шатун-
ная кривая для точки Болла, координаты которой, определенные по
формулам (16.200), будут:
хБ = —0,80895, уБ = — 0,79995.
Точки Бурместера находим, как указано в пункте 5° настоящего
Корни уравнения (16.210) в нашем примере будут:
tg?! =-4-0,11195, tg8H = — 3,57301.
Этим корням соответствуют круговые точки kx и шатунной
плоскости:
Xkt = — 1,58020,
yki = — 0,17690,
и центры Afj и Л12 в неподвижной
хм =-4-0,20173,
№,=4- 0,02258,
^ = —0,11622,
A 0,41526,
плоскости:
x«s = —0,09103,
Ул'а = +0,32525.
Точки Бурместера лежат на окружности (16.213). Поэтому их
шатунные кривые также будут симметричными, и следовательно,
мы получаем в них касание не 4-го, а сразу 5-го порядка. Точки
Бурместера и k2 и соответствующие им шатунные кривые показаны
на рис. 862. Однако механизмы с остановкой, получаемые при помощи
1068 КИНЕМАТИЧЕСКАЯ ГЕОМЕТРИЯ БЕСКОНЕЧНО БЛИЗКИХ ПОЛОЖЕНИЙ [ГЛ. XVI
этих точек, получаются неудачными в конструктивном отношении,
хотя и дают остановку на большем угле размаха ведомого звена по
сравнению с механизмами, получаемыми при использовании круговых
точек окружности (16.213).
Рис. 864.
На рис. 863 показан механизм с остановкой, у которого в каче-
стве круговой точки Е взята точка окружности а, а на рис. 864 —-
механизм с остановкой, в котором используется шатунная кривая
точки Болла.
ЛИТЕРАТУРА
1. Алексеев Н. И., О прямолинейно-направляющем механизме Гарта.
Научные записки Моск, гидрометеорол. ин-та, вып. VI, 1939.
2. А н т о в и л ь А. М., Бицентроида и центроиды в относительном движении.
Вестник инженеров и техников, 1940, № 7.
3. Артоболевский И. И.
а) Синтез плоских механизмов, Изд. АН СССР, 1939.
б) Атлас по кинематическому расчету кривошипно-шатунных механизмов,
Изд. АН СССР, 1942.
в) О двух новых геометрических местах в кинематике плоских механизмов.
Доклады АН СССР, новая серия, 1944, т. 44, № 6.
г) Роль и значение П. Л. Чебышева в истории развития теории механизмов.
Изв. ОТН АН СССР, 1945, № 4—5.
д) Механизмы для огибания конических сечений. Вестник инженеров и
техников, 1946, № 11—12.
е) Геометрические методы решения некоторых задач теории плоских меха-
низмов. Труды семинара по ТММ, 1947, т. I, вып. 3.
ж) Механизмы коникографов с огибанием. Доклады АН СССР, 1955, т. 104,
№ 5.
з) Механизмы для огибания эллипсов. Доклады АН СССР, 1949, т. 65,
№ 4.
и) О некоторых механизмах для черчения линий. Изв. ОТН АН СССР,
1946, № 7.
к) Два механизма для черчения кривых высших порядков. Доклады АН СССР,
1951, т. 80, № 5.
л) Об одном механизме инверсора. Доклады АН СССР, 1955, т. 104, № 6.
м) Механизмы для образования подэр к коническим сечениям. Доклады
АН СССР, 1955, т. 105, № 1.
н) О механизмах для образования циссоидальных кривых. Изв. ОТН АН СССР,
1955, № 11.
о) Теория механизмов для образования кривых, являющихся гиперболизмами
конических сечений. Изв. ОТН АН CGCP, 1955, № 11.
п) Механизмы, т. I, II, III и IV, 1947—1951.
р) Теория механизмов и машин, 1953.
с) Об эволютах шатунных кривых. Доклады АН СССР, т. 45, № 3, 1944.
т) Механизмы для возведения в куб. Доклады АН СССР, 1951, т. 79, № 6.
у) Механизм для решения квадратных уравнений вида Xs — рх -|- q = 0.
Доклады АН СССР, г. 79, 1951, № 3.
4. Артоболевский И. И., Добровольский В. В., Блох 3. Ш.,
Синтез механизмов, ГТТИ, 1944.
5. Артоболевский И. И., Леви тс кий Н. И.
а) Механизмы П. Л. Чебышева. Сборник «Научное наследие Чебышева»
АН СССР, 1945, вып. 2.
б) П. Л. Чебышев и русская теория механизмов. Труды семинара ТММ,
1947, вып. 5,
1070
ЛИТЕРАТУРА
в) Работа П. Л. Чебышева «Теория механизмов, известных под названием
параллелограммов, и применение метода поправок к решению задач син-
теза механизмов». Приложение к книге: П. Л. Чебышев, Теория меха-
низмов, известных под названием параллелограммов, Изд. АН СССР, 1949.
6. Артоболевский С. И., Машины-автоматы, Машгиз, 1949.
7. А ч е р к а н Н. С., Расчет и проектирование металлорежущих станков, 1950.
8. Б а р а н о в Г. Г.
а) Определение основных размеров прицепного механизма. Труды ВВА РККА,
1936, № 15.
б) К синтезу четырехзвенных механизмов. Труды Москов. авиац. ин-та,
1939, Сборник 1.
в) О решении некоторых задач Чебышева. Труды семинара по ТММ, 1948,
т. V, вып. 20.
9. Блох 3. Ш.
а) Синтез плоских кинематических цепей с низшими парами. Прикл. матем.
и механ., т. 2, вып. 3, 1938.
6) К синтезу четырехзвенных механизмов. Изв. ОТН АН СССР, 1940, № 1.
в) Применение шатунных кривых при решении задач синтеза плоских меха-
низмов. Изв. ОТН АН СССР, 1940, № 7.
г) Проектирование четырехзвенных механизмов по предельному значению
ускорения рабочего звена. Изв. ОТН АН СССР, 1940, № 8.
д) Проектирование плоских механизмов с низшими парами (Всес. НИИ
сельхоз. машиностр.), 1941.
е) К теории конхоидальных кривых. Изв. ОТН АН СССР, 1941, № 4.
ж) К синтезу кривошипно-шатунных прямолинейных направляющих меха-
низмов. Изв. ОТН АН СССР, 1941, № 5.
з) К теории симметричных механизмов Чебышева и их модификаций. Изв.
ОТН АН СССР, 1941, № 6.
и) К синтезу механизмов с остановкой. Изв. ОТН АН СССР, 1941, № 7—8.
к) Задача о наилучшем приближении шатунной кривой к заданной. В кн.
«Исследования в области машиноведения», Изд. АН СССР, 1944.
л) К теории Х-образного механизма Чебышева. Изв. ОТН АН СССР, 1944,
№ 9.
м) Основные результаты работ П. Л. Чебышева по метрическому синтезу
плоских механизмов. В кн. «Научное наследие П. Л. Чебышева», вып. 2,
Изд. АН СССР, 1945.
н) Приближенный синтез шарнирных механизмов, осуществляющих равномер-
ное движение. Изв. ОТН АН СССР, 1945, № 6.
о) Приближенный синтез механизмов, Машгиз, 1948.
10. Блох 3. Ш., Карпин Е. Б., Практические методы синтеза плоских
четырехзвенных .механизмов, Изд. АН СССР, 1943.
11. Бооль В. Г., фон, Инструменты и приборы для геометрического черчения
с изложением их теорий, Москва, 1892.
12. Бруевич Н. Г.
а) О проектировании прицепного кривошипного механизма. Труды ВВА
РККА, 1936, № 15.
б) Механизмы точной механики, Москва, 1938.
в) Точность механизмов, ГТТИ, 1946.
13. Г е р а с и м о в Ю. И., Обобщенная теория дезаксинальных и радиальных
мальтийских механизмов. Труды семинара по ТММ, 1948, т. IV, вып. 15.
14. Г е р о н и м у с Я. Л.
а) О наилучшем приближении посредством функций, не образующих си-
стему Чебышева. Доклады АН СССР, 1947, т. VII, № 1.
б) О применении метода Чебышева к задаче уравновешивания механизмов,
ГТТИ, 1948.
в) О законе подъема с наименьшим пиком ускорений. Труды семинара но
ТММ, 1948, т. IV, вып. 15.
ЛИТЕРАТУРА
1071
г) О некоторых вопросах синтеза кулачковых механизмов. Труды семинара
по ТММ, 1948, т. V, вып. 19.
д) Нахождение Профиля кулака ио заданному движению толкателя, «Тех-
ника воздушного флота», 1933, № 3.
15. Г ерш горин С. А., О механизмах для построения функций комплекс-
ного переменного. Журнал Ленингр. физ.-мат. об-ва, 1926, т. 1.
16. Гончаров В. Д., Теория интерполирования и приближения функций,
ГТТИ, 1954.
17. Делоне Н. Б.
а) Передача вращения и механическое черчение кривых шарнирно-рычаж-
ными механизмами, СПб, 1894.
б) О некоторых новых механизмах. Журнал Русск. физ.-хим. об-ва, 1893,
т. XXV.
18. Добровольский В. В.
а) Основы теории сферических механизмов. Изв. ОТН АН СССР, 1940, № 5.
б) Вопросы структуры механизмов в работах П. Л. Чебышева. Статья
в сборнике «Научное наследие Чебышева», Изд. АН СССР, 1945, вып. 2.
в) О точках Бурместера в сферическом движении. Прикл. матем. и механ.,
т. 9, вып. 6, 1945.
г) Синтез сферических механизмов. Труды семинара по ТММ, 1947, т. 1,
вып. 1.
д) Теория сферических механизмов, Машгиз, 1947.
е) Теория механизмов для образования плоских кривых. Изд. АН СССР,
1953.
ж) Динамическое проектирование кулачковых механизмов. Труды ВВА
им. Жуковского, сборник № 15, 1936.
з) Введение в динамику статически неопределимых механизмов. Труды
семинара по ТММ, вып. 30, Изд. АН СССР, 1949.
и) Теория механизмов, 1946.
к) Траектории пятизвенного механизма. Труды Моск, станкоинструмент.
ин-та, сборник III, 1938.
19. Е з и к а ш в и л и О. С., Кинематический метод обработки кулачков. Труды
семинара по ТММ, 1953, вып. 50.
20. Жуковский Н. Е., Приложение теории центров ускорений высших по-
рядков к направляющему механизму Чебышева. Журнал Русского физ.-хим.
об-ва, т. XV, стр. 134—141. Собр. соч., т. 1, 1937, стр. 227—234.
21. Зернов Д. С., Прикладная механика, 1925.
22. Зиновьев В. А.
а) Проектирование шарнирного четырехзвенника по заданным положениям
кривошипа и коромысла. Труды семинара по ТММ, 1949, т. VII, вып. 25.
б) Проектирование пространственных четырехзвенных механизмов по пол-
ному числу параметров. Труды семинара по ТММ, 1954, т. XIV, вып. 55.
23. 14 в а щ е н к о Н. Н.
а) Новые прямолинейные направляющие четырехзвенные механизмы. В сб.
«Регулирование машин и синтез механизмов», Машгиз, 1950.
б) Об основных параметрах механизма вылета стрелы в кранах с шарнирно-
сочлененной укосиной и гибкой отметкой. В том же сборнике.
24. Каминский В. П., Новый коникограф и устройства для универсальной
обработки по способу «обкатки» поверхностей вращения и цилиндров вто-
рого порядка. Вестник металлопромышл., 1939, № 8.
25. К е т о в X. Ф., Геометрическая теория механизмов. Труды Ленингр. поли-
техи. ин-та, № 4, 1953.
26. Кобринский А. Е.
а) Некоторые вопросы практического расчета на точность механизмов
с низшими парами. Труды семинара по ТММ, 1950, т. VIII, вып. 31.
б) О кинематических ошибках механизмов в положениях близких и край-
них. Труды семинара по ТММ, 1950, т. IX, вып. 33.
1072
ЛИТЕРАТУРА
в) Динамические нагрузки в кулачковых механизмах с упругими толкате-
лями. Труды семинара но ТММ, 1949, вып. 24.
г) К выбору закона движения толкателя. Труды семинара по ТММ, 1950,
вып. 35.
д) Кулачки с оптимальными динамическими характеристиками и схема при-
способлений для их обкатки. В сб. «Вопросы машиностроения», АН СССР,
1950.
27. Кобринск ий Н. Е., Математические машины непрерывного действия,
Гостехиздат, 1954.
28. Кожевников С. Н.
а) Выбор закона движения ведомого звена кулачкового механизма. Труды
Днепропетр. металлург, ин-та, 1949, вып. XVII.
б) Выбор параметров кулачковых механизмов. В сб. «Эксплуатация и кон-
струирование металлургического оборудования», Труды Днепропетр.
металлург, ин-та, 1954, вып. ХХХП.
29. Колчин Н. И., Раскрытие геометрических свойств механизмов на основе
синтеза их кинематических элементов первого порядка. Труды Ленингр.
политехи, ин-та, 1953, № 4.
30. Костицын В. Т.
а) Об одном шарнирном направляющем механизме. Изв. ОТН АН СССР,
1940, № 4.
б) О наименьших размерах кулачковых механизмов. Изв. ОТН АН СССР,
1948, № 10.
31. Котельников А. П., Точки Бурместера, их свойства и построение.
Матем. сборник Матсм. об-ва, 1927, вып. 3—4.
32. Кучер И. М., Конструирование специализированных станков автоматов и
полуавтоматов, Машгиз, 1952.
33. Л е в и т с к и й Н. И.
а) Синтез механизмов по Чебышеву, Изд. АН СССР, 1946.
б) О некоторых преобразованиях плоских механизмов с низшими парами.
Труды семинара по ТММ, 1947, т. II, вып. 5.
в) Применение квадратического приближения функций к решению задач
синтеза механизмов. Труды семинара по ТММ, 1948, вып. 17.
г) Синтез шарнирного четырехзвенника по заданной траектории точки
шатуна. Изв. ОТН АН СССР, 1948, № 10.
д) Симметричные шатунные кривые. Труды семинара по ТММ, 1948, т. IV,
вып. 13.
е) Несимметричные шатунные кривые. Труды семинара по ТММ, 1948,
т. IV, вып. 15.
ж) Синтез шарнирного четырехзвенника ио заданному закону движения,
Труды семинара по ТММ, 1949, г. VII, вып. 28.
з) Проектирование плоских механизмов с низшими парами, Изд. АН СССР, 1950.
и) Методы расчета кулачковых механизмов, Машгиз, 1950.
34. Л ев ит с к ий Н. И. и Степанов Б. И., Проектирование плоских пере-
даточных механизмов с низшими парами. В сб. «Вопросы машиноведения»,
АН СССР, 1950.
35. Л е в и т с к и й Н. И. и Ш а х б а з я н К. X.
а) К вопросу о проектировании механизмов по способу наименьших квад-
ратов. Сб". трудов Всесоюзн. заочн. политехи, ин-та, 1953, вып. 5.
б) Синтез пространственных четырехзвенных механизмов с низшими парами.
Труды семинара по ТММ, 1953, т. XI, вып. 54.
36. Литвин Ф. Л.
а) Некруглые зубчатые колеса, 1950.
б) Проектирование некруглых зубчатых колес, применяющихся в машино-
строении. Труды семинара по ТММ, 1954, т. XIV, вып. 55.
в) Проектирование некруглых зубчатых колес, применяющихся в машино-
строении. Труды семинара по ТММ, 19оЗ, т. XIV,. вып. 53.
ЛИТЕРАТУРА
1073
37. Малышев А. 11., Кинематика механизмов, Гизлегпром, 1933.
38. Мерцалов Н. И., Кинематика механизмов, 1914.
39. Н и к у л и н Н. А., Инструмент для вычерчивания циркулярных кривых
третьего порядка с двойной точкой. «Прикл. матем. и механ.», 1910, № 4.
40. Н о в о д в о р с к и й Е. П., Об одном способе синтеза механизмов. Труды
семинара по ТММ, 1951, вып. 42.
41. Новодворский Е. П. и Пинск ер И. Ш., Точностной и конструктив-
ный синтез шарнирных механизмов, Оборонгиз, 1953.
42. Орликов М. Л., Кулачковые механизмы машин-автоматов, Машгиз, 1955.
43. Парницкий А. Б., Шарнирно-сочлененные укосины кранов, Машгиз,
1948.
44. П и н с к е р И. Ш.
а) Приближенный синтез механизмов с низшими нарами. Труды семинара
по ТММ, 1948, т. V, вып. 18.
б) Подбор шарнирного четырехзвенника по специальному атласу кривых.
Труды семинара по ТММ, 1950, вып. 33.
45. Полы новс кий Г. Л., Механическое построение кривых при помощи
механизмов скольжения. Сталинград, механ. ин-т, Научно-техн, об-во, 1941,
вып. 6.
46. Рагул ьскис К. М., Метод динамического проектирования кулачковых
механизмов автоматов. Автореферат диссертации, Ин-т машиноведения
АН СССР, 1953.
47. Решетов Л. Н.
а) Кулачковые механизмы токарных автоматов, Изд. МВТУ, 1934.
б) Кулачковые механизмы, 1953.
48. Семенов М. В.
а) Аналитический метод синтеза стержневых механизмов, заданных двумя
и тремя положениями. Вести, инжен. и техн., 1938, № 12.
б) Шатунные кривые четырехзвенных механизмов. Труды семинара по ТММ,
1947, т. 111, вып. 10.
49. Сомов П. О., Об одной кинематической цепи с двумя степенями сво-
боды, Изд. Варшавского ун-та, Варшава, 1894, т. VII.
50. Сперанский Н. В.
а) О проектировании механизмов мальтийских крестов с приводом от шар-
нирного четырехзвенника. Труды семинара по ТММ, 1951, т. XII,
выи. 45.
б) Мальтийский механизм с Приводом от эллиптических зубчатых колес.
Там же, т. XVII, вып. 67.
51. Степанов Б. И., Проектирование пространственных передаточных меха-
низмов с низшими парами. Труды семинара по ТММ, 1952, т. XI, вып. 45.
52. Тир К. В.
а) К вопросу о рациональном профилировании кулачков полиграфических
машин. Автореферат диссертации, Моск, полиграф, ин-т, 1952.
б) Критерий качественной оценки и классификация законов периодического
движения. В сб. «Вопросы машиноведения и прочности в машинострое-
нии», т. Ill, вып. 2, Изд. Укр. АН, 1954.
в) Сравнительный анализ качественных характеристик исходных законов
периодического движения. Научные записки Института машиноведения
и автоматики Укр. АН, т. IV, вып. 3, 1955.
г) Синтез и качественная оценка комбинированных законов периодического.
движения. Там же, т. IV, вып. 4, 1956.
53. Тишин М. М.
а) Профилирование кулачков газораспределения авиационных моторов.
Труды семинара по ТММ, 1947, вып. 7.
б) Проектирование кулачковых механизмов с качающимся плоским рычагом.
Труды семинара по ТММ, вып. 7, 1947.
54. Урин Д. М„ Графоаналитическая теория мальтийского креста. МВТУ, 1936.
1074
ЛитёратурА
55. Чебышев П. J1.
а) Теория механизмов, известных под названием параллелограммов, АН
СССР, 1949.
б) Вопросы о наименьших величинах, связанные с приближенным пред-
ставлением функций. Собр. соч., АН СССР, т. II, 1948.
в) О некотором видоизменении коленчатого параллелограмма Уатта. Собр.
соч., АН СССР, т. IV, 1948.
г) Теорема относительно кривой Уатта. Там же.
д) О центробежном уравнителе. Там же.
е) Об одном механизме. Там же.
ж) О параллелограмме. Там же.
з) О зубчатых колесах. Там же.
и) О простейших параллелограммах, симметрических около одной оси. Там же.
к) О простейших сочленениях. Там же.
л) О параллелограммах, состоящих из трех элементов и симметрических
около одной оси. Там же.
м) О простейших параллелограммах, доставляющих прямолинейное движе-
ние с точностью до четвертой степени. Там же.
н) О параллелограммах, состоящих из трех каких-либо элементов. Там же.
о) О преобразовании вращательного движения в движение по некоторым
линиям при помощи сочлененных систем. Там же.
н) О простейшей суставчатой системе, доставляющей движения, симметри-
ческие около оси. Там же.
56. Ч е р к у д и н о в С. А.
а) Механизмы для вычерчивания геометрических мест метрического синтеза,
связанных с параметром г. Труды Ленингр. промышл. академии, 1939, т. II.
б) Геометрические места заданного угла поворота кривошипа. Труды
Ленингр. политехи, ин-та, 1940, вып. 1, № 2.
в) О кривых Альта и о механизмах для их вычерчивания. Там же.
г) К общей теории геометрических мест метрического синтеза. Труды
семинара по ТММ, 1947, т. I, вып. 4.
д) Об одном семействе двукривошипных четырехзвенных механизмов.
Там же, 1947, т. II, вып. 8.
е) Об экстремальных скоростях кулисных механизмов. Там же, 1948, т. II ,вып. 8.
ж) О мертвых положениях механизмов. Там же, 1947, т. II, вып. 8.
з) Угол передачи в шарнирном четырехзвеннике. Там же, 1947, т. III,
вып. 9.
и) К синтезу шарнирных четырехзвенников, осуществляющих приближенно
равномерное движение. Там же, 1947, т. III, вып. 9.
к) О некоторых общих вопросах синтеза шарнирных механизмов. Там же,
1947, т. 111, вып. 10.
л) К синтезу кривошипно-шатунных механизмов, осуществляющих прибли-
женно равномерное движение. Там же, 1948, т. V, вып. 18.
м) Об одном методе приближения в синтезе механизмов. Там же, 1948,
т. VII, вып. 20.
н) Метод наилучшего приближения в синтезе механизмов. Изв. ОТН
АН СССР, 1948, № 10.
о) Синтез некоторых механизмов приближенно равномерного движения. Труды
семинара по ТММ, АН СССР, 1949, т. VI, вып. 21.
п) О некоторых приложениях метода обращения движения. Там же, 1949,
т. VI, вып. 24.
р) Метод кратного интерполирования в синтезе механизмов. Там же, 1951,
т. IX, вып. 40.
57. Ч е р к у д и н о в С. А. и С п е р а н с к и й Н. В.
а) К синтезу плоских шарнирных механизмов с остановками. Труды семи-
нара по ТММ, 1951, т. XI, вып. 43.
б) Об одной схеме мальтийского механизма. Там же, т. XV, вып. 60,
ЛИТЕРАТУРА
1075
в) Синтез четырехзвенных передаточных механизмов методом интерполяцион-
ного приближения с одним узлом высокой кратности. I. Труды семи-
нара по ТММ, т. XVII, вып. 67, 1957.
г) То же ч. II. Там же, т. XVI1J, вып. 71.
58. Ш а с к о л ь с к и й Б. В., Расчет предельных углов подъема станков-
автоматов. «Станки и инструменты», 1947, № 8.
59. Шаумян Г. А.
а) Основы теории проектирования станков-автоматов и автоматических
линий, Машгиз, 1949.
б) Автоматы, М., 1952.
60. Юдин В. А., Динамический синтез плоских и пространственных кулачко-
вых механизмов, Изд. Военно-инженерной академии РККА, 1940.
61. Alt Н.
a) Zur Synthese der ebencn Mechanismen. Zeitschrift fur angewandte Ma-
thematik und Mechanic, 1921, т. 1, стр. 373.
6) Uber die Totlagen des Gelenkvierecks. Там же, 1925, т. V, стр. 337.
в) Die Bedeutung der Getriebelehre fiir den Ban von Verarbeitungsmaschi-
nen. Zeitschr. VDI, 1930, стр. 139.
г) Regelmassige und unregelmassige Maltheser Kreuzgetriebe. Maschinen-
bau, 1930, стр. 202.
д) Zur Getriebetechnik der Verpackmaschinen. Zeitschr. VDI, 1931, стр. 245.
e) Zur Geometrie der Koppelrastgetriebe. Ingenieur-Archiv, 1932, t. 3,
стр. 394.
ж) Koppelgetriebe als Rastgetriebe. Zeitschr. VDI, 1932, стр. 456 и 533.
з) Sonderfalle der RCT-Kurve und der Burmesterschen Mittelpunktkurve.
Maschinenbau, 1936, стр. 277.
и) Die Mittelpunkt- und die Kreispunktkurve in dem Sonderfall, bei dem
vier Lagen einer Ebene paarweise parallel sind. Maschinenbau, 1937,
стр. 105.
к) Mittelpunktkurve in dem Sonderfall, bei dem drei von vier Lagen einer
Ebene einander parallel sind. Maschinenbau, 1937, стр. 377.
л) Uber die Totlagen von Getriebegliedern. Maschinenbau, 1940, стр. 173.
м) Sonderfalle der Mittelpunktkurven. Maschinenbau, 1940, стр. 309 и 401.
н) Das Konstruieren von Gelenkvierecken unter Benutzung einer Kurven-
tafel. Zeitschr. VDI, 1941, стр. 69.
о) Koppelrastgetriebe mit grosser Giite der Rast und vorgeschrieben Zeiten
fiir Beginn und Ende der Rast. Maschinenbau, 1941, стр. 1933.
62. Bach K., Die Verwirklichung vorgegebener Winkelgeschwindigkeitsge-
setze bei Doppelkurvengetrieben. Ingenieur-Archiv, 1950, стр. 167.
63. Beyer R.
a) Technische Kinematik, 1931.
6) Anwendung von Schmiegungskegelschnitten in der Getriebetechnik,
Maschinenbau, 1938, стр. 253.
в) Kreispunktkurve in rechnerischer Behandlung. Maschinenbau, 1938,
стр. 595.
г) Zur Synthese ebener und raumlicher Kurbeltriebe. VDI-Forschungsheft
1939, 394.
д) Kinematische Getriebesynthese, Berlin, 1953.
e) Einfache getriebesynthetische Hilfsmittel zur angenaherten getribelichen
Erzeugung vorgeschriebener Bewegungen, Konstruktion, вып. 8, 1955.
64. В1 a s c h k e W. und M ii 11 e r H. R., Ebene Kinematik. Mijnchen, 1956.
65. Bobillier E., Cours de geometrie, 1870.
66. В о c k, Sternradgetriebe. VDI, 1929, стр. 397.
67. В u r m e s t e r L.
a) Uber die Geradfflhrung durch das Kurbelgebriebe. Civilingenieur, 1876,
t. 22, стр. 597 и 1877, т. 33, стр. 227.
б) Lehrbuch der Kinematik. Leipzig, 1888, 249—254,
1076
ЛИТЕРАТУРА
68. CamusL Sur 1e figure des dents des roues et des afles des pignons
pour rendre les horloges plus parfaites. Memoires de 1’ Academic, 1773.
69. Crawford W. R., The mechanical construction of the general conic
section. Engineer, 1936, t. 162, 4207.
70. Euler L., Novi Commentarii Academiae Metropolitanae, 1765.
71. F i n к e 1 n b u r g H.
a) Systematik der Bewegungsgesetze. Maschinenbau, 1936, стр. 695 и 1937,
стр. 221 и 425.
б) A'lehrspindelautomaten, 1938.
72. F 1 о с к е К. А.
a) Konstruktion von Koppelgetrieben. Zeitschrift VD1, 1934, стр. 49.
6) Zur Konstruktion von Kurvenscheiben bei Verarbeitungsmaschinen. VDI-
Forschungsheft, 1931.
73. Freudenschein F.
a) An analytical approach to the Design of Four-Link Mechanisms. Trans-
action of ASME, 1954, №3.
6) Aproximate Synthesis of Four-Bar Linkages. Там же, 1955, № 6.
в) On the maximum and minimum velocities and the acceleration in Four-
Link Mechanisms. Trans. ASME, № 4, 1956.
74. G r u b 1 e r M.
a) Ober die Kreispunkte einer komplan bewegten Ebene. Zeitschrift Mathe-
matik und Physik. 1892, t. 37, стр. 35.
6) Getriebelehre. Berlin, 1917.
75. Hackmuller E.
a) Zur Konstruktion der Burmesterschen Punkte. Maschinenbau, 1938,стр. 648.
6) Zur Synthese des ebenen Gelenkviereckes. Maschinenbau, 1940, стр. 402.
в) Eine analytisch durchgefiihrte Ableitung der Kreispunkts- und Mittel-
punktskurve. Zeitschr. fiir angewandte Math, und Meeh., t. 18, 1938,
стр. 252.
76. Hain K.
a) Die Weiterentwicklung der Schaltwerke. Zeitschr. VDI, 1949, № 22.
6) Angewandte Getriebelehre, Hannover, 1953.
в) Sechsgliederige Verbindungsgetriebe fiir Aufbaugerate an Ackerschlep-
pern. Zeitschr. VDI, № 30, 1954.
r) Die Analyse und Synthese der achtgliederigen Gelenkgetriebe. VDI-
Berichte, t. 5, 1955.
A) Voile Ausnutzung des Gelenkvierecks als Funktionsgetriebe. Regelungs-
technik, № 2, 1956.
77. Наг! H., On the production of circular and rectilinear motion. Messeng.
of Mathem., 1877, т. VII.
78. Hartmann W., Die Maschinengetriebe, 1913.
79. H о e с к e r, Sternradgetriebe. Zeitschr. VDI, 1930, стр. 265.
80. Holzer H., Walzhebel. Zeitschr. VDI, 1908, стр. 51.
81. H rones J. A., Nelson G. L., Analysis of the Four-Bar Linkage, 1951,
New York.
82. J a h r W. und К n e c h t e 1 P., Grundzilge der Getriebelehre, 1949.
83. Kempe A.
a) How to draw a straight line. Nature, 1877, t. 16.
6) On a general method of describing plane curves of the и-th degree of
linkwork. Proc, the London Math. Society, 1877—1878.
84. К i p e r G.
a) Synthese der ebenen Gelenkgetriebe. VDI, Forschungsheft, № 433,
1952, стр. 433.
6) Getriebefragen bei Verarbeitungsmaschinen in Karusellbauweisen. Zeitschr.
VDI, № 29, 1953.
в) Einfache Konstruktion von Gelenksvierecken fiir vier Lagenzuordnungen.
Konstruktion, Ns 1, 1954,
ЛИТЕРАТУРА
1077
г) Das Hilfsmittel der Gegenpunkte und seine Anwendung beim Konstrui-
ren von Gelenkvierecken, Konstruktion, № 8, 1954.
д) Die Konstruktion von Zweistandgetrieben mit Hilfe von Gegenpunkten.
Konstruktion, № 9, 1955.
85. Kraus R.
a) Lagenreduktion als Hilfsmittel sur Synthese ebener Kurbelgetriebe. Ma-
schinenbau, 1935, стр. 637.
6) Wertigkeitsbilanz und ihre Anwendung auf eine Geradfiihrung fiir
MeBgerate. Feinwerktechnik, № 3, 1952.
в) Geradfiihrungen durch das Gelenkviereck. Dusseldorf, 1955.
r) Gelenkvierecke fur gegebene Koppelpunktslagen und Steggelenke. Zeitschr.
VDI, 1949, стр. 607.
д) Die Angel- und Kreisungspunktkurve beim rechenden Gelenkviereck.
Feinwerktechnik, 1954, стр. 186.
e) Getriebeaufbau, 1952.
86. L e a u t e N.
a) Methode d’approximation graphique applicable a un grand nombre des
questions de mecanique pratique. Journal de 1’Ecole polytechnique,
t. XXV11I, вып. 46, стр. 166—225, 1879.
6) Sur une perfectionnement applicable a tous les regulateurs a force cen-
trifuge. Journal de 1’Ecole polytechnique, т. XXVIII, вып. 47, 1880.
в) Sur une famille des courbes que Гоп rencontre dans les transmissions de
mouvement et sur leur application dans les machines. Journal de i’Ecole
polytechnique, вып. 53, стр. 59—78, 1883.
г) Sur la trajectoire des drivers points d’un bielle en monvement. Comptes
Rendus, 1883, t. XCVI, стр. 639.
д) Regies pratiques la substitution a une arc donne des certaines courbes fer-
mees, engendrees par le point d’unbielle en mouvement. Там же, стр. 1256.
87. L i c h t w i t z O., Getriebe fiir aussetzende Bewegung, Berlin, 1953.
88. Liechtenheldt W.
a) Ober den Schlagmechanismus des mechanischen Webstuhles. Maschinen-
bau, 1936, стр. 405.
6) Zur Konstruktion von Schaftmaschinengetrieben. Maschinenbau,1938,стр. 145.
в) Einfache Konstruktionsverfahren zur Ermittlung der Abmessungen von
Kurbelgetrieben. VDl-Forschungsheft, № 408, 1941.
r) Kinematische und dynamische Untersuchung der Webladenantriebe. Faser-
forschung und Textiltechnik, t. 2, вып. 3 и 4, 1951.
д) Konstruktionstafel fiir die Bestimmung der Abmessungen von gelenk-
getrieben, VDI-Berichte, t. 5, 1955.
e) Rationalisierung der Konstruktionarbeit. Wiss. Z. TH Dresden, 1953—1954.
ж) Die Methode der Partialsynthese. Wiss. Z. TH Dresden, 1955—1956.
з) Lenkergeradfiihrungen in Feingeratebau. Feingeratetechnik, № 4, 1955.
и) Konstruktionstafeln fiir Gelenkmechanismen, VDI-Berichte, t. 12, 1956.
89. L i g u i n e V., Sur les systemes articule de M. M. Peaucellier, Hart et
Kempe. Nouv. Ann. de Math., 3-я серия, 1882, т. 11.
90. L i p к i n e L., Ober eine genaue Gelenk-Geradfiihrung. Bull, de 1’Acad. de
S. Petersbourg, 1871, т. XVI.
91. Mannheim A., Principes et developpements de geometrie cinematique.
Paris, 1894.
92. Meyer zur Capellen, Mathematische Instrumente. Leipzig, 1947
(имеется русский перевод).
93. Mitchell D. В., Cam Follower Dynamics. Machine Design, июнь 1950.
91. M ii 11 e r J.
a) Sur Synthese acht- und zehngliedriger Gelenkgetriebe. Wissenschaftliche
Zeitschrifte der technischen Hochschule, Dresden, 1953—1954, вып. 2.
6) Zur Analyse und Synthese achtgliedriger Gelenkgetriebe ohne gelenk-
vierecke. Там же, вып. 3.
1078
литература
95. Muller R.
a) Konstruktion der Burniesterschen Punkte fiir ein ebenes Gelenksviereck.
Zeitschrift fiir Mathematik und Physik, 1892, t. 37.
6) Einfiihrung in die theoretischc Kinematik. Berlin, 1932.
96. Nicaise M., Les mouvements mecaniques, 1931.
97. Peaucellier A., Note sur un balancier articule a mouvement rectiligne.
Journal de Phys., 1873.
98. Pike E. W. and Silverberg Th. A., Designing Mechanical Computers.
Machine Design, 1952, июль и август.
99. P о с к e r L е о S., An exact computing linkage. Machine Design, сентябрь,
1953.
100. Pone el et J., Traite de mecanique appliquee aux machines. Liege, 1845.
101. R a p p о p о r t, Kinematics of intermittent mechanisms. Product Engineer-
ing, 1949, июль, стр. НО; август, стр. 10Э; октябрь, стр. 137; 1950,
январь, стр. 120; апрель, стр. 183.
102. Reuleaux F., Lehrbuch der Kinematik, 1875.
103. Roberts S., On three bar motion in plane Space. Proc. Sond. Meeh. Soc.,
1875—1876, t. VII.
104. Rodenberg C., Die Bestimmung der Kreispunktkurven eines ebenen
Gelenkvierseits. Zeitschr. fiir Mathematik und Physik, 1891, t. 36, стр. 267.
105. Rosenauer N., Gelenkvierecke mit vorgeschriebenen Grosst- und
Kleinstwerten der Abtriebswinkelgeschwindigkeit. Maschinenbau, 1944.
106. Rossner W., Ermittling der Burmesterschen Punkte in Sonderfallen und
gebriebesynthetische Anwendung. Maschinenbautechnik, № 5, 1955.
107. Rothbart H., Cams, 1956.
108. Sauer, Hubbeschleunigung fiir die geneigte Sinuslinie. Maschinenbau,
1938, стр. 1038.
109. S a v a г у, Note pour letrace de 1’epare d’un eagrenage cylindrigne. Note
litographiee de 1’Ecole Polytechnigue. Paris, 1831. Euler L. Supplementem
de figura dentium rotarum. Novi Comment. Acad. Sc. Imp. Petropolitanae,
t. 11, 1767.
110. Schnarbach K.
a) Kurventriebe und Koppelgetriebe als Steuerorgane an Verarbeitungsma-
schinen. Zeitschr. VD1, 1951, стр. 223.
6) Gelenkgetriebe rail grossem Abtriebswinkel der Schwinge. Zeitschr.
VD1, 1954, стр. 279.
111. S i e к e г К. H.
a) Ermittlung von Gelenkvierecken aus den Kriimmungshalbmesseren' und
deren Anderungen. Die Technik, 1948, стр. 170.
6) Das Gelenkviereck als Functionsgetriebe. Feinwerktechnik, 1952,
стр. 182.
в) Analytische Betrachtung des Gelenkviereckcs, insbesondere der Bur-
mesterschen Punkte, VDI-Berichte, t. 5, 1955.
r) Zur algebreischen MaBsynthese ebener Kurbelgetriebe. Ing. Arch.,
t. XXIV вып. 3 и 4, 1956.
112. Svoboda A., Computing mechanisms and linkage. 1948 (имеется рус-
ский перевод).
113. Trank net G., Die Bedeutung der Getriebetechnik fiir die Konstruktion
automatischer Maschinen. Maschinenbautechnik, вып. 8, 1953.
114. Wade H. S host er, Cam Designing Analysis with Formulas for Deter-
mining Cam motion Factores. Product. Eng. май, июнь, 1940.
115. Willers F., Mathematische Instrumente, 1943 (имеется русский перевод).
116. Willis К., Principles of mechanisms, London, 1841.
ИМЕННОЙ УКАЗАТЕЛЬ
Адлер A. (Adler А.) 327
Алексеев Н. Н. 15, 275, 1069
Альт Г. (Alt Н.) 24, 25, 26, 773, 988,
1075
Антовиль А. М. 13, 1069
Артоболевский И. И. 12, 13, 15, Г8,
26, 641, 721, 1069
Артоболевский С. И. 13, 343, 1070
Ачеркан Н. С. 14, 440, 1070
Баранов Г. Г. 21, 24, 683, 1070
Бах К. (Bach К.) 1075
Бейер Р. (Beyer R.) 12, 24, 1075
Бернштейн С. Н. 529
Блашке В. (Blaschke W.1 12, 1075
Блох 3. Ш. 13, 18, 21, 26, 592, 601,
613, 614, 641, 689, 997, 1069,
1070
Бобилье Е. (Bobilier Е.) 12, 1075
Бок (Воск) 1076
Бооль В. Г. 14, 1070
Брикар 275
Бруевич Н. Г. 15, 24, 1070
Бурместер Л. (Burmester L.) 13, 23,
24, 151, 727, 730, 732, 751, 773, 988,
1076
Виллере Ф. (Willers F.) 15, 1079
Виллис К. (Willis К.) 12, 1079
Вяткин Г. П. 298
Гарт Г. (Hart Н.) 14, 1076
Гартман В. (Hartman W.) 1076
Герасимов Ю. Н. 14, 1070
Геронимус Я. Л. 13, 22, 354, 916, 1070
Гершгорин С. А. 15, 1071
Гольцер Г. (Holzer Н.) 13, 1076
Гончаров В. Д, 1071
Грасгоф Ф. (Grashoff F.),47
Грюблер М. (Griibler М.) 24, 25, 1076
Дарбу (Darboux) 275
Делоне Н. Б. 15, 295, 296, 1071
Добровольский В. В. 13, 15, 25, 254,
_ 260, 261, 301, 641, 1069, 1071
Езикашвили О. С. 13, 1071
Жуковский Н. Е. 1071
Зауэр (Sauer) 13, 1078
Зернов Д. С. 13, 1071
Зикер К. (Sieker К.) 21, 26, 647, 1078
Зиновьев В. А. 21, 643, 1071
Иващенко Н. Н. 1071
Каминский В. П. 1071
Камус Л. (Camus L.) 12, 1076
Карпин Е. Б. 26, 1070
Кемпе A. (Kempe А.) 14, 262, 264,
1076
Кетов X. Ф. 1071
Кипер Г. (Kiper G.) 24, 1077
Кнехтель П. (Knechtel Р.) 13, 1076
Кобринский А. Е. 13, 1071
Кобринский Н. Е. 15, 1072
Кожевников С. Н. 13, 1072
Колчин Н. И. 26, 1072
Костицын В. Т. 26, 1072
Котельников А. П. 25, 1017, 1072
Краус Р. (Kraus R.) 13, 24, 26, 1018,
1077
Крауфорд В. (Crawford W.) 1076
Кучер И. М. 14, 394, 396, 1072
Левитский Н. И. 13, 14, 18, 21. 22,
23, 26, 891, 1069, 1072
Литии В. (Liguine V.) 14, 1077
Линкин А. 14, 1077
Литвин Ф. Л. 13, 150, 160, 169, 1072
Лихтвип О. (Lichtwiz О.) 1077
Лихтенхельдт В. (Lichtenheldt W.) 24,
25, 988, 1077
Ломоносов М. В. 11
Лориа Г. (Loria) 261
Малышев А. П. 1073
Манхейм A. (Mannheim А.) 12, 1078
Мейер цур Капеллен В. (Meyer zur
Kapellen W.) 15, 1078
1080
ИМЕННОЙ УКАЗАТЕЛЬ
Мерцалов Н. И. 12, 13, 14, 1073
Митчел Д. (Mitchell D.) 13, 1078
Мюллер И. (Milller J.) 12, 24, 1078
Мюллер Р. (Milller R.) 25, 105, 1017,
1078
Нахапетян Е. Г. 443
Нельсон Г. (Nelson G.) 26, 993,
1076
Никез М. (Nicaise М.) 13, 1078
Никулин Н. А. 15, 1073
Новодворский Е. П. 21, 23, 644, 726,
922, 1073
Ньютон И. 279
Орликов М. Л. 1073
Пайк Е. (Pike Е.) 1078
Парницкий А. Б. 24, 1073
Линекер И. III. 21, 23, 726, 1073
Поккер Л. (Pocker L.) 15, 1078
Полыновский Г. Л. 15, 1073
Понселе Г. (Poncelet J.) 12, 1078
Поселье A. (Peaucellier А.) 14, 1078
Рагульскис К. М. 1073
Раппопорт (Rappoport) 1078
Рело Ф. (Reullaux F.) 12, 23, 1078
Ремез Я. Я. 540
Рёсснер В. (Reissner W.) 24, 1078
Решетов Л. Н. 13, 422, 1073
Робертс С. (Roberts S.) 1078
Роденберг К. (Rodenberg С.) 25, 1078
Розенауэр Н. (Rosenauer N.) 1078
Ротбарт Г. (Rotbart Н.) 14, 1078
Савари (Savary) 12, 83, 1078
Свобода A. (Svoboda А.) 21, 718, 891,
1078
Семенов М. В. 21, 1073
Сильверберг Т. (Silverberg Т.) 1078
Сомов П. О. 15, 296, 1073
Сперанский Н. В. 14, 25, 1073, 1075
Степанов Б. И. 23, 1072, 1073
Тир К. В. 13, 343, 1073
Тишин М. М. 13, 1073
Тренкер Г. (Tranker G.) 1079
Урин Д. М. 1073
Уэйд X. (Wade Н.) 13, 1079
Финкельнбург X. (Finkelnburg Н.) 13,
343, 1076
Флокке К. (Flocke К.) 14, 24, 1076
Фрейденштейн Ф (Freudenstein F.) 21,
26, 1076
Хайн К. (Hain К.) 13, 25, 1076
Хакмюллер Е. (Hackmiiller Е.) 24, 1076
Хоккер (Hoecker) 1076
Хронс Дж. 26, 993, 1076
Чебышев П. Л. 17,505,531, 676,684,988,
997, 1074
Черкудинов С. А. 14, 20, 23, 25, 26,
1074, 1075
Шаль 732
Шаскольский Б. В. 14, 1075
Шаумян Г. А. 14, 394, 1075
Шахбазян К. X. 23, 1072
Шнарбах К. (Schnarbach К.) 24, 1078
Шостер 13, 1079
Эйлер Л. 11, 12, 83, 1076
Юдин В. А. 14, 1075
Яр В. (Jahr W.) 13, 1076
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Альта диаграмма 827
Аналог круга перемены 98
— — поворотного 98, 108, 109, 111,
113
Антипараллелограмм шарнирный 48
Аньезера 304
Астроида 312, 314
Бицентроида 120, 127
Болла точка 1030
Бурместера задача 730
— кривая 745, 751
— точка 789, 791, 1063
— центр 789, 791, 793, 794, 801
Версьера 304
Вес параметрический 504
Воспроизведение заданной функции 144
— функциональной зависимости 319
Геометрия кинематическая 70, 727,
1017
Геронимуса теорема 541, 916
Гипоциклоида 317
Грасгофа теорема 47
Диаграмма Альта 827
Диада Чебышева 652
Задача Бурместера 730
Зацепление реечно-зубчатое 41
— цевочное 209
Инверсия 266
Инверсор 265, 267, 268
— Гарта 269
— Поселье 268
Интерполирование кратное 595
— функций 506, 545
Кардиоида 244, 308
Качение центроиды 70
Кемпе теорема 265
Колесо зубчатое 205
— логарифмическое 146
Колесо овальное 146
— эллиптическое 146, 148
Коникограф 277
— Богуславского 279
— для огибания конических сечений
280
— для одновременного обкатывания
двумя прямыми одного конического
сечения или двух софокусных кони-
ческих сечений 286
.— Каминского 277
— Кроуфорда 278
Конхоиде Никомеда 309
Координаты однородные 745
Коэффициент возрастания усилий 378
— времени работы мальтийского кре-
ста 431
— динамичности нагрузки 359
— заполнения площади графика уско-
рений 358
— полезного действия кулачкового
механизма 384
— изменения скорости хода 830
Крест мальтийский 62, 241, 262, 428,
429, 444, 449, 452, 457, 461, 464,
479, 485
Кривая Бурместера 301, 745, 751
— круговых точек 23, 301, 745, 751,
778,’ 780, 782, 1061
— фокального типа 301
— центров 24, 301, 745, 748, 752, 754,
757, 768, 772, 780, 782
— циркулярная 301, 747
— четвертого порядка типа Панкина
101
- шатунная 649, 654, 988, 990, 996,
998, 1056
Кривизна взаимоогибаемых кривых
75, 85
— траектории 80
— центроид 75
Кривые взаимоогибаемые 75, 80
Круг катания 86
— перегибов 78, 1021
— перемены 78, 94
1082
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Круг поворотный 78, 94
Кулачок 197, 333, 409, 412, 418
— гиперболоидный 337
— дисковый 337
— комбинированный 338
— конический 337
— открытый 337
— пазовый 338
— торцовый 338
— цилиндрический 337
Лемниската Бернулли 309
Линия зацепления 186
Лист Декарта 305
Метод Блоха 641
- дополнительных групп 87
--- центроид 206, 207
— Зикера 644
— комплексных чисел 638
— присоединения 87
— разверток 206, 217
— эвольвент 217
Методы синтеза механизмов алгебраи-
ческие 16
геометрические 16
приближенные 15
------------точные 15
Механизм выталкивателя кусков теста
в делительной машине 338
— Вяткина 298
— Гарта 275
— двойного кулачка 239
— двухкоромысловый 47
— для возведения в квадрат 423
-------- в куб 324
--- воспроизведения кривой Бурме-
стера 30)
— для вычерчивания астроиды 313
— для вычерчивания версьеры (аиь-
езеры) 304
—-------взаимно-обратных кривых 267
---— гиперболы 293, 297, 298
—-------гипоциклоиды 318
—-------кардиоды 308
—-------------- конических сечений 277
— — — конхоиды Нпкомеда 309
— ------кривых высшего порядка 300
— — — лемнискаты 310
-------- листа Декарта 305
—- — -— параболы 294, 299
----------- полукубической 315
---------- рулетты 315
----------- конических сечений 316
—-- ---— окружности 317
— эллипса 317
Механизм для вычерчивания строфоиды
300
— -----улитки Паскаля 308
-------- циклической кривой 315
•-------циссоиды 320
•---------Диоклеса 303
-------- четырехлепестковой розы 312
-------- эпициклоиды 318
— для извлечения корня квадратного
423
•--------- кубического 324
— для обкатывания эволют 291
— для огибания двумя взаимно-пер-
пендикулярными прямыми гиперболы
и параболы 290
— для огибания конических сечений
277
--------кривых высших порядков
,300
---- — параболы 284
-------- эллипса 280
— для одновременного огибания двух
софокусных эллипсов 288
-------- вычерчивания и огибания ги-
перболы 291
---------------- параболы 291
---------------- эллипса 290
— для перемещения точки по заданной
прямой 262
— для получения пропорциональных
отрезков на двух прямых, проходя-
щих через заданную точку 262
— для проведения через заданную
точку прямой, параллельной данной
262
— для проектирования заданной точки
на заданную прямую 262
— для решения уравнений квадратных
325, 327
----------кубических 330
----------- четвертой степени 330
— для сложения заданных отрезков
262
— закатывающего ролика машины для
закатки консервных банок 338
— звездчатый 40, 214, 216
----с реечным зацеплением 217
— зубчаторычажный 242
----с цевочным зацеплением 209
----цевочный Гриссона 211
---------- с остановками 213
— кардановых кругов 36
— клапанного распределения кулачко-
вый 54
— клиновый 37
— крестовой муфты 49
--------Ольдгейма 89
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
1083
— Механизм кривошипно-шатунный
48, 88, 108, 554, 612, 712, 834, 838,
880, 881, 888, 892, 950, 1046, 1052
— кулачковый 57, 59, 60, 63, 65, 66,
90; 109, 196, 197, 241, 333, 340, 343
Механизм кулачковый определение его
основных размеров 399
-----пространственный 335
-----с качающимся толкателем 40
— — с плоским коромыслом 335
----- с плоским толкателем 335
-----с поступательно движущимся
толкателем 41
-----с центральным толкателем 335
-----со смещенным толкателем 335
----- цевочный 428
— кулисно-коромысловый 335
— кулисный 48, 49, 89, 203, 205, 231,
555, 562, 840, 893, 901
— кулисный с криволинейной кули-
сой 41, 196, 225
-----с неподвижной криволинейной
кулисой 232
-----с поступательно-движущейся ку-
лисой 49, 229
— — с прямолинейной кулисой 196
— — со скользящей кулисой 44
— мальтийского креста 62, 241, 261,
428, 452, 457, 461, 464, 479, 485
--------с внешним зацеплением 429
-------с внутренним зацеплением
444, 449
- некруглых колес 134
— овальных центроид 158
— перекатывающихся рычагов 36, 40,
43, 44, 50, 134, 169, 176, 180, 196, 222
— планетарно-реечный 33
— планетарный 45, 315
— Поселье-Ляпкина 267
— прижимного ползуна кривошипного
пресса 1005
— прямолинейно-направляющий Гарта
270
-----Чебышева 675
— реечно-планетарный 36
— реечно-цевочный 41
— ротационного насоса кулачковый 54
— рычажно-планетарный 63
— с мгновенно равномерным движе-
нием 610
— с одной центроидной парой 182
— с остановками 67, 68, 213, 986,
1005
— с равномерным движением ведомого
звена 600
— симметричный, направляющий по
гиперболе 688
Механизм симметричный, направляю-
щий по дуге окружности 683
— синусный 557, 563
— суммирующий 262
— тангенсный 558, 564
— трехзвенный 27, 28, 37
—• фрикционно-рычажный 51, 52
— храповой 428
— цевочный 40
— цевочных колес Рело 210
— центроидный 29, 32, 33, 34, 129,
167
— — некруглых колес 134
---- перекатывающихся рычагов 169
— — планетарный 29, 30, 32
----трехзвенный 117
— четырехзвенный с двумя парами
качения и скольжения 236
—с двумя центроидными парами
— — с одной центроидной парой
— шарнирный антипараллелограмма 48
— — параллелограмма 47
— — .ромба 48
— — Чебышева с остановками 684
— шестизвенный с тремя поступатель-
ными парами 68
— — С четырьмя поступательными
парами 68
— эллипсографа 49, 89, 557, 563
----Делоне 295
— — четырехзвенный 294
— эллиптический центроидный 157
Многочлен, наименее уклоняющийся
от нуля 532
— Чебышева 532
Муфта крестовая 49
----Ольдгейма 89
Нарезание зубцов 206
----— некруглых колес 169
Обработка профилей зубцов некруглых
колес 142
---- центроид 142
— профиля кулачка 368
Огибающая 71, 73, 75
Отклонение взвешенное 504
— среднее квадратическое 514
Пантограф 265, 273
- — Сильвестра 273, 669
— Шейпера 274, 670
Парабола полукубическая Нейля 315
Параллелограмм шарнирный 48
Передача планетарная 464
1084
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Полюс относительных Положений 808,
815, 835
— поворота 78
— поворота конечного 732
Построение огибающей 71, 73
— Робертса 669
Преобразование Робертса 23
— направляющего механизма 669
Преобразование шатунной кривой 998,
1001
Приближение взвешенное 505
— интерполяционное с двукратными
узлами 843, 846
— квадратическое 514, 545, 564
— наилучшее 570, 916, 950, 977
Проектор Делоне 29
Прямая бесконечно удаленная 746
— несобственная 746
Радиус кривизны 80, 81, 92
---- траектории 104, 105
Разность взвешенная 504
Редуктор планетарный 45
— цевочный 210
Робертса построение 23
— преобразование 669
Роза четырехлепестковая 311
Ромб шарнирный 48
Рулетта 73, 315
Синтез механизмов 11
— • — аналитический 11
----приближенный 15, 501
---- структурный 11
---- точный 15
Система функций Чебышева 527, 916
Строфоида 300
Теорема Геронимуса 541, 916
— Грасгофа 47
Теорема Кемпе 265
— Чебышева 528
Толкатель 197, 333
Точка бесконечно удаленная 746
— Болла 1030
— Бурместера 789, 791, 1063
— круговая 23, 785
— несобственная 746
— нулевая 907, 909, 911, 913, 933
— узловая 906, 909, 911, 913
Точка циклическая 747
Треугольник полюсный 735, 760
Угол входа 864, 940
— выстоя 1007
— выхода 805, 940
— давления 373, 393, 811
— передачи 132, 191, 200, 810, 812
933
— поворота 732
----относительных положений 809
— размаха малого 1007
Улитка Паскаля 244, 307
Уравнение бицентроиды 127
— кривой центров 752
— центроиды 125, 126
----в полярных координатах 140
— шатунной кривой 649
— Эйлера — Савари 83
Уравнения сопряженных центроид в
параметрической форме 140
Фокус циркулярной кривой 748
Функция передаточного отношения 118
---- числа 118
— положения 117
— положения механизма 840
Центр Бурместера 789, 791, 793, 794,
801
— кривизны траектории 83, 101, 103,
105, 106
Центроида 70, 87
Цепь кинематическая восьмизвенная 68
— — шестизвениая 53
Циклоида 317
Циссоида 320
— Диоклеса 302
Чебышева диада 652
— многочлен 532
— теорема 528
Четырехзвенник шарнирный 547, 558,
581, 600, 654, 699, 806, 811, 819,
821, 825, 829, 830, 832, 834, 850, 872,
874, 950, 1003, 1033, 1043
---- симметричный 17
Эллипсограф 49
Эпициклоида 317